Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T13:29:11.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Multivalued action languages with constraints in CLP(FD)1

Published online by Cambridge University Press:  18 February 2010

AGOSTINO DOVIER ,
ANDREA FORMISANO  and
ENRICO PONTELLI
AGOSTINO DOVIER
Affiliation:
Università di Udine, Dipartimento di Matematica e Informatica, Via delle Scienze 206, 33100 UDINE (Italy) (e-mail: dovier@dimi.uniud.it)
ANDREA FORMISANO
Affiliation:
Università di Perugia, Dipartimento di Matematica e Informatica, Via Vanvitelli 1, 06123 Perugia (Italy) (e-mail: formis@dmi.unipg.it)
ENRICO PONTELLI
Affiliation:
New Mexico State University, Department of Computer Science, P.O. Box 30001, MSC CS, Las Cruces, NM 88003 (USA) (e-mail: epontell@cs.nmsu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Action description languages, such as 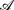and ℬ (Gelfond and Lifschitz, Electronic Transactions on Artificial Intelligence, 1998, vol. 2, pp. 193—210), are expressive instruments introduced for formalizing planning domains and planning problem instances. The paper starts by proposing a methodology to encode an action language (with conditional effects and static causal laws), a slight variation of ℬ, using Constraint Logic Programming over Finite Domains. The approach is then generalized to raise the use of constraints to the level of the action language itself. A prototype implementation has been developed, and the preliminary results are presented and discussed.

Keywords

action description languagesknowledge representationplanningconstraint logic programming
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 10 , Issue 2 , March 2010 , pp. 167 - 235
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apt, K. R. 2003. Principles of Constraint Programming. Cambridge University Press.CrossRefGoogle Scholar
Baral, C. 2003. Knowledge Representation, Reasoning and Declarative Problem Solving. Cambridge University Press.CrossRefGoogle Scholar
Baral, C., Son, T. and Tuan, L.-C. 2002. A transition function based characterization of actions with delayed and continuous effects. In Principles and Practice of Knowledge Representation and Reasoning, Morgan Kaufmann, 291–302.Google Scholar
Caseau, Y., Josset, F.-X. and Laburthe, F. 2002. CLAIRE: Combining sets, search and rules to better express algorithms. Theory and Practice of Logic Programming 2 (6), 769–805.CrossRefGoogle Scholar
Dovier, A., Formisano, A. and Pontelli, E. 2005. A comparison of CLP(FD) and ASP solutions to NP-complete problems. In Proc. of ICLP 2008, Gabbrielli, M. and Gupta, G., Eds. Lecture Notes in Computer Science, vol. 3668. Springer Verlag, 67–82.Google Scholar
Dovier, A., Formisano, A. and Pontelli, E. 2007. An experimental comparison of constraint logic programming and answer set programming. In Proc. of the Twenty-Second AAAI Conference on Artificial Intelligence. AAAI Press, Vancouver, British Columbia, Canada, 1622–1625.Google Scholar
Dovier, A., Formisano, A. and Pontelli, E. 2009a. An empirical study of CLP and ASP solutions of combinatorial problems. Journal of Experimental & Theoretical Artificial Intelligence 21 (2) (June), 79–121.CrossRefGoogle Scholar
Dovier, A., Formisano, A. and Pontelli, E. 2009b. Representing multi-agent planning in CLP. In Logic Programming and Non-monotonic Reasoning, 10th International Conference, LPNMR 2009, Potsdam, Germany, September 14–18, 2009, Proceedings, Erdem, E., Lin, F., and Schaub, T., Eds. Lecture Notes in Computer Science, vol. 5753. Springer, 423–429.Google Scholar
Eiter, T., Faber, W., Leone, N., Pfeifer, G. and Polleres, A. 2004. A logic programming approach to knowledge-state planning: Semantics and complexity. ACM Transactions on Computational Logic 5 (2) (April), 206–263.CrossRefGoogle Scholar
Gabaldon, A. 2002. Non-Markovian control in the situation calculus. In Proc. of the Eighteenth National Conference on Artificial Intelligence, Dechter, R., Kearns, M., and Sutton, R. S., Eds. American Association for Artificial Intelligence, AAAI Press, Menlo Park, California, 519–524.Google Scholar
Gebser, M., Kaufmann, B., Neumann, A. and Schaub, T. 2007. Clasp: A conflict-driven answer set solver. In Logic Programming and Non-Monotonic Reasoning, Baral, C., Brewka, G., and Schlipf, J. S., Eds. Springer Verlag, 260–265.CrossRefGoogle Scholar
Gelfond, M. and Lifschitz, V. 1998. Action languages. Electronic Transactions on Artificial Intelligence 2, 193–210.Google Scholar
Giunchiglia, E., Lee, J., Lifschitz, V., McCain, N. and Turner, H. 2004a. Non-monotonic causal theories. Artificial Intelligence 153 (1–2), 49–104.CrossRefGoogle Scholar
Giunchiglia, E., Lierler, Y. and Maratea, M. 2004b. SAT-based answer set programming. In AAAI-04, McGuinness, D. L. and Ferguson, G., Eds. The MIT Press, 61–66.Google Scholar
Hoffmann, M. J., Porteous, J. and Sebastia, L. 2004. Ordered landmarks in planning. Journal of Artificial Intelligence Research 22, 215–278.CrossRefGoogle Scholar
Jaffar, J. and Maher, M. 1994. Constraint logic programming: A survey. Journal of Logic Programming 19/20, 503–581.CrossRefGoogle Scholar
Lee, J. and Lifschitz, V. 2003. Describing additive fluents in action language C+. In IJCAI-03, Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, Acapulco, Mexico, August 9–15, 2003, Gottlob, G. and Walsh, T., Eds. Morgan Kaufmann, 1079–1084.Google Scholar
Levesque, H. J., Pirri, F. and Reiter, R. 1997. GOLOG: A logic programming language for dynamic domains. Journal of Logic Programming 31 (1–3), 59–83.CrossRefGoogle Scholar
Levesque, H. J., Pirri, F. and Reiter, R. 1998. Foundations for the situation calculus. Electronic Transactions on Artificial Intelligence 2, 159–178.Google Scholar
Lifschitz, V. 1999. Answer set planning. In Proc. of the 16th Intl. Conference on Logic Programming, Schreye, D. de, Ed. MIT Press, 23–37.Google Scholar
Lin, F. and Zhao, Y. 2004. ASSAT: Computing answer sets of a logic program by SAT solvers. Artificial Intelligence 157 (1–2), 115–137.CrossRefGoogle Scholar
Lopez, A. and Bacchus, F. 2003. Generalizing Graphplan by formulating planning as a CSP. In IJCAI-03, Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence, Acapulco, Mexico, August 9–15, 2003, Gottlob, G. and Walsh, T., Eds. Morgan Kaufmann, 954–960.Google Scholar
Marriott, K. and Stuckey, P. J. 1998. Programming with Constraints. The MIT Press.CrossRefGoogle Scholar
McCarthy, J. 1998. Elephant 2000 – A programming language based on speech acts February 1st 2010. [Online] URL: www.formal.stanford.edu/jmcGoogle Scholar
Reiter, R. 2001. Knowledge in Action: Logical Foundations for Describing and Implementing Dynamical Systems. MIT Press, Bradford Books, Cambridge, MA.CrossRefGoogle Scholar
Simons, P. 2000. Extending and Implementing the Stable Model Semantics. Ph.D. thesis, Helsinki University of Technology.Google Scholar
Son, T. C., Baral, C. and McIlraith, S. A. 2001. Planning with different forms of domain-dependent control knowledge – An answer set programming approach. In Logic Programming and Non-monotonic Reasoning, 6th International Conference, LPNMR 2001, Vienna, Austria, September 17–19, 2001, Proceedings, Eiter, T., Faber, W., and Truszczyński, M., Eds. Lecture Notes in Computer Science, vol. 2173. Springer, 226–239.Google Scholar
Son, T. C., Tu, P. H. and Baral, C. 2007. Reasoning and planning with sensing actions, incomplete information, and static causal laws using answer set programming. Theory and Practice of Logic Programming 7 (4), 377–450.Google Scholar
Thielscher, M. 1999. From situation calculus to fluent calculus: State update axioms as a solution to the inferential frame problem. In Artificial Intelligence 111 (1–2), 277–299.CrossRefGoogle Scholar
Thielscher, M. 2002a. Reasoning about actions with CHRs and finite domain constraints. Lecture Notes in Computer Science 2401, 70–84.CrossRefGoogle Scholar
Thielscher, M. 2002b. Pushing the envelope: Programming reasoning agents. In AAAI Workshop on Cognitive Robotics, Baral, C. and McIlraith, S., Eds. AAAI Press.Google Scholar
Tu, P. H., Son, T. C. and Pontelli, E. 2007. CPP: A constraint logic programming based planner with preferences. In Logic Programming and Non-monotonic Reasoning, 9th International Conference, LPNMR 2007, Tempe, AZ, USA, May 15-17, 2007, Proceedings, Baral, C., Brewka, G., and Schlipf, J. S., Eds. Lecture Notes in Computer Science, vol. 4483. Springer, 290–296.Google Scholar
Vidal, V. and Geffner, G. 2006. Branching and pruning: An optimal temporal POCL planner based in constraint programming. Artificial Intelligence 170, 298–335.CrossRefGoogle Scholar