1 Introduction
Answering queries over incomplete databases is crucial in many different scenarios such as data integration (Lenzerini Reference Lenzerini, Popa, Abiteboul and Kolaitis2002), data exchange (Arenas et al. Reference Arenas, Barceló, Libkin and Murlak2014), inconsistency management (Bertossi Reference Bertossi2011), data cleaning (Geerts et al. Reference Geerts, Mecca, Papotti and Santoro2013), ontology-based data access (OBDA) (Bienvenu and Ortiz Reference Bienvenu and Ortiz2015), and many others. The common thread running through all these applications lies in computing certain answers (Imielinski and Lipski Reference Imielinski and Lipski1984). Intuitively, this produces answers that are true in all possible worlds, that is, complete databases that an incomplete database represents. An incomplete database in itself is a set of tuples with missing information, plus integrity constraints. One can think, for example, of relations with nulls on which keys can be specified. Then, a possible world is obtained by substituting values for nulls so that all the keys are satisfied.
The notion of certain answers is sometimes too restrictive (for example, for some queries no answers are certain). In that case, an alternative is best answers: for them, there is no other tuple that is an answer in more possible worlds. However, computationally one encounters serious problems with both approaches. To start with, computing certain answers and best answers is intractable for first-order queries (Abiteboul et al. Reference Abiteboul, Kanellakis and Grahne1991; Libkin Reference Libkin, den Bussche and Arenas2018) (already for data complexity). Finding such answers in restricted subclasses of first-order queries often relies on sophisticated algorithms – not naturally expressible by other queries – that are therefore difficult to implement in a DBMS. We know that restricting to unions of conjunctive queries allows one to overcome this difficulty by using naïve evaluation which computes certain answers in polynomial time (Imielinski and Lipski Reference Imielinski and Lipski1984). This amounts to evaluating queries over incomplete databases as if nulls were usual data values, thus merely using the standard database query engine to compute certain answers.
We address these problems in the present paper whose goal is two-fold.
-
1. We start by filling gaps in our knowledge of the complexity of answering queries over incomplete databases. Intractable bounds on certain and best answers cited above were obtained under different formulations of query answering as a decision problem. We show that there are three natural ways to represent query answering as a decision problem and classify the complexity of certain and best answers for all of them.
-
2. We then look at a way of finding query answers by leveraging the existing database technology, namely by finding query rewritings which, when evaluated on the incomplete database, give us certain answers. We show that for a class extending unions of conjunctive queries with a form of negation (but still falling short of all first-order queries), such rewritings can be found in Datalog with negation, thus giving us a tractable complexity bound.
To elaborate on the first point, the two existing decision versions of the query answering problem are as follows: (a) is a tuple in the answer? and (b) is the answer a member of a given family of sets? We add a third: (c) is the answer equal to a given set. We then prove that for certain answers, the complexity is coNP,![]() , and DP-complete for (a), (b), (c). The result for (a) has long been known of course. For best answers, the complexity is uniform:
, and DP-complete for (a), (b), (c). The result for (a) has long been known of course. For best answers, the complexity is uniform:![]() -complete for all variations (the result for (b) was previously known). We shall define these complexity classes in the next section; for the reader not familiar with them, they all lie within the second level of the polynomial hierarchy.
-complete for all variations (the result for (b) was previously known). We shall define these complexity classes in the next section; for the reader not familiar with them, they all lie within the second level of the polynomial hierarchy.
For the second theme of the paper, we look at query rewritings. This is a standard way of leveraging database technology in the case of incomplete or imperfect information, and such rewritings were heavily used in data integration, data exchange, OBDA, query answering using views, consistent query answering, etc. (Calvanese et al. 2000; Reference Calvanese, Giacomo, Lenzerini and Vardi2007; Calí et al. Reference Cal, Calvanese and Lenzerini2013; 2003b). First-order rewritings are particularly useful, as they allow to use the power of standard database query engines. In fact when they exist, the rewritten queries can be implemented in any relational query engine by expressing them in SQL, with no need to implement ad-hoc algorithms. Next best are rewritings into Datalog (with negation): these let us express queries using recursive features of SQL.
As already mentioned, for unions of conjunctive queries (and even some mild restrictions with guarded negation Gheerbrant et al. Reference Gheerbrant, Libkin and Sirangelo2014) certain answers are computed by na ve evaluation without the presence of constraints. Under constraints, even such simple ones as keys, the picture is less complete. Indeed, keys and in general equality-generating dependencies (EGD) change the syntactic shape of a query that makes naive evaluation work.
-
Certain answers to a conjunctive query Q (or a union of CQs) on a database D under key constraints
 $\Sigma$
can be found by na ve evaluation of Q on the result of the chase of D with
$\Sigma$
can be found by na ve evaluation of Q on the result of the chase of D with
 $\Sigma$
. Mathematically,
$\Sigma$
. Mathematically,
 $\mathsf{cert}_\Sigma(Q,D)=Q(\mathsf{chase}_\Sigma(D))$
, where on the left-hand side we have certain answers under constraints and on the right-hand side the na ve evaluation of Q over the result of the chase. Here,
$\mathsf{cert}_\Sigma(Q,D)=Q(\mathsf{chase}_\Sigma(D))$
, where on the left-hand side we have certain answers under constraints and on the right-hand side the na ve evaluation of Q over the result of the chase. Here,
 $\mathsf{chase}_\Sigma$
refers to the classical textbook chase procedure with keys or more generally functional dependencies. In fact, the above result applies when
$\mathsf{chase}_\Sigma$
refers to the classical textbook chase procedure with keys or more generally functional dependencies. In fact, the above result applies when
 $\Sigma$
is a set of functional dependencies or equality generating dependencies (EGDs), not just keys.
$\Sigma$
is a set of functional dependencies or equality generating dependencies (EGDs), not just keys.
Unfortunately, the above result does not work when we move outside the class of select-project-join-union queries or unions of CQs. In fact even without constraints, certain answers to a query of the form
![]() $Q_1-Q_2$
, where both
$Q_1-Q_2$
, where both
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
are CQs, are not necessarily produced by na ve evaluation. To see why, take a database containing one fact
$Q_2$
are CQs, are not necessarily produced by na ve evaluation. To see why, take a database containing one fact
![]() $R(1,\bot)$
where
$R(1,\bot)$
where
![]() $\bot$
is a null and
$\bot$
is a null and
![]() $Q_1$
returning R while
$Q_1$
returning R while
![]() $Q_2$
is given by a formula
$Q_2$
is given by a formula
![]() $R(x,y) \wedge x=y$
. Here, na ve evaluation of
$R(x,y) \wedge x=y$
. Here, na ve evaluation of
![]() $Q_1-Q_2$
returns R (as 1 is not equal to
$Q_1-Q_2$
returns R (as 1 is not equal to
![]() $\bot$
), while certain answers is empty (as 0 is a possible value for
$\bot$
), while certain answers is empty (as 0 is a possible value for
![]() $\bot$
).
$\bot$
).
This motivates our question whether we can extend the class of CQs and their unions to obtain tractable evaluation of certain answers under constraints such as functional dependencies and EGDs. The answer is positive; in fact the query of the form
![]() $Q_1-Q_2$
above will be an example of a query in this class. To start with, the class must be such that finding certain answers for its queries without constraints is already tractable. We know one such class: it consists of arbitrary Boolean combinations of CQs, not just their union. We shall denote it by BCCQ. It was proved in Gheerbrant and Libkin (Reference Gheerbrant and Libkin2015) that certain answers for it can be found in polynomial time (for data complexity), though the procedure was tableau-based and not suitable for implementation in a database system.
$Q_1-Q_2$
above will be an example of a query in this class. To start with, the class must be such that finding certain answers for its queries without constraints is already tractable. We know one such class: it consists of arbitrary Boolean combinations of CQs, not just their union. We shall denote it by BCCQ. It was proved in Gheerbrant and Libkin (Reference Gheerbrant and Libkin2015) that certain answers for it can be found in polynomial time (for data complexity), though the procedure was tableau-based and not suitable for implementation in a database system.
This is precisely what we do in the second part of this paper. We establish three main results:
-
1. For an arbitrary BCCQ Q and a set of EGDs
 $\Sigma,$
one can construct a Datalog (with negation) query Q’ whose naive evaluation computes certain answers, thereby ensuring their polynomial-time data complexity.
$\Sigma,$
one can construct a Datalog (with negation) query Q’ whose naive evaluation computes certain answers, thereby ensuring their polynomial-time data complexity. -
2. There are however simple BCCQs, in fact even CQs, and keys, such that certain answers cannot be expressed as a first-order queries. Therefore, using Datalog was necessary.
-
3. Without constraints present, certain answers to BCCQs are not only polynomial-time computable as had been shown previously, but also can be expressed by first-order queries and thus efficiently implemented in SQL databases without using recursion.
The Sections 4.2, 4.3, and 4.4 address these items, respectively.
Note that the material from this paper is based on the two conference papers Gheerbrant and Sirangelo (Reference Gheerbrant and Sirangelo2019) and Gheerbrant et al. (Reference Gheerbrant, Libkin, Rogova, Sirangelo and Workshop Proceedings2022).
2 Preliminaries
2.1 Incomplete databases and constraints
We represent missing information in relational databases in the standard way using nulls (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995; Imielinski and Lipski Reference Imielinski and Lipski1984; van der Meyden Reference van der Meyden, Chomicki and Saake1998). Incomplete databases are populated by constants and nulls, coming respectively from two countably infinite sets
![]() ${\sf Const}$
and
${\sf Const}$
and
![]() ${\sf Null}$
. We denote nulls by
${\sf Null}$
. We denote nulls by
![]() $\bot$
, sometimes with sub- or superscript. We also allow them to repeat, thus adopting the model of marked nulls, as customary in the context of applications such as OBDA or data integration and exchange.
$\bot$
, sometimes with sub- or superscript. We also allow them to repeat, thus adopting the model of marked nulls, as customary in the context of applications such as OBDA or data integration and exchange.
A relational schema, or vocabulary
![]() $\sigma$
, is a set of relation names with associated arities. A database D over
$\sigma$
, is a set of relation names with associated arities. A database D over
![]() $\sigma$
associates to each relation name of arity k in
$\sigma$
associates to each relation name of arity k in
![]() $\sigma$
, a k-ary relation which is a finite subset of
$\sigma$
, a k-ary relation which is a finite subset of
![]() $({\sf Const} \cup {\sf Null})^k$
. Sets of constants and nulls occurring in D are denoted by
$({\sf Const} \cup {\sf Null})^k$
. Sets of constants and nulls occurring in D are denoted by
![]() ${\sf Const}(D)$
and
${\sf Const}(D)$
and
![]() ${\sf Null}(D)$
. A database is complete if it contains no nulls, that is
${\sf Null}(D)$
. A database is complete if it contains no nulls, that is
![]() ${\sf Null}(D) = \emptyset$
.
${\sf Null}(D) = \emptyset$
.
The active domain of D is the set of all values appearing in D, that is
![]() $\text{adom}(D)={\sf Const}(D)\cup{\sf Null}(D)$
.
$\text{adom}(D)={\sf Const}(D)\cup{\sf Null}(D)$
.
A valuation
![]() $v : {\sf Null}(D) \rightarrow {\sf Const}$
on a database D is a map that assigns constant values to nulls occurring in D. By v(D) and
$v : {\sf Null}(D) \rightarrow {\sf Const}$
on a database D is a map that assigns constant values to nulls occurring in D. By v(D) and
![]() $v(\bar a),$
we denote the result of replacing each null
$v(\bar a),$
we denote the result of replacing each null
![]() $\bot$
by
$\bot$
by
![]() $v(\bot)$
in a database D or in a tuple
$v(\bot)$
in a database D or in a tuple
![]() $\bar a$
. The semantics
$\bar a$
. The semantics
![]() $[\![ D ]\!]$
of an incomplete database D is the set
$[\![ D ]\!]$
of an incomplete database D is the set![]() of all complete databases it can represent. Here as is common in research on incomplete data, we use closed-world assumption (Imielinski and Lipski Reference Imielinski and Lipski1984; Reiter Reference Reiter, Gallaire and Minker1977) (i.e. everything we do not know to be true is automatically assumed to be false and no new tuple can be added).
of all complete databases it can represent. Here as is common in research on incomplete data, we use closed-world assumption (Imielinski and Lipski Reference Imielinski and Lipski1984; Reiter Reference Reiter, Gallaire and Minker1977) (i.e. everything we do not know to be true is automatically assumed to be false and no new tuple can be added).
An equality-generating dependency (EGD) is a first-order sentence of the form
![]() $\forall \bar x ~~(\varphi(\bar x)~\rightarrow~z=z')$
, where
$\forall \bar x ~~(\varphi(\bar x)~\rightarrow~z=z')$
, where
![]() $\varphi(\bar x)$
is a conjunction of atoms (without constants), each variable in
$\varphi(\bar x)$
is a conjunction of atoms (without constants), each variable in
![]() $\bar x$
occurs in some atom of
$\bar x$
occurs in some atom of
![]() $\varphi$
, and z, z’ are distinct variables in
$\varphi$
, and z, z’ are distinct variables in
![]() $\bar x$
. As a special case, a functional dependency (FD) over a relation name R is of the form
$\bar x$
. As a special case, a functional dependency (FD) over a relation name R is of the form
![]() $\forall \bar x, \bar y, z, z'~~(R(\bar x, \bar y, z) \wedge R(\bar x, \bar y', z') \rightarrow z = z')$
. Throughout this paper, we will assume that a (possibly empty) set of EGDs
$\forall \bar x, \bar y, z, z'~~(R(\bar x, \bar y, z) \wedge R(\bar x, \bar y', z') \rightarrow z = z')$
. Throughout this paper, we will assume that a (possibly empty) set of EGDs
![]() $\Sigma$
is associated with the database schema
$\Sigma$
is associated with the database schema
![]() $\sigma$
.
$\sigma$
.
A valuation v is consistent with
![]() $\Sigma$
(or just consistent, when
$\Sigma$
(or just consistent, when
![]() $\Sigma$
is clear from the context) if
$\Sigma$
is clear from the context) if
![]() $v(D) \models \Sigma$
. We denote by
$v(D) \models \Sigma$
. We denote by![]() the set of all consistent valuations defined on D.
the set of all consistent valuations defined on D.
2.2 Query answering
An m-ary query Q of active domain
![]() $\text{adom}(Q) \subseteq {\sf Const}$
is a map that associates with a database D a subset of
$\text{adom}(Q) \subseteq {\sf Const}$
is a map that associates with a database D a subset of
![]() $(\text{adom}(D)\cup \text{adom}(Q))^m$
. To answer an m-ary query Q over an incomplete database D, we follow (Lipski Reference Lipski, Rosenkrantz and Fagin1984) and adopt a slight generalization of the usual intersection-based certain answers notion, defined as
$(\text{adom}(D)\cup \text{adom}(Q))^m$
. To answer an m-ary query Q over an incomplete database D, we follow (Lipski Reference Lipski, Rosenkrantz and Fagin1984) and adopt a slight generalization of the usual intersection-based certain answers notion, defined as
![]() $\cap_vQ(v(D))$
, and furthermore incorporate constraints into query answering.
$\cap_vQ(v(D))$
, and furthermore incorporate constraints into query answering.
The set of certain answers to Q over D, with respect to a set of constraints
![]() $\Sigma$
, is
$\Sigma$
, is
For queries that explicitly use constants, we shall expand this to allow
![]() $\bar a$
range over
$\bar a$
range over
![]() $\text{adom}(D)$
and those constants. The only difference with the usual notion is that we allow answers to contain nulls, to avoid pathological situations when answers known with certainty are not returned (e.g. in a query returning a relation R one would expect R to be returned while the intersection-based certain answer will only return null-free tuples). If the set of constraints
$\text{adom}(D)$
and those constants. The only difference with the usual notion is that we allow answers to contain nulls, to avoid pathological situations when answers known with certainty are not returned (e.g. in a query returning a relation R one would expect R to be returned while the intersection-based certain answer will only return null-free tuples). If the set of constraints
![]() $\Sigma$
is empty, we omit it and write simply
$\Sigma$
is empty, we omit it and write simply
![]() $\mathsf{cert}(Q,D)$
. Of course, every valuation is consistent with the empty set of constraints.
$\mathsf{cert}(Q,D)$
. Of course, every valuation is consistent with the empty set of constraints.
Following Libkin (Reference Libkin, den Bussche and Arenas2018), given a query Q, a database D, a set of constraints
![]() $\Sigma$
, and a tuple
$\Sigma$
, and a tuple
![]() $\bar a$
over
$\bar a$
over
![]() $\text{adom}(D)\cup \text{adom}(Q)$
, we let the support of
$\text{adom}(D)\cup \text{adom}(Q)$
, we let the support of
![]() $\bar a$
be the set of all valuations that witness it:
$\bar a$
be the set of all valuations that witness it:
Again if
![]() $\Sigma=\emptyset$
we omit the subscript.
$\Sigma=\emptyset$
we omit the subscript.
Supports thus measure how close a tuple is to certainty. We consider one answer to be better than another if it has more support. That is, given a database D, a k-ary query Q, and k-tuples
![]() $\bar a, \bar b$
over
$\bar a, \bar b$
over
![]() $\text{adom}(D)\cup\text{adom}(Q)$
, we let
$\text{adom}(D)\cup\text{adom}(Q)$
, we let
The set of best answers to Q over D is defined as the set of answers for which there is no better one:
As the set of certain answers to Q over D is the set of answers that are witnessed by all valuations, note that it could also be defined using the notion of support. Namely,
![]() $\mathsf{cert}_\Sigma(Q,D)$
consists of all tuples
$\mathsf{cert}_\Sigma(Q,D)$
consists of all tuples
![]() $\bar{a} \in \text{adom}(D)^m$
for which
$\bar{a} \in \text{adom}(D)^m$
for which![]() contains all consistent valuations in
contains all consistent valuations in![]() .
.
Example 2.1 Let
![]() $Q(x)=\exists y (R(y) \wedge S(y,x))$
and
$Q(x)=\exists y (R(y) \wedge S(y,x))$
and
![]() $D = \{R(\bot_1), R(1), S(\bot_2, \bot_2)\}$
.
$D = \{R(\bot_1), R(1), S(\bot_2, \bot_2)\}$
.
We have![]() ,
,![]() and
and![]() .
.
It follows that
![]() $\mathsf{cert}(Q,D) = \emptyset$
and
$\mathsf{cert}(Q,D) = \emptyset$
and![]() .
.
2.3 Naïve evaluation and certain answers
For a query Q written in FO or Datalog, we write Q(D) to mean that such a query is evaluated na ve ly. That is, if D contains nulls, nulls of D are treated as new constants in the domain of D, distinct from each other, and distinct from all the other constants in D and
![]() $\varphi$
. For example, the query
$\varphi$
. For example, the query
![]() $\varphi(x,y) = \exists z~(R(x, z) \wedge R(z, y))$
, on the database
$\varphi(x,y) = \exists z~(R(x, z) \wedge R(z, y))$
, on the database
![]() $D = \{R(1, \bot_1), R(\bot_1, \bot_2), R(\bot_3, 2)\}$
selects only the tuple
$D = \{R(1, \bot_1), R(\bot_1, \bot_2), R(\bot_3, 2)\}$
selects only the tuple
![]() $(1, \bot_2)$
.
$(1, \bot_2)$
.
There are known connections between na ve evaluation and certain answers. If
![]() $\Sigma$
is empty and Q is a union of conjunctive queries, then
$\Sigma$
is empty and Q is a union of conjunctive queries, then
![]() $\mathsf{cert}_\Sigma(Q,D)=Q(D)$
, see Imielinski and Lipski (Reference Imielinski and Lipski1984). If
$\mathsf{cert}_\Sigma(Q,D)=Q(D)$
, see Imielinski and Lipski (Reference Imielinski and Lipski1984). If
![]() $\Sigma$
contains a set of EGDs, then
$\Sigma$
contains a set of EGDs, then
![]() $\mathsf{cert}_\Sigma(Q,D)=Q\big(\mathsf{chase}_\Sigma(D)\big)$
; cf. Greco et al. (Reference Greco, Molinaro and Spezzano2012). Here
$\mathsf{cert}_\Sigma(Q,D)=Q\big(\mathsf{chase}_\Sigma(D)\big)$
; cf. Greco et al. (Reference Greco, Molinaro and Spezzano2012). Here
![]() $\mathsf{chase}_\Sigma$
refers to the standard chase procedure with a set of EGDs, see Abiteboul et al. (Reference Abiteboul, Hull and Vianu1995).
$\mathsf{chase}_\Sigma$
refers to the standard chase procedure with a set of EGDs, see Abiteboul et al. (Reference Abiteboul, Hull and Vianu1995).
2.4 Query languages
Here we shall study best and certain answers to first-order (
![]() ${{{{\mathsf{FO}}}}}$
) queries, possibly in the presence of constraints, by means of their rewriting in
${{{{\mathsf{FO}}}}}$
) queries, possibly in the presence of constraints, by means of their rewriting in
![]() ${{{{\mathsf{FO}}}}}$
and Datalog. FO queries of vocabulary
${{{{\mathsf{FO}}}}}$
and Datalog. FO queries of vocabulary
![]() $\sigma$
use atomic relational and equality formulae and are closed under Boolean connectives
$\sigma$
use atomic relational and equality formulae and are closed under Boolean connectives
![]() $\wedge, \vee, \neg$
and quantifiers
$\wedge, \vee, \neg$
and quantifiers
![]() $\exists, \forall$
. We write
$\exists, \forall$
. We write
![]() $\varphi(\bar x)$
for an
$\varphi(\bar x)$
for an
![]() ${{{{\mathsf{FO}}}}}$
-formula
${{{{\mathsf{FO}}}}}$
-formula
![]() $\varphi$
with free variables
$\varphi$
with free variables
![]() $\bar x$
. With slight abuse of notation,
$\bar x$
. With slight abuse of notation,
![]() $\bar x$
will denote both a tuple of variables and the set of variables occurring in it. The set of constants used by
$\bar x$
will denote both a tuple of variables and the set of variables occurring in it. The set of constants used by
![]() $\varphi$
is denoted by
$\varphi$
is denoted by
![]() $\text{adom}(\varphi)$
. We interpret
$\text{adom}(\varphi)$
. We interpret
![]() ${{{{\mathsf{FO}}}}}$
-formulas under active domain semantics, that is quantified variables range over
${{{{\mathsf{FO}}}}}$
-formulas under active domain semantics, that is quantified variables range over
![]() $\text{adom}(D) \cup \text{adom}(\varphi)$
. Thus, an
$\text{adom}(D) \cup \text{adom}(\varphi)$
. Thus, an
![]() ${{{{\mathsf{FO}}}}}$
-formula
${{{{\mathsf{FO}}}}}$
-formula
![]() $\varphi(\bar x)$
represents a query (of active domain
$\varphi(\bar x)$
represents a query (of active domain
![]() $\text{adom}(\varphi)$
) mapping each database D into the set of tuples
$\text{adom}(\varphi)$
) mapping each database D into the set of tuples
![]() $\{\bar t \textrm { over } \text{adom}(D)\cup\text{adom}(\varphi)~|~D \models \varphi(\bar t)\}$
.
$\{\bar t \textrm { over } \text{adom}(D)\cup\text{adom}(\varphi)~|~D \models \varphi(\bar t)\}$
.
To evaluate
![]() ${{{{\mathsf{FO}}}}}$
-formulas with free variables, we use assignments
${{{{\mathsf{FO}}}}}$
-formulas with free variables, we use assignments
![]() $\nu$
from variables to constants in the active domain. Note that with a little abuse of notation, we write
$\nu$
from variables to constants in the active domain. Note that with a little abuse of notation, we write
![]() $D \models \varphi(\bar t)$
for
$D \models \varphi(\bar t)$
for
![]() $D \models_\nu \varphi(\bar x)$
under the assignment
$D \models_\nu \varphi(\bar x)$
under the assignment
![]() $\nu$
sending
$\nu$
sending
![]() $\bar x$
to
$\bar x$
to
![]() $\bar t$
.
$\bar t$
.
Here it is important to note that the query associated with
![]() $\varphi$
is a mapping defined on all databases D, possibly with nulls. If D contains nulls,
$\varphi$
is a mapping defined on all databases D, possibly with nulls. If D contains nulls,
![]() $D \models \varphi(\bar t)$
is to be intended “navely,” that is nulls of D are treated as new constants in the domain of D, distinct from each other, and distinct from all the other constants in D and
$D \models \varphi(\bar t)$
is to be intended “navely,” that is nulls of D are treated as new constants in the domain of D, distinct from each other, and distinct from all the other constants in D and
![]() $\varphi$
. For example, the query
$\varphi$
. For example, the query
![]() $\varphi(x,y) = \exists z~(R(x, z) \wedge R(z, y))$
, on the database
$\varphi(x,y) = \exists z~(R(x, z) \wedge R(z, y))$
, on the database
![]() $D = \{R(1, \bot_1), R(\bot_1, \bot_2), R(\bot_3, 2)\}$
selects only the tuple
$D = \{R(1, \bot_1), R(\bot_1, \bot_2), R(\bot_3, 2)\}$
selects only the tuple
![]() $(1, \bot_2)$
.
$(1, \bot_2)$
.
Conjunctive queries (CQs) are given by the
![]() $\exists,\wedge$
-fragment of
$\exists,\wedge$
-fragment of
![]() ${{{{\mathsf{FO}}}}}$
, and their unions (UCQs) by the
${{{{\mathsf{FO}}}}}$
, and their unions (UCQs) by the
![]() $\exists,\wedge,\vee$
-fragment of
$\exists,\wedge,\vee$
-fragment of
![]() ${{{{\mathsf{FO}}}}}$
; these are also captured by the positive fragment of relational algebra (select-project-union-join queries).
${{{{\mathsf{FO}}}}}$
; these are also captured by the positive fragment of relational algebra (select-project-union-join queries).
We also consider Boolean combination of conjunctive queries (BCCQs), that is, the closure of conjunctive queries under operations
![]() $q \cap q'$
,
$q \cap q'$
,
![]() $q \cup q'$
, and
$q \cup q'$
, and
![]() $q - q'$
.
$q - q'$
.
A Datalog rule (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995) is an expression of the form
![]() $R_1(u_1) \leftarrow R_2(u_2), \ldots , R_n (u_n )$
where
$R_1(u_1) \leftarrow R_2(u_2), \ldots , R_n (u_n )$
where
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $R_1, \ldots , R_n$
are relation names and
$R_1, \ldots , R_n$
are relation names and
![]() $u_1,\ldots, u_n$
are tuples of appropriate arities. Each variable occurring in
$u_1,\ldots, u_n$
are tuples of appropriate arities. Each variable occurring in
![]() $u_1$
must occur in at least one of
$u_1$
must occur in at least one of
![]() $u_2, \ldots , u_n$
. A Datalog program is a finite set of Datalog rules. The head of the rule is the expression
$u_2, \ldots , u_n$
. A Datalog program is a finite set of Datalog rules. The head of the rule is the expression
![]() $R_1(u_1)$
; and
$R_1(u_1)$
; and
![]() $R_2(u_2), \ldots, R_n(u_n )$
forms the body. The semantics is the standard fixed-point semantics.
$R_2(u_2), \ldots, R_n(u_n )$
forms the body. The semantics is the standard fixed-point semantics.
As the language of our rewritings, we shall be using
![]() ${{{{\mathsf{FO}}}}}$
, but also a fragment of stratified Datalog with negation in bodies that can be seen in two different ways.
${{{{\mathsf{FO}}}}}$
, but also a fragment of stratified Datalog with negation in bodies that can be seen in two different ways.
-
1. A program is evaluated in two steps. First, we can have a Datalog program P defining new idb predicates
 $S_1,\ldots,S_\ell$
. Then, we ask an
$S_1,\ldots,S_\ell$
. Then, we ask an
 ${{{{\mathsf{FO}}}}}$
query over the schema extended with these predicates
${{{{\mathsf{FO}}}}}$
query over the schema extended with these predicates
 $S_1,\ldots,S_\ell$
.
$S_1,\ldots,S_\ell$
. -
2. We evaluate a stratified Datalog with negation program in which the first stratum has no negation (but may have recursion) and the second stratum has no recursion (but may have negation).
From the rewritings, we produce it will be clear that they fall in these classes. The key point about them is that they can be implemented in recursive SQL and that they both have PTIME data complexity, making their evaluation feasible. Note that recursive SQL as it is currently implemented, for example, in PostgreSQL 8.4, is actually Turing complete (Gierth Reference Gierth2011; Coelho Reference Coelho2013).
2.5 Complexity classes
In order to study the complexity of best and certain answer computation, we shall need two classes in the second level of the polynomial hierarchy. Both of these contain NP and coNP and are contained in
![]() $\Sigma^p_2\cap\Pi^p_2$
. The class DP consists of languages
$\Sigma^p_2\cap\Pi^p_2$
. The class DP consists of languages
![]() $L_1\cap L_2$
where
$L_1\cap L_2$
where![]() and
and![]() . This class has appeared in database applications (Fagin et al. Reference Fagin, Kolaitis and Popa2005; Barceló et al. Reference Barceló, Libkin and Romero2014). The class
. This class has appeared in database applications (Fagin et al. Reference Fagin, Kolaitis and Popa2005; Barceló et al. Reference Barceló, Libkin and Romero2014). The class![]() consists of problems that can be solved in polynomial time with a logarithmic number of calls to an NP oracle (Buss and Hay Reference Buss and Hay1991). Equivalently, it can be described as the class of problems solved in P with an NP oracle where calls to the oracle are done in parallel, that is, independent of each other. This class has appeared in the context of AI, modal logic, OBDA (Gottlob Reference Gottlob1995; Eiter and Gottlob Reference Eiter and Gottlob1997; Calvanese et al. Reference Calvanese, Giacomo, Lembo, Lenzerini and Rosati2006; Bienvenu and Bourgaux Reference Bienvenu and Bourgaux2016), data exchange (Arenas et al. Reference Arenas, Pérez and Reutter2013).
consists of problems that can be solved in polynomial time with a logarithmic number of calls to an NP oracle (Buss and Hay Reference Buss and Hay1991). Equivalently, it can be described as the class of problems solved in P with an NP oracle where calls to the oracle are done in parallel, that is, independent of each other. This class has appeared in the context of AI, modal logic, OBDA (Gottlob Reference Gottlob1995; Eiter and Gottlob Reference Eiter and Gottlob1997; Calvanese et al. Reference Calvanese, Giacomo, Lembo, Lenzerini and Rosati2006; Bienvenu and Bourgaux Reference Bienvenu and Bourgaux2016), data exchange (Arenas et al. Reference Arenas, Pérez and Reutter2013).
3 Complexity of best and certain answers
We start by looking at complexity of certain and best answers of first-order queries and answer a few questions that are (perhaps somewhat surprisingly) missing in the literature. In this case, we look at arbitrary first-order queries; thus, we do not mention constraints since
![]() $\mathsf{cert}_\Sigma(Q,D)=\mathsf{cert}(\Sigma\to Q,D)$
and likewise for best answers. In the subsequent sections, when we consider rewritings for sublanguages of first order, we shall again mention constraints explicitly since queries of the form
$\mathsf{cert}_\Sigma(Q,D)=\mathsf{cert}(\Sigma\to Q,D)$
and likewise for best answers. In the subsequent sections, when we consider rewritings for sublanguages of first order, we shall again mention constraints explicitly since queries of the form
![]() $\Sigma\to Q$
will normally not belong to the same syntactic class as Q itself. In this context, we will refer to
$\Sigma\to Q$
will normally not belong to the same syntactic class as Q itself. In this context, we will refer to![]() .
.
As is common in database theory, we look at complexity in terms of complexity classes, which necessitates looking at decision versions of problems. The most common one that is found, stated here for![]() , is the following problem:
, is the following problem:

We are thus interested in data complexity: the query is fixed. We do not study combined complexity in this paper. In the remainder, we thus often omit the query and write![]() instead of
instead of![]() . Recall that in this case, for a language L, we say that the problem
. Recall that in this case, for a language L, we say that the problem![]() is C- complete in data complexity for a complexity class C, if
is C- complete in data complexity for a complexity class C, if![]() is solvable in C for every
is solvable in C for every
![]() $Q\in L$
, and there exists a specific
$Q\in L$
, and there exists a specific
![]() $Q_0\in L$
so that
$Q_0\in L$
so that![]() is hard for C. We know from Abiteboul et al. (Reference Abiteboul, Kanellakis and Grahne1991) that
is hard for C. We know from Abiteboul et al. (Reference Abiteboul, Kanellakis and Grahne1991) that![]() is coNP-complete in data complexity for first-order queries.
is coNP-complete in data complexity for first-order queries.
For best answers, it is a different version of the decision problem for which the complexity is known. Specifically, Libkin (Reference Libkin, den Bussche and Arenas2018) considered the problem of checking whether the set![]() belongs to a specified family of sets:
belongs to a specified family of sets:

For this decision version, the complexity of the problem was shown to be![]() -complete. This version looks a bit artificial, but we include it for the sake of completeness, because it has appeared in the literature.
-complete. This version looks a bit artificial, but we include it for the sake of completeness, because it has appeared in the literature.
However, this presentation of a decision suggests another rather natural presentation of a decision version, namely asking if a given set is![]() :
:

Our current state of knowledge is the complexity of CertainAnswer (coNP-complete) and BestAnswer
![]() $^\in$
(
$^\in$
(![]() -complete). Thus, we now fill the gap and classify complexities of all the problems – for data complexity – in the case of FO queries.
-complete). Thus, we now fill the gap and classify complexities of all the problems – for data complexity – in the case of FO queries.
We start by showing that all the alternatives for best answers – BestAnswer
![]() $_\Sigma$
, BestAnswer
$_\Sigma$
, BestAnswer
![]() $^=$
, and BestAnswer
$^=$
, and BestAnswer
![]() $^\in$
– are computationally equivalent.
$^\in$
– are computationally equivalent.
Theorem 3.1 For
![]() ${{{{\mathsf{FO}}}}}$
queries, the problems BestAnswer
${{{{\mathsf{FO}}}}}$
queries, the problems BestAnswer
![]() $_\Sigma$
, BestAnswer
$_\Sigma$
, BestAnswer
![]() $^\in,$
and BestAnswer
$^\in,$
and BestAnswer
![]() $^=$
are
$^=$
are![]() -complete in data complexity.
-complete in data complexity.
Proof. The upper bound for BestAnswer
![]() $^=$
immediately follows from the upper bound for BestAnswer
$^=$
immediately follows from the upper bound for BestAnswer
![]() $^\in$
(take the family
$^\in$
(take the family
![]() $\mathcal{X}$
to be a singleton
$\mathcal{X}$
to be a singleton
![]() $\{X\}$
). As for BestAnswer
$\{X\}$
). As for BestAnswer
![]() $_\Sigma,$
we only need a slight modification of the upper bound proof in Libkin (Reference Libkin, den Bussche and Arenas2018). To check whether
$_\Sigma,$
we only need a slight modification of the upper bound proof in Libkin (Reference Libkin, den Bussche and Arenas2018). To check whether![]() we proceed as follows. Since the query is fixed, and has therefore fixed arity k, in polynomial time we can enumerate all the k-tuples of
we proceed as follows. Since the query is fixed, and has therefore fixed arity k, in polynomial time we can enumerate all the k-tuples of
![]() $\text{adom}(D)$
. Then, using parallel calls to the NP oracle, we can check for each such tuple
$\text{adom}(D)$
. Then, using parallel calls to the NP oracle, we can check for each such tuple
![]() $\bar b$
whether
$\bar b$
whether![]() and whether
and whether![]() . With this information, in polynomial time we know whether
. With this information, in polynomial time we know whether
![]() $\bar a \lhd_{Q,D} \bar b$
for some
$\bar a \lhd_{Q,D} \bar b$
for some
![]() $\bar b$
.
$\bar b$
.
Assuming
![]() $\Sigma$
empty, we prove the two remaining lower bounds, reducing from the same
$\Sigma$
empty, we prove the two remaining lower bounds, reducing from the same![]() -complete problem (Wagner Reference Wagner1990): given an undirected graph G, is its chromatic number
-complete problem (Wagner Reference Wagner1990): given an undirected graph G, is its chromatic number
![]() $\chi(G)$
odd? With each undirected graph
$\chi(G)$
odd? With each undirected graph
![]() $G=\langle N, E\rangle$
with nodes N and edges E, we associate a database
$G=\langle N, E\rangle$
with nodes N and edges E, we associate a database
![]() $D_G$
over binary relations L,E and unary relations C,O as follows. We use a null
$D_G$
over binary relations L,E and unary relations C,O as follows. We use a null
![]() $\bot_n$
in
$\bot_n$
in
![]() $D_G$
for each node n of G. For each edge
$D_G$
for each node n of G. For each edge
![]() $\{n,n'\}$
of G, we have pairs
$\{n,n'\}$
of G, we have pairs
![]() $(\bot_n,\bot_{n'})$
and
$(\bot_n,\bot_{n'})$
and
![]() $(\bot_{n'},\bot_n)$
in the relation E of
$(\bot_{n'},\bot_n)$
in the relation E of
![]() $D_G$
. In relation C, we have m constants
$D_G$
. In relation C, we have m constants
![]() $\{c_1,\ldots,c_m\}$
(intuitively representing possible colors), where m is the number of nodes of G. Relation O of
$\{c_1,\ldots,c_m\}$
(intuitively representing possible colors), where m is the number of nodes of G. Relation O of
![]() $D_G$
is defined as
$D_G$
is defined as
![]() $\{c_i ~|~ i ~ \textrm{is odd}\},$
and L is a linear ordering on them, that is,
$\{c_i ~|~ i ~ \textrm{is odd}\},$
and L is a linear ordering on them, that is,
![]() $(c_i,c_j)\in L$
iff
$(c_i,c_j)\in L$
iff
![]() $i\leq j$
, for
$i\leq j$
, for
![]() $i,j\leq m$
.
$i,j\leq m$
.
Remark that any valuation v of
![]() $D_G$
that maps each null into a constant of C represents an assignment of colors in
$D_G$
that maps each null into a constant of C represents an assignment of colors in
![]() $\{c_1,\ldots,c_m\}$
to nodes of G. Then, we define a query
$\{c_1,\ldots,c_m\}$
to nodes of G. Then, we define a query
For any valuation v,
![]() $\phi(c)$
holds in
$\phi(c)$
holds in
![]() $v(D_G)$
iff (1)
$v(D_G)$
iff (1)
![]() $c = c_j$
for some
$c = c_j$
for some
![]() $j=1..m$
(ensured by the first conjunct). (2) For such a
$j=1..m$
(ensured by the first conjunct). (2) For such a
![]() $c_j$
, the valuation v maps each null into
$c_j$
, the valuation v maps each null into
![]() $\{c_1,\ldots,c_j\}$
(second conjunct), that is v represents an assignment of colors to nodes of G, using at most the first j colors. (3) Each color
$\{c_1,\ldots,c_j\}$
(second conjunct), that is v represents an assignment of colors to nodes of G, using at most the first j colors. (3) Each color
![]() $\{c_1,\ldots,c_j\}$
is used by v, that is v represents an assignment of colors to nodes of G, using precisely the first j colors (third conjunct). (4) There are no loops in E (fourth conjunct).
$\{c_1,\ldots,c_j\}$
is used by v, that is v represents an assignment of colors to nodes of G, using precisely the first j colors (third conjunct). (4) There are no loops in E (fourth conjunct).
Thus, for a valuation v, the formula
![]() $\phi(c_j)$
is true in
$\phi(c_j)$
is true in
![]() $v(D_G)$
iff v represents a coloring of G using precisely the first j colors
$v(D_G)$
iff v represents a coloring of G using precisely the first j colors
![]() $\{c_1,\ldots,c_j\}$
(which in the sequel we refer to as an exact j-coloring of G).
$\{c_1,\ldots,c_j\}$
(which in the sequel we refer to as an exact j-coloring of G).
Next, we define:
For a valuation v, we have that
![]() $Q(c_i)$
holds in
$Q(c_i)$
holds in
![]() $v(D_G)$
iff either v represents an exact i-coloring of G; or v represents an exact j-coloring of G with j odd, and
$v(D_G)$
iff either v represents an exact i-coloring of G; or v represents an exact j-coloring of G with j odd, and
![]() $i \leq j$
. In other words, valuations representing exact j-colorings, with j even, support only the maximal color
$i \leq j$
. In other words, valuations representing exact j-colorings, with j even, support only the maximal color
![]() $c_j$
; while valuations representing exact j-colorings, with j odd, support all colors
$c_j$
; while valuations representing exact j-colorings, with j odd, support all colors
![]() $\{c_1...c_j\}$
.
$\{c_1...c_j\}$
.
With this in place, we can conclude the reduction for the BestAnswer
![]() $_\Sigma$
problem:
$_\Sigma$
problem:
Claim.
![]() iff the chromatic number of G is odd.
iff the chromatic number of G is odd.
First, we prove the above claim. Let
![]() $\chi_G$
be the chromatic number of G. Then, there exist no exact colorings of G which are prefixes of
$\chi_G$
be the chromatic number of G. Then, there exist no exact colorings of G which are prefixes of
![]() $\{c_1, \dots c_{\chi_G}\}$
, while
$\{c_1, \dots c_{\chi_G}\}$
, while
![]() $\{c_1, \dots c_{\chi_G}\}$
is an exact coloring of G.
$\{c_1, \dots c_{\chi_G}\}$
is an exact coloring of G.
Assume first that
![]() $\chi_G$
is even. Then, there exist no valuations representing the exact coloring
$\chi_G$
is even. Then, there exist no valuations representing the exact coloring
![]() $\{c_1\}$
. Thus, the support of
$\{c_1\}$
. Thus, the support of
![]() $c_1$
is the set of valuation representing an exact coloring
$c_1$
is the set of valuation representing an exact coloring
![]() $\{c_1...c_j\}$
of G with j odd and
$\{c_1...c_j\}$
of G with j odd and
![]() $j > \chi_G$
. This support is not maximal. In fact, the support of
$j > \chi_G$
. This support is not maximal. In fact, the support of
![]() $c_{\chi_G}$
is:
$c_{\chi_G}$
is:
-
the valuations representing the exact coloring
 $\{c_1...c_{\chi_G}\}$
(there exists at least one);
$\{c_1...c_{\chi_G}\}$
(there exists at least one); -
the valuations representing an exact coloring
 $\{c_1...c_j\}$
of G with j odd and
$\{c_1...c_j\}$
of G with j odd and
 $j > \chi_G$
.
$j > \chi_G$
.
This support strictly contains the support of
![]() $c_1$
; in fact valuations in the first item cannot be also in the second.
$c_1$
; in fact valuations in the first item cannot be also in the second.
Assume now that
![]() $\chi_G$
is odd. Then, the support of
$\chi_G$
is odd. Then, the support of
![]() $c_1$
is the set of valuations representing an exact coloring
$c_1$
is the set of valuations representing an exact coloring
![]() $\{c_1...c_j\}$
of G with j odd and
$\{c_1...c_j\}$
of G with j odd and
![]() $j \geq \chi_G$
. We show that this set is maximal; that is, no color
$j \geq \chi_G$
. We show that this set is maximal; that is, no color
![]() $c_k$
can have a support strictly containing it.
$c_k$
can have a support strictly containing it.
-
if
 $k \leq \chi_G$
then the support of
$k \leq \chi_G$
then the support of
 $c_k$
is the set of valuations representing an exact coloring
$c_k$
is the set of valuations representing an exact coloring
 $\{c_1...c_j\}$
of G with j odd, and
$\{c_1...c_j\}$
of G with j odd, and
 $j \geq \chi_G$
. So same support as
$j \geq \chi_G$
. So same support as
 $c_1$
.
$c_1$
. -
if
 $k > \chi_G$
, the support of
$k > \chi_G$
, the support of
 $c_k$
cannot contain the valuations representing
$c_k$
cannot contain the valuations representing
 $\{c_1, \dots c_{\chi_G}\}$
. There exists at least one such valuation and it belongs to the support of
$\{c_1, \dots c_{\chi_G}\}$
. There exists at least one such valuation and it belongs to the support of
 $c_1$
. Thus, the support of
$c_1$
. Thus, the support of
 $c_k$
does not contain the support of
$c_k$
does not contain the support of
 $c_1$
.
$c_1$
.
We now move to BestAnswer
![]() $^=$
. With any undirected graph G, we associate a relational structure
$^=$
. With any undirected graph G, we associate a relational structure
![]() $D'_G$
obtained from
$D'_G$
obtained from
![]() $D_G$
by adding a new color
$D_G$
by adding a new color
![]() $c_0$
in C with
$c_0$
in C with
![]() $L(c_0,c_i)$
for every
$L(c_0,c_i)$
for every
![]() $0 \leq i \leq m$
. We define a restriction
$0 \leq i \leq m$
. We define a restriction
![]() $\psi$
of the original formula
$\psi$
of the original formula
![]() $\phi$
by disallowing
$\phi$
by disallowing
![]() $c_0$
in colorings: to obtain
$c_0$
in colorings: to obtain
![]() $\psi$
it suffices to replace L(y,x) in
$\psi$
it suffices to replace L(y,x) in
![]() $\phi$
by
$\phi$
by
![]() $L(y,x) \wedge y \neq c_0$
, and C(x) by
$L(y,x) \wedge y \neq c_0$
, and C(x) by
![]() $C(x) \wedge x\neq c_0$
. Thus, it is still true that
$C(x) \wedge x\neq c_0$
. Thus, it is still true that
![]() $\psi(c_j)$
is true in
$\psi(c_j)$
is true in
![]() $v(D_G')$
iff v represents a coloring of G using precisely
$v(D_G')$
iff v represents a coloring of G using precisely
![]() $\{c_1,\ldots,c_j\}$
.
$\{c_1,\ldots,c_j\}$
.
We define a new query:
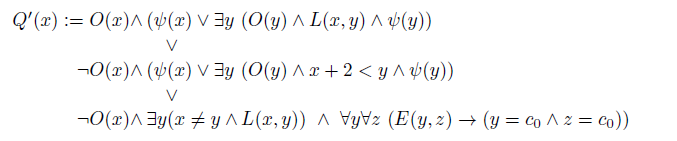
Note that
![]() $x+2 < y$
is used as a shorthand, as it is definable in our language.
$x+2 < y$
is used as a shorthand, as it is definable in our language.
![]() $Q'(c_i)$
holds in
$Q'(c_i)$
holds in
![]() $v(D'_G$
) iff
$v(D'_G$
) iff
-
either i is odd and v represents an exact j-coloring of G, with j odd and
 $i \leq j$
;
$i \leq j$
; -
or i is even and:
-
— either v represents an exact coloring
 $\{c_1...c_j\}$
of G with j odd, and
$\{c_1...c_j\}$
of G with j odd, and
 $i+2 < j$
;
$i+2 < j$
; -
— or v represents an exact coloring
 $\{c_1...c_i\}$
of G;
$\{c_1...c_i\}$
of G; -
— or
 $i<m$
and
$i<m$
and
 $v(\bot_j)=c_0$
for all
$v(\bot_j)=c_0$
for all
 $1 \leq j \leq m$
;
$1 \leq j \leq m$
;
-
The following claim completes the reduction for BestAnswer
![]() $^=$
:
$^=$
:
Claim.
![]() iff
iff
![]() $\chi(G)$
is even.
$\chi(G)$
is even.
In the following, we call
![]() $v_0$
the unique valuation such that
$v_0$
the unique valuation such that
![]() $v_0(\bot_j)=c_0$
for all
$v_0(\bot_j)=c_0$
for all
![]() $1 \leq j \leq m$
. First assume that
$1 \leq j \leq m$
. First assume that
![]() $\chi_G$
is even. For all
$\chi_G$
is even. For all
![]() $0 < i \leq m$
odd,
$0 < i \leq m$
odd,
![]() $Supp(c_i)$
is not maximal as
$Supp(c_i)$
is not maximal as
![]() $Supp(c_0) \supset Supp(c_i) \cup \{v_0\}$
. Hence,
$Supp(c_0) \supset Supp(c_i) \cup \{v_0\}$
. Hence,![]() , so we show
, so we show![]() . The inclusion holds whenever
. The inclusion holds whenever
![]() $c_i \geq \chi(G)$
, as
$c_i \geq \chi(G)$
, as
![]() $Supp(c_i)$
contains all valuations representing exact colorings
$Supp(c_i)$
contains all valuations representing exact colorings
![]() $\{c_1...c_i\}$
of G, while no other
$\{c_1...c_i\}$
of G, while no other
![]() $Supp(c_j)$
with
$Supp(c_j)$
with
![]() $i \neq j$
contains them. Now take
$i \neq j$
contains them. Now take
![]() $c_i < \chi(G)$
with i even, then
$c_i < \chi(G)$
with i even, then
![]() $Supp(c_i)$
contains
$Supp(c_i)$
contains
![]() $v_0$
together with all exact odd colorings (if there are any). First assume that there exists odd exact colorings of G, so there are
$v_0$
together with all exact odd colorings (if there are any). First assume that there exists odd exact colorings of G, so there are
![]() $\chi(G)+1$
ones and valuations representing them are not contained in
$\chi(G)+1$
ones and valuations representing them are not contained in
![]() $Supp(\chi(G))$
. Also,
$Supp(\chi(G))$
. Also,
![]() $v_0 \not \in Supp(c_k)$
with k odd and
$v_0 \not \in Supp(c_k)$
with k odd and
![]() $k < \chi(G)$
. It follows that
$k < \chi(G)$
. It follows that
![]() $Supp(c_i)$
, which is the union of
$Supp(c_i)$
, which is the union of
![]() $v_0$
and of all valuations representing odd exact colorings, is maximal. Now assume that there is no exact odd coloring. This corresponds to the special case
$v_0$
and of all valuations representing odd exact colorings, is maximal. Now assume that there is no exact odd coloring. This corresponds to the special case
![]() $\chi(G)=m$
where
$\chi(G)=m$
where
![]() $Supp(c_m)$
contains only the exact colorings
$Supp(c_m)$
contains only the exact colorings
![]() $\{c_1...c_{m}\}$
of G, but not
$\{c_1...c_{m}\}$
of G, but not
![]() $v_0$
; while
$v_0$
; while
![]() $Supp(c_j)=\emptyset$
whenever j odd. In such a case,
$Supp(c_j)=\emptyset$
whenever j odd. In such a case,
![]() $Supp(c_i)=\{v_0\}$
is also maximal.
$Supp(c_i)=\{v_0\}$
is also maximal.
We assume now
![]() $\chi(G)$
is odd and show
$\chi(G)$
is odd and show![]() . First notice that
. First notice that
![]() $Supp(c_1)$
is maximal whenever
$Supp(c_1)$
is maximal whenever
![]() $\chi(G)=1$
, as neither
$\chi(G)=1$
, as neither
![]() $Supp(c_0)$
nor any
$Supp(c_0)$
nor any
![]() $Supp(c_i)$
with
$Supp(c_i)$
with
![]() $i \geq 2$
contain valuations representing the exact
$i \geq 2$
contain valuations representing the exact
![]() $\{c_1\}$
colorings. So we assume
$\{c_1\}$
colorings. So we assume
![]() $\chi(G)\geq 3$
, from which it follows that there exists a constant
$\chi(G)\geq 3$
, from which it follows that there exists a constant
![]() $c_{\chi(G)-3}$
in the active domain which support contains
$c_{\chi(G)-3}$
in the active domain which support contains
![]() $v_0$
together with all valuations representing exact odd colorings. As
$v_0$
together with all valuations representing exact odd colorings. As
![]() $Supp(c_{\chi(G)-1})$
contains exactly the same set of valuations, to the exclusion of those representing
$Supp(c_{\chi(G)-1})$
contains exactly the same set of valuations, to the exclusion of those representing
![]() $\{c_1...c_{\chi(G)}\}$
colorings, it follows that
$\{c_1...c_{\chi(G)}\}$
colorings, it follows that
![]() $Supp(c_{\chi(G)-3}) \supset Supp(c_{\chi(G)-1})$
and so
$Supp(c_{\chi(G)-3}) \supset Supp(c_{\chi(G)-1})$
and so![]() .
.
Now that we showed that all three formulations of best answers actually collapse computationally, another natural question arises. Does a similar result hold for certain answers ? It is well known that data complexity of CertainAnswer
![]() $_\Sigma$
is coNP-complete for
$_\Sigma$
is coNP-complete for
![]() ${{{{\mathsf{FO }}}}}$
queries (Abiteboul et al. Reference Abiteboul, Kanellakis and Grahne1991). We complete the picture as follows and summarize results in Figure 1.
${{{{\mathsf{FO }}}}}$
queries (Abiteboul et al. Reference Abiteboul, Kanellakis and Grahne1991). We complete the picture as follows and summarize results in Figure 1.

Fig. 1. Summary of data complexity results for
![]() ${\mathsf{FO}}$
queries.
${\mathsf{FO}}$
queries.
1Abiteboul et al. (Reference Abiteboul, Kanellakis and Grahne1991); 2Libkin (Reference Libkin, den Bussche and Arenas2018).
Theorem 3.2 For
![]() ${{{{\mathsf{FO}}}}}$
queries, CertainAnswer
${{{{\mathsf{FO}}}}}$
queries, CertainAnswer
![]() $^=$
is
$^=$
is![]() -complete and CertainAnswer
-complete and CertainAnswer
![]() $^\in$
is
$^\in$
is![]() -complete in data complexity.
-complete in data complexity.
Proof. To prove membership of CertainAnswer
![]() $^=$
in
$^=$
in![]() , notice that for a query Q, this problem is the intersection of two languages
, notice that for a query Q, this problem is the intersection of two languages
![]() $L_1 \cap L_2$
where
$L_1 \cap L_2$
where
![]() $L_1=\{(D,X)~|~X \subseteq \mathsf{cert}(Q,D)\}$
and
$L_1=\{(D,X)~|~X \subseteq \mathsf{cert}(Q,D)\}$
and
![]() $L_2=\{(D,X)~|~\overline{X} \subseteq \overline{\mathsf{cert}(Q,D)}\}$
.
$L_2=\{(D,X)~|~\overline{X} \subseteq \overline{\mathsf{cert}(Q,D)}\}$
.
![]() $L_1$
is known to be in coNP : we guess a tuple
$L_1$
is known to be in coNP : we guess a tuple
![]() $\bar a \in X$
and a valuation
$\bar a \in X$
and a valuation
![]() $v\in V(D)$
with
$v\in V(D)$
with
![]() $v(\bar a)\not \in Q(v(D))$
. Similarly,
$v(\bar a)\not \in Q(v(D))$
. Similarly,
![]() $L_2$
is in NP : we guess a tuple
$L_2$
is in NP : we guess a tuple
![]() $\bar b \in \overline{X}$
and a valuation
$\bar b \in \overline{X}$
and a valuation
![]() $v'\in V(D)$
with
$v'\in V(D)$
with
![]() $v'(\bar b) \in Q(v(D))$
.
$v'(\bar b) \in Q(v(D))$
.
To prove membership of CertainAnswer
![]() $^\in$
in
$^\in$
in![]() , suppose the query Q is k-ary, and we are given a family of sets of k-ary tuples
, suppose the query Q is k-ary, and we are given a family of sets of k-ary tuples
![]() $\mathcal{X}=\{X_1, \ldots, X_n\}$
and a database D. For each
$\mathcal{X}=\{X_1, \ldots, X_n\}$
and a database D. For each
![]() $X_i \in \mathcal{X}$
, we use the NP oracle to decide in parallel whether
$X_i \in \mathcal{X}$
, we use the NP oracle to decide in parallel whether
![]() $X_i=\mathsf{cert}(Q,D)$
(for each
$X_i=\mathsf{cert}(Q,D)$
(for each
![]() $X_i,$
the two calls to the oracle do not depend on each other and they can also be done in parallel).
$X_i,$
the two calls to the oracle do not depend on each other and they can also be done in parallel).
For![]() -hardness, we reduce from the problem of checking whether
-hardness, we reduce from the problem of checking whether
![]() $\chi(G)$
, the chromatic number of an undirected graph G, equals 4 (Rothe Reference Rothe2003) and for
$\chi(G)$
, the chromatic number of an undirected graph G, equals 4 (Rothe Reference Rothe2003) and for![]() -hardness, we reduce from the related problem of checking whether
-hardness, we reduce from the related problem of checking whether
![]() $\chi(G)$
is odd. With such a graph G, we associate the same database
$\chi(G)$
is odd. With such a graph G, we associate the same database
![]() $D_G$
as in the proof of Theorem 3.1. Using the exact coloring formula
$D_G$
as in the proof of Theorem 3.1. Using the exact coloring formula
![]() $\varphi$
in the proof of Theorem 3.1, we define a query
$\varphi$
in the proof of Theorem 3.1, we define a query
We claim that
![]() $\mathsf{cert}(Q,D)=\{c_1, \ldots, c_n\}$
iff
$\mathsf{cert}(Q,D)=\{c_1, \ldots, c_n\}$
iff
![]() $\chi(G)=n$
, which entails
$\chi(G)=n$
, which entails
![]() $\mathsf{cert}(Q,D)=\{c_1, \ldots, c_4\}$
iff
$\mathsf{cert}(Q,D)=\{c_1, \ldots, c_4\}$
iff
![]() $\chi(G)=4$
and
$\chi(G)=4$
and
![]() $\mathsf{cert}(Q,D) \in \{\{c_1,\ldots,c_j\}~|~ j \text{ is odd and }1 \leq j \leq |G|\}$
iff
$\mathsf{cert}(Q,D) \in \{\{c_1,\ldots,c_j\}~|~ j \text{ is odd and }1 \leq j \leq |G|\}$
iff
![]() $\chi(G)$
is odd. Recall that
$\chi(G)$
is odd. Recall that
![]() $v(D_G)\models \varphi(c_i)$
iff
$v(D_G)\models \varphi(c_i)$
iff
![]() $c_i$
is a color in
$c_i$
is a color in
![]() $\{c_1, ..., c_{|G|}\}$
and v represents an exact i-coloring of the graph. Now
$\{c_1, ..., c_{|G|}\}$
and v represents an exact i-coloring of the graph. Now
![]() $v(D_G)\models Q(c_j)$
iff
$v(D_G)\models Q(c_j)$
iff
![]() $c_j$
is a color and there is no
$c_j$
is a color and there is no
![]() $i < j$
such that v represents an exact i-coloring of the graph, which holds exactly whenever
$i < j$
such that v represents an exact i-coloring of the graph, which holds exactly whenever
![]() $c_j \in \{c_1, ..., c_{\chi(G)}\}$
.
$c_j \in \{c_1, ..., c_{\chi(G)}\}$
.
4 Query rewritings for tractable fragments
Considering arbitrary
![]() ${{{{\mathsf{FO}}}}}$
queries brought us an intrinsic intractability result for all variants of the considered decision problems. This motivates restricting to well-behaved fragments such as CQs and UCQs. Recall that conjunctive queries (CQs) are given by the
${{{{\mathsf{FO}}}}}$
queries brought us an intrinsic intractability result for all variants of the considered decision problems. This motivates restricting to well-behaved fragments such as CQs and UCQs. Recall that conjunctive queries (CQs) are given by the
![]() $\exists,\wedge$
-fragment of
$\exists,\wedge$
-fragment of
![]() ${{{{\mathsf{FO}}}}}$
, and their unions (UCQs) by the
${{{{\mathsf{FO}}}}}$
, and their unions (UCQs) by the
![]() $\exists,\wedge,\vee$
-fragment of
$\exists,\wedge,\vee$
-fragment of
![]() ${{{{\mathsf{FO}}}}}$
. We extend them with a mild form of negation (since adding negation leads to coNP-hardness of certain answers). This mild form comes in the shape of Boolean combination of conjunctive queries (BCCQs), that is, the closure of conjunctive queries under operations
${{{{\mathsf{FO}}}}}$
. We extend them with a mild form of negation (since adding negation leads to coNP-hardness of certain answers). This mild form comes in the shape of Boolean combination of conjunctive queries (BCCQs), that is, the closure of conjunctive queries under operations
![]() $q \cap q'$
,
$q \cap q'$
,
![]() $q \cup q'$
, and
$q \cup q'$
, and
![]() $q - q'$
.
$q - q'$
.
If there are no constraints in
![]() $\Sigma$
, finding certain answers to BCCQs is known to be tractable (Gheerbrant and Libkin Reference Gheerbrant and Libkin2015), though by tableau-based techniques that are hard to implement in a database system. We now extend this in two ways. First, we show that tractability is preserved even in the presence of EGDs (and thus functional dependencies and keys). Second, we show that certain answers can be obtained by rewriting into a fragment of Datalog as described in Section 2. In particular, it means that certain answers can be found by a query expressible in recursive SQL (and even in SQL in the absence of constraints).
$\Sigma$
, finding certain answers to BCCQs is known to be tractable (Gheerbrant and Libkin Reference Gheerbrant and Libkin2015), though by tableau-based techniques that are hard to implement in a database system. We now extend this in two ways. First, we show that tractability is preserved even in the presence of EGDs (and thus functional dependencies and keys). Second, we show that certain answers can be obtained by rewriting into a fragment of Datalog as described in Section 2. In particular, it means that certain answers can be found by a query expressible in recursive SQL (and even in SQL in the absence of constraints).
For BestAnswer
![]() $_\Sigma$
a polynomial-time evaluation algorithm (in data complexity) already exists (Libkin Reference Libkin, den Bussche and Arenas2018). The resolution-based procedure is however in sharp contrast with naïve evaluation, which allows to compute certain answers to unions of conjunctive queries via usual model checking. We thus show how to apply our query rewriting techniques to the best answers problem.
$_\Sigma$
a polynomial-time evaluation algorithm (in data complexity) already exists (Libkin Reference Libkin, den Bussche and Arenas2018). The resolution-based procedure is however in sharp contrast with naïve evaluation, which allows to compute certain answers to unions of conjunctive queries via usual model checking. We thus show how to apply our query rewriting techniques to the best answers problem.
4.1 A normal form for queries: neutralizing variable repetition
Towards our rewritings, we start by putting each conjunctive query in a normal form which eliminates repetition of variables, by introducing new equality atoms.
Definition 4.1. (NRV normal form) A conjunctive query Q is in non-repeating variable normal form (NRV normal form) whenever it is of the form
![]() $Q(\bar{x})~=~\exists \bar{w} ~ (q(\bar{w}) \wedge e(\bar{x}, \bar{w}))$
where variables in
$Q(\bar{x})~=~\exists \bar{w} ~ (q(\bar{w}) \wedge e(\bar{x}, \bar{w}))$
where variables in
![]() $\bar x\bar w$
are pairwise distinct, and:
$\bar x\bar w$
are pairwise distinct, and:
-
 $q(\bar{w})$
is a conjunction of relational atoms without constants, where each free variable in
$q(\bar{w})$
is a conjunction of relational atoms without constants, where each free variable in
 $\bar{w}$
has at most one occurrence in q,
$\bar{w}$
has at most one occurrence in q, -
 $e(\bar{x},\bar{w})$
is a conjunction of equality atoms, possibly using constants, where each variable of
$e(\bar{x},\bar{w})$
is a conjunction of equality atoms, possibly using constants, where each variable of
 $\bar x$
is involved in at least one equality.
$\bar x$
is involved in at least one equality.
We say that
![]() $q(\bar{w})$
is the relational subquery of Q, and
$q(\bar{w})$
is the relational subquery of Q, and
![]() $e(\bar{x}, \bar{w})$
is the equality subquery of Q. A BCCQ is in NRV normal form if it is a Boolean combination of CQs in NRV normal form.
$e(\bar{x}, \bar{w})$
is the equality subquery of Q. A BCCQ is in NRV normal form if it is a Boolean combination of CQs in NRV normal form.
Example 4.2 The query Q(x) from Example 2.1 is equivalent to
![]() $\exists w_1 w_2 w_3 (R(w_1) \wedge S(w_2,w_3) \wedge w_1=w_2 \wedge w_3=x)$
, which is in NRV normal form.
$\exists w_1 w_2 w_3 (R(w_1) \wedge S(w_2,w_3) \wedge w_1=w_2 \wedge w_3=x)$
, which is in NRV normal form.
Clearly every conjunctive query Q is equivalent to a query in NRV normal form; moreover, Q can be easily rewritten in NRV normal form (in linear time in the size of the query). Thus in what follows, we assume w.l.o.g. that conjunctive queries are given in NRV normal form. Intuitively, the NRV normal form allows us to separate the two ingredients of a conjunctive query: the existence of facts in some relations of the database, on the one side, and a set of equality conditions on data values occurring in these facts, on the other side. The existence of facts does not depend on the valuation of nulls and thus can be directly tested on the incomplete database. Instead equality atoms in an NRV normal form imply conditions that valuations need to satisfy in order for the query to hold. We can thus first concentrate on the support of equality subqueries. This will be encoded in
![]() ${{{{\mathsf{FO}}}}}$
and then integrated in the rewriting of the whole conjunctive query.
${{{{\mathsf{FO}}}}}$
and then integrated in the rewriting of the whole conjunctive query.
We introduce a notion of equivalence of database elements w.r.t. to a set of equalities. Intuitively, equivalent elements of a tuple
![]() $\bar t$
are the ones which should be collapsed into a single value in order for a valuation of
$\bar t$
are the ones which should be collapsed into a single value in order for a valuation of
![]() $\bar t$
to satisfy all the given equalities.
$\bar t$
to satisfy all the given equalities.
Definition 4.3 Given a database D, a conjunction of equality atoms
![]() $\gamma(\bar{y})$
and an assignment
$\gamma(\bar{y})$
and an assignment
![]() $\nu: \bar y \cup \text{adom}(\gamma) \rightarrow\text{adom}(D)\cup \text{adom}(\gamma)$
preserving constants, we say that
$\nu: \bar y \cup \text{adom}(\gamma) \rightarrow\text{adom}(D)\cup \text{adom}(\gamma)$
preserving constants, we say that
![]() $u,u' \in \text{adom}(D)\cup\text{adom}(\gamma)$
are equivalent w.r.t.
$u,u' \in \text{adom}(D)\cup\text{adom}(\gamma)$
are equivalent w.r.t.
![]() $\gamma$
and
$\gamma$
and
![]() $\nu$
and write
$\nu$
and write
![]() $u \equiv_\gamma^\nu u'$
, if either
$u \equiv_\gamma^\nu u'$
, if either
![]() $u=u'$
or (u, u’) belongs to the reflexive symmetric transitive closure of
$u=u'$
or (u, u’) belongs to the reflexive symmetric transitive closure of
![]() $\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
.
$\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
.
The relation
![]() $\equiv_\gamma^\nu$
is clearly an equivalence relation over
$\equiv_\gamma^\nu$
is clearly an equivalence relation over
![]() $\text{adom}(D) \cup\text{adom}(\gamma)$
, where each element outside the range of
$\text{adom}(D) \cup\text{adom}(\gamma)$
, where each element outside the range of
![]() $\nu$
forms a singleton equivalence class.
$\nu$
forms a singleton equivalence class.
Example 4.4 Let
![]() $\gamma$
be
$\gamma$
be
![]() $x_1=x_2 \wedge x_2=x_3 \wedge x_4=x_5 \wedge x_6=1$
. Let
$x_1=x_2 \wedge x_2=x_3 \wedge x_4=x_5 \wedge x_6=1$
. Let
![]() $\nu$
assign
$\nu$
assign
![]() $\bot_i$
to
$\bot_i$
to
![]() $x_i$
for
$x_i$
for
![]() $i \leq 5$
, and
$i \leq 5$
, and
![]() $\bot_5$
to
$\bot_5$
to
![]() $x_6$
. The equivalence classes of
$x_6$
. The equivalence classes of
![]() $\equiv_\gamma^\nu$
are
$\equiv_\gamma^\nu$
are
![]() $\{\bot_i~|~i \leq 3\}$
and
$\{\bot_i~|~i \leq 3\}$
and
![]() $\{1, \bot_4, \bot_5\}$
, plus one singleton for each other element of the active domain.
$\{1, \bot_4, \bot_5\}$
, plus one singleton for each other element of the active domain.
In what follows, we denote by
![]() $\sim_{\gamma}$
the reflexive symmetric transitive closure of
$\sim_{\gamma}$
the reflexive symmetric transitive closure of
![]() $\{ (x,w) ~|~ x = w \in \gamma \}$
. Note that this is an equivalence relation among variables and constants of
$\{ (x,w) ~|~ x = w \in \gamma \}$
. Note that this is an equivalence relation among variables and constants of
![]() $\gamma$
. We will provide two syntactic encodings of this relation, one in Datalog and one in FO.
$\gamma$
. We will provide two syntactic encodings of this relation, one in Datalog and one in FO.
4.2 Datalog rewriting for certain answers for BCCQs with EGDs
Recall that, given a query Q, a database D, and a tuple
![]() $\bar{a}$
over
$\bar{a}$
over
![]() $\text{adom}(D) \cup \text{adom}(Q)$
we let the support of
$\text{adom}(D) \cup \text{adom}(Q)$
we let the support of
![]() $\bar{a}$
be the set of all valuations that witness it:
$\bar{a}$
be the set of all valuations that witness it:
In order to look for rewritings of BCCQs, a key observation is that
![]() $\bar a$
is a certain answer to Q iff
$\bar a$
is a certain answer to Q iff![]() . When Q is a BCCQ, so is
. When Q is a BCCQ, so is
![]() $\neg Q$
, thus we look for ways of expressing (non-)emptiness of the support for BCCQs.
$\neg Q$
, thus we look for ways of expressing (non-)emptiness of the support for BCCQs.
We start by concentrating on the support of equality subqueries. This will be encoded in Datalog and then integrated, as a key ingredient, in the rewriting of the whole query. We let
![]() $\gamma(\bar y)$
be an arbitrary set of equality atoms among variables
$\gamma(\bar y)$
be an arbitrary set of equality atoms among variables
![]() $\bar y$
and possibly constants. Intuitively, we will be interested in the case that
$\bar y$
and possibly constants. Intuitively, we will be interested in the case that
![]() $\gamma (\bar y)$
is the equality subquery
$\gamma (\bar y)$
is the equality subquery
![]() $e(\bar x, \bar w)$
of a CQ in NRV normal form (thus notice that in the Datalog program below
$e(\bar x, \bar w)$
of a CQ in NRV normal form (thus notice that in the Datalog program below
![]() $\bar y$
encompasses variables
$\bar y$
encompasses variables
![]() $\bar x \bar w $
of an equality subquery).
$\bar x \bar w $
of an equality subquery).
Remark that we can always write an EGD so that no variable in its body occurs more than once; it suffices to add to the body a set of variable equalities. Thus, we assume that EGDs in
![]() $\Sigma$
are of the form
$\Sigma$
are of the form
![]() $\forall \bar u ((\varphi(\bar{u}) \wedge \psi) \rightarrow z=z')$
where z, z’ are in
$\forall \bar u ((\varphi(\bar{u}) \wedge \psi) \rightarrow z=z')$
where z, z’ are in
![]() $\bar u$
, the conjunction of atoms
$\bar u$
, the conjunction of atoms
![]() $\varphi(\bar u)$
contains no constants, no variable occurs twice in
$\varphi(\bar u)$
contains no constants, no variable occurs twice in
![]() $\varphi(\bar u)$
, and
$\varphi(\bar u)$
, and
![]() $\psi$
is a set of equalities among variables of
$\psi$
is a set of equalities among variables of
![]() $\bar u$
. Remark also that membership in the set
$\bar u$
. Remark also that membership in the set
![]() $\text{adom}(D) \cup\text{adom}(\gamma)$
can be expressed by a UCQ formula that we call Dom(x). We encode equivalence of database elements in
$\text{adom}(D) \cup\text{adom}(\gamma)$
can be expressed by a UCQ formula that we call Dom(x). We encode equivalence of database elements in
![]() $\text{adom}(D) \cup\text{adom}(\gamma)$
w.r.t. a set of equalities
$\text{adom}(D) \cup\text{adom}(\gamma)$
w.r.t. a set of equalities
![]() $\gamma(\bar y)$
using the following Datalog program
Footnote 1
:
$\gamma(\bar y)$
using the following Datalog program
Footnote 1
:
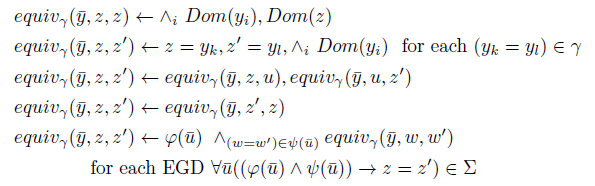
Intuitively, if
![]() $\bar t$
is a tuple of database elements assigned to
$\bar t$
is a tuple of database elements assigned to
![]() $\bar y$
, equivalent elements of D are the ones which should be collapsed into a single value in order for a valuation of D to satisfy all the equalities
$\bar y$
, equivalent elements of D are the ones which should be collapsed into a single value in order for a valuation of D to satisfy all the equalities
![]() $\gamma (\bar t)$
and the EGDs. For fixed
$\gamma (\bar t)$
and the EGDs. For fixed
![]() $\gamma$
and
$\gamma$
and
![]() $\bar t$
, the relation
$\bar t$
, the relation
![]() $\{(s,s') ~|~ D \models equiv_{\gamma}(\bar t, s, s')\}$
is an equivalence relation over
$\{(s,s') ~|~ D \models equiv_{\gamma}(\bar t, s, s')\}$
is an equivalence relation over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
where each element of
$\text{adom}(D) \cup \text{adom}(\gamma)$
where each element of
![]() $\text{adom}(D)$
neither in
$\text{adom}(D)$
neither in
![]() $\bar t$
nor in
$\bar t$
nor in
![]() $\text{adom}(\gamma)$
forms a singleton equivalence class.
$\text{adom}(\gamma)$
forms a singleton equivalence class.
The formula
![]() $equiv_\gamma$
is a key ingredient in our rewriting; as formalized in the following lemma, it selects precisely the pairs of elements that a consistent valuation needs to collapse to satisfy a set of equalities.
$equiv_\gamma$
is a key ingredient in our rewriting; as formalized in the following lemma, it selects precisely the pairs of elements that a consistent valuation needs to collapse to satisfy a set of equalities.
Lemma 4.5 Let
![]() $\gamma(\bar y)$
be a conjunction of equality atoms, D a database, and
$\gamma(\bar y)$
be a conjunction of equality atoms, D a database, and
![]() $\nu(\bar{y})=\bar{t}$
an assignment over
$\nu(\bar{y})=\bar{t}$
an assignment over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
. Assume v is a consistent valuation of nulls, then
$\text{adom}(D) \cup \text{adom}(\gamma)$
. Assume v is a consistent valuation of nulls, then
![]() $v(D) \models \gamma(v(\bar{t}))$
if and only if
$v(D) \models \gamma(v(\bar{t}))$
if and only if
![]() $v(s)=v(s')$
for all s, s’ such that
$v(s)=v(s')$
for all s, s’ such that
![]() $D \models equiv_{\gamma}(\bar{t},s,s')$
.
$D \models equiv_{\gamma}(\bar{t},s,s')$
.
Proof.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $v(D) \models \gamma(v(\bar{t}))$
and let s, s’ such that
$v(D) \models \gamma(v(\bar{t}))$
and let s, s’ such that
![]() $D \models equiv_{\gamma}(\bar{t},s,s')$
. We prove
$D \models equiv_{\gamma}(\bar{t},s,s')$
. We prove
![]() $v(s) = v(s')$
. We proceed by induction on the derivation of
$v(s) = v(s')$
. We proceed by induction on the derivation of
![]() $equiv_{\gamma}(\bar{t},s,s')$
by the fixpoint evaluation of the Datalog program. Assume
$equiv_{\gamma}(\bar{t},s,s')$
by the fixpoint evaluation of the Datalog program. Assume
![]() $equiv_{\gamma}(\bar{t},s,s')$
is derived at the first iteration, and then, it follows from one of the first two rules. If it is derived by the fist rule then
$equiv_{\gamma}(\bar{t},s,s')$
is derived at the first iteration, and then, it follows from one of the first two rules. If it is derived by the fist rule then
![]() $s = s'$
and therefore
$s = s'$
and therefore
![]() $v(s) = v(s')$
trivially. Assume
$v(s) = v(s')$
trivially. Assume
![]() $equiv_{\gamma}(\bar{t},s,s')$
is derived using the second rule then there exists
$equiv_{\gamma}(\bar{t},s,s')$
is derived using the second rule then there exists
![]() $(y_k = y_l) \in \gamma$
, and
$(y_k = y_l) \in \gamma$
, and
![]() $s= t_k$
and
$s= t_k$
and
![]() $s'=t_l$
; now since
$s'=t_l$
; now since
![]() $v(D) \models \gamma(v(\bar{t}))$
, we have
$v(D) \models \gamma(v(\bar{t}))$
, we have
![]() $v(t_k) = v(t_l)$
. Now assume that
$v(t_k) = v(t_l)$
. Now assume that
![]() $equiv_{\gamma}(\bar{t},s,s')$
is derived at some subsequent step. If it follows from the second rule, then it follows from
$equiv_{\gamma}(\bar{t},s,s')$
is derived at some subsequent step. If it follows from the second rule, then it follows from
![]() $equiv_{\gamma}(\bar{t},s,p)$
and
$equiv_{\gamma}(\bar{t},s,p)$
and
![]() $equiv_{\gamma}(\bar{t},p,s')$
derived at previous steps, thus by the induction hypothesis
$equiv_{\gamma}(\bar{t},p,s')$
derived at previous steps, thus by the induction hypothesis
![]() $v(s) = v(p)=v(s')$
. Similarly if
$v(s) = v(p)=v(s')$
. Similarly if
![]() $equiv_{\gamma}(\bar{t},s,s')$
is derived by the third rule, then it follows from
$equiv_{\gamma}(\bar{t},s,s')$
is derived by the third rule, then it follows from
![]() $equiv_{\gamma}(\bar{t},s',s)$
, and thus by induction
$equiv_{\gamma}(\bar{t},s',s)$
, and thus by induction
![]() $v(s) = v(s')$
. The last case is that
$v(s) = v(s')$
. The last case is that
![]() $equiv_{\gamma}(\bar{t},s,s')$
is derived by the last rule for some EGD
$equiv_{\gamma}(\bar{t},s,s')$
is derived by the last rule for some EGD
![]() $(\varphi(\bar{u})\wedge \psi(\bar u)) \rightarrow z=z')$
. So there exists a mapping
$(\varphi(\bar{u})\wedge \psi(\bar u)) \rightarrow z=z')$
. So there exists a mapping
![]() $\mu$
of
$\mu$
of
![]() $\bar u$
such that
$\bar u$
such that
![]() $D \models \phi(\mu(\bar u))$
and
$D \models \phi(\mu(\bar u))$
and
![]() $D\models equiv_\gamma(\bar t, \mu(w), \mu(w'))$
for each
$D\models equiv_\gamma(\bar t, \mu(w), \mu(w'))$
for each
![]() $(w=w') \in \psi(\bar u))$
and
$(w=w') \in \psi(\bar u))$
and
![]() $s =\mu(z)$
and
$s =\mu(z)$
and
![]() $s'=\mu(z')$
; so by the induction hypothesis
$s'=\mu(z')$
; so by the induction hypothesis
![]() $v(\mu(w)) = v(\mu(w'))$
. It follows that
$v(\mu(w)) = v(\mu(w'))$
. It follows that
![]() $v(D) \models \phi(v(\mu(\bar u)) ) \wedge \psi(v(\mu(\bar u)))$
and because v(D) satisfies the EGDs (v being consistent),
$v(D) \models \phi(v(\mu(\bar u)) ) \wedge \psi(v(\mu(\bar u)))$
and because v(D) satisfies the EGDs (v being consistent),
![]() $v(\mu(z)) = v(\mu(z'))$
, thus
$v(\mu(z)) = v(\mu(z'))$
, thus
![]() $v(s) = v(s')$
.
$v(s) = v(s')$
.
![]() $\Leftarrow$
Assume
$\Leftarrow$
Assume
![]() $\forall s, s'$
,
$\forall s, s'$
,
![]() $D \models equiv_{\gamma}(\bar{t},s,s')$
implies
$D \models equiv_{\gamma}(\bar{t},s,s')$
implies
![]() $v(s)=v(s')$
. We show that
$v(s)=v(s')$
. We show that
![]() $v(D) \models \gamma(v(\bar{t}))$
. In fact for each
$v(D) \models \gamma(v(\bar{t}))$
. In fact for each
![]() $(y_k = y_l) \in \gamma$
, we have
$(y_k = y_l) \in \gamma$
, we have
![]() $D \models equiv_\gamma(\bar t, t_k, t_l)$
(derived by the second rule). By our hypothesis
$D \models equiv_\gamma(\bar t, t_k, t_l)$
(derived by the second rule). By our hypothesis
![]() $v(t_k) = v(t_l)$
, thus
$v(t_k) = v(t_l)$
, thus
![]() $\gamma(v(\bar t))$
holds.
$\gamma(v(\bar t))$
holds.
Example 4.6 Let
![]() $\gamma$
and
$\gamma$
and
![]() $\nu$
be as in Example 4.4, then Lemma 4.5 implies that a valuation
$\nu$
be as in Example 4.4, then Lemma 4.5 implies that a valuation
![]() $v(D) \models \gamma(v(\bar{t}))$
iff
$v(D) \models \gamma(v(\bar{t}))$
iff
![]() $v(\bot_i) = v(\bot_j)$
for all
$v(\bot_i) = v(\bot_j)$
for all
![]() $i, j = 1..3$
, and
$i, j = 1..3$
, and
![]() $v(\bot_i) = 1$
for all
$v(\bot_i) = 1$
for all
![]() $i = 4,5$
.
$i = 4,5$
.
Formulas we write in the remainder are over signature
![]() $\sigma\cup Null$
, where
$\sigma\cup Null$
, where
![]() $\sigma$
is the database schema. In any incomplete database D over
$\sigma$
is the database schema. In any incomplete database D over
![]() $\sigma \cup Null$
, Null is always interpreted by the set of nulls occurring in D (in accordance with the semantics of the SQL construct IS NULL). That is we allow rewritings to test whether a database element is null or not.
$\sigma \cup Null$
, Null is always interpreted by the set of nulls occurring in D (in accordance with the semantics of the SQL construct IS NULL). That is we allow rewritings to test whether a database element is null or not.
For
![]() $\gamma(\bar y)$
a conjunction of equality atoms, using
$\gamma(\bar y)$
a conjunction of equality atoms, using
![]() $equiv_\gamma$
we define a new formula
$equiv_\gamma$
we define a new formula
![]() $comp_\gamma(\bar{y})$
stating the existence of a consistent valuation that collapses all equivalent elements of a tuple:
$comp_\gamma(\bar{y})$
stating the existence of a consistent valuation that collapses all equivalent elements of a tuple:
Proposition 4.7 Let
![]() $\gamma(\bar y)$
be a conjunction of equality atoms, D a database, and
$\gamma(\bar y)$
be a conjunction of equality atoms, D a database, and
![]() $\nu(\bar{y})=\bar{t}$
an assignment over
$\nu(\bar{y})=\bar{t}$
an assignment over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
, then
$\text{adom}(D) \cup \text{adom}(\gamma)$
, then
![]() $D \models comp_{\gamma} (\bar{t})$
if and only if there exists a consistent valuation v of nulls such that
$D \models comp_{\gamma} (\bar{t})$
if and only if there exists a consistent valuation v of nulls such that
![]() $v(D) \models \gamma(v(\bar{t}))$
. Moreover if such valuation exists, there exists one further satisfying
$v(D) \models \gamma(v(\bar{t}))$
. Moreover if such valuation exists, there exists one further satisfying
![]() $v(s) = v(s')$
iff
$v(s) = v(s')$
iff
![]() $ D \models equiv_\gamma(\bar t, s,s')$
, for all
$ D \models equiv_\gamma(\bar t, s,s')$
, for all
![]() $s, s' \in \text{adom}(D)\cup\text{adom}(\gamma)$
.
$s, s' \in \text{adom}(D)\cup\text{adom}(\gamma)$
.
Proof.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $D \models comp_{\gamma} (\bar{t})$
. Then,
$D \models comp_{\gamma} (\bar{t})$
. Then,
![]() $\forall c, c'$
constants,
$\forall c, c'$
constants,
![]() $D\models equiv_\gamma(\bar t, c, c')$
implies
$D\models equiv_\gamma(\bar t, c, c')$
implies
![]() $c=c'$
. As
$c=c'$
. As
![]() $\{(s,s') | D \models equiv_\gamma(\bar t, s,s')\}$
is an equivalence relation over
$\{(s,s') | D \models equiv_\gamma(\bar t, s,s')\}$
is an equivalence relation over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
, its equivalence classes form a partition of this set. In each equivalence class, there is at most one constant, so we define a valuation v mapping all nulls of a class to the unique constant of that class (or to a new fresh constant if the class does not contain any). Note that v has the property that
$\text{adom}(D) \cup \text{adom}(\gamma)$
, its equivalence classes form a partition of this set. In each equivalence class, there is at most one constant, so we define a valuation v mapping all nulls of a class to the unique constant of that class (or to a new fresh constant if the class does not contain any). Note that v has the property that
![]() $v(s) = v(s')$
iff
$v(s) = v(s')$
iff
![]() $ D \models equiv_\gamma(\bar t, s,s')$
; this allows to prove that v is a consistent valuation.
$ D \models equiv_\gamma(\bar t, s,s')$
; this allows to prove that v is a consistent valuation.
In fact, consider an arbitrary EGD
![]() $(\varphi(\bar{u})\wedge \psi(\bar u)) \rightarrow z=z')$
in
$(\varphi(\bar{u})\wedge \psi(\bar u)) \rightarrow z=z')$
in
![]() $\Sigma$
and assume
$\Sigma$
and assume
![]() $v(D) \models \varphi(\mu(\bar{u}))\wedge \psi(\mu(\bar u))$
for some
$v(D) \models \varphi(\mu(\bar{u}))\wedge \psi(\mu(\bar u))$
for some
![]() $\mu$
; we prove
$\mu$
; we prove
![]() $\mu(z) = \mu(z')$
. Since
$\mu(z) = \mu(z')$
. Since
![]() $\varphi$
is a conjunction of atoms with no constants and no repeated variables, there exists
$\varphi$
is a conjunction of atoms with no constants and no repeated variables, there exists
![]() $\mu'$
such that
$\mu'$
such that
![]() $D \models \varphi(\mu'(\bar u))$
and
$D \models \varphi(\mu'(\bar u))$
and
![]() $v(\mu'(\bar u)) = \mu(\bar u)$
. Take any equality
$v(\mu'(\bar u)) = \mu(\bar u)$
. Take any equality
![]() $w = w'$
in
$w = w'$
in
![]() $\psi(\bar u)$
, we show that
$\psi(\bar u)$
, we show that
![]() $D \models equiv_\gamma(\bar t, \mu'(w), \mu'(w'))$
. In fact because
$D \models equiv_\gamma(\bar t, \mu'(w), \mu'(w'))$
. In fact because
![]() $v(D) \models \psi(\mu(\bar u))$
we have
$v(D) \models \psi(\mu(\bar u))$
we have
![]() $\mu(w) = \mu(w')$
, and therefore
$\mu(w) = \mu(w')$
, and therefore
![]() $v(\mu'(w)) = v(\mu'(w'))$
. By definition of v then
$v(\mu'(w)) = v(\mu'(w'))$
. By definition of v then
![]() $D \models equiv_\gamma(\bar t, \mu'(w),\mu'(w'))$
. By the last rule of the Datalog program defining
$D \models equiv_\gamma(\bar t, \mu'(w),\mu'(w'))$
. By the last rule of the Datalog program defining
![]() $equiv_\gamma$
, we thus have that
$equiv_\gamma$
, we thus have that
![]() $D \models equiv_\gamma(\bar t, \mu'(z), \mu'(z'))$
; then again by definition of v, we have
$D \models equiv_\gamma(\bar t, \mu'(z), \mu'(z'))$
; then again by definition of v, we have
![]() $v(\mu'(z))=v(\mu'(z')$
, and therefore
$v(\mu'(z))=v(\mu'(z')$
, and therefore
![]() $\mu(z) = \mu(z')$
. This shows that v(D) satisfies all the EGDs; thus, v is consistent.
$\mu(z) = \mu(z')$
. This shows that v(D) satisfies all the EGDs; thus, v is consistent.
We have proved that v satisfies the characterization of Lemma 4.5, and can conclude that
![]() $v(D) \models \gamma(v(\bar t))$
.
$v(D) \models \gamma(v(\bar t))$
.
![]() $\Leftarrow$
Assume v is a consistent valuation and
$\Leftarrow$
Assume v is a consistent valuation and
![]() $v(D) \models \gamma(v(\bar{t}))$
. Let s,s’ such that
$v(D) \models \gamma(v(\bar{t}))$
. Let s,s’ such that
![]() $D \models equiv_\gamma(\bar{t},s,s')\wedge \neg Null(s') \wedge \neg Null(s)$
. By Lemma 4.5 we have
$D \models equiv_\gamma(\bar{t},s,s')\wedge \neg Null(s') \wedge \neg Null(s)$
. By Lemma 4.5 we have
![]() $v(s)=v(s')$
. Moreover, s,s’ are both constants, then
$v(s)=v(s')$
. Moreover, s,s’ are both constants, then
![]() $s=s'$
. Hence,
$s=s'$
. Hence,
![]() $D \models equiv_\gamma(\bar{t},s,s')\wedge \neg Null(s') \wedge \neg Null(s)\rightarrow s=s'$
, that is,
$D \models equiv_\gamma(\bar{t},s,s')\wedge \neg Null(s') \wedge \neg Null(s)\rightarrow s=s'$
, that is,
![]() $D \models comp_{\gamma} (\bar{t})$
.
$D \models comp_{\gamma} (\bar{t})$
.
We are now ready to define a formula capturing the inclusion of supports between two conjunctions of equality atoms, which will be a crucial ingredient in our rewriting. Let
![]() $\gamma(\bar{x})$
and
$\gamma(\bar{x})$
and
![]() $\gamma'({\bar y})$
be conjunctions of equality atoms with
$\gamma'({\bar y})$
be conjunctions of equality atoms with![]() . We define:
. We define:
Using Proposition 4.7 and Lemma 4.5, we obtain:
Proposition 4.8 Let
![]() $\gamma(\bar{x})$
,
$\gamma(\bar{x})$
,
![]() $\gamma'({\bar y})$
be conjunctions of equality atoms with
$\gamma'({\bar y})$
be conjunctions of equality atoms with![]() , D a database and
, D a database and
![]() $\nu(\bar{y})=\bar{t}$
,
$\nu(\bar{y})=\bar{t}$
,
![]() $\nu'(\bar{y})=\bar{t'}$
assignments over
$\nu'(\bar{y})=\bar{t'}$
assignments over![]() . Then
. Then
![]() $D \models imply_{\gamma, \gamma'}(\bar t, \bar t') \vee \neg comp_\gamma(\bar t)$
iff for all consistent valuations v, one has
$D \models imply_{\gamma, \gamma'}(\bar t, \bar t') \vee \neg comp_\gamma(\bar t)$
iff for all consistent valuations v, one has
![]() $v(D) \models \gamma(v(\bar t))$
implies
$v(D) \models \gamma(v(\bar t))$
implies
![]() $v(D) \models \gamma'(v(\bar t'))$
.
$v(D) \models \gamma'(v(\bar t'))$
.
Proof.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $D \models imply_{\gamma, \gamma'}(\bar t, \bar t') \vee \neg comp_\gamma(\bar t)$
. If
$D \models imply_{\gamma, \gamma'}(\bar t, \bar t') \vee \neg comp_\gamma(\bar t)$
. If
![]() $D \models \neg comp_\gamma(\bar t)$
then by Proposition 4.7, there is no consistent valuation v such that
$D \models \neg comp_\gamma(\bar t)$
then by Proposition 4.7, there is no consistent valuation v such that
![]() $v(D) \models \gamma(v(\bar{t}))$
and so the implication trivially holds. Now assume
$v(D) \models \gamma(v(\bar{t}))$
and so the implication trivially holds. Now assume
![]() $D \models imply_{\gamma, \gamma'}(\bar t, \bar t')$
, that is:
$D \models imply_{\gamma, \gamma'}(\bar t, \bar t')$
, that is:
We want to show that for all consistent valuations v of nulls such that
![]() $v(D) \models \gamma(v(\bar t))$
, one also has
$v(D) \models \gamma(v(\bar t))$
, one also has
![]() $v(D) \models \gamma'(v(\bar t'))$
. Consider a valuation v of nulls such that
$v(D) \models \gamma'(v(\bar t'))$
. Consider a valuation v of nulls such that
![]() $v(D) \models \gamma(v(\bar t))$
. Using Lemma 4.5, it is enough to show that
$v(D) \models \gamma(v(\bar t))$
. Using Lemma 4.5, it is enough to show that
![]() $\forall s,s'$
such that
$\forall s,s'$
such that
![]() $D \models equiv_{\gamma'}(\bar{t'},s,s')$
one has
$D \models equiv_{\gamma'}(\bar{t'},s,s')$
one has
![]() $v(s)=v(s')$
. So assume
$v(s)=v(s')$
. So assume
![]() $D \models equiv_{\gamma'}(\bar{t'},s,s')$
, by our assumption it follows that
$D \models equiv_{\gamma'}(\bar{t'},s,s')$
, by our assumption it follows that
![]() $D \models equiv_{\gamma}(\bar{t},s,s'))$
, and therefore, again by Lemma 4.5,
$D \models equiv_{\gamma}(\bar{t},s,s'))$
, and therefore, again by Lemma 4.5,
![]() $v(s)=v(s')$
.
$v(s)=v(s')$
.
![]() $\Leftarrow$
Assume for all consistent valuations v of nulls such that
$\Leftarrow$
Assume for all consistent valuations v of nulls such that
![]() $v(D) \models \gamma(v(\bar t))$
, one also has
$v(D) \models \gamma(v(\bar t))$
, one also has
![]() $v(D) \models \gamma'(v(\bar t'))$
. By Proposition 4.7, if there is no such valuation, then
$v(D) \models \gamma'(v(\bar t'))$
. By Proposition 4.7, if there is no such valuation, then
![]() $D \models \neg comp_\gamma(\bar t)$
. So assume now there is one such valuation. This entails that in particular, there exists a consistent
$D \models \neg comp_\gamma(\bar t)$
. So assume now there is one such valuation. This entails that in particular, there exists a consistent
![]() $v^*$
satisfying
$v^*$
satisfying
![]() $v^*(D) \models \gamma(v^*(\bar t))$
and
$v^*(D) \models \gamma(v^*(\bar t))$
and
![]() $v^*(s) = v^*(s')$
iff
$v^*(s) = v^*(s')$
iff
![]() $ D \models equiv_\gamma(\bar t, s,s')$
. By our assumption we have
$ D \models equiv_\gamma(\bar t, s,s')$
. By our assumption we have
![]() $v^*(D) \models \gamma'(v^*(\bar t'))$
. Hence, by Lemma 4.5,
$v^*(D) \models \gamma'(v^*(\bar t'))$
. Hence, by Lemma 4.5,
![]() $\forall s,s'$
such that
$\forall s,s'$
such that
![]() $D \models equiv_{\gamma'}(\bar{t'},s,s')$
one has
$D \models equiv_{\gamma'}(\bar{t'},s,s')$
one has
![]() $v^*(s)=v^*(s')$
. By the properties of
$v^*(s)=v^*(s')$
. By the properties of
![]() $v^*$
mentioned above, this implies
$v^*$
mentioned above, this implies
![]() $D \models equiv_\gamma(\bar t,s,s')$
. We have thus shown that
$D \models equiv_\gamma(\bar t,s,s')$
. We have thus shown that
![]() $D \models imply_{\gamma, \gamma'}(\bar t, \bar t')$
.
$D \models imply_{\gamma, \gamma'}(\bar t, \bar t')$
.
So far, we have dealt with equality subqueries and we have characterized the emptiness and inclusion of their supports (cf. Propositions 4.7 and 4.8, respectively). We can now use this machinery to characterize the support of a BCCQ. We start by expressing membership in the support of an individual CQ:
Lemma 4.9 Let D be a database, v a consistent valuation of D and
![]() $Q(\bar{x})$
a conjunctive query in NRV normal form, with relational subquery
$Q(\bar{x})$
a conjunctive query in NRV normal form, with relational subquery
![]() $q(\bar w)$
and equality subquery
$q(\bar w)$
and equality subquery
![]() $\gamma(\bar x, \bar w)$
. Then,
$\gamma(\bar x, \bar w)$
. Then,![]() if and only there exists
if and only there exists
![]() $\bar{s}$
such that
$\bar{s}$
such that
![]() $D \models q(\bar{s})\wedge comp_{\gamma} (\bar{r} \bar{s})$
and
$D \models q(\bar{s})\wedge comp_{\gamma} (\bar{r} \bar{s})$
and
![]() $v(D) \models \gamma(v(\bar{r}\bar{s}))$
.
$v(D) \models \gamma(v(\bar{r}\bar{s}))$
.
Proof.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $v \in Supp(Q,D, \bar{r})$
, that is v is consistent and
$v \in Supp(Q,D, \bar{r})$
, that is v is consistent and
![]() $v(\bar{r}) \in Q(v(D))$
and so there exists an assignment
$v(\bar{r}) \in Q(v(D))$
and so there exists an assignment
![]() $\mu$
of
$\mu$
of
![]() $\bar x \bar w$
over
$\bar x \bar w$
over
![]() $\text{adom}(v(D)) \cup \text{adom}(Q)$
such that
$\text{adom}(v(D)) \cup \text{adom}(Q)$
such that
![]() $\mu(\bar x) = v(\bar r)$
and
$\mu(\bar x) = v(\bar r)$
and
![]() $v(D) \models q(\mu(\bar w)) \wedge \gamma(\mu(\bar x\bar w))$
.
$v(D) \models q(\mu(\bar w)) \wedge \gamma(\mu(\bar x\bar w))$
.
Recall that
![]() $q(\bar{w})$
is a conjunction of relational atoms, with no constants and where each one of the free variables
$q(\bar{w})$
is a conjunction of relational atoms, with no constants and where each one of the free variables
![]() $\bar{w}$
has at most one occurrence in q. Thus, there exists a mapping
$\bar{w}$
has at most one occurrence in q. Thus, there exists a mapping
![]() $\nu$
of
$\nu$
of
![]() $\bar w$
over
$\bar w$
over
![]() $\text{adom}(D)$
such that
$\text{adom}(D)$
such that
![]() $D \models q(\nu(\bar w))$
and
$D \models q(\nu(\bar w))$
and
![]() $v(\nu(\bar w))=\mu(\bar w)$
. We let
$v(\nu(\bar w))=\mu(\bar w)$
. We let
![]() $\bar s = \nu(\bar w)$
. Recall that
$\bar s = \nu(\bar w)$
. Recall that
![]() $\bar x$
and
$\bar x$
and
![]() $\bar w$
do not share variables, so we can extend the mapping
$\bar w$
do not share variables, so we can extend the mapping
![]() $\nu$
by setting
$\nu$
by setting
![]() $\nu(\bar x) = \bar r$
. We thus have that
$\nu(\bar x) = \bar r$
. We thus have that
![]() $\nu(\bar x \bar w) = \bar r \bar s$
and
$\nu(\bar x \bar w) = \bar r \bar s$
and
![]() $v(\bar r \bar s) = \mu(\bar x \bar w)$
. It follows that v is a consistent valuation for which
$v(\bar r \bar s) = \mu(\bar x \bar w)$
. It follows that v is a consistent valuation for which
![]() $v(D) \models \gamma(v(\bar r\bar s))$
; then by Proposition 4.7, we also have
$v(D) \models \gamma(v(\bar r\bar s))$
; then by Proposition 4.7, we also have
![]() $D\models comp_\gamma(\bar r\bar s)$
.
$D\models comp_\gamma(\bar r\bar s)$
.
![]() $\Leftarrow$
Since
$\Leftarrow$
Since
![]() $D\models q(\bar s),$
we have
$D\models q(\bar s),$
we have
![]() $v(D) \models q(v(\bar s))$
. Moreover by the hypothesis
$v(D) \models q(v(\bar s))$
. Moreover by the hypothesis
![]() $v(D) \models \gamma (v(\bar r \bar s))$
, thus
$v(D) \models \gamma (v(\bar r \bar s))$
, thus
![]() $v(D) \models Q(v(\bar r))$
.
$v(D) \models Q(v(\bar r))$
.
In the remainder, we consider BCCQs
![]() $Q(\bar{x})~:=~Q_1(\bar{x}) \vee \ldots \vee Q_n(\bar{x})$
in NRV disjunctive normal form (DNF) where for all
$Q(\bar{x})~:=~Q_1(\bar{x}) \vee \ldots \vee Q_n(\bar{x})$
in NRV disjunctive normal form (DNF) where for all
![]() $1 \leq i \leq n$
:
$1 \leq i \leq n$
:
and for all
![]() $1 \leq j \leq m$
:
$1 \leq j \leq m$
:
For convenience, we assume w.l.o.g every conjunction of literals to be of the same length m. We can also assume without loss of generality that for each i we have
![]() $\text{adom}(\gamma_{i_j}) = \text{adom}(\gamma_{i_0})$
for all j. In fact, we can always pad any
$\text{adom}(\gamma_{i_j}) = \text{adom}(\gamma_{i_0})$
for all j. In fact, we can always pad any
![]() $\gamma_{i_j}$
with dummy equalities
$\gamma_{i_j}$
with dummy equalities
![]() $c = c$
to extend its active domain.
$c = c$
to extend its active domain.
Given a disjunct
![]() $Q_i$
in a BCCQ in DNF, we now define poss
$Q_i$
in a BCCQ in DNF, we now define poss
![]() $_{Q_i}$
, encoding the set of possible answers to
$_{Q_i}$
, encoding the set of possible answers to
![]() $Q_i$
, and cons
$Q_i$
, and cons
![]() $_{Q_i}$
, checking the compatibility of an answer with the negative literals in
$_{Q_i}$
, checking the compatibility of an answer with the negative literals in
![]() $Q_i$
.
$Q_i$
.
Using these new formulae, we show that the non-emptiness of![]() can be expressed as the existence of a possible answer.
can be expressed as the existence of a possible answer.
Proposition 4.10 Let D be a database and
![]() $Q(\bar{x})$
a DNF BCCQ in NRV normal form, then
$Q(\bar{x})$
a DNF BCCQ in NRV normal form, then![]() if and only if
if and only if
![]() $D \models \bigvee_{\substack{1\leq i \leq n}} \exists \bar{w}$
$D \models \bigvee_{\substack{1\leq i \leq n}} \exists \bar{w}$
![]() $poss_{Q_i}(\bar{r}\bar{w})$
.
$poss_{Q_i}(\bar{r}\bar{w})$
.
Proof.
![]() $\Leftarrow$
Let
$\Leftarrow$
Let
![]() $D \models \bigvee_{\substack{1\leq i \leq n}}\exists \bar{w}$
$D \models \bigvee_{\substack{1\leq i \leq n}}\exists \bar{w}$
![]() $poss_{Q_i}(\bar{r}\bar{w})$
, then there exists
$poss_{Q_i}(\bar{r}\bar{w})$
, then there exists
![]() $1 \leq i \leq n$
and an assignment
$1 \leq i \leq n$
and an assignment
![]() $\nu$
with
$\nu$
with
![]() $\nu(\bar{w})=\bar{s}$
,
$\nu(\bar{w})=\bar{s}$
,
![]() $D \models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and for all
$D \models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and for all
![]() $1 \leq j\leq m$
, for all
$1 \leq j\leq m$
, for all
![]() $\bar{s'}$
such that
$\bar{s'}$
such that
![]() $D\models q_{i_j}(\bar{s'})\wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
, one has
$D\models q_{i_j}(\bar{s'})\wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
, one has
![]() $D \models \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar r \bar s , \bar r \bar s')$
. Since
$D \models \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar r \bar s , \bar r \bar s')$
. Since
![]() $D \models comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
, by Proposition 4.7 there exists a consistent valuation
$D \models comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
, by Proposition 4.7 there exists a consistent valuation
![]() $v^*$
, such that
$v^*$
, such that
![]() $v^*(D) \models \gamma_{i_0}(v^*(\bar{r}\bar{s}))$
and for all
$v^*(D) \models \gamma_{i_0}(v^*(\bar{r}\bar{s}))$
and for all
![]() $s, s' \in \text{adom}(D)\cup\text{adom}(\gamma_{i_0})$
, we have
$s, s' \in \text{adom}(D)\cup\text{adom}(\gamma_{i_0})$
, we have
![]() $v^*(s) = v^*(s')$
iff
$v^*(s) = v^*(s')$
iff
![]() $D \models equiv_{\gamma_{i_0}}(\bar r \bar s,s,s')$
.
$D \models equiv_{\gamma_{i_0}}(\bar r \bar s,s,s')$
.
Moreover, we can prove the following claim:
Claim 4.11 For all conjunction of equalities
![]() $\gamma'(\bar y)$
with
$\gamma'(\bar y)$
with
![]() $\text{adom}(\gamma') = \text{adom} (\gamma_{i_0})$
and all
$\text{adom}(\gamma') = \text{adom} (\gamma_{i_0})$
and all
![]() $\bar t$
over
$\bar t$
over
![]() $\text{adom}(D) \cup \text{adom}(\gamma_{i_0})$
, one has
$\text{adom}(D) \cup \text{adom}(\gamma_{i_0})$
, one has
![]() $v^*(D) \models \gamma'(v^*(\bar t))$
iff for all consistent valuations v,
$v^*(D) \models \gamma'(v^*(\bar t))$
iff for all consistent valuations v,
![]() $v(D) \models \gamma_{i_0}(v(\bar{r}\bar{s}))$
implies
$v(D) \models \gamma_{i_0}(v(\bar{r}\bar{s}))$
implies
![]() $v(D) \models \gamma'(v(\bar t))$
.
$v(D) \models \gamma'(v(\bar t))$
.
Proof of the Claim.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $v^*(D) \models \gamma'(v^*(\bar t))$
and let v be a consistent valuation such that
$v^*(D) \models \gamma'(v^*(\bar t))$
and let v be a consistent valuation such that
![]() $v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
. We want to show
$v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
. We want to show
![]() $v(D) \models \gamma'(v(\bar t))$
. By Lemma 4.5, it is enough to show that
$v(D) \models \gamma'(v(\bar t))$
. By Lemma 4.5, it is enough to show that
![]() $\forall s, s' \in \text{adom}(D) \cup\text{adom}(\gamma_{i_0})$
,
$\forall s, s' \in \text{adom}(D) \cup\text{adom}(\gamma_{i_0})$
,
![]() $D \models equiv_{\gamma'}(\bar{t},s,s')$
implies
$D \models equiv_{\gamma'}(\bar{t},s,s')$
implies
![]() $v(s)=v(s')$
. So let s, s’ be such that
$v(s)=v(s')$
. So let s, s’ be such that
![]() $D \models equiv_{\gamma'}(\bar{t},s,s')$
. As
$D \models equiv_{\gamma'}(\bar{t},s,s')$
. As
![]() $v^*(D) \models \gamma'(v^*(\bar t))$
, by Lemma 4.5,
$v^*(D) \models \gamma'(v^*(\bar t))$
, by Lemma 4.5,
![]() $v^*(s)=v^*(s')$
. By the properties of
$v^*(s)=v^*(s')$
. By the properties of
![]() $v^*$
, so
$v^*$
, so
![]() $D \models equiv_{\gamma_{i_0}}(\bar r \bar s,s,s')$
. As
$D \models equiv_{\gamma_{i_0}}(\bar r \bar s,s,s')$
. As
![]() $v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
, by Lemma 4.5 it follows that
$v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
, by Lemma 4.5 it follows that
![]() $v(s)=v(s')$
.
$v(s)=v(s')$
.
![]() $\Leftarrow$
Assume for all consistent valuations v,
$\Leftarrow$
Assume for all consistent valuations v,
![]() $v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
implies
$v(D) \models \gamma_{i_0}(v(\bar r \bar s))$
implies
![]() $v(D) \models \gamma'(v(\bar t))$
. By Lemma 4.5,
$v(D) \models \gamma'(v(\bar t))$
. By Lemma 4.5,
![]() $v^*$
being consistent
$v^*$
being consistent
![]() $v^*(D) \models \gamma'(v^*(\bar{t}))$
.
$v^*(D) \models \gamma'(v^*(\bar{t}))$
.
Now fix some arbitrary
![]() $j \geq 1$
and
$j \geq 1$
and
![]() $\bar{s'}$
with
$\bar{s'}$
with
![]() $D\models q_{i_j}(\bar{s'})\wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
. By Proposition 4.8, it follows from
$D\models q_{i_j}(\bar{s'})\wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
. By Proposition 4.8, it follows from
![]() $D \models \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar{r}\bar{s},\bar{r}\bar{s'}) \wedge comp_{\gamma_{i_0}}(\bar r \bar s)$
that there exists a consistent valuation v’ with
$D \models \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar{r}\bar{s},\bar{r}\bar{s'}) \wedge comp_{\gamma_{i_0}}(\bar r \bar s)$
that there exists a consistent valuation v’ with
![]() $v'(D) \models \gamma_{i_0}(v'(\bar{r}\bar{s}))$
but
$v'(D) \models \gamma_{i_0}(v'(\bar{r}\bar{s}))$
but
![]() $v'(D) \not \models \gamma_{i_j}(v'(\bar{r}\bar{s'}))$
. By the above claim
$v'(D) \not \models \gamma_{i_j}(v'(\bar{r}\bar{s'}))$
. By the above claim
![]() $v^*(D) \not \models \gamma_{i_j}(v^*(\bar{r}\bar{s'}))$
. In summary, we have:
$v^*(D) \not \models \gamma_{i_j}(v^*(\bar{r}\bar{s'}))$
. In summary, we have:
-
(i)
 $D\models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and
$D\models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and
 $v^*(D)\models \gamma_{i_0}(v^*(\bar{r}\bar{s}))$
and so by Lemma 4.9, we have
$v^*(D)\models \gamma_{i_0}(v^*(\bar{r}\bar{s}))$
and so by Lemma 4.9, we have , that is,
, that is,
 $v^*(D) \models Q_{i_0}(v^*(\bar{r}))$
.
$v^*(D) \models Q_{i_0}(v^*(\bar{r}))$
. -
(ii) For all
 $1 \leq j \leq m$
and assignment
$1 \leq j \leq m$
and assignment
 $\nu'$
with
$\nu'$
with
 $\nu'(\bar{w})=\bar{s'}$
, if
$\nu'(\bar{w})=\bar{s'}$
, if
 $D \models q_{i_j}(\bar{s'}) \wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
then
$D \models q_{i_j}(\bar{s'}) \wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
then
 $v^*(D) \not \models \gamma_{i_j}(v^*(\bar{r}\bar{s'}))$
and so by Lemma 4.9, we have
$v^*(D) \not \models \gamma_{i_j}(v^*(\bar{r}\bar{s'}))$
and so by Lemma 4.9, we have , that is, for all
, that is, for all
 $1 \leq j \leq m$
,
$1 \leq j \leq m$
,
 $v^*(D) \models \neg Q_j(v^*(\bar{r}))$
.
$v^*(D) \models \neg Q_j(v^*(\bar{r}))$
.
This means we have![]() for all
for all
![]() $1 \leq i \leq n$
and so
$1 \leq i \leq n$
and so![]() .
.
![]() $\Rightarrow$
Let
$\Rightarrow$
Let![]() , so v is consistent and there is some
, so v is consistent and there is some
![]() $1 \leq i \leq n$
with: (i)
$1 \leq i \leq n$
with: (i)![]() , (ii) for all
, (ii) for all
![]() $1 \leq j \leq m$
,
$1 \leq j \leq m$
,![]() . Using Lemma 4.9 (i) implies that there exists
. Using Lemma 4.9 (i) implies that there exists
![]() $\bar{s}$
such that
$\bar{s}$
such that
![]() $D \models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and
$D \models q_{i_0}(\bar{s})\wedge comp_{\gamma_{i_0}}(\bar{r}\bar{s})$
and
![]() $v(D) \models \gamma_{i_0}(v(\bar{r}\bar{s}))$
. Again by Lemma 4.9, (ii) implies that for all
$v(D) \models \gamma_{i_0}(v(\bar{r}\bar{s}))$
. Again by Lemma 4.9, (ii) implies that for all
![]() $1 \leq j \leq m$
and
$1 \leq j \leq m$
and
![]() $\bar{s'}$
, if
$\bar{s'}$
, if
![]() $D \models q_{i_j}(\bar{s'}) \wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
then
$D \models q_{i_j}(\bar{s'}) \wedge comp_{\gamma_{i_j}}(\bar{r}\bar{s'})$
then
![]() $v(D) \not \models \gamma_{i_j}(v(\bar{r}\bar{s'}))$
. This entails by Proposition 4.8 that
$v(D) \not \models \gamma_{i_j}(v(\bar{r}\bar{s'}))$
. This entails by Proposition 4.8 that
![]() $D \models comp_{\gamma_{i_0}}(\bar{r}\bar{s}) \wedge \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar{r}\bar{s},\bar{r}\bar{s'})$
. This shows
$D \models comp_{\gamma_{i_0}}(\bar{r}\bar{s}) \wedge \neg imply_{\gamma_{i_0},\gamma_{i_j}}(\bar{r}\bar{s},\bar{r}\bar{s'})$
. This shows
![]() $D \models \bigvee_{\substack{1\leq i \leq n}} \exists \bar{w}$
$D \models \bigvee_{\substack{1\leq i \leq n}} \exists \bar{w}$
![]() $poss_{Q_i}(\bar{r}\bar{w})$
.
$poss_{Q_i}(\bar{r}\bar{w})$
.
Now that we have defined the formula expressing for a BCCQ Q non-emptiness of![]() (Proposition 4.10), we can easily define a rewriting for the problem CertainAnswer
(Proposition 4.10), we can easily define a rewriting for the problem CertainAnswer
![]() $_\Sigma$
(Q). To do so, we rely on the fact that
$_\Sigma$
(Q). To do so, we rely on the fact that
![]() $\bar r \in \mathsf{cert}_\Sigma(Q,D)$
iff
$\bar r \in \mathsf{cert}_\Sigma(Q,D)$
iff![]() .
.
Theorem 4.12 (Datalog rewriting)
Let D be a database whose schema contains a set of equality-generating dependencies
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $Q(\bar{x})$
be a BCCQ in NRV normal form. Let
$Q(\bar{x})$
be a BCCQ in NRV normal form. Let
![]() $Q' = Q_1'(\bar{x}) \vee \ldots \vee Q_n'(\bar{x})$
be
$Q' = Q_1'(\bar{x}) \vee \ldots \vee Q_n'(\bar{x})$
be
![]() $\neg Q$
in DNF normal form. Then,
$\neg Q$
in DNF normal form. Then,
![]() $\bar r \in \mathsf{cert}_\Sigma(Q,D)$
if and only if
$\bar r \in \mathsf{cert}_\Sigma(Q,D)$
if and only if
![]() $D \models \rho(\bar r)$
where
$D \models \rho(\bar r)$
where
![]() $\rho(\bar x) = \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
$\rho(\bar x) = \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
![]() $\neg poss_{Q'_i}(\bar{x}\bar{w})$
.
$\neg poss_{Q'_i}(\bar{x}\bar{w})$
.
Proof. One has that
![]() $\bar r \in \mathsf{cert}_\Sigma(Q,D)$
iff
$\bar r \in \mathsf{cert}_\Sigma(Q,D)$
iff
![]() $Supp(Q', D, \bar r) = \emptyset$
. Q’ being still a BCCQ, Proposition 4.10 tells us that
$Supp(Q', D, \bar r) = \emptyset$
. Q’ being still a BCCQ, Proposition 4.10 tells us that
![]() $Supp(Q', D, \bar r) =\emptyset$
iff
$Supp(Q', D, \bar r) =\emptyset$
iff
![]() $D \models \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
$D \models \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
![]() $\neg poss_{Q'_i}(\bar{r}\bar{w})$
.
$\neg poss_{Q'_i}(\bar{r}\bar{w})$
.
Corollary 4.13 For each fixed BCCQ query Q and a set of EGDs
![]() $\Sigma$
, the complexity of CertainAnswer
$\Sigma$
, the complexity of CertainAnswer
![]() $_\Sigma$
$_\Sigma$
![]() $_(Q)$
is in PTIME.
$_(Q)$
is in PTIME.
4.3 Non-rewritability in FO
The basic starting points for our investigation was the fact that
![]() $\mathsf{cert}_\Sigma(Q,D)=Q(\mathsf{chase}_\Sigma(D))$
for a CQ Q and a set
$\mathsf{cert}_\Sigma(Q,D)=Q(\mathsf{chase}_\Sigma(D))$
for a CQ Q and a set
![]() $\Sigma$
of FDs, for every database D. This remained true for unions of CQs, but failed for BCCQs, forcing us to produce a Datalog rewriting to obtain certain answers. But can a first-order rewriting be obtained instead? This would make it possible to produce certain answers using the core of SQL as opposed to its recursive features which do not always perform as well in practice.
$\Sigma$
of FDs, for every database D. This remained true for unions of CQs, but failed for BCCQs, forcing us to produce a Datalog rewriting to obtain certain answers. But can a first-order rewriting be obtained instead? This would make it possible to produce certain answers using the core of SQL as opposed to its recursive features which do not always perform as well in practice.
In this section, we show that the answer, in general, is negative even for CQs (and thus for BCCQs). In the next section, however we show that such rewritings can be obtained in FO for BCCQs whenever
![]() $\Sigma$
is empty.
$\Sigma$
is empty.
The main result of this section is the following.
Theorem 4.14 There exists a Boolean CQ Q and single FD
![]() $\Sigma$
over a relational schema of binary and unary relations such that
$\Sigma$
over a relational schema of binary and unary relations such that
![]() $\mathsf{cert}_\Sigma(Q,D)$
is not expressible as an FO query.
$\mathsf{cert}_\Sigma(Q,D)$
is not expressible as an FO query.
Proof. Consider a schema with one binary relation E and two unary relations A and B. The only FD in
![]() $\Sigma$
is
$\Sigma$
is
![]() $\forall x \forall y \forall z\ \big(E(x,y) \wedge E(x,z) \to y =z\big)$
; in other words, the first attribute of E is a key. The query Q is a Boolean CQ
$\forall x \forall y \forall z\ \big(E(x,y) \wedge E(x,z) \to y =z\big)$
; in other words, the first attribute of E is a key. The query Q is a Boolean CQ
![]() $\exists x\ (A(x)\wedge B(x))$
.
$\exists x\ (A(x)\wedge B(x))$
.
To prove inexpressibility of
![]() $\mathsf{cert}_\Sigma(Q,\cdot)$
in FO, for each
$\mathsf{cert}_\Sigma(Q,\cdot)$
in FO, for each
![]() $n > 0$
we create two databases
$n > 0$
we create two databases
![]() $D_n$
and
$D_n$
and
![]() $D_n'$
. In both of them, E is interpreted as a disjoint union
$D_n'$
. In both of them, E is interpreted as a disjoint union
![]() $T_1\cup T_2$
where
$T_1\cup T_2$
where
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are balanced binary trees of depth n in which all nodes are distinct nulls. In both A and B are singleton sets. In
$T_2$
are balanced binary trees of depth n in which all nodes are distinct nulls. In both A and B are singleton sets. In
![]() $D_n$
, the set A contains a leaf of
$D_n$
, the set A contains a leaf of
![]() $T_1$
and B contains a leaf of
$T_1$
and B contains a leaf of
![]() $T_2$
. In
$T_2$
. In
![]() $D_n'$
, both A and B contain leaves of
$D_n'$
, both A and B contain leaves of
![]() $T_1$
such that their only common ancestor in the tree is the root (in other words, they are leaves of subtrees rooted at different children of the root of
$T_1$
such that their only common ancestor in the tree is the root (in other words, they are leaves of subtrees rooted at different children of the root of
![]() $T_1$
).
$T_1$
).
Because of the constraint
![]() $\Sigma$
, for every valuation v such that the resulting database satisfies it we have that both
$\Sigma$
, for every valuation v such that the resulting database satisfies it we have that both
![]() $v(T_1)$
and
$v(T_1)$
and
![]() $v(T_2)$
are chains. Indeed, consider any node
$v(T_2)$
are chains. Indeed, consider any node
![]() $\bot$
with children
$\bot$
with children
![]() $\bot_1,\bot_2$
in
$\bot_1,\bot_2$
in
![]() $T_i$
. If
$T_i$
. If
![]() $v(\bot_1)\neq v(\bot_2)$
then the resulting tuples
$v(\bot_1)\neq v(\bot_2)$
then the resulting tuples
![]() $(v(\bot), v(\bot_1))$
and
$(v(\bot), v(\bot_1))$
and
![]() $(v(\bot),v(\bot_2))$
violate the constraint. Thus,
$(v(\bot),v(\bot_2))$
violate the constraint. Thus,
![]() $v(\bot_1)=v(\bot_2)$
and applying this construction inductively we see that
$v(\bot_1)=v(\bot_2)$
and applying this construction inductively we see that
![]() $v(T_i)$
is a chain. Hence, it has a single leaf, and thus
$v(T_i)$
is a chain. Hence, it has a single leaf, and thus
![]() $\mathsf{cert}_\Sigma(Q,D_n')$
is true, since A and B must be interpreted as that leaf. On the other hand,
$\mathsf{cert}_\Sigma(Q,D_n')$
is true, since A and B must be interpreted as that leaf. On the other hand,
![]() $\mathsf{cert}_\Sigma(Q,D_n)$
is false, since there is a valuation v that sends
$\mathsf{cert}_\Sigma(Q,D_n)$
is false, since there is a valuation v that sends
![]() $T_1$
and
$T_1$
and
![]() $T_2$
into two disjoint chains, and thus, A and B are interpreted as two distinct elements.
$T_2$
into two disjoint chains, and thus, A and B are interpreted as two distinct elements.
Assume now that
![]() $\mathsf{cert}_\Sigma(Q,\cdot)$
is rewritable as an FO sentence
$\mathsf{cert}_\Sigma(Q,\cdot)$
is rewritable as an FO sentence
![]() $\phi$
. Then, for every
$\phi$
. Then, for every
![]() $n > 0$
, we have
$n > 0$
, we have
![]() $D_n'\models\phi$
and
$D_n'\models\phi$
and
![]() $D_n\models\neg\phi$
. We next show that such a sentence cannot exist, thereby proving non-FO-rewritability.
$D_n\models\neg\phi$
. We next show that such a sentence cannot exist, thereby proving non-FO-rewritability.
Recall that in a database (with one binary relation, like considered here), a radius r neighborhood of an element a is its restriction to the set of all elements reachable from a by a path of length at most r, where the path does not take into account the orientation of edges of E (e.g. if we have E(a,b) and E(c,a) then both b and c are in the radius 1 neighborhood of a). When two neighborhoods, of elements a and b, are isomorphic, it means that there is an isomorphism between them that sends a to b. In other words, centers of neighborhoods are viewed as distinguished elements when it comes to defining neighborhoods. It is known that each first-order sentence
![]() $\psi$
is Hanf-local (Fagin et al. Reference Fagin, Stockmeyer and Vardi1995): that is, there exists a number
$\psi$
is Hanf-local (Fagin et al. Reference Fagin, Stockmeyer and Vardi1995): that is, there exists a number
![]() $r > 0$
such that for any two databases
$r > 0$
such that for any two databases
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, if there is a bijection f between
$D_2$
, if there is a bijection f between
![]() $D_1$
and
$D_1$
and
![]() $D_2$
such that the radius r neighborhoods of a in
$D_2$
such that the radius r neighborhoods of a in
![]() $D_1$
and f(a) in
$D_1$
and f(a) in
![]() $D_2$
are isomorphic then
$D_2$
are isomorphic then
![]() $D_1$
and
$D_1$
and
![]() $D_2$
agree on
$D_2$
agree on
![]() $\psi$
, that is either both satisfy it or both do not.
$\psi$
, that is either both satisfy it or both do not.
Now let r be such a number for the sentence
![]() $\phi$
we assumed exists. Consider
$\phi$
we assumed exists. Consider
![]() $D_n$
and
$D_n$
and
![]() $D_n'$
and let
$D_n'$
and let
![]() $T_{1a},T_{1*}$
be the subtrees of the root of
$T_{1a},T_{1*}$
be the subtrees of the root of
![]() $T_1$
in
$T_1$
in
![]() $D_n$
such that the first contains A while the second contains neither A not B, and let
$D_n$
such that the first contains A while the second contains neither A not B, and let
![]() $T_{2b},T_{2*}$
be defined similarly for subtrees of the root of
$T_{2b},T_{2*}$
be defined similarly for subtrees of the root of
![]() $T_2$
with respect to B. In
$T_2$
with respect to B. In
![]() $D_n'$
we define
$D_n'$
we define
![]() $T_{1a}',T_{1b}'$
as subtrees of the root of the tree containing A,B such that the first contains the A leaf and the second contains the B leaf, while
$T_{1a}',T_{1b}'$
as subtrees of the root of the tree containing A,B such that the first contains the A leaf and the second contains the B leaf, while
![]() $T_{2*}',T_{2**}'$
be the subtrees of the root of the tree having neither A nor B elements. Then, it is easy to see that the following pairs of trees are isomorphic:
$T_{2*}',T_{2**}'$
be the subtrees of the root of the tree having neither A nor B elements. Then, it is easy to see that the following pairs of trees are isomorphic:
![]() $T_{1a}$
and
$T_{1a}$
and
![]() $T_{1a}'$
,
$T_{1a}'$
,
![]() $T_{2b}$
and
$T_{2b}$
and
![]() $T_{1b}'$
,
$T_{1b}'$
,
![]() $T_{1*}$
and
$T_{1*}$
and
![]() $T_{2*}'$
,
$T_{2*}'$
,
![]() $T_{2*}$
and
$T_{2*}$
and
![]() $T_{2**}'$
.
$T_{2**}'$
.
We now define the bijection f as the union of those isomorphisms plus mapping roots of trees
![]() $T_i$
in D into roots of
$T_i$
in D into roots of
![]() $T_i$
in D’. It is an immediate observation that if
$T_i$
in D’. It is an immediate observation that if
![]() $n > r+1$
(i.e. leaves are not in the radius r neighborhood of children of roots) then f satisfies the condition that neighborhoods of a and f(a) of radius r are isomorphic. This would tell us that
$n > r+1$
(i.e. leaves are not in the radius r neighborhood of children of roots) then f satisfies the condition that neighborhoods of a and f(a) of radius r are isomorphic. This would tell us that
![]() $D_n$
and
$D_n$
and
![]() $D_n'$
agree on
$D_n'$
agree on
![]() $\phi$
but we know they do not. This contradiction completes the proof.
$\phi$
but we know they do not. This contradiction completes the proof.
As a corollary to the proof, we obtain the following result showing that non-recursive SQL is incapable of computing
![]() $\mathsf{cert}_\Sigma(Q,D)$
in the setting of Theorem 4.14.
$\mathsf{cert}_\Sigma(Q,D)$
in the setting of Theorem 4.14.
Corollary 4.15 There exists a Boolean CQ Q and single FD
![]() $\Sigma$
over a relational schema of binary and unary relations such that
$\Sigma$
over a relational schema of binary and unary relations such that
![]() $\mathsf{cert}_\Sigma(Q,D)$
is not expressible in the basic SELECT-FROM-WHERE-GROUP BY-HAVING fragment of SQL with arbitrary aggregate functions.
$\mathsf{cert}_\Sigma(Q,D)$
is not expressible in the basic SELECT-FROM-WHERE-GROUP BY-HAVING fragment of SQL with arbitrary aggregate functions.
This is due to the fact that queries in this fragment of SQL with grouping and aggregation can be translated into a logic with aggregate functions (Libkin Reference Libkin2003) which itself is known to be Hanf-local (Hella et al. Reference Hella, Libkin, Nurmonen and Wong2001).
4.4 FO rewriting for certain answers
We now focus on the special case where
![]() $\Sigma$
is empty. First notice that the only Datalog component in our rewriting was the
$\Sigma$
is empty. First notice that the only Datalog component in our rewriting was the
![]() $equiv_{\gamma}$
formula; moreover, notice that without constraints,
$equiv_{\gamma}$
formula; moreover, notice that without constraints,
![]() $equiv_{\gamma}$
simply computes a reflexive symmetric transitive closure. More precisely, for a given
$equiv_{\gamma}$
simply computes a reflexive symmetric transitive closure. More precisely, for a given
![]() $\bar t = \nu(\bar y)$
, one has that
$\bar t = \nu(\bar y)$
, one has that
![]() $equiv_{\gamma}(\bar t, s, s')$
holds in D iff (s,s’) belongs to the reflexive symmetric transitive closure of
$equiv_{\gamma}(\bar t, s, s')$
holds in D iff (s,s’) belongs to the reflexive symmetric transitive closure of
![]() $\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma(\bar y)\}$
over
$\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma(\bar y)\}$
over
![]() $\text{adom}(D) \cup\text{adom}(\gamma)$
.
$\text{adom}(D) \cup\text{adom}(\gamma)$
.
Definition 4.16 Given a database D, a conjunction of equality atoms
![]() $\gamma(\bar{y})$
and an assignment
$\gamma(\bar{y})$
and an assignment
![]() $\nu: \bar y \cup \text{adom}(\gamma) \rightarrow\text{adom}(D)\cup \text{adom}(\gamma)$
preserving constants, we say that
$\nu: \bar y \cup \text{adom}(\gamma) \rightarrow\text{adom}(D)\cup \text{adom}(\gamma)$
preserving constants, we say that
![]() $u,u' \in \text{adom}(D)\cup\text{adom}(\gamma)$
are equivalent w.r.t.
$u,u' \in \text{adom}(D)\cup\text{adom}(\gamma)$
are equivalent w.r.t.
![]() $\gamma$
and
$\gamma$
and
![]() $\nu$
and write
$\nu$
and write
![]() $u \equiv_\gamma^\nu u'$
, if either
$u \equiv_\gamma^\nu u'$
, if either
![]() $u=u'$
or (u, u’) belongs to the reflexive symmetric transitive closure of
$u=u'$
or (u, u’) belongs to the reflexive symmetric transitive closure of
![]() $\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
.
$\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
.
As
![]() $\Sigma$
is empty, we can rewrite as follows the
$\Sigma$
is empty, we can rewrite as follows the
![]() $equiv_{\gamma}$
formula in FO, where m is the number of equivalence classes of
$equiv_{\gamma}$
formula in FO, where m is the number of equivalence classes of
![]() $\sim_{\gamma}$
:
$\sim_{\gamma}$
:
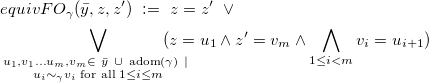
Proposition 4.17 Given an incomplete database D, a conjunction of equality atoms
![]() $\gamma(\bar{y})$
and an assignment
$\gamma(\bar{y})$
and an assignment
![]() $\nu(\bar{y})=\bar{t}$
over
$\nu(\bar{y})=\bar{t}$
over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
, given s,s’ in
$\text{adom}(D) \cup \text{adom}(\gamma)$
, given s,s’ in
![]() $\bar t\cup\text{adom}(\gamma)$
, we have that
$\bar t\cup\text{adom}(\gamma)$
, we have that
![]() $D \models equivFO_{\gamma} (\bar{t},s,s')$
if and only if
$D \models equivFO_{\gamma} (\bar{t},s,s')$
if and only if
![]() $s\equiv_\gamma^\nu s'$
.
$s\equiv_\gamma^\nu s'$
.
Intuitively, this holds because each disjunct of
![]() $equivFO_\gamma(\bar t, s, s') $
corresponds to a possible derivation of (s, s’) in the reflexive symmetric transitive closure of
$equivFO_\gamma(\bar t, s, s') $
corresponds to a possible derivation of (s, s’) in the reflexive symmetric transitive closure of
![]() $\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
, and one can prove that there is a bound only depending on
$\{(\nu(x), \nu(w)) ~|~ x = w \in \gamma\}$
, and one can prove that there is a bound only depending on
![]() $\gamma$
on the number of steps of this derivation.
$\gamma$
on the number of steps of this derivation.
Proof. To start with we naturally extend
![]() $\nu$
to be the identity on
$\nu$
to be the identity on
![]() $\text{adom}(\gamma)$
. Assume first
$\text{adom}(\gamma)$
. Assume first
![]() $D \models equivFO_{\gamma} (\bar{t},s,s')$
. If
$D \models equivFO_{\gamma} (\bar{t},s,s')$
. If
![]() $s=s'$
then
$s=s'$
then
![]() $s\equiv_\gamma^\nu s'$
. Now assume
$s\equiv_\gamma^\nu s'$
. Now assume
![]() $s \neq s'$
. Then, there exist variables and/or constants
$s \neq s'$
. Then, there exist variables and/or constants
![]() $u_1, v_1\ldots u_m, v_m \in~\bar{y}~\cup~\text{adom}(\gamma)$
with
$u_1, v_1\ldots u_m, v_m \in~\bar{y}~\cup~\text{adom}(\gamma)$
with
![]() $u_i \sim_\gamma v_i$
for all i, such that
$u_i \sim_\gamma v_i$
for all i, such that
![]() $s = \nu(u_1), s' = \nu(v_m)$
and
$s = \nu(u_1), s' = \nu(v_m)$
and
![]() $\nu(v_i) = \nu (u_{i+1})$
for all
$\nu(v_i) = \nu (u_{i+1})$
for all
![]() $i < m$
. Clearly
$i < m$
. Clearly
![]() $u_i\sim_\gamma v_i$
implies
$u_i\sim_\gamma v_i$
implies
![]() $\nu(u_i) \equiv_\gamma^\nu \nu(v_i)$
. Then,
$\nu(u_i) \equiv_\gamma^\nu \nu(v_i)$
. Then,
![]() $\nu(u_i) \equiv_\gamma^\nu \nu (u_{i+1})$
for all
$\nu(u_i) \equiv_\gamma^\nu \nu (u_{i+1})$
for all
![]() $i < m$
. We conclude by transitivity that
$i < m$
. We conclude by transitivity that
![]() $s= \nu(u_i) \equiv_\gamma^\nu \nu(u_m) \equiv_\gamma^\nu \nu(v_m)=s'$
, and therefore,
$s= \nu(u_i) \equiv_\gamma^\nu \nu(u_m) \equiv_\gamma^\nu \nu(v_m)=s'$
, and therefore,
![]() $s \equiv_\gamma^\nu s'$
.
$s \equiv_\gamma^\nu s'$
.
Assume now that
![]() $s \equiv_\gamma^\nu s'$
. If
$s \equiv_\gamma^\nu s'$
. If
![]() $s = s'$
then clearly
$s = s'$
then clearly
![]() $D \models equivFO_{\gamma} (\bar{t},s,s')$
. Thus, assume
$D \models equivFO_{\gamma} (\bar{t},s,s')$
. Thus, assume
![]() $s \neq s'$
. We proceed by induction on the number of transitive closure steps needed to derive (s,s’) starting for the base relation
$s \neq s'$
. We proceed by induction on the number of transitive closure steps needed to derive (s,s’) starting for the base relation
![]() $\{(\nu(x), \nu(w)) | x = w \in \gamma\}$
. In the base case,
$\{(\nu(x), \nu(w)) | x = w \in \gamma\}$
. In the base case,
![]() $(s,s') = (\nu(x), \nu(w))$
for some equality
$(s,s') = (\nu(x), \nu(w))$
for some equality
![]() $x=w \in \gamma$
. Then, D satisfies the following disjunct of
$x=w \in \gamma$
. Then, D satisfies the following disjunct of
![]() $equivFO_{\gamma} (\bar{t},s,s')$
: take
$equivFO_{\gamma} (\bar{t},s,s')$
: take
![]() $u_1 = x$
,
$u_1 = x$
,
![]() $v_1 = w$
,
$v_1 = w$
,
![]() $u_i = v_i = w$
for all
$u_i = v_i = w$
for all
![]() $i = 2..m$
(this is a disjunct since
$i = 2..m$
(this is a disjunct since
![]() $u_i \sim_\gamma v_i$
for all
$u_i \sim_\gamma v_i$
for all
![]() $i = 1..m$
). The disjunct is satisfied since
$i = 1..m$
). The disjunct is satisfied since
![]() $s = \nu(x) = \nu(u_1)$
,
$s = \nu(x) = \nu(u_1)$
,
![]() $s' = \nu(w) = \nu(v_m)$
, and for all
$s' = \nu(w) = \nu(v_m)$
, and for all
![]() $i = 1..m-1, \nu(v_i) = \nu(u_{i+1}) = \nu(w)$
.
$i = 1..m-1, \nu(v_i) = \nu(u_{i+1}) = \nu(w)$
.
In the general inductive case, there exists r such that
![]() $(r, s') = (\nu(x), \nu(w))$
for some equality
$(r, s') = (\nu(x), \nu(w))$
for some equality
![]() $x = w$
(or
$x = w$
(or
![]() $w=x$
)
$w=x$
)
![]() $\in \gamma$
, with
$\in \gamma$
, with
![]() $s \equiv_\gamma^\nu r$
derived at the previous step. By the induction hypothesis
$s \equiv_\gamma^\nu r$
derived at the previous step. By the induction hypothesis
![]() $D \models equivFO_\gamma(\bar t, s, r)$
. We can assume
$D \models equivFO_\gamma(\bar t, s, r)$
. We can assume
![]() $s \neq r$
since otherwise (s,s’) would be in the base relation. Therefore, D satisfies one of the disjuncts of
$s \neq r$
since otherwise (s,s’) would be in the base relation. Therefore, D satisfies one of the disjuncts of
![]() $equivFO_\gamma(\bar t, s, r)$
. Then, there exists a sequence of
$equivFO_\gamma(\bar t, s, r)$
. Then, there exists a sequence of
![]() $m+1$
pairs in
$m+1$
pairs in
![]() $\bar y \cup \text{adom}(\gamma)$
$\bar y \cup \text{adom}(\gamma)$
such that
-
 $u_{m+1} = x$
and
$u_{m+1} = x$
and
 $v_{m+1} = w$
,
$v_{m+1} = w$
, -
 $u_i \sim_\gamma v_i, i =1..m+1$
,
$u_i \sim_\gamma v_i, i =1..m+1$
, -
 $s = \nu(u_1)$
,
$s = \nu(u_1)$
,
 $r = \nu(v_m)$
,
$r = \nu(v_m)$
,
 $s' = \nu(v_{m+1})$
,
$s' = \nu(v_{m+1})$
, -
 $\nu(v_i) = \nu(u_{i+1})$
, for all
$\nu(v_i) = \nu(u_{i+1})$
, for all
 $i \leq m$
,
$i \leq m$
,
We now show that from this sequence of pairs, one can construct another one of exactly m pairs,
![]() $(u'_i, v'_i), i =1..m$
still connecting s ans s’, that is such that:
$(u'_i, v'_i), i =1..m$
still connecting s ans s’, that is such that:
-
(a)
 $u'_i \sim_\gamma v'_i, i =1..m$
$u'_i \sim_\gamma v'_i, i =1..m$
-
(b)
 $s = \nu(u'_1)$
,
$s = \nu(u'_1)$
,
 $s' = \nu(v'_{m})$
$s' = \nu(v'_{m})$
-
(c)
 $\nu(v'_i) = \nu(u'_{i+1})$
, for all
$\nu(v'_i) = \nu(u'_{i+1})$
, for all
 $i < m$
.
$i < m$
.
The idea is to first cut the sequence
![]() $(u_i, v_i), i =1..m+1$
, removing at least one pair, then pad it to size m if necessary.
$(u_i, v_i), i =1..m+1$
, removing at least one pair, then pad it to size m if necessary.
In order to cut the original sequence, remark that it contains
![]() $m+1$
pairs where m is the number of
$m+1$
pairs where m is the number of
![]() $\sim_\gamma$
equivalence classes. Thus, there exist
$\sim_\gamma$
equivalence classes. Thus, there exist
![]() $i < j$
such that
$i < j$
such that
![]() $u_i \sim_\gamma u_j$
. We remove from the sequence all elements between
$u_i \sim_\gamma u_j$
. We remove from the sequence all elements between
![]() $u_i$
and
$u_i$
and
![]() $v_j$
(excluded), the new sequence is
$v_j$
(excluded), the new sequence is
Note that this sequence satisfies (a) (b) and (c) above since
![]() $u_i \sim_\gamma u_j \sim_\gamma v_j$
. Let the new sequence contain k pairs. We know
$u_i \sim_\gamma u_j \sim_\gamma v_j$
. Let the new sequence contain k pairs. We know
![]() $k \leq m$
because we have removed at least one pair from the original sequence (recall
$k \leq m$
because we have removed at least one pair from the original sequence (recall
![]() $i < j$
). If
$i < j$
). If
![]() $k < m,$
we pad the sequence on the right with
$k < m,$
we pad the sequence on the right with
![]() $m-k$
pairs
$m-k$
pairs
![]() $(v_{m+1}, v_{m+1})$
. The new sequence still satisfies (a), (b), and (c); therefore, the corresponding disjunct of
$(v_{m+1}, v_{m+1})$
. The new sequence still satisfies (a), (b), and (c); therefore, the corresponding disjunct of
![]() $equivFO_\gamma(\bar t, s, s')$
is satisfied by D.
$equivFO_\gamma(\bar t, s, s')$
is satisfied by D.
Example 4.18 Let
![]() $\gamma:=y_1=y_2 \wedge z=x$
be the equality subquery of the query Q(x) in Example 4.2. Up to logical equivalence,
$\gamma:=y_1=y_2 \wedge z=x$
be the equality subquery of the query Q(x) in Example 4.2. Up to logical equivalence,
![]() $equivFO_{\gamma}(y_1,y_2,z,x,w,w')$
contains precisely the disjuncts
$equivFO_{\gamma}(y_1,y_2,z,x,w,w')$
contains precisely the disjuncts
![]() $w=w'$
,
$w=w'$
,
![]() $w=y_1 \wedge w'=y_2$
,
$w=y_1 \wedge w'=y_2$
,
![]() $w=z \wedge w'=x$
,
$w=z \wedge w'=x$
,
![]() $w=y_1 \wedge w'=x \wedge y_2=z$
, plus all disjuncts obtained from them by applying one or more of the following transformations: switch w and w’, switch
$w=y_1 \wedge w'=x \wedge y_2=z$
, plus all disjuncts obtained from them by applying one or more of the following transformations: switch w and w’, switch
![]() $y_1$
and
$y_1$
and
![]() $y_2$
, switch x and z. Let D be the database from Example 2.1, then we have for instance
$y_2$
, switch x and z. Let D be the database from Example 2.1, then we have for instance
![]() $D \models equivFO_{\gamma}(1,\bot_2,\bot_2,1,a,a')$
and
$D \models equivFO_{\gamma}(1,\bot_2,\bot_2,1,a,a')$
and
![]() $D \models equivFO_{\gamma}(1,\bot_2,\bot_2,\bot_2,a,a')$
for all
$D \models equivFO_{\gamma}(1,\bot_2,\bot_2,\bot_2,a,a')$
for all
![]() $a,a' \in \{1,\bot_2\}$
. Similarly
$a,a' \in \{1,\bot_2\}$
. Similarly
![]() $D \models equivFO_{\gamma}(\bot_1,\bot_2,\bot_2,1,a,a')$
for all
$D \models equivFO_{\gamma}(\bot_1,\bot_2,\bot_2,1,a,a')$
for all
![]() $a,a' \in \{1,\bot_1,\bot_2\}$
.
$a,a' \in \{1,\bot_1,\bot_2\}$
.
As a consequence of Proposition 4.17, for fixed
![]() $\gamma$
and
$\gamma$
and
![]() $\bar t$
, the relation
$\bar t$
, the relation
![]() $\{(s,s') ~|~ D \models equivFO_{\gamma}(\bar t, s, s')\}$
is an equivalence relation over
$\{(s,s') ~|~ D \models equivFO_{\gamma}(\bar t, s, s')\}$
is an equivalence relation over
![]() $\text{adom}(D) \cup \text{adom}(\gamma)$
where each element of
$\text{adom}(D) \cup \text{adom}(\gamma)$
where each element of
![]() $\text{adom}(D)$
neither in
$\text{adom}(D)$
neither in
![]() $\bar t$
nor in
$\bar t$
nor in
![]() $\text{adom}(\gamma)$
forms a singleton equivalence class.
$\text{adom}(\gamma)$
forms a singleton equivalence class.
As in Section 4.2,
![]() $ equivFO_{\gamma}$
selects precisely the pairs of elements of a tuple that a valuation needs to collapse to satisfy a set of equalities.
$ equivFO_{\gamma}$
selects precisely the pairs of elements of a tuple that a valuation needs to collapse to satisfy a set of equalities.
As a consequence, we can rewrite in FO the formula poss
![]() $_{Q_i}$
of Subsection 4.2 encoding the set of possible answers to
$_{Q_i}$
of Subsection 4.2 encoding the set of possible answers to
![]() $Q_i$
. It is enough to replace each occurrence of the Datalog
$Q_i$
. It is enough to replace each occurrence of the Datalog
![]() $equiv_{\gamma}(\bar{y},z,z')$
program in it by
$equiv_{\gamma}(\bar{y},z,z')$
program in it by
![]() $equiv^{FO}_{\gamma}(\bar{y},z,z')$
. We denote by poss
$equiv^{FO}_{\gamma}(\bar{y},z,z')$
. We denote by poss
![]() $^{FO}_{Q_i}$
the rewriting so obtained.
$^{FO}_{Q_i}$
the rewriting so obtained.
Theorem 4.19 (FO rewriting) Let D be a database,
![]() $\Sigma=\emptyset$
and let
$\Sigma=\emptyset$
and let
![]() $Q(\bar{x})$
be a BCCQ in NRV normal form. Let
$Q(\bar{x})$
be a BCCQ in NRV normal form. Let
![]() $Q' = Q_1'(\bar{x}) \vee \ldots \vee Q_n'(\bar{x})$
be
$Q' = Q_1'(\bar{x}) \vee \ldots \vee Q_n'(\bar{x})$
be
![]() $\neg Q$
in DNF normal form. Then,
$\neg Q$
in DNF normal form. Then,
![]() $\bar r \in \mathsf{cert}_\Sigma(Q,D)$
if and only if
$\bar r \in \mathsf{cert}_\Sigma(Q,D)$
if and only if
![]() $D \models \rho(\bar r)$
where
$D \models \rho(\bar r)$
where
![]() $\rho(\bar x) = \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
$\rho(\bar x) = \bigwedge_{\substack{1\leq i \leq n}} \forall \bar{w}$
![]() $\neg poss^{FO}_{Q'_i}(\bar{x}\bar{w})$
.
$\neg poss^{FO}_{Q'_i}(\bar{x}\bar{w})$
.
Note that tractability of BCCQ was already proved in Gheerbrant and Libkin (Reference Gheerbrant and Libkin2015) using tableau-based methods. We now refine complexity as follows.
Corollary 4.20 For each fixed BCCQ query Q, the complexity of CertainAnswer
![]() $_\Sigma$
$_\Sigma$
![]() $_(Q)$
is in DLOGSPACE whenever
$_(Q)$
is in DLOGSPACE whenever
![]() $\Sigma=\emptyset$
.
$\Sigma=\emptyset$
.
4.5 FO rewriting for best answers
Considering arbitrary
![]() ${{{{\mathsf{FO}}}}}$
queries brought us an intrinsic intractability result for all variants of best answers. This motivates restricting to unions of conjunctive queries, for which a polynomial-time evaluation algorithm (in data complexity) already exists(Libkin Reference Libkin, den Bussche and Arenas2018). The resolution-based procedure is however in sharp contrast with naïve evaluation, which allows to compute certain answers to unions of conjunctive queries via usual model checking. We thus initiate a descriptive complexity analysis of the best answers problem, showing that for unions of conjunctive queries, it can essentially be reduced – modulo a preprocessing of the query – to (naïve) evaluation of an
${{{{\mathsf{FO}}}}}$
queries brought us an intrinsic intractability result for all variants of best answers. This motivates restricting to unions of conjunctive queries, for which a polynomial-time evaluation algorithm (in data complexity) already exists(Libkin Reference Libkin, den Bussche and Arenas2018). The resolution-based procedure is however in sharp contrast with naïve evaluation, which allows to compute certain answers to unions of conjunctive queries via usual model checking. We thus initiate a descriptive complexity analysis of the best answers problem, showing that for unions of conjunctive queries, it can essentially be reduced – modulo a preprocessing of the query – to (naïve) evaluation of an
![]() ${{{{\mathsf{FO}}}}}$
-formula.
${{{{\mathsf{FO}}}}}$
-formula.
Given a union of conjunctive queries Q, our starting point towards an
![]() ${{{{\mathsf{FO}}}}}$
rewriting for best answers is finding an
${{{{\mathsf{FO}}}}}$
rewriting for best answers is finding an
![]() ${{{{\mathsf{FO}}}}}$
-formula
${{{{\mathsf{FO}}}}}$
-formula
![]() $Q_\subseteq(\bar{x}, \bar{y})$
encoding the inclusion of supports, that is selecting tuples
$Q_\subseteq(\bar{x}, \bar{y})$
encoding the inclusion of supports, that is selecting tuples
![]() $\bar s, \bar t$
over
$\bar s, \bar t$
over
![]() $\text{adom}(D)\cup\text{adom}(Q)$
iff
$\text{adom}(D)\cup\text{adom}(Q)$
iff![]() . From
. From
![]() $Q_\subseteq,$
one can easily define an
$Q_\subseteq,$
one can easily define an
![]() ${{{{\mathsf{FO}}}}}$
-formula selecting precisely all best answers to Q on D:
${{{{\mathsf{FO}}}}}$
-formula selecting precisely all best answers to Q on D:
As in Section 4.2, we assume all CQs to be in NRV normal form. We can thus first concentrate on the support of equality subqueries. This will be encoded in
![]() ${{{{\mathsf{FO}}}}}$
and then integrated in the rewriting of the whole conjunctive query.
${{{{\mathsf{FO}}}}}$
and then integrated in the rewriting of the whole conjunctive query.
We now go back to an arbitrary union of conjunctive queries of vocabulary
![]() $\sigma$
in NRV-normal form:
$\sigma$
in NRV-normal form:
where each
![]() $Q_i$
is in NRV normal form with relational subquery
$Q_i$
is in NRV normal form with relational subquery
![]() $q_i(\bar y_i, \bar z_i)$
and equality subquery
$q_i(\bar y_i, \bar z_i)$
and equality subquery
![]() $eq_i(\bar x, \bar y_i, \bar z_i)$
.
$eq_i(\bar x, \bar y_i, \bar z_i)$
.
Recall the formula
![]() $comp_{\gamma}$
, defined in Section 4.2, stating the existence of a valuation that collapses all equivalent elements of a tuple:
$comp_{\gamma}$
, defined in Section 4.2, stating the existence of a valuation that collapses all equivalent elements of a tuple:
Notice that if
![]() $D \models comp_\gamma(\bar t)$
then for each
$D \models comp_\gamma(\bar t)$
then for each
![]() $s \in adom(D)\cup\text{adom}(\gamma)$
there exists at most one constant c such that
$s \in adom(D)\cup\text{adom}(\gamma)$
there exists at most one constant c such that
![]() $D \models equivFO_\gamma(\bar t, s, c)$
. In fact if for constants
$D \models equivFO_\gamma(\bar t, s, c)$
. In fact if for constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
,
$c_2$
,
![]() $D \models equivFO_\gamma(\bar t, s, c_1)$
and
$D \models equivFO_\gamma(\bar t, s, c_1)$
and
![]() $D \models equivFO_\gamma(\bar t, s, c_2)$
, by transitivity
$D \models equivFO_\gamma(\bar t, s, c_2)$
, by transitivity
![]() $D \models equivFO_\gamma(\bar t, c_1, c_2)$
, implying
$D \models equivFO_\gamma(\bar t, c_1, c_2)$
, implying
![]() $c_1 = c_2$
.
$c_1 = c_2$
.
Example 4.21 Let D and
![]() $\gamma$
be as in Example 4.18. Consider
$\gamma$
be as in Example 4.18. Consider
![]() $comp_\gamma(y_1,y_2,z,x)$
. Given the tuples selected by
$comp_\gamma(y_1,y_2,z,x)$
. Given the tuples selected by
![]() $equivFO_\gamma$
in Example 4.18, we can conclude that
$equivFO_\gamma$
in Example 4.18, we can conclude that
![]() $D \models comp_\gamma(1,\bot_2,\bot_2,1)$
.
$D \models comp_\gamma(1,\bot_2,\bot_2,1)$
.
We now define a formula capturing the inclusion of supports between two conjunctions of equality atoms, which will be a crucial ingredient in our rewriting.
Let
![]() $\gamma(\bar{x})$
and
$\gamma(\bar{x})$
and
![]() $\gamma'({\bar y})$
be conjunctions of equality atoms with
$\gamma'({\bar y})$
be conjunctions of equality atoms with![]() . We define:
. We define:
Example 4.22 Let
![]() $\gamma$
and D be as in Example 4.18. Let
$\gamma$
and D be as in Example 4.18. Let
![]() $\gamma':=y'_1=y'_2 \wedge z'=x'$
, then it follows from Example 4.18 that
$\gamma':=y'_1=y'_2 \wedge z'=x'$
, then it follows from Example 4.18 that
![]() $D \models imply_{\gamma\gamma'}(\bot_1\bot_2\bot_21,1\bot_2\bot_2\bot_2)$
and
$D \models imply_{\gamma\gamma'}(\bot_1\bot_2\bot_21,1\bot_2\bot_2\bot_2)$
and
![]() $D \models imply_{\gamma\gamma'}(1\bot_2\bot_21,1\bot_2\bot_2\bot_2)$
.
$D \models imply_{\gamma\gamma'}(1\bot_2\bot_21,1\bot_2\bot_2\bot_2)$
.
By combining Propositions 4.8 and 4.7, we get:
Corollary 4.23 Let
![]() $\gamma(\bar y)$
,
$\gamma(\bar y)$
,
![]() $\gamma'(\bar y)$
be conjunctions of equality atoms with
$\gamma'(\bar y)$
be conjunctions of equality atoms with![]() , D a database and
, D a database and
![]() $\nu(\bar{y})=\bar{t}$
,
$\nu(\bar{y})=\bar{t}$
,
![]() $\nu'(\bar{y})=\bar{t'}$
assignments over
$\nu'(\bar{y})=\bar{t'}$
assignments over![]() . If
. If
![]() $D \models comp_{\gamma}(\bar{t}) \wedge imply_{\gamma, \gamma'}(\bar{t},\bar{t'})$
, then
$D \models comp_{\gamma}(\bar{t}) \wedge imply_{\gamma, \gamma'}(\bar{t},\bar{t'})$
, then
![]() $D \models comp_{\gamma'}(\bar{t'})$
.
$D \models comp_{\gamma'}(\bar{t'})$
.
Proof. Assume
![]() $D \models comp_{\gamma}(\bar{t}) \wedge imply_{\gamma, \gamma'}(\bar{t},\bar{t'})$
, that is,
$D \models comp_{\gamma}(\bar{t}) \wedge imply_{\gamma, \gamma'}(\bar{t},\bar{t'})$
, that is,
![]() $D \models \forall z z'~(equivFO_{\gamma}(\bar{t},z,z') \wedge \neg Null(z) \wedge \neg Null(z') \rightarrow z=z')$
and
$D \models \forall z z'~(equivFO_{\gamma}(\bar{t},z,z') \wedge \neg Null(z) \wedge \neg Null(z') \rightarrow z=z')$
and
![]() $D \models \forall z z'~(equivFO_{\gamma'}(\bar{t'},z,z')\rightarrow equivFO_{\gamma}(\bar{t},z,z'))$
. Now let
$D \models \forall z z'~(equivFO_{\gamma'}(\bar{t'},z,z')\rightarrow equivFO_{\gamma}(\bar{t},z,z'))$
. Now let
![]() $s,s' \in\text{adom}(D) \cup \text{adom}(\gamma)$
with
$s,s' \in\text{adom}(D) \cup \text{adom}(\gamma)$
with
![]() $D \models equivFO_{\gamma'}(\bar{t'},s,s') \wedge \neg Null(s) \wedge \neg Null(s')$
. As
$D \models equivFO_{\gamma'}(\bar{t'},s,s') \wedge \neg Null(s) \wedge \neg Null(s')$
. As
![]() $D \models imply_{\gamma, \gamma'}(\bar{t},\bar{t'}),$
it follows that
$D \models imply_{\gamma, \gamma'}(\bar{t},\bar{t'}),$
it follows that
![]() $D \models equivFO_{\gamma}(\bar{t},s,s')$
and so
$D \models equivFO_{\gamma}(\bar{t},s,s')$
and so
![]() $D \models \neg Null(s) \wedge \neg Null(s') \rightarrow s=s'$
now follows from
$D \models \neg Null(s) \wedge \neg Null(s') \rightarrow s=s'$
now follows from
![]() $D \models comp_{\gamma}(\bar{t})$
. Hence
$D \models comp_{\gamma}(\bar{t})$
. Hence
![]() $D \models comp_{\gamma'}(\bar{t'})$
.
$D \models comp_{\gamma'}(\bar{t'})$
.
We are now ready to define the
![]() ${{{{\mathsf{FO}}}}}$
-formula encoding the inclusion of supports.
${{{{\mathsf{FO}}}}}$
-formula encoding the inclusion of supports.
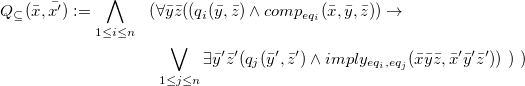 \begin{align}Q_\subseteq(\bar{x}, \bar{x'}) := \bigwedge\limits_{1\leq i \leq n} ~~(&\forall \bar{y}\bar{z} ((q_i(\bar{y},\bar{z})\wedge comp_{eq_i}(\bar{x},\bar{y},\bar{z})) \rightarrow\nonumber\\&\bigvee\limits_{1 \leq j \leq n}\exists \bar{y}' \bar{z}'(q_j(\bar{y}',\bar{z}') \wedge imply_{eq_i, eq_j}(\bar{x}\bar{y}\bar{z}, \bar{x}'\bar{y}'\bar{z}') )~ )~)\nonumber\end{align}
\begin{align}Q_\subseteq(\bar{x}, \bar{x'}) := \bigwedge\limits_{1\leq i \leq n} ~~(&\forall \bar{y}\bar{z} ((q_i(\bar{y},\bar{z})\wedge comp_{eq_i}(\bar{x},\bar{y},\bar{z})) \rightarrow\nonumber\\&\bigvee\limits_{1 \leq j \leq n}\exists \bar{y}' \bar{z}'(q_j(\bar{y}',\bar{z}') \wedge imply_{eq_i, eq_j}(\bar{x}\bar{y}\bar{z}, \bar{x}'\bar{y}'\bar{z}') )~ )~)\nonumber\end{align}
Combining Lemmas 4.5, 4.9, Propositions 4.7, 4.8, and Corollary 4.23, we get:
Proposition 4.24
![]() $D \models Q_\subseteq(\bar{s}, \bar{t})$
iff
$D \models Q_\subseteq(\bar{s}, \bar{t})$
iff
![]() $Supp(Q, D, \bar s) \subseteq Supp(Q,D, \bar t)$
.
$Supp(Q, D, \bar s) \subseteq Supp(Q,D, \bar t)$
.
Proof.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $D \models Q_{\subseteq}(\bar{s}, \bar{t})$
and let
$D \models Q_{\subseteq}(\bar{s}, \bar{t})$
and let
![]() $v \in Supp(Q, D, \bar s)$
be a valuation of D. By Lemma 4.9,
$v \in Supp(Q, D, \bar s)$
be a valuation of D. By Lemma 4.9,
![]() $\exists i\bar{a} \bar{b}~D\models q_i(\bar{a}\bar{b})\wedge comp_{eq_i}(\bar{s}\bar{a}\bar{b})$
and
$\exists i\bar{a} \bar{b}~D\models q_i(\bar{a}\bar{b})\wedge comp_{eq_i}(\bar{s}\bar{a}\bar{b})$
and
![]() $v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
. So by our assumption there exists
$v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
. So by our assumption there exists
![]() $j,\bar{a}'\bar{b}'$
with
$j,\bar{a}'\bar{b}'$
with
![]() $D \models~q_j(\bar{a}'\bar{b}') \wedge imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}')$
and by Corollary 4.23
$D \models~q_j(\bar{a}'\bar{b}') \wedge imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}')$
and by Corollary 4.23
![]() $D \models comp_{eq_j}(\bar{t}\bar{a}'\bar{b}')$
. Now let
$D \models comp_{eq_j}(\bar{t}\bar{a}'\bar{b}')$
. Now let
![]() $t_1,t_2$
such that
$t_1,t_2$
such that
![]() $D \models equiv_{eq_j}(\bar{t}\bar{a}'\bar{b}',t_1,t_2)$
. By
$D \models equiv_{eq_j}(\bar{t}\bar{a}'\bar{b}',t_1,t_2)$
. By
![]() $D \models~imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}'),$
we have
$D \models~imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}'),$
we have
![]() $D \models equiv_{eq_i}(\bar{s}\bar{a}\bar{b},t_1,t_2),$
and by Lemma 4.5,
$D \models equiv_{eq_i}(\bar{s}\bar{a}\bar{b},t_1,t_2),$
and by Lemma 4.5,
![]() $v(t_1)=v(t_2)$
. But then, again by Lemma 4.5,
$v(t_1)=v(t_2)$
. But then, again by Lemma 4.5,
![]() $v(D) \models eq_i(v(\bar{t}\bar{a}'\bar{b}'))$
and by Lemma 4.9 it follows that
$v(D) \models eq_i(v(\bar{t}\bar{a}'\bar{b}'))$
and by Lemma 4.9 it follows that
![]() $v \in Supp(Q,D,\bar{t})$
.
$v \in Supp(Q,D,\bar{t})$
.
![]() $\Leftarrow$
Assume
$\Leftarrow$
Assume
![]() $Supp(Q, D, \bar s) \subseteq Supp(Q,D, \bar t)$
and let
$Supp(Q, D, \bar s) \subseteq Supp(Q,D, \bar t)$
and let
![]() $i, \bar{a}$
,
$i, \bar{a}$
,
![]() $\bar{b}$
with
$\bar{b}$
with
![]() $D \models q_i(\bar{a},\bar{b})\wedge comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
. By Proposition 4.7, there exists a valuation v (that we assume w.l.o.g. to be tight) such that
$D \models q_i(\bar{a},\bar{b})\wedge comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
. By Proposition 4.7, there exists a valuation v (that we assume w.l.o.g. to be tight) such that
![]() $v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
and so by Lemma 4.9
$v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
and so by Lemma 4.9
![]() $v \in Supp(Q,D,\bar{s})$
. Hence by our assumption, we also have
$v \in Supp(Q,D,\bar{s})$
. Hence by our assumption, we also have
![]() $v \in Supp(Q,D,\bar{t}),$
and so by Lemma 4.9, there exists
$v \in Supp(Q,D,\bar{t}),$
and so by Lemma 4.9, there exists
![]() $j,\bar{a}'\bar{b}'$
with
$j,\bar{a}'\bar{b}'$
with
![]() $D \models~ q_j(\bar{a}'\bar{b}') \wedge comp_{eq_j}(\bar{t}\bar{a}'\bar{b}')$
and
$D \models~ q_j(\bar{a}'\bar{b}') \wedge comp_{eq_j}(\bar{t}\bar{a}'\bar{b}')$
and
![]() $v(D) \models eq_j(v(\bar{t}\bar{a}'\bar{b}'))$
.
$v(D) \models eq_j(v(\bar{t}\bar{a}'\bar{b}'))$
.
Claim 4.25 Let D be a database,
![]() $\gamma(\bar y)$
,
$\gamma(\bar y)$
,
![]() $\gamma'(\bar y)$
conjunctions of equality atoms with
$\gamma'(\bar y)$
conjunctions of equality atoms with![]() ,
,
![]() $\nu(\bar{y})=\bar{t}$
,
$\nu(\bar{y})=\bar{t}$
,
![]() $\nu'(\bar{y})=\bar{t'}$
assignments over
$\nu'(\bar{y})=\bar{t'}$
assignments over![]() and
and
![]() $v^*$
a valuation of D w.r.t.
$v^*$
a valuation of D w.r.t.
![]() $\nu$
and
$\nu$
and
![]() $\gamma$
satisfying the conditions of Lemma 4.7 (i.e.,
$\gamma$
satisfying the conditions of Lemma 4.7 (i.e.,
![]() $v^*(s) = v^*(s')$
iff
$v^*(s) = v^*(s')$
iff
![]() $ D \models equiv_\gamma(\bar t, s,s')$
, for all
$ D \models equiv_\gamma(\bar t, s,s')$
, for all![]() ). Then
). Then
![]() $v^*(D) \models \gamma'(v^*(\bar t'))$
iff for all valuations v,
$v^*(D) \models \gamma'(v^*(\bar t'))$
iff for all valuations v,
![]() $v(D) \models \gamma(v(\bar t))$
implies
$v(D) \models \gamma(v(\bar t))$
implies
![]() $v(D) \models \gamma'(v(\bar t'))$
.
$v(D) \models \gamma'(v(\bar t'))$
.
Proof of the claim.
![]() $\Rightarrow$
Assume
$\Rightarrow$
Assume
![]() $v^*(D) \models \gamma'(v^*(\bar t'))$
and let v be a valuation such that
$v^*(D) \models \gamma'(v^*(\bar t'))$
and let v be a valuation such that
![]() $v(D) \models \gamma(v(\bar t))$
. We want to show
$v(D) \models \gamma(v(\bar t))$
. We want to show
![]() $v(D) \models \gamma'(v(\bar t'))$
. By Lemma 4.5 it is enough to show that
$v(D) \models \gamma'(v(\bar t'))$
. By Lemma 4.5 it is enough to show that
![]() $\forall s, s' \in \bar{t'}$
,
$\forall s, s' \in \bar{t'}$
,
![]() $D \models equiv_{\gamma'}(\bar{t'},s,s')$
implies
$D \models equiv_{\gamma'}(\bar{t'},s,s')$
implies
![]() $v(D) \models v(s)=v(s')$
. So let
$v(D) \models v(s)=v(s')$
. So let
![]() $s, s' \in \bar{t'}$
such that
$s, s' \in \bar{t'}$
such that
![]() $D \models equiv_{\gamma'}(\bar{t'},s,s')$
. As
$D \models equiv_{\gamma'}(\bar{t'},s,s')$
. As
![]() $v^*(D) \models \gamma'(v^*(\bar t'))$
, by Lemma 4.5,
$v^*(D) \models \gamma'(v^*(\bar t'))$
, by Lemma 4.5,
![]() $v^*(D) \models v^*(s)=v^*(s')$
. Now
$v^*(D) \models v^*(s)=v^*(s')$
. Now
![]() $v^*$
satisfies the conditions of Lemma 4.7, so
$v^*$
satisfies the conditions of Lemma 4.7, so
![]() $D \models equiv_{\gamma}(\bar{t},s,s')$
. As
$D \models equiv_{\gamma}(\bar{t},s,s')$
. As
![]() $v(D) \models \gamma(v(\bar t))$
, by Lemma 4.5 it follows that
$v(D) \models \gamma(v(\bar t))$
, by Lemma 4.5 it follows that
![]() $v(D) \models v(s)=v(s')$
.
$v(D) \models v(s)=v(s')$
.
![]() $\Leftarrow$
Assume for all valuations v,
$\Leftarrow$
Assume for all valuations v,
![]() $v(D) \models \gamma(v(\bar t))$
implies
$v(D) \models \gamma(v(\bar t))$
implies
![]() $v(D) \models \gamma'(v(\bar t'))$
. By Lemma 4.5,
$v(D) \models \gamma'(v(\bar t'))$
. By Lemma 4.5,
![]() $v^*$
satisfying the conditions of Lemma 4.7, we have
$v^*$
satisfying the conditions of Lemma 4.7, we have
![]() $v^*(D) \models \gamma(v^*(\bar{t}))$
and so by our assumption
$v^*(D) \models \gamma(v^*(\bar{t}))$
and so by our assumption
![]() $v^*(D) \models \gamma'(v^*(\bar{t'}))$
.
$v^*(D) \models \gamma'(v^*(\bar{t'}))$
.
As v satisfies the conditions of Lemma 4.7, by Claim 4.25 it follows from
![]() $v(D) \models eq_j(v(\bar{t}\bar{a}'\bar{b}'))$
that
$v(D) \models eq_j(v(\bar{t}\bar{a}'\bar{b}'))$
that
![]() $\forall v$
with
$\forall v$
with
![]() $v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
, also
$v(D) \models eq_i(v(\bar{s}\bar{a}\bar{b}))$
, also
![]() $v(D) \models eq_i(v(\bar{t}\bar{a}'\bar{b}'))$
. Now by Proposition 4.8
$v(D) \models eq_i(v(\bar{t}\bar{a}'\bar{b}'))$
. Now by Proposition 4.8
![]() $D \models imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}') \vee \neg comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
. But
$D \models imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{a}'\bar{b}') \vee \neg comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
. But
![]() $D \models comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
, so
$D \models comp_{eq_i}(\bar{s},\bar{a},\bar{b})$
, so
![]() $D \models \exists \bar{y}\bar{z}(~q_j(\bar{y},\bar{z}) \wedge imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{y}\bar{z}))$
.
$D \models \exists \bar{y}\bar{z}(~q_j(\bar{y},\bar{z}) \wedge imply_{eq_i, eq_j}(\bar{s}\bar{a}\bar{b}, \bar{t}\bar{y}\bar{z}))$
.
ecall that from
![]() $Q_\subseteq$
one can easily define a first-order rewriting
$Q_\subseteq$
one can easily define a first-order rewriting
![]() $best_Q (\bar x)$
for best answers as in (1).
$best_Q (\bar x)$
for best answers as in (1).
Theorem 4.26 Given Q a union of conjunctive queries over schema
![]() $\sigma$
and an incomplete database D,
$\sigma$
and an incomplete database D,![]() .
.
Proof. By Proposition 4.24,
![]() $D \models best_Q(\bar t)$
if and only if
$D \models best_Q(\bar t)$
if and only if
![]() $\forall s Supp(Q,D,\bar{t}) \subseteq Supp(Q,D,\bar{s})$
implies
$\forall s Supp(Q,D,\bar{t}) \subseteq Supp(Q,D,\bar{s})$
implies
![]() $Supp(Q,D,\bar{s}) \subseteq Supp(Q,D,\bar{t})$
. Notice that this holds exactly whenever
$Supp(Q,D,\bar{s}) \subseteq Supp(Q,D,\bar{t})$
. Notice that this holds exactly whenever
![]() $\neg \exists \bar{s}$
with
$\neg \exists \bar{s}$
with
![]() $Supp(Q,D,\bar{t}) \subset Supp(Q,D,\bar{s})$
, that is, whenever
$Supp(Q,D,\bar{t}) \subset Supp(Q,D,\bar{s})$
, that is, whenever![]() .
.
Example 4.27 For
![]() $Q,D,\gamma, \gamma'$
as in Examples 2.1 and 4.22:
$Q,D,\gamma, \gamma'$
as in Examples 2.1 and 4.22:
This allows to derive for instance![]() (as observed in Example 2.1). In fact the subquery
(as observed in Example 2.1). In fact the subquery
![]() $R(y_1)\wedge S(y_2,z)\wedge comp_\gamma(y_1,y_2,z,x)$
with free variables
$R(y_1)\wedge S(y_2,z)\wedge comp_\gamma(y_1,y_2,z,x)$
with free variables
![]() $y_1,y_2,z,x$
selects on D tuples
$y_1,y_2,z,x$
selects on D tuples
![]() $(1,\bot_2,\bot_2,1),(\bot_1,\bot_2,\bot_2,1)$
, and no other tuple with last element 1. Moreover, as shown in Example 4.22
$(1,\bot_2,\bot_2,1),(\bot_1,\bot_2,\bot_2,1)$
, and no other tuple with last element 1. Moreover, as shown in Example 4.22
Thus,
![]() $D \models Q_\subseteq(1,\bot_2)\nonumber$
. Similarly, one can show
$D \models Q_\subseteq(1,\bot_2)\nonumber$
. Similarly, one can show
![]() $D \models Q_\subseteq(\bot_1,\bot_2),$
and therefore
$D \models Q_\subseteq(\bot_1,\bot_2),$
and therefore
![]() $D\models best_Q(\bot_2)$
.
$D\models best_Q(\bot_2)$
.
As a corollary of Theorem 4.26, for a union of conjunctive queries Q one can compute![]() by first computing the formula
by first computing the formula
![]() $best_Q(\bar x)$
from Q, then evaluating
$best_Q(\bar x)$
from Q, then evaluating
![]() $best_Q$
on D. Since data complexity of
$best_Q$
on D. Since data complexity of
![]() ${{{{\mathsf{FO}}}}}$
query evaluation is DLogSpace (and in particular AC
${{{{\mathsf{FO}}}}}$
query evaluation is DLogSpace (and in particular AC
![]() $^0$
), this gives the following corollary:
$^0$
), this gives the following corollary:
Corollary 4.28 For each fixed union of conjunctive queries Q, the data complexity of BestAnswer
![]() $_\Sigma$
is DLogSpace.
$_\Sigma$
is DLogSpace.
Note that it was known from Libkin (Reference Libkin, den Bussche and Arenas2018) that the data complexity of computing best answers for unions of conjunctive queries is polynomial time. In terms of combined complexity (i.e. when either Q, D and
![]() $\bar a$
are in the input), the rewriting approach (i.e. the procedure of computing
$\bar a$
are in the input), the rewriting approach (i.e. the procedure of computing
![]() $best_Q$
from Q and then evaluating
$best_Q$
from Q and then evaluating
![]() $best_Q$
on D), can be easily shown to be in PSPACE. In fact it is well known that a first-order query
$best_Q$
on D), can be easily shown to be in PSPACE. In fact it is well known that a first-order query
![]() $\phi$
can be evaluated on a database D in space at most
$\phi$
can be evaluated on a database D in space at most
![]() $qr(\phi) \log |D| + log|\phi|$
, where
$qr(\phi) \log |D| + log|\phi|$
, where
![]() $qr(\phi)$
is the quantifier rank of
$qr(\phi)$
is the quantifier rank of
![]() $\phi$
. Note that although
$\phi$
. Note that although
![]() $best_Q$
has size exponential in Q, the quantifier rank of
$best_Q$
has size exponential in Q, the quantifier rank of
![]() $best_Q$
is linear in the size of Q. Thus whether
$best_Q$
is linear in the size of Q. Thus whether
![]() $\bar a \in best(Q,D)$
can be checked using space
$\bar a \in best(Q,D)$
can be checked using space
![]() $O(|Q|, |D|)$
. Moreover one can easily check that
$O(|Q|, |D|)$
. Moreover one can easily check that
![]() $best_Q$
can be computed from Q in space polynomial in the size of
$best_Q$
can be computed from Q in space polynomial in the size of
![]() $|Q|$
. Since space bounded computations can be composed without storing the intermediate output, computing
$|Q|$
. Since space bounded computations can be composed without storing the intermediate output, computing
![]() $best_Q$
from Q and then evaluating
$best_Q$
from Q and then evaluating
![]() $best_Q$
on D can be done overall in PSPACE in the size of
$best_Q$
on D can be done overall in PSPACE in the size of
![]() $|Q|$
and
$|Q|$
and
![]() $|D|$
. The rewriting approach thus implies a PSPACE upper bound for the combined complexity of BestAnswer
$|D|$
. The rewriting approach thus implies a PSPACE upper bound for the combined complexity of BestAnswer
![]() $_\Sigma$
for unions of conjunctive queries. However, we can show that the problem actually stands in the third level of the polynomial hierarchy.
$_\Sigma$
for unions of conjunctive queries. However, we can show that the problem actually stands in the third level of the polynomial hierarchy.
Theorem 4.29 For unions of conjunctive queries, combined complexity of BestAnswer
![]() $_\Sigma$
is
$_\Sigma$
is
![]() $\Pi^p_3$
-complete. Hardness already holds for conjunctive queries.
$\Pi^p_3$
-complete. Hardness already holds for conjunctive queries.
Proof. For membership, first note that one can check in
![]() $\Pi^p_2$
whether
$\Pi^p_2$
whether
![]() $Supp(Q,D,\bar a) \subseteq Supp(Q,D,\bar b)$
on input given by a database D, a UCQ Q, and tuples
$Supp(Q,D,\bar a) \subseteq Supp(Q,D,\bar b)$
on input given by a database D, a UCQ Q, and tuples
![]() $\bar a$
and
$\bar a$
and
![]() $\bar b$
. In fact in order to check
$\bar b$
. In fact in order to check
![]() $Supp(Q,D,\bar a) \nsubseteq Supp(Q,D,\bar b)$
one guesses a valuation v of D, then calls an NP oracle to check
$Supp(Q,D,\bar a) \nsubseteq Supp(Q,D,\bar b)$
one guesses a valuation v of D, then calls an NP oracle to check
![]() $v(\bar a) \in Q(v(D))$
and
$v(\bar a) \in Q(v(D))$
and
![]() $v(\bar b) \notin Q(v(D))$
.
$v(\bar b) \notin Q(v(D))$
.
On input given by a database D, a UCQ Q, and a tuple
![]() $\bar a$
one can check
$\bar a$
one can check![]() as follows. First guess a tuple
as follows. First guess a tuple
![]() $\bar b$
over
$\bar b$
over
![]() $\text{adom}(D)$
of the same arity as
$\text{adom}(D)$
of the same arity as
![]() $\bar a$
; then, using two calls to a
$\bar a$
; then, using two calls to a
![]() $\Sigma^p_2$
oracle, check that
$\Sigma^p_2$
oracle, check that
![]() $Supp(Q,D,\bar a) \subseteq Supp(Q,D,\bar b)$
and
$Supp(Q,D,\bar a) \subseteq Supp(Q,D,\bar b)$
and
![]() $Supp(Q,D,\bar b) \nsubseteq Supp(Q,D,\bar a)$
.
$Supp(Q,D,\bar b) \nsubseteq Supp(Q,D,\bar a)$
.
For hardness, we reduce from
![]() $\forall\exists\forall 3DNF$
, which is known to be
$\forall\exists\forall 3DNF$
, which is known to be
![]() $\Pi^p_3$
-complete (Schaefer and Umans Reference Schaefer and Umans2002). We take as input a
$\Pi^p_3$
-complete (Schaefer and Umans Reference Schaefer and Umans2002). We take as input a
![]() $\forall\exists\forall 3DNF$
-formula of the form
$\forall\exists\forall 3DNF$
-formula of the form
where the each
![]() $conj_i$
is a conjunction of 3 (not necessarily distinct) literals over variables
$conj_i$
is a conjunction of 3 (not necessarily distinct) literals over variables
![]() $z_1,\ldots z_l, x_1, \ldots, x_k, y_1, \ldots, y_p$
.
$z_1,\ldots z_l, x_1, \ldots, x_k, y_1, \ldots, y_p$
.
We construct a database
![]() $D_F$
with
$D_F$
with
![]() $\text{adom}(D_F) = \{0, 1, good, bad\}\cup \{i, \bar i, \bot_i, \bar \bot_i, | i=1..k\}$
, and a conjunctive query
$\text{adom}(D_F) = \{0, 1, good, bad\}\cup \{i, \bar i, \bot_i, \bar \bot_i, | i=1..k\}$
, and a conjunctive query
![]() $Q_F(z_1, ..z_l, z)$
such that
$Q_F(z_1, ..z_l, z)$
such that![]() if and only if F is true.
if and only if F is true.
![]() $D_F$
is of signature
$D_F$
is of signature
![]() $\{S^4,C^2,A^2,B^3\}$
as follows:
$\{S^4,C^2,A^2,B^3\}$
as follows:
-
The extension of S and A and B is fixed and does not depend on F:
-
- S contains tuple (1,1,1,good), and tuples
 $(b_1,b_2,b_3,good)$
and
$(b_1,b_2,b_3,good)$
and
 $(b_1,b_2,b_3,bad)$
for every
$(b_1,b_2,b_3,bad)$
for every
 $b_1,b_2,b_3 \in \{0,1\}$
with
$b_1,b_2,b_3 \in \{0,1\}$
with
 $(b_1,b_2,b_3)\neq (1,1,1)$
. Intuitively, S encodes the possible truth assignment of each disjunct of F. Note that only the satisfying assignment (i.e. (1,1,1)) appears together with the only constant good, all the others appear both with good and bad.
$(b_1,b_2,b_3)\neq (1,1,1)$
. Intuitively, S encodes the possible truth assignment of each disjunct of F. Note that only the satisfying assignment (i.e. (1,1,1)) appears together with the only constant good, all the others appear both with good and bad. -
- A contains only two tuples: (0,1) and (1,0). Intuitively, A will be used to encode truth values for pairs of literals
 $(w, \neg w), w \in y_1, \ldots y_p, z_1, \ldots z_l$
.
$(w, \neg w), w \in y_1, \ldots y_p, z_1, \ldots z_l$
. -
- B contains tuples (0,0, bad), (1,1, bad) and tuples
 $(b_1, b_2, good)$
and
$(b_1, b_2, good)$
and
 $(b_1, b_2, bad)$
for every
$(b_1, b_2, bad)$
for every
 $b_1, b_2 \in \{0,1\}$
,
$b_1, b_2 \in \{0,1\}$
,
 $b_1 \neq b_2$
. Intuitively, B encodes assignments for pairs of literals
$b_1 \neq b_2$
. Intuitively, B encodes assignments for pairs of literals
 $(w, \neg w), w \in \{x_1, \ldots x_k\}$
. Note that here inconsistent pairs (i.e. same truth value) are possible, but these are the only ones which do not appear together with constant good.
$(w, \neg w), w \in \{x_1, \ldots x_k\}$
. Note that here inconsistent pairs (i.e. same truth value) are possible, but these are the only ones which do not appear together with constant good.
-
-
The extension of C depends on F and contains tuples
 $\{(\bot_i, i) | i=1..k\}$
and
$\{(\bot_i, i) | i=1..k\}$
and
 $\{(\bar \bot_i, \bar i) | i=1..k\}$
. Intuitively, a valuation (b, i) (resp.
$\{(\bar \bot_i, \bar i) | i=1..k\}$
. Intuitively, a valuation (b, i) (resp.
 $(b, \bar i)$
) of one of these tuples, with
$(b, \bar i)$
) of one of these tuples, with
 $b \in \{0,1\}$
, will encode truth value b for the literal
$b \in \{0,1\}$
, will encode truth value b for the literal
 $x_i$
(resp,
$x_i$
(resp,
 $\neg x_i$
) of F.
$\neg x_i$
) of F.
![]() $Q_F$
is defined as follows. For each variable w of F, the conjunctive query
$Q_F$
is defined as follows. For each variable w of F, the conjunctive query
![]() $Q_F$
will use variables w and
$Q_F$
will use variables w and
![]() $\bar w$
(either quantified or free). For a literal
$\bar w$
(either quantified or free). For a literal
![]() $\alpha$
of F, the corresponding variable of
$\alpha$
of F, the corresponding variable of
![]() $Q_F$
will be denoted as
$Q_F$
will be denoted as
![]() $enc(\alpha)$
. More precisely if
$enc(\alpha)$
. More precisely if
![]() $\alpha = w$
is a positive literal, then,
$\alpha = w$
is a positive literal, then,
![]() $enc(\alpha):=w$
, otherwise if
$enc(\alpha):=w$
, otherwise if
![]() $\alpha = \neg w$
then
$\alpha = \neg w$
then
![]() $enc(\alpha) := \bar w$
.
$enc(\alpha) := \bar w$
.
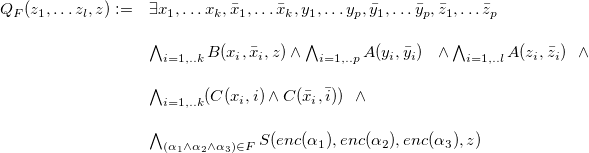 $$\begin{array}{ll} Q_F(z_1, \ldots z_l, z) := & \exists x_1, \ldots x_k, \bar x_1, \ldots \bar x_k, y_1, \ldots y_p, \bar y_1, \ldots \bar y_p, \bar z_1, \ldots \bar z_p \\ \\& \bigwedge_{i=1,..k} B(x_i, \bar x_i, z) \wedge \bigwedge_{i=1,..p} A(y_i, \bar y_i) ~ ~\wedge \bigwedge_{i=1,..l} A(z_i, \bar z_i) ~ ~\wedge \\\\& \bigwedge_{i=1,..k} (C(x_i, i) \wedge C(\bar x_i, \bar i)) ~ ~\wedge \\\\& \bigwedge_{(\alpha_1 \wedge \alpha_2 \wedge \alpha_3)\in F} S(enc(\alpha_1), enc(\alpha_2), enc(\alpha_3), z) \end{array} $$
$$\begin{array}{ll} Q_F(z_1, \ldots z_l, z) := & \exists x_1, \ldots x_k, \bar x_1, \ldots \bar x_k, y_1, \ldots y_p, \bar y_1, \ldots \bar y_p, \bar z_1, \ldots \bar z_p \\ \\& \bigwedge_{i=1,..k} B(x_i, \bar x_i, z) \wedge \bigwedge_{i=1,..p} A(y_i, \bar y_i) ~ ~\wedge \bigwedge_{i=1,..l} A(z_i, \bar z_i) ~ ~\wedge \\\\& \bigwedge_{i=1,..k} (C(x_i, i) \wedge C(\bar x_i, \bar i)) ~ ~\wedge \\\\& \bigwedge_{(\alpha_1 \wedge \alpha_2 \wedge \alpha_3)\in F} S(enc(\alpha_1), enc(\alpha_2), enc(\alpha_3), z) \end{array} $$
We can prove that all tuples of the form
![]() $(\bar t, good)$
(which we refer to as good tuples) have the same support. This is given by the set of all consistent boolean valuations (i.e. valuations of
$(\bar t, good)$
(which we refer to as good tuples) have the same support. This is given by the set of all consistent boolean valuations (i.e. valuations of
![]() $\bot_i, \bar\bot_i$
in
$\bot_i, \bar\bot_i$
in
![]() $\{0,1\}$
such that
$\{0,1\}$
such that
![]() $v(\bot_i) \neq v(\bar \bot_i)$
for all i). Moreover we can prove that if there exists a
$v(\bot_i) \neq v(\bar \bot_i)$
for all i). Moreover we can prove that if there exists a
![]() $(\bar t, bad)$
whose support contains all consistent boolean valuations then the support of
$(\bar t, bad)$
whose support contains all consistent boolean valuations then the support of
![]() $(\bar t, bad)$
strictly contains the support of good tuples. Therefore, any good tuple (including
$(\bar t, bad)$
strictly contains the support of good tuples. Therefore, any good tuple (including
![]() $(\bar 0, good)$
) is a best answer iff for all tuples
$(\bar 0, good)$
) is a best answer iff for all tuples
![]() $\bar t$
there exists a consistent boolean valuation which is not in the support of
$\bar t$
there exists a consistent boolean valuation which is not in the support of
![]() $(\bar t, bad)$
. We can finally show that the last holds iff F is true.
$(\bar t, bad)$
. We can finally show that the last holds iff F is true.
Therefore, under standard complexity theoretic assumptions, our rewriting approach is not optimal in terms of combined complexity, as it is often the case with generic approaches. However, it has the advantage of exploiting standard
![]() ${{{{\mathsf{FO}}}}}$
query evaluation, which despite the PSPACE combined complexity is highly optimized in database systems and works well in practice.
${{{{\mathsf{FO}}}}}$
query evaluation, which despite the PSPACE combined complexity is highly optimized in database systems and works well in practice.
5 Future work
Our rewriting techniques are closer to a practical implementation than the previous tableau-based method from Gheerbrant and Libkin (Reference Gheerbrant and Libkin2015). This is due to their expressibility in recursive SQL (or even non-recursive in the case of Theorems 4.19 and 4.26). However, while theoretically feasible, an actual implementation will need additional techniques to achieve acceptable performance. To see why, notice that the first rule in the definition of
![]() $equiv_\gamma$
creates a cross product over the full active domain, that is, the set of all elements that appeared in the database. This of course will be prohibitively large. While this may appear to be a significant obstacle, a similar situation with computing or approximating certain answers is not new in the literature. For instance, the first approximation scheme for certain answers to SQL queries that appeared in Libkin (Reference Libkin2016) has done exactly the same, and generated very large Cartesian products even for simple queries with negation. Nonetheless, an alternative was found quickly (Guagliardo and Libkin Reference Guagliardo, Libkin, Milo and Tan2016) that completely avoided the need for such expensive queries, and it was shown to work well on several TPC-H queries. Thus, looking for a practical and implementable rewriting is one of the possible directions for future work.
$equiv_\gamma$
creates a cross product over the full active domain, that is, the set of all elements that appeared in the database. This of course will be prohibitively large. While this may appear to be a significant obstacle, a similar situation with computing or approximating certain answers is not new in the literature. For instance, the first approximation scheme for certain answers to SQL queries that appeared in Libkin (Reference Libkin2016) has done exactly the same, and generated very large Cartesian products even for simple queries with negation. Nonetheless, an alternative was found quickly (Guagliardo and Libkin Reference Guagliardo, Libkin, Milo and Tan2016) that completely avoided the need for such expensive queries, and it was shown to work well on several TPC-H queries. Thus, looking for a practical and implementable rewriting is one of the possible directions for future work.
As another open problem, we note that the query for which we have shown certain answers to be non-rewritable in FO has DLOGSPACE data complexity. Indeed the problem is essentially reachability over trees, which can be easily encoded using deterministic transitive closure (Immerman Reference Immerman1987). To express DLOGSPACE problems, we need a language weaker than Datalog with negation. Thus, it is natural to ask whether a low complexity Datalog fragment would be sufficient to express rewritings of BCCQ, or a separating example that is PTIME-complete can be found.
Another direction would be to investigate how our techniques can be extended to different semantics of incompleteness. We used here the closed-world semantics (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995; Imielinski and Lipski Reference Imielinski and Lipski1984; van der Meyden Reference van der Meyden, Chomicki and Saake1998), in which data values are the only missing information, but there are other possible semantics, for example needed in order to cope with data inconsistencies (Calì et al. 2003a), where query rewritings could still be found. Quantitative variations of the notion of certainty as proposed in Libkin (Reference Libkin, den Bussche and Arenas2018) could also be investigated.




