Article contents
Modeling the effect of temperature on rhizome sprouting in the invasive weed silverleaf nightshade (Solanum elaeagnifolium)
Published online by Cambridge University Press: 12 February 2024
Abstract
Silverleaf nightshade (Solanum elaeagnifolium Cav.), a noxious, highly invasive perennial weed, poses a significant threat to irrigated summer crops, vegetables, and orchards. This weed has the ability to reproduce both sexually through seed production and asexually via an extensive underground rhizome network, the latter playing a major role in the weed’s invasion, establishment, and persistence. Our aims were thus to assess the impact of temperature on rhizome sprouting for fragments of different lengths and to model the sprouting dynamics. The influence of temperature on the sprouting of rhizome fragments (2.5-, 5-, 7.5-, or 10-cm long) was investigated in growth chambers at eight temperatures ranging from 10 to 45 C. The highest sprouting proportions for 10-cm rhizome fragments were recorded at 30 and 35 C in complete darkness. The highest sprouting time for all fragment lengths was observed at 15 C in complete darkness. Modeling sprouting rates as a function of temperature gave the cardinal temperatures for the four different rhizome fragment lengths, with Tb (base temperature) values of 12.80, 9.34, 9.14, and 9.50 C, To (optimal temperature) values of 38.9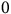 $$0$$, 36.60, 35.16, and 34.86 C, and Tc (ceiling temperature) values of 39.80, 40.08, 40.50, and 40.80 C for rhizome lengths of 2.5, 5, 7.5, and 10 cm, respectively. Based on these findings, the potential for S. elaeagnifolium to spread to new areas and possible new management strategies are discussed; these offer a novel approach for informed decision making regarding the control of this weed.
$$0$$, 36.60, 35.16, and 34.86 C, and Tc (ceiling temperature) values of 39.80, 40.08, 40.50, and 40.80 C for rhizome lengths of 2.5, 5, 7.5, and 10 cm, respectively. Based on these findings, the potential for S. elaeagnifolium to spread to new areas and possible new management strategies are discussed; these offer a novel approach for informed decision making regarding the control of this weed.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Weed Science Society of America
Footnotes
Associate Editor: Nicholas Basinger, University of Georgia
References
- 1
- Cited by


