Article contents
Setting Conventional Force Requirements: Roughly Right or Precisely Wrong?
Review products
Published online by Cambridge University Press: 13 June 2011
Abstract
The author analyzes the basic quanititative methodologies employed in the open literature to assess conventional forces and evaluates the extent to which they can be used to set military requirements with a new degree of reliability and accuracy. The recent proliferation of literature on conventional forces has begun to fill an important gap in the strategic studies field. Insufficient understanding of essential elements of ground combat, the context sensitivity of key variables, and inaccurate and unreliable data bases mean, however, that the output of both static and dynamic methodologies contains high levels of uncertainty. This seemingly irreducible uncertainty precludes the use of existing models to make definitive judgment about military needs. Nevertheless, because such uncertainty enhances deterrence, it may not only be unavoidable, but also preferable.
- Type
- Review Articles
- Information
- Copyright
- Copyright © Trustees of Princeton University 1989
References
1 This proliferation of research has in fact led to a growing divergence of opinion on the East-West balance. In very broad terms, official U.S. government assessments tend to be more pessimistic than those produced by outside analysts and scholars, but there is by no means a consensus on the military balance within the academic community.
2 Several developments have fostered the proliferation of literature on the conventional balance. Because the United States may soon face a period of economic austerity, it has become important to assess carefully in what ways defense spending can be reduced without eroding military capability and jeopardizing national security. There has also been a rapid growth in the number and quality of national security experts within the academic community. William Kaufmann has played a central role in teaching conventional force analysis to students at M.I.T., Harvard, and The Brookings Institution. These scholars are devoting increased attention to conventional forces and strategy because preoccupation with nuclear weapons led to a neglect of conventional issues during the 1950s and 1960s, because a greater reliance on nonnuclear options emerged with flexible response, and because study of conventional war lends itself more easily to historical and comparative methodologies. The 1987 U.S.-Soviet agreement to remove intermediate-range nuclear weapons from Europe and Secretary Gorbachev's announcement of the planned withdrawal of Soviet troops from Eastern Europe has also heightened interest in the conventional balance.
3 The equations used in the Epstein volume under review are set forth in his The Calculus of Conventional War: Dynamic Analysis without Lanchester Theory (Washington, DC: The Brookings Institution, 1985)Google Scholar. His other important works include Measuring Military Power — The Soviet Air Threat to Europe (Princeton: Princeton University Press, 1984)Google Scholar; The 1988 Defense Budget (Washington, DC: The Brookings Institution, 1987)Google Scholar; “Dynamic Analysis and the Conventional Balance in Europe,” International Security 12 (Spring 1988), 154–65CrossRefGoogle Scholar; “The 3:1 Rule, the Adaptive Dynamic Model, and the Future of Security Studies,” International Security 13 (Spring 1989), 90–127CrossRefGoogle Scholar; and “Soviet Vulnerabilities in Iran and the RDF Deterrent,” in the Miller volume under review. Mearsheimer's contributions to the Miller volume include “Why the Soviets Can't Win Quickly in Central Europe,” and “Maneuver, Mobile Defense, and the NATO Central Front.” A broader treatment of some of the main concepts discussed. in these articles is contained in Conventional Deterrence (Ithaca, NY: Cornell University Press, 1983)Google Scholar. Mearsheimer has also contributed to the debate in “Numbers, Strategy, and the European Balance,” International Security (Spring 1988), 174–85Google Scholar; “Assessing the Conventional Balance: The 3:1 Rule and Its Critics,” International Security 13 (Spring 1989), 54–89CrossRefGoogle Scholar; Correspondence, International Security 13 (Spring 1989), 128–44CrossRefGoogle Scholar; “A Strategic Misstep: The Maritime Strategy and Deterrence in Europe,” International Security 11 (Fall 1986), 3–57CrossRefGoogle Scholar. Other relevant contributions to the Miller volume include Richard Betts, “Conventional Strategy: New Critics, Old Choices”; Samuel Huntington, “Conventional Deterrence and Conventional Retaliation in Europe”; Edward Luttwak, “The Operational Level of War”; Barry Posen, “Measuring the European Conventional Balance”; Barry Posen and Stephen Van Evera, “Defense Policy and the Reagan Administration: Departure from Containment.” Other works discussed in this essay include: Biddle, Stephen, “The European Conventional Balance,” Survival 30 (March/April 1988), 99–121CrossRefGoogle Scholar; Biddle, , “The European Conventional Balance: A Reinterpretation,” in Wander, W. Thomas, ed., Nuclear and Conventional Forces in Europe—Implications for Arms Control and Security (Washington, DC: American Association for the Advancement of Science, 1987)Google Scholar; Brooks, Linton, “Naval Power and National Security—The Case for the Maritime Strategy,” International Security 11 (Fall 1986), 58–88CrossRefGoogle Scholar; Steven Canby, “The Alliance and Europe: Part IV—Military Doctrine and Technology,” Adelphi Paper No. 109 (London: International Institute for Strategic Studies, 1975); Cohen, Eliot, “Toward Better Net Assessment: Rethinking the European Conventional Balance,” International Security 13 (Summer 1988), 50–89CrossRefGoogle Scholar; Cohen, , Correspondence, International Security 13 (Spring 1989), 160–79Google Scholar; Congressional Budget Office, Assessing the NATO-Warsaw Pact Military Balance (Washington, DC: G.P.O., 1977)Google Scholar; Hamilton, Andrew, “Redressing the Conventional Balance: NATO's Reserve Military Manpower,” International Security 10 (Summer 1985), 111–36CrossRefGoogle Scholar; Holmes, Kim, “Measuring the Conventional Balance in Europe,” International Security 12 (Spring 1988), 166–73CrossRefGoogle Scholar; Kaufmann, William, “Nonnuclear Deterrence” and “The Arithmetic of Force Planning,” in Steinbruner, John and Sigal, Leon, eds., Alliance Security: NATO and the No-First-Use Question (Washington, DC: The Brookings Institution, 1983)Google Scholar; Lepingwell, John, “The Laws of Combat? Lanchester Reexamined,” International Security 12 (Summer 1987), 89–134CrossRefGoogle Scholar; Mako, William, U.S. Ground Forces and the Defense of Central Europe (Washington, DC: The Brookings Institution, 1983)Google Scholar; Posen, Barry, “Inadvertent Nuclear War? Escalation and NATO's Northern Flank,” International Security 7 (Fall 1982), 28–54CrossRefGoogle Scholar; Posen, , Correspondence, International Security 13 (Spring 1989), 144–60Google Scholar; J. A. Stockfisch, “Models, Data, and War: A Critique of the Study of Conventional Forces,” R-1526-PR (Santa Monica, CA: Rand Corporation, 1975); U.S. General Accounting Office, Models, Data, and War: A Critique of the Foundationfor Defense Analyses, PAD-80–21 (Washington, DC: G.A.O., 1980)Google Scholar.
4 In a static model, outcomes are determined by input measures alone and are not time-dependent. In dynamic models, outputs are recycled as inputs in successive iterations, making outcomes change as a function of time.
5 I do not mean to suggest that all combat models face precisely the same conceptual and methodological obstacles discussed in this essay. I do maintain, however, that the outputs of all combat models contain significant uncertainties because of the conceptual difficulties involved in modeling war and because of shortcomings in the existing data bases.
6 Epstein's equations are now being used by a government agency to undertake assessments of the balance. See Congressional Budget Office, U.S. Ground Forces and the Conventional Balance in Europe (Washington, DC: G.P.O., 1988)Google Scholar.
7 Some of the high-resolution models developed in or for the Pentagon are so complex that few individuals have the technical expertise to use them and few agencies have computers sufficiently powerful to run them. Moreover, such models are of little use to the policy community because of the “inability of OR [operations research] analysts to communicate model methodology (and hence the quality of study-generated information) to decision makers.” See Taylor, James, Force-on-Force Attrition Modeling (Arlington, VA: Operations Research Society of America, 1981), 112Google Scholar.
8 To examine the analytic limitations of formal combat modeling, it makes sense to focus on models for which bold claims have been set forth. Barry Posen, for example, bases his assessment of the conventional balance in Europe on a combat model (the Attrition-FEBA Expansion model devised by Richard Kugler), but he makes less ambitious claims about its analytic value and its accuracy and reliability. Variables that the analyst must use as inputs for Posen's model are outputs in Epstein's model. In the Attrition-FEBA model, attrition is not affected by movement of the front, and both casualty rates and movement of the front are inputs provided by the analyst. In Posen's own words, “build-up rates, tactical air power, force-to-space ratios, attrition rates, exchange rates, and advance rates—can be set by the user as he or she sees fit” (Posen in Miller, 93; see also 91–92, 115–16). In Epstein's model, attrition rates and velocity of the front are related and are outputs. An examination of Posen's model would indeed be instructive, but not necessarily useful as a means of assessing the limitations of the modeling enterprise.
9 In studying U.S. requirements in the Persian Gulf, for example, Epstein uses the output of his models to show that the current size of the Rapid Deployment Force (up to seven divisions and ten air wings) is too large and that “a force of 5 U.S. divisions plus 6 wings of close air support is adequate to contend with the force that the Soviets could sustain (logistically) in combat.…” Similarly, Epstein asserts that, for Western Europe, there is “no reason why NATO… should fail to meet its requirements and mount an imposing nonnuclear deterrent to conventional attack, especially if all allies honor their commitments, if a U.S. heavy division equivalent is reallocated from the Gulf to NATO, and if a program of terrain enhancement and obstacle preparation is instituted.…” See Epstein, The 1988 Defense Budget (in. 3), 35,45. See also Strategy and Force Planning, 97.
10 Public Records Office (P.R.O.), London, CAB 16/112, D.P.R. 9, February 6, 1936, “Defence Requirements,” 2.
11 See Gaddis, John Lewis, Strategies of Containment (New York: Oxford University Press, 1982), 297Google Scholar.
12 Mearsheimer, Conventional Deterrence (fn. 3).
13 The terms strategy and doctrine have been used rather haphazardly and have come to take on many different meanings. I distinguish between these two terms in the following manner: strategy refers to the way in which military means are used to achieve military ends; doctrine refers to a set of suppositions, principles, or rules about how to apply means to ends. Doctrine therefore informs the formulation of strategy.
14 On the offense/defense issue, for example, Samuel Huntington argues that NATO should adopt an offensive strategy of retaliation to respond to Soviet aggression in Central Europe. According to Huntington, adoption of an offensive retaliatory option would “restore some element of flexibility to a strategy that is rapidly becoming inflexible … [and] pose new uncertainties for the Soviet Union” (Huntington in Miller, 273). Both Stephen Van Evera and Jack Snyder, on the other hand, warn against the dangers inherent in offensive conventional strategies. They argue that offensive doctrines increase the likelihood of war by encouraging states to attack in order to reap the benefits of preemption. See Evera, Van, “The Cult of the Offensive and the Origins of the First World War,” International Security 9 (Summer 1983), 58–107CrossRefGoogle Scholar; and Snyder, Jack, The Ideology of the Offensive (Ithaca, NY: Cornell University Press, 1984)Google Scholar. On forward defense versus defense in depth, and maneuver warfare versus attrition warfare, see Betts in Miller, Luttwak in Miller, and John Mearsheimer, “Maneuver, Mobile Defense, and the NATO Central Front” in Miller.
15 Mearsheimer, “A Strategic Misstep” (fn. 3).
16 On the risks of escalation, see Posen, “Inadvertent Nuclear War” (fn. 3).
17 As discussed below, the ADE is only one type of firepower measure. Most are similar in methodology, and subject to the same types of criticism. I focus specifically on the ADE because it is the scoring system most widely used in the open literature.
18 Until the mid-1960s, the United States overestimated Soviet ground-troop strength by erroneously assuming that Warsaw Pact divisions were equivalent in strength to NATO divisions. Intelligence analysts began to reassess this assumption when they realized that the Warsaw Pact had neither the funds nor the manpower necessary to support their reported 175 divisions. For a detailed and fascinating description of this realization, see Smith, K. Wayne and Enthoven, Alain, How Much Is Enough? Shaping the Defense Program, 1967–1969 (New York: Harper & Row, 1971), 132–42Google Scholar. Smith and Enthoven confirm that this erroneous assessment produced resignation in Washington: “Even the simple, inexpensive step of making adequate plans and logistic provision for existing forces was largely ignored because of the presumed hopeless inadequacy of the forces” (p. 158).
19 The methodology was originally presented in “Weighted Effectiveness Indices/ Weighted Unit Values (WEI/WUV),” Study Report CAA-SR-73–18 (Bethesda, MD: War Gaming Directorate, U.S. Army Concepts Analysis Agency, April 1974) [hereafter referred to as WEI/WUV]. The methodology and the scores it produces have been updated twice: WEI/WUV II and WEI/WUV HI. The material presented in this essay relies upon “Weighted Effectiveness Indices/Weighted Unit Values III,” Study Report CAA-SR-79–12 (Bethesda, MD: War Gaming Directorate, U.S. Army Concepts Analysis Agency, 1979). The new versions of WEI/WUV were intended to update the scores assigned to individual weapons and to weapon categories. A new category—Infantry Fighting Vehicle—was also added. The revised scoring increased the importance of survivability and mobility and decreased the importance of firepower. See WEI/WUV III, 1–6. The U.S. Defense Department has recently developed a new scoring system: the division equivalent firepower (DEF) methodology. The DEF methodology is classified, but does not appear to differ substantially from the WEI/WUV scoring system. See Posen, “Is NATO Decisively Outnumbered?” (fn. 3), 190, n. 12.
20 Category weights vary depending on the projected theater of engagement and on whether the unit is in an offensive or defensive posture. Scores have been calculated for Central Europe, Northeast Asia, and the Persian Gulf/Middle East. Examples are presented in Appendix A.
21 For further discussion of this method of comparison and examples of scoring for different units, see Congressional Budget Office (fn. 3), 53–61; Mako (fn. 3), 105–25. These WUV-ADE equivalents refer to 1974 scores.
22 WEI/WUV (fn. 19, 1974), 13.
23 Revised versions of WEI/WUV scores have been updated to compensate for this bias in favor of firepower.
24 Because of this bias in the scoring methodology, Posen applies a multiplier of 1.5 to NATO wuv scores (Posen in Miller, 101).
25 See U.S. General Accounting Office (fn. 3), 54–55, and Stockfisch (fn. 3), 6–10,
26 WEI/WUV (fn. 19, 1979), 23; emphasis added.
27 Each of these three measures takes a different unit as the baseline for comparison and uses a different computational method. An ADE is roughly equivalent to an average U.S. armored division; a standard division equivalent (SDE) to an average Soviet division stationed in East Germany; and a heavy division equivalent (HDE) to an average U.S. heavy division. These three types of division equivalent and the force balances they produce are presented in Andrew Hamilton (fn. 3), 115–20, 134–36. Hamilton uses HDES in his own analysis, HDES give more weight to the infantry than to the armored component of divisions. William Kaufmann uses firepower units (FPUS) in his scoring system. He assesses the FPU of each unit in NATO and the Warsaw Pact and aggregates these scores to derive overall firepower potential. (The SDE is Hamilton's terminology.) See Kaufmann, “Nonnuclear Deterrence” and “The Arithmetic of Force Planning” (fn. 3). William Mako uses ADES in U.S. Ground Forces (fn. 3).
28 Hamilton (fn. 3), 115.
29 Mearsheimer, “Numbers, Strategy, and the European Balance” (fn. 3), 176–77, n. 5. Other assessments of the balance also point to the operational importance of the 3:1 and 2:1 offense-defense ratios. Andrew Hamilton, for example, writes that “the Pact-NATO ratio exceeds 2:1 after about two weeks of mobilization. In that situation, most analysts would agree that NATO needs to add forces if it wishes to have a better than even probability of preventing a large-scale conventional attack from achieving a breakthrough in the Central Region” (fn. 3), 121. Hamilton also uses the 3:1 rule as a measure of tactical effectiveness when he computes force attrition over time (ibid., 124). Barry Posen uses the 3:1 figure as a guide to judge the plausibility of his assumptions (Posen in Miller, 88, no).
30 See General DePuy, William E., “Technology and Tactics in Defense of Europe,” Army 29 (April 1979), 15Google Scholar. Mearsheimer in Miller, 133, n. 30; and Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 61, ns. 18 and 19.
31 This assumes that the Soviets would not attack if they calculated that they had poor chances of success. It is possible, however, that a Soviet attack would be the result, not of premeditated aggressive intent, but of fear or desperation triggered by political chaos in Eastern Europe and NATO mobilization. As Richard Betts argues, “the probability of armed conflict depends not only on the actual dangers of war to the attacker, but also on the perceived dangers of peace.” See Betts, , Surprise Attach Lessons for Defense Planning (Washington, DC: The Brookings Institution, 1982), 128Google Scholar. 141–44. This scenario does not suggest, however, that larger NATO forces are needed to ensure deterrence; in fact, a less favorable balance for the Soviets might only increase their feelings of desperation and raise their incentives for attack. Under these circumstances, political reassurance—in the form of defensive force postures and diplomatic gestures—would be the most effective tool to enhance deterrence. See also Betts, Richard K., “Conventional Deterrence: Predictive Uncertainty and Policy Confidence,” World Politics 37 (January 1985), 153–79CrossRefGoogle Scholar.
32 The most widely used studies of past battles available in the open literature include Dupuy, Trevor N., Numbers, Predictions and War: Using History to Evaluate Combat Factors and Predict the Outcome of Battles (Indianapolis: Bobbs-Merrill, 1979)Google Scholar; Dupuy, Understanding War: History and Theory in Combat (New York: Paragon House, 1987)Google Scholar; and Combat History Analysis Study Effort (CHASE): Progress Report for the Period August 1984-June 1985 [CHASE Report], CAA-TP-88–2 or AD-A179 734 (Bethesda, MD: Requirements and Resources Directorate, U.S. Army Concepts Analysis Agency, August 1986)Google Scholar. The CHASE Report is based on data prepared by the Historical Evaluation and Research Organization (HERO).
33 ibid., iii, v. For further discussion of the reliability of the data base, see Epstein, “The 3:1 Rule” (fn. 3), 104–5. The data base actually draws on 601 battles, but only 598 were used in the analysis of force ratios.
34 Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 66.
35 ibid., 62–64, 66–67.
36 In “Dynamic Analysis and the Conventional Balance in Europe” (fn. 3), Joshua Epstein presents nine breakthrough battles in which, he argues, the attacker won with less than a 3:1 advantage. Mearsheimer, in “Assessing the Conventional Balance” (fn. 3), maintains that Epstein's analysis is flawed by incorrect data and a failure to take qualitative factors and surprise into consideration. Epstein, in “The 3.1 Rule” (fn. 3), 90–95, 99–106, responds that Mearsheimer's critique is plagued by obscurity about what measures of firepower to use to test the rule and about the conditions under which the rule applies (i.e., what constitutes a breakthrough battle, should reserves be included in initial force ratios, etc.). In his earlier writings on the European balance, Mearsheimer uses ADES to assess the sufficiency of NATO forces (Mearshei-mer in Miller, 126–28, and “Numbers, Strategy and the European Balance,” fn. 3, 175–76). In his most recent presentation, he asserts that ADES are appropriate measures in Europe “because the fighting skills of the troops in NATO and Warsaw Pact armies are roughly equal.” In other cases, however, “ADE scores must be adjusted before they can fairly represent the relative combat power of opposing forces having unequal fighting skills …” (“Assessing the Conventional Balance,” fn. 3,63). As Epstein correctly notes, Mearsheimer provides no instructions as to how such adjustments are to be made (“The 3:1 Rule,” fn. 3, 91–92). Despite and because of these definitional problems, Mearsheimer does succeed in showing that the cases selected by Epstein do not constitute a clear refutation of the 3:1 rule. But Mearsheimer's argument also raises problematic questions about the relative importance of force ratios in determining outcomes and about how to set up rigorous empirical tests of the rule (see n. 47 below).
37 Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 57,56. For further discussion of the problems involved in empirically verifying the 3:1 rule, see Epstein, “The 3:1 Rule” (fn. 3). 8
38 An example of the use of the rule in pre-World War II planning can be found in P.R.O., CAB 38/26/13, April 15, 1914, Standing Sub-Committee of the Committee on Imperial Defence, “Attack on the British Isles from Overseas,” 9.
39 See U.S. Army, Operations, FM 100–5 (Washington, DC: U.S. Department of the Army, 1976)Google Scholar, and Posen in Miller, 83–84, n. 4. For Soviet Sources, see fns. 30 and 42.
40 DePuy (fn. 30), 15.
41 Posen in Miller, 84, n. 4; Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 60, n. 17.
42 DePuy (fn. 30), 15; Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 61; Sidorenko, A. A., The Offensive: A Soviet View (Moscow: 1970)Google Scholar, trans. U.S. Air Force (Washington, DC: G.P.O., 1976), 29; Epstein, “The 3:1 Rule” (fn. 3), 96; Posen in Miller, 84, n. 4; 113.
43 These examples are cited in Mako (fn. 3), 38. See also Congressional Budget Office (fn. 3), 60.
44 Holmes (fn. 3), 166.
45 The simple calculation below bears out this point. According to Hamilton (fn. 3,115), the Warsaw Pact would have roughly 81 ADES in central Europe after 100 days of mobilization while NATO would have about 46. Depending on desired force ratios, NATO requirements would be as follows:
The magnitude of these margins appears even greater when we consider that the scope of the debate in the United States is limited to the possibility of adding or subtracting a very small number of ADES, say one or two.
46 Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 66–68, Table 1. Dupuy also maintains that the 3:1 rule sometimes fails when force ratios are expressed in terms of firepower because the analysis neglects “the respective quality of the opposing forces.” See Dupuy (fn. 32, 1987), 36.
47 Mearsheimer shows that, when adjusted to reflect quality of troops and combat circumstances and environment (Dupuy's Combat Power Formula), the force ratios in the nine successful breakthrough battles presented by Epstein were greater than 3:1 in seven cases and close to 3:1 in the other two. See “Assessing the Conventional Balance” (fn. 3), 68; and Dupuy (fn. 32, 1987), 81–89, '56. Dupuy's Combat Power Formula, however, is not the same as the ADE or other firepower scores that are usually used in static comparisons; the latter do not take quality, tactics, and environment into consideration. The use of Combat Power ratios instead of ADE ratios therefore changes the methodology substantially and grants that firepower indexes alone are insufficient to serve as units of comparison in static models. If the 3:1 rule is to be subjected to rigorous empirical testing, this existing confusion over what constitutes an appropriate measure of combat power must be remedied. See also Epstein, “The 3:1 Rule” (fn. 3), 103–4.
48 CHASE Report (fn. 32), 3–20. This does not in itself disconfirm the 3:1 rule because of the analytic inconsistencies in the data base that are discussed above: not all the engagements are breakthrough battles; the defender does not always have prepared positions; force ratios have not been adjusted to reflect quality; etc.
49 ibid., 1–6.
50 Merritt, Jack and Sprey, Pierre, “Negative Marginal Returns in Weapon Acquisitions,” in Head, Richard and Rokke, Ervin, eds., American Defense Policy, 3rd ed. (Baltimore: The Johns Hopkins University Press, 1973), 491–92Google Scholar.
51 Betts, “Conventional Deterrence” (fn. 31), 170.
52 DePuy (fn. 30), 18–19.
53 These equations were originally published in Lanchester, F. W., Aircraft in Warfare: The Dawn of the Fourth Arm (London: Constable & Co., 1916)Google Scholar.
54 In direct fire, a unit concentrates its fire on specific and visible targets in its line of sight; it can determine when a target has been incapacitated, and move its fire to another target. In indirect fire, a unit fires at targets for which it does not have an uninterrupted line of sight. For a detailed discussion of Lanchester equations, see Taylor, James, Lanchester Models of Warfare, 2 vols. (Arlington, VA: Operations Research Society of America, 1983)Google Scholar, and Taylor (fn. 7). For a more condensed treatment and criticism, see Lepingwell (fn. 3).
55 I am drawing on Lepingwell's “The Laws of Combat?” (fn. 3) in this brief description of Lanchester theory. Readers seeking a fuller exposition should consult his article and the volumes by James Taylor cited in the previous note.
56 r* and b* denote that the effectiveness coefficients are not the same for the square law and the linear law. In the square law, the coefficient reflects enemy shooters killed per time per friendly shooter. In the linear law, the coefficient reflects the fraction of enemy shooters killed per time per friendly shooter.
57 See Robert L. Helmbold, “Historical Data and Lanchester's Theory of Combat” (Fort Belvoir, VA: Combat Operations Research Group), Part I: CORG-SP-128 (AD 480 975), 1961; and Part II: CORG-SP-190 (AD 480 109), 1964. See also Helmbold, , “Some Observations on the Use of Lanchester's Theory for Prediction,” Operations Research 12 (September-October 1964), 778–81CrossRefGoogle Scholar; Lepingwell (fn. 3), 113–21; and Epstein, The Calculus of Conventional War (fn. 3), 8–9. These studies face the same problems of data availability and reliability discussed above.
58 Homer-Dixon, , “A Common Misapplication of the Lanchester Square Law: A Research Note,” International Security 12 (Summer 1987), 138–39CrossRefGoogle Scholar; Lepingwell (fn. 3), 103–11.
59 Homer-Dixon (fn. 58), 137; emphasis in original.
60 For Epstein's detailed critique of Lanchester theory, see Strategy and Force Planning, 146–55. See also Epstein, The Calculus of Conventional War (fn. 3).
61 ibid., 7–13.
62 Because of limitations of space, Epstein's airpower equations will not be treated fully in this essay.
63 The innovation introduced by Epstein allows the defender to trade space for time. If the defender's losses exceed his threshold attrition rate, he can withdraw from the front until daily attrition decreases to below the threshold rate. For detailed discussion of the model, see Epstein, 69–80, 117–25.
64 Subscripts (r and b) are used to denote red (attacker) and blue (defender); t denotes threshold rate. Ab(d) and Ab(d — 1) represent blue attrition rate on day d and blue attrition rate on day d — 1, respectively. I have relabeled Epstein's variables to clarify the presentation.
65 Epstein, The Calculus of Conventional War (fn. 3), 4.
66 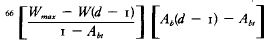 is a function designed to ensure that the defender's withdrawal rate approaches the maximum (Wmar) when Ab approaches 1.0 (100% daily attrition). Appendix B provides a more detailed explanation of the feedback mechanism and the variables used in Epstein's equations.
is a function designed to ensure that the defender's withdrawal rate approaches the maximum (Wmar) when Ab approaches 1.0 (100% daily attrition). Appendix B provides a more detailed explanation of the feedback mechanism and the variables used in Epstein's equations.
67 ![]() ensures that the changes in the prosecution rate (Arg) approach zero when the attacker's attrition rate (Ar) reaches his threshold (Art) and that the prosecution rate adjusts accordingly when attrition diverges from the threshold.
ensures that the changes in the prosecution rate (Arg) approach zero when the attacker's attrition rate (Ar) reaches his threshold (Art) and that the prosecution rate adjusts accordingly when attrition diverges from the threshold.
68 Epstein, Measuring Military Power (fn. 3), xxix; emphasis in original.
69 It is important to recall the level of accuracy that Epstein claims for this “gauge.” As was mentioned in the introduction, he uses his models to prescribe force levels accurate to one or two divisions.
70 For further discussion of this basic problem, see U.S. General Accounting Office (fn. 3), 3–31, 87–109, 147–53; and Stockfisch (fn. 3), esp, 1–10, 128–31.
71 Dupuy uses the term “intangible variables,” which he defines as “those which are—at least for the present—impossible to quantify with confidence, either because they are essentially qualitative in nature, or because for some other reason they currently defy precise delineation or measurement.” See Dupuy (fn. 32, 1979), 34.
72 I am indebted to Stephen Biddle for this point. See also Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 71. By “outcome,” I mean winners and losers, not force levels at some interim point in the battle. While Epstein's model does integrate air and ground components, it is somewhat counterintuitive that the feedback mechanism, by which the model is made adaptive, can affect outcomes only by buying time for air power (a nonadaptive component of the model) to drive results. This is not meant to suggest that, in reality, such a relationship between withdrawal and attrition due to air power does not exist. As discussed below, one could also postulate that withdrawal can affect outcomes by allowing the retreating party to alter the ground battle by changing its position, force mix, or tactics in order to exact a more favorable exchange ratio. When the air model is included in the analysis, withdrawal will affect outcomes if the air balance differs substantially from the ground balance, causing attrition to diverge from its ground-only values. See Biddle, “The European Conventional Balance” (fn. 3, 1988), 119, n. 22. This criticism of the model does not take into consideration the possibility that prolongation of the battle could affect the outcome because of extenuating political circumstances, or that victory could be measured in terms of territorial gains/losses (movement of the battle front) rather than in terms of attrition of the enemy's capabilities. These assumptions, however, are consistent with Epstein's assertion that “the wartime objective … is taken to be the attrition of the adversary'sforce” (p. 73, emphasis in original). It should also be noted that withdrawal can buy time for the arrival of reinforcements, though reinforcements are not explicitly considered in the original model. For an extension of the model allowing reinforcements, see Epstein, “The 3:1 Rule” (fn. 3), 114, n. 59.
73 It should be noted that withdrawal does not necessarily reduce the defender's attrition; the attacker can increase his prosecution rate to offset the defender's withdrawal. See Strategy and Force Planning, 123, ns. 11 and 12. Nevertheless, because the defender's attrition would be lower than if he had not withdrawn (assuming an advancing attacker), the feedback mechanism rests on the central assumption that withdrawal always benefits the retreating party.
74 Two historical trends are relevant here. First, the better prepared a defender's position, the lower his attrition. Second, the faster the movement of the front, the lower the casualty rates for both attacker and defender. This is due to the fact that troops are engaged in maneuver and have less time to utilize their weapons. (See Dupuy, fn. 32, 1987, pp. 157, 176.) It is therefore reasonable to assume that when the defender first abandons his positions, the attacker should, at least temporarily, be able to inflict increasing casualties on the exposed defender. Attrition on both sides may then fall temporarily when the attacker begins his pursuit, and rise when he again engages the defender.
75 Two examples illustrate the point. Between May 6 and 11, 1943, British and American troops battled Axis forces in the Medjerda Valley near Tunis. Allied troops first broke through enemy lines on the 6th and 7th, inflicting enough casualties to cause the Germans and Italians to withdraw toward Hammam Lif and Hammamet—areas that offered formidable natural barriers. By pursuing and attacking while the Germans and Italians were still withdrawing, however, the Allies routed the Axis powers and secured a surrender. The Allies took advantage of the confusion and disorganization that accompanied the retreat: “The brain and nerve-centre of the army was paralyzed, and nothing could function coherently any more.” Alexander Clifford, quoted in Major-General Fuller, J.F.C., The Second World War 1929–45 (London: Eyre & Spottiswoode, 1948), 249Google Scholar. The Battle of Jitra (Malaya, December 1941) also illustrates the potential dangers of withdrawal. The following details are drawn from Major GeneralKirby, S. Woodburn, et al. ., The War Against Japan — The Loss of Singapore, vol. 1, Official British History of World War II (London: H.M.S.O., 1957), 205–15Google Scholar. See also Mearsheimer, “Assessing the Conventional Balance” (fn. 3), 75, n. 47; 88–89. At 8 A.M. on December 11, a Punjabi detachment of the Eleventh Indian Division, not without losing some ground, succeeded in halting an attempted Japanese breakthrough. At 3 P.M., the unit was withdrawn from the front, whereupon the Japanese almost immediately took the offensive again. By 4:30, the advancing Japanese had routed the Indians and “all attempts to withdraw the battalion in an orderly fashion failed.…” Similar efforts to withdraw proved equally disastrous on succeeding days. Units leaving their prepared positions often came under heavy enemy pressure, leading to disorganization and interrupted communications. Moreover, the Eleventh Division had been ordered to withdraw to Gurun (where there were no prepared defenses) rather than to Sungei Kedah (where formidable tank obstacles already existed). This decision facilitated the success of the continuing Japanese offensive and demonstrated the importance of withdrawing to protected positions.
76 Epstein does acknowledge that factors other than attrition can affect withdrawal. See Epstein, “Dynamic Analysis” (fn. 3), 163, n. 19.
77 For discussion of the ambiguous effect of attrition on disengagement and battle termination—phenomena related to withdrawal—see Robert L. Helmbold, “Decision in Battle: Breakpoint Hypotheses and Engagement Termination Data,” R-772-PR (Santa Monica, CA: Rand Corporation, 1971), v. See also CHASE Report (fn. 32), chap. 6.
78 In Strategy and Force Planning, Epstein discusses possible modifications to his model, including the introduction of a variable exchange ratio (p. 125, n. 16). Since the publication of his initial models, Epstein appears to have become aware of the rigidities introduced by a fixed exchange rate. In “The 3:1 Rule” (fn. 3), he notes that he is at work on an extension of his equations for ground combat. Epstein presents a mechanism to be included in his new equations that will allow E to vary with changes in the quality of the defender's position. He also discusses a possible generalization of E that would make the exchange ratio dependent on time, on the force ratio, and on standard effectiveness terms (pp. 112–13, ns. 55 and 56).
79 Follow-on-Forces-Attack is a case in point. This plan calls for NATO forces to respond to a Warsaw Pact invasion with selected offensive strikes well into the enemy's rear. On the role of offensive conventional retaliation in NATO strategy, see Huntington in Miller.
80 Taylor (fn. 7), 36. It is important to note that study of force-to-space constraints is still in a rudimentary stage. No rigorous studies exist of when diminishing returns set in, or of the extent to which optimal concentration levels depend upon terrain, weather, weapon system, or other variables. Furthermore, the mechanism through which high levels of concentration constrain effectiveness is underspecified. Is the crucial factor the simple absence of space for more units, the lack of mobility, the difficulties involved in target acquisition, or the extent to which concentrated forces are lucrative targets for the adversary? For assessments of numerical values for force-to-space constraints, see Posen in Miller, 106–10. Posen specifies one ADE per 12.5 kilometers as the “theoretical maximum” (p. 110, n. 44). See also Mearsheimer, “Numbers, Strategy, and the European Balance” (fn. 3), 177–79, and Epstein, “The 3:1 Rule” (fn. 3), 123–24, n. 84. For Soviet thinking on force density in the breakthrough zone, see Siderenko (fn. 42), 30–31.
81 Merritt and Sprey (fn. 50), 491.
82 For an example of a model in which fire effectiveness is modified to take into consideration efficiencies of scale, see Taylor (fn. 7), 37ff. Many of the classified models used by government agencies do use variable exchange ratios. For further discussion of this problem, see Lowell Bruce Anderson, “A General Method for Relating Bounds on Attrition to the Average Rate of Movement of Ground Forces,” unpub. (Alexandria, VA: Institute for Defense Analyses, July 1986), 2–3.
83 In a stable equilibrium model, force imbalances would not grow wider over time, or would converge toward an equilibrium ratio. This is not to suggest that an unstable model may not be an appropriate reflection of reality, but that instability has important implications for policy and for the levels of uncertainty contained in the model's output. It should be noted that Epstein's model is less unstable than others frequently used within the policy community. See Biddle, “The European Conventional Balance” (fn. 3,1988).
84 ibid., 99. If the force ratio is below the level at which equilibrium occurs, the force imbalance grows progressively smaller until parity is reached; then the defender's force advantage grows progressively larger. These remarks assume that some level of attrition is occurring—that is, that the defender has not completely withdrawn from the engagement.
85 ibid., 100. The following example illustrates this property of the model. Assume that R begins an engagement with 1400 units and B with 1000, an initial force ratio of 1.4:1. Daily attrition (Ar) is 5%, and the exchange rate is 1.4:1. Using equations 8 and 9 above to compute the values for R and B surviving after one day of combat, we find that R(d + 1) = 1400 – .05(1400) = 1330. B(d + 1) = 1000 – 1/1.4(70) = 950. As we can see, the force ratio is still 1.4:1. One more day of combat would produce the following results: R(d + 2) = 1330 – .05(1330) = 1263.5. B(d + 2) = 950 – 1/1.4(66.5) = 902.5. Again the force ratio after two days is still 1.4:1. Now assume that the initial force levels are R = 2800 and B = 1000, a ratio of 2.8:1. With the exchange ratio and attrition rates unchanged, we compute two days of combat as follows: R(d + 1) = 2800 – .05(2800) = 2660. B(d + 1) = 1000 – 1/1.4(140) = 900; the force ratio after one day of combat has shifted to 2.95:1. R(d + 2) = 2660 — .05(2660) = 2527. B(d + 2) = 900 – 1/1.4(133) = 805; the force ratio after the second day of battle is 3.13:1. If we continued the calculation, the force ratio would quickly grow grossly imbalanced.
86 Taylor (fn. 7), no.
87 See U.S. General Accounting Office (fn. 3), 87–96, and Stockfisch (fn. 3), vi-viii. Information collected from historical battles is, as discussed above, unreliable and difficult to verify. Information collected from operational testing is sparse and of questionable worth in terms of its ability to represent the values that would obtain on an actual battlefield.
88 Dupuy (fn. 32, 1979), x.
89 Assume, for example, that a tank crew normally consists of four men. If one crew member is killed, the tank could still function, although at a possibly reduced level of effectiveness. It is therefore of questionable value to assume direct proportionality between personnel losses and firepower losses. In fact, it is unclear whether the attrition rates Epstein uses refer to personnel, armored vehicles, or overall firepower, but most historical studies express attrition in terms of personnel casualties. (See Appendix D, 128, note j.)
90 My consultations with military officers do not suggest that a 5% attrition rate—or any specific attrition rate—would lead to withdrawal with any degree of consistency or predictability.
91 Epstein does present a sensitivity analysis in which he uses a 3% rather than a 5% threshold attrition rate. This small change does not alter who wins, but it does affect the displacement of the front by as much as 300 kilometers. (See pp. 144–45.) Douglas Karo has run a series of sensitivity analyses using Epstein's equations for the Persian Gulf scenario. He shows that small and very plausible changes in the value of variables such as the exchange ratio or initial force levels do, in fact, produce a Soviet victory in several of Epstein's cases. In Karo's words, “a small number of seemingly plausible adjustments [on the order of 5% of original value] to estimates of force size or effectiveness lead to vastly different outcomes for battle details such as front movement and even for the identification of winners and losers.” In the scenario in which U.S. and Soviet forces are most closely matched (Case 3), “the conclusions reached by Epstein … appear to require accuracies in parameter estimation on the order of a few percent.” See Karo, “The 'Adaptive Model of War' and Security Policy Decisions: A Technical Note,” unpub. (Cambridge: M.I.T. Center for International Studies, 1988), 1, 4.
92 Epstein, Measuring Military Power (fn. 3), xxix.
93 Epstein assumes that the Soviets would be drawing on the trucks of 24 divisions. (For his computations, see pp. 112–16.) It should also be noted that Epstein calculates the logistical constraints facing Soviet forces by computing the maximum number of trucks that could operate on the limited roadways through the Zagros Mountains. Thus, even if the Soviets diverted trucks from other theaters, they could not put them to use unless they improved or expanded existing roadways. (See pp. 66–67, 11–63.) If the Soviets were to upgrade one roadway from stone/gravel (type 2) to cement/bituminous (type 1), their logistical capability would rise considerably. This would allow for another 2,061 three-ton trucks per day. With half arriving loaded and half returning empty, the upgraded road would supply an extra 3,091 tons of provisions per day. Assuming Soviet troops are consuming 1,675 tons of supplies per division per day, the upgraded road would support close to another two divisions.
94 Epstein acknowledges that deployment of the RDF would utilize “the full U.S. fleet of C-5 strategic transports” (pp. 63–65). Thomas McNaugher argues that when all lift procurement programs for the RDF are completed in 1988, the timely deployment of the RDF to the Gulf (five divisions in five weeks) would require “that all lift assets are set in motion simultaneously and that other contingencies do not rob CENTCOM of lift assets.” (Arms and Oil, Washington, DC: The Brookings Institution, 1985, 67Google Scholar; emphasis added.) Note that Mc-Naugher's calculations refer only to the time required from loading in the United States to unloading in the Gulf, not to the total time required from receipt of warning, to mobilization, to full deployment in Khuzistan.
95 U.S. Congressional Budget Office, Rapid Deployment Forces — Policy and Budgetary Implications (Washington, DC: G.P.O., 1983), 29–34Google Scholar. See also Kupchan, Charles A., The Persian Gulf and the West (Boston: Allen & Unwin, 1987), 120Google Scholar. 189–93.
96 Classified models used within the government planning community fall prey to similar methodological obstacles and face similar levels of uncertainty. See Paul K. Davis, “The Role of Uncertainty in Assessing the NATO-Pact Central-Region Balance,” Rand Paper P-7427 (Santa Monica, CA: Rand Corporation, April 1988).
97 P.R.O., CAB 38/5/43, May 5, 1904, “Defence of India: Observations on the Records of a War Game Played at Simla, 1903.”
98 Stockfisch (fn. 3), 122–23.
99 For further discussion of the differing assumptions that produce pessimistic and optimistic assessments, see Congressional Budget Office (fn. 3), 27–37, Posen in Miller, 83–91, and Biddle, “The European Conventional Balance” (fn. 3, 1988).
100 There is a striking parallel between this conclusion and the eventual result of the “revolution” in force planning that occurred in the McNamara Pentagon in the 1960s. The effort to calibrate the determination of requirements is, to a considerable extent, a rerun of the attempt to micro-manage defense policy under the Planning-Programming-Budgeting System (PPBS). In both periods, analysts have attempted to rationalize the planning and procurement process through quantification and modeling. Both efforts have confronted the same obstacles: a neglect of those variables that cannot be quantified and the quantification of other variables in a manner that is of dubious reliability and methodological rigor. It is of no small significance that in their published account of the PPBS years, Smith and Enthoven reveal their frustration over an inability to answer the question, “How much is enough?” and conclude that we must “quit pretending that there is a decisive authoritative basis for the military's stated 'requirements'.” Smith and Enthoven (fn. 18), 224.
101 Many of the models employed within the planning community already use variable exchange ratios; see fn. 82.
102 See Lebow, Richard Ned, Between Peace and War (Baltimore: The Johns Hopkins University Press, 1981), 242–47Google Scholar, and Mearsheimer, Conventional Deterrence (fn. 3).
103 This assessment of the effects of uncertainty on decision making is admittedly contestable. Uncertainty and complexity do not in all cases lead to indecision and conservatism; they can also lead to cognitive distortion and misinterpretation or to simplification of incoming information. Yet such reactions are most pronounced when decision makers are under considerable stress and when the alternatives to not going to war are extremely unattractive. See Lebow (fn. 107), 114. For example, the Allies decided to reopen the Eastern Front in 1918 despite pervasive pessimism about the ability of a new front to affect the course of the war. They were, however, driven by panic over Russia's collapse and Germany's consequent ability to focus all its forces on the Western Front. See Jervis, Robert, Perception and Misperception in International Politics (Princeton: Princeton University Press, 1976), 379Google Scholar. Similarly, the Japanese attacked Pearl Harbor in 1941 despite their awareness that they would probably not be able to defeat the United States in an extended war. The problem was that the costs of not going to war—halting the expansion of, if not dismantling, the empire—were intolerable. See Betts, Surprise Attach (fn. 31), 130–38. In both of these cases, neither a more optimistic assessment of the balance of forces nor more certainty about the likelihood of defeat would probably have affected decision making: the Allies in 1918 as well as the Japanese in 1941 saw little chance of success to begin with. In the absence of an international crisis and a belief in the imminence of war, the uncertainty surrounding conventional assessment should thus breed caution among the decision makers of both potential adversaries. During periods of crisis, when the decision to attack may well be the result of desperation and fear rather than of rational calculation about the chances of success, levels of uncertainty about the balance of forces are unlikely to either enhance or erode deterrence. For a general work on decision making and coping with uncertainty, see Steinbruner, John, The Cybernetic Theory of Decision (Princeton: Princeton University Press, 1974)Google Scholar, esp. 65–71.
104 Similar arguments have been put forward with respect to nuclear deterrence: uncertainty about the adversary's intentions and capabilities raises the barriers to first use. Edward Rhodes, for example, argues that the United States could enhance deterrence by deliberately making the Soviets more uncertain about U.S. intentions and about Washington's ability to control nuclear war once it starts. (Power and MADness, New York: Columbia University Press, forthcoming 1989Google Scholar). Donald Snow argues that technological breakthroughs in missile accuracy or in antisubmarine warfare could erode strategic stability by removing the uncertainty about the effects of nuclear exchanges upon which deterrence rests: “This ability to calculate profitability from first-striking is absolutely anathema to developed deterrent notions. …” (Nuclear Strategy in a Dynamic World, University, AL: University of Alabama Press, 1981, 208Google Scholar.)
page 577 note 1 These calculations are approximate and intended only to outline how very plausible lift constraints would affect force requirements for the RDF. Of the scenarios presented by Epstein, I am choosing that which seems most plausible: a Soviet build-up in northern Iran before attacking the United States in Khuzistan. Epstein's calculations for this scenario, upon which the following analysis is based, can be found in Appendix D-6 of Strategy and Force Planning.
2 To simplify the calculation, I am assuming a direct proportionality between lift used and divisions deployed. The exact number of divisions that could be deployed in Iran within three months would depend upon which divisions were sent (air mobile or mechanized) and upon which lift assets were allocated to the European mission (aircraft or ships).
3 That a 75% decrease in lift produces a 75% decrease in the initial U.S. force level (wuv score) is a conservative assumption (favorable to the Soviets) inasmuch as it is the arrival of the heavier divisions—such as the 24th Mechanized—that would be delayed.
4 I am assuming that units do not enter the battle as they arrive, but that they must await arrival of command-and-control infrastructure, logistical support, etc.
5 McNaugher (fn. 96, p. 68), shows that the United States could send four divisions to the Gulf in four weeks, but this assumes use of a prepositioned Marine division and the lighter 82nd Airborne and 101st Airmobile Divisions.
- 6
- Cited by


