1 Introduction
About a half century ago, using a perturbation method (at the third order) that has been widely applied in fluid mechanics for a long time, Phillips (Reference Phillips1960) gave the criterion of wave resonance
where
![]() $\boldsymbol{k}_{i}$
is wavenumber and
$\boldsymbol{k}_{i}$
is wavenumber and
![]() ${\it\omega}_{i}=\sqrt{gk_{i}}$
(with the gravity acceleration
${\it\omega}_{i}=\sqrt{gk_{i}}$
(with the gravity acceleration
![]() $g$
and the definition
$g$
and the definition
![]() $k_{i}=|\boldsymbol{k}_{i}|$
) is the linear frequency. In addition, Phillips (Reference Phillips1960) revealed that amplitude of resonant wave component grows linearly with time, if it is zero initially. Thereafter, the exactly and nearly resonant waves have been widely studied and applied (Benney Reference Benney1962; Longuet-Higgins Reference Longuet-Higgins1962; Bretherton Reference Bretherton1964; Longuet-Higgins & Smith Reference Longuet-Higgins and Smith1966; Stiassnie & Shemer Reference Stiassnie and Shemer1984; Hammack & Henderson Reference Hammack and Henderson1993; Mei, Stiassnie & Yue Reference Mei, Stiassnie and Yue2005; Onorato et al.
Reference Onorato, Osborne, Janssen and Resio2009). In particular, Benney (Reference Benney1962) established the evolution equations of wave-mode amplitudes, and demonstrated the time-dependent periodic exchange of wave energy for exactly resonant waves. Benney (Reference Benney1962) mentioned that ‘if all three modes are initially present then the energy distribution will vary with time’ and thus ‘no stable equilibrium amplitudes can be expected as the system is conservative.’ To the best of our knowledge, the so-called steady-state resonant waves (with time-independent spectrum) have not been found analytically at a order higher than three from the full water wave equations, because perturbation results contain secular terms when Phillips’ criterion is satisfied so that ‘the perturbation theory breaks down due to singularities in the transfer functions’, as pointed out by Madsen & Fuhrman (Reference Madsen and Fuhrman2012).
$k_{i}=|\boldsymbol{k}_{i}|$
) is the linear frequency. In addition, Phillips (Reference Phillips1960) revealed that amplitude of resonant wave component grows linearly with time, if it is zero initially. Thereafter, the exactly and nearly resonant waves have been widely studied and applied (Benney Reference Benney1962; Longuet-Higgins Reference Longuet-Higgins1962; Bretherton Reference Bretherton1964; Longuet-Higgins & Smith Reference Longuet-Higgins and Smith1966; Stiassnie & Shemer Reference Stiassnie and Shemer1984; Hammack & Henderson Reference Hammack and Henderson1993; Mei, Stiassnie & Yue Reference Mei, Stiassnie and Yue2005; Onorato et al.
Reference Onorato, Osborne, Janssen and Resio2009). In particular, Benney (Reference Benney1962) established the evolution equations of wave-mode amplitudes, and demonstrated the time-dependent periodic exchange of wave energy for exactly resonant waves. Benney (Reference Benney1962) mentioned that ‘if all three modes are initially present then the energy distribution will vary with time’ and thus ‘no stable equilibrium amplitudes can be expected as the system is conservative.’ To the best of our knowledge, the so-called steady-state resonant waves (with time-independent spectrum) have not been found analytically at a order higher than three from the full water wave equations, because perturbation results contain secular terms when Phillips’ criterion is satisfied so that ‘the perturbation theory breaks down due to singularities in the transfer functions’, as pointed out by Madsen & Fuhrman (Reference Madsen and Fuhrman2012).
The nonlinear interactions of steady-state periodic travelling water waves were investigated by many researchers, but mostly without considering wave resonance. Concus (Reference Concus1962) analytically investigated the standing capillary-gravity waves of finite amplitude by means of perturbation methods, but without considering the exact or near resonance of the wave. Hammack, Scheffner & Segur (Reference Hammack, Scheffner and Segur1989), Hammack, Henderson & Segur (Reference Hammack, Henderson and Segur2005) experimentally studied in a wave tank the interaction of two families of periodic travelling waves in shallow water, and observed pictures where symmetric and asymmetric hexagons were formed by wave crests. They also analytically reproduced such solutions using the Kadomtsev–Petviashvili (KP) equation which models this behaviour well. Note that Hammack et al. (Reference Hammack, Scheffner and Segur1989, Reference Hammack, Henderson and Segur2005) did not consider exact/near resonance of the wave either. In addition, Dubrovin, Flickinger & Segur (Reference Dubrovin, Flickinger and Segur1997) gave closed-form analytic solutions of the KP equation with three phases for travelling waves in shallow water, and found that ‘almost every three-phase solution is time dependent, in every coordinate system’. In addition, Iooss & Plotnikov (Reference Iooss and Plotnikov2009, Reference Iooss and Plotnikov2011) seriously proved the existence of the symmetrical and non-symmetrical three-dimensional travelling gravity waves without exact/near resonance.
Meiron, Saffman & Yuen (Reference Meiron, Saffman and Yuen1982) numerically solved the full wave equations for steady three-dimensional symmetric gravity waves with finite amplitude on deep water, and obtained results in good agreement with the experimental observations of Su (Reference Su1982) and Su et al. (Reference Su, Bergin, Marler and Myrick1982). Note that the exact/near resonance was not considered by Su (Reference Su1982), Su et al. (Reference Su, Bergin, Marler and Myrick1982) and Meiron et al. (Reference Meiron, Saffman and Yuen1982). For free surface waves with arbitrary uniform depth, Milewski & Keller (Reference Milewski and Keller1996) derived an isotropic pseudo-differential equation at the second order of small perturbation quantities, i.e. the ratio of wave amplitude to the wavelength and the ratio of depth to wavelength, from which one can reduce to the Benney–Luke equation, the Korteweg–de Vries (KdV) equation, the KP equation, and to the nonlinear shallow-water equations in the appropriate limits. Using their second-order perturbation equations together with the resonance criterion given by Phillips (Reference Phillips1960) at the third order, Milewski & Keller (Reference Milewski and Keller1996) numerically obtained steady-state resonant and non-resonant waves in finite water depth, although no multiple solutions were reported. Using a spectral collocation discretization together with the continuous method, Nicholls (Reference Nicholls1998) investigated travelling wave solutions to the Zakharov–Craig–Sulem (ZCS) formulation of the water wave problem, which is equivalent to the full water wave equations, but without considering exactly or nearly resonant waves. Based on a kind of integro-differential equations, Craig & Nicholls (Reference Craig and Nicholls2002) numerically investigated the bifurcation of travelling surface water waves, using the fast Fourier transform and surface spectral methods proposed by Nicholls (Reference Nicholls1998). However, as pointed out by Craig & Nicholls (Reference Craig and Nicholls2002), the three-dimensional waves (cross-waves) without surface tension exhibits the phenomenon of small divisors, which could make the behaviour of their numerical scheme very difficult to control. Nicholls & Reitich (Reference Nicholls and Reitich2006) proposed a stable high-order boundary perturbation algorithm for the numerical simulation of travelling water waves, but pointed out that the resonance ‘lies outside the scope’ of their method. Meiron et al. (Reference Meiron, Saffman and Yuen1982) also mentioned that, ‘the small-divisor problem appears if an attempt is made to calculate solutions by developing expansions in wave height’, and that ‘we are faced with a situation where increasing the accuracy of a calculation may lead to an increase in the number of close solutions and a decrease in the physical precision.’ To the best of our knowledge, numerical methods were not successful to the full water wave equations for either exactly or nearly resonant waves, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006). Neither do perturbation methods for the full wave equations at an order higher than three, as mentioned by Madsen & Fuhrman (Reference Madsen and Fuhrman2012).
By means of the homotopy analysis method (HAM) (Liao Reference Liao1992, Reference Liao1997, Reference Liao2003, Reference Liao2004, Reference Liao2012, Reference Liao2014; Vajravelu & Van Gorder Reference Vajravelu and Van Gorder2013), an analytic approximation method for highly nonlinear problems, the multiple solutions of steady-state resonant waves were obtained in the form of analytic approximations from the full water wave equations, not only in deep water (Liao Reference Liao2011; Liu & Liao Reference Liu and Liao2014) but also in uniform water depth (Xu et al. Reference Xu, Lin, Liao and Stiassnie2012) and over a bottom with an infinite number of periodic ripples (Xu, Lin & Liao Reference Xu, Lin and Liao2015). In particular, the multiple steady-state resonant waves were even observed experimentally (Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015) in a basin at State Key Laboratory of Ocean Engineering (in Shanghai, China), with excellent agreement with their theoretical predictions given by means of the HAM.
When Phillips’ resonance criterion (1.1) is exactly satisfied, it is traditionally called the exact resonance. When it is not exactly but nearly satisfied, it is called the nearly resonant wave. However, it is well known that near-resonance leads to the famous ‘small divisor problem’ (Poincaré Reference Poincaré1892; Yoccoz Reference Yoccoz1992), which is difficult to handle in mathematics (even numerically), as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006). To the best the authors’ knowledge, the multiple steady-state nearly resonant surface waves with time-independent spectrum have not been gained from the full water equations by means of perturbation methods either (Madsen & Fuhrman Reference Madsen and Fuhrman2012).
In this paper, we further applied the HAM to the full water wave equations in deep water and successfully gained such kind of steady-state nearly resonant waves with time-independent spectrum in a way rather similar to that for the exactly resonant waves (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014). In the frame of the HAM, by means of choosing a new linear operator that is a little different from the linear part of the original equations (here, it should be emphasized that it is impossible to do the same thing in the frame of perturbation methods), we can easily avoid the small divisor at the low wave frequency, or at least move it far away to a quite high frequency with physically negligible wave energy. From the physical and numerical viewpoints, it is found that the steady-state nearly resonant waves have nothing fundamentally different from the steady-state exactly resonant ones. These conclusions are confirmed and verified numerically by means of the Zakharov’s equation in a similar way to the steady-state exactly resonant case (Xu et al. Reference Xu, Lin, Liao and Stiassnie2012). Therefore, the steady-state nearly resonant waves have nothing fundamentally different from the steady-state exactly resonant ones, from the viewpoints of the HAM.
In this paper, the mathematical formulae are described in § 2, and results of a case study are given in § 3. The concluding remarks and discussions are given in § 4. The detailed analytic approximation approach based on the HAM for the full wave equation is given in appendix A and the numerical algorithm based on Zakharov’s equation is briefly described in appendix B.
2 Mathematical formulae
Consider the nonlinear interactions of two trains of progressive gravity waves with small amplitudes in deep water. Assume that the fluid is inviscid and incompressible, the flow is irrotational and the surface tension is neglected. The coordinate system
![]() $(x,y,z)$
is set on the free surface, with
$(x,y,z)$
is set on the free surface, with
![]() $z$
-axis positive vertically upwards. The velocity potential
$z$
-axis positive vertically upwards. The velocity potential
![]() ${\it\varphi}(x,y,z,t)$
is governed by the Laplace equation
${\it\varphi}(x,y,z,t)$
is governed by the Laplace equation
subject to the kinematic and dynamic conditions on the unknown free surface
![]() $z={\it\eta}(x,y,t)$
:
$z={\it\eta}(x,y,t)$
:
respectively, and the impermeable condition at the bottom:
where
![]() ${\it\eta}(x,y,t)$
denotes the wave elevation,
${\it\eta}(x,y,t)$
denotes the wave elevation,
![]() $t$
denotes the time and
$t$
denotes the time and
is a differential operator with
![]() $\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$
denoting the unit vector in the
$\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$
denoting the unit vector in the
![]() $x,y,z$
direction, respectively.
$x,y,z$
direction, respectively.
Consider the nonlinear interaction of a steady-state wave system of two periodic travelling waves. Write
where
![]() $\boldsymbol{k}_{i}$
is the wavenumber,
$\boldsymbol{k}_{i}$
is the wavenumber,
![]() ${\it\sigma}_{i}$
denotes actual wave frequency and
${\it\sigma}_{i}$
denotes actual wave frequency and
![]() $\boldsymbol{r}=x\,\boldsymbol{i}+y\,\boldsymbol{j}$
, respectively. In this paper, we focus on the steady-state cases, say, all wavenumbers
$\boldsymbol{r}=x\,\boldsymbol{i}+y\,\boldsymbol{j}$
, respectively. In this paper, we focus on the steady-state cases, say, all wavenumbers
![]() $\boldsymbol{k}_{i}$
and actual wave frequency
$\boldsymbol{k}_{i}$
and actual wave frequency
![]() ${\it\sigma}_{i}$
, where
${\it\sigma}_{i}$
, where
![]() $i=1,2$
, are time-independent. Due to the nonlinearity, the actual wave frequency
$i=1,2$
, are time-independent. Due to the nonlinearity, the actual wave frequency
![]() ${\it\sigma}_{i}$
is larger than the linear frequency
${\it\sigma}_{i}$
is larger than the linear frequency
![]() ${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
. Thus, the wave elevation can be expressed in the form
${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
. Thus, the wave elevation can be expressed in the form
where
![]() $A_{m,n}$
is a real number. Thus,
$A_{m,n}$
is a real number. Thus,
![]() $A_{m,n}^{2}$
versus
$A_{m,n}^{2}$
versus
![]() $|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|$
gives a wave spectrum. Here,
$|m\boldsymbol{k}_{1}+n\boldsymbol{k}_{2}|$
gives a wave spectrum. Here,
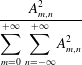 $$\begin{eqnarray}\frac{A_{m,n}^{2}}{\displaystyle \mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }A_{m,n}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{A_{m,n}^{2}}{\displaystyle \mathop{\sum }_{m=0}^{+\infty }\mathop{\sum }_{n=-\infty }^{+\infty }A_{m,n}^{2}}\end{eqnarray}$$
gives the percentage of wave energy of the wave component
![]() $\cos (m{\it\xi}_{1}+n{\it\xi}_{2})$
. As pointed out by Benney (Reference Benney1962), in a special case of exact resonance
$\cos (m{\it\xi}_{1}+n{\it\xi}_{2})$
. As pointed out by Benney (Reference Benney1962), in a special case of exact resonance
there exist periodic exchanges of wave energy between different wave components, i.e.
![]() $A_{m,n}$
is time-dependent in general. In this case, the corresponding wave spectrum is time-dependent. Note that the wave spectrum is time-independent when
$A_{m,n}$
is time-dependent in general. In this case, the corresponding wave spectrum is time-dependent. Note that the wave spectrum is time-independent when
![]() $A_{m,n}$
,
$A_{m,n}$
,
![]() $\boldsymbol{k}_{i}$
and
$\boldsymbol{k}_{i}$
and
![]() ${\it\sigma}_{i}$
are constants, corresponding to the so-called ‘steady-state waves’. In this paper, the wavenumber
${\it\sigma}_{i}$
are constants, corresponding to the so-called ‘steady-state waves’. In this paper, the wavenumber
![]() $\boldsymbol{k}_{i}$
and actual wave frequency
$\boldsymbol{k}_{i}$
and actual wave frequency
![]() ${\it\sigma}_{i}>{\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
, where
${\it\sigma}_{i}>{\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
, where
![]() $i=1,2$
, are given as constants, and the unknown, time-independent coefficient
$i=1,2$
, are given as constants, and the unknown, time-independent coefficient
![]() $A_{m,n}$
is determined in the way mentioned below. In addition, without loss of generality, we consider here only the so-called ‘nearly resonant’ case when (2.9) is nearly satisfied.
$A_{m,n}$
is determined in the way mentioned below. In addition, without loss of generality, we consider here only the so-called ‘nearly resonant’ case when (2.9) is nearly satisfied.
Since all of the wave amplitudes, the wavenumbers
![]() $\boldsymbol{k}_{i}$
and the actual wave frequencies
$\boldsymbol{k}_{i}$
and the actual wave frequencies
![]() ${\it\sigma}_{i}$
of the steady-state travelling waves are constant, i.e. independent of time, the original initial/boundary-value problem governed by (2.1)–(2.4) can be transformed into a boundary-value one by means of the new variables
${\it\sigma}_{i}$
of the steady-state travelling waves are constant, i.e. independent of time, the original initial/boundary-value problem governed by (2.1)–(2.4) can be transformed into a boundary-value one by means of the new variables
![]() ${\it\xi}_{1}$
and
${\it\xi}_{1}$
and
![]() ${\it\xi}_{2}$
. In the new coordinate system (
${\it\xi}_{2}$
. In the new coordinate system (
![]() ${\it\xi}_{1},{\it\xi}_{2},z$
), the Laplace equation (2.1) reads
${\it\xi}_{1},{\it\xi}_{2},z$
), the Laplace equation (2.1) reads
subject to the two boundary conditions on the unknown wave elevation
![]() $z={\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
:
$z={\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
:
 $$\begin{eqnarray}\displaystyle \mathscr{N}_{1}[{\it\varphi}] & = & \displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}{\it\sigma}_{i}{\it\sigma}_{j}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{i}\partial {\it\xi}_{j}}+g\frac{\partial {\it\varphi}}{\partial z}-2\mathop{\sum }_{i=1}^{2}{\it\sigma}_{i}\frac{\partial f}{\partial {\it\xi}_{i}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{i}}\frac{\partial f}{\partial {\it\xi}_{j}}+\frac{\partial {\it\varphi}}{\partial z}\frac{\partial f}{\partial z}=0,\quad \text{on }z={\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{N}_{1}[{\it\varphi}] & = & \displaystyle \mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}{\it\sigma}_{i}{\it\sigma}_{j}\frac{\partial ^{2}{\it\varphi}}{\partial {\it\xi}_{i}\partial {\it\xi}_{j}}+g\frac{\partial {\it\varphi}}{\partial z}-2\mathop{\sum }_{i=1}^{2}{\it\sigma}_{i}\frac{\partial f}{\partial {\it\xi}_{i}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{2}\mathop{\sum }_{j=1}^{2}\boldsymbol{k}_{i}\boldsymbol{\cdot }\boldsymbol{k}_{j}\frac{\partial {\it\varphi}}{\partial {\it\xi}_{i}}\frac{\partial f}{\partial {\it\xi}_{j}}+\frac{\partial {\it\varphi}}{\partial z}\frac{\partial f}{\partial z}=0,\quad \text{on }z={\it\eta}({\it\xi}_{1},{\it\xi}_{2}),\end{eqnarray}$$
and also the impermeable condition at the bottom
where
![]() $\mathscr{N}_{1}$
and
$\mathscr{N}_{1}$
and
![]() $\mathscr{N}_{2}$
are two nonlinear operators defined above, and
$\mathscr{N}_{2}$
are two nonlinear operators defined above, and
For a steady-state wave system with time-independent spectrum, there is no exchange of wave energy between different wave components, i.e. all physical quantities (such as wave amplitude and frequency) are constant. Thus, the steady-state wave elevation
![]() ${\it\eta}$
reads
${\it\eta}$
reads
where
![]() $A_{m,n}$
is a constant to be determined. Similarly, the velocity potential
$A_{m,n}$
is a constant to be determined. Similarly, the velocity potential
![]() ${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
should be in the form
${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
should be in the form
with the definition
where
![]() $B_{m,n}$
is a constant to be determined. Note that the linear governing equation (2.10) and the bottom condition (2.13) are automatically satisfied by (2.16). So, the unknown coefficients
$B_{m,n}$
is a constant to be determined. Note that the linear governing equation (2.10) and the bottom condition (2.13) are automatically satisfied by (2.16). So, the unknown coefficients
![]() $A_{m,n}$
and
$A_{m,n}$
and
![]() $B_{m,n}$
are determined by the two nonlinear boundary conditions (2.11) and (2.12).
$B_{m,n}$
are determined by the two nonlinear boundary conditions (2.11) and (2.12).
In the special case (2.9) of the exact resonance, Liao (Reference Liao2011) successfully applied the HAM to gain the (numerically) convergent analytic approximation solutions of the full wave equations for the steady-state exactly resonant waves in deep water with time-independent spectrum. The same approach was further used by Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) to the full wave equations for the steady-state exactly resonant waves in finite water depth, and by Liu & Liao (Reference Liu and Liao2014) to the full wave equation for steady-state exactly resonant waves in deep water in more general cases. The steady-state nearly resonant waves can be obtained in a rather similar way, as shown below. Since almost all mathematical formulae are the same as those given by Liao (Reference Liao2011), we only describe here this approach briefly. For details, please refer to appendix A.
In the HAM-based approach (Liao Reference Liao2011), the velocity potential
![]() ${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
and the free surface elevation
${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
and the free surface elevation
![]() ${\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
are expressed by two infinite series
${\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
are expressed by two infinite series
where
with the definition
![]() ${\it\chi}_{1}=0$
and
${\it\chi}_{1}=0$
and
![]() ${\it\chi}_{m}=1$
for
${\it\chi}_{m}=1$
for
![]() $m>1$
,
$m>1$
,
![]() ${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
is an initial guess of the velocity potential, and
${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
is an initial guess of the velocity potential, and
![]() ${\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z)$
(
${\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z)$
(
![]() $m\geqslant 1$
) is governed by the so-called
$m\geqslant 1$
) is governed by the so-called
![]() $m$
th-order deformation equation
$m$
th-order deformation equation
subject to the linear boundary condition
and the bed condition
Here,
![]() $\mathscr{L}$
is an auxiliary linear operator and
$\mathscr{L}$
is an auxiliary linear operator and
![]() $c_{0}$
is an auxiliary parameter, called ‘the convergence-control parameter’. In addition, all of the terms
$c_{0}$
is an auxiliary parameter, called ‘the convergence-control parameter’. In addition, all of the terms
![]() ${\it\Delta}_{m-1}^{{\it\eta}},{\it\Delta}_{m-1}^{{\it\phi}},S_{m-1},\bar{S}_{m}$
on the right-hand side are determined by the known previous approximations
${\it\Delta}_{m-1}^{{\it\eta}},{\it\Delta}_{m-1}^{{\it\phi}},S_{m-1},\bar{S}_{m}$
on the right-hand side are determined by the known previous approximations
![]() ${\it\eta}_{j}$
and
${\it\eta}_{j}$
and
![]() ${\it\varphi}_{j}$
, where
${\it\varphi}_{j}$
, where
![]() $j=0,1,2,\ldots ,m-1$
. For details, please refer to appendix A. Thus, as long as the initial guess
$j=0,1,2,\ldots ,m-1$
. For details, please refer to appendix A. Thus, as long as the initial guess
![]() ${\it\varphi}_{0}$
of the velocity potential, the auxiliary linear operator
${\it\varphi}_{0}$
of the velocity potential, the auxiliary linear operator
![]() $\mathscr{L}$
and the convergence-control parameter
$\mathscr{L}$
and the convergence-control parameter
![]() $c_{0}$
are properly chosen, one can gain
$c_{0}$
are properly chosen, one can gain
![]() ${\it\eta}_{j}$
and
${\it\eta}_{j}$
and
![]() ${\it\varphi}_{j}$
one by one.
${\it\varphi}_{j}$
one by one.
It should be emphasized that, in the above-mentioned HAM-based approach (Liao Reference Liao2011), we have great freedom to choose the auxiliary linear operator
![]() ${\mathcal{L}}$
, the initial guesses
${\mathcal{L}}$
, the initial guesses
![]() ${\it\varphi}_{0}$
of the velocity potential and the convergence-control parameter
${\it\varphi}_{0}$
of the velocity potential and the convergence-control parameter
![]() $c_{0}$
. As mentioned by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014), it is the freedom of the HAM on the choice of the initial guess that provides us a way to handle the singularity of the steady-state exactly resonant waves. In addition, although the so-called ‘convergence-control parameter’
$c_{0}$
. As mentioned by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014), it is the freedom of the HAM on the choice of the initial guess that provides us a way to handle the singularity of the steady-state exactly resonant waves. In addition, although the so-called ‘convergence-control parameter’
![]() $c_{0}$
in (2.19) and (2.21) has no physical meanings, it provides us a simple way to guarantee the convergence of the solution series (2.18), as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014) for the steady-state exactly resonant waves.
$c_{0}$
in (2.19) and (2.21) has no physical meanings, it provides us a simple way to guarantee the convergence of the solution series (2.18), as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014) for the steady-state exactly resonant waves.
For the steady-state exactly resonant water waves satisfying the criterion (2.9), Liao (Reference Liao2011) chose the following auxiliary linear operator
which has the property
and
where
![]() $\mathscr{L}^{-1}$
is the inverse operator of
$\mathscr{L}^{-1}$
is the inverse operator of
![]() $\mathscr{L}$
,
$\mathscr{L}$
,
![]() ${\it\Psi}_{m,n}$
defined by (2.17) is the eigenfunction, and
${\it\Psi}_{m,n}$
defined by (2.17) is the eigenfunction, and
is an eigenvalue of
![]() ${\mathcal{L}}$
for arbitrary wavenumber
${\mathcal{L}}$
for arbitrary wavenumber
![]() $\boldsymbol{k}_{i}$
and the linear frequency
$\boldsymbol{k}_{i}$
and the linear frequency
![]() ${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
of the primary waves, where
${\it\omega}_{i}=\sqrt{g|\boldsymbol{k}_{i}|}$
of the primary waves, where
![]() $i=1,2$
, with the property
$i=1,2$
, with the property
In addition, in the case (2.9) for the exactly resonant waves, it holds
So, from a mathematical viewpoint, the exactly resonant wave system (2.9) has three eigenvalues to be zero, i.e.
Owing to (2.25), it is the additional zero eigenvalue (such as
![]() ${\it\lambda}_{2,-1}$
in the above-mentioned case) that brings singularity to the exactly resonant wave problems. Such kind of singularity is mathematically difficult to handle in the frame of perturbation methods, as mentioned by Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, it is easy to overcome in the frame of the HAM, as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014).
${\it\lambda}_{2,-1}$
in the above-mentioned case) that brings singularity to the exactly resonant wave problems. Such kind of singularity is mathematically difficult to handle in the frame of perturbation methods, as mentioned by Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, it is easy to overcome in the frame of the HAM, as illustrated by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Liu & Liao (Reference Liu and Liao2014).
Write
Thus,
corresponds to the exact resonance. So, it is reasonable to define
for the nearly resonant waves. Here
![]() $10^{-3}$
is a small number, which can be replaced by others such as
$10^{-3}$
is a small number, which can be replaced by others such as
![]() $10^{-4}$
, but the conclusions given in this paper are qualitatively the same.
$10^{-4}$
, but the conclusions given in this paper are qualitatively the same.
From a mathematical viewpoint, when the resonance criterion (2.9) is nearly satisfied, we have two zero eigenvalues
![]() ${\it\lambda}_{1.0}$
and
${\it\lambda}_{1.0}$
and
![]() ${\it\lambda}_{0,1}$
, and one eigenvalue
${\it\lambda}_{0,1}$
, and one eigenvalue
![]() ${\it\lambda}_{2,-1}$
very close to zero. In this case, the famous ‘small divisor problem’ (Poincaré Reference Poincaré1892; Yoccoz Reference Yoccoz1992) arises, and the above-mentioned HAM-based approach for steady-state exactly resonant waves (Liao Reference Liao2011; Xu et al.
Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) does not work, due to the same mathematical difficulties mentioned by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006) for three-dimensional periodic travelling waves.
${\it\lambda}_{2,-1}$
very close to zero. In this case, the famous ‘small divisor problem’ (Poincaré Reference Poincaré1892; Yoccoz Reference Yoccoz1992) arises, and the above-mentioned HAM-based approach for steady-state exactly resonant waves (Liao Reference Liao2011; Xu et al.
Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) does not work, due to the same mathematical difficulties mentioned by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006) for three-dimensional periodic travelling waves.
How to overcome this ‘small divisor problem’ in the frame of the HAM?
Note that the HAM-based approach (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) works well for the steady-state exactly resonant waves that have more than two zero eigenvalues. Can we transfer the nearly resonant wave problems into exactly resonant ones? If yes, the nearly resonant wave problems can be solved almost in the same way as the exactly resonant ones.
It should be emphasized that the HAM-based approach (Liao Reference Liao2011; Xu et al.
Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014) provides us great freedom to choose the auxiliary linear operator
![]() $\mathscr{L}$
. For the steady-state exactly resonant waves in case of (2.9), Liao (Reference Liao2011) simply chose the auxiliary linear operator (2.23), which is exactly the linear part of (2.11). However, if we choose the same auxiliary linear operator (2.23) for the nearly resonant waves, the small divisor
$\mathscr{L}$
. For the steady-state exactly resonant waves in case of (2.9), Liao (Reference Liao2011) simply chose the auxiliary linear operator (2.23), which is exactly the linear part of (2.11). However, if we choose the same auxiliary linear operator (2.23) for the nearly resonant waves, the small divisor
![]() ${\it\lambda}_{m,n}$
appears due to (2.25). Fortunately, in the frame of the HAM, it is not absolutely necessary to do so: the freedom provided by the HAM is so large that, for the steady-state nearly resonant waves, we can choose here such a new, generalized auxiliary linear operator
${\it\lambda}_{m,n}$
appears due to (2.25). Fortunately, in the frame of the HAM, it is not absolutely necessary to do so: the freedom provided by the HAM is so large that, for the steady-state nearly resonant waves, we can choose here such a new, generalized auxiliary linear operator
where
is a constant in the case that (2.9) is nearly satisfied, with the property
and
in which
![]() ${\it\Psi}_{m,n}$
defined by (2.17) is the eigenfunction,
${\it\Psi}_{m,n}$
defined by (2.17) is the eigenfunction,
is an eigenvalue of the generalized auxiliary linear operator (2.33), respectively.
This is mainly because we have great freedom to choose the auxiliary linear operator in the frame of the HAM-based approach (Liao Reference Liao2011). Note that, for the nearly resonant waves with the small eigenvalue
![]() $0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$
, there are only two zero eigenvalues
$0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$
, there are only two zero eigenvalues
![]() ${\it\lambda}_{1,0}={\it\lambda}_{0,1}=0$
, where
${\it\lambda}_{1,0}={\it\lambda}_{0,1}=0$
, where
![]() ${\it\lambda}_{m,n}$
defined by (2.26) is the eigenvalue of the auxiliary linear operator (2.23) that comes from the linear part of the original wave equations. However, using the generalized auxiliary linear operator (2.33), we have now three zero eigenvalues
${\it\lambda}_{m,n}$
defined by (2.26) is the eigenvalue of the auxiliary linear operator (2.23) that comes from the linear part of the original wave equations. However, using the generalized auxiliary linear operator (2.33), we have now three zero eigenvalues
where
![]() $\bar{{\it\lambda}}_{m,n}$
is the eigenvalue of (2.33), with the same eigenfunction
$\bar{{\it\lambda}}_{m,n}$
is the eigenvalue of (2.33), with the same eigenfunction
![]() ${\it\Psi}_{m,n}$
defined by (2.17). In this way, the small divisor (due to small eigenvalue such as
${\it\Psi}_{m,n}$
defined by (2.17). In this way, the small divisor (due to small eigenvalue such as
![]() ${\it\lambda}_{2,-1}$
) at low frequency is avoided, or at least moved far away to rather high frequency with physically negligible wave energy, as illustrated below.
${\it\lambda}_{2,-1}$
) at low frequency is avoided, or at least moved far away to rather high frequency with physically negligible wave energy, as illustrated below.
In the case (2.9) of the exactly resonant waves with
![]() ${\it\lambda}_{2,-1}=0$
, corresponding to
${\it\lambda}_{2,-1}=0$
, corresponding to
due to the definition (2.26), we have
![]() ${\it\mu}=2$
according to the definition (2.34). However, when (2.9) is nearly satisfied,
${\it\mu}=2$
according to the definition (2.34). However, when (2.9) is nearly satisfied,
![]() ${\it\mu}$
deviates from 2 a little, so that the generalized auxiliary linear operator (2.33) is a little different from (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves. Therefore, the auxiliary linear operator (2.33) works not only for the nearly resonant cases (such as
${\it\mu}$
deviates from 2 a little, so that the generalized auxiliary linear operator (2.33) is a little different from (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves. Therefore, the auxiliary linear operator (2.33) works not only for the nearly resonant cases (such as
![]() $0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$
) but also for exactly resonant ones (such as
$0<|{\it\lambda}_{2,-1}|\leqslant 10^{-3}$
) but also for exactly resonant ones (such as
![]() ${\it\lambda}_{2,-1}=0$
), since all other mathematical formulae are the same (Liao Reference Liao2011), as described in appendix A. In other words, the auxiliary linear operator (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves is only a special case of the new auxiliary linear operator (2.33) for the nearly resonant ones. Thus, as long as the generalized auxiliary linear operator (2.33) is used, there always exist three zero eigenvalues
${\it\lambda}_{2,-1}=0$
), since all other mathematical formulae are the same (Liao Reference Liao2011), as described in appendix A. In other words, the auxiliary linear operator (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves is only a special case of the new auxiliary linear operator (2.33) for the nearly resonant ones. Thus, as long as the generalized auxiliary linear operator (2.33) is used, there always exist three zero eigenvalues
no matter whether the criterion (2.9) is either exactly or nearly satisfied. In other words, we can solve the steady-state nearly resonant waves almost in the same way as the exactly resonant ones. Therefore, from the viewpoints of the HAM, the steady-state nearly resonant water waves have nothing fundamentally different from the exactly resonant waves, except the more general definition (2.33) of the auxiliary linear operator
![]() $\mathscr{L}$
. We will illustrate this point in § 3 by means of a case study.
$\mathscr{L}$
. We will illustrate this point in § 3 by means of a case study.
In summary, our strategy is to transfer the nearly resonant wave problem (with two zero eigenvalues
![]() $\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=0$
and one small eigenvalue
$\bar{{\it\lambda}}_{1,0}=\bar{{\it\lambda}}_{0,1}=0$
and one small eigenvalue
![]() $\bar{{\it\lambda}}_{2,-1}$
that leads to small divisor problem) into the corresponding exactly resonant wave problem with three zero eigenvalues
$\bar{{\it\lambda}}_{2,-1}$
that leads to small divisor problem) into the corresponding exactly resonant wave problem with three zero eigenvalues
by means of choosing a generalized auxiliary linear operator (2.33) in the frame of the HAM. Note that the steady-state exactly resonant travelling waves in deep water and in finite depth governed by the full wave equations were successfully solved by means of the HAM (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012; Liu & Liao Reference Liu and Liao2014), and also observed experimentally in a laboratory with good agreement between analytic approximation and experimental results (Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). Here, it should be emphasized that, it is the HAM that provides us such kind of freedom to choose the generalized auxiliary linear operator (2.33), which is different from the linear part (2.23) of the original wave equations. This is quite different from perturbation methods (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and the numerical approaches (Meiron et al. Reference Meiron, Saffman and Yuen1982; Craig & Nicholls Reference Craig and Nicholls2002; Nicholls & Reitich Reference Nicholls and Reitich2006), which always regard the linear part (2.23) of the original wave equations as a linear operator. As a result, perturbation methods and these numerical approaches had to directly handle the small divisor problem, which is mathematically very difficult to overcome, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002), Nicholls & Reitich (Reference Nicholls and Reitich2006) and Madsen & Fuhrman (Reference Madsen and Fuhrman2012). This is the novelty value of our HAM-based approach for the steady-state nearly resonant travelling waves.
3 A case study
Without loss of generality, we consider here such a case that the resonance criterion (2.9) is satisfied either exactly or nearly, which can be solved by means of the HAM-based approach (Liao Reference Liao2011) using the generalized auxiliary linear operator (2.33). Moreover, without loss of generality, we consider a special case
where
![]() ${\it\alpha}$
denotes the angle between the wavenumbers
${\it\alpha}$
denotes the angle between the wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
,
$\boldsymbol{k}_{2}$
,
![]() ${\it\sigma}_{i}$
is the actual frequency,
${\it\sigma}_{i}$
is the actual frequency,
![]() ${\it\omega}_{i}=\sqrt{gk_{i}}$
with
${\it\omega}_{i}=\sqrt{gk_{i}}$
with
![]() $k_{i}=|\boldsymbol{k}_{i}|$
is the linear frequency and
$k_{i}=|\boldsymbol{k}_{i}|$
is the linear frequency and
![]() ${\it\epsilon}$
is a constant, respectively. Note that the resonance criterion (2.9) is exactly satisfied when
${\it\epsilon}$
is a constant, respectively. Note that the resonance criterion (2.9) is exactly satisfied when
![]() $k_{2}/k_{1}=0.8925$
, a case studied by Liao (Reference Liao2011) in detail. Except the generalized auxiliary linear operator (2.33), all other formulae are exactly the same as those for the steady-state exactly resonant waves (Liao Reference Liao2011), as mentioned in appendix A. The (numerically) convergent analytic approximations of the steady-state wave systems for
$k_{2}/k_{1}=0.8925$
, a case studied by Liao (Reference Liao2011) in detail. Except the generalized auxiliary linear operator (2.33), all other formulae are exactly the same as those for the steady-state exactly resonant waves (Liao Reference Liao2011), as mentioned in appendix A. The (numerically) convergent analytic approximations of the steady-state wave systems for
![]() $0.89\leqslant k_{2}/k_{1}\leqslant 0.895$
in the case of (3.1) with
$0.89\leqslant k_{2}/k_{1}\leqslant 0.895$
in the case of (3.1) with
![]() ${\it\epsilon}=1.0003$
are obtained almost in the same way to that described by Liao (Reference Liao2011) for the steady-state exactly resonant waves. For details, please refer to appendix A.
${\it\epsilon}=1.0003$
are obtained almost in the same way to that described by Liao (Reference Liao2011) for the steady-state exactly resonant waves. For details, please refer to appendix A.
We emphasize here that, unlike perturbation techniques and other analytic approximation methods, our HAM-based approach contains the so-called ‘convergence-control parameter’
![]() $c_{0}$
, which has no physical meanings but can provide us a convenient way to guarantee the convergence of solution series. For example, in case of
$c_{0}$
, which has no physical meanings but can provide us a convenient way to guarantee the convergence of solution series. For example, in case of
![]() $k_{2}/k_{1}=0.8915$
(corresponding to a case of nearly resonant waves), the solution series converges (strictly speaking, here it is a kind of ‘numerical’ convergence, since we just numerically show the decrease of residual errors versus the order of approximation, which however is not a mathematical proof), rather quickly by means of
$k_{2}/k_{1}=0.8915$
(corresponding to a case of nearly resonant waves), the solution series converges (strictly speaking, here it is a kind of ‘numerical’ convergence, since we just numerically show the decrease of residual errors versus the order of approximation, which however is not a mathematical proof), rather quickly by means of
![]() $-1.25\leqslant c_{0}\leqslant -0.75$
, with the optimal value of
$-1.25\leqslant c_{0}\leqslant -0.75$
, with the optimal value of
![]() $c_{0}$
near
$c_{0}$
near
![]() $-0.95$
, as shown in table 1. In fact, the numerical convergence of solution series given by the HAM for exactly resonant waves was generally guaranteed in the same way, as shown by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), Liu & Liao (Reference Liu and Liao2014) and Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). Note that the numerically convergent analytic approximations for the steady-state exactly resonant waves in deep water given by the HAM-based approach agreed well with the experimental observation in a laboratory, as mentioned by Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015).
$-0.95$
, as shown in table 1. In fact, the numerical convergence of solution series given by the HAM for exactly resonant waves was generally guaranteed in the same way, as shown by Liao (Reference Liao2011), Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), Liu & Liao (Reference Liu and Liao2014) and Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015). Note that the numerically convergent analytic approximations for the steady-state exactly resonant waves in deep water given by the HAM-based approach agreed well with the experimental observation in a laboratory, as mentioned by Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015).
Table 1. Averaged residual errors versus order of approximation for nearly resonant waves in case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}=1.0003$
and
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}=1.0003$
and
![]() $k_{2}/k_{1}=0.8915$
by means of different values of the convergence-control parameter
$k_{2}/k_{1}=0.8915$
by means of different values of the convergence-control parameter
![]() $c_{0}$
, with the corresponding distribution of wave energy 81.9 % (the first primary wave component), 9.7 % (the second primary one) and 8.2 % (the nearly resonant one). The angle between two wavenumbers
$c_{0}$
, with the corresponding distribution of wave energy 81.9 % (the first primary wave component), 9.7 % (the second primary one) and 8.2 % (the nearly resonant one). The angle between two wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
.
${\rm\pi}/36$
.
![]() $\mathscr{E}_{{\it\phi}}$
and
$\mathscr{E}_{{\it\phi}}$
and
![]() $\mathscr{E}_{{\it\eta}}$
denote the averaged residual errors of the two boundary conditions on the free surface.
$\mathscr{E}_{{\it\eta}}$
denote the averaged residual errors of the two boundary conditions on the free surface.

Table 2. Energy distribution of the steady-state exactly or nearly resonant waves in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
. The angle between two wavenumbers
$k_{2}/k_{1}$
. The angle between two wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
, and
${\rm\pi}/36$
, and
![]() $^{\ast }$
denotes the exactly resonant wave.
$^{\ast }$
denotes the exactly resonant wave.

In addition, unlike perturbation techniques, the HAM provides us great freedom to choose auxiliary linear operator
![]() $\mathscr{L}$
. The original linear operator (2.23) is widely used in perturbation approaches, which unfortunately leads to the so-called ‘small divisor problem’ at a low frequency (say,
$\mathscr{L}$
. The original linear operator (2.23) is widely used in perturbation approaches, which unfortunately leads to the so-called ‘small divisor problem’ at a low frequency (say,
![]() $m=2,n=-1$
, corresponding to the wave component
$m=2,n=-1$
, corresponding to the wave component
![]() $\cos (2{\it\xi}_{1}-{\it\xi}_{2})$
) for the nearly resonant case considered in this paper. Such kind of ‘small divisor problem’ is very difficult to overcome in mathematics, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002), Nicholls & Reitich (Reference Nicholls and Reitich2006) and Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, by means of simply choosing a new auxiliary linear operator (2.33) in the frame of the HAM, such kind of ‘small divisor problem’ can be easily avoided: it is found that, in the case considered in table 1, the so-called ‘small divisor problem’, corresponding to
$\cos (2{\it\xi}_{1}-{\it\xi}_{2})$
) for the nearly resonant case considered in this paper. Such kind of ‘small divisor problem’ is very difficult to overcome in mathematics, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002), Nicholls & Reitich (Reference Nicholls and Reitich2006) and Madsen & Fuhrman (Reference Madsen and Fuhrman2012). However, by means of simply choosing a new auxiliary linear operator (2.33) in the frame of the HAM, such kind of ‘small divisor problem’ can be easily avoided: it is found that, in the case considered in table 1, the so-called ‘small divisor problem’, corresponding to
![]() ${\it\delta}_{m,n}<10^{-3}$
with the definition (2.30), does not occur at least for
${\it\delta}_{m,n}<10^{-3}$
with the definition (2.30), does not occur at least for
by means of using the generalized auxiliary linear operator (2.33). From physical viewpoints, the kinetic energy of wave components with very high frequency, such as
is rather small and thus can be ignored. Therefore, in the frame of the HAM, the small divisor problem does not appear even at the 1000th-order of approximations. Note that such high-order analytic approximations are unnecessary from numerical viewpoint, since the averaged residual errors of the two boundary conditions are at the level of
![]() $10^{-20}$
by means of the optimal convergence-control parameter
$10^{-20}$
by means of the optimal convergence-control parameter
![]() $c_{0}=-0.95$
, as shown in table 1. In this way, the ‘small divisor’ at the low frequency of the steady-state nearly resonant waves is successfully moved far away to much higher frequencies, or even to infinity (although we cannot strictly prove this point right now for the considered case). This is mainly because the HAM is fundamentally different from other perturbation approaches, since it has nothing to do with any small physical parameters at all. Note that all other perturbation approaches cannot avoid such kind of ‘small divisor problems’. In other words, our HAM-based approach for the nearly resonant waves is novel, even only from the viewpoint that it can easily move the ‘small divisors’ at low frequency far away to rather high frequency by means of simply choosing the generalized auxiliary linear operator (2.33) that is different from the linear part (2.23) of the original wave equations.
$c_{0}=-0.95$
, as shown in table 1. In this way, the ‘small divisor’ at the low frequency of the steady-state nearly resonant waves is successfully moved far away to much higher frequencies, or even to infinity (although we cannot strictly prove this point right now for the considered case). This is mainly because the HAM is fundamentally different from other perturbation approaches, since it has nothing to do with any small physical parameters at all. Note that all other perturbation approaches cannot avoid such kind of ‘small divisor problems’. In other words, our HAM-based approach for the nearly resonant waves is novel, even only from the viewpoint that it can easily move the ‘small divisors’ at low frequency far away to rather high frequency by means of simply choosing the generalized auxiliary linear operator (2.33) that is different from the linear part (2.23) of the original wave equations.

Figure 1. Wave energy distribution (%) of the first primary wave of the steady-state exactly and nearly resonant wave system in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.

Figure 2. Wave energy distribution (%) of the second primary wave of the steady-state exactly and nearly resonant wave system in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.

Figure 3. Wave energy distribution (%) of the wave component
![]() $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
of the steady-state exactly and nearly resonant wave system in the case of
$\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
of the steady-state exactly and nearly resonant wave system in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
Here, we use another extraordinary advantage of the HAM, i.e. its freedom on choice of equation type for high-order approximations. In fact, such kind of advantage of the HAM has been successfully applied to many nonlinear problems, as illustrated by Liao & Tan (Reference Liao and Tan2007) who applied the HAM to successfully solve a second-order two-dimensional Gelfand equation even by means of a fourth-order auxiliary linear operator, and a second-order three-dimensional Gelfand equation even by means of a sixth-order auxiliary linear operator, respectively. In this paper, we further illustrate that, by means of simply choosing the generalized auxiliary linear operator (2.33) in the frame of the HAM, the so-called ‘small divisor’ can be easily moved far away from the low frequency to a very high one, where kinetic energy of wave components can be ignored from a physical viewpoint.
Given a value of
![]() $k_{2}/k_{1}$
, we search for the corresponding steady-state nearly (or exactly) resonant waves by means of the HAM-based approach mentioned above, and then gain the distribution of wave energy by means of (2.8). It is found that there exist multiple solutions in most cases, as shown in figures 1–3. The energy distribution (%) of the two primary waves (with the wavenumbers
$k_{2}/k_{1}$
, we search for the corresponding steady-state nearly (or exactly) resonant waves by means of the HAM-based approach mentioned above, and then gain the distribution of wave energy by means of (2.8). It is found that there exist multiple solutions in most cases, as shown in figures 1–3. The energy distribution (%) of the two primary waves (with the wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
) and the nearly (or exactly) resonant wave component (with the wavenumber
$\boldsymbol{k}_{2}$
) and the nearly (or exactly) resonant wave component (with the wavenumber
![]() $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
) is given in table 2.
$\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
) is given in table 2.
Note that the resonance criterion (2.9) is exactly satisfied when
![]() $k_{2}/k_{1}=0.8925$
in the case of (3.1). The results of the exact resonance are marked by the filled squares in figures 1–3. It is very interesting that the exactly resonant results are not fundamentally different from other nearly resonant ones: from figures 1–3, one cannot distinguish the exactly resonant results from the nearly resonant ones. It suggests that, from physical viewpoints, nothing is fundamentally different between the steady-state exactly resonant waves and the steady-state nearly resonant ones. Note also that, mathematically speaking, both of the exactly and nearly resonant results are obtained in the same way by means of the same auxiliary linear operator (2.33) in the frame of the HAM. Therefore, from numerical viewpoints, nothing is fundamentally different between the exactly resonant waves and the nearly resonant ones either.
$k_{2}/k_{1}=0.8925$
in the case of (3.1). The results of the exact resonance are marked by the filled squares in figures 1–3. It is very interesting that the exactly resonant results are not fundamentally different from other nearly resonant ones: from figures 1–3, one cannot distinguish the exactly resonant results from the nearly resonant ones. It suggests that, from physical viewpoints, nothing is fundamentally different between the steady-state exactly resonant waves and the steady-state nearly resonant ones. Note also that, mathematically speaking, both of the exactly and nearly resonant results are obtained in the same way by means of the same auxiliary linear operator (2.33) in the frame of the HAM. Therefore, from numerical viewpoints, nothing is fundamentally different between the exactly resonant waves and the nearly resonant ones either.
We studied many cases different from (3.1) in a similar way, and always obtained the corresponding steady-state nearly resonant waves. In all of our considered cases, the results of steady-state exactly resonant waves have nothing fundamentally different from those of nearly resonant ones. Thus, from physical viewpoints and in the frame of the HAM, nothing is fundamentally different between the steady-state exactly and nearly resonant waves.
All of our above-mentioned conclusions are based on the HAM-based approach for the full wave equations in deep water. Like Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012), we further numerically solve the Zakharov’s equation so as to verify the correctness of our above-mentioned conclusions. The numerical approach based on the Zakharov’s equation is described briefly in appendix B. For the same cases, numerical results given by the Zakharov’s equation are fundamentally the same as the analytical ones given by our HAM-based approach for the full wave equations, as shown in figures 4–6. In particular, from a physical viewpoint, the results of the steady-state exactly resonant waves (marked by the filled squares) have nothing fundamentally different from those of the nearly resonant ones either. This verifies the validity of the above-mentioned HAM-based approach and our analytic approximations gained from the full wave equations.

Figure 4. Wave energy distribution (%) obtained by Zakharov equation of the first primary wave of the steady-state exactly and nearly resonant wave system in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.

Figure 5. Wave energy distribution (%) obtained by Zakharov equation of the second primary wave of the steady-state exactly and nearly resonant wave system in case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.

Figure 6. Wave energy distribution (%) obtained by Zakharov equation of the wave component
![]() $\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
of the steady-state exactly and nearly resonant wave system in the case of
$\boldsymbol{k}_{3}=2\boldsymbol{k}_{1}-\boldsymbol{k}_{2}$
of the steady-state exactly and nearly resonant wave system in the case of
![]() ${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
${\it\sigma}_{1}/\sqrt{gk_{1}}={\it\sigma}_{2}/\sqrt{gk_{2}}={\it\epsilon}=1.0003$
with various
![]() $k_{2}/k_{1}$
, when the angle between wavenumbers
$k_{2}/k_{1}$
, when the angle between wavenumbers
![]() $\boldsymbol{k}_{1}$
and
$\boldsymbol{k}_{1}$
and
![]() $\boldsymbol{k}_{2}$
of the two primary waves is
$\boldsymbol{k}_{2}$
of the two primary waves is
![]() ${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
${\rm\pi}/36$
. The filled squares correspond to the exactly resonant wave.
4 Concluding remarks and discussions
In this paper, the HAM-based approach given by Liao (Reference Liao2011) for the steady-state exactly resonant waves is generalized for the steady-state nearly resonant waves by simply choosing the generalized auxiliary linear operator (2.33) but keeping all other formulae the same. In this way, we successfully gained, for the first time, the steady-state nearly resonant waves with time-independent spectrum in deep water. To the best of the authors’ knowledge, this kind of steady-state nearly resonant wave has not been obtained analytically from the full wave equations. Therefore, considering the published results about the steady-state exactly resonant waves (Liao Reference Liao2011; Xu et al. Reference Xu, Lin, Liao and Stiassnie2012, Reference Xu, Lin and Liao2015; Liu & Liao Reference Liu and Liao2014; Liu et al. Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015), steady-state gravity waves with time-independent amplitudes widely exist, no matter whether the resonance criterion is exactly or nearly satisfied.
Note that the HAM-based approach for the exactly resonant waves does not work for the nearly resonant ones, since the famous ‘small divisor problem’ appears. Even for numerical approaches, the small divisor problem is rather difficult to overcome in mathematics, as pointed out by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006). Our strategy is to mathematically transfer the steady-state nearly resonant wave problem into the corresponding exactly resonant ones by means of choosing a more general auxiliary linear operator (2.33) than the linear part (2.23) of the original wave equations. In this way, the ‘small divisor problem’ at low frequency is moved far away to rather high frequency with physically negligible wave energy, such as the wave component
with a tiny wave amplitude
![]() $A_{m,n}$
much smaller than the small divisor, illustrated in a case study in § 3. Note that it is the HAM that provides us such kind of freedom to choose the generalized auxiliary linear operator (2.33): perturbation and numerical approaches often directly use the linear part (2.23) of the original wave equations, and thus had to directly handle the small divisor problems. So, our HAM-based analytic approximation approach is fundamentally different from other perturbation methods (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and numerical approaches (Meiron et al.
Reference Meiron, Saffman and Yuen1982; Craig & Nicholls Reference Craig and Nicholls2002; Nicholls & Reitich Reference Nicholls and Reitich2006). This also shows the novelty and originality of our approach for the steady-state nearly resonant travelling waves.
$A_{m,n}$
much smaller than the small divisor, illustrated in a case study in § 3. Note that it is the HAM that provides us such kind of freedom to choose the generalized auxiliary linear operator (2.33): perturbation and numerical approaches often directly use the linear part (2.23) of the original wave equations, and thus had to directly handle the small divisor problems. So, our HAM-based analytic approximation approach is fundamentally different from other perturbation methods (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and numerical approaches (Meiron et al.
Reference Meiron, Saffman and Yuen1982; Craig & Nicholls Reference Craig and Nicholls2002; Nicholls & Reitich Reference Nicholls and Reitich2006). This also shows the novelty and originality of our approach for the steady-state nearly resonant travelling waves.
When the resonance criterion (2.9) is exactly satisfied, the general auxiliary linear operator (2.33) is the same (with
![]() ${\it\mu}=2$
) as (2.23) for the exact resonance (Liao Reference Liao2011), with three eigenvalues being zero. However, using the more general auxiliary linear operator (2.33), we always have three eigenvalues being zero, even in the case of the nearly resonant waves. So, from the viewpoint of the HAM, nothing is fundamentally different between the steady-state exactly and nearly resonant waves. Moreover, from figures 1–3, one cannot distinguish the results of the exact resonance from all other near-resonances. So, from the physical viewpoint, the results of the steady-state exactly resonant waves also have nothing fundamentally different from the nearly resonant ones, either.
${\it\mu}=2$
) as (2.23) for the exact resonance (Liao Reference Liao2011), with three eigenvalues being zero. However, using the more general auxiliary linear operator (2.33), we always have three eigenvalues being zero, even in the case of the nearly resonant waves. So, from the viewpoint of the HAM, nothing is fundamentally different between the steady-state exactly and nearly resonant waves. Moreover, from figures 1–3, one cannot distinguish the results of the exact resonance from all other near-resonances. So, from the physical viewpoint, the results of the steady-state exactly resonant waves also have nothing fundamentally different from the nearly resonant ones, either.
Therefore, from the physical viewpoints and in the frame of the HAM, nothing is fundamentally different between the steady-state exactly/nearly resonant waves with time-independent spectrum. Then, a question arises: why should we define the so-called ‘exactly resonant waves’? Let us consider such a thought experiment. Suppose that a person, who does not know Phillips’ criterion of wave resonance at all, applies the above-mentioned HAM-based approach to solve the steady-state travelling waves with time-independent spectrum. For them, the results in the case (2.9) at
![]() $k_{2}/k_{1}=0.8925$
have nothing special at all from physical viewpoints. In addition, in the frame of the HAM, all results are gained by using the same mathematical formulae with the same auxiliary linear operator (2.33). Thus, it seems unnecessary for them to define the special case
$k_{2}/k_{1}=0.8925$
have nothing special at all from physical viewpoints. In addition, in the frame of the HAM, all results are gained by using the same mathematical formulae with the same auxiliary linear operator (2.33). Thus, it seems unnecessary for them to define the special case
![]() $k_{2}/k_{1}=0.8925$
, which is traditionally called the ‘exactly resonant waves’ in the frame of perturbation methods. Note that the physics behind the same experimental observations should be independent of the used mathematical methods. So, this thought experiment suggests that the essence of the so-called ‘wave resonance’ should be reconsidered carefully from both physical and mathematical viewpoints.
$k_{2}/k_{1}=0.8925$
, which is traditionally called the ‘exactly resonant waves’ in the frame of perturbation methods. Note that the physics behind the same experimental observations should be independent of the used mathematical methods. So, this thought experiment suggests that the essence of the so-called ‘wave resonance’ should be reconsidered carefully from both physical and mathematical viewpoints.
The KP equation is a simplified model for water waves in shallow water. As pointed out by Hammack et al. (Reference Hammack, Scheffner and Segur1989, Reference Hammack, Henderson and Segur2005) and Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997), the KP equation has a closed-form solution with arbitrary two phase variables. Thus, there exist the steady-state exactly and nearly resonant waves of the KP equation in shallow water, although Hammack et al. (Reference Hammack, Scheffner and Segur1989, Reference Hammack, Henderson and Segur2005) and Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997) did not mention the wave resonance at all. However, the KP equation is only valid for waves in shallow water, and thus cannot describe waves in deep water. For example, Dubrovin et al. (Reference Dubrovin, Flickinger and Segur1997) gave closed-form analytic solutions of the KP equation with three phases for travelling waves in shallow water, and found that ‘almost every three-phase solution is time-dependent, in every coordinate system’. This conclusion is not correct for waves in deep water, since rather complicated steady-state exactly resonant waves in deep water are indeed found by Liu & Liao (Reference Liu and Liao2014) for the full wave equations. To the best of the authors’ knowledge, the steady-state nearly resonant waves in deep water with time-independent spectrum have never been obtained from the full wave equations in the form of analytic approximations. Neither have they been gained by other perturbation techniques (Madsen & Fuhrman Reference Madsen and Fuhrman2012) and numerical approaches due to the small divisor problem, as mentioned by Meiron et al. (Reference Meiron, Saffman and Yuen1982), Craig & Nicholls (Reference Craig and Nicholls2002) and Nicholls & Reitich (Reference Nicholls and Reitich2006).
Certainly, a lot of work should be done in future. Similarly, it is straightforward to gain the steady-state nearly resonant waves in a constant water depth and over a bottom with an infinite number of periodic ripples, in a similar manner to Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) and Xu et al. (Reference Xu, Lin and Liao2015) for the exactly resonant ones. In addition, it is quite possible to observe the steady-state nearly resonant waves in deep water experimentally (For this purpose, the steady-state nearly resonant water waves with large enough nonlinearity should be used.) in a basin, just like Liu et al. (Reference Liu, Xu, Li, Peng, Alsaedi and Liao2015) did for the steady-state exactly resonant waves.
The HAM-based analytic approximation approach can successfully avoid the small-divisor problem (related to the nearly resonant wave propagation) by means of moving small divisor at low frequency far away to rather high frequencies with physically negligible wave energy. This is reasonable from physical and numerical viewpoints. However, from strictly mathematical viewpoints, the small divisor might be still an obstacle, since it is even unknown whether or not a solution exists mathematically (Craig & Nicholls (Reference Craig and Nicholls2000) gave a rigorous proof of an existence theorem for two- and three-dimensional travelling water waves in the presence of capillarity. No existence theorems have been strictly proved for water waves in general, to the best of the authors’ knowledge). This is similar to the famous Navier–Stokes equations, whose numerical solutions are widely used, but solution existence of the Navier–Stokes equations is not strictly proved mathematically in general.
Acknowledgements
Sincere thanks are due to the anonymous reviewers for their helpful comments. This work is partly supported by the National Natural Science Foundation of China (approval numbers 11272209 and 11432009) and National Key Basic Research Program of China (approval number 2014CB046801). This research was also supported by the Israel Science Foundation (grant number 464/13).
Appendix A. Detailed mathematical formulae
The full water wave equations (2.10)–(2.13) for the steady-state nearly resonant waves in deep water can be solved by means of the HAM nearly in the same way as that mentioned by Liao (Reference Liao2011). Shortly speaking, our strategy is to transfer the steady-state nearly resonant waves into a steady-state exactly resonant ones, by means of choosing a generalized auxiliary linear operator that is a little different from the linear part of the original wave equations.
Let
![]() ${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
denote a initial guess solution of velocity potential
${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
denote a initial guess solution of velocity potential
![]() ${\it\varphi}$
satisfying the Laplace equation (2.10) and the bottom boundary condition (2.13),
${\it\varphi}$
satisfying the Laplace equation (2.10) and the bottom boundary condition (2.13),
![]() ${\mathcal{L}}$
an auxiliary linear operator with the property
${\mathcal{L}}$
an auxiliary linear operator with the property
![]() $\mathscr{L}[0]=0$
, and
$\mathscr{L}[0]=0$
, and
![]() $q\in [0,1]$
an embedding parameter without physical meaning, respectively. In the frame of the HAM, we first construct a family of solution
$q\in [0,1]$
an embedding parameter without physical meaning, respectively. In the frame of the HAM, we first construct a family of solution
![]() ${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
and
${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
and
![]() ${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
in
${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
in
![]() $q\in [0,1]$
by means of the so-called zeroth-order deformation equation
$q\in [0,1]$
by means of the so-called zeroth-order deformation equation
subject to the two boundary conditions on the unknown wave elevation
![]() $z={\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
:
$z={\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
:
and also the impermeable condition at the bottom
where
![]() $\mathscr{N}_{1}$
and
$\mathscr{N}_{1}$
and
![]() $\mathscr{N}_{2}$
are two nonlinear operators defined by (2.11) and (2.12),
$\mathscr{N}_{2}$
are two nonlinear operators defined by (2.11) and (2.12),
![]() $c_{0}\neq 0$
is the so-called ‘convergence-control parameter’ without physical meanings, respectively.
$c_{0}\neq 0$
is the so-called ‘convergence-control parameter’ without physical meanings, respectively.
When
![]() $q=0$
, the two boundary conditions (A 2) and (A 3) are automatically satisfied, thus we have the solution
$q=0$
, the two boundary conditions (A 2) and (A 3) are automatically satisfied, thus we have the solution
since
![]() $\mathscr{L}[0]=0$
and the initial guess
$\mathscr{L}[0]=0$
and the initial guess
![]() ${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
satisfies the Laplace equation (2.10) and the bottom boundary condition (2.13). When
${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
satisfies the Laplace equation (2.10) and the bottom boundary condition (2.13). When
![]() $q=1$
, since
$q=1$
, since
![]() $c_{0}\neq 0$
, the zeroth-order deformation equations (A 1)–(A 4) are equivalent to the original equations (2.10)–(2.13), so that we have
$c_{0}\neq 0$
, the zeroth-order deformation equations (A 1)–(A 4) are equivalent to the original equations (2.10)–(2.13), so that we have
Therefore, as
![]() $q$
increases from 0 to 1,
$q$
increases from 0 to 1,
![]() ${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
varies from the initial guess
${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
varies from the initial guess
![]() ${\it\varphi}_{0}$
to the unknown velocity potential
${\it\varphi}_{0}$
to the unknown velocity potential
![]() ${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
, so does
${\it\varphi}({\it\xi}_{1},{\it\xi}_{2},z)$
, so does
![]() ${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
from
${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
from
![]() $z=0$
to the unknown wave elevation
$z=0$
to the unknown wave elevation
![]() ${\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
, respectively. Note that, in the frame of the HAM, we have great freedom to choose the auxiliary linear operator
${\it\eta}({\it\xi}_{1},{\it\xi}_{2})$
, respectively. Note that, in the frame of the HAM, we have great freedom to choose the auxiliary linear operator
![]() $\mathscr{L}$
, the initial guess
$\mathscr{L}$
, the initial guess
![]() ${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
and the convergence-control parameter
${\it\varphi}_{0}({\it\xi}_{1},{\it\xi}_{2},z)$
and the convergence-control parameter
![]() $c_{0}$
. Assume that all of them are so properly chosen that both of
$c_{0}$
. Assume that all of them are so properly chosen that both of
![]() ${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
and
${\it\Phi}({\it\xi}_{1},{\it\xi}_{2},z;q)$
and
![]() ${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
vary continuously and in addition that they are analytic with respect to the embedding parameter
${\it\zeta}({\it\xi}_{1},{\it\xi}_{2};q)$
vary continuously and in addition that they are analytic with respect to the embedding parameter
![]() $q\in [0,1]$
. Then, we have the Maclaurin series with respect to
$q\in [0,1]$
. Then, we have the Maclaurin series with respect to
![]() $q$
:
$q$
:
where
Furthermore, assuming that the auxiliary linear operator
![]() $\mathscr{L}$
and especially the convergence-control parameter
$\mathscr{L}$
and especially the convergence-control parameter
![]() $c_{0}$
are so properly chosen that the above two Maclaurin series (A 7) and (A 8) are convergent at
$c_{0}$
are so properly chosen that the above two Maclaurin series (A 7) and (A 8) are convergent at
![]() $q=1$
, we have according to (A 6) the homotopy-series solution
$q=1$
, we have according to (A 6) the homotopy-series solution
respectively.
Substituting the Maclaurin series (A 7) and (A 8) into the zeroth-order deformation equations (A 1)–(A 4) and then equating the like-power of
![]() $q$
, we have the so-called high-order deformation equation
$q$
, we have the so-called high-order deformation equation
subject to the linear boundary condition
and the bed condition
together with
where
![]() ${\it\chi}_{1}=0$
and
${\it\chi}_{1}=0$
and
![]() ${\it\chi}_{m}=1$
for
${\it\chi}_{m}=1$
for
![]() $m>1$
, and all of the terms
$m>1$
, and all of the terms
![]() ${\it\Delta}_{m-1}^{{\it\eta}},{\it\Delta}_{m-1}^{{\it\phi}},S_{m-1},\bar{S}_{m}$
on the right-hand side of (A 13) are determined by the known previous approximations
${\it\Delta}_{m-1}^{{\it\eta}},{\it\Delta}_{m-1}^{{\it\phi}},S_{m-1},\bar{S}_{m}$
on the right-hand side of (A 13) are determined by the known previous approximations
![]() ${\it\eta}_{j}$
and
${\it\eta}_{j}$
and
![]() ${\it\varphi}_{j}$
(
${\it\varphi}_{j}$
(
![]() $j=0,1,2,\ldots ,m-1$
), whose definitions are exactly the same as those given by Liao (Reference Liao2011). For the sake of simplicity, we neglect their detailed definitions here.
$j=0,1,2,\ldots ,m-1$
), whose definitions are exactly the same as those given by Liao (Reference Liao2011). For the sake of simplicity, we neglect their detailed definitions here.
Note that
![]() ${\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z)$
is in the form
${\it\varphi}_{m}({\it\xi}_{1},{\it\xi}_{2},z)$
is in the form
where
automatically satisfies the Laplace equation (A 12) and the bed condition (A 14). Note that it is straightforward to gain
![]() ${\it\eta}_{m}$
by means of (A 15). So, only the linear boundary condition (A 13) need be satisfied. Thus, we have a special solution
${\it\eta}_{m}$
by means of (A 15). So, only the linear boundary condition (A 13) need be satisfied. Thus, we have a special solution
where
![]() $\mathscr{L}^{-1}$
is the inverse operator of the auxiliary linear operator
$\mathscr{L}^{-1}$
is the inverse operator of the auxiliary linear operator
![]() $\mathscr{L}$
.
$\mathscr{L}$
.
Note that the high-order deformation equations (A 12)–(A 14) are linear. Thus, in the frame of the HAM, we transfer the original nonlinear problem into an infinite number of linear sub-problems. However, unlike perturbation methods, such kind of transform does not need the existence of any small/large physical parameters. More importantly, different from other approximation techniques, we now have great freedom to choose the convergence-control parameter
![]() $c_{0}$
, which has no physical meanings but provides us a simple way to guarantee the convergence of solution series. In particular, the HAM also provides us great freedom to choose the auxiliary linear operator
$c_{0}$
, which has no physical meanings but provides us a simple way to guarantee the convergence of solution series. In particular, the HAM also provides us great freedom to choose the auxiliary linear operator
![]() $\mathscr{L}$
: in fact, it is this kind of freedom that provides us a straightforward way to handle the nearly resonant waves, as described below.
$\mathscr{L}$
: in fact, it is this kind of freedom that provides us a straightforward way to handle the nearly resonant waves, as described below.
When the resonance criterion (2.9) is nearly satisfied, we choose a generalized auxiliary linear operator
![]() $\mathscr{L}$
defined by (2.33) with the definition (2.34), which has the property
$\mathscr{L}$
defined by (2.33) with the definition (2.34), which has the property
where
![]() $\bar{{\it\lambda}}_{m,n}$
defined by (2.26) is the eigenvalue of the generalized auxiliary linear operator (2.33). Therefore, its inverse operator has the property
$\bar{{\it\lambda}}_{m,n}$
defined by (2.26) is the eigenvalue of the generalized auxiliary linear operator (2.33). Therefore, its inverse operator has the property
Using this property, it is easy to gain the special solution
![]() ${\it\varphi}_{m}^{\ast }$
by means of (A 18).
${\it\varphi}_{m}^{\ast }$
by means of (A 18).
Note that the generalized auxiliary linear operator (2.33) always have three eigenvalues being zero:
Therefore,
![]() ${\it\Psi}_{1,0},{\it\Psi}_{0,1}$
and
${\it\Psi}_{1,0},{\it\Psi}_{0,1}$
and
![]() ${\it\Psi}_{2,-1}$
are three primary solutions. So, the common solution reads
${\it\Psi}_{2,-1}$
are three primary solutions. So, the common solution reads
where
![]() ${\it\varphi}_{m}^{\ast }$
is a special solution, and
${\it\varphi}_{m}^{\ast }$
is a special solution, and
![]() $a_{m}^{0,1},a_{m}^{1,0}$
and
$a_{m}^{0,1},a_{m}^{1,0}$
and
![]() $a_{m}^{2,-1}$
are three constants to be determined.
$a_{m}^{2,-1}$
are three constants to be determined.
In the frame of the HAM, we have freedom to choose such an initial guess
where
![]() $a_{0}^{0,1},a_{0}^{1,0}$
and
$a_{0}^{0,1},a_{0}^{1,0}$
and
![]() $a_{0}^{2,-1}$
are three constants, which are determined by enforcing the disappearance of the terms
$a_{0}^{2,-1}$
are three constants, which are determined by enforcing the disappearance of the terms
on the right-hand side of (A 13), since the corresponding eigenvalues
![]() $\bar{{\it\lambda}}_{1,0},\bar{{\it\lambda}}_{0,1}$
and
$\bar{{\it\lambda}}_{1,0},\bar{{\it\lambda}}_{0,1}$
and
![]() $\bar{{\it\lambda}}_{2,-1}$
are zero so that (A 20) is invalid. This provides us three coupled, nonlinear algebraic equations about the unknown constants
$\bar{{\it\lambda}}_{2,-1}$
are zero so that (A 20) is invalid. This provides us three coupled, nonlinear algebraic equations about the unknown constants
![]() $a_{0}^{0,1},a_{0}^{0,1}$
and
$a_{0}^{0,1},a_{0}^{0,1}$
and
![]() $a_{0}^{2,-1}$
, which often have multiple solutions with real values, indicating multiple steady-state resonant waves, as pointed out by Liao (Reference Liao2011). In this way, we gain the initial guess
$a_{0}^{2,-1}$
, which often have multiple solutions with real values, indicating multiple steady-state resonant waves, as pointed out by Liao (Reference Liao2011). In this way, we gain the initial guess
![]() ${\it\varphi}_{0}$
, which further gives
${\it\varphi}_{0}$
, which further gives
![]() ${\it\eta}_{1}$
by means of (A 15). Then, it is straightforward to gain the special solution
${\it\eta}_{1}$
by means of (A 15). Then, it is straightforward to gain the special solution
![]() ${\it\varphi}_{1}^{\ast }$
by means of (A 18), and furthermore to have the common solution
${\it\varphi}_{1}^{\ast }$
by means of (A 18), and furthermore to have the common solution
where
![]() $a_{1}^{1,0},a_{1}^{0,1}$
and
$a_{1}^{1,0},a_{1}^{0,1}$
and
![]() $a_{1}^{2,-1}$
are unknown constants, which can be determined in a similar way. In this way, we can gain
$a_{1}^{2,-1}$
are unknown constants, which can be determined in a similar way. In this way, we can gain
![]() ${\it\varphi}_{m}$
and
${\it\varphi}_{m}$
and
![]() ${\it\eta}_{m}$
at high enough order of approximation, especially by means of computer algebra software such as Mathematica, Maple and so on.
${\it\eta}_{m}$
at high enough order of approximation, especially by means of computer algebra software such as Mathematica, Maple and so on.
Note that the right-hand side of (A 13) contains the convergence-control parameter
![]() $c_{0}$
, which provides us a simple way to guarantee the convergence of the solution series. The optimal value of the convergence-control parameter
$c_{0}$
, which provides us a simple way to guarantee the convergence of the solution series. The optimal value of the convergence-control parameter
![]() $c_{0}$
is determined by the minimum of the sum of residual error square of the two free surface boundary conditions. For example, please refer to table 1.
$c_{0}$
is determined by the minimum of the sum of residual error square of the two free surface boundary conditions. For example, please refer to table 1.
Note that we have
![]() ${\it\mu}=2$
when the resonance criterion (2.9) is exactly satisfied. Therefore, the auxiliary linear operator (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves is only a special case of the generalized auxiliary linear operator (2.33) for the nearly resonant waves. In addition, all mathematical formulae for the steady-state nearly resonant waves are the same as those given by Liao (Reference Liao2011) for the exactly resonant ones, only except the generalized auxiliary linear operator (2.33). So, the above-mentioned HAM-based approach is valid for both of the exactly resonant waves and nearly resonant waves. This indicates from the viewpoint of the HAM that exactly resonant waves have no fundamental difference from nearly resonant ones. The results given in § 3 also confirm this viewpoint.
${\it\mu}=2$
when the resonance criterion (2.9) is exactly satisfied. Therefore, the auxiliary linear operator (2.23) used by Liao (Reference Liao2011) for the exactly resonant waves is only a special case of the generalized auxiliary linear operator (2.33) for the nearly resonant waves. In addition, all mathematical formulae for the steady-state nearly resonant waves are the same as those given by Liao (Reference Liao2011) for the exactly resonant ones, only except the generalized auxiliary linear operator (2.33). So, the above-mentioned HAM-based approach is valid for both of the exactly resonant waves and nearly resonant waves. This indicates from the viewpoint of the HAM that exactly resonant waves have no fundamental difference from nearly resonant ones. The results given in § 3 also confirm this viewpoint.
In general, no matter either the resonance criterion
is satisfied exactly or nearly, the above-mentioned HAM-based approach is valid, as long as we choose
in the generalized auxiliary linear operator (2.23), where
![]() $m^{\prime }$
and
$m^{\prime }$
and
![]() $n^{\prime }$
are integers.
$n^{\prime }$
are integers.
Appendix B. Approach based on the Zakharov’s equation
Xu et al. (Reference Xu, Lin, Liao and Stiassnie2012) first gained the steady-state exactly resonant waves by means of the exact wave equations, and then confirmed their results by means of the Zakharov’s equation, which is a simplified wave model for exactly resonant and nearly resonant waves with weak nonlinearity. Here, to verify the HAM-based approach described in § 2 and the results of the case study reported in § 3, we solve here the same case by means of the Zakharov’s equation.
Let us consider a degenerate quartet in a linear near-resonance:
which give
where
For the same case (3.1), we take
Substituting
into Zakharov’s equation
and using (B 1), we have
where
![]() ${\it\beta}_{j}=|{\it\beta}_{j}|\text{e}^{\text{i}arg{\it\beta}_{j}}$
with
${\it\beta}_{j}=|{\it\beta}_{j}|\text{e}^{\text{i}arg{\it\beta}_{j}}$
with
![]() $|{\it\beta}_{j}|$
,
$|{\it\beta}_{j}|$
,
![]() $\arg {\it\beta}_{j}$
being unknown real constants, and
$\arg {\it\beta}_{j}$
being unknown real constants, and
Substituting (B 10) into (B 9a–c ) and using (B 3), we have the nonlinear algebraic equations
And for steady-state quartets with time-independent spectrum, one must set
Note that the steady-state free-surface elevation for the quartet is
where the wave amplitudes
![]() $a_{j}$
are related to
$a_{j}$
are related to
![]() ${\it\beta}_{j}$
by
${\it\beta}_{j}$
by
Thus, as soon as we get the solution
![]() $|{\it\beta}_{1}|,|{\it\beta}_{2}|,|{\it\beta}_{3}|$
from the algebraic equations (B 12)–(B 14) with (B 15) for given
$|{\it\beta}_{1}|,|{\it\beta}_{2}|,|{\it\beta}_{3}|$
from the algebraic equations (B 12)–(B 14) with (B 15) for given
![]() ${\it\omega}_{j}$
and
${\it\omega}_{j}$
and
![]() ${\it\epsilon}_{j}$
,
${\it\epsilon}_{j}$
,
![]() $j=1,2,3$
, the corresponding wave amplitudes are determined by (B 17).
$j=1,2,3$
, the corresponding wave amplitudes are determined by (B 17).











