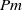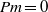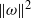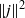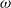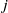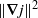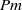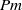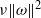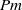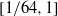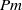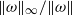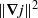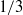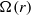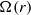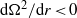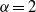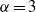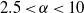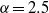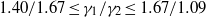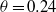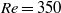Papers
Sensitivity of stratified turbulence to the buoyancy Reynolds number
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 1-22
-
- Article
- Export citation
Pressure losses in grooved channels
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 23-54
-
- Article
- Export citation
Balance model for equatorial long waves
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 55-90
-
- Article
-
- You have access
- Open access
- Export citation
A simplified vortex model of propeller and wind-turbine wakes
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 91-116
-
- Article
- Export citation
Inertial and barotropic instabilities of a free current in three-dimensional rotating flow
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 117-151
-
- Article
- Export citation
Physical processes influencing acoustic radiation from jet engine inlets
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 152-194
-
- Article
- Export citation
Two-dimensional magnetohydrodynamic turbulence in the limits of infinite and vanishing magnetic Prandtl number
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 195-215
-
- Article
-
- You have access
- Open access
- Export citation
Shear-induced mixing in geophysical flows: does the route to turbulence matter to its efficiency?
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 216-261
-
- Article
- Export citation
The stably stratified Taylor–Couette flow is always unstable except for solid-body rotation
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 262-280
-
- Article
- Export citation
Spatial structure of spectral transport in two-dimensional flow
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 281-298
-
- Article
- Export citation
Flow of a viscous nematic fluid around a sphere
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 299-331
-
- Article
- Export citation
Spectral non-locality, absolute equilibria and Kraichnan–Leith–Batchelor phenomenology in two-dimensional turbulent energy cascades
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 332-371
-
- Article
-
- You have access
- Open access
- Export citation
Growth rate of a shocked mixing layer with known initial perturbations
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 372-401
-
- Article
- Export citation
Faraday instability in floating liquid lenses: the spontaneous mutual adaptation due to radiation pressure
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 402-427
-
- Article
- Export citation
Electromagnetically driven zonal flows in a rapidly rotating spherical shell
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 428-445
-
- Article
- Export citation
Moffatt-type flows in a trihedral cone
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 446-461
-
- Article
- Export citation
Droplet motion on inclined heterogeneous substrates
-
- Published online by Cambridge University Press:
- 14 May 2013, pp. 462-491
-
- Article
- Export citation
The classical hydraulic jump in a model of shear shallow-water flows
-
- Published online by Cambridge University Press:
- 16 May 2013, pp. 492-521
-
- Article
- Export citation
Control of amplifier flows using subspace identification techniques
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 522-565
-
- Article
- Export citation
Spreading and bistability of droplets on differentially heated substrates
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 566-587
-
- Article
- Export citation