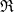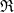1. Introduction
With the increasing demand for manufacturing, academia and industry around the world have explored new processing methods [Reference Yong, Zhifu and Yuan1–Reference Zhang, Chen and Peng4]. The parallel mechanism is widely used in complex surface machining because of its outstanding advantages of dexterity and rigidity [Reference Jin, Fang, Qu and Guo5–Reference Zhang, Mu, Liu, Bi and Wang8]. According to different work requirements, parallel mechanisms with different motion performances can be synthesized. Liu et al. proposed three-degree-of-freedom(3-DoF) [Reference Xie, Liu and Wang9], 4-DoF [Reference Bi, Xie, Liu and Luo10], and 5-DoF [Reference Shen, Xie, Liu and Xie11] parallel machine tools for milling workpieces with different morphologies and achieved good manufacturing performance. Fang et al. proposed a parallel machine tool with a large stretching ability for machining task requirements [Reference Yang, Fang, Li and Fang12–Reference He, Fang and Zhang14], which can greatly improve the workspace under the premise of ensuring the milling stiffness. As a typical machine tool structure, Exechon parallel mechanism is widely used in many manufacturing scenarios and has been deeply studied by many scholars [Reference Lian, Sun, Song, Jin and Price15–Reference López-Custodio, Fu, Dai and Jin18].
The workspace is the intersection of all reachable positions and reachable postures during the movement of the mechanism. Solving the workspace of the parallel mechanism is the most intuitive expression of its kinematic performance. Because the parallel mechanism has the structural characteristics of multiple branches, the forward kinematics model of the moving platform needs to couple the forward kinematics equations of all branches, and the calculation amount is large as a result. At present, the Newton-Raphson numerical calculation method is widely used in the above process [Reference Dharmalingum, Padayachee and Bright19, Reference Budaklı and Yılmaz20]. Therefore, the parallel mechanism usually adopts the workspace solution method based on inverse kinematics equations. Wang et al. solved the workspace of the mechanism based on inverse kinematics and proposed the concept of dexterous workspace utilization to measure the rationality of the mechanism design parameters [Reference Wang, Ji, Sun, Wan, Yuan and Zheng21]. Guo et al. proposed a method for solving the workspace of a series-parallel mechanism. First, based on the inverse kinematics, the boundary is explored to solve the workspace of the first-level parallel mechanism. Then, the workspace of the second-level mechanism is solved in the same way, and the spatial scatter points are transformed based on the first-level mechanism coordinate system, and then the workspace of the two-level series-parallel mechanism is obtained. By analogy, the workspace of the N-level mechanism can be quickly obtained. Antonov et al. analyzed the kinematics of the proposed series-parallel hybrid structure. Based on the inverse kinematics, the tracking motion of the mechanism under a given trajectory was realized, and the workspace was further obtained [Reference Guo, Zhao, Li, Liu, Deng and Tian22, Reference Antonov, Fomin, Glazunov, Kiselev and Carbone23]. Jin et al. established the inverse kinematics equation of the parallel mechanism and explored the workspace with a given step size in a given space by using the length of the rod as a variable to transform the numerical boundary constraints [Reference Jin, Fang, Zhang and Zhang24]. This is a convenient solution method and has been widely used for a long period [Reference Liu, Fan and Ding25–Reference Wu, Guo, Li, Niu and Li30].
The workspace solution method based on inverse kinematics greatly reduces the computational complexity compared with the forward kinematics workspace solution method using numerical iterative calculation. However, this method also has some drawbacks. For example, in the process of reachable workspace exploration, a traversal area needs to be given first. Under the condition of constant calculation step size, the larger the volume of this area is, the greater the amount of calculation is. The selection of too small a traversal area may lead to the coverage of an incomplete workspace, and thus we have to repeatedly run the solution model in a bigger traversal area. Therefore, a sufficiently large traversal area is usually selected in the calculation process [Reference Snyman, Du Plessis and Duffy31–Reference Rahman, Krouglicof and Lye36]. At the same time, the workspace solution method based on inverse kinematics needs to establish a solution model and calculate separately when solving the reachable position space and the reachable posture space (For example, the work posture is fixed to solve the work position space, and the work posture space is fixed to solve the work position space) [Reference Jin, Jiang and Li37–Reference Nigatu and Kim42]. In summary, although this workspace solution method has better solution performance, there is still a waste of computing resources. If the problem of large traversal area and separate modeling of position/posture space solution can be overcome, the computational efficiency will be further improved.
Mechanisms consisting of one constrained branch chain with the same number of DoFs as the mechanism and several redundant branches with more DoFs are typical [Reference Zhang and Gosselin43–Reference Zhang and Gao49]. In this study, we defined these mechanisms as (1+n) type parallel mechanisms with the aim to improve the computational efficiency of kinematics modeling of (1+n) type parallel mechanism. Additionally, we propose a novel method to solve the position and posture space simultaneously.
The chapters of this study are arranged as follows: The first section summarizes the research status and the problems existing in the existing research methods and then puts forward the research direction. The second section introduces the novel modeling method proposed in this study. By analyzing the similarities and differences between the traditional method and the new method, the superiority of the novel method is revealed, and the characteristics of the novel method are further summarized. In the third section, the performance evaluation system of the method is established. Based on the conditions of the same number of calculations, the solution experiments of the novel method and the traditional method are established, respectively. The calculation time and the calculated output rate of the workspace points are used as the evaluation criteria to compare the two methods. In the fourth section, the classical PPU-3RUS parallel mechanism [Reference Zhang50] and the new RS-3UPRU parallel mechanism proposed in this study are selected, and the workspace is solved based on the novel method proposed in this study. Several sets of workspace subsets of the specific moving platform posture are obtained from the solution set to prove the effectiveness and applicability of the novel method. In the fifth section, the method performance experiment is carried out, and the results of the novel method and the traditional method are compared to prove the superiority of the novel method. The sixth section summarizes the full text.
2. Proposal of modeling method based on the combination of forward and inverse kinematics
2.1. Structural characteristics of (1+n) type parallel mechanism
The characteristic of (1+n) parallel mechanism is composed of one constrained branch chain and n branch chains with redundant degrees-of-freedom. According to the corollary obtained from Lie group theory, the mechanism degrees-of-freedom are the intersection of the degrees-of-freedom of each branch chain. Therefore, the degree-of-freedom of the constrained branch chain is less than or equal to the redundant branch chain, and at the same time, the driving unit of such a mechanism is installed in the redundant branch chain in most cases. Thanks to this configuration, the singularities of such mechanisms are usually located at the edge of the reachable space. Therefore, (1+n) parallel mechanisms are widely used in machine tools and parts assembly in the manufacturing industry.
2.2. Core algorithm of novel solution method
The core algorithm of the solution method proposed in this study (as shown in Fig. 1) is to select a constrained branch of the parallel mechanism for a forward kinematics solution. The traversal space is obtained by traversing its joint angle and joint displacement, and then the space is judged point by point to determine whether it satisfies the inverse kinematics equation of the remaining branches. Finally, the position and posture workspace of the parallel mechanism can be obtained simultaneously.

Figure 1. Core algorithm of method.
The specific solution method is as follows:
According to the process shown in Fig. 2, this novel method introduces forward kinematics into the solution based on inverse kinematics. First, a branch chain is selected and regarded as an independent series mechanism. As we all know, the forward kinematics solution of the series mechanism and the inverse kinematics solution of the parallel mechanism are relatively simple, so we usually select the simplest branch chain in this step (Typically, constrained branch is chosen such that their number of DoF and number of joints is less than or equal to 6). According to a certain range, all the rotational and translational pairs of the branched chain are traversed, and a series of T matrices can be obtained.

Figure 2. The solution process of novel modeling method.
Next, the inverse kinematics of the remaining branches is solved. First, the O-xyz coordinate system is established at the static platform, and the O-uvw coordinate system is established at the moving platform. The point j and j′ of the branch chain i are described in the O-xyz system and the O-uvw system, respectively, and the coordinates of the two points in the two coordinate systems are further obtained. Then, the coordinate transformation of j′ from O-uvw system to O-xyz system is completed by left multiplying the R term and adding the P term to j′ . The driving points value expression (usually a length or angle expression) of the branched chain i can be obtained by using j and j′ in the O-xyz system.
Finally, the driving value is judged. When it exceeds the range, the next T matrix is brought into the branch chain solution process to obtain the next driving value; when the driving value meets the variation range of branch i, the position and posture of the mechanism at this time are recorded, and whether the traversal is over at this time is judged. When the traversal is not over, it enters the solution cycle again. When the traversal is completed, it is judged whether the branch chain at this time is the last. When the answer is negative, the i= i + 1 command is executed, and the loop is continued. When the answer is yes, jump out of the loop to end the solving process.
2.3. Analysis and characteristics of the novel method
The traditional method based on inverse kinematics has two situations when solving the workspace: (1) solve the reachable posture space at the determined position; (2) solve the reachable position space under the determined posture. The end pose transformation of the mechanism can be expressed by the T matrix in the base coordinate system, including the 3 × 3 R term that expresses the rotation transformation and the 3 × 1 P term that expresses the position transformation. When solving the reachable posture space, the P term is known. At this time, the values of the x-axis, y-axis, and z-axis are taken from 0° to 360° according to a certain degree, and several R matrices can be obtained, and then the same number of T matrices can be obtained. When the reachable position space is solved, the R term is known. At this time, the values along the x-axis, y-axis, and z-axis are taken according to a certain degree, and several P vectors can be obtained, and then the same number of T matrices can be obtained.
In the traditional method, the number of traversals in the length, width, and height directions of the traversal space is a
1, b
1
,
and c
1, respectively, and the number of rotations of the moving platform around the three coordinate axes is
![]() $\alpha$
1,
$\alpha$
1,
![]() $\beta$
1, and γ
1, respectively. Therefore, the number of traversals when solving the position space can be expressed as (a
1 × b
1 × c
1), and the number of traversals when solving the posture space can be expressed as (a
1 × b
1 × c
1)×(
$\beta$
1, and γ
1, respectively. Therefore, the number of traversals when solving the position space can be expressed as (a
1 × b
1 × c
1), and the number of traversals when solving the posture space can be expressed as (a
1 × b
1 × c
1)×(
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1). If you want to solve the position and posture space, the total number of traversals should be (a
1 × b
1 × c
1) + (a
1 × b
1 × c
1) × (
$\beta$
1 × γ
1). If you want to solve the position and posture space, the total number of traversals should be (a
1 × b
1 × c
1) + (a
1 × b
1 × c
1) × (
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1) = (a
1 × b
1 × c
1) × [1 + (
$\beta$
1 × γ
1) = (a
1 × b
1 × c
1) × [1 + (
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1)]. If the reachable position is judged when solving the posture space, the total number of traversals is at least (a
1 × b
1 × c
1)×(
$\beta$
1 × γ
1)]. If the reachable position is judged when solving the posture space, the total number of traversals is at least (a
1 × b
1 × c
1)×(
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1).
$\beta$
1 × γ
1).
In the novel method, it is assumed that the number of branch DoFs for forward kinematics in the parallel mechanism is 6, and the number of traversal values is a
2, b
2, c
2,
![]() $\alpha$
2,
$\alpha$
2,
![]() $\beta$
2, and γ
2, respectively. The number of traversals for solving the position and posture space can be expressed as (a
2 × b
2 × c
2) × (
$\beta$
2, and γ
2, respectively. The number of traversals for solving the position and posture space can be expressed as (a
2 × b
2 × c
2) × (
![]() $\alpha$
2 ×
$\alpha$
2 ×
![]() $\beta$
2 × γ
2).
$\beta$
2 × γ
2).
According to the introduction of traditional methods in Section 1, the value range of the traversed space is larger than the actual workspace range. So usually, a
1, b
1, c
1,
![]() $\alpha$
1,
$\alpha$
1,
![]() $\beta$
1, and γ
1 are bigger than a
2, b
2, c
2,
$\beta$
1, and γ
1 are bigger than a
2, b
2, c
2,
![]() $\alpha$
2,
$\alpha$
2,
![]() $\beta$
2, and γ
2, respectively. And it can be further known that:
$\beta$
2, and γ
2, respectively. And it can be further known that:
Moreover, when the number of DoFs of the parallel mechanism is smaller, the number of traversal parameters under the novel method will be less than 6, while traversal in the traditional method will be still 6-DoFs (as shown in Eq. (3)), and then the right end of Eq. (2) will be further reduced. When the left and right of Eq. (2) are equal, the novel method will obtain a more accurate workspace than the traditional method:
 \begin{align} \begin{cases} 5\text{DoFs}: & C_{6DoFs}^{5DoFs} = 6\\[4pt] 4\text{DoFs}: & C_{6DoFs}^{4DoFs}=15\\[4pt]3\text{DoFs}: & C_{6DoFs}^{3DoFs}=20\\[4pt]2\text{DoFs}: & C_{6DoFs}^{2DoFs}=15\\[4pt] 1\text{DoFs}: & C_{6DoFs}^{1DoFs}=6 \end{cases}\end{align}
\begin{align} \begin{cases} 5\text{DoFs}: & C_{6DoFs}^{5DoFs} = 6\\[4pt] 4\text{DoFs}: & C_{6DoFs}^{4DoFs}=15\\[4pt]3\text{DoFs}: & C_{6DoFs}^{3DoFs}=20\\[4pt]2\text{DoFs}: & C_{6DoFs}^{2DoFs}=15\\[4pt] 1\text{DoFs}: & C_{6DoFs}^{1DoFs}=6 \end{cases}\end{align}
Furthermore, the following inference can be obtained: if the same calculation workspace-point density is guaranteed, the calculation amount of the novel method is smaller; if the same amount of calculation is guaranteed, the computational workspace-point density of the novel method is larger.
Based on the above analysis of the novel method, its characteristics can be summarized as follows:
a. Constrained branch chain of the parallel mechanism is selected as a series branch chain for forward kinematics solution and traversal to ensure that the traversal space meets the working range of at least one branch chain. Compared with the traditional method, which traverses in the unknown space, the invalid traversal range is greatly reduced, and the solution speed can be improved.
b. Compared with the traditional method, which can only output the posture space of the determined position and the position space under the determined posture in a single solution, the novel method can output the posture space and the position space at the same time in a single solution. It can reduce computational complexity and redundancy.
c. Although the novel method will lead to uneven sampling, especially high sampling density at locations far from the FK (FK, forward kinematic) branch chain and low sampling density at locations close to the FK branch chain, the purpose of our workspace solution is to determine the working range boundary of the mechanism. Therefore, this characteristic of the method does not affect the practical effect.
d. Since the novel method utilizes forward kinematics, trigonometric function calculations are introduced. It is understandable to have concerns regarding the increased computation time of the novel method compared with the traditional one. However, it is important to note that the constrained branch chain for the forward kinematics calculation has a maximum of 6-DoFs and usually even fewer than that. Consequently, the number of joints in this branched chain also tends to be less than 6. Hence, by appropriately selecting the computational workload, the incremental computation time in the model application process will not be significantly noticeable. As demonstrated in the following example, while an increase in calculation workload does lead to an increase in computation time, when considering the substantial improvement in computational efficiency, we believe that sacrificing some of the calculation time is justifiable.
3. Performance evaluation system of novel modeling method for parallel mechanism
3.1. Method performance evaluation process
To verify that the novel method proposed in this study is superior to the traditional method, this part establishes the method performance evaluation system. The performance of the two methods is evaluated according to the calculation time and the calculated output rate. These above two indicators can be obtained as follows:
a. To obtain calculation time: we use the MATLAB platform to write and run the relevant calculation model code and use the built-in function to call the system clock to record the time of model calculation.
b. To obtain the calculated output rate: the ratio of the number of workspace recording points that meet the judgment conditions (n) to the total number of calculations (N) is the calculation output rate, as Eq. (4) shows:
These above two indicators are weighted to establish a comprehensive evaluation index as a result.
The computer parameter configurations and software versions used in the experiment are shown in Table I.
Table I. Experimental computer parameter configurations and software versions.

3.2. Performance evaluation conditions of method
The pseudo-codes of the novel method and traditional method are shown in Table II. In this part, we use the way described in Section 2 with less calculation to establish the solution model of the traditional method. In order to obtain the performance evaluation parameters of the algorithm more objectively, the same number of calculations is input into the two calculation models, and the calculation time and output rate of the two models are obtained, respectively. Repeat the above process for five times and record relevant data. Then, different sets of calculation input times are used to explore the performance change rule of the calculation models.
Table II. Solution method pseudo-code.

From Table II(b), the calculation model of the traditional method has a six-layer cyclic structure, and the required number of calculations can be expressed as (a
1 × b
1 × c
1)×(
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1) according to the previous text. In the novel method, the same number of calculations are assigned to each joint of the constrained chain, which can be expressed as [(a
1 × b
1 × c
1) × (
$\beta$
1 × γ
1) according to the previous text. In the novel method, the same number of calculations are assigned to each joint of the constrained chain, which can be expressed as [(a
1 × b
1 × c
1) × (
![]() $\alpha$
1 ×
$\alpha$
1 ×
![]() $\beta$
1 × γ
1)]1/n, where n is the count of joints of the constrained chain.
$\beta$
1 × γ
1)]1/n, where n is the count of joints of the constrained chain.
3.3. Establishment of comprehensive evaluation index
A dimensionless index
![]() $\mathfrak{R}$
is established to evaluate the performance of the model, which is obtained by weighting the calculation time (CT) and output rate (OR), respectively. The entropy weight method is used to determine the weights of the above two parameters, and the specific process is shown in Eqs. (5)–(9).
$\mathfrak{R}$
is established to evaluate the performance of the model, which is obtained by weighting the calculation time (CT) and output rate (OR), respectively. The entropy weight method is used to determine the weights of the above two parameters, and the specific process is shown in Eqs. (5)–(9).
First, data standardization is carried out. We can obtain a set of CT (CT = ct 1, ct 2,…, ct n ) and OR (OR = or 1, or 2,…, or n ) from the two computational models, respectively, by conducting multiple trials based on each count of input calculation times. Then normalize the data separately:
 \begin{align} \left\{\begin{array}{l} CTN_{i}=\dfrac{\frac{1}{CT_{i}}-\min \left\{\frac{1}{CT}\right\}}{\max \left\{\frac{1}{CT}\right\}-\min \left\{\frac{1}{CT}\right\}}\\[12pt] ORN_{i}=\dfrac{OR_{i}-\min \left\{OR\right\}}{\max \left\{OR\right\}-\min \left\{OR\right\}} \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{l} CTN_{i}=\dfrac{\frac{1}{CT_{i}}-\min \left\{\frac{1}{CT}\right\}}{\max \left\{\frac{1}{CT}\right\}-\min \left\{\frac{1}{CT}\right\}}\\[12pt] ORN_{i}=\dfrac{OR_{i}-\min \left\{OR\right\}}{\max \left\{OR\right\}-\min \left\{OR\right\}} \end{array}\right. \end{align}
Second, the information entropy of each set of parameters is calculated:
 \begin{align} \left\{\begin{array}{l} E_{CT}=-\ln\!(n)^{-1}\sum\limits_{i=1}^{n}{}^{CT}{p}{_{i}^{}}\ln {}^{CT}{p}{_{i}^{}}\\[6pt] E_{OR}=-\ln\!(n)^{-1}\sum\limits_{i=1}^{n}{}^{OR}{p}{_{i}^{}}\ln {}^{OR}{p}{_{i}^{}} \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{l} E_{CT}=-\ln\!(n)^{-1}\sum\limits_{i=1}^{n}{}^{CT}{p}{_{i}^{}}\ln {}^{CT}{p}{_{i}^{}}\\[6pt] E_{OR}=-\ln\!(n)^{-1}\sum\limits_{i=1}^{n}{}^{OR}{p}{_{i}^{}}\ln {}^{OR}{p}{_{i}^{}} \end{array}\right. \end{align}
where,
 \begin{align} \left\{\begin{array}{l} {}^{CT}{p}{_{i}^{}}=CTN_{i}/\sum\limits_{j=1}^{n}CTN_{j}\\[6pt] {}^{OR}{p}{_{i}^{}}=ORN_{i}/\sum\limits_{j=1}^{n}ORN_{j} \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{l} {}^{CT}{p}{_{i}^{}}=CTN_{i}/\sum\limits_{j=1}^{n}CTN_{j}\\[6pt] {}^{OR}{p}{_{i}^{}}=ORN_{i}/\sum\limits_{j=1}^{n}ORN_{j} \end{array}\right. \end{align}
Third, the weights of the two indicators are obtained:
 \begin{align} \left\{\begin{array}{l} W_{CT}=\dfrac{1-E_{CT}}{2-\left(E_{CT}+E_{OR}\right)}\\[6pt] W_{OR}=\dfrac{1-E_{OR}}{2-\left(E_{CT}+E_{OR}\right)} \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{l} W_{CT}=\dfrac{1-E_{CT}}{2-\left(E_{CT}+E_{OR}\right)}\\[6pt] W_{OR}=\dfrac{1-E_{OR}}{2-\left(E_{CT}+E_{OR}\right)} \end{array}\right. \end{align}
Finally, the original
![]() $\mathfrak{R}$
can be expressed as shown in Eq. (8); the greater
$\mathfrak{R}$
can be expressed as shown in Eq. (8); the greater
![]() $\mathfrak{R}$
is, the better performance the model has:
$\mathfrak{R}$
is, the better performance the model has:
4. Workspace analysis of parallel mechanism based on novel modeling method
4.1. Analysis of classical (1+n) type parallel mechanism
The PPU-3RUS parallel mechanism commonly used in parallel machine tools is selected for analysis. The mechanism is a typical (1+n) type parallel mechanism. As shown in Fig. 3, this configuration has 4-DoF moving along the y and z axes and rotating around the x and y axes.

Figure 3. Experimental device model: (a) Is the structure diagram; (b) Is a 3D solid model; (c) Is forward kinematic model of PPU branched chain.
The solution model of the PPU-3RUS parallel mechanism is established, as shown in Fig. 9(a). The O point at the center of the static platform is selected as the coordinate origin of the O-xyz system, and the O′ point at the center of the moving platform is selected as the coordinate origin of the O′ -uvw system.
Next, the basic geometric parameters of the structure are determined: where L OQ = 30, L SO’ = 5, r= L O’ A’ = 10, and R= L OA = 20. The RUS branches are arranged at equal intervals on the circumference, that is, ∠AOC, ∠AOB, ∠BOC, ∠A′O′C′ , ∠A′O′B′, and ∠B′O′C′ are all 120°.
Then the first step of the workspace solution is to derive the kinematic positive solution of the constrained branch chain. The two moving joint variables a and b and the two rotational joint variables
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
are traversed in the intervals of [−5,5], [Reference Liang, Zeng, Li, Su and He40, Reference Zhang50], [−π/2,−π/2], and [−π/2,−π/2], respectively, and several sets of T matrices can be further obtained, as shown in formula 10. The calculation details can be seen in Eq. (11):
$\beta$
are traversed in the intervals of [−5,5], [Reference Liang, Zeng, Li, Su and He40, Reference Zhang50], [−π/2,−π/2], and [−π/2,−π/2], respectively, and several sets of T matrices can be further obtained, as shown in formula 10. The calculation details can be seen in Eq. (11):
 \begin{align} \left\{\begin{array}{ll} {}^{O}{T}{_{Q}^{}} & =\textit{Trans}(0,a,0)\textit{Trans}(0,0,L_{OQ})\\[5pt] {}^{Q}{T}{_{S}^{}} & =\textit{Trans}(0,0,b)\\[5pt] {}^{S}{T}{_{O^{\prime}}^{}} & =Rot(Y,\frac{\pi }{2})Rot(Z,\alpha )Rot(X,\frac{\pi }{2})Rot (Z,\beta)\textit{Trans}(-L_{SO^{\prime}},0,0)Rot(Y,-\frac{\pi }{2})Rot(\mathrm{Z},-\frac{\pi }{2}) \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{ll} {}^{O}{T}{_{Q}^{}} & =\textit{Trans}(0,a,0)\textit{Trans}(0,0,L_{OQ})\\[5pt] {}^{Q}{T}{_{S}^{}} & =\textit{Trans}(0,0,b)\\[5pt] {}^{S}{T}{_{O^{\prime}}^{}} & =Rot(Y,\frac{\pi }{2})Rot(Z,\alpha )Rot(X,\frac{\pi }{2})Rot (Z,\beta)\textit{Trans}(-L_{SO^{\prime}},0,0)Rot(Y,-\frac{\pi }{2})Rot(\mathrm{Z},-\frac{\pi }{2}) \end{array}\right. \end{align}
The results can be obtained:
 \begin{align} {}^{O}{T}{_{O^{\prime}}^{}}= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} R(1,1) & R(1,2) & R(1,3) & P(1,1)\\[3pt] R(2,1) & R(2,2) & R(2,3) & P(2,1)\\[3pt] R(3,1) & R(3,2) & R(3,3) & P(3,1)\\ 0 & 0 & 0 & 1 \end{array}\right] \end{align}
\begin{align} {}^{O}{T}{_{O^{\prime}}^{}}= \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} R(1,1) & R(1,2) & R(1,3) & P(1,1)\\[3pt] R(2,1) & R(2,2) & R(2,3) & P(2,1)\\[3pt] R(3,1) & R(3,2) & R(3,3) & P(3,1)\\ 0 & 0 & 0 & 1 \end{array}\right] \end{align}
where the parameters in the T matrix are shown in Eqs. (13)−(14), respectively. Meanwhile, s is sin, and c is cos:
 \begin{align} R= \left \{\begin{array}{ll} R(1,1) & =c\beta \\[3pt] R(1,2) & =0\\[3pt] R(1,3) & =s\beta \\[3pt] R(2,1) & =s\alpha s\beta \\[3pt] R(2,2) & =c\alpha \\[3pt] R(2,3) & =-s\alpha c\beta \\[3pt] R(3,1) & =-c\alpha s\beta \\[3pt] R(3,2) & =s\alpha \\[3pt] R(3,3) & =c\alpha c\beta \end{array}\right. \end{align}
\begin{align} R= \left \{\begin{array}{ll} R(1,1) & =c\beta \\[3pt] R(1,2) & =0\\[3pt] R(1,3) & =s\beta \\[3pt] R(2,1) & =s\alpha s\beta \\[3pt] R(2,2) & =c\alpha \\[3pt] R(2,3) & =-s\alpha c\beta \\[3pt] R(3,1) & =-c\alpha s\beta \\[3pt] R(3,2) & =s\alpha \\[3pt] R(3,3) & =c\alpha c\beta \end{array}\right. \end{align}
 \begin{align} P=\left\{\begin{array}{l} P(1,1)=L_{SO^{\prime}}s\beta \\[3pt] P(2,1)=a-L_{SO^{\prime}}c\beta s\alpha \\[3pt] P(3,1)=b+L_{OQ}+L_{SO^{\prime}}c\alpha c\beta \end{array}\right. \end{align}
\begin{align} P=\left\{\begin{array}{l} P(1,1)=L_{SO^{\prime}}s\beta \\[3pt] P(2,1)=a-L_{SO^{\prime}}c\beta s\alpha \\[3pt] P(3,1)=b+L_{OQ}+L_{SO^{\prime}}c\alpha c\beta \end{array}\right. \end{align}
The second step: The inverse kinematics solutions of three RUS branches are obtained, respectively. The coordinates of A′ , B′, and C′ points were expressed under the O′ -uvw system and transformed into the coordinate expression under the O-xyz system by using Eq. (15):
 \begin{align*} \left\{\begin{array}{ll} A^{\prime}_{uvw} & =\left[r\times s\!\left(\frac{4\pi }{3}\right)\!,r\times c\!\left(\frac{4\pi }{3}\right)\!,0\right]^{T}\\[3pt] B^{\prime}_{uvw} & =\left[0,r,0\right]^{T}\\[3pt] C^{\prime}_{uvw} & =\left[r\times s\!\left(\frac{2\pi }{3}\right)\!,r\times c\!\left(\frac{2\pi }{3}\right)\!,0\right]^{T} \end{array}\right. \end{align*}
\begin{align*} \left\{\begin{array}{ll} A^{\prime}_{uvw} & =\left[r\times s\!\left(\frac{4\pi }{3}\right)\!,r\times c\!\left(\frac{4\pi }{3}\right)\!,0\right]^{T}\\[3pt] B^{\prime}_{uvw} & =\left[0,r,0\right]^{T}\\[3pt] C^{\prime}_{uvw} & =\left[r\times s\!\left(\frac{2\pi }{3}\right)\!,r\times c\!\left(\frac{2\pi }{3}\right)\!,0\right]^{T} \end{array}\right. \end{align*}
 \begin{align} \left\{\begin{array}{ll} A^{\prime}_{xyz} & =R\cdot A^{\prime}_{uvw}+P\\[3pt] B^{\prime}_{xyz} & =R\cdot B^{\prime}_{uvw}+P\\[3pt] C^{\prime}_{xyz} & =R\cdot C^{\prime}_{uvw}+P \end{array}\right. \end{align}
\begin{align} \left\{\begin{array}{ll} A^{\prime}_{xyz} & =R\cdot A^{\prime}_{uvw}+P\\[3pt] B^{\prime}_{xyz} & =R\cdot B^{\prime}_{uvw}+P\\[3pt] C^{\prime}_{xyz} & =R\cdot C^{\prime}_{uvw}+P \end{array}\right. \end{align}
Meanwhile, the coordinates of A, B, and C points are expressed in the O-xyz system:
 \begin{align*} \left\{\begin{array}{ll} A_{xyz} & =\left[R\times s\!\left(\frac{4\pi }{3}\right)\!,R\times c\!\left(\frac{4\pi }{3}\right)\!,0\right]^{T}\\[3pt] B_{xyz} & =\left[0,R,0\right]^{T}\\[3pt] C_{xyz} & =\left[R\times s\!\left(\frac{2\pi }{3}\right)\!,R\times c\!\left(\frac{2\pi }{3}\right)\!,0\right]^{T} \end{array}\right. \end{align*}
\begin{align*} \left\{\begin{array}{ll} A_{xyz} & =\left[R\times s\!\left(\frac{4\pi }{3}\right)\!,R\times c\!\left(\frac{4\pi }{3}\right)\!,0\right]^{T}\\[3pt] B_{xyz} & =\left[0,R,0\right]^{T}\\[3pt] C_{xyz} & =\left[R\times s\!\left(\frac{2\pi }{3}\right)\!,R\times c\!\left(\frac{2\pi }{3}\right)\!,0\right]^{T} \end{array}\right. \end{align*}
Finally, the distance expression between two fixed points on the static platform and the moving platform is derived, as shown in Eqs. (16)−(19). The space where the branch chain can move can be represented by constraining its value in a certain range, respectively:
where,
 \begin{align} L_{AA^{\prime}}=\left| \begin{array}{l} \left(b+L_{OQ}-\frac{rs\alpha }{2}+L_{SO^{\prime}}c\alpha c\beta +\frac{\sqrt{3}}{2}\textit{rc}\alpha s\beta \right)^{2}+\left(\frac{rc\alpha }{2}-a-\frac{R}{2}+L_{SO^{\prime}}c\beta s\alpha +\frac{\sqrt{3}}{2}\textit{rs}\alpha s\beta \right)^{2}\\[3pt] +\left(\frac{\sqrt{3}}{2}R+L_{SO^{\prime}}s\beta -\frac{\sqrt{3}}{2}Rc\beta \right)^{2} \end{array}\right| ^{\frac{1}{2}} \end{align}
\begin{align} L_{AA^{\prime}}=\left| \begin{array}{l} \left(b+L_{OQ}-\frac{rs\alpha }{2}+L_{SO^{\prime}}c\alpha c\beta +\frac{\sqrt{3}}{2}\textit{rc}\alpha s\beta \right)^{2}+\left(\frac{rc\alpha }{2}-a-\frac{R}{2}+L_{SO^{\prime}}c\beta s\alpha +\frac{\sqrt{3}}{2}\textit{rs}\alpha s\beta \right)^{2}\\[3pt] +\left(\frac{\sqrt{3}}{2}R+L_{SO^{\prime}}s\beta -\frac{\sqrt{3}}{2}Rc\beta \right)^{2} \end{array}\right| ^{\frac{1}{2}} \end{align}
 \begin{align} L_{CC^{\prime}}=\left| \begin{array}{l} \left(b+L_{OQ}-\frac{rs\alpha }{2}+L_{SO^{\prime}}c\alpha s\beta -\frac{\sqrt{3}}{2}\textit{rc}\alpha s\beta \right)^{2}+\left(\frac{R}{2}+a-\frac{rc\alpha }{2}-L_{SO^{\prime}}c\beta s\alpha +\frac{\sqrt{3}}{2}\textit{rs}\alpha s\beta \right)^{2}\\[3pt] +\left(L_{SO^{\prime}}s\beta -\frac{\sqrt{3}}{2}R+\frac{\sqrt{3}}{2}rc\beta \right)^{2} \end{array}\right| ^{\frac{1}{2}} \end{align}
\begin{align} L_{CC^{\prime}}=\left| \begin{array}{l} \left(b+L_{OQ}-\frac{rs\alpha }{2}+L_{SO^{\prime}}c\alpha s\beta -\frac{\sqrt{3}}{2}\textit{rc}\alpha s\beta \right)^{2}+\left(\frac{R}{2}+a-\frac{rc\alpha }{2}-L_{SO^{\prime}}c\beta s\alpha +\frac{\sqrt{3}}{2}\textit{rs}\alpha s\beta \right)^{2}\\[3pt] +\left(L_{SO^{\prime}}s\beta -\frac{\sqrt{3}}{2}R+\frac{\sqrt{3}}{2}rc\beta \right)^{2} \end{array}\right| ^{\frac{1}{2}} \end{align}
The variables a, b,
![]() $\alpha$
, and
$\alpha$
, and
![]() $\beta$
of the positive kinematics part in the PPU-3RUS model are traversed according to a∈[−5, 5], b∈ [Reference Liang, Zeng, Li, Su and He40, Reference Zhang50],
$\beta$
of the positive kinematics part in the PPU-3RUS model are traversed according to a∈[−5, 5], b∈ [Reference Liang, Zeng, Li, Su and He40, Reference Zhang50],
![]() $\alpha$
∈[−π/2, −π/2] and
$\alpha$
∈[−π/2, −π/2] and
![]() $\beta$
∈[−π/2, −π/2], respectively. At the same time, the L
AA’
, L
BB’
, and L
CC’
branched chains in the inverse kinematics part of the model are constrained within the range of [60, 150]. The points that satisfy the variation range of the branch chains are recorded in the traversal space, and finally, the workspace of the PPU-3RUS mechanism is obtained as shown in Fig. 4. The upper part of the figure is a three-dimensional workspace, and the lower part is the scatter projection of the workspace. The workspace of the PPU-3RUS mechanism is shown in the figure, which is distributed in the spatial range of x-axis direction [−5,5], y-axis direction [−10,10], and z-axis direction [70,85]. The shape of the workspace conforms to the characteristics of the mechanism joint configuration.
$\beta$
∈[−π/2, −π/2], respectively. At the same time, the L
AA’
, L
BB’
, and L
CC’
branched chains in the inverse kinematics part of the model are constrained within the range of [60, 150]. The points that satisfy the variation range of the branch chains are recorded in the traversal space, and finally, the workspace of the PPU-3RUS mechanism is obtained as shown in Fig. 4. The upper part of the figure is a three-dimensional workspace, and the lower part is the scatter projection of the workspace. The workspace of the PPU-3RUS mechanism is shown in the figure, which is distributed in the spatial range of x-axis direction [−5,5], y-axis direction [−10,10], and z-axis direction [70,85]. The shape of the workspace conforms to the characteristics of the mechanism joint configuration.

Figure 4. Workspace of P PU-3 R US.
To verify the correctness of the novel modeling method, several groups of specific motion postures of moving platforms are selected, respectively, and the corresponding workspace subset is obtained from the workspace. Figure 5 shows the workspace of the moving platform with y-axis rotation [−π/6, π/6] and z-axis moving within a range of up to 75 mm. Figure 6 shows the workspace of the moving platform with x-axis and y-axis rotation [−π/6, π/6] and z-axis moving within a range of up to 85 mm. So far, we have proved the effectiveness of the novel method proposed in this study.

Figure 5. The workspace in which the moving platform rotates around the y-axis [−π/6, π/6], and the z-axis moves within a working space of 75 mm.

Figure 6. The workspace in which the moving platform rotates around the x-axis and y-axis [−π/6, π/6] and the z-axis moves in the range of 85 mm.
4.2. Analysis of a novel (1+n) type parallel mechanism
In order to verify that the novel method proposed in this study has wide applicability in solving the (1+n) type parallel mechanism, the novel RS-3UPRU parallel mechanism proposed in this study is selected for analysis. As shown in Fig. 7, this configuration has three rotational degrees-of-freedom around the x, y, and z axes and is suitable as a carrier for milling cutters in curved and curved surface machining.

Figure 7. Experimental device model: (a) Is the structure diagram; (b) Is a three-dimensional solid model; (c) Is forward kinematic model of RS branched chain.
The solution model of the RS-3UPRU parallel mechanism is established, as shown in Fig. 7 (a). Point A at the center of the static platform is selected as the coordinate origin of the O-xyz system. Since there is no kinematic pair at point C, which is in the center of the moving platform, the end kinematic pair of the RS branch is located at point B, so point B is selected as the coordinate origin of the O′ -uvw system.
Next, the basic geometric parameters of the structure are determined: L AD = 72.66, L AB = 70.88, L BC = 5.34, L CE = 33.27. The UPRU branches are arranged at equal intervals on the circumference, that is, ∠DAF, ∠FAH, ∠DAH, ∠ECG, ∠GCI, and ∠ECI are all 120°. Then, according to the same analysis process mentioned above, the kinematic solution model is established by using the proposed method.
In the RS-3UPRU model, the variables γ 1, γ 2, and γ 3 of the positive kinematics part are traversed according to γ1∈[−π, π], γ2∈[−π/4, π/4], and γ3∈[−π/4, π/4], respectively. At the same time, the L DE , L FG , and L HI branch chains in the inverse kinematics part of the solution model are constrained within the range of [60, 250]. The points satisfying the variation range of the branched chains are recorded in the traversal space, and the workspace of the RS-3UPRU mechanism is finally obtained as shown in Fig. 8. The upper part of the figure is the projection of the spatial scatter fitting surface, the middle part is the spatial scatter fitting surface, and the lower part is the spatial scatter projection. The workspace of the RS-3UPRU mechanism is shown, which is distributed in the x-axis direction [−5,5], y-axis direction [−5,5], and z-axis direction [73,76.5]. The shape feature of the workspace is a spherical crown surface that conforms to the configuration characteristics of the mechanism.

Figure 8. Workspace of RS-3UPRU mechanism.
Similarly, we can obtain subsets of the workspace satisfying particular poses from the workspace, as Figs. 9–12 shown. So far, we have proved the wide applicability of the novel method proposed in this study.

Figure 9. The workspace of the moving platform rotating around the x-axis [−π/3, π/3].

Figure 10. The workspace of the moving platform rotating around the y-axis [−π/9, π/9].

Figure 11. The workspace of the moving platform rotating around the z-axis [−π/18, π/18].

Figure 12. The workspace of the moving platform rotating π/6 around the x-axis, y-axis, and z-axis, respectively.
5. Method performance analysis
5.1. Method performance analysis based on PPU-3RUS parallel mechanism
The PPU-3RUS parallel mechanism is analyzed by the traditional modeling method and the novel modeling method. For groups 1, 2, and 3, 105,205, and 305 calculations are performed, respectively. This is repeated five times for each group.
The experimental results based on the traditional modeling method and the novel modeling method correspond up and down in Fig. 13, where Fig. 13 (a) and (e) shows the calculation time, Fig 13 (b) and (e) shows the output rate, Fig. 13 (c1) and (f1) shows the calculated results for group 1, and Fig. 13 (c2) and (f2) shows the calculated results for the group 3.
Table III. Method performance evaluation index for PPU-3RUS parallel mechanism.


Figure 13. Analysis of P PU-3 R US parallel mechanism in two models.
It can be observed that the output rate obtained by using the traditional modeling method decreases with the increase of the number of computations, and the output rate is not ideal regardless of the number of computations. The result is shown in Fig. 12 (c1) and (c2), and it is difficult to obtain the accurate topography of the workspace with this method.
Compared with the traditional modeling method, the novel modeling method takes more time, but the output rate increases with the increase of the number of calculations, especially in group 2 and group 3, where the output rate is nearly 100%. Surprisingly, even for group 1 with the least number of calculations, the resulting workspace still exhibits complete topography.
According to the above experimental results, the weights of calculation time and output rate can be obtained by using Eqs. (4)–(8), and then the evaluation index
![]() $\mathfrak{R}$
value can be obtained. As the results are shown in Table III, the
$\mathfrak{R}$
value can be obtained. As the results are shown in Table III, the
![]() $\mathfrak{R}$
values of the novel methods are all larger than those of the traditional methods, and the group 2 obtained the highest evaluation score due to its excellent calculation time and output rate, which is the optimal solution among the three groups of experiments.
$\mathfrak{R}$
values of the novel methods are all larger than those of the traditional methods, and the group 2 obtained the highest evaluation score due to its excellent calculation time and output rate, which is the optimal solution among the three groups of experiments.
5.2. Method performance analysis based on RS-3UPRU parallel mechanism
For groups 1, 2 and 3, 106,156, and 206 calculations are performed, respectively. This is repeated five times for each group.
The analytical results of the RS-3UPRU parallel mechanism based on the traditional modeling method and the novel modeling method are similar to those described above, as shown in Fig. 1 4. The difference is Fig. 14 (c1), which shows the calculation result of group 2 because the output rate of group 1 is 0.
Table IV. Method performance evaluation index for RS-3UPRU parallel mechanism.


Figure 14. Analysis of RS-3U P RU parallel mechanism under two models.
It can be observed that the performance of the traditional modeling method is still worse than that of the novel modeling method. At the same time, it can be found that groups 1, 2, and 3 have achieved 100% output rate based on the novel method.
According to the above experimental results, the weights of calculation time and output rate can be obtained by using Eqs. (4)–(8), and then the evaluation index
![]() $\mathfrak{R}$
value can be obtained. As the results shown in Table IV, although in group 1 the traditional modeling method achieved a higher
$\mathfrak{R}$
value can be obtained. As the results shown in Table IV, although in group 1 the traditional modeling method achieved a higher
![]() $\mathfrak{R}$
value, the obtained score is invalid considering that its output rate is 0. In both groups 2 and 3, it was the novel modeling method that achieved higher scores. Group 1 obtained the highest evaluation score due to its excellent calculation time and output rate, which is the optimal solution among the three groups of experiments.
$\mathfrak{R}$
value, the obtained score is invalid considering that its output rate is 0. In both groups 2 and 3, it was the novel modeling method that achieved higher scores. Group 1 obtained the highest evaluation score due to its excellent calculation time and output rate, which is the optimal solution among the three groups of experiments.
5.3. Summary of analysis
Although the computation time of the novel modeling method is longer than that of the traditional modeling method in each experimental group, the high output rate obtained by the novel modeling method is incomparable to that of the traditional method. Thanks to this, the novel method can obtain the accurate workspace of the parallel mechanism with a small amount of calculation; in contrast to the traditional method, even with more calculation (resulting in more computing time), it is difficult to obtain comparable results with the novel method.
The evaluation index
![]() $\mathfrak{R}$
proposed in this study is used to objectively compare the two methods. The maximum
$\mathfrak{R}$
proposed in this study is used to objectively compare the two methods. The maximum
![]() $\mathfrak{R}$
value obtained by the novel method is 250% and 430% higher than that obtained by the traditional method for the PPU-3RUS parallel mechanism and RS-3UPRU parallel mechanism, respectively.
$\mathfrak{R}$
value obtained by the novel method is 250% and 430% higher than that obtained by the traditional method for the PPU-3RUS parallel mechanism and RS-3UPRU parallel mechanism, respectively.
6. Conclusion
In this study, a novel kinematics modeling method of (1+n) type parallel mechanism is proposed by combining forward kinematics and inverse kinematics. Compared with the traditional method based on inverse kinematics, the traversal space can satisfy the inverse kinematics equation of at least one branch chain when solving the workspace, so the solution efficiency can be greatly improved. The main contributions of this study can be summarized as follows:
(1) The solution model of position and posture space simultaneously is established. Compared with the traditional method, which can only solve the position space or posture space in a single model, the solution model established under the guidance of the novel method can solve the position space and posture space at the same time.
(2) Taking the classical PPU-3RUS parallel mechanism and the RS-3UPRU new parallel mechanism proposed in this study as an example, which verifies the effectiveness of the method and has wide applicability to the (1+n) type parallel mechanism.
(3) The original evaluation index
![]() $\mathfrak{R}$
value is proposed to evaluate the performance of modeling methods. The experimental system is built, and the analysis shows that the novel modeling method proposed in this study is better than the traditional modeling method.
$\mathfrak{R}$
value is proposed to evaluate the performance of modeling methods. The experimental system is built, and the analysis shows that the novel modeling method proposed in this study is better than the traditional modeling method.
Financial support
This work was supported by the Basic Research Fund for Central Universities of China, which is Research on Multi-robot Integrated Control Technology and Software Development (no. M23JBZX00010).
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this study.