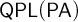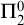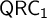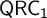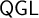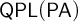1 Introduction
Provability is a fundamental concept in mathematics, logic, and philosophy alike. Gödel proved his famous incompleteness results in [Reference Gödel22] by formalizing provability. Thus, for formal theories like Peano Arithmetic (
![]() $\mathsf {PA}$
), we have a natural arithmetical predicate
$\mathsf {PA}$
), we have a natural arithmetical predicate
![]() $\Box _{\mathsf {PA}}(\cdot )$
that is true exactly for the Gödel numbers of
$\Box _{\mathsf {PA}}(\cdot )$
that is true exactly for the Gödel numbers of
![]() $\mathsf {PA}$
-provable sentences:
$\mathsf {PA}$
-provable sentences:
For readability we shall not distinguish formulas from their Gödel numbers or from syntactic terms (numerals) denoting these Gödel numbers in the future.
Gödel observed various provable structural properties of the provability predicate. For example, for any formula A, if
![]() $\mathsf {PA}\vdash A$
then
$\mathsf {PA}\vdash A$
then
![]() $\mathsf {PA}\vdash \Box _{\mathsf {PA}} A$
. Moreover, this can be formalized itself: for any formula A,
$\mathsf {PA}\vdash \Box _{\mathsf {PA}} A$
. Moreover, this can be formalized itself: for any formula A,
![]() $\mathsf {PA} \vdash \Box _{\mathsf {PA}} A \to \Box _{\mathsf {PA}} \Box _{\mathsf {PA}} A$
. Using such properties, and after showing how self-reference can be obtained in
$\mathsf {PA} \vdash \Box _{\mathsf {PA}} A \to \Box _{\mathsf {PA}} \Box _{\mathsf {PA}} A$
. Using such properties, and after showing how self-reference can be obtained in
![]() $\mathsf {PA}$
, Gödel derived his first incompleteness theorem (here presented in a slightly weakened form for
$\mathsf {PA}$
, Gödel derived his first incompleteness theorem (here presented in a slightly weakened form for
![]() $\mathsf {PA}$
) by observing that the sentence B such that
$\mathsf {PA}$
) by observing that the sentence B such that
![]() $\mathsf {PA} \vdash B \leftrightarrow \neg \Box _{\mathsf {PA}} B$
can neither be proved nor refuted in
$\mathsf {PA} \vdash B \leftrightarrow \neg \Box _{\mathsf {PA}} B$
can neither be proved nor refuted in
![]() $\mathsf {PA}$
, provided that
$\mathsf {PA}$
, provided that
![]() $\mathsf {PA}$
only proves true theorems.
$\mathsf {PA}$
only proves true theorems.
In light of this, it makes sense to design a system that collects all provable structural properties of the provability predicate. The language
![]() $\mathcal L_\Box $
of propositional modal logic is optimally suited for this purpose. The formulas of this language are as the ones of propositional logic together with a unary modality
$\mathcal L_\Box $
of propositional modal logic is optimally suited for this purpose. The formulas of this language are as the ones of propositional logic together with a unary modality
![]() $\Box $
that is syntactically treated as negation. Thus we can write
$\Box $
that is syntactically treated as negation. Thus we can write
![]() $\mathsf {Form}_\Box ::= \bot \mid \mathsf {Prop} \mid \mathsf {Form}_\Box \to \mathsf {Form}_\Box \mid \Box \mathsf { Form}_\Box $
, where
$\mathsf {Form}_\Box ::= \bot \mid \mathsf {Prop} \mid \mathsf {Form}_\Box \to \mathsf {Form}_\Box \mid \Box \mathsf { Form}_\Box $
, where
![]() $\mathsf {Prop}$
represents propositional symbols.
$\mathsf {Prop}$
represents propositional symbols.
The modal logical formulas are linked to arithmetic using so-called realizations. A particular realization
![]() $\cdot ^{*}$
maps propositional variables to sentences in the language of
$\cdot ^{*}$
maps propositional variables to sentences in the language of
![]() $\mathsf {PA}$
and this map is extended to any formula by stipulating that it commutes with implication,
$\mathsf {PA}$
and this map is extended to any formula by stipulating that it commutes with implication,
![]() $\bot $
is mapped to
$\bot $
is mapped to
![]() $(0=1)$
, and the modal operator is mapped to formalized provability, i.e.,
$(0=1)$
, and the modal operator is mapped to formalized provability, i.e.,
![]() $(\Box A)^{*_{\mathsf {PA}}} = \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}$
.
$(\Box A)^{*_{\mathsf {PA}}} = \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}$
.
We can now express what it means to be a provable structural property. For example, for any realization
![]() $\cdot ^{*}$
we have
$\cdot ^{*}$
we have
![]() $\mathsf {PA} \vdash (\Box (p \to q) \to (\Box p \to \Box q))^{*_{\mathsf {PA}}}$
, since
$\mathsf {PA} \vdash (\Box (p \to q) \to (\Box p \to \Box q))^{*_{\mathsf {PA}}}$
, since
![]() $\mathsf {PA} \vdash \Box _{\mathsf {PA}} (p^{*} \to q^{*}) \to (\Box _{\mathsf {PA}} p^{*} \to \Box _{\mathsf {PA}} q^{*} )$
for any formulas
$\mathsf {PA} \vdash \Box _{\mathsf {PA}} (p^{*} \to q^{*}) \to (\Box _{\mathsf {PA}} p^{*} \to \Box _{\mathsf {PA}} q^{*} )$
for any formulas
![]() $p^{*}$
and
$p^{*}$
and
![]() $q^{*}$
. The structural properties are thus captured by the modal formulas that are provable under any realization. We call this
$q^{*}$
. The structural properties are thus captured by the modal formulas that are provable under any realization. We call this
![]() $\mathsf {PL}(\mathsf {PA})$
, the provability logic of
$\mathsf {PL}(\mathsf {PA})$
, the provability logic of
![]() $\mathsf {PA}$
, and write
$\mathsf {PA}$
, and write
Via (1) we know that (
![]() $\mathsf {PA} \vdash A^{*_{\mathsf {PA}}}$
for any
$\mathsf {PA} \vdash A^{*_{\mathsf {PA}}}$
for any
![]() $\cdot ^{*}$
) if and only if (
$\cdot ^{*}$
) if and only if (
![]() $\mathbb {N} \vDash \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}$
for any
$\mathbb {N} \vDash \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}$
for any
![]() $\cdot ^{*}$
). Clearly
$\cdot ^{*}$
). Clearly
![]() $A^{*_{\mathsf {PA}}}$
only depends on the value of
$A^{*_{\mathsf {PA}}}$
only depends on the value of
![]() $\cdot ^{*}$
for the finitely many propositional variables that occur in A, and so the universal quantifier “for any
$\cdot ^{*}$
for the finitely many propositional variables that occur in A, and so the universal quantifier “for any
![]() $\cdot ^{*}$
” can be coded and made internal, making it possible to characterize
$\cdot ^{*}$
” can be coded and made internal, making it possible to characterize
![]() $\mathsf {PL}(\mathsf {PA})$
by
$\mathsf {PL}(\mathsf {PA})$
by
![]() $\{ A \mid \mathbb N \vDash \forall \cdot ^{*} \, \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}\}$
. We now observe that
$\{ A \mid \mathbb N \vDash \forall \cdot ^{*} \, \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}\}$
. We now observe that
![]() $\Box _{\mathsf {PA}} B$
is a
$\Box _{\mathsf {PA}} B$
is a
![]() $\Sigma ^0_1$
formula. That is,
$\Sigma ^0_1$
formula. That is,
![]() $\Box _{\mathsf {PA}} B$
is of the form
$\Box _{\mathsf {PA}} B$
is of the form
![]() $\exists p \, {\mathrm {Prf}}_{\mathsf {PA}}(p, B)$
, where
$\exists p \, {\mathrm {Prf}}_{\mathsf {PA}}(p, B)$
, where
![]() ${\mathrm {Prf}}_{\mathsf {PA}}(\cdot , \cdot )$
is a decidable predicate. Thus,
${\mathrm {Prf}}_{\mathsf {PA}}(\cdot , \cdot )$
is a decidable predicate. Thus,
![]() $\mathsf {PL}(\mathsf {PA})= \{ A \mid \mathbb N \vDash \forall \cdot ^{*} \, \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}\}$
has a
$\mathsf {PL}(\mathsf {PA})= \{ A \mid \mathbb N \vDash \forall \cdot ^{*} \, \Box _{\mathsf {PA}} A^{*_{\mathsf {PA}}}\}$
has a
![]() $\Pi ^0_2$
definition. If we moreover realize that
$\Pi ^0_2$
definition. If we moreover realize that
![]() $\Box _{\mathsf {PA}} (\cdot )$
is
$\Box _{\mathsf {PA}} (\cdot )$
is
![]() $\Sigma ^0_1$
complete in that any computably enumerableFootnote
1
set U can be defined using a formula
$\Sigma ^0_1$
complete in that any computably enumerableFootnote
1
set U can be defined using a formula
![]() $A_U$
as
$A_U$
as
![]() $\{ n \mid \mathbb N \vDash \Box _{\mathsf {PA}} (A_U(n))\}$
, then it seems that there is little hope that the
$\{ n \mid \mathbb N \vDash \Box _{\mathsf {PA}} (A_U(n))\}$
, then it seems that there is little hope that the
![]() $\Pi ^0_2$
set
$\Pi ^0_2$
set
![]() $\mathsf {PL}(\mathsf {PA})$
allows for a simple characterization.
$\mathsf {PL}(\mathsf {PA})$
allows for a simple characterization.
However, a little miracle happens and by Solovay’s Completeness Theorem [Reference Solovay34] we know that
![]() $\mathsf {PL}(\mathsf {PA})$
is decidable, corresponding to what we nowadays call the Gödel–Löb provability logic
$\mathsf {PL}(\mathsf {PA})$
is decidable, corresponding to what we nowadays call the Gödel–Löb provability logic
![]() $\mathsf {GL}$
. Likewise, Solovay proved that the set of true structural provability principles
$\mathsf {GL}$
. Likewise, Solovay proved that the set of true structural provability principles
is also decidable and described by the well-behaved modal logic
![]() $\mathsf {GLS}$
. We observe that, a priori,
$\mathsf {GLS}$
. We observe that, a priori,
![]() $\mathsf {TPL}(\mathsf {PA})$
falls outside the arithmetical hierarchy due to Tarski’s [Reference Tarski35] result on the undefinability of arithmetical truth.
$\mathsf {TPL}(\mathsf {PA})$
falls outside the arithmetical hierarchy due to Tarski’s [Reference Tarski35] result on the undefinability of arithmetical truth.
After these positive results, there was hope that the nice characterizations could be extended to the realm of quantified modal logic. Thus, the focus switched to the language
![]() $\mathcal {L}_{\Box , \forall }$
of quantified modal logic without identity, which contains
$\mathcal {L}_{\Box , \forall }$
of quantified modal logic without identity, which contains
![]() $\bot $
, relation symbols, Boolean connectives,
$\bot $
, relation symbols, Boolean connectives,
![]() $\forall x$
, and
$\forall x$
, and
![]() $\Box $
, as well as the usual abbreviations such as
$\Box $
, as well as the usual abbreviations such as
![]() $\Diamond $
and
$\Diamond $
and
![]() $\exists x$
. We define arithmetical realizations
$\exists x$
. We define arithmetical realizations
![]() $\cdot ^{*}$
for
$\cdot ^{*}$
for
![]() $\mathcal {L}_{\Box , \forall }$
formulas as before with the only difference that we now map n-ary relation symbols to arithmetical formulas with n free variables and set
$\mathcal {L}_{\Box , \forall }$
formulas as before with the only difference that we now map n-ary relation symbols to arithmetical formulas with n free variables and set
![]() $(\forall x \, \varphi )^{*_{\mathsf {PA}}}:= \forall y \, \varphi ^{*_{\mathsf {PA}}}$
, where y is the arithmetical variable corresponding to x. The quantified provability logic of
$(\forall x \, \varphi )^{*_{\mathsf {PA}}}:= \forall y \, \varphi ^{*_{\mathsf {PA}}}$
, where y is the arithmetical variable corresponding to x. The quantified provability logic of
![]() $\mathsf {PA}$
can now be defined by analogy (cf. [Reference Boolos11]):Footnote
2
$\mathsf {PA}$
can now be defined by analogy (cf. [Reference Boolos11]):Footnote
2
as well as
It is not hard to see that
![]() $\Box \forall x \, A \to \forall x \, \Box A$
is in
$\Box \forall x \, A \to \forall x \, \Box A$
is in
![]() $\mathsf {QPL}(\mathsf {PA})$
, and for some time it was believed that one could obtain
$\mathsf {QPL}(\mathsf {PA})$
, and for some time it was believed that one could obtain
![]() $\mathsf {QPL}(\mathsf {PA})$
by adding such principles together with predicate logical reasoning to
$\mathsf {QPL}(\mathsf {PA})$
by adding such principles together with predicate logical reasoning to
![]() $\mathsf {GL}$
. A first wrinkle in this hope appeared when Montagna [Reference Montagna32] published a new always provable principle falling outside this easily generated set. Soon after, Artemov [Reference Artemov2] proved that
$\mathsf {GL}$
. A first wrinkle in this hope appeared when Montagna [Reference Montagna32] published a new always provable principle falling outside this easily generated set. Soon after, Artemov [Reference Artemov2] proved that
![]() $\mathsf {TQPL}(\mathsf {PA})$
is not even arithmetically definable. Last hopes were scattered when Vardanyan [Reference Vardanyan36] and McGee [Reference McGee31] independently proved that
$\mathsf {TQPL}(\mathsf {PA})$
is not even arithmetically definable. Last hopes were scattered when Vardanyan [Reference Vardanyan36] and McGee [Reference McGee31] independently proved that
![]() $\mathsf {QPL}(\mathsf {PA})$
is as complex as it can possibly be:
$\mathsf {QPL}(\mathsf {PA})$
is as complex as it can possibly be:
![]() $\Pi ^0_2$
complete. Moreover, Boolos and McGee [Reference Boolos and McGee12] showed that
$\Pi ^0_2$
complete. Moreover, Boolos and McGee [Reference Boolos and McGee12] showed that
![]() $\mathsf {TQPL}(\mathsf {PA})$
is also as complex as possible:
$\mathsf {TQPL}(\mathsf {PA})$
is also as complex as possible:
![]() $\Pi ^0_1$
complete in the set of true arithmetic.
$\Pi ^0_1$
complete in the set of true arithmetic.
These negative results are quite robust in various ways. For example, Vardanyan [Reference Vardanyan and Adyan37] showed that restricting the language to the fragment with a single unary predicate and without any modality nesting doesn’t break the
![]() $\Pi ^0_2$
completeness.
$\Pi ^0_2$
completeness.
Restricting the complexity of the realizations to, for example,
![]() $\Sigma ^0_1$
formulas doesn’t help either: the corresponding set is still
$\Sigma ^0_1$
formulas doesn’t help either: the corresponding set is still
![]() $\Pi ^0_2$
complete, as shown by Berarducci [Reference Berarducci10].
$\Pi ^0_2$
complete, as shown by Berarducci [Reference Berarducci10].
One can consider
![]() $\mathsf {QPL}(T)$
for an arbitrary c.e. theory T. It is easy to see that the degenerate case of
$\mathsf {QPL}(T)$
for an arbitrary c.e. theory T. It is easy to see that the degenerate case of
![]() $\mathsf {QPL}(\mathsf {PA} + \Box _{\mathsf {PA}} \bot )$
is axiomatized by predicate logic together with
$\mathsf {QPL}(\mathsf {PA} + \Box _{\mathsf {PA}} \bot )$
is axiomatized by predicate logic together with
![]() $\Box \bot $
. However, Visser and de Jonge [Reference Visser and de Jonge38] proved that for most theories T,
$\Box \bot $
. However, Visser and de Jonge [Reference Visser and de Jonge38] proved that for most theories T,
![]() $\mathsf {QPL}(T)$
is indeed
$\mathsf {QPL}(T)$
is indeed
![]() $\Pi ^0_2$
complete. The title of their paper is No Escape from Vardanyan’s Theorem.
$\Pi ^0_2$
complete. The title of their paper is No Escape from Vardanyan’s Theorem.
Be that as it may, there have already been some “escapes” from Vardanyan’s Theorem. For example, the one-variable fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
is decidable, as shown by Artemov and Japaridze [Reference Artemov and Japaridze4]. Furthermore, an arithmetically complete quantified modal logic was proposed by Yavorsky [Reference Yavorsky, Wolter, Wansing, de Rijke and Zakharyaschev40] (see also [Reference Hao and Tourlakis24]). This logic, called
$\mathsf {QPL}(\mathsf {PA})$
is decidable, as shown by Artemov and Japaridze [Reference Artemov and Japaridze4]. Furthermore, an arithmetically complete quantified modal logic was proposed by Yavorsky [Reference Yavorsky, Wolter, Wansing, de Rijke and Zakharyaschev40] (see also [Reference Hao and Tourlakis24]). This logic, called
![]() $\mathsf {QGL}^b$
, assumes that in
$\mathsf {QGL}^b$
, assumes that in
![]() $\Box A$
every free variable of A is bound under the box. In other words,
$\Box A$
every free variable of A is bound under the box. In other words,
![]() $\mathsf {QGL}^b$
is roughly
$\mathsf {QGL}^b$
is roughly
![]() $\mathsf {QGL}$
extended with the axiom schema
$\mathsf {QGL}$
extended with the axiom schema
![]() $\Box A \to \Box \forall x \, A$
.
$\Box A \to \Box \forall x \, A$
.
Our proposed fragment includes countably many variables and allows for open variables under the box. In order to “escape,” we restrict the language to its strictly positive fragment instead. This work already began in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], where we described the system
![]() $\mathsf {QRC_1}$
and proved its decidability. Here we improve on the modal results presented there and prove the arithmetical completeness theorem for
$\mathsf {QRC_1}$
and proved its decidability. Here we improve on the modal results presented there and prove the arithmetical completeness theorem for
![]() $\mathsf {QRC_1}$
, previously left as a conjecture.
$\mathsf {QRC_1}$
, previously left as a conjecture.
There is an ongoing formalizationFootnote 3 of this paper in the Coq Proof Assistant [14], covering Sections 3 and 4 (and part of Section 5) as of May 2022.
1.1 Overview of the paper
We start with a brief overview of strictly positive logics in Section 2, followed by the definition of
![]() $\mathsf {QRC_1}$
, our main object of study, in Section 3.
$\mathsf {QRC_1}$
, our main object of study, in Section 3.
After that the paper is divided into two parts, the first dealing with purely modal results (Sections 4–6), and the second delving into arithmetic (Sections 7–10). The two parts are not completely independent, but a reader who wishes to skip to Section 7 need only be familiar with the definition of Kripke model with constant domain (Definition 4.1) and the constant domain completeness theorem for
![]() $\mathsf {QRC_1}$
(Theorem 5.11).
$\mathsf {QRC_1}$
(Theorem 5.11).
In the first part, Section 4 starts by presenting an extended definition of Kripke model that does not depend on inclusive models, with a respective soundness proof for
![]() $\mathsf {QRC_1}$
. Then in Section 5 we show that
$\mathsf {QRC_1}$
. Then in Section 5 we show that
![]() $\mathsf {QRC_1}$
is complete with respect to constant domain Kripke models. Section 6 remarks that
$\mathsf {QRC_1}$
is complete with respect to constant domain Kripke models. Section 6 remarks that
![]() $\mathsf {QRC_1}$
is the strictly positive fragment of every logic between
$\mathsf {QRC_1}$
is the strictly positive fragment of every logic between
![]() $\mathsf {QK}4$
and
$\mathsf {QK}4$
and
![]() $\mathsf {QGL}$
, and also of other quantified modal logics such as
$\mathsf {QGL}$
, and also of other quantified modal logics such as
![]() $\mathsf {QK}4 + \mathsf {BF}$
, where
$\mathsf {QK}4 + \mathsf {BF}$
, where
![]() $\mathsf {BF} = \forall x \, \Box A \to \Box \forall x \, A$
is the well-known and arithmetically unsound Barcan Formula.
$\mathsf {BF} = \forall x \, \Box A \to \Box \forall x \, A$
is the well-known and arithmetically unsound Barcan Formula.
In the second part, Section 7 explains our arithmetic reading of strictly positive formulas, followed by Section 8, where we prove the arithmetical completeness of
![]() $\mathsf {QRC_1}$
. Section 9 then makes use of the arithmetical completeness theorem to show that
$\mathsf {QRC_1}$
. Section 9 then makes use of the arithmetical completeness theorem to show that
![]() $\mathsf {QRC_1}$
is a fragment of
$\mathsf {QRC_1}$
is a fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
. Section 10, which can be read right after Section 7, shows the arithmetical soundness of
$\mathsf {QPL}(\mathsf {PA})$
. Section 10, which can be read right after Section 7, shows the arithmetical soundness of
![]() $\mathsf {QRC_1}$
with respect to Heyting Arithmetic.
$\mathsf {QRC_1}$
with respect to Heyting Arithmetic.
We end with some proposed avenues for future work in Section 11.
2 Strictly positive logics
A key feature of our escape is given by restricting the language. Given variables
![]() $x, x_i, \ldots $
and a signature
$x, x_i, \ldots $
and a signature
![]() $\Sigma $
fixing the constants
$\Sigma $
fixing the constants
![]() $c, c_i, \ldots $
and relation symbols
$c, c_i, \ldots $
and relation symbols
![]() $S, S_i, \ldots $
, the formulas of
$S, S_i, \ldots $
, the formulas of
![]() $\mathsf {QRC_1}$
are built up from
$\mathsf {QRC_1}$
are built up from
![]() $\top $
, n-ary relation symbols applied to n terms (which are either variables or constants), the binary
$\top $
, n-ary relation symbols applied to n terms (which are either variables or constants), the binary
![]() $\land $
, the unary
$\land $
, the unary
![]() $\Diamond $
, and the quantifier
$\Diamond $
, and the quantifier
![]() $\forall x$
. The provable judgments in
$\forall x$
. The provable judgments in
![]() $\mathsf {QRC_1}$
are all of the form
$\mathsf {QRC_1}$
are all of the form
![]() $\varphi \vdash \psi $
with
$\varphi \vdash \psi $
with
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
in the above language.
$\psi $
in the above language.
Our formulas are related to arithmetic through realizations
![]() $\cdot ^{\circ }$
that map n-ary predicate symbols to c.e. axiomatizations of theories indexed by n parameters (details can be found in Section 7). Given a
$\cdot ^{\circ }$
that map n-ary predicate symbols to c.e. axiomatizations of theories indexed by n parameters (details can be found in Section 7). Given a
![]() $\Sigma ^0_1$
axiomatization
$\Sigma ^0_1$
axiomatization
![]() $\tau $
of some theory T, we extend
$\tau $
of some theory T, we extend
![]() $\cdot ^{\circ }$
to non-predicate formulas such that conjunctions are interpreted as the unions of the corresponding axiom sets (
$\cdot ^{\circ }$
to non-predicate formulas such that conjunctions are interpreted as the unions of the corresponding axiom sets (
![]() $(\varphi \land \psi )^{\circ _{\tau }} := \varphi ^{\circ _{\tau }} \lor \psi ^{\circ _{\tau }}$
), and universal quantification corresponds to an infinite union (
$(\varphi \land \psi )^{\circ _{\tau }} := \varphi ^{\circ _{\tau }} \lor \psi ^{\circ _{\tau }}$
), and universal quantification corresponds to an infinite union (
![]() $(\forall x \, \varphi )^{\circ _{\tau }} := \exists y \, \varphi ^{\circ _{\tau }}$
, where y is the arithmetical variable corresponding to the modal variable x).
$(\forall x \, \varphi )^{\circ _{\tau }} := \exists y \, \varphi ^{\circ _{\tau }}$
, where y is the arithmetical variable corresponding to the modal variable x).
This interpretation is common in the study of reflection calculi [Reference Beklemishev7] and is more general than the usual, finitary one, mentioned in the previous section as
![]() $\cdot ^{*}$
. In the latter case, conjunctions of modal formulas are simply interpreted as conjunctions of their arithmetical counterparts. We further define and make use of this finitary notion in Section 8. While it is possible to represent finite extensions of a base theory through the finitary
$\cdot ^{*}$
. In the latter case, conjunctions of modal formulas are simply interpreted as conjunctions of their arithmetical counterparts. We further define and make use of this finitary notion in Section 8. While it is possible to represent finite extensions of a base theory through the finitary
![]() $\cdot ^{*}$
-style realizations, the
$\cdot ^{*}$
-style realizations, the
![]() $\cdot ^{\circ }$
approach allows for the possibility of infinitary extensions.
$\cdot ^{\circ }$
approach allows for the possibility of infinitary extensions.
Using this restricted fragment and infinitary arithmetical interpretation, we define the Strictly Positive Quantified Provability Logic of a theory T as follows.
The main result of this paper is that, for a large class of theories T, the logic
![]() $\mathsf {QPL}^{\mathsf {SP}}(T)$
is decidable and given by the system
$\mathsf {QPL}^{\mathsf {SP}}(T)$
is decidable and given by the system
![]() $\mathsf {QRC_1}$
as introduced in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. As such our paper was inspired by and contributes to three recent developments in the literature: strictly positive logics, reflection calculi, and polymodal logics.
$\mathsf {QRC_1}$
as introduced in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. As such our paper was inspired by and contributes to three recent developments in the literature: strictly positive logics, reflection calculi, and polymodal logics.
The quintessential polymodal provability logic is
![]() $\mathsf {GLP}$
, introduced by Japaridze in 1986 [Reference Japaridze26]. The Reflection Calculus,
$\mathsf {GLP}$
, introduced by Japaridze in 1986 [Reference Japaridze26]. The Reflection Calculus,
![]() $\mathsf {RC}$
, was first introduced by Dashkov [Reference Dashkov16] as the set of
$\mathsf {RC}$
, was first introduced by Dashkov [Reference Dashkov16] as the set of
![]() $\mathsf {GLP}$
-equivalences between strictly positive formulas. It was then axiomatized by Beklemishev [Reference Beklemishev, Bolander, Braüner, Ghilardi and Moss6], and it is the latter formulation that appears in most of the ensuing literature.
$\mathsf {GLP}$
-equivalences between strictly positive formulas. It was then axiomatized by Beklemishev [Reference Beklemishev, Bolander, Braüner, Ghilardi and Moss6], and it is the latter formulation that appears in most of the ensuing literature.
Even though
![]() $\mathsf {RC}$
has a strictly positive language, it is remarkably expressive, giving rise to an ordinal notation system [Reference Fernández-Duque19] and being an appropriate tool for
$\mathsf {RC}$
has a strictly positive language, it is remarkably expressive, giving rise to an ordinal notation system [Reference Fernández-Duque19] and being an appropriate tool for
![]() $\Pi ^0_1$
ordinal analysis [Reference Beklemishev and Pakhomov9]. This is remarkable because, while
$\Pi ^0_1$
ordinal analysis [Reference Beklemishev and Pakhomov9]. This is remarkable because, while
![]() $\mathsf {GLP}$
is
$\mathsf {GLP}$
is
![]() $\mathsf {PSPACE}$
complete [Reference Shapirovsky, Areces and Goldblatt33],
$\mathsf {PSPACE}$
complete [Reference Shapirovsky, Areces and Goldblatt33],
![]() $\mathsf {RC}$
has a polynomial-time decision procedure. Thus, at least in the case of
$\mathsf {RC}$
has a polynomial-time decision procedure. Thus, at least in the case of
![]() $\mathsf {GLP}$
, restricting the language to the strictly positive fragment is very worthwhile.
$\mathsf {GLP}$
, restricting the language to the strictly positive fragment is very worthwhile.
![]() $\mathsf {QRC_1}$
was inspired by
$\mathsf {QRC_1}$
was inspired by
![]() $\mathsf {RC}_1$
, which is the unimodal fragment of
$\mathsf {RC}_1$
, which is the unimodal fragment of
![]() $\mathsf {RC}$
. We hoped to emulate
$\mathsf {RC}$
. We hoped to emulate
![]() $\mathsf {RC}$
’s success in these two dimensions, obtaining a useful calculus with a simpler complexity than the original (
$\mathsf {RC}$
’s success in these two dimensions, obtaining a useful calculus with a simpler complexity than the original (
![]() $\mathsf {QPL}(\mathsf {PA})$
in this case). We already see in this paper that the latter goal was achieved, since
$\mathsf {QPL}(\mathsf {PA})$
in this case). We already see in this paper that the latter goal was achieved, since
![]() $\mathsf {QRC_1}$
is decidable while
$\mathsf {QRC_1}$
is decidable while
![]() $\mathsf {QPL}(\mathsf {PA})$
is
$\mathsf {QPL}(\mathsf {PA})$
is
![]() $\Pi ^0_2$
complete. However, the main expressibility tool available in
$\Pi ^0_2$
complete. However, the main expressibility tool available in
![]() $\mathsf {RC}$
, the iterated consistency statements (also known as worms [Reference Beklemishev, Chatzidakis, Koepke and Pohlers5]), are not very interesting when there is only one modality. Thus we plan to extend
$\mathsf {RC}$
, the iterated consistency statements (also known as worms [Reference Beklemishev, Chatzidakis, Koepke and Pohlers5]), are not very interesting when there is only one modality. Thus we plan to extend
![]() $\mathsf {QRC_1}$
to
$\mathsf {QRC_1}$
to
![]() $\mathsf {QRC}_\Lambda $
in the future.
$\mathsf {QRC}_\Lambda $
in the future.
When considering a strictly positive logic P, one may ask whether there is some modal logic L whose strictly positive fragment
![]() $L^{\mathsf {SP}}$
coincides with P (cf. [Reference Beklemishev and Odintsov8]). In that case we would have
$L^{\mathsf {SP}}$
coincides with P (cf. [Reference Beklemishev and Odintsov8]). In that case we would have
where
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are strictly positive formulas.
$\psi $
are strictly positive formulas.
We know that
![]() $\mathsf {RC}$
is the strictly positive fragment of
$\mathsf {RC}$
is the strictly positive fragment of
![]() $\mathsf {GLP}$
(in the sense of (2)), and in Section 6 we show that
$\mathsf {GLP}$
(in the sense of (2)), and in Section 6 we show that
![]() $\mathsf {QRC_1}$
is the strictly positive fragment of
$\mathsf {QRC_1}$
is the strictly positive fragment of
![]() $\mathsf {QGL}$
. However, there are strictly positive logics with no such counterpart, such as
$\mathsf {QGL}$
. However, there are strictly positive logics with no such counterpart, such as
![]() $\mathsf {RC}$
together with the persistence axiom
$\mathsf {RC}$
together with the persistence axiom
![]() $\langle \omega \rangle \varphi \vdash \varphi $
. This system was described in [Reference Beklemishev7] as
$\langle \omega \rangle \varphi \vdash \varphi $
. This system was described in [Reference Beklemishev7] as
![]() $\mathsf {RC}\omega $
.
$\mathsf {RC}\omega $
.
The study of strictly positive logics has also been developed in other communities, most notably in the field of description logics, as in [Reference Kikot, Kurucz, Tanaka, Wolter and Zakharyaschev27, Reference Kurucz, Wolter, Zakharyaschev, Beklemishev, Goranko and Shehtman30]. Furthermore, there is a significant body of work done about (non-strictly) positive logics (see [Reference Celani and Jansana13, Reference Dunn17]).
3 Quantified Reflection Calculus with one modality
The Quantified Reflection Calculus with one modality, or
![]() $\mathsf {QRC_1}$
, is a sequent logic in a strictly positive predicate modal language introduced in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1].
$\mathsf {QRC_1}$
, is a sequent logic in a strictly positive predicate modal language introduced in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1].
The free variables of a formula
![]() $\varphi $
are defined as usual, and denoted by
$\varphi $
are defined as usual, and denoted by
![]() ${\mathrm {fv}}(\varphi )$
. The expression
${\mathrm {fv}}(\varphi )$
. The expression
![]() $\varphi [x {\leftarrow } t]$
denotes the formula
$\varphi [x {\leftarrow } t]$
denotes the formula
![]() $\varphi $
with all free occurrences of the variable x simultaneously replaced by the term t. We say that t is free for x in
$\varphi $
with all free occurrences of the variable x simultaneously replaced by the term t. We say that t is free for x in
![]() $\varphi $
if no occurrence of a free variable in t becomes bound in
$\varphi $
if no occurrence of a free variable in t becomes bound in
![]() $\varphi [x {\leftarrow } t]$
.
$\varphi [x {\leftarrow } t]$
.
The axioms and rules of
![]() $\mathsf {QRC_1}$
are listed in the following definition from [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we removed the axiom
$\mathsf {QRC_1}$
are listed in the following definition from [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we removed the axiom
![]() $\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
because it is an easy consequence of the calculus without it.
$\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
because it is an easy consequence of the calculus without it.
Definition 3.1 (
 $\mathsf {QRC_1}$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
$\mathsf {QRC_1}$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Let
![]() $\Sigma $
be a signature and
$\Sigma $
be a signature and
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
, and
$\psi $
, and
![]() $\chi $
be any formulas in that language. The axioms and rules of
$\chi $
be any formulas in that language. The axioms and rules of
![]() $\mathsf {QRC_1}$
are the following:
$\mathsf {QRC_1}$
are the following:
-
(i)
 $\varphi \vdash \top $
and
$\varphi \vdash \top $
and
 $\varphi \vdash \varphi $
;
$\varphi \vdash \varphi $
; -
(ii)
 $\varphi \land \psi \vdash \varphi $
and
$\varphi \land \psi \vdash \varphi $
and
 $\varphi \land \psi \vdash \psi $
;
$\varphi \land \psi \vdash \psi $
; -
(iii) if
 $\varphi \vdash \psi $
and
$\varphi \vdash \psi $
and
 $\varphi \vdash \chi $
, then
$\varphi \vdash \chi $
, then
 $\varphi \vdash \psi \land \chi $
;
$\varphi \vdash \psi \land \chi $
; -
(iv) if
 $\varphi \vdash \psi $
and
$\varphi \vdash \psi $
and
 $\psi \vdash \chi $
, then
$\psi \vdash \chi $
, then
 $\varphi \vdash \chi $
;
$\varphi \vdash \chi $
; -
(v) if
 $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
 $\Diamond \varphi \vdash \Diamond \psi $
;
$\Diamond \varphi \vdash \Diamond \psi $
; -
(vi)
 $\Diamond \Diamond \varphi \vdash \Diamond \varphi $
;
$\Diamond \Diamond \varphi \vdash \Diamond \varphi $
; -
(vii) if
 $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
 $\varphi \vdash \forall x \, \psi $
(
$\varphi \vdash \forall x \, \psi $
(
 $x \notin {\mathrm {fv}}(\varphi )$
);
$x \notin {\mathrm {fv}}(\varphi )$
); -
(viii) if
 $\varphi [x {\leftarrow } t] \vdash \psi $
, then
$\varphi [x {\leftarrow } t] \vdash \psi $
, then
 $\forall x \, \varphi \vdash \psi $
(t free for x in
$\forall x \, \varphi \vdash \psi $
(t free for x in
 $\varphi $
);
$\varphi $
); -
(ix) if
 $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
 $\varphi [x {\leftarrow } t] \vdash \psi [x {\leftarrow } t]$
(t free for x in
$\varphi [x {\leftarrow } t] \vdash \psi [x {\leftarrow } t]$
(t free for x in
 $\varphi $
and
$\varphi $
and
 $\psi $
);
$\psi $
); -
(x) if
 $\varphi [x {\leftarrow } c] \vdash \psi [x {\leftarrow } c]$
, then
$\varphi [x {\leftarrow } c] \vdash \psi [x {\leftarrow } c]$
, then
 $\varphi \vdash \psi $
(c not in
$\varphi \vdash \psi $
(c not in
 $\varphi $
nor
$\varphi $
nor
 $\psi $
).
$\psi $
).
If
![]() $\varphi \vdash \psi $
, we say that
$\varphi \vdash \psi $
, we say that
![]() $\psi $
follows from
$\psi $
follows from
![]() $\varphi $
in
$\varphi $
in
![]() $\mathsf {QRC_1}$
. When the signature is not clear from the context, we write
$\mathsf {QRC_1}$
. When the signature is not clear from the context, we write
![]() $\varphi \vdash _\Sigma \psi $
instead.
$\varphi \vdash _\Sigma \psi $
instead.
We observe that our axioms do not include universal quantifier elimination. However, this and various other rules are readily available via the following easy lemma.
Lemma 3.2. The following are theorems (or derivable rules) of
![]() $\mathsf {QRC_1}$
:
$\mathsf {QRC_1}$
:
-
1.
 $\forall x \, \forall y \, \varphi \vdash \forall y \, \forall x \, \varphi $
;
$\forall x \, \forall y \, \varphi \vdash \forall y \, \forall x \, \varphi $
; -
2.
 $\forall x \, \varphi \vdash \varphi [x {\leftarrow } t]$
(t free for x in
$\forall x \, \varphi \vdash \varphi [x {\leftarrow } t]$
(t free for x in
 $\varphi $
);
$\varphi $
); -
3.
 $\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
;Footnote
4
$\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
;Footnote
4
-
4.
 $\forall x \, \varphi \vdash \forall y \, \varphi [x {\leftarrow } y]$
(y free for x in
$\forall x \, \varphi \vdash \forall y \, \varphi [x {\leftarrow } y]$
(y free for x in
 $\varphi $
and
$\varphi $
and
 $y \notin {\mathrm {fv}}(\varphi )$
);
$y \notin {\mathrm {fv}}(\varphi )$
); -
5. if
 $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
 $\varphi \vdash \psi [x {\leftarrow } t]$
(x not free in
$\varphi \vdash \psi [x {\leftarrow } t]$
(x not free in
 $\varphi $
and t free for x in
$\varphi $
and t free for x in
 $\psi $
);
$\psi $
); -
6. if
 $\varphi \vdash \psi [x {\leftarrow } c]$
, then
$\varphi \vdash \psi [x {\leftarrow } c]$
, then
 $\varphi \vdash \forall x \, \psi $
(x not free in
$\varphi \vdash \forall x \, \psi $
(x not free in
 $\varphi $
and c not in
$\varphi $
and c not in
 $\varphi $
nor
$\varphi $
nor
 $\psi $
).
$\psi $
).
The following are two useful complexity measures on the formulas of
![]() $\mathsf {QRC_1}$
.
$\mathsf {QRC_1}$
.
Definition 3.3 (
 ${\mathrm {d}}_\Diamond $
,
${\mathrm {d}}_\Diamond $
,
 ${\mathrm {d}}_\forall $
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
${\mathrm {d}}_\forall $
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Given a formula
![]() $\varphi $
, its modal depth
$\varphi $
, its modal depth
![]() ${\mathrm {d}}_\Diamond (\varphi )$
is defined inductively as follows:
${\mathrm {d}}_\Diamond (\varphi )$
is defined inductively as follows:
-
•
 ${\mathrm {d}}_\Diamond (\top ) := {\mathrm {d}}_\Diamond (S(x_0, \ldots , x_{n-1})) := 0$
;
${\mathrm {d}}_\Diamond (\top ) := {\mathrm {d}}_\Diamond (S(x_0, \ldots , x_{n-1})) := 0$
; -
•
 ${\mathrm {d}}_\Diamond (\psi \land \chi ) := \max \{{\mathrm {d}}_\Diamond (\psi ), {\mathrm {d}}_\Diamond (\chi )\}$
;
${\mathrm {d}}_\Diamond (\psi \land \chi ) := \max \{{\mathrm {d}}_\Diamond (\psi ), {\mathrm {d}}_\Diamond (\chi )\}$
; -
•
 ${\mathrm {d}}_\Diamond (\forall x \, \psi ) := {\mathrm {d}}_\Diamond (\psi )$
;
${\mathrm {d}}_\Diamond (\forall x \, \psi ) := {\mathrm {d}}_\Diamond (\psi )$
; -
•
 ${\mathrm {d}}_\Diamond (\Diamond \psi ) := {\mathrm {d}}_\Diamond (\psi ) + 1$
.
${\mathrm {d}}_\Diamond (\Diamond \psi ) := {\mathrm {d}}_\Diamond (\psi ) + 1$
.
Given a finite set of formulas
![]() $\Gamma $
, its modal depth is
$\Gamma $
, its modal depth is
![]() ${\mathrm {d}}_\Diamond (\Gamma ) := \max _{\varphi \in \Gamma }\{{\mathrm {d}}_\Diamond (\varphi )\}$
.
${\mathrm {d}}_\Diamond (\Gamma ) := \max _{\varphi \in \Gamma }\{{\mathrm {d}}_\Diamond (\varphi )\}$
.
The definition of quantifier depth
![]() ${\mathrm {d}}_\forall $
is analogous except for:
${\mathrm {d}}_\forall $
is analogous except for:
-
•
 ${\mathrm {d}}_\forall (\forall x \, \psi ) := {\mathrm {d}}_\forall (\psi ) + 1$
and
${\mathrm {d}}_\forall (\forall x \, \psi ) := {\mathrm {d}}_\forall (\psi ) + 1$
and -
•
 ${\mathrm {d}}_\forall (\Diamond \psi ) := {\mathrm {d}}_\forall (\psi )$
.
${\mathrm {d}}_\forall (\Diamond \psi ) := {\mathrm {d}}_\forall (\psi )$
.
The modal depth provides a necessary condition for derivability, which in particular implies irreflexivity.
Lemma 3.4 [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1].
Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be formulas in the language of
$\psi $
be formulas in the language of
![]() $\mathsf {QRC_1}$
.
$\mathsf {QRC_1}$
.
-
• If
 $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
 ${\mathrm {d}}_\Diamond (\varphi ) \geq {\mathrm {d}}_\Diamond (\psi )$
.
${\mathrm {d}}_\Diamond (\varphi ) \geq {\mathrm {d}}_\Diamond (\psi )$
. -
•
 $\varphi \not \vdash \Diamond \varphi $
.
$\varphi \not \vdash \Diamond \varphi $
.
Finally, the signature of
![]() $\mathsf {QRC_1}$
can be extended without strengthening the calculus.
$\mathsf {QRC_1}$
can be extended without strengthening the calculus.
Lemma 3.5 [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1].
Let
![]() $\Sigma $
be a signature and let C be a collection of constants not yet occurring in
$\Sigma $
be a signature and let C be a collection of constants not yet occurring in
![]() $\Sigma $
. By
$\Sigma $
. By
![]() $\Sigma _C$
we denote the signature obtained by including these new constants C in
$\Sigma _C$
we denote the signature obtained by including these new constants C in
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\varphi , \psi $
be formulas in the language of
$\varphi , \psi $
be formulas in the language of
![]() $\Sigma $
. Then, if
$\Sigma $
. Then, if
![]() $\varphi \vdash _{\Sigma _C} \psi $
, so does
$\varphi \vdash _{\Sigma _C} \psi $
, so does
![]() $\varphi \vdash _\Sigma \psi $
.
$\varphi \vdash _\Sigma \psi $
.
4 Relational semantics
![]() $\mathsf {QRC_1}$
was proven sound and complete with respect to relational semantics in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we extend both of those results in the following ways: we relax the requirement for the adequateness of a frame, and we prove constant domain completeness: that if
$\mathsf {QRC_1}$
was proven sound and complete with respect to relational semantics in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we extend both of those results in the following ways: we relax the requirement for the adequateness of a frame, and we prove constant domain completeness: that if
![]() $\varphi \not \vdash \psi $
then there exists a counter model that, in addition to being finite and irreflexive, also has a constant domain.
$\varphi \not \vdash \psi $
then there exists a counter model that, in addition to being finite and irreflexive, also has a constant domain.
We begin by slightly changing the definition of frame and relational model presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. There, models for
![]() $\mathsf {QRC_1}$
were described as a number of first-order models (the worlds) connected through a transitive relation R. We additionally required inclusiveness: that whenever w and u are worlds connected through R, the domain of w be included in the domain of u. We then used the inclusion (identity) function
$\mathsf {QRC_1}$
were described as a number of first-order models (the worlds) connected through a transitive relation R. We additionally required inclusiveness: that whenever w and u are worlds connected through R, the domain of w be included in the domain of u. We then used the inclusion (identity) function
![]() $\iota _{w, u}$
to refer to the element of the domain of u corresponding to an element in the domain of w.
$\iota _{w, u}$
to refer to the element of the domain of u corresponding to an element in the domain of w.
Here, we no longer have the inclusiveness restriction. In fact, as we will see bellow, any configuration of domains is sound as long as the functions
![]() $\eta _{w, u}$
relating the domain of w with the domain of u respect the transitivity of R. This is clearly the case if the frame is inclusive and
$\eta _{w, u}$
relating the domain of w with the domain of u respect the transitivity of R. This is clearly the case if the frame is inclusive and
![]() $\eta _{w, u} = \iota _{w, u}$
, so the definitions presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] are a particular case of the ones presented here.
$\eta _{w, u} = \iota _{w, u}$
, so the definitions presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] are a particular case of the ones presented here.
Definition 4.1. A relational model
![]() $\mathcal {M}$
in a signature
$\mathcal {M}$
in a signature
![]() $\Sigma $
is a tuple
$\Sigma $
is a tuple
![]() $\langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, v}\}_{wRv}, \{I_w\}_{w \in W},\{J_w\}_{w \in W} \rangle $
where:
$\langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, v}\}_{wRv}, \{I_w\}_{w \in W},\{J_w\}_{w \in W} \rangle $
where:
-
• W is a non-empty set (the set of worlds, where individual worlds are referred to as
 $w, u, v$
, etc.);
$w, u, v$
, etc.); -
• R is a binary relation on W (the accessibility relation);
-
• each
 $M_w$
is a finite set (the domain of the world w, whose elements are referred to as
$M_w$
is a finite set (the domain of the world w, whose elements are referred to as
 $d, d_0, d_1$
, etc.);
$d, d_0, d_1$
, etc.); -
• if
 $wRv$
, then
$wRv$
, then
 $\eta _{w, v}$
is a function from
$\eta _{w, v}$
is a function from
 $M_w$
to
$M_w$
to
 $M_v$
;
$M_v$
; -
• for each
 $w \in W$
, the interpretation
$w \in W$
, the interpretation
 $I_w$
assigns an element of the domain
$I_w$
assigns an element of the domain
 $M_w$
to each constant
$M_w$
to each constant
 $c \in \Sigma $
, written
$c \in \Sigma $
, written
 $c^{I_w}$
; and
$c^{I_w}$
; and -
• for each
 $w \in W$
, the interpretation
$w \in W$
, the interpretation
 $J_w$
assigns a set of tuples
$J_w$
assigns a set of tuples
 $S^{J_w} \subseteq \wp ((M_w)^n)$
to each n-ary relation symbol
$S^{J_w} \subseteq \wp ((M_w)^n)$
to each n-ary relation symbol
 $S \in \Sigma $
.
$S \in \Sigma $
.
The
![]() $\langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, v}\}_{wRv} \rangle $
part of the model is called its frame. We say that the frame (or model) is finite if W is finite, and that it is constant domain if all the
$\langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, v}\}_{wRv} \rangle $
part of the model is called its frame. We say that the frame (or model) is finite if W is finite, and that it is constant domain if all the
![]() $M_w$
coincide and all the
$M_w$
coincide and all the
![]() $\eta _{w, u}$
are the identity function.
$\eta _{w, u}$
are the identity function.
The relevant frames and models will need to satisfy a number of requisites.
Definition 4.2. A frame
![]() $\mathcal {F}$
is adequate if:
$\mathcal {F}$
is adequate if:
-
• R is transitive: if
 $wRu$
and
$wRu$
and
 $uRv$
, then
$uRv$
, then
 $wRv$
; and
$wRv$
; and -
•
 $\eta $
functions respect transitivity: if
$\eta $
functions respect transitivity: if
 $wRu$
and
$wRu$
and
 $uRv$
, then
$uRv$
, then
 $\eta _{w, v} = \eta _{u, v} \circ \eta _{w, u}$
.Footnote
5
$\eta _{w, v} = \eta _{u, v} \circ \eta _{w, u}$
.Footnote
5
A model is adequate if it is based on an adequate frame and it is:
-
• concordant: if
 $wRu$
, then
$wRu$
, then
 $c^{I_u} = \eta _{w, u}(c^{I_w})$
for every constant c.
$c^{I_u} = \eta _{w, u}(c^{I_w})$
for every constant c.
Note that in an adequate and rooted model the interpretation of the constants is fully determined by their interpretation at the root.
As in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], we use assignments to define truth at a world in a first-order model. A
![]() $w$
-assignment g is a function assigning a member of the domain
$w$
-assignment g is a function assigning a member of the domain
![]() $M_w$
to each variable in the language. Any
$M_w$
to each variable in the language. Any
![]() $w$
-assignment can be seen as a
$w$
-assignment can be seen as a
![]() $v$
-assignment as long as
$v$
-assignment as long as
![]() $wRv$
, by composing it with
$wRv$
, by composing it with
![]() $\eta _{w, v}$
on the left. We write
$\eta _{w, v}$
on the left. We write
![]() $g^v$
to shorten
$g^v$
to shorten
![]() $\eta _{w, v} \circ g$
when
$\eta _{w, v} \circ g$
when
![]() $w$
is clear from the context.
$w$
is clear from the context.
Two
![]() $w$
-assignments g and h are x-alternative, written
$w$
-assignments g and h are x-alternative, written
![]() $g \sim _{x} h$
, if they coincide on all variables other than x. A
$g \sim _{x} h$
, if they coincide on all variables other than x. A
![]() $w$
-assignment g is extended to terms by defining
$w$
-assignment g is extended to terms by defining
![]() $g(c) := c^{I_w}$
for any constant c. Note that this meshes nicely with the concordant restriction of an adequate model: for any term t, if
$g(c) := c^{I_w}$
for any constant c. Note that this meshes nicely with the concordant restriction of an adequate model: for any term t, if
![]() $wRv$
then
$wRv$
then
![]() $g^v(t) = \eta _{w, v}(g(t))$
.
$g^v(t) = \eta _{w, v}(g(t))$
.
We are finally ready to define satisfaction at a world. This definition is a straightforward adaptation of the one presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] to our current definition of model. The only difference is in the case of
![]() $\Diamond \varphi $
, where we use
$\Diamond \varphi $
, where we use
![]() $g^v$
instead of
$g^v$
instead of
![]() $g^\iota $
.
$g^\iota $
.
Definition 4.3. Let
![]() $\mathcal {M} = \langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, u}\}_{wRu}, \{I_w\}_{w \in W}, \{J_w\}_{w \in W} \rangle $
be an adequate model in some signature
$\mathcal {M} = \langle W, R, \{M_w\}_{w \in W}, \{\eta _{w, u}\}_{wRu}, \{I_w\}_{w \in W}, \{J_w\}_{w \in W} \rangle $
be an adequate model in some signature
![]() $\Sigma $
, and let
$\Sigma $
, and let
![]() $w \in W$
be a world, g be a
$w \in W$
be a world, g be a
![]() $w$
-assignment, S be an n-ary relation symbol, and
$w$
-assignment, S be an n-ary relation symbol, and
![]() $\varphi , \psi $
be formulas in the language of
$\varphi , \psi $
be formulas in the language of
![]() $\Sigma $
.
$\Sigma $
.
We define
![]() $\mathcal {M}, w \Vdash ^g \varphi $
(
$\mathcal {M}, w \Vdash ^g \varphi $
(
![]() $\varphi $
is true at w under g) by induction on
$\varphi $
is true at w under g) by induction on
![]() $\varphi $
as follows.
$\varphi $
as follows.
-
•
 $\mathcal {M}, w \Vdash ^g \top $
;
$\mathcal {M}, w \Vdash ^g \top $
; -
•
 $\mathcal {M}, w \Vdash ^g S(t_0, \ldots , t_{n-1})$
iff
$\mathcal {M}, w \Vdash ^g S(t_0, \ldots , t_{n-1})$
iff
 $\langle g(t_0), \ldots , g(t_{n-1}) \rangle \in S^{J_w}$
;
$\langle g(t_0), \ldots , g(t_{n-1}) \rangle \in S^{J_w}$
; -
•
 $\mathcal {M}, w \Vdash ^g \varphi \land \psi $
iff both
$\mathcal {M}, w \Vdash ^g \varphi \land \psi $
iff both
 $\mathcal {M}, w \Vdash ^g \varphi $
and
$\mathcal {M}, w \Vdash ^g \varphi $
and
 $\mathcal {M}, w \Vdash ^g \psi $
;
$\mathcal {M}, w \Vdash ^g \psi $
; -
•
 $\mathcal {M}, w \Vdash ^g \Diamond \varphi $
iff there is a
$\mathcal {M}, w \Vdash ^g \Diamond \varphi $
iff there is a
 $v \in W$
such that
$v \in W$
such that
 $wRv$
and
$wRv$
and
 $\mathcal {M}, v \Vdash ^{g^v} \varphi $
;
$\mathcal {M}, v \Vdash ^{g^v} \varphi $
; -
•
 $\mathcal {M}, w \Vdash ^g \forall x \, \varphi $
iff for all
$\mathcal {M}, w \Vdash ^g \forall x \, \varphi $
iff for all
 $w$
-assignments h such that
$w$
-assignments h such that
 $h \sim _{x} g$
, we have
$h \sim _{x} g$
, we have
 ${\mathcal {M}, w \Vdash ^{h} \varphi }$
.
${\mathcal {M}, w \Vdash ^{h} \varphi }$
.
Theorem 4.4 (Relational soundness).
If
![]() $\varphi \vdash \psi $
, then for any adequate model
$\varphi \vdash \psi $
, then for any adequate model
![]() $\mathcal {M}$
, for any world
$\mathcal {M}$
, for any world
![]() $w \in W$
, and for any
$w \in W$
, and for any
![]() $w$
-assignment g,
$w$
-assignment g,
Proof. By induction on the proof of
![]() $\varphi \vdash \psi $
, making the same arguments as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we highlight only the transitivity axiom, where the transitivity of the
$\varphi \vdash \psi $
, making the same arguments as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]. Here we highlight only the transitivity axiom, where the transitivity of the
![]() $\eta $
functions comes into play, and also remark on the generalization on constants rule.
$\eta $
functions comes into play, and also remark on the generalization on constants rule.
The transitivity axiom is
![]() $\Diamond \Diamond \varphi \vdash \Diamond \varphi $
, so assume that
$\Diamond \Diamond \varphi \vdash \Diamond \varphi $
, so assume that
![]() $\mathcal {M}, w \Vdash ^g \Diamond \Diamond \varphi $
. Then there is a world
$\mathcal {M}, w \Vdash ^g \Diamond \Diamond \varphi $
. Then there is a world
![]() $v$
such that
$v$
such that
![]() $wRv$
and
$wRv$
and
![]() $\mathcal {M}, v \Vdash ^{\eta _{w, v} \circ g} \Diamond \varphi $
, and also a subsequent world u such that
$\mathcal {M}, v \Vdash ^{\eta _{w, v} \circ g} \Diamond \varphi $
, and also a subsequent world u such that
![]() $vRu$
and
$vRu$
and
![]() $\mathcal {M}, u \Vdash ^{\eta _{v, u} \circ (\eta _{w, v} \circ g)} \varphi $
. Since R is transitive, we know that
$\mathcal {M}, u \Vdash ^{\eta _{v, u} \circ (\eta _{w, v} \circ g)} \varphi $
. Since R is transitive, we know that
![]() $wRu$
and thus that
$wRu$
and thus that
![]() $\eta _{v, u} \circ (\eta _{w, v} \circ g)$
coincides with
$\eta _{v, u} \circ (\eta _{w, v} \circ g)$
coincides with
![]() $\eta _{w, u} \circ g$
. Then
$\eta _{w, u} \circ g$
. Then
![]() $\mathcal {M}, u \Vdash ^{\eta _{w, u} \circ g} \psi $
, and consequently
$\mathcal {M}, u \Vdash ^{\eta _{w, u} \circ g} \psi $
, and consequently
![]() $\mathcal {M}, w \Vdash ^{g} \Diamond \varphi $
, as desired.
$\mathcal {M}, w \Vdash ^{g} \Diamond \varphi $
, as desired.
The soundness of the generalization on constants rule, Rule 3.1(x), is the most involved part of the proof presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] and depends on the construction of a model where the interpretation of a constant is changed. Building that model in this context is a simple matter of taking care to propagate that change to all future worlds using the
![]() $\eta $
functions.⊣
$\eta $
functions.⊣
We end this section by noting that, even though the language of
![]() $\mathsf {QRC_1}$
is quite restricted, even its
$\mathsf {QRC_1}$
is quite restricted, even its
![]() $\forall $
fragment requires counter-models with arbitrarily large domains. For example, the sequent
$\forall $
fragment requires counter-models with arbitrarily large domains. For example, the sequent
is unprovable in
![]() $\mathsf {QRC_1}$
, but satisfied by every world with at most two domain elements. This reasoning can be extended to any n: if S is an n-ary predicate symbol, let
$\mathsf {QRC_1}$
, but satisfied by every world with at most two domain elements. This reasoning can be extended to any n: if S is an n-ary predicate symbol, let
![]() $\varphi _n$
be the conjunction of the
$\varphi _n$
be the conjunction of the
![]() $n(n-1)/2$
formulas of the form
$n(n-1)/2$
formulas of the form
![]() $\forall x_0, \ldots , x_{n-2} \, S(\ldots , x_0, \ldots , x_0, \ldots )$
, with
$\forall x_0, \ldots , x_{n-2} \, S(\ldots , x_0, \ldots , x_0, \ldots )$
, with
![]() $x_0$
appearing in every possible pair of positions and every other position filled by a unique variable. Then
$x_0$
appearing in every possible pair of positions and every other position filled by a unique variable. Then
![]() $\varphi _n$
does not entail
$\varphi _n$
does not entail
![]() $ \psi _n := \forall x_0, \ldots , x_{n-1} \, S(x_0, \ldots , x_{n-1})$
but any world with at most
$ \psi _n := \forall x_0, \ldots , x_{n-1} \, S(x_0, \ldots , x_{n-1})$
but any world with at most
![]() $n-1$
domain elements that satisfies
$n-1$
domain elements that satisfies
![]() $\varphi _n$
must also satisfy
$\varphi _n$
must also satisfy
![]() $\psi _n$
.
$\psi _n$
.
5 Constant domain completeness
In [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] we proved relational completeness by building a term model that satisfies
![]() $\varphi $
and doesn’t satisfy
$\varphi $
and doesn’t satisfy
![]() $\psi $
when
$\psi $
when
![]() $\varphi \not \vdash \psi $
. That construction provides a finite, irreflexive, and rooted model with increasing domains. Here we show that it is possible to build a constant domain model instead, that is, a model where the domain of every world is exactly the same. This is extremely useful to prove the arithmetical completeness theorem in Section 8.
$\varphi \not \vdash \psi $
. That construction provides a finite, irreflexive, and rooted model with increasing domains. Here we show that it is possible to build a constant domain model instead, that is, a model where the domain of every world is exactly the same. This is extremely useful to prove the arithmetical completeness theorem in Section 8.
Before starting the formal proof, we briefly describe the main idea. The term models we build are such that each world is a pair of sets of closed formulas
![]() $p = \langle p^+, p^- \rangle $
. The first set,
$p = \langle p^+, p^- \rangle $
. The first set,
![]() $p^+$
, is the set of formulas that will be satisfied at that world, or the positive part. The second set,
$p^+$
, is the set of formulas that will be satisfied at that world, or the positive part. The second set,
![]() $p^-$
, is the set of formulas that will not be satisfied at that world, or the negative part. All worlds must be well-formed with respect to some finite set of closed formulas
$p^-$
, is the set of formulas that will not be satisfied at that world, or the negative part. All worlds must be well-formed with respect to some finite set of closed formulas
![]() $\Phi $
, which means that:
$\Phi $
, which means that:
-
• p is closed: every formula in
 $p^+$
and every formula in
$p^+$
and every formula in
 $p^-$
is closed;
$p^-$
is closed; -
• p is
 $\Phi $
-maximal: every formula of
$\Phi $
-maximal: every formula of
 $\Phi $
is in either
$\Phi $
is in either
 $p^+$
or
$p^+$
or
 $p^-$
(and there are no formulas in p but not in
$p^-$
(and there are no formulas in p but not in
 $\Phi $
);
$\Phi $
); -
• p is consistent: if
 $\delta \in p^-$
then
$\delta \in p^-$
then
 $\bigwedge p^+ \not \vdash \delta $
; and
$\bigwedge p^+ \not \vdash \delta $
; and -
• p is fully-witnessed: if
 $\forall x \, \varphi \in p^-$
then there is a constant c such that
$\forall x \, \varphi \in p^-$
then there is a constant c such that
 ${\varphi [x {\leftarrow } c] \in p^-}$
.
${\varphi [x {\leftarrow } c] \in p^-}$
.
In that case we say that p is
![]() $\Phi $
-maximal consistent and fully witnessed, or
$\Phi $
-maximal consistent and fully witnessed, or
![]() $\Phi $
-MCW for short (the closeness condition is included in the concept, although in practice almost every formula in this section will be closed). If p and q are pairs, we write
$\Phi $
-MCW for short (the closeness condition is included in the concept, although in practice almost every formula in this section will be closed). If p and q are pairs, we write
![]() $p \subseteq q$
when
$p \subseteq q$
when
![]() $p^+ \subseteq q^+$
and
$p^+ \subseteq q^+$
and
![]() $p^- \subseteq q^-$
. Furthermore, if
$p^- \subseteq q^-$
. Furthermore, if
![]() $\Gamma $
is a set of formulas we write
$\Gamma $
is a set of formulas we write
![]() $p \subseteq \Gamma $
instead of
$p \subseteq \Gamma $
instead of
![]() $p^+ \cup p^- \subseteq \Gamma $
.
$p^+ \cup p^- \subseteq \Gamma $
.
We want to have
![]() $\Phi $
-MCW pairs where
$\Phi $
-MCW pairs where
![]() $\Phi $
is closed under subformulas. However, the naive subformulas of
$\Phi $
is closed under subformulas. However, the naive subformulas of
![]() $\forall x \, \varphi $
might be open. In order to avoid that, we use the notion of closure with respect to a set of constants C defined in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], where
$\forall x \, \varphi $
might be open. In order to avoid that, we use the notion of closure with respect to a set of constants C defined in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], where
![]() $\varphi [x {\leftarrow } c]$
is a valid subformula of
$\varphi [x {\leftarrow } c]$
is a valid subformula of
![]() $\forall x \, \varphi $
as long as
$\forall x \, \varphi $
as long as
![]() $c \in C$
.
$c \in C$
.
Definition 5.1 (
 $\mathcal {C}\ell _C$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
$\mathcal {C}\ell _C$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Given a set of constants C, the closure of a formula
![]() $\varphi $
under C, written
$\varphi $
under C, written
![]() $\mathcal {C}\ell _C(\varphi )$
, is defined by induction on the formula as such:
$\mathcal {C}\ell _C(\varphi )$
, is defined by induction on the formula as such:
![]() $\mathcal {C}\ell _C(\top ) := \{\top \}$
;
$\mathcal {C}\ell _C(\top ) := \{\top \}$
;
![]() $\mathcal {C}\ell _C(S(t_0, \ldots , t_{n-1})) := \{S(t_0, \ldots , t_{n-1}), \top \}$
;
$\mathcal {C}\ell _C(S(t_0, \ldots , t_{n-1})) := \{S(t_0, \ldots , t_{n-1}), \top \}$
;
![]() $\mathcal {C}\ell _C(\varphi \land \psi ) := \{\varphi \land \psi \} \cup \mathcal {C}\ell _C(\varphi ) \cup \mathcal {C}\ell _C(\psi )$
;
$\mathcal {C}\ell _C(\varphi \land \psi ) := \{\varphi \land \psi \} \cup \mathcal {C}\ell _C(\varphi ) \cup \mathcal {C}\ell _C(\psi )$
;
![]() $\mathcal {C}\ell _C(\Diamond \varphi ) := \{\Diamond \varphi \} \cup \mathcal {C}\ell _C(\varphi )$
; and
$\mathcal {C}\ell _C(\Diamond \varphi ) := \{\Diamond \varphi \} \cup \mathcal {C}\ell _C(\varphi )$
; and
The closure under C of a set of formulas
![]() $\Gamma $
is the union of the closures under C of each of the formulas in
$\Gamma $
is the union of the closures under C of each of the formulas in
![]() $\Gamma $
:
$\Gamma $
:
The closure of a pair p is defined as the closure of
![]() $p^+ \cup p^-$
.
$p^+ \cup p^-$
.
Going back to the overview of the completeness proof, suppose that
![]() $\varphi \not \vdash \psi $
, (assuming for now that
$\varphi \not \vdash \psi $
, (assuming for now that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are closed). Defining
$\psi $
are closed). Defining
![]() $p := \langle \{\varphi \}, \{\psi \} \rangle $
, the counter-model will be rooted on a
$p := \langle \{\varphi \}, \{\psi \} \rangle $
, the counter-model will be rooted on a
![]() $\mathcal {C}\ell _C(p)$
-MCW extension of p, where C is a set of constants to determine. The set of constants C will be used as the domain of the root. Note that p is already closed and consistent, so taking the step to maximality is as simple as deciding whether to add each
$\mathcal {C}\ell _C(p)$
-MCW extension of p, where C is a set of constants to determine. The set of constants C will be used as the domain of the root. Note that p is already closed and consistent, so taking the step to maximality is as simple as deciding whether to add each
![]() $\chi \in \mathcal {C}\ell _C(p)$
to the positive or negative part of the root without ruining its consistency. The hard part is doing so in a way that guarantees that the resulting pair is fully witnessed.
$\chi \in \mathcal {C}\ell _C(p)$
to the positive or negative part of the root without ruining its consistency. The hard part is doing so in a way that guarantees that the resulting pair is fully witnessed.
The completeness proof shown in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] uses the observation that if
![]() $\bigwedge p^+ \not \vdash \forall x \, \chi $
, then also
$\bigwedge p^+ \not \vdash \forall x \, \chi $
, then also
![]() $\bigwedge p^+ \not \vdash \chi [x {\leftarrow } c]$
, as long as c does not appear in either
$\bigwedge p^+ \not \vdash \chi [x {\leftarrow } c]$
, as long as c does not appear in either
![]() $p^+$
or
$p^+$
or
![]() $\chi $
(Lemma 3.2.6). This suggests a way of sorting the formulas of
$\chi $
(Lemma 3.2.6). This suggests a way of sorting the formulas of
![]() $\mathcal {C}\ell _C(p)$
into positive and negative: mark a formula as positive if and only if it is a consequence of
$\mathcal {C}\ell _C(p)$
into positive and negative: mark a formula as positive if and only if it is a consequence of
![]() $p^+$
. This guarantees that there are witnesses for the negative universal formulas as long as there are enough constants to go around. The way to make sure that there are enough constants is precisely the difference between the proof presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] and the proof presented here. To that end, we introduce the following definition.
$p^+$
. This guarantees that there are witnesses for the negative universal formulas as long as there are enough constants to go around. The way to make sure that there are enough constants is precisely the difference between the proof presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] and the proof presented here. To that end, we introduce the following definition.
Definition 5.2 (
 ${\mathrm {d}}_{{\mathrm {const}}}$
).
${\mathrm {d}}_{{\mathrm {const}}}$
).
The number of different constants in a formula
![]() $\varphi $
is represented by
$\varphi $
is represented by
![]() ${\mathrm {d}}_{{\mathrm {const}}}(\varphi )$
. The maximum number of different constants per formula in a set of formulas
${\mathrm {d}}_{{\mathrm {const}}}(\varphi )$
. The maximum number of different constants per formula in a set of formulas
![]() $\Gamma $
is defined as
$\Gamma $
is defined as
![]() ${\mathrm {d}}_{{\mathrm {const}}}(\Gamma ) := \max _{\varphi \in \Gamma }\{{\mathrm {d}}_{{\mathrm {const}}}(\varphi )\}$
.
${\mathrm {d}}_{{\mathrm {const}}}(\Gamma ) := \max _{\varphi \in \Gamma }\{{\mathrm {d}}_{{\mathrm {const}}}(\varphi )\}$
.
Note that
![]() ${\mathrm {d}}_{{\mathrm {const}}}(\Gamma )$
is not the number of different constants appearing in
${\mathrm {d}}_{{\mathrm {const}}}(\Gamma )$
is not the number of different constants appearing in
![]() $\Gamma $
, but the maximum number of different constants in any single formula of
$\Gamma $
, but the maximum number of different constants in any single formula of
![]() $\Gamma $
. For example,
$\Gamma $
. For example,
![]() ${\mathrm {d}}_{{\mathrm {const}}}(\{S_0(c_0, c_1), S_1(c_2)\}) = 2$
.
${\mathrm {d}}_{{\mathrm {const}}}(\{S_0(c_0, c_1), S_1(c_2)\}) = 2$
.
We observe that the maximum number of distinct constants per formula in the closure under C of a set of formulas can be bounded by a number that does not depend on C.
Fact 5.3. For any formula
![]() $\varphi $
, set of formulas
$\varphi $
, set of formulas
![]() $\Phi $
, and set of constants C:
$\Phi $
, and set of constants C:
-
•
 ${\mathrm {d}}_{{\mathrm {const}}}(\varphi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi [x {\leftarrow } c]) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi ) + 1$
;
${\mathrm {d}}_{{\mathrm {const}}}(\varphi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi [x {\leftarrow } c]) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi ) + 1$
; -
•
 ${\mathrm {d}}_{{\mathrm {const}}}(\varphi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\varphi )) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi ) + {\mathrm {d}}_\forall (\varphi )$
;
${\mathrm {d}}_{{\mathrm {const}}}(\varphi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\varphi )) \leq {\mathrm {d}}_{{\mathrm {const}}}(\varphi ) + {\mathrm {d}}_\forall (\varphi )$
; -
•
 ${\mathrm {d}}_{{\mathrm {const}}}(\Phi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\Phi )) \leq {\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + {\mathrm {d}}_\forall (\Phi )$
.
${\mathrm {d}}_{{\mathrm {const}}}(\Phi ) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\Phi )) \leq {\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + {\mathrm {d}}_\forall (\Phi )$
.
We are now ready to prove a Lindenbaum-like lemma.
Lemma 5.4. Given a finite signature
![]() $\Sigma $
with constants C and a finite set of closed formulas
$\Sigma $
with constants C and a finite set of closed formulas
![]() $\Phi $
in the language of
$\Phi $
in the language of
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $|C|> 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
, if
$|C|> 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
, if
![]() $p \subseteq \mathcal {C}\ell _C(\Phi )$
is a closed consistent pair and
$p \subseteq \mathcal {C}\ell _C(\Phi )$
is a closed consistent pair and
![]() $p^+$
is a singleton, then there is a pair
$p^+$
is a singleton, then there is a pair
![]() $q \supseteq p$
in the language of
$q \supseteq p$
in the language of
![]() $\Sigma $
such that q is
$\Sigma $
such that q is
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW, and
$\mathcal {C}\ell _C(\Phi )$
-MCW, and
![]() ${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (p^+)$
.
${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (p^+)$
.
Proof. Like in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], we start by defining a pair
![]() $q \supseteq p$
such that for each
$q \supseteq p$
such that for each
![]() $\chi \in \mathcal {C}\ell _C(\Phi )$
,
$\chi \in \mathcal {C}\ell _C(\Phi )$
,
![]() $\chi \in q^+$
if and only if
$\chi \in q^+$
if and only if
![]() $p^+ \vdash \chi $
(otherwise
$p^+ \vdash \chi $
(otherwise
![]() $\chi \in q^-$
). It is easy to see that this pair q is
$\chi \in q^-$
). It is easy to see that this pair q is
![]() $\mathcal {C}\ell _C(\Phi )$
-maximal consistent, and we have
$\mathcal {C}\ell _C(\Phi )$
-maximal consistent, and we have
![]() ${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (p^+)$
by Lemma 3.4.
${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (p^+)$
by Lemma 3.4.
It remains to show that q is fully witnessed. Let
![]() $\forall x \, \psi $
be a formula in
$\forall x \, \psi $
be a formula in
![]() $q^-$
. We claim that there is
$q^-$
. We claim that there is
![]() $d \in C$
such that d does not appear either in
$d \in C$
such that d does not appear either in
![]() $p^+$
or in
$p^+$
or in
![]() $\forall x \, \psi $
. For this it is enough to see that
$\forall x \, \psi $
. For this it is enough to see that
![]() $|C|> {\mathrm {d}}_{{\mathrm {const}}}(\bigwedge p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi )$
, which is the same as
$|C|> {\mathrm {d}}_{{\mathrm {const}}}(\bigwedge p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi )$
, which is the same as
![]() $|C|> {\mathrm {d}}_{{\mathrm {const}}}(p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi )$
because
$|C|> {\mathrm {d}}_{{\mathrm {const}}}(p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi )$
because
![]() $p^+$
is a singleton by assumption. Since
$p^+$
is a singleton by assumption. Since
![]() $p^+ \subseteq \mathcal {C}\ell _C(\Phi )$
, we know that
$p^+ \subseteq \mathcal {C}\ell _C(\Phi )$
, we know that
![]() ${\mathrm {d}}_{{\mathrm {const}}}(p^+) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\Phi ))$
, and similarly for
${\mathrm {d}}_{{\mathrm {const}}}(p^+) \leq {\mathrm {d}}_{{\mathrm {const}}}(\mathcal {C}\ell _C(\Phi ))$
, and similarly for
![]() $\forall x \, \psi $
. Then by Fact 5.3 we may conclude that
$\forall x \, \psi $
. Then by Fact 5.3 we may conclude that
![]() ${\mathrm {d}}_{{\mathrm {const}}}(p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi ) \leq 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
, which suffices by our assumption on the size of C.
${\mathrm {d}}_{{\mathrm {const}}}(p^+) + {\mathrm {d}}_{{\mathrm {const}}}(\forall x \, \psi ) \leq 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
, which suffices by our assumption on the size of C.
Since
![]() $d \in C$
does not appear in either
$d \in C$
does not appear in either
![]() $p^+$
or
$p^+$
or
![]() $\forall x \, \psi $
, we conclude that
$\forall x \, \psi $
, we conclude that
![]() $p^+ \not \vdash \psi [x {\leftarrow } d]$
by Lemma 3.2.6, and consequently
$p^+ \not \vdash \psi [x {\leftarrow } d]$
by Lemma 3.2.6, and consequently
![]() $\psi [x {\leftarrow } d] \in q^-$
as desired.⊣
$\psi [x {\leftarrow } d] \in q^-$
as desired.⊣
We now recall the definition of
![]() $\hat {R}$
from [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], which is the relation we use to connect the worlds of the term model.
$\hat {R}$
from [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], which is the relation we use to connect the worlds of the term model.
Definition 5.5 (
 $p\hat {R}q$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
$p\hat {R}q$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
The relation
![]() $\hat {R}$
between pairs is such that
$\hat {R}$
between pairs is such that
![]() $p\hat {R}q$
if and only if both of following hold:
$p\hat {R}q$
if and only if both of following hold:
-
• for any formula
 $\Diamond \varphi \in p^-$
we have
$\Diamond \varphi \in p^-$
we have
 $\varphi , \Diamond \varphi \in q^-$
; and
$\varphi , \Diamond \varphi \in q^-$
; and -
• there is some formula
 $\Diamond \psi \in p^+ \cap q^-$
.
$\Diamond \psi \in p^+ \cap q^-$
.
Lemma 5.6 [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1].
The relation
![]() $\hat {R}$
restricted to consistent pairs is transitive and irreflexive.
$\hat {R}$
restricted to consistent pairs is transitive and irreflexive.
We now see that if
![]() $w$
is a
$w$
is a
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW pair with
$\mathcal {C}\ell _C(\Phi )$
-MCW pair with
![]() $\Diamond \varphi \in w^+$
, we can find a
$\Diamond \varphi \in w^+$
, we can find a
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW pair
$\mathcal {C}\ell _C(\Phi )$
-MCW pair
![]() $v$
with
$v$
with
![]() $\varphi \in v^+$
and
$\varphi \in v^+$
and
![]() $w\hat {R}v$
. The proof is the same as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], except that we now use Lemma 5.4 to obtain constant domains throughout the model.
$w\hat {R}v$
. The proof is the same as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], except that we now use Lemma 5.4 to obtain constant domains throughout the model.
Lemma 5.7 (Pair existence).
Let
![]() $\Sigma $
be a signature with a finite set of constants C, and
$\Sigma $
be a signature with a finite set of constants C, and
![]() $\Phi $
be a finite set of closed formulas in the language of
$\Phi $
be a finite set of closed formulas in the language of
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $|C|> 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
. If p is a
$|C|> 2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi )$
. If p is a
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW pair and
$\mathcal {C}\ell _C(\Phi )$
-MCW pair and
![]() $\Diamond \varphi \in p^+$
, then there is a
$\Diamond \varphi \in p^+$
, then there is a
![]() $\mathcal {C}\ell _{C}(\Phi )$
-MCW pair q such that
$\mathcal {C}\ell _{C}(\Phi )$
-MCW pair q such that
![]() $p\hat {R}q$
,
$p\hat {R}q$
,
![]() $\varphi \in q^+$
, and
$\varphi \in q^+$
, and
![]() ${\mathrm {d}}_\Diamond (q^+) < {\mathrm {d}}_\Diamond (p^+)$
.
${\mathrm {d}}_\Diamond (q^+) < {\mathrm {d}}_\Diamond (p^+)$
.
Proof. Consider the pair r defined as
![]() $r^+ := \{\varphi \}$
and
$r^+ := \{\varphi \}$
and
![]() $r^- := \{\delta , \Diamond \delta \mid \Diamond \delta \in p^-\} \cup \{\Diamond \varphi \}$
. It is easy to check that r is consistent and that
$r^- := \{\delta , \Diamond \delta \mid \Diamond \delta \in p^-\} \cup \{\Diamond \varphi \}$
. It is easy to check that r is consistent and that
![]() $p\hat {R}r$
(details can be found in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]), and clearly
$p\hat {R}r$
(details can be found in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]), and clearly
![]() $r \subseteq \mathcal {C}\ell _C(\Phi )$
. We then use Lemma 5.4 to obtain a
$r \subseteq \mathcal {C}\ell _C(\Phi )$
. We then use Lemma 5.4 to obtain a
![]() $\mathcal {C}\ell _{C}(\Phi )$
-MCW pair
$\mathcal {C}\ell _{C}(\Phi )$
-MCW pair
![]() $q \supseteq r$
such that
$q \supseteq r$
such that
![]() ${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (r^+) = {\mathrm {d}}_\Diamond (\varphi ) < {\mathrm {d}}_\Diamond (p^+)$
. We obtain
${\mathrm {d}}_\Diamond (q^+) = {\mathrm {d}}_\Diamond (r^+) = {\mathrm {d}}_\Diamond (\varphi ) < {\mathrm {d}}_\Diamond (p^+)$
. We obtain
![]() $p\hat {R}q$
as a straightforward consequence of
$p\hat {R}q$
as a straightforward consequence of
![]() $p\hat {R}r$
.⊣
$p\hat {R}r$
.⊣
We can now define an adequate and constant domain model
![]() $\mathcal {M}[p]$
from any given finite and consistent pair p such that
$\mathcal {M}[p]$
from any given finite and consistent pair p such that
![]() $\mathcal {M}[p]$
satisfies the formulas in
$\mathcal {M}[p]$
satisfies the formulas in
![]() $p^+$
and doesn’t satisfy the formulas in
$p^+$
and doesn’t satisfy the formulas in
![]() $p^-$
. The idea is exactly the same as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]: build a term model where each world w is a
$p^-$
. The idea is exactly the same as in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]: build a term model where each world w is a
![]() $\mathcal {C}\ell _{M}(p)$
-MCW pair, and the worlds are related by (a sub-relation of)
$\mathcal {C}\ell _{M}(p)$
-MCW pair, and the worlds are related by (a sub-relation of)
![]() $\hat {R}$
.
$\hat {R}$
.
Definition 5.8. Let
![]() $\Sigma $
be a signature. Given a finite consistent pair p of closed formulas in
$\Sigma $
be a signature. Given a finite consistent pair p of closed formulas in
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $p^+$
is a singleton,Footnote
6
we define an adequate model
$p^+$
is a singleton,Footnote
6
we define an adequate model
![]() $\mathcal {M}[p]$
. Here we will use
$\mathcal {M}[p]$
. Here we will use
![]() $\Phi := p^+ \cup p^-$
.
$\Phi := p^+ \cup p^-$
.
Let C be a set of at least
![]() $2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi ) + 1$
different constants, including all of the ones appearing in
$2{\mathrm {d}}_{{\mathrm {const}}}(\Phi ) + 2{\mathrm {d}}_\forall (\Phi ) + 1$
different constants, including all of the ones appearing in
![]() $\Sigma $
and adding more if necessary. The pairs of formulas we work with are in the signature
$\Sigma $
and adding more if necessary. The pairs of formulas we work with are in the signature
![]() $\Sigma $
extended by C.
$\Sigma $
extended by C.
We start by defining the underlying frame in an iterative manner. The root is given by Lemma 5.4 applied to C and p, obtaining the
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW pair q. Frame
$\mathcal {C}\ell _C(\Phi )$
-MCW pair q. Frame
![]() $\mathcal {F}^0$
is then defined such that its set of worlds is
$\mathcal {F}^0$
is then defined such that its set of worlds is
![]() $W^0 := \{q\}$
, its relation
$W^0 := \{q\}$
, its relation
![]() $R^0$
is empty, and the domain of q is
$R^0$
is empty, and the domain of q is
![]() $M^0_{q} := C$
.
$M^0_{q} := C$
.
Assume now that we already have a frame
![]() $\mathcal {F}^i$
, and we set out to define
$\mathcal {F}^i$
, and we set out to define
![]() $\mathcal {F}^{i+1}$
as an extension of
$\mathcal {F}^{i+1}$
as an extension of
![]() $\mathcal {F}^i$
. For each leaf
$\mathcal {F}^i$
. For each leaf
![]() $w$
of
$w$
of
![]() $\mathcal {F}^i$
, i.e., each world such that there is no world
$\mathcal {F}^i$
, i.e., each world such that there is no world
![]() $v \in \mathcal {F}^i$
with
$v \in \mathcal {F}^i$
with
![]() $w R^i v$
, and for each formula
$w R^i v$
, and for each formula
![]() $\Diamond \varphi \in w^+$
, use Lemma 5.7 to obtain a
$\Diamond \varphi \in w^+$
, use Lemma 5.7 to obtain a
![]() $\mathcal {C}\ell _C(\Phi )$
-MCW pair
$\mathcal {C}\ell _C(\Phi )$
-MCW pair
![]() $v$
such that
$v$
such that
![]() $w\hat {R}v$
,
$w\hat {R}v$
,
![]() $\varphi \in v^+$
, and
$\varphi \in v^+$
, and
![]() ${\mathrm {d}}_\Diamond (v^+) < {\mathrm {d}}_\Diamond (w^+)$
. Now add
${\mathrm {d}}_\Diamond (v^+) < {\mathrm {d}}_\Diamond (w^+)$
. Now add
![]() $v$
to
$v$
to
![]() $W^{i+1}$
, add
$W^{i+1}$
, add
![]() $\langle w, v \rangle $
to
$\langle w, v \rangle $
to
![]() $R^{i+1}$
, define
$R^{i+1}$
, define
![]() $M^{i+1}_v$
as C, and define
$M^{i+1}_v$
as C, and define
![]() $\eta _{w, v}$
as the identity function.
$\eta _{w, v}$
as the identity function.
The process described above terminates because each pair is finite and the modal depth of
![]() $\mathcal {C}\ell _C(\Phi )$
(and consequently of
$\mathcal {C}\ell _C(\Phi )$
(and consequently of
![]() $w^+$
, for any
$w^+$
, for any
![]() $w \subseteq \mathcal {C}\ell _C(\Phi )$
) is also finite. Thus there is a final frame
$w \subseteq \mathcal {C}\ell _C(\Phi )$
) is also finite. Thus there is a final frame
![]() $\mathcal {F}^m$
, for some natural number m. This frame is constant domain by construction, but not transitive. We obtain
$\mathcal {F}^m$
, for some natural number m. This frame is constant domain by construction, but not transitive. We obtain
![]() $\mathcal {F}[p]$
as the transitive closure of
$\mathcal {F}[p]$
as the transitive closure of
![]() $\mathcal {F}^m$
, which is clearly still constant domain. The
$\mathcal {F}^m$
, which is clearly still constant domain. The
![]() $\eta $
functions are all the identity in C, thus satisfying the transitivity condition. We conclude that the frame
$\eta $
functions are all the identity in C, thus satisfying the transitivity condition. We conclude that the frame
![]() $\mathcal {F}[p]$
is adequate.
$\mathcal {F}[p]$
is adequate.
In order to obtain the model
![]() $\mathcal {M}[p]$
based on the frame
$\mathcal {M}[p]$
based on the frame
![]() $\mathcal {F}[p]$
, let
$\mathcal {F}[p]$
, let
![]() $I_q$
take constants in
$I_q$
take constants in
![]() $\Sigma $
to their corresponding version as domain elements. If
$\Sigma $
to their corresponding version as domain elements. If
![]() $w$
is any other world, let
$w$
is any other world, let
![]() $I_w$
coincide with
$I_w$
coincide with
![]() $I_q$
. This is necessary to make sure that the model is concordant, because q sees every other world, and is sufficient to see that
$I_q$
. This is necessary to make sure that the model is concordant, because q sees every other world, and is sufficient to see that
![]() $\mathcal {M}[p]$
is adequate. Finally, given an n-ary predicate letter S and a world
$\mathcal {M}[p]$
is adequate. Finally, given an n-ary predicate letter S and a world
![]() $w$
, define
$w$
, define
![]() $S^{J_w}$
as the set of n-tuples
$S^{J_w}$
as the set of n-tuples
![]() $\langle d_0, \ldots , d_{n-1}\rangle \subseteq (M_w)^n$
such that
$\langle d_0, \ldots , d_{n-1}\rangle \subseteq (M_w)^n$
such that
![]() $S(d_0, \ldots , d_{n-1}) \in w^+$
.
$S(d_0, \ldots , d_{n-1}) \in w^+$
.
Since everything up until now was meant for closed formulas, and furthermore we are potentially adding new constants to the signature of the formulas we care about, we provide a way of replacing the free variables of a formula with constants.
Definition 5.9 (
 $\varphi ^g$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
$\varphi ^g$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Given a formula
![]() $\varphi $
in a signature
$\varphi $
in a signature
![]() $\Sigma $
and a function g from the set of variables to a set of constants in some signature
$\Sigma $
and a function g from the set of variables to a set of constants in some signature
![]() $\Sigma ' \supseteq \Sigma $
, we define the formula
$\Sigma ' \supseteq \Sigma $
, we define the formula
![]() $\varphi ^g$
in the signature
$\varphi ^g$
in the signature
![]() $\Sigma '$
as
$\Sigma '$
as
![]() $\varphi $
with each free variable x simultaneously replaced by
$\varphi $
with each free variable x simultaneously replaced by
![]() $g(x)$
.
$g(x)$
.
The constant domain model defined above coincides with the non-constant domain definition provided in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] in everything other than that it refers to the stronger Lemmas 5.4 and 5.7 that keep the domain constant. Thus the Truth Lemma holds with exactly the same proof.
Lemma 5.10 (Truth Lemma [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Let
![]() $\Sigma $
be a signature. For any finite non-empty consistent pair p of closed formulas in the language of
$\Sigma $
be a signature. For any finite non-empty consistent pair p of closed formulas in the language of
![]() $\Sigma $
, world
$\Sigma $
, world
![]() $w \in \mathcal {M}[p]$
,
$w \in \mathcal {M}[p]$
,
![]() $w$
-assignment g, and formula
$w$
-assignment g, and formula
![]() $\varphi $
in the language of
$\varphi $
in the language of
![]() $\Sigma $
such that
$\Sigma $
such that
![]() $\varphi ^g \in \mathcal {C}\ell _{M_w}(p)$
, we have that
$\varphi ^g \in \mathcal {C}\ell _{M_w}(p)$
, we have that
We are now ready to prove the constant domain completeness theorem.
Theorem 5.11 (Constant domain completeness).
Let
![]() $\Sigma $
be a signature and
$\Sigma $
be a signature and
![]() $\varphi , \psi $
be formulas in
$\varphi , \psi $
be formulas in
![]() $\Sigma $
. If
$\Sigma $
. If
![]() $\varphi \not \vdash \psi $
, then there is an adequate, finite, irreflexive, and constant domain model
$\varphi \not \vdash \psi $
, then there is an adequate, finite, irreflexive, and constant domain model
![]() $\mathcal {M}$
, a world
$\mathcal {M}$
, a world
![]() $w \in W$
, and a
$w \in W$
, and a
![]() $w$
-assignment g such that
$w$
-assignment g such that
Proof. As in the original proof of relational completeness presented in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1], define a new constant
![]() $c_x$
for each free variable x of
$c_x$
for each free variable x of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
and let
$\psi $
and let
![]() $\Sigma '$
be the signature
$\Sigma '$
be the signature
![]() $\Sigma $
augmented with these new constants and a dummy constant
$\Sigma $
augmented with these new constants and a dummy constant
![]() $c_0$
. Let g be the assignment taking each free variable x of
$c_0$
. Let g be the assignment taking each free variable x of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
to
$\psi $
to
![]() $c_x$
and every other variable to
$c_x$
and every other variable to
![]() $c_0$
. Note that
$c_0$
. Note that
![]() $\varphi ^g \not \vdash _{\Sigma '} \psi ^g$
by Rule 3.1(x) and Lemma 3.5. Build
$\varphi ^g \not \vdash _{\Sigma '} \psi ^g$
by Rule 3.1(x) and Lemma 3.5. Build
![]() $\mathcal {M} := \mathcal {M}[\langle \{\varphi ^g\}, \{\psi ^g\} \rangle ]$
as described in Definition 5.8, with root
$\mathcal {M} := \mathcal {M}[\langle \{\varphi ^g\}, \{\psi ^g\} \rangle ]$
as described in Definition 5.8, with root
![]() $w$
. Then by Lemma 5.10 we have both
$w$
. Then by Lemma 5.10 we have both
![]() $\mathcal {M}, w \Vdash ^g \varphi $
and
$\mathcal {M}, w \Vdash ^g \varphi $
and
![]() $\mathcal {M}, w \not \Vdash ^g \psi $
, as desired.⊣
$\mathcal {M}, w \not \Vdash ^g \psi $
, as desired.⊣
6 The strictly positive fragment of
 $\mathsf {QK}4$
and
$\mathsf {QK}4$
and
 $\mathsf {QGL}$
$\mathsf {QGL}$
Consider the language of full quantified modal logic with no equality nor constant nor function symbols,
![]() $\mathcal {L}_{\Box , \forall }$
. We use upper case letters to refer to formulas in this language. A propositional modal logic
$\mathcal {L}_{\Box , \forall }$
. We use upper case letters to refer to formulas in this language. A propositional modal logic
![]() $\mathsf {S}$
can be extend to a quantified modal logic
$\mathsf {S}$
can be extend to a quantified modal logic
![]() $\mathsf {QS}$
as described in [Reference Hughes and Cresswell25] by extending the language and adding the following axiom schema and rule:
$\mathsf {QS}$
as described in [Reference Hughes and Cresswell25] by extending the language and adding the following axiom schema and rule:
-
•
 $[\forall \mathsf {E}]$
$[\forall \mathsf {E}]$
 $\forall x \, A \to A[x {\leftarrow } y]$
(y free for x in A);
$\forall x \, A \to A[x {\leftarrow } y]$
(y free for x in A); -
•
 $[\forall \mathsf {I}]$
if
$[\forall \mathsf {I}]$
if
 $\mathsf {QS} \vdash A \to B$
, then
$\mathsf {QS} \vdash A \to B$
, then
 $\mathsf {QS} \vdash A \to \forall x \, B$
(
$\mathsf {QS} \vdash A \to \forall x \, B$
(
 $x \notin {\mathrm {fv}}(A)$
).
$x \notin {\mathrm {fv}}(A)$
).
The logic
![]() $\mathsf {K}4$
is obtained from the smallest normal modal logic
$\mathsf {K}4$
is obtained from the smallest normal modal logic
![]() $\mathsf {K}$
by adding the 4 Axiom
$\mathsf {K}$
by adding the 4 Axiom
![]() $\Box A \to \Box \Box A$
. The logic
$\Box A \to \Box \Box A$
. The logic
![]() $\mathsf {GL}$
is
$\mathsf {GL}$
is
![]() $\mathsf {K}4$
extended with Löb’s Axiom
$\mathsf {K}4$
extended with Löb’s Axiom
![]() $\Box (\Box A \to A) \to \Box A$
. Dashkov [Reference Dashkov16] showed that
$\Box (\Box A \to A) \to \Box A$
. Dashkov [Reference Dashkov16] showed that
![]() $\mathsf {RC}_1$
is the strictly positive fragment of both
$\mathsf {RC}_1$
is the strictly positive fragment of both
![]() $\mathsf {K}4$
and
$\mathsf {K}4$
and
![]() $\mathsf {GL}$
(and of any logic between them), in the sense that, if
$\mathsf {GL}$
(and of any logic between them), in the sense that, if
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are built up from
$\psi $
are built up from
![]() $\top $
, propositional symbols, conjunctions, and diamonds, then
$\top $
, propositional symbols, conjunctions, and diamonds, then
![]() $\varphi \vdash _{\mathsf {RC}_1} \psi $
if and only if
$\varphi \vdash _{\mathsf {RC}_1} \psi $
if and only if
![]() $\mathsf {K}4 \vdash \varphi \to \psi $
, and similarly for
$\mathsf {K}4 \vdash \varphi \to \psi $
, and similarly for
![]() $\mathsf {GL}$
. In this section we show that this equivalence is maintained in the predicate case.
$\mathsf {GL}$
. In this section we show that this equivalence is maintained in the predicate case.
Since
![]() $\mathsf {QRC_1}$
includes constants in its language and predicate modal logics are often presented without them, we define a map from the language of
$\mathsf {QRC_1}$
includes constants in its language and predicate modal logics are often presented without them, we define a map from the language of
![]() $\mathsf {QRC_1}$
to its constant-free subset, replacing constants with fresh variables. Thus, given a finite set of
$\mathsf {QRC_1}$
to its constant-free subset, replacing constants with fresh variables. Thus, given a finite set of
![]() $\mathsf {QRC_1}$
formulas
$\mathsf {QRC_1}$
formulas
![]() $\Phi $
where the constants appearing in
$\Phi $
where the constants appearing in
![]() $\Phi $
are
$\Phi $
are
![]() $\boldsymbol {c} = c_0, \ldots , c_{n-1}$
, let
$\boldsymbol {c} = c_0, \ldots , c_{n-1}$
, let
![]() $\boldsymbol {x} = x_0, \ldots , x_{n-1}$
be fresh variables with respect to
$\boldsymbol {x} = x_0, \ldots , x_{n-1}$
be fresh variables with respect to
![]() $\Phi $
. Then we define
$\Phi $
. Then we define
![]() $\varphi ^\Phi := \varphi [c_0 {\leftarrow } x_0]\cdots [c_{n-1} {\leftarrow } x_{n-1}]$
for each
$\varphi ^\Phi := \varphi [c_0 {\leftarrow } x_0]\cdots [c_{n-1} {\leftarrow } x_{n-1}]$
for each
![]() $\varphi \in \Phi $
, and abbreviate this long substitution with the notation
$\varphi \in \Phi $
, and abbreviate this long substitution with the notation
![]() $\varphi [\boldsymbol {c} {\leftarrow } \boldsymbol {x}]$
. Thus we also have
$\varphi [\boldsymbol {c} {\leftarrow } \boldsymbol {x}]$
. Thus we also have
![]() $\varphi = \varphi ^\Phi [\boldsymbol {x} {\leftarrow } \boldsymbol {c}]$
.
$\varphi = \varphi ^\Phi [\boldsymbol {x} {\leftarrow } \boldsymbol {c}]$
.
It is straightforward to iterate Rules 3.1(x) and 3.1(ix) in order to confirm that the above translation is harmless when it comes to provability.
Fact 6.1. Let
![]() $\Phi $
be a finite set of
$\Phi $
be a finite set of
![]() $\mathsf {QRC_1}$
formulas such that
$\mathsf {QRC_1}$
formulas such that
![]() $\varphi , \psi \in \Phi $
. Then
$\varphi , \psi \in \Phi $
. Then
The semantics presented here for
![]() $\mathsf {QRC_1}$
is a generalization of more traditional semantics for quantified modal logics, since it uses maps between domains. However, for this section, we will only need constant domain models. These can be easily interpreted in the usual framework as described in [Reference Hughes and Cresswell25]. The following is a well-known (and easily provable) result.
$\mathsf {QRC_1}$
is a generalization of more traditional semantics for quantified modal logics, since it uses maps between domains. However, for this section, we will only need constant domain models. These can be easily interpreted in the usual framework as described in [Reference Hughes and Cresswell25]. The following is a well-known (and easily provable) result.
Theorem 6.2 (Soundness for
 $\mathsf {QS}$
[Reference Hughes and Cresswell25]).
$\mathsf {QS}$
[Reference Hughes and Cresswell25]).
If
![]() $\mathcal {F} = \langle W, R \rangle $
satisfies every theorem of
$\mathcal {F} = \langle W, R \rangle $
satisfies every theorem of
![]() $\mathsf {S}$
, then any constant domain model based on
$\mathsf {S}$
, then any constant domain model based on
![]() $\mathcal {F}$
satisfies every theorem of
$\mathcal {F}$
satisfies every theorem of
![]() $\mathsf {QS}$
.
$\mathsf {QS}$
.
Thus any transitive constant domain model is a
![]() $\mathsf {QK}4$
model, and any transitive and conversely well-founded constant domain model is a
$\mathsf {QK}4$
model, and any transitive and conversely well-founded constant domain model is a
![]() $\mathsf {QGL}$
model.Footnote
7
$\mathsf {QGL}$
model.Footnote
7
We are now ready to show the main theorem of this section.
Theorem 6.3. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be
$\psi $
be
![]() $\mathsf {QRC_1}$
formulas and let
$\mathsf {QRC_1}$
formulas and let
![]() $\mathsf {QS}$
be any logic between
$\mathsf {QS}$
be any logic between
![]() $\mathsf {QK}4$
and
$\mathsf {QK}4$
and
![]() $\mathsf {QGL}$
. Then
$\mathsf {QGL}$
. Then
![]() $\varphi \vdash \psi $
if and only if there is a finite set
$\varphi \vdash \psi $
if and only if there is a finite set
![]() $\Phi $
such that
$\Phi $
such that
![]() $\varphi , \psi \in \Phi $
and
$\varphi , \psi \in \Phi $
and
![]() $\mathsf {QS} \vdash \varphi ^\Phi \to \psi ^\Phi $
.
$\mathsf {QS} \vdash \varphi ^\Phi \to \psi ^\Phi $
.
Proof. For the left-to-right implication, let
![]() $\Phi $
be the set of formulas appearing in the proof of
$\Phi $
be the set of formulas appearing in the proof of
![]() $\varphi \vdash \psi $
. It is easy to see by induction on the length of the
$\varphi \vdash \psi $
. It is easy to see by induction on the length of the
![]() $\mathsf {QRC_1}$
proof that
$\mathsf {QRC_1}$
proof that
![]() $\mathsf {QK}4 \vdash \varphi ^\Phi \to \psi ^\Phi $
, which then implies that
$\mathsf {QK}4 \vdash \varphi ^\Phi \to \psi ^\Phi $
, which then implies that
![]() $\mathsf {QS} \vdash \varphi ^\Phi \to \psi ^\Phi $
.
$\mathsf {QS} \vdash \varphi ^\Phi \to \psi ^\Phi $
.
For the right-to-left implication, we prove the contrapositive. If
![]() $\varphi \not \vdash \psi $
, then by Fact 6.1 we know that
$\varphi \not \vdash \psi $
, then by Fact 6.1 we know that
![]() $\varphi ^\Phi \not \vdash \psi ^\Phi $
for any
$\varphi ^\Phi \not \vdash \psi ^\Phi $
for any
![]() $\Phi $
including both
$\Phi $
including both
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. Let
$\psi $
. Let
![]() $\mathcal {M}$
be a
$\mathcal {M}$
be a
![]() $\mathsf {QRC_1}$
model satisfying
$\mathsf {QRC_1}$
model satisfying
![]() $\varphi ^\Phi $
and not satisfying
$\varphi ^\Phi $
and not satisfying
![]() $\psi ^\Phi $
, as given by Theorem 5.11. This model is transitive, irreflexive, and has finitely-many worlds, which means it is a
$\psi ^\Phi $
, as given by Theorem 5.11. This model is transitive, irreflexive, and has finitely-many worlds, which means it is a
![]() $\mathsf {QGL}$
model by Theorem 6.2. We conclude that
$\mathsf {QGL}$
model by Theorem 6.2. We conclude that
![]() $\mathsf {QGL} \not \vdash \varphi ^\Phi \to \psi ^\Phi $
, and consequently that
$\mathsf {QGL} \not \vdash \varphi ^\Phi \to \psi ^\Phi $
, and consequently that
![]() $\mathsf {QS} \not \vdash \varphi ^\Phi \to \psi ^\Phi $
.⊣
$\mathsf {QS} \not \vdash \varphi ^\Phi \to \psi ^\Phi $
.⊣
We end with the following observation. The proof of Theorem 6.3 holds for any quantified modal logic that extends
![]() $\mathsf {QK}4$
and is sound for any combination of constant-domain, finite, transitive, and irreflexive models. The Barcan Formula (
$\mathsf {QK}4$
and is sound for any combination of constant-domain, finite, transitive, and irreflexive models. The Barcan Formula (
![]() $\mathsf {BF}$
),
$\mathsf {BF}$
),
![]() $\forall x \, \Box A \to \Box \forall x \, A$
, is popular in the world of quantified modal logic and is always sound in constant-domain models. Thus the proof of Theorem 6.3 also serves to see that, for example,
$\forall x \, \Box A \to \Box \forall x \, A$
, is popular in the world of quantified modal logic and is always sound in constant-domain models. Thus the proof of Theorem 6.3 also serves to see that, for example,
![]() $\varphi \vdash \psi $
if and only if
$\varphi \vdash \psi $
if and only if
![]() $\mathsf {QK}4 + \mathsf {BF} \vdash \varphi ^\Phi \to \psi ^\Phi $
. This is curious because
$\mathsf {QK}4 + \mathsf {BF} \vdash \varphi ^\Phi \to \psi ^\Phi $
. This is curious because
![]() $\mathsf {BF}$
does not hold in
$\mathsf {BF}$
does not hold in
![]() $\mathsf {QGL}$
and is in fact unsound with the usual provability interpretation of
$\mathsf {QGL}$
and is in fact unsound with the usual provability interpretation of
![]() $\Box $
. From this we conclude that it would be worthwhile to study
$\Box $
. From this we conclude that it would be worthwhile to study
![]() $\mathsf {QRC_1}$
from points of view unrelated to provability.
$\mathsf {QRC_1}$
from points of view unrelated to provability.
7 Arithmetical semantics
Recall that the language of arithmetic is that of first-order logic together with the symbols
![]() $\{ 0, 1, +, \times , \leq , = \}$
with their usual arities (see [Reference Hájek and Pudlák23] for details). We will rely on
$\{ 0, 1, +, \times , \leq , = \}$
with their usual arities (see [Reference Hájek and Pudlák23] for details). We will rely on
![]() $\Sigma ^0_1$
collection throughout the sections on arithmetic, so we take
$\Sigma ^0_1$
collection throughout the sections on arithmetic, so we take
![]() ${\mathrm {I}\Sigma _{1}}$
as our base theory.
${\mathrm {I}\Sigma _{1}}$
as our base theory.
Let T be an elementary presented extension of
![]() ${\mathrm {I}\Sigma _{1}}$
, meaning that there is a bounded formula
${\mathrm {I}\Sigma _{1}}$
, meaning that there is a bounded formula
![]() ${\mathrm {Ax}}_T(u)$
that is true in the standard model if and only if u is (the Gödel number of) an axiom of T. In this setting it is traditional to define Gödel’s provability predicate
${\mathrm {Ax}}_T(u)$
that is true in the standard model if and only if u is (the Gödel number of) an axiom of T. In this setting it is traditional to define Gödel’s provability predicate
![]() $\Box _T \varphi $
as
$\Box _T \varphi $
as
![]() $\exists p \, {\mathrm {Prf}}_T(p, \ulcorner \varphi \urcorner )$
, where
$\exists p \, {\mathrm {Prf}}_T(p, \ulcorner \varphi \urcorner )$
, where
 $$ \begin{align*} {\mathrm{Prf}}_T(p, n) &:= \text{sequence}(p) \land p_{|p|-1} = n \land {}\\ & \forall k < |p| \, ( {\mathrm{Ax}}_T(p_k) \lor \exists i, j < k \, \text{MP}(p_i, p_j, p_k) \lor \exists i < k \, \text{Gen}(p_i, p_k) ). \end{align*} $$
$$ \begin{align*} {\mathrm{Prf}}_T(p, n) &:= \text{sequence}(p) \land p_{|p|-1} = n \land {}\\ & \forall k < |p| \, ( {\mathrm{Ax}}_T(p_k) \lor \exists i, j < k \, \text{MP}(p_i, p_j, p_k) \lor \exists i < k \, \text{Gen}(p_i, p_k) ). \end{align*} $$
Roughly,
![]() $\Box _T \varphi $
formalizes that there is a Hilbert-style proof of
$\Box _T \varphi $
formalizes that there is a Hilbert-style proof of
![]() $\varphi $
, that is, a finite sequence
$\varphi $
, that is, a finite sequence
![]() $p_0, \ldots , p_{m}$
such that
$p_0, \ldots , p_{m}$
such that
![]() $p_{m}$
is
$p_{m}$
is
![]() $\varphi $
and that each
$\varphi $
and that each
![]() $p_k$
is either (the Gödel number of) an axiom of T or follows from previous elements of the sequence through either modus ponens or generalization.
$p_k$
is either (the Gödel number of) an axiom of T or follows from previous elements of the sequence through either modus ponens or generalization.
Note that all the functions used in the definition of
![]() ${\mathrm {Prf}}_T$
can be naturally defined as bounded formulas in
${\mathrm {Prf}}_T$
can be naturally defined as bounded formulas in
![]() ${\mathrm {I}\Sigma _{1}}$
, and thus
${\mathrm {I}\Sigma _{1}}$
, and thus
![]() ${\mathrm {Prf}}_T$
is itself a bounded formula. This means that
${\mathrm {Prf}}_T$
is itself a bounded formula. This means that
![]() $\Box _T \varphi $
is
$\Box _T \varphi $
is
![]() $\Sigma ^0_1$
. We write
$\Sigma ^0_1$
. We write
![]() $\Diamond _T \varphi $
as shorthand for
$\Diamond _T \varphi $
as shorthand for
![]() $\neg \Box _T \neg \varphi $
.
$\neg \Box _T \neg \varphi $
.
In what follows we will be interested in c.e. theories, which are theories whose axioms can be defined by a
![]() $\Sigma ^0_1$
formula. It is known by Craig’s Trick [Reference Craig15, Reference Feferman18] that any such theory has an equivalent elementary presentation, allowing us to use the regular definition of
$\Sigma ^0_1$
formula. It is known by Craig’s Trick [Reference Craig15, Reference Feferman18] that any such theory has an equivalent elementary presentation, allowing us to use the regular definition of
![]() $\Box _T$
. However, we will work with specific axiomatizations and thus it is sometimes more convenient to allow
$\Box _T$
. However, we will work with specific axiomatizations and thus it is sometimes more convenient to allow
![]() ${\mathrm {Prf}}$
to be a
${\mathrm {Prf}}$
to be a
![]() $\Sigma ^0_1$
formula. For a given
$\Sigma ^0_1$
formula. For a given
![]() $\Sigma ^0_1$
axiomatization
$\Sigma ^0_1$
axiomatization
![]() $\tau $
of T, we define
$\tau $
of T, we define
![]() $\Box _\tau \varphi := \exists p \, {\mathrm {Prf}}_\tau (p, \ulcorner \varphi \urcorner )$
, where
$\Box _\tau \varphi := \exists p \, {\mathrm {Prf}}_\tau (p, \ulcorner \varphi \urcorner )$
, where
 $$ \begin{align*} {\mathrm{Prf}}_\tau(p, n) := &\text{sequence}(p) \land p_{|p|-1} = n \land \\ & \forall k < |p| \, ( \tau(p_k) \lor \exists i, j < k \, \text{MP}(p_i, p_j, p_k) \lor \exists i < k \, \text{Gen}(p_i, p_k) ) , \end{align*} $$
$$ \begin{align*} {\mathrm{Prf}}_\tau(p, n) := &\text{sequence}(p) \land p_{|p|-1} = n \land \\ & \forall k < |p| \, ( \tau(p_k) \lor \exists i, j < k \, \text{MP}(p_i, p_j, p_k) \lor \exists i < k \, \text{Gen}(p_i, p_k) ) , \end{align*} $$
the only difference from
![]() ${\mathrm {Prf}}_T$
being that we use the
${\mathrm {Prf}}_T$
being that we use the
![]() $\Sigma ^0_1$
formula
$\Sigma ^0_1$
formula
![]() $\tau $
instead of the bounded
$\tau $
instead of the bounded
![]() ${\mathrm {Ax}}_T$
. Thus
${\mathrm {Ax}}_T$
. Thus
![]() ${\mathrm {Prf}}_\tau $
is equivalent to a
${\mathrm {Prf}}_\tau $
is equivalent to a
![]() $\Sigma ^0_1$
formula (provably in
$\Sigma ^0_1$
formula (provably in
![]() ${\mathrm {I}\Sigma _{1}}$
), and so
${\mathrm {I}\Sigma _{1}}$
), and so
![]() $\Box _\tau \varphi $
is still
$\Box _\tau \varphi $
is still
![]() $\Sigma ^0_1$
. We define
$\Sigma ^0_1$
. We define
![]() $\Diamond _\tau \varphi $
as
$\Diamond _\tau \varphi $
as
![]() $\neg \Box _\tau \neg \varphi $
, as usual.
$\neg \Box _\tau \neg \varphi $
, as usual.
We wish to interpret the strictly positive formulas in the language of
![]() $\mathsf {QRC_1}$
as parameterized axiomatizations of arithmetical theories extending
$\mathsf {QRC_1}$
as parameterized axiomatizations of arithmetical theories extending
![]() ${\mathrm {I}\Sigma _{1}}$
. Let
${\mathrm {I}\Sigma _{1}}$
. Let
![]() $\tau $
be a bounded axiomatization of a sound c.e. base theory T extending
$\tau $
be a bounded axiomatization of a sound c.e. base theory T extending
![]() ${\mathrm {I}\Sigma _{1}}$
.
${\mathrm {I}\Sigma _{1}}$
.
A realization
![]() $\cdot ^{\circ }$
interprets each n-ary relation symbol
$\cdot ^{\circ }$
interprets each n-ary relation symbol
![]() $S(\boldsymbol {x}, \boldsymbol {c})$
as an
$S(\boldsymbol {x}, \boldsymbol {c})$
as an
![]() $(n+1)$
-ary
$(n+1)$
-ary
![]() $\Sigma ^0_1$
formula
$\Sigma ^0_1$
formula
![]() $\sigma (u, \boldsymbol {y}, \boldsymbol {z})$
in the language of arithmetic, where
$\sigma (u, \boldsymbol {y}, \boldsymbol {z})$
in the language of arithmetic, where
![]() $\boldsymbol {y}$
matches with
$\boldsymbol {y}$
matches with
![]() $\boldsymbol {x}$
and
$\boldsymbol {x}$
and
![]() $\boldsymbol {z}$
matches with
$\boldsymbol {z}$
matches with
![]() $\boldsymbol {c}$
.Footnote
8
We then extend this notion to any formula as follows (we add
$\boldsymbol {c}$
.Footnote
8
We then extend this notion to any formula as follows (we add
![]() $\tau (u)$
to the axioms of the interpretation of any relation symbol to guarantee that every theory is an extension of T).
$\tau (u)$
to the axioms of the interpretation of any relation symbol to guarantee that every theory is an extension of T).
Definition 7.1 (
 $\cdot ^{\circ _{\tau }}$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
$\cdot ^{\circ _{\tau }}$
[Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
Let
![]() $\cdot ^{\circ }$
be a realization such that, for a given n-ary predicate S and terms
$\cdot ^{\circ }$
be a realization such that, for a given n-ary predicate S and terms
![]() $\boldsymbol {t}$
,
$\boldsymbol {t}$
,
![]() $S(\boldsymbol {t})^{\circ }$
is an
$S(\boldsymbol {t})^{\circ }$
is an
![]() $(n+1)$
-ary
$(n+1)$
-ary
![]() $\Sigma ^0_1$
arithmetical formula where modal variables
$\Sigma ^0_1$
arithmetical formula where modal variables
![]() $x_k$
are interpreted as
$x_k$
are interpreted as
![]() $y_k$
and modal constants
$y_k$
and modal constants
![]() $c_k$
are interpreted as
$c_k$
are interpreted as
![]() $z_k$
. We extend this realization to
$z_k$
. We extend this realization to
![]() $\mathsf {QRC_1}$
formulas as follows:
$\mathsf {QRC_1}$
formulas as follows:
-
•
 $\top ^{\circ _{\tau }} := \tau (u)$
;
$\top ^{\circ _{\tau }} := \tau (u)$
; -
•
 $S(\boldsymbol {x}, \boldsymbol {c})^{\circ _{\tau }} : = S(\boldsymbol {x},\boldsymbol {c})^{\circ } \lor \tau (u)$
;
$S(\boldsymbol {x}, \boldsymbol {c})^{\circ _{\tau }} : = S(\boldsymbol {x},\boldsymbol {c})^{\circ } \lor \tau (u)$
; -
•
 $(\psi \land \delta )^{\circ _{\tau }} := \psi ^{\circ _{\tau }} \lor \delta ^{\circ _{\tau }}$
;
$(\psi \land \delta )^{\circ _{\tau }} := \psi ^{\circ _{\tau }} \lor \delta ^{\circ _{\tau }}$
; -
•
 $(\lozenge \psi )^{\circ _{\tau }} := \tau (u) \lor (u = \ulcorner \Diamond _{\psi ^{\circ _{\tau }}} \top \urcorner )$
;
$(\lozenge \psi )^{\circ _{\tau }} := \tau (u) \lor (u = \ulcorner \Diamond _{\psi ^{\circ _{\tau }}} \top \urcorner )$
; -
•
 $(\forall x_i \, \psi )^{\circ _{\tau }} := \exists y_i \, \psi ^{\circ _{\tau }}$
.
$(\forall x_i \, \psi )^{\circ _{\tau }} := \exists y_i \, \psi ^{\circ _{\tau }}$
.
We remark that, if the free variables of
![]() $\varphi $
are
$\varphi $
are
![]() $x_0, \ldots , x_{n-1}$
and the constants appearing in
$x_0, \ldots , x_{n-1}$
and the constants appearing in
![]() $\varphi $
are
$\varphi $
are
![]() $c_0, \ldots , c_{m-1}$
, then the free variables of
$c_0, \ldots , c_{m-1}$
, then the free variables of
![]() $\varphi ^{\circ _{\tau }}$
are u,
$\varphi ^{\circ _{\tau }}$
are u,
![]() $y_0, \ldots , y_{n-1}$
,
$y_0, \ldots , y_{n-1}$
,
![]() $z_0, \ldots , z_{m-1}$
. For example, if
$z_0, \ldots , z_{m-1}$
. For example, if
![]() $S(x_0, c_1)^{\circ _{\tau }} = \sigma (u, y_0, z_1) \lor \tau (u)$
, then
$S(x_0, c_1)^{\circ _{\tau }} = \sigma (u, y_0, z_1) \lor \tau (u)$
, then
The dotted variables
![]() $\dot {y_0}$
and
$\dot {y_0}$
and
![]() $\dot {z_1}$
in the expression
$\dot {z_1}$
in the expression
![]() $u = \ulcorner \Diamond _{\sigma (u, \dot {y_0}, \dot {z_1}) \lor \tau (u)} \top \urcorner $
indicate that
$u = \ulcorner \Diamond _{\sigma (u, \dot {y_0}, \dot {z_1}) \lor \tau (u)} \top \urcorner $
indicate that
![]() $y_0$
and
$y_0$
and
![]() $z_1$
are free variables of this expression that, upon being instantiated by natural numbers n and m, shall be replaced by the numerals
$z_1$
are free variables of this expression that, upon being instantiated by natural numbers n and m, shall be replaced by the numerals
![]() $\bar {n}$
and
$\bar {n}$
and
![]() $\bar {m}$
instead.
$\bar {m}$
instead.
Since we have
![]() $\Sigma ^0_1$
collection,
$\Sigma ^0_1$
collection,
![]() $\varphi ^{\circ _{\tau }}$
is always provably equivalent to a
$\varphi ^{\circ _{\tau }}$
is always provably equivalent to a
![]() $\Sigma ^0_1$
formula, and it represents the axiomatization of an extension of T.
$\Sigma ^0_1$
formula, and it represents the axiomatization of an extension of T.
We briefly inspect our intuitions regarding this arithmetic interpretation and the interaction between
![]() $\forall $
and
$\forall $
and
![]() $\Diamond $
. As mentioned in Lemma 3.2, the sequent
$\Diamond $
. As mentioned in Lemma 3.2, the sequent
![]() $\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
is provable in
$\Diamond \forall x \, \varphi \vdash \forall x \, \Diamond \varphi $
is provable in
![]() $\mathsf {QRC_1}$
. In the arithmetical reading it says that if the union of many theories (the
$\mathsf {QRC_1}$
. In the arithmetical reading it says that if the union of many theories (the
![]() $\forall x \, \varphi $
part) is consistent, then so is each individual theory. The converse, on the other hand, must not be a consequence of
$\forall x \, \varphi $
part) is consistent, then so is each individual theory. The converse, on the other hand, must not be a consequence of
![]() $\mathsf {QRC_1}$
, for it is not in general the case that the union of many consistent theories is itself consistent.
$\mathsf {QRC_1}$
, for it is not in general the case that the union of many consistent theories is itself consistent.
We can now define
![]() $\mathcal {QRC}_1(T)$
:
$\mathcal {QRC}_1(T)$
:
where
![]() $\theta $
is a closed formula and
$\theta $
is a closed formula and
![]() $\varphi ^{\circ _{\tau }}, \psi ^{\circ _{\tau }}$
in general depend on
$\varphi ^{\circ _{\tau }}, \psi ^{\circ _{\tau }}$
in general depend on
![]() $\boldsymbol {y}$
and
$\boldsymbol {y}$
and
![]() $\boldsymbol {z}$
.
$\boldsymbol {z}$
.
We will show that
for any sound c.e theory T extending
![]() ${\mathrm {I}\Sigma _{1}}$
. The left-to-right inclusion was already proved in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] for
${\mathrm {I}\Sigma _{1}}$
. The left-to-right inclusion was already proved in [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1] for
![]() ${\mathrm {I}\Sigma _{1}}$
, and the same proof goes through for any such T. The most notable part of the proof is the case of Rule 3.1(vii) (
${\mathrm {I}\Sigma _{1}}$
, and the same proof goes through for any such T. The most notable part of the proof is the case of Rule 3.1(vii) (
![]() $\forall $
introduction on the right), which uses
$\forall $
introduction on the right), which uses
![]() $\Sigma ^0_1$
collection. We go into detail on the very similar proof of Theorem 10.3.
$\Sigma ^0_1$
collection. We go into detail on the very similar proof of Theorem 10.3.
Theorem 7.2 (Arithmetical soundness [Reference de Almeida Borges, Joosten, Olivetti, Verbrugge, Negri and Sandu1]).
![]() $\mathsf {QRC_1} \subseteq \mathcal {QRC}_1(T)$
.
$\mathsf {QRC_1} \subseteq \mathcal {QRC}_1(T)$
.
We dedicate the next section to the proof of the other inclusion.
8 Arithmetical completeness
The proof of arithmetical completeness closely follows the proof of Solovay’s Theorem found in [Reference Boolos11]. The arithmetical semantics used there is different from the one presented in the previous section, allowing only for finite extensions of the base theory instead of arbitrary c.e. ones. This is not a problem because finite axiomatizations are enough to show completeness. We use
![]() $\cdot ^{\circ }$
in the general setting and
$\cdot ^{\circ }$
in the general setting and
![]() $\cdot ^{*}$
in the finite one. The base theory T considered here is any sound c.e. extension of
$\cdot ^{*}$
in the finite one. The base theory T considered here is any sound c.e. extension of
![]() ${\mathrm {I}\Sigma _{1}}$
. Note that we use the bounded
${\mathrm {I}\Sigma _{1}}$
. Note that we use the bounded
![]() ${\mathrm {Prf}}_T$
formula in the definition of
${\mathrm {Prf}}_T$
formula in the definition of
![]() $\cdot ^{*_{T}}$
(depending on an elementary axiomatization
$\cdot ^{*_{T}}$
(depending on an elementary axiomatization
![]() $\tau $
of T), as otherwise Solovay’s proof wouldn’t go through.
$\tau $
of T), as otherwise Solovay’s proof wouldn’t go through.
Definition 8.1 (
 $\cdot ^{*_{T}}$
).
$\cdot ^{*_{T}}$
).
Let
![]() $\cdot ^{*}$
be a realization such that, for a given predicate S and terms
$\cdot ^{*}$
be a realization such that, for a given predicate S and terms
![]() $\boldsymbol {t}$
,
$\boldsymbol {t}$
,
![]() $S(\boldsymbol {t})^{*}$
is an arithmetical formula with the same arity as S where modal variables
$S(\boldsymbol {t})^{*}$
is an arithmetical formula with the same arity as S where modal variables
![]() $x_k$
are interpreted as
$x_k$
are interpreted as
![]() $y_k$
and modal constants
$y_k$
and modal constants
![]() $c_k$
are interpreted as
$c_k$
are interpreted as
![]() $z_k$
. We extend this realization to
$z_k$
. We extend this realization to
![]() $\mathsf {QRC_1}$
formulas as follows:
$\mathsf {QRC_1}$
formulas as follows:
-
•
 $\top ^{*_{T}} := \top $
;
$\top ^{*_{T}} := \top $
; -
•
 $S(\boldsymbol {t})^{*_{T}} := S(\boldsymbol {t})^{*}$
;
$S(\boldsymbol {t})^{*_{T}} := S(\boldsymbol {t})^{*}$
; -
•
 $(\varphi \land \psi )^{*_{T}} := \varphi ^{*_{T}} \land \psi ^{*_{T}}$
;
$(\varphi \land \psi )^{*_{T}} := \varphi ^{*_{T}} \land \psi ^{*_{T}}$
; -
•
 $(\Diamond \varphi )^{*_{T}} := \Diamond _T \varphi ^{*_{T}}$
;
$(\Diamond \varphi )^{*_{T}} := \Diamond _T \varphi ^{*_{T}}$
; -
•
 $(\forall x_k \, \varphi )^{*_{T}} := \forall y_k \, \varphi ^{*_{T}}$
.
$(\forall x_k \, \varphi )^{*_{T}} := \forall y_k \, \varphi ^{*_{T}}$
.
The idea of Solovay’s proof is to embed a Kripke model not satisfying the desired unprovable formula in the language of arithmetic. If the embedding is done correctly, it is possible to prove that a formula is satisfied at a world of the Kripke model exactly when it is a consequence of the representation of that world in the desired theory T.
Given two strictly positive formulas
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
such that
$\psi $
such that
![]() $\varphi \not \vdash \psi $
in
$\varphi \not \vdash \psi $
in
![]() $\mathsf {QRC_1}$
, let
$\mathsf {QRC_1}$
, let
![]() $\mathcal {M}_{\varphi , \psi }$
be a finite, irreflexive, and constant domain adequate model satisfying
$\mathcal {M}_{\varphi , \psi }$
be a finite, irreflexive, and constant domain adequate model satisfying
![]() $\varphi $
and not satisfying
$\varphi $
and not satisfying
![]() $\psi $
at the root
$\psi $
at the root
![]() $1$
under a
$1$
under a
![]() $1$
-assignment
$1$
-assignment
![]() $g_{\varphi , \psi }$
. This model and assignment exist by Theorem 5.11. Since
$g_{\varphi , \psi }$
. This model and assignment exist by Theorem 5.11. Since
![]() $\mathcal {M}_{\varphi , \psi }$
has constant domain, we refer to
$\mathcal {M}_{\varphi , \psi }$
has constant domain, we refer to
![]() $g_{\varphi , \psi }$
and any other i-assignments as just assignments, omitting the relevant world.
$g_{\varphi , \psi }$
and any other i-assignments as just assignments, omitting the relevant world.
We assume that the worlds of
![]() $\mathcal {M}_{\varphi , \psi }$
are
$\mathcal {M}_{\varphi , \psi }$
are
![]() $W = \{ 1, 2, \ldots , N \}$
, where
$W = \{ 1, 2, \ldots , N \}$
, where
![]() $1$
is the root. We define a new (adequate) model
$1$
is the root. We define a new (adequate) model
![]() $\mathcal {M}$
that is a copy of
$\mathcal {M}$
that is a copy of
![]() $\mathcal {M}_{\varphi , \psi }$
, except that it has an extra world
$\mathcal {M}_{\varphi , \psi }$
, except that it has an extra world
![]() $0$
as the new root. This world
$0$
as the new root. This world
![]() $0$
is connected to all the other worlds through R and has the same domain, constant interpretation, and relational symbol interpretation as
$0$
is connected to all the other worlds through R and has the same domain, constant interpretation, and relational symbol interpretation as
![]() $1$
. The functions
$1$
. The functions
![]() $\eta _{0, i}$
with
$\eta _{0, i}$
with
![]() $0 < i \leq N$
are all defined as the identity function.
$0 < i \leq N$
are all defined as the identity function.
Let
![]() $\lambda _i$
be the Solovay sentences for T as defined in [Reference Boolos11], satisfying the following Embedding Lemma.
$\lambda _i$
be the Solovay sentences for T as defined in [Reference Boolos11], satisfying the following Embedding Lemma.
Lemma 8.2 (Embedding [Reference Boolos11]).
-
1.
 $\mathbb {N} \vDash \lambda _0$
;
$\mathbb {N} \vDash \lambda _0$
; -
2.
 $T \vdash \bigvee _{i \leq N} \lambda _i$
;
$T \vdash \bigvee _{i \leq N} \lambda _i$
; -
3.
 $T \vdash \lambda _i \to \bigwedge _{j \leq N, j \neq i} \neg \lambda _j$
, for
$T \vdash \lambda _i \to \bigwedge _{j \leq N, j \neq i} \neg \lambda _j$
, for
 $i \leq N$
;
$i \leq N$
; -
4.
 $T \vdash \lambda _i \to \bigwedge _{j \leq N, iRj} \Diamond _T \lambda _j$
, for
$T \vdash \lambda _i \to \bigwedge _{j \leq N, iRj} \Diamond _T \lambda _j$
, for
 $i \leq N$
;
$i \leq N$
; -
5.
 $T \vdash \lambda _i \to \Box _T \bigvee _{j \leq N, iRj} \lambda _j$
, for
$T \vdash \lambda _i \to \Box _T \bigvee _{j \leq N, iRj} \lambda _j$
, for
 $0 < i \leq N$
.
$0 < i \leq N$
.
The domain of every world is M. Let m be the size of M, and
![]() be a bijection between M and the set of numerals
be a bijection between M and the set of numerals
![]() $\{\overline {0}, \ldots , \overline {m - 1}\}$
.
$\{\overline {0}, \ldots , \overline {m - 1}\}$
.
We now define for a given n-ary predicate symbol S and terms
![]() $\boldsymbol {t} = t_0, \ldots , t_{n-1}$
the
$\boldsymbol {t} = t_0, \ldots , t_{n-1}$
the
![]() $\cdot ^{\circledast }$
interpretation as follows:
$\cdot ^{\circledast }$
interpretation as follows:

Here
![]() $x_k$
is any
$x_k$
is any
![]() $\mathsf {QRC_1}$
variable,
$\mathsf {QRC_1}$
variable,
![]() $y_k$
is the corresponding T variable,
$y_k$
is the corresponding T variable,
![]() $c_k$
is any
$c_k$
is any
![]() $\mathsf {QRC_1}$
constant,
$\mathsf {QRC_1}$
constant,
![]() $z_k$
is the corresponding T variable, and
$z_k$
is the corresponding T variable, and
![]() $\cdot ^{J_i}$
is the denotation of a predicate symbol at world i. Note that
$\cdot ^{J_i}$
is the denotation of a predicate symbol at world i. Note that
![]() $x_k \in {\mathrm {fv}}(S(\boldsymbol {t}))$
if and only if
$x_k \in {\mathrm {fv}}(S(\boldsymbol {t}))$
if and only if
![]() $y_k \in {\mathrm {fv}}(S(\boldsymbol {t})^{\circledast })$
and
$y_k \in {\mathrm {fv}}(S(\boldsymbol {t})^{\circledast })$
and
![]() $c_k$
appears in
$c_k$
appears in
![]() $S(\boldsymbol {t})$
if and only if
$S(\boldsymbol {t})$
if and only if
![]() $z_k \in {\mathrm {fv}}(S(\boldsymbol {t})^{\circledast })$
. The
$z_k \in {\mathrm {fv}}(S(\boldsymbol {t})^{\circledast })$
. The
![]() $\cdot ^{\circledast }$
interpretation is extended to non-predicate formulas as described in Definition 8.1.
$\cdot ^{\circledast }$
interpretation is extended to non-predicate formulas as described in Definition 8.1.
Fact 8.3. For any
![]() $\mathsf {QRC_1}$
formula
$\mathsf {QRC_1}$
formula
![]() $\varphi $
, variable
$\varphi $
, variable
![]() $x_k$
, and constant
$x_k$
, and constant
![]() $c_k$
, we have that
$c_k$
, we have that
![]() $x_k \in {\mathrm {fv}}(\varphi )$
if and only if
$x_k \in {\mathrm {fv}}(\varphi )$
if and only if
![]() $y_k \in {\mathrm {fv}}(\varphi ^{\circledast _{T}})$
and that
$y_k \in {\mathrm {fv}}(\varphi ^{\circledast _{T}})$
and that
![]() $c_k$
appears in
$c_k$
appears in
![]() $\varphi $
if and only if
$\varphi $
if and only if
![]() $z_k \in {\mathrm {fv}}(\varphi ^{\circledast _{T}})$
.
$z_k \in {\mathrm {fv}}(\varphi ^{\circledast _{T}})$
.
We further note that
![]() $\varphi ^{\circledast _{T}}$
is invariant under replacing variables by themselves modulo m, provably in T.
$\varphi ^{\circledast _{T}}$
is invariant under replacing variables by themselves modulo m, provably in T.
Lemma 8.4. For any
![]() $\mathsf {QRC_1}$
formula
$\mathsf {QRC_1}$
formula
![]() $\varphi $
and any arithmetical variable y:
$\varphi $
and any arithmetical variable y:
-
1.
 $ T \vdash \varphi ^{\circledast _{T}} \leftrightarrow \varphi ^{\circledast _{T}}[y {\leftarrow } y \ {\mathrm {mod}} \ m] $
;
$ T \vdash \varphi ^{\circledast _{T}} \leftrightarrow \varphi ^{\circledast _{T}}[y {\leftarrow } y \ {\mathrm {mod}} \ m] $
; -
2.
 $ T \vdash \forall y \, \varphi ^{\circledast _{T}} \leftrightarrow \forall y < m \, \varphi ^{\circledast _{T}} $
.
$ T \vdash \forall y \, \varphi ^{\circledast _{T}} \leftrightarrow \forall y < m \, \varphi ^{\circledast _{T}} $
.
Proof. The second item is a straightforward consequence of the first, which is proved by an external induction on the complexity of
![]() $\varphi $
, noting that T proves
$\varphi $
, noting that T proves
![]() $(y \ {\mathrm {mod}} \ m) \ {\mathrm {mod}} \ m = y \ {\mathrm {mod}} \ m$
for any y.⊣
$(y \ {\mathrm {mod}} \ m) \ {\mathrm {mod}} \ m = y \ {\mathrm {mod}} \ m$
for any y.⊣
We now prove two versions of a Truth Lemma, one for when
![]() $\varphi $
is forced at a world i of
$\varphi $
is forced at a world i of
![]() $\mathcal {M}$
, and one for when it isn’t. We wish to show that T proves
$\mathcal {M}$
, and one for when it isn’t. We wish to show that T proves
![]() $\varphi ^{\circledast _{T}}$
(respectively
$\varphi ^{\circledast _{T}}$
(respectively
![]() $\neg \varphi ^{\circledast _{T}}$
) as a consequence of
$\neg \varphi ^{\circledast _{T}}$
) as a consequence of
![]() $\lambda _i$
, as long as the free variables of
$\lambda _i$
, as long as the free variables of
![]() $\varphi $
are interpreted in the same way in both settings.
$\varphi $
are interpreted in the same way in both settings.
In order to use concise notation, we shall say
![]() $\boldsymbol {y}$
instead of
$\boldsymbol {y}$
instead of
![]() $y_0, \ldots , y_{n-1}$
, and similarly for other terms. We also abbreviate iterated substitutions, writing
$y_0, \ldots , y_{n-1}$
, and similarly for other terms. We also abbreviate iterated substitutions, writing
![]() instead of
instead of
![]() and writing
and writing
![]() instead of
instead of
![]() .
.
Lemma 8.5 (Truth Lemma: positive).
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\mathsf {QRC_1}$
formula with free variables
$\mathsf {QRC_1}$
formula with free variables
![]() $\boldsymbol {x} = x_0, \ldots , x_{n-1}$
and constants
$\boldsymbol {x} = x_0, \ldots , x_{n-1}$
and constants
![]() $\boldsymbol {c} = c_0, \ldots , c_{n'-1}$
. Then for any world
$\boldsymbol {c} = c_0, \ldots , c_{n'-1}$
. Then for any world
![]() $i \leq N$
and any assignment g,
$i \leq N$
and any assignment g,
Proof. By external induction on the complexity of
![]() $\varphi $
. The cases of
$\varphi $
. The cases of
![]() $\top $
and
$\top $
and
![]() $\land $
are straightforward.
$\land $
are straightforward.
In the case of relational symbols, we assume without loss of generality that the relevant formula is
![]() $S(x_0, c_0)$
. If
$S(x_0, c_0)$
. If
![]() $\mathcal {M}, i \Vdash ^g S(x_0, c_0)$
, then
$\mathcal {M}, i \Vdash ^g S(x_0, c_0)$
, then
![]() $\langle g(x_0), (c_0)^{I_i} \rangle \in S^{J_i}$
. Reason in T and assume
$\langle g(x_0), (c_0)^{I_i} \rangle \in S^{J_i}$
. Reason in T and assume
![]() $\lambda _i$
. It suffices to prove
$\lambda _i$
. It suffices to prove
which implies
under the assumption of
![]() $\lambda _i$
. We need to find
$\lambda _i$
. We need to find
![]() $\langle a_0, a_1 \rangle \in S^{J_i}$
such that
$\langle a_0, a_1 \rangle \in S^{J_i}$
such that
and
. Noting that
is provably equal to
for any b, we pick
![]() $a_0 := g(x_0)$
and
$a_0 := g(x_0)$
and
![]() $a_1 := (c_0)^{I_0}$
. This concludes this step of the proof because
$a_1 := (c_0)^{I_0}$
. This concludes this step of the proof because
![]() $(c_0)^{I_0}$
is equal to
$(c_0)^{I_0}$
is equal to
![]() $(c_0)^{I_i}$
, for any world i.
$(c_0)^{I_i}$
, for any world i.
For
![]() $\forall x_0 \, \varphi $
, assume without loss of generality that the free variables of
$\forall x_0 \, \varphi $
, assume without loss of generality that the free variables of
![]() $\varphi $
are
$\varphi $
are
![]() $x_0$
and
$x_0$
and
![]() $x_1$
. If
$x_1$
. If
![]() $\mathcal {M}, i \Vdash ^g \forall x_0 \, \varphi $
then for every assignment
$\mathcal {M}, i \Vdash ^g \forall x_0 \, \varphi $
then for every assignment
![]() $h \sim _{x_0} g$
we have
$h \sim _{x_0} g$
we have
![]() $\mathcal {M}, i \Vdash ^h \varphi $
. We wish to show
$\mathcal {M}, i \Vdash ^h \varphi $
. We wish to show
Reason in T and assume
![]() $\lambda _i$
. By Lemma 8.4, it is enough to show
$\lambda _i$
. By Lemma 8.4, it is enough to show
Since
![]() $y_0$
,
$y_0$
,
![]() $y_1$
, and
$y_1$
, and
![]() $\boldsymbol {z}$
are all different, we can push the substitutions inside and prove
$\boldsymbol {z}$
are all different, we can push the substitutions inside and prove
instead. Let
![]() $y_0 < m$
be arbitrary. Since
$y_0 < m$
be arbitrary. Since
is a bijection, there is
![]() $a \in M$
such that
$a \in M$
such that
. We define an assignment h such that
![]() $h \sim _{x_0} g$
and
$h \sim _{x_0} g$
and
![]() $h(x_0) := a$
. By assumption,
$h(x_0) := a$
. By assumption,
![]() $\mathcal {M}, i \Vdash ^h \varphi $
, so by the induction hypothesis we obtain
$\mathcal {M}, i \Vdash ^h \varphi $
, so by the induction hypothesis we obtain
This concludes the argument because
and
![]() $h(x_1) = g(x_1)$
.
$h(x_1) = g(x_1)$
.
Finally, consider the case of
![]() $\Diamond \varphi $
. If
$\Diamond \varphi $
. If
![]() $\mathcal {M}, i \Vdash ^g \Diamond \varphi $
, then there is
$\mathcal {M}, i \Vdash ^g \Diamond \varphi $
, then there is
![]() $j \leq N$
such that
$j \leq N$
such that
![]() $iRj$
and
$iRj$
and
![]() $\mathcal {M}, j \Vdash ^g \varphi $
. Reason in T and assume
$\mathcal {M}, j \Vdash ^g \varphi $
. Reason in T and assume
![]() $\lambda _i$
. By Lemma 8.2.4, we obtain
$\lambda _i$
. By Lemma 8.2.4, we obtain
![]() $\Diamond _T \lambda _j$
. Then the induction hypothesis under the box gives us the desired
$\Diamond _T \lambda _j$
. Then the induction hypothesis under the box gives us the desired
![]() .⊣
.⊣
Lemma 8.6 (Truth Lemma: negative).
Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\mathsf {QRC_1}$
formula with free variables
$\mathsf {QRC_1}$
formula with free variables
![]() $\boldsymbol {x} = x_0, \ldots , x_{n-1}$
and constants
$\boldsymbol {x} = x_0, \ldots , x_{n-1}$
and constants
![]() $\boldsymbol {c} = c_0, \ldots , c_{n'-1}$
. Then for any world
$\boldsymbol {c} = c_0, \ldots , c_{n'-1}$
. Then for any world
![]() $0 < i \leq N$
and any assignment g,
$0 < i \leq N$
and any assignment g,
Proof. By external induction on the complexity of
![]() $\varphi $
. The cases of
$\varphi $
. The cases of
![]() $\top $
and
$\top $
and
![]() $\land $
are straightforward.
$\land $
are straightforward.
For the relational symbols, consider
![]() $S(x_0, c_0)$
without loss of generality. If
$S(x_0, c_0)$
without loss of generality. If
![]() $\mathcal {M}, i \not \Vdash ^g S(x_0, c_0)$
, then
$\mathcal {M}, i \not \Vdash ^g S(x_0, c_0)$
, then
![]() $\langle g(x_0), (c_0)^{I_i} \rangle \notin S^{J_i}$
. Reason in T and assume
$\langle g(x_0), (c_0)^{I_i} \rangle \notin S^{J_i}$
. Reason in T and assume
![]() $\lambda _i$
. We obtain
$\lambda _i$
. We obtain
![]() $\neg \lambda _j$
for every
$\neg \lambda _j$
for every
![]() $j \neq i$
by Lemma 8.2.3, and hence need only show
$j \neq i$
by Lemma 8.2.3, and hence need only show
![]() . In other words, we need to check that if
. In other words, we need to check that if
![]() $\langle a_0, a_1 \rangle \in S^{J_i}$
, either
$\langle a_0, a_1 \rangle \in S^{J_i}$
, either
![]() , or
, or
![]() . This follows from our observation that
. This follows from our observation that
![]() $\langle g(x_0), (c_0)^{I_i} \rangle \notin S^{J_i}$
, taking into account that
$\langle g(x_0), (c_0)^{I_i} \rangle \notin S^{J_i}$
, taking into account that
![]() is equal to
is equal to
![]() for any b, that
for any b, that
![]() is injective, and that
is injective, and that
![]() $(c_0)^{I_0} = (c_0)^{I_i}$
.
$(c_0)^{I_0} = (c_0)^{I_i}$
.
Consider now the case of
![]() $\forall x_0 \, \varphi $
. We assume without loss of generality that
$\forall x_0 \, \varphi $
. We assume without loss of generality that
![]() ${\mathrm {fv}}(\varphi ) = \{x_0, x_1\}$
. If
${\mathrm {fv}}(\varphi ) = \{x_0, x_1\}$
. If
![]() $\mathcal {M}, i \not \Vdash ^g \forall x_0 \, \varphi $
, then there is an assignment
$\mathcal {M}, i \not \Vdash ^g \forall x_0 \, \varphi $
, then there is an assignment
![]() $h \sim _{x_0} g$
such that
$h \sim _{x_0} g$
such that
![]() $\mathcal {M}, i \not \Vdash ^h \varphi $
. Reason in T and assume
$\mathcal {M}, i \not \Vdash ^h \varphi $
. Reason in T and assume
![]() $\lambda _i$
. From the induction hypothesis we obtain
$\lambda _i$
. From the induction hypothesis we obtain
![]() , which then implies
, which then implies
![]() . This is what we wanted, taking into account that
. This is what we wanted, taking into account that
![]() $h(x_1) = g(x_1)$
.
$h(x_1) = g(x_1)$
.
Finally, in the case of
![]() $\Diamond \varphi $
, assume that
$\Diamond \varphi $
, assume that
![]() $\mathcal {M}, i \not \Vdash ^g \Diamond \varphi $
. Then for every j such that
$\mathcal {M}, i \not \Vdash ^g \Diamond \varphi $
. Then for every j such that
![]() $iRj$
, we have
$iRj$
, we have
![]() $\mathcal {M}, j \not \Vdash ^g \varphi $
and thus for each such j the induction hypothesis gives us
$\mathcal {M}, j \not \Vdash ^g \varphi $
and thus for each such j the induction hypothesis gives us
![]() , which put together implies
, which put together implies
![]() . Reason in T and assume
. Reason in T and assume
![]() $\lambda _i$
. By Lemma 8.2.5 and our assumption, we obtain
$\lambda _i$
. By Lemma 8.2.5 and our assumption, we obtain
![]() $\Box _T \bigvee _{iRj} \lambda _j$
. Taking the previous observation under the box, we conclude
$\Box _T \bigvee _{iRj} \lambda _j$
. Taking the previous observation under the box, we conclude
![]() , which is precisely
, which is precisely
![]() .⊣
.⊣
We are ready to prove something analogous to Solovay’s Theorem, which is the precursor to our desired completeness theorem.
Theorem 8.7. If
![]() $\varphi , \psi $
are
$\varphi , \psi $
are
![]() $\mathsf {QRC_1}$
formulas with free variables
$\mathsf {QRC_1}$
formulas with free variables
![]() $\boldsymbol {x}$
and constants
$\boldsymbol {x}$
and constants
![]() $\boldsymbol {c}$
such that
$\boldsymbol {c}$
such that
![]() $\varphi \not \vdash \psi $
, we have
$\varphi \not \vdash \psi $
, we have
![]() .
.
Proof. Recall that
![]() $\mathcal {M}$
satisfies
$\mathcal {M}$
satisfies
![]() $\varphi $
and not
$\varphi $
and not
![]() $\psi $
at world
$\psi $
at world
![]() $1$
under the assignment
$1$
under the assignment
![]() $g := g_{\varphi , \psi }$
.
$g := g_{\varphi , \psi }$
.
Since
![]() $\mathcal {M}, 1 \Vdash ^g \varphi $
, we obtain
$\mathcal {M}, 1 \Vdash ^g \varphi $
, we obtain
![]() from Lemma 8.5. Since
from Lemma 8.5. Since
![]() $\mathcal {M}, 1 \not \Vdash ^g \psi $
, we obtain
$\mathcal {M}, 1 \not \Vdash ^g \psi $
, we obtain
![]() from Lemma 8.6. Thus
from Lemma 8.6. Thus
![]() .
.
By Lemma 8.2.4 and the fact that
![]() $0R1$
, we obtain
$0R1$
, we obtain
![]() $T \vdash \lambda _0 \to \Diamond _T \lambda _1$
, so putting this together with the previous observation under the box,
$T \vdash \lambda _0 \to \Diamond _T \lambda _1$
, so putting this together with the previous observation under the box,
![]() .
.
By Lemma 8.2.1, we know that
![]() $\mathbb {N} \vDash \lambda _0$
, and thus by the soundness of T, we know that
$\mathbb {N} \vDash \lambda _0$
, and thus by the soundness of T, we know that
![]() . Then it must be the case that
. Then it must be the case that
![]() .⊣
.⊣
We now define an arithmetical realization
![]() $\cdot ^{\circledcirc }$
in the style of Section 7 that behaves like
$\cdot ^{\circledcirc }$
in the style of Section 7 that behaves like
![]() $\cdot ^{\circledast }$
. Recall that if
$\cdot ^{\circledast }$
. Recall that if
![]() $\tau $
is a
$\tau $
is a
![]() $\Sigma ^0_1$
formula axiomatizing T, the realization
$\Sigma ^0_1$
formula axiomatizing T, the realization
![]() $\cdot ^{\circ _{\tau }}$
sends
$\cdot ^{\circ _{\tau }}$
sends
![]() $\mathsf {QRC_1}$
formulas to
$\mathsf {QRC_1}$
formulas to
![]() $\Sigma ^0_1$
axiomatizations of theories extending T. So in particular we always have
$\Sigma ^0_1$
axiomatizations of theories extending T. So in particular we always have
![]() $(\varphi \land \psi )^{\circ _{\tau }} = \varphi ^{\circ _{\tau }} \lor \psi ^{\circ _{\tau }}$
, because
$(\varphi \land \psi )^{\circ _{\tau }} = \varphi ^{\circ _{\tau }} \lor \psi ^{\circ _{\tau }}$
, because
![]() $\chi $
is an axiom of the union of the theories axiomatized by
$\chi $
is an axiom of the union of the theories axiomatized by
![]() $\varphi ^{\circ _{\tau }}$
and
$\varphi ^{\circ _{\tau }}$
and
![]() $\psi ^{\circ _{\tau }}$
precisely when
$\psi ^{\circ _{\tau }}$
precisely when
![]() $\chi $
is an axiom of one of them. This is different from
$\chi $
is an axiom of one of them. This is different from
![]() $\cdot ^{*_{T}}$
realizations such as
$\cdot ^{*_{T}}$
realizations such as
![]() $\cdot ^{\circledast _{T}}$
, which send
$\cdot ^{\circledast _{T}}$
, which send
![]() $\mathsf {QRC_1}$
formulas to generic arithmetical formulas. We then interpret these formulas as finite extensions of T, so in particular
$\mathsf {QRC_1}$
formulas to generic arithmetical formulas. We then interpret these formulas as finite extensions of T, so in particular
![]() $(\varphi \land \psi )^{*_{T}} = \varphi ^{*_{T}} \land \psi ^{*_{T}}$
, because the union of
$(\varphi \land \psi )^{*_{T}} = \varphi ^{*_{T}} \land \psi ^{*_{T}}$
, because the union of
![]() $T + \varphi ^{*_{T}}$
and
$T + \varphi ^{*_{T}}$
and
![]() $T + \psi ^{*_{T}}$
is the same as
$T + \psi ^{*_{T}}$
is the same as
![]() $T + \varphi ^{*_{T}} \land \psi ^{*_{T}}$
.
$T + \varphi ^{*_{T}} \land \psi ^{*_{T}}$
.
We define
![]() $\cdot ^{\circledcirc }$
such that
$\cdot ^{\circledcirc }$
such that
![]() $S(\boldsymbol {t})^{\circledcirc } := \tau (u) \lor (u = \ulcorner S(\boldsymbol {t})^{\circledast } \urcorner )$
, and extend it to non-atomic formulas as described in Definition 7.1. Note that
$S(\boldsymbol {t})^{\circledcirc } := \tau (u) \lor (u = \ulcorner S(\boldsymbol {t})^{\circledast } \urcorner )$
, and extend it to non-atomic formulas as described in Definition 7.1. Note that
![]() $x_k \in {\mathrm {fv}}(\varphi )$
if and only if
$x_k \in {\mathrm {fv}}(\varphi )$
if and only if
![]() $y_k \in {\mathrm {fv}}(\varphi ^{\circledcirc _{\tau }})$
and
$y_k \in {\mathrm {fv}}(\varphi ^{\circledcirc _{\tau }})$
and
![]() $c_k$
appears in
$c_k$
appears in
![]() $\varphi $
if and only if
$\varphi $
if and only if
![]() $z_k \in {\mathrm {fv}}(\varphi ^{\circledcirc _{\tau }})$
.
$z_k \in {\mathrm {fv}}(\varphi ^{\circledcirc _{\tau }})$
.
Lemma 8.8. For any
![]() $\mathsf {QRC_1}$
formula
$\mathsf {QRC_1}$
formula
![]() $\varphi $
with free variables
$\varphi $
with free variables
![]() $\boldsymbol {x}$
and constants
$\boldsymbol {x}$
and constants
![]() $\boldsymbol {c}$
,
$\boldsymbol {c}$
,
where
![]() $\theta $
is (the Gödel number of) a closed formula.
$\theta $
is (the Gödel number of) a closed formula.
Proof. By external induction on
![]() $\varphi $
. There is nothing to show for
$\varphi $
. There is nothing to show for
![]() $\top $
, because since
$\top $
, because since
![]() $\tau $
is a bounded formula,
$\tau $
is a bounded formula,
![]() $\Box _{\tau }$
is the same as
$\Box _{\tau }$
is the same as
![]() $\Box _T$
.
$\Box _T$
.
The case of relational symbols is a straightforward consequence of the formalized Deduction Theorem [Reference Feferman18].
In the case of
![]() $\land $
, we take
$\land $
, we take
![]() $\varphi = \psi \land \delta $
, and we omit the variables
$\varphi = \psi \land \delta $
, and we omit the variables
![]() $\boldsymbol {y}$
and
$\boldsymbol {y}$
and
![]() $\boldsymbol {z}$
, as they introduce visual clutter but don’t make the proof any more complex.
$\boldsymbol {z}$
, as they introduce visual clutter but don’t make the proof any more complex.
(
![]() $\to $
) Reason in T and fix an arbitrary
$\to $
) Reason in T and fix an arbitrary
![]() $\theta $
, assuming
$\theta $
, assuming
![]() $\Box _{\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}} \theta $
. Then there is a finite sequence
$\Box _{\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}} \theta $
. Then there is a finite sequence
![]() $\boldsymbol {\pi } = \pi _0, \ldots ,\pi _n$
with
$\boldsymbol {\pi } = \pi _0, \ldots ,\pi _n$
with
![]() $\pi _n = \theta $
that is a proof of
$\pi _n = \theta $
that is a proof of
![]() $\theta $
in the theory axiomatized by
$\theta $
in the theory axiomatized by
![]() $\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}$
. Each formula
$\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}$
. Each formula
![]() $\chi _i$
occurring in
$\chi _i$
occurring in
![]() $\boldsymbol {\pi }$
that is not a consequence of previous formulas in the sequence through a rule satisfies either
$\boldsymbol {\pi }$
that is not a consequence of previous formulas in the sequence through a rule satisfies either
![]() $\psi ^{\circledcirc _{\tau }}$
or
$\psi ^{\circledcirc _{\tau }}$
or
![]() $\delta ^{\circledcirc _{\tau }}$
. Then we have in particular that either
$\delta ^{\circledcirc _{\tau }}$
. Then we have in particular that either
![]() $\Box _{\psi ^{\circledcirc _{\tau }}} \chi _i$
or
$\Box _{\psi ^{\circledcirc _{\tau }}} \chi _i$
or
![]() $\Box _{\delta ^{\circledcirc _{\tau }}} \chi _i$
for each such
$\Box _{\delta ^{\circledcirc _{\tau }}} \chi _i$
for each such
![]() $\chi _i$
, whence by the induction hypothesis either
$\chi _i$
, whence by the induction hypothesis either
![]() $\Box _T(\psi ^{\circledast _{T}} \to \chi _i)$
or
$\Box _T(\psi ^{\circledast _{T}} \to \chi _i)$
or
![]() $\Box _T(\delta ^{\circledast _{T}} \to \chi _i)$
holds. In both cases we have
$\Box _T(\delta ^{\circledast _{T}} \to \chi _i)$
holds. In both cases we have
![]() $\Box _T(\psi ^{\circledast _{T}} \wedge \delta ^{\circledast _{T}} \to \chi _i)$
, and thus the proof of
$\Box _T(\psi ^{\circledast _{T}} \wedge \delta ^{\circledast _{T}} \to \chi _i)$
, and thus the proof of
![]() $\theta $
can be repeated in T under the assumption of
$\theta $
can be repeated in T under the assumption of
![]() $(\psi \land \delta )^{\circledast _{T}}$
, as desired.
$(\psi \land \delta )^{\circledast _{T}}$
, as desired.
![]() $(\leftarrow )$
Fix
$(\leftarrow )$
Fix
![]() $\theta $
,
$\theta $
,
![]() $\boldsymbol {y}$
, and
$\boldsymbol {y}$
, and
![]() $\boldsymbol {z}$
. By the induction hypothesis (taking
$\boldsymbol {z}$
. By the induction hypothesis (taking
![]() $\theta $
to be
$\theta $
to be
![]() $\psi ^{\circledast _{T}}$
) we see that
$\psi ^{\circledast _{T}}$
) we see that
![]() $\Box _{\psi ^{\circledcirc _{\tau }}}\psi ^{\circledast _{T}}$
and likewise
$\Box _{\psi ^{\circledcirc _{\tau }}}\psi ^{\circledast _{T}}$
and likewise
![]() $\Box _{\delta ^{\circledcirc _{\tau }}} \delta ^{\circledast _{T}}$
. Thus
$\Box _{\delta ^{\circledcirc _{\tau }}} \delta ^{\circledast _{T}}$
. Thus
![]() $\Box _{\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}} (\psi ^{\circledast _{T}} \land \delta ^{\circledast _{T}})$
. By assumption we have
$\Box _{\psi ^{\circledcirc _{\tau }} \lor \delta ^{\circledcirc _{\tau }}} (\psi ^{\circledast _{T}} \land \delta ^{\circledast _{T}})$
. By assumption we have
![]() $\Box _T(\psi ^{\circledast _{T}} \land \delta ^{\circledast _{T}} \to \theta )$
, and since
$\Box _T(\psi ^{\circledast _{T}} \land \delta ^{\circledast _{T}} \to \theta )$
, and since
![]() $\varphi ^{\circledcirc _{\tau }}$
extends T, we may conclude
$\varphi ^{\circledcirc _{\tau }}$
extends T, we may conclude
![]() $\Box _{\varphi ^{\circledcirc _{\tau }}} \theta $
as desired.
$\Box _{\varphi ^{\circledcirc _{\tau }}} \theta $
as desired.
The
![]() $\forall $
case follows the same idea as the
$\forall $
case follows the same idea as the
![]() $\land $
case. Consider
$\land $
case. Consider
![]() $\varphi = \forall x_0 \, \psi $
, with
$\varphi = \forall x_0 \, \psi $
, with
![]() ${\mathrm {fv}}(\psi ) = \{x_0, x_1\}$
without loss of generality. Note that
${\mathrm {fv}}(\psi ) = \{x_0, x_1\}$
without loss of generality. Note that
![]() $x_0$
is represented by
$x_0$
is represented by
![]() $y_0$
in T, and this is always a different variable from any z used to represent
$y_0$
in T, and this is always a different variable from any z used to represent
![]() $\mathsf {QRC_1}$
constants. As there is no further complication with constants, we omit them. Let
$\mathsf {QRC_1}$
constants. As there is no further complication with constants, we omit them. Let
![]() $\theta $
and l be arbitrary and reason in T.
$\theta $
and l be arbitrary and reason in T.
![]() $(\to )$
If
$(\to )$
If
![]() $\Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \theta $
, then there is a proof
$\Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \theta $
, then there is a proof
![]() $\boldsymbol {\pi } = \pi _0, \ldots , \pi _n$
where
$\boldsymbol {\pi } = \pi _0, \ldots , \pi _n$
where
![]() $\pi _n = \theta $
and each axiom
$\pi _n = \theta $
and each axiom
![]() $\chi _i$
in
$\chi _i$
in
![]() $\boldsymbol {\pi }$
satisfies
$\boldsymbol {\pi }$
satisfies
![]() $\psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l][y_0 {\leftarrow } k_i]$
for some number
$\psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l][y_0 {\leftarrow } k_i]$
for some number
![]() $k_i$
, and consequently
$k_i$
, and consequently
![]() $\Box _T (\psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k_i] \to \chi _i)$
by the induction hypothesis for each i. Then by weakening we conclude
$\Box _T (\psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k_i] \to \chi _i)$
by the induction hypothesis for each i. Then by weakening we conclude
![]() $\Box _T (\forall y_0 \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \chi _i)$
for each i, and we are done.
$\Box _T (\forall y_0 \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \chi _i)$
for each i, and we are done.
![]() $(\leftarrow )$
Assume
$(\leftarrow )$
Assume
![]() $\Box _T (\forall y_0 \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \theta )$
. By Lemma 8.4 under the box, we obtain
$\Box _T (\forall y_0 \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \theta )$
. By Lemma 8.4 under the box, we obtain
![]() $\Box _T (\forall y_0 < m \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \theta )$
, where m is the size of the domain of
$\Box _T (\forall y_0 < m \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l] \to \theta )$
, where m is the size of the domain of
![]() $\mathcal {M}$
. Using the induction hypothesis for each
$\mathcal {M}$
. Using the induction hypothesis for each
![]() $k < m$
with
$k < m$
with
![]() $\theta := \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
,
$\theta := \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
,
![]() $y_0 := k$
, and
$y_0 := k$
, and
![]() $y_1 := l$
, we get
$y_1 := l$
, we get
![]() $\forall k < m \, \Box _{\psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]} \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
, and in particular
$\forall k < m \, \Box _{\psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]} \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
, and in particular
![]() $\forall k < m \, \Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
. Then by
$\forall k < m \, \Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \psi ^{\circledast _{T}}[y_1 {\leftarrow } l][y_0 {\leftarrow } k]$
. Then by
![]() $\Sigma ^0_1$
collection we can change the order of the quantifier and the box, concluding
$\Sigma ^0_1$
collection we can change the order of the quantifier and the box, concluding
![]() $\Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \forall y_0 < m \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l]$
, which is enough to conclude this part of the proof.
$\Box _{\exists y_0 \, \psi ^{\circledcirc _{\tau }}[y_1 {\leftarrow } l]} \forall y_0 < m \, \psi ^{\circledast _{T}}[y_1 {\leftarrow } l]$
, which is enough to conclude this part of the proof.
Finally, for the case of
![]() $\varphi = \Diamond \psi $
, we start by observing that applying the induction hypothesis to
$\varphi = \Diamond \psi $
, we start by observing that applying the induction hypothesis to
![]() $\bot $
yields
$\bot $
yields
![]() $ T \vdash \forall \boldsymbol {y}, \boldsymbol {z} \, ( \Diamond _{\varphi ^{\circledcirc _{\tau }}} \top \leftrightarrow \Diamond _T \varphi ^{\circledast _{T}} ) $
. Note that
$ T \vdash \forall \boldsymbol {y}, \boldsymbol {z} \, ( \Diamond _{\varphi ^{\circledcirc _{\tau }}} \top \leftrightarrow \Diamond _T \varphi ^{\circledast _{T}} ) $
. Note that
![]() $(\Diamond \psi )^{\circledcirc _{\tau }} = \tau (u) \lor (u = \ulcorner \Diamond _{\psi ^{\circledcirc _{\tau }}} \top \urcorner )$
, and thus
$(\Diamond \psi )^{\circledcirc _{\tau }} = \tau (u) \lor (u = \ulcorner \Diamond _{\psi ^{\circledcirc _{\tau }}} \top \urcorner )$
, and thus
![]() $\Box _{(\Diamond \psi )^{\circledcirc _{\tau }}} \theta $
is equivalent to
$\Box _{(\Diamond \psi )^{\circledcirc _{\tau }}} \theta $
is equivalent to
![]() $\Box _T (\Diamond _{\psi ^{\circledcirc _{\tau }}} \top \to \theta )$
by the formalized Deduction Theorem. The previous observation under the box then suffices to finish the proof.⊣
$\Box _T (\Diamond _{\psi ^{\circledcirc _{\tau }}} \top \to \theta )$
by the formalized Deduction Theorem. The previous observation under the box then suffices to finish the proof.⊣
We are finally ready to prove arithmetical completeness for any sound c.e. theory extending
![]() ${\mathrm {I}\Sigma _{1}}$
.
${\mathrm {I}\Sigma _{1}}$
.
Theorem 8.9 (Arithmetical completeness).
![]() $\mathsf {QRC_1} \supseteq \mathcal {QRC}_1(T)$
.
$\mathsf {QRC_1} \supseteq \mathcal {QRC}_1(T)$
.
Proof. Recall the definition of
![]() $\mathcal {QRC}_1(T)$
:
$\mathcal {QRC}_1(T)$
:
where
![]() $\theta $
is closed.
$\theta $
is closed.
We show that if
![]() $\varphi \not \vdash \psi $
, then the realization
$\varphi \not \vdash \psi $
, then the realization
![]() $\cdot ^{\circledcirc }$
defined above is such that
$\cdot ^{\circledcirc }$
defined above is such that
Suppose towards a contradiction that T does prove this formula. Then by Lemma 8.8,
Taking
,
, and
, we conclude
This together with the soundness of T contradicts Theorem 8.7.⊣
We have seen that
![]() $\mathsf {QRC_1} = \mathcal {QRC}_1(T)$
for any sound c.e. theory T extending
$\mathsf {QRC_1} = \mathcal {QRC}_1(T)$
for any sound c.e. theory T extending
![]() ${\mathrm {I}\Sigma _{1}}$
. Thus
${\mathrm {I}\Sigma _{1}}$
. Thus
![]() $\mathcal {QRC}_1(T)$
is constant over a large class of theories, and for these theories it does not depend on the specific axiomatization
$\mathcal {QRC}_1(T)$
is constant over a large class of theories, and for these theories it does not depend on the specific axiomatization
![]() $\tau $
chosen. This is similar to the propositional case, but simpler than the full predicate case, where
$\tau $
chosen. This is similar to the propositional case, but simpler than the full predicate case, where
![]() $\mathsf {QPL}(T)$
is known to depend on both T (as shown by Montagna [Reference Montagna32]) and
$\mathsf {QPL}(T)$
is known to depend on both T (as shown by Montagna [Reference Montagna32]) and
![]() $\tau $
(as shown by Artemov [Reference Artemov3]; see also [Reference Kurahashi28, Reference Kurahashi29]).
$\tau $
(as shown by Artemov [Reference Artemov3]; see also [Reference Kurahashi28, Reference Kurahashi29]).
9 A decidable fragment of
 $\mathsf {QPL}(\mathsf {PA})$
$\mathsf {QPL}(\mathsf {PA})$
As we mentioned before, Vardanyan’s results are very robust and
![]() $\Pi ^0_2$
completeness can already be obtained for the language with just one unary predicate symbol and no nested occurrences of
$\Pi ^0_2$
completeness can already be obtained for the language with just one unary predicate symbol and no nested occurrences of
![]() $\Box $
, as shown in [Reference Vardanyan and Adyan37]. However, Artemov and Japaridze [Reference Artemov and Japaridze4] managed to carve out a non-trivial decidable fragment of
$\Box $
, as shown in [Reference Vardanyan and Adyan37]. However, Artemov and Japaridze [Reference Artemov and Japaridze4] managed to carve out a non-trivial decidable fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
: all formulas that are decidable on finite Kripke frames correspond directly to a fragment of
$\mathsf {QPL}(\mathsf {PA})$
: all formulas that are decidable on finite Kripke frames correspond directly to a fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
. They further observed that as a corollary one can conclude the decidability of the one variable fragment of
$\mathsf {QPL}(\mathsf {PA})$
. They further observed that as a corollary one can conclude the decidability of the one variable fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
.
$\mathsf {QPL}(\mathsf {PA})$
.
The above may seem contradictory with Vardanyan’s result on
![]() $\Pi ^0_2$
completeness of the fragment of
$\Pi ^0_2$
completeness of the fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
with just one unary predicate symbol. However, although it is easy to see that in predicate logic any sentence with just one unary predicate is equivalent to one in the one-variable fragment, this does not hold when modalities are involved, as exhibited by the formula
$\mathsf {QPL}(\mathsf {PA})$
with just one unary predicate symbol. However, although it is easy to see that in predicate logic any sentence with just one unary predicate is equivalent to one in the one-variable fragment, this does not hold when modalities are involved, as exhibited by the formula
![]() $\forall x \, \forall y \, \Box (P(x) \lor \neg P(y))$
.
$\forall x \, \forall y \, \Box (P(x) \lor \neg P(y))$
.
In this section we shall see that
![]() $\mathsf {QRC_1}$
gives rise to a new decidable fragment of
$\mathsf {QRC_1}$
gives rise to a new decidable fragment of
![]() $\mathsf {QPL}(\mathsf {PA})$
. Let
$\mathsf {QPL}(\mathsf {PA})$
. Let
![]() $\mathcal {L}_{\Box , \forall }$
be the language of full quantified modal logic, based on the same signatures as the language of
$\mathcal {L}_{\Box , \forall }$
be the language of full quantified modal logic, based on the same signatures as the language of
![]() $\mathsf {QRC_1}$
and extending the latter with
$\mathsf {QRC_1}$
and extending the latter with
![]() $\to $
,
$\to $
,
![]() $\bot $
, and the usual abbreviations. We extend the notion of finite arithmetical realization described in Definition 8.1 to
$\bot $
, and the usual abbreviations. We extend the notion of finite arithmetical realization described in Definition 8.1 to
![]() $\mathcal {L}_{\Box , \forall }$
as follows:
$\mathcal {L}_{\Box , \forall }$
as follows:
-
•
 $\bot ^{*_{\mathsf {PA}}} := \bot $
;
$\bot ^{*_{\mathsf {PA}}} := \bot $
; -
•
 $(A \to B)^{*_{\mathsf {PA}}} := A^{*_{\mathsf {PA}}} \to B^{*_{\mathsf {PA}}}$
.
$(A \to B)^{*_{\mathsf {PA}}} := A^{*_{\mathsf {PA}}} \to B^{*_{\mathsf {PA}}}$
.
We now define the quantified provability logic of
![]() $\mathsf {PA}$
as the set of always provable
$\mathsf {PA}$
as the set of always provable
![]() $\mathcal {L}_{\Box , \forall }$
formulas:
$\mathcal {L}_{\Box , \forall }$
formulas:
where
![]() $\boldsymbol {y}$
are the arithmetical counterpart of
$\boldsymbol {y}$
are the arithmetical counterpart of
![]() $\boldsymbol {x}$
and
$\boldsymbol {x}$
and
![]() $\boldsymbol {z}$
the arithmetical counterpart of
$\boldsymbol {z}$
the arithmetical counterpart of
![]() $\boldsymbol {c}$
, as before.
$\boldsymbol {c}$
, as before.
Theorem 9.1. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be
$\psi $
be
![]() $\mathsf {QRC_1}$
formulas. Then
$\mathsf {QRC_1}$
formulas. Then
Proof. The left-to-right implication is proved by induction on
![]() $\varphi \vdash \psi $
. We note that the formalized converse Barcan formula is used in the case of the necessitation rule and provable
$\varphi \vdash \psi $
. We note that the formalized converse Barcan formula is used in the case of the necessitation rule and provable
![]() $\Sigma ^0_1$
completeness is used in the case of the transitivity axiom (see [Reference Boolos11] for details on these results).
$\Sigma ^0_1$
completeness is used in the case of the transitivity axiom (see [Reference Boolos11] for details on these results).
For the right-to-left implication, we take the contrapositive. Thus, let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be strictly positive formulas with free variables
$\psi $
be strictly positive formulas with free variables
![]() $\boldsymbol {x}$
and constants
$\boldsymbol {x}$
and constants
![]() $\boldsymbol {c}$
such that
$\boldsymbol {c}$
such that
![]() $\varphi \not \vdash \psi $
. By Theorem 8.7, we have
$\varphi \not \vdash \psi $
. By Theorem 8.7, we have
and thus
![]() $\varphi \to \psi \notin \mathsf {QPL}(\mathsf {PA})$
.⊣
$\varphi \to \psi \notin \mathsf {QPL}(\mathsf {PA})$
.⊣
10 Heyting Arithmetic
We end this paper with a foray into intuitionistic arithmetic. We show that
![]() $\mathsf {QRC_1}$
is sound with respect to Heyting Arithmetic (
$\mathsf {QRC_1}$
is sound with respect to Heyting Arithmetic (
![]() $\mathsf {HA}$
) and conjecture that it is complete as well.
$\mathsf {HA}$
) and conjecture that it is complete as well.
Let
![]() $\eta (u)$
be a
$\eta (u)$
be a
![]() $\Sigma ^0_1$
formula naturally axiomatizing
$\Sigma ^0_1$
formula naturally axiomatizing
![]() $\mathsf {HA}$
.Footnote
9
The
$\mathsf {HA}$
.Footnote
9
The
![]() $\mathsf {HA}$
-provability of
$\mathsf {HA}$
-provability of
![]() $\varphi $
can thus be expressed by
$\varphi $
can thus be expressed by
![]() $\Box _\eta \varphi $
, as defined in Section 7.
$\Box _\eta \varphi $
, as defined in Section 7.
We observe that a number of standard results in the realm of classical provability logic still hold in the intuitionistic case.
Lemma 10.1 (Derivability conditions [Reference Visser and Zoethout39]).
Let
![]() $\tau $
be a
$\tau $
be a
![]() $\Sigma ^0_1$
axiomatization of an arithmetical theory T extending
$\Sigma ^0_1$
axiomatization of an arithmetical theory T extending
![]() $\mathsf {HA}$
, and
$\mathsf {HA}$
, and
![]() $\varphi , \psi $
be formulas in the language of arithmetic. Then:
$\varphi , \psi $
be formulas in the language of arithmetic. Then:
-
1. if
 $T \vdash \varphi $
then
$T \vdash \varphi $
then
 $\mathsf {HA} \vdash \Box _\tau \varphi $
;
$\mathsf {HA} \vdash \Box _\tau \varphi $
; -
2.
 $\mathsf {HA} \vdash \Box _\tau (\varphi \to \psi ) \to (\Box _\tau \varphi \to \Box _\tau \psi )$
;
$\mathsf {HA} \vdash \Box _\tau (\varphi \to \psi ) \to (\Box _\tau \varphi \to \Box _\tau \psi )$
; -
3.
 $\mathsf {HA} \vdash \Box _\tau \varphi \to \Box _\eta \Box _\tau \varphi $
.
$\mathsf {HA} \vdash \Box _\tau \varphi \to \Box _\eta \Box _\tau \varphi $
.
Lemma 10.2 (Collection [Reference Fujiwara and Kurahashi21, Proposition 5.13]).
Let
![]() $\varphi $
be an arithmetical formula without x as a free variable. Then
$\varphi $
be an arithmetical formula without x as a free variable. Then
Note that, since
![]() $\mathsf {HA}$
proves full collection,
$\mathsf {HA}$
proves full collection,
![]() ${\mathrm {Prf}}_\eta $
is equivalent to a
${\mathrm {Prf}}_\eta $
is equivalent to a
![]() $\Sigma ^0_1$
formula, provably in
$\Sigma ^0_1$
formula, provably in
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
As in the classical case, we define
![]() $\Diamond _\tau \varphi $
as
$\Diamond _\tau \varphi $
as
![]() $\neg \Box _\tau \neg \varphi $
when
$\neg \Box _\tau \neg \varphi $
when
![]() $\tau $
is an axiomatization of an extension of
$\tau $
is an axiomatization of an extension of
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
We extend a generic realization
![]() $\cdot ^{\circ }$
to non-predicate formulas as in the classical case (cf. Definition 7.1). Note that
$\cdot ^{\circ }$
to non-predicate formulas as in the classical case (cf. Definition 7.1). Note that
![]() $\varphi ^{\circ _{\eta }}$
is equivalent to a
$\varphi ^{\circ _{\eta }}$
is equivalent to a
![]() $\Sigma ^0_1$
formula and extends
$\Sigma ^0_1$
formula and extends
![]() $\mathsf {HA}$
, both of these provably in
$\mathsf {HA}$
, both of these provably in
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
Theorem 10.3 (Arithmetical soundness w.r.t.
 $\mathsf {HA}$
).
$\mathsf {HA}$
).
Proof. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be formulas such that
$\psi $
be formulas such that
![]() $\varphi \vdash \psi $
. The proof is similar to the classical case, and proceeds by external induction on
$\varphi \vdash \psi $
. The proof is similar to the classical case, and proceeds by external induction on
![]() $\varphi \vdash \psi $
.
$\varphi \vdash \psi $
.
The soundness of
![]() $\varphi \vdash \top $
states that
$\varphi \vdash \top $
states that
![]() $\varphi ^{\circ _{\eta }}$
extends
$\varphi ^{\circ _{\eta }}$
extends
![]() $\mathsf {HA}$
, which can readily be checked by induction on
$\mathsf {HA}$
, which can readily be checked by induction on
![]() $\varphi $
. The soundness of
$\varphi $
. The soundness of
![]() $\varphi \vdash \varphi $
and of the cut rule are straightforward, and the soundness of
$\varphi \vdash \varphi $
and of the cut rule are straightforward, and the soundness of
![]() $\varphi \land \psi \vdash \varphi $
is a simple weakening.
$\varphi \land \psi \vdash \varphi $
is a simple weakening.
We proceed with the soundness of the conjunction introduction rule, that if
![]() $\varphi \vdash \psi $
and
$\varphi \vdash \psi $
and
![]() $\varphi \vdash \chi $
then
$\varphi \vdash \chi $
then
![]() $\varphi \vdash \psi \land \chi $
. Reason in
$\varphi \vdash \psi \land \chi $
. Reason in
![]() $\mathsf {HA}$
and let
$\mathsf {HA}$
and let
![]() $\theta $
be a closed formula, and
$\theta $
be a closed formula, and
![]() $\boldsymbol {y}$
and
$\boldsymbol {y}$
and
![]() $\boldsymbol {z}$
be arbitrary. Assume
$\boldsymbol {z}$
be arbitrary. Assume
![]() $\Box _{\psi ^{\circ _{\eta }} \lor \chi ^{\circ _{\eta }}} \theta $
, taking
$\Box _{\psi ^{\circ _{\eta }} \lor \chi ^{\circ _{\eta }}} \theta $
, taking
![]() $\boldsymbol {\pi } = \pi _0, \ldots , \pi _{n-1}$
as a proof of this fact. Some of the
$\boldsymbol {\pi } = \pi _0, \ldots , \pi _{n-1}$
as a proof of this fact. Some of the
![]() $\pi _i$
are axioms of
$\pi _i$
are axioms of
![]() $\psi ^{\circ _{\eta }}$
, some are axioms of
$\psi ^{\circ _{\eta }}$
, some are axioms of
![]() $\chi ^{\circ _{\eta }}$
, and some follow from previous steps in the proof through a rule. Let
$\chi ^{\circ _{\eta }}$
, and some follow from previous steps in the proof through a rule. Let
![]() $\{\delta _i\}_{i \in I}$
be the finite set of
$\{\delta _i\}_{i \in I}$
be the finite set of
![]() $\psi ^{\circ _{\eta }}$
axioms appearing in
$\psi ^{\circ _{\eta }}$
axioms appearing in
![]() $\boldsymbol {\pi }$
. Thus
$\boldsymbol {\pi }$
. Thus
![]() $\Box _{\psi ^{\circ _{\eta }}} \bigwedge _{i \in I} \delta _i$
and by the induction hypothesis for
$\Box _{\psi ^{\circ _{\eta }}} \bigwedge _{i \in I} \delta _i$
and by the induction hypothesis for
![]() $\varphi \vdash \psi $
we obtain
$\varphi \vdash \psi $
we obtain
![]() $\Box _{\varphi ^{\circ _{\eta }}} \bigwedge _{i \in I} \delta _i$
. On the other hand, we know
$\Box _{\varphi ^{\circ _{\eta }}} \bigwedge _{i \in I} \delta _i$
. On the other hand, we know
![]() $\Box _{\chi ^{\circ _{\eta }}} (\bigwedge _{i \in I} \delta _i \to \theta )$
by the Deduction Theorem. Through the induction hypothesis for
$\Box _{\chi ^{\circ _{\eta }}} (\bigwedge _{i \in I} \delta _i \to \theta )$
by the Deduction Theorem. Through the induction hypothesis for
![]() $\varphi \vdash \chi $
we conclude
$\varphi \vdash \chi $
we conclude
![]() $\Box _{\varphi ^{\circ _{\eta }}} (\bigwedge _{i \in I} \delta _i \to \theta )$
. Putting these two observations together, we obtain the desired
$\Box _{\varphi ^{\circ _{\eta }}} (\bigwedge _{i \in I} \delta _i \to \theta )$
. Putting these two observations together, we obtain the desired
![]() $\Box _{\varphi ^{\circ _{\eta }}} \theta $
.
$\Box _{\varphi ^{\circ _{\eta }}} \theta $
.
We turn to the necessitation rule, that if
![]() $\varphi \vdash \psi $
then
$\varphi \vdash \psi $
then
![]() $\Diamond \varphi \vdash \Diamond \psi $
. Reason in
$\Diamond \varphi \vdash \Diamond \psi $
. Reason in
![]() $\mathsf {HA}$
and let
$\mathsf {HA}$
and let
![]() $\theta,\ \boldsymbol{y}$
, and
$\theta,\ \boldsymbol{y}$
, and
![]() $\boldsymbol {z}$
be arbitrary. Consider the induction hypothesis with
$\boldsymbol {z}$
be arbitrary. Consider the induction hypothesis with
![]() $\theta := \neg \top $
(and
$\theta := \neg \top $
(and
![]() $\boldsymbol {y}$
,
$\boldsymbol {y}$
,
![]() $\boldsymbol {z}$
as given by our assumption):
$\boldsymbol {z}$
as given by our assumption):
![]() $\Box _{\psi ^{\circ _{\eta }}} \neg \top \to \Box _{\varphi ^{\circ _{\eta }}} \neg \top $
. Taking the contrapositive, we conclude
$\Box _{\psi ^{\circ _{\eta }}} \neg \top \to \Box _{\varphi ^{\circ _{\eta }}} \neg \top $
. Taking the contrapositive, we conclude
![]() $\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\psi ^{\circ _{\eta }}} \top $
, and consequently
$\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\psi ^{\circ _{\eta }}} \top $
, and consequently
![]() $\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\psi ^{\circ _{\eta }}} \top )$
by Lemma 10.1. Assume now that
$\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\psi ^{\circ _{\eta }}} \top )$
by Lemma 10.1. Assume now that
![]() $\Box _{(\Diamond \psi )^{\circ _{\eta }}} \theta $
. By the Deduction Theorem, we obtain
$\Box _{(\Diamond \psi )^{\circ _{\eta }}} \theta $
. By the Deduction Theorem, we obtain
![]() $\Box _\eta (\Diamond _{\psi ^{\circ _{\eta }}} \top \to \theta )$
. Thus our previous observation gives us
$\Box _\eta (\Diamond _{\psi ^{\circ _{\eta }}} \top \to \theta )$
. Thus our previous observation gives us
![]() $\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
, which is
$\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
, which is
![]() $\Box _{(\Diamond \varphi )^{\circ _{\eta }}} \theta $
by the Deduction Theorem.
$\Box _{(\Diamond \varphi )^{\circ _{\eta }}} \theta $
by the Deduction Theorem.
Consider the transitivity axiom:
![]() $\Diamond \Diamond \varphi \to \Diamond \varphi $
. We start by observing that
$\Diamond \Diamond \varphi \to \Diamond \varphi $
. We start by observing that
![]() $(\Diamond \Diamond \varphi )^{\circ _{\eta }}$
is equivalent to
$(\Diamond \Diamond \varphi )^{\circ _{\eta }}$
is equivalent to
![]() $\eta (u) \lor u = \ulcorner \Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \urcorner $
. Note that we can derive
$\eta (u) \lor u = \ulcorner \Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \urcorner $
. Note that we can derive
![]() $\Box _\eta (\Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\varphi ^{\circ _{\eta }}} \top )$
from Lemma 10.1. Assume now
$\Box _\eta (\Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \to \Diamond _{\varphi ^{\circ _{\eta }}} \top )$
from Lemma 10.1. Assume now
![]() $\Box _{(\Diamond \varphi )^{\circ _{\eta }}} \theta $
. By the Deduction Theorem we have
$\Box _{(\Diamond \varphi )^{\circ _{\eta }}} \theta $
. By the Deduction Theorem we have
![]() $\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
. Then we obtain
$\Box _\eta (\Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
. Then we obtain
![]() $\Box _\eta (\Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
by our previous observation, and we finish with one more application of the Deduction Theorem.
$\Box _\eta (\Diamond _\eta \Diamond _{\varphi ^{\circ _{\eta }}} \top \to \theta )$
by our previous observation, and we finish with one more application of the Deduction Theorem.
The
![]() $\forall $
introduction rule on the right states that if
$\forall $
introduction rule on the right states that if
![]() $x_0 \notin {\mathrm {fv}}(\varphi )$
and
$x_0 \notin {\mathrm {fv}}(\varphi )$
and
![]() $\varphi \vdash \psi $
, then
$\varphi \vdash \psi $
, then
![]() $\varphi \vdash \forall x_0 \, \psi $
. Reason in
$\varphi \vdash \forall x_0 \, \psi $
. Reason in
![]() $\mathsf {HA}$
and let
$\mathsf {HA}$
and let
![]() $\theta , \boldsymbol {y}$
, and
$\theta , \boldsymbol {y}$
, and
![]() $\boldsymbol {z}$
be arbitrary, where
$\boldsymbol {z}$
be arbitrary, where
![]() $y_0$
does not appear in
$y_0$
does not appear in
![]() $\boldsymbol {y}$
. Assume
$\boldsymbol {y}$
. Assume
![]() $\Box _{\exists y_0 \, \psi ^{\circ _{\eta }}} \theta $
and let
$\Box _{\exists y_0 \, \psi ^{\circ _{\eta }}} \theta $
and let
![]() $\boldsymbol {\pi } = \pi _0, \ldots , \pi _{n-1}$
be a proof of this fact. Let
$\boldsymbol {\pi } = \pi _0, \ldots , \pi _{n-1}$
be a proof of this fact. Let
![]() $\{\delta \}_{i \in I}$
be the finite set of axioms of
$\{\delta \}_{i \in I}$
be the finite set of axioms of
![]() $\exists y_0 \, \psi ^{\circ _{\eta }}$
appearing in
$\exists y_0 \, \psi ^{\circ _{\eta }}$
appearing in
![]() $\boldsymbol {\pi }$
. Note that
$\boldsymbol {\pi }$
. Note that
![]() $\Box _\eta (\forall i \in I \, \delta _i \to \theta )$
holds by the Deduction Theorem. Then for each
$\Box _\eta (\forall i \in I \, \delta _i \to \theta )$
holds by the Deduction Theorem. Then for each
![]() $i \in I$
there is
$i \in I$
there is
![]() $k_i$
such that
$k_i$
such that
![]() $\delta _i$
is an axiom of
$\delta _i$
is an axiom of
![]() $\psi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]$
, so in particular
$\psi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]$
, so in particular
![]() $\Box _{\psi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]} \delta _i$
. We can use the induction hypothesis for each
$\Box _{\psi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]} \delta _i$
. We can use the induction hypothesis for each
![]() $i \in I$
to conclude
$i \in I$
to conclude
![]() $\Box _{\varphi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]} \delta _i$
, and since
$\Box _{\varphi ^{\circ _{\eta }}[y_0 {\leftarrow } k_i]} \delta _i$
, and since
![]() $x_0 \not \in {\mathrm {fv}}(\varphi )$
, we also know that
$x_0 \not \in {\mathrm {fv}}(\varphi )$
, we also know that
![]() $y_0 \not \in {\mathrm {fv}}(\varphi ^{\circ _{\eta }})$
, and thus we obtain
$y_0 \not \in {\mathrm {fv}}(\varphi ^{\circ _{\eta }})$
, and thus we obtain
![]() $\forall i \in I \, \Box _{\varphi ^{\circ _{\eta }}} \delta _i$
. We now use collection to obtain
$\forall i \in I \, \Box _{\varphi ^{\circ _{\eta }}} \delta _i$
. We now use collection to obtain
![]() $\Box _{\varphi ^{\circ _{\eta }}} \forall i \in I \, \delta _i$
, and the result follows from our observation that
$\Box _{\varphi ^{\circ _{\eta }}} \forall i \in I \, \delta _i$
, and the result follows from our observation that
![]() $\Box _\eta (\forall i \in I \, \delta _i \to \theta )$
, noting that
$\Box _\eta (\forall i \in I \, \delta _i \to \theta )$
, noting that
![]() $\varphi ^{\circ _{\eta }}$
extends
$\varphi ^{\circ _{\eta }}$
extends
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
The
![]() $\forall $
introduction rule on the left states that if
$\forall $
introduction rule on the left states that if
![]() $\varphi [x_0 {\leftarrow } t] \vdash \psi $
, then
$\varphi [x_0 {\leftarrow } t] \vdash \psi $
, then
![]() $\forall x_0 \, \varphi \vdash \psi $
. Let
$\forall x_0 \, \varphi \vdash \psi $
. Let
![]() $w$
be the arithmetical counterpart of t (so if t is
$w$
be the arithmetical counterpart of t (so if t is
![]() $x_k$
then
$x_k$
then
![]() $w := y_k$
and if t is
$w := y_k$
and if t is
![]() $c_k$
then
$c_k$
then
![]() $w := z_k$
). We have
$w := z_k$
). We have
![]() $\varphi [x_0 {\leftarrow } t]^{\circ _{\eta }} = \varphi ^{\circ _{\eta }}[y_0 {\leftarrow } w]$
. Let
$\varphi [x_0 {\leftarrow } t]^{\circ _{\eta }} = \varphi ^{\circ _{\eta }}[y_0 {\leftarrow } w]$
. Let
![]() $\theta , \boldsymbol {y}$
, and
$\theta , \boldsymbol {y}$
, and
![]() $\boldsymbol {z}$
be arbitrary, where
$\boldsymbol {z}$
be arbitrary, where
![]() $y_0$
appears in
$y_0$
appears in
![]() $\boldsymbol {y}$
if and only if
$\boldsymbol {y}$
if and only if
![]() $x_0$
is a free variable of
$x_0$
is a free variable of
![]() $\psi $
. We assume
$\psi $
. We assume
![]() $\Box _{\psi ^{\circ _{\eta }}} \theta $
. If t appears in
$\Box _{\psi ^{\circ _{\eta }}} \theta $
. If t appears in
![]() $\varphi $
or in
$\varphi $
or in
![]() $\psi $
, then the value of w was already fixed when we picked arbitrary
$\psi $
, then the value of w was already fixed when we picked arbitrary
![]() $\boldsymbol {y}$
and
$\boldsymbol {y}$
and
![]() $\boldsymbol {z}$
. Otherwise, fix
$\boldsymbol {z}$
. Otherwise, fix
![]() $w := 0$
and use the induction hypothesis to obtain
$w := 0$
and use the induction hypothesis to obtain
![]() $\Box _{\varphi ^{\circ _{\eta }}[y_0 {\leftarrow } w]} \theta $
. It is then clear that
$\Box _{\varphi ^{\circ _{\eta }}[y_0 {\leftarrow } w]} \theta $
. It is then clear that
![]() $\Box _{\exists y_0 \, \varphi ^{\circ _{\eta }}} \theta $
holds as well.
$\Box _{\exists y_0 \, \varphi ^{\circ _{\eta }}} \theta $
holds as well.
Finally, the term instantiation and constant elimination rules boil down to variable renaming.⊣
The arithmetical completeness of
![]() $\mathsf {QRC_1}$
with respect to
$\mathsf {QRC_1}$
with respect to
![]() $\mathsf {HA}$
remains an open question. We conjecture that the fact that the substitutions in the completeness proofs are of restricted complexity, and the fact that
$\mathsf {HA}$
remains an open question. We conjecture that the fact that the substitutions in the completeness proofs are of restricted complexity, and the fact that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi ^0_2$
conservative over
$\Pi ^0_2$
conservative over
![]() $\mathsf {HA}$
(see [Reference Friedman, Scott and Muller20]) can be essential ingredients in a possible completeness proof.
$\mathsf {HA}$
(see [Reference Friedman, Scott and Muller20]) can be essential ingredients in a possible completeness proof.
11 Future work
There are many unexplored paths surrounding
![]() $\mathsf {QRC_1}$
. It would be worthwhile to extend it to a polymodal language (in analogy with
$\mathsf {QRC_1}$
. It would be worthwhile to extend it to a polymodal language (in analogy with
![]() $\mathsf {RC}$
, as in [Reference Beklemishev, Bolander, Braüner, Ghilardi and Moss6]), and to the positive setting (as in [Reference Celani and Jansana13, Reference Dunn17]). Whether this is possible without loosing decidability remains to be seen. A hypothetical
$\mathsf {RC}$
, as in [Reference Beklemishev, Bolander, Braüner, Ghilardi and Moss6]), and to the positive setting (as in [Reference Celani and Jansana13, Reference Dunn17]). Whether this is possible without loosing decidability remains to be seen. A hypothetical
![]() $\mathsf {QRC}_\Lambda $
would presumably lead to some interesting applications to
$\mathsf {QRC}_\Lambda $
would presumably lead to some interesting applications to
![]() $\Pi ^0_1$
ordinal analysis and ordinal notation systems.
$\Pi ^0_1$
ordinal analysis and ordinal notation systems.
There are several proof theoretical properties of interest, such as interpolation, cut-free proofs, fixpoints, etc. One could also strive for uniform completeness.
Moreover, the set of always true
![]() $\mathsf {QRC_1}$
sequents should be a productive avenue of study.
$\mathsf {QRC_1}$
sequents should be a productive avenue of study.
The completeness of
![]() $\mathsf {QRC_1}$
with respect to
$\mathsf {QRC_1}$
with respect to
![]() $\mathsf {HA}$
remains an open question.
$\mathsf {HA}$
remains an open question.
Finally, the current approximation for the computational complexity of
![]() $\mathsf {QRC_1}$
is super-exponential space, since the canonical model grows quite large. A more dedicated study might lead to a significant reduction in complexity.
$\mathsf {QRC_1}$
is super-exponential space, since the canonical model grows quite large. A more dedicated study might lead to a significant reduction in complexity.