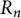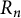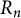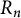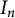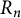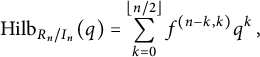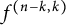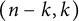Quasisymmetric harmonics of the exterior algebra

Abstract

We study the ring of quasisymmetric polynomials in n anticommuting (fermionic) variables. Let $R_n$ denote the ring of polynomials in n anticommuting variables. The main results of this paper show the following interesting facts about quasisymmetric polynomials in anticommuting variables:

1. (1) The quasisymmetric polynomials in $R_n$ form a commutative subalgebra of $R_n$.

2. (2) There is a basis of the quotient of $R_n$ by the ideal $I_n$ generated by the quasisymmetric polynomials in $R_n$ that is indexed by ballot sequences. The Hilbert series of the quotient is given by

   $$ \begin{align*}\text{Hilb}_{R_n/I_n}(q) = \sum_{k=0}^{\lfloor{n/2}\rfloor} f^{(n-k,k)} q^k\,,\end{align*} $$
   where $f^{(n-k,k)}$ is the number of standard tableaux of shape $(n-k,k)$.

3. (3) There is a basis of the ideal generated by quasisymmetric polynomials that is indexed by sequences that break the ballot condition.

1 Introduction

The study of coinvariants of groups dates back to Shephard—Todd and Chevalley [5, 27] and has fruitfully produced many connections between algebra, combinatorics, and physics. Motivated by recent developments in coinvariants of symmetric groups and symmetric functions theory incorporating fermionic variables, we study a coinvariant-like quotient of an exterior algebra obtained by the quotient of the ideal generated by quasisymmetric functions in fermionic variables. The quotient has a dimension that can be interpreted as the number of ballot sequences (or other interpretations; see, for instance, the OEIS [26] sequences A008315 and A001405).

A notable feature of many quotients similar to coinvariants is their amenability to combinatorial methods. One well-known example is the coinvariant ring of the symmetric group. It is the quotient of the polynomial ring $\mathbb {Q}[x_{1},\dots ,x_{n}]$ in commuting variables by the ideal generated by the symmetric polynomials with no constant term. As an $\mathcal {S}_{n}$ representation, this quotient is naturally graded and is well known to be isomorphic to the regular representation. Many useful bases of this space have been found by studying combinatorics related to permutations. For more details, see the nice surveys of [3, 13, 24, 25].

This line of inquiry inspired Garsia and Haiman [12, 18] to consider the ring of diagonal harmonics, a similar quotient in two sets of commuting variables as an $\mathcal {S}_{n}$ module. Haiman’s work [19] showed that the diagonal harmonics have a deep connection to the theory of Macdonald polynomials. A combinatorial expression for the Frobenius image of the diagonal harmonics known as the Shuffle Conjecture [16] showed that the module structure is closely related to the combinatorics of parking functions and can be described in terms of certain labeled Catalan paths. This connection relating the symmetric functions and the combinatorial expression was proved in [4] and is now known as the Shuffle Theorem.

The connection between the combinatorics and the symmetric function expressions of the Shuffle Theorem has been generalized [17] and proved [8] to an expression known as the Delta Conjecture. The last author with the group at the Fields Institute [31] proposed a deformation of diagonal harmonics to two sets of commuting variables and one set of anticommuting variables. In this case, the connection of representation theoretic interpretation to the symmetric function expression remains open. The symmetric function expressions and representation theoretic interpretation were extended further to include the quotient of two sets of commuting and two sets of anticommuting variables in [7] to what is known as the Theta Conjecture. At present, this also remains an open conjecture, but progress has been made on some special cases [21, 22, 29, 30].

The ring of quasisymmetric polynomials $QSym_{n}$ contains the ring of symmetric polynomials $Sym_{n}$ . Many combinatorial structures of $QSym_{n}$ parallel that of $Sym_{n}$ . Hivert described a Temperley–Lieb $TL_{n}$ action on $\mathbb {Q}[x_{1},\dots ,x_{n}]$ making $QSym_{n}$ exactly its trivial representation [20]. In 2003, Aval, F. Bergeron, and the first author studied $QSym$ coinvariant spaces obtained by replacing the ideal of nonconstant symmetric functions with the ideal of nonconstant quasisymmetric functions [1, 2]. Surprisingly, they found that dimensions of $QSym$ coinvariants are equal to the Catalan numbers. At the heart of their argument is a recursion built from Catalan paths. Li extended this argument to study some components of coinvariant spaces of diagonally quasisymmetric functions [23].

Motivated by physics, Desrosiers, Lapointe, and Mathieu [9, 10] introduced symmetric functions with one set of commuting and one set of anticommuting variables known as symmetric function in superspace. The commuting variables encode bosons, whereas the anticommuting ones encode fermions; hence, the anticommuting variables are sometimes referred to as “fermionic variables.” The Hopf algebra structure of the ring of symmetric functions in superspace was extended to quasisymmetric functions in superspace [11] and so a natural question is to extend the study of coinvariants of polynomial rings with commuting and anticommuting variables to the quotients of these polynomial rings by the ideal generated by “super” quasisymmetric polynomials.

Parallel to the Delta Conjecture or Theta Conjecture, one ideally would like to understand quasisymmetric coinvariants in multiple sets of commuting and anticommuting variables. Our study of quasisymmetric coinvariant spaces in one set of anticommuting variables is a first step in that study. We denote polynomials in anticommuting variables by $R_n$ . The main results of this paper show the following interesting facts about symmetric and quasisymmetric functions in anticommuting variables:

1. (1) The quasisymmetric polynomials in $R_n$ form a commutative subalgebra of $R_n$ (Proposition 2.3).

2. (2) That $R_n$ is free over the ring of symmetric polynomials in $R_n$ (Proposition 2.5).

3. (3) There is a basis of the quotient of $R_n$ by the ideal $I_n$ generated by the quasisymmetric polynomials in $R_n$ that is indexed by ballot sequences (Proposition 2.10). The Hilbert series of the quotient is given by

   $$ \begin{align*}\text{Hilb}_{R_n/I_n}(q) = \sum_{k=0}^{\lfloor{n/2}\rfloor} f^{(n-k,k)} q^k\,,\end{align*} $$
   where $f^{(n-k,k)}$ is the number of standard tableaux of shape $(n-k,k)$ (Corollary 4.4).

4. (4) There is a basis of the ideal generated by quasisymmetric polynomials that is indexed by sequences that break the ballot condition (Theorem 4.2) and a minimal Gröbner basis that is a subset of this basis (Corollary 4.6).

2 Quasisymmetric invariants on the exterior algebra

Fix n a positive integer, and let $R_n = {\mathbb Q}[\theta _1, \theta _2, \ldots , \theta _n]$ be the polynomial ring in anticommuting variables. The ring $R_n$ is isomorphic to the exterior algebra of a vector space of dimension n. The variables of this ring satisfy the relations

$$\begin{align*}\theta_i \theta_j = - \theta_j \theta_i\quad \text{ if } 1 \leq i \neq j \leq n \quad\text{and}\quad \theta_i^2 = 0\quad \text{ for }1 \leq i \leq n~. \end{align*}$$

Since these conditions impose that a monomial in $R_n$ has no repeated variables, the monomials are in bijection with subsets of $\{1,2,\ldots , n\}$ and the dimension of $R_n$ is therefore equal to $2^n$ .

Denote $[n] := \{1,2, \ldots ,n\}$ , and let $A = \{a_1 < a_2 < \cdots < a_r \} \subseteq [n]$ . We define $\theta _A := \theta _{a_1} \theta _{a_2} \cdots \theta _{a_r}$ , then the set of monomials $\{ \theta _A \}_{A \subseteq [n]}$ is a basis of $R_n$ .

We define an action on monomials of $R_n$ and extend this action linearly. For each integer $1 \leq i < n$ , let $\pi _i$ be an operator on $R_n$ that is defined by

(2.1) $$ \begin{align} \pi_i(\theta_A) = \begin{cases} \theta_{A}, & \text{ if } i, i+1 \in A\text{ or }i, i+1 \notin A,\\ \theta_{A \cup \{i+1\} \backslash \{i\}}, & \text{ if } i\in A\text{ and }i+1 \notin A,\\ \theta_{A \cup \{i\} \backslash \{i+1\}}, & \text{ if } i+1\in A\text{ and }i \notin A. \end{cases} \end{align} $$

These operators, instead of exchanging an i for an $i+1$ like the symmetric group action, have the effect of shifting the indices of the variables (if possible). They are therefore known as quasisymmetric operators. They were studied in depth by Hivert [20]. The operators are not multiplicative on $R_n$ in general since, for example,

$$\begin{align*}\pi_1( \theta_{1} \theta_{2}) = \theta_1 \theta_2 = - \pi_1( \theta_{1}) \pi_1(\theta_{2})~. \end{align*}$$

They are also not multiplicative when they act on the polynomial ring in commuting variables.

A polynomial that is invariant under the action of quasisymmetric operators is said to be quasisymmetric invariant (or just “quasisymmetric”). The quasisymmetric invariants of $R_n$ are linearly spanned by the elements:

(2.2) $$ \begin{align} F_{1^r}(\theta_1, \theta_2, \ldots, \theta_n) := \sum_{\substack{A \subseteq [n]\\|A|=r}} \theta_A~. \end{align} $$

The symbols $F_{1^r}$ for the elements borrows the notation from the polynomial ring in commuting variable invariants known as the “fundamental quasisymmetric polynomials”. The commuting polynomial quasisymmetric invariants are indexed by compositions.

Remark 2.1 As expressing polynomials with listing the variables (e.g., $p(\theta _1, \theta _2, \ldots , \theta _n)$ ) can be notational cumbersome, there will be points where we will drop the variables in the expressions and this will indicate that the polynomials are in the variables $\theta _1, \theta _2, \ldots , \theta _n$ . There will also be expressions where some polynomials have fewer variables and there we will indicate this by listing the variables.

2.1 Quasisymmetric functions generate a commutative subalgebra

In [11], the authors showed that the quasisymmetric functions in one set of commuting variables and one set of anticommuting variables form a graded Hopf algebra. This implies that the quasisymmetric functions in one set of anticommuting variables are closed under multiplication and the space is spanned by one element at each nonnegative degree. It follows that for $r, s \geq 0$ , there exists a (possibly $0$ ) coefficient $a_{r,s}$ such that

(2.3) $$ \begin{align} F_{1^r} F_{1^s} = a_{r,s} F_{1^{r+s}}\,. \end{align} $$

If $r+s>n$ , then $F_{1^{r+s}} = 0$ by definition and so the only relevant coefficient $a_{r,s}$ is when $r+s \leq n$ .

Remark 2.2 In the notation of [11], $F_{1^r}=M_{\dot {0}^r}=L_{\dot {0}^r}$ where $\dot {0}^r=(\dot {0},\dot {0},\ldots ,\dot {0})$ is a composition of length r. The “ $\dot {\ }$ ” over a part in [11] is to indicate a fermionic component. Therefore, the fermionic degree of $F_{1^r}$ is exactly r. In [11], they show that $a_{r,s}$ exists and express it as a sum of $\pm 1$ , but they do not give an explicit formula. Furthermore, they indicate that $a_{r,s}=(-1)^{rs}a_{s,r}$ . Here, we shall compute exactly $a_{r,s}$ and the formula shows that the subalgebra generated by the $F_{1^r}$ is commutative.

Proposition 2.3 The constants $a_{r,s}$ in equation ( 2.3 ) satisfy the following equation:

$$ \begin{align*}a_{r,s}= \begin{cases} 0, &\text{if }r,s\text{ are both odd,}\\ \\ \left({\lfloor \frac{r+s}{2} \rfloor \atop \lfloor \frac{r}{2} \rfloor}\right),&\text{otherwise.} \end{cases} \end{align*} $$

A remark brought to our attention by D. Grinberg [14] shows that $a_{r,s}$ is equal to the q-binomial coefficient $\left [ \begin {smallmatrix}r+s\\r\end {smallmatrix} \right ]_q$ evaluated at $q \rightarrow -1$ [15, Equation (185) on page 291].

Proof For completeness, we give a proof not assuming any results of [11]. Using equation (2.2), we have

$$ \begin{align*}F_{1^r}F_{1^s}= \sum_{\substack{A \subseteq [n]\\|A|=r}} \sum_{\substack{B \subseteq [n]\\|B|=s}} \theta_A \theta_B = \sum_{\substack{C \subseteq [n]\\|C|=r+s}} \Big(\sum_{\substack{A\subseteq C \\|A|=r}} (-1)^{|\{b<a\,|\,a\in A,\, b\in C\setminus A\}|} \Big) \theta_C\,. \end{align*} $$

To see the second equality, we remark that the product $\theta _A\theta _B=0$ if $A\cap B\ne \emptyset $ . Furthermore, if $A\cap B= \emptyset $ , then for $C=A\cup B$ , we have $B=C\setminus A$ and $\theta _A\theta _B=(-1)^{|\{b<a\,|\,a\in A, b\in C\setminus A\}|} \theta _C$ , where the sign is the number of interchanges needed to sort A followed by B into C. This does not depend on the values of the elements of C, but only on how A is chosen inside C. This shows that we get the same coefficient for all C of size $r+s$ and therefore $F_{1^r} F_{1^s} = a_{r,s} F_{1^{r+s}}$ with

(2.4) $$ \begin{align} a_{r,s}=\sum_{\substack{A\subseteq \{1,2,\ldots, r+s\}\\ |A|=r}} (-1)^{|\{1\le b<a\le r+s\,|\,a\in A, b\not\in A\}|} \end{align} $$

by choosing $C=\{1,2,\ldots ,r+s\}$ .

Let ${C\choose r}=\{A\subseteq C, |A|=r\}$ . We define a sign-reversing involution $\Phi \colon {C\choose r}\to {C\choose r}$ as follows. For $A\in {C\choose r}$ , let $\gamma (A)=\gamma _1\gamma _2\cdots \gamma _{r+s}\in \{0,1\}^{r+s}$ be the sequence such that $\gamma _i=1$ if $i\in A$ , and $\gamma _i=0$ otherwise. We look at the entries of $\gamma (A)$ two by two and find the smallest j (if it exists) such that the pair $\gamma _{2j-1}\gamma _{2j}$ is not $00$ or $11$ . If there is no such pair, we let $\Phi (A)=A$ . If we find such pair, we define the involution $\Phi (A)=A'$ , where $A'$ is such that $\gamma (A')$ is obtained from $\gamma (A)$ by interchanging $01\leftrightarrow 10$ in position $2j-1,2j$ . If r and s are both odd, then there must be at least one occurrence of $01$ or $10$ and there are no fixed points of this involution.

We let

$$ \begin{align*}\mathrm{Inv}(A)=\{1\le b<a\le r+s\,|\,a\in A, b\not\in A\}=\{1\le \ell<t\le r+s\,|\,\gamma_\ell=0,\gamma_t=1 \},\,\end{align*} $$

where $\gamma (A)=\gamma _1\gamma _2\cdots \gamma _{r+s}$ . As long as $(t,\ell )\ne (2j-1,2j)$ , there is a bijection between $(t,\ell )\in \mathrm{Inv}(A)$ and $(t',\ell )\in \mathrm{Inv}(A')$ interchanging the 1 and 0 in positions $2j-1$ and $2j$ . The pair $(2j-1,2j)$ is in only one of $\mathrm{Inv}(A)$ or $\mathrm{Inv}(A')$ but not the other. Therefore,

$$ \begin{align*}(-1)^{|\{1\le b<a\le r+s\,|\,a\in A, b\not\in A\}|} = -(-1)^{|\{1\le b<a\le r+s\,|\,a\in A', b\not\in A'\}|}\,.\end{align*} $$

If $\Phi (A)=A$ , we have that $|\mathrm{Inv}(A)|$ is even since we can match the pairs two by two. If r is odd and s is even, then the only $A \in \binom {C}{r}$ have $r+s \in A$ and $|\mathrm{Inv}(A)| = |\mathrm{Inv}(A \backslash \{ r+s \})| + s$ . Therefore, $\Phi $ is a sign reversing involution and all fixed points contribute in equation (2.4) with a $+1$ . Therefore,

$$ \begin{align*}a_{r,s}=\Bigg|\bigg\{ A\in {C\choose r}\bigg| \Phi(A)=A\bigg\}\bigg|=\left({\lfloor \frac{r+s}{2} \rfloor \atop \lfloor \frac{r}{2} \rfloor}\right)\,,\end{align*} $$

since there are a total of $\lfloor \frac {r+s}{2} \rfloor $ pairs $2j-1,2j$ in a sequence of length $r+s$ and we must have $\lfloor \frac {r}{2} \rfloor $ of them equal to $11$ and all others equal to $00$ in order to get $\Phi (A)=A$ .

The generating series for the coefficients $F(x,y) = \sum _{r,s \ge 0} a_{r,s} x^{r}y^{s}$ is equal to $\frac {1 + x + y}{1 - x^{2} - y^{2}}$ , and the OEIS [26] sequence number is A051159. This can be derived from Proposition 2.3 using standard techniques of generating functions.

One consequence of Proposition 2.3 is that $a_{r,s}=a_{s,r}$ for all $r,s\ge 0$ . Remark that this does not contradict the fermionic law stating that $a_{r,s}=(-1)^{rs}a_{s,r}$ since $a_{r,s}=0$ when both $r,s$ are odd. Therefore, we have shown the following corollary.

Corollary 2.4 The subalgebra generated by quasisymmetric invariants $\{F_{1^r}|r\ge 0\}$ is commutative.

2.2 The ideal generated by symmetric invariants

The symmetric invariants $\mathrm {Sym}_{R_n}$ of $R_n$ are very small since a basis consists of only two elements $1$ and $F_1(\theta _1, \theta _2, \ldots , \theta _n)$ . Therefore, the ideal generated by the invariants of nonzero degree, which we shall denote $J_n$ , is generated by a single element $F_1$ . We begin by considering the symmetric coinvariants of $R_n$ , the quotient ring $R_n/J_n$ . Because the ideal $J_n$ is principal, we can understand this quotient with much more detail. This quotient ring is a special case of the ring recently studied in [21, 22].

Recall that $\mathrm {dim}~R_n = 2^n$ , and if we consider the quotient $R_n/J_n$ , it is isomorphic to $R_{n-1}$ since in this algebra $\theta _n = - \theta _1 -\theta _2 - \cdots - \theta _{n-1}$ . Let $A \subseteq [n-1]$ and $A' = A \cup \{n\}$ , then the map which sends $\theta _{A'}$ to

$$ \begin{align*}-\theta_{A}(\theta_1 + \theta_2 + \cdots + \theta_{n-1}) \otimes 1 + \theta_{A} \otimes F_1\quad \in\ R_n/J_n \otimes \mathrm{Sym}_{R_n}\end{align*} $$

and $\theta _{A}$ to

$$ \begin{align*}\theta_{A} \otimes 1 \quad \in \ R_n/J_n \otimes \mathrm{Sym}_{R_n}\end{align*} $$

is an algebra isomorphism. Since this map describes the image for each monomial in $R_n$ , we have the following proposition.

Proposition 2.5 For each $n \geq 1$ ,

$$ \begin{align*}R_n \cong R_n/J_n \otimes \mathrm{Sym}_{R_n},\end{align*} $$

as an algebra. That is, $R_n$ is free over $\mathrm {Sym}_{R_n}$ .

2.3 The ideal generated by the quasisymmetric invariants

Define an ideal of $R_n$ generated by the quasisymmetric invariants as

$$\begin{align*}I_n := \left< F_{1^r}(\theta_1, \theta_2, \ldots, \theta_n) : 1 \leq r \leq n \right>. \end{align*}$$

Remark 2.6 Note that since the operators $\pi _i$ are not multiplicative, it is unlikely to be the case that $I_n$ as an ideal is invariant under the action of the $\pi _i$ . Indeed, we find that for $n=4$ ,

$$\begin{align*}\theta_2 F_{1}(\theta_1, \theta_2, \theta_3, \theta_4) = -\theta_1 \theta_2 + \theta_2 \theta_3 + \theta_2 \theta_4. \end{align*}$$

If we apply $\pi _1$ to this element, we obtain

$$\begin{align*}\pi_1(\theta_2 F_{1}(\theta_1, \theta_2, \theta_3, \theta_4)) = -\theta_1 \theta_2 + \theta_1 \theta_3 + \theta_1 \theta_4. \end{align*}$$

This is not in $I_4$ .

The exterior quasisymmetric coinvariants are defined to be

$$\begin{align*}EQC_n := R_n/I_n. \end{align*}$$

We borrow the name “coinvariant” space even though the generators, and not the whole ideal, are invariant under the quasisymmetric operators.

2.4 Differential operators on the exterior algebra

We can define a set of differential operators on $R_n$ which will permit us to define the orthogonal complement to the ideal and a notion of quasisymmetric harmonics.

The operators $\partial _{\theta _i}$ act on monomials in $R_n$ by

$$\begin{align*}\partial_{\theta_i}( \theta_A ) = \begin{cases} (-1)^{\#\{ j \in A: j<i\}}\theta_{A \backslash \{i\}},&\text{ if }i \in A,\\ 0,&\text{ if }i \notin A. \end{cases}~ \end{align*}$$

The operators can equally be characterized by the action that $\partial _{\theta _i}(1) = 0$ and the commutation relations

$$\begin{align*}\partial_{\theta_i} \partial_{\theta_j}=-\partial_{\theta_j} \partial_{\theta_i}\quad \text{ if } 1 \leq i \neq j \leq n \quad\text{and}\quad \partial_{\theta_i}^2 = 0\quad \text{ for }1 \leq i \leq n\,, \end{align*}$$

$$\begin{align*}\partial_{\theta_i} \theta_j=-\theta_j \partial_{\theta_i}\quad \text{ if } 1 \leq i \neq j \leq n \quad\text{and}\quad \partial_{\theta_i} \theta_i = 1\quad \text{ for }1 \leq i \leq n. \end{align*}$$

For a monomial $\theta _A = \theta _{a_1} \theta _{a_2} \cdots \theta _{a_r}$ , let $\overline {\theta _A} = \theta _{a_r} \theta _{a_{r-1}} \cdots \theta _{a_1}$ represent reversing the order of the variables in the monomial. Extend this notation to both differential operators and polynomials (and polynomials of differential operators) by extending the notation linearly.

We can define an inner product on $R_n$ by setting for $p,q \in R_n$ .

$$\begin{align*}\left< p, q \right> = \overline{p(\partial_{\theta_1}, \partial_{\theta_2}, \ldots, \partial_{\theta_n})} q( \theta_1, \theta_2, \ldots, \theta_n)|_{\theta_1=\theta_2 = \cdots=\theta_n=0}. \end{align*}$$

The monomials of $R_n$ form an orthonormal basis of the space with respect to this inner product.

Define the orthogonal complement to $I_n$ with respect to the inner product as the set

(2.5) $$ \begin{align} EQH_n :&= \left\{ q \in R_n : \left< p, q \right> = 0 \text{ for all } p \in I_n \right\} \end{align} $$

(2.6) $$ \begin{align} &=\left\{ q \in R_n : p(\partial_{\theta_1}, \partial_{\theta_2}, \ldots, \partial_{\theta_n}) q= 0 \text{ for all } p \in I_n \right\}. \end{align} $$

The second equality follows from the fact that $I_n$ is an ideal and shows that $EQH_n$ is also the solution space of a system of differential equations. The containment of the set in equation (2.6) inside the set in equation (2.5) is clear. For the reverse inclusion, take an element q which is not in the set in equation (2.6), and we assume for some $p \in I_n$ that $p(\partial _\theta ) q = c \theta ^\alpha $ plus possibly some other terms, but then $\overline {p \theta ^\alpha } \in I_n$ and $\left < \overline {p \theta ^\alpha }, q \right> = c$ , which implies that q is not in the set in equation (2.5).

We refer to $EQH_n$ as the exterior quasisymmetric harmonics. The harmonics and diagonal harmonics borrow the name from the physics literature because the harmonic operator $\partial _1^2 + \partial _2^2 + \cdots + \partial _n^2$ is symmetric in the differential operators. In the case of the exterior algebra, this operator acts as zero and yet we persist by borrowing the name from the analogous spaces of commuting variables.

It is clear that the monomials of $R_n$ form an orthonormal basis of the space with respect to the inner product; hence, the inner product is positive-definite. It follows that since $EQH_n$ is the orthogonal complement of the ideal $I_n$ in $R_n$ , then the following result must hold.

Proposition 2.7 For all $n \geq 1$ , as graded vector spaces,

$$\begin{align*}EQC_n \simeq EQH_n. \end{align*}$$

We will conclude this section by constructing a set of linearly independent elements inside $EQH_n$ , which will give us a lower bound on the dimension of $EQC_n$ . In Section 4, we will see that this is also an upper bound, thus concluding that our set is in fact a basis. To compute $EQH_n$ , we need to solve the differential equations in equation (2.6). Remark first that since $I_n$ is an ideal, we do not need to take all $p\in I_n$ , but it is enough to solve for the generators $p=F_{1^r}$ for $1\le r\le n$ . We can reduce that further using Proposition 2.3 as noted in the following lemma.

Lemma 2.8 For $n\ge 2$ , we have that $I_n$ is the ideal generated by $F_1$ and $F_{1^2}$ .

Proof Clearly, we have that the ideal generated by $F_1, F_{1^2}$ is contained in $I_n$ . For the converse, we note that for each $k\geq 1$ , there are nonzero coefficients a and $a'$ such that

$$\begin{align*}a F_{1^{2k}} = (F_{1^2})^k \hskip .2in\text{ and }\hskip .2in a' F_{1^{2k+1}} = (F_{1^2})^k F_1; \end{align*}$$

hence, all of the generators of $I_n$ are contained in the ideal generated by $F_1, F_{1^2}$ .

From this, we conclude that

(2.7) $$ \begin{align} EQH_n = \Bigg\{ q \in R_n : \quad\sum_{1\le i\le n} \partial_{\theta_i}q= 0 \quad\text{ and }\quad \sum_{1\le i<j\le n} \partial_{\theta_j}\partial_{\theta_i}q= 0 \Bigg\}~. \end{align} $$

Given $0\le k\le \lfloor \frac {n}{2}\rfloor $ , a noncrossing pairing of length k is a list $(C_1, C_2, \ldots , C_k)$ with

$$ \begin{align*} &C_r=(i_r,j_r) \text{ for }1\le i_r<j_r\le n\text{ for each }1 \leq r \leq k\text{ and,}\\ &\qquad \text{either } i_r<j_r<i_s<j_s \text{ or } i_s<i_r<j_r<j_s\,\text{ for any }1\le r<s\le k. \end{align*} $$

Given a noncrossing pairing $C=(C_1,C_2,\ldots C_k)$ , we define

(2.8) $$ \begin{align} \Delta_C = \big(\theta_{j_1}-\theta_{i_1}\big)\big(\theta_{j_2}-\theta_{i_2}\big)\cdots \big(\theta_{j_k}-\theta_{i_k}\big)\,. \end{align} $$

Here, $\Delta _C=1$ if $k=0$ . Remark that $j_1<j_2<\cdots < j_k$ . The following proposition shows that there is a relationship between the noncrossing pairing condition and the differential equations from equation (2.7).

Proposition 2.9 The set

$$ \begin{align*}{\mathcal D}^{\prime}_n =\bigg\{ \Delta_C: C=(C_1,C_2,\ldots, C_k)\text{ noncrossing pairing and }0\le k\le \left\lfloor \frac{n}{2}\right\rfloor\bigg\} \end{align*} $$

is contained in $EQH_n $ .

Proof To show that $\Delta _C$ is contained in $EQH_n $ , we fix C. We need to show that $\Delta _C$ satisfies the differential equation conditions in equation (2.7).

For the first defining equation of $EQH_n$ , we have

$$ \begin{align*} \sum_{1\le i\le n} \partial_{\theta_i}\Delta_C&=\sum_{1\le r\le k} (\partial_{\theta_{i_r}}+\partial_{\theta_{j_r}})\Delta_C + \sum_{i\notin \bigcup_{r=1}^k C_r} \partial_{\theta_i}\Delta_C\\ &=\sum_{1\le r\le k} (\partial_{\theta_{i_r}}+\partial_{\theta_{j_r}})\Delta_C =0\,. \end{align*} $$

For the last equality, fix $1\le r\le k$ and note that $\Delta _C =(-1)^{r-1}(\theta _{j_r}-\theta _{i_r}) q$ for some polynomial q and so for each r,

$$ \begin{align*}(\partial_{\theta_{i_r}}+\partial_{\theta_{j_r}})\Delta_C=(-1)^{r-1} (\partial_{\theta_{i_r}}+\partial_{\theta_{j_r}})(\theta_{j_r}-\theta_{i_r})q =0~. \end{align*} $$

For the second defining equation of $EQH_n $ , we decompose the sum over pairs $1\le i<j\le n$ according to whether (a) $|\{i,j\}\cap \bigcup _{r=1}^k C_r|<2$ , (b) $C_r = (i,j)$ for some r, or (c) $i,j$ appear in two different $C_{r},C_{s}$ .

In case (a), if $|\{i,j\}\cap \bigcup C|<2$ , then one of $\theta _i$ or $\theta _j$ does not appear in $\Delta _C$ and we have $ \partial _{\theta _j} \partial _{\theta _i}\Delta _C=0$ .

In case (b), we have that the product $\theta _{j_r}\theta _{i_r}$ does not appear in $\Delta _C$ and we also have $ \partial _{\theta _{j_r}} \partial _{\theta _{i_r}}\Delta _C=0$ .

Thus, we know that only case (c) contributes to the sum and we can thus write

$$ \begin{align*} \sum_{1\le i<j\le n} \partial_{\theta_j}\partial_{\theta_i}\Delta_C &= \sum_{1\le r<s\le k} \sum_{i\in C_{r} \atop j\in C_{s}} \pm \partial_{\theta_j}\partial_{\theta_i}\Delta_C~. \end{align*} $$

In the second sum on the right-hand side, we have to be careful as when we pick $i\in C_{r}$ and $ j\in C_{s}$ we are not guaranteed that $i<j$ , so a sign may be needed in order to keep the equality. We will make a careful study of all possibilities for fixed $1\le r<s\le k$ . First, we rearrange the terms of $\Delta _C$ in equation (2.8) to bring the terms $(\theta _{j_{r}}-\theta _{i_{r}})(\theta _{j_{s}}-\theta _{i_{s}})$ in front performing $(r-1)+(s-2)$ anticommutations, we have

$$ \begin{align*}\Delta_C =(-1)^{r+s-1}(\theta_{j_{r}}-\theta_{i_{r}})(\theta_{j_{s}}-\theta_{i_{s}})q\end{align*} $$

for some polynomial q. Remark that $i_{r},j_{r},i_{s},j_{s}$ satisfy either the inequalities

$$ \begin{align*}i_r<j_r<i_s<j_s \qquad \text{ or }\qquad i_s<i_r<j_r<j_s.\end{align*} $$

The only concern is their relative order, and we can thus assume that we have the numbers $1,2,3,4$ . There are two possibilities: $((i_r,j_r), (i_s,j_s))$ is equal to $((1,2),(3,4))$ or $((2,3),(1,4))$ . In the first case, we have

$$ \begin{align*}\big( \partial_{\theta_3}\partial_{\theta_1} + \partial_{\theta_3}\partial_{\theta_2} + \partial_{\theta_4}\partial_{\theta_1} + \partial_{\theta_4}\partial_{\theta_2}\big) (\theta_{2}-\theta_{1})(\theta_{4}-\theta_{3}) =0, \end{align*} $$

and in the second case, we get

$$ \begin{align*}\big( \partial_{\theta_2}\partial_{\theta_1} + \partial_{\theta_4}\partial_{\theta_2} + \partial_{\theta_3}\partial_{\theta_1} + \partial_{\theta_4}\partial_{\theta_3}\big) (\theta_{3}-\theta_{2})(\theta_{4}-\theta_{1}) =0. \end{align*} $$

Furthermore, this shows that $\Delta _C\in EQH_n $ for all noncrossing pairings C.

The set ${\mathcal D}^{\prime }_n$ is not linearly independent, for example, for $n=3$ and $k=1$ , we have the following three noncrossing pairings: $((1,2))$ , $((1,3))$ , and $((2,3))$ , but

$$\begin{align*}\Delta_{((1,2))} - \Delta_{((1,3))} + \Delta_{((2,3))} =0. \end{align*}$$

We want to select a linearly independent subset of ${\mathcal D}^{\prime }_n$ . We proceed as follows: consider a sequence $\alpha = (a_1, a_2, \ldots , a_n) \in \{0, 1\}^n$ such that $\sum _{i=1}^r a_i \leq r/2$ for all $1 \leq r \leq n$ . Such sequences are known as ballot sequences. If ever it is the case that $\sum _{i=1}^r a_i> r/2$ , then we say that $\alpha $ breaks the ballot condition at position r.

Given a ballot sequence $\alpha $ , we build a noncrossing pairing $C(\alpha )$ by first replacing all $0$ s by open parentheses $0\mapsto $ “(,” and all $1$ s by close parentheses $1\mapsto $ “),” and then do the natural maximal pairing of parenthesis. The positions of the pairings give us in lexicographic order a noncrossing pairing which we shall denote $C(\alpha )$ . Since $\alpha $ is a ballot sequence, every closed parenthesis is matched and some open parentheses might remain unpaired. The natural pairing of parenthesis guarantees that the result will be noncrossing. For example,

$$\begin{align*}\alpha=0010001101 ~~~~\mapsto~~~~ (()((())() ~~~~\mapsto~~~~ C(\alpha)=((2,3),(6,7),(5,8),(9,10)). \end{align*}$$

The total number of ballot sequences of size n is equal to $\binom {n}{\lfloor {n/2}\rfloor }$ (see [26, A001405]). The number of ballot sequences graded by the number of $1$ s in the sequence (see [26, A008315]) is given in Figure 1.

Figure 1 The number of ballot sequences of length n with exactly $k 1$ s with $1 \leq n \leq 9$ and $1 \leq k \leq \lfloor \frac {n}{2} \rfloor $ . These will be shown to be the graded dimensions of $EQH_n \simeq EQC_n$ .

Given this construction, we have the following proposition.

Proposition 2.10 The set

$$ \begin{align*}{\mathcal D}_n =\big\{ \Delta_{C(\alpha)}: \alpha \in \{0, 1\}^n \text{ a ballot sequence}\big\} \end{align*} $$

is contained in $EQH_n$ and is linearly independent.

Proof The first statement follows from Proposition 2.9 since ${\mathcal D}_n \subseteq {\mathcal D}^{\prime }_n \subseteq EQH_n$ . To show the linear independence, fix $\alpha $ a ballot sequence and let $C(\alpha )=((i_1,j_1),\ldots ,(i_k,j_k))$ be its noncrossing pairing. We remark that the sequence of numbers $j_1<j_2<\cdots <j_k$ corresponds to the position of the $1$ s in $\alpha $ . Using the monomial ordering described in Section 3 and by inspection of the product in equation (2.8), we observe that the term $\theta _{j_1}\theta _{j_2}\cdots \theta _{j_k}$ is the smallest lexicographic monomial in $\Delta _{C(\alpha )}$ . For different ballot sequences $\alpha $ , we get different positions of the $1$ s in $\alpha $ and thus different smallest lexicographic monomials, which shows the independence of ${\mathcal D}_n$ .

Remark 2.11 For a fixed $0\le k\le \lfloor \frac {n}{2}\rfloor $ , the set

$$ \begin{align*}{\mathcal D}^{(k)}_n =\big\{ \Delta_{C(\alpha)}: \alpha \in \{0, 1\}^n \text{ a ballot sequence with }k \text{ 1s}\big\}\end{align*} $$

spans a subspace of $R_n$ of degree k. It is known that the ballot sequences with k 1s are in bijection with standard tableaux of shape $(n-k,k)$ . If the variables $\theta $ were commutative, the space spanned by ${\mathcal D}^{(k)}_n$ would be the same as the space spanned by the Specht polynomials indexed by standard tableaux and therefore would be an irreducible symmetric group module. Here, the situation appears to be related, but is in fact quite different.

A small example is informative. Consider $n=4$ and $k=2$ . There are two ballot sequences $0101$ and $0011$ . The associated two noncrossing pairings are $((1,2),(3,4))$ and $((2,3),(1,4))$ , and we have

$$ \begin{align*}\Delta_{C(0101)}= (\theta_{2}-\theta_{1})(\theta_{4}-\theta_{3}) \quad\text{ and }\quad \Delta_{C(0011)}=(\theta_{3}-\theta_{2})(\theta_{4}-\theta_{1}). \end{align*} $$

On the other hand, the two standard tableaux associated with $0101$ and $0011$ are

A standard construction of the symmetric group irreducible of shape $(2,2)$ from the tableaux $T_1$ and $T_2$ is to use the Garnir polynomials

$$ \begin{align*} \Delta_{T_1} &= (\theta_{2}-\theta_{1})(\theta_{4}-\theta_{3}) =\Delta_{C(0101)},\\ \Delta_{T_2} &= (\theta_{3}-\theta_{1})(\theta_{4}-\theta_{2}). \end{align*} $$

Unfortunately, $ \Delta _{T_2}\notin EQH_n$ . In commutative variables, the span of the $\{\Delta _{T_1},\Delta _{T_2}\}$ (an irreducible module) would be the same as the span of $\{\Delta _{C(0101)},\Delta _{C(0011)}\}$ . However, for anticommutative variables, it is a different story. ¹

3 A linear basis of the ring

Again, let n be a fixed positive integer and $R_n = {\mathbb Q}[\theta _1, \theta _2, \ldots , \theta _n]$ . We have thus far represented the basis for $R_n$ as the elements $\theta _A$ with $A \subseteq [n]$ . Define $\alpha (A) \in \{ 0,1\}^n$ to be the sequence $a_1 a_2 a_3 \cdots a_n$ with $a_i = 1$ if $i \in A$ and $a_i = 0$ if $i \notin A$ so that

$$\begin{align*}\theta_A = \theta_1^{a_1} \theta_2^{a_2} \cdots \theta_n^{a_n} := \theta^{\alpha(A)}~. \end{align*}$$

For such a sequence $\alpha \in \{0,1\}^n$ , let $m_1(\alpha ) := \sum _{i=1}^n a_i$ represent the number of $1$ s in the string. This will also be the degree of the monomial $\theta ^{\alpha }$ .

For sequences $\alpha \in \{ 0, 1 \}^n$ , define elements $G_\alpha $ by

(3.1) $$ \begin{align} G_{1^s0^{n-s}} = F_{1^s} \end{align} $$

and if $\alpha \neq 1^s 0^{n-s}$ , then $\alpha $ is of the form $u01^s0^{n-k-s}$ for some string u of length $k-1$ and we recursively define

(3.2) $$ \begin{align} G_{u01^s0^{n-k-s}} = G_{u1^s0^{n-k-s+1}} - (-1)^{m_1(u)} \theta_k G_{u1^{s-1}0^{n-k-s+2}}~. \end{align} $$

We will show below that the recurrence for the $G_\alpha $ is defined so that they are S-polynomials [6] for elements of the ideal $I_n$ . In commutative variables, similar polynomials were defined by Aval–Bergeron–Bergeron [1, 2] as a (complete) subset of S-polynomials needed to compute all possible S-polynomials in the Buchburger algorithm for a Gröbner basis. It is not given that one can easily describe such a set of S-polynomials and here we have adapted the definition for working in the exterior algebra.

Example 3.1 For $\alpha = 010110$ and $\beta = 001100$ , we compute the elements $G_\alpha $ and $G_\beta $ using the definition.

$$ \begin{align*} G_{010110} &= G_{011100} + \theta_3 G_{011000} = (G_{111000} - \theta_1 G_{110000}) + \theta_3(G_{110000} - \theta_1 G_{100000})\\ &= \theta_2 \theta_4 \theta_5 + \theta_2 \theta_4 \theta_6 + \theta_2 \theta_5 \theta_6 + 2 \theta_3 \theta_4 \theta_5 + 2 \theta_3 \theta_4 \theta_6 + 2 \theta_3 \theta_5 \theta_6 + \theta_4 \theta_5 \theta_6, \end{align*} $$

and we have that

$$ \begin{align*} G_{001100} &= G_{011000} - \theta_2 G_{010000} = (G_{110000} - \theta_1 G_{100000}) - \theta_2 (G_{100000} - \theta_1 G_{000000})\\ &= \theta_3 \theta_4 + \theta_3 \theta_5 + \theta_3 \theta_6 + \theta_4 \theta_5 + \theta_4 \theta_6 + \theta_5 \theta_6. \end{align*} $$

We follow [6] for the convention of lexicographical ordering on monomials. Given vectors $u,v$ with nonnegative integer entries, we say that $u < v$ lexicographically if there exists an index $j \ge 1$ such that $u_{i} = v_{i}$ for all $1 \le i < j$ , but $u_{j} < v_{j}$ . Monomials of $R_{n}$ are ordered by their exponent vectors. More precisely, $\theta _{A} < \theta _{B}$ if $\alpha (A) < \alpha (B)$ lexicographically. For example, we have $\theta _{1}> \cdots > \theta _{n}$ and the lexicographically largest monomial in the above example $G_{001100}$ is $\theta _{3}\theta _{4}$ . The latter demonstrates an important property of these elements stated in the following proposition.

Proposition 3.2 The largest lexicographic term in $G_\alpha $ is $\theta ^\alpha $ .

The proof of Proposition 3.2 follows by induction on the length of $\alpha $ and from a lemma that is analogous to Lemma 3.3 of [2]. The recursion in this result is really the origin of the definition of $G_\alpha $ because equation (3.2) was adapted so that this lemma holds. It follows that the set $\{ G_\alpha \}_{\alpha \in \{0,1\}^n}$ is a basis for $R_n$ .

The argument for the proposition is elementary (chasing the largest lexicographic term in (3.3) and (3.4)) and so we do not include it; however, the proof of the following result comes from a careful analysis of the terms arising in the recursive definition of the $G_\alpha $ .

Lemma 3.3 Let $\alpha \in \{0,1\}^{n-1}$ , then

(3.3) $$ \begin{align} G_{0\alpha} &= G_\alpha(\theta_2, \theta_3, \ldots, \theta_n) \text{ and } \end{align} $$

(3.4) $$ \begin{align} \hspace{13pt}G_{1\alpha} &= \theta_1 G_{0\alpha} + P_{\alpha}(\theta_2, \theta_3, \ldots, \theta_n) \end{align} $$

for some polynomial $P_{\alpha }(\theta _2, \theta _3, \ldots , \theta _n) \in {\mathbb Q}[\theta _2, \theta _3, \ldots , \theta _n]$ .

Remark 3.4 By convention, the length of the index for our polynomials indicates in which polynomial space we are. For example, if $\beta \in \{0,1\}^{n}$ , then $G_\beta \in R_n$ . For $\alpha \in \{0,1\}^{n-1}$ in Lemma 3.3, when we write $G_\alpha (\theta _2, \theta _3, \ldots , \theta _n)$ , we mean $G_\alpha \in R_{n-1}$ embedded in $R_n$ with the substitution $\theta _i:=\theta _{i+1}$ . A similar convention will be followed for $P_\alpha $ .

Proof of Lemma 3.3

The proof will proceed by induction on $n-i$ where i is the number of trailing $0$ s in $\alpha $ . The base case $0=n-n$ with n zeros is $0\alpha = 0^n$ , and we have

$$\begin{align*}G_{0^n} = F_{1^0}(\theta_1,\theta_2 ,\ldots,\theta_n) = 1 = G_{0^{n-1}}(\theta_2, \theta_3, \ldots, \theta_n)~. \end{align*}$$

We then consider the case $0\alpha =01^s0^{n-s-1}$ . The polynomials $F_{1^s}$ satisfy the following identity:

(3.5) $$ \begin{align} F_{1^s}(\theta_1,\theta_2 ,\ldots,\theta_n) = \theta_1 F_{1^{s-1}}(\theta_2 ,\ldots,\theta_n) + F_{1^s}(\theta_2,\theta_3 ,\ldots,\theta_n). \end{align} $$

This follows directly from the definition (2.2) where we split the sum in two parts depending if $1\in A$ or not. The definition of $G_{01^s0^{n-s-1}}$ gives us

$$ \begin{align*} G_{01^s0^{n-s-1}}&= G_{1^s0^{n-s}} - \theta_1 G_{1^{s-1}0^{n-s+1}} =F_{1^s}(\theta_1,\theta_2 ,\ldots,\theta_n) - \theta_1 F_{1^{s-1}}(\theta_2 ,\ldots,\theta_n) \\ &= F_{1^s}(\theta_2,\theta_3 ,\ldots,\theta_n)= G_{\alpha}(\theta_2,\theta_3 ,\ldots,\theta_n). \end{align*} $$

To finish the proof of equation (3.3) by induction, let us assume that $\alpha $ is not of the form $01^s0^{n-s-1}$ for some $s>0$ . Instead, we have $0\alpha =0w01^s0^{n-k-s}$ for some $s>0$ and some string w of length $k-2$ . For $0\alpha =0w01^s0^{n-k-s}$ , we have $n-k-s$ trailing zeros. Remark that for $0w1^s0^{n-k-s+1}$ and $0w1^{s-1}0^{n-k-s+2}$ , we have more trailing zeros than that of $0\alpha $ and we will use the induction hypothesis with (3.3) in the equality (3.6).

(3.6) $$ \begin{align} G&_{0w01^s0^{n-k-s}}= G_{0w1^s0^{n-k-s+1}} - (-1)^{m_1(0w)} \theta_k G_{0w1^{s-1}0^{n-k-s+2}} \nonumber \\ & = G_{w1^s0^{n-k-s+1}}(\theta_2,\theta_3 ,\ldots,\theta_n) - (-1)^{m_1(0w)} \theta_k G_{w1^{s-1}0^{n-k-s+2}}(\theta_2,\theta_3 ,\ldots,\theta_n) \end{align} $$

(3.7) $$ \begin{align} &\hspace{-31pt} = \big[G_{w1^s0^{n-k-s+1}} - (-1)^{m_1(w)} \theta_{k-1} G_{w1^{s-1}0^{n-k-s+2}}\big](\theta_2,\theta_3 ,\ldots,\theta_n) \end{align} $$

(3.8) $$ \begin{align} &\hspace{-67pt} = G_{w01^s0^{n-k-s}} (\theta_2,\theta_3 ,\ldots,\theta_n) = G_{\alpha} (\theta_2,\theta_3 ,\ldots,\theta_n). \end{align} $$

In (3.7), the expression inside the square bracket $[\cdots ]$ is treated as a polynomial in the variables $\theta _1,\ldots ,\theta _{n-1}$ in $R_{n-1}$ (see Remark 3.4). Hence, the variable $\theta _{k}$ from (3.6) must be replaced by $\theta _{k-1}$ in (3.7). Furthermore, $m_1(0w)=m_1(w)$ . The expression we get is exactly the definition of $G_{w01^s0^{n-k-s}} \in R_{n-1}$ and equation (3.8) follows. This concludes the proof of (3.3).

We next prove equation (3.4) by induction. The base case is if $1\alpha = 1^{s+1}0^{n-s-1}$ , then using equation (3.5) we have

(3.9) $$ \begin{align} G_{1^{s+1}0^{n-s-1}} &= F_{1^{s+1}}(\theta_1,\theta_2 ,\ldots,\theta_n) \nonumber\\ &= \theta_1 F_{1^s} (\theta_2, \theta_3, \ldots, \theta_n)+ F_{1^{s+1}}(\theta_2, \theta_3, \ldots, \theta_n)\nonumber \\ &= \theta_1 G_{01^s0^{n-s-1}} + F_{1^{s+1}}(\theta_2, \theta_3, \ldots, \theta_n)~. \end{align} $$

In (3.9), we use (3.3) with $G_{01^s0^{n-s-1}}=G_{1^s0^{n-s-1}} (\theta _2, \ldots , \theta _n)=F_{1^s} (\theta _2, \ldots , \theta _n)$ . We then let $P_{1^{s}0^{n-s-1}} = F_{1^{s+1}}(\theta _1,\ldots ,\theta _{n-1})$ , and this shows that (3.4) holds in this case.

We now assume that $1\alpha \ne 1^{s+1}0^{n-s-1}$ . Therefore, $1\alpha =1w01^s0^{n-k-s}$ for some string w of length $k-2$ . We have

(3.10) $$ \begin{align} G&_{1w01^s0^{n-k-s}}= G_{1w1^s0^{n-k-s+1}} - (-1)^{m_1(1w)} \theta_k G_{1w1^{s-1}0^{n-k-s+2}} \nonumber \\ & = \big(\theta_1G_{0w1^s0^{n-k-s+1}} +P_{w1^s0^{n-k-s+1}}(\theta_2,\theta_3 ,\ldots,\theta_n)\big) \end{align} $$

(3.11) $$ \begin{align} &\qquad\qquad - (-1)^{m_1(1w)} \theta_k \big(\theta_1G_{0w1^{s-1}0^{n-k-s+2}} +P_{w1^{s-1}0^{n-k-s+2}}(\theta_2,\theta_3 ,\ldots,\theta_n)\big) \nonumber\\ & = \theta_1\big(G_{0w1^s0^{n-k-s+1}} - (-1)^{m_1(w)} \theta_k G_{0w1^{s-1}0^{n-k-s+2}}\big) \\ &\qquad\qquad + \big[P_{w1^s0^{n-k-s+1}} - (-1)^{m_1(1w)} \theta_{k-1} P_{w1^{s-1}0^{n-k-s+2}}\big] (\theta_2,\theta_3 ,\ldots,\theta_n). \nonumber \end{align} $$

In (3.10), we have used the induction hypothesis of (3.4) on both terms. In (3.11), we group together the terms with $\theta _1$ in front, using the identity $(-1)^{m_1(1w)} \theta _k \theta _1 = (-1)^{m_1(1w)+1} \theta _1 \theta _k = (-1)^{m_1(w)} \theta _1 \theta _k $ . The term with $\theta _1$ in (3.11) is the definition of $G_{0\alpha }$ . The expression inside the square bracket is a polynomial in $R_{n-1}$ that we take as the definition for $P_\alpha $ . This shows by induction that (3.4) holds in all cases and concludes the proof of the lemma.

4 A basis for the quotient

The elements $G_\alpha $ are defined so that we could use them to identify a nice basis of the ideal $I_n$ . Our first result establishes that the $G_\alpha $ such that $\alpha $ is not a ballot sequence are in the ideal. The slightly more difficult step is to show that these elements also span the ideal.

Proposition 4.1 If $\alpha \in \{0,1\}^n$ is not a ballot sequence, then $G_\alpha \in I_n$ .

Proof A sequence $\alpha \in \{ 0, 1\}^n$ is either of the form $\alpha = 1^s0^{n-s}$ for some $s> 0$ or $\alpha = u01^s0^{n-s-k}$ for some $s>0$ and some $u \in \{0,1\}^{k-1}$ .

In the first case, $\alpha $ breaks the ballot condition in position $1$ and by equation (3.1), $G_{1^s0^{n-s}} = F_{1^s}$ is in the ideal $I_n$ .

Now, the other case is established by induction on the position of the last $1$ in $\alpha $ . We assume that $\alpha = u01^s0^{n-s-k}$ and, by equation (3.2), $G_\alpha $ is in $I_n$ if both $G_{u1^s0^{n-k-s+1}}$ and $G_{u1^{s-1}0^{n-k-s+2}}$ are elements of $I_n$ .

Assume that $u01^s0^{n-s-k}$ breaks the ballot condition for the first time at position r. If $r<k$ , then $u1^s0^{n-k-s+1}$ and $u1^{s-1}0^{n-k-s+2}$ both break the ballot condition also at position r. Since $\alpha _k=0$ , $\alpha $ does not break the ballot condition for the first time at $r=k$ , so the other possibility is that $r>k$ . In this case, $u01^{r-k}$ with $r-k \leq s$ breaks the ballot condition for the first time and therefore so does $u1^{r-k-1}$ and so do both $u1^s0^{n-k-s+1}$ and $u1^{s-1}0^{n-k-s+2}$ . By our inductive hypothesis, this implies that $G_\alpha \in I_n$ .

Therefore, by induction, $\alpha $ breaking the ballot condition implies that $G_\alpha \in I_n$ for all $\alpha \in \{0,1\}^n$ .

We will show that the ideal lies in the span of the $G_\alpha $ such that $\alpha $ breaks the ballot condition, therefore establishing our main theorem.

Theorem 4.2 The set $A_n:=\big \{ G_\alpha : \alpha \in \{0,1\}^n \mathit { breaks the ballot condition}\big \}$ is a $\mathbb Q$ -linear basis of the ideal $I_n$ .

The proof of this theorem uses our understanding of the harmonic space $EQH_n\cong EQC_n$ . In Proposition 2.10, we found that $\dim (EQH_n)=\dim (EQC_n)$ is at least the number of ballot sequences. We first establish a small lemma about a spanning set for the quotient $EQC_n$ showing that the dimension is at most the number of ballot sequences. Therefore, we have equality and the set ${\mathcal D}_n$ in Proposition 2.10 is in fact a basis of $EQH_n$ .

Lemma 4.3 The set $B_n=\big \{ \theta ^\beta : \beta \in \{0,1\}^n \mathit { is\ a\ ballot\ sequence}\big \}$ $\mathbb Q$ -spans the quotient $R_n\big /I_n$ .

Proof Order the monomials lexicographically, and let $\theta ^\gamma $ be the smallest monomial that is not in the $\mathbb Q$ -span of $B_n$ (modulo $I_n$ ). We must have that $\gamma $ breaks the ballot condition, since otherwise $\theta ^\gamma \in B_n$ . Therefore, Proposition 4.1 tells us that $G_\gamma \in I_n$ . Proposition 3.2 says that $G_\gamma = \theta ^\gamma + \sum _{\beta <\gamma } c_\beta \theta ^\beta $ . Hence, modulo $I_n$ , we have

$$ \begin{align*}\theta^\gamma \equiv \theta^\gamma - G_\gamma = - \sum_{\beta<\gamma} c_\beta \theta^\beta.\end{align*} $$

The right-hand side is a linear combination of monomials strictly smaller than $\theta ^\gamma $ . By the choice of $\theta ^\gamma $ , all such monomials are in the $\mathbb Q$ -span of $B_n$ . Therefore, $\theta ^\gamma $ is also in the $\mathbb Q$ -span of $B_n$ , a contradiction. We must conclude that there are no such $\theta ^\gamma $ and all monomials are in the $\mathbb Q$ -span of $B_n$ modulo the ideal $I_n$ .

Proof of (Theorem 4.2)

Let $d_n$ be the number of ballot sequences of size n. We have

$$ \begin{align*}d_n \leq \dim EQH_{n} = \dim EQC_{n} \leq d_n,\end{align*} $$

where the first inequality follows from Proposition 2.10 and the second follows from Lemma 4.3. By Proposition 2.7, we have $d_{n} = \dim EQC_{n}$ . Let ${\mathbb Q}A_n$ be the ${\mathbb Q}\text {-span}$ of the elements of $A_n$ . Similarly, let ${\mathbb Q}B^{\prime }_n$ be the ${\mathbb Q}\text {-span}$ of the set $\big \{ G_\beta : \beta \in \{0,1\}^n \mathit { is\ a\ ballot\ sequence}\big \}$ . Using Proposition 3.2, we have that

$$ \begin{align*}R_n ={\mathbb Q}B^{\prime}_n \oplus {\mathbb Q}A_n. \end{align*} $$

Since ${\mathbb Q}A_n \subseteq I_n$ and $\dim {\mathbb Q}B^{\prime }_n = d_n$ , we conclude that ${\mathbb Q}A_n = I_n\,.$

There are several straightforward consequences of this theorem which we state here.

Corollary 4.4 The number of ballot sequences of length n with k entries $1$ is known [28] to be equal to the number $f^{(n-k,k)}$ of standard tableaux of shape $(n-k,k)$ . Therefore, we have that the Hilbert series of $EQH_n$ is

$$ \begin{align*}\text{Hilb}_{EQH_n}(q) = \sum_{k=0}^{\lfloor{n/2}\rfloor} f^{(n-k,k)} q^k\,.\end{align*} $$

Corollary 4.5 The set ${\mathcal D}_n$ is a basis of $EQH_n$ and of $EQC_n$ .

Corollary 4.6 The set $A_n$ is a (nonreduced, nonminimal) Gröbner basis of $I_n$ . A minimal Gröbner basis for $I_n$ is given by

$$ \begin{align*}\big\{ G_\alpha : \alpha \in \{0,1\}^n \mathit{ breaks\ the\ ballot\ condition\ only\ at\ the\ rightmost\ 1\ of } \alpha\big\}. \end{align*} $$

Remark 4.7 In this paper, we have adopted the language of ballot sequences. An alternative (as in [2, 3]) is to use northeast lattice paths in the first quadrant from $(0,0)$ with a north step for every $0$ and an east step for every $1$ as we read in a $0$ – $1$ sequence. In such representation, a sequence is ballot if and only if it remains above the diagonal.