Article contents
Parasitic waves and micro-breaking on highly nonlinear gravity–capillary waves in a convergent channel
Published online by Cambridge University Press: 08 May 2023
Abstract
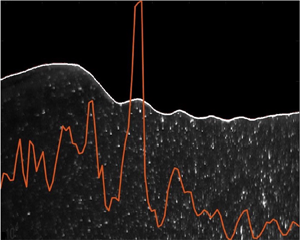
Gravity–capillary waves are waves influenced by both the effects of surface tension and gravity; these waves are at small scales with wavelength range from approximately 10 cm to less than 1 cm. Gravity–capillary waves play a significant role in air–sea interactions, and they exhibit much different features compared with gravity waves. They can be observed widely on the sea surface. Parasitic waves (capillary waves generated by and that ride on gravity and/or gravity–capillary waves) and micro-breaking can be observed on the water surface with winds; however, the presence of wind makes it difficult to analyse the mechanisms of the wave itself. In this paper, parasitic waves and micro-breaking on gravity–capillary waves are examined experimentally, both in the absence of wind. Parasitic waves and axisymmetric micro-breaking waves are generated mechanically in a convergent channel, where energy density increases due to spatial convergence. Three experimental techniques are used to measure wave properties: planar laser-induced fluorescence, particle image velocimetry and shadowgraphs. The wave profile evolution and vortices beneath the parasitic waves are studied. The micro-breaking of gravity–capillary waves is observed on a surface with added surfactant. The surfactant increases the Bond number, and makes breaking possible in these small-scale waves. Energy dissipation of parasitic waves and micro-breaking is quantified, and the enhanced dissipation caused by parasitic waves is identified through the experiments. In this study, mechanically generated breaking waves with wavelengths less than 10 cm are studied for the first time, without the effect of wind. The results yield insight into wave characteristics and energy dissipation on the air–sea interface at small scales.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



