I. INTRODUCTION
Emerging applications such as low-power sensor networks and wireless video surveillance require lightweight video encoding with high coding efficiency and resilience to transmission errors. Distributed video coding (DVC) is a different coding paradigm offering such benefits, where conventional video standards such as H.264/AVC are disadvantageous. DVC based on the information-theoretic results of Slepian and Wolf [Reference Slepian and Wolf1] and Wyner and Ziv [Reference Wyner and Ziv2] exploits the source statistics at the decoder instead of at the encoder. This significantly reduces the computational burden at the encoder compared with conventional video coding solutions.
Transform domain Wyner–Ziv (TDWZ) video coding from Stanford University [Reference Girod, Aaron, Rane and Rebollo-Monedero3] is one popular approach to DVC. The DISCOVER codec [4] brought some improvements of the coding efficiency, thanks to more accurate side information generation and correlation noise modeling. Other researchers have improved upon this approach, for example, by developing advanced refinement techniques [Reference Martins, Brites, Ascenso and Pereira5,Reference Huang and Forchhammer6]. Using a cross-band noise refinement technique [Reference Huang and Forchhammer6], the rate distortion (RD) performance of TDWZ has been improved. More recently, motion and residual re-estimation and a generalized reconstruction were proposed in the MORE codec [Reference Luong, Rakêt and Forchhammer7], which significantly improved the TDWZ coding efficiency. A motion re-estimation based on optical flow (OF) and residual motion compensation (MC) with motion updating were used to improve side information and noise modeling by taking partially decoded information into account. To improve noise modeling, a noise residual motion re-estimation technique was also proposed [Reference Luong, Rakêt and Forchhammer7].
Despite advances in practical TDWZ video coding, the RD performance of TDWZ video coding is still not matching that of conventional video coding approaches such as H.264/AVC. Including different coding modes as in conventional video compression may be a promising solution for further improving the DVC RD performance.
As in classical video coding schemes (e.g., based on H.264/AVC or HEVC), the use of different coding modes has also shown to bring benefits in {DVC}. However, the challenge here is that the encoder typically does not have access to the side information, while the decoder has no access to the original, so both the encoder and decoder do not have perfect information to base mode decision on. In general, mode decision in DVC can be classified into techniques for encoder-side or decoder-side mode decision, in the pixel-domain or transform domain. Techniques for encoder-side mode decision have been proposed by a number of researchers. In [Reference Ascenso and Pereira8], new techniques were proposed for intra and Wyner–Ziv (WZ) rate estimation, which drive a block-based encoder-side mode decision module deciding whether or not intra-coded information needs to be sent to the decoder in addition to the WZ bits. The work in [Reference Lee, Chiang, Tsai and Lie9] proposed to decide between WZ and intra blocks based on spatiotemporal features, including the temporal difference and spatial pixel variance. This reduces temporal flickering significantly, according to the authors. Instead of a pixel-domain approach, in [Reference Verbist, Deligiannis, Satti, Schelkens and Munteanu10] it was proposed to use Lagrange-based transform-domain mode decision in a feedback-channel free DVC system. In this system, a coarse estimation of the side information is generated at the encoder to aid the mode decision and rate estimation process. In contrast to these techniques, decoder-side mode decision has been proposed as well.
In [Reference Slowack, Skorupa, Mys, Lambert, Grecos and Van de Walle11–Reference Slowack13], it was proposed to exploit different coding modes, where the coding modes are entirely decided at the decoder. In [Reference Slowack, Skorupa, Mys, Lambert, Grecos and Van de Walle11,Reference Chien and Karam12], skipping or deciding between skipping or WZ coding for coefficient bands or bitplanes is proposed. The modes were decided based on a threshold using estimated rate and distortion values. More theoretically, the work in [Reference Slowack13] has developed techniques for RD-based decoder-side mode decision. The decoder-side mode decision takes the side information position in the quantization bin into account to determine the coding modes at the coefficient and bitplane levels. At coefficient level, whether to skip the entire coefficient band or not is decided using a coefficient band skip criterion. At the bitplane level, if the coefficient band is not skipped, the decoder is granted the choice between three different coding modes namely skip, WZ coding, and intra coding modes. More recently, a method for deciding among temporal, inter-view, and fused side information was developed in [Reference Petrazzuoli, Cagnazzo and Pesquet-Popescu14], which is based on observing the parity bitrate needed to correct the temporal and interview interpolations for a small number of WZ frames.
In this paper, we continue with the decoder-side mode decision for a TDWZ codec extending the work of [Reference Luong, Slowack, Forchhammer, Cock and Van de Walle15]. The mode decisions are significantly impacted by the correlation model that was enhanced by the refinement techniques proposed in DVC [Reference Huang and Forchhammer6,Reference Luong, Rakêt and Forchhammer7]. To take advantage of both the refinement techniques in [Reference Huang and Forchhammer6,Reference Luong, Rakêt and Forchhammer7] and the decoder-side mode decision in [Reference Slowack13], this paper proposes a decoder side adaptive mode decision (AMD) technique for TDWZ video coding. The mode decision uses estimated rate values to form an AMD and develop a residual MC to generate a more accurate correlation noise. The proposed AMD is integrated with the DVC codec in [Reference Huang and Forchhammer6] to enhance the RD performance of the TDWZ scheme and evaluate the benefits of AMD as in [Reference Luong, Slowack, Forchhammer, Cock and Van de Walle15]. Thereafter, the AMD technique is also integrated with a state-of-the-art, but also more complex DVC codec [Reference Luong, Rakêt and Forchhammer7].
To sum up, in this paper we extend the presentation of AMD initially presented in [Reference Luong, Slowack, Forchhammer, Cock and Van de Walle15] and additionally integrate the techniques with the advanced MORE DVC [Reference Luong, Rakêt and Forchhammer7] to achieve state-of-the-art results by integration in two highly efficient DVC codecs and evaluate the generality of the AMD techniques presented. The rest of this paper is organized as follows. In Section II, the proposed DVC architecture, including the AMD technique is presented. The AMD and residual MC techniques proposed are described in Section III. Section IV evaluates and compares the performance of our approach to other existing methods.
II. THE PROPOSED DVC ARCHITECTURE
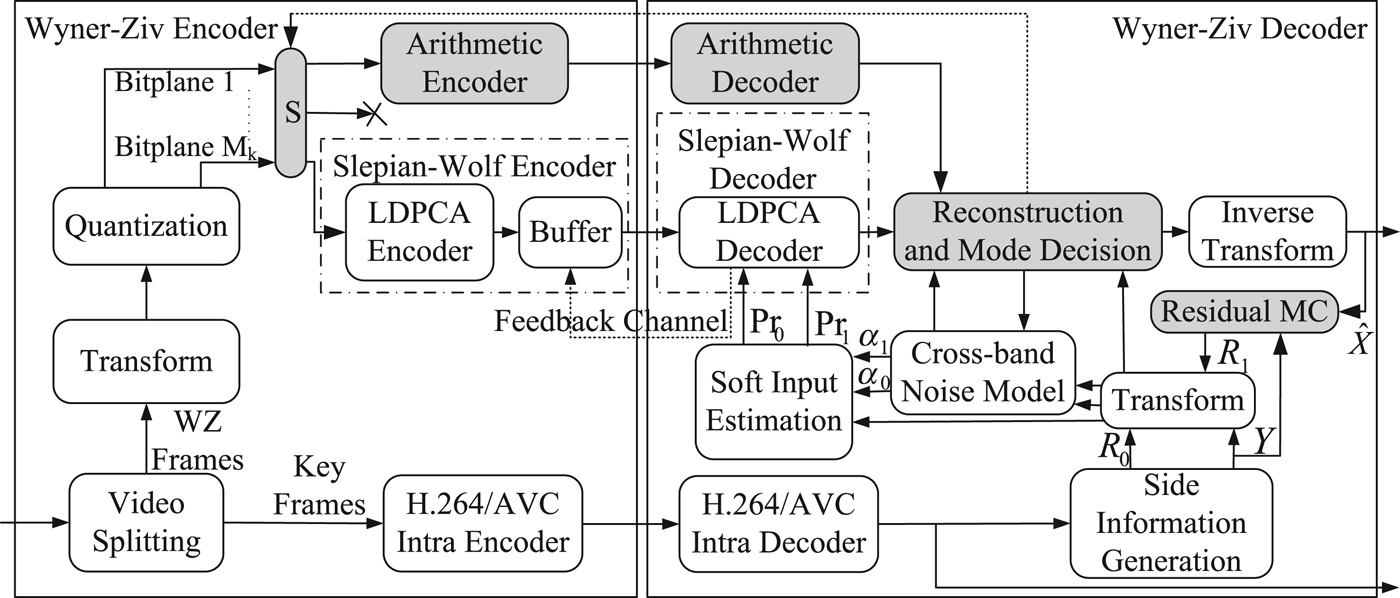
The architecture of an efficient TDWZ video codec with a feedback channel [Reference Girod, Aaron, Rane and Rebollo-Monedero3,4] is depicted in Fig. 1. The input video sequence is split into key frames and WZ frames, where the key frames are intra coded using conventional video coding techniques such as H.264/AVC intra coding. The WZ frames are transformed (4 × 4 DCT), quantized and decomposed into bitplanes. Each bitplane is in turn fed to a rate-compatible LDPC accumulate (LDPCA) encoder [Reference Varodayan, Aaron and Girod16] from most significant bitplane to least significant bitplane. The parity information from the output of the LDPCA encoder is stored in a buffer from which bits are requested by the decoder through a feedback channel.

Fig. 1. AMD TDWZ video architecture enhancing the cross-band DVC [6].
At the decoder side, overlapped block motion compensation (OBMC) [Reference Huang and Forchhammer6] is applied to generate a prediction of each WZ frame available at the encoder side. This prediction is referred to as the side information (Y). The decoder also estimates the noise residue (R 0) between the SI and the original frame at the encoder. This noise residue is used to derive the noise parameter α0 that is used to calculate soft-input information (conditional probabilities Pr0) for each bit in each bitplane. Given the SI and correlation model, soft input information is calculated for each bit in one bitplane. This serves as the input to the LDPCA decoder. For each bitplane (ordered from most to least significant bitplane), the decoder requests bits from the encoder's buffer via the feedback channel until decoding is successful (using a CRC as confirmation). After all bitplanes are successfully decoded, the WZ frame can be reconstructed through centroid reconstruction followed by inverse transformation.
To improve RD performance of TDWZ video coding as in DISCOVER [4], a cross-band noise model [Reference Huang and Forchhammer6] utilizing cross-band correlation based on the previously decoded neighboring bands and a mode decision technique [Reference Slowack13] have been introduced. In this paper, we integrate these and additionally propose an AMD by adapting mode decisions based on the estimated rate and compensating residual motions to further improve the RD performance.
The proposed techniques including the novel AMD in Section IIIA and the residual MC in Section IIIB are integrated in the cross-band DVC scheme [Reference Huang and Forchhammer6] as shown in Fig. 1. The mode decision, S, selects among the three modes skip, arithmetic, or WZ coding for each bitplane to be coded. The mode information is updated and sent by the decoder to the encoder after each bitplane is completely processed. The residual MC generates the additional residue R 1 along with the original residue R 0 generated by the OBMC technique [Reference Huang and Forchhammer6] of the side information generation. Thereafter, the cross-band noise model [Reference Huang and Forchhammer6] produces the parameters α0, α1 for estimating the corresponding soft inputs Pr0, Pr1 for the multiple input LDPCA decoder [Reference Luong, Rakêt, Huang and Forchhammer17]. When all bitplanes are decoded, the coefficients are reconstructed and the inverse transform converts the results to the decoded WZ frames ![]() $\widehat{X}$. These frames
$\widehat{X}$. These frames ![]() $\widehat{X}$ are also used along with SI frame Y for the residual MC to generate the residual frame R 1 for the next frame to be decoded.
$\widehat{X}$ are also used along with SI frame Y for the residual MC to generate the residual frame R 1 for the next frame to be decoded.
It can be noted that the techniques proposed in this architecture are require most processing on the decoder side. At the encoder, mode selection, S, is added, reacting to the mode selected by the decoder, and arithmetic coding is included as a mode, i.e. only minor changes are applied to the encoder. The skip mode added simplifies, when selected, the processing at both the encoder and decoder. The mode decision feed-back has the bitplane as finest granularity, i.e. a coarser granularity than that used with the LDPCA decoder. Thus the complexity of the encoder is still low. On the decoder side, on the one hand the proposed techniques consume additional computations, but on the other hand the number of feedback messages is reduced and when selected arithmetic decoding is simpler than repeated iterative LDPCA decoding. In this paper, we focus on the encoder complexity. In [Reference Slowack, Skorupa, Deligiannis, Lambert, Munteanu and Van de Walle18], a frame work to reduce the number of feedback requests is presented. This could be extended and adapted to the DVC codec presented here.
III. AMD WITH RESIDUAL MOTION COMPENSATION FOR DISTRIBUTED VIDEO CODING
This section proposes the AMD integrated with the residual MC. The AMD determines coding modes using not only the estimated cost for WZ coding as in [Reference Slowack13], but also utilizing the estimated WZ rate to optimize the mode decision during decoding. Moreover, the novel residual MC is integrated to make the noise modeling more accurate and thus the mode decision more effective by exploiting information from previously decoded frames. These proposed techniques are integrated in the cross-band DVC scheme [Reference Huang and Forchhammer6] as shown in Fig. 1 to improve the coding efficiency.
A) The AMD using estimated rate
The techniques for mode decision as employed in our codec extend the method in [Reference Slowack13]. Let X denote the original WZ frame and Y denote the side information frame. The cost for WZ coding a coefficient X k with index k in a particular coefficient band is defined as [Reference Slowack13]:
The first term in this sum denotes the conditional entropy of the quantized coefficient Q(X k) given the side information. The second term consists of the Lagrange parameter λ multiplied by the mean absolute distortion between the original coefficient X k and its reconstruction ![]() $\widehat{X}_{k}$, given the side information. Entropy and distortion are calculated as in [Reference Slowack13].
$\widehat{X}_{k}$, given the side information. Entropy and distortion are calculated as in [Reference Slowack13].
To calculate cost for skipping using (1) for the coefficient X k [Reference Slowack13], we set the entropy, H() = 0, representing the variable contribution after coding the mode. This gives:
where α is the noise parameter and 1/α gives the expected value, E[].
Often RD optimization in video coding is based on a Lagrangian expression J = D + λR, where D is the distortion and the rate. The expression we use (1) is, in these terms, based on the cost C = R + λD. One reason is that in skip mode R is small, thus by shifting lambda to the distortion term, the exact value of R is less important and we can even set the contribution of having coded the mode to 0 for skip.
If C skipk < C WZk for all coefficients in a coefficient band, all bitplanes in the coefficient band are skipped and the side information is used as the result. Otherwise, bitplane-level mode decision is performed to decide between bitplane-level skip, intra, or WZ coding as described in [Reference Slowack13]. The coding mode for each bitplane is communicated to the encoder through the feedback channel. It can be remarked that the mode information for each band is coded by 1 bit, e.g. 0 for skipped and 1 for not skipped. Thereafter, for a band which is not skipped, the information for each bitplane mode is coded by two bits for skip, intra, and WZ modes. Thus the number of feedback instances is reduced especially for skip coding at band level, but also for skip and intra at the bitplane level. We shall include the mode decision feedback bits in the code length when reporting results. Depending on the number of bands and corresponding bitplanes which are used for each QP point, the contribution by mode decision to the rates is relatively small compared to the total coding rate. For example, the mode information for QP 8, which has 15 bands coded in 63 bitplanes, needs the highest bits with 141 bits at most for coding modes (1 × 15 bands + 2 × 63 bitplanes not skipped).
One of the contributions in this paper is to extend the method above. Instead of using a sequence-independent formula for λ as in [Reference Slowack13], we propose to vary the Lagrange parameter depending on the sequence characteristics.
As a first step, results are generated for a range of lambdas and WZ quantization points, using the sequences Foreman, Coastguard, Hall Monitor, and Soccer (QCIF, 15Hz, and GOP2), which are typical for DVC, for training. Wherever necessary, the intra quantization parameter (QP) of the key frames is adjusted, so that the qualities of WZ frames and intra frames are comparable (i.e., within a 0.3 dB difference) for each of the RD points. For each sequence and WZ quantization matrix, the optimal lambda(s) are identified by selecting the set providing the best RD curve. These points are then used to create a graph of (optimal) lambdas as a function of the intra QP, as in Fig. 2. For each test sequence, the points were fitted with a continuous exponential function, where it can be noted that four reasonable QP points are considered sufficient in this work. This results in an approximation of the optimal lambda as a function of the intra QP, for each test sequence, i.e.

Fig. 2. Experiments on optimal λ.
where QP denotes the intra QP of the key frames, and a and b are constants. The optimal λ is obtained by the work in [Reference Slowack13] with fixed a = 7.6 and b = 0.1 for all sequences.
As shown in Fig. 2, the optimal λ differs among the sequences. Typically, for sequences with less motion (such as Hall Monitor), the optimal λ is lower to give more weight to the rate term in (1) and consequently encourage skip mode. On the other hand, for sequences with complex motion such as Soccer, the distortion introduced in the case of skip mode is significant due to errors in the side information, so that higher values for λ give better RD results.
The results in Fig. 2 are exploited to estimate the optimal λ on a frame-by-frame basis during decoding. The approach taken is – relatively simple – to look at the rate. Apart from the graph (Fig. 2) we also store the average rate per WZ frame associated with each of the points. For sequences with simple motion characteristics (e.g., Hall Monitor, Coastguard), for the same intra QP, the WZ rate is typically lower than for more complex sequences such as Foreman and Soccer. Therefore, during decoding, we first estimate the WZ rate and compare this estimate with the results in Fig. 2 to estimate the optimal lambda. Specifically, the WZ rate r i for the current frame is estimated as the median (med ) of the WZ rates r i−3, r i−2r i−1 of the three previously decoded WZ frames (as in [Reference Slowack, Skorupa, Deligiannis, Lambert, Munteanu and Van de Walle18]):
It can be noted that the first three WZ frames are coded using only intra and skip mode as in [Reference Slowack, Skorupa, Deligiannis, Lambert, Munteanu and Van de Walle18]. The estimated r i (4) is compared with rate points from the training sequences, which are shown in Fig. 2. We then obtain an estimate of the optimal lambda parameter for the current WZ frame to be decoded through interpolation.
In the training step, it may be noted that the optimal λs (in Fig. 2) are obtained along with the corresponding rate points. It is assumed that we have found the two closest rate points r 1, r 2, r 1 ≤ r i ≤ r 2, from the training sequences with the corresponding λr 1, λr 2, respectively. By means of a linear interpolation, the relations are expressed as:
As a result, we obtained λr i by
In summary, we can obtain λr i for each WZ frame with the estimated rate r i given the optimal λ versus IntraQP (in Fig. 2) and rate points from the training sequences as follows:
• Estimating the rate r i of the WZ frame based on the three previously decoded WZ frames by (4);
• Looking up the given rate points of the training sequences to get the two closest rate points r 1, r 2 with the corresponding λr 1, λr 2 satisfying r 1 ≤ r i ≤ r 2;
• Obtaining λr i by interpolation given by equation (6).
B) The residual MC
Noise modeling is one of the main issues impacting the accuracy of mode decisions. Both the WZ and skip costs as in (1) and (2) depend on the α parameter of the noise modeling. To improve performance and the noise modeling, this paper integrates the AMD (Section IIIA) with a technique exploiting information from previously decoded frames based on the assumption of useful correlation between the previous and current residual frames [Reference Luong, Rakêt and Forchhammer7]. This correlation was initially experimentally observed. This correlation can be expressed using the motion between the previous residue and the current residue, which we may hope to be similar to the motion between the previous SI and the current SI. This technique generates residual frames by compensating the motion between the previous SI frames and the current SI frame to the current residual frame to generate a more accurate noise distribution for noise modeling.
For a GOP of size two, let ![]() $\widehat{X}_{2n-2\omega}$ and
$\widehat{X}_{2n-2\omega}$ and ![]() $\widehat{X}_{2n}$ denote two decoded WZ frames at time 2n − 2ω and 2n, where ω denotes the index of the previously decoded ωth WZ frame before the current WZ frame at time 2n. Their associated SI frames are denoted by Y 2n−2ω and Y 2n, respectively. For objects that appear in the previous and current WZ frames, we expect the quality of the estimated SI, expressed by the distribution parameter to be similar. We shall try to capture this correlation using MC from frame 2n − 2ω to frame 2n. The motion between two the SI frames provides a way to capture this correlation. Here, each frame is split into N non-overlapped 8 × 8 blocks indexed by k, where 1 ≤ k ≤ N. It makes sense to assume that the motion vector v k of block k at position z k between
$\widehat{X}_{2n}$ denote two decoded WZ frames at time 2n − 2ω and 2n, where ω denotes the index of the previously decoded ωth WZ frame before the current WZ frame at time 2n. Their associated SI frames are denoted by Y 2n−2ω and Y 2n, respectively. For objects that appear in the previous and current WZ frames, we expect the quality of the estimated SI, expressed by the distribution parameter to be similar. We shall try to capture this correlation using MC from frame 2n − 2ω to frame 2n. The motion between two the SI frames provides a way to capture this correlation. Here, each frame is split into N non-overlapped 8 × 8 blocks indexed by k, where 1 ≤ k ≤ N. It makes sense to assume that the motion vector v k of block k at position z k between ![]() $\widehat{X}_{2n-2\omega}$ and
$\widehat{X}_{2n-2\omega}$ and ![]() $\widehat{X}_{2n}$ is the same as between Y 2n−2ω and Y 2n. This is represented as follows:
$\widehat{X}_{2n}$ is the same as between Y 2n−2ω and Y 2n. This is represented as follows:
A motion compensated estimate of ![]() $\widehat{X}_{2n}$ based on the motion v k,
$\widehat{X}_{2n}$ based on the motion v k, ![]() $\widehat{X}_{2n}^{MC}$, can be obtained by
$\widehat{X}_{2n}^{MC}$, can be obtained by
Based on the estimated SI frames Y 2n−2ω and Y 2n, the vectors v k are calculated using (7) within a search range (Φ of [16 × 16] pixels) as
where ![]() $\sum\nolimits_{\rm block}$ is the sum over all pixel positions z k. Thereafter,
$\sum\nolimits_{\rm block}$ is the sum over all pixel positions z k. Thereafter, ![]() $\widehat{X}_{2n}^{MC}$ is estimated by compensating
$\widehat{X}_{2n}^{MC}$ is estimated by compensating ![]() $\widehat{X}_{2n-2\omega}$ (8) for the selected motion v (9). Let R 2n denote the current residue at time 2n, generated by OBMC, and let
$\widehat{X}_{2n-2\omega}$ (8) for the selected motion v (9). Let R 2n denote the current residue at time 2n, generated by OBMC, and let ![]() $\widehat{R}_{2n}^{MC}$ denote the motion compensated residue, where R 2n and
$\widehat{R}_{2n}^{MC}$ denote the motion compensated residue, where R 2n and ![]() $\widehat{R}_{2n}^{MC}$ are equivalent to R 0 and R 1 (Section II, Fig. 1). Other motion estimation techniques may also be applied, e.g. OF [Reference Luong, Rakêt, Huang and Forchhammer17]. In the tests (Section IV), we shall apply both OBMC and OF.
$\widehat{R}_{2n}^{MC}$ are equivalent to R 0 and R 1 (Section II, Fig. 1). Other motion estimation techniques may also be applied, e.g. OF [Reference Luong, Rakêt, Huang and Forchhammer17]. In the tests (Section IV), we shall apply both OBMC and OF. ![]() $\widehat{R}_{2n}^{MC}$ can be estimated from
$\widehat{R}_{2n}^{MC}$ can be estimated from ![]() $\widehat{X}_{2n}^{MC}$ and Y 2n as follows:
$\widehat{X}_{2n}^{MC}$ and Y 2n as follows:
Finally, the compensated residue is obtained by inserting (8) in (10)
A motion compensated residue ![]() $\widehat{R}_{18}^{MC}$ (11) is predicted based on the decoded frame
$\widehat{R}_{18}^{MC}$ (11) is predicted based on the decoded frame ![]() $\widehat{X}_{2n-2}$ and the motion v between the SI frames Y 2n and Y 2n−2. To show the efficiency of the proposed technique, we calculate a difference between the motion compensated residue and an ideal residue calculated by X 2n − Y 2n−2 and compared this with a difference between the OBMC residue and the ideal residue. Figure 3 illustrates the frame by frame mean-square error (MSE) for Soccer (key frames QP=26) in order to compare the MSE between the OBMC residue and the ideal residue with the MSE between the motion compensated residue, denoted Motion, and the ideal residue. The MSE for Motion in Fig. 3 is consistently smaller than the MSE of the OBMC, i.e. the Motion residue is closer to the ideal residue than the OBMC residue.
$\widehat{X}_{2n-2}$ and the motion v between the SI frames Y 2n and Y 2n−2. To show the efficiency of the proposed technique, we calculate a difference between the motion compensated residue and an ideal residue calculated by X 2n − Y 2n−2 and compared this with a difference between the OBMC residue and the ideal residue. Figure 3 illustrates the frame by frame mean-square error (MSE) for Soccer (key frames QP=26) in order to compare the MSE between the OBMC residue and the ideal residue with the MSE between the motion compensated residue, denoted Motion, and the ideal residue. The MSE for Motion in Fig. 3 is consistently smaller than the MSE of the OBMC, i.e. the Motion residue is closer to the ideal residue than the OBMC residue.

Fig. 3. MSE (denoted OBMC) between the OBMC residue and the ideal residue versus MSE (denoted Motion) between the motion compensated residue and the ideal residue (for Frame 18 of Soccer).
C) The AMD MORE2SI codec
In order to further enhance the RD performance and test AMD, we shall also integrate AMD into the state-of-the-art, but also more complex, MORE2SI codec [Reference Luong, Rakêt and Forchhammer7], which is based on the SING2SI scheme [Reference Luong, Rakêt, Huang and Forchhammer17] additionally employing motion and residual re-estimation and a generalized reconstruction (Fig. 4). The MORE2SI scheme is here enhanced by integrating the AMD using the (decoder side) estimated rate of WZ frames to obtain a Lagrange parameter (Section IIIA). Figure 4 depicts the Adaptive Mode Decision MORE architecture using 2SI, which combines the powers of the MORE2SI scheme [Reference Luong, Rakêt and Forchhammer7] and the AMD technique (Sections IIIA + B) determining the three modes skip, arithmetic, or WZ coding of each bitplane. Initial experiments are reported in Section IV. It may be noted (Fig. 4) that the MORE2SI scheme [Reference Luong, Rakêt and Forchhammer7] applies OF as well as OBMC in the SI generation.

Fig. 4. Adaptive mode decision MORE video architecture.
IV. PERFORMANCE EVALUATION
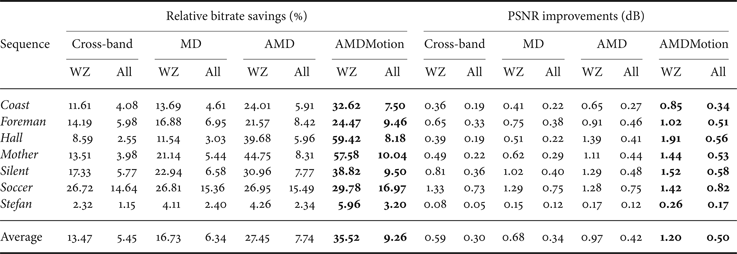
The RD performance of the proposed techniques are evaluated for the test sequences (149 frames of) Coastguard, Foreman, Hall Monitor, Mother–daughter, Silent, Soccer, and Stefan. In this work, the popular DVC benchmark sequences (QCIF, 15Hz, and GOP2) and only the luminance component of each frame are used for the performance evaluation and comparisons. The GOP size is 2, where odd frames are coded as key frames using H.264/AVC Intra and even frames are coded using WZ coding. Four RD points are considered corresponding to four predefined 4 × 4 quantization matrices Q1, Q4, Q7, and Q8 [4]. H.264/AVC Intra corresponds to the intra coding mode of the H.264/AVC codec JM 9.5 [19] in main profile. H.264/AVC Motion is obtained using the H.264/AVC main profile [19] exploiting temporal redundancy in an IBI structure. H.264/AVC No Motion denotes the H.264/AVC Motion but without applying any motion estimation. The proposed techniques are first integrated and tested in the cross-band DVC scheme in [Reference Huang and Forchhammer6], using the AMD as in Section IIIA and combined with the residual MC, as in Section IIIB, denoted by AMD and AMDMotion, respectively. Results of the proposed techniques are compared with those of the cross-band [Reference Huang and Forchhammer6] and the mode decision in [Reference Slowack13] integrated in the cross-band [Reference Huang and Forchhammer6], denoted by MD.
Table 1 presents the average bitrate savings, which are calculated as the increase of rate by DISCOVER over the rate of proposed technique, and equivalently the average PSNR improvements using the Bjøntegaard metric [Reference Bjøntegaard20] compared with the DISCOVER codec for WZ frames as well as for all frames. Compared with DISCOVER, the average bitrate saving for the proposed AMDMotion scheme is 35.5 and 9.26% (or equivalently the average improvement in PSNR is 1.2 and 0.5 dB) for WZ frames and all frames, respectively. Comparing AMDMotion with AMD, the AMDMotion scheme improves from 27.5% (0.97 dB) to 35.5% (1.2 dB) the average relative bitrate saving on WZ frames. In particular, the performance improvement is 59.4% (1.91 dB) and 8.18% (0.56 dB) for WZ frames and all frames for the low motion Hall Monitor sequence. Compared with the mode decision in [Reference Slowack13], AMD outperforms MD [Reference Slowack13] with average relative bitrate savings of 27.5% (0.97 dB) and 7.74% (0.42 dB) compared with 16.7 and 6.34% on WZ frames and all frames. Average bitrate savings (Bjøntegaard) of 22.1% (0.61 dB) and 3.8% (0.2 dB) are observed on WZ frames and all frames, compared with the cross-band [Reference Huang and Forchhammer6]. In these comparisons, it may be noted that LDPCA feedback bits is, as usual, not included, but the mode decision feedback bits for MD, AMD, and AMDMotion are included. As described in Section IIIA, only 1 bit is used to code skip mode at band level. If the mode is not a band level skip mode, even using the simple binary two bit code to signal the bit-plane mode contributes few bits compared with bits required by WZ coding of the bit-plane. Thus in comparison with cross-band and DISCOVER, the codecs using the new mode decision, MD, AMD, and AMDMotion furthermore require fewer LDPCA feedback requests as the skip and arithmetic coding modes do not invoke these requests.
Table 1. Bjøntegaard relative bitrate savings (%) and PSNR improvements (dB) over DISCOVER for WZ and all frames

The RD performance of the proposed AMD and AMDMotion codecs and H.264/AVC coding is also depicted in Fig. 5 for WZ frames and all frames. The AMDMotion codec gives a better RD performance than H.264/AVC Intra coding for all the sequences except Soccer and Stefan and also better than H.264/AVC No Motion for Coastguard. Furthermore, the proposed AMDMotion codec improves performance in particular for the lower motion sequences Hall Monitor, Silent, and Mother–daughter and lower rate points, e.g. Q1 and Q4, which are closer to the H264/AVC Motion and No Motion. In general, the RD performance of the AMDMotion codec clearly outperforms those of the cross-band scheme [Reference Huang and Forchhammer6] and DISCOVER [4].

Fig. 5. PSNR versus rate for the proposed codecs. (a) Hall Monitor, WZ frames, (b) Hall Monitor, all frames, (c) Mother–daughter, WZ frames, (d) Mother–daughter, all frames, (e) Coastguard, WZ frames, (f) Silent, WZ frames.
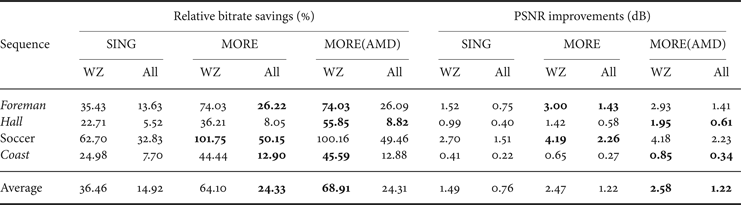
Furthermore, we performed an initial experiment by integrating the AMD technique with the recent advanced MORE2SI codec [Reference Luong, Rakêt and Forchhammer7] to test the performance experimentally. As the MORE2SI codec significantly improved both SI and noise modeling, the coding mode selected for higher rates is dominantly the WZ mode. Consequently, the results for MORE(AMD) are relatively improved the most at lower bitrates. For the higher bitrates, the results are expected to be close to those of the MORE2SI version. Therefore, the initial experiments were only conducted using the Adaptive Mode Decision MORE scheme (Section IIIC) by integrating the AMD for the RD points with the lowest rate. AMD is used for two RD points for Hall Monitor and one for Foreman, Soccer, and Coastguard (Section IIIC). The resulting codec called MORE(AMD) only applies skip mode and WZ coding mode (without considering intra mode). It achieved 68.9% in average bitrate saving (or equivalent the average improvement in PSNR is 2.6 dB) on WZ frames for GOP2 improving the 64.1% of MORE(2SI) (Table 2). For all frames GOP2, the MORE(AMD) gained 23.1% in average bitrate saving (or equivalent the average improvement in PSNR is 1.2 dB). The improvement over MORE(2SI) [Reference Luong, Rakêt and Forchhammer7] was mainly achieved by a significant improvement of the RD performance for the low motion sequence Hall Monitor with an average bitrate saving of 55.8% (1.9 dB) to the 36.2% (1.4 dB) achieved by the MORE(2SI) scheme [Reference Luong, Rakêt and Forchhammer7]. The performance of SING [Reference Luong, Rakêt, Huang and Forchhammer17] is also given for comparison. The RD performance of the proposed MORE(AMD) and other DVC codecs as well as H.264/AVC coding is also depicted in Fig. 6 for Hall Monitor for WZ frames. The code length obtained by replacing LDPCA coding with the Ideal Code Length (ICL) (Fig. 6), i.e. summing log of the inverse of the soft input values used to decode, is also given (MORE(AMD)) ICL. This may be interpreted as the potential gain in performance if a better Slepian-Wolf coder than LCPCA is developed and used.

Fig. 6. PSNR versus rate for the proposed DVC schemes for Hall on WZ frames.
Table 2. Bjøntegaard relative bitrate savings (%) and PSNR improvements (dB) over DISCOVER for WZ and all frames.

V. CONCLUSION
AMD DVC with residual MC was introduced to efficiently utilize skip, intra, and WZ modes based on rate estimation and combined with a more accurate correlation noise estimate. The AMD was based on the estimated rate to more accurately determine the modes during decoding. Moreover, the residual MC generated an additional residue to take advantage of correlation between the previously decoded and current noise residues. Experimental results show that the coding efficiency of the proposed AMDMotion scheme can robustly improve the RD performance of TDWZ DVC without changing the encoder. For a GOP size of 2 the average bitrate saving of the AMDMotion codec is 35.5 and 9.26% (or equivalently the average improvement in PSNR is 1.2 and 0.5 dB) on WZ frames and all frames compared with the DISCOVER codec. Furthermore, the MORE(AMD) codec integrating the AMD into the MORE codec, achieves 68.9% in average bitrate saving (or equivalently an average improvement in PSNR of 2.6 dB) on WZ frames for GOP2. The ICL result may be used to evaluate the potential for increased performance if SW coding is developed, which is more efficient than the LDPCA code applied.
Huynh Van Luong received the M.Sc. degree in Computer Engineering from the University of Ulsan, Korea in 2009. He received the Ph.D. degree with the Coding and Visual Communication Group in the Technical University of Denmark, Denmark in 2013. His research interests include image and video processing and coding, distributed source coding, visual communications, and multimedia systems.
Søren Forchhammer received the M.S. degree in Engineering and the Ph.D. degree from the Technical University of Denmark, Lyngby, in 1984 and 1988, respectively. Currently, he is a Professor with DTU Fotonik, Technical University of Denmark. He is the Head of the Coding and Visual Communication Group. His main interests include source coding, image and video coding, distributed source coding, distributed video coding, video quality, processing for image displays, communication theory, two-dimensional information theory, and visual communications.
Jürgen Slowack received the M.S. degree in Computer Engineering from Ghent University, Ghent Belgium, in 2006. From 2006 to 2012, he worked at Multimedia Laboratory, Ghent University – iMinds, obtaining the Ph.D. degree in 2010 and afterwards continuing his research as a post-doctoral researcher. Since 2012, he is working at Barco (Kortrijk, Belgium) in the context of video coding, streaming, networking, and transmission.
Jan De Cock obtained the M.S. and Ph.D. degrees in Engineering from Ghent University, Belgium, in 2004 and 2009, respectively. Since 2004 he has been working at Multimedia Laboratory, Ghent University, iMinds, where he is currently an Assistant Professor. In 2010, he obtained a post-doctoral research fellowship from the Flemish Agency for Innovation by Science and Technology (IWT) and in 2012, a post-doctoral research fellowship from the Research Foundation Flanders (FWO). His research interests include high-efficiency video coding and transcoding, scalable video coding, and multimedia applications.
Rik Van de Walle received master and Ph.D. degrees in Engineering from Ghent University, Belgium in July 1994 and February 1998, respectively. After a post-doctoral fellowship at the University of Arizona (Tucson, USA) he returned to Ghent, became a full-time Lecturer in 2001, and founded the Multimedia Lab at the Faculty of Engineering and Architecture. In 2004, he was appointed Full Professor, and in 2010 he became Senior Full Professor. In 2012, he became the Dean of Ghent University's Faculty of Engineering and Architecture. Within iMinds, Rik has been leading numerous research projects, and he is acting as the Head of Department of iMinds' Multimedia Technologies Research Department. His research interests include video coding and compression, game technology, media adaptation and delivery, multimedia information retrieval and understanding, knowledge representation and reasoning, and standardization activities in the domain of multimedia applications and services.