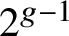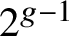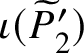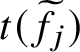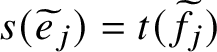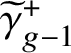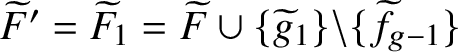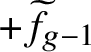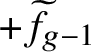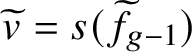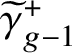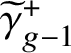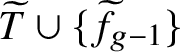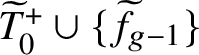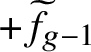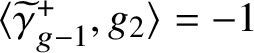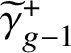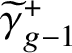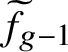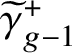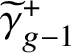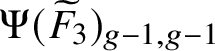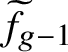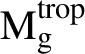1 Introduction
Kirchhoff’s celebrated matrix tree theorem states that the number of spanning trees of a connected finite graph G, also known as the complexity of G, is equal to the absolute value of the determinant of the reduced Laplacian matrix of G. From a tropical viewpoint, this number is also equal to the order of the Jacobian group
![]() $\operatorname {\mathrm {Jac}}(G)$
of G.
$\operatorname {\mathrm {Jac}}(G)$
of G.
In [Reference An, Baker, Kuperberg and ShokriehABKS14], Kirchhoff’s theorem was generalised to metric graphs and given a geometric interpretation. The Jacobian variety
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
of a metric graph
$\operatorname {\mathrm {Jac}}(\Gamma )$
of a metric graph
![]() $\Gamma $
of genus g is a real torus of dimension g, and its volume can be computed as a weighted sum over all spanning trees of
$\Gamma $
of genus g is a real torus of dimension g, and its volume can be computed as a weighted sum over all spanning trees of
![]() $\Gamma $
. Given a set
$\Gamma $
. Given a set
![]() $F\subset E(\Gamma )$
of g edges of
$F\subset E(\Gamma )$
of g edges of
![]() $\Gamma $
(with respect to a choice of model), denote by
$\Gamma $
(with respect to a choice of model), denote by
![]() $w(F)$
the product of the lengths of the edges in F. Then (see Theorem 1.5 in [Reference An, Baker, Kuperberg and ShokriehABKS14])
$w(F)$
the product of the lengths of the edges in F. Then (see Theorem 1.5 in [Reference An, Baker, Kuperberg and ShokriehABKS14])
 $$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\sum_{F}w(F),\\[-18pt]\nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\sum_{F}w(F),\\[-18pt]\nonumber \end{align} $$
where the sum is taken over those subsets F such that
![]() $\Gamma \backslash F$
is a spanning tree of
$\Gamma \backslash F$
is a spanning tree of
![]() $\Gamma $
.
$\Gamma $
.
The weighted matrix-tree theorem can be proved by a direct application of the Cauchy–Binet formula (see Remark 5.7 in [Reference An, Baker, Kuperberg and ShokriehABKS14]), but the authors give a geometric proof in terms of a canonical representability result for tropical divisor classes, which we briefly recall. Let
![]() $\Phi :\operatorname {\mathrm {Sym}}^g(\Gamma )\to \operatorname {\mathrm {Pic}}^g(\Gamma )$
be the tropical Abel–Jacobi map, sending an effective degree g divisor D to its linear equivalence class. A divisor
$\Phi :\operatorname {\mathrm {Sym}}^g(\Gamma )\to \operatorname {\mathrm {Pic}}^g(\Gamma )$
be the tropical Abel–Jacobi map, sending an effective degree g divisor D to its linear equivalence class. A divisor
![]() $D=P_1+\cdots +P_g$
is called a break divisor if each
$D=P_1+\cdots +P_g$
is called a break divisor if each
![]() $P_i$
is supported on an edge
$P_i$
is supported on an edge
![]() $e_i$
in such a way that
$e_i$
in such a way that
![]() $\{e_1,\ldots ,e_g\}$
is the complement of a spanning tree of
$\{e_1,\ldots ,e_g\}$
is the complement of a spanning tree of
![]() $\Gamma $
. By a result of Mikhalkin and Zharkov [Reference Mikhalkin and ZharkovMZ08], the map
$\Gamma $
. By a result of Mikhalkin and Zharkov [Reference Mikhalkin and ZharkovMZ08], the map
![]() $\Phi $
has a canonical continuous section, whose image is the set of break divisors in
$\Phi $
has a canonical continuous section, whose image is the set of break divisors in
![]() $\operatorname {\mathrm {Sym}}^g(\Gamma )$
. Hence,
$\operatorname {\mathrm {Sym}}^g(\Gamma )$
. Hence,
![]() $\operatorname {\mathrm {Pic}}^g(\Gamma )$
(and, by translation,
$\operatorname {\mathrm {Pic}}^g(\Gamma )$
(and, by translation,
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
) has a canonical cellular decomposition coming from the cells of
$\operatorname {\mathrm {Jac}}(\Gamma )$
) has a canonical cellular decomposition coming from the cells of
![]() $\operatorname {\mathrm {Sym}}^g(\Gamma )$
parametrised by the spanning trees of
$\operatorname {\mathrm {Sym}}^g(\Gamma )$
parametrised by the spanning trees of
![]() $\Gamma $
. Computing the volume of
$\Gamma $
. Computing the volume of
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
in terms of this decomposition gives equation (1), where the terms in the right-hand side correspond to the volumes of the individual cells. We note that the results of [Reference An, Baker, Kuperberg and ShokriehABKS14] can be reinterpreted as saying that the Abel–Jacobi map
$\operatorname {\mathrm {Jac}}(\Gamma )$
in terms of this decomposition gives equation (1), where the terms in the right-hand side correspond to the volumes of the individual cells. We note that the results of [Reference An, Baker, Kuperberg and ShokriehABKS14] can be reinterpreted as saying that the Abel–Jacobi map
![]() $\Phi $
is a harmonic morphism of polyhedral spaces of degree 1 (see Remark 2.5).
$\Phi $
is a harmonic morphism of polyhedral spaces of degree 1 (see Remark 2.5).
The purpose of this article is to prove analogous results for the tropical Prym variety associated to a free double cover of metric graphs. Given an étale double cover
![]() $f:\widetilde {C}\to C$
of smooth algebraic curves of genera
$f:\widetilde {C}\to C$
of smooth algebraic curves of genera
![]() $2g-1$
and g respectively, the kernel of the norm map
$2g-1$
and g respectively, the kernel of the norm map
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {C})\to \operatorname {\mathrm {Jac}}(C)$
has two connected components and the even component is an abelian variety of dimension
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {C})\to \operatorname {\mathrm {Jac}}(C)$
has two connected components and the even component is an abelian variety of dimension
![]() $g-1$
, known as the Prym variety
$g-1$
, known as the Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
of the double cover. Prym varieties have been extensively studied following Mumford’s seminal paper [Reference MumfordMum74], as they are one of only few instances of abelian varieties that can be described explicitly. Furthermore, they play a key role in rationality questions for threefolds [Reference Clemens and GriffithsCG72] and in constructing compact hyper-Kähler manifolds [Reference Laza, Saccà and VoisinLSV17].
$\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
of the double cover. Prym varieties have been extensively studied following Mumford’s seminal paper [Reference MumfordMum74], as they are one of only few instances of abelian varieties that can be described explicitly. Furthermore, they play a key role in rationality questions for threefolds [Reference Clemens and GriffithsCG72] and in constructing compact hyper-Kähler manifolds [Reference Laza, Saccà and VoisinLSV17].
The notion of an étale cover of algebraic curves has two natural analogues in tropical geometry. One can consider free covers
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
, which are covering spaces in the topological sense: the map
$\pi :\widetilde {\Gamma }\to \Gamma $
, which are covering spaces in the topological sense: the map
![]() $\pi $
is a local homeomorphism at each point and an isometry if the graphs are metric. It is often necessary to consider the more general unramified covers, which are finite harmonic morphisms of metric graphs satisfying a numerical Riemann–Hurwitz condition. This notion does not have an analogue for finite graphs. The tropicalisation of an étale cover of algebraic curves is an unramified cover of metric graphs but not necessarily free.
$\pi $
is a local homeomorphism at each point and an isometry if the graphs are metric. It is often necessary to consider the more general unramified covers, which are finite harmonic morphisms of metric graphs satisfying a numerical Riemann–Hurwitz condition. This notion does not have an analogue for finite graphs. The tropicalisation of an étale cover of algebraic curves is an unramified cover of metric graphs but not necessarily free.
The tropical Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
associated to an unramified double cover
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
associated to an unramified double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is defined in analogy with its algebraic counterpart [Reference Jensen and LenJL18, Definition 6.2]. Specifically,
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is defined in analogy with its algebraic counterpart [Reference Jensen and LenJL18, Definition 6.2]. Specifically,
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is the connected component of the identity of the kernel of the tropical norm map
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is the connected component of the identity of the kernel of the tropical norm map
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
(note that in the tropical case, the kernel has two connected components if
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
(note that in the tropical case, the kernel has two connected components if
![]() $\pi $
is free and one if
$\pi $
is free and one if
![]() $\pi $
is unramified but not free). As shown in [Reference Len and UlirschLU19, Theorem B], this construction commutes with tropicalisation. Namely, if
$\pi $
is unramified but not free). As shown in [Reference Len and UlirschLU19, Theorem B], this construction commutes with tropicalisation. Namely, if
![]() $\pi $
is the tropicalisation of an étale double cover
$\pi $
is the tropicalisation of an étale double cover
![]() $f:\widetilde {C}\to C$
of algebraic curves, then the tropical abelian variety
$f:\widetilde {C}\to C$
of algebraic curves, then the tropical abelian variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is the skeleton of the Berkovich analytification of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is the skeleton of the Berkovich analytification of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
and the corresponding Abel–Prym maps commute (the corresponding result for Jacobians was proved in [Reference Baker and RabinoffBR15]). This observation has recently led to new results concerning the dimensions of Brill–Noether loci in Prym varieties [Reference Creech, Len, Ritter and WuCLRW20, Corollary B].
$\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
and the corresponding Abel–Prym maps commute (the corresponding result for Jacobians was proved in [Reference Baker and RabinoffBR15]). This observation has recently led to new results concerning the dimensions of Brill–Noether loci in Prym varieties [Reference Creech, Len, Ritter and WuCLRW20, Corollary B].
In the current article, we consider only free double covers of finite and metric graphs. We first compute the order of the Prym group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
of a free double cover
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
of a free double cover
![]() $p:\widetilde {G}\to G$
of a finite graph G of genus g. The finite group
$p:\widetilde {G}\to G$
of a finite graph G of genus g. The finite group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is a canonically defined index 2 subgroup of the kernel of the norm map
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is a canonically defined index 2 subgroup of the kernel of the norm map
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(G)$
. In the spirit of Kirchhoff’s formula, the order of
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(G)$
. In the spirit of Kirchhoff’s formula, the order of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is a weighted sum over certain
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is a weighted sum over certain
![]() $(g-1)$
-element subsets of
$(g-1)$
-element subsets of
![]() $E(G)$
: given a subset
$E(G)$
: given a subset
![]() $F\subset E(G)$
of
$F\subset E(G)$
of
![]() $g-1$
edges of G, we say that F is an odd genus 1 decomposition of rank r if
$g-1$
edges of G, we say that F is an odd genus 1 decomposition of rank r if
![]() $G\backslash F$
consists of r connected components of genus 1, each having connected preimage in
$G\backslash F$
consists of r connected components of genus 1, each having connected preimage in
![]() $\widetilde {G}$
.
$\widetilde {G}$
.
Kirchhoff–Prym formula (Proposition 3.2)
The order of the Prym group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
of a free double cover
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
of a free double cover
![]() $p:\widetilde {G}\to G$
of finite graphs is equal to
$p:\widetilde {G}\to G$
of finite graphs is equal to
 $$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\sum_{r=1}^g 4^{r-1}C_r,\\[-18pt] \end{align*} $$
$$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\sum_{r=1}^g 4^{r-1}C_r,\\[-18pt] \end{align*} $$
where
![]() $C_r$
is the number of odd genus 1 decompositions of G of rank r.
$C_r$
is the number of odd genus 1 decompositions of G of rank r.
This formula has already been obtained by Zaslavsky in the seminal paper [Reference ZaslavskyZas82] as the determinant of the signed Laplacian matrix of the graph G (see Theorem 8A.4 in [Reference ZaslavskyZas82]) and was later explicitly interpreted as the order of the kernel of the norm map by Reiner and Tseng (see Proposition 9.9 in [Reference Reiner and TsengRT14]). We give an alternative proof, by comparing the Ihara zeta functions
![]() $\zeta (s,\widetilde {G})$
and
$\zeta (s,\widetilde {G})$
and
![]() $\zeta (s,G)$
of the graphs
$\zeta (s,G)$
of the graphs
![]() $\widetilde {G}$
and G. By the work of Stark and Terras [Reference Stark and TerrasST96, Reference Stark and TerrasST00], the quotient
$\widetilde {G}$
and G. By the work of Stark and Terras [Reference Stark and TerrasST96, Reference Stark and TerrasST00], the quotient
![]() $\zeta (s,\widetilde {G})/\zeta (s,G)$
for a free double cover
$\zeta (s,\widetilde {G})/\zeta (s,G)$
for a free double cover
![]() $p:\widetilde {G}\to G$
is the L-function of the cover evaluated at the nontrivial representation of the Galois group
$p:\widetilde {G}\to G$
is the L-function of the cover evaluated at the nontrivial representation of the Galois group
![]() $\mathbb {Z}/2\mathbb {Z}$
, and we use the L-function to compute the order of the Prym group. To the best of our knowledge, this is the first application of the Ihara zeta function to tropical geometry.
$\mathbb {Z}/2\mathbb {Z}$
, and we use the L-function to compute the order of the Prym group. To the best of our knowledge, this is the first application of the Ihara zeta function to tropical geometry.
We then derive a weighted version of the Kirchhoff–Prym formula for the volume of the Prym variety of a free double cover of metric graphs, in the same way that equation (1) generalises Kirchhoff’s theorem.
Theorem A Theorem 3.4
The volume of the tropical Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
of a free double cover
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
of a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is given by
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is given by
 $$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align*} $$
where the sum is taken over all odd genus 1 decompositions F of
![]() $\Gamma $
and where
$\Gamma $
and where
![]() $w(F)$
is the product of the lengths of the edges in F.
$w(F)$
is the product of the lengths of the edges in F.
In the second part of our article, we derive a geometric interpretation for the volume formula for the tropical Prym variety, in the spirit of [Reference An, Baker, Kuperberg and ShokriehABKS14]. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs and let
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs and let
![]() $\iota :\widetilde {\Gamma }\to \widetilde {\Gamma }$
be the associated involution. Consider the Abel–Prym map
$\iota :\widetilde {\Gamma }\to \widetilde {\Gamma }$
be the associated involution. Consider the Abel–Prym map
![]() $\Psi $
associated to
$\Psi $
associated to
![]() $\pi $
,
$\pi $
,
where
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
denotes the component of
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
denotes the component of
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
of the same parity as
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
of the same parity as
![]() $g-1$
.
$g-1$
.
Our principal result states that
![]() $\Psi $
is a harmonic morphism of polyhedral spaces of degree
$\Psi $
is a harmonic morphism of polyhedral spaces of degree
![]() $2^{g-1}$
(as in Definition 2.12). The space
$2^{g-1}$
(as in Definition 2.12). The space
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
has a natural polyhedral decomposition, with the top-dimensional cells
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
has a natural polyhedral decomposition, with the top-dimensional cells
![]() $C(\widetilde {F})$
indexed by multisets
$C(\widetilde {F})$
indexed by multisets
![]() $\widetilde {F}\subset E(\widetilde {\Gamma })$
of
$\widetilde {F}\subset E(\widetilde {\Gamma })$
of
![]() $g-1$
edges of
$g-1$
edges of
![]() $\widetilde {\Gamma }$
. We define the degree of a top-dimensional cell to be
$\widetilde {\Gamma }$
. We define the degree of a top-dimensional cell to be
 $\deg _{\Psi }(\widetilde {F})=2^{r(\widetilde {F})-1}$
if
$\deg _{\Psi }(\widetilde {F})=2^{r(\widetilde {F})-1}$
if
![]() $p(\widetilde {F})$
consists of distinct edges and is an odd genus 1 decomposition of rank
$p(\widetilde {F})$
consists of distinct edges and is an odd genus 1 decomposition of rank
![]() $r(\widetilde {F})$
and zero otherwise. Then the Abel–Prym map
$r(\widetilde {F})$
and zero otherwise. Then the Abel–Prym map
![]() $\Psi $
contracts the cell
$\Psi $
contracts the cell
![]() $C(\widetilde {F})$
if and only if
$C(\widetilde {F})$
if and only if
![]() $\deg _{\Psi }(\widetilde {F})=0$
. Furthermore,
$\deg _{\Psi }(\widetilde {F})=0$
. Furthermore,
![]() $\Psi $
is harmonic with respect to the degree, meaning that it satisfies a balancing condition around every codimension 1 cell of
$\Psi $
is harmonic with respect to the degree, meaning that it satisfies a balancing condition around every codimension 1 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
. This implies that we can extend the degree function to all of
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
. This implies that we can extend the degree function to all of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
in such a way that the sum of the degrees in each fibre of
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
in such a way that the sum of the degrees in each fibre of
![]() $\Psi $
is a finite constant, called the global degree of
$\Psi $
is a finite constant, called the global degree of
![]() $\Psi $
. To compute the global degree, we first observe that the harmonicity of the Abel–Prym map allows us to express the volume of
$\Psi $
. To compute the global degree, we first observe that the harmonicity of the Abel–Prym map allows us to express the volume of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
in terms of its degree. Comparing the result with Theorem A, we find that the global degree is in fact
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
in terms of its degree. Comparing the result with Theorem A, we find that the global degree is in fact
![]() $2^{g-1}$
. The factors
$2^{g-1}$
. The factors
![]() $4^{r(F)-1}$
in the weighted Kirchhoff–Prym formula represent squares of the local degrees of
$4^{r(F)-1}$
in the weighted Kirchhoff–Prym formula represent squares of the local degrees of
![]() $\Psi $
.
$\Psi $
.
Summarising, we obtain a semi-canonical representability result for tropical Prym divisors.
Theorem B Theorem 5.1
The Abel–Prym map
![]() $\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
associated to a free double cover
$\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
associated to a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is a harmonic morphism of polyhedral spaces of degree
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is a harmonic morphism of polyhedral spaces of degree
![]() $2^{g-1}$
. In particular, there is a degree map
$2^{g-1}$
. In particular, there is a degree map
![]() $\deg _{\Psi }:\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \mathbb {Z}_{\geq 0}$
such that any element of
$\deg _{\Psi }:\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \mathbb {Z}_{\geq 0}$
such that any element of
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
has exactly
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
has exactly
![]() $2^{g-1}$
representatives of the form
$2^{g-1}$
representatives of the form
![]() $\widetilde {D}-\iota (\widetilde {D})$
counted with multiplicity
$\widetilde {D}-\iota (\widetilde {D})$
counted with multiplicity
![]() $\deg _{\Psi } (\widetilde {D})$
, where
$\deg _{\Psi } (\widetilde {D})$
, where
![]() $\widetilde {D}$
is an effective divisor of degree
$\widetilde {D}$
is an effective divisor of degree
![]() $g-1$
.
$g-1$
.
We note that a divisor in
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
may have infinitely many representatives of the form
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
may have infinitely many representatives of the form
![]() $\widetilde {D}-\iota (\widetilde {D})$
with
$\widetilde {D}-\iota (\widetilde {D})$
with
![]() $\deg _{\Psi }(\widetilde {D})=0$
, but a generic divisor in
$\deg _{\Psi }(\widetilde {D})=0$
, but a generic divisor in
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
only has representatives
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
only has representatives
![]() $\widetilde {D}-\iota (\widetilde {D})$
with
$\widetilde {D}-\iota (\widetilde {D})$
with
![]() $\deg _{\Psi }(\widetilde {D})>0$
and hence finitely many in total.
$\deg _{\Psi }(\widetilde {D})>0$
and hence finitely many in total.
The canonical representability result of [Reference An, Baker, Kuperberg and ShokriehABKS14] also holds in the integral setting, after fixing a generic element
![]() $\lambda \in \operatorname {\mathrm {Jac}}(\Gamma )$
: given a model G of
$\lambda \in \operatorname {\mathrm {Jac}}(\Gamma )$
: given a model G of
![]() $\Gamma $
, any class in
$\Gamma $
, any class in
![]() $\operatorname {\mathrm {Pic}}^g(G)$
is represented by a unique break divisor
$\operatorname {\mathrm {Pic}}^g(G)$
is represented by a unique break divisor
![]() $D\in \operatorname {\mathrm {Sym}}^g(G)$
. Shifting the break divisor by
$D\in \operatorname {\mathrm {Sym}}^g(G)$
. Shifting the break divisor by
![]() $\lambda $
, we obtain a divisor supported on the complement of a spanning tree of G. See [Reference An, Baker, Kuperberg and ShokriehABKS14, Remark 4.26] and [Reference Backman, Baker and C. H.BBY19, Example 1.3.4] for more detail. An analogous correspondence result does not hold for Prym groups. In fact, the discrete Abel–Prym map
$\lambda $
, we obtain a divisor supported on the complement of a spanning tree of G. See [Reference An, Baker, Kuperberg and ShokriehABKS14, Remark 4.26] and [Reference Backman, Baker and C. H.BBY19, Example 1.3.4] for more detail. An analogous correspondence result does not hold for Prym groups. In fact, the discrete Abel–Prym map
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {G})\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {G}/G)$
associated to a free double cover
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {G})\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {G}/G)$
associated to a free double cover
![]() $p:\widetilde {G}\to G$
of finite graphs is not even surjective in general (see Example 2.9).
$p:\widetilde {G}\to G$
of finite graphs is not even surjective in general (see Example 2.9).
We believe that suitable generalisations of Theorems A and B hold for unramified double covers of metric graphs, which is the more general framework considered in [Reference Jensen and LenJL18] and [Reference Len and UlirschLU19]. To derive and prove them using the methods of our article, it would first be necessary to develop a theory of L-functions of unramified Galois covers of graphs, extending the theory for free covers developed in [Reference Stark and TerrasST96] and [Reference Stark and TerrasST00]. Such a theory should be a part of a more general theory of Ihara zeta functions of graphs of groups. This first step in this direction is the paper [Reference ZakharovZak20] by the second author. It would also be interesting to determine whether the Prym construction generalises to other tropical abelian covers (see [Reference Len, Ulirsch and ZakharovLUZ19]).
1.1 The algebraic Abel–Prym map and its tropicalisation
Let C be a smooth algebraic curve of genus g and let
![]() $\Phi ^d:\operatorname {\mathrm {Sym}}^d(C)\to \operatorname {\mathrm {Pic}}^d(C)$
be the degree d Abel–Jacobi map. It is a classical result that
$\Phi ^d:\operatorname {\mathrm {Sym}}^d(C)\to \operatorname {\mathrm {Pic}}^d(C)$
be the degree d Abel–Jacobi map. It is a classical result that
![]() $\Phi ^d$
has degree 1 when
$\Phi ^d$
has degree 1 when
![]() $d\leq g$
and is birational when
$d\leq g$
and is birational when
![]() $d=g$
[Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Chapter 1.3]. The degree d Abel–Prym map
$d=g$
[Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Chapter 1.3]. The degree d Abel–Prym map
![]() $\Psi ^d:\operatorname {\mathrm {Sym}}^d(\widetilde {C})\to \operatorname {\mathrm {Prym}}^{[d]}(\widetilde {C}/C)$
corresponding to an unramified double cover
$\Psi ^d:\operatorname {\mathrm {Sym}}^d(\widetilde {C})\to \operatorname {\mathrm {Prym}}^{[d]}(\widetilde {C}/C)$
corresponding to an unramified double cover
![]() $\pi :\widetilde {C}\to C$
of smooth algebraic curves is defined by
$\pi :\widetilde {C}\to C$
of smooth algebraic curves is defined by
![]() $\Psi ^d(\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
. Unlike the Abel–Jacobi map, the degree of
$\Psi ^d(\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
. Unlike the Abel–Jacobi map, the degree of
![]() $\Psi ^d$
depends nontrivially on the Brill–Noether type of C. For example, if
$\Psi ^d$
depends nontrivially on the Brill–Noether type of C. For example, if
![]() $d=1$
, then the degree is equal to
$d=1$
, then the degree is equal to
![]() $2$
if C is hyperelliptic and
$2$
if C is hyperelliptic and
![]() $1$
otherwise. However, the degree of the Abel–Prym map when
$1$
otherwise. However, the degree of the Abel–Prym map when
![]() $d=g-1$
is always
$d=g-1$
is always
![]() $2^{g-1}$
. We are very grateful to Sebastian Casalaina-Martin for a proof of this result (and a number of others) about the Abel–Prym map, which we have included as an Appendix to this article.
$2^{g-1}$
. We are very grateful to Sebastian Casalaina-Martin for a proof of this result (and a number of others) about the Abel–Prym map, which we have included as an Appendix to this article.
Given that the algebraic Abel–Prym map
![]() $\Psi ^{g-1}$
has degree
$\Psi ^{g-1}$
has degree
![]() $2^{g-1}$
, it is tempting to derive Theorem B from the corresponding algebraic statement by a tropicalisation argument (the same argument would also give an alternative proof of one of the principal results of [Reference An, Baker, Kuperberg and ShokriehABKS14], namely, the existence of a canonical section of the Abel–Jacobi map). It is well known that the tropicalisation of a degree d map of algebraic curves is a harmonic morphism of metric graphs of the same degree d. However, we are unaware of a suitable generalisation of this result to higher dimension, and the derivation of such a result is beyond the scope of this article.
$2^{g-1}$
, it is tempting to derive Theorem B from the corresponding algebraic statement by a tropicalisation argument (the same argument would also give an alternative proof of one of the principal results of [Reference An, Baker, Kuperberg and ShokriehABKS14], namely, the existence of a canonical section of the Abel–Jacobi map). It is well known that the tropicalisation of a degree d map of algebraic curves is a harmonic morphism of metric graphs of the same degree d. However, we are unaware of a suitable generalisation of this result to higher dimension, and the derivation of such a result is beyond the scope of this article.
Motivated by this similarity and by the results of the Appendix, we propose the following conjecture.
Conjecture 1.1. Let
![]() $f:\widetilde {C}\to C$
be an étale double cover of algebraic curves tropicalising to a free double cover
$f:\widetilde {C}\to C$
be an étale double cover of algebraic curves tropicalising to a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs. Then the degrees of the algebraic and tropical Abel–Prym maps
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs. Then the degrees of the algebraic and tropical Abel–Prym maps
![]() $\Psi ^d$
for
$\Psi ^d$
for
![]() $d\leq g-2$
associated to f and
$d\leq g-2$
associated to f and
![]() $\pi $
coincide. In particular, the degree of
$\pi $
coincide. In particular, the degree of
![]() $\Psi ^d$
is bounded by
$\Psi ^d$
is bounded by
![]() $2^d$
.
$2^d$
.
We stress that the tropical and algebraic results presented in this article are derived via entirely different techniques and are independent of each other.
1.2 Degenerations of abelian varieties
Polyhedral decompositions of real tori, such as the ones described above, suggest an interesting connection with degenerations of abelian varieties and compactifications of their moduli spaces.
The Jacobian of a nodal curve is a semi-abelian variety that is not proper in general. There are numerous compactifications constructed by various authors that depend on a choice of degree and an ample line bundle (e.g., [Reference EstevesEst01, Reference SimpsonSim94]). In degree g, these constructions coincide [Reference CaporasoCap94] and the strata in the compactification are in bijection with certain orientations on the dual graph of the curve [Reference ChristChr18, Theorem 3.2.8]. In fact, the same strata are in an order reversing bijection with the cells in the ABKS decomposition of the tropical Jacobian [Reference CaporasoCap18, Theorem 4.3.4]. More generally, each Simpson and Esteves compactified Jacobian of C can be constructed from a polyhedral decomposition of the tropical Jacobian of the dual graph of C [Reference Christ, Payne and ShenCPS19, Theorem 1.1]. An analogous statement in degree g holds uniformly over the moduli space of curves [Reference Abreu, Andria, Pacini and TaboadaAAPT19].
The situation is more subtle for Prym varieties. Given an admissible double cover
![]() $\widetilde {C}\to C$
of nodal curves, the identity component of the kernel of the norm map is, again, a nonproper semi-abelian variety. There are various approaches for compactifying the Prym variety (e.g., [Reference Alexeev, Birkenhake and HulekABH02, Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMGHL17]). However, unlike the case of Jacobians, the Prym–Torelli map
$\widetilde {C}\to C$
of nodal curves, the identity component of the kernel of the norm map is, again, a nonproper semi-abelian variety. There are various approaches for compactifying the Prym variety (e.g., [Reference Alexeev, Birkenhake and HulekABH02, Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMGHL17]). However, unlike the case of Jacobians, the Prym–Torelli map
![]() $\mathcal {R}_g\to A_{g-1}$
from the moduli space of étale double covers to the moduli space of abelian varieties does not extend to the boundary for any reasonable toroidal compactification of
$\mathcal {R}_g\to A_{g-1}$
from the moduli space of étale double covers to the moduli space of abelian varieties does not extend to the boundary for any reasonable toroidal compactification of
![]() $A_{g-1}$
[Reference VologodskyVol02, Reference Friedman and SmithFS86].
$A_{g-1}$
[Reference VologodskyVol02, Reference Friedman and SmithFS86].
We therefore ask the following.
Question 1.2. Given an admissible double cover
![]() $\widetilde {C}\to C$
with tropicalisation
$\widetilde {C}\to C$
with tropicalisation
![]() $\widetilde {\Gamma }\to \Gamma $
, do the cells of the semi-canonical decomposition of the tropical Prym variety
$\widetilde {\Gamma }\to \Gamma $
, do the cells of the semi-canonical decomposition of the tropical Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
described in Theorem B correspond to the boundary strata of an appropriate compactification of the Prym variety
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
described in Theorem B correspond to the boundary strata of an appropriate compactification of the Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
?
$\operatorname {\mathrm {Prym}}(\widetilde {C}/C)$
?
A positive answer would suggest a path to a natural compactification of the moduli space of abelian varieties such that the map
![]() $\mathcal {R}_g\to A_{g-1}$
extends to the boundary.
$\mathcal {R}_g\to A_{g-1}$
extends to the boundary.
2 Preliminaries
In this section, we review the necessary material about graphs, metric graphs, tropical ppavs, Jacobians, Prym varieties and polyhedral spaces. The only new material is found in Subsection 2.5, where we define the Prym group of a free double cover of graphs. Throughout this article, we consider both finite and metric graphs, which we distinguish by using Latin and Greek letters, respectively. Graphs are allowed to have loops and multi-edges but not legs, and we do not consider the more general setting of graphs with vertex weights. All graphs are assumed to be connected unless stated otherwise.
2.1 Graphs and free double covers
We denote the vertex and edge sets of a finite graph G respectively by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
and its genus by
$E(G)$
and its genus by
![]() $g(G)=|E(G)|-|V(G)|+1$
. An orientation of a graph G is a choice of direction for each edge, allowing us to define source and target maps
$g(G)=|E(G)|-|V(G)|+1$
. An orientation of a graph G is a choice of direction for each edge, allowing us to define source and target maps
![]() $s,t:E(G)\to V(G)$
. For a vertex
$s,t:E(G)\to V(G)$
. For a vertex
![]() $v\in V(G)$
, the tangent space
$v\in V(G)$
, the tangent space
![]() $T_vG$
is the set of edges emanating from v and the valency is
$T_vG$
is the set of edges emanating from v and the valency is
![]() $\operatorname {\mathrm {val}}(v)=\#T_vG$
(where each loop at v counts twice towards the valency). A metric graph
$\operatorname {\mathrm {val}}(v)=\#T_vG$
(where each loop at v counts twice towards the valency). A metric graph
![]() $\Gamma $
is the compact metric space obtained from a finite graph G by assigning positive lengths
$\Gamma $
is the compact metric space obtained from a finite graph G by assigning positive lengths
![]() $\ell :E(G)\to \mathbb {R}_{>0}$
to its edges and identifying each edge
$\ell :E(G)\to \mathbb {R}_{>0}$
to its edges and identifying each edge
![]() $e\in E(G)$
with a closed interval of length
$e\in E(G)$
with a closed interval of length
![]() $\ell (e)$
. The pair
$\ell (e)$
. The pair
![]() $(G,\ell )$
is called a model of
$(G,\ell )$
is called a model of
![]() $\Gamma $
and we define
$\Gamma $
and we define
![]() $g(\Gamma )=g(G)$
. A metric graph has infinitely many models, obtained by arbitrarily subdividing edges, but the genus
$g(\Gamma )=g(G)$
. A metric graph has infinitely many models, obtained by arbitrarily subdividing edges, but the genus
![]() $g(\Gamma )$
does not depend on the choice of model.
$g(\Gamma )$
does not depend on the choice of model.
The only maps of finite graphs that we consider in our article are free double covers
![]() $p:\widetilde {G}\to G$
. Such a map consists of a pair of surjective 2-to-1 maps
$p:\widetilde {G}\to G$
. Such a map consists of a pair of surjective 2-to-1 maps
![]() $p:V(\widetilde {G})\to V(G)$
and
$p:V(\widetilde {G})\to V(G)$
and
![]() $p:E(\widetilde {G})\to E(G)$
that preserve adjacency and such that the map is an isomorphism in the neighbourhood of every vertex of
$p:E(\widetilde {G})\to E(G)$
that preserve adjacency and such that the map is an isomorphism in the neighbourhood of every vertex of
![]() $\widetilde {G}$
. Specifically, for any pair of vertices
$\widetilde {G}$
. Specifically, for any pair of vertices
![]() $\widetilde {v}$
and v with
$\widetilde {v}$
and v with
![]() $p(\widetilde {v})=v$
and for each edge
$p(\widetilde {v})=v$
and for each edge
![]() $e\in E(G)$
attached to v, there is a unique edge
$e\in E(G)$
attached to v, there is a unique edge
![]() $\widetilde {e}\in E(G)$
attached to
$\widetilde {e}\in E(G)$
attached to
![]() $\widetilde {v}$
that maps to e. We say that
$\widetilde {v}$
that maps to e. We say that
![]() $p:\widetilde {G}\to G$
is oriented if
$p:\widetilde {G}\to G$
is oriented if
![]() $\widetilde {G}$
and G are oriented graphs and if the map p preserves the orientation. There is a naturally defined involution
$\widetilde {G}$
and G are oriented graphs and if the map p preserves the orientation. There is a naturally defined involution
![]() $\iota :\widetilde {G}\to \widetilde {G}$
on the source graph that exchanges the two sheets of the cover. It is easy to see that if G has genus g, then any connected double cover
$\iota :\widetilde {G}\to \widetilde {G}$
on the source graph that exchanges the two sheets of the cover. It is easy to see that if G has genus g, then any connected double cover
![]() $\widetilde {G}$
of G has genus
$\widetilde {G}$
of G has genus
![]() $2g-1$
.
$2g-1$
.
Remark 2.1. If
![]() $p:\widetilde {G}\to G$
is a free double cover and
$p:\widetilde {G}\to G$
is a free double cover and
![]() $e\in E(G)$
is a loop at v, then the preimage of e is either a pair of loops, one at each of the two vertices in
$e\in E(G)$
is a loop at v, then the preimage of e is either a pair of loops, one at each of the two vertices in
![]() $p^{-1}(v)$
, or a pair of edges connecting the two vertices in
$p^{-1}(v)$
, or a pair of edges connecting the two vertices in
![]() $p^{-1}(v)$
(oriented in the opposite directions if e is oriented).
$p^{-1}(v)$
(oriented in the opposite directions if e is oriented).
A free double cover of metric graphs
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
is a free double cover
$\pi :\widetilde {\Gamma }\to \Gamma $
is a free double cover
![]() $p:\widetilde {G}\to G$
of appropriate models
$p:\widetilde {G}\to G$
of appropriate models
![]() $(\widetilde {G},\ell )$
and
$(\widetilde {G},\ell )$
and
![]() $(G,\ell )$
respectively of
$(G,\ell )$
respectively of
![]() $\widetilde {\Gamma }$
and
$\widetilde {\Gamma }$
and
![]() $\Gamma $
that preserves edge length, so that
$\Gamma $
that preserves edge length, so that
![]() $\ell (p(\widetilde {e}))=\ell (\widetilde {e})$
for all
$\ell (p(\widetilde {e}))=\ell (\widetilde {e})$
for all
![]() $\widetilde {e}\in E(\widetilde {\Gamma })$
. A free double cover is the same as a finite harmonic morphism of global degree 2 and local degree 1 everywhere and we do not consider the more general case of unramified harmonic morphisms of degree 2 studied in [Reference Jensen and LenJL18] and [Reference Len and UlirschLU19]. From a topological viewpoint, free double covers are the same as normal covering spaces with Galois group
$\widetilde {e}\in E(\widetilde {\Gamma })$
. A free double cover is the same as a finite harmonic morphism of global degree 2 and local degree 1 everywhere and we do not consider the more general case of unramified harmonic morphisms of degree 2 studied in [Reference Jensen and LenJL18] and [Reference Len and UlirschLU19]. From a topological viewpoint, free double covers are the same as normal covering spaces with Galois group
![]() $\mathbb {Z}/2\mathbb {Z}$
.
$\mathbb {Z}/2\mathbb {Z}$
.
We consistently use the following construction, due to [Reference WallerWal76], to describe a double cover
![]() $p:\widetilde {G}\to G$
of a graph G of genus g.
$p:\widetilde {G}\to G$
of a graph G of genus g.
Construction A. Let G be a graph of genus g. Fix a spanning tree
![]() $T\subset G$
and a subset
$T\subset G$
and a subset
![]() $S\subset \{e_0,\ldots ,e_{g-1}\} $
of the edges in the complement of T. Let
$S\subset \{e_0,\ldots ,e_{g-1}\} $
of the edges in the complement of T. Let
![]() $\widetilde {T}^+$
and
$\widetilde {T}^+$
and
![]() $\widetilde {T}^-$
be two copies of T and for a vertex
$\widetilde {T}^-$
be two copies of T and for a vertex
![]() $v\in V(T)=V(G)$
denote
$v\in V(T)=V(G)$
denote
![]() $\widetilde {v}^{\pm }$
the corresponding vertices in
$\widetilde {v}^{\pm }$
the corresponding vertices in
![]() $\widetilde {T}^{\pm }$
. We define the graph
$\widetilde {T}^{\pm }$
. We define the graph
![]() $\widetilde {G}$
as
$\widetilde {G}$
as
 $$ \begin{align*}\widetilde{G}=\widetilde{T}^+\cup \widetilde{T}^- \cup \{\widetilde{e}_0^{{\kern1.5pt}\pm},\ldots,\widetilde{e}_{g-1}^{{\kern1.5pt}\pm}\}. \end{align*} $$
$$ \begin{align*}\widetilde{G}=\widetilde{T}^+\cup \widetilde{T}^- \cup \{\widetilde{e}_0^{{\kern1.5pt}\pm},\ldots,\widetilde{e}_{g-1}^{{\kern1.5pt}\pm}\}. \end{align*} $$
The map
![]() $p:\widetilde {G}\to G$
sends
$p:\widetilde {G}\to G$
sends
![]() $\widetilde {T}^{\pm }$
isomorphically to T and
$\widetilde {T}^{\pm }$
isomorphically to T and
![]() $\widetilde {e}_i^{{\kern1.5pt}\pm }$
to
$\widetilde {e}_i^{{\kern1.5pt}\pm }$
to
![]() $e_i$
. For
$e_i$
. For
![]() $e_i\in S$
, each of the two edges
$e_i\in S$
, each of the two edges
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_i$
above it has one vertex on
$\widetilde {e}^{{\kern1.5pt}\pm }_i$
above it has one vertex on
![]() $\widetilde {T}^+$
and one on
$\widetilde {T}^+$
and one on
![]() $\widetilde {T}^-$
, while for
$\widetilde {T}^-$
, while for
![]() $e_i\notin S$
both vertices of
$e_i\notin S$
both vertices of
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_i$
lie on the tree
$\widetilde {e}^{{\kern1.5pt}\pm }_i$
lie on the tree
![]() $\widetilde {T}^{\pm }$
. It is clear that if G is connected, then
$\widetilde {T}^{\pm }$
. It is clear that if G is connected, then
![]() $\widetilde {G}$
is connected if and only if S is nonempty. In the latter case, we may and will assume that
$\widetilde {G}$
is connected if and only if S is nonempty. In the latter case, we may and will assume that
![]() $e_0\in S$
and then
$e_0\in S$
and then
 $\widetilde {T}=\widetilde {T}^+\cup \widetilde {T}^-\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
is a spanning tree for
$\widetilde {T}=\widetilde {T}^+\cup \widetilde {T}^-\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
is a spanning tree for
![]() $\widetilde {G}$
. We furthermore always assume that the starting and ending vertices of
$\widetilde {G}$
. We furthermore always assume that the starting and ending vertices of
![]() $\widetilde {e}^{{\kern1.5pt}+}_0$
lie respectively on
$\widetilde {e}^{{\kern1.5pt}+}_0$
lie respectively on
![]() $\widetilde {T}^+$
and
$\widetilde {T}^+$
and
![]() $\widetilde {T}^-$
and conversely for
$\widetilde {T}^-$
and conversely for
![]() $\widetilde {e}^{-}_0$
:
$\widetilde {e}^{-}_0$
:
 $$ \begin{align*}s(\widetilde{e}^{{\kern1.5pt}\pm}_0)=\widetilde{s(e_0)}^{\pm},\quad t(\widetilde{e}^{{\kern1.5pt}\pm}_0)=\widetilde{t(e_0)}^{\mp}. \end{align*} $$
$$ \begin{align*}s(\widetilde{e}^{{\kern1.5pt}\pm}_0)=\widetilde{s(e_0)}^{\pm},\quad t(\widetilde{e}^{{\kern1.5pt}\pm}_0)=\widetilde{t(e_0)}^{\mp}. \end{align*} $$
We do not make the same assumptions about the lifts of the remaining edges
![]() $e_i\in S$
.
$e_i\in S$
.
The set of connected free double covers of G is thus identified with the set of nonempty subsets of
![]() $\{e_0,\ldots ,e_{g-1}\}$
. Alternatively, the fundamental cycle construction defines a basis for
$\{e_0,\ldots ,e_{g-1}\}$
. Alternatively, the fundamental cycle construction defines a basis for
![]() $H_1(G,\mathbb {Z})$
corresponding to the edges
$H_1(G,\mathbb {Z})$
corresponding to the edges
![]() $e_i$
(the ith basis element is the unique cycle supported on
$e_i$
(the ith basis element is the unique cycle supported on
![]() $T\cup \{e_i\}$
and containing
$T\cup \{e_i\}$
and containing
![]() $+e_i$
). The set of nonempty subsets of
$+e_i$
). The set of nonempty subsets of
![]() $\{e_0,\ldots ,e_{g-1}\}$
is then identified with the set of nonzero elements of
$\{e_0,\ldots ,e_{g-1}\}$
is then identified with the set of nonzero elements of
![]() $\operatorname {\mathrm {Hom}}(H_1(G,\mathbb {Z}),\mathbb {Z}/2\mathbb {Z})=H^1(G,\mathbb {Z}/2\mathbb {Z})$
(a subset is identified with its indicator function) and the latter is canonically identified with the set of connected free double covers of G by covering space theory.
$\operatorname {\mathrm {Hom}}(H_1(G,\mathbb {Z}),\mathbb {Z}/2\mathbb {Z})=H^1(G,\mathbb {Z}/2\mathbb {Z})$
(a subset is identified with its indicator function) and the latter is canonically identified with the set of connected free double covers of G by covering space theory.
Remark 2.2. Let
![]() $p:\widetilde {G}\to G$
be a free double cover corresponding to a tree
$p:\widetilde {G}\to G$
be a free double cover corresponding to a tree
![]() $T\subset G$
and a subset
$T\subset G$
and a subset
![]() $S\subset E(G)\backslash E(T)$
and let
$S\subset E(G)\backslash E(T)$
and let
![]() $G'\subset G$
be a subgraph. Then the preimage
$G'\subset G$
be a subgraph. Then the preimage
![]() $p^{-1}(G')$
is connected (equivalently, the restricted cover
$p^{-1}(G')$
is connected (equivalently, the restricted cover
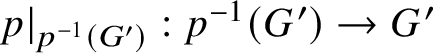 $p|_{p^{-1}(G')}:p^{-1}(G')\to G'$
is a nontrivial free double cover) if and only if there is a cycle on
$p|_{p^{-1}(G')}:p^{-1}(G')\to G'$
is a nontrivial free double cover) if and only if there is a cycle on
![]() $G'$
that contains an odd number of edges from S.
$G'$
that contains an odd number of edges from S.
2.2 Chip-firing and linear equivalence
We now briefly recall the basic notions of divisor theory for finite and metric graphs (see [Reference Baker and NorineBN07, Section 1] and [Reference Lim, Payne and PotashnikLPP12, Section 2] respectively for details).
Let G be a finite graph. The divisor group
![]() $\operatorname {\mathrm {Div}}(G)$
of G is the free abelian group on
$\operatorname {\mathrm {Div}}(G)$
of G is the free abelian group on
![]() $V(G)$
and the degree of a divisor is the sum of its coefficients:
$V(G)$
and the degree of a divisor is the sum of its coefficients:
 $$ \begin{align*}\operatorname{\mathrm{Div}}(G)=\left\{\sum a_v v:a_v\in \mathbb{Z}\right\},\quad \deg \sum a_v v=\sum a_v. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Div}}(G)=\left\{\sum a_v v:a_v\in \mathbb{Z}\right\},\quad \deg \sum a_v v=\sum a_v. \end{align*} $$
A divisor
![]() $D=\sum a_vv$
is called effective if all
$D=\sum a_vv$
is called effective if all
![]() $a_v\geq 0$
, and we denote the set of divisors of degree d by
$a_v\geq 0$
, and we denote the set of divisors of degree d by
![]() $\operatorname {\mathrm {Div}}^d(G)$
.
$\operatorname {\mathrm {Div}}^d(G)$
.
Let
![]() $n=|V(G)|$
be the number of vertices and let Q and A be the
$n=|V(G)|$
be the number of vertices and let Q and A be the
![]() $n\times n$
valency and adjacency matrices:
$n\times n$
valency and adjacency matrices:
The Laplacian
![]() $L=Q-A$
of G is a symmetric degenerate matrix whose rows and columns sum to zero. Given a vertex v, the divisor obtained via chip-firing from v is
$L=Q-A$
of G is a symmetric degenerate matrix whose rows and columns sum to zero. Given a vertex v, the divisor obtained via chip-firing from v is
 $$ \begin{align*}D_v=-\sum_{u\in V(G)}L_{uv}u. \end{align*} $$
$$ \begin{align*}D_v=-\sum_{u\in V(G)}L_{uv}u. \end{align*} $$
Such a divisor has degree 0; hence, the set of principal divisors
![]() $\operatorname {\mathrm {Prin}}(G)$
, which are defined as the image of the chip-firing map
$\operatorname {\mathrm {Prin}}(G)$
, which are defined as the image of the chip-firing map
lies inside
![]() $\operatorname {\mathrm {Div}}^0(G)$
. The Picard group and Jacobian of G are defined as
$\operatorname {\mathrm {Div}}^0(G)$
. The Picard group and Jacobian of G are defined as
Since any principal divisor has degree 0, the degree function descends to
![]() $\operatorname {\mathrm {Pic}}(G)$
and we denote
$\operatorname {\mathrm {Pic}}(G)$
and we denote
![]() $\operatorname {\mathrm {Pic}}^k(G)$
the set of equivalence classes of degree k divisors, so that
$\operatorname {\mathrm {Pic}}^k(G)$
the set of equivalence classes of degree k divisors, so that
![]() $\operatorname {\mathrm {Jac}}(G)=\operatorname {\mathrm {Pic}}^0(G)$
. The group
$\operatorname {\mathrm {Jac}}(G)=\operatorname {\mathrm {Pic}}^0(G)$
. The group
![]() $\operatorname {\mathrm {Pic}}(G)$
is infinite, but
$\operatorname {\mathrm {Pic}}(G)$
is infinite, but
![]() $\operatorname {\mathrm {Jac}}(G)$
is a finite group whose order is equal to the absolute value of any cofactor of the Laplacian L. Kirchhoff’s matrix tree theorem states that
$\operatorname {\mathrm {Jac}}(G)$
is a finite group whose order is equal to the absolute value of any cofactor of the Laplacian L. Kirchhoff’s matrix tree theorem states that
![]() $|\operatorname {\mathrm {Jac}}(G)|$
is equal to the number of spanning trees of G (see [Reference Baker and ShokriehBS13, Theorem 6.2]).
$|\operatorname {\mathrm {Jac}}(G)|$
is equal to the number of spanning trees of G (see [Reference Baker and ShokriehBS13, Theorem 6.2]).
The Picard variety of a metric graph
![]() $\Gamma $
of genus g is defined as follows (see [Reference Baker and FaberBF11]). A divisor on a metric graph
$\Gamma $
of genus g is defined as follows (see [Reference Baker and FaberBF11]). A divisor on a metric graph
![]() $\Gamma $
is a finite linear combination of the form
$\Gamma $
is a finite linear combination of the form
where
![]() $a_i\in \mathbb {Z}$
and
$a_i\in \mathbb {Z}$
and
![]() $p_i$
can be any point of
$p_i$
can be any point of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\deg D=a_1+\cdots +a_k$
. We denote by
$\deg D=a_1+\cdots +a_k$
. We denote by
![]() $\operatorname {\mathrm {Div}}(\Gamma )$
the divisor group and by
$\operatorname {\mathrm {Div}}(\Gamma )$
the divisor group and by
![]() $\operatorname {\mathrm {Div}}^k(\Gamma )$
the set of divisors of degree k. A rational function M on
$\operatorname {\mathrm {Div}}^k(\Gamma )$
the set of divisors of degree k. A rational function M on
![]() $\Gamma $
is a piecewise-linear real-valued function with integer slopes. The principal divisor
$\Gamma $
is a piecewise-linear real-valued function with integer slopes. The principal divisor
![]() $\operatorname {\mathrm {div}} (M)$
associated to M is the degree 0 divisor whose value at each point
$\operatorname {\mathrm {div}} (M)$
associated to M is the degree 0 divisor whose value at each point
![]() $p\in \Gamma $
is the sum of the incoming slopes of M at p. It is clear that
$p\in \Gamma $
is the sum of the incoming slopes of M at p. It is clear that
![]() $\operatorname {\mathrm {div}}(M+N)=\operatorname {\mathrm {div}}(M)+\operatorname {\mathrm {div}}(N)$
and
$\operatorname {\mathrm {div}}(M+N)=\operatorname {\mathrm {div}}(M)+\operatorname {\mathrm {div}}(N)$
and
![]() $\operatorname {\mathrm {div}}(-M)=-\operatorname {\mathrm {div}}(M)$
, so the principal divisors
$\operatorname {\mathrm {div}}(-M)=-\operatorname {\mathrm {div}}(M)$
, so the principal divisors
![]() $\operatorname {\mathrm {Prin}}(\Gamma )$
form a subgroup of
$\operatorname {\mathrm {Prin}}(\Gamma )$
form a subgroup of
![]() $\operatorname {\mathrm {Div}}^0(\Gamma )$
and the degree function descends to the quotient:
$\operatorname {\mathrm {Div}}^0(\Gamma )$
and the degree function descends to the quotient:
The Picard variety
![]() $\operatorname {\mathrm {Pic}}^0(\Gamma )$
is a real torus of dimension g and is isomorphic to the Jacobian variety of
$\operatorname {\mathrm {Pic}}^0(\Gamma )$
is a real torus of dimension g and is isomorphic to the Jacobian variety of
![]() $\Gamma $
, which we review in the next section, while each
$\Gamma $
, which we review in the next section, while each
![]() $\operatorname {\mathrm {Pic}}^k(\Gamma )$
is a torsor over
$\operatorname {\mathrm {Pic}}^k(\Gamma )$
is a torsor over
![]() $\operatorname {\mathrm {Pic}}^0(\Gamma )$
.
$\operatorname {\mathrm {Pic}}^0(\Gamma )$
.
2.3 Tropical abelian varieties
The Jacobian variety of a metric graph
![]() $\Gamma $
is a tropical principally polarised abelian variety (tropical ppav for short). We review the theory of tropical ppavs, following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] and [Reference Len and UlirschLU19], though we have found it convenient to slightly modify the main definitions (see Remark 2.3). In brief, a tropical ppav is a real torus
$\Gamma $
is a tropical principally polarised abelian variety (tropical ppav for short). We review the theory of tropical ppavs, following [Reference Foster, Rabinoff, Shokrieh and SotoFRSS18] and [Reference Len and UlirschLU19], though we have found it convenient to slightly modify the main definitions (see Remark 2.3). In brief, a tropical ppav is a real torus
![]() $\Sigma $
whose universal cover is equipped with a distinguished lattice (used to define integral local coordinates on
$\Sigma $
whose universal cover is equipped with a distinguished lattice (used to define integral local coordinates on
![]() $\Sigma $
and in general distinct from the lattice defining the torus itself) and an inner product.
$\Sigma $
and in general distinct from the lattice defining the torus itself) and an inner product.
Let
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
be finitely generated free abelian groups of the same rank and let
$\Lambda '$
be finitely generated free abelian groups of the same rank and let
![]() $[\cdot ,\cdot ]:\Lambda '\times \Lambda \to \mathbb {R}$
be a nondegenerate pairing. The triple
$[\cdot ,\cdot ]:\Lambda '\times \Lambda \to \mathbb {R}$
be a nondegenerate pairing. The triple
![]() $(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
defines a real torus with integral structure
$(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
defines a real torus with integral structure
![]() $\Sigma =\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})/\Lambda '$
, where the ‘integral structure’ refers to the lattice
$\Sigma =\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})/\Lambda '$
, where the ‘integral structure’ refers to the lattice
![]() $\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {Z})\subset \operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
and where
$\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {Z})\subset \operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
and where
![]() $\Lambda '$
is embedded in
$\Lambda '$
is embedded in
![]() $\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
via the assignment
$\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
via the assignment
![]() $\lambda '\mapsto [\lambda ',\cdot ]$
. The transposed data
$\lambda '\mapsto [\lambda ',\cdot ]$
. The transposed data
![]() $(\Lambda ',\Lambda ,[\cdot ,\cdot ]^t)$
define the dual torus
$(\Lambda ',\Lambda ,[\cdot ,\cdot ]^t)$
define the dual torus
![]() $\Sigma '=\operatorname {\mathrm {Hom}}(\Lambda ',\mathbb {R})/\Lambda $
.
$\Sigma '=\operatorname {\mathrm {Hom}}(\Lambda ',\mathbb {R})/\Lambda $
.
Let
![]() $\Sigma _1=(\Lambda _1,\Lambda ^{\prime }_1,[\cdot ,\cdot ]_1)$
and
$\Sigma _1=(\Lambda _1,\Lambda ^{\prime }_1,[\cdot ,\cdot ]_1)$
and
![]() $\Sigma _2=(\Lambda _2,\Lambda ^{\prime }_2,[\cdot ,\cdot ]_2)$
be two real tori with integral structure and let
$\Sigma _2=(\Lambda _2,\Lambda ^{\prime }_2,[\cdot ,\cdot ]_2)$
be two real tori with integral structure and let
![]() $f_*:\Lambda _1'\to \Lambda _2'$
and
$f_*:\Lambda _1'\to \Lambda _2'$
and
![]() $f^*:\Lambda _2\to \Lambda _1$
be a pair of maps satisfying
$f^*:\Lambda _2\to \Lambda _1$
be a pair of maps satisfying
for all
![]() $\lambda ^{\prime }_1\in \Lambda ^{\prime }_1$
and
$\lambda ^{\prime }_1\in \Lambda ^{\prime }_1$
and
![]() $\lambda _2\in \Lambda _2$
. The map
$\lambda _2\in \Lambda _2$
. The map
![]() $f^*$
defines a dual map
$f^*$
defines a dual map
![]() $\overline {f}:\operatorname {\mathrm {Hom}}(\Lambda _1,\mathbb {R})\to \operatorname {\mathrm {Hom}} (\Lambda _2,\mathbb {R})$
, and condition (3) implies that
$\overline {f}:\operatorname {\mathrm {Hom}}(\Lambda _1,\mathbb {R})\to \operatorname {\mathrm {Hom}} (\Lambda _2,\mathbb {R})$
, and condition (3) implies that
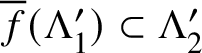 $\overline {f}(\Lambda ^{\prime }_1)\subset \Lambda ^{\prime }_2$
(in fact,
$\overline {f}(\Lambda ^{\prime }_1)\subset \Lambda ^{\prime }_2$
(in fact,
 $\overline {f}|_{\Lambda ^{\prime }_1}=f_*$
). Hence, the pair
$\overline {f}|_{\Lambda ^{\prime }_1}=f_*$
). Hence, the pair
![]() $(f_*,f^*)$
defines a homomorphism
$(f_*,f^*)$
defines a homomorphism
![]() $f:\Sigma _1\to \Sigma _2$
of real tori with integral structures. The transposed pair
$f:\Sigma _1\to \Sigma _2$
of real tori with integral structures. The transposed pair
![]() $(f^*,f_*)$
defines the dual homomorphism
$(f^*,f_*)$
defines the dual homomorphism
![]() $f':\Sigma ^{\prime }_2\to \Sigma ^{\prime }_1$
.
$f':\Sigma ^{\prime }_2\to \Sigma ^{\prime }_1$
.
Let
![]() $f=(f_*,f^*):\Sigma _1\to \Sigma _2$
be a homomorphism of real tori with integral structures
$f=(f_*,f^*):\Sigma _1\to \Sigma _2$
be a homomorphism of real tori with integral structures
![]() $\Sigma _i=(\Lambda _i,\Lambda ^{\prime }_i,[\cdot ,\cdot ]_i)$
. We can naturally associate two real tori to f: the connected component of the identity of the kernel of f, denoted
$\Sigma _i=(\Lambda _i,\Lambda ^{\prime }_i,[\cdot ,\cdot ]_i)$
. We can naturally associate two real tori to f: the connected component of the identity of the kernel of f, denoted
![]() $(\operatorname {\mathrm {Ker}} f)_0$
, and the cokernel
$(\operatorname {\mathrm {Ker}} f)_0$
, and the cokernel
![]() $\operatorname {\mathrm {Coker}} f$
. It is easy to see that
$\operatorname {\mathrm {Coker}} f$
. It is easy to see that
![]() $(\operatorname {\mathrm {Ker}} f)_0$
and
$(\operatorname {\mathrm {Ker}} f)_0$
and
![]() $\operatorname {\mathrm {Coker}} f$
also have integral structures and the natural maps
$\operatorname {\mathrm {Coker}} f$
also have integral structures and the natural maps
![]() $i:(\operatorname {\mathrm {Ker}} f)_0\to \Sigma _1$
and
$i:(\operatorname {\mathrm {Ker}} f)_0\to \Sigma _1$
and
![]() $p:\Sigma _2\to \operatorname {\mathrm {Coker}} f$
are homomorphisms of real tori with integral structure.
$p:\Sigma _2\to \operatorname {\mathrm {Coker}} f$
are homomorphisms of real tori with integral structure.
Indeed, let
![]() $K=(\operatorname {\mathrm {Coker}} f^*)^{tf}$
be the quotient of
$K=(\operatorname {\mathrm {Coker}} f^*)^{tf}$
be the quotient of
![]() $\operatorname {\mathrm {Coker}} f^*$
by its torsion subgroup (equivalently, the quotient of
$\operatorname {\mathrm {Coker}} f^*$
by its torsion subgroup (equivalently, the quotient of
![]() $\Lambda _1$
by the saturation of
$\Lambda _1$
by the saturation of
![]() $\operatorname {\mathrm {Im}} f^*$
) and let
$\operatorname {\mathrm {Im}} f^*$
) and let
![]() $K'=\operatorname {\mathrm {Ker}} f_*$
. Then
$K'=\operatorname {\mathrm {Ker}} f_*$
. Then
![]() $\operatorname {\mathrm {Hom}}(K,\mathbb {R})$
is naturally identified with the kernel of the map
$\operatorname {\mathrm {Hom}}(K,\mathbb {R})$
is naturally identified with the kernel of the map
![]() $\operatorname {\mathrm {Hom}}(\Lambda _1,\mathbb {R})\to \operatorname {\mathrm {Hom}} (\Lambda _2,\mathbb {R})$
dual to
$\operatorname {\mathrm {Hom}}(\Lambda _1,\mathbb {R})\to \operatorname {\mathrm {Hom}} (\Lambda _2,\mathbb {R})$
dual to
![]() $f^*$
, and therefore
$f^*$
, and therefore
![]() $(\operatorname {\mathrm {Ker}} f)_0=(K,K',[\cdot ,\cdot ]_K)$
, where
$(\operatorname {\mathrm {Ker}} f)_0=(K,K',[\cdot ,\cdot ]_K)$
, where
![]() $[\cdot ,\cdot ]_K:K'\times K\to \mathbb {R}$
is the pairing induced by
$[\cdot ,\cdot ]_K:K'\times K\to \mathbb {R}$
is the pairing induced by
![]() $[\cdot ,\cdot ]_1$
. We note that this pairing is well-defined: given
$[\cdot ,\cdot ]_1$
. We note that this pairing is well-defined: given
![]() $\lambda ^{\prime }_1\in K'$
and
$\lambda ^{\prime }_1\in K'$
and
![]() $\lambda _2\in \Lambda _2$
, equation (3) implies that
$\lambda _2\in \Lambda _2$
, equation (3) implies that
Therefore, for
![]() $\lambda '\in K'$
and
$\lambda '\in K'$
and
![]() $\lambda \in K$
, the pairing
$\lambda \in K$
, the pairing
![]() $[\lambda ',\lambda ]_K=[\lambda ',\lambda ]_1$
does not depend on a choice of representative for
$[\lambda ',\lambda ]_K=[\lambda ',\lambda ]_1$
does not depend on a choice of representative for
![]() $\lambda \in K$
. The natural maps
$\lambda \in K$
. The natural maps
![]() $i^*:\Lambda _1\to K$
and
$i^*:\Lambda _1\to K$
and
![]() $i_*:K'\to \Lambda _1'$
define
$i_*:K'\to \Lambda _1'$
define
![]() $(\operatorname {\mathrm {Ker}} f)_0$
as an integral subtorus of
$(\operatorname {\mathrm {Ker}} f)_0$
as an integral subtorus of
![]() $\Sigma _1$
. Similarly,
$\Sigma _1$
. Similarly,
![]() $\operatorname {\mathrm {Coker}} f=(C,C',[\cdot ,\cdot ]_C)$
, where
$\operatorname {\mathrm {Coker}} f=(C,C',[\cdot ,\cdot ]_C)$
, where
![]() $C=\operatorname {\mathrm {Ker}} f^*$
,
$C=\operatorname {\mathrm {Ker}} f^*$
,
![]() $C'=(\operatorname {\mathrm {Coker}} f_*)^{tf}$
, the pairing
$C'=(\operatorname {\mathrm {Coker}} f_*)^{tf}$
, the pairing
![]() $[\cdot ,\cdot ]_C$
is induced by
$[\cdot ,\cdot ]_C$
is induced by
![]() $[\cdot ,\cdot ]_2$
and p is given by the natural maps
$[\cdot ,\cdot ]_2$
and p is given by the natural maps
![]() $p_*:\Lambda ^{\prime }_2\to C'$
and
$p_*:\Lambda ^{\prime }_2\to C'$
and
![]() $p^*:C\to \Lambda _2$
. We note that a morphism f of real tori with integral structure has finite kernel if and only if K and
$p^*:C\to \Lambda _2$
. We note that a morphism f of real tori with integral structure has finite kernel if and only if K and
![]() $K'$
are trivial; in other words, if
$K'$
are trivial; in other words, if
![]() $f_*$
is injective (equivalently, if
$f_*$
is injective (equivalently, if
![]() $\operatorname {\mathrm {Im}} f^*$
has finite index in
$\operatorname {\mathrm {Im}} f^*$
has finite index in
![]() $\Lambda _1$
).
$\Lambda _1$
).
Let
![]() $\Sigma =(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
be a real torus with integral structure. A polarisation on
$\Sigma =(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
be a real torus with integral structure. A polarisation on
![]() $\Sigma $
is a map
$\Sigma $
is a map
![]() $\xi :\Lambda '\to \Lambda $
(necessarily injective) with the property that the induced bilinear form
$\xi :\Lambda '\to \Lambda $
(necessarily injective) with the property that the induced bilinear form
is symmetric and positive definite. Given a polarisation
![]() $\xi $
on
$\xi $
on
![]() $\Sigma $
, the pair
$\Sigma $
, the pair
![]() $(\xi ,\xi )$
defines a homomorphism
$(\xi ,\xi )$
defines a homomorphism
![]() $\eta :\Sigma \to \Sigma '$
to the dual, whose finite kernel is identified with
$\eta :\Sigma \to \Sigma '$
to the dual, whose finite kernel is identified with
![]() $\Lambda /\operatorname {\mathrm {Im}} \xi $
. The pair
$\Lambda /\operatorname {\mathrm {Im}} \xi $
. The pair
![]() $(\Sigma ,\xi )$
is called a tropical polarised abelian variety. The map
$(\Sigma ,\xi )$
is called a tropical polarised abelian variety. The map
![]() $\eta $
is an isomorphism if and only if
$\eta $
is an isomorphism if and only if
![]() $\xi $
is an isomorphism, in which case we say that the polarisation
$\xi $
is an isomorphism, in which case we say that the polarisation
![]() $\xi $
is principal.
$\xi $
is principal.
Let
![]() $\Sigma =(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
be a g-dimensional tropical polarised abelian variety. The associated bilinear form
$\Sigma =(\Lambda ,\Lambda ',[\cdot ,\cdot ])$
be a g-dimensional tropical polarised abelian variety. The associated bilinear form
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\Lambda '$
extends to an inner product on the universal cover
$\Lambda '$
extends to an inner product on the universal cover
![]() $V=\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
, which we also denote
$V=\operatorname {\mathrm {Hom}}(\Lambda ,\mathbb {R})$
, which we also denote
![]() $(\cdot ,\cdot )$
, and hence to a translation-invariant Riemannian metric on
$(\cdot ,\cdot )$
, and hence to a translation-invariant Riemannian metric on
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $C\subset \Sigma $
be a parallelotope framed by vectors
$C\subset \Sigma $
be a parallelotope framed by vectors
![]() $v_1,\ldots ,v_g\in V$
; then the volume of C is equal to the square root
$v_1,\ldots ,v_g\in V$
; then the volume of C is equal to the square root
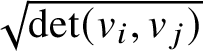 $\sqrt {\det (v_i,v_j)}$
of the Gramian determinant of the
$\sqrt {\det (v_i,v_j)}$
of the Gramian determinant of the
![]() $v_i$
. In particular, if
$v_i$
. In particular, if
![]() $\lambda ^{\prime }_1,\ldots ,\lambda ^{\prime }_g$
is a basis of
$\lambda ^{\prime }_1,\ldots ,\lambda ^{\prime }_g$
is a basis of
![]() $\Lambda '$
, then
$\Lambda '$
, then
 $$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\Sigma)=\det(\lambda^{\prime}_i,\lambda^{\prime}_j). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\Sigma)=\det(\lambda^{\prime}_i,\lambda^{\prime}_j). \end{align*} $$
Finally, let
![]() $f:\Sigma _1\to \Sigma _2$
be a homomorphism of real tori with integral structures given by
$f:\Sigma _1\to \Sigma _2$
be a homomorphism of real tori with integral structures given by
![]() $f^*:\Lambda _2\to \Lambda _1$
and
$f^*:\Lambda _2\to \Lambda _1$
and
![]() $f_*:\Lambda ^{\prime }_1\to \Lambda ^{\prime }_2$
and assume that f has finite kernel (equivalently,
$f_*:\Lambda ^{\prime }_1\to \Lambda ^{\prime }_2$
and assume that f has finite kernel (equivalently,
![]() $f_*$
is injective). Given a polarisation
$f_*$
is injective). Given a polarisation
![]() $\xi _2:\Lambda ^{\prime }_2\to \Lambda _2$
on
$\xi _2:\Lambda ^{\prime }_2\to \Lambda _2$
on
![]() $\Sigma _2$
with associated bilinear form
$\Sigma _2$
with associated bilinear form
![]() $(\cdot ,\cdot )_2$
, we define the induced polarisation
$(\cdot ,\cdot )_2$
, we define the induced polarisation
![]() $\xi _1:\Lambda ^{\prime }_1\to \Lambda _1$
by
$\xi _1:\Lambda ^{\prime }_1\to \Lambda _1$
by
![]() $\xi _1=f^*\circ \xi _2\circ f_*$
. This is indeed a polarisation, because by (3) the associated bilinear form
$\xi _1=f^*\circ \xi _2\circ f_*$
. This is indeed a polarisation, because by (3) the associated bilinear form
![]() $(\cdot ,\cdot )_1$
on
$(\cdot ,\cdot )_1$
on
![]() $\Lambda ^{\prime }_1$
is given by
$\Lambda ^{\prime }_1$
is given by
so it is symmetric and positive definite because
![]() $f_*$
is injective. Hence, in particular, an integral subtorus
$f_*$
is injective. Hence, in particular, an integral subtorus
![]() $i:\Pi \to \Sigma $
of a tropical polarised abelian variety
$i:\Pi \to \Sigma $
of a tropical polarised abelian variety
![]() $(\Sigma ,\xi )$
has an induced polarisation, which we denote
$(\Sigma ,\xi )$
has an induced polarisation, which we denote
![]() $i^*\xi $
. We note that the polarisation induced by a principal polarisation is not necessarily itself principal.
$i^*\xi $
. We note that the polarisation induced by a principal polarisation is not necessarily itself principal.
Remark 2.3. In [Reference Len and UlirschLU19], a real torus with integral structure is defined as a torus
![]() $\Sigma =N_{\mathbb {R}}/\Lambda $
with a distinguished lattice
$\Sigma =N_{\mathbb {R}}/\Lambda $
with a distinguished lattice
![]() $N\subset N_R$
in the universal cover and a morphism
$N\subset N_R$
in the universal cover and a morphism
![]() $f:\Sigma _1\to \Sigma _2$
as a map
$f:\Sigma _1\to \Sigma _2$
as a map
![]() $\overline {f}:N_{1,\mathbb {R}}\to N_{2,\mathbb {R}}$
satisfying
$\overline {f}:N_{1,\mathbb {R}}\to N_{2,\mathbb {R}}$
satisfying
![]() $\overline {f}(\Lambda _1)\subset \Lambda _2$
and induced by a
$\overline {f}(\Lambda _1)\subset \Lambda _2$
and induced by a
![]() $\mathbb {Z}$
-linear map
$\mathbb {Z}$
-linear map
![]() $N_1\to N_2$
. It is easy to see that this definition is equivalent to ours.
$N_1\to N_2$
. It is easy to see that this definition is equivalent to ours.
2.4 The Jacobian of a metric graph
We now construct the Jacobian variety
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
of a metric graph
$\operatorname {\mathrm {Jac}}(\Gamma )$
of a metric graph
![]() $\Gamma $
of genus g as a tropical ppav, following [Reference Baker and FaberBF11] and [Reference Len and UlirschLU19]. We first pick an oriented model G of
$\Gamma $
of genus g as a tropical ppav, following [Reference Baker and FaberBF11] and [Reference Len and UlirschLU19]. We first pick an oriented model G of
![]() $\Gamma $
and consider the corresponding simplicial homology groups. Let A be either
$\Gamma $
and consider the corresponding simplicial homology groups. Let A be either
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $\mathbb {R}$
and let
$\mathbb {R}$
and let
![]() $C_0(G,A)=A^{V(G)}$
and
$C_0(G,A)=A^{V(G)}$
and
![]() $C_1(G,A)=A^{E(G)}$
be respectively the simplicial
$C_1(G,A)=A^{E(G)}$
be respectively the simplicial
![]() $0$
-chain and
$0$
-chain and
![]() $1$
-chain groups of G with coefficients in A. The source and target maps
$1$
-chain groups of G with coefficients in A. The source and target maps
![]() $s,t:E(G)\to V(G)$
induce a boundary map
$s,t:E(G)\to V(G)$
induce a boundary map
 $$ \begin{align*}d_A:C_1(G,A)\to C_0(G,A), \quad \sum_{e\in E(G)}a_e e\mapsto \sum_{e\in E(G)}a_e[t(e)-s(e)], \end{align*} $$
$$ \begin{align*}d_A:C_1(G,A)\to C_0(G,A), \quad \sum_{e\in E(G)}a_e e\mapsto \sum_{e\in E(G)}a_e[t(e)-s(e)], \end{align*} $$
and the first simplicial homology group of G with coefficients in A is
![]() $H_1(G,A)=\operatorname {\mathrm {Ker}} d_A$
. We also consider the group of A-valued harmonic
$H_1(G,A)=\operatorname {\mathrm {Ker}} d_A$
. We also consider the group of A-valued harmonic
![]() $1$
-forms
$1$
-forms
![]() $\Omega (G,A)$
on G, which is a subgroup of the free A-module with basis
$\Omega (G,A)$
on G, which is a subgroup of the free A-module with basis
![]() $\{de:e\in E(G)\}$
:
$\{de:e\in E(G)\}$
:
 $$ \begin{align*}\Omega(G,A)=\left\{\sum_{e\in E(G)} \omega_e de:\sum_{e:t(e)=v}\omega_e=\sum_{e:s(e)=v}\omega_e\mbox{ for all }v\in V(G)\right\}. \end{align*} $$
$$ \begin{align*}\Omega(G,A)=\left\{\sum_{e\in E(G)} \omega_e de:\sum_{e:t(e)=v}\omega_e=\sum_{e:s(e)=v}\omega_e\mbox{ for all }v\in V(G)\right\}. \end{align*} $$
We note that mathematically
![]() $H_1(G,A)$
and
$H_1(G,A)$
and
![]() $\Omega (G,A)$
are the same object, but it is convenient to distinguish them, both for historical purposes and for clarity of exposition.
$\Omega (G,A)$
are the same object, but it is convenient to distinguish them, both for historical purposes and for clarity of exposition.
We now define an integration pairing
by
 $$ \begin{align*}[\gamma, \omega]=\int_{\gamma}\omega=\sum_{e\in E(G)}\gamma_e \omega_e \ell(e),\quad \gamma=\sum_{e\in E(G)}\gamma_ee,\quad \omega=\sum_{e\in E(G)}\omega_ede. \end{align*} $$
$$ \begin{align*}[\gamma, \omega]=\int_{\gamma}\omega=\sum_{e\in E(G)}\gamma_e \omega_e \ell(e),\quad \gamma=\sum_{e\in E(G)}\gamma_ee,\quad \omega=\sum_{e\in E(G)}\omega_ede. \end{align*} $$
By Lemma 2.1 in [Reference Baker and FaberBF11], the integration pairing restricts to a perfect pairing on
![]() $H_1(G,A)\times \Omega (G,A)$
.
$H_1(G,A)\times \Omega (G,A)$
.
Let
![]() $G'$
be the model of
$G'$
be the model of
![]() $\Gamma $
obtained by subdividing the edge
$\Gamma $
obtained by subdividing the edge
![]() $e\in E(G)$
into two edges
$e\in E(G)$
into two edges
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, oriented in the same way as e, with
$e_2$
, oriented in the same way as e, with
![]() $\ell (e_1)+\ell (e_2)=\ell (e)$
. The natural embedding
$\ell (e_1)+\ell (e_2)=\ell (e)$
. The natural embedding
![]() $C_1(G,A)\to C_1(G',A)$
sending e to
$C_1(G,A)\to C_1(G',A)$
sending e to
![]() $e_1+e_2$
restricts to an isomorphism
$e_1+e_2$
restricts to an isomorphism
![]() $H_1(G,A)\to H_1(G',A)$
. Similarly, the groups
$H_1(G,A)\to H_1(G',A)$
. Similarly, the groups
![]() $\Omega (G,A)$
and
$\Omega (G,A)$
and
![]() $\Omega (G',A)$
are naturally isomorphic, and these isomorphisms preserve the integration pairing. Hence, we can define
$\Omega (G',A)$
are naturally isomorphic, and these isomorphisms preserve the integration pairing. Hence, we can define
![]() $\Omega (\Gamma ,A)=\Omega (G,A)$
and
$\Omega (\Gamma ,A)=\Omega (G,A)$
and
![]() $H_1(\Gamma ,A)=H_1(G,A)$
for any model G, and by a
$H_1(\Gamma ,A)=H_1(G,A)$
for any model G, and by a
![]() $1$
-chain, or path, on
$1$
-chain, or path, on
![]() $\Gamma $
we mean a
$\Gamma $
we mean a
![]() $1$
-chain on any model of
$1$
-chain on any model of
![]() $\Gamma $
.
$\Gamma $
.
We now let
![]() $\Lambda =\Omega (\Gamma ,\mathbb {Z})$
and
$\Lambda =\Omega (\Gamma ,\mathbb {Z})$
and
![]() $\Lambda '=H_1(\Gamma ,\mathbb {Z})$
, let
$\Lambda '=H_1(\Gamma ,\mathbb {Z})$
, let
![]() $[\cdot ,\cdot ]:\Lambda '\times \Lambda \to \mathbb {R}$
be the integration pairing and let
$[\cdot ,\cdot ]:\Lambda '\times \Lambda \to \mathbb {R}$
be the integration pairing and let
![]() $\xi :H_1(\Gamma ,\mathbb {Z})\to \Omega (\Gamma ,\mathbb {Z})$
be the natural isomorphism sending the
$\xi :H_1(\Gamma ,\mathbb {Z})\to \Omega (\Gamma ,\mathbb {Z})$
be the natural isomorphism sending the
![]() $1$
-cycle
$1$
-cycle
![]() $\sum a_e e$
to the
$\sum a_e e$
to the
![]() $1$
-form
$1$
-form
![]() $\sum a_e de$
. We denote
$\sum a_e de$
. We denote
![]() $\Omega ^*(\Gamma )=\operatorname {\mathrm {Hom}}(\Omega (\Gamma ,\mathbb {Z}),\mathbb {R})$
, and by the universal coefficient theorem the group
$\Omega ^*(\Gamma )=\operatorname {\mathrm {Hom}}(\Omega (\Gamma ,\mathbb {Z}),\mathbb {R})$
, and by the universal coefficient theorem the group
![]() $\operatorname {\mathrm {Hom}}(H_1(\Gamma ,\mathbb {Z}),\mathbb {R})$
is canonically isomorphic to
$\operatorname {\mathrm {Hom}}(H_1(\Gamma ,\mathbb {Z}),\mathbb {R})$
is canonically isomorphic to
![]() $H^1(\Gamma ,\mathbb {R})$
. The Jacobian variety and the Albanese variety of
$H^1(\Gamma ,\mathbb {R})$
. The Jacobian variety and the Albanese variety of
![]() $\Gamma $
are the dual tropical ppavs
$\Gamma $
are the dual tropical ppavs
The group
![]() $H_1(\Gamma ,\mathbb {Z})$
carries an intersection form
$H_1(\Gamma ,\mathbb {Z})$
carries an intersection form
 $$ \begin{align} (\cdot,\cdot)=[\cdot,\xi(\cdot)]:H_1(\Gamma,\mathbb{Z})\times H_1(\Gamma,\mathbb{Z})\to \mathbb{R},\quad \left(\sum_{e\in E(G)}\gamma_ee,\sum_{e\in E(G)}\delta_ee\right)=\sum_{e\in E(G)} \gamma_e\delta_e \ell(e) \end{align} $$
$$ \begin{align} (\cdot,\cdot)=[\cdot,\xi(\cdot)]:H_1(\Gamma,\mathbb{Z})\times H_1(\Gamma,\mathbb{Z})\to \mathbb{R},\quad \left(\sum_{e\in E(G)}\gamma_ee,\sum_{e\in E(G)}\delta_ee\right)=\sum_{e\in E(G)} \gamma_e\delta_e \ell(e) \end{align} $$
that induces an inner product on
![]() $\Omega ^*(\Gamma )$
.
$\Omega ^*(\Gamma )$
.
Fix a point
![]() $q\in \Gamma $
and for any
$q\in \Gamma $
and for any
![]() $p\in \Gamma $
choose a path
$p\in \Gamma $
choose a path
![]() $\gamma (q,p)\in C_1(\Gamma ,\mathbb {Z})$
from q to p. Integrating along
$\gamma (q,p)\in C_1(\Gamma ,\mathbb {Z})$
from q to p. Integrating along
![]() $\gamma (q,p)$
defines an element of
$\gamma (q,p)$
defines an element of
![]() $\Omega (\Gamma )^*$
, and choosing a different path
$\Omega (\Gamma )^*$
, and choosing a different path
![]() $\gamma '(q,p)$
defines the same element modulo
$\gamma '(q,p)$
defines the same element modulo
![]() $H_1(\Gamma ,\mathbb {Z})\subset \Omega (\Gamma )^*$
. Hence, we have a well-defined Abel–Jacobi map
$H_1(\Gamma ,\mathbb {Z})\subset \Omega (\Gamma )^*$
. Hence, we have a well-defined Abel–Jacobi map
![]() $\Phi _q:\Gamma \to \operatorname {\mathrm {Jac}}(\Gamma )$
with base point q:
$\Phi _q:\Gamma \to \operatorname {\mathrm {Jac}}(\Gamma )$
with base point q:
 $$ \begin{align} \Phi_q:\Gamma\to \operatorname{\mathrm{Jac}}(\Gamma),\quad p\mapsto\left(\omega\mapsto \int_{\gamma(q,p)}\omega\right). \end{align} $$
$$ \begin{align} \Phi_q:\Gamma\to \operatorname{\mathrm{Jac}}(\Gamma),\quad p\mapsto\left(\omega\mapsto \int_{\gamma(q,p)}\omega\right). \end{align} $$
The map
![]() $\Phi _q$
extends by linearity to
$\Phi _q$
extends by linearity to
![]() $\operatorname {\mathrm {Div}}(\Gamma )$
, and its restriction to
$\operatorname {\mathrm {Div}}(\Gamma )$
, and its restriction to
![]() $\operatorname {\mathrm {Div}}^0(\Gamma )$
does not depend on the choice of base point q. The tropical analogue of the Abel–Jacobi theorem (see [Reference Mikhalkin and ZharkovMZ08], Theorem 6.3) states that
$\operatorname {\mathrm {Div}}^0(\Gamma )$
does not depend on the choice of base point q. The tropical analogue of the Abel–Jacobi theorem (see [Reference Mikhalkin and ZharkovMZ08], Theorem 6.3) states that
![]() $\Phi _q$
descends to a canonical isomorphism
$\Phi _q$
descends to a canonical isomorphism
![]() $\operatorname {\mathrm {Pic}}^0(\Gamma )\simeq \operatorname {\mathrm {Jac}}(\Gamma )$
. Since any
$\operatorname {\mathrm {Pic}}^0(\Gamma )\simeq \operatorname {\mathrm {Jac}}(\Gamma )$
. Since any
![]() $\operatorname {\mathrm {Pic}}^k(\Gamma )$
is a torsor over
$\operatorname {\mathrm {Pic}}^k(\Gamma )$
is a torsor over
![]() $\operatorname {\mathrm {Pic}}^0(\Gamma )$
, we can define
$\operatorname {\mathrm {Pic}}^0(\Gamma )$
, we can define
![]() $\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Pic}}^k(\Gamma ))=\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))$
.
$\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Pic}}^k(\Gamma ))=\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))$
.
Finally, we recall the principal results [Reference An, Baker, Kuperberg and ShokriehABKS14], which concern the tropical Jacobi inversion problem. Consider the degree g Abel–Jacobi map
A choice of model G for
![]() $\Gamma $
defines a cellular decomposition
$\Gamma $
defines a cellular decomposition
 $$ \begin{align*}\operatorname{\mathrm{Sym}}^g(\Gamma)=\bigcup_{F\in \operatorname{\mathrm{Sym}}^g(E(G))}C(F), \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Sym}}^g(\Gamma)=\bigcup_{F\in \operatorname{\mathrm{Sym}}^g(E(G))}C(F), \end{align*} $$
where for a multiset
![]() $F=\{e_1,\ldots ,e_g\}\in \operatorname {\mathrm {Sym}}^g(E(G))$
of g edges of G the cell
$F=\{e_1,\ldots ,e_g\}\in \operatorname {\mathrm {Sym}}^g(E(G))$
of g edges of G the cell
![]() $C(F)$
consists of divisors supported on F:
$C(F)$
consists of divisors supported on F:
We say that F is a break set if all
![]() $e_i$
are distinct and
$e_i$
are distinct and
![]() $G\backslash F$
is a tree and the set of break divisors is the union of the cells
$G\backslash F$
is a tree and the set of break divisors is the union of the cells
![]() $C(F)$
over all break sets F.
$C(F)$
over all break sets F.
The map
![]() $\Phi $
is affine linear on each cell
$\Phi $
is affine linear on each cell
![]() $C(F)$
and has maximal rank precisely when F is a break set. Specifically, the following is true:
$C(F)$
and has maximal rank precisely when F is a break set. Specifically, the following is true:
-
(1) If
 $F=\{e_1,\ldots ,e_g\}$
is a break set, then the restriction of
$F=\{e_1,\ldots ,e_g\}$
is a break set, then the restriction of
 $\Phi $
to
$\Phi $
to
 $C(F)$
is injective and (6)
$C(F)$
is injective and (6) $$ \begin{align} \operatorname{\mathrm{Vol}}(\Phi(C(F)))=\frac{w(F)}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Jac}}(\Gamma))},\quad w(F)=\operatorname{\mathrm{Vol}} (C(F))=\ell(e_1)\cdots \ell(e_g). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}(\Phi(C(F)))=\frac{w(F)}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Jac}}(\Gamma))},\quad w(F)=\operatorname{\mathrm{Vol}} (C(F))=\ell(e_1)\cdots \ell(e_g). \end{align} $$
-
(2) If F is not a break set, then the restriction of
 $\Phi $
to
$\Phi $
to
 $C(F)$
does not have maximal rank and
$C(F)$
does not have maximal rank and
 $\operatorname {\mathrm {Vol}}(\Phi (C(F)))=0$
.
$\operatorname {\mathrm {Vol}}(\Phi (C(F)))=0$
.
Furthermore, the map
![]() $\Phi $
has a unique continuous section whose image is the set of break divisors. Hence, the images of the break cells
$\Phi $
has a unique continuous section whose image is the set of break divisors. Hence, the images of the break cells
![]() $C(F)$
cover
$C(F)$
cover
![]() $\operatorname {\mathrm {Pic}}^g(\Gamma )$
with no overlaps in the interior of cells and summing together their volumes gives
$\operatorname {\mathrm {Pic}}^g(\Gamma )$
with no overlaps in the interior of cells and summing together their volumes gives
![]() $\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))=\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Pic}}^g(\Gamma ))$
.
$\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))=\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Pic}}^g(\Gamma ))$
.
Theorem 2.4 Theorem 1.5 of [Reference An, Baker, Kuperberg and ShokriehABKS14]
The volume of the Jacobian variety of a metric graph
![]() $\Gamma $
of genus g is given by
$\Gamma $
of genus g is given by
 $$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\sum_{F\subset E(\Gamma)}w(F), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\sum_{F\subset E(\Gamma)}w(F), \end{align} $$
where the sum is taken over g-element subsets
![]() $F\subset E(\Gamma )$
such that
$F\subset E(\Gamma )$
such that
![]() $\Gamma \backslash F$
is a tree.
$\Gamma \backslash F$
is a tree.
Remark 2.5. This result can be interpreted as saying that
![]() $\Phi $
is a harmonic morphism of polyhedral spaces of degree 1, where we define the local degree of
$\Phi $
is a harmonic morphism of polyhedral spaces of degree 1, where we define the local degree of
![]() $\Phi $
on a cell
$\Phi $
on a cell
![]() $C(F)$
to be
$C(F)$
to be
![]() $1$
if F is a break set and
$1$
if F is a break set and
![]() $0$
otherwise. Indeed, the harmonicity condition ensures that such a map has a unique continuous section, since each cell of
$0$
otherwise. Indeed, the harmonicity condition ensures that such a map has a unique continuous section, since each cell of
![]() $\operatorname {\mathrm {Pic}}^g(\Gamma )$
has a unique preimage in
$\operatorname {\mathrm {Pic}}^g(\Gamma )$
has a unique preimage in
![]() $\operatorname {\mathrm {Sym}}^g(\Gamma )$
, and these preimages fit together along codimension 1 cells. Formula (6) then implies that the map
$\operatorname {\mathrm {Sym}}^g(\Gamma )$
, and these preimages fit together along codimension 1 cells. Formula (6) then implies that the map
![]() $\Phi $
has a common volume dilation factor
$\Phi $
has a common volume dilation factor
![]() $1/\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))$
on all noncontracted cells.
$1/\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Jac}}(\Gamma ))$
on all noncontracted cells.
Remark 2.6. We also note that, from the point of view of the Riemannian geometry of
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
, the edge lengths on
$\operatorname {\mathrm {Jac}}(\Gamma )$
, the edge lengths on
![]() $\Gamma $
are measured in units of
$\Gamma $
are measured in units of
![]() $[\mbox {length}]^2$
, not
$[\mbox {length}]^2$
, not
![]() $[\mbox {length}]$
. This is already clear from formula (4) for the intersection form. Hence, for example, if
$[\mbox {length}]$
. This is already clear from formula (4) for the intersection form. Hence, for example, if
![]() $\Gamma $
is a circle of length L (in other words, consists of a single loop of length L attached to a vertex), then
$\Gamma $
is a circle of length L (in other words, consists of a single loop of length L attached to a vertex), then
![]() $\Gamma $
is canonically isomorphic to
$\Gamma $
is canonically isomorphic to
![]() $\operatorname {\mathrm {Pic}}^1(\Gamma )$
, but the volume of
$\operatorname {\mathrm {Pic}}^1(\Gamma )$
, but the volume of
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
is
$\operatorname {\mathrm {Jac}}(\Gamma )$
is
![]() $\sqrt {L}$
, rather than L.
$\sqrt {L}$
, rather than L.
2.5 Prym groups
We now discuss the Prym group of a free double cover of finite graphs. Unlike the case of metric graphs (which we treat in Subsection 2.6), finite groups do not have a distinguished connected component of the identity. We therefore require a notion of parity on elements of the kernel of the norm map.
Let
![]() $p:\widetilde {G}\to G$
be a free double cover of graphs. The induced maps
$p:\widetilde {G}\to G$
be a free double cover of graphs. The induced maps
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Div}}(\widetilde {G})\to \operatorname {\mathrm {Div}}(G)$
and
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Div}}(\widetilde {G})\to \operatorname {\mathrm {Div}}(G)$
and
![]() $\iota :\operatorname {\mathrm {Div}}(\widetilde {G})\to \operatorname {\mathrm {Div}}(\widetilde {G})$
given by
$\iota :\operatorname {\mathrm {Div}}(\widetilde {G})\to \operatorname {\mathrm {Div}}(\widetilde {G})$
given by
 $$ \begin{align*}\operatorname{\mathrm{Nm}}\left(\sum a_v v\right)=\sum a_v p(v),\quad \iota\left(\sum a_v v\right)=\sum a_v \iota(v) \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Nm}}\left(\sum a_v v\right)=\sum a_v p(v),\quad \iota\left(\sum a_v v\right)=\sum a_v \iota(v) \end{align*} $$
preserve degree and linear equivalence and descend to give a surjective map
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(G)$
and an isomorphism
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(G)$
and an isomorphism
![]() $\iota :\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(\widetilde {G})$
.
$\iota :\operatorname {\mathrm {Jac}}(\widetilde {G})\to \operatorname {\mathrm {Jac}}(\widetilde {G})$
.
A divisor in the kernel
![]() $D\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
has degree 0 and can be uniquely represented as
$D\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
has degree 0 and can be uniquely represented as
![]() $D=E-\iota (E)$
, where E is an effective divisor and the supports of E and
$D=E-\iota (E)$
, where E is an effective divisor and the supports of E and
![]() $\iota (E)$
are disjoint. We define the parity of D as
$\iota (E)$
are disjoint. We define the parity of D as
It turns out that parity respects addition and linear equivalence and hence gives a surjective homomorphism from
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Jac}}(\widetilde {G})$
to
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Jac}}(\widetilde {G})$
to
![]() $\mathbb {Z}/2\mathbb {Z}$
:
$\mathbb {Z}/2\mathbb {Z}$
:
Proposition 2.7. Let
![]() $D_1,D_2\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}^0(\widetilde {G})$
.
$D_1,D_2\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}^0(\widetilde {G})$
.
-
(1)
 $\epsilon (D_1+D_2)=\epsilon (D_1)+\epsilon (D_2)$
.
$\epsilon (D_1+D_2)=\epsilon (D_1)+\epsilon (D_2)$
. -
(2) If
 $D_1\simeq D_2$
then
$D_1\simeq D_2$
then
 $\epsilon (D_1)=\epsilon (D_2)$
.
$\epsilon (D_1)=\epsilon (D_2)$
.
Proof. Suppose that
![]() $p:\widetilde {G}\to G$
is defined by a spanning tree
$p:\widetilde {G}\to G$
is defined by a spanning tree
![]() $T\subset G$
and a nonempty subset
$T\subset G$
and a nonempty subset
![]() $S\subset E(G)\backslash E(T)$
, as in Construction A. Every divisor
$S\subset E(G)\backslash E(T)$
, as in Construction A. Every divisor
![]() $D\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
is of the form
$D\in \operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
is of the form
 $$ \begin{align*}D=\sum_{v\in V(G)}(a_{\widetilde{v}^+}\widetilde{v}^++a_{\widetilde{v}^-}\widetilde{v}^-), \end{align*} $$
$$ \begin{align*}D=\sum_{v\in V(G)}(a_{\widetilde{v}^+}\widetilde{v}^++a_{\widetilde{v}^-}\widetilde{v}^-), \end{align*} $$
where
![]() $a_{\widetilde {v}^+}+a_{\widetilde {v}^-}=0$
for each
$a_{\widetilde {v}^+}+a_{\widetilde {v}^-}=0$
for each
![]() $v\in V(G)$
. It follows that if
$v\in V(G)$
. It follows that if
![]() $D=E-\iota (E)$
, then
$D=E-\iota (E)$
, then
![]() $\deg E=\sum |a_{\widetilde {v}^+}|$
; hence,
$\deg E=\sum |a_{\widetilde {v}^+}|$
; hence,
 $$ \begin{align*}\epsilon(D)=\sum |a_{\widetilde{v}^+}|\bmod 2=\sum a_{\widetilde{v}^+}\bmod 2, \end{align*} $$
$$ \begin{align*}\epsilon(D)=\sum |a_{\widetilde{v}^+}|\bmod 2=\sum a_{\widetilde{v}^+}\bmod 2, \end{align*} $$
which is clearly preserved by addition.
To complete the proof, we need to show that any principal divisor in
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
is even. Consider an arbitrary principal divisor
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\subset \operatorname {\mathrm {Div}}(\widetilde {G})$
is even. Consider an arbitrary principal divisor
 $$\begin{align*}D=\sum_{v\in V(G)}(c_{\widetilde{v}^+}D_{\widetilde{v}^+}+c_{\widetilde{v}^-}D_{\widetilde{v}^-}) \end{align*}$$
$$\begin{align*}D=\sum_{v\in V(G)}(c_{\widetilde{v}^+}D_{\widetilde{v}^+}+c_{\widetilde{v}^-}D_{\widetilde{v}^-}) \end{align*}$$
on
![]() $\widetilde {G}$
. Its norm is
$\widetilde {G}$
. Its norm is
![]() $\operatorname {\mathrm {Nm}}(D)=\sum (c_{\widetilde {v}^+}+c_{\widetilde {v}^-})D_v\in \operatorname {\mathrm {Div}}(G)$
, which is the trivial divisor if and only if
$\operatorname {\mathrm {Nm}}(D)=\sum (c_{\widetilde {v}^+}+c_{\widetilde {v}^-})D_v\in \operatorname {\mathrm {Div}}(G)$
, which is the trivial divisor if and only if
![]() $c_{\widetilde {v}^+}+c_{\widetilde {v}^-}=c$
for a fixed
$c_{\widetilde {v}^+}+c_{\widetilde {v}^-}=c$
for a fixed
![]() $c\in \mathbb {Z}$
and for all
$c\in \mathbb {Z}$
and for all
![]() $v\in V(G)$
. Therefore, if
$v\in V(G)$
. Therefore, if
![]() $\operatorname {\mathrm {Nm}}(D)=0$
in
$\operatorname {\mathrm {Nm}}(D)=0$
in
![]() $\operatorname {\mathrm {Div}}(G)$
, then setting
$\operatorname {\mathrm {Div}}(G)$
, then setting
![]() $a_v=c_{\widetilde {v}^+}-c=-c_{\widetilde {v}^-}$
, we see that
$a_v=c_{\widetilde {v}^+}-c=-c_{\widetilde {v}^-}$
, we see that
 $$\begin{align*}D=cD^+ + \sum_{v\in V(G)} a_v (D_{\widetilde{v}^+} - D_{\widetilde{v}^-}), \end{align*}$$
$$\begin{align*}D=cD^+ + \sum_{v\in V(G)} a_v (D_{\widetilde{v}^+} - D_{\widetilde{v}^-}), \end{align*}$$
where
![]() $D^+$
the principal divisor obtained by firing each vertex
$D^+$
the principal divisor obtained by firing each vertex
![]() $\widetilde {v}^+$
of the top sheet once and
$\widetilde {v}^+$
of the top sheet once and
![]() $a_v\in \mathbb {Z}$
. We now show that each summand above is even, so D is even as well by the first part of the proof.
$a_v\in \mathbb {Z}$
. We now show that each summand above is even, so D is even as well by the first part of the proof.
First, we consider divisors of the form
![]() $D_{\widetilde {v}^+}-D_{\widetilde {v}^-}$
for
$D_{\widetilde {v}^+}-D_{\widetilde {v}^-}$
for
![]() $v\in V(G)$
. Suppose that the double cover p is described by Construction A. For any vertex
$v\in V(G)$
. Suppose that the double cover p is described by Construction A. For any vertex
![]() $u\in V(G)$
, denote
$u\in V(G)$
, denote
![]() $a_u$
and
$a_u$
and
![]() $b_u$
as the number of edges between u and v in
$b_u$
as the number of edges between u and v in
![]() $E(G)\backslash S$
and S, respectively. Then
$E(G)\backslash S$
and S, respectively. Then
and
 $$\begin{align*}(D_{\widetilde{v}^+} - D_{\widetilde{v}^-}) (\widetilde{v}^{{\kern1.5pt}\pm})= -\sum_{u\neq v} \mp{}(a_u + b_u). \end{align*}$$
$$\begin{align*}(D_{\widetilde{v}^+} - D_{\widetilde{v}^-}) (\widetilde{v}^{{\kern1.5pt}\pm})= -\sum_{u\neq v} \mp{}(a_u + b_u). \end{align*}$$
It follows that the contribution from each vertex u to the positive part of
![]() $D_{\widetilde {v}^+} - D_{\widetilde {v}^-}$
is
$D_{\widetilde {v}^+} - D_{\widetilde {v}^-}$
is
![]() $|a_u-b_u| + a_u + b_u = \max (2 a_u, 2 b_u)$
, which is even.
$|a_u-b_u| + a_u + b_u = \max (2 a_u, 2 b_u)$
, which is even.
As for
![]() $D^+$
, a direct calculation shows that
$D^+$
, a direct calculation shows that
 $$\begin{align*}D^+=\sum_{v\in V(G)}D_{\widetilde{v}^+}=\sum_{e\in S} \left(\widetilde{s(e)}^-+\widetilde{t(e)}^--\widetilde{s(e)}^+-\widetilde{t(e)}^+\right); \end{align*}$$
$$\begin{align*}D^+=\sum_{v\in V(G)}D_{\widetilde{v}^+}=\sum_{e\in S} \left(\widetilde{s(e)}^-+\widetilde{t(e)}^--\widetilde{s(e)}^+-\widetilde{t(e)}^+\right); \end{align*}$$
hence,
![]() $D^+$
is even and the proof is complete.
$D^+$
is even and the proof is complete.
Definition 2.8. The Prym group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)\subset \operatorname {\mathrm {Jac}}(\widetilde {G})$
of a free double cover
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)\subset \operatorname {\mathrm {Jac}}(\widetilde {G})$
of a free double cover
![]() $p:\widetilde {G}\to G$
is the subgroup of even divisors in
$p:\widetilde {G}\to G$
is the subgroup of even divisors in
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
.
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
.
It is clear that the order of the Prym group is equal to
 $$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}, \end{align*} $$
$$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}, \end{align*} $$
and one of the principal results of our article is a combinatorial formula (14) for
![]() $|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|$
. For now, we illustrate with an example.
$|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|$
. For now, we illustrate with an example.
Example 2.9. Consider the free double cover
![]() $p:\widetilde {G}\to G$
shown in Figure 1. In terms of Construction A, we can describe it by choosing
$p:\widetilde {G}\to G$
shown in Figure 1. In terms of Construction A, we can describe it by choosing
![]() $T\subset G$
to be the tree containing
$T\subset G$
to be the tree containing
![]() $e_3$
,
$e_3$
,
![]() $e_4$
and
$e_4$
and
![]() $e_5$
and setting
$e_5$
and setting
![]() $S=\{e_1,e_2\}$
. Using Kirchhoff’s theorem, we find that
$S=\{e_1,e_2\}$
. Using Kirchhoff’s theorem, we find that
![]() $|\operatorname {\mathrm {Jac}} (G')|=64$
and
$|\operatorname {\mathrm {Jac}} (G')|=64$
and
![]() $|\operatorname {\mathrm {Jac}}(G)|=4$
; therefore,
$|\operatorname {\mathrm {Jac}}(G)|=4$
; therefore,
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
and
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
have orders
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
have orders
![]() $16$
and
$16$
and
![]() $8$
, respectively. The group
$8$
, respectively. The group
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
is spanned by the divisors
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
is spanned by the divisors
![]() $D_i=\widetilde {v}_i^+-\widetilde {v}_i^-$
, where
$D_i=\widetilde {v}_i^+-\widetilde {v}_i^-$
, where
![]() $i=1,2,3,4$
and an exhaustive calculation using Dhar’s burning algorithm give a complete set of relations on the
$i=1,2,3,4$
and an exhaustive calculation using Dhar’s burning algorithm give a complete set of relations on the
![]() $D_i$
:
$D_i$
:
It follows that
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/8\mathbb {Z}$
with generators
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}\simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/8\mathbb {Z}$
with generators
![]() $D_1$
and
$D_1$
and
![]() $D_2$
and hence
$D_2$
and hence
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)\simeq \mathbb {Z}/8\mathbb {Z}$
with generator
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)\simeq \mathbb {Z}/8\mathbb {Z}$
with generator
![]() $D_1+D_2$
.
$D_1+D_2$
.

Figure 1 An example of a free double cover.
We note that the Abel–Prym map
![]() $\widetilde {G}=\operatorname {\mathrm {Sym}}^1(\widetilde {G})\to \operatorname {\mathrm {Prym}}^1(\widetilde {G}/G)$
sending
$\widetilde {G}=\operatorname {\mathrm {Sym}}^1(\widetilde {G})\to \operatorname {\mathrm {Prym}}^1(\widetilde {G}/G)$
sending
![]() $\widetilde {v}^{\pm }_i$
to
$\widetilde {v}^{\pm }_i$
to
![]() $\pm D_i$
is not surjective: both sets have eight elements, but the images of
$\pm D_i$
is not surjective: both sets have eight elements, but the images of
![]() $\widetilde {v}^{\pm }_1$
are equal, as well as those of
$\widetilde {v}^{\pm }_1$
are equal, as well as those of
![]() $\widetilde {v}^{\pm }_4$
.
$\widetilde {v}^{\pm }_4$
.
2.6 Prym varieties
Finally, we recall the definition of the Prym variety of a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs (see [Reference Jensen and LenJL18] and [Reference Len and UlirschLU19]). As in the finite case, the cover
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs (see [Reference Jensen and LenJL18] and [Reference Len and UlirschLU19]). As in the finite case, the cover
![]() $\pi $
induces a surjective norm map
$\pi $
induces a surjective norm map
 $$ \begin{align*}\operatorname{\mathrm{Nm}}:\operatorname{\mathrm{Pic}}^0(\widetilde{\Gamma})\to \operatorname{\mathrm{Pic}}^0(\Gamma),\quad \operatorname{\mathrm{Nm}}\left(\sum a_i \widetilde{p}_i\right) = \sum a_i\pi(\widetilde{p}_i), \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Nm}}:\operatorname{\mathrm{Pic}}^0(\widetilde{\Gamma})\to \operatorname{\mathrm{Pic}}^0(\Gamma),\quad \operatorname{\mathrm{Nm}}\left(\sum a_i \widetilde{p}_i\right) = \sum a_i\pi(\widetilde{p}_i), \end{align*} $$
and a corresponding involution
![]() $\iota :\operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })\to \operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })$
.
$\iota :\operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })\to \operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })$
.
The kernel
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
consists of divisors having a representative of the form
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
consists of divisors having a representative of the form
![]() $E-\iota (E)$
for some effective divisor E on
$E-\iota (E)$
for some effective divisor E on
![]() $\widetilde {\Gamma }$
. Indeed, suppose that
$\widetilde {\Gamma }$
. Indeed, suppose that
![]() $\widetilde {D}$
is a divisor on
$\widetilde {D}$
is a divisor on
![]() $\widetilde \Gamma $
such that
$\widetilde \Gamma $
such that
![]() $\operatorname {\mathrm {Nm}}(\widetilde {D})\simeq 0$
. Then
$\operatorname {\mathrm {Nm}}(\widetilde {D})\simeq 0$
. Then
![]() $\operatorname {\mathrm {Nm}}(\widetilde {D}) +\operatorname {\mathrm {div}}{f} = 0$
for some piecewise linear function f. Defining
$\operatorname {\mathrm {Nm}}(\widetilde {D}) +\operatorname {\mathrm {div}}{f} = 0$
for some piecewise linear function f. Defining
![]() $\tilde f(x) = f(\pi (x))$
, we see that
$\tilde f(x) = f(\pi (x))$
, we see that
![]() $\widetilde {D}$
is equivalent to a divisor whose pushforward is the zero divisor on the nose. Furthermore, the parity of E is well-defined and
$\widetilde {D}$
is equivalent to a divisor whose pushforward is the zero divisor on the nose. Furthermore, the parity of E is well-defined and
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
has two connected components corresponding to the parity of E [Reference Jensen and LenJL18, Proposition 6.1] (note that, in the more general case when
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
has two connected components corresponding to the parity of E [Reference Jensen and LenJL18, Proposition 6.1] (note that, in the more general case when
![]() $\pi $
is a dilated unramified double cover,
$\pi $
is a dilated unramified double cover,
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
has only one connected component).
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
has only one connected component).
Definition 2.10. The Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )\subset \operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })$
of the free double cover
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )\subset \operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })$
of the free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is the connected component of the identity of
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is the connected component of the identity of
![]() $\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
.
$\operatorname {\mathrm {Ker}} \operatorname {\mathrm {Nm}}$
.
The Prym variety
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
has the structure of a tropical ppav, which we now describe. Denote
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
has the structure of a tropical ppav, which we now describe. Denote
![]() $\widetilde {\Lambda }=\Omega (\widetilde {\Gamma },\mathbb {Z})$
,
$\widetilde {\Lambda }=\Omega (\widetilde {\Gamma },\mathbb {Z})$
,
![]() $\widetilde {\Lambda }'=H_1(\widetilde {\Gamma },\mathbb {Z})$
,
$\widetilde {\Lambda }'=H_1(\widetilde {\Gamma },\mathbb {Z})$
,
![]() $\Lambda =\Omega (\Gamma ,\mathbb {Z})$
and
$\Lambda =\Omega (\Gamma ,\mathbb {Z})$
and
![]() $\Lambda '=H_1(\Gamma ,\mathbb {Z})$
. Choose an oriented model
$\Lambda '=H_1(\Gamma ,\mathbb {Z})$
. Choose an oriented model
![]() $p:\widetilde {G}\to G$
for
$p:\widetilde {G}\to G$
for
![]() $\pi $
and consider the pushforward and pullback maps
$\pi $
and consider the pushforward and pullback maps
![]() $\pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
and
$\pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
and
![]() $\pi ^*:\Omega (\Gamma ,\mathbb {Z})\to \Omega (\widetilde {\Gamma },\mathbb {Z})$
defined by
$\pi ^*:\Omega (\Gamma ,\mathbb {Z})\to \Omega (\widetilde {\Gamma },\mathbb {Z})$
defined by
 $$ \begin{align*}\pi_*\left[\sum_{\widetilde{e}\in E(\widetilde{G})} a_{\widetilde{e}} \widetilde{e}\right]=\sum_{\widetilde{e}\in E(\widetilde{G})} a_{\widetilde{e}} \pi(\widetilde{e}),\quad \pi^* \left[\sum_{e\in E(G)}a_e de\right]= \sum_{e\in E(G)}a_e (d\widetilde{e}^{{\kern2pt}+}+d\widetilde{e}^{{\kern2pt}-}). \end{align*} $$
$$ \begin{align*}\pi_*\left[\sum_{\widetilde{e}\in E(\widetilde{G})} a_{\widetilde{e}} \widetilde{e}\right]=\sum_{\widetilde{e}\in E(\widetilde{G})} a_{\widetilde{e}} \pi(\widetilde{e}),\quad \pi^* \left[\sum_{e\in E(G)}a_e de\right]= \sum_{e\in E(G)}a_e (d\widetilde{e}^{{\kern2pt}+}+d\widetilde{e}^{{\kern2pt}-}). \end{align*} $$
It is easy to verify that the maps
![]() $\pi _*$
and
$\pi _*$
and
![]() $\pi ^*$
satisfy equation (3) with respect to the integration pairings on
$\pi ^*$
satisfy equation (3) with respect to the integration pairings on
![]() $\widetilde {\Gamma }$
and
$\widetilde {\Gamma }$
and
![]() $\Gamma $
. Therefore, the pair
$\Gamma $
. Therefore, the pair
![]() $(\pi _*,\pi ^*)$
defines a homomorphism
$(\pi _*,\pi ^*)$
defines a homomorphism
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
of real tori with integral structure (by Proposition 2.2.3 in [Reference Len and UlirschLU19], this homomorphism is identified with the norm homomorphism
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
of real tori with integral structure (by Proposition 2.2.3 in [Reference Len and UlirschLU19], this homomorphism is identified with the norm homomorphism
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })\to \operatorname {\mathrm {Pic}}^0(\Gamma )$
under the Abel–Jacobi isomorphism, justifying the notation). Hence,
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Pic}}^0(\widetilde {\Gamma })\to \operatorname {\mathrm {Pic}}^0(\Gamma )$
under the Abel–Jacobi isomorphism, justifying the notation). Hence,
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is in fact the real torus with integral structure
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is in fact the real torus with integral structure
![]() $(\operatorname {\mathrm {Ker}}\operatorname {\mathrm {Nm}})_0=(K,K',[\cdot ,\cdot ]_K)$
, where
$(\operatorname {\mathrm {Ker}}\operatorname {\mathrm {Nm}})_0=(K,K',[\cdot ,\cdot ]_K)$
, where
![]() $K=(\operatorname {\mathrm {Coker}} \pi ^*)^{tf}$
,
$K=(\operatorname {\mathrm {Coker}} \pi ^*)^{tf}$
,
![]() $K'=\operatorname {\mathrm {Ker}} \pi _*$
and
$K'=\operatorname {\mathrm {Ker}} \pi _*$
and
![]() $[\cdot ,\cdot ]_K$
is the pairing induced by the integration pairing on
$[\cdot ,\cdot ]_K$
is the pairing induced by the integration pairing on
![]() $\widetilde {\Gamma }$
. Alternatively, we can describe
$\widetilde {\Gamma }$
. Alternatively, we can describe
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
as the quotient
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
as the quotient
 $$ \begin{align*}\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma)=\frac{\operatorname{\mathrm{Ker}} \overline{\pi}:\Omega^*(\widetilde{\Gamma})\to \Omega^*(\Gamma)}{\operatorname{\mathrm{Ker}} \pi_*:H_1(\widetilde{\Gamma},\mathbb{Z})\to H^1(\Gamma,\mathbb{Z})}, \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma)=\frac{\operatorname{\mathrm{Ker}} \overline{\pi}:\Omega^*(\widetilde{\Gamma})\to \Omega^*(\Gamma)}{\operatorname{\mathrm{Ker}} \pi_*:H_1(\widetilde{\Gamma},\mathbb{Z})\to H^1(\Gamma,\mathbb{Z})}, \end{align*} $$
where
![]() $\overline {\pi }$
is the map dual to
$\overline {\pi }$
is the map dual to
![]() $\pi ^*$
.
$\pi ^*$
.
The polarisation
![]() $\widetilde {\xi }:H_1(\widetilde {\Gamma },\mathbb {Z})\to \Omega (\widetilde {\Gamma },\mathbb {Z})$
on
$\widetilde {\xi }:H_1(\widetilde {\Gamma },\mathbb {Z})\to \Omega (\widetilde {\Gamma },\mathbb {Z})$
on
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
induces a polarisation
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
induces a polarisation
![]() $i^*\widetilde {\xi }:K'\to K$
on
$i^*\widetilde {\xi }:K'\to K$
on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, and Theorem 2.2.7 in [Reference Len and UlirschLU19] states that there exists a principal polarisation
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, and Theorem 2.2.7 in [Reference Len and UlirschLU19] states that there exists a principal polarisation
![]() $\psi :K'\to K$
on
$\psi :K'\to K$
on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
such that
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
such that
![]() $i^*\widetilde {\xi }=2\psi $
. Hence,
$i^*\widetilde {\xi }=2\psi $
. Hence,
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is a tropical ppav. We note that the inner product
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is a tropical ppav. We note that the inner product
![]() $(\cdot ,\cdot )_P$
on
$(\cdot ,\cdot )_P$
on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
induced by the principal polarisation
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
induced by the principal polarisation
![]() $\psi $
is half of the restriction of the inner product
$\psi $
is half of the restriction of the inner product
![]() $(\cdot ,\cdot )_{\widetilde {\Gamma }}$
from
$(\cdot ,\cdot )_{\widetilde {\Gamma }}$
from
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
. In other words, for
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
. In other words, for
![]() $\gamma , \delta \in \operatorname {\mathrm {Ker}} \pi _*$
we have
$\gamma , \delta \in \operatorname {\mathrm {Ker}} \pi _*$
we have
 $$ \begin{align} (\gamma,\delta)_P{\,=\,}[\gamma,\psi(\delta)]{\,=\,}\frac{1}{2}[\gamma,\widetilde{\xi}(\delta)]{\,=\,}\frac{1}{2}(\gamma,\delta)_{\widetilde{\Gamma}}{\,=\,}\frac{1}{2}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\gamma_{\widetilde{e}}\delta_{\widetilde{e}}\ell(\widetilde{e}),\quad \gamma{\,=\,}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\gamma_{\widetilde{e}}\widetilde{e},\quad \delta{\,=\,}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\delta_{\widetilde{e}}\widetilde{e}, \end{align} $$
$$ \begin{align} (\gamma,\delta)_P{\,=\,}[\gamma,\psi(\delta)]{\,=\,}\frac{1}{2}[\gamma,\widetilde{\xi}(\delta)]{\,=\,}\frac{1}{2}(\gamma,\delta)_{\widetilde{\Gamma}}{\,=\,}\frac{1}{2}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\gamma_{\widetilde{e}}\delta_{\widetilde{e}}\ell(\widetilde{e}),\quad \gamma{\,=\,}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\gamma_{\widetilde{e}}\widetilde{e},\quad \delta{\,=\,}\sum_{\widetilde{e}\in E(\widetilde{\Gamma})}\delta_{\widetilde{e}}\widetilde{e}, \end{align} $$
and similarly for the induced product on
![]() $\operatorname {\mathrm {Ker}} \overline {\pi }$
. When discussing the metric properties of
$\operatorname {\mathrm {Ker}} \overline {\pi }$
. When discussing the metric properties of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, such as its volume, we always employ the inner product
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, such as its volume, we always employ the inner product
![]() $(\cdot ,\cdot )_P$
induced by the principal polarisation.
$(\cdot ,\cdot )_P$
induced by the principal polarisation.
We use a set of explicit coordinates on the torus
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
or, more accurately, on its universal cover
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
or, more accurately, on its universal cover
![]() $\operatorname {\mathrm {Ker}} \overline {\pi }$
. Choose a basis
$\operatorname {\mathrm {Ker}} \overline {\pi }$
. Choose a basis
 $$ \begin{align*}\widetilde{\gamma}_j=\sum_{\widetilde{e}\in E(\widetilde{G})} \widetilde{\gamma}_{j,\widetilde{e}}\widetilde{e},\quad j=1,\ldots,g-1 \end{align*} $$
$$ \begin{align*}\widetilde{\gamma}_j=\sum_{\widetilde{e}\in E(\widetilde{G})} \widetilde{\gamma}_{j,\widetilde{e}}\widetilde{e},\quad j=1,\ldots,g-1 \end{align*} $$
for
![]() $\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
. The principal polarisation
$\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
. The principal polarisation
 $\psi =\frac {1}{2}\widetilde {\xi }$
gives a corresponding basis of the second lattice
$\psi =\frac {1}{2}\widetilde {\xi }$
gives a corresponding basis of the second lattice
![]() $(\operatorname {\mathrm {Coker}} \pi ^*)^{tf}$
:
$(\operatorname {\mathrm {Coker}} \pi ^*)^{tf}$
:
 $$ \begin{align*}\omega_j=\psi(\widetilde{\gamma}_j)=\frac{1}{2}\sum_{\widetilde{e}\in E(\widetilde{G})} \widetilde{\gamma}_{j,\widetilde{e}}d\widetilde{e},\quad j=1,\ldots,g-1. \end{align*} $$
$$ \begin{align*}\omega_j=\psi(\widetilde{\gamma}_j)=\frac{1}{2}\sum_{\widetilde{e}\in E(\widetilde{G})} \widetilde{\gamma}_{j,\widetilde{e}}d\widetilde{e},\quad j=1,\ldots,g-1. \end{align*} $$
Let
![]() $\omega ^*_j$
denote the basis of
$\omega ^*_j$
denote the basis of
![]() $\operatorname {\mathrm {Ker}} \overline {\pi }:\Omega ^*(\widetilde {\Gamma })\to \Omega ^*(\Gamma )$
dual to the
$\operatorname {\mathrm {Ker}} \overline {\pi }:\Omega ^*(\widetilde {\Gamma })\to \Omega ^*(\Gamma )$
dual to the
![]() $\omega _j$
, so that
$\omega _j$
, so that
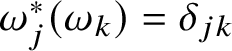 $\omega ^*_j(\omega _k)=\delta _{jk}$
; then elements of
$\omega ^*_j(\omega _k)=\delta _{jk}$
; then elements of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
can be given (locally uniquely) as linear combinations of the
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
can be given (locally uniquely) as linear combinations of the
![]() $\omega ^*_j$
.
$\omega ^*_j$
.
We compute for future reference the volume of the unit cube
 $C(\omega ^*_1,\ldots ,\omega ^*_{g-1})$
in the coordinate system defined by the
$C(\omega ^*_1,\ldots ,\omega ^*_{g-1})$
in the coordinate system defined by the
![]() $\omega ^*_j$
. We know that
$\omega ^*_j$
. We know that
![]() $\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))=\sqrt {\det G}$
, where
$\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))=\sqrt {\det G}$
, where
![]() $G_{ij}=(\widetilde {\gamma }_i,\widetilde {\gamma }_j)_P$
is the Gramian matrix of the basis
$G_{ij}=(\widetilde {\gamma }_i,\widetilde {\gamma }_j)_P$
is the Gramian matrix of the basis
![]() $\widetilde {\gamma }_j$
. The
$\widetilde {\gamma }_j$
. The
![]() $\widetilde {\gamma }_j$
, viewed as elements of
$\widetilde {\gamma }_j$
, viewed as elements of
![]() $\operatorname {\mathrm {Ker}} \overline {\pi }$
, are themselves a basis, so we can write
$\operatorname {\mathrm {Ker}} \overline {\pi }$
, are themselves a basis, so we can write
![]() $\omega ^*_i=\sum _j A_{ij}\widetilde {\gamma }_j$
for some matrix
$\omega ^*_i=\sum _j A_{ij}\widetilde {\gamma }_j$
for some matrix
![]() $A_{ij}$
. Pairing with
$A_{ij}$
. Pairing with
![]() $\omega _j$
and using that
$\omega _j$
and using that
![]() $[\widetilde {\gamma }_i,\omega _j]=G_{ij}$
, we see that A is in fact the inverse matrix of G. Hence, we see that
$[\widetilde {\gamma }_i,\omega _j]=G_{ij}$
, we see that A is in fact the inverse matrix of G. Hence, we see that
 $$ \begin{align} \operatorname{\mathrm{Vol}}(C(\omega^*_1,\ldots,\omega^*_{g-1}))=\det (\omega^*_i,\omega^*_j)=\det G^{-1} \det(\widetilde{\gamma}_i,\widetilde{\gamma}_j)\det G^{-1}=\frac{1}{\det G}=\frac{1}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}(C(\omega^*_1,\ldots,\omega^*_{g-1}))=\det (\omega^*_i,\omega^*_j)=\det G^{-1} \det(\widetilde{\gamma}_i,\widetilde{\gamma}_j)\det G^{-1}=\frac{1}{\det G}=\frac{1}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}. \end{align} $$
In particular, this volume does not depend on the choice of basis
![]() $\widetilde {\gamma }_j$
.
$\widetilde {\gamma }_j$
.
Remark 2.11. The definition of the Prym group for a free double cover of finite graphs is consistent with the definition for metric graphs in the following sense. Let
![]() $p:\widetilde {G}\to G$
be a free double cover of finite graphs and let
$p:\widetilde {G}\to G$
be a free double cover of finite graphs and let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be the corresponding double cover of metric graphs, where
$\pi :\widetilde {\Gamma }\to \Gamma $
be the corresponding double cover of metric graphs, where
![]() $\widetilde {\Gamma }$
and
$\widetilde {\Gamma }$
and
![]() $\Gamma $
are obtained respectively from
$\Gamma $
are obtained respectively from
![]() $\widetilde {G}$
and G by setting all edge lengths to
$\widetilde {G}$
and G by setting all edge lengths to
![]() $1$
. Then
$1$
. Then
![]() $\operatorname {\mathrm {Jac}}(\widetilde {G})$
is naturally a subgroup of
$\operatorname {\mathrm {Jac}}(\widetilde {G})$
is naturally a subgroup of
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
, consisting of divisors supported at the vertices and
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
, consisting of divisors supported at the vertices and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)=\operatorname {\mathrm {Jac}}(\widetilde {G})\cap \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
.
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)=\operatorname {\mathrm {Jac}}(\widetilde {G})\cap \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
.
2.7 Polyhedral spaces and harmonic morphisms
The spaces
![]() $\operatorname {\mathrm {Sym}}^d(\Gamma )$
,
$\operatorname {\mathrm {Sym}}^d(\Gamma )$
,
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
and
$\operatorname {\mathrm {Jac}}(\Gamma )$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are examples of rational polyhedral spaces, which are topological spaces locally modelled on rational polyhedral sets in
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are examples of rational polyhedral spaces, which are topological spaces locally modelled on rational polyhedral sets in
![]() $\mathbb {R}^n$
. A rational polyhedral space comes equipped with a structure sheaf, pulled back from the sheaf of affine
$\mathbb {R}^n$
. A rational polyhedral space comes equipped with a structure sheaf, pulled back from the sheaf of affine
![]() $\mathbb {Z}$
-linear functions on the embedded polyhedra. We shall not require the general theory of rational polyhedral spaces; in particular, we shall use only the polyhedral decomposition and not the sheaf of affine functions. See [Reference Mikhalkin and ZharkovMZ14], [Reference Gross and ShokriehGS19] for details.
$\mathbb {Z}$
-linear functions on the embedded polyhedra. We shall not require the general theory of rational polyhedral spaces; in particular, we shall use only the polyhedral decomposition and not the sheaf of affine functions. See [Reference Mikhalkin and ZharkovMZ14], [Reference Gross and ShokriehGS19] for details.
A rational polyhedral space P is a finite union of polyhedra, which we call cells. We only consider compact polyhedral spaces. The intersection of any two cells is either empty or a face of each. A polyhedral space P is equidimensional of dimension n if each maximal cell of P (with respect to inclusion) has dimension n and is connected through codimension 1 if the complement in P of all cells of codimension 2 is connected. A map
![]() $f:P\to Q$
of polyhedral spaces is locally given by affine
$f:P\to Q$
of polyhedral spaces is locally given by affine
![]() $\mathbb {Z}$
-linear transformations and is required to map each cell of P surjectively onto a cell of Q. We say that f contracts a cell C of P if
$\mathbb {Z}$
-linear transformations and is required to map each cell of P surjectively onto a cell of Q. We say that f contracts a cell C of P if
![]() $\dim (f(C))<\dim (C)$
.
$\dim (f(C))<\dim (C)$
.
We use an ad hoc definition of harmonic morphisms of polyhedral spaces, modelled on the corresponding definition for metric graphs.
Definition 2.12. [cf. Definition 2.5 in [Reference Len and RanganathanLR18]] Let
![]() $f:P\to Q$
be a map of equidimensional polyhedral spaces of the same dimension and let
$f:P\to Q$
be a map of equidimensional polyhedral spaces of the same dimension and let
![]() $\deg _f$
be a nonnegative integer-valued function defined on the top-dimensional cells of P. Let C be a codimension 1 cell of P mapping surjectively onto a codimension 1 cell D of Q. We say that f is harmonic at C (with respect to the degree function
$\deg _f$
be a nonnegative integer-valued function defined on the top-dimensional cells of P. Let C be a codimension 1 cell of P mapping surjectively onto a codimension 1 cell D of Q. We say that f is harmonic at C (with respect to the degree function
![]() $\deg _f$
) if the following condition holds: for any codimension 0 cell N of Q adjacent to D, the sum
$\deg _f$
) if the following condition holds: for any codimension 0 cell N of Q adjacent to D, the sum
 $$ \begin{align} \deg_f(C)=\sum_{M\subset f^{-1}(N),\, M\supset C} \deg_f (M) \end{align} $$
$$ \begin{align} \deg_f(C)=\sum_{M\subset f^{-1}(N),\, M\supset C} \deg_f (M) \end{align} $$
of the degrees
![]() $\deg _f M$
over all codimension 0 cells M of P adjacent to C and mapping to N is the same; in other words, does not depend on the choice of N. We say that f is harmonic if f is harmonic at every codimension 1 cell of P and, in addition, if
$\deg _f M$
over all codimension 0 cells M of P adjacent to C and mapping to N is the same; in other words, does not depend on the choice of N. We say that f is harmonic if f is harmonic at every codimension 1 cell of P and, in addition, if
![]() $f(C)=0$
on a codimension 0 cell C if and only if f contracts C.
$f(C)=0$
on a codimension 0 cell C if and only if f contracts C.
Given a harmonic morphism
![]() $f:P\to Q$
, equation (10) extends the degree function
$f:P\to Q$
, equation (10) extends the degree function
![]() $\deg _f$
to codimension 1 cells of P. If Q is connected through codimension 1, we can similarly define the degree on cells of any codimension and hence on all of P (note, however, that for a cell C of positive codimension,
$\deg _f$
to codimension 1 cells of P. If Q is connected through codimension 1, we can similarly define the degree on cells of any codimension and hence on all of P (note, however, that for a cell C of positive codimension,
![]() $\deg _f(C)=0$
does not imply that C is contracted). The function
$\deg _f(C)=0$
does not imply that C is contracted). The function
![]() $\deg _f$
is locally constant in fibres: given
$\deg _f$
is locally constant in fibres: given
![]() $p\in P$
and an open neighbourhood
$p\in P$
and an open neighbourhood
![]() $V\ni f(p)$
, there exists an open neighbourhood
$V\ni f(p)$
, there exists an open neighbourhood
![]() $U\ni p$
such that
$U\ni p$
such that
![]() $f(U)\subset V$
and such that for any
$f(U)\subset V$
and such that for any
![]() $q\in V$
the sum of the degrees over all points of
$q\in V$
the sum of the degrees over all points of
![]() $f^{-1}(q)\cap U$
is the same (in particular, this sum is finite). It follows that a harmonic morphism to a target connected through codimension 1 is surjective and has a well-defined global degree, which is the sum of the degrees over all points of any fibre.
$f^{-1}(q)\cap U$
is the same (in particular, this sum is finite). It follows that a harmonic morphism to a target connected through codimension 1 is surjective and has a well-defined global degree, which is the sum of the degrees over all points of any fibre.
The structure of a rational polyhedral space on a tropical abelian variety, such as
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
and
$\operatorname {\mathrm {Jac}}(\Gamma )$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, is induced by the integral structure: an affine linear function is
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, is induced by the integral structure: an affine linear function is
![]() $\mathbb {Z}$
-linear if it has integer slopes with respect to the embedded lattice. The correct definition of a rational polyhedral structure on
$\mathbb {Z}$
-linear if it has integer slopes with respect to the embedded lattice. The correct definition of a rational polyhedral structure on
![]() $\operatorname {\mathrm {Sym}}^d(\Gamma )$
, however, requires some care. The space
$\operatorname {\mathrm {Sym}}^d(\Gamma )$
, however, requires some care. The space
![]() $\operatorname {\mathrm {Sym}}^d(\Gamma )$
has a natural cellular decomposition, with top-dimensional cells
$\operatorname {\mathrm {Sym}}^d(\Gamma )$
has a natural cellular decomposition, with top-dimensional cells
![]() $C(F)$
indexed by d-tuples
$C(F)$
indexed by d-tuples
![]() $F\subset E(G)$
of edges of a suitably chosen model G of
$F\subset E(G)$
of edges of a suitably chosen model G of
![]() $\Gamma $
(see equation (21)). If the d-tuple
$\Gamma $
(see equation (21)). If the d-tuple
![]() $F=\{e_1,\ldots ,e_d\}$
contains neither loops nor repeated edges, then
$F=\{e_1,\ldots ,e_d\}$
contains neither loops nor repeated edges, then
![]() $C(F)$
is the parallelotope obtained by taking the Cartesian product of the
$C(F)$
is the parallelotope obtained by taking the Cartesian product of the
![]() $e_i$
inside
$e_i$
inside
![]() $\mathbb {R}^d$
. If F contains loop edges, then the corresponding cell will have self-gluings along some of its boundary cells. A more serious issue arises if F has repeated edges; in this case, the cell
$\mathbb {R}^d$
. If F contains loop edges, then the corresponding cell will have self-gluings along some of its boundary cells. A more serious issue arises if F has repeated edges; in this case, the cell
![]() $C(F)$
is a quotient of a parallelotope by a finite permutation action, which requires introducing additional cells at the appropriate diagonals.
$C(F)$
is a quotient of a parallelotope by a finite permutation action, which requires introducing additional cells at the appropriate diagonals.
A complete description of the polyhedral structure on
![]() $\operatorname {\mathrm {Sym}}^d(\Gamma )$
is given in the paper [Reference Brandt and UlirschBU18]. However, neither of the aforementioned issues arise in our article. First, we can always choose a loopless model for any tropical curve. Second, and more important, all of the calculations in this article concern only those cells
$\operatorname {\mathrm {Sym}}^d(\Gamma )$
is given in the paper [Reference Brandt and UlirschBU18]. However, neither of the aforementioned issues arise in our article. First, we can always choose a loopless model for any tropical curve. Second, and more important, all of the calculations in this article concern only those cells
![]() $C(F)$
for which F has no repeated edges. Specifically, we are interested in the structure of the Abel–Prym map
$C(F)$
for which F has no repeated edges. Specifically, we are interested in the structure of the Abel–Prym map
![]() $\Psi ^d:\operatorname {\mathrm {Sym}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
associated to a double cover
$\Psi ^d:\operatorname {\mathrm {Sym}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
associated to a double cover
![]() $\widetilde {\Gamma }\to \Gamma $
, and one of our first results (Theorem 4.1 part (1)) states that
$\widetilde {\Gamma }\to \Gamma $
, and one of our first results (Theorem 4.1 part (1)) states that
![]() $\Psi ^d$
contracts all of those cells
$\Psi ^d$
contracts all of those cells
![]() $C(F)$
where F has repeated edges. Hence, all top-dimensional cells of the symmetric product
$C(F)$
where F has repeated edges. Hence, all top-dimensional cells of the symmetric product
![]() $\operatorname {\mathrm {Sym}}^d(\Gamma )$
can be assumed to be parallelotopes.
$\operatorname {\mathrm {Sym}}^d(\Gamma )$
can be assumed to be parallelotopes.
3 Kirchhoff’s theorem for the Prym group and the Prym variety
In this section, we give combinatorial formulas for the order (14) of the Prym group of a free double cover
![]() $p:\widetilde {G}\to G$
of finite graphs and the volume (17) of the Prym variety of a free double cover
$p:\widetilde {G}\to G$
of finite graphs and the volume (17) of the Prym variety of a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs.
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs.
Formula (14) had already been obtained by Zaslavsky (see Theorem 8A.4 in [Reference ZaslavskyZas82]). Specifically, a free double cover
![]() $p:\widetilde {G}\to G$
induces the structure of a signed graph on G: defining the cover p in terms of Construction A with respect to a spanning tree
$p:\widetilde {G}\to G$
induces the structure of a signed graph on G: defining the cover p in terms of Construction A with respect to a spanning tree
![]() $T\subset G$
, we attach a negative sign
$T\subset G$
, we attach a negative sign
![]() $-$
to each edge
$-$
to each edge
![]() $e\in S\subset E(G)\backslash E(T)$
and a positive sign
$e\in S\subset E(G)\backslash E(T)$
and a positive sign
![]() $+$
to all other edges. Zaslavsky then defines the signed Laplacian matrix of G and shows that its determinant is given by (14) (note that the signed Laplacian is nonsingular, unlike the ordinary Laplacian). Reiner and Tseng specifically interpret the determinant of the signed Laplacian as the order of the Prym group
$+$
to all other edges. Zaslavsky then defines the signed Laplacian matrix of G and shows that its determinant is given by (14) (note that the signed Laplacian is nonsingular, unlike the ordinary Laplacian). Reiner and Tseng specifically interpret the determinant of the signed Laplacian as the order of the Prym group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
(see Proposition 9.9 in [Reference Reiner and TsengRT14]).
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
(see Proposition 9.9 in [Reference Reiner and TsengRT14]).
We give an alternative proof of (14) using the Ihara zeta function. Given a free double cover
![]() $p:\widetilde {G}\to G$
, the orders of
$p:\widetilde {G}\to G$
, the orders of
![]() $\operatorname {\mathrm {Jac}}(\widetilde {G})$
and
$\operatorname {\mathrm {Jac}}(\widetilde {G})$
and
![]() $\operatorname {\mathrm {Jac}}(G)$
can be computed from the corresponding zeta functions
$\operatorname {\mathrm {Jac}}(G)$
can be computed from the corresponding zeta functions
![]() $\zeta (\widetilde {G},s)$
and
$\zeta (\widetilde {G},s)$
and
![]() $\zeta (G,s)$
using Northshield’s class number formula [Reference NorthshieldNor98]. Hence, the ratio
$\zeta (G,s)$
using Northshield’s class number formula [Reference NorthshieldNor98]. Hence, the ratio
![]() $|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|=|\operatorname {\mathrm {Jac}}(\widetilde {G})|/2|\operatorname {\mathrm {Jac}}(G)|$
is given by the ratio of the zeta functions. This is equal to the Artin–Ihara L-function of the cover and can be explicitly computed from the corresponding determinantal formula, derived by Stark and Terras (see [Reference Stark and TerrasST96] and [Reference Stark and TerrasST00]).
$|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|=|\operatorname {\mathrm {Jac}}(\widetilde {G})|/2|\operatorname {\mathrm {Jac}}(G)|$
is given by the ratio of the zeta functions. This is equal to the Artin–Ihara L-function of the cover and can be explicitly computed from the corresponding determinantal formula, derived by Stark and Terras (see [Reference Stark and TerrasST96] and [Reference Stark and TerrasST00]).
The volume formula (17) is new, to the best of our knowledge, and is derived from (14) by a scaling argument.
3.1 The Ihara zeta function and the Artin–Ihara L-function
The Ihara zeta function
![]() $\zeta (s,G)$
of a finite graph G is the graph-theoretic analogue of the Dedekind zeta function of a number field and is defined as an Euler product over certain equivalence classes of closed paths on G. We recall its definition and properties (see [Reference TerrasTer10] for an elementary treatment).
$\zeta (s,G)$
of a finite graph G is the graph-theoretic analogue of the Dedekind zeta function of a number field and is defined as an Euler product over certain equivalence classes of closed paths on G. We recall its definition and properties (see [Reference TerrasTer10] for an elementary treatment).
Let G be a graph with
![]() $n=\#(V(G))$
vertices and
$n=\#(V(G))$
vertices and
![]() $m=\#(E(G))$
edges. A path P of length
$m=\#(E(G))$
edges. A path P of length
![]() $k=\ell (P)$
is a sequence
$k=\ell (P)$
is a sequence
![]() $P=e_1\cdots e_k$
of oriented edges of G such that
$P=e_1\cdots e_k$
of oriented edges of G such that
![]() $t(e_i)=s(e_{i+1})$
for
$t(e_i)=s(e_{i+1})$
for
![]() $i=1,\ldots ,k-1$
. We say that a path P is closed if
$i=1,\ldots ,k-1$
. We say that a path P is closed if
![]() $t(e_k)=s(e_1)$
and reduced if
$t(e_k)=s(e_1)$
and reduced if
![]() $e_{i+1}\neq \overline {e}_i$
for
$e_{i+1}\neq \overline {e}_i$
for
![]() $i=1,\ldots ,k-1$
and
$i=1,\ldots ,k-1$
and
![]() $e_1\neq \overline {e}_k$
. We can define positive integer powers of closed paths by concatenation, and a closed reduced path P is called primitive if there does not exist a closed path Q such that
$e_1\neq \overline {e}_k$
. We can define positive integer powers of closed paths by concatenation, and a closed reduced path P is called primitive if there does not exist a closed path Q such that
![]() $P=Q^k$
for some
$P=Q^k$
for some
![]() $k\geq 2$
. We consider two reduced paths to be equivalent if they differ by a choice of starting point; that is, we set
$k\geq 2$
. We consider two reduced paths to be equivalent if they differ by a choice of starting point; that is, we set
![]() $e_1\cdots e_k\sim e_j\cdots e_k\cdot e_1\cdots e_{j-1}$
for all
$e_1\cdots e_k\sim e_j\cdots e_k\cdot e_1\cdots e_{j-1}$
for all
![]() $j=1,\ldots k$
. A prime
$j=1,\ldots k$
. A prime
![]() $\mathfrak {p}$
of G is an equivalence class of primitive paths and has a well-defined length
$\mathfrak {p}$
of G is an equivalence class of primitive paths and has a well-defined length
![]() $\ell (\mathfrak {p})$
. We note that a primitive path and the same path traversed in the opposite direction represent distinct primes.
$\ell (\mathfrak {p})$
. We note that a primitive path and the same path traversed in the opposite direction represent distinct primes.
The Ihara zeta function
![]() $\zeta (s,G)$
of a graph G is the product
$\zeta (s,G)$
of a graph G is the product
 $$ \begin{align*}\zeta(s,G)=\prod_{\mathfrak{p}}(1-s^{\ell(\mathfrak{p})})^{-1} \end{align*} $$
$$ \begin{align*}\zeta(s,G)=\prod_{\mathfrak{p}}(1-s^{\ell(\mathfrak{p})})^{-1} \end{align*} $$
over all primes
![]() $\mathfrak {p}$
of G, where s is a complex variable. This product is usually infinite, converges for sufficiently small s and extends to rational function.
$\mathfrak {p}$
of G, where s is a complex variable. This product is usually infinite, converges for sufficiently small s and extends to rational function.
The three-term determinant formula, due to Bass [Reference BassBas92] (see also [Reference TerrasTer10]), expresses the reciprocal
![]() $\zeta (s,G)^{-1}$
as an explicit polynomial
$\zeta (s,G)^{-1}$
as an explicit polynomial
where Q and A are the valency and adjacency matrices (see (2)) and
![]() $g=m-n+1$
is the genus of G. It is clear from this formula that
$g=m-n+1$
is the genus of G. It is clear from this formula that
![]() $\zeta (s,G)^{-1}$
vanishes at
$\zeta (s,G)^{-1}$
vanishes at
![]() $s=1$
to order at least g, because for
$s=1$
to order at least g, because for
![]() $s=1$
the matrix inside the determinant is equal to the Laplacian L of G and
$s=1$
the matrix inside the determinant is equal to the Laplacian L of G and
![]() $\det L=0$
. In fact, the order of vanishing is equal to g, and Northshield [Reference NorthshieldNor98] shows that the leading Taylor coefficient computes the complexity; that is, the order of the Jacobian of G:
$\det L=0$
. In fact, the order of vanishing is equal to g, and Northshield [Reference NorthshieldNor98] shows that the leading Taylor coefficient computes the complexity; that is, the order of the Jacobian of G:
This result may be viewed as a graph-theoretic analogue of the class number formula.
The analogy with number theory was further reinforced by Stark and Terras, who developed (see [Reference Stark and TerrasST96] and [Reference Stark and TerrasST00]) a theory of L-functions of Galois covers of graphs, as follows. Let
![]() $p:\widetilde {G}\to G$
be a free Galois cover of graphs with Galois group K (we do not define these, since we only consider free double covers, which are Galois covers with
$p:\widetilde {G}\to G$
be a free Galois cover of graphs with Galois group K (we do not define these, since we only consider free double covers, which are Galois covers with
![]() $K=\mathbb {Z}/2\mathbb {Z}$
) and fix a representation
$K=\mathbb {Z}/2\mathbb {Z}$
) and fix a representation
![]() $\rho $
of K. Given a prime
$\rho $
of K. Given a prime
![]() $\mathfrak {p}$
of G, choose a representative P with starting vertex
$\mathfrak {p}$
of G, choose a representative P with starting vertex
![]() $v\in V(G)$
and choose a vertex
$v\in V(G)$
and choose a vertex
![]() $\widetilde {v}\in V(\widetilde {G})$
lying over v. The path P lifts to a unique path
$\widetilde {v}\in V(\widetilde {G})$
lying over v. The path P lifts to a unique path
![]() $\widetilde {P}$
in
$\widetilde {P}$
in
![]() $\widetilde {G}$
starting at
$\widetilde {G}$
starting at
![]() $\widetilde {v}$
and mapping to P and the terminal vertex of
$\widetilde {v}$
and mapping to P and the terminal vertex of
![]() $\widetilde {P}$
also maps to v. The Frobenius element
$\widetilde {P}$
also maps to v. The Frobenius element
![]() $F(P,\widetilde {G}/G)\in K$
is the unique element of the Galois group mapping
$F(P,\widetilde {G}/G)\in K$
is the unique element of the Galois group mapping
![]() $\widetilde {v}$
to the terminal vertex of
$\widetilde {v}$
to the terminal vertex of
![]() $\widetilde {P}$
. The Artin–Ihara L-function is now defined as the product
$\widetilde {P}$
. The Artin–Ihara L-function is now defined as the product
 $$ \begin{align*}L(s,\rho,\widetilde{G}/G)=\prod_{\mathfrak{p}} \det(1-\rho(F(P,\widetilde{G}/G))s^{\ell(\mathfrak{p})})^{-1} \end{align*} $$
$$ \begin{align*}L(s,\rho,\widetilde{G}/G)=\prod_{\mathfrak{p}} \det(1-\rho(F(P,\widetilde{G}/G))s^{\ell(\mathfrak{p})})^{-1} \end{align*} $$
taken over the primes
![]() $\mathfrak {p}$
of G, where for each prime
$\mathfrak {p}$
of G, where for each prime
![]() $\mathfrak {p}$
we pick an arbitrary representative P (Frobenius elements corresponding to different representatives of
$\mathfrak {p}$
we pick an arbitrary representative P (Frobenius elements corresponding to different representatives of
![]() $\mathfrak {p}$
are conjugate, so the determinant is well-defined).
$\mathfrak {p}$
are conjugate, so the determinant is well-defined).
Similar to the zeta function, the product defining the L-function converges to a rational function and is given by a determinant formula. Pick a spanning tree
![]() $T\subset G$
and index its preimages in
$T\subset G$
and index its preimages in
![]() $\widetilde {G}$
, called the sheets of the cover, by the elements of K. Given an edge
$\widetilde {G}$
, called the sheets of the cover, by the elements of K. Given an edge
![]() $e\in E(G)$
, the Frobenius element
$e\in E(G)$
, the Frobenius element
![]() $F(e)\in K$
is equal to
$F(e)\in K$
is equal to
![]() $h^{-1}g$
, where h and g are respectively the indices of the sheets of the source and the target of e. Let d be the degree of
$h^{-1}g$
, where h and g are respectively the indices of the sheets of the source and the target of e. Let d be the degree of
![]() $\rho $
and define the
$\rho $
and define the
![]() $nd\times nd$
Artinised valency and Artinised adjacency matrices as
$nd\times nd$
Artinised valency and Artinised adjacency matrices as
 $$ \begin{align*}Q_{\rho}=Q\otimes I_d,\quad (A_{\rho})_{uv}=\sum\rho(F(e)), \end{align*} $$
$$ \begin{align*}Q_{\rho}=Q\otimes I_d,\quad (A_{\rho})_{uv}=\sum\rho(F(e)), \end{align*} $$
where in the right-hand side we sum over all edges e between u and v. The three-term determinant formula for the L-function states that
 $$ \begin{align} L(s,\rho,\widetilde{G}/G)^{-1}=(1-s^2)^{(g-1)d}\det(I_{nd}-A_{\rho}s+(Q_{\rho}-I_{nd})s^2). \end{align} $$
$$ \begin{align} L(s,\rho,\widetilde{G}/G)^{-1}=(1-s^2)^{(g-1)d}\det(I_{nd}-A_{\rho}s+(Q_{\rho}-I_{nd})s^2). \end{align} $$
Finally, we relate the zeta and L-functions associated to a free Galois cover
![]() $p:\widetilde {G}\to G$
with Galois group K. First of all, the zeta functions of
$p:\widetilde {G}\to G$
with Galois group K. First of all, the zeta functions of
![]() $\widetilde {G}$
and G are equal to the L-function evaluated respectively at the right regular and trivial representations
$\widetilde {G}$
and G are equal to the L-function evaluated respectively at the right regular and trivial representations
![]() $\rho _K$
and
$\rho _K$
and
![]() $1_K$
:
$1_K$
:
Furthermore, for a reducible representation
![]() $\rho =\rho _1\oplus \rho _2$
the L-function factors as
$\rho =\rho _1\oplus \rho _2$
the L-function factors as
It follows that the zeta function of
![]() $\widetilde {G}$
has a factorisation
$\widetilde {G}$
has a factorisation
 $$ \begin{align} \zeta(s,\widetilde{G})=\zeta(s,G)\prod_{\rho}L(s,\rho,\widetilde{G}/G)^{d(\rho)}, \\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \zeta(s,\widetilde{G})=\zeta(s,G)\prod_{\rho}L(s,\rho,\widetilde{G}/G)^{d(\rho)}, \\[-15pt]\nonumber \end{align} $$
where the product is taken over the distinct nontrivial irreducible representations of K.
3.2 The order of the Prym group
We now specialise to the case where
![]() $K=\mathbb {Z}/2\mathbb {Z}$
in order to compute the order of the Prym group of a free double cover
$K=\mathbb {Z}/2\mathbb {Z}$
in order to compute the order of the Prym group of a free double cover
![]() $p:\widetilde {G}\to G$
of finite graphs. By (11), the leading Taylor coefficients of the zeta functions
$p:\widetilde {G}\to G$
of finite graphs. By (11), the leading Taylor coefficients of the zeta functions
![]() $\zeta (s,\widetilde {G})^{-1}$
and
$\zeta (s,\widetilde {G})^{-1}$
and
![]() $\zeta (s,G)^{-1}$
at
$\zeta (s,G)^{-1}$
at
![]() $s=1$
respectively compute the orders
$s=1$
respectively compute the orders
![]() $|\operatorname {\mathrm {Jac}}(\widetilde {G})|$
and
$|\operatorname {\mathrm {Jac}}(\widetilde {G})|$
and
![]() $|\operatorname {\mathrm {Jac}}(G)|$
. Since
$|\operatorname {\mathrm {Jac}}(G)|$
. Since
![]() $\zeta ^{-1}(s,\widetilde {G})$
is the product of
$\zeta ^{-1}(s,\widetilde {G})$
is the product of
![]() $\zeta ^{-1}(s,G)$
with the inverse of the L-function evaluated at the nontrivial representation of
$\zeta ^{-1}(s,G)$
with the inverse of the L-function evaluated at the nontrivial representation of
![]() $\mathbb {Z}/2\mathbb {Z}$
, the leading Taylor coefficient of the latter computes the order of the Prym.
$\mathbb {Z}/2\mathbb {Z}$
, the leading Taylor coefficient of the latter computes the order of the Prym.
By the results of [Reference An, Baker, Kuperberg and ShokriehABKS14], the Jacobian group of a graph G of genus g (and, by extension, the Jacobian variety of a metric graph) admits a noncanonical combinatorial description in terms of certain g-element subsets of
![]() $E(G)$
, specifically the complements of spanning trees. We now give an analogous definition for
$E(G)$
, specifically the complements of spanning trees. We now give an analogous definition for
![]() $(g-1)$
-element subsets of
$(g-1)$
-element subsets of
![]() $E(G)$
, which, as we shall see, enumerate the elements of
$E(G)$
, which, as we shall see, enumerate the elements of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
and control the geometry of the Prym varieties of double covers of metric graphs.
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
and control the geometry of the Prym varieties of double covers of metric graphs.
Definition 3.1. Let G be a graph of genus g and let
![]() $p:\widetilde {G}\to G$
be a connected free double cover. A subset
$p:\widetilde {G}\to G$
be a connected free double cover. A subset
![]() $F\subset E(G)$
of
$F\subset E(G)$
of
![]() $g-1$
edges of G is called a genus 1 decomposition of rank r if the graph
$g-1$
edges of G is called a genus 1 decomposition of rank r if the graph
![]() $G\backslash F=G_0\cup \cdots \cup G_{r-1}$
has r connected components, each of which has genus 1. We say that a genus 1 decomposition F is odd if the preimage of each
$G\backslash F=G_0\cup \cdots \cup G_{r-1}$
has r connected components, each of which has genus 1. We say that a genus 1 decomposition F is odd if the preimage of each
![]() $G_k$
in
$G_k$
in
![]() $\widetilde {G}$
is connected.
$\widetilde {G}$
is connected.
We note that when removing edges from a graph we never remove vertices – even isolated ones. A simple counting argument shows that if
![]() $F\subset E(G)$
is a subset such that each connected component of
$F\subset E(G)$
is a subset such that each connected component of
![]() $G\backslash F$
has genus 1, then F consists of
$G\backslash F$
has genus 1, then F consists of
![]() $g-1$
edges and a genus 1 decomposition cannot have rank greater than g.
$g-1$
edges and a genus 1 decomposition cannot have rank greater than g.
A genus 1 graph has two free double covers: the disconnected trivial cover and a unique nontrivial connected cover. Hence, we can equivalently require that the restriction of the cover p to each
![]() $G_k$
is a nontrivial free double cover. If the cover p is described by Construction A with respect to a choice of spanning tree
$G_k$
is a nontrivial free double cover. If the cover p is described by Construction A with respect to a choice of spanning tree
![]() $T\subset G$
and a nonempty subset
$T\subset G$
and a nonempty subset
![]() $S\subset E(G)\backslash E(T)$
, then a genus 1 decomposition
$S\subset E(G)\backslash E(T)$
, then a genus 1 decomposition
![]() $F\subset E(G)$
is odd if and only if each
$F\subset E(G)$
is odd if and only if each
![]() $G_k$
has an odd number of edges from S on its unique cycle (see Remark 2.2).
$G_k$
has an odd number of edges from S on its unique cycle (see Remark 2.2).
Theorem 3.2. Let G be a graph of genus g and let
![]() $p:\widetilde {G}\to G$
be the connected free double cover determined by
$p:\widetilde {G}\to G$
be the connected free double cover determined by
![]() $T\subset G$
and
$T\subset G$
and
![]() $S\subset E(G)\backslash E(T)$
. The order of the Prym group
$S\subset E(G)\backslash E(T)$
. The order of the Prym group
![]() $\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is equal to
$\operatorname {\mathrm {Prym}}(\widetilde {G}/G)$
is equal to
 $$ \begin{align} |\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\sum_{r=1}^g 4^{r-1}C_r, \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{2}|\operatorname{\mathrm{Ker}} \operatorname{\mathrm{Nm}}|=\sum_{r=1}^g 4^{r-1}C_r, \\[-15pt]\nonumber\end{align} $$
where
![]() $C_r$
is the number of odd genus 1 decompositions of G of rank r.
$C_r$
is the number of odd genus 1 decompositions of G of rank r.
Proof. Denote
![]() $n=|V(G)|$
and
$n=|V(G)|$
and
![]() $m=|E(G)|=n+g-1$
. According to (13), the zeta function of
$m=|E(G)|=n+g-1$
. According to (13), the zeta function of
![]() $\widetilde {G}$
is the product of the zeta function of G and the L-function of the cover
$\widetilde {G}$
is the product of the zeta function of G and the L-function of the cover
![]() $\widetilde {G}/G$
evaluated at the nontrivial representation
$\widetilde {G}/G$
evaluated at the nontrivial representation
![]() $\rho $
of the Galois group
$\rho $
of the Galois group
![]() $\mathbb {Z}/2\mathbb {Z}$
:
$\mathbb {Z}/2\mathbb {Z}$
:
The class number formula (11) gives the leading Taylor coefficients at
![]() $s=1$
:
$s=1$
:
 $$ \begin{align*}\zeta(s,\widetilde{G})^{-1}=2^{2g-1} (2g-2)|\operatorname{\mathrm{Jac}}(\widetilde{G})|(s-1)^{2g-1}+O\left((s-1)^{2g}\right), \end{align*} $$
$$ \begin{align*}\zeta(s,\widetilde{G})^{-1}=2^{2g-1} (2g-2)|\operatorname{\mathrm{Jac}}(\widetilde{G})|(s-1)^{2g-1}+O\left((s-1)^{2g}\right), \end{align*} $$
 $$ \begin{align*}\zeta(s,G)^{-1}=(-1)^{g-1}2^g (g-1)|\operatorname{\mathrm{Jac}}(G)|(s-1)^g+O\left((s-1)^{g+1}\right). \end{align*} $$
$$ \begin{align*}\zeta(s,G)^{-1}=(-1)^{g-1}2^g (g-1)|\operatorname{\mathrm{Jac}}(G)|(s-1)^g+O\left((s-1)^{g+1}\right). \end{align*} $$
The leading coefficient of the L-function is found directly from (12) (note that, unlike in formula (11), the determinant does not vanish at
![]() $s=1$
):
$s=1$
):
 $$ \begin{align*}L(s,\rho,\widetilde{G}/G)^{-1}=(-1)^{g-1}2^{g-1} \det(Q_{\rho}-A_{\rho}) (s-1)^{g-1}+O\left((s-1)^g\right). \end{align*} $$
$$ \begin{align*}L(s,\rho,\widetilde{G}/G)^{-1}=(-1)^{g-1}2^{g-1} \det(Q_{\rho}-A_{\rho}) (s-1)^{g-1}+O\left((s-1)^g\right). \end{align*} $$
Therefore, comparing the expansions of
![]() $L(s,\rho ,\widetilde {G}/G)^{-1}$
with
$L(s,\rho ,\widetilde {G}/G)^{-1}$
with
![]() $\zeta (s,\widetilde {G})^{-1}/\zeta (s,G)^{-1}$
, we see that
$\zeta (s,\widetilde {G})^{-1}/\zeta (s,G)^{-1}$
, we see that
 $$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}=\frac{1}{4}\det (Q_{\rho}-A_\rho). \end{align*} $$
$$ \begin{align*}|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}=\frac{1}{4}\det (Q_{\rho}-A_\rho). \end{align*} $$
We now calculate this
![]() $n\times n$
determinant. First of all,
$n\times n$
determinant. First of all,
![]() $Q_{\rho }=Q$
since
$Q_{\rho }=Q$
since
![]() $\rho $
is 1-dimensional. The Frobenius element
$\rho $
is 1-dimensional. The Frobenius element
![]() $F(e)$
of an edge
$F(e)$
of an edge
![]() $e\in E(G)$
is the nontrivial element of
$e\in E(G)$
is the nontrivial element of
![]() $\mathbb {Z}/2\mathbb {Z}$
, and hence
$\mathbb {Z}/2\mathbb {Z}$
, and hence
![]() $\rho (F(e))=-1$
, if and only if
$\rho (F(e))=-1$
, if and only if
![]() $e\in S$
. Putting this together, we see that the matrix
$e\in S$
. Putting this together, we see that the matrix
![]() $Q_{\rho }-A_{\rho }$
has the following form:
$Q_{\rho }-A_{\rho }$
has the following form:
 $$ \begin{align*}(Q_\rho-A_\rho)_{uv}=\left\{\begin{array}{c@{\quad}c}|\{\text{edges from}\ u\ \text{to}\ v\ \text{in}\ S\}|- |\{\text{edges from}\ u\ \text{to}\ v\ \text{not in}\ S\}|, & u\neq v, \\ 4|\{\text{loops at}\ u\ \text{in}\ S\}|+|\{\text{non-loops at}\ u\}|,& u=v. \end{array}\right. \end{align*} $$
$$ \begin{align*}(Q_\rho-A_\rho)_{uv}=\left\{\begin{array}{c@{\quad}c}|\{\text{edges from}\ u\ \text{to}\ v\ \text{in}\ S\}|- |\{\text{edges from}\ u\ \text{to}\ v\ \text{not in}\ S\}|, & u\neq v, \\ 4|\{\text{loops at}\ u\ \text{in}\ S\}|+|\{\text{non-loops at}\ u\}|,& u=v. \end{array}\right. \end{align*} $$
The matrix
![]() $Q_{\rho }-A_{\rho }$
turns out to be equal to the signed Laplacian matrix of the graph G (see Proposition 9.5 in [Reference Reiner and TsengRT14]), and its determinant is computed using a standard argument involving an appropriate factorisation and the Cauchy–Binet formula. We only give a sketch of these calculations, since they are not new (see Proposition 9.9 in loc. cit.).
$Q_{\rho }-A_{\rho }$
turns out to be equal to the signed Laplacian matrix of the graph G (see Proposition 9.5 in [Reference Reiner and TsengRT14]), and its determinant is computed using a standard argument involving an appropriate factorisation and the Cauchy–Binet formula. We only give a sketch of these calculations, since they are not new (see Proposition 9.9 in loc. cit.).
Pick an orientation on G. We factorise the signed Laplacian as
![]() $Q_\rho -A_\rho =B_S(G){}^tB_S(G)$
, where
$Q_\rho -A_\rho =B_S(G){}^tB_S(G)$
, where
 $$ \begin{align*}(B_S(G))_{ve}=\left\{\begin{array}{c@{\quad}c} 1, & t(e)=v\ \text{and}\ s(e)\neq v, \text{or}\ s(e)=v, t(e)\neq v\ \text{and}\ e\in S,\\ -1, & s(e)=v, t(e)\neq v\ \text{and}\ e\notin S,\\ 2, & s(e)=t(e)=v\ \text{and}\ e\in S,\\ 0, & \text{otherwise}\end{array}\right. \end{align*} $$
$$ \begin{align*}(B_S(G))_{ve}=\left\{\begin{array}{c@{\quad}c} 1, & t(e)=v\ \text{and}\ s(e)\neq v, \text{or}\ s(e)=v, t(e)\neq v\ \text{and}\ e\in S,\\ -1, & s(e)=v, t(e)\neq v\ \text{and}\ e\notin S,\\ 2, & s(e)=t(e)=v\ \text{and}\ e\in S,\\ 0, & \text{otherwise}\end{array}\right. \end{align*} $$
is the
![]() $n\times m S$
-twisted adjacency matrix
$n\times m S$
-twisted adjacency matrix
![]() $B_S(G)$
of the graph G, whose rows and columns are indexed respectively by
$B_S(G)$
of the graph G, whose rows and columns are indexed respectively by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
. By the Cauchy–Binet formula, we have
$E(G)$
. By the Cauchy–Binet formula, we have
 $$ \begin{align} |\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{4}\det (Q_{\rho}-A_\rho)=\frac{1}{4}\sum_{F\subset E(G),\,|F|=g-1} \det B_S(G\backslash F)^2. \end{align} $$
$$ \begin{align} |\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|=\frac{1}{4}\det (Q_{\rho}-A_\rho)=\frac{1}{4}\sum_{F\subset E(G),\,|F|=g-1} \det B_S(G\backslash F)^2. \end{align} $$
Here the sum is taken over all subsets F of
![]() $E(G)$
consisting of
$E(G)$
consisting of
![]() $m-n=g-1$
elements and
$m-n=g-1$
elements and
![]() $B_S(G\backslash F)$
is the matrix obtained from
$B_S(G\backslash F)$
is the matrix obtained from
![]() $B_S(G)$
by deleting the columns corresponding to the edges that are in F or, equivalently, the S-twisted adjacency matrix of the graph
$B_S(G)$
by deleting the columns corresponding to the edges that are in F or, equivalently, the S-twisted adjacency matrix of the graph
![]() $G\backslash F$
.
$G\backslash F$
.
Let
![]() $F\subset E(G)$
be such a subset and let
$F\subset E(G)$
be such a subset and let
![]() $G\backslash F=G_0\cup \cdots \cup G_{r-1}$
be the decomposition of G into connected components. The matrix
$G\backslash F=G_0\cup \cdots \cup G_{r-1}$
be the decomposition of G into connected components. The matrix
![]() $B_S(G\backslash F)$
is block-diagonal, with blocks
$B_S(G\backslash F)$
is block-diagonal, with blocks
![]() $B_S(G_k)$
corresponding to the
$B_S(G_k)$
corresponding to the
![]() $G_k$
. A block-diagonal matrix has nonzero determinant only if all blocks are square, meaning that
$G_k$
. A block-diagonal matrix has nonzero determinant only if all blocks are square, meaning that
![]() $g(G_k)=1$
for all k, in which case
$g(G_k)=1$
for all k, in which case
 $$ \begin{align} \det B_S(G\backslash F)^2=\prod_{k=0}^{r-1} \det B_S(G_k)^2. \end{align} $$
$$ \begin{align} \det B_S(G\backslash F)^2=\prod_{k=0}^{r-1} \det B_S(G_k)^2. \end{align} $$
The quantity
![]() $\det B_S(G_k)^2$
for a genus 1 graph
$\det B_S(G_k)^2$
for a genus 1 graph
![]() $G_k$
is computed by induction on the extremal edges (if any) and turns out to be equal to
$G_k$
is computed by induction on the extremal edges (if any) and turns out to be equal to
![]() $4$
if the unique cycle of
$4$
if the unique cycle of
![]() $G_k$
has an odd number of edges from S and
$G_k$
has an odd number of edges from S and
![]() $0$
if the number is even. Hence, only odd genus 1 decompositions contribute to the sum (15) and the contribution of a decomposition of rank r is equal to
$0$
if the number is even. Hence, only odd genus 1 decompositions contribute to the sum (15) and the contribution of a decomposition of rank r is equal to
![]() $4^r$
. This completes the proof.
$4^r$
. This completes the proof.
Example 3.3. Consider the free double cover
![]() $p:\widetilde {G}\to G$
shown in Figure 1. Here
$p:\widetilde {G}\to G$
shown in Figure 1. Here
![]() $g-1=1$
, and it is easy to see that any edge of G is an odd genus 1 decomposition. The edges
$g-1=1$
, and it is easy to see that any edge of G is an odd genus 1 decomposition. The edges
![]() $e_1$
,
$e_1$
,
![]() $e_2$
,
$e_2$
,
![]() $e_4$
and
$e_4$
and
![]() $e_5$
are decompositions of rank 1, while
$e_5$
are decompositions of rank 1, while
![]() $e_3$
is a decomposition of rank 2. Hence, by (14)
$e_3$
is a decomposition of rank 2. Hence, by (14)
which agrees with the calculations in Example 2.9.
3.3 The volume of the tropical Prym variety
In this subsection, we prove a weighted version of Theorem 3.2 that gives the volume of the Prym variety of a free double cover of metric graphs. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be such a cover, where
$\pi :\widetilde {\Gamma }\to \Gamma $
be such a cover, where
![]() $\widetilde {\Gamma }$
and
$\widetilde {\Gamma }$
and
![]() $\Gamma $
have genera
$\Gamma $
have genera
![]() $2g-1$
and
$2g-1$
and
![]() $g-1$
, respectively. Choose a model G for
$g-1$
, respectively. Choose a model G for
![]() $\Gamma $
. Similar to the discrete case, an odd genus 1 decomposition F of
$\Gamma $
. Similar to the discrete case, an odd genus 1 decomposition F of
![]() $\Gamma $
of rank
$\Gamma $
of rank
![]() $r(F)$
(with respect to the choice of model G) is a subset
$r(F)$
(with respect to the choice of model G) is a subset
![]() $F\subset E(G)$
of (necessarily)
$F\subset E(G)$
of (necessarily)
![]() $g-1$
edges of G such that
$g-1$
edges of G such that
![]() $E(G)\backslash F$
consists of
$E(G)\backslash F$
consists of
![]() $r(F)$
connected components of genus 1, each having a connected preimage in
$r(F)$
connected components of genus 1, each having a connected preimage in
![]() $\widetilde {\Gamma }$
. For such an F, we denote by
$\widetilde {\Gamma }$
. For such an F, we denote by
![]() $w(F)$
the product of the lengths of the edges in F.
$w(F)$
the product of the lengths of the edges in F.
Theorem 3.4. The volume of the Prym variety of a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is given by
$\pi :\widetilde {\Gamma }\to \Gamma $
of metric graphs is given by
 $$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align} $$
where the sum is taken over all odd genus 1 decompositions F of
![]() $\Gamma $
.
$\Gamma $
.
Remark 3.5. The right-hand side of formula (17) is defined with respect to a choice of model G for
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $G'$
be the model obtained from G by subdividing an edge
$G'$
be the model obtained from G by subdividing an edge
![]() $e\in E(G)$
into edges
$e\in E(G)$
into edges
![]() $e^{\prime }_1$
and
$e^{\prime }_1$
and
![]() $e^{\prime }_2$
, so that
$e^{\prime }_2$
, so that
![]() $\ell (e)=\ell (e^{\prime }_1)+\ell (e^{\prime }_2)$
. If
$\ell (e)=\ell (e^{\prime }_1)+\ell (e^{\prime }_2)$
. If
![]() $e\in F$
for some odd genus 1 decomposition F of G, then
$e\in F$
for some odd genus 1 decomposition F of G, then
![]() $(F\backslash \{e\})\cup \{e^{\prime }_1\}$
and
$(F\backslash \{e\})\cup \{e^{\prime }_1\}$
and
![]() $(F\backslash \{e\})\cup \{e^{\prime }_2\}$
are odd genus 1 decompositions of
$(F\backslash \{e\})\cup \{e^{\prime }_2\}$
are odd genus 1 decompositions of
![]() $G'$
of the same rank as F and vice versa. It follows that the right-hand side is invariant under edge subdivision and hence does not depend on the choice of model for
$G'$
of the same rank as F and vice versa. It follows that the right-hand side is invariant under edge subdivision and hence does not depend on the choice of model for
![]() $\Gamma $
. We also note that
$\Gamma $
. We also note that
![]() $\operatorname {\mathrm {Vol}}^2(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))$
is computed with respect to the intrinsic principal polarisation on
$\operatorname {\mathrm {Vol}}^2(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))$
is computed with respect to the intrinsic principal polarisation on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, which is half of the restriction of the principal polarisation on
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, which is half of the restriction of the principal polarisation on
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
.
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
.
We first establish the relationship between the volumes of the three tropical ppavs
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
,
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
,
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
and
$\operatorname {\mathrm {Jac}}(\Gamma )$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. To compute the last of the three volumes, we define (building on Construction A) an explicit basis for the kernel of the pushforward map
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. To compute the last of the three volumes, we define (building on Construction A) an explicit basis for the kernel of the pushforward map
![]() $\pi _*:H_1(\widetilde {\Gamma },/\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
, which we also use later.
$\pi _*:H_1(\widetilde {\Gamma },/\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
, which we also use later.
Let G be a graph. Introduce the
![]() $\mathbb {Z}$
-valued bilinear pairing
$\mathbb {Z}$
-valued bilinear pairing
 $$ \begin{align} \langle\cdot,\cdot\rangle:C_1(G,\mathbb{Z})\times C_1(G,\mathbb{Z})\to \mathbb{Z},\quad \left\langle \sum_{e\in E(G)} a_e e,\sum_{e\in E(G)} b_e e\right\rangle=\sum_{e\in E(G)}a_eb_e. \end{align} $$
$$ \begin{align} \langle\cdot,\cdot\rangle:C_1(G,\mathbb{Z})\times C_1(G,\mathbb{Z})\to \mathbb{Z},\quad \left\langle \sum_{e\in E(G)} a_e e,\sum_{e\in E(G)} b_e e\right\rangle=\sum_{e\in E(G)}a_eb_e. \end{align} $$
We note that this pairing does not take edge lengths into account and is not to be confused with the integration pairing
![]() $(\cdot ,\cdot )$
on a metric graph.
$(\cdot ,\cdot )$
on a metric graph.
Construction B. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a connected free double cover of metric graphs. Choose an oriented model
$\pi :\widetilde {\Gamma }\to \Gamma $
be a connected free double cover of metric graphs. Choose an oriented model
![]() $p:\widetilde {G}\to G$
and suppose that the cover p is given by Construction A with respect to a spanning tree
$p:\widetilde {G}\to G$
and suppose that the cover p is given by Construction A with respect to a spanning tree
![]() $T\subset G$
and a nonempty subset
$T\subset G$
and a nonempty subset
![]() $S\subset E(G)\backslash E(T)=\{e_0,\ldots ,e_{g-1}\}$
containing
$S\subset E(G)\backslash E(T)=\{e_0,\ldots ,e_{g-1}\}$
containing
![]() $e_0$
. In this construction, we define an explicit basis of the kernel of the pushforward map
$e_0$
. In this construction, we define an explicit basis of the kernel of the pushforward map
![]() $p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, as well as bases for
$p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, as well as bases for
![]() $H_1(\widetilde {G},\mathbb {Z})$
and
$H_1(\widetilde {G},\mathbb {Z})$
and
![]() $H_1(G,\mathbb {Z})$
. We use these bases to compute Gramian determinants; hence, we view them to be unordered sets.
$H_1(G,\mathbb {Z})$
. We use these bases to compute Gramian determinants; hence, we view them to be unordered sets.
We first construct a basis for
![]() $H_1(G,\mathbb {Z})$
. Let
$H_1(G,\mathbb {Z})$
. Let
![]() $\gamma _i\in H_1(G,\mathbb {Z})$
for
$\gamma _i\in H_1(G,\mathbb {Z})$
for
![]() $i=0,\ldots ,g-1$
denote the unique cycle of
$i=0,\ldots ,g-1$
denote the unique cycle of
![]() $T\cup \{e_i\}$
such that
$T\cup \{e_i\}$
such that
![]() $\langle \gamma _i,e_i\rangle =1$
. It is a standard fact that
$\langle \gamma _i,e_i\rangle =1$
. It is a standard fact that
is a basis of
![]() $H_1(G,\mathbb {Z})$
and, furthermore, any
$H_1(G,\mathbb {Z})$
and, furthermore, any
![]() $\gamma \in H_1(G,\mathbb {Z})$
can be explicitly decomposed in terms of
$\gamma \in H_1(G,\mathbb {Z})$
can be explicitly decomposed in terms of
![]() $\mathcal {B}$
as follows:
$\mathcal {B}$
as follows:
Similarly, let
![]() $\widetilde {\gamma }_0\in H_1(\widetilde {G},\mathbb {Z})$
and
$\widetilde {\gamma }_0\in H_1(\widetilde {G},\mathbb {Z})$
and
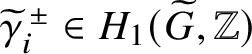 $\widetilde {\gamma }_i^{{\kern1.5pt}\pm }\in H_1(\widetilde {G},\mathbb {Z})$
for
$\widetilde {\gamma }_i^{{\kern1.5pt}\pm }\in H_1(\widetilde {G},\mathbb {Z})$
for
![]() $i=1,\ldots ,g-1$
denote the unique cycle respectively of
$i=1,\ldots ,g-1$
denote the unique cycle respectively of
 $\widetilde {T}\cup \{\widetilde{e}^{{\kern2pt}-}_0\}$
and
$\widetilde {T}\cup \{\widetilde{e}^{{\kern2pt}-}_0\}$
and
 $\widetilde {T}\cup \{\widetilde {e}_i^{{\kern1.5pt}\pm }\}$
such that
$\widetilde {T}\cup \{\widetilde {e}_i^{{\kern1.5pt}\pm }\}$
such that
![]() $\langle \widetilde {\gamma }_0,\widetilde{e}^{{\kern2pt}-}_0\rangle =1$
and
$\langle \widetilde {\gamma }_0,\widetilde{e}^{{\kern2pt}-}_0\rangle =1$
and
![]() $\langle \widetilde {\gamma }^{\pm }_i,\widetilde {e}^{{\kern1.5pt}\pm }_i\rangle =1$
respectively for
$\langle \widetilde {\gamma }^{\pm }_i,\widetilde {e}^{{\kern1.5pt}\pm }_i\rangle =1$
respectively for
![]() $i=1,\ldots ,g-1$
. Then
$i=1,\ldots ,g-1$
. Then
 $$ \begin{align*}\widetilde{\mathcal{B}}=\{\widetilde{\gamma}_0,\widetilde{\gamma}_1^{{\kern1.5pt}\pm},\ldots,\widetilde{\gamma}_{g-1}^{{\kern1.5pt}\pm}\} \end{align*} $$
$$ \begin{align*}\widetilde{\mathcal{B}}=\{\widetilde{\gamma}_0,\widetilde{\gamma}_1^{{\kern1.5pt}\pm},\ldots,\widetilde{\gamma}_{g-1}^{{\kern1.5pt}\pm}\} \end{align*} $$
is a basis of
![]() $H_1(\widetilde {G},\mathbb {Z})$
and we similarly have
$H_1(\widetilde {G},\mathbb {Z})$
and we similarly have
 $$ \begin{align*}\widetilde{\gamma}=\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_0\rangle\widetilde{\gamma}_0+\langle\widetilde{\gamma},\widetilde{e}^{{\kern2pt}+}_1\rangle \widetilde{\gamma}^+_1+\cdots+\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}+}_{g-1}\rangle \widetilde{\gamma}^+_{g-1}+\langle\widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_1\rangle \widetilde{\gamma}^-_1+\cdots+\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_{g-1}\rangle \widetilde{\gamma}^-_{g-1} \end{align*} $$
$$ \begin{align*}\widetilde{\gamma}=\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_0\rangle\widetilde{\gamma}_0+\langle\widetilde{\gamma},\widetilde{e}^{{\kern2pt}+}_1\rangle \widetilde{\gamma}^+_1+\cdots+\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}+}_{g-1}\rangle \widetilde{\gamma}^+_{g-1}+\langle\widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_1\rangle \widetilde{\gamma}^-_1+\cdots+\langle \widetilde{\gamma},\widetilde{e}^{{\kern2pt}-}_{g-1}\rangle \widetilde{\gamma}^-_{g-1} \end{align*} $$
for any
![]() $\widetilde {\gamma }\in H_1(\widetilde {G},\mathbb {Z})$
.
$\widetilde {\gamma }\in H_1(\widetilde {G},\mathbb {Z})$
.
We now compute the action of the pushforward map
![]() $p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
and the involution map
$p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
and the involution map
![]() $\iota _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(\widetilde {G},\mathbb {Z})$
on the basis
$\iota _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(\widetilde {G},\mathbb {Z})$
on the basis
![]() $\widetilde {\mathcal {B}}$
. The cycle
$\widetilde {\mathcal {B}}$
. The cycle
![]() $\widetilde {\gamma }_0$
starts at the vertex
$\widetilde {\gamma }_0$
starts at the vertex
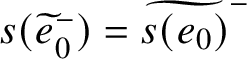 $s(\widetilde {e}_0^-)=\widetilde {s(e_0)}^-$
on the lower sheet
$s(\widetilde {e}_0^-)=\widetilde {s(e_0)}^-$
on the lower sheet
![]() $\widetilde {T}^-$
and then proceeds via
$\widetilde {T}^-$
and then proceeds via
![]() $+\widetilde {e}_0^-$
to the vertex
$+\widetilde {e}_0^-$
to the vertex
 $t(\widetilde {e}_0^-)=\widetilde {t(e_0)}^+$
on the upper sheet
$t(\widetilde {e}_0^-)=\widetilde {t(e_0)}^+$
on the upper sheet
![]() $\widetilde {T}^+$
, then to
$\widetilde {T}^+$
, then to
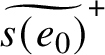 $\widetilde {s(e_0)}^+$
via a unique path in
$\widetilde {s(e_0)}^+$
via a unique path in
![]() $\widetilde {T}^+$
, then back to
$\widetilde {T}^+$
, then back to
 $t(\widetilde {e}_0^{{\kern1.5pt}+})=\widetilde {t(e_0)}^-$
on
$t(\widetilde {e}_0^{{\kern1.5pt}+})=\widetilde {t(e_0)}^-$
on
![]() $T^-$
via
$T^-$
via
![]() $+\widetilde {e}_0^{{\kern1.5pt}+}$
and then back to
$+\widetilde {e}_0^{{\kern1.5pt}+}$
and then back to
 $\widetilde {s(e_0)}^-$
via a unique path in
$\widetilde {s(e_0)}^-$
via a unique path in
![]() $\widetilde {T}^-$
. In other words,
$\widetilde {T}^-$
. In other words,
 $$ \begin{align*}\widetilde{\gamma}_0=\widetilde{e}_0^++\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\quad \iota_*(\widetilde{\gamma}_0)=\widetilde{e}_0^++\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\quad p_*(\widetilde{\gamma}_0)=2e_0+\mbox{edges of }T; \end{align*} $$
$$ \begin{align*}\widetilde{\gamma}_0=\widetilde{e}_0^++\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\quad \iota_*(\widetilde{\gamma}_0)=\widetilde{e}_0^++\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\quad p_*(\widetilde{\gamma}_0)=2e_0+\mbox{edges of }T; \end{align*} $$
therefore, computing the intersection numbers with
![]() $\widetilde {\mathcal {B}}$
and
$\widetilde {\mathcal {B}}$
and
![]() $\mathcal {B}$
we see that
$\mathcal {B}$
we see that
Now consider the cycle
![]() $\widetilde {\gamma }_i^+$
for
$\widetilde {\gamma }_i^+$
for
![]() $e_i\in S\backslash \{e_0\}$
. We introduce the index
$e_i\in S\backslash \{e_0\}$
. We introduce the index
 $$ \begin{align*}\sigma_i=\left\{\begin{array}{c@{\quad}c} +1,& s(\widetilde{e}_i^+)=s(e_i)^+,\\ -1, & s(\widetilde{e}_i^+)=s(e_i)^-.\end{array}\right. \end{align*} $$
$$ \begin{align*}\sigma_i=\left\{\begin{array}{c@{\quad}c} +1,& s(\widetilde{e}_i^+)=s(e_i)^+,\\ -1, & s(\widetilde{e}_i^+)=s(e_i)^-.\end{array}\right. \end{align*} $$
If
![]() $\sigma _i=1$
, then the cycle
$\sigma _i=1$
, then the cycle
![]() $\widetilde {\gamma }_i^+$
starts at
$\widetilde {\gamma }_i^+$
starts at
 $s(\widetilde {e}_i^{{\kern1.5pt}+})=\widetilde {s(e_i)}^+$
on
$s(\widetilde {e}_i^{{\kern1.5pt}+})=\widetilde {s(e_i)}^+$
on
![]() $\widetilde {T}^+$
and then moves to
$\widetilde {T}^+$
and then moves to
 $t(\widetilde {e}_i^{{\kern1.5pt}+})=\widetilde {t(e_i)}^-$
on
$t(\widetilde {e}_i^{{\kern1.5pt}+})=\widetilde {t(e_i)}^-$
on
![]() $\widetilde {T}^-$
via
$\widetilde {T}^-$
via
![]() $\widetilde {e}_i^{{\kern1.5pt}+}$
and then back to
$\widetilde {e}_i^{{\kern1.5pt}+}$
and then back to
 $\widetilde {s(e_i)}^+$
on
$\widetilde {s(e_i)}^+$
on
![]() $\widetilde {T}^+$
via a unique path in
$\widetilde {T}^+$
via a unique path in
![]() $\widetilde {T}$
. This path crosses from
$\widetilde {T}$
. This path crosses from
![]() $\widetilde {T}^-$
to
$\widetilde {T}^-$
to
![]() $\widetilde {T}^+$
and hence must contain the edge
$\widetilde {T}^+$
and hence must contain the edge
![]() $-\widetilde {e}_0^{{\kern1.5pt}+}$
. If
$-\widetilde {e}_0^{{\kern1.5pt}+}$
. If
![]() $\sigma _i=-1$
, then
$\sigma _i=-1$
, then
![]() $\widetilde {\gamma }_i^+$
crosses from
$\widetilde {\gamma }_i^+$
crosses from
![]() $\widetilde {T}^+$
to
$\widetilde {T}^+$
to
![]() $\widetilde {T}^-$
and hence contains
$\widetilde {T}^-$
and hence contains
![]() $\widetilde {e}_0^{{\kern1.5pt}+}$
. Similarly, we calculate that the cycle
$\widetilde {e}_0^{{\kern1.5pt}+}$
. Similarly, we calculate that the cycle
![]() $\widetilde {\gamma }_i^-$
contains the edge
$\widetilde {\gamma }_i^-$
contains the edge
![]() $\sigma _i\widetilde {e}_0^{{\kern1.5pt}+}$
. In other words, for
$\sigma _i\widetilde {e}_0^{{\kern1.5pt}+}$
. In other words, for
![]() $e_i\in S\backslash \{e_0\}$
we have
$e_i\in S\backslash \{e_0\}$
we have
 $$ \begin{align*}\widetilde{\gamma}_i^{{\kern1.5pt}\pm}=\widetilde{e}_i^{{\kern1.5pt}\pm}\mp \sigma_i\widetilde{e}_0^++\mbox{edges of }\widetilde{T}^{\pm},\quad \iota_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=\widetilde{e}_i^{\mp}\mp \sigma_i\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\ \ p_*(\widetilde{\gamma}^{\pm}_i)=e_i\mp \sigma_ie_0+\mbox{edges of }T; \end{align*} $$
$$ \begin{align*}\widetilde{\gamma}_i^{{\kern1.5pt}\pm}=\widetilde{e}_i^{{\kern1.5pt}\pm}\mp \sigma_i\widetilde{e}_0^++\mbox{edges of }\widetilde{T}^{\pm},\quad \iota_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=\widetilde{e}_i^{\mp}\mp \sigma_i\widetilde{e}_0^-+\mbox{edges of }\widetilde{T}^{\pm},\ \ p_*(\widetilde{\gamma}^{\pm}_i)=e_i\mp \sigma_ie_0+\mbox{edges of }T; \end{align*} $$
hence, computing the intersection numbers, we see that
Finally, for
![]() $e_i\notin S$
the cycle
$e_i\notin S$
the cycle
![]() $\gamma _i^{\pm }$
is contained in
$\gamma _i^{\pm }$
is contained in
 $\widetilde {T}^{\pm }\cup \{\widetilde {e}_i^{{\kern1.5pt}\pm }\}$
and hence does not contain the edge
$\widetilde {T}^{\pm }\cup \{\widetilde {e}_i^{{\kern1.5pt}\pm }\}$
and hence does not contain the edge
![]() $\widetilde {e}_0^{{\kern1.5pt}+}$
. It follows that
$\widetilde {e}_0^{{\kern1.5pt}+}$
. It follows that
 $$ \begin{align*}\iota_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=\widetilde{e}_i^{\mp}+\mbox{edges of }\widetilde{T}^{\pm},\quad p_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=e_i+\mbox{edges of }T,\quad e_i\notin S, \end{align*} $$
$$ \begin{align*}\iota_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=\widetilde{e}_i^{\mp}+\mbox{edges of }\widetilde{T}^{\pm},\quad p_*(\widetilde{\gamma}_i^{{\kern1.5pt}\pm})=e_i+\mbox{edges of }T,\quad e_i\notin S, \end{align*} $$
and therefore
It is now clear that
 $$ \begin{align} \widetilde{\mathcal{B}}^{\prime}_2=\{\widetilde{\gamma}_i^+-\iota_*(\widetilde{\gamma}_i^+)\}_{i=1}^{g-1}= \{\widetilde{\gamma}_i^+-\widetilde{\gamma}_i^-+\sigma_i\widetilde{\gamma}_0\}_{e_i\in S\backslash\{e_0\}}\cup \{\widetilde{\gamma}_i^+-\widetilde{\gamma}_i^-\}_{e_i\notin S} \end{align} $$
$$ \begin{align} \widetilde{\mathcal{B}}^{\prime}_2=\{\widetilde{\gamma}_i^+-\iota_*(\widetilde{\gamma}_i^+)\}_{i=1}^{g-1}= \{\widetilde{\gamma}_i^+-\widetilde{\gamma}_i^-+\sigma_i\widetilde{\gamma}_0\}_{e_i\in S\backslash\{e_0\}}\cup \{\widetilde{\gamma}_i^+-\widetilde{\gamma}_i^-\}_{e_i\notin S} \end{align} $$
is a basis for
![]() $\operatorname {\mathrm {Ker}} p_*$
.
$\operatorname {\mathrm {Ker}} p_*$
.
In Example 5.5, we explicitly construct this basis for a double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
with
$\pi :\widetilde {\Gamma }\to \Gamma $
with
![]() $g=3$
.
$g=3$
.
We now establish the relationship between the volumes of our three tropical ppavs.
Proposition 3.6. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs. Then the volumes of
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs. Then the volumes of
![]() $\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
,
$\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })$
,
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
and
$\operatorname {\mathrm {Jac}}(\Gamma )$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are related as
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are related as
 $$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}, \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}, \end{align*} $$
where the volume of each tropical ppav is calculated using its intrinsic principal polarisation.
Proof. We first introduce the following alternative basis
![]() $\mathcal {B}'$
for
$\mathcal {B}'$
for
![]() $H_1(G,\mathbb {Z})$
:
$H_1(G,\mathbb {Z})$
:
We now compute the pullback
![]() $\widetilde {\mathcal {B}}^{\prime }_1$
of
$\widetilde {\mathcal {B}}^{\prime }_1$
of
![]() $\mathcal {B}'$
to
$\mathcal {B}'$
to
![]() $H_1(\widetilde {G},\mathbb {Z})$
via the map
$H_1(\widetilde {G},\mathbb {Z})$
via the map
 $$ \begin{align*}p^*:H_1(G,\mathbb{Z})\to H_1(\widetilde{G},\mathbb{Z}),\quad \sum_{e\in E(G)} a_e e\mapsto \sum_{e\in E(G)} a_e (\widetilde{e}^{{\kern2pt}+}+\widetilde{e}^{{\kern2pt}-}). \end{align*} $$
$$ \begin{align*}p^*:H_1(G,\mathbb{Z})\to H_1(\widetilde{G},\mathbb{Z}),\quad \sum_{e\in E(G)} a_e e\mapsto \sum_{e\in E(G)} a_e (\widetilde{e}^{{\kern2pt}+}+\widetilde{e}^{{\kern2pt}-}). \end{align*} $$
Since
![]() $\gamma _i$
consists of
$\gamma _i$
consists of
![]() $+e_i$
and edges of T, we have
$+e_i$
and edges of T, we have
for
![]() $i=0,\ldots ,g-1$
. Computing intersection numbers as before, we see that
$i=0,\ldots ,g-1$
. Computing intersection numbers as before, we see that
Hence,
 $$\begin{align*}\widetilde{\mathcal{B}}^{\prime}_1=p^*(\mathcal{B}')=\{\widetilde{\gamma}_0\}\cup \{\widetilde{\gamma}_i^++\widetilde{\gamma}_i^--\sigma_i\widetilde{\gamma}_0\}_{e_i\in S\backslash\{e_0\}}\cup \{\widetilde{\gamma}_i^++\widetilde{\gamma}_i^-\}_{e_i\notin S}. \end{align*}$$
$$\begin{align*}\widetilde{\mathcal{B}}^{\prime}_1=p^*(\mathcal{B}')=\{\widetilde{\gamma}_0\}\cup \{\widetilde{\gamma}_i^++\widetilde{\gamma}_i^--\sigma_i\widetilde{\gamma}_0\}_{e_i\in S\backslash\{e_0\}}\cup \{\widetilde{\gamma}_i^++\widetilde{\gamma}_i^-\}_{e_i\notin S}. \end{align*}$$
Let
![]() $(\cdot ,\cdot )_{\widetilde {G}}$
and
$(\cdot ,\cdot )_{\widetilde {G}}$
and
![]() $(\cdot ,\cdot )_G$
denote the intersection pairings (4) on
$(\cdot ,\cdot )_G$
denote the intersection pairings (4) on
![]() $H_1(\widetilde {G},\mathbb {Z})$
and
$H_1(\widetilde {G},\mathbb {Z})$
and
![]() $H_1(G,\mathbb {Z})$
, respectively, and let
$H_1(G,\mathbb {Z})$
, respectively, and let
 $(\cdot ,\cdot )_P=\frac {1}{2}(\cdot ,\cdot )_{\widetilde {G}}$
denote the intersection pairing on
$(\cdot ,\cdot )_P=\frac {1}{2}(\cdot ,\cdot )_{\widetilde {G}}$
denote the intersection pairing on
![]() $\operatorname {\mathrm {Ker}} p_*$
corresponding to the principal polarisation on
$\operatorname {\mathrm {Ker}} p_*$
corresponding to the principal polarisation on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. We add the corresponding subscripts to each Gramian determinant, in order to keep track of the inner product that is used to compute it. Thus, the volumes of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. We add the corresponding subscripts to each Gramian determinant, in order to keep track of the inner product that is used to compute it. Thus, the volumes of
![]() $\operatorname {\mathrm {Jac}}(G)$
and
$\operatorname {\mathrm {Jac}}(G)$
and
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are given by
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are given by
 $$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\operatorname{\mathrm{Gram}}_G(\mathcal{B}'),\quad \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))=\operatorname{\mathrm{Gram}}_G(\mathcal{B}'),\quad \operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
We now consider the set
 $\widetilde {\mathcal {B}}'=\widetilde {\mathcal {B}}^{\prime }_1\cup \widetilde {\mathcal {B}}^{\prime }_2$
, which is a basis for the vector space
$\widetilde {\mathcal {B}}'=\widetilde {\mathcal {B}}^{\prime }_1\cup \widetilde {\mathcal {B}}^{\prime }_2$
, which is a basis for the vector space
![]() $H_1(\widetilde {\Gamma },\mathbb {Q})$
. By appropriately ordering the basis elements, the change-of-basis matrix from
$H_1(\widetilde {\Gamma },\mathbb {Q})$
. By appropriately ordering the basis elements, the change-of-basis matrix from
![]() $\widetilde {\mathcal {B}}$
to
$\widetilde {\mathcal {B}}$
to
![]() $\widetilde {\mathcal {B}}'$
becomes block-triangular with a
$\widetilde {\mathcal {B}}'$
becomes block-triangular with a
![]() $1$
in the top left corner and a block
$1$
in the top left corner and a block
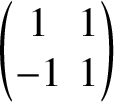 $\begin {pmatrix} 1 & 1\\ -1 & 1 \end {pmatrix}$
for each edge
$\begin {pmatrix} 1 & 1\\ -1 & 1 \end {pmatrix}$
for each edge
![]() $e_i, i=1,2\ldots ,g-1$
. Its determinant is therefore
$e_i, i=1,2\ldots ,g-1$
. Its determinant is therefore
![]() $\pm 2^{g-1}$
and it follows that
$\pm 2^{g-1}$
and it follows that
 $$\begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))=\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}})=2^{2-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}'). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))=\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}})=2^{2-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}'). \end{align*}$$
We now compute
 $\operatorname {\mathrm {Gram}}(\widetilde {\mathcal {B}}')$
using its block structure. First, we note that
$\operatorname {\mathrm {Gram}}(\widetilde {\mathcal {B}}')$
using its block structure. First, we note that
![]() $\iota _*(\widetilde {\gamma }^{\prime }_1)=\widetilde {\gamma }^{\prime }_1$
for all
$\iota _*(\widetilde {\gamma }^{\prime }_1)=\widetilde {\gamma }^{\prime }_1$
for all
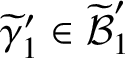 $\widetilde {\gamma }^{\prime }_1\in \widetilde {\mathcal {B}}^{\prime }_1$
and
$\widetilde {\gamma }^{\prime }_1\in \widetilde {\mathcal {B}}^{\prime }_1$
and
![]() $\iota _*(\widetilde {\gamma }^{\prime }_2)=-\widetilde {\gamma }^{\prime }_2$
for all
$\iota _*(\widetilde {\gamma }^{\prime }_2)=-\widetilde {\gamma }^{\prime }_2$
for all
 $\widetilde {\gamma }^{\prime }_2\in \widetilde {\mathcal {B}}^{\prime }_2$
. Since
$\widetilde {\gamma }^{\prime }_2\in \widetilde {\mathcal {B}}^{\prime }_2$
. Since
![]() $\iota _*$
preserves the pairing
$\iota _*$
preserves the pairing
![]() $(\cdot ,\cdot )_{\widetilde {G}}$
, it follows that
$(\cdot ,\cdot )_{\widetilde {G}}$
, it follows that
![]() $(\widetilde {\gamma }^{\prime }_1,\widetilde {\gamma }^{\prime }_2)_{\widetilde {G}}=0$
for all
$(\widetilde {\gamma }^{\prime }_1,\widetilde {\gamma }^{\prime }_2)_{\widetilde {G}}=0$
for all
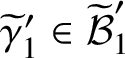 $\widetilde {\gamma }^{\prime }_1\in \widetilde {\mathcal {B}}^{\prime }_1$
and all
$\widetilde {\gamma }^{\prime }_1\in \widetilde {\mathcal {B}}^{\prime }_1$
and all
 $\widetilde {\gamma }^{\prime }_2\in \widetilde {\mathcal {B}}^{\prime }_2$
; therefore,
$\widetilde {\gamma }^{\prime }_2\in \widetilde {\mathcal {B}}^{\prime }_2$
; therefore,
 $$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}')=\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}')=\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
Since
 $(\cdot ,\cdot )_P=\frac {1}{2}(\cdot ,\cdot )_{\widetilde {G}}$
, it is clear that
$(\cdot ,\cdot )_P=\frac {1}{2}(\cdot ,\cdot )_{\widetilde {G}}$
, it is clear that
 $$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2)=2^{g-1}\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2)=2^{g-1}\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2). \end{align*} $$
Finally, for any
![]() $\gamma _1,\gamma _2\in H_1(G,\mathbb {Z})$
, we have
$\gamma _1,\gamma _2\in H_1(G,\mathbb {Z})$
, we have
![]() $(p^*(\gamma _1),p^*(\gamma _2))_{\widetilde {G}}=2(\gamma _1,\gamma _2)_G$
and therefore
$(p^*(\gamma _1),p^*(\gamma _2))_{\widetilde {G}}=2(\gamma _1,\gamma _2)_G$
and therefore
 $$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)=2^g\operatorname{\mathrm{Gram}}_G(\mathcal{B}'), \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)=2^g\operatorname{\mathrm{Gram}}_G(\mathcal{B}'), \end{align*} $$
because
![]() $\widetilde {\mathcal {B}}^{\prime }_1$
is the pullback of
$\widetilde {\mathcal {B}}^{\prime }_1$
is the pullback of
![]() $\mathcal {B}'$
. Putting all this together, we have
$\mathcal {B}'$
. Putting all this together, we have
 $$ \begin{align*}\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}=\frac{2^{2-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}')}{2\operatorname{\mathrm{Gram}}_G(\mathcal{B}')}= \frac{2^{1-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2)}{\operatorname{\mathrm{Gram}}_G(\mathcal{B}')}=\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2), \end{align*} $$
$$ \begin{align*}\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}=\frac{2^{2-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}')}{2\operatorname{\mathrm{Gram}}_G(\mathcal{B}')}= \frac{2^{1-2g}\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_1)\operatorname{\mathrm{Gram}}_{\widetilde{G}}(\widetilde{\mathcal{B}}^{\prime}_2)}{\operatorname{\mathrm{Gram}}_G(\mathcal{B}')}=\operatorname{\mathrm{Gram}}_P(\widetilde{\mathcal{B}}^{\prime}_2), \end{align*} $$
which is equal to
![]() $\operatorname {\mathrm {Vol}}^2(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))$
, as required.
$\operatorname {\mathrm {Vol}}^2(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))$
, as required.
The proof of Theorem 3.4 now follows from Theorem 3.2 and equation (7) by an elementary scaling argument.
Proof of Theorem 3.4.
The right-hand side of (17) is a homogeneous degree
![]() $g-1$
polynomial in the edge lengths of
$g-1$
polynomial in the edge lengths of
![]() $\Gamma $
and so is the left-hand side, being the determinant of a
$\Gamma $
and so is the left-hand side, being the determinant of a
![]() $(g-1)\times (g-1)$
Gramian matrix. Hence, it is sufficient to prove equation (17) in the case when
$(g-1)\times (g-1)$
Gramian matrix. Hence, it is sufficient to prove equation (17) in the case when
![]() $\Gamma $
, and hence
$\Gamma $
, and hence
![]() $\widetilde {\Gamma }$
, have integer edge lengths. Choose a model
$\widetilde {\Gamma }$
, have integer edge lengths. Choose a model
![]() $p:\widetilde {G}\to G$
for
$p:\widetilde {G}\to G$
for
![]() $\pi $
such that each edge of
$\pi $
such that each edge of
![]() $\widetilde {G}$
and G has length 1. In this case,
$\widetilde {G}$
and G has length 1. In this case,
![]() $\operatorname {\mathrm {Vol}}(F)=1$
for any set of edges; hence, by Kirchhoff’s theorem and (7) we have
$\operatorname {\mathrm {Vol}}(F)=1$
for any set of edges; hence, by Kirchhoff’s theorem and (7) we have
It follows by Proposition 3.6 that
 $$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}=|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\widetilde{\Gamma}))}{2\operatorname{\mathrm{Vol}}^2(\operatorname{\mathrm{Jac}}(\Gamma))}=\frac{|\operatorname{\mathrm{Jac}}(\widetilde{G})|}{2|\operatorname{\mathrm{Jac}}(G)|}=|\operatorname{\mathrm{Prym}}(\widetilde{G}/G)|. \end{align*} $$
But
![]() $|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|$
can be computed using (14), which agrees with the right-hand side of (17) when all edge lengths are equal to 1. This completes the proof.
$|\operatorname {\mathrm {Prym}}(\widetilde {G}/G)|$
can be computed using (14), which agrees with the right-hand side of (17) when all edge lengths are equal to 1. This completes the proof.
Example 3.7. Let
![]() $\Gamma $
be the genus 2 dumbbell graph, with loops
$\Gamma $
be the genus 2 dumbbell graph, with loops
![]() $e_1$
and
$e_1$
and
![]() $e_2$
of lengths
$e_2$
of lengths
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, connected by a bridge
$x_2$
, connected by a bridge
![]() $e_3$
of length
$e_3$
of length
![]() $x_3$
. The unique spanning tree of
$x_3$
. The unique spanning tree of
![]() $\Gamma $
consists of the edge
$\Gamma $
consists of the edge
![]() $e_3$
. The graph
$e_3$
. The graph
![]() $\Gamma $
has two topologically distinct connected free double covers
$\Gamma $
has two topologically distinct connected free double covers
![]() $\pi _1:\widetilde {\Gamma }_1\to \Gamma $
and
$\pi _1:\widetilde {\Gamma }_1\to \Gamma $
and
![]() $\pi _2:\widetilde {\Gamma }_2\to \Gamma $
, corresponding to flipping the edges
$\pi _2:\widetilde {\Gamma }_2\to \Gamma $
, corresponding to flipping the edges
![]() $S_1=\{e_1,e_2\}$
and
$S_1=\{e_1,e_2\}$
and
![]() $S_2=\{e_1\}$
(see Figure 2).
$S_2=\{e_1\}$
(see Figure 2).

Figure 2 Two free double covers of the dumbbell graph. Flipped edges are blue.
For the cover
![]() $\pi _1$
, the odd genus 1 decompositions are
$\pi _1$
, the odd genus 1 decompositions are
![]() $\{e_1\}$
and
$\{e_1\}$
and
![]() $\{e_2\}$
of rank 1 and
$\{e_2\}$
of rank 1 and
![]() $\{e_3\}$
of rank 2. For
$\{e_3\}$
of rank 2. For
![]() $\pi _2$
, the only odd genus 1 decomposition is
$\pi _2$
, the only odd genus 1 decomposition is
![]() $\{e_2\}$
of rank 1. Hence, Theorem 3.4 states that
$\{e_2\}$
of rank 1. Hence, Theorem 3.4 states that
Note that in each case the Prym variety is a circle and the square of its volume is its circumference (see Remark 2.6).
4 The local structure of the Abel–Prym map
In the remaining two sections, we provide a geometrisation of the volume formula (17) for the Prym variety of a free double cover of graphs, in the spirit of the analogous formula (7) for the volume of the Jacobian variety of a metric graph derived in [Reference An, Baker, Kuperberg and ShokriehABKS14].
Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs and let
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs and let
![]() $\iota :\widetilde {\Gamma }\to \widetilde {\Gamma }$
be the associated involution. For any integer d, we denote
$\iota :\widetilde {\Gamma }\to \widetilde {\Gamma }$
be the associated involution. For any integer d, we denote
![]() $\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
as the connected component of the kernel of the pushforward map
$\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
as the connected component of the kernel of the pushforward map
![]() $\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
having the same parity as d, so that
$\operatorname {\mathrm {Nm}}:\operatorname {\mathrm {Jac}}(\widetilde {\Gamma })\to \operatorname {\mathrm {Jac}}(\Gamma )$
having the same parity as d, so that
![]() $\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )=\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
if d is even and
$\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )=\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
if d is even and
![]() $\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
is the odd connected component if d is odd. In this section, we study the Abel–Prym map
$\operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
is the odd connected component if d is odd. In this section, we study the Abel–Prym map
for
![]() $d\leq g-1$
. The space
$d\leq g-1$
. The space
![]() $\operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })$
has a natural cellular structure, with cells enumerated by the edges and vertices of
$\operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })$
has a natural cellular structure, with cells enumerated by the edges and vertices of
![]() $\widetilde {\Gamma }$
supporting the divisor. The restriction of
$\widetilde {\Gamma }$
supporting the divisor. The restriction of
![]() $\Psi ^d$
to each cell is an affine linear map and we determine the cells on which
$\Psi ^d$
to each cell is an affine linear map and we determine the cells on which
![]() $\Psi ^d$
has maximal rank.
$\Psi ^d$
has maximal rank.
Choose an oriented model
![]() $p:\widetilde {G}\to G$
for
$p:\widetilde {G}\to G$
for
![]() $\pi $
such that
$\pi $
such that
![]() $\widetilde {G}$
and G have no loops. Let
$\widetilde {G}$
and G have no loops. Let
![]() $0\leq k\leq d$
, let
$0\leq k\leq d$
, let
![]() $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_k\}$
be a multiset of k edges of
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_k\}$
be a multiset of k edges of
![]() $\widetilde {G}$
and let
$\widetilde {G}$
and let
![]() $\widetilde {Z}$
be an effective divisor of degree
$\widetilde {Z}$
be an effective divisor of degree
![]() $d-k$
supported on
$d-k$
supported on
![]() $V(\widetilde {G})$
. Denote by
$V(\widetilde {G})$
. Denote by
![]() $C^k(\widetilde {F},\widetilde {Z})$
the k-dimensional set of effective divisors on
$C^k(\widetilde {F},\widetilde {Z})$
the k-dimensional set of effective divisors on
![]() $\widetilde {\Gamma }$
of the form
$\widetilde {\Gamma }$
of the form
![]() $\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_k+\widetilde {Z}$
, where each
$\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_k+\widetilde {Z}$
, where each
![]() $\widetilde {P}_i$
lies on
$\widetilde {P}_i$
lies on
![]() $\widetilde {f}_i$
. Any effective degree d divisor on
$\widetilde {f}_i$
. Any effective degree d divisor on
![]() $\widetilde {\Gamma }$
can be split up in such a way (uniquely if each point lies in the interior of an edge); hence, we have a cellular decomposition
$\widetilde {\Gamma }$
can be split up in such a way (uniquely if each point lies in the interior of an edge); hence, we have a cellular decomposition
 $$ \begin{align} \operatorname{\mathrm{Sym}}^d(\widetilde{\Gamma})=\bigcup_{k=0}^d \bigcup_{\widetilde{F},\widetilde{Z}} C^k(\widetilde{F},\widetilde{Z}),\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Sym}}^d(\widetilde{\Gamma})=\bigcup_{k=0}^d \bigcup_{\widetilde{F},\widetilde{Z}} C^k(\widetilde{F},\widetilde{Z}),\\[-15pt]\nonumber \end{align} $$
where the union is taken over all
![]() $\widetilde {F}\in \operatorname {\mathrm {Sym}}^k(E(\widetilde {G}))$
and
$\widetilde {F}\in \operatorname {\mathrm {Sym}}^k(E(\widetilde {G}))$
and
![]() $\widetilde {Z}\in \operatorname {\mathrm {Sym}}^{d-k}(V(\widetilde {G}))$
.
$\widetilde {Z}\in \operatorname {\mathrm {Sym}}^{d-k}(V(\widetilde {G}))$
.
The principal result of this section describes the cells
![]() $C^k(\widetilde {F},\widetilde {Z})$
that are not contracted by the Abel–Prym map
$C^k(\widetilde {F},\widetilde {Z})$
that are not contracted by the Abel–Prym map
![]() $\Psi ^d$
. It is clear that the divisor
$\Psi ^d$
. It is clear that the divisor
![]() $\widetilde {Z}$
plays no role in this question; hence, we assume that
$\widetilde {Z}$
plays no role in this question; hence, we assume that
![]() $k=d$
,
$k=d$
,
![]() $\widetilde {Z}=0$
and only consider the top-dimensional cells, which we denote
$\widetilde {Z}=0$
and only consider the top-dimensional cells, which we denote
Theorem 4.1. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs with oriented loopless model
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs with oriented loopless model
![]() $p:\widetilde {G}\to G$
and let
$p:\widetilde {G}\to G$
and let
![]() $\Psi ^d:\operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
be the degree d Abel–Prym map, where
$\Psi ^d:\operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[d]}(\widetilde {\Gamma }/\Gamma )$
be the degree d Abel–Prym map, where
![]() $1\leq d\leq g-1$
. Let
$1\leq d\leq g-1$
. Let
![]() $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}\subset E(\widetilde {G})$
be a multiset of edges of
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}\subset E(\widetilde {G})$
be a multiset of edges of
![]() $\widetilde {G}$
, let
$\widetilde {G}$
, let
![]() $C(\widetilde {F})\subset \operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })$
be the corresponding top-dimensional cell and denote
$C(\widetilde {F})\subset \operatorname {\mathrm {Sym}}^d(\widetilde {\Gamma })$
be the corresponding top-dimensional cell and denote
![]() $F=\{f_1,\ldots ,f_d\}$
, where
$F=\{f_1,\ldots ,f_d\}$
, where
![]() $f_i=p(\widetilde {f}_i)$
.
$f_i=p(\widetilde {f}_i)$
.
-
(1) If the edges in F are not distinct (in particular, if the edges in
 $\widetilde {F}$
are not distinct), then
$\widetilde {F}$
are not distinct), then
 $\Psi ^d$
contracts
$\Psi ^d$
contracts
 $C(\widetilde {F})$
.
$C(\widetilde {F})$
. -
(2) If the edges in F are distinct, then
 $\Psi ^d$
does not contract
$\Psi ^d$
does not contract
 $C(\widetilde {F})$
if and only if the preimage under p of each connected component of
$C(\widetilde {F})$
if and only if the preimage under p of each connected component of
 $G\backslash F$
is connected.
$G\backslash F$
is connected.
The proof of the first part of the theorem is quite elementary: for any
![]() $\widetilde {D}\in C(\widetilde {F})$
we construct a nearby divisor
$\widetilde {D}\in C(\widetilde {F})$
we construct a nearby divisor
![]() $\widetilde {D}'$
such that
$\widetilde {D}'$
such that
![]() $\Psi ^d(\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
is linearly equivalent to
$\Psi ^d(\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
is linearly equivalent to
![]() $\Psi ^d(\widetilde {D}')=\widetilde {D}'-\iota (\widetilde {D}')$
via an explicit rational function. To prove the second part, we calculate the matrix of
$\Psi ^d(\widetilde {D}')=\widetilde {D}'-\iota (\widetilde {D}')$
via an explicit rational function. To prove the second part, we calculate the matrix of
![]() $\Psi ^d$
with respect to a convenient basis and compute its rank. This part and the necessary constructions will occupy the greater part of this section.
$\Psi ^d$
with respect to a convenient basis and compute its rank. This part and the necessary constructions will occupy the greater part of this section.
Proof of Theorem 4.1, part (1).
Let
![]() $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}$
be a multiset such that not all
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}$
be a multiset such that not all
![]() $f_i=p(\widetilde {f}_i)$
are distinct. Without loss of generality, we assume that
$f_i=p(\widetilde {f}_i)$
are distinct. Without loss of generality, we assume that
![]() $f_1=f_2$
, which means that either
$f_1=f_2$
, which means that either
![]() $\widetilde {f}_1=\widetilde {f}_2$
or
$\widetilde {f}_1=\widetilde {f}_2$
or
![]() $\widetilde {f}_1=\iota (\widetilde {f}_2)$
. Let
$\widetilde {f}_1=\iota (\widetilde {f}_2)$
. Let
![]() $\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_d$
be a point of
$\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_d$
be a point of
![]() $C(\widetilde {F})$
, where each
$C(\widetilde {F})$
, where each
![]() $\widetilde {P}_i$
lies in the interior of
$\widetilde {P}_i$
lies in the interior of
![]() $\widetilde {f}_i$
.
$\widetilde {f}_i$
.
If
![]() $\widetilde {f}_1=\widetilde {f}_2$
, we can assume that either
$\widetilde {f}_1=\widetilde {f}_2$
, we can assume that either
![]() $\widetilde {P}_1=\widetilde {P}_2$
or that the direction from
$\widetilde {P}_1=\widetilde {P}_2$
or that the direction from
![]() $\widetilde {P}_1$
to
$\widetilde {P}_1$
to
![]() $\widetilde {P}_2$
is positive with respect to the orientation. Denote
$\widetilde {P}_2$
is positive with respect to the orientation. Denote
 $\widetilde {D}'=\widetilde {P}^{\prime }_1+\widetilde {P}^{\prime }_2+\widetilde {P}_3+\cdots +\widetilde {P}_d$
, where
$\widetilde {D}'=\widetilde {P}^{\prime }_1+\widetilde {P}^{\prime }_2+\widetilde {P}_3+\cdots +\widetilde {P}_d$
, where
![]() $\widetilde {P}^{\prime }_1$
and
$\widetilde {P}^{\prime }_1$
and
![]() $\widetilde {P}^{\prime }_2$
are obtained by moving
$\widetilde {P}^{\prime }_2$
are obtained by moving
![]() $\widetilde {P}_1$
and
$\widetilde {P}_1$
and
![]() $\widetilde {P}_2$
a small distance of
$\widetilde {P}_2$
a small distance of
![]() $\varepsilon>0$
respectively in the negative and the positive directions along
$\varepsilon>0$
respectively in the negative and the positive directions along
![]() $\widetilde {f}_1=\widetilde {f}_2$
. Then the divisor
$\widetilde {f}_1=\widetilde {f}_2$
. Then the divisor
 $$ \begin{align*}\Psi^d(\widetilde{D})-\Psi^d(\widetilde{D}')=\widetilde{D}-\iota(\widetilde{D})-\widetilde{D}'+\iota(\widetilde{D}')=\widetilde{P}_1+\widetilde{P}_2-\widetilde{P}^{\prime}_1-\widetilde{P}^{\prime}_2-\iota(\widetilde{P}_1)-\iota(\widetilde{P}_2)+\iota(\widetilde{P}^{\prime}_1)+\iota(\widetilde{P}^{\prime}_2) \end{align*} $$
$$ \begin{align*}\Psi^d(\widetilde{D})-\Psi^d(\widetilde{D}')=\widetilde{D}-\iota(\widetilde{D})-\widetilde{D}'+\iota(\widetilde{D}')=\widetilde{P}_1+\widetilde{P}_2-\widetilde{P}^{\prime}_1-\widetilde{P}^{\prime}_2-\iota(\widetilde{P}_1)-\iota(\widetilde{P}_2)+\iota(\widetilde{P}^{\prime}_1)+\iota(\widetilde{P}^{\prime}_2) \end{align*} $$
is the principal divisor of a piecewise linear function on
![]() $\widetilde {\Gamma }$
. Indeed, consider the function
$\widetilde {\Gamma }$
. Indeed, consider the function
![]() $M:\widetilde {\Gamma }\to \mathbb {R}$
having the following slopes on the edges of
$M:\widetilde {\Gamma }\to \mathbb {R}$
having the following slopes on the edges of
![]() $\widetilde {\Gamma }$
:
$\widetilde {\Gamma }$
:
-
• On
 $\widetilde {f}_1=\widetilde {f}_2$
, M has slope 0 to the left of
$\widetilde {f}_1=\widetilde {f}_2$
, M has slope 0 to the left of
 $\widetilde {P}_1'$
, slope
$\widetilde {P}_1'$
, slope
 $+1$
on
$+1$
on
 $[\widetilde {P}^{\prime }_1,\widetilde {P}_1]$
, slope 0 on
$[\widetilde {P}^{\prime }_1,\widetilde {P}_1]$
, slope 0 on
 $[\widetilde {P}_1,\widetilde {P}_2]$
, slope
$[\widetilde {P}_1,\widetilde {P}_2]$
, slope
 $-1$
on
$-1$
on
 $[\widetilde {P}_2,\widetilde {P}^{\prime }_2]$
and slope 0 to the right of
$[\widetilde {P}_2,\widetilde {P}^{\prime }_2]$
and slope 0 to the right of
 $\widetilde {P}^{\prime }_2$
.
$\widetilde {P}^{\prime }_2$
. -
• On
 $\iota (\widetilde {f}_1)=\iota (\widetilde {f}_2)$
, M has slope 0 to the left of
$\iota (\widetilde {f}_1)=\iota (\widetilde {f}_2)$
, M has slope 0 to the left of
 $\iota (\widetilde {P}_1)$
, slope
$\iota (\widetilde {P}_1)$
, slope
 $-1$
on
$-1$
on
 $[\iota (\widetilde {P}^{\prime }_1),\iota (\widetilde {P}_1)]$
, slope 0 on
$[\iota (\widetilde {P}^{\prime }_1),\iota (\widetilde {P}_1)]$
, slope 0 on
 $[\iota (\widetilde {P}_1),\iota (\widetilde {P}_2)]$
, slope
$[\iota (\widetilde {P}_1),\iota (\widetilde {P}_2)]$
, slope
 $+1$
on
$+1$
on
 $[\iota (\widetilde {P}_2),\iota (\widetilde {P}^{\prime }_2)]$
and slope 0 to the right of
$[\iota (\widetilde {P}_2),\iota (\widetilde {P}^{\prime }_2)]$
and slope 0 to the right of
 $\iota (\widetilde {P}^{\prime }_2)$
.
$\iota (\widetilde {P}^{\prime }_2)$
. -
• The function M has zero slope on all other edges of
 $\widetilde {\Gamma }$
.
$\widetilde {\Gamma }$
.
The net changes of M along
![]() $\widetilde {f}_1=\widetilde {f}_2$
and
$\widetilde {f}_1=\widetilde {f}_2$
and
![]() $\iota (\widetilde {f}_1)=\iota (\widetilde {f}_2)$
cancel out; hence, the function M is continuous and it is clear that
$\iota (\widetilde {f}_1)=\iota (\widetilde {f}_2)$
cancel out; hence, the function M is continuous and it is clear that
![]() $\Psi ^d(\widetilde {D})-\Psi ^d(\widetilde {D}')$
is the divisor of M. Therefore,
$\Psi ^d(\widetilde {D})-\Psi ^d(\widetilde {D}')$
is the divisor of M. Therefore,
![]() $\Psi ^d$
is not locally injective at
$\Psi ^d$
is not locally injective at
![]() $\widetilde {D}$
.
$\widetilde {D}$
.
The case
![]() $\widetilde {f}_1=\iota (\widetilde {f}_2)$
is similar. We consider
$\widetilde {f}_1=\iota (\widetilde {f}_2)$
is similar. We consider
 $\widetilde {D}'=\widetilde {P}^{\prime }_1+\widetilde {P}^{\prime }_2+\widetilde {P}_3+\cdots +\widetilde {P}_d$
, where
$\widetilde {D}'=\widetilde {P}^{\prime }_1+\widetilde {P}^{\prime }_2+\widetilde {P}_3+\cdots +\widetilde {P}_d$
, where
![]() $\widetilde {P}^{\prime }_1$
and
$\widetilde {P}^{\prime }_1$
and
![]() $\widetilde {P}^{\prime }_2$
are obtained by moving
$\widetilde {P}^{\prime }_2$
are obtained by moving
![]() $\widetilde {P}_1$
and
$\widetilde {P}_1$
and
![]() $\widetilde {P}_2$
a small distance of
$\widetilde {P}_2$
a small distance of
![]() $\varepsilon>0$
in the same direction along
$\varepsilon>0$
in the same direction along
![]() $\widetilde {f}_1$
and
$\widetilde {f}_1$
and
![]() $\widetilde {f}_2=\iota (\widetilde {f}_1)$
respectively. It is easy to check that
$\widetilde {f}_2=\iota (\widetilde {f}_1)$
respectively. It is easy to check that
![]() $\Psi ^d(\widetilde {D})-\Psi ^d(\widetilde {D}')$
is a principal divisor; hence,
$\Psi ^d(\widetilde {D})-\Psi ^d(\widetilde {D}')$
is a principal divisor; hence,
![]() $\Psi ^d$
is not locally injective at
$\Psi ^d$
is not locally injective at
![]() $\widetilde {D}$
.
$\widetilde {D}$
.
To prove part (2) of Theorem 4.1, we give an explicit description of the Abel–Prym map
![]() $\Psi ^d$
on a cell
$\Psi ^d$
on a cell
![]() $C(\widetilde {F})$
. We first consider the case
$C(\widetilde {F})$
. We first consider the case
![]() $d=1$
. Fix a base point
$d=1$
. Fix a base point
![]() $q\in \widetilde {\Gamma }$
and for each point
$q\in \widetilde {\Gamma }$
and for each point
![]() $p\in \widetilde {\Gamma }$
fix a path
$p\in \widetilde {\Gamma }$
fix a path
![]() $\gamma (q,p)$
from q to p. The Abel–Prym map
$\gamma (q,p)$
from q to p. The Abel–Prym map
![]() $\Psi ^1$
is a difference of Abel–Jacobi maps (5):
$\Psi ^1$
is a difference of Abel–Jacobi maps (5):
 $$ \begin{align*}\Psi^1:\widetilde{\Gamma}\to \operatorname{\mathrm{Prym}}^{[1]}(\widetilde{\Gamma}/\Gamma)\subset \operatorname{\mathrm{Jac}}(\widetilde{\Gamma}),\quad \Psi^1(p)(\omega)=\int_{\gamma(q,p)}\omega-\int_{\gamma(q,\iota(p))}\omega. \end{align*} $$
$$ \begin{align*}\Psi^1:\widetilde{\Gamma}\to \operatorname{\mathrm{Prym}}^{[1]}(\widetilde{\Gamma}/\Gamma)\subset \operatorname{\mathrm{Jac}}(\widetilde{\Gamma}),\quad \Psi^1(p)(\omega)=\int_{\gamma(q,p)}\omega-\int_{\gamma(q,\iota(p))}\omega. \end{align*} $$
It is more convenient to work with the even component
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. The odd component
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. The odd component
![]() $\operatorname {\mathrm {Prym}}^{[1]}(\widetilde {\Gamma }/\Gamma )$
is a torsor over
$\operatorname {\mathrm {Prym}}^{[1]}(\widetilde {\Gamma }/\Gamma )$
is a torsor over
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, and we can pass to the even component by translating by any element of the odd component; for example, the element
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, and we can pass to the even component by translating by any element of the odd component; for example, the element
 $\Psi ^1(\iota (q))=\int _{\gamma (q,\iota (q))}$
. We can further assume that the path
$\Psi ^1(\iota (q))=\int _{\gamma (q,\iota (q))}$
. We can further assume that the path
![]() $\gamma (q,\iota (p))$
in the formula above consists of
$\gamma (q,\iota (p))$
in the formula above consists of
![]() $\gamma (q,\iota (q))$
followed by the path
$\gamma (q,\iota (q))$
followed by the path
![]() $\iota _*(\gamma (q,p))$
. Putting this together, we obtain the translated Abel–Prym map, which we also denote
$\iota _*(\gamma (q,p))$
. Putting this together, we obtain the translated Abel–Prym map, which we also denote
![]() $\Psi ^1$
by abuse of notation:
$\Psi ^1$
by abuse of notation:
 $$ \begin{align} \Psi^1:\widetilde{\Gamma}\to \operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma),\quad \Psi^1(p)(\omega)=\int_{\gamma(q,p)}\omega-\int_{\iota_*(\gamma(q,p))}\omega. \end{align} $$
$$ \begin{align} \Psi^1:\widetilde{\Gamma}\to \operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma),\quad \Psi^1(p)(\omega)=\int_{\gamma(q,p)}\omega-\int_{\iota_*(\gamma(q,p))}\omega. \end{align} $$
Choose a basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
![]() $\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
. As explained in Subsection 2.6, the functionals
$\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
. As explained in Subsection 2.6, the functionals
 $\omega ^*_j\in \Omega ^*(\widetilde {\Gamma })$
dual to
$\omega ^*_j\in \Omega ^*(\widetilde {\Gamma })$
dual to
![]() $\omega _j=\psi (\widetilde {\gamma }_j)$
define a coordinate system on
$\omega _j=\psi (\widetilde {\gamma }_j)$
define a coordinate system on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, so we can write
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, so we can write
 $$ \begin{align*}\Psi^1(p)=\int_{\gamma(q,p)}-\int_{\iota_*(\gamma(q,p))}=\sum_{j=1}^{g-1}a_j(p)\omega_j^*, \end{align*} $$
$$ \begin{align*}\Psi^1(p)=\int_{\gamma(q,p)}-\int_{\iota_*(\gamma(q,p))}=\sum_{j=1}^{g-1}a_j(p)\omega_j^*, \end{align*} $$
where we find the coefficients
![]() $a_j(p)$
by pairing with
$a_j(p)$
by pairing with
![]() $\omega _j$
:
$\omega _j$
:
 $$ \begin{align*}a_j(p)=\int_{\gamma(q,p)}\omega_j-\int_{\iota_*(\gamma(q,p))}\omega_j. \end{align*} $$
$$ \begin{align*}a_j(p)=\int_{\gamma(q,p)}\omega_j-\int_{\iota_*(\gamma(q,p))}\omega_j. \end{align*} $$
We now assume that p lies on the interior of an edge
![]() $\widetilde {f}\in E(\widetilde {\Gamma })$
, which we identify using the orientation with the segment
$\widetilde {f}\in E(\widetilde {\Gamma })$
, which we identify using the orientation with the segment
![]() $(0,\ell (\widetilde {f}))$
. Pick
$(0,\ell (\widetilde {f}))$
. Pick
![]() $x_1,x_2\in (0,\ell (\widetilde {f}))$
such that
$x_1,x_2\in (0,\ell (\widetilde {f}))$
such that
![]() $x_1<x_2$
; then we see that
$x_1<x_2$
; then we see that
 $$ \begin{align*}a_j(x_2)-a_j(x_1)&=\int_{\gamma(q,x_2)}\omega_j-\int_{\iota_*(\gamma(q,x_2))}\omega_j-\int_{\gamma(q,x_1)}\omega_j+\int_{\iota_*(\gamma(q,x_1))}\omega_j\\ &=\int_{\gamma(x_1,x_2)}\omega_j-\int_{\iota_*(\gamma(x_1,x_2))}\omega_j. \end{align*} $$
$$ \begin{align*}a_j(x_2)-a_j(x_1)&=\int_{\gamma(q,x_2)}\omega_j-\int_{\iota_*(\gamma(q,x_2))}\omega_j-\int_{\gamma(q,x_1)}\omega_j+\int_{\iota_*(\gamma(q,x_1))}\omega_j\\ &=\int_{\gamma(x_1,x_2)}\omega_j-\int_{\iota_*(\gamma(x_1,x_2))}\omega_j. \end{align*} $$
We can assume that
![]() $\gamma (x_1,x_2)$
is the segment
$\gamma (x_1,x_2)$
is the segment
![]() $[x_1,x_2]\subset (0,\ell (\widetilde {f}))$
. The integral of
$[x_1,x_2]\subset (0,\ell (\widetilde {f}))$
. The integral of
![]() $\omega _j$
over
$\omega _j$
over
![]() $\gamma (x_1,x_2)$
is equal to the length
$\gamma (x_1,x_2)$
is equal to the length
![]() $x_2-x_1$
multiplied by the coefficient with which
$x_2-x_1$
multiplied by the coefficient with which
![]() $\widetilde {f}$
occurs in
$\widetilde {f}$
occurs in
![]() $\omega _j$
, which is
$\omega _j$
, which is
 $\frac {1}{2}\langle \widetilde {\gamma }_j,\widetilde {f}\rangle $
(the
$\frac {1}{2}\langle \widetilde {\gamma }_j,\widetilde {f}\rangle $
(the
![]() $\frac {1}{2}$
coefficient comes from using the principal polarisation of the Prym). Similarly, the integral of
$\frac {1}{2}$
coefficient comes from using the principal polarisation of the Prym). Similarly, the integral of
![]() $\omega _j$
over
$\omega _j$
over
![]() $\iota _*(\gamma (x_1,x_2))$
is equal to
$\iota _*(\gamma (x_1,x_2))$
is equal to
 $\frac {1}{2}(x_2-x_1)\langle \widetilde {\gamma }_j,\iota (\widetilde {f})\rangle $
and therefore
$\frac {1}{2}(x_2-x_1)\langle \widetilde {\gamma }_j,\iota (\widetilde {f})\rangle $
and therefore
 $$ \begin{align*}a_j(x_2)-a_j(x_1)=\frac{1}{2}(x_2-x_1) \langle \widetilde{\gamma}_j,\widetilde{f}-\iota(\widetilde{f})\rangle, \end{align*} $$
$$ \begin{align*}a_j(x_2)-a_j(x_1)=\frac{1}{2}(x_2-x_1) \langle \widetilde{\gamma}_j,\widetilde{f}-\iota(\widetilde{f})\rangle, \end{align*} $$
where
![]() $\langle \cdot ,\cdot \rangle $
is the edge pairing (18). It follows that, with respect to the coordinate vectors
$\langle \cdot ,\cdot \rangle $
is the edge pairing (18). It follows that, with respect to the coordinate vectors
![]() $\omega ^*_j$
defined by the basis
$\omega ^*_j$
defined by the basis
![]() $\widetilde {\gamma }_j$
, the restriction of the Abel–Prym map (23) to an edge
$\widetilde {\gamma }_j$
, the restriction of the Abel–Prym map (23) to an edge
![]() $\widetilde {f}=[0,\ell (\widetilde {f})]$
is an affine
$\widetilde {f}=[0,\ell (\widetilde {f})]$
is an affine
![]() $\mathbb {Z}$
-linear map of the form
$\mathbb {Z}$
-linear map of the form
 $$ \begin{align*}\Psi^1(x)=\frac{1}{2}\sum_{j=1}^{g-1}\langle \widetilde{\gamma}_j,\widetilde{f}-\iota(\widetilde{f})\rangle \omega^*_jx+C, \end{align*} $$
$$ \begin{align*}\Psi^1(x)=\frac{1}{2}\sum_{j=1}^{g-1}\langle \widetilde{\gamma}_j,\widetilde{f}-\iota(\widetilde{f})\rangle \omega^*_jx+C, \end{align*} $$
where C is a constant vector.
This formula readily generalises to any degree. Let
![]() $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}$
be a set of distinct edges of
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}$
be a set of distinct edges of
![]() $\widetilde {G}$
. We identify the cell
$\widetilde {G}$
. We identify the cell
![]() $C(\widetilde {F})$
with the parallelotope
$C(\widetilde {F})$
with the parallelotope
![]() $[0,\ell (\widetilde {f}_1)]\times \cdots \times [0,\ell (\widetilde {f}_d)]$
, where the point
$[0,\ell (\widetilde {f}_1)]\times \cdots \times [0,\ell (\widetilde {f}_d)]$
, where the point
![]() $(x_1,\ldots ,x_d)$
corresponds to the divisor
$(x_1,\ldots ,x_d)$
corresponds to the divisor
![]() $\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_d$
, where
$\widetilde {D}=\widetilde {P}_1+\cdots +\widetilde {P}_d$
, where
![]() $\widetilde {P}_i$
lies on
$\widetilde {P}_i$
lies on
![]() $\widetilde {f}_i$
at a distance of
$\widetilde {f}_i$
at a distance of
![]() $x_i$
from the starting vertex. Translating by any odd Prym divisor and moving to the even component if d is odd, we see that the restriction of the Abel–Prym map (21) to the cell
$x_i$
from the starting vertex. Translating by any odd Prym divisor and moving to the even component if d is odd, we see that the restriction of the Abel–Prym map (21) to the cell
![]() $C(\widetilde {F})$
is affine
$C(\widetilde {F})$
is affine
![]() $\mathbb {Z}$
-linear:
$\mathbb {Z}$
-linear:
 $$ \begin{align*}\Psi^d(x_1,\ldots,x_d)=\sum_{i=1}^d\sum_{j=1}^{g-1}(\Psi^d)_{ji}\omega^*_jx_i+C\in \operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma), \end{align*} $$
$$ \begin{align*}\Psi^d(x_1,\ldots,x_d)=\sum_{i=1}^d\sum_{j=1}^{g-1}(\Psi^d)_{ji}\omega^*_jx_i+C\in \operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma), \end{align*} $$
where
![]() $(\Psi ^d)_{ji}$
is the
$(\Psi ^d)_{ji}$
is the
![]() $(g-1)\times d$
matrix
$(g-1)\times d$
matrix
 $$ \begin{align} (\Psi^d)_{ji}=\frac{1}{2}\left\langle \widetilde{\gamma}_j, \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle \end{align} $$
$$ \begin{align} (\Psi^d)_{ji}=\frac{1}{2}\left\langle \widetilde{\gamma}_j, \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle \end{align} $$
and C is some constant vector.
To prove part (2) of Theorem 4.1, we compute the rank of
![]() $(\Psi ^d)_{ji}$
with respect to a carefully chosen basis
$(\Psi ^d)_{ji}$
with respect to a carefully chosen basis
![]() $\widetilde {\gamma }_j$
of
$\widetilde {\gamma }_j$
of
![]() $\operatorname {\mathrm {Ker}} \pi _*$
. Specifically, the ‘if’ and ‘only if’ statements will require slightly different choices of basis.
$\operatorname {\mathrm {Ker}} \pi _*$
. Specifically, the ‘if’ and ‘only if’ statements will require slightly different choices of basis.
Proof of Theorem 4.1, part (2).
We consider the decomposition of
![]() $G\backslash F$
into connected components, which we enumerate as follows:
$G\backslash F$
into connected components, which we enumerate as follows:
Before proceeding, we derive a relationship between the genera
![]() $g_k=|E(G_k)|-|V(G_k)|+1$
of the components
$g_k=|E(G_k)|-|V(G_k)|+1$
of the components
![]() $G_k$
:
$G_k$
:
 $$ \begin{align} g_0+\cdots+g_{r-1}=\sum_{k=0}^{r-1}|E(G_k)|-\sum_{k=0}^{r-1}|V(G_k)|+r=|E(G)|-d-|V(G)|+r=g+r-d-1. \end{align} $$
$$ \begin{align} g_0+\cdots+g_{r-1}=\sum_{k=0}^{r-1}|E(G_k)|-\sum_{k=0}^{r-1}|V(G_k)|+r=|E(G)|-d-|V(G)|+r=g+r-d-1. \end{align} $$
We now consider the two possibilities.
The preimage of one of the connected components is disconnected. Equivalently, we assume that the restriction of the cover p to one of the connected components is isomorphic to the trivial free double cover. Let
![]() $G_k$
be a connected component of genus
$G_k$
be a connected component of genus
![]() $g_k$
. If
$g_k$
. If
![]() $p^{-1}(G_k)$
is connected, then Construction B, applied to the cover
$p^{-1}(G_k)$
is connected, then Construction B, applied to the cover
 $p|_{p^{-1}(G_k)}:p^{-1}(G_k)\to G_k$
, produces
$p|_{p^{-1}(G_k)}:p^{-1}(G_k)\to G_k$
, produces
![]() $g_k-1$
linearly independent cycles
$g_k-1$
linearly independent cycles
![]() $\gamma _{kl}\in H_1(\widetilde {G},\mathbb {Z})$
that are supported on
$\gamma _{kl}\in H_1(\widetilde {G},\mathbb {Z})$
that are supported on
![]() $p^{-1}(G_k)$
and that lie in
$p^{-1}(G_k)$
and that lie in
![]() $\operatorname {\mathrm {Ker}} p_*$
. However, if the restriction of p to, say,
$\operatorname {\mathrm {Ker}} p_*$
. However, if the restriction of p to, say,
![]() $G_k$
is trivial, then we can find
$G_k$
is trivial, then we can find
![]() $g_k$
such cycles, by applying
$g_k$
such cycles, by applying
![]() $(\operatorname {\mathrm {Id}}-\iota )_*$
to the lifts of a linearly independent collection of cycles on
$(\operatorname {\mathrm {Id}}-\iota )_*$
to the lifts of a linearly independent collection of cycles on
![]() $G_k$
. In this case, it follows from (25) that there are at least
$G_k$
. In this case, it follows from (25) that there are at least
linearly independent cycles
![]() $\gamma _{kl}\in H_1(\widetilde {G},\mathbb {Z})$
, lying in the kernel of
$\gamma _{kl}\in H_1(\widetilde {G},\mathbb {Z})$
, lying in the kernel of
![]() $p_*$
and supported on
$p_*$
and supported on
Any such cycle
![]() $\gamma _{kl}$
pairs trivially with each
$\gamma _{kl}$
pairs trivially with each
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $\iota (\widetilde {f}_i)$
. Therefore, by completing these cycles to a basis of
$\iota (\widetilde {f}_i)$
. Therefore, by completing these cycles to a basis of
![]() $\operatorname {\mathrm {Ker}} p_*$
(passing to
$\operatorname {\mathrm {Ker}} p_*$
(passing to
![]() $\mathbb {Q}$
-coefficients if necessary), we see that the matrix (24) of
$\mathbb {Q}$
-coefficients if necessary), we see that the matrix (24) of
![]() $\Psi ^d$
with respect to this basis has at least
$\Psi ^d$
with respect to this basis has at least
![]() $g-d$
rows of zeroes and hence has rank less than d and contracts
$g-d$
rows of zeroes and hence has rank less than d and contracts
![]() $C(\widetilde {F})$
.
$C(\widetilde {F})$
.
The preimage of each connected component is connected. Equivalently, the restriction of p to each connected component is a nontrivial free double cover. This implies that
![]() $g_k\geq 1$
for each k, since any free double cover of a tree is trivial.
$g_k\geq 1$
for each k, since any free double cover of a tree is trivial.
We show that the matrix (24) has rank d with respect to an explicit choice of basis
![]() $\widetilde {\gamma }_i$
of
$\widetilde {\gamma }_i$
of
![]() $\operatorname {\mathrm {Ker}} \pi _*$
. The construction of this basis is somewhat involved and will be used again in the proof of Theorem 5.1, so we typeset it separately.
$\operatorname {\mathrm {Ker}} \pi _*$
. The construction of this basis is somewhat involved and will be used again in the proof of Theorem 5.1, so we typeset it separately.
Construction C. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a connected free double cover of metric graphs of genera
$\pi :\widetilde {\Gamma }\to \Gamma $
be a connected free double cover of metric graphs of genera
![]() $2g-1$
and g, respectively, and let
$2g-1$
and g, respectively, and let
![]() $p:\widetilde {G}\to G$
be an oriented model. Let
$p:\widetilde {G}\to G$
be an oriented model. Let
![]() $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}\subset E(\widetilde {G})$
be a set of d edges so that the edges
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_d\}\subset E(\widetilde {G})$
be a set of d edges so that the edges
![]() $f_i=p(\widetilde {f}_i)$
are distinct and denote
$f_i=p(\widetilde {f}_i)$
are distinct and denote
![]() $F=p(\widetilde {F})$
. Let
$F=p(\widetilde {F})$
. Let
be the decomposition of
![]() $G\backslash F$
into connected components and further assume that
$G\backslash F$
into connected components and further assume that
![]() $p^{-1}(G_k)$
is connected for each k. In this construction, we elaborate on Constructions A and B by carefully choosing a spanning tree
$p^{-1}(G_k)$
is connected for each k. In this construction, we elaborate on Constructions A and B by carefully choosing a spanning tree
![]() $T\subset G$
and a corresponding basis
$T\subset G$
and a corresponding basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
![]() $\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, with respect to which the matrix of the Abel–Prym map on the cell
$\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, with respect to which the matrix of the Abel–Prym map on the cell
![]() $C(\widetilde {F})$
has a convenient triangular structure. This construction involves a number of choices and relabellings, so we break it down into steps. At the same time, we will contract the portions of the graphs
$C(\widetilde {F})$
has a convenient triangular structure. This construction involves a number of choices and relabellings, so we break it down into steps. At the same time, we will contract the portions of the graphs
![]() $\widetilde {G}$
and G that are irrelevant to our intersection calculations.
$\widetilde {G}$
and G that are irrelevant to our intersection calculations.
Contracting the
![]() $G_k$
and choosing the spanning tree
$G_k$
and choosing the spanning tree
![]() $T\subset G$
. Choose a spanning tree
$T\subset G$
. Choose a spanning tree
![]() $T_k$
for each connected component
$T_k$
for each connected component
![]() $G_k$
. Denote by
$G_k$
. Denote by
![]() $G^c$
the graph obtained from G by contracting each subtree
$G^c$
the graph obtained from G by contracting each subtree
![]() $T_k$
to a separate vertex
$T_k$
to a separate vertex
![]() $v_k$
. Specifically, the vertex set of
$v_k$
. Specifically, the vertex set of
![]() $G^c$
is
$G^c$
is
![]() $V(G^c)=\{v_0,\ldots ,v_{r-1}\}$
and the edge set of
$V(G^c)=\{v_0,\ldots ,v_{r-1}\}$
and the edge set of
![]() $G^c$
is the set of edges G that are not in any
$G^c$
is the set of edges G that are not in any
![]() $T_k$
. There is a natural contraction map
$T_k$
. There is a natural contraction map
![]() $(\cdot )^c:G\to G^c$
; this map sends each vertex and edge of
$(\cdot )^c:G\to G^c$
; this map sends each vertex and edge of
![]() $T_k$
to
$T_k$
to
![]() $v_k$
and sends each edge of G that is not in any
$v_k$
and sends each edge of G that is not in any
![]() $T_k$
to the corresponding edge of
$T_k$
to the corresponding edge of
![]() $G^c$
. The contracted graph
$G^c$
. The contracted graph
![]() $G^c$
has the same genus g as G; hence, it has
$G^c$
has the same genus g as G; hence, it has
![]() $g+r-1$
edges, namely, the edges
$g+r-1$
edges, namely, the edges
![]() $F=\{f_1,\ldots ,f_d\}$
and
$F=\{f_1,\ldots ,f_d\}$
and
![]() $g+r-d-1$
loops corresponding to the uncontracted edges of the
$g+r-d-1$
loops corresponding to the uncontracted edges of the
![]() $G_k$
. Choose a spanning tree
$G_k$
. Choose a spanning tree
![]() $T^c$
for the contracted graph
$T^c$
for the contracted graph
![]() $G^c$
; the
$G^c$
; the
![]() $r-1$
edges of
$r-1$
edges of
![]() $T^c$
are a subset of the edges
$T^c$
are a subset of the edges
![]() $\{f_1,\ldots ,f_d\}$
.
$\{f_1,\ldots ,f_d\}$
.
Before proceeding, we relabel the edges
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $f_i=p(\widetilde {f}_i)$
so that
$f_i=p(\widetilde {f}_i)$
so that
![]() $E(T^c)=\{f_1,\ldots ,f_{r-1}\}$
. We then choose
$E(T^c)=\{f_1,\ldots ,f_{r-1}\}$
. We then choose
![]() $v_0$
as the root vertex of
$v_0$
as the root vertex of
![]() $T_c$
and further relabel and reorient the edges
$T_c$
and further relabel and reorient the edges
![]() $f_1,\ldots ,f_{r-1}$
away from
$f_1,\ldots ,f_{r-1}$
away from
![]() $v_0$
. Specifically, we require that, along the unique path in
$v_0$
. Specifically, we require that, along the unique path in
![]() $T^c$
starting at
$T^c$
starting at
![]() $v_0$
and ending at any other vertex, the edges are oriented in the direction of the path and appear in increasing order. Finally, we relabel the vertices
$v_0$
and ending at any other vertex, the edges are oriented in the direction of the path and appear in increasing order. Finally, we relabel the vertices
![]() $v_1,\ldots ,v_{r-1}$
so that
$v_1,\ldots ,v_{r-1}$
so that
![]() $t(f_j)=v_j$
for
$t(f_j)=v_j$
for
![]() $j=1,\ldots ,r-1$
; this implies that
$j=1,\ldots ,r-1$
; this implies that
![]() $s(f_j)=v_{\alpha (j)}$
for some index
$s(f_j)=v_{\alpha (j)}$
for some index
![]() $\alpha (j)<j$
.
$\alpha (j)<j$
.
We now form a spanning tree T for G by joining the subtrees
![]() $T_k$
with the edges of
$T_k$
with the edges of
![]() $T^c$
(viewed as edges of G):
$T^c$
(viewed as edges of G):
We denote the complementary edges of T in G by
![]() $E(G)\backslash E(T)=\{e_0,e_1,\ldots ,e_{g-1}\}$
, and we explain below how the
$E(G)\backslash E(T)=\{e_0,e_1,\ldots ,e_{g-1}\}$
, and we explain below how the
![]() $e_j$
are chosen.
$e_j$
are chosen.
Choosing
![]() $e_0$
and contracting the preimages of the
$e_0$
and contracting the preimages of the
![]() $G_k$
. We now describe the cover p using the spanning tree T and Construction A. The tree T has two disjoint lifts
$G_k$
. We now describe the cover p using the spanning tree T and Construction A. The tree T has two disjoint lifts
![]() $\widetilde {T}^{\pm }$
to
$\widetilde {T}^{\pm }$
to
![]() $\widetilde {G}$
, and we denote
$\widetilde {G}$
, and we denote
 $\widetilde {T}^{\pm }_k=\widetilde {T}^{\pm }\cap p^{-1}(T_k)$
the corresponding lifts of the
$\widetilde {T}^{\pm }_k=\widetilde {T}^{\pm }\cap p^{-1}(T_k)$
the corresponding lifts of the
![]() $T_k$
. For each
$T_k$
. For each
![]() $i=1,\ldots ,d$
, each of the trees
$i=1,\ldots ,d$
, each of the trees
![]() $\widetilde {T}^{\pm }$
contains exactly one of the two edges
$\widetilde {T}^{\pm }$
contains exactly one of the two edges
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $\iota (\widetilde {f}_i)$
. The cover
$\iota (\widetilde {f}_i)$
. The cover
![]() $p:f^{-1}(G_0)\to G_0$
is not trivial, so we can pick an edge
$p:f^{-1}(G_0)\to G_0$
is not trivial, so we can pick an edge
![]() $e_0\in E(G_0)\backslash E(T_0)$
having a lift
$e_0\in E(G_0)\backslash E(T_0)$
having a lift
![]() $\widetilde {e}_0=\widetilde {e}_0^{{\kern1.5pt}+}$
that connects
$\widetilde {e}_0=\widetilde {e}_0^{{\kern1.5pt}+}$
that connects
![]() $\widetilde {T}_0^+$
and
$\widetilde {T}_0^+$
and
![]() $\widetilde {T}_0^-$
. Then
$\widetilde {T}_0^-$
. Then
 $$ \begin{align*}\widetilde{T}=\widetilde{T}^+\cup \widetilde{T}^-\cup\{\widetilde{e}_0^+\} \end{align*} $$
$$ \begin{align*}\widetilde{T}=\widetilde{T}^+\cup \widetilde{T}^-\cup\{\widetilde{e}_0^+\} \end{align*} $$
is a spanning tree for
![]() $\widetilde {G}$
. We note that, by our labelling convention, for
$\widetilde {G}$
. We note that, by our labelling convention, for
![]() $k=1,\ldots ,r-1$
the target vertex
$k=1,\ldots ,r-1$
the target vertex
![]() $t(\widetilde {f}_k)$
lies on either
$t(\widetilde {f}_k)$
lies on either
![]() $\widetilde {T}^+_k$
or
$\widetilde {T}^+_k$
or
![]() $\widetilde {T}^-_k$
, while
$\widetilde {T}^-_k$
, while
![]() $t(\iota (\widetilde {f}_k))$
lies on the other subtree.
$t(\iota (\widetilde {f}_k))$
lies on the other subtree.
We now perform a contraction on the graph
![]() $\widetilde {G}$
that is consistent with the contraction
$\widetilde {G}$
that is consistent with the contraction
![]() $(\cdot )^c:G\to G^c$
defined above. The tree
$(\cdot )^c:G\to G^c$
defined above. The tree
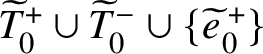 $\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
is a spanning tree for the preimage
$\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
is a spanning tree for the preimage
![]() $p^{-1}(G_0)$
, while for each
$p^{-1}(G_0)$
, while for each
![]() $k=1,\ldots ,r-1$
the two disjoint trees
$k=1,\ldots ,r-1$
the two disjoint trees
![]() $\widetilde {T}^+_k$
and
$\widetilde {T}^+_k$
and
![]() $\widetilde {T}^-_k$
form a spanning forest for
$\widetilde {T}^-_k$
form a spanning forest for
![]() $p^{-1}(G_k)$
. Let
$p^{-1}(G_k)$
. Let
![]() $\widetilde {G}^c$
denote the graph obtained from
$\widetilde {G}^c$
denote the graph obtained from
![]() $\widetilde {G}$
by contracting
$\widetilde {G}$
by contracting
 $\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
to a vertex
$\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
to a vertex
![]() $\widetilde {v}_0$
and contracting each
$\widetilde {v}_0$
and contracting each
![]() $\widetilde {T}^{\pm }_k$
to a separate vertex
$\widetilde {T}^{\pm }_k$
to a separate vertex
![]() $\widetilde {v}^{\pm }_k$
. We denote the contraction map by
$\widetilde {v}^{\pm }_k$
. We denote the contraction map by
![]() $(\cdot )^c:\widetilde {G}\to \widetilde {G}^c$
and for a noncontracted edge
$(\cdot )^c:\widetilde {G}\to \widetilde {G}^c$
and for a noncontracted edge
![]() $\widetilde {e}\in E(\widetilde {G})$
(i.e., for any edge not in
$\widetilde {e}\in E(\widetilde {G})$
(i.e., for any edge not in
 $\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
or in any
$\widetilde {T}^+_0\cup \widetilde {T}^-_0\cup \{\widetilde {e}_0^{{\kern1.5pt}+}\}$
or in any
![]() $\widetilde {T}^{\pm }_k$
) we denote
$\widetilde {T}^{\pm }_k$
) we denote
![]() $(\widetilde {e})^c=\widetilde {e}$
by abuse of notation. The double cover
$(\widetilde {e})^c=\widetilde {e}$
by abuse of notation. The double cover
![]() $p:\widetilde {G}\to G$
descends to a map
$p:\widetilde {G}\to G$
descends to a map
![]() $p:\widetilde {G}^c\to G^c$
(which is almost a double cover of graphs, except that
$p:\widetilde {G}^c\to G^c$
(which is almost a double cover of graphs, except that
![]() $v_0$
and
$v_0$
and
![]() $e_0$
each have a single preimage) and the projections commute with the contractions. The contraction
$e_0$
each have a single preimage) and the projections commute with the contractions. The contraction
![]() $\widetilde {T}^c$
of
$\widetilde {T}^c$
of
![]() $\widetilde {T}$
is a spanning tree for
$\widetilde {T}$
is a spanning tree for
![]() $\widetilde {G}^c$
, having vertex and edge sets
$\widetilde {G}^c$
, having vertex and edge sets
 $$ \begin{align*}V(\widetilde{T}^c)=V(\widetilde{G}^c)=\{\widetilde{v}_0,\widetilde{v}^{\pm}_1,\ldots,\widetilde{v}^{\pm}_{r-1}\},\quad E(\widetilde{T}^c)=\{\widetilde{f}_1,\ldots,\widetilde{f}_{r-1},\iota(\widetilde{f}_1),\ldots,\iota(\widetilde{f}_{r-1})\}. \end{align*} $$
$$ \begin{align*}V(\widetilde{T}^c)=V(\widetilde{G}^c)=\{\widetilde{v}_0,\widetilde{v}^{\pm}_1,\ldots,\widetilde{v}^{\pm}_{r-1}\},\quad E(\widetilde{T}^c)=\{\widetilde{f}_1,\ldots,\widetilde{f}_{r-1},\iota(\widetilde{f}_1),\ldots,\iota(\widetilde{f}_{r-1})\}. \end{align*} $$
The tree
![]() $\widetilde {T}^c$
can be viewed as two copies of
$\widetilde {T}^c$
can be viewed as two copies of
![]() $T^c$
joined at the common vertex
$T^c$
joined at the common vertex
![]() $\widetilde {v}_0$
.
$\widetilde {v}_0$
.
Labeling the complementary edges. Finally, we label the complementary edges
Each of the
![]() $e_j$
is either an edge of a subgraph
$e_j$
is either an edge of a subgraph
![]() $G_k$
that does not lie on the spanning tree
$G_k$
that does not lie on the spanning tree
![]() $T_k$
or one of the
$T_k$
or one of the
![]() $f_k$
. Since the restriction of the double cover
$f_k$
. Since the restriction of the double cover
![]() $p:\widetilde {G}\to G$
to each of the
$p:\widetilde {G}\to G$
to each of the
![]() $G_k$
is nontrivial, for each
$G_k$
is nontrivial, for each
![]() $k=1,\ldots ,r-1$
we can choose an edge in
$k=1,\ldots ,r-1$
we can choose an edge in
![]() $E(G_k)\backslash E(T_k)$
whose preimages cross
$E(G_k)\backslash E(T_k)$
whose preimages cross
![]() $\widetilde {T}^{\pm }_k$
, and we label this edge
$\widetilde {T}^{\pm }_k$
, and we label this edge
![]() $e_k$
. We pick the preimage
$e_k$
. We pick the preimage
 $\widetilde {e}_k=\widetilde {e}_k^{{\kern1.5pt}+}\in E(\widetilde {G})\backslash E(\widetilde {T})$
in such a way that the source vertex
$\widetilde {e}_k=\widetilde {e}_k^{{\kern1.5pt}+}\in E(\widetilde {G})\backslash E(\widetilde {T})$
in such a way that the source vertex
![]() $s(\widetilde {e}_k)$
lies on the same subtree
$s(\widetilde {e}_k)$
lies on the same subtree
![]() $\widetilde {T}^+_k$
or
$\widetilde {T}^+_k$
or
![]() $\widetilde {T}^-_k$
as the target vertex
$\widetilde {T}^-_k$
as the target vertex
![]() $t(\widetilde {f}_k)$
. Furthermore, for
$t(\widetilde {f}_k)$
. Furthermore, for
![]() $k=r,\ldots ,d$
, we denote
$k=r,\ldots ,d$
, we denote
![]() $e_k=f_k$
and
$e_k=f_k$
and
 $\widetilde {e}_k=\widetilde {e}^{{\kern1.5pt}+}_k=\widetilde {f}_k$
. The remaining edges
$\widetilde {e}_k=\widetilde {e}^{{\kern1.5pt}+}_k=\widetilde {f}_k$
. The remaining edges
![]() $e_k$
for
$e_k$
for
![]() $k=d+1,\ldots ,g-1$
and their preimages
$k=d+1,\ldots ,g-1$
and their preimages
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_k$
are labelled arbitrarily. We note that in this case,
$\widetilde {e}^{{\kern1.5pt}\pm }_k$
are labelled arbitrarily. We note that in this case,
![]() $e_k\in S$
for
$e_k\in S$
for
![]() $k=0,\ldots ,r-1$
.
$k=0,\ldots ,r-1$
.
To help follow the intersection calculations in the following proofs, we summarise the structure of the graphs
![]() $\widetilde {G}^c$
and
$\widetilde {G}^c$
and
![]() $G^c$
and the map
$G^c$
and the map
![]() $p:\widetilde {G}^c\to G^c$
:
$p:\widetilde {G}^c\to G^c$
:
-
(1) The vertices of the graphs
 $\widetilde {G}^c$
and
$\widetilde {G}^c$
and
 $G^c$
are The map p sends
$G^c$
are The map p sends $$ \begin{align*}V(\widetilde{G}^c)=\{\widetilde{v}_0,\widetilde{v}^{\pm}_1,\ldots,\widetilde{v}^{\pm}_{r-1}\},\quad V(G^c)=\{v_0,v_1,\ldots,v_{r-1}\}. \end{align*} $$
$$ \begin{align*}V(\widetilde{G}^c)=\{\widetilde{v}_0,\widetilde{v}^{\pm}_1,\ldots,\widetilde{v}^{\pm}_{r-1}\},\quad V(G^c)=\{v_0,v_1,\ldots,v_{r-1}\}. \end{align*} $$
 $\widetilde {v}_0$
to
$\widetilde {v}_0$
to
 $v_0$
and
$v_0$
and
 $\widetilde {v}^{\pm }_k$
to
$\widetilde {v}^{\pm }_k$
to
 $v_k$
.
$v_k$
.
-
(2) The edges of the graph
 $G^c$
are as follows: The
$G^c$
are as follows: The $$ \begin{align*}E(G^c)=\{f_1,\ldots,f_{r-1},e_0,\ldots,e_{r-1},e_r=f_r,\ldots,e_d=f_d,e_{d+1},\ldots,e_{g-1}\}. \end{align*} $$
$$ \begin{align*}E(G^c)=\{f_1,\ldots,f_{r-1},e_0,\ldots,e_{r-1},e_r=f_r,\ldots,e_d=f_d,e_{d+1},\ldots,e_{g-1}\}. \end{align*} $$
 $r-1$
edges
$r-1$
edges
 $\{f_1,\ldots ,f_{r-1}\}$
are the edges of the spanning tree
$\{f_1,\ldots ,f_{r-1}\}$
are the edges of the spanning tree
 $T_c$
; these are oriented in increasing order away from the root vertex
$T_c$
; these are oriented in increasing order away from the root vertex
 $v_0$
, so that
$v_0$
, so that
 $t(f_j)=v_j$
for
$t(f_j)=v_j$
for
 $j=1,\ldots ,r-1$
. The remaining g edges
$j=1,\ldots ,r-1$
. The remaining g edges
 $\{e_0,\ldots ,e_{g-1}\}$
are split into three groups: for
$\{e_0,\ldots ,e_{g-1}\}$
are split into three groups: for
 $j=0,\ldots ,r-1$
the edge
$j=0,\ldots ,r-1$
the edge
 $e_j$
is a loop at
$e_j$
is a loop at
 $v_j$
, for
$v_j$
, for
 $j=r,\ldots ,d$
the edge
$j=r,\ldots ,d$
the edge
 $e_j=f_j$
may or may not be a loop and for
$e_j=f_j$
may or may not be a loop and for
 $j=d+1,\ldots ,g-1$
each remaining
$j=d+1,\ldots ,g-1$
each remaining
 $e_j$
is a loop at one of the
$e_j$
is a loop at one of the
 $v_k$
.
$v_k$
.
-
(3) The edges of the graph
 $\widetilde {G}^c$
are as follows. For
$\widetilde {G}^c$
are as follows. For
 $j=1,\ldots ,r-1$
, each
$j=1,\ldots ,r-1$
, each
 $f_j$
has two preimages labelled
$f_j$
has two preimages labelled
 $\widetilde {f}_j$
and
$\widetilde {f}_j$
and
 $\iota (\widetilde {f}_j)$
; these
$\iota (\widetilde {f}_j)$
; these
 $2r-2$
edges form the spanning tree
$2r-2$
edges form the spanning tree
 $\widetilde {T}^c$
. Furthermore, for
$\widetilde {T}^c$
. Furthermore, for
 $j=1,\ldots ,r-1$
the target vertex
$j=1,\ldots ,r-1$
the target vertex
 $t(\widetilde {f}_j)$
is one of the two vertices
$t(\widetilde {f}_j)$
is one of the two vertices
 $\widetilde {v}_j^{{\kern1.5pt}\pm }$
. The edge
$\widetilde {v}_j^{{\kern1.5pt}\pm }$
. The edge
 $e_0$
has a unique preimage
$e_0$
has a unique preimage
 $\widetilde{e}^{{\kern2pt}-}_0$
, while for
$\widetilde{e}^{{\kern2pt}-}_0$
, while for
 $j=1,\ldots ,g-1$
each
$j=1,\ldots ,g-1$
each
 $e_j$
has two preimages
$e_j$
has two preimages
 $\widetilde {e}_j^{{\kern1.5pt}+}=\widetilde {e}_j$
and
$\widetilde {e}_j^{{\kern1.5pt}+}=\widetilde {e}_j$
and
 $\widetilde {e}_j^-=\iota (\widetilde {e}_j)$
. For
$\widetilde {e}_j^-=\iota (\widetilde {e}_j)$
. For
 $j=1,\ldots ,r-1$
the edges
$j=1,\ldots ,r-1$
the edges
 $\widetilde {e}_j$
and
$\widetilde {e}_j$
and
 $\iota (\widetilde {e}_j)$
(lying over the loop
$\iota (\widetilde {e}_j)$
(lying over the loop
 $e_j$
) connect
$e_j$
) connect
 $\widetilde {v}_j^+$
and
$\widetilde {v}_j^+$
and
 $\widetilde {v}_j^-$
in opposite directions, in such a way that
$\widetilde {v}_j^-$
in opposite directions, in such a way that
 $s(\widetilde {e}_j)=t(\widetilde {f}_j)$
. For
$s(\widetilde {e}_j)=t(\widetilde {f}_j)$
. For
 $j=r,\ldots ,d$
, we have
$j=r,\ldots ,d$
, we have
 $\widetilde {e}_j=\widetilde {f}_j$
and for each
$\widetilde {e}_j=\widetilde {f}_j$
and for each
 $j=d+1,\ldots ,g-1$
the two edges
$j=d+1,\ldots ,g-1$
the two edges
 $\widetilde {e}_j$
and
$\widetilde {e}_j$
and
 $\iota (\widetilde {e}_j)$
over
$\iota (\widetilde {e}_j)$
over
 $e_j$
are either parallel edges between
$e_j$
are either parallel edges between
 $\widetilde {v}^+_k$
and
$\widetilde {v}^+_k$
and
 $\widetilde {v}^-_k$
for some k or form a pair of loops.
$\widetilde {v}^-_k$
for some k or form a pair of loops.
We now employ Construction B to produce a basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
of
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
of
![]() $\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, with respect to the chosen spanning tree
$\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
, with respect to the chosen spanning tree
![]() $T\subset G$
. Let
$T\subset G$
. Let
![]() $\widetilde {\gamma }_0$
and
$\widetilde {\gamma }_0$
and
![]() $\widetilde {\gamma }_j^{{\kern1.5pt}\pm }$
for
$\widetilde {\gamma }_j^{{\kern1.5pt}\pm }$
for
![]() $j=1,\ldots ,g-1$
be the unique cycle respectively of
$j=1,\ldots ,g-1$
be the unique cycle respectively of
 $\widetilde {T}\cup \{\widetilde{e}^{{\kern2pt}-}_0\}$
and
$\widetilde {T}\cup \{\widetilde{e}^{{\kern2pt}-}_0\}$
and
 $\widetilde {T}\cup \{\widetilde {e}^{{\kern1.5pt}\pm }_j\}$
such that
$\widetilde {T}\cup \{\widetilde {e}^{{\kern1.5pt}\pm }_j\}$
such that
![]() $\langle \widetilde {\gamma }_0,\widetilde{e}^{{\kern2pt}-}_0\rangle =1$
and
$\langle \widetilde {\gamma }_0,\widetilde{e}^{{\kern2pt}-}_0\rangle =1$
and
 $\langle \widetilde {\gamma }^{\pm }_j,\widetilde {e}^{{\kern1.5pt}\pm }_j\rangle =1$
for
$\langle \widetilde {\gamma }^{\pm }_j,\widetilde {e}^{{\kern1.5pt}\pm }_j\rangle =1$
for
![]() $j=1,\ldots ,g-1$
. Then the cycles
$j=1,\ldots ,g-1$
. Then the cycles
 $$ \begin{align} \widetilde{\gamma}_j=\widetilde{\gamma}_j^+-\iota_*(\widetilde{\gamma}_j^+)=\left\{\begin{array}{c@{\quad}c}\widetilde{\gamma}^+_j-\widetilde{\gamma}^-_j+\sigma_j\widetilde{\gamma}_0, & e_j\in S, \\ \widetilde{\gamma}^+_j-\widetilde{\gamma}^-_j, & e_j\notin S,\end{array}\right.,\quad j=1,\ldots,g-1 \end{align} $$
$$ \begin{align} \widetilde{\gamma}_j=\widetilde{\gamma}_j^+-\iota_*(\widetilde{\gamma}_j^+)=\left\{\begin{array}{c@{\quad}c}\widetilde{\gamma}^+_j-\widetilde{\gamma}^-_j+\sigma_j\widetilde{\gamma}_0, & e_j\in S, \\ \widetilde{\gamma}^+_j-\widetilde{\gamma}^-_j, & e_j\notin S,\end{array}\right.,\quad j=1,\ldots,g-1 \end{align} $$
form a basis for
![]() $\operatorname {\mathrm {Ker}} \pi _*$
.
$\operatorname {\mathrm {Ker}} \pi _*$
.
In Example 5.5, we deploy this construction for a specific cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
with
$\pi :\widetilde {\Gamma }\to \Gamma $
with
![]() $g=3$
.
$g=3$
.
We now return to the proof. We need to compute the rank of the matrix (24) with respect to the basis (26)
 $$ \begin{align*}(\Psi^d)_{ji}=\frac{1}{2}\left\langle \widetilde{\gamma}_j, \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle=\frac{1}{2}\left\langle \widetilde{\gamma}^+_j-\iota_*(\widetilde{\gamma}^+_j), \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle. \end{align*} $$
$$ \begin{align*}(\Psi^d)_{ji}=\frac{1}{2}\left\langle \widetilde{\gamma}_j, \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle=\frac{1}{2}\left\langle \widetilde{\gamma}^+_j-\iota_*(\widetilde{\gamma}^+_j), \widetilde{f}_i-\iota(\widetilde{f}_i)\right\rangle=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle. \end{align*} $$
To compute the intersection numbers
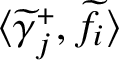 $\langle \widetilde {\gamma }^+_j,\widetilde {f}_i\rangle $
and
$\langle \widetilde {\gamma }^+_j,\widetilde {f}_i\rangle $
and
 $\langle \widetilde {\gamma }^+_j,\iota (\widetilde {f}_i)\rangle $
, we pass to the contracted graph
$\langle \widetilde {\gamma }^+_j,\iota (\widetilde {f}_i)\rangle $
, we pass to the contracted graph
![]() $\widetilde {G}^c$
. First of all, we note that none of edges
$\widetilde {G}^c$
. First of all, we note that none of edges
![]() $\widetilde {f}_i$
or
$\widetilde {f}_i$
or
![]() $\iota (\widetilde {f}_i)$
on
$\iota (\widetilde {f}_i)$
on
![]() $\widetilde {G}$
are contracted. Therefore, for any cycle
$\widetilde {G}$
are contracted. Therefore, for any cycle
![]() $\widetilde {\gamma }$
on
$\widetilde {\gamma }$
on
![]() $\widetilde {G}$
, its intersection with
$\widetilde {G}$
, its intersection with
![]() $\widetilde {f}_i$
or
$\widetilde {f}_i$
or
![]() $\iota (\widetilde {f}_i)$
can be computed on the contracted graph
$\iota (\widetilde {f}_i)$
can be computed on the contracted graph
![]() $\widetilde {G}^c$
:
$\widetilde {G}^c$
:
Furthermore, we observe that, since
![]() $\widetilde {\gamma }^+_j$
is the unique cycle on
$\widetilde {\gamma }^+_j$
is the unique cycle on
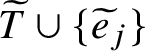 $\widetilde {T}\cup \{\widetilde {e}_j\}$
such that
$\widetilde {T}\cup \{\widetilde {e}_j\}$
such that
 $\langle \widetilde {\gamma }^+_j,\widetilde {e}_j\rangle =1$
, the contracted cycle
$\langle \widetilde {\gamma }^+_j,\widetilde {e}_j\rangle =1$
, the contracted cycle
![]() $(\widetilde {\gamma }_j)^c$
is the unique cycle on
$(\widetilde {\gamma }_j)^c$
is the unique cycle on
 $\widetilde {T}^c\cup \{\widetilde {e}_j\}$
such that
$\widetilde {T}^c\cup \{\widetilde {e}_j\}$
such that
 $\langle (\widetilde {\gamma }^+_j)^c,\widetilde {e}_j\rangle =1$
.
$\langle (\widetilde {\gamma }^+_j)^c,\widetilde {e}_j\rangle =1$
.
We first look at the cycles
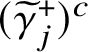 $(\widetilde {\gamma }^+_j)^c$
for
$(\widetilde {\gamma }^+_j)^c$
for
![]() $j=1,\ldots ,r-1$
. The edge
$j=1,\ldots ,r-1$
. The edge
![]() $e_j\in E(G^c)$
is a loop at
$e_j\in E(G^c)$
is a loop at
![]() $v_j$
. Its lift
$v_j$
. Its lift
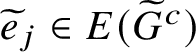 $\widetilde {e}_j\in E(\widetilde {G}^c)$
starts at
$\widetilde {e}_j\in E(\widetilde {G}^c)$
starts at
 $t(\widetilde {f}_j)$
, which is one of the two vertices
$t(\widetilde {f}_j)$
, which is one of the two vertices
![]() $\widetilde {v}^{\pm }_j$
(say
$\widetilde {v}^{\pm }_j$
(say
![]() $\widetilde {v}^+_j$
), and ends at the other vertex
$\widetilde {v}^+_j$
), and ends at the other vertex
![]() $\widetilde {v}^-_j$
(by our labelling convention
$\widetilde {v}^-_j$
(by our labelling convention
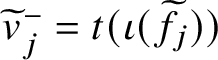 $\widetilde {v}^-_j=t(\iota (\widetilde {f}_j))$
). The contracted cycle
$\widetilde {v}^-_j=t(\iota (\widetilde {f}_j))$
). The contracted cycle
 $(\widetilde {\gamma }^+_j)^c$
is the unique cycle of the graph
$(\widetilde {\gamma }^+_j)^c$
is the unique cycle of the graph
 $\widetilde {T}^c\cup \{\widetilde {e}_j\}$
containing
$\widetilde {T}^c\cup \{\widetilde {e}_j\}$
containing
![]() $+\widetilde {e}_j$
: it starts at
$+\widetilde {e}_j$
: it starts at
![]() $\widetilde {v}^+_j$
, proceeds to
$\widetilde {v}^+_j$
, proceeds to
![]() $\widetilde {v}^-_j$
via
$\widetilde {v}^-_j$
via
![]() $\widetilde {e}_j$
and then to
$\widetilde {e}_j$
and then to
![]() $\widetilde {v}_0$
via the unique path on
$\widetilde {v}_0$
via the unique path on
![]() $\widetilde {T}^c$
from
$\widetilde {T}^c$
from
![]() $\widetilde {v}^+_j$
(the first edge of this path being
$\widetilde {v}^+_j$
(the first edge of this path being
 $-\iota (\widetilde {f}_j)$
) and then from
$-\iota (\widetilde {f}_j)$
) and then from
![]() $\widetilde {v}_0$
to
$\widetilde {v}_0$
to
![]() $\widetilde {v}^-_j$
via a unique path (the last edge of this path being
$\widetilde {v}^-_j$
via a unique path (the last edge of this path being
 $+\widetilde {f}_j$
). By the ordering convention that we chose for
$+\widetilde {f}_j$
). By the ordering convention that we chose for
![]() $T^c$
and hence
$T^c$
and hence
![]() $\widetilde {T}^c$
, the only edges that can occur on this (other than the generating edge
$\widetilde {T}^c$
, the only edges that can occur on this (other than the generating edge
![]() $\widetilde {e}_j$
, which does not lie on
$\widetilde {e}_j$
, which does not lie on
![]() $\widetilde {T}^c$
) are
$\widetilde {T}^c$
) are
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $\iota (\widetilde {f}_i)$
with
$\iota (\widetilde {f}_i)$
with
![]() $i\leq j$
. Furthermore,
$i\leq j$
. Furthermore,
![]() $\widetilde {f}_j$
and
$\widetilde {f}_j$
and
 $\iota (\widetilde {f}_j)$
occur, as we have seen, with coefficients
$\iota (\widetilde {f}_j)$
occur, as we have seen, with coefficients
![]() $+1$
and
$+1$
and
![]() $-1$
, respectively. It follows that for
$-1$
, respectively. It follows that for
![]() $j=1,\ldots ,r-1$
we have
$j=1,\ldots ,r-1$
we have
 $$ \begin{align*}(\Psi^d)_{ji}=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle=\langle (\widetilde{\gamma}^+_j)^c,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle=\left\{\begin{array}{c@{\quad}c} 0\mbox{ or }\pm 2,& i<j, \\ 2, & i=j, \\ 0, & i>j. \end{array}\right. \end{align*} $$
$$ \begin{align*}(\Psi^d)_{ji}=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle=\langle (\widetilde{\gamma}^+_j)^c,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle=\left\{\begin{array}{c@{\quad}c} 0\mbox{ or }\pm 2,& i<j, \\ 2, & i=j, \\ 0, & i>j. \end{array}\right. \end{align*} $$
We now calculate the intersection numbers
 $\langle \widetilde {\gamma }^+_j,\widetilde {f}_i-\iota (\widetilde {f}_i)\rangle $
for
$\langle \widetilde {\gamma }^+_j,\widetilde {f}_i-\iota (\widetilde {f}_i)\rangle $
for
![]() $j=r,\ldots ,d$
. Recall that we have chosen
$j=r,\ldots ,d$
. Recall that we have chosen
 $\widetilde {e}_j=\widetilde {f}_j$
, so the cycle
$\widetilde {e}_j=\widetilde {f}_j$
, so the cycle
 $(\widetilde {\gamma }^+_j)^c$
is the unique cycle on
$(\widetilde {\gamma }^+_j)^c$
is the unique cycle on
 $\widetilde {T}^c\cup \{\widetilde {f}_j\}$
containing
$\widetilde {T}^c\cup \{\widetilde {f}_j\}$
containing
 $+\widetilde {f}_j$
. By our ordering convention, the edges of the tree
$+\widetilde {f}_j$
. By our ordering convention, the edges of the tree
![]() $\widetilde {T}^c$
are
$\widetilde {T}^c$
are
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $\iota (\widetilde {f}_i)$
for
$\iota (\widetilde {f}_i)$
for
![]() $1\leq i\leq r-1$
. Hence,
$1\leq i\leq r-1$
. Hence,
 $(\widetilde {\gamma }^+_j)^c$
intersects
$(\widetilde {\gamma }^+_j)^c$
intersects
![]() $\widetilde {f}_j$
with multiplicity
$\widetilde {f}_j$
with multiplicity
![]() $+1$
and does not intersect any
$+1$
and does not intersect any
![]() $\widetilde {f}_i$
or
$\widetilde {f}_i$
or
![]() $\iota (\widetilde {f}_i)$
with
$\iota (\widetilde {f}_i)$
with
![]() $i\geq r$
. Therefore, for
$i\geq r$
. Therefore, for
![]() $j\geq r$
we have
$j\geq r$
we have
 $$ \begin{align*}(\Psi^d)_{ji}=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle=\langle (\widetilde{\gamma}^+_j)^c,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \left\{ \begin{array}{c@{\quad}c} 0,\pm 1,\mbox{ or }\pm 2,& i\leq r-1, \\ 1, & i=j, \\ 0, & i\geq r,i\neq j. \end{array}\right. \end{align*} $$
$$ \begin{align*}(\Psi^d)_{ji}=\left\langle \widetilde{\gamma}^+_j, \widetilde{f}_i -\iota(\widetilde{f}_i)\right\rangle=\langle (\widetilde{\gamma}^+_j)^c,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \left\{ \begin{array}{c@{\quad}c} 0,\pm 1,\mbox{ or }\pm 2,& i\leq r-1, \\ 1, & i=j, \\ 0, & i\geq r,i\neq j. \end{array}\right. \end{align*} $$
Putting everything together, we see that the
![]() $d\times d$
minor of
$d\times d$
minor of
![]() $(\Psi ^d)_{ji}$
corresponding to the partial basis
$(\Psi ^d)_{ji}$
corresponding to the partial basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_d$
is a lower-triangular matrix, whose first
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_d$
is a lower-triangular matrix, whose first
![]() $r-1$
diagonal entries are 2 and the remaining equal to 1. Hence,
$r-1$
diagonal entries are 2 and the remaining equal to 1. Hence,
![]() $\Psi ^d$
has rank d.
$\Psi ^d$
has rank d.
We now restrict our attention to the Abel–Prym map in degree
![]() $d=g-1$
, which we denote
$d=g-1$
, which we denote
![]() $\Psi $
:
$\Psi $
:
In this case the source has the same dimension as the target and we can compute the determinant of the matrix (24) of
![]() $\Psi $
on any top-dimensional cell
$\Psi $
on any top-dimensional cell
![]() $C(\widetilde {F})$
. This determinant depends on a choice of basis
$C(\widetilde {F})$
. This determinant depends on a choice of basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
for
![]() $\operatorname {\mathrm {Ker}} \pi _*$
but only up to sign; hence, the quantity
$\operatorname {\mathrm {Ker}} \pi _*$
but only up to sign; hence, the quantity
which we call the degree of
![]() $\Psi $
on
$\Psi $
on
![]() $C(\widetilde {F})$
, is well-defined.
$C(\widetilde {F})$
, is well-defined.
We now compute the degree of
![]() $\Psi $
on the top-dimensional cells of
$\Psi $
on the top-dimensional cells of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
. We recall from Subsection 3.2 that, given a connected free double cover
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
. We recall from Subsection 3.2 that, given a connected free double cover
![]() $p:\widetilde {G}\to G$
of a graph G of genus g, a subset
$p:\widetilde {G}\to G$
of a graph G of genus g, a subset
![]() $F\subset E(G)$
of
$F\subset E(G)$
of
![]() $g-1$
edges of G is called an odd genus 1 decomposition of rank r if
$g-1$
edges of G is called an odd genus 1 decomposition of rank r if
![]() $G\backslash F$
consists of r connected components of genus 1 and each of them has connected preimage in
$G\backslash F$
consists of r connected components of genus 1 and each of them has connected preimage in
![]() $\widetilde {G}$
.
$\widetilde {G}$
.
Corollary 4.2. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover with model
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover with model
![]() $p:\widetilde {G}\to G$
, let
$p:\widetilde {G}\to G$
, let
![]() $\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
be the Abel–Prym map, let
$\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
be the Abel–Prym map, let
![]() $C(\widetilde {F})=C^{g-1}(\widetilde {F},0)\subset \operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
be a top-dimensional cell corresponding to the multiset
$C(\widetilde {F})=C^{g-1}(\widetilde {F},0)\subset \operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
be a top-dimensional cell corresponding to the multiset
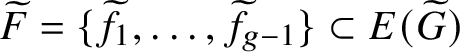 $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-1}\}\subset E(\widetilde {G})$
and let
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-1}\}\subset E(\widetilde {G})$
and let
![]() $F=p(\widetilde {F})$
. Then
$F=p(\widetilde {F})$
. Then
![]() $\deg _{\Psi }(\widetilde {F})$
is equal to
$\deg _{\Psi }(\widetilde {F})$
is equal to
 $$ \begin{align} \deg_{\Psi}(\widetilde{F})=\left\{\begin{array}{c@{\quad}c} 2^{r-1}, & \mbox{edges of }F\mbox{ are distinct and form an odd genus 1 decomposition of rank }r, \\ 0 & \mbox{otherwise.} \end{array}\right. \end{align} $$
$$ \begin{align} \deg_{\Psi}(\widetilde{F})=\left\{\begin{array}{c@{\quad}c} 2^{r-1}, & \mbox{edges of }F\mbox{ are distinct and form an odd genus 1 decomposition of rank }r, \\ 0 & \mbox{otherwise.} \end{array}\right. \end{align} $$
In particular, the volume of the image of
![]() $C(\widetilde {F})$
in
$C(\widetilde {F})$
in
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
is equal to
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
is equal to
 $$ \begin{align} \operatorname{\mathrm{Vol}}(\Psi(C(\widetilde{F})))=\frac{2^{r(\widetilde{F})-1}w(F)}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))},\quad w(F)=w(\widetilde{F})=\ell(\widetilde{f}_1)\cdots \ell(\widetilde{f}_{g-1}) \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Vol}}(\Psi(C(\widetilde{F})))=\frac{2^{r(\widetilde{F})-1}w(F)}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))},\quad w(F)=w(\widetilde{F})=\ell(\widetilde{f}_1)\cdots \ell(\widetilde{f}_{g-1}) \end{align} $$
if F is an odd genus 1 decomposition of rank
![]() $r(\widetilde {F})$
and zero otherwise.
$r(\widetilde {F})$
and zero otherwise.
Proof. This follows directly from the proof of Theorem 4.1. If the edges of
![]() $F=p(\widetilde {F})$
are not all distinct, then
$F=p(\widetilde {F})$
are not all distinct, then
![]() $\Psi $
contracts the cell
$\Psi $
contracts the cell
![]() $C(\widetilde {F})$
and hence
$C(\widetilde {F})$
and hence
![]() $\det \Psi =0$
on
$\det \Psi =0$
on
![]() $C(\widetilde {F})$
. If F consists of distinct edges, let
$C(\widetilde {F})$
. If F consists of distinct edges, let
![]() $G\backslash F=G_0\cup \cdots \cup G_{r-1}$
be the decomposition into connected components. By (25) we have that
$G\backslash F=G_0\cup \cdots \cup G_{r-1}$
be the decomposition into connected components. By (25) we have that
![]() $g_0+\cdots +g_{r-1}=r$
; hence, either
$g_0+\cdots +g_{r-1}=r$
; hence, either
![]() $g_k=0$
for some k or all
$g_k=0$
for some k or all
![]() $g_k=1$
. In the former case
$g_k=1$
. In the former case
![]() $G_k$
is a tree, so the restriction of the cover p to
$G_k$
is a tree, so the restriction of the cover p to
![]() $G_k$
is trivial and hence
$G_k$
is trivial and hence
![]() $\det \Psi =0$
on
$\det \Psi =0$
on
![]() $\widetilde {F}$
. In the latter case,
$\widetilde {F}$
. In the latter case,
![]() $\Psi $
has rank
$\Psi $
has rank
![]() $d=g-1$
if and only if the restriction of p to each
$d=g-1$
if and only if the restriction of p to each
![]() $G_k$
is nontrivial, which is true precisely when F is an odd genus 1 decomposition. Furthermore, the matrix of
$G_k$
is nontrivial, which is true precisely when F is an odd genus 1 decomposition. Furthermore, the matrix of
![]() $\Psi $
with respect to the basis (26) is lower triangular, with the first
$\Psi $
with respect to the basis (26) is lower triangular, with the first
![]() $r-1$
diagonal entries equal to 2 and the remaining equal to 1. Hence,
$r-1$
diagonal entries equal to 2 and the remaining equal to 1. Hence,
![]() $\det \Psi =2^{r-1}$
on
$\det \Psi =2^{r-1}$
on
![]() $C(\widetilde {F})$
, as required.
$C(\widetilde {F})$
, as required.
To prove (4.2), it is sufficient to note that
![]() $C(\widetilde {F})$
is a parallelotope with volume
$C(\widetilde {F})$
is a parallelotope with volume
![]() $w(\widetilde {F})$
and that
$w(\widetilde {F})$
and that
![]() $\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))^{-1}$
is the volume of the unit cube in the coordinate system on
$\operatorname {\mathrm {Vol}}(\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma ))^{-1}$
is the volume of the unit cube in the coordinate system on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
that we used to compute the matrix of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
that we used to compute the matrix of
![]() $\Psi $
(see equation (9)).
$\Psi $
(see equation (9)).
5 Harmonicity of the Abel–Prym map
In this section, we consider the degree
![]() $g-1$
Abel–Prym map
$g-1$
Abel–Prym map
![]() $\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
associated to a free double cover
$\Psi :\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
associated to a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
. The cellular decomposition of
$\pi :\widetilde {\Gamma }\to \Gamma $
. The cellular decomposition of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
induces a decomposition of
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
induces a decomposition of
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
(which is locally modelled on
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
(which is locally modelled on
![]() $\mathbb {R}^{g-1}$
). Pulling this decomposition back to
$\mathbb {R}^{g-1}$
). Pulling this decomposition back to
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
and refining cells as needed, the Abel–Prym map
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
and refining cells as needed, the Abel–Prym map
![]() $\Psi $
is a map of polyhedral spaces. We show that
$\Psi $
is a map of polyhedral spaces. We show that
![]() $\Psi $
is a harmonic map of polyhedral spaces of global degree
$\Psi $
is a harmonic map of polyhedral spaces of global degree
![]() $2^{g-1}$
, with respect to the degree function (28).
$2^{g-1}$
, with respect to the degree function (28).
Theorem 5.1. Let
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs. Then the Abel–Prym map
$\pi :\widetilde {\Gamma }\to \Gamma $
be a free double cover of metric graphs. Then the Abel–Prym map
is a harmonic map of polyhedral spaces of global degree
![]() $2^{g-1}$
, with respect to the degree function
$2^{g-1}$
, with respect to the degree function
![]() $\deg _{\Psi }$
defined on the codimension 0 cells of
$\deg _{\Psi }$
defined on the codimension 0 cells of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
by (28).
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
by (28).
The proof consists of two parts. First, we show that
![]() $\Psi $
is harmonic at each codimension 1 cell of
$\Psi $
is harmonic at each codimension 1 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
and hence has a well-defined global degree d because the polyhedral space
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
and hence has a well-defined global degree d because the polyhedral space
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is connected through codimension 1. We then show that
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is connected through codimension 1. We then show that
![]() $d=2^{g-1}$
. The proof of the first part is a somewhat involved calculation. We separate this result into a proposition and give its proof after the proof of the main Theorem 5.1.
$d=2^{g-1}$
. The proof of the first part is a somewhat involved calculation. We separate this result into a proposition and give its proof after the proof of the main Theorem 5.1.
Proposition 5.2. The degree
![]() $g-1$
Abel–Prym map
$g-1$
Abel–Prym map
is harmonic at each codimension 1 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
.
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
.
Proof of Theorem 5.1.
By Proposition 5.2, the Abel–Prym map has a certain global degree d. It may be possible to directly show that
![]() $d=2^{g-1}$
by somehow counting the preimages in a single fibre of
$d=2^{g-1}$
by somehow counting the preimages in a single fibre of
![]() $\Psi $
, but we employ a different method. Namely, we use the harmonicity of the map
$\Psi $
, but we employ a different method. Namely, we use the harmonicity of the map
![]() $\Psi $
to give an alternative calculation of the volume of the Prym variety, in terms of the unknown global degree d (similar to how the volume of
$\Psi $
to give an alternative calculation of the volume of the Prym variety, in terms of the unknown global degree d (similar to how the volume of
![]() $\operatorname {\mathrm {Jac}}(\Gamma )$
is computed in [Reference An, Baker, Kuperberg and ShokriehABKS14]). However, we have already computed the volume of the Prym variety in Theorem 3.4, using an entirely different method. Comparing the two formulas, we find that in fact
$\operatorname {\mathrm {Jac}}(\Gamma )$
is computed in [Reference An, Baker, Kuperberg and ShokriehABKS14]). However, we have already computed the volume of the Prym variety in Theorem 3.4, using an entirely different method. Comparing the two formulas, we find that in fact
![]() $d=2^{g-1}$
.
$d=2^{g-1}$
.
Let
![]() $M_i$
for
$M_i$
for
![]() $i=1,\ldots ,N$
be the codimension 0 cells of
$i=1,\ldots ,N$
be the codimension 0 cells of
![]() $\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
and let
$\operatorname {\mathrm {Prym}}^{[g-1]}(\widetilde {\Gamma }/\Gamma )$
and let
 $\widetilde {M}_{ij}$
for
$\widetilde {M}_{ij}$
for
![]() $j=1,\ldots ,k_i$
be the codimension 0 cells of
$j=1,\ldots ,k_i$
be the codimension 0 cells of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
mapping surjectively to
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
mapping surjectively to
![]() $M_i$
. The cells
$M_i$
. The cells
 $\widetilde {M}_{ij}$
are obtained by refining the natural cellular decomposition of
$\widetilde {M}_{ij}$
are obtained by refining the natural cellular decomposition of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
; in other words, each
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
; in other words, each
 $\widetilde {M}_{ij}$
is a subset of a cell
$\widetilde {M}_{ij}$
is a subset of a cell
 $C(\widetilde {F}_{ij})$
, where
$C(\widetilde {F}_{ij})$
, where
 $\widetilde {F}_{ij}\subset E(\widetilde {\Gamma })$
is a subset of edges such that
$\widetilde {F}_{ij}\subset E(\widetilde {\Gamma })$
is a subset of edges such that
 $p(\widetilde {F}_{ij})$
is an odd genus 1 decomposition of
$p(\widetilde {F}_{ij})$
is an odd genus 1 decomposition of
![]() $\Gamma $
of some rank
$\Gamma $
of some rank
 $r_{ij}=r(p(\widetilde {F}_{ij}))$
. Equation (29) gives the volume dilation factor of
$r_{ij}=r(p(\widetilde {F}_{ij}))$
. Equation (29) gives the volume dilation factor of
![]() $\Psi $
on the cell
$\Psi $
on the cell
 $C(\widetilde {F}_{ij})$
and hence on
$C(\widetilde {F}_{ij})$
and hence on
 $\widetilde {M}_{ij}$
. Therefore,
$\widetilde {M}_{ij}$
. Therefore,
 $$ \begin{align*}\operatorname{\mathrm{Vol}}(M_i)=\frac{2^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij})}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))} \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}(M_i)=\frac{2^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij})}{\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))} \end{align*} $$
for all i and j. On the other hand, the harmonicity condition implies that for each i we have
 $$ \begin{align*}d=\sum_{j=1}^{k_i} \deg_{\Psi}(\widetilde{M}_{ij})=\sum_{j=1}^{k_i} 2^{r_{ij}-1}. \end{align*} $$
$$ \begin{align*}d=\sum_{j=1}^{k_i} \deg_{\Psi}(\widetilde{M}_{ij})=\sum_{j=1}^{k_i} 2^{r_{ij}-1}. \end{align*} $$
Putting this together, we can write
 $$ \begin{align*}\operatorname{\mathrm{Vol}}(M_i)= \frac{1}{d}\sum_{j=1}^{k_i} 2^{r_{ij}-1}\cdot \operatorname{\mathrm{Vol}}(M_i)=\frac{1}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{j=1}^{k_i}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij}). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}(M_i)= \frac{1}{d}\sum_{j=1}^{k_i} 2^{r_{ij}-1}\cdot \operatorname{\mathrm{Vol}}(M_i)=\frac{1}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{j=1}^{k_i}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij}). \end{align*} $$
The sum of the volumes of the
![]() $M_i$
is the volume of the Prym variety:
$M_i$
is the volume of the Prym variety:
 $$ \begin{align*}\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}^{[g-1]}(\widetilde{\Gamma}/\Gamma))=\sum_{i=1}^N\operatorname{\mathrm{Vol}}(M_i)= \frac{1}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{i,j}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij}). \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}^{[g-1]}(\widetilde{\Gamma}/\Gamma))=\sum_{i=1}^N\operatorname{\mathrm{Vol}}(M_i)= \frac{1}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{i,j}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(\widetilde{M}_{ij}). \end{align*} $$
On the other hand, corresponding to each odd genus 1 decomposition F of
![]() $\Gamma $
there are
$\Gamma $
there are
![]() $2^{g-1}$
subsets
$2^{g-1}$
subsets
![]() $\widetilde {F}\subset E(\widetilde {\Gamma })$
such that
$\widetilde {F}\subset E(\widetilde {\Gamma })$
such that
![]() $p(\widetilde {F})=F$
, because each decomposition has exactly
$p(\widetilde {F})=F$
, because each decomposition has exactly
![]() $g-1$
edges. The volume
$g-1$
edges. The volume
![]() $\operatorname {\mathrm {Vol}}(C(\widetilde {F}))$
of each of these cells is equal to
$\operatorname {\mathrm {Vol}}(C(\widetilde {F}))$
of each of these cells is equal to
![]() $w(F)$
. Each cell
$w(F)$
. Each cell
![]() $C(\widetilde {F})$
corresponding to an odd genus 1 decomposition
$C(\widetilde {F})$
corresponding to an odd genus 1 decomposition
![]() $F=p(\widetilde {F})$
is a disjoint union of some of the
$F=p(\widetilde {F})$
is a disjoint union of some of the
![]() $M_{ij}$
and each
$M_{ij}$
and each
![]() $M_{ij}$
lies in some
$M_{ij}$
lies in some
![]() $C(\widetilde {F})$
. Hence, in fact the sum in the right-hand side can be written as
$C(\widetilde {F})$
. Hence, in fact the sum in the right-hand side can be written as
 $$ \begin{align*}\sum_{i,j}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(M_{ij})=\sum_{\widetilde{F}\subset E(\widetilde{\Gamma})} 4^{r(p(\widetilde{F}))-1}\operatorname{\mathrm{Vol}} (\widetilde{F})= 2^{g-1}\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align*} $$
$$ \begin{align*}\sum_{i,j}4^{r_{ij}-1}\operatorname{\mathrm{Vol}}(M_{ij})=\sum_{\widetilde{F}\subset E(\widetilde{\Gamma})} 4^{r(p(\widetilde{F}))-1}\operatorname{\mathrm{Vol}} (\widetilde{F})= 2^{g-1}\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F), \end{align*} $$
where the last sum is over all odd genus 1 decompositions F of
![]() $\Gamma $
. Therefore,
$\Gamma $
. Therefore,
 $$ \begin{align*}\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{2^{g-1}}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F).\\[-15pt] \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))=\frac{2^{g-1}}{d\cdot\operatorname{\mathrm{Vol}}(\operatorname{\mathrm{Prym}}(\widetilde{\Gamma}/\Gamma))}\sum_{F\subset E(\Gamma)} 4^{r(F)-1}w(F).\\[-15pt] \end{align*} $$
Comparing this formula with (17), we see that
![]() $d=2^{g-1}$
.
$d=2^{g-1}$
.
Remark 5.3. Given a Prym divisor class represented by
![]() $\Psi (\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
, the degree of
$\Psi (\widetilde {D})=\widetilde {D}-\iota (\widetilde {D})$
, the degree of
![]() $\Psi $
at
$\Psi $
at
![]() $\widetilde {D}\in \operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
in general depends on the choice of representative (in other words, the degree of
$\widetilde {D}\in \operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
in general depends on the choice of representative (in other words, the degree of
![]() $\Psi $
is not constant in fibres). We give an example of a free double cover
$\Psi $
is not constant in fibres). We give an example of a free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
and effective divisors
$\pi :\widetilde {\Gamma }\to \Gamma $
and effective divisors
![]() $\widetilde {D}_1$
and
$\widetilde {D}_1$
and
![]() $\widetilde {D}_2$
on the source, such that
$\widetilde {D}_2$
on the source, such that
![]() $\widetilde {D}_1-\iota (\widetilde {D}_1)\simeq \widetilde {D}_2-\iota (\widetilde {D}_2)$
, but the degrees of
$\widetilde {D}_1-\iota (\widetilde {D}_1)\simeq \widetilde {D}_2-\iota (\widetilde {D}_2)$
, but the degrees of
![]() $\Psi $
at
$\Psi $
at
![]() $\widetilde {D}_1$
and
$\widetilde {D}_1$
and
![]() $\widetilde {D}_2$
are different.
$\widetilde {D}_2$
are different.
Consider the free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
shown on Figure 3. The curves
$\pi :\widetilde {\Gamma }\to \Gamma $
shown on Figure 3. The curves
![]() $\widetilde {\Gamma }$
and
$\widetilde {\Gamma }$
and
![]() $\Gamma $
have genera
$\Gamma $
have genera
![]() $5$
and
$5$
and
![]() $3$
, respectively. The edge
$3$
, respectively. The edge
![]() $\widetilde {e}_3$
has length at least
$\widetilde {e}_3$
has length at least
![]() $3$
, while all other edges have length
$3$
, while all other edges have length
![]() $1$
. Fix real numbers
$1$
. Fix real numbers
![]() $0<y<x<1$
. Let
$0<y<x<1$
. Let
![]() $\widetilde {P}_1$
,
$\widetilde {P}_1$
,
![]() $\widetilde {Q}_1$
,
$\widetilde {Q}_1$
,
![]() $\widetilde {P}_2$
and
$\widetilde {P}_2$
and
![]() $\widetilde {Q}_2$
be the points on the edges
$\widetilde {Q}_2$
be the points on the edges
![]() $\widetilde {e}_1^{{\kern1.5pt}+}$
,
$\widetilde {e}_1^{{\kern1.5pt}+}$
,
![]() $\widetilde {e}_2^{{\kern1.5pt}+}$
,
$\widetilde {e}_2^{{\kern1.5pt}+}$
,
![]() $\widetilde{e}^{{\kern2pt}-}_1$
and
$\widetilde{e}^{{\kern2pt}-}_1$
and
![]() $\widetilde {e}_3^{{\kern1.5pt}+}$
, respectively, located at the following distances from the corresponding end vertices:
$\widetilde {e}_3^{{\kern1.5pt}+}$
, respectively, located at the following distances from the corresponding end vertices:
 $$ \begin{align*}d(\widetilde{v}_1^+,\widetilde{P}_1)=x,\quad d(\widetilde{v}_3^+,\widetilde{Q}_1)=y,\quad d(\widetilde{v}_2^-,\widetilde{P}_2)=x-y,\quad d(\widetilde{v}_2^+,\widetilde{Q}_2)=1+2y.\\[-15pt] \end{align*} $$
$$ \begin{align*}d(\widetilde{v}_1^+,\widetilde{P}_1)=x,\quad d(\widetilde{v}_3^+,\widetilde{Q}_1)=y,\quad d(\widetilde{v}_2^-,\widetilde{P}_2)=x-y,\quad d(\widetilde{v}_2^+,\widetilde{Q}_2)=1+2y.\\[-15pt] \end{align*} $$
Let
![]() $\widetilde {D}_1=\widetilde {P}_1+\widetilde {Q}_1$
and
$\widetilde {D}_1=\widetilde {P}_1+\widetilde {Q}_1$
and
![]() $\widetilde {D}_2=\widetilde {P}_2+\widetilde {Q}_2$
. The divisor
$\widetilde {D}_2=\widetilde {P}_2+\widetilde {Q}_2$
. The divisor
![]() $(\widetilde {D}_1-\iota \widetilde {D}_1) - (\widetilde {D}_2-\iota \widetilde {D}_2)$
is seen to be equivalent to 0 by repeatedly applying Dhar’s burning algorithm [Reference Baker and ShokriehBS13, Section 5.1] at each point where the divisor has a negative number of chips. As a consequence,
$(\widetilde {D}_1-\iota \widetilde {D}_1) - (\widetilde {D}_2-\iota \widetilde {D}_2)$
is seen to be equivalent to 0 by repeatedly applying Dhar’s burning algorithm [Reference Baker and ShokriehBS13, Section 5.1] at each point where the divisor has a negative number of chips. As a consequence,
![]() $\widetilde {D}_1-\iota \widetilde {D}_1$
and
$\widetilde {D}_1-\iota \widetilde {D}_1$
and
![]() $\widetilde {D}_2-\iota \widetilde {D}_2$
are linearly equivalent. However,
$\widetilde {D}_2-\iota \widetilde {D}_2$
are linearly equivalent. However,
![]() $\pi (\widetilde {D}_1)$
is supported on the odd genus 1 decomposition
$\pi (\widetilde {D}_1)$
is supported on the odd genus 1 decomposition
![]() $\{\widetilde {e}_1,\widetilde {e}_2\}$
of rank
$\{\widetilde {e}_1,\widetilde {e}_2\}$
of rank
![]() $2$
, while
$2$
, while
![]() $\pi (\widetilde {D}_2)$
is supported on the odd genus 1 decomposition
$\pi (\widetilde {D}_2)$
is supported on the odd genus 1 decomposition
![]() $\{\widetilde {e}_1,\widetilde {e}_3\}$
of rank
$\{\widetilde {e}_1,\widetilde {e}_3\}$
of rank
![]() $1$
, so the degrees of
$1$
, so the degrees of
![]() $\Psi $
at
$\Psi $
at
![]() $\widetilde {D}_1$
and
$\widetilde {D}_1$
and
![]() $\widetilde {D}_2$
are distinct.
$\widetilde {D}_2$
are distinct.

Figure 3 A double cover with a Prym divisor with representatives of distinct degrees.
By varying x and y, we obtain two polyhedral cells in
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
having the same image in
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
having the same image in
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
: the subset
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
: the subset
![]() $C_1=\{(x-y,1+2y):0<y<x<1\}$
of
$C_1=\{(x-y,1+2y):0<y<x<1\}$
of
![]() $\widetilde{e}^{{\kern2pt}-}_1\times \widetilde {e}^{{\kern1.5pt}+}_3$
and the subset
$\widetilde{e}^{{\kern2pt}-}_1\times \widetilde {e}^{{\kern1.5pt}+}_3$
and the subset
![]() $C_2=\{(x,y):0<y<x<1\}$
of
$C_2=\{(x,y):0<y<x<1\}$
of
![]() $\widetilde {e}^{{\kern1.5pt}+}_1\times \widetilde {e}^{{\kern1.5pt}+}_2$
. The volumes of
$\widetilde {e}^{{\kern1.5pt}+}_1\times \widetilde {e}^{{\kern1.5pt}+}_2$
. The volumes of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are equal to
$C_2$
are equal to
![]() $1$
and
$1$
and
![]() $1/2$
, respectively, which agrees with the fact that the degree of
$1/2$
, respectively, which agrees with the fact that the degree of
![]() $\Psi $
, equal to
$\Psi $
, equal to
![]() $1$
on
$1$
on
![]() $C_1$
and
$C_1$
and
![]() $2$
on
$2$
on
![]() $C_2$
, is the volume dilation factor. We also observe that the global degree of
$C_2$
, is the volume dilation factor. We also observe that the global degree of
![]() $\Psi $
is equal to
$\Psi $
is equal to
![]() $2^{g-1}=4$
. Therefore, Theorem B implies that there is a third divisor
$2^{g-1}=4$
. Therefore, Theorem B implies that there is a third divisor
![]() $\widetilde {D}_3$
(effective of degree 2) such that
$\widetilde {D}_3$
(effective of degree 2) such that
![]() $\widetilde {D}_1-\iota \widetilde {D}_1 \simeq \widetilde {D}_3-\iota \widetilde {D}_3$
and such that
$\widetilde {D}_1-\iota \widetilde {D}_1 \simeq \widetilde {D}_3-\iota \widetilde {D}_3$
and such that
![]() $\Gamma \setminus \pi (\widetilde {D}_3)$
consists of a single connected component.
$\Gamma \setminus \pi (\widetilde {D}_3)$
consists of a single connected component.
Before giving the proof of Proposition 5.2, we describe the structure of the Abel–Prym map for the covers of a genus 2 dumbbell graph.
Example 5.4. Consider the two covers
![]() $\pi _1:\widetilde {\Gamma }_1\to \Gamma $
and
$\pi _1:\widetilde {\Gamma }_1\to \Gamma $
and
![]() $\pi _2:\widetilde {\Gamma }_2\to \Gamma $
of the dumbbell graph
$\pi _2:\widetilde {\Gamma }_2\to \Gamma $
of the dumbbell graph
![]() $\Gamma $
described in Example 3.7. In this case,
$\Gamma $
described in Example 3.7. In this case,
![]() $g-1=1$
and the Abel–Prym maps
$g-1=1$
and the Abel–Prym maps
![]() $\Psi _1:\widetilde {\Gamma }_1\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_1/\Gamma )$
and
$\Psi _1:\widetilde {\Gamma }_1\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_1/\Gamma )$
and
![]() $\Psi _2:\widetilde {\Gamma }_2\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_2/\Gamma )$
are harmonic morphisms of metric graphs of degree 2, which we now describe.
$\Psi _2:\widetilde {\Gamma }_2\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_2/\Gamma )$
are harmonic morphisms of metric graphs of degree 2, which we now describe.
With respect to the cover
![]() $\pi _1$
, each edge of
$\pi _1$
, each edge of
![]() $\Gamma $
is an odd genus 1 decomposition; hence,
$\Gamma $
is an odd genus 1 decomposition; hence,
![]() $\Psi _1$
does not contract any edges. The edges
$\Psi _1$
does not contract any edges. The edges
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_1$
and
$\widetilde {e}^{{\kern1.5pt}\pm }_1$
and
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_2$
are mapped onto edges
$\widetilde {e}^{{\kern1.5pt}\pm }_2$
are mapped onto edges
![]() $f_1$
and
$f_1$
and
![]() $f_2$
, respectively. The degree of
$f_2$
, respectively. The degree of
![]() $\Psi _1$
on these edges is equal to 1; hence, the lengths of
$\Psi _1$
on these edges is equal to 1; hence, the lengths of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are
$f_2$
are
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, respectively. Each of the two edges
$x_2$
, respectively. Each of the two edges
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_3$
is mapped onto an edge
$\widetilde {e}^{{\kern1.5pt}\pm }_3$
is mapped onto an edge
![]() $f^{\pm }_3$
, of length
$f^{\pm }_3$
, of length
![]() $2x_3$
, because the degree of
$2x_3$
, because the degree of
![]() $\Psi _1$
is equal to 2. Hence,
$\Psi _1$
is equal to 2. Hence,
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_1/\Gamma )$
is a circle of circumference
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_1/\Gamma )$
is a circle of circumference
![]() $x_1+x_2+4x_3$
, as we have already seen in Example 3.7.
$x_1+x_2+4x_3$
, as we have already seen in Example 3.7.
The map
![]() $\Psi _2$
, on the other hand, contracts the edges
$\Psi _2$
, on the other hand, contracts the edges
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_1$
and
$\widetilde {e}^{{\kern1.5pt}\pm }_1$
and
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_3$
because
$\widetilde {e}^{{\kern1.5pt}\pm }_3$
because
![]() $\{e_1\}$
and
$\{e_1\}$
and
![]() $\{e_3\}$
are not genus 1 decompositions and maps
$\{e_3\}$
are not genus 1 decompositions and maps
![]() $\widetilde {e}^{{\kern1.5pt}\pm }_2$
to a unique loop edge
$\widetilde {e}^{{\kern1.5pt}\pm }_2$
to a unique loop edge
![]() $f_2$
of
$f_2$
of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_2/\Gamma )$
of length
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }_2/\Gamma )$
of length
![]() $x_2$
. The morphisms
$x_2$
. The morphisms
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Psi _2$
are given in Figure 4.
$\Psi _2$
are given in Figure 4.

Figure 4 Abel–Prym maps corresponding to the covers in Example 3.7.
Proof of Proposition 5.2.
Let
![]() $\widetilde {C}$
be a codimension 1 cell of
$\widetilde {C}$
be a codimension 1 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
such that its image
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
such that its image
![]() $C=\Psi (\widetilde {C})$
is a codimension 1 cell in
$C=\Psi (\widetilde {C})$
is a codimension 1 cell in
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Since
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Since
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is a torus, it locally looks like
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
is a torus, it locally looks like
![]() $\mathbb {R}^{g-1}$
, and we can think of the cell C as lying in a hyperplane
$\mathbb {R}^{g-1}$
, and we can think of the cell C as lying in a hyperplane
![]() $H_0\subset \mathbb {R}^{g-1}$
, with respect to an appropriate local coordinate system. There are exactly two codimension 0 cells
$H_0\subset \mathbb {R}^{g-1}$
, with respect to an appropriate local coordinate system. There are exactly two codimension 0 cells
![]() $M^{\pm }$
attached to C, each contained in a corresponding half-space of
$M^{\pm }$
attached to C, each contained in a corresponding half-space of
![]() $\mathbb {R}^{g-1}$
, which we also denote
$\mathbb {R}^{g-1}$
, which we also denote
![]() $M^{\pm }$
by abuse of notation. To show that
$M^{\pm }$
by abuse of notation. To show that
![]() $\Psi $
is harmonic at
$\Psi $
is harmonic at
![]() $\widetilde {C}$
, we need to show that the sum of
$\widetilde {C}$
, we need to show that the sum of
![]() $|\det \Psi |$
over the codimension 0 cells of
$|\det \Psi |$
over the codimension 0 cells of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
mapping to
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
mapping to
![]() $M^+$
is the same as the sum over those mapping to
$M^+$
is the same as the sum over those mapping to
![]() $M^-$
, in which case this sum is the degree of
$M^-$
, in which case this sum is the degree of
![]() $\Psi $
on
$\Psi $
on
![]() $\widetilde {C}$
.
$\widetilde {C}$
.
If
![]() $\Psi $
contracts every codimension 0 cell of
$\Psi $
contracts every codimension 0 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
attached to
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
attached to
![]() $\widetilde {C}$
, then the harmonicity condition is trivially verified and we set
$\widetilde {C}$
, then the harmonicity condition is trivially verified and we set
 $\deg _{\Psi }(\widetilde {C})=0$
. Hence, we assume that
$\deg _{\Psi }(\widetilde {C})=0$
. Hence, we assume that
![]() $\Psi $
does not contract some codimension 0 cell attached to
$\Psi $
does not contract some codimension 0 cell attached to
![]() $\widetilde {C}$
. By Corollary 4.2, this cell is a subset of
$\widetilde {C}$
. By Corollary 4.2, this cell is a subset of
![]() $C(\widetilde {F})$
, where
$C(\widetilde {F})$
, where
![]() $F=p(\widetilde {F})$
is an odd genus 1 decomposition of G. If
$F=p(\widetilde {F})$
is an odd genus 1 decomposition of G. If
![]() $\widetilde {C}$
lies in the interior of
$\widetilde {C}$
lies in the interior of
![]() $C(\widetilde {F})$
, then
$C(\widetilde {F})$
, then
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
also locally looks like
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
also locally looks like
![]() $\mathbb {R}^n$
in a neighbourhood of
$\mathbb {R}^n$
in a neighbourhood of
![]() $\widetilde {C}$
, the map
$\widetilde {C}$
, the map
![]() $\Psi $
is simply an affine linear map near
$\Psi $
is simply an affine linear map near
![]() $\widetilde {C}$
and therefore harmonic (such cells
$\widetilde {C}$
and therefore harmonic (such cells
![]() $\widetilde {C}$
do not occur in the standard polyhedral decomposition (22) of
$\widetilde {C}$
do not occur in the standard polyhedral decomposition (22) of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
but may occur in the refined decomposition induced by the map
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
but may occur in the refined decomposition induced by the map
![]() $\Psi $
).
$\Psi $
).
We therefore assume that
![]() $\widetilde {C}$
lies on the boundary of a cell
$\widetilde {C}$
lies on the boundary of a cell
![]() $C(\widetilde {F})$
, where
$C(\widetilde {F})$
, where
 $\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-1}\}$
is a set of edges of
$\widetilde {F}=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-1}\}$
is a set of edges of
![]() $\widetilde {G}$
such that
$\widetilde {G}$
such that
![]() $F=\{f_1,\ldots ,f_{g-1}\}$
,
$F=\{f_1,\ldots ,f_{g-1}\}$
,
![]() $f_i=p(\widetilde {f}_i)$
is an odd genus 1 decomposition of G of rank r. To simplify notation, we assume that in fact
$f_i=p(\widetilde {f}_i)$
is an odd genus 1 decomposition of G of rank r. To simplify notation, we assume that in fact
![]() $\widetilde {C}$
is a codimension 1 cell of
$\widetilde {C}$
is a codimension 1 cell of
![]() $C(\widetilde {F})$
with respect to the standard polyhedral decomposition (22) of
$C(\widetilde {F})$
with respect to the standard polyhedral decomposition (22) of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
. In other words, we assume that
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
. In other words, we assume that
![]() $\widetilde {C}=C^{g-2}(\widetilde {F}\backslash \{\widetilde {f}_a\},\widetilde {v})$
for some
$\widetilde {C}=C^{g-2}(\widetilde {F}\backslash \{\widetilde {f}_a\},\widetilde {v})$
for some
![]() $a\in \{1,\ldots ,g-1\}$
and where
$a\in \{1,\ldots ,g-1\}$
and where
![]() $\widetilde {v}=s(\widetilde {f}_a)$
is the starting vertex of
$\widetilde {v}=s(\widetilde {f}_a)$
is the starting vertex of
![]() $\widetilde {f}_a$
with respect to an appropriate orientation (we shall later specify which edge
$\widetilde {f}_a$
with respect to an appropriate orientation (we shall later specify which edge
![]() $\widetilde {f}_a$
we pick, in order to make our notation consistent with Construction C).
$\widetilde {f}_a$
we pick, in order to make our notation consistent with Construction C).
The top dimensional cells of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
that are adjacent to
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma })$
that are adjacent to
![]() $\widetilde {C}$
have the form
$\widetilde {C}$
have the form
![]() $C(\widetilde {F}')$
, where
$C(\widetilde {F}')$
, where
![]() $\widetilde {F}'=(\widetilde {F}\backslash \{\widetilde {f}_a\})\cup \{\widetilde {f}'\}$
and where
$\widetilde {F}'=(\widetilde {F}\backslash \{\widetilde {f}_a\})\cup \{\widetilde {f}'\}$
and where
![]() $\widetilde {f}'$
is any edge rooted at
$\widetilde {f}'$
is any edge rooted at
![]() $\widetilde {v}$
. We assume that all edges
$\widetilde {v}$
. We assume that all edges
![]() $\widetilde {f}'$
are oriented in such a way that
$\widetilde {f}'$
are oriented in such a way that
![]() $s(\widetilde {f}')=\widetilde {v}$
. By Corollary 4.2,
$s(\widetilde {f}')=\widetilde {v}$
. By Corollary 4.2,
![]() $\Psi $
does not contract
$\Psi $
does not contract
![]() $C(\widetilde {F}')$
if and only if
$C(\widetilde {F}')$
if and only if
![]() $p(\widetilde {F}')$
is an odd genus 1 decomposition of G. To prove harmonicity, we need to show that the sum of
$p(\widetilde {F}')$
is an odd genus 1 decomposition of G. To prove harmonicity, we need to show that the sum of
![]() $|\det \Psi |$
on those cells
$|\det \Psi |$
on those cells
![]() $C(\widetilde {F}')$
mapping to
$C(\widetilde {F}')$
mapping to
![]() $M^+$
is equal to the sum of those that map to
$M^+$
is equal to the sum of those that map to
![]() $M^-$
. By Corollary 4.2, the value of
$M^-$
. By Corollary 4.2, the value of
![]() $|\det \Psi |$
on a noncontracted cell
$|\det \Psi |$
on a noncontracted cell
![]() $C(\widetilde {F}')$
is a power of 2. In fact, as we shall see, adjacent to any cell
$C(\widetilde {F}')$
is a power of 2. In fact, as we shall see, adjacent to any cell
![]() $\widetilde {C}$
there are either two, three, or four noncontracted cells
$\widetilde {C}$
there are either two, three, or four noncontracted cells
![]() $C(\widetilde {F})$
, with the degrees distributed as shown on Figure 5 (plus an arbitrary number of contracted cells).
$C(\widetilde {F})$
, with the degrees distributed as shown on Figure 5 (plus an arbitrary number of contracted cells).

Figure 5 The Abel–Prym map near a noncontracted codimension 1 cell.
We calculate the matrix of
![]() $\Psi $
(or, rather, some of its entries) on each cell
$\Psi $
(or, rather, some of its entries) on each cell
![]() $C(\widetilde {F}')$
with respect to an appropriate coordinate system, in the same way that we proved part (2) of Theorem 4.1. First, we choose local coordinates on
$C(\widetilde {F}')$
with respect to an appropriate coordinate system, in the same way that we proved part (2) of Theorem 4.1. First, we choose local coordinates on
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
. As before, we identify
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
. As before, we identify
![]() $C(\widetilde {F})$
with the parallelotope
$C(\widetilde {F})$
with the parallelotope
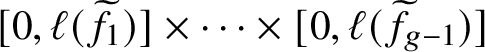 $[0,\ell (\widetilde {f}_1)]\times \cdots \times [0,\ell (\widetilde {f}_{g-1})]$
lying in the half-space
$[0,\ell (\widetilde {f}_1)]\times \cdots \times [0,\ell (\widetilde {f}_{g-1})]$
lying in the half-space
![]() $H^+=\{x:x_a\geq 0\}\subset \mathbb {R}^{g-1}$
. Under this identification, the cell
$H^+=\{x:x_a\geq 0\}\subset \mathbb {R}^{g-1}$
. Under this identification, the cell
![]() $\widetilde {C}$
lies in the hyperplane
$\widetilde {C}$
lies in the hyperplane
![]() $H^0=\{x:x_a=0\}$
and the corresponding cells of
$H^0=\{x:x_a=0\}$
and the corresponding cells of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
are
![]() $C=\Psi (\widetilde {C})\subset \Psi (H^0)$
and
$C=\Psi (\widetilde {C})\subset \Psi (H^0)$
and
![]() $M^{\pm }=\Psi (H^{\pm })$
, where
$M^{\pm }=\Psi (H^{\pm })$
, where
![]() $H^-=\{x:x_a\leq 0\}\subset \mathbb {R}^{g-1}$
. Similarly, we think of each of the other
$H^-=\{x:x_a\leq 0\}\subset \mathbb {R}^{g-1}$
. Similarly, we think of each of the other
![]() $C(\widetilde {F}')$
as lying in its own
$C(\widetilde {F}')$
as lying in its own
![]() $H^+$
.
$H^+$
.
To construct coordinates on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, we apply Construction C to the set
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, we apply Construction C to the set
![]() $\widetilde {F}$
. The output is a basis
$\widetilde {F}$
. The output is a basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
of
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
of
![]() $\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
given by equation (26). As explained in Subsection 2.6, the basis
$\operatorname {\mathrm {Ker}} \pi _*:H_1(\widetilde {\Gamma },\mathbb {Z})\to H_1(\Gamma ,\mathbb {Z})$
given by equation (26). As explained in Subsection 2.6, the basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
defines a coordinate system on
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
defines a coordinate system on
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, with respect to which the map
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
, with respect to which the map
![]() $\Psi $
on the cell
$\Psi $
on the cell
![]() $C(\widetilde {F})$
is affine linear and the
$C(\widetilde {F})$
is affine linear and the
![]() $(g-1)\times (g-1)$
matrix of the linear part is given by equation (24):
$(g-1)\times (g-1)$
matrix of the linear part is given by equation (24):
 $$ \begin{align*}\Psi(\widetilde{F})_{ji}=\frac{1}{2}\langle \widetilde{\gamma}_j,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \frac{1}{2}\langle \widetilde{\gamma}^+_j-\iota_*(\widetilde{\gamma}^+_j),\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \langle \widetilde{\gamma}^+_j,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F})_{ji}=\frac{1}{2}\langle \widetilde{\gamma}_j,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \frac{1}{2}\langle \widetilde{\gamma}^+_j-\iota_*(\widetilde{\gamma}^+_j),\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle= \langle \widetilde{\gamma}^+_j,\widetilde{f}_i-\iota(\widetilde{f}_i)\rangle. \end{align*} $$
We recall that we showed in Theorem 4.1 and Corollary 4.2 that
 $\Psi (\widetilde {F})_{ij}$
is a lower triangular matrix with determinant
$\Psi (\widetilde {F})_{ij}$
is a lower triangular matrix with determinant
![]() $2^{r-1}$
, where r is the rank of
$2^{r-1}$
, where r is the rank of
![]() $\widetilde {F}$
.
$\widetilde {F}$
.
Now let
![]() $C(\widetilde {F}')$
be another codimension 0 cell of
$C(\widetilde {F}')$
be another codimension 0 cell of
![]() $\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
adjacent to
$\operatorname {\mathrm {Sym}}^{g-1}(\widetilde {\Gamma }/\Gamma )$
adjacent to
![]() $\widetilde {C}$
, so
$\widetilde {C}$
, so
![]() $\widetilde {F}'=(\widetilde {F}\backslash \{\widetilde {f}_a\})\cup \{\widetilde {f}'\}$
, where
$\widetilde {F}'=(\widetilde {F}\backslash \{\widetilde {f}_a\})\cup \{\widetilde {f}'\}$
, where
![]() $\widetilde {f}'$
is an edge rooted at
$\widetilde {f}'$
is an edge rooted at
![]() $\widetilde {v}$
other than
$\widetilde {v}$
other than
![]() $f_a$
. We calculate the matrix of
$f_a$
. We calculate the matrix of
![]() $\Psi $
on
$\Psi $
on
![]() $C(\widetilde {F}')$
using the same basis
$C(\widetilde {F}')$
using the same basis
![]() $\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
(in other words, we do not recalculate the basis by replacing
$\widetilde {\gamma }_1,\ldots ,\widetilde {\gamma }_{g-1}$
(in other words, we do not recalculate the basis by replacing
![]() $\widetilde {F}$
with
$\widetilde {F}$
with
![]() $\widetilde {F}'$
in Construction C). The resulting matrix differs from
$\widetilde {F}'$
in Construction C). The resulting matrix differs from
 $\Psi (\widetilde {F})_{ji}$
by a single column only:
$\Psi (\widetilde {F})_{ji}$
by a single column only:
 $$ \begin{align} \Psi(\widetilde{F}')_{ji}=\left\{\begin{array}{c@{\quad}c} \Psi(\widetilde{F})_{ji}, & i\neq a, \\ \langle \widetilde{\gamma}^+_j,\widetilde{f}'-\iota(\widetilde{f}')\rangle, & i=a. \end{array}\right. \end{align} $$
$$ \begin{align} \Psi(\widetilde{F}')_{ji}=\left\{\begin{array}{c@{\quad}c} \Psi(\widetilde{F})_{ji}, & i\neq a, \\ \langle \widetilde{\gamma}^+_j,\widetilde{f}'-\iota(\widetilde{f}')\rangle, & i=a. \end{array}\right. \end{align} $$
To check the harmonicity of
![]() $\Psi $
around
$\Psi $
around
![]() $\widetilde {C}$
, it suffices to compute the determinants
$\widetilde {C}$
, it suffices to compute the determinants
![]() $\det \Psi (\widetilde {F}')$
for all
$\det \Psi (\widetilde {F}')$
for all
![]() $\widetilde {F}'$
. Indeed, the Abel–Prym map
$\widetilde {F}'$
. Indeed, the Abel–Prym map
![]() $\Psi $
contracts the cell
$\Psi $
contracts the cell
![]() $C(\widetilde {F}')$
if and only if
$C(\widetilde {F}')$
if and only if
![]() $\det \Psi (\widetilde {F}')=0$
. Furthermore,
$\det \Psi (\widetilde {F}')=0$
. Furthermore,
![]() $C(\widetilde {F}')$
maps to
$C(\widetilde {F}')$
maps to
![]() $M^+$
if
$M^+$
if
![]() $\det \Psi (\widetilde {F}')>0$
and to
$\det \Psi (\widetilde {F}')>0$
and to
![]() $M^-$
if
$M^-$
if
![]() $\det \Psi (\widetilde {F}')<0$
, and to prove harmonicity we need to check that the positive determinants exactly cancel the negative determinants.
$\det \Psi (\widetilde {F}')<0$
, and to prove harmonicity we need to check that the positive determinants exactly cancel the negative determinants.
The set F is an odd genus 1 decomposition of G of some rank r and we denote
the decomposition into connected components. Each
![]() $G_k$
has genus 1 and each
$G_k$
has genus 1 and each
![]() $p^{-1}(G_k)$
is connected. We denote
$p^{-1}(G_k)$
is connected. We denote
There are two separate cases that we need to consider: either both endpoints u and v of the edge
![]() $f_a=p(\widetilde {f}_a)$
that we are removing lie on one connected component or the edge
$f_a=p(\widetilde {f}_a)$
that we are removing lie on one connected component or the edge
![]() $f_a$
connects two different components.
$f_a$
connects two different components.
Both endpoints of the edge
![]() $f_a$
lie on a single connected component of
$f_a$
lie on a single connected component of
![]() $G\backslash F$
. Without loss of generality, we assume that
$G\backslash F$
. Without loss of generality, we assume that
![]() $f_a$
is rooted on the component
$f_a$
is rooted on the component
![]() $G_0$
. The edge
$G_0$
. The edge
![]() $f_a$
is a loop on the contracted graph
$f_a$
is a loop on the contracted graph
![]() $G^c$
rooted at the vertex
$G^c$
rooted at the vertex
![]() $v_0$
. Since a loop cannot be part of a spanning tree, we can further assume without loss of generality that
$v_0$
. Since a loop cannot be part of a spanning tree, we can further assume without loss of generality that
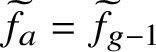 $\widetilde {f}_a=\widetilde {f}_{g-1}$
. We observe that, on the contracted graph
$\widetilde {f}_a=\widetilde {f}_{g-1}$
. We observe that, on the contracted graph
![]() $\widetilde {G}^c$
, the edge
$\widetilde {G}^c$
, the edge
 $\widetilde {f}_{g-1}$
is a loop rooted at
$\widetilde {f}_{g-1}$
is a loop rooted at
![]() $\widetilde {v}_0$
. The contraction of the cycle
$\widetilde {v}_0$
. The contraction of the cycle
 $\widetilde {\gamma }^+_{g-1}$
is the unique cycle containing
$\widetilde {\gamma }^+_{g-1}$
is the unique cycle containing
 $+\widetilde {f}_{g-1}$
, but since this is already a loop, we see that
$+\widetilde {f}_{g-1}$
, but since this is already a loop, we see that
 $(\widetilde {\gamma }^+_{g-1})^c=\widetilde {f}_{g-1}$
.
$(\widetilde {\gamma }^+_{g-1})^c=\widetilde {f}_{g-1}$
.
It follows that the intersection of
 $\widetilde {\gamma }^+_{g-1}$
with all other edges
$\widetilde {\gamma }^+_{g-1}$
with all other edges
![]() $\widetilde {f}_i$
and
$\widetilde {f}_i$
and
![]() $\iota (\widetilde {f}_i)$
for
$\iota (\widetilde {f}_i)$
for
![]() $i=1,\ldots ,g-2$
is 0. Hence, the matrix
$i=1,\ldots ,g-2$
is 0. Hence, the matrix
![]() $\Psi _{ji}$
is block upper triangular, having a
$\Psi _{ji}$
is block upper triangular, having a
![]() $(g-2)\times (g-2)$
lower triangular block with determinant
$(g-2)\times (g-2)$
lower triangular block with determinant
![]() $2^{r-1}$
in the upper left corner and a 1 in the lower right corner. Therefore, the images of the subspaces
$2^{r-1}$
in the upper left corner and a 1 in the lower right corner. Therefore, the images of the subspaces
![]() $H^{\pm }$
and the hyperplane
$H^{\pm }$
and the hyperplane
![]() $H^0$
are
$H^0$
are
 $$ \begin{align*}M^+=\Psi(H^+)=\{y:y_{g-1}\geq 0\}, \quad M^-=\Psi(H^-)=\{y:y_{g-1}\leq 0\}, \quad \Psi(H^0)=\{y:y_{g-1}=0\}. \end{align*} $$
$$ \begin{align*}M^+=\Psi(H^+)=\{y:y_{g-1}\geq 0\}, \quad M^-=\Psi(H^-)=\{y:y_{g-1}\leq 0\}, \quad \Psi(H^0)=\{y:y_{g-1}=0\}. \end{align*} $$
Now let
![]() $\widetilde {f}'$
be an edge at
$\widetilde {f}'$
be an edge at
![]() $\widetilde {v}$
, so that
$\widetilde {v}$
, so that
 $\widetilde {F}'=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {f}'\}$
defines a cell
$\widetilde {F}'=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {f}'\}$
defines a cell
![]() $C(\widetilde {F}')$
adjacent to
$C(\widetilde {F}')$
adjacent to
![]() $C(\widetilde {F})$
via
$C(\widetilde {F})$
via
![]() $C'$
. The matrix
$C'$
. The matrix
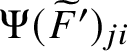 $\Psi (\widetilde {F}')_{ji}$
is given by (30) and is obtained from the matrix
$\Psi (\widetilde {F}')_{ji}$
is given by (30) and is obtained from the matrix
![]() $\Psi (\widetilde {F})$
by replacing the last column. Hence, it is also block upper triangular, and to compute
$\Psi (\widetilde {F})$
by replacing the last column. Hence, it is also block upper triangular, and to compute
![]() $\det \Psi (\widetilde {F}')$
it suffices to find the new entry
$\det \Psi (\widetilde {F}')$
it suffices to find the new entry
 $$ \begin{align} \Psi(\widetilde{F}')_{g-1,g-1}=\langle \widetilde{\gamma}^+_{g-1},\widetilde{f}'-\iota(\widetilde{f}')\rangle \end{align} $$
$$ \begin{align} \Psi(\widetilde{F}')_{g-1,g-1}=\langle \widetilde{\gamma}^+_{g-1},\widetilde{f}'-\iota(\widetilde{f}')\rangle \end{align} $$
in the lower right corner. Furthermore, the sign of this entry determines the sign of
![]() $\det \Psi (\widetilde {F}')$
and hence the image cell
$\det \Psi (\widetilde {F}')$
and hence the image cell
![]() $\Psi (C(\widetilde {F}'))$
of
$\Psi (C(\widetilde {F}'))$
of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
: if the entry is positive, then
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
: if the entry is positive, then
![]() $\Psi $
maps
$\Psi $
maps
![]() $C(\widetilde {F}')$
to the same half-space
$C(\widetilde {F}')$
to the same half-space
![]() $M^+$
as
$M^+$
as
![]() $C(\widetilde {F})$
, while if it is negative then
$C(\widetilde {F})$
, while if it is negative then
![]() $\Psi (C(\widetilde {F}'))\subset M^-$
and if it is zero then
$\Psi (C(\widetilde {F}'))\subset M^-$
and if it is zero then
![]() $C(\widetilde {F}')$
is contracted.
$C(\widetilde {F}')$
is contracted.
There are several possibilities to consider, depending on the relative positions of
![]() $v=s(f_{g-1})$
and
$v=s(f_{g-1})$
and
![]() $u=t(f_{g-1})$
on the component
$u=t(f_{g-1})$
on the component
![]() $G_0$
. Let
$G_0$
. Let
![]() $\gamma (G_0)$
denote the unique cycle on
$\gamma (G_0)$
denote the unique cycle on
![]() $G_0$
(oriented in any direction); then any vertex of
$G_0$
(oriented in any direction); then any vertex of
![]() $G_0$
has a unique (possibly trivial) shortest path to
$G_0$
has a unique (possibly trivial) shortest path to
![]() $\gamma (G_0)$
. For two distinct vertices
$\gamma (G_0)$
. For two distinct vertices
![]() $v_1,v_2\in V(G_0)$
, we write
$v_1,v_2\in V(G_0)$
, we write
![]() $v_1<v_2$
if the unique path from
$v_1<v_2$
if the unique path from
![]() $v_2$
to
$v_2$
to
![]() $\gamma (G_0)$
passes through
$\gamma (G_0)$
passes through
![]() $v_1$
; this defines a partial order on
$v_1$
; this defines a partial order on
![]() $V(G_0)$
.
$V(G_0)$
.
-
(1) The vertex v does not lie on
 $\gamma (G_0)$
and
$\gamma (G_0)$
and
 $v\nless u$
. In other words, v lies on a tree attached to
$v\nless u$
. In other words, v lies on a tree attached to
 $\gamma (G_0)$
and u does not lie higher up on the same tree.
$\gamma (G_0)$
and u does not lie higher up on the same tree.Let
 $g_1$
be the unique edge rooted at v that points in the direction of the cycle
$g_1$
be the unique edge rooted at v that points in the direction of the cycle
 $\gamma (G_0)$
. Since the unique path from u to
$\gamma (G_0)$
. Since the unique path from u to
 $\gamma (G_0)$
avoids v, the graph
$\gamma (G_0)$
avoids v, the graph
 $G_0'=G_0\cup \{f_{g-1}\}\backslash \{g_1\}$
is connected, has genus 1 and has connected preimage, since the unique cycle of
$G_0'=G_0\cup \{f_{g-1}\}\backslash \{g_1\}$
is connected, has genus 1 and has connected preimage, since the unique cycle of
 $G_0'$
is
$G_0'$
is
 $\gamma (G_0)$
. Therefore,
$\gamma (G_0)$
. Therefore,
 $F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
is an odd genus 1 decomposition of G, of the same length r as F. For any other edge
$F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
is an odd genus 1 decomposition of G, of the same length r as F. For any other edge
 $e'$
rooted at v, removing it disconnects the corresponding branch of the tree from
$e'$
rooted at v, removing it disconnects the corresponding branch of the tree from
 $G_0$
and attaching
$G_0$
and attaching
 $f_{g-1}$
does not reconnect this branch. Hence,
$f_{g-1}$
does not reconnect this branch. Hence,
 $G\backslash \{f_1,\ldots ,f_{g-2}, e'\}$
has a connected component of genus 0 and
$G\backslash \{f_1,\ldots ,f_{g-2}, e'\}$
has a connected component of genus 0 and
 $\{f_1,\ldots ,f_{g-2}, e'\}$
is not a genus 1 decomposition. The graph
$\{f_1,\ldots ,f_{g-2}, e'\}$
is not a genus 1 decomposition. The graph
 $G_0$
and its preimage
$G_0$
and its preimage
 $\pi ^{-1}(G_0)$
are shown on Figure 6.
$\pi ^{-1}(G_0)$
are shown on Figure 6.
Figure 6 The cycle
 $\widetilde {\gamma }^+_{g-1}$
in Case (1).
$\widetilde {\gamma }^+_{g-1}$
in Case (1).We see that the only cell
 $C(\widetilde {F}')$
adjacent to
$C(\widetilde {F}')$
adjacent to
 $C(\widetilde {F})$
through
$C(\widetilde {F})$
through
 $C'$
on which
$C'$
on which
 $|\det \Psi |$
is nonzero corresponds to
$|\det \Psi |$
is nonzero corresponds to
 $\widetilde {F}'=\widetilde {F}_1=\widetilde {F}\cup \{\widetilde {g}_1\}\backslash \{\widetilde {f}_{g-1}\}$
, where
$\widetilde {F}'=\widetilde {F}_1=\widetilde {F}\cup \{\widetilde {g}_1\}\backslash \{\widetilde {f}_{g-1}\}$
, where
 $\widetilde {g}_1$
is the unique edge rooted at
$\widetilde {g}_1$
is the unique edge rooted at
 $\widetilde {v}$
that maps to
$\widetilde {v}$
that maps to
 $g_1$
. Furthermore, F and
$g_1$
. Furthermore, F and
 $F_1=p(\widetilde {F}_1)$
have the same rank r; hence, the value of
$F_1=p(\widetilde {F}_1)$
have the same rank r; hence, the value of
 $|\det \Psi |$
on the two cells
$|\det \Psi |$
on the two cells
 $C(\widetilde {F})$
and
$C(\widetilde {F})$
and
 $C(\widetilde {F}_1)$
is equal to
$C(\widetilde {F}_1)$
is equal to
 $2^{r-1}$
, so to prove harmonicity we only need to show that
$2^{r-1}$
, so to prove harmonicity we only need to show that
 $\Psi $
maps
$\Psi $
maps
 $C(\widetilde {F}_1)$
to the half-space
$C(\widetilde {F}_1)$
to the half-space
 $M^-$
. As explained above, it suffices to compute the last diagonal entry (31) of
$M^-$
. As explained above, it suffices to compute the last diagonal entry (31) of
 $\Psi (\widetilde {F}_1)$
, where
$\Psi (\widetilde {F}_1)$
, where
 $\widetilde {f}'=\widetilde {g}_1$
.
$\widetilde {f}'=\widetilde {g}_1$
.The cycle
 $\widetilde {\gamma }^+_{g-1}$
is the unique cycle of the graph
$\widetilde {\gamma }^+_{g-1}$
is the unique cycle of the graph
 $\widetilde {T}\cup \{\widetilde {f}_{g-1}\}$
containing
$\widetilde {T}\cup \{\widetilde {f}_{g-1}\}$
containing
 $+\widetilde {f}_{g-1}$
. It starts at the vertex
$+\widetilde {f}_{g-1}$
. It starts at the vertex
 $\widetilde {v}=s(\widetilde {f}_{g-1})$
, proceeds to
$\widetilde {v}=s(\widetilde {f}_{g-1})$
, proceeds to
 $\widetilde {u}=t(\widetilde {f}_{g-1})$
via
$\widetilde {u}=t(\widetilde {f}_{g-1})$
via
 $+\widetilde {f}_{g-1}$
and then from
$+\widetilde {f}_{g-1}$
and then from
 $\widetilde {u}$
back to
$\widetilde {u}$
back to
 $\widetilde {v}$
via the unique path in the tree
$\widetilde {v}$
via the unique path in the tree
 $\widetilde {T}$
. This path actually lies in the spanning tree
$\widetilde {T}$
. This path actually lies in the spanning tree
 $\widetilde {T}_0^+\cup \widetilde {T}_0^-\cup \{\widetilde {e}^{{\kern1.5pt}+}_0\}$
of
$\widetilde {T}_0^+\cup \widetilde {T}_0^-\cup \{\widetilde {e}^{{\kern1.5pt}+}_0\}$
of
 $p^{-1}(G_0)$
. The last edge of the path is
$p^{-1}(G_0)$
. The last edge of the path is
 $\widetilde {g}_1$
, oriented in the opposite direction, since we have assumed that
$\widetilde {g}_1$
, oriented in the opposite direction, since we have assumed that
 $s(\widetilde {g}_1)=\widetilde {v}$
; hence,
$s(\widetilde {g}_1)=\widetilde {v}$
; hence,
 $\langle \widetilde {\gamma }^+_{g-1},\widetilde {g}_1\rangle =-1$
. In addition, the path does not contain
$\langle \widetilde {\gamma }^+_{g-1},\widetilde {g}_1\rangle =-1$
. In addition, the path does not contain
 $\iota (\widetilde {g}_1)$
. It follows that Therefore,
$\iota (\widetilde {g}_1)$
. It follows that Therefore, $$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-1. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-1. \end{align*} $$
 $\Psi $
maps the cell
$\Psi $
maps the cell
 $C(\widetilde {F}_1)$
to the half-space
$C(\widetilde {F}_1)$
to the half-space
 $M^-$
, hence
$M^-$
, hence
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
(2) The vertex v does not lie on
 $\gamma (G_0)$
and
$\gamma (G_0)$
and
 $v<u$
. As before, let
$v<u$
. As before, let
 $g_1$
denote the unique edge at v pointing towards
$g_1$
denote the unique edge at v pointing towards
 $\gamma (G_0)$
and let
$\gamma (G_0)$
and let
 $g_2$
be the unique edge rooted at v which lies on the path from v to u (this path, when reversed, is part of the unique path from u to
$g_2$
be the unique edge rooted at v which lies on the path from v to u (this path, when reversed, is part of the unique path from u to
 $\gamma (G_0)$
). Attaching
$\gamma (G_0)$
). Attaching
 $f_{g-1}$
to
$f_{g-1}$
to
 $G_0$
produces a graph of genus 2. Any edge
$G_0$
produces a graph of genus 2. Any edge
 $e'$
rooted at v other than
$e'$
rooted at v other than
 $f_{g-1}$
,
$f_{g-1}$
,
 $g_1$
or
$g_1$
or
 $g_2$
is the starting edge of a separate branch of
$g_2$
is the starting edge of a separate branch of
 $G_0\cup \{f_{g-1}\}$
, so removing
$G_0\cup \{f_{g-1}\}$
, so removing
 $e'$
creates a genus 0 connected component. Hence, the only genus 1 decompositions of the form
$e'$
creates a genus 0 connected component. Hence, the only genus 1 decompositions of the form
 $(F\backslash \{f'\})\cup \{f_{g-1}\}$
are
$(F\backslash \{f'\})\cup \{f_{g-1}\}$
are
 $F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
,
$F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
,
 $F_2=\{f_1,\ldots ,f_{g-2},g_2\}$
and F itself. The decompositions F and
$F_2=\{f_1,\ldots ,f_{g-2},g_2\}$
and F itself. The decompositions F and
 $F_2$
have length r, while
$F_2$
have length r, while
 $F_1$
has length
$F_1$
has length
 $r+1$
, because the edge
$r+1$
, because the edge
 $g_1$
is a bridge edge of
$g_1$
is a bridge edge of
 $G_0\cup \{f_{g-1}\}$
and removing it produces two genus 1 connected components.
$G_0\cup \{f_{g-1}\}$
and removing it produces two genus 1 connected components.We now consider the edges
 $\widetilde {g}_1$
,
$\widetilde {g}_1$
,
 $\widetilde {g}_2$
and
$\widetilde {g}_2$
and
 $\widetilde {f}_{g-1}$
on
$\widetilde {f}_{g-1}$
on
 $\widetilde {G}$
, lying above
$\widetilde {G}$
, lying above
 $g_1$
,
$g_1$
,
 $g_2$
and
$g_2$
and
 $f_{g-1}$
and rooted at
$f_{g-1}$
and rooted at
 $\widetilde {v}=s(\widetilde {f}_{g-1})$
. Denote
$\widetilde {v}=s(\widetilde {f}_{g-1})$
. Denote
 $\widetilde {F}_1=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_1\}$
and
$\widetilde {F}_1=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_1\}$
and
 $\widetilde {F}_2=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_2\}$
. The edges
$\widetilde {F}_2=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_2\}$
. The edges
 $g_1$
and
$g_1$
and
 $g_2$
lie on the same tree attached to the cycle
$g_2$
lie on the same tree attached to the cycle
 $\gamma (G_0)$
as the vertex v and the lift of a tree is a tree. Hence, the endpoints of the edges
$\gamma (G_0)$
as the vertex v and the lift of a tree is a tree. Hence, the endpoints of the edges
 $\widetilde {g}_1$
and
$\widetilde {g}_1$
and
 $\widetilde {g}_2$
both lie on the same subtree
$\widetilde {g}_2$
both lie on the same subtree
 $\widetilde {T}_0^{{\kern1.5pt}\pm }$
of
$\widetilde {T}_0^{{\kern1.5pt}\pm }$
of
 $p^{-1}(G_0)$
as
$p^{-1}(G_0)$
as
 $\widetilde {v}$
and we assume without loss of generality that this component is
$\widetilde {v}$
and we assume without loss of generality that this component is
 $\widetilde {T}_0^+$
. For
$\widetilde {T}_0^+$
. For
 $t(\widetilde {f}_{g-1})$
, however, there are two sub-possibilities, as shown on Figure 7.
$t(\widetilde {f}_{g-1})$
, however, there are two sub-possibilities, as shown on Figure 7.
Figure 7 The cycle
 $\widetilde {\gamma }^+_{g-1}$
in the two sub-cases of Case (2).
$\widetilde {\gamma }^+_{g-1}$
in the two sub-cases of Case (2).-
(a) The target vertex
 $\widetilde {u}=t(f_{g-1})$
lies on
$\widetilde {u}=t(f_{g-1})$
lies on
 $\widetilde {T}_0^+$
. In this case, the unique cycle
$\widetilde {T}_0^+$
. In this case, the unique cycle
 $\widetilde {\gamma }^+_{g-1}$
of the graph
$\widetilde {\gamma }^+_{g-1}$
of the graph
 $\widetilde {T}\cup \{\widetilde {f}_{g-1}\}$
actually lies on
$\widetilde {T}\cup \{\widetilde {f}_{g-1}\}$
actually lies on
 $\widetilde {T}_0^+\cup \{\widetilde {f}_{g-1}\}$
: it starts at
$\widetilde {T}_0^+\cup \{\widetilde {f}_{g-1}\}$
: it starts at
 $\widetilde {v}$
, proceeds to
$\widetilde {v}$
, proceeds to
 $\widetilde {u}$
via
$\widetilde {u}$
via
 $+\widetilde {f}_{g-1}$
and then returns to
$+\widetilde {f}_{g-1}$
and then returns to
 $\widetilde {v}$
via the unique path that ends with the edge
$\widetilde {v}$
via the unique path that ends with the edge
 $-\widetilde {g}_2$
. It follows that
$-\widetilde {g}_2$
. It follows that
 $\langle \widetilde {\gamma }^+_{g-1},g_2\rangle =-1$
and
$\langle \widetilde {\gamma }^+_{g-1},g_2\rangle =-1$
and
 $\langle \widetilde {\gamma }^+_{g-1},\iota (g_2)\rangle =0$
. Furthermore, the cycle
$\langle \widetilde {\gamma }^+_{g-1},\iota (g_2)\rangle =0$
. Furthermore, the cycle
 $\widetilde {\gamma }^+_{g-1}$
does not intersect the edges
$\widetilde {\gamma }^+_{g-1}$
does not intersect the edges
 $\widetilde {g}_1$
and
$\widetilde {g}_1$
and
 $\iota (\widetilde {g}_1)$
. Hence, we can compute the last diagonal entries of the upper-triangular matrices
$\iota (\widetilde {g}_1)$
. Hence, we can compute the last diagonal entries of the upper-triangular matrices
 $\Psi (\widetilde {F}_1)$
and
$\Psi (\widetilde {F}_1)$
and
 $\Psi (\widetilde {F}_2)$
: It follows that
$\Psi (\widetilde {F}_2)$
: It follows that $$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=0,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle=-1. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=0,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle=-1. \end{align*} $$
 $|\det \Psi (\widetilde {F}_1)|=0$
; hence, the cell
$|\det \Psi (\widetilde {F}_1)|=0$
; hence, the cell
 $C(\widetilde {F}_1)$
is contracted. Also,
$C(\widetilde {F}_1)$
is contracted. Also,
 $\Psi $
maps the cell
$\Psi $
maps the cell
 $C(\widetilde {F}_2)$
to the opposite half-space
$C(\widetilde {F}_2)$
to the opposite half-space
 $M^-$
as
$M^-$
as
 $C(\widetilde {F})$
but with the same determinant, since
$C(\widetilde {F})$
but with the same determinant, since
 $\widetilde {F}$
and
$\widetilde {F}$
and
 $\widetilde {F}_2$
have the same rank r. Hence,
$\widetilde {F}_2$
have the same rank r. Hence,
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
(b) The target vertex
 $\widetilde {u}=t(f_{g-1})$
lies on
$\widetilde {u}=t(f_{g-1})$
lies on
 $\widetilde {T}_0^-$
. In this case, the cycle
$\widetilde {T}_0^-$
. In this case, the cycle
 $\widetilde {\gamma }^+_{g-1}$
starts at
$\widetilde {\gamma }^+_{g-1}$
starts at
 $\widetilde {v}$
, proceeds to
$\widetilde {v}$
, proceeds to
 $\widetilde {u}$
via
$\widetilde {u}$
via
 $\widetilde {f}_{g-1}$
and proceeds to
$\widetilde {f}_{g-1}$
and proceeds to
 $\iota (\widetilde {v})$
via a unique path that ends with the edge
$\iota (\widetilde {v})$
via a unique path that ends with the edge
 $-\iota (\widetilde {g}_2)$
. From there the path returns from
$-\iota (\widetilde {g}_2)$
. From there the path returns from
 $\iota (\widetilde {v})$
to
$\iota (\widetilde {v})$
to
 $\widetilde {v}$
via the unique path that passes through the edge
$\widetilde {v}$
via the unique path that passes through the edge
 $\widetilde {e}^{{\kern1.5pt}+}_0$
that links the two trees
$\widetilde {e}^{{\kern1.5pt}+}_0$
that links the two trees
 $\widetilde {T}^{\pm }_0$
; this path starts with the edge
$\widetilde {T}^{\pm }_0$
; this path starts with the edge
 $\iota (\widetilde {g}_1)$
and ends with
$\iota (\widetilde {g}_1)$
and ends with
 $-\widetilde {g}_1$
. Summarising, we see that Hence, we calculate the final diagonal entries of
$-\widetilde {g}_1$
. Summarising, we see that Hence, we calculate the final diagonal entries of $$ \begin{align*}\langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_1 \rangle=-1,\quad \langle \widetilde{\gamma}^+_{g-1},\iota(\widetilde{g}_1) \rangle=1,\quad \langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_2 \rangle=0,\quad \langle \widetilde{\gamma}^+_{g-1},\iota(\widetilde{g}_1) \rangle=-1. \end{align*} $$
$$ \begin{align*}\langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_1 \rangle=-1,\quad \langle \widetilde{\gamma}^+_{g-1},\iota(\widetilde{g}_1) \rangle=1,\quad \langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_2 \rangle=0,\quad \langle \widetilde{\gamma}^+_{g-1},\iota(\widetilde{g}_1) \rangle=-1. \end{align*} $$
 $\Psi (\widetilde {F}_1)$
and
$\Psi (\widetilde {F}_1)$
and
 $\Psi (\widetilde {F}_2)$
: It follows that
$\Psi (\widetilde {F}_2)$
: It follows that $$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle =-2,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle =1. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle =-2,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle =1. \end{align*} $$
 $\Psi $
maps
$\Psi $
maps
 $C(\widetilde {F}_2)$
to the same half-space
$C(\widetilde {F}_2)$
to the same half-space
 $M^+$
with the same determinant
$M^+$
with the same determinant
 $|\det d \Psi (\widetilde {F}_2)|=|\det d \Psi (\widetilde {F})|=2^{r-1}$
, while
$|\det d \Psi (\widetilde {F}_2)|=|\det d \Psi (\widetilde {F})|=2^{r-1}$
, while
 $C(\widetilde {F}_1)$
is mapped to the opposite space
$C(\widetilde {F}_1)$
is mapped to the opposite space
 $M^-$
with determinant
$M^-$
with determinant
 $|\det d \Psi (\widetilde {F}_1)|=2^r$
. Since
$|\det d \Psi (\widetilde {F}_1)|=2^r$
. Since
 $2^r=2^{r-1}+2^{r-1}$
, the map
$2^r=2^{r-1}+2^{r-1}$
, the map
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
-
(3) The vertex v lies on
 $\gamma (G_0)$
and
$\gamma (G_0)$
and
 $v\nless u$
. Let
$v\nless u$
. Let
 $g_1$
and
$g_1$
and
 $g_2$
be the two edges of
$g_2$
be the two edges of
 $G_0$
rooted at v that lie on the cycle
$G_0$
rooted at v that lie on the cycle
 $\gamma (G_0)$
; then
$\gamma (G_0)$
; then
 $F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
and
$F_1=\{f_1,\ldots ,f_{g-2},g_1\}$
and
 $F_2=\{f_1,\ldots ,f_{g-2},g_2\}$
are genus 1 decompositions of
$F_2=\{f_1,\ldots ,f_{g-2},g_2\}$
are genus 1 decompositions of
 $G_0$
of the same rank r as F, since removing
$G_0$
of the same rank r as F, since removing
 $g_1$
or
$g_1$
or
 $g_2$
from
$g_2$
from
 $G_0\cup \{f_{g-1}\}$
gives a connected graph of genus 1. Any edge
$G_0\cup \{f_{g-1}\}$
gives a connected graph of genus 1. Any edge
 $f'\in T_vG_0$
other than
$f'\in T_vG_0$
other than
 $g_1$
and
$g_1$
and
 $g_2$
is the starting edge of a separate tree which does not contain
$g_2$
is the starting edge of a separate tree which does not contain
 $u=t(f_{g-1})$
, so
$u=t(f_{g-1})$
, so
 $G_0\cup \{f_{g-1}\}\backslash \{f'\}$
has a genus 0 connected component and
$G_0\cup \{f_{g-1}\}\backslash \{f'\}$
has a genus 0 connected component and
 $\{f_1,\ldots ,f_{g-2},f'\}$
is not a genus 1 decomposition.
$\{f_1,\ldots ,f_{g-2},f'\}$
is not a genus 1 decomposition.Let
 $\widetilde {g}_1$
and
$\widetilde {g}_1$
and
 $\widetilde {g}_2$
be the edges of
$\widetilde {g}_2$
be the edges of
 $\widetilde {G}$
at
$\widetilde {G}$
at
 $\widetilde {v}$
lying above
$\widetilde {v}$
lying above
 $g_1$
and
$g_1$
and
 $g_2$
, respectively, and denote
$g_2$
, respectively, and denote
 $\widetilde {F}_1=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_1\}$
and
$\widetilde {F}_1=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_1\}$
and
 $\widetilde {F}_2=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_2\}$
. The preimage of the cycle
$\widetilde {F}_2=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_2\}$
. The preimage of the cycle
 $\gamma (G_0)$
is the unique cycle
$\gamma (G_0)$
is the unique cycle
 $\gamma (p^{-1}(G_0))$
of the genus 1 graph
$\gamma (p^{-1}(G_0))$
of the genus 1 graph
 $p^{-1}(G_0)$
. We orient this cycle so that it starts with the edge
$p^{-1}(G_0)$
. We orient this cycle so that it starts with the edge
 $\widetilde {g}_1$
, passes through
$\widetilde {g}_1$
, passes through
 $\iota (\widetilde {v})$
and ends with
$\iota (\widetilde {v})$
and ends with
 $-\widetilde {g}_2$
. Let
$-\widetilde {g}_2$
. Let
 $\widetilde {u}'$
be the end vertex of the unique shortest path from
$\widetilde {u}'$
be the end vertex of the unique shortest path from
 $\widetilde {u}$
to
$\widetilde {u}$
to
 $\gamma (p^{-1}(G_0))$
; this vertex may be
$\gamma (p^{-1}(G_0))$
; this vertex may be
 $\widetilde {u}$
itself but cannot be
$\widetilde {u}$
itself but cannot be
 $\widetilde {v}$
or
$\widetilde {v}$
or
 $\iota (\widetilde {v})$
, since we have assumed that the shortest path from u to
$\iota (\widetilde {v})$
, since we have assumed that the shortest path from u to
 $\gamma (G_0)$
does not pass through v. We now assume without loss of generality that
$\gamma (G_0)$
does not pass through v. We now assume without loss of generality that
 $\widetilde {u}'$
lies on the same path from
$\widetilde {u}'$
lies on the same path from
 $\widetilde {v}$
to
$\widetilde {v}$
to
 $\iota (\widetilde {v})$
as
$\iota (\widetilde {v})$
as
 $\widetilde {g}_1$
; otherwise, exchange
$\widetilde {g}_1$
; otherwise, exchange
 $\widetilde {g}_1$
and
$\widetilde {g}_1$
and
 $\widetilde {g}_2$
(see Figure 8).
$\widetilde {g}_2$
(see Figure 8).
Figure 8 The cycle
 $\widetilde {\gamma }^+_{g-1}$
in Case (3).
$\widetilde {\gamma }^+_{g-1}$
in Case (3).All cells adjacent to
 $\widetilde {C}$
other than
$\widetilde {C}$
other than
 $C(\widetilde {F})$
,
$C(\widetilde {F})$
,
 $C(\widetilde {F}_1)$
and
$C(\widetilde {F}_1)$
and
 $C(\widetilde {F}_2)$
are contracted. For the last two, we need to compute the matrix entry (31). We now calculate the relevant intersection numbers. The path
$C(\widetilde {F}_2)$
are contracted. For the last two, we need to compute the matrix entry (31). We now calculate the relevant intersection numbers. The path
 $\widetilde {\gamma }^+_{g-1}$
starts at
$\widetilde {\gamma }^+_{g-1}$
starts at
 $\widetilde {v}$
, proceeds via
$\widetilde {v}$
, proceeds via
 $+\widetilde {f}_{g-1}$
to
$+\widetilde {f}_{g-1}$
to
 $\widetilde {u}$
and then to
$\widetilde {u}$
and then to
 $\widetilde {u}'$
and then back to
$\widetilde {u}'$
and then back to
 $\widetilde {v}$
along a path lying in
$\widetilde {v}$
along a path lying in
 $\gamma (p^{-1}(G_0))$
that ends with
$\gamma (p^{-1}(G_0))$
that ends with
 $-\widetilde {g}_1$
and does not contain
$-\widetilde {g}_1$
and does not contain
 $\iota (\widetilde {g}_1)$
,
$\iota (\widetilde {g}_1)$
,
 $\widetilde {g}_2$
or
$\widetilde {g}_2$
or
 $\iota (\widetilde {g}_2)$
. It follows that Therefore,
$\iota (\widetilde {g}_2)$
. It follows that Therefore, $$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle =-1,\quad\Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle =0. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle =-1,\quad\Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle =0. \end{align*} $$
 $\Psi $
maps
$\Psi $
maps
 $C(\widetilde {F}_1)$
to the opposite side
$C(\widetilde {F}_1)$
to the opposite side
 $M^-$
as
$M^-$
as
 $C(\widetilde {F})$
but with the same determinant
$C(\widetilde {F})$
but with the same determinant
 $|\det \Psi |=2^{r-1}$
. On the other hand,
$|\det \Psi |=2^{r-1}$
. On the other hand,
 $C(\widetilde {F}_2)$
is contracted (this can also be seen by noting that the preimage of the graph
$C(\widetilde {F}_2)$
is contracted (this can also be seen by noting that the preimage of the graph
 $G_0\cup \{f_{g-1}\}\backslash \{g_2\}$
is disconnected). Hence,
$G_0\cup \{f_{g-1}\}\backslash \{g_2\}$
is disconnected). Hence,
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
(4) Finally, we consider the possibility that v lies on
 $\gamma (G_0)$
and that
$\gamma (G_0)$
and that
 $v<u$
; in other words, u lies on a tree attached to v. In this case, there are three edges at v that give genus 1 decompositions: the two edges
$v<u$
; in other words, u lies on a tree attached to v. In this case, there are three edges at v that give genus 1 decompositions: the two edges
 $g_1$
and
$g_1$
and
 $g_2$
lying on the cycle
$g_2$
lying on the cycle
 $\gamma (G_0)$
and the edge
$\gamma (G_0)$
and the edge
 $g_3$
that starts the unique path from v to u. All other edges
$g_3$
that starts the unique path from v to u. All other edges
 $e'$
at v support trees, and their removal from
$e'$
at v support trees, and their removal from
 $G_0\cup \{f_{g-1}\}$
produces a connected component of genus 0.
$G_0\cup \{f_{g-1}\}$
produces a connected component of genus 0.For
 $i=1,2,3$
denote
$i=1,2,3$
denote
 $\widetilde {g}_i$
the lift of
$\widetilde {g}_i$
the lift of
 $g_i$
rooted at
$g_i$
rooted at
 $\widetilde {v}$
and denote
$\widetilde {v}$
and denote
 $\widetilde {F}_i=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_i\}$
. As in Case 2 above, there are two subcases, depending on whether the target vertex
$\widetilde {F}_i=\{\widetilde {f}_1,\ldots ,\widetilde {f}_{g-2},\widetilde {g}_i\}$
. As in Case 2 above, there are two subcases, depending on whether the target vertex
 $\widetilde {u}$
lies on the same tree
$\widetilde {u}$
lies on the same tree
 $T^{\pm }_0$
as
$T^{\pm }_0$
as
 $\widetilde {v}$
(say
$\widetilde {v}$
(say
 $T^+_0$
) or on the other tree. The two possibilities are shown on Figure 9.
$T^+_0$
) or on the other tree. The two possibilities are shown on Figure 9.
Figure 9 The cycle
 $\widetilde {\gamma }^+_{g-1}$
in the two sub-cases of Case (4).
$\widetilde {\gamma }^+_{g-1}$
in the two sub-cases of Case (4).-
(a) The vertex
 $\widetilde {u}$
lies on
$\widetilde {u}$
lies on
 $T^+_0$
. In this case, any path on the graph
$T^+_0$
. In this case, any path on the graph
 $p^{-1}(G_0\cup \{f_{g-1}\})$
starting at
$p^{-1}(G_0\cup \{f_{g-1}\})$
starting at
 $\widetilde {v}$
and ending at
$\widetilde {v}$
and ending at
 $\iota (\widetilde {v})$
passes through the preimage
$\iota (\widetilde {v})$
passes through the preimage
 $p^{-1}(\gamma (G_0))$
of the unique cycle of
$p^{-1}(\gamma (G_0))$
of the unique cycle of
 $G_0$
. Removing either
$G_0$
. Removing either
 $\{\widetilde {g}_1,\iota (\widetilde {g}_1)\}$
or
$\{\widetilde {g}_1,\iota (\widetilde {g}_1)\}$
or
 $\{\widetilde {g}_2,\iota (\widetilde {g}_2)\}$
from
$\{\widetilde {g}_2,\iota (\widetilde {g}_2)\}$
from
 $p^{-1}(\gamma (G_0))$
disconnects the cycle and therefore the entire preimage graph
$p^{-1}(\gamma (G_0))$
disconnects the cycle and therefore the entire preimage graph
 $p^{-1}(G_0\cup \{f_{g-1}\})$
. It follows that
$p^{-1}(G_0\cup \{f_{g-1}\})$
. It follows that
 $F_1$
and
$F_1$
and
 $F_2$
are not odd genus 1 decompositions. To prove harmonicity, we need to compute
$F_2$
are not odd genus 1 decompositions. To prove harmonicity, we need to compute
 $\Psi (\widetilde {F}_3)_{g-1,g-1}$
. The cycle
$\Psi (\widetilde {F}_3)_{g-1,g-1}$
. The cycle
 $\widetilde {\gamma }^+_{g-1}$
starts at
$\widetilde {\gamma }^+_{g-1}$
starts at
 $\widetilde {v}$
, proceeds to
$\widetilde {v}$
, proceeds to
 $\widetilde {u}$
via
$\widetilde {u}$
via
 $\widetilde {f}_{g-1}$
and then back to
$\widetilde {f}_{g-1}$
and then back to
 $\widetilde {v}$
via a path in
$\widetilde {v}$
via a path in
 $T_0^+$
that ends in
$T_0^+$
that ends in
 $-\widetilde {g}_3$
and does not contain
$-\widetilde {g}_3$
and does not contain
 $\iota (\widetilde {g}_3)$
. It follows that Therefore,
$\iota (\widetilde {g}_3)$
. It follows that Therefore, $$ \begin{align*}\Psi(\widetilde{F}_3)_{g-1,g-1}=\langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_3-\iota(\widetilde{g}_3)\rangle =-1. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_3)_{g-1,g-1}=\langle \widetilde{\gamma}^+_{g-1},\widetilde{g}_3-\iota(\widetilde{g}_3)\rangle =-1. \end{align*} $$
 $\Psi $
maps
$\Psi $
maps
 $C(\widetilde {F}_3)$
to the opposite side
$C(\widetilde {F}_3)$
to the opposite side
 $M^-$
as
$M^-$
as
 $C(\widetilde {F})$
but with the same determinant
$C(\widetilde {F})$
but with the same determinant
 $2^{r-1}$
. Hence,
$2^{r-1}$
. Hence,
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
(b) The vertex
 $\widetilde {u}$
lies on
$\widetilde {u}$
lies on
 $T^-_0$
. In this case, all three genus 1 decompositions
$T^-_0$
. In this case, all three genus 1 decompositions
 $F_1$
,
$F_1$
,
 $F_2$
and
$F_2$
and
 $F_3$
are odd. There are two paths from
$F_3$
are odd. There are two paths from
 $\widetilde {v}$
to
$\widetilde {v}$
to
 $\iota (\widetilde {v})$
along the cycle
$\iota (\widetilde {v})$
along the cycle
 $p^{-1}(\gamma (G_0))$
, starting with edges
$p^{-1}(\gamma (G_0))$
, starting with edges
 $\widetilde {g}_1$
and
$\widetilde {g}_1$
and
 $\widetilde {g}_2$
. We assume without loss of generality that the path that contains the edge
$\widetilde {g}_2$
. We assume without loss of generality that the path that contains the edge
 $\widetilde {e}^{{\kern1.5pt}+}_0$
(and hence lies in the spanning tree
$\widetilde {e}^{{\kern1.5pt}+}_0$
(and hence lies in the spanning tree
 $\widetilde {T}$
) begins with
$\widetilde {T}$
) begins with
 $\widetilde {g}_1$
. In this case, the path
$\widetilde {g}_1$
. In this case, the path
 $\widetilde {\gamma }^+_{g-1}$
begins at
$\widetilde {\gamma }^+_{g-1}$
begins at
 $\widetilde {v}$
, moves to
$\widetilde {v}$
, moves to
 $\widetilde {u}$
via
$\widetilde {u}$
via
 $\widetilde {f}_{g-1}$
and then to
$\widetilde {f}_{g-1}$
and then to
 $\iota (\widetilde {v})$
via a path ending in
$\iota (\widetilde {v})$
via a path ending in
 $-\iota (\widetilde {g}_3)$
and finally from
$-\iota (\widetilde {g}_3)$
and finally from
 $\iota (\widetilde {v})$
via the path (passing through
$\iota (\widetilde {v})$
via the path (passing through
 $\widetilde {e}^{{\kern1.5pt}+}_0$
) that starts with
$\widetilde {e}^{{\kern1.5pt}+}_0$
) that starts with
 $\iota (\widetilde {g}_2)$
and ends with
$\iota (\widetilde {g}_2)$
and ends with
 $-\widetilde {g}_1$
. Hence,
$-\widetilde {g}_1$
. Hence,
 $\widetilde {\gamma }^+_{g-1}$
contains
$\widetilde {\gamma }^+_{g-1}$
contains
 $-\widetilde {g}_1+\iota (\widetilde {g}_2)-\iota (\widetilde {g}_3)$
and does not contain the edges
$-\widetilde {g}_1+\iota (\widetilde {g}_2)-\iota (\widetilde {g}_3)$
and does not contain the edges
 $\iota (\widetilde {g}_1)$
,
$\iota (\widetilde {g}_1)$
,
 $\widetilde {g}_2$
or
$\widetilde {g}_2$
or
 $\widetilde {g}_3$
and therefore the diagonal entries are
$\widetilde {g}_3$
and therefore the diagonal entries are  $$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-1,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle=-1, \end{align*} $$
Therefore,
$$ \begin{align*}\Psi(\widetilde{F}_1)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-1,\quad \Psi(\widetilde{F}_2)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_2-\iota(\widetilde{g}_2)\rangle=-1, \end{align*} $$
Therefore, $$ \begin{align*}\Psi(\widetilde{F}_3)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_3-\iota(\widetilde{g}_3)\rangle=1. \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_3)_{g-1,g-1}=\langle\widetilde{\gamma}^+_{g-1},\widetilde{g}_3-\iota(\widetilde{g}_3)\rangle=1. \end{align*} $$
 $\Psi $
maps the two cells
$\Psi $
maps the two cells
 $C(\widetilde {F})$
and
$C(\widetilde {F})$
and
 $C(\widetilde {F}_3)$
to the half-space
$C(\widetilde {F}_3)$
to the half-space
 $M^+$
and the two cells
$M^+$
and the two cells
 $C(\widetilde {F}_1)$
and
$C(\widetilde {F}_1)$
and
 $C(\widetilde {F}_2)$
to the half-space
$C(\widetilde {F}_2)$
to the half-space
 $M^-$
, all with the same determinant
$M^-$
, all with the same determinant
 $2^{r-1}$
. Hence,
$2^{r-1}$
. Hence,
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
The endpoints of
![]() $f_a$
lie on different connected components of
$f_a$
lie on different connected components of
![]() $G\backslash F$
. We assume without loss of generality that
$G\backslash F$
. We assume without loss of generality that
![]() $v=s(f_a)$
lies on
$v=s(f_a)$
lies on
![]() $G_0$
and that
$G_0$
and that
![]() $u=t(f_a)$
lies on
$u=t(f_a)$
lies on
![]() $G_1$
. Furthermore, we assume that
$G_1$
. Furthermore, we assume that
![]() $f_a$
lies in the spanning tree
$f_a$
lies in the spanning tree
![]() $T^c$
, and the ordering convention then implies that
$T^c$
, and the ordering convention then implies that
![]() $f_a=f_1$
and
$f_a=f_1$
and
![]() $\widetilde {f}_a=\widetilde {f}_1$
. Since the matrix
$\widetilde {f}_a=\widetilde {f}_1$
. Since the matrix
![]() $\Psi (\widetilde {F})$
is lower triangular, we see that
$\Psi (\widetilde {F})$
is lower triangular, we see that
![]() $M^+=\Psi (H^+)=\{y:y_1\geq 0\}$
and
$M^+=\Psi (H^+)=\{y:y_1\geq 0\}$
and
![]() $M^-=\Psi (H^-)=\{y:y_1\leq 0\}$
.
$M^-=\Psi (H^-)=\{y:y_1\leq 0\}$
.
Let
![]() $\widetilde {f}'$
be an edge at
$\widetilde {f}'$
be an edge at
![]() $\widetilde {v}$
and let
$\widetilde {v}$
and let
 $\widetilde {F}'=\{\widetilde {f}',\widetilde {f}_2,\ldots ,\widetilde {f}_{g-1}\}$
define a cell
$\widetilde {F}'=\{\widetilde {f}',\widetilde {f}_2,\ldots ,\widetilde {f}_{g-1}\}$
define a cell
![]() $C(\widetilde {F}')$
adjacent to
$C(\widetilde {F}')$
adjacent to
![]() $C(\widetilde {F})$
via
$C(\widetilde {F})$
via
![]() $C'$
. The matrix
$C'$
. The matrix
![]() $\Psi (\widetilde {F}')$
is obtained from the matrix
$\Psi (\widetilde {F}')$
is obtained from the matrix
![]() $\Psi (\widetilde {F})$
by replacing the first column, so we are only interested in the new entry
$\Psi (\widetilde {F})$
by replacing the first column, so we are only interested in the new entry
 $\Psi (\widetilde {F}')_{11}=\langle \widetilde {\gamma }^+_1,\widetilde {f}'-\iota (\widetilde {f}')\rangle $
in the top left: if it is zero, then
$\Psi (\widetilde {F}')_{11}=\langle \widetilde {\gamma }^+_1,\widetilde {f}'-\iota (\widetilde {f}')\rangle $
in the top left: if it is zero, then
![]() $p(\widetilde {F}')$
is not an odd genus 1 decomposition, and if it is nonzero, then its sign determines whether
$p(\widetilde {F}')$
is not an odd genus 1 decomposition, and if it is nonzero, then its sign determines whether
![]() $\Psi $
maps
$\Psi $
maps
![]() $C(\widetilde {F}')$
to
$C(\widetilde {F}')$
to
![]() $M^+$
or
$M^+$
or
![]() $M^-$
.
$M^-$
.
The edge
![]() $f_1$
is a bridge edge of the graph
$f_1$
is a bridge edge of the graph
![]() $G_0\cup G_1\cup \{f_1\}$
. We need to consider two possibilities:
$G_0\cup G_1\cup \{f_1\}$
. We need to consider two possibilities:
-
(1) The vertex
 $v=s(f_1)$
does not lie on the unique cycle
$v=s(f_1)$
does not lie on the unique cycle
 $\gamma (G_0)$
of the graph
$\gamma (G_0)$
of the graph
 $G_0$
. There is a unique edge
$G_0$
. There is a unique edge
 $g_1$
at v pointing in the direction of
$g_1$
at v pointing in the direction of
 $\gamma (G_0)$
and the graph
$\gamma (G_0)$
and the graph
 $G_0\cup G_1\cup \{f_1\}\backslash \{g_1\}$
has two connected components of genus 1, namely,
$G_0\cup G_1\cup \{f_1\}\backslash \{g_1\}$
has two connected components of genus 1, namely,
 $G_0\backslash \{g_1\}$
and
$G_0\backslash \{g_1\}$
and
 $G_1$
. Therefore,
$G_1$
. Therefore,
 $F_1=\{g_1,f_2,\ldots ,f_{g-1}\}$
is an odd genus 1 decomposition of the same length r as F. Any other edge
$F_1=\{g_1,f_2,\ldots ,f_{g-1}\}$
is an odd genus 1 decomposition of the same length r as F. Any other edge
 $f'$
at v supports a tree rooted at v; hence, removing
$f'$
at v supports a tree rooted at v; hence, removing
 $f'$
from
$f'$
from
 $G_0\cup G_1\cup \{f\}$
separates a genus 0 connected component and the corresponding decomposition is not genus 1 (see Figure 10).
$G_0\cup G_1\cup \{f\}$
separates a genus 0 connected component and the corresponding decomposition is not genus 1 (see Figure 10).
Figure 10 The cycle
 $\widetilde {\gamma }^+_1$
in Case (1).
$\widetilde {\gamma }^+_1$
in Case (1).Let
 $\widetilde {g}_1$
denote the lift of
$\widetilde {g}_1$
denote the lift of
 $g_1$
at
$g_1$
at
 $\widetilde {v}$
and denote
$\widetilde {v}$
and denote
 $\widetilde {F}_1=\{\widetilde {g}_1,\widetilde {f}_2,\ldots ,\widetilde {f}_{g-1}\}$
. To show that
$\widetilde {F}_1=\{\widetilde {g}_1,\widetilde {f}_2,\ldots ,\widetilde {f}_{g-1}\}$
. To show that
 $\Psi $
is harmonic, it remains to show that
$\Psi $
is harmonic, it remains to show that
 $\Psi $
maps the cell
$\Psi $
maps the cell
 $C(\widetilde {F}_1)$
to the opposite side
$C(\widetilde {F}_1)$
to the opposite side
 $M^-$
; in other words, we need to show that the diagonal entry
$M^-$
; in other words, we need to show that the diagonal entry
 $\Psi (\widetilde {F}_1)_{11}=\langle \widetilde {\gamma }^+_1,\widetilde {g}_1-\iota (\widetilde {g}_1)\rangle $
is negative.
$\Psi (\widetilde {F}_1)_{11}=\langle \widetilde {\gamma }^+_1,\widetilde {g}_1-\iota (\widetilde {g}_1)\rangle $
is negative.We have chosen an edge
 $e_1$
lying on the unique cycle
$e_1$
lying on the unique cycle
 $\gamma (G_1)$
of
$\gamma (G_1)$
of
 $G_1$
and a lift
$G_1$
and a lift
 $\widetilde {e}^{{\kern1.5pt}+}_1$
lying on the unique cycle of
$\widetilde {e}^{{\kern1.5pt}+}_1$
lying on the unique cycle of
 $p^{-1}(G_1)$
, with the property that the path from
$p^{-1}(G_1)$
, with the property that the path from
 $\widetilde {u}=t(\widetilde {f})$
to
$\widetilde {u}=t(\widetilde {f})$
to
 $\iota (\widetilde {u})$
that passes through
$\iota (\widetilde {u})$
that passes through
 $\widetilde {e}^{{\kern1.5pt}+}_1$
has the same orientation as
$\widetilde {e}^{{\kern1.5pt}+}_1$
has the same orientation as
 $\widetilde {e}^{{\kern1.5pt}+}_1$
. Hence, the path
$\widetilde {e}^{{\kern1.5pt}+}_1$
. Hence, the path
 $\widetilde {\gamma }^+_1$
is constructed as follows: it starts at
$\widetilde {\gamma }^+_1$
is constructed as follows: it starts at
 $\widetilde {v}$
, proceeds via
$\widetilde {v}$
, proceeds via
 $\widetilde {f}_1$
to
$\widetilde {f}_1$
to
 $\widetilde {u}$
and then via the aforementioned path to
$\widetilde {u}$
and then via the aforementioned path to
 $\iota (\widetilde {u})$
, then to
$\iota (\widetilde {u})$
, then to
 $\iota (\widetilde {v})$
via
$\iota (\widetilde {v})$
via
 $-\iota (\widetilde {f}_1)$
and then from
$-\iota (\widetilde {f}_1)$
and then from
 $\iota (\widetilde {v})$
to
$\iota (\widetilde {v})$
to
 $\widetilde {v}$
via the unique path in
$\widetilde {v}$
via the unique path in
 $p^{-1}(G_0)$
containing the edge
$p^{-1}(G_0)$
containing the edge
 $\widetilde {e}^{{\kern1.5pt}+}_0$
. This path begins with
$\widetilde {e}^{{\kern1.5pt}+}_0$
. This path begins with
 $\iota (\widetilde {g}_1)$
and ends with
$\iota (\widetilde {g}_1)$
and ends with
 $-\widetilde {g}_1$
; hence, Therefore,
$-\widetilde {g}_1$
; hence, Therefore, $$ \begin{align*}\Psi(\widetilde{F}_1)_{11}=\langle \widetilde{\gamma}^+_1,\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-2.\\[-17pt] \end{align*} $$
$$ \begin{align*}\Psi(\widetilde{F}_1)_{11}=\langle \widetilde{\gamma}^+_1,\widetilde{g}_1-\iota(\widetilde{g}_1)\rangle=-2.\\[-17pt] \end{align*} $$
 $\Psi $
maps
$\Psi $
maps
 $C(\widetilde {F})$
and
$C(\widetilde {F})$
and
 $C(\widetilde {F}_1)$
to different sides of
$C(\widetilde {F}_1)$
to different sides of
 $\widetilde {C}$
with the same determinant, so
$\widetilde {C}$
with the same determinant, so
 $\Psi $
is harmonic.
$\Psi $
is harmonic.
-
(2) The vertex
 $v=s(f_1)$
lies on the unique cycle
$v=s(f_1)$
lies on the unique cycle
 $\gamma (G_0)$
of
$\gamma (G_0)$
of
 $G_0$
. It is easy to see that this case is in fact a relabelling of Case 2b described above. Indeed, let
$G_0$
. It is easy to see that this case is in fact a relabelling of Case 2b described above. Indeed, let
 $g^{\prime }_1$
and
$g^{\prime }_1$
and
 $g^{\prime }_2$
be the two edges at v lying on
$g^{\prime }_2$
be the two edges at v lying on
 $\gamma (G_0)$
. Replacing
$\gamma (G_0)$
. Replacing
 $f_1$
,
$f_1$
,
 $g^{\prime }_1$
and
$g^{\prime }_1$
and
 $g^{\prime }_2$
with respectively
$g^{\prime }_2$
with respectively
 $g_1$
,
$g_1$
,
 $f_{g-1}$
and
$f_{g-1}$
and
 $g_2$
, we obtain the same picture as in Case 2b (see Figure 11).
$g_2$
, we obtain the same picture as in Case 2b (see Figure 11).
Figure 11 The configuration in Case (2).
This completes the proof of Proposition 5.2.
Example 5.5. We now illustrate Theorem 5.1, the structure of the Abel–Prym map, as well as Constructions A, B and C, using the free double cover
![]() $\pi :\widetilde {\Gamma }\to \Gamma $
shown in Figure 12. We note that
$\pi :\widetilde {\Gamma }\to \Gamma $
shown in Figure 12. We note that
![]() $g=3$
; hence, the Abel–Prym map
$g=3$
; hence, the Abel–Prym map
maps to the identity connected component of the Prym variety. The graph
![]() $\widetilde {\Gamma }$
has no loops, so it is sufficient to use the minimal model
$\widetilde {\Gamma }$
has no loops, so it is sufficient to use the minimal model
![]() $p:\widetilde {G}\to G$
, which is obtained by not subdividing any edges.
$p:\widetilde {G}\to G$
, which is obtained by not subdividing any edges.

Figure 12 Free double cover with
![]() $g=3$
.
$g=3$
.
We begin by using Construction C to define a basis
![]() $\widetilde {\gamma }_1,\widetilde {\gamma }_2$
for
$\widetilde {\gamma }_1,\widetilde {\gamma }_2$
for
![]() $\operatorname {\mathrm {Ker}} p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
. This basis defines a coordinate system on
$\operatorname {\mathrm {Ker}} p_*:H_1(\widetilde {G},\mathbb {Z})\to H_1(G,\mathbb {Z})$
. This basis defines a coordinate system on
![]() $\operatorname {\mathrm {Prym}} (\widetilde {\Gamma }/\Gamma )$
. We will write down the matrix of
$\operatorname {\mathrm {Prym}} (\widetilde {\Gamma }/\Gamma )$
. We will write down the matrix of
![]() $\Psi $
with respect to this coordinate system on each noncontracted cell of
$\Psi $
with respect to this coordinate system on each noncontracted cell of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. First, we need to choose two edges
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. First, we need to choose two edges
![]() $\widetilde {f}_1,\widetilde {f}_2\in E(\widetilde {G})$
mapping to distinct edges of G. It is convenient to set
$\widetilde {f}_1,\widetilde {f}_2\in E(\widetilde {G})$
mapping to distinct edges of G. It is convenient to set
 $\widetilde {f}_1=\widetilde {h}^+_3$
and
$\widetilde {f}_1=\widetilde {h}^+_3$
and
 $\widetilde {f}_2=\widetilde {h}^-_6$
. Removing
$\widetilde {f}_2=\widetilde {h}^-_6$
. Removing
![]() $f_1=h_3$
and
$f_1=h_3$
and
![]() $f_2=h_6$
decomposes G into three connected components, which we denote as follows:
$f_2=h_6$
decomposes G into three connected components, which we denote as follows:
For
![]() $G_0$
we choose the spanning tree
$G_0$
we choose the spanning tree
![]() $T_0=\{h_5\}$
, while
$T_0=\{h_5\}$
, while
![]() $G_1$
and
$G_1$
and
![]() $G_2$
have trivial spanning trees. The corresponding spanning tree T of G is
$G_2$
have trivial spanning trees. The corresponding spanning tree T of G is
To construct a spanning tree
![]() $\widetilde {T}$
for
$\widetilde {T}$
for
![]() $\widetilde {G}$
, we join the two lifts
$\widetilde {G}$
, we join the two lifts
![]() $\widetilde {T}^{\pm }$
of T with one of the lifts of
$\widetilde {T}^{\pm }$
of T with one of the lifts of
![]() $h_4$
. We choose
$h_4$
. We choose
 $\widetilde {e}^{{\kern1.5pt}+}_0=\widetilde {h}^+_4$
, so that
$\widetilde {e}^{{\kern1.5pt}+}_0=\widetilde {h}^+_4$
, so that
 $$ \begin{align*}\widetilde{T}=\widetilde{T}^+\cup\widetilde{T}^-\cup\{\widetilde{e}^{{\kern2pt}+}_0\}=\{\widetilde{h}^{\pm}_3,\widetilde{h}^+_4,\widetilde{h}^{\pm}_5, \widetilde{h}^{\pm}_6\}. \end{align*} $$
$$ \begin{align*}\widetilde{T}=\widetilde{T}^+\cup\widetilde{T}^-\cup\{\widetilde{e}^{{\kern2pt}+}_0\}=\{\widetilde{h}^{\pm}_3,\widetilde{h}^+_4,\widetilde{h}^{\pm}_5, \widetilde{h}^{\pm}_6\}. \end{align*} $$
In order to agree with the notation of Constructions A-C, we denote
![]() $e_0=h_4$
,
$e_0=h_4$
,
![]() $e_1=h_1$
,
$e_1=h_1$
,
![]() $e_2=h_7$
,
$e_2=h_7$
,
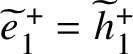 $\widetilde {e}^{{\kern1.5pt}+}_1=\widetilde {h}^+_1$
and
$\widetilde {e}^{{\kern1.5pt}+}_1=\widetilde {h}^+_1$
and
 $\widetilde {e}^{{\kern1.5pt}+}_2=\widetilde {h}^+_7$
(recall that we require
$\widetilde {e}^{{\kern1.5pt}+}_2=\widetilde {h}^+_7$
(recall that we require
![]() $t(\widetilde {f}_k)=s(\widetilde {e}_k)$
).
$t(\widetilde {f}_k)=s(\widetilde {e}_k)$
).
According to Construction B, the cycles
![]() $\widetilde {\gamma }^+_1$
and
$\widetilde {\gamma }^+_1$
and
![]() $\widetilde {\gamma }^+_2$
are the unique cycles of
$\widetilde {\gamma }^+_2$
are the unique cycles of
![]() $\widetilde {G}$
containing the spanning tree
$\widetilde {G}$
containing the spanning tree
![]() $\widetilde {T}$
and the edges
$\widetilde {T}$
and the edges
 $\widetilde {e}^{{\kern1.5pt}+}_1=\widetilde {h}^+_1$
and
$\widetilde {e}^{{\kern1.5pt}+}_1=\widetilde {h}^+_1$
and
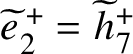 $\widetilde {e}^{{\kern1.5pt}+}_2=\widetilde {h}^+_7$
, respectively. In other words,
$\widetilde {e}^{{\kern1.5pt}+}_2=\widetilde {h}^+_7$
, respectively. In other words,
 $$ \begin{align*}\widetilde{\gamma}^+_1=\widetilde{h}_1^+-\widetilde{h}^-_3-\widetilde{h}^+_4-\widetilde{h}^+_5+\widetilde{h}^+_3,\quad \widetilde{\gamma}^+_2=\widetilde{h}^+_7-\widetilde{h}^+_6+\widetilde{h}^+_4+\widetilde{h}^-_5+\widetilde{h}^-_6. \end{align*} $$
$$ \begin{align*}\widetilde{\gamma}^+_1=\widetilde{h}_1^+-\widetilde{h}^-_3-\widetilde{h}^+_4-\widetilde{h}^+_5+\widetilde{h}^+_3,\quad \widetilde{\gamma}^+_2=\widetilde{h}^+_7-\widetilde{h}^+_6+\widetilde{h}^+_4+\widetilde{h}^-_5+\widetilde{h}^-_6. \end{align*} $$
The cycles
![]() $\widetilde {\gamma }^+_1-\iota _*(\widetilde {\gamma }^+_1)$
and
$\widetilde {\gamma }^+_1-\iota _*(\widetilde {\gamma }^+_1)$
and
![]() $\widetilde {\gamma }^+_2-\iota _*(\widetilde {\gamma }^+_2)$
form a basis for
$\widetilde {\gamma }^+_2-\iota _*(\widetilde {\gamma }^+_2)$
form a basis for
![]() $\operatorname {\mathrm {Ker}} p_*$
.
$\operatorname {\mathrm {Ker}} p_*$
.
We now determine the matrix of the linear map
![]() $\Psi $
on each noncontracted cell of
$\Psi $
on each noncontracted cell of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. There are 15 two-element subsets of
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. There are 15 two-element subsets of
![]() $E(G)$
, and all of them are odd genus 1 decompositions except for
$E(G)$
, and all of them are odd genus 1 decompositions except for
![]() $\{h_1,h_3\}$
and
$\{h_1,h_3\}$
and
![]() $\{h_6,h_7\}$
. Therefore, there are 52 cells of
$\{h_6,h_7\}$
. Therefore, there are 52 cells of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
on which
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
on which
![]() $\Psi $
has maximal rank, corresponding to the 13 odd genus 1 decompositions. The matrix of
$\Psi $
has maximal rank, corresponding to the 13 odd genus 1 decompositions. The matrix of
![]() $\Psi $
on a cell
$\Psi $
on a cell
 $\widetilde {h}^+_i\times \widetilde {h}^+_j$
is the
$\widetilde {h}^+_i\times \widetilde {h}^+_j$
is the
![]() $2\times 2$
matrix whose columns are obtained by respectively intersecting
$2\times 2$
matrix whose columns are obtained by respectively intersecting
 $\widetilde {h}^+_i-\widetilde {h}^-_i$
and
$\widetilde {h}^+_i-\widetilde {h}^-_i$
and
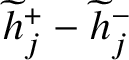 $\widetilde {h}^+_j-\widetilde {h}^-_j$
with the cycles
$\widetilde {h}^+_j-\widetilde {h}^-_j$
with the cycles
![]() $\widetilde {\gamma }^+_1$
and
$\widetilde {\gamma }^+_1$
and
![]() $\widetilde {\gamma }^+_2$
, and the matrix of
$\widetilde {\gamma }^+_2$
, and the matrix of
![]() $\Psi $
on the other three cells
$\Psi $
on the other three cells
 $\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j$
is obtained by appropriately changing the signs of the columns.
$\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j$
is obtained by appropriately changing the signs of the columns.
Table 1 lists the 13 odd genus 1 decompositions of the graph G. For each odd genus 1 decomposition
![]() $F=\{h_i,h_j\}$
, we provide the rank
$F=\{h_i,h_j\}$
, we provide the rank
![]() $r(F)$
(the number of connected components of
$r(F)$
(the number of connected components of
![]() $G\backslash F)$
, the local degree
$G\backslash F)$
, the local degree
![]() $\deg \Psi =2^{r(F)-1}$
on each cell of
$\deg \Psi =2^{r(F)-1}$
on each cell of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
corresponding to the odd genus 1 decomposition and the matrix of
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
corresponding to the odd genus 1 decomposition and the matrix of
![]() $\Psi $
on the cell
$\Psi $
on the cell
 $\widetilde {h}^+_i\times \widetilde {h}^-_i$
(the absolute value of its determinant is
$\widetilde {h}^+_i\times \widetilde {h}^-_i$
(the absolute value of its determinant is
![]() $\deg \Psi $
). We also assign a colour to each odd genus 1 decomposition.
$\deg \Psi $
). We also assign a colour to each odd genus 1 decomposition.
Table 1 The 13 odd genus 1 decompositions of the graph G.

We now explain how to construct the Abel–Prym map
![]() $\Psi :\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. We first choose a starting cell; it is convenient to begin with the cell
$\Psi :\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. We first choose a starting cell; it is convenient to begin with the cell
 $\widetilde {f}_1\times \widetilde {f}_2=\widetilde {h}^+_3\times \widetilde {h}^-_6$
. According to our calculations, the matrix of
$\widetilde {f}_1\times \widetilde {f}_2=\widetilde {h}^+_3\times \widetilde {h}^-_6$
. According to our calculations, the matrix of
![]() $\Psi $
on this cell is
$\Psi $
on this cell is
 $$ \begin{align*}\Psi|_{\widetilde{h}^+_3\times \widetilde{h}^-_6}=\left[\begin{array}{c@{\quad}c} 2 & 0 \\ 0 & 2 \end{array}\right]; \end{align*} $$
$$ \begin{align*}\Psi|_{\widetilde{h}^+_3\times \widetilde{h}^-_6}=\left[\begin{array}{c@{\quad}c} 2 & 0 \\ 0 & 2 \end{array}\right]; \end{align*} $$
note that this matrix is lower-triangular with
![]() $r(\{h_3,h_6)\})-1=2$
diagonal entries equal to
$r(\{h_3,h_6)\})-1=2$
diagonal entries equal to
![]() $2$
, in accordance with Corollary 4.2. Viewing
$2$
, in accordance with Corollary 4.2. Viewing
 $\widetilde {h}^+_3\times \widetilde {h}^-_6$
as the rectangle
$\widetilde {h}^+_3\times \widetilde {h}^-_6$
as the rectangle
![]() $[0,\ell (h_3)]\times [0,\ell (h_6)]$
in
$[0,\ell (h_3)]\times [0,\ell (h_6)]$
in
![]() $\mathbb {R}^2$
, we see that
$\mathbb {R}^2$
, we see that
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
is a rectangle with sides
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
is a rectangle with sides
![]() $2\ell (h_3)$
and
$2\ell (h_3)$
and
![]() $2\ell (h_6)$
in
$2\ell (h_6)$
in
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
(with respect to the coordinate system defined by
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
(with respect to the coordinate system defined by
![]() $\widetilde {\gamma }_1$
and
$\widetilde {\gamma }_1$
and
![]() $\widetilde {\gamma }_2$
). We note that since
$\widetilde {\gamma }_2$
). We note that since
![]() $\deg \Psi =4$
on the cell
$\deg \Psi =4$
on the cell
 $\widetilde {h}^+_3\times \widetilde {h}^-_6$
, the Abel–Prym map is one-to-one over the interior of the cell; in other words, there are no other cells of
$\widetilde {h}^+_3\times \widetilde {h}^-_6$
, the Abel–Prym map is one-to-one over the interior of the cell; in other words, there are no other cells of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
lying over
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
lying over
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
.
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
.
We now look at the graph to locate the cells in
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
that are adjacent to
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
that are adjacent to
 $\widetilde {h}^+_3\times \widetilde {h}^-_6$
, by changing one of the two edges to an adjacent edge. We then use Table 1 to determine their images in
$\widetilde {h}^+_3\times \widetilde {h}^-_6$
, by changing one of the two edges to an adjacent edge. We then use Table 1 to determine their images in
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. For example, the terminal vertex of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. For example, the terminal vertex of
![]() $\widetilde {h}^+_3$
is the starting vertex of
$\widetilde {h}^+_3$
is the starting vertex of
![]() $\widetilde {h}^+_1$
and the terminal vertex of
$\widetilde {h}^+_1$
and the terminal vertex of
![]() $\widetilde {h}^-_1$
. Therefore, the images of the two cells
$\widetilde {h}^-_1$
. Therefore, the images of the two cells
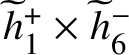 $\widetilde {h}^+_1\times \widetilde {h}^-_6$
and
$\widetilde {h}^+_1\times \widetilde {h}^-_6$
and
 $\widetilde {h}^-_1\times \widetilde {h}^-_6$
are glued to the right side of the rectangle
$\widetilde {h}^-_1\times \widetilde {h}^-_6$
are glued to the right side of the rectangle
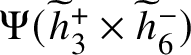 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
. According to the table, each of the images
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
. According to the table, each of the images
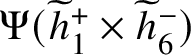 $\Psi (\widetilde {h}^+_1\times \widetilde {h}^-_6)$
and
$\Psi (\widetilde {h}^+_1\times \widetilde {h}^-_6)$
and
 $\Psi (\widetilde {h}^+_1\times \widetilde {h}^-_6)$
is a rectangle with sides
$\Psi (\widetilde {h}^+_1\times \widetilde {h}^-_6)$
is a rectangle with sides
![]() $\ell (h_1)$
and
$\ell (h_1)$
and
![]() $2\ell (h_6)$
; this implies that these images coincide. Similarly, along the top edge of the rectangle
$2\ell (h_6)$
; this implies that these images coincide. Similarly, along the top edge of the rectangle
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
we glue two identical rectangles
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
we glue two identical rectangles
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^+_7)$
and
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^+_7)$
and
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_7)$
. On the other hand, the two cells that are glued along the left side of the rectangle
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_7)$
. On the other hand, the two cells that are glued along the left side of the rectangle
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
are the noncongruent parallelograms
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
are the noncongruent parallelograms
 $\Psi (\widetilde {h}^+_5\times \widetilde {h}^-_6)$
and
$\Psi (\widetilde {h}^+_5\times \widetilde {h}^-_6)$
and
 $\Psi (\widetilde {h}^-_4\times \widetilde {h}^-_6)$
and, similarly, there are two noncongruent parallelograpms along the bottom side of
$\Psi (\widetilde {h}^-_4\times \widetilde {h}^-_6)$
and, similarly, there are two noncongruent parallelograpms along the bottom side of
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
.
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_6)$
.
We then proceed in the same way for all noncontracted cells. For example, the right sides of the two identical rectangles
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^+_7)$
and
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^+_7)$
and
 $\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_7)$
are attached to the left side of the rectangle
$\Psi (\widetilde {h}^+_3\times \widetilde {h}^-_7)$
are attached to the left side of the rectangle
 $\Psi (\widetilde {h}^-_3\times \widetilde {h}^-_6)$
and so on. The result is a collection of overlapping parallelograms
$\Psi (\widetilde {h}^-_3\times \widetilde {h}^-_6)$
and so on. The result is a collection of overlapping parallelograms
 $\Psi (\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j)$
tiling the torus
$\Psi (\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j)$
tiling the torus
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Each parallelogram tile comes equipped with the degree of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Each parallelogram tile comes equipped with the degree of
![]() $\Psi $
(equal to 1, 2 or 4) and the total degree of all tiles above each point is equal to 4, so any point not lying on the boundary of a tile lies in anywhere between one and four tiles. The structure of the overlaps strongly depends on the exact values of the edge lengths
$\Psi $
(equal to 1, 2 or 4) and the total degree of all tiles above each point is equal to 4, so any point not lying on the boundary of a tile lies in anywhere between one and four tiles. The structure of the overlaps strongly depends on the exact values of the edge lengths
![]() $\ell (h_i)$
.
$\ell (h_i)$
.
The result, for a specific choice of edge lengths, is shown in Figure 13. The top part is an exploded view of the noncontracted cells of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. Each cell
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. Each cell
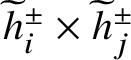 $\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j$
is represented by a parallelogram and is coloured according to the corresponding odd genus 1 decomposition
$\widetilde {h}^{\pm }_i\times \widetilde {h}^{\pm }_j$
is represented by a parallelogram and is coloured according to the corresponding odd genus 1 decomposition
![]() $\{h_i,h_j\}$
(see Table 1). The cells are arranged in several horizontal layers and are oriented and aligned according to their images in
$\{h_i,h_j\}$
(see Table 1). The cells are arranged in several horizontal layers and are oriented and aligned according to their images in
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. For example, the four large dark grey cells in the middle layer represent the four cells
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. For example, the four large dark grey cells in the middle layer represent the four cells
 $\widetilde {h}^{\pm }_3\times \widetilde {h}^{\pm }_6$
, which are the only cells of degree 4. No attempt has been made to show the incidence relations between the cells in
$\widetilde {h}^{\pm }_3\times \widetilde {h}^{\pm }_6$
, which are the only cells of degree 4. No attempt has been made to show the incidence relations between the cells in
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
, since this complex is not embeddable in
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
, since this complex is not embeddable in
![]() $\mathbb {R}^3$
and the numerous cells that are contracted by
$\mathbb {R}^3$
and the numerous cells that are contracted by
![]() $\Psi $
are not shown.
$\Psi $
are not shown.

Figure 13 The structure of the Abel–Prym map
![]() $\Psi :\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
of the cover shown in Figure 12. The tesselated parallelogram on the bottom is
$\Psi :\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })\to \operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
of the cover shown in Figure 12. The tesselated parallelogram on the bottom is
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
with the cell decomposition induced by
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
with the cell decomposition induced by
![]() $\Psi $
. The top and middle parts are an exploded view of the noncontracted cells of
$\Psi $
. The top and middle parts are an exploded view of the noncontracted cells of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. Cells of
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
. Cells of
![]() $\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
are coloured according to the type of the odd genus 1 decomposition; these colours are mixed in cells of
$\operatorname {\mathrm {Sym}}^2(\widetilde {\Gamma })$
are coloured according to the type of the odd genus 1 decomposition; these colours are mixed in cells of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Edge lengths are
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
. Edge lengths are
![]() $\ell (h_1)=2.4$
,
$\ell (h_1)=2.4$
,
![]() $\ell (h_3)=0.8$
,
$\ell (h_3)=0.8$
,
![]() $\ell (h_4)=1$
,
$\ell (h_4)=1$
,
![]() $\ell (h_5)=1.4$
,
$\ell (h_5)=1.4$
,
![]() $\ell (h_6)=1.1$
,
$\ell (h_6)=1.1$
,
![]() $\ell (h_7)=1.4$
.
$\ell (h_7)=1.4$
.
The multicoloured parallelogram on the bottom layer is
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
with the induced cellular decomposition, obtained by intersecting all of the tiles. A cell corresponding to a single parallelogram has the same colour, while if parallelograms of different colours intersect, we blend the corresponding colours. The central point of the parallelogram is the identity element of
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
with the induced cellular decomposition, obtained by intersecting all of the tiles. A cell corresponding to a single parallelogram has the same colour, while if parallelograms of different colours intersect, we blend the corresponding colours. The central point of the parallelogram is the identity element of
![]() $\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
.
$\operatorname {\mathrm {Prym}}(\widetilde {\Gamma }/\Gamma )$
.
A The algebraic Abel–Prym map (by Sebastian Casalaina-Martin)
Let
![]() $\pi :\widetilde C\to C$
be a connected étale double cover of a smooth projective curve C of genus
$\pi :\widetilde C\to C$
be a connected étale double cover of a smooth projective curve C of genus
![]() $g\ge 2$
over an algebraically closed field k of characteristic not equal to
$g\ge 2$
over an algebraically closed field k of characteristic not equal to
![]() $2$
, let
$2$
, let
![]() $\iota :\widetilde C\to \widetilde C$
be the associated involution and denote by
$\iota :\widetilde C\to \widetilde C$
be the associated involution and denote by
![]() $\operatorname {\mathrm {Nm}}:J(\widetilde C)\to J(C)$
the norm map for
$\operatorname {\mathrm {Nm}}:J(\widetilde C)\to J(C)$
the norm map for
![]() $\pi $
, where for a smooth projective curve X over k we denote by
$\pi $
, where for a smooth projective curve X over k we denote by
 $J(X)=\operatorname {Pic}^0_{X/k}$
the Jacobian of X. For any natural number d the Abel–Prym map in degree d is defined to be the map
$J(X)=\operatorname {Pic}^0_{X/k}$
the Jacobian of X. For any natural number d the Abel–Prym map in degree d is defined to be the map
 $$ \begin{align*}\widetilde D\mapsto \mathcal O_{\widetilde C}(\widetilde D-\iota \widetilde D), \end{align*} $$
$$ \begin{align*}\widetilde D\mapsto \mathcal O_{\widetilde C}(\widetilde D-\iota \widetilde D), \end{align*} $$
where
![]() $\widetilde C^{(d)}$
is the d-fold symmetric product of the curve. The kernel of the norm map has two connected components, namely, the Prym variety
$\widetilde C^{(d)}$
is the d-fold symmetric product of the curve. The kernel of the norm map has two connected components, namely, the Prym variety
![]() $P=P(\widetilde C/C):=(\ker \operatorname {\mathrm {Nm}})^\circ $
, the connected component of the identity and the remaining component, which we will denote by
$P=P(\widetilde C/C):=(\ker \operatorname {\mathrm {Nm}})^\circ $
, the connected component of the identity and the remaining component, which we will denote by
![]() $P'$
; P admits a principal polarisation
$P'$
; P admits a principal polarisation
![]() $\Xi $
with the property that if
$\Xi $
with the property that if
![]() $\Theta _{\widetilde C}$
is the canonical principal polarisation on
$\Theta _{\widetilde C}$
is the canonical principal polarisation on
![]() $J(\widetilde C)$
, then
$J(\widetilde C)$
, then
![]() $\Theta _{\widetilde C}|_P = 2\cdot \Xi $
(e.g., [Reference MumfordMum74, §6]). The image of
$\Theta _{\widetilde C}|_P = 2\cdot \Xi $
(e.g., [Reference MumfordMum74, §6]). The image of
![]() $\delta _d$
is contained in P if d is even and contained in
$\delta _d$
is contained in P if d is even and contained in
![]() $P'$
if d is odd (e.g., [Reference BeauvilleBea77, Lem. 3.3, and p. 159]).
$P'$
if d is odd (e.g., [Reference BeauvilleBea77, Lem. 3.3, and p. 159]).
The Abel–Prym map in degree
![]() $1$
has been studied quite extensively, and we recall this case in Subsection A.1. In particular, the map
$1$
has been studied quite extensively, and we recall this case in Subsection A.1. In particular, the map
![]() $\delta _1$
is a closed embedding if and only if
$\delta _1$
is a closed embedding if and only if
![]() $\widetilde C$
is not hyperelliptic and has degree
$\widetilde C$
is not hyperelliptic and has degree
![]() $2$
otherwise. The purpose of this appendix is to provide a proof of some basic facts regarding the Abel–Prym map for
$2$
otherwise. The purpose of this appendix is to provide a proof of some basic facts regarding the Abel–Prym map for
![]() $d>1$
. We expect that these are well known but are not aware of a reference in the literature.
$d>1$
. We expect that these are well known but are not aware of a reference in the literature.
Proposition A.1 Corollary A.9, Corollary A.13 and Proposition A.14
The Abel–Prym map
![]() $\delta _d$
is generically finite if and only if
$\delta _d$
is generically finite if and only if
![]() $d\le g-1$
and surjects onto P (respectively
$d\le g-1$
and surjects onto P (respectively
![]() $P'$
) if and only if
$P'$
) if and only if
![]() $d\ge g-1$
and d is even (respectively d is odd). Moreover,
$d\ge g-1$
and d is even (respectively d is odd). Moreover,
![]() $\deg \delta _{g-1}=2^{g-1}$
, and if
$\deg \delta _{g-1}=2^{g-1}$
, and if
![]() $\operatorname {char}(k)=0$
, then for
$\operatorname {char}(k)=0$
, then for
![]() $d\le g-2$
we have
$d\le g-2$
we have
![]() $\deg \delta _d=2^n\le 2^d$
for some integer
$\deg \delta _d=2^n\le 2^d$
for some integer
![]() $n\le d$
, with equality holding if
$n\le d$
, with equality holding if
![]() $\widetilde C$
is hyperelliptic.
$\widetilde C$
is hyperelliptic.
Remark A.2 Degree bound in positive characteristic
If
![]() $\operatorname {char}(k)=p>0$
, then for
$\operatorname {char}(k)=p>0$
, then for
![]() $d\le g-2$
we show that
$d\le g-2$
we show that
![]() $\deg \delta _d=p^{m}2^n$
for some integers m and n with
$\deg \delta _d=p^{m}2^n$
for some integers m and n with
![]() $n\le d$
. The reason for the uncontrolled power of p in the formula is that we compute the degree via a cohomology class computation in
$n\le d$
. The reason for the uncontrolled power of p in the formula is that we compute the degree via a cohomology class computation in
![]() $\ell $
-adic cohomology, with
$\ell $
-adic cohomology, with
![]() $\ell \ne p$
. A similar computation in crystalline cohomology allows one to remove the powers of p.
$\ell \ne p$
. A similar computation in crystalline cohomology allows one to remove the powers of p.
For general covers one has the following.
Proposition A.3 Corollary A.15
Let
![]() $\widetilde C/C$
be a general cover. Then
$\widetilde C/C$
be a general cover. Then
![]() $\deg \delta _d=1$
for
$\deg \delta _d=1$
for
![]() $d<g/2$
.
$d<g/2$
.
While
![]() $\delta _1$
is finite, in contrast, for all
$\delta _1$
is finite, in contrast, for all
![]() $d\ge 2$
there exist positive dimensional fibres of
$d\ge 2$
there exist positive dimensional fibres of
![]() $\delta _d$
. Indeed, it suffices to show this for d even since for all d, fibres of
$\delta _d$
. Indeed, it suffices to show this for d even since for all d, fibres of
![]() $\delta _{d}$
can be included in fibres of
$\delta _{d}$
can be included in fibres of
![]() $\delta _{d+1}$
using the observation that if
$\delta _{d+1}$
using the observation that if
![]() $\delta _{d}(\widetilde D) = \delta _{d}(\widetilde D')$
, then
$\delta _{d}(\widetilde D) = \delta _{d}(\widetilde D')$
, then
![]() $\delta _{d+1}(\widetilde D+\tilde p) = \delta _{d+1}(\widetilde D' + \tilde p)$
for any
$\delta _{d+1}(\widetilde D+\tilde p) = \delta _{d+1}(\widetilde D' + \tilde p)$
for any
![]() $\tilde p\in \widetilde C$
. For d even, we note that the composition
$\tilde p\in \widetilde C$
. For d even, we note that the composition
 $C^{(d/2)}\stackrel {\pi ^*}{\to } \widetilde C^{(d)}\stackrel {\delta _{d}}{\to } P\subseteq J(\widetilde C)$
has image
$C^{(d/2)}\stackrel {\pi ^*}{\to } \widetilde C^{(d)}\stackrel {\delta _{d}}{\to } P\subseteq J(\widetilde C)$
has image
![]() $\mathcal O_{\widetilde C}$
.
$\mathcal O_{\widetilde C}$
.
Sometimes in the presentation it will be convenient to fix a divisor
![]() $\widetilde D_0\in \widetilde C^{(d)}$
and then consider the associated pointed Abel–Prym map
$\widetilde D_0\in \widetilde C^{(d)}$
and then consider the associated pointed Abel–Prym map
 $$ \begin{align*}\delta_{d,\widetilde D_0}: \widetilde C^{(d)}\longrightarrow P \subseteq J(\widetilde C) \end{align*} $$
$$ \begin{align*}\delta_{d,\widetilde D_0}: \widetilde C^{(d)}\longrightarrow P \subseteq J(\widetilde C) \end{align*} $$
 $$ \begin{align*}D\mapsto \mathcal O_{\widetilde C}(\widetilde D-\iota \widetilde D)\otimes \mathcal O_{\widetilde C}(\iota \widetilde D_0-\widetilde D_0), \end{align*} $$
$$ \begin{align*}D\mapsto \mathcal O_{\widetilde C}(\widetilde D-\iota \widetilde D)\otimes \mathcal O_{\widetilde C}(\iota \widetilde D_0-\widetilde D_0), \end{align*} $$
which simply differs from the canonical Abel–Prym map
![]() $\delta _d$
by translation by
$\delta _d$
by translation by
 $\mathcal O_{\widetilde C}(\iota \widetilde D_0-\widetilde D_0)$
and has image contained in the Prym variety. We emphasise for clarity that the Abel–Prym map and pointed Abel–Prym map defined here are different from the map obtained by restricting the Abel map in degree d to a chosen translate of the Prym variety (e.g., [Reference BeauvilleBea82, Reference Smith and VarleySV01]).
$\mathcal O_{\widetilde C}(\iota \widetilde D_0-\widetilde D_0)$
and has image contained in the Prym variety. We emphasise for clarity that the Abel–Prym map and pointed Abel–Prym map defined here are different from the map obtained by restricting the Abel map in degree d to a chosen translate of the Prym variety (e.g., [Reference BeauvilleBea82, Reference Smith and VarleySV01]).
A.1 The Abel–Prym map in degree
 $1$
$1$
We recall the following well-known result.
Proposition A.4. For any prime number
![]() $\ell \ne \operatorname {char}(k)$
and any point
$\ell \ne \operatorname {char}(k)$
and any point
![]() $\tilde p_0\in \widetilde C$
, the class of the pushforward of
$\tilde p_0\in \widetilde C$
, the class of the pushforward of
![]() $\widetilde C$
by the pointed Abel–Prym map is
$\widetilde C$
by the pointed Abel–Prym map is
 $$ \begin{align} (\delta_{1,\tilde p_0})_*[\widetilde C]=2\cdot \frac{[\Xi]^{\rho-1}}{(\rho-1)!} \in H^{2\rho -2}(P,\mathbb Z_\ell(\rho-1)), \end{align} $$
$$ \begin{align} (\delta_{1,\tilde p_0})_*[\widetilde C]=2\cdot \frac{[\Xi]^{\rho-1}}{(\rho-1)!} \in H^{2\rho -2}(P,\mathbb Z_\ell(\rho-1)), \end{align} $$
where
![]() $\rho =\dim P=g-1$
. In addition, if
$\rho =\dim P=g-1$
. In addition, if
![]() $\widetilde C$
is not hyperelliptic, then the Abel–Prym map
$\widetilde C$
is not hyperelliptic, then the Abel–Prym map
![]() $\delta _1$
is an embedding, so that
$\delta _1$
is an embedding, so that
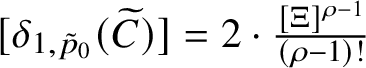 $[\delta _{1,\tilde p_0}(\widetilde C)]= 2\cdot \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
. If
$[\delta _{1,\tilde p_0}(\widetilde C)]= 2\cdot \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
. If
![]() $\widetilde C$
is hyperelliptic, then
$\widetilde C$
is hyperelliptic, then
![]() $\delta _1$
has degree
$\delta _1$
has degree
![]() $2$
and the image
$2$
and the image
![]() $\Sigma :=\delta _1(\widetilde C)\subseteq P'$
is a smooth hyperelliptic curve of genus
$\Sigma :=\delta _1(\widetilde C)\subseteq P'$
is a smooth hyperelliptic curve of genus
![]() $g-1$
so that setting
$g-1$
so that setting
 $\Sigma _{\tilde p_0}:=\delta _{1,\tilde p_0}(\widetilde C)\subseteq P$
, we have
$\Sigma _{\tilde p_0}:=\delta _{1,\tilde p_0}(\widetilde C)\subseteq P$
, we have
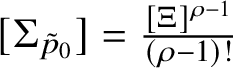 $[\Sigma _{\tilde p_0}]= \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
and
$[\Sigma _{\tilde p_0}]= \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
and
![]() $(P,\Xi )$
is isomorphic to the principally polarised Jacobian
$(P,\Xi )$
is isomorphic to the principally polarised Jacobian
![]() $(J(\Sigma ),\Theta _\Sigma )$
.
$(J(\Sigma ),\Theta _\Sigma )$
.
Proof. Computing the degree of
![]() $\delta _1$
is a basic computation from the definition; the details can be found in [Reference Birkenhake and LangeBL04, Prop. 12.5.2] where the arguments are made over
$\delta _1$
is a basic computation from the definition; the details can be found in [Reference Birkenhake and LangeBL04, Prop. 12.5.2] where the arguments are made over
![]() $\mathbb C$
but which hold over any algebraically closed field of characteristic not equal to
$\mathbb C$
but which hold over any algebraically closed field of characteristic not equal to
![]() $2$
. The statements regarding the differential of
$2$
. The statements regarding the differential of
![]() $\delta _1$
can be found in [Reference Birkenhake and LangeBL04, Cor. 12.5.5–7] over
$\delta _1$
can be found in [Reference Birkenhake and LangeBL04, Cor. 12.5.5–7] over
![]() $\mathbb C$
; those arguments also hold over any algebraically closed field of characteristic not equal to
$\mathbb C$
; those arguments also hold over any algebraically closed field of characteristic not equal to
![]() $2$
, and we also review this in Subsection A.2.1. As the map
$2$
, and we also review this in Subsection A.2.1. As the map
![]() $\delta _1$
is finite, computing the class of
$\delta _1$
is finite, computing the class of
 $(\delta _{1,\tilde p_0})_*[\widetilde C]$
is a standard argument using the fact that
$(\delta _{1,\tilde p_0})_*[\widetilde C]$
is a standard argument using the fact that
![]() $H^{2\rho - 2}(P,\mathbb Z_\ell )= \bigwedge ^{2\rho -2}H^1(P,\mathbb Z_\ell )$
and facts about first Chern classes of symmetric polarisations on abelian varieties. This is essentially the same argument that is used to prove Poincaré’s formula in [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 25], and the arguments there are easily adapted to the Abel–Prym map and the positive characteristic case (see [Reference MasiewickiMas76, Lem. 3.2] over
$H^{2\rho - 2}(P,\mathbb Z_\ell )= \bigwedge ^{2\rho -2}H^1(P,\mathbb Z_\ell )$
and facts about first Chern classes of symmetric polarisations on abelian varieties. This is essentially the same argument that is used to prove Poincaré’s formula in [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p. 25], and the arguments there are easily adapted to the Abel–Prym map and the positive characteristic case (see [Reference MasiewickiMas76, Lem. 3.2] over
![]() $\mathbb C$
).
$\mathbb C$
).
The fact that
![]() $\Sigma $
is smooth and that
$\Sigma $
is smooth and that
![]() $(P,\Xi )$
is isomorphic to the principally polarised Jacobian
$(P,\Xi )$
is isomorphic to the principally polarised Jacobian
![]() $(J(\Sigma ),\Theta _\Sigma )$
follows from the fact that
$(J(\Sigma ),\Theta _\Sigma )$
follows from the fact that
 $[\Sigma _{\tilde p_0}]= \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
and the criterion of Matsusaka–Ran [Reference CollinoCol84]. One can conclude that
$[\Sigma _{\tilde p_0}]= \frac {[\Xi ]^{\rho -1}}{(\rho -1)!} $
and the criterion of Matsusaka–Ran [Reference CollinoCol84]. One can conclude that
![]() $\Sigma $
is hyperelliptic by considering the image of the
$\Sigma $
is hyperelliptic by considering the image of the
![]() $g^1_2$
on
$g^1_2$
on
![]() $\widetilde C$
under the norm map for
$\widetilde C$
under the norm map for
![]() $\widetilde C\to \Sigma $
.
$\widetilde C\to \Sigma $
.
Remark A.5. If
![]() $\widetilde C$
is hyperellptic, then C is hyperelliptic as well (consider the image of the
$\widetilde C$
is hyperellptic, then C is hyperelliptic as well (consider the image of the
![]() $g^1_2$
on
$g^1_2$
on
![]() $\widetilde C$
under the norm map for
$\widetilde C$
under the norm map for
![]() $\pi $
). Thus, the conclusion in Proposition A.4 that if
$\pi $
). Thus, the conclusion in Proposition A.4 that if
![]() $\widetilde C$
is hyperelliptic then
$\widetilde C$
is hyperelliptic then
![]() $(P,\Xi )$
is a hyperelliptic Jacobian is a special case of a result of Mumford, which states that for any
$(P,\Xi )$
is a hyperelliptic Jacobian is a special case of a result of Mumford, which states that for any
![]() $\pi :\widetilde C\to C$
with C hyperelliptic, the Prym variety is a product of hyperelliptic Jacobians [Reference MumfordMum74, p. 346].
$\pi :\widetilde C\to C$
with C hyperelliptic, the Prym variety is a product of hyperelliptic Jacobians [Reference MumfordMum74, p. 346].
Remark A.6. In the case where
![]() $\widetilde C$
is hyperelliptic, we can say more. From the definition, we have that
$\widetilde C$
is hyperelliptic, we can say more. From the definition, we have that
![]() $\delta _1(\tilde p)=\delta _1(\tilde p')$
for distinct points
$\delta _1(\tilde p)=\delta _1(\tilde p')$
for distinct points
![]() $\tilde p,\tilde p'\in \widetilde C$
if and only if
$\tilde p,\tilde p'\in \widetilde C$
if and only if
![]() $\tilde p+\iota (\tilde p')$
is in the (unique)
$\tilde p+\iota (\tilde p')$
is in the (unique)
![]() $g^1_2$
on
$g^1_2$
on
![]() $\widetilde C$
. By Riemann–Hurwitz,
$\widetilde C$
. By Riemann–Hurwitz,
![]() $\delta _1$
is ramified at four points. The ramification points
$\delta _1$
is ramified at four points. The ramification points
![]() $\tilde r \in \widetilde C$
of
$\tilde r \in \widetilde C$
of
![]() $\delta _1$
are distinguished by the fact that the
$\delta _1$
are distinguished by the fact that the
![]() $2$
-torsion line bundle
$2$
-torsion line bundle
![]() $\eta $
determining the cover
$\eta $
determining the cover
![]() $\pi $
satisfies
$\pi $
satisfies
![]() $\eta =\mathcal O_C(\pi (\tilde r)-p)$
for some
$\eta =\mathcal O_C(\pi (\tilde r)-p)$
for some
![]() $p\in C$
. Note that this forces
$p\in C$
. Note that this forces
![]() $\pi (\tilde r)$
and p to be branch points for the hyperelliptic involution on C. In summary, if
$\pi (\tilde r)$
and p to be branch points for the hyperelliptic involution on C. In summary, if
![]() $\widetilde C$
is hyperelliptic, then
$\widetilde C$
is hyperelliptic, then
![]() $\eta \cong \mathcal O_C(p'-p)$
for some distinct ramification points
$\eta \cong \mathcal O_C(p'-p)$
for some distinct ramification points
![]() $p,p'\in C$
for the
$p,p'\in C$
for the
![]() $g^1_2$
on C and the four ramification points of
$g^1_2$
on C and the four ramification points of
![]() $\delta _1$
are the points
$\delta _1$
are the points
![]() $\pi ^{-1}(\{p,p'\})$
. The details can be found in [Reference Birkenhake and LangeBL04, §12.5], where again the arguments hold in positive characterstic, as well; see also Subsection A.2.1.
$\pi ^{-1}(\{p,p'\})$
. The details can be found in [Reference Birkenhake and LangeBL04, §12.5], where again the arguments hold in positive characterstic, as well; see also Subsection A.2.1.
A.2 The differential of the Abel–Prym map
We next show that the Abel–Prym map is generically finite for
![]() $d\le g-1$
by showing that the differential is generically injective in that range.
$d\le g-1$
by showing that the differential is generically injective in that range.
Proposition A.7. For
![]() $d\le g-1$
, the differential of
$d\le g-1$
, the differential of
![]() $\delta _d$
is generically injective. For all d the differential generically has rank equal to
$\delta _d$
is generically injective. For all d the differential generically has rank equal to
![]() $\min (d,g-1)$
. The differential of
$\min (d,g-1)$
. The differential of
![]() $\delta _d$
is injective if and only if
$\delta _d$
is injective if and only if
![]() $d=1$
and
$d=1$
and
![]() $\widetilde C$
is not hyperelliptic.
$\widetilde C$
is not hyperelliptic.
More precisely, the differential
![]() $\delta _d$
is injective at
$\delta _d$
is injective at
![]() $\widetilde D\in \widetilde C^{(d)}$
if and only if the support of
$\widetilde D\in \widetilde C^{(d)}$
if and only if the support of
![]() $\widetilde D$
satisfies
$\widetilde D$
satisfies
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
and, setting
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
and, setting
![]() $D=\operatorname {\mathrm {Nm}}\widetilde D$
, there does not exist an effective divisor
$D=\operatorname {\mathrm {Nm}}\widetilde D$
, there does not exist an effective divisor
![]() $E\in C^{(d)}$
such that
$E\in C^{(d)}$
such that
![]() $\eta =\mathcal O_C(D-E)$
, where
$\eta =\mathcal O_C(D-E)$
, where
![]() $\eta $
is the
$\eta $
is the
![]() $2$
-torsion line bundle determining the cover
$2$
-torsion line bundle determining the cover
![]() $\widetilde C/C$
.
$\widetilde C/C$
.
Proof. The case
![]() $d=1$
is handled in Proposition A.4. Since there exist positive dimensional fibres of
$d=1$
is handled in Proposition A.4. Since there exist positive dimensional fibres of
![]() $\delta _d$
for all
$\delta _d$
for all
![]() $d\ge 2$
, the differential cannot be injective for
$d\ge 2$
, the differential cannot be injective for
![]() $d\ge 2$
. For the statements on the generic rank, once we have shown that the differential of
$d\ge 2$
. For the statements on the generic rank, once we have shown that the differential of
![]() $\delta _{g-1}$
is generically injective, by a dimension count it is generically surjective and one can easily check that this implies that
$\delta _{g-1}$
is generically injective, by a dimension count it is generically surjective and one can easily check that this implies that
![]() $\delta _d$
surjects onto P or
$\delta _d$
surjects onto P or
![]() $P'$
for all
$P'$
for all
![]() $d\ge g-1$
. Thus, for the generic rank of the differential of
$d\ge g-1$
. Thus, for the generic rank of the differential of
![]() $\delta _d$
, it only remains to show that for
$\delta _d$
, it only remains to show that for
![]() $d\le g-1$
, the differential of
$d\le g-1$
, the differential of
![]() $\delta _d$
is generically injective.
$\delta _d$
is generically injective.
For this, we factor
![]() $\delta _d$
as follows:
$\delta _d$
as follows:

where
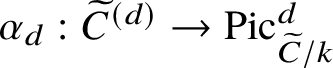 ${\alpha _d}:\widetilde C^{(d)}\to \operatorname {Pic}^d_{\widetilde C/k}$
is the Abel map
${\alpha _d}:\widetilde C^{(d)}\to \operatorname {Pic}^d_{\widetilde C/k}$
is the Abel map
 $\widetilde D\mapsto \mathcal O_{\widetilde C}(\widetilde D)$
. Then at the level of the differential, at a divisor
$\widetilde D\mapsto \mathcal O_{\widetilde C}(\widetilde D)$
. Then at the level of the differential, at a divisor
![]() $\widetilde D\in \widetilde C^{(d)}$
, these are given by the maps
$\widetilde D\in \widetilde C^{(d)}$
, these are given by the maps

The composition of the maps above agrees with the composition of the maps

which in turn factors as

where we denote by
 $+:H^0(\mathcal O_{\widetilde D}(\widetilde D)) \times H^0(\mathcal O_{\iota \widetilde D}(\iota \widetilde D)) \to H^0( \mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D))$
the differential of the map
$+:H^0(\mathcal O_{\widetilde D}(\widetilde D)) \times H^0(\mathcal O_{\iota \widetilde D}(\iota \widetilde D)) \to H^0( \mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D))$
the differential of the map
![]() $+:\widetilde C^{(d)}\times \widetilde C^{(d)}\to \widetilde C^{(2d)}$
at the point
$+:\widetilde C^{(d)}\times \widetilde C^{(d)}\to \widetilde C^{(2d)}$
at the point
![]() $(\widetilde D,\iota \widetilde D)$
, we set
$(\widetilde D,\iota \widetilde D)$
, we set
![]() $\beta _d:= +\circ (1\times (-\iota ))$
and
$\beta _d:= +\circ (1\times (-\iota ))$
and
![]() $T\alpha _{2d}$
is the differential of the Abel map
$T\alpha _{2d}$
is the differential of the Abel map
 $\alpha _{2d}: \widetilde C^{(2d)}\to \operatorname {Pic}^{2d}_{\widetilde C/k}$
at the point
$\alpha _{2d}: \widetilde C^{(2d)}\to \operatorname {Pic}^{2d}_{\widetilde C/k}$
at the point
![]() $\widetilde D+\iota \widetilde D$
. Recall that
$\widetilde D+\iota \widetilde D$
. Recall that
![]() $T\alpha _{2d}$
is identified with the coboundary map
$T\alpha _{2d}$
is identified with the coboundary map

from the long exact sequence associated to the short exact sequence
 $$ \begin{align} 0\to \mathcal O_{\widetilde C}\to \mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D)\to \mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D)\to 0. \end{align} $$
$$ \begin{align} 0\to \mathcal O_{\widetilde C}\to \mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D)\to \mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D)\to 0. \end{align} $$
Returning now to showing that the differential of
![]() $\delta _d$
is generically injective, note that
$\delta _d$
is generically injective, note that
![]() $\beta _d$
in (34) is injective if and only if
$\beta _d$
in (34) is injective if and only if
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Thus, under the assumption
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Thus, under the assumption
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
, it suffices to show that the coboundary map
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
, it suffices to show that the coboundary map
![]() $\partial _{\widetilde D+\iota \widetilde D}$
in (35) is injective for general
$\partial _{\widetilde D+\iota \widetilde D}$
in (35) is injective for general
![]() $\widetilde D$
of degree
$\widetilde D$
of degree
![]() $d\le g-1$
. From the long exact sequence in cohomology, it is enough to show that
$d\le g-1$
. From the long exact sequence in cohomology, it is enough to show that
 $h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))=1$
. For this, set
$h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))=1$
. For this, set
![]() $D=\operatorname {\mathrm {Nm}}(\widetilde D)$
so that we have
$D=\operatorname {\mathrm {Nm}}(\widetilde D)$
so that we have
![]() $\widetilde D+\iota \widetilde D=\pi ^*D$
. Then using that
$\widetilde D+\iota \widetilde D=\pi ^*D$
. Then using that
![]() $\pi _*\mathcal O_{\widetilde C}=\mathcal O_C\oplus \eta $
, where
$\pi _*\mathcal O_{\widetilde C}=\mathcal O_C\oplus \eta $
, where
![]() $\eta ^{\otimes 2}\cong \mathcal O_C$
is the
$\eta ^{\otimes 2}\cong \mathcal O_C$
is the
![]() $2$
-torsion line bundle defining the cover and the projection formula, we have
$2$
-torsion line bundle defining the cover and the projection formula, we have
 $h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))= h^0(C,\mathcal O_C(D))+h^0(C,\eta (D))$
. Thus, it suffices to show that
$h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))= h^0(C,\mathcal O_C(D))+h^0(C,\eta (D))$
. Thus, it suffices to show that
![]() $h^0(C,\mathcal O_C(D))=1$
and
$h^0(C,\mathcal O_C(D))=1$
and
![]() $ h^0(C,\eta (D))=0$
, if D is general of degree
$ h^0(C,\eta (D))=0$
, if D is general of degree
![]() $d\le g-1$
(since if
$d\le g-1$
(since if
![]() $\widetilde D$
is generic, then D will be, too). By Riemann–Roch, this is equivalent to showing that
$\widetilde D$
is generic, then D will be, too). By Riemann–Roch, this is equivalent to showing that
![]() $h^0(C,K_C(-D))=g-d$
and
$h^0(C,K_C(-D))=g-d$
and
![]() $h^0(C,K_C(-D)\otimes \eta )=(g-1)-d$
; if D is general of degree
$h^0(C,K_C(-D)\otimes \eta )=(g-1)-d$
; if D is general of degree
![]() $d\le g-1$
, then these conditions are satisfied. This completes the proof regarding generic injectivity of the differential.
$d\le g-1$
, then these conditions are satisfied. This completes the proof regarding generic injectivity of the differential.
For the final statement of the proposition, still under the assumption
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
, we observe that the coboundary map (35) is identified with the direct sum of the coboundary maps
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
, we observe that the coboundary map (35) is identified with the direct sum of the coboundary maps

associated to the short exact sequence
![]() $0\to \mathcal O_C\to \mathcal O_C(D)\to \mathcal O_C(D)|_D\to 0$
and the short exact sequence obtained by tensoring with
$0\to \mathcal O_C\to \mathcal O_C(D)\to \mathcal O_C(D)|_D\to 0$
and the short exact sequence obtained by tensoring with
![]() $\eta $
. For this, apply
$\eta $
. For this, apply
![]() $\pi _*$
to (36) and use
$\pi _*$
to (36) and use
 $R^1\pi _*\mathcal O_{\widetilde C}=0$
and the projection formula to obtain the direct sum of the short exact sequences together with the identification
$R^1\pi _*\mathcal O_{\widetilde C}=0$
and the projection formula to obtain the direct sum of the short exact sequences together with the identification
 $\pi _*\mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D)= \mathcal O_C(D)|_D\oplus \eta (D)|_D$
. Since the image of
$\pi _*\mathcal O_{\widetilde D+\iota \widetilde D}(\widetilde D+\iota \widetilde D)= \mathcal O_C(D)|_D\oplus \eta (D)|_D$
. Since the image of
![]() $\beta _d$
in (34) is equal to the anti-invariant part of the target, which is in turn identified with
$\beta _d$
in (34) is equal to the anti-invariant part of the target, which is in turn identified with
![]() $H^0(\eta (D))|_D)$
, one is reduced to checking the injectivity of
$H^0(\eta (D))|_D)$
, one is reduced to checking the injectivity of
![]() $\partial _{\eta (D)}$
. From the long exact sequence in cohomology, this coboundary map is injective if and only if
$\partial _{\eta (D)}$
. From the long exact sequence in cohomology, this coboundary map is injective if and only if
![]() $0=h^0(C,\eta )= h^0(C,\eta (D))$
. This fails if and only if
$0=h^0(C,\eta )= h^0(C,\eta (D))$
. This fails if and only if
![]() $\eta \cong \mathcal O_C(D-E)$
for some effective divisor
$\eta \cong \mathcal O_C(D-E)$
for some effective divisor
![]() $E\in C^{(d)}$
, completing the proof.
$E\in C^{(d)}$
, completing the proof.
Remark A.8. It is elementary to see from the definition of the Abel–Prym map, or from (33), that if
 $h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))\ge 2$
, then the differential of
$h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))\ge 2$
, then the differential of
![]() $\delta _d$
fails to be injective at
$\delta _d$
fails to be injective at
![]() $\widetilde D$
. Therefore, Proposition A.7 implies that if
$\widetilde D$
. Therefore, Proposition A.7 implies that if
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
and
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
and
 $h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))\ge 2$
, then
$h^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))\ge 2$
, then
![]() $h^0(C,\eta (D))>0$
. Here we give an elementary proof of this fact. Indeed, let
$h^0(C,\eta (D))>0$
. Here we give an elementary proof of this fact. Indeed, let
 $\tilde \sigma \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))$
be such that its divisor of zeros is
$\tilde \sigma \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))$
be such that its divisor of zeros is
![]() $(\tilde \sigma )_0=\widetilde D$
. Then for general
$(\tilde \sigma )_0=\widetilde D$
. Then for general
 $\tilde \sigma ' \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))$
, with divisor of zeros
$\tilde \sigma ' \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D))$
, with divisor of zeros
![]() $(\tilde \sigma ')_0=\widetilde D'$
, we have that the section
$(\tilde \sigma ')_0=\widetilde D'$
, we have that the section
 $\tilde \sigma \cdot \iota \tilde \sigma ' \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))$
, with divisor of zeros
$\tilde \sigma \cdot \iota \tilde \sigma ' \in H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))$
, with divisor of zeros
![]() $(\tilde \sigma \cdot \iota \tilde \sigma ' )_0=\widetilde D+\iota \widetilde D'$
, has support that is not equal to the support of
$(\tilde \sigma \cdot \iota \tilde \sigma ' )_0=\widetilde D+\iota \widetilde D'$
, has support that is not equal to the support of
![]() $\iota \widetilde D+\widetilde D'$
; here we are using that
$\iota \widetilde D+\widetilde D'$
; here we are using that
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Therefore,
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Therefore,
![]() $\tilde \sigma \cdot \iota \tilde \sigma '\ne \tilde \sigma ' \cdot \iota \tilde \sigma $
, since their associated divisors have different supports. Consequently,
$\tilde \sigma \cdot \iota \tilde \sigma '\ne \tilde \sigma ' \cdot \iota \tilde \sigma $
, since their associated divisors have different supports. Consequently,
![]() $\tilde \sigma \cdot \iota \tilde \sigma '- \tilde \sigma ' \cdot \iota \tilde \sigma \ne 0$
gives a nontrivial element of
$\tilde \sigma \cdot \iota \tilde \sigma '- \tilde \sigma ' \cdot \iota \tilde \sigma \ne 0$
gives a nontrivial element of
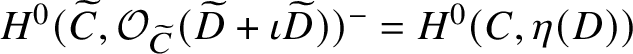 $H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))^-= H^0(C,\eta (D))$
.
$H^0(\widetilde C,\mathcal O_{\widetilde C}(\widetilde D+\iota \widetilde D))^-= H^0(C,\eta (D))$
.
Corollary A.9. The Abel–Prym map
![]() $\delta _d$
is generically finite if and only if
$\delta _d$
is generically finite if and only if
![]() $d\le g-1$
and surjects onto P (respectively
$d\le g-1$
and surjects onto P (respectively
![]() $P'$
) if and only if
$P'$
) if and only if
![]() $d\ge g-1$
and d is even (respectively d is odd).
$d\ge g-1$
and d is even (respectively d is odd).
Corollary A.10. Suppose that
![]() $\eta $
is not in the image of the difference map
$\eta $
is not in the image of the difference map
![]() $C^{(d)}\times C^{(d)}\to J(C)$
, which requires
$C^{(d)}\times C^{(d)}\to J(C)$
, which requires
![]() $d<g/2$
and holds if in addition
$d<g/2$
and holds if in addition
![]() $\widetilde C/C$
is general. Then the exceptional locus of
$\widetilde C/C$
is general. Then the exceptional locus of
![]() $\delta _d$
is exactly the locus of
$\delta _d$
is exactly the locus of
![]() $\widetilde D\in \widetilde C^{(d)}$
such that
$\widetilde D\in \widetilde C^{(d)}$
such that
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
.
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
.
Proof. First, we explain that if
![]() $\widetilde C/C$
is general and
$\widetilde C/C$
is general and
![]() $d<g/2$
, then
$d<g/2$
, then
![]() $\eta $
is not in the image of the difference map
$\eta $
is not in the image of the difference map
![]() $C^{(d)}\times C^{(d)}\to J(C)$
. Indeed, if
$C^{(d)}\times C^{(d)}\to J(C)$
. Indeed, if
![]() $\eta = \mathcal O_C(D-E)$
for some effective divisors D and E of degree d on C, then since
$\eta = \mathcal O_C(D-E)$
for some effective divisors D and E of degree d on C, then since
![]() $\pi ^*\eta \cong \mathcal O_{\widetilde C}$
(e.g., [Reference MumfordMum74, Lem. p.332]), we would have
$\pi ^*\eta \cong \mathcal O_{\widetilde C}$
(e.g., [Reference MumfordMum74, Lem. p.332]), we would have
![]() $\pi ^*D \sim \pi ^*E$
, so that in this case
$\pi ^*D \sim \pi ^*E$
, so that in this case
![]() $\widetilde C$
would have a
$\widetilde C$
would have a
 $g^1_{2d}$
, which is not possible due to [Reference Aprodu and FarkasAF12, Thm. 1.4], which states that for a general cover
$g^1_{2d}$
, which is not possible due to [Reference Aprodu and FarkasAF12, Thm. 1.4], which states that for a general cover
![]() $\widetilde C/C$
, there is no
$\widetilde C/C$
, there is no
![]() $g^1_e$
on
$g^1_e$
on
![]() $\widetilde C$
for
$\widetilde C$
for
![]() $e<g$
(in positive characteristic combine the proof of [Reference Aprodu and FarkasAF12, Thm. 1.4] given in [Reference Aprodu and FarkasAF12, Prop. 3.1] with [Reference OssermanOss14, Thm. 1.1]).
$e<g$
(in positive characteristic combine the proof of [Reference Aprodu and FarkasAF12, Thm. 1.4] given in [Reference Aprodu and FarkasAF12, Prop. 3.1] with [Reference OssermanOss14, Thm. 1.1]).
Now assuming that
![]() $\eta $
is not in the image of the difference map
$\eta $
is not in the image of the difference map
![]() $C^{(d)}\times C^{(d)}\to J(C)$
, which implies that
$C^{(d)}\times C^{(d)}\to J(C)$
, which implies that
![]() $d<g/2\le g-1$
(e.g., [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Ex. D-1, p.223]; the argument holds in positive characteristic, as well), then Proposition A.7 implies that the exceptional locus is contained in the locus of
$d<g/2\le g-1$
(e.g., [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, Ex. D-1, p.223]; the argument holds in positive characteristic, as well), then Proposition A.7 implies that the exceptional locus is contained in the locus of
![]() $\widetilde D\in \widetilde C^{(d)}$
such that
$\widetilde D\in \widetilde C^{(d)}$
such that
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
. On the other hand, it is easy to see that the exceptional locus of
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
. On the other hand, it is easy to see that the exceptional locus of
![]() $\delta _d$
contains the locus of
$\delta _d$
contains the locus of
![]() $\widetilde D\in \widetilde C^{(d)}$
such that
$\widetilde D\in \widetilde C^{(d)}$
such that
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
. Indeed, suppose that
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)\ne \emptyset $
. Indeed, suppose that
![]() $\widetilde D=\tilde p+\iota \tilde p+\widetilde E= \pi ^*p +\widetilde E$
for some
$\widetilde D=\tilde p+\iota \tilde p+\widetilde E= \pi ^*p +\widetilde E$
for some
![]() $\tilde p\in \widetilde C$
,
$\tilde p\in \widetilde C$
,
![]() $p\in C$
and
$p\in C$
and
![]() $\widetilde E\in \widetilde C^{(d-2)}$
. Then for all
$\widetilde E\in \widetilde C^{(d-2)}$
. Then for all
![]() $p'\in C$
set
$p'\in C$
set
 $\widetilde D_{p'}=\pi ^*p'+\widetilde E$
and we have
$\widetilde D_{p'}=\pi ^*p'+\widetilde E$
and we have
 $\delta _d(\widetilde D_{p'})= \delta _d(\widetilde D)$
.
$\delta _d(\widetilde D_{p'})= \delta _d(\widetilde D)$
.
A.2.1 Geometric interpretation of the differential of the Abel–Prym map
The projectivised differential of
![]() $\delta _1$
factors as
$\delta _1$
factors as

where
![]() $\eta $
is the
$\eta $
is the
![]() $2$
-torsion line bundle on C determining the cover
$2$
-torsion line bundle on C determining the cover
![]() $\pi $
; the bottom row is the Prym canonical map, given by the linear system
$\pi $
; the bottom row is the Prym canonical map, given by the linear system
![]() $|K_C\otimes \eta |$
; and the right vertical map is the projection onto the second factor. Moreover,
$|K_C\otimes \eta |$
; and the right vertical map is the projection onto the second factor. Moreover,
![]() $\mathbb P T\delta _1$
is defined at
$\mathbb P T\delta _1$
is defined at
![]() $\tilde p\in \widetilde C$
if and only if
$\tilde p\in \widetilde C$
if and only if
![]() $\phi _{K_C\otimes \eta }$
is defined at
$\phi _{K_C\otimes \eta }$
is defined at
![]() $p=\pi (\tilde p)$
; that is, p is not a base point of
$p=\pi (\tilde p)$
; that is, p is not a base point of
![]() $|K_C\otimes \eta |$
. One can find all of this in [Reference Birkenhake and LangeBL04, Prop. 12.5.2] over
$|K_C\otimes \eta |$
. One can find all of this in [Reference Birkenhake and LangeBL04, Prop. 12.5.2] over
![]() $\mathbb C$
; the arguments hold in positive characteristic as well. Indeed, factoring
$\mathbb C$
; the arguments hold in positive characteristic as well. Indeed, factoring
![]() $\delta _1$
as
$\delta _1$
as
 $\widetilde C\stackrel {\alpha _1}{\to } \operatorname {Pic}^1_{\widetilde C/k}\stackrel {1-\iota }{\to } P'\subseteq J(\widetilde C)$
where
$\widetilde C\stackrel {\alpha _1}{\to } \operatorname {Pic}^1_{\widetilde C/k}\stackrel {1-\iota }{\to } P'\subseteq J(\widetilde C)$
where
![]() $\alpha _1$
is the Abel map and taking the differential at a point
$\alpha _1$
is the Abel map and taking the differential at a point
![]() $\tilde p\in \widetilde C$
, one obtains the maps
$\tilde p\in \widetilde C$
, one obtains the maps
 $H^0(\mathcal O_{\tilde p}(\tilde p))\stackrel {T\alpha _1}{\to } H^1(\mathcal O_{\widetilde C}) \stackrel {1-\iota }{\to } H^1(\mathcal O_{\widetilde C})^-\subseteq H^1(\mathcal O_{\widetilde C})$
. Identifying
$H^0(\mathcal O_{\tilde p}(\tilde p))\stackrel {T\alpha _1}{\to } H^1(\mathcal O_{\widetilde C}) \stackrel {1-\iota }{\to } H^1(\mathcal O_{\widetilde C})^-\subseteq H^1(\mathcal O_{\widetilde C})$
. Identifying
 $H^1(\widetilde C,\mathcal O_{\widetilde C})=H^0(\widetilde C,K_{\widetilde C})^\vee $
and
$H^1(\widetilde C,\mathcal O_{\widetilde C})=H^0(\widetilde C,K_{\widetilde C})^\vee $
and
 $H^1(\widetilde C,\mathcal O_{\widetilde C})^-=H^0(C,K_C\otimes \eta )^\vee $
, one uses the fact that the projectivised differential of the Abel map is the canonical map
$H^1(\widetilde C,\mathcal O_{\widetilde C})^-=H^0(C,K_C\otimes \eta )^\vee $
, one uses the fact that the projectivised differential of the Abel map is the canonical map
![]() $\phi _{K_{\widetilde C}}$
on
$\phi _{K_{\widetilde C}}$
on
![]() $\widetilde C$
.
$\widetilde C$
.
A Riemann–Roch computation gives that
![]() $|K_C\otimes \eta |$
has a base point if and only if
$|K_C\otimes \eta |$
has a base point if and only if
![]() $\eta =\mathcal O_C(p'-p)$
for some
$\eta =\mathcal O_C(p'-p)$
for some
![]() $p,p'\in C$
, in which case C is hyperelliptic and p and
$p,p'\in C$
, in which case C is hyperelliptic and p and
![]() $p'$
are the base points of
$p'$
are the base points of
![]() $|K_C\otimes \eta |$
(e.g., [Reference Ciliberto, Dedieu, Concettina and KnutsenCDCK19, Lem. 2.1(i)]). Note that
$|K_C\otimes \eta |$
(e.g., [Reference Ciliberto, Dedieu, Concettina and KnutsenCDCK19, Lem. 2.1(i)]). Note that
![]() $\pi ^*p'\sim \pi ^*p$
gives a
$\pi ^*p'\sim \pi ^*p$
gives a
![]() $g^1_2$
on
$g^1_2$
on
![]() $\widetilde C$
. In particular, this recovers the statements about the differential of
$\widetilde C$
. In particular, this recovers the statements about the differential of
![]() $\delta _1$
in Proposition A.4 and Remark A.6.
$\delta _1$
in Proposition A.4 and Remark A.6.
As a consequence, if
![]() $K_C\otimes \eta $
is very ample, then given
$K_C\otimes \eta $
is very ample, then given
![]() $\widetilde D\in \widetilde C^{(d)}$
and setting
$\widetilde D\in \widetilde C^{(d)}$
and setting
![]() $D=\operatorname {\mathrm {Nm}}\widetilde D$
, the projectivisation of
$D=\operatorname {\mathrm {Nm}}\widetilde D$
, the projectivisation of
 $(T_{\widetilde D}\delta _d)(T_{\widetilde D}\widetilde C^{(d)}) $
is identified with the span of the scheme
$(T_{\widetilde D}\delta _d)(T_{\widetilde D}\widetilde C^{(d)}) $
is identified with the span of the scheme
![]() $\phi _{K_C\otimes \eta }(D)$
in
$\phi _{K_C\otimes \eta }(D)$
in
![]() $\mathbb PH^0(C,K_C\otimes \eta )^\vee $
. The same result holds more generally as long as the Prym canonical map is defined at the support of D and the Prym canonical model of C is smooth at the image of the support of D. Note that another Riemann–Roch computation gives that if
$\mathbb PH^0(C,K_C\otimes \eta )^\vee $
. The same result holds more generally as long as the Prym canonical map is defined at the support of D and the Prym canonical model of C is smooth at the image of the support of D. Note that another Riemann–Roch computation gives that if
![]() $|K_C\otimes \eta |$
is base point free, then
$|K_C\otimes \eta |$
is base point free, then
![]() $K_C\otimes \eta $
fails to be very ample if and only if
$K_C\otimes \eta $
fails to be very ample if and only if
![]() $\eta \cong \mathcal O_C(p+q - p'-q')$
for some
$\eta \cong \mathcal O_C(p+q - p'-q')$
for some
![]() $p,q,p',q'\in C$
, in which case C is tetragonal, and p and q are not separated by
$p,q,p',q'\in C$
, in which case C is tetragonal, and p and q are not separated by
![]() $|K_C\otimes \eta |$
; as usual, when
$|K_C\otimes \eta |$
; as usual, when
![]() $p=q$
, we mean the differential drops rank at
$p=q$
, we mean the differential drops rank at
![]() $p=q$
(e.g., [Reference Ciliberto, Dedieu, Concettina and KnutsenCDCK19, Lem. 2.1(ii)]).
$p=q$
(e.g., [Reference Ciliberto, Dedieu, Concettina and KnutsenCDCK19, Lem. 2.1(ii)]).
A.3 Pushforward of the fundamental class under the Abel–Prym map
The main result of this subsection is the following proposition.
Proposition A.11. Let
![]() $\ell $
be a prime number not equal to
$\ell $
be a prime number not equal to
![]() $\operatorname {char}(k)$
. For
$\operatorname {char}(k)$
. For
![]() $d\le g-1$
and taking
$d\le g-1$
and taking
![]() $\widetilde D_0\in \widetilde C^{(d)}$
, the class of the pushforward of the symmetric product under the pointed Abel–Prym map
$\widetilde D_0\in \widetilde C^{(d)}$
, the class of the pushforward of the symmetric product under the pointed Abel–Prym map
![]() $\delta _{d,\widetilde D_0}$
is given by
$\delta _{d,\widetilde D_0}$
is given by
 $$ \begin{align*}( \delta_{d,\widetilde D_0})_*[\widetilde C^{(d)}] = 2^d\frac{[\Xi]^{\rho-d}}{(\rho-d)!}\in H^{2\rho-2d}(P,\mathbb Z_\ell(\rho-d)), \end{align*} $$
$$ \begin{align*}( \delta_{d,\widetilde D_0})_*[\widetilde C^{(d)}] = 2^d\frac{[\Xi]^{\rho-d}}{(\rho-d)!}\in H^{2\rho-2d}(P,\mathbb Z_\ell(\rho-d)), \end{align*} $$
where
![]() $\rho =g-1=\dim P$
.
$\rho =g-1=\dim P$
.
While Proposition A.11 can be proven exactly as in the
![]() $d=1$
case (i.e., as in the proof of (32) in Proposition A.4), that computation is somewhat laborious, and we prefer to give an alternate proof using (32) as the starting point. Similar computations can be found in [Reference BeauvilleBea82, §1] and [Reference SmithSmi89].
$d=1$
case (i.e., as in the proof of (32) in Proposition A.4), that computation is somewhat laborious, and we prefer to give an alternate proof using (32) as the starting point. Similar computations can be found in [Reference BeauvilleBea82, §1] and [Reference SmithSmi89].
For this, we take a brief detour. If
![]() $X,Y\subseteq A$
are subvarieties of an abelian variety and the map
$X,Y\subseteq A$
are subvarieties of an abelian variety and the map
![]() $a:X\times Y\to X+Y\subseteq A$
given by addition is generically finite, then it essentially follows from the definition of the Pontryagin product that in the Chow ring or in the cohomology ring,
$a:X\times Y\to X+Y\subseteq A$
given by addition is generically finite, then it essentially follows from the definition of the Pontryagin product that in the Chow ring or in the cohomology ring,
We will want a slight generalisation. If we suppose that
![]() $f_X:X'\to X\subseteq A$
and
$f_X:X'\to X\subseteq A$
and
![]() $f_Y:Y'\to Y\subseteq A$
are generically finite surjective morphisms and we set
$f_Y:Y'\to Y\subseteq A$
are generically finite surjective morphisms and we set
![]() $a' = a\circ (f_X\times f_Y)$
to be the composition
$a' = a\circ (f_X\times f_Y)$
to be the composition

then, still under the assumption that a is generically finite, we have
Indeed, we have the following string of equalities:
 $$ \begin{align*} a^{\prime}_*[X'\times Y']&=(\deg a')[X+Y]=(\deg (f_X\times f_Y))(\deg a) [X+Y]=(\deg f_X)( \deg f_Y)(\deg a) [X+Y]\\ &=(\deg f_X)(\deg f_Y) [X]\star [Y] = ((\deg f_X) [X'])\star ((\deg f_Y)[Y'])=f_{X,*}[X']\star f_{Y,*}[Y']. \end{align*} $$
$$ \begin{align*} a^{\prime}_*[X'\times Y']&=(\deg a')[X+Y]=(\deg (f_X\times f_Y))(\deg a) [X+Y]=(\deg f_X)( \deg f_Y)(\deg a) [X+Y]\\ &=(\deg f_X)(\deg f_Y) [X]\star [Y] = ((\deg f_X) [X'])\star ((\deg f_Y)[Y'])=f_{X,*}[X']\star f_{Y,*}[Y']. \end{align*} $$
Finally, we will want to use the standard result that for a principally polarised abelian variety
![]() $(A,\Theta )$
of dimension g, in the Chow ring we have
$(A,\Theta )$
of dimension g, in the Chow ring we have
 $$ \begin{align} \frac{[\Theta]^{g-a}}{(g-a)!}\star \frac{[\Theta]^{g-b}}{(g-b)!}=\binom{a+b}{a}\frac{[\Theta]^{g-(a+b)}}{(g-(a+b))!}, \end{align} $$
$$ \begin{align} \frac{[\Theta]^{g-a}}{(g-a)!}\star \frac{[\Theta]^{g-b}}{(g-b)!}=\binom{a+b}{a}\frac{[\Theta]^{g-(a+b)}}{(g-(a+b))!}, \end{align} $$
which we will use in the form
 $$ \begin{align} \left(\frac{[\Theta]^{g-1}}{(g-1)!}\right)^{\star d}=d!\frac{[\Theta]^{g-d}}{(g-d)!}. \end{align} $$
$$ \begin{align} \left(\frac{[\Theta]^{g-1}}{(g-1)!}\right)^{\star d}=d!\frac{[\Theta]^{g-d}}{(g-d)!}. \end{align} $$
A reference for (38) over
![]() $\mathbb C$
is [Reference Birkenhake and LangeBL04, Cor. 16.5.8, p.538], which uses as its starting point [Reference BeauvilleBea86, Thm., p.647], also proven over
$\mathbb C$
is [Reference Birkenhake and LangeBL04, Cor. 16.5.8, p.538], which uses as its starting point [Reference BeauvilleBea86, Thm., p.647], also proven over
![]() $\mathbb C$
. However, [Reference Deninger and MurreDM91, Thm. 2.19] shows that Beauville’s result holds over any algebraically closed field and, consequently, the arguments for [Reference Birkenhake and LangeBL04, Cor. 16.5.8, p.538] go through in positive characteristic as well. Of course, (38) is elementary to prove in
$\mathbb C$
. However, [Reference Deninger and MurreDM91, Thm. 2.19] shows that Beauville’s result holds over any algebraically closed field and, consequently, the arguments for [Reference Birkenhake and LangeBL04, Cor. 16.5.8, p.538] go through in positive characteristic as well. Of course, (38) is elementary to prove in
![]() $\ell $
-adic cohomology and this is, in fact, all we need.
$\ell $
-adic cohomology and this is, in fact, all we need.
Proof of Proposition A.11.
Let
![]() $\tilde p_0\in \widetilde C$
and set
$\tilde p_0\in \widetilde C$
and set
![]() $\widetilde D_0=d\tilde p_0$
. From Corollary A.9 we know that
$\widetilde D_0=d\tilde p_0$
. From Corollary A.9 we know that
![]() $\delta _d$
is generically finite; therefore, if we factor the composition
$\delta _d$
is generically finite; therefore, if we factor the composition
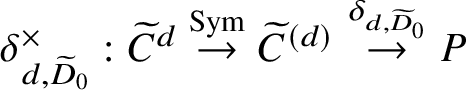 $\delta _{d,\widetilde D_0}^\times :\widetilde C^d\stackrel {\operatorname {\mathrm {Sym}}}{\to } \widetilde C^{(d)}\stackrel {\delta _{d,\widetilde D_0}}{\to } P $
as
$\delta _{d,\widetilde D_0}^\times :\widetilde C^d\stackrel {\operatorname {\mathrm {Sym}}}{\to } \widetilde C^{(d)}\stackrel {\delta _{d,\widetilde D_0}}{\to } P $
as

then from the left-hand side of (37), (32) and (39), we have
 $$ \begin{align*}(\delta^\times_{d,\widetilde D_0})_*[\widetilde C^d]= \left((\delta_{1,\tilde p_0})_*[\widetilde C]\right)^{\star^d}= \left(2\frac{[\Xi]^{\rho-1}}{(\rho-1)!}\right)^{\star^d} = 2^d d! \frac{[\Xi]^{\rho-d}}{(\rho-d)!}. \end{align*} $$
$$ \begin{align*}(\delta^\times_{d,\widetilde D_0})_*[\widetilde C^d]= \left((\delta_{1,\tilde p_0})_*[\widetilde C]\right)^{\star^d}= \left(2\frac{[\Xi]^{\rho-1}}{(\rho-1)!}\right)^{\star^d} = 2^d d! \frac{[\Xi]^{\rho-d}}{(\rho-d)!}. \end{align*} $$
On the other hand, we have
 $$ \begin{align*}(\delta^\times_{d,\widetilde D_0})_*[\widetilde C^d]= (\delta_{d,\widetilde D_0})_* \operatorname{\mathrm{Sym}}_*[\widetilde C^d] = d!(\delta_{d,\widetilde D_0})_* [\widetilde C^{(d)}], \end{align*} $$
$$ \begin{align*}(\delta^\times_{d,\widetilde D_0})_*[\widetilde C^d]= (\delta_{d,\widetilde D_0})_* \operatorname{\mathrm{Sym}}_*[\widetilde C^d] = d!(\delta_{d,\widetilde D_0})_* [\widetilde C^{(d)}], \end{align*} $$
completing the proof.
A.4 The degree of the Abel–Prym map
We start with the following consequence of Proposition A.11.
Corollary A.12. Let
![]() $\ell $
be a prime number not equal to
$\ell $
be a prime number not equal to
![]() $\operatorname {char}(k)$
. For
$\operatorname {char}(k)$
. For
![]() $d\le g-1$
and taking
$d\le g-1$
and taking
![]() $\widetilde D_0\in \widetilde C^{(d)}$
, the class
$\widetilde D_0\in \widetilde C^{(d)}$
, the class
![]() $[\operatorname {Im} \delta _{d,\widetilde D_0}]$
of the image of the pointed Abel–Prym map
$[\operatorname {Im} \delta _{d,\widetilde D_0}]$
of the image of the pointed Abel–Prym map
![]() $ \delta _{d,\widetilde D_0}$
(as a set or, rather, as an irreducible scheme, with the reduced induced scheme structure) is
$ \delta _{d,\widetilde D_0}$
(as a set or, rather, as an irreducible scheme, with the reduced induced scheme structure) is
 $$ \begin{align*}[\operatorname{Im} \delta_{d,\widetilde D_0}] = \frac{2^d}{\deg \delta_{d,\widetilde D_0}}\frac{[\Xi]^{\rho-d}}{(\rho-d)!}\in H^{2\rho-2d}(P,\mathbb Z_\ell (\rho-d)), \end{align*} $$
$$ \begin{align*}[\operatorname{Im} \delta_{d,\widetilde D_0}] = \frac{2^d}{\deg \delta_{d,\widetilde D_0}}\frac{[\Xi]^{\rho-d}}{(\rho-d)!}\in H^{2\rho-2d}(P,\mathbb Z_\ell (\rho-d)), \end{align*} $$
where
![]() $\rho =g-1=\dim P$
.
$\rho =g-1=\dim P$
.
Proof. This follows from Proposition A.11 using the fact that
![]() $\delta _d$
is generically finite (Corollary A.9) so that
$\delta _d$
is generically finite (Corollary A.9) so that
 $(\delta _{d,\widetilde D_0})_*[\widetilde C^{(d)}]= \deg (\delta _{d,\widetilde D_0})[\operatorname {Im} \delta _{d,\widetilde D_0}]$
.
$(\delta _{d,\widetilde D_0})_*[\widetilde C^{(d)}]= \deg (\delta _{d,\widetilde D_0})[\operatorname {Im} \delta _{d,\widetilde D_0}]$
.
This gives the following corollary.
Corollary A.13. We have
![]() $\deg \delta _{g-1}=2^{g-1}$
, and if
$\deg \delta _{g-1}=2^{g-1}$
, and if
![]() $\operatorname {char}(k)=0$
, then for
$\operatorname {char}(k)=0$
, then for
![]() $d\le g-2$
we have
$d\le g-2$
we have
![]() $\deg \delta _d=2^n\le 2^d$
for some integer
$\deg \delta _d=2^n\le 2^d$
for some integer
![]() $n\le d$
. If
$n\le d$
. If
![]() $\operatorname {char}(k)=p>0$
, then for
$\operatorname {char}(k)=p>0$
, then for
![]() $d\le g-2$
we have
$d\le g-2$
we have
![]() $\deg \delta _d=p^{m}2^n$
for some integers m and n with
$\deg \delta _d=p^{m}2^n$
for some integers m and n with
![]() $n\le d$
.
$n\le d$
.
Proof. In the case where
![]() $d=g-1$
, we know, in addition, the class of the image
$d=g-1$
, we know, in addition, the class of the image
 $\operatorname {Im}(\delta _{g-1,\widetilde D_0})$
; indeed,
$\operatorname {Im}(\delta _{g-1,\widetilde D_0})$
; indeed,
![]() $\delta _{g-1,\widetilde D_0}$
surjects onto P (Corollary A.9), so that
$\delta _{g-1,\widetilde D_0}$
surjects onto P (Corollary A.9), so that
 $\operatorname {Im}(\delta _{g-1,\widetilde D_0})=P$
. The fact that
$\operatorname {Im}(\delta _{g-1,\widetilde D_0})=P$
. The fact that
![]() $\deg \delta _{g-1}=2^{g-1}$
then follows immediately from Corollary A.12, completing the proof.
$\deg \delta _{g-1}=2^{g-1}$
then follows immediately from Corollary A.12, completing the proof.
The case where
![]() $d\le g-2$
follows from the fact that
$d\le g-2$
follows from the fact that
 $\frac {[\Xi ]^{\rho -d}}{(\rho -d)!}\in H^{2\rho -2d}(P,\mathbb Z_\ell (\rho -d))$
is a minimal cohomology class (i.e., it is not divisible by
$\frac {[\Xi ]^{\rho -d}}{(\rho -d)!}\in H^{2\rho -2d}(P,\mathbb Z_\ell (\rho -d))$
is a minimal cohomology class (i.e., it is not divisible by
![]() $\ell $
), so that Corollary A.12 (considered for all primes
$\ell $
), so that Corollary A.12 (considered for all primes
![]() $\ell \ne \operatorname {char}(k)$
) implies that
$\ell \ne \operatorname {char}(k)$
) implies that
![]() $\deg \delta _d$
must be a power of the characteristic exponent of k times a power of
$\deg \delta _d$
must be a power of the characteristic exponent of k times a power of
![]() $2$
that is at most
$2$
that is at most
![]() $2^d$
.
$2^d$
.
A.5 The Abel–Prym map for hyperelliptic covers
We now discuss the degree of the Abel–Prym map in the case where
![]() $\widetilde C$
is hyperelliptic.
$\widetilde C$
is hyperelliptic.
Proposition A.14. Assume that
![]() $\widetilde C$
is hyperelliptic. Then for
$\widetilde C$
is hyperelliptic. Then for
![]() $d\le g-1$
, we have
$d\le g-1$
, we have
![]() $\deg \delta _d=2^d$
.
$\deg \delta _d=2^d$
.
Proof. From Corollary A.13 we only need to show that
![]() $\deg \delta _d\ge 2^d$
. So fix
$\deg \delta _d\ge 2^d$
. So fix
![]() $\widetilde D=\tilde p_1+\cdots +\tilde p_d\in \widetilde C^{(d)}$
to be general; in particular, such that the fibre of
$\widetilde D=\tilde p_1+\cdots +\tilde p_d\in \widetilde C^{(d)}$
to be general; in particular, such that the fibre of
![]() $\delta _d$
over
$\delta _d$
over
![]() $\delta _d(\widetilde D)$
is finite. For
$\delta _d(\widetilde D)$
is finite. For
 $\widetilde D'=\tilde p_1'+\cdots +\tilde p_d'\in \widetilde C^{(d)}$
we have
$\widetilde D'=\tilde p_1'+\cdots +\tilde p_d'\in \widetilde C^{(d)}$
we have
![]() $\delta _d(\widetilde D')=\delta _d(\widetilde D)$
if and only if
$\delta _d(\widetilde D')=\delta _d(\widetilde D)$
if and only if
![]() $ \tilde p_1 -\iota \tilde p_1 +\cdots +\tilde p_d -\iota \tilde p_d \sim \tilde p_1' -\iota \tilde p_1' +\cdots +\tilde p_d' -\iota \tilde p_d' $
or, equivalently,
$ \tilde p_1 -\iota \tilde p_1 +\cdots +\tilde p_d -\iota \tilde p_d \sim \tilde p_1' -\iota \tilde p_1' +\cdots +\tilde p_d' -\iota \tilde p_d' $
or, equivalently,
Denoting by h the hyperelliptic involution on
![]() $\widetilde C$
, the assumption that
$\widetilde C$
, the assumption that
![]() $\widetilde D$
is general means that we can assume that the
$\widetilde D$
is general means that we can assume that the
![]() $\tilde p_i$
and
$\tilde p_i$
and
![]() $\iota h (\tilde p_j)$
are all distinct. Therefore, there are
$\iota h (\tilde p_j)$
are all distinct. Therefore, there are
![]() $2^d$
distinct choices of
$2^d$
distinct choices of
![]() $\widetilde D'$
such that
$\widetilde D'$
such that
![]() $\delta _d(\widetilde D')=\delta _d(\widetilde D)$
, determined by the
$\delta _d(\widetilde D')=\delta _d(\widetilde D)$
, determined by the
![]() $2^d$
choices of taking
$2^d$
choices of taking
![]() $\tilde p_i'$
either equal to
$\tilde p_i'$
either equal to
![]() $\tilde p_i$
or to
$\tilde p_i$
or to
![]() $\iota h(\tilde p_i)$
; note that since the
$\iota h(\tilde p_i)$
; note that since the
![]() $g^1_2$
on
$g^1_2$
on
![]() $\widetilde C$
is unique,
$\widetilde C$
is unique,
![]() $\tilde p + h(\tilde p)$
is in the
$\tilde p + h(\tilde p)$
is in the
![]() $g^1_2$
if and only if
$g^1_2$
if and only if
![]() $\iota \tilde p +\iota h(\tilde p)$
is in the
$\iota \tilde p +\iota h(\tilde p)$
is in the
![]() $g^1_2$
.
$g^1_2$
.
A.6 The Abel–Prym map for general covers
We now prove that for a general cover
![]() $\widetilde C/C$
, the degree of the Abel–Prym map is
$\widetilde C/C$
, the degree of the Abel–Prym map is
![]() $1$
for
$1$
for
![]() $d<g/2$
.
$d<g/2$
.
Corollary A.15 The Abel–Prym map for general covers
Let
![]() $\widetilde C/C$
be a general cover. Then
$\widetilde C/C$
be a general cover. Then
![]() $\deg \delta _d=1$
for
$\deg \delta _d=1$
for
![]() $d<g/2$
.
$d<g/2$
.
Proof. Let
![]() $\widetilde D\in \widetilde C^{(d)}$
be a general point; in particular, assume that
$\widetilde D\in \widetilde C^{(d)}$
be a general point; in particular, assume that
![]() $\widetilde D$
is reduced and
$\widetilde D$
is reduced and
![]() $\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Now suppose that
$\operatorname {Supp}(\widetilde D)\cap \operatorname {Supp}(\iota \widetilde D)=\emptyset $
. Now suppose that
![]() $\widetilde D'\in \widetilde C^{(d)}$
and
$\widetilde D'\in \widetilde C^{(d)}$
and
![]() $\delta _d(\widetilde D)=\delta _d(\widetilde D')$
. Then we have
$\delta _d(\widetilde D)=\delta _d(\widetilde D')$
. Then we have
![]() $\widetilde D+\iota \widetilde D'\sim \widetilde D'+\iota \widetilde D$
. If
$\widetilde D+\iota \widetilde D'\sim \widetilde D'+\iota \widetilde D$
. If
![]() $\widetilde D+\iota \widetilde D'= \widetilde D'+\iota \widetilde D$
, then considering the supports of the divisors, we must have that
$\widetilde D+\iota \widetilde D'= \widetilde D'+\iota \widetilde D$
, then considering the supports of the divisors, we must have that
![]() $\widetilde D'=\widetilde D$
. Otherwise,
$\widetilde D'=\widetilde D$
. Otherwise,
![]() $\widetilde C$
admits a
$\widetilde C$
admits a
 $g^1_{2d}$
. However, by [Reference Aprodu and FarkasAF12, Thm. 1.4], for a general cover
$g^1_{2d}$
. However, by [Reference Aprodu and FarkasAF12, Thm. 1.4], for a general cover
![]() $\widetilde C/C$
, there is no
$\widetilde C/C$
, there is no
![]() $g^1_e$
on
$g^1_e$
on
![]() $\widetilde C$
for
$\widetilde C$
for
![]() $e<g$
. Thus, if
$e<g$
. Thus, if
![]() $d<g/2$
, then
$d<g/2$
, then
![]() $\widetilde C$
does not admit a
$\widetilde C$
does not admit a
 $g^1_{2d}$
, and so
$g^1_{2d}$
, and so
![]() $\delta _d$
is generically injective.
$\delta _d$
is generically injective.
Remark A.16. The Donagi–Smith [Reference Donagi and SmithDS81, §3] approach to computing the degree of a generically finite morphism by computing the local degree along a fibre, together with the general position theorem (e.g., [Reference Arbarello, Cornalba, Griffiths and HarrisACGH85, p.109] or [Reference Eisenbud and HarrisEH92, Thm. 3.1]) allows one to compute
![]() $\deg \delta _d=1$
in characteristic
$\deg \delta _d=1$
in characteristic
![]() $0$
for
$0$
for
![]() $\widetilde C/C$
general and
$\widetilde C/C$
general and
![]() $d\le g-2$
.
$d\le g-2$
.
Acknowledgements
The author thanks Angela Ortega and Roy Smith for useful comments that pointed to an error in an earlier draft regarding fibres of the Abel–Prym map. He also thanks Gavril Farkas for pointing out an error in an earlier draft regarding Brill–Noether theory for connected étale double covers and directing the author to [Reference Aprodu and FarkasAF12, Reference SchwarzSch17] where the correct statements are proven, providing the needed result to complete the proof of Proposition A.3.
Acknowledgements
We thank Matthew Baker, Samuel Grushevsky, Sam Payne and Dhruv Ranganathan for useful discussions and David Jensen, Martin Ulirsch and Chi-Ho Yuen for comments on an older version of the article. We are very thankful to Victor Reiner for pointing out the history of the Kirchhoff–Prym formula in the context of critical groups and signed graphs. We are deeply grateful to Sebastian Casalaina-Martin for a comprehensive Appendix dedicated to the algebraic Abel–Prym map.
Conflict of Interest
None.