I. INTRODUCTION
Piezoelectric materials have been used for many applications such as sensors and actuators, Reference Uchino1 and recently studied for vibration energy harvesters. Reference Priya2,Reference Harigai, Adachi and Fujii3 For most of these applications, the piezoelectric material used is lead zirconate titanate because of the large piezoelectric properties and high Curie temperature. Reference Jaffe, Cook and Jaffe4 However, lead is a toxic element and therefore lead-free piezoelectric materials have been studied. Reference Takenaka and Nagata5,Reference Shrout and Zhang6 So far, the most promising lead-free piezoelectric materials are (K, Na)NbO3 and (Bi, Na)TiO3–BaTiO3, and proto-type devices and actual products were developed using them. Reference Takenaka, Maruyama and Sakata7–Reference Saito, Wada, Adachi and Kanno12 However, because of lower piezoelectric properties of both materials than those of lead zirconate titanate, other lead-free piezoelectric materials with superior properties are desired.
Bismuth ferrite, BiFeO3, is piezoelectric, rhombohedral perovskite oxide with the high Curie temperature of ∼825 °C. Reference Rojac, Bencan, Malic, Tutuncu, Jones, Daniels and Damjanovic13 Because the synthesis of second-phase-free BiFeO3 was difficult and also because a ceramic sample was so leaky and the coercive field was so large that a measurement of a well-saturated ferroelectric loop was difficult, BiFeO3 ceramics were less studied until a large remanent polarization of ∼60 µC/cm2 was reported for a BiFeO3 epitaxial film and a single crystal. Reference Wang, Neaton, Zheng, Nagarajan, Ogale, Liu, Viehland, Vaithyanathan, Schlom, Waghmare, Spaldin, Rabe, Wuttig and Ramesh14,Reference Lebeugle, Colson, Forget and Viret15 Intensive studies suggested that the leaky response was associated with the formation of Bi25FeO39 and the vaporization of Bi2O3 at high temperature and subsequent oxygen filling (VO˙˙ + 1/2 O2 → OO × + 2 h˙) on cooling, leading to p-type conductivity, Reference Rojac, Bencan, Malic, Tutuncu, Jones, Daniels and Damjanovic13,Reference Chishima, Noguchi, Kitanaka and Miyayama16 and a large coercive field was believed to be due to Bi and O vacancies forming dipolar defect complexes, which pinned domain walls and made the ceramics ferroelectrically hard. For BiFeO3 ceramics prepared from a mechanochemically activated powder to minimize the Bi2O3 vaporization, high electrical resistivity, a saturated polarization–electric field loops with the remanent polarization of ∼20 µC/cm2, and the large electric-field-induced strain of 0.3% were reported with relatively low piezoelectric constant d 33 values of 26–35 pC/N. Reference Rojac, Kosec, Budic, Setter and Damjanovic17
One of the methods to improve the piezoelectric responses is to induce compositional phase transition by making solid-solutions with different crystal systems (ex. PbZrO3–PbTiO3, (Bi1/2Na1/2)TiO3–BaTiO3, etc.). So far, orthorhombic ReFeO3 (Re: La, Sm, and Dy), Reference Fujino, Murakami, Anbusathaiah, Lim, Nagarajan, Fennie, Wuttig, Salamanca-Riba and Takeuchi18,Reference Kan, Cheng, Nagarajan and Takeuchi19 tetragonal BiCoO3, Reference Azuma, Niitaka, Hayashi, Oka, Takano, Funakubo and Shimakawa20,Reference Nakamura, Kawai, Azuma, Kubota, Shimada, Aiba and Shimakawa21 tetragonal Bi(Zn1/2Ti1/2)O3, Reference Yazawa, Yasui, Morioka, Yamada, Uchida, Gruverman and Funakubo22 cubic SrTiO3, Reference Itoh, Shimura, Sakamoto and Yogo23 orthorhombic CaTiO3, Reference Wang, Wang, Liu and Chen24 tetragonal BaTiO3, Reference Kumar, Srinivas and Suryanarayana25–Reference Futakuchi, Kakuda and Sakai27 tetragonal (Bi1/2K1/2)TiO3 (Ref. Reference Matsuo, Noguchi, Miyayama, Suzuki, Watanabe, Sasabe, Ozaki, Mori, Torii and Kamiyama28–Reference Hagiwara and Fujihara30) were studied as end-members for solid-solutions with rhombohedral BiFeO3. In the form of thin film, increased piezoelectric responses were reported in solid-solutions with orthoferrite SmFeO3 with a high-field piezoelectric constant d 33* value (calculated from a strain–electric field curve) of 110 pm/V at the rhombohedral–pseudo-orthorhombic phase boundary composition of (Bi0.86Sm0.14)FeO3, Reference Fujino, Murakami, Anbusathaiah, Lim, Nagarajan, Fennie, Wuttig, Salamanca-Riba and Takeuchi18 and solid solutions with tetragonal BiCoO3 with a high-field d 33* value of 100 pm/V at the rhombohedral–tetragonal phase boundary composition of Bi(Fe0.9Co0.1)O3. Reference Nakamura, Kawai, Azuma, Kubota, Shimada, Aiba and Shimakawa21 In the form of bulk, increased piezoelectric responses were reported for solid-solutions with titanates such as tetragonal BaTiO3 (Refs. Reference Kumar, Srinivas and Suryanarayana25–Reference Futakuchi, Kakuda and Sakai27) and (Bi1/2K1/2)TiO3. Reference Matsuo, Noguchi, Miyayama, Suzuki, Watanabe, Sasabe, Ozaki, Mori, Torii and Kamiyama28–Reference Hagiwara and Fujihara30 For both solid-solution ceramics, the crystal system changed from rhombohedral to pseudocubic to tetragonal phases with increasing tetragonal end-member content, and the piezoelectric response was increased with keeping high Curie temperature at the composition that the crystal system changed from rhombohedral to pseudocubic phases: that is, the piezoelectric constant d 33 of 116 pC/N and the Curie temperature of 619 °C for Mn-doped 0.75BaTiO3–0.25BiFeO3 ceramics Reference Leontsev and Eitel26 and d 33 of ∼130 pC/N and the Curie temperature of 450 °C for 0.6(Bi0.5K0.5)TiO3–0.4BiFeO3 ceramics. Reference Matsuo, Noguchi, Miyayama, Suzuki, Watanabe, Sasabe, Ozaki, Mori, Torii and Kamiyama28,Reference Hagiwara and Fujihara30
Another method to increase the piezoelectric properties is to alter lattice distortion. An example is the solid-solution of BaTiO3 and (Bi1/2K1/2)TiO3. The crystal system is tetragonal throughout composition, but the piezoelectric properties can be increased with decreasing tetragonal distortion (c/a) at compositions between 0.8BaTiO3–0.2(Bi1/2K1/2)TiO3 and 0.4BaTiO3–0.6(Bi1/2K1/2)TiO3. Reference Hiruma, Aoyagi, Nagata and Takenaka31 The solid-solution of BiFeO3 with rhombohedral (Bi1/2Na1/2) TiO3, [(1−x) (Bi1/2Na1/2)TiO3–xBiFeO3] is this type. The crystal system of the solid-solution is rhombohedral throughout composition and does not experience a compositional phase transformation at room temperature. Reference Dorcet, Marchet and Trolliard32,Reference Ramana, Suryanarayana and Sankaram33 However, the crystal structure does change with composition; the rhombohedral distortion (90° − α) (α is measured based on a pseudocubic perovskite unit cell) is minimized at x = 0.2, while the lattice constant, a, is linearly increased with BiFeO3 content. Reference Dorcet, Marchet and Trolliard32 Therefore, it is interesting to study how the dielectric, ferroelectric, and piezoelectric properties change with the crystal structure. However, reports on ferroelectric and piezoelectric properties for the system were limited, Reference Ramana, Suryanarayana and Sankaram33–Reference Tian, Zhang, Yuan, Wu, Wang, Ma, Huo and Duan36 and a systematic study on electric properties was not reported.
In this study, (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 (x = 0–0.9) ceramics were prepared with solid-state synthesis, and the dielectric, ferroelectric, and piezoelectric properties along with the crystal structure and microstructure were investigated.
II. EXPERIMENTAL PROCEDURES
(1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics were prepared by solid-state synthesis. Raw powders of Bi2O3 (99.99%; Kojundo Chemical Lab. Co., Ltd., Saitama, Japan), Na2CO3 (99.99%; Rare Metallic Co. Ltd., Tokyo, Japan), TiO2 (99.9%, Kojundo Chemical Lab. Co., Ltd.), and α-Fe2O3 (99.9%, Kojundo Chemical Lab. Co., Ltd.) were batched according to the chemical formula with a total amount of 20 g, and they were initially mixed at 500 rpm for 20 min using a planetary ball mill (classic line P-7, Fritsch) with ethanol (20 mL) and stabilized zirconia balls with the diameter of 3 mm (40 g). After drying at 120 °C, the powders were calcined at 750 °C for 4 h in a closed alumina crucible in air. Crystal structure of the calcined powder was checked by x-ray diffraction (XRD, RINT 2500; Rigaku Corporation, Tokyo, Japan) with Cu Kα radiation. The calcined powder was milled again using the planetary ball mill with the same condition. After drying, the powder was mixed with 5 wt% polyvinyl alcohol binder and sieved through a mesh with 0.8 mm openings. Disc compacts (the diameter of 1 cm) pressed uniaxially at 200 MPa were initially heated at 700 °C for 2 h to remove the binder and then sintered at 980–1100 °C for 2 h in air.
Density was measured by an Archimedes method. Crystal structure was determined by XRD for powders crushed from sintered ceramics. Several diffraction peaks were used to determine lattice parameters by a least-square method. Lattice parameters were initially calculated on a hexagonal unit cell and then they were converted to those calculated on a pseudocubic cell (rhombohedral angle was nearly 90°) with using equations shown in literature. Reference Cullity37,Reference Moreau, Michel, Gerson and James38 The diffraction patterns were corrected by an external Si standard. For microstructural observation, a surface of the sintered ceramics was mirror-polished and then the polished ceramics were thermally etched at temperatures lower than the sintering temperatures by 100 °C for 15 min in air. The surface was observed by scanning electron microscopy (SEM, VE-9800; Keyence Corporation, Osaka, Japan). Grain size and the error bar were determined to be the average and the standard deviation of the diameters of 60–80 grains observed on an SEM image. The ceramics were polished down to approximately 0.3 mm in thickness. For electrical measurements, silver paste was applied on the top and bottom surfaces of the ceramics and heated at 550 °C, and the samples were sawed to the size of 2.5 × 2.5 × 0.3 mm3. The dielectric properties were determined from impedance measured at 1, 10, and 100 kHz using an impedance analyzer (4194A; Hewlett–Packard, Palo Alto, California) at temperatures from room temperature to 500 °C (on heating). Polarization–electric field (P–E) loops were measured at 0.1, 1, and 100 Hz and strain–electric field (S–E) curves were measured at 0.1 Hz using a ferroelectric tester (TF analyzer 2000; aixACCT Systems GmbH, Aachen, Germany) and a polarization and strain measuring system (Model JP005-SE; Lead Techno, Shiga, Japan) with a displacement meter (Millitron 1240; Mahr, Esslingen, Germany). The ceramic samples were poled at room temperature at 50–65 kV/cm for 5 min, and the piezoelectric constant d 33 was measured by a d 33 meter (Model ZJ-6B; Chinese Academy of Science, Beijing, China).
III. RESULTS AND DISCUSSION
A. Microstructure and crystal structure
The microstructures of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics were observed by SEM. As examples, the SEM images of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics with x = 0, 0.2, 0.5, and 0.9 are shown in Fig. 1. Dense microstructures were observed. The relative density of all the ceramics prepared was 95–99%, as listed in Table I. Grain sizes were 2–3 µm at x = 0–0.3 and about 1 µm at x = 0.4–0.9 (which are also listed in Table I). The larger grain sizes for the (Bi1/2Na1/2)TiO3-rich compositions were mainly attributed to higher sintering temperatures required to densify the ceramics. Here, the melting points of (Bi1/2Na1/2)TiO3 and BiFeO3 are 1290 °C (Ref. Reference Park, Chung, Kim and Hong39) and 960–970 °C, Reference Chaudhuri, Mitra, Mandal and Mandal40 respectively.

FIG. 1. SEM images of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 (x = 0, 0.2, 0.5, and 0.9) ceramics.
TABLE I. Sintering temperature, relative density, grain size of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics.

XRD patterns of the powders crushed from the sintered ceramics of (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 (x = 0–0.9) are shown in Fig. 2. Only diffraction peaks of a perovskite phase were observed for the ceramics. The 113 diffraction peak (the diffraction peaks were indexed on the basis of the hexagonal symmetry) was observed for the perovskite phase, which meant that the samples could be assigned to the rhombohedral R3c symmetry. The diffraction peaks were shifted to lower angle sides with x. Figure 3 shows the lattice constant and rhombohedral angle based on a pseudocubic cell for the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. The lattice constant increased linearly with x, while the rhombohedral angle showed a nonlinear behavior; it was maximized and approached to 90° at x = 0.1. Similar results were reported in literature, Reference Dorcet, Marchet and Trolliard32,Reference Ramana, Suryanarayana and Sankaram33 except that the rhombohedral angles observed in this study at x = 0.05–0.4 was much closer to 90°, that is, 89.9–90°, compared to the α values of 89.7–89.8° at x = 0.1–0.4 from the literature. It was explained that the linear increase in the lattice constant with the BF content was mainly caused by the larger ionic radius of the Fe3+ ion (0.645 Å) than that of the Ti4+ (0.604 Å) while the ionic radii of the Na+ ion (1.39 Å) and the Bi3+ (1.38 Å) were virtually unchanged. Reference Dorcet, Marchet and Trolliard32,Reference Shannon41 On the other hand, the reason for the nonlinear behavior of the rhombohedral angle was not understood.

FIG. 2. XRD patterns of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. Diffraction peaks were indexed on the basis of the hexagonal symmetry.

FIG. 3. Lattice constant a and rhombohedral angle α for the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics.
B. Electric properties
The dielectric constant and loss measured at 1 kHz and room temperature for the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 (x = 0–0.9) ceramics are shown in Fig. 4. At x = 0, the dielectric constant was about 580. It increased to 600–660 at x = 0.05–0.2, and then decreased with x. It was speculated that the dielectric constant was increased because the samples became ferroelectrically soft owing to the reduction in the rhombohedral distortion (90° − α). On the other hand, the decrease in the dielectric constant at x = 0.3–0.9 was attributed to the increase in the temperature of the dielectric maximum, T m, with x, as shown in the next paragraph. The dielectric loss was lower than 0.1 at x = 0–0.7. At x = 0.8 and 0.9, it increased to about 0.2, which might be attributed to electric conduction.

FIG. 4. Room temperature dielectric constant and loss of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics.
Figure 5 shows the temperature dependence of the dielectric constant and loss of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics (x = 0–0.5). At x = 0, two anomalies were observed for the dielectric constant profile: that is, a hump around 200 °C at which the dielectric constant was frequency dependent, and the nearly frequency-independent diffused dielectric maximum peak at 331 °C. These results were consistent with previous studies. Reference Dorcet, Marchet, Pena and Trolliard42,Reference Yao, Ge, Luo, Li, Viehland and Luo43 The hump could be related to a phase transition from a ferroelectric rhombohedral phase to an antiferroelectric modulated phase, and the diffused peak could be related to an antiferroelectric orthorhombic phase to a paraelectric tetragonal phase. Reference Dorcet, Trolliard and Boullay44,Reference Trolliard and Dorcet45 Note that there is one more dielectric anomaly reported at 520–540 °C, which was not measured in this study and was associated with the tetragonal to cubic phase transition. Reference Jones and Thomas46 The frequency dependence of the dielectric constant measured at 100 kHz and 1MHz was disappeared at 264 °C. Here, such a temperature was defined at which the frequency dispersion disappeared by comparing dielectric constant measured at 100 kHz and 1 MHz was defined as T FD. This temperature was close to the temperature that the rhombohedral phase disappeared in the modulated phase of the rhombohedral and orthorhombic phases at 280 °C. Reference Trolliard and Dorcet45 With increasing x, the temperature at which the dielectric constant measured at 1 MHz was maximized, T m, tends to increase from 331 to 404 °C at x = 0–0.4. At x = 0.5, the T m value could not be determined due to increased conduction. On the other hand, T FD was not strongly altered. The T FD and T m values are summarized in Table II. It was found that the T m value of this study was lower than that of previous study, which might be in part associated with the smaller rhombohedral distortion (90° − α).

FIG. 5. Temperature dependence of the dielectric properties of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. T m is the temperature at which the dielectric constant measured at 1 MHz was maximized, and T FD is the temperature at which the frequency dispersion of the dielectric constant measured at 100 kHz and 1 MHz disappeared.
TABLE II. T m, T FD, d 33*, and d 33 of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. T m is the dielectric constant maximum temperature measured at 1 MHz. T FD is the temperature, at which the frequency dependence disappeared for the dielectric constant measured at 100 kHz and 1 MHz. d 33* is the maximum strain divided by the applied electric field for the unipolar strain–electric field curve shown in Fig. 9. d 33 is the piezoelectric constant measured by the berlincourt d 33 meter for poled ceramics.
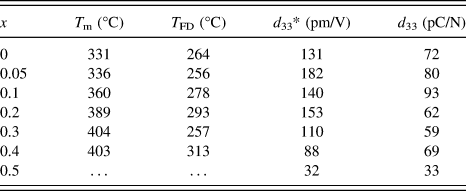
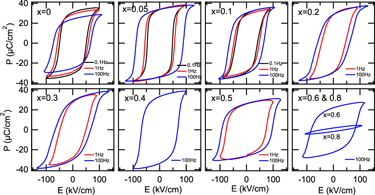
Figure 6 shows the P–E loops measured at 0.1, 1, and 100 Hz for the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 (x = 0–0.8) ceramics. At x = 0, ferroelectric hysteresis loops with the remanent polarization ∼30 µC/cm2 were observed at 0.1 and 1 Hz. The remanent polarization measured at 1 and 100 Hz was lower than that at 0.1 Hz. This was because an electric field which was large enough to saturate the polarization could not be applied to the sample. With increasing frequency, the coercive field increased due to a slow response of domains to the electric field. Reference Jona and Shirane47 At x = 0.05–0.4, well-developed hysteresis loops with the remanent polarization of 30–35 µC/cm2 were observed. Note that these values were much larger than those of previously reported P–E loops which were not fully saturated. Reference Ramana, Suryanarayana and Sankaram33,Reference Tian, Zhang, Yuan, Wu, Wang, Ma, Huo and Duan36 On the other hand, the coercive field was lowered compared to that at x = 0. This was attributed to the reduction of the rhombohedral distortion (90° − α) which facilitated domain wall motion. At x = 0.5–0.8, the polarization and the opening of the ferroelectric P–E loops decreased with x, especially at x = 0.8. This reduction was attributed to the increased content of BiFeO3 which was a hard ferroelectric material due to strongly pinned domain walls. Reference Rojac, Kosec, Budic, Setter and Damjanovic17 Note that the P–E loops measured at 0.1 and/or 1 Hz were not shown at x = 0.2–0.8 because the loops appeared leaky or the samples were electrically broken down. The remanent polarization and coercive field are summarized in Fig. 7.

FIG. 6. P-E loops of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. The frequency was 0.1, 1, and 100 Hz.

FIG. 7. Remanent polarization and coercive field of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics.
The bipolar and unipolar S–E curves measured at 0.1 Hz for the (1 − x) (Bi1/2Na1/2) TiO3–xBiFeO3 ceramics with x = 0–0.5 are shown in Figs. 8 and 9, respectively. Typical butterfly curves were observed for the bipolar measurements. At x = 0–0.2, the induced unipolar strain was 0.12–0.16% for the applied electric field of 80–100 kV/cm, and it was maximized at x = 0.05 with the d 33* value (= maximum strain/applied electric field) of 182 pm/V. At x = 0.3–0.5, the strain was decreased with x, due to the hardening. The piezoelectric constant measured by the d 33 meter for poled ceramics as well as the d 33* value is listed in Table II. The d 33 value of 72 pC/N at x = 0 was increased to 93 pC/N at x = 0.1, and then decreased to about 60–70 pC/N at x = 0.2–0.4, followed by the sudden drop to 33 pC/N at x = 0.5. A similar highest d 33 value was reported by Ryu et al., Reference Ryu, Song, Kim, Lee, Seong, Jeong and Song34 but their composition dependence was different. That is, the d 33 value was maximized at x = 0.05, and it dropped to about 30 and 5 pC/N at x = 0.1 and 0.2, respectively. The reason for the difference is unknown, but could be related to the quality of the samples or poling conditions.

FIG. 8. Bipolar S–E curves of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. The frequency was 0.1 Hz.

FIG. 9. Unipolar S–E curves of the (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics. The frequency was 0.1 Hz.
In this study, it was found that the well-developed P–E loops could be obtained at x = 0–0.6, and the decrease in the rhombohedral distortion at x = 0.05–0.1 was coincident with the increased in the dielectric and piezoelectric properties while keeping T FD and T m high. These findings could be useful in development of high performance lead-free piezoelectric materials.
IV. CONCLUSIONS
The dense (1 − x) (Bi1/2Na1/2)TiO3–xBiFeO3 ceramics with the single perovskite phase were prepared by the solid-state synthesis. The crystal system of the ceramics was rhombohedral with the R3c symmetry. The rhombohedral distortion (90° − α) was minimized at x = 0.1, while the lattice constant increased linearly with x. T FD was between 256–313 °C and T m tended to increase from 331–404 °C with x for the samples with x = 0–0.5, where T FD is the temperature at which the frequency dispersion of the dielectric constant measured at 100 kHz and 1 MHz disappeared and T m is the temperature at which the dielectric constant measured at 1 MHz was maximized. With increasing x, the dielectric constant increased at x = 0.05, and then decreased. Saturated ferroelectric P–E hysteresis and S–E butterfly responses were observed at x = 0–0.6 and x = 0–0.5, respectively. The coercive field was reduced at x = 0.05–0.2 and the large remanent polarization of 30–35 µC/cm2 was obtained at x = 0–0.4. The piezoelectric constants d 33 and d 33* were maximized to 93 pC/N at x = 0.1 and 183 p.m./V at x = 0.05, respectively.
ACKNOWLEDGMENT
The authors would like thank Profs. Kuroiwa and Moriyoshi of Hiroshima University and Prof. Wada of University of Yamanashi for synchrotron radiation experiments for crystal structure analyses which supported our XRD data. This work was in part supported by Ryukoku University Science and Technology Fund.