1. Introduction
Recent laser fusion research, represented by the remarkable exploitation of the NIF (National Ignition Facility) Program and NIC (National Ignition Campaign) Program at LLNL (Lawrence Livermore National Laboratory) in America, has made excellent progress towards attaining the conditions required for ignition. Achieving ignition, however, is still a challenge. Some scientific cliff difficulties[Reference Chandal1] appeared in NIC ignition experiments and need to be further explored. These difficulties cover a number of physical areas. Firstly, the value of the efficiency of the coupling of the input ![]() $3\omega _{0}$ laser to the ignition fuel target was lower than the expected simulation values; for example, the implosion velocity and fuel target stagnation pressure were 13% and
$3\omega _{0}$ laser to the ignition fuel target was lower than the expected simulation values; for example, the implosion velocity and fuel target stagnation pressure were 13% and ![]() $\sim $50% lower. Secondly, the radiation driving target ablation ratio was
$\sim $50% lower. Secondly, the radiation driving target ablation ratio was ![]() $\sim $20%–60% higher than the simulation value. Thirdly, the target deuterium-tritium (DT) fuel met an earlier “mix cliff” limitation at the time when the residual ablator’s mass is 0.4 mg instead of the designed 0.28 mg. Fourthly, the laser–plasma interaction (LPI) process occurs during the
$\sim $20%–60% higher than the simulation value. Thirdly, the target deuterium-tritium (DT) fuel met an earlier “mix cliff” limitation at the time when the residual ablator’s mass is 0.4 mg instead of the designed 0.28 mg. Fourthly, the laser–plasma interaction (LPI) process occurs during the ![]() $3\omega _{0}$ energy deposition on the corona of the hohlraum inner surface. In addition, it should be noted that LPI might have a significant effect on the other three difficulties, though many efforts have been made to increase the ignition threshold factor exp(ITF
$3\omega _{0}$ energy deposition on the corona of the hohlraum inner surface. In addition, it should be noted that LPI might have a significant effect on the other three difficulties, though many efforts have been made to increase the ignition threshold factor exp(ITF![]() $_x$) and the experimental results have been getting better in the past two years.
$_x$) and the experimental results have been getting better in the past two years.
Until now, the under-used classical theory of LPI (CTLPI)[Reference Liu, Rosenbluth and White2–Reference Jones, Mead, Coggeshall, Aldrich, Norton, Pollak and Wallace6] has been based on the boundary condition hypothesis of uniform incident light and bulk homogeneous plasmas. However, it is known that the far-field profile of the incident laser beam has a strong speckle irradiance contrast with severe self-phase modulation on the wavefront. Meanwhile, laser produced plasma jetting always appears and develops, which definitively spoils the corona plasma homogeneity. Therefore, it is necessary to investigate and analyze precisely in detail the features of the production and development of small scale filamentation instability, which may spatially and temporally modify the plasma homogeneity and can be easily induced by the leading laser interaction with the plasmas.
Self-focusing filamentation instability was studied separately and individually together with the other important nonlinear three-wave interaction processes in the 1970s and 1980s[Reference Liu, Rosenbluth and White2–Reference Jones, Mead, Coggeshall, Aldrich, Norton, Pollak and Wallace6]. In the years of 1976 and 1977, Eidman et al. [Reference Eidman, Key and Sigel7] and Hass et al. [Reference Hass, Shay, Kruer, Phillion, Rainer, Ruper and Kornblum8] found in the X-ray pinhole camera images from laser-irradiated targets that the whole X-ray spot size was smaller than the incident laser hot spot size, which indicated that the laser hot spots had self-focused due to the thermal effect to a smaller size, resulting in a stronger X-ray emitting spot. Baldis et al. [Reference Baldis and Corkum9] measured the filaments in 1980 using Thomson scattering and optical probe beam reflection. Following the early investigations, Lin et al. [Reference Lin, Will and Rumsby10, Reference Lin, Willi, Toner and Gibson12–Reference Lin, Zhang, Lin, Wang, Zhuang, Wei, Lu, Shi, Dai, Tian, Fan and Li16], Willi et al. [Reference Willi, Rumsby, Hooker, Raven and Lin11], Giulietti et al. [Reference Giulietti, Afshar-Rad, Coe, Will, Lin and Yu17], and Jones et al. [Reference Jones, Mead, Coggeshall, Aldrich, Norton, Pollak and Wallace6] investigated the small scale filamentation instability further in the 1980s and 1990s.
Recently the effect of phase front deformation on the growth of the filamentation instability was studied[Reference Higson, Trines, Jiang, Bingham, Lancaster, Davies and Norreys18]. Filamentation instability and its connection to two-plasmon decay (TPD) instability were also investigated by using energetic proton radiography[Reference Séguin, Li, Manuel, Rinderknecht, Sinenian, Frenje, Rygg, Hicks, Petrasso, Delettrez, Marshall and Smalyuk19, Reference Manuel, Li, Séguin, Sinenian, Frenje, Casey, Petrasso, Hager, Betti, Hu, Delettrez and Meyerhofer20], a diagnostic technique appropriate for the observation of electromagnetic fields[Reference Séguin, Li, Manuel, Rinderknecht, Sinenian, Frenje, Rygg, Hicks, Petrasso, Delettrez, Marshall and Smalyuk19–Reference Ahmed, Dieckmann, Romagnani, Doria, Sarri, Cerchez, Ianni, Kourakis, Giesecke, Notley, Prasad, Willi and Borghesi21].
2. Collection and re-analysis for some of the earlier experimental results on small scale unstable filamentation
The early experimental investigation of the connection of TPD instability with filamentation instability is re-analyzed in a new way. Differing from the old approach, which considered more the details of the ![]() $3\omega _{0}/2$ emission features and separately the link of some contribution from the filamentation process, our approach provides in this paper more qualitative filamentation features, from the original experimental graphs, and more detailed analysis for the experiments. Several important pieces of evidence are given now to show that the unstable small scale self-focusing filamentation instability (SSSFI) should be the first important factor for stimulating the TPD instability and, as a deduction, the other three instabilities (i.e., stimulated Raman scattering (SRS), stimulated Brillouin scattering (SBS), and resonance absorption (RA)) in laser plasma corona, though the evidence was not completely recognized in the previous articles. Following the new recognition of LPI physics, the contribution of LPI to some of the branches of scientific difficulties of laser fusion ignition physics are discussed.
$3\omega _{0}/2$ emission features and separately the link of some contribution from the filamentation process, our approach provides in this paper more qualitative filamentation features, from the original experimental graphs, and more detailed analysis for the experiments. Several important pieces of evidence are given now to show that the unstable small scale self-focusing filamentation instability (SSSFI) should be the first important factor for stimulating the TPD instability and, as a deduction, the other three instabilities (i.e., stimulated Raman scattering (SRS), stimulated Brillouin scattering (SBS), and resonance absorption (RA)) in laser plasma corona, though the evidence was not completely recognized in the previous articles. Following the new recognition of LPI physics, the contribution of LPI to some of the branches of scientific difficulties of laser fusion ignition physics are discussed.

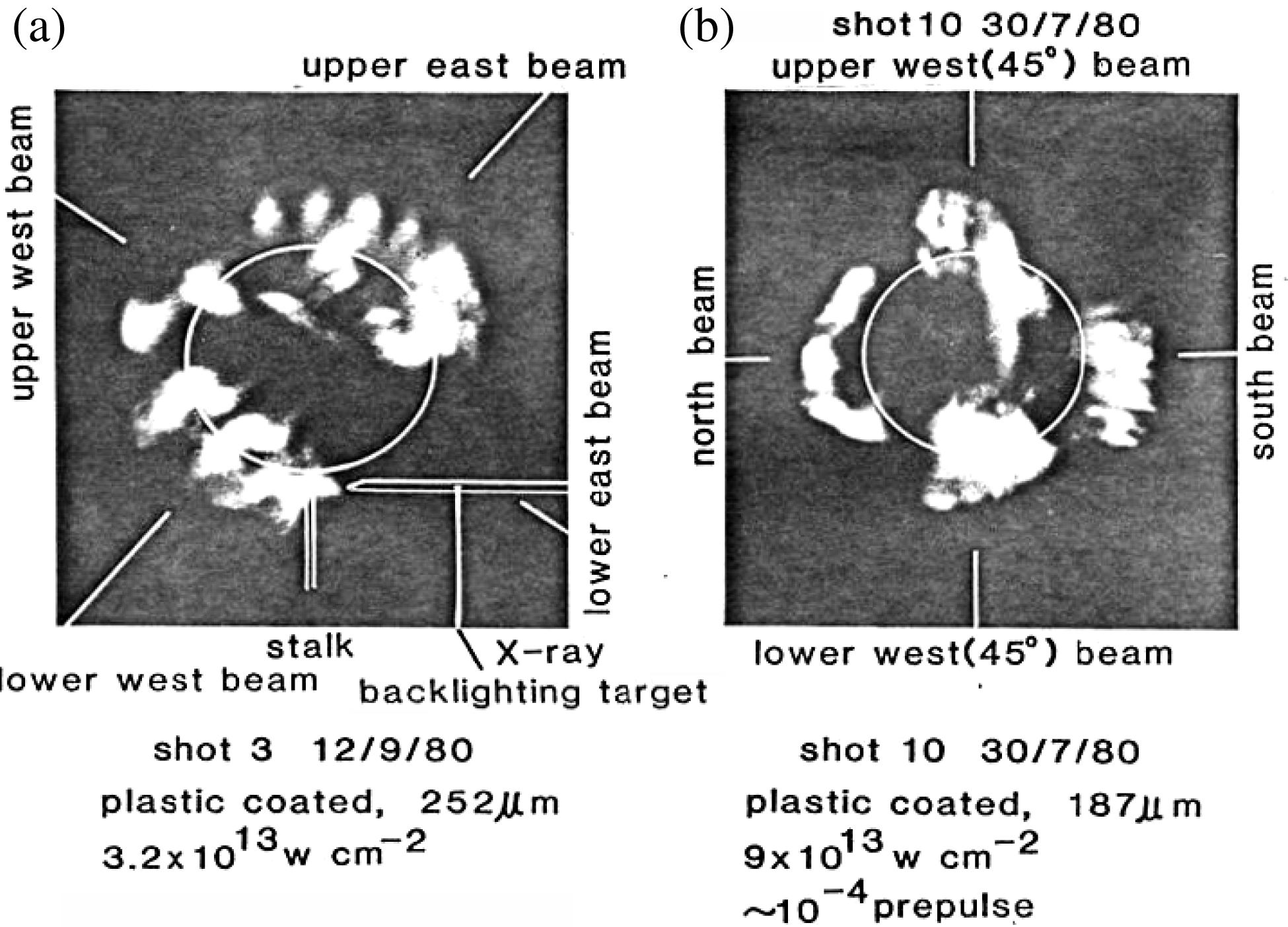
Figure 1. Photographs of the ![]() $3\omega _{0}/2$ harmonic emission from six-beam-irradiated spherical targets taken from two perpendicular directions. (a) 1
$3\omega _{0}/2$ harmonic emission from six-beam-irradiated spherical targets taken from two perpendicular directions. (a) 1 ![]() $\mathrm {\mu} {\rm m}$ polymer coated target, initial diameter 252
$\mathrm {\mu} {\rm m}$ polymer coated target, initial diameter 252 ![]() $\mathrm {\mu} {\rm m}$, irradiance
$\mathrm {\mu} {\rm m}$, irradiance ![]() $3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$. (b) 1
$3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$. (b) 1 ![]() $\mathrm {\mu} {\rm m}$ polymer coated target, initial diameter 187
$\mathrm {\mu} {\rm m}$ polymer coated target, initial diameter 187 ![]() $\mathrm {\mu} {\rm m}$, irradiance
$\mathrm {\mu} {\rm m}$, irradiance ![]() $9 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$[Reference Lin, Will and Rumsby10].
$9 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$[Reference Lin, Will and Rumsby10].
2.1. The observation of the connection of filamentation instability to the TPD instability
Lin et al. [Reference Lin, Will and Rumsby10] obtained the time integrated ![]() $3\omega _{0}/2$ bunched filament structures from a cubic six-laser-beam-irradiated spherical glass micro-balloon target corona in 1981. Figure 1 shows the 2D space resolved experimental images of time integrated
$3\omega _{0}/2$ bunched filament structures from a cubic six-laser-beam-irradiated spherical glass micro-balloon target corona in 1981. Figure 1 shows the 2D space resolved experimental images of time integrated ![]() $3\omega _{0}/2$ filament emission bunches, each defined as the integration or overlapping of many individual filaments in space and/or time dimensions. The earlier work[Reference Lin, Will and Rumsby10] concluded that “The
$3\omega _{0}/2$ filament emission bunches, each defined as the integration or overlapping of many individual filaments in space and/or time dimensions. The earlier work[Reference Lin, Will and Rumsby10] concluded that “The ![]() $3\omega _{0}/2$ emission structures imply that the plasma corona is no longer homogeneous in which an
$3\omega _{0}/2$ emission structures imply that the plasma corona is no longer homogeneous in which an ![]() $n_{c}/4$ layer can exist within a background plasma of much higher density. As the
$n_{c}/4$ layer can exist within a background plasma of much higher density. As the ![]() $3\omega _{0}/2$ emission structures are aligned along the laser beam directions, the results reported here are clear evidence for self-focusing and filamentation in the underdense corona plasma surrounding the target.” However, many succeeding investigations showed that the fine
$3\omega _{0}/2$ emission structures are aligned along the laser beam directions, the results reported here are clear evidence for self-focusing and filamentation in the underdense corona plasma surrounding the target.” However, many succeeding investigations showed that the fine ![]() $3\omega _{0}/2$ emission structures with rather high time, space, and spectrum resolutions opened some new phases. Some questions should be proposed and answered, such as:
$3\omega _{0}/2$ emission structures with rather high time, space, and spectrum resolutions opened some new phases. Some questions should be proposed and answered, such as:
Is the small scale self-focusing filamentation instability (SSSFI) stable or unstable?
What are the effective physical boundary conditions for SSSFI? Classical bulk plasmas interacting with classically uniform incoherent light? Or the leading section of the laser pulse, or the added prepulse, produced plasmas interacting with the real incident laser light profile with severe phase modulation and strong amplitude modulation?
What is the connection between SSSFI and TPD, SRS, SBS, and RA?
What role does the SSSFI play in LPI? Is it very important or negligible?
The filaments in figure 1 could be composed of many temporarily existing ![]() $n_{c}/4$ layers, which indicate that the corona plasma is already very inhomogeneous. These temporarily existing
$n_{c}/4$ layers, which indicate that the corona plasma is already very inhomogeneous. These temporarily existing ![]() $n_{c}/4$ layers are produced transiently by the self-phase modulation (SPM) of the incident laser light driving forward the filament ends and increasing the electron density to higher than
$n_{c}/4$ layers are produced transiently by the self-phase modulation (SPM) of the incident laser light driving forward the filament ends and increasing the electron density to higher than ![]() $n_{c}/4$, with much higher laser intensity inside the filaments than in background plasmas. That perhaps was the first experiment to study the connection of filamentation instability with the other kinds of instabilities in the laser plasma corona. On the foundation of CTLPI, another unexpected result was that there was no uniform
$n_{c}/4$, with much higher laser intensity inside the filaments than in background plasmas. That perhaps was the first experiment to study the connection of filamentation instability with the other kinds of instabilities in the laser plasma corona. On the foundation of CTLPI, another unexpected result was that there was no uniform ![]() $3\omega _{0}/2$ emission around the bulk spherical shell plasma
$3\omega _{0}/2$ emission around the bulk spherical shell plasma ![]() $n_{c}/4$ density layer during the whole laser pulse period, except the strong
$n_{c}/4$ density layer during the whole laser pulse period, except the strong ![]() $3\omega _{0}/2$ filament bunches which are just along the direction of the laser light normally or tangentially incident on the glass micro-balloon target. One explanation is that the laser average power intensities outside the
$3\omega _{0}/2$ filament bunches which are just along the direction of the laser light normally or tangentially incident on the glass micro-balloon target. One explanation is that the laser average power intensities outside the ![]() $n_{{c}}/4$ layer of the individual and the integrated filament bunches were still lower than the predicted threshold of TPD instability, which was considered as
$n_{{c}}/4$ layer of the individual and the integrated filament bunches were still lower than the predicted threshold of TPD instability, which was considered as ![]() $5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$ according to the earliest CTLPI. This implies that the laser intensity in the laser produced filament ends should be several tens of times higher than that outside. In addition, since the irradiance at the ends (“bottoms” was adopted on the original paper[Reference Lin, Will and Rumsby10]) of the filament channels was considerably larger than that in the surrounding areas, one would expect the emission to have been caused by the modulated moving
$5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$ according to the earliest CTLPI. This implies that the laser intensity in the laser produced filament ends should be several tens of times higher than that outside. In addition, since the irradiance at the ends (“bottoms” was adopted on the original paper[Reference Lin, Will and Rumsby10]) of the filament channels was considerably larger than that in the surrounding areas, one would expect the emission to have been caused by the modulated moving ![]() $n_{c}/4$ trajectories of the filament self-focusing ends.
$n_{c}/4$ trajectories of the filament self-focusing ends.

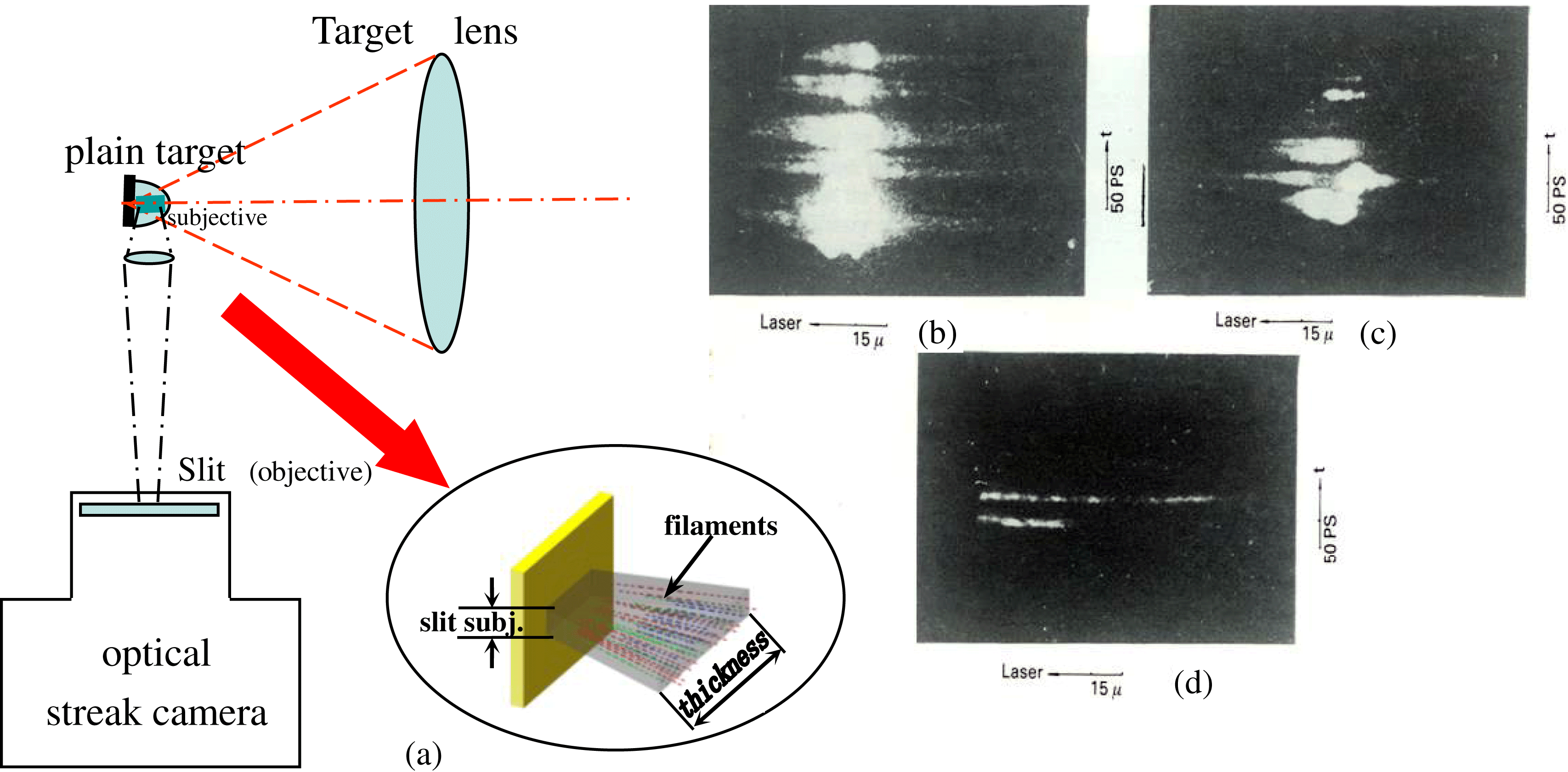
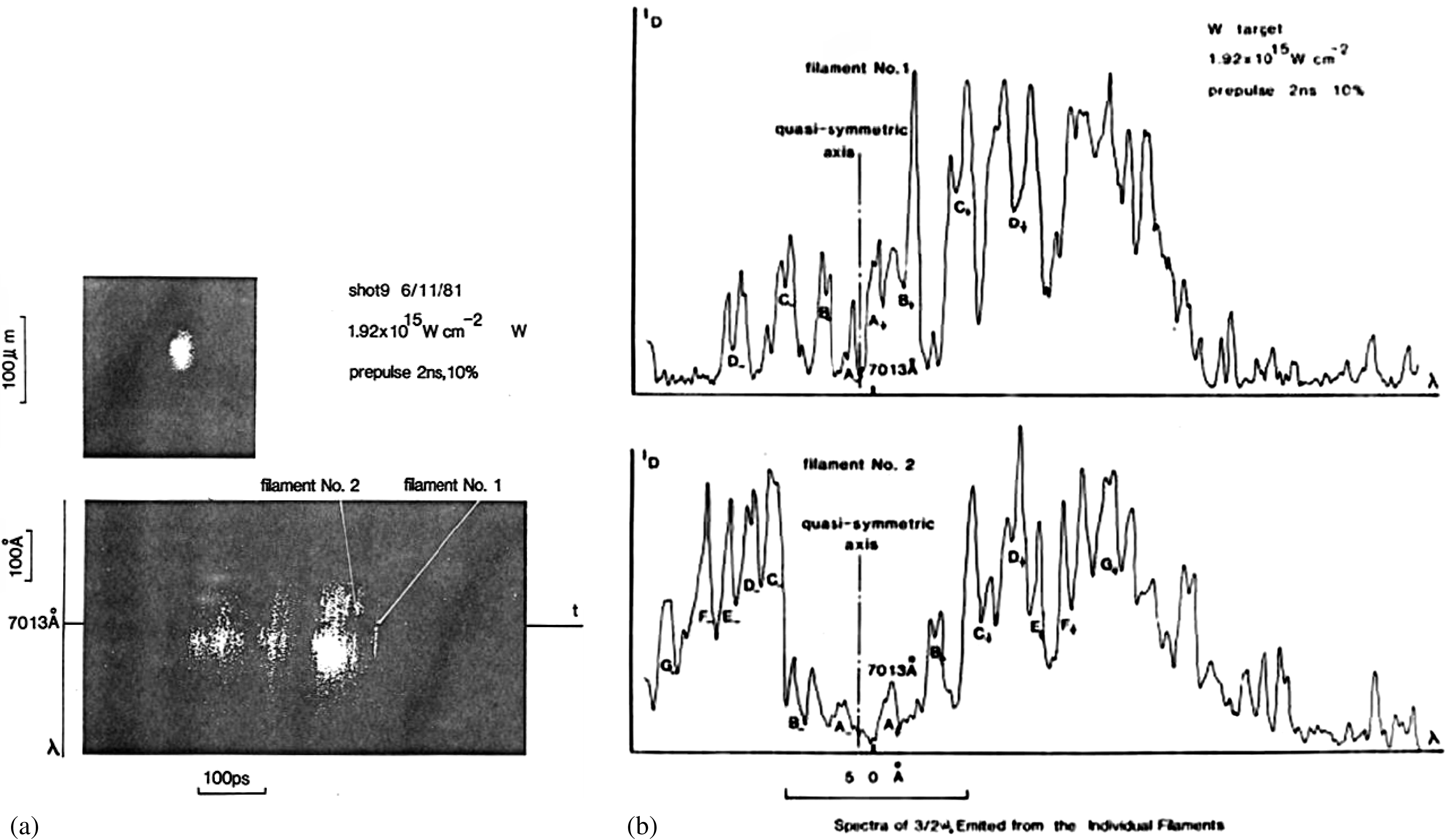
Figure 2. ![]() $(3/2)\omega _{0}$ time and space resolved photographs, along the filament channels. (a) The experimental setup. The magnification of the imaging optics was 19, with the temporal resolution of 5–10 ps and the spatial resolution of 5
$(3/2)\omega _{0}$ time and space resolved photographs, along the filament channels. (a) The experimental setup. The magnification of the imaging optics was 19, with the temporal resolution of 5–10 ps and the spatial resolution of 5 ![]() $\mathrm {\mu} {\rm m}$. (b) Shot No. 107; narrow band laser irradiation on a Ta plain target with laser incidence angle
$\mathrm {\mu} {\rm m}$. (b) Shot No. 107; narrow band laser irradiation on a Ta plain target with laser incidence angle ![]() $\sim 10^{\circ }$, energy 8.3 J and pulse width 250 ps. (c) Shot No. 124; narrow band laser irradiation on an Al plain target with laser incidence angle
$\sim 10^{\circ }$, energy 8.3 J and pulse width 250 ps. (c) Shot No. 124; narrow band laser irradiation on an Al plain target with laser incidence angle ![]() $\sim 20^{\circ }$, energy 8.1 J and pulse width 250 ps. (d) Shot No. 113; broad band laser irradiation on a Ta target with laser incidence angle
$\sim 20^{\circ }$, energy 8.1 J and pulse width 250 ps. (d) Shot No. 113; broad band laser irradiation on a Ta target with laser incidence angle ![]() $\sim 10^{\circ }$, energy 3.6 J and pulse width 250 ps [Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15].
$\sim 10^{\circ }$, energy 3.6 J and pulse width 250 ps [Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15].
2.2. The experimental evidence for the unstable SSSFI phenomenon and the features of spatially and temporally resolved  $3\omega _{0}/2$ emission
$3\omega _{0}/2$ emission
The spatially and temporally resolved ![]() $3\omega _{0}/2$ emission was investigated in 1986[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15] and 1992[Reference Lin, Zhang, Lin, Wang, Zhuang, Wei, Lu, Shi, Dai, Tian, Fan and Li16]. The optical streak camera slit was horizontally aligned parallel to the driving laser central axis for observing the laser focal center produced filaments along the filament channels by imaging optics. The experimental arrangement is shown in figure 2(a)[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15].
$3\omega _{0}/2$ emission was investigated in 1986[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15] and 1992[Reference Lin, Zhang, Lin, Wang, Zhuang, Wei, Lu, Shi, Dai, Tian, Fan and Li16]. The optical streak camera slit was horizontally aligned parallel to the driving laser central axis for observing the laser focal center produced filaments along the filament channels by imaging optics. The experimental arrangement is shown in figure 2(a)[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15].
It can be found in the spatially and temporally resolved ![]() $3\omega _{0}/2$ emission photograph in figure 2(d) that two individual filaments were caught with filament lengths of 120
$3\omega _{0}/2$ emission photograph in figure 2(d) that two individual filaments were caught with filament lengths of 120 ![]() $\mathrm {\mu} {\rm m}$ and 43
$\mathrm {\mu} {\rm m}$ and 43 ![]() $\mathrm {\mu} {\rm m}$, respectively. The longest and the shortest filament lengths in figures 2(b) and (c) were 130
$\mathrm {\mu} {\rm m}$, respectively. The longest and the shortest filament lengths in figures 2(b) and (c) were 130 ![]() $\mathrm {\mu} {\rm m}$ and 15
$\mathrm {\mu} {\rm m}$ and 15 ![]() $\mathrm {\mu} {\rm m}$, respectively. The temporal existence duration at all of the spatial filament positions was
$\mathrm {\mu} {\rm m}$, respectively. The temporal existence duration at all of the spatial filament positions was ![]() $\sim $5 ps, and along with the lifetime of each filament from the beginning of the stimulated
$\sim $5 ps, and along with the lifetime of each filament from the beginning of the stimulated ![]() $3\omega _{0}/2$ emission to the ending of the emission, came to around
$3\omega _{0}/2$ emission to the ending of the emission, came to around ![]() $\sim $15 ps–20 ps. One should pay attention here to the difference of the real inner aperture of a filament from the outer aperture of the
$\sim $15 ps–20 ps. One should pay attention here to the difference of the real inner aperture of a filament from the outer aperture of the ![]() $3\omega _{0}/2$ emission filaments. The former could be reduced to the minimum diameter scale of the incident laser wavelength at the ends of the second section of the filament duration of the lifetime, while the latter
$3\omega _{0}/2$ emission filaments. The former could be reduced to the minimum diameter scale of the incident laser wavelength at the ends of the second section of the filament duration of the lifetime, while the latter ![]() $3\omega _{0}/2$ emission aperture and the existence time mainly or only depend on the interaction region and the period in terms of the TPD produced
$3\omega _{0}/2$ emission aperture and the existence time mainly or only depend on the interaction region and the period in terms of the TPD produced ![]() $\omega _{0}/2$ plasmon interaction with the incident laser photons at the transient ends or nodes of filaments.
$\omega _{0}/2$ plasmon interaction with the incident laser photons at the transient ends or nodes of filaments.
We may define, among the filaments with different lengths, the long length filaments as the strong filaments, which have higher laser intensities on the filament ends with stronger laser self-phase modulation drive (SPMD) or pondermotive force drive (PFD) ability to drive the filament ends to penetrate deeper into the plasma corona, even to the region of a quarter of the critical layer. We may, in the same way, define the moderate and the weak filaments. It should be noted here that the above defined ![]() $3\omega _{0}/2$ emission filament length could be the temporally first half-section of the whole filament temporal development process, in which the self-phase modulation will be enhanced by further PFD self-focusing such that the axial plasmas are pushed forward to build up the filament ends or nodes with higher plasma density to a level higher than
$3\omega _{0}/2$ emission filament length could be the temporally first half-section of the whole filament temporal development process, in which the self-phase modulation will be enhanced by further PFD self-focusing such that the axial plasmas are pushed forward to build up the filament ends or nodes with higher plasma density to a level higher than ![]() $n_{c}/4$, or even
$n_{c}/4$, or even ![]() $n_{c}$, to construct the limited laser imprinting.
$n_{c}$, to construct the limited laser imprinting.
From figures 2(b), (c), and (d) it is found that: (i) The individually weak filaments appeared at the temporal pulse profile valleys of the amplitude modulated laser pulse. At the pulse profile peak region, the total filament sampling numbers integrated along the thickness direction, shown in figure 2(a), increased quickly in an overlapped short transient period, even bringing about a signal saturation. However, the distinct features of unstable filamentation effects, such as the temporal existence period and the long spatial length, and the position of the low density corona area, are displayed and easy to examine. (ii) From the analysis of above experimental results, there is still no evidence for CTLPI produced ![]() $3\omega _{0}/2$ emission from bulk homogeneous plasma corona. (iii) It seems that the
$3\omega _{0}/2$ emission from bulk homogeneous plasma corona. (iii) It seems that the ![]() $3\omega _{0}/2$ emission intensity arising from laser–plasma interaction of TPD instability for high
$3\omega _{0}/2$ emission intensity arising from laser–plasma interaction of TPD instability for high ![]() $Z$ target material (Ta) in figure 2(b) was stronger than that for the target with intermediate
$Z$ target material (Ta) in figure 2(b) was stronger than that for the target with intermediate ![]() $Z$ (Al) in figure 2(c). (iv) Figure 2(d) illustrates that the power of each single
$Z$ (Al) in figure 2(c). (iv) Figure 2(d) illustrates that the power of each single ![]() $3\omega _{0}/2$ filament depends on the total fraction of the incident laser power assigned to the related first half-section of the filaments. And the fraction of assignment depends on the random distribution of the very inhomogeneous bulk plasmas.
$3\omega _{0}/2$ filament depends on the total fraction of the incident laser power assigned to the related first half-section of the filaments. And the fraction of assignment depends on the random distribution of the very inhomogeneous bulk plasmas.
The work in the article[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15] adopted a group of ![]() $\sim $3 nm bandwidth incident laser interaction experiments to examine the
$\sim $3 nm bandwidth incident laser interaction experiments to examine the ![]() $3\omega _{0}/2$ emission feature. It is described in the paper that the wide band laser focal spot size is much larger and more uniform than the narrow one[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15], resulting in quite a large percentage laser irradiance reduction, leading to the
$3\omega _{0}/2$ emission feature. It is described in the paper that the wide band laser focal spot size is much larger and more uniform than the narrow one[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15], resulting in quite a large percentage laser irradiance reduction, leading to the ![]() $3\omega _{0}/2$ filamentation being seldom produced[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15]. For many shots of the broad band laser, there were no appearances of
$3\omega _{0}/2$ filamentation being seldom produced[Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15]. For many shots of the broad band laser, there were no appearances of ![]() $3\omega _{0}/2$ filaments. When the broad band laser irradiance increased, the
$3\omega _{0}/2$ filaments. When the broad band laser irradiance increased, the ![]() $3\omega _{0}/2$ filaments seldom appeared and were seldom caught.
$3\omega _{0}/2$ filaments seldom appeared and were seldom caught.
Comparing the observed ![]() $3\omega _{0}/2$ filament images in figures 2(b), (c) and (d), one should find that all of the
$3\omega _{0}/2$ filament images in figures 2(b), (c) and (d), one should find that all of the ![]() $3\omega _{0}/2$ signal was produced and
$3\omega _{0}/2$ signal was produced and ![]() ${{\sim }}90^{\circ }$ side scattered from the individual or bunched filament channels, with intense node modulations along their own filament channel axes, though the intensity modulation appeared a bit weaker than that observed from the backscattered spectrum node modulations of filaments, which will be described and re-analyzed below. The weakening mechanism could be caused by the transformation astigmatic distortion of the
${{\sim }}90^{\circ }$ side scattered from the individual or bunched filament channels, with intense node modulations along their own filament channel axes, though the intensity modulation appeared a bit weaker than that observed from the backscattered spectrum node modulations of filaments, which will be described and re-analyzed below. The weakening mechanism could be caused by the transformation astigmatic distortion of the ![]() $3\omega _{0}/2$ node signals during the imagery process while the light emitted from one node subject passed through a large gradient plasma density area, in the left side in figures 2(b) and (c), along different directions transversely, at about
$3\omega _{0}/2$ node signals during the imagery process while the light emitted from one node subject passed through a large gradient plasma density area, in the left side in figures 2(b) and (c), along different directions transversely, at about ![]() $80^{\circ }$ orientation relative to the incident laser major axis.
$80^{\circ }$ orientation relative to the incident laser major axis.
The above time and space resolved ![]() $3\omega _{0}/2$ emission experiments have provided further clear evidence for the origin, existence, and features of the unstable SSSFI, qualitatively, in detail. All the results directly further support the assertion that the unstable filament instability provides a decisive contribution to the TPD instability process in laser produced plasmas. It is unlikely that the filamentation instability behaves as a transient phenomenon “flicker” effect, predicted by the simulation.
$3\omega _{0}/2$ emission experiments have provided further clear evidence for the origin, existence, and features of the unstable SSSFI, qualitatively, in detail. All the results directly further support the assertion that the unstable filament instability provides a decisive contribution to the TPD instability process in laser produced plasmas. It is unlikely that the filamentation instability behaves as a transient phenomenon “flicker” effect, predicted by the simulation.
It should be recognized that in the above analyses of Sections 2.1 and 2.2 the ![]() $3\omega _{0}/2$ filament channels appeared mainly in the bulk plasma corona area with average electron density from
$3\omega _{0}/2$ filament channels appeared mainly in the bulk plasma corona area with average electron density from ![]() $n_{c}/4$ to
$n_{c}/4$ to ![]() $n_{c}/10{-}n_{c}/20$. This implies that, firstly, the TPD process is induced in the rather low electron density area instead of the macroscale
$n_{c}/10{-}n_{c}/20$. This implies that, firstly, the TPD process is induced in the rather low electron density area instead of the macroscale ![]() $n_{c}/4$ density region which is predicted by early classical theory of TPD, and, secondly, the transient
$n_{c}/4$ density region which is predicted by early classical theory of TPD, and, secondly, the transient ![]() $3\omega _{0}/2$ emission and decay process, including all the TPD stimulation, the three-wave interaction of
$3\omega _{0}/2$ emission and decay process, including all the TPD stimulation, the three-wave interaction of ![]() $\omega _{0}/2$ plasmons with the incident laser photons, the
$\omega _{0}/2$ plasmons with the incident laser photons, the ![]() $\omega _{0}/2$ plasma electron wave fast decay by Landau damping and the accompanying fast electron and hard X-ray emission from the ends, nodes, or channels, occurred in the low density region of laser produced plasmas in a 5–10 ps period.
$\omega _{0}/2$ plasma electron wave fast decay by Landau damping and the accompanying fast electron and hard X-ray emission from the ends, nodes, or channels, occurred in the low density region of laser produced plasmas in a 5–10 ps period.
2.3. The experimental study of the dynamics of a small scale unstable filament growth and damping process
The features of space and spectrum resolved  $3\omega _{0}/2$ emission
$3\omega _{0}/2$ emission
Some earlier work[Reference Lin, Willi, Toner and Gibson12, Reference Lin, Willi and Rumsby13] investigated spatially resolved spectra of ![]() $3\omega _{0}/2$ emission, induced by the TPD instability process, in 1981, and obtained a finest
$3\omega _{0}/2$ emission, induced by the TPD instability process, in 1981, and obtained a finest ![]() $3\omega _{0}/2$ emission photograph with the spatial and spectral resolutions of 5
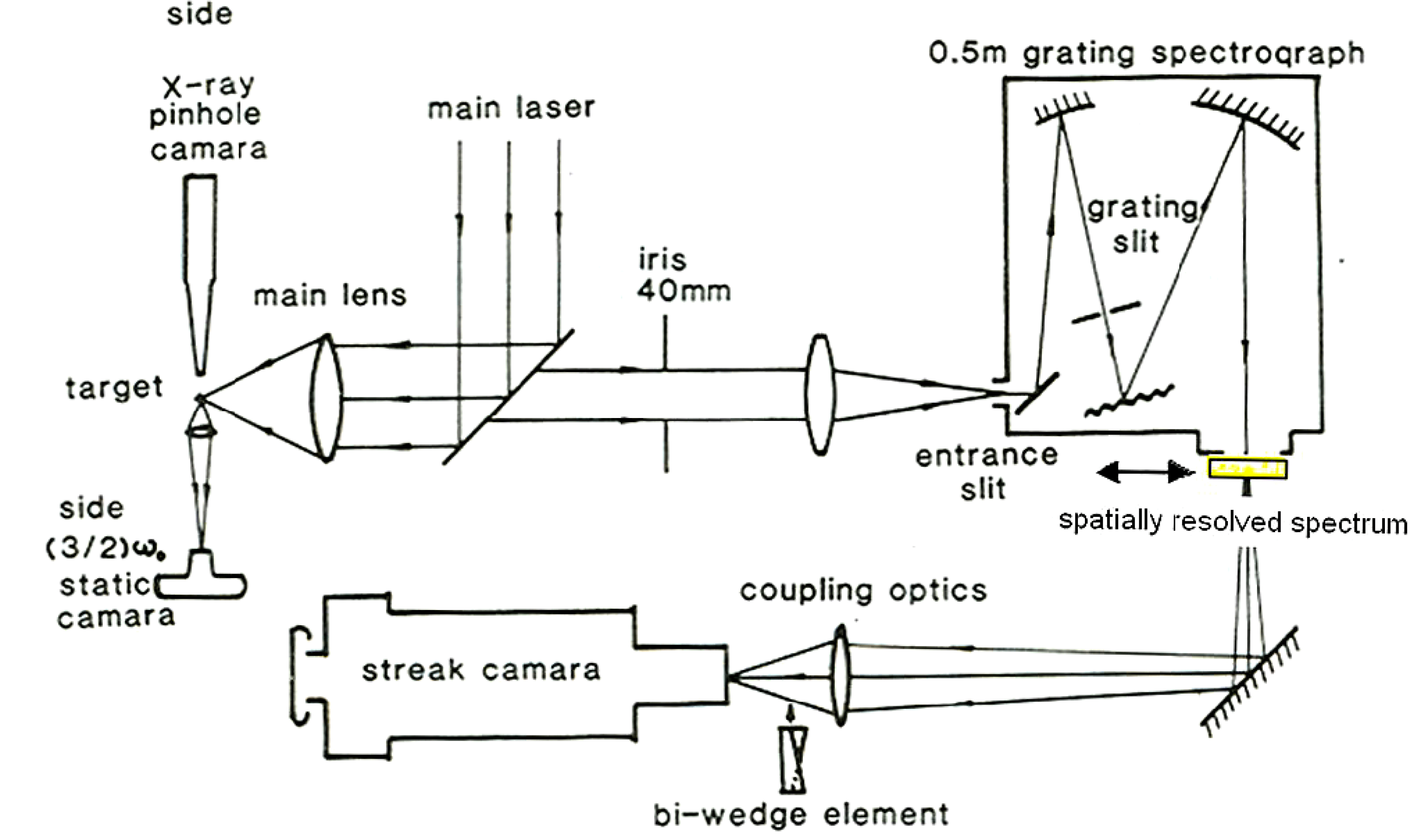
$3\omega _{0}/2$ emission photograph with the spatial and spectral resolutions of 5 ![]() $\mathrm {\mu} {\rm m}$ and 0.3 nm, respectively. The experimental setup is shown in figure 3 and the spectrum was obtained at the imagery output plane position of the 0.5 m spectrometer with the spectrum entrance slit at around 100
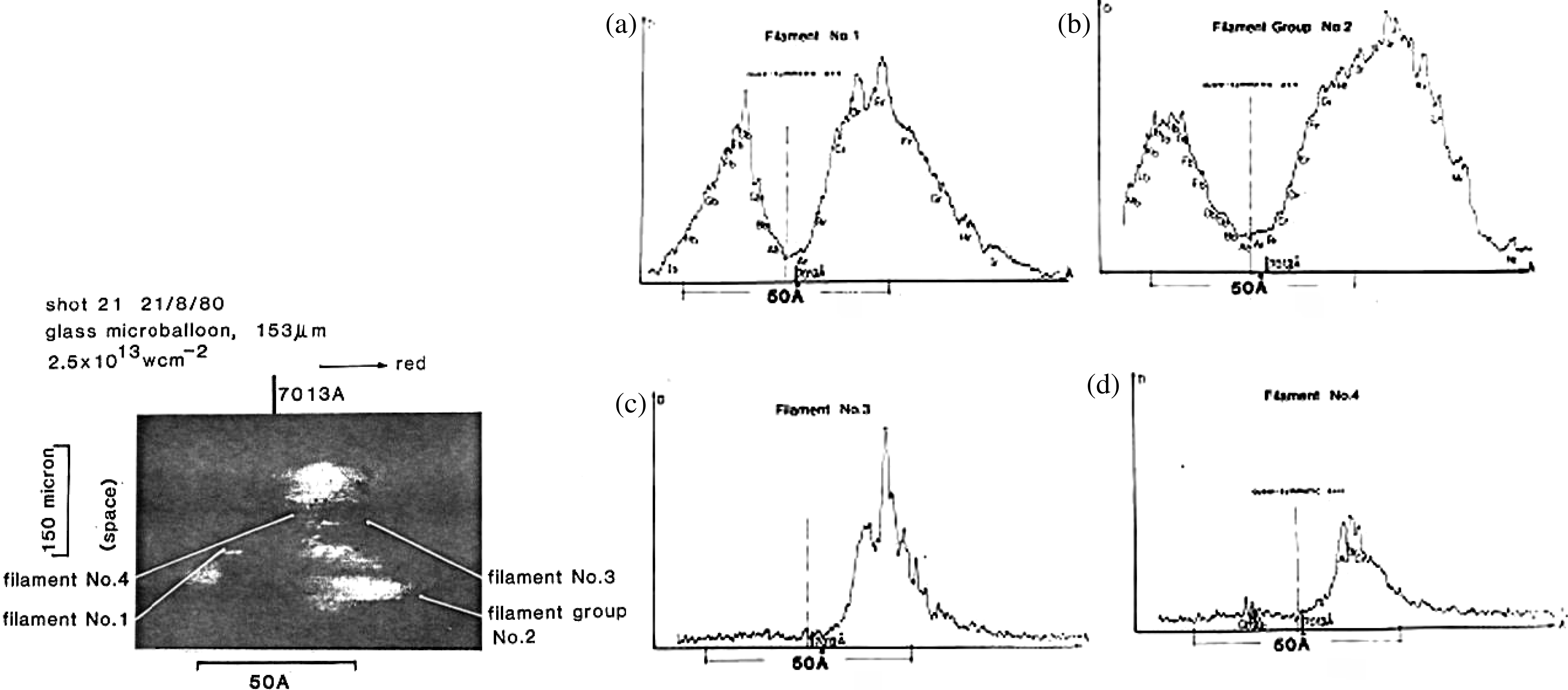
$\mathrm {\mu} {\rm m}$ and 0.3 nm, respectively. The experimental setup is shown in figure 3 and the spectrum was obtained at the imagery output plane position of the 0.5 m spectrometer with the spectrum entrance slit at around 100 ![]() $\mathrm {\mu} {\rm m}$. The backscattering spectrum structures for single and bunched filaments (figure 4) were observed with a single hump and/or double humps corresponding to the differently sampled spatial filament positions. In the experiment, the 153
$\mathrm {\mu} {\rm m}$. The backscattering spectrum structures for single and bunched filaments (figure 4) were observed with a single hump and/or double humps corresponding to the differently sampled spatial filament positions. In the experiment, the 153 ![]() $\mathrm {\mu} {\rm m}$ diameter glass micro-ball was irradiated with a laser of intensity
$\mathrm {\mu} {\rm m}$ diameter glass micro-ball was irradiated with a laser of intensity ![]() $2.5\times 10^{13}\ {\rm W}/{\rm cm}^{2}$. The moderately low laser irradiance led to relatively few sampled filament numbers. Therefore the spatial position of the
$2.5\times 10^{13}\ {\rm W}/{\rm cm}^{2}$. The moderately low laser irradiance led to relatively few sampled filament numbers. Therefore the spatial position of the ![]() $3\omega _{0}/2$ filament spectral signals could be easily distinguished on the target corona area.
$3\omega _{0}/2$ filament spectral signals could be easily distinguished on the target corona area.

Figure 3. Experimental arrangement for space and time resolved spectroscopy of the ![]() $(3\omega _{0}/2)$ emission[Reference Lin, Willi, Toner and Gibson12].
$(3\omega _{0}/2)$ emission[Reference Lin, Willi, Toner and Gibson12].

Figure 4. The ![]() $3\omega _{0}/2$ spatially resolved spectrum[Reference Lin, Willi and Rumsby13].
$3\omega _{0}/2$ spatially resolved spectrum[Reference Lin, Willi and Rumsby13].
The features of the filament spectral structures from figure 4 can be derived as:
(i) All of the ![]() $3\omega _{0}/2$ spectrum signals obtained from the experiment originated from individual single filaments or a number of filament bunches. No sign of a homogeneous bulk plasma produced signal was found at the
$3\omega _{0}/2$ spectrum signals obtained from the experiment originated from individual single filaments or a number of filament bunches. No sign of a homogeneous bulk plasma produced signal was found at the ![]() $n_{c}/4$ density layer.
$n_{c}/4$ density layer.
(ii) Spectrum filaments No. 1 and No. 2 are double-humped strong filaments with a large gap width between the red spectrum hump peak and the blue one, which are at 3.1 nm and 5.6 nm, respectively. They can be denominated as strong spectrum filaments. The weak spectrum filaments No. 3 and No. 4 with the single red humps and the almost disappearing blue humps have the narrow gap widths of 3.4 nm and 3.1 nm, respectively.
(iii) The spatial node size from all individual filament emissions in the time and spectrum resolved photograph was measured as 4–5 ![]() $\mathrm {\mu} {\rm m}$ in diameter, which coincides with the Willi[Reference Willi, Rumsby, Hooker, Raven and Lin11] X-ray pinhole camera experimental results described in Section 2.4 below, with the 1.5 keV band X-ray wavelength and with each of the spot sizes in the 4–5
$\mathrm {\mu} {\rm m}$ in diameter, which coincides with the Willi[Reference Willi, Rumsby, Hooker, Raven and Lin11] X-ray pinhole camera experimental results described in Section 2.4 below, with the 1.5 keV band X-ray wavelength and with each of the spot sizes in the 4–5 ![]() $\mathrm {\mu} {\rm m}$ diameter range.
$\mathrm {\mu} {\rm m}$ diameter range.
The space and spectrum resolved filamentation instability investigation is an important diagnostic means for not only ![]() $3\omega _{0}/2$ (TPD), but also SRS,
$3\omega _{0}/2$ (TPD), but also SRS, ![]() $\omega _{0}$ (SBS), and even
$\omega _{0}$ (SBS), and even ![]() $2\omega _{0}$ (RA). In particular, when the spatial slit width of the spectrometer can be adjusted to as narrow as possible, the total number of samples of filaments is decreased to the smallest, and the laser irradiance on the target surface is moderate.
$2\omega _{0}$ (RA). In particular, when the spatial slit width of the spectrometer can be adjusted to as narrow as possible, the total number of samples of filaments is decreased to the smallest, and the laser irradiance on the target surface is moderate.
The time and spectrum resolved  $3\omega _{0}/2$ emission[Reference Lin, Willi, Toner and Gibson12, Reference Lin14, Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15]
$3\omega _{0}/2$ emission[Reference Lin, Willi, Toner and Gibson12, Reference Lin14, Reference Lin, Tan, Gu, Mei, Pan, Yu and Deng15]
The experimental setup is given in figure 3 and the spectrum photograph is in figure 5. The temporally and spectrally resolved ![]() $3\omega _{0}/2$ emission appeared a bit ambiguous in the photographs, making it difficult to distinguish a single-filament feature due to the much higher laser irradiance
$3\omega _{0}/2$ emission appeared a bit ambiguous in the photographs, making it difficult to distinguish a single-filament feature due to the much higher laser irradiance ![]() $(2.8\mbox{--}14\times 10^{14}\ {\rm W}/{\rm cm}^{2})$ on the micro-balloon target surface, which led to the emissions of too many filaments being squeezed together in a narrow picosecond range.
$(2.8\mbox{--}14\times 10^{14}\ {\rm W}/{\rm cm}^{2})$ on the micro-balloon target surface, which led to the emissions of too many filaments being squeezed together in a narrow picosecond range.

Figure 5. The temporally resolved spectrum[Reference Lin, Willi, Toner and Gibson12].
The intensity scanning for the two distinguishable spectrum filaments is shown in figure 5(b). The temporal widths of the spectrum trajectories from the two spectrum filaments are both around 4–5 ps. The spectrum scanning results support a spectrally quasi-symmetrical feature for the ![]() $3\omega _{0}/2$ backscattering spectrum, lending support to the Doppler shift model, which described the dynamics of the filament production and decay. Meanwhile, the theoretical framework and the complicated simulation of the generation of a series of strong
$3\omega _{0}/2$ backscattering spectrum, lending support to the Doppler shift model, which described the dynamics of the filament production and decay. Meanwhile, the theoretical framework and the complicated simulation of the generation of a series of strong ![]() $3\omega _{0}/2$ nodes along the filament channels are still awaiting construction. However, the
$3\omega _{0}/2$ nodes along the filament channels are still awaiting construction. However, the ![]() $3\omega _{0}/2$ emission inside the unstable filament is always accompanied with filament node or end initiation and very fast collapse due to the low density plasma environment. Those processes will produce a large amount of intense X-ray node bursts in a very underdense surrounding corona plasma area. This picture is at variance with the previous common scenario wherein the intense X-rays, including X-ray spots or nodes, should be produced in the critical or ablation layer plasma area[Reference Willi, Rumsby, Hooker, Raven and Lin11]. In addition, the picture may interpret the above mentioned 1.5 keV X-ray spotty spots, which are scattered and are larger than those of the laser-irradiated far-field intensity profile.
$3\omega _{0}/2$ emission inside the unstable filament is always accompanied with filament node or end initiation and very fast collapse due to the low density plasma environment. Those processes will produce a large amount of intense X-ray node bursts in a very underdense surrounding corona plasma area. This picture is at variance with the previous common scenario wherein the intense X-rays, including X-ray spots or nodes, should be produced in the critical or ablation layer plasma area[Reference Willi, Rumsby, Hooker, Raven and Lin11]. In addition, the picture may interpret the above mentioned 1.5 keV X-ray spotty spots, which are scattered and are larger than those of the laser-irradiated far-field intensity profile.
From figure 5, the small temporal difference of ![]() $\sim $10–20 ps could still be seen clearly, from the very beginning of the red shift spectrum to the end of the blue one. The single and double humps with quasi-symmetrical distribution were also analyzed in earlier work[Reference Lin, Willi, Toner and Gibson12, Reference Lin14].
$\sim $10–20 ps could still be seen clearly, from the very beginning of the red shift spectrum to the end of the blue one. The single and double humps with quasi-symmetrical distribution were also analyzed in earlier work[Reference Lin, Willi, Toner and Gibson12, Reference Lin14].
2.4. Evidence of the filament end or node dynamic collapse process induced large amount of 1.5 keV hot X-ray spot bursts
The large amount of spotty 1.5 keV X-ray hot spots with each spot size about 4–5 ![]() $\mathrm {\mu} {\rm m}$ is shown in figure 6(c)[Reference Willi, Rumsby, Hooker, Raven and Lin11]. The target was a smooth glass plate with the laser irradiance
$\mathrm {\mu} {\rm m}$ is shown in figure 6(c)[Reference Willi, Rumsby, Hooker, Raven and Lin11]. The target was a smooth glass plate with the laser irradiance ![]() $3.3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$ and the laser spot size 250
$3.3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$ and the laser spot size 250 ![]() $\mathrm {\mu} {\rm m}$ in diameter. On the basis of the unstable SSSFI process, this spotty X-ray photograph can be attributed to the laser hot speckles, shown in figure 6(b), having split or been trapped randomly into the huge amount of self-focusing small scale filaments and the subsequent TPD decay induced X-ray emission with each spotty size in the range 4–5
$\mathrm {\mu} {\rm m}$ in diameter. On the basis of the unstable SSSFI process, this spotty X-ray photograph can be attributed to the laser hot speckles, shown in figure 6(b), having split or been trapped randomly into the huge amount of self-focusing small scale filaments and the subsequent TPD decay induced X-ray emission with each spotty size in the range 4–5 ![]() $\mathrm {\mu} {\rm m}$, contrasting with the early description[Reference Willi, Rumsby, Hooker, Raven and Lin11] which stated “the spotty X-ray spots originate from dense regions of the expanding plasma with similar temperature as the background plasma and are caused by higher ablation rates in the more intense spots of the laser beam”. These SPMD and/or finally PFD small scale filaments will be stimulated and collapsed, resulting in the generation of the
$\mathrm {\mu} {\rm m}$, contrasting with the early description[Reference Willi, Rumsby, Hooker, Raven and Lin11] which stated “the spotty X-ray spots originate from dense regions of the expanding plasma with similar temperature as the background plasma and are caused by higher ablation rates in the more intense spots of the laser beam”. These SPMD and/or finally PFD small scale filaments will be stimulated and collapsed, resulting in the generation of the ![]() $\sim $1.5 keV X-ray band bursts, and even the superhard X-ray bursts at the filament ends or nodes, mostly in underdense corona plasmas. The deduction shows that most of the 1.5 keV X-ray hot spots were generated in quite a large area of the very low density plasma region, which illustrates why the X-ray hot spot distribution area from figure 6(c) is larger than the incident laser speckle distribution area from figure 6(b) and why the plasma jetting shadowgraph areas from figures 6(a) and (d) are also obviously larger than those from figure 6(b).
$\sim $1.5 keV X-ray band bursts, and even the superhard X-ray bursts at the filament ends or nodes, mostly in underdense corona plasmas. The deduction shows that most of the 1.5 keV X-ray hot spots were generated in quite a large area of the very low density plasma region, which illustrates why the X-ray hot spot distribution area from figure 6(c) is larger than the incident laser speckle distribution area from figure 6(b) and why the plasma jetting shadowgraph areas from figures 6(a) and (d) are also obviously larger than those from figure 6(b).

Figure 6. (a) Shadowgraph recorded on a glass target 1 ns after the beginning of the laser pulse, showing pronounced plasma jets with the clear filament node modulation. (b) Laser beam profile taken in the equivalent target plane. (c) X-ray pinhole camera image in the 1.5 keV energy band (pinhole filtered with 40 ![]() $\mathrm {\mu} {\rm m}$ of beryllium). The scale for all the images is 50
$\mathrm {\mu} {\rm m}$ of beryllium). The scale for all the images is 50 ![]() $\mathrm {\mu} {\rm m}$, for (a), (b), and (c). (d) Shadowgraph 1.4 ns delayed from the beginning of the laser pulse, showing pronounced plasma jets without filament node modulation. (e) Temporal profile of the green heating laser pulse[Reference Willi, Rumsby, Hooker, Raven and Lin11].
$\mathrm {\mu} {\rm m}$, for (a), (b), and (c). (d) Shadowgraph 1.4 ns delayed from the beginning of the laser pulse, showing pronounced plasma jets without filament node modulation. (e) Temporal profile of the green heating laser pulse[Reference Willi, Rumsby, Hooker, Raven and Lin11].
Another interesting phenomenon is displayed in figure 6(a), where the shadowgraph with 50 ps temporal gate duration was just at the pulse trailing edge position of the incident heating laser, shown in figure 6(e), with a sixth of the laser power intensity, ![]() $5.5 \times 10^{12}\ {\rm W}/{\rm cm}^{2}$, on the target surface. In this case the LPI produced filamentation process still existed, bringing about the display of a clear filament, and the filament node or end modulation structures for the heating laser reached the rather underdense plasma region.
$5.5 \times 10^{12}\ {\rm W}/{\rm cm}^{2}$, on the target surface. In this case the LPI produced filamentation process still existed, bringing about the display of a clear filament, and the filament node or end modulation structures for the heating laser reached the rather underdense plasma region.
Inferring from the shadowgraphs in figure 6(a), the experimental result shown in figure 6(d) showed no filament node or end modulation structures at all due to the probe laser gate position being 1.4 ns delayed from the 1.1 ns full width main laser starting time. At that time, there was no main heating laser energy irradiated on the target. This was further important evidence for the massive filaments displayed with the end or node modulation on the very underdense plasma corona.

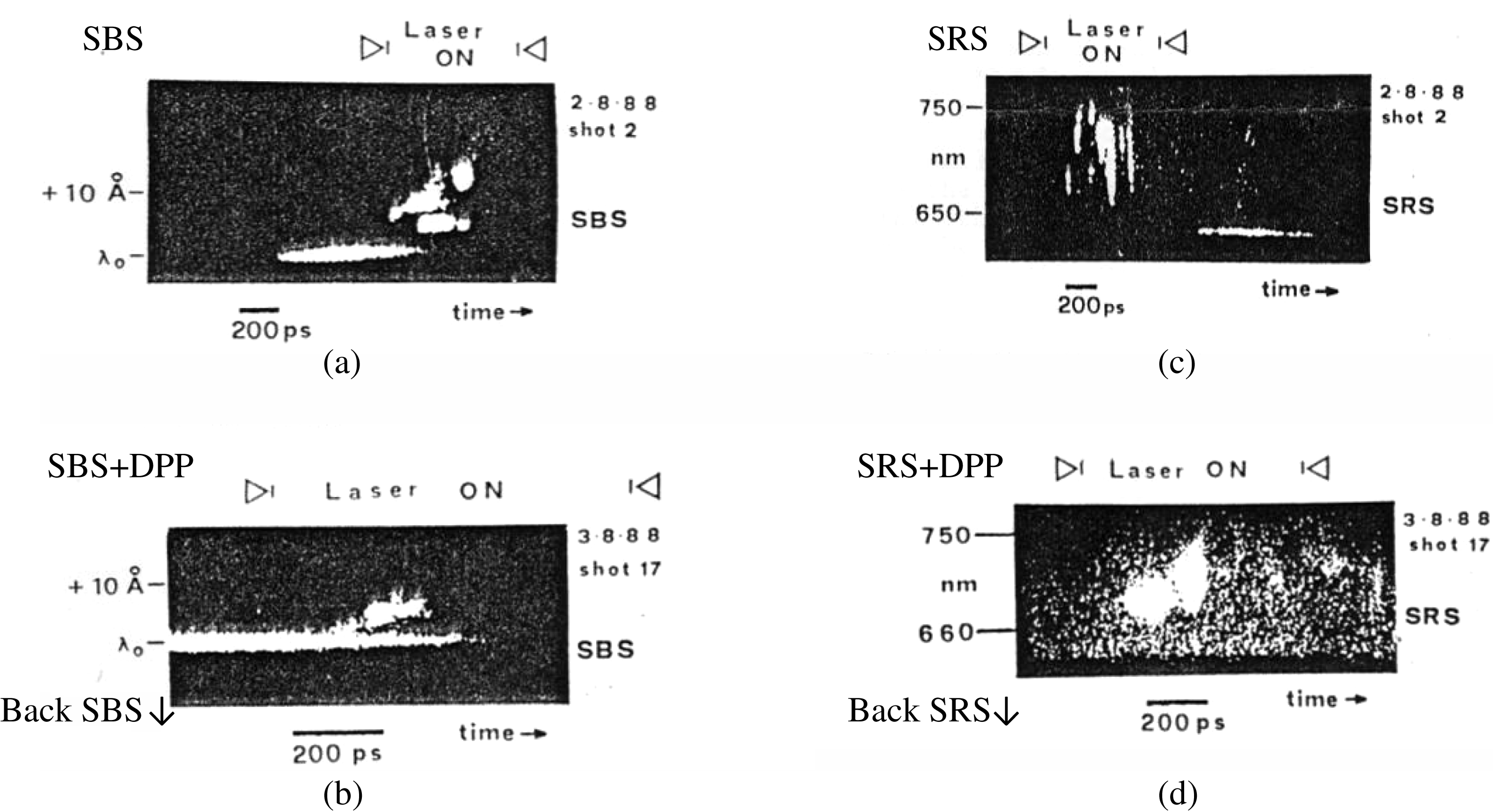
Figure 7. (a) SBS time resolved spectrum with an unsmoothed beam. (b) SBS time resolved spectrum with an RPP smoothed beam. (c) SRS time resolved spectrum with an unsmoothed beam. (d) SRS time resolved spectrum with an RPP smoothed beam[Reference Giulietti, Afshar-Rad, Coe, Will, Lin and Yu17].
A sign of X-ray emissions from the modulated nodes of filaments along with the incident light could also be distinguished in figure 6(c) if the heating laser light came from the upper left front corner direction of the picture’s central region. One may carefully resolve a number of spot linked strings along with the above mentioned incident laser light lines.
Therefore, there is actually, for the first time, simultaneously obtained new evidence of filament node modulation from figure 6(a), obtained by optical shadowgraph technology, and an extremely feasible proof of hot X-rays emitting from the modulated filament nodes and ends in an extremely low density plasma corona, without any other reasonable options for consideration, as shown in figure 6(c), from the 1.5 keV band X-ray spot pinhole imagery, though this phenomenon was not recognized in the originally published article[Reference Willi, Rumsby, Hooker, Raven and Lin11].
2.5. The time and spectrum resolved SRS and SBS emission
Giulietti et al. [Reference Giulietti, Afshar-Rad, Coe, Will, Lin and Yu17] investigated the SRS and SBS emission features, in 1988. The temporally and spectrally resolved SRS and SBS emissions were observed using a ![]() $2\omega _{0}$ green heating laser as the incident laser in the experiments. The experimental results are shown in figures 7(a), (b), (c), and (d). The experimental parameters are labeled in the picture.
$2\omega _{0}$ green heating laser as the incident laser in the experiments. The experimental results are shown in figures 7(a), (b), (c), and (d). The experimental parameters are labeled in the picture.
Figure 7(a) shows the low temporally resolved SBS spectrum signal. The spectrum was divided to both red and blue shift macroscale humps. The spectrum double-hump separation increases and decreases following the heating laser power intensity changes. On the basis of the unstable SSSFI model, integration of the total transient individual filament intensities will yield the SBS spectrum. However, the temporal resolution of the diagnostics was rather low, and the laser irradiance on the target with intermediate ![]() ${Z}$ was too high, so the experiment could not show the detailed filamentation effect in that experiment.
${Z}$ was too high, so the experiment could not show the detailed filamentation effect in that experiment.
Figure 7(b) shows the experimental result on the random phase plate (RPP) application for the field beam smoothing. The random phase plate breaks the laser field speckles into a quite large number of fine speckles with much less energy and intensity for each speckle, resulting in a weakened filamentation process, if it should be stimulated, leading to the spectrally blue hump nearly vanishing and the red one being weakened.
Figure 7(c) displays the temporally resolved SRS spectrum emission with a serious temporal modulation, as a sign of the appearance of filamentation instability. However, it might be difficult to distinguish the filament temporal width and the other features, also due to the temporally low resolving power.
Figure 7(d) displays the spectrum feature weakened due to the application of the RPP.
Although the filamentations are weakened with the distributed phase plate (DPP) or RPP, this was not because of the action of the DPP or RPP itself, but because of the much larger heating region with the completely decreased incident laser average power intensity on the target surface.
2.6. The transfer from the SPMD unstable SSSFI to the PFD unstable SSSFI
The very serious node modulated damage produced inside the laser glasses and the final optics of the high power laser driver have, at a very early time, been clearly explained, while the laser output average power intensities, in the damage region, reach a level of about ![]() $10^{10}\ {\rm W}/{\rm cm}^{2}$ or less[Reference Campbell, Maney, Atherton, Montesanti, DeYoreo, Sheehan, Kozlowski and Barker22, Reference Jedamzik and Elsmann23]. Figure 8(a) shows a typical example of damage to a few individual and/or several bunches of small scale self-focusing filamentation (SSSFF) produced inside the material output position of the Nd doped glass rod amplifier at the laser power intensity of
$10^{10}\ {\rm W}/{\rm cm}^{2}$ or less[Reference Campbell, Maney, Atherton, Montesanti, DeYoreo, Sheehan, Kozlowski and Barker22, Reference Jedamzik and Elsmann23]. Figure 8(a) shows a typical example of damage to a few individual and/or several bunches of small scale self-focusing filamentation (SSSFF) produced inside the material output position of the Nd doped glass rod amplifier at the laser power intensity of ![]() $10^{10}\ {\rm W}/{\rm cm}^{2}$ on the damage region.
$10^{10}\ {\rm W}/{\rm cm}^{2}$ on the damage region.
The enhancement of the nonlinear refractive index can be expressed as
Here ![]() $n_{0}$ represents the linear refractive index of solid material, and
$n_{0}$ represents the linear refractive index of solid material, and ![]() $n_{2}$ is the nonlinear index. As
$n_{2}$ is the nonlinear index. As ![]() $n_{0}\sim 1.5$,
$n_{0}\sim 1.5$, ![]() $n_{2}=1.13\times 10^{-13}$ esu (Shanghai, Nd:glass),
$n_{2}=1.13\times 10^{-13}$ esu (Shanghai, Nd:glass), ![]() $\gamma = 4.19 \times 10^{-3}\ {\rm cm}^{2}/{\rm W}$[Reference Koechner24] is the unit transfer factor. Assuming
$\gamma = 4.19 \times 10^{-3}\ {\rm cm}^{2}/{\rm W}$[Reference Koechner24] is the unit transfer factor. Assuming ![]() $I=10^{10}\ {\rm W}/{\rm cm}^{2}$, which is strong enough to decisively produce, for the filaments of SSSFF, serious damage in the laser glass and the final optic quartz solid materials, we estimate the index enhancement
$I=10^{10}\ {\rm W}/{\rm cm}^{2}$, which is strong enough to decisively produce, for the filaments of SSSFF, serious damage in the laser glass and the final optic quartz solid materials, we estimate the index enhancement ![]() $\Delta n= 4.7\times 10^{-6}$.
$\Delta n= 4.7\times 10^{-6}$.
In the case of laser produced plasmas, the refractive index ![]() $n_{pe}$ can be described as
$n_{pe}$ can be described as
Here ![]() $n_{e}$ is the locally sampled electron density in corona plasma, and
$n_{e}$ is the locally sampled electron density in corona plasma, and ![]() $n_{c}$ is the critical density, where the frequency of the plasma electron wave is just the heating laser frequency. Assuming
$n_{c}$ is the critical density, where the frequency of the plasma electron wave is just the heating laser frequency. Assuming ![]() $n_{e}$ to be equal to
$n_{e}$ to be equal to ![]() $n_{c}/30$, then
$n_{c}/30$, then ![]() $n_{pe}$ will be approximately equal to 0.96667 and the refractive index enhancement
$n_{pe}$ will be approximately equal to 0.96667 and the refractive index enhancement ![]() $\Delta n_{pe}$ will be
$\Delta n_{pe}$ will be ![]() ${\sim }3.45 \times 10^{-2}$. The
${\sim }3.45 \times 10^{-2}$. The ![]() $n_{pe}$ enhancement amplitude is four orders of magnitude larger than the SSSFI modulation induced index enhancement
$n_{pe}$ enhancement amplitude is four orders of magnitude larger than the SSSFI modulation induced index enhancement ![]() $\Delta n$ in solid-state material. The above estimation implies that the generation of SSSFI with node modulation in the laser plasma corona should be much easier and the result more massive than in the glass or final optics of the heating laser driver.
$\Delta n$ in solid-state material. The above estimation implies that the generation of SSSFI with node modulation in the laser plasma corona should be much easier and the result more massive than in the glass or final optics of the heating laser driver.

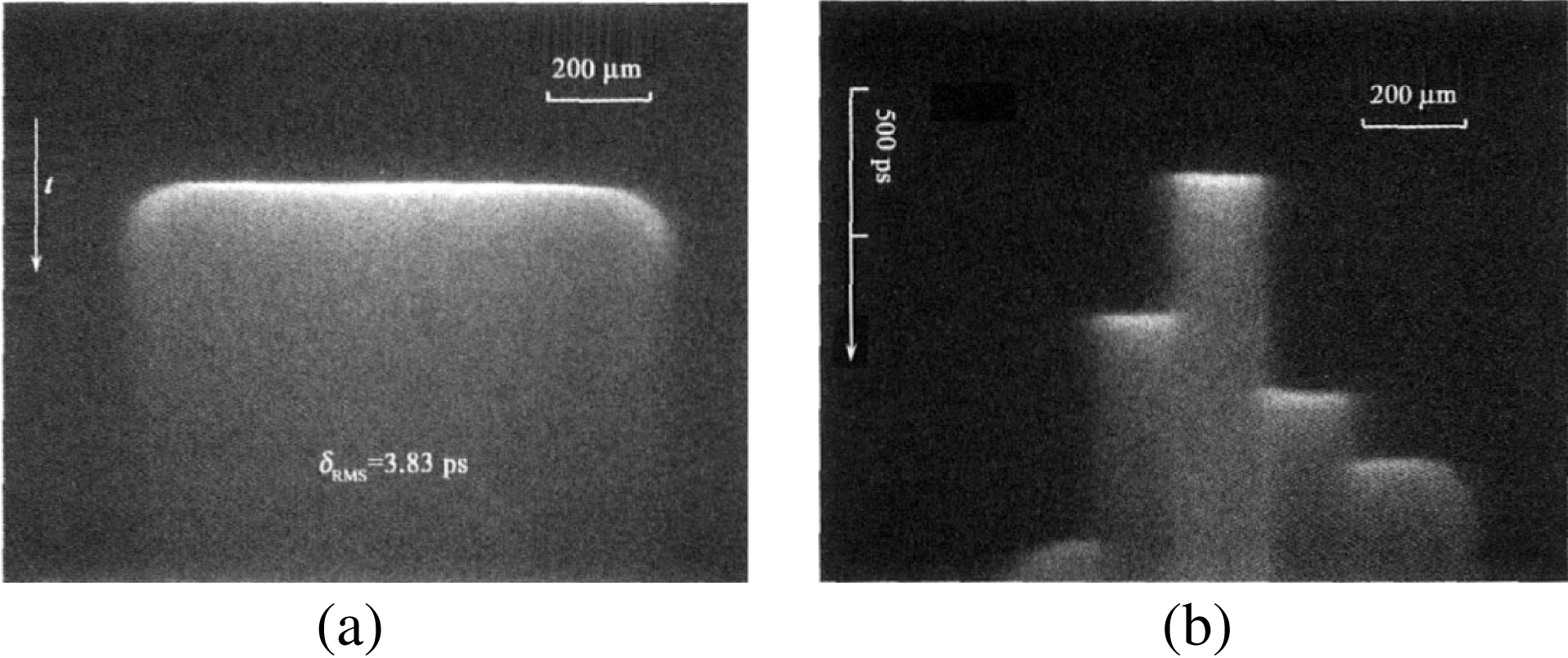
Figure 8. Small scale self-focusing filaments in the rod amplifier[Reference Zhou25].
Figure 8 displays the SSSFF process induced strong or weak, individual or bunched, filaments with node modulations inside the output area of a laser Nd:glass rod amplifier[Reference Zhou25]. It should be noted that the uniformity and the other qualities of the laser glass and the final optics are extremely good, with the material homogeneity of ![]() $1\mbox{--}5 \times 10^{-6}/{\rm cm}$ and with no bobbles and defects affecting the SSSFI process.
$1\mbox{--}5 \times 10^{-6}/{\rm cm}$ and with no bobbles and defects affecting the SSSFI process.
To keep the laser facility safe and to maintain the output capability, laser scientists usually employ all of the methods that will prevent the laser facility from sustaining self-focusing filament damage. However, SPM damage effects are still seldom presented seriously. This is because there are deep phase and amplitude modulations at the laser near-field and far-field output, leading to the focal spot being full of highly intense spikes, which are quite evident from the reported results from NIF[Reference Zhou25].
Considering the physical boundary conditions for LPI processes, it is well known that when a typical ![]() $3\omega _{0}$ heating laser irradiates a target surface, the irradiance distribution profile can be selected as shown in figure 9. These simulations and experimental results display quite heavy amplitude modulations with seriously non-erasable self-phase modulations. Moreover, the absolutely heaviest burden of intensity for solid-state material has already been increased to 3–5 orders of magnitude for the laser produced plasmas, by the laser focusing optics, from the intensity
$3\omega _{0}$ heating laser irradiates a target surface, the irradiance distribution profile can be selected as shown in figure 9. These simulations and experimental results display quite heavy amplitude modulations with seriously non-erasable self-phase modulations. Moreover, the absolutely heaviest burden of intensity for solid-state material has already been increased to 3–5 orders of magnitude for the laser produced plasmas, by the laser focusing optics, from the intensity ![]() $10^{10}\ {\rm W}/{\rm cm}^{2}$ to
$10^{10}\ {\rm W}/{\rm cm}^{2}$ to ![]() $10^{13-15}\ {\rm W}/{\rm cm}^{2}$. As the central ignition mechanism requires four steps of incident driving laser pulse profile, which cover the laser power intensity range from
$10^{13-15}\ {\rm W}/{\rm cm}^{2}$. As the central ignition mechanism requires four steps of incident driving laser pulse profile, which cover the laser power intensity range from ![]() $10^{12}\ {\rm W}/{\rm cm}^{2}$ to
$10^{12}\ {\rm W}/{\rm cm}^{2}$ to ![]() $10^{15}\ {\rm W}/{\rm cm}^{2}$, the study of LPI physical processes in these ranges is essential. This is re-analyzed above Section 2.4 of this paper for the filament generation feature, shown in figure 6(a), for the power intensity of
$10^{15}\ {\rm W}/{\rm cm}^{2}$, the study of LPI physical processes in these ranges is essential. This is re-analyzed above Section 2.4 of this paper for the filament generation feature, shown in figure 6(a), for the power intensity of ![]() $5.5 \times 10^{12}\ {\rm W}/{\rm cm}^{2}$. In the picture of figure 6(a), the gaps between the neighboring modulated nodes are estimated as around 20
$5.5 \times 10^{12}\ {\rm W}/{\rm cm}^{2}$. In the picture of figure 6(a), the gaps between the neighboring modulated nodes are estimated as around 20 ![]() $\mathrm {\mu} {\rm m}$ and the scales of individual filament apertures for very low density plasma are around 10
$\mathrm {\mu} {\rm m}$ and the scales of individual filament apertures for very low density plasma are around 10 ![]() $\mathrm {\mu} {\rm m}$. Therefore it is easy to estimate the light focusing angle inside each of the filament channels as approximately
$\mathrm {\mu} {\rm m}$. Therefore it is easy to estimate the light focusing angle inside each of the filament channels as approximately ![]() $20^{\circ }$–
$20^{\circ }$–![]() $25^{\circ }$ with respect to the filament channel axes, implying that
$25^{\circ }$ with respect to the filament channel axes, implying that ![]() $\sim $25% of the total energy of laser light inside each filament could be used to generate filament walls and ends or nodes with plasma density higher than the surrounding plasma, bringing about the generation of the new transient denser layer pieces including
$\sim $25% of the total energy of laser light inside each filament could be used to generate filament walls and ends or nodes with plasma density higher than the surrounding plasma, bringing about the generation of the new transient denser layer pieces including ![]() $n_{c}/4$ density plasmas.
$n_{c}/4$ density plasmas.

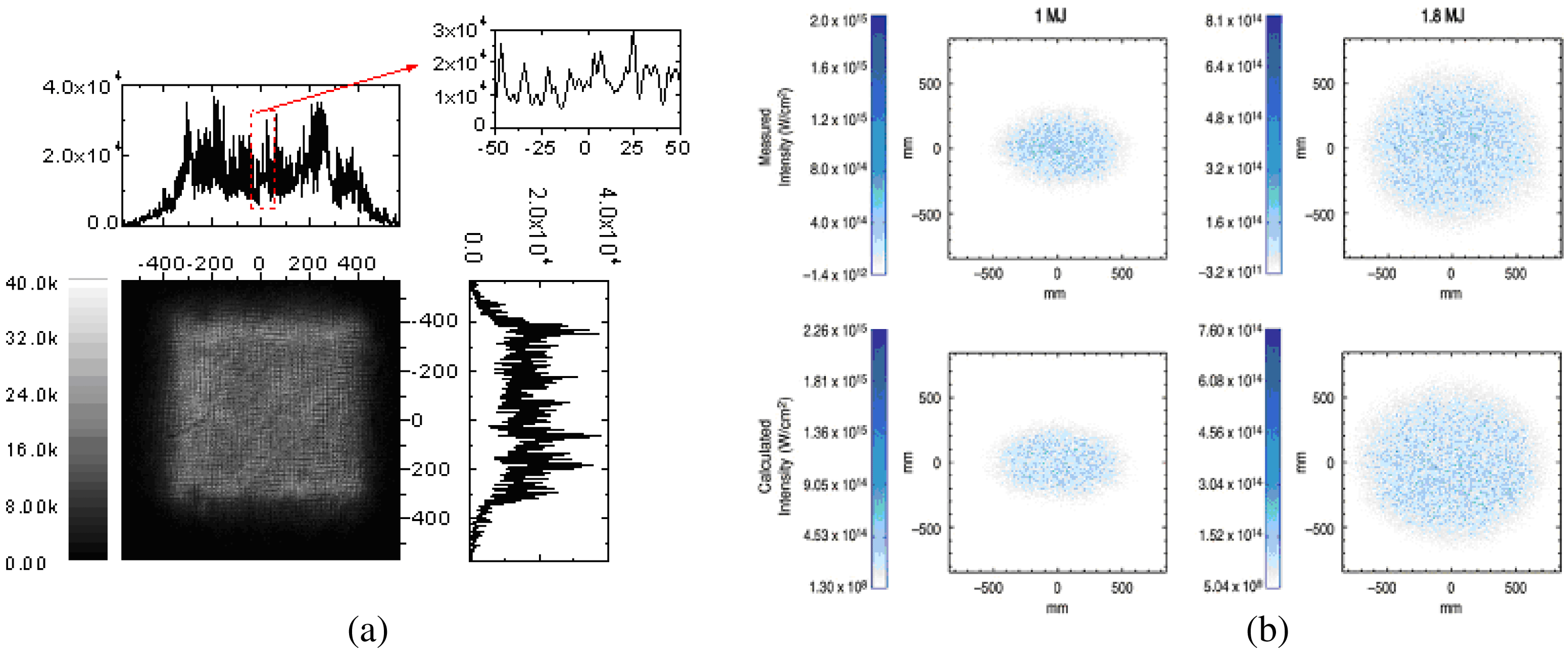
Figure 9. Two samples of focal spot intensity distribution are given with different spatial smoothing mechanisms. (a) The measured focal spot and profiles along two dimensions of SG-II laser facility from a CCD (charge coupled device) of ![]() $1024\times 1024$ elements with each pixel size being 13
$1024\times 1024$ elements with each pixel size being 13 ![]() $\mathrm {\mu} {\rm m}$ at
$\mathrm {\mu} {\rm m}$ at ![]() ${\sim }12\times $ magnification when a lens array is applied to the laser beam, and the measured speckle contrast is 0.46 rms. (b) The measured (top) and calculated (below) far-field speckle profile on NIF when CPP is applied to the laser beam, and the measured contrast is 0.79 rms[Reference Jiang, Zhou, Wu, Li, Li and Lin26, Reference Haynam, Wegner, Auerbach, Bowers, Dixit, Erbert, Heestand, Henesian, Hermann, Jancaitis, Manes, Marshall, Mehta, Menapace, Moses, Murray, Nostrand, Orth, Patterson, Sacks, Shaw, Spaeth, Sutton, Williams, Widmayer, White, Yang and Van27].
${\sim }12\times $ magnification when a lens array is applied to the laser beam, and the measured speckle contrast is 0.46 rms. (b) The measured (top) and calculated (below) far-field speckle profile on NIF when CPP is applied to the laser beam, and the measured contrast is 0.79 rms[Reference Jiang, Zhou, Wu, Li, Li and Lin26, Reference Haynam, Wegner, Auerbach, Bowers, Dixit, Erbert, Heestand, Henesian, Hermann, Jancaitis, Manes, Marshall, Mehta, Menapace, Moses, Murray, Nostrand, Orth, Patterson, Sacks, Shaw, Spaeth, Sutton, Williams, Widmayer, White, Yang and Van27].
If we regard the heating laser in an earlier article[Reference Willi, Rumsby, Hooker, Raven and Lin11] as the preheating laser, the shadowgraph of figure 6(d) in fact provides the physical boundary condition for the under-irradiated plasma corona, at 300 ps after the complete ending of the preheating laser pulse. The photograph illustrates firstly that the corona plasma could never be homogeneous, and is seriously jetting modulated. Secondly, the distribution of the energy assignment of each filament will to a considerable degree be decided by the jet structures, at least in the transient shadowgraph gate period of 50 ps, while the following main heating laser could be arranged to be just arrived.
It could be concluded that the SPMD induced SSSFI process has settled a foundation and framework for transferring to the next ponderomotive force driving SSSFI process, while the average laser irradiances reach a level larger than approximately ![]() $5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$. At such levels, the self-focusing filaments have the ability to focus further to the minimum level of the incident laser wavelength scale under the required ponderomotive force driving, resulting in the extremely high irradiance of
$5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$. At such levels, the self-focusing filaments have the ability to focus further to the minimum level of the incident laser wavelength scale under the required ponderomotive force driving, resulting in the extremely high irradiance of ![]() $10^{16-17}\ {\rm W}/{\rm cm}^{2}$ at the filament nodes or ends, bringing about a huge amount of plasmon generation and decay bursts, accompanying the relativistic electrons and superhard X-ray bursts. All of these effects could stir the plasma into an extremely inhomogeneous form, inducing a strong scattering of the heating laser light, and resulting in a serious reduction of the inverse bremsstrahlung absorption for the designed black cavity (Hohlraum) inner surface.
$10^{16-17}\ {\rm W}/{\rm cm}^{2}$ at the filament nodes or ends, bringing about a huge amount of plasmon generation and decay bursts, accompanying the relativistic electrons and superhard X-ray bursts. All of these effects could stir the plasma into an extremely inhomogeneous form, inducing a strong scattering of the heating laser light, and resulting in a serious reduction of the inverse bremsstrahlung absorption for the designed black cavity (Hohlraum) inner surface.
3. Discussion
3.1. Outcomes and judgments
To summarize the above early precise experimental results and the re-analyzed data, several outcomes and judgments can be extracted as follows.
(1) All of the ![]() $3\omega _{0}/2$ emission features were carefully re-studied, examined, and re-analyzed for the above early experiments, including 2D space, space spectrum, time spectrum, and space–time resolved experimental data. The
$3\omega _{0}/2$ emission features were carefully re-studied, examined, and re-analyzed for the above early experiments, including 2D space, space spectrum, time spectrum, and space–time resolved experimental data. The ![]() $3\omega _{0}/2$ filament diameter was about 4–5
$3\omega _{0}/2$ filament diameter was about 4–5 ![]() $\mathrm {\mu} {\rm m}$. The length was 15
$\mathrm {\mu} {\rm m}$. The length was 15 ![]() $\mathrm {\mu} {\rm m}$–130
$\mathrm {\mu} {\rm m}$–130 ![]() $\mathrm {\mu} {\rm m}$. And the
$\mathrm {\mu} {\rm m}$. And the ![]() $3\omega _{0}/2$ emission existence time at any local position along the filament channel from each individual filament is about 5 ps. Each filament’s stimulated to collapsed period is about 10–20 ps.
$3\omega _{0}/2$ emission existence time at any local position along the filament channel from each individual filament is about 5 ps. Each filament’s stimulated to collapsed period is about 10–20 ps.
(2) There were no signs of the ![]() $3\omega _{0}/2$ signal in terms of the CTLPI predicted features that have appeared at the average bulk plasma density
$3\omega _{0}/2$ signal in terms of the CTLPI predicted features that have appeared at the average bulk plasma density ![]() $n_{c}/4$ shell layer until now. These results indicate that the TPD process was not generated, or did not exist, in “the bulk homogeneous plasma environment”, and was only stimulated inside the transient small scale self-focused filaments. In this sense, the filamentation instability could be extremely unlikely to show a “flicker” effect.
$n_{c}/4$ shell layer until now. These results indicate that the TPD process was not generated, or did not exist, in “the bulk homogeneous plasma environment”, and was only stimulated inside the transient small scale self-focused filaments. In this sense, the filamentation instability could be extremely unlikely to show a “flicker” effect.
Moreover, because of the self-focusing effects, a very large part of the most intense heating laser light energy with higher light irradiance has been almost all trapped inside the filament channels transiently, and this could have no opportunity to go over the filament channels horizontally outside to realize their production, growth and saturation process for bulk homogeneous plasma, although, via spatial and temporal averaging, the corona laser plasma seems to be smoothing. In this sense, the unstable small scale filamentation instability should be regarded as the instability of first priority in the LPI corona area.
(3) Each filament can be temporally divided into two sections. For the leading first section, the focusing filament is constructed in terms of a serious self-phase modulation and also serious amplitude fluctuations from the heating laser beam profile with a bit lower power intensity with a larger inner aperture at the filament ends. As soon as the end power intensity increased to the threshold of the ponderomotive force production in the second section, the self-focus process will be accelerated to push forward the leading end electron density to much higher density, to the level of ![]() $n_{c}/4$ or even more, resulting in a transient
$n_{c}/4$ or even more, resulting in a transient ![]() $3\omega _{0}/2$ emission at the filament surrounding plasma density of approximately
$3\omega _{0}/2$ emission at the filament surrounding plasma density of approximately ![]() $n_{c}/20$ to
$n_{c}/20$ to ![]() $n_{c}/30$, shown in figures 2(b), (c), and (d). The appearance of a transient
$n_{c}/30$, shown in figures 2(b), (c), and (d). The appearance of a transient ![]() $3\omega _{0}/2$ emission spatially extending filament line at such a low surrounding plasma density, as one of the most important features of the unstable SSSFI, is among the solid evidence of the massive generation of mainly SPMD and PFD filaments in a low average laser irradiance of the
$3\omega _{0}/2$ emission spatially extending filament line at such a low surrounding plasma density, as one of the most important features of the unstable SSSFI, is among the solid evidence of the massive generation of mainly SPMD and PFD filaments in a low average laser irradiance of the ![]() $10^{13}\ {\rm W}/{\rm cm}^{2}$ scale. In addition, it should be understandable that the CTLPI filamentation model would not be able to stimulate the TPD process and the
$10^{13}\ {\rm W}/{\rm cm}^{2}$ scale. In addition, it should be understandable that the CTLPI filamentation model would not be able to stimulate the TPD process and the ![]() $3\omega _{0}/2$ emission in the region of very low surrounding plasma density, about
$3\omega _{0}/2$ emission in the region of very low surrounding plasma density, about ![]() $n_{c}/20$ to
$n_{c}/20$ to ![]() $n_{c}/30$, for the corona area.
$n_{c}/30$, for the corona area.
(4) After the stimulation of TPD and ![]() $3\omega _{0}/2$ emission in a filament, the rapid decay of the stimulated plasma electron wave by Landau damping or wave breaking occurs, and fast electrons and hot X-rays are emitted, leading to stirring of the corona plasma by the convection between the hot and/or superhot electrons and the surrounding cold electrons, producing more turbulent plasma jets, which will cause more seriously inhomogeneous distribution of plasma, and the acceleration of the next process of the succeeding filamentation process.
$3\omega _{0}/2$ emission in a filament, the rapid decay of the stimulated plasma electron wave by Landau damping or wave breaking occurs, and fast electrons and hot X-rays are emitted, leading to stirring of the corona plasma by the convection between the hot and/or superhot electrons and the surrounding cold electrons, producing more turbulent plasma jets, which will cause more seriously inhomogeneous distribution of plasma, and the acceleration of the next process of the succeeding filamentation process.
(5) The hot X-ray emission phenomena were studied with very high spatial resolution of an X-ray pinhole camera by Willi et al. [Reference Willi, Rumsby, Hooker, Raven and Lin11] in 1982. A large amount of very spotty small 1.5 keV hot X-ray spots with different distribution to the large scale laser speckles was obtained. The target was a smooth glass plate with the laser irradiance of ![]() $3.3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$. The heating laser far-field irradiation size was 250
$3.3 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$. The heating laser far-field irradiation size was 250 ![]() $\mathrm {\mu} {\rm m}$ in diameter and each of the 1.5 keV hot X-ray spot sizes were 4–5
$\mathrm {\mu} {\rm m}$ in diameter and each of the 1.5 keV hot X-ray spot sizes were 4–5 ![]() $\mathrm {\mu} {\rm m}$. The X-ray spot intensities were varied from weak to strong randomly, which just coincided very well with the SSSFI induced filament features for both sizes and intensities. These phenomena indicated that the heating laser speckles had further split into a huge amount of self-focused small scale filaments with the outer diameter of 4–5
$\mathrm {\mu} {\rm m}$. The X-ray spot intensities were varied from weak to strong randomly, which just coincided very well with the SSSFI induced filament features for both sizes and intensities. These phenomena indicated that the heating laser speckles had further split into a huge amount of self-focused small scale filaments with the outer diameter of 4–5 ![]() $\mathrm {\mu} {\rm m}$. These small scale filaments will be stimulated and collapsed, resulting in the production of the
$\mathrm {\mu} {\rm m}$. These small scale filaments will be stimulated and collapsed, resulting in the production of the ![]() $\sim $1.5 keV X-ray bursts at the ends or nodes.
$\sim $1.5 keV X-ray bursts at the ends or nodes.
The further re-analysis of previous work by Willi et al. [Reference Willi, Rumsby, Hooker, Raven and Lin11] proves that the precise experiments have simultaneously obtained both new evidence of filament node modulation, from figure 6(a), by temporally gated optical shadowgraph technology, and also a feasibly reasonable deduction of the extremely important proof of the hot X-ray emission from the modulated filament nodes or ends in an underdense plasma corona, shown in figure 6(c), from the 1.5 keV band X-ray pinhole imagery.
We note that the recent work by Séguin et al. discussed the relation between the filaments and the TPD instability[Reference Séguin, Li, Manuel, Rinderknecht, Sinenian, Frenje, Rygg, Hicks, Petrasso, Delettrez, Marshall and Smalyuk19], and they concluded that the filaments were not caused by TPD. Firstly, we have not declared that the filaments were caused by TPD. Actually, from the above analysis, we have recognized that the plasma density distribution is extremely inhomogeneous. Even if the laser spot intensity profile is uniform, it is easy to produce small scale self-focusing filaments (see figure 6(d)). Moreover, the laser phase front at the focus plane has already been severely modulated by self-phase modulation. Therefore, in complete LPI processes the first priority should be the filaments driven by self-phase modulation (small scale). TPD will be generated inside some strong filaments where the laser intensity reaches the TPD threshold (usually considered to be about ![]() $5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$). In this case, we regard the serious self-focusing of the filaments as the origin of the TPD process. And TPD will then stir the plasma, further leading to more serious plasma density inhomogeneity. As a result, the laser intensities at the filament channels are able to reach levels of even up to 1–
$5 \times 10^{14}\ {\rm W}/{\rm cm}^{2}$). In this case, we regard the serious self-focusing of the filaments as the origin of the TPD process. And TPD will then stir the plasma, further leading to more serious plasma density inhomogeneity. As a result, the laser intensities at the filament channels are able to reach levels of even up to 1–![]() $5 \times 10^{17}\ {\rm W}/{\rm cm}^{2}$, resulting in ponderomotive force driven strong filament bunches. For figure 2(d), we consider the filaments in terms of
$5 \times 10^{17}\ {\rm W}/{\rm cm}^{2}$, resulting in ponderomotive force driven strong filament bunches. For figure 2(d), we consider the filaments in terms of ![]() $3\omega _{0}/2$ light emission. Only when the drive laser is on and interacts with the plasma is there (filamented)
$3\omega _{0}/2$ light emission. Only when the drive laser is on and interacts with the plasma is there (filamented) ![]() $3\omega _{0}/2$ light emission (via TPD). The temporal existence duration of filaments is
$3\omega _{0}/2$ light emission (via TPD). The temporal existence duration of filaments is ![]() $\sim $10 ps, obtained by an optical streak camera with the temporal resolution of around 3 ps (see figures 2(b), 2(c), 2(d), and figure 5(a)). Long time strong small scale filaments were not observed. The filament (Fig. 3 in Ref. 19) observed by Séguin et al. is considered in terms of the electromagnetic field. This electromagnetic field is associated with the (filamented) plasma jet. The plasma jet may exist for a long time during the drive laser interaction with the plasma and even long after the end of the drive laser part. The existence of a large number of filamented plasma jets and their long lifetime indicate that the plasma density is very inhomogeneous during and after the drive laser part. Though the average laser intensity outside the filaments is lower than the predicted threshold of TPD instability, the laser intensity in the laser produced filament channels should be several tens of times higher than that outside due to laser self-focusing, and reach the TPD threshold. While Séguin et al. consider that the filaments are not caused by the TPD instability due to the average laser intensity being below the TPD threshold, they have not considered laser self-focusing.
$\sim $10 ps, obtained by an optical streak camera with the temporal resolution of around 3 ps (see figures 2(b), 2(c), 2(d), and figure 5(a)). Long time strong small scale filaments were not observed. The filament (Fig. 3 in Ref. 19) observed by Séguin et al. is considered in terms of the electromagnetic field. This electromagnetic field is associated with the (filamented) plasma jet. The plasma jet may exist for a long time during the drive laser interaction with the plasma and even long after the end of the drive laser part. The existence of a large number of filamented plasma jets and their long lifetime indicate that the plasma density is very inhomogeneous during and after the drive laser part. Though the average laser intensity outside the filaments is lower than the predicted threshold of TPD instability, the laser intensity in the laser produced filament channels should be several tens of times higher than that outside due to laser self-focusing, and reach the TPD threshold. While Séguin et al. consider that the filaments are not caused by the TPD instability due to the average laser intensity being below the TPD threshold, they have not considered laser self-focusing.
3.2. Discussion and comments
The negative and positive effects on the laser fusion physical processes
The unstable SSSFI induced transient TPD and SRS processes play some essentially negative roles on the LPI at corona plasma with respect to the roles played by SBS and RA due to the plasma electron wave collapse processes generating hot and superhot electrons which are accompanied with hard and superhard X-ray emission. The investigation of the connection of the SRS to the unstable SSSFI has not been so precise and deep as that of TPD processes due to the lower space and time resolution of the SRS experiments. However, the temporally resolved SRS spectrum from figure 7(c) and (d) still clearly displays an SRS spectrum with seriously short temporal period filament modulation. These results imply that all of the conclusions from the connection of the SSSFI to the TPD instability could be transformed to qualitative conclusions regarding SRS instability.
For the indirect drive experiment, the heating laser will unavoidably, from the very beginning, construct a huge number of filaments with extremely long lengths, by SPMD induced SSSFI, for the extremely low density plasma inside the cylindrical black cavity. However, each individual filament will hold a much larger fraction of the total of the incident heating laser energy caused by the high ![]() $Z$ gold plasma induced stronger inhomogeneous plasma jetting with a relatively long jetting scale horizontally. The succeeding process will accelerate the SRS and TPD instability being transiently stimulated and collapsed at the filament ends, nodes or channel walls, all around the fusion micro-balloon target. Finally, the huge amount of ends or nodes of plasma electron wave collapse, this being accompanied with hot electrons and/or hard X-ray emission, resulting in an increased ablation rate of the fusion target ablator arising from the burst hot electrons and the entropy enhancement of the iced target fuel for those several keV hard X-rays, leading possibly to the scaling of some of the scientific cliffs.
$Z$ gold plasma induced stronger inhomogeneous plasma jetting with a relatively long jetting scale horizontally. The succeeding process will accelerate the SRS and TPD instability being transiently stimulated and collapsed at the filament ends, nodes or channel walls, all around the fusion micro-balloon target. Finally, the huge amount of ends or nodes of plasma electron wave collapse, this being accompanied with hot electrons and/or hard X-ray emission, resulting in an increased ablation rate of the fusion target ablator arising from the burst hot electrons and the entropy enhancement of the iced target fuel for those several keV hard X-rays, leading possibly to the scaling of some of the scientific cliffs.
It should be mentioned that it may be the case that the backscattered SRS signals can represent the accurate SRS fraction (percentage) of the total heating laser energy. In this case, is the optical SRS production mechanism completely confirmed for the percentage?

Figure 10. The laser produced a very smooth and flat shock front yielded by a seriously fluctuating irradiance of less than around ![]() $5 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$, and a rather low laser power intensity on the target surface. (a) Rear shock luminescence signal images of a 30
$5 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$, and a rather low laser power intensity on the target surface. (a) Rear shock luminescence signal images of a 30 ![]() $\mathrm {\mu} {\rm m}$ Al planar target measured using the optical streak camera. The measured scope size on the planar target is about 800
$\mathrm {\mu} {\rm m}$ Al planar target measured using the optical streak camera. The measured scope size on the planar target is about 800 ![]() $\mathrm {\mu} {\rm m}$, and the time fluctuation of the laser produced shock front is 3.83 ps (rms) with a good planarity, compared to the time of 1.5 ns when a shock wave is transmitting in the target. (b) Four-step Al target experiments with the Al substrate thickness of 20
$\mathrm {\mu} {\rm m}$, and the time fluctuation of the laser produced shock front is 3.83 ps (rms) with a good planarity, compared to the time of 1.5 ns when a shock wave is transmitting in the target. (b) Four-step Al target experiments with the Al substrate thickness of 20 ![]() $\mathrm {\mu} {\rm m}$: experimental results with the average shock velocity of 20.9 km s
$\mathrm {\mu} {\rm m}$: experimental results with the average shock velocity of 20.9 km s![]() $^{-1}$, with the velocity contrast at less than 0.5% and the linear correlation coefficient of 0.999,96. The two results show that planarity of the shock wave can still be maintained although there are many intensity modulations in the focal spot[Reference Gu, Fu, Huang, Wu, Ye, Shu, Ma, He and Wang28].
$^{-1}$, with the velocity contrast at less than 0.5% and the linear correlation coefficient of 0.999,96. The two results show that planarity of the shock wave can still be maintained although there are many intensity modulations in the focal spot[Reference Gu, Fu, Huang, Wu, Ye, Shu, Ma, He and Wang28].
It is well known that a single filament, produced in a very low ![]() $Z$ target plasma corona, is able to occupy a rather small fraction of the incident laser energy. This is because the ions with light weight and low charge in laser produced plasmas possess a better balance ability for the plasma electrical field. This is very important for constructing a more homogeneous plasma to avoid the strong filament production for direct drive fusion. In the direct drive case, the low
$Z$ target plasma corona, is able to occupy a rather small fraction of the incident laser energy. This is because the ions with light weight and low charge in laser produced plasmas possess a better balance ability for the plasma electrical field. This is very important for constructing a more homogeneous plasma to avoid the strong filament production for direct drive fusion. In the direct drive case, the low ![]() $Z$ ablator material of the fusion target micro-balloon will generate much more electrically balanced corona plasma, leading also to the production of unavoidable, but weak, filaments via the heating laser far-field speckle smoothing technology, resulting in a smaller influence on the implosion target physics process, including weaker fuel preheating and a lower ablation rate for the ablator. Therefore, the smallest energy filaments produced in the lowest
$Z$ ablator material of the fusion target micro-balloon will generate much more electrically balanced corona plasma, leading also to the production of unavoidable, but weak, filaments via the heating laser far-field speckle smoothing technology, resulting in a smaller influence on the implosion target physics process, including weaker fuel preheating and a lower ablation rate for the ablator. Therefore, the smallest energy filaments produced in the lowest ![]() $Z$ laser plasma may have the most positive effect for direct drive ignition.
$Z$ laser plasma may have the most positive effect for direct drive ignition.
The heating laser wavelength effect
The smallest filament inner aperture in laser produced plasmas has a scale of about one wavelength for the heating laser, resulting in the smallest holding energy in an individual filament obtained by adopting the ![]() $3\omega _{0}$ heating laser being a ninth of the energy of the
$3\omega _{0}$ heating laser being a ninth of the energy of the ![]() $1\omega _{0}$ heating laser. In this sense, choosing the
$1\omega _{0}$ heating laser. In this sense, choosing the ![]() $3\omega _{0}$ heating laser will be absolutely necessary to avoid the essentially negative effect of the unstable SSSFI.
$3\omega _{0}$ heating laser will be absolutely necessary to avoid the essentially negative effect of the unstable SSSFI.
The other positive effect on the laser fusion physical process
The ![]() $3\omega _{0}/2$ filaments would be formed at the leading half-section of the self-focusing process, induced from the inhomogeneous corona plasma; a small fraction of laser light will be collected inside the filament with moderate laser power intensity, while most of the other fractions of the light will be diverged forward easily by the corona plasma inhomogeneity, bringing about a slightly more uniform illumination on the critical density surface—this effect could be described as the “first” physical uniformization, in order to differentiate from the “second” physical uniformization by the electron thermal conduction between the critical surface and the ablation surface.
$3\omega _{0}/2$ filaments would be formed at the leading half-section of the self-focusing process, induced from the inhomogeneous corona plasma; a small fraction of laser light will be collected inside the filament with moderate laser power intensity, while most of the other fractions of the light will be diverged forward easily by the corona plasma inhomogeneity, bringing about a slightly more uniform illumination on the critical density surface—this effect could be described as the “first” physical uniformization, in order to differentiate from the “second” physical uniformization by the electron thermal conduction between the critical surface and the ablation surface.
As the laser power intensity increases, following the power intensity increase of the incident laser pulse leading edge, a larger fraction of the laser light will trap into the bunched filaments and later join the TPD process transiently, in a picosecond scale period. Moreover, there is still enough light, which can pass forward via the filament outer walls or ends, to diverge and to deposit the light energy randomly on the critical surface. Figure 10 shows that the laser produced a very smooth and flat shock front yielded by a seriously fluctuating irradiance less than around ![]() $5 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$, and a rather low laser power intensity on the target surface. Although the laser irradiance distribution was just like that of figure 9(a) with the measured speckle contrast at 0.46 rms, or even larger actually, the laser produced shock front flatness was extremely good due to the two-step physical smoothing mentioned above.
$5 \times 10^{13}\ {\rm W}/{\rm cm}^{2}$, and a rather low laser power intensity on the target surface. Although the laser irradiance distribution was just like that of figure 9(a) with the measured speckle contrast at 0.46 rms, or even larger actually, the laser produced shock front flatness was extremely good due to the two-step physical smoothing mentioned above.
In the fast collapse phase of the bunch of individual filaments, some percentage of the light energy trapped inside the filaments, which did not take part in the TPD and the ![]() $3\omega _{0}/2$ composition process, will quickly escape outside and divergently deposit its energy on the critical surface.
$3\omega _{0}/2$ composition process, will quickly escape outside and divergently deposit its energy on the critical surface.
Therefore, the unstable SSSFI process only has a moderate effect on the uniform target illumination except as regards the too bad boundary conditions for the corona plasma homogeneity.
4. Conclusions
We show that the SSSFI from either the SPMD or the PFD or both are almost the only origins of the TPD instability stimulated and collapsed experimentally in the leading fraction laser pulse produced plasmas in this paper. Also the other parametric instabilities, including SRS, SBS and RA ones, from the re-analysis of the early experimental results, were deduced to support an inseparable similar conclusion.
Actually there always are massive filaments generated and collapsed by the unstable SSSFI process unavoidably in the laser produced plasma corona for each filament lifetime of 10–20 ps. While the laser power intensities at the ends of the strong SPMD filaments reach the PFD self-focusing threshold, the strong filaments will be turned into PFD filaments, which will produce superhot electrons and hard X-rays, affecting the laser fusion physical process.
The SPMD unstable SSSFI itself on one hand ought to play a positive role in being the first laser intensity uniformization in the laser plasma corona, which is beneficial for laser fusion; on the other hand it plays a slightly negative role, due to the TPD collapse produced hot electrons and the 1.5–10 keV hard X-ray bursts in the duration of about 5 ps. The PFD unstable SSSFI process generated filaments will produce superhot electrons and superhard X-rays, and stir the high density plasma seriously, leading to the so called laser imprinting effect and a moderately harmful effect on the laser fusion physics.
To solve the laser irradiance uniformization problem, recently developed procedures including the CPP, DPP, RPP, and LA ones have been widely utilized and have partially improved the LPI physical boundary conditions. A further procedure should be carried out to break the laser field speckles into a quite large number of fine speckles, each with much less energy and intensity for all fine speckles. This smoothing of the laser irradiance will suppress the PFD unstable SSSFI generated filaments and superhot electrons and hard X-rays.
Adopting a very low ![]() $Z$ material for laser target illumination is important for realizing the fluid balance more easily and quickly in laser produced plasmas in order to reduce the passively assigned fractions of the incident laser energy in each individual filament, resulting in a further suppression of the process of generation of PFD induced unstable filaments. Therefore a reasonable fusion target design will mitigate superhot electron and hard X-ray generation, bringing about a beneficial effect for laser fusion.
$Z$ material for laser target illumination is important for realizing the fluid balance more easily and quickly in laser produced plasmas in order to reduce the passively assigned fractions of the incident laser energy in each individual filament, resulting in a further suppression of the process of generation of PFD induced unstable filaments. Therefore a reasonable fusion target design will mitigate superhot electron and hard X-ray generation, bringing about a beneficial effect for laser fusion.
Acknowledgements
The authors would like to acknowledge fruitful discussions with R. Li, B. Shen, and several other colleagues abroad. We thank the referees for their helpful suggestions. We thank B. Chen and D. Huang for assistance with the technical management for this paper.