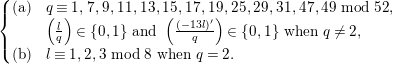1 Introduction
Let
![]() $B$
be an indefinite quaternion division algebra over
$B$
be an indefinite quaternion division algebra over
![]() $\mathbb{Q}$
, and
$\mathbb{Q}$
, and
![]() $d(B)$
its discriminant. Choose and fix a maximal order
$d(B)$
its discriminant. Choose and fix a maximal order
![]() ${\mathcal{O}}$
of
${\mathcal{O}}$
of
![]() $B$
, which is unique up to conjugation. A QM-abelian surface by
$B$
, which is unique up to conjugation. A QM-abelian surface by
![]() ${\mathcal{O}}$
over a field
${\mathcal{O}}$
over a field
![]() $K$
is a pair
$K$
is a pair
![]() $(A,i)$
, where
$(A,i)$
, where
![]() $A$
is a two-dimensional abelian variety over
$A$
is a two-dimensional abelian variety over
![]() $K$
and
$K$
and
![]() $i:{\mathcal{O}}{\hookrightarrow}\operatorname{End}_{K}(A)$
is an injective ring homomorphism sending
$i:{\mathcal{O}}{\hookrightarrow}\operatorname{End}_{K}(A)$
is an injective ring homomorphism sending
![]() $1$
to
$1$
to
![]() $id$
(cf. [Reference Buzzard4, p. 591]). Here,
$id$
(cf. [Reference Buzzard4, p. 591]). Here,
![]() $\operatorname{End}_{K}(A)$
is the ring of endomorphisms of
$\operatorname{End}_{K}(A)$
is the ring of endomorphisms of
![]() $A$
defined over
$A$
defined over
![]() $K$
. We assume that
$K$
. We assume that
![]() ${\mathcal{O}}$
acts on
${\mathcal{O}}$
acts on
![]() $A$
from the left. Let
$A$
from the left. Let
![]() $M^{B}$
be the Shimura curve over
$M^{B}$
be the Shimura curve over
![]() $\mathbb{Q}$
associated to
$\mathbb{Q}$
associated to
![]() $B$
, which parameterizes the isomorphism classes of QM-abelian surfaces by
$B$
, which parameterizes the isomorphism classes of QM-abelian surfaces by
![]() ${\mathcal{O}}$
(cf. [Reference Jordan7, p. 93]). Then
${\mathcal{O}}$
(cf. [Reference Jordan7, p. 93]). Then
![]() $M^{B}$
is a proper smooth curve over
$M^{B}$
is a proper smooth curve over
![]() $\mathbb{Q}$
. Note that its isomorphism class over
$\mathbb{Q}$
. Note that its isomorphism class over
![]() $\mathbb{Q}$
depends only on
$\mathbb{Q}$
depends only on
![]() $d(B)$
.
$d(B)$
.
We study rational points on
![]() $M^{B}$
. By [Reference Shimura9, Theorem 0], we have
$M^{B}$
. By [Reference Shimura9, Theorem 0], we have
![]() $M^{B}(\mathbb{R})=\emptyset$
. Let
$M^{B}(\mathbb{R})=\emptyset$
. Let
![]() $k$
be a number field. If
$k$
be a number field. If
![]() $k$
has a real place, then
$k$
has a real place, then
![]() $M^{B}(k)=\emptyset$
. We have a natural question: If
$M^{B}(k)=\emptyset$
. We have a natural question: If
![]() $k$
has no real place and if
$k$
has no real place and if
![]() $d(B)$
is large enough, does
$d(B)$
is large enough, does
![]() $M^{B}(k)$
become small? In some cases,
$M^{B}(k)$
become small? In some cases,
![]() $M^{B}(k)$
is expected to become empty when
$M^{B}(k)$
is expected to become empty when
![]() $d(B)$
grows; in other cases, it might consist of only CM points (in the sense of [Reference González and Rotger6, Definition 5.5]). In this context, Jordan obtained a criterion of the emptiness of
$d(B)$
grows; in other cases, it might consist of only CM points (in the sense of [Reference González and Rotger6, Definition 5.5]). In this context, Jordan obtained a criterion of the emptiness of
![]() $M^{B}(k)$
when
$M^{B}(k)$
when
![]() $k$
is imaginary quadratic and
$k$
is imaginary quadratic and
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
(see [Reference Jordan7, Theorems 6.3 and 6.6]). In the situation of [Reference Jordan7, Theorem 6.3], Skorobogatov proved that counterexamples to the Hasse principle for
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
(see [Reference Jordan7, Theorems 6.3 and 6.6]). In the situation of [Reference Jordan7, Theorem 6.3], Skorobogatov proved that counterexamples to the Hasse principle for
![]() $M^{B}$
is accounted for by the Manin obstruction in the sense of [Reference Skorobogatov10, Section 5.2] (see [Reference Skorobogatov11, Theorem 3.1]). Rotger and de Vera-Piquero expanded these results to the case where
$M^{B}$
is accounted for by the Manin obstruction in the sense of [Reference Skorobogatov10, Section 5.2] (see [Reference Skorobogatov11, Theorem 3.1]). Rotger and de Vera-Piquero expanded these results to the case where
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
by using projective Galois representations (see [Reference Rotger and de Vera-Piquero8, Theorem 1.1]). Note that a point of
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
by using projective Galois representations (see [Reference Rotger and de Vera-Piquero8, Theorem 1.1]). Note that a point of
![]() $M^{B}(k)$
is represented by a QM-abelian surface by
$M^{B}(k)$
is represented by a QM-abelian surface by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $k$
if and only if
$k$
if and only if
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
(see [Reference Jordan7, Theorem 1.1]). So one cannot use the geometry over
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
(see [Reference Jordan7, Theorem 1.1]). So one cannot use the geometry over
![]() $k$
to study rational points on
$k$
to study rational points on
![]() $M^{B}$
over
$M^{B}$
over
![]() $k$
when
$k$
when
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
. The author gave a criterion of the emptiness of
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
. The author gave a criterion of the emptiness of
![]() $M^{B}(k)$
with no restriction on the degree
$M^{B}(k)$
with no restriction on the degree
![]() $[k:\mathbb{Q}]$
in a form of expanding the above results, without relevance to the Manin obstruction (see [Reference Arai2, Theorem 1.1]). In this article, we give another criterion of the emptiness of
$[k:\mathbb{Q}]$
in a form of expanding the above results, without relevance to the Manin obstruction (see [Reference Arai2, Theorem 1.1]). In this article, we give another criterion of the emptiness of
![]() $M^{B}(k)$
and obtain new counterexamples to the Hasse principle for
$M^{B}(k)$
and obtain new counterexamples to the Hasse principle for
![]() $M^{B}$
. We also prove that such counterexamples obtained from these results are accounted for by the Manin obstruction. As for [Reference Jordan7, Theorem 6.6], the author expanded the result to the case where
$M^{B}$
. We also prove that such counterexamples obtained from these results are accounted for by the Manin obstruction. As for [Reference Jordan7, Theorem 6.6], the author expanded the result to the case where
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
by imposing a certain congruent condition on a prime divisor of
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
by imposing a certain congruent condition on a prime divisor of
![]() $d(B)$
(see [Reference Arai1]).
$d(B)$
(see [Reference Arai1]).
There is an attempt to produce a family of counterexamples to the Hasse principle for Shimura curves. Skorobogatov–Yafaev and Clark obtained some results in this direction (see [Reference Skorobogatov and Yafaev12] and [Reference Clark5, Theorems 1, 2 and 3], respectively). The results of this article enable us to produce an explicit infinite family of such counterexamples which are accounted for by the Manin obstruction.
2 Main results
To state the main results, we give several notations.
∙
 $k$
: a number field;
$k$
: a number field;∙
 $\overline{k}$
: an algebraic closure of
$\overline{k}$
: an algebraic closure of
 $k$
;
$k$
;∙
 ${\mathcal{O}}_{k}$
: the integer ring of
${\mathcal{O}}_{k}$
: the integer ring of
 $k$
;
$k$
;∙
 $\mathbb{A}_{k}$
: the adèle ring of
$\mathbb{A}_{k}$
: the adèle ring of
 $k$
;
$k$
;∙
 $Cl_{k}$
: the ideal class group of
$Cl_{k}$
: the ideal class group of
 $k$
;
$k$
;∙
 $h_{k}^{\prime }$
: the largest order of the elements in
$h_{k}^{\prime }$
: the largest order of the elements in
 $Cl_{k}$
;
$Cl_{k}$
;∙
 $\unicode[STIX]{x1D6FA}_{k}$
: the set of places of
$\unicode[STIX]{x1D6FA}_{k}$
: the set of places of
 $k$
;
$k$
;∙
 $k_{v}$
: the completion of
$k_{v}$
: the completion of
 $k$
at
$k$
at
 $v\in \unicode[STIX]{x1D6FA}_{k}$
;
$v\in \unicode[STIX]{x1D6FA}_{k}$
;∙
 $\operatorname{Br}(k_{v})$
: the Brauer group of
$\operatorname{Br}(k_{v})$
: the Brauer group of
 $k_{v}$
;
$k_{v}$
;∙
 $\operatorname{Br}(M^{B})=H_{\acute{\text{e}}\text{t}}^{2}(M^{B},\mathbb{G}_{m})$
: the Brauer group of
$\operatorname{Br}(M^{B})=H_{\acute{\text{e}}\text{t}}^{2}(M^{B},\mathbb{G}_{m})$
: the Brauer group of
 $M^{B}$
;
$M^{B}$
;∙
 ${\mathcal{K}}_{1}(k,B)$
: the set of quadratic extensions
${\mathcal{K}}_{1}(k,B)$
: the set of quadratic extensions
 $K$
of
$K$
of
 $k$
(contained in
$k$
(contained in
 $\overline{k}$
) such that
$\overline{k}$
) such that
 $B\otimes _{\mathbb{Q}}K\cong \text{M}_{2}(K)$
;
$B\otimes _{\mathbb{Q}}K\cong \text{M}_{2}(K)$
;∙
 ${\mathcal{K}}_{2}(k,B)$
: the set of quadratic extensions
${\mathcal{K}}_{2}(k,B)$
: the set of quadratic extensions
 $K$
of
$K$
of
 $k$
(contained in
$k$
(contained in
 $\overline{k}$
) such that for any prime divisor
$\overline{k}$
) such that for any prime divisor
 $p$
of
$p$
of
 $d(B)$
, any prime
$d(B)$
, any prime
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $k$
above
$k$
above
 $p$
is ramified in
$p$
is ramified in
 $K/k$
.
$K/k$
.
Note that
![]() ${\mathcal{K}}_{2}(k,B)$
is contained in
${\mathcal{K}}_{2}(k,B)$
is contained in
![]() ${\mathcal{K}}_{1}(k,B)$
(cf. Proof of Lemma 2.2). For positive integers
${\mathcal{K}}_{1}(k,B)$
(cf. Proof of Lemma 2.2). For positive integers
![]() $N$
and
$N$
and
![]() $e$
, let
$e$
, let
∙
 ${\mathcal{C}}(N,e):=\{\unicode[STIX]{x1D6FD}^{e}+\overline{\unicode[STIX]{x1D6FD}}^{e}\in \mathbb{Z}\mid \unicode[STIX]{x1D6FD},\overline{\unicode[STIX]{x1D6FD}}\in \mathbb{C}\text{ are the roots of }T^{2}+sT+N=0\text{ for some }s\in \mathbb{Z},s^{2}\leqslant 4N\}$
;
${\mathcal{C}}(N,e):=\{\unicode[STIX]{x1D6FD}^{e}+\overline{\unicode[STIX]{x1D6FD}}^{e}\in \mathbb{Z}\mid \unicode[STIX]{x1D6FD},\overline{\unicode[STIX]{x1D6FD}}\in \mathbb{C}\text{ are the roots of }T^{2}+sT+N=0\text{ for some }s\in \mathbb{Z},s^{2}\leqslant 4N\}$
;∙
 ${\mathcal{D}}(N,e):=\{a,a\pm N^{e/2},a\pm 2N^{e/2},a^{2}-3N^{e}\in \mathbb{R}\mid a\in {\mathcal{C}}(N,e)\}$
.
${\mathcal{D}}(N,e):=\{a,a\pm N^{e/2},a\pm 2N^{e/2},a^{2}-3N^{e}\in \mathbb{R}\mid a\in {\mathcal{C}}(N,e)\}$
.
If
![]() $e$
is even, then
$e$
is even, then
![]() ${\mathcal{D}}(N,e)\subseteq \mathbb{Z}$
. For a subset
${\mathcal{D}}(N,e)\subseteq \mathbb{Z}$
. For a subset
![]() ${\mathcal{D}}\subseteq \mathbb{Z}$
, let
${\mathcal{D}}\subseteq \mathbb{Z}$
, let
∙
 ${\mathcal{P}}({\mathcal{D}})$
: the set of prime divisors of some of the nonzero integers in
${\mathcal{P}}({\mathcal{D}})$
: the set of prime divisors of some of the nonzero integers in
 ${\mathcal{D}}$
.
${\mathcal{D}}$
.
For a later use, we give:
Lemma 2.1. If
![]() $e$
is even, then
$e$
is even, then
![]() ${\mathcal{P}}({\mathcal{D}}(N,e))$
contains
${\mathcal{P}}({\mathcal{D}}(N,e))$
contains
![]() $2,3$
and every prime divisor of
$2,3$
and every prime divisor of
![]() $N$
.
$N$
.
Proof. Assume that
![]() $e$
is even. Let
$e$
is even. Let
![]() $\unicode[STIX]{x1D6FD},\overline{\unicode[STIX]{x1D6FD}}$
be the roots of
$\unicode[STIX]{x1D6FD},\overline{\unicode[STIX]{x1D6FD}}$
be the roots of
![]() $T^{2}+N=0$
. Then
$T^{2}+N=0$
. Then
![]() $\unicode[STIX]{x1D6FD}^{2}=\overline{\unicode[STIX]{x1D6FD}}^{2}=-N$
and
$\unicode[STIX]{x1D6FD}^{2}=\overline{\unicode[STIX]{x1D6FD}}^{2}=-N$
and
![]() $\unicode[STIX]{x1D6FD}^{e}=\overline{\unicode[STIX]{x1D6FD}}^{e}=(-N)^{e/2}$
. Hence
$\unicode[STIX]{x1D6FD}^{e}=\overline{\unicode[STIX]{x1D6FD}}^{e}=(-N)^{e/2}$
. Hence
![]() ${\mathcal{C}}(N,e)$
and
${\mathcal{C}}(N,e)$
and
![]() ${\mathcal{D}}(N,e)$
contain
${\mathcal{D}}(N,e)$
contain
![]() $\unicode[STIX]{x1D6FD}^{e}+\overline{\unicode[STIX]{x1D6FD}}^{e}=2(-N)^{e/2}$
. Therefore
$\unicode[STIX]{x1D6FD}^{e}+\overline{\unicode[STIX]{x1D6FD}}^{e}=2(-N)^{e/2}$
. Therefore
![]() ${\mathcal{P}}({\mathcal{D}}(N,e))$
contains
${\mathcal{P}}({\mathcal{D}}(N,e))$
contains
![]() $2$
and every prime divisor of
$2$
and every prime divisor of
![]() $N$
.
$N$
.
In the following, we prove
![]() $3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
.
$3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
.
[Case
![]() $3\mid N$
]. It has already been proved.
$3\mid N$
]. It has already been proved.
[Case
![]() $3\nmid N$
]. Let
$3\nmid N$
]. Let
![]() $a:=2(-N)^{e/2}$
. Then
$a:=2(-N)^{e/2}$
. Then
![]() $a\in {\mathcal{C}}(N,e)$
and
$a\in {\mathcal{C}}(N,e)$
and
![]() $a\not \equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
.
$a\not \equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
.
(i) Case
![]() $a\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. First, assume
$a\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. First, assume
![]() $N^{e/2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Then
$N^{e/2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Then
![]() $a-N^{e/2},a+2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Since
$a-N^{e/2},a+2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Since
![]() ${\mathcal{D}}(N,e)$
contains two distinct elements
${\mathcal{D}}(N,e)$
contains two distinct elements
![]() $a-N^{e/2},a+2N^{e/2}$
, we have
$a-N^{e/2},a+2N^{e/2}$
, we have
![]() $3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
. Next, assume
$3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
. Next, assume
![]() $N^{e/2}\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Then
$N^{e/2}\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Then
![]() $a+N^{e/2},a-2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Since
$a+N^{e/2},a-2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. Since
![]() $a+N^{e/2},a-2N^{e/2}\in {\mathcal{D}}(N,e)$
, we have
$a+N^{e/2},a-2N^{e/2}\in {\mathcal{D}}(N,e)$
, we have
![]() $3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
.
$3\in {\mathcal{P}}({\mathcal{D}}(N,e))$
.
(ii) Case
![]() $a\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. If
$a\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
. If
![]() $N^{e/2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, then
$N^{e/2}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, then
![]() $a+N^{e/2},a-2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
and
$a+N^{e/2},a-2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
and
![]() $a+N^{e/2},a-2N^{e/2}\in {\mathcal{D}}(N,e)$
. If
$a+N^{e/2},a-2N^{e/2}\in {\mathcal{D}}(N,e)$
. If
![]() $N^{e/2}\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, then
$N^{e/2}\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
, then
![]() $a-N^{e/2},a+2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
and
$a-N^{e/2},a+2N^{e/2}\equiv 0\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
and
![]() $a-N^{e/2},a+2N^{e/2}\in {\mathcal{D}}(N,e)$
.◻
$a-N^{e/2},a+2N^{e/2}\in {\mathcal{D}}(N,e)$
.◻
For a prime number
![]() $q$
and a prime
$q$
and a prime
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
![]() $k$
above
$k$
above
![]() $q$
, let
$q$
, let
∙
 $k_{\mathfrak{q}}$
: the completion of
$k_{\mathfrak{q}}$
: the completion of
 $k$
at
$k$
at
 $\mathfrak{q}$
;
$\mathfrak{q}$
;∙
 $\unicode[STIX]{x1D705}(\mathfrak{q})$
: the residue field of
$\unicode[STIX]{x1D705}(\mathfrak{q})$
: the residue field of
 $\mathfrak{q}$
;
$\mathfrak{q}$
;∙
 $\text{N}_{\mathfrak{q}}$
: the cardinality of
$\text{N}_{\mathfrak{q}}$
: the cardinality of
 $\unicode[STIX]{x1D705}(\mathfrak{q})$
;
$\unicode[STIX]{x1D705}(\mathfrak{q})$
;∙
 $e_{\mathfrak{q}}$
: the ramification index of
$e_{\mathfrak{q}}$
: the ramification index of
 $\mathfrak{q}$
in
$\mathfrak{q}$
in
 $k/\mathbb{Q}$
;
$k/\mathbb{Q}$
;∙
 $f_{\mathfrak{q}}$
: the degree of the extension
$f_{\mathfrak{q}}$
: the degree of the extension
 $\unicode[STIX]{x1D705}(\mathfrak{q})/\mathbb{F}_{q}$
;
$\unicode[STIX]{x1D705}(\mathfrak{q})/\mathbb{F}_{q}$
;∙
 ${\mathcal{B}}(q)$
: the set of the isomorphism classes of indefinite quaternion division algebras
${\mathcal{B}}(q)$
: the set of the isomorphism classes of indefinite quaternion division algebras
 $B$
over
$B$
over
 $\mathbb{Q}$
such that
$\mathbb{Q}$
such that  $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-q})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-q}))\quad & \displaystyle \text{if }q\neq 2,\\ \displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-1})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-1}))\text{ and }\quad & \\ \displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-2})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-2}))\quad & \displaystyle \text{if }q=2;\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-q})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-q}))\quad & \displaystyle \text{if }q\neq 2,\\ \displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-1})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-1}))\text{ and }\quad & \\ \displaystyle B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-2})\not \cong \text{M}_{2}(\mathbb{Q}(\sqrt{-2}))\quad & \displaystyle \text{if }q=2;\end{array}\right.\end{eqnarray}$$
∙
 ${\mathcal{S}}(k,\mathfrak{q})$
: the set of the isomorphism classes of indefinite quaternion division algebras
${\mathcal{S}}(k,\mathfrak{q})$
: the set of the isomorphism classes of indefinite quaternion division algebras
 $B$
over
$B$
over
 $\mathbb{Q}$
such that every prime divisor of
$\mathbb{Q}$
such that every prime divisor of
 $d(B)$
belongs to
$d(B)$
belongs to  $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))\quad & \displaystyle \text{if }B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)\text{ and }e_{\mathfrak{q}}\text{ is even},\\ \displaystyle {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2e_{\mathfrak{q}}))\quad & \displaystyle \text{if }B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k);\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))\quad & \displaystyle \text{if }B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)\text{ and }e_{\mathfrak{q}}\text{ is even},\\ \displaystyle {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2e_{\mathfrak{q}}))\quad & \displaystyle \text{if }B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k);\end{array}\right.\end{eqnarray}$$
∙
 ${\mathcal{K}}(k,\mathfrak{q})$
: the set of quadratic extensions
${\mathcal{K}}(k,\mathfrak{q})$
: the set of quadratic extensions
 $K$
of
$K$
of
 $k$
(contained in
$k$
(contained in
 $\overline{k}$
) such that
$\overline{k}$
) such that
 $\mathfrak{q}$
is ramified in
$\mathfrak{q}$
is ramified in
 $K/k$
.
$K/k$
.
Note that
![]() ${\mathcal{S}}(k,\mathfrak{q})$
is a finite set, while
${\mathcal{S}}(k,\mathfrak{q})$
is a finite set, while
![]() ${\mathcal{K}}_{2}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
is an infinite set (cf. [Reference Arai and Momose3, Remark 4.4]). We have the following criterion of
${\mathcal{K}}_{2}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
is an infinite set (cf. [Reference Arai and Momose3, Remark 4.4]). We have the following criterion of
![]() $B\in {\mathcal{B}}(q)$
.
$B\in {\mathcal{B}}(q)$
.
Lemma 2.2.
(1) Assume
 $q\neq 2$
. Then
$q\neq 2$
. Then
 $B\in {\mathcal{B}}(q)$
if and only if there is a prime divisor of
$B\in {\mathcal{B}}(q)$
if and only if there is a prime divisor of
 $d(B)$
which splits in
$d(B)$
which splits in
 $\mathbb{Q}(\sqrt{-q})$
.
$\mathbb{Q}(\sqrt{-q})$
.(2) We have
 $B\in {\mathcal{B}}(2)$
if and only if there are prime divisors
$B\in {\mathcal{B}}(2)$
if and only if there are prime divisors
 $p_{1},p_{2}$
of
$p_{1},p_{2}$
of
 $d(B)$
satisfying
$d(B)$
satisfying
 $p_{1}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
and
$p_{1}\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
and
 $p_{2}\equiv 1,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. Here, the case where
$p_{2}\equiv 1,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
. Here, the case where
 $p_{1}=p_{2}$
is allowed.
$p_{1}=p_{2}$
is allowed.
Proof. By the Hasse principle, we have
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
if and only if
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
if and only if
![]() $B\otimes _{\mathbb{Q}}k_{v}\cong \text{M}_{2}(k_{v})$
for any
$B\otimes _{\mathbb{Q}}k_{v}\cong \text{M}_{2}(k_{v})$
for any
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
(see [Reference Vignéras13, Propriété I in p. 74]). Let
$v\in \unicode[STIX]{x1D6FA}_{k}$
(see [Reference Vignéras13, Propriété I in p. 74]). Let
![]() $l$
be a prime number and
$l$
be a prime number and
![]() $D_{l}$
the quaternion division algebra over
$D_{l}$
the quaternion division algebra over
![]() $\mathbb{Q}_{l}$
. If
$\mathbb{Q}_{l}$
. If
![]() $L$
is a quadratic extension of
$L$
is a quadratic extension of
![]() $\mathbb{Q}_{l}$
, then
$\mathbb{Q}_{l}$
, then
![]() $D_{l}\otimes _{\mathbb{Q}_{l}}L\cong \text{M}_{2}(L)$
(see [Reference Vignéras13, Théorème 1.3 in Chapitre II]). Therefore (1) follows.
$D_{l}\otimes _{\mathbb{Q}_{l}}L\cong \text{M}_{2}(L)$
(see [Reference Vignéras13, Théorème 1.3 in Chapitre II]). Therefore (1) follows.
We see that
![]() $l$
splits in
$l$
splits in
![]() $\mathbb{Q}(\sqrt{-1})$
(resp.
$\mathbb{Q}(\sqrt{-1})$
(resp.
![]() $\mathbb{Q}(\sqrt{-2})$
) if and only if
$\mathbb{Q}(\sqrt{-2})$
) if and only if
![]() $l\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
(resp.
$l\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$
(resp.
![]() $l\equiv 1,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
). Then (2) follows.◻
$l\equiv 1,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8$
). Then (2) follows.◻
Note that
![]() ${\mathcal{B}}(q)$
is an infinite set for any
${\mathcal{B}}(q)$
is an infinite set for any
![]() $q$
. Since
$q$
. Since
![]() $M^{B}$
is proper over
$M^{B}$
is proper over
![]() $\mathbb{Q}$
, we have
$\mathbb{Q}$
, we have
![]() $M^{B}(\mathbb{A}_{k})=\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}M^{B}(k_{v})$
. Define a pairing
$M^{B}(\mathbb{A}_{k})=\prod _{v\in \unicode[STIX]{x1D6FA}_{k}}M^{B}(k_{v})$
. Define a pairing
by
![]() $(c,\{x_{v}\}_{v\in \unicode[STIX]{x1D6FA}_{k}})=\sum _{v\in \unicode[STIX]{x1D6FA}_{k}}\operatorname{inv}_{v}(x_{v}^{\ast }c)$
. Here,
$(c,\{x_{v}\}_{v\in \unicode[STIX]{x1D6FA}_{k}})=\sum _{v\in \unicode[STIX]{x1D6FA}_{k}}\operatorname{inv}_{v}(x_{v}^{\ast }c)$
. Here,
![]() $\operatorname{inv}_{v}:\operatorname{Br}(k_{v})\longrightarrow \mathbb{Q}/\mathbb{Z}$
is the local invariant at
$\operatorname{inv}_{v}:\operatorname{Br}(k_{v})\longrightarrow \mathbb{Q}/\mathbb{Z}$
is the local invariant at
![]() $v$
, and
$v$
, and
![]() $x_{v}^{\ast }:\operatorname{Br}(M^{B})\longrightarrow \operatorname{Br}(k_{v})$
is the map associated to
$x_{v}^{\ast }:\operatorname{Br}(M^{B})\longrightarrow \operatorname{Br}(k_{v})$
is the map associated to
![]() $x_{v}:\operatorname{Spec}(k_{v})\longrightarrow M^{B}$
. In this sum, we have
$x_{v}:\operatorname{Spec}(k_{v})\longrightarrow M^{B}$
. In this sum, we have
![]() $\operatorname{inv}_{v}(x_{v}^{\ast }c)=0$
for all but finitely many
$\operatorname{inv}_{v}(x_{v}^{\ast }c)=0$
for all but finitely many
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
. Let
$v\in \unicode[STIX]{x1D6FA}_{k}$
. Let
![]() $M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}$
be the right kernel of this pairing. Then
$M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}$
be the right kernel of this pairing. Then
![]() $M^{B}(k)\subseteq M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}\subseteq M^{B}(\mathbb{A}_{k})$
(see [Reference Skorobogatov10, Section 5.2]). The main results of this article are:
$M^{B}(k)\subseteq M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}\subseteq M^{B}(\mathbb{A}_{k})$
(see [Reference Skorobogatov10, Section 5.2]). The main results of this article are:
Theorem 2.3. Assume that
![]() $k/\mathbb{Q}$
has even degree. Let
$k/\mathbb{Q}$
has even degree. Let
![]() $q$
be a prime number such that
$q$
be a prime number such that
∙ there is a unique prime
 $\mathfrak{q}$
of
$\mathfrak{q}$
of
 $k$
above
$k$
above
 $q$
;
$q$
;∙
 $f_{\mathfrak{q}}$
is odd (and so
$f_{\mathfrak{q}}$
is odd (and so
 $e_{\mathfrak{q}}$
is even);
$e_{\mathfrak{q}}$
is even);∙
 $B\in {\mathcal{B}}(q)\setminus {\mathcal{S}}(k,\mathfrak{q})$
.
$B\in {\mathcal{B}}(q)\setminus {\mathcal{S}}(k,\mathfrak{q})$
.
Then
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.
Theorem 2.4. Let
![]() $p,q$
be distinct prime numbers, and let
$p,q$
be distinct prime numbers, and let
![]() $\mathfrak{q}$
be a prime of
$\mathfrak{q}$
be a prime of
![]() $k$
above
$k$
above
![]() $q$
. Assume that
$q$
. Assume that
∙
 $f_{\mathfrak{p}}$
is odd for any prime
$f_{\mathfrak{p}}$
is odd for any prime
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $k$
above
$k$
above
 $p$
;
$p$
;∙
 $f_{\mathfrak{q}}$
is odd;
$f_{\mathfrak{q}}$
is odd;∙
 $B\in {\mathcal{B}}(q)$
;
$B\in {\mathcal{B}}(q)$
;∙
 $p\mid d(B)$
;
$p\mid d(B)$
;∙
 $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
.
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
.
Then
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.
Remark 2.5.
(1) If
 $k/\mathbb{Q}$
has odd degree, then
$k/\mathbb{Q}$
has odd degree, then
 $k$
has a real place, and so
$k$
has a real place, and so
 $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=M^{B}(\mathbb{A}_{k})=\emptyset$
.
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=M^{B}(\mathbb{A}_{k})=\emptyset$
.(2) In [Reference Arai2], we proved only
 $M^{B}(k)=\emptyset$
in the setting of Theorem 2.3.
$M^{B}(k)=\emptyset$
in the setting of Theorem 2.3.(3) Theorem 2.3 for imaginary quadratic fields was proved in [Reference Jordan7, Theorem 6.3], [Reference Rotger and de Vera-Piquero8, Theorem 1.1], [Reference Skorobogatov11, Theorem 3.1].
From these theorems, we obtain the following counterexamples to the Hasse principle for Shimura curves, which are accounted for by the Manin obstruction. Especially, we obtain an infinite family of such counterexamples.
Proposition 2.6.
(1) Let
 $n\in \mathbb{Z}$
be an odd integer. Assume that
$n\in \mathbb{Z}$
be an odd integer. Assume that
 $n$
is square free and that
$n$
is square free and that
 $(d(B),k)=(39,\mathbb{Q}(\sqrt{2n},\sqrt{-13}))$
. Then
$(d(B),k)=(39,\mathbb{Q}(\sqrt{2n},\sqrt{-13}))$
. Then
 $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
,
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
,
 $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
 $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.(2) Assume
 $(d(B),k)=(39,\mathbb{Q}(\sqrt{3},\sqrt{-13}))$
or
$(d(B),k)=(39,\mathbb{Q}(\sqrt{3},\sqrt{-13}))$
or
 $(39,\mathbb{Q}(\sqrt{17},\sqrt{-13}))$
. Then
$(39,\mathbb{Q}(\sqrt{17},\sqrt{-13}))$
. Then
 $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
,
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
,
 $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
 $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.(3) Let
 $L$
be the subfield of
$L$
be the subfield of
 $\mathbb{Q}(\unicode[STIX]{x1D701}_{9})$
satisfying
$\mathbb{Q}(\unicode[STIX]{x1D701}_{9})$
satisfying
 $[L:\mathbb{Q}]=3$
, where
$[L:\mathbb{Q}]=3$
, where
 $\unicode[STIX]{x1D701}_{9}$
is a primitive
$\unicode[STIX]{x1D701}_{9}$
is a primitive
 $9$
th root of unity. Assume
$9$
th root of unity. Assume
 $(d(B),k)=(62,L(\sqrt{-39}))$
or
$(d(B),k)=(62,L(\sqrt{-39}))$
or
 $(86,L(\sqrt{-15}))$
. Then
$(86,L(\sqrt{-15}))$
. Then
 $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
,
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
,
 $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
 $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.(4) Assume
 $(d(B),k)=(122,\mathbb{Q}(\sqrt{-39},\sqrt{-183}))$
. Then
$(d(B),k)=(122,\mathbb{Q}(\sqrt{-39},\sqrt{-183}))$
. Then
 $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
,
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
,
 $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
 $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
In Sections 3–4, we review the classification of characters associated to QM-abelian surfaces, which plays a key role in the proof. In Section 5 (resp. Section 6), we prove Theorem 2.4 (resp. Theorem 2.3). In Section 7, we deduce Proposition 2.6(1)(3) (resp. Proposition 2.6(2)(4)) from Theorem 2.3 (resp. Theorem 2.4). Note that we cannot apply Theorem 2.3 to
![]() $k=\mathbb{Q}(\sqrt{3},\sqrt{-13})$
,
$k=\mathbb{Q}(\sqrt{3},\sqrt{-13})$
,
![]() $\mathbb{Q}(\sqrt{17},\sqrt{-13})$
or
$\mathbb{Q}(\sqrt{17},\sqrt{-13})$
or
![]() $\mathbb{Q}(\sqrt{-39},\sqrt{-183})$
, because no prime number
$\mathbb{Q}(\sqrt{-39},\sqrt{-183})$
, because no prime number
![]() $q$
is totally ramified in these fields.
$q$
is totally ramified in these fields.
3 Canonical isogeny characters
We review canonical isogeny characters associated to QM-abelian surfaces, which were introduced in [Reference Jordan7, Section 4]. Let
![]() $K$
be a field of characteristic
$K$
be a field of characteristic
![]() $0$
possessing an algebraic closure
$0$
possessing an algebraic closure
![]() $\overline{K}$
,
$\overline{K}$
,
![]() $(A,i)$
a QM-abelian surface by
$(A,i)$
a QM-abelian surface by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $K$
, and
$K$
, and
![]() $p$
a prime divisor of
$p$
a prime divisor of
![]() $d(B)$
. The
$d(B)$
. The
![]() $p$
-torsion subgroup
$p$
-torsion subgroup
![]() $A[p](\overline{K})$
of
$A[p](\overline{K})$
of
![]() $A$
has exactly one nonzero proper left
$A$
has exactly one nonzero proper left
![]() ${\mathcal{O}}$
-submodule, which we shall denote by
${\mathcal{O}}$
-submodule, which we shall denote by
![]() $C_{p}$
. Then
$C_{p}$
. Then
![]() $C_{p}$
has order
$C_{p}$
has order
![]() $p^{2}$
, and is called the canonical torsion subgroup of
$p^{2}$
, and is called the canonical torsion subgroup of
![]() $(A,i)$
of reduced order
$(A,i)$
of reduced order
![]() $p$
; it is stable under the action of the Galois group
$p$
; it is stable under the action of the Galois group
![]() $\text{G}_{K}=\operatorname{Gal}(\overline{K}/K)$
. Let
$\text{G}_{K}=\operatorname{Gal}(\overline{K}/K)$
. Let
![]() $\mathfrak{P}_{{\mathcal{O}}}\subseteq {\mathcal{O}}$
be the unique left ideal of reduced norm
$\mathfrak{P}_{{\mathcal{O}}}\subseteq {\mathcal{O}}$
be the unique left ideal of reduced norm
![]() $p\mathbb{Z}$
. In fact,
$p\mathbb{Z}$
. In fact,
![]() $\mathfrak{P}_{{\mathcal{O}}}$
is a two-sided ideal of
$\mathfrak{P}_{{\mathcal{O}}}$
is a two-sided ideal of
![]() ${\mathcal{O}}$
. Then
${\mathcal{O}}$
. Then
![]() $C_{p}$
is free of rank
$C_{p}$
is free of rank
![]() $1$
over
$1$
over
![]() ${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}$
. Fix an isomorphism
${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}$
. Fix an isomorphism
![]() ${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}\cong \mathbb{F}_{p^{2}}$
. The action of
${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}\cong \mathbb{F}_{p^{2}}$
. The action of
![]() $\text{G}_{K}$
on
$\text{G}_{K}$
on
![]() $C_{p}$
yields a character
$C_{p}$
yields a character
where
![]() $\operatorname{Aut}_{{\mathcal{O}}}(C_{p})$
is the group of
$\operatorname{Aut}_{{\mathcal{O}}}(C_{p})$
is the group of
![]() ${\mathcal{O}}$
-linear automorphisms of
${\mathcal{O}}$
-linear automorphisms of
![]() $C_{p}$
. The character
$C_{p}$
. The character
![]() $\unicode[STIX]{x1D71A}_{p}$
depends on the choice of the isomorphism
$\unicode[STIX]{x1D71A}_{p}$
depends on the choice of the isomorphism
![]() ${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}\cong \mathbb{F}_{p^{2}}$
, but the pair
${\mathcal{O}}/\mathfrak{P}_{{\mathcal{O}}}\cong \mathbb{F}_{p^{2}}$
, but the pair
![]() $\{\unicode[STIX]{x1D71A}_{p},(\unicode[STIX]{x1D71A}_{p})^{p}\}$
does not depend on this choice. Either of the characters
$\{\unicode[STIX]{x1D71A}_{p},(\unicode[STIX]{x1D71A}_{p})^{p}\}$
does not depend on this choice. Either of the characters
![]() $\unicode[STIX]{x1D71A}_{p},(\unicode[STIX]{x1D71A}_{p})^{p}$
is called a canonical isogeny character at
$\unicode[STIX]{x1D71A}_{p},(\unicode[STIX]{x1D71A}_{p})^{p}$
is called a canonical isogeny character at
![]() $p$
.
$p$
.
Let
![]() $\widehat{\mathbb{Z}}$
be the profinite completion of
$\widehat{\mathbb{Z}}$
be the profinite completion of
![]() $\mathbb{Z}$
, and let
$\mathbb{Z}$
, and let
Let
![]() $M_{p}^{B}$
be the Shimura curve over
$M_{p}^{B}$
be the Shimura curve over
![]() $\mathbb{Q}$
associated to
$\mathbb{Q}$
associated to
![]() $D_{p}$
. Then it parameterizes the isomorphism classes of triples
$D_{p}$
. Then it parameterizes the isomorphism classes of triples
![]() $(A,i,c)$
, where
$(A,i,c)$
, where
![]() $(A,i)$
is a QM-abelian surface by
$(A,i)$
is a QM-abelian surface by
![]() ${\mathcal{O}}$
and
${\mathcal{O}}$
and
![]() $c$
is a generator of its canonical torsion subgroup
$c$
is a generator of its canonical torsion subgroup
![]() $C_{p}$
as an
$C_{p}$
as an
![]() ${\mathcal{O}}$
-module. Note that the curve
${\mathcal{O}}$
-module. Note that the curve
![]() $M_{p}^{B}$
over
$M_{p}^{B}$
over
![]() $\mathbb{Q}$
is not geometrically connected if
$\mathbb{Q}$
is not geometrically connected if
![]() $p\neq 2$
(see [Reference Skorobogatov11, p. 780] for details). The map
$p\neq 2$
(see [Reference Skorobogatov11, p. 780] for details). The map
![]() $(A,i,c)\longmapsto (A,i)$
defines a covering
$(A,i,c)\longmapsto (A,i)$
defines a covering
![]() $M_{p}^{B}\longrightarrow M^{B}$
(over
$M_{p}^{B}\longrightarrow M^{B}$
(over
![]() $\mathbb{Q}$
) whose automorphism group
$\mathbb{Q}$
) whose automorphism group
![]() $\operatorname{Aut}(M_{p}^{B}/M^{B})$
is isomorphic to
$\operatorname{Aut}(M_{p}^{B}/M^{B})$
is isomorphic to
 $$\begin{eqnarray}\mathbb{F}_{p^{2}}^{\times }/\{\pm 1\}\cong \left\{\begin{array}{@{}ll@{}}\displaystyle \mathbb{Z}/\frac{p^{2}-1}{2}\mathbb{Z}\quad & \displaystyle \text{if }p\neq 2,\\ \displaystyle \mathbb{Z}/3\mathbb{Z}\quad & \displaystyle \text{if }p=2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}_{p^{2}}^{\times }/\{\pm 1\}\cong \left\{\begin{array}{@{}ll@{}}\displaystyle \mathbb{Z}/\frac{p^{2}-1}{2}\mathbb{Z}\quad & \displaystyle \text{if }p\neq 2,\\ \displaystyle \mathbb{Z}/3\mathbb{Z}\quad & \displaystyle \text{if }p=2.\end{array}\right.\end{eqnarray}$$
If
![]() $p\geqslant 5$
, then
$p\geqslant 5$
, then
![]() $\mathbb{F}_{p^{2}}^{\times }/\{\pm 1\}$
has a unique subgroup
$\mathbb{F}_{p^{2}}^{\times }/\{\pm 1\}$
has a unique subgroup
![]() $C(6)$
which is isomorphic to
$C(6)$
which is isomorphic to
![]() $\mathbb{Z}/6\mathbb{Z}$
. The quotient of
$\mathbb{Z}/6\mathbb{Z}$
. The quotient of
![]() $M_{p}^{B}$
by
$M_{p}^{B}$
by
![]() $C(6)$
defines an unramified subcovering
$C(6)$
defines an unramified subcovering
which is an
![]() $M^{B}$
-torsor under the constant group scheme
$M^{B}$
-torsor under the constant group scheme
![]() $(\mathbb{F}_{p^{2}}^{\times })^{12}\cong \mathbb{Z}/\frac{p^{2}-1}{12}\mathbb{Z}$
(see [Reference Skorobogatov11, Corollary 1.2]). Let
$(\mathbb{F}_{p^{2}}^{\times })^{12}\cong \mathbb{Z}/\frac{p^{2}-1}{12}\mathbb{Z}$
(see [Reference Skorobogatov11, Corollary 1.2]). Let
![]() $x\in M^{B}(K)$
. Then the action of
$x\in M^{B}(K)$
. Then the action of
![]() $\text{G}_{K}$
on the fiber of
$\text{G}_{K}$
on the fiber of
![]() $f_{p}^{B}$
at
$f_{p}^{B}$
at
![]() $x$
yields a character
$x$
yields a character
Lemma 3.1. [Reference Skorobogatov11, Lemma 2.1]
Assume
![]() $p\geqslant 5$
. If
$p\geqslant 5$
. If
![]() $x$
is represented by a QM-abelian surface
$x$
is represented by a QM-abelian surface
![]() $(A,i)$
by
$(A,i)$
by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $K$
, then
$K$
, then
![]() $\unicode[STIX]{x1D71A}_{(A,i,p)}^{12}=\unicode[STIX]{x1D719}_{x}$
.
$\unicode[STIX]{x1D71A}_{(A,i,p)}^{12}=\unicode[STIX]{x1D719}_{x}$
.
4 Classification of characters
We review the classification of characters associated to QM-abelian surfaces over local fields of characteristic
![]() $0$
. Let
$0$
. Let
![]() $m$
be a prime number,
$m$
be a prime number,
![]() $M$
a finite extension of
$M$
a finite extension of
![]() $\mathbb{Q}_{m}$
, and
$\mathbb{Q}_{m}$
, and
![]() $\mathfrak{M}$
(resp.
$\mathfrak{M}$
(resp.
![]() $\unicode[STIX]{x1D705}(M)$
) the maximal ideal (resp. the residue field) of
$\unicode[STIX]{x1D705}(M)$
) the maximal ideal (resp. the residue field) of
![]() $M$
. For a QM-abelian surface
$M$
. For a QM-abelian surface
![]() $(A,i)$
by
$(A,i)$
by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $M$
, fix a canonical isogeny character
$M$
, fix a canonical isogeny character
![]() $\unicode[STIX]{x1D71A}_{p}=\unicode[STIX]{x1D71A}_{(A,i,p)}:\text{G}_{M}\longrightarrow \mathbb{F}_{p^{2}}^{\times }$
, where
$\unicode[STIX]{x1D71A}_{p}=\unicode[STIX]{x1D71A}_{(A,i,p)}:\text{G}_{M}\longrightarrow \mathbb{F}_{p^{2}}^{\times }$
, where
![]() $p$
is a prime divisor of
$p$
is a prime divisor of
![]() $d(B)$
. Let
$d(B)$
. Let
![]() $\text{G}_{M}^{\text{ab}}$
be the Galois group of the maximal abelian extension
$\text{G}_{M}^{\text{ab}}$
be the Galois group of the maximal abelian extension
![]() $M^{\text{ab}}/M$
. Then we have an induced character
$M^{\text{ab}}/M$
. Then we have an induced character
![]() $\unicode[STIX]{x1D71A}_{p}^{\text{ab}}:\text{G}_{M}^{\text{ab}}\longrightarrow \mathbb{F}_{p^{2}}^{\times }$
. Let
$\unicode[STIX]{x1D71A}_{p}^{\text{ab}}:\text{G}_{M}^{\text{ab}}\longrightarrow \mathbb{F}_{p^{2}}^{\times }$
. Let
![]() $\unicode[STIX]{x1D714}_{M}:{\mathcal{O}}_{M}^{\times }\longrightarrow \text{G}_{M}^{\text{ab}}$
be the Artin map, and let
$\unicode[STIX]{x1D714}_{M}:{\mathcal{O}}_{M}^{\times }\longrightarrow \text{G}_{M}^{\text{ab}}$
be the Artin map, and let
In this local setting, we have:
Proposition 4.1. [Reference Jordan7, Proposition 4.7(2)]
If
![]() $m\neq p$
, then
$m\neq p$
, then
![]() $r_{(A,i,p)}^{12}=1$
.
$r_{(A,i,p)}^{12}=1$
.
Let
![]() $e_{M}$
(resp.
$e_{M}$
(resp.
![]() $f_{M}$
) be the ramification index of
$f_{M}$
) be the ramification index of
![]() $M/\mathbb{Q}_{m}$
(resp. the degree of the residue field extension
$M/\mathbb{Q}_{m}$
(resp. the degree of the residue field extension
![]() $\unicode[STIX]{x1D705}(M)/\mathbb{F}_{m}$
). Let
$\unicode[STIX]{x1D705}(M)/\mathbb{F}_{m}$
). Let
![]() $\text{N}_{M}:=m^{f_{M}}$
,
$\text{N}_{M}:=m^{f_{M}}$
,
![]() $t_{M}:=\text{gcd}(2,f_{M})\in \{1,2\}$
.
$t_{M}:=\text{gcd}(2,f_{M})\in \{1,2\}$
.
Proposition 4.2. [Reference Jordan7, Proposition 4.8]
Assume
![]() $m=p$
. Then there is a unique element
$m=p$
. Then there is a unique element
![]() $c\in \mathbb{Z}/(p^{t_{M}}-1)\mathbb{Z}$
satisfying
$c\in \mathbb{Z}/(p^{t_{M}}-1)\mathbb{Z}$
satisfying
for any
![]() $u\in {\mathcal{O}}_{M}^{\times }$
, where
$u\in {\mathcal{O}}_{M}^{\times }$
, where
![]() $\widetilde{u}\in \unicode[STIX]{x1D705}(M)^{\times }$
is the reduction of
$\widetilde{u}\in \unicode[STIX]{x1D705}(M)^{\times }$
is the reduction of
![]() $u$
modulo
$u$
modulo
![]() $\mathfrak{M}$
. Furthermore, we have
$\mathfrak{M}$
. Furthermore, we have
Let
![]() $l$
be a prime number,
$l$
be a prime number,
![]() $T_{l}A$
the
$T_{l}A$
the
![]() $l$
-adic Tate module of
$l$
-adic Tate module of
![]() $A$
, and
$A$
, and
![]() $\operatorname{Aut}_{{\mathcal{O}}}(T_{l}A)$
the group of
$\operatorname{Aut}_{{\mathcal{O}}}(T_{l}A)$
the group of
![]() $\mathbb{Z}_{l}$
-linear automorphisms of
$\mathbb{Z}_{l}$
-linear automorphisms of
![]() $T_{l}A$
commuting with the action of
$T_{l}A$
commuting with the action of
![]() ${\mathcal{O}}$
. Let
${\mathcal{O}}$
. Let
![]() ${\mathcal{O}}_{l}:={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Z}_{l}$
,
${\mathcal{O}}_{l}:={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Z}_{l}$
,
![]() $B_{l}:=B\otimes _{\mathbb{Q}}\mathbb{Q}_{l}$
, and fix an isomorphism
$B_{l}:=B\otimes _{\mathbb{Q}}\mathbb{Q}_{l}$
, and fix an isomorphism
![]() $\operatorname{Aut}_{{\mathcal{O}}}(T_{l}A)\cong {\mathcal{O}}_{l}^{\times }$
. Let
$\operatorname{Aut}_{{\mathcal{O}}}(T_{l}A)\cong {\mathcal{O}}_{l}^{\times }$
. Let
be the representation determined by the action of
![]() $\text{G}_{M}$
on
$\text{G}_{M}$
on
![]() $T_{l}A$
. Let
$T_{l}A$
. Let
![]() $\operatorname{Trd}_{B_{l}/\mathbb{Q}_{l}}$
(resp.
$\operatorname{Trd}_{B_{l}/\mathbb{Q}_{l}}$
(resp.
![]() $\operatorname{Nrd}_{B_{l}/\mathbb{Q}_{l}}$
) be the reduced trace (resp. the reduced norm) on
$\operatorname{Nrd}_{B_{l}/\mathbb{Q}_{l}}$
) be the reduced trace (resp. the reduced norm) on
![]() $B_{l}$
, and
$B_{l}$
, and
![]() $\operatorname{Fr}\in \text{G}_{M}$
a Frobenius element. For each positive integer
$\operatorname{Fr}\in \text{G}_{M}$
a Frobenius element. For each positive integer
![]() $e$
, let
$e$
, let
![]() $a_{l}(\operatorname{Fr}^{e}):=\operatorname{Trd}_{B_{l}/\mathbb{Q}_{l}}(R_{l}(\operatorname{Fr}^{e}))$
. If
$a_{l}(\operatorname{Fr}^{e}):=\operatorname{Trd}_{B_{l}/\mathbb{Q}_{l}}(R_{l}(\operatorname{Fr}^{e}))$
. If
![]() $l\neq m$
, then
$l\neq m$
, then
![]() $a_{l}(\operatorname{Fr}^{e})\in \mathbb{Z}$
and it does not depend on
$a_{l}(\operatorname{Fr}^{e})\in \mathbb{Z}$
and it does not depend on
![]() $l$
. We shall denote it by
$l$
. We shall denote it by
![]() $a(\operatorname{Fr}^{e})$
. Then
$a(\operatorname{Fr}^{e})$
. Then
if
![]() $l\neq m$
.
$l\neq m$
.
Proposition 4.3. [Reference Jordan7, Proposition 5.3]
(1)
 $a(\operatorname{Fr}^{e})\in {\mathcal{C}}(\text{N}_{M},e)$
for any
$a(\operatorname{Fr}^{e})\in {\mathcal{C}}(\text{N}_{M},e)$
for any
 $e\geqslant 1$
.
$e\geqslant 1$
.(2) If
 $m\neq p$
, then for any
$m\neq p$
, then for any $$\begin{eqnarray}a(\operatorname{Fr}^{e})\equiv \unicode[STIX]{x1D71A}_{p}(\operatorname{Fr}^{e})+(\text{N}_{M})^{e}\unicode[STIX]{x1D71A}_{p}(\operatorname{Fr}^{e})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\end{eqnarray}$$
$$\begin{eqnarray}a(\operatorname{Fr}^{e})\equiv \unicode[STIX]{x1D71A}_{p}(\operatorname{Fr}^{e})+(\text{N}_{M})^{e}\unicode[STIX]{x1D71A}_{p}(\operatorname{Fr}^{e})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\end{eqnarray}$$
 $e\geqslant 1$
.
$e\geqslant 1$
.
5 Proof of Theorem 2.4
Suppose that the assumptions of Theorem 2.4 hold. Since
![]() $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
, we have
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
, we have
![]() $p\geqslant 5$
and
$p\geqslant 5$
and
![]() $p\neq q$
(see Lemma 2.1). If
$p\neq q$
(see Lemma 2.1). If
![]() $M^{B}(\mathbb{A}_{k})=\emptyset$
, then
$M^{B}(\mathbb{A}_{k})=\emptyset$
, then
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. So, in the following, assume
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. So, in the following, assume
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
. Then for any
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
. Then for any
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
, there is a point
$v\in \unicode[STIX]{x1D6FA}_{k}$
, there is a point
![]() $x_{v}\in M^{B}(k_{v})$
. Note that
$x_{v}\in M^{B}(k_{v})$
. Note that
![]() $k$
has no real place in this case. We have a family of characters
$k$
has no real place in this case. We have a family of characters
associated to the covering
![]() $f_{p}^{B}:Y_{p}^{B}\longrightarrow M^{B}$
.
$f_{p}^{B}:Y_{p}^{B}\longrightarrow M^{B}$
.
Assume that there is a global character
![]() $\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
such that
$\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
such that
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{k_{v}}}=\unicode[STIX]{x1D719}_{x_{v}}$
for any
$\unicode[STIX]{x1D6F7}|_{\text{G}_{k_{v}}}=\unicode[STIX]{x1D719}_{x_{v}}$
for any
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
. If
$v\in \unicode[STIX]{x1D6FA}_{k}$
. If
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
, fix
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
, fix
![]() $K_{0}\in {\mathcal{K}}_{2}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
. Let
$K_{0}\in {\mathcal{K}}_{2}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
. Let
Then
![]() $B\otimes _{\mathbb{Q}}K\cong \text{M}_{2}(K)$
because
$B\otimes _{\mathbb{Q}}K\cong \text{M}_{2}(K)$
because
![]() $K_{0}\in {\mathcal{K}}_{2}(k,B)\subseteq {\mathcal{K}}_{1}(k,B)$
. Let
$K_{0}\in {\mathcal{K}}_{2}(k,B)\subseteq {\mathcal{K}}_{1}(k,B)$
. Let
![]() $\mathfrak{M}$
be a prime of
$\mathfrak{M}$
be a prime of
![]() $K$
,
$K$
,
![]() $\mathfrak{m}$
the prime of
$\mathfrak{m}$
the prime of
![]() $k$
below
$k$
below
![]() $\mathfrak{M}$
, and
$\mathfrak{M}$
, and
![]() $v(\mathfrak{m})$
the place of
$v(\mathfrak{m})$
the place of
![]() $k$
corresponding to
$k$
corresponding to
![]() $\mathfrak{m}$
. Since
$\mathfrak{m}$
. Since
![]() $B\otimes _{\mathbb{Q}}K_{\mathfrak{M}}\cong \text{M}_{2}(K_{\mathfrak{M}})$
, the point
$B\otimes _{\mathbb{Q}}K_{\mathfrak{M}}\cong \text{M}_{2}(K_{\mathfrak{M}})$
, the point
![]() $x_{v(\mathfrak{m})}$
is represented by a QM-abelian surface
$x_{v(\mathfrak{m})}$
is represented by a QM-abelian surface
![]() $(A_{\mathfrak{M}},i_{\mathfrak{M}})$
by
$(A_{\mathfrak{M}},i_{\mathfrak{M}})$
by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $K_{\mathfrak{M}}$
(see [Reference Jordan7, Theorem 1.1]). Then
$K_{\mathfrak{M}}$
(see [Reference Jordan7, Theorem 1.1]). Then
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D719}_{x_{v(\mathfrak{m})}}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
by Lemma 3.1. Since
$\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D719}_{x_{v(\mathfrak{m})}}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
by Lemma 3.1. Since
![]() $K_{0}\in {\mathcal{K}}(k,\mathfrak{q})$
, there is a unique prime
$K_{0}\in {\mathcal{K}}(k,\mathfrak{q})$
, there is a unique prime
![]() $\mathfrak{Q}$
of
$\mathfrak{Q}$
of
![]() $K$
above
$K$
above
![]() $\mathfrak{q}$
. We also have
$\mathfrak{q}$
. We also have
Let
![]() $\operatorname{Fr}_{\mathfrak{Q}}\in \text{G}_{K_{\mathfrak{Q}}}(\subseteq \text{G}_{K})$
be a Frobenius element. Fix an element
$\operatorname{Fr}_{\mathfrak{Q}}\in \text{G}_{K_{\mathfrak{Q}}}(\subseteq \text{G}_{K})$
be a Frobenius element. Fix an element
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{k}$
satisfying
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{k}$
satisfying
We see that the character
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is unramified away from
$\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is unramified away from
![]() $p$
. In fact, its restriction to
$p$
. In fact, its restriction to
![]() $\text{G}_{K_{\mathfrak{M}}}$
is
$\text{G}_{K_{\mathfrak{M}}}$
is
![]() $\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
, which is unramified if
$\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
, which is unramified if
![]() $\mathfrak{M}\nmid p$
(see Proposition 4.1). Then
$\mathfrak{M}\nmid p$
(see Proposition 4.1). Then
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is identified with a character
$\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is identified with a character
![]() $\mathfrak{I}_{K}(p)\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
, where
$\mathfrak{I}_{K}(p)\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
, where
![]() $\mathfrak{I}_{K}(p)$
is the group of fractional ideals of
$\mathfrak{I}_{K}(p)$
is the group of fractional ideals of
![]() $K$
prime to
$K$
prime to
![]() $p$
.
$p$
.
For
![]() $\mathfrak{M}=\mathfrak{Q}$
, we claim
$\mathfrak{M}=\mathfrak{Q}$
, we claim
![]() $\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\equiv \operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
.
$\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\equiv \operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
.
[Case
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
]. In this case,
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
]. In this case,
![]() $[K:k]=2$
and
$[K:k]=2$
and
![]() $\mathfrak{q}{\mathcal{O}}_{K}=\mathfrak{Q}^{2}$
. Then
$\mathfrak{q}{\mathcal{O}}_{K}=\mathfrak{Q}^{2}$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{Q}}}}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{2h_{k}^{\prime }})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{q}^{h_{k}^{\prime }}{\mathcal{O}}_{K})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{K})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((1)_{\infty },(1)_{p},(\unicode[STIX]{x1D6FC})^{\infty ,p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((\unicode[STIX]{x1D6FC}^{-1})_{\infty },(\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{\infty ,p})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{p})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{12}(\unicode[STIX]{x1D6FC}^{-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{Q}}}}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{2h_{k}^{\prime }})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{q}^{h_{k}^{\prime }}{\mathcal{O}}_{K})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\unicode[STIX]{x1D6FC}{\mathcal{O}}_{K})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((1)_{\infty },(1)_{p},(\unicode[STIX]{x1D6FC})^{\infty ,p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((\unicode[STIX]{x1D6FC}^{-1})_{\infty },(\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{\infty ,p})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{p})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{12}(\unicode[STIX]{x1D6FC}^{-1}).\nonumber\end{eqnarray}$$
Here,
![]() $\infty$
is the infinite place of
$\infty$
is the infinite place of
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $((1)_{\infty },(1)_{p},(\unicode[STIX]{x1D6FC})^{\infty ,p})$
(resp.
$((1)_{\infty },(1)_{p},(\unicode[STIX]{x1D6FC})^{\infty ,p})$
(resp.
![]() $((\unicode[STIX]{x1D6FC}^{-1})_{\infty },(\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{\infty ,p})$
, resp.
$((\unicode[STIX]{x1D6FC}^{-1})_{\infty },(\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{\infty ,p})$
, resp.
![]() $((\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{p})$
) is the element of
$((\unicode[STIX]{x1D6FC}^{-1})_{p},(1)^{p})$
) is the element of
![]() $\mathbb{A}_{K}^{\times }$
where the components above
$\mathbb{A}_{K}^{\times }$
where the components above
![]() $\infty$
,
$\infty$
,
![]() $p$
are
$p$
are
![]() $1$
and the others
$1$
and the others
![]() $\unicode[STIX]{x1D6FC}$
(resp. where the components above
$\unicode[STIX]{x1D6FC}$
(resp. where the components above
![]() $\infty$
,
$\infty$
,
![]() $p$
are
$p$
are
![]() $\unicode[STIX]{x1D6FC}^{-1}$
and the others
$\unicode[STIX]{x1D6FC}^{-1}$
and the others
![]() $1$
, resp. where the components above
$1$
, resp. where the components above
![]() $p$
are
$p$
are
![]() $\unicode[STIX]{x1D6FC}^{-1}$
and the others
$\unicode[STIX]{x1D6FC}^{-1}$
and the others
![]() $1$
), and
$1$
), and
![]() $\mathfrak{P}$
runs through the primes of
$\mathfrak{P}$
runs through the primes of
![]() $K$
above
$K$
above
![]() $p$
. Note that the components above
$p$
. Note that the components above
![]() $\infty$
have no contribution since
$\infty$
have no contribution since
![]() $K$
has no real place. Since
$K$
has no real place. Since
![]() $K_{0}\in {\mathcal{K}}_{2}(k,B)$
, we have
$K_{0}\in {\mathcal{K}}_{2}(k,B)$
, we have
![]() $f_{\mathfrak{P}}=f_{\mathfrak{p}}$
where
$f_{\mathfrak{P}}=f_{\mathfrak{p}}$
where
![]() $\mathfrak{p}$
is the prime of
$\mathfrak{p}$
is the prime of
![]() $k$
below
$k$
below
![]() $\mathfrak{P}$
. By the assumption,
$\mathfrak{P}$
. By the assumption,
![]() $f_{\mathfrak{p}}$
is odd. Then
$f_{\mathfrak{p}}$
is odd. Then
![]() $t_{K_{\mathfrak{P}}}=1$
for any
$t_{K_{\mathfrak{P}}}=1$
for any
![]() $\mathfrak{P}$
. By Proposition 4.2, we have
$\mathfrak{P}$
. By Proposition 4.2, we have
and so
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }}) & = & \displaystyle \mathop{\prod }_{\mathfrak{P}\mid p}\operatorname{Norm}_{\unicode[STIX]{x1D705}(\mathfrak{P})/\mathbb{F}_{p}}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{P})^{6e_{\mathfrak{P}}}\equiv \operatorname{Norm}_{K/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{6}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }}) & = & \displaystyle \mathop{\prod }_{\mathfrak{P}\mid p}\operatorname{Norm}_{\unicode[STIX]{x1D705}(\mathfrak{P})/\mathbb{F}_{p}}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{P})^{6e_{\mathfrak{P}}}\equiv \operatorname{Norm}_{K/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{6}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
[Case
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
]. In this case,
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
]. In this case,
![]() $K=k$
and
$K=k$
and
![]() $\mathfrak{Q}=\mathfrak{q}$
. Then
$\mathfrak{Q}=\mathfrak{q}$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\unicode[STIX]{x1D6FC}^{2}{\mathcal{O}}_{K})=\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{24}(\unicode[STIX]{x1D6FC}^{-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{\mathfrak{P}\mid p}\operatorname{Norm}_{\unicode[STIX]{x1D705}(\mathfrak{P})/\mathbb{F}_{p}}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{P})^{12e_{\mathfrak{P}}}\equiv \operatorname{Norm}_{K/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{2h_{k}^{\prime }})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\unicode[STIX]{x1D6FC}^{2}{\mathcal{O}}_{K})=\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{24}(\unicode[STIX]{x1D6FC}^{-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{\mathfrak{P}\mid p}\operatorname{Norm}_{\unicode[STIX]{x1D705}(\mathfrak{P})/\mathbb{F}_{p}}(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{P})^{12e_{\mathfrak{P}}}\equiv \operatorname{Norm}_{K/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\nonumber\\ \displaystyle & & \displaystyle \quad =\operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}\hspace{0.2em}{\rm mod}\hspace{0.2em}p,\nonumber\end{eqnarray}$$
as claimed. Here,
![]() $\mathfrak{P}$
runs through the primes of
$\mathfrak{P}$
runs through the primes of
![]() $K=k$
above
$K=k$
above
![]() $p$
.
$p$
.
Since
![]() $\mathfrak{q}^{h_{k}^{\prime }}=\unicode[STIX]{x1D6FC}{\mathcal{O}}_{k}$
, we have
$\mathfrak{q}^{h_{k}^{\prime }}=\unicode[STIX]{x1D6FC}{\mathcal{O}}_{k}$
, we have
![]() $\text{N}_{\mathfrak{q}}^{h_{k}^{\prime }}=|\text{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})|$
and
$\text{N}_{\mathfrak{q}}^{h_{k}^{\prime }}=|\text{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})|$
and
![]() $\text{N}_{\mathfrak{q}}^{12h_{k}^{\prime }}=\operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}$
. Then
$\text{N}_{\mathfrak{q}}^{12h_{k}^{\prime }}=\operatorname{Norm}_{k/\mathbb{Q}}(\unicode[STIX]{x1D6FC})^{12}$
. Then
On the other hand, we have
 $$\begin{eqnarray}\displaystyle a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }}) & \equiv & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})+\text{N}_{\mathfrak{Q}}^{2h_{k}^{\prime }}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})+q^{2h_{k}^{\prime }f_{\mathfrak{ Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }}) & \equiv & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})+\text{N}_{\mathfrak{Q}}^{2h_{k}^{\prime }}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})+q^{2h_{k}^{\prime }f_{\mathfrak{ Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\nonumber\end{eqnarray}$$
by Proposition 4.3(2), where
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})$
is the integer associated to
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})$
is the integer associated to
![]() $(A_{\mathfrak{Q}},i_{\mathfrak{Q}})$
as in the last section. Let
$(A_{\mathfrak{Q}},i_{\mathfrak{Q}})$
as in the last section. Let
![]() $\unicode[STIX]{x1D700}:=q^{-h_{k}^{\prime }f_{\mathfrak{ Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in \mathbb{F}_{p^{2}}^{\times }$
. Recall that
$\unicode[STIX]{x1D700}:=q^{-h_{k}^{\prime }f_{\mathfrak{ Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in \mathbb{F}_{p^{2}}^{\times }$
. Recall that
![]() $f_{\mathfrak{Q}}=f_{\mathfrak{q}}$
. Then
$f_{\mathfrak{Q}}=f_{\mathfrak{q}}$
. Then
Therefore
By Proposition 4.3(1), we have
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in {\mathcal{C}}(\text{N}_{\mathfrak{Q}},2h_{k}^{\prime })={\mathcal{C}}(q^{f_{\mathfrak{q}}},2h_{k}^{\prime })$
. Then
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in {\mathcal{C}}(\text{N}_{\mathfrak{Q}},2h_{k}^{\prime })={\mathcal{C}}(q^{f_{\mathfrak{q}}},2h_{k}^{\prime })$
. Then
Since
![]() $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
, we have
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
, we have
(1)
 $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=0,\pm q^{h_{k}^{\prime }f_{\mathfrak{ q}}},\pm 2q^{h_{k}^{\prime }f_{\mathfrak{ q}}}$
; or
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})=0,\pm q^{h_{k}^{\prime }f_{\mathfrak{ q}}},\pm 2q^{h_{k}^{\prime }f_{\mathfrak{ q}}}$
; or(2)
 $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{2}=3q^{2h_{k}^{\prime }f_{\mathfrak{ q}}}$
.
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})^{2}=3q^{2h_{k}^{\prime }f_{\mathfrak{ q}}}$
.
[Case (1)]. In this case,
![]() $q$
divides
$q$
divides
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})$
. Then by [Reference Arai2, Lemma 2.6],
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})$
. Then by [Reference Arai2, Lemma 2.6],
![]() $q$
divides
$q$
divides
![]() $a(\operatorname{Fr}_{\mathfrak{Q}})$
. We have
$a(\operatorname{Fr}_{\mathfrak{Q}})$
. We have
![]() $f_{\mathfrak{Q}}=f_{\mathfrak{q}}$
, which is odd by the assumption. Then we obtain
$f_{\mathfrak{Q}}=f_{\mathfrak{q}}$
, which is odd by the assumption. Then we obtain
![]() $B\not \in {\mathcal{B}}(q)$
(see [Reference Jordan7, Theorem 2.1, Propositions 2.3 and 5.1(1)]). This is a contradiction.
$B\not \in {\mathcal{B}}(q)$
(see [Reference Jordan7, Theorem 2.1, Propositions 2.3 and 5.1(1)]). This is a contradiction.
[Case (2)]. Since
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in \mathbb{Z}$
, this case cannot happen.
$a(\operatorname{Fr}_{\mathfrak{Q}}^{2h_{k}^{\prime }})\in \mathbb{Z}$
, this case cannot happen.
Then we have proved that the family
![]() $\{\unicode[STIX]{x1D719}_{x_{v}}\}_{v\in \unicode[STIX]{x1D6FA}_{k}}$
does not come from a global character
$\{\unicode[STIX]{x1D719}_{x_{v}}\}_{v\in \unicode[STIX]{x1D6FA}_{k}}$
does not come from a global character
![]() $\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. This means that the subset
$\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. This means that the subset
![]() $M^{B}(\mathbb{A}_{k})^{f_{p}^{B}}$
of
$M^{B}(\mathbb{A}_{k})^{f_{p}^{B}}$
of
![]() $M^{B}(\mathbb{A}_{k})$
associated to
$M^{B}(\mathbb{A}_{k})$
associated to
![]() $f_{p}^{B}$
(see [Reference Skorobogatov10, Definition 5.3.1]) is empty. Then by [Reference Skorobogatov10, Theorem 6.1.2], we conclude
$f_{p}^{B}$
(see [Reference Skorobogatov10, Definition 5.3.1]) is empty. Then by [Reference Skorobogatov10, Theorem 6.1.2], we conclude
![]() $M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.◻
$M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.◻
6 Proof of Theorem 2.3
Suppose that the assumptions of Theorem 2.3 hold. Assume
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
. Then for any
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
. Then for any
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
, there is a point
$v\in \unicode[STIX]{x1D6FA}_{k}$
, there is a point
![]() $x_{v}\in M^{B}(k_{v})$
. Since
$x_{v}\in M^{B}(k_{v})$
. Since
![]() $B\not \in {\mathcal{S}}(k,\mathfrak{q})$
, there is a prime divisor
$B\not \in {\mathcal{S}}(k,\mathfrak{q})$
, there is a prime divisor
![]() $p$
of
$p$
of
![]() $d(B)$
such that
$d(B)$
such that
Fix such
![]() $p$
. Then
$p$
. Then
![]() $p\geqslant 5$
,
$p\geqslant 5$
,
![]() $p\neq q$
and we have a family of characters
$p\neq q$
and we have a family of characters
associated to
![]() $f_{p}^{B}$
.
$f_{p}^{B}$
.
Assume that there is a global character
![]() $\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
such that
$\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
such that
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{k_{v}}}=\unicode[STIX]{x1D719}_{x_{v}}$
for any
$\unicode[STIX]{x1D6F7}|_{\text{G}_{k_{v}}}=\unicode[STIX]{x1D719}_{x_{v}}$
for any
![]() $v\in \unicode[STIX]{x1D6FA}_{k}$
. If
$v\in \unicode[STIX]{x1D6FA}_{k}$
. If
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
, fix
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
, fix
![]() $K_{0}\in {\mathcal{K}}_{1}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
. Let
$K_{0}\in {\mathcal{K}}_{1}(k,B)\cap {\mathcal{K}}(k,\mathfrak{q})$
. Let
![]() $K,\mathfrak{M},\mathfrak{m},v(\mathfrak{m}),(A_{\mathfrak{M}},i_{\mathfrak{M}})$
be the same as in the last section. Note that
$K,\mathfrak{M},\mathfrak{m},v(\mathfrak{m}),(A_{\mathfrak{M}},i_{\mathfrak{M}})$
be the same as in the last section. Note that
![]() $[K:\mathbb{Q}]$
is even since
$[K:\mathbb{Q}]$
is even since
![]() $k/\mathbb{Q}$
has even degree. Then
$k/\mathbb{Q}$
has even degree. Then
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D719}_{x_{v(\mathfrak{m})}}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
. Let
$\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D719}_{x_{v(\mathfrak{m})}}|_{\text{G}_{K_{\mathfrak{M}}}}=\unicode[STIX]{x1D71A}_{(A_{\mathfrak{M}},i_{\mathfrak{M}},p)}^{12}$
. Let
![]() $\mathfrak{Q}$
be the unique prime of
$\mathfrak{Q}$
be the unique prime of
![]() $K$
above
$K$
above
![]() $\mathfrak{q}$
, and let
$\mathfrak{q}$
, and let
![]() $\operatorname{Fr}_{\mathfrak{Q}}\in \text{G}_{K_{\mathfrak{Q}}}(\subseteq \text{G}_{K})$
be a Frobenius element. Note that
$\operatorname{Fr}_{\mathfrak{Q}}\in \text{G}_{K_{\mathfrak{Q}}}(\subseteq \text{G}_{K})$
be a Frobenius element. Note that
![]() $\mathfrak{Q}$
is the unique prime of
$\mathfrak{Q}$
is the unique prime of
![]() $K$
above
$K$
above
![]() $q$
. Then
$q$
. Then
![]() $q{\mathcal{O}}_{K}=\mathfrak{Q}^{e_{\mathfrak{Q}}}$
and
$q{\mathcal{O}}_{K}=\mathfrak{Q}^{e_{\mathfrak{Q}}}$
and
![]() $\text{N}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}}=q^{[K:\mathbb{Q}]}$
.
$\text{N}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}}=q^{[K:\mathbb{Q}]}$
.
For
![]() $\mathfrak{M}=\mathfrak{Q}$
, we prove
$\mathfrak{M}=\mathfrak{Q}$
, we prove
![]() $\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\equiv q^{6[K:\mathbb{Q}]}\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
. The character
$\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\equiv q^{6[K:\mathbb{Q}]}\hspace{0.2em}{\rm mod}\hspace{0.2em}p$
. The character
![]() $\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is unramified away from
$\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}$
is unramified away from
![]() $p$
, and it is identified with a character
$p$
, and it is identified with a character
![]() $\mathfrak{I}_{K}(p)\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. Then
$\mathfrak{I}_{K}(p)\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{Q}}}}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(q{\mathcal{O}}_{K})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((1)_{\infty },(1)_{p},(q)^{\infty ,p})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((q^{-1})_{\infty },(q^{-1})_{p},(1)^{\infty ,p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((q^{-1})_{p},(1)^{p})=\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{12}(q^{-1})\equiv \mathop{\prod }_{\mathfrak{P}\mid p}q^{6e_{\mathfrak{P}}f_{\mathfrak{P}}}=q^{6[K:\mathbb{Q}]}\hspace{0.2em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}^{12}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K_{\mathfrak{Q}}}}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(\mathfrak{Q}^{e_{\mathfrak{Q}}})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}(q{\mathcal{O}}_{K})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((1)_{\infty },(1)_{p},(q)^{\infty ,p})=\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((q^{-1})_{\infty },(q^{-1})_{p},(1)^{\infty ,p})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6F7}|_{\text{G}_{K}}((q^{-1})_{p},(1)^{p})=\mathop{\prod }_{\mathfrak{P}\mid p}r_{(A_{\mathfrak{P}},i_{\mathfrak{P}},p)}^{12}(q^{-1})\equiv \mathop{\prod }_{\mathfrak{P}\mid p}q^{6e_{\mathfrak{P}}f_{\mathfrak{P}}}=q^{6[K:\mathbb{Q}]}\hspace{0.2em}{\rm mod}\hspace{0.2em}p.\nonumber\end{eqnarray}$$
Here,
![]() $((1)_{\infty },(1)_{p},(q)^{\infty ,p}),((q^{-1})_{\infty },(q^{-1})_{p},(1)^{\infty ,p}),((q^{-1})_{p},(1)^{p})\in \mathbb{A}_{K}^{\times }$
are defined in the same way as in the last section,
$((1)_{\infty },(1)_{p},(q)^{\infty ,p}),((q^{-1})_{\infty },(q^{-1})_{p},(1)^{\infty ,p}),((q^{-1})_{p},(1)^{p})\in \mathbb{A}_{K}^{\times }$
are defined in the same way as in the last section,
![]() $\mathfrak{P}$
runs through the primes of
$\mathfrak{P}$
runs through the primes of
![]() $K$
above
$K$
above
![]() $p$
, and the congruence follows from Proposition 4.2 (or [Reference Arai2, Corollary 2.3]).
$p$
, and the congruence follows from Proposition 4.2 (or [Reference Arai2, Corollary 2.3]).
In the following, we repeat the argument in [Reference Arai2, Section 3] and deduce a contradiction. We have
 $$\begin{eqnarray}\displaystyle a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}}) & \equiv & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})+\text{N}_{\mathfrak{ Q}}^{e_{\mathfrak{Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})+q^{[K:\mathbb{Q}]}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}}) & \equiv & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})+\text{N}_{\mathfrak{ Q}}^{e_{\mathfrak{Q}}}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{-1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})+q^{[K:\mathbb{Q}]}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{-1}\hspace{0.2em}{\rm mod}\hspace{0.2em}p\nonumber\end{eqnarray}$$
by Proposition 4.3(2). Let
![]() $\unicode[STIX]{x1D700}:=q^{-[K:\mathbb{Q}]/2}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in \mathbb{F}_{p^{2}}^{\times }$
. Then
$\unicode[STIX]{x1D700}:=q^{-[K:\mathbb{Q}]/2}\unicode[STIX]{x1D71A}_{(A_{\mathfrak{Q}},i_{\mathfrak{Q}},p)}(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in \mathbb{F}_{p^{2}}^{\times }$
. Then
Therefore
By Proposition 4.3(1), we have
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in {\mathcal{C}}(\text{N}_{\mathfrak{Q}},e_{\mathfrak{Q}})$
. Moreover, we have
$a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in {\mathcal{C}}(\text{N}_{\mathfrak{Q}},e_{\mathfrak{Q}})$
. Moreover, we have
Then
Since
![]() $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{Q}}))$
, we have
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{Q}}))$
, we have
(1)
 $a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=0,\pm q^{[K:\mathbb{Q}]/2},\pm 2q^{[K:\mathbb{Q}]/2}$
; or
$a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})=0,\pm q^{[K:\mathbb{Q}]/2},\pm 2q^{[K:\mathbb{Q}]/2}$
; or(2)
 $a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{2}=3q^{[K:\mathbb{Q}]}$
.
$a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})^{2}=3q^{[K:\mathbb{Q}]}$
.
[Case (1)]. In this case,
![]() $q$
divides
$q$
divides
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})$
and
$a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})$
and
![]() $a(\operatorname{Fr}_{\mathfrak{Q}})$
. Since
$a(\operatorname{Fr}_{\mathfrak{Q}})$
. Since
![]() $f_{\mathfrak{Q}}$
is odd, we have
$f_{\mathfrak{Q}}$
is odd, we have
![]() $B\not \in {\mathcal{B}}(q)$
. This is a contradiction.
$B\not \in {\mathcal{B}}(q)$
. This is a contradiction.
[Case (2)]. Since
![]() $[K:\mathbb{Q}]$
is even and
$[K:\mathbb{Q}]$
is even and
![]() $a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in \mathbb{Z}$
, this case cannot happen.
$a(\operatorname{Fr}_{\mathfrak{Q}}^{e_{\mathfrak{Q}}})\in \mathbb{Z}$
, this case cannot happen.
Then we have proved that the family
![]() $\{\unicode[STIX]{x1D719}_{x_{v}}\}_{v\in \unicode[STIX]{x1D6FA}_{k}}$
does not come from
$\{\unicode[STIX]{x1D719}_{x_{v}}\}_{v\in \unicode[STIX]{x1D6FA}_{k}}$
does not come from
![]() $\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. Therefore
$\unicode[STIX]{x1D6F7}:\text{G}_{k}\longrightarrow (\mathbb{F}_{p^{2}}^{\times })^{12}$
. Therefore
![]() $M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.◻
$M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
.◻
7 Counterexamples to the Hasse principle
Jordan obtained the following counterexamples to the Hasse principle, and Skorobogatov proved that it is accounted for by the Manin obstruction.
Proposition 7.1. ([Reference Jordan7, Example 6.4] and [Reference Skorobogatov11, Section 4.1])
If
![]() $(d(B),k)$
$(d(B),k)$
![]() $=(39,\mathbb{Q}(\sqrt{-13}))$
, then
$=(39,\mathbb{Q}(\sqrt{-13}))$
, then
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
and
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
Especially, the existence of adelic points help us produce counterexamples to the Hasse principle for
![]() $d(B)=39$
and number fields containing
$d(B)=39$
and number fields containing
![]() $\mathbb{Q}(\sqrt{-13})$
. In Lemma 7.2 below, we restrict our attention to the special case and study the assumptions of Theorem 2.4.
$\mathbb{Q}(\sqrt{-13})$
. In Lemma 7.2 below, we restrict our attention to the special case and study the assumptions of Theorem 2.4.
For a prime number
![]() $q\neq 2$
, let
$q\neq 2$
, let
![]() $(\frac{\cdot }{q})\in \{0,1,-1\}$
be the Legendre symbol. For a nonzero integer
$(\frac{\cdot }{q})\in \{0,1,-1\}$
be the Legendre symbol. For a nonzero integer
![]() $N\in \mathbb{Z}$
, let
$N\in \mathbb{Z}$
, let
![]() $(N)^{\prime }$
be the square free part of
$(N)^{\prime }$
be the square free part of
![]() $N$
. Precisely, if
$N$
. Precisely, if
![]() $N=ab^{2}$
where
$N=ab^{2}$
where
![]() $a,b\in \mathbb{Z}$
,
$a,b\in \mathbb{Z}$
,
![]() $a$
is square free and
$a$
is square free and
![]() $\text{gcd}(a,b)=1$
, then
$\text{gcd}(a,b)=1$
, then
![]() $(N)^{\prime }=a$
. For a finite Galois extension
$(N)^{\prime }=a$
. For a finite Galois extension
![]() $k$
of
$k$
of
![]() $\mathbb{Q}$
and a prime number
$\mathbb{Q}$
and a prime number
![]() $l$
, let
$l$
, let
![]() $e_{l}(k)$
(resp.
$e_{l}(k)$
(resp.
![]() $f_{l}(k)$
, resp.
$f_{l}(k)$
, resp.
![]() $g_{l}(k)$
) be the ramification index of
$g_{l}(k)$
) be the ramification index of
![]() $l$
in
$l$
in
![]() $k/\mathbb{Q}$
(resp. the degree of the residue field extension above
$k/\mathbb{Q}$
(resp. the degree of the residue field extension above
![]() $l$
in
$l$
in
![]() $k/\mathbb{Q}$
, resp. the number of primes of
$k/\mathbb{Q}$
, resp. the number of primes of
![]() $k$
above
$k$
above
![]() $l$
).
$l$
).
Lemma 7.2.
(1) Assume
 $d(B)=39$
. Then:
$d(B)=39$
. Then:(i)
 $B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
.
$B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
.(ii)
 $B\in {\mathcal{B}}(q)$
if and only if
$B\in {\mathcal{B}}(q)$
if and only if
 $q\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
or
$q\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
or
 $q\equiv 1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.
$q\equiv 1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.
(2) Let
 $l$
be a prime number, and assume
$l$
be a prime number, and assume
 $(d(B),k)=(39,\mathbb{Q}(\sqrt{l},\sqrt{-13}))$
. Let
$(d(B),k)=(39,\mathbb{Q}(\sqrt{l},\sqrt{-13}))$
. Let
 $p,q$
be distinct prime numbers, and let
$p,q$
be distinct prime numbers, and let
 $\mathfrak{q}$
be a prime of
$\mathfrak{q}$
be a prime of
 $k$
above
$k$
above
 $q$
. Then the conditions
$q$
. Then the conditions
 $p\mid d(B)$
and
$p\mid d(B)$
and
 $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
imply
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))$
imply
 $p=13$
. In this case, we have:
$p=13$
. In this case, we have:(i)
 $f_{\mathfrak{p}}$
is odd for any prime
$f_{\mathfrak{p}}$
is odd for any prime
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $k$
above
$k$
above
 $p$
if and only if
$p$
if and only if
 $l\equiv 0,1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.
$l\equiv 0,1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.(ii)
 $f_{\mathfrak{q}}$
is odd if and only if
$f_{\mathfrak{q}}$
is odd if and only if  $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle (\text{a}) & \displaystyle q\equiv 1,7,9,11,13,15,17,19,25,29,31,47,49\hspace{0.2em}{\rm mod}\hspace{0.2em}52,\\ \displaystyle & \displaystyle \left(\frac{l}{q}\right)\in \{0,1\}\text{and }\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ \displaystyle (\text{b}) & \displaystyle l\equiv 1,2,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\displaystyle (\text{a}) & \displaystyle q\equiv 1,7,9,11,13,15,17,19,25,29,31,47,49\hspace{0.2em}{\rm mod}\hspace{0.2em}52,\\ \displaystyle & \displaystyle \left(\frac{l}{q}\right)\in \{0,1\}\text{and }\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ \displaystyle (\text{b}) & \displaystyle l\equiv 1,2,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.\end{eqnarray}$$
Proof. (1) (i) The prime number
![]() $3$
(resp.
$3$
(resp.
![]() $13$
) is inert (resp. ramified) in
$13$
) is inert (resp. ramified) in
![]() $\mathbb{Q}(\sqrt{-13})$
. Then
$\mathbb{Q}(\sqrt{-13})$
. Then
![]() $B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
(cf. Proof of Lemma 2.2).
$B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
(cf. Proof of Lemma 2.2).
(ii) By taking
![]() $p_{1}=13$
and
$p_{1}=13$
and
![]() $p_{2}=3$
in Lemma 2.2(2), we have
$p_{2}=3$
in Lemma 2.2(2), we have
![]() $B\in {\mathcal{B}}(2)$
. We see that
$B\in {\mathcal{B}}(2)$
. We see that
![]() $3$
(resp.
$3$
(resp.
![]() $13$
) splits in
$13$
) splits in
![]() $\mathbb{Q}(\sqrt{-q})$
if and only if
$\mathbb{Q}(\sqrt{-q})$
if and only if
![]() $q\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
(resp.
$q\equiv 2\hspace{0.2em}{\rm mod}\hspace{0.2em}3$
(resp.
![]() $q\equiv 1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
). Then the assertion follows from Lemma 2.2(1).
$q\equiv 1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
). Then the assertion follows from Lemma 2.2(1).
(2) (i) Since
![]() $p=13$
is ramified in
$p=13$
is ramified in
![]() $\mathbb{Q}(\sqrt{-13})$
, we have
$\mathbb{Q}(\sqrt{-13})$
, we have
![]() $e_{p}(k)=2$
or
$e_{p}(k)=2$
or
![]() $4$
. Since a prime number except
$4$
. Since a prime number except
![]() $2$
is not totally ramified in a biquadratic field, we have
$2$
is not totally ramified in a biquadratic field, we have
![]() $e_{p}(k)=2$
. Then the following conditions are equivalent.
$e_{p}(k)=2$
. Then the following conditions are equivalent.
∙
 $f_{\mathfrak{p}}$
is odd for any prime
$f_{\mathfrak{p}}$
is odd for any prime
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $k$
above
$k$
above
 $p$
.
$p$
.∙
 $f_{p}(k)=1$
.
$f_{p}(k)=1$
.∙
 $(e_{p}(k),f_{p}(k),g_{p}(k))=(2,1,2)$
.
$(e_{p}(k),f_{p}(k),g_{p}(k))=(2,1,2)$
.∙
 $13$
splits in
$13$
splits in
 $\mathbb{Q}(\sqrt{l})$
or
$\mathbb{Q}(\sqrt{l})$
or
 $l=13$
.
$l=13$
.∙
 $l\equiv 0,1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.
$l\equiv 0,1,3,4,9,10,12\hspace{0.2em}{\rm mod}\hspace{0.2em}13$
.
(ii) The following conditions are equivalent.
∙
 $f_{\mathfrak{q}}$
is odd.
$f_{\mathfrak{q}}$
is odd.∙
 $f_{q}(k)=1$
.
$f_{q}(k)=1$
.∙
 $q$
is not inert in
$q$
is not inert in
 $\mathbb{Q}(\sqrt{-13})$
,
$\mathbb{Q}(\sqrt{-13})$
,
 $\mathbb{Q}(\sqrt{l})$
or
$\mathbb{Q}(\sqrt{l})$
or
 $\mathbb{Q}(\sqrt{(-13l)^{\prime }})$
.
$\mathbb{Q}(\sqrt{(-13l)^{\prime }})$
.∙
 $\left\{\begin{array}{@{}ll@{}}(\text{a}) & \left(\frac{-13}{q}\right),\left(\frac{l}{q}\right),\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ (\text{b}) & l\not \equiv 5,7\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.$
$\left\{\begin{array}{@{}ll@{}}(\text{a}) & \left(\frac{-13}{q}\right),\left(\frac{l}{q}\right),\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ (\text{b}) & l\not \equiv 5,7\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.$
∙
 $\left\{\begin{array}{@{}ll@{}}(\text{a}) & q\equiv 1,7,9,11,13,15,17,19,25,29,31,47,49\hspace{0.2em}{\rm mod}\hspace{0.2em}52,\\ & \left(\frac{l}{q}\right)\in \{0,1\}\text{and }\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ (\text{b}) & l\equiv 1,2,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.$
$\left\{\begin{array}{@{}ll@{}}(\text{a}) & q\equiv 1,7,9,11,13,15,17,19,25,29,31,47,49\hspace{0.2em}{\rm mod}\hspace{0.2em}52,\\ & \left(\frac{l}{q}\right)\in \{0,1\}\text{and }\left(\frac{(-13l)^{\prime }}{q}\right)\in \{0,1\}\text{when }q\neq 2,\\ (\text{b}) & l\equiv 1,2,3\hspace{0.2em}{\rm mod}\hspace{0.2em}8\text{ when }q=2.\end{array}\right.$
◻
Lemma 7.2 and a similar study combined with Proposition 7.1, [Reference Rotger and de Vera-Piquero8, Table 1] help us prove Proposition 2.6 as follows.
(1) By Lemma 7.2(1)(i), we have
![]() $B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
. Then
$B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
. Then
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
. Let
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
. Let
![]() $q=2$
. Then
$q=2$
. Then
![]() $(e_{q}(k),f_{q}(k),g_{q}(k))=(4,1,1)$
. Let
$(e_{q}(k),f_{q}(k),g_{q}(k))=(4,1,1)$
. Let
![]() $\mathfrak{q}$
be the unique prime of
$\mathfrak{q}$
be the unique prime of
![]() $k$
above
$k$
above
![]() $q$
. Then
$q$
. Then
![]() ${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))={\mathcal{P}}({\mathcal{D}}(2,4))=\{2,3,5,7,47\}$
(see [Reference Arai2, Table 1]). By Lemma 7.2(1)(ii), we have
${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))={\mathcal{P}}({\mathcal{D}}(2,4))=\{2,3,5,7,47\}$
(see [Reference Arai2, Table 1]). By Lemma 7.2(1)(ii), we have
![]() $B\in {\mathcal{B}}(q)$
. Let
$B\in {\mathcal{B}}(q)$
. Let
![]() $p=13$
. Then
$p=13$
. Then
![]() $p\mid d(B)$
and
$p\mid d(B)$
and
![]() $p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))$
. Hence
$p\not \in {\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},e_{\mathfrak{q}}))$
. Hence
![]() $B\not \in {\mathcal{S}}(k,\mathfrak{q})$
. Applying Theorem 2.3, we obtain
$B\not \in {\mathcal{S}}(k,\mathfrak{q})$
. Applying Theorem 2.3, we obtain
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. By Proposition 7.1, we have
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. By Proposition 7.1, we have
![]() $M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-13})})\neq \emptyset$
. Therefore
$M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-13})})\neq \emptyset$
. Therefore
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
(2) Since
![]() $B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
, we have
$B\otimes _{\mathbb{Q}}\mathbb{Q}(\sqrt{-13})\cong \text{M}_{2}(\mathbb{Q}(\sqrt{-13}))$
, we have
![]() $B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
. Assume
$B\otimes _{\mathbb{Q}}k\cong \text{M}_{2}(k)$
. Assume
![]() $k=\mathbb{Q}(\sqrt{3},\sqrt{-13})$
(resp.
$k=\mathbb{Q}(\sqrt{3},\sqrt{-13})$
(resp.
![]() $k=\mathbb{Q}(\sqrt{17},\sqrt{-13})$
). Then
$k=\mathbb{Q}(\sqrt{17},\sqrt{-13})$
). Then
![]() $Cl_{k}\cong \mathbb{Z}/4\mathbb{Z}$
(resp.
$Cl_{k}\cong \mathbb{Z}/4\mathbb{Z}$
(resp.
![]() $Cl_{k}\cong \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
) and
$Cl_{k}\cong \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
) and
![]() $h_{k}^{\prime }=4$
. These are due to the mathematics software system Sage. In any case, let
$h_{k}^{\prime }=4$
. These are due to the mathematics software system Sage. In any case, let
![]() $(p,q)=(13,2)$
. Then by Lemma 7.2, we have
$(p,q)=(13,2)$
. Then by Lemma 7.2, we have
![]() $B\in {\mathcal{B}}(q)$
and
$B\in {\mathcal{B}}(q)$
and
![]() $f_{p}(k),f_{q}(k)$
are odd. In fact,
$f_{p}(k),f_{q}(k)$
are odd. In fact,
![]() $(e_{p}(k),f_{p}(k),g_{p}(k))=(e_{q}(k),f_{q}(k),g_{q}(k))=(2,1,2)$
. Let
$(e_{p}(k),f_{p}(k),g_{p}(k))=(e_{q}(k),f_{q}(k),g_{q}(k))=(2,1,2)$
. Let
![]() $\mathfrak{q}$
be a prime of
$\mathfrak{q}$
be a prime of
![]() $k$
above
$k$
above
![]() $q$
. Then
$q$
. Then
![]() ${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))={\mathcal{P}}({\mathcal{D}}(2,8))=\{2,3,5,7,31,47,193\}$
does not contain
${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))={\mathcal{P}}({\mathcal{D}}(2,8))=\{2,3,5,7,31,47,193\}$
does not contain
![]() $p=13$
. By Theorem 2.4, we have
$p=13$
. By Theorem 2.4, we have
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. Since
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. Since
![]() $M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-13})})\neq \emptyset$
, we have
$M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-13})})\neq \emptyset$
, we have
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.
(3) The assertion follows from Theorem 2.3 with
![]() $q=3$
. See [Reference Arai2, Proof of Proposition 4.1(2)].
$q=3$
. See [Reference Arai2, Proof of Proposition 4.1(2)].
(4) We have
![]() $B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
since
$B\otimes _{\mathbb{Q}}k\not \cong \text{M}_{2}(k)$
since
![]() $2$
splits completely in
$2$
splits completely in
![]() $k$
. In this case,
$k$
. In this case,
![]() $Cl_{k}\cong \mathbb{Z}/8\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
and
$Cl_{k}\cong \mathbb{Z}/8\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
and
![]() $h_{k}^{\prime }=8$
. Let
$h_{k}^{\prime }=8$
. Let
![]() $(p,q)=(61,3)$
. Then
$(p,q)=(61,3)$
. Then
![]() $(e_{p}(k),f_{p}(k),g_{p}(k))=(e_{q}(k),f_{q}(k),g_{q}(k))=(2,1,2)$
. Since
$(e_{p}(k),f_{p}(k),g_{p}(k))=(e_{q}(k),f_{q}(k),g_{q}(k))=(2,1,2)$
. Since
![]() $61$
splits in
$61$
splits in
![]() $\mathbb{Q}(\sqrt{-3})$
, we have
$\mathbb{Q}(\sqrt{-3})$
, we have
![]() $B\in {\mathcal{B}}(q)$
(see Lemma 2.2(1)). Then
$B\in {\mathcal{B}}(q)$
(see Lemma 2.2(1)). Then
![]() ${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))={\mathcal{P}}({\mathcal{D}}(3,16))=\{2,3,5,7,11,17,23,31,47,97,113,191,193,353,383,2113,$
${\mathcal{P}}({\mathcal{D}}(\text{N}_{\mathfrak{q}},2h_{k}^{\prime }))={\mathcal{P}}({\mathcal{D}}(3,16))=\{2,3,5,7,11,17,23,31,47,97,113,191,193,353,383,2113,$
![]() $3457,30529,36671\}$
does not contain
$3457,30529,36671\}$
does not contain
![]() $p=61$
. Applying Theorem 2.4, we have
$p=61$
. Applying Theorem 2.4, we have
![]() $M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. By [Reference Rotger and de Vera-Piquero8, Table 1], we have
$M^{B}(k)=M^{B}(\mathbb{A}_{k})^{\operatorname{Br}}=\emptyset$
. By [Reference Rotger and de Vera-Piquero8, Table 1], we have
![]() $M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-183})})\neq \emptyset$
. Therefore
$M^{B}(\mathbb{A}_{\mathbb{Q}(\sqrt{-183})})\neq \emptyset$
. Therefore
![]() $M^{B}(\mathbb{A}_{k})\neq \emptyset$
.◻
$M^{B}(\mathbb{A}_{k})\neq \emptyset$
.◻
Acknowledgments
The author would like to thank the anonymous referee for helpful comments, which have contributed to improving the article.