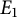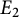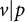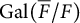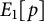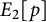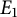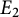1 Introduction
The Iwasawa theory of Galois representations, especially those arising from elliptic curves and Hecke eigencuspforms, affords deep insights into the arithmetic of such objects. Let p be a fixed odd prime. Mazur [Reference Mazur23] and Greenberg [Reference Greenberg6] initiated the Iwasawa theory of p-ordinary elliptic curves E defined over
![]() $\mathbb {Q}$
. The main object of study is the
$\mathbb {Q}$
. The main object of study is the
![]() $p^{\infty }$
-Selmer group over the cyclotomic
$p^{\infty }$
-Selmer group over the cyclotomic
![]() $\mathbb {Z}_{p}$
-extension, denoted by
$\mathbb {Z}_{p}$
-extension, denoted by
![]() $\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
. Let
$\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
. Let
![]() $\Gamma $
denote the Galois group of the cyclotomic
$\Gamma $
denote the Galois group of the cyclotomic
![]() $\mathbb {Z}_{p}$
-extension over
$\mathbb {Z}_{p}$
-extension over
![]() $\mathbb {Q}$
. When E has good ordinary reduction at the prime p, it was conjectured by Mazur that the Selmer group
$\mathbb {Q}$
. When E has good ordinary reduction at the prime p, it was conjectured by Mazur that the Selmer group
![]() $\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
is cotorsion as a module over the Iwasawa algebra
$\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
is cotorsion as a module over the Iwasawa algebra
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
. This is now a celebrated theorem of Kato [Reference Kato12]. The corresponding theory for p-supersingular elliptic curves was initiated by Perrin-Riou in [Reference Perrin-Riou26] and has since gained considerable momentum, see [Reference Iovita and Pollack10, Reference Kim13, Reference Kitajima and Otsuki16–Reference Kurihara19, Reference Lei, Loeffler and Zerbes22, Reference Pollack28, Reference Sprung34]. If E has supersingular reduction at p, then
$\mathbb {Z}_{p}[[\Gamma ]]$
. This is now a celebrated theorem of Kato [Reference Kato12]. The corresponding theory for p-supersingular elliptic curves was initiated by Perrin-Riou in [Reference Perrin-Riou26] and has since gained considerable momentum, see [Reference Iovita and Pollack10, Reference Kim13, Reference Kitajima and Otsuki16–Reference Kurihara19, Reference Lei, Loeffler and Zerbes22, Reference Pollack28, Reference Sprung34]. If E has supersingular reduction at p, then
![]() $\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
is no longer
$\operatorname {Sel}(E/\mathbb {Q}^{\operatorname {cyc}})$
is no longer
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion. Kobayashi considered plus and minus Selmer groups, which were defined using plus and minus norm groups, that were introduced in [Reference Perrin-Riou26]. These signed Selmer groups are cotorsion over
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion. Kobayashi considered plus and minus Selmer groups, which were defined using plus and minus norm groups, that were introduced in [Reference Perrin-Riou26]. These signed Selmer groups are cotorsion over
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
.
$\mathbb {Z}_{p}[[\Gamma ]]$
.
Suppose E is an elliptic curve defined over a number field F. Let
![]() $\Sigma _{p}$
denote the set of primes of F above p. In the case when E has good reduction at all primes in
$\Sigma _{p}$
denote the set of primes of F above p. In the case when E has good reduction at all primes in
![]() $\Sigma _{p}$
, and
$\Sigma _{p}$
, and
![]() $F_{v}\simeq \mathbb {Q}_{p}$
for all
$F_{v}\simeq \mathbb {Q}_{p}$
for all
![]() $v\in \Sigma _{p}$
such that E is supersingular at v, generalizations of the plus/minus Selmer groups have been studied in [Reference Iovita and Pollack10, Reference Kim15, Reference Nuccio and Sujatha25]. The case where E has semistable reduction at the primes in
$v\in \Sigma _{p}$
such that E is supersingular at v, generalizations of the plus/minus Selmer groups have been studied in [Reference Iovita and Pollack10, Reference Kim15, Reference Nuccio and Sujatha25]. The case where E has semistable reduction at the primes in
![]() $\Sigma _{p}$
(i.e., good ordinary, multiplicative or good supersingular) has also been considered, see [Reference Lei and Lim20, Reference Lei and Lim21]. In this paper, we assume that E has semistable reduction at the primes in
$\Sigma _{p}$
(i.e., good ordinary, multiplicative or good supersingular) has also been considered, see [Reference Lei and Lim20, Reference Lei and Lim21]. In this paper, we assume that E has semistable reduction at the primes in
![]() $\Sigma _{p}$
. In this mixed-reduction setting, a plethora of Selmer groups depending on the reduction-types at the primes in
$\Sigma _{p}$
. In this mixed-reduction setting, a plethora of Selmer groups depending on the reduction-types at the primes in
![]() $\Sigma _{p}$
can be defined. This collection of Selmer groups is referred to as the multisigned Selmer groups.
$\Sigma _{p}$
can be defined. This collection of Selmer groups is referred to as the multisigned Selmer groups.
Denote by
![]() $\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
the set of primes of F above p at which E has good supersingular reduction. Associated to each vector
$\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
the set of primes of F above p at which E has good supersingular reduction. Associated to each vector
![]() $\ddagger \in \{+,-\}^{d}$
, there is a multisigned Selmer group
$\ddagger \in \{+,-\}^{d}$
, there is a multisigned Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
, defined in Section 2. There are
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
, defined in Section 2. There are
![]() $2^{d}$
vectors
$2^{d}$
vectors
![]() $\ddagger $
and hence
$\ddagger $
and hence
![]() $2^{d}$
Selmer groups to consider.
$2^{d}$
Selmer groups to consider.
Two elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
over F are said to be p-congruent if their associated residual representations are isomorphic, i.e.,
$E_{2}$
over F are said to be p-congruent if their associated residual representations are isomorphic, i.e.,
![]() $E_{1}[p]$
and
$E_{1}[p]$
and
![]() $E_{2}[p]$
are isomorphic as Galois modules. It is of particular interest in Iwasawa theory to study the relationship between Iwasawa invariants of the Selmer groups of p-congruent elliptic curves. Such investigations were initiated by Greenberg and Vatsal [Reference Greenberg and Vatsal8], who considered p-congruent, p-ordinary elliptic curves
$E_{2}[p]$
are isomorphic as Galois modules. It is of particular interest in Iwasawa theory to study the relationship between Iwasawa invariants of the Selmer groups of p-congruent elliptic curves. Such investigations were initiated by Greenberg and Vatsal [Reference Greenberg and Vatsal8], who considered p-congruent, p-ordinary elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
defined over
$E_{2}$
defined over
![]() $\mathbb {Q}$
. They showed that the main conjecture is true for
$\mathbb {Q}$
. They showed that the main conjecture is true for
![]() $E_{1}$
if and only if the main conjecture is true for
$E_{1}$
if and only if the main conjecture is true for
![]() $E_{2}$
. To this end, they study the relationship between the algebraic and analytic Iwasawa invariants of
$E_{2}$
. To this end, they study the relationship between the algebraic and analytic Iwasawa invariants of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Their method involves examining the algebraic structure of certain imprimitive Selmer groups associated to
$E_{2}$
. Their method involves examining the algebraic structure of certain imprimitive Selmer groups associated to
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
in comparing the Iwasawa-invariants. Let
$E_{2}$
in comparing the Iwasawa-invariants. Let
![]() $\Sigma _{0}$
be the set of primes
$\Sigma _{0}$
be the set of primes
![]() $v\nmid p$
of F at which
$v\nmid p$
of F at which
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. Greenberg and Vatsal compare the
$E_{2}$
has bad reduction. Greenberg and Vatsal compare the
![]() $\Sigma _{0}$
-imprimitive Selmer groups of
$\Sigma _{0}$
-imprimitive Selmer groups of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Their results were generalized to the p-supersingular case for the plus and minus Selmer groups by Kim in [Reference Kim13] and Ponsinet [Reference Ponsinet29].
$E_{2}$
. Their results were generalized to the p-supersingular case for the plus and minus Selmer groups by Kim in [Reference Kim13] and Ponsinet [Reference Ponsinet29].
In this paper, the above mentioned results of Greenberg-Vatsal and Kim are generalized to the mixed reduction setting. Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be two elliptic curves defined over a number field F that are p-congruent for an odd prime p. Assume that both
$E_{2}$
be two elliptic curves defined over a number field F that are p-congruent for an odd prime p. Assume that both
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
have semistable reduction at all primes of F above p. In other words,
$E_{2}$
have semistable reduction at all primes of F above p. In other words,
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
both have good reduction or multiplicative reduction at the primes above p. Assume further that the conditions of Hypothesis 2.1 are satisfied. Since
$E_{2}$
both have good reduction or multiplicative reduction at the primes above p. Assume further that the conditions of Hypothesis 2.1 are satisfied. Since
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
are p-congruent, it follows that the sets
$E_{2}$
are p-congruent, it follows that the sets
![]() $\Sigma _{\operatorname {ss}}(E_{1})$
and
$\Sigma _{\operatorname {ss}}(E_{1})$
and
![]() $\Sigma _{\operatorname {ss}}(E_{2})$
are equal (see [Reference Nuccio and Sujatha25, Proposition 3.9]). Set
$\Sigma _{\operatorname {ss}}(E_{2})$
are equal (see [Reference Nuccio and Sujatha25, Proposition 3.9]). Set
![]() $\Sigma _{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
to denote the set of supersingular primes
$\Sigma _{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
to denote the set of supersingular primes
![]() $v|p$
of
$v|p$
of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, and let
$E_{2}$
, and let
![]() $\ddagger \in \{+,-\}^{d}$
be a signed vector. The signed vector prescribes a choice of local condition at each prime in
$\ddagger \in \{+,-\}^{d}$
be a signed vector. The signed vector prescribes a choice of local condition at each prime in
![]() $\Sigma _{\operatorname {ss}}$
. Associated with
$\Sigma _{\operatorname {ss}}$
. Associated with
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
and
$E_{2}$
and
![]() $\ddagger $
, we consider p-primary Selmer groups
$\ddagger $
, we consider p-primary Selmer groups
![]() $\operatorname {Sel}^{\ddagger }(E_{1}/F^{\operatorname {cyc}})$
and
$\operatorname {Sel}^{\ddagger }(E_{1}/F^{\operatorname {cyc}})$
and
![]() $\operatorname {Sel}^{\ddagger }(E_{2}/F^{\operatorname {cyc}})$
. We refer to Definition 2.2 for the precise definition. We shall assume throughout for
$\operatorname {Sel}^{\ddagger }(E_{2}/F^{\operatorname {cyc}})$
. We refer to Definition 2.2 for the precise definition. We shall assume throughout for
![]() $i=1,2$
that the Selmer groups
$i=1,2$
that the Selmer groups
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion over the Iwasawa algebra.
$\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion over the Iwasawa algebra.
Given
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, recall that
$E_{2}$
, recall that
![]() $\Sigma _{0}$
is the set of all primes
$\Sigma _{0}$
is the set of all primes
![]() $v\nmid p$
at which either
$v\nmid p$
at which either
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. There is a subset
$E_{2}$
has bad reduction. There is a subset
![]() $\Sigma _{1}$
of the set of primes
$\Sigma _{1}$
of the set of primes
![]() $\Sigma _{0}$
which plays a role in the statement of our results (see Definition 4.1). The imprimitive Selmer group
$\Sigma _{0}$
which plays a role in the statement of our results (see Definition 4.1). The imprimitive Selmer group
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
is defined by relaxing the Selmer conditions at the primes in
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
is defined by relaxing the Selmer conditions at the primes in
![]() $\Sigma _{1}$
. The precise definition is given in the discussion preceding Proposition 2.3. Our first result in this paper is Theorem 4.5. We show that if the
$\Sigma _{1}$
. The precise definition is given in the discussion preceding Proposition 2.3. Our first result in this paper is Theorem 4.5. We show that if the
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}/F^{\operatorname {cyc}})$
is zero, then the
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}/F^{\operatorname {cyc}})$
is zero, then the
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}/F^{\operatorname {cyc}})$
is also zero. Further, if these
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}/F^{\operatorname {cyc}})$
is also zero. Further, if these
![]() $\mu $
-invariants are both zero, then the imprimitive
$\mu $
-invariants are both zero, then the imprimitive
![]() $\lambda $
-invariants of
$\lambda $
-invariants of
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}/F^{\operatorname {cyc}})$
and
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}/F^{\operatorname {cyc}})$
and
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}/F^{\operatorname {cyc}})$
are equal. This result does more than simply generalize the aforementioned results. Over the rational numbers, if Theorem 4.5 is specialized to the case of p-ordinary reduction (resp. p-supersingular reduction), we obtain refinements of the results Greenberg-Vatsal (resp. Kim, Ponsinet). This is due to the fact that the set of primes
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}/F^{\operatorname {cyc}})$
are equal. This result does more than simply generalize the aforementioned results. Over the rational numbers, if Theorem 4.5 is specialized to the case of p-ordinary reduction (resp. p-supersingular reduction), we obtain refinements of the results Greenberg-Vatsal (resp. Kim, Ponsinet). This is due to the fact that the set of primes
![]() $\Sigma _{1}$
is optimal in the sense that it is smaller than the full set of primes
$\Sigma _{1}$
is optimal in the sense that it is smaller than the full set of primes
![]() $\Sigma _{0}$
(considered in previous works).
$\Sigma _{0}$
(considered in previous works).
The Euler characteristic of the p-primary Selmer group an elliptic curve over
![]() $\mathbb {Q}$
with p-ordinary reduction may be defined when the Selmer group over
$\mathbb {Q}$
with p-ordinary reduction may be defined when the Selmer group over
![]() $\mathbb {Q}$
is finite. Furthermore, it is of significant interest from the point of view of the p-adic Birch and Swinnerton-Dyer conjecture. The truncated Euler characteristic is a derived version of the usual Euler characteristic, which may be defined in the positive rank setting. Setting
$\mathbb {Q}$
is finite. Furthermore, it is of significant interest from the point of view of the p-adic Birch and Swinnerton-Dyer conjecture. The truncated Euler characteristic is a derived version of the usual Euler characteristic, which may be defined in the positive rank setting. Setting
![]() $\Gamma :=\operatorname {Gal}(F^{\operatorname {cyc}}/F)$
, consider the natural map
$\Gamma :=\operatorname {Gal}(F^{\operatorname {cyc}}/F)$
, consider the natural map
for which
![]() $\phi (x)$
is the residue class of x in
$\phi (x)$
is the residue class of x in
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})_{\Gamma }$
. The truncated Euler characteristic of
$\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})_{\Gamma }$
. The truncated Euler characteristic of
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
can be defined if both the kernel and cokernel of
$\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
can be defined if both the kernel and cokernel of
![]() $\phi $
are finite (see Definition 3.1). If this is the case, we set
$\phi $
are finite (see Definition 3.1). If this is the case, we set
 $$ \begin{align*}\chi_{t}^{\ddagger}(\Gamma,E_{i}):=\frac{\#\operatorname{ker} \phi}{\# \operatorname{cok} \phi}. \end{align*} $$
$$ \begin{align*}\chi_{t}^{\ddagger}(\Gamma,E_{i}):=\frac{\#\operatorname{ker} \phi}{\# \operatorname{cok} \phi}. \end{align*} $$
The reader is referred to Lemma 3.3 for precise conditions under which the truncated Euler characteristic
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{i})$
is well defined (also see Remark 5.0.1).
$\chi _{t}^{\ddagger }(\Gamma , E_{i})$
is well defined (also see Remark 5.0.1).
Leveraging our results on
![]() $\mu $
-invariants and imprimitive
$\mu $
-invariants and imprimitive
![]() $\lambda $
-invariants, we prove congruence relations for the truncated Euler characteristics of multisigned Selmer groups of the p-congruent elliptic curves
$\lambda $
-invariants, we prove congruence relations for the truncated Euler characteristics of multisigned Selmer groups of the p-congruent elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Theorem 5.5 is the main result of the paper, in which
$E_{2}$
. Theorem 5.5 is the main result of the paper, in which
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{1})$
is precisely related to
$\chi _{t}^{\ddagger }(\Gamma , E_{1})$
is precisely related to
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{2})$
. We impose Hypothesis (4.2), which states that for
$\chi _{t}^{\ddagger }(\Gamma , E_{2})$
. We impose Hypothesis (4.2), which states that for
![]() $i=1,2$
, the Selmer groups
$i=1,2$
, the Selmer groups
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion over the Iwasawa algebra, and that the truncated Euler characteristics
$\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion over the Iwasawa algebra, and that the truncated Euler characteristics
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{i})$
are well defined. At a prime v,
$\chi _{t}^{\ddagger }(\Gamma , E_{i})$
are well defined. At a prime v,
![]() $L_{v}(E_{i}, s)$
is the local L-function of
$L_{v}(E_{i}, s)$
is the local L-function of
![]() $E_{i}$
at v. We set
$E_{i}$
at v. We set
![]() $\delta _{E_{i}, \Sigma _{1}}$
to be the product of local-factors at the primes in
$\delta _{E_{i}, \Sigma _{1}}$
to be the product of local-factors at the primes in
![]() $\Sigma _{1}$
$\Sigma _{1}$
(see Definition 5.2). Here,
![]() $|\cdot |_{p}$
is the absolute value normalized by
$|\cdot |_{p}$
is the absolute value normalized by
![]() $|p|_{p}^{-1}=p$
. It is shown that there is an explicit relationship between
$|p|_{p}^{-1}=p$
. It is shown that there is an explicit relationship between
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})$
and
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})$
and
![]() $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{2})$
, and the reader is referred to Theorem 5.5 for the precise statement. The set of primes
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{2})$
, and the reader is referred to Theorem 5.5 for the precise statement. The set of primes
![]() $\Sigma _{1}$
can be smaller than the set
$\Sigma _{1}$
can be smaller than the set
![]() $\Sigma _{0}$
, and hence the relation between truncated Euler characteristics is more refined. This is why it is of considerable importance that the set of primes
$\Sigma _{0}$
, and hence the relation between truncated Euler characteristics is more refined. This is why it is of considerable importance that the set of primes
![]() $\Sigma _{1}$
be carefully chosen to be as small as possible. Theorem 6.7 extends Theorem 5.5 to the multisigned Selmer groups of certain
$\Sigma _{1}$
be carefully chosen to be as small as possible. Theorem 6.7 extends Theorem 5.5 to the multisigned Selmer groups of certain
![]() $\mathbb {Z}_{p}^{m}$
-extensions. Furthermore, we compare the Akashi series for p-congruent elliptic curves over such
$\mathbb {Z}_{p}^{m}$
-extensions. Furthermore, we compare the Akashi series for p-congruent elliptic curves over such
![]() $\mathbb {Z}_{p}^{m}$
-extensions. Our results are informed by explicit examples which are listed in Section 7.
$\mathbb {Z}_{p}^{m}$
-extensions. Our results are informed by explicit examples which are listed in Section 7.
2 Preliminaries
Throughout, we fix an odd prime number p and number field F. Let
![]() $F^{\operatorname {cyc}}$
be the cyclotomic
$F^{\operatorname {cyc}}$
be the cyclotomic
![]() $\mathbb {Z}_{p}$
-extension of F. Denote by
$\mathbb {Z}_{p}$
-extension of F. Denote by
![]() $\Sigma _{p}$
the set of primes of F above p. Let E be an elliptic curve over F and denote by
$\Sigma _{p}$
the set of primes of F above p. Let E be an elliptic curve over F and denote by
![]() $\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
the set of primes in
$\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
the set of primes in
![]() $\Sigma _{p}$
at which E has supersingular reduction. Let
$\Sigma _{p}$
at which E has supersingular reduction. Let
![]() $\mathcal {F}_{\infty }/F$
be a Galois extension of F containing
$\mathcal {F}_{\infty }/F$
be a Galois extension of F containing
![]() $F^{\operatorname {cyc}}$
such that
$F^{\operatorname {cyc}}$
such that
![]() $\operatorname {Gal}(\mathcal {F}_{\infty }/F)\simeq \mathbb {Z}_{p}^{m}$
for an integer
$\operatorname {Gal}(\mathcal {F}_{\infty }/F)\simeq \mathbb {Z}_{p}^{m}$
for an integer
![]() $m\geq 1$
. Set
$m\geq 1$
. Set
![]() $\operatorname {G}:=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
,
$\operatorname {G}:=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
,
![]() $H:=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
and let
$H:=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
and let
![]() $\Gamma $
be the Galois group
$\Gamma $
be the Galois group
![]() $\operatorname {Gal}(F^{\operatorname {cyc}}/F)$
, which is identified with
$\operatorname {Gal}(F^{\operatorname {cyc}}/F)$
, which is identified with
![]() $\operatorname {G}/\operatorname {H}$
. Associated to any pro-p group
$\operatorname {G}/\operatorname {H}$
. Associated to any pro-p group
![]() $\mathcal {G}$
, the Iwasawa algebra
$\mathcal {G}$
, the Iwasawa algebra
![]() $\mathbb {Z}_{p}[[\mathcal {G}]]$
is the inverse limit
$\mathbb {Z}_{p}[[\mathcal {G}]]$
is the inverse limit
![]() $\varprojlim _{U} \mathbb {Z}_{p}[\mathcal {G}/U]$
, where U ranges over all open normal subgroups of
$\varprojlim _{U} \mathbb {Z}_{p}[\mathcal {G}/U]$
, where U ranges over all open normal subgroups of
![]() $\mathcal {G}$
. Set
$\mathcal {G}$
. Set
![]() $\mathcal {F}_{0}:=F$
and for
$\mathcal {F}_{0}:=F$
and for
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathcal {F}_{n}$
denote the unique subextension
$\mathcal {F}_{n}$
denote the unique subextension
![]() $F\subseteq \mathcal {F}_{n}\subset \mathcal {F}_{\infty }$
such that
$F\subseteq \mathcal {F}_{n}\subset \mathcal {F}_{\infty }$
such that
![]() $\operatorname {Gal}(\mathcal {F}_{n}/F)\simeq (\mathbb {Z}/p^{n}\mathbb {Z})^{m}$
. We introduce the following hypothesis on the elliptic curve E.
$\operatorname {Gal}(\mathcal {F}_{n}/F)\simeq (\mathbb {Z}/p^{n}\mathbb {Z})^{m}$
. We introduce the following hypothesis on the elliptic curve E.
Hypothesis 2.1 Throughout, E is required to satisfy the following hypotheses:
-
(1) E has semistable reduction at all primes
 $v\in \Sigma _{p}$
(i.e., either good ordinary, good supersingular or bad multiplicative reduction).
$v\in \Sigma _{p}$
(i.e., either good ordinary, good supersingular or bad multiplicative reduction). -
(2) The residual representation
 $E[p]$
is a
$E[p]$
is a
 $2$
-dimensional
$2$
-dimensional
 $\mathbb {F}_{p}$
-vector space which is irreducible as a
$\mathbb {F}_{p}$
-vector space which is irreducible as a
 $\operatorname {Gal}(\overline {F}/F)$
-module.
$\operatorname {Gal}(\overline {F}/F)$
-module. -
(3) For every prime
 $v\in \Sigma _{\operatorname {ss}}(E)$
, the completion
$v\in \Sigma _{\operatorname {ss}}(E)$
, the completion
 $F_{v}$
is isomorphic to
$F_{v}$
is isomorphic to
 $\mathbb {Q}_{p}$
.
$\mathbb {Q}_{p}$
. -
(4) For
 $v\in \Sigma _{\operatorname {ss}}(E)$
, set
$v\in \Sigma _{\operatorname {ss}}(E)$
, set
 $a_{v}(E):=1+p-\# \widetilde {E}_{v}(\mathbb {F}_{p})$
, where
$a_{v}(E):=1+p-\# \widetilde {E}_{v}(\mathbb {F}_{p})$
, where
 $\widetilde {E}_{v}$
is the reduction of E at v. Assume that
$\widetilde {E}_{v}$
is the reduction of E at v. Assume that
 $a_{v}(E)=0$
for all
$a_{v}(E)=0$
for all
 $v\in \Sigma _{\operatorname {ss}}(E)$
.
$v\in \Sigma _{\operatorname {ss}}(E)$
.
Note that for
![]() $v\in \Sigma _{\operatorname {ss}}(E)$
, it follows from Hasse’s theorem that
$v\in \Sigma _{\operatorname {ss}}(E)$
, it follows from Hasse’s theorem that
![]() $|a_{v}(E)|< 2\sqrt {p}$
. Since E has supersingular reduction at v, we find that p divides
$|a_{v}(E)|< 2\sqrt {p}$
. Since E has supersingular reduction at v, we find that p divides
![]() $\# \widetilde {E}_{v}(\mathbb {F}_{p})$
. Therefore, condition (4) above is satisfied for all primes
$\# \widetilde {E}_{v}(\mathbb {F}_{p})$
. Therefore, condition (4) above is satisfied for all primes
![]() $p\geq 7$
.
$p\geq 7$
.
Lemma 2.1 Let
![]() $\mathcal {F}_{\infty }$
a
$\mathcal {F}_{\infty }$
a
![]() $\mathbb {Z}_{p}^{m}$
-extension of F as above. The following conditions are satisfied:
$\mathbb {Z}_{p}^{m}$
-extension of F as above. The following conditions are satisfied:
-
(1) The only primes that ramify in
 $\mathcal {F}_{\infty }$
are the primes v of F above p.
$\mathcal {F}_{\infty }$
are the primes v of F above p. -
(2) Let
 $\mathfrak {p}_{i}|p$
be a prime of F at which E has supersingular reduction. Let
$\mathfrak {p}_{i}|p$
be a prime of F at which E has supersingular reduction. Let
 $n\geq 1$
and let
$n\geq 1$
and let
 $\eta $
be a prime of
$\eta $
be a prime of
 $\mathcal {F}_{n}$
above
$\mathcal {F}_{n}$
above
 $\mathfrak {p}_{i}$
. Then,
$\mathfrak {p}_{i}$
. Then,
 $\mathcal {F}_{n,\eta }$
is isomorphic to
$\mathcal {F}_{n,\eta }$
is isomorphic to
 $K_{n}$
for some finite unramified extension K of
$K_{n}$
for some finite unramified extension K of
 $\mathbb {Q}_{p}$
. Here,
$\mathbb {Q}_{p}$
. Here,
 $K_{n}$
is the nth layer in the cyclotomic
$K_{n}$
is the nth layer in the cyclotomic
 $\mathbb {Z}_{p}$
-extension of K.
$\mathbb {Z}_{p}$
-extension of K.
Proof Note that in any
![]() $\mathbb {Z}_{p}$
-extension of F, the only primes that ramify are the primes above p, see [Reference Washington36, Proposition 13.2]. Any
$\mathbb {Z}_{p}$
-extension of F, the only primes that ramify are the primes above p, see [Reference Washington36, Proposition 13.2]. Any
![]() $\mathbb {Z}_{p}^{m}$
-extension is a composite of m independent
$\mathbb {Z}_{p}^{m}$
-extension is a composite of m independent
![]() $\mathbb {Z}_{p}$
-extensions, part (1) follows.
$\mathbb {Z}_{p}$
-extensions, part (1) follows.
Recall that it is assumed that
![]() $\mathcal {F}_{\infty }$
contains
$\mathcal {F}_{\infty }$
contains
![]() $F^{\operatorname {cyc}}$
. We identify
$F^{\operatorname {cyc}}$
. We identify
![]() $F_{\mathfrak {p}_{i}}$
with
$F_{\mathfrak {p}_{i}}$
with
![]() $\mathbb {Q}_{p}$
. By local class field theory, the maximal pro-p extension of
$\mathbb {Q}_{p}$
. By local class field theory, the maximal pro-p extension of
![]() $\mathbb {Q}_{p}$
is the composite of the cyclotomic
$\mathbb {Q}_{p}$
is the composite of the cyclotomic
![]() $\mathbb {Z}_{p}$
-extension
$\mathbb {Z}_{p}$
-extension
![]() $\mathbb {Q}_{p}^{\operatorname {cyc}}$
and the unramified
$\mathbb {Q}_{p}^{\operatorname {cyc}}$
and the unramified
![]() $\mathbb {Z}_{p}$
-extension
$\mathbb {Z}_{p}$
-extension
![]() $\mathbb {Q}_{p}^{\operatorname {nr}}$
. Letting
$\mathbb {Q}_{p}^{\operatorname {nr}}$
. Letting
![]() $\mathbb {Q}_{p,n}\subset \mathbb {Q}_{p}^{\operatorname {cyc}}$
be the nth layer, we find that
$\mathbb {Q}_{p,n}\subset \mathbb {Q}_{p}^{\operatorname {cyc}}$
be the nth layer, we find that
![]() $\mathcal {F}_{n,\eta }$
is the composite of an unramified extension
$\mathcal {F}_{n,\eta }$
is the composite of an unramified extension
![]() $K/\mathbb {Q}_{p}$
and
$K/\mathbb {Q}_{p}$
and
![]() $\mathbb {Q}_{p, n}$
, and (2) follows.▪
$\mathbb {Q}_{p, n}$
, and (2) follows.▪
Part (2) of Lemma 2.1 ensures that the signed norm groups of E over
![]() $F_{n,\eta }$
may be defined. This is used in Definition 2.2, where the multisigned Selmer groups associated to E over
$F_{n,\eta }$
may be defined. This is used in Definition 2.2, where the multisigned Selmer groups associated to E over
![]() $\mathcal {F}_{\infty }$
are defined. We shall now define local conditions at each of the primes
$\mathcal {F}_{\infty }$
are defined. We shall now define local conditions at each of the primes
![]() $\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
. By Hypothesis (2.1), the local field
$\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
. By Hypothesis (2.1), the local field
![]() $F_{\mathfrak {p}_{i}}$
is isomorphic to
$F_{\mathfrak {p}_{i}}$
is isomorphic to
![]() $\mathbb {Q}_{p}$
. Denote by
$\mathbb {Q}_{p}$
. Denote by
![]() $\widehat {E}_{\mathfrak {p}_{i}}$
the formal group of E over
$\widehat {E}_{\mathfrak {p}_{i}}$
the formal group of E over
![]() $F_{\mathfrak {p}_{i}}$
. For any algebraic extension L of
$F_{\mathfrak {p}_{i}}$
. For any algebraic extension L of
![]() $F_{\mathfrak {p}_{i}}\simeq \mathbb {Q}_{p}$
, denote by
$F_{\mathfrak {p}_{i}}\simeq \mathbb {Q}_{p}$
, denote by
![]() $\widehat {E}_{\mathfrak {p}_{i}}(L):=\widehat {E}_{\mathfrak {p}_{i}}(\mathfrak {m}_{L})$
, where
$\widehat {E}_{\mathfrak {p}_{i}}(L):=\widehat {E}_{\mathfrak {p}_{i}}(\mathfrak {m}_{L})$
, where
![]() $\mathfrak {m}_{L}$
is the maximal ideal of
$\mathfrak {m}_{L}$
is the maximal ideal of
![]() $\mathcal {O}_{L}$
. Let K be a finite unramified extension of
$\mathcal {O}_{L}$
. Let K be a finite unramified extension of
![]() $\mathbb {Q}_{p}$
and
$\mathbb {Q}_{p}$
and
![]() $K^{\operatorname {cyc}}$
the cyclotomic
$K^{\operatorname {cyc}}$
the cyclotomic
![]() $\mathbb {Z}_{p}$
-extension of K. Denote by
$\mathbb {Z}_{p}$
-extension of K. Denote by
![]() $K_{n}$
the unique subextension of
$K_{n}$
the unique subextension of
![]() $K^{\operatorname {cyc}}/K$
of degree
$K^{\operatorname {cyc}}/K$
of degree
![]() $p^{n}$
. Kobayashi introduced plus and minus norm groups:
$p^{n}$
. Kobayashi introduced plus and minus norm groups:
where
![]() $\operatorname {tr}_{n/m+1}:\widehat {E}_{\mathfrak {p}_{i}}(K_{n})\rightarrow \widehat {E}_{\mathfrak {p}_{i}}(K_{m+1})$
denotes the trace map with respect to the formal group law on
$\operatorname {tr}_{n/m+1}:\widehat {E}_{\mathfrak {p}_{i}}(K_{n})\rightarrow \widehat {E}_{\mathfrak {p}_{i}}(K_{m+1})$
denotes the trace map with respect to the formal group law on
![]() $\widehat {E}_{\mathfrak {p}_{i}}$
.
$\widehat {E}_{\mathfrak {p}_{i}}$
.
Let
![]() $\ddagger =(\ddagger _{1},\dots , \ddagger _{d})\in \{+,-\}^{d}$
be a multisigned vector, so that each component
$\ddagger =(\ddagger _{1},\dots , \ddagger _{d})\in \{+,-\}^{d}$
be a multisigned vector, so that each component
![]() $\ddagger _{i}$
is either a
$\ddagger _{i}$
is either a
![]() $+$
or
$+$
or
![]() $-$
sign. For each finite prime
$-$
sign. For each finite prime
![]() $v\notin \Sigma _{\operatorname {ss}}(E)$
, and each integer
$v\notin \Sigma _{\operatorname {ss}}(E)$
, and each integer
![]() $n\geq 1$
, set
$n\geq 1$
, set
 $$ \begin{align}\mathcal{H}_{v}(\mathcal{F}_{n}, E[p^{\infty}]):=\prod_{\eta|v} \frac{H^{1}(\mathcal{F}_{n,\eta}, E[p^{\infty}])}{E(\mathcal{F}_{n,\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}},\end{align} $$
$$ \begin{align}\mathcal{H}_{v}(\mathcal{F}_{n}, E[p^{\infty}]):=\prod_{\eta|v} \frac{H^{1}(\mathcal{F}_{n,\eta}, E[p^{\infty}])}{E(\mathcal{F}_{n,\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}},\end{align} $$
where
![]() $\eta $
runs through the primes of
$\eta $
runs through the primes of
![]() $\mathcal {F}_{n}$
above v. For each prime
$\mathcal {F}_{n}$
above v. For each prime
![]() $\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
, set
$\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
, set
 $$ \begin{align}\mathcal{H}_{\mathfrak{p}_{i}}^{\pm}(\mathcal{F}_{n}, E[p^{\infty}]):=\prod_{\eta|\mathfrak{p}_{i}} \frac{H^{1}(\mathcal{F}_{n,\eta}, E[p^{\infty}])}{\widehat{E}_{\mathfrak{p}_{i}}^{\pm}(\mathcal{F}_{n,\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}}.\end{align} $$
$$ \begin{align}\mathcal{H}_{\mathfrak{p}_{i}}^{\pm}(\mathcal{F}_{n}, E[p^{\infty}]):=\prod_{\eta|\mathfrak{p}_{i}} \frac{H^{1}(\mathcal{F}_{n,\eta}, E[p^{\infty}])}{\widehat{E}_{\mathfrak{p}_{i}}^{\pm}(\mathcal{F}_{n,\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}}.\end{align} $$
Let
![]() $\eta $
be a prime of
$\eta $
be a prime of
![]() $\mathcal {F}_{\infty }$
above
$\mathcal {F}_{\infty }$
above
![]() $\mathfrak {p}_{i}$
. By (2) of Lemma 2.1,
$\mathfrak {p}_{i}$
. By (2) of Lemma 2.1,
![]() $\mathcal {F}_{n,\eta }$
is isomorphic to
$\mathcal {F}_{n,\eta }$
is isomorphic to
![]() $K_{n}$
for some finite unramified extension K over
$K_{n}$
for some finite unramified extension K over
![]() $\mathbb {Q}_{p}$
. Thus the norm groups
$\mathbb {Q}_{p}$
. Thus the norm groups
![]() $\widehat {E}_{\mathfrak {p}_{i}}^{\pm } (\mathcal {F}_{n,\eta })$
are defined. We now come to the definition of the multisigned Selmer groups.
$\widehat {E}_{\mathfrak {p}_{i}}^{\pm } (\mathcal {F}_{n,\eta })$
are defined. We now come to the definition of the multisigned Selmer groups.
Definition 2.2 Let d be the cardinality of
![]() $\Sigma _{\operatorname {ss}}(E)$
and let
$\Sigma _{\operatorname {ss}}(E)$
and let
![]() $\ddagger =(\ddagger _{1},\dots , \ddagger _{d})$
be a multi-signed vector, so that each component
$\ddagger =(\ddagger _{1},\dots , \ddagger _{d})$
be a multi-signed vector, so that each component
![]() $\ddagger _{i}$
is either a
$\ddagger _{i}$
is either a
![]() $+$
sign or
$+$
sign or
![]() $-$
sign. Let
$-$
sign. Let
![]() $\Sigma $
be a finite primes of F containing
$\Sigma $
be a finite primes of F containing
![]() $\Sigma _{p}$
and the primes at which E has bad reduction. Let
$\Sigma _{p}$
and the primes at which E has bad reduction. Let
![]() $\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}$
be the primes in
$\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}$
be the primes in
![]() $\Sigma _{\operatorname {ss}}(E)$
. For
$\Sigma _{\operatorname {ss}}(E)$
. For
![]() $i=1,\dots , d$
, let
$i=1,\dots , d$
, let
![]() $\mathcal {H}_{\mathfrak {p}_{i}}^{\ddagger _{i}}(\mathcal {F}_{n}, E[p^{\infty }])$
be the group defined above, see (2.2). The multisigned Selmer group
$\mathcal {H}_{\mathfrak {p}_{i}}^{\ddagger _{i}}(\mathcal {F}_{n}, E[p^{\infty }])$
be the group defined above, see (2.2). The multisigned Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{n})$
is the kernel of the map:
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{n})$
is the kernel of the map:
 $$ \begin{align*}\Phi_{E,\mathcal{F}_{n}}^{\ddagger}:H^{1}(\mathcal{F}_{n},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash \Sigma_{\operatorname{ss}}(E)} \mathcal{H}_{v}(\mathcal{F}_{n}, E[p^{\infty}])\times \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(\mathcal{F}_{n}, E[p^{\infty}]).\end{align*} $$
$$ \begin{align*}\Phi_{E,\mathcal{F}_{n}}^{\ddagger}:H^{1}(\mathcal{F}_{n},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash \Sigma_{\operatorname{ss}}(E)} \mathcal{H}_{v}(\mathcal{F}_{n}, E[p^{\infty}])\times \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(\mathcal{F}_{n}, E[p^{\infty}]).\end{align*} $$
Let
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
be the direct limit
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
be the direct limit
![]() $\varinjlim _{n} \operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{n})$
and write
$\varinjlim _{n} \operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{n})$
and write
![]() $\operatorname {X}^{\ddagger }(E/\mathcal {F}_{\infty })$
for its Pontryagin-dual.
$\operatorname {X}^{\ddagger }(E/\mathcal {F}_{\infty })$
for its Pontryagin-dual.
For practical purposes, it is convenient to work with an alternative description of
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
. For
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
. For
![]() $v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}(E)$
denote by
$v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}(E)$
denote by
![]() $E_{v}$
the curve over the local field
$E_{v}$
the curve over the local field
![]() $F_{v}$
. Since
$F_{v}$
. Since
![]() $E_{v}$
has good ordinary or multiplicative reduction, it fits in a short exact sequence of
$E_{v}$
has good ordinary or multiplicative reduction, it fits in a short exact sequence of
![]() $\operatorname {Gal}(\overline {F_{v}}/F_{v})$
-modules:
$\operatorname {Gal}(\overline {F_{v}}/F_{v})$
-modules:
Here,
![]() $C_{v}$
and
$C_{v}$
and
![]() $D_{v}$
are both of corank one over
$D_{v}$
are both of corank one over
![]() $\mathbb {Z}_{p}$
with the property that
$\mathbb {Z}_{p}$
with the property that
![]() $C_{v}$
is a divisible subgroup and
$C_{v}$
is a divisible subgroup and
![]() $D_{v}$
is the maximal subgroup on which
$D_{v}$
is the maximal subgroup on which
![]() $\operatorname {I}_{v}:=\operatorname {Gal}(\overline {F_{v}}/F_{v}^{\operatorname {nr}})$
acts via a finite order quotient. In fact,
$\operatorname {I}_{v}:=\operatorname {Gal}(\overline {F_{v}}/F_{v}^{\operatorname {nr}})$
acts via a finite order quotient. In fact,
![]() $D_{v}$
is specified as follows:
$D_{v}$
is specified as follows:
 $$ \begin{align}D_{v}=\begin{cases} \widetilde{E_{v}}[p^{\infty}] \quad \text{if }E_{v} \text{ has good ordinary reduction},\\ \mathbb{Q}_{p}/\mathbb{Z}_{p}(\phi) \quad \text{if }E_{v} \text{ has multiplicative reduction,} \end{cases}\end{align} $$
$$ \begin{align}D_{v}=\begin{cases} \widetilde{E_{v}}[p^{\infty}] \quad \text{if }E_{v} \text{ has good ordinary reduction},\\ \mathbb{Q}_{p}/\mathbb{Z}_{p}(\phi) \quad \text{if }E_{v} \text{ has multiplicative reduction,} \end{cases}\end{align} $$
where
![]() $\phi $
is an unramified quadratic character, which is trivial if and only if
$\phi $
is an unramified quadratic character, which is trivial if and only if
![]() $E_{v}$
has split multiplicative reduction. For further details, the reader is referred to the discussions in [Reference Coates and Greenberg2, p. 150] and [Reference Greenberg and Vatsal8, section 2].
$E_{v}$
has split multiplicative reduction. For further details, the reader is referred to the discussions in [Reference Coates and Greenberg2, p. 150] and [Reference Greenberg and Vatsal8, section 2].
Note that above each prime v of F, there are finitely many primes
![]() $\eta |v$
of
$\eta |v$
of
![]() $F^{\operatorname {cyc}}$
. For
$F^{\operatorname {cyc}}$
. For
![]() $\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
, set
$\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}(E)$
, set
 $$ \begin{align*}\mathcal{H}_{\mathfrak{p}_{i}}^{\pm}(F^{\operatorname{cyc}}, E[p^{\infty}]):=\prod_{\eta|\mathfrak{p}_{i}} \frac{H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])}{\widehat{E}^{\pm}(F^{\operatorname{cyc}}_{\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}},\end{align*} $$
$$ \begin{align*}\mathcal{H}_{\mathfrak{p}_{i}}^{\pm}(F^{\operatorname{cyc}}, E[p^{\infty}]):=\prod_{\eta|\mathfrak{p}_{i}} \frac{H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])}{\widehat{E}^{\pm}(F^{\operatorname{cyc}}_{\eta})\otimes \mathbb{Q}_{p}/\mathbb{Z}_{p}},\end{align*} $$
where
![]() $\eta $
runs through the primes of
$\eta $
runs through the primes of
![]() $F^{\operatorname {cyc}}$
above
$F^{\operatorname {cyc}}$
above
![]() $\mathfrak {p}_{i}$
. For
$\mathfrak {p}_{i}$
. For
![]() $v\in \Sigma \backslash \Sigma _{\operatorname {ss}}(E)$
, set
$v\in \Sigma \backslash \Sigma _{\operatorname {ss}}(E)$
, set
 $$ \begin{align} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}]):=\begin{cases}\prod_{\eta|v} \operatorname{im}\left(H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\rightarrow H^{1}(\operatorname{I}_{\eta}, D_{v})\right)\text{ if }v\in \Sigma_{p}\backslash \Sigma_{\operatorname{ss}}(E),\\ \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\text{ if }v\in \Sigma\backslash \Sigma_{p}, \end{cases} \end{align} $$
$$ \begin{align} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}]):=\begin{cases}\prod_{\eta|v} \operatorname{im}\left(H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\rightarrow H^{1}(\operatorname{I}_{\eta}, D_{v})\right)\text{ if }v\in \Sigma_{p}\backslash \Sigma_{\operatorname{ss}}(E),\\ \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\text{ if }v\in \Sigma\backslash \Sigma_{p}, \end{cases} \end{align} $$
where
![]() $\operatorname {I}_{\eta }$
is the inertia subgroup of
$\operatorname {I}_{\eta }$
is the inertia subgroup of
![]() $\operatorname {Gal}(\overline {F_{\eta }^{\operatorname {cyc}}}/F_{\eta }^{\operatorname {cyc}})$
. The Selmer group
$\operatorname {Gal}(\overline {F_{\eta }^{\operatorname {cyc}}}/F_{\eta }^{\operatorname {cyc}})$
. The Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
coincides with the kernel of the restriction map
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
coincides with the kernel of the restriction map
 $$ \begin{align*} \Phi_{E,F^{\operatorname{cyc}}}^{\ddagger}:H^{1}(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash \Sigma_{\operatorname{ss}}(E)} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}])\times \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
$$ \begin{align*} \Phi_{E,F^{\operatorname{cyc}}}^{\ddagger}:H^{1}(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash \Sigma_{\operatorname{ss}}(E)} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}])\times \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
For further details, see [Reference Greenberg and Vatsal8, pp. 32, 42] and the discussion in [Reference Greenberg6, Section 5]. Let
![]() $\Sigma _{0}$
be a finite set of primes of F which does not contain any prime
$\Sigma _{0}$
be a finite set of primes of F which does not contain any prime
![]() $v\in \Sigma _{p}$
. The
$v\in \Sigma _{p}$
. The
![]() $\Sigma _{0}$
-imprimitive Selmer group
$\Sigma _{0}$
-imprimitive Selmer group
![]() $\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
is the kernel of the restriction map
$\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
is the kernel of the restriction map
 $$ \begin{align*} \Phi_{E,F^{\operatorname{cyc}}}^{\Sigma_{0},\ddagger}:H^{1}(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow\! \prod_{v\in \Sigma\backslash (\Sigma_{\operatorname{ss}}(E)\cup \Sigma_{0}\kern-1pt)} \!\mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\kern-1pt\infty}])\kern1pt{\times}\kern1pt \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
$$ \begin{align*} \Phi_{E,F^{\operatorname{cyc}}}^{\Sigma_{0},\ddagger}:H^{1}(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow\! \prod_{v\in \Sigma\backslash (\Sigma_{\operatorname{ss}}(E)\cup \Sigma_{0}\kern-1pt)} \!\mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\kern-1pt\infty}])\kern1pt{\times}\kern1pt \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
The Pontryagin dual of
![]() $\operatorname {Sel}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
is denoted by
$\operatorname {Sel}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
is denoted by
![]() $\operatorname {X}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
. The next Proposition follows from [Reference Greenberg and Vatsal8, Proposition 2.1] and [Reference Lei and Lim21, Proposition 4.6].
$\operatorname {X}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
. The next Proposition follows from [Reference Greenberg and Vatsal8, Proposition 2.1] and [Reference Lei and Lim21, Proposition 4.6].
Proposition 2.3 Assume that the Selmer group
![]() $\operatorname {Sel}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
is cotorsion as a
$\operatorname {Sel}^{\Sigma _{0}, \ddagger }(E/F^{\operatorname {cyc}})$
is cotorsion as a
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module. Then, the maps
$\mathbb {Z}_{p}[[\Gamma ]]$
-module. Then, the maps
![]() $\Phi _{E,F^{\operatorname {cyc}}}^{\ddagger }$
and
$\Phi _{E,F^{\operatorname {cyc}}}^{\ddagger }$
and
![]() $\Phi _{E,F^{\operatorname {cyc}}}^{\Sigma _{0},\ddagger }$
are surjective.
$\Phi _{E,F^{\operatorname {cyc}}}^{\Sigma _{0},\ddagger }$
are surjective.
Thus we have a short exact sequence relating the
![]() $\Sigma _{0}$
-imprimitive Selmer group
$\Sigma _{0}$
-imprimitive Selmer group
![]() $\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
with the Selmer group
$\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
with the Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
 $$ \begin{align*} 0\rightarrow \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})\rightarrow \operatorname{Sel}^{\Sigma_0,\ddagger}(E/F^{\operatorname{cyc}})\xrightarrow{\Phi_{E,F^{\operatorname{cyc}}}^{\ddagger, \Sigma_0}}\prod_{v\in \Sigma_0} \mathcal{H}_v(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow 0.\end{align*} $$
$$ \begin{align*} 0\rightarrow \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})\rightarrow \operatorname{Sel}^{\Sigma_0,\ddagger}(E/F^{\operatorname{cyc}})\xrightarrow{\Phi_{E,F^{\operatorname{cyc}}}^{\ddagger, \Sigma_0}}\prod_{v\in \Sigma_0} \mathcal{H}_v(F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow 0.\end{align*} $$
Choose a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
and identify
$\Gamma $
and identify
![]() $\gamma -1$
with T in choosing an isomorphism
$\gamma -1$
with T in choosing an isomorphism
![]() $\mathbb {Z}_{p}[[\Gamma ]]\simeq \mathbb {Z}_{p}[[T]]$
. A polynomial
$\mathbb {Z}_{p}[[\Gamma ]]\simeq \mathbb {Z}_{p}[[T]]$
. A polynomial
![]() $f(T)\in \mathbb {Z}_{p}[T]$
is said to be distinguished if it is a monic polynomial and all nonleading coefficients are divisible by p. By the structure theorem of finitely generated torsion
$f(T)\in \mathbb {Z}_{p}[T]$
is said to be distinguished if it is a monic polynomial and all nonleading coefficients are divisible by p. By the structure theorem of finitely generated torsion
![]() $\mathbb {Z}_{p}[[T]]$
-modules, there is a pseudo-isomorphism
$\mathbb {Z}_{p}[[T]]$
-modules, there is a pseudo-isomorphism
 $$ \begin{align*}\operatorname{X}^{\ddagger}(E/F^{cyc})\sim \left(\bigoplus_{i=1}^{n} \mathbb{Z}_{p}[[T]]/(f_{i}(T))\right)\oplus \left(\bigoplus_{j=1}^{m} \mathbb{Z}_{p}[[T]]/(p^{\mu_{j}}) \right).\end{align*} $$
$$ \begin{align*}\operatorname{X}^{\ddagger}(E/F^{cyc})\sim \left(\bigoplus_{i=1}^{n} \mathbb{Z}_{p}[[T]]/(f_{i}(T))\right)\oplus \left(\bigoplus_{j=1}^{m} \mathbb{Z}_{p}[[T]]/(p^{\mu_{j}}) \right).\end{align*} $$
For,
![]() $i=1,\dots , n$
, the elements
$i=1,\dots , n$
, the elements
![]() $f_{i}(T)$
above are distinguished polynomials and the product
$f_{i}(T)$
above are distinguished polynomials and the product
![]() $f_{E}^{\ddagger }(T):=p^{\sum _{j} \mu _{j}} \prod _{i} f_{i}(T)$
is called the characteristic polynomial. The signed Iwasawa invariants are defined by
$f_{E}^{\ddagger }(T):=p^{\sum _{j} \mu _{j}} \prod _{i} f_{i}(T)$
is called the characteristic polynomial. The signed Iwasawa invariants are defined by
![]() $\lambda _{E}^{\ddagger }:=\operatorname {deg} f_{E}^{\ddagger }(T)$
and
$\lambda _{E}^{\ddagger }:=\operatorname {deg} f_{E}^{\ddagger }(T)$
and
![]() $\mu _{E}^{\ddagger }:=\sum _{j=1}^{m} \mu _{j}$
. Denote by
$\mu _{E}^{\ddagger }:=\sum _{j=1}^{m} \mu _{j}$
. Denote by
![]() $f_{E}^{\Sigma _{0},\ddagger }(T)$
,
$f_{E}^{\Sigma _{0},\ddagger }(T)$
,
![]() $\lambda _{E}^{\Sigma _{0},\ddagger }$
and
$\lambda _{E}^{\Sigma _{0},\ddagger }$
and
![]() $\mu _{E}^{\Sigma _{0},\ddagger }$
the characteristic polynomial,
$\mu _{E}^{\Sigma _{0},\ddagger }$
the characteristic polynomial,
![]() $\lambda $
-invariant and
$\lambda $
-invariant and
![]() $\mu $
-invariant of the imprimitive Selmer group
$\mu $
-invariant of the imprimitive Selmer group
![]() $\operatorname {X}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
.
$\operatorname {X}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
.
3 The truncated Euler characteristic
In this section, we recall the notion of the truncated Euler characteristic, which is a generalization of the usual Euler characteristic. We then discuss explicit formulas for the truncated Euler characteristic, as predicted by the p-adic Birch and Swinnerton-Dyer conjecture. For a more detailed exposition, the reader may refer to [Reference Coates, Schneider and Sujatha3, Section 3] and [Reference Zerbes37]. For a discrete p-primary cofinitely generated
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module M for which the cohomology groups
$\mathbb {Z}_{p}[[\Gamma ]]$
-module M for which the cohomology groups
![]() $H^{i}(\Gamma , M)$
have finite order, the Euler characteristic is defined to be the quotient
$H^{i}(\Gamma , M)$
have finite order, the Euler characteristic is defined to be the quotient
 $$ \begin{align*} \chi(\Gamma, M):=\frac{\# H^{0}(\Gamma, M)}{\# H^{1}(\Gamma, M)}. \end{align*} $$
$$ \begin{align*} \chi(\Gamma, M):=\frac{\# H^{0}(\Gamma, M)}{\# H^{1}(\Gamma, M)}. \end{align*} $$
For an elliptic curve E with potentially good ordinary reduction at all primes above p, the Euler characteristic of the Selmer group is defined, provided the Selmer group of E over the base field is finite. This definition does not extend to the case when the Selmer group of E is infinite. The natural substitute is the truncated Euler characteristic.
Definition 3.1 Let M be a discrete p-primary
![]() $\Gamma $
-module let
$\Gamma $
-module let
![]() $\phi _{M}$
be the natural map
$\phi _{M}$
be the natural map
for which
![]() $\phi _{M}(x)$
is the residue class of x in
$\phi _{M}(x)$
is the residue class of x in
![]() $M_{\Gamma }$
. The truncated Euler characteristic
$M_{\Gamma }$
. The truncated Euler characteristic
![]() $\chi _{t}\left (\Gamma , M\right )$
is defined if both
$\chi _{t}\left (\Gamma , M\right )$
is defined if both
![]() $\operatorname {ker}(\phi _{M})$
and
$\operatorname {ker}(\phi _{M})$
and
![]() $\operatorname {cok}(\phi _{M})$
are finite. In this case,
$\operatorname {cok}(\phi _{M})$
are finite. In this case,
![]() $\chi _{t}(\Gamma , M)$
is defined by
$\chi _{t}(\Gamma , M)$
is defined by
 $$ \begin{align*}\chi_{t}\left(\Gamma, M\right):=\frac{\#\operatorname{ker}(\phi_{M})}{\#\operatorname{cok}(\phi_{M})}.\end{align*} $$
$$ \begin{align*}\chi_{t}\left(\Gamma, M\right):=\frac{\#\operatorname{ker}(\phi_{M})}{\#\operatorname{cok}(\phi_{M})}.\end{align*} $$
For a discrete
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module M, set
$\mathbb {Z}_{p}[[\Gamma ]]$
-module M, set
![]() $f_{M}(T)$
to be the characteristic polynomial of the Pontryagin dual of M and write
$f_{M}(T)$
to be the characteristic polynomial of the Pontryagin dual of M and write
![]() $f_{M}(T)= T^{r_{M}} g_{M}(T)$
, where
$f_{M}(T)= T^{r_{M}} g_{M}(T)$
, where
![]() $g_{M}(0)\neq 0$
. In other words,
$g_{M}(0)\neq 0$
. In other words,
![]() $r_{M}$
is the order of vanishing of
$r_{M}$
is the order of vanishing of
![]() $f_{M}(T)$
at
$f_{M}(T)$
at
![]() $T=0$
.
$T=0$
.
Lemma 3.2 Assume that M is cofinitely generated and cotorsion as a
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module. The Euler characteristic
$\mathbb {Z}_{p}[[\Gamma ]]$
-module. The Euler characteristic
![]() $\chi (\Gamma , M)$
is defined if and only if
$\chi (\Gamma , M)$
is defined if and only if
![]() $r_{M}=0$
.
$r_{M}=0$
.
Proof Let X be the Pontryagin dual of M. The invariant submodule
![]() $M^{\Gamma }$
is dual to
$M^{\Gamma }$
is dual to
![]() $X_{\Gamma }$
and the quotient
$X_{\Gamma }$
and the quotient
![]() $M_{\Gamma }$
is dual to
$M_{\Gamma }$
is dual to
![]() $X^{\Gamma }$
. By an application of the structure theorem for finitely generated torsion
$X^{\Gamma }$
. By an application of the structure theorem for finitely generated torsion
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-modules, there is a pseudoisomorphism
$\mathbb {Z}_{p}[[\Gamma ]]$
-modules, there is a pseudoisomorphism
for some elements
![]() $f_{i}(T)\in \mathbb {Z}_{p}[[\Gamma ]]$
. The module
$f_{i}(T)\in \mathbb {Z}_{p}[[\Gamma ]]$
. The module
![]() $X_{\Gamma }$
may be identified with
$X_{\Gamma }$
may be identified with
![]() $X/TX$
and
$X/TX$
and
![]() $X^{\Gamma }$
is the kernel of the multiplication by T map
$X^{\Gamma }$
is the kernel of the multiplication by T map
![]() $\times T: X\rightarrow X$
. It is easy to see that the groups
$\times T: X\rightarrow X$
. It is easy to see that the groups
![]() $X_{\Gamma }$
and
$X_{\Gamma }$
and
![]() $X^{\Gamma }$
are finite precisely when
$X^{\Gamma }$
are finite precisely when
![]() $T\nmid f_{i}(T)$
for
$T\nmid f_{i}(T)$
for
![]() $i=1,\dots , m$
. Therefore,
$i=1,\dots , m$
. Therefore,
![]() $X_{\Gamma }$
and
$X_{\Gamma }$
and
![]() $X^{\Gamma }$
are finite precisely when
$X^{\Gamma }$
are finite precisely when
![]() $r_{M}=0$
.▪
$r_{M}=0$
.▪
The following lemma is a criterion for the truncated Euler characteristic to be well defined.
Lemma 3.3 Assume that M is a p-primary, discrete
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module. Let X be the Pontryagin dual of M. Assume that X is a finitely generated torsion
$\mathbb {Z}_{p}[[\Gamma ]]$
-module. Let X be the Pontryagin dual of M. Assume that X is a finitely generated torsion
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module. Denote by
$\mathbb {Z}_{p}[[\Gamma ]]$
-module. Denote by
![]() $X[p^{\infty }]$
the
$X[p^{\infty }]$
the
![]() $p^{\infty }$
-torsion submodule of X. Let
$p^{\infty }$
-torsion submodule of X. Let
![]() $f_{1}(T), \dots , f_{n}(T)$
be distinguished polynomials such that
$f_{1}(T), \dots , f_{n}(T)$
be distinguished polynomials such that
![]() $X/X[p^{\infty }]$
is pseudo-isomorphic to
$X/X[p^{\infty }]$
is pseudo-isomorphic to
![]() $\bigoplus _{i=1}^{n} \mathbb {Z}_{p}[[T]]/(f_{i}(T))$
. Suppose that none of the polynomials
$\bigoplus _{i=1}^{n} \mathbb {Z}_{p}[[T]]/(f_{i}(T))$
. Suppose that none of the polynomials
![]() $f_{i}(T)$
is divisible by
$f_{i}(T)$
is divisible by
![]() $T^{2}$
. Then, the kernel and cokernel of
$T^{2}$
. Then, the kernel and cokernel of
![]() $\phi _{M}$
are finite and the truncated Euler characteristic
$\phi _{M}$
are finite and the truncated Euler characteristic
![]() $\chi _{t}(\Gamma , M)$
is defined. In particular, the truncated Euler characteristic
$\chi _{t}(\Gamma , M)$
is defined. In particular, the truncated Euler characteristic
![]() $\chi _{t}(\Gamma , M)$
is defined when
$\chi _{t}(\Gamma , M)$
is defined when
![]() $r_{M}\leq 1$
.
$r_{M}\leq 1$
.
Proof The assertion of the lemma follows from the proof of [Reference Zerbes37, Lemma 2.11].▪
Let
![]() $|\cdot |_{p}$
denote the absolute value on
$|\cdot |_{p}$
denote the absolute value on
![]() $\mathbb {Q}_{p}$
normalized by
$\mathbb {Q}_{p}$
normalized by
![]() $|p|_{p}=p^{-1}$
. When both
$|p|_{p}=p^{-1}$
. When both
![]() $\operatorname {ker}(\phi _{M})$
and
$\operatorname {ker}(\phi _{M})$
and
![]() $\operatorname {cok}(\phi _{M})$
are finite, the truncated Euler characteristic
$\operatorname {cok}(\phi _{M})$
are finite, the truncated Euler characteristic
![]() $\chi _{t}(\Gamma , M)$
is related to the quantity
$\chi _{t}(\Gamma , M)$
is related to the quantity
![]() $|g_{M}(0)|_{p}$
.
$|g_{M}(0)|_{p}$
.
Lemma 3.4 Let M be a discrete
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
module which is cofinitely generated and cotorsion. If the kernel and cokernel of
$\mathbb {Z}_{p}[[\Gamma ]]$
module which is cofinitely generated and cotorsion. If the kernel and cokernel of
![]() $\phi _{M}$
are finite, then
$\phi _{M}$
are finite, then
and further,
![]() $r_{M}=\operatorname {cork}_{\mathbb {Z}_{p}} M^{\Gamma }=\operatorname {cork}_{\mathbb {Z}_{p}} M_{\Gamma }$
.
$r_{M}=\operatorname {cork}_{\mathbb {Z}_{p}} M^{\Gamma }=\operatorname {cork}_{\mathbb {Z}_{p}} M_{\Gamma }$
.
Proof The assertion follows from [Reference Zerbes37, Lemma 2.11].▪
Evidently, it follows that
![]() $\chi _{t}(\Gamma , M)=p^{N}$
, where
$\chi _{t}(\Gamma , M)=p^{N}$
, where
![]() $N\in \mathbb {Z}_{\geq 0}$
. Let
$N\in \mathbb {Z}_{\geq 0}$
. Let
![]() $\mu _{M}$
(resp.
$\mu _{M}$
(resp.
![]() $\lambda _{M}$
) denote its
$\lambda _{M}$
) denote its
![]() $\mu $
-invariant (resp.
$\mu $
-invariant (resp.
![]() $\lambda $
-invariant) of
$\lambda $
-invariant) of
![]() $M^{\vee }$
as a
$M^{\vee }$
as a
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module.
$\mathbb {Z}_{p}[[\Gamma ]]$
-module.
Lemma 3.5 Let M be a cofinitely generated cotorsion
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module such that
$\mathbb {Z}_{p}[[\Gamma ]]$
-module such that
![]() $\phi _{M}:M^{\Gamma }\rightarrow M_{\Gamma }$
has finite kernel and cokernel. Then, the following are equivalent:
$\phi _{M}:M^{\Gamma }\rightarrow M_{\Gamma }$
has finite kernel and cokernel. Then, the following are equivalent:
-
(a)
 $\chi _{t}(\Gamma , M)=1$
and
$\chi _{t}(\Gamma , M)=1$
and -
(b)
 $\mu _{M}=0$
and
$\mu _{M}=0$
and
 $\lambda _{M}=r_{M}$
.
$\lambda _{M}=r_{M}$
.
Proof Suppose that
![]() $\chi _{t}(\Gamma , M)=1$
. Recall that
$\chi _{t}(\Gamma , M)=1$
. Recall that
![]() $g_{M}(T)$
is a polynomial such that
$g_{M}(T)$
is a polynomial such that
![]() $f_{M}(T)=T^{r_{M}} g_{M}(T)$
and
$f_{M}(T)=T^{r_{M}} g_{M}(T)$
and
![]() $T\nmid g_{M}(T)$
. By Lemma 3.4,
$T\nmid g_{M}(T)$
. By Lemma 3.4,
As a result,
![]() $f_{M}(T)$
and
$f_{M}(T)$
and
![]() $g_{M}(T)$
are distinguished polynomials. Since
$g_{M}(T)$
are distinguished polynomials. Since
![]() $g_{M}(0)$
is a unit, it follows that
$g_{M}(0)$
is a unit, it follows that
![]() $g_{M}(T)$
is a unit. Since
$g_{M}(T)$
is a unit. Since
![]() $g_{M}(T)$
is a distinguished polynomial, it follows that
$g_{M}(T)$
is a distinguished polynomial, it follows that
As a result,
![]() $\mu _{M}=1$
and
$\mu _{M}=1$
and
![]() $\lambda _{M}=\operatorname {deg} f_{M}(T)=r_{M}$
.
$\lambda _{M}=\operatorname {deg} f_{M}(T)=r_{M}$
.
Conversely, suppose that
![]() $\mu _{M}=0$
and
$\mu _{M}=0$
and
![]() $\lambda _{M}=r_{M}$
. Since
$\lambda _{M}=r_{M}$
. Since
![]() $\mu _{M}=0$
, it follows that
$\mu _{M}=0$
, it follows that
![]() $f_{M}(T)$
and
$f_{M}(T)$
and
![]() $g_{M}(T)$
are distinguished polynomials. The degree of
$g_{M}(T)$
are distinguished polynomials. The degree of
![]() $f_{M}(T)$
is
$f_{M}(T)$
is
![]() $\lambda _{M}=r_{M}$
, it follows that
$\lambda _{M}=r_{M}$
, it follows that
![]() $g_{M}(T)$
is a constant polynomial and hence,
$g_{M}(T)$
is a constant polynomial and hence,
![]() $g_{M}(T)=1$
. By Lemma 3.4,
$g_{M}(T)=1$
. By Lemma 3.4,
▪
Let
![]() $r_{E}^{\ddagger }$
denote the order of vanishing of
$r_{E}^{\ddagger }$
denote the order of vanishing of
![]() $f_{E}^{\ddagger }(T)$
at
$f_{E}^{\ddagger }(T)$
at
![]() $T=0$
, and write
$T=0$
, and write
Note that
![]() $g_{E}^{\ddagger }(0)\neq 0$
. According to Lemma 3.4, the truncated Euler characteristic
$g_{E}^{\ddagger }(0)\neq 0$
. According to Lemma 3.4, the truncated Euler characteristic
![]() $\chi _{t}^{\ddagger }(\Gamma , E):=\chi _{t}(\Gamma , \operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}}))$
is determined by the constant term of
$\chi _{t}^{\ddagger }(\Gamma , E):=\chi _{t}(\Gamma , \operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}}))$
is determined by the constant term of
![]() $g_{E}^{\ddagger }(T)$
. By Lemma 3.5, if the truncated Euler characteristic is defined (in the sense of Definition 3.1), then
$g_{E}^{\ddagger }(T)$
. By Lemma 3.5, if the truncated Euler characteristic is defined (in the sense of Definition 3.1), then
![]() $\chi _{t}^{\ddagger }(\Gamma , E)=1$
if and only if
$\chi _{t}^{\ddagger }(\Gamma , E)=1$
if and only if
![]() $\mu _{E}^{\ddagger }=0$
and
$\mu _{E}^{\ddagger }=0$
and
![]() $\lambda _{E}^{\ddagger }=r_{E}^{\ddagger }$
.
$\lambda _{E}^{\ddagger }=r_{E}^{\ddagger }$
.
We next discuss the p-adic Birch and Swinnerton-Dyer conjecture and its relationship with explicit formulas for truncated Euler characteristics. Note that there are formulations of the p-adic Birch and Swinnerton-Dyer conjecture in very general contexts (see for instance [Reference Rubin31, p. 6]). For ease of exposition, we restrict ourselves to the case where the elliptic curves E are defined over
![]() $\mathbb {Q}$
. For elliptic curves with good ordinary or multiplicative reduction, the p-adic Birch and Swinnerton-Dyer conjecture in its current form was formulated by Mazur et al. [Reference Mazur, Tate and Teitelbaum24, p. 38]. This is a p-adic analog of the classical Birch and Swinnerton-Dyer conjecture which predicts the order of vanishing of the Mazur and Swinnerton-Dyer p-adic L-function
$\mathbb {Q}$
. For elliptic curves with good ordinary or multiplicative reduction, the p-adic Birch and Swinnerton-Dyer conjecture in its current form was formulated by Mazur et al. [Reference Mazur, Tate and Teitelbaum24, p. 38]. This is a p-adic analog of the classical Birch and Swinnerton-Dyer conjecture which predicts the order of vanishing of the Mazur and Swinnerton-Dyer p-adic L-function
![]() $\mathcal {L}(E/\mathbb {Q},T)$
at
$\mathcal {L}(E/\mathbb {Q},T)$
at
![]() $T=0$
, and postulates an explicit formula for the leading term (see also [Reference Bernardi and Perrin-Riou1]). When E has good supersingular reduction at p, a version of the p-adic Birch and Swinnerton-Dyer conjecture for signed p-adic L-functions was formulated by Sprung [Reference Sprung35]. The conjecture of loc. cit. is equivalent to that of Bernardi and Perrin-Riou [Reference Bernardi and Perrin-Riou1]. Lemma 3.4 asserts that the truncated Euler-characteristic is related to the leading coefficient of the characteristic element of the Selmer group. The main conjecture and the p-adic Birch and Swinnerton-Dyer conjecture together predict precise formulas for the truncated Euler characteristic.
$T=0$
, and postulates an explicit formula for the leading term (see also [Reference Bernardi and Perrin-Riou1]). When E has good supersingular reduction at p, a version of the p-adic Birch and Swinnerton-Dyer conjecture for signed p-adic L-functions was formulated by Sprung [Reference Sprung35]. The conjecture of loc. cit. is equivalent to that of Bernardi and Perrin-Riou [Reference Bernardi and Perrin-Riou1]. Lemma 3.4 asserts that the truncated Euler-characteristic is related to the leading coefficient of the characteristic element of the Selmer group. The main conjecture and the p-adic Birch and Swinnerton-Dyer conjecture together predict precise formulas for the truncated Euler characteristic.
Assume that E has either good ordinary or multiplicative reduction at p. When E has split multiplicative reduction at p, set
![]() $\mathcal {L}_{p}(E)$
to denote the
$\mathcal {L}_{p}(E)$
to denote the
![]() $\mathcal {L}$
-invariant associated to the Galois representation on the p-adic Tate module of E (see [Reference Greenberg and Vatsal8, p. 407]). The p-adic height pairing (cf. [Reference Schneider32] and [Reference Schneider33]) is a p-adic analog of the usual height pairing. This pairing is conjectured to be non-degenerate (cf. [Reference Schneider33]) and the p-adic regulator
$\mathcal {L}$
-invariant associated to the Galois representation on the p-adic Tate module of E (see [Reference Greenberg and Vatsal8, p. 407]). The p-adic height pairing (cf. [Reference Schneider32] and [Reference Schneider33]) is a p-adic analog of the usual height pairing. This pairing is conjectured to be non-degenerate (cf. [Reference Schneider33]) and the p-adic regulator
![]() $R_{p}(E/\mathbb {Q})$
is defined to be the determinant of this pairing. Let
$R_{p}(E/\mathbb {Q})$
is defined to be the determinant of this pairing. Let
![]() $\kappa $
denote the p-adic cyclotomic character. Fix a branch of the p-adic logarithm and set
$\kappa $
denote the p-adic cyclotomic character. Fix a branch of the p-adic logarithm and set
![]() $\mathcal {R}_{\gamma }(E/\mathbb {Q})$
to denote the normalized height pairing
$\mathcal {R}_{\gamma }(E/\mathbb {Q})$
to denote the normalized height pairing
![]() $(\log _{p}\kappa (\gamma ))^{-r} R_{p}(E/\mathbb {Q})$
, where r denotes the rank of the Mordell Weil group
$(\log _{p}\kappa (\gamma ))^{-r} R_{p}(E/\mathbb {Q})$
, where r denotes the rank of the Mordell Weil group
![]() $E(\mathbb {Q})$
. Let
$E(\mathbb {Q})$
. Let
![]() $E_{0}(\mathbb {Q}_{l})\subset E(\mathbb {Q}_{l})$
be the subgroup of l-adic points with nonsingular reduction modulo l. Denote by
$E_{0}(\mathbb {Q}_{l})\subset E(\mathbb {Q}_{l})$
be the subgroup of l-adic points with nonsingular reduction modulo l. Denote by
![]() $\mathcal {\tau }(E)$
the Tamagawa product
$\mathcal {\tau }(E)$
the Tamagawa product
![]() $\prod _{l} c_{l}$
, where
$\prod _{l} c_{l}$
, where
![]() $c_{l}$
is the index of
$c_{l}$
is the index of
![]() $E_{0}(\mathbb {Q}_{l})$
in
$E_{0}(\mathbb {Q}_{l})$
in
![]() $E(\mathbb {Q}_{l})$
. Let
$E(\mathbb {Q}_{l})$
. Let
![]() $a_{l}(E)$
be the lth coefficient of the normalized eigenform associated to E. For p-adic numbers a and b, write
$a_{l}(E)$
be the lth coefficient of the normalized eigenform associated to E. For p-adic numbers a and b, write
![]() $a\sim b$
if
$a\sim b$
if
![]() $a=ub$
for a p-adic unit u. Let
$a=ub$
for a p-adic unit u. Let
![]() $r^{\prime }$
be the order of vanishing at
$r^{\prime }$
be the order of vanishing at
![]() $T=0$
of the characteristic element of the Selmer group
$T=0$
of the characteristic element of the Selmer group
![]() $\operatorname {Sel}(E/\mathbb {Q}_{\operatorname {cyc}})$
. The following result does not assume the main conjecture.
$\operatorname {Sel}(E/\mathbb {Q}_{\operatorname {cyc}})$
. The following result does not assume the main conjecture.
Theorem 3.6 (Perrin-Riou [Reference Perrin-Riou27], Schneider [Reference Schneider33], Jones [Reference Jones11])
Suppose that E has either good ordinary reduction or multiplicative reduction at p. Assume that
-
(1) the p-adic regulator
 $R_{p}(E/\mathbb {Q})$
is non-zero and
$R_{p}(E/\mathbb {Q})$
is non-zero and -
(2)
 has finite cardinality.
has finite cardinality.
Then, the following assertions are true:
-
(a) If E has either good ordinary reduction or non-split multiplicative reduction at p, then
 $r^{\prime }=r$
. If E has split multiplicative reduction at p, then
$r^{\prime }=r$
. If E has split multiplicative reduction at p, then
 $r^{\prime }=r+1$
.
$r^{\prime }=r+1$
. -
(b) Assume further that the truncated Euler-characteristic
 $\chi _{t}(\Gamma , E)$
is defined (in the sense of Definition 3.1). If E has either good ordinary reduction at p or nonsplit multiplicative reduction at p, then Here,
$\chi _{t}(\Gamma , E)$
is defined (in the sense of Definition 3.1). If E has either good ordinary reduction at p or nonsplit multiplicative reduction at p, then Here,
 $\epsilon _{p}(E)$
is set to be
$\epsilon _{p}(E)$
is set to be
 $(1-\frac {1}{\alpha })^{s}$
, where
$(1-\frac {1}{\alpha })^{s}$
, where
 $\alpha $
is the unit root of the Hecke polynomial
$\alpha $
is the unit root of the Hecke polynomial
 $X^{2}-a_{p}(E) X+p$
and
$X^{2}-a_{p}(E) X+p$
and  $$ \begin{align*}s=\begin{cases}s=2 \quad \text{if }E\text{ has good ordinary reduction at }p,\\ s=1 \quad \text{if }E\text{ has non-split multiplicative reduction at }\textit{p}. \end{cases}\end{align*} $$
$$ \begin{align*}s=\begin{cases}s=2 \quad \text{if }E\text{ has good ordinary reduction at }p,\\ s=1 \quad \text{if }E\text{ has non-split multiplicative reduction at }\textit{p}. \end{cases}\end{align*} $$
-
(c) If E has split-multiplicative reduction, the
 $\mathcal {L}$
-invariant
$\mathcal {L}$
-invariant
 $\mathcal {L}_{p}(E)$
plays a role and we have
$\mathcal {L}_{p}(E)$
plays a role and we have 
4 Iwasawa invariants of congruent elliptic curves
In this section, we show that the imprimitive Iwasawa-invariants associated to congruent elliptic curves satisfy certain relations. Throughout, E is an elliptic curve over F which satisfies Hypothesis (2.1). Denote by
![]() $T_{p}(E):=\varprojlim _{n} E[p^{n}]$
the p-adic Tate-module equipped with natural
$T_{p}(E):=\varprojlim _{n} E[p^{n}]$
the p-adic Tate-module equipped with natural
![]() $\operatorname {Gal}(\overline {F}/F)$
action and set
$\operatorname {Gal}(\overline {F}/F)$
action and set
![]() $V_{p}(E):=T_{p} (E)\otimes \mathbb {Q}_{p}$
. At a prime
$V_{p}(E):=T_{p} (E)\otimes \mathbb {Q}_{p}$
. At a prime
![]() $v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}(E)$
, recall that there are corank one
$v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}(E)$
, recall that there are corank one
![]() $\mathbb {Z}_{p}$
-modules which fit into a short exact sequence
$\mathbb {Z}_{p}$
-modules which fit into a short exact sequence
When E has good ordinary reduction at v, the quotient
![]() $D_{v}$
may be identified with
$D_{v}$
may be identified with
![]() $\widetilde {E}_{v}[p^{\infty }]$
, where
$\widetilde {E}_{v}[p^{\infty }]$
, where
![]() $\widetilde {E}_{v}$
is the reduction of E at v. On the other hand, when E has multiplicative reduction at v, identify
$\widetilde {E}_{v}$
is the reduction of E at v. On the other hand, when E has multiplicative reduction at v, identify
![]() $D_{v}$
with a twist of
$D_{v}$
with a twist of
![]() $\mathbb {Q}_{p}/\mathbb {Z}_{p}$
by an unramified quadratic character.
$\mathbb {Q}_{p}/\mathbb {Z}_{p}$
by an unramified quadratic character.
Hypothesis 4.1 Let E be an elliptic curve over F which satisfies Hypothesis (2.1). Let
![]() $\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
be the set of primes
$\Sigma _{\operatorname {ss}}(E)=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
be the set of primes
![]() $v|p$
of F at which E has supersingular reduction. Let
$v|p$
of F at which E has supersingular reduction. Let
![]() $\ddagger \in \{+,-\}^{d}$
be a signed vector. Then
$\ddagger \in \{+,-\}^{d}$
be a signed vector. Then
![]() $(E, \ddagger )$
satisfies the following conditions:
$(E, \ddagger )$
satisfies the following conditions:
-
(1) The Selmer group
 $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
 $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion.
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion. -
(2) The truncated Euler characteristic
 $\chi _{t}^{\ddagger }(\Gamma , E)$
is defined. In other words, the natural map has finite kernel and cokernel.
$\chi _{t}^{\ddagger }(\Gamma , E)$
is defined. In other words, the natural map has finite kernel and cokernel. $$ \begin{align*}\phi_{E}^{\ddagger}: \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})^{\Gamma}\rightarrow \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})_{\Gamma}\end{align*} $$
$$ \begin{align*}\phi_{E}^{\ddagger}: \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})^{\Gamma}\rightarrow \operatorname{Sel}^{\ddagger}(E/F^{\operatorname{cyc}})_{\Gamma}\end{align*} $$
Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be p-congruent elliptic curves over F. It follows from the proof of [Reference Nuccio and Sujatha25, Proposition 3.9] that
$E_{2}$
be p-congruent elliptic curves over F. It follows from the proof of [Reference Nuccio and Sujatha25, Proposition 3.9] that
![]() $\Sigma _{\operatorname {ss}}(E_{1})$
is equal to
$\Sigma _{\operatorname {ss}}(E_{1})$
is equal to
![]() $\Sigma _{\operatorname {ss}}(E_{2})$
. Set
$\Sigma _{\operatorname {ss}}(E_{2})$
. Set
![]() $\Sigma _{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
to denote the set of supersingular primes
$\Sigma _{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
to denote the set of supersingular primes
![]() $v|p$
of
$v|p$
of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, and let
$E_{2}$
, and let
![]() $\ddagger \in \{+,-\}^{d}$
be a signed vector. We introduce the following hypothesis on the triple
$\ddagger \in \{+,-\}^{d}$
be a signed vector. We introduce the following hypothesis on the triple
![]() $(E_{1},E_{2},\ddagger )$
.
$(E_{1},E_{2},\ddagger )$
.
Hypothesis 4.2 Hypothesis (4.1) holds for both
![]() $(E_{1},\ddagger )$
and
$(E_{1},\ddagger )$
and
![]() $(E_{2},\ddagger )$
.
$(E_{2},\ddagger )$
.
We now define the imprimitive Selmer group associated to the residual Galois representation
![]() $E_{i}[p]$
. Let
$E_{i}[p]$
. Let
![]() $\Sigma $
be a set of finite primes of F containing
$\Sigma $
be a set of finite primes of F containing
![]() $\Sigma _{p}$
and the primes at which
$\Sigma _{p}$
and the primes at which
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. For a prime
$E_{2}$
has bad reduction. For a prime
![]() $v\in \Sigma _{p}$
let
$v\in \Sigma _{p}$
let
![]() $\eta _{v}$
be the unique prime of
$\eta _{v}$
be the unique prime of
![]() $F^{\operatorname {cyc}}$
above v. Let
$F^{\operatorname {cyc}}$
above v. Let
![]() $\operatorname {I}_{\eta _{v}}$
be the inertia subgroup of
$\operatorname {I}_{\eta _{v}}$
be the inertia subgroup of
![]() $\operatorname {Gal}(\overline {F_{\eta _{v}}^{\operatorname {cyc}}}/F_{\eta _{v}}^{\operatorname {cyc}})$
. For a prime
$\operatorname {Gal}(\overline {F_{\eta _{v}}^{\operatorname {cyc}}}/F_{\eta _{v}}^{\operatorname {cyc}})$
. For a prime
![]() $v\in \Sigma _{\operatorname {ss}}$
, and
$v\in \Sigma _{\operatorname {ss}}$
, and
![]() $i=1,2$
, define
$i=1,2$
, define
 $$ \begin{align*} \mathcal{H}_{v}^{\pm}(F^{\operatorname{cyc}},E_{i}[p]):=\frac{H^{1}(F^{\operatorname{cyc}}_{\eta_{v}}, E_{i}[p])}{\widehat{E}_{i}^{\pm}(F^{\operatorname{cyc}}_{\eta_{v}})/p\widehat{E}_{i}^{\pm}(F^{\operatorname{cyc}}_{\eta_{v}})}. \end{align*} $$
$$ \begin{align*} \mathcal{H}_{v}^{\pm}(F^{\operatorname{cyc}},E_{i}[p]):=\frac{H^{1}(F^{\operatorname{cyc}}_{\eta_{v}}, E_{i}[p])}{\widehat{E}_{i}^{\pm}(F^{\operatorname{cyc}}_{\eta_{v}})/p\widehat{E}_{i}^{\pm}(F^{\operatorname{cyc}}_{\eta_{v}})}. \end{align*} $$
For
![]() $v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
, set
$v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
, set
 $$ \begin{align*}\mathcal{H}_{v}(F^{\operatorname{cyc}},E_{i}[p]):=\begin{cases}\prod_{\eta| v} H^{1}(F^{\operatorname{cyc}}_{\eta}, E_{i}[p])\quad \text{if }v\in \Sigma\backslash \Sigma_{p},\\ H^{1}(\operatorname{I}_{\eta_{v}}, D_{v}(E_{i})[p])\quad \text{if }v\in \Sigma_{p}\backslash \Sigma_{\operatorname{ss}}. \end{cases}\end{align*} $$
$$ \begin{align*}\mathcal{H}_{v}(F^{\operatorname{cyc}},E_{i}[p]):=\begin{cases}\prod_{\eta| v} H^{1}(F^{\operatorname{cyc}}_{\eta}, E_{i}[p])\quad \text{if }v\in \Sigma\backslash \Sigma_{p},\\ H^{1}(\operatorname{I}_{\eta_{v}}, D_{v}(E_{i})[p])\quad \text{if }v\in \Sigma_{p}\backslash \Sigma_{\operatorname{ss}}. \end{cases}\end{align*} $$
For an elliptic curve E over F, denote by
![]() $\mathcal {N}_{E}$
the conductor of E and
$\mathcal {N}_{E}$
the conductor of E and
![]() $\overline {\mathcal {N}}_{E}$
the prime to p part of the Artin conductor of the residual representation
$\overline {\mathcal {N}}_{E}$
the prime to p part of the Artin conductor of the residual representation
![]() $E[p]$
. Let
$E[p]$
. Let
![]() $v\nmid p$
be a finite prime of F. Note that v divides
$v\nmid p$
be a finite prime of F. Note that v divides
![]() $\mathcal {N}_{E}$
(resp.
$\mathcal {N}_{E}$
(resp.
![]() $\overline {\mathcal {N}}_{E}$
) is and only if it is a bad reduction prime of E (resp. the residual Galois representation
$\overline {\mathcal {N}}_{E}$
) is and only if it is a bad reduction prime of E (resp. the residual Galois representation
![]() $E[p]$
is ramified at v). To ease notation, let
$E[p]$
is ramified at v). To ease notation, let
![]() $\mathcal {N}_{1}$
and
$\mathcal {N}_{1}$
and
![]() $\mathcal {N}_{2}$
denote the conductors of
$\mathcal {N}_{2}$
denote the conductors of
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, respectively. Denote by
$E_{2}$
, respectively. Denote by
![]() $\overline {\mathcal {N}}$
the prime to p part of the Artin conductor of
$\overline {\mathcal {N}}$
the prime to p part of the Artin conductor of
![]() $E_{1}[p]$
. Note that since
$E_{1}[p]$
. Note that since
![]() $E_{1}[p]$
is isomorphic to
$E_{1}[p]$
is isomorphic to
![]() $E_{2}[p]$
,
$E_{2}[p]$
,
![]() $\overline {\mathcal {N}}$
is the conductor of
$\overline {\mathcal {N}}$
is the conductor of
![]() $E_{2}[p]$
.
$E_{2}[p]$
.
Definition 4.1 Let E be an elliptic curve over F. If
![]() $p\geq 5$
, let
$p\geq 5$
, let
![]() $\Sigma _{1}(E)$
denote the subset of primes of F such that
$\Sigma _{1}(E)$
denote the subset of primes of F such that
![]() $(\mathrm {i})\ v\nmid p$
,
$(\mathrm {i})\ v\nmid p$
,
![]() $(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
, and
$(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
, and
![]() $(\mathrm {iii})$
if
$(\mathrm {iii})$
if
![]() $\mu _{p}$
is contained in
$\mu _{p}$
is contained in
![]() $F_{v}$
, then E has split multiplicative reduction at v. In the case
$F_{v}$
, then E has split multiplicative reduction at v. In the case
![]() $p=3$
, set
$p=3$
, set
![]() $\Sigma _{1}(E)$
to be the set of primes of F such that
$\Sigma _{1}(E)$
to be the set of primes of F such that
![]() $(\mathrm {i}) \ v\nmid p$
,
$(\mathrm {i}) \ v\nmid p$
,
![]() $(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
.
$(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
.
The
![]() $\Sigma _{1}$
-imprimitive mod-p Selmer group
$\Sigma _{1}$
-imprimitive mod-p Selmer group
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}[p]/F^{\operatorname {cyc}})$
is defined to be the kernel of the restriction map:
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}[p]/F^{\operatorname {cyc}})$
is defined to be the kernel of the restriction map:
 $$ \begin{align*}\overline{\Phi}_{E_{i}}^{\Sigma_{1},\ddagger}:H^{1}(F_{\Sigma}/F^{\operatorname{cyc}}, E_{i}[p])\rightarrow \prod_{\Sigma/(\Sigma_{\operatorname{ss}}\cup \Sigma_{1})} \mathcal{H}_{v}(F^{\operatorname{cyc}},E_{i}[p])\times \prod_{j=1}^{d}\mathcal{H}_{\mathfrak{p}_{j}}^{\ddagger_{j}}(F^{\operatorname{cyc}},E_{i}[p]).\end{align*} $$
$$ \begin{align*}\overline{\Phi}_{E_{i}}^{\Sigma_{1},\ddagger}:H^{1}(F_{\Sigma}/F^{\operatorname{cyc}}, E_{i}[p])\rightarrow \prod_{\Sigma/(\Sigma_{\operatorname{ss}}\cup \Sigma_{1})} \mathcal{H}_{v}(F^{\operatorname{cyc}},E_{i}[p])\times \prod_{j=1}^{d}\mathcal{H}_{\mathfrak{p}_{j}}^{\ddagger_{j}}(F^{\operatorname{cyc}},E_{i}[p]).\end{align*} $$
Proposition 4.2 Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be elliptic curves over F which are p-congruent. Let
$E_{2}$
be elliptic curves over F which are p-congruent. Let
![]() $\ddagger $
be a signed vector and assume that
$\ddagger $
be a signed vector and assume that
![]() $(E_{1},E_{2},\ddagger )$
satisfies Hypothesis (4.2). Let
$(E_{1},E_{2},\ddagger )$
satisfies Hypothesis (4.2). Let
![]() $\Sigma _{1}$
be the set of primes as in Definition 4.1. Then the isomorphism
$\Sigma _{1}$
be the set of primes as in Definition 4.1. Then the isomorphism
![]() $E_{1}[p]\simeq E_{2}[p]$
induces an isomorphism of Selmer groups
$E_{1}[p]\simeq E_{2}[p]$
induces an isomorphism of Selmer groups
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}[p]/F^{\operatorname {cyc}})\simeq \operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}[p]/F^{\operatorname {cyc}})$
.
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{1}[p]/F^{\operatorname {cyc}})\simeq \operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{2}[p]/F^{\operatorname {cyc}})$
.
Proof Let
![]() $\Phi :E_{1}[p]\xrightarrow {\sim } E_{2}[p]$
be a choice of isomorphism of Galois modules. Clearly,
$\Phi :E_{1}[p]\xrightarrow {\sim } E_{2}[p]$
be a choice of isomorphism of Galois modules. Clearly,
![]() $\Phi $
induces an isomorphism
$\Phi $
induces an isomorphism
![]() $H^{1}(F_{\Sigma }/F^{\operatorname {cyc}}, E_{1}[p])\xrightarrow {\sim } H^{1}(F_{\Sigma }/F^{\operatorname {cyc}}, E_{2}[p])$
. It suffices to show that for
$H^{1}(F_{\Sigma }/F^{\operatorname {cyc}}, E_{1}[p])\xrightarrow {\sim } H^{1}(F_{\Sigma }/F^{\operatorname {cyc}}, E_{2}[p])$
. It suffices to show that for
![]() $v\in \Sigma $
, the isomorphism
$v\in \Sigma $
, the isomorphism
![]() $\Phi :E_{1}[p]\xrightarrow {\sim } E_{2}[p]$
induces an isomorphism
$\Phi :E_{1}[p]\xrightarrow {\sim } E_{2}[p]$
induces an isomorphism
This is clear for
![]() $v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
. For
$v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
. For
![]() $v\in \Sigma _{\operatorname {ss}}$
, this assertion follows from the arguments in [Reference Kim13, p. 186].▪
$v\in \Sigma _{\operatorname {ss}}$
, this assertion follows from the arguments in [Reference Kim13, p. 186].▪
Proposition 4.3 Let E be an elliptic curve over F satisfying Hypothesis (2.1) and
![]() $\ddagger $
a signed vector. Let
$\ddagger $
a signed vector. Let
![]() $\Sigma _{0}$
be a finite set of primes
$\Sigma _{0}$
be a finite set of primes
![]() $v\nmid p$
containing
$v\nmid p$
containing
![]() $\Sigma _{1}(E)$
. Then, there is an isomorphism
$\Sigma _{1}(E)$
. Then, there is an isomorphism
Proof Let
![]() $\Sigma $
be a finite set of primes containing
$\Sigma $
be a finite set of primes containing
![]() $\Sigma _{0}$
, the primes at which E has bad reduction and
$\Sigma _{0}$
, the primes at which E has bad reduction and
![]() $\Sigma _{p}$
. We consider the diagram relating the two Selmer groups:
$\Sigma _{p}$
. We consider the diagram relating the two Selmer groups:

Since
![]() $\Gamma $
is pro-p and
$\Gamma $
is pro-p and
![]() $E[p]$
is an irreducible Galois module, clearly
$E[p]$
is an irreducible Galois module, clearly
Hence, we deduce that
![]() $H^{0}(F^{\operatorname {cyc}}, E[p^{\infty }])=0$
and have shown that g is an isomorphism.
$H^{0}(F^{\operatorname {cyc}}, E[p^{\infty }])=0$
and have shown that g is an isomorphism.
It only remains to show that h is injective. For
![]() $v\in \Sigma /(\Sigma _{\operatorname {ss}}(E)\cup \Sigma _{0})$
denote by
$v\in \Sigma /(\Sigma _{\operatorname {ss}}(E)\cup \Sigma _{0})$
denote by
![]() $h_{v}$
the natural map
$h_{v}$
the natural map
and for
![]() $v\in \Sigma _{\operatorname {ss}}(E)$
,
$v\in \Sigma _{\operatorname {ss}}(E)$
,
We show that the maps
![]() $h_{v}$
are injective for
$h_{v}$
are injective for
![]() $v\in \Sigma \backslash \Sigma _{0}$
. This has been shown in the proof of [Reference Greenberg and Vatsal8, Proposition 2.8] for
$v\in \Sigma \backslash \Sigma _{0}$
. This has been shown in the proof of [Reference Greenberg and Vatsal8, Proposition 2.8] for
![]() $v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}$
and in [Reference Kim13, Proposition 2.10] for
$v\in \Sigma _{p}\backslash \Sigma _{\operatorname {ss}}$
and in [Reference Kim13, Proposition 2.10] for
![]() $v\in \Sigma _{\operatorname {ss}}$
. Therefore, it remains to consider primes
$v\in \Sigma _{\operatorname {ss}}$
. Therefore, it remains to consider primes
![]() $v\in \Sigma \backslash (\Sigma _{0}\cup \Sigma _{p})$
.
$v\in \Sigma \backslash (\Sigma _{0}\cup \Sigma _{p})$
.
First consider the case when
![]() $p\geq 5$
. Recall that
$p\geq 5$
. Recall that
![]() $\Sigma _{1}(E)$
consists of primes of F such that
$\Sigma _{1}(E)$
consists of primes of F such that
![]() $(\mathrm {i}) \ v\nmid p$
,
$(\mathrm {i}) \ v\nmid p$
,
![]() $(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
, and
$(\mathrm {ii}) \ v|(\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
, and
![]() $(\mathrm {iii})$
if
$(\mathrm {iii})$
if
![]() $\mu _{p}$
is contained in
$\mu _{p}$
is contained in
![]() $F_{v}$
, then E has split multiplicative reduction at v. Since
$F_{v}$
, then E has split multiplicative reduction at v. Since
![]() $v\notin \Sigma _{0}$
, one of the above conditions is not satisfied. Since
$v\notin \Sigma _{0}$
, one of the above conditions is not satisfied. Since
![]() $v\notin \Sigma _{p}$
,
$v\notin \Sigma _{p}$
,
![]() $(\mathrm {i})$
is satisfied. Hence, there are two cases to consider:
$(\mathrm {i})$
is satisfied. Hence, there are two cases to consider:
-
(1)
 $(\mathrm {ii})$
is not satisfied and
$(\mathrm {ii})$
is not satisfied and -
(2)
 $(\mathrm {ii})$
is satisfied, but
$(\mathrm {ii})$
is satisfied, but
 $(\mathrm {iii})$
is not.
$(\mathrm {iii})$
is not.
First consider the case when
![]() $(\mathrm {ii})$
is not satisfied, i.e.,
$(\mathrm {ii})$
is not satisfied, i.e.,
![]() $v\nmid (\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
. In this case, the injectivity of
$v\nmid (\mathcal {N}_{E}/\overline {\mathcal {N}}_{E})$
. In this case, the injectivity of
![]() $h_{v}$
follows from the proof of [Reference Emerton, Pollack and Weston5, Lemma 4.1.2]. Next, consider the case when
$h_{v}$
follows from the proof of [Reference Emerton, Pollack and Weston5, Lemma 4.1.2]. Next, consider the case when
![]() $(\mathrm {ii})$
is satisfied, but
$(\mathrm {ii})$
is satisfied, but
![]() $(\mathrm {iii})$
is not. Since
$(\mathrm {iii})$
is not. Since
![]() $(\mathrm {ii})$
is satisfied,
$(\mathrm {ii})$
is satisfied,
![]() $v\mid \mathcal {N}_{E}$
, hence, E has bad reduction at v. Since
$v\mid \mathcal {N}_{E}$
, hence, E has bad reduction at v. Since
![]() $(\mathrm {iii})$
is not satisfied, it follows that
$(\mathrm {iii})$
is not satisfied, it follows that
![]() $\mu _{p}$
is contained in
$\mu _{p}$
is contained in
![]() $F_{v}$
and E has either non-split multiplicative reduction or additive reduction at v. In this case, the injectivity of
$F_{v}$
and E has either non-split multiplicative reduction or additive reduction at v. In this case, the injectivity of
![]() $h_{v}$
follows from [Reference Hachimori and Matsuno9, Proposition 5.1]. When
$h_{v}$
follows from [Reference Hachimori and Matsuno9, Proposition 5.1]. When
![]() $p=3$
, the injectivity of
$p=3$
, the injectivity of
![]() $h_{v}$
follows from the same reasoning as above.▪
$h_{v}$
follows from the same reasoning as above.▪
Proposition 4.4 Let E be an elliptic curve over a number field F and
![]() $\Sigma _{0}$
any finite set of primes
$\Sigma _{0}$
any finite set of primes
![]() $v\nmid p$
. Assume that:
$v\nmid p$
. Assume that:
![]() $(\mathrm {i}) \ E(F)[p]=0$
,
$(\mathrm {i}) \ E(F)[p]=0$
,
![]() $(\mathrm {ii}) \ \operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})$
is cotorsion as a
$(\mathrm {ii}) \ \operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})$
is cotorsion as a
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-module. Then the Selmer group
$\mathbb {Z}_{p}[[\Gamma ]]$
-module. Then the Selmer group
![]() $\operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})$
contains no proper finite index
$\operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})$
contains no proper finite index
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-submodules.
$\mathbb {Z}_{p}[[\Gamma ]]$
-submodules.
Proof We adapt the proof of [Reference Greenberg7, Proposition 4.14], which is due to Greenberg. Let
![]() $\Sigma $
be a finite set of primes containing
$\Sigma $
be a finite set of primes containing
![]() $\Sigma _{0}\cup \Sigma _{p}$
and the primes of E at which E has bad reduction. Consider the
$\Sigma _{0}\cup \Sigma _{p}$
and the primes of E at which E has bad reduction. Consider the
![]() $\Sigma _{0}\cup \Sigma _{p}$
-strict and relaxed Selmer groups:
$\Sigma _{0}\cup \Sigma _{p}$
-strict and relaxed Selmer groups:
 $$ \begin{align*} \operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}}):=\operatorname{ker}\left\{H^{1} (F_{\Sigma}/F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash (\Sigma_{0}\cup \Sigma_{p})} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}])\right\}, \end{align*} $$
$$ \begin{align*} \operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}}):=\operatorname{ker}\left\{H^{1} (F_{\Sigma}/F^{\operatorname{cyc}},E[p^{\infty}])\rightarrow \prod_{v\in \Sigma\backslash (\Sigma_{0}\cup \Sigma_{p})} \mathcal{H}_{v}(F^{\operatorname{cyc}}, E[p^{\infty}])\right\}, \end{align*} $$
 $$ \begin{align*} \operatorname{Sel}^{\operatorname{str}}(E/F^{\operatorname{cyc}}):= \operatorname{ker}\left\{\operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}})\rightarrow \prod_{v\in \Sigma_{0}\cup \Sigma_{p}} \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{Sel}^{\operatorname{str}}(E/F^{\operatorname{cyc}}):= \operatorname{ker}\left\{\operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}})\rightarrow \prod_{v\in \Sigma_{0}\cup \Sigma_{p}} \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, E[p^{\infty}])\right\}. \end{align*} $$
By Proposition 2.3, it follows that
 $$ \begin{align*} \operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}})/\operatorname{Sel}^{\Sigma_{0}, \ddagger} (E/F^{\operatorname{cyc}})\simeq \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
$$ \begin{align*} \operatorname{Sel}^{\operatorname{rel}}(E/F^{\operatorname{cyc}})/\operatorname{Sel}^{\Sigma_{0}, \ddagger} (E/F^{\operatorname{cyc}})\simeq \prod_{i=1}^{d} \mathcal{H}_{\mathfrak{p}_{i}}^{\ddagger_{i}}(F^{\operatorname{cyc}}, E[p^{\infty}]). \end{align*} $$
For
![]() $i=1,\dots , d$
, it follows from standard arguments (see the proof of [Reference Kim13, Proposition 2.11]) that
$i=1,\dots , d$
, it follows from standard arguments (see the proof of [Reference Kim13, Proposition 2.11]) that
![]() $ \mathcal {H}_{\mathfrak {p}_{i}}^{\ddagger _{i}}(F^{\operatorname {cyc}}, E[p^{\infty }])^{\vee }$
is isomorphic to
$ \mathcal {H}_{\mathfrak {p}_{i}}^{\ddagger _{i}}(F^{\operatorname {cyc}}, E[p^{\infty }])^{\vee }$
is isomorphic to
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
. By [Reference Greenberg and Vatsal8, Lemma 2.6], it suffices to show that
$\mathbb {Z}_{p}[[\Gamma ]]$
. By [Reference Greenberg and Vatsal8, Lemma 2.6], it suffices to show that
![]() $\operatorname {Sel}^{\operatorname {rel}} (E/F^{\operatorname {cyc}})$
has no proper finite index
$\operatorname {Sel}^{\operatorname {rel}} (E/F^{\operatorname {cyc}})$
has no proper finite index
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-submodules. Since
$\mathbb {Z}_{p}[[\Gamma ]]$
-submodules. Since
![]() $\operatorname {Sel}^{\operatorname {str}}(E/F^{\operatorname {cyc}})^{\vee }$
is a quotient of
$\operatorname {Sel}^{\operatorname {str}}(E/F^{\operatorname {cyc}})^{\vee }$
is a quotient of
![]() $\operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})^{\vee }$
, it is
$\operatorname {Sel}^{\Sigma _{0}, \ddagger } (E/F^{\operatorname {cyc}})^{\vee }$
, it is
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-torsion.
$\mathbb {Z}_{p}[[\Gamma ]]$
-torsion.
Recall that
![]() $\kappa $
denotes the p-adic cyclotomic character. For
$\kappa $
denotes the p-adic cyclotomic character. For
![]() $s\in \mathbb {Z}$
, let
$s\in \mathbb {Z}$
, let
![]() $A_{s}$
denote the twisted Galois module
$A_{s}$
denote the twisted Galois module
![]() $E[p^{\infty }]\otimes \kappa ^{s} $
. Since
$E[p^{\infty }]\otimes \kappa ^{s} $
. Since
![]() $E(F)[p]=0$
and
$E(F)[p]=0$
and
![]() $\Gamma $
is pro-p, it follows that
$\Gamma $
is pro-p, it follows that
![]() $E(F^{\operatorname {cyc}})[p]=0$
, and as a result,
$E(F^{\operatorname {cyc}})[p]=0$
, and as a result,
![]() $H^{0}(F^{\operatorname {cyc}}, A_{s})=0$
. Since
$H^{0}(F^{\operatorname {cyc}}, A_{s})=0$
. Since
![]() $\Gamma $
is pro-p it follows from standard arguments that
$\Gamma $
is pro-p it follows from standard arguments that
![]() $H^{0}(F, A_{s})=0$
for all s. For a subfield K of
$H^{0}(F, A_{s})=0$
for all s. For a subfield K of
![]() $F^{\operatorname {cyc}}$
, and v a prime of F which does not divide p, set
$F^{\operatorname {cyc}}$
, and v a prime of F which does not divide p, set
![]() $\mathcal {H}_{v}(K, A_{s})$
to be the product
$\mathcal {H}_{v}(K, A_{s})$
to be the product
![]() $\prod _{\eta |v} H^{1}(K_{\eta }, A_{s})/(A_{s}(K_{\eta })\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p})$
, where
$\prod _{\eta |v} H^{1}(K_{\eta }, A_{s})/(A_{s}(K_{\eta })\otimes \mathbb {Q}_{p}/\mathbb {Z}_{p})$
, where
![]() $\eta $
ranges the finitely many primes of K above v. Set
$\eta $
ranges the finitely many primes of K above v. Set
![]() $P^{\Sigma , \operatorname {rel}}(K, A_{s})$
to be the product
$P^{\Sigma , \operatorname {rel}}(K, A_{s})$
to be the product
and set
![]() $P^{\Sigma , \operatorname {str}}(K, A_{s})$
to be the product
$P^{\Sigma , \operatorname {str}}(K, A_{s})$
to be the product
Let
![]() $S_{A_{s}}^{\operatorname {rel}}(K)$
and
$S_{A_{s}}^{\operatorname {rel}}(K)$
and
![]() $S_{A_{s}}^{\operatorname {str}}(K)$
be the Selmer groups defined as follows
$S_{A_{s}}^{\operatorname {str}}(K)$
be the Selmer groups defined as follows
Since
![]() $\operatorname {Sel}^{\operatorname {str}}(E/F^{\operatorname {cyc}})$
is
$\operatorname {Sel}^{\operatorname {str}}(E/F^{\operatorname {cyc}})$
is
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion, we have that
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion, we have that
![]() $S_{A_{s}}^{\operatorname {str}}(F^{\operatorname {cyc}})^{\Gamma }$
is finite for all but finitely many values of s. Hence,
$S_{A_{s}}^{\operatorname {str}}(F^{\operatorname {cyc}})^{\Gamma }$
is finite for all but finitely many values of s. Hence,
![]() $S_{A_{s}}^{\operatorname {str}}(F)$
is finite for all but finitely many values of s. We set
$S_{A_{s}}^{\operatorname {str}}(F)$
is finite for all but finitely many values of s. We set
![]() $M=A_{s}$
, and in accordance with the proof of [Reference Greenberg7, Proposition 4.14],
$M=A_{s}$
, and in accordance with the proof of [Reference Greenberg7, Proposition 4.14],
![]() $M^{*}=A_{-s}$
. Denote by
$M^{*}=A_{-s}$
. Denote by
![]() $S_{M}(F)$
the Selmer group defined by the relaxed conditions
$S_{M}(F)$
the Selmer group defined by the relaxed conditions
![]() $S_{A_{s}}^{\operatorname {rel}}(F)$
and in accordance with the discussion on [Reference Greenberg7, p. 100],
$S_{A_{s}}^{\operatorname {rel}}(F)$
and in accordance with the discussion on [Reference Greenberg7, p. 100],
![]() $S_{M^{*}}(F)$
is the strict Selmer group
$S_{M^{*}}(F)$
is the strict Selmer group
![]() $S_{A_{-s}}^{\operatorname {str}}(F)$
. Let s be such that
$S_{A_{-s}}^{\operatorname {str}}(F)$
. Let s be such that
![]() $S_{M^{*}}(F)$
is finite. Since
$S_{M^{*}}(F)$
is finite. Since
![]() $S_{M^{*}}(F)$
is finite and
$S_{M^{*}}(F)$
is finite and
![]() $M^{*}(F)=0$
, it follows that the map
$M^{*}(F)=0$
, it follows that the map
![]() $H^{1}(F_{\Sigma }/F, M)\rightarrow P^{\Sigma , \operatorname {rel}}(K, M)$
is surjective (see [Reference Greenberg7, Proposition 4.13]). It follows from the proof of [Reference Greenberg7, Proposition 4.14] that
$H^{1}(F_{\Sigma }/F, M)\rightarrow P^{\Sigma , \operatorname {rel}}(K, M)$
is surjective (see [Reference Greenberg7, Proposition 4.13]). It follows from the proof of [Reference Greenberg7, Proposition 4.14] that
![]() $\operatorname {Sel}^{\operatorname {rel}} (E/F^{\operatorname {cyc}})$
has no proper finite index
$\operatorname {Sel}^{\operatorname {rel}} (E/F^{\operatorname {cyc}})$
has no proper finite index
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-submodules. This completes the proof.▪
$\mathbb {Z}_{p}[[\Gamma ]]$
-submodules. This completes the proof.▪
Recall that for
![]() $i=1,2$
, the
$i=1,2$
, the
![]() $\mu $
-invariant (resp.
$\mu $
-invariant (resp.
![]() $\lambda $
-invariant) of the Selmer group
$\lambda $
-invariant) of the Selmer group
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
is denoted by
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
is denoted by
![]() $\mu _{E_{i}}^{\Sigma _{1},\ddagger }$
(resp.
$\mu _{E_{i}}^{\Sigma _{1},\ddagger }$
(resp.
![]() $\lambda _{E_{i}}^{\Sigma _{1},\ddagger }$
).
$\lambda _{E_{i}}^{\Sigma _{1},\ddagger }$
).
Theorem 4.5 Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be elliptic curves over F which are p-congruent. Let
$E_{2}$
be elliptic curves over F which are p-congruent. Let
![]() $\ddagger $
be a signed vector and assume that
$\ddagger $
be a signed vector and assume that
![]() $(E_{1},E_{2},\ddagger )$
satisfies Hypothesis (4.2). Let
$(E_{1},E_{2},\ddagger )$
satisfies Hypothesis (4.2). Let
![]() $\Sigma _{1}$
be the set of primes as in Definition 4.1. Then the following assertions hold:
$\Sigma _{1}$
be the set of primes as in Definition 4.1. Then the following assertions hold:
-
(1) The
 $\mu $
-invariant
$\mu $
-invariant
 $\mu _{E_{1}}^{\Sigma _{1},\ddagger }$
is equal to zero if and only if
$\mu _{E_{1}}^{\Sigma _{1},\ddagger }$
is equal to zero if and only if
 $\mu _{E_{2}}^{\Sigma _{1},\ddagger }$
is equal to zero.
$\mu _{E_{2}}^{\Sigma _{1},\ddagger }$
is equal to zero. -
(2) If
 $\mu _{E_{1}}^{\Sigma _{1},\ddagger }=0$
(or equivalently
$\mu _{E_{1}}^{\Sigma _{1},\ddagger }=0$
(or equivalently
 $\mu _{E_{2}}^{\Sigma _{1},\ddagger }=0$
), then the
$\mu _{E_{2}}^{\Sigma _{1},\ddagger }=0$
), then the
 $\Sigma _{1}$
-imprimitive
$\Sigma _{1}$
-imprimitive
 $\lambda $
-invariants
$\lambda $
-invariants
 $\lambda _{E_{1}}^{\Sigma _{1},\ddagger }$
and
$\lambda _{E_{1}}^{\Sigma _{1},\ddagger }$
and
 $\lambda _{E_{2}}^{\Sigma _{1}, \ddagger }$
are equal.
$\lambda _{E_{2}}^{\Sigma _{1}, \ddagger }$
are equal.
Proof For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $M_{i}$
denote the Pontryagin dual of
$M_{i}$
denote the Pontryagin dual of
![]() $\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
. It follows from Propositions 4.2 and 4.3 that
$\operatorname {Sel}^{\Sigma _{1},\ddagger }(E_{i}/F^{\operatorname {cyc}})$
. It follows from Propositions 4.2 and 4.3 that
![]() $M_{1}/pM_{1}$
is isomorphic to
$M_{1}/pM_{1}$
is isomorphic to
![]() $M_{2}/pM_{2}$
. Note that
$M_{2}/pM_{2}$
. Note that
![]() $\mu _{E_{i}}^{\Sigma _{1},\ddagger }$
is equal to
$\mu _{E_{i}}^{\Sigma _{1},\ddagger }$
is equal to
![]() $0$
if and only if
$0$
if and only if
![]() $M_{i}/pM_{i}$
is finite. Thus, it follows that if
$M_{i}/pM_{i}$
is finite. Thus, it follows that if
![]() $\mu _{E_{1}}^{\Sigma _{1},\ddagger }$
is zero, then so is
$\mu _{E_{1}}^{\Sigma _{1},\ddagger }$
is zero, then so is
![]() $\mu _{E_{2}}^{\Sigma _{1},\ddagger }$
.
$\mu _{E_{2}}^{\Sigma _{1},\ddagger }$
.
Next, assume that
![]() $\mu _{E_{1}}^{\ddagger }$
and
$\mu _{E_{1}}^{\ddagger }$
and
![]() $\mu _{E_{2}}^{\ddagger }$
are both zero. Proposition 4.4 asserts that
$\mu _{E_{2}}^{\ddagger }$
are both zero. Proposition 4.4 asserts that
![]() $M_{i}$
contains no finite
$M_{i}$
contains no finite
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-submodules, and thus,
$\mathbb {Z}_{p}[[\Gamma ]]$
-submodules, and thus,
![]() $M_{i}$
is a free
$M_{i}$
is a free
![]() $\mathbb {Z}_{p}$
-module of rank equal to
$\mathbb {Z}_{p}$
-module of rank equal to
![]() $\lambda _{E_{i}}^{\Sigma _{1}, \ddagger }$
. Since
$\lambda _{E_{i}}^{\Sigma _{1}, \ddagger }$
. Since
![]() $M_{1}/pM_{1}$
is isomorphic to
$M_{1}/pM_{1}$
is isomorphic to
![]() $M_{2}/pM_{2}$
, it follows that
$M_{2}/pM_{2}$
, it follows that
![]() $\lambda _{E_{1}}^{\Sigma _{1}, \ddagger }$
is equal to
$\lambda _{E_{1}}^{\Sigma _{1}, \ddagger }$
is equal to
![]() $\lambda _{E_{2}}^{\Sigma _{1}, \ddagger }$
.▪
$\lambda _{E_{2}}^{\Sigma _{1}, \ddagger }$
.▪
5 Congruences for Euler characteristics
Consider elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
that are p-congruent and let
$E_{2}$
that are p-congruent and let
![]() $\Sigma ^{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
be the set of supersingular primes v of
$\Sigma ^{\operatorname {ss}}=\{\mathfrak {p}_{1},\dots , \mathfrak {p}_{d}\}$
be the set of supersingular primes v of
![]() $E_{1}$
such that
$E_{1}$
such that
![]() $v|p$
. As noted earlier, these are also the supersingular primes v of
$v|p$
. As noted earlier, these are also the supersingular primes v of
![]() $E_{2}$
such that
$E_{2}$
such that
![]() $v|p$
. Let
$v|p$
. Let
![]() $\ddagger \in \{+,-\}^{d}$
be a signed vector and assume that Hypothesis (4.2) is satisfied for the triple
$\ddagger \in \{+,-\}^{d}$
be a signed vector and assume that Hypothesis (4.2) is satisfied for the triple
![]() $(E_{1}, E_{2}, \ddagger )$
. Associated to
$(E_{1}, E_{2}, \ddagger )$
. Associated to
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
is the set of primes
$E_{2}$
is the set of primes
![]() $\Sigma _{1}$
, see Definition 4.1. In this section, it is shown that there is an explicit relationship between the multisigned Euler characteristics
$\Sigma _{1}$
, see Definition 4.1. In this section, it is shown that there is an explicit relationship between the multisigned Euler characteristics
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{1})$
and
$\chi _{t}^{\ddagger }(\Gamma , E_{1})$
and
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{2})$
.
$\chi _{t}^{\ddagger }(\Gamma , E_{2})$
.
Let E be an elliptic curve satisfying Hypothesis (2.1) and
![]() $\Sigma _{0}$
a finite set of primes
$\Sigma _{0}$
a finite set of primes
![]() $v\nmid p$
. Recall that
$v\nmid p$
. Recall that
![]() $r_{E}^{\ddagger }$
is the order of vanishing of the characteristic polynomial
$r_{E}^{\ddagger }$
is the order of vanishing of the characteristic polynomial
![]() $f_{E}^{\ddagger }(T)$
at
$f_{E}^{\ddagger }(T)$
at
![]() $T=0$
. The following Proposition shows that the quantity
$T=0$
. The following Proposition shows that the quantity
![]() $r_{E}^{\ddagger }$
is related to the Mordell Weil rank of E and the reduction type of E at the primes
$r_{E}^{\ddagger }$
is related to the Mordell Weil rank of E and the reduction type of E at the primes
![]() $v|p$
. The proof of the following result is based on an adaptation of the control theorem from the ordinary setting, see [Reference Mazur23].
$v|p$
. The proof of the following result is based on an adaptation of the control theorem from the ordinary setting, see [Reference Mazur23].
Proposition 5.1 Let E be as above and assume that the following two conditions are satisfied:
-
(i) the truncated Euler characteristic
 $\chi _{t}^{\ddagger }(\Gamma , E)$
is defined (in the sense of Definition 3.1).
$\chi _{t}^{\ddagger }(\Gamma , E)$
is defined (in the sense of Definition 3.1). -
(ii) The p-primary part of the Tate-Shafarevich group
 is finite.
is finite.
Let r be the Mordell-Weil rank of E and
![]() $\operatorname {sp}_{E}$
the number of primes
$\operatorname {sp}_{E}$
the number of primes
![]() $v|p$
at which E has split multiplicative reduction. Then, we have that
$v|p$
at which E has split multiplicative reduction. Then, we have that
![]() $r\leq r_{E}^{\ddagger }\leq r+\operatorname {sp}_{E}$
. In particular, if there are no primes
$r\leq r_{E}^{\ddagger }\leq r+\operatorname {sp}_{E}$
. In particular, if there are no primes
![]() $v\in \Sigma _{p}$
at which E has split multiplicative reduction, then
$v\in \Sigma _{p}$
at which E has split multiplicative reduction, then
![]() $r_{E}^{\ddagger }$
is equal to r.
$r_{E}^{\ddagger }$
is equal to r.
Proof Let
![]() $\Sigma $
be a finite set of primes containing
$\Sigma $
be a finite set of primes containing
![]() $\Sigma _{p}$
and the primes at which E has bad reduction. By Lemma 3.4, the multisigned rank
$\Sigma _{p}$
and the primes at which E has bad reduction. By Lemma 3.4, the multisigned rank
![]() $r_{E}^{\ddagger }$
is equal to the
$r_{E}^{\ddagger }$
is equal to the
![]() $\mathbb {Z}_{p}$
-corank of
$\mathbb {Z}_{p}$
-corank of
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})^{\Gamma }$
. We compare
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})^{\Gamma }$
. We compare
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})^{\Gamma }$
with the usual Selmer group
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})^{\Gamma }$
with the usual Selmer group
![]() $\operatorname {Sel}(E/F)$
. Let
$\operatorname {Sel}(E/F)$
. Let
![]() ${\Phi }_{E,F}: H^{1}(F_{\Sigma }/F, E[p^{\infty }])\rightarrow \prod _{v\in \Sigma } \mathcal {H}_{v}(F, E[p^{\infty }])$
be the defining map for the Selmer group
${\Phi }_{E,F}: H^{1}(F_{\Sigma }/F, E[p^{\infty }])\rightarrow \prod _{v\in \Sigma } \mathcal {H}_{v}(F, E[p^{\infty }])$
be the defining map for the Selmer group
![]() $\operatorname {Sel}(E/F)$
. Consider the fundamental diagram
$\operatorname {Sel}(E/F)$
. Consider the fundamental diagram

where the vertical maps are induced by restriction. Since
![]() $E(F)[p]=0$
and
$E(F)[p]=0$
and
![]() $\Gamma $
is pro-p, it follows that
$\Gamma $
is pro-p, it follows that
![]() $H^{0}(F^{\operatorname {cyc}}, E[p^{\infty }])=0$
. It follows from the inflation-restriction sequence that g is an isomorphism. Thus, we have the following short exact sequence:
$H^{0}(F^{\operatorname {cyc}}, E[p^{\infty }])=0$
. It follows from the inflation-restriction sequence that g is an isomorphism. Thus, we have the following short exact sequence:
It suffices to show that the kernel of h has corank less than or equal to
![]() $\operatorname {sp}_{E}$
. For
$\operatorname {sp}_{E}$
. For
![]() $v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
, let
$v\in \Sigma \backslash \Sigma _{\operatorname {ss}}$
, let
![]() $h_{v}^{\prime }$
denote the natural map
$h_{v}^{\prime }$
denote the natural map
For
![]() $\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}$
, set
$\mathfrak {p}_{i}\in \Sigma _{\operatorname {ss}}$
, set
![]() $h_{\mathfrak {p}_{i}}^{\prime }$
denotes the map
$h_{\mathfrak {p}_{i}}^{\prime }$
denotes the map
Let
![]() $h^{\prime }$
be the product of the maps
$h^{\prime }$
be the product of the maps
![]() $h_{v}^{\prime }$
as v ranges over
$h_{v}^{\prime }$
as v ranges over
![]() $\Sigma $
. Note that the kernel of h is contained in the kernel of
$\Sigma $
. Note that the kernel of h is contained in the kernel of
![]() $h^{\prime }$
. Let
$h^{\prime }$
. Let
![]() $\Sigma _{\operatorname {sp}}(E)$
be the set of primes
$\Sigma _{\operatorname {sp}}(E)$
be the set of primes
![]() $v|p$
at which E has split multiplicative reduction. We show that
$v|p$
at which E has split multiplicative reduction. We show that
![]() $\operatorname {ker} h_{v}^{\prime }$
is finite if
$\operatorname {ker} h_{v}^{\prime }$
is finite if
![]() $v\notin \Sigma _{\operatorname {sp}}(E)$
and of corank one for
$v\notin \Sigma _{\operatorname {sp}}(E)$
and of corank one for
![]() $v\in \Sigma _{\operatorname {sp}}(E)$
. For
$v\in \Sigma _{\operatorname {sp}}(E)$
. For
![]() $v\in \Sigma \backslash \Sigma _{p}$
, this follows from [Reference Coates and Sujatha4, Lemma 3.4], for
$v\in \Sigma \backslash \Sigma _{p}$
, this follows from [Reference Coates and Sujatha4, Lemma 3.4], for
![]() $v\in \Sigma _{p}$
at which E has good ordinary reduction, it follows from [Reference Coates and Sujatha4, Proposition 3.5]. Next consider the case where
$v\in \Sigma _{p}$
at which E has good ordinary reduction, it follows from [Reference Coates and Sujatha4, Proposition 3.5]. Next consider the case where
![]() $v|p$
and E has multiplicative reduction at v.
$v|p$
and E has multiplicative reduction at v.
The Galois representation of the local Galois group
![]() $\operatorname {G}_{F_{v}}$
on
$\operatorname {G}_{F_{v}}$
on
![]() $E[p]$
is of the form
$E[p]$
is of the form
 ${ \left (\!\!\! {\begin {array}{cc} {\varphi _{v} \kappa } & {\ast } \\ {} & {\varphi _{v}^{-1}} \\ \end {array} } \!\!\!\right )}$
, where
${ \left (\!\!\! {\begin {array}{cc} {\varphi _{v} \kappa } & {\ast } \\ {} & {\varphi _{v}^{-1}} \\ \end {array} } \!\!\!\right )}$
, where
![]() $\varphi _{v}$
is an unramified character. Let w be a prime of
$\varphi _{v}$
is an unramified character. Let w be a prime of
![]() $F^{\operatorname {cyc}}$
above v and let
$F^{\operatorname {cyc}}$
above v and let
![]() $\Gamma _{v}$
denote
$\Gamma _{v}$
denote
![]() $\operatorname {Gal}(F_{w}^{\operatorname {cyc}}/F_{v})$
. By Shapiro’s Lemma,
$\operatorname {Gal}(F_{w}^{\operatorname {cyc}}/F_{v})$
. By Shapiro’s Lemma,
 $$ \begin{align*} H^{0}\left(\Gamma, \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, D_{v})\right)\simeq H^{0}(\Gamma_{v}, H^{1}(F_{w}^{\operatorname{cyc}}, D_{v})). \end{align*} $$
$$ \begin{align*} H^{0}\left(\Gamma, \prod_{\eta|v} H^{1}(F_{\eta}^{\operatorname{cyc}}, D_{v})\right)\simeq H^{0}(\Gamma_{v}, H^{1}(F_{w}^{\operatorname{cyc}}, D_{v})). \end{align*} $$
The kernel of
![]() $h_{v}^{\prime }$
is contained in the kernel of the restriction map
$h_{v}^{\prime }$
is contained in the kernel of the restriction map
and by the inflation restriction sequence, the kernel of
![]() $h_{v}^{\prime }$
is contained in
$h_{v}^{\prime }$
is contained in
![]() $H^{1}(\Gamma _{v}, H^{0}(F_{w}^{\operatorname {cyc}},D_{v}))$
. When E has nonsplit multiplicative reduction at v, the character
$H^{1}(\Gamma _{v}, H^{0}(F_{w}^{\operatorname {cyc}},D_{v}))$
. When E has nonsplit multiplicative reduction at v, the character
![]() $\varphi _{v}$
is nontrivial and thus
$\varphi _{v}$
is nontrivial and thus
![]() $H^{0}(F_{v}, D_{v})=0$
. Since
$H^{0}(F_{v}, D_{v})=0$
. Since
![]() $\Gamma _{v}$
is pro-p, it follows that
$\Gamma _{v}$
is pro-p, it follows that
![]() $H^{0}(F_{w}^{\operatorname {cyc}},D_{v})=0$
when
$H^{0}(F_{w}^{\operatorname {cyc}},D_{v})=0$
when
![]() $\varphi _{v}\neq 1$
. On the other hand, when
$\varphi _{v}\neq 1$
. On the other hand, when
![]() $\varphi _{v}=1$
, the Galois action on
$\varphi _{v}=1$
, the Galois action on
![]() $H^{0}(F_{w}^{\operatorname {cyc}}, D_{v})\simeq \mathbb {Q}_{p}/\mathbb {Z}_{p}$
is trivial. As a result, the corank of
$H^{0}(F_{w}^{\operatorname {cyc}}, D_{v})\simeq \mathbb {Q}_{p}/\mathbb {Z}_{p}$
is trivial. As a result, the corank of
![]() $H^{1}(\Gamma _{v}, H^{0}(F_{w}^{\operatorname {cyc}}, D_{v}))$
is one when E has split multiplicative reduction at v.
$H^{1}(\Gamma _{v}, H^{0}(F_{w}^{\operatorname {cyc}}, D_{v}))$
is one when E has split multiplicative reduction at v.
Finally, consider the case when
![]() $v|p$
and E has supersingular reduction at v. In this case,
$v|p$
and E has supersingular reduction at v. In this case,
![]() $h_{v}^{\prime }$
is injective, as shown in the proof of [Reference Lei and Lim21, Theorem 5.3].
$h_{v}^{\prime }$
is injective, as shown in the proof of [Reference Lei and Lim21, Theorem 5.3].
Putting all this together, we have that
![]() $\operatorname {corank}_{\mathbb {Z}_{p}} \operatorname {ker} h\leq \operatorname {sp}_{E}$
, and thus, from the short exact sequence (5.1), we have
$\operatorname {corank}_{\mathbb {Z}_{p}} \operatorname {ker} h\leq \operatorname {sp}_{E}$
, and thus, from the short exact sequence (5.1), we have
Since it is assumed that
is finite, the result follows.▪
Remark 5.0.1 It is generally expected that for any signed vector
![]() $\ddagger $
, the order of vanishing
$\ddagger $
, the order of vanishing
![]() $r_{E}^{\ddagger }$
should equal the rank of
$r_{E}^{\ddagger }$
should equal the rank of
![]() $E(F)$
when E has good reduction at the primes above p. This can be verified through computation when
$E(F)$
when E has good reduction at the primes above p. This can be verified through computation when
![]() $F=\mathbb {Q}$
. The above result shows that if certain additional conditions are met, then this statement is indeed true. In particular, in the case when
$F=\mathbb {Q}$
. The above result shows that if certain additional conditions are met, then this statement is indeed true. In particular, in the case when
![]() $\operatorname {rank} E(F)=1$
(and
$\operatorname {rank} E(F)=1$
(and
![]() is finite), one should expect that
is finite), one should expect that
![]() $r_{E}^{\ddagger }=1$
as well. Assuming this, it follows from Lemma 3.3 that the truncated Euler characteristic is defined in this setting. Of course, in the rank zero setting, the truncated Euler characteristic matches the classical Euler characteristic which is defined if
$r_{E}^{\ddagger }=1$
as well. Assuming this, it follows from Lemma 3.3 that the truncated Euler characteristic is defined in this setting. Of course, in the rank zero setting, the truncated Euler characteristic matches the classical Euler characteristic which is defined if
![]() is finite. We believe that the conditions of Lemma 3.3 should always be satisfied for multisigned Selmer groups, however, this expectation has not been written down explicitly in any references that we are aware of.
is finite. We believe that the conditions of Lemma 3.3 should always be satisfied for multisigned Selmer groups, however, this expectation has not been written down explicitly in any references that we are aware of.
We now study congruences for truncated Euler characteristics. For
![]() $v\in \Sigma _{0}$
, set
$v\in \Sigma _{0}$
, set
![]() $h_{E}^{(v)}(T)$
to be the characteristic polynomial of the Pontryagin dual of
$h_{E}^{(v)}(T)$
to be the characteristic polynomial of the Pontryagin dual of
![]() $\mathcal {H}_{v}(F^{\operatorname {cyc}},E[p^{\infty }])$
. Since
$\mathcal {H}_{v}(F^{\operatorname {cyc}},E[p^{\infty }])$
. Since
![]() $ \operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
$ \operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion, it follows from Proposition 2.3 that there is a short exact sequence:
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion, it follows from Proposition 2.3 that there is a short exact sequence:
As a result, we arrive at the following relation:
Recall that
![]() $V_{p}(E)$
is the p-adic vector space
$V_{p}(E)$
is the p-adic vector space
![]() $T_{p}(E)\otimes \mathbb {Q}_{p}$
, equipped with
$T_{p}(E)\otimes \mathbb {Q}_{p}$
, equipped with
![]() $\operatorname {Gal}(\overline {F}/F)$
-action. Let
$\operatorname {Gal}(\overline {F}/F)$
-action. Let
![]() $P_{v}(E,T)$
denote the characteristic polynomial
$P_{v}(E,T)$
denote the characteristic polynomial
where
![]() $\operatorname {I}_{v}$
is the inertia group at v. For
$\operatorname {I}_{v}$
is the inertia group at v. For
![]() $s\in \mathbb {C}$
, set
$s\in \mathbb {C}$
, set
![]() $L_{v}(E,s)$
to denote
$L_{v}(E,s)$
to denote
![]() $P_{v}(E,Nv^{-s})^{-1}$
, where
$P_{v}(E,Nv^{-s})^{-1}$
, where
![]() $Nv$
denotes the norm
$Nv$
denotes the norm
![]() $N_{L/\mathbb {Q}}v$
. Recall that
$N_{L/\mathbb {Q}}v$
. Recall that
![]() $\gamma $
is a topological generator of
$\gamma $
is a topological generator of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\rho :\Gamma \rightarrow \mu _{p^{\infty }}$
be a finite order character and let
$\rho :\Gamma \rightarrow \mu _{p^{\infty }}$
be a finite order character and let
![]() $\sigma _{v}$
denote the Frobenius at v. Let
$\sigma _{v}$
denote the Frobenius at v. Let
![]() $\mathcal {P}_{v}(E,T)$
be the element in
$\mathcal {P}_{v}(E,T)$
be the element in
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
defined by the relation
$\mathbb {Z}_{p}[[\Gamma ]]$
defined by the relation
![]() $\mathcal {P}_{v}(E,\rho (\gamma )-1)=P_{v}(E,\rho (\sigma _{v}) Nv^{-1})$
. According to [Reference Greenberg and Vatsal8, Proposition 2.4], the polynomial
$\mathcal {P}_{v}(E,\rho (\gamma )-1)=P_{v}(E,\rho (\sigma _{v}) Nv^{-1})$
. According to [Reference Greenberg and Vatsal8, Proposition 2.4], the polynomial
![]() $\mathcal {P}_{v}(E,T)$
generates the Pontryagin dual of
$\mathcal {P}_{v}(E,T)$
generates the Pontryagin dual of
![]() $\mathcal {H}_{v}(F^{\operatorname {cyc}}, E[p^{\infty }])$
and thus coincides with
$\mathcal {H}_{v}(F^{\operatorname {cyc}}, E[p^{\infty }])$
and thus coincides with
![]() $h^{(v)}(T)$
up to a unit in
$h^{(v)}(T)$
up to a unit in
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
.
$\mathbb {Z}_{p}[[\Gamma ]]$
.
Definition 5.2 Set
![]() $\delta _{E,\Sigma _{0}}$
to be the product
$\delta _{E,\Sigma _{0}}$
to be the product
![]() $\prod _{v\in \Sigma _{0}} |L_{v}(E, 1)|_{p}$
. Here,
$\prod _{v\in \Sigma _{0}} |L_{v}(E, 1)|_{p}$
. Here,
![]() $|L_{v}(E, 1)|_{p}$
is set to be equal to
$|L_{v}(E, 1)|_{p}$
is set to be equal to
![]() $0$
if
$0$
if
![]() $L_{v}(E, 1)^{-1}=0$
.
$L_{v}(E, 1)^{-1}=0$
.
Write
and set
![]() $|g_{E,\Sigma _{0}}(0)|_{p}^{-1}$
to be zero if
$|g_{E,\Sigma _{0}}(0)|_{p}^{-1}$
to be zero if
![]() $g_{E,\Sigma _{0}}(0)$
equals zero. It follows from the relation (5.2) that
$g_{E,\Sigma _{0}}(0)$
equals zero. It follows from the relation (5.2) that
One has the following result.
Lemma 5.3 Let E be an elliptic curve satisfying Hypothesis (2.1) and let
![]() $\ddagger $
be a signed vector, for a finite set
$\ddagger $
be a signed vector, for a finite set
![]() $\Sigma _{0}$
consisting of primes
$\Sigma _{0}$
consisting of primes
![]() $v\nmid p$
. Then we have the following equality:
$v\nmid p$
. Then we have the following equality:
Proof Note that
![]() $\mathcal {P}_{v}(E,0)$
equals
$\mathcal {P}_{v}(E,0)$
equals
![]() $P_{v}(E,l^{-1})=L_{v}(E,1)^{-1}$
. Therefore, it follows that
$P_{v}(E,l^{-1})=L_{v}(E,1)^{-1}$
. Therefore, it follows that
![]() $h^{(v)}(0)$
coincides with
$h^{(v)}(0)$
coincides with
![]() $|L_{v}(E,1)|_{p}$
up to a unit in
$|L_{v}(E,1)|_{p}$
up to a unit in
![]() $\mathbb {Z}_{p}$
. From the relation (5.4), we have that
$\mathbb {Z}_{p}$
. From the relation (5.4), we have that
Lemma 3.4 asserts that
![]() $\chi _{t}^{\ddagger }(\Gamma , E)$
is equal to
$\chi _{t}^{\ddagger }(\Gamma , E)$
is equal to
![]() $|g_{E}^{\ddagger }(0)|_{p}^{-1}$
, and this completes the proof. ▪
$|g_{E}^{\ddagger }(0)|_{p}^{-1}$
, and this completes the proof. ▪
Denote the
![]() $\mu $
-invariants of
$\mu $
-invariants of
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
and
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
and
![]() $\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
by
$\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
by
![]() $\mu _{E}^{ \ddagger }$
and
$\mu _{E}^{ \ddagger }$
and
![]() $\mu _{E}^{\Sigma _{0}, \ddagger }$
, respectively. Denote the
$\mu _{E}^{\Sigma _{0}, \ddagger }$
, respectively. Denote the
![]() $\lambda $
-invariants by
$\lambda $
-invariants by
![]() $\lambda _{E}^{ \ddagger }$
and
$\lambda _{E}^{ \ddagger }$
and
![]() $\lambda _{E}^{\Sigma _{0}, \ddagger }$
respectively. It is easy to show that for
$\lambda _{E}^{\Sigma _{0}, \ddagger }$
respectively. It is easy to show that for
![]() $v\in \Sigma _{0}$
, the
$v\in \Sigma _{0}$
, the
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $h_{E}^{(v)}(T)$
is equal to zero, and hence
$h_{E}^{(v)}(T)$
is equal to zero, and hence
![]() $\mu _{E}^{\Sigma _{0}, \ddagger }$
is equal to
$\mu _{E}^{\Sigma _{0}, \ddagger }$
is equal to
![]() $\mu _{E}^{\ddagger }$
.
$\mu _{E}^{\ddagger }$
.
Lemma 5.4 Let E be an elliptic curve satisfying Hypothesis (2.1) and let
![]() $\ddagger $
be a signed vector. For a finite set
$\ddagger $
be a signed vector. For a finite set
![]() $\Sigma _{0}$
consisting of primes
$\Sigma _{0}$
consisting of primes
![]() $v\nmid p$
, we have that
$v\nmid p$
, we have that
Proof First assume that
![]() $\delta _{E,\Sigma _{0}}\times \chi _{t}^{\ddagger }(\Gamma , E)=1$
, it is then shown that
$\delta _{E,\Sigma _{0}}\times \chi _{t}^{\ddagger }(\Gamma , E)=1$
, it is then shown that
![]() $\mu _{E}^{\ddagger }=0$
and
$\mu _{E}^{\ddagger }=0$
and
![]() $\lambda _{E}^{\Sigma _{0}, \ddagger }=r_{E}^{\ddagger }$
. Recall that
$\lambda _{E}^{\Sigma _{0}, \ddagger }=r_{E}^{\ddagger }$
. Recall that
![]() $f_{E}^{\Sigma _{0},\ddagger }(T)$
is the characteristic polynomial for the Selmer group
$f_{E}^{\Sigma _{0},\ddagger }(T)$
is the characteristic polynomial for the Selmer group
![]() $\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
and is written as
$\operatorname {Sel}^{\Sigma _{0},\ddagger }(E/F^{\operatorname {cyc}})$
and is written as
![]() $T^{r_{E}^{\ddagger }}g_{E}^{\Sigma _{0},\ddagger }(T)$
. It follows from Lemma 5.3 that
$T^{r_{E}^{\ddagger }}g_{E}^{\Sigma _{0},\ddagger }(T)$
. It follows from Lemma 5.3 that
![]() $g_{E}^{\Sigma _{0},\ddagger }(0)$
is a unit in
$g_{E}^{\Sigma _{0},\ddagger }(0)$
is a unit in
![]() $\mathbb {Z}_{p}$
, and thus
$\mathbb {Z}_{p}$
, and thus
![]() $g_{E}^{\Sigma _{0},\ddagger }(T)$
is a unit in
$g_{E}^{\Sigma _{0},\ddagger }(T)$
is a unit in
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
. It follows from this that
$\mathbb {Z}_{p}[[\Gamma ]]$
. It follows from this that
![]() $\mu _{E,\Sigma _{0}}^{\ddagger }=0$
and
$\mu _{E,\Sigma _{0}}^{\ddagger }=0$
and
![]() $\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. The following relation is satisfied:
$\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. The following relation is satisfied:
(see (5.2)). According to [Reference Greenberg and Vatsal8, Proposition 2.4], the polynomial
![]() $\mathcal {P}_{v}(E,T)$
generates the Pontryagin dual of
$\mathcal {P}_{v}(E,T)$
generates the Pontryagin dual of
![]() $\mathcal {H}_{v}(F^{\operatorname {cyc}}, E[p^{\infty }])$
and thus coincides with
$\mathcal {H}_{v}(F^{\operatorname {cyc}}, E[p^{\infty }])$
and thus coincides with
![]() $h^{(v)}(T)$
up to a unit in
$h^{(v)}(T)$
up to a unit in
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
. It is easy to see that
$\mathbb {Z}_{p}[[\Gamma ]]$
. It is easy to see that
![]() $\mathcal {P}_{v}(E,T)$
is equal to a monic polynomial, up to a unit in
$\mathcal {P}_{v}(E,T)$
is equal to a monic polynomial, up to a unit in
![]() $\mathbb {Z}_{p}$
. As a result, p does not divide
$\mathbb {Z}_{p}$
. As a result, p does not divide
![]() $h^{(v)}(T)$
. It follows that
$h^{(v)}(T)$
. It follows that
![]() $\mu _{E}^{\ddagger }=\mu _{E,\Sigma _{0}}^{\ddagger }=0$
.
$\mu _{E}^{\ddagger }=\mu _{E,\Sigma _{0}}^{\ddagger }=0$
.
Conversely, suppose that
![]() $\mu _{E}^{\ddagger }=0$
and that
$\mu _{E}^{\ddagger }=0$
and that
![]() $\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. The degree of
$\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. The degree of
![]() $f_{E,\Sigma _{0}}^{\ddagger }(T)$
is equal to
$f_{E,\Sigma _{0}}^{\ddagger }(T)$
is equal to
![]() $\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. Since
$\lambda _{E,\Sigma _{0}}^{\ddagger }=r_{E}^{\ddagger }$
. Since
![]() $f_{E,\Sigma _{0}}^{\ddagger }(T)$
is expressed as
$f_{E,\Sigma _{0}}^{\ddagger }(T)$
is expressed as
![]() $T^{r_{E}^{\ddagger }} g_{E,\Sigma _{0}}(T)$
, the degree of
$T^{r_{E}^{\ddagger }} g_{E,\Sigma _{0}}(T)$
, the degree of
![]() $g_{E,\Sigma _{0}}(T)$
is equal to zero. It has been shown that
$g_{E,\Sigma _{0}}(T)$
is equal to zero. It has been shown that
![]() $\mu _{E,\Sigma _{0}}^{\ddagger }=\mu _{E}^{\ddagger }=0$
. It follows that
$\mu _{E,\Sigma _{0}}^{\ddagger }=\mu _{E}^{\ddagger }=0$
. It follows that
![]() $g_{E,\Sigma _{0}}(T)$
is a unit in
$g_{E,\Sigma _{0}}(T)$
is a unit in
![]() $\mathbb {Z}_{p}$
. Lemma 5.3 asserts that
$\mathbb {Z}_{p}$
. Lemma 5.3 asserts that
![]() $\delta _{E,\Sigma _{0}}\times \chi _{t}^{\ddagger }(\Gamma , E)$
is equal to
$\delta _{E,\Sigma _{0}}\times \chi _{t}^{\ddagger }(\Gamma , E)$
is equal to
![]() $|g_{E,\Sigma _{0}}(0)|_{p}^{-1}$
and therefore equal to
$|g_{E,\Sigma _{0}}(0)|_{p}^{-1}$
and therefore equal to
![]() $1$
.▪
$1$
.▪
Next, we come to the main theorem of the section. It is shown that the truncated Euler characteristic of
![]() $E_{1}$
is related to that of
$E_{1}$
is related to that of
![]() $E_{2}$
after one accounts for the auxiliary set of primes
$E_{2}$
after one accounts for the auxiliary set of primes
![]() $\Sigma _{1}$
. The smaller the set of primes
$\Sigma _{1}$
. The smaller the set of primes
![]() $\Sigma _{1}$
, the more refined the congruence relation between truncated Euler characteristics is. This is why it is of considerable importance that the set of primes
$\Sigma _{1}$
, the more refined the congruence relation between truncated Euler characteristics is. This is why it is of considerable importance that the set of primes
![]() $\Sigma _{1}$
be carefully chosen to be as small as possible. We note that in the statement of [Reference Ray and Sujatha30, Theorem 3.3], the elliptic curves
$\Sigma _{1}$
be carefully chosen to be as small as possible. We note that in the statement of [Reference Ray and Sujatha30, Theorem 3.3], the elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
were defined over
$E_{2}$
were defined over
![]() $\mathbb {Q}$
with good ordinary reduction at p. Furthermore, the set of auxiliary primes
$\mathbb {Q}$
with good ordinary reduction at p. Furthermore, the set of auxiliary primes
![]() $\Sigma _{0}$
was the full set of primes
$\Sigma _{0}$
was the full set of primes
![]() $v\nmid p$
at which
$v\nmid p$
at which
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. The set of primes
$E_{2}$
has bad reduction. The set of primes
![]() $\Sigma _{1}$
is smaller and hence, when
$\Sigma _{1}$
is smaller and hence, when
![]() $F=\mathbb {Q}$
the result below refines the result [Reference Ray and Sujatha30, Theorem 3.3].
$F=\mathbb {Q}$
the result below refines the result [Reference Ray and Sujatha30, Theorem 3.3].
Theorem 5.5 Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be elliptic curves which satisfy Hypothesis (4.2) mentioned in the introduction. Then, the following assertions hold.
$E_{2}$
be elliptic curves which satisfy Hypothesis (4.2) mentioned in the introduction. Then, the following assertions hold.
-
(1) Suppose
 $r_{E_{1}}^{\ddagger }$
is equal to
$r_{E_{1}}^{\ddagger }$
is equal to
 $r_{E_{2}}^{\ddagger }$
. Then,
$r_{E_{2}}^{\ddagger }$
. Then,
 $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})$
is equal to
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})$
is equal to
 $1$
if and only if
$1$
if and only if
 $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})$
is equal to
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})$
is equal to
 $1$
.
$1$
. -
(2) If
 $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
, then
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
, then
 $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is divisible by p.
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is divisible by p. -
(3) If
 $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is divisible by p and
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is divisible by p and
 $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})=1$
, then,
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})=1$
, then,
 $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
.
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
.
Proof We first assume consider the case when
![]() $r_{E_{1}}^{\ddagger }$
is equal to
$r_{E_{1}}^{\ddagger }$
is equal to
![]() $r_{E_{2}}^{\ddagger }$
. It follows from Lemma 5.4 that
$r_{E_{2}}^{\ddagger }$
. It follows from Lemma 5.4 that
![]() $\delta _{E_{i},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{i})=1$
if and only if
$\delta _{E_{i},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{i})=1$
if and only if
![]() $\mu _{E_{i}}^{\ddagger }=0$
and
$\mu _{E_{i}}^{\ddagger }=0$
and
![]() $\lambda _{E_{i}}^{\Sigma _{1},\ddagger }=r_{E_{i}}^{\ddagger }$
. Suppose that
$\lambda _{E_{i}}^{\Sigma _{1},\ddagger }=r_{E_{i}}^{\ddagger }$
. Suppose that
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})=1$
, then it follows that
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{1})=1$
, then it follows that
![]() $\mu _{E_{1}}^{\ddagger }=0$
and
$\mu _{E_{1}}^{\ddagger }=0$
and
![]() $\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. It follows from Corollary 4.5 that
$\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. It follows from Corollary 4.5 that
![]() $\mu _{E_{2}}^{\ddagger }=0$
and
$\mu _{E_{2}}^{\ddagger }=0$
and
![]() $\lambda _{E_{2}}^{\Sigma _{1},\ddagger }=r_{E_{2}}^{\ddagger }$
. Thus, by Lemma 5.4, we have that
$\lambda _{E_{2}}^{\Sigma _{1},\ddagger }=r_{E_{2}}^{\ddagger }$
. Thus, by Lemma 5.4, we have that
![]() $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{2})=1$
. This proves part (1).
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma , E_{2})=1$
. This proves part (1).
Next, it is assumed that
![]() $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
and it shown that p divides
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
and it shown that p divides
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. Suppose by way of contradiction that p does not divide
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. Suppose by way of contradiction that p does not divide
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. This means that
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. This means that
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is equal to
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
is equal to
![]() $1$
. Lemma 5.4 asserts that
$1$
. Lemma 5.4 asserts that
![]() $\mu _{E_{1}}^{\ddagger }=0$
and
$\mu _{E_{1}}^{\ddagger }=0$
and
![]() $\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. It follows from Corollary 4.5 that
$\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. It follows from Corollary 4.5 that
![]() $\mu _{E_{2}}^{\ddagger }=0$
and
$\mu _{E_{2}}^{\ddagger }=0$
and
![]() $\lambda _{E_{2}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. Recall that
$\lambda _{E_{2}}^{\Sigma _{1},\ddagger }=r_{E_{1}}^{\ddagger }$
. Recall that
![]() $\lambda _{E_{2}}^{\Sigma _{1},\ddagger }$
is the degree of the characteristic polynomial
$\lambda _{E_{2}}^{\Sigma _{1},\ddagger }$
is the degree of the characteristic polynomial
![]() $f_{E_{2}}^{\ddagger }(T)$
. Since
$f_{E_{2}}^{\ddagger }(T)$
. Since
![]() $r_{E_{2}}^{\ddagger }$
is the order of vanishing of
$r_{E_{2}}^{\ddagger }$
is the order of vanishing of
![]() $f_{E_{2}}^{\ddagger }(T)$
at
$f_{E_{2}}^{\ddagger }(T)$
at
![]() $T=0$
, it follows that
$T=0$
, it follows that
![]() $\lambda _{E_{2}}^{\Sigma _{1},\ddagger }\geq r_{E_{2}}^{\ddagger }$
. This is a contradiction, as it is assumed that
$\lambda _{E_{2}}^{\Sigma _{1},\ddagger }\geq r_{E_{2}}^{\ddagger }$
. This is a contradiction, as it is assumed that
![]() $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
. Hence, p divides
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
. Hence, p divides
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. This proves part (2).
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
. This proves part (2).
Next, we prove part (3). Since
![]() $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})=1$
, we deduce from Lemma 5.4 that
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{2})=1$
, we deduce from Lemma 5.4 that
![]() $\mu _{E_{2}}^{\ddagger }=0$
and
$\mu _{E_{2}}^{\ddagger }=0$
and
![]() $\lambda _{E_{2}}^{\Sigma _{1},\ddagger }= r_{E_{2}}^{\ddagger }$
. It follows from Corollary 4.5 that
$\lambda _{E_{2}}^{\Sigma _{1},\ddagger }= r_{E_{2}}^{\ddagger }$
. It follows from Corollary 4.5 that
![]() $\mu _{E_{1}}^{\ddagger }=0$
and
$\mu _{E_{1}}^{\ddagger }=0$
and
![]() $\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{2}}^{\ddagger }$
. Since p divides
$\lambda _{E_{1}}^{\Sigma _{1},\ddagger }=r_{E_{2}}^{\ddagger }$
. Since p divides
![]() $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
, it follows from Lemma 5.4 that
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\Gamma ,E_{1})$
, it follows from Lemma 5.4 that
![]() $r_{E_{1}}^{\ddagger }<\lambda _{E_{1}}^{\Sigma _{1},\ddagger }$
. Therefore, we have shown that
$r_{E_{1}}^{\ddagger }<\lambda _{E_{1}}^{\Sigma _{1},\ddagger }$
. Therefore, we have shown that
![]() $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
.▪
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
.▪
Consider the case when
![]() $r_{E_{1}}^{\ddagger }=r_{E_{2}}^{\ddagger }$
. It is natural to ask if
$r_{E_{1}}^{\ddagger }=r_{E_{2}}^{\ddagger }$
. It is natural to ask if
![]() $\chi _{t}^{\ddagger }(\Gamma ,E_{1})=1$
implies that
$\chi _{t}^{\ddagger }(\Gamma ,E_{1})=1$
implies that
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{2})=1$
? This statement is false, as is shown in [Reference Ray and Sujatha30, Example 5.2], where it is shown that there are
$\chi _{t}^{\ddagger }(\Gamma , E_{2})=1$
? This statement is false, as is shown in [Reference Ray and Sujatha30, Example 5.2], where it is shown that there are
![]() $5$
-congruent elliptic curves
$5$
-congruent elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
over
$E_{2}$
over
![]() $\mathbb {Q}$
which both have Mordell-Weil rank
$\mathbb {Q}$
which both have Mordell-Weil rank
![]() $1$
and good ordinary reduction at
$1$
and good ordinary reduction at
![]() $5$
, such that
$5$
, such that
![]() $\chi _{t}(\Gamma , E_{1})=1$
and
$\chi _{t}(\Gamma , E_{1})=1$
and
![]() $\chi _{t}(\Gamma , E_{2})=5^{2}$
. Therefore it is necessary to account the factors
$\chi _{t}(\Gamma , E_{2})=5^{2}$
. Therefore it is necessary to account the factors
![]() $\delta _{E_{i}, \Sigma _{1}}$
, i.e.,
$\delta _{E_{i}, \Sigma _{1}}$
, i.e.,
6 Results over
 $\mathbb {Z}_{p}^{m}$
-extensions
$\mathbb {Z}_{p}^{m}$
-extensions
We show that our results on truncated Euler characteristics generalize to
![]() $\mathbb {Z}_{p}^{m}$
-extensions. The multisigned Selmer groups have not been defined for more general p-adic Lie extensions. In the good ordinary reduction setting, the reader is referred to [Reference Zerbes37] for a discussion on truncated Euler characteristics over general p-adic Lie extensions. In [Reference Ray and Sujatha30, Section 4], congruence relations are proved for truncated Euler characteristics over p-adic Lie extensions for elliptic curves with good ordinary reduction at p.
$\mathbb {Z}_{p}^{m}$
-extensions. The multisigned Selmer groups have not been defined for more general p-adic Lie extensions. In the good ordinary reduction setting, the reader is referred to [Reference Zerbes37] for a discussion on truncated Euler characteristics over general p-adic Lie extensions. In [Reference Ray and Sujatha30, Section 4], congruence relations are proved for truncated Euler characteristics over p-adic Lie extensions for elliptic curves with good ordinary reduction at p.
Let
![]() $\mathcal {F}_{\infty }/F$
be a Galois extension of F containing
$\mathcal {F}_{\infty }/F$
be a Galois extension of F containing
![]() $F^{\operatorname {cyc}}$
such that
$F^{\operatorname {cyc}}$
such that
![]() $\operatorname {Gal}(\mathcal {F}_{\infty }/F)\simeq \mathbb {Z}_{p}^{m}$
for an integer
$\operatorname {Gal}(\mathcal {F}_{\infty }/F)\simeq \mathbb {Z}_{p}^{m}$
for an integer
![]() $m\geq 1$
. Set
$m\geq 1$
. Set
![]() $\operatorname {G}:=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
,
$\operatorname {G}:=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
,
![]() $H:=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
and identify
$H:=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
and identify
![]() $\Gamma $
with
$\Gamma $
with
![]() $\operatorname {Gal}(F^{\operatorname {cyc}}/F)\simeq \operatorname {G}/\operatorname {H}$
. Let E be an elliptic curve and
$\operatorname {Gal}(F^{\operatorname {cyc}}/F)\simeq \operatorname {G}/\operatorname {H}$
. Let E be an elliptic curve and
![]() $\ddagger $
be a signed vector, assume that
$\ddagger $
be a signed vector, assume that
![]() $(E,\ddagger )$
satisfies Hypothesis (4.1). Another natural hypothesis is that the Selmer groups be in
$(E,\ddagger )$
satisfies Hypothesis (4.1). Another natural hypothesis is that the Selmer groups be in
![]() $\mathfrak {M}_{H}(\operatorname {G})$
. The precise definition is given below.
$\mathfrak {M}_{H}(\operatorname {G})$
. The precise definition is given below.
Definition 6.1 Let M be a cofinitely generated cotorsion
![]() $\mathbb {Z}_{p}[[\operatorname {G}]]$
-module and let
$\mathbb {Z}_{p}[[\operatorname {G}]]$
-module and let
![]() $M(p)$
be the p-primary submodule of M. The category
$M(p)$
be the p-primary submodule of M. The category
![]() $\mathfrak {M}_{H}(\operatorname {G})$
consists of all such modules M such that
$\mathfrak {M}_{H}(\operatorname {G})$
consists of all such modules M such that
![]() $M/M(p)$
is a finitely generated
$M/M(p)$
is a finitely generated
![]() $\mathbb {Z}_{p}[[H]]$
-module.
$\mathbb {Z}_{p}[[H]]$
-module.
We introduce the following hypothesis.
Hypothesis 6.1 Assume that the Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
is in
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
is in
![]() $\mathfrak {M}_{H}(\operatorname {G})$
.
$\mathfrak {M}_{H}(\operatorname {G})$
.
We recall the notion of the truncated
![]() $\operatorname {G}$
-Euler characteristic of
$\operatorname {G}$
-Euler characteristic of
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
.
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
.
Definition 6.2 Let M be a discrete p-primary
![]() $\operatorname {G}$
-module, define
$\operatorname {G}$
-module, define
as the composite of the natural map
![]() $\phi _{D^{H}}:H^{0}(\Gamma , M^{H})\rightarrow H^{1}(\Gamma , M^{H})$
with the inflation map
$\phi _{D^{H}}:H^{0}(\Gamma , M^{H})\rightarrow H^{1}(\Gamma , M^{H})$
with the inflation map
![]() $H^{1}(\Gamma , M^{H})\rightarrow H^{1}(\operatorname {G},M)$
. The
$H^{1}(\Gamma , M^{H})\rightarrow H^{1}(\operatorname {G},M)$
. The
![]() $\operatorname {G}$
-Euler characteristic of the module M is defined if the following two conditions are satisfied:
$\operatorname {G}$
-Euler characteristic of the module M is defined if the following two conditions are satisfied:
-
(1) both
 $\operatorname {ker}(\psi _{M})$
and
$\operatorname {ker}(\psi _{M})$
and
 $\operatorname {cok}(\psi _{M})$
are finite and
$\operatorname {cok}(\psi _{M})$
are finite and -
(2)
 $H^{i}(\operatorname {G}, M)$
is finite for
$H^{i}(\operatorname {G}, M)$
is finite for
 $i\geq 2$
.
$i\geq 2$
.
The truncated
![]() $\operatorname {G}$
-Euler characteristic is then defined by
$\operatorname {G}$
-Euler characteristic is then defined by
 $$ \begin{align*} \chi_{t}(\operatorname{G},M):=\frac{\# \operatorname{ker}(\psi_{M})}{\# \operatorname{cok}(\psi_{M})}\times \prod_{i= 2}^{m} \# \left(H^{i}(\operatorname{G},M)\right)^{(-1)^{i}}\kern-2pt. \end{align*} $$
$$ \begin{align*} \chi_{t}(\operatorname{G},M):=\frac{\# \operatorname{ker}(\psi_{M})}{\# \operatorname{cok}(\psi_{M})}\times \prod_{i= 2}^{m} \# \left(H^{i}(\operatorname{G},M)\right)^{(-1)^{i}}\kern-2pt. \end{align*} $$
Next, we recall the notion of the Akashi series. For a cofinitely generated
![]() $\Gamma $
-module M, let
$\Gamma $
-module M, let
![]() $\operatorname {char}_{\Gamma }(M)$
be the characteristic polynomial of its Pontryagin dual
$\operatorname {char}_{\Gamma }(M)$
be the characteristic polynomial of its Pontryagin dual
![]() $M^{\vee }$
. This is the unique polynomial generating the characteristic ideal which can be expressed as the product of a power of p and a distinguished polynomial.
$M^{\vee }$
. This is the unique polynomial generating the characteristic ideal which can be expressed as the product of a power of p and a distinguished polynomial.
Definition 6.3 Let D be a discrete p-primary
![]() $\operatorname {G}$
-module. The Akashi series of D is defined if
$\operatorname {G}$
-module. The Akashi series of D is defined if
![]() $H^{i}(H, D)$
is cotorsion and cofinitely generated for all
$H^{i}(H, D)$
is cotorsion and cofinitely generated for all
![]() $i\geq 0$
. In this case, the Akashi series
$i\geq 0$
. In this case, the Akashi series
![]() $\operatorname {Ak}_{H}(D)$
is taken to be the following alternating product:
$\operatorname {Ak}_{H}(D)$
is taken to be the following alternating product:
 $$ \begin{align*} \operatorname{Ak}_{H}(D):=\prod_{i= 0}^{m-1} \left(\operatorname{char}_{\Gamma} H^{i}(H, D)\right)^{(-1)^{i}}\kern-2pt. \end{align*} $$
$$ \begin{align*} \operatorname{Ak}_{H}(D):=\prod_{i= 0}^{m-1} \left(\operatorname{char}_{\Gamma} H^{i}(H, D)\right)^{(-1)^{i}}\kern-2pt. \end{align*} $$
Note that the Akashi series coincides with the characteristic polynomial when
![]() $\mathcal {F}_{\infty }=F^{\operatorname {cyc}}$
. The following Proposition describes the relationship between the Akashi series and truncated
$\mathcal {F}_{\infty }=F^{\operatorname {cyc}}$
. The following Proposition describes the relationship between the Akashi series and truncated
![]() $\operatorname {G}$
-Euler characteristic.
$\operatorname {G}$
-Euler characteristic.
Proposition 6.4 [Reference Zerbes37, Proposition 2.10]
Let D be a discrete p-primary
![]() $\operatorname {G}$
-module such that the Pontryagin dual
$\operatorname {G}$
-module such that the Pontryagin dual
![]() $D^{\vee }$
is in
$D^{\vee }$
is in
![]() $\mathfrak {M}_{H}(\operatorname {G})$
. Then, the Akashi series
$\mathfrak {M}_{H}(\operatorname {G})$
. Then, the Akashi series
![]() $\operatorname {Ak}_{H}(D)$
is defined. Furthermore, suppose that the truncated
$\operatorname {Ak}_{H}(D)$
is defined. Furthermore, suppose that the truncated
![]() $\operatorname {G}$
-Euler characteristic of D is defined in the sense of Definition
6.2
. Let
$\operatorname {G}$
-Euler characteristic of D is defined in the sense of Definition
6.2
. Let
![]() $\beta T^{k}$
be the leading term of
$\beta T^{k}$
be the leading term of
![]() $\operatorname {Ak}_{H}(D)$
. Then, the following assertions hold:
$\operatorname {Ak}_{H}(D)$
. Then, the following assertions hold:
-
(1) the order of vanishing k is given by
 $$ \begin{align*} k = \sum_{i\geq 0} (-1)^{i} \operatorname{corank}_{\mathbb{Z}_{p}} H^{i}(H,D)^{\Gamma}, \end{align*} $$
$$ \begin{align*} k = \sum_{i\geq 0} (-1)^{i} \operatorname{corank}_{\mathbb{Z}_{p}} H^{i}(H,D)^{\Gamma}, \end{align*} $$
-
(2) the truncated
 $\operatorname {G}$
-Euler characteristic is given by
$\operatorname {G}$
-Euler characteristic is given by  $$ \begin{align*} \chi_{t}(\operatorname{G},D) = |\beta|_{p}^{-1}. \end{align*} $$
$$ \begin{align*} \chi_{t}(\operatorname{G},D) = |\beta|_{p}^{-1}. \end{align*} $$
The truncated
![]() $\operatorname {G}$
-Euler characteristic of
$\operatorname {G}$
-Euler characteristic of
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
is denoted by
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
is denoted by
![]() $\chi _{t}^{\ddagger }(\operatorname {G}, E)$
. When the truncated
$\chi _{t}^{\ddagger }(\operatorname {G}, E)$
. When the truncated
![]() $\operatorname {G}$
-Euler characteristic is defined, it is related to the Akashi series of
$\operatorname {G}$
-Euler characteristic is defined, it is related to the Akashi series of
![]() $\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
, which we denote by
$\operatorname {Sel}^{\ddagger }(E/\mathcal {F}_{\infty })$
, which we denote by
![]() $\operatorname {Ak}_{H}^{\ddagger }(E)$
. The following theorem due to Lei and Lim describes the link between Akashi series
$\operatorname {Ak}_{H}^{\ddagger }(E)$
. The following theorem due to Lei and Lim describes the link between Akashi series
![]() $\operatorname {Ak}_{H}^{\ddagger }(E)$
and the characteristic polynomial
$\operatorname {Ak}_{H}^{\ddagger }(E)$
and the characteristic polynomial
![]() $f_{E}^{\ddagger }(T)$
of the Selmer group
$f_{E}^{\ddagger }(T)$
of the Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
.
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
.
Theorem 6.5 [Reference Lei and Lim21, Theorem 1.1]
Let E be an elliptic curve over a number field F, and let
![]() $\ddagger $
be a signed vector. Let
$\ddagger $
be a signed vector. Let
![]() $\mathcal {F}_{\infty }$
be a
$\mathcal {F}_{\infty }$
be a
![]() $\mathbb {Z}_{p}^{m}$
-extension of F which contains
$\mathbb {Z}_{p}^{m}$
-extension of F which contains
![]() $F^{\operatorname {cyc}}$
. Assume that:
$F^{\operatorname {cyc}}$
. Assume that:
-
(2) The Selmer group
 $\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
$\operatorname {Sel}^{\ddagger }(E/F^{\operatorname {cyc}})$
is
 $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion.
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion.
Then, the Akashi series
![]() $\operatorname {Ak}_{H}^{\ddagger }(E)$
is well-defined and is given by
$\operatorname {Ak}_{H}^{\ddagger }(E)$
is well-defined and is given by
where
![]() $\gamma _{E}$
is the number of primes of
$\gamma _{E}$
is the number of primes of
![]() $F^{\operatorname {cyc}}$
above p with nontrivial decomposition group in
$F^{\operatorname {cyc}}$
above p with nontrivial decomposition group in
![]() $\mathcal {F}_{\infty }/F^{\operatorname {cyc}}$
and at which E has split multiplicative reduction.
$\mathcal {F}_{\infty }/F^{\operatorname {cyc}}$
and at which E has split multiplicative reduction.
Corollary 6.6 Let E be an elliptic curve over a number field F, and let
![]() $\ddagger $
be a signed vector. Let
$\ddagger $
be a signed vector. Let
![]() $\mathcal {F}_{\infty }$
be a
$\mathcal {F}_{\infty }$
be a
![]() $\mathbb {Z}_{p}^{m}$
-extension of F which contains
$\mathbb {Z}_{p}^{m}$
-extension of F which contains
![]() $F^{\operatorname {cyc}}$
. Assume that
$F^{\operatorname {cyc}}$
. Assume that
-
(2) The truncated
 $\operatorname {G}$
-Euler characteristic
$\operatorname {G}$
-Euler characteristic
 $\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is well defined.
$\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is well defined.
Then, the truncated
![]() $\operatorname {G}$
-Euler characteristic
$\operatorname {G}$
-Euler characteristic
![]() $\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is equal to the truncated
$\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is equal to the truncated
![]() $\Gamma $
-Euler characteristic
$\Gamma $
-Euler characteristic
![]() $\chi _{t}^{\ddagger }(\Gamma , E)$
.
$\chi _{t}^{\ddagger }(\Gamma , E)$
.
Theorem 6.7 Let
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
be p-congruent elliptic curves over a number field F. Let
$E_{2}$
be p-congruent elliptic curves over a number field F. Let
![]() $\ddagger $
be a signed vector. Assume that
$\ddagger $
be a signed vector. Assume that
-
(2) The truncated
 $\operatorname {G}$
-Euler characteristic
$\operatorname {G}$
-Euler characteristic
 $\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is well defined.
$\chi _{t}^{\ddagger }(\operatorname {G}, E)$
is well defined.
Then, the following assertions hold.
-
(1) Suppose that
 $r^{\ddagger }_{E_{1}}=r^{\ddagger }_{E_{2}}$
. Then, we have that the truncated
$r^{\ddagger }_{E_{1}}=r^{\ddagger }_{E_{2}}$
. Then, we have that the truncated
 $\operatorname {G}$
-Euler characteristics are defined, then
$\operatorname {G}$
-Euler characteristics are defined, then
 $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G},E_{1})$
is equal to
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G},E_{1})$
is equal to
 $1$
if and only if
$1$
if and only if
 $\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G}, E_{2})$
is equal to
$\delta _{E_{2},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G}, E_{2})$
is equal to
 $1$
. Furthermore,
$1$
. Furthermore,
 $\delta _{E_{1},\Sigma _{1}}\times \operatorname {Ak}_{H}^{\ddagger }(E_{1})$
is equal to
$\delta _{E_{1},\Sigma _{1}}\times \operatorname {Ak}_{H}^{\ddagger }(E_{1})$
is equal to
 $T^{r_{E_{1}}+\gamma _{E_{1}}}$
if and only if
$T^{r_{E_{1}}+\gamma _{E_{1}}}$
if and only if
 $\delta _{E_{2},\Sigma _{1}}\times \operatorname {Ak}_{H}^{\ddagger }(E_{2})$
is equal to
$\delta _{E_{2},\Sigma _{1}}\times \operatorname {Ak}_{H}^{\ddagger }(E_{2})$
is equal to
 $T^{r_{E_{1}}+\gamma _{E_{2}}}$
.
$T^{r_{E_{1}}+\gamma _{E_{2}}}$
. -
(2) Suppose that
 $r^{\ddagger }_{E_{1}}<r^{\ddagger }_{E_{2}}$
. Then, p divides
$r^{\ddagger }_{E_{1}}<r^{\ddagger }_{E_{2}}$
. Then, p divides
 $\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G},E_{1})$
.
$\delta _{E_{1},\Sigma _{1}}\times \chi _{t}^{\ddagger }(\operatorname {G},E_{1})$
.
7 Examples
We discuss two concrete examples which illustrate our results for
![]() $p=5$
. Our computations are aided by Sage. The reader is referred to [Reference Ray and Sujatha30, Section 5] for examples when both elliptic curves are defined over
$p=5$
. Our computations are aided by Sage. The reader is referred to [Reference Ray and Sujatha30, Section 5] for examples when both elliptic curves are defined over
![]() $\mathbb {Q}$
and have good ordinary reduction at
$\mathbb {Q}$
and have good ordinary reduction at
![]() $p=5$
.
$p=5$
.
7.1 Example 1
Consider elliptic curves
![]() $E_{1}=66a1$
and
$E_{1}=66a1$
and
![]() $E_{2}=462d1$
. The elliptic curves
$E_{2}=462d1$
. The elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
are
$E_{2}$
are
![]() $5$
-congruent and supersingular at
$5$
-congruent and supersingular at
![]() $5$
. Both elliptic curves
$5$
. Both elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
have Mordell-Weil rank zero, hence the Euler characteristic
$E_{2}$
have Mordell-Weil rank zero, hence the Euler characteristic
![]() $\chi (\Gamma , E_{i})$
is well defined for
$\chi (\Gamma , E_{i})$
is well defined for
![]() $i=1,2$
. Hypothesis (2.1) is satisfied for the elliptic curves
$i=1,2$
. Hypothesis (2.1) is satisfied for the elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
. Let
$E_{2}$
. Let
![]() $\ddagger \in \{+,-\}$
be a choice of sign. Assume that for
$\ddagger \in \{+,-\}$
be a choice of sign. Assume that for
![]() $i=1,2$
, the Selmer group
$i=1,2$
, the Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/\mathbb {Q}^{\operatorname {cyc}})$
is
$\operatorname {Sel}^{\ddagger }(E_{i}/\mathbb {Q}^{\operatorname {cyc}})$
is
![]() $\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion. Therefore, Hypothesis (4.2) is satisfied. We show that
$\mathbb {Z}_{p}[[\Gamma ]]$
-cotorsion. Therefore, Hypothesis (4.2) is satisfied. We show that
![]() $\delta _{E_{i}, \Sigma _{1}}=1$
and
$\delta _{E_{i}, \Sigma _{1}}=1$
and
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{i})=1$
for
$\chi _{t}^{\ddagger }(\Gamma , E_{i})=1$
for
![]() $i=1,2$
. This demonstrates Theorem 5.5 which asserts that
$i=1,2$
. This demonstrates Theorem 5.5 which asserts that
The conductor
![]() $N_{1}$
of
$N_{1}$
of
![]() $E_{1}$
(resp.
$E_{1}$
(resp.
![]() $N_{2}$
of
$N_{2}$
of
![]() $E_{2}$
) is
$E_{2}$
) is
![]() $66=2\times 3\times 11$
(resp.
$66=2\times 3\times 11$
(resp.
![]() $462=2\times 3\times 7\times 11$
). The set
$462=2\times 3\times 7\times 11$
). The set
![]() $\Sigma _{0}$
consists of the primes
$\Sigma _{0}$
consists of the primes
![]() $v\neq 5$
at which
$v\neq 5$
at which
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. We have that
$E_{2}$
has bad reduction. We have that
![]() $\Sigma _{0}=\{2,3,7,11\}$
. We calculate the optimal set of primes
$\Sigma _{0}=\{2,3,7,11\}$
. We calculate the optimal set of primes
![]() $\Sigma _{1}\subseteq \Sigma _{0}$
. Let
$\Sigma _{1}\subseteq \Sigma _{0}$
. Let
![]() $\overline {N}$
denote the prime to
$\overline {N}$
denote the prime to
![]() $5$
Artin conductor of the residual representation. Recall that
$5$
Artin conductor of the residual representation. Recall that
![]() $\Sigma _{1}$
is the set of primes
$\Sigma _{1}$
is the set of primes
![]() $\Sigma (E_{1})\cup \Sigma (E_{2})$
, where
$\Sigma (E_{1})\cup \Sigma (E_{2})$
, where
![]() $\Sigma (E_{i})$
consists of the primes
$\Sigma (E_{i})$
consists of the primes
![]() $v\neq 5$
such that
$v\neq 5$
such that
![]() $v|(N_{i}/\overline {N})$
, and if
$v|(N_{i}/\overline {N})$
, and if
![]() $\mu _{5}$
is contained in
$\mu _{5}$
is contained in
![]() $\mathbb {Q}_{v}$
, then E has split multiplicative reduction at v. Note that
$\mathbb {Q}_{v}$
, then E has split multiplicative reduction at v. Note that
![]() $\mathbb {Q}_{11}$
contains
$\mathbb {Q}_{11}$
contains
![]() $\mu _{5}$
and both elliptic curves
$\mu _{5}$
and both elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
have nonsplit multiplicative reduction at
$E_{2}$
have nonsplit multiplicative reduction at
![]() $11$
. Hence,
$11$
. Hence,
![]() $\Sigma _{1}\subseteq \{2,3,7\}$
is strictly smaller than
$\Sigma _{1}\subseteq \{2,3,7\}$
is strictly smaller than
![]() $\Sigma _{0}=\{2,3,7,11\}$
. Recall that
$\Sigma _{0}=\{2,3,7,11\}$
. Recall that
![]() $\delta _{E,\Sigma _{1}}$
is the product
$\delta _{E,\Sigma _{1}}$
is the product
![]() $\prod _{v\in \Sigma _{1}} |L_{v}(E, 1)|_{5}$
. From the discussion in [Reference Ray and Sujatha30, p. 7],
$\prod _{v\in \Sigma _{1}} |L_{v}(E, 1)|_{5}$
. From the discussion in [Reference Ray and Sujatha30, p. 7],
![]() $L_{v}(E_{i},1)^{-1}$
is equal to
$L_{v}(E_{i},1)^{-1}$
is equal to
![]() $v^{-1}(l+\beta _{v}(E_{i})-a_{l}(E))$
, where
$v^{-1}(l+\beta _{v}(E_{i})-a_{l}(E))$
, where
![]() $\beta _{v}(E_{i})$
is
$\beta _{v}(E_{i})$
is
![]() $1$
when
$1$
when
![]() $E_{i}$
has good reduction at v and is
$E_{i}$
has good reduction at v and is
![]() $0$
otherwise. These values are calculated from the following:
$0$
otherwise. These values are calculated from the following:
 $$ \begin{align*} \begin{split} &2+\beta_{2}(E_{1})-a_{2}(E_{1})=3, 3+\beta_{3}(E_{1})-a_{3}(E_{1})=2, 7+\beta_{7}(E_{1})-a_{7}(E_{1})=6,\\ &2+\beta_{2}(E_{2})-a_{2}(E_{2})=3, 3+\beta_{3}(E_{2})-a_{3}(E_{2})=3, 7+\beta_{7}(E_{2})-a_{7}(E_{2})=8.\\ \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &2+\beta_{2}(E_{1})-a_{2}(E_{1})=3, 3+\beta_{3}(E_{1})-a_{3}(E_{1})=2, 7+\beta_{7}(E_{1})-a_{7}(E_{1})=6,\\ &2+\beta_{2}(E_{2})-a_{2}(E_{2})=3, 3+\beta_{3}(E_{2})-a_{3}(E_{2})=3, 7+\beta_{7}(E_{2})-a_{7}(E_{2})=8.\\ \end{split} \end{align*} $$
None of the above values are not divisible by
![]() $5$
and hence,
$5$
and hence,
![]() $\delta _{E_{1},\Sigma _{1}}$
and
$\delta _{E_{1},\Sigma _{1}}$
and
![]() $\delta _{E_{2}, \Sigma _{1}}$
are both
$\delta _{E_{2}, \Sigma _{1}}$
are both
![]() $1$
. The Euler characteristics
$1$
. The Euler characteristics
![]() $\chi ^{\pm }(\Gamma , E_{i})$
may be calculated explicitly. The Euler characteristic
$\chi ^{\pm }(\Gamma , E_{i})$
may be calculated explicitly. The Euler characteristic
![]() $\chi (\Gamma , E_{i})$
is given up to
$\chi (\Gamma , E_{i})$
is given up to
![]() $5$
-adic unit by
$5$
-adic unit by
see [Reference Kim14, Theorem 1.2]. For both elliptic curves,
![]() and
and
![]() $E_{i}(\mathbb {Q})$
has no
$E_{i}(\mathbb {Q})$
has no
![]() $5$
-torsion. It follows that
$5$
-torsion. It follows that
![]() $\#\operatorname {Sel}(E/\mathbb {Q})\sim 1$
. Furthermore, the Tamagawa products
$\#\operatorname {Sel}(E/\mathbb {Q})\sim 1$
. Furthermore, the Tamagawa products
![]() $\prod c_{v}(E_{1})=6$
and
$\prod c_{v}(E_{1})=6$
and
![]() $\prod c_{v}(E_{1})=16$
. It thus follows that both Euler characteristics
$\prod c_{v}(E_{1})=16$
. It thus follows that both Euler characteristics
![]() $\chi ^{\pm }(\Gamma , E_{i})=1$
for
$\chi ^{\pm }(\Gamma , E_{i})=1$
for
![]() $i=1,2$
. We have thus demonstrated the relationship between Euler characteristics via explicit computation.
$i=1,2$
. We have thus demonstrated the relationship between Euler characteristics via explicit computation.
7.2 Example 2
We work out an example over the field
![]() $F:=\mathbb {Q}(i)$
. Let
$F:=\mathbb {Q}(i)$
. Let
![]() $E_{1}$
(resp.
$E_{1}$
(resp.
![]() $E_{2}$
) be the curves
$E_{2}$
) be the curves
![]() $38a1$
(resp.
$38a1$
(resp.
![]() $114b1$
), base-changed to F. The elliptic curves
$114b1$
), base-changed to F. The elliptic curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
are
$E_{2}$
are
![]() $5$
-congruent. The prime
$5$
-congruent. The prime
![]() $p=5$
splits into
$p=5$
splits into
![]() $\mathfrak {p}\mathfrak {p}^{*}$
, where
$\mathfrak {p}\mathfrak {p}^{*}$
, where
![]() $\mathfrak {p}=(2+i)$
and
$\mathfrak {p}=(2+i)$
and
![]() $\mathfrak {p}^{*}=(2-i)$
. Both curves
$\mathfrak {p}^{*}=(2-i)$
. Both curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
are supersingular at the primes
$E_{2}$
are supersingular at the primes
![]() $\mathfrak {p}$
and
$\mathfrak {p}$
and
![]() $\mathfrak {p}^{*}$
. The Mordell-Weil ranks of
$\mathfrak {p}^{*}$
. The Mordell-Weil ranks of
![]() $E_{1}$
(resp.
$E_{1}$
(resp.
![]() $E_{2}$
) over F are
$E_{2}$
) over F are
![]() $0$
(resp.
$0$
(resp.
![]() $1$
). Let
$1$
). Let
![]() $\ddagger =(\ddagger _{1}, \ddagger _{2})$
be a signed vector. It thus makes sense to assume that the order of vanishing of the signed Selmer group at
$\ddagger =(\ddagger _{1}, \ddagger _{2})$
be a signed vector. It thus makes sense to assume that the order of vanishing of the signed Selmer group at
![]() $T=0$
is given by
$T=0$
is given by
![]() $r_{E_{1}}^{\ddagger }=0$
and
$r_{E_{1}}^{\ddagger }=0$
and
![]() $r_{E_{2}}^{\ddagger }=1$
. Since
$r_{E_{2}}^{\ddagger }=1$
. Since
![]() $r_{E_{2}}^{\ddagger }\leq 1$
, it follows from Lemma 3.3 that the truncated Euler characteristic
$r_{E_{2}}^{\ddagger }\leq 1$
, it follows from Lemma 3.3 that the truncated Euler characteristic
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{2})$
is well defined. On the other hand, since
$\chi _{t}^{\ddagger }(\Gamma , E_{2})$
is well defined. On the other hand, since
![]() $r_{E_{1}}^{\ddagger }=0$
, the truncated Euler characteristic
$r_{E_{1}}^{\ddagger }=0$
, the truncated Euler characteristic
![]() $\chi _{t}^{\ddagger }(\Gamma , E_{1})$
is well defined and coincides with the usual Euler characteristic
$\chi _{t}^{\ddagger }(\Gamma , E_{1})$
is well defined and coincides with the usual Euler characteristic
![]() $\chi (\Gamma , E_{1})$
. Since
$\chi (\Gamma , E_{1})$
. Since
![]() $r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
, Theorem 5.5 asserts that
$r_{E_{1}}^{\ddagger }<r_{E_{2}}^{\ddagger }$
, Theorem 5.5 asserts that
![]() $5$
divides
$5$
divides
![]() $\delta _{E_{1}, \Sigma _{1}}\times \chi (\Gamma , E_{1})$
. We demonstrate this via direct calculation by showing that
$\delta _{E_{1}, \Sigma _{1}}\times \chi (\Gamma , E_{1})$
. We demonstrate this via direct calculation by showing that
![]() $\delta _{E_{1}, \Sigma _{1}}$
is divisible by
$\delta _{E_{1}, \Sigma _{1}}$
is divisible by
![]() $5$
.
$5$
.
We shall assume that the Selmer groups
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion. The optimal set of primes
$\operatorname {Sel}^{\ddagger }(E_{i}/F^{\operatorname {cyc}})$
are cotorsion. The optimal set of primes
![]() $\Sigma _{1}$
is contained in
$\Sigma _{1}$
is contained in
![]() $\{(i+1), 3, 19\}$
, the set of primes
$\{(i+1), 3, 19\}$
, the set of primes
![]() $v\nmid 5$
at which either
$v\nmid 5$
at which either
![]() $E_{1}$
or
$E_{1}$
or
![]() $E_{2}$
has bad reduction. Both curves
$E_{2}$
has bad reduction. Both curves
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
have split multiplicative reduction at
$E_{2}$
have split multiplicative reduction at
![]() $19$
, and hence
$19$
, and hence
![]() $19\in \Sigma _{1}$
. The prime
$19\in \Sigma _{1}$
. The prime
![]() $19$
is inert in F and its norm is
$19$
is inert in F and its norm is
![]() $19^{2}=361$
. The curve
$19^{2}=361$
. The curve
![]() $E_{1}$
has split multiplicative reduction at
$E_{1}$
has split multiplicative reduction at
![]() $19$
, hence
$19$
, hence
![]() $a_{19}(E_{1})=1$
. Recall that
$a_{19}(E_{1})=1$
. Recall that
![]() $L_{19}(E_{1}, 1)^{-1}$
is equal to
$L_{19}(E_{1}, 1)^{-1}$
is equal to
![]() $P_{19}(E_{1},19^{-2})$
, see the discussion following (5.3). The characteristic polynomial
$P_{19}(E_{1},19^{-2})$
, see the discussion following (5.3). The characteristic polynomial
![]() $P_{19}(E_{1},T)$
is equal to
$P_{19}(E_{1},T)$
is equal to
![]() $1-a_{19}(E_{1})T$
. Therefore,
$1-a_{19}(E_{1})T$
. Therefore,
![]() $L_{19}(E_{1}, 1)^{-1}=\frac {19^{2}-a_{19}(E_{1})}{19^{2}}=\frac {360}{361}$
. This implies that
$L_{19}(E_{1}, 1)^{-1}=\frac {19^{2}-a_{19}(E_{1})}{19^{2}}=\frac {360}{361}$
. This implies that
![]() $|L_{19}(E_{1},1)|_{5}=5$
. Since
$|L_{19}(E_{1},1)|_{5}=5$
. Since
![]() $19\in \Sigma _{1}$
, it follows that
$19\in \Sigma _{1}$
, it follows that
![]() $\delta _{E_{1}, \Sigma _{1}}$
is divisible by
$\delta _{E_{1}, \Sigma _{1}}$
is divisible by
![]() $5$
.
$5$
.
Let
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
be the maximal pro-p abelian extension of F unramified outside
$F_{2}$
be the maximal pro-p abelian extension of F unramified outside
![]() $\mathfrak {p}$
, resp.
$\mathfrak {p}$
, resp.
![]() $\mathfrak {p}^{*}$
. Both
$\mathfrak {p}^{*}$
. Both
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are
$F_{2}$
are
![]() $\mathbb {Z}_{p}$
-extensions of F. Let
$\mathbb {Z}_{p}$
-extensions of F. Let
![]() $\mathcal {F}_{\infty }$
be the composite of
$\mathcal {F}_{\infty }$
be the composite of
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
. We discuss results for truncated Euler characteristics over
$F_{2}$
. We discuss results for truncated Euler characteristics over
![]() $\mathcal {F}_{\infty }$
. Assume that for
$\mathcal {F}_{\infty }$
. Assume that for
![]() $i=1,2$
, the Selmer group
$i=1,2$
, the Selmer group
![]() $\operatorname {Sel}^{\ddagger }(E_{i}/\mathcal {F}_{\infty })$
is in
$\operatorname {Sel}^{\ddagger }(E_{i}/\mathcal {F}_{\infty })$
is in
![]() $\mathfrak {M}_{H}(\operatorname {G})$
. Recall that
$\mathfrak {M}_{H}(\operatorname {G})$
. Recall that
![]() $\operatorname {G}=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
and
$\operatorname {G}=\operatorname {Gal}(\mathcal {F}_{\infty }/F)$
and
![]() $H=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
. Corollary 6.6 asserts that
$H=\operatorname {Gal}(\mathcal {F}_{\infty }/F^{\operatorname {cyc}})$
. Corollary 6.6 asserts that
![]() $\chi _{t}^{\ddagger }(\operatorname {G}, E_{i})$
is equal to
$\chi _{t}^{\ddagger }(\operatorname {G}, E_{i})$
is equal to
![]() $\chi _{t}^{\ddagger }(\operatorname {G}, E_{i})$
for
$\chi _{t}^{\ddagger }(\operatorname {G}, E_{i})$
for
![]() $i\,{=}\,1,2$
.
$i\,{=}\,1,2$
.