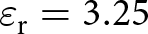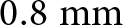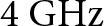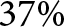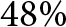Dual UWB bandpass filter with highly band-to-band rejection using stepped impedance stub-loaded resonators for WBAN health-care applications

Abstract

With the rapid development of communication technology, the researches of multi-band filtering circuits have become more and more important. Multimode resonator (MMR) is one of the vital methods to provide multi-resonant modes within a single design. In this paper, a dual-band ultra-wideband bandpass filter (UWB-BPF) using stepped impedance stub-loaded resonators (SI-SLR) is presented. The main advantage of using SI-SLR is to have better performance with multimode behavior and more parameters to control resonant modes. SI-SLR combines the advantages of SIR and SLR structures, which gives a compact, high-performance multiband filter. The proposed filter design has compact size, sharp and flat response with low insertion loss (IL), low return loss (RL), and high band-to-band rejection. The filter is designed for UWB communication in wireless body area networks and fabricated on Arlon substrate with relative permittivity ${\varepsilon_{\textrm{r}}} = 3.25$, thickness $0.8\;{\textrm{mm}}$. The resulted dual-bands are centered at $4{\textrm{ GHz}}$ and $8.3{\textrm{ GHz}}$ with fractional bandwidths $37{\textrm{% }}$ and $48{\textrm{%}}$. The simulation was carried out using CST Microwave Studio. The filter provides good passband performances, with IL 0.49 dB and 0.31 dB at the center frequency of lower and higher bands, respectively. The band-to-band 40 dB rejection is realized by adding circular spiral at the input/output of the filter.

Introduction

Wireless body area networks (WBANs) are special-purpose wireless sensor networks designed to operate in the human body and its surroundings to continuously monitor a patient’s health conditions while not imposing restrictions on the patient’s lifestyle [1, 2]. These are mainly used to monitor the human body and some of its vital functions, such as recording heart electrical signals, measuring glucose levels, performing periodic medical examinations, or in emergency cases in which the patient needs immediate attention [1]. WBAN is defined as a set of different intelligent elements such as sensors, nodes, and actuators [2] and has three different bands designated by IEEE [2, 3]: Human body communication (16 and 27 MHz), narrowband body communication (402–405, 420–450, 863–870, 902–928, 956–956 MHz), ultra-wideband (UWB) communication (Low-band: 3.24–4.74 GHz, Hi-band: 6.2–10.3 GHz). UWB systems has been defined in 2003 by the Federal Communication Commission as any system occupying a fractional bandwidth (FBW) greater than 0.2 [4]. As UWB technology is a low data rate in short range, it is one of the most popular technologies used in WBAN [1] for various applications, such as health care and precise localization in indoor environments [3]. Designing UWB-bandpass filters (BPFs) is a difficult job for microwave researchers compared to other types of BPFs [5]. Different approaches for designing UWB BPFs have been recently proposed, such as parallel-coupled-line [6, 7], asymmetric coplanar waveguide defect ground structure (ACPW-DGS) [8], and tapered resonators [9]. Although the proposed design in paper [6] is compact and highly selective, the stop-band used to reject the unwanted wireless local area network (WLAN) signal is narrow, and the RL is high (12 dB). In paper [7], a straightforward method of designing the BPF is proposed by cascading a low-pass filter and a high-pass filter, and inductively compensated parallel-coupled lines (ICPCL) has been used to achieve compactness. Results give high RL in passbands (12 dB). In paper [8], the design is compact but the IL degrades as the frequency gets higher. Tapered resonator design in paper [9] achieves good results with large size. To achieve UWB BPF with compact size, and simple design process MMR has been proposed. The most popular MMR structures are stepped impedance resonators (SIRs), stub-loaded resonators (SLRs), and ring resonators [10]. SIR has a simple structure and can be implemented in small size area, but it is difficult to extend to more resonant modes. SLR has compact size, is easy to extend to more resonant modes, and has high flexibility of the frequency arrangements. Ring resonator resonant frequencies can be controlled individually, but designs are large in size and difficult to extend to more resonant modes [11]. Multiple modes can be used to realize multiple passbands [12]. To maximize the filtering circuit performance, the appropriate method in designing actual multi-band filtering circuit is to combine different types of MMR structures [11]. Superposition of SIR and SLR (SI-SLR) gives the filter better performance with multimode behavior and more parameters to control resonant modes. SI-SLR combines the advantages of SIR and SLR structures, which implies the possibility of designing compact, high-performance multiband filters [13]. Recently, many approaches to MMR multiband BPF design have been reported. The most common structure used to design dual-band BPFs is SIR [14, 15]. In paper [14], a dual-band BPF with a tunable band is demonstrated. The band can be tuned between 5.7 and 8.4 GHz without any increment in the circuit size. In paper [15], the design uses loop resonator with double T-shaped and open-bended stubs (OBSs) to have low IL, good suppression level, and compact size dual-band BPF. Although designs proposed in papers [14] and [15] have attractive characteristics, they are narrow band designs and lack FBW information. Another dual-band BPF design is proposed in paper [16]. The design uses octagonal loop resonators, tapered resonators, and OBSs. The design has two bands with FBW 11% and 26% for lower and higher band, respectively. The higher band bandwidth (BW) can be adjusted (max FBW 26%). Different SLR BPF designs are presented in paper [17] for Global System for Mobile (GSM) and WLAN bands with considerable size reduction. The design has high IL and large circuit dimension. A quad-band BPF was investigated using (λ/2) SLR in paper [18]; three of the demonstrated bands has 3-dB FBW less than 15% with high IL (0.9 dB). Another quad-band BPF design in paper [19] was realized by multi-embedded SLR, which had an IL higher than 1.3 dB. Some approaches investigated getting more passbands such as in paper [20] with a BPF design with six bands using a multimode resonator (MMR) loaded with branches. However, the bands are narrow (FBW < 6%) except the first band has FBW equal to 29.27%. A controllable sept-band BPF design in paper [21] aimed at GSM, WLAN, WIFI, and 4G/5G communication using coupled SLRs. Similar to the previous mentioned designs, the bands are narrow with IL changes from band to another between the values 0.5 and 1.6 dB. In paper [22], the design was a compact wideband microstrip BPF based on SLR for the next-generation mobile standards “5G” 3–6 GHz with a center frequency of 4.75 GHz. Many different approaches have been designed for UWB systems. The proposed UWB filter design in paper [23] uses a circular ring-shaped resonator attached to a uniform impedance microstrip line, with a high RL (13 dB). In paper [24], the design is based on quintuple mode resonator with IL (0.8 dB) and RL (10 dB). Basit et al. [5] used SIR to implement a simple UWB topology with two notches at 3.5 GHz for WiMAX with a 7.5 GHz C-band satellite downlink communication system. The IL for this design was 1.1 dB and RL was 18 dB. Chakraborty et al. [25] investigated a novel design for UWB indoor applications with three sharp notches at 6 GHz for the Wi-Fi 6E, 6.53 GHz for super-extended C band, and 8.35 GHz for satellite TV networks or raw satellite feeds. The topology used is an open-ended SIR attached to an interdigitated uniform impedance resonance. The rejection at 6 GHz is split into two narrow rejection bands (<1.47%) with a passband 6.19–6.46 GHz between them, the third rejection band at 8.35 GHz is also very narrow (0.47%). In paper [26], an UWB BPF is based on SLR with a reconfigurable stop-band in the notched frequency from 3 to 9.5 GHz controlled by PIN diode effect. The use of PIN diode makes it so difficult to have good selectivity, and not good out of band performance.

This paper is involved in designing a novel dual-band UWB for high and low WBAN bands using SI-SLR BPF topology. The most important characteristics of the proposed BPF are compact size, sharp and flat response with low IL, low RL, and high band-to-band rejection.

The paper is organized as follows: The following section analyzes of the dual-mode resonator structures (SLR and SIR) used in the proposed design, followed by an analysis of SI-SLR structure. The proposed geometry of the MMR filter is described in the “Filter geometry” section. The simulation and experimental results are described in the “Results and discussion” and “Experimental results” sections, respectively, followed by the “Conclusion” section.

Analysis of the dual-mode resonators

Figure 1 shows different dual-mode resonators used in designing multiband filters. The resonant condition of $\lambda /4{\ }$ SIR (Fig. 1a) is given by [13]

(1)\begin{equation}K = \tan {\theta_1}\tan {\theta_2}\end{equation}

Figure 1. (a) $\lambda /4{\ }$ SIR; (b) short-end SLR; (c) open-end SLR.

where $K = {Y_1}/{Y_2}$, ${Y_1}$ and ${Y_2}$ are the characteristic admittance. ${\theta_1}$ and ${\theta_2}$ are the electrical lengths.

Due to the symmetry of the SLR, the resonator can be analyzed using even-/odd-mode analysis [13]. The even-mode and odd-mode input admittances ${Y_{{\textrm{in,e}}}}$ and ${Y_{{\textrm{in,o}}}}$ for open-stub SLR can be calculated as [11]

(2)\begin{equation}{Y_{{\textrm{in}},{\textrm{e}}}} = j{Y_1}{{2{Y_1}\tan {\theta_1} + {Y_2}\tan {\theta_2}} \over {2{Y_1} - {Y_2}\tan {\theta_1}\tan {\theta_2}}}\end{equation}

(3)\begin{equation}{Y_{{\textrm{in,o}}}} = - j{Y_1}{1 \over {\tan {\theta_1}}}\end{equation}

where $Y$ and $\theta $ denote the characteristic admittance and electrical length, respectively. Resonance is obtained when $Im\left( {{Y_{{\textrm{in}}}}} \right) = 0$ [27]. Thus, the structure has two resonance frequencies ${f_{\textrm{e}}}$ and ${f_{\textrm{o}}}$ which can be calculated as following, for ${Y_{{\textrm{in,o}}}} = 0$ we have

(4)\begin{equation}\tan {\theta_1} = \infty \Rightarrow {\theta_1} = {\pi \over 2} + n\pi \end{equation}

The electrical length of a transmission line is defined as

(5)\begin{equation}{\theta_i} = \beta {L_i} = {{2\pi f\sqrt {{\varepsilon_{{\textrm{eff}}}}} } \over c}{L_i}\end{equation}

where ${L_i}$ is the physical length of the transmission line $i$, $f$ is the resonant frequency, ${\varepsilon_{{\textrm{eff}}}}$ is the effective relative permittivity, and $c$ is the velocity of light in vacuum. Substituting (5) in (4) gives the odd-mode resonant frequency as

(6)\begin{equation}{f_{\textrm{o}}} = {{\left( {2n + 1} \right)c} \over {4{L_1}\sqrt {{\varepsilon_{{\textrm{eff}}}}} }}\end{equation}

For ${Y_{{\textrm{in,e}}}} = 0$

(7)\begin{equation}\cot \left( {{\theta_1}} \right)\tan \left( {{\theta_2}} \right) = - {{2{Y_1}} \over {{Y_2}}}\end{equation}

If we let ${Y_2} = 2{Y_1}$, the resonance condition can be deduced as

(8)\begin{align} \tan \left( {{\theta_2}} \right) & = - \tan \left( {{\theta_1}} \right) \\ \Rightarrow {\theta_2} & = n\pi - {\tan ^{ - 1}}\left[ {\tan \left( {{\theta_1}} \right)} \right] \\ &\Rightarrow {\theta_2} + {\theta_1} = n\pi \end{align}

This leads to even-mode resonant frequency:

(9)\begin{equation}{f_{\textrm{e}}} = {{nc} \over {2\left( {{L_1} + {L_2}} \right)\sqrt {{\varepsilon_{{\textrm{eff}}}}} }}\end{equation}

In a similar manner, we can find the even/odd -mode resonant frequency for short stub SLR. The input admittances ${Y_{{\textrm{in,e}}}}$ and ${Y_{{\textrm{in,o}}}}$ can be calculated as [11]

(10)\begin{equation}{Y_{{\textrm{in,e}}}} = j{Y_1}{{2{Y_1}\tan {\theta_1}\tan {\theta_2} - {Y_2}} \over {2{Y_1}\tan {\theta_2} + {Y_2}\tan {\theta_1}}}\end{equation}

(11)\begin{equation}{Y_{{\textrm{in,o}}}} = - j{Y_1}{1 \over {\tan {\theta_1}}}\end{equation}

The odd-mode resonant frequency is calculated in the same way as open-stub SLR (Eq. 6). For even-mode resonance, we have

(12)\begin{equation}{Y_{{\textrm{in,e}}}} = 0 \Rightarrow \tan \left( {{\theta_1}} \right)\tan \left( {{\theta_2}} \right) = {{{Y_2}} \over {2{Y_1}}}\end{equation}

If we let ${Y_2} = 2{Y_1}$, the resonance condition can be deduced as

(13)\begin{align} & \tan \left( {{\theta_1}} \right)\tan \left( {{\theta_2}} \right) = 1 \\ & \Rightarrow {\theta_1} + {\theta_2} = {\pi \over 2} + n\pi \end{align}

This leads to even-mode resonant frequency:

(14)\begin{equation}{f_{\textrm{e}}} = {{\left( {2n + 1} \right)c} \over {4\left( {{L_2} + {L_1}} \right)\sqrt {{\varepsilon_{{\textrm{eff}}}}} }}\end{equation}

The proposed SI-SLR structure used to design the filter is shown in Fig. 2.

Figure 2. The proposed SI-SLR structure.

Even-mode and odd-mode input admittances (see Fig. 3a and b) can be calculated as

(15)\begin{equation}{Y_{{\textrm{in}},1}} = j{Y_1}{{2{Y_1}\tan {\theta_1}\tan {\theta_3} - {Y_3}} \over {2{Y_1}\tan {\theta_3} + {Y_3}\tan {\theta_1}}}\end{equation}

(16)\begin{align} {Y_{in,e}} &= {Y_2}{{{Y_{in,1}} + j{Y_2}\tan {\theta_2}} \over {{Y_2} + j{Y_{in,1}}\tan {\theta_2}}} \\ \,\;\;\;\;\; & = - j{Y_2}{{\begin{array}{c}2Y_1^2\tan \theta_1^\prime\tan {\theta_3} - {Y_1}{Y_3} \\ + 2{Y_1}{Y_2}\tan {\theta_2}\tan {\theta_3} + {Y_2}{Y_3}\tan \theta_1^\prime\tan {\theta_2}\end{array}} \over {\begin{array}{c} 2Y_1^2\tan \theta_1^\prime\tan {\theta_2}\tan {\theta_3} - 2{Y_1}{Y_2}\tan {\theta_3}\\ - {Y_2}{Y_3}\tan \theta_1^\prime - {Y_1}{Y_3}\tan {\theta_2}\end{array}}} \end{align}

(17)\begin{equation}{Y_{in,o}} = - j{Y_2}{{K - \tan \theta_1^\prime\tan {\theta_2}} \over {\tan \theta_1^\prime + K\tan {\theta_2}}}\end{equation}

Figure 3. The proposed SI-SLR structure equivalent circuit. (a) even-mode; (b) odd-mode.

where $K = {{{Y_1}} \over {{Y_2}}} = {{{Z_2}} \over {{Z_1}}}$, $\theta_1^\prime = \beta \left( {{L_1}/2} \right)$,$ {\theta_2} = \beta {L_2}$, ${\theta_3} = \beta {L_3}$.

Equation (17) determines the first resonant frequency ${f_1}$ which can be obtained with resonance condition introduced in Eq. (12). So ${f_1}$ is related to parameters $K$, $\theta_1^\prime\left( {{L_1}} \right)$, ${\theta_2}\left( {{L_2}} \right)$. Equation (16) introduces two other frequencies and ${f_2}$ and ${f_3}$ under condition ${Y_{{\textrm{in,e}}}} = 0$.

(18)\begin{align} \tan {\theta_3} & = {{{Y_1}{Y_3} - {Y_2}{Y_3}\tan \theta_1^\prime\tan {\theta_2}} \over {2Y_1^2\tan \theta_1^\prime + 2{Y_1}{Y_2}\tan {\theta_2}}} \\ & = {{K{K_1} - K1\tan \theta_1^\prime\tan {\theta_2}} \over {2K\tan \theta_1^\prime + 2\tan {\theta_2}}}\end{align}

where ${K_1} = {{{Y_3}} \over {{Y_1}}}$.

The main advantage of using SIR in this design is to have more resonant frequency with compact design. The periodic nature of ($\tan \theta $) gives spurious harmonic frequencies [27]. Figure 4 shows three normalized spurious resonant frequencies (${f_{{\textrm{sp}}}})$ for the $\lambda /2$-SIR, we can see that the separation of the spurious resonance increases with the lowering of the value of K and decreases with higher value of K [13, 27].

Figure 4. Spurious resonance frequency of $\lambda /2$-SIR [27].

Filter geometry

Figure 5 shows the proposed UWB dual-band filter design, which is composed of SI-SLR coupled with open-stub SLR, and a circular spiral for band rejection. We set the widths of SIR to have K high enough, so that the spurious resonant frequencies lay in the desired band.

Figure 5. The proposed UWB dual-band filter design.

We set $\theta_1^\prime = 3{\theta_2}$. The resonance condition from Eq. (17) can be written as

(19)\begin{equation}K = \tan \theta_1^\prime\tan {\theta_2} = \tan \left( {3{\theta_2}} \right)\tan \left( {{\theta_2}} \right)\end{equation}

Using the mathematical fact of

(20)\begin{equation}\tan \left( {3x} \right) = {{3\tan x - {{\tan }^3}x} \over {1 - 3\tan x}} \end{equation}

We get

(21)\begin{equation}K = {{3{{\tan }^2}{\theta_2} - {{\tan }^4}{\theta_2}} \over {1 - 3\tan {\theta_2}}} \end{equation}

Figure 6 shows the changes of $K$ when frequency changes in range $f = \left[ {0 - 12} \right]{\textrm{GHz}}$. We determine the value of $K$ high enough. We can see that the range of K to choose is wide, so we determine K in a way that the resonant frequency lays in the lower band and spurious resonant frequencies lay in the higher band of the required filter. For $K = 1.$

Figure 6. Impedance ratio $K$ as a function of frequency.

We choose $K = 1.6$, then ${f_0} = 3.5\;{\textrm{GHz}}$, ${f_{s{\rm{p}}1}} = 1.8 \times {f_0} = 6.3\;{\rm{GHz}}$, ${f_{{\rm{sp}}2}} = 2.5 \times {f_0} = 8.7\;{\textrm{GHz}}$, ${f_{{\rm{sp}}3}} = 3.5 \times {f_0} = 12.25\;{\rm{GHz}}$ which is out of desired band. As a result, we get ${\theta_2} = {24^{\textrm{o}}}$, and ${\theta_1} = {72^{\textrm{o}}}$. Even-mode resonant frequencies can be found by fixing Eq. (16) by letting $\left( {{\theta_3} = {\theta_2} = {{24}^{\textrm{o}}}} \right)$ and using the Eq. (20) to have

(22)\begin{equation} {Y_{{\textrm{in,e}}}} = - j{Y_2}{{\begin{array}{c} - \left( {2Y_1^2 + {Y_2}{Y_3}} \right){{\tan }^4}{\theta_2} - 6{Y_1}{Y_3}{{\tan }^3}{\theta_2}\\ + \left( {6Y_1^2 + 3{Y_2}{Y_3} + 2{Y_1}{Y_2}} \right){{\tan }^2}{\theta_2} \\ + 3{Y_1}{Y_3}\tan {\theta_2} - {Y_1}{Y_3}\end{array}} \over {\begin{array}{c} \tan {\theta_2}\left( - 2Y_1^2{{\tan }^4}{\theta_2} + \left( {6Y_1^2 - {Y_2}{Y_3}} \right){{\tan }^2}{\theta_2}\right.\\ \left. + 3\left( {2{Y_1}{Y_2} + {Y_1}{Y_3}} \right)\tan {\theta_3}\right. \\ \left. - 2{Y_1}{Y_2} - 3{Y_2}{Y_3} - {Y_1}{Y_3}\vphantom{{2Y_1^2 + {Y_2}{Y_3}}} \right)\end{array}}}\end{equation}

We get two resonant frequencies when ${Y_{{\textrm{in,e}}}} = 0$ at 4.375 and 7.48 GHz. By extending the SI-SLR structure with open-stub SLR and optimizing design lengths we get the dimensions of the filter geometry as shown in Table 1.

Table 1. Dimensions of the filter

We added a high Q circular spiral to introduce a transmission zero (TZ) without influencing the passband loss much [11]. The design of a circular inductor may be with a single turn or more. It may be observed that the inductance of a single turn is less than the inductance of a straight line with the same length and width [28].

Results and discussion

We used CST for filter simulation, and as a result of the proposed design, we get six resonance modes: (${f_1} = 3.8{\textrm{ GHz}}$, ${f_2} = 4.1{\textrm{ GHz}}$, ${f_3} = 6.75{\textrm{ GHz}}$, ${f_4} = 7.6{\rm{ GHz}}$, ${f_5} = 8.96{\textrm{ GHz}}$, and ${f_6} = 9.9{\rm{ GHz}}$), with three TZs at (${f_{{\rm{T}}{{\rm{Z}}_1}}} = 1.6\;{\rm{GHz}}$, ${f_{{\rm{T}}{{\rm{Z}}_2}}} = 5.7\;{\rm{GHz}}$, ${f_{{\rm{T}}{{\rm{Z}}_3}}} = 10.95\;{\rm{GHz}}$). This gives two transmission bands centered at (${f_{{C_1}}} = 4{\textrm{ GHz}}$ and ${f_{{C_2}}} = 8.3{\rm{ GHz}}$). The FBWs are ($B{W_1} = 37{\textrm{% }}$, $B{W_2} = 48{\textrm{% }}$). Figure 7 shows the magnitude of the simulated ${S_{11}}$ and ${S_{21}}$. The operational mechanism of the proposed filter is described in Fig. 8 by the surface current distribution through the filter. We chose three operating frequencies, which are the center frequencies of the two passbands (4 and 8 GHz) and 6 GHz. As can be noted at the center frequencies of the dual bands of filter (Fig. 8a and b), the current at the resonator is strong, which means that all of the radiated electromagnetic waves transit through this filter, while we can see at 6 GHz (Fig. 8c) the current is very weak, which means that no radiated electromagnetic waves go through this filter at this frequency. The filter exhibited flat group delay less than 2 ns with sharp increases at the resonance frequencies (<5 ns) as illustrated in Fig. 9.

Figure 7. Simulated ${S_{11}}$ and ${S_{21}}$ of the proposed filter.

Figure 8. Surface current of the filter at (a) 4 GHz, (b) 8 GHz, and (c) 6 GHz.

Figure 9. Group delay performance.

The structure of the filter gives many parameters that can be altered to adjust the filter bands as required. The key parameter is the impedance ratio K, which determines the fundamental frequency in the lower band. The impedance ratio K is related to parameters ${W_1}$ and ${W_2}$. Figure 10 shows the filter response w.r.t. K. As seen in figure, the resonance in the lower band is heavily dependent on the value of K because it determines the fundamental resonant frequency introduced in Eq. (21). The higher band resonant frequencies also shifted up as a result. So, choosing K is one of the most important parameters in our design which can determine the frequency response in the higher band of the filter.

Figure 10. Simulated ${S_{11}}$ and ${S_{21}}$ w.r.t. impedance ratio $K$.

The circular spiral affects the band-to-band rejection. The number of turns for the spiral affects TZs ${f_{{\textrm{T}}{{\textrm{Z}}_2}}}$ and ${f_{{\textrm{T}}{{\textrm{Z}}_3}}}$. Which gives the ability to control the BW of the filter bands. As the turns of the spiral increased, ${f_{{\textrm{T}}{{\textrm{Z}}_2}}}$ and ${f_{{\textrm{T}}{{\textrm{Z}}_3}}}$ shifts down, but with ${f_{{\textrm{T}}{{\textrm{Z}}_3}}}$ affects more than ${f_{{\textrm{T}}{{\textrm{Z}}_2}}}.$ Figure 11 shows the filter performance for 3-turns, 2-turns, and one turn spiral. The spiral length $H$ has the same effect of the number of spiral turns. as H gets smaller, the rejection band shifts lower. The same happens to the TZ frequency ${f_{T{Z_3}}}$ (Fig. 12). The fact that the spiral parameters affect ${f_{{\textrm{T}}{{\textrm{Z}}_2}}}$ and ${f_{{\textrm{T}}{{\textrm{Z}}_3}}}$ gives the ability to control and determine the required BW. Other parameters to get into consideration are the length of the coupling between SI-SLR and the open-stub SLR ${L_c}$ (Fig. 13) and the length of the SLR line ${L_4}$ which can be adjusted in the final place to adjust and enhance the matching of the filter.

Figure 11. Simulated ${S_{11}}$ and ${S_{21}}$ w.r.t. number of spiral turns.

Figure 12. Simulated ${S_{11}}$ and ${S_{21}}$ w.r.t. parameter $H$.

Figure 13. Simulated ${S_{11}}$ and ${S_{21}}$ w.r.t. parameter ${L_c}$.

Experimental results

We fabricate the proposed filter using Arlon substrate with relative permittivity ${\varepsilon_{\rm{r}}} = 3.25$ and thickness $h = 0.8\;{\textrm{mm}}$. The top view of the fabricated prototype is shown in Fig. 14a, where the overall effective area occupied by the filter is $20.2\;{\rm{mm}} \times 12.3\;{\rm{mm}}$. Alternatively, the size can be expressed by guided wavelength ${\lambda_{\textrm{g}}}$ which can be calculated as

(23)\begin{equation}{\lambda_{\textrm{g}}} = {c \over {{f_{\textrm{c}}}\sqrt {{\varepsilon_{{\textrm{eff}}}}} }}\end{equation}

Figure 14. Proposed filter implementation. (a) Fabricated prototype, (b) Comparison of the simulated and measured responses of the filter.

for ${f_{\rm{c}}} = 6.75\;{\textrm{GHz}}$. The size of the fabricated prototype is $0.72\;{\lambda_{\rm{g}}} \times 0.44\;{\lambda_{\rm{g}}}$. The measured filter performances are compared to the simulated results in Fig. 14b, where it can be observed that the measured results almost match the simulated output. The proposed notched filter characteristics are compared in Table 2 with recent available filters found in the literature. The column-wise entries stand for the total passbands in GHz with FBW (%),IL in dB, RL in dB, notch frequency in GHz/notch attenuation in dB, filter size in respect of the guided wavelength, and finally the technique used, respectively.

Table 2. Comparison of performance with the available filters

The available filters mentioned in Table 2 is separated into three categories, UWB filter designs, UWB filter with notch characteristics, and multi-band BPF. Based on Table 2, it can be seen that the proposed filter has relatively better characteristics among mentioned filter designs.

By comparing The IL and RL parameters, the proposed filter has the lowest IL and the highest RL.

The FBW of the proposed design is 37% and 48% which are higher than the mentioned “Multi-band BPF” designs. As shown in Table 2, the passbands achieved by those designs are narrow FBW < 18% except a band in paper [20], $FBW = 29.27{\textrm{ % }}$ in paper [19], and $26{\textrm{ % }}$ in paper [16].

Another feature to compare is the notch characteristics. The proposed structure has higher stopband BW than designs mentioned under “UWB filter with notch characteristic” designs. The notches implemented in these designs are narrow 280 MHz@6.3 GHz [6] 310 MHz@3.5 GHz, and 690 MHz@7.5 GHz [5], 1 GHz@9.28 GHz and 450 MHz@10.48 GHz [8]. 180 MHz@6 GHz, 160 MHz@6.53 GHz, and 80 MHz@8.35 GHz [25]. In this work, the proposed filter achieved wider stopband 1.65 GHz@5.57 GHz. Also the band-to-band rejection is relatively among the highest between other designs.

It should be noted here that there is a trade-off between designing parameter of a filter. As the proposed design has lowest IL, highest RL, highest FBW, and good band-to-band rejection characteristics, it has larger size than other topology mentioned in Table 2. The obtained dual-band cannott be tuned such as dual-band designs in [14–16]. It also does not have as high band-to-band rejection as filter design in [20].

Conclusion

In this paper, we proposed a dual UWB-BPF based on the SI-SLR structure. The combination of SLR and SIR was adopted to have more resonant modes with good performance and a compact design. The impedance ratio K was chosen to be large, so we can have the spurious resonant frequencies construct the higher band of the filter. The proposed UWB-BPF is compact in size $0.72\;{\lambda_{\rm{g}}} \times 0.44\;{\lambda_{\rm{g}}}$. It operates in frequencies 4 and 8.3 GHz with FBWs 37% and 48%, respectively. The measured RL at the lower band is better than 24 dB, while at the higher band it is better than 20 dB. The measured IL is 0.49 and 0.31 dB at the center frequency of lower and higher bands, respectively. The wide rejection band is implemented using a circular spiral. The measured attenuation at the notch is 40 dB. The experimental results almost match the simulated results. The proposed filter match very well with UWB communication bands in WBANs, so it can be used as one of its important elements that gives the ability to operate at both bands.