A variable stiffness robotic gripper based on parallel beam with vision-based force sensing for flexible grasping

Abstract

The demand for flexible grasping of various objects by robotic hands in the industry is rapidly growing. To address this, we propose a novel variable stiffness gripper (VSG). The VSG design is based on a parallel-guided beam structure inserted by a slider from one end, allowing stiffness variation by changing the length of the parallel beams participating in the system. This design enables continuous adjustment between high compliance and high stiffness of the gripper fingers, providing robustness through its mechanical structure. The linear analytical model of the deflection and stiffness of the parallel beam is derived, which is suitable for small and medium deflections. The contribution of each parameter of the parallel beam to the stiffness is analyzed and discussed. Also, a prototype of the VSG is developed, achieving a stiffness ratio of 70.9, which is highly competitive. Moreover, a vision-based force sensing method utilizing ArUco markers is proposed as a replacement for traditional force sensors. By this method, the VSG is capable of closed-loop control during the grasping process, ensuring efficiency and safety under a well-defined grasping strategy framework. Experimental tests are conducted to emphasize the importance and safety of stiffness variation. In addition, it shows the high performance of the VSG in adaptive grasping for asymmetric scenarios and its ability to flexible grasping for objects with various hardness and fragility. These findings provide new insights for future developments in the field of variable stiffness grippers.

1. Introduction

Robotic hands, usually mounted on a robotic arm, are widely utilized in various industrial production tasks [1]. Traditional robotic hands are typically rigid [2], offering numerous advantages such as structural stability, excellent robustness, high holding force, substantial load capacity, high precision, great durability, and fast operation [3]. However, the rigid robotic hand is poorly adapted to irregularly shaped, complexly structured, and fragile objects, such as a piece of bread and a glass of water. They may not be able to grab such objects effectively or cause damage. Moreover, during human-robot interaction, a rigid robotic hand may injure humans in a collision due to its rigid structure [4].

Unlike rigid robotic hands [5, 6], compliant robotic hands are more suitable for applications that require adaptability, safe interaction, and flexibility [7–9]. Compliant robotic hands exhibit high flexibility, enabling them to adapt to objects of irregular shapes and various sizes [10, 11]. For instance, refs. [12, 13] proposed grippers based on the jamming of granular materials, allowing them to grasp irregularly shaped objects with a strong grasping force. However, such grippers may struggle with gripping sharp objects. Additionally, grippers made of soft materials [14] or composites [15] have been explored. Pneumatic [16, 17] and underactuated [18, 19] grippers have also demonstrated high adaptability and the ability to conform to irregularly shaped objects without the need for precise control inputs. Fin Ray effect-inspired grippers [20–22] based on bionics have also been proposed. Compliant robotic hands provide inherent safety when interacting with humans or delicate objects, as they apply gentle grips, minimizing the risk of injury or damage [23]. As a result, more and more compliant robotic hands have been applied in industry in recent years, such as in food and agricultural product processing lines [24, 25]. Nevertheless, compared to rigid robotic hands, compliant robotic hands have limited strength and load-carrying capacity, making them unsuitable for handling heavy loads or tasks that require significant force. Moreover, the control accuracy of compliant robotic hands may be compromised, which is a disadvantage in applications requiring high precision or fine manipulation.

However, some scenarios necessitate both the high holding force and precision of a rigid robotic hand and the adaptability and flexibility of a compliant robotic hand. For instance, in flexible production lines in factories [26], the robotic hand must be capable of gripping parts with different characteristics. Furthermore, for service robots expected to become commonplace in households, ensuring safety while handling a variety of tasks is crucial [27].

Therefore, researchers have proposed the concept of variable stiffness robotic grippers [28], which combine the functions and advantages of rigid and flexible robotic hands. One feasible principle for achieving stiffness variation is altering the physical properties of materials. For instance, ref. [29] employs permanent magnets to adjust the magnetic force between two fingers, thereby enabling variable stiffness in the gripper. Ref. [30] utilizes pneumatic pouch actuators to control the folding and unfolding of adaptable flaps on flexure hinges, consequently altering the hinge’s stiffness. Also using pneumatic air actuation, the gripper proposed by ref. [31] combines layer jamming technique to achieve stiffness adjustment. Ref. [32] adopts a similar method to reduce or increase the stiffness of the gripper by converting between positive and negative pressure. Refs. [33, 34] proposed a 3D printed gripper by imitating human fingers, using a method of heating the shape-memory polymer located at the finger joints to reduce stiffness. Similarly, the use of shape-memory alloy [35] and low-melting-point materials [36] allows for stiffness adjustment by controlling the temperature of the material. Nevertheless, a common drawback of grippers that employ these innovative methods is that they may lack sufficient stiffness to accommodate high-load scenarios.

Altering the mechanical structure is an alternative stiffness adjustment principle with a high degree of robustness compared to utilizing the inherent properties of the material. Ref. [37] presents a gripper capable of adjusting stiffness by altering the state of a pangolin scale structure through the actuation of a toothed pneumatic actuator to enhance the stiffness of pneumatic gripper. In ref. [38], another pneumatic-driven gripper is introduced, based on an exoskeleton structure equipped with a self-locking mechanism to improve grabbing stability. Ref. [39] elaborates on a gripper that achieves stiffness changes through the manipulation of tendons in each finger to achieve high flexibility. Ref. [40] employs a hybrid variable stiffness actuator to directly modulate the stiffness of a conventional 1-DOF gripper to accomplish a high stiffness ratio. Ref. [41] introduces a gripper with an enhanced Fin Ray structure that can discretely adjust stiffness by rotating the ribs within the frame of the Fin Ray to perform adaptive and flexible grasping. Additionally, ref. [42] presents a gripper with variable stiffness fingers capable of achieving continuous stiffness changes through a built-in flexure hinge shaft, which has a relatively wide range of stiffness variations.

In contrast to the aforementioned methods, this paper presents a novel design of a variable stiffness gripper (VSG) for flexible grasping. The two fingers of the VSG employ a parallel-guided beam structure [43], with a slider block inserted from one end. By controlling the position of the slider within the beam’s cavity, the length of the parallel leaf springs participating in the system can be adjusted, thereby achieving changes in stiffness. This design enables the continuous variation of VSG fingers from highly compliant to fully rigid states, encompassing a wide range of varying stiffness levels. Theoretically, the VSG can achieve a stiffness ratio of 391.5. Additionally, the VSG possesses other advantageous features. This mechanism based on mechanical structures rather than soft materials or electrical sensors makes the VSG highly robust and durable. The movement of the slider on the finger requires relatively low extrusion and retraction forces, enabling rapid online stiffness changes. The stiffness of the two fingers can be independently adjusted to accommodate various grasping tasks. Also, multifarious types of fingertips can be added to expand the functionality of the VSG and enhance its grasping capability.

The paper proceeds as follows: Section 2 elucidates the principles and design of stiffness variation in the VSG. Section 3 establishes an analytical model of the parallel-guided beam. Section 4 illustrates the features and performance of the VSG. The flexible grasping capabilities are demonstrated in Section 5.

2. Design of proposed gripper

2.1. Principle of stiffness variation

Figure 1 illustrates a parallel-guided beam with a cavity. Similar to the structure of a syringe, the stiffness of this beam can be adjusted by introducing a long solid block into one end, which has the same height and width as the cavity of the beam, while keeping other beam parameters constant. The stiffness variation is achieved by changing the length of the parallel beam involved in the system, akin to two parallel leaf springs. As the solid block is inserted deeper into the cavity, the length of the leaf spring involved in the system decreases, resulting in increased stiffness of the beam. At full insertion, the entire parallel beam structure can be regarded as a solid cantilever beam, exhibiting maximum stiffness. Conversely, by gradually retracting the solid block from the cavity, the length of the leaf springs involved in the system increases, leading to a reduction in beam stiffness. Ultimately, the stiffness of the beam reaches its minimum value when the solid block is fully removed from the cavity.

Figure 1. The principle of continuous stiffness change.

2.2. Mechanical design

Utilizing the aforementioned principle as a basis, a VSG was devised, comprising a base, driving mechanism, and variable stiffness mechanism, as depicted in Fig. 2. The primary function of the VSG base is to accommodate diverse components, featuring threaded holes atop that facilitate connection to robotic arms via a connector. Positioned at the front of the base are two horizontal slides and one vertical slide, collectively forming the T-tracks along with six attached cover plates. These T-tracks enable sliders to undergo translational motion within their confines. In addition, the shell of the VSG is connected to the base through six brackets, which are not shown in the figure.

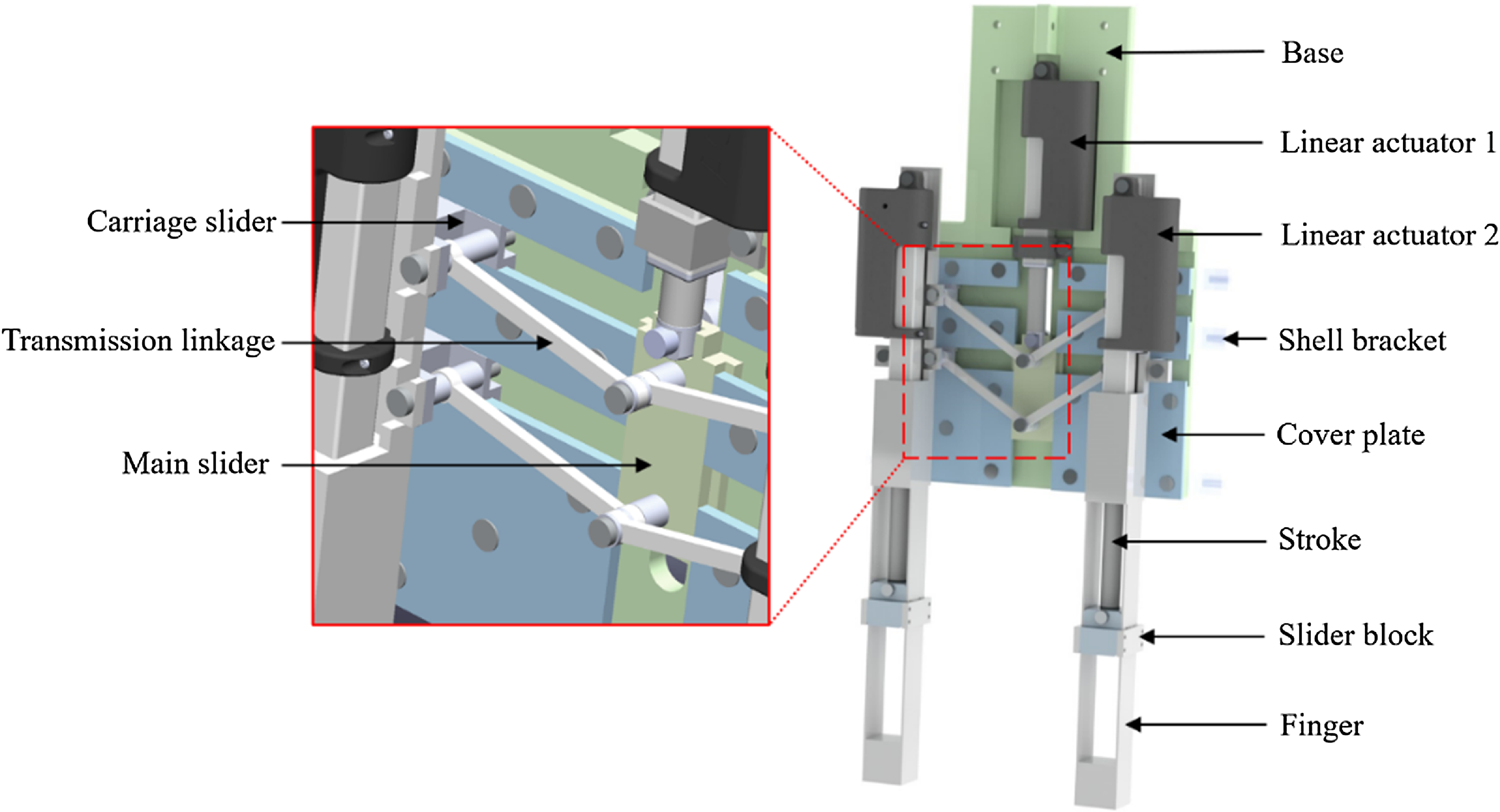
Figure 2. 3D model of the variable stiffness gripper.

The driving mechanism of the VSG is designed to open and close the two fingers in parallel. Four carriage blocks have been symmetrically positioned on both the left and right sides, enabling lateral sliding along the track. Each of the two fingers is affixed to a set of carriage slides located on their respective sides. To establish a connection between the carriage slides and the main slider, a transmission linkage is employed. Every two neighboring linkages are not in the same plane to prevent any potential interference during movement. The rear end of the main slider is securely attached to the front end of the stroke of the linear actuator (P16-50-64-12-P), which features a stroke length of 50 mm and a back drive force of 200 N. The linear actuator is fixed onto the base and is responsible for driving the main slider and affecting the sliding motion of the carriage sliders along the track, thus facilitating the opening and closing of the fingers.

According to the principle in Section 2.1, the variable stiffness mechanism of the fingers is mainly performed by a linear actuator (P16-100-22-12-P) installed on each finger. It has a 100 mm long stroke, which is the same length as the parallel-guided beam section of the finger. The head of the stroke is connected with the bottom of the slider block, and the slider block is set on the parallel beam as a track. Since the stroke is rigid, the region of the parallel-guided beam propelled forward by the stroke can be treated as a solid component, while the remaining portion of the beam housing the cavity retains its compliant characteristics. Therefore, this mechanism can achieve continuous online stiffness adjustment and only takes 2.2 s from the minimum stiffness to the maximum stiffness under no load condition. Theoretically, the VSG can achieve a 367-fold stiffness change. The stiffness of the two fingers can be adjusted independently to adapt to variable grasping tasks. The cube-shaped head of the finger, featuring a side length of 20 mm, serves as a mounting platform for various accessories, including the fingertip.

In contrast to the angular gripper, the parallel gripper mechanism offers notable advantages in terms of precision and facile fingertip replacement, enhancing modularity. However, one drawback of this mechanism is the limited finger opening, which can be addressed by employing appropriately shaped fingertips. The entire VSG is customizable in terms of size and performance parameters, and the fingers and fingertips can be modularized to suit a variety of demands.

3. Modeling and validation

3.1. Force modeling

First, the static force analysis of the VSG holding an object has been conducted. As shown in Fig. 3, the object is subject to a downward gravity G and two upward friction f located at the contact points with the fingers. Noteworthily, one of the characteristics of the parallel beams is that, under small to middle deflections, its end only moves in translation and hardly produces rotation. Therefore, the angle of the fingertips can be disregarded in this case. Establishing force equilibrium equation in the vertical direction:

Figure 3. Free body diagram of the variable stiffness gripper.

(1) \begin{equation}G=2f\end{equation}

In the horizontal direction, the two fingers exert a pair of equal but oppositely directed gripping forces F, on the object. The relationship between the f and F is as follows:

(2) \begin{equation}f=\mu F\end{equation}

where μ is the coefficient of friction.

The above equations provide a discernible insight that the grasping load of the VSG could be enhanced by increasing μ while F remains constant, which can be achieved by attaching high-friction materials to the fingertips.

3.2. Stiffness modeling

To investigate the force-deflection relationship of a parallel-guided beam, it is essential to establish a model that characterizes its stiffness. Building upon previous work [44, 45], we have developed and simplified a linear analysis model suitable for small to medium deflections [46] (within 10% of the beam length) in a specific range of parameters.

Figure 4 depicts the force applied to a parallel-guided beam. Employing a Cartesian coordinate system, the x-axis is oriented horizontally to the left, the y-axis vertically to the x-axis, while the z-axis is omitted for simplicity. The beam, with length L, is divided into three segments: l ₁ and l ₃ represent solid bodies with respective moments of inertia I ₁ and I ₃, while segment l ₂ denotes a compliant parallel beam with moment of inertia I ₂, regarded as two parallel leaf springs. Assuming the right end of the beam is fixed, a downward force F is applied perpendicular to the beam axis at the left end.

Figure 4. Sketch for the stiffness modeling of the parallel-guided beam.

In this model, we neglect parasitic error motions [47] in the x-axis direction, pertaining to undesired movements within the constraints, as their magnitude is considerably smaller compared to displacements in the y-axis direction. While the compliant segment l ₂ primarily contributes to the beam deflection, it is important not to overlook the solid segments l ₁ and l ₃. Accounting for these sections is critical in improving the accuracy of the model since, in practical applications, segments l ₁ and l ₃ possess certain lengths rather than being thin-walled [48].

Next, we proceed to compute the deflection and stiffness of the parallel beam. As illustrated in Fig. 3, points A, B, C, and D lie on the central auxiliary line of the beam. Point A corresponds to the load-bearing end of the beam, while points B and C are situated at the ends of the l ₂ section, and point D represents the fixed end. The height of the beam is denoted as H, while the height of the cavity is h. The thickness of a leaf spring is determined as t = (H – h)/2. The width W of the beam is not shown in the figure, which will be used to calculate the moment of inertia.

(3) \begin{equation}I_{1}=I_{3}=\frac{WH^{3}}{12}\end{equation}

(4) \begin{equation}I_{2}=\frac{Wt^{3}}{12}\end{equation}

Using segment-by-segment analysis and superposition methods, the parallel beam can be divided into three segments: AB, BC, and CD, corresponding to l ₁, l ₂, and l ₃, respectively. Calculating the deflection and rotation angles at points A, B, and C individually, and cumulatively acting on point A, the maximum deflection of the entire beam in the y-axis direction can be obtained.

Initially, focusing solely on segment AB, segments BC and CD are assumed to be rigid. At this time, point B can be regarded as being fixed on the wall, and point A is affected by downward force F. Because segment l ₁ is solid, using the deflection formula of a cantilever beam, the deflection $\delta$ _AA at point A can be obtained, where E represents Young’s modulus.

(5) \begin{equation}\delta _{\mathrm{AA}}=\frac{Fl_{1}^{3}}{3E_{1}I_{1}}\end{equation}

The deflection angle of segment AB does not need to be calculated, as the orientation of point A has no impact on its own coordinates. Subsequently, setting segments AB and CD as rigid, and only consider segment BC. Here, point C is fixed on the wall, and point B is acted on by downward force F and bending moment Fl ₁ from segment AB. Based on the theory of parallel-guided beam mechanism [49, 50], the deflection formula of parallel beam is deduced. This can be used to calculate the deflection angle θ _B of the segment BC, which results from the combined action of force and bending moment. θ _B is transmitted to point A through l ₁, causing point A to have a certain deflection. At the same time, the deflection $\delta$ _B of point B can also be obtained, which is produced by the joint action of force and bending moment and makes point A produce the same deflection. In summary, the deflection and deflection of point B will act on point A, making point A produce deflection $\delta$ _AB.

(6) \begin{equation}\theta _{\mathrm{B}}=\frac{t^{2}}{6h^{2}}\left(\frac{Fl_{1}l_{2}}{E_{2}I_{2}}+\frac{Fl_{2}^{2}}{2E_{2}I_{2}}\right)\end{equation}

(7) \begin{equation}\delta _{\mathrm{B}}=\frac{Fl_{2}^{3}}{24E_{2}I_{2}}+\frac{t^{2}}{12h^{2}}\left(\frac{Fl_{1}l_{2}^{2}}{E_{2}I_{2}}+\frac{Fl_{2}^{3}}{2E_{2}I_{2}}\right)\end{equation}

(8) \begin{equation}\delta _{\mathrm{AB}}=\delta _{B}+\theta _{B}l_{1}\end{equation}

Similarly, the segments AB and BC are regarded as rigid bodies, and only the segment CD is considered. At this time, point D is fixed on the wall, and point C is subjected to the downward force F and the bending moment F(l ₁ + l ₂) from segment AC. Use the deflection formula of a cantilever beam to obtain the deflection angle C of CD, and the deflection $\delta$ _C of point C. Consequently, the deflection and deflection of point C act upon point A, resulting in the deflection $\delta$ _AC at point A.

(9) \begin{equation}\theta _{\mathrm{C}}=\frac{Fl_{3}^{2}}{2E_{3}I_{3}}+\frac{F(l_{1}+l_{2})l_{3}}{E_{3}I_{3}}\end{equation}

(10) \begin{equation}\delta _{\mathrm{C}}=\frac{Fl_{3}^{3}}{3E_{3}I_{3}}+\frac{F(l_{1}+l_{2})l_{3}^{2}}{2E_{3}I_{3}}\end{equation}

(11) \begin{align}\delta _{\mathrm{AC}}={\delta _{C}}+\theta _{C}(l_{1}+l_{2})\end{align}

Finally, add up all the deflections acting on point A to get its total deflection $\delta$ _A under the action of force F, and then get the stiffness of the whole beam K.

(12) \begin{equation}\delta _{\mathrm{A}}=\delta _{\mathrm{AA}}+\delta _{\mathrm{AB}}+\delta _{\mathrm{AC}}\end{equation}

(13) \begin{equation}K=\frac{F}{\delta _{\mathrm{A}}}\end{equation}

3.3. Validation discussion

To validate the analytical model proposed above, we adopt the control variable method, whereby the length l ₂, thickness t, and width W of the compliant parallel beam section are taken as independent variables. Deflection and stiffness are then determined under varying forces through theoretical calculations, finite element analysis (FEA) simulations, and experimental measurements. Keeping other parameters unchanged, select ten values for each of the aforementioned three parameters for investigation.

Before proceeding, the Young’s modulus (E) of the Polylactic acid (PLA) material used in the validation process needs to be determined. The deflection formula of the cantilever beam, as Eq. (5), is utilized, the force and deflection are measured through experiments, and then substituted into the size parameters to calculate E. To ensure accuracy, multiple cantilever beams with identical dimensions to a single sheet of parallel beams are utilized, employing the same print configuration. Then, the final results are averaged to reduce errors. Traditional testing methods [51] based on the definition of Young’s modulus are omitted due to the anisotropic nature of 3D printed parts caused by different patterns and fillings, leading to inaccurate outcomes. Finally, Young’s modulus of the PLA material used is determined to be E = 2530 MPa at 80% filling and a 0.1 mm layer height.

The selected parallel beam models are subjected to theoretical calculations using MATLAB, based on the obtained E and other known dimensional parameters. 3D modeling is then conducted for these models, which are subsequently imported into ANSYS for FEA simulations, where one end of the beam is fixed, and the other end is stressed. Next, these models were printed using a 3D printer. One end of the beam was fixed in a bench vise, and the other end was applied with a probe of a force gauge, enabling the measurement of force and deflection during deformation.

The obtained results are compared and analyzed to identify the factors influencing stiffness and the relationship between parameters. To facilitate finding regularities, the existing parameters are normalized. For instance, l ₂/L is used to represent the ratio of the compliant segment of the parallel beam, whereby a smaller value indicates a reduced proportion of the total length of the compliant segment, resulting in increased beam stiffness. Similarly, h/H represents the thickness ratio of the leaf spring, with a smaller value indicating greater stiffness and thicker leaf springs. Additionally, W/L represents the width ratio of the beam, where a smaller value corresponds to a thinner beam width and lower stiffness.

In Fig. 5(a), the relationship between l ₂/L and beam stiffness is illustrated, showing that an increase in the ratio of l ₂/L is associated with a decrease in beam stiffness. When l ₂/L is less than 0.2, the error between FEA and experimental values increases significantly but remains within 5% relative to the theoretical values and FEA results. This discrepancy can be attributed to deflection values in these cases being less than 1 mm, causing the percentage error to be amplified. Thus, this discrepancy is attributed to experimental error rather than systematic error. Figure 5(b) presents the relationship between h/H and stiffness. When the h/H ratio is less than 0.5, it indicates that the combined thickness of the two parallel beams exceeds half of the overall beam thickness, which is no longer applicable formulas for compliant parallel beams. This abnormal range should be avoided in design, as it cannot produce lower stiffness. However, when h/H exceeds 0.5, it falls within the normal design range, with the error between the analytical model and FEA not exceeding 5%. When h/H is less than 0.7, a large error is observed between the experimental values and FEA results. This difference is likely attributed to the beam becoming thicker, resulting in minimal deformation of the entire beam, similar to the situation with l ₂/L. Figure 5(c) depicts the relationship between W/L and parallel beam stiffness, which generally exhibits a positive correlation. The errors of all theoretical values, FEA results, and experimental values are less than 5%. The above analysis reveals that increasing the length of the parallel beam, reducing the thickness of the leaf spring, and decreasing the width contribute to lower stiffness values and higher stiffness ratios.

Figure 5. Comparison of finite element analysis, theoretical value, and experimental value: (a) l₂/L; (b) h/H; (c) W/L.

4. Features and performance of the VSG

4.1. Prototype

In accordance with the principles and design outlined in Section 2, a prototype of the VSG was fabricated, as shown in Fig. 6. To enable the gripping of larger objects, a 15 × 20 × 20 mm cube was affixed as a fingertip to each finger. In addition, a rubber pad with a thickness of 1 mm was applied to the surface of the fingertips to enhance friction. The structural components of the prototype were produced through 3D printing, utilizing PLA material with Young’s modulus of 2530 MPa with 80% filling and a 0.1 mm layer height. In practical applications, alternative metal materials such as aluminum alloy and titanium alloy can be used to enhance the longevity and performance of the VSG.

Figure 6. Prototype of the variable stiffness gripper.

Table I lists the values of the main design parameters of the VSG. Based on this configuration, it can theoretically achieve a stiffness ratio of 391.5, covering sufficiently low and sufficiently high stiffnesses, which enables the VSG to be capable of grasping various objects with different weights, volumes, and shapes. The stiffness of the two fingers can be adjusted individually, which enables the VSG to grip irregular objects. In the regular grasping task, the two fingers were set to identical stiffness to maintain the stability of the system.

Table I. Main specifications of the variable stiffness gripper.

4.2. Performance of the finger stiffness

Following the establishment of the prototype of the VSG, an analysis of its stiffness performance is conducted. To facilitate analysis, one of the fingers is selected, and the effective length of its parallel beam mechanism is 140 mm, including a compliant parallel beam segment of 100 mm. Use $\lambda$ to represent the ratio of the distance stuck out by the stroke of the linear actuator to the length of the original compliant segment. As $\lambda$ increases, the effective length of the compliant parallel beam decreases, leading to a reduction in finger stiffness. The range of $\lambda$ is divided into 11 stiffness levels, with values ranging from 0 to 1 in increments of 0.1.

First, the theoretical values of deflection and stiffness are calculated for each stiffness level. Subsequently, FEA simulations are conducted as depicted in Fig. 7(a), where the base of the finger is fixed, and a downward force is applied to the other end. Similarly, experimental measurements are performed, as shown in Fig. 7(b), where one end of the finger is fixed in a bench vise and a probe connected to a force gauge is used to measure the force and deflection during deformation. To eliminate the effect of gravity, the reading of the force gauge is reset to zero when the probe touches the beam. Each configuration is measured five times, and the results are averaged to reduce error.

Figure 7. (a) Finite element analysis simulation and (b) experimental measurements of a finger prototype.

Figure 8 illustrates the relationship between $\lambda$ and the stiffness of the VSG, including the comparison of theoretical values, FEA results, and experimental measurements. When $\lambda$ is below 0.8, the error between theoretical values and FEA results consistently remains within 5%. For $\lambda$ greater than or equal to 0.8, the error remains below 10%, aligning with the findings in Section 3.2. Moreover, when $\lambda$ is below 0.5, the error between FEA results and experimental measurements is consistently below 10%. However, as $\lambda$ increases, the error also increases. One possible reason deflections of the experimental values are small, in which case the numerical error is small, so the percentage error is exaggerated. Another factor could be the slider block at the head of the stroke cannot lock the parallel beam, and there is a certain slippage after a large force is applied. As a result, at higher stiffness levels, the error between experimental measurements and theoretical values increases, leading to actual stiffness performance lower than the theoretical predictions. In the experiment, the VSG demonstrates a minimum stiffness of 0.1 N/mm, a maximum stiffness of 7.2 N/mm, and a stiffness ratio of 70.9. However, in theory, it can achieve a stiffness change of up to 391.5 times, corresponding to a maximum stiffness of 40.7 N/mm.

Figure 8. Stiffness varying with different slider filling ratio $\lambda$ .

Figure 9 shows the relationship between force and deflection for different $\lambda$ values in the experiment. It is evident that when $\lambda$ is below 0.8, the differences between each stiffness level are more pronounced, while the differences become relatively less significant when $\lambda$ is above or equal to 0.8. Consequently, in subsequent experiments, three $\lambda$ values (0, 0.5, and 1) will be selected to study the performance of different stiffness levels, while simplifying the calculation workload.

Figure 9. Relationship between force and deflection for various $\lambda$ .

Table II provides a comparison of the VSG performance with other variable stiffness grippers, highlighting the advantages of our VSG in terms of achieving higher stiffness values and a wider range of stiffness variation. The stiffness ratio of the VSG is among the highest, second only to ref. [30], which utilized a self-locking mechanism driven by pneumatic actuation. However, despite its high stiffness ratio, the maximum stiffness of ref. [38] was only 0.9 N/mm, which is in the compliant category rather than the rigid one. In contrast, our prototype achieves a much higher maximum stiffness. If we were to base our VSG prototype on aluminum alloy instead of 3D printing, it would further increase the maximum stiffness and stiffness ratio, enhancing its capabilities in rigid grasping tasks.

Table II. Performance comparison among variable stiffness grippers.

4.3. Vision-based force sensing

To enable precise closed-loop control, it becomes imperative to acquire real-time force feedback during the gripping process of the gripper, which enables the gripper to have the ability to adjust the magnitude of the gripping force, and successfully grab the object without damage. Conventionally, force sensors are integrated into the gripper, thereby increasing its structural complexity. We propose a novel approach by using ArUco marker detection to achieve force sensing to reduce cost and structural complexity. ArUco is a binary square fiducial marker, that is utilized to determine the position and orientation of objects through QR code recognition. The inherent advantages of ArUco markers lie in their robust, fast, and straightforward detection capabilities. Hence, the positioning function of ArUco can be exploited to monitor the deflection of the finger of VSG, allowing the retrieval of the corresponding force value from a pre-established database and facilitating force sensing. Figure 10 shows the experimental setup using this method, and a detailed description is provided below.

Figure 10. Experimental setup of grasping.

Initially, we establish a database of force and deflection relationships by utilizing experimental data from the previous section. The force and deflection data for each $\lambda$ are interpolated to an accuracy of 0.1 N and 0.01 mm, respectively. Furthermore, the $\lambda$ is interpolated with a resolution of 0.01. Consequently, we obtain a dataset encompassing the force-deflection relationship for various $\lambda$ values. In the application, the interval of $\lambda$ when collecting data in the experiment can be shortened to reduce the error of the data set.

Next, the camera for marker detection is calibrated. Instead of a depth camera, a regular monocular camera can be utilized. A calibration board, which comprises a calibration image with multiple ArUco markers, is generated and printed. The calibration image should contain as many markers as possible to improve the calibration accuracy. Then, the calibration plate is positioned within the camera’s field of view, and multiple calibration images are captured from different angles and distances. Based on Python, use the ArUco module in the OpenCV library to extract the information of the markers in the calibration image. We can calculate the intrinsic and extrinsic camera parameters by relying on this information. The intrinsic parameters involve the camera’s focal length, the principal point’s position, and distortion coefficients, while the extrinsic parameters encompass the camera’s position and orientation. Finally, the calibration image undergoes distortion correction to verify the calibration results, thereby deriving the camera parameter matrix.

Subsequently, position recognition is performed on the ArUco markers. Two 20 × 20 mm markers with IDs 0 and 1, respectively, obtained from the dictionary DICT_4X4_50, are affixed to the solid part of one of the fingers. The camera is positioned to focus on the finger, maintaining an appropriate distance. Figure 11 is an image captured by the camera in real-time, where the axes of two ArUco markers are displayed, and the y-axis is marked in red. The y-coordinates of their centers are continually read in real-time, and the difference $\delta$ _y, representing the finger’s deflection, is calculated. This process operates at a rate of 30 frames per second. Then, by inputting $\lambda$ and $\delta$ _y, the corresponding force value is retrieved from the database. To minimize noise during data acquisition and reduce errors, a Kalman filter is employed. The error remains below 7.4% when $\delta$ _y exceeds 5 mm. For deflections below 5 mm, the error increases but remains within 19.5%. One possible reason is that the marker size used is not large enough to recognize the location with insufficient precision. Another reason is that the numerical difference between the value of ArUco and the experimental value is small, but the percentage is relatively large.

Figure 11. Force sensing.

4.4. Grasping control and strategy

The closed-loop control block diagram for the VSG is depicted in Fig. 12. The input of the linear actuator is V _a which represents the velocity of the linear actuator’s stroke. The displacement of the linear actuator’s stroke at the center of the VSG is denoted as x _a , which is responsible for driving the finger to close. On the other hand, x _g represents the translation distance of a finger during closing. According to the Pythagorean theorem, the relationship between x _a and x _g is shown in the box of the control diagram. The output force, represented by F, is derived from the product of x _g and the gain K. The desired output force is denoted by F _d . The discrepancy between F and F _d is characterized as the error e. To obtain the desired control output, a proportional-integral differential controller is applied to the error signal and gains the desired control output. Additionally, x _s denotes the stroke displacement of the linear actuator on the two fingers, which is designed to adjust the stiffness of the fingers. The relationship between stiffness K and x _s is described as K = f(x _s ). The stiffness K corresponding to $\lambda$ can be obtained from Fig. 7, where $\lambda$ = x _s /100. The control system is combined with vision-based force sensing, which enables precise control of the gripping force, and ensures that it is not damaged while successfully gripping the target object, especially fragile objects.

Figure 12. Control system of the variable stiffness gripper.

The strategy of the VSG to grasp the target object is shown in Fig. 13. Prior to the grasping task, it is essential to classify the objects based on parameters such as volume, shape, weight, hardness, and fragility. Experimental investigations are conducted to determine the appropriate grasping force for each object category, which will be elaborated in Section 5. To mitigate the impact of contact and protect the object from damage, a preset stiffness slightly smaller than the required stiffness is employed. For instance, when grasping a tomato, the corresponding stiffness is determined when $\lambda$ equals 0.5. We could set the initial value of $\lambda$ as 0.3 instead of 0, which reduces the impact force while also saving time for stiffness adjustment. Additionally, instead of keeping the maximum opening, the gripper is preset to open slightly larger than the object’s size. This approach reduces finger closure distance, thereby improving operational efficiency. Next, the VSG is maneuvered to the object’s location using a robotic arm, aligning the two fingers with the grasping point on the target object. The fingers are then closed to contact the object. Simultaneously, the stiffness K _a of the finger is adjusted by positioning the linear actuator’s stroke at the corresponding $\lambda$ position. Moreover, the fingertip’s deflection is captured using the camera, enabling the retrieval of the corresponding force F from the database, which is then transmitted to the control system. If the desired grasping force is achieved, it indicates a successful grasping task, and the object is placed at the target position. Conversely, if the desired grip is not attained, the fingers will continue to pinch until the aim is reached.

Figure 13. Grasping strategy.

4.5. Importance of stiffness adjustment

To demonstrate the importance of stiffness adjustment for robotic grippers, a step response test was conducted on the VSG across different stiffness configurations. This test aimed to evaluate the dynamic grasping force of the VSG under closed-loop force control. The experimental setup, as shown in Fig. 11, involved the rapid grasping of a load cell by the fingertip of the VSG fingers. Through closed-loop force control, the final grasping force was maintained consistently on various stiffness modes during the test.

Figure 14 illustrates the impact on the dynamic grasping performance of the VSG at maximum and minimum stiffness settings, with the dashed line representing the final force required. It is observed that the instantaneous grasping force of the VSG exhibits approximately 10% overshoot at maximum stiffness, whereas the minimum stiffness allows for smooth attainment of the desired force. At high stiffness, a minimal finger closure distance leads to a large force increase, while at low stiffness, the force increment is relatively smaller for the same distance. Notably, this overshooting force may pose a risk of object damage, particularly when delicate or fragile objects are involved, as they are highly sensitive to grasping force. Additionally, the response time to reach the desired force in the low stiffness mode is slower than that in the high stiffness mode state, which also helps to protect the target object from damage. These findings underscore the necessity of employing variable stiffness in dynamic grasping tasks. While the low stiffness mode mitigates overshoot and potential damage, it is accompanied by slower response times. Conversely, the high stiffness mode enables faster response at the expense of increased overshoot and potential damage, which is suitable for objects that are not fragile or solid. Therefore, adjusting the stiffness of a robotic gripper according to the specific application scenario is crucial to achieving optimal grasping performance.

Figure 14. Dynamic grasping performance in various stiffness.

5. Demonstration of flexible grasping

5.1. Adaptive grasping

In the preceding section, a step response test was conducted with the load cell positioned at the center. However, in practical applications, robotic grippers frequently encounter scenarios necessitating asymmetric grasping, where each finger does not make contact with the object simultaneously. In these situations, avoiding damage to the object is crucial. In this case, achieving asymmetric grasping with a small contact force is a necessary capability to exhibit the flexible grasping performance of robotic grippers. Therefore, an adaptive grasping experiment was performed on the VSG to verify its ability to grasp objects with irregular shapes or uncertain positions.

The experimental setup remains unchanged in Fig. 10, except for the placement of the load cell in an asymmetric position between the two fingers of the VSG. The VSG is initially set to the maximum opening while maintaining the minimum stiffness, followed by a gradual closure of the fingers until one finger makes contact with one side of the load cell. During this process, the finger’s displacement and the load cell’s force are recorded, as illustrated in Fig. 15. The maximum deflection of the finger reached approximately 4 mm, while the maximum recorded force was approximately 0.7 N when successfully grasping the load cell.

Figure 15. Adaptive grasping in minimum stiffness.

The experimental results demonstrate that VSG possesses the capability to adapt passively to objects with uncertain positions and irregular shapes by adjusting the finger stiffness, thereby preventing damage to fragile objects. By maintaining minimal stiffness, the VSG can exert small contact forces on the object during asymmetric grasping. If the initial contact force is insufficient to successfully grip the target object, the stiffness of fingers can be gradually increased online until the grasping task is accomplished.

5.2. Grasping of various objects

Different from adaptive grasping, which mainly studies the irregular shape and asymmetric position of objects, here we focus on the characteristics of objects such as weight, hardness, and fragility. When grasping objects with known properties, they are positioned between the two fingers at the center during the grasping process. Based on the classification of objects, appropriate stiffness, and opening configurations are preset for the VSG, which enhances the gripping efficiency compared to adaptive grasping scenarios.

A series of grasping tests were conducted on over thirty objects, all of which resulted in successful grasping. The success criterion was defined as the VSG lifting the target object and elevating it to a height greater than 100 mm from the table, then moving back 100 mm at a speed of 0.1 m/s to put it down. In cases where the object did not lift off the table or fell during the process, it was deemed a grasping failure. Similarly, it was considered a failure if excessive gripping force caused the object to break.

Table III illustrates the characteristics of eight representative target objects. Each object was individually weighed, and a pre-grip test was conducted to determine the required force for successful grasping. The procedure involved gradually increasing the grasping force for each object until the grasping was successful. Furthermore, objects were roughly categorized based on their hardness and fragility to determine the optimal stiffness for grasping. Initially, objects were classified as either soft (S) or hard (H) based on common sense, such as considering a sponge as soft and an aluminum block as hard. Objects are then further classified based on their fragility (F). Fragile objects were assigned positive values above 0, while robust objects were assigned negative values. For instance, eggshells, bulbs, aluminum frames, and aluminum blocks were all classified as hard objects. However, both eggshells and light bulbs were fragile, whereas aluminum frames and aluminum blocks were not. For further differentiation, the eggshell was considered more fragile than the bulb, resulting in assigning +1 to the eggshell and +2 to the light bulb. Similarly, the aluminum frame was relatively more fragile than the aluminum block, leading to assigning −1 to the frame and −2 to the block. To obtain intuitive results, three values of $\lambda$ – 0, 0.5, and 1 – were selected for examination, corresponding to minimum, low, and maximum stiffness settings, respectively. For example, a light and fragile eggshell is suitable for grasping with minimum stiffness; a disposable cup for holding water is suitable for low stiffness; and a heavy and strong aluminum block is suitable for maximum stiffness.

Table III. Properties of the grasping object.

Figure 16 shows the various target objects that were grasped in the experiments. These experiments validate the ability of the VSG to perform flexible grasping tasks on objects with varying weights, hardness levels, and fragilities.

Figure 16. Demonstration of flexing grasping in various objects: (a) cup of water; (b) tomato; (c) sponge; (d) rubber ball; (e) eggshell; (f) bulb; (g) aluminum frame; and (h) aluminum block.

6. Conclusions

This research proposed a novel VSG for flexible gripping. Based on the parallel-guided beam structure where a slider is inserted from one end of the beam, the stiffness of the two fingers could be individually adjusted by changing the length of the parallel beams participating in the system. This design allowed for continuous variation in the compliance of the gripper’s fingers, ranging from highly compliant to completely rigid states. The linear analytical model of deflection and stiffness of the parallel beam was derived segment by segment, using the principle of superposition, making it suitable for small and medium deflections. Deflection and stiffness data for the parallel beams were collected through ANSYS simulations, MATLAB calculations, and experimental tests, considering different parameters and configurations. The collected data were then compared and verified using the control variable method, with most cases showing an error within 10%. The fabricated VSG prototype exhibited a minimum stiffness of 0.1 N/mm, a maximum stiffness of 7.2 N/mm, and a stiffness ratio of 70.9. The theoretical analysis indicated a remarkable stiffness change of up to 391.5 times, corresponding to a maximum stiffness of 40.7 N/mm. A new vision-based force sensing method utilizing ArUco markers was proposed as an alternative to traditional force sensors, and it demonstrated errors within 20%. By leveraging this method, closed-loop control for the object-grasping process was achieved. A grasping strategy was specified to ensure efficiency and safety during the gripping operation. To elucidate the importance of stiffness variation, a step response test was conducted. Furthermore, the VSG demonstrated its adaptability in grasping asymmetric objects and delicate items with varying hardness. These findings underscored the exceptional performance of the VSG in the flexible grasping of objects with diverse characteristics. Future research will focus on further optimizing the analytical model, refining the structural design, and enhancing the force sensing method to improve accuracy and overall performance. Additionally, a more detailed object classification will be conducted to determine the required grasping force and stiffness parameters more precisely.