Computational aerodynamics: Advances and challenges

Abstract

Computational aerodynamics, which complement more expensive empirical approaches, are critical for developing aerospace vehicles. During the past three decades, computational aerodynamics capability has improved remarkably, following advances in computer hardware and algorithm development. However, most of the fundamental computational capability realised in recent applications is derived from earlier advances, where specific gaps in solution procedures have been addressed only incrementally. The present article presents our view of the state of the art in computational aerodynamics and assessment of the issues that drive future aerodynamics and aerospace vehicle development. Requisite capabilities for perceived future needs are discussed, and associated grand challenge problems are presented.

1.0 INTRODUCTION

Computational aerodynamics research can be traced back to more than a century ago (e.g. see the landmark paper by Richardson⁽¹⁾). However, much of the groundbreaking work for the modern-day electronic computations was performed during the 1960s at Los Alamos Scientific Laboratory (now Los Alamos National Laboratory). Since the 1970s, computational technology for flow analysis has developed rapidly, in parallel with advances in computing hardware. During the 1980s and 1990s, flow simulation tools of varying fidelity were developed for aerodynamics applications. Numerous individuals contributed to algorithm research, and many organisations developed computational tools in such areas as meteorology and aerospace vehicle development. It is an almost impossible task to review these activities comprehensively and give proper credit to all major contributors in this review. For a more comprehensive historical review, readers are referred to existing literature such as Roache⁽²⁾, Tannehill et al⁽³⁾, and Chapman⁽⁴⁾. In this review, we focus on the advances in computational aerodynamics, or, more narrowly, on the computational fluid dynamics (CFD) that impacted aerospace engineering and sciences. We also discuss what challenges need to be addressed to support aerospace engineering for the foreseeable future.

Computational flow analysis complements the experimental approach. As the computational aerodynamics technology became more developed in parallel with advances in computing hardware, computational flow analysis became a key element in providing data for fluid engineering and fundamentally changed how aircrafts and spacecraft are designed. In aeronautics, aircraft design demands high precision and rapid design cycles, requiring integrated work with other disciplines such as structures and control. Johnson et al⁽⁵⁾ summarise how computational analysis became an indispensable part of aircraft design.

In the space exploration area, however, applications of computational aerodynamics have lagged aeronautics, partially because space-related flow problems involve largely time-dependent and complex flow phenomena, which require an advanced unsteady flow algorithm and physical modelling (e.g. see Kiris et al^(6,7) ). Moreover, limited amounts of experimental and flight data are available for validation, especially for new vehicle configurations. Advanced computational technology suitable for space transportation vehicle development requires maturation through experiences in realistic applications. When a new vehicle concept like the Space Shuttle launch vehicle was on the drawing board, flow simulation capabilities or CFD tools were not mature enough to make a significant impact. Therefore, until recently, most operational space vehicles were designed heavily relying on empiricism. Later, the CFD technology suitable for space applications was developed in parallel with vehicles’ operational period. Subsequently, CFD became useful to support operational aspects, to retrofit for improved components and to investigate accidents. Since post-Shuttle human space exploration requires new or replacement vehicles, conceptual design evaluations rely on databases generated by CFD, which has not, however, been thoroughly validated for the types of flow encountered in new vehicle concepts. Therefore, the so-called best-practices protocols have been developed in conjunction with new vehicle development tasks. In this report, the state of the art in computational aerodynamics and requisite capabilities for supporting future tasks are discussed with a list of grand challenge problems.

Regarding the development of requisite capabilities for aerospace problem solving, steady investment has been made, especially during the 1980s and 1990s, to develop flow simulation tools of varying fidelity. As a result, computational technology has become an indispensable part of the design and operation of aerospace vehicles. However, there are several fundamental elements of these tools that need continued advances such as efficient algorithms, geometry definition and grid generation procedures, boundary condition procedures, physical modelling, and pre- and post-processing methods. Furthermore, in a practical problem-solving environment, computer architecture, data management tools and networking play a very important role in producing results in a timely manner. To obtain solutions within a reasonable turnaround time, approximate formulations and simplified geometries were utilised first. Then, in the 1980s and 1990s, increasing the fidelity of formulation and inclusion of more complete geometry were the focus largely in a single discipline. The high-speed scientific computing environment has grown to the point that vehicles and components are to some degree amenable to computer simulations. Despite these advances, unsolved problems still exist in several areas critical to aerospace mission successes. For example, high-fidelity simulation of unsteady flow for the prediction of vibration loads on launch vehicles and prediction of massively separated flow is among the remaining challenges. Of course, CFD-related issues can vary depending on the primary flow features of interest, and resolving all scales and features of complex problems is not necessarily needed in all flow analyses or in all tasks.

Following the early successes in developing solution algorithms and flow solvers, reduction of solution time has been realised more through computer hardware speed-up than algorithm advancement. Thus, the parallel computing methods and associated data management schemes have played an important role in utilising compute resources. As problem sizes continue to grow, development of both advanced methods and advanced computer hardware remains very important.

It is to be noted that successful application of computational technology requires the synergy of the computing facility, software, simulation tools, data analysis tools and networks, coupled with a combined knowledge of engineering, flow physics and computer science. Contrary to the common impression that CFD is mature enough to the point that it is usable by non-experts, available tools still lack prediction capability in many critical areas and require experts to conduct successful simulation of surprisingly many problems in aerospace vehicle applications. Thus, it is necessary to advance the state of the art in CFD and to gain critical skills in both numerical methods and physics. Lack of support has been listed as a main culprit for the slow progress in advancing the state of the art in CFD. However, the primary questions to ask are as follows: What advances can be made given resources? Is the slow progress due to limited resources or limited innovations? Or do we simply wait for the computing hardware to increase its capability by several orders of magnitude compared to current computers?

In this article, a brief summary of the state of the art in computational aerodynamics will be given first, followed by a discussion on what needs to be done realistically to solve grand challenge problems we face today in supporting aeronautics and space exploration. Some features are cross-cutting in nature for both exploration and aeronautics. The examples selected are based primarily on our experience. We will discuss best practices utilising current and projected tools and computers rather than based on conjectures about the new but uncertain ‘revolutionary’ computational technology.

2.0 STATE OF THE ART IN COMPUTATIONAL AERODYNAMICS

In this section, we will review the state of the art (SOA) in computational aerodynamics from the flow simulation capability point of view. This assessment can then be used to determine the areas that need further advances to produce credible and predictive results for the flow analysis of a wide range of vehicle configurations and operating scenarios.

2.1 Reynolds Averaged Navier-Stokes (RANS) modelling for viscous flow simulation

Key areas for describing computational capabilities for viscous flow simulations are listed in the following sections based on our observations.

2.1.1 Flow solver capabilities

Many viscous flow solvers were developed primarily by research organisations such as government laboratories and later distributed to industries and software developers. Subsequently, many variations of vendor-developed software or flow simulation codes became available to users. More recently, there are open-source solvers available such as openFoam or SU2. In general, the capabilities of these and other in-house viscous codes in research laboratories can be characterised as follows.

a) Simulation of attached flows

Steady-state solutions for attached flows about complex configurations are routinely solved reliably and are being used for aerospace vehicle development and operations. Supercomputers are now readily available, and thus simulations with a hundred million grid points are fairly common. Unsteady or time-dependent flow can be solved when the flow is primarily attached about relatively simple geometries.

b) Simulation of massively separated or unsteady/transient flow involving complex geometry

Massively separated flows and vortex-dominated flows are difficult to solve accurately. For more complex geometries, unsteady simulations require guidelines on spatial and temporal resolutions. For good convergence, accuracy and reliability, best-practice guidelines are required on mesh resolution and time step size.

c) Grid generation

Dependence on grid quality continues to be an important factor to get consistent and accurate CFD predictions. Many grid generators are available, but to utilise beneficial grid characteristics of different grid topologies, it is desirable to be able to seamlessly couple different grids in simulation. Also, at the present time, grid generation typically requires an expert for more than a week to go from CAD to grid. Therefore, more automation is highly desirable.

d) Post-processing

Post-processing massive datasets for extracting aerodynamic loads is routinely done, but flow feature extraction, especially for unsteady flow, still remains challenging.

2.1.2 Physical modelling capabilities

Physical modelling is of major importance for obtaining accurate and reliable solutions. The following lists provide a summary of current physical modelling status for engineering-level viscous flow simulation.

a) Turbulence models

Details of current turbulence modelling practices will be presented in the next sub-section. A short summary is listed here:

• • Engineering-level turbulence models exist, but the modelling approach has not been improved much since the early days of CFD. To be economically viable, one- or two-equation models are frequently used in conjunction with aerospace flight vehicles.

• • Current models are not capable of predicting massively separated and unsteady flows.

• • Separated flows need ad hoc tuning or can be more accurately computed by utilising large eddy simulation (LES) variants such as hybrid Reynolds Averaged Navier-Stokes (RANS)-LES, wall-modelled LES, Wall-Resolved LES, or implicit LES (ILES) approaches (e.g. detached eddy simulation [DES]-based models are gaining popularity, despite accuracy issues in the wall region).

• • Internal flow applications of existing turbulence models, most of which are tuned for external flows, are not very well evaluated and may require the development and calibration of models using new approaches.

Accurate models for transition are practically non-existent for engineering; for multi-phase or multi-material flow, models are further behind in producing even engineering-level solutions.

b) Criteria for engineering models of turbulence

Current models, which are mostly tuned to boundary-layer flow, have been successfully used in many vehicle calculations where flow is largely attached and steady-state solutions are the main quantities of interest. Users of legacy CFD codes may not have in-depth knowledge of turbulence modelling. Following are some of the issues that need to be considered when selecting turbulence models for mission computing:

• • Sensitivity: Impact of the model on the accuracy of the overall computed results needs to be assessed relative to the impact on the accuracy stemming from algorithm and grid quality.

• • Consistency and robustness: It should be usable by non-experts.

• • Range of applicability: Most engineering-level models are tuned for limited cases, and therefore the applicable range needs to be defined.

With advances in computer hardware, resolution and turnaround time have improved substantially, but there are problems that require advanced algorithm and enhanced methods such as in- and out-flow boundary condition procedures. Algorithms for the RANS approach may need to be reevaluated for applications to turbulent eddy simulation, which may offer a possibility for obtaining more physical and consistent solutions⁽⁸⁾. Turbulent eddy simulations will be discussed in the next sub-section.

2.2 Turbulent flow simulations

Although RANS will continue to be used in the computation of flows around and inside complex geometries, more researchers and practitioners will increasingly use LES and hybrid methods, which combine LES and near-wall RANS-type modeling. Direct numerical simulations (DNSs) will also continue to be used on finely resolved meshes. Note that DNS should not be considered as validation data but rather as a benchmark, and as a simulation result must contain some assessment of the numerical errors. A brief overview of the previous approaches with particular focus on channel flows where there is an extensive body of work is given later.

A recent overview of the progress made regarding DNS of wall-bounded turbulent flows with particular emphasis on channel and pipe flow geometries is given in Refs 8-11 and references therein. Most of the DNS studies have used finite differences, Legendre polynomials and/or spectral methods based on Fourier representations or Chebychev-tau formulations. More recently, Discontinuous Galerkin (DG) methods have also been applied to DNS of turbulent channel flow^(12,13) .

Incompressible DNS of fully developed channel flow has been published^(14-21). These studies shed light on the turbulent flow physics, as well as provide data for the validation of numerical methods and turbulence models. A recent study⁽²²⁾ compared two fundamentally different DNS codes to assess the accuracy and reproducibility of standard and non-standard turbulence statistics, showing that the maximum relative deviations were below 0.2% for the mean flow, below 1% for the root-mean-square velocity and pressure fluctuations, and below 2% for the three components of the turbulent dissipation. In comparison to incompressible DNS, there is only a limited number of compressible DNS studies and those have primarily been conducted for supersonic flows^(23-26).

The DNS data obtained by Tsuji et al⁽²⁷⁾ and Philip et al⁽²⁸⁾ were initially verified against experimental results and then used to further probe and shed light on the turbulent flow physics. Other studies tried to ascertain the differences between channel and pipe turbulent flows through numerical computations^(29,30) and experiments^(31,32) . Monty et al⁽³¹⁾ presented a comparison of experimental data with well-documented high Reynolds number (Re_τ = 934) DNS⁽¹⁷⁾. An excellent agreement for the streamwise velocity statistics between the two datasets was reported. Although the energy spectra were very similar, the DNS predicted a lower-energy value in the logarithmic region, possibly due to the (shorter) dimension of the DNS box. The high computational cost required to successfully resolve all turbulent length scales limits the applicability of DNS to relatively low Reynolds numbers and the incompressible Navier-Stokes equations. Note that DNS should be used (cautiously) as a benchmark rather than as validation data as a simulation result must ideally contain some assessment of the numerical errors and an error bar; however, this is not the case in the literature.

There are several research studies concerning LES, both classical and implicit. One of the early ILES concepts was originated from the observations made by Boris et al⁽³³⁾ that the embedded dissipation of a certain class of numerical methods can be used in lieu of explicit sub-grid scale (SGS) models in classical LES of turbulent flows. Modified equation analysis (MEA) was developed⁽³⁴⁾ in an effort to determine the stability of a difference equation by examining the truncation errors. The process begins from reducing a differential equation to a discretised equation by expanding each of its terms in a Taylor series. Such an analysis has been performed for the truncation error of certain schemes^(35-41), leading to a better understanding of the implicit subgrid dissipation. In ILES, the Navier-Stokes equations (NSE) are discretised using high-resolution/high-order non-oscillatory methods without involving a low-pass filtering operation, which gives rise to SGS terms that require additional modelling. Instead, only the (implicit) de facto filtering introduced through the finite volume integration of the NSE over the grid cells is utilised in conjunction with non-linear numerical schemes that adhere to a number of principles; see Refs 42 and 43, and review Refs 40, 44, and 45. It has been shown⁽³⁵⁾ that ILES methods need to be carefully⁽¹³⁾ designed, optimised and validated for the particular differential equation to be solved. Direct MEA of high-resolution schemes for the Navier-Stokes equations is extremely difficult to perform; thus, understanding of the numerical properties of these methods to date still relies on performing computational experiments.

Classical LES studies have dealt with the development of SGS models and error contributions from SGS modelling (Stolz et al^(46,47) , Hickel et al^(48,49) and references therein) and numerical schemes^(50-54); error control through explicit filtering^(53,55,56) ; and the effects of different filtering procedures^(57-59). Recent developments of explicit SGS models include the approximate deconvolution model (ADM)⁽⁴⁶⁾, which is an approximation of the non-filtered field by means of a truncated series expansion of the inverse filter operator. For an incompressible channel flow, ADM compared well against DNS data and showed a significant improvement⁽⁴⁷⁾ over the results obtained from typical SGS models such as the classical and dynamic Smagorinsky model. An evolution of the ADM is the adaptive local deconvolution model (ALDM)⁽⁴⁸⁾. The ALDM is based on a non-linear discretisation scheme, which contains several free deconvolution parameters that allow control of the truncation error. The ALDM was applied to incompressible, turbulent channel flow to analyse its implicit SGS modelling capability in wall-bounded turbulence⁽⁴⁹⁾. In the framework of classical LES, the accuracy of the SGS model is strongly influenced by the numerical contamination of the smallest resolved turbulent structures near the filter cut-off length^(51,52,60) .

Furthermore, it was found that the numerical error and SGS model interact with each other^(50,52-54) . It was reported⁽⁵⁰⁾ that for low-order finite-difference schemes, the truncation errors can exceed in magnitude the contribution of the SGS term. High-order numerical schemes are thus important in resolving the large energy-containing scales more accurately. However, they can also lead to contamination of the smallest resolved scales by truncation errors, in particular when using non-spectral methods. It was shown⁽⁵⁶⁾ that these errors could be controlled using an explicit filter. Nonetheless, mesh refinement still improved the results at a faster rate than the explicit filter size. Furthermore, previous studies⁽⁵³⁾ have shown that a minimum ratio of explicit filter width to cell size is necessary to be defined in order to prevent numerical errors from becoming larger than the contribution of the SGS turbulence closure terms and consequently saturating the solution period.

The influence of the numerical errors and SGS models in LES of channel flows, with and without explicit filtering, was studied by Gullbrand et al^(61,62) . When comparing to LES without explicit filtering, the difference in the mean velocity profiles was not large; however, the turbulence intensities were improved when explicit filtering was used. Gullbrand⁽⁶²⁾ investigated various dynamic SGS models to obtain the true filtered LES solution for an incompressible turbulent channel flow. It was hypothesised that the true LES solution should depend only on the filter width, regardless of the grid resolution. On the other hand, in ILES, the solution converges towards DNS as the grid is refined because the filter width is implicitly and directly connected to the grid spacing. The effect of the different filtering methods was also examined in a subsequent study⁽⁵⁸⁾ showing that three-dimensional filtering gives better results than two-dimensional filtering. Brandt⁽⁵⁹⁾ reported that the effect of filtering can be significant, with smooth filters increasing the total simulation error. Recently, Bose et al⁽⁵⁷⁾ investigated the use of explicit filtering in LES for obtaining grid-independent numerical solutions similar to the work of Gullbrand⁽⁶²⁾. The convergence of the simulations was analysed for a turbulent channel flow at various friction Reynolds numbers (Re_τ = 180, 395 and 640), and it was shown that by using an explicit filter, the turbulent statistics and energy spectra became independent of mesh resolution. Other LES approaches include spectral-based LES⁽⁶³⁾ and ‘variational multiscale residual-based turbulence modeling’^(64,65) .

Although LES is computationally less demanding than DNS, it still requires significant computational resources for simulating near-wall turbulence at high Reynolds numbers. An alternative to LES is to make use of wall-layer models near the wall and use LES to resolve the outer region of the boundary layer, thus ‘relaxing’ the grid resolution requirements near the wall. The wall-layer models can be broadly classified as (i) equilibrium laws based on the logarithmic law, or some other assumed velocity profile (wall functions); (ii) zonal models, in which the turbulent boundary-layer equations (TBLEs) are solved, weakly coupled to the outer-layer LES; and (iii) hybrid methods employing a RANS-based turbulence model near the wall and LES in the outer layer. A thorough review of these is provided by Piomelli⁽⁶⁶⁾. The best-known realisation of the hybrid framework is the DES method by Spalart et al⁽⁶⁷⁾. In DES, the interface location is dictated by the grid parameters through a switching condition. Nikitin et al⁽⁶⁸⁾ used DES in the simulation of a turbulent channel flow. The results showed a non-physical boundary layer developing near the RANS/LES interface caused by the misalignment of the log layers between the RANS and LES regions. Due to the log-layer mismatch, the skin-friction coefficient was under-predicted by approximately 15%. In the most commonly used DES implementation, the entire boundary layer is modelled by RANS^(69,70) . Using the k-ε model, Hamba^(69,70) carried out hybrid simulations of channel flow and introduced additional filtering at the interface to reduce the log-layer mismatch. Although these methods are promising, the amplitude of the stochastic forcing and the width of the additional filtering both need to be determined empirically. Piomelli et al⁽⁷¹⁾ applied a stochastic backscatter model to the wall-modelled DES of a channel flow showing improvements in the prediction of the mean velocity profile.

Other DES studies^(72,73) also reported issues in coupling the modelled and LES resolved regions, especially when more complex geometries and flows were considered in comparison to a plane flat surface^(74-77). More recently, a dynamic slip wall boundary condition for wall-modelled LES⁽⁷⁸⁾ was proposed, which gave encouraging results for separated flows over Airfoils. Chen et al⁽⁷⁹⁾ showed that both ILES and the immersed-interface treatment of the wall boundaries provide high computational efficiency on very coarse meshes for backward-facing step and periodic hill flows. Another category of near-wall models has been proposed,⁽⁸⁰⁾ which has been used in RANS but may also prove promising for DES. Although there is an extensive body of published research regarding the solution of turbulent channel flows using DNS, classical LES, and DES, ILES investigations are still limited in number^(81-84). Previous research^(81-84) has indicated that ILES is capable of reproducing first- and second-order statistical moments of the velocity field. Reviews examining the accuracy of ILES in other canonical problems such as the turbulence decay in a Taylor-Green vortex have also been published^(85,86) . Despite this literature, there has been no systematic attempt to investigate the behaviour of different high-order compressible ILES methods in compressible turbulent channel flows.

3.0 MULTI-PHYSICS MODELLING

Modelling and simulation is increasingly becoming a powerful tool in designing and manufacturing new aerospace products. Multi-physics simulations involve continuum and/or atomistic methods for a range of temporal and spatial scales and physical processes involved. Multi-physics consists of three main attributes: ‘multi-field’, ’multi-domain’, and ‘multi-scale’⁽⁸⁷⁾. The combination of these attributes can lead to the understanding of the natural behaviour of physical systems by generating relational mathematical and computational models.

Product development requires extended investigation of its behaviour in various environmental conditions, which may include thermal, mechanical and humidity stimuli. Coupling techniques to address these types of multi-physics (also known as multi-field) problems include electrodynamic and thermoelasticity. Multi-field theories have also been extended to three fields that include thermo-electroelasticity^(88,89) and hygro-thermoelasticity⁽⁹⁰⁾.

Multi-domain modelling refers to the physical problems that focus on the interaction of continuum systems characterised by different properties, such as multi-phase flows, liquid-solid interaction and moving boundaries. A typical example of multi-domain modelling application is the field of aeroelasticity. Coupled formulations have been developed⁽⁹¹⁾ for cases where (i) neither domain can be solved separately from each other or (ii) neither set of dependent variables can be explicitly eliminated. The first attempts to study aeroelasticity were based on linear mathematical models⁽⁹²⁾. Linear aeroelastic models have successfully managed to predict the basic features of aeroelastic behaviour of a structure both in the subsonic^(93,94) and in the supersonic regimes⁽⁹⁵⁾. However, the advances in the aircraft industry have pushed towards critical design conditions in the transonic regime in terms of flutter, which linear models failed to predict.

Nowadays, non-linear CFD and computational structural dynamics (CSD) are widely used in aeroelastic simulations. CFD is used for the estimation of the flow temperature, pressure and density by solving the Navier-Stokes equations. On the other hand, CSD is used for modelling the non-linear geometrical and material behaviour of solids. However, the solution of such a dynamic problem requires the constant exchange of input information between CFD and CSD, as the latter one needs information on the airflow while CFD requires the knowledge of the temperature or the deformation of the solid. Coupling CFD and CSD is one of the most challenging tasks. There are two main coupling strategies, namely, the monolithic approach^(96,97) and the partitioned energy approach^(98,99) . In the monolithic approach, the coupled system is regarded as a whole and ensures convergence provided that the non-linearities of the sub-systems can be resolved. On the other hand, in the partitioned solution approach, solid and structure are spatially decomposed and the different physical fields (partitions) interact through the exchange of boundary conditions. In the case of very weak fluid-solid interaction, partitioned solvers are more effective than the monolithic ones as they converge in fewer time steps. On the contrary, for strongly coupled problems, partitioned solvers can hardly converge and monolithic ones become essential⁽¹⁰⁰⁾.

Continuum models (e.g. CFD, finite element analysis [FEA]) have been the staple of computational simulations of many engineering problems. However, the development of nano-devices such as micro-electromechanical systems (MEMSs) over the last few decades created the need to study micro-/nano-scale systems, where many of the laws of continuum mechanics break down⁽¹⁰¹⁾. Fortunately, recent advances in computing have made the investigation of the mechanics of fluids and materials on nano-scales feasible with the use of molecular models. Molecular models can be simulated using two techniques: molecular dynamics⁽¹⁰²⁾ and Monte Carlo⁽¹⁰³⁾. The computational expense limits the use of these methods to a number of atoms relatively small compared to macro-scale problems. Multi-scale methods (Fig. 1) attempt to bridge the accurate microscopic models with efficient continuum ones.

Figure 1. Multi-scale modelling of materials and multi-material interfaces across length scales.

Multi-scale methods can be divided into two groups: the meso-scale and the hybrid ones. Meso-scale methods work with intermediate resolution, i.e. a single solver that can simulate large physical phenomena taking into account the essential detail of the molecular interactions. This is achieved by replacing an atomic description by larger particles while averaging fine detail out. The most common meso-scale methods are (a) lattice gas cellular automata (LGA)^(104,105) , (b) the lattice-Boltzmann (LB) method^(106,107) , (c) dissipative particle dynamics (DPD)⁽¹⁰⁸⁾ and (d) direct simulation Monte Carlo (DSMC)^(109,110) . On the other hand, hybrid models employ two solvers, a molecular (e.g. molecular dynamics, Monte Carlo) and a continuum one (e.g. CFD, FEA). The challenge in such an approach is the transparent exchange of information between the two. Hybrid models can be classified into geometric decomposition (GD) and embedded-based techniques (EBT) depending on how the length scales are decoupled^(111-118).

It is expected that in the future, the interface between the three basic components needed to address multi-scale problems, governing equations, experimental data and simulation software, will become integrated. This will enhance the accuracy of the existing modelling methods and lead to the evolution of the design of aerospace products intended to operate under complex environmental conditions. As far as multi-domain systems are concerned, current modelling software should evolve and become capable of handling a larger number of domains to represent effectively real environmental and operating conditions.

Multi-scale methods need to be further developed to enable the fabrication of devices that incorporate design characteristics ranging from nano- to macro-scale, such as the aircraft skin^(119,120) . In the future, new, more robust methods efficiently linking the atomistic and the continuum domains should be developed. This will enable modelling of materials for particular applications. For example, selecting and designing a proper material for a morphing skin of an aircraft is not a trivial task, as candidate materials should be able to withstand the aerodynamic loads and simultaneously be flexible enough to alter their shape during flight. Therefore, a large number of experiments should be carried out to identify the most suitable choice. An alternative and cost-effective approach would be to perform multi-physics simulations based on an integrated framework.

Besides multi-scale material modelling, hybrid multi-scale simulations have been extended to static and quasi-static physical problems, where relaxation time scales in atomic models can be matched by the continuum ones, but not to fully dynamic problems where the macroscopic evolution in time affects the molecular structure of a system. Such cases include adsorption, sedimentation, fouling and fatigue. For example, in the case of a flow over an elastic surface, the long time scales over which the structure of the surface is deformed cannot be simulated by a molecular solver and the dynamics of the build-up, which are being calculated by a continuum solver, cannot be fed into the molecular domain, as a re-initialisation of the molecular solver would be required. Therefore, the development of integrated hybrid approaches capable of linking macroscopic changes with the molecular structure and meso-scale methods is needed. Other challenges that have to be addressed in the future involve parallelisation of hybrid codes, which, in combination with complex geometries, poses a number of challenges regarding the molecular solver and the boundary conditions at multi-material interfaces.

4.0 VISION

Computational aerodynamics can play a significant role for developing aerospace vehicles during the conceptual design and trade study phases. This requires consistency in computed results and quick turnaround to evaluate different ideas. In applying current simulation tools to determine fluid dynamic loads on aerospace vehicles, flow physics such as turbulence are approximated by models. Modelling that ensures prediction of the proper non-linear physical phenomena is crucially important. Predictive simulation capability, usually with a range of limited applicability, will alleviate the need for extensive ground- or flight-testing. The requisite capabilities listed to follow are the ones needed for enhancing aerodynamics analysis for developing the next-generation vehicles. The list is intended to identify the major advances in computational aerodynamics required in the near or medium-term future. This will help minimise the expensive ‘test-fail-fix’ cycle of past practices.

4.1 Requisite capabilities

Some of the capabilities required for computational aerodynamics facing current and mid-term future applications are:

• • Quantification of grid effects relative to physics model sensitivity and versatile grid generation capability to couple various grid topologies as needed.

• • Advanced algorithms, such as space-time correlation, and high-accuracy methods especially for unsteady flows.

• • Guidelines for selecting turbulence modelling approach for real-world applications such as RANS, DES variants, LES, hybrid wall-modelled or wall-resolved LES, and ILES suitable for flow solvers in use.

• • Aeroacoustics modelling and computation capability.

• • Simulation capability for integrated vehicle-propulsion configuration. For launch vehicle design applications such as for determining structural loading and for designing the guidance and control system, computed results using clean vehicles without plume and protuberances seem adequate. However, with plume or wake, the prediction capability for the separated region can drastically be reduced.

• • Practical model for predicting combustion instability.

• • Parallel implementation of flow solver codes on ever-evolving high-performance computer architecture.

• • Improved speed of CAD to solution so that CFD can be utilised in post-concept trades for revising the design with very specific goals.

4.2 Target research areas

Selected research areas are listed as follows where requisite capabilities discussed previously can be advanced.

4.2.1 Unsteady and separated flow research

To improve current practices for establishing CFD application procedures, advances in algorithms will be desired, such as enhanced time integration schemes/procedures combined with high-accuracy and grid adaption schemes.

4.2.2 Range of applicability for turbulence models

Even though intensive research on turbulence physics has been performed for several decades, models useful for vehicle development and operations have been developed by CFD practitioners at the engineering level. To meet the near-term needs, it will be necessary to enhance CFD tools to simulate turbulent flow more consistently. Therefore, establishing a usable recipe for turbulence modelling will be very valuable, possibly using existing models and/or enhanced versions.

4.2.3 Practical turbulent eddy simulation method

Uncertainties in turbulent flow simulation can be reduced by modelling small eddies only. However, the computing requirements for turbulent eddy simulation are still an issue. In 1979, Chapman⁽⁴⁾ projected that a full aircraft can be solved using LES in the 1990s. This projection has been delayed more than ten years now, and most simulations are still performed with wall models. Now computers are at the petaflop level, but only if the entire system of a supercomputing facility can be allocated to one user. In reality, it is reasonable to assume that about 10% or less of a system will be available to solve one problem. Therefore, it will make practical sense to develop efficient new methods while computer hardware is being advanced further.

4.2.4 Engineering-level physics model

No usable guidelines are available for multi-phase, cavitation and combustion instability. However, in a number of important applications, such as the turbopump, cavitation phenomena need to be included in CFD simulation. In propulsion simulation, prediction of combustion instability has been a major challenge and still requires longer-term research combined with systematic validation experiments.

4.3 Outlook for organised or directed research

Research in many of the areas discussed previously is already in progress but lacks coordination. Strategic investments are rare because of the erroneous assumption that CFD has reached its maximum potential and further development will result in only incremental improvement at best. However, CFD is not accurate enough for many major design decisions except in limited regions of operational conditions in aerodynamics and engineering, and largely is not reliable when extrapolated to un-experimented flow regimes. It is to be noted that CFD has made a profound impact on aircraft design, especially commercial transport aircrafts. Similar impacts can be expected in aerospace sciences and engineering in general when ‘prediction’ capability is improved to produce consistent and credible results. To close the current gap in computational aerodynamics, strategic investment at a fundamental technology level would be desirable.

5.0 GRAND CHALLENGE APPLICATIONS

The goal of grand challenge (GC) problems is to develop several key capabilities of computational aerodynamics procedures to handle current bottleneck issues. Therefore, we are looking at medium term, three- to five-year, realistic advances to facilitate development of computational capability for aerodynamics analysis and vehicle development. The GC cases presented here are to advance several realistic and practical capabilities. There are also open-ended issues not extensively discussed here, such as developing general turbulence models applicable to a wide variety of flows.

Our assumptions in selecting these GC problems are that (1) we do not anticipate significant long-term research and technology development funding to generally advance fundamental CFD capability, and (2) there are immediate needs for developing specific capabilities to make tangible impacts on current missions. Typically, aerospace vehicles, once developed, will be in operation for a long time. Therefore, the impacts of computational aerodynamics will be the greatest during the conceptual and preliminary design phases. Significant impacts will be made in the subsequent applications for retrofitting and operational support. For example, the Space Shuttle was designed without much help from CFD and has flown for 30 years since its maiden flight. Subsequent advances in CFD and computer hardware have made major impacts on many aspects of retrofitting, operational support and accident investigation.

5.1 Grand Challenge #1 (GC1): Simulation of a full aircraft configuration

Accurate CFD simulations around a full aircraft configuration still remain a major CFD challenge. Although RANS simulations on relatively fine grids are feasible, achieving acceptable accuracy at takeoff and landing conditions is an extremely difficult task. The RANS prediction uncertainties at high angles of attack are associated with the inherent inability of RANS methods to capture flow unsteadiness, in general, and unsteady flow separation and turbulent wakes, in particular. Some of these challenges have been discussed in the American Institute of Aeronautics and Astronautics (AIAA) high-lift workshops⁽¹²¹⁾. The computational challenges include (1) an accurate representation of the full aircraft configuration – usually, the simulations are preformed on simplified geometries that do not include the slat-track and flap-track fairings and the slat pressure tubes; (2) high aspect ratio skewed elements with non-planar face definition that are often present, thus increasing the complexity in implementing high-order spatial discretisation schemes, which are more sensitive to grid quality issues compared to second-order schemes; and (3) accurate prediction of the drag coefficient, which has been partially attributed to installation effects of the model in the wind tunnel but also to the turbulence modelling as well as numerical accuracy particularly in the flow separation regions and in the wake. Large eddy simulations of a full aircraft configuration, including the near-wall region at adequate mesh resolution, are unlikely to be performed at least within the next decade. However, the use of high-order methods in conjunction with hybrid approaches may increasingly allow the use of LES, and ILES more specifically, to model flows around full aircraft configurations.

Figure 2 shows the hybrid unstructured mesh around the DLR-F6 geometry, which had been proposed as a test problem in the 2nd AIAA CFD Drag Prediction Workshop⁽¹²²⁾. The RANS version of a high-order code^(123-125) was implemented in the simulation of the DLR-F6 geometry from the 2nd AIAA CFD Drag Prediction Workshop. The flow conditions were Mach number of 0.75, zero angle-of-attack, and Reynolds number of 3×10⁶ based on the mean aerodynamic chord.

Figure 2. Computational grid for the DLR-F6 geometry; a) surface mesh of the DLR-F6 quadrature points; b) corresponding quadrature points.

The objective of this study was to assess the uncertainty associated with different numerical schemes with respect to the drag coefficient prediction. In Fig. 3, the results on the coarsest mesh, which consists of approximately 5 million elements, are shown in conjunction with different numerical schemes, namely, second-order MUSCL and third-order WENO schemes. The reduction of error in the drag prediction is faster when increasing the numerical order of the scheme than when increasing the grid size (Fig. 3). This is also reflected in the computing time, where the coarse grid simulation using the WENO third-order scheme requires less time than the standard MUSCL second-order scheme on the medium-size grid. The present results are compared with the mean values of drag from all the available solutions of the 2nd AIAA CFD Drag Prediction Workshop.

Figure 3. Predicted drag coefficient (C_D) error for DLR-F6 obtained from second- and third-order methods and comparison with the mean values of the solutions of the 2nd Drag Prediction Workshop. The blue line (labelled as present) has been obtained using a high-order RANS code (Azure)⁽¹²³⁾ in conjunction with the second-order MUSCL and third-order WENO schemes on the coarsest grid.

In light of these results, this GC should perform simulation of a full aircraft configuration.

5.2 Grand Challenge #2 (GC2): Rotorcraft flow simulation

The simulations of the flow field of a rotorcraft in hover as well as in forward flight involve blade-vortex interactions and turbulence modelling for near and far wake. Even though fine-resolution simulations are possible with advances in computer hardware, there are many challenging issues for routine simulations. Local grid resolution, grid adaptation and turbulence modelling for near and far wake are some of the pacing issues in simulation.

Figure 4 illustrates the latest simulation capability using Overflow code by Chaderjian et al^(126,127) . In Fig. 4(a), the CFD generated flow is visualised using an iso-surface of the q-criterion and coloured by vorticity magnitude, where red is high and blue is low. In Fig. 4(b), the green turbulent structures show vortex stretching as the boundary-layer wake shear layers that form at the blade trailing edge descend and interact with the vortices.

Figure 4. Rotorcraft flow simulations in top view in forward flight and hover.

5.3 Grand Challenge #3 (GC3): Integration of multiple grid topologies for complex geometry simulation

One of the most important first steps for CFD simulation is grid generation. For example, surface grid is important in representing geometry accurately. The selection of grid topology is directly related to the type of flow being simulated, whether it is a boundary-layer type, free shear layer, or wake flow. Grid quality has been an important issue from the early days of CFD, but rigorous guidelines such as the criteria for determining the grid density, optimum distribution, stretching rates and allowable skewness have not been established yet.

Currently the most commonly used grids are Cartesian, unstructured, or overset structured grids. Each approach is well developed, but it is desirable to be able to combine these to benefit from the best features of each. GC2 calls for an automated high-fidelity multiple-grid technique using a conservative overset grid approach.

Three representative samples of different grid approaches are shown in Fig. 5 for launch vehicle simulation as discussed by Moini-Yekta et al⁽¹²⁸⁾. These are Cartesian (Fig. 5(a)), unstructured (Fig. 5(b)) and overset structured grids (Fig. 5(c)). The benefits and shortcomings of each are listed in the figure for comparison.

Figure 5. Examples of three different grid topologies for launch environment simulation.

The proposed task is to apply the grid integration technology developed under GC3 to generate a combined grid and to compare grid generation efficiency and flow solution accuracy to other single-grid approaches.

5.4 Grand Challenge #4 (GC4): Space-time resolution guideline for unsteady flow simulation

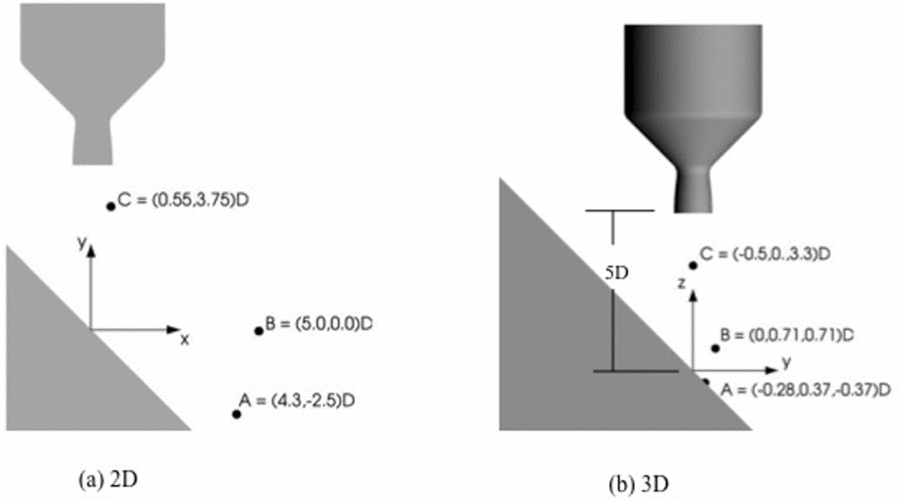
For unsteady flow simulation, space-time convergence is a major issue. Current practices require establishing guidelines for temporal and spatial resolution. However, it is very expensive and case dependent to computationally determine the sensitivity related to space-time resolution as well as to establish a sub-iteration requirement for a dual-time stepping approach. The goal of GC4 is to establish a guideline for space-time resolution and then test this criterion against well-established test cases. A suitable test case for GC4 is to apply the criterion developed for the experimental study case by Nakanishi et al⁽¹²⁹⁾. The geometry and the probe locations for comparing experiments and computed results are indicated in Fig. 6.

Figure 6. Geometry and point probe locations for jet impingement test case for space-time convergence study. Flow conditions are from the experiment by Nakanishi et al⁽¹²⁹⁾: Nozzle exit temperature = 300K, jet Mach number, M = 1.8.

Brehm et al⁽¹³⁰⁾ used this case to study space-time convergence as illustrated in Fig. 7. Results from the space-time resolution guideline can then be compared with the best-practice results by Brehm et al⁽¹³⁰⁾.

Figure 7. Spatial convergence study for 2D case⁽¹²⁹⁾.

5.5 Grand Challenge #5 (GC5): Effects of turbulence models on simulation accuracy

Several issues need to be considered with respect to turbulence models required for mission support involving complex geometry and time-dependent turbulent flows. For attached boundary-layer flows, turbulence scale is small and the usual RANS-based model works well. In general, the major bottleneck for flow simulation stems from uncertainties in modelling turbulence and transition. Especially for massively separated flows and unsteady shear-layer interaction problems such as the jet-plume interaction problem, adequacy of the particular turbulence model in use needs to be examined. When RANS models, such as Spalart-Allmaras (S-A)⁽¹³¹⁾, Baldwin-Barth (B-B)⁽¹³²⁾, or SST⁽¹³³⁾, have difficulties, LES or the LES-RANS hybrid model might offer an avenue to overcome these difficulties. However, they are expensive and have their own limitations, especially for wall-bounded flows.

The goal of GC5 is to evaluate LES, DES and ILES and assess the pros and cons of these approaches. The results of these evaluations and assessments are then expected to provide directions on what needs to be developed further to mature these modelling approaches to a wider range of flows.

Basic test cases for GC5 are to compare LES, various versions of DES, and ILES for a selected number of basic flows such as the decaying box turbulence, flow over a cylinder and back step flow. Then, to test model performances in a real-world situation, simulation of plume-induced flow separation (PIFS) for the Apollo 6 flight is proposed where flight data and RANS computed results are available (Gusman et al⁽¹³⁴⁾). This test case offers the opportunity to examine in detail the performance of DNS- and LES-based modelling approaches, which are particularly relevant to complex geometry applications such as separated flow, shear-layer interaction, plume-separated boundary-layer interaction and interaction of multiple jets and wakes. An example of RANS computed results is illustrated in Fig. 8. Sensitivity to grids and time-step sizes can also be assessed by comparing the best solutions to the results from other codes and experimental data. Specific modelling requirements can also be derived for supporting vehicle development and operations.

Figure 8. Mach number distribution for four points in the Apollo 6 trajectory using SST turbulence model⁽¹³³⁾ with hybrid grid⁽¹³⁴⁾.

5.6 Grand Challenge #6 (GC6): Aeroacoustics – computational issues

Requirements for aero-acoustic computations are different from CFD. For example, numerical dispersion and dissipation errors can cause major errors in acoustic wave propagation. Spatial and temporal discretisation schemes and far-field non-reflecting boundary conditions play very important roles.

For acoustics involving complex geometry, it is a common practice to develop an acoustic surface about a RANS solution and apply Lighthill's method for propagation to the far field. To study noise generation mechanisms associated with jets and jet-solid interfaces, fine-scale turbulence computations are needed (at the DNS or LES level). The primary question to be answered is whether we can compute noise sources directly and accurately propagate acoustic radiation with a wave propagation model. This approach can be compared to a RANS-acoustic surface modelling combination such as reported by Kiris et al⁽¹³⁵⁾ and Brehm et al⁽¹³⁶⁾.

6.0 CONCLUDING REMARKS

The opinions presented in this article are based on the authors’ experience related to computational aerodynamics and engineering and may represent only a small portion of the flow simulation challenges we face today. Those requisite capabilities listed previously, if made available in the near term, can significantly impact the next generation of air- and space-vehicle development and operations. We also believe that longer-term strategic research and development, especially for the development of more universally applicable turbulence and possibly transition models, will have far-reaching impacts on computational fluid engineering for flight vehicles as well as aerospace engineering in general.