Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-13T07:04:54.498Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit Sets of Typical Homeomorphisms

Published online by Cambridge University Press:  20 November 2018

Nilson C. Bernardes Jr.
Nilson C. Bernardes Jr.*
Affiliation:
Departamento de Matemática Aplicada, Instituto de Matemática, Universidade Federal do Rio de Janeiro, Caixa Postal 68530, Rio de Janeiro, RJ, 21945-970, Brasile-mail: bernardes@im.ufrj.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an integer 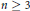$n\,\ge \,3$, a metrizable compact topological $n$-manifold 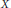$X$ with boundary, and a finite positive Borel measure $\mu $ on 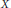$X$, we prove that for the typical homeomorphism 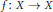$f\,:\,X\,\to \,X$, it is true that for $\mu $-almost every point $x$ in 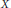$X$ the limit set 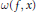$\omega (f,\,x)$ is a Cantor set of Hausdorff dimension zero, each point of 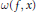$\omega (f,\,x)$ has a dense orbit in 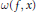$\omega (f,\,x)$, 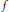$f$ is non-sensitive at each point of 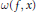$\omega (f,\,x)$, and the function 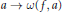$a\,\to \,\omega (f,\,a)$ is continuous at $x$.

Keywords

37B2054H2028C1554C3554E52topological manifoldshomeomorphismsmeasuresBaire categorylimit sets
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 225 - 232
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Agronsky, S. J., Bruckner, A. M., and Laczkovich, M., Dynamics of typical continuous functions. J. London Math. Soc. (2) 40(1989), no. 2, 227–243. http://dx.doi.org/10.1112/jlms/s2-40.2.227 Google Scholar
[2] Akin, E., On chain continuity. Discrete Contin. Dynam. Systems 2(1996), no. 1, 111–120. http://dx.doi.org/10.3934/dcds.1996.2.111 Google Scholar
[3] Akin, E., Hurley, M., and Kennedy, J. A., Dynamics of topologically generic homeomorphisms. Mem. Amer. Math. Soc. 164(2003), no. 783.Google Scholar
[4] Bernardes, N. C. Jr., On the predictability of discrete dynamical systems. Proc. Amer. Math. Soc. 130(2002), no. 7, 1983–1992. http://dx.doi.org/10.1090/S0002-9939-01-06247-5 Google Scholar
[5] Bernardes, N. C. Jr., On the predictability of discrete dynamical systems. II. Proc. Amer. Math. Soc. 133(2005), no. 12, 3473–3483. http://dx.doi.org/10.1090/S0002-9939-05-07924-4 Google Scholar
[6] Bernardes, N. C. Jr., Limit sets of typical continuous functions. J. Math. Anal. Appl. 319(2006), no. 2, 651–659. http://dx.doi.org/10.1016/j.jmaa.2005.06.056 Google Scholar
[7] Bernardes, N. C. Jr., On the predictability of discrete dynamical systems. III. J. Math. Anal. Appl. 339(2008), no. 1, 58–69. http://dx.doi.org/10.1016/j.jmaa.2007.06.029 Google Scholar
[8] Diestel, R., Graph theory. Graduate Texts in Mathematics, 173, Springer-Verlag, New York, 1997.Google Scholar
[9] Lehning, H., Dynamics of typical continuous functions. Proc. Amer. Math. Soc. 123(1995), no. 6, 1703–1707.Google Scholar
[10] Munkres, J. R., Elements of algebraic topology. Addison-Wesley Publishing Company, Menlo Park, CA, 1984.Google Scholar