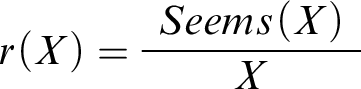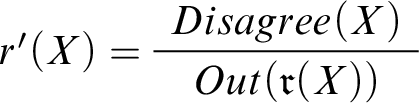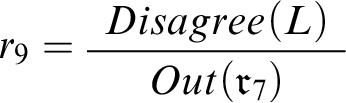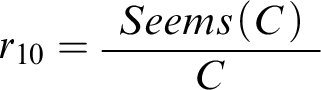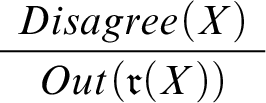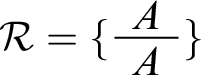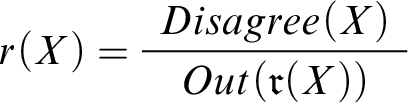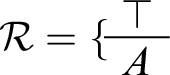CONCILIATORY REASONING, SELF-DEFEAT, AND ABSTRACT ARGUMENTATION

Abstract

According to conciliatory views on the significance of disagreement, it’s rational for you to become less confident in your take on an issue in case your epistemic peer’s take on it is different. These views are intuitively appealing, but they also face a powerful objection: in scenarios that involve disagreements over their own correctness, conciliatory views appear to self-defeat and, thereby, issue inconsistent recommendations. This paper provides a response to this objection. Drawing on the work from defeasible logics paradigm and abstract argumentation, it develops a formal model of conciliatory reasoning and explores its behavior in the troubling scenarios. The model suggests that the recommendations that conciliatory views issue in such scenarios are perfectly reasonable—even if outwardly they may look odd.

1 Introduction

Think of your favorite philosophical problem. You’ve likely thought about it for a long time, and you must have some idea regarding how to resolve it. And odds are you know someone who has thought about it for at least as long, whose credential are as good as yours, and whose solution to the problem is incompatible with yours. If so, you’re in disagreement with an epistemic peer. ¹ Should this fact make you less confident that your solution to the problem is the correct one? According to the so-called conciliatory or conciliationist views, it should. This answer has much intuitive appeal: the problem is complex, you are not infallible, and one straightforward explanation for the disagreement is that you’ve made a subtle mistake when reasoning. An equally good explanation is that your opponent has made a mistake. But given that there’s no good reason to favor the latter, reducing confidence still seems appropriate. ²

But their intuitive appeal notwithstanding, conciliatory views are said to run into problems when applied to themselves, or when answering the question of what should one do when disagreeing about the epistemic significance of disagreement. The problems are most transparent and easiest to explain for the more extreme conciliatory views. According to such views, when you hold a well-reasoned belief that X and an equally informed colleague disagrees with you about whether X, you should lower your confidence in X dramatically, or—to state it in terms of categorical beliefs—you should abandon your belief and suspend judgment on the issue.

Let’s imagine that you’ve reasoned your way toward such a view, and that you’re the sort of person who acts on the views they hold. Imagine further that you have a well-reasoned belief on some other complex issue, say, you believe that we have libertarian free will. Now, to your dismay, you find yourself in a crossfire: your friend metaphysician Milo thinks that there’s no libertarian free will, while your friend epistemologist Evelyn thinks that one should not abandon one’s well-reasoned belief when faced with a disagreeing peer. Call this scenario Double Disagreement. The question now is how should you adjust your beliefs. For starters, your conciliatory view appears to self-defeat, or call for abandoning itself. Just instantiate X with it! There’s disagreement of the right sort, and so you should abandon your view. And to make the matters worse, there’s something in the vicinity of inconsistency around the corner. Think about what are you to do about your belief in free will. Since there’s no antecedent reason to start by applying the conciliatory view to itself, you’ve two lines of argument supporting opposing conclusions: that you should abandon your belief in the existence of free will, and that it’s not the case that you should. On the one hand, it’d seem that you should drop the belief, in light of your disagreement with Milo and your conciliatory view. On the other, there’s the following line of argument too. Your conciliatory view self-defeats, and, once it does, your disagreement with Milo loses its epistemic significance. But if the disagreement isn’t significant for you, then it’s fine for you to keep your belief in the existence of free will, implying that it’s not the case that you should abandon it. ³

Although this was sketchy and quick, you should agree that the advocates of strong conciliatory views face a challenge: it looks like their views issue inconsistent recommendations in Double Disagreement and other scenarios sharing its structure. What’s more, Christensen [8], Elga [16], and others have forcefully argued that this challenge generalizes to all types of conciliatory views, whether they be calling for strong, moderate, or even minimal conciliation. ⁴ We’ll call this challenge the self-defeat objection to conciliatory views. ⁵

Advocates of conciliatory views have taken this objection very seriously, offering various ingenious responses to it. Thus, Bogardus [3] argues that we have a special rational insight into the truth of conciliationism, making it immune from disagreements about it. ⁶ Elga proposes modifying conciliationism, with the view of making beliefs in it exempt from its scope of application. Christensen [8] suggests that cases like Double Disagreement are inherently unfortunate or tragic, and that what they reveal is that conciliatory views can lead to inevitable violations of “epistemic ideals,” as opposed to showing that these views themselves are mistaken. Matheson [33] invokes “higher-order recommendations” and evidentialism to respond to the objection. ⁷ And Pittard [37] argues that the agent who finds herself in Double Disagreement has no way of “deferring” to her opponent both at the level of belief and the level of reasoning, and that, therefore, it’s rational for her to refuse to abandon her belief in conciliationism. Even without looking at these responses in any more detail, it should be clear that they all either incur intuitive costs or substantially modify conciliationism. ⁸ So the advocates of conciliatory views should welcome a less committal and more conservative response to the objection.

One of the two main goals of this paper, then, is to develop such a response. The second one is to present a formal model that captures the core idea behind conciliatory views using the resources from the defeasible logic paradigm. This model, I contend, is particularly useful for exploring the structure of conciliatory reasoning in cases like Double Disagreement and, therefore, also working out a response to the self-defeat objection. In a word, it’ll help us see two things. First, the recommendations that conciliatory views issue in such cases aren’t, in fact, inconsistent. And second, in those cases where these recommendations may appear incoherent to us—that is, when they say, roughly, that you should abandon your belief in conciliationism and still conciliate in response to the disagreement about free will—they actually call for the correct and perfectly reasonable response. ⁹

The remainder of this paper is structured as follows. Section 2 sets up the model and sharpens the objection: Section 2.1 formulates a defeasible reasoner, or a simple logic with a consequence relation at its core; Section 2.2 embeds the core idea behind conciliationism in it; and Section 2.3 turns to cases like Double Disagreement, leading to a formal version of the concern that conciliatory views self-defeat. We then address it in two steps. Section 3 is concerned with a, by and large, technical problem, but, by solving it, we will have shown that conciliatory views do not issue inconsistent recommendations when they turn on themselves. Section 4, in turn, is concerned with explaining why even those recommendations of conciliatory views that may, at first, strike us as incoherent actually call for rational responses. The key role in this is played by the notion of (rational) degrees of confidence. These three sections are followed by a brief conclusion and an appendix, verifying the main observations.

2 Conciliatory reasoning in default logic

2.1 Basic defeasible reasoner

This section defines a simple defeasible reasoner. The particular reasoner we’ll be working with is a form of default logic. ¹⁰ The core idea behind it is to supplement the standard (classical) logic with a special set of default rules representing defeasible generalizations, with a view of being able to derive a stronger set of conclusions from a given set of premises. We assume the language of ordinary propositional logic as our background and represent default rules as pairs of (vertically) ordered formulas: where X and Y are arbitrary propositions, 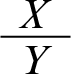will stand for the rule that lets us conclude Y from X by default. To take an example, let B be the proposition that Tweety is a bird and F the proposition that Tweety flies. Then 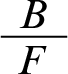says that we can conclude that Tweety flies as soon as we have established that he is a bird. We use the letter r (with subscripts) to denote default rules, and make use of the functions $Premise[\cdot ]$ and $Conclusion[\cdot ]$ to pick out, respectively, the premise and the conclusion of some given rule: if 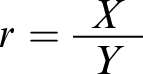, then $Premise[r] = X$ and $Conclusion[r] = Y$ . The second function can be applied to sets of rules too: where $\mathcal {S}$ is a set of default rules, $Conclusion[\mathcal {S}]$ picks out the conclusions of all rules in $\mathcal {S}$ , or, formally, $Conclusion[\mathcal {S}] = \{Conclusion[r]: r\in \mathcal {S}\}$ .

We envision an agent reasoning on the basis of a two-part structure $\langle \mathcal {W},\mathcal {R}\rangle $ where $\mathcal {W}$ is a set of ordinary propositional formulas—the hard information, or the information that the agent is certain of—and $\mathcal {R}$ is a set of default rules—the rules the agent relies on when reasoning. We call such structures contexts and denote them by the letter c (with subscripts).

Definition 1 (Contexts)

A context c is a structure of the form $\langle \mathcal {W},\mathcal {R}\rangle $ , where $\mathcal {W}$ is a set of propositional formulas and $\mathcal {R}$ is a set of default rules.

Let’s illustrate the notion using a standard example from the artificial intelligence literature, the Tweety Triangle: in the first step, the reasoning agent learns that Tweety is a bird and concludes that Tweety flies. In the second, it learns that Tweety is a penguin, retracts the previous conclusion, and concludes that Tweety doesn’t fly. Since the scenario unfolds in two steps, there are two contexts, $c_1 = \langle \mathcal {W},\mathcal {R}\rangle $ and $c_2 = \langle \mathcal {W}',\mathcal {R}\rangle $ . Let B and F be as before, and let P stand for the proposition that Tweety is a penguin. The hard information $\mathcal {W}$ of $c_1$ must include B and $P\supset B$ , expressing an instance of the fact that all penguins are birds. The set of rules $\mathcal {R}$ of $c_1$ (and $c_2)$ , in turn, contains the two rules and . The first lets the reasoner infer that Tweety can fly, by default, once it has concluded that Tweety is a bird. The second lets the reasoner infer that Tweety cannot fly, by default, once it has concluded that he is a penguin. Notice that $r_1$ and $r_2$ can be thought of as instances of two sensible, yet defeasible principles for reasoning, namely, that birds usually fly and that penguins usually do not. As for $c_2 = \langle \mathcal {W}',\mathcal {R}\rangle $ , it is just like $c_1$ , except for its hard information also contains P, saying that Tweety is a penguin.

Now we will specify a procedure determining which formulas follow from any given context. It will rely on an intermediary notion of a proper scenario. Given some context $c = \langle \mathcal {W},\mathcal {R}\rangle $ , any subset of its rules $\mathcal {R}$ counts as a scenario based on c, but proper scenarios are going to be special, in the sense that, by design, they will contain all and only those rules from $\mathcal {R}$ of which we’ll want to say that they should be applied or that they should be in force. As long as this is kept in mind, the following definition of consequence should make good intuitive sense: ¹¹

Definition 2 (Consequence)

Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context. Then the statement X follows from c, written as , just in case $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ for each proper scenario $\mathcal {S}$ based on c.

Of course, the notion of a proper scenario still has to be defined. It will emerge as a combination of three conditions on the rules included in them. The first of these captures the intuitive idea that a rule has to come into operation, or that it has to be triggered:

Definition 3 (Triggered rules)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ a scenario based on it. Then the default rules from $\mathcal {R}$ that are triggered in $\mathcal {S}$ are those that belong to the set $Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}) = \{r \in \mathcal {R}: \mathcal {W}\cup Conclusion[S]\vdash Premise[r]\}$ .

Applying this definition to the empty scenario $\emptyset $ , against the background of the context $c_1$ , it’s easy to see that $Triggered_{\mathcal {W},\mathcal {R}}(\emptyset ) = \{r_1\}$ : the hard information $\mathcal {W} = \{B, P\supset B\}$ entails B, and $B = Premise[r_1]$ .

The need for further conditions on proper scenarios reveals itself once we apply $Triggered(\cdot )$ to any scenario against the background of $c_2$ . While both rules $r_1$ and $r_2$ come out triggered in every scenario based on it, the only scenario that seems intuitively correct is $\{r_2\}$ . This means that we need to specify a further condition, precluding the addition of $r_1$ to $\{r_2\}$ . And here’s one that does the trick:

Definition 4 (Conflicted rules)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context, and $\mathcal {S}$ a scenario based on it. Then the rules from $\mathcal {R}$ that are conflicted in the context of $\mathcal {S}$ are those that belong to the set $Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S}) = \{r\in \mathcal {R}: \mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]\}$ .

Notice that we have $Conflicted_{\mathcal {W},\mathcal {R}}(\{r_2\}) = \{r_1\}$ , saying that the rule $r_1$ is conflicted in the context of the scenario $\{r_2\}$ , as desired. Now consider the following preliminary definition for proper scenarios:

Definition 5 (Proper scenarios, first pass)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ a scenario based on it. Then $\mathcal {S}$ is a proper scenario based on c just in case

$$ \begin{align*}\begin{array}{llll} \mathcal{S} &= &\{ r\in \mathcal{R} : & r \in Triggered_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Conflicted_{\mathcal{W},\mathcal{R}}(\mathcal{S}) \}. \end{array} \end{align*} $$

The definition gives us the correct result when applied to $c_1$ , since the singleton $\mathcal {S}_1 = \{r_1\}$ comes out as its only proper scenario. But it falls flat when applied to $c_2$ , since both $\mathcal {S}_1$ and $\mathcal {S}_2 = \{r_2\}$ qualify as proper. There are multiple ways to resolve this problem formally. The one I adopt here is motivated by the broader goal of having the resources which will let us model conciliatory reasoning.

We introduce a new type of exclusionary rules, letting the reasoner take other rules out of consideration. To be able to formulate such rules, we extend the background language in two ways. First, we introduce rule names: every default rule $r_X$ is assigned a unique name $\mathfrak {r}_X$ —the Fraktur script is used to distinguish rule names from the rules themselves. Second, we introduce a special predicate $Out(\cdot )$ , with a view of forming expressions of the form $Out(\mathfrak {r}_X)$ . The intended meaning of $Out(\mathfrak {r}_x)$ is that the rule $r_x$ is excluded or taken out of consideration. ¹² For concreteness, let $\mathfrak {r}_1$ be the name of the familiar rule $r_1$ . Then $Out(\mathfrak {r}_1)$ says that $r_1$ is excluded.

With names and the new predicate in hand, we can formulate a second negative condition on a rule’s inclusion in a proper scenario:

Definition 6 (Excluded rules)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context, and $\mathcal {S}$ a scenario based on this context. Then the rules from $\mathcal {R}$ that are excluded in the context of $\mathcal {S}$ are those that belong to the set $Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S}) = \{r\in \mathcal {R}: \mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Out(\mathfrak {r})\}$ .

Our full definition of proper scenarios, then, runs thus: ¹³

Definition 7 (Proper scenarios)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ a scenario based on it. Then $\mathcal {S}$ is a proper scenario based on c just in case

$$ \begin{align*}\begin{array}{llll} \mathcal{S} &= &\{ r\in \mathcal{R} : & r \in Triggered_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Conflicted_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Excluded_{\mathcal{W},\mathcal{R}}(\mathcal{S}) \}. \end{array} \end{align*} $$

According to this definition, a proper scenario $\mathcal {S}$ contains all and only those rules that are triggered and neither conflicted, nor excluded in it.

Returning to the example, $c_1$ and $c_2$ must be supplemented with the rule , saying that the rule $r_1$ must be taken out of consideration in case Tweety is a penguin. This should make good sense. Since penguins form a peculiar type of birds, it’s not reasonable to base one’s conclusion that a penguin flies on the idea that birds usually do. It’s easy to see that $\mathcal {S}_1$ is still the only proper scenario based on $c_1$ , and that $\mathcal {S}_3 = \{r_2,r_3\}$ is the only proper scenario based on $c_2$ . So the addition of $r_3$ leaves us with a unique proper scenario in each case. ¹⁴ And this gives us the intuitively correct results: given our definition of consequence, the formula F, saying that Tweety is able to fly, follows from $c_1$ , and the formula $\neg F$ , saying that Tweety isn’t able to fly, follows from $c_2$ .

With this, our basic defeasible reasoner is complete. We interpret it as a model reasoner: if it outputs X in the context c, then it’s rational for one to, or one ought to, believe that X in the situation c stands for. And if the reasoner doesn’t output X in c, then it’s not rational for one to, or it’s not the case that one ought to, believe that X in the situation c stands for. It may look like the model is committed to the all-or-nothing picture of doxastic attitudes, but it actually can accommodate degree-of-confidence talk as well—more on this in Section 4.

I will sometimes represent contexts as inference graphs. The ones in Figure 1 represent the two contexts capturing the Tweety Triangle. Here’s how such graphs should be read: a black node at the bottom of the graph—a node that isn’t grayed out, that is—represents an atomic formula from the hard information. A double link from X to Y stands for a proposition of the form $X\supset Y$ . A single link from X to Y stands for an ordinary default rule of the form 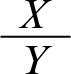, while a crossed out single link from X to Y stands for a default rule of the form . A crossed out link that starts from a node X and points to another link stands for an exclusionary default of the form 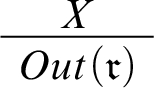, with the second link representing the rule r.

Fig. 1 Tweety Triangle, $c_1$ (left) and $c_2$ (right).

2.2 Capturing conciliationism

Now let’s see how the core idea motivating conciliatory views can be captured in the defeasible reasoner. As a first step, consider the following case, in which the conciliatory response seems particularly intuitive:

Mental Math. My friend and I have been going out to dinner for many years. We always tip 20% and divide the bill equally, and we always do the math in our heads. We’re quite accurate, but on those occasions where we’ve disagreed in the past, we’ve been right equally often. This evening seems typical, in that I don’t feel unusually tired or alert, and neither my friend nor I have had more wine or coffee than usual. I get $43 in my mental calculation, and become quite confident of this answer. But then my friend says she got $45. I dramatically reduce my confidence that $43 is the right answer. ¹⁵

Mental Math describes fairly complex reasoning, and we shouldn’t miss three of its features: first, we can distinguish two components in it, the mathematical calculations and the reasoning prompted by the friend’s announcement. What’s more, it seems perfectly legitimate to call the former the agent’s first-order reasoning and the latter her second-order reasoning. Second, the agent’s initial confidence in $43 being the correct answer is based on her calculations, and it gets reduced because the agent becomes suspicious of them. And third, the friend’s announcement provides for a very good reason for the agent to suspect that she may have erred in her calculations.

Bearing this in mind, let’s capture the agent’s reasoning in the model. To this end, we introduce a new predicate $Seems(\cdot )$ to our language. Now, $Seems(X)$ is meant to express the thought that the agent has reasoned to the best of her ability about whether some proposition X is true and come to the conclusion that it is true as a result. I doubt that there’s much informative we can say about the reasoning implied in $Seems(\cdot )$ . One thing should be clear though: it’s going to depend on X and thus also differ from one case to another. If X is a mathematical claim, $Seems(X)$ implies calculations of the sort described in Mental Math. If X is a philosophical claim, $Seems(X)$ implies a careful philosophical investigation. Also, note that $Seems(X)$ is perfectly compatible with $\neg X$ . Since the agent is fallible, the fact that she has reasoned to the best of her ability about the issue doesn’t guarantee that the conclusion is correct.

Presumably, though, situations where the agent’s best reasoning leads her astray are relatively rare, and so it’s reasonable for her to go by her best reasoning. After all, she doesn’t have any other alternative. This motivates the following default rule schema:

1. Significance of first-order reasoning: , or if your best first-order (or domain-specific) reasoning suggests that X, conclude X by default.

In Mental Math, we would instantiate the schema with the rule 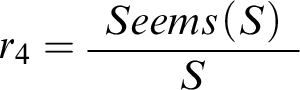, with S standing for the proposition that my share of the bill is $43. What the friend’s announcement brings into question, then, is exactly the connection between $Seems(S)$ and S. While my mental calculations usually are reliable, now and then I make a mistake. The announcement suggests that this may have happened when I reasoned toward S.

To capture the effects of the announcement, we use another designated predicate $Disagree(\cdot )$ . The formula $Disagree(X)$ is meant to express the idea that the agent is in genuine disagreement about whether X. And I say genuine to distinguish the sorts of disagreements that conciliationists take to be epistemically significant from merely apparent disagreements, such as verbal disagreements and disagreements based on misunderstandings. ¹⁶ So $Disagree(S)$ means that there’s a genuine disagreement—between me and my friend—over whether my share of the bill is $43. We capture the effects of this disagreement by means of the default rule , which says, roughly, that in case there’s genuine disagreement about whether S, the rule $r_4$ , which lets me conclude S on the basis of $Seems(S)$ , is to be excluded. The rule $r_5$ , then, is what expresses the distinctively conciliatory component of the complex reasoning discussed in Mental Math.

Now notice that $r_5$ too instantiates a default rule schema, namely:

1. Significance of disagreement: , or if there’s genuine disagreement about whether X, stop relying on your first-order reasoning about X by default.

This schema expresses the core idea motivating conciliatory views, or the core of conciliationism, in our model. ¹⁷

As a first pass, we might try to express Mental Math in the context $c_3 = \langle \mathcal {W},\mathcal {R}\rangle $ where $\mathcal {W} = \{Seems(S)$ , $Disagree(S)\}$ and $\mathcal {R} = \{r_4,r_5\}$ —see Figure 2 for a picture. While S doesn’t follow from $c_3$ , as desired, this context doesn’t represent some important features of the scenario. In particular, it misleadingly suggests that the agent doesn’t reason to the conclusion that there’s genuine disagreement over the bill’s amount, but, rather, starts off knowing it for a fact. Admittedly, the description glances over this component of the reasoning, but it’s clearly implied by the background story:“.. my friend and I have been going out to dinner for many years.. we’ve been right equally often.. neither my friend nor I have had more wine or coffee than usual.” And nothing stands in the way of capturing the reasoning implied by this description by instantiating the familiar schema with $Disagree(S)$ .

Fig. 2 Mental Math, first pass.

We represent Mental Math using the pair of contexts $c_4 = \langle \mathcal {W},\mathcal {R}\rangle $ and $c_5 = \langle \mathcal {W}', \mathcal {R}\rangle $ , with the first standing for the situation before the friend’s announcement and the second right after it. The set $\mathcal {W}$ is comprised of the formula $Seems(S)$ , and $\mathcal {W}'$ of the formulas $Seems(S)$ and $Seems(Disagree(S))$ . Both contexts share the same set of rules $\mathcal {R}$ , comprised of the familiar rules $r_4$ and $r_5$ , as well as the new rule 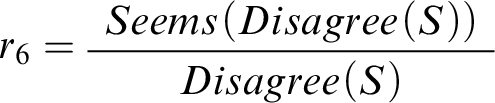, another instance of the first-order reasoning schema. The two contexts are depicted in Figure 3. It’s not hard to verify that $\{r_4\}$ is the unique proper scenario based on $c_4$ , and that, therefore, S follows from $c_4$ , suggesting that, before the announcement, it’s rational for the agent to believe that her share of the bill is $43. As for $c_5$ , here again we have only one proper scenario, namely, $\{r_5,r_6\}$ . This implies that S does not follow from $c_5$ , suggesting that, after the announcement, it’s not rational for the agent to believe that her share of the bill is $43. So our model delivers the intuitive result.

Fig. 3 Mental Math, final, $c_4$ (left) and $c_5$ (right).

It also supports the following take on conciliationism: it’s not a simple view, on which you’re invariably required to give up your belief in X as soon as you find yourself in disagreement over X with an epistemic peer—or, perhaps, as soon as it’s rational for you to think that you’re in such a disagreement. Instead, it’s a more structured view, saying roughly the following: if your best first-order (or domain-specific) reasoning suggests that X and it’s rational for you to believe that you’re in disagreement over X with an epistemic peer, then, under normal circumstances, you should bracket your first-order reasoning about X and avoid forming beliefs on its basis. ¹⁸

2.3 Disagreements over disagreement

Now we can turn to the self-defeat objection. Here’s the scenario I used to illustrated it, presented in the first-person perspective:

Double Disagreement. I consider myself an able philosopher with special interests in metaphysics and social epistemology. I’ve reasoned very carefully about the vexed topic of free will, and I’ve come to the conclusion that we have libertarian free will. I’ve also spent a fair amount of time thinking about the issues surrounding peer disagreement, becoming convinced that conciliationism is correct and that one has to give up one’s well-reasoned opinion when faced with a disagreeing peer. Then, to my surprise, I discover that my friend metaphysician Milo disagrees with me about the existence of free will, and that my friend epistemologist Evelyn disagrees with me about conciliationism. ¹⁹

Elga [16] famously argued that cases like this show that conciliatory views are inconsistent. ²⁰ His line of reasoning runs roughly thus. On the one hand, conciliationism seems to recommend that I abandon my belief in the existence of free will in response to my disagreement with Milo. On the other, conciliationism seems to recommend that I do not abandon my belief in the existence of free will. How? Well, it recommends that I abandon my belief in conciliationism in response to my disagreement with Evelyn. But with this belief gone, my disagreement with Milo seems to lose its epistemic significance for me, implying that it must be okay for me to retain the belief in the existence of free will. Putting the two together, conciliationism appears to support two inconsistent conclusions, that I ought to abandon the belief in free will, and that it’s not the case that I ought to.

Now let’s see if our model reasoner supports this train of thought. The first step is to capture Double Disagreement in a context, and here already we face a difficulty: we need to model the agent’s becoming convinced that conciliationism is correct. We know that conciliationism can be modeled as a specific reasoning policy, but we don’t yet know how to model the reasoning that puts such a policy in place. What we’ll do, then, is start with a partial representation, and then gradually add the missing pieces. Let C stand for the proposition that conciliationism is correct—and think of C as a placeholder to be made precise later on—and L for the proposition that we have libertarian free will. As our first pass, we represent Double Disagreement as the context $c_6 = \langle \mathcal {W},\mathcal {R}\rangle $ where $\mathcal {W}$ is comprised of $Seems(L)$ , $Seems(C)$ , $Seems(Disagree(L))$ , and $Seems(Disagree(C))$ , and where $\mathcal {R}$ contains the following rules:

1. : If my first-order reasoning about free will suggests that it exists, I conclude that it does indeed exist by default.

2. : If my (first-order) reasoning about my disagreement with Milo suggests that it’s genuine, I conclude that this disagreement is genuine by default.

3. : If there’s genuine disagreement over free will, I back off from my first-order reasoning about it by default.

4. : If my reasoning about the epistemic significance of disagreement suggests that conciliationism is correct, I conclude that it is by default.

5. : If my reasoning about my disagreement with Evelyn suggests that it’s genuine, I conclude that this disagreement is genuine by default.

6. : If there’s genuine disagreement over conciliationism, I back off from my first-order reasoning about it by default.

The context $c_6$ is depicted in Figure 4.

Fig. 4 Double Disagreement, first pass.

There’s one proper scenario based on $c_6$ , namely, $\{r_{8},r_{9},r_{11},r_{12}\}$ , and this implies that neither C, nor L follow from this context. There’s nothing inconsistent here, but the reasoner’s response may seem odd: it doesn’t draw the conclusion that conciliationism is correct, and yet backs off from its reasoning about free will on distinctively conciliatory grounds. (I’ll have much more to say about this seeming oddness below.) However, the main problem is that, in $c_6$ , there’s no connection between the proposition saying that conciliationism is correct and the conciliatory reasoning policy, or between C and the rules $r_{9}$ and $r_{12}$ .

We’re going to put the connection in place, proceeding in two steps and starting by linking C and $r_9$ . To this end, let’s focus on a curtailed version of Double Disagreement in which I never find out that Evelyn disagrees with me over conciliationism—call this case Disagreement with Milo. We can express it in the context $c_7 = \langle \mathcal {W},\mathcal {R}\rangle $ , which is like $c_6$ , except for its hard information $\mathcal {W}$ lacks the formula $Seems(Disagree(C))$ , and its set of rules lacks $r_{11}$ and $r_{12}$ . ²¹

Since C says that conciliationism is correct and $r_9$ is an instance of the conciliatory schema , it seems reasonable to arrange things in such a way that C is what puts $r_9$ in place. To this end, we extend our language with another designated predicate $Reasonable(\cdot )$ . Where $Out(\mathfrak {r})$ says that r is taken out of consideration, $Reasonable(\mathfrak {r})$ says that r is a prima facie reasonable rule to follow, or that r is among the rules that the agent could base her conclusions on. The formula $Reasonable(\mathfrak {r}_9)$ , in particular, says that $r_9$ is a prima facie reasonable rule to follow. ²² We’re going to have to update our defeasible reasoner so that it can take this predicate into account. But first let’s connect C and $r_9$ by adding the rule to $c_7$ . The complete context is depicted in Figure 5. Notice that the graph depicting it includes two types of links we haven’t seen before. First, there’s a single link (standing for $r_{13}$ ) that points to another one and that isn’t crossed out. From now on, links of this type will represent rules of the form . Second, there’s a dashed link (standing for $r_9$ ). From now on, links of this type will represent rules that, intuitively, the reasoner can start relying on only after it has concluded that they are prima facie reasonable to follow. ²³

Fig. 5 Disagreement with Milo.

An easy check reveals that $Reasonable(\mathfrak {r}_9)$ and C do, while L does not follow from $c_7$ . This is the intuitive result, but we can’t rest content with what we have here. To see why, consider the context $c_8 = \langle \mathcal {W}\cup \{Out(\mathfrak {r}_{10})\},\mathcal {R}\rangle $ that extends the hard information of $c_7$ with the formula $Out(\mathfrak {r}_{10})$ , saying that the rule is to be taken out of consideration. It can be verified that the only proper scenario based on $c_8$ is $\{r_8,r_9\}$ , and that, therefore, neither C, nor $Reasonable(\mathfrak {r}_9)$ , nor L follow from it. But this is the wrong result: the formula L doesn’t follow because it gets excluded by the rule $r_9$ which was supposed to depend on the reasoner concluding C and $Reasonable(\mathfrak {r}_9)$ . Thus, a rule that, intuitively, should have no effects whatsoever ends up precluding the reasoner from deriving L.

To make the new predicate and rules like $r_9$ do real work, the inner workings of the reasoner have to be modified. And my general strategy here is to let the reasoner use a rule r only on the condition that it can infer a formula of the form $Reasonable(\mathfrak {r})$ , just like currently it can use a rule r only on the condition that it can infer its triggering condition, $Premise[r]$ . So, from now on, the reasoner is allowed to use a rule r only in case it can infer both $Premise[r]$ and $Reasonable(\mathfrak {r})$ . And there are two ways for it to infer a formula of the form $Reasonable(\mathfrak {r})$ : from the hard information or by means of other rules. One immediate implication of this is that some $Reasonable$ -formulas are going to have to be included in the hard information. But this should make good sense: the presence of $Reasonable(\mathfrak {r})$ in $\mathcal {W}$ can be understood in terms of the reasoner taking r to be a prima facie reasonable rule to follow from the outset. ²⁴

In Section 2.1, the central notion of a proper scenario was defined by appealing to three conditions on rules. Now we amend it by adding a fourth one:

Definition 8 (Reasonable rules)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context, and $\mathcal {S}$ a scenario based on it. Then the rules from $\mathcal {R}$ that are prima facie reasonable (to follow) in the context of the scenario $\mathcal {S}$ are those that belong to the set $Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S}) = \{r \in \mathcal {R}: \mathcal {W}\cup Conclusion[S]\vdash Reasonable(\mathfrak {r})\}$ .

Definition 9 (Proper scenarios, revised)

Let $\langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ a scenario based on it. Then $\mathcal {S}$ is a proper scenario based on $\langle \mathcal {W},\mathcal {R}\rangle $ just in case

$$ \begin{align*}\begin{array}{llll} \mathcal{S} &= &\{ r\in \mathcal{R} : & r\in Reasonable_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r \in Triggered_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Conflicted_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Excluded_{\mathcal{W},\mathcal{R}}(\mathcal{S}) \}. \end{array} \end{align*} $$

With this, we’re all done. There’s no need to change the definition of consequence. ²⁵ The next observation shows that our revised reasoner is a conservative generalization of the original one—the proof is provided in the Appendix:

Observation 2.1. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be an arbitrary regular context where no $Reasonable$ -formulas occur—or, more precisely, a context where no subformula of any of the formulas in $\mathcal {W}$ or any of the premises or conclusions of the rules in $\mathcal {R}$ is of the form $Reasonable(\mathfrak {r})$ . Then there’s a context $c' = \langle \mathcal {W}\cup \{Reasonable(\mathfrak {r}):r\in \mathcal {R}\},\mathcal {R}\rangle $ that’s equivalent to c. Or more explicitly, X follows from c if and only if X follows from $c'$ for all X such that no subformula of X is of the form $Reasonable(\mathfrak {r})$ .

Our final rendering of Disagreement with Milo is the context $c_9 = \langle \mathcal {W},\mathcal {R}\rangle $ , which is like $c_7$ , except for its hard information $\mathcal {W}$ also includes the formulas saying that the reasoner takes the rules $r_7$ , $r_8$ , $r_{10}$ , and $r_{13}$ to be prima facie reasonable to follow, that is, $\mathcal {W}$ includes the formulas $Reasonable(\mathfrak {r}_{7})$ , $Reasonable(\mathfrak {r}_{8})$ , $Reasonable(\mathfrak {r}_{10})$ , and $Reasonable(\mathfrak {r}_{13})$ . It’s not difficult to see that the only proper scenario based on $c_9$ is $\{r_8,r_9,r_{10},r_{13}\}$ , and so that C does, while L doesn’t follow from this context. Thus, our analysis suggests that the correct response to the scenario is to stick to the belief in conciliationism and to abandon the belief in free will. This seems perfectly intuitive. ²⁶

Now let’s zoom in on the other half of the story in Double Disagreement, forgetting about free will for a second and restricting attention to conciliationism. Our preliminary formalization included the formulas $Seems(C)$ and $Seems(Disagree(C))$ , as well as the following three rules: , , and 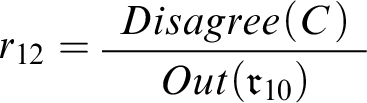. We found it wanting because it didn’t connect C and $r_{12}$ . Now, however, we can complete this formalization by supplementing it with the rule 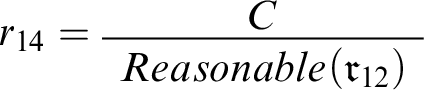, as well as $Reasonable$ -formulas saying that $r_{10}$ , $r_{11}$ , and $r_{14}$ are prima facie reasonable rules. The resulting context $c_{10}$ is depicted in Figure 6. (Note that here and elsewhere formulas of the form $Reasonable(\mathfrak {r})$ are not explicitly represented.)

Fig. 6 Disagreement with Evelyn.

As it turns out, however, there are no proper scenarios based on $c_{10}$ . ²⁷ This is bad news for the advocates of conciliatory views, since no proper scenarios means that we get for any formula X whatsoever: on our definition of consequence, a formula X follows from a context $c = \langle \mathcal {W},\mathcal {R}\rangle $ if and only if $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ for every proper scenario based on c. But when there are no proper scenarios, every formula satisfies the right-hand side of the biconditional vacuously, and so every formula follows from the context. What’s more, the context capturing the entire story recounted in Double Disagreement delivers the same result. Merging $c_9$ and $c_{10}$ , we acquire the context $c_{11}$ , our final representation of the scenario—see Figure 7. Yet again, there are no proper scenarios based on $c_{11}$ , and we get for all X. Thus, our carefully designed model reasoner seems to suggest that the correct conciliatory response to Double Disagreement is to conclude everything. ²⁸

Fig. 7 Double Disagreement, final.

We can think of this problem as the formal version of the self-defeat objection to conciliatory views that we started with. In the end, putting forth a model (conciliatory) reasoner which suggests that concluding everything is the correct response to scenarios of a certain shape is much like advancing a (conciliatory) view that can issue inconsistent recommendations. The fact that this formal problem obtains lends support to Elga’s pessimistic conclusion that conciliatory views are inherently flawed.

Luckily, though, the problem can be addressed.

3 Moving to argumentation theory

The fact that conciliationism turns on itself in Double Disagreement is only part of the reason why our model reasoner suggests concluding everything. Its other part is something of a technical nuisance: default logic—which our reasoner is based on—isn’t particularly well-suited to handle contexts containing what we can call vicious cycles or self-defeating chains of rules. ²⁹ The main goal of this section is to clear this nuisance. Once it’s been cleared, we’ll see that conciliatory views do not have to issue inconsistent directives in Double Disagreement and other scenarios like it.

In order to be in a position to handle contexts containing vicious cycles adequately—including the context $c_{11}$ that expresses Double Disagreement and happens to contain such a cycle in the form of the chain of rules $r_{10}$ – $r_{14}$ – $r_{12}$ —we go beyond default logic and draw on the resources of a more general formal framework called abstract argumentation theory. As Dung [13] has shown in his seminal work, default logic, as well as many other formalisms for defeasible reasoning can be seen as special cases of argumentation theory. One implication of this is that it’s possible to formulate an argumentation theory-based reasoner that picks out the same consequence relation as our default-logic based reasoner from the previous section. And that’s just what we’re going to do. For, first, a simple tweak to the new reasoner will let it handle cycles adequately, and, second, we’ll need the additional resources of argumentation theory later anyway (to capture degrees of confidence in Section 4).

The remainder of this section is structured as follows. Sections 3.1–3.3 introduce abstract argumentation, relate it to default logic, and formulate the more sophisticated reasoner. Section 3.4 returns to Double Disagreement, explains how this reasoner handles it, and contrasts its recommendations with the proposals for responding to the self-defeat objection from the literature.

3.1 Argument frameworks

In default logic, conclusions are derived on the basis of contexts. In argumentation theory, they are derived on the basis of argument (or argumentation) frameworks. Formally, such frameworks are pairs of the from $\langle \mathcal {A}, \leadsto \rangle $ , where $\mathcal {A}$ is a set of arguments—the elements of which can be anything—and $\leadsto $ is a defeat relation among them. ³⁰ Thus, for any two arguments $\mathcal {S}$ and $\mathcal {S}'$ in $\mathcal {A}$ , the relation $\leadsto $ can tell us whether $\mathcal {S}$ defeats $\mathcal {S}'$ or not. ³¹ We denote argument frameworks with the letter $\mathcal {F}$ . What argumentation theory does is provide a number of sensible ways for selecting the set of winning arguments of any given framework $\mathcal {F}$ , the set which, in its turn, determines the conclusions that can be drawn on the basis of $\mathcal {F}$ . Since the frameworks we focus on will be constructed from contexts, argumentation theory will let us determine the conclusions that can be drawn on the basis of any given context c.

Our logic-based reasoner relies on the notion of a proper scenario to determine the consequences of a context. This notion specifies something like the necessary and sufficient conditions for a rule’s counting as admissible or good—that the rule be reasonable, triggered, not conflicted, and not excluded—and the reasoner can be thought of as selecting such rules in one single step. However, nothing stands in the way of selecting the good rules in a more stepwise fashion. That is, instead of jumping from a context to the scenario containing all and only the admissible rules, we could first select all scenarios whose members satisfy the positive conditions—reasonable and triggered—and later filter out the scenarios whose members do not satisfy the remaining negative conditions—conflicted and excluded. Let’s restate the idea, using our formal notation: starting with a context $c = \langle \mathcal {W},\mathcal {R}\rangle $ , in the first step we’d select all and only those scenarios $\mathcal {S} \subseteq \mathcal {R}$ such that, for every r in $\mathcal {S}$ ,

1. $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Reasonable(r)\& Premise[r]$ ,

and, in the second step, we’d filter out all of those scenarios $\mathcal {S}$ for which it holds that there’s some r in $\mathcal {S}$ such that

1. $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Out(\mathfrak {r})$ .

After the second step, we’d have access to all and only the good rules. Applying argumentation theory to contexts can be naturally thought of as proceeding in these two steps. The scenarios selected in the first step are the arguments of the argumentation framework based on the given context. And the scenarios that remain standing after the second step are the winning arguments of the framework. The definition of an argument based on a context, then, runs thus:

Definition 10 (Arguments)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ a scenario based on it, $\mathcal {S} \subseteq \mathcal {R}$ . Then $\mathcal {S}$ is an argument based on c just in case $\mathcal {S} \subseteq Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $\mathcal {S} \subseteq Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . The set of arguments based on c is the set $Arguments(c) = \{\mathcal {S}\subseteq \mathcal {R} : \mathcal {S}\text { is an argument based on }c\}$ .

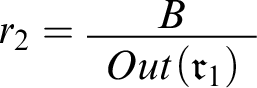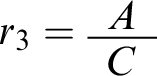To see the definition at work, let’s apply it to a toy case. Consider the context $c_{12} =\langle \mathcal {W},\mathcal {R}\rangle $ where $\mathcal {W}$ contains A, $Reasonable(\mathfrak {r}_1)$ , $Reasonable(\mathfrak {r}_2)$ , and $Reasonable(\mathfrak {r}_3)$ and $\mathcal {R}$ contains , , and . The context is depicted in Figure 8. There are eight scenarios based on $c_{12}$ , namely, $\mathcal {S}_0 = \emptyset $ , $\mathcal {S}_1 = \{r_1\}$ , $\mathcal {S}_2 = \{r_2\}$ , $\mathcal {S}_3 = \{r_3\}$ , $\mathcal {S}_4 = \{r_1,r_2\}$ , $\mathcal {S}_5 = \{r_1,r_3\}$ , $\mathcal {S}_6 = \{r_2,r_3\}$ , and $\mathcal {S}_7 = \{r_1,r_2,r_3\}$ . Two of these, $\mathcal {S}_2$ and $\mathcal {S}_6$ , fail to qualify as arguments. Each contains a rule that’s not triggered in it. Indeed, one glance at the graph depicting $c_{12}$ in Figure 8 is enough to see that $r_2$ can’t be triggered in any scenario based on $c_{12}$ that doesn’t include $r_1$ . This leaves us with six arguments that comprise the first element $\mathcal {A}$ of the argument framework based on $c_{12}$ .

Fig. 8 Sample context with a vicious cycle.

Our next definition specifies the conditions under which one argument defeats another:

Definition 11 (Defeat)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ and $\mathcal {S}'$ two arguments based on it. Then $\mathcal {S}$ defeats $\mathcal {S}'$ , written as $\mathcal {S}\leadsto \mathcal {S}'$ , if and only if there is some rule $r\in \mathcal {S}'$ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash \neg Conclusion[r]$ , or $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ .

Notice how the ideas behind the notions of conflicted and excluded rules get repurposed in this definition. A rule r came out conflicted in the context of a scenario $\mathcal {S}$ just in case $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ . Now an argument $\mathcal {S}$ defeats another one $\mathcal {S}'$ just in case there’s a rule r in $\mathcal {S}'$ such that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ . A similar parallel holds of exclusion. Let’s apply the definition to the arguments 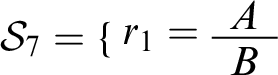, , and . Since $Conclusion[\mathcal {S}_7]$ entails $Out(\mathfrak {r}_1)$ and $r_1$ is in $\mathcal {S}_1$ , the argument $\mathcal {S}_7$ defeats $\mathcal {S}_1$ . What’s more, given that $r_1$ is an element of $\mathcal {S}_7$ , this argument also self-defeats.

Now we have all that’s needed to specify how to construct argument frameworks from contexts:

Definition 12 (Argument frameworks based on contexts)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be an epistemic context. Then the argument framework $\mathcal {F}(c)$ based on c is the pair $\langle \mathcal {A}, \leadsto \rangle $ where $\mathcal {A} = Arguments(c)$ and $\leadsto $ is the set $\{(\mathcal {S},\mathcal {S}') \in \mathcal {A}\times \mathcal {A} : \mathcal {S}\text { defeats } \mathcal {S}' \}$ .

Figure 9 represents the argument framework $\mathcal {F}(c_{12})$ constructed from $c_{12}$ . Here’s how it should be read: the nodes of the graph represent the arguments in $\mathcal {A}$ , and the double arrows between the nodes stand for the defeat relations between arguments. A node with an arrow pointing to itself means that the argument it represent self-defeats.

Fig. 9 Argument framework based on the sample context $c_{12}$ .

It’ll be useful to introduce some shorthand notation: let $\mathcal {F} = \langle \mathcal {A}, \leadsto \rangle $ be an arbitrary argument framework and $\Gamma $ and $\Gamma '$ two sets of arguments from $\mathcal {A}$ . When there’s an argument $\mathcal {S}$ in $\Gamma $ that defeats some argument $\mathcal {S}'$ from $\mathcal {A}$ , we write $\Gamma \leadsto \mathcal {S}'$ ; and when there’s a pair of arguments $\mathcal {S}$ and $\mathcal {S}'$ such that $\mathcal {S}$ is in $\Gamma $ , $\mathcal {S}'$ is in $\Gamma '$ , and $\mathcal {S} \leadsto \mathcal {S}'$ , we write $\Gamma \leadsto \Gamma '$ . As an illustration, in the case of $\mathcal {F}(c_{12})$ , we have $\{\mathcal {S}_0,\mathcal {S}_7\}\leadsto \mathcal {S}_5$ , while we do not have $\{\mathcal {S}_0,\mathcal {S}_7\}\leadsto \mathcal {S}_3$ ; and we have $\{\mathcal {S}_0,\mathcal {S}_7\}\leadsto \{\mathcal {S}_1,\mathcal {S}_3,\mathcal {S}_4\}$ , while we do not have $\{\mathcal {S}_0,\mathcal {S}_7\}\leadsto \{\mathcal {S}_3\}$ . Further, when there’s no argument $\mathcal {S}$ in $\Gamma $ such that $\mathcal {S}$ defeats $\mathcal {S}'$ , we write ; and when there’s no pair of arguments $\mathcal {S}$ and $\mathcal {S}'$ such that $\mathcal {S}$ is in $\Gamma $ , $\mathcal {S}'$ is in $\Gamma '$ , and $\mathcal {S}\leadsto \mathcal {S}'$ , we write .

3.2 Selecting winning arguments

Now we can turn to argumentation theory proper. As flagged above, the winning argument set of a framework is selected solely on the basis of defeat relations between its arguments. ³² In the literature, the collection of definitions letting one select such sets is called admissibility semantics. You may find it helpful to think of this semantics as serving a function that’s similar to the one served by the notion of a proper scenario in the context of default logic. There’s one important difference, however. Where default logic didn’t offer any choice, the admissibility semantics provides a number of different sensible ways of selecting winning arguments. We’re going to focus on two such ways here, beginning with what’s called stability semantics:

Definition 13 (Stability semantics)

Let $\mathcal {F} = \langle \mathcal {A}, \leadsto \rangle $ be an argument framework and $\Gamma $ a set of arguments from $\mathcal {A}$ . Then:

1. (i) $\Gamma $ is conflict-free if and only if there are no two arguments $\mathcal {S}$ , $\mathcal {S}'$ in $\Gamma $ such that $\mathcal {S}\leadsto \mathcal {S}'$ .

2. (ii) $\Gamma $ is stable, or a stable extension of $\mathcal {F}$ , if and only if

   1. (1) $\Gamma $ is conflict-free, and

   2. (2) $\Gamma $ defeats all the arguments that are not in it, that is, for all $\mathcal {S} \in \mathcal {A}\backslash \Gamma $ , $\Gamma \leadsto \mathcal {S}$ .

Stability semantics is closely related to default logic, and we’ll state the precise connection between the two in a moment. For now, simply note that there are no stable argument sets based on the framework $\mathcal {F}(c_{12})$ , just like there are no proper scenarios based on the context $c_{12}$ . ³³ The argument sets that are conflict-free, such as $\{\mathcal {S}_0,\mathcal {S}_3\}$ , fail to defeat all of the arguments that are not in them, and the argument sets that defeat all of the arguments that are not in them, such as $\{\mathcal {S}_0,\mathcal {S}_3,\mathcal {S}_4\}$ , fail to be conflict-free. This is due to the self-defeating chain $r_1$ - $r_2$ .

The alternative to stability semantics we’ll use is called preference semantics.

Definition 14 (Preference semantics)

Let $\mathcal {F} = \langle \mathcal {A}, \leadsto \rangle $ be an argument framework and $\Gamma $ a set of arguments from $\mathcal {A}$ . Then:

1. (i) $\Gamma $ is conflict-free if and only if there are no arguments $\mathcal {S}$ , $\mathcal {S}'$ in $\Gamma $ such that $\mathcal {S}\leadsto \mathcal {S}'$ .

2. (ii) An argument $\mathcal {S}$ in $\mathcal {A}$ is defended by $\Gamma $ if and only if, for all $\mathcal {S}'$ (with $\mathcal {S}'$ in $\mathcal {A}\backslash \Gamma $ ) such that $\mathcal {S}'\leadsto \mathcal {S}$ , we have $\Gamma \leadsto \mathcal {S}'$ .

3. (iii) $\Gamma $ is a complete extension of $\mathcal {F}$ if and only if

   1. (1) $\Gamma $ is conflict-free, and

   2. (2) $\Gamma $ contains all of the arguments it defends.

4. (iv) $\Gamma $ is preferred, or a preferred extension of $\mathcal {F}$ , if and only if $\Gamma $ is a maximal complete extension of $\mathcal {F}$ , that is, if and only if there’s no other complete extension $\Gamma '$ of $\mathcal {F}$ such that $\Gamma \subset \Gamma '$ .

Let’s apply this definition to $\mathcal {F}(c_{12})$ . The largest conflict-free set of arguments is $\{\mathcal {S}_0$ , $\mathcal {S}_1$ , $\mathcal {S}_3$ , $\mathcal {S}_5\}$ . However, it does not defend all of its members: both $\mathcal {S}_4$ and $\mathcal {S}_7$ defeat $\mathcal {S}_5$ , and there’s nothing in the set that defeats either of them. There are a few sets that are both conflict-free and defend all of their members, namely, $\emptyset $ , $\{\mathcal {S}_0\}$ , $\{\mathcal {S}_3\}$ , and $\{\mathcal {S}_0,\mathcal {S}_3\}$ . However, only one of them qualifies as a complete extension, namely, $\{\mathcal {S}_0,\mathcal {S}_3\}$ . Why do the other sets fail to qualify? Well, take $\{\mathcal {S}_0\}$ as an example. A complete set is supposed to contain all the arguments it defends, and a minute’s reflection reveals that there’s an argument that $\{\mathcal {S}_0\}$ defends that’s not in it, namely, $\mathcal {S}_3$ . What’s more, the set $\{\mathcal {S}_0,\mathcal {S}_3\}$ also happens to be the unique preferred extension of $\mathcal {F}(c_{12})$ .

Preference semantics has a clear intuitive rationale. Any conflict-free set of arguments that defends itself—that is, any complete extension—is a desirable state to occupy: it is consistent, and it has a rejoinder to every attack on it. And there’s a clear sense in which a preferred set of arguments is an even more desirable state: it’s still consistent, it still has a rejoinder to every attack on it, and it’s also as big of an argument set of this sort as there can be. So if we’re looking to select winning argument sets, preferred extensions are very natural candidates. ³⁴

While we have labeled various kinds of argument sets, we haven’t stated the conditions under which a formula follows from such a set. The following definition rectifies the omission:

Definition 15. Where $\mathcal {F}(c)$ is an argument framework constructed from some context $c = \langle \mathcal {W},\mathcal {R}\rangle $ and $\Gamma $ is a set of arguments based on $\mathcal {F}(c)$ , a statement X is a conclusion of $\Gamma $ if and only if there is some argument $\mathcal {S}$ in $\Gamma $ such that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ .

With this, we have all the elements we need to define two distinct consequence relations. Both specify when a formula X follows from a context c. Both take a circuitous route, utilizing the resources of argumentation theory. The only difference between them is that the first relies on stability and the second on preference semantics:

Definition 16 (Consequence, stable)

Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context. Then the statement X follows from c according to stability semantics, written as , just in case it is a conclusion of every stable extension of the argument framework $\mathcal {F}(c)$ .

Definition 17 (Consequence, preferred)

Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context. Then the statement X follows from c according to preference semantics, written as , just in case it is a conclusion of every preferred extension of the argument framework $\mathcal {F}(c)$ .

The promised connection between default logic and stability semantics can now be stated in the form of an observation—the proof of which is provided in the Appendix:

Observation 3.1. Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context and X an arbitrary formula. Then X follows from c in default logic, , if and only if X follows from c according to stability semantics, .

So stability semantics expresses default logic in argumentation-theoretic terms, inheriting its virtues and vices. We have seen one of its vices: default logic collapses in the presence of self-defeating chains. ³⁵

My proposal is that we switch from the consequence relation picked out by both default logics and stability semantics to the one picked out by the preference semantics. The move is not ad hoc, because there is a clear sense in which preference semantics is a conservative generalization of stability semantics, and, thus, also of default logic. This sense is captured by the following observation—its proof is, again, given in the Appendix:

Observation 3.2. Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {F}(c) = \langle \mathcal {A}, \leadsto \rangle $ an argument framework constructed from it. If $\mathcal {F}(c)$ does not contain either odd cycles of defeat or infinite chains of defeat, then if and only if .

From this, it immediately follows that preference semantics gives the same results as default logic in all contexts that do not contain any self-defeating chains of rules. ³⁶ If a context contains such a chain, default logic returns the trivial set, while preference semantics returns more meaningful consequences. The toy context $c_{12}$ is a case in point. When we run default logic on it, we get for any formula X whatsoever, while, when we rely on the preference semantics, we get the more reasonable and . Here and in general, preference semantics effectively disregards self-defeating chains of rules and draws conclusions on the basis of those rules only that are independent of such chains.

3.3 Minimal arguments and basic defeat

Before we return to Double Disagreement, it’ll be useful to introduce an alternative way of thinking about argumentation frameworks that makes analyzing complex frameworks easier.

If we take another look at the framework $\mathcal {F}(c_{12})$ —depicted alongside the context $c_{12}$ it’s constructed from in Figure 10—we should realize that there’s an intuitive sense in which some of its arguments are basic and others are not. While $\mathcal {S}_1 = \{r_1\}$ , $\mathcal {S}_3 = \{r_3\}$ , $\mathcal {S}_4 = \{r_1, r_2\}$ , $\mathcal {S}_{5} = \{r_1,r_3\}$ , and $\mathcal {S}_7 = \{r_1, r_2,r_3\}$ all qualify as arguments based on $c_{12}$ , there seems to be a qualitative difference between the first three, $\mathcal {S}_1$ , $\mathcal {S}_3$ , and $\mathcal {S}_4$ , on the one hand, and $\mathcal {S}_5$ and $\mathcal {S}_7$ , on the other. First off, $\mathcal {S}_1$ , $\mathcal {S}_3$ , and $\mathcal {S}_4$ are the (set-theoretically) smallest arguments allowing us to derive, respectively, B, $Out(\mathfrak {r}_1)$ , and C. Thus, while we have both $\mathcal {W}\cup Conclusion[\mathcal {S}_1]\vdash B$ and $\mathcal {W}\cup Conclusion[\mathcal {S}_7]\vdash B$ , only in the case of $\mathcal {S}_1$ can we say that there’s no smaller argument that would let us derive B. And second, $\mathcal {S}_5$ and $\mathcal {S}_7$ are naturally thought of as aggregates of the basic arguments: $\mathcal {S}_5$ combines $\mathcal {S}_1$ and $\mathcal {S}_3$ , while $\mathcal {S}_7$ combines $\mathcal {S}_1$ , $\mathcal {S}_3$ , and $\mathcal {S}_4$ . What’s more, we can identify a basic defeat relation between arguments. There’s, again, an intuitive sense in which the real action happens between the smallest argument supporting the conclusion $Out(\mathfrak {r}_1)$ , namely, $\mathcal {S}_4$ , and the smallest argument containing $r_1$ , namely, $\mathcal {S}_1$ . (In Figure 10, this relation is represented by the highlighted arrow.) The defeat relations between the other arguments depend on it in a way we can make precise: for any two arguments $\mathcal {S}$ , $\mathcal {S}'$ in $\mathcal {F}(c_{12})$ , we have $\mathcal {S} \leadsto \mathcal {S}'$ only if the basic argument $\mathcal {S}_4$ is a part of $\mathcal {S}$ , $\mathcal {S}_4\subseteq \mathcal {S}$ , and the basic argument $\mathcal {S}_1$ is a part of $\mathcal {S}'$ , $\mathcal {S}_1 \subseteq \mathcal {S}'$ .

Fig. 10 Sample context $c_{12}$ and the argumentation framework $\mathcal {F}(c_{12})$ , again.

We’re going to capture these intuitive ideas of basic arguments and defeat in a mathematically precise way, and then show how they let us define an alternative relation of defeat between the arguments based on some context c that is extensionally equivalent to the one we’re already familiar with.

The first step in specifying this relation is to select those arguments from $Arguments(c)$ that seem basic. Notice here that an argument that’s basic with respect to one rule or one formula doesn’t have to count as basic with respect to another rule or formula. Consider our example again. The scenario $\mathcal {S}_4 = \{r_1,r_2\}$ seems basic with respect to both the rule $r_2$ and the formula $Out(\mathfrak {r}_1)$ , since there’s no smaller argument that would either contain $r_2$ , or let us derive $Out(\mathfrak {r}_1)$ . However, $\mathcal {S}_4$ is not basic with respect to $r_1$ and the formula B, since there’s the smaller $\mathcal {S}_1 = \{r_1\}$ which contains $r_1$ and let’s us derive B. What this means is that the formal notion capturing the intuitive idea of basicness must be relativized, to a rule or a formula. But otherwise, the basic, or minimal, arguments just are the (set-theoretically) smallest arguments we can find:

Definition 18 (Minimal arguments, with respect to rules)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and r a rule from $\mathcal {R}$ . Then the r- minimal arguments, in the context of c, are those arguments that belong to the set

$$ \begin{align*}\begin{array}{lllll} Minimal_{\mathcal{F}(c)}(r) &= &\{\mathcal{S} \in Arguments(c) : &r\in \mathcal{S} \text{ and } \\ &&& \not\exists\mathcal{S}'\in Arguments(c) \text{ such that } \\ &&&\mbox{ }\mbox{ }(1)\mbox{ }r\in\mathcal{S}'\text{, and } \\ &&&\mbox{ }\mbox{ }(2)\mbox{ }\mathcal{S}'\subset \mathcal{S} \}. \end{array} \end{align*} $$

Definition 19 (Minimal arguments, with respect to formulas)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and X a formula of our language. Then the X- minimal arguments, in the context of c, are those arguments that belong to the set

$$ \begin{align*}\begin{array}{llll} Minimal_{\mathcal{F}(c)}(X) = &\{\mathcal{S} \in Arguments(c) : & \mathcal{W}\cup Conclusion[\mathcal{S}]\vdash X \text{ and } & \\ && \not\exists\mathcal{S}'\in Arguments(c) \text{ such that } \\ && \mbox{ }\mbox{ }(1)\mbox{ }\mathcal{W}\cup Conclusion[\mathcal{S}']\vdash X\text{, and} \\ && \mbox{ }\mbox{ }(2)\mbox{ }\mathcal{S}'\subset \mathcal{S} \}. \end{array} \end{align*} $$

The plural in the definitions isn’t accidental. In general, there can be multiple r- or X-minimal arguments, as our next example makes plain. Consider the context $c_{13} = \langle \mathcal {W},\mathcal {R}\rangle $ with $\mathcal {W} = \{A$ , C, $Reasonable(\mathfrak {r}_1)$ , $Reasonable(\mathfrak {r}_4)$ , $Reasonable(\mathfrak {r}_5)\}$ and $\mathcal {R}$ consisting of the rules , , and A glance at the inference graph depicting this context (see Figure 11) is enough to realize that there are two alternative ways of reaching D, by means of the chain $r_1$ – $r_4$ and by means of the chain $r_5$ – $r_4$ . And, indeed, if we apply Definition 19 to $c_{13}$ , two arguments come out as D-minimal, namely, $\{r_1,r_4\}$ and $\{r_4,r_5\}$ .

Fig. 11 Multiple basic arguments.

Now let’s turn to basic defeat. Our next definition might look somewhat involved, but all it does is capture the intuition we started with. For two arguments $\mathcal {S}$ and $\mathcal {S}'$ to stand in the relation of basic defeat, there has to be a rule r such that $\mathcal {S}'$ is r-minimal and $\mathcal {S}$ is either $\neg Conclusion[r]$ - or $Out(\mathfrak {r})$ -minimal.

Definition 20 (Basic defeat)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ and $\mathcal {S}'$ two arguments of the framework $\mathcal {F}(c)$ . Then $\mathcal {S}$ stands in the relation of basic defeat to $\mathcal {S}'$ , written as $\mathcal {S}\leadsto _b \mathcal {S}'$ , if and only if there is some rule $r \in \mathcal {R}$ such that

1. (i) $\mathcal {S}'$ is in $Minimal_{\mathcal {F}(c)}(r)$ , and

2. (ii) either (1) or (2):

   1. (1) $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ and $\mathcal {S}$ is in $Minimal_{\mathcal {F}(c)} (\neg Conclusion[r])$ ,

   2. (2) $\mathcal {W}\cup Conclsuion[\mathcal {S}]\vdash Out(\mathfrak {r})$ and S is in $Minimal_{\mathcal {F}(c)}(Out(\mathfrak {r}))$ .

Returning to $c_{12}$ , it can be verified that the only two arguments that stand in the basic defeat relation are $\mathcal {S}_4$ and $\mathcal {S}_1$ . For $\mathcal {S}_4$ is the only element of the set $Minimal_{\mathcal {F}(c_{12})}(Out(\mathfrak {r}_1))$ and $\mathcal {S}_1$ is the only element of $Minimal_{\mathcal {F}(c_{12})}(r_1)$ . And given that $Conclusion[\mathcal {S}_4]$ entails $Out(\mathfrak {r}_1)$ , we have $\mathcal {S}_4\leadsto _b \mathcal {S}_1$ .

The relation of basic defeat can then be extrapolated to arguments of arbitrary complexity, as follows:

Definition 21 (Defeat, alternative definition)

Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ and $\mathcal {S}'$ two arguments based on it. Then $\mathcal {S}$ defeats $\mathcal {S}'$ , written as $\mathcal {S} \leadsto _a \mathcal {S}'$ , if and only if there is an $\mathcal {S}'' \subseteq \mathcal {S}$ and an $\mathcal {S}'''\subseteq \mathcal {S}'$ such that $\mathcal {S}''$ and $\mathcal {S}'''$ stand in the basic defeat relation, $\mathcal {S}''\leadsto _b \mathcal {S}'''$ .

It’s not difficult to verify that this definition lets us recover the defeat relations of the argument framework $\mathcal {F}(c_{12})$ from $\mathcal {S}_4\leadsto _b \mathcal {S}_1$ . This is not a coincidence, as our next observation makes clear—its proof is given in the Appendix:

Observation 3.3. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ and $\mathcal {S}'$ arguments from the argument framework $\mathcal {F}(c)$ constructed from it. Then $\mathcal {S}$ defeats $\mathcal {S}'$ , according to Definition 11, $\mathcal {S}\leadsto \mathcal {S}'$ , if and only if $\mathcal {S}$ defeats $\mathcal {S}'$ , according to Definition 21, $\mathcal {S}\leadsto _a\mathcal {S}'$ .

Since Definitions 11 and 21 are extensionally equivalent, we can go back and forth between the two ways of thinking about argument frameworks constructed from contexts: we can look at a given framework in its entirety and apply the preference semantics to it to determine its consequences. Alternatively, we can restrict attention to the fragment of this framework that contains only the minimal arguments and apply the semantics to it.

3.4 Disagreements over disagreement revisited

Recall the Double Disagreement scenario in which a committed conciliationist is confronted with two disagreeing peers: the metaphysician Milo disagrees with her about the existence of free will, and the epistemologist Evelyn disagrees with her about conciliationism. We expressed this scenario in the context $c_{11}$ , depicted again for convenience in Figure 12. Our original model reasoner would derive any formula from it, suggesting that the correct response to the scenario is to conclude everything. But now let’s see how the more sophisticated reasoner handles it.

Fig. 12 Double Disagreement, again.

Since $c_{11}$ is a fairly complex context, it’d be difficult to explore the entire argumentation framework $\mathcal {F}(c_{11})$ constructed from it. In light of Section 3.3, however, we can restrict attention to a fragment of it that contains only its most informative minimal arguments and the defeat relations among them. This fragment is comprised of:

1. the C-minimal argument $\mathcal {S}_8 = \{r_{10}\}$ ;

2. the $Out(\mathfrak {r}_{10})$ -minimal $\mathcal {S}_9 = \{r_{10},r_{11},r_{12},r_{14}\}$ , which defeats $\mathcal {S}_8$ , itself, and $\mathcal {S}_{12}$ ;

3. the $Disagree(C)$ -minimal $\mathcal {S}_{10} =\{r_{11}\}$ ;

4. the L-minimal $\mathcal {S}_{11} = \{r_{7}\}$ ;

5. the $Out(\mathfrak {r}_{7})$ -minimal $\mathcal {S}_{12} = \{r_{8},r_{9},r_{10},r_{13}\}$ , which defeats $\mathcal {S}_{11}$ ; and

6. the $Disagree(L)$ -minimal argument $\mathcal {S}_{13} = \{r_{8}\}$ .

The fragment is depicted in Figure 13. The lightly shaded region shows which of its arguments are in the preferred extension of $\mathcal {F}(c_{11})$ .

Fig. 13 Core arguments from $\mathcal {F}(c_{11})$ .

It’s not difficult to see why the defeat relations obtain: the argument $\mathcal {S}_9$ supports the formula $Out(\mathfrak {r}_{10})$ , suggesting that the rule $r_{10}$ be taken out of consideration, and, since the arguments $\mathcal {S}_8$ , $\mathcal {S}_9$ itself, and $\mathcal {S}_{12}$ have this rule as an element, they all come out defeated by $\mathcal {S}_9$ . Similarly, the argument $\mathcal {S}_{12}$ supports the formula $Out(\mathfrak {r}_{7})$ , suggesting that $r_{7}$ be taken out of consideration, and, given that $\mathcal {S}_{11}$ has this rule as an element, it gets defeated by $\mathcal {S}_{12}$ . As the picture makes clear, the arguments $\mathcal {S}_8$ and $\mathcal {S}_{11}$ are not included in the preferred extension of $\mathcal {F}(c_{11})$ . Hence, neither C, nor L follow from the context, or and . And this means that our sophisticated reasoner—henceforth the reasoner, without qualification—suggests that the correct response to Double Disagreement is to abandon both the belief in conciliationism and the belief in the existence of free will.

What should we make of this recommendation? The first thing to note is that it’s perfectly consistent. Our model captures an extreme version of conciliationism, and yet it does not issue inconsistent recommendations in a paradigm case involving a disagreement over the epistemic significance of disagreement. ³⁷ So, assuming our model captures conciliationism adequately—which, I think, it does—we can conclude that Elga [16] is mistaken: it’s not the case that (all) conciliatory views lead to inconsistency when they turn on themselves.

But the fact that a view doesn’t issue inconsistent recommendations does not make it plausible, let alone show that it is correct. And there’s reason to feel uneasy about the reasoner’s response: it appears to be incoherent. If one is to abandon the belief in conciliationism, why on Earth would one respond to the disagreement over the existence of free will as a conciliationist would? I contend, however, that this is the correct response, and most of what I do in the remainder of this paper will be directed toward explaining why it looks incoherent, but in fact isn’t. Before I turn to this task, however, it’ll be informative to take a brief look at the constructive responses to the self-defeat objection that have been offered in the literature.

These fall in three categories, depending on how they respond to two crucial questions about the behavior of conciliatory views in cases like Double Disagreement. The first one is whether or not a committed conciliationist ought to abandon her belief in conciliationism in such cases. The second is whether or not she also ought to abandon the belief in free will—or the belief in whatever the first-order disagreement happens to be about—once she has abandoned the belief in conciliationism. The first category of responses includes those of Bogardus [3], Christensen [8], Elga [16], and Pittard [37] all of whom reply to the first question in the negative. ³⁸ The second category is comprised of Matheson’s [33, 34] response who replies to the first question in the affirmative and the second one in the negative. These two types of replies—no to the first question and yes to the first and no to the second—were taken to be the only sensible replies up until very recently. But now there is a third category too that includes the responses of Christensen [10] and Littlejohn [32] both of whom suggest that there may be nothing wrong with replying to both questions in the affirmative. Littlejohn seems to appeal to burden of proof: as long the opponents of conciliatory views haven’t explained what’s wrong with the apparently incoherent responses—which they haven’t—their advocates don’t have anything to worry about. ³⁹ And Christensen offers a compelling positive argument for the conclusion that the incoherent (or “akratic”) response can be rational. ⁴⁰

Thus, our formal analysis points to the same response as the most recent replies to the self-defeat objection. This suggests that we may well be on the right track, even if the reasoner’s response may seem odd to us. Now, I think that the reason it seems odd to us stems from the fact that the story recounted in Double Disagreement is underdescribed. Notice that it’s very natural to think that the answer to the question of which response to the scenario is rational depends, in part, on the agent’s rational degrees of confidence in the conclusions of her (first-order) reasoning about conciliationism, free will, and the disagreements over these two matters. ⁴¹ If the agent is much more confident in the reasoning that led her to conclude that she and Milo are in genuine disagreement than in the reasoning that led her to conclude that free will exists, then, intuitively, she should abandon her belief in free will. If, by contrast, she is much more confident in the reasoning that led her to conclude that free will exists than in the reasoning that led her to conclude that there’s genuine disagreement over it, then, intuitively, it’s fine for her to retain the belief in free will. ⁴² So the agent’s degrees of confidence can make a difference for how she is to respond to Double Disagreement, and yet its description doesn’t provide us with enough detail to figure out what the agent’s relevant degrees of confidence are. ⁴³

This observation supports two conclusions. First, given the importance of degrees of confidence, any fully adequate model of conciliatory reasoning should be able to accommodate them, and so our model, in particular, needs to be modified further. And second, given that the description doesn’t fully specify all normatively relevant details, we shouldn’t expect there to be only one context representing Double Disagreement and only one rational response to it. Instead, we should expect that there are going to be many such contexts—representing various versions of the scenario in which different degrees of confidence (in the reasoning about conciliationism, free will, and the disagreements about them) are rational—and that they won’t necessarily call for the same rational response.

In light of this, it shouldn’t be surprising that by embedding Double Disagreement in the context $c_{11}$ we have implicitly filled in the missing information about the agent’s degrees of confidence in a particular way. Once we make this information explicit, the reasoner’s response will look much more plausible, or so I’m going to argue.

4 Adding degrees of confidence

This section has two main goals. The first is to extend our model reasoner, so that it is sensitive to the information about (rational) degrees of confidence. The second is to explore how the agent’s degrees of confidence might determine what’s rational for her to do in Double Disagreement. As flagged, this will shed light on the seemingly incoherent response we saw above.

It’s natural to expect that degree-of-confidence talk will go together with numerical values. In the present context, however, degrees of confidence will be represented not by means of numerical values, but, rather, by means of a comparative relation. This means that it won’t make sense to ask about one’s degree of confidence in some proposition unless it’s compared to one’s degree of confidence in another proposition, or that we’ll always be concerned only with relative degrees of confidence.

The rest of this section is structured as follows. Section 4.1 is concerned with relative degrees of support (not confidence): it introduces the idea of a priority relation over rules of a context and shows how it can be used to relativize the relation of support between arguments and their conclusions. Once this is done, it won’t necessarily hold that any two arguments support their conclusions to the same degree. Instead, what will typically happen is that one argument supports its conclusion to a greater degree, or more strongly, than another argument supports its conclusion. Section 4.2 returns to Double Disagreement, explains how the relevant degrees of confidence—that is, the agent’s degrees of confidence in the reasoning about conciliationism, free will, and the disagreements about these two questions—can be mapped on the priority relation over rules, and works through an illustrative example. Finally, Section 4.3 provides a general answer to the question of how do the reasoner’s responses depend on what the rational degrees of confidence in Double Disagreement are, situates this answer in the literature, and revisits the seemingly incoherent response from Section 3.4.

4.1 Relativizing support to degrees of support

Our model reasoner determines the formulas that follow from a given context roughly as follows. It starts by constructing an argument framework from the context, then it selects its set of winning arguments, and, finally, it outputs the conclusions this set supports. However, throughout this process, the reasoner takes all arguments to support their conclusions equally well, or to the same degree. The first step toward factoring degrees of confidence in the model is to relativize support to degrees of support. This will have a direct effect on how conflicts between arguments get resolved and, thus, on which set of arguments comes out winning.

The idea that (defeasible) arguments can support their conclusions to varying degrees, and that this can affect resolution of conflicts between arguments is both natural and familiar. ⁴⁴ We’re going to implement this idea in our model, drawing on two principles I call Weakest Link and Winner Takes All, both of which come from Pollock’s [39, 40, 42] work.

Before we turn to these principles, we need to extend contexts with a priority relation on rules. Let the statement $r \leq r'$ mean that the premise of the rule $r'$ , $Premise[r']$ , confers at least as much support on its conclusion, $Conclusion[r']$ , as the premise of the rule r, $Premise[r]$ , confers on its respective conclusion, $Conclusion[r]$ . For the sake of brevity, in what follows we often omit the reference to rule premises and conclusions, reading $r \leq r'$ as saying, simply, that $r'$ is at least as strong as r. We also require that $\leq $ satisfies some natural properties. First, it must be reflexive, meaning that each rule must be at least as strong as itself:

$$ \begin{align*} r \leq r. \end{align*} $$

Second, it must be transitive, meaning that whenever $r'$ is at least as strong as r and $r''$ is at least as strong as $r'$ , the rule $r''$ has to be at least as strong as r:

$$ \begin{align*} \text{if } r \leq r' \text{ and } r'\leq r'', \text{ then } r\leq r''. \end{align*} $$

Third, the relation $\leq $ must satisfy connectivity, which says that any two rules can be compared with respect to their strength:

$$ \begin{align*} r \leq r', r' \leq r, \text{ or both}. \end{align*} $$

Requiring that all rules are comparable should make good sense here: for any two considerations conferring support to different conclusions, we’d seem to always be able to ask which of the two confers more. ⁴⁵ It’ll also be useful to introduce some shorthand notation: when we have $r \leq r'$ without $r' \leq r$ , we write $r < r'$ . And when we have both $r \leq r'$ and $r' \leq r$ (for distinct rules), we write $r \sim r'$ .

In the remainder of this paper, we will be concerned with weighted contexts:

Definition 22 (Weighted contexts)

A weighted context c is a structure of the form $\langle \mathcal {W},\mathcal {R},\leq \rangle $ where $\langle \mathcal {W},\mathcal {R}\rangle $ is a context and $\leq $ is a reflexive, transitive, and connected relation (or a connected preorder) on $\mathcal {R}$ .

As our first example, consider the context $c_{14} = \langle \mathcal {W},\mathcal {R},\leq \rangle $ with $\mathcal {W} = \{A\}$ , , , , , and $r_1 < r_2 < r_3 < r_4$ . ⁴⁶ The ordering tells us that the rule $r_4$ is the strongest, that it’s followed by $r_3$ , then by $r_2$ , and that $r_1$ is the weakest. Figure 14 represents this context graphically.

Fig. 14 Weakest Link Principle.

Now let’s zoom in on two arguments based on $c_{14}$ , namely, $\mathcal {S}_1 = \{r_1, r_4\}$ and $\mathcal {S}_2 = \{r_2,r_3\}$ . Since we have $\mathcal {W}\cup Conclusion[\mathcal {S}_1]\vdash D$ and $\mathcal {W}\cup Conclusion[\mathcal {S}_2]\vdash \neg D$ , these two arguments support opposing conclusions. Given that the four rules now have relative weights, we can ask about the support that each of these arguments confers on their conclusion. According to our next definition, their relative degrees of support are determined using the Weakest Link Principle. ⁴⁷

Definition 23 (Argument Strengths, using Weakest Link)

Let $c = \langle \mathcal {W},\mathcal {R},\leq \rangle $ be a weighted context and $\mathcal {S}$ and $\mathcal {S}'$ two scenarios based on it. Then $\mathcal {S}'$ is at least as strong as $\mathcal {S}$ , written as $\mathcal {S} \preceq \mathcal {S}'$ , if and only if there is a rule r in $\mathcal {S}$ such that, for all $r'\in \mathcal {S}'$ , $r \leq r'$ .

As its name suggests, the Weakest Link Principle says that an argument is exactly as strong as its weakest element. With regard to $\mathcal {S}_1$ and $\mathcal {S}_2$ , in particular, it says that $\mathcal {S}_1$ is only as strong as $r_1$ , that $\mathcal {S}_2$ is only as strong as $r_2$ , and that, therefore, $\mathcal {S}_2$ supports $\neg D$ to a greater degree than $\mathcal {S}_1$ supports D. Notice how this happens: since $\mathcal {S}_1$ contains the rule $r_1$ that’s (strictly) weaker than both rules in $\mathcal {S}_2$ —that is, we have both $r_1 < r_2$ and $r_1 < r_3$ —the argument $\mathcal {S}_2$ is at least as strong as $\mathcal {S}_1$ , or $\mathcal {S}_1 \preceq \mathcal {S}_2$ . But even though $\mathcal {S} \preceq \mathcal {S}'$ doesn’t exclude the possibility that $\mathcal {S}' \preceq \mathcal {S}$ holds, in the particular case at hand this doesn’t happen. While $r_4$ is stronger than both elements of $\mathcal {S}_2$ , its other element $r_1$ is (strictly) weaker than both of them. Thus, there’s no rule in $\mathcal {S}_2$ that would be only as strong as all the rules in $\mathcal {S}_1$ . So we have $\mathcal {S}_1 \preceq \mathcal {S}_2$ and not $\mathcal {S}_2 \preceq \mathcal {S}_1$ , or $\mathcal {S}_1 \prec \mathcal {S}_2$ in the shorthand.

Notice that Definition 23 lets us compare any two scenarios. Our next example illustrates why this may seem problematic. In Section 3.3, we looked at the context $c_{13}$ with $\mathcal {W} = \{A, C\}$ and $\mathcal {R}$ consisting of the rules , , and . Now we extend it in two ways. First, we supplement ${\mathcal {R}}$ with the rule . Second, we add an ordering on $\mathcal {R}\cup \{r_3\}$ , namely, ${r_1 < r_3 < r_4 \sim r_5}$ . The result is the weighted context ${c_{15} = \langle \mathcal {W},\mathcal {R}\cup \{r_3\},\leq \rangle }$ , depicted in Figure 15.

Fig. 15 Minimal arguments and Weakest Link.

Let’s zoom in on the arguments $\mathcal {S}_3 = \{r_1,r_4,r_5\}$ and $\mathcal {S}_4 = \{r_3\}$ based on $c_{15}$ . The first supports the formula D, and the second supports the contrary formula $\neg D$ . And it’s easy to see that, on Definition 23, $\mathcal {S}_4$ comes out stronger than $\mathcal {S}_3$ : there’s a rule in $\mathcal {S}_3$ , namely, $r_1$ , that is weaker than every rule in $\mathcal {S}_4$ . This verdict may seem counterintuitive, since $\mathcal {S}_3$ allows one to reach D without relying on the relatively weak rule $r_1$ at all, using the chain $r_5$ – $r_4$ whose elements are both (strictly) stronger than $r_3$ . However, the fault here doesn’t lie with Definition 23, but, rather, with the fact that we are juxtaposing $\mathcal {S}_3$ and $\mathcal {S}_4$ . The argument $\mathcal {S}_3$ actually combines two D-minimal arguments, namely, $\mathcal {S}_5 = \{r_1,r_4\}$ and $\mathcal {S}_6 = \{r_4,r_5\}$ . When we juxtapose $\mathcal {S}_5$ and $\mathcal {S}_6$ with $\mathcal {S}_4$ , we get the intuitive result—or the result we’d expect the Weakest Link to deliver—namely, that $\mathcal {S}_5 \prec \mathcal {S}_4$ and $\mathcal {S}_4 \prec \mathcal {S}_6$ . Since what’s important for whether D does or doesn’t follow from the context $c_{15}$ is whether or not there’s some argument supporting D that’s not undermined by the rule $r_3$ , the definition does just fine.

Although the Weakest Link tells us how to compare strengths of arguments, it doesn’t tell us how to resolve conflicts between arguments. This is why we need a second principle. Intuitively, the conflict between $\mathcal {S}_1$ and $\mathcal {S}_2$ should be resolved in favor of the stronger argument $\mathcal {S}_2$ . However, an important question remains: what’s the all-things-considered degree of support conferred on $\neg D$ , or how well is it supported after all the relevant information has been taken into consideration? There seem to be two prima facie reasonable answers to this question. According to the first, all-things-considered degree of support conferred on $\neg D$ equals the degree of support that $\mathcal {S}_2$ confers on $\neg D$ . According to the second, the degree of support that $\mathcal {S}_2$ confers on $\neg D$ is to be taken as a starting point and it is to be attenuated, in one way or another, factoring in the strength of the contrary argument $\mathcal {S}_1$ . I’m going to adopt the first response here, or the response that goes with the Winner Takes All Principle. This is not because I have a knockdown argument against the alternative, but because I have no idea how to capture the alternative formally. ⁴⁸

Also, note that the Winner Takes All doesn’t only let us resolve conflicts between arguments supporting contrary conclusions, but can also determine if the support that an argument confers on its conclusion gets undermined by some other argument: suppose that we have two arguments $\mathcal {S}$ and $\mathcal {S}'$ , that $\mathcal {S}$ supports some formula X, and that $\mathcal {S}'$ contests the support that $\mathcal {S}$ confers on X by supporting the proposition $Out(\mathfrak {r})$ , with r being a rule that the support $\mathcal {S}$ lends to X crucially depends on—see Figure 16 for a schematic representation. Applying the principle here amounts to saying that $\mathcal {S}'$ cancels all the support that $\mathcal {S}$ confers on X if $\mathcal {S}'$ is at least as strong as $\mathcal {S}$ , and that it has no effects otherwise. ⁴⁹

Fig. 16 Winner Takes All and exclusionary rules.

Our next definition, then, specifies a notion of defeat, taking into account varying degrees of support and drawing on the two principles. The first is manifest in the definition’s reliance on the $\preceq $ relation. The second in its binary character, or the fact that a potential defeater $\mathcal {S}$ of $\mathcal {S}'$ either fully defeats $\mathcal {S}'$ , or has absolutely no effect on it.

Definition 24 (Defeat with degrees)

Let $c = \langle \mathcal {W},\mathcal {R},\leq \rangle $ be a weighted context and $\mathcal {S}$ and $\mathcal {S}'$ two arguments based on it. Then $\mathcal {S}$ defeats $\mathcal {S}'$ , written as $\mathcal {S}\leadsto _\leq \mathcal {S}'$ , if and only if there is some rule $r\in \mathcal {S}'$ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash \neg Conclusion[r]$ , or $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ and $\mathcal {S}' \preceq \mathcal {S}$ .

There’s only one difference between this definition and Definition 11 (Defeat) from Section 3.1, namely, the requirement that the defeating argument is at least as strong as the defeated one. An easy check will convince you that this definition delivers the intuitive results in the examples that we looked at. We get $\mathcal {S}_2 \leadsto _\leq \mathcal {S}_1$ , but not $\mathcal {S}_1 \leadsto _\leq \mathcal {S}_2$ , as well as $\mathcal {S}_4 \leadsto _\leq \mathcal {S}_3$ and $\mathcal {S}_4 \leadsto _\leq \mathcal {S}_5$ , but not $\mathcal {S}_4 \leadsto _\leq \mathcal {S}_6$ .

With the new definition of defeat in hand, we can construct argument frameworks from weighted contexts:

Definition 25 (Argument frameworks based on weighted contexts)

Let $c = {\langle \mathcal {W},\mathcal {R},{\leq}\rangle} $ be some weighted context. Then the argument framework $\mathcal {F}(c)$ based on c is the pair $\langle \mathcal {A},\leadsto _\leq \rangle $ where $\mathcal {A}$ is the set $Arguments(c)$ and $\leadsto _\leq $ is the set $\{(\mathcal {S},\mathcal {S}') \in \mathcal {A}\times \mathcal {A} : \mathcal {S} \leadsto _\leq \mathcal {S}' \}$ .

Stability and preference semantics can be applied to argument frameworks, whether they be built from regular or weighted contexts. This means that there’s no need to change the definitions from Section 3.2. Also, it’s straightforward to define the analogue of basic defeat from Section 3.3, taking into account the relative strengths of rules, as well as an alternative procedure for acquiring argument frameworks based on it. But we won’t do it here for reasons of space. We close this section with an observation, showing that the addition of weights to contexts is a conservative generalization of our original model—its proof can be found in the Appendix:

Observation 4.1. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a regular context and $c' = \langle \mathcal {W},\mathcal {R},\leq \rangle $ be the same context with a connected preorder $\leq $ assigning all the rules r in $\mathcal {R}$ the same weight—so, for all r, $r' \in \mathcal {R}$ , $r \sim r'$ . Then $\mathcal {F}(c) = \mathcal {F}(c')$ .

4.2 From degrees of confidence to degrees of support

Having developed some new tools, we can return to Double Disagreement. We expressed it in the context $c_{11} = \langle \mathcal {W},\mathcal {R}\rangle $ , which is depicted in Figure 17 one final time. In Section 3.4, we noted that it needs to be supplemented with the information about the agent’s degrees of confidence in the conclusions of her domain-specific reasoning. Now recall which propositions the formulas $Seems(C)$ , $Seems(L)$ , $Seems(Disagree(C))$ , and $Seems(Disagree(L))$ express. They are, respectively, that the agent’s (first-order) reasoning suggests that conciliationism is true, that her reasoning suggests that we have free will, that her reasoning suggests that she’s in genuine disagreement over conciliationism, and that it suggests that she’s in genuine disagreement over free will. In light of this, it’s very natural to associate the agent’s degrees of confidence with these formulas.

Fig. 17 Double Disagreement, once more.

However, given that, in weighted contexts, weights are associated with rules, and not formulas, we need to express the degrees of confidence associated with the $Seems$ -formulas in terms of a priority relation on rules. As a first step, notice that every rule in $c_{11}$ is of one of three forms, namely, 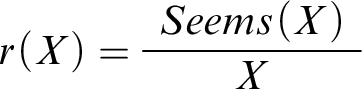, , or 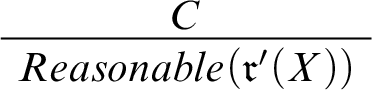. Now notice that the (relative) strengths of the rules fitting the first form correspond directly to the (relative) degrees of confidence associated with the $Seems$ -formulas. Thus, suppose we want to capture a version of Double Disagreement where the agent is least confident in the reasoning leading her to conclude that she’s in genuine disagreement over conciliationism, $Seems(Disagree(C))$ , more confident in the reasoning leading her to conclude that she’s in genuine disagreement over free will, $Seems(Disagree(L))$ , even more confident in her reasoning about free will, $Seems(L)$ , and most confident in her reasoning about conciliationism, $Seems(C)$ . Here we’d order the four rules instantiating the $r(X)$ -schema as follows: $r_{11} < r_{8} < r_7 < r_{10}$ .

Turning to the rules that don’t fit this schema, notice that every argument based on $c_{11}$ containing either the rule 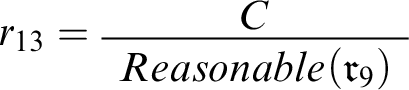or the rule has to contain , and that every argument containing or has to contain $r_{10}$ too, as well as at least one additional rule of the form 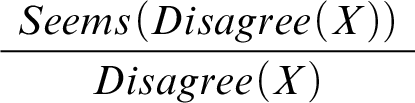. This is due to the structure of $c_{11}$ and the fact that all rules comprising an argument have to be triggered and deemed reasonable in it. For illustration, consider some scenario $\mathcal {S}$ based on $c_{11}$ that contains the rule 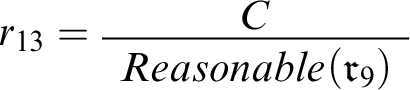. Does $\mathcal {S}$ qualify as an argument based on $c_{11}$ ? Well, it can qualify only in case $r_{13}$ is triggered in it, and, for $r_{13}$ to be triggered in it, $\mathcal {S}$ has to contain $r_{10}$ . This is important because our model reasoner relies on the Weakest Link Principle to determine the relative strengths of arguments. One direct consequence is that any argument based on $c_{11}$ can be only as strong as the rules of the form it contains. Thus, there’s a clear sense in which what really matters for the relative strengths of arguments—and, thus, also for the overall conclusions the reasoner draws—are the relative strengths of the four rules that have this form, namely, $r_7$ , $r_8$ , $r_{10}$ , and $r_{11}$ .

What’s more, on a certain plausible assumption, the relative strengths of these rules are all that matters. We can see what’s at stake here by looking at the argument 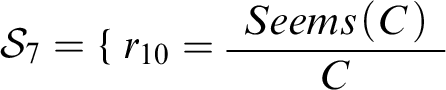, 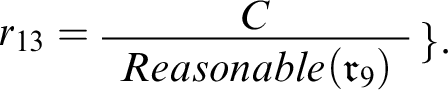Because of the Weakest Link Principle, the support that $\mathcal {S}_7$ confers on $Reasonable(\mathfrak {r}_9)$ can be only as strong as $r_{10}$ . It is, however, possible for this support to be much lower, and it will be lower in all cases where the strength of $r_{13}$ is lower than that of $r_{10}$ . That’s why we are going to rule out such cases, assuming that the following principle holds true:

1. No Support Lost: The relative weights of rules whose form is either or must be at least as high as the weights of rules of form that they depend on.

The intuitive idea of dependency between rules which this assumption appeals to can be made precise in terms of the relations between the arguments based on $c_{11}$ . If there’s no argument $\mathcal {S}$ based on $c_{11}$ that contains r but not $r'$ , then r depends on $r'$ . Notice that No Support Lost formalizes the intuitive idea that the strengths of the arguments based on $c_{11}$ should depend only on the agent’s relevant degrees of confidence. ⁵⁰ So it looks like a perfectly reasonable assumption.

With No Support Lost in place, there’s a general answer to the question of how do the reasoner’s responses depend on the relative strengths of the four crucial rules. The next section stars with this answer. The remainder of this one works through an example, illustrating how the addition of an ordering on rules in $c_{11}$ affects the reasoner’s response.

Let $c_{16} = \langle \mathcal {W},\mathcal {R},\leq \rangle $ be the weighted context we acquire by extending $c_{11}$ with the ordering $r_{11}\sim r_{12} < r_{9}\sim r_{10}\sim r_{13}\sim r_{14} < r_{7} < r_{8}$ . It expresses a version of Double Disagreement where the agent is least confident in the reasoning leading her to conclude that the disagreement over conciliationism is genuine, $Seems(Disagree(C))$ , more confident in the reasoning leading her to conclude that conciliationism is true, $Seems(C)$ , even more confident in the reasoning suggesting that free will exists, $Seems(L)$ , and most confident in the reasoning suggesting that the disagreement over free will is genuine, $Seems(Disagree(L))$ . Notice that the ordering assigns the rules whose form is either or the same relative weights as the weakest rules of the form 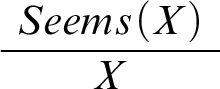that they depend on. This is only for the sake of simplicity. Nothing would change if these rules were assigned different relative weights, as long as No Support Lost wasn’t violated.

We restrict attention to a fragment of the argument framework $\mathcal {F}(c_{16})$ , containing its most informative minimal arguments and the defeat relations between them—this is the same fragment we looked at when considering the framework $\mathcal {F}(c_{11})$ in Section 3.4:

1. the C-minimal argument $\mathcal {S}_8 = \{r_{10}\}$ ;

2. the $Out(\mathfrak {r}_{10})$ -minimal $\mathcal {S}_9 = \{r_{10},r_{11},r_{12},r_{14}\}$ , which defeats itself;

3. the $Disagree(C)$ -minimal $\mathcal {S}_{10} =\{r_{11}\}$ ;

4. the L-minimal $\mathcal {S}_{11} = \{r_{7}\}$ ;

5. the $Out(\mathfrak {r}_{7})$ -minimal $\mathcal {S}_{12} = \{r_{8},r_{9},r_{10},r_{13}\}$ ; and

6. the $Disagree(L)$ -minimal argument $\mathcal {S}_{13} = \{r_{8}\}$ .

The fragment is depicted in Figure 18. Notice that there are fewer defeat relations between arguments, when compared to $\mathcal {F}(c_{11})$ . There the self-defeating argument $\mathcal {S}_9$ defeated both $\mathcal {S}_8$ and $\mathcal {S}_{12}$ . Now it does not, and it’s easy to see why: since $\mathcal {S}_9$ contains $r_{11}$ and $r_{12}$ that are strictly weaker than the only element of $\mathcal {S}_8$ , namely, $r_{10}$ , it’s not the case that $\mathcal {S}_8 \preceq \mathcal {S}_9$ . And that’s a prerequisite for $\mathcal {S}_9$ to defeat $\mathcal {S}_8$ . Similarly, the $Out(\mathfrak {r}_{7})$ -minimal $\mathcal {S}_{12}$ no longer defeats the L-minimal $\mathcal {S}_{11}$ . Yet again, $r_7$ is stronger than some of the elements of $\mathcal {S}_{12}$ , and so $\mathcal {S}_{11} \preceq \mathcal {S}_{12}$ doesn’t hold.

Fig. 18 Core arguments from $\mathcal {F}(c_{16})$ .

Since $\mathcal {S}_8$ and $\mathcal {S}_{11}$ are in the preferred extension of $\mathcal {F}(c_{16})$ —the shaded region in Figure 18—both C and L follow from $c_{16}$ . So the reasoner suggests that, in the particular version of Double Disagreement that is captured by $c_{16}$ , one should stick to one’s belief in conciliationism, as well as one’s belief in free will. At first blush, this recommendation might look incoherent. Since the agent retains the belief in conciliationism, why wouldn’t she conciliate in response to the disagreement over free will—especially, given the fact that she’s more confident in it being genuine than her own reasoning about free will?

We shouldn’t forget, however, that we’re dealing with a situation where the agent is more confident in the reasoning that led her to conclude that we have free will than the reasoning that led her to conclude that conciliationism is correct. And it’s not difficult to imagine her reasoning as follows:

After deliberating about the epistemic significance of disagreement, conciliationism seems to me to be correct. If it is, I should abandon my belief in the existence of free will in response to my disagreement with Milo. However, I’ve more faith in my deliberation about the question of free will than my deliberation about the epistemic significance of disagreement, and it would be foolish of me to abandon a view on the basis of another view that seems to me to be correct, but that I’m also less confident of.

It’s not only that there’s nothing incoherent about this line of thought. It also seems very intuitive. So the reasoner’s response to $c_{16}$ is perfectly reasonable.

4.3 Disagreements over disagreement with degrees

Now we can turn to the following question: how does the reasoner’s response depend on the degrees of confidence associated with the conclusions reached through first-order reasoning? It’ll be useful to introduce some simple notation. Recall that $Seems(X)$ says that the agent has arrived at the conclusion that X after deliberating about whether X to the best of her ability. Now, let $Seems(X) \leq Seems(Y)$ express the idea that the agent is at least as confident in the conclusion of her reasoning about whether Y as she is in the conclusion of her reasoning about whether X; and let $Seems(X) < Seems(Y)$ be shorthand for $Seems(X)\leq Seems(Y)$ and not $Seems(Y) \leq Seems(X)$ .

As far as the belief in conciliationism is concerned, the reasoner’s response depends on the degrees of confidence in $Seems(C)$ and $Seems(Disagree(C))$ : it abandons this belief, if the degree of confidence in the truth of conciliationism is only as high as the degree of confidence in the disagreement over it being genuine—that is, if $Seems(C) \leq Seems(Disagree(C))$ —and retains it otherwise—that is, when $Seems(C)> Seems(Disagree(C))$ . This response seems perfectly intuitive. It’s also well in line with the literature, in the following sense: those authors who think that conciliatory views can turn on themselves, but also that this isn’t fatal for them—that is, Christensen [10], Littlejohn [32], and Matheson [33, 34]—would agree that, in such situations, the belief in conciliationism should be abandoned. ⁵¹ As for the belief in free will, the reasoner’s response here depends on the relative degrees of confidence in $Seems(C)$ , $Seems(L)$ , and $Seems(Disagree(L))$ : it abandons this belief, in case the degree of confidence in the reasoning leading to the conclusion that free will exists is only as high as both the degree of confidence in the disagreement over it being genuine and the degree of confidence in the truth of conciliationism—that is, in case both $Seems(L) \leq Seems(Disagree(L))$ and $Seems(L) \leq Seems(C)$ —and retains the belief otherwise—that is, if either $Seems(L)> Seems(Disagree(L))$ , or $Seems(L)> Seems(C)$ .

Although the reasoner’s response with regard to the belief in free will is perfectly reasonable—or so I shall argue—it may go against pre-theoretic intuitions about the behavior of conciliatory views and what’s made of their behavior in much of the literature. Three features, in particular, make the reasoner’s response surprising—and the first two are independent of the self-defeat objection. The first is that the question of whether it’s rational to retain the belief in free will turns out to depend on the relative degrees of confidence in the reasoning that led the agent to conclude that free will exists and the reasoning that led her to conclude that the disagreement over free will is genuine, $Seems(L)$ and $Seems(Disagree(L))$ . In particular, it turns out that, in some cases, a committed conciliationist can rationally retain her belief in free will even if she has a high degree of confidence that there’s a genuine disagreement over it. At first blush, this might look like a reductio: if the view expressed in the formal model allows for such a possibility, then the view is conciliatory in name only. I contend, however, that the view expressed in the model is genuinely conciliatory, in the sense that it preserves the core conciliationist intuition that the only rational response to a genuine disagreement is conciliation. It’s just that it is combined with the natural ideas that an agent is typically uncertain about whether or not the disagreement she faces is genuine, and that some beliefs are more rational for an agent to hold than others. And these ideas make space for cases under discussion. Let’s try putting ourselves into the shoes of a committed conciliationist who is more confident in her reasoning about free will than her reasoning about the relevant disagreement:

After thinking hard about the issue of epistemic significance of disagreement, I’m quite sure that conciliation is the only rational response to a genuine disagreement. I’ve also thought very carefully about the vexed issue of free will, and I’m quite sure that free will exists. My colleague Milo has also worked on free will, and he’s told me a few times that free will is nonsense—although we haven’t been able to find a time to sit down and discuss the question at length. So while I’m fairly confident that we’re in genuine disagreement, it’s not impossible that our disagreement is merely verbal. If it turned out that it is not merely verbal, I’d immediately suspend judgment on whether free will exists. However, as things stand, I can rationally retain the belief in free will. For I can’t say—in good conscience—that Milo’s publication record in metaphysics and the few interactions that we have had make me as confident that our disagreement is genuine as my own work makes me confident that free will exists.

I, for my part, think that the agent’s train of thought here is perfectly reasonable, and, more importantly, that there’s no good reason to question her allegiance to conciliationism—at least, if it’s kept in mind that, by assumption, the agent’s degrees of confidence are rational, or, roughly, in accordance with her evidence. ⁵²

The second feature that makes the reasoner’s response to the free will issue surprising is that it depends on the relative degrees of confidence in the conclusions of the reasoning about free will and the reasoning about conciliationism, $Seems(L)$ and $Seems(C)$ . Most proponents of conciliatory views take on board the idea that the correct doxastic response to a mundane case of disagreement—that is, one in which a committed conciliationist finds out that she’s in disagreement over some nontrivial issue with an epistemic peer—depends on how confident the conciliationist is in her take on the issue: the higher her pre-disagreement degree of confidence in her view on X, the higher her post-disagreement degree of confidence in her view on X should be. Some proponents of conciliatory views may also accept the idea that the response to mundane cases of disagreement should depend on one’s degrees of confidence in conciliationism: the higher one’s degree of confidence in conciliationism, the lower one’s post-disagreement degree of confidence in one’s view on X should be. Nevertheless the literature proceeds under the assumption that demands that one lowers one’s confidence in one’s view on X, no matter how it compares to one’s confidence in conciliationism. ⁵³ But, as we have seen, it’s easy to make intuitive sense of an agent who thinks that conciliationism is correct, finds herself in disagreement with a peer over the question of whether free will exists, and nevertheless retains her belief in the latter: her degree of confidence in the reasoning supporting the conclusion that free will exists is simply higher than her degree of confidence in the reasoning supporting the conclusion that conciliationism is true. So even though our model reasoner’s response goes against the orthodoxy, it seems perfectly reasonable.

Thus, the answer to the question of whether or not it is rational to conciliate in a mundane case of disagreement depends on more details than standardly thought. The details that let the agent decide if the disagreement she finds herself in is genuine are important. But so are the details that determine the agent’s relative degrees of confidence in conciliationism and her take on the question that’s under dispute. In the end, even though the agent holds conciliationism to be true, it’s a view on a complex issue she isn’t fully certain of, and it’s but one among many other views on complex issues she isn’t fully certain of. And there doesn’t seem to be anything speaking in favor of granting conciliationism hegemony over all these other views.

Finally, the third surprising feature of the reasoner’s response to the free will issue is that it does not depend on whether or not conciliationism turns on itself in the scenario—or, to use our notation, on whether $Seems(C) \leq Seems(Disagree(C))$ or, rather, $Seems(C)> Seems(Disagree(C))$ obtains. With few, and mostly recent, exceptions, authors writing on the self-defeat objection have thought that conciliationism’s turning on itself either leads, or would lead, to problems having to do specifically with the belief in free will. Ever since Elga [16] argued that it leads to inconsistent recommendations—to abandon this belief and not to abandon it—most authors have responded to the objection in one of two ways. The majority has tried to argue that conciliationism actually never turns on itself, or that its turning on itself doesn’t mean that one has to abandon the belief in it and cease to follow its recommendations. And Matheson [33, 34] has tried to argue that, whenever conciliationism turns on itself, its recommendation regarding the belief in free will loses its normative force. ⁵⁴ But all of this literature took it for granted that the answer to the question of what’s the correct response regarding the belief in free will depends on whether or not conciliationism turns on itself.

As we saw in Section 3.4, this dependency has been called into question only recently, and now our analysis provides further evidence against it: it suggests that there are some cases where it’s rational to retain the belief in free will and the belief in conciliationism, and that there are others where it’s rational to abandon the belief in free will and the belief in conciliationism. ⁵⁵ We have already discussed cases fitting the former pattern. Now let’s turn to those that fit the latter.

In a typical scenario where the reasoner abandons both the belief in free will and the belief in conciliationism, the degree of confidence in the reasoning leading to the conclusion that free will exists is lower than the degree of confidence in the reasoning leading to the conclusion that conciliationism is correct, $Seems(L) < Seems(C)$ . (This degree of confidence is also lower than the degree of confidence in the disagreement with Milo being genuine, $Seems(L) < Seems(Disagree(L))$ , but this latter point is less important for our purposes.) Now, putting ourselves into the shoes of an agent with these degrees of confidence, it seems compelling to reason about the situation as follows:

I’ve thought about the epistemic significance of disagreement to the best of my ability, and, as far as I can tell, conciliationism is correct. If it is correct, I should back off from the reasoning that led me to conclude that free will exists, since my disagreement with Milo gives me good reason to suspect that this reasoning rests on a mistake. Also, I’m more confident in my reasoning about conciliationism than my reasoning about free will, and yet my disagreement with Evelyn gives me good reason to suspect that the former reasoning rests on a mistake. ⁵⁶ Clearly, my conclusion regarding conciliationism is either correct, or it is not. If it is—in spite of the evidence to the contrary—I shouldn’t trust my reasoning about free will. And if it is not, then the reasoning that I’m more confident in than my reasoning about free will has led me astray. Should I rely on the reasoning I’m less confident in if the reasoning that I am more confident in turned out to be mistaken? Perhaps, it’s safer not to. So, I shouldn’t believe that free will exists.

While one might find this train of thought overly cautious, it’s perfectly coherent and sensible. So our formal analysis suggests that Littlejohn [32] is right to think that there isn’t necessarily anything wrong with suspending judgment on conciliationism and still conciliating in response to the disagreement over free will. ⁵⁷ However, it also suggests that calling the agent’s backing off from her belief in free will in such cases conciliating is misleading.

The analysis also sheds light on the reasoner’s response that we discussed back in Section 3.4, before introducing degrees of confidence. And what it suggests is that we think of the version of Double Disagreement the reasoner was responding to as an atypical case fitting the pattern just discussed. Not making the degrees of confidence explicit in the model amounts to assuming that all the relevant degrees of confidence are equal, $Seems(L) = Seems(C) = Seems(Disagree(L)) = Seems(Disagree(L))$ . But the above train of thought can be extrapolated to cases where all degrees are equal—although it does become slightly less intuitive. Still, this seems to be enough to conclude that the reasoner’s response that looked incoherent to us back in Section 3.4 is, in fact, perfectly reasonable.

Given that our analysis of Double Disagreement readily generalizes to other cases involving disagreements over conciliationism, we have a fully general response to the self-defeat objection. ⁵⁸

5 Conclusion

Let’s take a look back at the distance covered. Our starting point was an important worry about conciliatory views: they would seem to self-defeat and issue inconsistent recommendations in scenarios involving disagreements over their own correctness. Drawing on the work from the defeasible logic paradigm, I devised a model conciliatory reasoner and focused on its behavior in the troublesome scenarios. At first, this reasoner suggested that one is to conclude everything in them, seemingly only reinforcing the worry. However, this was largely due to a technical problem, having to do with the particular framework used. The problem was resolved by moving to the more general framework of argumentation theory. Once modified, the reasoner suggested that, in response to a case where one finds oneself in disagreement over conciliationism, as well as over some other independent question X, one is to back off from both one’s belief in conciliationism and one’s take on X. Having noted the seeming incoherence of this response, I went on to suggest that it seems to us incoherent only because the scenario is underdescribed, and that, in particular, what’s missing is the information about the reasoning agent’s degrees of confidence. In the last third of the paper, I enhanced the model reasoner so that it can take this information into account, and we saw how its responses to the troublesome scenario correlate with the differences in the (relative) degrees of confidence. There were three important upshots. The first was independent of the self-defeat objection: contrary to the common assumption, a committed conciliationist can rationally retain her view on some issue even if she has good or even excellent evidence suggesting that there’s genuine disagreement over it—this is due to the importance of her relative degrees of confidence in conciliationism, in the issue under dispute, and in the disagreement being genuine. The second upshot was that—again, contrary to a widely-held assumption—whether one is to back off from one’s take on X in the troublesome scenarios does not depend on whether or not it’s rational for one to retain the belief in conciliationism. Notably, this is well in line with the recent ideas of Christensen [10] and Littlejohn [32]. Finally, the third upshot was that the reasoner’s recommendation to adopt the seemingly incoherent doxastic state is perfectly reasonable, given the circumstances it’s issued in. So, assuming our model reasoner is true to the spirit of conciliatory views—which, I think, we have all reasons to think it is—we have a response to the self-defeat objection against conciliatory views.

6 Appendix: proofs of the central observations

Observation 2.1. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be an arbitrary regular context where no $Reasonable$ -formulas occur—or, more precisely, a context where no subformula of any of the formulas in $\mathcal {W}$ or any of the premises or conclusions of the rules in $\mathcal {R}$ is of the form $Reasonable(\mathfrak {r})$ . Then there’s a context $c' = \langle \mathcal {W}\cup \{Reasonable(\mathfrak {r}):r\in \mathcal {R}\},\mathcal {R}\rangle $ that’s equivalent to c. Or more explicitly, X follows from c if and only if X follows from $c'$ for all X such that no subformula of X is of the form $Reasonable(\mathfrak {r})$ .

Proof. Left-to-right: Take some arbitrary formula X that follows from c, according to the original definition of consequence. Then we know that, for every proper scenario $\mathcal {S}$ based on c, we have $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ . Now zoom in on one such proper scenario $\mathcal {S}$ . By the definition of the notion, for all $r\in \mathcal {S}$ , we have $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ , $r\notin Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ , and $r\notin Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Now let’s refocus on the new context $c'$ . It’s not difficult to see that $\mathcal {S}$ qualifies as a proper scenario based on $c'$ . Since all the original information is present in $c'$ , we can be sure that, for all $r\in \mathcal {S}$ , we have $r \in Triggered_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ , $r\notin Conflicted_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ , and $r\notin Excluded_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ . What’s more, by the construction of $c'$ , we know that, for every $r \in \mathcal {S}$ , there’s a formula of the form $Reasonable(\mathfrak {r})$ in the hard information of $c'$ . Hence, for every $r\in \mathcal {S}$ , we have $r\in Reasonable_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ . So $\mathcal {S}$ is proper. The same applies to other proper scenarios based on c, and so X follows from $c'$ , according to the modified definition.

Right-to-left: Suppose that X doesn’t contain the predicate $Reasonable$ and that X follows from $c'$ , according to the modified definition of consequence. Then for every proper scenario $\mathcal {S}$ based on $c'$ , it holds that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ . Take an arbitrary $\mathcal {S}$ . Then, by the definition of proper scenarios, we know that, for all $r \in \mathcal {S}$ , $r\in Triggered_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ , $r \notin Conflicted_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ , and $r\notin Excluded_{\mathcal {W}',\mathcal {R}}(\mathcal {S})$ . By construction, there’s no information in $c'$ that would have to do with the new predicate and wouldn’t be contained in c. Hence, for all $r \in \mathcal {S}$ , $r\in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ , $r \notin Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ , and $r\notin Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . So $\mathcal {S}$ qualifies as a proper scenario based on c, implying that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ . The same applies to the other proper scenarios based on $c'$ , and so X follows from c, according to the original definition.□

Observation 3.1. Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context and X an arbitrary formula. Then X follows from c in default logic, , if and only if X follows from c according to stability semantics, .

Proof. Left-to-right: Suppose that . The, for every proper scenario $\mathcal {S}$ based on c, we have $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash X$ . Consider an arbitrary $\mathcal {S}$ of this sort. Since $\mathcal {S} \subseteq Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $\mathcal {S} \subseteq Triggered_{\mathcal {W},\mathcal {R}} (\mathcal {S})$ , the set $\mathcal {S}$ is an element of $Arguments(c)$ . Now we will show that that $\mathcal {S}$ defeats every argument $\mathcal {S}'$ in $Arguments(c)$ such that $\mathcal {S}' \not \subseteq \mathcal {S}$ . So take an arbitrary $\mathcal {S}'$ of this sort and consider $\mathcal {S}'' = \mathcal {S}\cap \mathcal {S}'$ . Now take some rule r from $\mathcal {S}'$ such that $r\in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S}'')$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}'')$ . Such an r has to exist because $\mathcal {S}' \in Argument(c)$ and $\mathcal {S}'' \subset \mathcal {S}'$ . In light of the fact that $r\in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S}'')$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}'')$ , it has to be the case that $r\in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . So, given that $\mathcal {S}$ is a proper scenario, it must be the case that either $r \in Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ or $r\in Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . So either $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Out(\mathfrak {r})$ . But in either case we get $\mathcal {S} \leadsto \mathcal {S}'$ . Set $\Gamma = \{\mathcal {S}' \in Arguments(c): \mathcal {S}' \subseteq \mathcal {S}\}$ . Since $\mathcal {S}$ defeats every $\mathcal {S}'$ in $Arguments(c)$ , the set of arguments $\Gamma $ defeats every argument that is not contained in $\Gamma $ . And given that $\mathcal {S}$ is a proper scenario, $\Gamma $ has to be consistent. So $\Gamma $ is a stable extension of $\mathcal {F}(c)$ . What’s more, X follows from $\Gamma $ , as it contains $\mathcal {S}$ and $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ . Notice that we can run the same argument for every other proper scenario based on c. Consequently, .

Right-to-left: Suppose that . This means that, for every stable extension $\Gamma $ of $\mathcal {F}(c)$ , it holds that $\Gamma $ contains some argument $\mathcal {S}$ such that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash X$ . Let’s now focus on one such stable extension $\Gamma $ .

The first step is to show that this $\Gamma $ has a maximal element, that is, an argument $\mathcal {S}$ such that, for all $\mathcal {S}'\in \Gamma $ , we have $\mathcal {S}' \subseteq \mathcal {S}$ . To show that this holds, we use a proof by contradiction. Suppose that there’s no single maximal element in $\Gamma $ . Now take some $\mathcal {S} \in \Gamma $ such that there’s no $\mathcal {S}' \in \Gamma $ with $\mathcal {S} \subset \mathcal {S}'$ . Consider an arbitrary rule r from $\mathcal {R}$ such that $r \notin \mathcal {S}$ , but $r \in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Since $\mathcal {S}$ is maximal, $\mathcal {S}\cup \{r\} \notin \Gamma $ . And given that $\Gamma $ is stable, it must hold that $\Gamma \leadsto \mathcal {S}\cup \{r\}$ . So there has to be some argument $\mathcal {S}' \in \Gamma $ such that $\mathcal {S}' \leadsto \mathcal {S}\cup \{r\}$ . The expression $\mathcal {S}' \leadsto \mathcal {S}\cup \{r\}$ means that there has to be some rule $r'$ in $\mathcal {S}\cup \{r\}$ such that $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash \neg Conclusion[r']$ or $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash \neg Out(\mathfrak {r}')$ . However, if the rule $r'$ in question is anything but r itself, then we would also have $\mathcal {S}' \leadsto \mathcal {S}$ , making $\Gamma $ inconsistent. So the argument $\mathcal {S}'$ is such that either $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash \neg Out(\mathfrak {r})$ . Notice that has to be such an argument $\mathcal {S}'$ for every r with $r \notin \mathcal {S}$ , but $r \in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ —if there are any such rules at all.

Now let’s zoom in on a different set $\mathcal {S}^\dagger \in \Gamma $ such that there’s no $\mathcal {S}' \in \Gamma $ with $\mathcal {S}^\dagger \subset \mathcal {S}$ . So $\mathcal {S}^\dagger \neq \mathcal {S}$ . Consider $\mathcal {S}\cap \mathcal {S}^\dagger $ . Take the rule $r^\dagger $ such that $r^\dagger \in \mathcal {S}^\dagger $ , $r^\dagger \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}\cap \mathcal {S}^\dagger )$ , and $r^\dagger \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}\cap \mathcal {S}^\dagger )$ . Since $\mathcal {S}$ and $\mathcal {S}^\dagger $ are both in $Arguments(c)$ and $\mathcal {S}^\dagger \not \subseteq \mathcal {S}$ , such a rule $r^\dagger $ must exist. But given the proof in the previous paragraph, we can be sure that there has to be an argument $\mathcal {S}' \in \Gamma $ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash \neg Conclusion[r^\dagger ]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}']\vdash Out(\mathfrak {r}^\dagger )$ . Since $r^\dagger \in \mathcal {S}^\dagger $ , we have $\mathcal {S} \leadsto \mathcal {S}^\dagger $ which entails, contrary to our assumption, that $\Gamma $ is inconsistent. So $\Gamma $ must have a maximal element after all.

It’s not difficult to see that the maximal element of $\Gamma $ , call it, $\mathcal {S}$ , is such that, for all $\mathcal {S}'\in Argument(c)$ with $\mathcal {S}'\not \subseteq \mathcal {S}$ , it holds that $\mathcal {S} \leadsto \mathcal {S}'$ . Consider some $\mathcal {S}'$ that fits the description. Given that $\Gamma $ is stable, we know that $\Gamma \leadsto \mathcal {S}'$ . So there’s some argument $\mathcal {S}'' \in \Gamma $ such that $\mathcal {S}'' \leadsto \mathcal {S}'$ , meaning that $\mathcal {W}\cup Conclusion[\mathcal {S}'']\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}'']\vdash Out(\mathfrak {r})$ for some rule $r \in \mathcal {S}'$ . But since $\mathcal {S}$ is maximal, it must be the case that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Out(\mathfrak {r})$ for some rule $r \in \mathcal {S}'$ . Consequently, $\mathcal {S} \leadsto \mathcal {S}'$ . Another thing that should be clear is that $\mathcal {W} \cup Conclusion[\mathcal {S}]\vdash X$ : If there’s an argument in $\Gamma $ that lets us conclude X, then X follows from the maximal element too.

The final step is to show that the maximal element $\mathcal {S}$ of $\Gamma $ is a proper scenario based on c. What we need to establish, then, is that $\mathcal {S} = \mathcal {S}'$ where

$$ \begin{align*}\begin{array}{llll} \mathcal{S}' &= &\{ r\in \mathcal{R} : & r\in Reasonable_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r \in Triggered_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Conflicted_{\mathcal{W},\mathcal{R}}(\mathcal{S}), \\ &&& r\notin Excluded_{\mathcal{W},\mathcal{R}}(\mathcal{S}) \}. \end{array} \end{align*} $$

$\mathcal {S} \subseteq \mathcal {S}'$ : Take an arbitrary r from $\mathcal {S}$ . Since $\mathcal {S}$ is in $Argument(c)$ , we know that $r \in Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $r \in Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Suppose we had $r \in Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . In that case, $\mathcal {S}$ would self-defeat, and $\Gamma $ couldn’t be a stable extension. So $r\notin Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Now suppose we had $r \in Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Again, $\mathcal {S}$ would self-defeat, and $\Gamma $ couldn’t be a stable extension. So $r\notin Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ .

$\mathcal {S}' \subseteq \mathcal {S}$ : Take an arbitrary r such that r is an element of $Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and $ Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ and r is not an element of either $Conflicted_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ , or $Excluded_{\mathcal {W},\mathcal {R}}(\mathcal {S})$ . Now suppose, toward a contradiction, that $r\notin \mathcal {S}$ . Let $\mathcal {S}^\dagger = \mathcal {S}\cup \{r\}$ . Since $\mathcal {S}^\dagger \subseteq Triggered_{\mathcal {W},\mathcal {R}}(\mathcal {S}^\dagger )$ and $\mathcal {S}^\dagger \subseteq Reasonable_{\mathcal {W},\mathcal {R}}(\mathcal {S}^\dagger )$ , $\mathcal {S}^\dagger $ must be in $Argument(c)$ . What’s more, we do not have $\mathcal {S} \leadsto \mathcal {S}$ , and so . This is enough to conclude that $\Gamma $ is not a stable extension after all.

This shows that $\mathcal {S}$ is proper. Since we can run the same argument for every other stable extension, we know that .□

Observation 3.2. Let $c =\langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {F}(c) = \langle \mathcal {A}, \leadsto \rangle $ an argument framework constructed from it. If $\mathcal {F}(c)$ does not contain either odd cycles of defeat or infinite chains of defeat, then if and only if .

Proof. We will show that an argument set $\Gamma $ is a stable extension of $\mathcal {F}(c)$ if and only if it is a preferred extensions of $\mathcal {F}(c)$ . The result follows immediately.

Left-to-right [13]: This direction holds independently of the assumption. Let $\Gamma $ be a stable extension of $\mathcal {F}(c)$ . So, for all $\mathcal {S}\in \mathcal {A}\backslash \Gamma $ , $\Gamma \leadsto \mathcal {S}$ . It’s easy to see that $\Gamma $ is complete: Consider an argument $\mathcal {S}$ such that $\Gamma $ defends $\mathcal {S}$ . If $\mathcal {S} \in \Gamma $ , we’re done. So suppose $\mathcal {S} \notin \Gamma $ . Since $\Gamma $ is stable, we have it that $\Gamma \leadsto \mathcal {S}$ . Thus, there’s an argument $\mathcal {S}' \in \Gamma $ such that $\mathcal {S}'\leadsto \mathcal {S}$ . Given that $\Gamma $ defends $\mathcal {S}$ , there has to be an $\mathcal {S}^\dagger $ in $\Gamma $ such that $\mathcal {S}^\dagger \leadsto \mathcal {S}'$ . But this would mean that $\Gamma $ is not conflict-free, which contradicts it being stable. Now let’s verify that $\Gamma $ is not only a complete extension, but also a maximal complete extensions: Suppose that it wasn’t. There would be another complete extension $\Gamma '$ such that $\Gamma \subset \Gamma '$ . Let $\mathcal {S}$ be an argument such that $\mathcal {S}\notin \Gamma $ and $\mathcal {S}\in \Gamma '$ . Since $\Gamma $ is stable, $\Gamma \leadsto \mathcal {S}$ , and so $\Gamma ' \leadsto \mathcal {S}$ . Then, however, $\Gamma '$ is not conflict-free, which contradicts it being complete.

Right-to-left: Suppose that $\Gamma $ is a preferred, but not a stable extension of $\mathcal {F}(c)$ . So $\Gamma $ is a maximal complete extension, and yet there is some argument $\mathcal {S}_1 \in \mathcal {A}$ such that $\mathcal {S}_1\notin \Gamma $ and . Since $\Gamma $ is complete, it can’t defend $\mathcal {S}_1$ . So there has to be an argument $\mathcal {S}_2 \in \mathcal {A}$ such that $\mathcal {S}_2 \notin \Gamma $ , $\mathcal {S}_2\leadsto \mathcal {S}_1$ , and . And then, again, given that $\Gamma $ is complete, it can’t defend $\mathcal {S}_2$ . So there has to be an argument $\mathcal {S}_3 \in \mathcal {A}$ such that $\mathcal {S}_3\notin \Gamma $ , $\mathcal {S}_3\leadsto \mathcal {S}_2$ , and . We can apply the same line of reasoning to $\mathcal {S}_4$ and further, but eventually it has to stop, since, by assumption, there are no infinitely ascending chains of defeat in $\mathcal {F}(c)$ . So we will end up with the following possibly very long, but finite chain:

$$ \begin{align*} \mathcal{S}_n \leadsto \mathcal{S}_{n-1} \leadsto \cdots \leadsto \mathcal{S}_3\leadsto \mathcal{S}_2\leadsto\mathcal{S}_1, \end{align*} $$

and we will have established on the way that, for all i with $1\leq i < n$ , $S_i \notin \Gamma $ . Call the set containing the arguments in this chain $\Delta $ . Now there are two possibilities: either $\mathcal {S}_n = \mathcal {S}_j$ for some $1 \leq j < n$ or not. If the latter, no arguments in $\mathcal {A}$ defeats $\mathcal {S}_n$ . This implies that $\mathcal {S}_n$ is defended by $\Gamma $ , and, in light of $\Gamma $ being complete, that $\mathcal {S}_n \in \Gamma $ . So we have a contradiction showing that every defeat chain between arguments from $\mathcal {A}$ that aren’t in $\Gamma $ has to end in a cycle. In particular, we have $\mathcal {S}_n = \mathcal {S}_j$ for some $1 \leq j < n$ . What’s more, $\mathcal {S}_j\leadsto \mathcal {S}_{n-1} \leadsto \cdots \leadsto \mathcal {S}_{j+1}\leadsto \mathcal {S}_j$ must be an even cycle—since, by assumption, $\mathcal {F}(c)$ doesn’t contain any odd cycles of defeat.

Now let $\Delta ' = \{\mathcal {S}_i\in \Delta : i = n - 2k\text { with } k\in \mathbb {N} \}$ and $\Delta '' = \{\mathcal {S}_i\in \Delta : i = n - {(2k+1)}\text { with } k\in \mathbb {N} \}$ . Notice that $\Delta '$ is consistent, and that it defends all of its arguments from $\Delta ''$ . If $\Delta '$ was inconsistent, there would be and odd cycle of defeat in $\mathcal {F}(c)$ after all. And if $\Delta '$ didn’t defend one of its arguments from $\Delta ''$ , $\mathcal {S}_n \leadsto \mathcal {S}_{n-1} \leadsto \cdots \leadsto \mathcal {S}_2\leadsto \mathcal {S}_1$ couldn’t be a chain ending in a cycle.

Next, consider some arbitrary argument $\mathcal {S}^\dagger $ from $\Delta '$ . It’s in principle possible that $\mathcal {A}$ contains an argument $\mathcal {S}_1'$ such that $\mathcal {S}_1'\leadsto \mathcal {S}^\dagger $ and $\mathcal {S}_1'\notin \Delta ''$ . Above we have already established that $\mathcal {S}_1'\notin \Gamma $ . And, given that we have also established that every chain of defeat between arguments from $\mathcal {A}$ that are not in $\Gamma $ has to end in an even cycle, we can be sure that the chain

$$ \begin{align*} \mathcal{S}^{\prime}_m \leadsto\cdots \leadsto \mathcal{S}_1' \leadsto \mathcal{S}^\dagger \leadsto \cdots \leadsto \mathcal{S}_2\leadsto\mathcal{S}_1 \end{align*} $$

ends in an even cycle too. Notice that it’s possible that $\mathcal {S}^{\prime }_m = \mathcal {S}_i$ for some $1 \leq i \leq n$ (where the $\mathcal {S}_i$ is also in $\Delta '$ , see below). Let $\Theta = \{\mathcal {S}_1',\ldots , \mathcal {S}_m'\}$ and $\Theta ' = \{S_i'\in \Theta : {i = 2k}\text { with } 2k\in \mathbb {N}\text { and }1<i\leq m\}$ . It’s not difficult to see that the set $\Delta '\cup \Theta '$ defends $\mathcal {S}^\dagger $ and also that $\Delta '\cup \Theta '$ defends all of the arguments in it from the set $\Delta ''\cup \Theta ''$ where $\Theta ''=\Theta \backslash \Theta '$ . This follows from what we already know about the relation between $\Delta '$ and $\Delta ''$ and the fact that $\mathcal {S}_m'\leadsto \cdots \leadsto \mathcal {S}_1'$ ends in a cycle. Now it remains to show that $\Delta '\cup \Theta '$ is disjoint from $\Delta ''$ (and so consistent). So suppose, toward a contradiction, that it’s not. Then there has to be some argument $\mathcal {S}^\ddagger $ such that $\mathcal {S}^\ddagger \in \Theta '$ and $\mathcal {S}^\ddagger \in \Delta ''$ (clearly, $\Delta '$ and $\Delta ''$ are disjoint). Given how we defined $\Theta '$ , it’s clear that the chain $\mathcal {S}^\ddagger \leadsto \cdots \leadsto \mathcal {S}_1'\leadsto \mathcal {S}^\dagger $ is of even length. Further, given that $\mathcal {S}^\ddagger \in \Delta $ , a subchain of $\mathcal {S}_n \leadsto \cdots \leadsto \mathcal {S}_2\leadsto \mathcal {S}_1$ has to connect $\mathcal {S}^\dagger $ to $\mathcal {S}^\ddagger $ . Since $\mathcal {S}^\dagger $ is in $\Delta '$ and $\mathcal {S}^\ddagger $ is in $\Delta ''$ , this chain has to be of odd length. But the two chains that connect $\mathcal {S}^\dagger $ and $\mathcal {S}^\ddagger $ form a cycle, and, since one of them is of even and the other of odd length, we get a contradiction: $\mathcal {F}(c)$ contains an odd cycle of defeat. Thus, $\Delta '\cup \Theta '$ has to be disjoint from $\Delta ''$ .

Notice that we have effectively shown how to extend $\Delta '$ into a larger set of arguments $\Delta '\cup \Theta '$ that defends $\mathcal {S}^\dagger $ from a defeat that doesn’t come from $\Delta ''$ (if there’s one). Since $\mathcal {S}^\dagger $ was chosen arbitrary, the same line of reasoning can be applied to any argument from $\Delta '$ and the larger set $\Delta '\cup \Theta '$ .

Now let’s assume, without loss of generality, that there is no argument $\mathcal {S}$ in $\mathcal {A}$ such that $\mathcal {S}\leadsto \Delta '\cup \Theta '$ and $\mathcal {S}\notin \Delta ''\cup \Theta ''$ . Let $\Gamma ' = \Gamma \cup \Delta '\cup \Theta '$ . Clearly, $\Gamma '$ is a consistent and a complete extension of $\mathcal {F}(c)$ . The facts that $\Gamma '$ is complete and that $\Gamma \subset \Gamma '$ imply that $\Gamma $ is not a maximal complete extension after all. Thus, we get a contradiction and can conclude that $\Gamma $ has to be a stable extension.□

Observation 3.3. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a context and $\mathcal {S}$ and $\mathcal {S}'$ arguments from the argument framework $\mathcal {F}(c)$ constructed from it. Then $\mathcal {S}$ defeats $\mathcal {S}'$ , according to Definition 11, $\mathcal {S}\leadsto \mathcal {S}'$ , if and only if $\mathcal {S}$ defeats $\mathcal {S}'$ , according to Definition 21, $\mathcal {S}\leadsto _a\mathcal {S}'$ .

Proof. Right-to-left: Suppose that $\mathcal {S}\leadsto _a \mathcal {S}'$ . This implies that there are arguments $\mathcal {S}^\dagger $ and $\mathcal {S}^\ddagger $ in the set $Arguments(c)$ such that $\mathcal {S}^\dagger \subseteq \mathcal {S}$ , $\mathcal {S}^\ddagger \subseteq \mathcal {S}'$ , and $\mathcal {S}^\dagger \leadsto _b \mathcal {S}^\ddagger $ . From here, either $\mathcal {W}\cup Conclusion[\mathcal {S}^\dagger ]\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}^\dagger ]\vdash Out(\mathfrak {r})$ for some rule r from $\mathcal {S}^\ddagger $ . Since $\mathcal {S}^\dagger \subseteq \mathcal {S}$ and $\mathcal {S}^\ddagger \subseteq \mathcal {S}'$ , it follows that $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash \neg Conclusion[r]$ or $\mathcal {W}\cup Conclusion[\mathcal {S}]\vdash Out(\mathfrak {r})$ for some rule r from $\mathcal {S}'$ . And this is enough to conclude that $\mathcal {S}\leadsto \mathcal {S}'$ .

Left-to-right: Suppose that $\mathcal {S} \leadsto \mathcal {S}'$ . This means that there is a rule $r\in \mathcal {S}'$ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash \neg Conclusion[r]$ , or $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ . Without loss of generality, suppose that $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ . Now take the (set-theoretically) smallest argument $\mathcal {S}^\dagger $ in $Arguments(c)$ such that $\mathcal {W}\cup Conclusion[\mathcal {S}^\dagger ]\vdash Out(\mathfrak {r})$ and $\mathcal {S}^\dagger \subseteq \mathcal {S}$ . Since $\mathcal {S}$ is in $Arguments(c)$ , we know that $\mathcal {S}^\dagger $ exists. It’s easy to see that $\mathcal {S}^\dagger $ is in the set $Minimal_{\mathcal {F}(c)}(Out(\mathfrak {r}))$ : If not, then there must be another set $\mathcal {S}^\ddagger \subset \mathcal {S}^\dagger $ in $Arguments(c)$ such that $\mathcal {W}\cup Conclusion[\mathcal {S}^\ddagger ]\vdash Out(\mathfrak {r})$ . In that case, however, we’d also have $\mathcal {S}^\ddagger \subset \mathcal {S}$ , contradicting our assumption that $\mathcal {S}^\dagger $ is the smallest arguments that’s also a subset of $\mathcal {S}$ that entails $Out(\mathfrak {r})$ with $\mathcal {W}$ . Given our definition of basic defeat, $\mathcal {S}^\dagger \leadsto _b \mathcal {S}''$ , for any $\mathcal {S}''$ such that $\mathcal {S}''$ is in $Minimal_{\mathcal {F}(c)}(r)$ . Let $\mathcal {S}^\ddagger $ be the (set-theoretically) smallest argument from $Arguments(c)$ with both $r \in \mathcal {S}^\ddagger $ and $\mathcal {S}^\ddagger \subseteq \mathcal {S}'$ . Since $\mathcal {S}'$ is in $Arguments(c)$ , we can be sure that $\mathcal {S}^\ddagger $ exists. It’s again easy to see that $\mathcal {S}^\ddagger $ is among the arguments in $Minimal_{\mathcal {F}(c)}(r)$ , from which it follows that $\mathcal {S}^\dagger \leadsto _b \mathcal {S}^\ddagger $ . Finally, given that $\mathcal {S}^\dagger \subseteq \mathcal {S}$ and $\mathcal {S}^\ddagger \subseteq \mathcal {S}'$ , we also have $\mathcal {S}\leadsto _a \mathcal {S}'$ .□

Observation 4.1. Let $c = \langle \mathcal {W},\mathcal {R}\rangle $ be a regular context and $c' = \langle \mathcal {W},\mathcal {R},\leq \rangle $ be the same context with a connected preorder $\leq $ assigning all the rules r in $\mathcal {R}$ the same weight—so, for all r, $r' \in \mathcal {R}$ , $r \sim r'$ . Then $\mathcal {F}(c) = \mathcal {F}(c')$ .

Proof. The sets of arguments of $\mathcal {F}(c)$ and $\mathcal {F}(c')$ are clearly the same. So it remains to show that the defeat relations among the arguments in them coincide.

Left-to-right: Take two arbitrary arguments $\mathcal {S}$ and $\mathcal {S}'$ from $\mathcal {F}(c)$ with $\mathcal {S} \leadsto \mathcal {S}'$ . Since $\mathcal {S} \leadsto \mathcal {S}'$ , we know that there’s some rule r in $\mathcal {S}'$ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash \neg Conclusion[r]$ , or $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ . Now, the fact that all rules $\mathcal {R}$ are assigned the same weights immediately entails that $r \leq r'$ , for all $r' \in \mathcal {S}$ , which is enough to conclude that $\mathcal {S}' \preceq \mathcal {S}$ . And thus, $\mathcal {S}\leadsto _\leq \mathcal {S}'$ .

Right-to-left: Take two arbitrary arguments $\mathcal {S}$ and $\mathcal {S}'$ from $\mathcal {F}(c')$ such that $\mathcal {S} \leadsto _\leq \mathcal {S}'$ . Since $\mathcal {S} \leadsto _\leq \mathcal {S}'$ , we know that there’s some rule r in $\mathcal {S}'$ such that either $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash \neg Conclusion[r]$ , or $\mathcal {W}\cup Conclusion[\mathcal {S}] \vdash Out(\mathfrak {r})$ . And this is enough to conclude that $\mathcal {S} \leadsto \mathcal {S}'$ .