Introduction
The West Antarctic ice streams are some of the most energetic parts of any ice sheet, achieving speeds in excess of several hundreds of meters per year, despite exceptionally small gravitational action. The gravitational driving stress on Ice Stream B, Antarctica, is about 15 kPa (Whillans and Van der Veen, 1993). On other fast-moving glaciers, such as Byrd Glacier, Antarctica, the driving stress is an order of magnitude larger, ranging from 100 to 300 kPa (Whillans and others, 1989). In this respect, the ice streams bear more resemblance to floating ice shelves, with typical driving stresses of 10 kPa and large speeds, than to other grounded glaciers.
As on other fast glaciers, such as Columbia Glacier, Alaska (Van der Veen and Whillans, 1993), or Byrd Glacier (Whillans and others, 1989), longitudinal stresses on Ice Stream B play only a minor role. Whillans and Van der Veen (1993) used velocities measured along a flowline extending from the inland catchment region to the calving front of the Ross Ice Shelf to assess the importance of resistance to flow from gradients in longitudinal stress. Their conclusion was that these stresses contribute little to the large-scale balance of forces, except very close to the ice-shelf iront. For the ice shelf, this Ending confirms earlier work of Thomas and MacAveal (1982), who concluded from surface strain-rate measurements on the Ross Ice Shelf that the weight-induced spreading stress is balanced mostly by friction originating from the sides and, to a lesser extent, grounded ice rises.
The ice streams are embedded in the more sluggishly moving main body of the ice sheet. The speed contrast between the very active Ice Stream B and the neighboring inter-stream ridges is enormous, On the ridges, ice velocities are typically a few m year−1, compared to several hundred m year−1 on the ice stream (Whillans and Van der Veen, 1993). The transition from slow to rapid flow occurs over a narrow region a few kilometers wide. It may be expected that friction associated with this intense lateral shear is of importance in the budget of forces acting on the ice stream. Measurements of transects of surface velocity across the ice stream seem to confirm this notion. In the region near UpB Camp on Ice Stream B, lateral drag balances as much as 50% or more of the driving stress (Echelmeyer and others, 1994). Farther down-glacier, on the ice plain upstream of the grounding line, lateral drag supports almost all of the (very small) driving stress (Bindschadler and others, 1987), On Ice Sircam E, the picture appears to be similar, with basal drag only supporting about 29% of the areally averaged driving stress (MacAyeal and others, 1995).
The picture emerging from these observations is that the ice streams may represent the transition from grounded sheet flow to ice-shelf flow. In earlier models (e.g. Van der Veen, 1987; Hughes, 1992) this transition was believed to be achieved by longitudinal stress gradients. However, the data collected on the West Antarctic ice streams and on the Ross Ice Shelf indicate that the transition from sheet flow to ice-shelf spreading is achieved by a switch in resistance from the glacier bed to the lateral margins.
It is not clear how the reduction in basal drag under the ice streams is achieved. The bed under Ice Stream B has been .studied only in a small area near UpB Camp. This being one of the few crevasse-free regions of the ice stream (chosen for its accessibility, allowing safe surface operations), results obtained in this region may not be representative for the entire ice stream. Seismic studies near UpB Camp have revealed the presence of a meters thick porous laver of sediment at high pore pressure (Blankenship and others, 1986). These measurements have been interpreted as indicating the existence of an actively deforming layer of subglacial till (Alley and others, 1986). The commonly held view is that deformation within this layer is responsible for the large speeds observed on Ice Stream B, and the majority of recent ice-stream models are based on the assumption that the flow of the ice stream is controlled by the mechanical properties of the subglacial material (e.g. Alley and others, 1989; MacAyeal, 1989). However, this view may be challenged, as was recently done by MacAyeal and others (1995). These authors argued that the small basal friction under ice streams depends on the interaction between glacier flow, geological properties of the bedrock, subglacial drainage of meltwater, and erosion and deposition of unconsolidated material. Whillans and Van der Veen (1993) suggested that the reduction in basal resistance may be associated with a change in the geologic nature of the bed under the ice.
At this stage of understanding, there is little, if any, point in incorporating (unknown or poorly constrained) basal processes in detail into a numerical ice-stream model. While this may limit the ability of models to realistically describe ice-stream evolution, numerical models can be valuable tools in identifying potentially important processes that warrant further studies. One such process is the interaction between width and speed of an ice stream. This coupling is the focus of the model discussed in this contribution.
Ice streams have the potential to expand laterally by incorporating slow ridge ice into the ice stream. Because the width of an ice stream may change, and the speed of the ice stream could be proportional to the fourth power of its width (if the driving stress is balanced in large proportion by lateral drag), the possibility fur a positive feed-back exists. A widening ice stream will flow increasingly faster, which may further widen the ice stream through enhanced erosion of the inter-stream ridges and so forth. To study this feed-back, a process that describes erosion of the ridges is included in the present model. The width of the ice stream can change according to a balance between side erosion or entrainment and advection of ice from the inter-stream ridges.
The strength of the bed is important to the development of ice streams. In this study, the basal strength is treated in a very simple manner to avoid the use of potentially complex (or ill-constrained) parameterizations for erosion and advection of subglacial material, drainage of water, strength of the basal till, etc. The onset of a weakened ice–bed interface is incorporated by means of a “friction parameter” that accounts for reduced strength of the underlying material due to action of meltwater and deformable or unconsolidated till. If the bed is weakened, the driving force is taken up by the sides, and with time evolution of the glacier, by a change in driving force. The present model for bed strength bears resemblance to that used by Budd (1975) to model periodically surging glaciers. The difference is that, in Budd’s model, reduction in basal resistance must lead to an increase in basal drag up- and down-glacier to preserve gross force balance. In the present model, any part of the driving stress not supported by drag at the glacier bed is supported by the lateral margins, and a local reduction in basal friction does not directly affect friction elsewhere along the ice stream.
The above considerations have led to the numerical model described in this contribution. The model is a one-dimensional flowline model but the width of the flow band is allowed to vary along the flowline as well as with time. Temperature calculations are not included: instead, the bed is taken to be at its pressure-melting point throughout. The onset of fast ice-stream flow does not appear to be simply a matter of switching from a frozen to a partly or fully melted bed. Under most of the recently halted Ice Stream C, the bed appears to be well lubricated (Alley and others, 1994), yet this ice stream is moving only at very small speeds. Apparently, ice streams are not simple manifestations of temperature-controlled “binge–purge cycles”.
Model Description
Force balance
Glacier flow is driven by gradients in the gravitational stress, as described by the driving stress
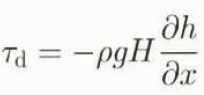
where ρ represents the density of ice, g the acceleration due to gravity, H the ice thickness and h the elevation of the surface above sea level. In this study, flow along a flowline oriented along the flow direction, represented by the x axis, is considered.
The driving stress is balanced by resistive forces that may act at the glacier bed, at the glacier margins and resistance associated with gradients in longitudinal stress. As noted earlier, Whillans and Van der Veen (1993) found that gradients in longitudinal stress contribute little to the large-scale force balance of Ice Stream B and, in this study, this source of flow resistance is neglected. Thus, equilibrium of forces may be expressed as

in which the first term on the righthand side represents basal drag and the second term resistance due to lateral drag. The transverse coordinate is denoted by y. The resistive stress, R xy , is the lateral shear stress, which may be estimated from the transverse variation in velocity, as discussed below. Integrating Equation (2) over the width of the ice stream (from y = −W to y = +W) gives

where the overbar denotes the widih-averaged value and τ s represents the lateral shearing stress at the margins (taken to be the same, but of opposite sign, at both margins), This equation has been used many limes before in numerical models (e.g. Thomas, 1973; Van der Veen, 1986; Hughes, 1992).
The balance Equation (3) provides the basis for the present model. The driving stress on the lefthand side can be calculated from the glacier geometry (ice thickness and surface slope; Equation (1)). By adopting a sliding relation, basal drag can be linked to the glacier speed, while resistance from lateral drag can be estimated from the center-line speed. The result is Equation (12) given below, which allows the width-averaged glacier speed to be calculated from the glacier geometry. An important assumption made here is that lateral shear and basal, or near-basal motion, are mechanically independent and do not influence one another through an effective shear stress, or some such thing. In that case, both sources of flow resistance may be considered independently. To be fully correct, basal and lateral drag should be expressed in terms of glacier speed and transverse gradients in speed. However, this leads to a non-linear differential equation that cannot be solved analytically (e.g. Nye, 1965; Harbor. 1992). To avoid the complicated numerics involved in solving the balance equation explicitly along a transect, both resistive terms are estimated separately, with the requirement that the net resistance to flow must balance the driving stress. This procedure is appropriate if either basal drag or lateral drag .supports most of the driving stress but may be less realistic during the transition stage when both drags are equally important. As it turns out, the transition from flow controlled at the bed to flow controlled by lateral drag occurs rather rapidly and over short distances in the present model, justifying a posteriori the treatment of resistive terms adopted here.
Basal drag
The processes controlling basal motion are not well understood, The mechanics could be dominated by a layer of deforming till (Alley and others, 1986, 1989), in which case the speed of the glacier is determined by the thickness and material properties of the subglacial layer. Alternatively, there could be Weertman-type sliding due to a combination of regelation and creep round obstructions but adjusted for subglacial water pressure, as was done by Bindschadler (1983), for example. In either case, the equation for glacier speed is similar in form and the sliding relation used by Bindschadler (1983) is adopted here, remarking that the most important model results are not overly sensitive to the particular form of the relation used. That is,
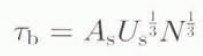
where U s represents the sliding velocity, A s, a sliding parameter and N the effective basal pressure, taken here equal to the height above buoyancy.
The weakening of the bed under ice streams must be included in the model. The cause of this weakening is not known. According to most theories, the speed of basal slip increases with the amount of basal water. One suggested process envisions that the more water the larger the fraction of basal protuberances that may be drowned, or the more subglacial ponds. Subglacial water may also render the mobile drift more fluid or affect erosion of the bed, In any case, water is considered to reduce the friction between the ice and the bed. In the present model, this mechanism is included by multiplying the sliding parameter, A s (kept constant), by a friction parameter denoted by μ. Replacing the effective basal pressure, N, by the height above buoyancy, the modified width-averaged sliding relation becomes

where ρ w represents the density of sea water and H b the elevation of the bed (negative if below sea level). For a regular bed, μ = 1, while μ = 0 corresponds to a completely weakened bed unable to provide any resistance to flow.
Softening of the glacier bed
The friction parameter is a measure of the resistance that the lied can offer. A reasonable assumption is that this friction parameter is proportional to a conservative quantity such as the amount of subglacial water or deformable material. Accordingly, the lime evolution of μ is determined from considerations of continuity for the lubricating material. However, rather than including calculations of continuity of lubricant, and adding a parameterization to link the friction parameter to this quantity, a simpler approach is to calculate changes in μ directly from a continuity equation. In the present model, a diffusion-type continuity equation is used, with diffusivity D μ (including advection would not change the behavior of the model in an important way but diffusion equations are numerically more stable and easier to solve), That is

with t representing time. The value of the diffusivity determines flow rapidly spatial variations in basal strength are eliminated by dispersion of the lubricant.
The second term on the rigthand side of Equation (6) describes local weakening of the bed–ice interlace. Weakening of the bed is primarily due to heat generated at the glacier base, that is, the product of basal drag and sliding speed, with the constant of proportionality denoted by C μ . A feature of till observed under Ice Stream B is its large water content. This suggests that the apparent weakness of this till is caused by saturation with meltwater. If so, the controlling parameter may be the amount of water produced rather than the actual thickness of the subglacial laver of till. In either case, the production of lubricant in the continuity equation for μ is taken to be proportional to basal heat generation.
Lateral drag
In the present model, lateral drag is considered independently from basal drag. The lateral shearing stress is simply linked with the shear-strain rate (transverse gradient in ice velocity) using Glen’s flow law with exponent n = 3. That is,

In this expression, B represents the flow-law parameter.
The assumption is now made that lateral drag is equally important across the full width of the ice stream or, equivakntly, lateral drag supports the same fraction of driving stress at each point on a transect across the ice stream. In that case, the second term on the righthand side of the balance Equation (2) may be taken constant along a transect. If the thickness of the ice is also constant in the transverse direction, it follows that the lateral shearing stress, R xy varies linearly across the ice stream as
in which τ s represents the value of the shear stress at the margins. Using this expression to eliminate the lateral shearing stress from Equation (7), and integrating the resulting expression with respect to the transverse direction, y, subject to the no-slip boundary conditions at both lateral margins, gives the transverse velocity profile

with the center-line speed given by
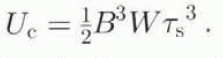
The width-averaged velocity equals four-fifths of the center-line speed, and the shear stress at the margin can be written as

To avoid unrealistically large values of τ s when the half-width becomes very small, W is constrained to be greater than 2 km.
Ice speed
Equations (5) and (11) link basal drag ![]() and lateral drag (τ
s) to the width-averaged ice speed, using these expressions in the balance Equation (3) gives, after some re-arranging, the following relation between the ice velocity and driving stress:
and lateral drag (τ
s) to the width-averaged ice speed, using these expressions in the balance Equation (3) gives, after some re-arranging, the following relation between the ice velocity and driving stress:

This is the central equation used here to study ice-stream flow. It allows the width-averaged velocity (and thus the discharge through a cross-section) to be calcula Led from the ice-stream geometry (thickness and slope in τ d, and half-width, W), provided that the friction parameter, μ, is known. The time evolution of the friction parameter is described by the continuity Equation (6).
Change in width
Entrainment of ice from the inter-stream ridges must be included in order to model the width evolution of the ice stream. Entrainment is a term often used in oceanography to describe the set of processes involved when turbulence spreads into adjacent non-turbulent fluid (Phillips, 1977). In the present context, the term is used to describe the incorporation of ridge ice into the ice stream, resulting in a widening of the ice stream, and a minor increase in discharge (this process is termed “discerpment” by Hughes (1992)). The outward movement of the margins is taken equal to the rate of entrainment, V e , less the transverse velocity into the ice stream. V a , which will be prescribed. That is
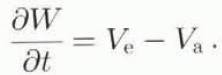
Experiments are conducted with two potential processes for entrainment. In the first formulation, entrainment is taken proportional to the shear stress at the margin
with C e a constant. In the second formulation, the rate of entrainment is taken proportional to the drag force that must be supported by the bed just outboard of the ice stream (or, equivalently, to the resistance offered by lateral drag, as described by the second term on the righthand side of the force-balance Equation (3)), Thus
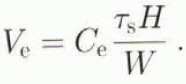
The first model is probably more in line with physical intuition but it leads to great instability and so the second model was developed.
Softening of the margins
There may be softening or stiffening of the ice in the lateral shear margins due to strain. Strain heating associated with intense lateral shear in the margins must raise the temperature of the marginal ice, thereby making this ice softer and reducing resistance from lateral drag. The increase in temperature as the ice travels across the shear margin can be readily estimated from the rate of shearing and the transverse speed of the ice (e.g. Whillans and others, 1993; Echelmeyer and others, 1994). Adopting the temperature-dependence of the flow-law parameter given in Hooke (1981), the effect of strain heating is incorporated into the present model.
Additionally, the strength of the ice in the shear margin may be altered if a pronounced fabric develops. Ice subjected to simple shear becomes progressively stiffer as crystals rotate out of favorable alignment for shearing. This strain hardening may be offset by recrystallization, which leads to the development of a single-maximum Fabric that makes the ice soft with respect to the applied stress. The model simulations of Van der Veen and Whillans (1994) indicate that after undergoing sufficient strain (about 30%), the ice is about four times softer than isotropic ice. Such strain is readily accumulated by the ice travelling through the shear margin. In the present model, softening is taken to increase linearly with strain across the shear margin, tip to a maximum .softening by a factor of 4 for a total strain of 30% or more. If recrystallization does not occur, the margins become stiller with time due to fabric development, tending to offset strain heating. A stiffening option is not included in the present model because held measurements suggest a net softening (Echelmeyer and others, 1994).
Synthesis
The processes described above are used to construct a flowline model that calculates the evolution of an ice stream from the divide to the grounding line. Time evolution is governed by mass continuity and, to keep the numerical scheme stable, the continuity equation for ice is written as a diffusion equation (Oerlemans ana1 Van der Veen, 1984). Two boundary conditions are imposed; one at each end of the model domain. At the up-glacial end, the surface slope is held fixed at zero (an immobile ice divide). At the down-glacial end, the profile is extended two grid points beyond the grounding line, using expressions for the equilibrium profile of an ice shelf controlled entirely by lateral drag. The position of the grounding line is determined by the flotation criterion and is allowed to advance or retreat as the ice stream develops.
The numerical model contains a number of parameterizations and parameter values that may affect the behavior of the ice stream. In the following, the sensitivity of the model to inherent uncertainties is investigated. As it turns out, the most critical process is the parameterization of entrainment. Changing values of other parameters over a wide range has only a small effect on the model behavior.
Model Results
Constant width
In the first experiments, the width of the model ice stream is kept fixed and softening of ice in the shear margins is neglected. The important model parameters are the constant. C μ , that links the increase in bed softness to basal-heat production, and the diffusivity, D μ , describing how effectively the lubricating material is spatially distributed and discharged. For all values selected, the model ice sheet reaches a steady state in which the profile is determined by the relative magnitude of C μ , and D μ . Within two orders of magnitude, the value of the diffusivity affects, in a minor way, how rapidly this steady state is reached and, for simplicity, D μ , is kept constant at the value 107 m2. The range of values selected for C μ (10−5 − 10−7 year kPa−1 m−1), relative to D μ , covers the extremes from a fairly sharp to a broad region of onset of fast flow. All steady-state profiles exhibit a convex surface elevation. Examples are shown in Figure 1 and these illustrate that the steady-state profile depends only weakly on the relative magnitudes of C μ and D μ . In the model ice sheet, basal friction decreases to zero in these experiments. The driving stress is supported entirely by lateral drag and the partitioning factor (defined as the fraction of flow resistance originating at the lateral margins) equals 1.

Fig. 1. Steady-state ice-stream profiles calculated with the present model, keeping the half-width constant (W = 10 km), for different values of the softening parameter: Cμ = 10−5 year kPa−1 m−1 (short-dashed curves), Cμ = 10−6 year kPa−1 m−1 (full curves), Cμ = 10−7 year kPa−1 m−1 (long-dashed curves). The diffusivity for softness is kept constant, Dμ = 107 m2. Residual strength of the bed, τyield, is zero and softening of the ice in the margins from strain heating and fabric development is not included.
The bed may provide some residual resistance. Shear tests performed on basal till retrieved from beneath Ice Stream B suggest a yield strength of a few kPa (Kamb, 1991). In the model, this effect can he included by prescribing a minimum basal drag, corresponding to the yield strength of the basal material. That is, calculated basal drag cannot become smaller than the yield strength, τ yield, unless the driving stress becomes smaller than this value. As shown in Figure 2, incorporating a residual basal strength has little effect on the model ice stream; the ice stream becomes slightly thicker and not all of the driving stress is opposed by lateral drag in the lower regions (partitioning factor < 1).

Fig. 2. Steady-state profiles calculated with the present model, keeping the half-width constant (W = 10 km). Cμ = 10–6 year kPa−1 m−1 and Dμ = 107 m2 in all three model runs. The full curves represent the model ice stream with zero residual basal strength and no softening of the margins. The short-dashed curves are the result of a calculation with a residual basal strength of 2 kPa. The long-dashed curves refer to the calculation that also includes the effect of softening of the ice in the margins.
Figure 2 also shows flow softening of the ice in the margins affects the model ice stream. The effects are minor and the partitioning factor is slightly smaller than in the other calculations shown in this figure. This is because the profile is flatter with smaller driving stress. The minimum basal drag is fixed at 2 kPa, so lateral drag supports somewhat less of the driving stress than before.
Variable width
A steady-state width may develop in which erosion of the inter-stream ridge ice is exactly counteracted by advection of ice from the ridges into the ice stream. Two parameterizations for the rate of entrainment are explored here. The first formulation is inspired by physical intuition but it leads to unstable behavior and so the second parameterization was developed, based on the observation that, at least on short time-scales, the ice streams appear to be stable.
In the first parameterization, entrainment is taken proportional to the shear stress transmitted between the ice stream and the nearly stagnant ridge, and
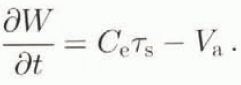
The physical concept is that entrainment may be governed by the drag, τ s, acting at the margins. This drag captures ridge ice by traction. However, this formulation necessarily leads to unstable ice-stream widths.
The instability may be understood by writing the shear stress at the margins as
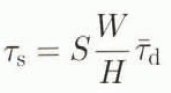
in which S represents the partitioning factor, that is, the fraction of driving stress supported by lateral drag. Substitution in Equation (16) gives

In practice, the partitioning factor, driving stress and thickness change slowly with time. As the ice stream becomes wider, this equation predicts that the rate of entrainment increases, causing a run-away widening of the ice stream. However, the ice streams are known to be stable on the decadal time-scale, at least some of the time. Thus, this first formulation is not suitable.
For the second parameterization, entrainment is taken to be proportional to some rough measure of the extra-basal drag under the inter-stream ridge. With the flow of the ice stream controlled by lateral drag, there must be a region of large basal drag outboard of the shear margin, under the inter-stream ridge. This is because integrated over the full width of the ice stream and adjacent ridges, the driving stress must be balanced by drag at the bed. Thus, basal drag under the ridges must be larger than the local driving stress to compensate for the reduced basal friction under the main body of ice stream. This large basal drag may weaken and mobilize the underlying bed, allowing the ice stream to widen. Therefore, in the second parameterization, the rate of entrainment is linked to the magnitude of this excess basal drag or, equivalently, to the fraction of driving stress on the ice stream supported from the sides (Equation (15)). Assuming that the width of the zone under the ridges over which the extra-basal drag is deposited is proportional to the width of the ice stream, the second formulation for the rate of change in ice-stream width is

in which the parameter C e. includes the proportionality between the width of the zone of large basal drag and the width of the ice stream. Figure 3 shows some of the steady-state profiles using the second parameterization calculated for different values of the entrainment parameter C e and transverse velocity into the ice stream.

Fig. 3. Effect of lateral erosion on the steady-state model ice stream. The initial half-width of the ice stream is 2 km. Entrainment is taken proportional to the part of driving stress supported by lateral drag. Short-dashed curves: Ce. = 0.1 m kPa−1 year−1, Va = 5 m year−1. Full curves: Ce = 0.3 m kPa−1 year−1, Va = 5 m year−1. Dash-dot-dot curves: Ce = 2.0 m kPa−1 year−1 Va = 5 m year−1. Long-dashed curves: Ce = 0.3 m kPa−1 year−1, Va = 10 m year−1. Other parameters used: Cμ = 10−6 year kPa−1 m, Dμ = 107 m2, τyield = 2 kPa. Softening of the marginal ice is included.
The isoline plots in Figure 4 show flow the steady state is approached with the second parameterization. As the bed weakens, lateral drag becomes more important and entrainment causes the ice stream to widen (the initial half-width is 2 km). The glacier-elevation profile adjusts slowly to the increased discharge. The relatively steep surface slopes result in a wave of large speed travelling up-glacier. The associated thinning leads to a drop in driving stress and hence in resistance offered by lateral drag. As a result, entrainment of the inter-stream ridges decreases somewhat, allowing the ice stream to contract due to advection from the ridges. This process of adjustment of glacier width and surface slope continues until a steady state is readied (after about 50 000 years; the waves apparent in Figure 4 continue after 25000 years but with decreasing amplitude).
It may be noted that the amplitude of the ice-stream adjustment (the waves in Figure 4) depends on the initial profile chosen. In this experiment, before the start of the simulation, the model was run to a steady state, assuming that the driving stress is balanced entirely by basal drag, That is, the friction parameter was kept fixed at μ = 1 until a steady state was reached, which was used as starting geometry for the calculations shown in Figure 4. Choosing an initial geometry that is closer to the steady-State profiles shown in Figure 3 reduces the amplitude of the adjustment waves (because the driving stress is smaller, so that the surface profile requires less adjustment as the ice stream widens), but has no effect on the final steady state reached by the model.
The value of the entrainment parameter. C e , can be estimated using data from Ice Stream B. Echelmeyer and others (1994) used a transect of velocity across this ice stream to estimate the partitioning of flow resistance between lateral and basal drags. For the region near the UpB Camp, where the driving stress is about 12 kPa, they estimated basal drag to be 6 kPa or less, with the shear stress at the margin 150–200 kPa. The advection velocity from the ridges into the ice stream is typically 5–10 m year−1 (Whillans and Van der Veen, 1993). Making the assumption that the width at the transect considered by Echelmeyer and others is close to steady state, the entrainment parameter, C e, ranges from 0.01−0.1 m kPa−1 year−1 in the first parameterization, while in the second formulation C e. is 0.5–2.0 m kPa−1 year−1.
Discussion
The modelling is successful in many respects. The fast speed of the ice stream, long length, simple shape of the margins and gradual onset of fast flow at the head, are all features of both the model and Nature. The principal difficulty lies in the manner in which entrainment should be treated.
At the headward onset, the switch between inland-ice Style of flow and ice-stream flow is achieved through a reduction in strength of the bed. This seems realistic as the leading theories for the onset of ice-stream flow entail a change in bed character. Perhaps fewer rock knobs stand up into the ice streams and so there is less retarding force. Perhaps the ice-stream bed is more moldable through glacial erosion and deposition, so there are fewer roughness elements at the 0.1−1.0 m scale to provide friction. Perhaps a water-and-till slurry forms at the bed due to sufficient traction, water and erodable debris; the slurry may be as thin as a few millimeters, or meters thick. These are all viable hypotheses and by [inking the strength of the bed to the rate of basal-water production the onset of ice-stream flow is determined internally by the model rather than being- geographically determined.

Fig. 4. Growth of the model ice stream to steady state, represented by the full curve in Figure 3.
A special feature of the model is that resistance to flow can be switched from the bed to the lateral margins. This is an important switch. Up-glacier, the motion is controlled by basal slip, down-glacier motion is controlled largely by Lateral drag- and the speed becomes strongly dependent cm the width of the ice stream. Changes in the ice-stream width resulting from entrainment or erosion of the ridge ice may therefore play a crucial role in the development of the ice stream.
The process of entrainment is critical to ice-stream evolution. The present model incorporates some attempts at parameterizing the process of entrainment. The first formulation, in which the rate of entrainment is linked to lateral shear stress at the margins, generates extreme instabilities. An important result of the present work is that such a formulation is not viable. In order for even short-term stability, entrainment of ridge ice must be more sensitive to thickness (a decrease in thickness of the ice stream must lead to a more than proportional decrease in entrainment rate) or entrainment must become less for wider ice streams. There are likely other formulations but, for the second model, entrainment was chosen to be sensitive to ice-stream width.
The physical basis for the second formulation is tenuous. In it, the width of the zone of large basal drag outboard of the shear margins is considered to be proportional to ice-stream width. There is probably no such direct linkage in Nature and this formulation may be considered to be a stand-in for any formulation that allows for more than linear linkage to ice-stream thickness.
In Nature, wider ice streams may he older and have caused thinning of the neighboring ridge ice, a process that is sometimes called “draw-down”. This may bring colder ice closer to the bed and a more secure grip by ridge ice on the bed. In effect, wider ice streams may cause the inter-Stream ridges to fasten themselves better to their beds. This is the sort of process that is being crudely modelled with the second formulation.
The views presented in this model follow general wisdom for basal mechanics but there are some deviations. The model does not specifically invoke imported water or mobile drill to lubricate the ice streams (as proposed by Alley and others (1994)). Rather, lubrication is locally generated and allowed to spread. Nor does the model consider the stability of a sheet of basal water or dilated till (as done by Retzlaff and Bentley (1993)). The exact process occurring at the bed is not known and we prefer to hold with a model of little complexity for the bed that predicts the main features.
Acknowledgements
This work was supported by the U.S. National Science Foundation (grant No. DPP-9017445 and OPP-9316509). This is Byrd Polar Research Center contribution No. C-987.






