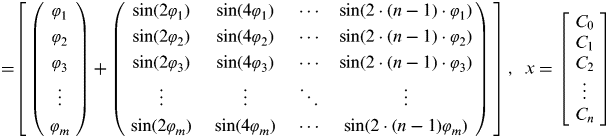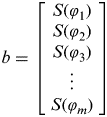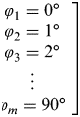1. INTRODUCTION
The least squares method was first used in the fields of astronomy and geodesy as researchers and mathematicians solved the navigation problems of crossing oceans. Celestial navigation was the key to enabling ships to cross open oceans. Obtaining dependable celestial information was crucial, so the prediction of stars, planets, and previous sightings of the celestial objects were used together with the least squares method to produce accurate almanacs. Centuries later, scientists in the field of errors and statistics found many different ways to utilise least squares, such as the regression analysis used for estimating the relationships among variables in statistics.
The meridian arc length calculation is a fundamental element for many navigational methods, especially for rhumb-line and great elliptic sailings on the earth (presumed to be an ellipsoid). As traditional navigation is carried out on the “navigational sphere” and because all modern navigational software, such as Geographical Information Systems (GIS), Electronic Chart Display and Information Systems (ECDIS) and other Electronic Chart Systems (ECS) use the WGS-84 ellipsoid datum, this makes traditional mathematical navigation solutions not accurate enough for modern navigational computerisation. With “black box” navigational software methods unknown to the public and the lack of official standardisations implied, this causes a need to review and investigate the computerisation of current methods.
With least squares methods being widely used in other areas of science, it has inspired us to re-approach its original use in geodesy. This paper presents the research as follows: In Section 2, a simple revision of the current meridian arc length formulae in sailing calculations is presented, including the general meridian arc length formula, which can be numerated directly making it the same as the formulae proposed in a number of textbooks. We then introduce the meridian arc formulae presented by Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009), which have two coefficients with regard to geodetic latitude and sine functions. By further using their method, we obtain new extended meridian arc formulae with different constraints for comparison. In Section 3 we introduce overdetermined systems and their approximated solutions.
From an overdetermined system with known components of the traditional meridian arc formula, as the coefficients of standard geodetic meridian arc formulas are not “closed forms”, the least squares method can be used to approximate the coefficients of a truncated traditional formula and in doing so, gives us the new compact formulae. This is presented in Section 4. The main difference between the new and traditional formulae is that the traditional formulae are often truncated to the first few terms for practical use and in doing so neglect the values not truncated, whereas the new formulae presented in this paper include the non-truncated values and fit the formulae with the best fitting coefficients, making the new formulae more accurate than the traditional method with the same number of terms. With no official standard of how many terms the meridian arc equation must take, the combinations of the terms are endless, and are not discussed here. A comparison between the new formulae and existing methods is presented in Section 5, where the maximum and minimum errors and accuracy of the different formulae are shown. Finally, the work is concluded in Section 6.
2. FORMULAE FOR MERIDIAN ARC LENGTH IN SAILING CALCULATIONS
2.1. Revision of current meridian arc length formulae
In this section, an overview of the most important geodetic formulae is given. The methods and formulae used to calculate the meridian arc length for sailing calculations on the ellipsoid are included in navigational software and are important to the accuracy embedded within them. The formulae for the meridian arc length on an ellipsoid presumed Earth originate from integrating the curvature of the meridian, which is the curvature of an ellipse. The integration of the curvature from the equator to a reduced latitude (β) is expressed in Equation (1).
 $$M(\beta ) = \int\limits_0^\beta {(a^2 \sin ^2 \beta + b^2 \cos ^2 \beta )^{1/2} d\beta} $$
$$M(\beta ) = \int\limits_0^\beta {(a^2 \sin ^2 \beta + b^2 \cos ^2 \beta )^{1/2} d\beta} $$where, a=Major radius; b=Semi-Minor radius.
This integral (Equation (1)) is a famous integral called the “complete elliptic integral of the second type”, an integral which cannot be expressed in closed forms with terms of familiar calculus, except when e, the eccentricity of the spheroid equals zero, then it transforms the ellipse into a circle. As geodetic latitude (φ) is the most common latitude used in navigational systems and for practical use, there is a need to transfer the relationship between geodetic latitude (φ) and reduced latitude (β). Taking the relationship between geodetic latitude and reduced latitude (Equation (2), Figure 1) gives the meridian arc length integral with respect to geodetic latitude (φ) (Equation (3).

Figure 1. Meridian plane with reduced (β) and geodetic (ϕ) latitude of point P on the spheroid.
As Equation (3) originates from an elliptic integral of the second type, it also cannot be evaluated in a “closed” form. The calculation can be performed by the binomial expansion of the denominator with integration by parts. In the binomial expansion of Equation (3), since the powers of the denominator are not a positive integer (here it is −3/2), the expansion would be infinite, and when expressed in a general formula form yields Equation (4).
 $$S(\varphi ) = a(1 - e^2 )\int_0^\varphi {\left[ {\sum\limits_{k = 0}^\infty {( - 1)^k \left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)} (e^2 \sin ^2 \varphi )^k} \right]d\varphi} $$
$$S(\varphi ) = a(1 - e^2 )\int_0^\varphi {\left[ {\sum\limits_{k = 0}^\infty {( - 1)^k \left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)} (e^2 \sin ^2 \varphi )^k} \right]d\varphi} $$Since the powers of e are very small, Equation (4) is a rapidly converging series, so the number of terms retained depends on the accuracy required. By rearranging Equation (4) with general terms of even powers of sine and further integrating by parts gives the following general formula of the meridian arc length in Equation (5):
 $$S(\varphi ) = a(1 - e^2 )\left[ {M_0 \varphi + \sum\limits_{i = 1}^\infty {M_{2i} \sin (2 \cdot i \cdot \varphi} )} \right]$$
$$S(\varphi ) = a(1 - e^2 )\left[ {M_0 \varphi + \sum\limits_{i = 1}^\infty {M_{2i} \sin (2 \cdot i \cdot \varphi} )} \right]$$where
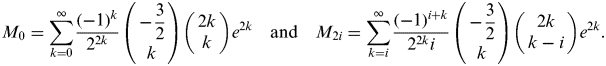 $$M_0 = \sum\limits_{k = 0}^\infty {\displaystyle{{( - 1)^k} \over {2^{2k}}} \left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)\left( {\matrix{ {2k} \cr k \cr}} \right)e^{2k}} \quad {\rm and}\quad M_{2i} = \sum\limits_{k = i}^\infty {\displaystyle{{( - 1)^{i + k}} \over {2^{2k} i}}\left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)\left( {\matrix{ {2k} \cr {k - i} \cr}} \right)e^{2k}}. $$
$$M_0 = \sum\limits_{k = 0}^\infty {\displaystyle{{( - 1)^k} \over {2^{2k}}} \left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)\left( {\matrix{ {2k} \cr k \cr}} \right)e^{2k}} \quad {\rm and}\quad M_{2i} = \sum\limits_{k = i}^\infty {\displaystyle{{( - 1)^{i + k}} \over {2^{2k} i}}\left( {\matrix{ { - \displaystyle{3 \over 2}} \cr k \cr}} \right)\left( {\matrix{ {2k} \cr {k - i} \cr}} \right)e^{2k}}. $$The binomial series for half integer multiples is defined by:
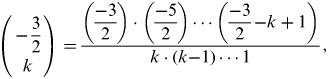 $$\left( {\matrix{ {{\rm -} \displaystyle{3 \over 2}} \cr k \cr}} \right) = \displaystyle{{\left( {\displaystyle{{{\rm -} 3} \over 2}} \right) \cdot \left( {\displaystyle{{{\rm -} 5} \over 2}} \right) \cdots \left( {\displaystyle{{{\rm -} 3} \over 2}{\rm -} k + 1} \right)} \over {k \cdot (k{\rm -} 1) \cdots 1}},$$
$$\left( {\matrix{ {{\rm -} \displaystyle{3 \over 2}} \cr k \cr}} \right) = \displaystyle{{\left( {\displaystyle{{{\rm -} 3} \over 2}} \right) \cdot \left( {\displaystyle{{{\rm -} 5} \over 2}} \right) \cdots \left( {\displaystyle{{{\rm -} 3} \over 2}{\rm -} k + 1} \right)} \over {k \cdot (k{\rm -} 1) \cdots 1}},$$where k is the truncated term.
After expanding and collecting the coefficients of Equation (5) truncated at order e 20 and M 20 with computer programs that do symbolic calculating, the coefficients are shown below in Equation (6). This confirms the results of Equation (5) to be accurate, as the coefficients up to M 8 first given by Delambre (Reference Delambre1799) are the same.
 $${\eqalign{\left[ {.5 \matrix{ {M_0} \cr {M_2} \cr {M_4} \cr {M_6} \cr {M_8} \cr {M_{10}} \cr {M_{12}} \cr {M_{14}} \cr {M_{16}} \cr {M_{18}} \cr {M_{20}} \cr}} \right] = & \left[ {\matrix{ 1 & {{\displaystyle{3 \over 4}}} & {{\displaystyle{{45} \over {64}}}} & {{\displaystyle{{175} \over {256}}}} & {{\displaystyle{{11025} \over {16384}}}} & {{\displaystyle{{43659} \over {65536}}}} & {{\displaystyle{{693693} \over {1048576}}}} & {{\displaystyle{{2760615} \over {1073741824}}}} \cr 0 & { - {\displaystyle{3 \over 8}}} & { - {\displaystyle{{15} \over {32}}}} & { - {\displaystyle{{525} \over {1024}}}} & { - {\displaystyle{{2205} \over {4096}}}} & { - {\displaystyle{{72765} \over {131072}}}} & { - {\displaystyle{{297297} \over {524288}}}} & { - {\displaystyle{{19324305} \over {33554432}}}} \cr 0 & 0 & {{\displaystyle{{15} \over {256}}}} & {{\displaystyle{{105} \over {1024}}}} & {{\displaystyle{{2205} \over {16384}}}} & {{\displaystyle{{10395} \over {65536}}}} & {{\displaystyle{{1486485} \over {8388608}}}} & {{\displaystyle{{6441435} \over {33554432}}}} \cr 0 & 0 & 0 & { - {\displaystyle{{35} \over {3072}}}} & { - {\displaystyle{{105} \over {4096}}}} & { - {\displaystyle{{10395} \over {262144}}}} & { - {\displaystyle{{55055} \over {1048576}}}} & { - {\displaystyle{{2147145} \over {335544332}}}} \cr 0 & 0 & 0 & 0 & {{\displaystyle{{315} \over {131072}}}} & {{\displaystyle{{3465} \over {524288}}}} & {{\displaystyle{{99099} \over {8388608}}}} & {{\displaystyle{{585585} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & { - {\displaystyle{{693} \over {1310720}}}} & { - {\displaystyle{{9009} \over {5242880}}}} & { - {\displaystyle{{117117} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & {{\displaystyle{{1001} \over {8388608}}}} & {{\displaystyle{{15015} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - {\displaystyle{{6435} \over {234881024}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr}} \right. \cr \cr & \left. {.5\matrix{ {{\displaystyle{{703956825} \over {1073741824}}}} & {{\displaystyle{{2807136475} \over {4294967296}}}} & {{\displaystyle{{44801898141} \over {68719476736}}}} \cr { - {\displaystyle{{78217425} \over {134217728}}}} & { - {\displaystyle{{5052845655} \over {8589934592}}}} & { - {\displaystyle{{20364499155} \over {34359738368}}}} \cr {{\displaystyle{{109504395} \over {536870912}}}} & {{\displaystyle{{459349605} \over {2147483648}}}} & {{\displaystyle{{61093497465} \over {274877906944}}}} \cr { - {\displaystyle{{9954945} \over {134217728}}}} & { - {\displaystyle{{357271915} \over {4294967296}}}} & { - {\displaystyle{{1566499935} \over {17179869184}}}} \cr {{\displaystyle{{49774725} \over {2147483648}}}} & {{\displaystyle{{247342095} \over {8589934592}}}} & {{\displaystyle{{4699499805} \over {137438953472}}}} \cr { - {\displaystyle{{765765} \over {134217728}}}} & { - {\displaystyle{{35334585} \over {4294967296}}}} & { - {\displaystyle{{939899961} \over {85899345920}}}} \cr {{\displaystyle{{546975} \over {536870912}}}} & {{\displaystyle{{3926065} \over {2147483648}}}} & {{\displaystyle{{1566499935} \over {549755813888}}}} \cr { - {\displaystyle{{109395} \over {939524096}}}} & { - {\displaystyle{{35334585} \over {120259084288}}}} & { - {\displaystyle{{39491595} \over {68719476736}}}} \cr {{\displaystyle{{109395} \over {17179869184}}}} & {{\displaystyle{{2078505} \over {68719476736}}}} & {{\displaystyle{{92147055} \over {1099511627776}}}} \cr 0 & { - {\displaystyle{{230945} \over {154618822656}}}} & { - {\displaystyle{{1616615} \over {206158430208}}}} \cr 0 & 0 & {{\displaystyle{{969969} \over {2748779069440}}}} \cr}} \right]\left[ {.5\matrix{ 1 \cr {e^2} \cr {e^4} \cr {e^6} \cr {e^8} \cr {e^{10}} \cr {e^{12}} \cr {e^{14}} \cr {e^{16}} \cr {e^{18}} \cr {e^{20}} \cr}} \right]} $
$${\eqalign{\left[ {.5 \matrix{ {M_0} \cr {M_2} \cr {M_4} \cr {M_6} \cr {M_8} \cr {M_{10}} \cr {M_{12}} \cr {M_{14}} \cr {M_{16}} \cr {M_{18}} \cr {M_{20}} \cr}} \right] = & \left[ {\matrix{ 1 & {{\displaystyle{3 \over 4}}} & {{\displaystyle{{45} \over {64}}}} & {{\displaystyle{{175} \over {256}}}} & {{\displaystyle{{11025} \over {16384}}}} & {{\displaystyle{{43659} \over {65536}}}} & {{\displaystyle{{693693} \over {1048576}}}} & {{\displaystyle{{2760615} \over {1073741824}}}} \cr 0 & { - {\displaystyle{3 \over 8}}} & { - {\displaystyle{{15} \over {32}}}} & { - {\displaystyle{{525} \over {1024}}}} & { - {\displaystyle{{2205} \over {4096}}}} & { - {\displaystyle{{72765} \over {131072}}}} & { - {\displaystyle{{297297} \over {524288}}}} & { - {\displaystyle{{19324305} \over {33554432}}}} \cr 0 & 0 & {{\displaystyle{{15} \over {256}}}} & {{\displaystyle{{105} \over {1024}}}} & {{\displaystyle{{2205} \over {16384}}}} & {{\displaystyle{{10395} \over {65536}}}} & {{\displaystyle{{1486485} \over {8388608}}}} & {{\displaystyle{{6441435} \over {33554432}}}} \cr 0 & 0 & 0 & { - {\displaystyle{{35} \over {3072}}}} & { - {\displaystyle{{105} \over {4096}}}} & { - {\displaystyle{{10395} \over {262144}}}} & { - {\displaystyle{{55055} \over {1048576}}}} & { - {\displaystyle{{2147145} \over {335544332}}}} \cr 0 & 0 & 0 & 0 & {{\displaystyle{{315} \over {131072}}}} & {{\displaystyle{{3465} \over {524288}}}} & {{\displaystyle{{99099} \over {8388608}}}} & {{\displaystyle{{585585} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & { - {\displaystyle{{693} \over {1310720}}}} & { - {\displaystyle{{9009} \over {5242880}}}} & { - {\displaystyle{{117117} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & {{\displaystyle{{1001} \over {8388608}}}} & {{\displaystyle{{15015} \over {33554432}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & { - {\displaystyle{{6435} \over {234881024}}}} \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr}} \right. \cr \cr & \left. {.5\matrix{ {{\displaystyle{{703956825} \over {1073741824}}}} & {{\displaystyle{{2807136475} \over {4294967296}}}} & {{\displaystyle{{44801898141} \over {68719476736}}}} \cr { - {\displaystyle{{78217425} \over {134217728}}}} & { - {\displaystyle{{5052845655} \over {8589934592}}}} & { - {\displaystyle{{20364499155} \over {34359738368}}}} \cr {{\displaystyle{{109504395} \over {536870912}}}} & {{\displaystyle{{459349605} \over {2147483648}}}} & {{\displaystyle{{61093497465} \over {274877906944}}}} \cr { - {\displaystyle{{9954945} \over {134217728}}}} & { - {\displaystyle{{357271915} \over {4294967296}}}} & { - {\displaystyle{{1566499935} \over {17179869184}}}} \cr {{\displaystyle{{49774725} \over {2147483648}}}} & {{\displaystyle{{247342095} \over {8589934592}}}} & {{\displaystyle{{4699499805} \over {137438953472}}}} \cr { - {\displaystyle{{765765} \over {134217728}}}} & { - {\displaystyle{{35334585} \over {4294967296}}}} & { - {\displaystyle{{939899961} \over {85899345920}}}} \cr {{\displaystyle{{546975} \over {536870912}}}} & {{\displaystyle{{3926065} \over {2147483648}}}} & {{\displaystyle{{1566499935} \over {549755813888}}}} \cr { - {\displaystyle{{109395} \over {939524096}}}} & { - {\displaystyle{{35334585} \over {120259084288}}}} & { - {\displaystyle{{39491595} \over {68719476736}}}} \cr {{\displaystyle{{109395} \over {17179869184}}}} & {{\displaystyle{{2078505} \over {68719476736}}}} & {{\displaystyle{{92147055} \over {1099511627776}}}} \cr 0 & { - {\displaystyle{{230945} \over {154618822656}}}} & { - {\displaystyle{{1616615} \over {206158430208}}}} \cr 0 & 0 & {{\displaystyle{{969969} \over {2748779069440}}}} \cr}} \right]\left[ {.5\matrix{ 1 \cr {e^2} \cr {e^4} \cr {e^6} \cr {e^8} \cr {e^{10}} \cr {e^{12}} \cr {e^{14}} \cr {e^{16}} \cr {e^{18}} \cr {e^{20}} \cr}} \right]} $Further extension of the equation can give the direct calculation of the meridian arc length between two geodetic latitudes φA and φB; this is shown in Equation (7).
 $$S(\varphi )_{\varphi _B} ^{\varphi _A} = a(1 - e^2 )\left[ {M_0 (\varphi _B - \varphi _A ) + \sum\limits_{i = 1}^\infty {M_{2i} (\sin (2 \cdot i \cdot \varphi _B} ) - \sin (2 \cdot i \cdot \varphi _A ))} \right]$$
$$S(\varphi )_{\varphi _B} ^{\varphi _A} = a(1 - e^2 )\left[ {M_0 (\varphi _B - \varphi _A ) + \sum\limits_{i = 1}^\infty {M_{2i} (\sin (2 \cdot i \cdot \varphi _B} ) - \sin (2 \cdot i \cdot \varphi _A ))} \right]$$ Very accurate results are obtained by Equation (5) with M 4 or M 6 terms of up to eight or ten powers of e (e 8, e 10). For sailing calculations on the ellipsoid, using M 2 terms up to eight or ten powers of e will be sufficient, whereas in other areas of application it will be determined on the degree of accuracy needed. The formulae above are presented in textbooks such as the Admiralty Manual of Navigation (1987), and Bowditch's American Practical Navigator (Reference Bowditch1977) in non-general forms. Equation (5) can be further manipulated and transformed into other forms, such as Bessel's formula and Helmert's formula which require the introduction of new terms of n ![]() $\left( {n = (1{\rm -} \sqrt {1 + e^2} )/1 + \sqrt {1 + e^2}} \right)$. (Kawase, Reference Kawase2011; Deakin and Hunter, Reference Deakin and Hunter2009; Krüger, Reference Krüger1912).
$\left( {n = (1{\rm -} \sqrt {1 + e^2} )/1 + \sqrt {1 + e^2}} \right)$. (Kawase, Reference Kawase2011; Deakin and Hunter, Reference Deakin and Hunter2009; Krüger, Reference Krüger1912).
2.2. The Proposed Formulae by Pallikaris, Tsoulos and Paradissis
Since the WGS-84 datum is used for electronic chart systems. Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) proposed new formulae to calculate the meridian arc, by calculating Equation (5) with M 0 and M 2 terms of up to the eighth powers of e then neglecting M 4 and above terms in WGS-84 standards. They give the following formula used to calculate the meridian arc:
These coefficients are obtained by simply truncating the M 0, M2 values up to the eighth powers of e with the ellipsoid major radius in metres. Taking into account that computer programs use radian units in trigonometry calculations, the transformation of degree units into radians must be allowed for (1° equals π/180 radian units).
The main concept of Pallikaris, Tsoulos and Paradissis's methods is to calculate and only use the desired coefficient terms (M 0, M2 and so on) up to certain powers of e. This neglects the above coefficient terms which are not desired and truncates each term to a certain value of e to the desired accuracy. The reason they do this is that in the meridian arc general formula Equation (5), the powers of e are very small causing the values of each coefficient term to approximate a certain value if the truncated powers of e terms are enough, and in the binominal theorem which the meridian arc formula uses for its coefficient terms, the denominator will greatly surpass its numerator upon reaching certain high coefficient terms, causing the influences of higher terms in the meridian arc formula to greatly decrease after a certain first few terms.
By further expanding their method to M 0, M2 and M 4 terms of up to the eighth powers of e, we can obtain new 3 coefficient formulas as below:
 $$\hskip-10pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi - 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\hskip-22pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$
$$\hskip-10pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi - 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\hskip-22pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$Correspondingly, expanding their method up to M 6 terms of up to the eighth powers of e are shown below:
 $$\hskip-35pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi \!-\! 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)}\! \right)\hskip-35pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\cr & - 0.021980996\left( {\sin \left( {\displaystyle{{6 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{6 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$
$$\hskip-35pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi \!-\! 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)}\! \right)\hskip-35pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\cr & - 0.021980996\left( {\sin \left( {\displaystyle{{6 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{6 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$And whereas up to M 8 terms and eighth powers of e is the equation below:
 $$\hskip-35pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi \!-\! 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)}\! \right)\hskip-35pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\cr & - 0.021980996\left( {\sin \left( {\displaystyle{{6 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{6 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right) \cr & + 0.000030579\left( {\sin \left( {\displaystyle{{8 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{8 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$
$$\hskip-35pt\eqalign{ M_{\varphi _A} ^{\varphi _B} =& 111132.952546922 \cdot \Delta \varphi \!-\! 16038.508615363\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)}\! \right)\hskip-35pt \cr & + 16.832599651\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\cr & - 0.021980996\left( {\sin \left( {\displaystyle{{6 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{6 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right) \cr & + 0.000030579\left( {\sin \left( {\displaystyle{{8 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{8 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$In the method presented (Pallikaris et al., Reference Pallikaris, Tsoulos and Paradissis2009), terms up to the eighth power of e are used. For accuracy comparisons, we further extend this method and present Pallikaris, Tsoulos and Paradissis's formula with up to 20 powers of e with M 0 and M 2 terms to see how they affect the accuracy of the equation, the new two coefficient meridian arc formula is presented as below:
And in addition, the 3 coefficient Pallikaris, Tsoulos and Paradissis's meridian arc formula up to 20 powers of e with M 0, M2 and M 4 terms is:
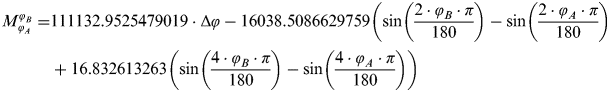 $$\hskip-15pt\eqalign{M_{\varphi _A} ^{\varphi _B} =& 111132.9525479019 \cdot \Delta \varphi - 16038.5086629759\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\hskip-35pt \cr & + 16.832613263\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$
$$\hskip-15pt\eqalign{M_{\varphi _A} ^{\varphi _B} =& 111132.9525479019 \cdot \Delta \varphi - 16038.5086629759\left( {\sin \left( {\displaystyle{{2 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{2 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)\hskip-35pt \cr & + 16.832613263\left( {\sin \left( {\displaystyle{{4 \cdot \varphi _B \cdot \pi} \over {180}}} \right) - \sin \left( {\displaystyle{{4 \cdot \varphi _A \cdot \pi} \over {180}}} \right)} \right)} $$These formulae are compared in Section 5 of this paper, and in addition we present the errors and influences they have on the meridian arc formula. Where in the above meridian arc length equations, the distances are calculated in metres, conversion to nautical units is achieved by dividing the equation by 1852, as 1 nautical mile equals 1852 metres.
3. OVERDETERMINED SYSTEMS AND APPROXIMATE SOLUTIONS FROM THE LEAST SQUARES METHOD
A system of linear equations in mathematics is considered overdetermined if there are more equations than the unknown. The method of ordinary least squares can be used to find an approximate solution for overdetermined systems with the least errors, as for example in astronomy for predicting the orbits of celestial objects.
“Least squares” means that the overall solution minimizes the sum of the squares of the errors made in every single equation. To find the best-fitting curve to a given set of points by minimizing the sum of the squares of the errors, the most important application is the data fitting (Figure 2). The sum of the squares of the errors is used instead of the error absolute values because it allows the offsets to be treated as a continuous differentiable quantity.

Figure 2. Best-fitting curve to a given set of data points. Here, one can find the best fitting curve of equation Y=kX2+p with ten given data points with least squares method.
4. THE NEW PROPOSED ARC LENGTH BY THE LEAST SQUARES METHOD
As previously mentioned, the meridian arc length formula can be presented in the form of Equation (5), and with modern navigational and GPS systems implementing the WGS 84 datum, by taking a(1−e 2) of WGS 84 parameters into Equation (5), we obtain a new general formula of the meridian arc length as shown in Equation (14).
Now, finding the coefficients C i, i=0,1,2,3…with the least squares method is the aim here, Equation (14) with restricted n+1 numbers of coefficients are the proposed new meridian arc formulas as shown below in Equation (15)
with n+1 numbers of coefficients depending on the accuracy needed. The accuracy of the first few terms is discussed in the following comparison paragraph.
To acquire the coefficients of the new formulae, we calculate the meridian arc distance with standard geodetic methods (by Equation (5)). Then, by forming an overdetermined system with the proposed new equations, the method of least squares gives an approximate solution to the meridian arc length coefficients in a matrix form.
To achieve the above, we take m (finite) φ values with the same intervals starting from 0° to 90° into Equation (5) to calculate the accurate meridian arc values. For accuracy reasons, we take up to M 20 terms with 20 powers of e in Equation (5) to represent the actual meridian arc distance; calculations were done with the WGS-84 datum to be compatible with modern electronic navigational systems. With this done, we obtain m number of equations that represent the actual meridian arc with equal intervals starting from 0° to 90° of latitude.
Next, depending on the accuracy desired, we form an overdetermined system by setting n+1 number of coefficients wanted for the new equation; the more coefficients, the more the new formula will resemble the original meridian arc formula. Now there are m linear equations with n+1 unknown coefficients, to make this system overdetermined, m must be more than n+1 (m > n+1). This overdetermined system can be written in matrix form as Ax=b, and shown below in Equation (16).
 $$\hskip-10pt\left[\!\! {\matrix{ {\left( {\matrix{ {\varphi _1} \cr {\varphi _2} \cr {\varphi _3} \cr {\matrix{ \vdots \cr {\varphi _m} \cr}} \cr}} \right)}\!\!\!\!\! & +\!\!\!\!\! & {\left( {\matrix{ {\sin (2\varphi _1 )} & {\sin (4\varphi _1 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _1 )} \cr {\sin (2\varphi _2 )} & {\sin (4\varphi _2 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _2 )} \cr {\sin (2\varphi _3 )} & {\sin (4\varphi _3 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _3 )} \cr {\matrix{ \vdots \cr {\sin (2\varphi _m )} \cr}} & {\matrix{ \vdots \cr {\sin (4\varphi _m )} \cr}} & {\matrix{ \ddots \cr \cdots \cr}} & {\matrix{ \vdots \cr {\sin (2 \cdot (n - 1)\varphi _m )} \cr}} \cr}} \right)}\!\! \cr}} \right]\! \cdot\! \left[\! {\matrix{ {C_0} \cr {C_1} \cr {C_2} \cr {\matrix{ \vdots \cr {C_n} \cr}} \cr}} \!\right]\! =\! \left[\! {\matrix{ {S(\varphi _1 )} \cr {S(\varphi _2 )} \cr {S(\varphi _3 )} \cr {\matrix{ \vdots \cr {S(\varphi _m )} \cr}} \cr}} \!\right]$$
$$\hskip-10pt\left[\!\! {\matrix{ {\left( {\matrix{ {\varphi _1} \cr {\varphi _2} \cr {\varphi _3} \cr {\matrix{ \vdots \cr {\varphi _m} \cr}} \cr}} \right)}\!\!\!\!\! & +\!\!\!\!\! & {\left( {\matrix{ {\sin (2\varphi _1 )} & {\sin (4\varphi _1 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _1 )} \cr {\sin (2\varphi _2 )} & {\sin (4\varphi _2 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _2 )} \cr {\sin (2\varphi _3 )} & {\sin (4\varphi _3 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _3 )} \cr {\matrix{ \vdots \cr {\sin (2\varphi _m )} \cr}} & {\matrix{ \vdots \cr {\sin (4\varphi _m )} \cr}} & {\matrix{ \ddots \cr \cdots \cr}} & {\matrix{ \vdots \cr {\sin (2 \cdot (n - 1)\varphi _m )} \cr}} \cr}} \right)}\!\! \cr}} \right]\! \cdot\! \left[\! {\matrix{ {C_0} \cr {C_1} \cr {C_2} \cr {\matrix{ \vdots \cr {C_n} \cr}} \cr}} \!\right]\! =\! \left[\! {\matrix{ {S(\varphi _1 )} \cr {S(\varphi _2 )} \cr {S(\varphi _3 )} \cr {\matrix{ \vdots \cr {S(\varphi _m )} \cr}} \cr}} \!\right]$$where,
 $$\hskip-12pt\eqalign{ A =& \left[ {\matrix{ {\left( {\matrix{ {\varphi _1} \cr {\varphi _2} \cr {\varphi _3} \cr {\matrix{ \vdots \cr {\varphi _m} \cr}} \cr}} \right)}\!\!\!\!\! & + &\!\!\!\!\! {\left( {\matrix{ {\sin (2\varphi _1 )} & {\sin (4\varphi _1 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _1 )} \cr {\sin (2\varphi _2 )} & {\sin (4\varphi _2 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _2 )} \cr {\sin (2\varphi _3 )} & {\sin (4\varphi _3 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _3 )} \cr {\matrix{ \vdots \cr {\sin (2\varphi _m )} \cr}} & {\matrix{ \vdots \cr {\sin (4\varphi _m )} \cr}} & {\matrix{ \ddots \cr \cdots \cr}} & {\matrix{ \vdots \cr {\sin (2 \cdot (n - 1)\varphi _m )} \cr}} \cr}} \right)} \cr}} \right]}, & \enspace x = \left[ {\matrix{ {C_0} \cr {C_1} \cr {C_2} \cr {\matrix{ \vdots \cr {C_n} \cr}} \cr}} \right]$$are the wanted coefficents.
$$\hskip-12pt\eqalign{ A =& \left[ {\matrix{ {\left( {\matrix{ {\varphi _1} \cr {\varphi _2} \cr {\varphi _3} \cr {\matrix{ \vdots \cr {\varphi _m} \cr}} \cr}} \right)}\!\!\!\!\! & + &\!\!\!\!\! {\left( {\matrix{ {\sin (2\varphi _1 )} & {\sin (4\varphi _1 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _1 )} \cr {\sin (2\varphi _2 )} & {\sin (4\varphi _2 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _2 )} \cr {\sin (2\varphi _3 )} & {\sin (4\varphi _3 )} & \cdots & {\sin (2 \cdot (n - 1) \cdot \varphi _3 )} \cr {\matrix{ \vdots \cr {\sin (2\varphi _m )} \cr}} & {\matrix{ \vdots \cr {\sin (4\varphi _m )} \cr}} & {\matrix{ \ddots \cr \cdots \cr}} & {\matrix{ \vdots \cr {\sin (2 \cdot (n - 1)\varphi _m )} \cr}} \cr}} \right)} \cr}} \right]}, & \enspace x = \left[ {\matrix{ {C_0} \cr {C_1} \cr {C_2} \cr {\matrix{ \vdots \cr {C_n} \cr}} \cr}} \right]$$are the wanted coefficents. $$b = \left[ {\matrix{ {S(\varphi _1 )} \cr {S(\varphi _2 )} \cr {S(\varphi _3 )} \cr {\matrix{ \vdots \cr {S(\varphi _m )} \cr}} \cr}} \right]$are the values of Equation (5) up to M 20 terms and 20 powers of e.
$$b = \left[ {\matrix{ {S(\varphi _1 )} \cr {S(\varphi _2 )} \cr {S(\varphi _3 )} \cr {\matrix{ \vdots \cr {S(\varphi _m )} \cr}} \cr}} \right]$are the values of Equation (5) up to M 20 terms and 20 powers of e. $\hskip-12pt\left[ {\matrix{ {\varphi _1 = 0{\curr { \char "000B0}}} \cr {\varphi _2 = 1{\curr { \char "000B0}}} \cr {\varphi _3 = 2{\curr { \char "000B0}}} \cr {\matrix{ \vdots \cr {\varphi _m = 90{\curr { \char "000B0}}} \cr}} \cr}} \right]$, degree intervals differ depending on how many intervals to m is decided.
$\hskip-12pt\left[ {\matrix{ {\varphi _1 = 0{\curr { \char "000B0}}} \cr {\varphi _2 = 1{\curr { \char "000B0}}} \cr {\varphi _3 = 2{\curr { \char "000B0}}} \cr {\matrix{ \vdots \cr {\varphi _m = 90{\curr { \char "000B0}}} \cr}} \cr}} \right]$, degree intervals differ depending on how many intervals to m is decided.
Since latitudes range from 0° to 90°, it would be adequate to at least put less than 1° intervals from 0° to 90° latitude for the overdetermined system.
For the overdetermined system Ax=b, the least squares formula is obtained from the problem ![]() $\mathop {\min} \limits_x \left\| {Ax - b} \right\|$, provided that (ATA)−1 exists, the solution can be written with the normal Equations (17):
$\mathop {\min} \limits_x \left\| {Ax - b} \right\|$, provided that (ATA)−1 exists, the solution can be written with the normal Equations (17):
where the T sign indicates a matrix transpose.
With this method, approximated solutions for the new meridian arc formula coefficients are given. For example, for the new arc length formula (Equation (15)) with two coefficients equation, n=1, and if it also uses 1° intervals from 0° to 90°, then m=91, this gives a 91-by-2 matrix A ([A]91×2), a 2-by1 matrix x ([x]2×1), and another 2-by-1 matrix b ([b]2×1), by taking in the least squares method solution, then this gives the x matrix solution, and forms the new meridian arc formula with two corresponding coefficients C 0 and C 1. Following the method above, the solved coefficients for the new formulae with terms of up to n=5 with 1° intervals for m are shown in Table 1, each row (n=1,2,…,5) is a new arc length formula with restricted n+1 number of coefficients; put the values back into Equation (15) for the full corresponding formulae.
Table 1. Solved coefficients for the new formulas with terms of up to n=5, m=91 with 1° intervals, ![]() $M_0^\varphi $ is calculated in nautical miles for these coefficients.
$M_0^\varphi $ is calculated in nautical miles for these coefficients.

5. COMPARISON OF FORMULA PERFORMANCE
5.1. Comparison
Comparison of the different formulae for calculating the meridian arc distance are evaluated and shown below, the compared formulae are
1. The original formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) (Equation (8)).
2. The extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with up to eighth powers of e and M 4 terms (Equation (9)).
3. The extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with up to eighth powers of e and M 6 terms (Equation (10)).
4. The extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with up to eighth powers of e and M 8 terms (Equation (11)).
5. The extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with up to 20th powers of e and M 2 terms (Equation (12)).
6. The extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with up to eighth powers of e and M 4 terms (Equation (13)).
7. The propsosed new formulae in this paper with n=0∼5 (Equation (15), n=0∼5, m=91).
A comparison must always have a standard to be compared with to determine whether the outcomes are good or bad. The comparison standard used here is Equation (5) with up to M 20 terms and 20 powers of e, as this formula provides micrometre accuracies for the meridian arc length on an ellipsoid presumed Earth. The distances calculated in this formula are compared with Vincenty's formula (Vincenty, Reference Vincenty1975), which give accuracies within 0·5 mm on the ellipsoid, and are shown in Table 2. With Vincenty's formula being considered as one of the most precise methods with millimetre accuracies on the WGS-84 ellipsoid, the results in Table 2 show that Equation (5) with up to M 20 terms and 20 powers of e should be sufficient as the comparison standard used here.
Table 2. Comparison of Equation (5) with M 20 terms up to 20 powers of e with Vincenty's formula (1975).

*above distances are calculated in metres.
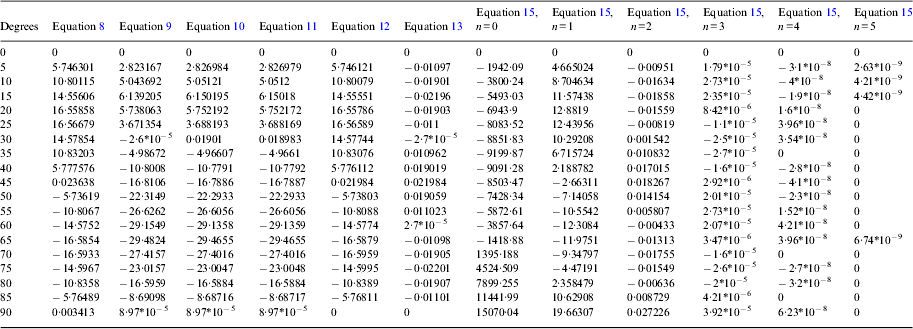
The errors between the compared formulae with Equation (5) having M 20 terms and up to 20 powers of e are shown in Table 3 expressed with the units of metres. These comparisons are based on the calculations of 91 meridian arcs lengths contained from the equator to parallel latitudes starting from 0° to 90° latitude with 1° increments.
Table 3 is expressed in units of metres. These comparisons are based on the calculations of 91 meridian arcs lengths contained from the equator to parallel latitudes starting from 0° to 90° latitude with 1° increments. For a simple and clear view on how the discrepancies compare to each another, they are also presented in Figures 3 and 4, where Figure 3 shows the error differences of Equations (8) and (15), (where n=0 and m=91) and Figure 4 shows the differences between Equations (8), (9), (10), (11), (12), (13) and (15) (where n=1∼5 and m=91), vertical axis of these figures represent the errors when compared to Equation (5) with M 20 terms and 20 powers of e, where the horizontal axis is the corresponding latitude of the compared meridian arc length distances.
Table 3. The errors between the compared formulae and the standard arc length.

* For brevity, only intervals of 5° are shown, m=91 for Equation 13, units are in metres.
This paper also presents the maximum deviation, minimum deviation and standard deviation of each new formula as shown in Table 4. It must be noted as we want the error difference from the standard, this means when calculating the average, maximum and minimum errors an absolute value is used instead of simply using such positive and negative errors provided in Table 3, as this will give a non-meaningful average, maximum and minimum errors. Note that the minimum deviations do not include the initial values for latitude 0°. If included, all minimum deviations shall be zero because at 0° latitude, the meridian arc length of all equations equal zero.
Table 4. Error averages, maximums and minimums and standard deviation.

* above units are calculated in metres.
As data fitting in overdetermined systems is essential for the accuracy of the approximated solution, we compare whether more data inputs (m>91) influence the accuracy of the formulae. Here, we compare the accuracy of the new two coefficients formula (Equation (15), n=1), as this formula with its high accuracy and compactness in calculations would be used most in practical needs. We compare the accuracy of the method when m=91 with 1° increments to 90°, and when m=181 with 0·5° increments to 90°. The results are shown in Table 5, again, the minimum deviations do not include the initial values for 0° latitude.
Table 5. Comparisons between differing m.

*above units are calculated in metres.
5.2. Discussion of comparison results
As shown in Tables 3 and 4, the new formula Equation (15) with one coefficient (n=0) is not accurate enough for precise sailing calculations.
The new formula (Equation (15)) with two coefficients (n=1) is sufficient for practical sailing calculations with an average error of 8 m with a range of 20∼0·2 m errors. It is to be noted that when compared to the formulas presented by Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) (Equation (8), 2009) and extended formula Equation (12) with near identical values, although they all have the same coefficient terms (M 0 and M 2) and have almost the same accuracy, our maximum error is larger (20 m vs 17 m), this is because the least squares method includes the non-truncated terms causing the values to not be a sine curve as shown in Equation (8). This causes a continuing rise for latitudes of about 70° and higher. But as one can see from Figure 4, Equation (15) with two terms of coefficients (n=1) maintains a lower maximum error between 0∼70° degrees, and as most shipping routes are between 70° latitude north and south, the new formula (Equation (15) with two terms of coefficients can be considered an acceptable alternative for Equation (8).
In Equations (9), (10), and (11), the extended formulae of Pallikaris, Tsoulos and Paradissis's method which are calculated up to eight powers of e and up to M 4, M6 and M 8 terms respectively have no significant difference between each other and also can be considered appropriate for navigational sailing with maximum errors up to 30 metres. Yet, it is to be noted that these all have more than two coefficient terms, and only at below approximately 35° latitude do these equations have a better accuracy than those of the above two coefficient term formula.
The new formula (Equation (15)) with three coefficients (n=2) drastically lowers the errors to millimetre range, which should be sufficient when needing very high accuracy calculations. When compared to the extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with three coefficient terms (Equations (9) and (13)), only Equation (13) of up to 20 powers of e will give repeatable millimetre level accuracy. It is to be noted that although our new least square formula with three coefficient terms (Equation (15), n=2) and the extended formulae of Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009) with three coefficient terms up to 20 powers of e powers (Equation (13)) have near identical values and both are viable for high accuracy calculations, the least square method is a slightly more accurate (approximately about 3∼4 mm). This is because our method takes account of the non-truncated higher term values and as such demonstrates the use of the least square method implied here.
The new formula (Equation (15)) with four and above coefficients (n=3 and above) shows no significant difference between Equation (5) with M 10 terms up to 20 powers of e, and Vicenty's formula (Vicenty, Reference Vincenty1975), making this new formula with four coefficients a suitable alternative to save computer resources when requiring such high accuracies.
In the extended formulae of Pallikaris, Tsoulos and Paradissis's method, it is to be noted that when calculating up to eight powers of e, taking in more terms of M 4 to M 8 does not improve its accuracy drastically. And when taking more powers of e (here, 20 powers of e), their formula with two terms of coefficient does not differ much to those of eight powers of e, it is only when taking three terms and above with more powers of e that the formula becomes drastically more accurate for high accuracy calculations.
There is no significant difference between m=91 and m=181, yet of course m=181 should be more accurate, as more information is given, then the data fitting should be more accurate and a better curve line equation is fitted. It can also be seen that the standard deviation of m=181 is more compact than m=91, meaning the errors do not diverge as far as the origin of zero when compared to m=91.
6. CONCLUSIONS
According to the calculation tests carried out above, the proposed new formulae (Equation (15)) in this paper which use the least square method have the benefits of:
• Better accuracy than simply truncating at a certain point for lower accuracy needs.
• Depending on the accuracies required, how many coefficients the formula has is chosen by the user. At least three coefficients (n=2) should be chosen for high accuracy mapping such as GPS navigation on land, whereas for very rough estimates, assuming the meridian arc length equals the latitude times 3432·9672 is a quick and useful technique. For sailing applications, the two coefficient formula would be sufficient as it only has a maximum error of 20 metres whereas seeking a higher accuracy for sailing calculations does not have any practical value for marine navigation and costs more resources than needed. This can be seen as an evaluation of accuracy and calculation speeds deemed most efficient for the user.
• Since our new formula with two coefficients (n=1) uses the same computer algorithm resources as those original formulae presented by Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009), and as their formulae have already be proven to be about twice as fast as the other geodetic methods formulae of the same accuracy, we can also assume that our new presented formulae shall also be faster than those compared in Pallikaris et al. (Reference Pallikaris, Tsoulos and Paradissis2009).
We must note that directly calculating Equation (5) up to multiple terms and storing the coefficients in a memory space for computer algorithms would take up a lot of space. If one wants the most accurate values of the meridian arc, this would be the correct way, but with the least squares method above, we could acquire near identical accuracies with fewer terms, and in doing so, save computer memory space. In practical use, such high accuracies are often not needed and only cost unnecessary resources, thus making the efficient formulae presented in this paper well suited for practical use. Although modern computers perform at very high speed, and can handle more complex geodetic formulas, saving computing resources is an important aspect in the design of navigational systems. Navigational systems are becoming even more compact, and the saved computer resources can be readily used for other functions such as more user friendly and customized interfaces, 3-D presentations and more information-packed integrated maps and charts.
The new proposed formulae in this paper are diverse and adaptable to many different conditions of accuracy, ranging from road maps that require sub-metre accuracies, to simple estimates of long distances. These new formulae can be used for the development of new algorithms without diminishing the accuracies required for the situation. The least squares method can be expanded to other fields of science for future studies.
ACKNOWLEDGEMENT
This work was supported in part by the National Science Council of Taiwan, Republic of China, under grant NSC 98-2410-H-019-019-, NSC 99-2410-H-019-023-, NSC 100-2410-H-019-018-, and NSC 101-2410-H-019-025-.