1. INTRODUCTION
Estimating uncertainties associated with ice-volume estimates is important for, among others, sea-level rise (SLR) studies. For instance, as discussed by Farinotti and Huss (Reference Farinotti and Huss2013), the errors in individual glacier volume data compiled in calibration datasets for volume/area scaling have an impact on the expected accuracy of the SLR estimates from glacier ensembles based on such scaling relationships.
In spite of their importance, errors in ice-volume estimates are often not well described, or even quantified in the literature. For instance, none of the earliest reported glacier volumes of Svalbard based on the Soviet and Norwegian/British airborne echo-soundings (Macheret and Zhuravlev, Reference Macheret and Zhuravlev1982; Dowdeswell and others, Reference Dowdeswell, Drewry, Liestøl and Orheim1984) were accompanied by estimates of their errors. Two different studies of Bamber and others (Reference Bamber, Layberry and Gogineni2001, Reference Bamber2013) derived the volume of the entire Greenland ice sheet discussing the different error sources involved; however, these studies lacked an estimate of the total error in volume. Other studies, such as Saintenoy and others (Reference Saintenoy2013) and Fischer and Kuhn (Reference Fischer and Kuhn2013), use ground-penetrating radar (GPR)-retrieved DEMs of ice thickness to calculate the volume of Austre Lovénbreen (Svalbard) and 64 Austrian glaciers, respectively. They report some of the most significant error sources (e.g. interpolation error, error in radio-wave velocity and error in area), but they do not provide details of the statistics used to combine these errors to derive an error in volume. Moreover, they assume a linear relation between the ice-thickness errors at the grid points when obtaining the final volume error estimate, an assumption that leads to overestimating the error, as we will discuss later. On the contrary, Pettersson and others (Reference Pettersson2011) obtained an extremely small error for the volume estimate of Vestfonna ice cap, because their method implicitly assumed independence between the errors at grid cells of the ice-thickness DEM, which leads to underestimating the error, as it will be discussed in Section 2.1.
The aim of this work is to assess the error involved in the computation of the volume of an ice mass, delimited by a given boundary, from its ice-thickness DEM. We thus focus on ice volumes, and do not address density issues. Consequently, the volumes considered in the case study presented in this paper, as well as most of the individual glacier volumes reported in the literature, are not ice (or water) equivalent. However, we note that, for SLR applications, the density assumption used for volume-to-mass conversion becomes a major source of uncertainty, particularly in alpine glaciers, where the firn layer can make up a large fraction of thickness in the accumulation area.
Estimation of ice-volume errors requires determination of: (1) the ice-thickness error of the DEM, generally calculated from ice-thickness data retrieved from prospective methods such as the GPR; (2) the degree of correlation existing among the ice-thickness errors at the grid points; and (3) the impact on the volume computation of the errors in boundary delineation. In what follows, we will pay attention to these and other related aspects.
2. METHODOLOGY
The volume, in an ice-thickness DEM, of a glacier can be computed as the sum of the individual volumes at the grid-cell level, i.e. the sum of cell area times the average ice thickness for the cell,
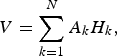 $$V = \sum\limits_{k = 1}^N {A_kH_k}, $$
$$V = \sum\limits_{k = 1}^N {A_kH_k}, $$
where A k is the area of each grid cell and H k is the ice thickness associated with the cell. This will be the basis for our estimate of the total error in volume. The basic terminology on errors used in this study is the same as that of the previous companion papers (Lapazaran and others, Reference Lapazaran, Otero, Martín-Español and Navarro2016a, Reference Lapazaran, Otero, Martín-Español and Navarrob; this issue (Papers I and II)).
Our starting point assumes that the error of the DEM is known or can be estimated following, e.g. the techniques described in Papers I and II, either as an ice-thickness standard deviation error map (
![]() $\varepsilon _{H_k}$
at each grid point) or as an ice-thickness average error of the whole DEM, ε
H DEM. We can characterize the latter as the RMS average value of the ice-thickness error throughout the grid (Eqn (4) in Paper II).
$\varepsilon _{H_k}$
at each grid point) or as an ice-thickness average error of the whole DEM, ε
H DEM. We can characterize the latter as the RMS average value of the ice-thickness error throughout the grid (Eqn (4) in Paper II).
To estimate the accuracy of the volume calculation, we separate its errors conceptually into two main components: the error in volume arising from the ice-thickness errors of a DEM with a given fixed boundary assumed to be free from positioning errors, ε VH , and the error in volume stemming from the uncertainty in boundary delineation, ε VB . We analyse both error components separately and their combination below.
2.1. Error in volume due to the error in ice thickness
To estimate ε VH we need to consider the degree of spatial correlation among the ice-thickness errors at the grid cells. These are often correlated, because:
-
(1) There is an inherent spatial correlation among the ice thickness due to the continuity of both glacier surface and bed, and thus the ice-thickness-dependent data errors are likely correlated.
-
(2) Some of the errors of the raw data are correlated along the profiles. Examples for the directly retrieved ice-thickness measurements are systematic errors in the velocity used for two-way-travel-time to ice-thickness conversion, in the identification and picking of the ice bed, and in the locations of the measurement points along profiles. For synthetic data, examples are errors in the ice-thickness-estimation equation or in its parameters, or data positioning errors. For boundary data, a typical example is the systematic misplacement of the boundary due to, e.g. presence of debris or snow cover.
-
(3) The interpolator propagates the data errors to the grid points, increasing their correlation. Although the ice-thickness interpolation is performed using values at neighbouring data points, and these change as the interpolator moves through the grid, the estimations at neighbouring locations are computed from nearly the same set of data points.
If the errors at the N grid points,
![]() $\varepsilon _{H_k}$
, were all independent, and we characterized them by means of ε
H DEM, the error in volume due to ice-thickness errors would be
$\varepsilon _{H_k}$
, were all independent, and we characterized them by means of ε
H DEM, the error in volume due to ice-thickness errors would be
![]() $\varepsilon _{VH} = {{A\varepsilon _{H\,{\rm DEM}}} / {\sqrt N}} $
. This means that the error would decrease with the size of the DEM cells. This is an excessively optimistic assumption (i.e. it underestimates the error), given that not all the errors are expected to be independent. If, alternatively, they were all linearly dependent, the expression would simply be ε
VH
= A
ε
H DEM. However, this is an overly pessimistic assumption (i.e. it overestimates the error), which considers the error as a mean value rather than a standard deviation, thus preventing any statistical compensation.
$\varepsilon _{VH} = {{A\varepsilon _{H\,{\rm DEM}}} / {\sqrt N}} $
. This means that the error would decrease with the size of the DEM cells. This is an excessively optimistic assumption (i.e. it underestimates the error), given that not all the errors are expected to be independent. If, alternatively, they were all linearly dependent, the expression would simply be ε
VH
= A
ε
H DEM. However, this is an overly pessimistic assumption (i.e. it overestimates the error), which considers the error as a mean value rather than a standard deviation, thus preventing any statistical compensation.
Taking into account that some spatial correlation between grid values exists, but that there is no linear dependence among them, we aim to determine the equivalent number of independent values within the grid, N R , which should not depend on the grid size. Assuming there are N R independent values, we can estimate ε VH as
To estimate N R we use the integral range as defined by Lantuéjoul (Reference Lantuéjoul1991), which allows a comparison between the scale of the phenomenon under study and the scale of observation. If the domain of observations is large with respect to the integral range, the ratio between the former and the latter represents the equivalent number of independent values in the domain (e.g. Garrigues and others, Reference Garrigues, Allard, Baret and Weiss2006). The definition of the integral range varies with the dimension of the space of the domain of observations. For instance, Blanchin and Chilès (Reference Blanchin and Chilès1993) used a similar approach in a one-dimensional (1-D) continuous sampling along a profile with a length L greater than the 1-D integral range, IR 1, leading asymptotically to N R = L/IR 1. In our case, the 2-D integral range, IR 2, can be considered as the equivalent area of influence of each independent value, and thus, in a typical scenario with many intersecting profiles covering the whole glacier area A, we can approximate
hence estimating ε VH as
The estimate of IR
2 requires the calculation of the variogram of the ice-thickness errors at the grid points. The variogram function,
![]() $\gamma (h)$
, measures the correlation between pairs of points as a function of the distance between them, h, and the range, R, of the variogram indicates the maximum distance where we can expect correlation between pairs of points (e.g. Cressie, Reference Cressie1993; p. 131), i.e. the distance at which the variogram fits its maximum value (referred to as its sill, σ
2). The theoretical variogram results from fitting a certain function to the experimental variogram, which is a cloud of squared dissimilarities between pairs of points (e.g. Wackernagel, Reference Wackernagel2003). However, some of the possible variogram function models (e.g. Stable, Gaussian and Exponential models; Table 1) grow asymptotically to their sill, and thus their range is necessarily infinite. For this type of function model, a practical range is defined as the distance at which the variogram reaches the 95% of its sill. Since for each variogram model there is a proportionality between the integral range and the range (or the practical range, when applied), and the estimate of the latter is straightforward from the variogram, we prefer working in terms of range rather than of integral range. Table 1 shows the relation between IR
2 and R, and the derived changes in Eqns (3) and (4), for the most common variogram models. These relations can be derived by applying the definition of integral range (e.g. Lantuéjoul, Reference Lantuéjoul1991, Reference Lantuéjoul2002; Garrigues and others, Reference Garrigues, Allard, Baret and Weiss2006) to each particular variogram model. Examples of variogram functions can be obtained e.g. from Wackernagel (Reference Wackernagel2003). Additional results of integral ranges in 1, 2 and 3 dimensions, for a wider set of models, can be found in Lantuéjoul (Reference Lantuéjoul2002). The choice of a specific variogram model is achieved due to its optimal fitting to the experimental variogram of the ice-thickness errors at the grid points, as compared with the other models.
$\gamma (h)$
, measures the correlation between pairs of points as a function of the distance between them, h, and the range, R, of the variogram indicates the maximum distance where we can expect correlation between pairs of points (e.g. Cressie, Reference Cressie1993; p. 131), i.e. the distance at which the variogram fits its maximum value (referred to as its sill, σ
2). The theoretical variogram results from fitting a certain function to the experimental variogram, which is a cloud of squared dissimilarities between pairs of points (e.g. Wackernagel, Reference Wackernagel2003). However, some of the possible variogram function models (e.g. Stable, Gaussian and Exponential models; Table 1) grow asymptotically to their sill, and thus their range is necessarily infinite. For this type of function model, a practical range is defined as the distance at which the variogram reaches the 95% of its sill. Since for each variogram model there is a proportionality between the integral range and the range (or the practical range, when applied), and the estimate of the latter is straightforward from the variogram, we prefer working in terms of range rather than of integral range. Table 1 shows the relation between IR
2 and R, and the derived changes in Eqns (3) and (4), for the most common variogram models. These relations can be derived by applying the definition of integral range (e.g. Lantuéjoul, Reference Lantuéjoul1991, Reference Lantuéjoul2002; Garrigues and others, Reference Garrigues, Allard, Baret and Weiss2006) to each particular variogram model. Examples of variogram functions can be obtained e.g. from Wackernagel (Reference Wackernagel2003). Additional results of integral ranges in 1, 2 and 3 dimensions, for a wider set of models, can be found in Lantuéjoul (Reference Lantuéjoul2002). The choice of a specific variogram model is achieved due to its optimal fitting to the experimental variogram of the ice-thickness errors at the grid points, as compared with the other models.
Table 1. Relation between the range, R, and the 2-D integral range, IR
2, for the most common variogram models,
![]() $\gamma (h)$
. The last two columns relate Eqns (3) and (4) with the range of the variogram. The integral range of the Stable model depends on its power, λ, and on the value of the gamma function (Γ, Euler integral of the second kind), becoming the Exponential model when λ = 1, and the Gaussian model when λ = 2. For values 0.5 ≤ λ ≤ 2, ε
VH
for the Stable model becomes very close to that obtained from Eqn (4) using R
2 instead of IR
2, i.e.
$\gamma (h)$
. The last two columns relate Eqns (3) and (4) with the range of the variogram. The integral range of the Stable model depends on its power, λ, and on the value of the gamma function (Γ, Euler integral of the second kind), becoming the Exponential model when λ = 1, and the Gaussian model when λ = 2. For values 0.5 ≤ λ ≤ 2, ε
VH
for the Stable model becomes very close to that obtained from Eqn (4) using R
2 instead of IR
2, i.e.
![]() $\varepsilon _{VH} \approx \varepsilon _{H\,{\rm DEM}}R\sqrt A $
$\varepsilon _{VH} \approx \varepsilon _{H\,{\rm DEM}}R\sqrt A $

Sometimes the range does not only depend on the distance between points, but also on the direction between them (anisotropy in the correlation). To detect it, half the circle of directions must be divided into different angular sectors and an experimental variogram must be generated for each sector, taking into account only the pairs of points within its corresponding directions. Then, the same variogram model must be fitted to each of these experimental variograms to find the corresponding range. Both the maximum range and the range in its orthogonal direction will be the ranges defining this anisotropy, R a and R b (e.g. Wackernagel, Reference Wackernagel2003). In this case, R 2 in Table 1 must be replaced by the product R a R b .
The range of interest to estimate the error in the volume via Eqn (4) and Table 1 is that derived from the DEM of errors at the grid points,
![]() $\varepsilon _{H_k}$
. However, if a DEM of errors were not available we suggest using the range of the variogram of ice-thickness values at the grid points (H
k
) as the best solution to approximate its range. This approach is generally conservative, since ice thicknesses at grid points are usually more correlated than their errors, thus generating a larger range, i.e. a larger error in volume. On the other hand, we do not use the variogram of the errors of the dataset instead of those in the DEM, for two reasons. First, the errors in the dataset are biased, since both the GPR profiles and the glacier boundary are oversampled (in particular, the variogram is more realistic if the boundary values are excluded), while the rest of the glacier surface is devoid of data. Second, the dataset does not contain interpolation errors. Consequently, it should not be expected that the variogram of the errors of the dataset will generate a good estimate of the range representative for the entire glacier.
$\varepsilon _{H_k}$
. However, if a DEM of errors were not available we suggest using the range of the variogram of ice-thickness values at the grid points (H
k
) as the best solution to approximate its range. This approach is generally conservative, since ice thicknesses at grid points are usually more correlated than their errors, thus generating a larger range, i.e. a larger error in volume. On the other hand, we do not use the variogram of the errors of the dataset instead of those in the DEM, for two reasons. First, the errors in the dataset are biased, since both the GPR profiles and the glacier boundary are oversampled (in particular, the variogram is more realistic if the boundary values are excluded), while the rest of the glacier surface is devoid of data. Second, the dataset does not contain interpolation errors. Consequently, it should not be expected that the variogram of the errors of the dataset will generate a good estimate of the range representative for the entire glacier.
2.2. Error in volume due to the error in boundary delineation
Each DEM of ice thickness implicitly includes its own fixed boundary, which is undoubtedly affected by an error. We aim here to estimate the error in glacier volume resulting from this uncertainty in glacier-boundary delineation.
Delineating a glacier boundary accurately is not an easy task. Snow patches or debris cover over valley walls and glacier fronts hinder the proper definition of the glacier boundary (Paper II, Section 3.2). Even when glacier boundaries are delineated from ground-based GPS measurements, the main error source will be the subjective glacier-boundary determination carried out by the operator. These errors are not easy to estimate and strongly depend on the conditions involved. Several examples can be found in the literature. For instance, Bernard and others (Reference Bernard2014) analysed this type of error for Austre Lovénbreen – a small (~4.6 km2) valley glacier in Northwestern Spitsbergen. They observed that the ice extent was typically from 25 to 30 m, occasionally up to 100 m, under the marginal slopes, producing an uncertainty in area of ~10%, although they always found an area underestimation in all zones of this glacier (i.e. a bias). This uncertainty is much larger than those cited by Paul and others (Reference Paul2013), in which the different glacier delineations by multiple authors had average standard deviation of area between 2.6% (Ötztal Alps) and 5.7% (Alaska), depending on the geographical settings. Another example is the relative error in area for the glaciers of the most recent Svalbard glacier inventory (König and others, Reference König, Nuth, Kohler, Moholdt and Pettersen2014). Its accuracy is estimated to be typically better than 5%, but it shows a discrepancy of ~8% when compared with the delineations done by Hagen and others (Reference Hagen, Liestøl, Roland and Jørgensen1993) using the same set of aerial images from 1990 (Nuth and others, Reference Nuth2013).
This error in boundary delineation not only has an impact on the glacier area, but also on the calculation of glacier volume. We will refer to it as error in volume related to the boundary-delineation error (ε VB ). Although the uncertainty in boundary delineation affects the areas where the glacier is thinnest (this statement does not apply to divides, calving fronts or artificial boundaries), ε VB is not necessarily small. Often, GPR coverage near steep-slope walls at the glacier margins is relatively scarce. As a consequence, a mischaracterization of the glacier boundary will affect the ice-thickness DEM extending well into the glacier. This inwards propagation of the boundary error becomes an important source of error.
In spite of the boundary uncertainty, ice-thickness DEMs are defined based on a fixed glacier mask. The DEM boundary is a pixelation of the glacier boundary, generated to accommodate it to a regular grid. However, we will not consider pixelation errors, since this pixelation is overlapped with (and often much smaller than) the uncertainty in boundary delineation.
In what follows, two scenarios are considered that differ in whether: (1) the error in ice thickness arising from the uncertainty in glacier boundary has not been considered in the ice-thickness DEM (Scenario 1); or (2) it has already been taken into account as assumed in Paper II (Scenario 2).
2.2.1. Scenario 1 – Boundary uncertainty is not considered in the available DEM
To estimate the error in volume associated with the boundary uncertainty, we characterize the latter by the fraction (p) of the total glacier area (A) affected by the error. In other words, we evaluate ε VB as the change in volume of the ice-thickness DEM when the glacier boundary is shifted inwards/outwards by an amount equal to pA.
We start by analysing ε VB for a land-based glacier with a zero ice-thickness boundary. Figure 1a shows, in a cross-section of a glacier, how a shift in the boundary has an impact on the ice-thickness estimate of the inner parts extending up to the nearest GPR measurement. To model this error in volume, we simplify its section to a triangle (yellow in Fig. 1b), whose height is characterized by H m, which we conservatively approximate by the mean ice thickness of the glacier. Making a 3-D extension of this error section, we get an error band along the glacier boundary with a triangular section. The base of this band is the error in area, pA, and the height of the triangle is the mean ice thickness of the glacier (H m = V/A). It then results in

Fig. 1. Volume error arising from the uncertainty in the glacier boundary, for zero ice-thickness segments of the boundary. (a) An example of a boundary error produced by a debris cover at the glacier contour; in yellow the section of this volume error; the dashed orange line marks the location of the GPR ice-thickness measurement (H GPR) closest to the glacier's lateral margin. (b) The volume error is conservatively modelled as a band with triangular section, based on the error area, pA; its height is characterized as H m, the mean value, over the glacier surface, of the ice thickness at the closest GPR measurement to each boundary point, which we approximate by the mean ice thickness of the glacier.
This strip-based conservative error estimate for ε VB is valid for both inwards and outwards shifts of the boundary (e.g. in cases in which we respectively underestimate or overestimate the glacier area due to debris/snow cover).
If the glacier boundary is not completely land based, e.g. it includes calving fronts, or if it includes divides or artificial sections (so not the entire boundary has zero ice thickness), the different boundary zones must be studied separately. For the zone with zero ice-thickness boundary, the error in volume can be estimated using Eqn (5), weighted by the fraction of the boundary with zero ice thickness, α:
For the remaining zones of the boundary, errors in volume (
![]() $\varepsilon _{VB_\alpha} $
) are obtained multiplying the error in area, pA, by the corresponding fraction of the boundary with nonzero ice thickness, 1−α, and by the mean ice thickness in this boundary zone, H
b.
$\varepsilon _{VB_\alpha} $
) are obtained multiplying the error in area, pA, by the corresponding fraction of the boundary with nonzero ice thickness, 1−α, and by the mean ice thickness in this boundary zone, H
b.
ε
VB
will then be obtained by adding
![]() $\varepsilon _{VB_\alpha} $
and
$\varepsilon _{VB_\alpha} $
and
![]() $\varepsilon _{VB_{1 - \alpha}} $
.
$\varepsilon _{VB_{1 - \alpha}} $
.
Assuming the independence of the error in volume due to the uncertainty in boundary delineation of Scenario 1, ε VB , and the error in volume associated with the error in ice thickness, ε VH , we can estimate the total error in glacier volume as
2.2.2. Scenario 2 – Boundary uncertainty is already considered in the available DEM
If the boundary uncertainty was taken into account when estimating the error in ice thickness of the DEM (as in Paper II), then its contribution to the error in volume has already been partly considered in ε VH . Just partly, because the DEM of ice thickness was generated on the basis of a particular glacier mask, with a fixed area, and this will produce an additional error in volume associated to the boundary uncertainty, not yet taken into account. To estimate it, we cannot proceed as in Scenario 1, because then we would be double counting part of the error in volume related to boundary uncertainty. However, as shown in Figure 2, the error in volume can be separated into two parts. The first part, denoted ε 1, is the error in ice volume that has already been considered within the contribution of the error in ice thickness of the DEM. It encompasses the ice-thickness errors at the boundary points and their propagation to the interior through the interpolation at the grid points (Paper II). The other component, denoted ε 2, is the error in volume not yet considered and that we aim to estimate now.

Fig. 2. (a) Two components of the error in volume arising from the uncertainty in boundary, for zero ice-thickness segments of the boundary: ε
1, already considered as part of the error in ice thickness of the DEM; ε
2, the part of the error in volume not accounted for in the error in ice thickness of the DEM. (b) ε
2 can be idealized as a band with triangular section, based on the error area, pA, with height assumed to be equal to
![]() $\varepsilon _{H_b}$
.
$\varepsilon _{H_b}$
.
From Figure 2 we can derive, for segments of the boundary with zero ice thickness (fraction α of the boundary),
where
![]() $\varepsilon _{H_{\rm b}}$
is the RMS value of the ice-thickness error along the glacier boundary with zero ice thickness.
$\varepsilon _{H_{\rm b}}$
is the RMS value of the ice-thickness error along the glacier boundary with zero ice thickness.
Note that, in this scenario, Eqn (7) is still applicable to the segments with non-zero ice thickness (e.g. calving fronts or ice divides), and ε
VB
will be obtained by adding ε
2 and
![]() $\varepsilon _{VB_{1 - \alpha}} $
.
$\varepsilon _{VB_{1 - \alpha}} $
.
If there is not enough information to obtain
![]() $\varepsilon _{H_{\rm b}}$
, it can be conservatively approximated by the global error in ice thickness of the DEM, ε
H DEM.
$\varepsilon _{H_{\rm b}}$
, it can be conservatively approximated by the global error in ice thickness of the DEM, ε
H DEM.
In neither Scenario, 1 nor 2, is ε 1 calculated. However, the implicit estimate of ε 1 obtained via the triangular-section strip of Scenario 1 is much more conservative (likely produces an overestimate of the error) than its estimate via the propagation of the boundary uncertainty to the ice-thickness error (Paper II) followed in Scenario 2. In the latter scenario, there is a statistical propagation of the boundary uncertainty to the ice-thickness error of the DEM. It will also be statistically combined within the error in volume through the parameter N R in Eqn (2). On the other hand, the triangular-section-strip approach of Scenario 1 linearly propagates the ice-thickness error to the whole area of error, which generates an extremely conservative error estimate. Therefore, we strongly recommend following, whenever possible, the procedure described in Scenario 2.
The assumption of independence between ε VH and ε VB underlying Eqn (8) is realistic in Scenario 1, but questionable in Scenario 2, since in the latter ε VH includes part of the error in volume resulting from the error in area, but ε VB also stems from the error in area. Thus, we conservatively estimate the total error in volume by simple addition of both ε VB of Scenario 2, and ε VH ,
3. CASE STUDY: WERENSKIOLDBREEN
We now apply the error-estimate techniques discussed above to the volume calculated from a DEM of ice thickness of Werenskioldbreen, a land-terminating polythermal glacier in Svalbard (Fig. 3). This glacier was also used as case study in Papers I and II. This case study aims to explore the similarities and differences between the approaches to estimate ε VB used in Scenarios 1 and 2 discussed above.

Fig. 3. (a) Location of Werenskioldbreen in Southern Spitsbergen, Svalbard. (b) DEM of ice thickness of Werenskioldbreen. The arrows to the southeast indicate the limits of the ice divide with Tuvbreen. (c) DEM of error in thickness, corresponding to the DEM of ice thickness in (b).
Figures 3b, c show respectively, the ice-thickness DEM of Werenksioldbreen and its corresponding uncertainty map, obtained from Papers I and II. We assume Figure 3c as the starting point of the error analysis performed under Scenario 2. The area and volume of the glacier are, respectively, A = 26.62 km2 and V = 2.86 km3, obtained as the product of the number of grid cells within the glacier-boundary times the cell area, and using Eqn (1). To estimate ε VB we need to know the complementary fractions of zero and nonzero ice-thickness boundary, α and 1−α, respectively. For Werenskioldbreen, we set the ice thickness at the boundary as zero everywhere except at the ice divide with Tuvbreen (a tributary of Hansbreen), to the southeast (Fig. 3b), resulting α = 0.9914. As explained in Paper II, we adopted an error in area of 8%, i.e. p = 0.08.
In Table 2 we show, for both Scenarios 1 and 2, the results for the different errors and parameters involved in the final estimate of the error in volume. The range of the variogram, R, is computed, in both scenarios, using Stable variograms of the error at the grid cells,
![]() $\varepsilon _{H_k}$
(λ = 1.3 in Scenario 1 and λ = 1.4 in Scenario 2) since we have found that these variogram models optimally fit each case, compared with the other models. The value of ε
H DEM is estimated from Eqn (4) in Paper II. The estimate of
$\varepsilon _{H_k}$
(λ = 1.3 in Scenario 1 and λ = 1.4 in Scenario 2) since we have found that these variogram models optimally fit each case, compared with the other models. The value of ε
H DEM is estimated from Eqn (4) in Paper II. The estimate of
![]() $\varepsilon _{H_{\rm b}}$
is only needed in Scenario 2 when applying Eqn (9). ε
VH
is obtained from Table 1, using the Stable variogram in both scenarios. The ε
VB
value to be used in Eqn (8) is calculated as the sum of the results from Eqns (6) and (7) in Scenario 1 or from Eqns (9) and (7) in Scenario 2. The final error in the volume estimate, ε
V
, calculated by means of Eqn (8) in Scenario 1 and of Eqn (10) in Scenario 2, is shown both in km3 and in percentage of the total volume of Werenskioldbreen.
$\varepsilon _{H_{\rm b}}$
is only needed in Scenario 2 when applying Eqn (9). ε
VH
is obtained from Table 1, using the Stable variogram in both scenarios. The ε
VB
value to be used in Eqn (8) is calculated as the sum of the results from Eqns (6) and (7) in Scenario 1 or from Eqns (9) and (7) in Scenario 2. The final error in the volume estimate, ε
V
, calculated by means of Eqn (8) in Scenario 1 and of Eqn (10) in Scenario 2, is shown both in km3 and in percentage of the total volume of Werenskioldbreen.
Table 2. Results for the main parameters and error components involved in the computation of the error in volume for Werenskioldbreen, together with the corresponding final error in volume, for Scenarios 1 and 2. In the last column Eqns (8) and (10) have been used for Scenarios 1 and 2, respectively

The ranges obtained for Scenarios 1 and 2 are quite similar. We find this reasonable, as their respective variograms are based on two ice-thickness error DEMs, differing only in the contribution of the boundary error (absent in Scenario 1).
3.1. Differences between Scenarios 1 and 2
Comparing the error estimates for Scenarios 1 and 2, we observe that ε VH is smaller in Scenario 1 than in Scenario 2 despite the smaller range obtained in Scenario 2. This is because Scenario 1 includes neither the error in the boundary cells nor its inwards propagation to the grid nodes. On the other hand, ε VB in Scenario 1 is much larger than in Scenario 2. This is also expected, because the whole volume of the triangular-section strip is considered in Scenario 1 (Fig. 1), while in Scenario 2 only a small part of that volume is involved (Fig. 2). As earlier noted (Section 2.2), we consider that the results obtained in Scenario 2 are more realistic than those from Scenario 1, which are extremely pessimistic.
3.2. Range of the DEM of ice-thickness versus range of the DEM of errors
For comparison, we also calculate the range associated with the variogram based on the ice-thickness DEM, H k , using a similar variogram function (Stable with power λ = 1.5, which fits optimally). We find a value of 1529 m, which is larger than those in Table 2 since the ice thicknesses are more correlated than their corresponding errors. Consequently, if this value is used as an estimate of R, it will generate, using the expressions in Table 1, a more pessimistic estimate of ε VH , 0.1026 km3 in Scenario 1 and 0.1078 km3 in Scenario 2, giving 0.1531 km3 (5.4%) and 0.1170 km3 (4.1%), respectively, as final estimates of ε V .
3.3. Error of the DEM versus error in the boundary
In Scenario 2, ε
H DEM is ~2 times larger than
![]() $\varepsilon _{H_{\rm b}}$
. Therefore, if we use ε
H DEM as a proxy for
$\varepsilon _{H_{\rm b}}$
. Therefore, if we use ε
H DEM as a proxy for
![]() $\varepsilon _{H_{\rm b}}$
, we will obtain a ε
VB
~ 2 times larger than the value given in Table 2 (following Eqn (9)). Although this produces a more pessimistic error estimate, both are of the same order of magnitude, hence this approximation would be acceptable if enough information to obtain
$\varepsilon _{H_{\rm b}}$
, we will obtain a ε
VB
~ 2 times larger than the value given in Table 2 (following Eqn (9)). Although this produces a more pessimistic error estimate, both are of the same order of magnitude, hence this approximation would be acceptable if enough information to obtain
![]() $\varepsilon _{H_{\rm b}}$
were not available.
$\varepsilon _{H_{\rm b}}$
were not available.
3.4. Separate contributions of the boundary uncertainty and the error in ice thickness to the error in volume
ε
VB
in Scenario 2 represents only ε
2, a small portion of the total error in volume due to boundary uncertainty (Fig. 2). The remaining part is embedded within ε
VH
. To evaluate separately the total contributions to the error in volume of the boundary uncertainty ε
VB
and the error in ice thickness ε
VH
, we can take the value for ε
VH
from Scenario 1 (
![]() $\varepsilon _{VH_1}$
, which does not include error in boundary uncertainty at all) and that for ε
V
from Scenario 2 (
$\varepsilon _{VH_1}$
, which does not include error in boundary uncertainty at all) and that for ε
V
from Scenario 2 (
![]() $\varepsilon _{V_2}$
, our best estimate of the total error in volume). Splitting errors in this way
$\varepsilon _{V_2}$
, our best estimate of the total error in volume). Splitting errors in this way
![]() $\varepsilon _{VH_1}$
and ε
VB
are independent. Thus, solving for ε
VB
in
$\varepsilon _{VH_1}$
and ε
VB
are independent. Thus, solving for ε
VB
in
![]() $\varepsilon _{V_2}^2 = \varepsilon _{VH_1}^2 + \varepsilon _{VB}^2 $
, we could obtain an estimate of the total error in volume derived from the boundary uncertainty.
$\varepsilon _{V_2}^2 = \varepsilon _{VH_1}^2 + \varepsilon _{VB}^2 $
, we could obtain an estimate of the total error in volume derived from the boundary uncertainty.
Applying this rationale to the values given in Table 2 (
![]() $\varepsilon _{VH_1}$
= 0.0368 km3 and
$\varepsilon _{VH_1}$
= 0.0368 km3 and
![]() $\varepsilon _{V_2}$
= 0.0474 km3), we find ε
VB
= 0.0299 km3. Proceeding similarly, but recalculating
$\varepsilon _{V_2}$
= 0.0474 km3), we find ε
VB
= 0.0299 km3. Proceeding similarly, but recalculating
![]() $\varepsilon _{VH_1}$
with the variogram parameters from Scenario 2 (
$\varepsilon _{VH_1}$
with the variogram parameters from Scenario 2 (
![]() $\varepsilon _{VH_1}$
= 0.0364 km3), we find ε
VB
= 0.0304 km3. Summarizing, assuming Scenario 2, the two components of the total error in volume of Werenskioldbreen, ε
VH
and ε
VB
, have the same order of magnitude.
$\varepsilon _{VH_1}$
= 0.0364 km3), we find ε
VB
= 0.0304 km3. Summarizing, assuming Scenario 2, the two components of the total error in volume of Werenskioldbreen, ε
VH
and ε
VB
, have the same order of magnitude.
3.5. Comparison with previous studies of the error in volume
We conclude this case study by comparing the volume error estimates obtained following our methodology with those obtained following some simplifications often found in the literature (e.g. Pettersson and others, Reference Pettersson2011, in bullet 1; Saintenoy and others, Reference Saintenoy2013 in bullet 2). These rarely take into account the error in volume due to boundary uncertainty, so they represent estimates of ε VH rather than of ε V :
-
(1) Assuming uncorrelated errors, for N = 10 648 grid values of ice thickness of the DEM, we get
 $\varepsilon _V = A\varepsilon _{H\,{\rm DEM}}/\sqrt N $
= 0.0038 km3 (0.1% of the total volume, an overly optimistic estimate).
$\varepsilon _V = A\varepsilon _{H\,{\rm DEM}}/\sqrt N $
= 0.0038 km3 (0.1% of the total volume, an overly optimistic estimate). -
(2) The error estimate that treats the error as a mean value, rather than as a standard deviation, thus implicitly assuming linear dependence of the gridded values, gives ε V = A ε H DEM = 0.3912 km3 (13.7% of the total volume, an extremely pessimistic estimate).
The difference between the estimates above spans two orders of magnitude (note that N ~ 10 000). Our estimate from Scenario 2 is one order of magnitude larger than the former, and one order of magnitude smaller than the latter, although far from their mean value.
4. CONCLUSIONS
We have presented a methodology to estimate the error in volume of a glacier DEM of ice thickness, accounting for the two main error sources: the ice-thickness error at the DEM grid cells and the uncertainty in the glacier-boundary delineation. The method is robust and provides error estimates more realistic than those often found in the literature.
To accurately capture the volume error stemming from the ice-thickness DEM error, it is crucial to estimate the correlation existing among the errors at the grid cells, as they are far from being independent of each other. Estimates of the error in volume are underestimated when the ice-thickness errors computed at the grid points are assumed to be uncorrelated, and overestimated if they are considered to be linearly dependent. These estimates differ in orders of magnitude, both between themselves and when compared to our more realistic estimate of the error in volume, revealing the importance of providing the statistics used along with the individual error sources to obtain uncertainty estimates. We have shown that the integral range of the variogram function of an ice-thickness error DEM is a good parameter to estimate the number of independent values at the grid cells. It is obtained via the range of the variogram, and is used to obtain an estimate of the error in volume resulting from the errors in ice thickness.
In the case study of Werenskioldbreen, adopting an error in area of 8%, both components of the error in volume, related to errors in thickness and to errors in area, have the same order of magnitude, although the value of the latter is strongly dependent on the accuracy of the glacier delineation. We expect that, in glaciers with larger errors in area, the error in boundary delineation could become the largest error component of the total error in volume.
ACKNOWLEDGEMENTS
We thank the scientific editor, Jo Jacka, and two anonymous reviewers for their valuable comments and suggestions that helped improving the quality of this paper. This research was supported by grants CTM2011-28980 and CTM2014-56473-R from the Spanish National Plan for R&D. We thank Jacek Jania and Mariusz Grabiec (Faculty of Earth Sciences, University of Silesia) and Dariusz Puczko (Institute of Geophysics, Polish Academy of Sciences) for making available to us Werenskioldbreen GPR data.







