Buoyancy-driven lacustrine calving, Glaciar Nef, Chilean Patagonia

Abstract

Glaciar Nef, a 164 km² eastern outlet of Hielo Patagónico Norte (the northern Patagonia icefield), terminates in a proglacial lake that has formed in conjunction with 20th-century glacier retreat. The terminus is inferred to be transiently afloat. A hinge-calving mechanism is proposed in which buoyant forces impose a torque on the glacier tongue, resulting in the release of coherent sections of the glacier tongue as “tabular” icebergs. A simple model shows how torque and tensile stress reach a maximum at the up-glacier limit of the buoyant zone, and that glacier thinning causes this point to migrate up-glacier. Empirical evidence supporting this model includes elevated thermo-erosional notches ≤6.5 m above lake level, and the ubiquitous presence since 1975 of “tabular” icebergs with surface areas ≤0.3 km². Flow speeds of 1.2–1.3 m d⁻¹ were measured near the terminus in February 1998. Extrapolations from these short-term data yield a calving rate of 785–835 m a⁻¹ and a calving flux of 232 × 10⁶ m³ a⁻¹ or 0.2 km³ a⁻¹. The calculated mean water depth at the terminus is 190 m. This calving rate is higher than at grounded temperate glaciers calving in fresh water, but is nevertheless almost an order of magnitude less than calving rates at both grounded and floating tidewater glaciers.

Introduction

Despite its obvious importance for the dynamics of many ice masses worldwide, calving remains a poorly understood process (Van der Veen, 1996). Of the three known categories of calving glacier — polar/floating, polar/grounded and temperate/grounded — the last is probably the best understood, as a consequence of detailed studies of tidewater glaciers in Alaska (Meier and Post, 1987; Powell, 1990, 1991; Meier, 1997; Van der Veen, 1997). Lacustrine calving, however, has received relatively little attention. Studies in Europe in connection with hydropower schemes (Funk and Röthlisberger, 1989; Hooke and others, 1989; Kennett and others, 1997) have shown that the well-established correlation between calving rates (u _c) and water depth (h _w) at tidewater glaciers in which u _c increases linearly with h _w (Brown and others, 1982; Pelto and Warren, 1991) also applies in lacustrine settings.

However, for any given depth of water, calving rates appear to be at least an order of magnitude less in fresh water than in tidewater. Explaining this surprising contrast is an important glaciological challenge (Meier, 1997; Hanson and Hooke, 2000) and has stimulated studies of the dynamics and glacio-climatic response of lacustrine calving glaciers in Greenland (Warren, 1991), New Zealand (Kirkbride and Warren, 1997, 1999) and Patagonia (Warren, 1994, 1999; Warren and others, 1995c; Naruse and others, 1997; Skvarca and Naruse, 1997; Harrison and Winchester, 1998; Rott and others, 1998; Naruse and Skvarca, 2000; Harrison and others, in press). These studies have confirmed the contrast in calving rates and proposed some preliminary process explanations. Although calving rates correlate positively with water depth, this may not be a causative correlation. The water-depth model has been challenged by Van der Veen and co-workers, who argue that terminus position is controlled by the ice thickness in excess of flotation (Van der Veen, 1996, 1997; Venteris and others, 1997; Venteris, 1999). The significance of the salinity of the proglacial water body has also been questioned using comparative data from Alaska and Patagonia (Venteris, 1999). A physical basis for the water-depth–calving-speed relation has been proposed by Hanson and Hooke (2000), who conclude that the influence of water depth on longitudinal deviatoric stresses near the terminus is one of many possible controls on calving speeds.

The primary aims of research carried out at Glaciar Nef, Patagonia, in February 1998 were to derive a calving rate, examine calving mechanisms and to chart the evolution of terminus geometry during historic glacier retreat. The results reported here contribute to the emerging regional dataset of calving statistics for Patagonia (Warren and Aniya, 1999). The building of such regional databases of calving-glacier statistics was one of several key recommendations of an international workshop on calving (Van der Veen, 1997) because “little progress can be made towards the goal of understanding calving processes without observational data” (Krimmel, 1997, p. 17). At present such data are limited.

Geographical Setting and Description

Three mountain icefields with a total area of some 19 200 km² exist in southernmost South America (Warren and Aniya, 1999), nourished by the westerlies which deliver 6000–8000 mm a⁻¹ of precipitation (Escobar and others, 1992; Rott and others, 1998). Although they remain poorly known (Warren and Sugden, 1993; Lliboutry, 1998), knowledge is increasing rapidly, especially through the use of satellite imagery (Aniya and others, 1996; Aniya, 1999) and spaceborne radar imagery (Rignot and others, 1996a, b; Forster and others, 1999; Michel and Rignot, 1999; Skvarca and others, 1999; Aniya and others, 2000). Since calving glaciers constitute a large and increasing majority of all outlet glaciers, icefield behaviour is inextricably linked with calving dynamics (Naruse and others, 1995a; Aniya and others, 2000), significantly complicating climatic and palaeoclimatic interpretations of glacier behaviour (Aniya, 1999; Luckman and Villalba, 2001). This has focused attention on calving dynamics (Naruse and others, 1995a, 1997; Warren and others, 1995a, b, 1997; Rott and others, 1998; Warren, in press).

Glaciar Nef (47°06′ S, 73° 11′ W) is one of eight major outlet glaciers which drain the eastern flank of Hielo Patagónico Norte (HPN; northern Patagonia icefield) (Fig. 1). The glacier has a surface area of 164 km² and is 33 km long, descending from its icefield accumulation area at 2800 m a.s.l. to a 1.4 km wide calving terminus in Lago Nef at 420 m a.s.l. (Aniya, 1988). The equilibrium line lies at around 1350 m a.s.l., indicating an accumulation-area ratio of 0.60 (Aniya, 1988). In 1975 the average surface gradient of the lower 10 km was 2° or 1 : 38.The northeastern side of the glacier currently consists of profusely crevassed clean ice (Fig. 2), but on its southwestern side, upstream of a large embayment, medial and lateral moraines merge to mantle the glacier with supraglacial debris. This area derives from a tributary glacier whereas the calving terminus is sourced from the icefield. The calving front rises some 25–30 m above lake level at its centre, becoming lower towards both margins, and descending to water level at its northeastern end where, for a short distance, the ice margin parallels the shoreline and transverse crevasses form drowned re-entrants (Fig. 2). This configuration has changed little since November 1995 (personal communication from M. Aniya, 1997).

Fig. 1. The location of Glaciar Nef The terminus is shown at its 1975 position. Simplified from 1 : 50 000 “Cordón Soler” sheet (Instituto Geográfico Militar de Chile). Insets: Hielo Patagonico Norte highlighting Glaciar Nef drainage basin (based on Aniya (1988)), and the location of HPN in South America.

Fig. 2. The terminus of Glaciar Nef from the northeast, February 1998.

Previous work on the glacier is limited. Yoshida (1981) undertook preliminary geomorphological observations around Lago Nef, and Casassa (1987) reported a maximum ice thickness of 1000 ± 250 m in the upper part of Glaciar Nef. From a firn core obtained in the accumulation area, Matsuoka and Naruse (1999) derived accumulation and ablation values for 1996 of +5.6 and −3.4 m w.e., respectively, yielding a net balance of +2.2 m w.e. The only other work relating to the glacier has been low-level aerial observations of glacier-terminus change around HPN by Aniya and co-workers (Aniya and Enomoto, 1986; Aniya, 1992, 1999; Wada and Aniya, 1995; Aniya and Wakao, 1997) and analysis of change using RADARSAT and Landsat imagery (Aniya and others, 2000).

Glaciar Nef retreated during the 20th century, in common with the broad regional trend (Aniya and Enomoto, 1986; Aniya, 1999), and Lago Nef has formed and grown in conjunction with this retreat. Lichenometric evidence suggests that the terminus lost contact with its terminal moraine in the late 1930s (V. Winchester and others, unpublished data), and by 1944 a small arcuate ice-contact lake existed (Aniya and Enomoto, 1986). The lake is now some 4.5 km long and about 1.5 km wide. In February 1998 a profusion of icebergs choked almost the entire lake, with only small areas of open water at the northwest and southeast ends (Fig. 3). Prominent vegetation trimlines along the valley sides mark the 19th-century maximum (Fig. 3; Fig. 7, shown later), retreat from which is dated to about 1860 by lichenometry and dendrochronology (Winchester and others, in press). The southeastern end of the lake consists of a composite terminal moraine ridge some 500 m wide and rising ≤40 m above the lake. Río Nef, a tributary of Río Baker, at present begins at a prominent breach in this morainic rampart, but several large palaeo-channels cut across and skirt around the moraines. Some meltwater also drains northwards to the Río Soler down a side valley up-glacier from the terminus (Fig. 1).

Fig. 3. Lago Nef and Glaciar Nef from the terminal moraines at the southeastern corner of the lake, February 1998. Note the 3 m long inflatable boat for scale. 19th-century vegetation trimlines are visible on the valley sides.

Methods

Ice velocities

Surface ice velocities near the terminus were measured over an 8 day period (15–23 February 1998) with intermediate surveys on 17, 19 and 21 February. Displacement of prominent seracs was surveyed with an electronic distance meter (EDM)/theodolite from a 146 m baseline established on the southwestern (true right) valley side some 2.3 km from the glacier terminus (Fig. 4). Precipitous, unstable valley sides and the profusion of icebergs made closer approach impossible. The choice of the baseline and the seracs was dictated by the topography of the valley side and of the glacier surface.

Fig. 4. Measured and inferred bathymetry of Lago Nef Solid isobaths (25 m interval) indicate measured bathymetry, and dotted isobaths (50 m interval) represent inferred bathymetry (for explanation see text). Also shown are the seracs (A–D) on Glaciar Nef used for the velocity survey, the velocity survey baseline, the location of the survey station for the bathymetric survey, and the location of the meteorological station.

Bathymetry

Water depths in the southeastern third of the lake were measured with a Lowrance X-60 echo sounder with an instrumental accuracy of 3% of water depth, mounted on a small inflatable boat. Because icebergs prevented shore-to-shore transects, spot soundings were measured in all accessible open-water areas. The location of each sounding was surveyed with an EDM/theodolite sighting onto a prism in the boat from a survey station 58 m above lake level on the southwestern lateral moraines (Fig. 4).

Water temperatures

Five vertical water-temperature profiles were measured in the southeastern sector of the lake using an electronic water sensor with a maximum depth capability of 100 m that was designed and calibrated in the U.K. by the Institute of Freshwater Ecology. The temperature at each depth was averaged from down- and up-profiles. Laboratory calibration proves an accuracy of ±0.02°C, but under field conditions an accuracy closer to ±0.1°C is more likely.

Iceberg dimensions and meteorological observations

The heights and long axes of the largest icebergs were surveyed from the valley side. Subaqueous, near-surface geometry of icebergs near the southeastern end of the lake was investigated from the boat. Daily observations of air temperature (maximum and minimum), rainfall and sun hours were made at a station at the southeast end of Lago Nef (Fig. 4).

Results

Characteristics of historic glacier retreat

The pattern of retreat of Glaciar Nef from the 19th-century maximum to 1998 is summarized in Figure 5. Two aspects are noteworthy. Firstly, retreat from the 1860s to the 1930s was slow despite significant surface lowering; 70 years after the onset of retreat the terminus was still in contact with part of the terminal moraine complex, and even as recently as 1984 the glacier was only 150 m from the moraine, a linear net retreat rate of just 3 m a⁻¹ over the previous 50 years.

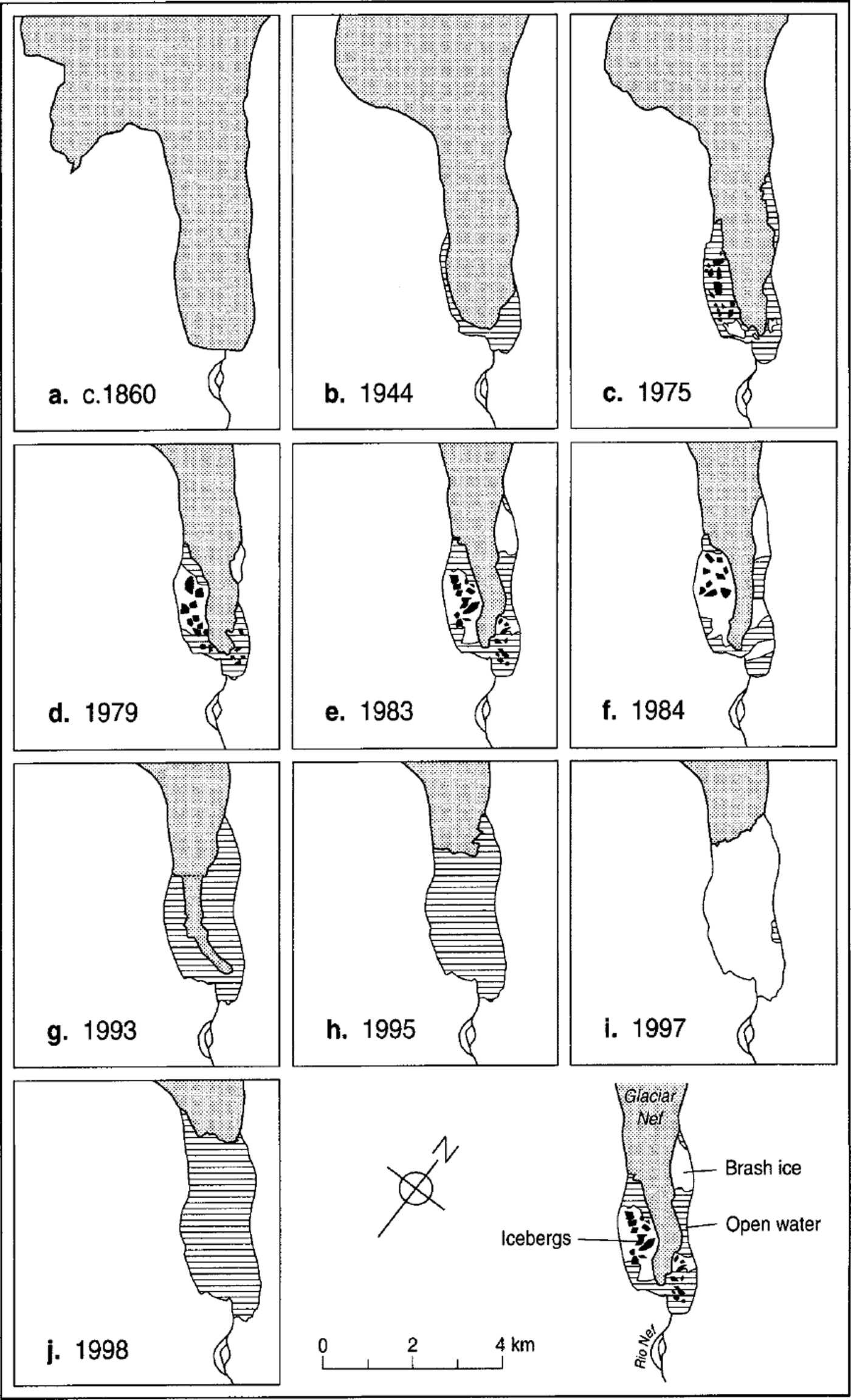
Fig. 5. Fluctuation history of Glaciar Nef from the mid-19th century to 1998. The 19th-century position is based on trimline evidence, and the date of about 1860 on lichenometric and dendrochronological data collected in 1998 (Winchester and others, in press). Icebergs, areas of brash ice and locations of transverse crevassing are shown only for the years with vertical aerial photographs; in 1997 almost the entire lake was choked with icebergs and brash ice, but the RADARSAT image does not permit icebergs to be resolved. The inferred transverse crevasse in panel h shows the line along which the tongue fractured between December 1993 and May 1994 (Wada and Aniya, 1995). Sources: vertical aerial photographs of November 1944, March 1975, March 1979, January 1983, March 1984; oblique aerial photographs of December 1993 (M. Aniya), November 1995 ( M. Aniya ); RADARSAT image of January 1997 (from Aniya and others, 2000); fieldwork in February 1998.

Secondly, from 1944 to 1984 the terminus narrowed by about 1000 m and thinned vertically by ≤90 m (= 2.25 m a⁻¹) (Aniya and Enomoto, 1986), but the location of its front point changed little, even advancing a few tens of metres between 1975 and 1979. Even in the early 1990s when it was narrowing at ≤117 m a⁻¹, little retreat occurred (Wada and Aniya, 1995). Then, at some time between 29 December 1993 and 10 May 1994, the 2.25 km long tongue of ice calved and broke up in the lake (Wada and Aniya, 1995), fracturing along the line shown in Figure 5g. This event contributed significantly to the total area lost during 1987–97 of 2.07 km²; in terms of percentage change to glacier surface area, this is the largest recent loss at any HPN glacier (Aniya and others, 2000). Just prior to its disintegration, the whole tongue drifted south a short distance (Aniya and others, 2000). The position of the northeastern glacier/rock junction remained almost unchanged between 1993 and 1998 while the terminus retreated 3.5 km at 875 m a⁻¹. Thus the dramatic onset of runaway recession in 1994 lagged the transition from a land-terminating to a calving terminus by 50–60 years.

Crevasse patterns, thermo-erosional notches and iceberg characteristics

During the 1944–94 period when the terminus consisted of a narrowing tongue, surface crevassing was dominantly longitudinal (Fig. 6). However, from 1975 all the vertical aerial photographs also show a narrow zone of transverse crevasses cutting the longitudinal set at 70–90° (Fig. 5). In all cases, the transverse crevasses exist either at −635 ± 35 m up-glacier from the terminus and/or at twice that distance up-glacier at −1300 ± 80 m. In the 1984 vertical aerial photograph and in a low-level oblique aerial photograph taken by the first author on 29 January 1991, the final few hundred metres of the glacier exhibit a reverse slope. In 1984 the transverse crevassing coincides with a zone in which the lateral ice margins are at lake level, down-glacier from which the ice surface rises towards a cliffed terminus.

Fig. 6. Vertical aerial photograph of the lower part of Glaciar Nef in March 1979 (Instituto Geográfico Militar de Chile). Note the large icebergs and the dominantly longitudinal crevassing.

In 1998, a set of horizontal thermo-erosional notches was present along the entirety of the 700 m long cliffed section of the glacier terminus (Fig. 7). The highest and most pronounced of these notches was 6.5 m above the waterline. One possible explanation for these would be a high lake stand. However, a recent 6.5 m rise of lake level would have left abundant evidence on the unconsolidated valley sides around Lago Nef, as well as downstream along the valley of Río Nef, but there was no evidence of lake stands greater than +0.5 m. The notches are therefore interpreted as having been formed at lake level by thermal erosion and subsequently raised to their observed position by buoyancy-driven upward displacement of the glacier terminus.

Fig. 7. Part of the calving terminus of Glaciar Nef, showing the highest thermo-erosional notch (arrowed) 6.5 m above the waterline. Note also the vegetation trimlines on the valley sides.

In combination, these observations of transverse crevassing, reverse slopes and elevated thermo-erosional notches suggest that the terminus of Glaciar Nef has been close to or at flotation (i.e. transiently afloat) since 1975. The preservation of these notches along 700 m of the terminus shows that large calving events are infrequent, and that even small-scale calving is rare between the large events. No calving was observed during the fieldwork in 1998.At least since 1975, calving has typically consisted of low-frequency, high-magnitude events. All the vertical aerial photographs show icebergs with long axes of several hundred metres (e.g. ≤460 m, 1979; ≤540 m, 1983) (Figs 5 and 6). In 1998, many of the large icebergs had long axes in excess of 300 m (maximum = 600 m), surface areas of the order of 0.05–0.3 km², and were floating 30–50 m above water level. This is ≤20 m higher than the highest sections of the calving terminus. The preservation of the surface morphology of the lower glacier on many large icebergs (Fig. 8) demonstrates that they have calved without overturning. These characteristics are also apparent in 1995 oblique aerial photographs taken by M. Aniya. Several of the large icebergs were observed to drift, showing that they were free-floating, not grounded.

Fig. 8. Large “tabular” icebergs on Lago Nef, February 1998, showing the preservation of the surface morphology of the lower glacier.

Despite surface water temperatures <0.5°C, most of the icebergs at the southeast end of the lake possessed subaqueous shelves 0.2–1.0 m below the waterline and projecting as much as 25 m beyond their subaerial portions. These unusually extensive subaqueous projections are probably formed by the combination of intense insolation and very cold water, together with the effect of subaerial meltwater runoff.

Bathymetry

The measured and inferred bathymetry of Lago Nef is shown in Figure 4. Minimum estimates of water depth in the parts of Lago Nef that were inaccessible in 1998 can be inferred using two lines of evidence: the height of the glacier terminus, and estimates of the draughts of the largest icebergs.

If the glacier terminus is in hydrostatic equilibrium, the evidence for upward displacement of the terminus permits a calculation of the water depth (h _w) at the terminus. For hydrostatic equilibrium, the minimum water depth required for flotation is:

(1a)

where h ₀ is the thickness of ice above the waterline. Since, in the present case, the prominent thermo-erosional notch is 6.5 m above the present waterline, this must be the minimum depth of water beneath the ice, created by uplift. Thus,

(1b)

For h ₀ = 25 m, this yields a water depth of 231.5 m. High void ratios in greatly crevassed glaciers can reduce the height of the effective ice surface relative to that of mean visible (serac top) surface by several metres (Meier and others, 1994). Thus, the calculated water depth should be regarded as a maximum. Note that the glacier margin could have been in hydrostatic equilibrium both at the time the thermo-erosional notch was cut and at the time of observation, if uplift was driven by surface ice ablation.

However, the fact that the upper surfaces of several of the large, free-floating “tabular” icebergs are at a height ≤20 m above the glacier terminus indicates that it is not in hydrostatic equilibrium and that, upon release, the icebergs rise to achieve equilibrium. If so, Equation (1b) underestimates h _w. The wide distribution of large, non-grounded icebergs in the lake indicates that it is steep-sided with a substantial area of deep water. Taking account of void space, the geometry and surface heights of the icebergs suggest that parts of the lake must be >300 m deep. In support of this inference, ice-thickness data from 1985 (Casassa, 1987) indicate a maximum water depth close to the present terminus of 307 m. For testing the correlation between calving speed and water depth, the crucial information is the width-averaged water depth at the glacier terminus. Figure 4, constructed using the above inferences, suggests that the mean water depth at the calving front is 190 m.

Water temperatures

Water temperatures were low and varied insignificantly, either spatially, temporally or with depth. This is unsurprising in a lake dominated by floating ice. The southeast end of the lake was essentially isothermal. Maximum and minimum recorded temperatures were 0.48° and 0.28°C, respectively, and even during windless, sunny days the surface temperature rose by <0.1°C. Thin lake ice formed most nights and melted by mid-morning.

Ice velocities

Ice-velocity data are given in Table 1. Results were obtained from only four points due to the limited number of distinctive seracs with flow vectors that were suitably oriented with respect to the baseline. Ice velocities for the southwestern part of the terminus could not be determined, because ice flow in this area was towards the baseline. Some of the early intermediate surveys of seracs A and B yielded spurious results, so data for later periods were used. Extrapolations to annual values are given to facilitate comparison with other calving data which are conventionally expressed as annual figures. There is evidence that seasonal variability in flow speed in Patagonia is limited (cf. discussion in Warren (1999)), and thus that extrapolations from seasonal to annual values can be meaningful. Nevertheless, given the short measurement period, these data permit only the provisional estimate that the width-averaged flow speed close to the terminus is of the order of 0.8–1.0 m d⁻¹ or 300–350 m a⁻¹.

Table 1. Displacements of seracs near the terminus of Glaciar Nef, 15–23 February 1998. Locations of seracs are shown in Figure 4

Meteorological observations: the 1997/98 El Niño

One of the strongest El Niño events in recent decades peaked in February 1998. It affected Patagonia to an unusual extent due to a Southern Oceans anticyclone that was anomalously intense and east-shifted relative to previous large El Niño–Southern Oscillation (ENSO) events (Winchester and others, 1999). The sustained calm, sunny conditions which resulted may have contributed to the minimal calving activity. Mean daily maximum and minimum temperatures were 17° and 4.5°C, respectively.

Discussion

Characteristics of glacier retreat

During the 20th century, most HPN outlet glaciers have retreated, coincident with a warming of 0.4–1.4°C south of latitude 46° S since the beginning of the century (Rosenblüth and others, 1995). In the period 1944–96, HPN lost 1% of its surface area (Aniya, 1999). However, the rates and timings of glacier recession have been rather variable (Aniya and Enomoto, 1986; Aniya, 1999). In particular, an east–west contrast is apparent in the historic and current behaviour of many of the outlet glaciers (Aniya, 1988; Warren and Sugden, 1993). Recession generally accelerated during the 1970s and 1980s (Lliboutry, 1998), but during the 1990s retreat rates of most glaciers decreased, with several achieving stability or readvancing small distances. This probably reflects a delayed response to a marked precipitation increase from the 1970s (Winchester and Harrison, 1996; Harrison and Winchester, 1998; Aniya, 1999). However, four lacustrine calving glaciers (Reicher, Gualas, Steffen, Nef) experienced accelerated retreat in the 1990s as narrowing termini calved and/or broke up in ice-contact lakes (Wada and Aniya, 1995; Aniya and Wakao, 1997). Since 1990 the climatically-driven trend seems to have been towards more positive mass balances, with some dynamically induced noise superimposed (e.g. calving; debris cover). As suggested by Aniya (1999), the rapid calving retreats during the 1990s are most probably delayed responses to negative mass balance during earlier decades.

The geometry of the recent retreat at Glaciar Nef is noteworthy for two reasons. Firstly, a pattern of terminus narrowing and downwasting followed by rapid recession seems to be characteristic of lake-calving glaciers following the noncalving/calving transition. In recent decades, for example, such a pattern has been observed at lacustrine glaciers in Norway (Theakstone, 1989), Patagonia (Warren, 1994; Aniya, 1999) and New Zealand (Kirkbride, 1993; Hochstein and others, 1998). The formation of long, narrow tongues of this kind is not, however, known to occur at tidewater glaciers. This concurs with previous work which concluded that lacustrine glaciers are inherently more stable than tidewater glaciers (Warren, 1991). Secondly, the unchanging position of the northeastern glacier/rock junction while the terminus retreated >3.5 km in pivotal fashion during the 1990s is an interesting example of the role of topographic pinning points (cf. Mercer, 1961; Warren, 1991) in the stability and evolution of calving termini.

Buoyancy-driven calving

Evidence and interpretation

Calving at Glaciar Nef consists of high-magnitude, low-frequency events, producing some of the largest icebergs in Patagonia. Four lines of evidence demonstrate the importance of buoyant forces at this site since 1975:

thermo-erosional notches ≤6.5 m above lake level, indicating upward displacement of the glacier terminus.

transverse crevasses cutting the narrow ice tongues of the 1970s and 1980s; in 1984 and 1991 these are coincident with a transition from normal to reverse slopes.

the ubiquitous presence of large “tabular” icebergs floating ≤20 m above the terminus and in their original orientation (i.e. not having overturned). The vertical aerial photographs and observations by Aniya in 1995 show that this has been typical at least since 1975 (cf. Fig. 6).

the southward drift of the narrow glacier tongue just prior to its disintegration early in 1994 is interpreted by Aniya and others (2000) as being indicative of flotation.

What combination of processes and factors simultaneously inhibits “normal” calving (with the production of prismatic icebergs) while promoting buoyancy-driven calving (with the production of “tabular” icebergs)? Two primary candidates are:

rapid thinning combined with slow terminus retreat progressively reducing the surface gradient until buoyant uplift of the glacier tongue occurs.

ice near the terminus approaching flotation, causing basal shear stress to decrease to zero.

Aerial photographs show that open transverse crevasses are absent from most of the lower part of the glacier, indicating that the glacier terminus is not undergoing longitudinal extension. This will inhibit small-scale calving, especially given near-freezing water temperatures which will result in low rates of waterline and subaqueous melting (cf. Kirkbride and Warren, 1997). In the absence of tidal flexure and wave action, both of which can promote calving in tidewater settings, surface melting becomes the dominant ablation process. Limited data on ablation rates and ice-thickness change on eastern outlet glaciers of the Patagonian icefields suggest that Glaciar Nef could lose 4–11 m a⁻¹ of ice thickness close to the terminus (Kobayashi and Saito, 1985; Naruse and others, 1995a, b, 1997). We suggest that it is surface ice loss which causes large, coherent sections of the tongue to reach flotation, creating an upward bending moment which causes calving.

A model of buoyant calving

The principle of buoyancy-driven calving is illustrated and tested in a simple model of a water-terminating glacier tongue (Fig. 9a). The ice terminates in water with depth h _w, rests on a horizontal bed and has a constant gradient a. We assume that longitudinal stresses are negligible. The ice thickness required for flotation is:

(2)

where ρ _w and ρ _i are the densities of water and ice, respectively. The ice tongue will be buoyant where the ice thickness, h _i, is less than h _n. The magnitude of the buoyant force is found from:

(3)

where g is gravitational acceleration. σ_z is positive downwards, and negative σ_z corresponds to buoyant ice. Buoyancy produces a torque in the ice, and at a distance x _i from the ice margin the torque (bending moment) is given by:

(4)

Fig. 9. (a) Definition sketch of an ice tongue with a buoyant margin. (b) Development of torque (M) and longitudinal stresses σ_x arising from the buoyant forces.

The torque acts around a horizontal neutral axis located at y = 0.5 h _i and results in compressive stresses in the x direction above the neutral axis, and corresponding tensile stresses below the neutral axis, rising to a maximum at the ice base (Fig. 9b). The tensile stresses are opposed by cryostatic pressure, and the tensile stress at the ice base is given by:

(5)

(positive σ_{x max} = compressive; negative σ_{x max} = tensile). I is the moment of inertia, and is related to the shape of the cross-section. For a rectangular cross-section of unit width,

(6)

For an ice tongue with an initial terminal thickness h_n , surface ablation will result in the formation of a buoyant marginal zone, which will lengthen as the ice progressively thins. The torque and σ_{x max} produced by the buoyant ice are at a maximum at the up-glacier limit of the buoyant zone, where h _i = h_n . Figure 10 shows calculated values of σ_{x max} for α = 5° and a = 2°, for a range of terminal ice thicknesses. As ice thickness decreases, the basal tensile stress increases, and the point of greatest tensile stress migrates up-glacier. For a given terminal ice thickness, basal tensile stresses are greater for α = 2° than α = 5° because low-gradient ice tongues can become buoyant over a greater length of the snout.

Fig. 10. Basal tensile stresses resulting from buoyant forces for a range of terminus ice thicknesses and surface gradients of 5° and 2°. The calculated stresses are based on the assumption that the ice remains in contact with the bed, and that buoyant forces are unresolved by upwarping of the ice. Upwarping rates will increase, and fracture becomes increasingly likely as the length of the buoyant zone increases. Fracture will be encouraged by high ablation rates.

The evolution of basal tensile stresses with decreasing ice thickness shown in Figure 10 assumes that the position of the ice base does not change through time, and that buoyant forces are unresolved by ice creep. However, upward bending of the ice will occur in response to the torque imposed by the buoyant forces, due to longitudinal extension and thinning below 0.5 h _i and longitudinal shortening and thickening above h _i. Upward bending will reduce the buoyant forces acting on the ice tongue, and thus, at any point in time, the tensile stresses at the ice base will arise from the remaining buoyant forces unresolved by creep. Brittle failure will occur at the base of the ice when σ_{x max} exceeds the tensile strength of the ice: σ_{x max} > σ _crit. Since σ_{x max} occurs at the base of the ice, failure will commence at the glacier bed and propagate upwards. Failure is likely to be catastrophic, because fracture growth reduces the local ice thickness h _i, thus reducing the moment of inertia I, and increasing the tensile stress at the fracture tip (Equation (5)).

The tensile strength of glacier ice has been determined experimentally by Gagnon and Gammon (1995), who showed that for intact ice close to the pressure-melting point, tensile strength is about 1 MPa. Lower values (about 0.1–0.2 MPa) were calculated by Vaughan (1993) from the occurrence of crevasses on temperate glaciers, although these values relate to low-density near-surface firn rather than deep ice. Taking a value of 1 MPa as an upper limit, the model predicts that, in the absence of ice creep, buoyancy-driven fracture will occur on low-gradient glaciers at distances of 200–400 m from the terminus, depending on ice surface gradient. Despite the idealized nature of the model, it is interesting to note that during the last 25 years, while the glacier’s surface gradient has been ≤2°, icebergs have typically had dimensions of several hundred metres.

Determining rates of ice creep and upward bending for given ablation rates and ice geometries is beyond the scope of this paper. However, as a general point, it can be said that ice creep is more likely to fully accommodate evolving buoyant forces when ablation rates are low, and that unresolved tensile stresses are more likely to exceed the tensile strength of ice when ablation rates are high. Thus, for a buoyant ice tongue, upward bending of the snout is more likely to occur during the winter months, and fracture of the buoyant portion is more likely to occur in summer when ablation rates are high.

Adopting aspects of the model of Lingle and others (1993), the observations at Glaciar Nef in 1998 are suggestive of a three-stage response of the glacier as the terminus accommodates the increasing buoyancy-driven torque:

1. 1. In the initial stage, when terminal ice is slightly less than h_n , the buoyant zone is confined to a small portion at the end of the tongue. Because the torque and basal tensile stresses are small, ice-creep rates are low, and the buoyant terminal ice is held below hydrostatic equilibrium by the non-buoyant ice upstream. Thermal erosion at the waterline forms a notch.

2. 2. During the second stage, glacier thinning by surface ablation causes the limit of the buoyant zone to migrate up-glacier. Torque increases and the terminus begins to up-warp, lifting the thermo-erosional notch above lake level.

3. 3. The final stage involves catastrophic failure, either at the point of maximum moment (the up-glacier limit of the buoyant zone) or at a point where bottom topography introduces a local stress concentration. The entire terminal zone down-glacier of this point is then released as one or more icebergs. If the terminus does not achieve hydrostatic equilibrium through up-warping prior to calving, these icebergs will float higher than the glacier terminus.

The existence of multiple thermo-erosional notches demonstrates that the up-warping of the terminus is not instantaneous upon reaching flotation, but occurs progressively. In the late 1970s and 1980s, the up-glacier limit of the buoyant zone (inferred from the transverse crevassing) was located about 635 ± 35 m up-glacier from the terminus. Icebergs with long axes ≤600 m were present in Lago Nef in both November 1995 and February 1998, suggesting that even with a very different glacier-terminus geometry (cf. Fig. 5) the point of maximum moment may still be located approximately the same distance up-glacier of the calving front.

Comparison with previous observations

A role for buoyant forces in triggering lacustrine calving has previously been suggested from observations in Alaska (Lingle and others, 1993), Norway (Theakstone and Knudsen, 1986; Theakstone, 1989), Arctic Canada (Holdsworth, 1973) and in Iceland by Howarth and Price (1969) who propose a buoyancy-driven hinge-calving mechanism from work at Breiðamerkurjökull. At the same site, Derbyshire (1974) infers that sections of the terminus are close to or at flotation, and presents photographic evidence (plate IVb) showing many of the features reported at Glaciar Nef (e.g. large, flat-topped icebergs floating significantly higher than the terminal ice cliff). Additionally, the terminus zone exhibits a reverse slope, increasing in height from the base of an icefall a short distance up-glacier. This situation is also reported at Austerdalsisen, Norway, by Theakstone (1989).

Most pertinently, buoyant forces are invoked by Lingle and others (1993) in their proposal of an “inverse Reeh” calving mechanism (cf. Reeh, 1968) from observations at Bering Glacier. Prior to the arrival of the 1993 surge front, the terminus in Vitus Lake was held below hydrostatic equilibrium by the tensile strength of the uncrevassed ice; due to this positive buoyancy, icebergs which calved from the low calving cliff “popped up” and floated substantially higher than the general level of the terminus. “Normal” calving was apparently inhibited by the absence of crevasse-forming deformation during the 28 year quiescent period. Upon the arrival of the surge front in 1994, profuse, large-scale calving immediately ensued as substantial areas became afloat and broke up (personal communication from A. Post, 1995).

Powell (1990) and Alley (1991) argue that temperate glaciers cannot form floating ice shelves because abundant englacial and inter-crystalline water makes the ice too weak to resist calving in the absence of restraint from basal shear stress. The evidence reported here and in the studies cited above indicates that they can, albeit only locally and briefly. Lliboutry (1998) also infers periods of terminus flotation of several Patagonian glaciers from their 20th-century oscillations, and A. Post (personal communication, 1995) cites examples of temperate glacier tongues floating in lakes in Alaska. He stresses, however, that they can only survive when lateral or bottom topography provides stability; when they become free-floating they break up rapidly.

It has also been argued by Van der Veen and co-workers (Van der Veen, 1996, 1997; Venteris and others, 1997; Venteris, 1999) that once a calving glacier terminus thins below a flotation criterion (suggested to be about 50 m in excess of flotation) rapid calving ensues until the terminus has retreated to a position where its thickness exceeds flotation. It seems that this threshold is indeed significant for many calving glaciers. Equally, however, it is clear from this study and the observations of buoyant calving cited above that some glaciers thin beyond the flotation criterion without undergoing rapid calving retreat. At such glaciers, the key threshold is not 50 m in excess of flotation, but flotation itself. An important but unanswered question arises: what determines which of these two thresholds controls calving behaviour? It may well be significant that all the glaciers at which calving has been linked to buoyancy-induced stresses calve into lakes, not into tidewater. Longitudinal strain rates (or their absence) are also likely to be a significant factor.

Several studies have noted that the size/frequency distribution of icebergs produced by lacustrine calving is typically distinct from that in tidewater, with the former producing a higher percentage of large icebergs than the latter (Qamar, 1988; Warren, 1991; Kirkbride, 1993). Glaciar Nef represents an end member of this spectrum, with very large icebergs produced by hinge calving. Large, flat-topped icebergs have also been noted in ice-contact lakes in front of slow-flowing, debris-mantled glaciers (e.g. Miller Lake, Alaska (Reid and Callender, 1965); Hooker Lake, New Zealand (Warren and Kirkbride, 1998)), but these have been interpreted as the products of subaqueous calving from a submerged “ice foot” of the kind inferred by Kirkbride and Warren (1997) and described by Hunter and Powell (1998).

Calving rates

Tidewater vs fresh water

Mean calving rate (u _c in m a⁻¹) can be obtained from the equation:

(7)

where calving rate, u _c, is related to the rate of terminus change, u, and ice velocity, u _i, both averaged over the terminus width. Taking u to be 300–350 m a⁻¹, and u (January 1997–February 1998) to be −485 m a⁻¹, Equation (7) yields a calving speed of 785–835 m a⁻¹.This estimate does not incorporate melt rates along the calving face of Glaciar Nef. These are unknown, but are likely to be small (<20 m a⁻¹) relative to u _c, especially given water temperatures <0.5°C.

The standard form in which the u _c/h _w relationship is expressed is

(8)

where k is an empirical constant. For temperate tidewater glaciers in Alaska, k = 27.1 ± 2 a⁻¹ (Brown and others, 1982). The recent behaviour of Glaciar Nef is consistent with k = 4.3. Combining the ice-cliff height with a mean water depth of 190 m, the mean ice thickness at the calving front is taken to be 205 m. Given that u _i = 300–350 m a⁻¹ and that the glacier is 1400 m wide, this yields an annual mass flux at the terminus of approximately 86–100 × 10⁶ m³ a⁻¹.If u _c = 810 m a⁻¹, the annual calving flux is about 232 × 10⁶ m³ a⁻¹ or 0.2 km³ a⁻¹. Given that h _w is likely to be >190 m, these are minimum estimates.

These figures are approximate, but all of them indicate that the calving speed at Glaciar Nefis far below typical tidewater rates. For h _w = 190 m, the tidewater value of k predicts a calving speed of 5150 m a⁻¹, more than six times greater than the calculated calving rate. If h _w is in fact >250 m, a calving speed >6750 m a⁻¹ would be expected in tidewater, eight times faster than the calculated rate. These data thus strengthen the growing consensus that calving rates in fresh water are almost an order of magnitude less than in an equivalent depth of tidewater. Further, they indicate that even in deep lakes where the glacier terminus is intensely crevassed and reaches flotation, calving rates are still many times slower than tidewater calving speeds, despite the fact that they exceed typical rates for lacustrine calving.

Grounded vs floating

For grounded lake-calving glaciers, Funk and Röthlisberger (1989) and Warren and others (1995c) derived best estimates of k = 1.9 + 12 m a⁻¹ and k = 2.5 ± 0.5 m a⁻¹, respectively. The fact that k = 4.3 at Glaciar Nef is unsurprising given that buoyancy-driven hinge calving and grounded calving are different processes. It is unreasonable to apply a u _c/h _w relationship to a floating calving terminus, as it would imply that u _c increases with increasing h _w below the floating tongue. This is most improbable, unless basal melt rates are progressively enhanced, in turn accelerating calving in some way.

Although the value of k at Glaciar Nef is higher than that found in studies of lacustrine calving at grounded termini, it is nevertheless broadly compatible with such studies. Given the transiently floating condition of Glaciar Nef, this is curious, but it is consistent with Pelto and Warren’s (1991) study which found that u _c correlated with h _w at both grounded and floating termini. It is likely that glacier thickness (h _i) rather than h _w explains this apparent anomaly because calving studies have consistently found strong correlations between u _c, on the one hand, and both h _w and h _i on the other (Brown and others, 1982; Reeh, 1994). This highlights the difficulty of identifying the dependent and independent variables in the calving problem (cf. Venteris, 1999), and the perennial danger of interpreting correlation as causation.

Conclusions

The key findings of this work are:

1. 1. Imbalanced hydrostatic stresses at calving termini which reach flotation impose an upward-bending moment which leads to infrequent but high-magnitude hinge calving. At Glaciar Nef, such buoyancy-driven calving has been significant at least since 1975, and appears to have become dominant since 1994.

2. 2. Glaciar Nef flows at about 300–350 m a⁻¹ and calves at some 785–835 m a⁻¹ in a mean water depth ≥190 m. Much of Lago Nef is probably >200 m deep, and water temperatures are close to freezing. These results support existing data which indicate that calving rates in freshwater are many times smaller than in tidewater, and show that this is so even when the calving front is afloat and intensely crevassed.

3. 3. Unlike tidewater glaciers, at which the non-calving/calving transition typically leads to fast recession without delay, lacustrine glacier termini frequently undergo a phase of downwasting and narrowing prior to the onset of rapid terminus retreat. At Glaciar Nef, this phase lasted >50 years. In common with many previous studies of calving glaciers, the 20th-century fluctuation history of Glaciar Nef shows that dynamic and topographic controls can partially decouple glacier-terminus behaviour from the climatic signal over decadal time-scales.

4. 4. Available information from lacustrine calving glaciers shows that in terms of stability, dynamics and climatic sensitivity they form a population distinct from both tidewater glaciers and non-calving glaciers.