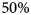Introduction
Bandpass filters are essential components in many microwave systems. The ever increasing system complexity requires filters that are compact and show good electrical performance.
Substrate integrated waveguides (SIWs) [Reference Xu, Zhang, Hong, Wu and Cui1, Reference Xu and Wu2] have been the object of extensive research in the last few years. They exhibit excellent shielding properties and can be manufactured in conventional printed circuit board (PCB) technology. As standard SIWs are rather bulky, miniaturized variants have been proposed. Folded SIWs [Reference Grigoropoulos and Young3], which require a multilayer PCB stack, achieve up to $50\%$![]() surface reduction [Reference Che, Geng, Deng and Chow4] and allow for compact filter designs [Reference Grigoropoulos, Sanz-Izquierdo and Young5]. Miniaturization can be pushed further by altering the cavity shape, as demonstrated with folded circular SIWs (FCSIWs) in [Reference Zhang, Wang, Yan and Xu6, Reference Sieganschin, Tegowski, Jaschke and Jacob7]. A subsystem based on such components has been successfully implemented in [Reference Sieganschin, Albrecht, Tegowski, Jaschke, Waldhelm, Lamann and Jacob8], while the authors in [Reference Sieganschin, Tegowski, Koelpin and Jacob9] address their application to higher-order filters. The multimode operation provides another – intrinsic – means to reduce the circuit size [Reference Huang, Zhou and Mao10, Reference Moro, Moscato, Bozzi and Perregrini11]. Besides, loading of SIW cavities is an alternative miniaturization approach [Reference Dong, Yang and Itoh12]. However, in contrast to folded SIWs, it impairs the shielding properties.
surface reduction [Reference Che, Geng, Deng and Chow4] and allow for compact filter designs [Reference Grigoropoulos, Sanz-Izquierdo and Young5]. Miniaturization can be pushed further by altering the cavity shape, as demonstrated with folded circular SIWs (FCSIWs) in [Reference Zhang, Wang, Yan and Xu6, Reference Sieganschin, Tegowski, Jaschke and Jacob7]. A subsystem based on such components has been successfully implemented in [Reference Sieganschin, Albrecht, Tegowski, Jaschke, Waldhelm, Lamann and Jacob8], while the authors in [Reference Sieganschin, Tegowski, Koelpin and Jacob9] address their application to higher-order filters. The multimode operation provides another – intrinsic – means to reduce the circuit size [Reference Huang, Zhou and Mao10, Reference Moro, Moscato, Bozzi and Perregrini11]. Besides, loading of SIW cavities is an alternative miniaturization approach [Reference Dong, Yang and Itoh12]. However, in contrast to folded SIWs, it impairs the shielding properties.
This work proposes miniaturization techniques for filters based on the FCSIW cavity introduced in [Reference Sieganschin, Tegowski and Jacob13]. Here, a compact 10 GHz filter with a large stopband is shown. The design relies on a novel type of FCSIW cavity. Compared to [Reference Zhang, Wang, Yan and Xu6] and [Reference Sieganschin, Tegowski, Jaschke and Jacob7], it possesses a modified septum with a gap along the outer edge instead of the tip. This septum shape leads to a significantly reduced cavity size and a larger stopband. Further miniaturization is achieved by tuning a higher-order mode for dual-mode operation. The present work proposes yet another step to substantially improve compactness by reducing the cavity dimensions while preserving its resonant frequency. To demonstrate this miniaturization concept, a novel X-band filter is presented and compared with the reference design from [Reference Sieganschin, Tegowski and Jacob13] as well as to the state of the art.
The remainder of this paper is organized as follows. Section “Cavity properties” presents the geometry and analyzes the electrical properties of the FCSIW cavity. Section “Filter designs” describes the design, the optimization, and the realization of both filters. Additionally, it compares the implemented components with the state of the art. Section “Conclusion” concludes the paper.
Cavity properties
Figure 1 illustrates the proposed FCSIW cavity. The vias with diameter d and pitch p form a sector cylinder with angle α, radius R, and height 2 h. The permittivity of the substrate inside the cavity is $\epsilon _r$![]() . A septum with a slot of width s and length x s is positioned in the middle.
. A septum with a slot of width s and length x s is positioned in the middle.

Fig. 1. Model of the FCSIW cavity with a slotted septum.
As R ≫ h, only modes that are transverse magnetic (TM) with respect to z need to be considered in the analysis. They are labeled TMnp0, with p = 1, 2, 3, … being the radial order and n = 0, 1, 2, … the azimuthal one. For n ≥ 1, the superscripts O and E distinguish between modes with a perfect electric conductor (PEC) and a perfect magnetic conductor (PMC) in the septum plane, respectively. Unless otherwise stated, it is assumed that $\epsilon _r = 3.62$![]() , s 0 = 0.35 mm, h = 0.3 mm, d = 0.4 mm, and p = 0.7 mm. The slot length x s is initially set to 0 mm. The electrical field magnitude of the fundamental TM010 mode and of the higher-order TM$_{110}^E$
, s 0 = 0.35 mm, h = 0.3 mm, d = 0.4 mm, and p = 0.7 mm. The slot length x s is initially set to 0 mm. The electrical field magnitude of the fundamental TM010 mode and of the higher-order TM$_{110}^E$![]() , TM$_{110}^O$
, TM$_{110}^O$![]() , and TM020 modes is shown in Fig. 2.
, and TM020 modes is shown in Fig. 2.

Fig. 2. Magnitude of the electrical field for (a) the TM010, (b) the TM$_{110}^E$![]() , (c) the TM$_{110}^O$
, (c) the TM$_{110}^O$![]() , and (d) the TM020 mode.
, and (d) the TM020 mode.
Figure 3(a) illustrates the resonant frequency of the fundamental TM010 mode versus the angle α for different R. The resonant frequency increases for smaller angles. However, when changing the angle from 90 to 30°, i.e. reducing the surface area by a factor of three, the resonant frequency increases by only about $20\%$![]() . Hence, the cavity can be significantly downsized without severely affecting the resonant frequency. The frequency shift can be compensated by increasing the cavity radius R.
. Hence, the cavity can be significantly downsized without severely affecting the resonant frequency. The frequency shift can be compensated by increasing the cavity radius R.

Fig. 3. Resonant frequency versus angle α of (a) the fundamental TM010 mode for different radii R (in mm) and (b) higher-order modes with R = 5.5 mm. An FCSIW cavity with b 0/R = 0.45 is assumed.
Higher-order modes need to be considered prior to the filter design, since they may create parasitic passbands and impair the stopband characteristics. As depicted in Fig. 3(b), the resonances of the fundamental and higher-order modes are quite far apart for smaller angles. However, due to the pronounced angular dependence of the higher-order mode resonances, the mode separation is reduced as α increases.
Cavity miniaturization
As will be shown in this section, the cavity can be miniaturized by controlling the parameter b 0 (see Fig. 1). As presented in Fig. 4, the resonant frequency of the fundamental TM010 mode decreases as b 0/R is reduced. This property enables to control the miniaturization of the FCSIW cavity.

Fig. 4. Resonant frequency of the fundamental TM010 mode of an unloaded FCSIW cavity versus the ratio b 0/R for different R (in mm) with α = 45°.
As an example, consider a design resonant frequency of f res = 10 GHz. For a cavity with R = 6 mm, b 0/R ≈ 0.45 has to be adjusted. Suppose b 0/R is reduced to 0.35. To maintain the resonant frequency of 10 GHz, the radius needs to be reduced to R′ = 5 mm. Thus, the cavity area is miniaturized according to the scaling factor
where R is the radius of the initial cavity and R′ is the radius of the scaled one. For the above example, $S = 30\%$![]() . Thus, a significant size reduction of the cavity is possible by reducing b 0/R while preserving its resonant frequency. It is noted that this miniaturization is an inherent property of the FCSIW cavity. Scaling the area of conventional cavity types, e.g.rectangular SIW cavities always increases their resonant frequency.
. Thus, a significant size reduction of the cavity is possible by reducing b 0/R while preserving its resonant frequency. It is noted that this miniaturization is an inherent property of the FCSIW cavity. Scaling the area of conventional cavity types, e.g.rectangular SIW cavities always increases their resonant frequency.
However, cavity miniaturization is geometrically limited. For very small b 0 values, the septum corners, marked with blue circles in Fig. 1, overlap, yielding completely different electromagnetic properties. Hence, the miniaturization needs an adjustment of technological parameters, i.e. the reduction of s 0, d, and p. This, on the other hand, increases the sensitivity to manufacturing tolerances.
Dual-mode operation
Besides the geometrical means already addressed, the compactness of the cavity can be improved even further by shaping its mode spectrum. In the following, the tuning of a higher-order mode is discussed, which enables dual-mode operation.
Figure 5 illustrates the surface current flow on the septum for the four relevant modes. Along the edge around φ = α/2, the currents of the TM010, TM$_{110}^O$![]() , and TM020 modes flow in radial direction and those of the TM$_{110}^E$
, and TM020 modes flow in radial direction and those of the TM$_{110}^E$![]() mode in azimuthal direction. Hence, a slot placed there (see Fig. 1) has almost no effect on the former modes, but strongly disturbs the latter one. This is confirmed in Fig. 6 which reports their resonant frequencies versus the slot length x s. The slot lowers the resonant frequency of only the TM$_{110}^E$
mode in azimuthal direction. Hence, a slot placed there (see Fig. 1) has almost no effect on the former modes, but strongly disturbs the latter one. This is confirmed in Fig. 6 which reports their resonant frequencies versus the slot length x s. The slot lowers the resonant frequency of only the TM$_{110}^E$![]() mode, which, for x s ≈ 3 mm, is about 10 GHz and thus very close to that of the TM010 mode. Figure 7 illustrates this effect. The slot forces the current of the TM$_{110}^E$
mode, which, for x s ≈ 3 mm, is about 10 GHz and thus very close to that of the TM010 mode. Figure 7 illustrates this effect. The slot forces the current of the TM$_{110}^E$![]() mode around the slot, which causes the resonant frequency to decrease. This enables dual-mode operation and simultaneously keeps spurious modes almost 30 GHz away.
mode around the slot, which causes the resonant frequency to decrease. This enables dual-mode operation and simultaneously keeps spurious modes almost 30 GHz away.

Fig. 5. Current density on the septum of (a) the TM010, (b) the TM$_{110}^E$![]() , (c) the TM$_{110}^O$
, (c) the TM$_{110}^O$![]() , and (d) the TM020 mode.
, and (d) the TM020 mode.

Fig. 6. Resonant frequencies of the first four modes and their dependence on the slot length x s for an FCSIW cavity with R = 5.5 mm, α = 45°, b 0/R = 0.45, and s = 0.2 mm.

Fig. 7. Magnitude of the electrical field of (a) the TM010 and (b) the TM$_{110}^E$![]() mode of a slotted FCSIW cavity. Current density on the septum of a slotted FCSIW cavity of (c) the TM010, and (d) the TM$_{110}^E$
mode of a slotted FCSIW cavity. Current density on the septum of a slotted FCSIW cavity of (c) the TM010, and (d) the TM$_{110}^E$![]() mode.
mode.
Intracavity mode coupling
Next, the coupling between the TM010 and the TM$_{110}^E$![]() modes within a cavity is analyzed. For this, the cavity is weakly coupled by a stripline at in- and output, as depicted in Fig. 8. The simulated transmission S 21 (Fig. 9) shows two resonances, with f 01 being the eigen-mode frequency of TM010. To clarify, whether they result from mode-splitting, the eigen-frequencies of the cavity are determined. For this, the TM010 (TM$_{110}^E$
modes within a cavity is analyzed. For this, the cavity is weakly coupled by a stripline at in- and output, as depicted in Fig. 8. The simulated transmission S 21 (Fig. 9) shows two resonances, with f 01 being the eigen-mode frequency of TM010. To clarify, whether they result from mode-splitting, the eigen-frequencies of the cavity are determined. For this, the TM010 (TM$_{110}^E$![]() ) mode must be excited by an even (odd) stimulus, as it satisfies the PMC (PEC) condition at the symmetry plane φ = α/2. According to [Reference Hong14], this translates into
) mode must be excited by an even (odd) stimulus, as it satisfies the PMC (PEC) condition at the symmetry plane φ = α/2. According to [Reference Hong14], this translates into
where S 11,e and S 11,o are the even- and the odd-mode S-parameters, respectively. The associated group delays are shown in Fig. 9. Their maxima, which mark the eigen-frequencies of the cavity, coincide with the magnitude peaks of S 21. Thus, no mode-splitting occurs and the modes are not coupled [Reference Hong14].

Fig. 8. Slotted FCSIW cavity coupled with a stripline at input (port 1) and output (port 2).

Fig. 9. S 21 (blue line) and group delays of S 11,e (red, solid line) and S 11,o (red, dashed line) of a weakly coupled dual-mode cavity.
Input/output coupling
The in- and output coupling of the slotted dual-mode cavity is discussed in this section. The coupling is controlled by the position of the stripline. Figure 10(a) illustrates a loaded two-port cavity with R = 5.5 mm. The previous subsection demonstrated no coupling between the TM010 and TM$_{110}^E$![]() modes within the cavity. Thus, the stripline at the input has to excite both modes and their external quality factors Q e must be similar. The latter can be independently extracted by an even and an odd stimulus [Reference Hong14], respectively.
modes within the cavity. Thus, the stripline at the input has to excite both modes and their external quality factors Q e must be similar. The latter can be independently extracted by an even and an odd stimulus [Reference Hong14], respectively.

Fig. 10. Loaded slotted dual-mode FCSIW cavity with (a) R = 5.5 mm and (b) R = 4 mm.
Figures 11(a) and 11(b) show the dependencies for both modes as b 0 varies. To match the resonant frequency of 10 GHz, the parameter b 0 needs to be 2.25 mm, which corresponds to an external quality factor of Q e ≈ 11.

Fig. 11. (a) External quality factor and (b) resonant frequency of the TM010 and TM$_{110}^E$![]() modes of the loaded slotted cavity with R = 5.5 mm and x s = 3.5 mm.
modes of the loaded slotted cavity with R = 5.5 mm and x s = 3.5 mm.
According to (1), the cavity is downsized by $S = 47\%$![]() as the radius reduces to R = 4 mm. Figure 12 reports the dependence of the cavity characteristics on b 0. To achieve a resonant frequency of 10 GHz, b 0 needs to be reduced to 1.7 mm, which also guarantees sufficient coupling. Thus, a filter based on a miniaturized cavity is feasible.
as the radius reduces to R = 4 mm. Figure 12 reports the dependence of the cavity characteristics on b 0. To achieve a resonant frequency of 10 GHz, b 0 needs to be reduced to 1.7 mm, which also guarantees sufficient coupling. Thus, a filter based on a miniaturized cavity is feasible.

Fig. 12. (a) External quality factor and (b) resonant frequency of the TM010 and TM$_{110}^E$![]() modes of the loaded slotted cavity with R = 4 mm and x s = 3 mm.
modes of the loaded slotted cavity with R = 4 mm and x s = 3 mm.
The downside of this scaling is marked in Fig. 10(b) with a blue circle. Here, the gaps around the feeding stripline and the septum slot become very small, which increases the demands on the manufacturing process.
Filter designs
In this section, two FCSIW cavity filters are designed. The first filter from [Reference Sieganschin, Tegowski and Jacob13] serves as a reference filter. The second filter additionally relies on the miniaturization techniques from Section “Cavity miniaturization.” Both filters possess a fourth-order Chebyshev characteristic in the passband, a center frequency of f 0 = 10 GHz, and a fractional bandwidth (FBW) of $10\%$![]() . Figure 13(a) shows the corresponding layout. It consists of two symmetrically arranged dual-mode cavities with α = 45°.
. Figure 13(a) shows the corresponding layout. It consists of two symmetrically arranged dual-mode cavities with α = 45°.

Fig. 13. (a) Schematic of the proposed filter and (b) the PCB stack.
Corresponding to the analysis from Section “Input/output coupling,” the parameter b 0 adjusts the in- and the output coupling, which is realized by a 50 Ω stripline. The interresonator coupling, which, among others, determines the filter bandwidth, is fine-tuned by b and b v. As explained above, the center frequency is controlled by the radius R, the slot length x s, and the length b 0. The coupling topology is depicted in Fig. 14. The operating modes TM010 and TM$_{110}^E$![]() of the same cavity are not coupled. The two dual-mode cavities thus lead to four transmission poles and two transmission zeros, which, due to symmetry, occur at the same frequency [Reference Guglielmi, Roquebrun, Jarry, Kerherve, Capurso and Piloni15]. The transmission zeros result from the simultaneous excitation of the TM010 and the TM$_{110}^E$
of the same cavity are not coupled. The two dual-mode cavities thus lead to four transmission poles and two transmission zeros, which, due to symmetry, occur at the same frequency [Reference Guglielmi, Roquebrun, Jarry, Kerherve, Capurso and Piloni15]. The transmission zeros result from the simultaneous excitation of the TM010 and the TM$_{110}^E$![]() modes. Indeed, the electrical field of the former one points in the same direction at the input and the output, whereas it changes the sign for the latter (see Figs 7(a,b)). This leads to destructive interference [Reference Guglielmi, Roquebrun, Jarry, Kerherve, Capurso and Piloni15, Reference Liu, Zhang, Tang, Deng and Zhou16]. The final dimensions are obtained from optimization with CST Microwave Studio Filter Designer 3D.
modes. Indeed, the electrical field of the former one points in the same direction at the input and the output, whereas it changes the sign for the latter (see Figs 7(a,b)). This leads to destructive interference [Reference Guglielmi, Roquebrun, Jarry, Kerherve, Capurso and Piloni15, Reference Liu, Zhang, Tang, Deng and Zhou16]. The final dimensions are obtained from optimization with CST Microwave Studio Filter Designer 3D.

Fig. 14. Coupling topology of the proposed filter with S and L representing source and load, respectively.
Both filters are manufactured on a multilayer PCB using Megtron 6 laminates from Panasonic with the stack shown in Fig. 13(b). The permittivity $\epsilon _r$![]() and the loss tangent tan (δ) are 3.62 and 0.005, respectively. Additionally, a hyper very low profile copper foil with a root mean square surface roughness of R q = 0.5 μm is used. The minimum realizable feature size is ≈100 μm.
and the loss tangent tan (δ) are 3.62 and 0.005, respectively. Additionally, a hyper very low profile copper foil with a root mean square surface roughness of R q = 0.5 μm is used. The minimum realizable feature size is ≈100 μm.
Reference filter
Figure 15 presents the manufactured reference filter [Reference Sieganschin, Tegowski and Jacob13]. For better manufacturability, the parameter b 0 is kept ≈2 mm. The operating modes of the manufactured cavities have simulated unloaded quality factors between 130 and 160. Table 1 lists the filter dimensions.

Fig. 15. Manufactured reference filter with the septum contour marked in blue. The reference planes for TRL calibration are indicated with RP.
Table 1. Dimensions of the manufactured reference filter

A Through-Reflect-Line (TRL) calibration is performed at the reference planes indicated in Fig. 15. Figures 16 and 17 show the narrowband and the wideband simulation and measurement results, respectively. Except for a frequency shift of 70 MHz, they agree very well. In the passband, the measured insertion loss remains below 2.4 dB and the reflection coefficient below −18 dB. The out-of-band rejection exceeds 40 dB between 11.2 and 30 GHz.

Fig. 16. Simulated (dashed) and measured (solid) filter responses S 11 (blue line) and S 21 (red line) of the reference filter.

Fig. 17. Simulated (dashed) and measured (solid) filter responses S 11 (blue line) and S 21 (red line) of the reference filter.
The measured stopband response does not show the pronounced transmission zeros which are both located at 13.77 GHz in simulation. This is due to the limited internal isolation of the used network analyzer.
Miniaturized filter
The cavity of the miniaturized filter is designed as mentioned in Section “Cavity miniaturization.” The miniaturization goal is to achieve scaling of $S = 50\%$![]() with respect to the reference filter [Reference Sieganschin, Tegowski and Jacob13]. To implement the miniaturized filter, parameters {d, s, p, s 0} are reduced to {0.2, 0.12, 0.4, 0.215} mm. This reduces the unloaded quality factor of the operating cavity modes to values between 116 and 120.
with respect to the reference filter [Reference Sieganschin, Tegowski and Jacob13]. To implement the miniaturized filter, parameters {d, s, p, s 0} are reduced to {0.2, 0.12, 0.4, 0.215} mm. This reduces the unloaded quality factor of the operating cavity modes to values between 116 and 120.
The manufactured filter is depicted in Fig. 18. Table 2 lists its dimensions. Similarly to the measurements of the reference filter, a TRL calibration is performed at the indicated reference planes. Figures 19 and 20 show the narrowband and the wideband simulation and measurement results of the miniaturized filter, respectively. They confirm its functionality and feasibility. The reflection coefficient is better than −10 dB and the insertion loss remains below 3.4 dB. The loss increase stems from the reduced unloaded quality factor.

Fig. 18. Manufactured miniaturized filter with the septum contour marked in blue. The reference planes for TRL calibration are indicated with RP.

Fig. 19. Simulated (dashed) and measured (solid) filter responses S 11 (blue line) and S 21 (red line) of the miniaturized filter.

Fig. 20. Simulated (dashed) and measured (solid) filter responses S 11 (blue line) and S 21 (red line) of the miniaturized filter.
Table 2. Dimensions of the manufactured miniaturized filter

The degraded reflection coefficient results from the increased tolerance sensitivity. The passband is shifted by 270 MHz. The out-of-band rejection exceeds 40 dB between 11.3 and 33 GHz. Additionally, the parasitic passband around 36 GHz is less pronounced for the miniaturized filter with a minimum isolation of 17 dB, in contrast to 5 dB for the reference filter (see Fig. 17). The reason for the significantly improved out-of-band behavior is the reduced radius R since it shifts the higher-order modes to higher frequencies. In general, a larger deviation between simulation and measurement in comparison with the reference filter results is observed. This is due to the smaller feature sizes which are more prone to tolerance effects. As an example, Fig. 21 analyzes the sensitivity of the reflection coefficient on the slot width s. Changing the slot width by 20 μm yields a reflection coefficient of −15 and −10 dB for the reference and for the miniaturized filter, respectively.

Fig. 21. Simulated S 11 of (a) the reference filter for s = 0.2 mm (blue) and s = 0.18 mm (red) and (b) the miniaturized filter for s = 0.12 mm (blue) and s = 0.1 mm (red).
Comparison with state of the art
Table 3 compares the presented filters with state-of-the-art SIW components, where the reference filter is labeled as F1 and the miniaturized one as F2. Here, λ 0 is the substrate wavelength at center frequency f 0. The last column reports the stopband normalized to f 0. The proposed filters exhibit the best performance in terms of real estate and out-of-band rejection. Compared to F1 [Reference Sieganschin, Tegowski and Jacob13], F2 is $50\%$![]() more compact, albeit having the same passband properties and even a better stopband behavior.
more compact, albeit having the same passband properties and even a better stopband behavior.
Table 3. Comparison with state-of-the-art SIW filters

Conclusion
This work presents two X-band filters with a center frequency of 10 GHz. They are based on a novel FCSIW cavity, where a slot in the septum enables dual-mode operation. Two such dual-mode cavities are connected to form fourth-order filters. Two filters are designed, which both are more compact than state-of-the-art components, the second one being even $50\%$![]() more compact than the first one. This is accomplished by exploiting the particular properties of the FCSIW cavity, which allow it to significantly downsize its dimensions without increasing its resonant frequency. This greatly improves the compactness as also verified experimentally. Besides, both filters exhibit a large stopband. The filters are especially suited for systems requiring a high integration density in conjunction with multilayer PCBs.
more compact than the first one. This is accomplished by exploiting the particular properties of the FCSIW cavity, which allow it to significantly downsize its dimensions without increasing its resonant frequency. This greatly improves the compactness as also verified experimentally. Besides, both filters exhibit a large stopband. The filters are especially suited for systems requiring a high integration density in conjunction with multilayer PCBs.
Acknowledgements
The authors acknowledge funding and support of this work by the German Aerospace Center (DLR) on behalf of the German Federal Ministry for Economic Affairs and Climate Action (BMWK) under research contracts 50 YB 1707 and 50 RK 1926.
Conflict of interest
The authors report no conflict of interest.
 Anton Sieganschin received his B.Sc. and M.Sc. degrees from the Hamburg University of Technology, Hamburg, Germany, in 2015 and 2017, respectively, where he is currently pursuing his Ph.D. degree at the Institute of High-Frequency Technology. His current research interest includes phased arrays, passive components, and component packaging.
Anton Sieganschin received his B.Sc. and M.Sc. degrees from the Hamburg University of Technology, Hamburg, Germany, in 2015 and 2017, respectively, where he is currently pursuing his Ph.D. degree at the Institute of High-Frequency Technology. His current research interest includes phased arrays, passive components, and component packaging.
 Bartosz Tegowski was born in 1997. He received his B.Sc. and M.Sc. degrees in electrical engineering from the Hamburg University of Technology, Hamburg, Germany, in 2019 and 2021, respectively, where he is currently pursuing his Ph.D. degree at the Institute of High-Frequency Technology. His current research interests include microwave filter design, electromagnetic theory, and radar system modeling.
Bartosz Tegowski was born in 1997. He received his B.Sc. and M.Sc. degrees in electrical engineering from the Hamburg University of Technology, Hamburg, Germany, in 2019 and 2021, respectively, where he is currently pursuing his Ph.D. degree at the Institute of High-Frequency Technology. His current research interests include microwave filter design, electromagnetic theory, and radar system modeling.
 Alexander Koelpin (S’ 04–M’ 10–SM’ 16) received his diploma in electrical engineering in 2005, his doctoral degree in 2010, and his habilitation in 2014 all from the University of Erlangen-Nuremberg (FAU), Germany. From 2005 to 05/2017 he was with the Institute for Electronics Engineering, FAU, Germany. From 2007 to 2010 he has been team leader, from 2010 to 2015 group leader of Circuits, Systems and Hardware Test and since 2015 leader of the group Electronic Systems. From 06/2017 to 02/2020 he was professor and head of the chair for Electronics and Sensor Systems with the Brandenburg University of Technology Cottbus-Senftenberg, Germany. Since 03/2020 he has been with the Hamburg University of Technology, Germany as professor and head of the Institute of High-Frequency Technology. Alexander Koelpin's research interests are in the areas of microwave circuits and systems, radar and wireless sensing, wireless communication systems, local positioning, and six-port technology. He has authored or co-authored more than 300 publications in his areas of interest. Furthermore, he serves as a reviewer for several journals and conferences, has been chair of the IEEE MTT-S technical committee MTT-24 from 2018 to 2020, since 2018 elected member and since 2020 vice chair of the IEEE MTT-S/AP German Chapter Executive Board, member of the Commission A: Electromagnetic Metrology of U.R.S.I., from 2012 to 2017 conference co-chair of the IEEE Topical Conference on Wireless Sensors and Sensor Networks, and served as conference chair for the 2020 German Microwave Conference as well as technical program chair for IEEE Radio and Wireless week 2021. In 2016 he has been awarded the IEEE MTT-S Outstanding Young Engineer Award and in 2017 with the ITG Award of the German VDE.
Alexander Koelpin (S’ 04–M’ 10–SM’ 16) received his diploma in electrical engineering in 2005, his doctoral degree in 2010, and his habilitation in 2014 all from the University of Erlangen-Nuremberg (FAU), Germany. From 2005 to 05/2017 he was with the Institute for Electronics Engineering, FAU, Germany. From 2007 to 2010 he has been team leader, from 2010 to 2015 group leader of Circuits, Systems and Hardware Test and since 2015 leader of the group Electronic Systems. From 06/2017 to 02/2020 he was professor and head of the chair for Electronics and Sensor Systems with the Brandenburg University of Technology Cottbus-Senftenberg, Germany. Since 03/2020 he has been with the Hamburg University of Technology, Germany as professor and head of the Institute of High-Frequency Technology. Alexander Koelpin's research interests are in the areas of microwave circuits and systems, radar and wireless sensing, wireless communication systems, local positioning, and six-port technology. He has authored or co-authored more than 300 publications in his areas of interest. Furthermore, he serves as a reviewer for several journals and conferences, has been chair of the IEEE MTT-S technical committee MTT-24 from 2018 to 2020, since 2018 elected member and since 2020 vice chair of the IEEE MTT-S/AP German Chapter Executive Board, member of the Commission A: Electromagnetic Metrology of U.R.S.I., from 2012 to 2017 conference co-chair of the IEEE Topical Conference on Wireless Sensors and Sensor Networks, and served as conference chair for the 2020 German Microwave Conference as well as technical program chair for IEEE Radio and Wireless week 2021. In 2016 he has been awarded the IEEE MTT-S Outstanding Young Engineer Award and in 2017 with the ITG Award of the German VDE.
 Arne F. Jacob received his Dr.-Ing. degree from the Technische Universität Braunschweig, Braunschweig, Germany, in 1986. From 1986 to 1988, he was a Fellow at CERN, the European Organization for Nuclear Research, Geneva, Switzerland. In 1988, he joined the Lawrence Berkeley (National) Laboratory, University of California at Berkeley, Berkeley, CA, USA, for almost 3 years as a staff scientist at the Accelerator and Fusion Research Division. In 1990, he became a professor at the Institut für Hochfrequenztechnik, Technische Universität Braunschweig. From 2004 until his retirement in April 2020, he was a professor and the head of the Institute of High-Frequency Technology at the Hamburg University of Technology, Hamburg, Germany. His current research interests include the design, packaging, and application of integrated (sub)systems up to millimeter frequencies, and the characterization of complex materials.
Arne F. Jacob received his Dr.-Ing. degree from the Technische Universität Braunschweig, Braunschweig, Germany, in 1986. From 1986 to 1988, he was a Fellow at CERN, the European Organization for Nuclear Research, Geneva, Switzerland. In 1988, he joined the Lawrence Berkeley (National) Laboratory, University of California at Berkeley, Berkeley, CA, USA, for almost 3 years as a staff scientist at the Accelerator and Fusion Research Division. In 1990, he became a professor at the Institut für Hochfrequenztechnik, Technische Universität Braunschweig. From 2004 until his retirement in April 2020, he was a professor and the head of the Institute of High-Frequency Technology at the Hamburg University of Technology, Hamburg, Germany. His current research interests include the design, packaging, and application of integrated (sub)systems up to millimeter frequencies, and the characterization of complex materials.