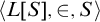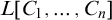1 Introduction
The first author introduced the inner model stable core while investigating under what circumstances the universe V is a class forcing extension of the inner model
![]() $\operatorname {HOD} $
, the collection of all hereditarily ordinal definable sets [Reference Friedman8, Reference Friedman9]. He showed in [Reference Friedman8] that there is a robust
$\operatorname {HOD} $
, the collection of all hereditarily ordinal definable sets [Reference Friedman8, Reference Friedman9]. He showed in [Reference Friedman8] that there is a robust
![]() $\Delta _2$
-definable class S contained in
$\Delta _2$
-definable class S contained in
![]() $\operatorname {HOD} $
such that V is a class-forcing extension of the structure
$\operatorname {HOD} $
such that V is a class-forcing extension of the structure
![]() $\langle L[S],\in , S\rangle $
, which he called the stable core, by an
$\langle L[S],\in , S\rangle $
, which he called the stable core, by an
![]() $\operatorname {Ord} $
-cc class partial order
$\operatorname {Ord} $
-cc class partial order
![]() $\mathbb P$
definable from S. Indeed, for any inner model M, V is a
$\mathbb P$
definable from S. Indeed, for any inner model M, V is a
![]() $\mathbb P$
-forcing extension of
$\mathbb P$
-forcing extension of
![]() $\langle M[S],\in ,S\rangle $
, so that in particular, since
$\langle M[S],\in ,S\rangle $
, so that in particular, since
![]() $\operatorname {HOD} [S]=\operatorname {HOD} $
, V is a
$\operatorname {HOD} [S]=\operatorname {HOD} $
, V is a
![]() $\mathbb P$
-forcing extension of
$\mathbb P$
-forcing extension of
![]() $\langle \operatorname {HOD} ,\in ,S\rangle $
.
$\langle \operatorname {HOD} ,\in ,S\rangle $
.
Let’s explain the result in more detail for the stable core
![]() $L[S]$
, noting that exactly the same analysis applies to
$L[S]$
, noting that exactly the same analysis applies to
![]() $\operatorname {HOD} $
. The partial order
$\operatorname {HOD} $
. The partial order
![]() $\mathbb P$
is definable in
$\mathbb P$
is definable in
![]() $\langle L[S],\in ,S\rangle $
and there is a generic filter G, meeting all dense sub-classes of
$\langle L[S],\in ,S\rangle $
and there is a generic filter G, meeting all dense sub-classes of
![]() $\mathbb P$
definable in
$\mathbb P$
definable in
![]() $\langle L[S],\in ,S\rangle $
, such that
$\langle L[S],\in ,S\rangle $
, such that
![]() $V=L[S][G]$
. All standard forcing theorems hold for
$V=L[S][G]$
. All standard forcing theorems hold for
![]() $\mathbb P$
since it has the
$\mathbb P$
since it has the
![]() $\operatorname {Ord} $
-cc. Thus, we get that the forcing relation for
$\operatorname {Ord} $
-cc. Thus, we get that the forcing relation for
![]() $\mathbb P$
is definable in
$\mathbb P$
is definable in
![]() $\langle L[S],\in ,S\rangle $
and the forcing extension
$\langle L[S],\in ,S\rangle $
and the forcing extension
![]() $\langle V,\in ,G\rangle \models \operatorname {ZFC} $
. However, this particular generic filter G is not definable in V. To obtain G, we first force with an auxiliary forcing
$\langle V,\in ,G\rangle \models \operatorname {ZFC} $
. However, this particular generic filter G is not definable in V. To obtain G, we first force with an auxiliary forcing
![]() $\mathbb Q$
to add a particular class F, without adding sets, such that
$\mathbb Q$
to add a particular class F, without adding sets, such that
![]() $V=L[F]$
. We then show that G is definable from F and F is in turn definable in the structure
$V=L[F]$
. We then show that G is definable from F and F is in turn definable in the structure
![]() $\langle L[S][G], \in , S,G\rangle $
, so that
$\langle L[S][G], \in , S,G\rangle $
, so that
![]() $L[S][G]=V$
. This gives a formulation of the result as a
$L[S][G]=V$
. This gives a formulation of the result as a
![]() $\operatorname {ZFC} $
-theorem because we can say (using the definitions of
$\operatorname {ZFC} $
-theorem because we can say (using the definitions of
![]() $\mathbb P$
and
$\mathbb P$
and
![]() $\mathbb Q$
) that it is forced by
$\mathbb Q$
) that it is forced by
![]() $\mathbb Q$
that
$\mathbb Q$
that
![]() $V=L[F]$
, where F is V-generic for
$V=L[F]$
, where F is V-generic for
![]() $\mathbb Q$
, and (the definition of) G is
$\mathbb Q$
, and (the definition of) G is
![]() $\langle L[S],\in ,S\rangle $
-generic, and finally that F is definable in
$\langle L[S],\in ,S\rangle $
-generic, and finally that F is definable in
![]() $\langle L[S][G],\in ,S,G\rangle $
. Of course, a careful formulation would say that the result holds for all sufficiently large natural numbers n, where n bounds the complexity of the formulas used.
$\langle L[S][G],\in ,S,G\rangle $
. Of course, a careful formulation would say that the result holds for all sufficiently large natural numbers n, where n bounds the complexity of the formulas used.
Without the niceness requirement on
![]() $\mathbb P$
that it has the
$\mathbb P$
that it has the
![]() $\operatorname {Ord} $
-cc, there is a much easier construction of a class forcing notion
$\operatorname {Ord} $
-cc, there is a much easier construction of a class forcing notion
![]() $\mathbb P$
, suggested by Woodin, such that V is a class forcing extension of
$\mathbb P$
, suggested by Woodin, such that V is a class forcing extension of
![]() $\langle \operatorname {HOD} ,\in , \mathbb P\rangle $
(see the end of Section 2). At the same time, some additional predicate must be added to
$\langle \operatorname {HOD} ,\in , \mathbb P\rangle $
(see the end of Section 2). At the same time, some additional predicate must be added to
![]() $\operatorname {HOD} $
in order to realize all of V as a class-forcing extension because, as Hamkins and Reitz observed in [Reference Hamkins and Reitz13], it is consistent that V is not a class-forcing extension of
$\operatorname {HOD} $
in order to realize all of V as a class-forcing extension because, as Hamkins and Reitz observed in [Reference Hamkins and Reitz13], it is consistent that V is not a class-forcing extension of
![]() $\operatorname {HOD} $
. To construct such a counterexample, we suppose that
$\operatorname {HOD} $
. To construct such a counterexample, we suppose that
![]() $\kappa $
is inaccessible in L and force over the Kelley–Morse model
$\kappa $
is inaccessible in L and force over the Kelley–Morse model
![]() $\mathcal L=\langle V_{\kappa }^L,\in , V_{\kappa +1}^L\rangle $
to code the truth predicate of
$\mathcal L=\langle V_{\kappa }^L,\in , V_{\kappa +1}^L\rangle $
to code the truth predicate of
![]() $V_{\kappa }^L$
(which is an element of
$V_{\kappa }^L$
(which is an element of
![]() $V_{\kappa +1}^L$
) into the continuum pattern below
$V_{\kappa +1}^L$
) into the continuum pattern below
![]() $\kappa $
. The first-order part
$\kappa $
. The first-order part
![]() $V_{\kappa }^L[G]$
of this extension cannot be a forcing extension of
$V_{\kappa }^L[G]$
of this extension cannot be a forcing extension of
![]() $\operatorname {HOD} ^{V_{\kappa }^L[G]}=V_{\kappa }^L$
(by the weak homogeneity of the coding forcing), because the truth predicate of
$\operatorname {HOD} ^{V_{\kappa }^L[G]}=V_{\kappa }^L$
(by the weak homogeneity of the coding forcing), because the truth predicate of
![]() $V_{\kappa }^L$
is definable there and this can be recovered via the forcing relation.
$V_{\kappa }^L$
is definable there and this can be recovered via the forcing relation.
While the definition of the partial order
![]() $\mathbb P$
is fairly involved, the stability predicate S simply codes the elementarity relations between sufficiently nice initial segments
$\mathbb P$
is fairly involved, the stability predicate S simply codes the elementarity relations between sufficiently nice initial segments
![]() $H_{\alpha }$
(the collection of all sets with transitive closure of size less than
$H_{\alpha }$
(the collection of all sets with transitive closure of size less than
![]() $\alpha $
) of V. Given a natural number
$\alpha $
) of V. Given a natural number
![]() $n\geq 1$
, call a cardinal
$n\geq 1$
, call a cardinal
![]() $\alpha \ n$
-good if it is a strong limit cardinal and
$\alpha \ n$
-good if it is a strong limit cardinal and
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $\Sigma _n$
-collection. The predicate S consists of triples
$\Sigma _n$
-collection. The predicate S consists of triples
![]() $(n,\alpha ,\beta )$
such that
$(n,\alpha ,\beta )$
such that
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are n-good cardinals and
$\beta $
are n-good cardinals and
![]() $H_{\alpha }\prec _{\Sigma _n}H_{\beta }$
. We will denote by
$H_{\alpha }\prec _{\Sigma _n}H_{\beta }$
. We will denote by
![]() $S_n$
the nth slice of the stability predicate S, namely
$S_n$
the nth slice of the stability predicate S, namely
![]() $S_n=\{(\alpha ,\beta )\mid (n,\alpha ,\beta )\in S\}$
.Footnote
1
$S_n=\{(\alpha ,\beta )\mid (n,\alpha ,\beta )\in S\}$
.Footnote
1
Clearly the stable core
![]() $L[S]\subseteq \operatorname {HOD} $
, and the first author showed in [Reference Friedman8] that it is consistent that
$L[S]\subseteq \operatorname {HOD} $
, and the first author showed in [Reference Friedman8] that it is consistent that
![]() $L[S]$
is smaller than
$L[S]$
is smaller than
![]() $\operatorname {HOD} $
. The stable core is much more forcing absolute than
$\operatorname {HOD} $
. The stable core is much more forcing absolute than
![]() $\operatorname {HOD} $
. The model
$\operatorname {HOD} $
. The model
![]() $L[S]$
is clearly unaffected by forcings of size less than the
$L[S]$
is clearly unaffected by forcings of size less than the
![]() $\omega $
th strong limit cardinal (because S is unaffected), and, assuming the
$\omega $
th strong limit cardinal (because S is unaffected), and, assuming the
![]() $\operatorname {GCH} $
, is preserved by forcing to code the universe into a real [Reference Friedman8]. Jensen showed that we can force over L to add a
$\operatorname {GCH} $
, is preserved by forcing to code the universe into a real [Reference Friedman8]. Jensen showed that we can force over L to add a
![]() $\Pi ^1_2$
-singleton r with a forcing of size continuum (a subposet of Sacks forcing) [Reference Jensen and Bar-Hillel16]. The real r is obviously in
$\Pi ^1_2$
-singleton r with a forcing of size continuum (a subposet of Sacks forcing) [Reference Jensen and Bar-Hillel16]. The real r is obviously in
![]() $\operatorname {HOD} ^{L[r]}$
, and thus, we can already change
$\operatorname {HOD} ^{L[r]}$
, and thus, we can already change
![]() $\operatorname {HOD} $
with a forcing of size continuum. Also, the forcing to code the universe into a real fails to preserve
$\operatorname {HOD} $
with a forcing of size continuum. Also, the forcing to code the universe into a real fails to preserve
![]() $\operatorname {HOD} $
whenever
$\operatorname {HOD} $
whenever
![]() $V\neq L[a]$
for a set a by Vopenka’s theorem that every set of ordinals is set-generic over
$V\neq L[a]$
for a set a by Vopenka’s theorem that every set of ordinals is set-generic over
![]() $\operatorname {HOD} $
.
$\operatorname {HOD} $
.
In order to motivate the many questions which arise about the stable core, let us briefly discuss the set-theoretic goals of studying inner models.
The study of canonical inner models has proved to be one of the most fruitful directions of modern set-theoretic research. The canonical inner models, of which Gödel’s constructible universe L was the first example, are built bottom-up by a canonical procedure. The resulting fine structure of the models leads to regularity properties, such as the
![]() $\operatorname {GCH} $
and
$\operatorname {GCH} $
and
![]() $\square $
, and sometimes even absoluteness properties. But all known canonical inner models are incompatible with sufficiently large large cardinals, and indeed each such inner model is very far from the universe in the presence of sufficiently large large cardinals in the sense, for example, that covering fails and the large cardinals are not downward absolute.
$\square $
, and sometimes even absoluteness properties. But all known canonical inner models are incompatible with sufficiently large large cardinals, and indeed each such inner model is very far from the universe in the presence of sufficiently large large cardinals in the sense, for example, that covering fails and the large cardinals are not downward absolute.
The inner model
![]() $\operatorname {HOD} $
was introduced by Gödel, who showed that in a universe of
$\operatorname {HOD} $
was introduced by Gödel, who showed that in a universe of
![]() $\mathrm {ZF}$
it is always a model of
$\mathrm {ZF}$
it is always a model of
![]() $\operatorname {ZFC} $
. But unlike the constructible universe which also shares this property,
$\operatorname {ZFC} $
. But unlike the constructible universe which also shares this property,
![]() $\operatorname {HOD} $
has turned out to be highly non-canonical. While L cannot be modified by forcing,
$\operatorname {HOD} $
has turned out to be highly non-canonical. While L cannot be modified by forcing,
![]() $\operatorname {HOD} $
can be easily changed by forcing because we can use forcing to code information into
$\operatorname {HOD} $
can be easily changed by forcing because we can use forcing to code information into
![]() $\operatorname {HOD} $
. For instance, any subset of the ordinals from V can be made ordinal definable in a set-forcing extension by coding its characteristic function into the continuum pattern, so that it becomes an element of the
$\operatorname {HOD} $
. For instance, any subset of the ordinals from V can be made ordinal definable in a set-forcing extension by coding its characteristic function into the continuum pattern, so that it becomes an element of the
![]() $\operatorname {HOD} $
of the extension. Indeed, by coding all of V into the continuum pattern of a class-forcing extension, Roguski showed that every universe V is the
$\operatorname {HOD} $
of the extension. Indeed, by coding all of V into the continuum pattern of a class-forcing extension, Roguski showed that every universe V is the
![]() $\operatorname {HOD} $
of one of its class-forcing extensions [Reference Roguski28]. Thus, any consistent set-theoretic property, including all known large cardinals, consistently holds in
$\operatorname {HOD} $
of one of its class-forcing extensions [Reference Roguski28]. Thus, any consistent set-theoretic property, including all known large cardinals, consistently holds in
![]() $\operatorname {HOD} $
. At the same time, the
$\operatorname {HOD} $
. At the same time, the
![]() $\operatorname {HOD} $
of a given universe can be very far from it. It is consistent that a universe can have measurable cardinals none of which are even weakly compact in
$\operatorname {HOD} $
of a given universe can be very far from it. It is consistent that a universe can have measurable cardinals none of which are even weakly compact in
![]() $\operatorname {HOD} $
, and that a universe can have a supercompact cardinal which is not even weakly compact in
$\operatorname {HOD} $
, and that a universe can have a supercompact cardinal which is not even weakly compact in
![]() $\operatorname {HOD} $
[Reference Cummings, Foreman and Kanamori2]. It is also consistent that
$\operatorname {HOD} $
[Reference Cummings, Foreman and Kanamori2]. It is also consistent that
![]() $\operatorname {HOD} $
is wrong about all successor cardinals [Reference Cummings, Friedman and Golshani4].
$\operatorname {HOD} $
is wrong about all successor cardinals [Reference Cummings, Friedman and Golshani4].
Does the stable core behave more like the canonical inner models or more like
![]() $\operatorname {HOD} $
? Is there a fine structural version of the stable core, does it satisfy regularity properties such as the
$\operatorname {HOD} $
? Is there a fine structural version of the stable core, does it satisfy regularity properties such as the
![]() $\operatorname {GCH} $
? Is there a bound on the large cardinals that are compatible with the stable core? Or, on the other hand, are the large cardinals downward absolute to the stable core? Can we code information into the stable core using forcing?
$\operatorname {GCH} $
? Is there a bound on the large cardinals that are compatible with the stable core? Or, on the other hand, are the large cardinals downward absolute to the stable core? Can we code information into the stable core using forcing?
In this article, we show the following results about the structure of the stable core, which answer some of the aforementioned questions as well as motivate further questions about the structure of the stable core in the presence of sufficiently large large cardinals.
Measurable cardinals are consistent with the stable core.
Theorem 1.1.
-
(1) The stable core of
 $L[\mu ]$
, the canonical model for one measurable cardinal, is
$L[\mu ]$
, the canonical model for one measurable cardinal, is
 $L[\mu ]$
. In particular, the stable core can have a measurable cardinal.
$L[\mu ]$
. In particular, the stable core can have a measurable cardinal. -
(2) Suppose that
 $\langle \kappa _{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
is an increasing discrete sequence of measurable cardinals. If
$\langle \kappa _{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
is an increasing discrete sequence of measurable cardinals. If
 $\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
, where
$\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
, where
 $U_{\alpha }$
is a normal measure on
$U_{\alpha }$
is a normal measure on
 $\kappa _{\alpha }$
, then the stable core of
$\kappa _{\alpha }$
, then the stable core of
 $L[\vec U]$
is
$L[\vec U]$
is
 $L[\vec U]$
. In particular, the stable core can have a discrete proper class of measurable cardinals.
$L[\vec U]$
. In particular, the stable core can have a discrete proper class of measurable cardinals.
Theorem 1.1(1) is Corollary 4.3(1) and Theorem 1.1(2) is Theorem 4.6.
We can code information into the stable core over L or
![]() $L[\mu ]$
using forcing.
$L[\mu ]$
using forcing.
Theorem 1.2. Suppose
![]() $\mathbb P\in L$
is a forcing notion and
$\mathbb P\in L$
is a forcing notion and
![]() $G\subseteq \mathbb P$
is L-generic. Then there is a further forcing extension
$G\subseteq \mathbb P$
is L-generic. Then there is a further forcing extension
![]() $L[G][H]$
such that
$L[G][H]$
such that
![]() $G\in L[S^{L[G][H]}]$
(the universe of the stable core). An analogous result holds for
$G\in L[S^{L[G][H]}]$
(the universe of the stable core). An analogous result holds for
![]() $L[\mu ]$
.
$L[\mu ]$
.
Theorem 1.2 is Theorems 3.1 and 4.7.
An extension of the coding results shows that the
![]() $\operatorname {GCH} $
can fail badly in the stable core.
$\operatorname {GCH} $
can fail badly in the stable core.
Theorem 1.3.
-
(1) There is a class-forcing extension of L such that in its stable core the
 $\operatorname {GCH} $
fails at every regular cardinal.
$\operatorname {GCH} $
fails at every regular cardinal. -
(2) There is a class-forcing extension of
 $L[\mu ]$
such that in its stable core there is a measurable cardinal and the
$L[\mu ]$
such that in its stable core there is a measurable cardinal and the
 $\operatorname {GCH} $
fails on a tail of regular cardinals.
$\operatorname {GCH} $
fails on a tail of regular cardinals.
Theorem 1.3(1) is Theorem 3.3 and Theorem 1.3(2) is Theorem 4.8.
Measurable cardinals need not be downward absolute to the stable core.
Theorem 1.4. There is a forcing extension of
![]() $L[\mu ]$
in which the measurable cardinal
$L[\mu ]$
in which the measurable cardinal
![]() $\kappa $
of
$\kappa $
of
![]() $L[\mu ]$
remains measurable, but it is not even weakly compact in the stable core.
$L[\mu ]$
remains measurable, but it is not even weakly compact in the stable core.
Although we don’t know whether the stable core can have a measurable limit of measurables, the stable core has inner models with measurable limits of measurables, and much more. Say that a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $1$
-measurable if it is measurable, and, for
$1$
-measurable if it is measurable, and, for
![]() $n < \omega $
,
$n < \omega $
,
![]() $(n+1)$
-measurable if it is measurable and a limit of n-measurable cardinals. Write
$(n+1)$
-measurable if it is measurable and a limit of n-measurable cardinals. Write
![]() $m_0^{\#}$
for
$m_0^{\#}$
for
![]() $0^{\#}$
and
$0^{\#}$
and
![]() $m_n^{\#}$
for the minimal mouse which is a sharp for a proper class of n-measurable cardinals, namely, an active mouse
$m_n^{\#}$
for the minimal mouse which is a sharp for a proper class of n-measurable cardinals, namely, an active mouse
![]() $\mathcal {M}$
such that the critical point of the top extender is a limit of n-measurable cardinals in
$\mathcal {M}$
such that the critical point of the top extender is a limit of n-measurable cardinals in
![]() $\mathcal {M}$
. Here we mean mouse in the sense of [Reference Mitchell, Foreman and Kanamori26, Sections 1 and 2], i.e., a mouse has only total measures on its sequence. The mouse
$\mathcal {M}$
. Here we mean mouse in the sense of [Reference Mitchell, Foreman and Kanamori26, Sections 1 and 2], i.e., a mouse has only total measures on its sequence. The mouse
![]() $m_n^{\#}$
can also be construed as a fine structural mouse with both total and partial extenders (see [Reference Zeman31], Section 4).
$m_n^{\#}$
can also be construed as a fine structural mouse with both total and partial extenders (see [Reference Zeman31], Section 4).
Theorem 1.5. For all
![]() $n<\omega $
, if
$n<\omega $
, if
![]() $m_{n+1}^{\#}$
exists, then
$m_{n+1}^{\#}$
exists, then
![]() $m_n^{\#}$
is in the stable core.
$m_n^{\#}$
is in the stable core.
Moreover, we obtain the following characterization of natural inner models of the stable core. Consider for
![]() $n<\omega $
, the following class clubs:
$n<\omega $
, the following class clubs:
We show in Proposition 2.3 that the clubs
![]() $C_n$
are definable in
$C_n$
are definable in
![]() $L[S]$
. It is not difficult then to see that they satisfy the hypothesis of the theorem below.
$L[S]$
. It is not difficult then to see that they satisfy the hypothesis of the theorem below.
Theorem 1.6. Let
![]() $n < \omega $
and suppose that
$n < \omega $
and suppose that
![]() $m_n^{\#}$
exists. Then whenever
$m_n^{\#}$
exists. Then whenever
are class clubs of uncountable cardinals such that for every
![]() $1<i\leq n$
and every
$1<i\leq n$
and every
![]() $\gamma \in C_i$
,
$\gamma \in C_i$
,
then
![]() $L[C_1,\ldots ,C_n]$
is a hyperclass-forcing extension of a (truncated) iterate of
$L[C_1,\ldots ,C_n]$
is a hyperclass-forcing extension of a (truncated) iterate of
![]() $m_n^{\#}$
.
$m_n^{\#}$
.
An
![]() $\operatorname {Ord} $
-length iteration of the mouse
$\operatorname {Ord} $
-length iteration of the mouse
![]() $m_n^{\#}$
produces a model M satisfying
$m_n^{\#}$
produces a model M satisfying
![]() $\operatorname {ZFC} $
without powerset whose largest cardinal is
$\operatorname {ZFC} $
without powerset whose largest cardinal is
![]() $\operatorname {Ord} $
. By truncating the model M at
$\operatorname {Ord} $
. By truncating the model M at
![]() $\operatorname {Ord} $
, we obtain the model
$\operatorname {Ord} $
, we obtain the model
![]() $V_{\operatorname {Ord} }^M\models \operatorname {ZFC} $
. The structure
$V_{\operatorname {Ord} }^M\models \operatorname {ZFC} $
. The structure
![]() $(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
is a model of the strong second-order set theory Kelley–Morse (with the Class Choice Principle). In second-order set theory, hyperclass-forcing notions are definable partial orders whose elements are classes (third-order objects). A forcing construction with hyperclass-forcing notions can be made sense of over models of Kelley–Morse (with the Class Choice Principle) for a certain class of nice enough partial orders. To obtain Theorem 1.6, we will force over the structure
$(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
is a model of the strong second-order set theory Kelley–Morse (with the Class Choice Principle). In second-order set theory, hyperclass-forcing notions are definable partial orders whose elements are classes (third-order objects). A forcing construction with hyperclass-forcing notions can be made sense of over models of Kelley–Morse (with the Class Choice Principle) for a certain class of nice enough partial orders. To obtain Theorem 1.6, we will force over the structure
![]() $(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
with an n-length iteration of
$(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
with an n-length iteration of
![]() $\operatorname {Ord} $
-length products of Prikry forcing. Since the
$\operatorname {Ord} $
-length products of Prikry forcing. Since the
![]() $\operatorname {Ord} $
-length product of Prikry forcing uses full support, conditions in this forcing are classes in the structure
$\operatorname {Ord} $
-length product of Prikry forcing uses full support, conditions in this forcing are classes in the structure
![]() $(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
, making it a hyperclass-forcing notion. Details of the construction are provided in Section 7. Theorem 1.6 is Theorem 7.10.
$(V_{\operatorname {Ord} }^M,\in , V_{\operatorname {Ord} +1}^M)$
, making it a hyperclass-forcing notion. Details of the construction are provided in Section 7. Theorem 1.6 is Theorem 7.10.
2 Preliminaries
Recall that, for a cardinal
![]() $\alpha $
,
$\alpha $
,
![]() $H_{\alpha }$
is the collection of all sets x with transitive closure of size less than
$H_{\alpha }$
is the collection of all sets x with transitive closure of size less than
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha $
is regular, then
$\alpha $
is regular, then
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $\operatorname {ZFC} ^-$
(
$\operatorname {ZFC} ^-$
(
![]() $\operatorname {ZFC} $
without the powerset axiom). But for singular
$\operatorname {ZFC} $
without the powerset axiom). But for singular
![]() $\alpha $
,
$\alpha $
,
![]() $H_{\alpha }$
may fail to satisfy even
$H_{\alpha }$
may fail to satisfy even
![]() $\Sigma _2$
-collection.
$\Sigma _2$
-collection.
The following proposition is standard.
Proposition 2.1. Suppose
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are uncountable cardinals.
$\beta $
are uncountable cardinals.
-
(1)
 $H_{\alpha }\prec _{\Sigma _1} V$
.
$H_{\alpha }\prec _{\Sigma _1} V$
. -
(2) If
 $H_{\alpha }\prec _{\Sigma _m} V$
, then
$H_{\alpha }\prec _{\Sigma _m} V$
, then
 $\Sigma _m$
-collection holds in
$\Sigma _m$
-collection holds in
 $H_{\alpha }$
. In particular, every
$H_{\alpha }$
. In particular, every
 $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
 $\Sigma _1$
-collection.
$\Sigma _1$
-collection. -
(3) If
 $H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
and
$H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
and
 $\Sigma _m$
-collection holds in
$\Sigma _m$
-collection holds in
 $H_{\beta }$
, then it also holds in
$H_{\beta }$
, then it also holds in
 $H_{\alpha }$
.
$H_{\alpha }$
.
Proof Let’s prove (1), which is a classical fact attributed to Lévy. Suppose
![]() $\exists x\,\varphi (x,a)$
holds in V, where
$\exists x\,\varphi (x,a)$
holds in V, where
![]() $\varphi (x,a)$
is a
$\varphi (x,a)$
is a
![]() $\Delta _0$
-formula and
$\Delta _0$
-formula and
![]() $a\in H_{\alpha }$
. We can assume without loss that a is transitive and has size at least
$a\in H_{\alpha }$
. We can assume without loss that a is transitive and has size at least
![]() $\omega $
. Let
$\omega $
. Let
![]() $X\prec _{\Sigma _1} V$
be a
$X\prec _{\Sigma _1} V$
be a
![]() $\Sigma _1$
-elementary substructure of size
$\Sigma _1$
-elementary substructure of size
![]() $|a|$
with
$|a|$
with
![]() $a\cup \{a\}\subseteq X$
, and let M be the Mostowski collapse of X. Since M is transitive and has size
$a\cup \{a\}\subseteq X$
, and let M be the Mostowski collapse of X. Since M is transitive and has size
![]() $|a|$
, it is in
$|a|$
, it is in
![]() $H_{\alpha }$
. Also, by elementarity, M satisfies
$H_{\alpha }$
. Also, by elementarity, M satisfies
![]() $\exists x\,\varphi (x,a)$
. So there is
$\exists x\,\varphi (x,a)$
. So there is
![]() $b\in M$
such that
$b\in M$
such that
![]() $M\models \varphi (b,a)$
. But since
$M\models \varphi (b,a)$
. But since
![]() $M\subseteq H_{\alpha }$
is transitive and
$M\subseteq H_{\alpha }$
is transitive and
![]() $\varphi (x,y)$
is a
$\varphi (x,y)$
is a
![]() $\Delta _0$
-assertion, it follows that
$\Delta _0$
-assertion, it follows that
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $\varphi (b,a)$
as well.
$\varphi (b,a)$
as well.
Next, let’s prove (2). Fix a
![]() $\Sigma _m$
-formula
$\Sigma _m$
-formula
![]() $\varphi (x,y,z)$
and sets
$\varphi (x,y,z)$
and sets
![]() $a,c\in H_{\alpha }$
. Suppose that
$a,c\in H_{\alpha }$
. Suppose that
![]() $H_{\alpha }\models \forall x\in a\,\exists y\,\varphi (x,y,c)$
. Then, by
$H_{\alpha }\models \forall x\in a\,\exists y\,\varphi (x,y,c)$
. Then, by
![]() $\Sigma _m$
-elementarity, for every
$\Sigma _m$
-elementarity, for every
![]() $\bar a\in a$
,
$\bar a\in a$
,
![]() $\exists y\,\varphi (\bar a,y,c)$
holds in V. Thus, V satisfies
$\exists y\,\varphi (\bar a,y,c)$
holds in V. Thus, V satisfies
![]() $\forall x\in a\,\exists y\,\varphi (x,y,c)$
. In V, by collection, there is a set b such that
$\forall x\in a\,\exists y\,\varphi (x,y,c)$
. In V, by collection, there is a set b such that
![]() $\forall x\in a\,\exists y\in b\,\varphi (x,y,c)$
holds. So V satisfies
$\forall x\in a\,\exists y\in b\,\varphi (x,y,c)$
holds. So V satisfies
If
![]() $m=1$
, then
$m=1$
, then
![]() $\psi (c)$
is a
$\psi (c)$
is a
![]() $\Sigma _1$
-assertion. Hence
$\Sigma _1$
-assertion. Hence
![]() $H_{\alpha }\models \psi (c)$
by elementarity. Thus, we have verified
$H_{\alpha }\models \psi (c)$
by elementarity. Thus, we have verified
![]() $\Sigma _1$
-collection in
$\Sigma _1$
-collection in
![]() $H_{\alpha }$
. If
$H_{\alpha }$
. If
![]() $m>1$
, we can suppose inductively that we have verified
$m>1$
, we can suppose inductively that we have verified
![]() $\Sigma _{m-1}$
-collection in
$\Sigma _{m-1}$
-collection in
![]() $H_{\alpha }$
. In this case, the formula
$H_{\alpha }$
. In this case, the formula
![]() $\psi (c)$
is equivalent by
$\psi (c)$
is equivalent by
![]() $\Sigma _{m-1}$
-collection to a
$\Sigma _{m-1}$
-collection to a
![]() $\Sigma _m$
-formula
$\Sigma _m$
-formula
![]() $\bar \psi (c)$
. By
$\bar \psi (c)$
. By
![]() $\Sigma _m$
-elementarity,
$\Sigma _m$
-elementarity,
![]() $H_{\alpha }\models \bar \psi (c)$
. But then
$H_{\alpha }\models \bar \psi (c)$
. But then
![]() $H_{\alpha }\models \psi (c)$
since it satisfies
$H_{\alpha }\models \psi (c)$
since it satisfies
![]() $\Sigma _{m-1}$
-collection by assumption. An analogous argument shows
$\Sigma _{m-1}$
-collection by assumption. An analogous argument shows
![]() $(3)$
.
$(3)$
.
It follows immediately from Proposition 2.1(1) that the strong limit cardinals of V are definable in the stable core.
Corollary 2.2. The class of strong limit cardinals of V is definable in the stable core
![]() $\langle L[S],\in ,S\rangle $
. Indeed,
$\langle L[S],\in ,S\rangle $
. Indeed,
![]() $\alpha $
is a strong limit cardinal if and only if there is a cardinal
$\alpha $
is a strong limit cardinal if and only if there is a cardinal
![]() $\beta $
such that
$\beta $
such that
![]() $(\alpha ,\beta )\in S_1$
.
$(\alpha ,\beta )\in S_1$
.
The stable core can also define, for each n, the class club
![]() $C_n$
(introduced in the introduction) of all strong limit cardinals
$C_n$
(introduced in the introduction) of all strong limit cardinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $H_{\alpha }\prec _{\Sigma _n}V$
.
$H_{\alpha }\prec _{\Sigma _n}V$
.
Proposition 2.3. For every
![]() $n<\omega $
, the class club
$n<\omega $
, the class club
![]() $C_n$
is definable in the stable core.
$C_n$
is definable in the stable core.
Proof The class club
![]() $C_1$
is definable because it is precisely the class of all strong limit cardinals. Now suppose inductively that the club
$C_1$
is definable because it is precisely the class of all strong limit cardinals. Now suppose inductively that the club
![]() $C_i$
is definable for some
$C_i$
is definable for some
![]() $i\geq 1$
. Let’s argue that
$i\geq 1$
. Let’s argue that
![]() $C_{i+1}$
is precisely the collection of all
$C_{i+1}$
is precisely the collection of all
![]() $\alpha \in C_i$
such that for cofinally many
$\alpha \in C_i$
such that for cofinally many
![]() $\beta \in C_i$
, we have
$\beta \in C_i$
, we have
![]() $\langle \alpha ,\beta \rangle \in S_{i+1}$
. If
$\langle \alpha ,\beta \rangle \in S_{i+1}$
. If
![]() $\alpha $
is a strong limit cardinal such that
$\alpha $
is a strong limit cardinal such that
![]() $H_{\alpha }\prec _{\Sigma _{i+1}}V$
, then clearly
$H_{\alpha }\prec _{\Sigma _{i+1}}V$
, then clearly
![]() $\alpha \in C_i$
and there are cofinally many
$\alpha \in C_i$
and there are cofinally many
![]() $\beta \in C_i$
for which
$\beta \in C_i$
for which
![]() $H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
. Next, suppose that
$H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
. Next, suppose that
![]() $\alpha \in C_i$
and for cofinally many
$\alpha \in C_i$
and for cofinally many
![]() $\beta \in C_i$
,
$\beta \in C_i$
,
![]() $H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
. Suppose V satisfies
$H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
. Suppose V satisfies
![]() $\exists x\,\varphi (x,a)$
, where
$\exists x\,\varphi (x,a)$
, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Pi _i$
-formula. Then there is a set b such that
$\Pi _i$
-formula. Then there is a set b such that
![]() $\varphi (b,a)$
holds in V. Choose a large enough
$\varphi (b,a)$
holds in V. Choose a large enough
![]() $\beta \in C_i$
with
$\beta \in C_i$
with
![]() $H_{\alpha }\prec _{\Sigma _{i+1}} H_{\beta }$
such that
$H_{\alpha }\prec _{\Sigma _{i+1}} H_{\beta }$
such that
![]() $b\in H_{\beta }$
. Thus,
$b\in H_{\beta }$
. Thus,
![]() $H_{\beta }\models \varphi (b,a)$
, and hence
$H_{\beta }\models \varphi (b,a)$
, and hence
![]() $H_{\beta }\models \exists x\,\varphi (x,a)$
. Since
$H_{\beta }\models \exists x\,\varphi (x,a)$
. Since
![]() $H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
,
$H_{\alpha }\prec _{\Sigma _{i+1}}H_{\beta }$
,
![]() $H_{\alpha }\models \exists x,\varphi (x,a)$
as well. This completes our verification that
$H_{\alpha }\models \exists x,\varphi (x,a)$
as well. This completes our verification that
![]() $H_{\alpha }\prec _{\Sigma _{i+1}} V$
.
$H_{\alpha }\prec _{\Sigma _{i+1}} V$
.
Given a cardinal
![]() $\alpha $
, let
$\alpha $
, let
![]() denote the relation consisting of pairs
denote the relation consisting of pairs
![]() $\langle \beta ,H_{\beta }\rangle $
for
$\langle \beta ,H_{\beta }\rangle $
for
![]() $\beta <\alpha $
.
$\beta <\alpha $
.
Proposition 2.4. For
![]() $m\geq 1$
and strong limit cardinals
$m\geq 1$
and strong limit cardinals
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
,
$\beta $
,
![]() $H_{\alpha }\prec _{\Sigma _{m+1}}H_{\beta }$
if and only if
$H_{\alpha }\prec _{\Sigma _{m+1}}H_{\beta }$
if and only if
![]() .
.
Proof For the forward direction, observe that the relation
![]() is
is
![]() $\Pi _1$
-definable and amenable over
$\Pi _1$
-definable and amenable over
![]() $H_{\alpha }$
, which implies that predicates which are
$H_{\alpha }$
, which implies that predicates which are
![]() $\Sigma _m$
-definable over
$\Sigma _m$
-definable over
![]() are
are
![]() $\Sigma _{m+1}$
-definable over
$\Sigma _{m+1}$
-definable over
![]() $H_{\alpha }$
. So let’s focus on the backward direction. First, observe that a
$H_{\alpha }$
. So let’s focus on the backward direction. First, observe that a
![]() $\Sigma _2$
-formula
$\Sigma _2$
-formula
![]() $\exists x\,\forall y\,\varphi (x,y,a)$
holds in
$\exists x\,\forall y\,\varphi (x,y,a)$
holds in
![]() $H_{\alpha }$
if and only if the
$H_{\alpha }$
if and only if the
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
holds in
![]() , and a
, and a
![]() $\Pi _2$
-formula
$\Pi _2$
-formula
![]() $\forall x\,\exists y\,\varphi (x,y,a)$
holds in
$\forall x\,\exists y\,\varphi (x,y,a)$
holds in
![]() $H_{\alpha }$
if and only if the
$H_{\alpha }$
if and only if the
![]() $\Pi _1$
-formula
$\Pi _1$
-formula
holds in
![]() . Both equivalences follow from Proposition 2.1(1) and the fact that
. Both equivalences follow from Proposition 2.1(1) and the fact that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are strong limits. Thus, the complexity of any assertion is reduced by 1.
$\beta $
are strong limits. Thus, the complexity of any assertion is reduced by 1.
Proposition 2.5. Suppose
![]() $1\leq m<\omega $
,
$1\leq m<\omega $
,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are strong limit cardinals,
$\beta $
are strong limit cardinals,
![]() $\mathbb P\in H_{\alpha }$
is a partial order, and
$\mathbb P\in H_{\alpha }$
is a partial order, and
![]() $G\subseteq \mathbb P$
is V-generic. For
$G\subseteq \mathbb P$
is V-generic. For
![]() $(1)$
and
$(1)$
and
![]() $(2)$
, suppose additionally that
$(2)$
, suppose additionally that
![]() $H_{\alpha }\models \Sigma _m$
-collection.
$H_{\alpha }\models \Sigma _m$
-collection.
-
(1) The Definability Lemma and Truth Lemma for
 $\Sigma _m$
-formulas hold for
$\Sigma _m$
-formulas hold for
 $\mathbb P$
in
$\mathbb P$
in
 $H_{\alpha }$
. Indeed, if
$H_{\alpha }$
. Indeed, if
 $\varphi (\bar x)$
is a
$\varphi (\bar x)$
is a
 $\Sigma _m$
-formula, then the relation
$\Sigma _m$
-formula, then the relation
 $p\Vdash \varphi (\bar x)$
is also
$p\Vdash \varphi (\bar x)$
is also
 $\Sigma _m$
in
$\Sigma _m$
in
 $H_{\alpha }$
.
$H_{\alpha }$
. -
(2)
 $H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
if and only if
$H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
if and only if  $$ \begin{align*}H_{\alpha}^{V[G]}=H_{\alpha}[G]\prec_{\Sigma_m}H_{\beta}[G]=H_{\beta}^{V[G]}.\end{align*} $$
$$ \begin{align*}H_{\alpha}^{V[G]}=H_{\alpha}[G]\prec_{\Sigma_m}H_{\beta}[G]=H_{\beta}^{V[G]}.\end{align*} $$
-
(3)
 $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
 $\Sigma _m$
-collection if and only if
$\Sigma _m$
-collection if and only if
 $H_{\alpha }[G]$
satisfies
$H_{\alpha }[G]$
satisfies
 $\Sigma _m$
-collection.
$\Sigma _m$
-collection.
Proof The argument for (1) actually works for all cardinals
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, not just strong limits. We argue that the standard definition of the forcing relation works in
$\beta $
, not just strong limits. We argue that the standard definition of the forcing relation works in
![]() $H_{\alpha }$
. Suppose, for instance, that
$H_{\alpha }$
. Suppose, for instance, that
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $p\Vdash \sigma =\tau $
for
$p\Vdash \sigma =\tau $
for
![]() $\mathbb P$
-names
$\mathbb P$
-names
![]() $\sigma ,\tau \in H_{\alpha }$
and let
$\sigma ,\tau \in H_{\alpha }$
and let
![]() $H\subseteq \mathbb P$
be V-generic with
$H\subseteq \mathbb P$
be V-generic with
![]() $p\in H$
. The relation
$p\in H$
. The relation
![]() $p\Vdash \sigma =\tau $
is a
$p\Vdash \sigma =\tau $
is a
![]() $\Sigma _1$
-assertion stating that a tree exists witnessing the recursive definition of
$\Sigma _1$
-assertion stating that a tree exists witnessing the recursive definition of
![]() $\sigma =\tau $
in terms of names of lower rank (in fact, the assertion is
$\sigma =\tau $
in terms of names of lower rank (in fact, the assertion is
![]() $\Delta _1$
because we can say “for every tree obeying the recursive definition…”). So by
$\Delta _1$
because we can say “for every tree obeying the recursive definition…”). So by
![]() $\Sigma _1$
-elementarity,
$\Sigma _1$
-elementarity,
![]() $p\Vdash \sigma =\tau $
holds in V, and hence
$p\Vdash \sigma =\tau $
holds in V, and hence
![]() $\sigma _H=\tau _H$
. Conversely, suppose that
$\sigma _H=\tau _H$
. Conversely, suppose that
![]() $\sigma _H=\tau _H$
for some V-generic filter
$\sigma _H=\tau _H$
for some V-generic filter
![]() $H\subseteq \mathbb P$
. Then there is
$H\subseteq \mathbb P$
. Then there is
![]() $p\in H$
such that
$p\in H$
such that
![]() $p\Vdash \sigma =\tau $
, and hence, by
$p\Vdash \sigma =\tau $
, and hence, by
![]() $\Sigma _1$
-elementarity,
$\Sigma _1$
-elementarity,
![]() $p\Vdash \sigma =\tau $
holds in
$p\Vdash \sigma =\tau $
holds in
![]() $H_{\alpha }$
as well. The remainder of the argument is by induction on the complexity of formulas. For instance, let’s argue for negations. Suppose that the standard definition of the forcing relation holds in
$H_{\alpha }$
as well. The remainder of the argument is by induction on the complexity of formulas. For instance, let’s argue for negations. Suppose that the standard definition of the forcing relation holds in
![]() $H_{\alpha }$
for a formula
$H_{\alpha }$
for a formula
![]() $\varphi $
. By definition of the forcing relation,
$\varphi $
. By definition of the forcing relation,
![]() $p\Vdash \neg \varphi $
if for every
$p\Vdash \neg \varphi $
if for every
![]() $q\leq p$
, q does not force
$q\leq p$
, q does not force
![]() $\varphi $
, but clearly this holds in
$\varphi $
, but clearly this holds in
![]() $H_{\alpha }$
if and only if it holds V provided that they agree on what it means for q to force
$H_{\alpha }$
if and only if it holds V provided that they agree on what it means for q to force
![]() $\varphi $
, which is the inductive assumption.
$\varphi $
, which is the inductive assumption.
The argument that the definition of the forcing relation for a
![]() $\Sigma _m$
-formula is itself
$\Sigma _m$
-formula is itself
![]() $\Sigma _m$
is also standard. The collection assumption is required to make sure that a formula is equivalent to its normal form where all the bounded quantifiers are pushed to the back. The argument above already shows that for formulae of the form “
$\Sigma _m$
is also standard. The collection assumption is required to make sure that a formula is equivalent to its normal form where all the bounded quantifiers are pushed to the back. The argument above already shows that for formulae of the form “
![]() $\sigma =\tau $
” the forcing relation is
$\sigma =\tau $
” the forcing relation is
![]() $\Delta _1$
. Let’s argue for instance that for
$\Delta _1$
. Let’s argue for instance that for
![]() $\Delta _0$
-formulas, the complexity of the forcing relation is
$\Delta _0$
-formulas, the complexity of the forcing relation is
![]() $\Delta _1$
. Say
$\Delta _1$
. Say
![]() $p\Vdash \exists x\in \sigma \,\varphi (x,\sigma )$
, where
$p\Vdash \exists x\in \sigma \,\varphi (x,\sigma )$
, where
![]() $\varphi (x,y)$
is a
$\varphi (x,y)$
is a
![]() $\Delta _0$
-formula and by induction
$\Delta _0$
-formula and by induction
![]() $q\Vdash \varphi (x,y)$
is a
$q\Vdash \varphi (x,y)$
is a
![]() $\Delta _1$
-relation. Then
$\Delta _1$
-relation. Then
![]() $p\Vdash \exists x\in \sigma \,\varphi (x,\sigma )$
holds if and only if for every
$p\Vdash \exists x\in \sigma \,\varphi (x,\sigma )$
holds if and only if for every
![]() $q\leq p$
, there is
$q\leq p$
, there is
![]() $r\leq q$
and
$r\leq q$
and
![]() $\tau \in \text {dom}(\sigma )$
such that
$\tau \in \text {dom}(\sigma )$
such that
![]() $r\Vdash \varphi (\tau ,\sigma )$
, and of course, quantification over elements of
$r\Vdash \varphi (\tau ,\sigma )$
, and of course, quantification over elements of
![]() $\mathbb P$
is obviously bounded.
$\mathbb P$
is obviously bounded.
Now let’s prove (2). We start with the forward direction, which is standard. Suppose that
![]() $H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
. Clearly, since
$H_{\alpha }\prec _{\Sigma _m} H_{\beta }$
. Clearly, since
![]() $\mathbb P\in H_{\alpha }$
, we have
$\mathbb P\in H_{\alpha }$
, we have
![]() $H_{\alpha }[G]=H_{\alpha }^{V[G]}$
and similarly for
$H_{\alpha }[G]=H_{\alpha }^{V[G]}$
and similarly for
![]() $H_{\beta }$
. If a
$H_{\beta }$
. If a
![]() $\Sigma _m$
-assertion
$\Sigma _m$
-assertion
![]() $\varphi $
holds in
$\varphi $
holds in
![]() $H_{\alpha }[G]$
, then there is some
$H_{\alpha }[G]$
, then there is some
![]() $p\in G$
such that
$p\in G$
such that
![]() $p\Vdash \varphi $
holds in
$p\Vdash \varphi $
holds in
![]() $H_{\alpha }$
, which is also a
$H_{\alpha }$
, which is also a
![]() $\Sigma _m$
-assertion by (1), and so
$\Sigma _m$
-assertion by (1), and so
![]() $p\Vdash \varphi $
holds in
$p\Vdash \varphi $
holds in
![]() $H_{\beta }$
, meaning that
$H_{\beta }$
, meaning that
![]() $H_{\beta }[G]$
satisfies
$H_{\beta }[G]$
satisfies
![]() $\varphi $
.
$\varphi $
.
Next, let’s prove the backward direction. Suppose that
![]() $H_{\alpha }[G]\prec _{\Sigma _m}H_{\beta }[G]$
. The argument for
$H_{\alpha }[G]\prec _{\Sigma _m}H_{\beta }[G]$
. The argument for
![]() $m=1$
is trivial since if
$m=1$
is trivial since if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are cardinals in
$\beta $
are cardinals in
![]() $V[G]$
, then they are also obviously cardinals in V, and so the result follows by Proposition 2.1(1). So suppose that
$V[G]$
, then they are also obviously cardinals in V, and so the result follows by Proposition 2.1(1). So suppose that
![]() $m\geq 2$
. Since
$m\geq 2$
. Since
![]() $\mathbb P\in H_{\alpha }$
,
$\mathbb P\in H_{\alpha }$
,
![]() $\alpha $
remains a strong limit in
$\alpha $
remains a strong limit in
![]() $V[G]$
. Thus,
$V[G]$
. Thus,
![]() $H_{\alpha }[G]=H_{\alpha }^{V[G]}$
has a definable hierarchy consisting of
$H_{\alpha }[G]=H_{\alpha }^{V[G]}$
has a definable hierarchy consisting of
![]() $H_{\beta }^{V[G]}$
for regular
$H_{\beta }^{V[G]}$
for regular
![]() $\beta <\alpha $
. The existence of such a hierarchy suffices for the standard
$\beta <\alpha $
. The existence of such a hierarchy suffices for the standard
![]() $\Delta _2$
-definition of the ground model in a forcing extension (due independently to Woodin [Reference Woodin30] and Laver [Reference Laver22]) to go through, so that
$\Delta _2$
-definition of the ground model in a forcing extension (due independently to Woodin [Reference Woodin30] and Laver [Reference Laver22]) to go through, so that
![]() $H_{\alpha }$
is
$H_{\alpha }$
is
![]() $\Delta _2$
-definable in
$\Delta _2$
-definable in
![]() $H_{\alpha }[G]$
. Indeed, examining the definition shows that
$H_{\alpha }[G]$
. Indeed, examining the definition shows that
is
![]() $\Delta _1$
-definable in
$\Delta _1$
-definable in
. Now suppose that
![]() $H_{\alpha }$
satisfies a
$H_{\alpha }$
satisfies a
![]() $\Pi _m$
-assertion
$\Pi _m$
-assertion
![]() $\varphi (a)$
, and let
$\varphi (a)$
, and let
![]() $\varphi ^*(a)$
be the equivalent
$\varphi ^*(a)$
be the equivalent
![]() $\Pi _{m-1}$
-assertion which holds in
$\Pi _{m-1}$
-assertion which holds in
. Since
is
![]() $\Delta _1$
-definable in
$\Delta _1$
-definable in
, there is a
![]() $\Pi _{m-1}$
-assertion
$\Pi _{m-1}$
-assertion
![]() $\varphi ^{**}(a)$
expressing in
$\varphi ^{**}(a)$
expressing in
that
![]() $\varphi ^*(a)$
holds in
$\varphi ^*(a)$
holds in
. By Proposition 2.4,
Thus,
satisfies
![]() $\varphi ^{**}(a)$
, and therefore
$\varphi ^{**}(a)$
, and therefore
![]() $\varphi ^*(a)$
holds in
$\varphi ^*(a)$
holds in
. So finally,
![]() $\varphi (a)$
holds in
$\varphi (a)$
holds in
![]() $H_{\beta }$
.
$H_{\beta }$
.
Finally, let’s prove (3). Again, we start with the standard forward direction. Suppose that
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $\Sigma _m$
-collection. Let
$\Sigma _m$
-collection. Let
![]() $\varphi (x,y)$
and a be such that
$\varphi (x,y)$
and a be such that
So there is some
![]() $p\in G$
and a name
$p\in G$
and a name
![]() $\dot a$
for a such that
$\dot a$
for a such that
![]() $p\Vdash \forall x\in \dot a\,\exists y\,\varphi (x,y)$
. Fix a name
$p\Vdash \forall x\in \dot a\,\exists y\,\varphi (x,y)$
. Fix a name
![]() $\sigma \in \operatorname {dom} \dot a$
and apply
$\sigma \in \operatorname {dom} \dot a$
and apply
![]() $\Sigma _m$
-collection in
$\Sigma _m$
-collection in
![]() $H_{\alpha }$
to the statement
$H_{\alpha }$
to the statement
to obtain a collecting set
![]() $y_{\sigma }$
. Next, apply
$y_{\sigma }$
. Next, apply
![]() $\Sigma _m$
-collection in
$\Sigma _m$
-collection in
![]() $H_{\alpha }$
, to the statement
$H_{\alpha }$
, to the statement
which holds by the previous step because
![]() $y_x$
witnesses it for x, to obtain a collecting set B. We can assume without loss that B consists only of
$y_x$
witnesses it for x, to obtain a collecting set B. We can assume without loss that B consists only of
![]() $\mathbb P$
-names and let
$\mathbb P$
-names and let
![]() $\dot b =\{(y,p)\mid y\in B\}$
. It is not difficult to see that
$\dot b =\{(y,p)\mid y\in B\}$
. It is not difficult to see that
![]() $\dot b_G$
gives the collecting set in
$\dot b_G$
gives the collecting set in
![]() $H_{\alpha }[G]$
.
$H_{\alpha }[G]$
.
For the backward direction, assume that
![]() $H_{\alpha }[G]$
satisfies
$H_{\alpha }[G]$
satisfies
![]() $\Sigma _m$
-collection and let
$\Sigma _m$
-collection and let
![]() $\varphi (x,y)$
and a be such that
$\varphi (x,y)$
and a be such that
![]() $H_{\alpha }$
satisfies
$H_{\alpha }$
satisfies
![]() $\forall x\in a\,\exists y\,\varphi (x,y)$
. Again, the case
$\forall x\in a\,\exists y\,\varphi (x,y)$
. Again, the case
![]() $m=1$
is trivial since cardinals are downward absolute, so we can assume
$m=1$
is trivial since cardinals are downward absolute, so we can assume
![]() $m\geq 2$
and use the
$m\geq 2$
and use the
![]() $\Delta _1$
-definability of
$\Delta _1$
-definability of
![]() in
in
![]() . Thus, we can apply
. Thus, we can apply
![]() $\Sigma _{m}$
-collection in
$\Sigma _{m}$
-collection in
![]() $H_{\alpha }[G]$
to obtain a set b collecting witnesses for
$H_{\alpha }[G]$
to obtain a set b collecting witnesses for
![]() $\varphi (x,y)$
. Since
$\varphi (x,y)$
. Since
![]() $\mathbb P$
can be assumed to have size less than
$\mathbb P$
can be assumed to have size less than
![]() $\alpha $
, we can cover
$\alpha $
, we can cover
![]() $b\cap V$
with a set
$b\cap V$
with a set
![]() $\bar b$
of size less than
$\bar b$
of size less than
![]() $\alpha $
in V. So
$\alpha $
in V. So
![]() $\bar b\in H_{\alpha }$
.
$\bar b\in H_{\alpha }$
.
It follows from Proposition 2.5(2) and (3) that only an initial segment of the stability predicate can be changed by set forcing. So the stable core is at least partially forcing absolute.
Corollary 2.6. If
![]() $\mathbb P\in H_{\gamma }$
is a forcing notion and
$\mathbb P\in H_{\gamma }$
is a forcing notion and
![]() $G\subseteq \mathbb P$
is V-generic, then
$G\subseteq \mathbb P$
is V-generic, then
![]() $(n,\alpha ,\beta )\in S$
if and only if
$(n,\alpha ,\beta )\in S$
if and only if
![]() $(n,\alpha ,\beta )\in S^{V[G]}$
for all
$(n,\alpha ,\beta )\in S^{V[G]}$
for all
![]() $\alpha , \beta \geq \gamma $
. So, in particular, S and
$\alpha , \beta \geq \gamma $
. So, in particular, S and
![]() $S^{V[G]}$
agree above the size of the forcing.
$S^{V[G]}$
agree above the size of the forcing.
Next, let’s give an argument that consistently the stable core can be a proper submodel of
![]() $\operatorname {HOD} $
. The fact follows from results in [Reference Friedman8], but here we give a simplified argument suggested to the second author by Woodin.
$\operatorname {HOD} $
. The fact follows from results in [Reference Friedman8], but here we give a simplified argument suggested to the second author by Woodin.
Proposition 2.7. It is consistent that
![]() $L[S]\subsetneq \operatorname {HOD} $
.
$L[S]\subsetneq \operatorname {HOD} $
.
Proof Start in L and force to add a Cohen real r. Next, force to code r into the continuum pattern on the
![]() $\aleph _n$
’s and let H be
$\aleph _n$
’s and let H be
![]() $L[r]$
-generic for the coding forcing
$L[r]$
-generic for the coding forcing
![]() $\mathbb P$
(the full support
$\mathbb P$
(the full support
![]() $\omega $
-length product forcing on coordinate n with
$\omega $
-length product forcing on coordinate n with
![]() $\operatorname {Add}(\aleph _n,\aleph _{n+2})$
whenever
$\operatorname {Add}(\aleph _n,\aleph _{n+2})$
whenever
![]() $n\in r$
and with trivial forcing otherwise). Observe that
$n\in r$
and with trivial forcing otherwise). Observe that
![]() $\operatorname {HOD} ^{L[r][H]}=L[r]$
because it has r, which the forcing
$\operatorname {HOD} ^{L[r][H]}=L[r]$
because it has r, which the forcing
![]() $\mathbb P$
made definable, and it must be contained in
$\mathbb P$
made definable, and it must be contained in
![]() $L[r]$
because
$L[r]$
because
![]() $\mathbb P$
is weakly homogeneous. We would like to argue that the stable core of
$\mathbb P$
is weakly homogeneous. We would like to argue that the stable core of
![]() $L[r][H]$
is L. By Corollary 2.6, the stable core of
$L[r][H]$
is L. By Corollary 2.6, the stable core of
![]() $L[r]$
is L. So it remains to argue that forcing with
$L[r]$
is L. So it remains to argue that forcing with
![]() $\mathbb P$
does not change the stable core. The forcing
$\mathbb P$
does not change the stable core. The forcing
![]() $\mathbb P$
preserves that
$\mathbb P$
preserves that
![]() $\aleph _{\omega }$
is a strong limit cardinal because it forces
$\aleph _{\omega }$
is a strong limit cardinal because it forces
![]() $2^{\aleph _n}\leq \aleph _{n+2}$
for all
$2^{\aleph _n}\leq \aleph _{n+2}$
for all
![]() $n<\omega $
, and it preserves all larger strong limit cardinals because it is small in size relative to them. So the strong limit cardinals of
$n<\omega $
, and it preserves all larger strong limit cardinals because it is small in size relative to them. So the strong limit cardinals of
![]() $L[r]$
are the same as in
$L[r]$
are the same as in
![]() $L[r][H]$
. By Corollary 2.6, only triples
$L[r][H]$
. By Corollary 2.6, only triples
![]() $(n,\aleph _{\omega },\gamma )$
with
$(n,\aleph _{\omega },\gamma )$
with
![]() $n\geq 2$
in S can be affected by
$n\geq 2$
in S can be affected by
![]() $\mathbb P$
. But for
$\mathbb P$
. But for
![]() $n\geq 2$
,
$n\geq 2$
,
![]() $(n,\aleph _{\omega },\gamma )$
can never make it into any stability predicate because
$(n,\aleph _{\omega },\gamma )$
can never make it into any stability predicate because
![]() $H_{\aleph _{\omega }}$
believes that there are no limit cardinals and
$H_{\aleph _{\omega }}$
believes that there are no limit cardinals and
![]() $H_{\gamma }$
sees
$H_{\gamma }$
sees
![]() $\aleph _{\omega }$
.
$\aleph _{\omega }$
.
We end the section with a brief description of a class forcing notion
![]() $\mathbb P$
making no use of the stability predicate such that V is a class generic extension of
$\mathbb P$
making no use of the stability predicate such that V is a class generic extension of
![]() $\langle \operatorname {HOD} ,\in , \mathbb P\rangle $
(this possibility was first suggested by Woodin). Conditions in
$\langle \operatorname {HOD} ,\in , \mathbb P\rangle $
(this possibility was first suggested by Woodin). Conditions in
![]() $\mathbb P$
are triples
$\mathbb P$
are triples
![]() $(\alpha ,\varphi ,\gamma )$
, where
$(\alpha ,\varphi ,\gamma )$
, where
![]() $\alpha <\gamma $
are ordinals,
$\alpha <\gamma $
are ordinals,
![]() $\varphi $
is a formula with ordinal parameters below
$\varphi $
is a formula with ordinal parameters below
![]() $\gamma $
which defines in
$\gamma $
which defines in
![]() $V_{\gamma }$
a non-empty subset
$V_{\gamma }$
a non-empty subset
![]() $X(\alpha ,\varphi ,\gamma )$
of
$X(\alpha ,\varphi ,\gamma )$
of
![]() $P(\alpha )$
. The ordering is given by
$P(\alpha )$
. The ordering is given by
![]() $(\alpha ^*,\varphi ^*,\gamma ^*)\leq (\alpha ,\varphi ,\gamma )$
whenever
$(\alpha ^*,\varphi ^*,\gamma ^*)\leq (\alpha ,\varphi ,\gamma )$
whenever
![]() $\alpha \leq \alpha ^*$
and for all
$\alpha \leq \alpha ^*$
and for all
![]() $y\in X(\alpha ^*,\varphi ^*,\gamma ^*)$
,
$y\in X(\alpha ^*,\varphi ^*,\gamma ^*)$
,
![]() $y\cap \alpha \in X(\alpha ,\varphi ,\gamma )$
. Observe that
$y\cap \alpha \in X(\alpha ,\varphi ,\gamma )$
. Observe that
![]() $\mathbb P$
is a V-definable class contained in
$\mathbb P$
is a V-definable class contained in
![]() $\operatorname {HOD} $
, and hence
$\operatorname {HOD} $
, and hence
![]() $\langle \operatorname {HOD} ,\in ,\mathbb P\rangle \models \operatorname {ZFC} $
. It is not difficult to see that if A is an
$\langle \operatorname {HOD} ,\in ,\mathbb P\rangle \models \operatorname {ZFC} $
. It is not difficult to see that if A is an
![]() $\operatorname {Ord} $
-Cohen generic class of ordinals, then the collection
$\operatorname {Ord} $
-Cohen generic class of ordinals, then the collection
![]() $G(A)=\{(\alpha ,\varphi ,\gamma )\in \mathbb P\mid A\cap \alpha \in X(\alpha ,\varphi ,\gamma )\}$
is
$G(A)=\{(\alpha ,\varphi ,\gamma )\in \mathbb P\mid A\cap \alpha \in X(\alpha ,\varphi ,\gamma )\}$
is
![]() $\mathbb P$
-generic over V. But since we can easily recover A from
$\mathbb P$
-generic over V. But since we can easily recover A from
![]() $G(A)$
and clearly
$G(A)$
and clearly
![]() $V=L[A]$
, we have that
$V=L[A]$
, we have that
![]() $V=L[G(A)]$
. In particular, we get that
$V=L[G(A)]$
. In particular, we get that
![]() $G(A)$
is
$G(A)$
is
![]() $\langle \operatorname {HOD} ,\in ,\mathbb P\rangle $
-generic and
$\langle \operatorname {HOD} ,\in ,\mathbb P\rangle $
-generic and
![]() $\operatorname {HOD} [G(A)]=L[G(A)]=L[A]=V$
. However, unlike the forcing in [Reference Friedman8],
$\operatorname {HOD} [G(A)]=L[G(A)]=L[A]=V$
. However, unlike the forcing in [Reference Friedman8],
![]() $\mathbb P$
does not have the
$\mathbb P$
does not have the
![]() $\operatorname {Ord} $
-cc.
$\operatorname {Ord} $
-cc.
3 Coding into the stable core over L
We will argue that any set added generically over L can be coded into the stable core of a further forcing extension. It is easiest to code into the strong limit cardinals (because these are always definable in the stable core), but we will show that we can actually code into any mth slice
![]() $S_m$
of the stability predicate.
$S_m$
of the stability predicate.
Theorem 3.1. Suppose
![]() $\mathbb P\in L$
is a forcing notion and
$\mathbb P\in L$
is a forcing notion and
![]() $G\subseteq \mathbb P$
is L-generic. Then for every
$G\subseteq \mathbb P$
is L-generic. Then for every
![]() $m\geq 1$
, there is a further forcing extension
$m\geq 1$
, there is a further forcing extension
![]() $L[G][H]$
such that
$L[G][H]$
such that
![]() $G\in L[S^{L[G][H]}_m]$
.
$G\in L[S^{L[G][H]}_m]$
.
Proof We can assume via coding that
![]() $G\subseteq \kappa $
for some cardinal
$G\subseteq \kappa $
for some cardinal
![]() $\kappa $
. Also, since
$\kappa $
. Also, since
![]() $\mathbb P$
is a set forcing,
$\mathbb P$
is a set forcing,
![]() $\operatorname {GCH} $
holds on a tail of the cardinals in
$\operatorname {GCH} $
holds on a tail of the cardinals in
![]() $L[G]$
, and so on a tail, the strong limit cardinals coincide with the limit cardinals. Also, on a tail,
$L[G]$
, and so on a tail, the strong limit cardinals coincide with the limit cardinals. Also, on a tail,
![]() $S^L$
agrees with
$S^L$
agrees with
![]() $S^{L[G]}$
by Corollary 2.6.
$S^{L[G]}$
by Corollary 2.6.
We work in L. High above
![]() $\kappa $
, we will define a sequence
$\kappa $
, we will define a sequence
![]() $\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi <\kappa \rangle $
of coding pairs such that
$\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi <\kappa \rangle $
of coding pairs such that
![]() $(\beta _{\xi },\beta _{\xi }^*)\in S^L_m$
. The coding forcing
$(\beta _{\xi },\beta _{\xi }^*)\in S^L_m$
. The coding forcing
![]() $\mathbb C$
will be defined so that if
$\mathbb C$
will be defined so that if
![]() $H\subseteq \mathbb C$
is
$H\subseteq \mathbb C$
is
![]() $L[G]$
-generic, then we will have
$L[G]$
-generic, then we will have
![]() $\xi \in G$
if and only if
$\xi \in G$
if and only if
![]() $(\beta _{\xi },\beta _{\xi }^*)\in S^{L[G][H]}_m$
. Since
$(\beta _{\xi },\beta _{\xi }^*)\in S^{L[G][H]}_m$
. Since
![]() $L[S^{L[G][H]}_m]$
can construct L, it will have the sequence of the coding pairs as well as
$L[S^{L[G][H]}_m]$
can construct L, it will have the sequence of the coding pairs as well as
![]() $S^{L[G][H]}_m$
, so that all the information put together will allow it to recover G.
$S^{L[G][H]}_m$
, so that all the information put together will allow it to recover G.
Call a strong limit cardinal
![]() $\alpha \ m$
-stable if
$\alpha \ m$
-stable if
![]() $H_{\alpha }\prec _{\Sigma _m} L$
. Observe that there is a proper class of m-stable cardinals and if
$H_{\alpha }\prec _{\Sigma _m} L$
. Observe that there is a proper class of m-stable cardinals and if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are both m-stable, then the pair
$\beta $
are both m-stable, then the pair
![]() $(\alpha ,\beta )\in S_m^L$
. Let
$(\alpha ,\beta )\in S_m^L$
. Let
![]() $\delta _0$
be the least strong limit cardinal above
$\delta _0$
be the least strong limit cardinal above
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\beta _0$
be the least m-stable cardinal above
$\beta _0$
be the least m-stable cardinal above
![]() $\delta _0$
of cofinality
$\delta _0$
of cofinality
![]() $\delta _0^+$
and let
$\delta _0^+$
and let
![]() $\beta _0^*$
be the least m-stable cardinal above
$\beta _0^*$
be the least m-stable cardinal above
![]() $\beta _0$
. Now supposing we have defined the pairs
$\beta _0$
. Now supposing we have defined the pairs
![]() $(\beta _{\eta },\beta _{\eta }^*)$
of m-stable cardinals for all
$(\beta _{\eta },\beta _{\eta }^*)$
of m-stable cardinals for all
![]() $\eta <\xi $
, let
$\eta <\xi $
, let
![]() $\delta _{\xi }$
be the supremum of the
$\delta _{\xi }$
be the supremum of the
![]() $\beta _{\eta }^*$
for
$\beta _{\eta }^*$
for
![]() $\eta <\xi $
, let
$\eta <\xi $
, let
![]() $\beta _{\xi }$
be the least m-stable cardinal above
$\beta _{\xi }$
be the least m-stable cardinal above
![]() $\delta _{\xi }$
of cofinality
$\delta _{\xi }$
of cofinality
![]() $\delta _{\xi }^+$
, and let
$\delta _{\xi }^+$
, and let
![]() $\beta _{\xi }^*$
be the least m-stable cardinal above
$\beta _{\xi }^*$
be the least m-stable cardinal above
![]() $\beta _{\xi }$
. In particular,
$\beta _{\xi }$
. In particular,
![]() $\beta _{\xi }>\delta _{\xi }^+$
since, by m-stability,
$\beta _{\xi }>\delta _{\xi }^+$
since, by m-stability,
![]() $\beta _{\xi }$
is a strong limit cardinal. Note that the sequence
$\beta _{\xi }$
is a strong limit cardinal. Note that the sequence
![]() $\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi <\kappa \rangle $
is
$\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi <\kappa \rangle $
is
![]() $\Sigma _{m+1}$
-definable over L. Note also that
$\Sigma _{m+1}$
-definable over L. Note also that
![]() $\beta _{\eta }<\beta _{\eta }^*<\beta _{\xi }<\beta _{\xi }^*$
for all
$\beta _{\eta }<\beta _{\eta }^*<\beta _{\xi }<\beta _{\xi }^*$
for all
![]() $\eta <\xi <\kappa $
and for limit
$\eta <\xi <\kappa $
and for limit
![]() $\lambda <\kappa $
,
$\lambda <\kappa $
,
![]() $\beta _{\lambda }>\bigcup _{\xi <\lambda }\beta _{\xi }$
, so that the sequence of the
$\beta _{\lambda }>\bigcup _{\xi <\lambda }\beta _{\xi }$
, so that the sequence of the
![]() $\beta _{\xi }$
will be purposefully discontinuous. Since the forcing
$\beta _{\xi }$
will be purposefully discontinuous. Since the forcing
![]() $\mathbb P$
is small relative to
$\mathbb P$
is small relative to
![]() $\delta _0$
, by Corollary 2.6, the coding pairs
$\delta _0$
, by Corollary 2.6, the coding pairs
![]() $(\beta _{\xi },\beta _{\xi }^*)\in S_m^{L[G]}$
.
$(\beta _{\xi },\beta _{\xi }^*)\in S_m^{L[G]}$
.
Now for
![]() $\xi <\kappa $
, let
$\xi <\kappa $
, let
![]() $\mathbb C_{\xi }$
be the following forcing. If
$\mathbb C_{\xi }$
be the following forcing. If
![]() $\xi \in G$
, then
$\xi \in G$
, then
![]() $\mathbb C_{\xi }$
is the trivial forcing. If
$\mathbb C_{\xi }$
is the trivial forcing. If
![]() $\xi \notin G$
, then
$\xi \notin G$
, then
![]() $\mathbb C_{\xi }=\operatorname {Coll}(\delta ^+_{\xi },\beta _{\xi })$
. Let
$\mathbb C_{\xi }=\operatorname {Coll}(\delta ^+_{\xi },\beta _{\xi })$
. Let
![]() $\mathbb C$
be the full support product
$\mathbb C$
be the full support product
![]() $\Pi _{\xi <\kappa }\mathbb C_{\xi }$
and let
$\Pi _{\xi <\kappa }\mathbb C_{\xi }$
and let
![]() $H\subseteq \mathbb C$
be
$H\subseteq \mathbb C$
be
![]() $L[G]$
-generic.
$L[G]$
-generic.
Let’s check that
![]() $\mathbb C$
collapses the minimum number of cardinals, namely
$\mathbb C$
collapses the minimum number of cardinals, namely
![]() $\mathbb C$
collapses a cardinal
$\mathbb C$
collapses a cardinal
![]() $\delta $
if and only if there is a non-trivial forcing stage
$\delta $
if and only if there is a non-trivial forcing stage
![]() $\xi $
such that
$\xi $
such that
![]() $\delta _{\xi }^+<\delta \leq \beta _{\xi }$
. For every
$\delta _{\xi }^+<\delta \leq \beta _{\xi }$
. For every
![]() $\xi <\kappa $
, the forcing
$\xi <\kappa $
, the forcing
![]() $\mathbb C$
factors as
$\mathbb C$
factors as
![]() $\Pi _{\eta <\xi }\mathbb C_{\eta }\times \Pi _{\xi \leq \eta <\kappa }\mathbb C_{\eta }$
, where the second part is
$\Pi _{\eta <\xi }\mathbb C_{\eta }\times \Pi _{\xi \leq \eta <\kappa }\mathbb C_{\eta }$
, where the second part is
![]() -closed (using full support), and so cannot collapse any cardinals
-closed (using full support), and so cannot collapse any cardinals
![]() $\leq \delta ^+_{\xi }$
. Observe next that the forcing
$\leq \delta ^+_{\xi }$
. Observe next that the forcing
![]() $\operatorname {Coll}(\delta ^+_{\xi },\beta _{\xi })$
has size
$\operatorname {Coll}(\delta ^+_{\xi },\beta _{\xi })$
has size
![]() $\beta _{\xi }^{\delta _{\xi }}=\beta _{\xi }$
because
$\beta _{\xi }^{\delta _{\xi }}=\beta _{\xi }$
because
![]() $\text {cf}(\beta _{\xi })>\delta _{\xi }$
by our choice of
$\text {cf}(\beta _{\xi })>\delta _{\xi }$
by our choice of
![]() $\beta _{\xi }$
, and so cannot collapse any cardinal
$\beta _{\xi }$
, and so cannot collapse any cardinal
![]() $\geq \beta _{\xi }^+$
. It follows that the forcing
$\geq \beta _{\xi }^+$
. It follows that the forcing
![]() $\mathbb C$
cannot collapse any
$\mathbb C$
cannot collapse any
![]() $\delta \in (\beta _{\xi }, \delta _{\xi +1}^+]$
. It remains to show that
$\delta \in (\beta _{\xi }, \delta _{\xi +1}^+]$
. It remains to show that
![]() $\delta _{\lambda }$
and
$\delta _{\lambda }$
and
![]() $\delta _{\lambda }^+$
for a limit
$\delta _{\lambda }^+$
for a limit
![]() $\lambda $
are preserved. By what we already showed,
$\lambda $
are preserved. By what we already showed,
![]() $\delta _{\lambda }$
is a limit of cardinals in the forcing extension, and therefore remains a cardinal. Also, by what we already showed, if
$\delta _{\lambda }$
is a limit of cardinals in the forcing extension, and therefore remains a cardinal. Also, by what we already showed, if
![]() $\delta ^+_{\lambda }$
is collapsed, then it must be collapsed to
$\delta ^+_{\lambda }$
is collapsed, then it must be collapsed to
![]() $\delta _{\lambda }$
. Suppose this happens and fix a bijection
$\delta _{\lambda }$
. Suppose this happens and fix a bijection
![]() $f:\delta _{\lambda }\to \delta _{\lambda }^+$
in the forcing extension. We can let
$f:\delta _{\lambda }\to \delta _{\lambda }^+$
in the forcing extension. We can let
![]() $f=\bigcup _{\xi <\lambda }f_{\xi }$
, where
$f=\bigcup _{\xi <\lambda }f_{\xi }$
, where
![]() $f_{\xi }:\gamma _{\xi }\to \delta _{\lambda }^+$
and the
$f_{\xi }:\gamma _{\xi }\to \delta _{\lambda }^+$
and the
![]() $\gamma _{\xi }$
are cofinal in
$\gamma _{\xi }$
are cofinal in
![]() $\delta _{\lambda }$
. Each function
$\delta _{\lambda }$
. Each function
![]() $f_{\xi }$
must be added by some proper initial segment of
$f_{\xi }$
must be added by some proper initial segment of
![]() $\Pi _{\xi <\lambda }\mathbb C_{\xi }$
by closure, and therefore its range must be bounded in
$\Pi _{\xi <\lambda }\mathbb C_{\xi }$
by closure, and therefore its range must be bounded in
![]() $\delta _{\lambda }^+$
. Now build a descending sequence of conditions
$\delta _{\lambda }^+$
. Now build a descending sequence of conditions
![]() $\langle p_{\xi }\mid \xi <\lambda \rangle $
in
$\langle p_{\xi }\mid \xi <\lambda \rangle $
in
![]() $\Pi _{\xi <\lambda }\mathbb C_{\xi }$
such that
$\Pi _{\xi <\lambda }\mathbb C_{\xi }$
such that
![]() $p_{\xi }$
decides the bound on the range of
$p_{\xi }$
decides the bound on the range of
![]() $f_{\xi }$
. But then any condition p below the entire sequence forces that f is bounded in
$f_{\xi }$
. But then any condition p below the entire sequence forces that f is bounded in
![]() $\delta _{\lambda }^+$
, which is the desired contradiction.
$\delta _{\lambda }^+$
, which is the desired contradiction.
By the following claim, the forcing
![]() $\mathbb C$
also preserves the
$\mathbb C$
also preserves the
![]() $\operatorname {GCH} $
where the coding forcing takes place, so the strong limit cardinals of
$\operatorname {GCH} $
where the coding forcing takes place, so the strong limit cardinals of
![]() $L[G][H]$
are precisely the limit cardinals there.
$L[G][H]$
are precisely the limit cardinals there.
Claim 1. The
![]() $\operatorname {GCH} $
continues to hold on the part where it holds in
$\operatorname {GCH} $
continues to hold on the part where it holds in
![]() $L[G]$
in the forcing extension
$L[G]$
in the forcing extension
![]() $L[G][H]$
by
$L[G][H]$
by
![]() $\mathbb C$
.
$\mathbb C$
.
Proof By closure, it is clear that wherever the
![]() $\operatorname {GCH} $
held below
$\operatorname {GCH} $
held below
![]() $\delta _0^+$
, it will continue to hold. Since
$\delta _0^+$
, it will continue to hold. Since
![]() $G \subseteq \kappa $
,
$G \subseteq \kappa $
,
![]() $\operatorname {GCH} $
holds in
$\operatorname {GCH} $
holds in
![]() $L[G]$
above
$L[G]$
above
![]() $\delta _0$
.
$\delta _0$
.
If there is trivial forcing at stage 0, then the
![]() $\operatorname {GCH} $
holds at
$\operatorname {GCH} $
holds at
![]() $\delta _0^+$
in
$\delta _0^+$
in
![]() $L[G][H]$
. So suppose that
$L[G][H]$
. So suppose that
![]() $\mathbb C_0=\operatorname {Coll}(\delta _0^+,\beta _0)$
is a non-trivial stage. Recall that
$\mathbb C_0=\operatorname {Coll}(\delta _0^+,\beta _0)$
is a non-trivial stage. Recall that
![]() $\operatorname {Coll}(\delta _0^+,\beta _0)$
has size
$\operatorname {Coll}(\delta _0^+,\beta _0)$
has size
![]() $\beta _0$
so that there are
$\beta _0$
so that there are
![]() $\beta _0^+$
-many nice names for subsets of
$\beta _0^+$
-many nice names for subsets of
![]() $\delta _0^+$
(and of course in
$\delta _0^+$
(and of course in
![]() $L[G][H]$
,
$L[G][H]$
,
![]() $(\delta _0^+)^+=(\beta _0^+)^{L[G]}$
), which shows that the
$(\delta _0^+)^+=(\beta _0^+)^{L[G]}$
), which shows that the
![]() $\operatorname {GCH} $
holds at
$\operatorname {GCH} $
holds at
![]() $\delta _0^+$
in
$\delta _0^+$
in
![]() $L[G][H]$
in this case as well.
$L[G][H]$
in this case as well.
Now suppose inductively that the
![]() $\operatorname {GCH} $
holds up to some cardinal
$\operatorname {GCH} $
holds up to some cardinal
![]() $\rho $
. If
$\rho $
. If
![]() $\rho =\delta _{\xi }^+$
for a successor ordinal
$\rho =\delta _{\xi }^+$
for a successor ordinal
![]() $\xi $
, we repeat the argument for
$\xi $
, we repeat the argument for
![]() $\xi =0$
. If
$\xi =0$
. If
![]() $\delta _{\xi }^+<\rho <\delta _{\xi +1}^+$
and there was non-trivial forcing at stage
$\delta _{\xi }^+<\rho <\delta _{\xi +1}^+$
and there was non-trivial forcing at stage
![]() $\xi $
, then
$\xi $
, then
![]() $\beta _{\xi }<\rho <\delta _{\xi +1}^+$
, and so the
$\beta _{\xi }<\rho <\delta _{\xi +1}^+$
, and so the
![]() $\operatorname {GCH} $
continues to hold because the initial forcing is small relative to
$\operatorname {GCH} $
continues to hold because the initial forcing is small relative to
![]() $\rho $
and the tail forcing is closed. Next, suppose
$\rho $
and the tail forcing is closed. Next, suppose
![]() $\rho =\delta _{\lambda }^+$
for a limit cardinal
$\rho =\delta _{\lambda }^+$
for a limit cardinal
![]() $\lambda <\kappa $
. Since
$\lambda <\kappa $
. Since
![]() $\lambda $
is a limit, the initial segment forcing
$\lambda $
is a limit, the initial segment forcing
![]() $\Pi _{\xi <\lambda }\mathbb C_{\xi }$
has size at most
$\Pi _{\xi <\lambda }\mathbb C_{\xi }$
has size at most
![]() $\delta _{\lambda }^+$
. This means that there are
$\delta _{\lambda }^+$
. This means that there are
![]() $(\delta ^+_{\lambda })^+$
-many nice-names for subsets of
$(\delta ^+_{\lambda })^+$
-many nice-names for subsets of
![]() $\delta _{\lambda }^+$
, so that the
$\delta _{\lambda }^+$
, so that the
![]() $\operatorname {GCH} $
holds at
$\operatorname {GCH} $
holds at
![]() $\rho =\delta _{\lambda }^+$
. Finally, suppose
$\rho =\delta _{\lambda }^+$
. Finally, suppose
![]() $\rho =\delta _{\lambda }$
. Each
$\rho =\delta _{\lambda }$
. Each
![]() $A\subseteq \delta _{\lambda }$
is uniquely determined by the sequence
$A\subseteq \delta _{\lambda }$
is uniquely determined by the sequence
![]() $\langle A_{\xi }\mid \xi <\lambda \rangle $
with
$\langle A_{\xi }\mid \xi <\lambda \rangle $
with
![]() $A_{\xi }=A\cap \beta _{\xi }$
. Let
$A_{\xi }=A\cap \beta _{\xi }$
. Let
![]() $\dot f_{\xi }$
be a name for an injection from
$\dot f_{\xi }$
be a name for an injection from
![]() $P(\beta _{\xi })$
into
$P(\beta _{\xi })$
into
![]() $\delta _{\lambda }$
, which exists since, by assumption, the
$\delta _{\lambda }$
, which exists since, by assumption, the
![]() $\operatorname {GCH} $
holds below
$\operatorname {GCH} $
holds below
![]() $\delta _{\lambda }$
in
$\delta _{\lambda }$
in
![]() $L[G][H]$
. Let’s argue that every sequence
$L[G][H]$
. Let’s argue that every sequence
![]() $\langle A_{\xi }\mid \xi <\lambda \rangle $
such that
$\langle A_{\xi }\mid \xi <\lambda \rangle $
such that
![]() $A_{\xi }\subseteq \beta _{\xi }$
in the extension has a name of the form
$A_{\xi }\subseteq \beta _{\xi }$
in the extension has a name of the form
![]() $\dot A$
, where
$\dot A$
, where
![]() $\dot A(\xi )=\dot f^{-1}_{\xi }(\gamma )$
for some
$\dot A(\xi )=\dot f^{-1}_{\xi }(\gamma )$
for some
![]() $\gamma \in \delta _{\lambda }$
. Let
$\gamma \in \delta _{\lambda }$
. Let
![]() $\dot B$
be any name for the sequence
$\dot B$
be any name for the sequence
![]() $\langle A_{\xi }\mid \xi <\lambda \rangle $
and
$\langle A_{\xi }\mid \xi <\lambda \rangle $
and
![]() $p'\in H$
be a condition forcing that
$p'\in H$
be a condition forcing that
![]() $\dot B$
is a sequence of the right form. Below
$\dot B$
is a sequence of the right form. Below
![]() $p'$
, we build a descending sequence
$p'$
, we build a descending sequence
![]() $p_{\xi }$
for
$p_{\xi }$
for
![]() $\xi <\lambda $
of conditions deciding that
$\xi <\lambda $
of conditions deciding that
![]() $\dot B(\xi )=\dot f_{\xi }^{-1}(\gamma _{\xi })$
for some fixed
$\dot B(\xi )=\dot f_{\xi }^{-1}(\gamma _{\xi })$
for some fixed
![]() $\gamma _{\xi }<\delta _{\lambda }$
. By closure, there is some p below the entire sequence. So by density, there is some such
$\gamma _{\xi }<\delta _{\lambda }$
. By closure, there is some p below the entire sequence. So by density, there is some such
![]() $p\in H$
. It follows that there are at most as many subsets of
$p\in H$
. It follows that there are at most as many subsets of
![]() $\delta _{\lambda }$
in the extension as there are functions
$\delta _{\lambda }$
in the extension as there are functions
![]() $f:\lambda \to \delta _{\lambda }$
in the ground model, and there are
$f:\lambda \to \delta _{\lambda }$
in the ground model, and there are
![]() $\delta _{\lambda }^+$
-many such functions.
$\delta _{\lambda }^+$
-many such functions.
Now we will argue that the pair
![]() $(\beta _{\xi },\beta _{\xi }^*)$
belongs in
$(\beta _{\xi },\beta _{\xi }^*)$
belongs in
![]() $S^{L[G][H]}_m$
if and only if
$S^{L[G][H]}_m$
if and only if
![]() $\xi \in G$
. If
$\xi \in G$
. If
![]() $\xi \notin G$
, then
$\xi \notin G$
, then
![]() $\beta _{\xi }$
is not even a cardinal in
$\beta _{\xi }$
is not even a cardinal in
![]() $L[G][H]$
, and therefore certainly
$L[G][H]$
, and therefore certainly
![]() $(\beta _{\xi },\beta _{\xi }^*)\notin S^{L[G][H]}_m$
. Suppose that
$(\beta _{\xi },\beta _{\xi }^*)\notin S^{L[G][H]}_m$
. Suppose that
![]() $\xi \in G$
, so that there is trivial forcing at stage
$\xi \in G$
, so that there is trivial forcing at stage
![]() $\xi $
. By what we already argued about which cardinals are collapsed in
$\xi $
. By what we already argued about which cardinals are collapsed in
![]() $L[G][H]$
, it follows that
$L[G][H]$
, it follows that
![]() $\beta _{\xi }$
and
$\beta _{\xi }$
and
![]() $\beta _{\xi }^*$
are limit cardinals there. Let
$\beta _{\xi }^*$
are limit cardinals there. Let
![]() $\mathbb C_{\text {small}}=\Pi _{\eta <\xi }\mathbb C_{\eta }$
and
$\mathbb C_{\text {small}}=\Pi _{\eta <\xi }\mathbb C_{\eta }$
and
![]() $\mathbb C_{\text {tail}}=\Pi _{\xi <\eta <\kappa }\mathbb C_{\eta }$
, and note that since there is no forcing at stage
$\mathbb C_{\text {tail}}=\Pi _{\xi <\eta <\kappa }\mathbb C_{\eta }$
, and note that since there is no forcing at stage
![]() $\xi $
,
$\xi $
,
![]() $\mathbb C$
factors as
$\mathbb C$
factors as
![]() $\mathbb C_{\text {small}}\times \mathbb C_{\text {tail}}$
. Let
$\mathbb C_{\text {small}}\times \mathbb C_{\text {tail}}$
. Let
![]() $H_{\text {small}}\times H_{\text {tail}}$
be the corresponding factoring of the generic filter H. Since
$H_{\text {small}}\times H_{\text {tail}}$
be the corresponding factoring of the generic filter H. Since
![]() $\mathbb C_{\text {tail}}$
is
$\mathbb C_{\text {tail}}$
is
![]() $\leq \beta ^*_{\xi }$
-closed, we have that
$\leq \beta ^*_{\xi }$
-closed, we have that
![]() $H_{\beta _{\xi }}^{L[G][H]}=H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}$
and
$H_{\beta _{\xi }}^{L[G][H]}=H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}$
and
![]() $H_{\beta _{\xi }^*}^{L[G][H]}=H_{\beta _{\xi }^*}^{L[G][H_{\text {small}}]}$
. By Proposition 2.5(3),
$H_{\beta _{\xi }^*}^{L[G][H]}=H_{\beta _{\xi }^*}^{L[G][H_{\text {small}}]}$
. By Proposition 2.5(3),
![]() $H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}$
satisfies
$H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}$
satisfies
![]() $\Sigma _m$
-collection and by Proposition 2.5(2),
$\Sigma _m$
-collection and by Proposition 2.5(2),
![]() $H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}\prec _{\Sigma _m} H_{\beta _{\xi }^*}^{L[G][H_{\text {small}}]}$
.
$H_{\beta _{\xi }}^{L[G][H_{\text {small}}]}\prec _{\Sigma _m} H_{\beta _{\xi }^*}^{L[G][H_{\text {small}}]}$
.
It follows from Theorem 3.1 that (consistently) the stable core is not a fine-structural or in any sense canonical inner model. Among the numerous corollaries of Theorem 3.1 are the following.
Corollary 3.2.
-
(1) The
 $\operatorname {GCH} $
can fail on an arbitrarily large initial segment of the regular cardinals in the stable core.
$\operatorname {GCH} $
can fail on an arbitrarily large initial segment of the regular cardinals in the stable core. -
(2) An arbitrarily large ordinal of L can be countable in the stable core.
-
(3)
 $\mathrm {MA}+\neg \mathrm {CH}$
can hold in the stable core.
$\mathrm {MA}+\neg \mathrm {CH}$
can hold in the stable core.
Proof For (1), we force over L to violate the
![]() $\operatorname {GCH} $
on an initial segment of the regular cardinals, and then code all the subsets we add into the stable core of the forcing extension by the coding forcing
$\operatorname {GCH} $
on an initial segment of the regular cardinals, and then code all the subsets we add into the stable core of the forcing extension by the coding forcing
![]() $\mathbb C$
. For (2), we force over L to collapse the ordinal, and then code the collapsing map into the stable core of the forcing extension by the coding forcing
$\mathbb C$
. For (2), we force over L to collapse the ordinal, and then code the collapsing map into the stable core of the forcing extension by the coding forcing
![]() $\mathbb C$
. For (3), we force Martin’s Axiom with
$\mathbb C$
. For (3), we force Martin’s Axiom with
![]() $2^{\omega }=\kappa $
, where
$2^{\omega }=\kappa $
, where
![]() $\kappa $
is uncountable and regular, to hold over L, and let
$\kappa $
is uncountable and regular, to hold over L, and let
![]() $L[G]$
be the forcing extension. We then code the G into the stable core of the forcing extension high above
$L[G]$
be the forcing extension. We then code the G into the stable core of the forcing extension high above
![]() $\kappa $
. Any ccc partial order
$\kappa $
. Any ccc partial order
![]() $\mathbb P$
on
$\mathbb P$
on
![]() $\kappa $
in the stable core of the coding extension already exists in
$\kappa $
in the stable core of the coding extension already exists in
![]() $L[G]$
, and therefore G will have added a partial generic filter (meeting some less than continuum many dense sets) for it.
$L[G]$
, and therefore G will have added a partial generic filter (meeting some less than continuum many dense sets) for it.
Theorem 3.3. It is consistent that the
![]() $\operatorname {GCH} $
fails at all regular cardinals in the stable core.
$\operatorname {GCH} $
fails at all regular cardinals in the stable core.
Proof The idea will be to force the
![]() $\operatorname {GCH} $
to fail at all regular cardinals over L, and then use
$\operatorname {GCH} $
to fail at all regular cardinals over L, and then use
![]() $\operatorname {Ord} $
-many coding pairs to code all the added subsets into the stable core of a forcing extension. In this argument, we will code into the limit cardinals, namely
$\operatorname {Ord} $
-many coding pairs to code all the added subsets into the stable core of a forcing extension. In this argument, we will code into the limit cardinals, namely
![]() $S_1$
, by using generalized Cohen forcing instead of the collapse forcing.
$S_1$
, by using generalized Cohen forcing instead of the collapse forcing.
In L, let
![]() $\mathbb P$
be the Easton support
$\mathbb P$
be the Easton support
![]() $\operatorname {Ord} $
-length product forcing with
$\operatorname {Ord} $
-length product forcing with
![]() $\operatorname {Add}(\kappa ,\kappa ^{++})$
at every regular cardinal
$\operatorname {Add}(\kappa ,\kappa ^{++})$
at every regular cardinal
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $G\subseteq \mathbb P$
be L-generic. Standard arguments show that in
$G\subseteq \mathbb P$
be L-generic. Standard arguments show that in
![]() $L[G]$
,
$L[G]$
,
![]() $2^{\kappa }=\kappa ^{++}$
for every regular cardinal
$2^{\kappa }=\kappa ^{++}$
for every regular cardinal
![]() $\kappa $
, while the
$\kappa $
, while the
![]() $\operatorname {GCH} $
continues to hold at singular cardinals (see, for example, [Reference Jech15]). Since
$\operatorname {GCH} $
continues to hold at singular cardinals (see, for example, [Reference Jech15]). Since
![]() $\langle L[G],\in , G\rangle $
has a definable global well-order, we can assume via coding that
$\langle L[G],\in , G\rangle $
has a definable global well-order, we can assume via coding that
![]() $G\subseteq \operatorname {Ord} $
(and define the coding forcing in this expanded structure).
$G\subseteq \operatorname {Ord} $
(and define the coding forcing in this expanded structure).
We first work in L. Let
![]() $\delta _0$
be the least strong limit cardinal. Above
$\delta _0$
be the least strong limit cardinal. Above
![]() $\delta _0$
, we will define a sequence
$\delta _0$
, we will define a sequence
![]() $\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi \in \operatorname {Ord} \rangle $
of coding pairs of strong limit cardinals. Let
$\langle (\beta _{\xi },\beta _{\xi }^*)\mid \xi \in \operatorname {Ord} \rangle $
of coding pairs of strong limit cardinals. Let
![]() $\beta _0<\beta _0^*$
be the next two strong limit cardinals above
$\beta _0<\beta _0^*$
be the next two strong limit cardinals above
![]() $\delta _0$
. Now supposing we have defined the pairs
$\delta _0$
. Now supposing we have defined the pairs
![]() $(\beta _{\eta },\beta _{\eta }^*)$
of strong limit cardinals for all
$(\beta _{\eta },\beta _{\eta }^*)$
of strong limit cardinals for all
![]() $\eta <\xi $
, let
$\eta <\xi $
, let
![]() $\delta _{\xi }$
be the supremum of the
$\delta _{\xi }$
be the supremum of the
![]() $\beta _{\eta }^*$
for
$\beta _{\eta }^*$
for
![]() $\eta <\xi $
and let
$\eta <\xi $
and let
![]() $\beta _{\xi }<\beta _{\xi }^*$
be the next two strong limit cardinals above
$\beta _{\xi }<\beta _{\xi }^*$
be the next two strong limit cardinals above
![]() $\delta _{\xi }$
. Observe that every strong limit cardinal of L remains a strong limit in
$\delta _{\xi }$
. Observe that every strong limit cardinal of L remains a strong limit in
![]() $L[G]$
, and so in particular, the elements
$L[G]$
, and so in particular, the elements
![]() $\beta _{\xi }$
and
$\beta _{\xi }$
and
![]() $\beta _{\xi }^*$
of the coding pairs are strong limits in
$\beta _{\xi }^*$
of the coding pairs are strong limits in
![]() $L[G]$
.
$L[G]$
.
For each ordinal
![]() $\xi $
, let
$\xi $
, let
![]() $\mathbb C_{\xi }$
be the following forcing. If
$\mathbb C_{\xi }$
be the following forcing. If
![]() $\xi \in G$
, then
$\xi \in G$
, then
![]() $\mathbb C_{\xi }$
is the trivial forcing. So suppose that
$\mathbb C_{\xi }$
is the trivial forcing. So suppose that
![]() $\xi \notin G$
. If
$\xi \notin G$
. If
![]() $\delta _{\xi }$
is singular, we let
$\delta _{\xi }$
is singular, we let
![]() $\mathbb C_{\xi }=\operatorname {Add}(\delta ^+_{\xi },\beta _{\xi })$
(the partial order to add
$\mathbb C_{\xi }=\operatorname {Add}(\delta ^+_{\xi },\beta _{\xi })$
(the partial order to add
![]() $\beta _{\xi }$
-many Cohen subsets to
$\beta _{\xi }$
-many Cohen subsets to
![]() $\delta ^+_{\xi }$
with bounded conditions), and otherwise, we let
$\delta ^+_{\xi }$
with bounded conditions), and otherwise, we let
![]() $\mathbb C_{\xi }=\operatorname {Add}(\delta _{\xi },\beta _{\xi })$
. Let’s argue that all forcing notions
$\mathbb C_{\xi }=\operatorname {Add}(\delta _{\xi },\beta _{\xi })$
. Let’s argue that all forcing notions
![]() $\mathbb C_{\xi }$
are cardinal preserving. If
$\mathbb C_{\xi }$
are cardinal preserving. If
![]() $\delta _{\xi }$
is singular, then the
$\delta _{\xi }$
is singular, then the
![]() $\operatorname {GCH} $
holds at
$\operatorname {GCH} $
holds at
![]() $\delta _{\xi }$
, and therefore
$\delta _{\xi }$
, and therefore
![]() $\operatorname {Add}(\delta ^+_{\xi },\beta _{\xi })$
has the
$\operatorname {Add}(\delta ^+_{\xi },\beta _{\xi })$
has the
![]() $(2^{{\mathrel {\scriptscriptstyle <}}\delta _{\xi }^+})^+=(2^{\delta _{\xi }})^+=\delta _{\xi }^{++}$
chain condition, which means that it preserves all cardinals. If
$(2^{{\mathrel {\scriptscriptstyle <}}\delta _{\xi }^+})^+=(2^{\delta _{\xi }})^+=\delta _{\xi }^{++}$
chain condition, which means that it preserves all cardinals. If
![]() $\delta _{\xi }$
is regular, then it is inaccessible because it is always a limit cardinal, and therefore
$\delta _{\xi }$
is regular, then it is inaccessible because it is always a limit cardinal, and therefore
![]() $\operatorname {Add}(\delta _{\xi },\beta _{\xi })$
preserves all cardinals. Obviously, every non-trivial forcing
$\operatorname {Add}(\delta _{\xi },\beta _{\xi })$
preserves all cardinals. Obviously, every non-trivial forcing
![]() $\mathbb C_{\xi }$
destroys the strong limit property of
$\mathbb C_{\xi }$
destroys the strong limit property of
![]() $\beta _{\xi }$
in the forcing extension.
$\beta _{\xi }$
in the forcing extension.
Let
![]() $\mathbb C$
be the
$\mathbb C$
be the
![]() $\operatorname {Ord} $
-length Easton support product
$\operatorname {Ord} $
-length Easton support product
![]() $\Pi _{\xi \in \operatorname {Ord} }\mathbb C_{\xi }$
. Let’s argue that the forcing notion
$\Pi _{\xi \in \operatorname {Ord} }\mathbb C_{\xi }$
. Let’s argue that the forcing notion
![]() $\mathbb C$
is also cardinal preserving. Observe first that if
$\mathbb C$
is also cardinal preserving. Observe first that if
![]() $\delta _{\xi }$
is singular, then the initial segment
$\delta _{\xi }$
is singular, then the initial segment
![]() $\Pi _{\eta <\xi }\mathbb C_{\eta }$
has size
$\Pi _{\eta <\xi }\mathbb C_{\eta }$
has size
![]() $\delta _{\xi }^{\delta _{\xi }}=\delta _{\xi }^+$
since the
$\delta _{\xi }^{\delta _{\xi }}=\delta _{\xi }^+$
since the
![]() $\operatorname {GCH} $
holds at
$\operatorname {GCH} $
holds at
![]() $\delta _{\xi }$
. If
$\delta _{\xi }$
. If
![]() $\delta _{\xi }$
is regular, then
$\delta _{\xi }$
is regular, then
![]() $\delta _{\xi }$
is inaccessible, so that conditions in
$\delta _{\xi }$
is inaccessible, so that conditions in
![]() $\Pi _{\eta <\xi }\mathbb C_{\eta }$
are bounded, and hence
$\Pi _{\eta <\xi }\mathbb C_{\eta }$
are bounded, and hence
![]() $\Pi _{\eta <\xi }\mathbb C_{\eta }$
has size
$\Pi _{\eta <\xi }\mathbb C_{\eta }$
has size
![]() $\delta _{\xi }^{{\mathrel {\scriptscriptstyle <}}\delta _{\xi }}=\delta _{\xi }$
. Now we can argue that if
$\delta _{\xi }^{{\mathrel {\scriptscriptstyle <}}\delta _{\xi }}=\delta _{\xi }$
. Now we can argue that if
![]() $\delta _{\xi }^+<\gamma <\delta _{\xi +1}$
is a cardinal, then it remains a cardinal in the forcing extension by
$\delta _{\xi }^+<\gamma <\delta _{\xi +1}$
is a cardinal, then it remains a cardinal in the forcing extension by
![]() $\mathbb C$
because by previous calculations, the initial segment
$\mathbb C$
because by previous calculations, the initial segment
![]() $\Pi _{\eta <\xi }\mathbb C_{\eta }\times \mathbb C_{\xi }$
cannot collapse
$\Pi _{\eta <\xi }\mathbb C_{\eta }\times \mathbb C_{\xi }$
cannot collapse
![]() $\gamma $
, and the tail forcing is highly closed. Cardinals of the form
$\gamma $
, and the tail forcing is highly closed. Cardinals of the form
![]() $\delta _{\xi +1}$
cannot be collapsed because the successor stage forcings are cardinal preserving. It remains to consider cardinals of the form
$\delta _{\xi +1}$
cannot be collapsed because the successor stage forcings are cardinal preserving. It remains to consider cardinals of the form
![]() $\delta _{\lambda }$
and
$\delta _{\lambda }$
and
![]() $\delta _{\lambda }^+$
for a limit cardinal
$\delta _{\lambda }^+$
for a limit cardinal
![]() $\lambda $
. By what we already showed,
$\lambda $
. By what we already showed,
![]() $\delta _{\lambda }$
is a limit of cardinals in the forcing extension, and hence must be a cardinal itself. If
$\delta _{\lambda }$
is a limit of cardinals in the forcing extension, and hence must be a cardinal itself. If
![]() $\delta _{\lambda }$
is regular, then it is inaccessible, and hence the initial segment
$\delta _{\lambda }$
is regular, then it is inaccessible, and hence the initial segment
![]() $\Pi _{\xi <\lambda }\mathbb C_{\xi }$
is too small to collapse
$\Pi _{\xi <\lambda }\mathbb C_{\xi }$
is too small to collapse
![]() $\delta _{\lambda }^+$
. So suppose that
$\delta _{\lambda }^+$
. So suppose that
![]() $\delta _{\lambda }$
is singular with
$\delta _{\lambda }$
is singular with
![]() $\text {cof}(\delta _{\lambda })=\mu <\delta _{\lambda }$
. By regrouping the product, we can view the forcing
$\text {cof}(\delta _{\lambda })=\mu <\delta _{\lambda }$
. By regrouping the product, we can view the forcing
![]() $\Pi _{\xi <\lambda }\mathbb C_{\xi }$
as a product of length
$\Pi _{\xi <\lambda }\mathbb C_{\xi }$
as a product of length
![]() $\mu $
, which is
$\mu $
, which is
![]() -closed on a tail. Thus, an analogous argument to the one given in the proof of Theorem 3.1 shows that
-closed on a tail. Thus, an analogous argument to the one given in the proof of Theorem 3.1 shows that
![]() $\delta _{\lambda }^+$
cannot be collapsed to
$\delta _{\lambda }^+$
cannot be collapsed to
![]() $\delta _{\lambda }$
in this case, completing the proof that
$\delta _{\lambda }$
in this case, completing the proof that
![]() $\mathbb C$
is cardinal preserving. In particular, this implies that the
$\mathbb C$
is cardinal preserving. In particular, this implies that the
![]() $\operatorname {GCH} $
continues to fail at all regular cardinals in any forcing extension by
$\operatorname {GCH} $
continues to fail at all regular cardinals in any forcing extension by
![]() $\mathbb C$
.
$\mathbb C$
.
Let
![]() $H\subseteq \mathbb C$
be
$H\subseteq \mathbb C$
be
![]() $L[G]$
-generic. For each
$L[G]$
-generic. For each
![]() $\xi \in \operatorname {Ord} $
, we can factor
$\xi \in \operatorname {Ord} $
, we can factor
![]() $\mathbb C$
as the product
$\mathbb C$
as the product
![]() $\Pi _{\eta <\xi }C_{\eta }\times \Pi _{\xi \leq \eta }C_{\eta }$
, where the tail forcing
$\Pi _{\eta <\xi }C_{\eta }\times \Pi _{\xi \leq \eta }C_{\eta }$
, where the tail forcing
![]() $\Pi _{\xi \leq \eta }C_{\eta }$
is
$\Pi _{\xi \leq \eta }C_{\eta }$
is
![]() -closed since we used Easton support. Note that since
-closed since we used Easton support. Note that since
![]() $\mathbb C$
is a progressively closed class product, it preserves
$\mathbb C$
is a progressively closed class product, it preserves
![]() $\operatorname {ZFC} $
to the forcing extension
$\operatorname {ZFC} $
to the forcing extension
![]() $L[G][H]$
[Reference Reitz27].
$L[G][H]$
[Reference Reitz27].
Suppose
![]() $\xi <\kappa $
is a trivial stage of forcing in
$\xi <\kappa $
is a trivial stage of forcing in
![]() $\mathbb C$
. Let
$\mathbb C$
. Let
![]() $\mathbb C_{\text {small}}=\Pi _{\eta <\xi }\mathbb C_{\eta }$
and
$\mathbb C_{\text {small}}=\Pi _{\eta <\xi }\mathbb C_{\eta }$
and
![]() $\mathbb C_{\text {tail}}=\Pi _{\xi <\eta }\mathbb C_{\eta }$
. The forcing
$\mathbb C_{\text {tail}}=\Pi _{\xi <\eta }\mathbb C_{\eta }$
. The forcing
![]() $\mathbb C_{\text {small}}$
has size at most
$\mathbb C_{\text {small}}$
has size at most
![]() $\delta _{\xi }^+$
, and therefore cannot destroy the strong limit property of
$\delta _{\xi }^+$
, and therefore cannot destroy the strong limit property of
![]() $\beta _{\xi }$
and
$\beta _{\xi }$
and
![]() $\beta _{\xi }^*$
, and neither can
$\beta _{\xi }^*$
, and neither can
![]() $\mathbb C_{\text {tail}}$
, which is
$\mathbb C_{\text {tail}}$
, which is
![]() -closed. It follows that
-closed. It follows that
![]() $\beta _{\xi }$
and
$\beta _{\xi }$
and
![]() $\beta _{\xi }^*$
remain strong limits in
$\beta _{\xi }^*$
remain strong limits in
![]() $L[G][H]$
.
$L[G][H]$
.
In the above result, we coded the subsets added by G into
![]() $S_1$
. Let’s see what it would take to code subsets added by G into the mth slice
$S_1$
. Let’s see what it would take to code subsets added by G into the mth slice
![]() $S_m$
of the stability predicate for
$S_m$
of the stability predicate for
![]() $m\geq 2$
. The main problem is that if
$m\geq 2$
. The main problem is that if
![]() $\alpha $
is a singular cardinal, then
$\alpha $
is a singular cardinal, then
![]() $\mathbb P\upharpoonright \alpha $
has unbounded support in
$\mathbb P\upharpoonright \alpha $
has unbounded support in
![]() $\alpha $
, and therefore
$\alpha $
, and therefore
![]() $\mathbb P\upharpoonright \alpha $
is not a class forcing over
$\mathbb P\upharpoonright \alpha $
is not a class forcing over
![]() $H_{\alpha }$
, which prevents us from using standard lifting arguments to go from
$H_{\alpha }$
, which prevents us from using standard lifting arguments to go from
![]() $H_{\alpha }^L\prec _{\Sigma _m}H_{\beta }^L$
to
$H_{\alpha }^L\prec _{\Sigma _m}H_{\beta }^L$
to
![]() $H_{\alpha }^{L[G]}\prec _{\Sigma _m} H_{\beta }^{L[G]}$
. The construction would go through for m, if we assume that L has a proper class of inaccessible cardinals
$H_{\alpha }^{L[G]}\prec _{\Sigma _m} H_{\beta }^{L[G]}$
. The construction would go through for m, if we assume that L has a proper class of inaccessible cardinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $H_{\alpha }^L\prec _{\Sigma _{m+1}} L$
. The class forcing
$H_{\alpha }^L\prec _{\Sigma _{m+1}} L$
. The class forcing
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\Delta _2$
-definable, so the forcing relation for
$\Delta _2$
-definable, so the forcing relation for
![]() $\Sigma _m$
-formulas is
$\Sigma _m$
-formulas is
![]() $\Sigma _{m+1}$
-definable. Using this, we can argue that if
$\Sigma _{m+1}$
-definable. Using this, we can argue that if
![]() $H_{\alpha }^L\prec _{\Sigma _{m+1}} H_{\beta }^L$
, then
$H_{\alpha }^L\prec _{\Sigma _{m+1}} H_{\beta }^L$
, then
![]() $H_{\alpha }^{L[G]}=H_{\alpha }^L[G]\prec _{\Sigma _{m}}H_{\beta }^L[G]=H_{\beta }^{L[G]}$
.
$H_{\alpha }^{L[G]}=H_{\alpha }^L[G]\prec _{\Sigma _{m}}H_{\beta }^L[G]=H_{\beta }^{L[G]}$
.
Finally, let’s note that if we only wanted the
![]() $\operatorname {GCH} $
to fail cofinally, then we could force in a single step to add
$\operatorname {GCH} $
to fail cofinally, then we could force in a single step to add
![]() $\kappa ^{++}$
-many subsets to some
$\kappa ^{++}$
-many subsets to some
![]() $\kappa $
, followed by the forcing to code the sets into the stable core, and do this for cofinally many cardinals, spacing them out enough to prevent interference.
$\kappa $
, followed by the forcing to code the sets into the stable core, and do this for cofinally many cardinals, spacing them out enough to prevent interference.
4 Measurable cardinals in the stable core
In [Reference Kennedy, Magidor and Väänänen18], Kennedy, Magidor, and Väänänen studied properties of the model
![]() $\langle L[\operatorname {Card}],\in ,\operatorname {Card}\rangle $
for the class
$\langle L[\operatorname {Card}],\in ,\operatorname {Card}\rangle $
for the class
![]() $\operatorname {Card}$
of cardinals of V. They showed that if there is a measurable cardinal, then
$\operatorname {Card}$
of cardinals of V. They showed that if there is a measurable cardinal, then
![]() $L[\mu ]$
, the canonical model for a single measurable cardinal, is contained in
$L[\mu ]$
, the canonical model for a single measurable cardinal, is contained in
![]() $L[\operatorname {Card}]$
. In particular,
$L[\operatorname {Card}]$
. In particular,
![]() $L[\operatorname {Card}]^{L[\mu ]}=L[\mu ]$
, which shows that
$L[\operatorname {Card}]^{L[\mu ]}=L[\mu ]$
, which shows that
![]() $L[\operatorname {Card}]$
can have a measurable cardinal. Recently, Welch showed that if
$L[\operatorname {Card}]$
can have a measurable cardinal. Recently, Welch showed that if
![]() $m_1^{\#}$
exists, then
$m_1^{\#}$
exists, then
![]() $L[\operatorname {Card}]$
is a certain Prikry-type forcing extension of an iterate of
$L[\operatorname {Card}]$
is a certain Prikry-type forcing extension of an iterate of
![]() $m_1^{\#}$
adding Prikry sequences to all measurable cardinals in it [Reference Welch29]. It follows from this that, in the presence of sufficiently large large cardinals, the model
$m_1^{\#}$
adding Prikry sequences to all measurable cardinals in it [Reference Welch29]. It follows from this that, in the presence of sufficiently large large cardinals, the model
![]() $L[\operatorname {Card}]$
satisfies the
$L[\operatorname {Card}]$
satisfies the
![]() $\operatorname {GCH} $
and has no measurable cardinals, although it does have an inner model with a proper class of measurables.
$\operatorname {GCH} $
and has no measurable cardinals, although it does have an inner model with a proper class of measurables.
We adapt techniques of [Reference Kennedy, Magidor and Väänänen18] to show that if there is a measurable cardinal, then, for every
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $L[\mu ]$
is contained in
$L[\mu ]$
is contained in
![]() $L[S_m]$
. In particular,
$L[S_m]$
. In particular,
![]() $L[S^{L[\mu ]}]=L[\mu ]$
, showing that the stable core can have a measurable cardinal. Indeed, we improve this result to show that the stable core can have a discrete proper class of measurable cardinals.
$L[S^{L[\mu ]}]=L[\mu ]$
, showing that the stable core can have a measurable cardinal. Indeed, we improve this result to show that the stable core can have a discrete proper class of measurable cardinals.
Let’s start with the following easy proposition showing that if
![]() $0^{\#}$
exists, then it is in the stable core.
$0^{\#}$
exists, then it is in the stable core.
Proposition 4.1. If
![]() $0^{\#}$
exists, then
$0^{\#}$
exists, then
![]() $0^{\#}\in L[S_m]$
for every
$0^{\#}\in L[S_m]$
for every
![]() $m\geq 1$
.
$m\geq 1$
.
Proof Every
![]() $L[S_m]$
has many increasing
$L[S_m]$
has many increasing
![]() $\omega $
-sequences of V-cardinals, so fix some such sequence
$\omega $
-sequences of V-cardinals, so fix some such sequence
![]() $\langle \alpha _n\mid n<\omega \rangle $
. We have that
$\langle \alpha _n\mid n<\omega \rangle $
. We have that
![]() $\varphi (x_0,\ldots ,x_{n-1})\in 0^{\#}$
if and only if
$\varphi (x_0,\ldots ,x_{n-1})\in 0^{\#}$
if and only if
![]() $L_{\alpha _n}\models \varphi (\alpha _0,\ldots ,\alpha _{n-1})$
.
$L_{\alpha _n}\models \varphi (\alpha _0,\ldots ,\alpha _{n-1})$
.
Theorem 4.2. Suppose that
![]() $\kappa $
is a measurable cardinal and
$\kappa $
is a measurable cardinal and
![]() $L[\mu ]$
is the canonical inner model with a normal measure
$L[\mu ]$
is the canonical inner model with a normal measure
![]() $\mu $
on
$\mu $
on
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $L[\mu ]\subseteq L[S_m]$
for every
$L[\mu ]\subseteq L[S_m]$
for every
![]() $m\geq 1$
.
$m\geq 1$
.
The proof of this theorem uses techniques from the proof of Kunen’s Uniqueness Theorem ([Reference Kunen19], [Reference Kunen20], for a modern account, see, for example, [Reference Jech15, Theorem 19.14]) and is following the idea of Theorem 9.1 in [Reference Kennedy, Magidor and Väänänen18].
Proof of Theorem 4.2
We will first argue that for some sufficiently large
![]() $\lambda $
, the normal measure
$\lambda $
, the normal measure
![]() $\mu _{\lambda }$
on the
$\mu _{\lambda }$
on the
![]() $\lambda $
th iterated ultrapower of
$\lambda $
th iterated ultrapower of
![]() $L[\mu ]$
by
$L[\mu ]$
by
![]() $\mu $
is in
$\mu $
is in
![]() $L[S_m]$
, and then find in
$L[S_m]$
, and then find in
![]() $L[S_m]$
an elementary substructure of size
$L[S_m]$
an elementary substructure of size
![]() $(\kappa ^+)^V$
of an initial segment
$(\kappa ^+)^V$
of an initial segment
![]() $L_{\theta }[\mu _{\lambda }]$
, for some very large
$L_{\theta }[\mu _{\lambda }]$
, for some very large
![]() $\theta $
(in particular, ensuring that
$\theta $
(in particular, ensuring that
![]() $\mu _{\lambda }\in L_{\theta }[\mu _{\lambda }]$
), of the iterate that will collapse to
$\mu _{\lambda }\in L_{\theta }[\mu _{\lambda }]$
), of the iterate that will collapse to
![]() $L_{\bar \theta }[\mu ]$
. Since we were able to choose the substructure to be of size
$L_{\bar \theta }[\mu ]$
. Since we were able to choose the substructure to be of size
![]() $(\kappa ^+)^V$
,
$(\kappa ^+)^V$
,
![]() $\bar \theta \geq (\kappa ^+)^{L[\mu ]}$
, ensuring that
$\bar \theta \geq (\kappa ^+)^{L[\mu ]}$
, ensuring that
![]() $L_{\bar \theta }[\mu ]$
contains
$L_{\bar \theta }[\mu ]$
contains
![]() $\mu $
.
$\mu $
.
We can assume that
![]() $\mu \in L[\mu ]$
. We work in V and fix
$\mu \in L[\mu ]$
. We work in V and fix
![]() $m\geq 1$
. Let
$m\geq 1$
. Let
![]() $\lambda> \kappa ^{+}$
be a strong limit cardinal with unboundedly many
$\lambda> \kappa ^{+}$
be a strong limit cardinal with unboundedly many
![]() $\alpha $
in
$\alpha $
in
![]() $\lambda $
such that
$\lambda $
such that
![]() $(\alpha ,\lambda )\in S_m$
. Let
$(\alpha ,\lambda )\in S_m$
. Let
![]() $j_{\lambda }: L[\mu ]\to L[\mu _{\lambda }]$
be the embedding given by the
$j_{\lambda }: L[\mu ]\to L[\mu _{\lambda }]$
be the embedding given by the
![]() $\lambda $
th iterated ultrapower of
$\lambda $
th iterated ultrapower of
![]() $L[\mu ]$
by
$L[\mu ]$
by
![]() $\mu $
, so that in
$\mu $
, so that in
![]() $L[\mu _{\lambda }]$
,
$L[\mu _{\lambda }]$
,
![]() $\mu _{\lambda }$
is a normal measure on the cardinal
$\mu _{\lambda }$
is a normal measure on the cardinal
![]() $\lambda =j_{\lambda }(\kappa )$
(by [Reference Kanamori17, Corollary 19.7], for all cardinals
$\lambda =j_{\lambda }(\kappa )$
(by [Reference Kanamori17, Corollary 19.7], for all cardinals
![]() $\lambda>\kappa ^+$
, the
$\lambda>\kappa ^+$
, the
![]() $\lambda $
th element of the critical sequence is
$\lambda $
th element of the critical sequence is
![]() $\lambda $
). Let
$\lambda $
). Let
![]() $\langle \kappa _{\xi } \mid \xi <\lambda \rangle $
be the critical sequence of the iteration by
$\langle \kappa _{\xi } \mid \xi <\lambda \rangle $
be the critical sequence of the iteration by
![]() $\mu $
. Finally, let
$\mu $
. Finally, let
![]() $\mathcal {F}$
denote the filter generated by the tails
$\mathcal {F}$
denote the filter generated by the tails
for
![]() $\xi < \lambda $
. We will argue that
$\xi < \lambda $
. We will argue that
![]() $L[\mu _{\lambda }]=L[\mathcal {F}]$
. It will follow that
$L[\mu _{\lambda }]=L[\mathcal {F}]$
. It will follow that
![]() $L[\mu _{\lambda }]\subseteq L[S_m]$
since
$L[\mu _{\lambda }]\subseteq L[S_m]$
since
![]() $L[S_m]$
can compute
$L[S_m]$
can compute
![]() $L[\mathcal {F}]$
from
$L[\mathcal {F}]$
from
![]() $S_m$
.
$S_m$
.
First, let’s argue that
![]() $\mu _{\lambda }\subseteq \mathcal {F}$
. Suppose
$\mu _{\lambda }\subseteq \mathcal {F}$
. Suppose
![]() $X \in \mu _{\lambda }$
. Then there must be a
$X \in \mu _{\lambda }$
. Then there must be a
![]() $\zeta < \lambda $
such that
$\zeta < \lambda $
such that
![]() $\{ \kappa _{\xi } \mid \zeta \leq \xi < \lambda \} \subseteq X$
(see [Reference Kanamori17, Lemma 19.5]). As
$\{ \kappa _{\xi } \mid \zeta \leq \xi < \lambda \} \subseteq X$
(see [Reference Kanamori17, Lemma 19.5]). As
![]() $\kappa _{\eta } = \eta $
for every sufficiently large cardinal
$\kappa _{\eta } = \eta $
for every sufficiently large cardinal
![]() $\eta < \lambda $
(see [Reference Kanamori17, Corollary 19.7]), it follows that
$\eta < \lambda $
(see [Reference Kanamori17, Corollary 19.7]), it follows that
for some
![]() $\zeta ^{\prime } < \lambda $
. In particular,
$\zeta ^{\prime } < \lambda $
. In particular,
![]() $A_{\zeta ^{\prime }} \subseteq X$
, and thus
$A_{\zeta ^{\prime }} \subseteq X$
, and thus
![]() $X \in \mathcal {F}$
. But now since
$X \in \mathcal {F}$
. But now since
![]() $\mu _{\lambda }$
is an ultrafilter in
$\mu _{\lambda }$
is an ultrafilter in
![]() $L[\mu _{\lambda }]$
and
$L[\mu _{\lambda }]$
and
![]() $\mathcal {F}$
is a filter, it follows that
$\mathcal {F}$
is a filter, it follows that
![]() $\mathcal {F}\cap L[\mu _{\lambda }]\subseteq \mu _{\lambda }$
and hence
$\mathcal {F}\cap L[\mu _{\lambda }]\subseteq \mu _{\lambda }$
and hence
![]() $\mathcal {F}\cap L[\mu _{\lambda }]=\mu _{\lambda }$
. From here it is not difficult to see that
$\mathcal {F}\cap L[\mu _{\lambda }]=\mu _{\lambda }$
. From here it is not difficult to see that
![]() $L[\mu _{\lambda }]=L[\mathcal {F}]$
, and hence
$L[\mu _{\lambda }]=L[\mathcal {F}]$
, and hence
![]() $L[\mu _{\lambda }]\subseteq L[S_m]$
.
$L[\mu _{\lambda }]\subseteq L[S_m]$
.
Now we will define in
![]() $L[S_m]$
, a sequence of length
$L[S_m]$
, a sequence of length
![]() $(\kappa ^+)^V$
whose elements will generate the desired elementary substructure. Recall that if
$(\kappa ^+)^V$
whose elements will generate the desired elementary substructure. Recall that if
![]() $\eta $
is a strong limit cardinal of cofinality greater than
$\eta $
is a strong limit cardinal of cofinality greater than
![]() $\kappa $
and moreover
$\kappa $
and moreover
![]() $\eta>\lambda $
(the length of the iteration), then
$\eta>\lambda $
(the length of the iteration), then
![]() $j_{\lambda }(\eta )=\eta $
(see [Reference Kanamori17, Corollary 19.7]). Let
$j_{\lambda }(\eta )=\eta $
(see [Reference Kanamori17, Corollary 19.7]). Let
![]() $\lambda ^* \gg \lambda $
be a strong limit cardinal of cofinality greater than
$\lambda ^* \gg \lambda $
be a strong limit cardinal of cofinality greater than
![]() $(\kappa ^+)^V$
such that the set
$(\kappa ^+)^V$
such that the set
![]() $S_m^{\lambda ^*} = \{ \eta \mid (\eta ,\lambda ^*) \in S_m \}$
is unbounded in
$S_m^{\lambda ^*} = \{ \eta \mid (\eta ,\lambda ^*) \in S_m \}$
is unbounded in
![]() $\lambda ^*$
. Let
$\lambda ^*$
. Let
![]() $\eta _0$
be the
$\eta _0$
be the
![]() $(\kappa ^+)^V$
th element of
$(\kappa ^+)^V$
th element of
![]() $S_m^{\lambda ^*}$
above
$S_m^{\lambda ^*}$
above
![]() $\lambda $
. Inductively, let
$\lambda $
. Inductively, let
![]() $\eta _{\xi +1}$
be the
$\eta _{\xi +1}$
be the
![]() $(\kappa ^+)^V$
th element of
$(\kappa ^+)^V$
th element of
![]() $S_m^{\lambda ^*}$
above
$S_m^{\lambda ^*}$
above
![]() $\eta _{\xi }$
and
$\eta _{\xi }$
and
![]() $\eta _{\delta } = \bigcup _{\xi < \delta } \eta _{\xi }$
for limit ordinals
$\eta _{\delta } = \bigcup _{\xi < \delta } \eta _{\xi }$
for limit ordinals
![]() $\delta $
. Let
$\delta $
. Let
![]() $A = \{ \eta _{\xi +1} \mid \xi < (\kappa ^+)^V\}$
. As
$A = \{ \eta _{\xi +1} \mid \xi < (\kappa ^+)^V\}$
. As
![]() $(\kappa ^+)^V$
is regular (in V), it follows that
$(\kappa ^+)^V$
is regular (in V), it follows that
![]() $\operatorname {cf}^V(\eta _{\xi +1})=(\kappa ^+)^V$
for all
$\operatorname {cf}^V(\eta _{\xi +1})=(\kappa ^+)^V$
for all
![]() $\eta _{\xi +1} \in A$
. Therefore each element of A is fixed by the iteration embedding
$\eta _{\xi +1} \in A$
. Therefore each element of A is fixed by the iteration embedding
![]() $j_{\lambda }$
.
$j_{\lambda }$
.
Fix
![]() $\theta $
above the supremum of A. Let
$\theta $
above the supremum of A. Let
![]() $X\prec L_{\theta }[\mu _{\lambda }]$
be the Skolem hull of
$X\prec L_{\theta }[\mu _{\lambda }]$
be the Skolem hull of
![]() $\kappa \cup A$
in
$\kappa \cup A$
in
![]() $L_{\theta }[\mu _{\lambda }]$
, and note that
$L_{\theta }[\mu _{\lambda }]$
, and note that
![]() $X \in L[S_m]$
. Let N denote the Mostowski collapse of X, and let
$X \in L[S_m]$
. Let N denote the Mostowski collapse of X, and let
be the inverse of the collapse embedding. Note that
![]() $\lambda $
is in X as it is definable as the unique measurable cardinal in
$\lambda $
is in X as it is definable as the unique measurable cardinal in
![]() $L_{\theta }[\mu _{\lambda }]$
. In fact,
$L_{\theta }[\mu _{\lambda }]$
. In fact,
![]() $\sigma (\kappa ) = \lambda $
by the following argument. As X is generated by elements from
$\sigma (\kappa ) = \lambda $
by the following argument. As X is generated by elements from
![]() $j_{\lambda }\mathbin {"} L[\mu ]$
, it is contained in
$j_{\lambda }\mathbin {"} L[\mu ]$
, it is contained in
![]() $j_{\lambda }\mathbin " L[\mu ]\prec L[\mu _{\lambda }]$
. But there is no
$j_{\lambda }\mathbin " L[\mu ]\prec L[\mu _{\lambda }]$
. But there is no
![]() $\gamma \in j_{\lambda }\mathbin " L[\mu ]$
with
$\gamma \in j_{\lambda }\mathbin " L[\mu ]$
with
![]() $\kappa < \gamma < \lambda $
, so
$\kappa < \gamma < \lambda $
, so
![]() $\lambda $
has to collapse to
$\lambda $
has to collapse to
![]() $\kappa $
. Finally, since
$\kappa $
. Finally, since
![]() $|A| = (\kappa ^+)^V$
and
$|A| = (\kappa ^+)^V$
and
![]() $\sigma (\kappa )=\lambda $
, the collapse N has the form
$\sigma (\kappa )=\lambda $
, the collapse N has the form
![]() $L_{\bar \theta }[\nu ]$
with
$L_{\bar \theta }[\nu ]$
with
![]() $\nu $
a normal measure on
$\nu $
a normal measure on
![]() $\kappa $
and
$\kappa $
and
![]() $\bar \theta $
an ordinal of size
$\bar \theta $
an ordinal of size
![]() $(\kappa ^+)^V$
. By Kunen’s Uniqueness Theorem (see, for example, [Reference Jech15, Theorem 19.14]),
$(\kappa ^+)^V$
. By Kunen’s Uniqueness Theorem (see, for example, [Reference Jech15, Theorem 19.14]),
![]() $N = L_{\bar \theta }[\mu ]$
, and thus
$N = L_{\bar \theta }[\mu ]$
, and thus
![]() $L_{\bar \theta }[\mu ] \in L[S_m]$
. So
$L_{\bar \theta }[\mu ] \in L[S_m]$
. So
![]() $L[\mu ]\subseteq L[S_m]$
, as desired.
$L[\mu ]\subseteq L[S_m]$
, as desired.
Corollary 4.3.
-
(1) We have
 $L[S^{L[\mu ]}] = L[\mu ]$
. In particular, it is consistent that the stable core has a measurable cardinal.
$L[S^{L[\mu ]}] = L[\mu ]$
. In particular, it is consistent that the stable core has a measurable cardinal. -
(2) Let
 $K^{DJ}$
denote the Dodd–Jensen core model below a measurable cardinal. Then
$K^{DJ}$
denote the Dodd–Jensen core model below a measurable cardinal. Then
 $K^{DJ} \subseteq L[S]$
, and hence
$K^{DJ} \subseteq L[S]$
, and hence
 $L[S^{K^{DJ}}]=K^{DJ}$
.
$L[S^{K^{DJ}}]=K^{DJ}$
. -
(3) If
 $0^{\dagger }$
exists, then
$0^{\dagger }$
exists, then
 $0^{\dagger } \in L[S]$
.
$0^{\dagger } \in L[S]$
.
Proof (1) follows immediately from Theorem 4.2 by applying it inside
![]() $V = L[\mu ]$
.
$V = L[\mu ]$
.
For (2) we first recall the definition of the Dodd–Jensen core model
![]() $K^{DJ}$
from [Reference Dodd and Jensen5]. We call a transitive model M of the form
$K^{DJ}$
from [Reference Dodd and Jensen5]. We call a transitive model M of the form
![]() $M=\langle J_{\alpha }[U],\in ,U\rangle $
a Dodd–Jensen mouse if M satisfies that U is a normal measure on some
$M=\langle J_{\alpha }[U],\in ,U\rangle $
a Dodd–Jensen mouse if M satisfies that U is a normal measure on some
![]() $\kappa < \alpha $
, all of the iterated ultrapowers of M by U are well-founded, and M has a fine structural property implying that
$\kappa < \alpha $
, all of the iterated ultrapowers of M by U are well-founded, and M has a fine structural property implying that
![]() $M = \operatorname {Hull}_1^M(\rho \cup p)$
(the
$M = \operatorname {Hull}_1^M(\rho \cup p)$
(the
![]() $\Sigma _1$
-Skolem closure of M) for some ordinal
$\Sigma _1$
-Skolem closure of M) for some ordinal
![]() $\rho < \kappa $
and some finite set of parameters
$\rho < \kappa $
and some finite set of parameters
![]() $p \subseteq \alpha $
(see [Reference Dodd and Jensen5, Definition 5.4]). The Dodd–Jensen core model
$p \subseteq \alpha $
(see [Reference Dodd and Jensen5, Definition 5.4]). The Dodd–Jensen core model
![]() $K^{DJ} = L[\mathcal {M}]$
, where
$K^{DJ} = L[\mathcal {M}]$
, where
![]() $\mathcal {M}$
is the class of all such Dodd–Jensen mice (see [Reference Dodd and Jensen5, Definition 6.3] or, for a modern account, [Reference Mitchell, Foreman and Kanamori26]). So we need to argue that every such mouse M is in
$\mathcal {M}$
is the class of all such Dodd–Jensen mice (see [Reference Dodd and Jensen5, Definition 6.3] or, for a modern account, [Reference Mitchell, Foreman and Kanamori26]). So we need to argue that every such mouse M is in
![]() $L[S]$
. We essentially follow the proof of Theorem 4.2 to show that some
$L[S]$
. We essentially follow the proof of Theorem 4.2 to show that some
![]() $\lambda $
th iterate
$\lambda $
th iterate
![]() $M_{\lambda }$
of M is in
$M_{\lambda }$
of M is in
![]() $L[S]$
. Then we argue that
$L[S]$
. Then we argue that
![]() $M \in L[M_{\lambda }]$
as, by
$M \in L[M_{\lambda }]$
as, by
![]() $\Sigma _1$
-elementarity of
$\Sigma _1$
-elementarity of
![]() $j_{\lambda }$
, M is isomorphic to
$j_{\lambda }$
, M is isomorphic to
![]() $\operatorname {Hull}_1^{M_{\lambda }}(\rho \cup j_{\lambda }(p))$
. Hence,
$\operatorname {Hull}_1^{M_{\lambda }}(\rho \cup j_{\lambda }(p))$
. Hence,
![]() $M \in L[S]$
.
$M \in L[S]$
.
For (3), since the strong limit cardinals of V are definable in
![]() $L[S]$
, the result for
$L[S]$
, the result for
![]() $0^{\dagger }$
follows from Theorem 4.2 as in the proof of Proposition 4.1.
$0^{\dagger }$
follows from Theorem 4.2 as in the proof of Proposition 4.1.
By analyzing the proof of Theorem 4.2, we see that what it really used was not
![]() $S_m$
, but the class club
$S_m$
, but the class club
![]() $C_m$
(of all strong limit cardinals
$C_m$
(of all strong limit cardinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $H_{\alpha }\prec _{\Sigma _m}V$
) which is, of course, definable from
$H_{\alpha }\prec _{\Sigma _m}V$
) which is, of course, definable from
![]() $S_m$
. Thus, abstracting away the argument, we see that the proof of Theorem 4.2 relied on the fact that for a certain club C of cardinals (namely
$S_m$
. Thus, abstracting away the argument, we see that the proof of Theorem 4.2 relied on the fact that for a certain club C of cardinals (namely
![]() $C_m$
),
$C_m$
),
![]() $L[\mu ]\subseteq L[C]$
and
$L[\mu ]\subseteq L[C]$
and
![]() $L[C]\subseteq L[S]$
. The following result shows that this argument with one club C cannot be pushed further to show that stronger large cardinals are in the stable core. Given a club C, we will denote by
$L[C]\subseteq L[S]$
. The following result shows that this argument with one club C cannot be pushed further to show that stronger large cardinals are in the stable core. Given a club C, we will denote by
![]() $\hat C$
, the collection of all successor elements of C together with its least element.
$\hat C$
, the collection of all successor elements of C together with its least element.
Theorem 4.4 [Reference Welch29].
Suppose that C is a class club of uncountable cardinals. Then there is an
![]() $\operatorname {Ord} $
-length iteration of the mouse
$\operatorname {Ord} $
-length iteration of the mouse
![]() $m_1^{\#}$
such that in the direct limit model
$m_1^{\#}$
such that in the direct limit model
![]() $M_C$
(truncated at
$M_C$
(truncated at
![]() $\operatorname {Ord} $
), the measurable cardinals are precisely the elements of
$\operatorname {Ord} $
), the measurable cardinals are precisely the elements of
![]() $\hat C$
.
$\hat C$
.
Proof Let
![]() $\bar \kappa $
be the critical point of the top measure of
$\bar \kappa $
be the critical point of the top measure of
![]() $m_1^{\#}$
. Let
$m_1^{\#}$
. Let
![]() $\langle \alpha _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
be the increasing enumeration of C.
$\langle \alpha _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
be the increasing enumeration of C.
Iterate the first measurable cardinal
![]() $\kappa _0$
of
$\kappa _0$
of
![]() $m_1^{\#}$
$m_1^{\#}$
![]() $\alpha _0$
-many times, so that
$\alpha _0$
-many times, so that
![]() $\kappa _0$
iterates to
$\kappa _0$
iterates to
![]() $\alpha _0$
, and let
$\alpha _0$
, and let
![]() $M_{\alpha _0}$
be the iterate. Since
$M_{\alpha _0}$
be the iterate. Since
![]() $m_1^{\#}$
is countable,
$m_1^{\#}$
is countable,
![]() $M_{\alpha _0}$
has cardinality
$M_{\alpha _0}$
has cardinality
![]() $\alpha _0$
, and hence the critical point of the top measure
$\alpha _0$
, and hence the critical point of the top measure
![]() $\bar \kappa _{\alpha _0}$
, the image of
$\bar \kappa _{\alpha _0}$
, the image of
![]() $\bar \kappa $
in
$\bar \kappa $
in
![]() $M_{\alpha _0}$
, is below
$M_{\alpha _0}$
, is below
![]() $\alpha _1$
. In particular, the next measurable cardinal
$\alpha _1$
. In particular, the next measurable cardinal
![]() $\kappa _1$
above
$\kappa _1$
above
![]() $\alpha _0$
in
$\alpha _0$
in
![]() $M_{\alpha _0}$
is below
$M_{\alpha _0}$
is below
![]() $\alpha _1$
and we can iterate it to
$\alpha _1$
and we can iterate it to
![]() $\alpha _1$
by iterating it
$\alpha _1$
by iterating it
![]() $\alpha _1$
-many times. Repeat this for all successor ordinals
$\alpha _1$
-many times. Repeat this for all successor ordinals
![]() $\xi $
and take direct limits along the iteration embeddings at limit stages with the following exception.
$\xi $
and take direct limits along the iteration embeddings at limit stages with the following exception.
Suppose we have carried out the construction for a limit
![]() $\xi $
-many steps resulting in the model
$\xi $
-many steps resulting in the model
![]() $M_{\xi }$
, where
$M_{\xi }$
, where
![]() $\bar \kappa _{\xi }$
is the critical point of the top measure, in which the measurable cardinals limit up to
$\bar \kappa _{\xi }$
is the critical point of the top measure, in which the measurable cardinals limit up to
![]() $\bar \kappa _{\xi }$
. In this case, we must have
$\bar \kappa _{\xi }$
. In this case, we must have
![]() $\xi =\alpha _{\xi }$
. When this happens we have run out of room and don’t have a measurable cardinal to iterate to the next element
$\xi =\alpha _{\xi }$
. When this happens we have run out of room and don’t have a measurable cardinal to iterate to the next element
![]() $\alpha _{\xi +1}$
of
$\alpha _{\xi +1}$
of
![]() $\hat C$
. To make more space, in the next step, we iterate up the top measure to obtain the model
$\hat C$
. To make more space, in the next step, we iterate up the top measure to obtain the model
![]() $M_{\xi +1}$
with more measurable cardinals. By cardinality considerations, the critical point
$M_{\xi +1}$
with more measurable cardinals. By cardinality considerations, the critical point
![]() $\bar \kappa _{\xi +1}$
of the top measure is obviously below
$\bar \kappa _{\xi +1}$
of the top measure is obviously below
![]() $\alpha _{\xi +1}$
. Hence, we can continue the construction, iterating the least measurable cardinal
$\alpha _{\xi +1}$
. Hence, we can continue the construction, iterating the least measurable cardinal
![]() $\kappa _{\xi +1}$
above
$\kappa _{\xi +1}$
above
![]() $\xi $
in
$\xi $
in
![]() $M_{\xi +1}$
to
$M_{\xi +1}$
to
![]() $\alpha _{\xi +1}$
.
$\alpha _{\xi +1}$
.
Let M be the resulting model obtained as the direct limit along the iteration embeddings and let
![]() $M_C$
be M truncated at
$M_C$
be M truncated at
![]() $\operatorname {Ord} $
, which is the cardinal on which the top measure of M lives. The construction ensures that we hit every element of
$\operatorname {Ord} $
, which is the cardinal on which the top measure of M lives. The construction ensures that we hit every element of
![]() $\hat C$
along the way, so that the measurable cardinals in
$\hat C$
along the way, so that the measurable cardinals in
![]() $M_C$
are exactly the elements
$M_C$
are exactly the elements
![]() $\hat C$
.
$\hat C$
.
A more elaborate version of this iteration argument is going to be used in Section 6 to generalize the results of [Reference Welch29] to a finite number of specially nested clubs.
Corollary 4.5. If C is a class club of uncountable V-cardinals, then
![]() $m_1^{\#}\notin L[C]$
.
$m_1^{\#}\notin L[C]$
.
Proof Suppose towards a contradiction that
![]() $m_1^{\#}\in L[C]$
. Iterate
$m_1^{\#}\in L[C]$
. Iterate
![]() $m_1^{\#}$
inside
$m_1^{\#}$
inside
![]() $L[C]$
to a model M as in the proof of Theorem 4.4, and let
$L[C]$
to a model M as in the proof of Theorem 4.4, and let
![]() $M_C$
be the truncation of M at
$M_C$
be the truncation of M at
![]() $\operatorname {Ord} $
. In particular, C is definable in
$\operatorname {Ord} $
. In particular, C is definable in
![]() $M_C$
by considering the closure of its measurable cardinals. It follows that
$M_C$
by considering the closure of its measurable cardinals. It follows that
![]() $L[C]$
is a definable sub-class of
$L[C]$
is a definable sub-class of
![]() $M_C$
, so that
$M_C$
, so that
![]() $L[C] = M_C$
. But this is impossible because
$L[C] = M_C$
. But this is impossible because
![]() $m_1^{\#}$
is a countable model (in
$m_1^{\#}$
is a countable model (in
![]() $L[C]$
), which means, in particular, that
$L[C]$
), which means, in particular, that
![]() $\omega _1^{m_1^{\#}}=\omega _1^{M_C}$
is countable in
$\omega _1^{m_1^{\#}}=\omega _1^{M_C}$
is countable in
![]() $L[C]$
.
$L[C]$
.
In the last section of the article we will show that, unlike
![]() $L[\operatorname {Card}]$
, the stable core, given sufficiently large large cardinals, can have inner models with a proper class of n-measurable cardinals for any
$L[\operatorname {Card}]$
, the stable core, given sufficiently large large cardinals, can have inner models with a proper class of n-measurable cardinals for any
![]() $n<\omega $
.
$n<\omega $
.
Now we can say more precisely what Welch showed about the model
![]() $L[\operatorname {Card}]$
in [Reference Welch29]. Let
$L[\operatorname {Card}]$
in [Reference Welch29]. Let
![]() $M_C$
, for the class club C of limit cardinals, be the iterate of
$M_C$
, for the class club C of limit cardinals, be the iterate of
![]() $m_1^{\#}$
(truncated at
$m_1^{\#}$
(truncated at
![]() $\operatorname {Ord} $
) obtained as in the proof of Theorem 4.4 in which the measurable cardinals are precisely the cardinals of V of the form
$\operatorname {Ord} $
) obtained as in the proof of Theorem 4.4 in which the measurable cardinals are precisely the cardinals of V of the form
![]() $\aleph _{\omega \cdot \alpha +\omega }$
(namely elements of
$\aleph _{\omega \cdot \alpha +\omega }$
(namely elements of
![]() $\hat C$
). Let
$\hat C$
). Let
![]() $U_{\alpha }\subseteq P^{M_C}(\aleph _{\omega \cdot \alpha +\omega })$
be the iteration measures on
$U_{\alpha }\subseteq P^{M_C}(\aleph _{\omega \cdot \alpha +\omega })$
be the iteration measures on
![]() $\aleph _{\omega \cdot \alpha +\omega }$
in
$\aleph _{\omega \cdot \alpha +\omega }$
in
![]() $M_C$
, and note that a subset of
$M_C$
, and note that a subset of
![]() $\aleph _{\omega \cdot \alpha +\omega }$
in
$\aleph _{\omega \cdot \alpha +\omega }$
in
![]() $M_C$
is in
$M_C$
is in
![]() $U_{\alpha }$
if and only if it contains some tail of the cardinals. Let
$U_{\alpha }$
if and only if it contains some tail of the cardinals. Let
![]() $\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
. The model
$\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
. The model
![]() $M_C$
has the form
$M_C$
has the form
![]() $L[\vec U]$
because it is an iterate of the mouse
$L[\vec U]$
because it is an iterate of the mouse
![]() $m^{\#}_1$
. Let
$m^{\#}_1$
. Let
![]() $W_{\alpha }\subseteq P^{L[\operatorname {Card}]}(\aleph _{\omega \cdot \alpha +\omega })$
consist of all subsets of
$W_{\alpha }\subseteq P^{L[\operatorname {Card}]}(\aleph _{\omega \cdot \alpha +\omega })$
consist of all subsets of
![]() $\aleph _{\omega \cdot \alpha +\omega }$
in
$\aleph _{\omega \cdot \alpha +\omega }$
in
![]() $L[\operatorname {Card}]$
containing some tail of cardinals
$L[\operatorname {Card}]$
containing some tail of cardinals
![]() $\aleph _{\omega \cdot \alpha +n}$
,
$\aleph _{\omega \cdot \alpha +n}$
,
![]() $n<\omega $
, and let
$n<\omega $
, and let
![]() $\vec W$
be the sequence of the
$\vec W$
be the sequence of the
![]() $W_{\alpha }$
. Now it is easy to see that
$W_{\alpha }$
. Now it is easy to see that
![]() $L[\vec W]=L[\vec U]$
, and hence, since
$L[\vec W]=L[\vec U]$
, and hence, since
![]() $\vec W$
is definable in
$\vec W$
is definable in
![]() $L[\operatorname {Card}]$
,
$L[\operatorname {Card}]$
,
![]() $M_C$
is contained in
$M_C$
is contained in
![]() $L[\operatorname {Card}]$
. Let f be a function on
$L[\operatorname {Card}]$
. Let f be a function on
![]() $\hat C$
such that
$\hat C$
such that
We clearly have that
![]() $L[\operatorname {Card}]=L[f]$
, and also
$L[\operatorname {Card}]=L[f]$
, and also
![]() $L[f]=L[\vec W][f]=M_C[f]$
because the sequence
$L[f]=L[\vec W][f]=M_C[f]$
because the sequence
![]() $\vec W$
can be recovered from f. Thus,
$\vec W$
can be recovered from f. Thus,
![]() $L[\operatorname {Card}]=M_C[f]$
, and it turns out that in some sense which we will explain in detail in Section 7,
$L[\operatorname {Card}]=M_C[f]$
, and it turns out that in some sense which we will explain in detail in Section 7,
![]() $M_C[f]$
is a Prikry-type forcing extension of
$M_C[f]$
is a Prikry-type forcing extension of
![]() $M_C$
adding Prikry sequences to all its measurable cardinals.
$M_C$
adding Prikry sequences to all its measurable cardinals.
Note that in this construction we iterated the measurable cardinals to elements of
![]() $\hat C$
, where C is the club of limit cardinals, instead of to all successor cardinals, because we need to have enough cardinals in between to be able to use them to define the measures in
$\hat C$
, where C is the club of limit cardinals, instead of to all successor cardinals, because we need to have enough cardinals in between to be able to use them to define the measures in
![]() $\vec U$
, so that
$\vec U$
, so that
![]() $L[\vec U]$
is contained in
$L[\vec U]$
is contained in
![]() $L[C]$
. If on the other hand, we iterate the measurable cardinals to all successor cardinals, then we can get an inclusion in the other direction:
$L[C]$
. If on the other hand, we iterate the measurable cardinals to all successor cardinals, then we can get an inclusion in the other direction:
![]() $L[C]$
is contained in the iterate
$L[C]$
is contained in the iterate
![]() $M_C$
.
$M_C$
.
We will now generalize the result that the stable core of
![]() $L[\mu ]$
is equal to
$L[\mu ]$
is equal to
![]() $L[\mu ]$
to show that if
$L[\mu ]$
to show that if
![]() $\vec U$
is a discrete proper class sequence of normal measures, then the stable core of
$\vec U$
is a discrete proper class sequence of normal measures, then the stable core of
![]() $L[\vec U]$
is
$L[\vec U]$
is
![]() $L[\vec U]$
. It follows that the stable core can have a proper class of measurable cardinals.
$L[\vec U]$
. It follows that the stable core can have a proper class of measurable cardinals.
Theorem 4.6. If
![]() $\vec U$
is a discrete proper class sequence of normal measures, then
$\vec U$
is a discrete proper class sequence of normal measures, then
![]() $L[S]^{L[\vec U]} = L[\vec U]$
. In particular, it is consistent that the stable core has a proper class of measurable cardinals.
$L[S]^{L[\vec U]} = L[\vec U]$
. In particular, it is consistent that the stable core has a proper class of measurable cardinals.
Proof Let
![]() $\vec U$
be a discrete proper class sequence of normal measures and work in
$\vec U$
be a discrete proper class sequence of normal measures and work in
![]() $V = L[\vec U]$
. Consider the stable core
$V = L[\vec U]$
. Consider the stable core
![]() $L[S]$
and the corresponding core models
$L[S]$
and the corresponding core models
![]() $K_0 = K^{L[S]}$
and
$K_0 = K^{L[S]}$
and
![]() $K = K^V$
. Recall that all measurable cardinals in V are measurable in K as witnessed by restrictions of the measures in
$K = K^V$
. Recall that all measurable cardinals in V are measurable in K as witnessed by restrictions of the measures in
![]() $\vec U$
, and therefore V and K have the same universes. Compare
$\vec U$
, and therefore V and K have the same universes. Compare
![]() $K_0$
and K in V. As both are proper class models they have a common iterate
$K_0$
and K in V. As both are proper class models they have a common iterate
![]() $K^*$
.
$K^*$
.
Case 1. The K-side of the coiteration drops.
Then
![]() $K^*$
is the
$K^*$
is the
![]() $\operatorname {Ord} $
-length iterate of some mouseFootnote
2
$\operatorname {Ord} $
-length iterate of some mouseFootnote
2
![]() $\mathcal {M}$
which appears after the last drop on the K-side of the coiteration such that
$\mathcal {M}$
which appears after the last drop on the K-side of the coiteration such that
![]() $K^*$
is the result of hitting a measure on some
$K^*$
is the result of hitting a measure on some
![]() $\kappa $
in
$\kappa $
in
![]() $\mathcal {M}$
and its images (truncated at
$\mathcal {M}$
and its images (truncated at
![]() $\operatorname {Ord} $
). The successive images of
$\operatorname {Ord} $
). The successive images of
![]() $\kappa $
form a V-definable club
$\kappa $
form a V-definable club
![]() $D_0$
of ordinals which are regular cardinals in
$D_0$
of ordinals which are regular cardinals in
![]() $K^*$
. The
$K^*$
. The
![]() $K_0$
-side of the coiteration does not drop, so there is an iteration map
$K_0$
-side of the coiteration does not drop, so there is an iteration map
![]() $\pi _0 \colon K_0 \rightarrow K^*$
and the ordinals
$\pi _0 \colon K_0 \rightarrow K^*$
and the ordinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $\pi _0 \mathbin " \alpha \subseteq \alpha $
form a V-definable club
$\pi _0 \mathbin " \alpha \subseteq \alpha $
form a V-definable club
![]() $D_1$
. Let
$D_1$
. Let
![]() $D = D_0 \cap D_1$
. Note that the iteration of
$D = D_0 \cap D_1$
. Note that the iteration of
![]() $K_0$
has set-length, since the measures on the K-side, and therefore also those on the
$K_0$
has set-length, since the measures on the K-side, and therefore also those on the
![]() $K_0$
-side, are bounded by the measurable
$K_0$
-side, are bounded by the measurable
![]() $\kappa $
which is sent to
$\kappa $
which is sent to
![]() $\operatorname {Ord} $
on the K-side of the iteration (by the discreteness of the measure sequence). It follows that for some
$\operatorname {Ord} $
on the K-side of the iteration (by the discreteness of the measure sequence). It follows that for some
![]() $\delta $
, all elements of D of cofinality at least
$\delta $
, all elements of D of cofinality at least
![]() $\delta $
are fixed by the iteration map
$\delta $
are fixed by the iteration map
![]() $\pi _0$
.
$\pi _0$
.
Let
![]() $n<\omega $
be large enough such that D is
$n<\omega $
be large enough such that D is
![]() $\Sigma _n$
-definable in V. Recall from Proposition 2.3 that the class club
$\Sigma _n$
-definable in V. Recall from Proposition 2.3 that the class club
![]() $C_n$
consisting of all strong limit
$C_n$
consisting of all strong limit
![]() $\beta $
such that
$\beta $
such that
![]() $H_{\beta } \prec _{\Sigma _n} V$
is definable from S. Let
$H_{\beta } \prec _{\Sigma _n} V$
is definable from S. Let
![]() $\beta \in C_n$
be sufficiently large. In V, D is cofinal in
$\beta \in C_n$
be sufficiently large. In V, D is cofinal in
![]() $\operatorname {Ord} $
. Therefore, in
$\operatorname {Ord} $
. Therefore, in
![]() $H_{\beta }$
,
$H_{\beta }$
,
![]() $D \cap H_{\beta }$
is cofinal in
$D \cap H_{\beta }$
is cofinal in
![]() $\beta $
, and hence
$\beta $
, and hence
![]() $\beta \in D$
. So a tail of
$\beta \in D$
. So a tail of
![]() $C_n$
is contained in D and there is a
$C_n$
is contained in D and there is a
![]() $\delta $
-sequence of adjacent elements of
$\delta $
-sequence of adjacent elements of
![]() $C_n$
contained in D such that its limit
$C_n$
contained in D such that its limit
![]() $\lambda $
is singular of uncountable cofinality in
$\lambda $
is singular of uncountable cofinality in
![]() $L[S]$
. But
$L[S]$
. But
![]() $\lambda \in D$
and all elements of D are regular in
$\lambda \in D$
and all elements of D are regular in
![]() $K^*$
. As
$K^*$
. As
![]() $\pi _0(\lambda ) = \lambda $
,
$\pi _0(\lambda ) = \lambda $
,
![]() $\lambda $
is also regular in
$\lambda $
is also regular in
![]() $K_0$
, contradicting the covering lemma for sequences of measures in
$K_0$
, contradicting the covering lemma for sequences of measures in
![]() $L[S]$
(see [Reference Mitchell24], [Reference Mitchell25]).
$L[S]$
(see [Reference Mitchell24], [Reference Mitchell25]).
Case 2. The
![]() $K_0$
-side of the coiteration drops.
$K_0$
-side of the coiteration drops.
Let
![]() $\mathcal {N}$
be the model on the
$\mathcal {N}$
be the model on the
![]() $K_0$
-side of the coiteration after the last drop. Then
$K_0$
-side of the coiteration after the last drop. Then
![]() $\mathcal {N} \cap \operatorname {Ord} < \operatorname {Ord} $
, but the coiteration of
$\mathcal {N} \cap \operatorname {Ord} < \operatorname {Ord} $
, but the coiteration of
![]() $\mathcal {N}$
and an iterate
$\mathcal {N}$
and an iterate
![]() $K^{\prime }$
of K results in the common proper class iterate
$K^{\prime }$
of K results in the common proper class iterate
![]() $K^*$
. The iteration from K to
$K^*$
. The iteration from K to
![]() $K^{\prime }$
is non-dropping and hence
$K^{\prime }$
is non-dropping and hence
![]() $K^{\prime }$
is universal. But this contradicts the fact that the coiteration of
$K^{\prime }$
is universal. But this contradicts the fact that the coiteration of
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $K^{\prime }$
does not terminate after set-many steps.
$K^{\prime }$
does not terminate after set-many steps.
Case 3. Both sides of the coiteration do not drop, i.e., there are elementary embeddings
![]() $\pi _0 \colon K_0 \rightarrow K^*$
and
$\pi _0 \colon K_0 \rightarrow K^*$
and
![]() $\pi \colon K \rightarrow K^*$
.
$\pi \colon K \rightarrow K^*$
.
As
![]() $K^*$
, and hence
$K^*$
, and hence
![]() $K_0$
, has a proper class discrete sequence of measures it is universal in
$K_0$
, has a proper class discrete sequence of measures it is universal in
![]() $V = L[\vec U]$
. Therefore, in fact,
$V = L[\vec U]$
. Therefore, in fact,
![]() $K_0 = K^*$
by the proof of Theorem 7.4.8 in [Reference Zeman31]. Finally, we argue that K cannot move in the iteration to
$K_0 = K^*$
by the proof of Theorem 7.4.8 in [Reference Zeman31]. Finally, we argue that K cannot move in the iteration to
![]() $K_0$
. Suppose this is not the case and let U on
$K_0$
. Suppose this is not the case and let U on
![]() $\kappa $
be the first measure that is used. Let
$\kappa $
be the first measure that is used. Let
![]() $\kappa ^*$
be the image of
$\kappa ^*$
be the image of
![]() $\kappa $
in
$\kappa $
in
![]() $K_0$
. For some large enough
$K_0$
. For some large enough
![]() $n < \omega $
,
$n < \omega $
,
![]() $C_n$
can define a proper class
$C_n$
can define a proper class
![]() $C^*$
of fixed points of
$C^*$
of fixed points of
![]() $\pi $
as follows. There is a V-definable club C of ordinals
$\pi $
as follows. There is a V-definable club C of ordinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $\pi \, " \alpha \subseteq \alpha $
. As in Case 1, a tail of
$\pi \, " \alpha \subseteq \alpha $
. As in Case 1, a tail of
![]() $C_n$
is contained in C. Let
$C_n$
is contained in C. Let
![]() $\beta \in C_n$
be an arbitrary element of that tail and let
$\beta \in C_n$
be an arbitrary element of that tail and let
![]() $\gamma $
be the
$\gamma $
be the
![]() $\omega $
-th element of
$\omega $
-th element of
![]() $C_n$
above
$C_n$
above
![]() $\beta $
. Then
$\beta $
. Then
![]() $\gamma $
is a closure point of
$\gamma $
is a closure point of
![]() $\pi $
and
$\pi $
and
![]() $\operatorname {cf}(\gamma ) = \omega $
in V and hence in K, since the universes of V and K agree. So the iteration map is continuous at
$\operatorname {cf}(\gamma ) = \omega $
in V and hence in K, since the universes of V and K agree. So the iteration map is continuous at
![]() $\gamma $
and therefore
$\gamma $
and therefore
![]() $\pi (\gamma ) = \gamma $
.
$\pi (\gamma ) = \gamma $
.
Let
![]() $\bar {K}_0$
be the transitive collapse of
$\bar {K}_0$
be the transitive collapse of
![]() $\operatorname {Hull}^{K_0}(\kappa \cup \{\kappa ^*\} \cup C^*)$
. Then
$\operatorname {Hull}^{K_0}(\kappa \cup \{\kappa ^*\} \cup C^*)$
. Then
![]() $\bar {K}_0$
has a proper class of measurable cardinals including
$\bar {K}_0$
has a proper class of measurable cardinals including
![]() $\kappa $
. In particular,
$\kappa $
. In particular,
![]() $\bar {K}_0$
is a universal weasel, and hence an iterate of K, where the first measure used in the iteration has critical point above
$\bar {K}_0$
is a universal weasel, and hence an iterate of K, where the first measure used in the iteration has critical point above
![]() $\kappa $
. Therefore
$\kappa $
. Therefore
![]() $\bar {K}_0$
and hence
$\bar {K}_0$
and hence
![]() $L[S]$
and
$L[S]$
and
![]() $K_0$
contain the measure U on
$K_0$
contain the measure U on
![]() $\kappa $
, contradicting the fact that this measure was used in the iteration.
$\kappa $
, contradicting the fact that this measure was used in the iteration.
Therefore, we obtain that
![]() $K_0 = K$
. As
$K_0 = K$
. As
![]() $L[\vec U]$
can be reconstructed from K it follows that
$L[\vec U]$
can be reconstructed from K it follows that
![]() $L[S] = L[\vec U]$
.
$L[S] = L[\vec U]$
.
The arguments of Section 3 generalize directly to coding sets added generically over
![]() $L[\mu ]$
into the stable core of a further forcing extension. If the forcing adding the generic sets is either small relative to the measurable cardinal
$L[\mu ]$
into the stable core of a further forcing extension. If the forcing adding the generic sets is either small relative to the measurable cardinal
![]() $\kappa $
of
$\kappa $
of
![]() $L[\mu ]$
or
$L[\mu ]$
or
![]() $\leq \kappa $
-closed, and the coding is done high above
$\leq \kappa $
-closed, and the coding is done high above
![]() $\kappa $
, then the stable core of the coding extension will continue to think that
$\kappa $
, then the stable core of the coding extension will continue to think that
![]() $\kappa $
is measurable.
$\kappa $
is measurable.
Theorem 4.7. Suppose
![]() $V=L[\mu ]$
. If
$V=L[\mu ]$
. If
![]() $\mathbb P$
is a forcing notion of size less than
$\mathbb P$
is a forcing notion of size less than
![]() $\kappa $
or
$\kappa $
or
![]() $\mathbb P$
is
$\mathbb P$
is
![]() $\leq \kappa $
-closed and
$\leq \kappa $
-closed and
![]() $G\subseteq \mathbb P$
is V-generic, then there is a further forcing extension
$G\subseteq \mathbb P$
is V-generic, then there is a further forcing extension
![]() $V[G][H]$
such that
$V[G][H]$
such that
![]() $G\in L[S^{V[G][H]}]$
, and
$G\in L[S^{V[G][H]}]$
, and
![]() $\kappa $
remains a measurable cardinal there.
$\kappa $
remains a measurable cardinal there.
Proof Suppose
![]() $\mathbb P$
is a small forcing. By the Lévy–Solovay theorem,
$\mathbb P$
is a small forcing. By the Lévy–Solovay theorem,
![]() $\kappa $
remains measurable in
$\kappa $
remains measurable in
![]() $V[G]$
, as witnessed by the normal measure
$V[G]$
, as witnessed by the normal measure
![]() $\nu $
on
$\nu $
on
![]() $\kappa $
such that
$\kappa $
such that
![]() $A\in \nu $
if and only if there is
$A\in \nu $
if and only if there is
![]() $\bar A\in \mu $
with
$\bar A\in \mu $
with
![]() $\bar A\subseteq A$
. Since the coding forcing defined in the proof of Theorem 3.1 is
$\bar A\subseteq A$
. Since the coding forcing defined in the proof of Theorem 3.1 is
![]() $\leq \kappa $
-closed,
$\leq \kappa $
-closed,
![]() $\nu $
continues to be a normal measure on
$\nu $
continues to be a normal measure on
![]() $\kappa $
in
$\kappa $
in
![]() $V[G][H]$
. Since
$V[G][H]$
. Since
![]() $L[\mu ]\subseteq L[S^{V[G][H]}]$
by Theorem 4.2, in
$L[\mu ]\subseteq L[S^{V[G][H]}]$
by Theorem 4.2, in
![]() $L[S^{V[G][H]}]$
, we can define
$L[S^{V[G][H]}]$
, we can define
![]() $\nu ^*$
such that
$\nu ^*$
such that
![]() $A\in \nu ^*$
if and only if there is
$A\in \nu ^*$
if and only if there is
![]() $\bar A\in \mu $
with
$\bar A\in \mu $
with
![]() $\bar A\subseteq A$
, and clearly
$\bar A\subseteq A$
, and clearly
![]() $\nu ^*$
must be a normal measure on
$\nu ^*$
must be a normal measure on
![]() $\kappa $
in
$\kappa $
in
![]() $L[S^{V[G][H]}]$
.
$L[S^{V[G][H]}]$
.
The argument for
![]() $\leq \kappa $
-closed
$\leq \kappa $
-closed
![]() $\mathbb P$
is even easier because
$\mathbb P$
is even easier because
![]() $\mu $
remains a normal measure on
$\mu $
remains a normal measure on
![]() $\kappa $
in
$\kappa $
in
![]() $V[G][H]$
.
$V[G][H]$
.
Moreover, we get the following variant of Theorem 3.3 in the presence of a measurable cardinal.
Theorem 4.8. It is consistent relative to the existence of a measurable cardinal that the stable core has a measurable cardinal above which the
![]() $\operatorname {GCH} $
fails at all regular cardinals.
$\operatorname {GCH} $
fails at all regular cardinals.
5 Measurable cardinals are not downward absolute to the stable core
In this section, we show that it is consistent that measurable cardinals are not downward absolute to the stable core. We will use a modification of Kunen’s classical argument that weakly compact cardinals are not downward absolute [Reference Kunen21].
Theorem 5.1. Measurable cardinals are not downward absolute to the stable core. Indeed, it is possible to have a measurable cardinal in V which is not even weakly compact in the stable core.
Proof Suppose
![]() $V=L[\mu ]$
, where
$V=L[\mu ]$
, where
![]() $\mu $
is a normal measure on a measurable cardinal
$\mu $
is a normal measure on a measurable cardinal
![]() $\kappa $
.
$\kappa $
.
Let
![]() $\mathbb P_{\kappa }$
be the Easton support iteration of length
$\mathbb P_{\kappa }$
be the Easton support iteration of length
![]() $\kappa $
forcing with
$\kappa $
forcing with
![]() $\operatorname {Add}(\alpha ,1)$
at every stage
$\operatorname {Add}(\alpha ,1)$
at every stage
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha $
is a regular cardinal in
$\alpha $
is a regular cardinal in
![]() $V^{\mathbb P_{\alpha }}$
. It is a standard fact that whenever the
$V^{\mathbb P_{\alpha }}$
. It is a standard fact that whenever the
![]() $\operatorname {GCH} $
holds, which is the case in
$\operatorname {GCH} $
holds, which is the case in
![]() $V=L[\mu ]$
,
$V=L[\mu ]$
,
![]() $\mathbb P_{\kappa }$
preserves all cardinals, cofinalities, and the
$\mathbb P_{\kappa }$
preserves all cardinals, cofinalities, and the
![]() $\operatorname {GCH} $
(see, for example, [Reference Cummings, Foreman and Kanamori3]). Let
$\operatorname {GCH} $
(see, for example, [Reference Cummings, Foreman and Kanamori3]). Let
![]() $G\subseteq \mathbb P_{\kappa }$
be V-generic. In
$G\subseteq \mathbb P_{\kappa }$
be V-generic. In
![]() $V[G]$
, let
$V[G]$
, let
![]() $\mathbb Q$
be the forcing to add a homogeneous
$\mathbb Q$
be the forcing to add a homogeneous
![]() $\kappa $
-Souslin tree and let T be the
$\kappa $
-Souslin tree and let T be the
![]() $V[G]$
-generic tree added by
$V[G]$
-generic tree added by
![]() $\mathbb Q$
(the forcing originally appeared in [Reference Kunen21] and a more modern version is written up in [Reference Gitman and Welch12]). In
$\mathbb Q$
(the forcing originally appeared in [Reference Kunen21] and a more modern version is written up in [Reference Gitman and Welch12]). In
![]() $V[G][T]$
, let
$V[G][T]$
, let
![]() $\mathbb C$
be the forcing, as in the proof of Theorem 3.1 for the case
$\mathbb C$
be the forcing, as in the proof of Theorem 3.1 for the case
![]() $m=1$
, to code T, using the strong limit cardinals, into the stable core of a forcing extension high above
$m=1$
, to code T, using the strong limit cardinals, into the stable core of a forcing extension high above
![]() $\kappa $
and let
$\kappa $
and let
![]() $H\subseteq \mathbb C$
be
$H\subseteq \mathbb C$
be
![]() $V[G][T]$
-generic. Finally, in
$V[G][T]$
-generic. Finally, in
![]() $V[G][T][H]$
, we force with T to add a branch to it, and let
$V[G][T][H]$
, we force with T to add a branch to it, and let
![]() $b\subseteq T$
be a
$b\subseteq T$
be a
![]() $V[G][T][H]$
-generic branch of T. Note that, as a notion of forcing, T is
$V[G][T][H]$
-generic branch of T. Note that, as a notion of forcing, T is
![]() -distributive and
-distributive and
![]() $\kappa $
-cc. As Kunen showed, the combined forcing
$\kappa $
-cc. As Kunen showed, the combined forcing
![]() $\mathbb Q*\dot T$
, where
$\mathbb Q*\dot T$
, where
![]() $\dot T$
is the canonical name for T, has a
$\dot T$
is the canonical name for T, has a
![]() -closed dense subset, and therefore is forcing equivalent to
-closed dense subset, and therefore is forcing equivalent to
![]() $\operatorname {Add}(\kappa ,1)$
[Reference Kunen21]. Thus, the iteration
$\operatorname {Add}(\kappa ,1)$
[Reference Kunen21]. Thus, the iteration
![]() $\mathbb P_{\kappa }*\dot {\mathbb Q}*\dot T$
is forcing equivalent to
$\mathbb P_{\kappa }*\dot {\mathbb Q}*\dot T$
is forcing equivalent to
![]() $\mathbb P_{\kappa }*\operatorname {Add}(\kappa ,1)$
.
$\mathbb P_{\kappa }*\operatorname {Add}(\kappa ,1)$
.
Obviously,
![]() $\kappa $
is not even weakly compact in
$\kappa $
is not even weakly compact in
![]() $V[G][T]$
, and hence also not in
$V[G][T]$
, and hence also not in
![]() $V[G][T][H]$
because the coding forcing
$V[G][T][H]$
because the coding forcing
![]() $\mathbb C$
is highly closed, and so cannot add a branch to T. Thus,
$\mathbb C$
is highly closed, and so cannot add a branch to T. Thus,
![]() $\kappa $
is also not weakly compact in the stable core of
$\kappa $
is also not weakly compact in the stable core of
![]() $V[G][T][H]$
because, by our coding,
$V[G][T][H]$
because, by our coding,
![]() $L[S^{V[G][T][H]}]$
has the
$L[S^{V[G][T][H]}]$
has the
![]() $\kappa $
-Souslin tree T.
$\kappa $
-Souslin tree T.
Next, let’s argue that the measurability of
![]() $\kappa $
is resurrected in the final model
$\kappa $
is resurrected in the final model
![]() $V[G][T][H][b]$
. Standard lifting arguments show that
$V[G][T][H][b]$
. Standard lifting arguments show that
![]() $\kappa $
is measurable in
$\kappa $
is measurable in
![]() $V[G][T][b]$
, which is a forcing extension by
$V[G][T][b]$
, which is a forcing extension by
![]() $\mathbb P_{\kappa }*\operatorname {Add}(\kappa ,1)$
. But
$\mathbb P_{\kappa }*\operatorname {Add}(\kappa ,1)$
. But
![]() $V[G][T][H][b]$
and
$V[G][T][H][b]$
and
![]() $V[G][T][b]$
have the same subsets of
$V[G][T][b]$
have the same subsets of
![]() $\kappa $
, which means that
$\kappa $
, which means that
![]() $\kappa $
is also measurable in
$\kappa $
is also measurable in
![]() $V[G][T][H][b]$
.
$V[G][T][H][b]$
.
For ease of reference, let
![]() $W=V[G][T][H]$
. We will argue that the stable core of
$W=V[G][T][H]$
. We will argue that the stable core of
![]() $W[b]$
is the same as the stable core of W, so that
$W[b]$
is the same as the stable core of W, so that
![]() $\kappa $
is not weakly compact there.
$\kappa $
is not weakly compact there.
Note, using Claim 1 in the proof of Theorem 3.1, that all forcing extensions in this argument satisfy the
![]() $\operatorname {GCH} $
. Observe now that since W and
$\operatorname {GCH} $
. Observe now that since W and
![]() $W[b]$
have the same cardinals (since forcing with T is
$W[b]$
have the same cardinals (since forcing with T is
![]() -distributive and
-distributive and
![]() $\kappa $
-cc), and the
$\kappa $
-cc), and the
![]() $\operatorname {GCH} $
holds in both models, they have the same strong limit cardinals (namely the limit cardinals). Thus, we have that
$\operatorname {GCH} $
holds in both models, they have the same strong limit cardinals (namely the limit cardinals). Thus, we have that
![]() $S_1^W=S_1^{W[b]}$
. The remaining arguments will therefore assume that
$S_1^W=S_1^{W[b]}$
. The remaining arguments will therefore assume that
![]() $n\geq 2$
in the triple
$n\geq 2$
in the triple
![]() $(n,\alpha ,\beta )$
.
$(n,\alpha ,\beta )$
.
It is easy to see that for
![]() $\alpha <\beta \leq \kappa $
, a triple
$\alpha <\beta \leq \kappa $
, a triple
![]() $(n,\alpha ,\beta )\in S^W$
if and only if it is in
$(n,\alpha ,\beta )\in S^W$
if and only if it is in
![]() $S^{W[b]}$
because forcing with the tree T does not add small subsets to
$S^{W[b]}$
because forcing with the tree T does not add small subsets to
![]() $\kappa $
.
$\kappa $
.
The case
![]() $\kappa <\alpha <\beta $
follows by Proposition 2.5 because
$\kappa <\alpha <\beta $
follows by Proposition 2.5 because
![]() $\alpha $
is above the size of the forcing T.
$\alpha $
is above the size of the forcing T.
Finally, we consider the remaining case
![]() $\alpha \leq \kappa <\beta $
. Observe that for every strong limit cardinal
$\alpha \leq \kappa <\beta $
. Observe that for every strong limit cardinal
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $H_{\alpha }^W$
satisfies the assertion that for every successor cardinal
$H_{\alpha }^W$
satisfies the assertion that for every successor cardinal
![]() $\gamma ^+$
, there is an
$\gamma ^+$
, there is an
![]() $L_{\alpha }(H_{\gamma ^+})$
-generic filter for
$L_{\alpha }(H_{\gamma ^+})$
-generic filter for
![]() $\operatorname {Add}(\gamma ^+,1)^{L_{\alpha }(H_{\gamma ^+})}$
. The reason is that
$\operatorname {Add}(\gamma ^+,1)^{L_{\alpha }(H_{\gamma ^+})}$
. The reason is that
![]() $H_{\gamma ^+}^{V[G]}=H_{\gamma ^+}^{V[G_{\gamma }]}$
, where we factor
$H_{\gamma ^+}^{V[G]}=H_{\gamma ^+}^{V[G_{\gamma }]}$
, where we factor
![]() $\mathbb P_{\kappa }\cong \mathbb P_{\gamma +1}*\mathbb P_{\text {tail}}$
and correspondingly factor
$\mathbb P_{\kappa }\cong \mathbb P_{\gamma +1}*\mathbb P_{\text {tail}}$
and correspondingly factor
![]() $G\cong G_{\gamma +1}*G_{\text {tail}}$
. The complexity of the assertion is
$G\cong G_{\gamma +1}*G_{\text {tail}}$
. The complexity of the assertion is
![]() $\Pi _2$
because we can express it as follows:
$\Pi _2$
because we can express it as follows:
However,
![]() $H_{\beta }^W$
cannot satisfy this assertion because it obviously cannot have an
$H_{\beta }^W$
cannot satisfy this assertion because it obviously cannot have an
![]() $L_{\beta }(H_{\gamma ^+})$
-generic filter for
$L_{\beta }(H_{\gamma ^+})$
-generic filter for
![]() $\operatorname {Add}(\gamma ^+,1)^{L_{\beta }(H_{\gamma ^+})}$
, where
$\operatorname {Add}(\gamma ^+,1)^{L_{\beta }(H_{\gamma ^+})}$
, where
![]() $\gamma =\kappa ^{++}$
, because the
$\gamma =\kappa ^{++}$
, because the
![]() $H_{\gamma ^+}$
of
$H_{\gamma ^+}$
of
![]() $L_{\beta }(H_{\gamma ^+})$
is the real
$L_{\beta }(H_{\gamma ^+})$
is the real
![]() $H_{\gamma ^+}$
of W. The same argument holds for
$H_{\gamma ^+}$
of W. The same argument holds for
![]() $W[b]$
showing that no triple
$W[b]$
showing that no triple
![]() $(n,\alpha ,\beta )$
can be in either
$(n,\alpha ,\beta )$
can be in either
![]() $S^W$
or
$S^W$
or
![]() $S^{W[b]}$
for
$S^{W[b]}$
for
![]() $n\geq 2$
.
$n\geq 2$
.
6 Separating the stable core and
 $L[\operatorname {Card}]$
$L[\operatorname {Card}]$
Finally, we would like to consider the possible relationships between the stable core
![]() $L[S]$
and the model
$L[S]$
and the model
![]() $L[\operatorname {Card}]$
.
$L[\operatorname {Card}]$
.
Even though the stable core can define the class of strong limit cardinals of V, there is no reason to believe that it can see the cardinals. Indeed, it is even possible to make
![]() $L[\operatorname {Card}]$
larger than the stable core.
$L[\operatorname {Card}]$
larger than the stable core.
Theorem 6.1. It is consistent that
![]() $L[S]\subsetneq L[\operatorname {Card}]$
.
$L[S]\subsetneq L[\operatorname {Card}]$
.
Proof We start in L. Force to add an L-generic Cohen real r. Next, force with the full support product
![]() $\mathbb P=\Pi _{k<\omega }\mathbb Q_k$
, where if
$\mathbb P=\Pi _{k<\omega }\mathbb Q_k$
, where if
![]() $k\in r$
, then
$k\in r$
, then
![]() $\mathbb Q_k=\operatorname {Coll}(\aleph _{2k},\aleph _{2k+1})$
, and otherwise
$\mathbb Q_k=\operatorname {Coll}(\aleph _{2k},\aleph _{2k+1})$
, and otherwise
![]() $\mathbb Q_k$
is the trivial forcing. The forcing
$\mathbb Q_k$
is the trivial forcing. The forcing
![]() $\mathbb P$
codes r into the cardinals of the forcing extension. Suppose
$\mathbb P$
codes r into the cardinals of the forcing extension. Suppose
![]() $H\subseteq \Pi _{k<\omega }\mathbb Q_k$
is
$H\subseteq \Pi _{k<\omega }\mathbb Q_k$
is
![]() $L[r]$
-generic, and observe that
$L[r]$
-generic, and observe that
![]() $r\in L[\operatorname {Card}^{L[r][H]}]$
because it can be constructed by comparing the cardinals of L with the cardinals of
$r\in L[\operatorname {Card}^{L[r][H]}]$
because it can be constructed by comparing the cardinals of L with the cardinals of
![]() $L[r][H]$
. However, the stable core
$L[r][H]$
. However, the stable core
![]() $L[S^{L[r][H]}]=L$
remains unchanged because we preserved the strong limit cardinals, and for the slices
$L[S^{L[r][H]}]=L$
remains unchanged because we preserved the strong limit cardinals, and for the slices
![]() $S_n$
of the stable core with
$S_n$
of the stable core with
![]() $n\geq 2$
, it suffices that the forcing has size smaller than the second strong limit cardinal.
$n\geq 2$
, it suffices that the forcing has size smaller than the second strong limit cardinal.
Next, let’s show that in various situations,
![]() $L[\operatorname {Card}]$
can be a proper submodel of the stable core
$L[\operatorname {Card}]$
can be a proper submodel of the stable core
![]() $L[S]$
.
$L[S]$
.
Theorem 6.2. It is consistent that
![]() $L[\operatorname {Card}]\subsetneq L[S]$
.
$L[\operatorname {Card}]\subsetneq L[S]$
.
Proof We start in L and force to add a Cohen real r. We then code r into the stable core of a further forcing extension using the coding forcing from the proof of Theorem 3.3. More precisely, we let
![]() $\delta _0$
be any sufficiently large singular strong limit cardinal, and let
$\delta _0$
be any sufficiently large singular strong limit cardinal, and let
![]() $\langle (\beta _n,\beta _n^*)\mid n<\omega \rangle $
be the sequence of
$\langle (\beta _n,\beta _n^*)\mid n<\omega \rangle $
be the sequence of
![]() $\omega $
-many pairs of successive strong limit cardinals above
$\omega $
-many pairs of successive strong limit cardinals above
![]() $\delta _0$
(note that they must all be singular), which will be our coding pairs. Now define that
$\delta _0$
(note that they must all be singular), which will be our coding pairs. Now define that
![]() $\mathbb C_n$
is trivial for
$\mathbb C_n$
is trivial for
![]() $n\not \in r$
, and otherwise let
$n\not \in r$
, and otherwise let
![]() $\mathbb C_n=\operatorname {Add}(\delta _n^+,\beta _n)$
, where
$\mathbb C_n=\operatorname {Add}(\delta _n^+,\beta _n)$
, where
![]() $\delta _n=\beta _{n-1}^*$
for
$\delta _n=\beta _{n-1}^*$
for
![]() $n>0$
. By the arguments given in the proof of Theorem 3.3, the full support forcing
$n>0$
. By the arguments given in the proof of Theorem 3.3, the full support forcing
![]() $\mathbb C=\Pi _{n<\omega }\mathbb C_n$
is cardinal preserving. Let
$\mathbb C=\Pi _{n<\omega }\mathbb C_n$
is cardinal preserving. Let
![]() $H\subseteq \mathbb C$
be
$H\subseteq \mathbb C$
be
![]() $L[r]$
-generic. Now observe that since we have
$L[r]$
-generic. Now observe that since we have
![]() $\operatorname {Card}^L=\operatorname {Card}^{L[r][H]}$
, it follows that
$\operatorname {Card}^L=\operatorname {Card}^{L[r][H]}$
, it follows that
![]() $L[\operatorname {Card}^{L[r][H]}]=L$
, but
$L[\operatorname {Card}^{L[r][H]}]=L$
, but
![]() $L[r]\subseteq L[S^{L[r][H]}]$
.
$L[r]\subseteq L[S^{L[r][H]}]$
.
Theorem 6.3. It is consistent that
![]() $L[S]$
has a measurable cardinal and
$L[S]$
has a measurable cardinal and
![]() $L[\operatorname {Card}]\subsetneq L[S]$
.
$L[\operatorname {Card}]\subsetneq L[S]$
.
Proof We start in a model
![]() $V=L[\mu ]$
with a measurable cardinal
$V=L[\mu ]$
with a measurable cardinal
![]() $\kappa $
and force to add a Cohen subset to some
$\kappa $
and force to add a Cohen subset to some
![]() $\delta \gg \kappa $
. Let
$\delta \gg \kappa $
. Let
![]() $G\subseteq \operatorname {Add}(\delta ,1)$
be V-generic. We then code G into the stable core using the cardinal preserving coding forcing
$G\subseteq \operatorname {Add}(\delta ,1)$
be V-generic. We then code G into the stable core using the cardinal preserving coding forcing
![]() $\mathbb C$
from the proof of Theorem 3.3. Let H be
$\mathbb C$
from the proof of Theorem 3.3. Let H be
![]() $V[G]$
-generic for
$V[G]$
-generic for
![]() $\mathbb C$
. Since we forced high above
$\mathbb C$
. Since we forced high above
![]() $\kappa $
,
$\kappa $
,
![]() $\kappa $
remains measurable in
$\kappa $
remains measurable in
![]() $L[S^{V[G][H]}]$
as in Theorem 4.7. Because
$L[S^{V[G][H]}]$
as in Theorem 4.7. Because
![]() $\mathbb C$
preserves cardinals,
$\mathbb C$
preserves cardinals,
![]() $L[\operatorname {Card}^{V[G][H]}]=L[\operatorname {Card}^V]=V$
, but
$L[\operatorname {Card}^{V[G][H]}]=L[\operatorname {Card}^V]=V$
, but
![]() $L[S^{V[G][H]}]$
contains G by construction.
$L[S^{V[G][H]}]$
contains G by construction.
We also separate the models
![]() $L[\operatorname {Card}]$
and
$L[\operatorname {Card}]$
and
![]() $L[S]$
by showing that, for each
$L[S]$
by showing that, for each
![]() $n < \omega $
, if
$n < \omega $
, if
![]() $m_{n+1}^{\#}$
exists, then
$m_{n+1}^{\#}$
exists, then
![]() $m_n^{\#}\in L[S]$
. Recall that even
$m_n^{\#}\in L[S]$
. Recall that even
![]() $m_1^{\#}$
cannot be an element of
$m_1^{\#}$
cannot be an element of
![]() $L[\operatorname {Card}]$
(Corollary 4.5).
$L[\operatorname {Card}]$
(Corollary 4.5).
Given a class A, we will say that a cardinal
![]() $\gamma $
is
$\gamma $
is
![]() $\Sigma _n$
-stable relative to A if
$\Sigma _n$
-stable relative to A if
![]() $\langle H_{\gamma },\in ,A\rangle \prec _{\Sigma _n} \langle V,\in ,A\rangle $
. We will say that a class B is
$\langle H_{\gamma },\in ,A\rangle \prec _{\Sigma _n} \langle V,\in ,A\rangle $
. We will say that a class B is
![]() $\Sigma _n$
-stable relative to A if every
$\Sigma _n$
-stable relative to A if every
![]() $\gamma \in B$
is
$\gamma \in B$
is
![]() $\Sigma _n$
-stable relative to A. Let us say that a cardinal is strictly n-measurable if it is n-measurable, but not
$\Sigma _n$
-stable relative to A. Let us say that a cardinal is strictly n-measurable if it is n-measurable, but not
![]() $n+1$
-measurable. Recall that given a club C, we denote by
$n+1$
-measurable. Recall that given a club C, we denote by
![]() $\hat C$
, the collection of all successor elements of C together with its least element.
$\hat C$
, the collection of all successor elements of C together with its least element.
Theorem 6.4. Suppose that
![]() $C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
$C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
![]() $C_2$
is
$C_2$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1$
. Then there is an
$C_1$
. Then there is an
![]() $\operatorname {Ord} $
-length iteration of the mouse
$\operatorname {Ord} $
-length iteration of the mouse
![]() $m_2^{\#}$
such that in the direct limit model
$m_2^{\#}$
such that in the direct limit model
![]() $M_{C_1,C_2}$
(truncated at
$M_{C_1,C_2}$
(truncated at
![]() $\operatorname {Ord} $
) the strictly
$\operatorname {Ord} $
) the strictly
![]() $1$
-measurable cardinals are precisely the elements of
$1$
-measurable cardinals are precisely the elements of
![]() $\hat C_1$
and the
$\hat C_1$
and the
![]() $2$
-measurable cardinals are precisely the elements of
$2$
-measurable cardinals are precisely the elements of
![]() $\hat C_2$
.
$\hat C_2$
.
Proof Let
![]() $C_1=\langle \alpha _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
and let
$C_1=\langle \alpha _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
and let
![]() $\langle \gamma _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
be a sequence such that
$\langle \gamma _{\xi }\mid \xi \in \operatorname {Ord} \rangle $
be a sequence such that
![]() $\alpha _{\gamma _{\xi }}$
is the
$\alpha _{\gamma _{\xi }}$
is the
![]() $\xi $
th element of
$\xi $
th element of
![]() $C_2$
in the enumeration of
$C_2$
in the enumeration of
![]() $C_1$
. The iteration will closely resemble the iteration from the proof of Theorem 4.4.
$C_1$
. The iteration will closely resemble the iteration from the proof of Theorem 4.4.
Iterate the first measurable cardinal
![]() $\kappa _0$
of
$\kappa _0$
of
![]() $m_2^{\#}$
$m_2^{\#}$
![]() $\alpha _0$
-many times, so that
$\alpha _0$
-many times, so that
![]() $\kappa _0$
iterates to
$\kappa _0$
iterates to
![]() $\alpha _0$
, and let
$\alpha _0$
, and let
![]() $M_{\alpha _0}$
be the iterate. Continue to iterate measurable cardinals onto elements of
$M_{\alpha _0}$
be the iterate. Continue to iterate measurable cardinals onto elements of
![]() $\hat C_1$
until we reach for the first time a direct limit stage
$\hat C_1$
until we reach for the first time a direct limit stage
![]() $\eta _0$
where in the model
$\eta _0$
where in the model
![]() $M_{\eta _0}$
all measurable cardinals below the first 2-measurable cardinal are elements of
$M_{\eta _0}$
all measurable cardinals below the first 2-measurable cardinal are elements of
![]() $\hat C_1$
. It is not difficult to see that
$\hat C_1$
. It is not difficult to see that
![]() $\eta _0$
is the first cardinal such that
$\eta _0$
is the first cardinal such that
![]() $\eta _0=\alpha _{\eta _0}$
, the
$\eta _0=\alpha _{\eta _0}$
, the
![]() $\eta _0$
th element of
$\eta _0$
th element of
![]() $C_1$
, and that in
$C_1$
, and that in
![]() $M_{\eta _0}$
,
$M_{\eta _0}$
,
![]() $\eta _0$
is the first 2-measurable cardinal. Since
$\eta _0$
is the first 2-measurable cardinal. Since
![]() $C_2$
is
$C_2$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1$
,
$C_1$
,
![]() $\eta _0$
must be below the first element of
$\eta _0$
must be below the first element of
![]() $C_2$
. To achieve our goal of making the least 2-measurable the least element of
$C_2$
. To achieve our goal of making the least 2-measurable the least element of
![]() $C_2$
, at this stage, we iterate up
$C_2$
, at this stage, we iterate up
![]() $\eta _0$
to obtain a model
$\eta _0$
to obtain a model
![]() $M_{\eta _0+1}$
with more strictly 1-measurable cardinals and continue iterating measurable cardinals onto elements of
$M_{\eta _0+1}$
with more strictly 1-measurable cardinals and continue iterating measurable cardinals onto elements of
![]() $\hat C_1$
. Let
$\hat C_1$
. Let
![]() $\eta _{\xi }$
be the
$\eta _{\xi }$
be the
![]() $\xi $
th stage where we iterate up the first 2-measurable cardinal
$\xi $
th stage where we iterate up the first 2-measurable cardinal
![]() $\eta _{\xi }$
as above. Since
$\eta _{\xi }$
as above. Since
![]() $\alpha _{\gamma _0}$
, the least element of
$\alpha _{\gamma _0}$
, the least element of
![]() $C_2$
, is
$C_2$
, is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1$
, it must be that
$C_1$
, it must be that
![]() $\eta _{\xi }<\alpha _{\gamma _0}$
for every
$\eta _{\xi }<\alpha _{\gamma _0}$
for every
![]() $\xi <\alpha _{\gamma _0}$
as every iteration of a shorter length
$\xi <\alpha _{\gamma _0}$
as every iteration of a shorter length
![]() $\beta <\alpha _{\gamma _0}$
(of the kind we have been doing) has to be an element of
$\beta <\alpha _{\gamma _0}$
(of the kind we have been doing) has to be an element of
![]() $H_{\alpha _{\gamma _0}}$
by
$H_{\alpha _{\gamma _0}}$
by
![]() $\Sigma _1$
-elementarity. We would like to argue that the thread t in the stage
$\Sigma _1$
-elementarity. We would like to argue that the thread t in the stage
![]() $\alpha _{\gamma _0}$
direct limit such that
$\alpha _{\gamma _0}$
direct limit such that
![]() $t(\xi )$
is the first 2-measurable cardinal maps to
$t(\xi )$
is the first 2-measurable cardinal maps to
![]() $\alpha _{\gamma _0}$
as desired. It suffices to observe that every ordinal thread s below t must be constant from some stage onward. So suppose that
$\alpha _{\gamma _0}$
as desired. It suffices to observe that every ordinal thread s below t must be constant from some stage onward. So suppose that
![]() $s<t$
, which by definition of direct limit means that on a tail of stages
$s<t$
, which by definition of direct limit means that on a tail of stages
![]() $\xi $
,
$\xi $
,
![]() $s(\xi )<t(\xi )$
. Fix some such
$s(\xi )<t(\xi )$
. Fix some such
![]() $\xi $
in the tail and consider a stage
$\xi $
in the tail and consider a stage
![]() $\eta _{\bar \xi }>\xi $
where we have
$\eta _{\bar \xi }>\xi $
where we have
![]() $s(\eta _{\bar \xi })<t(\eta _{\bar \xi })=\eta _{\bar \xi }$
. Here the equality holds by elementarity as
$s(\eta _{\bar \xi })<t(\eta _{\bar \xi })=\eta _{\bar \xi }$
. Here the equality holds by elementarity as
![]() $\eta _{\bar \xi }$
is the first
$\eta _{\bar \xi }$
is the first
![]() $2$
-measurable cardinal in
$2$
-measurable cardinal in
![]() $M_{\eta _{\bar \xi }}$
. Since the critical points of the iteration after this stage are above
$M_{\eta _{\bar \xi }}$
. Since the critical points of the iteration after this stage are above
![]() $\eta _{\bar \xi }$
, the thread s remains constant from that point onward.
$\eta _{\bar \xi }$
, the thread s remains constant from that point onward.
Thus,
![]() $\alpha _{\gamma _0}$
must be the first
$\alpha _{\gamma _0}$
must be the first
![]() $2$
-measurable cardinal in the direct limit model
$2$
-measurable cardinal in the direct limit model
![]() $M_{\alpha _{\gamma _0}}$
. Having correctly positioned the first
$M_{\alpha _{\gamma _0}}$
. Having correctly positioned the first
![]() $2$
-measurable cardinal, we proceed with iterating the strictly 1-measurable cardinals onto elements of
$2$
-measurable cardinal, we proceed with iterating the strictly 1-measurable cardinals onto elements of
![]() $\hat C_1$
below the next element of
$\hat C_1$
below the next element of
![]() $C_2$
. As in the proof of Theorem 4.4, it will be the case that at some limit stages in
$C_2$
. As in the proof of Theorem 4.4, it will be the case that at some limit stages in
![]() $C_2$
, we will need to use the top measure of
$C_2$
, we will need to use the top measure of
![]() $m_2^{\#}$
to create more room for the iteration to proceed.
$m_2^{\#}$
to create more room for the iteration to proceed.
Let M be the resulting model obtained as the direct limit along the iteration embeddings and let
![]() $M_{C_1,C_2}$
be M truncated at
$M_{C_1,C_2}$
be M truncated at
![]() $\operatorname {Ord} $
. The construction ensures that the strictly 1-measurable cardinals of
$\operatorname {Ord} $
. The construction ensures that the strictly 1-measurable cardinals of
![]() $M_{C_1,C_2}$
are precisely the elements of
$M_{C_1,C_2}$
are precisely the elements of
![]() $\hat C_1$
and
$\hat C_1$
and
![]() $2$
-measurable cardinals of
$2$
-measurable cardinals of
![]() $M_{C_1,C_2}$
are precisely the elements of
$M_{C_1,C_2}$
are precisely the elements of
![]() $\hat C_2$
.
$\hat C_2$
.
Given a club C, let
![]() $C^*$
denote the club of all limit points of C. Next, let’s argue that if
$C^*$
denote the club of all limit points of C. Next, let’s argue that if
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are clubs as above, then
$C_2$
are clubs as above, then
![]() $M_{C_1^*,C_2^*}$
is contained in
$M_{C_1^*,C_2^*}$
is contained in
![]() $L[C_1,C_2]$
.
$L[C_1,C_2]$
.
Theorem 6.5. Suppose that
![]() $C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
$C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
![]() $C_2$
is
$C_2$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1$
. Then
$C_1$
. Then
![]() $M_{C_1^*,C_2^*}$
(obtained as in Theorem 6.4) is contained in
$M_{C_1^*,C_2^*}$
(obtained as in Theorem 6.4) is contained in
![]() $L[C_1,C_2]$
.
$L[C_1,C_2]$
.
Proof Given
![]() $\alpha \in \hat C_1^*$
, let
$\alpha \in \hat C_1^*$
, let
![]() $U_{\alpha }\subseteq P(\alpha )^{M_{C_1^*,C_2^*}}$
be the iteration measures in
$U_{\alpha }\subseteq P(\alpha )^{M_{C_1^*,C_2^*}}$
be the iteration measures in
![]() $M_{C_1^*,C_2^*}$
, and note that a set from
$M_{C_1^*,C_2^*}$
, and note that a set from
![]() $M_{C_1^*,C_2^*}$
is in
$M_{C_1^*,C_2^*}$
is in
![]() $U_{\alpha }$
if and only if it contains a tail of
$U_{\alpha }$
if and only if it contains a tail of
![]() $C_1\cap \alpha $
. Let
$C_1\cap \alpha $
. Let
![]() $\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
. Similarly, for
$\vec U=\langle U_{\alpha }\mid \alpha \in \operatorname {Ord} \rangle $
. Similarly, for
![]() $\beta \in \hat C_2^*$
, let
$\beta \in \hat C_2^*$
, let
![]() $W_{\beta }\subseteq P(\beta )^{M_{C_1^*,C_2^*}}$
be the iteration measures in
$W_{\beta }\subseteq P(\beta )^{M_{C_1^*,C_2^*}}$
be the iteration measures in
![]() $M_{C_1^*,C_2^*}$
, and let
$M_{C_1^*,C_2^*}$
, and let
![]() $\vec W=\langle W_{\beta }\mid \beta \in \operatorname {Ord} \rangle $
. Here we also have that a set is in
$\vec W=\langle W_{\beta }\mid \beta \in \operatorname {Ord} \rangle $
. Here we also have that a set is in
![]() $W_{\beta }$
if and only if it contains a tail of
$W_{\beta }$
if and only if it contains a tail of
![]() $C_2\cap \beta $
because, as we noted in the proof of Theorem 6.4, at every stage in
$C_2\cap \beta $
because, as we noted in the proof of Theorem 6.4, at every stage in
![]() $C_2$
we iterate up the measure on the
$C_2$
we iterate up the measure on the
![]() $2$
-measurable cardinal until we reach an element of
$2$
-measurable cardinal until we reach an element of
![]() $\hat C_2^*$
. Finally, observe that
$\hat C_2^*$
. Finally, observe that
![]() $M_{C_1^*,C_2^*}=L[\vec U,\vec W]$
, and thus, it is contained in
$M_{C_1^*,C_2^*}=L[\vec U,\vec W]$
, and thus, it is contained in
![]() $L[C_1,C_2]$
.
$L[C_1,C_2]$
.
Theorems 6.4 and 6.5 easily generalize to n nested clubs
![]() $C_1,\ldots , C_n$
such that
$C_1,\ldots , C_n$
such that
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1,\ldots ,C_{i-1}$
(more precisely, relative to the class canonically coding the the sequence
$C_1,\ldots ,C_{i-1}$
(more precisely, relative to the class canonically coding the the sequence
![]() $\langle C_1,\ldots , C_{i-1}\rangle $
of classes) for all
$\langle C_1,\ldots , C_{i-1}\rangle $
of classes) for all
![]() $1<i\leq n$
.
$1<i\leq n$
.
Theorem 6.6. Suppose that
![]() $C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are class clubs of uncountable cardinals such that
$C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are class clubs of uncountable cardinals such that
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1,\ldots , C_{i-1}$
for all
$C_1,\ldots , C_{i-1}$
for all
![]() $1< i\leq n$
. Then there is an
$1< i\leq n$
. Then there is an
![]() $\operatorname {Ord} $
-length iteration of the mouse
$\operatorname {Ord} $
-length iteration of the mouse
![]() $m_n^{\#}$
such that in the direct limit model
$m_n^{\#}$
such that in the direct limit model
![]() $M_{C_1,\ldots ,C_n}$
(truncated at
$M_{C_1,\ldots ,C_n}$
(truncated at
![]() $\operatorname {Ord} $
), for
$\operatorname {Ord} $
), for
![]() $1\leq i\leq n$
, the strictly i-measurable cardinals are precisely the elements of
$1\leq i\leq n$
, the strictly i-measurable cardinals are precisely the elements of
![]() $\hat C_i$
.
$\hat C_i$
.
Theorem 6.7. Suppose that
![]() $C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are class clubs of uncountable cardinals such that
$C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are class clubs of uncountable cardinals such that
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1,\ldots , C_{i-1}$
for all
$C_1,\ldots , C_{i-1}$
for all
![]() $1<i\leq n$
. Then
$1<i\leq n$
. Then
![]() $M_{ C_1^*,\ldots ,C_n^*}$
(obtained as in Theorem 6.6) is contained in
$M_{ C_1^*,\ldots ,C_n^*}$
(obtained as in Theorem 6.6) is contained in
![]() $L[C_1,\ldots , C_n]$
.
$L[C_1,\ldots , C_n]$
.
Theorem 6.8. For all
![]() $n<\omega $
, if
$n<\omega $
, if
![]() $m_{n+1}^{\#}$
exists, then
$m_{n+1}^{\#}$
exists, then
![]() $m_n^{\#}$
is in the stable core.
$m_n^{\#}$
is in the stable core.
Proof By Proposition 2.3, for
![]() $i\geq 1$
, the stable core can define class clubs
$i\geq 1$
, the stable core can define class clubs
![]() $C_i$
of strong limit cardinals
$C_i$
of strong limit cardinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $H_{\alpha }\prec _{\Sigma _i} V$
. In particular, each
$H_{\alpha }\prec _{\Sigma _i} V$
. In particular, each
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1,\ldots ,C_{i-1}$
. Fix some
$C_1,\ldots ,C_{i-1}$
. Fix some
![]() $n<\omega $
. If
$n<\omega $
. If
![]() $m_{n+1}^{\#}$
exists, then by Theorem 6.7,
$m_{n+1}^{\#}$
exists, then by Theorem 6.7,
![]() $M_{C_1^*,\ldots ,C_{n+1}^*}$
is contained in the stable core, and so in particular, the stable core has
$M_{C_1^*,\ldots ,C_{n+1}^*}$
is contained in the stable core, and so in particular, the stable core has
![]() $m_n^{\#}$
.
$m_n^{\#}$
.
7 Characterizing models
 $L[C_1,\ldots ,C_n]$
$L[C_1,\ldots ,C_n]$
In this section, we will generalize Welch’s arguments in [Reference Welch29] to show that, in the presence of many measurable cardinals, models
![]() $L[C_1,\ldots ,C_n]$
, where
$L[C_1,\ldots ,C_n]$
, where
are class clubs of uncountable cardinals such that
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1,\ldots ,C_{i-1}$
, are truncations to
$C_1,\ldots ,C_{i-1}$
, are truncations to
![]() $\operatorname {Ord} $
of forcing extensions of an iterate of the mouse
$\operatorname {Ord} $
of forcing extensions of an iterate of the mouse
![]() $m_n^{\#}$
via a full support product of Prikry forcings.
$m_n^{\#}$
via a full support product of Prikry forcings.
In [Reference Fuchs10], Fuchs defined, given a discrete set D of measurable cardinals, a Prikry-type forcing
![]() $\mathbb P_D$
to singularize them all, as follows. For every
$\mathbb P_D$
to singularize them all, as follows. For every
![]() $\alpha \in D$
, we fix a normal measure
$\alpha \in D$
, we fix a normal measure
![]() $\mu _{\alpha }$
on
$\mu _{\alpha }$
on
![]() $\alpha $
with respect to which the forcing
$\alpha $
with respect to which the forcing
![]() $\mathbb P_D$
will be defined. Conditions in
$\mathbb P_D$
will be defined. Conditions in
![]() $\mathbb P_D$
are pairs
$\mathbb P_D$
are pairs
![]() $\langle h, H\rangle $
such that H is a function on D with
$\langle h, H\rangle $
such that H is a function on D with
![]() $H(\alpha )\in \mu _{\alpha }$
and h is a function on D with finite support such that
$H(\alpha )\in \mu _{\alpha }$
and h is a function on D with finite support such that
![]() is a finite sequence of elements of
is a finite sequence of elements of
![]() $\alpha $
below the least element of
$\alpha $
below the least element of
![]() $H(\alpha )$
and above all
$H(\alpha )$
and above all
![]() $\beta \in D$
with
$\beta \in D$
with
![]() $\beta <\alpha $
. Extension is defined by
$\beta <\alpha $
. Extension is defined by
![]() $(h,H)\leq (f,F)$
if for all
$(h,H)\leq (f,F)$
if for all
![]() $\alpha \in D$
,
$\alpha \in D$
,
![]() $H(\alpha )\subseteq F(\alpha )$
,
$H(\alpha )\subseteq F(\alpha )$
,
![]() $h(\alpha )$
end-extends
$h(\alpha )$
end-extends
![]() $f(\alpha )$
, and
$f(\alpha )$
, and
![]() $h(\alpha )\setminus f(\alpha )\subseteq F(\alpha )$
. Note that the first coordinate of the pair has finite support while the second coordinate has full support so that the forcing is a mix of a finite support and a full support-product. It is not difficult to see that the Magidor iteration of Prikry forcing for a discrete set D of measurable cardinals is equivalent to
$h(\alpha )\setminus f(\alpha )\subseteq F(\alpha )$
. Note that the first coordinate of the pair has finite support while the second coordinate has full support so that the forcing is a mix of a finite support and a full support-product. It is not difficult to see that the Magidor iteration of Prikry forcing for a discrete set D of measurable cardinals is equivalent to
![]() $\mathbb P_D$
. For the definition and properties of the Magidor iteration, see Section 6 of [Reference Gitik, Foreman and Kanamori11].
$\mathbb P_D$
. For the definition and properties of the Magidor iteration, see Section 6 of [Reference Gitik, Foreman and Kanamori11].
Theorem 7.1 (See [Reference Fuchs10]).
The forcing
![]() $\mathbb P_D$
has the
$\mathbb P_D$
has the
![]() $|D|^+$
-cc, preserves all cardinals, and preserves all cofinalities not in D.
$|D|^+$
-cc, preserves all cardinals, and preserves all cofinalities not in D.
The forcing
![]() $\mathbb P_D$
also has the Prikry property, namely, given a condition
$\mathbb P_D$
also has the Prikry property, namely, given a condition
![]() $(h,H)\in \mathbb P_D$
and a sentence
$(h,H)\in \mathbb P_D$
and a sentence
![]() $\varphi $
of the forcing language, there is a condition
$\varphi $
of the forcing language, there is a condition
![]() $(h,H^*)$
deciding
$(h,H^*)$
deciding
![]() $\varphi $
such that for every
$\varphi $
such that for every
![]() $\alpha \in D$
,
$\alpha \in D$
,
![]() $H^*(\alpha )\subseteq H(\alpha )$
(see [Reference Gitik, Foreman and Kanamori11, Section 6] for details).
$H^*(\alpha )\subseteq H(\alpha )$
(see [Reference Gitik, Foreman and Kanamori11, Section 6] for details).
For an ordinal
![]() $\lambda $
, let
$\lambda $
, let
![]() $D_{<\!\lambda }$
be
$D_{<\!\lambda }$
be
![]() $D\upharpoonright \lambda $
and
$D\upharpoonright \lambda $
and
![]() $D_{\geq \!\lambda }$
be the rest of D. The forcing
$D_{\geq \!\lambda }$
be the rest of D. The forcing
![]() $\mathbb P_D$
factors as
$\mathbb P_D$
factors as
![]() $\mathbb P_{D_{<\!\lambda }}\times \mathbb P_{D_{\geq \!\lambda }}$
.
$\mathbb P_{D_{<\!\lambda }}\times \mathbb P_{D_{\geq \!\lambda }}$
.
Proposition 7.2. Suppose f is V-generic for
![]() $\mathbb P_D$
. If
$\mathbb P_D$
. If
![]() $g:\gamma \to V_{\gamma }$
is a function in
$g:\gamma \to V_{\gamma }$
is a function in
![]() $V[f]$
with
$V[f]$
with
![]() $\gamma <\lambda $
, then g is added by
$\gamma <\lambda $
, then g is added by
![]() $f\upharpoonright \lambda $
.
$f\upharpoonright \lambda $
.
Proof It suffices to see that
![]() $\mathbb P_{D_{\geq \!\lambda }}$
cannot add g over
$\mathbb P_{D_{\geq \!\lambda }}$
cannot add g over
![]() $V[f\upharpoonright \lambda ]$
. Let
$V[f\upharpoonright \lambda ]$
. Let
![]() $\dot g$
be a
$\dot g$
be a
![]() $\mathbb P_{D_{\geq \!\lambda }}$
-name for g so that
$\mathbb P_{D_{\geq \!\lambda }}$
-name for g so that
![]() . By the Prikry property of
. By the Prikry property of
![]() $\mathbb P_{D_{\geq \!\lambda }}$
, for every
$\mathbb P_{D_{\geq \!\lambda }}$
, for every
![]() $x\in V_{\gamma }$
and
$x\in V_{\gamma }$
and
![]() $\alpha <\gamma $
, there is some condition
$\alpha <\gamma $
, there is some condition
![]() $(\emptyset , H_{x,\alpha })$
deciding whether
$(\emptyset , H_{x,\alpha })$
deciding whether
![]() $\dot g(\check \alpha )=\check x$
. There are less than
$\dot g(\check \alpha )=\check x$
. There are less than
![]() $\kappa $
many such conditions, where
$\kappa $
many such conditions, where
![]() $\kappa $
is the least measurable cardinal in D greater than or equal to
$\kappa $
is the least measurable cardinal in D greater than or equal to
![]() $\lambda $
. Thus, we can intersect all the measure one sets on each coordinate of
$\lambda $
. Thus, we can intersect all the measure one sets on each coordinate of
![]() $H_{x,\alpha }$
to obtain a condition
$H_{x,\alpha }$
to obtain a condition
![]() $(\emptyset , H)$
below all of the
$(\emptyset , H)$
below all of the
![]() $(\emptyset , H_{x,\alpha })$
. Clearly
$(\emptyset , H_{x,\alpha })$
. Clearly
![]() $(\emptyset , H)$
decides
$(\emptyset , H)$
decides
![]() $\dot g$
.
$\dot g$
.
Proposition 7.3. Suppose that
![]() $\kappa $
is inaccessible and D is contained in and unbounded in
$\kappa $
is inaccessible and D is contained in and unbounded in
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\kappa $
remains inaccessible after forcing with
$\kappa $
remains inaccessible after forcing with
![]() $\mathbb P_D$
.
$\mathbb P_D$
.
Proof By Theorem 7.1,
![]() $\kappa $
is regular after forcing with
$\kappa $
is regular after forcing with
![]() $\mathbb P_D$
. So it remains to show that
$\mathbb P_D$
. So it remains to show that
![]() $\kappa $
is a strong limit after forcing with
$\kappa $
is a strong limit after forcing with
![]() $\mathbb P_D$
. Fix a cardinal
$\mathbb P_D$
. Fix a cardinal
![]() $\alpha <\kappa $
and let
$\alpha <\kappa $
and let
![]() $\lambda $
be the least measurable cardinal in D above
$\lambda $
be the least measurable cardinal in D above
![]() $\alpha $
. Since
$\alpha $
. Since
![]() $D\subseteq \kappa $
,
$D\subseteq \kappa $
,
![]() $\lambda <\kappa $
. By Proposition 7.2, every subset of
$\lambda <\kappa $
. By Proposition 7.2, every subset of
![]() $\alpha $
added by
$\alpha $
added by
![]() $\mathbb P_D$
is already added by
$\mathbb P_D$
is already added by
![]() $\mathbb P_{D_{<\!\lambda }}$
. But since
$\mathbb P_{D_{<\!\lambda }}$
. But since
![]() $\kappa $
is an inaccessible,
$\kappa $
is an inaccessible,
![]() $\mathbb P_{D_{<\!\lambda }}$
clearly has a chain condition less than
$\mathbb P_{D_{<\!\lambda }}$
clearly has a chain condition less than
![]() $\lambda $
, and therefore a nice-name counting argument shows that it adds less than
$\lambda $
, and therefore a nice-name counting argument shows that it adds less than
![]() $\kappa $
-many subsets of
$\kappa $
-many subsets of
![]() $\alpha $
.
$\alpha $
.
Fuchs showed that the forcing
![]() $\mathbb P_D$
has a Mathias-like criterion for establishing when a collection of sequences is generic for it.
$\mathbb P_D$
has a Mathias-like criterion for establishing when a collection of sequences is generic for it.
Theorem 7.4 [Reference Fuchs10].
Suppose that M is a transitive model of
![]() $\operatorname {ZFC} $
, D is a discrete set of measurable cardinals in M, and the forcing
$\operatorname {ZFC} $
, D is a discrete set of measurable cardinals in M, and the forcing
![]() $\mathbb P_D^M$
is constructed in M as above. A function f on D such that
$\mathbb P_D^M$
is constructed in M as above. A function f on D such that
![]() $f(\alpha )\in [\alpha ]^{\omega }$
is an
$f(\alpha )\in [\alpha ]^{\omega }$
is an
![]() $\omega $
-sequence in
$\omega $
-sequence in
![]() $\alpha $
above
$\alpha $
above
![]() $\beta \in D$
for every
$\beta \in D$
for every
![]() $\beta <\alpha $
is M-generic for
$\beta <\alpha $
is M-generic for
![]() $\mathbb P_D^M$
if and only if for every function H on D with
$\mathbb P_D^M$
if and only if for every function H on D with
![]() $H(\alpha )\in \mu _{\alpha }$
,
$H(\alpha )\in \mu _{\alpha }$
,
![]() $\bigcup _{\alpha \in D}f(\alpha )\setminus H(\alpha )$
is finite.
$\bigcup _{\alpha \in D}f(\alpha )\setminus H(\alpha )$
is finite.
We will now give the technical set-up for the forcing construction that we want to perform over iterates of the mice
![]() $m_n^{\#}$
.
$m_n^{\#}$
.
Let
![]() $\operatorname {ZFC} ^-_I$
be the theory consisting of
$\operatorname {ZFC} ^-_I$
be the theory consisting of
![]() $\operatorname {ZFC} ^-$
together with the assertion that there is a largest cardinal
$\operatorname {ZFC} ^-$
together with the assertion that there is a largest cardinal
![]() $\kappa $
and that it is inaccessible, namely
$\kappa $
and that it is inaccessible, namely
![]() $\kappa $
is regular and for every
$\kappa $
is regular and for every
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $P(\alpha )$
exists and has size smaller than
$P(\alpha )$
exists and has size smaller than
![]() $\kappa $
. Note that, in particular,
$\kappa $
. Note that, in particular,
![]() $V_{\alpha }$
exists in models of
$V_{\alpha }$
exists in models of
![]() $\operatorname {ZFC} ^-_I$
for all ordinals
$\operatorname {ZFC} ^-_I$
for all ordinals
![]() $\alpha \leq \kappa $
. Natural models of
$\alpha \leq \kappa $
. Natural models of
![]() $\operatorname {ZFC} ^-_I$
are
$\operatorname {ZFC} ^-_I$
are
![]() $H_{\kappa ^+}$
for an inaccessible cardinal
$H_{\kappa ^+}$
for an inaccessible cardinal
![]() $\kappa $
. The theory
$\kappa $
. The theory
![]() $\operatorname {ZFC} ^-_I$
is bi-interpretable with the second-order class set theory
$\operatorname {ZFC} ^-_I$
is bi-interpretable with the second-order class set theory
![]() $\mathrm {KM}+\mathrm {CC}$
, Kelley–Morse set theory (
$\mathrm {KM}+\mathrm {CC}$
, Kelley–Morse set theory (
![]() $\mathrm {KM}$
) together with the Class Choice Principle
$\mathrm {KM}$
) together with the Class Choice Principle
![]() $(\mathrm {CC})$
[Reference Marek23]. Models of Kelley–Morse are two-sorted of the form
$(\mathrm {CC})$
[Reference Marek23]. Models of Kelley–Morse are two-sorted of the form
![]() $\mathscr V=(V,\in ,\mathcal C)$
, with V consisting of the sets,
$\mathscr V=(V,\in ,\mathcal C)$
, with V consisting of the sets,
![]() $\mathcal C$
consisting of classes, and
$\mathcal C$
consisting of classes, and
![]() $\in $
being a membership relation between sets as well as between sets and classes. The axioms of Kelley–Morse are
$\in $
being a membership relation between sets as well as between sets and classes. The axioms of Kelley–Morse are
![]() $\operatorname {ZFC} $
together with the following axioms for classes: extensionality, existence of a global well-order class, class replacement asserting that every class function restricted to a set is a set, and comprehension for all second-order assertions. The Class Choice Principle
$\operatorname {ZFC} $
together with the following axioms for classes: extensionality, existence of a global well-order class, class replacement asserting that every class function restricted to a set is a set, and comprehension for all second-order assertions. The Class Choice Principle
![]() $\mathrm {CC}$
is a scheme of assertions, which asserts for every second-order formula
$\mathrm {CC}$
is a scheme of assertions, which asserts for every second-order formula
![]() $\varphi (x,X,Y)$
that if for every set x, there is a class X such that
$\varphi (x,X,Y)$
that if for every set x, there is a class X such that
![]() $\varphi (x,X,Y)$
holds, then there is a single class Z choosing witnesses for every set x, in the sense that
$\varphi (x,X,Y)$
holds, then there is a single class Z choosing witnesses for every set x, in the sense that
![]() $\varphi (x,Z_x,Y)$
holds for every set x, where
$\varphi (x,Z_x,Y)$
holds for every set x, where
![]() $Z_x=\{y\mid \langle x,y\rangle \in Z\}$
is the xth slice of Z. If
$Z_x=\{y\mid \langle x,y\rangle \in Z\}$
is the xth slice of Z. If
![]() $\mathscr V=(V,\in ,\mathcal C)$
is a model of
$\mathscr V=(V,\in ,\mathcal C)$
is a model of
![]() $\mathrm {KM}+\mathrm {CC}$
, then the collection of all extensional well-founded relations in
$\mathrm {KM}+\mathrm {CC}$
, then the collection of all extensional well-founded relations in
![]() $\mathcal C$
, modulo isomorphism and with a natural membership relation, forms a model
$\mathcal C$
, modulo isomorphism and with a natural membership relation, forms a model
![]() $M_{\mathscr V}$
of
$M_{\mathscr V}$
of
![]() $\operatorname {ZFC} ^-_I$
, whose largest cardinal
$\operatorname {ZFC} ^-_I$
, whose largest cardinal
![]() $\kappa $
is (isomorphic to)
$\kappa $
is (isomorphic to)
![]() $\operatorname {Ord} $
, such that
$\operatorname {Ord} $
, such that
![]() $V_{\kappa }^{M_{\mathscr V}}\cong V$
and the collection of all subsets of
$V_{\kappa }^{M_{\mathscr V}}\cong V$
and the collection of all subsets of
![]() $V_{\kappa }^{M_{\mathscr V}}$
in
$V_{\kappa }^{M_{\mathscr V}}$
in
![]() $M_{\mathscr V}$
is precisely
$M_{\mathscr V}$
is precisely
![]() $\mathcal C$
(modulo the isomorphism).Footnote
3
On the other hand, given any model
$\mathcal C$
(modulo the isomorphism).Footnote
3
On the other hand, given any model
![]() $M\models \operatorname {ZFC} ^-_I$
, we have that
$M\models \operatorname {ZFC} ^-_I$
, we have that
![]() $\mathscr V=(V_{\kappa }^M,\in ,\mathcal C)$
, where
$\mathscr V=(V_{\kappa }^M,\in ,\mathcal C)$
, where
![]() $\mathcal C$
consists of all subsets of
$\mathcal C$
consists of all subsets of
![]() $V_{\kappa }^M$
in M, is a model of
$V_{\kappa }^M$
in M, is a model of
![]() $\mathrm {KM}+\mathrm {CC}$
, and moreover,
$\mathrm {KM}+\mathrm {CC}$
, and moreover,
![]() $M_{\mathscr V}$
is then precisely M.
$M_{\mathscr V}$
is then precisely M.
The bi-interpretability of the two theories was used by Antos and Friedman in [Reference Antos, Friedman, Antos, Friedman, Honzik and Ternullo1] to develop a theory of hyperclass forcing over models of
![]() $\mathrm {KM}+\mathrm {CC}$
. A hyperclass forcing over a model
$\mathrm {KM}+\mathrm {CC}$
. A hyperclass forcing over a model
![]() $\mathscr V=(V,\in ,\mathcal C)\models \mathrm { KM}+\mathrm {CC}$
is a partial order on a sub-collection of
$\mathscr V=(V,\in ,\mathcal C)\models \mathrm { KM}+\mathrm {CC}$
is a partial order on a sub-collection of
![]() $\mathcal C$
that is definable over
$\mathcal C$
that is definable over
![]() $\mathscr V$
. Suppose that G is
$\mathscr V$
. Suppose that G is
![]() $\mathbb P$
-generic for a hyperclass-forcing
$\mathbb P$
-generic for a hyperclass-forcing
![]() $\mathbb P$
over
$\mathbb P$
over
![]() $\mathscr V$
, meaning that it meets all the definable dense sub-collections of
$\mathscr V$
, meaning that it meets all the definable dense sub-collections of
![]() $\mathbb P$
. We move to
$\mathbb P$
. We move to
![]() $M_{\mathscr V}$
, over which
$M_{\mathscr V}$
, over which
![]() $\mathbb P$
is a definable class-forcing, and consider the forcing extension
$\mathbb P$
is a definable class-forcing, and consider the forcing extension
![]() $M_{\mathscr V}[G]$
. The forcing
$M_{\mathscr V}[G]$
. The forcing
![]() $\mathbb P$
may not preserve
$\mathbb P$
may not preserve
![]() $\operatorname {ZFC} ^-_I$
, but whenever it does, we define that the hyperclass-forcing extension
$\operatorname {ZFC} ^-_I$
, but whenever it does, we define that the hyperclass-forcing extension
![]() $\mathscr V[G]$
is the Kelley–Morse model consisting of
$\mathscr V[G]$
is the Kelley–Morse model consisting of
![]() $V_{\kappa }^{M_{\mathscr V}[G]}$
together with all the subsets of
$V_{\kappa }^{M_{\mathscr V}[G]}$
together with all the subsets of
![]() $V_{\kappa }^{M_{\mathscr V}[G]}$
in
$V_{\kappa }^{M_{\mathscr V}[G]}$
in
![]() $M_{\mathscr V}[G]$
.
$M_{\mathscr V}[G]$
.
An
![]() $\operatorname {Ord} $
-length iterate M of a mouse
$\operatorname {Ord} $
-length iterate M of a mouse
![]() $m^{\#}_n$
is obviously a model of
$m^{\#}_n$
is obviously a model of
![]() $\operatorname {ZFC} ^-_I$
with largest cardinal
$\operatorname {ZFC} ^-_I$
with largest cardinal
![]() $\operatorname {Ord} $
, and moreover it has a definable global well-ordering. Thus, M naturally gives rise to a model of
$\operatorname {Ord} $
, and moreover it has a definable global well-ordering. Thus, M naturally gives rise to a model of
![]() $\mathrm {KM}+\mathrm {CC}$
, namely its truncation at
$\mathrm {KM}+\mathrm {CC}$
, namely its truncation at
![]() $\operatorname {Ord} $
, whose classes are the subsets of
$\operatorname {Ord} $
, whose classes are the subsets of
![]() $V^M_{\operatorname {Ord} }$
in M.
$V^M_{\operatorname {Ord} }$
in M.
Let M be a model of
![]() $\operatorname {ZFC} ^-_I$
with a largest cardinal
$\operatorname {ZFC} ^-_I$
with a largest cardinal
![]() $\kappa $
and a definable well-ordering of the universe. Let D be a discrete set in M of measurable cardinals below
$\kappa $
and a definable well-ordering of the universe. Let D be a discrete set in M of measurable cardinals below
![]() $\kappa $
and suppose that D is unbounded in
$\kappa $
and suppose that D is unbounded in
![]() $\kappa $
. Over M,
$\kappa $
. Over M,
![]() $\mathbb P_D$
is a class forcing notion all of whose antichains are sets. Class forcing works the same way over models of
$\mathbb P_D$
is a class forcing notion all of whose antichains are sets. Class forcing works the same way over models of
![]() $\operatorname {ZFC} ^-$
as it does over models of
$\operatorname {ZFC} ^-$
as it does over models of
![]() $\operatorname {ZFC} $
. Pretame forcing (see [Reference Friedman7] for definition and properties) preserves
$\operatorname {ZFC} $
. Pretame forcing (see [Reference Friedman7] for definition and properties) preserves
![]() $\operatorname {ZFC} ^-$
to forcing extensions and has definable forcing relations (this is due to Stanley and can be found in [Reference Holy, Krapf and Schlicht14]). In a model with a definable global well-order, every class forcing all of whose antichains are sets is pretame. Although “mixing of names” is not always doable with class forcing that has proper class-sized antichains, it still works if all antichains are sets. Finally, the existence of a definable global well-order gives that the Mathias criterion of Theorem 7.4 still holds in this setting.
$\operatorname {ZFC} ^-$
to forcing extensions and has definable forcing relations (this is due to Stanley and can be found in [Reference Holy, Krapf and Schlicht14]). In a model with a definable global well-order, every class forcing all of whose antichains are sets is pretame. Although “mixing of names” is not always doable with class forcing that has proper class-sized antichains, it still works if all antichains are sets. Finally, the existence of a definable global well-order gives that the Mathias criterion of Theorem 7.4 still holds in this setting.
Forcing with
![]() $\mathbb P_D$
preserves the inaccessibility of
$\mathbb P_D$
preserves the inaccessibility of
![]() $\kappa $
by Proposition 7.3, while singularizing all the measurable cardinals below it. Thus, in particular, a forcing extension by
$\kappa $
by Proposition 7.3, while singularizing all the measurable cardinals below it. Thus, in particular, a forcing extension by
![]() $\mathbb P_D$
remains a model of
$\mathbb P_D$
remains a model of
![]() $\operatorname {ZFC} ^-_I$
.
$\operatorname {ZFC} ^-_I$
.
Proposition 7.5. Given a
![]() $\mathbb P_D$
-generic f, we have that
$\mathbb P_D$
-generic f, we have that
![]() $V_{\kappa }^{M[f]}=V_{\kappa }^M[f]$
.
$V_{\kappa }^{M[f]}=V_{\kappa }^M[f]$
.
Proof The one inclusion
![]() $V_{\kappa }^M[f]\subseteq V_{\kappa }^{M[f]}$
is clear. For the other inclusion suppose that
$V_{\kappa }^M[f]\subseteq V_{\kappa }^{M[f]}$
is clear. For the other inclusion suppose that
![]() $a\in V_{\kappa }^{M[f]}$
. There is some
$a\in V_{\kappa }^{M[f]}$
. There is some
![]() $\beth $
-fixed point cardinal
$\beth $
-fixed point cardinal
![]() $\alpha <\kappa $
in
$\alpha <\kappa $
in
![]() $M[f]$
such that
$M[f]$
such that
![]() $a\in V_{\alpha }^{M[f]}$
, so that a is coded there by a subset A of
$a\in V_{\alpha }^{M[f]}$
, so that a is coded there by a subset A of
![]() $\alpha $
in
$\alpha $
in
![]() $M[f]$
. By Proposition 7.2, A must be added by some initial segment of the product
$M[f]$
. By Proposition 7.2, A must be added by some initial segment of the product
![]() $\mathbb P_D$
, and therefore is an interpretation of a name in
$\mathbb P_D$
, and therefore is an interpretation of a name in
![]() $V_{\kappa }^M$
by an initial segment of f.
$V_{\kappa }^M$
by an initial segment of f.
We can also view
![]() $\mathbb P_D$
as a hyperclass forcing over the model
$\mathbb P_D$
as a hyperclass forcing over the model
![]() $\mathscr V=(V_{\kappa }^M,\in ,\mathcal C)$
, with
$\mathscr V=(V_{\kappa }^M,\in ,\mathcal C)$
, with
![]() $\mathcal C$
being the collection of all subsets of
$\mathcal C$
being the collection of all subsets of
![]() $V_{\kappa }^M$
in M. Since
$V_{\kappa }^M$
in M. Since
![]() $M[f]$
is a model of
$M[f]$
is a model of
![]() $\operatorname {ZFC} ^-_I$
(because
$\operatorname {ZFC} ^-_I$
(because
![]() $\kappa $
remains inaccessible), we can form the forcing extension
$\kappa $
remains inaccessible), we can form the forcing extension
![]() $\mathscr V[f]$
, and it is (by definition) the model
$\mathscr V[f]$
, and it is (by definition) the model
![]() $(V_{\kappa }[f],\in ,\mathcal C^*)$
with
$(V_{\kappa }[f],\in ,\mathcal C^*)$
with
![]() $\mathcal C^*$
being the collection of all subsets of
$\mathcal C^*$
being the collection of all subsets of
![]() $V_{\kappa }^M[f]$
in
$V_{\kappa }^M[f]$
in
![]() $M[f]$
.
$M[f]$
.
Now we go back to our specific setting in which we consider
![]() $\operatorname {Ord} $
-length iterates of the mice
$\operatorname {Ord} $
-length iterates of the mice
![]() $m^{\#}_n$
.
$m^{\#}_n$
.
Let C be the class club of limit cardinals and let M be the (non-truncated) iterate model of
![]() $m_1^{\#}$
constructed by Welch (see Section 4). The model M satisfies
$m_1^{\#}$
constructed by Welch (see Section 4). The model M satisfies
![]() $\operatorname {ZFC} ^-_I$
with the largest cardinal
$\operatorname {ZFC} ^-_I$
with the largest cardinal
![]() $\operatorname {Ord} $
and has a definable well-ordering of the universe. Let
$\operatorname {Ord} $
and has a definable well-ordering of the universe. Let
![]() $D=\hat C$
be the collection of all measurable cardinals of M. Let f be the function on D such that
$D=\hat C$
be the collection of all measurable cardinals of M. Let f be the function on D such that
![]() $f(\omega \cdot \alpha +\omega )=\langle \omega \cdot \alpha +n\mid n<\omega \rangle $
. Welch showed that f is generic for
$f(\omega \cdot \alpha +\omega )=\langle \omega \cdot \alpha +n\mid n<\omega \rangle $
. Welch showed that f is generic for
![]() $\mathbb P_D$
(defined using measures arising in the iteration) by verifying the Mathias criterion. As before, let
$\mathbb P_D$
(defined using measures arising in the iteration) by verifying the Mathias criterion. As before, let
![]() $M_C$
be M truncated at
$M_C$
be M truncated at
![]() $\operatorname {Ord} $
. Let
$\operatorname {Ord} $
. Let
![]() $\mathcal C$
be the collection of subsets of
$\mathcal C$
be the collection of subsets of
![]() $M_C$
in M and
$M_C$
in M and
![]() $\mathcal C^*$
be the collection of all subsets of
$\mathcal C^*$
be the collection of all subsets of
![]() $M_C[f]$
in
$M_C[f]$
in
![]() $M[f]$
. With this set-up, Welch proved the following theorem.
$M[f]$
. With this set-up, Welch proved the following theorem.
Theorem 7.6 (Welch [Reference Welch29]).
The model
![]() $M[\operatorname {Card}]$
is a class forcing extension of M by the class forcing
$M[\operatorname {Card}]$
is a class forcing extension of M by the class forcing
![]() $\mathbb P_D$
. Equivalently, the second-order model
$\mathbb P_D$
. Equivalently, the second-order model
![]() $(M_C[\operatorname {Card}], \in ,\mathcal C^*)$
is a hyperclass-forcing extension of
$(M_C[\operatorname {Card}], \in ,\mathcal C^*)$
is a hyperclass-forcing extension of
![]() $(M, \in ,\mathcal C)$
by the hyperclass forcing
$(M, \in ,\mathcal C)$
by the hyperclass forcing
![]() $\mathbb P_D$
.
$\mathbb P_D$
.
Indeed, it is not difficult to see that the function f cannot be added by any set forcing over M (or equivalently, cannot be added by any class forcing over
![]() $M_C$
).
$M_C$
).
Theorem 7.7. In the notation of Theorem 7.6, f is not set-generic over M. Equivalently, f is not class-generic over the second-order model
![]() $(M_C[f],\in , \mathcal C)$
.
$(M_C[f],\in , \mathcal C)$
.
Proof Consider the regressive function g with domain D defined by
![]() $g(\alpha ) = \text {min}(f(\alpha ))$
. If
$g(\alpha ) = \text {min}(f(\alpha ))$
. If
![]() $g_0$
is any regressive function in M on D then by genericity, g dominates
$g_0$
is any regressive function in M on D then by genericity, g dominates
![]() $g_0$
at all but finitely many elements of D. But if
$g_0$
at all but finitely many elements of D. But if
![]() $\mathbb P$
is any set-forcing of M,
$\mathbb P$
is any set-forcing of M,
![]() $\mathbb P$
has size at most
$\mathbb P$
has size at most
![]() $\operatorname {Ord} $
in M, and therefore we will argue that
$\operatorname {Ord} $
in M, and therefore we will argue that
![]() $\mathbb P$
cannot add such a dominating function. Let
$\mathbb P$
cannot add such a dominating function. Let
![]() $\{p_{\xi }\mid \xi \in \operatorname {Ord} \}$
be a listing of the elements of
$\{p_{\xi }\mid \xi \in \operatorname {Ord} \}$
be a listing of the elements of
![]() $\mathbb P$
in which every element of
$\mathbb P$
in which every element of
![]() $\mathbb P$
appears cofinally often. Let
$\mathbb P$
appears cofinally often. Let
![]() $\dot g$
be a
$\dot g$
be a
![]() $\mathbb P$
-name for a regressive function on D. For every
$\mathbb P$
-name for a regressive function on D. For every
![]() $\xi \in \operatorname {Ord} $
, choose a condition
$\xi \in \operatorname {Ord} $
, choose a condition
![]() $p^*_{\xi }$
extending
$p^*_{\xi }$
extending
![]() $p_{\xi }$
that decides
$p_{\xi }$
that decides
![]() $\dot g(\alpha _{\xi })=\beta _{\xi }$
, where
$\dot g(\alpha _{\xi })=\beta _{\xi }$
, where
![]() $\alpha _{\xi }$
is the
$\alpha _{\xi }$
is the
![]() $\xi $
th element of D. Define
$\xi $
th element of D. Define
![]() $g_0(\alpha _{\xi }) = \beta _{\xi } + 1$
. Then any condition
$g_0(\alpha _{\xi }) = \beta _{\xi } + 1$
. Then any condition
![]() $p_{\xi }$
in
$p_{\xi }$
in
![]() $\mathbb P$
has an extension forcing
$\mathbb P$
has an extension forcing
![]() $g_0(\alpha _{\xi })> \dot g(\alpha _{\xi })$
. Since every
$g_0(\alpha _{\xi })> \dot g(\alpha _{\xi })$
. Since every
![]() $p\in \mathbb P$
appears in our listing cofinally often, for cofinally many
$p\in \mathbb P$
appears in our listing cofinally often, for cofinally many
![]() $\xi < \kappa $
, every
$\xi < \kappa $
, every
![]() $p\in \mathbb P$
has an extension forcing
$p\in \mathbb P$
has an extension forcing
![]() $g_0(\alpha _{\xi })> \dot g(\alpha _{\xi })$
, which means that
$g_0(\alpha _{\xi })> \dot g(\alpha _{\xi })$
, which means that
![]() $\dot g$
cannot be forced to dominate all regressive
$\dot g$
cannot be forced to dominate all regressive
![]() $g_0$
on D in M on a final segment of D.
$g_0$
on D in M on a final segment of D.
We will need to make use of the following theorem.
Theorem 7.8. Forcing with
![]() $\mathbb P_D$
preserves all measurable cardinals not in D. Indeed, if
$\mathbb P_D$
preserves all measurable cardinals not in D. Indeed, if
![]() $\kappa \notin D$
is a measurable cardinal in M and
$\kappa \notin D$
is a measurable cardinal in M and
![]() $\mu $
is a normal measure on
$\mu $
is a normal measure on
![]() $\kappa $
that does not concentrate on measurable cardinals, then
$\kappa $
that does not concentrate on measurable cardinals, then
![]() $\kappa $
has a normal measure
$\kappa $
has a normal measure
![]() $\bar \mu \in M[f]$
, a forcing extension by
$\bar \mu \in M[f]$
, a forcing extension by
![]() $\mathbb P_D$
, such that
$\mathbb P_D$
, such that
![]() $\bar A\in \bar \mu $
if and only if there is
$\bar A\in \bar \mu $
if and only if there is
![]() $A\in \mu $
with
$A\in \mu $
with
![]() $A\subseteq \bar A$
.
$A\subseteq \bar A$
.
See Section 6 of [Reference Gitik, Foreman and Kanamori11] for a proof.
Suppose that
![]() $m^{\#}_2$
exists and
$m^{\#}_2$
exists and
![]() $C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
$C_1\supseteq C_2$
are class clubs of uncountable cardinals such that
![]() $C_2$
is
$C_2$
is
![]() $\Sigma _1$
-stable relative to
$\Sigma _1$
-stable relative to
![]() $C_1$
. Let M be the (untruncated) iterate of
$C_1$
. Let M be the (untruncated) iterate of
![]() $m^{\#}_2$
constructed as in the proof of Theorem 6.4 for the clubs
$m^{\#}_2$
constructed as in the proof of Theorem 6.4 for the clubs
![]() $C_1^*$
and
$C_1^*$
and
![]() $C_2^*$
consisting of the limit points of
$C_2^*$
consisting of the limit points of
![]() $C_1$
and
$C_1$
and
![]() $C_2$
respectively. With this set-up, we get the following generalization of Welch’s theorem. Recall that we denote by
$C_2$
respectively. With this set-up, we get the following generalization of Welch’s theorem. Recall that we denote by
![]() $M_{C_1^*,C_2*}$
the truncation at
$M_{C_1^*,C_2*}$
the truncation at
![]() $\operatorname {Ord} $
of the model M obtained by iterating the mouse
$\operatorname {Ord} $
of the model M obtained by iterating the mouse
![]() $m^{\#}_2$
so that its strictly 1-measurable cardinals are precisely the elements of
$m^{\#}_2$
so that its strictly 1-measurable cardinals are precisely the elements of
![]() $C_1^*$
and its 2-measurable cardinals are the precisely the elements of
$C_1^*$
and its 2-measurable cardinals are the precisely the elements of
![]() $C_2^*$
.
$C_2^*$
.
Let
![]() $D_i$
for
$D_i$
for
![]() $i=1,2$
, be the class of strictly i-measurable cardinals in M. For every measurable cardinal
$i=1,2$
, be the class of strictly i-measurable cardinals in M. For every measurable cardinal
![]() $\alpha \in M$
, let
$\alpha \in M$
, let
![]() $\mu _{\alpha }$
be the normal measure on
$\mu _{\alpha }$
be the normal measure on
![]() $\alpha $
arising from the iteration. Let
$\alpha $
arising from the iteration. Let
![]() ${\mathbb P}_{D_1}$
and
${\mathbb P}_{D_1}$
and
![]() ${\mathbb P}_{D_2}$
be the product Prikry forcings defined with respect to the measures
${\mathbb P}_{D_2}$
be the product Prikry forcings defined with respect to the measures
![]() $\mu _{\alpha }$
in M. Let f be M-generic for
$\mu _{\alpha }$
in M. Let f be M-generic for
![]() ${\mathbb P}_{D_2}$
. In
${\mathbb P}_{D_2}$
. In
![]() $M[f]$
, every measurable cardinal in
$M[f]$
, every measurable cardinal in
![]() $D_1$
remains measurable by Theorem 7.8. Since no
$D_1$
remains measurable by Theorem 7.8. Since no
![]() $\mu _{\alpha }$
concentrates on measurable cardinals (otherwise
$\mu _{\alpha }$
concentrates on measurable cardinals (otherwise
![]() $\alpha $
would have Mitchell order 2), by Theorem 7.8, every measurable cardinal
$\alpha $
would have Mitchell order 2), by Theorem 7.8, every measurable cardinal
![]() $\alpha \in D_1$
has, in
$\alpha \in D_1$
has, in
![]() $M[f]$
, a normal measure
$M[f]$
, a normal measure
![]() $\bar \mu _{\alpha }$
generated by
$\bar \mu _{\alpha }$
generated by
![]() $\mu _{\alpha }$
. Thus, we can define in
$\mu _{\alpha }$
. Thus, we can define in
![]() $M[f]$
, the Prikry product forcing
$M[f]$
, the Prikry product forcing
![]() $\bar {\mathbb P}_{D_1}$
with respect to the measures
$\bar {\mathbb P}_{D_1}$
with respect to the measures
![]() $\bar \mu _{\alpha }$
. Let
$\bar \mu _{\alpha }$
. Let
![]() $\dot {\mathbb P}_{D_1}$
be the
$\dot {\mathbb P}_{D_1}$
be the
![]() ${\mathbb P}_{D_2}$
-name for this Prikry forcing product. Notice that
${\mathbb P}_{D_2}$
-name for this Prikry forcing product. Notice that
![]() ${\mathbb P}_{D_1}$
is the product Prikry forcing defined in M, while
${\mathbb P}_{D_1}$
is the product Prikry forcing defined in M, while
![]() $\bar {\mathbb P}_{D_1}$
is the product Prikry forcing defined in a forcing extension of M by
$\bar {\mathbb P}_{D_1}$
is the product Prikry forcing defined in a forcing extension of M by
![]() ${\mathbb P}_{D_2}$
. Although these are potentially different forcing notions, we will show below that they are forcing equivalent.
${\mathbb P}_{D_2}$
. Although these are potentially different forcing notions, we will show below that they are forcing equivalent.
Theorem 7.9. The model
![]() $M[C_1,C_2]$
is a forcing extension of M by the class forcing iteration
$M[C_1,C_2]$
is a forcing extension of M by the class forcing iteration
![]() ${\mathbb P}_{D_2}*\dot {\mathbb P}_{D_1}$
. The iteration
${\mathbb P}_{D_2}*\dot {\mathbb P}_{D_1}$
. The iteration
![]() ${\mathbb P}_{D_2}*\dot {\mathbb P}_{D_1}$
is equivalent to the product
${\mathbb P}_{D_2}*\dot {\mathbb P}_{D_1}$
is equivalent to the product
![]() ${\mathbb P}_{D_2}\times {\mathbb P}_{D_1}$
. Moreover,
${\mathbb P}_{D_2}\times {\mathbb P}_{D_1}$
. Moreover,
![]() $M_{C_1^*,C_2^*}[C_1,C_2]=L[C_1,C_2]$
, and the latter is then the first-order part of a hyperclass-forcing extension of the Kelley–Morse model
$M_{C_1^*,C_2^*}[C_1,C_2]=L[C_1,C_2]$
, and the latter is then the first-order part of a hyperclass-forcing extension of the Kelley–Morse model
![]() $\langle V_{\operatorname {Ord} }^M,\in ,\mathcal C\rangle $
(where
$\langle V_{\operatorname {Ord} }^M,\in ,\mathcal C\rangle $
(where
![]() $\mathcal C$
consists of the subsets of
$\mathcal C$
consists of the subsets of
![]() $V_{\operatorname {Ord} }^M$
in M).
$V_{\operatorname {Ord} }^M$
in M).
Proof Let
![]() $f_1$
be the function on the elements
$f_1$
be the function on the elements
![]() $\alpha $
of
$\alpha $
of
![]() $\hat C_1^*$
such that
$\hat C_1^*$
such that
![]() $f_1(\alpha )$
is the
$f_1(\alpha )$
is the
![]() $\omega $
-sequence of elements of
$\omega $
-sequence of elements of
![]() $C_1$
limiting up to
$C_1$
limiting up to
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $f_2$
be the function on the elements
$f_2$
be the function on the elements
![]() $\alpha $
of
$\alpha $
of
![]() $\hat C_2^*$
such that
$\hat C_2^*$
such that
![]() $f_2(\alpha )$
is the
$f_2(\alpha )$
is the
![]() $\omega $
-sequence of elements of
$\omega $
-sequence of elements of
![]() $C_2$
limiting up to
$C_2$
limiting up to
![]() $\alpha $
. The arguments in [Reference Welch29] already verify that
$\alpha $
. The arguments in [Reference Welch29] already verify that
![]() $f_2$
satisfies the Mathias criterion for
$f_2$
satisfies the Mathias criterion for
![]() ${\mathbb P}_{D_2}$
and
${\mathbb P}_{D_2}$
and
![]() $f_1$
satisfies the Mathias criterion for
$f_1$
satisfies the Mathias criterion for
![]() ${\mathbb P}_{D_1}$
. Indeed, we will now argue that
${\mathbb P}_{D_1}$
. Indeed, we will now argue that
![]() ${\mathbb P}_{D_1}$
densely embeds into
${\mathbb P}_{D_1}$
densely embeds into
![]() $\bar {\mathbb P}_{D_1}=(\dot {\mathbb P}_{D_1})_{f_2}$
. Since class forcing notions with set-sized antichains which densely embed produce the same forcing extensions (see [Reference Holy, Krapf and Schlicht14]), we will be able to assume without loss that we are actually forcing with
$\bar {\mathbb P}_{D_1}=(\dot {\mathbb P}_{D_1})_{f_2}$
. Since class forcing notions with set-sized antichains which densely embed produce the same forcing extensions (see [Reference Holy, Krapf and Schlicht14]), we will be able to assume without loss that we are actually forcing with
![]() ${\mathbb P}_{D_1}$
.
${\mathbb P}_{D_1}$
.
It suffices to argue that for every function F on
![]() $D_1$
in
$D_1$
in
![]() $M[f_2]$
such that
$M[f_2]$
such that
![]() $F(\alpha )\in \mu _{\alpha }$
, there is a function
$F(\alpha )\in \mu _{\alpha }$
, there is a function
![]() $F^*\in M$
such that
$F^*\in M$
such that
![]() $F^*(\alpha )\in \mu _{\alpha }$
and
$F^*(\alpha )\in \mu _{\alpha }$
and
![]() $F^*(\alpha )\subseteq F(\alpha )$
for every
$F^*(\alpha )\subseteq F(\alpha )$
for every
![]() $\alpha \in D_1$
. Let
$\alpha \in D_1$
. Let
![]() $\dot F$
be a
$\dot F$
be a
![]() ${\mathbb P}_{D_2}$
-name for F such that
${\mathbb P}_{D_2}$
-name for F such that
![]() forces that
forces that
![]() $\dot F(\alpha )\in \check \mu _{\alpha }$
for every measurable
$\dot F(\alpha )\in \check \mu _{\alpha }$
for every measurable
![]() $\alpha $
(this requires mixing names). We will argue in M, by induction on
$\alpha $
(this requires mixing names). We will argue in M, by induction on
![]() $\beta \leq \operatorname {Ord} $
, that we can define cohering functions
$\beta \leq \operatorname {Ord} $
, that we can define cohering functions
![]() $f_{\beta }$
on
$f_{\beta }$
on
![]() $D_1\upharpoonright \beta $
such that
$D_1\upharpoonright \beta $
such that
![]() $f_{\beta }(\alpha )\in \mu _{\alpha }$
and
$f_{\beta }(\alpha )\in \mu _{\alpha }$
and
![]() for every
for every
![]() $\alpha \in D_1\upharpoonright \beta $
. Suppose inductively that we can construct
$\alpha \in D_1\upharpoonright \beta $
. Suppose inductively that we can construct
![]() $f_{\gamma }$
for
$f_{\gamma }$
for
![]() $\gamma <\beta $
as required. Let’s argue that we can construct
$\gamma <\beta $
as required. Let’s argue that we can construct
![]() $f_{\beta }$
. If
$f_{\beta }$
. If
![]() $\beta $
is a limit ordinal, then
$\beta $
is a limit ordinal, then
![]() $f_{\beta }$
is just the union of the
$f_{\beta }$
is just the union of the
![]() $f_{\gamma }$
. So suppose that
$f_{\gamma }$
. So suppose that
![]() $\beta =\beta ^*+1$
and assume that F is defined at
$\beta =\beta ^*+1$
and assume that F is defined at
![]() $\beta ^*$
because otherwise there is nothing to prove. Observe that
$\beta ^*$
because otherwise there is nothing to prove. Observe that
![]() $F\upharpoonright \beta $
must be added by
$F\upharpoonright \beta $
must be added by
![]() ${\mathbb P}_{{D_2}_{<\!\beta }}$
by Proposition 7.2. Since
${\mathbb P}_{{D_2}_{<\!\beta }}$
by Proposition 7.2. Since
![]() $\beta ^*\in C_1$
cannot be a limit of elements of
$\beta ^*\in C_1$
cannot be a limit of elements of
![]() $C_2$
,
$C_2$
,
![]() ${\mathbb P}_{{D_2}_{<\!\beta }}$
must have size
${\mathbb P}_{{D_2}_{<\!\beta }}$
must have size
![]() $\lambda <\beta ^*$
. Let
$\lambda <\beta ^*$
. Let
![]() $\dot f$
be a
$\dot f$
be a
![]() ${\mathbb P}_{{D_2}_{<\!\beta }}$
-name for
${\mathbb P}_{{D_2}_{<\!\beta }}$
-name for
![]() $F\upharpoonright \beta $
such that
$F\upharpoonright \beta $
such that
![]() . For every condition
. For every condition
![]() $p\in {\mathbb P}_{{D_2}_{<\!\beta }}$
, if p forces that some
$p\in {\mathbb P}_{{D_2}_{<\!\beta }}$
, if p forces that some
![]() $A\in \mu _{\beta ^*}$
is contained in
$A\in \mu _{\beta ^*}$
is contained in
![]() $\dot f(\beta ^*)$
, then choose some such
$\dot f(\beta ^*)$
, then choose some such
![]() $A_p$
. Since there are at most
$A_p$
. Since there are at most
![]() $\lambda $
-many such sets
$\lambda $
-many such sets
![]() $A_p\in \mu _{\beta ^*}$
and
$A_p\in \mu _{\beta ^*}$
and
![]() $\lambda <\beta ^*$
, we can intersect them all to obtain a set
$\lambda <\beta ^*$
, we can intersect them all to obtain a set
![]() $A\in \mu _{\beta ^*}$
such that
$A\in \mu _{\beta ^*}$
such that
![]() . It follows that
. It follows that
![]() $f_{\beta }$
defined to extend
$f_{\beta }$
defined to extend
![]() $f_{\beta ^*}$
with
$f_{\beta ^*}$
with
![]() $f_{\beta }(\beta ^*)=A$
satisfies our requirements.
$f_{\beta }(\beta ^*)=A$
satisfies our requirements.
This completes the argument that
![]() ${\mathbb P}_{D_1}$
densely embeds into
${\mathbb P}_{D_1}$
densely embeds into
![]() $\bar {\mathbb P}_{D_1}$
. The argument also shows that
$\bar {\mathbb P}_{D_1}$
. The argument also shows that
![]() $f_1$
meets the Mathias criterion for
$f_1$
meets the Mathias criterion for
![]() $\bar {\mathbb P}_{D_1}$
because it met the Mathias criterion for
$\bar {\mathbb P}_{D_1}$
because it met the Mathias criterion for
![]() ${\mathbb P}_{D_1}$
over M and every sequence of measure one sets from
${\mathbb P}_{D_1}$
over M and every sequence of measure one sets from
![]() $M[f_2]$
can be thinned out on each coordinate to a sequence of measure one sets which exists in M. Thus,
$M[f_2]$
can be thinned out on each coordinate to a sequence of measure one sets which exists in M. Thus,
![]() $f_1$
is
$f_1$
is
![]() $M[f_2]$
-generic for
$M[f_2]$
-generic for
![]() $\bar {\mathbb P}_{D_1}$
.
$\bar {\mathbb P}_{D_1}$
.
Finally, by Proposition 7.3, forcing with
![]() $\bar {\mathbb P}_{D_1}$
preserves the inaccessibility of
$\bar {\mathbb P}_{D_1}$
preserves the inaccessibility of
![]() $\operatorname {Ord} $
in
$\operatorname {Ord} $
in
![]() $M[f_2]$
, so that we can form the hyperclass forcing extension of the Kelley–Morse model whose first-order part is
$M[f_2]$
, so that we can form the hyperclass forcing extension of the Kelley–Morse model whose first-order part is
![]() $M_{C_1^*,C_2^*}$
and the first-order part of the forcing extension is then the model
$M_{C_1^*,C_2^*}$
and the first-order part of the forcing extension is then the model
![]() $M_{C_1^*,C_2^*}[f_2][f_1]=M_{C_1^*,C_2^*}[C_1,C_2]$
. Using Theorem 6.5, it is clear that
$M_{C_1^*,C_2^*}[f_2][f_1]=M_{C_1^*,C_2^*}[C_1,C_2]$
. Using Theorem 6.5, it is clear that
![]() $M_{C_1^*,C_2^*}[C_1,C_2]=L[C_1,C_2]$
.
$M_{C_1^*,C_2^*}[C_1,C_2]=L[C_1,C_2]$
.
The characterization easily generalizes to n-many clubs
![]() $C_1, \dots , C_n$
. Suppose that
$C_1, \dots , C_n$
. Suppose that
![]() $m_n^{\#}$
exists and
$m_n^{\#}$
exists and
![]() $C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are clubs of uncountable cardinals such that
$C_1\supseteq C_2\supseteq \cdots \supseteq C_n$
are clubs of uncountable cardinals such that
![]() $C_i$
is
$C_i$
is
![]() $\Sigma _1$
-stable relative to (the class canonically coding)
$\Sigma _1$
-stable relative to (the class canonically coding)
![]() $C_1,\ldots ,C_{i-1}$
for all
$C_1,\ldots ,C_{i-1}$
for all
![]() $1<i\leq n$
. Let M be the (untruncated) iterate of
$1<i\leq n$
. Let M be the (untruncated) iterate of
![]() $m_n^{\#}$
constructed as usual for the clubs
$m_n^{\#}$
constructed as usual for the clubs
![]() $C_1^*,\ldots ,C_n^*$
consisting of the limit points of the clubs
$C_1^*,\ldots ,C_n^*$
consisting of the limit points of the clubs
![]() $C_1,\ldots ,C_n$
respectively.
$C_1,\ldots ,C_n$
respectively.
Theorem 7.10. The model
![]() $M[C_1,\ldots ,C_n]$
is a forcing extension of M by the class forcing iteration
$M[C_1,\ldots ,C_n]$
is a forcing extension of M by the class forcing iteration
![]() ${\mathbb P}_{D_n}*\cdots *\dot {\mathbb P}_{D_1}$
, where
${\mathbb P}_{D_n}*\cdots *\dot {\mathbb P}_{D_1}$
, where
![]() $D_i$
, for
$D_i$
, for
![]() $1\leq i\leq n$
, is the class of strictly i-measurable cardinals. The iteration
$1\leq i\leq n$
, is the class of strictly i-measurable cardinals. The iteration
![]() ${\mathbb P}_{D_n}*\cdots *\dot {\mathbb P}_{D_1}$
is equivalent to the product
${\mathbb P}_{D_n}*\cdots *\dot {\mathbb P}_{D_1}$
is equivalent to the product
![]() ${\mathbb P}_{D_n}\times \cdots \times {\mathbb P}_{D_1}$
. Moreover,
${\mathbb P}_{D_n}\times \cdots \times {\mathbb P}_{D_1}$
. Moreover,
![]() $M_{C_1^*,\ldots ,C_n^*}[C_1,\ldots ,C_n]=L[C_1,\ldots ,C_n]$
, and the latter is then the first-order part of a hyperclass-forcing extension of the Kelley–Morse model
$M_{C_1^*,\ldots ,C_n^*}[C_1,\ldots ,C_n]=L[C_1,\ldots ,C_n]$
, and the latter is then the first-order part of a hyperclass-forcing extension of the Kelley–Morse model
![]() $\langle V_{\operatorname {Ord} }^M,\in ,\mathcal C\rangle $
(where
$\langle V_{\operatorname {Ord} }^M,\in ,\mathcal C\rangle $
(where
![]() $\mathcal C$
consists of the subsets of
$\mathcal C$
consists of the subsets of
![]() $V_{\operatorname {Ord} }^M$
in M).
$V_{\operatorname {Ord} }^M$
in M).
Theorem 7.7 also generalizes to show that such an extension cannot be obtained by a set forcing over M (or equivalently a class forcing over
![]() $M_{C_1^*,\ldots ,C_n^*}$
).
$M_{C_1^*,\ldots ,C_n^*}$
).
8 Open questions
The article did not answer several difficult questions about the structure of the stable core. In Sections 3 and 4, we showed how to code information into the stable core over small canonical inner models using the fact that these models must be contained in the stable core so that we can use them for decoding. In a very recent work Friedman showed that there is a large cardinal notion below a Woodin cardinal such that the stability predicate is definable over an iterate of a mouse with such a large cardinal. This immediately implies that we cannot code any set into the stable core and that there is a bound (below a Woodin cardinal) on the large cardinals that can exist in inner models of the stable core [Reference Friedman6]. This leaves the following open questions regarding the structure of the stable core.
We still don’t have a precise upper bound on the large cardinals that can exist in the stable core.
Question 1. Can the stable core have a measurable limit of measurable cardinals?
For
![]() $\operatorname {HOD} $
, we know that the
$\operatorname {HOD} $
, we know that the
![]() $\operatorname {HOD} $
of
$\operatorname {HOD} $
of
![]() $\operatorname {HOD} $
can be smaller than
$\operatorname {HOD} $
can be smaller than
![]() $\operatorname {HOD} $
and that any universe V is the
$\operatorname {HOD} $
and that any universe V is the
![]() $\operatorname {HOD} $
of a class forcing extension of itself.
$\operatorname {HOD} $
of a class forcing extension of itself.
Question 2. Can the stable core of the stable core be smaller than the stable core?
Question 3. When is V the stable core of an outer model? More precisely, is there a tame (
![]() $\operatorname {ZFC} $
-preserving) class forcing notion
$\operatorname {ZFC} $
-preserving) class forcing notion
![]() $\mathbb P$
such that for some V-generic filter
$\mathbb P$
such that for some V-generic filter
![]() $G\subseteq \mathbb P$
we have
$G\subseteq \mathbb P$
we have
![]() $V=L[S^{V[G]}]$
?
$V=L[S^{V[G]}]$
?
Finally, with regard to Section 7, we can ask whether the results there generalize to
![]() $\omega $
-many clubs.
$\omega $
-many clubs.
Question 4. Is there a version of Theorem 7.10 for
![]() $\omega $
-many clubs?
$\omega $
-many clubs?
Acknowledgment
We would like to thank Gabriel Goldberg for his valuable comments on an earlier draft of the article.
Funding
The first author wishes to acknowledge the support of the Austrian Science Fund (FWF) through Research Projects P28157 and P28420. The third author, formerly known as Sandra Uhlenbrock, wishes to acknowledge the support of the Austrian Science Fund (FWF) through Research Projects P28157 and V844.The authors acknowledge Tu Wein Bibliothek for financial support through its Open Access Funding Program.