Introduction
Radio-echo reflections from internal layers have been observed over widespread areas of the Antarctic and Greenland ice sheets. The presence of the internal layering has generated a great deal of interest among glaciologists because the layering provides an areal glimpse of the third dimension (depth) of ice sheets previously obtained only at single points through bore holes.
The origin of internal reflections has not been positively determined. There may in fact be several causes of internal reflections and a better understanding of the internal reflections is needed to increase their value as a glaciological tool. Although some of the reflections may originate in a single discrete layer, many apparently arise from the combined reflection coefficient of several layers.
Reference Robin de, Robin de , Evans and BaileyRobin and others (1969) showed that small changes in ice density in an isolated thin layer yield reflection coefficients large enough to produce the observed echoes for layering to depths of approximately 1 000 m.Reference Harrison Harrison (1973) suggested that the best explanation for most internal layering is a change in permittivity due to anisotropy in the value of permittivity parallel and perpendicular to the c-axis.
Reference Paren and Robin de.Paren and Robin (1975) concluded that reflections above a depth of c. 1 500 m are due to permittivity changes resulting from density changes and reflections from below c. 1 500 m are due to changes in the loss tangent.
Little work has been done to correlate the reflecting layers with physical properties of the ice obtained from cores. In a recent paper Reference GudmandsenGudmandsen (1975) pointed out that it is difficult to establish a good correlation due to the very small changes in physical properties required to produce reflections and the many variations in some physical properties over distances that are small compared to radar wavelength. Gudmandsen discusses a general comparison between layer echoes and gross changes in the oxygen-isotope ratios.
In this paper calculations of reflection coefficients indicate that multiple layering will not produce a significant increase in the reflection coefficient except that a zone of layers may be considered as a single thick layer with averaged properties. Calculation of reflection coefficients for dust and ash layers and for anisotropy in permittivity show these to be unlikely causes for observed reflections. Finally, a comparison between reflector depth and physical properties of the core at “Byrd” station, Antarctica, shows a good correlation between density variation and reflector depth in the top 1 000 m. This result is in good agreement with Reference Paren and Robin de.Paren and Robin (1975).
Reflection Coefficients—Single Thin Layer
The complex relative permittivity may be represented by
where ϵ’ is the relative permittivity, ϵ” is the relative loss factor and i = √ (—1) For ϵ” ≪ 1 the index of refraction n = √ ϵ’. In this paper ϵ⋆ = ϵ’ and changes in the relative permittivity shall be considered. (Changes in ϵ⋆ due to changes in ϵ”, or more specifically the loss factor, tan δ = ϵ”/ϵ’ are considered byReference Paren and Robin de. Paren and Robin (1975).)
The reflection coefficient R for a single layer of ice in terms of the reflection coefficients at the bottom and top interface is

(Reference BrekovskikhBrekhovskikh, 1957, p. 50 of the English translation) where R23 and R12 are the reflection coefficients for the interface between medium 2 and medium 3 (upper space), and medium 1 (lower half-space) and medium 2, respectively, k 2z is the vertical wave number in medium 2 and d is the thickness of the layer. For vertical incidence the reflection coefficient at the 1–2 boundary is (n 1—n 2)/(n 1+n 2) where n 1 and n 2 are the indices of refraction in medium one and medium two. Similar expressions obtain for any other boundary.
If medium 1 and medium 3 are the same, then R 23 = −R 12. For small changes in index of refraction let n 2 = n 1 + Δn With Δn the ≪ second term in the denominator of Equation (1) can be neglected as being of the order of (Δn)2, and R ≈ R 23(1 — exp (2ik 2z d)). If, further, d ≪ λ, exp(2ik 2z d) ≃ 1+2ik2z d/, and the expression for R becomes R ≈ — R 23(2ik2z d). Since R23 = Δn/2n, R ≈ (—i2πd/λ)(Δn/n).
This expression is identical to the formula for a single thin layer of Reference HarrisonHarrison (1973). Reference Robin de, Robin de , Evans and BaileyRobin and others (1969) derive an identical formula in terms of density variation Δp. Using the empirical relationship n = 1+0.85p between index of refraction n and density p (Reference Robin de, Robin de , Evans and BaileyRobin and others, 1969), Δn = 0.85Δp and 2Δn/n = 1.7Δp/n ≈ Δp The three equivalent expressions are

Some estimates of single-layer reflection coefficients to be found in the ice sheet are given later.
Reflection Coefficients—Multiple layers
When considering the propagation of a continuous wave with sinusoidal time variation exp (— iΩt), the reflection of waves from multiple layers can be described by a single reflection coefficient. This reflection coefficient can be calculated through repeated application of Equation (1) or alternatively in terms of the input impedance of the layers.
Consider first a single boundary between two media. The tangential components of the field vectors must be continuous across the boundary. Therefore the impedance
![]() for layered media is conveniently defined in terms of the tangential components E
t and H
t:
for layered media is conveniently defined in terms of the tangential components E
t and H
t:
![]() = E
t/H
t This impedance is called the “normal impedance”. The normal impedance for a wave whose E vector is parallel to the boundary (perpendicular to the plane of propagation) is defined for each medium as
= E
t/H
t This impedance is called the “normal impedance”. The normal impedance for a wave whose E vector is parallel to the boundary (perpendicular to the plane of propagation) is defined for each medium as
![]() = η/cos θ Where η is the intrinsic impedance of the medium, η = (μ0/ϵϵ0)½ (and θ is the angle between the direction of propagation and the normal to the boundary. μ0
and ϵ0 are the permeability and permittivity of free space. The reflection coefficient for a wave incident in medium 1 at the boundary of medium 2 is
= η/cos θ Where η is the intrinsic impedance of the medium, η = (μ0/ϵϵ0)½ (and θ is the angle between the direction of propagation and the normal to the boundary. μ0
and ϵ0 are the permeability and permittivity of free space. The reflection coefficient for a wave incident in medium 1 at the boundary of medium 2 is
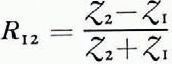
where
![]() 1 and
1 and
![]() 2 are the normal impedances in medium 1 and medium 2, respectively.
2 are the normal impedances in medium 1 and medium 2, respectively.
If instead of a half-space with impedance
![]() 2 we have a thick sequence of layers with differing impedance and thicknesses we can still use Equation (3) if we let
2 we have a thick sequence of layers with differing impedance and thicknesses we can still use Equation (3) if we let
![]() 2 continue to represent the ratio of Et/Ht at the boundary with medium 1. In other words, the impedance for the thick sequence of layers can be represented by the equivalent impedance of a single layer. This equivalent impedance “looking into” the sequence of layers is defined as the input impedance,
2 continue to represent the ratio of Et/Ht at the boundary with medium 1. In other words, the impedance for the thick sequence of layers can be represented by the equivalent impedance of a single layer. This equivalent impedance “looking into” the sequence of layers is defined as the input impedance,
![]() i = Et/Ht. The input impedance at the top of an individual layer
i = Et/Ht. The input impedance at the top of an individual layer
![]() i
t may be found from the input impedance at the bottom of that layer
i
t may be found from the input impedance at the bottom of that layer
![]() i
b from
i
b from

(Reference BrekovskikhBrekhovskikh, 1957), where
![]() 1 is the normal impedance of the layer and ϕ
1 is the phase change in the layer, equal to kd cos θ where k, θ and d are the wave number, angle of incidence, and thickness for the layer, respectively. Once the input impedance of the sequence of layers is found by the repeated application of Equation (4) from the bottom to the top of the sequence, the reflection coefficient may be found from Equation (3).
1 is the normal impedance of the layer and ϕ
1 is the phase change in the layer, equal to kd cos θ where k, θ and d are the wave number, angle of incidence, and thickness for the layer, respectively. Once the input impedance of the sequence of layers is found by the repeated application of Equation (4) from the bottom to the top of the sequence, the reflection coefficient may be found from Equation (3).
Reflection coefficients for a single layer and uniform multiple layers are shown in Figure 1. The reflection coefficient for a single layer increases as the layer thickness increases to thickness λ/4 where λ is the wavelength. At λ/4 the reflection from the top and bottom of the layer are in phase with each other and R is twice its half-space value. As the thickness increases further, R decreases until at λ/2, R is equal to zero. The function repeats periodically with thickness interval λ/2.
A similar function is obtained for multiple layering for a zone of thin, (thickness ≪ λ) uniform layers with equal layer thickness and spacing. The total thickness (plotted on the abscissa) is the distance from the top of the first layer to the bottom of the last layer of a zone of multiple layers. The zone of layers behaves like a single layer with an impedance equal to the mean value averaged over all the layers in the zone. Hence, in Figure 1 the maximum reflection coefficient for layers of uniform thickness and spacing is half the maximum reflection coefficient for a single layer. This is exactly the value for a half-space.

Fig. 1. The magnitude of the reflection coefficient for a single layer and uniform multiple layers plotted as a function of layer thickness with Δ n = 0.01. For uniform multiple layers the thickness and spacing = 0.01λ The total thickness represents the distance from the top of the first layer to the. bottom of the last layer in an increasingly thick zone of layers.
How well does this averaged layer represent a sequence of layers of non-uniform thickness and spacing? Reflection coefficients for non-uniform layer spacing and thickness were evaluated to determine if a zone of layers with variable spacing and thickness can be approximated by a single layer with averaged properties. If so, then the reflection coefficient for a single boundary (half-space) can be used to estimate maximum reflections from multiple layering.
First consider a case where thin layers are randomly spaced in such a manner that all phase delays are equally likely. In this case the mean reflection coefficient for all the layers is expected to be √N times the reflection coefficient for a single layer R 1 where N is the number of layers. Hence,
We now consider a gated sinusoidal (pulsed) signal. The analysis described above is still applicable as long as the reflected pulse from the upper layers and lower layers interfere with each other. For a time-limited signal with spatial pulse-width P w, the maximum distance over which the two signals will interfere will be P w/2. Hence, the input impedance for a zone of layers P w/2 in thickness can be used to calculate an upper bound to the reflection coefficient for a pulsed signal. Equation (5) can be applied where N is now the number of layers in a distance P w/2; however, in order for the phases of the various layers to add up in a truly random fashion, the distance between layers must be allowed to vary at least between 0 and λ/2 (0 < ϕ ≼ 2π). As a result, N for a pulsed signal will never in reality become very large when Equation (5) is relevant. For example, for a 35 MHz signal λ ≈ 4 m and the average value for the distance between layers would have to be approximately 1 m. For a pulse width 0.25 μα the spatial pulse width P w is about 40 m. The number of thin layers with a random phase relation in a zone of thickness P w/2 = 20 m is then approximately N = 20 and the reflection coefficient R is ≼ √20R 1.
Now we return to a zone of closely spaced layers. If we assume the layers are thin (0.1–10 cm for example) and the spacing between layers is of the same order of magnitude, then a large number of layers will occur in the distance P w/2 but the phase relationship between layers no longer varies in a completely random fashion and the expression R = √NR 1 no longer holds true. The reflection coefficient for an increasingly thick zone of layers will approach the periodic behavior of uniform layers as shown in Figure 1.

Fig. 2. The reflection coefficient for thin layers with variable thickness and spacing ≪.λ The variation in the average value (dashed line) is due to the random variation in thickness and spacing between 0.1 and 10 cm. The rapid oscillations arise from the multiples of λ/4 for the total zonal thickness. Pw/2 = 20 m.

Fig. 3. Reflection coefficients for layers with thickness and spacing uniformly distributed about 3 cm with a standard deviation of 1 cm.
To show that this is so, calculations of reflection coefficients for randomly varying layer spacing and thickness were obtained by high-speed computer. An example is shown in Figure 2 which shows the reflection coefficient for a zone of layers whose thickness and spacing vary randomly between 0.1 cm and 10 cm (λ = 4 m). The periodic peaks are due to the fact that the zone of layers acts very much like a single layer with e averaged over the zone.
The average reflection coefficient is essentially independent of P w/2. The variations in the average value, or shift of the baseline, is the result of the random variation in thickness and spacing of the layers. The results shown in Figure 2 are typical of more than ten separate models where the thickness and spacing were varied over the same interval (0.1–10 cm). A typical result for a model which may be yet more realistic is shown in Figure 3.
For uniform layers the maximum R (R max) is equal to the reflection coefficient for a half-space with the same impedance contrast (Fig. 1). For the models calculated with spacing and thickness varying from 0.1 cm to 10 cm, R max did not deviate from the half-space value of R by more than a factor of two over distances Pw/2 (total thickness ≈ 20 m). The approximation of replacing the zone of thin layers by a single layer with ∊ averaged over the zone is a good one, thus the value of R for a half-space is a good approximation for the expected value of Rmax for multiple layering.
Reflection Coefficient And Pulse Width
It is significant to note that although the value of R in Figure 2 fluctuates rapidly as the thick ness of the layered zone (or P w) is varied, the value of R max (or the average value of R) is not very sensitive to changes in P w. In contrast the value of R from Equation (5) is proportional to P w Unfortunately this difference probably cannot be used to determine the nature of the reflecting layers as suggested by Reference HarrisonHarrison (1973). Harrison observed internal reflection using two different pulse widths (0.25 μs and 1 μs) and found the reflected power with the longer pulse width to be 5 dB greater than with the short pulse width. Since the reflection coefficient for specular reflection from a single layer is not a function of pulse width whereas reflection from random multiple layering (Equation (5) is proportional to pulse width, Harrison concludes, with support from other evidence, that the reflections were produced by multiple reflections according to Equation (5). If, however, the reflecting surface is not perfectly specular, the average reflected power for a single reflecting surface also is a function of pulse width. For exampleReference Robin de, Robin de , Evans and Bailey Robin and others (1969) show that the reflected power is proportional to the pulse width and a four-fold increase in pulse width produces a 6 dB increase in reflected power, an effect very similar to that of Equation (5). In this case the signal is integrated over a horizontal rather than a vertical distance.
Although the observed echo strength is a function of P w this does not necessarily mean that integration is taking place over vertical distances rather than horizontal distances, hence the observed changes in reflected power do not rule out the possibility of reflections of the type shown in Figure 2 which are, on the average, independent of pulse width.
Origin of reflections
The most obvious cause of internal reflections in the relatively pure ice of the Antarctic ice sheet is density variations. Assuming thin layers of bubble-free ice in a generally bubbly ice and calculating bubble volume (bubble pressure) for different depths,Reference Paren and Robin de. Paren and Robin (1975) estimate Δp = 0.001 (Δϵ/ϵ ≈ 0.001) at 800 m. This value is in good agreement with the measured density variations shown in Figure 4 (A. J. Gow, personal communication in 1968).Reference Harrison Harrison (1973) estimated density variations using an exponential curve empirically derived by Reference SchyttSchytt (1958) from measurements on a core 100 m in length. Although the empirical equation fits the data points reasonably well (there is considerable scatter of the measured densities), extrapolation of his curve to 1 000 m results in estimates of Δϵ/ϵ of the order 10−12 compared with 10−3 found above; hence Harrison’s estimates of reflection coefficients due to density variation are several orders of magnitude too low for depths greater than a few hundred meters.

Fig. 4. Comparison of reflector depth (thin horizontal lines) with physical properties of the ice at “Byrd” station, Antarctica. The first column shows measured density variations (Δ p) (from A. J. Gow, personal communication in in(1968). The open triangles have values of 0.003 or less (R p < —80 dB). Column two shows the distribution of dust bands (solid line) and ash bands (heavy line segments) (from Cow and Williamson, 1971). Variations in seismic velocity (Reference BentleyBentley, 1972) are indicated in column three. The depth of the reflector at c. 1 300 m was picked with less precision from a flight profile ofReference Robin de., Robin de , Swithinbank and Smith. Robin and others (1970).
At “Byrd” station, the power reflection coefficient R p (R p = 20 log10|R|) for a layer at 1 000 m must be about —80 dB in order to be detected (Reference Robin de, Robin de , Evans and BaileyRobin and others, 1969). For a single layer 1 cm thick with Δϵ/ϵ = 0.OO1, Equation (2) yields R p = —102 dB. A layer thickness c. 10 cm would be required to produce R p = —80 dB.
In a detailed study of a 411 m ice core from Greenland,Reference Langway Langway (1970) found ice layers and structural features which were about 1–20 mm in thickness. Thick ice layers (3–5 mm) were less numerous than thin ice layers (1–2 mm) but were found more often in closely spaced groups of two or three individual layers.
Since layers up to 10 cm thick are probably rare, multiple-layer reflection coefficients or a zone of layers are required to account for the presence of numerous internal reflections. The average value of R p (dashed line in Figs 2 and 3) for a zone of multiple layering one meter or more in thickness with Δϵ/ϵ between layers equal to 0.001 is approximately —72 dB. For a zone 10 cm thick with Δϵ/ϵ = 0.002 (Δϵ/ϵ = 0.001 averaged over the zone) R p = —80 dB as found for a single 10 cm thick layer above. Hence, both zones of 1 m or 10 cm thickness containing density variations of the order of 1 cm thick can produce an ample signal return although a single layer 1 cm thick is not detectable. Reflections from density variations are considered in more detail below when discussing Figure 4.
The ice at “Byrd” station is completely bubble-free below a depth of 1 100 m. (Reference GowGow, 1970) and reflections from this depth cannot be explained by density variations. Reference Paren and Robin de.Paren and Robin (1975) have suggested recently that changes in tan δ may produce the echo observed below 1 100 m.
Another mechanism considered for producing internal reflections is the change in dielectric constant within layers of dust or dirt found in the ice sheet. Many layers of volcanic ash and dust have been observed in the ice core from “Byrd” station and described by Reference Gow and WilliamsonGow and Williamson (1971). Only two of these bands occur above a depth of 1 100 m. An ash band present at 788 m is about 1 mm thick, made up mainly of volcanic glass fragments with concentrations approximately 10−4 g/cm3 (A. J. Gow, personal communication in 1974). Assuming a relative dielectric constant for the glass and using the Wiener formula for calculating the dielectric constant of mixture of two dielectrics, a power reflection coefficient R p of — 150 dB is estimated. For a maximum layer thickness of 6 cm and maximum concentrations of 10−3 g/cm3 reported byReference Gow and Williamson Gow and Williamson (1971) (concentrations were generally very much less than this), R p for a single layer is still only about —95 dB, not sufficient to produce a signal at the surface.
The large number of dust layers present between 1 300–1 400 m might produce the reflection at about that depth observed on some flight records near “Byrd” station (Reference Robin de., Robin de , Swithinbank and Smith.Robin and others, 1970, see Fig. 3), but ash and dust bands cannot account for most of the internal reflection observed.
The calculation above was for the ash or dust bands alone. However, these dust and ash bands are accompanied by zones of bubble-free ice up to 10 mm thick and the bubble-free layer alone may produce a more significant reflection coefficient than the dust or ash bands themselves. Even so, R p for a 10 mm layer of bubble-free ice is only about —100 dB and below 1 200 m where most of the ash and dust bands occur the ice is completely bubble-free anyway. Large changes in tan δ may be associated with these bands and produce the reflections as suggested by Reference Paren and Robin de.Paren and Robin (1975).
Another possible source of reflections that has been suggested, most recently by Reference HarrisonHarrison (1973), is anisotropy in the ice. Harrison considers anisotropy to be the most likely source of deep reflections. That anisotropy exists is certain, and changes in ϵ due to anisotropy can produce significant reflections, but we can show that anisotropy is unlikely to produce adequate reflection coefficients for widespread internal layering at “Byrd” station.
Reference Humbel, Humbel von, Jona and Scherret·Humbel and others (1953) report an anisotropy of c. 14% in the static dielectric constant. This value has generally been accepted—at least until recently when Reference Wörz and ColeWörz and Cole (1969) found different results on measurements of polycrystalline ice with c-axes “nearly parallel”. They found “. . . little if any anisotropy of the static dielectric constant near the melting point, rather than a difference of order 10% reported by Humbel, Jona and Scherrer”.
Anisotropy in the optical frequency range (separated from radio frequencies by the infrared absorption bands) is very small; the difference in index of refraction between the extraordinary ray ne and ordinary ray n o is only n e—n o = 0.001 3 (Reference WeastWeast, 1975). This corresponds to c. 0.2% anisotropy in ϵ which compares well with the c. 0.2% difference in length of the O—O bonds parallel and perpendicular to the c-axis.
The frequency band of interest in radio-echo sounding (radio-frequency region) lies between the principal relaxation absorption band and the infrared absorption band. One unpublished measurement had been made in this region before 1975. At a frequency of 2 700 MHz no anisotropy was observed within an experimental accuracy of about 1% (W. Westphal, personal communication in 1974).
Reference Von Hippel, Von Hippel, Knoll and WestphalVon Hippel and others (1971) list different values of e for single crystals parallel and perpendicular to the caxis. Although the measurements were made from ice of the same origin, there may have been small differences between samples measured parallel and perpendicular. One of the authors (W. Westphal, personal communication in 1974) states that no inference of anisotropy should be drawn from these data; rather, the 2 700 MHz value (Δϵ <1%) should be used.
Reference Johari and CharetteJohari and Charette (1975) independently concluded that the measurements of Von Hippel and others, which were made for entirely different reasons, do not indicate anisotropy of greater than 1%. They made measurements on polycrystalline ice and single ice crystals (electric field perpendicular to the caxis) at 35 MHz and 60 MHz and found the values for ϵ’ to agree within ±0.2% corresponding to a maximum anisotropy parallel and perpendicular to the c-axis of c. 1%.
If we assume an anisotropy of ϵ equal to 1%, the boundary between a half-space with c-axes all vertical and a half-space with c-axes all horizontal and parallel, resulting in maximum Δϵ, would produce a maximum power reflection coefficient of c. —52 dB. The reflection coefficient would be zero if the electric field vector E were perpendicular to the c-axes and —52 dB if E were parallel to the c-axes. Maximum R p for a single layer 1 cm thick with caxes all horizontal and parallel in ice otherwise containing all vertical c-axes would be ≈ −79 dB.
Using the value 0.2% for the value between isotropic ice and anisotropic ice with ϵ perpendicular to the c-axis, maximum R p for an anisotropic layer 1 cm thick with c-axis vertical in normally isotropic ice would be approximately —95 dB. A significant reflection would not be produced.
Small changes in the angle of orientation for ice with c-axes all aligned will produce significant Δϵ/ϵ values if we assume that e varies uniformly between ϵ parallel and c perpendicular. For example, if the caxes are all parallel to the direction of propagation (vertical), E is everywhere normal to the caxes. Inclining the direction of the c-axes 10° to the direction of propagation would yield Δϵ/ϵ = (Δϵmax/ϵ) sin 10° ≈ 1.5 × 10−3 where (Δϵmax/ϵ), the value of anisotropy, is again taken as 1%. This value of Δϵ/ϵ is comparable to the value found for density variation. Any reflection produced would be a function of antenna orientation at the surface. If the c-axes were uniformly distributed within a cone forming an angle of 10° with the vertical then

where θ is the angle between the cone and vertical, ϕ is the azimuthal angle, and dΩ = sin θ d θ ϕ, yielding Δϵ/ϵ ≈ 0.75 × 10−3 again comparable to the dielectric contrast produced by density changes.
These values are obtained using a value of 1% for anisotropy which might be considered an upper limit, Furthermore, the change in crystal orientation must be sudden (over distance ≪ λ) in order to produce a significant reflection. Such changes in crystal orientation may exist in some glaciers and portions of the ice sheets, but the evidence from the “Byrd” station deep drill core suggests they are not widespread there. The orientation of the c-axes of crystals were observed from thin sections at 40 levels (22 measurements from depths above 1 300 m) throughout the 2 164 m core length taken from the deep drill hole at “Byrd” station (Reference Gow and WilliamsonA. J. Gow and T. Williamson, 1976). The c-axes above 300 m depth are quite random. Below 300 m there is a gradual concentration of c-axes toward the vertical to a depth of approximately 1 200 m where 60% of the c-axes lie within 25% of the vertical, Between 1 200 and 1 300 m there is a rapid increase in the vertical concentration. At 1 300 m about 90% of the c-axes lie within 25° of the vertical.
Ultrasonic compressional wave velocities which have a single-crystal anisotropy of about 7% were measured continuously up the “Byrd” deep drill hole from depths of 1 550 m (Reference BentleyBentley, 1972). The velocity-depth curve observed is shown in Figure 4. The general pattern of increasing c-axis concentration is reflected in the increasing velocities shown. There are several small variations of velocity (±25 m/s). The velocity changes presumably reflect small changes in crystal orientation. If all the c-axes were uniformly distributed within a cone forming an angle anywhere from 15° to 50° with the vertical, a change in the cone angle of only 5° would produce a 25 m/s change in the ultrasonic velocity (Reference BennettBennett, 1972, fig. 24). Such a change would produce a Δϵ/ϵ, again on the order of 4 × 10−4. The corresponding reflection coefficient for a half-space, R p = —80 dB, would produce a detectable signal.
The seismic velocities shown in Figure 3 were averaged over distances of approximately 2 m and the curve was further smoothed over distances of the order of 20 m, hence changes in crystal orientation larger than indicated by the velocity curve may exist. In order to produce a detectable echo, however, these changes would have to occur over a distance ≪ λ.
Sudden changes in crystal orientation have been observed within the dust and ash bands. The c-axes of ice crystals in these bands are nearly all vertical (A. J. Gow, personal communication in 1974) ; however, most of the dust and ash bands occur below 1 200 m where all of the ice has strong vertical preferred orientation and so the contrast between the bands and the surrounding ice cannot be very great. The single bands at 788 m and 911 m would produce a significant Δϵ/ϵ but the very thin layer (1-2 mm) would produce an R p of only c. — 100 dB. For the region near 1 350 m a maximum of 500 layers in a distance of P w/2 (20 m) can be expected. Estimating Δϵ/ϵ = 0.000 4 the maximum reflection coefficient for multiple layering is R p ≈ —80 dB. Although anisotropy may produce detectable reflections it seems unlikely that this is the cause for the widespread internal reflections observed in the interior portions of the ice sheet.
Correlation of reflector depth with physical properties of the ice
Radio-echo sounding measurements were made at “Byrd” station, Antarctica, where a 2 164 m core to the bottom of the ice sheet was obtained. A SPRI-Randall Mk II radar (Reference Evans and SmithEvans and Smith, 1969) retuned to 50 MHz was used to make a series of measurements aimed at determining the nature of internal reflections. Detailed wide-angle reflection measurements and vertical profiling were conducted near the station. The vertical profiles and the wide-angle reflection measurements were used together to determine the depth of the most prominent reflecting layers within the ice. These reflectors are represented in Figure 4 by the solid horizontal lines. The reflection at a depth of approximately 1 300 m shown by a dashed line was taken from Robin and others (1970, fig. 6). Also shown in the figure are physical properties of the ice measured on the core or in the drill hole. The three mechanisms for producing reflections that were discussed above are shown.
The first column shows density variation as a function of depth. Only 1% of the ice core was sampled for density (approximately 1 cm every 1.0 m). These values were plotted and the density variations were obtained using a graphically produced smooth curve. It is hard to justify correlation of these measurements with the reflecting layers, as so little of the ice is represented. It is shown here, however, as it is the most detailed comparison available to date. The correlation between density variation and reflector depth appears high. The large density variations at approximately 75 and 85 m do not correlate with a reflector because radar reflections could not be picked for depths less than about 200 in. The density variations shown by open triangles have values of 0.000 3 or less (R p < —80 dB) and at depths near 1 000 m probably would not be detected. Otherwise, only one density variation does not correlate with a reflecting layer; furthermore, nearly all reflecting layers lie within c. 10 m of a density variation. Because the density was measured at roughly 10 m intervals throughout the core, the measured variations may represent zones of density variation and the correlation of reflector depth with density variation does not imply reflection by single layers.
In column two, the results of Reference Gow and WilliamsonGow and Williamson (1971) are shown. The continuous curve shows the number of dust bands present in the ice column; ash bands are represented by the heavy individual lines. Only one ash band and one dust band occur above a depth of 1 200 m. Although reflecting layers are seen at nearly the same depths as these bands, correlation is difficult. In the case of the ash band, a significant density variation occurs at approximately the same depth, and in the case of the dust band, there is an apparent change in crystal orientation.
Column three shows the seismic velocity results of Reference BentleyBentley (1972), indicating changes in crystal orientation. Possible correlations are indicated at 420 m and 890 m; however, both variations of crystal orientation appear quite small.
The correlation between reflector depth and density variation is quite high. Contrarily, the other properties could, at most, account for only a few reflections.
This figure together with the estimates of reflection coefficients obtained for the various mechanisms leave little doubt that density variations are responsible for nearly all the internal echoes in the top 1 000 m observed in the vicinity of “Byrd” station.
Summary
Density variations appear to be the most likely cause of the internal layering observed within the top 1 000 m of the ice sheets of Greenland and Antarctica. Because the density variations occur over distances small compared to the radar wavelength, the reflections may result from many layers. Zones of multiple layering can be approximated by a single layer with averaged properties. It may never be possible to correlate the internal layering with density variations satisfactorily due to the small spatial variations of density within the ice and the small density contrasts which produce the observed echoes.
If the nature of these internal layers was better known they would serve as a powerful tool to the glaciologist modeling the dynamics of ice sheets. The internal reflection layers most probably represent ancient depositional surfaces. Reference Robin de, Robin de , Evans and BaileyRobin and others (1969) found that the depth of a prominent reflecting layer in Greenland corresponded to a buried surface layer when a steady-state model of dynamics was used for the ice sheet. Internal reflections due to density variations are consistent with the hypothesis of depositional surfaces. Glaciologists should not wait for verification of this hypothesis from the radio engineers and ice physicists but should use (with caution) the assumption of depositional surfaces. In the end, the results the glaciologists obtain when making this assumption may yield the most insight as to the true nature of these reflections.
Acknowledgements
The work was done at “Byrd” station in January 1970 with the assistance of Dr C. R. Bentley and Mr C. W. Nichols. G. R. Bentley provided valuable assistance with the manuscript. This work was supported by NSF Grant OPP72-05802.






