A Model for Scaling Avalanche Speeds

Abstract

Snow-avalanche speeds, run-out distances, and the concepts from dense granular flows are combined in a model for prediction of speeds along the incline. Field measurements indicate that speeds and run-out distances are nearly independent of path steepness once a length is chosen to scale them. Application of granular-flow concepts explains these results. The most important feature of the model (and the speed data) is the steep gradient of speeds in the run-out zone. These results emphasize the need for high precision in run-out prediction when construction or defences are contemplated.

Introduction

The two important elements for land-use planning in snow-avalanche terrain are prediction of avalanche run-out and expected avalanche speeds along the path. Avalanche run-out predictions are used to define safe areas and to aid in decisions on placement of structures. When structures must be built, estimates of avalanche speeds are essential for calculating design impact pressures. In some applications, defences are used to slow, stop, or deflect avalanche debris and the height and design of these barriers is very sensitive to the approach speed of the avalanche mass. These applications combine to make avalanche run-out and speed prediction among the most important topics in avalanche research.

The early attempts to define the engineering aspects of land-use planning and structure placement in avalanche terrain consisted of solving for avalanche speeds and run-out positions simultaneously by selecting friction coefficients for an avalanche-dynamics model. However, McClung and Lied (1987) gave an alternative method for definition of speeds and run-out positions. We proposed that the problem be divided into two parts: run-out prediction and speed definition.

There are good reasons to solve the problem in two stages. Of primary importance is the fact that calculation of avalanche speeds is physically and mathematically very difficult. The complex problem of flowing snow interacting with complicated terrain features is not likely to be solved soon. For the most part, the mechanical properties (including density) are unknown as well as the boundary conditions. Given these uncertainties, it is highly unlikely that presently available dynamics models can be used to predict where avalanches will stop with any certainty. However, there are methods available to define run-out distances independent of the dynamics problem. Once the run-out distance is predicted or found from field evidence, the dynamics problem can be simplified enough to make it possible.

When a stop position is defined (methods are given below), the path geometry is completely specified for the dynamics problem. This enables calibration of the dynamics model using avalanche-speed data scaled according to a (then known) path-length parameter and it enables definition of the mean value of the basal friction parameter over the entire length of travel of the avalanche. These considerations make it possible to attack the dynamics problem. There is also an additional advantage in defining the stop position first: avalanche-speed measurements show that the gradient of speeds in the deceleration phase is very steep. Therefore, friction is very high at the end of the run-out and speeds there are very sensitive to stop position. Examples are given in this paper which show that it is difficult to match (and therefore predict) speed data unless a stop position is chosen.

In this paper, the second part of the problem, that of speed definition, is developed. Since choice of a run-out position is necessary before speed calculations are attempted in the model, this topic is briefly reviewed first.

Part I. Avalanche Run-Out Distances

In practice, the most common methods of determining avalanche run-out distances are by field inspection at the sites for evidence of destructive effects from previous avalanches or by collection of long-term data on avalanche run-out at sites. When these methods are not available, I believe that statistical prediction (based upon terrain features) represents the most promising quantitative method thus far presented. Unlike physical models, statistical prediction allows run-out distance uncertainties to be defined in standard statistical terms.

The pioneering efforts in statistical run-out prediction (Bovis and Mears, 1976; Lied and Bakkehöi, 1980; Bakkehöi and others, 1983) were based on regression analyses of topographic parameters collected for a set of avalanche paths in a mountain range. However, McClung and others (1989) and McClung and Mears (in press) analyzed data from five mountain ranges and concluded that avalanche run-out distances obey a Gumbel (extreme value) distribution. I believe this approach is superior and I have employed it in this paper. However, some avalanche workers still use the regression approach and it could be employed as well in the first part of the model proposed in this paper.

The procedures for fitting a set of data points to an extreme-value distribution are well known but previous work of mine documents one of the simplest: fitting a linear regression line through a set of plotting positions defined from a data set of run-out distances. The parameter fitted to the distribution is defined as a dimensionless run-out ratio:

(1)

where α, β, δ are three angles defined for each avalanche path in the data set and Δx, X _β are two horizontal distance measurements defined in Figure 1. The angle δ is defined by sighting from the extreme point reached by avalanches in the past to the start position; β is obtained by sighting from the position where the slope angle first declines to 10° to the starting point; δ is defined by sighting between the positions marked for α and β.

Fig. 1. Definition of geometry to describe extreme avalanche run-out.

The position defined by β (the β point) is taken as a reference point from which to calculate run-out. The run-out distance (Δx) (time-scale ~ 100 years) is the horizontal reach from the β point to the extreme run-out position. The length (X_β ) is the horizontal distance between the starting point and the β point.

Given a data set for which these parameters are measured for a given mountain range, it becomes possible to predict the run-out ratio as a function of the non-excedance probability, p, of the Gumbel distribution. Let x ≡ Δx/X β, then if ƒ(x) is the probability density function, ρ = Pr(x ≤ x _p) where

(2)

Given a value, x _p, 100 _ρ (%) values of x in the distribution have values less than x _p. In Equation (2), u and b are the location and scale parameters for the distribution. For the extreme-value distribution, the equation of the regression line through the plotting positions is defined by:

(3)

Previous papers (McClung and others, 1989; McCIung and Mears, in press) give values for u (0.08–0.37) and b (0.07–0.21) for five individual mountain ranges including more than 500 avalanche paths.

From Equation (3), it is possible to define a mapping of run-out distances for a given avalanche path as a function of p. For example, with u and b determined for a given range, the position defined by (Δx/X β)_0.99 = u + 4.6b, gives a run-out position which 99% of avalanche run-out ratios in the data set will not exceed (usually a fairly safe location).

Once a run-out position (or a mapping of distances) is determined by one of the methods above, the path geometry is completely determined and the dynamics problem can be tackled by applying Part II of the model discussed below, which constitutes the main thrust of this paper.

Part II. Estimation of Avalanche Speeds along the Incline

Problem Definition and Physical Description

Large dry-snow avalanche flows have a dense core of flowing material in contact with the bed over which they flow. Experience and field data (e.g. McCIung and Schaerer, 1985) show that this type of avalanche produces the combination of highest impact pressures and longest run-out. Such a flow is called a dry-flowing avalanche: the design avalanche for a placement and design of structures.

Often for dry-flowing avalanches, the dense core of material at the base is obscured from view by material suspended in the air by turbulent eddies around the periphery of the avalanche. This material (called powder) tends to make the flowing material appear as a body of low-density material moving like a turbulent fluid. However, in almost all cases there is a dense core of material at the base and it is the internal deformation of this core and its interaction with the sliding surface which I believe dominates the motion resistance of large avalanches to determine their speeds.

Field observations and measurements show that avalanche speeds and run-out are quite sensitive to the physical condition of the surface over which the avalanche flows. Soft or wet surfaces introduce high friction which reduces avalanche speeds and run-out. In this paper, only one type of avalanche is modelled: one characterized by minimum friction, maximum run-out (time-scale ~ 100 years) and maximum speed. For this reason, effects such as plowing into new snow or flow over a wetted surface are not accounted for explicitly. Also, entrainment and deposition of snow as the avalanche travels along the path are not explicitly included; the present knowledge about these effects is too meager to introduce them without speculative assumptions.

In practical usage, simple models which do not attempt to describe the internal deformation of the flowing material or which do not call for precise boundary conditions have been dominant for 35 years. Since the mechanical properties of flowing snow have not been measured and the boundary conditions for avalanche flow can only be speculated about, it is clear that any of the more complicated models (e.g. Norem and others, 1987) must rely upon assumptions rather than data for model calibration.

The approach here is to develop a method for scaling speeds similar in scope to the popular models of the past (Voellmy, 1955; Perla and others, 1980). The scaling procedure is based upon trends expected from results on dense, granular flows including both the general form of the boundary conditions at the upper and lower flow boundaries and the deformation properties of dense granular materials. Using these results, the parameters in the model are determined from speed measurements and run-out distances. Since no attempt is made to describe the internal deformation or detailed physics of avalanche motion (see e.g. Norem and others (1987) for a more detailed model), the flow depth of the avalanche is not predicted and only the transport speed of the avalanche is given. My model is so simple there is no difference between the frontal speed and the center-of-mass speed.

Trends From Granular-Flow Results

Field observations of avalanche deposits show that significant heat is generated by particle collisions in the flow. Often, large dry avalanches have moist snow in their deposits. The small amounts of moisture present subsequently freeze to produce very hard snow in the deposit. The simple observations that mean particle size becomes smaller (due to fracturing and abrasion) the further the avalanche travels and, that the snow from dry avalanches can be moist in the deposit, strongly indicate that the volume fraction filled by particles is high in flowing avalanche snow. Simple arguments from avalanche speed and impact-pressure measurements were given by McClung and Schaerer (1985) to estimate roughly the volume fraction filled by solid material in the flowing snow. These estimates indicate that the volume fractions filled by snow particles and air are the same order of magnitude and therefore particle collisions are expected to be the dominant mechanism of momentum transport within and at the lower boundary of the flowing mass.

In flowing snow avalanches, the density of the mixture of air and solid particles in the core is high and the effects of the air can be entirely neglected in a mechanical description. There are two reasons for this: (1) large density ratio between the particles and the air (10²-10³); (2) presence of particles even in small amounts (Ackermann and Shen, 1978) will suppress any turbulence in the interstitial air. For dry-avalanche flows, the particles are a mixture of ice and air with densities that must range from about 200 kg/m³ for the larger particles (McClung and Schaerer, 1985) to 917 kg/m³ (ice) for the smallest fragments. Except for the initial stage of motion, I believe that the core of a dry flowing avalanche can be described as a dense granular flow. A dense granular flow is one in which the fraction of the flow volume filled by the grains (called the volume fraction, v, here) is high enough that particle collisions dominate the motion resistance within the flow and at a solid boundary over which the material flows. A list of relevant properties from dense granular-flow models (including computer studies) and laboratory measurements is given in Appendix A as they are used as a basis for the model developed.

The granular-flow results (Appendix A) may be interpreted along with field observations of avalanches to produce a rough qualitative picture of how friction might vary as an avalanche moves down-slope. In chronological order, the sequence is expected to be: (1) initial bed surface drops below static values to a low value by propagation of shear fractures underneath the slab to produce low friction initially (McClung, 1987); (2) break-up of slab material into particles and blocks of irregular shape and a distribution of sizes by destructive collisions with the roughness elements along the path and by particle-particle collisions; (3) as the material moves down-slope over steep terrain, granular flow becomes possible, the rate of deformation (basal shearing) increases, causing basal friction to increase; (4) at some point when low slope angles are traversed, locking begins to occur in the upper part of the flow; this effect forces the deformation to be contained in a narrower band at the base of the flow to maintain high shear rate and high friction there (e.g. Savage and Jeffrey, 1981) as locking moves towards the base; (5) at a low slope angle, the transport speed slows, the rate of basal shearing decreases, and rubbing friction emerges as the volume fraction increases in the basal region. This causes the friction to increase towards a high static value. No theories or data are available to describe precisely when one phase of motion stops and another begins.

The discussion above suggests that basal friction is generally expected to increase as the avalanche moves down-slope if the flowing material behaves as a dense granular flow. If shear and normal forces are strongly coupled throughout the core (including the basal region), avalanche-speed data are also consistent with this picture (shown in a later section).

Center of Mass Model with Granular Drag and Centripetal Effects

I believe the present knowledge about avalanche speeds and flow properties from field observations and measurements is only sufficient to describe the motion of the transport speed (either center of mass or frontal speed) of the mass along the incline. In my model, the flowing mass is treated as a continuum initially (in Appendix B) and then the formulation is collapsed to a simpler model in which only the transport speed is specified. Earlier models (Voellmy, 1955; Salm, 1979; Perla and others, 1980) of the same class as the present model were developed by specifying friction parameters on a largely ad hoc basis without sufficient attention to boundary conditions. The resulting model in this paper appears mathematically similar to the earlier models but the physical assumptions, the final mathematical formulation, and the assumed boundary conditions are entirely different. I believe it is important to develop the equations from a continuum approach to emphasize the differences between this and the earlier models. The equation to describe (see derivation in Appendix B) the center of mass speed u is:

(4)

In Equation (4), dS is an element of path length, ψ is local slope angle, and g is acceleration due to gravity. The friction terms are: (1) μ(S), speed-dependent drag from granular flow at the base of the flow, and (2) D ₀(S) is the sum of two terms: turbulent air/dust drag at the top of the flow and drag due to centripetal forces for motion on a curved path. Specifically,

(5)

where r(S) is radius of curvature of the path, ρ is mean value of density in the core of the avalanche, ρ _t is density (air/snow) at the top of the core, h is flow depth, and C _f is a drag coefficient for turbulent air/dust drag at the top of the core (see further details in Appendix B).

Equation (4) is mathematically similar to one derived by Salm (1979) and Perla and others (1980), henceforth called the PCM model. There are, however, important differences: only one drag term (granular) is assumed at the bottom of the flow and this is strongly coupled to the normal force there. Also, since μ is taken to vary with S, it describes speed-dependent drag; since μ = μ (S) and u = u(S), it is implied that μ = μ(u). McClung and Schaerer (1983) showed that taking μ and D ₀ constant (the usual assumptions for applying the PCM model, Salm’s model, or Voellmy’s model) makes it impossible to explain avalanche-speed data.

A second difference in the present model is that turbulent (air/dust) drag is assumed only at the top of the flow. In the formulations of PCM, SaIm or Voellmy, a drag term independent of normal force and proportional to u ² was included (on an ad hoc basis) to account for turbulent drag at the base of the flow or around the upper periphery. This drag term is negligible for a description of dense granular flow at the base of a flowing avalanche: the presence of particles in significant numbers will prevent turbulence from forming and the high volume fraction filled by solids will guarantee that shear and normal forces are transferred through collisions.

The PCM model also included a drag term proportional to u ² to account for plowing into new snow. The present model could account for plowing if the resistive forces are coupled in a Coulomb type of relationship (Equation (Bll)). Because the value of μ is the mean value over the length of the flow, plowing could be interpreted as implying higher mean basal resistance due to conditions at the front of the avalanche. Since my model is calibrated from field measurements of maximum speed and run-out, plowing effects of the type described above are implicitly included. The same remark applies to entrainment and deposition of snow and air into the moving avalanche: these effects are not included explicitly; however, since the model is calibrated from field data, they are implicitly included.

Even though Equation (4) appears mathematically similar to the PCM model, the physical and mathematical differences (outlined above) are crucial for calculating avalanche speeds (see McClung and Schaerer (1983) for a further discussion). The continuum development in Appendix B clarifies and emphasizes these differences.

Quantities used in Model Calibration

Once a run-out distance is selected by one of the methods given in Part I, it is possible to estimate two quantities necessary to calibrate the model: maximum speed and mean value of basal friction.

Consider an avalanche which reaches maximum speed, u _m, after traversing a length of path S ₁ (acceleration phase). Integration of Equation (4) (μ = μ(S), r = r(S), D ₀ = D ₀(S)) from 0 to S ₁ gives

(6)

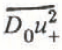where is the mean value of g(sin ψ - μcos ψ) and is the mean value of D ₀ u ² over S ₁.

Similarly, integration over the deceleration phase (S ₁ to S ₀) where S₀ is total path length to the stop position gives

(7)

where and are mean values over the deceleration phase.

Elimination of S ₁ from Equations (6) and (7) gives

(8)

where the constant C is a function of the constants , and .

Equation (8) shows that maximum speed may be scaled with (S ₀)_½ (a known quantity). Equation (8) is useful in two ways; (1) it gives a rough upper limit on design maximum speed for an avalanche path with known run-out once an upper-limit value for C is determined, and (2) the upper-limit value for C is used to calibrate the speed model in the present paper (in a later section).

From Figure t, with sin ψ = dy/dS and cos ψ = dx/dS, H vertical drop, integration of Equation (4) from 0 to S ₀ gives

(9)

where is the mean value over the range 0 to S ₀. Equation (9) restates a well-known result: if drag terms due to centripetal force and turbulent air/dust are negligible, the mean value of μ is defined by tan α (a known quantity in the present model). The results of Equations (8) and (9) will be used to calibrate the model in a later section.

Turbulent Air/Dust Drag

Dry avalanche flows are usually surrounded by a dust cloud of material over the dense core which contacts the sliding surface. 1 measured impact pressures using small load cells through the vertical cross-section of avalanches (McClung and Schaerer, 1985). The results show that the frequency of particle impacts decreases with height above the sliding surface. At the top of the core, the pressure cells recorded only sporadic impacts which suggests that the top of the core consists of saltating particles. It is likely that the effective surface roughness may be appreciable for turbulent snow dust interacting with saltating particles at the top of the flow.

For turbulent flow over a rough surface, Schlicting (1979, p. 653–59) gave an expression for the drag coefficient

(10)

where L ₀ is length and k is roughness height. Mellor (1968) suggested a value C _f = 2 × 10⁻³ from estimates of drifting snow over a smooth surface. With L ₀ = 100 m (length of avalanche flow) and k in the range 0.1–1 m, Equation (10) suggests that C _f can be an order of magnitude larger than that expected for a smooth surface.

From impact experiments, McClung and Schaerer (1985) estimated the average density for dry flowing avalanches to be ~ 100 kg/m³, and for a powder avalanche we estimated ρ to be near 10 kg/m³. From these results, an upper limit on the ratio () can be taken to be about 0.1 in Equation (5). Given that large avalanches have flow depths, h ≃ 2–5 m, an approximate maximum value for D ₀ can be estimated from the quantities above (, L ₀/k = 10⁻³, C _f = 1.2 × 10⁻², h = 2 m) to give D₀ ⁻¹ = 3333 m. Using this rough estimate, it is evident from Equation (4) that turbulent drag at the upper surface of flow is not usually expected to have much effect until speeds are near 30 m/s. The product D ₀ S ₀ must be greater than ½ for this drag term to have a significant effect on speeds. Since virtually all applications of speed models are in the run-out zone where speeds are less than 30 m/s, turbulent air/dust drag is expected to have minor importance in most engineering applications. In applications, it is recommended to input a value of D ₀ as constant all along the path; the determination of μ as a function of position is the most important part of the model offered here. Due to uncertainty in the air-drag coefficient (Equation (10)), it is most suitable to calculate speed profiles with no air drag and with maximum expected air drag in applications. These two solutions then give upper- and lower-bound estimates for the speed profiles on a given avalanche path.

Centripetal Drag Term

Avalanches often move on curved paths (usually concave on overall shape). The term in Equation (18) from centripetal acceleration is derived by depth-averaging using the normal force Equation (B7). The term was simplified by assuming a fairly blunt velocity profile and a depth-averaged density throughout the depth of flow to give D₀ in Equation (5). In view of the uncertainties, and rough approximations, I feel it is sufficient to input a constant value μ/r for this drag term over the entire length of path. A simple method to calculate r is to fit a curve to the avalanche profile (see Fig. 1), for example: y = ax ₂ + bx + c and then determine the radius of curvature by (negative if convex):

(11)

When the lengthr/μ becomes comparable to about one-half the total path length traversed, it will influence the avalanche speeds in the model. For steep profiles (β > 40°), this term can reduce speeds in the middle section of the path by 10% or more. For avalanche terrain, r generally increases with distance down-slope and, since the centripetal term is multiplied by u ², the centripetal term usually has little or no effect on speeds in the run-out zone.

Numerical Solutions

Perla and others (1980) gave a simple method for solving Equation (4). By dividing the slope into small segments so that ψ can be taken constant over each segment, numerical solutions are easy to obtain. Each segment is assigned an angle ψ _i , a length L_i, and friction

values μ _i , = tan ϕ _i , D _0i . If the speed at the beginning of a segment is then the speed at the end of the ith segment is given by (see Fig. 2):

(12)

where γ _i = g(sin ψ _i - tan ϕ_i cos γ _i ) and λ _i = 2L _i /D _0i . If the avalanche stops before the end of a segment, the distance from the beginning of the segment is:

(13)

Fig. 2. Definition of segments of length L_i and slope angle ψ _i for numerical solutions.

Equations (12) and (13) are easily programmed for numerical solutions. It is of interest that software developed by Cheng and Perla (1979) may be used in the general case by replacing their mass to drag parameter (MfD)_i with (1/D _oi ) and μ _i with tan ϕ _i on each segment.

Granular-Friction Scaling Model

In order to complete the dynamics model, values for μ and D ₀ must be specified all along the incline. My approach to the solution of Equation (4) consists of specifying a constant value of D ₀ (curvature and air drag) for a high-speed dry avalanche and the definition of μ = tan ϕ(S) at each position on the path. From the analysis of the air-drag term and Equation (10), variations in μ along he incline dominate the motion resistance almost entirely when speeds are less than about 30 m/s (large avalanches).

Specifying the variation of granular-flow friction along the path is the crux of the model presented here. The formulation must be consistent with the descriptive aspects of avalanche flows, avalanche-speed and run-out distance data, and the mechanics of rapid granular flows. It is tempting to try formulating constitutive equations relating μ to transport speed, and granular-flow parameters (v, coeff ic ients of restitution, overburden, depth of shearing). However, I believe such a relationship is still somewhat in the future even for engineering applications. Also, the complexity of such a relationship would not be appropriate for the model here which is intended to be as simple as possible.

From avalanche-speed measurements, field observations, and the granular-flow results, I expect that μ will generally increase as the avalanche moves down-slope. The initial value of friction, μ ₀, is expected to be very low. Visual observations of avalanches confirm the trends in speed measurements (e.g. Salm and Gubler, 1985) that the initial acceleration is very rapid. The final value of μ must approach high values close to the static limit in the deceleration phase. Avalanche-speed measurements show that deceleration is very rapid near the end of the run-out; this implies very high friction in the final stage of motion.

In the middle parts of the path, intermediate values of friction seem likely. In the acceleration phase (with slip at the basal boundary), as the rate of basal shearing builds up, v should decrease at the boundary to increase the dynamic friction. As the descent continues, the speed will reach a maximum (when driving force and drag forces are in balance). From granular-flow results (e.g. Campbell and Brennen, 1985a), it is possible that basal drag might decrease as v increases with decreasing slope angle to produce an inflection point in μ _S. However, once v increases to produce a significant rubbing component on the grains, static friction will begin to emerge and μ will increase. Therefore, it is possible that the magnitude of μ ₀ may oscillate, but I believe that μ must generally increase down-slope and I will ignore any inflection point of the relationship μ ₀. Calculation of such an inflection point will involve precise knowledge of locking mechanics. The analysis by Savage and Jeffrey (1981) shows one possible scenario implying that an inflection point may not exist. By ignoring an inflection point, a simple two-parameter equation relating μ and S provides an adequate starting point:

(14)

From Equation (10), a value for μ is available once run-out is specified:

(15)

Elimination of K from Equations (14) and (15) gives

(16)

Given an approximate initial value (μ ₀) (or a small range of values), n is the only parameter left to complete definition of the model. Run-out distances and avalanche-speed data provide the necessary information to estimate n I expect that d _μ /dS ≥ 0 due to the assumption that μ increases in the down-slope direction. The condition d₂ μ/dS ₂ ≤ 0 implies that friction increases asymptotically as motion proceeds to approach a limiting value (static value) at the stop position. Application of these conditions together implies 0 ≤ n ≤ 1. The value n = 0 defines a high friction limit:

(17)

In practice, a small initial value may be needed to initiate notion for n = 0. Physically, this limit implies that friction jumps to a high value almost immediately. The low friction limit is given by n = 1.

(18)

Further justification for the limits 0 ≤ n ≤ 1 is provided in the next section where data for maximum speed and run-out distances are used to find values of n as a function of β and ρ.

If air and centripetal drag are ignored, data from western Norway (McClung and Lied, 1987) suggest that μ (or tan α) ranges from 0.325 to 1.15 for the data set. If Equation (17) applies to the steepest profile (α = 49°) and Equation (18) for the gentlest (α = 18°), limits on μ are implied in the range 0.2 to 1.15. Given that initial values of μ are expected to be below granular-flow values, this is a reasonable range based on granular-flow models (e.g. Campbell and Gong, 1986) for a material with a fairly low coefficient of restitution.

Estimates of static values for μ for alpine snow are also of interest. Slow laboratory shearing experiments (McClung, 1987) show that the friction angle (ratio of peak shear stress to normal stress at failure) is in the range 1.19–5.67 for alpine snow. Avalanche-slope failure angles imply the ratio is in the range 0.47–1.43. Neither of these ranges will apply precisely to the physical problem here: a locked mass slowing by sliding over a rough surface. Granular-flow models (McTigue, 1978; Savage and Jeffrey, 1981) for hard spheres predict μ = 0.85 under rapid shearing when the granular temperature is zero. Static values are expected to exceed this value because the rubbing friction would add to it.

Definition Of Model Friction Coefficients From Run-Out And Speed Data

Once the run-out distance and a value for D ₀ are specified, the values of μ and S ₀ are determined in Equation (16). Analysis of initial avalanche-speed data shows that μ ₀ = 0.2 is an adequate approximation. Gubler (personal communication) suggests a value even less than 0.2. Therefore, in order to specify completely the friction along the path, the only parameter left to specify in Equation (16) is the power n. This parameter may be defined using Equation (8) and data from avalanche speeds. The procedure is to calibrate the model using the upper envelope of maximum avalanche-speed data scaled as a function of S ₀. This will allow values of и to be determined as a function of path steepness and run-out position for the design avalanche: the one with minimum friction and maximum speed in the middle part of the path

Figure 3 gives μ _m versus (S ₀)_½ for avalanches from Canada (Roger’s Pass, B.C.), Switzerland, and Norway. The data collection represents frontal speeds of avalanches with differing mass and mechanical properties moving over terrain with varying surface characteristics and topographic features (Schaerer, 1975; McClung and Schaerer, 1983).

Fig. 3. Maximum speed versus (S ₀)_½ for avalanches from Canada (o). Switzerland, and Norway (*). The envelope μ _m = 1.5(S ₀)_½ is shown.

Since the data from Canada are obtained from single estimates in the middle of the path, many will not represent precise estimates of maximum speeds. Also, the data set contains estimates from small avalanches, wet avalanches, and ones with less than optimum surface-friction conditions. Therefore, the upper limit envelope (shown in Figure 3) μ _m ≃ 1.5(S ₀)_½ is chosen to calibrate the model (the design case). From the data, the ratio μ _m/(S ₀)_½ has a range of 0.17–1.38 m_½ S⁻¹ (mean 0.70; standard deviation 0.28).

Rank correlation coefficients, R _s, were calculated for the Roger’s Pass data. Correlation of μ _m with S ₀)_½ gave 0.437 for the dry avalanches in the data set and this value changes very little if all 72 avalanches are used (R _s = 0.469).

The value of R _s for correlation of μ _m/(S ₀)_½ with respect to α is −0.34 for the sub-set of 50 dry avalanches and it is insignificant for the full data set (−0.13). Since tan α is the average slope all along the path, it is an index of path steepness. Correlation of μ _m/(S ₀)_½ with tan α gave a value 0.09 for the full data set and −0.08 for the sub-set of 50 dry avalanches. This important result suggests that maximum avalanche speeds are nearly independent of profile steepness once a suitable length scale (S ₀)_½ is chosen for scaling. The result seems paradoxical but it may be consistent with granular-flow results: steeper paths have higher driving force during acceleration but the rate of shearing at the base of the avalanche may be faster to produce higher dynamic friction which compensates so that maximum speed does not increase.

In order to determine the value of n (Equation (16)) in a fairly general manner, I have used a geometrical model of avalanche paths from western Norway derived by McClung and Lied (1987). The model consists of definition of the constants (a, b, c) in the equation y = ax ² + bx + c as a function of path steepness (geometry; Fig. 3). Run-out along the curve is defined by a mapping of values of the non-excedence probability p (0.5 ≤ ρ ≤ 0.99). Using Weibull plotting positions, a regression analysis gave u = 0.14, b = 0.08 using the data set from western Norway as an example (see Equation (3)).

By constraining maximum speed to match closely the maximum value of μ _m/(S ₀)_½ (from speed data) independent of path steepness (β), a set of values for n was derived as a function of path steepness (Table I). Figure 4 shows pre-dictions of the parameter μ _m/(S ₀)_½ as a function of path steepness and run-out position. This result shows that path steepness gives the major influence, so that in my model β is the only parameter used to determine n. Therefore, the values in Table I are recommended as guidelines for use in applications.

From Figure 4, the values of μ _m/(S ₀)_½ exceed the value 1.5 for the steepest profile (β = 50°) and they are less than 1.5 for the gentlest profile (β = 20°). This is due to steepness in the initial parts given by the geometrical model. The initial slope angle increases with ° in the geometrical model (29 for β = 20°; 66° for β = 50°). These values of initial slope angle are near the extremes measured for avalanche starting-zone angles (e.g. Perla, 1976). In this sense, the limits of 1.12 ≤ μ _m/(S ₀)_½ ≤ 2.13 in Figure 4 can be regarded as extreme limits: n = 0 implies 1.98 ≤ U_mZ(S₀) ≤ 2.13 (β = 50°) and n = 1 gives 1.12 ≤ μ _m/(S ₀)_½ ≤ 1.28 (β = 20°) for ρ in the range 0.50–0.99.

Fig. 4. Predictions of μ _m/(S ₀)_½ versus probability (ρ) and path steepness (β) for a geometrical terrain model (McClung and Lied. 1987) developed from run-out data in western Norway, 0, (β = 50°); *, (β = 40°); ��;μ (β = 30°); Δ (β = 20°).

Table I Suggested Values Of μ ₀ And n As A Function Of Path Steepness (β)

Calculations with actual avalanche profiles near the extremes of steepness gave a closer match to the upper limit of the field data: Ruby Peak, Colorado (β 16.7°, β = 23°, S ₀ = 2300 m) and PS-67, Norway (β = 49°, β = 51°, S = 1600 m) gave respectively μ _m/(S ₀)_½ = 1.45 and 1.88 in comparison with the extreme limits estimated from the geometrical model (Fig. 4). The recommendations of Table I put the value μ _m/(S ₀)_½ = 1.5 m^½ s⁻¹ in the middle (most of common values of path steepness).

The values in Table I are derived by neglecting the turbulent air/dust drag and centripetal force. I expect that this approximation will suffice in most engineering applications. To include these terms, I suggest estimating D ₀ and then reducing μ in Equation (9) while retaining the value of n appropriate to path steepness (β) from Table I. Using an iterative procedure, the stop position (known) can be matched to give the solution for speeds all along the incline. Including air drag and centripetal drag will reduce the estimates of maximum speed produced by application of the values in Table I, but these terms may not be important in most run-out zone applications.

The high friction limit for the model produces over-estimates of maximum speed for the steepest profiles. Such profiles are rare in practice (β = 50°). The path-steepness range for the Rogers Pass speed data is fairly broad, but most data are concentrated around the mean. It is entirely possible that there are not enough speed data to illustrate adequately path-steepness extremes because the data represent avalanches at differing mass and mechanical properties moving over paths with varying topography and surface friction. As well, steep paths represent the class which is most likely to be subjected to centripetal drag effects. If centripetal forces are included in the model calibration, a better match to the maximum speed envelope will be obtained.

Comparison With Field Measurements Of Avalanche Speeds

Recently, data have been published for speeds of large avalanches all along the incline (Norem and Kristensen, 1985, 1986; Norem and others, 1985; Salm and Gubler, 1985; Gubler and others, 1986). Comparison with these data requires care: the data represent frontal speeds but the assumptions in the model ignore the distinction between frontal and centre of mass speed. In addition, the run-out position for the model is taken as the extreme position (tip) of the debris. The model assumptions (ignoring differences between centre of mass and frontal speed) may not be accurate enough in some applications. In addition, the model predictions are intended for the rare design avalanche (≃100year); therefore, particular examples will not entirely match optimum friction conditions and model predictions will exceed measured speeds in most cases.

A complete speed profile for a large dry avalanche was reported bySalm and Gubler (1985) (β = 22°, α = 18°). Sensitivity with respect to values of air drag is shown in Figure 5. This figure shows that μ ₀ = 0.2, n = 1/2 provides a good match to the data in the acceleration and deceleration phases. Addition of the air-drag component reduces the speeds in the region of maximum speed to provide a closer match to the data for μ ₀ = 0.2, n = 1/2.

Fig. 5. Model predictions versus measured speeds (Aulta avalanche path. Switzerland). (-). measured; (). μ ₀ = 0.2. n = ½, D₀ ⁻¹ = 3333 m; (*). μ ₀ = 0.2. n = ½. D₀ ⁻¹ = 0.

Data for an avalanche with a shorter, steeper path, the Magergrond from Switzerland (α = 31°), were measured by Gubler and others (1986). They provide profiles for three avalanches with maximum speeds 19.7, 28.1, and 42.7 m/s. In Figure 6, model predictions are compared with the fastest of these for μ = μ μ ₀ = 0.2, n = 1/4, and μ ₀ = 0.2, n = 1/2. Figure 6 clearly shows that μ = μ produces speed values which underestimate the measured ones for a path of this steepness. The pair μ ₀ = 0.2, n = 1/4 provides an excellent match to the data except in the early deceleration phase, when both the pairs μ ₀ = 0.2, n = 1/4 and μ ₀ = 0.2, n = 1/2, D ₀ ⁻¹= 3333 m give speed predictions exceeding the measured ones. Again, addition of an air-drag term provides a closer match to measurements in the high-speed regions.

Fig. 6. Predicted speed profiles versus measured speeds (Madergrond avalanche path. Switzerland). (-). measured; (). μ = μ. D₀ ⁻¹ = 0; (*). μ ₀ = 0.2, n = ^¼, D₀ ⁻¹ = 0; (+). μ ₀ = 0.2. n = ½, D₀ ⁻¹ = 3333 m.

Variations of stop position (μ) with μ ₀ = 0.2, n 1/2, D ₀ ⁻¹ = 3333 m are shown in Figure 7 for the avalanche in Figure 5. This figure shows the importance of specifying the stop position in order to estimate closely speed profiles.

Fig. 7. Predicted speed profiles as a function of stop position (variations in μ) for μ ₀ = 0.2, n = ½, D₀ ⁻¹ = 3333 m for the same measured speed profile in Figure 6. (-). measured; (Δ), μ = 0.27; (o), μ=0.32, μ = 0.37.

Since the speed data show very rapid deceleration, it would not be possible to match speed data closely using the model without specifying a stop position. Since avalanche speeds are very sensitive to stop position, the model must also display such behaviour.

Data from Ryggfonn path, Norway (β = 28°), provide an indication that avalanche speeds are very sensitive to mechanical properties of flowing snow and the conditions of the sliding surface. Data for two large avalanches (April 1982, April 1983) are given in Figure 8 (from Norem and Kristensen, 1985; Norem and others, 1985). The 1982 avalanche was dry but the lower part of the path had a wet surface. The 1983 avalanche had partly wet snow in the flowing material and the surface was wet in the run-out zone. These conditions deviate from the model assumptions.

Fig. 8. Predicted speed profiles versus measured speeds for two avalanches of differing mechanical properties (Ryggfonn avalanche path. Norway). (�). 1982 avalanche; (−), 1983 avalanche; (+), μ ₀ = 0.2. n = ½. D₀ ⁻¹ = 3333 m; (*). μ ₀ = 0.2. n = ¾, D₀ ⁻¹ = 3333 m.

Also shown (Fig. 8) are the model predictions for μ ₀ 0.2, n = 1/2, n = 3/4, D₀ ⁻¹ = 3333 m, for Ryggfonn. Maximum speed is within about 15% of that measured. Again, the model speeds are too high in the deceleration phase but the wet sliding surface there could explain part of the difference. The 1982 avalanche fits the model assumptions more closely but, even for it, the comparison is not ideal. Except for the early high peak in speed (path length 800 m), the model does agree with data from both

speed profiles that generally the speeds accelerate for about 1500 m along the incline. It is interesting that Perla and others (1984) attributed the early peak in the speed data to a possible spurious effect for the 1982 avalanche. It is not known whether this is true.

Figures 5–8 illustrate a number of complicated effects in the speed profiles that were measured under conditions of the design high-speed avalanche described by the speed model. The model does, however, reproduce the major features of the data. In addition, the model has a much stronger physical basis (granular-flow concepts) than the earlier models of the VoelImy-PCM class which were constructed in an ad hoc fashion instead of being developed from a continuum approach.

Summary and Discussion

The model proposed consists of two parts: (1) definition of extreme avalanche run-out distance using statistical methods, field observations or a combination of these, and (2) calculation of approximate expected speeds along the incline for one type of avalanche: the one characterized by minimum friction and maximum speed. Since the model requires avalanche run-out as input and since it is calibrated from field measurements of maximum avalanche speed, it is (by definition) consistent with these field measurements.

The speed model appears mathematically similar to simple models of the past (Voellmy, 1955; Perla and others, 1980) but its application is entirely different: the run-out distance is used to define the mean value of granular (speed-dependent) friction and avalanche-speed data are used to determine the value of n in Equation (16). Application of the model consists of a suitable choice of μ ₀ and n for the given path-steepness parameter (β) from Table I. For a given run-out distance, S ₀ and μ are then determined to complete Equation (16) which is applied in numerical solutions on the path broken into path-length segments and slope angles.

Equation (17) may be regarded as the high friction limit for the present model (excluding air drag and centripetal effects). McClung and Schaerer (1983) showed that this is the low friction limit for models of the PCM-VoeIlmy class. We also provided some speed data which exceed the model speed limit (low friction limit) for the PCM class of models. A further example is provided in this paper (Fig. 7). These examples emphasize an undesirable characteristic of the PCM-VoeIlmy models. If constant mean values are used for the two friction coefficients in the models, then measured speeds can exceed the model speed limit. If both parameters are allowed to vary along the path (instead of taking constant mean values), then it is impossible to determine the parameters from currently available speed data and the predictions are arbitrary.

In the present model, no attempt is made to predict the flow depth. This is a quantity which engineers are anxious to know. In order to predict flow depth, the internal deformation of the avalanche flow must be defined. Until the mechanical properties and boundary conditions for flowing snow are determined, I do not believe flow-depth predictions are possible with any certainty. However, it should be possible to estimate roughly flow depths as a function of path-confinement geometry if an initial geometry (slab thickness and dimension) is specified for the flowing mass unless the avalanche entrains significant amounts of snow during descent (see e.g. Salm, 1979).

The simplicity and approximate nature of the model must be kept in mind. The true complexity of the avalanche-dynamics problem prevents solutions with the precision sought in many consulting applications for this and other models. Since the speed predictions are developed from scaling rather than a physical model, they must be integrated with as much information as possible collected in the field when applications are attempted.

Acknowledgements

This paper would not have been possible without speed data from the collections of P. Schaerer, NRCC; H. Gubler, Swiss Federal Institute for Snow and Avalanche Research; and H. Norem, Norwegian Geotechnical Institute. I am grateful for their contributions.