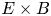1 Introduction
This paper discusses the stability of a pair plasma of arbitrary non-neutrality that is confined by the magnetic field of a long, straight, current-carrying wire. We are interested in this configuration because it is the large-aspect-ratio limit of a dipole trap, where the magnetic field is produced by a circular current hoop (Saitoh et al. Reference Saitoh, Yoshida, Morikawa, Yano, Hayashi, Mizushima, Kawai, Kobayashi and Mikami2010). The APEX collaboration plans to use a dipole trap with a levitated coil to confine a pair plasma. Depending on the injection scheme, a pure electron plasma is initially confined in the trap (Stoneking et al. Reference Stoneking, Pedersen, Helander, Chen, Hergenhahn, Stenson, Fiksel, von der Linden, Saitoh and Surko2020). Because of the mass symmetry of the electrons and positrons, the pair plasma is expected to provide insights into novel plasma physics (Helander & Connor Reference Helander and Connor2016; Stenson et al. Reference Stenson, Horn-Stanja, Stoneking and Pedersen2017; Mishchenko, Plunk & Helander Reference Mishchenko, Plunk and Helander2018).
We expect that the most important instabilities are of low frequency and long wavelength compared with the cyclotron motion and are electrostatic in nature, since the plasma pressure is typically low compared with the magnetic pressure ($\beta \ll 1$![]() ). Depending on the degree of non-neutrality, diocotron modes (Levy Reference Levy1965; Briggs, Daugherty & Levy Reference Briggs, Daugherty and Levy1970) and interchange modes (Krall, Trivelpiece & Gross Reference Krall, Trivelpiece and Gross1973; Garcia Reference Garcia2003) govern the stability.
). Depending on the degree of non-neutrality, diocotron modes (Levy Reference Levy1965; Briggs, Daugherty & Levy Reference Briggs, Daugherty and Levy1970) and interchange modes (Krall, Trivelpiece & Gross Reference Krall, Trivelpiece and Gross1973; Garcia Reference Garcia2003) govern the stability.
Stable and unstable diocotron modes are ubiquitous in the low-frequency dynamics of magnetically confined non-neutral plasmas. These modes have been studied extensively in Penning–Malmberg traps, where a non-neutral plasma column is confined radially by a uniform axial magnetic field and axially by electrostatic fields (Fine & Driscoll Reference Fine and Driscoll1998). The equilibrium plasma undergoes azimuthal $E\times B$![]() drift rotation because of the radial electric field of the plasma space charge. The perturbed electric potential of the diocotron mode is nearly constant along the magnetic field and propagates in the direction of the drifts. In the case of a Penning–Malmberg trap the mode potential is nearly constant axially and propagates azimuthally.
drift rotation because of the radial electric field of the plasma space charge. The perturbed electric potential of the diocotron mode is nearly constant along the magnetic field and propagates in the direction of the drifts. In the case of a Penning–Malmberg trap the mode potential is nearly constant axially and propagates azimuthally.
In contrast, the long straight wire produces a purely azimuthal magnetic field. The space charge electric field is still radial, resulting in an axial $E\times B$![]() drift. Thus, the diocotron mode potential is constant azimuthally and propagates axially. In addition, the inhomogeneity and curvature of the magnetic field for the long straight wire produce curvature and gradient-B drifts in the axial direction which compete with the $E\times B$
drift. Thus, the diocotron mode potential is constant azimuthally and propagates axially. In addition, the inhomogeneity and curvature of the magnetic field for the long straight wire produce curvature and gradient-B drifts in the axial direction which compete with the $E\times B$![]() drift. We will see that these drifts can have a stabilising influence on diocotron modes.
drift. We will see that these drifts can have a stabilising influence on diocotron modes.
Just as the $E\times B$![]() drift plays a key role in the dynamics of the diocotron mode, the curvature and gradient-B drifts play a key role in the dynamics of the interchange mode (Krall et al. Reference Krall, Trivelpiece and Gross1973; Garcia Reference Garcia2003). Because the curvature and gradient-B drifts depend on the sign of charge, the drifts can produce a perturbed charge density within a neutral plasma. If the gradient in the magnitude of the magnetic field and the gradient in the density are aligned, the perturbed charge density acts self-consistently to enhance the perturbation. These gradients both point radially inwards at the outboard side of the cylindrical plasma. There has been previous work on the interchange mode for a neutral pair plasma using a local theory (Mishchenko et al. Reference Mishchenko, Plunk and Helander2018). Here, we solve the mode equation taking into account the global plasma geometry and the boundary conditions on the perturbed potential at conductors surrounding the confinement region.
drift plays a key role in the dynamics of the diocotron mode, the curvature and gradient-B drifts play a key role in the dynamics of the interchange mode (Krall et al. Reference Krall, Trivelpiece and Gross1973; Garcia Reference Garcia2003). Because the curvature and gradient-B drifts depend on the sign of charge, the drifts can produce a perturbed charge density within a neutral plasma. If the gradient in the magnitude of the magnetic field and the gradient in the density are aligned, the perturbed charge density acts self-consistently to enhance the perturbation. These gradients both point radially inwards at the outboard side of the cylindrical plasma. There has been previous work on the interchange mode for a neutral pair plasma using a local theory (Mishchenko et al. Reference Mishchenko, Plunk and Helander2018). Here, we solve the mode equation taking into account the global plasma geometry and the boundary conditions on the perturbed potential at conductors surrounding the confinement region.
Section 2 of the paper combines the linearised drift kinetic equations for electrons and positrons and Poisson's equation to obtain the mode equation for the perturbed electric potential. This same mode equation describes both the diocotron mode and the interchange mode. When the equation is scaled properly, it contains two dimensionless parameters. The parameter $k^2\lambda _{\rm D}^2$![]() is a measure of the importance of the curvature and gradient-B drifts, where $k$
is a measure of the importance of the curvature and gradient-B drifts, where $k$![]() is the axial wavenumber and $\lambda _{\rm D}$
is the axial wavenumber and $\lambda _{\rm D}$![]() is a characteristic Debye length. The parameter $\eta = {n_{\rm p}^{(0)}(r)}/{n_{\rm e}^{(0)}(r)}$
is a characteristic Debye length. The parameter $\eta = {n_{\rm p}^{(0)}(r)}/{n_{\rm e}^{(0)}(r)}$![]() is the ratio of positron density to electron density. We assume that the two species are uniformly mixed and have in mind that the electron density is always larger than or equal to the positron density, allowing $0 \leqslant \eta \leqslant 1$
is the ratio of positron density to electron density. We assume that the two species are uniformly mixed and have in mind that the electron density is always larger than or equal to the positron density, allowing $0 \leqslant \eta \leqslant 1$![]() . In addition, the Debye length is defined using a density characteristic of the electrons. The temperature is assumed to be uniform in radius and to be common to both species. The rest of the paper examines solutions for diocotron and interchange modes that arise in various limits of these two parameters.
. In addition, the Debye length is defined using a density characteristic of the electrons. The temperature is assumed to be uniform in radius and to be common to both species. The rest of the paper examines solutions for diocotron and interchange modes that arise in various limits of these two parameters.
In the dimensionless mode equation, the scaled frequency is given by the expression $\varOmega = \omega /\alpha$![]() , where $\alpha = -{2{\rm \pi} c^2 e n_{0{\rm e}}}/{Ik}$
, where $\alpha = -{2{\rm \pi} c^2 e n_{0{\rm e}}}/{Ik}$![]() is an effective drift frequency. Here $n_{0{\rm e}}$
is an effective drift frequency. Here $n_{0{\rm e}}$![]() is a constant characterising the electron density, $I$
is a constant characterising the electron density, $I$![]() is the current in the wire, $c$
is the current in the wire, $c$![]() is the speed of light, $e$
is the speed of light, $e$![]() is the magnitude of the electron charge and $k$
is the magnitude of the electron charge and $k$![]() is the axial wavenumber for the mode. We will find solutions to the mode equation with scaled growth rate ${\rm Im}(\varOmega )$
is the axial wavenumber for the mode. We will find solutions to the mode equation with scaled growth rate ${\rm Im}(\varOmega )$![]() that is order unity. The unscaled growth rates are therefore of order $\alpha$
that is order unity. The unscaled growth rates are therefore of order $\alpha$![]() . The current $I$
. The current $I$![]() is taken to be negative so that the scaling factor $\alpha$
is taken to be negative so that the scaling factor $\alpha$![]() is positive.
is positive.
Section 3 considers the limit where both parameters are zero, that is, the case of a pure electron plasma with temperature low enough that the curvature and gradient-B drifts may be neglected. This is the limit where the diocotron mode takes its simplest form. The velocity variables drop out, yielding a simplified kinetic equation of reduced dimension. The reduced mode equation yields a necessary condition for instability; the derivative $\partial (r^2 n^{(0)}(r))/\partial r$![]() must be non-monotonic, where $n^{(0)}(r)$
must be non-monotonic, where $n^{(0)}(r)$![]() is the equilibrium density and $r$
is the equilibrium density and $r$![]() is the radial coordinate. This criterion is easily satisfied since the density must vanish at the two cylindrical conductors that bound the confinement region and be non-zero in between. The inner conductor is the surface of the cylindrical wire and the outer is a cylindrical boundary wall. Thus, it is not surprising that we find diocotron instabilities for various sample density profiles. In a Penning–Malmberg trap one finds the condition that $\partial (n^{(0)}(r))/\partial r$
is the radial coordinate. This criterion is easily satisfied since the density must vanish at the two cylindrical conductors that bound the confinement region and be non-zero in between. The inner conductor is the surface of the cylindrical wire and the outer is a cylindrical boundary wall. Thus, it is not surprising that we find diocotron instabilities for various sample density profiles. In a Penning–Malmberg trap one finds the condition that $\partial (n^{(0)}(r))/\partial r$![]() must be non-monotonic. The $r^2$
must be non-monotonic. The $r^2$![]() difference between the two criteria arises from the fact that the $E\times B$
difference between the two criteria arises from the fact that the $E\times B$![]() drift flow is incompressible in the canonical phase space of the reduced distribution, not in configuration space. Even in the limit where the curvature and gradient-B drifts are negligible, the difference in the magnetic field is important.
drift flow is incompressible in the canonical phase space of the reduced distribution, not in configuration space. Even in the limit where the curvature and gradient-B drifts are negligible, the difference in the magnetic field is important.
The mode equation is a differential equation for the electric potential. In § 3.2, a Green's function is used to rewrite the mode equation as a Van Kampen eigenvalue equation for the density perturbation (Van Kampen Reference Van Kampen1955; Case Reference Case1959; Schecter et al. Reference Schecter, Dubin, Cass, Driscoll, Lansky and O'Neil2000). Section 3.3 uses this approach to find an analytic solution for a plasma where $r^2 n^{(0)}$![]() is a flat-top profile. We show that the instability results from the linear interaction between a positive energy density perturbation and a negative energy density perturbation. Section 3.4 discusses numerical solutions for the Van Kampen eigenvalue equation and the mode equation for the case of a Gaussian density profile. The mode equation is solved using the shooting method and the Van Kampen equation is solved by discretising the radial coordinate and solving the resulting matrix-eigenvalue problem.
is a flat-top profile. We show that the instability results from the linear interaction between a positive energy density perturbation and a negative energy density perturbation. Section 3.4 discusses numerical solutions for the Van Kampen eigenvalue equation and the mode equation for the case of a Gaussian density profile. The mode equation is solved using the shooting method and the Van Kampen equation is solved by discretising the radial coordinate and solving the resulting matrix-eigenvalue problem.
Section 3.5 considers the limit where the parameter $\eta$![]() is zero but $k^2\lambda _{\rm D}^2$
is zero but $k^2\lambda _{\rm D}^2$![]() is finite. This limit corresponds to a warm, pure electron plasma. We consider a density distribution that leads to instability for $k^2\lambda _{\rm D}^2 = 0$
is finite. This limit corresponds to a warm, pure electron plasma. We consider a density distribution that leads to instability for $k^2\lambda _{\rm D}^2 = 0$![]() and examine the stability for a sequence of increasing values of this parameter. The growth rates drop smoothly to zero as $k^2\lambda _{\rm D}^2$
and examine the stability for a sequence of increasing values of this parameter. The growth rates drop smoothly to zero as $k^2\lambda _{\rm D}^2$![]() increases towards unity, demonstrating a stabilising influence of the curvature and gradient-B drifts on the diocotron mode.
increases towards unity, demonstrating a stabilising influence of the curvature and gradient-B drifts on the diocotron mode.
Section 4 discusses warm, partially neutral plasmas for which the parameters $\eta$![]() and $k^2\lambda _{\rm D}^2$
and $k^2\lambda _{\rm D}^2$![]() are non-zero. To clearly identify the interchange mode, we start in § 4.1 by considering the limit $\eta = 1$
are non-zero. To clearly identify the interchange mode, we start in § 4.1 by considering the limit $\eta = 1$![]() , where the plasma is neutral. In this limit, the equilibrium $E\times B$
, where the plasma is neutral. In this limit, the equilibrium $E\times B$![]() drift vanishes and there is no diocotron mode. Numerical solutions of the mode equation for Gaussian density distributions show that the mode growth rate is an increasing function of the parameter $k^2\lambda _{\rm D}^2$
drift vanishes and there is no diocotron mode. Numerical solutions of the mode equation for Gaussian density distributions show that the mode growth rate is an increasing function of the parameter $k^2\lambda _{\rm D}^2$![]() . This dependence reflects the central role played in the instability by the curvature and gradient-B drifts. We identify the instability as an interchange mode. Section 4.3 considers the modes under variation of both parameters $\eta$
. This dependence reflects the central role played in the instability by the curvature and gradient-B drifts. We identify the instability as an interchange mode. Section 4.3 considers the modes under variation of both parameters $\eta$![]() and $k^2\lambda _{\rm D}^2$
and $k^2\lambda _{\rm D}^2$![]() . As these two parameters vary, the relative importance of the $E\times B$
. As these two parameters vary, the relative importance of the $E\times B$![]() drift and of the curvature and gradient-B drifts vary, producing variation in the growth rates of the diocotron and interchange modes.
drift and of the curvature and gradient-B drifts vary, producing variation in the growth rates of the diocotron and interchange modes.
There are several important differences between the simplified model of a long, straight wire and the actual levitated dipole trap. Bending the straight wire into a coil has two implications. First, the axis of symmetry is no longer aligned with the wire but is given by the central axis of the coil. The magnetic field strength is no longer constant along a magnetic field line and magnetic mirroring has to be considered. Second, the possible wavenumbers are no longer continuous but take on discrete values. An additional difference comes with the cylindrical vacuum chamber that encloses the levitated dipole. The conducting surface is no longer aligned with a magnetic field line, more specifically, there is no conducting surface at the inboard side of the coil. Hence, the effect of a perturbation of the plasma on the opposing plasma at the inboard side has to be taken into account.
2 General mode equation
The purpose of this section is to obtain the governing equation for diocotron and interchange modes that propagate on an electron–positron plasma that is confined by the magnetic field of a long straight current carrying wire. The plasma is allowed to have arbitrary non-neutrality and finite temperature. The two modes have sufficiently low frequency and long wavelength that guiding-centre-drift theory can be used to describe the electron and positron dynamics, and the two modes are electrostatic in nature. Consequently, the mode equation for the perturbed electric potential can be obtained from the linearised drift kinetic equations for the electrons and positrons and Poisson's equation.
2.1 Drift kinetic equation
Let a long, straight, current carrying wire be coincident with the z-axis of a cylindrical coordinate system ($r,\theta, z$![]() ). The magnetic field in the vicinity of the wire is then given by the expression
). The magnetic field in the vicinity of the wire is then given by the expression
and the vector potential by the expression
The confinement region is bounded by the conducting surface of the wire at radius $r_{\rm wire}$![]() and an outer conducting cylinder at radius $r_{{\rm wall}}$
and an outer conducting cylinder at radius $r_{{\rm wall}}$![]() , where $r_{{\rm wire}} < r_{{\rm wall}}$
, where $r_{{\rm wire}} < r_{{\rm wall}}$![]() . A schematic of this configuration is given by figure 1.
. A schematic of this configuration is given by figure 1.

Figure 1. Schematic of the configuration with the wire in red, the plasma in blue and the wall in grey. The current through the wire is indicated by the black arrow and the magnetic field by the blue arrow.
Following Taylor (Reference Taylor1964), the guiding-centre-drift Lagrangian of a particle moving in the field of the wire can be written in the form
where $j = {\rm e}$![]() refers to electrons and $j = {\rm p}$
refers to electrons and $j = {\rm p}$![]() refers to positrons. The respective particle has charge $q_j$
refers to positrons. The respective particle has charge $q_j$![]() , mass $m_j$
, mass $m_j$![]() and magnetic moment $\mu _j = m_jv_{\perp }^2/2|B|$
and magnetic moment $\mu _j = m_jv_{\perp }^2/2|B|$![]() . Since the mass for electrons and positrons is the same we will drop that index from now on. The first term in the Lagrangian is the kinetic energy associated with the velocity component parallel to the magnetic field line, the second is the vector potential term, the third is the electrostatic potential energy and the last term is the potential energy associated with the magnetic moment. Both potential energy terms enter the Lagrangian with a minus sign. The canonical momenta for the species $j$
. Since the mass for electrons and positrons is the same we will drop that index from now on. The first term in the Lagrangian is the kinetic energy associated with the velocity component parallel to the magnetic field line, the second is the vector potential term, the third is the electrostatic potential energy and the last term is the potential energy associated with the magnetic moment. Both potential energy terms enter the Lagrangian with a minus sign. The canonical momenta for the species $j$![]() are given by the expressions
are given by the expressions
The corresponding guiding-centre-drift Hamiltonian is given by the expression
The canonically conjugate variables are ($\theta, p_{\theta }$![]() ) and ($z,p_{zj}$
) and ($z,p_{zj}$![]() ), where $p_{zj}$
), where $p_{zj}$![]() represents any dependence on the radius $r$
represents any dependence on the radius $r$![]() . Neglecting collisions for the relatively short time scales relevant to mode growth, the adiabatic invariant $\mu$
. Neglecting collisions for the relatively short time scales relevant to mode growth, the adiabatic invariant $\mu$![]() can be treated as a constant of the motion.
can be treated as a constant of the motion.
The distribution of guiding centres is given by the expression $f_j=f_j(\theta, p_{\theta },z,p_{zj},\mu,t)$![]() and satisfies the kinetic equation
and satisfies the kinetic equation
The number of guiding centres within a phase space volume is given by the expression
and the density of guiding centres in physical space is given by the expression
where use has been made of the relation $|{\rm d}p_{zj}| = |{2Iq_j}/{c^2 r}|\,{\rm d}r$![]() . The drift in the z-direction follows from the Hamiltonian in (2.5)
. The drift in the z-direction follows from the Hamiltonian in (2.5)
where ${\partial r}/{\partial p_{zj}} = -{c^2r}/{2q_jI}$![]() . The first two terms on the right-hand side of (2.9) are the curvature and gradient-B drifts and the last term is the $E\times B$
. The first two terms on the right-hand side of (2.9) are the curvature and gradient-B drifts and the last term is the $E\times B$![]() drift. For a given electric potential, the $E\times B$
drift. For a given electric potential, the $E\times B$![]() drift is independent of the sign of charge in contrast to the curvature and gradient-B drift.
drift is independent of the sign of charge in contrast to the curvature and gradient-B drift.
2.2 Linear mode equation
In linear theory the distribution for species $j$![]() can be written in the form
can be written in the form
where the first term is the equilibrium distribution and the second term is the perturbation. The corresponding electric potential is written in the form
We neglect the finite resistivity of the bounding conductors. Consequently, the mode potential vanishes at both boundaries. The $p_{zj}$![]() in the argument of the potential functions represents radial dependence and must be used in the corresponding Hamiltonian $H_j$
in the argument of the potential functions represents radial dependence and must be used in the corresponding Hamiltonian $H_j$![]() . Assume an equilibrium distribution of the form
. Assume an equilibrium distribution of the form
with the equilibrium Hamiltonian $H_j^{(0)} = {p_{\theta }^2}/{2mr^2} + \mu |B| + q_j \phi ^{(0)}$![]() . The second factor in (2.12) is a Maxwellian velocity distribution. We consider the case where the temperature is independent of the radius and is the same for both species. Carrying out the integrals in (2.8) shows that $g_j(p_{zj})$
. The second factor in (2.12) is a Maxwellian velocity distribution. We consider the case where the temperature is independent of the radius and is the same for both species. Carrying out the integrals in (2.8) shows that $g_j(p_{zj})$![]() is the equilibrium density up to a multiplicative constant.
is the equilibrium density up to a multiplicative constant.
Using the functional dependence of $f_j^{(0)}(p_{\theta }, p_{zj}, \mu )$![]() and $H_j^{(0)}(p_{\theta }, p_{zj}, \mu )$
and $H_j^{(0)}(p_{\theta }, p_{zj}, \mu )$![]() and linearising the kinetic equation in the perturbation yields the relation
and linearising the kinetic equation in the perturbation yields the relation

with the solution

Poisson's equation for the mode potential then takes the form

where use has been made of (2.8).
To solve (2.14) we divided by the resonance factor $\omega - k ({\partial H^{(0)}}/{\partial p_z})$![]() , which can be zero for some value of $p_z$
, which can be zero for some value of $p_z$![]() if ${\rm Im}(\omega )=0$
if ${\rm Im}(\omega )=0$![]() . This is the same problem as faced by Landau when solving the Vlasov equation (Landau Reference Landau1946). The underlying difficulty is that (2.15) is a proper initial value solution to (2.14) only for a growing wave where ${\rm Im}(\omega )>0$
. This is the same problem as faced by Landau when solving the Vlasov equation (Landau Reference Landau1946). The underlying difficulty is that (2.15) is a proper initial value solution to (2.14) only for a growing wave where ${\rm Im}(\omega )>0$![]() is positive. As ${\rm Im}(\omega )$
is positive. As ${\rm Im}(\omega )$![]() approaches zero the contour of integration must be deformed to stay on the same side of any pole or branch cut. We avoid this complication by solving the mode equation only for growing modes. This is sufficient to identify domains of instability. However, it is important to keep in mind that a growing mode is not a general solution for an arbitrary initial density perturbation. The eigenfunction of such a mode does not necessarily match the radial dependence of an arbitrary initial perturbation. However, if this mode is the fastest-growing mode and has a non-zero overlap integral with the initial perturbation, it is the time-asymptotic limit of the solution for the initial perturbation. Likewise, the plasma modes in Landau's solution dominate only in the time-asymptotic limit.
approaches zero the contour of integration must be deformed to stay on the same side of any pole or branch cut. We avoid this complication by solving the mode equation only for growing modes. This is sufficient to identify domains of instability. However, it is important to keep in mind that a growing mode is not a general solution for an arbitrary initial density perturbation. The eigenfunction of such a mode does not necessarily match the radial dependence of an arbitrary initial perturbation. However, if this mode is the fastest-growing mode and has a non-zero overlap integral with the initial perturbation, it is the time-asymptotic limit of the solution for the initial perturbation. Likewise, the plasma modes in Landau's solution dominate only in the time-asymptotic limit.
The integral on the right-hand side can be rewritten in the form

with the scaled velocities $x_{\parallel } = \sqrt {{m}/{T}} \,v_{\parallel }$![]() and $x_{\perp } = \sqrt {{m}/{T}} \, v_{\perp }$
and $x_{\perp } = \sqrt {{m}/{T}} \, v_{\perp }$![]() . Here, use had been made of ${\rm d}\mu \,{\rm d}p_{\theta } = ({\sqrt {m}T^{{3}/{2}}r}/{2B})\,{\rm d}\kern0.7pt x_{\perp }^2\,{\rm d}\kern0.7pt x_{\parallel }$
. Here, use had been made of ${\rm d}\mu \,{\rm d}p_{\theta } = ({\sqrt {m}T^{{3}/{2}}r}/{2B})\,{\rm d}\kern0.7pt x_{\perp }^2\,{\rm d}\kern0.7pt x_{\parallel }$![]() . Gauss's law and the relation ${\partial r}/{\partial p_{zj}} = -{c^2r}/{2q_jI}$
. Gauss's law and the relation ${\partial r}/{\partial p_{zj}} = -{c^2r}/{2q_jI}$![]() imply the result
imply the result
where $\eta = {n_{\rm p}^{(0)}(r)}/{n_{\rm e}^{(0)}(r)}$![]() is the ratio of positron to electron density. We have assumed that the two species are uniformly mixed. Expressing $g_j(p_{zj})$
is the ratio of positron to electron density. We have assumed that the two species are uniformly mixed. Expressing $g_j(p_{zj})$![]() in terms of the number density $n_j$
in terms of the number density $n_j$![]() according to (2.13) and plugging (2.17) back into Poisson's equation (2.16) yields the equation
according to (2.13) and plugging (2.17) back into Poisson's equation (2.16) yields the equation

We now want to bring (2.19) into a dimensionless form. To do so, we introduce the scaled radius $\xi = kr$![]() and the scaled density $\tilde {n}=n/n_0$
and the scaled density $\tilde {n}=n/n_0$![]() where $n_0$
where $n_0$![]() is a constant characteristic value of the density. As an example, consider the Gaussian density profile
is a constant characteristic value of the density. As an example, consider the Gaussian density profile
which when scaled takes the form
where $\xi _0 = kr_0$![]() is the scaled peak and $\Delta \xi = \Delta r k$
is the scaled peak and $\Delta \xi = \Delta r k$![]() is the scaled width. For notational simplicity, we denote $\tilde {n}(r) = \tilde {n}(\xi /k)$
is the scaled width. For notational simplicity, we denote $\tilde {n}(r) = \tilde {n}(\xi /k)$![]() by $\tilde {n}(\xi )$
by $\tilde {n}(\xi )$![]() remembering that all lengths are scaled by $k$
remembering that all lengths are scaled by $k$![]() . The mode equation (2.19) can be rewritten in the form
. The mode equation (2.19) can be rewritten in the form

The scaled frequency is given by $\varOmega = {\omega }/{\alpha } = -{I k \omega }/{2{\rm \pi} q_{\rm e} c^2 n_{0{\rm e}}}$![]() . The Debye length $\lambda _{\rm D} = \sqrt {T/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$
. The Debye length $\lambda _{\rm D} = \sqrt {T/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$![]() depends on the characteristic density $n_{0{\rm e}}$
depends on the characteristic density $n_{0{\rm e}}$![]() that was introduced before. The importance of finite-temperature effects depends on the ratio $a = {k^2\lambda _{\rm D}^2}/{\varOmega - (1-\eta )\int _0^{\xi } {\rm d}\xi ' \,\xi '\tilde {n}^{(0)}}$
that was introduced before. The importance of finite-temperature effects depends on the ratio $a = {k^2\lambda _{\rm D}^2}/{\varOmega - (1-\eta )\int _0^{\xi } {\rm d}\xi ' \,\xi '\tilde {n}^{(0)}}$![]() in regions where the plasma density is non-zero. We can simplify (2.22) further
in regions where the plasma density is non-zero. We can simplify (2.22) further

The remaining integral can be carried out analytically by following Zocco et al. (Reference Zocco, Xanthopoulos, Doerk, Connor and Helander2018)

where erfc is the complementary error function for a complex argument. Note that the parameter $a$![]() does not depend on the scaled velocity variables.
does not depend on the scaled velocity variables.
3 Cold pure electron plasma
This section considers the limit where both $k^2\lambda _{\rm D}^2$![]() and $\eta$
and $\eta$![]() are small compared with unity, taken here to be formally zero. Setting these parameters to zero in (2.22) and using the relation
are small compared with unity, taken here to be formally zero. Setting these parameters to zero in (2.22) and using the relation
yields the reduced equation

3.1 Reduced description
This equation can be obtained directly by noting that in the zero-temperature approximation the two kinetic energy terms in the Hamiltonian (2.5) may be neglected and we are left with $H_{\rm e} = q_{\rm e}\phi (z, p_z, t)$![]() . Because the velocity variables are not present in this reduced Hamiltonian, a reduced electron distribution can be used
. Because the velocity variables are not present in this reduced Hamiltonian, a reduced electron distribution can be used
The reduced distribution satisfies the reduced kinetic equation $\partial h_{\rm e} / \partial t + [h_{\rm e}, q_{\rm e}\phi ] = 0$![]() . Linearising the reduced kinetic equation and combining it with Poisson's equation yields (3.2).
. Linearising the reduced kinetic equation and combining it with Poisson's equation yields (3.2).
A necessary condition for instability can be established by following the same procedure as that used for a long, cylindrical, non-neutral plasma in a homogeneous magnetic field (Briggs et al. Reference Briggs, Daugherty and Levy1970). Let the scaled frequency be written as a real and an imaginary part, $\varOmega = \varOmega _r + {\rm i}\varGamma$![]() , multiply mode equation (3.2) by the mode complex conjugate, integrate over ${\rm d}\xi \xi$
, multiply mode equation (3.2) by the mode complex conjugate, integrate over ${\rm d}\xi \xi$![]() from the inner conductor to the outer conductor, use integration by parts on the partial derivative term and take the imaginary part of the resulting equation to obtain the requirement
from the inner conductor to the outer conductor, use integration by parts on the partial derivative term and take the imaginary part of the resulting equation to obtain the requirement

Equation (3.4) can be satisfied for positive $\varGamma$![]() only when $\tilde {n}_{\rm e}^{(0)}\xi ^2$
only when $\tilde {n}_{\rm e}^{(0)}\xi ^2$![]() is non-monotonic in $\xi$
is non-monotonic in $\xi$![]() . Since the density is zero at the inner cylinder and at the outer cylinder but finite in between this requirement is always satisfied. The inner conductor is the surface of the cylindrical wire and the outer surface is a cylindrical boundary wall. Thus, it is not surprising that we find diocotron instabilities for several sample density profiles. The corresponding condition for a plasma in a Penning–Malmberg trap is that $\partial n_{\rm e}^{(0)}(r)/\partial r$
. Since the density is zero at the inner cylinder and at the outer cylinder but finite in between this requirement is always satisfied. The inner conductor is the surface of the cylindrical wire and the outer surface is a cylindrical boundary wall. Thus, it is not surprising that we find diocotron instabilities for several sample density profiles. The corresponding condition for a plasma in a Penning–Malmberg trap is that $\partial n_{\rm e}^{(0)}(r)/\partial r$![]() be non-monotonic. The $r^2$
be non-monotonic. The $r^2$![]() difference between the two criteria is due to the $E\times B$
difference between the two criteria is due to the $E\times B$![]() flow being incompressible in the canonical phase space of the reduced distribution, not in configuration space. This is the same factor that enters the ratio between the phase space density and the physical density $r^2n_{\rm e} = |2Ie/c^2|h_{\rm e}$
flow being incompressible in the canonical phase space of the reduced distribution, not in configuration space. This is the same factor that enters the ratio between the phase space density and the physical density $r^2n_{\rm e} = |2Ie/c^2|h_{\rm e}$![]() , where $|2Ie/c^2|$
, where $|2Ie/c^2|$![]() is a constant. For the uniform axial magnetic field of a Penning–Malmberg trap, the two spaces are the same. Even in the limit where the curvature and gradient-B drifts are negligible, the difference in the magnetic field is important.
is a constant. For the uniform axial magnetic field of a Penning–Malmberg trap, the two spaces are the same. Even in the limit where the curvature and gradient-B drifts are negligible, the difference in the magnetic field is important.
Since the diocotron instability involves the requirement that the plasma cylinder is hollow, one might think that the plasma can be stabilised by charging the wire. However, this does not work for the case of a long straight wire, since both the electric field from the charged wire and the magnetic field fall off as $1/r$![]() . Hence, the $E\times B$
. Hence, the $E\times B$![]() drift from the charged wire is independent of $r$
drift from the charged wire is independent of $r$![]() and can be removed by a transformation to the drifting frame. In the lab frame, the drift produces a Doppler shift in the real part of the mode frequency, but does not change the imaginary part, that is, the growth rate.
and can be removed by a transformation to the drifting frame. In the lab frame, the drift produces a Doppler shift in the real part of the mode frequency, but does not change the imaginary part, that is, the growth rate.
3.2 Van Kampen method
An alternative to mode equation (3.2) for the electric potential is the Van Kampen eigenvalue equation for the density perturbation (Van Kampen Reference Van Kampen1955; Case Reference Case1959; Schecter et al. Reference Schecter, Dubin, Cass, Driscoll, Lansky and O'Neil2000). To this end, first note that the scaled Poisson equation for the mode potential takes the form
One can identify the left-hand side in (3.2) as the scaled, perturbed density $-4{\rm \pi} q n^{(1)}/k^2$![]() . Hence, we can write (3.2) as
. Hence, we can write (3.2) as

In Appendix A, we obtain Green's function

where ${I}_0(\xi )$![]() and ${K}_0(\xi )$
and ${K}_0(\xi )$![]() are Bessel functions of an imaginary argument. The perturbed potential can be written in terms of the perturbed density by using Green's function
are Bessel functions of an imaginary argument. The perturbed potential can be written in terms of the perturbed density by using Green's function

yielding the Van Kampen eigenvalue equation for the density perturbation

The derivation of (3.9) does not involve division by $\varOmega - \int _0^{\xi } {\rm d}\xi ' \,\xi '\tilde {n}^{(0)}$![]() . There is no restriction that $\varGamma$
. There is no restriction that $\varGamma$![]() be greater than zero. The Van Kampen method systematically finds all modes, stable and unstable, without the need for analytic continuation. As we show, the eigenmodes include discrete modes as well as continuum modes (Case Reference Case1959). As mentioned earlier, our focus here is on unstable modes.
be greater than zero. The Van Kampen method systematically finds all modes, stable and unstable, without the need for analytic continuation. As we show, the eigenmodes include discrete modes as well as continuum modes (Case Reference Case1959). As mentioned earlier, our focus here is on unstable modes.
For completeness, we note that the different eigenmodes can be combined to provide a solution to an arbitrary initial value problem. Let $n_1^{(1)} (\xi )$![]() and $n_2^{(1)} (\xi )$
and $n_2^{(1)} (\xi )$![]() be two eigenfunctions corresponding to frequencies $\varOmega _1$
be two eigenfunctions corresponding to frequencies $\varOmega _1$![]() and $\varOmega _2$
and $\varOmega _2$![]() and define the inner product
and define the inner product

From (3.9) one finds the orthogonality relation
This relation is useful in expanding an arbitrary initial density perturbation in eigenmodes
where $a_d$![]() and $a(\varOmega )$
and $a(\varOmega )$![]() are time-independent constants given in terms of the initial perturbation $n^{(1)} (\xi, t)$
are time-independent constants given in terms of the initial perturbation $n^{(1)} (\xi, t)$![]() by the relations
by the relations


the sum over $a_d$![]() covers the discrete modes and the integral over $a(\varOmega )$
covers the discrete modes and the integral over $a(\varOmega )$![]() covers the continuum modes.
covers the continuum modes.
3.3 Analytic solution
Analytic solutions to mode equation (3.2) and Van Kampen equation (3.9) are possible for the special case where the equilibrium density profile is given by the expression
where $\xi _{\rm in}$![]() and $\xi _{\rm out}$
and $\xi _{\rm out}$![]() are the inner and outer edge of the plasma density, which is generally not the same as the inner and outer boundary $\xi _{\rm wire}$
are the inner and outer edge of the plasma density, which is generally not the same as the inner and outer boundary $\xi _{\rm wire}$![]() and $\xi _{\rm wall}$
and $\xi _{\rm wall}$![]() and $\varTheta$
and $\varTheta$![]() is a step function. This density profile corresponds to a flat-top profile for the equilibrium distribution function $h_{\rm e}^{(0)}(\xi )$
is a step function. This density profile corresponds to a flat-top profile for the equilibrium distribution function $h_{\rm e}^{(0)}(\xi )$![]() . For this density distribution the radial derivative in (3.9)
. For this density distribution the radial derivative in (3.9)
is the sum of two delta functions. This feature simplifies both the mode equation and the Van Kampen equation, allowing analytic solutions. We will solve the Van Kampen equation since Green's function has already solved part of the problem. Equation (3.9) implies that the density perturbation is a sum of two delta functions as well:
Evaluating (3.9) at the inner and outer edge of the plasma respectively yields
Eliminating $C_{\rm in}$![]() and $C_{\rm out}$
and $C_{\rm out}$![]() between the two equations gives a quadratic equation for $\varOmega$
between the two equations gives a quadratic equation for $\varOmega$![]()
where the relation $G(\xi _{\rm in}, \xi _{\rm out}) = G(\xi _{\rm out}, \xi _{\rm in})$![]() has been used.
has been used.
Physically the dispersion relation describes the interaction between two charge density perturbations. There is one at $\xi = \xi _{\rm in}$![]() , where the step function $n^{(0)} (\xi ) \xi ^2$
, where the step function $n^{(0)} (\xi ) \xi ^2$![]() rises, which we labelled $C_{\rm in}$
rises, which we labelled $C_{\rm in}$![]() . The second charge density perturbations is labelled $C_{\rm out}$
. The second charge density perturbations is labelled $C_{\rm out}$![]() and is located at $\xi = \xi _{\rm out}$
and is located at $\xi = \xi _{\rm out}$![]() , where the step function falls back to zero. In the dispersion equation (3.20), the interaction between the two density perturbations is represented by $G(\xi _{\rm in}, \xi _{\rm out})$
, where the step function falls back to zero. In the dispersion equation (3.20), the interaction between the two density perturbations is represented by $G(\xi _{\rm in}, \xi _{\rm out})$![]() . When $\xi _{\rm out} - \xi _{\rm in}$
. When $\xi _{\rm out} - \xi _{\rm in}$![]() is large compared with unity, $G(\xi _{\rm in}, \xi _{\rm out}) \approx \exp [-(\xi _{\rm out} - \xi _{\rm in})]$
is large compared with unity, $G(\xi _{\rm in}, \xi _{\rm out}) \approx \exp [-(\xi _{\rm out} - \xi _{\rm in})]$![]() is exponentially small and the interaction between the two density perturbations is negligible. Equation (3.20) then simplifies yielding the two modes
is exponentially small and the interaction between the two density perturbations is negligible. Equation (3.20) then simplifies yielding the two modes
When $\xi _{\rm out}-\xi _{\rm in}$![]() is not large compared with unity, $G(\xi _{\rm in},\xi _{\rm out})$
is not large compared with unity, $G(\xi _{\rm in},\xi _{\rm out})$![]() is not exponentially small and must be retained in (3.20). The two density perturbations interact significantly and each mode involves both perturbations. The solution to (3.20) can be expressed in terms of the frequencies $\varOmega _{\rm in}$
is not exponentially small and must be retained in (3.20). The two density perturbations interact significantly and each mode involves both perturbations. The solution to (3.20) can be expressed in terms of the frequencies $\varOmega _{\rm in}$![]() and $\varOmega _{\rm out}$
and $\varOmega _{\rm out}$![]() :
:
The right-hand side of (3.23) contains an imaginary part if $(\varOmega _{\rm in} - \varOmega _{\rm out})^2 < 4\xi _{\rm in}^4G(\xi _{\rm in}, \xi _{\rm out})^2$![]() . In this case, the two solutions $\varOmega _{\pm }$
. In this case, the two solutions $\varOmega _{\pm }$![]() correspond to a growing and a damped diocotron mode. The growth rate is largest when the two frequencies $\varOmega _{\rm in}$
correspond to a growing and a damped diocotron mode. The growth rate is largest when the two frequencies $\varOmega _{\rm in}$![]() and $\varOmega _{\rm out}$
and $\varOmega _{\rm out}$![]() are nearly resonant and the interaction strength $4\xi _{\rm in}^4G(\xi _{\rm in}, \xi _{\rm out})^2$
are nearly resonant and the interaction strength $4\xi _{\rm in}^4G(\xi _{\rm in}, \xi _{\rm out})^2$![]() is large.
is large.
An interesting property of these two modes is the respective sign of the wave energies. If the frequencies are both positive, the energy associated with density perturbation $C_{\rm in}$![]() has positive energy, and the second mode, density perturbation $C_{\rm out}$
has positive energy, and the second mode, density perturbation $C_{\rm out}$![]() , has negative energy. In Appendix B we calculate the energy required to create the two density perturbations and find the signs of the energy associated with the two perturbations to be opposite. For the growing mode, the energy flow is from the negative energy perturbation to the positive energy perturbation, and for the damped mode, the energy flow is reversed. Such an interaction, also known as reactive instability, is known to happen both in plasma physics and fluid dynamics (Cairns Reference Cairns1979). The direction in which the energy flows is associated with the phase shift between the two perturbations. This phase shift is given by the expression
, has negative energy. In Appendix B we calculate the energy required to create the two density perturbations and find the signs of the energy associated with the two perturbations to be opposite. For the growing mode, the energy flow is from the negative energy perturbation to the positive energy perturbation, and for the damped mode, the energy flow is reversed. Such an interaction, also known as reactive instability, is known to happen both in plasma physics and fluid dynamics (Cairns Reference Cairns1979). The direction in which the energy flows is associated with the phase shift between the two perturbations. This phase shift is given by the expression
If the mode is growing ($\varGamma = {\rm Im}(\varOmega )>0$![]() ), the outer perturbation is ahead of the inner perturbation and vice versa. The ratio between the amplitudes of the two density perturbations for one distinct mode is given by the expression
), the outer perturbation is ahead of the inner perturbation and vice versa. The ratio between the amplitudes of the two density perturbations for one distinct mode is given by the expression
Figure 2 shows the changing mode structure for a decreasing sequence of the plasma thickness $\xi _{\rm out}-\xi _{\rm in}$![]() . The inner and outer conductors are located at $\xi _{\rm wire} = 1$
. The inner and outer conductors are located at $\xi _{\rm wire} = 1$![]() and $\xi _{\rm wall} = 8$
and $\xi _{\rm wall} = 8$![]() . The thickest plasma in figure 2(a) supports two modes consisting of separate density perturbations at the respective plasma edges. For the slightly thinner plasma in figure 2(b) a small density perturbation on the opposite edge in addition to the dominant one becomes apparent. This trend continues in figure 2(c). Note also that the difference between the frequencies of the two modes decreases. Finally, figure 2(d) shows the case of an unstable mode. The frequency becomes complex and the two solutions turn into their respective complex conjugate, a growing and a damped solution.
. The thickest plasma in figure 2(a) supports two modes consisting of separate density perturbations at the respective plasma edges. For the slightly thinner plasma in figure 2(b) a small density perturbation on the opposite edge in addition to the dominant one becomes apparent. This trend continues in figure 2(c). Note also that the difference between the frequencies of the two modes decreases. Finally, figure 2(d) shows the case of an unstable mode. The frequency becomes complex and the two solutions turn into their respective complex conjugate, a growing and a damped solution.

Figure 2. The normalised initial density distribution for a pure electron plasma (grey solid line) and the density perturbation at the inner plasma edge (red dashed line) as well as the outer edge (blue dotted line) plotted over the scaled radius $\xi = kr$![]() . The thickness of the initial density distribution decreases from the upper left to the lower right panel. For the thinnest case in panel (d), the frequency becomes complex. Both the damped (purple dashed line) and the growing mode (blue dotted line) are shown.
. The thickness of the initial density distribution decreases from the upper left to the lower right panel. For the thinnest case in panel (d), the frequency becomes complex. Both the damped (purple dashed line) and the growing mode (blue dotted line) are shown.
To understand the dependence on the plasma geometry, that is, on $r_{\rm in}$![]() and $r_{\rm out}$
and $r_{\rm out}$![]() , we allow these quantities to vary, holding $r_{\rm wire}$
, we allow these quantities to vary, holding $r_{\rm wire}$![]() , $r_{\rm wall}$
, $r_{\rm wall}$![]() and $k$
and $k$![]() constant. This translates to holding $\xi _{\rm wire}$
constant. This translates to holding $\xi _{\rm wire}$![]() and $\xi _{\rm wall}$
and $\xi _{\rm wall}$![]() constant and varying $\xi _{\rm in}$
constant and varying $\xi _{\rm in}$![]() and $\xi _{\rm out}$
and $\xi _{\rm out}$![]() independently. Figure 3 shows a contour plot of ${\rm Im}[\varOmega (\xi _{\rm in}, \xi _{\rm out}, \xi _{\rm wire}, \xi _{\rm wall})]$
independently. Figure 3 shows a contour plot of ${\rm Im}[\varOmega (\xi _{\rm in}, \xi _{\rm out}, \xi _{\rm wire}, \xi _{\rm wall})]$![]() , where the x-axis is $\xi _{\rm in}$
, where the x-axis is $\xi _{\rm in}$![]() and the y-axis is the difference $\xi _{\rm out}-\xi _{\rm in}$
and the y-axis is the difference $\xi _{\rm out}-\xi _{\rm in}$![]() . Again, the boundaries are fixed at $\xi _{\rm wire}=1$
. Again, the boundaries are fixed at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() .
.

Figure 3. Contour plot of the growth rate ${\rm Im}(\varOmega )$![]() of discrete modes, where the abscissa is $\xi _{\rm in}$
of discrete modes, where the abscissa is $\xi _{\rm in}$![]() and the ordinate is $\xi _{\rm out}-\xi _{\rm in}$
and the ordinate is $\xi _{\rm out}-\xi _{\rm in}$![]() . The inner and outer cylindrical conductors are located at $\xi _{\rm wire}=1$
. The inner and outer cylindrical conductors are located at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() , respectively. The white line marks the region in which the outer radius would be smaller than the inner radius $\xi _{\rm out}<\xi _{\rm in}$
, respectively. The white line marks the region in which the outer radius would be smaller than the inner radius $\xi _{\rm out}<\xi _{\rm in}$![]() .
.
As was discussed previously, good interaction between the two density perturbations requires that $\xi _{\rm out}-\xi _{\rm in}$![]() is not too large. This is in agreement with the vertical range of instability in figure 3 up to $\xi _{\rm out}-\xi _{\rm in} \approx 1$
is not too large. This is in agreement with the vertical range of instability in figure 3 up to $\xi _{\rm out}-\xi _{\rm in} \approx 1$![]() . Likewise, we expect that neither density perturbation can be too near to one of the conducting boundaries. Otherwise, the boundaries would shield the interaction potential. This is consistent with the gap between the last contour of finite growth rate and the ordinate on the left as well as the white solid line on the right in figure 3.
. Likewise, we expect that neither density perturbation can be too near to one of the conducting boundaries. Otherwise, the boundaries would shield the interaction potential. This is consistent with the gap between the last contour of finite growth rate and the ordinate on the left as well as the white solid line on the right in figure 3.
The unscaled growth rate is given by the expression
The growth rate varies linearly with the density and inversely with the current. The scaling of the growth rate with the wavelength is not directly apparent since the scaled distance $\xi =kr$![]() is a function of the wavelength. Consider a constant wavenumber $k_0$
is a function of the wavelength. Consider a constant wavenumber $k_0$![]() with the corresponding growth rate $\gamma (k_0) = \alpha \,{\rm Im}[\varOmega (k_0r_{\rm in}, k_0r_{\rm out}, k_0r_{\rm wire}, k_0r_{\rm wall})]$
with the corresponding growth rate $\gamma (k_0) = \alpha \,{\rm Im}[\varOmega (k_0r_{\rm in}, k_0r_{\rm out}, k_0r_{\rm wire}, k_0r_{\rm wall})]$![]() . Changing the wavenumber $k$
. Changing the wavenumber $k$![]() while keeping the position of the boundary and the plasma edges fixed results in a change of the growth rate according to the ratio
while keeping the position of the boundary and the plasma edges fixed results in a change of the growth rate according to the ratio
The pre-factor of $k_0/k$![]() on the right-hand side of (3.27) comes from the $k$
on the right-hand side of (3.27) comes from the $k$![]() -dependence in the scaling factor $\alpha$
-dependence in the scaling factor $\alpha$![]() . The change of the growth rate with wavelength is shown in figure 4.
. The change of the growth rate with wavelength is shown in figure 4.

Figure 4. Growth rate for different wavenumbers $k$![]() normalised by the growth rate for the reference wavenumber $k_0 = r_{\rm wire}^{-1}$
normalised by the growth rate for the reference wavenumber $k_0 = r_{\rm wire}^{-1}$![]() .
.
Instability is limited to wavenumbers with $k/k_0 < 1.3$![]() , where $k_0 = r_{\rm wire}^{-1}$
, where $k_0 = r_{\rm wire}^{-1}$![]() . Again this restriction comes from the requirement that $\xi _{\rm out}-\xi _{\rm in} = k(r_{\rm out}-r_{\rm in})$
. Again this restriction comes from the requirement that $\xi _{\rm out}-\xi _{\rm in} = k(r_{\rm out}-r_{\rm in})$![]() is not large compared with unity. The variation of this quantity in figure 4 comes from the variation of $k$
is not large compared with unity. The variation of this quantity in figure 4 comes from the variation of $k$![]() , rather than the variation of $r_{\rm out}-r_{\rm in}$
, rather than the variation of $r_{\rm out}-r_{\rm in}$![]() .
.
For an infinitely long plasma, the allowed wavenumbers $k$![]() lie on a continuum. That is not the case for the model of a plasma in a large-aspect-ratio dipole trap which implies a periodic boundary condition. Consequently, the allowed wavenumbers are restricted to the discrete values $k=n/R$
lie on a continuum. That is not the case for the model of a plasma in a large-aspect-ratio dipole trap which implies a periodic boundary condition. Consequently, the allowed wavenumbers are restricted to the discrete values $k=n/R$![]() , where $n$
, where $n$![]() is a positive integer and $R$
is a positive integer and $R$![]() is the radius of the coil. This restriction suggests the possibilities of eliminating unstable modes by choosing $R < (r_{\rm out}-r_{\rm in})/1.3$
is the radius of the coil. This restriction suggests the possibilities of eliminating unstable modes by choosing $R < (r_{\rm out}-r_{\rm in})/1.3$![]() . Unfortunately, this is inconsistent with our model of a large-aspect-ratio dipole. Nevertheless, this observation does suggest that the opposite limit, a dipole trap with near-unity aspect ratio, might have interesting stability properties.
. Unfortunately, this is inconsistent with our model of a large-aspect-ratio dipole. Nevertheless, this observation does suggest that the opposite limit, a dipole trap with near-unity aspect ratio, might have interesting stability properties.
3.4 Numerical results
For a general density profile, a numerical solution of the mode equation or of the Van Kampen equation is necessary. For solutions of the mode equation, we use the shooting method. This method relies on an initial guess for the complex scaled frequency $\varOmega$![]() . The boundary condition requires that the mode potential is zero at the inner boundary $\xi _{\rm wire}$
. The boundary condition requires that the mode potential is zero at the inner boundary $\xi _{\rm wire}$![]() and we choose a finite initial slope of the potential at that point. The specific value of the slope does not matter since the mode equation is linear. These two initial conditions allow the equation to be integrated outwards to the conductor at $\xi _{\rm wall}$
and we choose a finite initial slope of the potential at that point. The specific value of the slope does not matter since the mode equation is linear. These two initial conditions allow the equation to be integrated outwards to the conductor at $\xi _{\rm wall}$![]() . The outer boundary condition requires the potential to vanish which is generally not the case for the first guess of $\varOmega$
. The outer boundary condition requires the potential to vanish which is generally not the case for the first guess of $\varOmega$![]() . A root finder that is based on Powell's method (Powell Reference Powell1964) is used to find the complex value of $\varOmega$
. A root finder that is based on Powell's method (Powell Reference Powell1964) is used to find the complex value of $\varOmega$![]() , for which the boundary condition is satisfied. This value is the correct complex frequency of the mode.
, for which the boundary condition is satisfied. This value is the correct complex frequency of the mode.
There is a subtlety in the integration of the mode equation from the inner to the outer boundary. To solve (2.14), we divided by the resonance factor $\omega - k ({\partial H^{(0)}}/{\partial p_z})$![]() , which can be zero for some value of $\xi$
, which can be zero for some value of $\xi$![]() if $\omega$
if $\omega$![]() is real. The contour of integration must then be deformed to stay on the same side of the singularity. We avoid this complication by solving the mode equation only for growing modes. In this case the equation can be integrated along the real $\xi$
is real. The contour of integration must then be deformed to stay on the same side of the singularity. We avoid this complication by solving the mode equation only for growing modes. In this case the equation can be integrated along the real $\xi$![]() -axis. In subsequent plots of growth rates we use zero value whenever the shooting method does not return a positive value.
-axis. In subsequent plots of growth rates we use zero value whenever the shooting method does not return a positive value.
In order to solve the eigenvalue problem (3.9) for a general density profile we follow Schecter et al. (Reference Schecter, Dubin, Cass, Driscoll, Lansky and O'Neil2000). The radius is discretised such that (3.9) can be rewritten in matrix form. For every grid point we obtain one eigenvalue, the scaled frequency, and one eigenfunction, the density perturbation. As discussed in § 3.2 this method yields a discretised representation of all the modes without recourse to analytic continuation. We focus on the discrete unstable mode, which corresponds to the mode obtained by solving the mode equation.
Consider the Gaussian distribution in (2.21). Solving the mode equation (2.22) yields the scaled growth rate $\varGamma = {\rm Im}(\varOmega (\xi _{\rm in}, \xi _{\rm out}, \xi _{\rm wire}, \xi _{\rm wall})$![]() . Figure 5 shows a contour plot of this growth rate in the plane $(\Delta \xi, \xi _{0})$
. Figure 5 shows a contour plot of this growth rate in the plane $(\Delta \xi, \xi _{0})$![]() for fixed values $\xi _{\rm wire}=1$
for fixed values $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() . This figure illustrates the dependence of the growth rate on the plasma geometry for fixed wavenumber and fixed boundaries. The same results are obtained when solving the Van Kampen equation (3.9), selecting only the discrete unstable mode. The result for a Gaussian density profile agrees qualitatively with the analytic result for the profile given by (3.15). Some of the results in figure 5 resemble density profiles with a non-negligible value in the close proximity of a boundary. If a large fraction of the plasma is close to either boundary we expect a quick loss of particles and a consequent truncation of the density profile.
. This figure illustrates the dependence of the growth rate on the plasma geometry for fixed wavenumber and fixed boundaries. The same results are obtained when solving the Van Kampen equation (3.9), selecting only the discrete unstable mode. The result for a Gaussian density profile agrees qualitatively with the analytic result for the profile given by (3.15). Some of the results in figure 5 resemble density profiles with a non-negligible value in the close proximity of a boundary. If a large fraction of the plasma is close to either boundary we expect a quick loss of particles and a consequent truncation of the density profile.

Figure 5. Contour plot of the growth rate ${\rm Im}(\varOmega )$![]() of discrete modes for a Gaussian equilibrium density profile that is centred around $\xi _{0}$
of discrete modes for a Gaussian equilibrium density profile that is centred around $\xi _{0}$![]() and has the width $\Delta \xi$
and has the width $\Delta \xi$![]() as defined in (2.21). The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$
as defined in (2.21). The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() , respectively. The hatched areas highlight the density profiles for which the density in close proximity of a boundary is beyond 1 % of the maximum density.
, respectively. The hatched areas highlight the density profiles for which the density in close proximity of a boundary is beyond 1 % of the maximum density.
3.5 Finite-temperature effects
In this section, we allow the parameter $k^2\lambda _{\rm D}^2$![]() to be finite but retain zero value for the parameter $\eta = 0$
to be finite but retain zero value for the parameter $\eta = 0$![]() in mode equation (2.22). This is the case of a warm pure electron plasma. Using the shooting method, we solve the mode equation for the Gaussian equilibrium density distribution given in (2.21), with the scaled values $\xi _{\rm wire}=1$
in mode equation (2.22). This is the case of a warm pure electron plasma. Using the shooting method, we solve the mode equation for the Gaussian equilibrium density distribution given in (2.21), with the scaled values $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() . Figure 6 shows a plot of the scaled growth rate vs $k^2\lambda _{\rm D}^2$
. Figure 6 shows a plot of the scaled growth rate vs $k^2\lambda _{\rm D}^2$![]() for four values of the Gaussian thickness $\Delta \xi$
for four values of the Gaussian thickness $\Delta \xi$![]() . In all four cases, the scaled growth rate decreases to zero as $k^2\lambda _{\rm D}^2$
. In all four cases, the scaled growth rate decreases to zero as $k^2\lambda _{\rm D}^2$![]() increases towards unity, demonstrating a stabilising influence of the curvature and gradient-B drifts on the diocotron mode. As mentioned before, only solutions with ${\rm Im}(\varOmega )>0$
increases towards unity, demonstrating a stabilising influence of the curvature and gradient-B drifts on the diocotron mode. As mentioned before, only solutions with ${\rm Im}(\varOmega )>0$![]() can be accepted.
can be accepted.

Figure 6. The growth rate of the diocotron mode is plotted over $k^2\lambda _{\rm D}^2$![]() . The density profile of the plasma is given by the Gaussian in (2.21), centred in between the conducting surfaces. The thickness of the lines corresponds to the thickness $\Delta \xi$
. The density profile of the plasma is given by the Gaussian in (2.21), centred in between the conducting surfaces. The thickness of the lines corresponds to the thickness $\Delta \xi$![]() of the density profile. The velocity distribution is a Maxwellian. The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$
of the density profile. The velocity distribution is a Maxwellian. The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() , respectively.
, respectively.
The stabilisation might appear to be due to Debye screening of the potential perturbation, but note that the mode propagates perpendicular to the magnetic field. The plasma cannot rearrange itself freely such that it shields the potential perturbation. The factor $k^2\lambda _{\rm D}^2$![]() appears only in front of the gradient-B and curvature drift. Instead, we believe that the stabilisation is due to the spread in these drifts, not to the mere existence of a drift velocity.
appears only in front of the gradient-B and curvature drift. Instead, we believe that the stabilisation is due to the spread in these drifts, not to the mere existence of a drift velocity.
The spread comes from the Maxwellian velocity distribution. Thus, we ask what happens if the equilibrium velocity distribution is replaced by $f^{(0)} = g(p_z)\delta (v_{\parallel }-v_{\parallel 0})\delta (v^2_{\perp }-v^2_{\perp 0})$![]() . This distribution is a valid equilibrium, since the variables $v_{\parallel } = {p_{\theta }}/{mr(p_z)}$
. This distribution is a valid equilibrium, since the variables $v_{\parallel } = {p_{\theta }}/{mr(p_z)}$![]() and $v_{\perp } = \mu |{2I}/{mcr(p_z)}|$
and $v_{\perp } = \mu |{2I}/{mcr(p_z)}|$![]() are both constants of the motion in that $p_{\theta }$
are both constants of the motion in that $p_{\theta }$![]() , $p_z$
, $p_z$![]() and $\mu$
and $\mu$![]() are all constants of the motion. In Appendix C, we obtain the mode equation for this distribution and solve for the growth rate assuming the same Gaussian density distribution as used for figure 6. The velocity integral in the mode equation is evaluated trivially because of the delta function velocity dependence. As can be seen in figure 7 we find no evidence of stabilisation for large $k^2\hat {\lambda }_{\rm D}^2$
are all constants of the motion. In Appendix C, we obtain the mode equation for this distribution and solve for the growth rate assuming the same Gaussian density distribution as used for figure 6. The velocity integral in the mode equation is evaluated trivially because of the delta function velocity dependence. As can be seen in figure 7 we find no evidence of stabilisation for large $k^2\hat {\lambda }_{\rm D}^2$![]() when there is no spread in the drift velocities. Here, we define the characteristic length scale $\hat {\lambda }_{\rm D} = \sqrt {W/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$
when there is no spread in the drift velocities. Here, we define the characteristic length scale $\hat {\lambda }_{\rm D} = \sqrt {W/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$![]() which replaces the Debye length. Instead of the temperature $T$
which replaces the Debye length. Instead of the temperature $T$![]() , it depends on the total kinetic energy $W$
, it depends on the total kinetic energy $W$![]() . Accordingly, the scaled velocities are defined as $x_{\parallel } = \sqrt {{m}/{W}} \, v_{\parallel }$
. Accordingly, the scaled velocities are defined as $x_{\parallel } = \sqrt {{m}/{W}} \, v_{\parallel }$![]() and $x_{\perp } = \sqrt {{m}/{W}} \,v_{\perp }$
and $x_{\perp } = \sqrt {{m}/{W}} \,v_{\perp }$![]() .
.

Figure 7. The growth rate of the diocotron mode is plotted over $k^2\lambda _{\rm D}^2$![]() . The density profile of the plasma is given by the Gaussian in (2.21), centred in between the conducting surfaces. The thickness of the lines corresponds to the thickness $\Delta \xi$
. The density profile of the plasma is given by the Gaussian in (2.21), centred in between the conducting surfaces. The thickness of the lines corresponds to the thickness $\Delta \xi$![]() of the density profile. The velocity distribution is a delta distribution that peaks at $x_{\perp } = x_{\parallel } = 1$
of the density profile. The velocity distribution is a delta distribution that peaks at $x_{\perp } = x_{\parallel } = 1$![]() . The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$
. The inner and outer cylindrical conductors are at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() respectively.
respectively.
The linear stability analysis does not reveal the mechanism behind the stabilisation. However, figure 6 indicates that the stability threshold for $k^2\lambda _{\rm D}^2$![]() is a strictly increasing function of the growth rate in the cold limit $\varGamma (k^2\lambda _{\rm D}^2 = 0)$
is a strictly increasing function of the growth rate in the cold limit $\varGamma (k^2\lambda _{\rm D}^2 = 0)$![]() . We suspect that, if the spread in the drifts is comparable to $\varGamma (k^2\lambda _{\rm D}^2 = 0)$
. We suspect that, if the spread in the drifts is comparable to $\varGamma (k^2\lambda _{\rm D}^2 = 0)$![]() , the interaction between the negative and positive energy mode described in § 3.3 is mitigated.
, the interaction between the negative and positive energy mode described in § 3.3 is mitigated.
4 Pair plasma
In this section we consider a partially neutralised plasma of uniformly mixed electrons and positrons. For low temperature where the curvature and gradient-B drifts are small compared with the $E\times B$![]() drift, a trivial extension of results for a single-species plasma is possible. Since the $E\times B$
drift, a trivial extension of results for a single-species plasma is possible. Since the $E\times B$![]() drifts are independent of the sign of charge, the uniformly mixed pair plasma evolves as a single-species plasma of equilibrium density $(1-\eta )n^{(0)}(r)$
drifts are independent of the sign of charge, the uniformly mixed pair plasma evolves as a single-species plasma of equilibrium density $(1-\eta )n^{(0)}(r)$![]() . Consequently, the diocotron mode disappears in the quasi-neutral limit ($\eta = 1$
. Consequently, the diocotron mode disappears in the quasi-neutral limit ($\eta = 1$![]() ). In contrast to the $E\times B$
). In contrast to the $E\times B$![]() drift, the curvature and gradient-B drifts depend on the sign of charge and are in opposite directions for the two species.
drift, the curvature and gradient-B drifts depend on the sign of charge and are in opposite directions for the two species.
The purpose of this section is to understand the interchange mode for a pair plasma and to explore the relation of this mode to the diocotron mode for various degrees of non-neutrality and various temperatures. While the diocotron mode lives off the equilibrium $E\times B$![]() drift, the interchange mode lives off the equilibrium curvature and gradient-B drifts. Nevertheless, the modes have much in common. The electric potentials for both are constant along the magnetic field lines and sinusoidal in the direction of the drifts. Since the mode potential structure is the same, both modes are governed by the mode equation (2.22).
drift, the interchange mode lives off the equilibrium curvature and gradient-B drifts. Nevertheless, the modes have much in common. The electric potentials for both are constant along the magnetic field lines and sinusoidal in the direction of the drifts. Since the mode potential structure is the same, both modes are governed by the mode equation (2.22).
4.1 Neutral warm pair plasma
To identify the interchange mode in its simplest form, we first consider the limit of a neutral pair plasma, where $\eta =1$![]() . There is no diocotron mode in this limit. The mode equation reduces to the form
. There is no diocotron mode in this limit. The mode equation reduces to the form

This equation again can be solved by using the shooting method. Figure 8 shows the scaled growth rate $\varGamma ={\rm Im}(\varOmega )$![]() vs $k^2 \lambda _{\rm D}^2$
vs $k^2 \lambda _{\rm D}^2$![]() . Both the electron and the positron density distributions are given by the Gaussian from (2.21), centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$
. Both the electron and the positron density distributions are given by the Gaussian from (2.21), centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() with different widths $\Delta \xi = \xi _{\rm out}-\xi _{\rm in}$
with different widths $\Delta \xi = \xi _{\rm out}-\xi _{\rm in}$![]() . All curves start from $k^2 \lambda _{\rm D}^2=0$
. All curves start from $k^2 \lambda _{\rm D}^2=0$![]() and reach a peak for $k^2 \lambda _{\rm D}^2$
and reach a peak for $k^2 \lambda _{\rm D}^2$![]() of order unity, but then decrease with further increase in $k^2 \lambda _{\rm D}^2$
of order unity, but then decrease with further increase in $k^2 \lambda _{\rm D}^2$![]() . In the next section, analytic explanations for the rapid rise and fall will be obtained.
. In the next section, analytic explanations for the rapid rise and fall will be obtained.

Figure 8. The growth rate is plotted over $k^2\lambda _{\rm D}^2$![]() for a quasi-neutral pair plasma ($\eta =1$
for a quasi-neutral pair plasma ($\eta =1$![]() ) with different Gaussian density profiles and a Maxwellian velocity distribution. The Gaussian density profiles have different widths in the range $0.4 < \Delta \xi < 0.7$
) with different Gaussian density profiles and a Maxwellian velocity distribution. The Gaussian density profiles have different widths in the range $0.4 < \Delta \xi < 0.7$![]() and they are centred in between the conducting surfaces.
and they are centred in between the conducting surfaces.
In the scaled mode equation (2.22) the parameter $k^2 \lambda _{\rm D}^2$![]() enters as the coefficient of the curvature and gradient-B drifts. The rapid rise in growth rate in figure 8 with increasing $k^2 \lambda _{\rm D}^2$
enters as the coefficient of the curvature and gradient-B drifts. The rapid rise in growth rate in figure 8 with increasing $k^2 \lambda _{\rm D}^2$![]() reflects the central role played in the instability by the curvature and gradient-B drifts. We identify the instability as an interchange mode in that its mechanism involves the curvature and gradient-B drifts acting transverse to a density gradient. The magnetic field has bad curvature, and there is a negative density gradient on the outside of the Gaussian. The growth rate decreases for $k^2\lambda _{\rm D}^2 \gtrsim 1$
reflects the central role played in the instability by the curvature and gradient-B drifts. We identify the instability as an interchange mode in that its mechanism involves the curvature and gradient-B drifts acting transverse to a density gradient. The magnetic field has bad curvature, and there is a negative density gradient on the outside of the Gaussian. The growth rate decreases for $k^2\lambda _{\rm D}^2 \gtrsim 1$![]() . Again, this stabilisation for large $k^2 \hat {\lambda }_{\rm D}^2$
. Again, this stabilisation for large $k^2 \hat {\lambda }_{\rm D}^2$![]() disappears if we consider a delta distribution instead of a Maxwellian as shown in figure 9. The definition of the parameter $\hat {\lambda }_{\rm D}$
disappears if we consider a delta distribution instead of a Maxwellian as shown in figure 9. The definition of the parameter $\hat {\lambda }_{\rm D}$![]() is the same as in § 3.5. Similar to the diocotron mode, the interchange mode appears to be stabilised by a large spread in the drift velocities.
is the same as in § 3.5. Similar to the diocotron mode, the interchange mode appears to be stabilised by a large spread in the drift velocities.

Figure 9. The growth rate of the interchange mode is plotted over $k^2\hat {\lambda }_{\rm D}^2$![]() for a quasi-neutral pair plasma ($\eta =1$
for a quasi-neutral pair plasma ($\eta =1$![]() ) and different Gaussian density profiles. The Gaussian density profiles have different widths in the range $0.4 < \Delta \xi < 0.7$
) and different Gaussian density profiles. The Gaussian density profiles have different widths in the range $0.4 < \Delta \xi < 0.7$![]() and they are centred in between the conducting surfaces. The velocity distribution is a delta distribution that peaks at $x_{\perp } = x_{\parallel } = 1$
and they are centred in between the conducting surfaces. The velocity distribution is a delta distribution that peaks at $x_{\perp } = x_{\parallel } = 1$![]() .
.
The growth rate displayed in figure 8 might therefore be interpreted as a competition between the curvature and gradient-B drifts as drivers of the instability and the stabilisation due to the spread in those drifts leading to a maximum growth rate at $k^2 \hat {\lambda }_{\rm D}^2 \approx 1$![]() and stabilisation for $k^2 \hat {\lambda }_{\rm D}^2 > 5$
and stabilisation for $k^2 \hat {\lambda }_{\rm D}^2 > 5$![]() .
.
However, the instability is different from the standard description of an interchange instability. In the standard description, the curvature and gradient-B drifts are modelled by a drift due to an artificial gravity. The interchange instability is presented as an analogue of the Rayleigh–Taylor instability for a heavy fluid on top of a light fluid (Guzdar et al. Reference Guzdar, Satyanarayana, Huba and Ossakow1982). The large ion mass produces an ion gravitational drift that is large compared with the electron gravitational drift. For the electron–positron plasma the drifts for the two species are equal in magnitude. In the case of an electron–ion plasma the large ion mass gives rise to a large polarisation drift for the ions in the mode field or, equivalently, a large plasma dielectric constant $\epsilon =1+4{\rm \pi} n M_i c^2/B^2 \gg 1$![]() . Because of the small mass for the electrons and positrons, we have neglected the polarisation drift or, equivalently, assumed that the dielectric constant, $\epsilon =1+4{\rm \pi} n m_{\rm e} c^2/B^2$
. Because of the small mass for the electrons and positrons, we have neglected the polarisation drift or, equivalently, assumed that the dielectric constant, $\epsilon =1+4{\rm \pi} n m_{\rm e} c^2/B^2$![]() , is nearly unity. In addition, since the magnetic field is inhomogeneous, the $E \times B$
, is nearly unity. In addition, since the magnetic field is inhomogeneous, the $E \times B$![]() drift is not incompressible.
drift is not incompressible.
An interesting feature of the neutral case is that the real part of the frequency vanishes for all values of $k^2\lambda _{\rm D}^2$![]() (Kennedy Reference Kennedy2020). The mode is purely growing and does not propagate. To understand this result, note that (4.1) is invariant under interchange of $\varOmega \rightarrow -\varOmega$
(Kennedy Reference Kennedy2020). The mode is purely growing and does not propagate. To understand this result, note that (4.1) is invariant under interchange of $\varOmega \rightarrow -\varOmega$![]() . Consequently, there is nothing in the equation to choose a direction of propagation for the wave, so the real part of the frequency must be zero. We see this result explicitly in graphs of the ${\rm Re}(\varOmega )$
. Consequently, there is nothing in the equation to choose a direction of propagation for the wave, so the real part of the frequency must be zero. We see this result explicitly in graphs of the ${\rm Re}(\varOmega )$![]() vs $\eta$
vs $\eta$![]() in the next section.
in the next section.
4.2 Higher-order radial modes
Up to this point, no mention has been made of higher-order radial modes. The growth rates in figure 8 are all for the fundamental radial eigenmodes. However, higher-order radial modes occur for $\eta \approx 1$![]() and sufficiently small $k^2\lambda _{\rm D}^2$
and sufficiently small $k^2\lambda _{\rm D}^2$![]() . Figure 10 shows plots of the first three radial eigenmodes for $k^2\lambda _{\rm D}^2 = 0.2$
. Figure 10 shows plots of the first three radial eigenmodes for $k^2\lambda _{\rm D}^2 = 0.2$![]() and $\eta = 1$
and $\eta = 1$![]() . The eigenmodes are typically labelled by the number of zero crossings. One can see that the higher order mode potentials are oscillatory in the region where the slope of the density distribution is negative.
. The eigenmodes are typically labelled by the number of zero crossings. One can see that the higher order mode potentials are oscillatory in the region where the slope of the density distribution is negative.

Figure 10. The initial density distribution at different scaled radii $\xi = kr$![]() is given by the black dashed line. The black solid curves correspond to the potential perturbation for different mode numbers. The thickness of the lines decreases with increasing mode number.
is given by the black dashed line. The black solid curves correspond to the potential perturbation for different mode numbers. The thickness of the lines decreases with increasing mode number.
Likewise, figure 11 shows plots of the growth rates for these eigenmodes vs $k^2\lambda _{\rm D}^2$![]() . Note that the fundamental radial eigenmode is the fastest growing and so is the most important for stability considerations.
. Note that the fundamental radial eigenmode is the fastest growing and so is the most important for stability considerations.

Figure 11. The growth rates for different radial eigenmodes of the interchange mode are plotted over $k^2\lambda _{\rm D}^2$![]() assuming a quasi-neutral pair plasma ($\eta =1$
assuming a quasi-neutral pair plasma ($\eta =1$![]() ). The unperturbed density profile is a Gaussian with the width $\Delta \xi = 0.7$
). The unperturbed density profile is a Gaussian with the width $\Delta \xi = 0.7$![]() that is centred in between the conducting surfaces.
that is centred in between the conducting surfaces.
To understand these results intuitively, we rewrite (4.1) in a simpler form. Setting $\eta = 1$![]() and $\varOmega =i\varGamma$
and $\varOmega =i\varGamma$![]() yields
yields
where


As can be seen in figure 12, the function $f$![]() rises monotonically from $0$
rises monotonically from $0$![]() to the maximum value of ${\rm \pi}$
to the maximum value of ${\rm \pi}$![]() as $|a|^2 = {k^4\lambda _{\rm D}^4}/{\varGamma ^2}$
as $|a|^2 = {k^4\lambda _{\rm D}^4}/{\varGamma ^2}$![]() varies from $0$
varies from $0$![]() to $\infty$
to $\infty$![]() . The function $g$
. The function $g$![]() rises monotonically from $0$
rises monotonically from $0$![]() to the maximum value of $2$
to the maximum value of $2$![]() in the same interval.
in the same interval.

Figure 12. Evaluating the two integrals in (4.3) for different values of $|a|^2$![]() yields the solid curve for $g$
yields the solid curve for $g$![]() and the dashed curve for $f$
and the dashed curve for $f$![]() . The ratio $g/f$
. The ratio $g/f$![]() is given by the dotted line.
is given by the dotted line.
First, we look at (4.2) in the limit where $|a|^2 = k^4\lambda _{\rm D}^4/\varGamma ^2 \ll 1$![]() . The denominators in (4.3) can then be approximated by unity and performing the integrals yields $g(|a|^2) = 14|a|^2$
. The denominators in (4.3) can then be approximated by unity and performing the integrals yields $g(|a|^2) = 14|a|^2$![]() and $f(|a|^2) = 4|a|^2$
and $f(|a|^2) = 4|a|^2$![]() . The mode equation (4.2) takes the form of a Sturm–Liouville problem (Goedbloed & Poedts Reference Goedbloed and Poedts2004).
. The mode equation (4.2) takes the form of a Sturm–Liouville problem (Goedbloed & Poedts Reference Goedbloed and Poedts2004).
A Sturm–Liouville problem is an eigenvalue problem for which the eigenvalue $\lambda _n = 4k^2\lambda _{\rm D}^2/\varGamma _n^2$![]() increases with the number of zero-crossings $n$
increases with the number of zero-crossings $n$![]() of the eigenfunction. Hence, the lowest-order radial eigenmode ($n = 0$
of the eigenfunction. Hence, the lowest-order radial eigenmode ($n = 0$![]() ) has the largest scaled growth rate as was observed in figure 11. Likewise, the rapid increase of the growth rate in figures 8 and 11 as $k^2\lambda _{\rm D}^2 = \lambda _n \varGamma _n^2/4$
) has the largest scaled growth rate as was observed in figure 11. Likewise, the rapid increase of the growth rate in figures 8 and 11 as $k^2\lambda _{\rm D}^2 = \lambda _n \varGamma _n^2/4$![]() increases from zero can be understood in terms of this expression for the eigenvalue. All the modes in figure 8 are the fundamental, but with different values of the width for the Gaussian. The variation from curve to curve arises from changes in the eigenvalue as the width of the Gaussian is varied.
increases from zero can be understood in terms of this expression for the eigenvalue. All the modes in figure 8 are the fundamental, but with different values of the width for the Gaussian. The variation from curve to curve arises from changes in the eigenvalue as the width of the Gaussian is varied.
If $\frac {7}{2} \tilde {n}^{(0)} + \xi ({\partial \tilde {n}^{(0)}}/{\partial \xi }) > 0$![]() in the entire confinement region, the second derivative of the potential perturbation is purely positive (purely negative for $\phi ^{(1)} < 0$
in the entire confinement region, the second derivative of the potential perturbation is purely positive (purely negative for $\phi ^{(1)} < 0$![]() ). The boundary conditions cannot be satisfied in that case. Consequently, the interchange instability occurs for density profiles with a steep, negative gradient only. The same result was found in the local limit (Mishchenko et al. Reference Mishchenko, Plunk and Helander2018). When $k^2\lambda _{\rm D}^2$
). The boundary conditions cannot be satisfied in that case. Consequently, the interchange instability occurs for density profiles with a steep, negative gradient only. The same result was found in the local limit (Mishchenko et al. Reference Mishchenko, Plunk and Helander2018). When $k^2\lambda _{\rm D}^2$![]() approaches unity we have to go back to (4.2). The condition for instability of the interchange mode then generalises to $\frac {g}{f} \tilde {n}^{(0)} + \xi ({\partial \tilde {n}^{(0)}}/{\partial \xi }) < 0$
approaches unity we have to go back to (4.2). The condition for instability of the interchange mode then generalises to $\frac {g}{f} \tilde {n}^{(0)} + \xi ({\partial \tilde {n}^{(0)}}/{\partial \xi }) < 0$![]() . The fraction ${g}/{f}$
. The fraction ${g}/{f}$![]() monotonically decreases from $7/2$
monotonically decreases from $7/2$![]() to $2/{\rm \pi}$
to $2/{\rm \pi}$![]() as $|a|^2$
as $|a|^2$![]() goes from zero to infinity.
goes from zero to infinity.
Looking at regions where the density falls off steeply, such that $({\xi }/{\tilde {n}^{(0)}})({\partial \tilde {n}^{(0)}}/{\partial \xi }) \ll -1$![]() , we can think of the quantity $f/k^2\lambda _{\rm D}^2$
, we can think of the quantity $f/k^2\lambda _{\rm D}^2$![]() as the eigenvalue $\lambda _n$
as the eigenvalue $\lambda _n$![]() . The function $f(|a|^2)$
. The function $f(|a|^2)$![]() monotonically increases to the maximum value of ${\rm \pi}$
monotonically increases to the maximum value of ${\rm \pi}$![]() . Thus, as $\lambda _n k^2\lambda _{\rm D}^2$
. Thus, as $\lambda _n k^2\lambda _{\rm D}^2$![]() approaches ${\rm \pi}$
approaches ${\rm \pi}$![]() , the growth rate $\varGamma _n$
, the growth rate $\varGamma _n$![]() is forced to zero and there is no solution for $\lambda _n k^2\lambda _{\rm D}^2 > {\rm \pi}$
is forced to zero and there is no solution for $\lambda _n k^2\lambda _{\rm D}^2 > {\rm \pi}$![]() . This behaviour is seen in figure 8 and is probably related to the spread in drift velocities for the Maxwellian velocity distribution that was discussed before.
. This behaviour is seen in figure 8 and is probably related to the spread in drift velocities for the Maxwellian velocity distribution that was discussed before.
4.3 Arbitrary non-neutrality
Next, we investigate the stability of pair plasmas with arbitrary non-neutrality. Figure 13 shows the imaginary part of the scaled growth rate ${\rm Im}(\varOmega )$![]() vs the density ratio $\eta$
vs the density ratio $\eta$![]() for different values of $k^2\lambda _{\rm D}^2$
for different values of $k^2\lambda _{\rm D}^2$![]() . Figure 14 shows the corresponding real part of the scaled frequency. All of the curves assume that both the electrons and positrons have a Gaussian density distributions that is given by (2.21).
. Figure 14 shows the corresponding real part of the scaled frequency. All of the curves assume that both the electrons and positrons have a Gaussian density distributions that is given by (2.21).

Figure 13. The growth rate is plotted over the density ratio of positrons to electrons $\eta$![]() . The parameter $k^2\lambda _{\rm D}^2$
. The parameter $k^2\lambda _{\rm D}^2$![]() increases as the curves gradually change colour from blue to red. The density distribution is given by a Gaussian that is centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$
increases as the curves gradually change colour from blue to red. The density distribution is given by a Gaussian that is centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() and has the width $\Delta \xi = \xi _{\rm out}-\xi _{\rm in} = 0.4$
and has the width $\Delta \xi = \xi _{\rm out}-\xi _{\rm in} = 0.4$![]() .
.

Figure 14. The frequency plotted over the density ratio of positrons to electrons $\eta$![]() . The parameter $k^2\lambda _{\rm D}^2$
. The parameter $k^2\lambda _{\rm D}^2$![]() increases as the curves gradually change colour from blue to red. The density distribution is given by a Gaussian that is centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$
increases as the curves gradually change colour from blue to red. The density distribution is given by a Gaussian that is centred in between the conducting cylindrical boundaries at $\xi _{\rm wire}=1$![]() and $\xi _{\rm wall}=8$
and $\xi _{\rm wall}=8$![]() and has the width $\Delta \xi = \xi _{\rm out}-\xi _{\rm in} = 0.4$
and has the width $\Delta \xi = \xi _{\rm out}-\xi _{\rm in} = 0.4$![]() . We omit the values for which ${\rm Im}(\varOmega ) \leqslant 0$
. We omit the values for which ${\rm Im}(\varOmega ) \leqslant 0$![]() .
.
As we have seen, the diocotron instability depends crucially on the axial $E \times B$![]() drift, but is stabilised by the curvature and gradient-B drifts. In contrast, the interchange mode depends crucially on the curvature and gradient-B drifts, and shear associated with the $E \times B$
drift, but is stabilised by the curvature and gradient-B drifts. In contrast, the interchange mode depends crucially on the curvature and gradient-B drifts, and shear associated with the $E \times B$![]() drift has a stabilising influence. Thus, the growing mode is diocotron-like for small values of $\eta$
drift has a stabilising influence. Thus, the growing mode is diocotron-like for small values of $\eta$![]() and small values of $k^2\lambda _{\rm D}^2$
and small values of $k^2\lambda _{\rm D}^2$![]() . Likewise the interchange mode dominates for large values of $\eta$
. Likewise the interchange mode dominates for large values of $\eta$![]() and large values of $k^2\lambda _{\rm D}^2$
and large values of $k^2\lambda _{\rm D}^2$![]() . For intermediate values of $\eta$
. For intermediate values of $\eta$![]() and finite $k^2\lambda _{\rm D}^2$
and finite $k^2\lambda _{\rm D}^2$![]() , a mode is formed by the competition between the driving and stabilising influences of the different drifts.
, a mode is formed by the competition between the driving and stabilising influences of the different drifts.
Consistent with this picture, the blue curve in figure 13, for which $k^2\lambda _{\rm D}^2 = 0$![]() , exhibits the largest growth rate for small values of $\eta$
, exhibits the largest growth rate for small values of $\eta$![]() and completely vanishes for $\eta =1$
and completely vanishes for $\eta =1$![]() . This is the limit of a pure diocotron mode. With a small but finite temperature corresponding to $k^2\lambda _{\rm D}^2 = 0.01$
. This is the limit of a pure diocotron mode. With a small but finite temperature corresponding to $k^2\lambda _{\rm D}^2 = 0.01$![]() , the interchange mode becomes apparent for $\eta > 0.7$
, the interchange mode becomes apparent for $\eta > 0.7$![]() . The red curve, for which $k^2\lambda _{\rm D}^2 = 1$
. The red curve, for which $k^2\lambda _{\rm D}^2 = 1$![]() , illustrates the opposite limit where the diocotron mode is suppressed relative to the interchange mode. The plasma is stable for $\eta =0$
, illustrates the opposite limit where the diocotron mode is suppressed relative to the interchange mode. The plasma is stable for $\eta =0$![]() but the growth rate increases as $\eta$
but the growth rate increases as $\eta$![]() approaches unity. For $k^2\lambda _{\rm D}^2>1$
approaches unity. For $k^2\lambda _{\rm D}^2>1$![]() we see a stabilising effect on the interchange mode due to the relative drift motion of particles with different thermal velocities.
we see a stabilising effect on the interchange mode due to the relative drift motion of particles with different thermal velocities.
As mentioned in the previous section, the real part of the frequency in figure 14 goes to zero as the plasma becomes quasi-neutral. The mode does not propagate in that limit.
5 Conclusion
This paper has discussed the stability of diocotron and interchange modes in a pair plasma with arbitrary non-neutrality that is confined by the magnetic field of a long, straight, current-carrying wire. The linearised drift kinetic equations for the electrons and positrons were combined with Poisson's equation to obtain a comprehensive mode equation that describes both modes. This equation depends on the two dimensionless parameters: the parameter $k^2 \lambda _{\rm D}^2$![]() , where $k$
, where $k$![]() is the axial wavenumber of the mode and $\lambda _{\rm D}$
is the axial wavenumber of the mode and $\lambda _{\rm D}$![]() is the Debye length; and the parameter $\eta = {n_{\rm p}^{(0)}(r)}/{n_{\rm e}^{(0)}(r)}$
is the Debye length; and the parameter $\eta = {n_{\rm p}^{(0)}(r)}/{n_{\rm e}^{(0)}(r)}$![]() , which is the ratio of positron density to electron density. The stability of the modes is discussed as a function of these two parameters.
, which is the ratio of positron density to electron density. The stability of the modes is discussed as a function of these two parameters.
In the limit where both of the parameters are small compared with unity, that is, the limit of a relatively cold pure electron plasma, the equilibrium $E\times B$![]() drift dominates over the curvature and gradient-B drifts. Consequently, the diocotron mode dominates over the interchange mode. The mode equation yields a necessary condition for instability in this limit, namely that $r^2 n_{e}^{(0)}$
drift dominates over the curvature and gradient-B drifts. Consequently, the diocotron mode dominates over the interchange mode. The mode equation yields a necessary condition for instability in this limit, namely that $r^2 n_{e}^{(0)}$![]() must be non-monotonic in radius $r$
must be non-monotonic in radius $r$![]() . This criterion is typically satisfied, given that the density is zero at the inner and outer cylindrical conductor but non-zero in between. An analytic solution to the mode equation was obtained for the special case where $r^2 n_{e}^{(0)}$
. This criterion is typically satisfied, given that the density is zero at the inner and outer cylindrical conductor but non-zero in between. An analytic solution to the mode equation was obtained for the special case where $r^2 n_{e}^{(0)}$![]() is a flat-top profile. In this case, the instability results from the linear interaction of a positive energy density perturbation and a negative energy density perturbation. The order of magnitude of the growth rates obtained is the drift frequency ${Ik}/{2{\rm \pi} c^2 q_{\rm e}n_{0{\rm e}}}$
is a flat-top profile. In this case, the instability results from the linear interaction of a positive energy density perturbation and a negative energy density perturbation. The order of magnitude of the growth rates obtained is the drift frequency ${Ik}/{2{\rm \pi} c^2 q_{\rm e}n_{0{\rm e}}}$![]() . When the parameter $k^2 \lambda _{\rm D}^2$
. When the parameter $k^2 \lambda _{\rm D}^2$![]() approaches unity the equilibrium curvature and gradient-B drifts become comparable to the $E \times B$
approaches unity the equilibrium curvature and gradient-B drifts become comparable to the $E \times B$![]() drift and stabilise the diocotron mode. The stabilisation is due to the spread in the drift velocities, rather than the existence of a drift velocity.
drift and stabilise the diocotron mode. The stabilisation is due to the spread in the drift velocities, rather than the existence of a drift velocity.
When $\eta =1$![]() , the pair plasma is neutral and there is no equilibrium $E \times B$
, the pair plasma is neutral and there is no equilibrium $E \times B$![]() drift and, hence, no diocotron mode. For finite $k^2 \lambda _{\rm D}^2$
drift and, hence, no diocotron mode. For finite $k^2 \lambda _{\rm D}^2$![]() we find an interchange mode with a maximum growth rate at $k^2 \lambda _{\rm D}^2 \approx 1$
we find an interchange mode with a maximum growth rate at $k^2 \lambda _{\rm D}^2 \approx 1$![]() . The curvature and gradient-B drifts play a central role in this mode. However, if the temperature or the wavenumber is large ($k^2 \lambda _{\rm D}^2 \gg 1$
. The curvature and gradient-B drifts play a central role in this mode. However, if the temperature or the wavenumber is large ($k^2 \lambda _{\rm D}^2 \gg 1$![]() ), the relative drift motion mitigates the formation of the mode structure. For sufficiently small $k^2 \lambda _{\rm D}^2$
), the relative drift motion mitigates the formation of the mode structure. For sufficiently small $k^2 \lambda _{\rm D}^2$![]() and $\eta =1$
and $\eta =1$![]() , the mode equation admits higher-order radial modes, although the fundamental always has the largest growth rate.
, the mode equation admits higher-order radial modes, although the fundamental always has the largest growth rate.
When the two parameters are intermediate in value, we found a competition between the two modes.
The goal of this and future work is to help understand upcoming measurements of density and potential fluctuations in electron plasmas in the APEX levitated dipole. The current experiment (Deller et al. Reference Deller, Bayer, Steinbrunner, Card, Danielson, Stoneking and Schoenberg2024) runs with a cold electron plasma ($\eta = 0,\ k^2\lambda _{\rm D}^2 \ll 0$![]() ). A persistent potential perturbation is observed that is likely to be an $m=1$
). A persistent potential perturbation is observed that is likely to be an $m=1$![]() diocotron mode with confinement times on the order of several minutes. Even if the plasma is unstable in the linear regime, the perturbation may saturate due to nonlinear effects which does not necessarily lead to a loss of confinement. In future experiments, the number of positrons will be increased gradually with the goal of reaching $\eta = 1$
diocotron mode with confinement times on the order of several minutes. Even if the plasma is unstable in the linear regime, the perturbation may saturate due to nonlinear effects which does not necessarily lead to a loss of confinement. In future experiments, the number of positrons will be increased gradually with the goal of reaching $\eta = 1$![]() . In this case we expect the interchange mode to dominate over the diocotron mode. For the interchange mode we will probably see a wavelength comparable to the Debye length ($k^2 \lambda _{\rm D}^2 = 1$
. In this case we expect the interchange mode to dominate over the diocotron mode. For the interchange mode we will probably see a wavelength comparable to the Debye length ($k^2 \lambda _{\rm D}^2 = 1$![]() ) since this is the fastest growing mode. Generally, the confinement properties of a non-neutral plasma exceed those of a neutral electron–ion plasma. It is the main goal of the APEX collaboration to explore the (confinement) properties of a pair plasma. The results presented here provide a starting point for analysing these upcoming experiments.
) since this is the fastest growing mode. Generally, the confinement properties of a non-neutral plasma exceed those of a neutral electron–ion plasma. It is the main goal of the APEX collaboration to explore the (confinement) properties of a pair plasma. The results presented here provide a starting point for analysing these upcoming experiments.
Acknowledgements
We thank M.R. Stoneking, A. Mishchenko, C.F. Driscoll, D.H.E. Dubin, P. Helander, R. Kleiber, A. Zocco and E. Stenson for many helpful discussions.
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Funding
This work has received support from the National Science Foundation (NSF) grant number Phy21-06332.
Declaration of interests
The authors report no conflict of interest.
Appendix A
Green's function $G(\xi, \xi ')$![]() is defined through the equation
is defined through the equation
and the boundary conditions that $G(\xi, \xi ')$![]() vanish on the inner and outer cylindrical conductors. Hence, $G(\xi, \xi ')$
vanish on the inner and outer cylindrical conductors. Hence, $G(\xi, \xi ')$![]() depends parametrically on $\xi _{\rm wire}$
depends parametrically on $\xi _{\rm wire}$![]() and $\xi _{\rm wall}$
and $\xi _{\rm wall}$![]() . To simplify the notation we leave this dependence implicit. We postulate a Green's function of the form
. To simplify the notation we leave this dependence implicit. We postulate a Green's function of the form

where $\alpha (\xi, \xi _{x}) = {I}_0(\xi ){K}_0(\xi _x) - {I}_0(\xi _x){K}_0(\xi )$![]() is a combination of modified Bessel functions. The proposed Green's function satisfies (A1) everywhere except at the delta function and satisfies the boundary conditions at the two conducting boundaries. The equation is satisfied at the delta function if the following two conditions are satisfied as well:
is a combination of modified Bessel functions. The proposed Green's function satisfies (A1) everywhere except at the delta function and satisfies the boundary conditions at the two conducting boundaries. The equation is satisfied at the delta function if the following two conditions are satisfied as well:
Using ${\partial \alpha (\xi ', \xi _{x})}/{\partial \xi } = {I}_1(\xi ){K}_0(\xi _x) + {I}_0(\xi _x){K}_1(\xi )$![]() as well as $\xi [{I}_1(\xi ){K}_0(\xi ) + {I}_0(\xi ){K}_1(\xi )] = 1$
as well as $\xi [{I}_1(\xi ){K}_0(\xi ) + {I}_0(\xi ){K}_1(\xi )] = 1$![]() and solving for $A$
and solving for $A$![]() and $B$
and $B$![]() yields Green's function
yields Green's function

Note that Green's function satisfies the expected relation $G(\xi, \xi ')=G(\xi ', \xi )$![]() .
.
Appendix B
In this appendix, we calculate the sign of the energy for the analytic solutions found in § 3.3. We first introduce the mode action $\Delta J$![]() and recall that the mode energy and mode axial momentum are related to the action through the relations $\Delta W = \omega \Delta J$
and recall that the mode energy and mode axial momentum are related to the action through the relations $\Delta W = \omega \Delta J$![]() and $\Delta P_z = k \Delta J$
and $\Delta P_z = k \Delta J$![]() . These relations imply a simple relation between the mode energy and mode momentum $\Delta W = \omega /k \Delta P_z$
. These relations imply a simple relation between the mode energy and mode momentum $\Delta W = \omega /k \Delta P_z$![]() (Landau & Lifshitz Reference Landau and Lifshitz1976). This relation is useful since it is easier to calculate $\Delta P_z$
(Landau & Lifshitz Reference Landau and Lifshitz1976). This relation is useful since it is easier to calculate $\Delta P_z$![]() than $\Delta W$
than $\Delta W$![]() . The momentum of the plasma is
. The momentum of the plasma is
expressed in terms of the reduced distribution function $h = \int {\rm d}p_{\theta } \,{\rm d}\mu f$![]() . As the wave grows, the plasma momentum changes by the amount
. As the wave grows, the plasma momentum changes by the amount
where $\Delta h(z, p_z, t) = h^{(1)}(z,p_z)+h^{(2)}(z,p_z)$![]() is the corresponding change in the particle distribution. The term $h^{(1)}(z,p_z )$
is the corresponding change in the particle distribution. The term $h^{(1)}(z,p_z )$![]() is first order in the mode potential and is sinusoidal in its z-dependence. This term is removed by the z-integral. The second-order terms are characterised by wavenumber $k+k=2k$
is first order in the mode potential and is sinusoidal in its z-dependence. This term is removed by the z-integral. The second-order terms are characterised by wavenumber $k+k=2k$![]() and $k-k=0$
and $k-k=0$![]() . The term characterised by $2k$
. The term characterised by $2k$![]() also vanishes when integrating over $z$
also vanishes when integrating over $z$![]() . The only relevant term is the one with $k=0$
. The only relevant term is the one with $k=0$![]() . This term is given by a quasi-linear second-order perturbation theory (Davidson Reference Davidson2001)
. This term is given by a quasi-linear second-order perturbation theory (Davidson Reference Davidson2001)
Using the fact that ${\partial h^{(0)}}/{\partial p_z}$![]() is the sum of two delta functions and integrating by parts yields the expression
is the sum of two delta functions and integrating by parts yields the expression
where $L = \int {\rm d}z$![]() is the plasma length. The energy of the mode is then given by the expression
is the plasma length. The energy of the mode is then given by the expression
If the frequencies are both positive, the energy associated with density perturbation $C_{\rm in}$![]() has positive energy and the second mode density perturbation $C_{\rm out}$
has positive energy and the second mode density perturbation $C_{\rm out}$![]() has negative energy.
has negative energy.
Appendix C
We want to exclude the effect of a spread in the drift velocities that comes with a Maxwellian velocity distribution. Let us assume a distribution function of the form $f_j^{(0)} = g(p_{zj})\delta (v_{\parallel }-v_{\parallel 0})\delta (v^2_{\perp }-v^2_{\perp 0})$![]() . In order to derive the corresponding mode equation, we first evaluate the following integral
. In order to derive the corresponding mode equation, we first evaluate the following integral

where we have used integration by parts to evaluate the derivative of the delta distribution and used the relations ${\partial x_{\parallel }}/{\partial p_{zj}} = {c^2x_{\parallel }}/{2Iq_j}$![]() and ${\partial x^2_{\perp }}/{\partial p_{zj}} = {c^2x^2_{\perp }}/{2Iq_j}$
and ${\partial x^2_{\perp }}/{\partial p_{zj}} = {c^2x^2_{\perp }}/{2Iq_j}$![]() . We define the scaled velocities as $x_{\parallel } = \sqrt {{m}/{W}} \, v_{\parallel }$
. We define the scaled velocities as $x_{\parallel } = \sqrt {{m}/{W}} \, v_{\parallel }$![]() and $x_{\perp } = \sqrt {{m}/{W}} \,v_{\perp }$
and $x_{\perp } = \sqrt {{m}/{W}} \,v_{\perp }$![]() with the total kinetic energy $W$
with the total kinetic energy $W$![]() . In the following, we set $W_{\perp } = W_{\parallel } = W/2$
. In the following, we set $W_{\perp } = W_{\parallel } = W/2$![]() such that $x_{\parallel 0} = x_{\perp 0} = 1$
such that $x_{\parallel 0} = x_{\perp 0} = 1$![]() . For a direct comparison with previous results we define the characteristic length scale $\hat {\lambda }_{\rm D} = \sqrt {W/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$
. For a direct comparison with previous results we define the characteristic length scale $\hat {\lambda }_{\rm D} = \sqrt {W/4{\rm \pi} q_{\rm e}^2 n_{0{\rm e}}}$![]() which replaces the Debye length. Substituting this result in the mode equation (2.16) and expressing it in dimensionless form yields the mode equation
which replaces the Debye length. Substituting this result in the mode equation (2.16) and expressing it in dimensionless form yields the mode equation

where $\tilde {\varOmega }_{\pm } = \varOmega \pm k^2\hat {\lambda }_{\rm D}^2({x_{\perp 0}^2}/{2}+x_{\parallel 0}^2)$![]() is the mode frequency, Doppler shifted by the curvature and gradient-B drift. Integrating the distribution function over velocity space gives us the number density $n^{(0)}_j(r) = |q_j|({\sqrt {m}\hat {T}^{3/2}}/{2c}) g(p_{zj})$
is the mode frequency, Doppler shifted by the curvature and gradient-B drift. Integrating the distribution function over velocity space gives us the number density $n^{(0)}_j(r) = |q_j|({\sqrt {m}\hat {T}^{3/2}}/{2c}) g(p_{zj})$![]() . In the limit of a pure electron plasma ($\eta = 0$
. In the limit of a pure electron plasma ($\eta = 0$![]() ) we obtain
) we obtain

In the cold limit $k^2\hat {\lambda }_{\rm D}^2 = 0$![]() the mode equation reduces to the result we obtained in (3.2). For a quasi-neutral pair plasma the mode equation becomes
the mode equation reduces to the result we obtained in (3.2). For a quasi-neutral pair plasma the mode equation becomes

The resulting growth rate does not show any stabilisation with increasing $k^2\hat {\lambda }_{\rm D}^2$![]() .
.