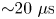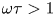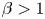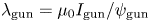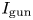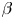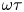1. Introduction
Weakly collisional plasmas (particle mean free paths ![]() $\lesssim$ system size) with ratio of thermal-to-magnetic pressure
$\lesssim$ system size) with ratio of thermal-to-magnetic pressure ![]() $\beta >1$ and, simultaneously, Hall magnetization parameter
$\beta >1$ and, simultaneously, Hall magnetization parameter ![]() $\omega \tau >1$ (i.e., gyro-frequency greater than collision frequency), represent a frontier regime of laboratory plasma physics research. By contrast, magnetically confined plasmas typically have
$\omega \tau >1$ (i.e., gyro-frequency greater than collision frequency), represent a frontier regime of laboratory plasma physics research. By contrast, magnetically confined plasmas typically have ![]() $\beta \ll 1$ and
$\beta \ll 1$ and ![]() $\omega \tau \gg 1$, whereas inertially confined and high-energy-density plasmas typically have
$\omega \tau \gg 1$, whereas inertially confined and high-energy-density plasmas typically have ![]() $\beta \gg 1$ and
$\beta \gg 1$ and ![]() $\omega \tau \ll 1$. If plasmas with both
$\omega \tau \ll 1$. If plasmas with both ![]() $\beta ,\omega \tau >1$ can be formed successfully, an interesting next step will be to attempt to generate small-scale, tangled magnetic field with connection length much longer than the characteristic scale size of the plasma. This paper focuses on the first step of forming and characterizing a transient plasma with both
$\beta ,\omega \tau >1$ can be formed successfully, an interesting next step will be to attempt to generate small-scale, tangled magnetic field with connection length much longer than the characteristic scale size of the plasma. This paper focuses on the first step of forming and characterizing a transient plasma with both ![]() $\beta >1$ and
$\beta >1$ and ![]() $\omega \tau >1$ in a laboratory setting.
$\omega \tau >1$ in a laboratory setting.
One motivation for this work is to help establish a new laboratory platform to study the fundamental physics of weakly collisional, magnetized, high-![]() $\beta$ plasmas (Kunz et al. Reference Kunz, Squire, Balbus, Bale, Chen, Churazov, Cowley, Forest, Gammie and Quataert2020) as a foundational aspect of the scientific discipline of plasma physics. These types of plasmas, while ubiquitous in the universe, are poorly understood in terms of their basic stability and transport properties (Chandran & Cowley Reference Chandran and Cowley1998; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008), on both macroscales and microscales. A better predictive understanding of the behaviour of these types of plasmas could potentially shed light on the dynamics and evolution of magnetohydrodynamic (MHD) turbulence (Schekochihin & Cowley Reference Schekochihin and Cowley2007; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) and magnetostatic turbulence (Ryutov & Remington Reference Ryutov and Remington2002; Ryutov et al. Reference Ryutov, Kane, Mizuta, Pound and Remington2004), which are fundamentally different compared with the drift-wave turbulence of low-
$\beta$ plasmas (Kunz et al. Reference Kunz, Squire, Balbus, Bale, Chen, Churazov, Cowley, Forest, Gammie and Quataert2020) as a foundational aspect of the scientific discipline of plasma physics. These types of plasmas, while ubiquitous in the universe, are poorly understood in terms of their basic stability and transport properties (Chandran & Cowley Reference Chandran and Cowley1998; Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008), on both macroscales and microscales. A better predictive understanding of the behaviour of these types of plasmas could potentially shed light on the dynamics and evolution of magnetohydrodynamic (MHD) turbulence (Schekochihin & Cowley Reference Schekochihin and Cowley2007; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009) and magnetostatic turbulence (Ryutov & Remington Reference Ryutov and Remington2002; Ryutov et al. Reference Ryutov, Kane, Mizuta, Pound and Remington2004), which are fundamentally different compared with the drift-wave turbulence of low-![]() $\beta$, magnetically confined plasmas; on astrophysical systems such as accretion flows around black holes (Balbus & Hawley Reference Balbus and Hawley1998), the intracluster medium (known as ICM) within galaxy clusters (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005; Peterson & Fabian Reference Peterson and Fabian2006), the interstellar medium where large-scale structures form (Scalo & Elmegreen Reference Scalo and Elmegreen2004; McKee & Ostriker Reference McKee and Ostriker2007), stellar/solar winds (Bruno & Carbone Reference Bruno and Carbone2013) and on outstanding cosmological questions such as the origin (magnetogenesis) and amplification (dynamo) of magnetic fields (Kulsrud & Zweibel Reference Kulsrud and Zweibel2008). In these systems, although the magnetic pressure is significantly less than the plasma thermal pressure, the magnetic fields can still influence plasma dynamics.
$\beta$, magnetically confined plasmas; on astrophysical systems such as accretion flows around black holes (Balbus & Hawley Reference Balbus and Hawley1998), the intracluster medium (known as ICM) within galaxy clusters (Schekochihin et al. Reference Schekochihin, Cowley, Kulsrud, Hammett and Sharma2005; Peterson & Fabian Reference Peterson and Fabian2006), the interstellar medium where large-scale structures form (Scalo & Elmegreen Reference Scalo and Elmegreen2004; McKee & Ostriker Reference McKee and Ostriker2007), stellar/solar winds (Bruno & Carbone Reference Bruno and Carbone2013) and on outstanding cosmological questions such as the origin (magnetogenesis) and amplification (dynamo) of magnetic fields (Kulsrud & Zweibel Reference Kulsrud and Zweibel2008). In these systems, although the magnetic pressure is significantly less than the plasma thermal pressure, the magnetic fields can still influence plasma dynamics.
A second motivation for this work is to discover how to form a novel, magnetized, ![]() $\beta >1$ target plasma for magneto-inertial fusion (MIF), also known as magnetized target fusion (known as MTF) (Kirkpatrick, Lindemuth & Ward Reference Kirkpatrick, Lindemuth and Ward1995; Lindemuth & Siemon Reference Lindemuth and Siemon2009). Magneto-inertial fusion is a class of pulsed fusion approaches, where a liner compresses a magnetized target plasma, in which the magnetic field reduces thermal transport and enhances fusion-charged-product (e.g.
$\beta >1$ target plasma for magneto-inertial fusion (MIF), also known as magnetized target fusion (known as MTF) (Kirkpatrick, Lindemuth & Ward Reference Kirkpatrick, Lindemuth and Ward1995; Lindemuth & Siemon Reference Lindemuth and Siemon2009). Magneto-inertial fusion is a class of pulsed fusion approaches, where a liner compresses a magnetized target plasma, in which the magnetic field reduces thermal transport and enhances fusion-charged-product (e.g. ![]() $\alpha$ particles) energy deposition within the plasma fuel. Many MIF efforts over several decades have focused on the use of
$\alpha$ particles) energy deposition within the plasma fuel. Many MIF efforts over several decades have focused on the use of ![]() $\beta \leq 1$ plasmas, e.g. spheromaks (Bellan Reference Bellan2000) and field-reversed configurations (FRC) (Steinhauer Reference Steinhauer2011), as the target plasma for subsequent liner compression. However, these
$\beta \leq 1$ plasmas, e.g. spheromaks (Bellan Reference Bellan2000) and field-reversed configurations (FRC) (Steinhauer Reference Steinhauer2011), as the target plasma for subsequent liner compression. However, these ![]() $\beta \leq 1$ plasmas suffer from MHD instabilities that have precluded the attainment of robust fusion conditions. This has motivated the consideration of magnetized plasmas that can avoid MHD instabilities while still benefitting from magnetic thermal insulation (Ryutov Reference Ryutov2009; Hsu & Langendorf Reference Hsu and Langendorf2019), which could potentially be enabled by the
$\beta \leq 1$ plasmas suffer from MHD instabilities that have precluded the attainment of robust fusion conditions. This has motivated the consideration of magnetized plasmas that can avoid MHD instabilities while still benefitting from magnetic thermal insulation (Ryutov Reference Ryutov2009; Hsu & Langendorf Reference Hsu and Langendorf2019), which could potentially be enabled by the ![]() $\beta ,\omega \tau >1$ regime. The lifetime of a
$\beta ,\omega \tau >1$ regime. The lifetime of a ![]() $\beta >1$ plasma target will be limited largely by hydrodynamic expansion rather than MHD instability growth, and thus fast liner compression is required, which has been demonstrated successfully in magnetized liner inertial fusion (known as MagLIF) (Slutz et al. Reference Slutz, Herrmann, Vesey, Sefkow, Sinars, Rovang, Peterson and Cuneo2010; Gomez et al. Reference Gomez, Slutz, Sefkow, Sinars, Hahn, Hansen, Harding, Knapp, Schmit and Jennings2014) and is the aim of plasma-jet-driven MIF (known as PJMIF) (Thio et al. Reference Thio, Panarella, Kirkpatrick, Knapp, Wysocki, Parks and Schmidt1999; Hsu et al. Reference Hsu, Awe, Brockington, Case, Cassibry, Kagan, Messer, Stanic, Tang and Welch2012a; Thio et al. Reference Thio, Hsu, Witherspoon, Cruz, Case, Langendorf, Yates, Dunn, Cassibry and Samulyak2019). The present work is a first step toward determining the viability of forming potential magnetized target plasmas with
$\beta >1$ plasma target will be limited largely by hydrodynamic expansion rather than MHD instability growth, and thus fast liner compression is required, which has been demonstrated successfully in magnetized liner inertial fusion (known as MagLIF) (Slutz et al. Reference Slutz, Herrmann, Vesey, Sefkow, Sinars, Rovang, Peterson and Cuneo2010; Gomez et al. Reference Gomez, Slutz, Sefkow, Sinars, Hahn, Hansen, Harding, Knapp, Schmit and Jennings2014) and is the aim of plasma-jet-driven MIF (known as PJMIF) (Thio et al. Reference Thio, Panarella, Kirkpatrick, Knapp, Wysocki, Parks and Schmidt1999; Hsu et al. Reference Hsu, Awe, Brockington, Case, Cassibry, Kagan, Messer, Stanic, Tang and Welch2012a; Thio et al. Reference Thio, Hsu, Witherspoon, Cruz, Case, Langendorf, Yates, Dunn, Cassibry and Samulyak2019). The present work is a first step toward determining the viability of forming potential magnetized target plasmas with ![]() $\beta ,\omega \tau > 1$ that may be suitable for subsequent, fast liner compression.
$\beta ,\omega \tau > 1$ that may be suitable for subsequent, fast liner compression.
In this work, performing experiments on the Big Red Ball (BRB) (Forest et al. Reference Forest, Flanagan, Brookhart, Clark, Cooper, Désangles, Egedal, Endrizzi, Khalzov and Li2015) at the Wisconsin Plasma Physics Laboratory (WiPPL), we launch and merge two ![]() $\beta \sim 1$ plasmas to transiently create
$\beta \sim 1$ plasmas to transiently create ![]() $\beta ,\omega \tau >1$ conditions for
$\beta ,\omega \tau >1$ conditions for ![]() ${\sim }20\ \mathrm {\mu }\textrm {s}$, and experimentally measure the plasma parameters in both the individual and merged plasmas. Compared with individual plasmas, the head-on collisions (i) increase the duration for which the desired plasma state exists at a particular location and (ii) increase the magnitudes of the density and radial and toroidal magnetic field components, which widens the parameter space compared with that achievable with individual plasmas. The transient nature is unavoidable for
${\sim }20\ \mathrm {\mu }\textrm {s}$, and experimentally measure the plasma parameters in both the individual and merged plasmas. Compared with individual plasmas, the head-on collisions (i) increase the duration for which the desired plasma state exists at a particular location and (ii) increase the magnitudes of the density and radial and toroidal magnetic field components, which widens the parameter space compared with that achievable with individual plasmas. The transient nature is unavoidable for ![]() $\beta > 1$ plasmas unless they are wall confined, which would bring in complications including plasma–wall interactions and impurities. Our plasma-formation approach is analogous to many prior studies that generated
$\beta > 1$ plasmas unless they are wall confined, which would bring in complications including plasma–wall interactions and impurities. Our plasma-formation approach is analogous to many prior studies that generated ![]() $\beta < 1$ spheromaks using magnetized coaxial guns (Bellan Reference Bellan2000) and the merging/collision of two
$\beta < 1$ spheromaks using magnetized coaxial guns (Bellan Reference Bellan2000) and the merging/collision of two ![]() $\beta < 1$ compact toroids, e.g. spheromaks (Bellan Reference Bellan2000) or field reversed configurations (FRC) (Steinhauer Reference Steinhauer2011), for magnetic-reconnection studies (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990; Ono et al. Reference Ono, Inomoto, Ueda, Matsuyama and Okazaki1999; Cothran et al. Reference Cothran, Falk, Fefferman, Landreman, Brown and Schaffer2003) and fusion concept exploration (Guo et al. Reference Guo, Binderbauer, Barnes, Putvinski, Rostoker, Sevier, Tuszewski, Anderson, Andow and Bonelli2011; Slough, Votroubek & Pihl Reference Slough, Votroubek and Pihl2011). To access various portions of the
$\beta < 1$ compact toroids, e.g. spheromaks (Bellan Reference Bellan2000) or field reversed configurations (FRC) (Steinhauer Reference Steinhauer2011), for magnetic-reconnection studies (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990; Ono et al. Reference Ono, Inomoto, Ueda, Matsuyama and Okazaki1999; Cothran et al. Reference Cothran, Falk, Fefferman, Landreman, Brown and Schaffer2003) and fusion concept exploration (Guo et al. Reference Guo, Binderbauer, Barnes, Putvinski, Rostoker, Sevier, Tuszewski, Anderson, Andow and Bonelli2011; Slough, Votroubek & Pihl Reference Slough, Votroubek and Pihl2011). To access various portions of the ![]() $\beta$,
$\beta$, ![]() $\omega \tau$ parameter space, we tune the experimentally adjustable parameter
$\omega \tau$ parameter space, we tune the experimentally adjustable parameter ![]() $\lambda _{\textrm {gun}} = \mu _0 I_{\textrm {gun}}/\psi _{\textrm {gun}}$, where
$\lambda _{\textrm {gun}} = \mu _0 I_{\textrm {gun}}/\psi _{\textrm {gun}}$, where ![]() $I_{\textrm {gun}}$ is the peak gun electrical current and
$I_{\textrm {gun}}$ is the peak gun electrical current and ![]() $\psi _{\textrm {gun}}$ is the applied vacuum poloidal magnetic flux linking the gun electrodes (Yee & Bellan Reference Yee and Bellan2000; Hsu & Bellan Reference Hsu and Bellan2005). Engineering improvements to our plasma injectors are presently underway to improve reliability and reproducibility of plasma formation.
$\psi _{\textrm {gun}}$ is the applied vacuum poloidal magnetic flux linking the gun electrodes (Yee & Bellan Reference Yee and Bellan2000; Hsu & Bellan Reference Hsu and Bellan2005). Engineering improvements to our plasma injectors are presently underway to improve reliability and reproducibility of plasma formation.
The paper is organized as follows. Section 2 provides background information on the scaling of ![]() $\beta$ and
$\beta$ and ![]() $\omega \tau$ and the plasma-formation process. Section 3 describes the experimental set-up and diagnostics. Section 4 presents experimental results for individual and merged plasmas. Section 5 discusses future work. Section 6 provides conclusions.
$\omega \tau$ and the plasma-formation process. Section 3 describes the experimental set-up and diagnostics. Section 4 presents experimental results for individual and merged plasmas. Section 5 discusses future work. Section 6 provides conclusions.
2. Background
In this section, we provide background information that further motivates this work and helps with understanding the experimental set-up, methods and the results presented later in the paper.
2.1. Plasma parameters
In this subsection, we describe the plasma parameters needed to achieve ![]() $\beta ,\omega \tau >1$ simultaneously. The definition of
$\beta ,\omega \tau >1$ simultaneously. The definition of ![]() $\beta$ is
$\beta$ is
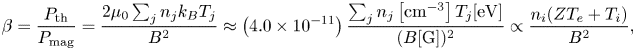 \begin{align} \beta = \frac{P_{\textrm{th}}}{P_{\textrm{mag}}} = \frac{2 \mu_{0} \sum_{j} n_{j} k_B T_{j} }{B^{2}} \approx \left(4.0 \times 10^{-11}\right) \frac{\sum_{j} n_{j}\left[\mathrm{cm}^{-3}\right] T_{j}[\mathrm{eV}] }{(B[\mathrm{G}])^2} \propto \frac{n_i (ZT_{e} + T_{i}) }{B^{2}}, \end{align}
\begin{align} \beta = \frac{P_{\textrm{th}}}{P_{\textrm{mag}}} = \frac{2 \mu_{0} \sum_{j} n_{j} k_B T_{j} }{B^{2}} \approx \left(4.0 \times 10^{-11}\right) \frac{\sum_{j} n_{j}\left[\mathrm{cm}^{-3}\right] T_{j}[\mathrm{eV}] }{(B[\mathrm{G}])^2} \propto \frac{n_i (ZT_{e} + T_{i}) }{B^{2}}, \end{align}
where ![]() $P_{\textrm {th}}$ is the plasma thermal pressure,
$P_{\textrm {th}}$ is the plasma thermal pressure, ![]() $P_{\textrm {mag}}$ the magnetic pressure,
$P_{\textrm {mag}}$ the magnetic pressure, ![]() $\mu _{0}$ the vacuum permeability,
$\mu _{0}$ the vacuum permeability, ![]() $n_{j}$ the ion or electron density (
$n_{j}$ the ion or electron density (![]() $j=i,e$),
$j=i,e$), ![]() $k_{B}$ the Boltzmann constant,
$k_{B}$ the Boltzmann constant, ![]() $T_{j}$ the ion or electron temperature,
$T_{j}$ the ion or electron temperature, ![]() $B$ the magnetic field strength and
$B$ the magnetic field strength and ![]() $Z$ the mean ion charge state. A thermal-pressure-dominated plasma has
$Z$ the mean ion charge state. A thermal-pressure-dominated plasma has ![]() $\beta > 1$. The definitions of the ion and electron Hall magnetization parameters,
$\beta > 1$. The definitions of the ion and electron Hall magnetization parameters, ![]() $\omega _i \tau _i$ and
$\omega _i \tau _i$ and ![]() $\omega _e \tau _e$, respectively, are
$\omega _e \tau _e$, respectively, are
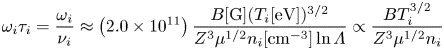 \begin{equation} \omega_{i}\tau_{i} = \frac{\omega_{i}}{\nu_{i}} \approx \left(2.0 \times 10^{11}\right) \frac{B[\mathrm{G}] (T_{i}[\mathrm{eV}])^{3/2}}{Z^{3} \mu^{1/2} n_{i}[\mathrm{cm}^{-3}] \ln{\varLambda}} \propto \frac{B T_{i}^{3/2}}{Z^3\mu^{1/2}n_i} \end{equation}
\begin{equation} \omega_{i}\tau_{i} = \frac{\omega_{i}}{\nu_{i}} \approx \left(2.0 \times 10^{11}\right) \frac{B[\mathrm{G}] (T_{i}[\mathrm{eV}])^{3/2}}{Z^{3} \mu^{1/2} n_{i}[\mathrm{cm}^{-3}] \ln{\varLambda}} \propto \frac{B T_{i}^{3/2}}{Z^3\mu^{1/2}n_i} \end{equation}and
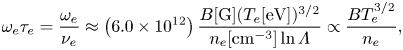 \begin{equation} \omega_{e}\tau_{e} =\frac{\omega_{e}}{\nu_e} \approx \left(6.0 \times 10^{12}\right) \frac{B[\mathrm{G}] (T_{e}[\mathrm{eV}])^{3/2}}{n_{e}[\mathrm{cm}^{-3}] \ln{\varLambda}} \propto \frac{B T_{e}^{3/2}}{n_e}, \end{equation}
\begin{equation} \omega_{e}\tau_{e} =\frac{\omega_{e}}{\nu_e} \approx \left(6.0 \times 10^{12}\right) \frac{B[\mathrm{G}] (T_{e}[\mathrm{eV}])^{3/2}}{n_{e}[\mathrm{cm}^{-3}] \ln{\varLambda}} \propto \frac{B T_{e}^{3/2}}{n_e}, \end{equation}
where ![]() $\omega _{i,e}$ are the ion and electron gyrofrequencies,
$\omega _{i,e}$ are the ion and electron gyrofrequencies, ![]() $\tau _{i,e}$ the ion and electron collision times,
$\tau _{i,e}$ the ion and electron collision times, ![]() $\nu _{i,e}$ the ion and electron collision rates,
$\nu _{i,e}$ the ion and electron collision rates, ![]() $\mu$ the atomic mass number and
$\mu$ the atomic mass number and ![]() $\ln {\varLambda } \approx 10$ the Coulomb logarithm. The condition
$\ln {\varLambda } \approx 10$ the Coulomb logarithm. The condition ![]() $\omega _{i}\tau _{i}>1$ is usually more stringent than
$\omega _{i}\tau _{i}>1$ is usually more stringent than ![]() $\omega _{e}\tau _{e}>1$.
$\omega _{e}\tau _{e}>1$.
Figure 1 illustrates contours of ![]() $\beta$,
$\beta$,![]() $\omega _{i}\tau _{i}=0.1, 1$ and 10 as a function of
$\omega _{i}\tau _{i}=0.1, 1$ and 10 as a function of ![]() $n$,
$n$, ![]() $T$ and
$T$ and ![]() $B$, assuming that
$B$, assuming that ![]() $n=n_i=n_e$ (and therefore
$n=n_i=n_e$ (and therefore ![]() $Z=1$),
$Z=1$), ![]() $T=T_{i} = T_{e}$ and
$T=T_{i} = T_{e}$ and ![]() $\mu =$ 1. The shaded regions in the plots denote the parameter spaces where
$\mu =$ 1. The shaded regions in the plots denote the parameter spaces where ![]() $\beta , \omega _i\tau _i >1$. Because
$\beta , \omega _i\tau _i >1$. Because ![]() $n$ is in the numerator of
$n$ is in the numerator of ![]() $\beta$ and denominator of
$\beta$ and denominator of ![]() $\omega \tau$, and vice versa for
$\omega \tau$, and vice versa for ![]() $B$, in general there are only limited ranges and combinations of
$B$, in general there are only limited ranges and combinations of ![]() $n$,
$n$, ![]() $T$ and
$T$ and ![]() $B$ for which
$B$ for which ![]() $\beta$ and
$\beta$ and ![]() $\omega \tau$ can be simultaneously greater than unity. In general, higher
$\omega \tau$ can be simultaneously greater than unity. In general, higher ![]() $T$ helps because
$T$ helps because ![]() $T$ is in the numerator for both
$T$ is in the numerator for both ![]() $\beta$ and
$\beta$ and ![]() $\omega \tau$. Additionally in figure 1, we plot the ratio of the ion cyclotron radius
$\omega \tau$. Additionally in figure 1, we plot the ratio of the ion cyclotron radius ![]() $\rho _{ci} \propto T_{i}^{1/2}/B$ to the characteristic plasma radius
$\rho _{ci} \propto T_{i}^{1/2}/B$ to the characteristic plasma radius ![]() $L_{0} = R = 30\ \textrm {cm}$, here. The dashed arrow shows the region in parameter space for which the characteristic plasma radius is larger than the ion cyclotron radius,
$L_{0} = R = 30\ \textrm {cm}$, here. The dashed arrow shows the region in parameter space for which the characteristic plasma radius is larger than the ion cyclotron radius, ![]() $\rho _{ci}/L_{0} < 1$. The dots in the plots denote approximately the values obtained experimentally in this research.
$\rho _{ci}/L_{0} < 1$. The dots in the plots denote approximately the values obtained experimentally in this research.
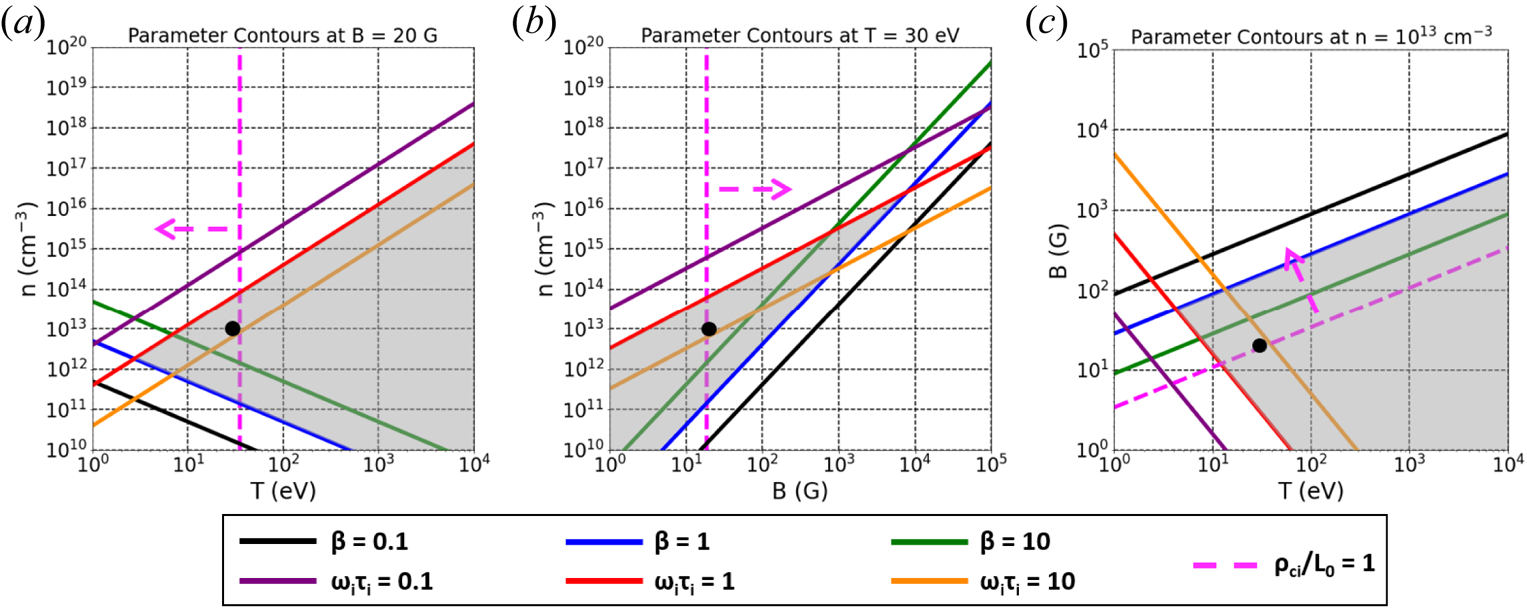
Figure 1. Contours of ![]() $\beta$,
$\beta$, ![]() $\omega _{i}\tau _{i}$ and
$\omega _{i}\tau _{i}$ and ![]() $\rho _{ci}/L_{0}$ in the (a)
$\rho _{ci}/L_{0}$ in the (a) ![]() $n$–
$n$–![]() $T$ plane at constant
$T$ plane at constant ![]() $B = 20\ \textrm {G}$, (b)
$B = 20\ \textrm {G}$, (b) ![]() $n$–
$n$–![]() $B$ plane at constant
$B$ plane at constant ![]() $T=T_{i} = T_{e} = 30\ \textrm {eV}$ and (c)
$T=T_{i} = T_{e} = 30\ \textrm {eV}$ and (c) ![]() $B$–
$B$–![]() $T$ plane at constant
$T$ plane at constant ![]() $n=n_{i} = n_{e} = 10^{13}\ \textrm {cm}^{-3}$. The shaded regions correspond to the desired regime of
$n=n_{i} = n_{e} = 10^{13}\ \textrm {cm}^{-3}$. The shaded regions correspond to the desired regime of ![]() $\beta , \omega \tau >1$. The dashed arrows show the regime for which
$\beta , \omega \tau >1$. The dashed arrows show the regime for which ![]() $\rho _{ci}/L_{0} < 1$, with
$\rho _{ci}/L_{0} < 1$, with ![]() $L_{0} = 30\ \textrm {cm}$. The dots correspond to the approximate values obtained in the present research.
$L_{0} = 30\ \textrm {cm}$. The dots correspond to the approximate values obtained in the present research.
2.2. Plasma formation
In this subsection, we describe the plasma-formation method and insights derived from previous work that we exploit to achieve the objectives of the present research. It has long been known that compact-toroid plasmas, i.e. spheromaks and FRCs, are formed in the ![]() $\beta \leq 1$,
$\beta \leq 1$, ![]() $\omega \tau >1$ regime, where the thermal pressure is confined by an equal or larger magnetic pressure.
$\omega \tau >1$ regime, where the thermal pressure is confined by an equal or larger magnetic pressure.
Spheromak and spheromak-like plasmas can be created using magnetized plasma guns with coaxial, cylindrical electrodes in the presence of an applied ‘bias’ poloidal magnetic flux ![]() $\psi _{\textrm {gun}} = \int B_{\textrm {pol}} \cdot \textrm {d}A$ linking the two electrodes (see figure 2). Electrical current
$\psi _{\textrm {gun}} = \int B_{\textrm {pol}} \cdot \textrm {d}A$ linking the two electrodes (see figure 2). Electrical current ![]() $I_{\textrm {gun}}$ in the electrodes (
$I_{\textrm {gun}}$ in the electrodes (![]() $z$ direction) and in the plasma (
$z$ direction) and in the plasma (![]() $r$ direction) that forms between the electrodes generates a toroidal magnetic field (
$r$ direction) that forms between the electrodes generates a toroidal magnetic field (![]() $B_{\textrm {tor}}$, in the
$B_{\textrm {tor}}$, in the ![]() $\phi$ direction), and the associated magnetic pressure accelerates the plasma out of the electrodes (
$\phi$ direction), and the associated magnetic pressure accelerates the plasma out of the electrodes (![]() $z$ direction). The moving plasma advects the poloidal bias magnetic field (
$z$ direction). The moving plasma advects the poloidal bias magnetic field (![]() $B_{\textrm {pol}}$, in the
$B_{\textrm {pol}}$, in the ![]() $r$–
$r$–![]() $z$ plane). Depending on the values of
$z$ plane). Depending on the values of ![]() $I_{\textrm {gun}}$ and
$I_{\textrm {gun}}$ and ![]() $\psi _{\textrm {gun}}$, the magnetic field lines associated with the plasma can reconnect and detach from the electrodes as the plasma propagates out of the gun. The resulting plasma has both (i)
$\psi _{\textrm {gun}}$, the magnetic field lines associated with the plasma can reconnect and detach from the electrodes as the plasma propagates out of the gun. The resulting plasma has both (i) ![]() $B_{\textrm {pol}}$ associated with toroidal currents and (ii)
$B_{\textrm {pol}}$ associated with toroidal currents and (ii) ![]() $B_{\textrm {tor}}$ associated with poloidal currents. The relative values of magnetic field, density and temperature in the plasma, and their evolution, determine the values of
$B_{\textrm {tor}}$ associated with poloidal currents. The relative values of magnetic field, density and temperature in the plasma, and their evolution, determine the values of ![]() $\beta$ and
$\beta$ and ![]() $\omega \tau$. For
$\omega \tau$. For ![]() $\beta > 1$, the magnetic field is not large enough to create an equilibrium with the plasma thermal pressure, so
$\beta > 1$, the magnetic field is not large enough to create an equilibrium with the plasma thermal pressure, so ![]() $\beta >1$ plasmas will exist only transiently.
$\beta >1$ plasmas will exist only transiently.
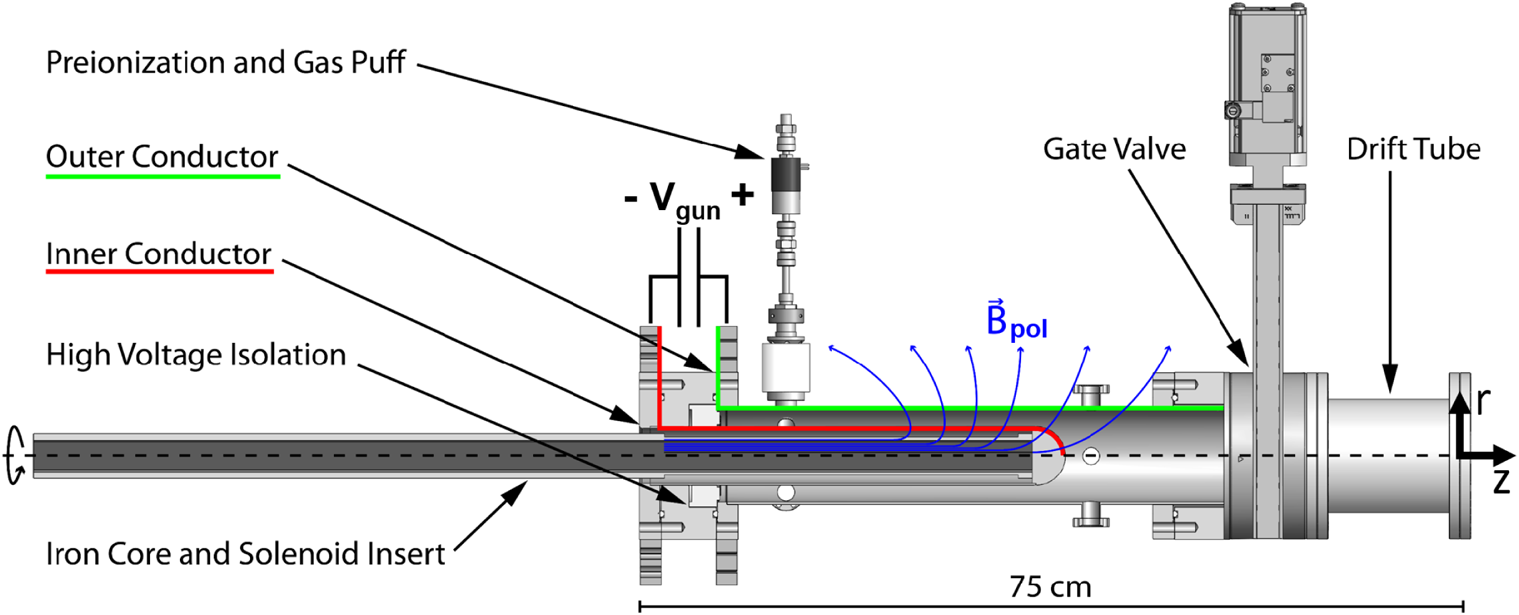
Figure 2. Diagram of a plasma gun/injector used in this research, showing the coordinate system, inner (cathode, red) and outer (anode, green) electrodes, and solenoid and iron core that generate the bias poloidal magnetic flux (blue). Gas is injected between the electrodes and preionized using a separate ‘washer gun’ system (Fiksel et al. Reference Fiksel, Almagri, Craig, Iida, Prager and Sarff1996). Finally, a discharge with gun voltage ![]() $V_{\textrm {gun}}$ between the electrodes accelerates the plasma out of the injector in the
$V_{\textrm {gun}}$ between the electrodes accelerates the plasma out of the injector in the ![]() $z$ direction.
$z$ direction.
The ![]() $\lambda _{\textrm {gun}}$ parameter,
$\lambda _{\textrm {gun}}$ parameter,
determines whether a spheromak forms (Bellan Reference Bellan2000; Yee & Bellan Reference Yee and Bellan2000; Hsu & Bellan Reference Hsu and Bellan2005). A spheromak (![]() $\beta < 1$,
$\beta < 1$, ![]() $\omega \tau >1$) will be formed under the condition (Bellan Reference Bellan2000)
$\omega \tau >1$) will be formed under the condition (Bellan Reference Bellan2000)
where 3.83 is the first root of the Bessel function of the first kind ![]() $J_{1}(x)$, and
$J_{1}(x)$, and ![]() $r_{\textrm {gun}}$ is the characteristic size (e.g. inner radius of the outer gun electrode). On the other hand, a plasma jet with rapidly decaying magnetic flux is formed when
$r_{\textrm {gun}}$ is the characteristic size (e.g. inner radius of the outer gun electrode). On the other hand, a plasma jet with rapidly decaying magnetic flux is formed when ![]() $\psi _{\textrm {gun}} = 0$ and
$\psi _{\textrm {gun}} = 0$ and ![]() $\lambda _{\textrm {gun}}=\infty$ (Hsu et al. Reference Hsu, Merritt, Moser, Awe, Brockington, Davis, Adams, Case, Cassibry and Dunn2012b; Merritt et al. Reference Merritt, Moser, Hsu, Adams, Dunn, Holgado and Gilmore2014), resulting in a plasma with
$\lambda _{\textrm {gun}}=\infty$ (Hsu et al. Reference Hsu, Merritt, Moser, Awe, Brockington, Davis, Adams, Case, Cassibry and Dunn2012b; Merritt et al. Reference Merritt, Moser, Hsu, Adams, Dunn, Holgado and Gilmore2014), resulting in a plasma with ![]() $\beta \gg 1$ and
$\beta \gg 1$ and ![]() $\omega \tau \ll 1$ after a few resistive decay times of the magnetic flux (of the order of several
$\omega \tau \ll 1$ after a few resistive decay times of the magnetic flux (of the order of several ![]() $\mathrm {\mu }\textrm {s}$). Given these two bracketing conditions, it is intuitive to expect that a plasma with both
$\mathrm {\mu }\textrm {s}$). Given these two bracketing conditions, it is intuitive to expect that a plasma with both ![]() $\beta ,\omega \tau > 1$ may occur for some
$\beta ,\omega \tau > 1$ may occur for some ![]() $\lambda _{\textrm {gun}}$ satisfying
$\lambda _{\textrm {gun}}$ satisfying ![]() $\lambda _{\textrm {crit}} < \lambda _{\textrm {gun}} < \infty$.
$\lambda _{\textrm {crit}} < \lambda _{\textrm {gun}} < \infty$.
In the present work, we launch and collide (head-on) two plasmas formed by coaxial guns. We orient the applied bias magnetic fields such that the plasmas have opposite magnetic helicities ![]() $H$, where
$H$, where ![]() $H= \int \boldsymbol {A} \boldsymbol {\cdot } \boldsymbol {B}\,\mathrm {d}V$ and
$H= \int \boldsymbol {A} \boldsymbol {\cdot } \boldsymbol {B}\,\mathrm {d}V$ and ![]() $\boldsymbol {A}$ is the magnetic vector potential with
$\boldsymbol {A}$ is the magnetic vector potential with ![]() $\boldsymbol {B}=\boldsymbol {\nabla } \times \boldsymbol {A}$. In the
$\boldsymbol {B}=\boldsymbol {\nabla } \times \boldsymbol {A}$. In the ![]() $\lambda _{\textrm {gun}}\gtrsim \lambda _{\textrm {crit}}$ regime, the helicity of merging compact-toroid plasmas determines the magnetic topology of the resultant plasma, i.e. the merging of two cohelicity or counter-helicity spheromaks creates a
$\lambda _{\textrm {gun}}\gtrsim \lambda _{\textrm {crit}}$ regime, the helicity of merging compact-toroid plasmas determines the magnetic topology of the resultant plasma, i.e. the merging of two cohelicity or counter-helicity spheromaks creates a ![]() $\beta \ll 1$ spheromak or a
$\beta \ll 1$ spheromak or a ![]() $\beta \lesssim 1$ FRC, respectively (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990; Ono et al. Reference Ono, Inomoto, Ueda, Matsuyama and Okazaki1999). However, this precludes the achievement of the
$\beta \lesssim 1$ FRC, respectively (Yamada et al. Reference Yamada, Ono, Hayakawa, Katsurai and Perkins1990; Ono et al. Reference Ono, Inomoto, Ueda, Matsuyama and Okazaki1999). However, this precludes the achievement of the ![]() $\beta ,\omega \tau >1$ regime that we seek. The goal of this research is to explore and characterize the head-on merging of two coaxial-gun-formed plasmas in the range
$\beta ,\omega \tau >1$ regime that we seek. The goal of this research is to explore and characterize the head-on merging of two coaxial-gun-formed plasmas in the range ![]() $\lambda _{\textrm {crit}}<\lambda _{\textrm {gun}}<\infty$ in order to form a transient plasma with
$\lambda _{\textrm {crit}}<\lambda _{\textrm {gun}}<\infty$ in order to form a transient plasma with ![]() $\beta ,\omega \tau >1$.
$\beta ,\omega \tau >1$.
2.3. Plasma propagation and merging
As the plasmas propagate into the vacuum chamber from the magnetized coaxial guns, they expand into an applied background magnetic field that is oriented along the propagation direction (![]() $z$ axis). The applied background field mitigates the amount of expansion. To estimate the range of plasma parameters during plasma propagation, we use a combination of measurements at the chamber centre and near the gun, along with basic scaling relationships. This expected range of plasma parameters dictates the range of
$z$ axis). The applied background field mitigates the amount of expansion. To estimate the range of plasma parameters during plasma propagation, we use a combination of measurements at the chamber centre and near the gun, along with basic scaling relationships. This expected range of plasma parameters dictates the range of ![]() $\beta$,
$\beta$, ![]() $\omega \tau$, Mach number
$\omega \tau$, Mach number ![]() $M$, Alfvén Mach number
$M$, Alfvén Mach number ![]() $M_A$ and mean free paths, as well as the nature of the plasma-merging dynamics. Further details are provided in § 4.1.
$M_A$ and mean free paths, as well as the nature of the plasma-merging dynamics. Further details are provided in § 4.1.
3. Experimental setup
In this work, we launch two ![]() $\beta > 1$ plasmas head-on within a vacuum chamber and measure the resulting plasma densities, temperatures and magnetic fields. The experiments are conducted on the BRB, which is part of the WiPPL, a frontier-plasma-science user facility.
$\beta > 1$ plasmas head-on within a vacuum chamber and measure the resulting plasma densities, temperatures and magnetic fields. The experiments are conducted on the BRB, which is part of the WiPPL, a frontier-plasma-science user facility.
3.1. Experimental chamber: the BRB
Figure 3 shows a diagram of the BRB experimental chamber at the WiPPL (Cooper et al. Reference Cooper, Wallace, Brookhart, Clark, Collins, Ding, Flanagan, Khalzov, Li and Milhone2014; Forest et al. Reference Forest, Flanagan, Brookhart, Clark, Cooper, Désangles, Egedal, Endrizzi, Khalzov and Li2015). The multicusp magnetic confinement of the BRB contributes ![]() $<1\ \textrm {G}$ to the plasma-merging region. Two plasma injectors are positioned on opposite poles (labelled south and north) of the 3 m diameter vacuum chamber at a base pressure of
$<1\ \textrm {G}$ to the plasma-merging region. Two plasma injectors are positioned on opposite poles (labelled south and north) of the 3 m diameter vacuum chamber at a base pressure of ![]() ${\sim }4\ \mathrm {\mu }\textrm {Torr}$. A 3 m diameter Helmholtz coil set outside of the chamber provides a 50 G (direct current) magnetic field pointing from south to north. This background magnetic field serves to prevent the
${\sim }4\ \mathrm {\mu }\textrm {Torr}$. A 3 m diameter Helmholtz coil set outside of the chamber provides a 50 G (direct current) magnetic field pointing from south to north. This background magnetic field serves to prevent the ![]() $\beta >1$ plasmas from expanding too much and reducing in density before colliding at the chamber centre. The magnetic field from the Helmholtz coil alters the magnetization of the iron core and thus the bias flux within the coaxial injectors, which is taken into account in the reported
$\beta >1$ plasmas from expanding too much and reducing in density before colliding at the chamber centre. The magnetic field from the Helmholtz coil alters the magnetization of the iron core and thus the bias flux within the coaxial injectors, which is taken into account in the reported ![]() $\lambda _{\textrm {gun}}$ values.
$\lambda _{\textrm {gun}}$ values.
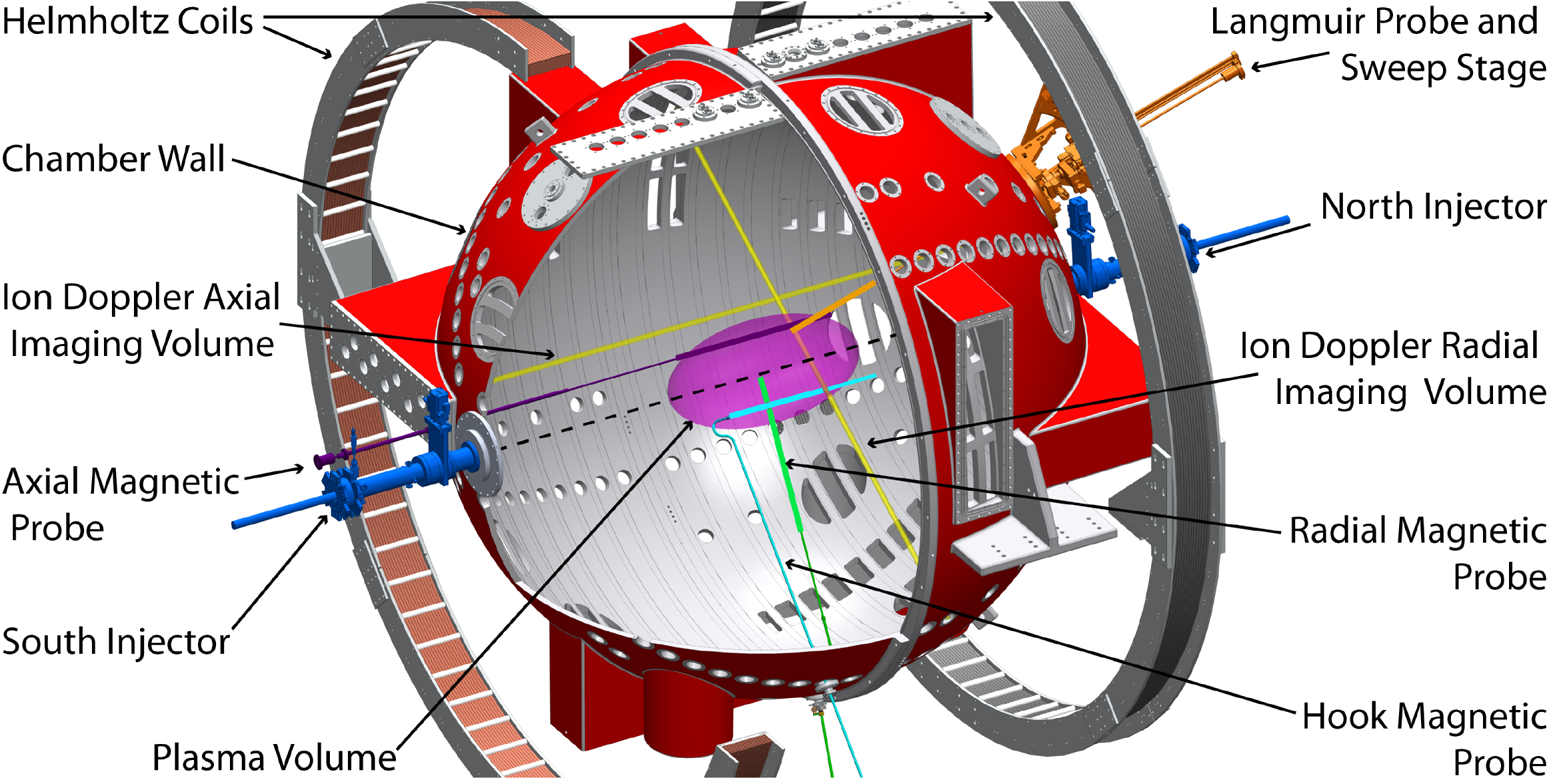
Figure 3. Diagram of the experimental set-up, showing relative locations of the plasma injectors, diagnostics, approximate plasma volume in the 3 m diameter BRB chamber, and external Helmholtz coils.
We define the chamber coordinates in the poloidal plane by ![]() $(r, z)$, where the south pole is
$(r, z)$, where the south pole is ![]() $(r = 0\ \mathrm {cm}, z = -150\ \mathrm {cm})$ and the north pole is
$(r = 0\ \mathrm {cm}, z = -150\ \mathrm {cm})$ and the north pole is ![]() $(r = 0\ \mathrm {cm}, z = +150\ \mathrm {cm})$. Diagnostics are placed at different toroidal angles
$(r = 0\ \mathrm {cm}, z = +150\ \mathrm {cm})$. Diagnostics are placed at different toroidal angles ![]() $\phi$, and toroidal symmetry of the plasma structure is assumed for estimating plasma parameters. Experimental results suggest that this assumption may not always be valid. However, toroidal symmetry is not a requirement for accessing the parameter regimes for the physics studies of interest, nor for the studies themselves.
$\phi$, and toroidal symmetry of the plasma structure is assumed for estimating plasma parameters. Experimental results suggest that this assumption may not always be valid. However, toroidal symmetry is not a requirement for accessing the parameter regimes for the physics studies of interest, nor for the studies themselves.
3.2. Plasma injector
Figure 2 illustrates the coaxial plasma injectors (Matsumoto et al. Reference Matsumoto, Roche, Allfrey, Sekiguchi, Asai, Gota, Cordero, Garate, Kinley and Valentine2016a,Reference Matsumoto, Sekiguchi, Asai, Gota, Garate, Allfrey, Valentine, Morehouse, Roche and Kinleyb; Edo et al. Reference Edo, Asai, Tanaka, Yamada, Hosozawa, Kaminou, Gota, Roche, Allfrey and Osin2018) that we use to create our plasmas. The inner radius of the outer electrode (anode) is ![]() $r_{\textrm {gun}} = 4.15\ \textrm {cm}$, leading to
$r_{\textrm {gun}} = 4.15\ \textrm {cm}$, leading to ![]() $\lambda _{\textrm {crit}} \approx 92\ \textrm {m}^{-1}$ for spheromak formation. Thus, we desire
$\lambda _{\textrm {crit}} \approx 92\ \textrm {m}^{-1}$ for spheromak formation. Thus, we desire ![]() $\lambda _{\textrm {gun}}>\lambda _{\textrm {crit}}$, by reducing
$\lambda _{\textrm {gun}}>\lambda _{\textrm {crit}}$, by reducing ![]() $\psi _{\textrm {gun}}$, in order to create
$\psi _{\textrm {gun}}$, in order to create ![]() $\beta >1,\omega \tau >1$ magnetized plasmas.
$\beta >1,\omega \tau >1$ magnetized plasmas.
The plasmas are created by (i) establishing a poloidal bias flux ![]() $\psi _{\textrm {gun}}$ between the coaxial electrodes, (ii) injecting neutral gas between the electrodes, (iii) preionizing the gas to create a plasma, (iv) accelerating the plasma by discharging current through the electrodes. To establish
$\psi _{\textrm {gun}}$ between the coaxial electrodes, (ii) injecting neutral gas between the electrodes, (iii) preionizing the gas to create a plasma, (iv) accelerating the plasma by discharging current through the electrodes. To establish ![]() $\psi _{\textrm {gun}}$, an iron core surrounded by a copper winding is inserted into the inner coaxial electrode (cathode). A current
$\psi _{\textrm {gun}}$, an iron core surrounded by a copper winding is inserted into the inner coaxial electrode (cathode). A current ![]() $<3\ \textrm {A}$ (direct current) through the 4.1 cm diameter winding supplies
$<3\ \textrm {A}$ (direct current) through the 4.1 cm diameter winding supplies ![]() $\psi _{\textrm {gun}}<0.4\ \textrm {mWb}$ within the
$\psi _{\textrm {gun}}<0.4\ \textrm {mWb}$ within the ![]() ${\sim }30\ \textrm {cm}$ length region of plasma formation and acceleration in the coaxial injector. To vary
${\sim }30\ \textrm {cm}$ length region of plasma formation and acceleration in the coaxial injector. To vary ![]() $\lambda _{\textrm {gun}}$, we vary
$\lambda _{\textrm {gun}}$, we vary ![]() $\psi _{\textrm {gun}}$ and fix
$\psi _{\textrm {gun}}$ and fix ![]() $I_{\textrm {gun}}$. Gas is injected by valves into the coaxial gun 3 ms before the trigger of the main electrode discharge.
$I_{\textrm {gun}}$. Gas is injected by valves into the coaxial gun 3 ms before the trigger of the main electrode discharge.
In the present work, we use H and He gases for the south and north injectors, respectively. Helium is used for ion Doppler spectroscopy measurements. We only use H in the south injector, for which we observe better performance with H than with He (not yet understood). The south injector is on loan from TAE Technologies, Inc., and the north injector was modified, designed and built at WiPPL based on the TAE injector. The injected gas diffuses through a ‘washer gun’ (Fiksel et al. Reference Fiksel, Almagri, Craig, Iida, Prager and Sarff1996), in which an applied preionization voltage ![]() ${<}1\ \textrm {kV}$ breaks down the gas, and a 1 kA current sustains 100 kW of heating power. The washer guns use a
${<}1\ \textrm {kV}$ breaks down the gas, and a 1 kA current sustains 100 kW of heating power. The washer guns use a ![]() $<1\ \textrm {kG}$ magnetic field produced with a small solenoid to assist in plasma breakdown. This field is roughly aligned with the poloidal magnetic field produced by the iron-core solenoid.
$<1\ \textrm {kG}$ magnetic field produced with a small solenoid to assist in plasma breakdown. This field is roughly aligned with the poloidal magnetic field produced by the iron-core solenoid.
The main current ![]() $I_{\textrm {gun}}$ that accelerates the plasma out of the coaxial gun by the
$I_{\textrm {gun}}$ that accelerates the plasma out of the coaxial gun by the ![]() $\boldsymbol {J}\times \boldsymbol {B}$ force has a peak of
$\boldsymbol {J}\times \boldsymbol {B}$ force has a peak of ![]() $\approx 130$ kA and a risetime of
$\approx 130$ kA and a risetime of ![]() $5\ \mathrm {\mu }\textrm {s}$. The current is crowbarred to prevent ringing. For each injector, the main discharge circuit has a capacitance of
$5\ \mathrm {\mu }\textrm {s}$. The current is crowbarred to prevent ringing. For each injector, the main discharge circuit has a capacitance of ![]() $70\ \mathrm {\mu }\textrm {F}$ operating at voltages of 10 kV, thereby storing 3.5 kJ. Accounting for losses in the transmission line, the energy delivered to the injector is
$70\ \mathrm {\mu }\textrm {F}$ operating at voltages of 10 kV, thereby storing 3.5 kJ. Accounting for losses in the transmission line, the energy delivered to the injector is ![]() ${\sim }0.5\ \textrm {kJ}$, estimated from time-resolved current and voltage measurements. After the plasma is accelerated along the length of the electrodes, it travels
${\sim }0.5\ \textrm {kJ}$, estimated from time-resolved current and voltage measurements. After the plasma is accelerated along the length of the electrodes, it travels ![]() ${\sim }35\ \textrm {cm}$ through the injector and drift tube before it enters the experimental chamber.
${\sim }35\ \textrm {cm}$ through the injector and drift tube before it enters the experimental chamber.
3.3. Diagnostics
3.3.1. Visible fast-framing camera imaging
We image the individual plasmas and plasma collisions using a fast-framing Phantom v710 camera with ![]() $1\ \mathrm {\mu }\textrm {s}$ exposure times and
$1\ \mathrm {\mu }\textrm {s}$ exposure times and ![]() $3\ \mathrm {\mu }\textrm {s}$ interframe time. The camera is positioned at an approximately
$3\ \mathrm {\mu }\textrm {s}$ interframe time. The camera is positioned at an approximately ![]() $45^{\circ }$ angle relative to the axial plasma-propagation direction. Narrow bandpass filters selectively admit
$45^{\circ }$ angle relative to the axial plasma-propagation direction. Narrow bandpass filters selectively admit ![]() $\textrm {H}_{\alpha }$,
$\textrm {H}_{\alpha }$, ![]() $\textrm {H}_{\beta }$, He-i and He-ii plasma line emission. The imaging helps verify magnetic-signal timings and with experimental troubleshooting.
$\textrm {H}_{\beta }$, He-i and He-ii plasma line emission. The imaging helps verify magnetic-signal timings and with experimental troubleshooting.
3.3.2. Langmuir probe
Electron densities and electron temperatures are measured using a multitip Langmuir probe. The 16 tips each have independent bias voltages to sample the current-voltage (![]() $I$-
$I$-![]() $V$) traces with
$V$) traces with ![]() $0.2\ \mathrm {\mu }\textrm {s}$ sampling period. The position of the Langmuir probe within the chamber can be adjusted, but for the data presented in this work, the probe was fixed at the chamber coordinates
$0.2\ \mathrm {\mu }\textrm {s}$ sampling period. The position of the Langmuir probe within the chamber can be adjusted, but for the data presented in this work, the probe was fixed at the chamber coordinates ![]() $(r=25\ \mathrm {cm}, z=10\ \mathrm {cm})$. The
$(r=25\ \mathrm {cm}, z=10\ \mathrm {cm})$. The ![]() $n_{e}$ is given by (Cherrington Reference Cherrington1982)
$n_{e}$ is given by (Cherrington Reference Cherrington1982)
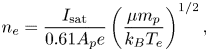 \begin{equation} n_{e} = \frac{I_{\textrm{sat}}}{0.61 A_{p} e} \left(\frac{\mu m_{p}}{k_{B} T_{e}} \right)^{1/2}, \end{equation}
\begin{equation} n_{e} = \frac{I_{\textrm{sat}}}{0.61 A_{p} e} \left(\frac{\mu m_{p}}{k_{B} T_{e}} \right)^{1/2}, \end{equation}
where ![]() $I_{\textrm {sat}}$ is the ion saturation current,
$I_{\textrm {sat}}$ is the ion saturation current, ![]() $A_{p}$ is the probe area,
$A_{p}$ is the probe area, ![]() $e$ is the elementary charge and
$e$ is the elementary charge and ![]() $m_{p}$ is the proton mass. We use
$m_{p}$ is the proton mass. We use ![]() $\mu =1$, 4 and 2.5 for H, He and merged H–He plasmas, respectively. The
$\mu =1$, 4 and 2.5 for H, He and merged H–He plasmas, respectively. The ![]() $T_e$ is inferred by fitting
$T_e$ is inferred by fitting
to the exponential part of the ![]() $I$–
$I$–![]() $V$ curve.
$V$ curve.
The discrete nature of sampling with a multitip probe introduces slightly more error than a typical swept Langmuir probe. All error bars presented here represent statistical uncertainties introduced via measurement and propagated in the analysis, but do not represent the typically much larger errors from Langmuir probe theory (Hutchinson Reference Hutchinson2002). Looking at the quiescent period after the plasmas have collided, we estimate the standard deviations in the measured ![]() $I$ and
$I$ and ![]() $V$ to be 0.2 V and 1 mA, respectively. Using these values, we take the
$V$ to be 0.2 V and 1 mA, respectively. Using these values, we take the ![]() $I$-
$I$-![]() $V$ data and generate an
$V$ data and generate an ![]() $N = 10^4$ size population of mock data with standard deviations around those values. By repeating these calculations at different times and for different shots, we find a 4 % uncertainty in
$N = 10^4$ size population of mock data with standard deviations around those values. By repeating these calculations at different times and for different shots, we find a 4 % uncertainty in ![]() $T_e$ and a 5 % uncertainty in
$T_e$ and a 5 % uncertainty in ![]() $n_e$, which are the combination of the (non-systematic) uncertainties in measurement and the fitting routine. These represent lower bounds in the error, as they only include noise and not theoretical or systematic error.
$n_e$, which are the combination of the (non-systematic) uncertainties in measurement and the fitting routine. These represent lower bounds in the error, as they only include noise and not theoretical or systematic error.
3.3.3. Magnetic probe arrays
The magnetic fields and velocities are measured using an array of Bdot probes (‘hook magnetic probe’ in figure 3), where the probe loop voltage ![]() $V \propto \partial B / \partial t$. The Bdot probe array consists of 11 locations equally spaced between
$V \propto \partial B / \partial t$. The Bdot probe array consists of 11 locations equally spaced between ![]() $(r = 16\ \mathrm {cm}, z = -20\ \mathrm {cm})$ and
$(r = 16\ \mathrm {cm}, z = -20\ \mathrm {cm})$ and ![]() $(r = 16\ \mathrm {cm}, z = 40\ \mathrm {cm})$ for the data presented in this work. At each array location there are six loops – three orthogonal pairs of oppositely wound loops – to measure the three spatial components of the magnetic field and minimize common mode noise. Data are recorded at a
$(r = 16\ \mathrm {cm}, z = 40\ \mathrm {cm})$ for the data presented in this work. At each array location there are six loops – three orthogonal pairs of oppositely wound loops – to measure the three spatial components of the magnetic field and minimize common mode noise. Data are recorded at a ![]() $0.1\ \mathrm {\mu }\textrm {s}$ sampling rate and numerically integrated to provide values of the magnetic field. The Bdot-coil areas are calibrated to within a few percent. There is a systematic uncertainty of the entire probe array of
$0.1\ \mathrm {\mu }\textrm {s}$ sampling rate and numerically integrated to provide values of the magnetic field. The Bdot-coil areas are calibrated to within a few percent. There is a systematic uncertainty of the entire probe array of ![]() ${\sim }1\ \textrm {cm}$.
${\sim }1\ \textrm {cm}$.
There are two other Bdot-probe arrays in the chamber (‘axial magnetic probe’ and ‘radial magnetic probe’ in figure 3), which provide magnetic signals at different radii and toroidal positions. These arrays help determine the radial extent of the plasma (![]() ${\sim }30\ \textrm {cm}$ radius) as a function of toroidal angle. We also observe
${\sim }30\ \textrm {cm}$ radius) as a function of toroidal angle. We also observe ![]() ${\sim }30\ \textrm {km}\,\textrm {s}^{-1}$ plasma radial expansion, which affects the ion Doppler spectroscopy data.
${\sim }30\ \textrm {km}\,\textrm {s}^{-1}$ plasma radial expansion, which affects the ion Doppler spectroscopy data.
3.3.4. Ion Doppler spectroscopy
Ion temperatures are measured using ion Doppler spectroscopy. We observe Doppler broadening of the 468.6 nm He-ii line along a radial viewing chord at ![]() $z=10\ \textrm {cm}$. Light is collected using a 2.54 cm collimator, a 10 nm bandwidth monochrometer,
$z=10\ \textrm {cm}$. Light is collected using a 2.54 cm collimator, a 10 nm bandwidth monochrometer, ![]() $3\ \mathrm {\mu }\textrm {m}$ fibre bundles and fed into a Czerny–Turner type spectrometer, as described in Den Hartog & Fonck (Reference Den Hartog and Fonck1994). We obtain measurements at a sampling rate of
$3\ \mathrm {\mu }\textrm {m}$ fibre bundles and fed into a Czerny–Turner type spectrometer, as described in Den Hartog & Fonck (Reference Den Hartog and Fonck1994). We obtain measurements at a sampling rate of ![]() ${\sim }1\ \mathrm {\mu }\textrm {s}$. The measured broadening is a convolution of broadening from the following sources: the ion temperature, the spectrometer instrumental broadening and the plasma radial-expansion velocity. The result is
${\sim }1\ \mathrm {\mu }\textrm {s}$. The measured broadening is a convolution of broadening from the following sources: the ion temperature, the spectrometer instrumental broadening and the plasma radial-expansion velocity. The result is ![]() $\sigma ^{2}_{\textrm {measured}} = \sigma ^{2}_{\textrm {Ti}} + \sigma ^{2}_{\textrm {instr}} + \sigma ^{2}_{\textrm {exp}}$, where
$\sigma ^{2}_{\textrm {measured}} = \sigma ^{2}_{\textrm {Ti}} + \sigma ^{2}_{\textrm {instr}} + \sigma ^{2}_{\textrm {exp}}$, where ![]() $\sigma$ is the Gaussian broadening, i.e. full-width at half-maximum (known as FWHM). The instrumental broadening at
$\sigma$ is the Gaussian broadening, i.e. full-width at half-maximum (known as FWHM). The instrumental broadening at ![]() $T_i=30\ \textrm {eV}$ is equivalent to
$T_i=30\ \textrm {eV}$ is equivalent to ![]() $\sigma _{\textrm {instr}}=1.5\ \textrm {eV}$, but the relative contribution increases for smaller
$\sigma _{\textrm {instr}}=1.5\ \textrm {eV}$, but the relative contribution increases for smaller ![]() $T_i$. Broadening from the
$T_i$. Broadening from the ![]() $\sim 30\ \textrm {km}\,\textrm {s}^{-1}$ plasma radial expansion is equivalent to
$\sim 30\ \textrm {km}\,\textrm {s}^{-1}$ plasma radial expansion is equivalent to ![]() $\sigma _{\textrm {exp}} \sim 9\ \textrm {eV}$. As
$\sigma _{\textrm {exp}} \sim 9\ \textrm {eV}$. As ![]() $T_e$ cools below
$T_e$ cools below ![]() ${\sim }10\ \textrm {eV}$, the emission drops rapidly, and
${\sim }10\ \textrm {eV}$, the emission drops rapidly, and ![]() $T_i$ cannot be measured.
$T_i$ cannot be measured.
4. Experimental results
4.1. Estimated plasma parameters
The nature of head-on merging of two plasmas, e.g. whether they interpenetrate or form sonic or MHD shocks, depends on the plasma parameters just prior to merging. As the plasmas propagate with axial speed ![]() $v \sim 70\ \textrm {km}\,\textrm {s}^{-1}$ into the chamber from the magnetized coaxial guns, they expand into a 50 G applied background magnetic field that is oriented along the propagation direction (
$v \sim 70\ \textrm {km}\,\textrm {s}^{-1}$ into the chamber from the magnetized coaxial guns, they expand into a 50 G applied background magnetic field that is oriented along the propagation direction (![]() $z$ axis). The plasmas expand radially (with instantaneous radius
$z$ axis). The plasmas expand radially (with instantaneous radius ![]() $R$) and axially (with instantaneous length
$R$) and axially (with instantaneous length ![]() $L$) each by a factor of
$L$) each by a factor of ![]() ${\sim }8$ from the initial size near the gun to the final size near the chamber centre, with volume
${\sim }8$ from the initial size near the gun to the final size near the chamber centre, with volume ![]() $V \propto L R^{2}$. Near the chamber centre, we measure the plasma
$V \propto L R^{2}$. Near the chamber centre, we measure the plasma ![]() $R$,
$R$, ![]() $L$,
$L$, ![]() $n_e$,
$n_e$, ![]() $T_e$,
$T_e$, ![]() $T_i$,
$T_i$, ![]() $\boldsymbol {B}$ and
$\boldsymbol {B}$ and ![]() $v$. In the drift tube near the gun, we measure
$v$. In the drift tube near the gun, we measure ![]() $B$ during separate experiments, and we infer the other quantities by making assumptions about the expansion scalings (i.e. conservation of particles and resistive diffusion of magnetic flux), and verify the consistency of the inferred parameters near the gun with that of prior work using similar plasma injectors (Matsumoto et al. Reference Matsumoto, Roche, Allfrey, Sekiguchi, Asai, Gota, Cordero, Garate, Kinley and Valentine2016a,Reference Matsumoto, Sekiguchi, Asai, Gota, Garate, Allfrey, Valentine, Morehouse, Roche and Kinleyb; Edo et al. Reference Edo, Asai, Tanaka, Yamada, Hosozawa, Kaminou, Gota, Roche, Allfrey and Osin2018).
$B$ during separate experiments, and we infer the other quantities by making assumptions about the expansion scalings (i.e. conservation of particles and resistive diffusion of magnetic flux), and verify the consistency of the inferred parameters near the gun with that of prior work using similar plasma injectors (Matsumoto et al. Reference Matsumoto, Roche, Allfrey, Sekiguchi, Asai, Gota, Cordero, Garate, Kinley and Valentine2016a,Reference Matsumoto, Sekiguchi, Asai, Gota, Garate, Allfrey, Valentine, Morehouse, Roche and Kinleyb; Edo et al. Reference Edo, Asai, Tanaka, Yamada, Hosozawa, Kaminou, Gota, Roche, Allfrey and Osin2018).
Making the assumptions of conservation of particle and exponentially decaying magnetic flux while the expanding plasma propagates from the gun to the chamber centre, we have the following relations: ![]() $n \propto L^{-1}R^{-2}$;
$n \propto L^{-1}R^{-2}$; ![]() $B_{r}, B_{\phi } \propto L^{-1}R^{-1}\textrm {e}^{-Ct}$; and
$B_{r}, B_{\phi } \propto L^{-1}R^{-1}\textrm {e}^{-Ct}$; and ![]() $B_{z} \propto R^{-2}\textrm {e}^{-Ct}$ with propagation time
$B_{z} \propto R^{-2}\textrm {e}^{-Ct}$ with propagation time ![]() $t$ and a constant
$t$ and a constant ![]() $C$. While it is tempting to assume adiabatic expansion (
$C$. While it is tempting to assume adiabatic expansion (![]() $PV^{\gamma } = \textrm {constant}$, with
$PV^{\gamma } = \textrm {constant}$, with ![]() $\gamma = 5/3$) to infer the dependence of
$\gamma = 5/3$) to infer the dependence of ![]() $T$ on plasma volume
$T$ on plasma volume ![]() $V$, the strict adiabatic-cooling rate
$V$, the strict adiabatic-cooling rate ![]() $T \propto L^{-2/3}r^{-4/3}$ would lead to unrealistic
$T \propto L^{-2/3}r^{-4/3}$ would lead to unrealistic ![]() $>\ \textrm {keV}$ temperatures near the gun when extrapolated from measured temperatures near the chamber centre. Instead, as a lower bound, we take
$>\ \textrm {keV}$ temperatures near the gun when extrapolated from measured temperatures near the chamber centre. Instead, as a lower bound, we take ![]() $T_{i} \approx$ constant. At higher densities near the gun,
$T_{i} \approx$ constant. At higher densities near the gun, ![]() $T_e$ and
$T_e$ and ![]() $T_i$ equilibrate over
$T_i$ equilibrate over ![]() ${\sim } 1\ \mathrm {\mu }\textrm {s}$ time scales, but at the lower densities near the chamber centre, the ion–electron equilibration time is longer than the
${\sim } 1\ \mathrm {\mu }\textrm {s}$ time scales, but at the lower densities near the chamber centre, the ion–electron equilibration time is longer than the ![]() ${\sim } 20\ \mathrm {\mu }\textrm {s}$ propagation time. Thus,
${\sim } 20\ \mathrm {\mu }\textrm {s}$ propagation time. Thus, ![]() $T_e$ decreases from the initial
$T_e$ decreases from the initial ![]() $T_{e} \approx T_{i}$ near the gun to the measured
$T_{e} \approx T_{i}$ near the gun to the measured ![]() $T_{e} < T_{i}$ near the chamber centre, due to radiation and
$T_{e} < T_{i}$ near the chamber centre, due to radiation and ![]() $P\mathrm {d}V$ work on the background magnetic field. Concurrently, resistive dissipation of the magnetic field causes Ohmic heating of the electrons. To put bounds on parameters rather than to be predictive of the precise plasma temperature between the gun and the chamber centre, we simply model a linear decrease in
$P\mathrm {d}V$ work on the background magnetic field. Concurrently, resistive dissipation of the magnetic field causes Ohmic heating of the electrons. To put bounds on parameters rather than to be predictive of the precise plasma temperature between the gun and the chamber centre, we simply model a linear decrease in ![]() $T_{e}$ during propagation.
$T_{e}$ during propagation.
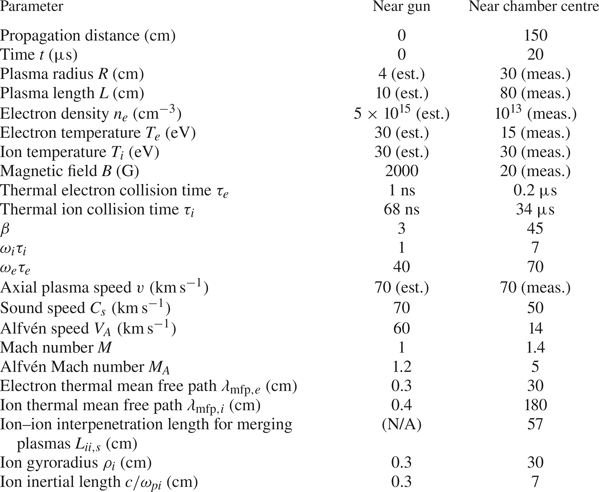
Based on the relations and information discussed above, we provide estimates of parameters near the gun and near the chamber centre in table 1, which suggests that thermal pressure is greater than magnetic pressure (i.e. ![]() $\beta >1$) both near the gun and near the chamber centre. While the radial expansion speed measured by the B-dot probe array near the chamber centre is
$\beta >1$) both near the gun and near the chamber centre. While the radial expansion speed measured by the B-dot probe array near the chamber centre is ![]() ${\sim }30\ \textrm {km}\,\textrm {s}^{-1}$, the average expansion speed calculated during propagation through the chamber (from figure 4) is
${\sim }30\ \textrm {km}\,\textrm {s}^{-1}$, the average expansion speed calculated during propagation through the chamber (from figure 4) is ![]() $\sim 13\ \textrm {km}\,\textrm {s}^{-1}$. Both observations of the radial expansion speed are less than the ion sound speed
$\sim 13\ \textrm {km}\,\textrm {s}^{-1}$. Both observations of the radial expansion speed are less than the ion sound speed ![]() $C_s$ or Alfvén speed
$C_s$ or Alfvén speed ![]() $V_A$ near the gun (in table 1). Near the chamber centre, the measured expansion speed is still subsonic. During head-on merging, the plasmas are super-Alfvénic and slightly supersonic, and thus it may be expected that MHD shocks could form. However, during initial head-on merging of two plasmas, the classical ion–ion Coulomb interpenetration length between the merging plasmas is an appreciable fraction of
$V_A$ near the gun (in table 1). Near the chamber centre, the measured expansion speed is still subsonic. During head-on merging, the plasmas are super-Alfvénic and slightly supersonic, and thus it may be expected that MHD shocks could form. However, during initial head-on merging of two plasmas, the classical ion–ion Coulomb interpenetration length between the merging plasmas is an appreciable fraction of ![]() $L$, and thus it may be expected that any shock formation will be delayed if it forms at all, as observed in prior work with merging supersonic plasmas (Moser & Hsu Reference Moser and Hsu2015; Langendorf et al. Reference Langendorf, Yates, Hsu, Thoma and Gilmore2019). By interpolating the data in table 1, we show in figure 4 the time evolution of parameters for an individual plasma as it propagates to the centre of the chamber before merging. Notably,
$L$, and thus it may be expected that any shock formation will be delayed if it forms at all, as observed in prior work with merging supersonic plasmas (Moser & Hsu Reference Moser and Hsu2015; Langendorf et al. Reference Langendorf, Yates, Hsu, Thoma and Gilmore2019). By interpolating the data in table 1, we show in figure 4 the time evolution of parameters for an individual plasma as it propagates to the centre of the chamber before merging. Notably, ![]() $\beta$,
$\beta$, ![]() $\omega _i \tau _i$ and
$\omega _i \tau _i$ and ![]() $\omega _e \tau _e$ are anticipated to be equal to or greater than unity for an individual plasma during propagation and expansion into the chamber. A key question is whether this is also true upon merging, where densities can be much higher than for an individual plasma.
$\omega _e \tau _e$ are anticipated to be equal to or greater than unity for an individual plasma during propagation and expansion into the chamber. A key question is whether this is also true upon merging, where densities can be much higher than for an individual plasma.
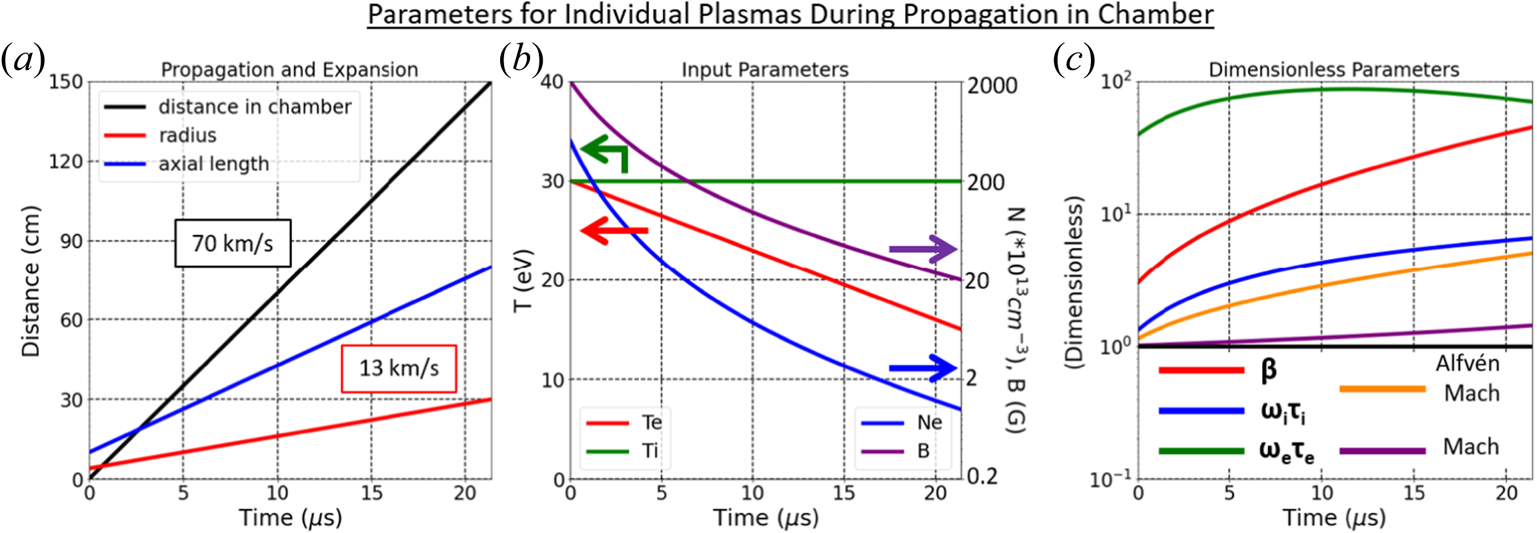
Figure 4. Anticipated plasma parameters versus time for individual plasmas as they propagate to the centre of the chamber. Values are based on interpolating the data in table 1 and serve to place bounds on parameters rather than to precisely predict behaviour during propagation.
Table 1. Measured (meas.) and estimated (est.) values of plasma parameters (for single plasmas) for the experiments reported in this paper, assuming ![]() $Z=1$,
$Z=1$, ![]() $\mu =1$,
$\mu =1$, ![]() $\gamma =5/3$ and
$\gamma =5/3$ and ![]() $\ln {\varLambda }=10$.
$\ln {\varLambda }=10$.
4.2. Negligible effect of neutrals
In this subsection, we show that the effect of neutrals should be negligible.
First, we consider ion–neutral collisionality (dominated by charge exchange) within the plasmas before merging. The plasmas generated from the coaxial injectors are highly ionized. We utilize the PrismSpect atomic modelling software (MacFarlane et al. Reference MacFarlane, Golovkin, Woodruff, Welch, Oliver, Melhorn and Campbell2004) with the temperature and density conditions in table 1 to estimate the fraction of neutral particles to be ![]() $<3 \times 10^{-6}$ near the gun and
$<3 \times 10^{-6}$ near the gun and ![]() $<2 \times 10^{-6}$ near the chamber centre. Within each plasma, the ion–neutral collision time is
$<2 \times 10^{-6}$ near the chamber centre. Within each plasma, the ion–neutral collision time is ![]() $\tau _{CX} = \nu _{CX}^{-1} \approx (n_{n} \sigma _{CX} v_{i,n})^{-1}$, where we assume that the relative speed between ions (
$\tau _{CX} = \nu _{CX}^{-1} \approx (n_{n} \sigma _{CX} v_{i,n})^{-1}$, where we assume that the relative speed between ions (![]() $T_{i}=30\ \textrm {eV}$) and cold neutrals is
$T_{i}=30\ \textrm {eV}$) and cold neutrals is ![]() $v_{i,n}=54\ \textrm {km}\,\textrm {s}^{-1}$. Based on the high ionization fraction, the neutral density is
$v_{i,n}=54\ \textrm {km}\,\textrm {s}^{-1}$. Based on the high ionization fraction, the neutral density is ![]() $n_{n} < 1.5 \times 10^{10}\ \textrm {cm}^{-3}$. The
$n_{n} < 1.5 \times 10^{10}\ \textrm {cm}^{-3}$. The ![]() $\textrm {H}^{1+}$–
$\textrm {H}^{1+}$–![]() $\textrm {H}^{0}$ charge exchange cross-section is
$\textrm {H}^{0}$ charge exchange cross-section is ![]() $\sigma _{CX} \sim 3 \times 10^{-15}\ \textrm {cm}^{2}$ (Smirnov Reference Smirnov2000). Therefore, we estimate that
$\sigma _{CX} \sim 3 \times 10^{-15}\ \textrm {cm}^{2}$ (Smirnov Reference Smirnov2000). Therefore, we estimate that ![]() $\tau _{CX} \approx 4\ \textrm {ms}$, much larger than the experimental duration. Comparatively, the thermal ion–ion collision times
$\tau _{CX} \approx 4\ \textrm {ms}$, much larger than the experimental duration. Comparatively, the thermal ion–ion collision times ![]() $\tau _i$ are
$\tau _i$ are ![]() ${\sim }68\ \textrm {ns}$ near the gun and
${\sim }68\ \textrm {ns}$ near the gun and ![]() ${\sim }34\ \mathrm {\mu }\textrm {s}$ near the chamber centre. Thus, ion–neutral collisionality within the plasma is a small effect.
${\sim }34\ \mathrm {\mu }\textrm {s}$ near the chamber centre. Thus, ion–neutral collisionality within the plasma is a small effect.
Next we consider the collisionality between the plasma ions and the background neutrals in the vacuum chamber. We expect plasmas injected into the chamber (![]() ${\sim }70\ \textrm {km}\,\textrm {s}^{-1}$) to run ahead of injected neutrals (at room temperature 0.026 eV, thermal velocity
${\sim }70\ \textrm {km}\,\textrm {s}^{-1}$) to run ahead of injected neutrals (at room temperature 0.026 eV, thermal velocity ![]() $v_{\textrm {th},n} < 1.5\ \textrm {km}\,\textrm {s}^{-1}$). The vacuum chamber base pressure
$v_{\textrm {th},n} < 1.5\ \textrm {km}\,\textrm {s}^{-1}$). The vacuum chamber base pressure ![]() ${\sim }4\ \mathrm {\mu }\textrm {Torr}$ corresponds to a neutral background density of
${\sim }4\ \mathrm {\mu }\textrm {Torr}$ corresponds to a neutral background density of ![]() $n_{n} \approx 1.3 \times 10^{11}\ \textrm {cm}^{-3}$. The collision time for plasma ions colliding with the stationary background neutrals is
$n_{n} \approx 1.3 \times 10^{11}\ \textrm {cm}^{-3}$. The collision time for plasma ions colliding with the stationary background neutrals is ![]() $\tau _{\textrm {background}} = \nu _{\textrm {background}}^{-1} \approx (n_{n} \sigma _{CX} v_{i})^{-1}$, where
$\tau _{\textrm {background}} = \nu _{\textrm {background}}^{-1} \approx (n_{n} \sigma _{CX} v_{i})^{-1}$, where ![]() $v_{i} \sim 70\ \textrm {km}\,\textrm {s}^{-1}$ is the ion speed. We calculate this collision time to be
$v_{i} \sim 70\ \textrm {km}\,\textrm {s}^{-1}$ is the ion speed. We calculate this collision time to be ![]() $\tau _{\textrm {background}} \approx 400\ \mathrm {\mu }\textrm {s}$, again larger than the experimental duration. Comparatively, the ion–ion collision time for the two counter-streaming merging plasmas is approximately equal to the ion–ion slowing time
$\tau _{\textrm {background}} \approx 400\ \mathrm {\mu }\textrm {s}$, again larger than the experimental duration. Comparatively, the ion–ion collision time for the two counter-streaming merging plasmas is approximately equal to the ion–ion slowing time ![]() $\tau _{ii,s} = \nu _{ii,s}^{-1} \approx (v_{\textrm {rel}}/4L_{ii,s})^{-1}$ (Messer et al. Reference Messer, Case, Wu, Brockington and Witherspoon2013; Merritt et al. Reference Merritt, Moser, Hsu, Adams, Dunn, Holgado and Gilmore2014), where
$\tau _{ii,s} = \nu _{ii,s}^{-1} \approx (v_{\textrm {rel}}/4L_{ii,s})^{-1}$ (Messer et al. Reference Messer, Case, Wu, Brockington and Witherspoon2013; Merritt et al. Reference Merritt, Moser, Hsu, Adams, Dunn, Holgado and Gilmore2014), where ![]() $v_{\textrm {rel}} = 2 v_{i} \sim 140\ \textrm {km}\,\textrm {s}^{-1}$ is the relative plasma velocity and
$v_{\textrm {rel}} = 2 v_{i} \sim 140\ \textrm {km}\,\textrm {s}^{-1}$ is the relative plasma velocity and ![]() $L_{ii,s} \approx$ 57 cm is the ion–ion slowing length, which gives
$L_{ii,s} \approx$ 57 cm is the ion–ion slowing length, which gives ![]() $\tau _{ii,s} \approx 16\ \mathrm {\mu }\textrm {s}$. This calculation is a characteristic slowing time for H–H merging; for H–He and He–H the calculated slowing times are
$\tau _{ii,s} \approx 16\ \mathrm {\mu }\textrm {s}$. This calculation is a characteristic slowing time for H–H merging; for H–He and He–H the calculated slowing times are ![]() $3\ \mathrm {\mu }\textrm {s}$ and
$3\ \mathrm {\mu }\textrm {s}$ and ![]() $27\ \mathrm {\mu }\textrm {s}$, respectively. Thus, the effect of neutral collisionality is also negligible in the merging between opposing plasmas.
$27\ \mathrm {\mu }\textrm {s}$, respectively. Thus, the effect of neutral collisionality is also negligible in the merging between opposing plasmas.
4.3. Measurements near the chamber centre
The primary results of this work are the measurement of plasma parameters – density, temperature, and magnetic field – from both individual plasmas and merged plasmas via head-on collisions, which occur near the (![]() $r<30\ \textrm {cm}$,
$r<30\ \textrm {cm}$, ![]() $z=10\ \textrm {cm}$) chamber position. We show evidence for obtaining transiently the desired state of
$z=10\ \textrm {cm}$) chamber position. We show evidence for obtaining transiently the desired state of ![]() $\beta >1$ and
$\beta >1$ and ![]() $\omega _{i}\tau _{i}>1$ for both situations. Figure 5(a,b) shows visible imaging of individual plasmas coming from the south and north sides of the chamber, respectively, and also of a head-on plasma collision (panel (c)) between the two individual plasmas. We use the emission seen on the sides of the probes to observe and verify from which direction the plasma is coming. Estimates of Bohm losses to probe surfaces are small compared with total particle inventories, and thus we expect the probes to not significantly perturb the plasma.
$\omega _{i}\tau _{i}>1$ for both situations. Figure 5(a,b) shows visible imaging of individual plasmas coming from the south and north sides of the chamber, respectively, and also of a head-on plasma collision (panel (c)) between the two individual plasmas. We use the emission seen on the sides of the probes to observe and verify from which direction the plasma is coming. Estimates of Bohm losses to probe surfaces are small compared with total particle inventories, and thus we expect the probes to not significantly perturb the plasma.

Figure 5. Fast-framing camera images of visible self-emission for plasmas from (a) south injector only, (b) north injector only, and (c) both injectors. The main purpose of these images is to verify which sides of the probes light up due to the incoming plasma(s).
Here, the south H plasma has ![]() $\lambda _{\textrm {gun},S} = 600\ \textrm {m}^{-1}$, and the north He plasma has
$\lambda _{\textrm {gun},S} = 600\ \textrm {m}^{-1}$, and the north He plasma has ![]() $\lambda _{\textrm {gun},N} = 1200\ \textrm {m}^{-1}$. Depending upon the formation and propagation dynamics, the ratio of toroidal to poloidal magnetic fields and corresponding
$\lambda _{\textrm {gun},N} = 1200\ \textrm {m}^{-1}$. Depending upon the formation and propagation dynamics, the ratio of toroidal to poloidal magnetic fields and corresponding ![]() $\lambda _{\textrm {plasma}}$ for the plasma can be different from
$\lambda _{\textrm {plasma}}$ for the plasma can be different from ![]() $\lambda _{\textrm {gun}}$, but
$\lambda _{\textrm {gun}}$, but ![]() $\lambda _{\textrm {gun}}$ influences the initial plasma state. Since
$\lambda _{\textrm {gun}}$ influences the initial plasma state. Since ![]() $\lambda _{\textrm {gun}}$ satisfies
$\lambda _{\textrm {gun}}$ satisfies ![]() $\infty > \lambda _{\textrm {gun}} > \lambda _{\textrm {crit}} = 92\ \textrm {m}^{-1}$, we are in the desired parameter regime for obtaining
$\infty > \lambda _{\textrm {gun}} > \lambda _{\textrm {crit}} = 92\ \textrm {m}^{-1}$, we are in the desired parameter regime for obtaining ![]() $\beta >1$ and
$\beta >1$ and ![]() $\omega _{i}\tau _{i}>1$ plasmas.
$\omega _{i}\tau _{i}>1$ plasmas.
Magnetic-field data are obtained by integrating the Bdot-probe-array signals. Figure 6 shows the spatio-temporal evolution of the magnetic-field components for an individual H plasma from the south (shot 46330), an individual He plasma from the north (shot 46338) and for an H–He collision (shot 46343). From left to right, the three columns of coloured contour plots are for the radial ![]() $B_r$, toroidal
$B_r$, toroidal ![]() $B_{\phi }$ and axial
$B_{\phi }$ and axial ![]() $B_z$ fields (
$B_z$ fields (![]() $z=0$ corresponds to the chamber centre). For the contour plots, the Bdot-probe array is oriented along
$z=0$ corresponds to the chamber centre). For the contour plots, the Bdot-probe array is oriented along ![]() $z$ and positioned at
$z$ and positioned at ![]() $r=16\ \textrm {cm}$. For reference, the arrival of the density signal can be seen in figure 7.
$r=16\ \textrm {cm}$. For reference, the arrival of the density signal can be seen in figure 7.
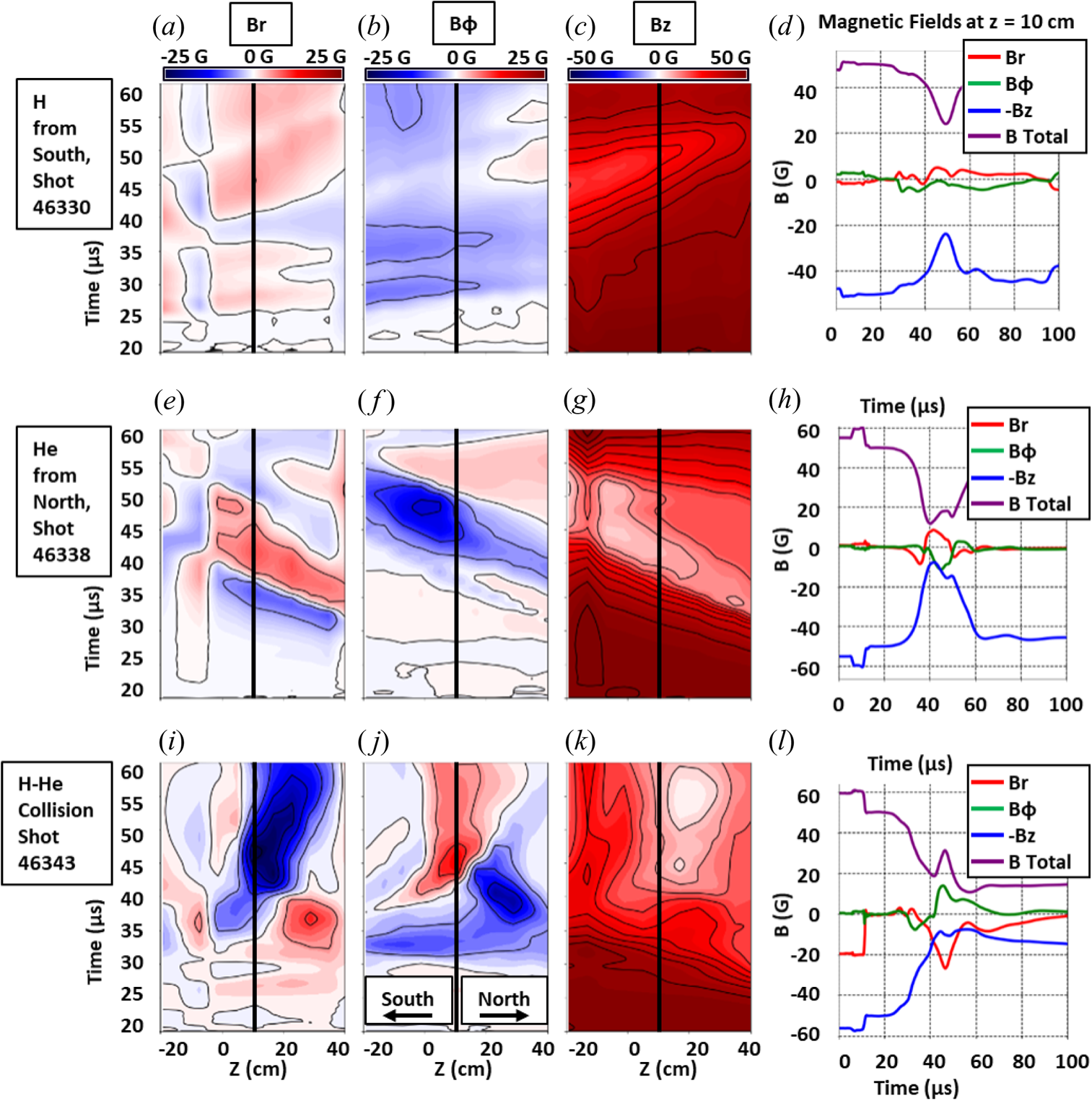
Figure 6. (a–c,e–g,i–k) Magnetic-field components versus ![]() $z$ (at
$z$ (at ![]() $r=16\ \textrm {cm}$) and
$r=16\ \textrm {cm}$) and ![]() $t$ for (a–d) an individual H plasma, (e–h) an individual He plasma and (i–l) an H–He collision. A signal travelling up and to the right is travelling through the chamber from south to north. The contour lines represent 5 G increments. (d,h,l) Lineouts (corresponding to the vertical black lines in the contour plots) of magnetic-field components and total
$t$ for (a–d) an individual H plasma, (e–h) an individual He plasma and (i–l) an H–He collision. A signal travelling up and to the right is travelling through the chamber from south to north. The contour lines represent 5 G increments. (d,h,l) Lineouts (corresponding to the vertical black lines in the contour plots) of magnetic-field components and total ![]() $B=(B_r^2 + B_{\phi }^2 + B_z^2)^{1/2}$ versus
$B=(B_r^2 + B_{\phi }^2 + B_z^2)^{1/2}$ versus ![]() $t$ at
$t$ at ![]() $z\approx 10\ \textrm {cm}$ (including the applied
$z\approx 10\ \textrm {cm}$ (including the applied ![]() $B_z$ from the Helmholtz coil). To avoid obscuring the
$B_z$ from the Helmholtz coil). To avoid obscuring the ![]() $B$-total trace,
$B$-total trace, ![]() $-B_z$ is plotted.
$-B_z$ is plotted.
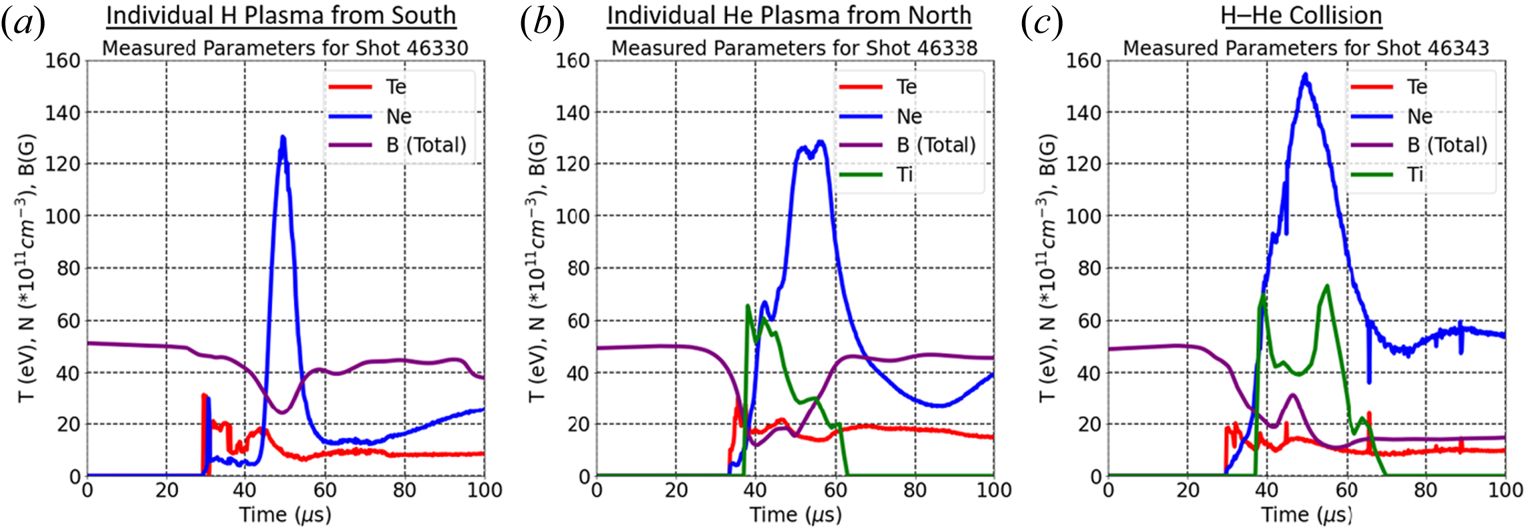
Figure 7. Plots of ![]() $T_e$ and
$T_e$ and ![]() $n_e$ (at
$n_e$ (at ![]() $z=10\ \textrm {cm}$,
$z=10\ \textrm {cm}$, ![]() $r=25\ \textrm {cm}$), total
$r=25\ \textrm {cm}$), total ![]() $B$ (at
$B$ (at ![]() $z=10\ \textrm {cm}$,
$z=10\ \textrm {cm}$, ![]() $r=16\ \textrm {cm}$, from figure 6) and
$r=16\ \textrm {cm}$, from figure 6) and ![]() $T_i$ (when He is present; radial viewing chord at
$T_i$ (when He is present; radial viewing chord at ![]() $z=10\ \textrm {cm}$) versus
$z=10\ \textrm {cm}$) versus ![]() $t$ for an (a) individual H plasma, (b) individual He plasma and (c) H–He collision.
$t$ for an (a) individual H plasma, (b) individual He plasma and (c) H–He collision.
Based on the slopes of the magnetic contours, we infer individual plasma axial velocities of ![]() ${\sim }70\ \textrm {km}\,\textrm {s}^{-1}$. As the plasmas propagate through the chamber and radially expand, they advect the 50 G background axial magnetic field in the radial direction, reducing the magnitude of the
${\sim }70\ \textrm {km}\,\textrm {s}^{-1}$. As the plasmas propagate through the chamber and radially expand, they advect the 50 G background axial magnetic field in the radial direction, reducing the magnitude of the ![]() $B_{z}$ component within the plasma radius. In the H–He collision case, we observe larger magnetic-field strengths of the non-axial components (
$B_{z}$ component within the plasma radius. In the H–He collision case, we observe larger magnetic-field strengths of the non-axial components (![]() ${\sim }30\ \textrm {G}$ compared with
${\sim }30\ \textrm {G}$ compared with ![]() $<20\ \textrm {G}$), and the axial field is reduced to
$<20\ \textrm {G}$), and the axial field is reduced to ![]() $B_{z} <20\ \textrm {G}$ for a longer duration. Due to stagnation of the colliding plasmas, the magnetic signals last for
$B_{z} <20\ \textrm {G}$ for a longer duration. Due to stagnation of the colliding plasmas, the magnetic signals last for ![]() $>40\ \mathrm {\mu }\textrm {s}$ near the chamber centre for the H–He collision case compared with
$>40\ \mathrm {\mu }\textrm {s}$ near the chamber centre for the H–He collision case compared with ![]() $\sim 20\ \mathrm {\mu }\textrm {s}$ for the individual plasmas that propagate past the chamber centre. In future work, we intend to better characterize the anticipated diamagnetic effects based on the relative polarities of the background field compared with the magnetized plasmas.
$\sim 20\ \mathrm {\mu }\textrm {s}$ for the individual plasmas that propagate past the chamber centre. In future work, we intend to better characterize the anticipated diamagnetic effects based on the relative polarities of the background field compared with the magnetized plasmas.
Figure 7 shows the time evolution of ![]() $T_e$ and
$T_e$ and ![]() $n_e$ (at
$n_e$ (at ![]() $r=25\ \mathrm {cm}, z= 10\ \textrm {cm}$) and total
$r=25\ \mathrm {cm}, z= 10\ \textrm {cm}$) and total ![]() $B$ (at
$B$ (at ![]() $r=16\ \mathrm {cm}, z= 10\ \mathrm {cm}$, from figure 6) for an individual H plasma from the south (shot 46330), an individual He plasma from the north (shot 46338) and for an H–He collision (shot 46343). For shots 46338 and 46343, for which there is He present,
$r=16\ \mathrm {cm}, z= 10\ \mathrm {cm}$, from figure 6) for an individual H plasma from the south (shot 46330), an individual He plasma from the north (shot 46338) and for an H–He collision (shot 46343). For shots 46338 and 46343, for which there is He present, ![]() $T_i$ is also plotted. Compared with the plasma from the north, the south plasma density persists for less time (
$T_i$ is also plotted. Compared with the plasma from the north, the south plasma density persists for less time (![]() $<20\ \mathrm {\mu }\textrm {s}$) and causes less reduction of the background magnetic field. The H–He collision case has a peak density above the value for the two individual plasmas, and at
$<20\ \mathrm {\mu }\textrm {s}$) and causes less reduction of the background magnetic field. The H–He collision case has a peak density above the value for the two individual plasmas, and at ![]() $>60\ \mathrm {\mu }\textrm {s}$, the magnetic signals decrease to
$>60\ \mathrm {\mu }\textrm {s}$, the magnetic signals decrease to ![]() $<15\ \textrm {G}$, although density is still present. Additionally,
$<15\ \textrm {G}$, although density is still present. Additionally, ![]() $T_e$ for both the individual and colliding plasmas are
$T_e$ for both the individual and colliding plasmas are ![]() $T_{e} \approx 15\ \textrm {eV}$. The
$T_{e} \approx 15\ \textrm {eV}$. The ![]() $T_i$ data show that
$T_i$ data show that ![]() $T_{i}>30\ \textrm {eV} > T_{e}$. At
$T_{i}>30\ \textrm {eV} > T_{e}$. At ![]() $>60\ \mathrm {\mu }\textrm {s}$, the
$>60\ \mathrm {\mu }\textrm {s}$, the ![]() $T_{i}$ signal falls to zero for low density and low electron temperature.
$T_{i}$ signal falls to zero for low density and low electron temperature.
Figure 8 shows the derived values of ![]() $\beta$ and
$\beta$ and ![]() $\omega _{i}\tau _{i}$ versus
$\omega _{i}\tau _{i}$ versus ![]() $t$, based on the quantities in figure 7. Because experiments with the individual plasma from the south (shot 46330) uses only H gas, we did not obtain direct
$t$, based on the quantities in figure 7. Because experiments with the individual plasma from the south (shot 46330) uses only H gas, we did not obtain direct ![]() $T_{i}$ measurements and therefore assume
$T_{i}$ measurements and therefore assume ![]() $T_i=T_e$ for those shots (which serves as a lower bound for
$T_i=T_e$ for those shots (which serves as a lower bound for ![]() $T_{i}$,
$T_{i}$, ![]() $\beta$ and
$\beta$ and ![]() $\omega _{i}\tau _{i}$). In figure 8(b,c), the red and blue traces (where
$\omega _{i}\tau _{i}$). In figure 8(b,c), the red and blue traces (where ![]() $T_i=T_e$ is assumed) can be compared with the green and purple traces (based on measured
$T_i=T_e$ is assumed) can be compared with the green and purple traces (based on measured ![]() $T_i$). We observe
$T_i$). We observe ![]() $\beta >1$ and
$\beta >1$ and ![]() $\omega _{i}\tau _{i}>1$ for
$\omega _{i}\tau _{i}>1$ for ![]() $>20\ \mathrm {\mu }\textrm {s}$ in both the individual H and He plasmas and in the H–He collision. In particular, at the
$>20\ \mathrm {\mu }\textrm {s}$ in both the individual H and He plasmas and in the H–He collision. In particular, at the ![]() $50\ \mathrm {\mu }\textrm {s}$ time of peak density in the collision, we obtain
$50\ \mathrm {\mu }\textrm {s}$ time of peak density in the collision, we obtain ![]() $\beta \approx 100$ and
$\beta \approx 100$ and ![]() $\omega _{i}\tau _{i}\approx 4$ (using the measured
$\omega _{i}\tau _{i}\approx 4$ (using the measured ![]() $T_{i}$ values). Compared with the individual-plasma cases, which also obtain the desired
$T_{i}$ values). Compared with the individual-plasma cases, which also obtain the desired ![]() $\beta ,\omega \tau >1$ regime due to plasma expansion, the collision case gives higher densities and durations which expands the parameter regime available for study, and is more relevant for scaling to regimes of interest for an MIF target.
$\beta ,\omega \tau >1$ regime due to plasma expansion, the collision case gives higher densities and durations which expands the parameter regime available for study, and is more relevant for scaling to regimes of interest for an MIF target.
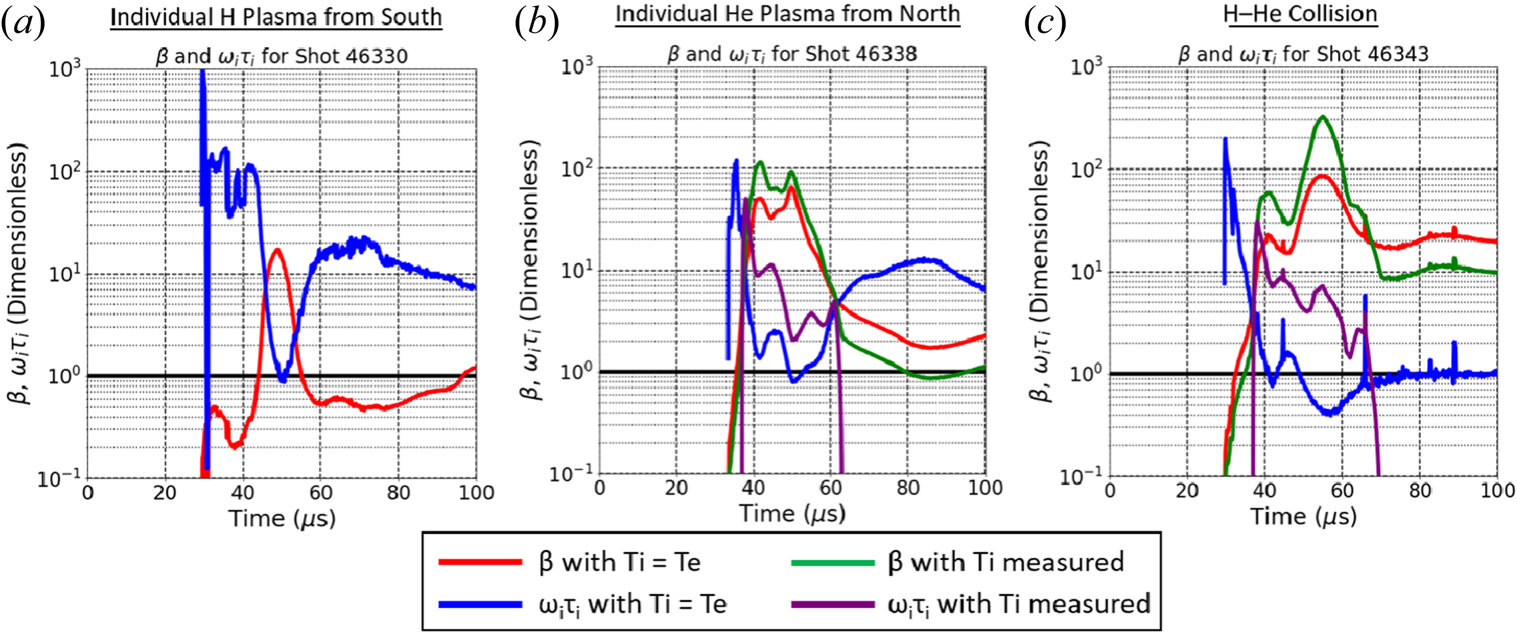
Figure 8. Derived values of ![]() $\beta$ and
$\beta$ and ![]() $\omega _i \tau _i$ versus
$\omega _i \tau _i$ versus ![]() $t$, based on the quantities from figure 7, showing that there are time windows up to
$t$, based on the quantities from figure 7, showing that there are time windows up to ![]() $20\ \mathrm {\mu }\textrm {s}$ in duration during which
$20\ \mathrm {\mu }\textrm {s}$ in duration during which ![]() $\beta$ and
$\beta$ and ![]() $\omega _i \tau _i$ are simultaneously greater than unity, for all three cases of (a) individual H plasma, (b) individual He plasma and (c) H–He collision.
$\omega _i \tau _i$ are simultaneously greater than unity, for all three cases of (a) individual H plasma, (b) individual He plasma and (c) H–He collision.
We find that the plasma from the north injector has larger ![]() $B_r$ and
$B_r$ and ![]() $B_{\phi }$ than the plasma from the south injector. The 50 G background
$B_{\phi }$ than the plasma from the south injector. The 50 G background ![]() $B_z$ from the Helmholtz coil is used to prevent radial expansion of the plasmas. Without the background field, we observe a significant decrease to near zero in the magnetic field signal in the plasma from the south injector, but we do still observe (smaller) magnetic signals in the plasma from the north injector. Studying the plasma collision without the background magnetic field is useful to support the future goals of studying collisions of more than two plasmas. In a possible future case of colliding six plasmas together (e.g. three orthogonal sets of head-on collisions), a Helmholtz-coil magnetic field would not be able to align with the propagation direction for six plasmas.
$B_z$ from the Helmholtz coil is used to prevent radial expansion of the plasmas. Without the background field, we observe a significant decrease to near zero in the magnetic field signal in the plasma from the south injector, but we do still observe (smaller) magnetic signals in the plasma from the north injector. Studying the plasma collision without the background magnetic field is useful to support the future goals of studying collisions of more than two plasmas. In a possible future case of colliding six plasmas together (e.g. three orthogonal sets of head-on collisions), a Helmholtz-coil magnetic field would not be able to align with the propagation direction for six plasmas.
5. Discussion and future work
We intend to build on this work in upcoming experimental campaigns by (i) exploring the time dynamics for the plasma collisions, especially looking into how the energy is distributed within the system, (ii) obtaining a spatial map of plasma parameters by scanning probe positions within the chamber, and (iii) performing a greater number of shots per position to obtain statistics on density, temperature and magnetic-field fluctuations. During the experimental campaigns reported here, we did not complete a probe spatial scan because the individual plasmas did not form as reproducibly as desired. A likely reason for the unrepeatable nature is preionization that is not toroidally symmetric within the coaxial injector. Future work will test more-uniform gas injection and preionization systems. Preliminary engineering improvements using a new more-uniform annular preionization system, a reduced gas injection timing delay from 3 ms to 2 ms, and four gas injectors instead of one around the annular gun nozzle have shown promise in creating more-reproducible plasmas with ![]() ${\sim }95\,\%$ reliability for obtaining similar plasma parameters shot-to-shot. Equivalent levels of engineering improvements to plasma guns and their subsystems have recently been demonstrated in Yates et al. (Reference Yates, Langendorf, Hsu, Dunn, Brockington, Case, Cruz, Witherspoon, Thio and Cassibry2020), which reported significantly improved balance of plasma mass injection in six- and seven-gun experiments as compared with Hsu et al. (Reference Hsu, Langendorf, Yates, Dunn, Brockington, Case, Cruz, Witherspoon, Gilmore and Cassibry2018). Continuation of these experiments on the BRB will focus on better characterization of and generation of small-scale, tangled fields in these merged,
${\sim }95\,\%$ reliability for obtaining similar plasma parameters shot-to-shot. Equivalent levels of engineering improvements to plasma guns and their subsystems have recently been demonstrated in Yates et al. (Reference Yates, Langendorf, Hsu, Dunn, Brockington, Case, Cruz, Witherspoon, Thio and Cassibry2020), which reported significantly improved balance of plasma mass injection in six- and seven-gun experiments as compared with Hsu et al. (Reference Hsu, Langendorf, Yates, Dunn, Brockington, Case, Cruz, Witherspoon, Gilmore and Cassibry2018). Continuation of these experiments on the BRB will focus on better characterization of and generation of small-scale, tangled fields in these merged, ![]() $\beta >1,\omega \tau >1$ plasmas, as well as the exploration and variation of additional parameters, such as radiative cooling, magnetic Prandtl number, etc., of relevance to fundamental plasma physics and plasma-astrophysics questions.
$\beta >1,\omega \tau >1$ plasmas, as well as the exploration and variation of additional parameters, such as radiative cooling, magnetic Prandtl number, etc., of relevance to fundamental plasma physics and plasma-astrophysics questions.
Future studies of processes related to astrophysical phenomena including MHD turbulence and magnetic dynamo will depend upon the plasma characteristics. Required resolution of spatial scales and time scales for MHD turbulence depend upon the Alfvén speed. From the approximate parameters obtained in the present work (see table 1), a 50 cm-scale plasma environment should last ![]() $>35\ \mathrm {\mu }\textrm {s}$ to support at least one crossing time associated with a
$>35\ \mathrm {\mu }\textrm {s}$ to support at least one crossing time associated with a ![]() ${\sim }14\ \textrm {km}\,\textrm {s}^{-1}$ Alfvén speed. The plasma needs to support
${\sim }14\ \textrm {km}\,\textrm {s}^{-1}$ Alfvén speed. The plasma needs to support ![]() ${\sim }10$ ion inertial lengths (0.3–7 cm) and ion gyroradii (0.3–30 cm) to allow turbulent cascades to develop. These turbulent cascades will be experimentally characterized while covering over two orders of magnitude in spatial scale by conducting millimetre-scale measurements. For studies of the magnetic dynamo, we plan to obtain large-enough (
${\sim }10$ ion inertial lengths (0.3–7 cm) and ion gyroradii (0.3–30 cm) to allow turbulent cascades to develop. These turbulent cascades will be experimentally characterized while covering over two orders of magnitude in spatial scale by conducting millimetre-scale measurements. For studies of the magnetic dynamo, we plan to obtain large-enough (![]() ${\gg }1$) magnetic Prandtl numbers (the ratio of magnetic Reynolds number to Reynolds number,
${\gg }1$) magnetic Prandtl numbers (the ratio of magnetic Reynolds number to Reynolds number, ![]() $Pr=R_{m}/Re \propto T^{4}$) and support at least one global turnover time over which the 50 cm-scale plasma can be advected by
$Pr=R_{m}/Re \propto T^{4}$) and support at least one global turnover time over which the 50 cm-scale plasma can be advected by ![]() ${\sim }50\ \textrm {km}\,\textrm {s}^{-1}$ flows, in
${\sim }50\ \textrm {km}\,\textrm {s}^{-1}$ flows, in ![]() ${\sim }10\ \mathrm {\mu }\textrm {s}$.
${\sim }10\ \mathrm {\mu }\textrm {s}$.
Meanwhile, upcoming experiments on the Plasma Liner Experiment (known as the PLX) (Hsu et al. Reference Hsu, Langendorf, Yates, Dunn, Brockington, Case, Cruz, Witherspoon, Gilmore and Cassibry2018; Yates et al. Reference Yates, Langendorf, Hsu, Dunn, Brockington, Case, Cruz, Witherspoon, Thio and Cassibry2020) at Los Alamos National Laboratory will explore the merging of six or more plasmas to create ![]() $\beta >1,\omega \tau >1$ plasmas, at higher densities and temperatures than on the BRB, as a potential MIF target. To advance this MIF concept, future work on the BRB will explore formation of tangled magnetic fields within
$\beta >1,\omega \tau >1$ plasmas, at higher densities and temperatures than on the BRB, as a potential MIF target. To advance this MIF concept, future work on the BRB will explore formation of tangled magnetic fields within ![]() $\beta >1,\omega \tau >1$ plasmas, for which the magnetic field connection length is much longer than the local magnetic field scale size. These studies will evaluate thermal transport properties compared with theoretical predictions for diffusion coefficients in plasmas with tangled magnetic fields (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1978; Rechester & Rosenbluth Reference Rechester and Rosenbluth1978; Chandran & Cowley Reference Chandran and Cowley1998).
$\beta >1,\omega \tau >1$ plasmas, for which the magnetic field connection length is much longer than the local magnetic field scale size. These studies will evaluate thermal transport properties compared with theoretical predictions for diffusion coefficients in plasmas with tangled magnetic fields (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1978; Rechester & Rosenbluth Reference Rechester and Rosenbluth1978; Chandran & Cowley Reference Chandran and Cowley1998).
6. Conclusions
In this work, we successfully used coaxial plasma-gun injectors to study individual and head-on-merging plasmas on the BRB at the WiPPL. By tuning the injector parameter ![]() $\lambda _{\textrm {gun}} = \mu _0 I_{\textrm {gun}}/\psi _{\textrm {gun}}$ within an intermediate range between
$\lambda _{\textrm {gun}} = \mu _0 I_{\textrm {gun}}/\psi _{\textrm {gun}}$ within an intermediate range between ![]() $\lambda _{\textrm {crit}} < \lambda _{\textrm {gun}} < \infty$, we were able to demonstrate the formation of a transient plasma with both
$\lambda _{\textrm {crit}} < \lambda _{\textrm {gun}} < \infty$, we were able to demonstrate the formation of a transient plasma with both ![]() $\beta >1$ and
$\beta >1$ and ![]() $\omega _{i}\tau _{i}>1$. This is a promising first step toward establishing a new experimental platform for studying frontier, weakly magnetized, high-
$\omega _{i}\tau _{i}>1$. This is a promising first step toward establishing a new experimental platform for studying frontier, weakly magnetized, high-![]() $\beta$ plasma physics, e.g. the topics described in § 5. Compared with individual plasmas, the head-on collisions (i) increase the duration for which the desired plasma state exists at a particular location and (ii) increase the magnitudes of
$\beta$ plasma physics, e.g. the topics described in § 5. Compared with individual plasmas, the head-on collisions (i) increase the duration for which the desired plasma state exists at a particular location and (ii) increase the magnitudes of ![]() $n$,
$n$, ![]() $B_r$, and
$B_r$, and ![]() $B_{\phi }$, which widens the parameter space compared with that achievable with individual plasmas.
$B_{\phi }$, which widens the parameter space compared with that achievable with individual plasmas.
Acknowledgements
T.B. and D.A.E. contributed equally to these experiments. The authors gratefully acknowledge J. Olson, J. Wallace, D. Den Hartog and the rest of the WiPPL team for their technical support. We acknowledge H. Gota, T. Roche, I. Allfrey and TAE Technologies for providing one of the plasma injectors and its design. Los Alamos National Laboratory (LANL) staff were supported by the LANL Laboratory Directed Research and Development (LDRD) program under DOE contract no. 89233218CNA000001. University of Wisconsin staff and the WiPPL user facility are supported by the DOE Office of Science, Fusion Energy Sciences under award no. DE-SC0018266. The BRB construction was supported by a National Science Foundation Major Research Instrumentation grant.
Editor Troy Carter thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.