Introduction
To understand and forecast avalanche release is one of the key objectives of avalanche research, with many problems still unsolved (Reference SchweizerSchweizer, 1999). In order to reach this goal the snow-deformation process should be understood, including pure deformation, damage, fracture and healing (sintering). Reference St. Lawrence and BradleySt. Lawrence and Bradley (1975) provided a good interpretation of the deformation process considering the microstructure, but omitted the effect of sintering. Reference De MontmollinDe Montmollin (1978) showed the importance of sintering, which he called fast metamorphism, for the deformation and fracturing process, as well as for the interpretation of mechanical tests. Even for small shear deformations the snow texture changes, some bonds break and others form, and the grams rearrange (Reference Feldt and BallardFeldt and Ballard, 1966). If the process is slow, the snow can sustain large strain since the sintering process is fast enough to balance the damage process. For large deformation rates, damage will accumulate and a fracture surface can form. Adequate quantification of the different processes related to bonding is still lacking. However, bonding between snow grams is the critical factor in determining the response of snow to applied loads (Reference Shapiro, Johnson, Sturm and BlaisdellShapiro and others, 1997). Only high-resolution (in space and time) measurements can provide the data required for detailed understanding; they are needed for future simulations of the snow-deformation and -failure process. A prerequisite for relating the snow-mechanical properties to texture is the successful quantitative characterization of snow texture. Finally, it should be possible to simulate the snow-mechanical response based on snow texture and ice-mechanical properties.
Determining the viscoelastic properties from simple tests can be misleading since the properties change during the tests (Reference MellorMellor, 1975) due to changes in bonding. Simple shear experiments were recently performed by Reference SchweizerSchweizer (1998), and the results of previous shear experiments are summarized there. The precision reached was often not high enough to differentiate between processes. Continuous monitoring of the snow-textural changes during the load experiments would be needed, but is not yet available.
The use of different snow samples for each experiment and the lack of adequate textural characterization leads in general to substantial scatter in the results. In order to perform shear measurements with high resolution and to take advantage of a measurement technique allowing the same snow sample to be loaded repeatedly without destroying it, we decided to use a so-called rheometer in an SLF cold laboratory at Weissfluhjoch, Switzerland (Fig. 1).

Fig. 1. The CVR50 rheometer in the SLFcold laboratory at Weissfluhjoch.
The rheometer is a rotational shear test apparatus which takes full advantage of a rotational measuring set-up (high precision) and of dynamic measuring methods. The method itself is not new. Torsional shear tests (e.g. Shinojima, 1966; Reference De Montmollinde Montmollin, 1978) as well as dynamic experiments (e.g. Reference YosidaYosida, 1956; Reference NakayaNakaya, 1959; Reference Chae and OuraChae, 1967) have been performed in the past. However, modern rheometers allow new possibilities for measuring the viscoelastic properties of snow with high resolution. In the following, the method used to perform rheological measurements with a rheometer is introduced, and a limited number of data are presented in order to show how the rheometer works and what kind of results can be obtained.
Methods
Rheometer
Rheometers are commonly used in industry and research at various levels to provide information for process engineering, stability evaluation, product development, quality control and consumer study (Reference WhorlowWhorlow, 1992). Rheological measurements today represent a standard method of determining the viscoelastic properties of a wide range of materials. However, a rheometer has not yet been used to study the viscoelastic deformation of snow. The advantages of using a rheometer for snow studies are the high precision at relatively low stress, and the possibility of determining the viscoelastic properties of a specific type of snow at various frequencies and temperatures with the same snow sample, provided it is loaded within the linear range (where the stress is proportional to the strain) so that no textural changes take place during the experiments. However, the nature of the snow does not always allow standard rheometric procedures to be applied.
Although the cone-plate configuration is common with the type of stress-controlled rheometer (CVR50 of Bohlin Instruments), the plate-plate configuration is best suited for testing snow. This configuration is generally used for more solid-like materials with low viscosity, for materials consisting of particles and if pre-formed sample discs are tested (Reference Carreau, de Kee and ChahabraCarreau and others, 1997). The distance between the two plates (or the sample thickness) should be about 5–10 times the particle dimension, and the sample diameter should be about 5–10 times the sample thickness. We used plates of 60 mm diameter, and prepared samples about 7 mm thick, thereby fulfilling the two scale conditions. Since the sample thickness or gap size is many times the particle diameter, small variations in gap size should not influence the results.
The coupling between the plates and the snow sample is ensured by using grooved plates, and by very slightly compressing the sample at the beginning. If the coupling is not given during an experiment, the upper plate starts to rotate very fast due to the loss of resistance, and material is torn away.
Uniform deformation over the sample thickness, i.e. also uniform distribution of the stresses within the sample (in transversal direction), is assumed, which seems reasonable based on previous work (Reference Navarre and DesruesNavarre and Desrues, 1978; Reference NaritaNarita, 1983) and observations during our own experiments. At low strain we have never observed a yield surface within a sample during deformation experiments. We would expect a yield surface to form, if at all, shortly before fracture. Stress concentrations are, in general, expected at the interface to the plates for any measuring set-up.
The disadvantage of the plate-plate configuration is that the strain, the strain rate and the stress are not distributed homogeneously within the sample in radial direction, but increase with increasing radius.
The CVR50 rheometer is a stress-controlled torsional shear apparatus composed principally of a constant torque motor that works on the base of a drag cup system, and a completely digital angular position sensor providing high resolution (Table 1). The torque is directly applied to the upper part of the measuring system, while the bottom part is fixed to the rheometer frame. In order to prevent friction, the upper part (moving) must have a very good bearing system (compressed air or mechanical bearing). The rheometer controls the torque and measures the resulting angular deformation. The strain rate
![]() , the strain ε and the stress τ are calculated according to:
, the strain ε and the stress τ are calculated according to:

where r is the plate radius, h is the distance between the two plates, the so-called gap, Ω is the angular velocity, 9 is the angular deformation and T is the measured torque. For the plate-plate configuration the shear stress, shear strain and strain rate are calculated for three-quarters of the plate radius (Carreau and others, Reference Carreau, de Kee and Chahabra1997). This averaging is used in the following. The experiments performed with the rheometer can be classified as stress-ramp and creep experiments, and as dynamic measurements (oscillation).
Table 1. Technical data of the CVR50 rheometer of Bohlin Instruments
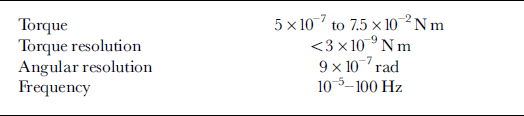
Creep and stress-ramp measuring methods
The so-called static measuring methods can be divided into two categories: stress-ramp and creep experiments. We will not show any results of our creep and creep-recovery experiments, but will focus on stress-ramp experiments. In a stress-ramp experiment the applied stress is increased (or decreased) from an initial to a final stress level, linearly or logarithmically, continuously or in steps. Such a load process can be used, for example, to simulate the loading process during a snowfall period. Stress-ramp experiments were performed in order to better understand the deformation process and possibly to validate the dynamically determined mechanical parameters.
Oscillation-measuring method
Dynamic experiments are performed by applying a harmonically varying torque to the sample. Thereby the deformation can be separated into a time-independent part (elastic) and a time-dependent part (viscous). Due to the high resolution, the applied torque can be very small so that destructive deformation is avoided.
If a small, harmonically varying stress τ(t) is applied to a viscoelastic material such as snow, the measured strain response ε(t) for linear viscoelastic deformation is also sinusoidal but there is a phase difference 6 between stress and strain (Fig. 2). The phase shift 6 can vary between 0° and 90° and depends on the viscoelastic nature of the material. The closer the phase shift is to 0°, the more solid-like (elastic) is the behaviour of the tested material. There are several equivalent ways of expressing the relation between stress and strain, and defining the viscoelastic properties. Using complex notation the complex dynamic shear modulus G* is
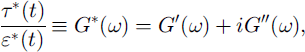
where ω is applied angular frequency, G’ is the shear storage modulus and G” is the shear loss modulus (Reference MakoskoMakosko, 1994).

Fig. 2. Raw data of amplitude-sweep experiment. The resulting strain is not in phase with the applied torque due to the viscoelastic nature of snow.
The software provided with the rheometer performs the calculations to divide the deformation into the elastic part (in phase with the stress) and the viscous part (in phase with the strain rate). However, these calculations are meaningful only if the deformation is small so that the material tested behaves linearly, i.e. the strain is proportional to the stress. As proportionality holds only for small strains, the application of oscillation experiments makes sense only if small stresses are applied. If the strain is large, the material response will be non-linear, i.e. the sample is “overstrained” and the initial (unloaded) snow texture is destroyed.
Three different types of dynamic experiment can be performed with the rheometer used. In constant-oscillation experiments the applied stress and the oscillation frequency are held constant. In amplitude-sweep experiments the oscillation frequency is held constant and the applied stress (oscillation amplitude) is linearly or logarithmically increased or decreased with time. In frequency-sweep tests a constant stress is applied with increasing or decreasing oscillation frequency. In the following we will focus on the results of amplitude-sweep experiments.
To determine the limit of linear viscoelastic behaviour, an amplitude sweep is performed by increasing the applied torque in small steps. The measured viscoelastic parameters will stay constant and not change as long as the proportional limit (Reference JaegerJaeger, 1969) is not reached. Beyond the linear range a change (decrease) of the viscoelastic parameters of snow is expected.
Determining the viscoelastic properties in the linear range is physically relevant since for a strain larger than the critical strain for linearity, textural changes are expected to take place. It does not make sense to measure the viscoelastic parameters beyond the proportional limit. Only within the linear range are elasticity and viscosity referred to a precise snow texture and not to a transitional stage.
Snow sampling
The snow used for testing was collected from the SLF study plot below Weissfluhjoch. Snow collection starts with a detailed snow profile which is important for identifying potential layers that can be used for laboratory tests. We paid particular attention to the snow hardness. Only snow with an in situ hand-hardness index between 2 (four fingers) and 4 (pencil) was collected. In order to have sufficient material for testing, only layers more than about 5 cm thick were taken. Several (two to five) blocks of about 45 cm × 20 cm × 30 cm were cut out from the snow cover and put into cold boxes of the same size, to be transported to the cold laboratory at Weissfluhjoch. In the laboratory the blocks were further analyzed and cut into thinner blocks of so-called homogeneous snow layers originating from a single snowfall with similar meteorological conditions (principally wind and temperature). The layers that could be used for snow testing were stored in plastic sacks to prevent sublimation, for a maximum period of about 1 month at a temperature of –40°C. At low temperature the metamorphism process is very slow, so the changes in texture are small.
The sample preparation was not easy since the sample thickness is quite small (about 7 mm). Therefore, we developed a simple cutting device to prepare the samples. It consists of a cutting cylinder (40 or 60 mm in diameter) containing the snow cut out from a snow block, and on top of it, of a swivelling sample-holder with the same dimensions as the sample used (40 or 60 mm in diameter and 7 mm thick). The snow in the cylinder is pushed from below into the sample-holder, and the sample is cut between the sample-holder and the cylinder, resulting in a thin snow disc. The sample-holder is rotated to the side, and the sample can be taken out. The snow was again characterized before testing: snow type, temperature and hardness, sample weight and thickness (density). The sample is then put between the two parallel grooved plates of the rheometer, and the upper plate is moved down till there is firm contact between the snow and the plate (Fig. 3).

Fig. 3. Snow sample (about 7 mm thick) mounted between the two grooved parallel plates (60 mm in diameter). The bottom plate is fixed to the rheometer frame, while the upper plate is rotating.
After the experiment the sample form, the hardness and the temperature are checked and recorded. For long experiments the sample temperature is measured continuously with a very thin thermocouple put directly into the snow sample.
For most of the snow types tested, single snow crystals were stored in isooctane before and after sample loading for subsequent objective microscopic analysis. Some loaded and corresponding unloaded samples were conserved with a pore-filler and analyzed with the serial cut technique.
Results and Interpretation
Dynamic measurements
The result of an amplitude-sweep experiment is given in Figure 4. The tested snow consisted of faceted and rounded particles with a diameter of 0.25–1 mm, a hand-hardness index of 2 (four fingers) and a density of 240 kg m−3. The measuring frequency was 1Hz. The applied stress was linearly increased from 40 to 500 Pa. The snow temperature was –9°C. The storage modulus G’ is initially about 0.8 MPa. At an applied stress of about 200 Pa it starts to decrease, i.e. the snow becomes weaker since textural changes are occurring. The strain at the proportional limit is therefore found to be about 2 × 10−4 . The dynamic viscosity η is about 2 × 104 Pas. Throughout the experiment the phase shift 6 hardly changes and is about 10°, showing that the deformation is mainly elastic.

Fig. 4. Result of an amplitude-sweep experiment. Storage modulus G’, dynamic viscosity η’, phase shift δ and the measured strain are shown vs the applied stress.
To demonstrate that textural changes (principally bond-breaking; Reference Kinosita and OuraKinosita, 1967) arise during deformation beyond the linear viscoelastic range, we repeated the same amplitude-sweep experiment several times with the same snow sample (snow type and measurement parameters as above, but with a larger stress amplitude) within and beyond the linear viscoelastic range (Fig. 5). The results clearly demonstrate that if the sample is deformed beyond the limit strain, the changes in texture and related mechanical parameters become very important. Already after one overloading cycle the snow sample is weaker, most likely due to bond-breaking. Figure 5 (see inset) shows the high reproducibility of the results within the linear range.

Fig. 5. Storage modulus G’ vs measured strain for six repeated amplitude-sweep experiments using the same snow sample (same snow type and measuring parameters as in Fig. 4). The first three experiments were performed within the linear range (below the proportional limit), the second three beyond the proportional limit. Inset shows detail within the linear range.
In Figure 6 the proportional limit strain is shown for two different snow types of similar density and snow temperature (–4°C). The first snow type consists of decomposed particles and in part small rounded grams of size 0.5–1 mm, and hand-hardness index 2 (four fingers). The second snow type consists of small rounded grams and decomposed particles, 0.25–0.75 mm in size and with the same hand-hardness index. For each snow type, nine identical amplitude-sweep experiments were performed to determine the proportional limit. At equal snow density, the proportional limit is larger for the snow with smaller than for the snow with larger crystals. The number of ice grams is larger for the snow with smaller grams, so the number of bonds is also larger than for the snow with larger grains. Assuming that bond dimensions are similar for both types of snow, and that the deformation occurs mainly in the bonds (due to the stress concentrations in the bonds), the proportional limit will be larger for the snow with smaller grains. The same explanation also applies to the density: the higher the density is, the higher will be the proportional limit strain.

Fig. 6. Proportional limit strain vs snow density for two snow types. Snow type 1: decomposed particles and partly small rounded grains, 0.5–1 mm in size and hand-hardness index 2 (four fingers). Snow type 2: small rounded and decomposed particles, 0.25–0.75mm in size and hand-hardness index 2
The dynamic mechanical properties (G’,η’) obtained from 20 identical amplitude-sweep tests with an oscillation frequency of 1 Hz are shown in Figure 7. All samples were cut out of the same snow layer which consisted of small rounded particles and partly decomposed particles, 0.25–0.75 mm in size, and hand-hardness index 2. Snow temperature was about –4°C. The density varied between 215 and 255 kg m–3. The storage modulus G’ was found to be 0.38–0.8 MPa, and despite the scatter, clearly increases with increasing snow density (p = 0.001) (Fig 7). Possible reasons for the scatter are measuring errors (very small strain, variation in normal stress, small temperature variations and density determination) and inhomogeneity of the tested snow. The density variations of the snow samples taken from a layer assumed to be homogeneous are obviously linked to small textural differences. So the mechanical parameters determined do not belong exactly to the same type of snow. As already discussed, for the proportional limit strain such a dependence of the storage modulus G’ on the density is reasonable in view of the snow texture.

Fig. 7. Storage modulus G’ and dynamic viscosity η vs snow density for a series of measurements with the same snow type (small rounded and partly decomposed particles, 0.25–0.75 mm in size and hand-hardness index 2). Measuring frequency 1 Hz, temperature-4° C.
The phase shift (ratio of elastic to viscous deformation; not shown) was found to be 9–18° and does not depend on snow density. This result is explained by the fact that the texture should not have any influence on the type of deformation. Inside the range of linear viscoelastic deformation, the phase difference 6 will depend only on external parameters that influence the mechanical behaviour of ice, such as temperature and strain rate.
The dynamic viscosity η’ (Fig 7) was found to be 1.6–3.4 × 10–4 Pa s, and shows the same dependence on the snow density as the storage modulus G’ since η’ is directly related to G’ and 6 as follows:
Stress-ramp measurements
The result of a stress-ramp experiment is plotted in Figure 8. The grains of the tested snow sample were classified as small rounded and partly decomposed particles, 0.25–0.75 mm in size. Hand-hardness index was 2 (four fingers). The stress was increased from 10 to 860 Pa in 15 000 s (about 4 h). Snow temperature during the test was about –5°C. At the beginning the strain rate increases at a low rate. The snow texture imposes a slow rate of deformation, but the damage process continues since the proportional limit (1 × 10–4) has long been crossed. After a considerable time the strain rate increases, and the sample finally breaks at a large strain (ε ≈ 0.35). The large value of strain reached before sample fracturing is surprising in view of the proportional limit at very small strain, when bond fracturing is supposed to start. The strain rate before sample breaking is about 8 × 10–4 s–1. In experiments performed at higher temperatures (e.g. –2°C) the fracture strain can reach values of > 1. Considering that the proportional limit for the sample tested in the experiment shown in Figure 8 was about 1 × 10–4, it seems impossible that the sample resists so long without breaking, unless another process is considered. The only explanation seems to be that a healing process (sintering) occurs during the experiments, as postulated by Reference De Montmollinde Montmollin (1982). The damage process is apparently balanced for a long time by the sintering process. Although bonds are continuously breaking, due to the proximity of the ice grains and the internal stresses new unstressed bonds are formed continuously as well. Only at high applied stress and at sufficiently large strain rate does the damage process exceed the healing process.

Fig. 8. Stress-strain and strain-rate-strain curves of a stress-ramp experiment.
The large strain reached in the stress-ramp experiment suggests that changes in texture should be noticeable. Therefore unloaded and loaded samples cut perpendicular to the disc faces at about three-quarters of the radius were conserved with an organic pore-filler. However, it was difficult to find a useful method for analyzing the two-dimensional images obtained with the serial cut technique. The existing methods are very time-consuming, and it does not seem possible to obtain results precise enough to detect small changes in snow texture (Reference Hansen and BrownHansen and Brown, 1987). The error might be larger than the textural changes searched for. Considering that the samples that we analyzed were composed of partly decomposed precipitation particles and of small rounded grains, 0.25–1 mm in size, we focused on the partly decomposed grains (not symmetrical particles). For each elongated particle in the digital image the angle between the horizontal axis and the major (longitudinal) axis of the ice particle was measured as shown in Figure 9 (inset). For the unloaded sample most of the elongated particles were parallel to the snow layering (Fig. 9). However, the analysis of a sample from the same snow layer loaded in a stress-ramp test (stress from 10 to 1600 Pa in 8250 s, ε = 0.13,
![]() , no fracture) showed that during the experiment the orientation of the elongated particles moved even more towards the horizontal. More elongated particles show horizontal orientation after the experiment, as would be expected since the strain was large and grain rearrangement was supposed to occur. Reference Feldt and BallardFeldt and Ballard (1966) made similar observations during compression tests.
, no fracture) showed that during the experiment the orientation of the elongated particles moved even more towards the horizontal. More elongated particles show horizontal orientation after the experiment, as would be expected since the strain was large and grain rearrangement was supposed to occur. Reference Feldt and BallardFeldt and Ballard (1966) made similar observations during compression tests.

Fig. 9. Angle between the horizontal axis and the major (longitudinal) axis of elongated ice particles vs the portion of particles (frequency); insert shows the definition of the angle.
From stress-ramp experiments it is possible to obtain at least one of the important mechanical parameters, the initial tangent modulus, commonly assumed to be the shear modulus. It is determined by a linear regression of the data points at the beginning of a stress-strain curve. The method was described by Reference MellorMellor (1975) and used, for example, by Reference SchweizerSchweizer (1998). Before each stress-ramp experiment an amplitude-sweep experiment with the same sample was performed to determine the proportional limit strain and the viscoelastic parameters. Thereby the dynamic storage modulus G’ and the initial tangent modulus G for the same snow sample can be compared (Fig. 10), in order to validate the dynamically measured data and to show the possible errors introduced by determining the shear modulus with the initial tangent method. Since the different data were measured at different strain rates, a transformation is needed. The stress-ramp experiments are performed at a strain rate of about 1 × 10–4 s–1, and the dynamic experiments at about 1 s−1. Based on unpublished data of the authors and the results of Reference SchweizerSchweizer (1998) for the strain-rate dependency of the shear modulus, the values of the initial tangent modulus are transformed so that they represent values at a strain rate of about 1 s−1. From the 21 measurements performed, 13 show a good agreement between the measured storage modulus G’ and the calculated shear modulus G (Fig. 10). All these points originate from inside the linear range which was determined with the amplitude-sweep experiment. For 8 out of the 21 measurements the initial deformation was already too large to calculate the tangent modulus inside the linear range. The interpolated stress-strain points were already beyond the proportional limit, so the determined initial tangent modulus clearly underestimates the true shear modulus for these experiments. The values obtained are the shear moduli for already damaged snow samples and depend directly on the strain reached, i.e. the damage stage.

Fig. 10. Initial tangent modulus from stress-ramp (static) measurements vs storage modulus from dynamic measurements. Both moduli are given for the same strain rate (about 1 s−1) and snow temperature.
Conclusions
The results obtained during two winters, partly presented above, showed that the use in a cold laboratory of the CVR50 rheometer of Bohlin Instruments is technically possible and represents a very good method of measuring the rheological parameters of snow. The experimental procedure has been established successfully. The reproducibility of the results confirms the applicability of the method.
Dynamic oscillation experiments allow the proportional limit strain for viscoelastic deformation to be determined. The limit was found to be 0.5–5 × 10−4 depending on snow type, density, loading rate and temperature. It is at least about a factor of 10 smaller than for ice (Reference Budd and JackaBudd and jacka, 1989; Reference Petrenko and WhitworthPetrenko and Whitworth, 1999). This is in accordance with the assumption that the deformation of snow should occur primarily in the bonds, which contribute only a few per cent to the snow volume. The mechanical parameters measured within the linear range (below the proportional limit) are not modified by microstructural changes, but are original material properties needed for future simulations of the deformation and failure process of snow. As could be shown, beyond the proportional limit important textural changes (damage) are taking place. So any significant shear deformation of snow implies grain rearrangement.
The values of the dynamically measured (at 1 Hz) storage modulus G’ vary between 0.2 and 2 MPa depending on snow type, density, temperature and frequency. Since under torsional shear the strain rate is not constant within the snow sample, it is difficult to directly compare the present results with values obtained by other methods, such as simple shear. However, the order of magnitude is correct (Reference MellorMellor, 1975), even if it is often not known whether other results were obtained below or beyond the proportional limit. Only simulations performed on the base of our measuring geometry could provide a relation between the shear storage modulus and the strain rate. This is the only drawback to rheometric measurements, but it is clear that the high precision needed (eg. for oscillation measurements within the linear range) can only be obtained with a torsional loading device. The dynamic viscosity η’ was found to be between 7 × 104 and 2 × 106 Pa s, and the phase shift 6 between about 5° and 20°, showing the predominance of the elastic part of the deformation. All values are determined at an oscillation frequency of 1Hz and are in agreement with the values compiled by Reference MellorMellor (1975).
Comparison of the results obtained with dynamic and static experiments showed good agreement. Whereas dynamic measurements must be performed to determine the viscoelastic parameters inside the linear range of viscoelastic deformation, the static methods are better for study of the damage and fracture process. The chaotic nature of the damage and fracture process will lead to higher scatter in the results obtained with experiments outside the linear range.
Future work will deal with the quantification of the dependence of the viscoelastic parameters on temperature and frequency, since the dynamic experimental set-up allows a snow sample to be tested over a large range of temperature and frequency. An update of the rheometer will make it possible to precisely control and measure the normal force, so that experiments under exactly the same measuring conditions can be performed.
Acoustic emission measurements should provide further insight into the damage process that sets in beyond the proportional limit. On a larger time-scale the crucial question is how the relation between the mechanical parameters and the snow texture is quantified. However, once it becomes possible to measure important textural parameters such as bond number and size, the rheometric measurements will be very useful since physically based, highly reproducible values of the mechanical properties can be obtained. Therefore the rheometer could be used as a standard test to determine the mechanical behaviour of snow. Since the deformation process below the proportional limit strain depends directly on the bonds, the mechanical parameters determined might even represent an index of strength.
Acknowledgements
We would like to thank L.J. Gauckler (Nonmetallic Inorganic Materials, ETH Zurich) for encouraging us to use a rheometer for studying the mechanical properties of snow. We gratefully acknowledge reviews by K. Hutter and C. Balan.













