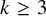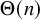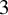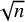1 Introduction
The study of cycles in graphs goes back to the early days of graph theory and has been fundamental ever since. Of particular interest are Hamilton cycles, i.e., cycles passing through all the vertices of a graph. Starting with the cornerstone theorem of Dirac [Reference Dirac8], there are many results giving sufficient conditions for a graph to be Hamiltonian, for some other classical examples see [Reference Bondy4, Reference Chvátal5, Reference Chvátal and Erdős6, Reference Fan12, Reference Ore22]. In 1973, Bondy [Reference Bondy3] made the ‘meta-conjecture’ that any nontrivial condition which guarantees the existence of a Hamilton cycle should also guarantee that the given graph is pancyclic, i.e., contains cycles of all possible lengths, with possibly a simple family of exceptions. This assertion turned out to be influential, and by now, there are numerous appealing results of this type. For example, Bondy himself [Reference Bondy2] proved that Ore’s sufficient condition for Hamiltonicity (that the sum of degrees of any pair of nonadjacent vertices is at least n) implies that the graph is either pancyclic or isomorphic to the complete bipartite graph
![]() $K_{n/2,n/2}$
. Bauer and Schmeichel [Reference Bauer and Schmeichel1], relying on previous results of Schmeichel and Hakimi [Reference Schmeichel and Hakimi23], have shown that the sufficient conditions for Hamiltonicity of Bondy [Reference Bondy4], Chvátal [Reference Chvátal5] and Fan [Reference Fan12] all imply pancyclicity, barring a small family of exceptions. Jackson and Ordaz [Reference Jackson and Ordaz17] conjectured that any graph G whose connectivity
$K_{n/2,n/2}$
. Bauer and Schmeichel [Reference Bauer and Schmeichel1], relying on previous results of Schmeichel and Hakimi [Reference Schmeichel and Hakimi23], have shown that the sufficient conditions for Hamiltonicity of Bondy [Reference Bondy4], Chvátal [Reference Chvátal5] and Fan [Reference Fan12] all imply pancyclicity, barring a small family of exceptions. Jackson and Ordaz [Reference Jackson and Ordaz17] conjectured that any graph G whose connectivity
![]() $\kappa (G)$
is strictly larger than its independence number
$\kappa (G)$
is strictly larger than its independence number
![]() $\alpha (G)$
must be pancyclic. This conjecture is motivated by the classical theorem of Chvátal and Erdős [Reference Chvátal and Erdős6] that a graph with
$\alpha (G)$
must be pancyclic. This conjecture is motivated by the classical theorem of Chvátal and Erdős [Reference Chvátal and Erdős6] that a graph with
![]() $\kappa (G) \geq \alpha (G)$
must be Hamiltonian. An approximate version of the conjecture was proven by Keevash and Sudakov [Reference Keevash and Sudakov18], who showed that
$\kappa (G) \geq \alpha (G)$
must be Hamiltonian. An approximate version of the conjecture was proven by Keevash and Sudakov [Reference Keevash and Sudakov18], who showed that
![]() $\kappa (G) \geq 600 \alpha (G)$
is sufficient for pancyclicity.
$\kappa (G) \geq 600 \alpha (G)$
is sufficient for pancyclicity.
Pancyclicity is just an instance of a wider class of problems, which study the properties of the set of cycle lengths of a graph with connection to other graph parameters. The set of cycle lengths of G is called its cycle spectrum and denoted
![]() $\mathcal {C}(G)$
. There are by now numerous results relating properties of
$\mathcal {C}(G)$
. There are by now numerous results relating properties of
![]() $\mathcal {C}(G)$
to various graph parameters. For example, Erdős [Reference Erdős10] conjectured that a graph G with girth g and average degree d must satisfy
$\mathcal {C}(G)$
to various graph parameters. For example, Erdős [Reference Erdős10] conjectured that a graph G with girth g and average degree d must satisfy
![]() $|\mathcal {C}(G)| \geq \Omega (d^{\lfloor \frac {g-1}{2} \rfloor })$
. The case
$|\mathcal {C}(G)| \geq \Omega (d^{\lfloor \frac {g-1}{2} \rfloor })$
. The case
![]() $g = 5$
was settled by Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp11]. Later, Sudakov and Verstraëte [Reference Sudakov and Verstraëte24] proved the full conjecture in a strong form. Another example is a result of Gould, Haxell and Scott [Reference Gould, Haxell and Scott15] that a graph with minimum degree
$g = 5$
was settled by Erdős, Faudree, Rousseau and Schelp [Reference Erdős, Faudree, Rousseau and Schelp11]. Later, Sudakov and Verstraëte [Reference Sudakov and Verstraëte24] proved the full conjecture in a strong form. Another example is a result of Gould, Haxell and Scott [Reference Gould, Haxell and Scott15] that a graph with minimum degree
![]() $cn$
must have a cycle of any even length between
$cn$
must have a cycle of any even length between
![]() $4$
and
$4$
and
![]() $ec(G) - K$
, where
$ec(G) - K$
, where
![]() $ec(G)$
is the length of a longest even cycle in G and K is a constant depending only on c. We should also mention the recent work of Gao, Huo, Liu and Ma [Reference Gao, Huo, Liu and Ma13], who proved several conjectures relating properties of
$ec(G)$
is the length of a longest even cycle in G and K is a constant depending only on c. We should also mention the recent work of Gao, Huo, Liu and Ma [Reference Gao, Huo, Liu and Ma13], who proved several conjectures relating properties of
![]() $\mathcal {C}(G)$
to the minimum degree, connectivity or chromatic number of G.
$\mathcal {C}(G)$
to the minimum degree, connectivity or chromatic number of G.
Bondy’s meta-conjecture is about conditions for Hamiltonicity which imply pancyclicity. A natural question in the opposite direction is as follows: Let us assume that a graph G is Hamiltonian; under which assumptions can we also guarantee that G is pancyclic? Since pancyclicity is sometimes too strong of a requirement, we can relax it and ask to find many cycle lengths. Questions of this type were first introduced by Jacobson and Lehel at the 1999 conference ‘Paul Erdős and His Mathematics’, where they asked for the minimum size of the cycle spectrum of a k-regular Hamiltonian graph G on n vertices. The aforementioned result of Bondy [Reference Bondy2] implies that if
![]() $k = \lceil n/2 \rceil $
, then G is pancyclic unless
$k = \lceil n/2 \rceil $
, then G is pancyclic unless
![]() $G = K_{n/2,n/2}$
. At the other extreme, if
$G = K_{n/2,n/2}$
. At the other extreme, if
![]() $k = 2$
, then G clearly has just one cycle. Jacobson and Lehel conjectured that, already for
$k = 2$
, then G clearly has just one cycle. Jacobson and Lehel conjectured that, already for
![]() $k \geq 3$
, the number of cycle lengths should be linear in n. This is best possible since they also observed that one cannot expect to have pancyclicity. Indeed, assuming
$k \geq 3$
, the number of cycle lengths should be linear in n. This is best possible since they also observed that one cannot expect to have pancyclicity. Indeed, assuming
![]() $2k$
divides n, take
$2k$
divides n, take
![]() $\frac {n}{2k}$
disjoint copies of
$\frac {n}{2k}$
disjoint copies of
![]() $K_{k,k}$
, ordered in a cycle, remove an edge from each of them and add an edge between any two consecutive copies such that the resulting graph is k-regular. It is not hard to see that, in this construction, the possible cycle lengths are precisely all the even integers between
$K_{k,k}$
, ordered in a cycle, remove an edge from each of them and add an edge between any two consecutive copies such that the resulting graph is k-regular. It is not hard to see that, in this construction, the possible cycle lengths are precisely all the even integers between
![]() $4$
and
$4$
and
![]() $2k$
and between
$2k$
and between
![]() $\frac {2n}{k}$
and n. This gives in total
$\frac {2n}{k}$
and n. This gives in total
![]() $\frac {n}{2} \cdot \frac {k-2}{k} + k$
different lengths.
$\frac {n}{2} \cdot \frac {k-2}{k} + k$
different lengths.
Soon after the above question was first circulated, Gould, Jacobson and Pfender proved that
![]() $|\mathcal {C}(G)| \geq \Omega (\sqrt {n})$
for every k-regular n-vertex Hamiltonian graph G (with
$|\mathcal {C}(G)| \geq \Omega (\sqrt {n})$
for every k-regular n-vertex Hamiltonian graph G (with
![]() $k \geq 3$
). This bound was subsequently obtained by several other authors. Yet, prior to our work, the
$k \geq 3$
). This bound was subsequently obtained by several other authors. Yet, prior to our work, the
![]() $\sqrt {n}$
bound was the best known result. In particular, Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] remarked that improving this estimate would be of considerable interest. Furthermore, the following strengthening of the above conjecture of Jacobson and Lehel, which replaces the k-regularity condition with the assumption that the minimum degree is at least
$\sqrt {n}$
bound was the best known result. In particular, Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] remarked that improving this estimate would be of considerable interest. Furthermore, the following strengthening of the above conjecture of Jacobson and Lehel, which replaces the k-regularity condition with the assumption that the minimum degree is at least
![]() $3$
, was proposed by Verstraëte [Reference Verstraëte28].
$3$
, was proposed by Verstraëte [Reference Verstraëte28].
Conjecture 1.1. An n-vertex Hamiltonian graph G with
![]() $\delta (G) \geq 3$
has
$\delta (G) \geq 3$
has
![]() $\Omega (n)$
different cycle lengths.
$\Omega (n)$
different cycle lengths.
While the special case of this conjecture for regular graphs already seems quite challenging, it is natural to expect that the full Conjecture 1.1 is even harder. The reason for this is that often problems become more difficult when the regularity requirement is replaced by a minimum degree assumption. One well-known example is a conjecture of Thomassen [Reference Thomassen25], that a graph with a large enough minimum degree contains a subgraph of large minimum degree and large girth. This conjecture is open even for girth
![]() $7$
. However, this statement becomes easy if the given graph is regular; see e.g., [Reference Montgomery, Pokrovskiy and Sudakov21]. Such situations arise also for questions related to the one studied here: A classical result of Smith (see [Reference Tutte27] and also [Reference Thomassen26]) states that every Hamiltonian
$7$
. However, this statement becomes easy if the given graph is regular; see e.g., [Reference Montgomery, Pokrovskiy and Sudakov21]. Such situations arise also for questions related to the one studied here: A classical result of Smith (see [Reference Tutte27] and also [Reference Thomassen26]) states that every Hamiltonian
![]() $3$
-regular graph G contains a second Hamilton cycle. As was shown by Entringer and Swart [Reference Entringer and Swart9], this is no longer true if instead of
$3$
-regular graph G contains a second Hamilton cycle. As was shown by Entringer and Swart [Reference Entringer and Swart9], this is no longer true if instead of
![]() $3$
-regularity we assume that
$3$
-regularity we assume that
![]() $\delta (G) \geq 3$
(even if all degrees are equal to
$\delta (G) \geq 3$
(even if all degrees are equal to
![]() $3$
or
$3$
or
![]() $4$
). Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] required an involved proof to even show that a Hamiltonian G with
$4$
). Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] required an involved proof to even show that a Hamiltonian G with
![]() $\delta (G) \geq 3$
contains a second cycle of length at least
$\delta (G) \geq 3$
contains a second cycle of length at least
![]() $n - o(n)$
. In contrast, for regular G, this proof can be simplified considerably and gives a better bound.
$n - o(n)$
. In contrast, for regular G, this proof can be simplified considerably and gives a better bound.
It is worth noting that if one replaces the minimum degree requirement
![]() $\delta (G) \geq 3$
, with the requirement that the average degree is at least
$\delta (G) \geq 3$
, with the requirement that the average degree is at least
![]() $3$
, then the aforementioned lower bound of
$3$
, then the aforementioned lower bound of
![]() $\Omega (\sqrt {n})$
is tight. More generally, Milans, Pfender, Rautenbach, Regen and West [Reference Milans, Pfender, Rautenbach, Regen and West20] have shown that a graph G with n vertices and m edges satisfies
$\Omega (\sqrt {n})$
is tight. More generally, Milans, Pfender, Rautenbach, Regen and West [Reference Milans, Pfender, Rautenbach, Regen and West20] have shown that a graph G with n vertices and m edges satisfies
![]() $|\mathcal {C}(G)| \geq (1-o(1))\sqrt {m - n}$
, and this is tight up to lower-order terms.
$|\mathcal {C}(G)| \geq (1-o(1))\sqrt {m - n}$
, and this is tight up to lower-order terms.
In this paper, we prove the following theorem, which resolves Conjecture 1.1 asymptotically:
Theorem 1.1. An n-vertex Hamiltonian graph G with
![]() $\delta (G) \geq 3$
contains cycles of
$\delta (G) \geq 3$
contains cycles of
![]() $n^{1-o(1)}$
different lengths.
$n^{1-o(1)}$
different lengths.
Our proof of Theorem 1.1 is constructive: It gives a polynomial-time algorithm for finding cycles of
![]() $n^{1-o(1)}$
different lengths in a Hamiltonian graph of minimum degree
$n^{1-o(1)}$
different lengths in a Hamiltonian graph of minimum degree
![]() $3$
, provided a Hamilton cycle is specified.
$3$
, provided a Hamilton cycle is specified.
2 A sketch and the main ideas
The overarching idea that we employ is to split the Hamilton cycle into pieces (usually paths or pairs of paths) and then find paths with lengths on a different ‘scale’ in different parts. To illustrate what we mean, let us consider the following situation. Suppose that we managed to split our Hamilton cycle into two paths
![]() $P_1,P_2$
such that there are many chords inside the vertex-set of each
$P_1,P_2$
such that there are many chords inside the vertex-set of each
![]() $P_i$
(or, more precisely, that inside each
$P_i$
(or, more precisely, that inside each
![]() $P_i$
there is a linear number of vertices touching a chord whose other endpoint is also on
$P_i$
there is a linear number of vertices touching a chord whose other endpoint is also on
![]() $P_i$
). Suppose that we found
$P_i$
). Suppose that we found
![]() $k = \Omega (\sqrt {n})$
paths
$k = \Omega (\sqrt {n})$
paths
![]() $Q_1,\dots ,Q_k$
between the endpoints of
$Q_1,\dots ,Q_k$
between the endpoints of
![]() $P_1$
(which only use the vertices of
$P_1$
(which only use the vertices of
![]() $P_1$
) such that
$P_1$
) such that
![]() $|Q_1|,\dots ,|Q_k|$
are all different and all belong to an interval of width
$|Q_1|,\dots ,|Q_k|$
are all different and all belong to an interval of width
![]() $\sqrt {n}$
. Suppose further that we found
$\sqrt {n}$
. Suppose further that we found
![]() $\ell = \Omega (\sqrt {n})$
paths
$\ell = \Omega (\sqrt {n})$
paths
![]() $R_1,\dots ,R_{\ell }$
between the endpoints of
$R_1,\dots ,R_{\ell }$
between the endpoints of
![]() $P_2$
(which only use the vertices of
$P_2$
(which only use the vertices of
![]() $P_2$
) such that the lengths of any two of these paths are at least
$P_2$
) such that the lengths of any two of these paths are at least
![]() $\sqrt {n}$
apart, namely,
$\sqrt {n}$
apart, namely,
![]() $||R_i| - |R_j||> \sqrt {n}$
for all
$||R_i| - |R_j||> \sqrt {n}$
for all
![]() $i \neq j$
. In this situation, we can combine any one of the
$i \neq j$
. In this situation, we can combine any one of the
![]() $Q_i$
’s with any one the
$Q_i$
’s with any one the
![]() $R_j$
’s, joining them into a cycle of length
$R_j$
’s, joining them into a cycle of length
![]() $|Q_i| + |R_j|$
. The crucial point is that the
$|Q_i| + |R_j|$
. The crucial point is that the
![]() $k\ell $
numbers
$k\ell $
numbers
![]() $|Q_i| + |R_j|$
are all different. In other words, we use the ‘condensed’ lengths
$|Q_i| + |R_j|$
are all different. In other words, we use the ‘condensed’ lengths
![]() $Q_1,\dots ,Q_k$
to ‘fill in the gaps’ between the ‘spread-out’ lengths
$Q_1,\dots ,Q_k$
to ‘fill in the gaps’ between the ‘spread-out’ lengths
![]() $R_1,\dots ,R_{\ell }$
(see Lemma 3.2 for the details on this). In total, this would give us
$R_1,\dots ,R_{\ell }$
(see Lemma 3.2 for the details on this). In total, this would give us
![]() $k\ell = \Omega (n)$
different cycle lengths. Hence, achieving both above goals would establish Conjecture 1.1.
$k\ell = \Omega (n)$
different cycle lengths. Hence, achieving both above goals would establish Conjecture 1.1.
We believe that both above statements should be true, namely, that one can find both
![]() $\Omega (\sqrt {n})$
distinct path lengths all contained in an interval of width
$\Omega (\sqrt {n})$
distinct path lengths all contained in an interval of width
![]() $\sqrt {n}$
and
$\sqrt {n}$
and
![]() $\Omega (\sqrt {n})$
path lengths which are
$\Omega (\sqrt {n})$
path lengths which are
![]() $\sqrt {n}$
apart. Observe that both of these statements are essentially implied by Conjecture 1.1 (see Section 5 for more details) and that our main result shows that both hold asymptotically (i.e., with
$\sqrt {n}$
apart. Observe that both of these statements are essentially implied by Conjecture 1.1 (see Section 5 for more details) and that our main result shows that both hold asymptotically (i.e., with
![]() $\sqrt {n}$
replaced by
$\sqrt {n}$
replaced by
![]() $n^{1/2-o(1)}$
). On the other hand, these statements shift the difficulty from finding many lengths (note that there have been a number of proofs that there are at least
$n^{1/2-o(1)}$
). On the other hand, these statements shift the difficulty from finding many lengths (note that there have been a number of proofs that there are at least
![]() $\sqrt {n}$
different lengths over the years) to controlling what kind of lengths we find.
$\sqrt {n}$
different lengths over the years) to controlling what kind of lengths we find.
Our actual strategy for tackling Conjecture 1.1 is a bit more involved. Instead of splitting our cycle into just two parts, we split it into a larger number k of parts (with k to be chosen as roughly
![]() $\sqrt {\log n}$
). Here, each part will be a pair of cycle sections (subpaths of the cycle) with at least
$\sqrt {\log n}$
). Here, each part will be a pair of cycle sections (subpaths of the cycle) with at least
![]() $n^{1-o(1)}$
chords between them, with different section pairs situated ‘on top of’ each other (see Figure 2). Now, with the goal of finding
$n^{1-o(1)}$
chords between them, with different section pairs situated ‘on top of’ each other (see Figure 2). Now, with the goal of finding
![]() $n^{1-\varepsilon }$
different lengths (where
$n^{1-\varepsilon }$
different lengths (where
![]() $\varepsilon $
is an appropriately chosen vanishing function of n), we shall proceed as follows. Inside the first of the k parts, we shall find
$\varepsilon $
is an appropriately chosen vanishing function of n), we shall proceed as follows. Inside the first of the k parts, we shall find
![]() $\Omega (n^{\varepsilon })$
path lengths all belonging to an interval of width
$\Omega (n^{\varepsilon })$
path lengths all belonging to an interval of width
![]() $n^{\varepsilon }$
. Then, inside the second part, we shall find about
$n^{\varepsilon }$
. Then, inside the second part, we shall find about
![]() $\Omega (n^{\varepsilon })$
lengths
$\Omega (n^{\varepsilon })$
lengths
![]() $\ell _1 < \ldots < \ell _t$
such that any two consecutive lengths are
$\ell _1 < \ldots < \ell _t$
such that any two consecutive lengths are
![]() $\Theta (n^{\varepsilon })$
apart, namely
$\Theta (n^{\varepsilon })$
apart, namely
![]() $\ell _{i+1} - \ell _i = \Theta (n^{\varepsilon })$
for all i. Now, by combining the paths we found in these two parts, we will get
$\ell _{i+1} - \ell _i = \Theta (n^{\varepsilon })$
for all i. Now, by combining the paths we found in these two parts, we will get
![]() $\Omega (n^{2\varepsilon })$
different path lengths, all belonging to an interval of width
$\Omega (n^{2\varepsilon })$
different path lengths, all belonging to an interval of width
![]() $O(n^{2\varepsilon })$
and only using vertices from the first two parts of the partition. Continuing in this manner, we will find inside the third part
$O(n^{2\varepsilon })$
and only using vertices from the first two parts of the partition. Continuing in this manner, we will find inside the third part
![]() $\Omega (n^{\varepsilon })$
lengths which are
$\Omega (n^{\varepsilon })$
lengths which are
![]() $\Theta (n^{2\varepsilon })$
apart, inside the fourth part
$\Theta (n^{2\varepsilon })$
apart, inside the fourth part
![]() $\Omega (n^{\varepsilon })$
lengths which are
$\Omega (n^{\varepsilon })$
lengths which are
![]() $\Theta (n^{3\varepsilon })$
apart and so on. This will always allow us to combine the new lengths we find with the lengths found so far to get
$\Theta (n^{3\varepsilon })$
apart and so on. This will always allow us to combine the new lengths we find with the lengths found so far to get
![]() $\Omega (n^{i\varepsilon })$
different path lengths, all belonging to an interval of width
$\Omega (n^{i\varepsilon })$
different path lengths, all belonging to an interval of width
![]() $O(n^{i\varepsilon })$
, only using vertices from the first i parts. Unfortunately, in each iteration, we will lose a polylogarithmic factor in the number of paths we find, which will result in the optimal number of iterations being
$O(n^{i\varepsilon })$
, only using vertices from the first i parts. Unfortunately, in each iteration, we will lose a polylogarithmic factor in the number of paths we find, which will result in the optimal number of iterations being
![]() $\sqrt {\frac {\log n}{\log \log n}}$
(this corresponds to having
$\sqrt {\frac {\log n}{\log \log n}}$
(this corresponds to having
![]() $\varepsilon = \sqrt {\frac {\log \log n}{\log n}}$
). After this number of iterations, we will find
$\varepsilon = \sqrt {\frac {\log \log n}{\log n}}$
). After this number of iterations, we will find
![]() $n^{1-o(1)}$
different lengths. This iterative process is handled in Lemma 4.8.
$n^{1-o(1)}$
different lengths. This iterative process is handled in Lemma 4.8.

Figure 1 A section pair with a chord
![]() $(x,y)$
and its corresponding trivial path marked in red.
$(x,y)$
and its corresponding trivial path marked in red.

Figure 2 A parallel collection of subsection pairs.
Let us now focus on a single iteration, and sketch the main ideas involved. For simplicity, suppose that this is the third iteration, namely, that our goal is to find (inside the third of the k parts of the partition)
![]() $\Omega (n^{\varepsilon })$
path lengths
$\Omega (n^{\varepsilon })$
path lengths
![]() $\ell _1 < \ldots <\ell _t$
with
$\ell _1 < \ldots <\ell _t$
with
![]() $\ell _{i+1} - \ell _i = \Theta (n^{2\varepsilon })$
for all i. Up to this step, we have already found
$\ell _{i+1} - \ell _i = \Theta (n^{2\varepsilon })$
for all i. Up to this step, we have already found
![]() $\Theta (n^{2\varepsilon })$
path lengths in an interval of width
$\Theta (n^{2\varepsilon })$
path lengths in an interval of width
![]() $O(n^{2\varepsilon })$
inside the first two parts. Now, we consider a maximum collection
$O(n^{2\varepsilon })$
inside the first two parts. Now, we consider a maximum collection
![]() $e_1,\dots ,e_m$
of chords inside the third part such that, for all
$e_1,\dots ,e_m$
of chords inside the third part such that, for all
![]() $i \neq j$
, the lengths of
$i \neq j$
, the lengths of
![]() $e_i$
and
$e_i$
and
![]() $e_j$
differ by at least
$e_j$
differ by at least
![]() $n^{2\varepsilon }$
. Each chord
$n^{2\varepsilon }$
. Each chord
![]() $e_i$
gives rise to a path inside the third part (namely, the path that consists of the chord and pieces of the cycle), and the lengths of any two of these m paths differ by at least
$e_i$
gives rise to a path inside the third part (namely, the path that consists of the chord and pieces of the cycle), and the lengths of any two of these m paths differ by at least
![]() $n^{2\varepsilon }$
. Now, observe that if
$n^{2\varepsilon }$
. Now, observe that if
![]() $m \geq n^{1-3\varepsilon }$
, then by combining these paths with the
$m \geq n^{1-3\varepsilon }$
, then by combining these paths with the
![]() $\Theta (n^{2\varepsilon })$
path lengths we found in the first two parts of the partition, we obtain altogether
$\Theta (n^{2\varepsilon })$
path lengths we found in the first two parts of the partition, we obtain altogether
![]() $m \cdot \Omega (n^{2\varepsilon }) = \Omega (n^{1-\varepsilon })$
different cycle lengths and thus achieve our goal already at this stage. So we may assume that
$m \cdot \Omega (n^{2\varepsilon }) = \Omega (n^{1-\varepsilon })$
different cycle lengths and thus achieve our goal already at this stage. So we may assume that
![]() $m \leq n^{1-3\varepsilon }$
. Since
$m \leq n^{1-3\varepsilon }$
. Since
![]() $e_1,\dots ,e_m$
is a maximal family, the length of any other chord must be at distance at most
$e_1,\dots ,e_m$
is a maximal family, the length of any other chord must be at distance at most
![]() $n^{2\varepsilon }$
to that of one of the
$n^{2\varepsilon }$
to that of one of the
![]() $e_i$
’s. By averaging (and as each part of the partition contains
$e_i$
’s. By averaging (and as each part of the partition contains
![]() $n^{1-o(1)}$
chords), we see that there is a family E of at least
$n^{1-o(1)}$
chords), we see that there is a family E of at least
![]() $n^{1-o(1)}/m \geq n^{3\varepsilon - o(1)}$
different chords, whose lengths all belong to an interval of width
$n^{1-o(1)}/m \geq n^{3\varepsilon - o(1)}$
different chords, whose lengths all belong to an interval of width
![]() $n^{2\varepsilon }$
. The reason such a family E is useful is as follows: Suppose we partition the two cycle sections of the third part into subpaths
$n^{2\varepsilon }$
. The reason such a family E is useful is as follows: Suppose we partition the two cycle sections of the third part into subpaths
![]() $X_1,X_2,\ldots $
of length
$X_1,X_2,\ldots $
of length
![]() $n^{2\varepsilon }$
. Then, for any two such subpaths
$n^{2\varepsilon }$
. Then, for any two such subpaths
![]() $X_i,X_j$
of the same cycle section, which are not consecutive (and hence are at distance larger than
$X_i,X_j$
of the same cycle section, which are not consecutive (and hence are at distance larger than
![]() $n^{2\varepsilon }$
on the path), any chord touching
$n^{2\varepsilon }$
on the path), any chord touching
![]() $X_i$
must interlace (i.e., cross) any chord touching
$X_i$
must interlace (i.e., cross) any chord touching
![]() $X_j$
. For if not, then the difference of the lengths of these two chords is larger than
$X_j$
. For if not, then the difference of the lengths of these two chords is larger than
![]() $n^{2\varepsilon }$
, contradicting the fact that both lengths belong to an interval of width
$n^{2\varepsilon }$
, contradicting the fact that both lengths belong to an interval of width
![]() $n^{2\varepsilon }$
. So we see that E decomposes into pairwise-interlacing pieces; see Figure 3 for an illustration. This structure, together with some additional arguments, then allows us to find the
$n^{2\varepsilon }$
. So we see that E decomposes into pairwise-interlacing pieces; see Figure 3 for an illustration. This structure, together with some additional arguments, then allows us to find the
![]() $\Omega (n^{\varepsilon })$
desired path lengths
$\Omega (n^{\varepsilon })$
desired path lengths
![]() $\ell _1 < \ldots < \ell _t$
. We remark that, while it is not hard to find such lengths with
$\ell _1 < \ldots < \ell _t$
. We remark that, while it is not hard to find such lengths with
![]() $\ell _{i+1}-\ell _i= \Omega (n^{2\varepsilon })$
, which already allows us to find
$\ell _{i+1}-\ell _i= \Omega (n^{2\varepsilon })$
, which already allows us to find
![]() $\Omega (n^{3\varepsilon })$
lengths, it is essential for the next iteration that these lengths are not too far apart, in other words ensuring in addition that
$\Omega (n^{3\varepsilon })$
lengths, it is essential for the next iteration that these lengths are not too far apart, in other words ensuring in addition that
![]() $\ell _{i+1}-\ell _i \le O(n^{2\varepsilon })$
is crucial in order to be able to continue our argument.
$\ell _{i+1}-\ell _i \le O(n^{2\varepsilon })$
is crucial in order to be able to continue our argument.

Figure 3 An interlacing collection of subsection pairs.
Executing the above strategy presents significant technical difficulties, in part due to the need to join the various pieces in suitable ways. This sometimes makes various parts of the argument a bit cumbersome, and we try to alleviate this situation with a number of figures illustrating the argument.
Finally, we note that splitting the cycle into pieces (i.e., subpaths or pairs of sections) is nontrivial and requires some work. To illustrate this, note that if our graph only consisted of ‘diameter’ chords (joining vertices which are as far apart on the cycle as possible), then it is not possible to split the cycle into two paths with each of them still containing many chords. The way we go around this issue is to show that one can ‘reroute’ the original Hamilton cycle using two chords (and large parts of the Hamilton cycle), thus obtaining a new cycle which admits the desired split.
3 Setting up the stage
Let us introduce some terminology that we will use in the proof. For a path P, denote by
![]() $|P|$
the number of edges in P. Given a path or a cycle, we will call its subpaths sections. We will often consider chords between two sections of a cycle, and hence, it is convenient to have the following setup. A section pair is a pair of vertex-disjoint paths
$|P|$
the number of edges in P. Given a path or a cycle, we will call its subpaths sections. We will often consider chords between two sections of a cycle, and hence, it is convenient to have the following setup. A section pair is a pair of vertex-disjoint paths
![]() $X,Y$
. We will always denote the endpoints of X by
$X,Y$
. We will always denote the endpoints of X by
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $x^{\text {b}}$
, where
$x^{\text {b}}$
, where
![]() $x^{\text {t}}$
is called the top and
$x^{\text {t}}$
is called the top and
![]() $x^{\text {b}}$
the bottom. Similarly, the endpoints of Y are denoted
$x^{\text {b}}$
the bottom. Similarly, the endpoints of Y are denoted
![]() $y^{\text {t}},y^{\text {b}}$
. For distinct
$y^{\text {t}},y^{\text {b}}$
. For distinct
![]() $x_1,x_2 \in X$
, we say that
$x_1,x_2 \in X$
, we say that
![]() $x_1$
is above
$x_1$
is above
![]() $x_2$
if
$x_2$
if
![]() $x_1$
is closer to
$x_1$
is closer to
![]() $x^{\text {t}}$
along X than
$x^{\text {t}}$
along X than
![]() $x_2$
; otherwise we say that
$x_2$
; otherwise we say that
![]() $x_1$
is below
$x_1$
is below
![]() $x_2$
. For sets
$x_2$
. For sets
![]() $X_1,X_2 \subseteq X$
, we say that
$X_1,X_2 \subseteq X$
, we say that
![]() $X_1$
is above (resp., below)
$X_1$
is above (resp., below)
![]() $X_2$
if every
$X_2$
if every
![]() $x_1 \in X_1$
is above (resp., below) every
$x_1 \in X_1$
is above (resp., below) every
![]() $x_2 \in X_2$
. When considering a sequence
$x_2 \in X_2$
. When considering a sequence
![]() $X_1,\dots ,X_t$
of disjoint subsets of X, unless otherwise specified, we assume they are labeled in such a way that
$X_1,\dots ,X_t$
of disjoint subsets of X, unless otherwise specified, we assume they are labeled in such a way that
![]() $X_i$
is below
$X_i$
is below
![]() $X_j$
for all
$X_j$
for all
![]() $1 \leq i < j \leq t$
. We use
$1 \leq i < j \leq t$
. We use
![]() $x_i^{\text {t}}$
(resp.,
$x_i^{\text {t}}$
(resp.,
![]() $x_i^{\text {b}}$
) to denote the top (resp., bottom) vertex of
$x_i^{\text {b}}$
) to denote the top (resp., bottom) vertex of
![]() $X_i$
.
$X_i$
.
For
![]() $x_1,x_2 \in X$
, denote by
$x_1,x_2 \in X$
, denote by
![]() $X[x_1,x_2]$
the subpath of X between
$X[x_1,x_2]$
the subpath of X between
![]() $x_1$
and
$x_1$
and
![]() $x_2$
and by
$x_2$
and by
![]() $d_X(x_1,x_2) = |X[x_1,x_2]|$
the length of this subpath, namely, the distance between
$d_X(x_1,x_2) = |X[x_1,x_2]|$
the length of this subpath, namely, the distance between
![]() $x_1$
and
$x_1$
and
![]() $x_2$
along X. Define
$x_2$
along X. Define
![]() $Y[y_1,y_2]$
and
$Y[y_1,y_2]$
and
![]() $d_Y(y_1,y_2)$
analogously for
$d_Y(y_1,y_2)$
analogously for
![]() $y_1,y_2 \in Y$
. A subsection pair of a section pair
$y_1,y_2 \in Y$
. A subsection pair of a section pair
![]() $X,Y$
is a section pair consisting of a subpath of X and a subpath of Y.
$X,Y$
is a section pair consisting of a subpath of X and a subpath of Y.
A chord is an edge with one endpoint in X and one in Y. Let
![]() $(x_1,y_1),(x_2,y_2)$
be two chords which have no common vertices. We say that
$(x_1,y_1),(x_2,y_2)$
be two chords which have no common vertices. We say that
![]() $(x_1,y_1),(x_2,y_2)$
are parallel if
$(x_1,y_1),(x_2,y_2)$
are parallel if
![]() $x_i$
is above
$x_i$
is above
![]() $x_{3-i}$
and
$x_{3-i}$
and
![]() $y_i$
is above
$y_i$
is above
![]() $y_{3-i}$
for some
$y_{3-i}$
for some
![]() $i = 1,2$
; otherwise we say that
$i = 1,2$
; otherwise we say that
![]() $(x_1,y_1),(x_2,y_2)$
are interlacing. In other words,
$(x_1,y_1),(x_2,y_2)$
are interlacing. In other words,
![]() $(x_1,y_1),(x_2,y_2)$
are interlacing if
$(x_1,y_1),(x_2,y_2)$
are interlacing if
![]() $x_1$
is above
$x_1$
is above
![]() $x_2$
but
$x_2$
but
![]() $y_1$
is below
$y_1$
is below
![]() $y_2$
, or vice versa.
$y_2$
, or vice versa.
The following statement is equivalent to (the symmetric case of) the Erdös-Szekeres lemma.
Lemma 3.1. Let
![]() $k \geq 1$
, and let
$k \geq 1$
, and let
![]() $X,Y$
be a section pair with at least
$X,Y$
be a section pair with at least
![]() $(k-1)^2 + 1$
chords, no two of which share vertices. Then there is a set E of k chords such that either every two chords in E are parallel or every two chords in E are interlacing.
$(k-1)^2 + 1$
chords, no two of which share vertices. Then there is a set E of k chords such that either every two chords in E are parallel or every two chords in E are interlacing.
Given a collection of disjoint subsection pairs
![]() $X_1,Y_1;\ldots; X_t,Y_t$
(where as usual we will assume that
$X_1,Y_1;\ldots; X_t,Y_t$
(where as usual we will assume that
![]() $X_i$
is below
$X_i$
is below
![]() $X_j$
for all
$X_j$
for all
![]() $i<j$
), we say that the collection is parallel if also
$i<j$
), we say that the collection is parallel if also
![]() $Y_i$
is below
$Y_i$
is below
![]() $Y_j$
for all
$Y_j$
for all
![]() $i<j$
, and we say that it is interlacing if
$i<j$
, and we say that it is interlacing if
![]() $Y_i$
is above
$Y_i$
is above
![]() $Y_j$
for all
$Y_j$
for all
![]() $i<j$
. See Figures 2 and 3.
$i<j$
. See Figures 2 and 3.
The length of a chord
![]() $(x,y)$
is defined as
$(x,y)$
is defined as
![]() $d_X(x^{\text {t}},x) + d_Y(y^{\text {t}},y)$
, which is one less than the length of the path
$d_X(x^{\text {t}},x) + d_Y(y^{\text {t}},y)$
, which is one less than the length of the path
![]() $X[x^{\text {t}},x],(x,y),Y[y,y^{\text {t}}]$
. This path will be called the trivial path corresponding to the chord
$X[x^{\text {t}},x],(x,y),Y[y,y^{\text {t}}]$
. This path will be called the trivial path corresponding to the chord
![]() $(x,y)$
.
$(x,y)$
.
A top-bottom path-pair (for the section pair
![]() $X,Y$
) is a pair of vertex-disjoint paths which are contained in
$X,Y$
) is a pair of vertex-disjoint paths which are contained in
![]() $X \cup Y$
, start at
$X \cup Y$
, start at
![]() $x^{\text {t}},y^{\text {t}}$
and end at
$x^{\text {t}},y^{\text {t}}$
and end at
![]() $x^{\text {b}},y^{\text {b}}$
. So, for example,
$x^{\text {b}},y^{\text {b}}$
. So, for example,
![]() $X,Y$
is a (trivial) top-bottom path-pair. The length of a top-bottom path-pair
$X,Y$
is a (trivial) top-bottom path-pair. The length of a top-bottom path-pair
![]() $\mathcal {P} = (P_1,P_2)$
is defined as
$\mathcal {P} = (P_1,P_2)$
is defined as
![]() $|P_1| + |P_2|$
and denoted by
$|P_1| + |P_2|$
and denoted by
![]() $|\mathcal {P}|$
.
$|\mathcal {P}|$
.
Given
![]() $x \in X, y \in Y$
, a path from x to y is called a below-path if it only uses vertices of X and Y which are below x and y, respectively.
$x \in X, y \in Y$
, a path from x to y is called a below-path if it only uses vertices of X and Y which are below x and y, respectively.
At several points in the proof, we will split our cycle into disjoint parts (paths or section pairs) and concatenate paths (or path-pairs) which we find in different parts. Evidently, the length of the concatenated path is the sum of lengths of the individual paths. Hence, the set of path lengths we obtain in this way is the sum-set of the sets of path lengths we find in each of the different parts. Formally, given a sequence of sets
![]() $L_1,\ldots , L_t$
, we define the sum-set
$L_1,\ldots , L_t$
, we define the sum-set
![]() $L_1+\ldots +L_t:=\{\ell _1+\ldots +\ell _t \mid \ell _i \in L_i\}$
. Given a set L of integers, we say that two elements of L are consecutive (with respect to L) if there is no element of L between them. By interval we always mean an interval of natural numbers. We will often use the trivial fact that if
$L_1+\ldots +L_t:=\{\ell _1+\ldots +\ell _t \mid \ell _i \in L_i\}$
. Given a set L of integers, we say that two elements of L are consecutive (with respect to L) if there is no element of L between them. By interval we always mean an interval of natural numbers. We will often use the trivial fact that if
![]() $x,y$
belong to an interval I, then
$x,y$
belong to an interval I, then
![]() $|x - y| \leq |I|-1$
. For numbers
$|x - y| \leq |I|-1$
. For numbers
![]() $x,y$
, we say that
$x,y$
, we say that
![]() $x,y$
are at least b apart (or just b apart) if
$x,y$
are at least b apart (or just b apart) if
![]() $|x - y| \geq b$
and at most b apart if
$|x - y| \geq b$
and at most b apart if
![]() $|x - y| \leq b$
. The following auxiliary lemmas about sum-sets will come in handy later.
$|x - y| \leq b$
. The following auxiliary lemmas about sum-sets will come in handy later.
Lemma 3.2. Let
![]() $L_1,\ldots , L_t \subseteq \mathbb {N}$
with the property that for all
$L_1,\ldots , L_t \subseteq \mathbb {N}$
with the property that for all
![]() $1\le i\le t$
, every two consecutive elements of
$1\le i\le t$
, every two consecutive elements of
![]() $L_i$
are at least a and at most b apart. Then there is a subset of
$L_i$
are at least a and at most b apart. Then there is a subset of
![]() $L_1+\ldots + L_t$
of size
$L_1+\ldots + L_t$
of size
![]() $1+\sum _{i=1}^t (|L_i|-1)$
in which every two consecutive elements are at least a and at most b apart.
$1+\sum _{i=1}^t (|L_i|-1)$
in which every two consecutive elements are at least a and at most b apart.
Proof. We will prove the lemma by induction on t. If
![]() $t=1$
, then the statement is trivial. Assume it holds for
$t=1$
, then the statement is trivial. Assume it holds for
![]() $t-1$
so that we can find a subset S of
$t-1$
so that we can find a subset S of
![]() $L_1+\ldots + L_{t-1}$
of size
$L_1+\ldots + L_{t-1}$
of size
![]() $1+\sum _{i=1}^{t-1} (|L_i|-1)$
with all consecutive elements being at least a and at most b apart. Let
$1+\sum _{i=1}^{t-1} (|L_i|-1)$
with all consecutive elements being at least a and at most b apart. Let
![]() $x_1 < \ldots < x_s$
be the elements of S, and let
$x_1 < \ldots < x_s$
be the elements of S, and let
![]() $y_1 < \ldots < y_r$
be the elements of
$y_1 < \ldots < y_r$
be the elements of
![]() $L_t$
. Then
$L_t$
. Then
![]() $\{ x_1 + y_1 < x_2 + y_1 < \ldots < x_s + y_1 < x_s + y_2 < \ldots < x_s + y_r\}$
is a subset of
$\{ x_1 + y_1 < x_2 + y_1 < \ldots < x_s + y_1 < x_s + y_2 < \ldots < x_s + y_r\}$
is a subset of
![]() $L_1 + \ldots + L_t$
of size
$L_1 + \ldots + L_t$
of size
![]() $|S| + |L_t| - 1 = 1+\sum _{i=1}^t (|L_i|-1)$
having the desired property.
$|S| + |L_t| - 1 = 1+\sum _{i=1}^t (|L_i|-1)$
having the desired property.
Lemma 3.3. Let
![]() $L_1,L_2$
be sets of positive integers. Suppose that each
$L_1,L_2$
be sets of positive integers. Suppose that each
![]() $L_i$
is a subset of an interval of size
$L_i$
is a subset of an interval of size
![]() $\ell _i$
and that any two elements of
$\ell _i$
and that any two elements of
![]() $L_1$
are at least
$L_1$
are at least
![]() $\ell _2$
apart. Then
$\ell _2$
apart. Then
![]() $L_1+L_2$
has
$L_1+L_2$
has
![]() $|L_1||L_2|$
elements, within some interval of size
$|L_1||L_2|$
elements, within some interval of size
![]() $\ell _1+\ell _2$
.
$\ell _1+\ell _2$
.
Proof. Let
![]() $r_1< \ldots < r_t$
be the elements of
$r_1< \ldots < r_t$
be the elements of
![]() $L_1$
and
$L_1$
and
![]() $s_1 < \ldots < s_p$
be the elements of
$s_1 < \ldots < s_p$
be the elements of
![]() $L_2$
. We claim that all
$L_2$
. We claim that all
![]() $r_i+s_j$
are distinct. To see this, assume that
$r_i+s_j$
are distinct. To see this, assume that
![]() $r_i+s_j=r_{i'}+s_{j'}$
. If
$r_i+s_j=r_{i'}+s_{j'}$
. If
![]() $i\neq i'$
, then we must have
$i\neq i'$
, then we must have
![]() $|r_i-r_{i'}| \ge \ell _2$
. However,
$|r_i-r_{i'}| \ge \ell _2$
. However,
![]() $|s_j-s_j^{\prime }| <\ell _2$
, and so this is impossible. Hence,
$|s_j-s_j^{\prime }| <\ell _2$
, and so this is impossible. Hence,
![]() $i=i'$
. This further implies that
$i=i'$
. This further implies that
![]() $j=j'$
and completes the proof. This shows that
$j=j'$
and completes the proof. This shows that
![]() $L_1+L_2$
indeed has
$L_1+L_2$
indeed has
![]() $|L_1||L_2|$
elements. Furthermore, notice that all elements in
$|L_1||L_2|$
elements. Furthermore, notice that all elements in
![]() $L_1+L_2$
belong into
$L_1+L_2$
belong into
![]() $[r_1+s_1,r_t+s_p]$
, and since
$[r_1+s_1,r_t+s_p]$
, and since
![]() $r_t-r_1 < \ell _1$
and
$r_t-r_1 < \ell _1$
and
![]() $s_p-s_1 < \ell _2$
, this interval indeed has size at most
$s_p-s_1 < \ell _2$
, this interval indeed has size at most
![]() $\ell _1+\ell _2$
.
$\ell _1+\ell _2$
.
All our logarithms are in base
![]() $2$
unless otherwise specified. We will omit floor/ceiling signs whenever these are not crucial.
$2$
unless otherwise specified. We will omit floor/ceiling signs whenever these are not crucial.
4 Finding cycles of many different lengths
In this section, we will prove our main result, Theorem 1.1. We begin, in the following subsection, by proving a number of lemmas which provide us with the main tools to attack the problem. We then proceed to put everything together in the subsequent subsection.
4.1 Main lemmas
The following lemma states that, in every section pair with many chords, one can find either a parallel or an interlacing collection of subsection pairs, each of which still has many chords.
Lemma 4.1. Let
![]() $X,Y$
be a section pair with m chords, and let
$X,Y$
be a section pair with m chords, and let
![]() $k \geq 1$
. Suppose that no vertex of
$k \geq 1$
. Suppose that no vertex of
![]() $X \cup Y$
is incident to more than
$X \cup Y$
is incident to more than
![]() $\frac {m}{10k^2}$
chords. Then there is either a parallel or an interlacing collection of subsection pairs
$\frac {m}{10k^2}$
chords. Then there is either a parallel or an interlacing collection of subsection pairs
![]() $X_1,Y_1;\dots ;X_k,Y_k$
such that
$X_1,Y_1;\dots ;X_k,Y_k$
such that
![]() $e(X_i,Y_i) \geq \Omega (\frac {m}{k^4})$
for all
$e(X_i,Y_i) \geq \Omega (\frac {m}{k^4})$
for all
![]() $1 \leq i \leq k$
.
$1 \leq i \leq k$
.
Proof. We partition X into subpaths
![]() $X^{\prime }_1,\dots ,X^{\prime }_{s},X^{\prime }_{s+1}$
such that, for each
$X^{\prime }_1,\dots ,X^{\prime }_{s},X^{\prime }_{s+1}$
such that, for each
![]() $1 \leq i \leq s$
,
$1 \leq i \leq s$
,
![]() $X^{\prime }_i$
touches at least
$X^{\prime }_i$
touches at least
![]() $\frac {m}{10k^2}$
and at most
$\frac {m}{10k^2}$
and at most
![]() $\frac {m}{5k^2}$
chords and such that
$\frac {m}{5k^2}$
chords and such that
![]() $X^{\prime }_{s+1}$
touches less than
$X^{\prime }_{s+1}$
touches less than
![]() $\frac {m}{10k^2}$
chords. We do this as follows: Take
$\frac {m}{10k^2}$
chords. We do this as follows: Take
![]() $X^{\prime }_1$
to be the minimum initial segment of X which touches at least
$X^{\prime }_1$
to be the minimum initial segment of X which touches at least
![]() $\frac {m}{10k^2}$
chords. By minimality, the segment obtained by removing the last vertex x of
$\frac {m}{10k^2}$
chords. By minimality, the segment obtained by removing the last vertex x of
![]() $X^{\prime }_1$
touches less than
$X^{\prime }_1$
touches less than
![]() $\frac {m}{10k^2}$
chords. Also, x itself touches at most
$\frac {m}{10k^2}$
chords. Also, x itself touches at most
![]() $\frac {m}{10k^2}$
chords by the assumption of the lemma. So overall,
$\frac {m}{10k^2}$
chords by the assumption of the lemma. So overall,
![]() $X^{\prime }_1$
touches at most
$X^{\prime }_1$
touches at most
![]() $\frac {m}{5k^2}$
chords. We now remove
$\frac {m}{5k^2}$
chords. We now remove
![]() $X^{\prime }_1$
and continue in this fashion. As long as the remaining subpath touches at least
$X^{\prime }_1$
and continue in this fashion. As long as the remaining subpath touches at least
![]() $\frac {m}{10k^2}$
chords, we can extract an initial segment of it which touches at least
$\frac {m}{10k^2}$
chords, we can extract an initial segment of it which touches at least
![]() $\frac {m}{10k^2}$
and at most
$\frac {m}{10k^2}$
and at most
![]() $\frac {m}{5k^2}$
chords. In the end, we are left with a, possibly empty, subpath touching less than
$\frac {m}{5k^2}$
chords. In the end, we are left with a, possibly empty, subpath touching less than
![]() $\frac {m}{10k^2}$
chords, and we take this subpath to be
$\frac {m}{10k^2}$
chords, and we take this subpath to be
![]() $X^{\prime }_{s+1}$
.
$X^{\prime }_{s+1}$
.
In the same way, partition Y into subpaths
![]() $Y^{\prime }_1,\dots ,Y^{\prime }_t,Y^{\prime }_{t+1}$
with each
$Y^{\prime }_1,\dots ,Y^{\prime }_t,Y^{\prime }_{t+1}$
with each
![]() $Y^{\prime }_i$
,
$Y^{\prime }_i$
,
![]() $1 \leq i \leq t$
, touching at least
$1 \leq i \leq t$
, touching at least
![]() $\frac {m}{10k^2}$
and at most
$\frac {m}{10k^2}$
and at most
![]() $\frac {m}{5k^2}$
chords and with
$\frac {m}{5k^2}$
chords and with
![]() $Y^{\prime }_{t+1}$
touching less than
$Y^{\prime }_{t+1}$
touching less than
![]() $\frac {m}{10k^2}$
chords. Clearly,
$\frac {m}{10k^2}$
chords. Clearly,
![]() $4k^2 \leq (m - \frac {m}{10k^2})/\frac {m}{5k^2} \leq s,t \leq 10k^2$
. Define an auxiliary bipartite graph G with sides
$4k^2 \leq (m - \frac {m}{10k^2})/\frac {m}{5k^2} \leq s,t \leq 10k^2$
. Define an auxiliary bipartite graph G with sides
![]() $[s]$
and
$[s]$
and
![]() $[t+1]$
, in which
$[t+1]$
, in which
![]() $(i,j)$
is an edge if
$(i,j)$
is an edge if
![]() $e(X^{\prime }_i,Y^{\prime }_j) \geq \frac {m}{400k^4}$
. Let
$e(X^{\prime }_i,Y^{\prime }_j) \geq \frac {m}{400k^4}$
. Let
![]() $I \subseteq [s]$
. We claim that
$I \subseteq [s]$
. We claim that
![]() $|N_G(I)| \geq |I|/4$
. To see this, note that
$|N_G(I)| \geq |I|/4$
. To see this, note that
 $$ \begin{align*} |I| \cdot \frac{m}{10k^2} &\leq \sum_{i \in I}{e(X^{\prime}_i,Y)} \leq \sum_{j \in N_G(I)}{e(X,Y^{\prime}_j)} + (t+1) \cdot |I| \cdot \frac{m}{400k^4} \\ &\leq |N_G(I)| \cdot \frac{m}{5k^2} + 2t \cdot |I| \cdot \frac{m}{400k^4} \leq |N_G(I)| \cdot \frac{m}{5k^2} + |I| \cdot \frac{m}{20k^2}. \end{align*} $$
$$ \begin{align*} |I| \cdot \frac{m}{10k^2} &\leq \sum_{i \in I}{e(X^{\prime}_i,Y)} \leq \sum_{j \in N_G(I)}{e(X,Y^{\prime}_j)} + (t+1) \cdot |I| \cdot \frac{m}{400k^4} \\ &\leq |N_G(I)| \cdot \frac{m}{5k^2} + 2t \cdot |I| \cdot \frac{m}{400k^4} \leq |N_G(I)| \cdot \frac{m}{5k^2} + |I| \cdot \frac{m}{20k^2}. \end{align*} $$
Rearranging gives
![]() $|N_G(I)| \geq |I|/4$
. Now, by a well-known generalization of Hall’s theorem, there is a matching in G which saturates at least
$|N_G(I)| \geq |I|/4$
. Now, by a well-known generalization of Hall’s theorem, there is a matching in G which saturates at least
![]() $s/4 \geq k^2$
of the elements of
$s/4 \geq k^2$
of the elements of
![]() $[s]$
. By Lemma 3.1, such a matching contains either a parallel or an interlacing family of chords of size k. It is easy to see that such a family gives sets
$[s]$
. By Lemma 3.1, such a matching contains either a parallel or an interlacing family of chords of size k. It is easy to see that such a family gives sets
![]() $X_1,\dots ,X_k,Y_1,\dots ,Y_k$
as in the statement of the lemma.
$X_1,\dots ,X_k,Y_1,\dots ,Y_k$
as in the statement of the lemma.
In a section pair
![]() $X,Y$
with many chords, we will be able to find many paths of different lengths, for example, between
$X,Y$
with many chords, we will be able to find many paths of different lengths, for example, between
![]() $x^t$
and
$x^t$
and
![]() $y^b$
. However, in order to be able to join these paths into cycles of many different lengths, we need to find top-bottom path-pairs that include these paths. This is necessary in order to combine these lengths with lengths found in other section pairs above or below
$y^b$
. However, in order to be able to join these paths into cycles of many different lengths, we need to find top-bottom path-pairs that include these paths. This is necessary in order to combine these lengths with lengths found in other section pairs above or below
![]() $X,Y$
. In order to find such top-bottom path-pairs, it is useful to have a special chord
$X,Y$
. In order to find such top-bottom path-pairs, it is useful to have a special chord
![]() $(x,y) \in E(X,Y)$
which interlaces all (or many) other chords in
$(x,y) \in E(X,Y)$
which interlaces all (or many) other chords in
![]() $E(X,Y)$
. Indeed, observe that we can use such a chord
$E(X,Y)$
. Indeed, observe that we can use such a chord
![]() $(x,y)$
to walk from
$(x,y)$
to walk from
![]() $y^t$
to
$y^t$
to
![]() $x^b$
, while using the chords which interlace
$x^b$
, while using the chords which interlace
![]() $(x,y)$
to obtain many path lengths from
$(x,y)$
to obtain many path lengths from
![]() $x^t$
to
$x^t$
to
![]() $y^b$
. This way, the two paths (one from
$y^b$
. This way, the two paths (one from
![]() $x^t$
to
$x^t$
to
![]() $y^b$
and one from
$y^b$
and one from
![]() $y^t$
to
$y^t$
to
![]() $x^b$
) do not intersect each other; see the left part of Figure 10 (where the special chord
$x^b$
) do not intersect each other; see the left part of Figure 10 (where the special chord
![]() $(x,y)$
is denoted by
$(x,y)$
is denoted by
![]() $(x_j,y_j)$
).
$(x_j,y_j)$
).

Figure 4 Different paths
![]() $P^{\prime }_i$
.
$P^{\prime }_i$
.

Figure 5 A combination of
![]() $P_2'$
and a path provided by induction (marked as zigzag in the figure).
$P_2'$
and a path provided by induction (marked as zigzag in the figure).

Figure 6
![]() $Q_1^R,Q_2^R$
are marked as red zigzag paths,
$Q_1^R,Q_2^R$
are marked as red zigzag paths,
![]() $Q^{\prime }_R$
is depicted in red,
$Q^{\prime }_R$
is depicted in red,
![]() $Q_1^B,Q_2^B$
are marked as blue zigzag paths,
$Q_1^B,Q_2^B$
are marked as blue zigzag paths,
![]() $Q^{\prime }_B$
is depicted in blue and some
$Q^{\prime }_B$
is depicted in blue and some
![]() $R_i$
is depicted in green.
$R_i$
is depicted in green.

Figure 7 The lower part of the path is provided by the induction and can be chosen among
![]() $\tilde {\Omega }(m^{i\varepsilon })$
paths with lengths in an interval of size
$\tilde {\Omega }(m^{i\varepsilon })$
paths with lengths in an interval of size
![]() $m^{i\varepsilon }$
. The upper top-bottom path-pair for
$m^{i\varepsilon }$
. The upper top-bottom path-pair for
![]() $X_{i+1},Y_{i+1}$
can be chosen among a collection of
$X_{i+1},Y_{i+1}$
can be chosen among a collection of
![]() $\tilde {\Omega }(m^{\varepsilon })$
of them with lengths
$\tilde {\Omega }(m^{\varepsilon })$
of them with lengths
![]() $m^{i\varepsilon }$
apart.
$m^{i\varepsilon }$
apart.

Figure 8 Case 1 of Lemma 4.2. Note that trivial paths using any two distinct edges of a star always have different lengths.

Figure 9 Case 2 of Lemma 4.2. Edges
![]() $(x_j,y_j)$
are depicted in red. Shaded regions have many chords and will become
$(x_j,y_j)$
are depicted in red. Shaded regions have many chords and will become
![]() $X_j^{\prime \prime },Y_j^{\prime \prime }$
.
$X_j^{\prime \prime },Y_j^{\prime \prime }$
.

Figure 10 Two options for how
![]() $(x_j,y_j)$
can interlace
$(x_j,y_j)$
can interlace
![]() $X_j^{\prime \prime },Y_j^{\prime \prime }$
and the corresponding top-bottom path-pairs we use.
$X_j^{\prime \prime },Y_j^{\prime \prime }$
and the corresponding top-bottom path-pairs we use.
Evidently, a chord
![]() $(x,y)$
as above does not exist if all chords in
$(x,y)$
as above does not exist if all chords in
![]() $E(X,Y)$
are pairwise-parallel. Hence, it is reasonable to try and partition
$E(X,Y)$
are pairwise-parallel. Hence, it is reasonable to try and partition
![]() $X,Y$
into parallel subsections and try and find such a chord
$X,Y$
into parallel subsections and try and find such a chord
![]() $(x,y)$
in each of them. This again may fail if in a given part there is a vertex of a very high degree. As the following lemma shows, this is essentially the only obstacle. For an illustration of the two outcomes of Lemma 4.2, we refer the reader to Figures 8 and 9. As the statement of Lemma 4.2 suggests, we cannot guarantee that the special chord
$(x,y)$
in each of them. This again may fail if in a given part there is a vertex of a very high degree. As the following lemma shows, this is essentially the only obstacle. For an illustration of the two outcomes of Lemma 4.2, we refer the reader to Figures 8 and 9. As the statement of Lemma 4.2 suggests, we cannot guarantee that the special chord
![]() $(x,y)$
interlaces a constant fraction of all other chords; we have to pay a log factor.
$(x,y)$
interlaces a constant fraction of all other chords; we have to pay a log factor.
Lemma 4.2. Let
![]() $X,Y$
be a section pair with
$X,Y$
be a section pair with
![]() $m\ge 2$
chords. Then there is a parallel collection of subsection pairs
$m\ge 2$
chords. Then there is a parallel collection of subsection pairs
![]() $X_1,Y_1;\dots ;X_t,Y_t$
such that
$X_1,Y_1;\dots ;X_t,Y_t$
such that
![]() $\sum _{i=1}^t {e(X_i,Y_i)} \geq m/24$
and one of the following holds:
$\sum _{i=1}^t {e(X_i,Y_i)} \geq m/24$
and one of the following holds:
-
1. For every i, there is a vertex in
 $X_i \cup Y_i$
which is incident to at least
$X_i \cup Y_i$
which is incident to at least
 $\frac {e(X_i,Y_i)}{6\log m}$
chords in
$\frac {e(X_i,Y_i)}{6\log m}$
chords in
 $E(X_i,Y_i)$
.
$E(X_i,Y_i)$
. -
2. For every i, there is a chord in
 $E(X_i,Y_i)$
which interlaces at least
$E(X_i,Y_i)$
which interlaces at least
 $\frac {e(X_i,Y_i)}{6\log m}$
of the chords in
$\frac {e(X_i,Y_i)}{6\log m}$
of the chords in
 $E(X_i,Y_i)$
.
$E(X_i,Y_i)$
.
Proof. We will produce a partition
![]() $X_1,\ldots ,X_{t'}$
of X and a partition
$X_1,\ldots ,X_{t'}$
of X and a partition
![]() $Y_1,\ldots , Y_{t'}$
of Y such that
$Y_1,\ldots , Y_{t'}$
of Y such that
![]() $\sum _{i=1}^{t'} {e(X_i,Y_i)} \geq m/12,$
and each pair
$\sum _{i=1}^{t'} {e(X_i,Y_i)} \geq m/12,$
and each pair
![]() $X_i,Y_i$
satisfies the condition of one of the items 1 or 2. Evidently, for one of the items, the pairs satisfying it would contribute at least half of all chords. Keeping only the pairs satisfying this item, we will obtain the desired collection.
$X_i,Y_i$
satisfies the condition of one of the items 1 or 2. Evidently, for one of the items, the pairs satisfying it would contribute at least half of all chords. Keeping only the pairs satisfying this item, we will obtain the desired collection.
We now construct such partitions
![]() $X_1,\ldots ,X_{t'}$
and
$X_1,\ldots ,X_{t'}$
and
![]() $Y_1,\ldots , Y_{t'}$
through the following process. We start with the trivial partition
$Y_1,\ldots , Y_{t'}$
through the following process. We start with the trivial partition
![]() $\{X\}$
of X and
$\{X\}$
of X and
![]() $\{Y\}$
of Y. Note that we may assume that
$\{Y\}$
of Y. Note that we may assume that
![]() $m\ge 16$
or the trivial partition already satisfies the condition of item 1. Suppose that, at a given step of the process, there is a pair of sets
$m\ge 16$
or the trivial partition already satisfies the condition of item 1. Suppose that, at a given step of the process, there is a pair of sets
![]() $X_i,Y_i$
which violates the conditions of both items 1 and 2. Partition
$X_i,Y_i$
which violates the conditions of both items 1 and 2. Partition
![]() $X_i$
into two subsections
$X_i$
into two subsections
![]() $X',X"$
with
$X',X"$
with
![]() $X'$
above
$X'$
above
![]() $X"$
, such that
$X"$
, such that
![]() $X'$
and
$X'$
and
![]() $X"$
each touch at least
$X"$
each touch at least
![]() $\left ( \frac {1}{2} - \frac {1}{6\log m} \right )e(X_i,Y_i)$
and at most
$\left ( \frac {1}{2} - \frac {1}{6\log m} \right )e(X_i,Y_i)$
and at most
![]() $\left ( \frac {1}{2} + \frac {1}{6\log m} \right )e(X_i,Y_i)$
of the chords between
$\left ( \frac {1}{2} + \frac {1}{6\log m} \right )e(X_i,Y_i)$
of the chords between
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
. This is possible since every vertex of
$Y_i$
. This is possible since every vertex of
![]() $X_i$
is incident to less than
$X_i$
is incident to less than
![]() $\frac {e(X_i,Y_i)}{6\log m}$
of these chords (by the assumption that item 1 fails). Let x be the lowest vertex of
$\frac {e(X_i,Y_i)}{6\log m}$
of these chords (by the assumption that item 1 fails). Let x be the lowest vertex of
![]() $X'$
which is incident to a chord, and let y be the lowest vertex of
$X'$
which is incident to a chord, and let y be the lowest vertex of
![]() $Y_i$
which is adjacent to x. Partition Y into subsections
$Y_i$
which is adjacent to x. Partition Y into subsections
![]() $Y',Y"$
such that
$Y',Y"$
such that
![]() $Y'$
is above
$Y'$
is above
![]() $Y"$
and y is the lowest vertex of
$Y"$
and y is the lowest vertex of
![]() $Y'$
. Observe that if a chord
$Y'$
. Observe that if a chord
![]() $e \in E(X',Y") \cup E(X",Y')$
does not contain y, then e interlaces
$e \in E(X',Y") \cup E(X",Y')$
does not contain y, then e interlaces
![]() $(x,y)$
. So the number of such chords is less than
$(x,y)$
. So the number of such chords is less than
![]() $\frac {e(X_i,Y_i)}{6\log m}$
. Also,
$\frac {e(X_i,Y_i)}{6\log m}$
. Also,
![]() $e(X_i,y) < \frac {e(X_i,Y_i)}{6\log m}$
. (Here, we used the assumption that
$e(X_i,y) < \frac {e(X_i,Y_i)}{6\log m}$
. (Here, we used the assumption that
![]() $X_i,Y_i$
violates both items 1 and 2). We conclude that
$X_i,Y_i$
violates both items 1 and 2). We conclude that
![]() $e(X',Y") + e(X",Y') < \frac {e(X_i,Y_i)}{3\log m}$
. It follows that
$e(X',Y") + e(X",Y') < \frac {e(X_i,Y_i)}{3\log m}$
. It follows that
![]() $e(X',Y') = e(X',Y_i) - e(X',Y") \geq \left ( \frac {1}{2} - \frac {1}{2\log m} \right )e(X_i,Y_i)$
, and similarly
$e(X',Y') = e(X',Y_i) - e(X',Y") \geq \left ( \frac {1}{2} - \frac {1}{2\log m} \right )e(X_i,Y_i)$
, and similarly
![]() $e(X",Y") \geq \left ( \frac {1}{2} - \frac {1}{2\log m} \right )e(X_i,Y_i)$
. Note that we also have the upper bound
$e(X",Y") \geq \left ( \frac {1}{2} - \frac {1}{2\log m} \right )e(X_i,Y_i)$
. Note that we also have the upper bound
![]() $e(X',Y'),e(X",Y") \leq \left ( \frac {1}{2} + \frac {1}{6\log m} \right )e(X_i,Y_i)$
. We now define new partitions by replacing
$e(X',Y'),e(X",Y") \leq \left ( \frac {1}{2} + \frac {1}{6\log m} \right )e(X_i,Y_i)$
. We now define new partitions by replacing
![]() $X_i$
with
$X_i$
with
![]() $X',X"$
and
$X',X"$
and
![]() $Y_i$
with
$Y_i$
with
![]() $Y',Y"$
. This way, we may continue the process until every pair
$Y',Y"$
. This way, we may continue the process until every pair
![]() $X_i,Y_i$
satisfies the condition of one of the items 1 or 2. Indeed, at each step, we replace some pair
$X_i,Y_i$
satisfies the condition of one of the items 1 or 2. Indeed, at each step, we replace some pair
![]() $X_i,Y_i$
with pairs having fewer edges than
$X_i,Y_i$
with pairs having fewer edges than
![]() $X_i,Y_i$
. If the number of edges of some pair is at most
$X_i,Y_i$
. If the number of edges of some pair is at most
![]() $6$
, then this pair trivially satisfies item 1. Hence, the process must terminate.
$6$
, then this pair trivially satisfies item 1. Hence, the process must terminate.
To each pair
![]() $(X_i,Y_i)$
appearing in the course of the process, we assign a binary string as follows. Assign the initial pair
$(X_i,Y_i)$
appearing in the course of the process, we assign a binary string as follows. Assign the initial pair
![]() $(X,Y)$
the empty string. If
$(X,Y)$
the empty string. If
![]() $(X',Y'),(X",Y")$
are obtained by splitting
$(X',Y'),(X",Y")$
are obtained by splitting
![]() $(X_i,Y_i)$
as above and
$(X_i,Y_i)$
as above and
![]() $(X_i,Y_i)$
is assigned the string
$(X_i,Y_i)$
is assigned the string
![]() $\sigma $
, then let
$\sigma $
, then let
![]() $(X',Y')$
be assigned the string
$(X',Y')$
be assigned the string
![]() $\sigma ,0$
and
$\sigma ,0$
and
![]() $(X",Y")$
the string
$(X",Y")$
the string
![]() $\sigma ,1$
. Let
$\sigma ,1$
. Let
![]() $h(X_i,Y_i)$
be the length of the string assigned to a pair
$h(X_i,Y_i)$
be the length of the string assigned to a pair
![]() $X_i,Y_i$
. It is easy to show, by induction, that
$X_i,Y_i$
. It is easy to show, by induction, that
 $$ \begin{align} \sum\left( \frac{1}{2} \right)^{h(X_i,Y_i)} = 1 \end{align} $$
$$ \begin{align} \sum\left( \frac{1}{2} \right)^{h(X_i,Y_i)} = 1 \end{align} $$
is preserved throughout the process, where the sum ranges over all pairs
![]() $X_i,Y_i$
at a given moment. Moreover, by our upper and lower bounds on
$X_i,Y_i$
at a given moment. Moreover, by our upper and lower bounds on
![]() $e(X',Y'),e(X",Y")$
, we get by induction that
$e(X',Y'),e(X",Y")$
, we get by induction that
 $$ \begin{align*}0<m \cdot \left( \frac{1}{2} - \frac{1}{2\log m} \right)^{h(X_i,Y_i)} \leq e(X_i,Y_i) \leq m \cdot \left( \frac{1}{2} + \frac{1}{6\log m} \right)^{h(X_i,Y_i)} \end{align*} $$
$$ \begin{align*}0<m \cdot \left( \frac{1}{2} - \frac{1}{2\log m} \right)^{h(X_i,Y_i)} \leq e(X_i,Y_i) \leq m \cdot \left( \frac{1}{2} + \frac{1}{6\log m} \right)^{h(X_i,Y_i)} \end{align*} $$
for every pair
![]() $(X_i,Y_i)$
appearing in the process. In particular,
$(X_i,Y_i)$
appearing in the process. In particular,
![]() $h(X_i,Y_i) \le 2\log m$
for each such pair
$h(X_i,Y_i) \le 2\log m$
for each such pair
![]() $(X_i,Y_i)$
. Hence,
$(X_i,Y_i)$
. Hence,
 $$ \begin{align*}e(X_i,Y_i) \geq m \cdot \left( \frac{1}{2} - \frac{1}{2\log m} \right)^{h(X_i,Y_i)} \geq m \cdot \left( 1 - \frac{1}{\log m} \right)^{2\log m} \left( \frac{1}{2} \right)^{h(X_i,Y_i)} \geq \frac{m}{12} \cdot \left( \frac{1}{2} \right)^{h(X_i,Y_i)}.\end{align*} $$
$$ \begin{align*}e(X_i,Y_i) \geq m \cdot \left( \frac{1}{2} - \frac{1}{2\log m} \right)^{h(X_i,Y_i)} \geq m \cdot \left( 1 - \frac{1}{\log m} \right)^{2\log m} \left( \frac{1}{2} \right)^{h(X_i,Y_i)} \geq \frac{m}{12} \cdot \left( \frac{1}{2} \right)^{h(X_i,Y_i)}.\end{align*} $$
Consider the partitions
![]() $X_1,\dots ,X_{t'}$
and
$X_1,\dots ,X_{t'}$
and
![]() $Y_1,\dots ,Y_{t'}$
at the end of the process. By equation (4.1) and the above, we have
$Y_1,\dots ,Y_{t'}$
at the end of the process. By equation (4.1) and the above, we have
![]() $\sum _{i=1}^{t'}{e(X_i,Y_i)} \ge m/12$
. This completes the proof of the lemma.
$\sum _{i=1}^{t'}{e(X_i,Y_i)} \ge m/12$
. This completes the proof of the lemma.
The final, main lemma of this subsection is Lemma 4.7 below. Before stating it, we will prove some auxiliary lemmas that will feature in its proof. We start with the following lemma.
Lemma 4.3. Let
![]() $X,Y$
be a section pair with m chords, and suppose that each vertex of X is incident to at most one chord. Then either there is a family of
$X,Y$
be a section pair with m chords, and suppose that each vertex of X is incident to at most one chord. Then either there is a family of
![]() $m/2$
pairwise-interlacing chords or we can find pairs of chords
$m/2$
pairwise-interlacing chords or we can find pairs of chords
![]() $(e_i,e^{\prime }_i)$
,
$(e_i,e^{\prime }_i)$
,
![]() $e_i = (x_i,y_i), e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
$e_i = (x_i,y_i), e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
![]() $i = 1,\dots ,t$
such that the following holds:
$i = 1,\dots ,t$
such that the following holds:
-
1. For every
 $1 \leq i \leq t$
,
$1 \leq i \leq t$
,
 $e_i,e^{\prime }_i$
are either parallel or share a vertex in Y.
$e_i,e^{\prime }_i$
are either parallel or share a vertex in Y. -
2. For every
 $1 \leq i < j \leq t$
, both
$1 \leq i < j \leq t$
, both
 $e_i$
and
$e_i$
and
 $e^{\prime }_i$
interlace both
$e^{\prime }_i$
interlace both
 $e_j$
and
$e_j$
and
 $e^{\prime }_j$
.
$e^{\prime }_j$
. -
3.
 $\sum _{i=1}^t d_X(x_i,x^{\prime }_i) \geq m/4$
.
$\sum _{i=1}^t d_X(x_i,x^{\prime }_i) \geq m/4$
.
Proof. We execute the following process. To start, set
![]() $E_1 = E(X,Y)$
. For each
$E_1 = E(X,Y)$
. For each
![]() $i \geq 1$
, we do as follows. If every two chords in
$i \geq 1$
, we do as follows. If every two chords in
![]() $E_i$
are interlacing, then stop. Otherwise, among all pairs of chords in
$E_i$
are interlacing, then stop. Otherwise, among all pairs of chords in
![]() $E_i$
which are parallel or share a vertex, choose one pair
$E_i$
which are parallel or share a vertex, choose one pair
![]() $e_i,e^{\prime }_i \in E_i$
,
$e_i,e^{\prime }_i \in E_i$
,
![]() $e_i = (x_i,y_i)$
,
$e_i = (x_i,y_i)$
,
![]() $e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
, which maximizes
$e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
, which maximizes
![]() $d_X(x_i,x^{\prime }_i)$
. Without loss of generality, let us assume that
$d_X(x_i,x^{\prime }_i)$
. Without loss of generality, let us assume that
![]() $x_i$
is above
$x_i$
is above
![]() $x^{\prime }_i$
(note that
$x^{\prime }_i$
(note that
![]() $x_i,x^{\prime }_i$
are distinct by our assumption that every vertex in X is incident to at most one chord;
$x_i,x^{\prime }_i$
are distinct by our assumption that every vertex in X is incident to at most one chord;
![]() $y_i,y^{\prime }_i$
may be equal). Since
$y_i,y^{\prime }_i$
may be equal). Since
![]() $e_i,e^{\prime }_i$
are parallel or share a vertex, it holds that either
$e_i,e^{\prime }_i$
are parallel or share a vertex, it holds that either
![]() $y_i = y^{\prime }_i$
or
$y_i = y^{\prime }_i$
or
![]() $y_i$
is above
$y_i$
is above
![]() $y^{\prime }_i$
. Let
$y^{\prime }_i$
. Let
![]() $X^*$
be the set of vertices of X between
$X^*$
be the set of vertices of X between
![]() $x_i$
and
$x_i$
and
![]() $x^{\prime }_i$
(including
$x^{\prime }_i$
(including
![]() $x_i,x^{\prime }_i$
), and let
$x_i,x^{\prime }_i$
), and let
![]() $Y^*$
be the set of vertices of Y between
$Y^*$
be the set of vertices of Y between
![]() $y_i$
and
$y_i$
and
![]() $y^{\prime }_i$
(including
$y^{\prime }_i$
(including
![]() $y_i,y^{\prime }_i$
). Observe that if
$y_i,y^{\prime }_i$
). Observe that if
![]() $e = (x,y) \in E_i$
is a chord with
$e = (x,y) \in E_i$
is a chord with
![]() $y \in Y^*$
, then x must be in
$y \in Y^*$
, then x must be in
![]() $X^*$
. Indeed, if x is above
$X^*$
. Indeed, if x is above
![]() $x_i$
, then
$x_i$
, then
![]() $e,e^{\prime }_i$
are parallel or share a vertex and
$e,e^{\prime }_i$
are parallel or share a vertex and
![]() $d_X(x,x^{\prime }_i)> d_X(x_i,x^{\prime }_i)$
; similarly, if x is below
$d_X(x,x^{\prime }_i)> d_X(x_i,x^{\prime }_i)$
; similarly, if x is below
![]() $x^{\prime }_i$
, then
$x^{\prime }_i$
, then
![]() $e,e_i$
are parallel or share a vertex and
$e,e_i$
are parallel or share a vertex and
![]() $d_X(x,x_i)> d_X(x_i,x^{\prime }_i)$
. In both cases, we get a contradiction to the maximality of
$d_X(x,x_i)> d_X(x_i,x^{\prime }_i)$
. In both cases, we get a contradiction to the maximality of
![]() $e_i,e^{\prime }_i$
.
$e_i,e^{\prime }_i$
.
Let F be the set of chords
![]() $(x,y) \in E_i$
with
$(x,y) \in E_i$
with
![]() $x \in X^*$
. Clearly,
$x \in X^*$
. Clearly,
![]() $|F| \geq 2$
because
$|F| \geq 2$
because
![]() $e_i,e^{\prime }_i \in F$
. Set
$e_i,e^{\prime }_i \in F$
. Set
![]() $E_{i+1} := E_i \setminus F$
. Note that
$E_{i+1} := E_i \setminus F$
. Note that
![]() $d_X(x_i,x^{\prime }_i) = |X^*| - 1 \geq |F| - 1 \geq |F|/2 = (|E_i| - |E_{i+1}|)/2$
, where the first inequality holds because every vertex of
$d_X(x_i,x^{\prime }_i) = |X^*| - 1 \geq |F| - 1 \geq |F|/2 = (|E_i| - |E_{i+1}|)/2$
, where the first inequality holds because every vertex of
![]() $X^*$
is incident to at most one chord. Above we have shown that F contains all chords
$X^*$
is incident to at most one chord. Above we have shown that F contains all chords
![]() $(x,y)$
with
$(x,y)$
with
![]() $y \in Y^*$
. It is now easy to see that each
$y \in Y^*$
. It is now easy to see that each
![]() $e = (x,y) \in E_{i+1}$
interlaces both
$e = (x,y) \in E_{i+1}$
interlaces both
![]() $e_i$
and
$e_i$
and
![]() $e^{\prime }_i$
. Indeed, let
$e^{\prime }_i$
. Indeed, let
![]() $e = (x,y) \in E_{i+1}$
. Then x is either above
$e = (x,y) \in E_{i+1}$
. Then x is either above
![]() $x_i$
or below
$x_i$
or below
![]() $x^{\prime }_i$
, and y is either above
$x^{\prime }_i$
, and y is either above
![]() $y_i$
or below
$y_i$
or below
![]() $y^{\prime }_i$
. If x is above
$y^{\prime }_i$
. If x is above
![]() $x_i$
and y is above
$x_i$
and y is above
![]() $y_i$
, then
$y_i$
, then
![]() $e,e^{\prime }_i$
are parallel with
$e,e^{\prime }_i$
are parallel with
![]() $d_X(x,x_i)> d(x_i,x^{\prime }_i)$
, contradicting the maximality of
$d_X(x,x_i)> d(x_i,x^{\prime }_i)$
, contradicting the maximality of
![]() $e_i,e^{\prime }_i$
. Similarly, it is impossible that x is below
$e_i,e^{\prime }_i$
. Similarly, it is impossible that x is below
![]() $x^{\prime }_i$
and y is below
$x^{\prime }_i$
and y is below
![]() $y^{\prime }_i$
. In the remaining two cases, e interlaces
$y^{\prime }_i$
. In the remaining two cases, e interlaces
![]() $e_i,e^{\prime }_i$
. This ensures that item 2 will be satisfied.
$e_i,e^{\prime }_i$
. This ensures that item 2 will be satisfied.
Suppose that the process continues for t steps. Then in
![]() $E_{t+1}$
, every two chords are interlacing. So if
$E_{t+1}$
, every two chords are interlacing. So if
![]() $|E_{t+1}| \geq m/2$
, then we are done. Suppose then that
$|E_{t+1}| \geq m/2$
, then we are done. Suppose then that
![]() $|E_{t+1}| < m/2$
. Consider the pairs of chords
$|E_{t+1}| < m/2$
. Consider the pairs of chords
![]() $e_i = (x_i,y_i),e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
$e_i = (x_i,y_i),e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
![]() $1 \leq i \leq t$
. We have already shown that items 1 and 2 hold. For item 3, we have
$1 \leq i \leq t$
. We have already shown that items 1 and 2 hold. For item 3, we have
 $$ \begin{align*}\sum_{i = 1}^t {d_X(x_i,x^{\prime}_i)} \geq \frac{1}{2}\sum_{i = 1}^t (|E_i| - |E_{i+1}|) = \frac{1}{2}(|E_1| - |E_{t+1}|) \geq m/4, \end{align*} $$
$$ \begin{align*}\sum_{i = 1}^t {d_X(x_i,x^{\prime}_i)} \geq \frac{1}{2}\sum_{i = 1}^t (|E_i| - |E_{i+1}|) = \frac{1}{2}(|E_1| - |E_{t+1}|) \geq m/4, \end{align*} $$
as required.
The next two lemmas are concerned with combining paths over a family of interlacing subsections.
Lemma 4.4. Let
![]() $X,Y$
be a section pair with
$X,Y$
be a section pair with
![]() $3t$
interlacing chords, whose lengths belong into an interval of size D. Then there are paths
$3t$
interlacing chords, whose lengths belong into an interval of size D. Then there are paths
![]() $P_1,\dots ,P_{t}$
between
$P_1,\dots ,P_{t}$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2D$
for every
$1 \leq |P_{i+1}| - |P_i| \leq 2D$
for every
![]() $1 \leq i \leq t - 1$
. In particular,
$1 \leq i \leq t - 1$
. In particular,
![]() $|P_{t}| \geq |P_1| + t - 1$
.
$|P_{t}| \geq |P_1| + t - 1$
.
Proof. Let
![]() $(x_1,y_1),\dots ,(x_{3t},y_{3t}) \in E(X,Y)$
be the given family of interlacing chords, with
$(x_1,y_1),\dots ,(x_{3t},y_{3t}) \in E(X,Y)$
be the given family of interlacing chords, with
![]() $x_i$
above
$x_i$
above
![]() $x_j$
and
$x_j$
and
![]() $y_i$
below
$y_i$
below
![]() $y_j$
for each
$y_j$
for each
![]() $1 \leq i < j \leq 3t$
. For
$1 \leq i < j \leq 3t$
. For
![]() $1 \leq i \leq 3t-1$
, put
$1 \leq i \leq 3t-1$
, put
![]() $d_i := d_Y(y_i,y_{i+1}) - d_X(x_i,x_{i+1})$
. Note that
$d_i := d_Y(y_i,y_{i+1}) - d_X(x_i,x_{i+1})$
. Note that
![]() $d_i$
is precisely the difference between the lengths of
$d_i$
is precisely the difference between the lengths of
![]() $(x_i,y_i)$
and
$(x_i,y_i)$
and
![]() $(x_{i+1},y_{i+1})$
, so by our assumption, we have
$(x_{i+1},y_{i+1})$
, so by our assumption, we have
![]() $|d_i|\le D-1.$
We prove the lemma by induction on t. In the base case
$|d_i|\le D-1.$
We prove the lemma by induction on t. In the base case
![]() $t=1$
, the desired path
$t=1$
, the desired path
![]() $P_1$
can be chosen as the trivial path of the chord
$P_1$
can be chosen as the trivial path of the chord
![]() $(x_1,y_1)$
.
$(x_1,y_1)$
.
For the induction step, we will first find two paths
![]() $Q_1,Q_2$
between
$Q_1,Q_2$
between
![]() $x_1$
and
$x_1$
and
![]() $x_3$
such that
$x_3$
such that
![]() $1 \leq |Q_2| - |Q_1| \leq 2D$
and such that
$1 \leq |Q_2| - |Q_1| \leq 2D$
and such that
![]() $Q_1,Q_2$
do not use any vertices of X below
$Q_1,Q_2$
do not use any vertices of X below
![]() $x_3$
or any vertices of Y above
$x_3$
or any vertices of Y above
![]() $y_3$
. To find such
$y_3$
. To find such
![]() $Q_1,Q_2$
, we proceed as follows. For
$Q_1,Q_2$
, we proceed as follows. For
![]() $i = 1,2$
, put
$i = 1,2$
, put
![]() $a_i := d_X(x_i,x_{i+1})$
and
$a_i := d_X(x_i,x_{i+1})$
and
![]() $b_i := d_Y(y_i,y_{i+1})$
so that
$b_i := d_Y(y_i,y_{i+1})$
so that
![]() $d_i = b_i - a_i$
. Consider the following four paths between
$d_i = b_i - a_i$
. Consider the following four paths between
![]() $x_1$
and
$x_1$
and
![]() $x_3$
.
$x_3$
.
-
•
 $P^{\prime }_1 = X[x_1,x_3]$
, depicted in blue in Figure 4;
$P^{\prime }_1 = X[x_1,x_3]$
, depicted in blue in Figure 4; -
•
 $P^{\prime }_2 = X[x_1,x_2],(x_2,y_2),Y[y_2,y_3],(y_3,x_3)$
, depicted in red in Figure 4;
$P^{\prime }_2 = X[x_1,x_2],(x_2,y_2),Y[y_2,y_3],(y_3,x_3)$
, depicted in red in Figure 4; -
•
 $P^{\prime }_3 = (x_1,y_1),Y[y_1,y_2],(y_2,x_2),X[x_2,x_3]$
, depicted in green in Figure 4;
$P^{\prime }_3 = (x_1,y_1),Y[y_1,y_2],(y_2,x_2),X[x_2,x_3]$
, depicted in green in Figure 4; -
•
 $P^{\prime }_4 = (x_1,y_1),Y[y_1,y_3],(y_3,x_3)$
, depicted in yellow in Figure 4.
$P^{\prime }_4 = (x_1,y_1),Y[y_1,y_3],(y_3,x_3)$
, depicted in yellow in Figure 4.
Observe that
![]() $P^{\prime }_1,\dots ,P^{\prime }_4$
do not use any vertices of X below
$P^{\prime }_1,\dots ,P^{\prime }_4$
do not use any vertices of X below
![]() $x_3$
or any vertices of Y above
$x_3$
or any vertices of Y above
![]() $y_3$
. We have
$y_3$
. We have
![]() $|P^{\prime }_1| = a_1 + a_2$
,
$|P^{\prime }_1| = a_1 + a_2$
,
![]() $|P^{\prime }_2| = a_1 + b_2 + 2$
,
$|P^{\prime }_2| = a_1 + b_2 + 2$
,
![]() $|P^{\prime }_3| = a_2 + b_1 + 2$
,
$|P^{\prime }_3| = a_2 + b_1 + 2$
,
![]() $|P^{\prime }_4| = b_1 + b_2 + 2$
. Hence,
$|P^{\prime }_4| = b_1 + b_2 + 2$
. Hence,
![]() $|P^{\prime }_2| - |P^{\prime }_1| = d_2 + 2$
,
$|P^{\prime }_2| - |P^{\prime }_1| = d_2 + 2$
,
![]() $|P^{\prime }_3| - |P^{\prime }_1| = d_1 + 2$
,
$|P^{\prime }_3| - |P^{\prime }_1| = d_1 + 2$
,
![]() $|P^{\prime }_4| - |P^{\prime }_1| = d_1 + d_2 + 2$
,
$|P^{\prime }_4| - |P^{\prime }_1| = d_1 + d_2 + 2$
,
![]() $|P^{\prime }_3| - |P^{\prime }_2| = d_1 - d_2$
,
$|P^{\prime }_3| - |P^{\prime }_2| = d_1 - d_2$
,
![]() $|P^{\prime }_4| - |P^{\prime }_2| = d_1$
and
$|P^{\prime }_4| - |P^{\prime }_2| = d_1$
and
![]() $|P^{\prime }_4| - |P^{\prime }_3| = d_2$
. So we see that, for all
$|P^{\prime }_4| - |P^{\prime }_3| = d_2$
. So we see that, for all
![]() $Q_1,Q_2 \in \{P^{\prime }_1,\dots ,P^{\prime }_4\}$
, it holds that
$Q_1,Q_2 \in \{P^{\prime }_1,\dots ,P^{\prime }_4\}$
, it holds that
![]() $||Q_2| - |Q_1|| \leq |d_1| + |d_2| + 2 \leq 2D$
.
$||Q_2| - |Q_1|| \leq |d_1| + |d_2| + 2 \leq 2D$
.
Observe that the four numbers
![]() $a_1 + a_2, a_1 + b_2 + 2, a_2 + b_1 + 2, b_1 + b_2 + 2$
cannot all be equal. Indeed, if the first three are equal, then
$a_1 + a_2, a_1 + b_2 + 2, a_2 + b_1 + 2, b_1 + b_2 + 2$
cannot all be equal. Indeed, if the first three are equal, then
![]() $b_1 = a_1 - 2$
and
$b_1 = a_1 - 2$
and
![]() $b_2 = a_2 - 2$
, which means that
$b_2 = a_2 - 2$
, which means that
![]() $b_1 + b_2 + 2 = a_1 + a_2 - 2 \neq a_1 + a_2$
. It follows that there are
$b_1 + b_2 + 2 = a_1 + a_2 - 2 \neq a_1 + a_2$
. It follows that there are
![]() $Q_1,Q_2 \in \{P^{\prime }_1,\dots ,P^{\prime }_4\}$
with
$Q_1,Q_2 \in \{P^{\prime }_1,\dots ,P^{\prime }_4\}$
with
![]() $|Q_1| \neq |Q_2|$
, say
$|Q_1| \neq |Q_2|$
, say
![]() $|Q_1| < |Q_2|$
. We have already shown that
$|Q_1| < |Q_2|$
. We have already shown that
![]() $|Q_2| - |Q_1| \leq 2D$
. So
$|Q_2| - |Q_1| \leq 2D$
. So
![]() $Q_1,Q_2$
satisfy all of our requirements.
$Q_1,Q_2$
satisfy all of our requirements.
We now complete the induction step using the paths
![]() $Q_1,Q_2$
found above. Let
$Q_1,Q_2$
found above. Let
![]() $t \geq 2$
, and apply the induction hypothesis with parameter
$t \geq 2$
, and apply the induction hypothesis with parameter
![]() $t - 1$
and with X and Y replaced by
$t - 1$
and with X and Y replaced by
![]() $X[x_4,x^{\text {b}}]$
and
$X[x_4,x^{\text {b}}]$
and
![]() $Y[y^{\text {t}},y_4]$
, which still contain
$Y[y^{\text {t}},y_4]$
, which still contain
![]() $3(t-1)$
of our interlacing chords. This way we obtain paths
$3(t-1)$
of our interlacing chords. This way we obtain paths
![]() $R_1,\dots ,R_{t-1}$
between
$R_1,\dots ,R_{t-1}$
between
![]() $x_4$
and
$x_4$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $1 \leq |R_{i+1}| - |R_i| \leq 2D$
for every
$1 \leq |R_{i+1}| - |R_i| \leq 2D$
for every
![]() $1 \leq i \leq t - 2$
. For
$1 \leq i \leq t - 2$
. For
![]() $1 \leq i \leq t-1$
, let
$1 \leq i \leq t-1$
, let
![]() $P_i$
be the concatenation of
$P_i$
be the concatenation of
![]() $X[x^{\text {t}},x_1]$
,
$X[x^{\text {t}},x_1]$
,
![]() $Q_1$
,
$Q_1$
,
![]() $X[x_3,x_4]$
and
$X[x_3,x_4]$
and
![]() $R_i$
. Let
$R_i$
. Let
![]() $P_{t}$
be the concatenation of
$P_{t}$
be the concatenation of
![]() $X[x^{\text {t}},x_1]$
,
$X[x^{\text {t}},x_1]$
,
![]() $Q_2$
,
$Q_2$
,
![]() $X[x_3,x_4]$
and
$X[x_3,x_4]$
and
![]() $R_{t-1}$
. See Figure 5 for an illustration of the resulting paths
$R_{t-1}$
. See Figure 5 for an illustration of the resulting paths
![]() $P_i$
. For each
$P_i$
. For each
![]() $1 \leq i \leq t-2$
, we have
$1 \leq i \leq t-2$
, we have
![]() $|P_{i+1}| - |P_i| = |R_{i+1}| - |R_i|$
, and hence
$|P_{i+1}| - |P_i| = |R_{i+1}| - |R_i|$
, and hence
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2D$
. Lastly,
$1 \leq |P_{i+1}| - |P_i| \leq 2D$
. Lastly,
![]() $|P_{t}| - |P_{t - 1}| = |Q_2| - |Q_1|$
, and hence
$|P_{t}| - |P_{t - 1}| = |Q_2| - |Q_1|$
, and hence
![]() $1 \leq |P_{t}| - |P_{t - 1}| \leq 2D$
as well. This completes the proof.
$1 \leq |P_{t}| - |P_{t - 1}| \leq 2D$
as well. This completes the proof.
Lemma 4.5. Let
![]() $X,Y$
be a section pair, let
$X,Y$
be a section pair, let
![]() $t \geq 1$
be odd and let
$t \geq 1$
be odd and let
![]() $X_1,Y_1;\dots ;X_t,Y_t$
be an interlacing collection of subsection pairs. Let
$X_1,Y_1;\dots ;X_t,Y_t$
be an interlacing collection of subsection pairs. Let
![]() $d_1,\dots ,d_t \geq 1$
. Suppose that for each
$d_1,\dots ,d_t \geq 1$
. Suppose that for each
![]() $1 \leq i \leq t$
, there are two paths
$1 \leq i \leq t$
, there are two paths
![]() $Q_i^R,Q_i^B \subseteq X_i \cup Y_i$
with
$Q_i^R,Q_i^B \subseteq X_i \cup Y_i$
with
![]() $|Q_i^R| - |Q_i^B| \geq d_i$
, which go between
$|Q_i^R| - |Q_i^B| \geq d_i$
, which go between
![]() $x^{\text {t}}_i$
and
$x^{\text {t}}_i$
and
![]() $y^{\text {t}}_i$
if i is odd and between
$y^{\text {t}}_i$
if i is odd and between
![]() $x^{\text {b}}_i$
and
$x^{\text {b}}_i$
and
![]() $y^{\text {b}}_i$
if i is even. Set
$y^{\text {b}}_i$
if i is even. Set
![]() $D := \max _{i = 1,\dots ,t}{(|X_i| + |Y_i|)}$
. Then there are paths
$D := \max _{i = 1,\dots ,t}{(|X_i| + |Y_i|)}$
. Then there are paths
![]() $P_1,\dots ,P_{(t+3)/2}$
between
$P_1,\dots ,P_{(t+3)/2}$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $|P_{(t+3)/2}| - |P_1| \geq \sum _{i = 1}^t{d_i}$
and such that
$|P_{(t+3)/2}| - |P_1| \geq \sum _{i = 1}^t{d_i}$
and such that
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2D$
for every
$1 \leq |P_{i+1}| - |P_i| \leq 2D$
for every
![]() $1 \leq i \leq (t+1)/2$
.
$1 \leq i \leq (t+1)/2$
.
Proof. Without loss of generality, assume that
![]() $X_i$
is above
$X_i$
is above
![]() $X_j$
for all
$X_j$
for all
![]() $i<j$
(and consequently, the opposite is true for the
$i<j$
(and consequently, the opposite is true for the
![]() $Y_i$
’s). The proof is by induction on t. For the case
$Y_i$
’s). The proof is by induction on t. For the case
![]() $t = 1$
, simply take
$t = 1$
, simply take
![]() $P_1/P_2$
to be the concatenation of
$P_1/P_2$
to be the concatenation of
![]() $X[x^{\text {t}},x^{\text {t}}_1]$
,
$X[x^{\text {t}},x^{\text {t}}_1]$
,
![]() $Q_1^B/Q_1^R$
and
$Q_1^B/Q_1^R$
and
![]() $Y[y^{\text {t}}_1,y^{\text {t}}]$
. Clearly,
$Y[y^{\text {t}}_1,y^{\text {t}}]$
. Clearly,
![]() $|P_2| - |P_1| = |Q_1^R| - |Q_1^B|$
, which immediately implies that
$|P_2| - |P_1| = |Q_1^R| - |Q_1^B|$
, which immediately implies that
![]() $|P_2| - |P_1| \geq d_1 \geq 1$
. On the other hand, since
$|P_2| - |P_1| \geq d_1 \geq 1$
. On the other hand, since
![]() $Q_1^R,Q_1^B$
are both contained in
$Q_1^R,Q_1^B$
are both contained in
![]() $X_1 \cup Y_1$
, we have
$X_1 \cup Y_1$
, we have
![]() $|P_2| - |P_1| = |Q_1^R| - |Q_1^B| \leq |X_1| + |Y_1| \leq D$
, as required.
$|P_2| - |P_1| = |Q_1^R| - |Q_1^B| \leq |X_1| + |Y_1| \leq D$
, as required.
Suppose now that
![]() $t \geq 3$
. For each
$t \geq 3$
. For each
![]() $c = R,B$
, define a path
$c = R,B$
, define a path
![]() $Q^{\prime }_c$
from
$Q^{\prime }_c$
from
![]() $x^{\text {t}}$
to
$x^{\text {t}}$
to
![]() $x_2^{\text {b}}$
as follows:
$x_2^{\text {b}}$
as follows:
See Figure 6 for an illustration. We have
![]() $|Q^{\prime }_R| - |Q^{\prime }_B| = \sum _{i = 1}^2(|Q_i^R| - |Q_i^B|) \geq d_1 + d_2$
. On the other hand, since
$|Q^{\prime }_R| - |Q^{\prime }_B| = \sum _{i = 1}^2(|Q_i^R| - |Q_i^B|) \geq d_1 + d_2$
. On the other hand, since
![]() $Q^R_i,Q^B_i \subseteq X_i \cup Y_i$
(for
$Q^R_i,Q^B_i \subseteq X_i \cup Y_i$
(for
![]() $i = 1,2$
), we have that
$i = 1,2$
), we have that
![]() $|Q^R_i| - |Q^B_i| \leq D$
and hence
$|Q^R_i| - |Q^B_i| \leq D$
and hence
![]() $|Q^{\prime }_R| - |Q^{\prime }_B| \leq 2D$
. Note that
$|Q^{\prime }_R| - |Q^{\prime }_B| \leq 2D$
. Note that
![]() $Q^{\prime }_B,Q^{\prime }_R$
do not use any vertices of X below
$Q^{\prime }_B,Q^{\prime }_R$
do not use any vertices of X below
![]() $x_2^{\text {b}}$
or any vertices of Y above
$x_2^{\text {b}}$
or any vertices of Y above
![]() $y_2^{\text {t}}$
. Now apply the induction hypothesis with parameter
$y_2^{\text {t}}$
. Now apply the induction hypothesis with parameter
![]() $t-2$
and with X and Y replaced by
$t-2$
and with X and Y replaced by
![]() $X[x_2^{\text {b}},x^{\text {b}}]$
and
$X[x_2^{\text {b}},x^{\text {b}}]$
and
![]() $Y[y^{\text {t}},y_3^{\text {b}}]$
. This gives paths
$Y[y^{\text {t}},y_3^{\text {b}}]$
. This gives paths
![]() $R_1,\dots ,R_{(t+1)/2}$
between
$R_1,\dots ,R_{(t+1)/2}$
between
![]() $x_2^{\text {b}}$
and
$x_2^{\text {b}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $|R_{(t+1)/2}| - |R_1| \geq \sum _{i = 3}^t{d_i}$
and such that
$|R_{(t+1)/2}| - |R_1| \geq \sum _{i = 3}^t{d_i}$
and such that
![]() $1 \leq |R_{i+1}| - |R_i| \leq 2D$
for every
$1 \leq |R_{i+1}| - |R_i| \leq 2D$
for every
![]() $1 \leq i \leq (t-1)/2$
. For
$1 \leq i \leq (t-1)/2$
. For
![]() $1 \leq i \leq (t+1)/2$
, let
$1 \leq i \leq (t+1)/2$
, let
![]() $P_i$
be the concatenation of
$P_i$
be the concatenation of
![]() $Q^{\prime }_B$
and
$Q^{\prime }_B$
and
![]() $R_i$
. Let
$R_i$
. Let
![]() $P_{(t+3)/2}$
be the concatenation of
$P_{(t+3)/2}$
be the concatenation of
![]() $Q^{\prime }_R$
and
$Q^{\prime }_R$
and
![]() $R_{(t+1)/2}$
. Then
$R_{(t+1)/2}$
. Then
![]() $|P_{(t+3)/2}| - |P_1| = |Q^{\prime }_R| - |Q^{\prime }_B| + |R_{(t+1)/2}| - |R_1| \geq \sum _{i = 1}^t{d_i}$
. Moreover, for every
$|P_{(t+3)/2}| - |P_1| = |Q^{\prime }_R| - |Q^{\prime }_B| + |R_{(t+1)/2}| - |R_1| \geq \sum _{i = 1}^t{d_i}$
. Moreover, for every
![]() $1 \leq i \leq (t-1)/2$
we have
$1 \leq i \leq (t-1)/2$
we have
![]() $|P_{i+1}| - |P_i| = |R_{i+1}| - |R_i|$
and hence
$|P_{i+1}| - |P_i| = |R_{i+1}| - |R_i|$
and hence
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2D$
. Finally, we have
$1 \leq |P_{i+1}| - |P_i| \leq 2D$
. Finally, we have
![]() $|P_{(t+3)/2}| - |P_{(t+1)/2}| = |Q^{\prime }_R| - |Q^{\prime }_B|$
and hence
$|P_{(t+3)/2}| - |P_{(t+1)/2}| = |Q^{\prime }_R| - |Q^{\prime }_B|$
and hence
![]() $1 \leq |P_{(t+3)/2}| - |P_{(t+1)/2}| \leq 2D$
. This completes the proof.
$1 \leq |P_{(t+3)/2}| - |P_{(t+1)/2}| \leq 2D$
. This completes the proof.
Using Lemmas 4.3, 4.4 and 4.5, we can now prove the following lemma, which states that in a section pair with m chords one can find two paths whose lengths differ by
![]() $\Omega (m)$
, provided every vertex on one side is incident to at most one chord.
$\Omega (m)$
, provided every vertex on one side is incident to at most one chord.
Lemma 4.6. Let
![]() $X,Y$
be a section pair with
$X,Y$
be a section pair with
![]() $m \geq 12$
chords, and suppose that each vertex of X is incident to at most one chord. Then there are two paths
$m \geq 12$
chords, and suppose that each vertex of X is incident to at most one chord. Then there are two paths
![]() $P,P'$
between
$P,P'$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $|P'| \geq |P| + \Omega (m)$
. By symmetry, there are two paths
$|P'| \geq |P| + \Omega (m)$
. By symmetry, there are two paths
![]() $Q,Q'$
between
$Q,Q'$
between
![]() $x^{\text {b}}$
and
$x^{\text {b}}$
and
![]() $y^{\text {b}}$
such that
$y^{\text {b}}$
such that
![]() $|Q'| \geq |Q| + \Omega (m)$
.
$|Q'| \geq |Q| + \Omega (m)$
.
Proof. Apply Lemma 4.3. If
![]() $E(X,Y)$
contains a family of
$E(X,Y)$
contains a family of
![]() $m/2$
pairwise-interlacing chords, then we are done by Lemma 4.4. Otherwise, let
$m/2$
pairwise-interlacing chords, then we are done by Lemma 4.4. Otherwise, let
![]() $e_i = (x_i,y_i)$
,
$e_i = (x_i,y_i)$
,
![]() $e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
$e^{\prime }_i = (x^{\prime }_i,y^{\prime }_i)$
,
![]() $1 \leq i \leq t$
, be as in Lemma 4.3. Without loss of generality we may assume, for each
$1 \leq i \leq t$
, be as in Lemma 4.3. Without loss of generality we may assume, for each
![]() $1 \leq i \leq t$
, that
$1 \leq i \leq t$
, that
![]() $x_i$
is above
$x_i$
is above
![]() $x^{\prime }_i$
, and hence either
$x^{\prime }_i$
, and hence either
![]() $y_i = y^{\prime }_i$
or
$y_i = y^{\prime }_i$
or
![]() $y_i$
is above
$y_i$
is above
![]() $y^{\prime }_i$
. For
$y^{\prime }_i$
. For
![]() $1 \leq i \leq t$
, let
$1 \leq i \leq t$
, let
![]() $X_i := X[x_i,x^{\prime }_i]$
,
$X_i := X[x_i,x^{\prime }_i]$
,
![]() $Y_i := Y[y_i,y^{\prime }_i]$
; so
$Y_i := Y[y_i,y^{\prime }_i]$
; so
![]() $x_i^{\text {t}} = x_i$
,
$x_i^{\text {t}} = x_i$
,
![]() $x_i^{\text {b}} = x^{\prime }_i$
,
$x_i^{\text {b}} = x^{\prime }_i$
,
![]() $y_i^{\text {t}} = y_i$
, and
$y_i^{\text {t}} = y_i$
, and
![]() $y_i^{\text {b}} = y^{\prime }_i$
. Item 2 of Lemma 4.3 guarantees that, after possibly permuting the coordinates
$y_i^{\text {b}} = y^{\prime }_i$
. Item 2 of Lemma 4.3 guarantees that, after possibly permuting the coordinates
![]() $1,\dots ,t$
, we have that
$1,\dots ,t$
, we have that
![]() $X_i$
is above
$X_i$
is above
![]() $X_j$
and
$X_j$
and
![]() $Y_i$
is below
$Y_i$
is below
![]() $Y_j$
for every
$Y_j$
for every
![]() $1 \leq i < j \leq t$
. Set
$1 \leq i < j \leq t$
. Set
![]() $d_i := d_X(x_i,x^{\prime }_i)$
. Observe that, for each
$d_i := d_X(x_i,x^{\prime }_i)$
. Observe that, for each
![]() $1 \leq i \leq t$
,
$1 \leq i \leq t$
,
![]() $Q^B_i := (x_i,y_i)$
and
$Q^B_i := (x_i,y_i)$
and
![]() $Q^R_i := X[x_i,x^{\prime }_i], (x^{\prime }_i,y^{\prime }_i), Y[y^{\prime }_i,y_i]$
are two paths between
$Q^R_i := X[x_i,x^{\prime }_i], (x^{\prime }_i,y^{\prime }_i), Y[y^{\prime }_i,y_i]$
are two paths between
![]() $x_i$
and
$x_i$
and
![]() $y_i$
, both contained in
$y_i$
, both contained in
![]() $X_i \cup Y_i$
such that
$X_i \cup Y_i$
such that
![]() $|Q^R_i| - |Q^B_i| = d_X(x_i,x^{\prime }_i) + d_Y(y_i,y^{\prime }_i) \geq d_i$
. Similarly,
$|Q^R_i| - |Q^B_i| = d_X(x_i,x^{\prime }_i) + d_Y(y_i,y^{\prime }_i) \geq d_i$
. Similarly,
![]() $Q^B_i := (x^{\prime }_i,y^{\prime }_i)$
and
$Q^B_i := (x^{\prime }_i,y^{\prime }_i)$
and
![]() $Q^R_i := X[x^{\prime }_i,x_i], (x_i,y_i), Y[y_i,y^{\prime }_i]$
are two paths between
$Q^R_i := X[x^{\prime }_i,x_i], (x_i,y_i), Y[y_i,y^{\prime }_i]$
are two paths between
![]() $x^{\prime }_i$
and
$x^{\prime }_i$
and
![]() $y^{\prime }_i$
, both contained in
$y^{\prime }_i$
, both contained in
![]() $X_i \cup Y_i$
such that
$X_i \cup Y_i$
such that
![]() $|Q^R_i| - |Q^B_i| \geq d_i$
. Hence, we are in the setting of Lemma 4.5. By item 3 of Lemma 4.3, we have
$|Q^R_i| - |Q^B_i| \geq d_i$
. Hence, we are in the setting of Lemma 4.5. By item 3 of Lemma 4.3, we have
![]() $\sum _{i=1}^t {d_i} \geq m/4$
. If t is even, then omit a pair
$\sum _{i=1}^t {d_i} \geq m/4$
. If t is even, then omit a pair
![]() $(X_i,Y_i)$
for which
$(X_i,Y_i)$
for which
![]() $d_i = \min \{d_1,\dots ,d_t\}$
; this way we guarantee that t is odd (which is necessary for invoking Lemma 4.5), while making sure that the sum
$d_i = \min \{d_1,\dots ,d_t\}$
; this way we guarantee that t is odd (which is necessary for invoking Lemma 4.5), while making sure that the sum
![]() $\sum d_i$
over the remaining i is at least
$\sum d_i$
over the remaining i is at least
![]() $m/8$
. To complete the proof, apply Lemma 4.5 and set
$m/8$
. To complete the proof, apply Lemma 4.5 and set
![]() $P := P_1$
and
$P := P_1$
and
![]() $P' := P_{(t+3)/2}$
.
$P' := P_{(t+3)/2}$
.
Finally, we are in a position to prove Lemma 4.7. This lemma states that if a section pair has many chords whose lengths are close to each other, say all contained in some (small) interval J, then one can find a sequence of path lengths, with any two consecutive lengths differing by
![]() $\Theta (|J|)$
. This lemma will play a key role in the proof of Theorem 1.1.
$\Theta (|J|)$
. This lemma will play a key role in the proof of Theorem 1.1.
Lemma 4.7. Let
![]() $X,Y$
be a section pair, and suppose that each vertex of X is incident to at most one chord. Let
$X,Y$
be a section pair, and suppose that each vertex of X is incident to at most one chord. Let
![]() $E \subseteq E(X,Y)$
be a set of chords, and let
$E \subseteq E(X,Y)$
be a set of chords, and let
![]() $J \subseteq \mathbb {N}$
be an interval such that, for each
$J \subseteq \mathbb {N}$
be an interval such that, for each
![]() $e \in E$
, the length of e belongs to J. Then for
$e \in E$
, the length of e belongs to J. Then for
![]() $k = \Omega (|E|/|J|)$
, there are paths
$k = \Omega (|E|/|J|)$
, there are paths
![]() $P_1,\dots ,P_{k}$
between
$P_1,\dots ,P_{k}$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $|P_{i+1}| - |P_i| = \Theta (|J|)$
for every
$|P_{i+1}| - |P_i| = \Theta (|J|)$
for every
![]() $1 \leq i \leq k-1$
.
$1 \leq i \leq k-1$
.
Proof. We will assume that
![]() $|E| \gg |J|$
, as otherwise, the assertion is trivial. We only consider the chords in E (removing all others). Partition X into subsections
$|E| \gg |J|$
, as otherwise, the assertion is trivial. We only consider the chords in E (removing all others). Partition X into subsections
![]() $X_1,\dots ,X_s$
such that
$X_1,\dots ,X_s$
such that
![]() $X_1,\dots ,X_{s-1}$
have
$X_1,\dots ,X_{s-1}$
have
![]() $|J|$
vertices each, and
$|J|$
vertices each, and
![]() $X_s$
has less than
$X_s$
has less than
![]() $|J|$
vertices. (As usual,
$|J|$
vertices. (As usual,
![]() $X_i$
is below
$X_i$
is below
![]() $X_j$
for
$X_j$
for
![]() $i < j$
.) Note that if
$i < j$
.) Note that if
![]() $i \neq j$
have the same parity, then for all
$i \neq j$
have the same parity, then for all
![]() $x_1 \in X_i, x_2 \in X_j$
we have
$x_1 \in X_i, x_2 \in X_j$
we have
![]() $d_X(x_1,x_2)> |J|$
. Without loss of generality, we shall assume that
$d_X(x_1,x_2)> |J|$
. Without loss of generality, we shall assume that
![]() $\sum _{i \text { even}}{e(X_i)} \geq \sum _{i \text { odd}}{e(X_i)}$
, and hence
$\sum _{i \text { even}}{e(X_i)} \geq \sum _{i \text { odd}}{e(X_i)}$
, and hence
![]() $\sum _{i \text { even}}{e(X_i)} \geq |E|/2$
(the other case is symmetrical). For convenience, let us set
$\sum _{i \text { even}}{e(X_i)} \geq |E|/2$
(the other case is symmetrical). For convenience, let us set
![]() $I_0 = \{i \in [s] : i \text { even}\}$
. For each
$I_0 = \{i \in [s] : i \text { even}\}$
. For each
![]() $i \in I_0$
, let
$i \in I_0$
, let
![]() $Y_i$
be the minimal subpath of Y containing all neighbours of
$Y_i$
be the minimal subpath of Y containing all neighbours of
![]() $X_i$
. Note that
$X_i$
. Note that
![]() $\sum _{i \in I_0}{e(X_i,Y_i)} \geq |E|/2$
.
$\sum _{i \in I_0}{e(X_i,Y_i)} \geq |E|/2$
.
Observe that, for all
![]() $(x_1,y_1),(x_2,y_2) \in E(X_i,Y_i)$
, we have
$(x_1,y_1),(x_2,y_2) \in E(X_i,Y_i)$
, we have
![]() $d_Y(y_1,y_2) \leq d_X(x_1,x_2) + |J| < 2|J|$
, where the first inequality follows from the fact that the lengths of
$d_Y(y_1,y_2) \leq d_X(x_1,x_2) + |J| < 2|J|$
, where the first inequality follows from the fact that the lengths of
![]() $(x_1,y_1)$
and
$(x_1,y_1)$
and
![]() $(x_2,y_2)$
both belong to J and hence differ by at most
$(x_2,y_2)$
both belong to J and hence differ by at most
![]() $|J|$
. So we see that
$|J|$
. So we see that
![]() $|Y_i| \leq 2|J|$
. Next, observe that, for every pair
$|Y_i| \leq 2|J|$
. Next, observe that, for every pair
![]() $i,j \in I_0$
with
$i,j \in I_0$
with
![]() $i < j$
and for all
$i < j$
and for all
![]() $(x_1,y_1) \in E(X_i,Y_i)$
,
$(x_1,y_1) \in E(X_i,Y_i)$
,
![]() $(x_2,y_2) \in E(X_j,Y_j)$
, it must be the case that
$(x_2,y_2) \in E(X_j,Y_j)$
, it must be the case that
![]() $y_2$
is below
$y_2$
is below
![]() $y_1$
. Indeed, if not, then
$y_1$
. Indeed, if not, then
![]() $(x_1,y_1),(x_2,y_2)$
either are parallel or share a vertex, which means that the difference between the lengths of
$(x_1,y_1),(x_2,y_2)$
either are parallel or share a vertex, which means that the difference between the lengths of
![]() $(x_1,y_1)$
and
$(x_1,y_1)$
and
![]() $(x_2,y_2)$
is at least
$(x_2,y_2)$
is at least
![]() $d_X(x_1,x_2)> |J|$
, contradicting that both of these lengths are in J. So we see that
$d_X(x_1,x_2)> |J|$
, contradicting that both of these lengths are in J. So we see that
![]() $Y_j$
is below
$Y_j$
is below
![]() $Y_i$
. In other words, every chord in
$Y_i$
. In other words, every chord in
![]() $E(X_i,Y_i)$
interlaces every chord in
$E(X_i,Y_i)$
interlaces every chord in
![]() $E(X_j,Y_j)$
.
$E(X_j,Y_j)$
.
Let
![]() $I'$
(resp.,
$I'$
(resp.,
![]() $I"$
) be the set of all
$I"$
) be the set of all
![]() $i \in I_0$
with
$i \in I_0$
with
![]() $0 < e(X_i,Y_i) < 12$
(resp.,
$0 < e(X_i,Y_i) < 12$
(resp.,
![]() $e(X_i,Y_i) \geq 12$
). Suppose first that
$e(X_i,Y_i) \geq 12$
). Suppose first that
![]() $\sum _{i \in I'}{e(X_i,Y_i)} \geq |E|/4$
. Then by picking one chord from
$\sum _{i \in I'}{e(X_i,Y_i)} \geq |E|/4$
. Then by picking one chord from
![]() $E(X_i,Y_i)$
for each
$E(X_i,Y_i)$
for each
![]() $i \in I'$
, we obtain a family of pairwise-interlacing chords of size
$i \in I'$
, we obtain a family of pairwise-interlacing chords of size
![]() $\Omega (|E|)$
. Let
$\Omega (|E|)$
. Let
![]() $(x_1,y_1),\dots ,(x_{3t},y_{3t})$
be such a family with
$(x_1,y_1),\dots ,(x_{3t},y_{3t})$
be such a family with
![]() $t = \Omega (|E|)$
. By Lemma 4.4, there are paths
$t = \Omega (|E|)$
. By Lemma 4.4, there are paths
![]() $P_1,\dots ,P_{t}$
between
$P_1,\dots ,P_{t}$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2|J|$
for every
$1 \leq |P_{i+1}| - |P_i| \leq 2|J|$
for every
![]() $1 \leq i \leq t - 1$
. It is easy to see that, under these conditions, we can find indices
$1 \leq i \leq t - 1$
. It is easy to see that, under these conditions, we can find indices
![]() $1 \leq i_1 < \dots < i_k$
with
$1 \leq i_1 < \dots < i_k$
with
![]() $k = \Omega (t/|J|) = \Omega (|E|/|J|)$
such that
$k = \Omega (t/|J|) = \Omega (|E|/|J|)$
such that
![]() $|P_{i_{j+1}}| - |P_{i_j}| = \Theta (|J|)$
for every
$|P_{i_{j+1}}| - |P_{i_j}| = \Theta (|J|)$
for every
![]() $1 \leq j \leq k-1$
. Thus, the assertion of the lemma holds in this case.
$1 \leq j \leq k-1$
. Thus, the assertion of the lemma holds in this case.
Suppose now that
![]() $\sum _{i \in I"}{e(X_i,Y_i)} \geq |E|/4$
. Write
$\sum _{i \in I"}{e(X_i,Y_i)} \geq |E|/4$
. Write
![]() $I" = \{i_1,\dots ,i_t\}$
, where
$I" = \{i_1,\dots ,i_t\}$
, where
![]() $i_1 < \dots < i_t$
. If t is even, then we only consider
$i_1 < \dots < i_t$
. If t is even, then we only consider
![]() $i_1,\dots ,i_{t-1}$
, thus making sure that the number of indices in consideration is odd. Observe that
$i_1,\dots ,i_{t-1}$
, thus making sure that the number of indices in consideration is odd. Observe that
![]() $e(X_{i_t},Y_{i_t}) \leq |X_{i_t}| \leq |J|$
(since every vertex of X is incident to at most one chord), and hence
$e(X_{i_t},Y_{i_t}) \leq |X_{i_t}| \leq |J|$
(since every vertex of X is incident to at most one chord), and hence
![]() $\sum _{j=1}^{t-1}{e(X_{i_j},Y_{i_j})} \geq |E|/4 - |J| \geq |E|/8$
. So with a slight abuse of notation, we will assume from now on that t is odd and
$\sum _{j=1}^{t-1}{e(X_{i_j},Y_{i_j})} \geq |E|/4 - |J| \geq |E|/8$
. So with a slight abuse of notation, we will assume from now on that t is odd and
![]() $\sum _{j=1}^{t}{e(X_{i_j},Y_{i_j})} \geq |E|/8$
.
$\sum _{j=1}^{t}{e(X_{i_j},Y_{i_j})} \geq |E|/8$
.
Fix any
![]() $1 \leq j \leq t$
. Applying Lemma 4.6 to
$1 \leq j \leq t$
. Applying Lemma 4.6 to
![]() $X_{i_j}$
and
$X_{i_j}$
and
![]() $Y_{i_j}$
gives paths
$Y_{i_j}$
gives paths
![]() $P,P' \subseteq X_{i_j} \cup Y_{i_j}$
between
$P,P' \subseteq X_{i_j} \cup Y_{i_j}$
between
![]() $x_{i_j}^{\text {t}}$
and
$x_{i_j}^{\text {t}}$
and
![]() $y_{i_j}^{\text {t}}$
with
$y_{i_j}^{\text {t}}$
with
![]() $|P'| \geq |P| + \Omega (e(X_{i_j},Y_{i_j}))$
, as well as paths
$|P'| \geq |P| + \Omega (e(X_{i_j},Y_{i_j}))$
, as well as paths
![]() $Q,Q' \subseteq X_{i_j} \cup Y_{i_j}$
between
$Q,Q' \subseteq X_{i_j} \cup Y_{i_j}$
between
![]() $x_{i_j}^{\text {b}}$
and
$x_{i_j}^{\text {b}}$
and
![]() $y_{i_j}^{\text {b}}$
with
$y_{i_j}^{\text {b}}$
with
![]() $|Q'| \geq |Q| + \Omega (e(X_{i_j},Y_{i_j}))$
. Hence, we are in the setting of Lemma 4.5 with
$|Q'| \geq |Q| + \Omega (e(X_{i_j},Y_{i_j}))$
. Hence, we are in the setting of Lemma 4.5 with
![]() $d_j = \Omega (e(X_{i_j},Y_{i_j}))$
. Moreover,
$d_j = \Omega (e(X_{i_j},Y_{i_j}))$
. Moreover,
![]() $D := \max _{j = 1,\dots ,t}{(|X_{i_j}| + |Y_{i_j}|)} \leq 3|J|$
. By Lemma 4.5, there are paths
$D := \max _{j = 1,\dots ,t}{(|X_{i_j}| + |Y_{i_j}|)} \leq 3|J|$
. By Lemma 4.5, there are paths
![]() $P_1,\dots ,P_{(t+3)/2}$
between
$P_1,\dots ,P_{(t+3)/2}$
between
![]() $x^{\text {t}}$
and
$x^{\text {t}}$
and
![]() $y^{\text {t}}$
such that
$y^{\text {t}}$
such that
![]() $|P_{(t+3)/2}| - |P_1| \geq \sum _{j = 1}^t{d_j} = \sum _{j = 1}^t{\Omega (e(X_{i_j},Y_{i_j}))} = \Omega (|E|)$
and such that
$|P_{(t+3)/2}| - |P_1| \geq \sum _{j = 1}^t{d_j} = \sum _{j = 1}^t{\Omega (e(X_{i_j},Y_{i_j}))} = \Omega (|E|)$
and such that
![]() $1 \leq |P_{i+1}| - |P_i| \leq 2D = O(|J|)$
for every
$1 \leq |P_{i+1}| - |P_i| \leq 2D = O(|J|)$
for every
![]() $1 \leq i \leq (t+1)/2$
. Again, it is easy to see that under these conditions, we can find indices
$1 \leq i \leq (t+1)/2$
. Again, it is easy to see that under these conditions, we can find indices
![]() $1 \leq i_1 < \dots < i_k$
with
$1 \leq i_1 < \dots < i_k$
with
![]() $k = \Omega (|E|/|J|)$
such that
$k = \Omega (|E|/|J|)$
such that
![]() $|P_{i_{j+1}}| - |P_{i_j}| = \Theta (|J|)$
for every
$|P_{i_{j+1}}| - |P_{i_j}| = \Theta (|J|)$
for every
![]() $1 \leq j \leq k-1$
. So we have established the assertion of the lemma in this case as well. This completes the proof.
$1 \leq j \leq k-1$
. So we have established the assertion of the lemma in this case as well. This completes the proof.
4.2 Putting it all together
The following is the main lemma in the proof of Theorem 1.1.
Lemma 4.8. Let
![]() $X,Y$
be a section pair, and suppose that each vertex of X is incident to at most one chord. Let
$X,Y$
be a section pair, and suppose that each vertex of X is incident to at most one chord. Let
![]() $X_1,Y_1;\ldots; X_t,Y_t$
be a parallel collection of subsection pairs such that for every i, there are m chords between
$X_1,Y_1;\ldots; X_t,Y_t$
be a parallel collection of subsection pairs such that for every i, there are m chords between
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
. Provided
$Y_i$
. Provided
![]() $ t \ge \sqrt {\log m}$
, there are at least
$ t \ge \sqrt {\log m}$
, there are at least
![]() $\Omega (m/2^{4\sqrt {\log m \log \log m}})$
different lengths of paths from
$\Omega (m/2^{4\sqrt {\log m \log \log m}})$
different lengths of paths from
![]() $x^{\text {t}}$
to
$x^{\text {t}}$
to
![]() $y^{\text {t}}$
.
$y^{\text {t}}$
.
Proof. We may and will assume throughout that m is sufficiently large. Let us for convenience define
![]() $\varepsilon :=\sqrt {\frac {\log \log m}{\log m}}$
. Observe that
$\varepsilon :=\sqrt {\frac {\log \log m}{\log m}}$
. Observe that
![]() $m^{\varepsilon }=2^{\sqrt {\log m \log \log m}}$
, so our goal is to find
$m^{\varepsilon }=2^{\sqrt {\log m \log \log m}}$
, so our goal is to find
![]() $\Omega (m^{1-4\varepsilon })$
different lengths of paths from
$\Omega (m^{1-4\varepsilon })$
different lengths of paths from
![]() $x^{\text {t}}$
to
$x^{\text {t}}$
to
![]() $y^{\text {t}}$
. Let us assume towards a contradiction that there are less than
$y^{\text {t}}$
. Let us assume towards a contradiction that there are less than
![]() $\Omega (m^{1-4\varepsilon })$
different lengths of paths from
$\Omega (m^{1-4\varepsilon })$
different lengths of paths from
![]() $x^{\text {t}}$
to
$x^{\text {t}}$
to
![]() $y^{\text {t}}$
. Recall that
$y^{\text {t}}$
. Recall that
![]() $x_i^{\text {t}}$
/
$x_i^{\text {t}}$
/
![]() $x_i^{\text {b}}$
denote the top/bottom vertices of
$x_i^{\text {b}}$
denote the top/bottom vertices of
![]() $X_i$
, and similarly
$X_i$
, and similarly
![]() $y_i^{\text {t}}$
/
$y_i^{\text {t}}$
/
![]() $y_i^{\text {b}}$
denote the top/bottom vertices of
$y_i^{\text {b}}$
denote the top/bottom vertices of
![]() $Y_i$
. We will prove the following claim by induction on i.
$Y_i$
. We will prove the following claim by induction on i.
Induction statement. For a large enough constant
![]() $C>0$
and for every
$C>0$
and for every
![]() $i \le 1/\varepsilon $
, there are below-paths from
$i \le 1/\varepsilon $
, there are below-paths from
![]() $x_i^{\text {t}}$
to
$x_i^{\text {t}}$
to
![]() $y_i^{\text {t}}$
of
$y_i^{\text {t}}$
of
![]() $\frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}}$
different lengths, all of which belong to an interval of size
$\frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}}$
different lengths, all of which belong to an interval of size
![]() $m^{i\varepsilon }$
.
$m^{i\varepsilon }$
.
Before turning to the proof of this statement, let us show that it indeed implies the lemma. By choosing
![]() $i= \left \lfloor 1/\varepsilon \right \rfloor $
, we have
$i= \left \lfloor 1/\varepsilon \right \rfloor $
, we have
![]() $m^{i\varepsilon } \ge m^{1-\varepsilon }$
and
$m^{i\varepsilon } \ge m^{1-\varepsilon }$
and
So, using, e.g., that
![]() $C^2 \leq \log m$
, we get
$C^2 \leq \log m$
, we get
 $$ \begin{align*}\frac{m^{i\varepsilon}}{(C\log m)^{2(i-1)}} \geq \frac{m^{1-\varepsilon}}{(\log m)^{3i}} \geq \frac{m^{1-\varepsilon}}{(\log m)^{3/\varepsilon}} \geq m^{1-4\varepsilon}. \end{align*} $$
$$ \begin{align*}\frac{m^{i\varepsilon}}{(C\log m)^{2(i-1)}} \geq \frac{m^{1-\varepsilon}}{(\log m)^{3i}} \geq \frac{m^{1-\varepsilon}}{(\log m)^{3/\varepsilon}} \geq m^{1-4\varepsilon}. \end{align*} $$
This implies we find at least
![]() $\Omega (m^{1-4\varepsilon })$
path lengths, as desired.
$\Omega (m^{1-4\varepsilon })$
path lengths, as desired.
From now on, our goal is to prove the above induction statement. For the base case of
![]() $i=1$
, note that, since for any chord
$i=1$
, note that, since for any chord
![]() $(x,y)$
, the trivial path
$(x,y)$
, the trivial path
![]() $X[x^{\text {t}},x],(x,y),Y[y,y^{\text {t}}]$
has length exactly the length of
$X[x^{\text {t}},x],(x,y),Y[y,y^{\text {t}}]$
has length exactly the length of
![]() $(x,y)$
plus one, there can be at most
$(x,y)$
plus one, there can be at most
![]() $m^{1-4\varepsilon } \leq m^{1-\varepsilon }$
different chord lengths. Since there are m chords between
$m^{1-4\varepsilon } \leq m^{1-\varepsilon }$
different chord lengths. Since there are m chords between
![]() $X_1$
and
$X_1$
and
![]() $Y_1$
, there must exist a length which appears at least
$Y_1$
, there must exist a length which appears at least
![]() $m^{\varepsilon }$
many times. Apply Lemma 4.4 with
$m^{\varepsilon }$
many times. Apply Lemma 4.4 with
![]() $t=\lfloor m^{\varepsilon }/3 \rfloor $
to the family of chords having this length, noting that chords of the same length must be interlacing and that for such chords the parameter D in Lemma 4.4 equals
$t=\lfloor m^{\varepsilon }/3 \rfloor $
to the family of chords having this length, noting that chords of the same length must be interlacing and that for such chords the parameter D in Lemma 4.4 equals
![]() $1$
. Lemma 4.4 gives us a collection of
$1$
. Lemma 4.4 gives us a collection of
![]() $t \geq m^{\varepsilon }/6$
lengths of paths between
$t \geq m^{\varepsilon }/6$
lengths of paths between
![]() $x_1^{\text {t}}$
and
$x_1^{\text {t}}$
and
![]() $y_1^{\text {t}}$
with all consecutive differences being either
$y_1^{\text {t}}$
with all consecutive differences being either
![]() $1$
or
$1$
or
![]() $2$
apart so in total belonging into an interval of size at most
$2$
apart so in total belonging into an interval of size at most
![]() $2t+1 \leq m^{\varepsilon }$
, as desired.
$2t+1 \leq m^{\varepsilon }$
, as desired.
Let us now move on to the induction step. So assume that for some
![]() $1\le i \le 1/\varepsilon -1$
, there are below-paths going from
$1\le i \le 1/\varepsilon -1$
, there are below-paths going from
![]() $x_{i}^{\text {t}}$
to
$x_{i}^{\text {t}}$
to
![]() $y_{i}^{\text {t}}$
of
$y_{i}^{\text {t}}$
of
![]() $\frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}}$
different lengths, all of which belong to an interval of size
$\frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}}$
different lengths, all of which belong to an interval of size
![]() $m^{i\varepsilon }$
. Note that we can extend all of these paths to below-paths from
$m^{i\varepsilon }$
. Note that we can extend all of these paths to below-paths from
![]() $x_{i+1}^{\text {b}}$
to
$x_{i+1}^{\text {b}}$
to
![]() $y_{i+1}^{\text {b}}$
by using
$y_{i+1}^{\text {b}}$
by using
![]() $X[x_{i}^{\text {t}},x_{i+1}^{\text {b}}]$
and
$X[x_{i}^{\text {t}},x_{i+1}^{\text {b}}]$
and
![]() $Y[y_{i}^{\text {t}},y_{i+1}^{\text {b}}]$
and still keep the same property concerning their lengths, as each length is increased by the same number.
$Y[y_{i}^{\text {t}},y_{i+1}^{\text {b}}]$
and still keep the same property concerning their lengths, as each length is increased by the same number.
Our goal now is to find in
![]() $X_{i+1},Y_{i+1}$
top-bottom path-pairs with many (roughly
$X_{i+1},Y_{i+1}$
top-bottom path-pairs with many (roughly
![]() $m^{\varepsilon }/\text {poly}\log m$
) different lengths, among which any two consecutive ones are
$m^{\varepsilon }/\text {poly}\log m$
) different lengths, among which any two consecutive ones are
![]() $\Theta (m^{i\varepsilon })$
apart. We can use any such top-bottom path-pair to extend any of our below-paths from
$\Theta (m^{i\varepsilon })$
apart. We can use any such top-bottom path-pair to extend any of our below-paths from
![]() $x_{i+1}^{\text {b}}$
to
$x_{i+1}^{\text {b}}$
to
![]() $y_{i+1}^{\text {b}}$
into a below-path from
$y_{i+1}^{\text {b}}$
into a below-path from
![]() $x_{i+1}^{\text {t}}$
to
$x_{i+1}^{\text {t}}$
to
![]() $y_{i+1}^{\text {t}}$
with the length being the sum of the lengths of our original path and that of the top-bottom path-pair we used. Lemma 3.3 will then allow us to ‘fill in the gaps’ of size
$y_{i+1}^{\text {t}}$
with the length being the sum of the lengths of our original path and that of the top-bottom path-pair we used. Lemma 3.3 will then allow us to ‘fill in the gaps’ of size
![]() $\Theta (m^{i\varepsilon })$
between the lengths of the top-bottom path-pairs we found, by using the path lengths given by the inductive assumption. This will complete the induction step. See Figure 7 for an illustration.
$\Theta (m^{i\varepsilon })$
between the lengths of the top-bottom path-pairs we found, by using the path lengths given by the inductive assumption. This will complete the induction step. See Figure 7 for an illustration.
Let us apply Lemma 4.2 to the section pair
![]() $X_{i+1},Y_{i+1}$
to obtain a parallel collection of subsection pairs
$X_{i+1},Y_{i+1}$
to obtain a parallel collection of subsection pairs
![]() $X_1^{\prime }, Y_1^{\prime }; \ldots; X_{t'}^{\prime },Y_{t'}^{\prime }$
such that
$X_1^{\prime }, Y_1^{\prime }; \ldots; X_{t'}^{\prime },Y_{t'}^{\prime }$
such that
![]() $\sum _{j=1}^{t'} e(X_j^{\prime },Y_j^{\prime }) \ge m/24$
and either for every j we have a vertex in
$\sum _{j=1}^{t'} e(X_j^{\prime },Y_j^{\prime }) \ge m/24$
and either for every j we have a vertex in
![]() $X_j^{\prime } \cup Y_j^{\prime }$
incident to
$X_j^{\prime } \cup Y_j^{\prime }$
incident to
![]() ${e(X_j^{\prime },Y_j^{\prime })}/{(6\log m)}$
chords, or for every j there is a chord
${e(X_j^{\prime },Y_j^{\prime })}/{(6\log m)}$
chords, or for every j there is a chord
![]() $(x_j,y_j)$
in
$(x_j,y_j)$
in
![]() $E(X_j^{\prime },Y_j^{\prime })$
interlacing at least
$E(X_j^{\prime },Y_j^{\prime })$
interlacing at least
![]() ${e(X_j^{\prime },Y_j^{\prime })}/{(6\log m)}$
chords in
${e(X_j^{\prime },Y_j^{\prime })}/{(6\log m)}$
chords in
![]() $E(X_j^{\prime },Y_j^{\prime })$
. See Figures 8 and 9. In the former case, we get
$E(X_j^{\prime },Y_j^{\prime })$
. See Figures 8 and 9. In the former case, we get
![]() $\Omega (m/\log m)\ge \Omega (m^{1-4\varepsilon })$
chords, any two of which are either parallel or share a vertex, which means that all of these chords have different lengths. This in turn means that we have
$\Omega (m/\log m)\ge \Omega (m^{1-4\varepsilon })$
chords, any two of which are either parallel or share a vertex, which means that all of these chords have different lengths. This in turn means that we have
![]() $\Omega (m^{1-4\varepsilon })$
different lengths of (trivial) paths from
$\Omega (m^{1-4\varepsilon })$
different lengths of (trivial) paths from
![]() $x^{\text {t}}$
to
$x^{\text {t}}$
to
![]() $y^{\text {t}}$
, giving us a contradiction. So we may assume that we are in the latter case.
$y^{\text {t}}$
, giving us a contradiction. So we may assume that we are in the latter case.
For each j, consider all chords in
![]() $E(X_j^{\prime },Y_j^{\prime })$
which interlace
$E(X_j^{\prime },Y_j^{\prime })$
which interlace
![]() $(x_j,y_j)$
. Observe that they can be of two types: Either their X-vertex is above
$(x_j,y_j)$
. Observe that they can be of two types: Either their X-vertex is above
![]() $x_j$
and their Y-vertex is below
$x_j$
and their Y-vertex is below
![]() $y_j$
, or vice versa. Consider only the interlacing chords of the more frequent type, and define
$y_j$
, or vice versa. Consider only the interlacing chords of the more frequent type, and define
![]() $X_j^{\prime \prime },Y_j^{\prime \prime }$
to be the smallest subsections of
$X_j^{\prime \prime },Y_j^{\prime \prime }$
to be the smallest subsections of
![]() $X^{\prime }_j,Y^{\prime }_j$
which contain all these chords. In particular,
$X^{\prime }_j,Y^{\prime }_j$
which contain all these chords. In particular,
![]() $x_j \notin X_j^{\prime \prime }$
,
$x_j \notin X_j^{\prime \prime }$
,
![]() $y_j \notin Y_j^{\prime \prime }$
, and
$y_j \notin Y_j^{\prime \prime }$
, and
![]() $(X^{\prime \prime }_j,Y^{\prime \prime }_j)$
is interlaced by
$(X^{\prime \prime }_j,Y^{\prime \prime }_j)$
is interlaced by
![]() $(x_j,y_j)$
as a section pair. Moreover, we still have
$(x_j,y_j)$
as a section pair. Moreover, we still have
![]() $\sum _{j=1}^{t'} e(X_j^{\prime \prime },Y_j^{\prime \prime }) \ge \Omega (m/\log m)$
chords altogether. Consider the intervals of the form
$\sum _{j=1}^{t'} e(X_j^{\prime \prime },Y_j^{\prime \prime }) \ge \Omega (m/\log m)$
chords altogether. Consider the intervals of the form
![]() $[k,2k]$
with k a power of
$[k,2k]$
with k a power of
![]() $2$
and
$2$
and
![]() $k \leq m/2$
. Each
$k \leq m/2$
. Each
![]() $e(X_j^{\prime \prime },Y_j^{\prime \prime })$
belongs to such an interval, of which there are
$e(X_j^{\prime \prime },Y_j^{\prime \prime })$
belongs to such an interval, of which there are
![]() $O(\log m)$
. So by averaging, there exists
$O(\log m)$
. So by averaging, there exists
![]() $1 \le k \le m/2$
and a subset
$1 \le k \le m/2$
and a subset
![]() $S \subseteq [t']$
such that for any
$S \subseteq [t']$
such that for any
![]() $j \in S$
we have
$j \in S$
we have
![]() $e(X_j^{\prime \prime },Y_j^{\prime \prime }) \in [k,2k]$
, and
$e(X_j^{\prime \prime },Y_j^{\prime \prime }) \in [k,2k]$
, and
![]() $\sum _{j \in S} e(X_j^{\prime \prime },Y_j^{\prime \prime }) \ge \Omega (m/\log ^2 m)$
. Furthermore, by deleting
$\sum _{j \in S} e(X_j^{\prime \prime },Y_j^{\prime \prime }) \ge \Omega (m/\log ^2 m)$
. Furthermore, by deleting
![]() $e(X_j^{\prime \prime },Y_j^{\prime \prime }) - k \leq \frac {1}{2}e(X_j^{\prime \prime },Y_j^{\prime \prime })$
chords from each pair
$e(X_j^{\prime \prime },Y_j^{\prime \prime }) - k \leq \frac {1}{2}e(X_j^{\prime \prime },Y_j^{\prime \prime })$
chords from each pair
![]() $X^{\prime \prime }_j,Y^{\prime \prime }_j$
with
$X^{\prime \prime }_j,Y^{\prime \prime }_j$
with
![]() $j \in S$
(so in total at most a half of all such chords), we may assume for convenience that
$j \in S$
(so in total at most a half of all such chords), we may assume for convenience that
![]() $e(X_j^{\prime \prime },Y_j^{\prime \prime })=k$
for all
$e(X_j^{\prime \prime },Y_j^{\prime \prime })=k$
for all
![]() $j \in S$
. Observe in particular that
$j \in S$
. Observe in particular that
We now construct a collection of top-bottom path-pairs for
![]() $X_j^{\prime },Y_j^{\prime }$
for each
$X_j^{\prime },Y_j^{\prime }$
for each
![]() $j \in S$
. Depending on which of the two types above was more frequent, we have two essentially symmetric cases. In the first one,
$j \in S$
. Depending on which of the two types above was more frequent, we have two essentially symmetric cases. In the first one,
![]() $X_j^{\prime \prime }$
is above
$X_j^{\prime \prime }$
is above
![]() $x_j$
and
$x_j$
and
![]() $Y_j^{\prime \prime }$
is below
$Y_j^{\prime \prime }$
is below
![]() $y_j$
. Here, we will take our path pairs to all contain the path which goes along
$y_j$
. Here, we will take our path pairs to all contain the path which goes along
![]() $X_j^{\prime }$
from the bottom to
$X_j^{\prime }$
from the bottom to
![]() $x_j$
, uses the chord
$x_j$
, uses the chord
![]() $(x_j,y_j)$
and then goes along
$(x_j,y_j)$
and then goes along
![]() $Y^{\prime }_j$
from
$Y^{\prime }_j$
from
![]() $y_j$
to the top of
$y_j$
to the top of
![]() $Y_j^{\prime }$
. The second path in each pair is going to follow
$Y_j^{\prime }$
. The second path in each pair is going to follow
![]() $X_j^{\prime }$
from the top until the top of
$X_j^{\prime }$
from the top until the top of
![]() $X_j^{\prime \prime }$
, then follow a path inside
$X_j^{\prime \prime }$
, then follow a path inside
![]() $X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
from the top of
$X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
from the top of
![]() $X_j^{\prime \prime }$
to the bottom of
$X_j^{\prime \prime }$
to the bottom of
![]() $Y_j^{\prime \prime }$
, and then follow along
$Y_j^{\prime \prime }$
, and then follow along
![]() $Y_j^{\prime }$
to its bottom. Symmetrically, in the second case, our path pairs will all use the path through
$Y_j^{\prime }$
to its bottom. Symmetrically, in the second case, our path pairs will all use the path through
![]() $(x_j,y_j)$
from the top of
$(x_j,y_j)$
from the top of
![]() $X_j^{\prime }$
to the bottom of
$X_j^{\prime }$
to the bottom of
![]() $Y_j^{\prime }$
, with the other path (from the bottom of
$Y_j^{\prime }$
, with the other path (from the bottom of
![]() $X_j^{\prime }$
to the top of
$X_j^{\prime }$
to the top of
![]() $Y_j^{\prime }$
) passing through
$Y_j^{\prime }$
) passing through
![]() $X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
. See Figure 10 for these two symmetric cases. Since the argument is analogous in both cases, from now on, let us assume we are in the first case.
$X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
. See Figure 10 for these two symmetric cases. Since the argument is analogous in both cases, from now on, let us assume we are in the first case.
Observe that if we find a collection of path lengths inside
![]() $X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
going from the top of
$X_j^{\prime \prime } \cup Y_j^{\prime \prime }$
going from the top of
![]() $X_j^{\prime \prime }$
to the bottom of
$X_j^{\prime \prime }$
to the bottom of
![]() $Y_j^{\prime \prime }$
, then we have the same collection of lengths of top-bottom path-pairs for
$Y_j^{\prime \prime }$
, then we have the same collection of lengths of top-bottom path-pairs for
![]() $X_j^{\prime },Y_j^{\prime }$
up to a possible translation by a fixed constant. This is because the top-bottom path-pairs we consider only differ in which path they use between the top of
$X_j^{\prime },Y_j^{\prime }$
up to a possible translation by a fixed constant. This is because the top-bottom path-pairs we consider only differ in which path they use between the top of
![]() $X_j^{\prime \prime }$
and the bottom of
$X_j^{\prime \prime }$
and the bottom of
![]() $Y_j^{\prime \prime }$
.
$Y_j^{\prime \prime }$
.
It will be convenient to consider the ‘flipped’ section pair
![]() $X_j^{\prime \prime},\bar {Y_j^{\prime \prime }}$
, which we obtain by reversing the path
$X_j^{\prime \prime},\bar {Y_j^{\prime \prime }}$
, which we obtain by reversing the path
![]() $Y_j^{\prime \prime }$
(and denote it as
$Y_j^{\prime \prime }$
(and denote it as
![]() $\bar {Y_j^{\prime \prime }}$
). In particular, the top of
$\bar {Y_j^{\prime \prime }}$
). In particular, the top of
![]() $\bar {Y_j^{\prime \prime }}$
is the bottom of
$\bar {Y_j^{\prime \prime }}$
is the bottom of
![]() $Y_j^{\prime \prime }$
and any top-to-top path in
$Y_j^{\prime \prime }$
and any top-to-top path in
![]() $X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
is just a path between the top of
$X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
is just a path between the top of
![]() $X_j^{\prime \prime }$
and the bottom of
$X_j^{\prime \prime }$
and the bottom of
![]() $Y_j^{\prime \prime }$
.
$Y_j^{\prime \prime }$
.
Claim 1. For each
![]() $j \in S$
, one of the following holds.
$j \in S$
, one of the following holds.
-
1. There are at least
 $2k^{1-(i+1)\varepsilon }$
lengths, any two at least
$2k^{1-(i+1)\varepsilon }$
lengths, any two at least
 $k^{i\varepsilon }$
apart, of top-to-top paths in
$k^{i\varepsilon }$
apart, of top-to-top paths in
 $X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
.
$X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
. -
2. There is an interval
 $I_j \subseteq \mathbb {N}$
of size
$I_j \subseteq \mathbb {N}$
of size
 $k^{i\varepsilon }$
such that the length with respect to
$k^{i\varepsilon }$
such that the length with respect to
 $X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
of at least
$X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
of at least
 $k^{(i+1)\varepsilon }/4$
chords belongs to
$k^{(i+1)\varepsilon }/4$
chords belongs to
 $I_j$
.
$I_j$
.
Proof. All our chord lengths in this proof will be with respect to
![]() $X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
. Take a minimal collection of disjoint intervals of size
$X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
. Take a minimal collection of disjoint intervals of size
![]() $k^{i\varepsilon }$
each, which cover all chord lengths (i.e., the length with respect to
$k^{i\varepsilon }$
each, which cover all chord lengths (i.e., the length with respect to
![]() $X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
of every chord in
$X_j^{\prime \prime },\bar {Y_j^{\prime \prime }}$
of every chord in
![]() $E(X_j^{\prime \prime },\bar {Y_j^{\prime \prime }})$
belongs to one of these intervals). For each such interval I, either I can be taken as the desired
$E(X_j^{\prime \prime },\bar {Y_j^{\prime \prime }})$
belongs to one of these intervals). For each such interval I, either I can be taken as the desired
![]() $I_j$
, or there must be less than
$I_j$
, or there must be less than
![]() $k^{(i+1)\varepsilon }/4$
chords with length in I. As there are k chords in
$k^{(i+1)\varepsilon }/4$
chords with length in I. As there are k chords in
![]() $E(X_j^{\prime \prime },\bar {Y_j^{\prime \prime }})$
, this means that we needed to use at least
$E(X_j^{\prime \prime },\bar {Y_j^{\prime \prime }})$
, this means that we needed to use at least
![]() $4k^{1-(i+1)\varepsilon }$
intervals to cover all chord lengths. Since we took a minimal collection, each interval is nonempty. By picking one length from every second interval, we find
$4k^{1-(i+1)\varepsilon }$
intervals to cover all chord lengths. Since we took a minimal collection, each interval is nonempty. By picking one length from every second interval, we find
![]() $2k^{1-(i+1)\varepsilon }$
chord lengths, any two separated by one of our intervals (since we took a length from every second interval). Hence, any two such lengths are at least
$2k^{1-(i+1)\varepsilon }$
chord lengths, any two separated by one of our intervals (since we took a length from every second interval). Hence, any two such lengths are at least
![]() $k^{i\varepsilon }$
apart. For each such length, take a chord of this length and take the trivial path between the top of
$k^{i\varepsilon }$
apart. For each such length, take a chord of this length and take the trivial path between the top of
![]() $X^{\prime \prime }_j$
and the top of
$X^{\prime \prime }_j$
and the top of
![]() $\bar {Y_j^{\prime \prime }}$
corresponding to this chord. This gives the
$\bar {Y_j^{\prime \prime }}$
corresponding to this chord. This gives the
![]() $2k^{1-(i+1)\varepsilon }$
path lengths required by item 1.
$2k^{1-(i+1)\varepsilon }$
path lengths required by item 1.
Let
![]() $S_1$
be the subset of S consisting of j for which case
$S_1$
be the subset of S consisting of j for which case
![]() $1$
of the above claim occurred. Let us first assume this was the more common case, namely that
$1$
of the above claim occurred. Let us first assume this was the more common case, namely that
![]() $|S_1|\ge |S|/2$
.
$|S_1|\ge |S|/2$
.
Claim 2. If
![]() $|S_1|\ge |S|/2$
, then there are
$|S_1|\ge |S|/2$
, then there are
![]() $\Omega (m^{1-(i+1)\varepsilon }/\log ^2 m)$
lengths of top-bottom path-pairs for
$\Omega (m^{1-(i+1)\varepsilon }/\log ^2 m)$
lengths of top-bottom path-pairs for
![]() $X_{i+1},Y_{i+1}$
which are all at least
$X_{i+1},Y_{i+1}$
which are all at least
![]() $m^{i\varepsilon}$
apart.
$m^{i\varepsilon}$
apart.
Proof. For each
![]() $j \in S_1$
, consider the
$j \in S_1$
, consider the
![]() $2k^{1-(i+1)\varepsilon }$
top-to-top paths for
$2k^{1-(i+1)\varepsilon }$
top-to-top paths for
![]() $X^{\prime \prime }_j,\bar {Y_j^{\prime \prime }}$
given by item 1 of Claim 1. Each of these paths is a path from the top of
$X^{\prime \prime }_j,\bar {Y_j^{\prime \prime }}$
given by item 1 of Claim 1. Each of these paths is a path from the top of
![]() $X_j^{\prime \prime }$
to the bottom of
$X_j^{\prime \prime }$
to the bottom of
![]() $Y_j^{\prime \prime }$
. Hence, as explained above, this gives rise to top-bottom path-pairs for
$Y_j^{\prime \prime }$
. Hence, as explained above, this gives rise to top-bottom path-pairs for
![]() $X_j^{\prime },Y_j^{\prime }$
with at least
$X_j^{\prime },Y_j^{\prime }$
with at least
![]() $2k^{1-(i+1)\varepsilon }\ge 2$
(recall that
$2k^{1-(i+1)\varepsilon }\ge 2$
(recall that
![]() $i \le 1/\varepsilon -1$
) lengths, any two of which are at least
$i \le 1/\varepsilon -1$
) lengths, any two of which are at least
![]() $k^{i\varepsilon }$
apart. Denote the set of these lengths by
$k^{i\varepsilon }$
apart. Denote the set of these lengths by
![]() $L_j$
. Now observe that by choosing a path-pair for
$L_j$
. Now observe that by choosing a path-pair for
![]() $X^{\prime }_j,Y^{\prime }_j$
of length
$X^{\prime }_j,Y^{\prime }_j$
of length
![]() $\ell _{j}\in L_j$
for each
$\ell _{j}\in L_j$
for each
![]() $j \in S_1$
and joining these paths with subpaths of
$j \in S_1$
and joining these paths with subpaths of
![]() $X,Y$
, we obtain a top-bottom path-pair for
$X,Y$
, we obtain a top-bottom path-pair for
![]() $X_{i+1},Y_{i+1}$
of length
$X_{i+1},Y_{i+1}$
of length
![]() $\sum _{j \in S_1} \ell _{j}+C_0$
, where
$\sum _{j \in S_1} \ell _{j}+C_0$
, where
![]() $C_0$
is the sum of the lengths of the subpaths we used to join our top-bottom path-pairs into a top-bottom path-pair for
$C_0$
is the sum of the lengths of the subpaths we used to join our top-bottom path-pairs into a top-bottom path-pair for
![]() $X_{i+1},Y_{i+1}$
; so
$X_{i+1},Y_{i+1}$
; so
![]() $C_0$
is independent of our choices for
$C_0$
is independent of our choices for
![]() $\ell _j$
. Lemma 3.2 now tells us that we can find
$\ell _j$
. Lemma 3.2 now tells us that we can find
![]() $|S_1|k^{1-(i+1)\varepsilon }$
lengths of top-bottom path-pairs for
$|S_1|k^{1-(i+1)\varepsilon }$
lengths of top-bottom path-pairs for
![]() $X_{i+1},Y_{i+1}$
which are at least
$X_{i+1},Y_{i+1}$
which are at least
![]() $k^{i\varepsilon }$
apart. By taking every
$k^{i\varepsilon }$
apart. By taking every
![]() $m^{i\varepsilon }/k^{i\varepsilon }$
-th such length, we get at least
$m^{i\varepsilon }/k^{i\varepsilon }$
-th such length, we get at least
 $\lfloor |S_1|k^{1-(i+1)\varepsilon }/(m^{i\varepsilon }/k^{i\varepsilon }) \rfloor \geq \frac 12 |S_1|k^{1-\varepsilon }/m^{i\varepsilon }\ge \frac 14 |S|k^{1-\varepsilon }/m^{i\varepsilon } \ge \frac 1{4} |S|k/m^{(i+1)\varepsilon } \ge \Omega (m^{1-(i+1)\varepsilon }/\log ^2 m)$
lengths which are at least
$\lfloor |S_1|k^{1-(i+1)\varepsilon }/(m^{i\varepsilon }/k^{i\varepsilon }) \rfloor \geq \frac 12 |S_1|k^{1-\varepsilon }/m^{i\varepsilon }\ge \frac 14 |S|k^{1-\varepsilon }/m^{i\varepsilon } \ge \frac 1{4} |S|k/m^{(i+1)\varepsilon } \ge \Omega (m^{1-(i+1)\varepsilon }/\log ^2 m)$
lengths which are at least
![]() $m^{i\varepsilon }$
apart, where the last inequality uses (4.3). This proves the claim.
$m^{i\varepsilon }$
apart, where the last inequality uses (4.3). This proves the claim.
Let us now use Claim 2 to complete the proof in the case that
![]() $|S_1| \geq |S|/2$
. Observe that we may combine our top-bottom path-pairs for
$|S_1| \geq |S|/2$
. Observe that we may combine our top-bottom path-pairs for
![]() $X_{i+1},Y_{i+1}$
(provided by Claim 2) with top-to-top below-paths from
$X_{i+1},Y_{i+1}$
(provided by Claim 2) with top-to-top below-paths from
![]() $x_i^{\text {t}}$
to
$x_i^{\text {t}}$
to
![]() $y_i^{\text {t}}$
, provided by the inductive assumption, to obtain below-paths from
$y_i^{\text {t}}$
, provided by the inductive assumption, to obtain below-paths from
![]() $x_{i+1}^{\text {t}}$
to
$x_{i+1}^{\text {t}}$
to
![]() $y_{i+1}^{\text {t}}$
, which can then be extended along
$y_{i+1}^{\text {t}}$
, which can then be extended along
![]() $X,Y$
into top-to-top paths for
$X,Y$
into top-to-top paths for
![]() $X,Y$
. Each such path length is of the form
$X,Y$
. Each such path length is of the form
![]() $\ell _1+\ell _2+C_0$
, where
$\ell _1+\ell _2+C_0$
, where
![]() $\ell _1$
may be chosen among our
$\ell _1$
may be chosen among our
![]() $\Omega (m^{1-(i+1)\varepsilon }/\log ^2m)$
lengths of top-bottom path-pairs for
$\Omega (m^{1-(i+1)\varepsilon }/\log ^2m)$
lengths of top-bottom path-pairs for
![]() $X_{i+1},Y_{i+1}$
, which are at least
$X_{i+1},Y_{i+1}$
, which are at least
![]() $m^{i\varepsilon }$
apart;
$m^{i\varepsilon }$
apart;
![]() $\ell _2$
may be chosen among
$\ell _2$
may be chosen among
![]() $\Omega (m^{i\varepsilon }/(C\log m)^{(2i-2)})$
lengths which belong in an interval of size
$\Omega (m^{i\varepsilon }/(C\log m)^{(2i-2)})$
lengths which belong in an interval of size
![]() $m^{i\varepsilon }$
(as guaranteed by the induction hypothesis), and
$m^{i\varepsilon }$
(as guaranteed by the induction hypothesis), and
![]() $C_0$
is independent of the choice of
$C_0$
is independent of the choice of
![]() $\ell _1,\ell _2$
. Therefore, by Lemma 3.3 we get at least
$\ell _1,\ell _2$
. Therefore, by Lemma 3.3 we get at least
![]() $\Omega (m^{1-\varepsilon }/(C\log m)^{2i}) \ge \Omega (m^{1-4\varepsilon })$
(see equation (4.2)) different lengths of top-to-top paths for
$\Omega (m^{1-\varepsilon }/(C\log m)^{2i}) \ge \Omega (m^{1-4\varepsilon })$
(see equation (4.2)) different lengths of top-to-top paths for
![]() $X,Y$
, contradicting our assumption that the number of such lengths is smaller than
$X,Y$
, contradicting our assumption that the number of such lengths is smaller than
![]() $\Omega (m^{1-4\varepsilon })$
. This completes the proof in the case
$\Omega (m^{1-4\varepsilon })$
. This completes the proof in the case
![]() $|S_1| \geq |S|/2$
.
$|S_1| \geq |S|/2$
.
So we must have the second case in Claim 1 occurring more often, namely that
![]() $S_2:=S \setminus S_1$
has size at least
$S_2:=S \setminus S_1$
has size at least
![]() $|S|/2$
. By definition, for any
$|S|/2$
. By definition, for any
![]() $j \in S_2$
there is an interval
$j \in S_2$
there is an interval
![]() $I_j$
of size
$I_j$
of size
![]() $k^{i\varepsilon }$
such that at least
$k^{i\varepsilon }$
such that at least
![]() $k^{(i+1)\varepsilon }/4$
chords in
$k^{(i+1)\varepsilon }/4$
chords in
![]() $E(X^{\prime \prime }_i,\bar {Y_{j}^{\prime \prime }})$
have their length with respect to the subsection pair
$E(X^{\prime \prime }_i,\bar {Y_{j}^{\prime \prime }})$
have their length with respect to the subsection pair
![]() $X_{j}^{\prime \prime }, \bar {Y_{j}^{\prime \prime }}$
belong in
$X_{j}^{\prime \prime }, \bar {Y_{j}^{\prime \prime }}$
belong in
![]() $I_j$
. Applying Lemma 4.7 (with
$I_j$
. Applying Lemma 4.7 (with
![]() $J = I_j$
), we find
$J = I_j$
), we find
![]() $\Omega (k^{\varepsilon })$
top-to-top paths in
$\Omega (k^{\varepsilon })$
top-to-top paths in
![]() $X_{j}^{\prime \prime }, \bar {Y_{j}^{\prime \prime }}$
whose lengths are
$X_{j}^{\prime \prime }, \bar {Y_{j}^{\prime \prime }}$
whose lengths are
![]() $\Theta (k^{i\varepsilon })$
apart. As before, this gives us top-bottom path-pairs for
$\Theta (k^{i\varepsilon })$
apart. As before, this gives us top-bottom path-pairs for
![]() $X_{j}^{\prime },Y_j^{\prime }$
of lengths which are
$X_{j}^{\prime },Y_j^{\prime }$
of lengths which are
![]() $\Theta (k^{i\varepsilon })$
apart. Once again, we can choose one such length for each
$\Theta (k^{i\varepsilon })$
apart. Once again, we can choose one such length for each
![]() $X_j^{\prime },Y_j^{\prime }$
and combine the corresponding top-bottom path-pairs into a top-bottom path-pair for
$X_j^{\prime },Y_j^{\prime }$
and combine the corresponding top-bottom path-pairs into a top-bottom path-pair for
![]() $X_{i+1},Y_{i+1}$
, with the resulting length being the sum of the lengths of the top-bottom path-pairs we chose plus a fixed number (which is independent of our choices). Lemma 3.2 then tells us that we can find top-bottom path-pairs for
$X_{i+1},Y_{i+1}$
, with the resulting length being the sum of the lengths of the top-bottom path-pairs we chose plus a fixed number (which is independent of our choices). Lemma 3.2 then tells us that we can find top-bottom path-pairs for
![]() $X_{i+1},Y_{i+1}$
of
$X_{i+1},Y_{i+1}$
of
![]() $\Omega (|S_2|k^{\varepsilon })\ge \Omega (|S|k^{\varepsilon })$
lengths which are
$\Omega (|S_2|k^{\varepsilon })\ge \Omega (|S|k^{\varepsilon })$
lengths which are
![]() $\Theta (k^{i \varepsilon })$
apart, say between
$\Theta (k^{i \varepsilon })$
apart, say between
![]() $c_1 k^{i \varepsilon }$
and
$c_1 k^{i \varepsilon }$
and
![]() $c_2 k^{i \varepsilon }$
. Once again, we only consider every
$c_2 k^{i \varepsilon }$
. Once again, we only consider every
![]() $m^{i\varepsilon }/c_1k^{i\varepsilon }$
-th length, thus guaranteeing that every two such lengths are at least
$m^{i\varepsilon }/c_1k^{i\varepsilon }$
-th length, thus guaranteeing that every two such lengths are at least
![]() $m^{i\varepsilon }$
and at most
$m^{i\varepsilon }$
and at most
![]() $\frac {c_2}{c_1}m^{i\varepsilon } = O(m^{i\varepsilon })$
apart. The number of these lengths is at least
$\frac {c_2}{c_1}m^{i\varepsilon } = O(m^{i\varepsilon })$
apart. The number of these lengths is at least
![]() $c_1k^{i\varepsilon }/m^{i\varepsilon }\cdot \Omega (|S|k^{\varepsilon })\ge \Omega (k^{(i+1)\varepsilon -1} m^{1-i\varepsilon }/\log ^2 m)\ge \Omega (m^{\varepsilon }/\log ^2 m)$
, with the first inequality using equation (4.3). Take the first
$c_1k^{i\varepsilon }/m^{i\varepsilon }\cdot \Omega (|S|k^{\varepsilon })\ge \Omega (k^{(i+1)\varepsilon -1} m^{1-i\varepsilon }/\log ^2 m)\ge \Omega (m^{\varepsilon }/\log ^2 m)$
, with the first inequality using equation (4.3). Take the first
![]() $\Theta (m^{\varepsilon }/\log ^2 m)$
of them. Since these lengths are at most
$\Theta (m^{\varepsilon }/\log ^2 m)$
of them. Since these lengths are at most
![]() $O(m^{i\varepsilon })$
apart, they are all contained in an interval of size
$O(m^{i\varepsilon })$
apart, they are all contained in an interval of size
![]() $O(m^{(i+1)\varepsilon })$
. Now similarly as in the previous case, we can combine any of these top-bottom path-pairs with our below paths from
$O(m^{(i+1)\varepsilon })$
. Now similarly as in the previous case, we can combine any of these top-bottom path-pairs with our below paths from
![]() $x_i^{\text {t}}$
to
$x_i^{\text {t}}$
to
![]() $y_i^{\text {t}}$
, which are provided by the induction hypothesis. Lemma 3.3 ensures that, by doing so, we get at least
$y_i^{\text {t}}$
, which are provided by the induction hypothesis. Lemma 3.3 ensures that, by doing so, we get at least
![]() $\Omega (m^{\varepsilon }/\log ^2 m) \cdot \frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}} = \Omega \left (\frac {m^{(i+1)\varepsilon }}{C^{2i-2}(\log m)^{2i}}\right )$
lengths which all belong to an interval of size
$\Omega (m^{\varepsilon }/\log ^2 m) \cdot \frac {m^{i\varepsilon }}{6(C\log m)^{2(i-1)}} = \Omega \left (\frac {m^{(i+1)\varepsilon }}{C^{2i-2}(\log m)^{2i}}\right )$
lengths which all belong to an interval of size
![]() $O(m^{(i+1)\varepsilon })$
. By potentially losing a constant proportion of the lengths, we can guarantee they all lie in an interval of size at most
$O(m^{(i+1)\varepsilon })$
. By potentially losing a constant proportion of the lengths, we can guarantee they all lie in an interval of size at most
![]() $m^{(i+1)\varepsilon }$
, and by choosing C to be large enough, we will have at least
$m^{(i+1)\varepsilon }$
, and by choosing C to be large enough, we will have at least
![]() $\frac {m^{(i+1)\varepsilon }}{(C\log m)^{2i}}$
of them, completing the induction step and hence the proof.
$\frac {m^{(i+1)\varepsilon }}{(C\log m)^{2i}}$
of them, completing the induction step and hence the proof.
We are now in a position to prove Theorem 1.1, which we rephrase in the following quantitative form:
Theorem 4.9. Every n-vertex Hamiltonian graph with minimum degree
![]() $3$
has cycle spectrum of size at least
$3$
has cycle spectrum of size at least
![]() $\Omega \Big ({n}/{2^{6\sqrt {\log n \log \log n}}}\Big ).$
$\Omega \Big ({n}/{2^{6\sqrt {\log n \log \log n}}}\Big ).$
Proof. Let us fix a Hamilton cycle H in our graph and a direction for this cycle. We define the length of a chord
![]() $\{x,y\}$
to be the length of the shorter of the two paths along the cycle between x and y; in particular, the length is always at most
$\{x,y\}$
to be the length of the shorter of the two paths along the cycle between x and y; in particular, the length is always at most
![]() $n/2$
. For every vertex v, we fix a single chord
$n/2$
. For every vertex v, we fix a single chord
![]() $c(v)$
incident to v. By the pigeonhole principle, there must exist an
$c(v)$
incident to v. By the pigeonhole principle, there must exist an
![]() $\ell \le n/4$
such that at least
$\ell \le n/4$
such that at least
![]() $n/\log n$
vertices have the length of their chosen chord in
$n/\log n$
vertices have the length of their chosen chord in
![]() $[\ell ,2\ell ]$
. Now let us partition H into consecutive sections
$[\ell ,2\ell ]$
. Now let us partition H into consecutive sections
![]() $B_1,\ldots , B_s,R$
(appearing in this order along H), where
$B_1,\ldots , B_s,R$
(appearing in this order along H), where
![]() $|B_s|=4\ell $
and
$|B_s|=4\ell $
and
![]() $s= \left \lfloor \frac {n}{4\ell } \right \rfloor \ge 1$
, and the starting vertex for
$s= \left \lfloor \frac {n}{4\ell } \right \rfloor \ge 1$
, and the starting vertex for
![]() $B_1$
is chosen uniformly at random among the vertices of the cycle. We will talk of the first half of
$B_1$
is chosen uniformly at random among the vertices of the cycle. We will talk of the first half of
![]() $B_j$
(which is just the set of the first
$B_j$
(which is just the set of the first
![]() $2\ell $
vertices of
$2\ell $
vertices of
![]() $B_j$
), the first quarter of
$B_j$
), the first quarter of
![]() $B_j$
(the set of the first
$B_j$
(the set of the first
![]() $\ell $
vertices), etc.
$\ell $
vertices), etc.
A vertex v is said to be good if
![]() $c(v)$
is contained in some
$c(v)$
is contained in some
![]() $B_j$
and if the two endpoints of
$B_j$
and if the two endpoints of
![]() $c(v)$
belong to different halves of
$c(v)$
belong to different halves of
![]() $B_j$
. We claim that the probability that a given v with
$B_j$
. We claim that the probability that a given v with
![]() $c(v) \in [\ell ,2\ell ]$
is good is at least
$c(v) \in [\ell ,2\ell ]$
is good is at least
![]() $\frac {1}{8}$
. To see this, write
$\frac {1}{8}$
. To see this, write
![]() $c(v) = \{v,w\}$
, and consider the shorter path (along the cycle) between v and w; recall that the length of
$c(v) = \{v,w\}$
, and consider the shorter path (along the cycle) between v and w; recall that the length of
![]() $c(v)$
is defined as the length of this path. There are two cases: If when walking on this path from v to w, we walk in the direction of the cycle (which was fixed at the beginning), then v is guaranteed to be good if it belongs to the second quarter of some
$c(v)$
is defined as the length of this path. There are two cases: If when walking on this path from v to w, we walk in the direction of the cycle (which was fixed at the beginning), then v is guaranteed to be good if it belongs to the second quarter of some
![]() $B_j$
. Otherwise, i.e., if we walk against the direction of the cycle, then v is guaranteed to be good if it belongs to the third quarter of some
$B_j$
. Otherwise, i.e., if we walk against the direction of the cycle, then v is guaranteed to be good if it belongs to the third quarter of some
![]() $B_j$
. In any case, the probability that v is good is at least
$B_j$
. In any case, the probability that v is good is at least
![]() $\frac {1}{4} \cdot \frac {|B_1| + \ldots + |B_s|}{n}$
. Since
$\frac {1}{4} \cdot \frac {|B_1| + \ldots + |B_s|}{n}$
. Since
![]() $|B_1| + \ldots + |B_s| \geq n/2$
, this probability is at least
$|B_1| + \ldots + |B_s| \geq n/2$
, this probability is at least
![]() $\frac {1}{8}$
, as claimed. By linearity of expectation, the expected number of good vertices is at least
$\frac {1}{8}$
, as claimed. By linearity of expectation, the expected number of good vertices is at least
![]() $\frac {n}{8 \log n}$
. Let us now fix an outcome
$\frac {n}{8 \log n}$
. Let us now fix an outcome
![]() $B_1,\ldots , B_s,R$
for which we have at least this many good vertices. Let I be the set of
$B_1,\ldots , B_s,R$
for which we have at least this many good vertices. Let I be the set of
![]() $i \in [s]$
such that
$i \in [s]$
such that
![]() $B_i$
contains at least
$B_i$
contains at least
![]() $\frac {\ell }{4\log n}$
good vertices. Observe that the sections
$\frac {\ell }{4\log n}$
good vertices. Observe that the sections
![]() $B_i$
,
$B_i$
,
![]() $i \notin I$
, contribute in total at most
$i \notin I$
, contribute in total at most
![]() $s\cdot \frac {\ell }{4\log n} \le \frac {n}{16\log n}$
to the overall number of good vertices. Therefore, at least
$s\cdot \frac {\ell }{4\log n} \le \frac {n}{16\log n}$
to the overall number of good vertices. Therefore, at least
![]() $\frac {n}{16 \log n}$
good vertices belong to sections
$\frac {n}{16 \log n}$
good vertices belong to sections
![]() $B_i$
with
$B_i$
with
![]() $i \in I$
. In particular,
$i \in I$
. In particular,
![]() $|I| \geq \frac {n}{64 \ell \log n}$
since each
$|I| \geq \frac {n}{64 \ell \log n}$
since each
![]() $B_i$
has
$B_i$
has
![]() $4\ell $
vertices.
$4\ell $
vertices.
For each
![]() $i \in I$
, we will later find inside
$i \in I$
, we will later find inside
![]() $B_i$
paths of at least
$B_i$
paths of at least
![]() $1+ \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
different lengths joining the endpoints of
$1+ \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
different lengths joining the endpoints of
![]() $B_i$
. Let us first complete the proof using this. To do so, choose for each
$B_i$
. Let us first complete the proof using this. To do so, choose for each
![]() $i \in I$
, one of these paths joining the endpoints of
$i \in I$
, one of these paths joining the endpoints of
![]() $B_i$
, and combine these paths into a cycle using H. The length of the resulting cycle is equal to the sum of the lengths of the paths we chose plus a fixed number, independent of our choices (i.e., the total length of the pieces of H we used to join the paths). So by Lemma 3.2, these cycles take at least
$B_i$
, and combine these paths into a cycle using H. The length of the resulting cycle is equal to the sum of the lengths of the paths we chose plus a fixed number, independent of our choices (i.e., the total length of the pieces of H we used to join the paths). So by Lemma 3.2, these cycles take at least
![]() $\Omega \left (\frac {n}{ \ell \log n}\cdot {\ell }/{2^{5\sqrt {\log n \log \log n}}}\right ) \ge \Omega \left ({n}/{2^{6\sqrt {\log n \log \log n}}}\right )$
different lengths, as desired.
$\Omega \left (\frac {n}{ \ell \log n}\cdot {\ell }/{2^{5\sqrt {\log n \log \log n}}}\right ) \ge \Omega \left ({n}/{2^{6\sqrt {\log n \log \log n}}}\right )$
different lengths, as desired.
What remains to be proved is that, for
![]() $i \in I$
,
$i \in I$
,
![]() $B_i$
contains paths of
$B_i$
contains paths of
![]() $1+ \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
different lengths joining its endpoints. By definition,
$1+ \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
different lengths joining its endpoints. By definition,
![]() $B_i$
has at least
$B_i$
has at least
![]() $\frac {\ell }{4\log n}$
good vertices. Since
$\frac {\ell }{4\log n}$
good vertices. Since
![]() $B_i$
contains at least one chord, we know it has at least two path lengths (one coming from the length of
$B_i$
contains at least one chord, we know it has at least two path lengths (one coming from the length of
![]() $B_i$
itself and the other from the path only using a single chord). In particular, we may assume that
$B_i$
itself and the other from the path only using a single chord). In particular, we may assume that
![]() $\ell \gg 2^{5\sqrt {\log n \log \log n}}$
or we are done. Let X denote the first half of
$\ell \gg 2^{5\sqrt {\log n \log \log n}}$
or we are done. Let X denote the first half of
![]() $B_i$
and Y its second half. We think of
$B_i$
and Y its second half. We think of
![]() $X,Y$
as a section pair (omitting the middle edge of
$X,Y$
as a section pair (omitting the middle edge of
![]() $B_i$
) and consider the endpoints of
$B_i$
) and consider the endpoints of
![]() $B_i$
to be the top vertices of X and Y. By definition, every chord
$B_i$
to be the top vertices of X and Y. By definition, every chord
![]() $c(v)$
which corresponds to a good vertex v has one endpoint in X and one in Y. Let us assume without loss of generality that X contains at least half (so at least
$c(v)$
which corresponds to a good vertex v has one endpoint in X and one in Y. Let us assume without loss of generality that X contains at least half (so at least
![]() $\frac {\ell }{8\log n}$
) of all good vertices in
$\frac {\ell }{8\log n}$
) of all good vertices in
![]() $B_i$
. Delete any chord which was not chosen by one of the good vertices in X. This way, we make sure that every vertex in X is incident to at most one chord. Also, at least
$B_i$
. Delete any chord which was not chosen by one of the good vertices in X. This way, we make sure that every vertex in X is incident to at most one chord. Also, at least
![]() $\frac {\ell }{8\log n}$
chords remain.
$\frac {\ell }{8\log n}$
chords remain.
Let us now apply Lemma 4.1 to this section pair
![]() $X,Y$
with parameter
$X,Y$
with parameter
![]() $m=\frac {\ell }{8\log n}$
and
$m=\frac {\ell }{8\log n}$
and
![]() $k=\sqrt {\log n}$
and thus obtain either a vertex
$k=\sqrt {\log n}$
and thus obtain either a vertex
![]() $v \in Y$
incident to at least
$v \in Y$
incident to at least
![]() $\Omega \left ({\ell }/{\log ^2 n}\right )$
chords or an interlacing or parallel collection of k subsection pairs
$\Omega \left ({\ell }/{\log ^2 n}\right )$
chords or an interlacing or parallel collection of k subsection pairs
![]() $X_1,Y_1;\ldots; X_k,Y_k$
, each containing at least
$X_1,Y_1;\ldots; X_k,Y_k$
, each containing at least
![]() $\Omega \left ({\ell }/{\log ^3 n}\right )$
chords.
$\Omega \left ({\ell }/{\log ^3 n}\right )$
chords.
Suppose first that there is a vertex
![]() $v \in Y$
incident to at least
$v \in Y$
incident to at least
![]() $\Omega \left ({\ell }/{\log ^2 n}\right )$
chords
$\Omega \left ({\ell }/{\log ^2 n}\right )$
chords
![]() $(v,x)$
,
$(v,x)$
,
![]() $x \in X$
. Observe that all these chords have different lengths. Now, for each such chord, consider the path between the endpoints of
$x \in X$
. Observe that all these chords have different lengths. Now, for each such chord, consider the path between the endpoints of
![]() $B_i$
, which uses only this chord and no others. These are paths of
$B_i$
, which uses only this chord and no others. These are paths of
![]() $\Omega \left ({\ell }/{\log ^2 n}\right )$
different lengths between the endpoints of
$\Omega \left ({\ell }/{\log ^2 n}\right )$
different lengths between the endpoints of
![]() $B_i$
, as required.
$B_i$
, as required.
Suppose now that we are in the second case, namely that there exists an interlacing or parallel collection
![]() $X_1,Y_1;\ldots; X_k,Y_k$
of subsection pairs with
$X_1,Y_1;\ldots; X_k,Y_k$
of subsection pairs with
![]() $e(X_i,Y_i) \geq \Omega \left ({\ell }/{\log ^3 n}\right )$
for each
$e(X_i,Y_i) \geq \Omega \left ({\ell }/{\log ^3 n}\right )$
for each
![]() $i = 1,\dots ,k$
. If these subsection pairs are parallel, then we may immediately apply Lemma 4.8 with
$i = 1,\dots ,k$
. If these subsection pairs are parallel, then we may immediately apply Lemma 4.8 with
![]() $t=k$
and
$t=k$
and
![]() $m=\Omega ({\ell }/{\log ^3 n})$
to get the desired number
$m=\Omega ({\ell }/{\log ^3 n})$
to get the desired number
![]() $\Omega \big ( \frac {\ell }{\log ^3n}/2^{4\sqrt {\log n \log \log n}} \big ) \geq \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
of different path lengths between the endpoints of
$\Omega \big ( \frac {\ell }{\log ^3n}/2^{4\sqrt {\log n \log \log n}} \big ) \geq \Omega (\ell /2^{5\sqrt {\log n \log \log n}})$
of different path lengths between the endpoints of
![]() $B_i$
. In the case that
$B_i$
. In the case that
![]() $X_1,Y_1;\ldots; X_k,Y_k$
are interlacing, we need an extra step, as follows. Suppose without loss of generality that
$X_1,Y_1;\ldots; X_k,Y_k$
are interlacing, we need an extra step, as follows. Suppose without loss of generality that
![]() $X_i$
is below
$X_i$
is below
![]() $X_j$
(and hence
$X_j$
(and hence
![]() $Y_i$
is above
$Y_i$
is above
![]() $Y_j$
) for each
$Y_j$
) for each
![]() $1 \leq i < j \leq k$
. Take
$1 \leq i < j \leq k$
. Take
![]() $(x_1,y_1) \in E(X_1,Y_1)$
and
$(x_1,y_1) \in E(X_1,Y_1)$
and
![]() $(x_2,y_2) \in E(X_2,Y_2)$
. Let us now ‘reroute’
$(x_2,y_2) \in E(X_2,Y_2)$
. Let us now ‘reroute’
![]() $B_i$
along the interlacing chords
$B_i$
along the interlacing chords
![]() $(x_1,y_1)$
,
$(x_1,y_1)$
,
![]() $(x_2,y_2)$
; in other words, we consider a new path
$(x_2,y_2)$
; in other words, we consider a new path
![]() $B_i^{\prime }$
, obtained by following X from the top until
$B_i^{\prime }$
, obtained by following X from the top until
![]() $x_2$
, jumping along
$x_2$
, jumping along
![]() $(x_2,y_2)$
, following
$(x_2,y_2)$
, following
![]() $B_i$
(now in the other direction) until
$B_i$
(now in the other direction) until
![]() $x_1$
, jumping along
$x_1$
, jumping along
![]() $(x_1,y_1)$
and finally following Y until its top. See Figure 11 for a picture. Note that
$(x_1,y_1)$
and finally following Y until its top. See Figure 11 for a picture. Note that
![]() $B_i^{\prime }$
splits into the section pair
$B_i^{\prime }$
splits into the section pair
![]() $X' := X[x^{\text {t}},x_2]$
,
$X' := X[x^{\text {t}},x_2]$
,
![]() $Y' := B_i[y_2,x_1],(x_1,y_1),Y[y_1,y^{\text {t}}]$
, with
$Y' := B_i[y_2,x_1],(x_1,y_1),Y[y_1,y^{\text {t}}]$
, with
![]() $X'$
having the same top as X and
$X'$
having the same top as X and
![]() $Y'$
the same top as Y. Observe that
$Y'$
the same top as Y. Observe that
![]() $X_k,\ldots , X_3$
still appear in this order along
$X_k,\ldots , X_3$
still appear in this order along
![]() $X'$
, but, crucially,
$X'$
, but, crucially,
![]() $Y_3,\dots ,Y_k$
now appear in the reverse order; see Figure 12. In other words, the subsection pairs
$Y_3,\dots ,Y_k$
now appear in the reverse order; see Figure 12. In other words, the subsection pairs
![]() $X_3,Y_3;\ldots; X_k,Y_k$
are parallel in
$X_3,Y_3;\ldots; X_k,Y_k$
are parallel in
![]() $X',Y'$
. So we may now apply Lemma 4.8 with
$X',Y'$
. So we may now apply Lemma 4.8 with
![]() $t=k-2$
and
$t=k-2$
and
![]() $m=\Omega ({\ell }/{\log ^3 n})$
to get the desired number of different path lengths between the endpoints of
$m=\Omega ({\ell }/{\log ^3 n})$
to get the desired number of different path lengths between the endpoints of
![]() $B_i$
. This completes the proof.
$B_i$
. This completes the proof.

Figure 11 Rerouting through a path
![]() $B^{\prime }_i$
marked in red.
$B^{\prime }_i$
marked in red.

Figure 12 Rerouted path
![]() $B^{\prime }_i$
with new relative positions of the section pairs.
$B^{\prime }_i$
with new relative positions of the section pairs.
5 Concluding remarks
In this paper, we proved that an n-vertex Hamiltonian graph of minimum degree
![]() $3$
has cycles of
$3$
has cycles of
![]() $n^{1-o(1)}$
different lengths, which shows that Conjecture 1.1 holds asymptotically. Moreover, for the original question of Jacobson and Lehel (dealing with graphs of bounded degree), we can use our ideas to get a better quantitative bound of
$n^{1-o(1)}$
different lengths, which shows that Conjecture 1.1 holds asymptotically. Moreover, for the original question of Jacobson and Lehel (dealing with graphs of bounded degree), we can use our ideas to get a better quantitative bound of
![]() $\frac {n}{\text {polylog}(n)}$
. Still, it would be very interesting to prove a linear bound on the number of cycles, even in the
$\frac {n}{\text {polylog}(n)}$
. Still, it would be very interesting to prove a linear bound on the number of cycles, even in the
![]() $3$
-regular case. Towards this, we propose the following natural intermediate steps:
$3$
-regular case. Towards this, we propose the following natural intermediate steps:
Conjecture 5.1. In an n-vertex Hamiltonian graph with minimum degree
![]() $3$
, there are:
$3$
, there are:
-
1.
 $\Omega (\sqrt {n})$
cycle lengths all belonging to an interval of size
$\Omega (\sqrt {n})$
cycle lengths all belonging to an interval of size
 $O(\sqrt {n})$
.
$O(\sqrt {n})$
. -
2.
 $\Omega (\sqrt {n})$
cycle lengths any two of which are at least
$\Omega (\sqrt {n})$
cycle lengths any two of which are at least
 $\Omega (\sqrt {n})$
apart.
$\Omega (\sqrt {n})$
apart.
Observe first that Conjecture 1.1 immediately implies Conjecture 5.1. On the other hand, a slight strengthening of Conjecture 5.1 already implies Conjecture 1.1. Indeed, suppose that in Conjecture 5.1, we replace the assumption of minimum degree
![]() $3$
with the assumption that linearly many vertices have degree at least
$3$
with the assumption that linearly many vertices have degree at least
![]() $3$
. Furthermore, suppose that instead of starting with a Hamilton cycle we start with a Hamilton path, and instead of cycle lengths we consider path lengths of paths going between the endpoints of the given Hamilton path. Then by splitting our Hamilton cycle (or a ‘rerouted’ cycle) into two paths (similarly to what is done in the proof of Theorem 4.9), we can apply this strengthened version of Conjecture 5.1 and obtain linearly many cycle lengths (see Section 2 for some details).
$3$
. Furthermore, suppose that instead of starting with a Hamilton cycle we start with a Hamilton path, and instead of cycle lengths we consider path lengths of paths going between the endpoints of the given Hamilton path. Then by splitting our Hamilton cycle (or a ‘rerouted’ cycle) into two paths (similarly to what is done in the proof of Theorem 4.9), we can apply this strengthened version of Conjecture 5.1 and obtain linearly many cycle lengths (see Section 2 for some details).
We note that ideas similar to the general approach described above, namely of controlling the large- and small-scale behavior separately in a way which allows us to combine the gains, have been very useful in a number of situations. This idea has been used in additive combinatorics for a long time; see, for example, Lemma 1 in a 1964 paper of Graham [Reference Graham16] and a more recent example of its use by Conlon, Fox and Pham in the context of subset sums, to settle a number of conjectures in the area [Reference Conlon, Fox and Pham7]. Another example is the recent remarkable work of Liu and Montgomery [Reference Liu and Montgomery19], resolving the Erdős-Hajnal odd cycle problem. In that paper, in order to find a path of some specific length
![]() $\ell $
between two given vertices, the authors first find a path of length somewhat close to
$\ell $
between two given vertices, the authors first find a path of length somewhat close to
![]() $\ell $
, and then ‘fill in the gap’ by repeatedly changing the path length by
$\ell $
, and then ‘fill in the gap’ by repeatedly changing the path length by
![]() $2$
, using certain gadgets (see Lemma 4.8 in [Reference Liu and Montgomery19]).
$2$
, using certain gadgets (see Lemma 4.8 in [Reference Liu and Montgomery19]).
Finally, let us also discuss the following related question, which was already mentioned in passing in the introduction. What is the minimum C such that every n-vertex Hamiltonian graph with minimum degree
![]() $3$
contains a second cycle of length at least
$3$
contains a second cycle of length at least
![]() $n - C$
? Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] show that
$n - C$
? Girão, Kittipassorn and Narayanan [Reference Girão, Kittipassorn and Narayanan14] show that
![]() $C = O(n^{4/5}) = o(n)$
, and conjecture that actually
$C = O(n^{4/5}) = o(n)$
, and conjecture that actually
![]() $C = O(1)$
. It is also interesting to ask whether the answer changes if we want in addition to have
$C = O(1)$
. It is also interesting to ask whether the answer changes if we want in addition to have
![]() $C>0$
(i.e., if we forbid this second cycle from being a Hamilton cycle). Such a result might be useful to completely settle the conjecture of Jacobson and Lehel.
$C>0$
(i.e., if we forbid this second cycle from being a Hamilton cycle). Such a result might be useful to completely settle the conjecture of Jacobson and Lehel.
Acknowledgements
We are grateful to the anonymous referees for their careful reading of the paper and several suggestions which improved the presentation.
Funding statement
Research supported in part by a grant from the SNSF(200021_196965) and by a grant from NSF (CCF-1900460).
Conflicts of Interest
None.