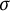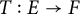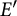1 Introduction
In [Reference Grothendieck16], Grothendieck introduced the notion of Dunford–Pettis operator between Banach spaces, which took a very important place in the mathematical literature, and several of its properties have been studied. In the case of Banach lattices, many authors focus on the various interrelationships between Dunford–Pettis and other types of operators (see, for instance, [Reference Aliprantis and Burkinshaw1, Reference Aqzzouz, Nouira and Zraoula4, Reference Aqzzouz, Nouira and Zraoula5, Reference Aqzzouz, Nouira and Zraoula6, Reference Chen, Chen and Ji10, Reference Dodds and Fremlin11, Reference Kalton and Saab17, Reference Wickstead20]). Next, a number of related notions have been studied in the literature.
In this context, in [Reference El Kaddouri, H’michane, Bouras and Moussa13], the authors introduced the class of weak* Dunford–Pettis operators and, in [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12], they studied Banach lattices on which all positive weak* Dunford–Pettis operators are weakly compact (resp. M-weakly compact and order weakly compact). Indeed, they gave a characterization of pair Banach lattices
![]() $(E,F)$
such that every positive weak* Dunford–Pettis operator
$(E,F)$
such that every positive weak* Dunford–Pettis operator
![]() $T:E\rightarrow F$
is weakly compact (resp. M-weakly compact and order weakly compact) when F has an order continuous norm (resp. F is Dedekind
$T:E\rightarrow F$
is weakly compact (resp. M-weakly compact and order weakly compact) when F has an order continuous norm (resp. F is Dedekind
![]() $\sigma $
-complete) (see [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.2, 2.4, and 2.5]). Also, they gave an example to prove that the condition “F has an order continuous norm” (resp. “F is Dedekind
$\sigma $
-complete) (see [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.2, 2.4, and 2.5]). Also, they gave an example to prove that the condition “F has an order continuous norm” (resp. “F is Dedekind
![]() $\sigma $
-complete”), that they added, is not an accessory.
$\sigma $
-complete”), that they added, is not an accessory.
The aim of this work is to continue this study and shed more light on it. In fact, we give necessary conditions on pair of Banach lattices
![]() $(E,F)$
such that every positive weak* Dunford–Pettis operator
$(E,F)$
such that every positive weak* Dunford–Pettis operator
![]() $T:E\rightarrow F$
is weakly compact (resp. M-weakly compact and order weakly compact) without any assumption on F (Propositions 2.2 and 2.3 and Theorem 3.2), and we characterize Banach lattices
$T:E\rightarrow F$
is weakly compact (resp. M-weakly compact and order weakly compact) without any assumption on F (Propositions 2.2 and 2.3 and Theorem 3.2), and we characterize Banach lattices
![]() $E,F$
such that every positive weak* Dunford–Pettis operator
$E,F$
such that every positive weak* Dunford–Pettis operator
![]() $T:E\rightarrow F$
is weakly compact when F is Dedekind
$T:E\rightarrow F$
is weakly compact when F is Dedekind
![]() $\sigma $
-complete (Theorem 3.3). Moreover, we present a more general class of Banach lattices for which Theorems 2.4 and 2.5 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] fail to be true if F is not Dedekind
$\sigma $
-complete (Theorem 3.3). Moreover, we present a more general class of Banach lattices for which Theorems 2.4 and 2.5 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] fail to be true if F is not Dedekind
![]() $\sigma $
-complete (Theorems 2.6 and 2.7). Also, we get, along the way, other interesting consequences. Finally, we characterize Banach lattice E and Banach space Y such that every weak* Dunford–Pettis operator
$\sigma $
-complete (Theorems 2.6 and 2.7). Also, we get, along the way, other interesting consequences. Finally, we characterize Banach lattice E and Banach space Y such that every weak* Dunford–Pettis operator
![]() $T:E\rightarrow Y$
(resp.
$T:E\rightarrow Y$
(resp.
![]() $T:Y\rightarrow E$
) is almost M-weakly (resp. L-weakly) compact (Theorem 4.1 (resp. Theorem 4.2)).
$T:Y\rightarrow E$
) is almost M-weakly (resp. L-weakly) compact (Theorem 4.1 (resp. Theorem 4.2)).
To state our results, we need to fix some notations and recall some definitions. A vector lattice E is an ordered vector space in which
![]() $\sup (x,y)$
exists for every
$\sup (x,y)$
exists for every
![]() $x,y \in E$
, and it is Dedekind
$x,y \in E$
, and it is Dedekind
![]() $\sigma $
-complete if every majorized countable nonempty subset of E has a supremum.
$\sigma $
-complete if every majorized countable nonempty subset of E has a supremum.
A Banach lattice is a Banach space
![]() $(E,\left \Vert .\right \Vert )$
such that E is a vector lattice and its norm satisfies the following property: for each
$(E,\left \Vert .\right \Vert )$
such that E is a vector lattice and its norm satisfies the following property: for each
![]() $x,y\in E$
such that
$x,y\in E$
such that
![]() $\left \vert x\right \vert \leq \left \vert y\right \vert $
, we have
$\left \vert x\right \vert \leq \left \vert y\right \vert $
, we have
![]() $\left \Vert x\right \Vert \leq \left \Vert y\right \Vert $
. This norm is said to be order-continuous if for each generalized sequence
$\left \Vert x\right \Vert \leq \left \Vert y\right \Vert $
. This norm is said to be order-continuous if for each generalized sequence
![]() $(x_{\alpha })$
such that
$(x_{\alpha })$
such that
![]() $ x_{\alpha }\downarrow 0$
in E, the sequence
$ x_{\alpha }\downarrow 0$
in E, the sequence
![]() $(x_{\alpha })$
converges to
$(x_{\alpha })$
converges to
![]() $0 $
for the norm,
$0 $
for the norm,
![]() $\left \Vert .\right \Vert $
, where the notation
$\left \Vert .\right \Vert $
, where the notation
![]() $x_{\alpha }\downarrow 0$
means that the sequence
$x_{\alpha }\downarrow 0$
means that the sequence
![]() $(x_{\alpha })$
is decreasing, its infimum exists, and
$(x_{\alpha })$
is decreasing, its infimum exists, and
![]() $\inf (x_{\alpha })=0$
. Recall that if E is a Banach lattice, its topological dual
$\inf (x_{\alpha })=0$
. Recall that if E is a Banach lattice, its topological dual
![]() $E^{\prime }$
, endowed with the dual norm, is also a Banach lattice.
$E^{\prime }$
, endowed with the dual norm, is also a Banach lattice.
We will use the term operator between two Banach lattices to mean a bounded linear mapping. Recall that an operator
![]() $T : E \longrightarrow F$
between two ordered vector spaces is said to be positive (in symbol
$T : E \longrightarrow F$
between two ordered vector spaces is said to be positive (in symbol
![]() $0 \leq T$
) if
$0 \leq T$
) if
![]() $T(x) \geq 0$
for all
$T(x) \geq 0$
for all
![]() $x \geq 0$
, and that the relation between two operators
$x \geq 0$
, and that the relation between two operators
![]() $S,T:E\longrightarrow F$
defined by
$S,T:E\longrightarrow F$
defined by
![]() $S\leq T$
whenever
$S\leq T$
whenever
![]() $0\leq T-S$
defines an order relation on the space of operators from E to F.
$0\leq T-S$
defines an order relation on the space of operators from E to F.
An operator T from a Banach space X into a Banach space Y is called weak* Dunford–Pettis if
![]() $f_{n}(T(x_{n}))\rightarrow 0$
whenever
$f_{n}(T(x_{n}))\rightarrow 0$
whenever
![]() $x_{n}\rightarrow 0$
for
$x_{n}\rightarrow 0$
for
![]() $\sigma (X,X^{\prime })$
in X and
$\sigma (X,X^{\prime })$
in X and
![]() $f_{n}\rightarrow 0$
for
$f_{n}\rightarrow 0$
for
![]() $\sigma (Y^{\prime },Y)$
in Y. A weak* Dunford–Pettis operator is not necessary weakly compact, and conversely, a weakly compact operator is not necessary weak* Dunford–Pettis. In fact, the identity operator of the Banach lattice
$\sigma (Y^{\prime },Y)$
in Y. A weak* Dunford–Pettis operator is not necessary weakly compact, and conversely, a weakly compact operator is not necessary weak* Dunford–Pettis. In fact, the identity operator of the Banach lattice
![]() $l^{2}$
is weakly compact, but it is not weak* Dunford–Pettis, and the identity operator of the Banach lattice
$l^{2}$
is weakly compact, but it is not weak* Dunford–Pettis, and the identity operator of the Banach lattice
![]() $l^{1}$
is weak* Dunford–Pettis, but it is not weakly compact. In general, for a Banach space X, the identity operator of X is weak* Dunford–Pettis if and only if X has the DP* property [Reference El Kaddouri, H’michane, Bouras and Moussa13, Corollary 3.3]. Recall that, from [Reference Borwein, Fabian and Vanderwerff7], a Banach space X has the Dunford–Pettis* property (DP*) if
$l^{1}$
is weak* Dunford–Pettis, but it is not weakly compact. In general, for a Banach space X, the identity operator of X is weak* Dunford–Pettis if and only if X has the DP* property [Reference El Kaddouri, H’michane, Bouras and Moussa13, Corollary 3.3]. Recall that, from [Reference Borwein, Fabian and Vanderwerff7], a Banach space X has the Dunford–Pettis* property (DP*) if
![]() $f_n(x_n)\rightarrow 0$
for every weakly null sequence
$f_n(x_n)\rightarrow 0$
for every weakly null sequence
![]() $(x_n) \in X$
and every weak* null sequence
$(x_n) \in X$
and every weak* null sequence
![]() $(f_n) \in X'$
. Note that, according to [Reference Borwein, Fabian and Vanderwerff7, Remark 3.2],
$(f_n) \in X'$
. Note that, according to [Reference Borwein, Fabian and Vanderwerff7, Remark 3.2],
![]() $\ell ^1$
and
$\ell ^1$
and
![]() $\ell ^\infty $
have the Dunford–Pettis* property.
$\ell ^\infty $
have the Dunford–Pettis* property.
If E is a Banach lattice and Y is a Banach space, an operator
![]() $T:E\rightarrow Y$
is said to be M-weakly compact if for every disjoint sequence
$T:E\rightarrow Y$
is said to be M-weakly compact if for every disjoint sequence
![]() $(x_{n})$
in the closed unit ball
$(x_{n})$
in the closed unit ball
![]() $B_{E}$
of E, we have
$B_{E}$
of E, we have
![]() $\left \Vert T(x_{n})\right \Vert \rightarrow 0$
. Also,
$\left \Vert T(x_{n})\right \Vert \rightarrow 0$
. Also,
![]() $T:E\rightarrow Y$
is said to be order weakly compact if it carries order bounded intervals of E to relatively weakly compact sets in Y; equivalently, for every disjoint order bounded sequence
$T:E\rightarrow Y$
is said to be order weakly compact if it carries order bounded intervals of E to relatively weakly compact sets in Y; equivalently, for every disjoint order bounded sequence
![]() $(x_n)$
in E, we have
$(x_n)$
in E, we have
![]() $\left \Vert T(x_{n})\right \Vert \rightarrow 0$
.
$\left \Vert T(x_{n})\right \Vert \rightarrow 0$
.
There exist weak* Dunford–Pettis operators that are not M-weakly compact. In fact, the identity operator
![]() $I_{l^{\infty }}:l^{\infty } \rightarrow l^{\infty }$
is weak* Dunford–Pettis, but it is not M-weakly compact.
$I_{l^{\infty }}:l^{\infty } \rightarrow l^{\infty }$
is weak* Dunford–Pettis, but it is not M-weakly compact.
We refer to [Reference Aliprantis and Burkinshaw2] for unexplained terminology on Banach lattice theory and operators.
2 M-weak and order weak compactness of positive weak* Dunford–Pettis operators
If E and F are Banach lattices, we denote by
![]() $\mathcal {P}_1$
the following property:
$\mathcal {P}_1$
the following property:
![]() $\mathcal {P}_1$
: every positive weak* Dunford–Pettis operator from E to F is M-weakly compact (resp. order weakly compact).
$\mathcal {P}_1$
: every positive weak* Dunford–Pettis operator from E to F is M-weakly compact (resp. order weakly compact).
In their paper [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and 2.5], the authors proved that if F is Dedekind
![]() $\sigma $
-complete, then E and F satisfy property
$\sigma $
-complete, then E and F satisfy property
![]() $\mathcal {P}_1$
if and only if one of the following is valid:
$\mathcal {P}_1$
if and only if one of the following is valid:
-
(a) The norms of
 $E'$
and F are order-continuous (resp. the norm of E is order-continuous).
$E'$
and F are order-continuous (resp. the norm of E is order-continuous). -
(b) E is finite-dimensional (resp. the norm of F is order-continuous).
And, in order to justify that the condition “F is Dedekind
![]() $\sigma $
-complete” is not necessary, they mentioned that it suffices to take
$\sigma $
-complete” is not necessary, they mentioned that it suffices to take
![]() $E=l^{\infty }$
and
$E=l^{\infty }$
and
![]() $F=c$
; every positive operator
$F=c$
; every positive operator
![]() $T:l^{\infty }\rightarrow c$
is M-weakly compact (and hence order weakly compact); however, neither of the two conditions (a) and (b) are satisfied.
$T:l^{\infty }\rightarrow c$
is M-weakly compact (and hence order weakly compact); however, neither of the two conditions (a) and (b) are satisfied.
The objective of this section is to shed more light on what happens in the case when F is not Dedekind
![]() $\sigma $
-complete. Indeed, we will give necessary (and not sufficient) conditions on Banach lattices to verify the property
$\sigma $
-complete. Indeed, we will give necessary (and not sufficient) conditions on Banach lattices to verify the property
![]() $\mathcal {P}_1$
. Also, we give a more general example of Banach lattices E and F for which any positive weak* Dunford–Pettis operator from E to F is M-weakly compact (and hence order weakly compact), without any of the conditions (a) and (b) being verified. This prove that, in the general case, the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and 2.5], which are sufficient, fail to be necessary for a large class of pair Banach lattices, not only for the pair
$\mathcal {P}_1$
. Also, we give a more general example of Banach lattices E and F for which any positive weak* Dunford–Pettis operator from E to F is M-weakly compact (and hence order weakly compact), without any of the conditions (a) and (b) being verified. This prove that, in the general case, the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and 2.5], which are sufficient, fail to be necessary for a large class of pair Banach lattices, not only for the pair
![]() $(\ell ^\infty , c)$
.
$(\ell ^\infty , c)$
.
First, we begin with a useful lemma.
Lemma 2.1 Let
![]() $X,Y,Z$
be Banach spaces, T an operator from X to Y, and S an operator from Y to Z.
$X,Y,Z$
be Banach spaces, T an operator from X to Y, and S an operator from Y to Z.
-
(1) If T or S is weak* Dunford–Pettis, then
 $S\circ T$
is weak* Dunford–Pettis.
$S\circ T$
is weak* Dunford–Pettis. -
(2) If X or Y has the DP* property, then T is weak* Dunford–Pettis.
-
(3) If X or Y or Z has the DP* property, then
 $S\circ T$
is weak* Dunford–Pettis.
$S\circ T$
is weak* Dunford–Pettis.
Proof
-
(1) Let
 $(x_n)$
and
$(x_n)$
and
 $(f_n)$
be two sequences in X and
$(f_n)$
be two sequences in X and
 $Z'$
, respectively, such that
$Z'$
, respectively, such that
 $x_n\overset {\sigma (X,X')}{\longrightarrow } 0$
and
$x_n\overset {\sigma (X,X')}{\longrightarrow } 0$
and
 $f_n\overset {\sigma (Z',Z)}{\longrightarrow } 0$
. Remark that
$f_n\overset {\sigma (Z',Z)}{\longrightarrow } 0$
. Remark that
 $Tx_n\overset {\sigma (Y,Y')}{\longrightarrow } 0$
and
$Tx_n\overset {\sigma (Y,Y')}{\longrightarrow } 0$
and
 $f_n \circ S\overset {\sigma (Y',Y)}{\longrightarrow } 0$
. Hence,
$f_n \circ S\overset {\sigma (Y',Y)}{\longrightarrow } 0$
. Hence,-
• if T is weak* Dunford–Pettis, then
 $(f_n \circ S)\circ T(x_n)\longrightarrow 0$
.
$(f_n \circ S)\circ T(x_n)\longrightarrow 0$
. -
• if S is weak* Dunford–Pettis, then
 $f_n \circ S ( T(x_n))\longrightarrow 0$
.
$f_n \circ S ( T(x_n))\longrightarrow 0$
.
In both cases, we have
 $f_n \circ (S\circ T)(x_n)\longrightarrow 0$
, so
$f_n \circ (S\circ T)(x_n)\longrightarrow 0$
, so
 $S\circ T$
is weak* Dunford–Pettis.
$S\circ T$
is weak* Dunford–Pettis. -
-
(2) It is a consequence of the first property of the current Lemma 2.1 and [Reference El Kaddouri, H’michane, Bouras and Moussa13, Corollary 3.3] since
 $T=id_Y\circ T=T\circ id_X $
.
$T=id_Y\circ T=T\circ id_X $
. -
(3) It is a direct consequence of (1) and (2).
Now, remark that, from the proofs of Theorems 2.4 and 2.5 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12], we can deduce, without any assumption on F, the following two propositions. For the sake of completeness, we present their proofs.
Proposition 2.2 Let E and F be two Banach lattices. If every positive weak* Dunford–Pettis operator
![]() $T : E \rightarrow F$
is M-weakly compact, then one of the following is valid:
$T : E \rightarrow F$
is M-weakly compact, then one of the following is valid:
-
(a) The norm of
 $E'$
is order-continuous.
$E'$
is order-continuous. -
(b)
 $F=\{0\}$
.
$F=\{0\}$
.
Proof Assume that the norm of
![]() $E'$
is not order-continuous and
$E'$
is not order-continuous and
![]() $F\neq \{0\}$
and consider
$F\neq \{0\}$
and consider
![]() $0 < y \in F^+$
. It follows from [Reference Meyer-Nieberg18, Theorem 2.4.14 and Proposition 2.3.11] the existence of a sublattice of E isomorphic to
$0 < y \in F^+$
. It follows from [Reference Meyer-Nieberg18, Theorem 2.4.14 and Proposition 2.3.11] the existence of a sublattice of E isomorphic to
![]() $\ell ^1$
, and hence also a positive projection
$\ell ^1$
, and hence also a positive projection
![]() $P : E \rightarrow \ell ^1$
. Consider the positive operator S defined by
$P : E \rightarrow \ell ^1$
. Consider the positive operator S defined by
 $$ \begin{align*}\begin{array}{llll} S :& \ell^1& \rightarrow &F \\ & (\lambda_n)_n & \mapsto &= (\sum\limits_{n=1}^{+\infty}\lambda_n)y \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{llll} S :& \ell^1& \rightarrow &F \\ & (\lambda_n)_n & \mapsto &= (\sum\limits_{n=1}^{+\infty}\lambda_n)y \end{array}\end{align*} $$
and put
![]() $T= S\circ P$
. According to Lemma 2.1, T is a positive weak* Dunford–Pettis (because
$T= S\circ P$
. According to Lemma 2.1, T is a positive weak* Dunford–Pettis (because
![]() $ \ell ^1$
has DP*property). However, T is not M-weakly compact. Indeed, if
$ \ell ^1$
has DP*property). However, T is not M-weakly compact. Indeed, if
![]() $(e_n)_n$
is the canonical basis of
$(e_n)_n$
is the canonical basis of
![]() $\ell ^1$
, then that
$\ell ^1$
, then that
![]() $T(e_n)=y \nrightarrow 0$
.
$T(e_n)=y \nrightarrow 0$
.
Note that it is clear that the condition (b) of Proposition 2.2 is sufficient, but the condition (a) is not. Indeed, it suffices to take E such that the norm of
![]() $E'$
is order-continuous, and F Dedekind
$E'$
is order-continuous, and F Dedekind
![]() $\sigma $
-complete with nonorder-continuous norm, and apply [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.4].
$\sigma $
-complete with nonorder-continuous norm, and apply [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.4].
Recall that, from [Reference Aliprantis and Burkinshaw2, p. 222], a Banach lattice E is said to be lattice embeddable into another Banach lattice F, whenever there exist a lattice homomorphism
![]() $T : E \rightarrow F$
and two positive constants
$T : E \rightarrow F$
and two positive constants
![]() $m,M$
satisfying
$m,M$
satisfying
T is called a lattice embedding from E into F. In this case,
![]() $T(E)$
is a closed sublattice of F which can be identified with E.
$T(E)$
is a closed sublattice of F which can be identified with E.
Proposition 2.3 Let
![]() $E,F$
be two Banach lattices. If every positive weak* Dunford–Pettis operator
$E,F$
be two Banach lattices. If every positive weak* Dunford–Pettis operator
![]() $T : E \rightarrow F$
is order-weakly compact, then one of the following is valid:
$T : E \rightarrow F$
is order-weakly compact, then one of the following is valid:
-
(a) The norm of E is order-continuous.
-
(b)
 $\ell ^\infty $
is not lattice embeddable in F.
$\ell ^\infty $
is not lattice embeddable in F.
Proof Assume that the norm of E is not order-continuous, and that there exists a lattice embedding
![]() $S : \ell ^\infty \rightarrow F$
from
$S : \ell ^\infty \rightarrow F$
from
![]() $\ell ^\infty $
to F. It follows from [Reference Aliprantis and Burkinshaw2, Theorem 4.14] that there exist
$\ell ^\infty $
to F. It follows from [Reference Aliprantis and Burkinshaw2, Theorem 4.14] that there exist
![]() $y \in E^+$
and a disjoint sequence
$y \in E^+$
and a disjoint sequence
![]() $(x_n)\in [0, y]$
which does not converge to zero in norm. We may assume that
$(x_n)\in [0, y]$
which does not converge to zero in norm. We may assume that
![]() $\Vert x_n\Vert = 1$
for all
$\Vert x_n\Vert = 1$
for all
![]() $n\in \mathbb {N}^*$
. Hence, by [Reference Aqzzouz, Elbour and H’michane3, Lemma 3.4], there exists a positive disjoint sequence
$n\in \mathbb {N}^*$
. Hence, by [Reference Aqzzouz, Elbour and H’michane3, Lemma 3.4], there exists a positive disjoint sequence
![]() $(g_n)$
of
$(g_n)$
of
![]() $E^+$
with
$E^+$
with
![]() $\Vert g_n\Vert = 1$
such that
$\Vert g_n\Vert = 1$
such that
![]() $g_n(x_m) =1$
if
$g_n(x_m) =1$
if
![]() $n = m$
and
$n = m$
and
![]() $g_n(x_m) =0$
if
$g_n(x_m) =0$
if
![]() $n \neq m$
for every
$n \neq m$
for every
![]() $m,n\in \mathbb {N}^*$
. We define the positive operator P as follows:
$m,n\in \mathbb {N}^*$
. We define the positive operator P as follows:
and put
![]() $T = S\circ P $
. Since
$T = S\circ P $
. Since
![]() $ \ell ^\infty $
has DP* property, according to Lemma 2.1, T is a positive weak* Dunford–Pettis. However, it is not order weakly compact, because
$ \ell ^\infty $
has DP* property, according to Lemma 2.1, T is a positive weak* Dunford–Pettis. However, it is not order weakly compact, because
![]() $(x_n)$
is an order bounded disjoint sequence in E, but
$(x_n)$
is an order bounded disjoint sequence in E, but
![]() $\Vert T(x_n)\Vert \nrightarrow 0$
.
$\Vert T(x_n)\Vert \nrightarrow 0$
.
Remark 2.4 It is clear here that the condition (b) of Proposition 2.3 is sufficient, but we do not know if the condition (a) is or not. Remark that the example
![]() $\ell _\infty $
given in [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] fails to verify the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and 2.5], but satisfies the conditions (a) and (b) of Propositions 2.2 and 2.3, which is logical.
$\ell _\infty $
given in [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] fails to verify the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and 2.5], but satisfies the conditions (a) and (b) of Propositions 2.2 and 2.3, which is logical.
As a consequence, we obtain Corollary 4.52 of [Reference Aliprantis and Burkinshaw2].
Corollary 2.5 Every separable Dedekind
![]() $\sigma $
-complete Banach lattice has an order-continuous norm.
$\sigma $
-complete Banach lattice has an order-continuous norm.
Proof Let E be a separable and Dedekind
![]() $\sigma $
-complete Banach lattices. According to [Reference Aliprantis and Burkinshaw2, Exercise 6, p. 337], every operator from E to
$\sigma $
-complete Banach lattices. According to [Reference Aliprantis and Burkinshaw2, Exercise 6, p. 337], every operator from E to
![]() $\ell ^\infty $
is order weakly compact, and then, by corollary 2.3, E has an order-continuous norm.
$\ell ^\infty $
is order weakly compact, and then, by corollary 2.3, E has an order-continuous norm.
Now, we give a class of pair
![]() $(E,Y)$
consisting of a Banach lattice E and a Banach space F for which every weak* Dunford–Pettis operator from E to Y is M-weakly compact (and hence order weakly compact). Moreover, we can choose Y as a Banach lattice so that none of the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and Theorem 2.5] are verified.
$(E,Y)$
consisting of a Banach lattice E and a Banach space F for which every weak* Dunford–Pettis operator from E to Y is M-weakly compact (and hence order weakly compact). Moreover, we can choose Y as a Banach lattice so that none of the conditions (a) and (b) of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorems 2.4 and Theorem 2.5] are verified.
Theorem 2.6 Let E be a Banach lattice, and let X be a separable Banach space. If the topological dual
![]() $E'$
has an order-continuous norm, then every weak* Dunford–Pettis operator
$E'$
has an order-continuous norm, then every weak* Dunford–Pettis operator
![]() $T:E\rightarrow X$
is M-weakly compact.
$T:E\rightarrow X$
is M-weakly compact.
Proof Let
![]() $(x_n)$
be a norm bounded disjoint sequence of
$(x_n)$
be a norm bounded disjoint sequence of
![]() $E^+$
. We have to show that
$E^+$
. We have to show that
![]() $\lim \Vert Tx_n\Vert = 0$
. To this end, assume by way of contradiction that
$\lim \Vert Tx_n\Vert = 0$
. To this end, assume by way of contradiction that
![]() $\lim \Vert Tx_n\Vert \neq 0$
. Then, there exist some
$\lim \Vert Tx_n\Vert \neq 0$
. Then, there exist some
![]() $\varepsilon> 0$
and a subsequence
$\varepsilon> 0$
and a subsequence
![]() $ (y_n)$
of
$ (y_n)$
of
![]() $(x_n)$
satisfying
$(x_n)$
satisfying
![]() $\Vert Ty_n\Vert>\varepsilon $
for all
$\Vert Ty_n\Vert>\varepsilon $
for all
![]() $n\in \mathbb {N}^*$
. For each n, there exists a continuous linear functional
$n\in \mathbb {N}^*$
. For each n, there exists a continuous linear functional
![]() $f_n$
on X such that
$f_n$
on X such that
![]() $\Vert f_n\Vert =1$
and
$\Vert f_n\Vert =1$
and
Since X is a separable Banach space, then
![]() $(f_n)$
has a weak*-convergent subsequence
$(f_n)$
has a weak*-convergent subsequence
![]() $\left (f_{\phi (n)}\right )$
(see [Reference Aliprantis and Burkinshaw2, Exercise 7, p. 167]). Let
$\left (f_{\phi (n)}\right )$
(see [Reference Aliprantis and Burkinshaw2, Exercise 7, p. 167]). Let
![]() $f\in X'$
be its weak*-limit, i.e.,
$f\in X'$
be its weak*-limit, i.e.,
![]() $f_{\phi (n)} \overset {\sigma (X',X)}{\longrightarrow } f$
. On the other hand, since
$f_{\phi (n)} \overset {\sigma (X',X)}{\longrightarrow } f$
. On the other hand, since
![]() $E'$
has an order-continuous norm and
$E'$
has an order-continuous norm and
![]() $(y_n)$
is disjoint, it follows from [Reference Meyer-Nieberg18, Corollary 2.4.3] that
$(y_n)$
is disjoint, it follows from [Reference Meyer-Nieberg18, Corollary 2.4.3] that
![]() $y_n \overset {\sigma (E,E')}{\longrightarrow } 0$
and hence
$y_n \overset {\sigma (E,E')}{\longrightarrow } 0$
and hence
![]() $f\left ( Ty_n\right ) \longrightarrow 0$
. Finally, since T is weak* Dunford–Pettis,
$f\left ( Ty_n\right ) \longrightarrow 0$
. Finally, since T is weak* Dunford–Pettis,
![]() $ (f_{\phi (n)}- f) (Ty_{\phi (n)} ) \longrightarrow 0$
, and consequently we have
$ (f_{\phi (n)}- f) (Ty_{\phi (n)} ) \longrightarrow 0$
, and consequently we have
![]() $f_{\phi (n)} (Ty_{\phi (n) }) \longrightarrow 0$
, which contradicts (2.1). Therefore,
$f_{\phi (n)} (Ty_{\phi (n) }) \longrightarrow 0$
, which contradicts (2.1). Therefore,
![]() $\lim \Vert Tx_n\Vert = 0$
must hold true.
$\lim \Vert Tx_n\Vert = 0$
must hold true.
Recall that, for a compact Hausdorff space K, the Banach space
![]() $\mathcal {C}(K):=\displaystyle {\mathcal {C}}(K,\mathbb {R} )$
of continuous real-valued functions on K with the supremum norm is separable if and only if K is metrizable. Hence, if K is a metric compact set and E is a Banach lattice such that
$\mathcal {C}(K):=\displaystyle {\mathcal {C}}(K,\mathbb {R} )$
of continuous real-valued functions on K with the supremum norm is separable if and only if K is metrizable. Hence, if K is a metric compact set and E is a Banach lattice such that
![]() $E'$
has an order-continuous norm, then every weak* Dunford–Pettis operator
$E'$
has an order-continuous norm, then every weak* Dunford–Pettis operator
![]() $T:E\rightarrow \mathcal {C} (K)$
is M-weakly compact.
$T:E\rightarrow \mathcal {C} (K)$
is M-weakly compact.
Next, we will prove that this result remains true if K is a Hausdorff compact and strictly semi-compact topological space. Recall from [Reference Grothendieck15] that a Hausdorff topological space K is said to be strictly semi-compact if every sequence in K admits a convergent subsequence in K. Metric compact spaces are examples of strictly semi-compacts, but uncountable products of compact intervals are not (see [Reference Grothendieck15, pp. 169 and 170]).
Theorem 2.7 Let E be a Banach lattice, and let K be a compact space which is strictly semi-compact. If the norm of
![]() $E'$
is order-continuous, then every weak* Dunford–Pettis operator
$E'$
is order-continuous, then every weak* Dunford–Pettis operator
![]() $T:E\rightarrow \mathcal {C}(K)$
is M-weakly compact.
$T:E\rightarrow \mathcal {C}(K)$
is M-weakly compact.
Proof Let
![]() $T:E\rightarrow \mathcal {C}(K)$
be a weak* Dunford–Pettis operator, and let
$T:E\rightarrow \mathcal {C}(K)$
be a weak* Dunford–Pettis operator, and let
![]() $(x_n)_n$
be a bounded disjoint sequence in E. We have to prove that
$(x_n)_n$
be a bounded disjoint sequence in E. We have to prove that
![]() $\lim \limits _{n} \Vert T(x_n) \Vert =0$
. Assume that
$\lim \limits _{n} \Vert T(x_n) \Vert =0$
. Assume that
![]() $\left (\Vert T(x_n) \Vert \right )$
does not converge to
$\left (\Vert T(x_n) \Vert \right )$
does not converge to
![]() $0$
. In this situation, we can suppose that there exists a sequence
$0$
. In this situation, we can suppose that there exists a sequence
![]() $(t_n)\in K^{\mathbb {N}}$
such that
$(t_n)\in K^{\mathbb {N}}$
such that
![]() $\vert T(x_n)(t_n) \vert \geq 1$
for every
$\vert T(x_n)(t_n) \vert \geq 1$
for every
![]() $n\in \mathbb {N}$
. Next, since K is strictly semi-compact, the sequence
$n\in \mathbb {N}$
. Next, since K is strictly semi-compact, the sequence
![]() $(t_n)$
has a subsequence (that we denote always
$(t_n)$
has a subsequence (that we denote always
![]() $(t_n)$
) which converges to
$(t_n)$
) which converges to
![]() $t\in K$
. Hence, the sequence
$t\in K$
. Hence, the sequence
![]() $(\delta _{t_n}-\delta _{t})$
converges to
$(\delta _{t_n}-\delta _{t})$
converges to
![]() $0$
for the topology
$0$
for the topology
![]() $\sigma \left (F',F \right )$
, where
$\sigma \left (F',F \right )$
, where
![]() $F=\mathcal {C}(K)$
and
$F=\mathcal {C}(K)$
and
![]() $\delta _{t_n},\delta _{t}$
are the Dirac measures. Once again, as the norm of
$\delta _{t_n},\delta _{t}$
are the Dirac measures. Once again, as the norm of
![]() $E'$
is order-continuous, the sequence
$E'$
is order-continuous, the sequence
![]() $(x_n)$
converges weakly to
$(x_n)$
converges weakly to
![]() $0$
. Hence,
$0$
. Hence,
![]() $\delta _{t}(T(x_n))\longrightarrow 0$
, and since T is weak* Dunford–Pettis,
$\delta _{t}(T(x_n))\longrightarrow 0$
, and since T is weak* Dunford–Pettis,
![]() $\left (\delta _{t_n}-\delta _{t}\right )\left (T(x_n)\right )\longrightarrow 0$
. We deduce then that
$\left (\delta _{t_n}-\delta _{t}\right )\left (T(x_n)\right )\longrightarrow 0$
. We deduce then that
![]() $\delta _{t_n}(T(x_n))\longrightarrow 0$
, which presents a contradiction, because
$\delta _{t_n}(T(x_n))\longrightarrow 0$
, which presents a contradiction, because
![]() $1\leq \vert T(x_n) (t_n)\vert $
for every
$1\leq \vert T(x_n) (t_n)\vert $
for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Remark 2.8 If we take
![]() $K=\beta \mathbb {N}$
, the Stone–Čech compactified set of
$K=\beta \mathbb {N}$
, the Stone–Čech compactified set of
![]() $\mathbb {N}$
, then
$\mathbb {N}$
, then
![]() $\mathcal {C}\left (\beta \mathbb {N}\right )=l^{\infty }$
, and we know that the identity operator
$\mathcal {C}\left (\beta \mathbb {N}\right )=l^{\infty }$
, and we know that the identity operator
![]() $id_{l^{\infty }}:l^{\infty } \rightarrow l^{\infty }$
is positive and weak* Dunford–Pettis, but it is not M-weakly compact. This shows the known result:
$id_{l^{\infty }}:l^{\infty } \rightarrow l^{\infty }$
is positive and weak* Dunford–Pettis, but it is not M-weakly compact. This shows the known result:
![]() $\beta \mathbb {N}$
is not strictly semi-compact. It has been shown in [Reference Carothers9, p. 157] that a sequence in
$\beta \mathbb {N}$
is not strictly semi-compact. It has been shown in [Reference Carothers9, p. 157] that a sequence in
![]() $\mathbb {N}$
converges in
$\mathbb {N}$
converges in
![]() $\beta \mathbb {N}$
if and only if it already converges in
$\beta \mathbb {N}$
if and only if it already converges in
![]() $\mathbb {N}$
. This also proves that Theorem 2.7 is not true if K is not strictly semi-compact.
$\mathbb {N}$
. This also proves that Theorem 2.7 is not true if K is not strictly semi-compact.
We end this section by mentioning that the result of Theorem 2.1 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] related to the domination problem, when
![]() $E=F$
and E is Dedekind
$E=F$
and E is Dedekind
![]() $\sigma $
-complete, remains true if
$\sigma $
-complete, remains true if
![]() $E\neq F$
without assuming that F is Dedekind
$E\neq F$
without assuming that F is Dedekind
![]() $\sigma $
-complete.
$\sigma $
-complete.
Proposition 2.9 If E and F are two Banach lattices, then the following assertions are equivalent:
-
(1) Every positive weak* Dunford–Pettis operator from E into F is M-weakly compact.
-
(2) For all operators,
 $S, T : E\rightarrow F$
such that
$S, T : E\rightarrow F$
such that
 $0\leq S\leq T$
and T is weak* Dunford–Pettis, S is M-weakly compact.
$0\leq S\leq T$
and T is weak* Dunford–Pettis, S is M-weakly compact.
Proof
-
 $(1) \Rightarrow (2)$
Let
$(1) \Rightarrow (2)$
Let
 $S, T : E\rightarrow F$
be two operators such that
$S, T : E\rightarrow F$
be two operators such that
 $0 \leq S \leq T$
and T is weak* Dunford–Pettis. So, T is M-weakly compact and hence it is clear that S is M-weakly compact.
$0 \leq S \leq T$
and T is weak* Dunford–Pettis. So, T is M-weakly compact and hence it is clear that S is M-weakly compact. -
 $(2) \Rightarrow (1)$
Obvious.
$(2) \Rightarrow (1)$
Obvious.
3 Weak compactness of positive weak* Dunford–Pettis operators
In the same paper [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12], the authors studied Banach lattices E and F verifying the following property:
![]() $\mathcal {P}_2$
: every positive weak* Dunford–Pettis operator from E to F is weakly compact.
$\mathcal {P}_2$
: every positive weak* Dunford–Pettis operator from E to F is weakly compact.
They gave a characterization of such Banach lattices, but only in the case when the norm of F is order-continuous, and in the case when
![]() $E=F$
and E is Dedekind
$E=F$
and E is Dedekind
![]() $\sigma $
-complete. It has been established [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.2] that if the norm of F is order-continuous, then every positive weak* Dunford–Pettis operator from E to F is weakly compact if and only if one of the following is valid:
$\sigma $
-complete. It has been established [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.2] that if the norm of F is order-continuous, then every positive weak* Dunford–Pettis operator from E to F is weakly compact if and only if one of the following is valid:
-
(a) The norm of
 $E'$
is order-continuous.
$E'$
is order-continuous. -
(b) F is reflexive.
In the particular case when
![]() $E=F$
, it has been established that, if E is Dedekind
$E=F$
, it has been established that, if E is Dedekind
![]() $\sigma $
-complete, then every positive weak* Dunford–Pettis operator from E to E is weakly compact if and only if the norms of E and
$\sigma $
-complete, then every positive weak* Dunford–Pettis operator from E to E is weakly compact if and only if the norms of E and
![]() $E'$
are order-continuous [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.1].
$E'$
are order-continuous [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.1].
The aim of this section is to give necessary conditions on Banach lattices to verify the property
![]() $\mathcal {P}_2$
in the general case, and a characterization when F is only Dedekind
$\mathcal {P}_2$
in the general case, and a characterization when F is only Dedekind
![]() $\sigma $
-complete. To do this, we will need the following lemma.
$\sigma $
-complete. To do this, we will need the following lemma.
Lemma 3.1 Let E be a Banach lattice. If
![]() $l^\infty $
(resp.
$l^\infty $
(resp.
![]() $c_0$
) is lattice embeddable in E, then there exist a lattice embedding T from
$c_0$
) is lattice embeddable in E, then there exist a lattice embedding T from
![]() $l^\infty $
(resp.
$l^\infty $
(resp.
![]() $c_0$
) to E and a positive operator
$c_0$
) to E and a positive operator
![]() $P : E \rightarrow l^\infty $
so that
$P : E \rightarrow l^\infty $
so that
![]() $P\circ T$
is the identity operator of
$P\circ T$
is the identity operator of
![]() $l^\infty $
(resp. the canonical injection from
$l^\infty $
(resp. the canonical injection from
![]() $c_0$
into
$c_0$
into
![]() $l^\infty $
).
$l^\infty $
).
Proof By definition, there exists a lattice embedding
![]() $T : E_1 \rightarrow E$
with
$T : E_1 \rightarrow E$
with
![]() $E_1=l^\infty $
(resp.
$E_1=l^\infty $
(resp.
![]() $E_1=c_0$
). Denote by
$E_1=c_0$
). Denote by
![]() $(e_n)$
the canonical basis of
$(e_n)$
the canonical basis of
![]() $E_1$
and put
$E_1$
and put
![]() $v_n=T(e_n)$
. Then
$v_n=T(e_n)$
. Then
![]() $\left ( v_n \right )$
is a bounded disjoint sequence in E, and by [Reference Aqzzouz, Elbour and H’michane3, Lemma 3.4], there exists a positive bounded and disjoint sequence
$\left ( v_n \right )$
is a bounded disjoint sequence in E, and by [Reference Aqzzouz, Elbour and H’michane3, Lemma 3.4], there exists a positive bounded and disjoint sequence
![]() $\left (f_n \right )$
in
$\left (f_n \right )$
in
![]() $E'$
such that for all
$E'$
such that for all
![]() $m,n\in \mathbb {N}$
, we have
$m,n\in \mathbb {N}$
, we have
 $$ \begin{align*}f_n(v_m)=\begin{cases} 1, \text{ if } m=n, \\ 0,\text{ if } m\neq n.\end{cases}\end{align*} $$
$$ \begin{align*}f_n(v_m)=\begin{cases} 1, \text{ if } m=n, \\ 0,\text{ if } m\neq n.\end{cases}\end{align*} $$
Now, the operator
answers the question.
Theorem 3.2 Let E and F be Banach lattices. If each positive weak* Dunford–Pettis operator
![]() $T:E\rightarrow F$
is weakly compact, then one of the following assertions is valid:
$T:E\rightarrow F$
is weakly compact, then one of the following assertions is valid:
-
(1) The norm of
 $E^{\prime }$
is order-continuous and
$E^{\prime }$
is order-continuous and
 $l^{\infty }$
is not embedded in F.
$l^{\infty }$
is not embedded in F. -
(2) E is reflexive.
-
(3) F is reflexive.
Proof
-
• Step 1. In [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.2], it has been proved that if every positive weak* Dunford–Pettis operator
 $T:E\rightarrow F$
is weakly compact, then either the norm of
$T:E\rightarrow F$
is weakly compact, then either the norm of
 $E^{\prime }$
is order-continuous or F is reflexive. We repeat here this proof. Assume that the norm of
$E^{\prime }$
is order-continuous or F is reflexive. We repeat here this proof. Assume that the norm of
 $E'$
is not order-continuous. As before E, there exists a positive projection
$E'$
is not order-continuous. As before E, there exists a positive projection
 $P : E \rightarrow \ell ^1$
. Consider the operator
$P : E \rightarrow \ell ^1$
. Consider the operator
 $S : \ell ^1 \rightarrow F$
defined by
$S : \ell ^1 \rightarrow F$
defined by
 $S((\alpha _i)) =\sum \limits _{i=1}^{+\infty }\alpha _ix_i$
for each
$S((\alpha _i)) =\sum \limits _{i=1}^{+\infty }\alpha _ix_i$
for each
 $(\alpha _i) \in \ell ^1$
. The composed operator
$(\alpha _i) \in \ell ^1$
. The composed operator
 $T = S\circ P $
is weak* Dunford–Pettis and hence by our hypothesis T is weakly compact. So, the sequence
$T = S\circ P $
is weak* Dunford–Pettis and hence by our hypothesis T is weakly compact. So, the sequence
 $(x_n) = (T(e_n))$
has a subsequence which converges weakly to an element of F, where
$(x_n) = (T(e_n))$
has a subsequence which converges weakly to an element of F, where
 $(e_n)$
is the canonical basis of
$(e_n)$
is the canonical basis of
 $ \ell ^1$
. So, by the Eberlein–Smulian’s theorem, F is reflexive.
$ \ell ^1$
. So, by the Eberlein–Smulian’s theorem, F is reflexive. -
• Step 2. Suppose by the way of contradiction that
 $l^{\infty }$
is lattice embeddable in F and E is not reflexive. According to the Lozanovsky theorem [Reference Aliprantis and Burkinshaw2, Theorem 4.71],
$l^{\infty }$
is lattice embeddable in F and E is not reflexive. According to the Lozanovsky theorem [Reference Aliprantis and Burkinshaw2, Theorem 4.71],
 $l^1$
or
$l^1$
or
 $c_0$
is lattice embeddable in E. If
$c_0$
is lattice embeddable in E. If
 $l^1$
is lattice embeddable in E, then the norm of
$l^1$
is lattice embeddable in E, then the norm of
 $E'$
is not order-continuous, in this case, by Step 1 of the current proof, F is reflexive, which contradicts the fact that
$E'$
is not order-continuous, in this case, by Step 1 of the current proof, F is reflexive, which contradicts the fact that
 $l^{\infty }$
is lattice embeddable in F. So, assume that
$l^{\infty }$
is lattice embeddable in F. So, assume that
 $c_0$
is lattice embeddable in E and apply Lemma 3.1. Then there exist positive operators
$c_0$
is lattice embeddable in E and apply Lemma 3.1. Then there exist positive operators
 $T_F:l^\infty \rightarrow F$
,
$T_F:l^\infty \rightarrow F$
,
 $P_F : F \rightarrow l^\infty $
,
$P_F : F \rightarrow l^\infty $
,
 $T_E:c_0\rightarrow E$
, and
$T_E:c_0\rightarrow E$
, and
 $P_E : E \rightarrow l^\infty $
so that
$P_E : E \rightarrow l^\infty $
so that
 $P_F\circ T_F$
is the identity operator of
$P_F\circ T_F$
is the identity operator of
 $l^\infty $
and
$l^\infty $
and
 $P_E\circ T_E$
is the canonical injection from
$P_E\circ T_E$
is the canonical injection from
 $c_0$
into
$c_0$
into
 $l^\infty $
. Since
$l^\infty $
. Since
 $l^\infty $
has the Dunford–Pettis* property, the composite operator
$l^\infty $
has the Dunford–Pettis* property, the composite operator
 $S:=T_F\circ P_E$
is weak* Dunford–Pettis, but it fails to be weakly compact because the composite
$S:=T_F\circ P_E$
is weak* Dunford–Pettis, but it fails to be weakly compact because the composite
 $P_F\circ S\circ T_E=P_F\circ T_F\circ P_E\circ T_E$
is the canonical injection from
$P_F\circ S\circ T_E=P_F\circ T_F\circ P_E\circ T_E$
is the canonical injection from
 $c_0$
to
$c_0$
to
 $l^\infty $
which is not weakly compact.
$l^\infty $
which is not weakly compact.
When F is Dedekind
![]() $\sigma $
-complete, we obtain the following characterization.
$\sigma $
-complete, we obtain the following characterization.
Theorem 3.3 Let E and F be Banach lattices. If F is Dedekind
![]() $\sigma $
-complete, then each positive weak* Dunford–Pettis operator
$\sigma $
-complete, then each positive weak* Dunford–Pettis operator
![]() $T:E\rightarrow F$
is weakly compact if and only if one of the following assertions is valid:
$T:E\rightarrow F$
is weakly compact if and only if one of the following assertions is valid:
-
(1) The norms of
 $E^{\prime }$
and F are order-continuous.
$E^{\prime }$
and F are order-continuous. -
(2) E is reflexive.
-
(3) F is reflexive.
Proof The direct implication follows from the previous theorem, since if F is Dedekind
![]() $\sigma $
-complete, its norm is order-continuous if and only if
$\sigma $
-complete, its norm is order-continuous if and only if
![]() $\ell ^\infty $
is not lattice embeddable in F (see [Reference Aliprantis and Burkinshaw2, Theorem 4.51 (Lozanovsky–Mekler–Meyer-Nieberg)]).
$\ell ^\infty $
is not lattice embeddable in F (see [Reference Aliprantis and Burkinshaw2, Theorem 4.51 (Lozanovsky–Mekler–Meyer-Nieberg)]).
For the converse, if E or F is reflexive, the result is obvious, and if the norms of
![]() $E'$
and F are order-continuous, the result follows from Theorem 2.2 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12].
$E'$
and F are order-continuous, the result follows from Theorem 2.2 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12].
Remark 3.4 To show that the condition “the norm of F is order-continuous” is necessary in [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12, Theorem 2.2], the authors gave the example of the identity operator of the Banach lattice
![]() $\ell ^\infty $
, which is weak* Dunford–Pettis but fails to be weakly compact, even if the norm of
$\ell ^\infty $
, which is weak* Dunford–Pettis but fails to be weakly compact, even if the norm of
![]() $\left (\ell ^\infty \right )'$
is order-continuous. This is now explained by Corollary 3.5. However, we do not know if the reciprocal of Theorem 3.2 is true or not.
$\left (\ell ^\infty \right )'$
is order-continuous. This is now explained by Corollary 3.5. However, we do not know if the reciprocal of Theorem 3.2 is true or not.
In the particular case when
![]() $E=F$
, we obtain Theorem 2.1 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] as a corollary.
$E=F$
, we obtain Theorem 2.1 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12] as a corollary.
Corollary 3.5 If E is a Dedekind
![]() $\sigma $
-complete Banach lattice, then the following assertions are equivalent:
$\sigma $
-complete Banach lattice, then the following assertions are equivalent:
-
(1) Each positive weak* Dunford–Pettis operator
 $T:E\rightarrow F$
is weakly compact.
$T:E\rightarrow F$
is weakly compact. -
(2) The norms of
 $E^{\prime }$
and E are order-continuous.
$E^{\prime }$
and E are order-continuous.
As consequence, we derive a characterization of reflexive Banach lattices in terms of weak compactness of weak* Dunford–Pettis operators and AL-spaces.
Corollary 3.6 (Compare with Corollary 2.3 of [Reference El Fahri, H’michane, El Kaddouri and Aboutafail12]). If F is a Banach lattice, then the following assertions are equivalent:
-
(1) F is reflexive.
-
(2) For any infinite-dimensional AL-space E, every positive weak* Dunford–Pettis operator from E into F is weakly compact.
-
(3) There exists an infinite-dimensional AL-space E such that every positive weak* Dunford–Pettis operator from E into F is weakly compact.
-
(4) Every positive weak* Dunford–Pettis operator from
 $\ell ^1$
into F is weakly compact.
$\ell ^1$
into F is weakly compact.
Proof
-
 $(1)\Rightarrow (2)$
In fact, in this case, according to [Reference Aliprantis and Burkinshaw2, Theorem 5.24], every operator from E to F is weakly compact.
$(1)\Rightarrow (2)$
In fact, in this case, according to [Reference Aliprantis and Burkinshaw2, Theorem 5.24], every operator from E to F is weakly compact. -
 $(2)\Rightarrow (4)$
Obvious.
$(2)\Rightarrow (4)$
Obvious. -
 $(4)\Rightarrow (3)$
Obvious.
$(4)\Rightarrow (3)$
Obvious. -
 $(3)\Rightarrow (1)$
According to [Reference Aliprantis and Burkinshaw2, Exercise 15, p. 254],
$(3)\Rightarrow (1)$
According to [Reference Aliprantis and Burkinshaw2, Exercise 15, p. 254],
 $\ell ^1$
is lattice embeddable in E; hence, the norm of
$\ell ^1$
is lattice embeddable in E; hence, the norm of
 $E'$
is not order-continuous and consequently, from Corollary 3.2, F is reflexive.
$E'$
is not order-continuous and consequently, from Corollary 3.2, F is reflexive.
In the same way, we also obtain a characterization of reflexive Banach lattices in terms of weak compactness of weak* Dunford–Pettis operators and AM-spaces.
Corollary 3.7 If E is a Banach lattice, then the following assertions are equivalent:
-
(1) E is reflexive.
-
(2) For any infinite-dimensional AM-space F, every positive weak* Dunford–Pettis operator from E into F is weakly compact.
-
(3) There exits an infinite-dimensional AM-space F such that every positive weak* Dunford–Pettis operator from E into F is weakly compact.
-
(4) Every positive weak* Dunford–Pettis operator from E to
 $\ell ^\infty $
is weakly compact.
$\ell ^\infty $
is weakly compact.
Other consequence is the following corollary.
Corollary 3.8 If K is a compact topological space which is strictly semi-compact, then
![]() $l^\infty $
is not embedded in
$l^\infty $
is not embedded in
![]() $\mathcal {C}(K)$
.
$\mathcal {C}(K)$
.
Also, we have the following corollary.
Corollary 3.9 Let K be a compact topological space which is strictly semi-compact. If
![]() $\mathcal {C}(K)$
is Dedekind
$\mathcal {C}(K)$
is Dedekind
![]() $\sigma $
-complete, then it is of finite-dimensional.
$\sigma $
-complete, then it is of finite-dimensional.
Proof By the preceding corollary, the norm of
![]() $\mathcal {C}(K)$
is order-continuous. Since its closed unit ball is an order interval, then it is weakly compact. Consequently,
$\mathcal {C}(K)$
is order-continuous. Since its closed unit ball is an order interval, then it is weakly compact. Consequently,
![]() $\mathcal {C}(K)$
is reflexive, and therefore it has a finite dimension [Reference Aliprantis and Burkinshaw2, Exercise 14, p. 253].
$\mathcal {C}(K)$
is reflexive, and therefore it has a finite dimension [Reference Aliprantis and Burkinshaw2, Exercise 14, p. 253].
Finally, we give sufficient conditions on a Banach lattice to have the positive Grothendieck property. Recall that a Banach space X is said to have the Grothendieck property if every weak* null sequence in
![]() $X^{\prime }$
is weakly null. The simplest nonreflexive Banach space with the Grothendieck property is
$X^{\prime }$
is weakly null. The simplest nonreflexive Banach space with the Grothendieck property is
![]() $ l^{\infty }$
. Other examples of nonreflexive Banach spaces with the Grothendieck property are the spaces
$ l^{\infty }$
. Other examples of nonreflexive Banach spaces with the Grothendieck property are the spaces
![]() $C(K)$
, where K is any compact Stonean space.
$C(K)$
, where K is any compact Stonean space.
A Banach lattice E is said to have the positive Grothendieck property if every positive weak* null sequence in
![]() $E^{\prime }$
is weakly null.
$E^{\prime }$
is weakly null.
Corollary 3.10 Let E be a Banach lattice. If E has the weak
![]() $^*$
Dunford–Pettis property and the norm of
$^*$
Dunford–Pettis property and the norm of
![]() $E'$
is order-continuous, then E has the positive Grothendieck property.
$E'$
is order-continuous, then E has the positive Grothendieck property.
Proof In this situation, each operator
![]() $T:E\rightarrow c_0$
is weak
$T:E\rightarrow c_0$
is weak
![]() $^*$
Dunford–Pettis and hence weakly compact. As consequence, E has the positive Grothendieck property (see [Reference Witold21, p. 762]).
$^*$
Dunford–Pettis and hence weakly compact. As consequence, E has the positive Grothendieck property (see [Reference Witold21, p. 762]).
4 Almost M-weak and almost L-weak compactness of weak* Dunford–Pettis operators
The notion of almost M-weakly (and almost L-weakly) compact operators was introduced in [Reference Bouras, Lhaimer and Moussa8] and studied in [Reference Elbour, Afkir and Sabiri14, Reference Nouira, Lhaimer and Elbour19]. An operator T from a Banach lattice E into a Banach space Y is called almost M-weakly compact if for every bounded and disjoint sequence
![]() $(x_n)$
in E, and every weakly convergent sequence
$(x_n)$
in E, and every weakly convergent sequence
![]() $( f_n)$
of Y, we have
$( f_n)$
of Y, we have
![]() $f_n(T (x_n)) \rightarrow 0$
.
$f_n(T (x_n)) \rightarrow 0$
.
An operator T from a Banach space X into a Banach lattice F is called almost L-weakly compact if T carries relatively weakly compact subsets of X onto L-weakly compact subsets of F. Recall that a nonempty bounded subset A of a Banach lattice E is said to be L-weakly compact if
![]() $\Vert x_n\Vert \rightarrow 0$
for every disjoint sequence
$\Vert x_n\Vert \rightarrow 0$
for every disjoint sequence
![]() $(x_n)$
contained in the solid hull of A. In [Reference Bouras, Lhaimer and Moussa8], it has been proved that an operator T from a Banach space X into a Banach lattice F is almost L-weakly compact if and only if
$(x_n)$
contained in the solid hull of A. In [Reference Bouras, Lhaimer and Moussa8], it has been proved that an operator T from a Banach space X into a Banach lattice F is almost L-weakly compact if and only if
![]() $f_n(T (x_n)) \rightarrow 0$
for every weakly convergent sequence
$f_n(T (x_n)) \rightarrow 0$
for every weakly convergent sequence
![]() $(x_n)$
of X and every bounded and disjoint sequence
$(x_n)$
of X and every bounded and disjoint sequence
![]() $( f_n)$
of F [Reference Bouras, Lhaimer and Moussa8, Theorem 2.2]. In [Reference Elbour, Afkir and Sabiri14], the authors gave a characterization of almost L-weakly compact and almost M-weakly compact operators involving the maximal ideal in a Banach lattice E on which the induced norm is order-continuous, denoted by
$( f_n)$
of F [Reference Bouras, Lhaimer and Moussa8, Theorem 2.2]. In [Reference Elbour, Afkir and Sabiri14], the authors gave a characterization of almost L-weakly compact and almost M-weakly compact operators involving the maximal ideal in a Banach lattice E on which the induced norm is order-continuous, denoted by
![]() $E^{a}$
[Reference Elbour, Afkir and Sabiri14, Propositions 1 and 2].
$E^{a}$
[Reference Elbour, Afkir and Sabiri14, Propositions 1 and 2].
Theorem 4.1 If E is a Banach lattice and Y is a non-null Banach space, then the following assertions are equivalent:
-
(1) The norm of
 $E'$
is order-continuous.
$E'$
is order-continuous. -
(2) Every weak* Dunford–Pettis operator from E to Y is almost M-weakly compact.
Proof
-
(1) Suppose that the norm of
 $E'$
is order-continuous and consider a weak* Dunford–Pettis operator
$E'$
is order-continuous and consider a weak* Dunford–Pettis operator
 $T:E\rightarrow Y$
. Let
$T:E\rightarrow Y$
. Let
 $(x_n)$
be a bounded and disjoint sequence in E and
$(x_n)$
be a bounded and disjoint sequence in E and
 $(f_n)$
a weakly convergent sequence in
$(f_n)$
a weakly convergent sequence in
 $Y'$
. Since the norm of
$Y'$
. Since the norm of
 $E'$
is order-continuous, according to [Reference Meyer-Nieberg18, Corollary 2.4.3], we have
$E'$
is order-continuous, according to [Reference Meyer-Nieberg18, Corollary 2.4.3], we have
 $x_n\overset {\sigma (E,E')}{\rightarrow } 0$
. Hence, if we put f the weak limit of
$x_n\overset {\sigma (E,E')}{\rightarrow } 0$
. Hence, if we put f the weak limit of
 $(f_n)$
, then
$(f_n)$
, then
 $f\circ T(x_n)\rightarrow 0$
and
$f\circ T(x_n)\rightarrow 0$
and
 $(f_n-f)\circ T (x_n)\rightarrow 0$
. Consequently, we have
$(f_n-f)\circ T (x_n)\rightarrow 0$
. Consequently, we have
 $f_n\circ T (x_n)\rightarrow 0$
.
$f_n\circ T (x_n)\rightarrow 0$
. -
(2) Suppose that the norm of
 $E'$
is not order-continuous. Then
$E'$
is not order-continuous. Then
 $(E')^{a}\subsetneq E'$
, and therefore there exists
$(E')^{a}\subsetneq E'$
, and therefore there exists
 $f\in E'$
such that
$f\in E'$
such that
 $f\notin (E')^{a}$
. Fix
$f\notin (E')^{a}$
. Fix
 $y\in Y$
nonnull and consider the operator
$y\in Y$
nonnull and consider the operator  $$ \begin{align*}\begin{array}{llll} T : & E & \longleftrightarrow & Y\\ & x & \longmapsto & f(x).y. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{llll} T : & E & \longleftrightarrow & Y\\ & x & \longmapsto & f(x).y. \end{array}\end{align*} $$
Let
 $(x_n)$
be a null weak sequence in E and
$(x_n)$
be a null weak sequence in E and
 $(f_n)$
a null weak* sequence in
$(f_n)$
a null weak* sequence in
 $Y'$
. Hence,
$Y'$
. Hence,
 $f_n\circ T (x_n)=f_n(y). f (x_n)\rightarrow 0$
. This proves that T is weak* Dunford–Pettis. On the other hand, there exists
$f_n\circ T (x_n)=f_n(y). f (x_n)\rightarrow 0$
. This proves that T is weak* Dunford–Pettis. On the other hand, there exists
 $g\in Y'$
satisfying
$g\in Y'$
satisfying
 $g(y)=1$
, so
$g(y)=1$
, so
 $T'(g)=f \notin (E')^{a}$
. Now, according to [Reference Elbour, Afkir and Sabiri14, Proposition 2], T is not almost M-weakly compact.
$T'(g)=f \notin (E')^{a}$
. Now, according to [Reference Elbour, Afkir and Sabiri14, Proposition 2], T is not almost M-weakly compact.
Theorem 4.2 If F is a Banach lattice and X is a non-null Banach space, then the following assertions are equivalent:
-
(1) The norm of F is order-continuous.
-
(2) Every weak* Dunford–Pettis operator from X to F is almost L-weakly compact.
Proof
-
(1) Suppose that the norm of F is order-continuous and consider a weak* Dunford–Pettis operator
 $T:X\rightarrow F$
. Let
$T:X\rightarrow F$
. Let
 $(x_n)$
be a weakly convergent sequence in X, x be its weak limit, and
$(x_n)$
be a weakly convergent sequence in X, x be its weak limit, and
 $(f_n)$
be a bounded and disjoint sequence in F. As above, since the norm of F is order-continuous and according to [Reference Meyer-Nieberg18, Corollary 2.4.3], we have
$(f_n)$
be a bounded and disjoint sequence in F. As above, since the norm of F is order-continuous and according to [Reference Meyer-Nieberg18, Corollary 2.4.3], we have
 $f_n\overset {\sigma (F',F)}{\longrightarrow } 0$
. Hence,
$f_n\overset {\sigma (F',F)}{\longrightarrow } 0$
. Hence,
 $f_n\circ T(x)\rightarrow 0$
,
$f_n\circ T(x)\rightarrow 0$
,
 $f_n\circ T (x_n-x)\rightarrow 0$
, and consequently
$f_n\circ T (x_n-x)\rightarrow 0$
, and consequently
 $f_n\circ T (x_n)\rightarrow 0$
.
$f_n\circ T (x_n)\rightarrow 0$
. -
(2) Suppose that the norm of F is not order-continuous. Again,
 $F^{a}\subsetneq F$
, and there exists
$F^{a}\subsetneq F$
, and there exists
 $y\in F$
such that
$y\in F$
such that
 $y\notin F^{a}$
. Fix
$y\notin F^{a}$
. Fix
 $f\in X'$
nonnull and consider the operator
$f\in X'$
nonnull and consider the operator  $$ \begin{align*}\begin{array}{llll} T : & X & \longleftrightarrow & F\\ & x & \longmapsto & f(x).y. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{llll} T : & X & \longleftrightarrow & F\\ & x & \longmapsto & f(x).y. \end{array}\end{align*} $$
T is weak* Dunford–Pettis and
 $T(X) \nsubseteq F^{a}$
, so according to [Reference Elbour, Afkir and Sabiri14, Proposition 1], T is not almost L-weakly compact.
$T(X) \nsubseteq F^{a}$
, so according to [Reference Elbour, Afkir and Sabiri14, Proposition 1], T is not almost L-weakly compact.