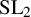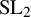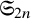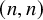1 Introduction and the main results
In this article, we study the transition matrix between two famous bases, the Specht basis and the
![]() $ \operatorname {SL}_2 $
-web basis, for the irreducible representation of the symmetric group
$ \operatorname {SL}_2 $
-web basis, for the irreducible representation of the symmetric group
![]() $ \mathfrak {S}_{2n} $
indexed by the partition
$ \mathfrak {S}_{2n} $
indexed by the partition
![]() $ (n,n) $
. Motivated by Rhoades’s work [Reference RhoadesRho19], we give a combinatorial interpretation for entries of the transition matrix as a certain class of permutations, and we present their interesting properties.
$ (n,n) $
. Motivated by Rhoades’s work [Reference RhoadesRho19], we give a combinatorial interpretation for entries of the transition matrix as a certain class of permutations, and we present their interesting properties.
For an integer
![]() $ n\ge 1 $
, let
$ n\ge 1 $
, let
![]() $ \mathfrak {S}_{2n} $
be the symmetric group on the set
$ \mathfrak {S}_{2n} $
be the symmetric group on the set
![]() $ [2n] = \{ 1,\dots ,2n \} $
. It is well-known that each irreducible representation of
$ [2n] = \{ 1,\dots ,2n \} $
. It is well-known that each irreducible representation of
![]() $ \mathfrak {S}_{2n} $
can be indexed by a partition of
$ \mathfrak {S}_{2n} $
can be indexed by a partition of
![]() $ 2n $
. For a partition
$ 2n $
. For a partition
![]() $ \lambda $
of
$ \lambda $
of
![]() $ 2n $
, we then denote by
$ 2n $
, we then denote by
![]() $ \mathcal {S}^\lambda $
the irreducible representation indexed by
$ \mathcal {S}^\lambda $
the irreducible representation indexed by
![]() $ \lambda $
, called the Specht module. In this article, we focus specifically on the Specht module indexed by the partition
$ \lambda $
, called the Specht module. In this article, we focus specifically on the Specht module indexed by the partition
![]() $(n,n)$
, and two well-studied bases for
$(n,n)$
, and two well-studied bases for
![]() $ \mathcal {S}^{(n,n)} $
.
$ \mathcal {S}^{(n,n)} $
.
A standard Young tableau of shape
![]() $ (n,n) $
is a
$ (n,n) $
is a
![]() $ 2\times n $
array of integers whose entries are
$ 2\times n $
array of integers whose entries are
![]() $ [2n] $
, and each row and each column are increasing. See Figure 1 for an example. The set of standard Young tableaux of shape
$ [2n] $
, and each row and each column are increasing. See Figure 1 for an example. The set of standard Young tableaux of shape
![]() $ (n,n) $
, denoted by
$ (n,n) $
, denoted by
![]() $ \operatorname {SYT}(n,n) $
, parametrizes the Specht basis
$ \operatorname {SYT}(n,n) $
, parametrizes the Specht basis
for
![]() $ \mathcal {S}^{(n,n)} $
. For more details on the Specht basis and related combinatorics, see [Reference FultonFul97, Reference SaganSag01].
$ \mathcal {S}^{(n,n)} $
. For more details on the Specht basis and related combinatorics, see [Reference FultonFul97, Reference SaganSag01].
A (perfect) matching on
![]() $ [2n] $
is a set partition of
$ [2n] $
is a set partition of
![]() $ [2n] $
such that each block has size 2. We also depict a matching on
$ [2n] $
such that each block has size 2. We also depict a matching on
![]() $ [2n] $
as a diagram consisting of
$ [2n] $
as a diagram consisting of
![]() $ 2n $
vertices and
$ 2n $
vertices and
![]() $ n $
arcs where any pair of arcs has no common vertex. A crossing is a pair of arcs
$ n $
arcs where any pair of arcs has no common vertex. A crossing is a pair of arcs
![]() $ \{a,c\} $
and
$ \{a,c\} $
and
![]() $ \{b,d\} $
with
$ \{b,d\} $
with
![]() $ a<b<c<d $
. A matching is called noncrossing if the matching has no crossing, and nonnesting if there is no pair of arcs
$ a<b<c<d $
. A matching is called noncrossing if the matching has no crossing, and nonnesting if there is no pair of arcs
![]() $ \{a,d\} $
and
$ \{a,d\} $
and
![]() $ \{b,c\} $
with
$ \{b,c\} $
with
![]() $ a<b<c<d $
; see Figure 2. For an arc
$ a<b<c<d $
; see Figure 2. For an arc
![]() $\{i,j\}$
with
$\{i,j\}$
with
![]() $i<j$
, i is called an opener and j is called a closer. Let
$i<j$
, i is called an opener and j is called a closer. Let
![]() $\operatorname {Mat}_{2n}$
(
$\operatorname {Mat}_{2n}$
(
![]() $\operatorname {NC}_{2n}$
and
$\operatorname {NC}_{2n}$
and
![]() $\operatorname {NN}_{2n}$
, respectively) stand for the set of (noncrossing and nonnesting, respectively) matchings on
$\operatorname {NN}_{2n}$
, respectively) stand for the set of (noncrossing and nonnesting, respectively) matchings on
![]() $ [2n] $
.
$ [2n] $
.

Figure 1 A standard Young tableau of shape
![]() $ (4,4) $
.
$ (4,4) $
.

Figure 2 Two matchings on
![]() $ [8] $
. The first one is nonnesting, while the second one is noncrossing.
$ [8] $
. The first one is nonnesting, while the second one is noncrossing.
Note that there is a natural bijection between
![]() $ \operatorname {SYT}(n,n) $
and
$ \operatorname {SYT}(n,n) $
and
![]() $\operatorname {NN}_{2n} $
. For
$\operatorname {NN}_{2n} $
. For
![]() $ T\in \operatorname {SYT}(n,n) $
, connect two vertices lying on the same column of
$ T\in \operatorname {SYT}(n,n) $
, connect two vertices lying on the same column of
![]() $ T $
via an arc; then we obtain a nonnesting matching. For instance, the tableau in Figure 1 and the first matching in Figure 2 are under this correspondence. Using this correspondence, we index the Specht basis for
$ T $
via an arc; then we obtain a nonnesting matching. For instance, the tableau in Figure 1 and the first matching in Figure 2 are under this correspondence. Using this correspondence, we index the Specht basis for
![]() $ \mathcal {S}^{(n,n)} $
by nonnesting matchings of
$ \mathcal {S}^{(n,n)} $
by nonnesting matchings of
![]() $ [2n] $
, instead of standard Young tableaux of shape
$ [2n] $
, instead of standard Young tableaux of shape
![]() $ (n,n) $
:
$ (n,n) $
:
We now consider the
![]() $ 2 \times 2n $
matrix
$ 2 \times 2n $
matrix
 $$\begin{align*}z = \begin{bmatrix} z_{1,1} & z_{1,2} & \dots & z_{1,2n} \\ z_{2,1} & z_{2,2} & \dots & z_{2,2n} \end{bmatrix}, \end{align*}$$
$$\begin{align*}z = \begin{bmatrix} z_{1,1} & z_{1,2} & \dots & z_{1,2n} \\ z_{2,1} & z_{2,2} & \dots & z_{2,2n} \end{bmatrix}, \end{align*}$$
where
![]() $ z_{i,j} $
’s are indeterminates. For
$ z_{i,j} $
’s are indeterminates. For
![]() $ 1\le i<j\le 2n $
, let
$ 1\le i<j\le 2n $
, let
![]() $ \Delta _{ij}:=\Delta _{ij}(z) $
be the maximal minor of
$ \Delta _{ij}:=\Delta _{ij}(z) $
be the maximal minor of
![]() $ z $
with respect to the
$ z $
with respect to the
![]() $ i $
th and
$ i $
th and
![]() $ j $
th columns (i.e.,
$ j $
th columns (i.e.,
![]() $ \Delta _{ij} = z_{1,i} z_{2,j} - z_{1,j} z_{2,i} $
). For a matching
$ \Delta _{ij} = z_{1,i} z_{2,j} - z_{1,j} z_{2,i} $
). For a matching
![]() $ M\in \operatorname {Mat}_{2n} $
, let
$ M\in \operatorname {Mat}_{2n} $
, let
 $$\begin{align*}\Delta_M := \Delta_M(z) = \prod_{\{i,j\}\in M} \Delta_{ij} \in \mathbb{C}[z_{1,1},\dots,z_{2,2n}]. \end{align*}$$
$$\begin{align*}\Delta_M := \Delta_M(z) = \prod_{\{i,j\}\in M} \Delta_{ij} \in \mathbb{C}[z_{1,1},\dots,z_{2,2n}]. \end{align*}$$
It is important to note that the polynomials
![]() $ \Delta _{ij} $
satisfy the following relation: For
$ \Delta _{ij} $
satisfy the following relation: For
![]() $ 1\le a<b<c< d \le 2n$
,
$ 1\le a<b<c< d \le 2n$
,
We define a vector space
![]() $ W_n $
to be the
$ W_n $
to be the
![]() $ \mathbb {C} $
-span of
$ \mathbb {C} $
-span of
![]() $ \Delta _M $
for all
$ \Delta _M $
for all
![]() $ M\in \operatorname {Mat}_{2n} $
. In [Reference Kung and RotaKR84], it turns out that the set
$ M\in \operatorname {Mat}_{2n} $
. In [Reference Kung and RotaKR84], it turns out that the set
forms a basis for
![]() $ W_n $
. We call this basis the web basis. (The web basis was developed in the
$ W_n $
. We call this basis the web basis. (The web basis was developed in the
![]() $ \operatorname {SL}_2 $
-invariant theory due to Kuperburg [Reference KuperbergKup96], and its original construction slightly differs from the one we describe above. But they are essentially the same; see [Reference RhoadesRho19].)
$ \operatorname {SL}_2 $
-invariant theory due to Kuperburg [Reference KuperbergKup96], and its original construction slightly differs from the one we describe above. But they are essentially the same; see [Reference RhoadesRho19].)
In addition, there is a natural
![]() $ \mathfrak {S}_{2n} $
-action on
$ \mathfrak {S}_{2n} $
-action on
![]() $ W_n $
as follows: Regarding a permutation
$ W_n $
as follows: Regarding a permutation
![]() $ \sigma \in \mathfrak {S}_{2n} $
as a
$ \sigma \in \mathfrak {S}_{2n} $
as a
![]() $ 2n\times 2n $
permutation matrix, define
$ 2n\times 2n $
permutation matrix, define
![]() $ \sigma \cdot \Delta _M(z) := \Delta _M(z\sigma ^{-1}) $
. Then the space
$ \sigma \cdot \Delta _M(z) := \Delta _M(z\sigma ^{-1}) $
. Then the space
![]() $ W_n $
is closed under this action and hence carries an
$ W_n $
is closed under this action and hence carries an
![]() $ \mathfrak {S}_{2n} $
-module structure. Furthermore, the
$ \mathfrak {S}_{2n} $
-module structure. Furthermore, the
![]() $ \mathfrak {S}_{2n} $
-module
$ \mathfrak {S}_{2n} $
-module
![]() $ W_n $
is isomorphic to the Specht module
$ W_n $
is isomorphic to the Specht module
![]() $ \mathcal {S}^{(n,n)} $
[Reference Petersen, Pylyavskyy and RhoadesPPR09]. Therefore, due to Schur’s lemma, there is a unique (up to scalar) isomorphism
$ \mathcal {S}^{(n,n)} $
[Reference Petersen, Pylyavskyy and RhoadesPPR09]. Therefore, due to Schur’s lemma, there is a unique (up to scalar) isomorphism
![]() $ \varphi :W_n \rightarrow \mathcal {S}^{(n,n)} $
.
$ \varphi :W_n \rightarrow \mathcal {S}^{(n,n)} $
.
Let
![]() $ M_0 $
be the unique matching which is simultaneously noncrossing and nonnesting (i.e.,
$ M_0 $
be the unique matching which is simultaneously noncrossing and nonnesting (i.e.,
![]() $ M_0 = \{ \{1,2\},\dots ,\{2n-1,2n\} \} $
). Due to [Reference Russell and TymoczkoRT19], the isomorphism
$ M_0 = \{ \{1,2\},\dots ,\{2n-1,2n\} \} $
). Due to [Reference Russell and TymoczkoRT19], the isomorphism
![]() $ \varphi $
maps
$ \varphi $
maps
![]() $ \Delta _{M_0} $
to
$ \Delta _{M_0} $
to
![]() $ v_{M_0} $
up to scalar, and thus we choose an appropriate scalar so that
$ v_{M_0} $
up to scalar, and thus we choose an appropriate scalar so that
![]() $ \varphi (\Delta _{M_0}) = v_{M_0} $
. We also let
$ \varphi (\Delta _{M_0}) = v_{M_0} $
. We also let
![]() $ w_M := \varphi (\Delta _M) $
for each
$ w_M := \varphi (\Delta _M) $
for each
![]() $ M\in \operatorname {NC}_{2n} $
. Then the Specht basis can expand into (the image of) the web basis: For
$ M\in \operatorname {NC}_{2n} $
. Then the Specht basis can expand into (the image of) the web basis: For
![]() $ M\in \operatorname {NN}_{2n} $
,
$ M\in \operatorname {NN}_{2n} $
,
In [Reference Russell and TymoczkoRT19], Russell and Tymoczko initiated the combinatorial study of the transition matrix
They constructed directed graphs on the standard Young tableaux and noncrossing matchings, and using them, showed the unitriangularity of the matrix. They also gave some open problems related to their results. One of them is the positivity of the entries of
![]() $ A $
, which was proved by Rhoades soon after.
$ A $
, which was proved by Rhoades soon after.
Theorem 1.1 [Reference RhoadesRho19].
The entries
![]() $ a_{MM'} $
of the transition matrix
$ a_{MM'} $
of the transition matrix
![]() $ A $
are nonnegative integers.
$ A $
are nonnegative integers.
Although Rhoades established the positivity phenomenon for entries of
![]() $ A $
, he did not find an explicit combinatorial interpretation of the nonnegative integer
$ A $
, he did not find an explicit combinatorial interpretation of the nonnegative integer
![]() $ a_{MM'} $
, c.f. [Reference RhoadesRho19, Problem 1.3]. Inspired by his work, we introduce a new family of permutations which are enumerated by the integers
$ a_{MM'} $
, c.f. [Reference RhoadesRho19, Problem 1.3]. Inspired by his work, we introduce a new family of permutations which are enumerated by the integers
![]() $ a_{MM'} $
, and we study their enumerative properties.
$ a_{MM'} $
, and we study their enumerative properties.
Our strategy is based on Rhoades’s observation [Reference RhoadesRho19]. He figured out that the entries
![]() $ a_{MM'} $
are related to resolving crossings of matchings in the following sense: For a matching
$ a_{MM'} $
are related to resolving crossings of matchings in the following sense: For a matching
![]() $ M\in \operatorname {Mat}_{2n} $
, let
$ M\in \operatorname {Mat}_{2n} $
, let
![]() $ \{ a,c \} $
and
$ \{ a,c \} $
and
![]() $ \{ b,d \} $
be a crossing pair in
$ \{ b,d \} $
be a crossing pair in
![]() $ M $
(if it exists), where
$ M $
(if it exists), where
![]() $ a<b<c<d $
. Let
$ a<b<c<d $
. Let
![]() $ M' $
and
$ M' $
and
![]() $ M" $
be the matchings identical to
$ M" $
be the matchings identical to
![]() $ M $
except that
$ M $
except that
![]() $ \{ a,b \} $
and
$ \{ a,b \} $
and
![]() $ \{ c,d \} $
in
$ \{ c,d \} $
in
![]() $ M' $
, and
$ M' $
, and
![]() $ \{ a,d \} $
and
$ \{ a,d \} $
and
![]() $ \{ b,c \} $
in
$ \{ b,c \} $
in
![]() $ M" $
. Then, by the relation (1), we have
$ M" $
. Then, by the relation (1), we have
In addition, the number of crossing pairs in
![]() $ M' $
(respectively,
$ M' $
(respectively,
![]() $ M" $
) is strictly less than the number of crossing pairs in
$ M" $
) is strictly less than the number of crossing pairs in
![]() $ M $
. Therefore, iterating the resolving procedure gives the expansion of
$ M $
. Therefore, iterating the resolving procedure gives the expansion of
![]() $ \Delta _M $
in terms of the basis (2). In other words, when we write
$ \Delta _M $
in terms of the basis (2). In other words, when we write
the coefficient
![]() $ c_{MM'} $
is equal to the number of occurrences of the noncrossing matching
$ c_{MM'} $
is equal to the number of occurrences of the noncrossing matching
![]() $ M' $
obtained by iteratively resolving crossings in
$ M' $
obtained by iteratively resolving crossings in
![]() $ M $
. Note that the order of the choice of crossing pairs does not affect the expansion of
$ M $
. Note that the order of the choice of crossing pairs does not affect the expansion of
![]() $ \Delta _M $
. Rhoades showed that for
$ \Delta _M $
. Rhoades showed that for
![]() $ M\in \operatorname {NN}_{2n} $
and
$ M\in \operatorname {NN}_{2n} $
and
![]() $ M'\in \operatorname {NC}_{2n} $
, the entry
$ M'\in \operatorname {NC}_{2n} $
, the entry
![]() $ a_{MM'} $
of the transition matrix equals
$ a_{MM'} $
of the transition matrix equals
![]() $ c_{MM'} $
. Hence, to give a combinatorial interpretation of
$ c_{MM'} $
. Hence, to give a combinatorial interpretation of
![]() $ a_{MM'} $
, we track the resolving process from a nonnesting matching to noncrossing matchings.
$ a_{MM'} $
, we track the resolving process from a nonnesting matching to noncrossing matchings.
To state our main result, we need some preliminaries. We first note that noncrossing matchings and nonnesting matchings are Catalan objects. In other words, they are enumerated by Catalan numbers. Another famous Catalan object is a Dyck path. A Dyck path of length
![]() $ 2n $
is a lattice path from
$ 2n $
is a lattice path from
![]() $ (0,0) $
to
$ (0,0) $
to
![]() $ (n,n) $
consisting of
$ (n,n) $
consisting of
![]() $ n $
north steps
$ n $
north steps
![]() $ (0,1) $
and
$ (0,1) $
and
![]() $ n $
east steps
$ n $
east steps
![]() $ (1,0) $
that does not pass below the line
$ (1,0) $
that does not pass below the line
![]() $ y=x $
. We write
$ y=x $
. We write
![]() $ \mathsf {N} $
and
$ \mathsf {N} $
and
![]() $ \mathsf {E} $
for the north step and the east step, respectively. We therefore regard a Dyck path as a sequence consisting of
$ \mathsf {E} $
for the north step and the east step, respectively. We therefore regard a Dyck path as a sequence consisting of
![]() $ n \ \mathsf {N} $
’s and
$ n \ \mathsf {N} $
’s and
![]() $ n \ \mathsf {E} $
’s. Let
$ n \ \mathsf {E} $
’s. Let
![]() $\operatorname {Dyck}_{2n}$
be the set of Dyck paths of length
$\operatorname {Dyck}_{2n}$
be the set of Dyck paths of length
![]() $ 2n $
. Identifying a Dyck path with the region below the path, we give a natural partial order on
$ 2n $
. Identifying a Dyck path with the region below the path, we give a natural partial order on
![]() $ \operatorname {Dyck}_{2n} $
by inclusion, denoted by
$ \operatorname {Dyck}_{2n} $
by inclusion, denoted by
![]() $ \subseteq $
. For instance, the Dyck path
$ \subseteq $
. For instance, the Dyck path
![]() $\mathsf {N}\cdots \mathsf {N}\mathsf {E}\cdots \mathsf {E}$
where
$\mathsf {N}\cdots \mathsf {N}\mathsf {E}\cdots \mathsf {E}$
where
![]() $n \ \mathsf {N}$
’s precede
$n \ \mathsf {N}$
’s precede
![]() $n \ \mathsf {E} $
’s is the maximum path in
$n \ \mathsf {E} $
’s is the maximum path in
![]() $\operatorname {Dyck}_{2n}$
with respect to the partial order, whereas the path
$\operatorname {Dyck}_{2n}$
with respect to the partial order, whereas the path
![]() $\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {E}\cdots \mathsf {N}\mathsf {E}$
is the minimum path. In Section 2, we define a map
$\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {E}\cdots \mathsf {N}\mathsf {E}$
is the minimum path. In Section 2, we define a map
![]() $D:\operatorname {Mat}_{2n}\rightarrow \operatorname {Dyck}_{2n}$
, and by abuse of notation, a map
$D:\operatorname {Mat}_{2n}\rightarrow \operatorname {Dyck}_{2n}$
, and by abuse of notation, a map
![]() $D:\mathfrak {S}_n\rightarrow \operatorname {Dyck}_{2n}$
. We also define a map
$D:\mathfrak {S}_n\rightarrow \operatorname {Dyck}_{2n}$
. We also define a map
![]() $ M:\mathfrak {S}_n\rightarrow \operatorname {NC}_{2n} $
. Finally, we introduce a new family of permutations, called web permutations. With these data, we now present one of our main results.
$ M:\mathfrak {S}_n\rightarrow \operatorname {NC}_{2n} $
. Finally, we introduce a new family of permutations, called web permutations. With these data, we now present one of our main results.
Theorem 1.2. For matchings
![]() $ M\in \operatorname {NN}_{2n} $
and
$ M\in \operatorname {NN}_{2n} $
and
![]() $ M'\in \operatorname {NC}_{2n} $
, the entry
$ M'\in \operatorname {NC}_{2n} $
, the entry
![]() $ a_{MM'} $
is equal to the number of web permutations
$ a_{MM'} $
is equal to the number of web permutations
![]() $ \sigma \in \mathfrak {S}_n $
such that
$ \sigma \in \mathfrak {S}_n $
such that
![]() $ D(\sigma )\subseteq D(M) $
and
$ D(\sigma )\subseteq D(M) $
and
![]() $M(\sigma )=M'$
.
$M(\sigma )=M'$
.
The theorem follows almost immediately from the definition of the novel permutations. However, the definition does not directly tell us whether a given permutation is a web permutation or not. Our second main result, Theorem 3.4, explains how to characterize these permutations in terms of their cycle structures. Using this characterization, we deduce the results in [Reference Russell and TymoczkoRT19, Reference Im and ZhuIZ22] concerning the unitriangularity of the transition matrix and a necessary and sufficient condition for additional vanishing entries. Furthermore, the characterization leads us to enumerative properties of web permutations. To be more precise, Euler numbers count web permutations (Corollary 4.2), and we present a conjecture related web permutations and the Seidel triangle, which generalizes a result of Nakamigawa [Reference NakamigawaNak20] (Conjecture 4.9).
The article is organized as follows. In Section 2, we give a new model, called a grid configuration, for representing matchings. Within this model, we resolve crossings in nonnesting matchings until there is no crossing. We then define web permutations from the noncrossing grid configurations, and we prove Theorem 1.2. In the next two sections, we study some properties of web permutations. In Section 3, we give a characterization of web permutations. We show that web permutations are closely related to André permutations. Section 4 provides some interesting enumerative properties of web permutations.
2 Grid configurations and web permutations
In this section, we define grid configurations which represent matchings in a ‘rigid’ setting. We describe the procedure of resolving crossings within this model. We then introduce a new class of permutations, called web permutations. This provides a combinatorial interpretation for the entries
![]() $ a_{MM'} $
of the transition matrix.
$ a_{MM'} $
of the transition matrix.
Consider an
![]() $n \times n$
grid in the
$n \times n$
grid in the
![]() $xy$
-plane with corners
$xy$
-plane with corners
![]() $(0,0), (0,n), (n,0)$
and
$(0,0), (0,n), (n,0)$
and
![]() $(n,n)$
. We denote each cell by
$(n,n)$
. We denote each cell by
![]() $(i,j)$
, where i and j are the x- and y-coordinates of its upper-right corner. Let
$(i,j)$
, where i and j are the x- and y-coordinates of its upper-right corner. Let
![]() $\sigma \in \mathfrak {S}_n$
be a permutation. For each
$\sigma \in \mathfrak {S}_n$
be a permutation. For each
![]() $1\le i\le n$
, mark the cell
$1\le i\le n$
, mark the cell
![]() $ (i,\sigma (i)) $
, and draw a horizontal line to the left and a vertical line to the top from the marked cell. We call this the empty grid configuration of
$ (i,\sigma (i)) $
, and draw a horizontal line to the left and a vertical line to the top from the marked cell. We call this the empty grid configuration of
![]() $ \sigma $
. A cell
$ \sigma $
. A cell
![]() $(i,j)$
is called a crossing of
$(i,j)$
is called a crossing of
![]() $ \sigma $
if there are both a vertical line and a horizontal line through the cell in the empty grid configuration; that is,
$ \sigma $
if there are both a vertical line and a horizontal line through the cell in the empty grid configuration; that is,
![]() $ \sigma (i) < j $
and
$ \sigma (i) < j $
and
![]() $ i < \sigma ^{-1}(j) $
. We denote by
$ i < \sigma ^{-1}(j) $
. We denote by
![]() $ \operatorname {Cr}(\sigma ) $
the set of all crossings of
$ \operatorname {Cr}(\sigma ) $
the set of all crossings of
![]() $ \sigma $
. For a subset
$ \sigma $
. For a subset
![]() $ E\subseteq \operatorname {Cr}(\sigma ) $
, the grid configuration
$ E\subseteq \operatorname {Cr}(\sigma ) $
, the grid configuration
![]() $ G(\sigma ,E) $
of a pair
$ G(\sigma ,E) $
of a pair
![]() $ (\sigma , E) $
is defined to be the empty grid configuration of
$ (\sigma , E) $
is defined to be the empty grid configuration of
![]() $ \sigma $
where each crossing in
$ \sigma $
where each crossing in
![]() $ E $
is replaced by an elbow as shown in Figure 3. In particular, the empty grid configuration of
$ E $
is replaced by an elbow as shown in Figure 3. In particular, the empty grid configuration of
![]() $ \sigma $
is
$ \sigma $
is
![]() $ G(\sigma ,\emptyset ) $
.
$ G(\sigma ,\emptyset ) $
.

Figure 3 A crossing to an elbow.
For the
![]() $ n \times n $
grid, we label leftmost vertical intervals from bottom to top with 1 through n and uppermost horizontal intervals from left to right with
$ n \times n $
grid, we label leftmost vertical intervals from bottom to top with 1 through n and uppermost horizontal intervals from left to right with
![]() $n+1$
through
$n+1$
through
![]() $2n$
. With this label of boundary intervals, a grid configuration can be considered as a matching on
$2n$
. With this label of boundary intervals, a grid configuration can be considered as a matching on
![]() $ [2n] $
as follows: Each strand joining ith and jth boundary intervals represents an arc connecting i and j; see Figure 4. We denote by
$ [2n] $
as follows: Each strand joining ith and jth boundary intervals represents an arc connecting i and j; see Figure 4. We denote by
![]() $M(\sigma ,E)$
the matching associated to the grid configuration
$M(\sigma ,E)$
the matching associated to the grid configuration
![]() $ G(\sigma ,E) $
. For short, we write
$ G(\sigma ,E) $
. For short, we write
![]() $ M(\sigma ) = M(\sigma , \operatorname {Cr}(\sigma )) $
.
$ M(\sigma ) = M(\sigma , \operatorname {Cr}(\sigma )) $
.

Figure 4 The grid configuration
![]() $G(1324,\{(1,3),(1,4)\})$
and the corresponding matching.
$G(1324,\{(1,3),(1,4)\})$
and the corresponding matching.
We define a partial order on cells of the
![]() $n \times n$
grid by
$n \times n$
grid by
![]() $(x,y)\succeq (x',y')$
if
$(x,y)\succeq (x',y')$
if
![]() $x\le x'$
and
$x\le x'$
and
![]() $y\ge y'$
. In other words,
$y\ge y'$
. In other words,
![]() $ (x,y)\succeq (x',y') $
if and only if the cell
$ (x,y)\succeq (x',y') $
if and only if the cell
![]() $ (x,y) $
lies on the upper-left quadrant at
$ (x,y) $
lies on the upper-left quadrant at
![]() $ (x', y') $
.
$ (x', y') $
.
In the relation (3), the crossing pair (
![]() $ \{a,c\} $
and
$ \{a,c\} $
and
![]() $ \{b,d\} $
in
$ \{b,d\} $
in
![]() $ M $
) is resolved in two different ways. Similarly, we introduce two operations to resolve a crossing in a grid configuration. For a permutation
$ M $
) is resolved in two different ways. Similarly, we introduce two operations to resolve a crossing in a grid configuration. For a permutation
![]() $ \sigma $
and
$ \sigma $
and
![]() $ E\subsetneq \operatorname {Cr}(\sigma ) $
, let
$ E\subsetneq \operatorname {Cr}(\sigma ) $
, let
![]() $c=(i,j)$
be a crossing in the grid configuration
$c=(i,j)$
be a crossing in the grid configuration
![]() $G(\sigma ,E)$
, i.e.,
$G(\sigma ,E)$
, i.e.,
![]() $ c\in \operatorname {Cr}(\sigma )\setminus E $
. Then one can resolve the crossing
$ c\in \operatorname {Cr}(\sigma )\setminus E $
. Then one can resolve the crossing
![]() $ c $
by replacing it with an elbow, which gives the grid configuration
$ c $
by replacing it with an elbow, which gives the grid configuration
![]() $ G(\sigma ,E\cup \{c\}) $
. We call this operation smoothing. Note that the smoothing operation coincides with the process giving
$ G(\sigma ,E\cup \{c\}) $
. We call this operation smoothing. Note that the smoothing operation coincides with the process giving
![]() $ M' $
from
$ M' $
from
![]() $ M $
in the relation (3). To obtain a grid configuration corresponding to
$ M $
in the relation (3). To obtain a grid configuration corresponding to
![]() $ M" $
, we need an additional assumption on the grid configuration
$ M" $
, we need an additional assumption on the grid configuration
![]() $ G(\sigma , E) $
and the crossing
$ G(\sigma , E) $
and the crossing
![]() $ c $
. We assume that
$ c $
. We assume that
Let
![]() $ c=(i,j) $
,
$ c=(i,j) $
,
![]() $ k=\sigma (i) $
and
$ k=\sigma (i) $
and
![]() $ \ell =\sigma ^{-1}(j) $
. Due to the assumption, the crossing is made by the vertical line from the marked cell
$ \ell =\sigma ^{-1}(j) $
. Due to the assumption, the crossing is made by the vertical line from the marked cell
![]() $ (i, k) $
and the horizontal line from the marked cell
$ (i, k) $
and the horizontal line from the marked cell
![]() $ (\ell ,j) $
. Let
$ (\ell ,j) $
. Let
![]() $ \sigma ' $
be a permutation given by
$ \sigma ' $
be a permutation given by
 $$\begin{align*}\sigma'(m) = \begin{cases} j, & \mbox{if } m=i , \\ k, & \mbox{if } m=\ell , \\ \sigma(m), & \mbox{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\sigma'(m) = \begin{cases} j, & \mbox{if } m=i , \\ k, & \mbox{if } m=\ell , \\ \sigma(m), & \mbox{otherwise.} \end{cases} \end{align*}$$
Equivalently, we let
![]() $ \sigma '=\sigma \cdot t_{i,\ell } $
, where
$ \sigma '=\sigma \cdot t_{i,\ell } $
, where
![]() $ t_{i,\ell } $
is the transposition which swaps
$ t_{i,\ell } $
is the transposition which swaps
![]() $ i $
and
$ i $
and
![]() $ \ell $
. Then
$ \ell $
. Then
![]() $ c\notin \operatorname {Cr}(\sigma ') $
, and every crossing in
$ c\notin \operatorname {Cr}(\sigma ') $
, and every crossing in
![]() $ \operatorname {Cr}(\sigma ) $
which is not less than
$ \operatorname {Cr}(\sigma ) $
which is not less than
![]() $ c $
belongs to
$ c $
belongs to
![]() $ \operatorname {Cr}(\sigma ') $
, and vice versa. Hence, we have
$ \operatorname {Cr}(\sigma ') $
, and vice versa. Hence, we have
![]() $ E\subseteq \operatorname {Cr}(\sigma ') $
. Moreover, at the level of matchings, the only two arcs going through the cell
$ E\subseteq \operatorname {Cr}(\sigma ') $
. Moreover, at the level of matchings, the only two arcs going through the cell
![]() $ c $
in
$ c $
in
![]() $ G(\sigma ,E) $
are changed in
$ G(\sigma ,E) $
are changed in
![]() $ M(\sigma ',E) $
. In other words, the crossing
$ M(\sigma ',E) $
. In other words, the crossing
![]() $ c $
is resolved in
$ c $
is resolved in
![]() $ G(\sigma ',E) $
, and the others leave unchanged. In addition,
$ G(\sigma ',E) $
, and the others leave unchanged. In addition,
![]() $ M(\sigma ,E\cup \{c\})\neq M(\sigma ',E)$
. Therefore, we conclude
$ M(\sigma ,E\cup \{c\})\neq M(\sigma ',E)$
. Therefore, we conclude
![]() $ M(\sigma ',E) = M" $
in the relation (3). We call this operation, giving
$ M(\sigma ',E) = M" $
in the relation (3). We call this operation, giving
![]() $ G(\sigma ',E) $
from
$ G(\sigma ',E) $
from
![]() $ G(\sigma ,E) $
, switching. Roughly speaking, the switching operation is that if two marked cells
$ G(\sigma ,E) $
, switching. Roughly speaking, the switching operation is that if two marked cells
![]() $ (i,k) $
and
$ (i,k) $
and
![]() $ (\ell ,j) $
make a crossing at
$ (\ell ,j) $
make a crossing at
![]() $ (i,j) $
, then move the marked cells to
$ (i,j) $
, then move the marked cells to
![]() $ (i,j) $
and
$ (i,j) $
and
![]() $ (\ell ,k) $
.
$ (\ell ,k) $
.
We consider a grid configuration G as the vector
![]() $\Delta _{M(G)}$
. We can then rewrite the relation (3) in terms of grid configurations as follows: For a permutation
$\Delta _{M(G)}$
. We can then rewrite the relation (3) in terms of grid configurations as follows: For a permutation
![]() $ \sigma $
,
$ \sigma $
,
![]() $ E\subsetneq \operatorname {Cr}(\sigma ) $
and a crossing
$ E\subsetneq \operatorname {Cr}(\sigma ) $
and a crossing
![]() $ c\in \operatorname {Cr}(\sigma )\setminus E $
satisfying the condition (5), we have
$ c\in \operatorname {Cr}(\sigma )\setminus E $
satisfying the condition (5), we have
For example, let
![]() $ \sigma =1324\in \mathfrak {S}_4 $
and
$ \sigma =1324\in \mathfrak {S}_4 $
and
![]() $ E=\{(1,3),(1,4)\} $
, and consider the grid configuration
$ E=\{(1,3),(1,4)\} $
, and consider the grid configuration
![]() $ G(\sigma , E) $
which is shown in Figure 4. Resolving a crossing
$ G(\sigma , E) $
which is shown in Figure 4. Resolving a crossing
![]() $ c=(2,4)\in \operatorname {Cr}(\sigma )\setminus E $
, we have
$ c=(2,4)\in \operatorname {Cr}(\sigma )\setminus E $
, we have

Here, the red dot indicates the crossing
![]() $ c $
.
$ c $
.
In what follows, we always choose a set
![]() $ E $
as an upper order ideal in
$ E $
as an upper order ideal in
![]() $ \operatorname {Cr}(\sigma ) $
, and a crossing
$ \operatorname {Cr}(\sigma ) $
, and a crossing
![]() $ c $
as a maximal crossing in
$ c $
as a maximal crossing in
![]() $ \operatorname {Cr}(\sigma )\setminus E $
. Then
$ \operatorname {Cr}(\sigma )\setminus E $
. Then
![]() $ E\cup \{c\} $
is also an upper order ideal in
$ E\cup \{c\} $
is also an upper order ideal in
![]() $ \operatorname {Cr}(\sigma ) $
, and furthermore, the condition (5) always will be satisfied.
$ \operatorname {Cr}(\sigma ) $
, and furthermore, the condition (5) always will be satisfied.
From the grid configuration
![]() $G(id, \emptyset )$
, we obtain two grid configurations by resolving the maximal crossing
$G(id, \emptyset )$
, we obtain two grid configurations by resolving the maximal crossing
![]() $ (1,n) $
by the smoothing and switching operations, respectively. By resolving crossings until there is no crossing left, we get grid configurations of the form
$ (1,n) $
by the smoothing and switching operations, respectively. By resolving crossings until there is no crossing left, we get grid configurations of the form
![]() $G(\sigma , \operatorname {Cr}(\sigma ))$
. For each remaining grid configuration
$G(\sigma , \operatorname {Cr}(\sigma ))$
. For each remaining grid configuration
![]() $G(\sigma , \operatorname {Cr}(\sigma ))$
, the permutation
$G(\sigma , \operatorname {Cr}(\sigma ))$
, the permutation
![]() $\sigma $
is called a web permutation of
$\sigma $
is called a web permutation of
![]() $[n]$
and we denote the set of web permutations of
$[n]$
and we denote the set of web permutations of
![]() $[n]$
by
$[n]$
by
![]() $\operatorname {Web}_n$
. We will see that web permutations do not depend on the choice of maximal crossings
$\operatorname {Web}_n$
. We will see that web permutations do not depend on the choice of maximal crossings
![]() $ c $
in the resolving processes (Proposition 2.1). We would like to highlight the following expression in terms of grid configurations:
$ c $
in the resolving processes (Proposition 2.1). We would like to highlight the following expression in terms of grid configurations:
Here, the summation on the right-hand side is over all permutations
![]() $\sigma $
that arise from resolving crossings in the grid configuration
$\sigma $
that arise from resolving crossings in the grid configuration
![]() $G(id, \emptyset )$
through the smoothing and switching operations, continuing until no crossings remain. This equation can be regarded as an enhanced representation of (4) with respect to grid configurations. For example, starting from the grid configuration
$G(id, \emptyset )$
through the smoothing and switching operations, continuing until no crossings remain. This equation can be regarded as an enhanced representation of (4) with respect to grid configurations. For example, starting from the grid configuration
![]() $G(id,\emptyset )$
for
$G(id,\emptyset )$
for
![]() $n=3$
, we have
$n=3$
, we have

Therefore, we conclude that
![]() $\operatorname {Web}_3=\{123, 213, 132, 231, 321\}$
. The following proposition justifies that web permutations are well-defined.
$\operatorname {Web}_3=\{123, 213, 132, 231, 321\}$
. The following proposition justifies that web permutations are well-defined.
Proposition 2.1. The expansion in (6) is unique. In other words, the grid configurations appearing in (6) do not depend on the order of resolving procedure (choice of maximal crossings). In addition, the permutations
![]() $\sigma $
in (6) are all distinct.
$\sigma $
in (6) are all distinct.
Proof. Let
![]() $ G(\sigma ,E) $
be a grid configuration obtained from
$ G(\sigma ,E) $
be a grid configuration obtained from
![]() $G(id,\emptyset )$
through a process of resolving crossings using the smoothing and switching operations. Let
$G(id,\emptyset )$
through a process of resolving crossings using the smoothing and switching operations. Let
![]() $ c $
and
$ c $
and
![]() $ c' $
denote two maximal crossings in
$ c' $
denote two maximal crossings in
![]() $G(\sigma ,E)$
, where the x-coordinate of c is less than the x-coordinate of
$G(\sigma ,E)$
, where the x-coordinate of c is less than the x-coordinate of
![]() $c'$
. There are two cases to consider: (a) The y-coordinate of c and the x-coordinate of
$c'$
. There are two cases to consider: (a) The y-coordinate of c and the x-coordinate of
![]() $c'$
are the same, and (b) they are different. These cases are illustrated in Figure 5, where the crossings c and
$c'$
are the same, and (b) they are different. These cases are illustrated in Figure 5, where the crossings c and
![]() $c'$
are indicated by red dots.
$c'$
are indicated by red dots.

Figure 5 Two cases of maximal crossings.
In the first case, if we resolve both c and
![]() $c'$
with the same operation (both by the smoothing operations or both by the switching operations), the order of resolving c and
$c'$
with the same operation (both by the smoothing operations or both by the switching operations), the order of resolving c and
![]() $c'$
becomes irrelevant. Hence, we only need to show that resolving c in a way and
$c'$
becomes irrelevant. Hence, we only need to show that resolving c in a way and
![]() $c'$
in the other way leads to the same grid configuration obtained by resolving
$c'$
in the other way leads to the same grid configuration obtained by resolving
![]() $c'$
first and then c. This can be directly verified. Furthermore, for the second case, it is evident that the order of resolving crossings c and
$c'$
first and then c. This can be directly verified. Furthermore, for the second case, it is evident that the order of resolving crossings c and
![]() $c'$
is irrelevant.
$c'$
is irrelevant.
In general, any total order that extends the partial order
![]() $ \succeq $
on cells can be derived from another total order by performing a sequence of interchanging the order of two incomparable cells. In our case, it yields that it is sufficient to demonstrate that we can interchange the order of two maximal crossings in
$ \succeq $
on cells can be derived from another total order by performing a sequence of interchanging the order of two incomparable cells. In our case, it yields that it is sufficient to demonstrate that we can interchange the order of two maximal crossings in
![]() $ G(\sigma ,E) $
.
$ G(\sigma ,E) $
.
We now verify the distinctness part. Fix a total order on cells which extends the partial order, and we resolve crossings in
![]() $ G(id, \emptyset ) $
to obtain (6) with respect to the total order. Let
$ G(id, \emptyset ) $
to obtain (6) with respect to the total order. Let
![]() $G(\sigma ,\operatorname {Cr}(\sigma ))$
and
$G(\sigma ,\operatorname {Cr}(\sigma ))$
and
![]() $G(\tau ,\operatorname {Cr}(\tau ))$
be two grid configurations obtained from
$G(\tau ,\operatorname {Cr}(\tau ))$
be two grid configurations obtained from
![]() $G(id,\emptyset )$
through two distinct processes of resolving crossings using the smoothing and switching operations, until no crossings remain. Suppose that the processes of resolving crossings to obtain
$G(id,\emptyset )$
through two distinct processes of resolving crossings using the smoothing and switching operations, until no crossings remain. Suppose that the processes of resolving crossings to obtain
![]() $G(\sigma ,\operatorname {Cr}(\sigma ))$
and
$G(\sigma ,\operatorname {Cr}(\sigma ))$
and
![]() $G(\tau ,\operatorname {Cr}(\tau ))$
are the same until we obtain a grid configuration
$G(\tau ,\operatorname {Cr}(\tau ))$
are the same until we obtain a grid configuration
![]() $G(\rho ,E)$
, and let
$G(\rho ,E)$
, and let
![]() $c=(i,j)$
be the maximum crossing in
$c=(i,j)$
be the maximum crossing in
![]() $\operatorname {Cr}(\rho )\setminus E$
under the fixed total order. Furthermore, suppose that we resolve c by applying the smoothing operation in the process giving
$\operatorname {Cr}(\rho )\setminus E$
under the fixed total order. Furthermore, suppose that we resolve c by applying the smoothing operation in the process giving
![]() $G(\sigma ,\operatorname {Cr}(\sigma ))$
and by applying the switching operation in the process giving
$G(\sigma ,\operatorname {Cr}(\sigma ))$
and by applying the switching operation in the process giving
![]() $G(\tau ,\operatorname {Cr}(\tau ))$
. As there is an elbow at
$G(\tau ,\operatorname {Cr}(\tau ))$
. As there is an elbow at
![]() $(i,j)$
in
$(i,j)$
in
![]() $ G(\sigma ,\operatorname {Cr}(\sigma )) $
, we have
$ G(\sigma ,\operatorname {Cr}(\sigma )) $
, we have
![]() $\sigma (i)<j$
. However, since there is a marking at
$\sigma (i)<j$
. However, since there is a marking at
![]() $(i,j)$
in
$(i,j)$
in
![]() $ G(\tau ,\operatorname {Cr}(\tau )) $
after applying the switching operation to c, we have
$ G(\tau ,\operatorname {Cr}(\tau )) $
after applying the switching operation to c, we have
![]() $\tau (i)=j$
. Therefore, we conclude that
$\tau (i)=j$
. Therefore, we conclude that
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are distinct.
$\tau $
are distinct.
For a matching M, record
![]() $\mathsf {N}$
for openers and
$\mathsf {N}$
for openers and
![]() $\mathsf {E}$
for closers reading M from left to right. This gives the Dyck path
$\mathsf {E}$
for closers reading M from left to right. This gives the Dyck path
![]() $D(M)$
in the
$D(M)$
in the
![]() $n \times n$
grid. It is well-known that the two restrictions of the map
$n \times n$
grid. It is well-known that the two restrictions of the map
![]() $ D:\operatorname {Mat}_{2n}\rightarrow \operatorname {Dyck}_{2n} $
to
$ D:\operatorname {Mat}_{2n}\rightarrow \operatorname {Dyck}_{2n} $
to
![]() $ \operatorname {NC}_{2n} $
and
$ \operatorname {NC}_{2n} $
and
![]() $ \operatorname {NN}_{2n} $
are bijections. To a permutation
$ \operatorname {NN}_{2n} $
are bijections. To a permutation
![]() $\sigma $
, we associate the minimum Dyck path
$\sigma $
, we associate the minimum Dyck path
![]() $ D(\sigma ) $
where every cell
$ D(\sigma ) $
where every cell
![]() $ (i,\sigma (i)) $
lies below the path; see Figure 6.
$ (i,\sigma (i)) $
lies below the path; see Figure 6.

Figure 6 The Dyck path
![]() $ D(\sigma ) $
associated to
$ D(\sigma ) $
associated to
![]() $ \sigma =21354 $
is
$ \sigma =21354 $
is
![]() $ \mathsf {N}\mathsf {N}\mathsf {E}\mathsf {E}\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {N}\mathsf {E}\mathsf {E} $
.
$ \mathsf {N}\mathsf {N}\mathsf {E}\mathsf {E}\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {N}\mathsf {E}\mathsf {E} $
.
Given a nonnesting matching
![]() $ M\in \operatorname {NN}_{2n} $
, let
$ M\in \operatorname {NN}_{2n} $
, let
![]() $ E(M) $
be the set of cells in the
$ E(M) $
be the set of cells in the
![]() $n \times n$
grid which are above the path
$n \times n$
grid which are above the path
![]() $D(M)$
. Consider the matching
$D(M)$
. Consider the matching
![]() $ M(id,E(M)) $
. In the region below
$ M(id,E(M)) $
. In the region below
![]() $ D(M) $
, if
$ D(M) $
, if
![]() $ \{i,j\} $
is an arc in
$ \{i,j\} $
is an arc in
![]() $ M $
, then the
$ M $
, then the
![]() $ i $
th step and
$ i $
th step and
![]() $ j $
th step of
$ j $
th step of
![]() $ D(M) $
are connected by an arc in
$ D(M) $
are connected by an arc in
![]() $ G(id,E(M)) $
. Moreover, in the region above
$ G(id,E(M)) $
. Moreover, in the region above
![]() $ D(M) $
, each
$ D(M) $
, each
![]() $ i $
th step is connected to the
$ i $
th step is connected to the
![]() $ i $
th boundary interval. Thus,
$ i $
th boundary interval. Thus,
![]() $ \{i,j\} $
is also an arc in
$ \{i,j\} $
is also an arc in
![]() $ M(id,E(M)) $
, so we conclude that the matchings
$ M(id,E(M)) $
, so we conclude that the matchings
![]() $ M $
and
$ M $
and
![]() $ M(id,E(M)) $
coincide. For example, let
$ M(id,E(M)) $
coincide. For example, let
![]() $ M $
be the first matching in Figure 2. Then the corresponding path
$ M $
be the first matching in Figure 2. Then the corresponding path
![]() $ D(M) $
is
$ D(M) $
is
![]() $ \mathsf {N}\mathsf {E}\mathsf {N}\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {E}\mathsf {E} $
, and
$ \mathsf {N}\mathsf {E}\mathsf {N}\mathsf {N}\mathsf {E}\mathsf {N}\mathsf {E}\mathsf {E} $
, and
![]() $ E(M) = \{ (1,2), (1,3), (1,4), (2,4) \} $
. The grid configuration
$ E(M) = \{ (1,2), (1,3), (1,4), (2,4) \} $
. The grid configuration
![]() $ G(id, E(M)) $
is shown in Figure 7, and one can see
$ G(id, E(M)) $
is shown in Figure 7, and one can see
![]() $ M(id, E(M)) = M $
. Similar to the definition of
$ M(id, E(M)) = M $
. Similar to the definition of
![]() $ \operatorname {Web}_n $
, we consider the equation
$ \operatorname {Web}_n $
, we consider the equation

Figure 7 The grid configuration
![]() $ G(id, E(M)) $
and the Dyck path
$ G(id, E(M)) $
and the Dyck path
![]() $ D(M) $
where
$ D(M) $
where
![]() $ M=\{ \{1,2\},\{3,5\},\{4,7\},\{6,8\} \} $
.
$ M=\{ \{1,2\},\{3,5\},\{4,7\},\{6,8\} \} $
.
Here, the summation on the right-hand side is over all permutations
![]() $\sigma $
that arise from resolving crossings in the grid configuration
$\sigma $
that arise from resolving crossings in the grid configuration
![]() $G(id, E(M))$
through the smoothing and switching operations, continuing until no crossings remain. We then define
$G(id, E(M))$
through the smoothing and switching operations, continuing until no crossings remain. We then define
![]() $ \operatorname {Web}_M $
to be the set of permutations
$ \operatorname {Web}_M $
to be the set of permutations
![]() $ \sigma $
appearing in the right-hand side of the above equation. In particular,
$ \sigma $
appearing in the right-hand side of the above equation. In particular,
![]() $ \operatorname {Web}_n = \operatorname {Web}_M $
, where
$ \operatorname {Web}_n = \operatorname {Web}_M $
, where
![]() $ M=\{ \{1,n+1\}, \{2,n+2\},\dots , \{n,2n\} \}. $
$ M=\{ \{1,n+1\}, \{2,n+2\},\dots , \{n,2n\} \}. $
Using the above notations, we prove one of our main results that tells us which web permutations contribute to the entry
![]() $a_{MM'}$
.
$a_{MM'}$
.
Proof of Theorem 1.2.
By the definition of web permutations, we have
Hence, it is enough to show that
We can obtain the grid configuration
![]() $ G(id,E(M)) $
from
$ G(id,E(M)) $
from
![]() $ G(id,\emptyset ) $
by applying the smoothing operation to all crossings in
$ G(id,\emptyset ) $
by applying the smoothing operation to all crossings in
![]() $ E(M) $
. Since Proposition 2.1 says that
$ E(M) $
. Since Proposition 2.1 says that
![]() $ \operatorname {Web}_n $
does not depend on the order of resolving processes, we obtain
$ \operatorname {Web}_n $
does not depend on the order of resolving processes, we obtain
![]() $ \operatorname {Web}_M \subseteq \operatorname {Web}_n $
. From this, it is clear that
$ \operatorname {Web}_M \subseteq \operatorname {Web}_n $
. From this, it is clear that
 $$ \begin{align*} \operatorname{Web}_M &= \{ \sigma\in \operatorname{Web}_n : E(M)\subseteq \operatorname{Cr}(\sigma)\} \\ &= \{ \sigma\in \operatorname{Web}_n : (i,\sigma(i)) \not\in E(M) \mbox{ for all } i \}, \end{align*} $$
$$ \begin{align*} \operatorname{Web}_M &= \{ \sigma\in \operatorname{Web}_n : E(M)\subseteq \operatorname{Cr}(\sigma)\} \\ &= \{ \sigma\in \operatorname{Web}_n : (i,\sigma(i)) \not\in E(M) \mbox{ for all } i \}, \end{align*} $$
which proves the claim (7).
3 Characterization of web permutations
In the previous section, we have introduced the new class of permutations which are obtained by tracking the resolving process. In fact, Theorem 1.2 is just a byproduct of the definition of web permutations. In this section, we provide a characterization of these permutations. This characterization depends only on their permutation structures, especially their cycle structures. Using this characterization, we prove the results in [Reference Russell and TymoczkoRT19, Reference Im and ZhuIZ22] concerning the unitriangularity of the transition matrix and a necessary and sufficient condition for additional vanishing entries.
We begin with recalling two ways to represent permutations. One way is the one-line notation which we have already used – that is, regarding a permutation as a word. More precisely, for a permutation
![]() $ \sigma :[n]\rightarrow [n] $
, we write
$ \sigma :[n]\rightarrow [n] $
, we write
![]() $ \sigma = \sigma _1 \sigma _2 \dots \sigma _n $
, where
$ \sigma = \sigma _1 \sigma _2 \dots \sigma _n $
, where
![]() $ \sigma _i = \sigma (i) $
. Another way to write permutations is the cycle notation. Instead of the precise definition of this notation, we give an example; for the definition, see [Reference StanleySta12]. Let
$ \sigma _i = \sigma (i) $
. Another way to write permutations is the cycle notation. Instead of the precise definition of this notation, we give an example; for the definition, see [Reference StanleySta12]. Let
![]() $ \sigma = 564132\in \mathfrak {S}_6 $
; then the cycle notation of
$ \sigma = 564132\in \mathfrak {S}_6 $
; then the cycle notation of
![]() $ \sigma $
is
$ \sigma $
is
![]() $ (1,5,3,4)(2,6) $
. We always use parentheses and commas when writing cycles.
$ (1,5,3,4)(2,6) $
. We always use parentheses and commas when writing cycles.
Let us examine how the two resolving operations on a grid configuration
![]() $ G(\sigma ,E) $
affect the permutation
$ G(\sigma ,E) $
affect the permutation
![]() $ \sigma $
, particularly its cycle structure. By definition, the smoothing operation does not change the permutation
$ \sigma $
, particularly its cycle structure. By definition, the smoothing operation does not change the permutation
![]() $\sigma $
, whereas the switching operation does. Figure 8 provides an illustrative example of the switching operation. The left one in Figure 8 is a grid configuration
$\sigma $
, whereas the switching operation does. Figure 8 provides an illustrative example of the switching operation. The left one in Figure 8 is a grid configuration
![]() $ G(\sigma , E) $
, where
$ G(\sigma , E) $
, where
![]() $ \sigma =(1,5,4,6)(2,3,7) $
and
$ \sigma =(1,5,4,6)(2,3,7) $
and
![]() $ E=\operatorname {Cr}(\sigma )\setminus \{(6,2)\} $
. Applying the switching operation to the crossing
$ E=\operatorname {Cr}(\sigma )\setminus \{(6,2)\} $
. Applying the switching operation to the crossing
![]() $ (6,2) $
in
$ (6,2) $
in
![]() $ G(\sigma ,E) $
yields the grid configuration
$ G(\sigma ,E) $
yields the grid configuration
![]() $ G(\tau , \operatorname {Cr}(\tau )) $
, where
$ G(\tau , \operatorname {Cr}(\tau )) $
, where
![]() $ \tau =(1,5,4,6, 2,3,7) $
; it is depicted on the right in Figure 8. Note that both permutations
$ \tau =(1,5,4,6, 2,3,7) $
; it is depicted on the right in Figure 8. Note that both permutations
![]() $ \sigma $
and
$ \sigma $
and
![]() $ \tau $
are web permutations. One can observe that in this example, the switching operation merges two cycles into one cycle. Keeping this example in mind might be helpful for comprehending this section.
$ \tau $
are web permutations. One can observe that in this example, the switching operation merges two cycles into one cycle. Keeping this example in mind might be helpful for comprehending this section.

Figure 8 Applying the switching operation to the left grid configuration with the crossing indicated as the red dot gives the right one.
To describe our characterization of web permutations, we review the notion of André permutations and define an analogue of them. André permutations were introduced by Foata and Schützenberger [Reference Foata and SchützenbergerFS73], and have been studied with several applications in the literature; see, for example, [Reference StanleySta94, Reference Foata and HanFH16]. One of the interesting properties of them is that they are enumerated by Euler numbers; see Section 4.
We now think of permutations as words consisting of distinct positive integers. André permutations are defined recursively as follows. First, the empty word and each one-letter word are André permutations. For a permutation
![]() $ w=w_1 w_2 \cdots w_n $
with
$ w=w_1 w_2 \cdots w_n $
with
![]() $ n\ge 2 $
, let
$ n\ge 2 $
, let
![]() $ w_k $
be the smallest letter in
$ w_k $
be the smallest letter in
![]() $ w $
. Then
$ w $
. Then
![]() $ w $
is an André permutation if both
$ w $
is an André permutation if both
![]() $ w_1 \cdots w_{k-1} $
and
$ w_1 \cdots w_{k-1} $
and
![]() $ w_{k+1}\cdots w_{n} $
are André permutations and
$ w_{k+1}\cdots w_{n} $
are André permutations and
![]() $ \max \{w_1,\dots ,w_{k-1}\} < \max \{w_{k+1},\dots ,w_n\} $
. For example, a word 546237 is an André permutation because the letter 2 is smallest, both two words 546 and 37 are André permutations, and
$ \max \{w_1,\dots ,w_{k-1}\} < \max \{w_{k+1},\dots ,w_n\} $
. For example, a word 546237 is an André permutation because the letter 2 is smallest, both two words 546 and 37 are André permutations, and
![]() $ \max \{5,4,6\}<\max \{3,7\} $
. Using this notion, we define a cycle analogue of André permutations.
$ \max \{5,4,6\}<\max \{3,7\} $
. Using this notion, we define a cycle analogue of André permutations.
Definition 3.1. Let
![]() $ C=(a_1,\dots ,a_k) $
be a cycle with
$ C=(a_1,\dots ,a_k) $
be a cycle with
![]() $ a_1 = \min \{a_1,\dots ,a_k\} $
. We say that
$ a_1 = \min \{a_1,\dots ,a_k\} $
. We say that
![]() $ C $
is an André cycle if the permutation
$ C $
is an André cycle if the permutation
![]() $ a_2\cdots a_k $
is an André permutation.
$ a_2\cdots a_k $
is an André permutation.
For instance, a cycle
![]() $ C = (2,3,7,1,5,4,6) $
is an André cycle since
$ C = (2,3,7,1,5,4,6) $
is an André cycle since
![]() $ C = (1,5,4,6,2,3,7) $
and the permutation 546237 is an André permutation.
$ C = (1,5,4,6,2,3,7) $
and the permutation 546237 is an André permutation.
For a cycle
![]() $ C=(a_1,\dots ,a_k) $
, we write
$ C=(a_1,\dots ,a_k) $
, we write
![]() $ \min C = \min \{a_1,\dots ,a_k\} $
and
$ \min C = \min \{a_1,\dots ,a_k\} $
and
![]() $ \max C = \max \{a_1,\dots ,a_k\}$
for short. The following lemma is useful in the sequel.
$ \max C = \max \{a_1,\dots ,a_k\}$
for short. The following lemma is useful in the sequel.
Lemma 3.2. Let
![]() $ C=(a_1,\dots ,a_k) $
be an André cycle with
$ C=(a_1,\dots ,a_k) $
be an André cycle with
![]() $ a_1=\min C $
. Then
$ a_1=\min C $
. Then
![]() $ a_k=\max C $
.
$ a_k=\max C $
.
Proof. By definition, the last letter of an André permutation is the largest element in the permutation. This fact directly gives the proof.
The following lemma gives how to obtain a new André cycle from old André cycles.
Lemma 3.3. Let
![]() $ C_1=(a_1,\dots ,a_k) $
and
$ C_1=(a_1,\dots ,a_k) $
and
![]() $ C_2=(b_1,\dots ,b_\ell ) $
be André cycles with
$ C_2=(b_1,\dots ,b_\ell ) $
be André cycles with
![]() $ a_1 = \min C_1 $
and
$ a_1 = \min C_1 $
and
![]() $ b_1=\min C_2 $
. If
$ b_1=\min C_2 $
. If
![]() $ a_1<b_1 $
and
$ a_1<b_1 $
and
![]() $ a_k<b_\ell $
, then the cycle
$ a_k<b_\ell $
, then the cycle
![]() $ (a_1,\dots ,a_k, b_1,\dots ,b_\ell ) $
is also an André cycle.
$ (a_1,\dots ,a_k, b_1,\dots ,b_\ell ) $
is also an André cycle.
Proof. We induct on
![]() $ k $
. First, consider the base case
$ k $
. First, consider the base case
![]() $ k=1 $
. Since
$ k=1 $
. Since
![]() $ a_1 = \min \{a_1,b_1,\dots ,b_\ell \} $
, we only need to show that the permutation
$ a_1 = \min \{a_1,b_1,\dots ,b_\ell \} $
, we only need to show that the permutation
![]() $ b_1\cdots b_k $
is an André permutation. This follows immediately from the definition of André permutations.
$ b_1\cdots b_k $
is an André permutation. This follows immediately from the definition of André permutations.
We now suppose
![]() $ k\ge 2 $
. Recall that the two permutations
$ k\ge 2 $
. Recall that the two permutations
![]() $ a_2\cdots a_k $
and
$ a_2\cdots a_k $
and
![]() $ b_2\cdots b_\ell $
are André permutations. In addition, by Lemma 3.2 and the assumption
$ b_2\cdots b_\ell $
are André permutations. In addition, by Lemma 3.2 and the assumption
![]() $ a_k< b_\ell $
, we have
$ a_k< b_\ell $
, we have
![]() $ \max \{a_2,\dots ,a_k\}<\max \{b_2,\dots ,b_\ell \} $
. Thus, if
$ \max \{a_2,\dots ,a_k\}<\max \{b_2,\dots ,b_\ell \} $
. Thus, if
![]() $ b_1< \min \{a_2,\dots ,a_k\} $
, then the permutation
$ b_1< \min \{a_2,\dots ,a_k\} $
, then the permutation
![]() $ a_2\cdots a_k b_1\cdots b_\ell $
is an André permutation. Otherwise, let
$ a_2\cdots a_k b_1\cdots b_\ell $
is an André permutation. Otherwise, let
![]() $ a_p=\min \{a_2,\dots ,a_k\} $
for some
$ a_p=\min \{a_2,\dots ,a_k\} $
for some
![]() $ p $
, so that
$ p $
, so that
![]() $ a_p < b_1 $
and both
$ a_p < b_1 $
and both
![]() $ a_2\cdots a_{p-1} $
and
$ a_2\cdots a_{p-1} $
and
![]() $ a_{p+1}\cdots a_k $
are André permutations. By the induction hypothesis, we have that the cycle
$ a_{p+1}\cdots a_k $
are André permutations. By the induction hypothesis, we have that the cycle
![]() $ (a_p,\dots ,a_k,b_1,\dots ,b_\ell ) $
is an André cycle. It is also clear that
$ (a_p,\dots ,a_k,b_1,\dots ,b_\ell ) $
is an André cycle. It is also clear that
![]() $ a_{p-1} < a_k < b_\ell $
. Again, by the induction hypothesis, we deduce that the cycle
$ a_{p-1} < a_k < b_\ell $
. Again, by the induction hypothesis, we deduce that the cycle
![]() $ (a_1,\dots ,a_k, b_1,\dots ,b_\ell ) $
is an André cycle, which yields the desired result.
$ (a_1,\dots ,a_k, b_1,\dots ,b_\ell ) $
is an André cycle, which yields the desired result.
We now show another main result of the article, which gives a characterization of web permutations.
Theorem 3.4. A permutation
![]() $ \sigma \in \mathfrak {S}_n $
is a web permutation if and only if each cycle of
$ \sigma \in \mathfrak {S}_n $
is a web permutation if and only if each cycle of
![]() $ \sigma $
is an André cycle.
$ \sigma $
is an André cycle.
Proof. Recall that the web permutations do not depend on the order of choices of maximal crossings. Hence, we fix the following total order on the cells in the
![]() $ n \times n $
grid, which completes the partial order, and we assume that our resolving process respects this total order: For two cells
$ n \times n $
grid, which completes the partial order, and we assume that our resolving process respects this total order: For two cells
![]() $ (i,j) $
and
$ (i,j) $
and
![]() $ (i',j') $
, we let
$ (i',j') $
, we let
![]() $ (i,j)>(i',j') $
if either
$ (i,j)>(i',j') $
if either
![]() $ j>j' $
, or
$ j>j' $
, or
![]() $ j=j' $
and
$ j=j' $
and
![]() $ i<i' $
.
$ i<i' $
.
We first prove the ‘only if’ part. Let
![]() $ \sigma $
be a web permutation, and
$ \sigma $
be a web permutation, and
be the sequence of grid configurations where
![]() $ G^{(k)} $
is obtained from
$ G^{(k)} $
is obtained from
![]() $ G^{(k-1)} $
by resolving a single crossing for each
$ G^{(k-1)} $
by resolving a single crossing for each
![]() $ k $
, with respect to the total order. We write
$ k $
, with respect to the total order. We write
![]() $ G^{(k)} = G(\sigma ^{(k)}, E^{(k)}) $
. Also let
$ G^{(k)} = G(\sigma ^{(k)}, E^{(k)}) $
. Also let
![]() $ c^{(k)} $
be the crossing in
$ c^{(k)} $
be the crossing in
![]() $ \operatorname {Cr}(\sigma ^{(k-1)})\setminus E^{(k-1)} $
such that
$ \operatorname {Cr}(\sigma ^{(k-1)})\setminus E^{(k-1)} $
such that
![]() $ G^{(k)} $
is obtained from
$ G^{(k)} $
is obtained from
![]() $ G^{(k-1)} $
by resolving
$ G^{(k-1)} $
by resolving
![]() $ c^{(k)} $
.
$ c^{(k)} $
.
It is obvious that the identity permutation
![]() $ \sigma ^{(0)}=id $
consists of André cycles. We claim that each
$ \sigma ^{(0)}=id $
consists of André cycles. We claim that each
![]() $ \sigma ^{(k)} $
also consists of André cycles for
$ \sigma ^{(k)} $
also consists of André cycles for
![]() $ 1\le k\le r $
; in particular, so does
$ 1\le k\le r $
; in particular, so does
![]() $ \sigma $
. Fix an integer
$ \sigma $
. Fix an integer
![]() $ 1\le k\le r $
. We use an inductive argument, so suppose that each cycle of
$ 1\le k\le r $
. We use an inductive argument, so suppose that each cycle of
![]() $ \sigma ^{(k-1)} $
is an André cycle. If
$ \sigma ^{(k-1)} $
is an André cycle. If
![]() $ G^{(k)} $
is obtained by applying the smoothing operation to the crossing
$ G^{(k)} $
is obtained by applying the smoothing operation to the crossing
![]() $ c^{(k)} $
in
$ c^{(k)} $
in
![]() $ G^{(k-1)} $
, then
$ G^{(k-1)} $
, then
![]() $ \sigma ^{(k-1)}=\sigma ^{(k)} $
, and thus there is nothing to prove. Therefore, we assume that
$ \sigma ^{(k-1)}=\sigma ^{(k)} $
, and thus there is nothing to prove. Therefore, we assume that
![]() $ G^{(k)} $
is obtained from
$ G^{(k)} $
is obtained from
![]() $ G^{(k-1)} $
by applying the switching operation to the crossing
$ G^{(k-1)} $
by applying the switching operation to the crossing
![]() $ c^{(k)}=(i,j) $
. Then
$ c^{(k)}=(i,j) $
. Then
Let
![]() $ C_1, \dots , C_\ell $
be cycles of
$ C_1, \dots , C_\ell $
be cycles of
![]() $ \sigma ^{(k-1)} $
. We first observe that for each
$ \sigma ^{(k-1)} $
. We first observe that for each
![]() $ 1\le p\le \ell $
, all entries in
$ 1\le p\le \ell $
, all entries in
![]() $ C_p $
except the minimum
$ C_p $
except the minimum
![]() $ \min C_p $
are greater than
$ \min C_p $
are greater than
![]() $ j $
. We justify this observation later. From this, we have that
$ j $
. We justify this observation later. From this, we have that
![]() $ i $
and
$ i $
and
![]() $ j $
are contained in different cycles of
$ j $
are contained in different cycles of
![]() $ \sigma ^{(k-1)} $
. Indeed, if
$ \sigma ^{(k-1)} $
. Indeed, if
![]() $ i $
and
$ i $
and
![]() $ j $
lie on the same cycle, then
$ j $
lie on the same cycle, then
![]() $ \sigma ^{(k-1)}(i) $
also lies on the cycle, but it is a contradiction to (8). Without loss of generality, let
$ \sigma ^{(k-1)}(i) $
also lies on the cycle, but it is a contradiction to (8). Without loss of generality, let
![]() $ C_1=(a_1,\dots ,a_s) $
and
$ C_1=(a_1,\dots ,a_s) $
and
![]() $ C_2=(b_1,\dots ,b_t) $
contain
$ C_2=(b_1,\dots ,b_t) $
contain
![]() $ i $
and
$ i $
and
![]() $ j $
, respectively, with
$ j $
, respectively, with
![]() $ a_1=\min C_1 $
and
$ a_1=\min C_1 $
and
![]() $ b_1 = \min C_2 $
. By the first inequality of (8) and the observation,
$ b_1 = \min C_2 $
. By the first inequality of (8) and the observation,
![]() $ a_1 = \sigma ^{(k-1)}(i) $
and
$ a_1 = \sigma ^{(k-1)}(i) $
and
![]() $ b_1 = j $
, so
$ b_1 = j $
, so
![]() $ a_s = i $
and
$ a_s = i $
and
![]() $ b_t = (\sigma ^{(k-1)})^{-1}(j) $
. By definition, resolving the crossing
$ b_t = (\sigma ^{(k-1)})^{-1}(j) $
. By definition, resolving the crossing
![]() $ (i,j) $
by applying the switching operation merges two cycles
$ (i,j) $
by applying the switching operation merges two cycles
![]() $ C_1 $
and
$ C_1 $
and
![]() $ C_2 $
into the cycle
$ C_2 $
into the cycle
![]() $ C=(a_1,\dots ,a_s,b_1,\dots ,b_t) $
, and leaves other cycles unchanged. It therefore follows from Lemma 3.3 and (8) that the cycle
$ C=(a_1,\dots ,a_s,b_1,\dots ,b_t) $
, and leaves other cycles unchanged. It therefore follows from Lemma 3.3 and (8) that the cycle
![]() $ C $
is an André cycle. Note that
$ C $
is an André cycle. Note that
![]() $ \min C = a_1 = \sigma ^{(k-1)}(i) < j $
, and there is no crossing on row
$ \min C = a_1 = \sigma ^{(k-1)}(i) < j $
, and there is no crossing on row
![]() $ j $
in the grid configuration
$ j $
in the grid configuration
![]() $ G^{(k)} $
. Hence the crossing
$ G^{(k)} $
. Hence the crossing
![]() $ c^{(k+1)} $
lies below row
$ c^{(k+1)} $
lies below row
![]() $ j $
, which implies the observation inductively.
$ j $
, which implies the observation inductively.
We now prove the ‘if’ part. It suffices to show that we obtain any André cycle by iterating resolving processes to the identity permutation along the total order. We induct on the length of an André cycle where the base case being trivial. Suppose that
![]() $ C=(a_1,\dots ,a_k) $
is an André cycle with
$ C=(a_1,\dots ,a_k) $
is an André cycle with
![]() $ k\ge 2 $
and
$ k\ge 2 $
and
![]() $ a_1=\min C $
. Then, by definition, the permutation
$ a_1=\min C $
. Then, by definition, the permutation
![]() $ a_2\cdots a_k $
is an André permutation. Let
$ a_2\cdots a_k $
is an André permutation. Let
![]() $ a_p = \min \{a_2,\dots ,a_k\} $
for some p, so
$ a_p = \min \{a_2,\dots ,a_k\} $
for some p, so
![]() $a_2\cdots a_{p-1}$
and
$a_2\cdots a_{p-1}$
and
![]() $a_{p+1}\cdots a_k$
are also André permutations. Thus, the cycles
$a_{p+1}\cdots a_k$
are also André permutations. Thus, the cycles
![]() $ (a_1,\dots ,a_{p-1}) $
and
$ (a_1,\dots ,a_{p-1}) $
and
![]() $ (a_p, \dots ,a_k) $
are André cycles. By the induction hypothesis, we can obtain the web permutation
$ (a_p, \dots ,a_k) $
are André cycles. By the induction hypothesis, we can obtain the web permutation
![]() $ \sigma =(a_1,\dots ,a_{p-1})(a_p,\dots ,a_k) $
by resolving processes. More precisely, we can obtain the grid configuration
$ \sigma =(a_1,\dots ,a_{p-1})(a_p,\dots ,a_k) $
by resolving processes. More precisely, we can obtain the grid configuration
![]() $ G(\sigma , E) $
such that for
$ G(\sigma , E) $
such that for
![]() $ 1\le i\le n $
and
$ 1\le i\le n $
and
![]() $ j\le a_p $
,
$ j\le a_p $
,
![]() $ (i,j)\notin E $
. Furthermore, one can easily check that the cell
$ (i,j)\notin E $
. Furthermore, one can easily check that the cell
![]() $ (a_{p-1}, a_p) $
belongs to
$ (a_{p-1}, a_p) $
belongs to
![]() $ \operatorname {Cr}(\sigma ) $
, so
$ \operatorname {Cr}(\sigma ) $
, so
![]() $ (a_{p-1}, a_p)\in \operatorname {Cr}(\sigma )\setminus E $
. We then obtain the desired cycle
$ (a_{p-1}, a_p)\in \operatorname {Cr}(\sigma )\setminus E $
. We then obtain the desired cycle
![]() $ C $
by switching the crossing
$ C $
by switching the crossing
![]() $ (a_{p-1}, a_p) $
in the grid configuration
$ (a_{p-1}, a_p) $
in the grid configuration
![]() $ G(\sigma , E) $
, which completes the proof.
$ G(\sigma , E) $
, which completes the proof.
As an application of the characterization, we show that the transition matrix
![]() $ (a_{MM'}) $
is unitriangular with respect to a certain order on
$ (a_{MM'}) $
is unitriangular with respect to a certain order on
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
, and we determine which entries
$ \operatorname {NC}_{2n} $
, and we determine which entries
![]() $ a_{MM'} $
vanish. These are already known due to Russell–Tymoczko [Reference Russell and TymoczkoRT19] and Im–Zhu [Reference Im and ZhuIZ22].
$ a_{MM'} $
vanish. These are already known due to Russell–Tymoczko [Reference Russell and TymoczkoRT19] and Im–Zhu [Reference Im and ZhuIZ22].
Before we give the vanishing condition, we first show that the set
![]() $ \operatorname {Web}_n $
includes a well-studied class of permutations. For a permutation
$ \operatorname {Web}_n $
includes a well-studied class of permutations. For a permutation
![]() $ \sigma = \sigma _1\cdots \sigma _n $
, we say that
$ \sigma = \sigma _1\cdots \sigma _n $
, we say that
![]() $\sigma $
contains a 312-pattern if there exist three indices
$\sigma $
contains a 312-pattern if there exist three indices
![]() $ 1\le i<j<k\le n $
such that
$ 1\le i<j<k\le n $
such that
![]() $ \sigma _j<\sigma _k<\sigma _i $
. A permutation is 312-avoiding if it does not contain a 312-pattern. Note that 312-avoiding permutations are a Catalan object. Furthermore, the restriction of
$ \sigma _j<\sigma _k<\sigma _i $
. A permutation is 312-avoiding if it does not contain a 312-pattern. Note that 312-avoiding permutations are a Catalan object. Furthermore, the restriction of
![]() $ D:\mathfrak {S}_n\rightarrow \operatorname {Dyck}_{2n} $
to the set of 312-avoiding permutations of
$ D:\mathfrak {S}_n\rightarrow \operatorname {Dyck}_{2n} $
to the set of 312-avoiding permutations of
![]() $ [n] $
is a bijection.
$ [n] $
is a bijection.
Corollary 3.5. A 312-avoiding permutation is a web permutation.
Proof. By Theorem 3.4, it suffices to show the following: For a permutation
![]() $ \sigma $
, if there is a cycle
$ \sigma $
, if there is a cycle
![]() $C=(a_1,\dots ,a_\ell )$
which is not an André cycle in
$C=(a_1,\dots ,a_\ell )$
which is not an André cycle in
![]() $\sigma $
, then
$\sigma $
, then
![]() $\sigma $
contains a 312-pattern which consists of
$\sigma $
contains a 312-pattern which consists of
![]() $a_i$
’s.
$a_i$
’s.
We use induction on the length of C. Since any cycle of length less than 3 is an André cycle, the base case is when the length of C is 3. The only case is of the form
![]() $(a_1,a_2,a_3)$
, where
$(a_1,a_2,a_3)$
, where
![]() $a_1<a_3<a_2$
. Thus,
$a_1<a_3<a_2$
. Thus,
![]() $\sigma $
contains a 312-pattern
$\sigma $
contains a 312-pattern
![]() $a_1<a_3<a_2$
.
$a_1<a_3<a_2$
.
Now assume that the length of C is larger than 3. Write
![]() $C=(a_1,a_2,\dots ,a_\ell , b_1,b_2,\dots ,b_r)$
, where
$C=(a_1,a_2,\dots ,a_\ell , b_1,b_2,\dots ,b_r)$
, where
![]() $ a_1 $
and
$ a_1 $
and
![]() $ b_1 $
is the smallest and the second smallest elements of
$ b_1 $
is the smallest and the second smallest elements of
![]() $ C $
, respectively. Then one of the following holds:
$ C $
, respectively. Then one of the following holds:
-
i)
 $C_1=(a_1,a_2,\dots ,a_\ell )$
is not an André cycle.
$C_1=(a_1,a_2,\dots ,a_\ell )$
is not an André cycle. -
ii)
 $C_2=(b_1,b_2,\dots ,b_r)$
is not an André cycle.
$C_2=(b_1,b_2,\dots ,b_r)$
is not an André cycle. -
iii) both
 $C_1$
, and
$C_1$
, and
 $C_2$
are André cycles and
$C_2$
are André cycles and
 $\max C_1=a_\ell>b_{r}=\max C_2$
.
$\max C_1=a_\ell>b_{r}=\max C_2$
.
For the first case, by the induction hypothesis, there exist integers
![]() $0\le i,j,k\le \ell $
such that
$0\le i,j,k\le \ell $
such that
![]() $a_i<a_j<a_k$
and
$a_i<a_j<a_k$
and
![]() $a_{j+1}<a_{k+1}<a_{i+1}$
, where the subscripts are interpreted modulo
$a_{j+1}<a_{k+1}<a_{i+1}$
, where the subscripts are interpreted modulo
![]() $\ell $
. Note that
$\ell $
. Note that
![]() $\sigma _{a_i}=a_{i+1}$
except for
$\sigma _{a_i}=a_{i+1}$
except for
![]() $\sigma _{a_\ell }=b_1$
. Since
$\sigma _{a_\ell }=b_1$
. Since
![]() $b_1$
is the second smallest element, replacing
$b_1$
is the second smallest element, replacing
![]() $a_1$
with
$a_1$
with
![]() $b_1$
does not change the pattern of
$b_1$
does not change the pattern of
![]() ${a_{i+1}}{a_{j+1}}{a_{k+1}}$
. Therefore,
${a_{i+1}}{a_{j+1}}{a_{k+1}}$
. Therefore,
![]() $\sigma $
contains a 312-pattern as we claimed. The second case can be proved similarly to the first case. For the last case,
$\sigma $
contains a 312-pattern as we claimed. The second case can be proved similarly to the first case. For the last case,
![]() $a_1<b_r<a_\ell $
forms a 312-pattern. Indeed,
$a_1<b_r<a_\ell $
forms a 312-pattern. Indeed,
![]() $\sigma _{a_1}=a_2, \sigma _{b_r}=a_1, \sigma _{a_\ell }=b_1$
and
$\sigma _{a_1}=a_2, \sigma _{b_r}=a_1, \sigma _{a_\ell }=b_1$
and
![]() $a_1<b_1<a_2$
.
$a_1<b_1<a_2$
.
Recall that the set
![]() $ \operatorname {Dyck}_{2n} $
has a partial order
$ \operatorname {Dyck}_{2n} $
has a partial order
![]() $ \subseteq $
, and there are bijections
$ \subseteq $
, and there are bijections
![]() $ D $
from
$ D $
from
![]() $ \operatorname {NN}_{2n} $
and from
$ \operatorname {NN}_{2n} $
and from
![]() $ \operatorname {NC}_{2n} $
to
$ \operatorname {NC}_{2n} $
to
![]() $ \operatorname {Dyck}_{2n} $
. Then the maps
$ \operatorname {Dyck}_{2n} $
. Then the maps
![]() $ D $
induce a partial order on
$ D $
induce a partial order on
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
. Furthermore, when we choose a total order on
$ \operatorname {NC}_{2n} $
. Furthermore, when we choose a total order on
![]() $ \operatorname {Dyck}_{2n} $
that completes the partial order
$ \operatorname {Dyck}_{2n} $
that completes the partial order
![]() $ \subseteq $
, the maps
$ \subseteq $
, the maps
![]() $ D $
give a total order on
$ D $
give a total order on
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
.
$ \operatorname {NC}_{2n} $
.
Remark 3.6. In [Reference Russell and TymoczkoRT19], Russell and Tymoczko defined a directed graph
![]() $ \Gamma $
on
$ \Gamma $
on
![]() $ \operatorname {NC}_{2n} $
and defined a partial order on
$ \operatorname {NC}_{2n} $
and defined a partial order on
![]() $ \operatorname {NC}_{2n} $
using the digraph. The graph
$ \operatorname {NC}_{2n} $
using the digraph. The graph
![]() $ \Gamma $
is an edge-labeled directed graph whose vertex set is the set of noncrossing matchings, and its labeled edges are given as follows. For
$ \Gamma $
is an edge-labeled directed graph whose vertex set is the set of noncrossing matchings, and its labeled edges are given as follows. For
![]() $ M,M'\in \operatorname {NC}_{2n} $
, assign a labeled, directed edge
$ M,M'\in \operatorname {NC}_{2n} $
, assign a labeled, directed edge
![]() $M \xrightarrow {i} M'$
if both of the following conditions hold:
$M \xrightarrow {i} M'$
if both of the following conditions hold:
-
i) M has arcs
 $\{j,k\}$
and
$\{j,k\}$
and
 $\{i,i+1\}$
, while
$\{i,i+1\}$
, while
 $M'$
has arcs
$M'$
has arcs
 $\{j,i\}$
and
$\{j,i\}$
and
 $\{i+1,k\}$
, where
$\{i+1,k\}$
, where
 $ j<i<k $
.
$ j<i<k $
. -
ii) Other arcs in M and
 $M'$
are the same.
$M'$
are the same.
The graph
![]() $\Gamma $
defines a partial order on
$\Gamma $
defines a partial order on
![]() $\operatorname {NC}_{2n}$
by letting
$\operatorname {NC}_{2n}$
by letting
![]() $M'\preceq M$
if there is a directed path from M to
$M'\preceq M$
if there is a directed path from M to
![]() $M'$
in
$M'$
in
![]() $\Gamma $
. Russell and Tymoczko also defined a partial order on
$\Gamma $
. Russell and Tymoczko also defined a partial order on
![]() $\operatorname {NN}_{2n}$
via a well-known bijection between
$\operatorname {NN}_{2n}$
via a well-known bijection between
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
.
$ \operatorname {NC}_{2n} $
.
In terms of Dyck paths, the labeled, directed edges defined by Russell and Tymoczko can be described as follows: For
![]() $ D,D'\in \operatorname {Dyck}_{2n} $
, assign a labeled, directed edge
$ D,D'\in \operatorname {Dyck}_{2n} $
, assign a labeled, directed edge
![]() $ D \xrightarrow {i} D' $
if both of the following conditions hold:
$ D \xrightarrow {i} D' $
if both of the following conditions hold:
-
i)
 $ D $
has
$ D $
has
 $ \mathsf {N} $
at
$ \mathsf {N} $
at
 $ i $
th step and
$ i $
th step and
 $ \mathsf {E} $
at
$ \mathsf {E} $
at
 $ (i+1) $
st step, while
$ (i+1) $
st step, while
 $ D' $
has
$ D' $
has
 $ \mathsf {E} $
at
$ \mathsf {E} $
at
 $ i $
th step and
$ i $
th step and
 $ \mathsf {N} $
at
$ \mathsf {N} $
at
 $ (i+1) $
st step.
$ (i+1) $
st step. -
ii) Other steps in D and
 $D'$
are the same.
$D'$
are the same.
In other words, we obtain
![]() $ D' $
from
$ D' $
from
![]() $ D $
by removing the cell containing
$ D $
by removing the cell containing
![]() $ i $
th and
$ i $
th and
![]() $ (i+1) $
st steps as edges in
$ (i+1) $
st steps as edges in
![]() $ D $
. Thus, the two partial orders on Dyck paths defined by the cover relation and inclusion are the same. Therefore, the partial order defined by Russell and Tymoczko in terms of
$ D $
. Thus, the two partial orders on Dyck paths defined by the cover relation and inclusion are the same. Therefore, the partial order defined by Russell and Tymoczko in terms of
![]() $ \operatorname {NC}_{2n} $
, as well as
$ \operatorname {NC}_{2n} $
, as well as
![]() $\operatorname {NN}_{2n}$
, coincides with ours.
$\operatorname {NN}_{2n}$
, coincides with ours.
We now take a total order on
![]() $ \operatorname {Dyck}_{2n} $
which completes the partial order
$ \operatorname {Dyck}_{2n} $
which completes the partial order
![]() $ \subseteq $
, and thus we have the induced total order on
$ \subseteq $
, and thus we have the induced total order on
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
. We assume that orderings of rows and columns of the transition matrix
$ \operatorname {NC}_{2n} $
. We assume that orderings of rows and columns of the transition matrix
![]() $ (a_{MM'}) $
are the decreasing orders with respect to the total order on
$ (a_{MM'}) $
are the decreasing orders with respect to the total order on
![]() $ \operatorname {NN}_{2n} $
and
$ \operatorname {NN}_{2n} $
and
![]() $ \operatorname {NC}_{2n} $
. Then the entry
$ \operatorname {NC}_{2n} $
. Then the entry
![]() $ a_{MM'} $
is on the diagonal if and only if
$ a_{MM'} $
is on the diagonal if and only if
![]() $ D(M)=D(M') $
.
$ D(M)=D(M') $
.
We are now ready to prove the unitriangularity of the transition matrix
![]() $(a_{MM'})$
and the conjecture of Russell and Tymoczko [Reference Russell and TymoczkoRT19, Conjecture 5.8] concerning the condition of the vanishing entries, which is later proved by Im and Zhu [Reference Im and ZhuIZ22, Theorem 1.1].
$(a_{MM'})$
and the conjecture of Russell and Tymoczko [Reference Russell and TymoczkoRT19, Conjecture 5.8] concerning the condition of the vanishing entries, which is later proved by Im and Zhu [Reference Im and ZhuIZ22, Theorem 1.1].
Corollary 3.7 [Reference Russell and TymoczkoRT19, Reference Im and ZhuIZ22].
Let
![]() $ M\in \operatorname {NN}_{2n} $
and
$ M\in \operatorname {NN}_{2n} $
and
![]() $ M'\in \operatorname {NC}_{2n} $
. Then
$ M'\in \operatorname {NC}_{2n} $
. Then
![]() $ a_{MM'}> 0 $
if and only if
$ a_{MM'}> 0 $
if and only if
![]() $ D(M') \subseteq D(M) $
. In particular, the transition matrix
$ D(M') \subseteq D(M) $
. In particular, the transition matrix
![]() $(a_{MM'})$
is upper-triangular with ones along the diagonal.
$(a_{MM'})$
is upper-triangular with ones along the diagonal.
Proof. Recall that by the argument in the proof of Theorem 1.2, we have
We first show that there are ones along the diagonal (i.e.,
![]() $ a_{MM'}=1 $
if
$ a_{MM'}=1 $
if
![]() $ D(M)=D(M') $
). Let
$ D(M)=D(M') $
). Let
![]() $\sigma $
be a permutation in
$\sigma $
be a permutation in
![]() $\operatorname {Web}_M$
satisfying
$\operatorname {Web}_M$
satisfying
![]() $M(\sigma )=M'$
. Denote the set of cells above the Dyck path
$M(\sigma )=M'$
. Denote the set of cells above the Dyck path
![]() $D(\sigma )$
by
$D(\sigma )$
by
![]() $E(\sigma )$
. We claim that
$E(\sigma )$
. We claim that
![]() $E(\sigma )=\operatorname {Cr}(\sigma )$
. Since
$E(\sigma )=\operatorname {Cr}(\sigma )$
. Since
![]() $E(\sigma )\subseteq \operatorname {Cr}(\sigma )$
is obvious, suppose that we have
$E(\sigma )\subseteq \operatorname {Cr}(\sigma )$
is obvious, suppose that we have
![]() $E(\sigma )\subsetneq \operatorname {Cr}(\sigma )$
, and let c be a maximal crossing in
$E(\sigma )\subsetneq \operatorname {Cr}(\sigma )$
, and let c be a maximal crossing in
![]() $ \operatorname {Cr}(\sigma )\setminus E(\sigma ) $
. Note that
$ \operatorname {Cr}(\sigma )\setminus E(\sigma ) $
. Note that
Thus, if we resolve all crossings by applying the smoothing operation to obtain
![]() $G(\sigma ,\operatorname {Cr}(\sigma ))$
, the associated Dyck path
$G(\sigma ,\operatorname {Cr}(\sigma ))$
, the associated Dyck path
![]() $D(M')=D(M(\sigma ))$
lies strictly below
$D(M')=D(M(\sigma ))$
lies strictly below
![]() $D(M)$
, which is a contradiction.
$D(M)$
, which is a contradiction.
It is well-known that 312-avoiding permutations are only permutations satisfying the condition
![]() $ \operatorname {Cr}(\sigma )=E(\sigma ) $
, and the map
$ \operatorname {Cr}(\sigma )=E(\sigma ) $
, and the map
![]() $D:\operatorname {Web}_n\rightarrow \operatorname {Dyck}_{2n}$
is a bijection when restricted to 312-avoiding permutations (see [Reference StanleySta12, §1.2]). Here, the restriction makes sense by Corollary 3.5. Combining these facts, it follows that each 312-avoiding permutation represents each one on the diagonal in the transition matrix.
$D:\operatorname {Web}_n\rightarrow \operatorname {Dyck}_{2n}$
is a bijection when restricted to 312-avoiding permutations (see [Reference StanleySta12, §1.2]). Here, the restriction makes sense by Corollary 3.5. Combining these facts, it follows that each 312-avoiding permutation represents each one on the diagonal in the transition matrix.
To show the ‘only if’ part of the first assertion, assume that
![]() $D(M') \nsubseteq D(M)$
. Then there exists a cell below the Dyck path
$D(M') \nsubseteq D(M)$
. Then there exists a cell below the Dyck path
![]() $D(M')$
and above the Dyck path
$D(M')$
and above the Dyck path
![]() $D(M)$
(i.e.,
$D(M)$
(i.e.,
![]() $ E(M)\setminus E(M')\neq \emptyset ). $
Choose a maximal cell
$ E(M)\setminus E(M')\neq \emptyset ). $
Choose a maximal cell
![]() $c=(i,j)$
in
$c=(i,j)$
in
![]() $ E(M)\setminus E(M')\neq \emptyset. $
Let
$ E(M)\setminus E(M')\neq \emptyset. $
Let
![]() $\sigma $
be a web permutation. If
$\sigma $
be a web permutation. If
![]() $\sigma $
is in
$\sigma $
is in
![]() $\operatorname {Web}_M$
, then we have
$\operatorname {Web}_M$
, then we have
![]() $c\in \operatorname {Cr}(\sigma )$
; thus,
$c\in \operatorname {Cr}(\sigma )$
; thus,
![]() $\sigma _i<j$
. However, if
$\sigma _i<j$
. However, if
![]() $M(\sigma )=M'$
, then we have
$M(\sigma )=M'$
, then we have
![]() $\sigma _i=j$
, which is a contradiction. Therefore, we have
$\sigma _i=j$
, which is a contradiction. Therefore, we have
![]() $ a_{MM'}=0 $
.
$ a_{MM'}=0 $
.
For the ‘if’ part, let
![]() $M"$
be the nonnesting matching such that
$M"$
be the nonnesting matching such that
![]() $D(M")=D(M')$
. Then we have
$D(M")=D(M')$
. Then we have
 $$ \begin{align*} a_{MM'} &= |\{\sigma \in \operatorname{Web}_n: D(\sigma)\subseteq D(M), M(\sigma)=M'\}| \\ &\ge |\{\sigma \in \operatorname{Web}_n: D(\sigma)\subseteq D(M')=D(M"), M(\sigma)=M'\}| \\ &= a_{M"M'}=1. \end{align*} $$
$$ \begin{align*} a_{MM'} &= |\{\sigma \in \operatorname{Web}_n: D(\sigma)\subseteq D(M), M(\sigma)=M'\}| \\ &\ge |\{\sigma \in \operatorname{Web}_n: D(\sigma)\subseteq D(M')=D(M"), M(\sigma)=M'\}| \\ &= a_{M"M'}=1. \end{align*} $$
This completes the proof.
4 Enumeration of web permutations
In this section, we focus on the number of web permutations. More precisely, we give a relation between web permutations and André cycles (Theorem 4.1), and we show that the numbers of web permutations equal Euler numbers. We also conjecture that the Seidel triangle can be recovered completely from the certain classes of web permutations.
We have characterized web permutations using André cycles (Theorem 3.4). We now present another relationship between web permutations and André cycles. Let us first review the Foata transformation
![]() $ \widehat {~~}:\mathfrak {S}_n\rightarrow \mathfrak {S}_n $
. For a permutation
$ \widehat {~~}:\mathfrak {S}_n\rightarrow \mathfrak {S}_n $
. For a permutation
![]() $\sigma \in \mathfrak {S}_n$
, the canonical cycle notation of
$\sigma \in \mathfrak {S}_n$
, the canonical cycle notation of
![]() $ \sigma $
is a cycle notation of
$ \sigma $
is a cycle notation of
![]() $ \sigma $
such that its cycles are sorted based on the smallest elements of the cycles, and the smallest element of each cycle is written in the last place of the cycle. We define
$ \sigma $
such that its cycles are sorted based on the smallest elements of the cycles, and the smallest element of each cycle is written in the last place of the cycle. We define
![]() $ \widehat {\sigma } $
to be the permutation obtained by dropping the parentheses in the canonical cycle notation of
$ \widehat {\sigma } $
to be the permutation obtained by dropping the parentheses in the canonical cycle notation of
![]() $ \sigma $
. A right-to-left minimum is an element
$ \sigma $
. A right-to-left minimum is an element
![]() $ \sigma _i $
such that
$ \sigma _i $
such that
![]() $ \sigma _i < \sigma _j $
for all
$ \sigma _i < \sigma _j $
for all
![]() $ j>i $
. Using right-to-left minima of
$ j>i $
. Using right-to-left minima of
![]() $ \sigma $
, one can easily construct the inverse of the Foata transformation. Note that the number of cycles of
$ \sigma $
, one can easily construct the inverse of the Foata transformation. Note that the number of cycles of
![]() $ \sigma $
equals the number of right-to-left minima of
$ \sigma $
equals the number of right-to-left minima of
![]() $ \widehat {\sigma } $
.
$ \widehat {\sigma } $
.
We now introduce a map
![]() $\phi : \mathfrak {S}_n \rightarrow \mathfrak {S}_{n+2}$
as a slight modification of the Foata transformation. For a permutation
$\phi : \mathfrak {S}_n \rightarrow \mathfrak {S}_{n+2}$
as a slight modification of the Foata transformation. For a permutation
![]() $\sigma \in \mathfrak {S}_n$
, define the one-cycle permutation
$\sigma \in \mathfrak {S}_n$
, define the one-cycle permutation
![]() $\phi (\sigma ) \in \mathfrak {S}_{n+2}$
by
$\phi (\sigma ) \in \mathfrak {S}_{n+2}$
by
It follows immediately from the bijectivity of the Foata transformation that the map
![]() $ \phi $
is injective, and its image
$ \phi $
is injective, and its image
![]() $ \phi (\mathfrak {S}_n) $
is the set of one-cycle permutations
$ \phi (\mathfrak {S}_n) $
is the set of one-cycle permutations
![]() $ \sigma \in \mathfrak {S}_{n+2} $
with
$ \sigma \in \mathfrak {S}_{n+2} $
with
![]() $ \sigma (n+2)=1 $
. For instance, let
$ \sigma (n+2)=1 $
. For instance, let
![]() $ \sigma =568479312\in \mathfrak {S}_9 $
. In the canonical cycle notation,
$ \sigma =568479312\in \mathfrak {S}_9 $
. In the canonical cycle notation,
![]() $ \sigma =(5,7,3,8,1)(6,9,2)(4) $
, so
$ \sigma =(5,7,3,8,1)(6,9,2)(4) $
, so
![]() $ \widehat {\sigma }=573816924 $
. Then we have
$ \widehat {\sigma }=573816924 $
. Then we have
The right-to-left minima of
![]() $ \widehat {\sigma } $
are
$ \widehat {\sigma } $
are
![]() $ 1,2 $
and
$ 1,2 $
and
![]() $ 4 $
, which are the minima of cycles of
$ 4 $
, which are the minima of cycles of
![]() $ \sigma $
. Note that the permutation
$ \sigma $
. Note that the permutation
![]() $ \sigma $
is a web permutation, and the cycle
$ \sigma $
is a web permutation, and the cycle
![]() $ \phi (\sigma ) $
is an André cycle. Surprisingly, this is not an accident.
$ \phi (\sigma ) $
is an André cycle. Surprisingly, this is not an accident.
Theorem 4.1. For
![]() $ n\ge 1 $
, let
$ n\ge 1 $
, let
![]() $ \operatorname {AC}_{n+2}\subset \mathfrak {S}_{n+2} $
be the set of André cycles consisting of
$ \operatorname {AC}_{n+2}\subset \mathfrak {S}_{n+2} $
be the set of André cycles consisting of
![]() $ [n+2] $
. Then we have
$ [n+2] $
. Then we have
![]() $ \phi (\operatorname {Web}_n) = \operatorname {AC}_{n+2} $
. In particular, the number of web permutations of
$ \phi (\operatorname {Web}_n) = \operatorname {AC}_{n+2} $
. In particular, the number of web permutations of
![]() $ [n] $
is equal to the number of André cycles consisting of
$ [n] $
is equal to the number of André cycles consisting of
![]() $ [n+2] $
.
$ [n+2] $
.
Proof. Let
![]() $\sigma $
be a web permutation of
$\sigma $
be a web permutation of
![]() $ [n] $
. In the canonical cycle notation, we write
$ [n] $
. In the canonical cycle notation, we write
where
![]() $ C_i = (c^{(i)}_{1}, \dots , c^{(i)}_{n_i}) $
is a cycle with
$ C_i = (c^{(i)}_{1}, \dots , c^{(i)}_{n_i}) $
is a cycle with
![]() $\min C_i = c^{(i)}_{n_i}$
for each
$\min C_i = c^{(i)}_{n_i}$
for each
![]() $ i=1,\dots ,k $
, and
$ i=1,\dots ,k $
, and
![]() $1=c^{(1)}_{n_1}<\cdots <c^{(k)}_{n_k}$
. Note that by Theorem 3.4, each cycle
$1=c^{(1)}_{n_1}<\cdots <c^{(k)}_{n_k}$
. Note that by Theorem 3.4, each cycle
![]() $ C_i $
is an André cycle; that is, each word
$ C_i $
is an André cycle; that is, each word
![]() $ c^{(i)}_1\cdots c^{(i)}_{n_i-1} $
is an André permutation. We claim that the word
$ c^{(i)}_1\cdots c^{(i)}_{n_i-1} $
is an André permutation. We claim that the word
obtained by appending
![]() $ n+1 $
to the end of
$ n+1 $
to the end of
![]() $ \widehat {\sigma } $
is an André permutation. Since
$ \widehat {\sigma } $
is an André permutation. Since
![]() $ c^{(1)}_{n_1} $
is the minimum in the word, and
$ c^{(1)}_{n_1} $
is the minimum in the word, and
![]() $ c^{(1)}_1\cdots c^{(1)}_{n_1-1} $
is an André permutation, it suffices to show that the suffix
$ c^{(1)}_1\cdots c^{(1)}_{n_1-1} $
is an André permutation, it suffices to show that the suffix
![]() $ c^{(2)}_{1}\cdots c^{(2)}_{n_2}\cdots c^{(k)}_{n_k} (n+1) $
is an André permutation. Then an appropriate inductive argument shows the claim. We now consider the cycle
$ c^{(2)}_{1}\cdots c^{(2)}_{n_2}\cdots c^{(k)}_{n_k} (n+1) $
is an André permutation. Then an appropriate inductive argument shows the claim. We now consider the cycle
![]() $ \phi (\sigma ) $
. Using the canonical cycle notation of
$ \phi (\sigma ) $
. Using the canonical cycle notation of
![]() $ \sigma $
, we have
$ \sigma $
, we have
Thus, by the claim,
![]() $\phi (\sigma )$
is an André permutation of
$\phi (\sigma )$
is an André permutation of
![]() $ [n+2] $
, as desired.
$ [n+2] $
, as desired.
Conversely, let
![]() $ \tau $
be an André cycle of
$ \tau $
be an André cycle of
![]() $ [n+2] $
. By Lemma 3.2,
$ [n+2] $
. By Lemma 3.2,
![]() $ \tau $
forms
$ \tau $
forms
![]() $ (1,a_1,\dots ,a_n, n+2) $
. Let
$ (1,a_1,\dots ,a_n, n+2) $
. Let
![]() $ a_{n_1},\dots ,a_{n_k} $
be the right-to-left minima of the permutation
$ a_{n_1},\dots ,a_{n_k} $
be the right-to-left minima of the permutation
![]() $ a_1\cdots a_n $
with
$ a_1\cdots a_n $
with
![]() $ n_1<\dots <n_k=n $
so that
$ n_1<\dots <n_k=n $
so that
![]() $ a_{n_1}<\dots <a_{n_k} $
. Then we only need to show that the permutation
$ a_{n_1}<\dots <a_{n_k} $
. Then we only need to show that the permutation
![]() $ (a_1,\dots ,a_{n_1})(a_{n_1+1},\dots ,a_{n_2})\cdots (a_{n_{k-1}+1},\dots ,a_{n_k}) $
is a web permutation, or equivalently, due to Theorem 3.4, each cycle
$ (a_1,\dots ,a_{n_1})(a_{n_1+1},\dots ,a_{n_2})\cdots (a_{n_{k-1}+1},\dots ,a_{n_k}) $
is a web permutation, or equivalently, due to Theorem 3.4, each cycle
![]() $ (a_{n_{i-1}+1},\dots ,a_{n_i}) $
is an André cycle. It is easily verified by a similar argument as in the previous claim and using the right-to-left minima. Hence, we leave the details to the reader.
$ (a_{n_{i-1}+1},\dots ,a_{n_i}) $
is an André cycle. It is easily verified by a similar argument as in the previous claim and using the right-to-left minima. Hence, we leave the details to the reader.
4.1 Euler and Entringer numbers
In this subsection, we give various enumerative properties of web permutations using Theorem 4.1.
We start with recalling Euler numbers. The Euler numbers
![]() $ E_n $
are defined via the exponential generating function
$ E_n $
are defined via the exponential generating function
 $$\begin{align*}E(z) := \sum_{n\ge 0} E_n \frac{x^n}{n!} = \sec z + \tan z. \end{align*}$$
$$\begin{align*}E(z) := \sum_{n\ge 0} E_n \frac{x^n}{n!} = \sec z + \tan z. \end{align*}$$
The first few Euler numbers are 1, 1, 1, 2, 5, 16, 61; see [Reference SloaneSlo20] with ID number A000111. There are numerous combinatorial objects enumerated by Euler numbers
![]() $ E_n $
(e.g., alternating permutations, complete increasing binary trees, etc.). For example, the Euler number
$ E_n $
(e.g., alternating permutations, complete increasing binary trees, etc.). For example, the Euler number
![]() $ E_n $
counts André permutations of
$ E_n $
counts André permutations of
![]() $ [n] $
. For details, we refer to [Reference StanleySta10], which is a wonderful survey of Euler numbers and related topics. We provide another occurrence of Euler numbers.
$ [n] $
. For details, we refer to [Reference StanleySta10], which is a wonderful survey of Euler numbers and related topics. We provide another occurrence of Euler numbers.
Corollary 4.2. The Euler number
![]() $ E_{n+1} $
enumerates the number of web permutations of
$ E_{n+1} $
enumerates the number of web permutations of
![]() $ [n] $
.
$ [n] $
.
Proof. By definition, the number of André permutations of
![]() $ [n] $
is equal to the number of André cycles of
$ [n] $
is equal to the number of André cycles of
![]() $ [n+1] $
. Then Theorem 4.1 implies the desired result.
$ [n+1] $
. Then Theorem 4.1 implies the desired result.
Remark 4.3. One can prove the corollary without using the fact that the number of André permutations is equal to the Euler number. Indeed, let
![]() $ w_n $
be the number of web permutations of
$ w_n $
be the number of web permutations of
![]() $ [n] $
,
$ [n] $
,
![]() $ ac_n $
the number of André cycles of
$ ac_n $
the number of André cycles of
![]() $ [n] $
, and
$ [n] $
, and
 $$\begin{align*}W(z) = \sum_{n\ge 0} w_n \frac{z^n}{n!}, \quad\mbox{and}\quad AC(z) = \sum_{n\ge 1} ac_n \frac{z^n}{n!}, \end{align*}$$
$$\begin{align*}W(z) = \sum_{n\ge 0} w_n \frac{z^n}{n!}, \quad\mbox{and}\quad AC(z) = \sum_{n\ge 1} ac_n \frac{z^n}{n!}, \end{align*}$$
where we set
![]() $ w_0 = 1 $
. Then by a standard fact of generating functionology [Reference StanleySta99, Corollary 5.1.6] and Theorem 3.4, we have
$ w_0 = 1 $
. Then by a standard fact of generating functionology [Reference StanleySta99, Corollary 5.1.6] and Theorem 3.4, we have
Meanwhile, Theorem 4.1 gives the ODE
 $$\begin{align*}W(z) = \frac{d^2}{dz^2} AC(z) = \frac{d^2}{dz^2} \log W(z), \end{align*}$$
$$\begin{align*}W(z) = \frac{d^2}{dz^2} AC(z) = \frac{d^2}{dz^2} \log W(z), \end{align*}$$
whose unique solution is
![]() $ W(z) = \sec z \tan z + \sec ^2 z = E'(z) $
, which implies
$ W(z) = \sec z \tan z + \sec ^2 z = E'(z) $
, which implies
![]() $ w_n = E_{n+1} $
.
$ w_n = E_{n+1} $
.
For a permutation
![]() $ \sigma $
, let
$ \sigma $
, let
![]() $ \operatorname {c}(\sigma ) $
be the number of cycles of
$ \operatorname {c}(\sigma ) $
be the number of cycles of
![]() $ \sigma $
, and
$ \sigma $
, and
![]() $ \operatorname {rlmin}(\sigma ) $
the number of right-to-left minima of
$ \operatorname {rlmin}(\sigma ) $
the number of right-to-left minima of
![]() $ \sigma $
. By convention, we set
$ \sigma $
. By convention, we set
![]() $ \operatorname {c}(\emptyset ) = 0 $
, where
$ \operatorname {c}(\emptyset ) = 0 $
, where
![]() $ \emptyset $
is the empty permutation, and
$ \emptyset $
is the empty permutation, and
![]() $ \operatorname {Web}_0=\{\emptyset \}. $
Since the Foata transformation gives the equidistribution of the two statistics
$ \operatorname {Web}_0=\{\emptyset \}. $
Since the Foata transformation gives the equidistribution of the two statistics
![]() $ \operatorname {c}(\sigma ) $
and
$ \operatorname {c}(\sigma ) $
and
![]() $ \operatorname {rlmin}(\sigma ) $
, we have the following corollary concerning the distribution of
$ \operatorname {rlmin}(\sigma ) $
, we have the following corollary concerning the distribution of
![]() $ \operatorname {c}(\sigma ) $
on
$ \operatorname {c}(\sigma ) $
on
![]() $ \operatorname {Web}_n $
.
$ \operatorname {Web}_n $
.
Corollary 4.4. We have
 $$ \begin{align*} \left( \frac{1}{1-\sin z} \right)^t = \sum_{n\ge 0} \sum_{\sigma\in \operatorname{Web}_n} t^{\operatorname{c}(\sigma)} \frac{z^{n}}{n!}. \end{align*} $$
$$ \begin{align*} \left( \frac{1}{1-\sin z} \right)^t = \sum_{n\ge 0} \sum_{\sigma\in \operatorname{Web}_n} t^{\operatorname{c}(\sigma)} \frac{z^{n}}{n!}. \end{align*} $$
Proof. In [Reference DisantoDis13, Proposition 1], the author showed that
 $$ \begin{align*} \left( \frac{1}{1-\sin z} \right)^t = \sum_{n\ge 1}\sum_{\sigma} t^{\operatorname{rlmin}(\sigma)-1} \frac{z^{n-1}}{(n-1)! }, \end{align*} $$
$$ \begin{align*} \left( \frac{1}{1-\sin z} \right)^t = \sum_{n\ge 1}\sum_{\sigma} t^{\operatorname{rlmin}(\sigma)-1} \frac{z^{n-1}}{(n-1)! }, \end{align*} $$
where the inner sum is over all André permutations of
![]() $ [n] $
. Therefore, the proof follows immediately from Theorem 4.1.
$ [n] $
. Therefore, the proof follows immediately from Theorem 4.1.
We also recall Entringer numbers. The Entringer numbers are given by the generating function
 $$\begin{align*}\frac{\cos x + \sin x}{\cos (x+y)} = \sum_{m,n \ge 0} E_{m+n,[m,n]} \frac{x^m}{m!} \frac{y^n}{n!}, \end{align*}$$
$$\begin{align*}\frac{\cos x + \sin x}{\cos (x+y)} = \sum_{m,n \ge 0} E_{m+n,[m,n]} \frac{x^m}{m!} \frac{y^n}{n!}, \end{align*}$$
where
![]() $ [m,n] $
is
$ [m,n] $
is
![]() $ m $
if
$ m $
if
![]() $ m+n $
is odd, and
$ m+n $
is odd, and
![]() $ n $
otherwise. These numbers refine Euler numbers in the following sense: For
$ n $
otherwise. These numbers refine Euler numbers in the following sense: For
![]() $ n\ge 1 $
,
$ n\ge 1 $
,
 $$\begin{align*}\sum_{k=1}^n E_{n,k} = E_{n+1}. \end{align*}$$
$$\begin{align*}\sum_{k=1}^n E_{n,k} = E_{n+1}. \end{align*}$$
We have a counterpart of this refinement.
Corollary 4.5. The Entringer number
![]() $ E_{n,k} $
is equal to the number of web permutations
$ E_{n,k} $
is equal to the number of web permutations
![]() $ \sigma $
of
$ \sigma $
of
![]() $ [n] $
with
$ [n] $
with
![]() $ \sigma _1 = n+1-k $
.
$ \sigma _1 = n+1-k $
.
Proof. In [Reference Foata and HanFH16, Theorem 1.1], the authors showed that
![]() $ E_{n,k} $
equals the number of André permutations
$ E_{n,k} $
equals the number of André permutations
![]() $ \sigma $
of
$ \sigma $
of
![]() $ [n+1] $
with
$ [n+1] $
with
![]() $ \sigma _1 = n+1-k $
. Combining this fact and Theorem 4.1 gives the proof.
$ \sigma _1 = n+1-k $
. Combining this fact and Theorem 4.1 gives the proof.
4.2 Genocchi numbers and the Seidel triangle
The Genocchi numbers are well-studied numbers with various combinatorial properties; see, for example, [Reference DumontDum74, Reference Lazar and WachsLW20]. The Genocchi numbers can be defined by the Seidel triangle as follows [Reference SeidelSei77]. The Seidel triangle is an array of integers
![]() $(s_{i,j})_{i,j\ge 1}$
such that
$(s_{i,j})_{i,j\ge 1}$
such that
![]() $s_{1,1}=s_{2,1}=1$
and
$s_{1,1}=s_{2,1}=1$
and
 $$\begin{align*}\begin{cases} s_{2i+1,j} = s_{2i+1,j-1} + s_{2i,j} \mbox{ for } j=1,2,\dots, i+1\\ s_{2i,j} = s_{2i,j+1} + s_{2i-1,j} \mbox{ for } j=i,i-1,\dots,1, \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} s_{2i+1,j} = s_{2i+1,j-1} + s_{2i,j} \mbox{ for } j=1,2,\dots, i+1\\ s_{2i,j} = s_{2i,j+1} + s_{2i-1,j} \mbox{ for } j=i,i-1,\dots,1, \end{cases} \end{align*}$$
where
![]() $s_{i,j}=0$
for
$s_{i,j}=0$
for
![]() $j<0$
or
$j<0$
or
![]() $j>\lceil i/2\rceil $
. The Genocchi numbers
$j>\lceil i/2\rceil $
. The Genocchi numbers
![]() $g_n$
are defined by
$g_n$
are defined by
In fact, the sequence
![]() $(g_n)$
is the interleaving of the Genocchi numbers of the first kind and the median Genocchi numbers. The first values of the Seidel triangle and Genocchi numbers (in red) are given in the following sequence:
$(g_n)$
is the interleaving of the Genocchi numbers of the first kind and the median Genocchi numbers. The first values of the Seidel triangle and Genocchi numbers (in red) are given in the following sequence:

Recall that we denote by
![]() $M_0$
for the unique matching which is simultaneously noncrossing and nonnesting (i.e.,
$M_0$
for the unique matching which is simultaneously noncrossing and nonnesting (i.e.,
![]() $ M_0 = \{ \{1,2\},\dots ,\{2n-1,2n\} \} $
). To emphasize the size of the matching, we denote this unique matching of
$ M_0 = \{ \{1,2\},\dots ,\{2n-1,2n\} \} $
). To emphasize the size of the matching, we denote this unique matching of
![]() $[2n]$
by
$[2n]$
by
![]() $M^{(n)}_0$
. Let
$M^{(n)}_0$
. Let
![]() $f(n)$
be the number of web permutations
$f(n)$
be the number of web permutations
![]() $\sigma $
of
$\sigma $
of
![]() $[n]$
with
$[n]$
with
![]() $M(\sigma )=M^{(n)}_0$
. In [Reference NakamigawaNak20], Nakamigawa studied expansions of certain chord diagrams. The author computed the multiplicity of the
$M(\sigma )=M^{(n)}_0$
. In [Reference NakamigawaNak20], Nakamigawa studied expansions of certain chord diagrams. The author computed the multiplicity of the
![]() $ n $
-necklace in the expansion of the
$ n $
-necklace in the expansion of the
![]() $ n $
-crossing chord diagram through an iterative process of resolving crossings. Here, the resolving rule employed in this process coincides with the resolving rule (3). In the context of matchings, this is equivalent to the problem of determining the number of occurrences of the noncrossing matching
$ n $
-crossing chord diagram through an iterative process of resolving crossings. Here, the resolving rule employed in this process coincides with the resolving rule (3). In the context of matchings, this is equivalent to the problem of determining the number of occurrences of the noncrossing matching
![]() $ M_0 $
obtained by iteratively resolving crossings in
$ M_0 $
obtained by iteratively resolving crossings in
![]() $ M = \{\{1,n+1\},\{2,n+2\},\dots ,\{n,2n\}\} $
via the rule (3). In our terminology, a result of Nakamigawa can be stated as follows.
$ M = \{\{1,n+1\},\{2,n+2\},\dots ,\{n,2n\}\} $
via the rule (3). In our terminology, a result of Nakamigawa can be stated as follows.
Theorem 4.6 [Reference NakamigawaNak20, Theorem 3.1].
For
![]() $ n\ge 1 $
, we have
$ n\ge 1 $
, we have
![]() $ f(n)=g_n $
.
$ f(n)=g_n $
.
Let
![]() $f(n,k)$
be the number of web permutations
$f(n,k)$
be the number of web permutations
![]() $\sigma $
of
$\sigma $
of
![]() $[n]$
such that
$[n]$
such that
![]() $ M(\sigma ) = M^{(n)}_0 $
and
$ M(\sigma ) = M^{(n)}_0 $
and
![]() $\sigma _1=k$
. Obviously,
$\sigma _1=k$
. Obviously,
![]() $ f(n)=\sum _{1\le k\le n} f(n,k) $
. Some of these numbers vanish in the following cases.
$ f(n)=\sum _{1\le k\le n} f(n,k) $
. Some of these numbers vanish in the following cases.
Proposition 4.7. For
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $1\le k \le \lfloor n/2\rfloor $
, we have
$1\le k \le \lfloor n/2\rfloor $
, we have
![]() $f(n,2k)=0$
.
$f(n,2k)=0$
.
Proof. Let
![]() $\sigma $
be a web permutation of
$\sigma $
be a web permutation of
![]() $[n]$
with
$[n]$
with
![]() $\sigma _1=2k$
. Then considering the grid configuration
$\sigma _1=2k$
. Then considering the grid configuration
![]() $ G(\sigma ,\operatorname {Cr}(\sigma )) $
, the associated matching
$ G(\sigma ,\operatorname {Cr}(\sigma )) $
, the associated matching
![]() $M(\sigma )$
has an arc connecting
$M(\sigma )$
has an arc connecting
![]() $2k$
and some j with
$2k$
and some j with
![]() $2k<j$
. Since there is the arc connecting
$2k<j$
. Since there is the arc connecting
![]() $2k-1$
and
$2k-1$
and
![]() $2k$
in
$2k$
in
![]() $M^{(n)}_0$
, we deduce
$M^{(n)}_0$
, we deduce
![]() $M(\sigma )\neq M^{(n)}_0$
.
$M(\sigma )\neq M^{(n)}_0$
.
Proposition 4.8. For
![]() $n>1$
, we have
$n>1$
, we have
![]() $f(n,n)=0$
.
$f(n,n)=0$
.
Proof. Let
![]() $\sigma $
be a web permutation of
$\sigma $
be a web permutation of
![]() $[n]$
with
$[n]$
with
![]() $\sigma _1=n$
. Since the elements
$\sigma _1=n$
. Since the elements
![]() $ 1 $
and
$ 1 $
and
![]() $ n $
are contained in the same cycle, we have
$ n $
are contained in the same cycle, we have
![]() $ \sigma _n = 1 $
by Lemma 3.2 and Theorem 3.4. Then there is a marking at
$ \sigma _n = 1 $
by Lemma 3.2 and Theorem 3.4. Then there is a marking at
![]() $(n,1)$
in the grid configuration
$(n,1)$
in the grid configuration
![]() $ G(\sigma ,\operatorname {Cr}(\sigma )) $
. Observe that the vertical line and horizontal line starting from the cell
$ G(\sigma ,\operatorname {Cr}(\sigma )) $
. Observe that the vertical line and horizontal line starting from the cell
![]() $(n,1)$
do not make a crossing. Hence, we deduce
$(n,1)$
do not make a crossing. Hence, we deduce
![]() $\{1,2n\}\in M(\sigma )$
, which implies that
$\{1,2n\}\in M(\sigma )$
, which implies that
![]() $M(\sigma )\neq M^{(n)}_0$
.
$M(\sigma )\neq M^{(n)}_0$
.
By Propositions 4.7 and 4.8, we have
We now propose a conjecture that the values appearing in the Seidel triangle are
![]() $f(n,k)$
.
$f(n,k)$
.
Conjecture 4.9 (Verified up to
 $ n=6 $
).
$ n=6 $
).
For
![]() $ n\ge 1 $
, we have
$ n\ge 1 $
, we have
 $$\begin{align*}\begin{cases} f(2n-1,2k-1)= s_{2n-2, k},\\ f(2n, 2k-1) = s_{2n-1, n-k+1}. \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} f(2n-1,2k-1)= s_{2n-2, k},\\ f(2n, 2k-1) = s_{2n-1, n-k+1}. \end{cases} \end{align*}$$
This conjecture includes Nakamigawa’s result. To elaborate, let
![]() $ \sigma $
be a web permutation of
$ \sigma $
be a web permutation of
![]() $ [n] $
such that
$ [n] $
such that
![]() $ M(\sigma )=M^{(n)}_0 $
and
$ M(\sigma )=M^{(n)}_0 $
and
![]() $ \sigma _1 = 1 $
. Deleting the cycle
$ \sigma _1 = 1 $
. Deleting the cycle
![]() $ (1) $
from
$ (1) $
from
![]() $ \sigma $
and decreasing each letter by 1, the resulting permutation is a web permutation of
$ \sigma $
and decreasing each letter by 1, the resulting permutation is a web permutation of
![]() $ [n-1] $
with
$ [n-1] $
with
![]() $ M(\sigma )=M^{(n-1)}_0 $
. In addition, this correspondence is bijective, so we deduce
$ M(\sigma )=M^{(n-1)}_0 $
. In addition, this correspondence is bijective, so we deduce
![]() $ f(n,1) = f(n-1) $
. Thus, the conjecture implies
$ f(n,1) = f(n-1) $
. Thus, the conjecture implies
![]() $ f(n-1) = g_{n-1} $
, which is Nakamigawa’s result.
$ f(n-1) = g_{n-1} $
, which is Nakamigawa’s result.
Acknowledgements
The authors are grateful to Jang Soo Kim for several suggestions which improved the manuscript. They would also like to thank to referees for numerous helpful comments.
Competing interest
The authors have no competing interest to declare.
Financial support
Jihyeug Jang was supported by NRF grant #2022R1A2C101100911. Jaeseong Oh was supported by KIAS Individual Grant (CG083401) at Korea Institute for Advanced Study.