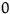Totality, Regularity, and Cardinality in Probability Theory

Abstract

Recent developments in generalized probability theory have renewed a debate about whether regularity (i.e., the constraint that only logical contradictions get assigned probability $0$) should be a necessary feature of both chances and credences. Crucial to this debate, however, are some mathematical facts regarding the interplay between the existence of regular generalized probability measures and various cardinality assumptions. We improve on several known results in the literature regarding the existence of regular generalized probability measures. In particular, we give necessary and sufficient conditions for the existence of regular generalized probability measures defined on the whole powerset of any sample space.

1. Regularity and classical probability theory

The standard Kolmogorovian approach to probability theory on infinite sample spaces is neither regular nor total. In Kolmogorov probability theory, a probability space is given by a triple $(\Omega, \rm{\mathfrak{A}},\mu )$ , where $\Omega $ is a set called the sample space, $\rm{\mathfrak{A}}$ is a $\sigma$ -algebra of subsets of $\Omega $ , and $\mu$ is a probability measure assigning a real number in the interval $[0,1]$ to every set in $\rm{\mathfrak{A}}$ .

Regularity corresponds to the constraint that only logical contradictions get assigned probability $0$ . ¹ It is often understood as a “bridge principle” between modality and probability (Hájek, 2011; Easwaran, 2014), stating that no possible event can receive a probability $0$ of occurring. Totality, on the other hand, requires every subset of the sample space $\Omega $ to be measurable, that is, to have a probability value.

A measure $\mu$ in a probability space $(\Omega, \rm{\mathfrak{A}},\mu )$ satisfies Kolmogorov’s axioms if:

• $\mu (U)\geq 0$ for all $U\in \rm{\mathfrak{A}}$ (nonnegativity);

• $\mu (\Omega )=1$ (normality); and

• whenever $\{A_{i}\}_{i\in \omega }$ is a family of pairwise disjoint sets in $\rm{\mathfrak{A}}, \mu (\cup _{i\in \omega }A_{i})\!\!=\sum _{i\in \omega }\mu (A_{i})$ (countable additivity).

Moreover:

• $\mu$ is regular if $\mu (A)=0$ implies $A=\emptyset $ for any $A\in \rm{\mathfrak{A}}$ ; and

• $\mu$ is total if $\rm{\mathfrak{A}}=\rm{\mathscr{P}}(\Omega )$ .

It is well known that (and this is one example among many) by letting $\Omega =[0,1]$ , we witness a failure of both regularity and totality for many standard Kolmogorovian probability measures. Indeed, suppose $\mu$ is a uniform probability measure defined on all singletons in $[0,1]$ ; that is, $\mu (\{x\})$ is defined for any $x\in [0,1]$ , and $\mu (\{x\})=\mu (\{y\})$ for any $x,y\in [0,1]$ . Then a standard argument that uses countable additivity ² establishes that $\mu (\{x\})=0$ for any $x\in [0,1]$ . One of the unpalatable consequences of this fact is that we have to accept that in a Kolmogorovian setup, whenever we throw a perfectly pointed dart at the interval [0, 1] and we assume uniformity, every single point $x\in [0,1]$ has probability $0$ to be hit, even though one of them will be hit (because $\mu ([0,1])=1$ ). But, and we will come back to this point later on, failure of regularity can also occur when the probability distribution is not uniform.

The failure of totality in the Kolmogorovian context often follows from the axiom of choice. For example, Vitali’s theorem establishes that there are subsets of the interval [0, 1] that are not Lebesgue measurable. ³ When one does not require the probability measure to be translation invariant, the existence of total probability measures on the interval $[0,1]$ becomes either trivial (for any $x\in [0,1]$ , the function $\mu _{x}\colon \rm{\mathscr{P}}([0,1])\rightarrow [0,1]$ given by $\mu (U)=1$ if $x\in U, \mu (U)=0$ otherwise is a two-valued, countably additive, total probability measure) or independent of $ZFC$ (the existence of a countably additive total measure $\mu$ such that $\mu (\{x\})=0$ for all $x\in [0,1]$ implies that $2^{\omega }$ is real-valued measurable; see Ciesielski [1989]).

The failure of regularity and totality ⁴ in the Kolmogorovian case raises the issue of whether there exist theorems relating regularity and totality that can be stated in more general terms and that apply beyond the context of Kolmogorovian probability. For instance, the failure of totality for the Lebesgue measure uses countable additivity. But what if we weaken our probability measures to finitely additive functions? ⁵

Philosophers of probability have devoted quite a bit of attention to regularity. ⁶ The discussion has recently been revitalized by the emergence of powerful infinitesimalist approaches to probability theory, which seem to open new possibilities for a defense of regularity by using infinitesimals in the range of the probability measure. But some philosophers have found this attempt to save regularity wanting. In particular, Williamson (2007), Easwaran (2014), and Hájek (2011) have claimed that the use of infinitesimals is not a satisfactory way of implementing regularity as a constraint on rational credences. For instance, Williamson (2007) provides a thought experiment with a countably infinite sequence of coin tosses and claims that even with infinitesimals at our disposal, the probability of such a sequence is $0$ (and yet such a sequence is possible). Meanwhile, Easwaran (2014) and Hájek (2011) argue that some of the issues for orthodox Bayesianism created by the failure of regularity are best addressed by a revision of orthodox Bayesianism altogether.

Regarding the introduction of infinitesimals as a solution to the regularity problem in standard probability theory, the dialectic that has emerged has been well characterized by Hájek:

I envisage a kind of arms race: we scotched regularity for real-valued probability measures by canvassing sufficiently large domains: making them uncountable. The friends of regularity fought back, enriching their ranges: making them hyperrealvalued. I counter with a still larger domain: making its values hyperreal-valued. Perhaps regularity can be preserved over that domain by enriching the range again, as it might be, making it hyper-hyperreal-valued. I counter again with a yet larger domain: making its values hyper-hyperreal-valued. And so it goes. Some latter-day Bernstein and Wattenberg would need to keep coming up with constructions that would uphold regularity, however big $\Omega $ gets—presumably with ever-richer fields of numbers to provide the values of the probability measures (2011, 21–22).

The thought contained here has received a tentative characterization by Hofweber (2014b) and a more formal one by Pruss (2013). Hofweber advocates “flexibility” in the choice of range and conjectures that by choosing a large enough range, one can preserve properties akin to regularity (he is especially concerned about preserving what he calls the “minimal constraint”):

The lesson from this for believers in infinitesimal chances is simply this: we don’t pick our numbers that measure chance once and for all. We don’t use a fixed number system once and for all, suitable for whatever events need their chances measured. Rather, we pick a suitable extension of the real numbers, one that is suitable for the task at hand and the events under consideration that need their chances measured. If we try to measure the chance of the dart to hit a certain point on the real line, or the chance that a countable sequence of coin tosses comes up heads, then any hyperreal extension of the real numbers will do. We can just pick one. If we hope to measure a larger set of events, then we should play it safe and pick a larger non-Archimedean extension of the real numbers. All that is needed, I conjecture, is one that has larger cardinality than the set of events to be measured. As long as the range of the probability measure is larger than the domain, we will be fine. Less might be fine in most cases, but more is a safe bet. Thus when we measure the chance of events in a certain set of events we pick some extension of the real numbers with infinitesimals that has a larger size than the set of events. Any one of them will do. But you can’t pick one first to be suitable for any possible sets of events that need their chances measured.

In keeping with the dialectic outlined so far, the formal results discussed in the literature on the topic can be roughly divided into two categories. On the one hand, existence theorems establish that under certain conditions on the sample space $\Omega $ and the range of probabilities $V$ , regular probability measures from $\rm{\mathscr{P}}(\Omega )$ to $V$ can be constructed. On the other hand, impossibility theorems identify conditions on $\Omega $ and $V$ under which there can be no regular probability measure from $\rm{\mathscr{P}}(\Omega )$ to $V$ . For results of the first kind, Hofweber (2014a) provides, for instance, the following result:

Theorem 1.1. Let $\Omega $ be any infinite sample space. There is a hyperreal field $\rm{\Re }^{\rm{*}}$ of at most cardinality $2^{| \Omega | }$ and a regular probability measure from $\rm{\mathscr{P}}(\Omega )$ into $\rm{\Re }^{\rm{*}}$ .

In other words, given any sample space $\Omega $ of cardinality $\kappa$ , one can always obtain a total and regular probability measure on $\rm{\mathscr{P}}(\Omega )$ by finding an appropriate hyperreal field of cardinality $2^{\kappa }$ .

By contrast, the best impossibility results existing in the literature are given by Pruss (2013) (see also sec. 2). Unlike Hofweber (2014a), who focuses on the size of the algebra of subsets of the sample space, Pruss focuses on the size of the sample space. Pruss (2013) shows that whenever $\Omega $ is strictly larger in cardinality than the range of a probability measure $\mu, \mu$ cannot be regular.

Our main contribution to the existing literature is an improvement of Pruss’s impossibility theorem. Using a notion of generalized probability measure inspired by Pruss’s setting, we establish the following:

Theorem 3.1. For any generalized probability range $(V,\leq,+,0)$ and any set $\Omega $ such that $| \Omega | \geq | V|$ , there is no total regular $V$ -probability measure for $\Omega $ .

Theorem 3.1 is a clear strengthening of Pruss’s result because it establishes that the assumption that $| \Omega | \gt | V|$ can be weakened to $| \Omega | \geq | V|$ . We also combine our novel impossibility theorem with existence theorems such as the ones noted by Hofweber (2014a) and Benci et al. (2018) to address the following question: Given a sample space $\Omega $ and a cardinal $\kappa$ , is there a generalized probability range $V$ (see Definition 2.1) of size $\kappa$ and a regular generalized $V$ -probability measure defined on $\rm{\mathscr{P}}(\Omega )$ ? We show that under the assumption of the generalized continuum hypothesis (GCH), the conjunction of the known existence theorems and our impossibility result yields a complete answer to the question:

Theorem 5.7. (GCH) Let $\kappa$ be a cardinal and $\Omega $ a set. Then there is a hyperreal field $\rm{\Re }$ of size $\kappa$ and a total and regular finitely additive probability measure $\mu \colon \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ if and only if (iff) $| \Omega | \lt \kappa$ .

Moreover, a related problem is to give necessary and sufficient conditions for when, given a sample space $\Omega $ and a field $V$ , there exists a regular probability measure defined on $\rm{\mathscr{P}}(\Omega )$ . Because we believe that the first question is the more relevant one for the current philosophical debate on regularity, we do not pursue this question here. However, we consider a similar question in the case where the algebra of events is the set of finite and cofinite subsets of $\Omega $ rather than the full powerset. Regarding this issue, we establish the following existence result:

Theorem 4.7. Let $\Omega $ be an infinite set, let $Fin(\Omega )$ be the algebra of finite and cofinite subsets of $\Omega $ , and let $V$ be a countable non-Archimedean field. Then there is a regular $V$ -probability measure $\mu \colon Fin(\Omega )\rightarrow V$ .

We then use this lemma together with well-known impossibility results to establish the following:

Theorem 4.8. Let $\Omega $ be an uncountable set and $F$ an infinite field. Then there is a regular generalized $F$ -probability measure defined on the algebra of finite and cofinite subsets of $\Omega $ iff $F$ is non-Archimedean.

The rest of the article is organized as follows. In Section 2, we introduce a framework for generalized probability measures inspired by the one in Pruss (2013) and connect the issue of regularity in probability theory to an old result of Zermelo (1904) regarding functions from the powerset of a set $X$ into $X$ itself. In Section 3, we show how Zermelo’s theorem can be used to establish several impossibility results about total and regular probability measures. In particular, we show how to improve the cardinality assumption in Pruss’s impossibility theorem. In Section 4, we investigate what happens when the requirement that a generalized probability measure be defined on the full powerset of an infinite sample space is relaxed, and we show that even in this case, Zermelo’s theorem allows us to prove some impossibility theorems. Finally, in Section 5, we discuss the connection between our results and some of the hyperreal fields that have been constructed as ranges of regular generalized probability measures.

2. Part-whole and regularity

In this section, we first introduce the general probabilistic setting in which we will work. Throughout this article, we will not assume that the range of a probability measure $\mu$ is contained in the real unit interval $[0,1]$ . The motivation for this is twofold. First, Hájek’s (2011) “arms race” description of the dialectic between proponents and opponents of regularity involves considering domains and codomains of ever-increasing cardinality. Second, as we shall see later on, the relationship between regularity, totality, and cardinality in the classical setting is muddled by the fact that the standard unit interval $[0,1]$ is Archimedean. We may therefore hope to gain a clearer understanding of the possible obstacles to the existence of a total and regular probability measure in a more general context in which Archimedeanity does not play a role anymore. However, given the importance of probability measures with a range contained in the real interval $[0,1]$ in the literature, we will often point out how the results we discuss apply in this specific case. We start with the following definitions adapted from Pruss (2013).

Definition 2.1. A generalized probability range is a tuple $(V,\leq,+,0)$ satisfying the following conditions:

• $(V,\leq )$ is a partial order, with $0$ being its least element;

• $(V,+,0)$ is a commutative monoid—that is, $+$ is a commutative and associative operation on $V$ , and $x+0=x$ for any $x\in V$ ; and

• for any $x,y,z\in V, x\lt y$ implies $x+z\lt y+z$ .

Definition 2.2. Let $(V,\leq,+,0)$ be a generalized probability range. A generalized $V$ -probability space is a triple $(\Omega, \rm{\mathfrak{A}},\mu )$ such that:

• $\Omega $ is a set, and $\rm{\mathfrak{A}}$ is a collection of subsets of $\Omega $ closed under finite unions and complements; and

• $\mu \colon \rm{\mathscr{P}}(\Omega )\rightarrow V$ is a function satisfying the following two conditions:

  • – $0\leq \mu (A)$ for any $A\in \rm{\mathfrak{A}}$ (nonnegativity); and

  • – whenever $A,B\in \rm{\mathfrak{A}}$ are such that $A\cap B=\emptyset, \mu (A\cup B)=\mu (A)+\mu (B)$ (finite additivity).

Given a generalized probability space, $(\Omega, \rm{\mathfrak{A}},\mu )$ , the generalized $V$ -probability measure $\mu$ is total if $\rm{\mathfrak{A}}=\rm{\mathscr{P}}(\Omega )$ , and it is regular if $\mu (A)=0$ implies $A=\emptyset $ for any $A\in \rm{\mathfrak{A}}$ .

For any ordered field $F$ , the nonnegative elements of $F$ form a generalized probability range. For this reason, we will sometimes consider fields as generalized probability ranges, despite the slight abuse of language. Note that in the classical setting, a finitely additive probability measure is a generalized $\rm{\mathbb{R}}$ -probability measure $(\Omega, \rm{\mathfrak{A}},\mu )$ satisfying the additional condition that $\mu (\Omega )=1$ .

Pruss (2013) shows a version of the following:

Theorem 2.3. Let $(V,\leq,+,0)$ be a generalized probability range and $\Omega $ a set such that $| \Omega | \gt | V|$ . Then there is no total and regular generalized $V$ -probability measure for $\Omega $ .

Our first main result (Theorem 3.1) is an improvement of Pruss’s result. In this section, we lay the groundwork for this theorem by establishing a connection between generalized regular probability measures and part-whole–preserving functions. We start by recalling a result that is well known in the literature (e.g., it is stated en passant in Benci et al. [2018], 516) but is worth proving expressly. We first need the following definition:

Definilabeltion 2.4. Let $V$ be a generalized probability range and $(\Omega, \rm{\mathfrak{A}},\mu )$ be a generalized $V$ -probability space. The generalized $V$ -probability measure $\mu$ preserves part-whole if for any $A,B\in \rm{\mathfrak{A}}$ such that $A\subsetneq B, \mu (A)\lt \mu (B)$ .

Lemmlabela 2.5. Let $\mu \colon \rm{\mathfrak{A}}\rightarrow V$ be a generalized $V$ -probability measure for some generalized probability range $V$ . Then $\mu$ satisfies regularity iff $\mu$ preserves part-whole.

Proof. First, it is a simple exercise to verify that any generalized $V$ -probability space $(\Omega, \rm{\mathfrak{A}},\mu )$ has the following two properties: $\mu (\emptyset )=0$ , and $\mu (A)\leq \mu (B)$ whenever $A,B\in \rm{\mathfrak{A}}$ and $A\subseteq B$ .

Fix $V, \Omega, \rm{\mathfrak{A}}$ , and $\mu \colon \rm{\mathfrak{A}}\rightarrow V$ . If $A\subsetneq B$ for some $A,B\in \rm{\mathfrak{A}}$ , then finite additivity implies that $\mu (B)=\mu (A)+\mu (B\backslash A)$ . If $\mu$ is regular, then we have $0\lt \mu (B\backslash A)$ , from which it follows that

$\mu \left(A\right)=\mu \left(A\right)+0\lt \mu \left(A\right)+\mu \left(B\backslash A\right)=\mu \left(B\right).$

Hence, $\mu$ preserves part-whole.

Now suppose $\mu$ preserves part-whole, and let $A$ be any nonempty set in $\rm{\mathfrak{A}}$ . Because $\emptyset \subsetneq A$ , by part-whole we have $\mu (\emptyset )\lt \mu (A)$ . Thus, $\mu (A) \neq \mu (\emptyset )=0$ for every nonempty subset $A$ , which means that $\mu$ is regular.□

We now introduce a theorem that will be of great use for our proofs. Its significance for the study of abstraction operators that are used in the context of neologicism has been highlighted by Mancosu and Siskind (2019) and for issues related to the axiom of choice in second-order logic by Siskind et al. (2023). The theorem, in its set-theoretic version, is implicit in Zermelo (1904) and was brought out explicitly by Kanamori (1997).

Theorem 2.6 (Zermelo, 1904). Given a set $X$ and an arbitrary function $f\,\colon\, \rm{\mathscr{P}}(X)\rightarrow X$ , there are sets $A,B\in \rm{\mathscr{P}}(X)$ such that $A\subsetneq B$ and $f(A)=f(B)$ .

The theorem can be proved without the axiom of choice, and it can be formalized in a second-order theory with only the additional symbol for $f$ (see Mancosu and Siskind, 2019). Here is a set-theoretic proof that uses transfinite induction:

Proof. Fix a set $X$ and a function $f\,\colon\, \rm{\mathscr{P}}(X)\rightarrow X$ . In order to violate part-whole, we must find two sets $A,B\in \rm{\mathscr{P}}(X)$ such that $A$ is a proper subset of $B$ and $f(A)=f(B)$ . Using transfinite recursion, define a function $G\,\colon\, Ord\rightarrow \rm{\mathscr{P}}(X)$ , where $Ord$ is the class of ordinals, as follows:

$G\left(0\right)=f\left(\emptyset \right);$

$G\left(\alpha \right)=f\left(ran\left(G| \alpha \right)\right),{\rm where\ }{ran}(G| \alpha )=\{G\left(\beta \right)| \beta \lt \alpha \}.$

One easily verifies that for any ordinal $\alpha, G(\alpha )\subseteq X$ . Because $\rm{\mathscr{P}}(X)$ is a set and $Ord$ is a proper class, there must be $\alpha \lt \beta \in Ord$ such that $G(\alpha )=G(\beta )$ . Letting $A=G| \alpha$ and $B=G| \beta$ , this means that $f(A)=G(\alpha )=G(\beta )=f(B)$ . At the same time, we clearly have that $A\subsetneq B$ , which shows that $A$ and $B$ are the required counterexamples to part-whole.□

The connection between the previous applications and the probabilistic setting is the following. Just as in neologicism we are concerned with functions defined by abstraction principles mapping concepts (conceived extensionally as subsets of the domain of individuals) on a certain domain into the domain itself, in many applications of probability theory, we are also mapping a collection of subsets (or the entire power set) of the sample space $\Omega $ into $\Omega $ itself.

The following result is the first immediate application of Zermelo’s (1904) result in the context of probability theory:

Theorem 2.7. Let $X$ be a subset of $[0,1]$ , and let $\mu$ from $\rm{\mathscr{P}}([0,1])$ into $X$ be a finitely additive probability measure. Then $\mu$ is not regular.

Proof. Fix a finitely additive probability measure $\mu \,\colon\, \rm{\mathscr{P}}([0,1])\rightarrow X$ , and notice that we may view $\mu$ as a finitely additive measure with codomain $[0,1]$ . By Lemma 2.5, $\mu$ is regular only if it preserves part-whole. But by Theorem 2.6, $\mu$ must violate part-whole and therefore cannot be regular.□

Theorem 2.7 only uses a special case of Zermelo’s theorem—namely, when the codomain of the function $f$ is a subset of the unit interval. As we shall now see, the generality of Zermelo’s theorem allows for a much more general impossibility result regarding the existence of regular probability measures.

3. Zermelo’s theorem and generalized probability measures

Our first generalization of Theorem 2.7 allows us to consider a much wider class of sample spaces and probability ranges.

Theorem 3.1. For any generalized probability range $(V,\leq,+,0)$ and any set $\Omega $ such that $| \Omega | \geq | V|$ , there is no total regular $V$ -probability measure for $\Omega $ .

Proof. Suppose toward a contradiction that $\mu$ is a regular generalized $V$ -probability measure for $\Omega $ . Because $| \Omega | \geq | V|$ , there is a surjection $f\,\colon\, \Omega \rightarrow V$ . Consider the inverse image lift $f_{\rm{*}}\,\colon\, \rm{\mathscr{P}}(V)\rightarrow \rm{\mathscr{P}}(\Omega )$ of the surjection $f$ , given by $f_{\rm{*}}(A)=\{y\in \Omega | f(y)\in A\}$ for any $A\subseteq V$ . One easily verifies the following:

• $f_{\rm{*}}(\emptyset )=\emptyset, f_{\rm{*}}(A)\subseteq f_{\rm{*}}(B)$ whenever $A,B\subseteq V$ and $A\subseteq B$ ; and

• for any $A,B\subseteq V, f_{\rm{*}}(A\cup B)=f_{\rm{*}}(A)\cup f_{\rm{*}}(B), f_{\rm{*}}(A\cap B)=f_{\rm{*}}(A)\cap f_{\rm{*}}(B)$ ;

• $f_{\rm{*}}$ is an injection.

Now consider the composition $\nu =\mu \circ f_{\rm{*}}\,\colon\, \rm{\mathscr{P}}(V)\rightarrow V$ . We then verify that $\nu$ is a regular generalized $V$ -probability measure. Indeed:

• For any $A\subseteq V, \nu (A)=\mu (f_{\rm{*}}(A))\geq 0$ by nonnegativity of $\mu$ .

• For any $A,B\subseteq V$ such that $A\cap B=\emptyset $ :

$\nu \left(A\cup B\right)=\mu \left(f_{\rm{*}}\left(A\cup B\right)\right)=\mu \left(f_{\rm{*}}\left(A\right)\cup f_{\rm{*}}\left(B\right)\right)=\mu \left(f_{\rm{*}}\left(A\right)\right)+\mu \left(f_{\rm{*}}\left(B\right)\right)$

by finite additivity of $\mu$ , and because $f_{\rm{*}}(A)\cap f_{\rm{*}}(B)=f_{\rm{*}}(A\cap B)=\emptyset $ . Hence,

$\nu \left(A\cup B\right)=\nu \left(A\right)+\nu \left(B\right),$

which shows that $\nu$ is finitely additive.

• For any $A\subseteq V, (A)=0$ implies that $\mu (f_{\rm{*}}(A))=0$ . Because $\mu$ is regular, this means that $f_{\rm{*}}(A)=\emptyset $ . Because $f_{\rm{*}}$ is injective and $f_{\rm{*}}(A)=f_{\rm{*}}(\emptyset )=\emptyset $ , it follows that $A=\emptyset $ , which establishes that $\nu$ is regular.

By Lemma 2.5, this means that there is a part-whole–preserving function $\mu \,\colon\, \rm{\mathscr{P}}(V)\rightarrow V$ , which contradicts Zermelo’s theorem. Hence, there is no generalized $V$ -probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow V$ .□

Theorem 3.1 is a clear generalization of Pruss’s (2013) result. By appealing to Zermelo’s theorem, we weakened the assumption that $\Omega $ has size strictly greater than $V$ to merely assuming the existence of a surjection from $\Omega $ to $V$ .

Moreover, Pruss’s (2013) result only shows that there must be at least one failure of regularity for any $V$ -probability measure. Using Theorem 3.1, however, we can actually show that there must be many failures of regularity, even in the generalized setting.

Lemma 3.2. Let $\Omega $ be a set and $V$ be a generalized probability range such that $| \Omega | =| V| =\kappa$ . Then for any $V$ -probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow V, \mu (\{x\})=0$ for $\kappa$ many elements $x\in \Omega $ .

Proof. Let $C=\{x\in \Omega | \mu (\{x\})=0\}$ , and let $\Omega \rm{'}=\Omega \backslash C$ . Consider the function $\nu \,\colon\, \rm{\mathscr{P}}(\Omega \rm{'})\rightarrow V$ determined by $\nu (A)=\mu (A)$ for any $A\subseteq \Omega \rm{'}$ . One easily verifies that $\nu$ is a $V$ -probability measure for $\Omega \rm{'}$ . Now suppose that $A\subsetneq B\in \rm{\mathscr{P}}(\Omega \rm{'})$ . This implies that there is $x\in B\backslash A$ , and note that because $B$ is disjoint from $C, \nu (\{x\})=\mu (\{x\})\gt 0$ , which implies that $\nu (B\backslash A)\gt 0$ . Because $\nu (B)=\nu (A)+\nu (B\backslash A)$ , it therefore follows that $\nu (A)\lt \nu (B)$ . Thus $\nu$ is a regular $V$ -probability measure for $\Omega \rm{'}$ . By Zermelo’s theorem (Theorem 3.1), it follows that $| \Omega \rm{'}| \lt | V| =\kappa$ . Now, because $\kappa =| \Omega | =| \Omega \rm{'}| +| C|$ , from $| \Omega \rm{'}| \lt \kappa$ and basic cardinal arithmetic, it follows that $| C| =\kappa$ . Thus, $\mu (\{x\})=0$ for $\kappa$ many elements $x$ of $\Omega $ .

Finally, we conclude this section by discussing in some detail the special case of real-valued finitely additive probability measures. As an immediate corollary of Theorem 3.1, we obtain the following:

Corollary 3.3. Let $\Omega $ be a set such that $| \Omega | =2^{{\aleph _{0}}}$ . Then no finitely additive probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow [0,1]$ is regular.

Corollary 3.3 is a weaker form of a well-known result establishing that there can be no finitely additive regular probability measure from a set $\Omega $ into $[0,1]$ when $\Omega $ is uncountable. The argument has been presented neatly by both Hájek (2003) and Williamson (2007). Let $\Omega $ be a set, and suppose that $\mu$ is a finitely additive probability measure into $[0,1]$ and defined on all singletons. For any natural number $n$ , let $A_{n}$ be the set of all $x\in \Omega $ such that $\mu \left( {\left\{ x \right\}} \right) \ge {1 \over n}$ . By finite additivity, each $A_{n}$ must be finite, which means that there can only be countably many singletons mapped to a nonzero value in $[0,1]$ . If $\Omega $ is uncountable, then this means that uncountably many singletons must be mapped to $0$ .

The Hájek–Williamson argument has three advantages. The first one is that it shows that the failure of regularity must occur in many places because uncountably many singletons must be mapped to $0$ . By contrast, Corollary 3.3 only guarantees that regularity must fail in some place, which is enough to conclude that any standard probability measure must assign probability $0$ to $\{x\}$ for some $x$ , but nothing more. Here, however, it is easy to see that one can adapt the proof of Lemma 3.2 in a straightforward way so as to obtain continuum many failures of regularity in the case of a probability measure defined on the full powerset of a sample space of size continuum. Second, although our application of Zermelo’s theorem requires the sample space $\Omega $ to have size continuum, one only needs $\Omega $ to be uncountable for the Hájek–Williamson argument to go through. In the absence of the continuum hypothesis, the Hájek–Williamson result is therefore stronger than ours. Finally, the Hájek–Williamson argument only requires the probability measure to be defined on all singletons, ⁷ whereas our results assume that the probability measure is total. However, the last two differences between the two results are connected to a third significant one: the Hájek–Williamson argument relies in an essential way on the fact that the real interval $[0,1]$ is Archimedean. By finite additivity, only finitely many singletons can have probability greater than ${1 \over n}$ for a fixed natural number $n$ , which means that uncountably many singletons must have a value smaller than ${1 \over n}$ for any $n$ . But this implies that uncountably many singletons must have probability $0$ only because $0$ is the unique element smaller than ${1 \over n}$ for any $n$ (i.e., $[0,1]$ is Archimedean). The Hájek–Williamson argument does not say anything about the failure of regularity in a non-Archimedean field, which contrasts with the generality of Theorem 3.1. We will return to the issue of Archimedeanity in the next section, in which we investigate to what extent totality is necessary to establish the impossibility results mentioned so far.

4. Relaxing totality

In this section, we investigate the consequences of relaxing the requirement that the algebra of events must be the entire powerset of $\Omega $ for the existence of regular measures. Let us start with an easy result.

Lemma 4.1. Let $\Omega $ be a set, and assume that there exists a total and regular generalized $V$ -probability measure $\mu$ on $\rm{\mathscr{P}}(\Omega )$ for some generalized probability range $V$ . Then for any infinite algebra $\rm{\mathbb{A}}$ of subsets of $\Omega $ , there is a generalized probability range $V\rm{'}$ of size at most $| \rm{\mathbb{A}}|$ and a regular probability measure $\nu \,\colon\, {\rm{\mathbb{A}}}\rightarrow V\rm{'}$ . Moreover, if $V$ is a field, then so is $V\rm{'}$ .

Proof. Let $\Omega, \rm{\mathbb{A}}, {\it V}$ , and $\mu \,\colon\, \rm{\mathbb{A}}\rightarrow {\it V}$ be as in the statement of the lemma, and let $S$ be the range of the restriction of $\mu$ to $\rm{\mathbb{A}}$ . Let $V\rm{'}$ be the substructure of $V$ generated by $S$ , and notice that because $| \rm{\mathbb{A}}| \geq \max \{\aleph _{0},| {\it S}| \}$ , we have that $| V\rm{'}| \leq \rm{\mathbb{A}}$ . But clearly, the restriction $\nu \,\colon\, \rm{\mathbb{A}}\rightarrow {\it V}\rm{'}$ of $\mu$ is the required regular probability measure. Moreover, if $V$ is a field, then we can take $V\rm{'}$ to be the substructure of $V$ generated by $S$ in the language of fields, and thus we may assume that $V\rm{'}$ is a field.

In the next section (Theorem 5.5), we will recall existing results in the literature establishing that for any set $\Omega $ there is a hyperreal field $V$ and a regular generalized $V$ -probability measure defined on $\rm{\mathscr{P}}(\Omega )$ . This entails that the assumption in the statement of Lemma 4.1 can in fact always be satisfied.

For now, let us investigate some consequences of this lemma for countable sample spaces and real-valued probability measures. In order to do this, we start by recalling a classical result of measure theory (e.g., it is a special case of theorem 2.5 in Horn and Tarski [1948]):

Lemma 4.2. Let $\Omega $ be a countable set. Then there is a regular finitely additive probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow [0,1]$ .

Proof. Let us first show this in the case $\Omega =\rm{\mathbb{N}}$ . Recall that any real number in the interval $[0,1]$ has a binary expansion; that is, it can be written as a (possibly infinite) sequence of negative powers of 2. For example, the rational number $0.625$ can be written as $0.5+0.125=1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3}$ . Conversely, any countable sequence $s$ of $0s$ and $1s$ determines the binary expansion of some real number $r(s)\in [0,1]$ . For any subset $U$ of $\rm{\mathbb{N}}$ , let $\mu _{0}(U)=r(\chi _{U})$ ; that is, let $\mu _{0}(U)$ be the real number whose binary expansion is determined by the characteristic function of $U$ . Formally, this means that for any $U\subseteq \rm{\mathbb{N}}$ :

$\mu _{0}\left(U\right)=\displaystyle\sum _{i\in \rm{\mathbb{N}}}\chi _{U}\left(i\right)\cdot 2^{-i}.$

For example, $\mu _{0}(\{1,3\})=1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3}=0.625$ . Then observe the following:

• $\mu _{0}(U)=0$ iff $\chi _{U}$ is constantly $0$ iff $U=\emptyset $ .

• Whenever $U\cap V=\emptyset $ , we have that:

$\mu _{0}\left(U\right)+\mu _{0}\left(V\right)=\sum _{i\in \rm{\mathbb{N}}}\chi _{U}\left(i\right)\cdot 2^{-i}+\sum _{i\in \rm{\mathbb{N}}}\chi _{V}\left(i\right)\cdot 2^{-i}$

$\hskip 2.2pc=\sum _{i\in N}\left(\chi _{U}\left(i\right)+\chi _{V}\left(i\right)\right)\cdot 2^{-i}$

$\hskip 3.1pc=\sum _{i\in N}\max \left(\chi _{U}\left(i\right),\chi _{V}\left(i\right)\right)\cdot 2^{-i}$

$\hskip -1.2pc=\sum _{i\in N}\chi _{U\cup V}\cdot 2^{-i}$

$\hskip -2.5pc=\mu _{0}\left(U\cup V\right),$

which shows that $\mu _{0}$ is finitely additive (in fact, the same argument shows that it is $\sigma$ -additive).

Hence, $\mu _{0}$ is a regular finitely additive probability measure defined on the whole of $\rm{\mathscr{P}}(\rm{\mathbb{N}})$ . Now if $\Omega $ is any countable set, there is a surjection $f\,\colon\, \rm{\mathbb{N}}\rightarrow \Omega $ , which can be lifted to an injection $f_{\rm{*}}\,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\mathscr{P}}(\rm{\mathbb{N}})$ , as in the proof of Theorem 3.1. But then $\mu _{0}\circ f_{\rm{*}}\,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow [0,1]$ is also a regular finitely additive probability measure defined on $\rm{\mathscr{P}}(\Omega )$ .□

Combined with a similar construction as in Lemma 4.1, we get the following as an immediate corollary of Lemma 4.2:

Corollary 4.3. Let $\Omega $ be a countable set, and let $Fin(\Omega )$ be the algebra of finite and cofinite subsets of $\Omega $ . Then there is a regular probability measure $\mu \,\colon\, Fin(\Omega )\rightarrow [0,1]\cap \rm{\mathbb{Q}}$ .

Proof. Let $f$ be a bijection between $\Omega $ and $\omega$ . This induces an isomorphism of fields of sets $\varphi \,\colon\, Fin(\Omega )\rightarrow Fin(\omega )$ . Note, moreover, that for any finite or cofinite subset $A$ of $\omega, \mu _{0}(A)$ is rational, where $\mu _{0}$ is the regular probability measure defined in the proof of Lemma 4.2. Then letting $\mu$ be the restriction of $\mu _{0}$ to $Fin(\omega )$ and $\nu =\mu \circ \varphi$ , we have that $\nu$ is a regular $\rm{\mathbb{Q}}$ -probability measure.□

Moreover, Lemmas 4.1 and 4.2 also have some immediate consequences regarding the interaction of probability theory and computability theory. For example, it is well known that there are only countably many recursive subsets of $\omega$ and that they form a Boolean subalgebra $\rm{\mathbb{A}}$ of $\rm{\mathscr{P}}(\omega )$ . By Lemma 4.1, we may consider the subfield $V\rm{'}$ of $\rm{\mathbb{R}}$ generated by the range of the restriction of $\mu _{0}$ to $\rm{\mathbb{A}}$ , where, again, $\mu _{0}$ is the function defined in the proof of Lemma 4.2. In fact, it is easy to verify that $V\rm{'}$ is exactly the field of all recursive reals in the interval $[0,1]$ . This has the following consequence:

Corollary 4.4. Let $\rm{\mathbb{R}}\rm{'}$ be the field of recursive reals in the interval $[0,1]$ . Then there is a countable algebra $\rm{\mathfrak{A}}\subseteq \rm{\mathscr{P}}(\rm{\mathbb{R}}\rm{'})$ and a regular probability measure $\nu \,\colon\, \rm{\mathfrak{A}}\rightarrow \rm{\mathbb{R}}\rm{'}$ .

Proof. Because $\rm{\mathbb{R}}\rm{'}$ is countable, fix a bijection $f\,\colon\, \rm{\mathbb{R}}\rm{'}\rightarrow \omega$ . As usual, this yields an isomorphism $f_{\rm{*}}\,\colon\, \rm{\mathscr{P}}(\omega )\rightarrow \rm{\mathscr{P}}(\rm{\mathbb{R}}\rm{'})$ , so let $\rm{\mathfrak{A}}={\it f}_{\rm{*}}[\rm{\mathbb{A}}]$ ; that is, $\rm{\mathfrak{A}}$ is the range of the restriction of $f$ to $\rm{\mathbb{A}}$ . Clearly, $\rm{\mathfrak{A}}$ is a countable subalgebra of $\rm{\mathbb{R}}\rm{'}$ . Moreover, let $\nu \,\colon\, \rm{\mathfrak{A}}\rightarrow \rm{\mathbb{R}}\rm{'}$ be defined as $\nu (f_{\rm{*}}(A))=\mu _{0}(A)$ . Notice that this is well defined because, by construction, any element in $\rm{\mathfrak{A}}$ is of the form $f_{\rm{*}}(A)$ for some $A\in \rm{\mathbb{A}}$ such that $\mu _{0}(A)\in \rm{\mathbb{R}}\rm{'}$ . But clearly, $\nu$ is regular, which completes the proof.□

In other words, when restricting our attention to a countable subalgebra of the powerset of the recursive reals in the interval $[0,1]$ , we are able to escape the conclusion of Zermelo’s theorem. Of course, this is only because $\rm{\mathfrak{A}}$ is not the full powerset of the set of recursive reals because there are uncountably many subsets of the recursive reals. Let us also note that the regular probability measure thus constructed is not itself recursive, nor is $\rm{\mathfrak{A}}$ the algebra of recursive subsets of $\rm{\mathbb{R}}\rm{'}$ .

The previous results establish that relaxing the assumption of totality may sometimes allow for the existence of regular probability measures. One is therefore led to wonder whether totality is in fact a necessary condition for the conclusion of Zermelo’s theorem to apply. The proof of Zermelo’s original theorem certainly seems to make essential use of the fact that the function $f\,\colon\, \rm{\mathscr{P}}(X)\rightarrow X$ that ends up violating part-whole is defined on all arbitrary subsets of $X$ . However, the obstacle to the existence of regular probability measures is not totality per se because it is sufficient that the algebra of events be merely isomorphic to the full powerset of the sample space, as the following straightforward lemma shows:

Lemma 4.5. Let $\Omega $ be an infinite set and $V$ a generalized probability range such that $| \Omega | \geq | V|$ . Then for any algebra of events $\rm{\mathfrak{A}}$ such that $\rm{\mathfrak{A}}$ and $\rm{\mathscr{P}}(\Omega )$ are isomorphic as fields of sets, there is no regular $V$ -probability measure $\mu \,\colon\, \rm{\mathfrak{A}}\rightarrow V$ .

Proof. Suppose $\rm{\mathfrak{A}}$ is an algebra of events isomorphic to $\rm{\mathscr{P}}(\Omega )$ , and let $\varphi \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\mathfrak{A}}$ be such an isomorphism. Clearly, if $\mu \,\colon\, \rm{\mathfrak{A}}\rightarrow V$ is a regular $V$ -probability measure, then so is $\mu \circ \varphi \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow V$ . Therefore, by Theorem 3.1 there can be no regular $V$ -probability measure defined on $\rm{\mathfrak{A}}$ .□

As a direct consequence of Lemma 4.5, we can now prove the following impossibility theorem for algebras of events that are far from being the full powerset of the sample space:

Corollary 4.6. Let $\Omega $ be an infinite set and $V$ be a generalized probability range such that $| \Omega | \geq | V|$ . Then there is a subalgebra $\rm{\mathfrak{A}}$ of $\rm{\mathscr{P}}(\Omega )$ such that $| \rm{\mathfrak{A}}| =| \rm{\mathscr{P}}(\Omega )\backslash \rm{\mathfrak{A}}| =| \rm{\mathscr{P}}(\Omega )|$ and for which there is no regular $V$ -probability measure defined on $\rm{\mathfrak{A}}$ .

Proof. Fix a bijection $f$ from $\Omega $ into $\Omega \times \{0,1\}$ , and let $\pi \,\colon\, \Omega \times \{0,1\}\rightarrow \Omega $ be defined as $\pi (x,i)=x$ for any $x\in \Omega, i\in \{0,1\}$ . Finally, let $g\,\colon\, \Omega \rightarrow \Omega $ be the composition $\pi \circ f$ . Because $g$ is a surjection, it induces an embedding $g^{\rm{*}}$ of $\rm{\mathscr{P}}(\Omega )$ into $\rm{\mathscr{P}}(\Omega )$ . Let $\rm{\mathfrak{A}}=g^{\rm{*}}[\rm{\mathscr{P}}(\Omega )]=\{g^{\rm{*}}(U)| U\subseteq \Omega \}$ . It is straightforward to verify that the map $\varphi \,\colon\, \rm{\mathfrak{A}}\rightarrow \rm{\mathscr{P}}(\Omega )$ given by $\varphi (g^{\rm{*}}(U))=U$ for any $U\in \rm{\mathscr{P}}(\Omega )$ is an isomorphism of fields of sets. By Lemma 4.5, this implies that there can be no regular $V$ -probability measure defined on $\rm{\mathfrak{A}}$ . Now for any $x\in \Omega $ , let $x_{0}=f^{-1}(x,0)$ and $x_{1}=f^{-1}(x,1)$ . Note that $x_{0}\neq x_{1}$ yet $g(x_{0})=g(x_{1})=x$ for any $x\in \Omega $ . Thus, for any $x\in \Omega $ and $U\subseteq \Omega, x_{0}\in g^{\rm{*}}(U)$ iff $g(x_{0})\in U$ iff $g(x_{1})\in U$ iff $x_{1}\in g^{\rm{*}}(U)$ . From this, it follows at once that $\{x_{0}\}\,\notin \,\rm{\mathfrak{A}}$ for any $x\in \Omega $ . Because $x_{0}\neq y_{0}$ whenever $x\neq y$ , we can therefore conclude that $\rm{\mathfrak{A}}$ is a proper subalgebra of $\rm{\mathscr{P}}(\Omega )$ such that $| \rm{\mathscr{P}}(\Omega )\backslash \rm{\mathfrak{A}}| =| \rm{\mathscr{P}}(\Omega )|$ .□

This result establishes that totality is not, after all, a necessary condition for the conclusion of Zermelo’s theorem to hold. Indeed, to guarantee that there can be no regular generalized $V$ -probability measure defined on a subalgebra $\rm{\mathfrak{A}}$ of $\rm{\mathscr{P}}(\Omega )$ for some set $\Omega $ of size $| V|$ , it is enough to assume that $\rm{\mathfrak{A}}$ is isomorphic to $\rm{\mathscr{P}}(\Omega )$ , which, as corollary 4.6 shows, does not coincide with $\rm{\mathfrak{A}}$ being the full powerset of $\Omega $ . Moreover, the real obstacle to the existence of a regular function also does not lie in the constraints put on the cardinality of the algebra of events, as the following result shows:

Lemma 4.7. Let $\Omega $ be an infinite set, let $Fin(\Omega )$ be the algebra of finite and cofinite subsets of $\Omega $ , and let $V$ be a countable non-Archimedean field. Then there is a regular $V$ -probability measure $\mu \,\colon\, Fin(\Omega )\rightarrow V$ .

Proof. Let $V$ be a countable non-Archimedean field. ⁸ Fix a positive infinitesimal $\varepsilon \in V$ . By definition, any element in $Fin(\Omega )$ is either a finite subset of $\Omega $ or the complement of such a finite subset. Define $\mu \,\colon\, Fin(\Omega )\rightarrow V$ by letting $\mu (A)=\varepsilon | A|$ if $A$ is finite, and $(A)=1-\varepsilon | \Omega \backslash A|$ otherwise. Let us show that $\mu$ is the required measure. Suppose $A,B\in Fin(\Omega )$ are such that $A\cap B=\emptyset $ . We distinguish two cases:

• Case 1: Both $A$ and $B$ are finite. In this case we have that $A\cup B$ is finite and $| A\cup B| =| A| +| B|$ , so

$\mu \left(A\cup B\right)=\varepsilon \left| A\cup B\right| =\varepsilon \left(\left| A\right| +\left| B\right| \right)=\varepsilon \left| A\right| +\varepsilon \left| B\right| =\mu \left(A\right)+\mu \left(B\right).$

• Case 2: Either $A$ or $B$ is infinite. Without loss of generality, assume $A$ is infinite. Note that this means that $\Omega \backslash A$ is finite. Because $A\cap B=\emptyset $ , we have that $B\subseteq \Omega \backslash A$ , so $B$ is also finite. By simple finite cardinality reasoning, we have that $| \Omega \backslash A| =| B| +| (\Omega \backslash A)\cap (\Omega \backslash B)|$ . Moreover, we have that $\Omega \backslash (A\cup B)=(\Omega \backslash A)\cap (\Omega \backslash B)$ . Because $A$ and $A\cup B$ are infinite but $B$ is finite, it follows that $\mu (A)=1-\varepsilon | \Omega \backslash A|, \mu (A\cup B)=1-\varepsilon | (\Omega \backslash A)\cap (\Omega \backslash B)|$ , and $\mu (B)=\varepsilon | B|$ . Now we compute:

$\left| \Omega \backslash A\right| =\left| B\right| +\left| \left(\Omega \backslash A\right)\cap \left(\Omega \backslash B\right)\right| \Leftrightarrow$

$\left| B\right| =\left| \Omega \backslash A\right| -\left| \left(\Omega \backslash A\right)\cap \left(\Omega \backslash B\right)\right| \Leftrightarrow$

$\varepsilon \left| B\right| =\varepsilon \left| \Omega \backslash A\right| -\varepsilon \left| \left(\Omega \backslash A\right)\cap \left(\Omega \backslash B\right)\right| \Leftrightarrow$

$1-\varepsilon \left| \Omega \backslash A\right| +\varepsilon \left| \Omega \backslash B\right| =1-\varepsilon \left| \left(\Omega \backslash A\right)\cap \left(\Omega \backslash B\right)\right| \Leftrightarrow$

$\mu \left(A\right)+\mu \left(B\right)=\mu \left(A\cup B\right).$

It follows that $\mu$ is a $V$ -probability measure. Moreover, by construction, $\mu$ is clearly regular.□

Lemma 4.7 shows that the cardinality of the algebra of events does not determine by itself how big the codomain of a regular generalized probability measure must be. Indeed, a countable codomain will suffice for a sample space $\Omega $ , provided that the algebra of events under consideration is generated by the singletons. But such an algebra has the same cardinality as $\Omega $ , which shows that a countable codomain is enough to find regular measures for arbitrarily large algebras.

We conclude this section by connecting this last result with our discussion of Archimedeanity in the previous section:

Corollary 4.8. Let $\Omega $ be an uncountable set and $F$ be an infinite field. Then there is a regular generalized $F$ -probability measure defined on the algebra of finite and cofinite subsets of $\Omega $ iff $F$ is non-Archimedean.

Proof. Suppose that $F$ is non-Archimedean. Because $F$ is infinite, it contains a countable non-Archimedean subfield. By Lemma 4.7, it follows that there is a regular generalized $F$ -probability measure defined on the Boolean algebra of finite and cofinite subsets of $F$ . Conversely, if $F$ is Archimedean, then the Hájek–Williamson argument shows that there can be no regular generalized $F$ -probability measure defined on all the singletons in $\Omega $ .

5. Regularity, cardinality, and hyperreal fields

In this final section, we connect our investigations on the relationship between totality, regularity, and cardinality to the nonstandard approach to probability and to hyperreal extensions of $\rm{\mathbb{R}}$ . We will limit ourselves to the model-theoretic approach to nonstandard analysis because our interest in the cardinality of domains and codomains of regular probability measures does not align with an axiomatic approach à la Nelson. We start by recalling the framework of enlargements that is central in Robinsonian nonstandard analysis. ⁹

Definition 5.1. The universe $\rm{\mathbb{U}}(\rm{\mathbb{X}})$ over a set $\rm{\mathbb{X}}$ is defined as follows:

• $\rm{\mathbb{U}}_{0}(\rm{\mathbb{X}})=\rm{\mathbb{X}}$ ;

• ${\rm{\mathbb{U}}}_{i+1}(\rm{\mathbb{X}})={\rm{\mathbb{U}}}_{\it i}(\rm{\mathbb{X}})\cup \rm{\mathscr{P}}({\rm{\mathbb{U}}}_{\it i}(\rm{\mathbb{X}}))$ for $i\lt \omega$ ; and

• $\rm{\mathbb{U}}({\rm{\mathbb{X}}})=\cup _{\it i\lt \omega } {\rm{\mathbb{U}}}_{\it i}(\rm{\mathbb{X}})$ .

Definition 5.2 An enlargement is a map $ ^{*}\,\colon\, \rm{\mathbb{U}}(\rm{\mathbb{X}})\rightarrow \rm{\mathbb{U}}(\rm{\mathfrak{X}})$ between universes such that:

• $\rm{\mathbb{X}}\subsetneq \rm{\mathfrak{X}}$ , and $^{\rm{*}}x=x$ for any $x\in \rm{\mathbb{X}}$ ;

• $\rm{\mathfrak{X}}=^{\rm{*}}\rm{\mathbb{X}}$ and $^{\rm{*}}\emptyset =\emptyset $ ;

• (Transfer Principle) for any first-order formula $\varphi (x_{1},..,x_{n})$ in the language of set theory and any $a_{1},\ldots,a_{n}\in \rm{\mathbb{U}}(\rm{\mathbb{X}})$ :

$\rm{\mathbb{U}}\left(\rm{\mathbb{X}}\right)| =\varphi \left(a_{1},\ldots,a_{n}\right)\Leftrightarrow ^{\rm{*}}\rm{\mathbb{U}}\left(\rm{\mathbb{X}}\right)| =\varphi (^{\rm{*}}a_{1},\ldots,^{\rm{*}}a_{n});\rm{and}$

• (Saturation Principle) whenever $A\in \rm{\mathbb{U}}(\rm{\mathbb{X}})$ is collection of sets such that for any $a_{1},\ldots,a_{n}\in A, \cap _{i\leq n}a_{i}\neq \emptyset $ , there is $b\in \rm{\mathbb{U}}(\rm{\mathbb{X}})$ such that $b\in \cap _{i\leq n}^{\rm{*}}a_{i}$ .

Whenever $^{\rm{*}}\,\colon\, \rm{\mathbb{U}}(\rm{\mathbb{R}})\rightarrow \rm{\mathbb{U}}(\rm{\Re })$ is an enlargement, $\rm{\Re }$ is a hyperreal extension of $\rm{\mathbb{R}}$ , meaning that it satisfies the same first-order theory in the language of fields as $\rm{\mathbb{R}}$ , but it contains infinitely small and infinitely large numbers. In particular, one obtains a nonstandard unit interval $[0,1]_{\rm{\Re }}=^{\rm{*}}[0,1]_{\rm{\mathbb{R}}}$ . Using a nonstandard framework similar to enlargements, Bernstein and Wattenberg (1969) showed the following:

Theorem 5.3 (Bernstein and Wattenberg, 1969). There is a hyperreal extension $\rm{\Re }$ and a total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}([0,1]_{\rm{\mathbb{R}}})\rightarrow [0,1]_{\rm{\Re }}$ such that for any Lebesgue measurable set $A\subseteq [0,1]$ , the Lebesgue measure of $A$ is equal to the standard part of $\mu (A)$ .

One must exert some care in distinguishing the hyperreal field $\rm{\Re }$ used by Bernstein and Wattenberg (1969) from the simplest type of hyperreal extensions obtained by taking an ultrapower of the reals modulo a nonprincipal ultrafilter on $\omega$ . Indeed, if $R$ is such an ultrapower, then

$| [0,1]_{R}\left| =\right| \{f| f\,\colon\, \omega \rightarrow [0,1]_{\rm{\mathbb{R}}}\}\left| =\right| [0,1]_{\rm{\mathbb{R}}}| ^{{\aleph _{0}}}=(2^{{\aleph _{0}}})^{{\aleph _{0}}}=2^{{\aleph _{0}}},$

and hence $[0,1]_{R}$ has the same size as $\rm{\mathbb{R}}$ . But then it follows directly from Theorem 3.1 that there can be no total and regular probability measure from $\rm{\mathscr{P}}(\rm{\mathbb{R}})$ into $[0,1]_{R}$ . Thus, the hyperreal field $\rm{\Re }$ considered by Bernstein and Wattenberg cannot be isomorphic to such a hyperreal extension $R$ because it must have size strictly greater than $2^{{\aleph _{0}}}$ .

Another important aspect of this nonstandard setting is the distinction between internal and external objects. Given an enlargement $^{\rm{*}}\,\colon\, \rm{\mathbb{U}}(\rm{\mathbb{X}})\rightarrow \rm{\mathbb{U}}(\rm{\mathfrak{X}})$ , an element $a\in \rm{\mathbb{U}}(\rm{\mathfrak{X}})$ is internal if $a\in \cup *\rm{\mathbb{U}}(\rm{\mathbb{X}})=\cup \{^{*}\it b| b\in \rm{\mathbb{U}}(\rm{\mathbb{X}})\}$ , and external otherwise. The distinction is crucial for many applications of nonstandard analysis because internal objects generally behave in a much more tractable fashion than external objects. An important example of internal objects is the internal subsets $\rm{\mathscr{P}}_{\rm{Int}}(^{\rm{*}}\it A)$ of the image $^{\rm{*}}A$ of some standard object $A$ . In particular, one has that for any $A\in \rm{\mathbb{U}}(\rm{\mathbb{X}})$ ,

$^{\rm{*}}\rm{\mathscr{P}}\left(\it A\right)=\rm{\mathscr{P}}_{\rm{Int}}(^{\rm{*}}\it A).$

In the context of an enlargement $^{\rm{*}}\,\colon\, \rm{\mathbb{U}}(\rm{\mathbb{R}})\rightarrow \rm{\mathbb{U}}(\rm{\Re })$ , one may therefore be interested in considering both internal and external entities when discussing the existence of total and regular probability measures on the nonstandard unit interval $[0,1]_{\rm{\Re }}$ . The following is straightforward to verify:

Lemma 5.4. Let $^{\rm{*}}\,\colon\, \rm{\mathbb{U}}(\rm{\mathbb{R}})\rightarrow \rm{\mathbb{U}}(\rm{\Re })$ be an enlargement. Then:

1. 1. There is no external total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}([0,1]_{\rm{\Re }})\rightarrow [0,1]_{\rm{\Re }}$ .

2. 2. There is no internal total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}_{\rm{Int}}([0,1]_{\rm{\Re }})\rightarrow [0,1]_{\rm{\Re }}$ .

Proof. Item $1$ is a direct application of Theorem 3.1. For item $2$ , note that $\rm{\mathbb{U}}(\rm{\mathbb{R}})$ satisfies the first-order statement that there is no total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}([0,1]_{\rm{\mathbb{R}}})\rightarrow [0,1]_{\rm{\mathbb{R}}}$ , so by the Transfer Principle $^{\rm{*}}\rm{\mathbb{U}}(\rm{\mathbb{R}})$ satisfies the corresponding statement that there is no total and regular probability measure $\mu \,\colon\, ^{\rm{*}}\rm{\mathscr{P}}([0,1]_{\rm{\mathbb{R}}})\rightarrow [0,1]_{\rm{\Re }}$ . But because $^{\rm{*}}\rm{\mathscr{P}}([0,1]_{\rm{\mathbb{R}}})=\rm{\mathscr{P}}_{\rm{Int}}([0,1]_{\rm{\mathbb{R}}})$ , it follows that there is no regular internal probability measure into $[0,1]_{\rm{\Re }}$ defined on all the internal subsets of $[0,1]_{\rm{\Re }}$ .□

It is worth mentioning that Lemma 5.4 does not address the issue of whether there can be an external $[0,1]_{\rm{\Re }}$ -valued regular probability measure that is defined on all the internal subsets of $[0,1]_{\rm{\Re }}$ . Note in particular that the results of Section 4 do not apply here because $\rm{\mathscr{P}}_{\rm{Int}}([0,1]_{\rm{\Re }})$ has the same size as the full powerset of $[0,1]_{\rm{\Re }}$ , but it is not a complete algebra, and thus it is not isomorphic to $\rm{\mathscr{P}}([0,1]_{\rm{\Re }})$ . ¹⁰ We leave this technical issue as an interesting open problem for the time being and limit ourselves to pointing out that nonstandard frameworks obtained as limits of enlargements might be a promising approach toward a positive answer to this problem. ¹¹

We conclude this section by discussing the connection between our results and an alternative approach to probability theory inspired by nonstandard analysis—namely, the non-Archimedean probability (NAP) theory developed by Benci et al. (2013, 2018). The main advantage of NAP over classical probability theory is that one can construct, for any set $\Omega $ , a total and regular probability measure on $\rm{\mathscr{P}}(\Omega )$ whose codomain is a reasonably small hyperreal extension of $\rm{\mathbb{R}}$ . We briefly review their construction here.

Let $\Omega $ be an infinite set. We write $\rm{\mathscr{P}}_{\rm{Fin}}(\Omega )$ for the set of all finite subsets of $\Omega $ , and we write $^{\Omega }\rm{\mathbb{R}}$ for the ring of functions from $\rm{\mathscr{P}}_{\rm{Fin}}(\Omega )$ into $\rm{\mathbb{R}}$ , where the operations $+$ and $\cdot$ and the order $\lt$ are defined pointwise. A fine ideal on $^{\Omega }\rm{\mathbb{R}}$ is a maximal ideal containing the set

$\{\varphi \,\colon\, \rm{\mathscr{P}}_{\rm{Fin}}\left(\Omega \right)\rightarrow \rm{\mathbb{R}}| \exists A\subseteq \rm{\mathbb{R}~ }\forall B\supseteq A\,\colon\, \varphi \left(B\right)=0\}.$

Given a fine ideal $I$ , the quotient $^{\Omega }\rm{\mathbb{R}}/I$ is a hyperreal field that extends $\rm{\mathbb{R}}$ and has size

$| ^{\Omega }\rm{\mathbb{R}}\left| =\right| \rm{\mathbb{R}}| ^{\left| \rm{\mathscr{P}}_{\rm{Fin}}\left(\Omega \right)\right| }=(2^{{\aleph _{0}}})^{\left| \Omega \right| }=2^{\left| \Omega \right| }.$

Benci et al. (2013) prove the following.

Theorem 5.5. For any infinite set $\Omega $ , there is a total, regular, finitely additive probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow ^{\Omega }\rm{\mathbb{R}}/I$ .

Benci et al. (2013) call such functions NAP measures and show that they exhibit a number of attractive properties. In particular, they satisfy a notion of additivity that is arguably a generalization of countable additivity in the non-Archimedean context. Combined with Theorem 3.1, this yields the following result regarding the interplay between cardinality, regularity, and totality for hyperreal fields:

Theorem 5.6. Let $\Omega $ be an infinite set and $\kappa$ be a cardinal. Then:

1. 1. If $| \Omega | \geq \kappa$ , then for any hyperreal field $\rm{\Re }$ of size at most $\kappa$ , there is no total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ .

2. 2. If $2^{| \Omega | }\leq \kappa$ , then there is a hyperreal field $\rm{\Re }$ of size at most $\kappa$ and a total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ .

Proof. Item $1$ follows directly from Theorem 3.1 because any hyperreal field is a generalized probability range, and item $2$ follows immediately from Theorem 5.5. □

Finally, let us note that under the assumption of GCH, Theorem 5.6 yields a complete answer to the question of the compatibility between regularity and totality as raised in Section 1.

Theorem 5.7 [GCH] Let $\kappa$ be a cardinal and $\Omega $ a set. Then there is a hyperreal field $\rm{\Re }$ of size $\kappa$ and a total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ iff $| \Omega | \lt \kappa$ .

Proof. Suppose that there is a hyperreal field $\rm{\Re }$ of size $\kappa$ and a total and regular probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ . Then by the contrapositive of Theorem 5.6.1, it follows that $| \Omega | \lt \kappa$ . Conversely, suppose that $| \Omega | \lt \kappa$ . Because GCH holds, it follows that $2^{| \Omega | }=| \Omega | ^{+}\leq \kappa$ . Hence, by theorem 5.6.2, there is a hyperreal field $\rm{\Re }$ of size at most $\kappa$ and a probability measure $\mu \,\colon\, \rm{\mathscr{P}}(\Omega )\rightarrow \rm{\Re }$ . But clearly, without loss of generality, we can assume that $\rm{\Re }$ has size $\kappa$ , which completes the proof. □

We conclude by briefly discussing the significance of our results to the debate regarding regularity in probability theory. In short, we see our results as confirming that the debate has been essentially well posed by Hofweber (2014b) and Hájek (2011). On the one hand, Theorem 5.7 can be viewed as the mathematical fact underlying Hájek’s (2011) “arms race.” Indeed, as a consequence of Zermelo’s theorem, for any possible range of probability values $V$ , any regular probability measure defined on the full powerset of $V$ must take its values in a range of cardinality strictly greater than $V$ . In that sense, no hyperreal field can be “large enough” to play the role of the reals in an alternative to Kolmogorov probability theory that would satisfy the regularity constraint. At the same time, Hofweber is correct in saying that the cardinality of the codomain is the only substantial obstacle to the existence of a regular probability measure for any sample space. In fact, under GCH, it is necessary and sufficient to take the successor cardinal of the size of the domain as the size of the codomain of such a regular probability measure. To make this point differently, this means that, at least under GCH, the existence theorems noted by Hofweber (2014a) and Benci et al. (2018) are the best possible. Interestingly, this also has a consequence for a slightly different question, regarding whether any standard probability function can be approximated by a regular function defined on a hyperreal field. ¹² Hofweber and Schindler (2016) give a positive answer to this question. Given a standard probability space $(\Omega, \rm{\mathfrak{A}},\overline{\mu })$ , they show that $\overline{\mu }$ can be approximated by a regular probability measure $\mu$ (in the sense that $\mu (U)$ is infinitesimally close to $\overline{\mu }(U)$ for any $U\in \rm{\mathfrak{A}}$ ) defined on a hyperreal field $V$ of size at most $2^{| \Omega | }$ . As an easy consequence of Theorem 5.7, we have that, under GCH, the cardinality bound obtained by Hofweber and Schindler is the best possible. In other words, this means that from the point of view of the cardinality of the range of probabilities, the existence problem (i.e., whether there exists a regular probability measure) and the approximation problem (i.e., whether any standard probability function can be approximated by a regular one) are equivalent.

Finally, let us make one final remark on the issue. As the results in Section 4 show, a lot hinges on the particular structure of the algebra of events under consideration. If one agrees with Hájek (2011) that the regularity constraint implicitly entails a totality constraint, then the “arms race” is indeed the only option. But if one only wants to consider events that are finite or cofinite sets of outcomes, then, as Lemma 4.7 shows, any countable non-Archimedean field would suffice. We take this as evidence that there is still much to explore regarding the interplay between regularity, totality, and cardinality in probability theory.