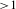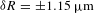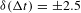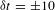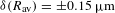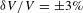Measurements of the ablation-front trajectory and low-mode nonuniformity in direct-drive implosions using x-ray self-emission shadowgraphy

Abstract

Self-emission x-ray shadowgraphy provides a method to measure the ablation-front trajectory and low-mode nonuniformity of a target imploded by directly illuminating a fusion capsule with laser beams. The technique uses time-resolved images of soft x-rays (${>}1$ keV) emitted from the coronal plasma of the target imaged onto an x-ray framing camera to determine the position of the ablation front. Methods used to accurately measure the ablation-front radius (${\it\delta}R=\pm 1.15~{\rm\mu}\text{m}$), image-to-image timing (${\it\delta}({\rm\Delta}t)=\pm 2.5$ ps) and absolute timing (${\it\delta}t=\pm 10$ ps) are presented. Angular averaging of the images provides an average radius measurement of ${\it\delta}(R_{\text{av}})=\pm 0.15~{\rm\mu}\text{m}$ and an error in velocity of ${\it\delta}V/V=\pm 3\%$. This technique was applied on the Omega Laser Facility [Boehly et al., Opt. Commun. 133, 495 (1997)] and the National Ignition Facility [Campbell and Hogan, Plasma Phys. Control. Fusion 41, B39 (1999)].

1. Introduction

In direct-drive inertial confinement fusion (ICF), laser beams are focused onto the surface of a fusion capsule that is imploded to reach thermonuclear ignition^[1]. The beams ablate the target surface and drive the shell to high velocities. At maximum compression, a fraction of the kinetic energy is transferred into the internal energy of the hot spot, where fusion reactions are initiated. The minimum laser energy required for ignition is a strong function of the shell’s maximum implosion velocity ($E_{\text{min}}\propto V_{\text{imp}}^{-6}$)^[2], which highlights the importance of accurately measuring it. During the compression, low-mode nonuniformities that grow at the ablation surface result in distortion of the hot spot and a reduction in implosion performance.

A self-emission x-ray shadowgraphy (SES) technique^[4] (Figure 1(a)) has been applied to ICF experiments to measure the ablation-front trajectory, velocity^[5] and low-mode nonuniformity^[6–8] of targets imploded on the Omega Laser Facility^[9] and the National Ignition Facility (NIF)^[10]. A pinhole array is used to image the soft x-rays (${>}1$ keV, spectrally filtered using $25.4~{\rm\mu}\text{m}$ Be) emitted in the coronal plasma of an imploding target onto a four-strip x-ray framing camera (XRFC) to obtain 12 (three per strip) time-resolved images of an imploding target. The steep inner edge observed in the intensity profile of the image is used to determine the position of the ablation surface (Figures 1(b) and (c)). This edge is created by the combination of the limb effect of soft x-rays emitted in the coronal plasma and the absorption of the x-rays, emitted at the back side of the target, in the cold dense shell. The absorption steepens the gradient by reducing the emission by a factor of 2 over a few microns in its direction (Figure 1(c)). Because this gradient is steep and governed by the absorption where the plasma temperature goes to zero, the position of the mid-intensity point in this edge is an excellent measure of the position of the ablation front (the position is defined by where the electron temperature is 100 eV).

Figure 1. (a) Schematic of the SES technique. X-rays emitted by the coronal plasma (dark green area) are imaged by a pinhole onto an XRFC. The shell (orange area) prevents the x-rays emitted at the back of the shell (light green area) from reaching the detector. The simulated shell density (red curve, left axis) and electron temperature (dashed blue curve, right axis) profiles (b) were post-processed with Spect3D ^[3] to calculate the intensity profile (c). The mid-intensity point in the inner gradient corresponds to the position of the ablation front (dashed black line). The intensity lineout calculated without absorption of the shell is plotted in (c) (dashed curve). The difference between the two intensity lineouts emphasizes the effect of the absorption of the x-rays emitted at the back of the target in the shell, which steepens the inner gradient significantly.

Figure 2. (a) The PSF for the x-ray imaging diagnostics calculated for the setup used on the OMEGA Laser System. A lineout of the PSF is plotted (dashed curve). (b) Comparison of an intensity profile (gray curve) measured along the dotted black lines displayed on the self-emission images (inset) with the calculated profiles (red curve). The position of the ablation front is indicated (dashed line). The profile azimuthally averaged over the entire image is plotted (dashed black curve). (c) Variation of the position of the mid-intensity point in the inner gradient relative to the best-fit circle is shown for all angles (red curve).

This paper describes different methods used to characterize the diagnostic, showing that the accuracy of the measurement of the ablation front position is ${\it\delta}R=\pm 1.15~{\rm\mu}\text{m}$. Two techniques were used to measure the image-to-image timing to within ${\it\delta}({\rm\Delta}t)=\pm 2.5$ ps. The method used to time the images to the laser pulse (absolute timing) was demonstrated to have an accuracy of ${\it\delta}t=\pm 10$ ps.

The SES technique is applied to symmetric implosions on the OMEGA Laser System and to polar-drive experiments on the NIF. The OMEGA Laser is configured for symmetric irradiation, while the beam geometry on the NIF is currently optimized for x-ray geometry with no beams located around the equator. Initial polar-direct-drive experiments repoint the beams toward the equator to generate a uniform ablation^[11]. In these experiments, the angularly averaged radius provides a measure of the ablation-front trajectory to within ${\it\delta}(R_{\text{av}})=\pm 0.15~{\rm\mu}\text{m}$ and velocity to within ${\it\delta}V/V=\pm 3\%$. In the symmetrically driven implosions, where the nonuniformity has a random phase, the amplitude and the phase of the modes are determined using a Fourier decomposition. In this case, the amplitude of mode 2 is measured to within ${\it\delta}(\text{Fou}_{2})=\pm 0.25\%$. In the polar-drive implosions, the dominant low-mode nonuniformities are axisymmetric around the polar axis, and the mode amplitudes are determined using a Legendre polynomial decomposition. With this method, the amplitudes of modes 2, 4 and 6 are determined to within ${\it\delta}(\text{Leg}_{n})=\pm 0.5\%$.

Figure 3. (a) Schematic of the XRFC high-voltage lines: four pulsers are launched by a trigger pulse and generate four pulses that are delayed independently by a delay box and sent to the four strips of the microchannel plate. (b) Comparison of the interstrip timing measured offline (method 1, red points) and on real shot (method 2, blue points). (c) Comparison of the trajectory measured by the reference camera (blue curve) with the trajectory measured by the uncalibrated camera (red circles). Differences of ${\it\delta}t_{(1{-}2)}=115$ ps, ${\it\delta}t_{(1{-}3)}=152$ ps and ${\it\delta}t_{(1{-}4)}=190$ ps were measured between the requested and real interstrip timings between the strips (1–2), (1–3) and (1–4) (dashed arrows). (d) Comparison of the trajectories measured on strip 1 (squares), strip 2 (triangles), strip 3 (inverse triangles) and strip 4 (circles) when the delay box was set to get 0 interstrip timing: residual delays of 10, 7 and 18 ps were measured between strips (1–2), (1–3) and (1–4), respectively.

2. Characterization of the framing camera

The accuracy in the time-resolved measurements of the ablation-front trajectory, velocity and low-mode nonuniformity using the SES technique is determined by the precision in the measurement of the ablation-front position ($R\pm {\it\delta}R$), the accuracy of the image-to-image timing (${\rm\Delta}t\pm {\it\delta}({\rm\Delta}t)$) and the absolute timing between the images and the laser pulse ($t\pm {\it\delta}t$)^{[12, 13]}.

2.1. Radial accuracy (pinhole imaging)

To optimize the resolution of the steep gradient generated by self-emission x-ray imaging, the optimal pinhole diameter was determined ($d_{\text{Opt}}=\sqrt{2.44{\it\lambda}L_{\text{tp}}[M/(M+1)]}$) by setting the diameter of the geometric image of a point ($d_{\text{G}}=(M+1)d$, where $d$ is the diameter of the pinhole) equal to the diameter of the diffraction image of a point ($d_{\text{D}}=(2.44{\it\lambda}/d)L_{\text{tp}}M$, where $M$ is the magnification of the pinhole imaging system, ${\it\lambda}$ is the x-ray wavelength and $L_{\text{tp}}$ is the distance between the target and the pinhole). On OMEGA, this corresponds to $d_{\text{Opt}}=10~{\rm\mu}\text{m}$ when using $M=6$, ${\it\lambda}=1.24$ nm and $L_{\text{tp}}=40$ mm. This configuration results in the point-spread function (PSF) shown in Figure 2(a) calculated using the coherent ray-tracing program FRED ^[14]. The calculation takes into account the pinhole imaging (geometry and diffraction) and the modulation transfer function of the microchannel plate of the XRFC ^[15]. From this PSF calculation, the minimum distance between two points in the object space that can be distinguished in the image plane is given by the full width at half maximum (FWHM) of the PSF ($12~{\rm\mu}\text{m}$).

Figure 2(b) compares intensity profiles from measured self-emission images with profiles calculated by post-processing hydrodynamic simulations with Spect3D. The synthetic x-ray images were convolved with the PSF of the diagnostic (Figure 2(a)). Excellent agreement was obtained, which shows that both the simulation of the soft x-rays emitted by the imploding target and the modeling of the response of the imaging system are well reproduced.

The center of the measured images was determined iteratively. Intensity profiles were taken along chords through the center of the image. The positions of the mid-intensity points on each profile were determined and a new center was calculated, fitting the points with a circle using a ${\it\chi}^{2}$ analysis. This process was repeated until the center position changed by no more than $0.1~{\rm\mu}\text{m}$.

The accuracy in the position of the mid-intensity point in the inner gradient of the measured profile can be determined using the intercept theorem $N/(2{\it\delta}R)=S/l_{\text{grad}}$, where ${\it\delta}R$ is the variation in the measured radius, $N=3{\it\sigma}_{\text{N}}$ and ${\it\sigma}_{\text{N}}$ is the standard deviation of the noise. The signal ($S=0.4$) is defined as the difference in x-ray intensities over the length of the inner gradient $l_{\text{grad}}$ (Figure 2(b)). Applying this to the example shown in Figure 2(b), ${\it\delta}R=0.5~l_{\text{grad}}/(S/N)\sim 1.4~{\rm\mu}\text{m}$, where $l_{\text{grad}}=9~{\rm\mu}\text{m}$ and $S/N=10$.

In spherical experiments, the position of the ablation front was determined by averaging the position of the mid-intensity point in the inner gradient over all angles. This improved the accuracy of the measured ablation-front position by a factor of $\sqrt{N_{p}}$, where $N_{p}=2{\it\pi}R/d_{\text{PSF}}$ is the number of independent measurements, $R$ is the averaged radius and $d_{\text{PSF}}$ is the FWHM of the PSF. On OMEGA, this resulted in an accuracy in the $360^{\circ }$ angularly averaged radius of ${\it\delta}R_{\text{av}}<0.15~{\rm\mu}\text{m}$, where $d_{\text{PSF}}\approx 12~{\rm\mu}\text{m}$ and $\sqrt{N_{p}}\approx 10$ for $R=200~{\rm\mu}\text{m}$.

Figure 2(c) shows that the 3-sigma variation in the measured radius around the image relative to the $360^{\circ }$ angularly averaged radius is $[3{\it\sigma}_{R}]_{360^{\circ }}\approx 3.5~{\rm\mu}\text{m}$. This is consistent with the peak-to-valley variation in the measured radius calculated from the intercept theorem ($[2{\it\delta}R]_{\text{Intercept}}\approx [3{\it\sigma}_{R}]_{360^{\circ }}$).

2.2. Image-to-image timing (interstrip timing)

The XRFC uses four microchannel plates to time-resolve the pinhole images. The microchannel plates are activated by independently timed high-voltage pulses, and the accuracy in the timing between images on subsequent plates (interstrip timing) is given by the accuracy of the high-voltage pulsers (Figure 3(a)). Each electrical pulse is created by a pulser and travels through a delay box that generates a different delay for each strip. The jitter in the interstrip timing corresponds primarily to the jitter between two pulsers.

The interstrip timing was determined by using an 8 GHz oscilloscope to measure the time difference between the electrical pulses that come from different delay lines. The timing error between two channels was calibrated by splitting an electrical pulse and sending each pulse to two different inputs of the oscilloscope through two cables of the same length. The jitter between two pulsers was determined by repeating the measurements several times. The interstrip timing was measured for the XRFC setup used on the OMEGA Laser System (Figure 3(b)). An error of $\pm 4$ ps in the interstrip timing was inferred from the 8 ps of drift in the oscilloscope determined before and after the measurements. The standard deviation of the jitter between two pulsers of ${\it\sigma}_{\text{p}}=1.5$ ps was determined by repeating each measurement five times. This resulted in a jitter of the interstrip timing of ${\it\delta}({\rm\Delta}t)=\pm 3{\it\sigma}_{\text{p}}/2=\pm 2.5$ ps.

To verify the interstrip timing, the ablation-front trajectory was simultaneously measured using two XRFCs (Figure 3(c)). First, the residual interstrip timings of the reference XRFC with the synchronized delay box were determined by measuring the ablation-front trajectory of an imploding target. Small differences in the radii of the ablation front between each strip were used to quantify the residual time difference between each strip (Figure 3(d)). To set the interstrip timing to calibrated values, precalibrated delay cables were connected to the output of the synchronized delay box. The reference XRFC was used to measure the reference trajectory, and the interstrip timing of the second XRFC was measured by comparing the difference between the requested interstrip timing and the measured interstrip timing (Figure 3(c)). The measurements were repeated three times to determine the interstrip timings to within a few ps. The interstrip timings are presented in Figure 3(b). An error in the interstrip measurement of ${\it\delta}({\rm\Delta}t)=\pm 3{\it\sigma}_{\text{s}}/2=\pm 2.5$ ps was determined, where ${\it\sigma}_{\text{s}}=1.7$ ps is the standard deviation of the measurement of the interstrip timing over multiple repeated shots. Excellent agreement was obtained between the two methods (Figure 3(b)).

2.3. Absolute timing

The variation of the absolute timing is determined on each shot by measuring the time difference between the electrical monitor pulse from the XRFC and the optical fiducial, which is a time reference for the laser pulse. To calibrate the absolute timing, the time difference between the laser and the XRFC was measured on a timing reference shot.

Figure 4. (a) Comparison of the rise of the normalized laser intensity (red points) calculated from the rise of the x-ray intensity generated by a gold sphere irradiated by six laser pulses measured on an XRFC with the optical laser pulse (dashed blue curve). Two beams were advanced by 400 ps to measure the flat field of the framing camera. The series of images recorded on the framing camera during the rise of the x-ray emission is shown at the top of the figure. (b) Comparison of the absolute-timing calibration measured over two campaigns (the open and solid squares correspond to two different campaigns). The standard deviation of the variation of this number is shown on the figure.

Figure 5. Comparison of the measured (red symbols, each of which corresponds to a different camera) mid-intensity point in (a) the inner gradient trajectory and (b) the velocity with the simulation (blue curve). In (a), the laser pulse is plotted as the solid black curve and the trajectory of the ablation front from the simulation as the dashed black curve.

The timing reference shot used a 4-mm-diameter gold target with multiple laser pulses that rose over 100 ps to a 1-ns-long flattop intensity. The time-resolved x-ray intensities emitted by the gold plasmas were measured on the XRFC (see images in Figure 4) and used to determine the rise of the laser intensity after adjusting for the conversion of the x-ray intensity to laser intensity ($I_{\text{laser}}\propto I_{\text{x-ray}}^{-3.4}$^[16], where $I_{\text{x-ray}}$ and $I_{\text{laser}}$ are the x-ray and laser intensities, respectively). The pulse shape measured by the XRFC was compared with the optical pulse shape (Figure 4(b)) to determine the absolute timing. To compare the x-ray signals measured between different beams, all measurements were normalized to the measured laser beam energy $I_{\text{norm}}=I_{\text{laser}}/E_{\text{laser}}$. To account for the variation in the sensitivity of the camera, a few beams were advanced in time by 400 ps to generate a constant x-ray flux (top images in Figure 4), and each x-ray intensity was normalized to the x-ray intensity measured on the closest flat-field (FF) spot ($I_{\text{FF}}=I_{\text{norm}}/I_{\text{norm,FF}}$). Figure 4(c) shows the variation of the absolute timing over multiple shots. An accuracy in the absolute timing of ${\it\delta}t=\pm 3{\it\sigma}_{{\rm\Delta}t}/2=\pm 10$ ps was determined, where ${\it\sigma}_{{\rm\Delta}t}$ is the standard deviation of the variation of the absolute-timing calibration number.

3. Application

The SES technique was applied to measure the ablation-front trajectory, velocity and nonuniformity of an imploding target in direct-drive implosions on the Omega Laser Facility and low-mode nonuniformities on the NIF.

3.1. Ablation-front trajectory and velocity on the OMEGA Laser System

The experiment employed 60 ultraviolet (${\it\lambda}_{0}=351$ nm) laser beams at the Omega Laser facility. The laser beams uniformly illuminated the target and were smoothed by polarization smoothing^[17], smoothing by spectral dispersion^[18] and distributed phase plates^[19] (fourth-order super-Gaussian with 95% of the energy contained within the initial target diameter). One 100-ps-long picket was used to set the target implosion onto a low adiabat^[20] followed by a 2 ns step pulse that drove the target to its final velocity (Figure 5(a)). The total laser energy on the target was 19.6 kJ, which resulted in a maximum laser power of 11 TW. The target had an $867.8~{\rm\mu}\text{m}$ outer diameter with a $26.8$-${\rm\mu}\text{m}$-thick CH ablator covered by $0.1~{\rm\mu}\text{m}$ of Al and filled with deuterium at 10.5 atm.

The images displayed at the top of Figure 5 correspond to self-emission images that were recorded using the setting of the SES diagnostic described in Section 1. Images were time integrated over ${\sim}40$ ps^[13], and interstrip timings of 250 ps were used. Three framing cameras were used to determine the trajectory of the ablation front over the entire length of the main drive.

Figure 5 compares the measured ablation-front trajectory and in-flight shell velocity with hydrodynamic simulations. The accuracy in the measurement of the ablation-front velocity calculated between two images of two consecutive strips (averaged over ${\rm\Delta}t\approx 250$ ps) is given by ${\it\delta}V/V={\it\delta}({\rm\Delta}t)/{\rm\Delta}t+\sqrt{2}{\it\delta}R_{\text{av}}/{\rm\Delta}R_{\text{av}}\approx 3\%$, where ${\it\delta}({\rm\Delta}t)\approx 4$ ps is the error in the interstrip timing (dominated by the error in the measurement of ${\rm\Delta}t$ (see Section 2.2)) and, for a velocity of 200 km/s, ${\rm\Delta}R_{\text{av}}=50~{\rm\mu}\text{m}$. Simulations were performed with the 1D hydrodynamic code LILAC ^[21], and included models for nonlocal electron transport^[22] and cross-beam energy transfer (CBET)^[23]. Synthetic x-ray self-emission images were calculated using Spect3D. The images were convolved with the PSF of the diagnostic. The simulated trajectory and velocities were obtained by post-processing the synthetic images following the same method as used on the experimental images. Excellent agreement between the position of the mid-intensity point and the position of the ablation front was obtained, showing that the hydrodynamic coupling was well modeled.

3.2. Ablation-front nonuniformity on the OMEGA Laser System

To investigate the uniformity of the drive, the angular variation in the ablation surface was decomposed using a Fourier series. Figure 6(a) shows that mode 2 dominates the low-mode nonuniformity. Figure 6(b) shows that the amplitude of the low-mode nonuniformity grows linearly with radius and that the phase is approximately constant (${\it\phi}_{2}=89\pm 14^{\circ }$).

Figure 6. (a) Comparison of the variation of ${\rm\Delta}R/R_{\text{av}}$ (red curve) with mode 2 calculated using a discrete Fourier transform of the contour defined by $f_{2}({\it\theta})=A_{2}\cos ({\it\theta}+{\it\phi}_{2})$ (blue curve). (b) Evolution of the amplitude (red points) and the phase (open blue triangles) of mode 2 during the implosion. The linear best fit to the growth of the mode amplitude is plotted (dashed black line).

Figure 7. (Top) Series of x-ray self-emission images recorded on the NIF. (a) Comparison of measured ${\rm\Delta}R/R_{\text{av}}$ (red curve) with the curve obtained by adding the first 10 Legendre polynomials of the decomposition. These are compared with the synthetic contour at an equivalent radius (dashed black curve). The vertical axis of symmetry is plotted (dashed black line) and the angle ${\it\theta}_{0}$ of this vertical axis is indicated in the inset. The measured growths (red points) of (b) mode 2, (c) mode 4 and (d) mode 6 using a Legendre polynomial decomposition are compared with simulations (blue curve). An accuracy better than $\pm 0.5\%$ in the mode-amplitude measurement was determined and corresponded to three times the standard deviation of the distance between the measurements and the best-fit line (dashed black line).

For each radius, the amplitude of mode 2 is defined by $\text{Fou}_{2}=2|\text{fou}_{2}|/N_{\text{DFT}}$, where $fo_{2}=\sum _{j=0}^{N_{\text{DFT}}-1}({\rm\Delta}R({\it\theta}_{j})/R_{\text{av}})e^{-4i{\it\pi}j/N_{\text{DFT}}}$ is the second coefficient of the Fourier transform of ${\rm\Delta}R({\it\theta})/R_{\text{av}}$ discretized over $N_{\text{DFT}}$ points equally spaced in angle around the contour, ${\rm\Delta}R({\it\theta}_{j})=R({\it\theta}_{j})-R_{\text{av}}$ and ${\it\theta}_{j}$ is the angle of the point $j$. When the contour is not defined over all angles, an algorithm is used to determine the discrete Fourier transform^[24].

A $\pm 0.25\%$ accuracy in the mode 2 measurement was determined and corresponds to three times the standard deviation of the distance between the points and the best-fit line (Figure 6(b)). This corresponds to an error in the mode amplitude of better than $\pm 0.5~{\rm\mu}\text{m}$, which is slightly larger than the accuracy in the measurement of the averaged shell radius. The facts that the phase of the nonuniformity does not change significantly over the nine measurements and that a variation of this constant phase was observed among different shots show that the mode is not an artifact of the diagnostic (Figure 6(b)).

3.3. Ablation-front nonuniformity on the NIF

The SES technique was implemented on the NIF to measure the shell trajectory, velocity and low-mode nonuniformities in polar-direct-drive experiments (the experimental setup is detailed in Ref. [8]). A series of images are presented at the top of Figure 7. To increase the signal-to-noise ratio on the NIF experiments, the pinholes were larger than the optimum diameter ($d_{\text{NIF}}=60~{\rm\mu}\text{m}>d_{\text{Opt}}=25~{\rm\mu}\text{m}$), which resulted in a $32.5~{\rm\mu}\text{m}$ FWHM of the PSF. In the polar-direct-drive configuration, the illumination is symmetric around the polar axis, so ${\rm\Delta}R/R_{\text{av}}$ is decomposed using Legendre polynomials with their axes of symmetry adjusted to be the polar axes. Figure 7(a) compares the contour with the curve that corresponds to the addition of the first 10 Legendre polynomials of the contour decomposition. The good agreement between the two curves shows that the contour is nearly symmetric around the polar axis.

Figures 7(b)–(d) compare the growth of modes 2, 4 and 6 of the ablation front with hydrodynamic simulations. In each case, the accuracy in the amplitude of the modes is better than $\pm 0.5\%$, which corresponds to three times the standard deviation of the distance between the points and the best-fit curves. Simulations were conducted using the 2D hydrodynamic code DRACO ^[25] with nonlocal electron transport and CBET models, and the axis of symmetry along the polar axis. The simulated modes were obtained by post-processing simulations with Spect3D, convolving them with the PSF of the diagnostic, and determining the position of the inner gradient in the synthetic images. The differences observed between the calculated and simulated mode amplitudes are primarily due to an overdriven pole (or underdriven equator) (Figure 7(a)), probably due to errors in the 2D nonlocal electron transport and CBET models.

The decomposition over Legendre polynomials is defined by ${\rm\Delta}R/R({\it\theta}_{j}-{\it\theta}_{0})=\sum _{n=1}^{\infty }\{\text{Leg}_{n}P_{n}[\cos ({\it\theta}_{j}-{\it\theta}_{0})]\}$, where $P_{n}$ is the Legendre polynomial $n$, $\text{Leg}_{n}$ is the coefficient, $n$ is the Legendre mode and ${\it\theta}_{0}=90^{\circ }$ corresponds to the angle of the axis of symmetry (Figure 7(a)). The mode amplitudes are normalized to the norm of the Legendre polynomials relative to the L2 inner product $\text{Leg}_{n}=\text{Leg}_{n}/[2/(2n+1)]^{0.5}$. With this normalization factor for a symmetric signal, the amplitudes of the modes defined with the Legendre polynomial are similar to the amplitudes of the modes calculated using the Fourier decomposition.

4. Conclusion

In summary, different methods used to characterize the SES technique in the configuration used on the OMEGA Laser System have been presented. The precise calculation of the PSF made it possible to determine the position of the ablation front to within $\pm 1.15~{\rm\mu}\text{m}$. Two methods – one offline, one on a shot – were compared to measure the interstrip timing of the XRFC to within $\pm 2.5$ ps; excellent agreement was obtained. A method to measure the timing between the images and the laser pulse to within $\pm 10$ ps was presented. The SES technique was applied to measure the ablation-front trajectory, velocity and mode 2 nonuniformity on symmetric implosions on OMEGA to within ${\it\delta}(R_{\text{av}})=\pm 0.15~{\rm\mu}\text{m}$, ${\it\delta}V/V=\pm 3\%$ and ${\it\delta}(Fo_{2})=\pm 0.25\%$, respectively. Excellent agreement was obtained with 1D hydrodynamic simulations conducted with the code LILAC. The technique was applied in polar-direct-drive experiments performed on the NIF. The ablation-front low-mode nonuniformities were characterized using Legendre polynomial decomposition. The amplitudes of modes 2, 4 and 6 were compared with 2D simulation results conducted with the hydrodynamic code DRACO. The observed differences are probably due to errors in the 2D nonlocal electron transport and CBET models.