The version of this manuscript originally published contained a error in Eq. (12b).
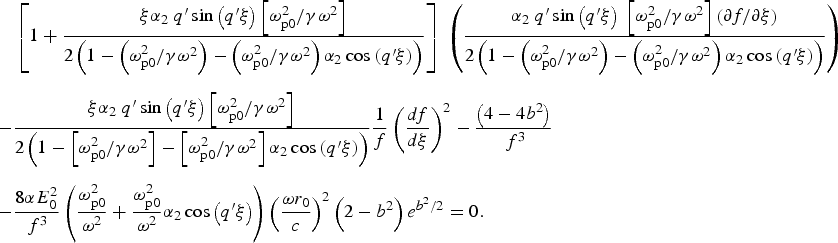 $$ \eqalign{& \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]} \over {2\left( {1 - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right) - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right){\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}} \right]\; \left( {\displaystyle{{{\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\; \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]\left( {\partial f/\partial {\rm \xi}} \right)} \over {2\left( {1 - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right) - \left( {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right){\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}} \right) \cr - &\displaystyle{{{\rm \xi} {\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\left[ {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right] - \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]{\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}\displaystyle{1 \over f}\left( {\displaystyle{{df} \over {d{\rm \xi}}}} \right)^2 - \displaystyle{{\left( {4 - 4b^2} \right)} \over {\,f^3}} \cr - & \displaystyle{{8{\rm \alpha} E_0^2} \over {\,f^3}} \left( {\displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} ^2}} + \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} ^2}} {\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)\left( {\displaystyle{{{\rm \omega} r_0} \over c}} \right)^2 \left( {2 - b^2} \right)e^{b^2 /2} = 0.} $$
$$ \eqalign{& \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]} \over {2\left( {1 - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right) - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right){\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}} \right]\; \left( {\displaystyle{{{\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\; \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]\left( {\partial f/\partial {\rm \xi}} \right)} \over {2\left( {1 - \left( {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right) - \left( {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right){\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}} \right) \cr - &\displaystyle{{{\rm \xi} {\rm \alpha} _{2\;} q^{\prime}\sin \left( {q^{\prime}{\rm \xi}} \right)\left[ {{\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} {\rm \omega} ^2} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right] - \left[ {{\rm \omega} _{{\rm p0}}^2 /{\rm \gamma} {\rm \omega} ^2} \right]{\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)}}\displaystyle{1 \over f}\left( {\displaystyle{{df} \over {d{\rm \xi}}}} \right)^2 - \displaystyle{{\left( {4 - 4b^2} \right)} \over {\,f^3}} \cr - & \displaystyle{{8{\rm \alpha} E_0^2} \over {\,f^3}} \left( {\displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} ^2}} + \displaystyle{{{\rm \omega} _{{\rm p}0}^2} \over {{\rm \omega} ^2}} {\rm \alpha} _2 \cos \left( {q^{\prime}{\rm \xi}} \right)} \right)\left( {\displaystyle{{{\rm \omega} r_0} \over c}} \right)^2 \left( {2 - b^2} \right)e^{b^2 /2} = 0.} $$
should be replaced by:
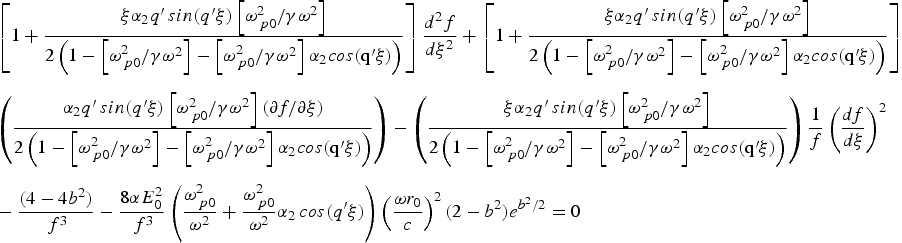 $$\eqalign{& \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right]\displaystyle{{d^2 f} \over {d{\rm \xi} ^2}} + \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right] \cr & \left( {\displaystyle{{{\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right](\partial f/\partial {\rm \xi} )} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right) - \left( {\displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right)\displaystyle{1 \over f}\left( {\displaystyle{{df} \over {d{\rm \xi}}}} \right)^2 \cr & - \displaystyle{{(4 - 4b^{\rm 2} )} \over {\,f^3}} - \displaystyle{{8\alpha E_0^2} \over {\,f^3}} \left( {\displaystyle{{{\rm \omega} _{\,p0}^2} \over {{\rm \omega} ^2}} + \displaystyle{{{\rm \omega} _{\,p0}^2} \over {{\rm \omega} ^2}} {\rm \alpha} _2 \,cos{\rm (}q{\rm ^{\prime}}{\rm \xi} {\rm )}} \right)\left( {\displaystyle{{{\rm \omega} r_0} \over c}} \right)^2 (2 - b^{\rm 2} )e^{b^2 /2} = 0} $$
$$\eqalign{& \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right]\displaystyle{{d^2 f} \over {d{\rm \xi} ^2}} + \left[ {1 + \displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right] \cr & \left( {\displaystyle{{{\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right](\partial f/\partial {\rm \xi} )} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right) - \left( {\displaystyle{{{\rm \xi} {\rm \alpha} _2 q^{\prime}\,sin{\rm (}q^{\prime}{\rm \xi} {\rm )}\left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]} \over {2\left( {1 - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right] - \left[ {{\rm \omega} _{\,p0}^2 {\rm /}{\rm \gamma} {\rm \omega} ^{\rm 2}} \right]{\rm \alpha} _2 cos{\rm (q^{\prime}}{\rm \xi} {\rm )}} \right)}}} \right)\displaystyle{1 \over f}\left( {\displaystyle{{df} \over {d{\rm \xi}}}} \right)^2 \cr & - \displaystyle{{(4 - 4b^{\rm 2} )} \over {\,f^3}} - \displaystyle{{8\alpha E_0^2} \over {\,f^3}} \left( {\displaystyle{{{\rm \omega} _{\,p0}^2} \over {{\rm \omega} ^2}} + \displaystyle{{{\rm \omega} _{\,p0}^2} \over {{\rm \omega} ^2}} {\rm \alpha} _2 \,cos{\rm (}q{\rm ^{\prime}}{\rm \xi} {\rm )}} \right)\left( {\displaystyle{{{\rm \omega} r_0} \over c}} \right)^2 (2 - b^{\rm 2} )e^{b^2 /2} = 0} $$


