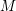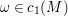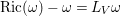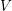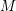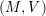1 Introduction
Let ![]() $M$ be an
$M$ be an ![]() $n$-dimensional Fano manifold, that is,
$n$-dimensional Fano manifold, that is, ![]() $M$ is a compact complex manifold and
$M$ is a compact complex manifold and ![]() $c_{1}(M)$ is represented by some Kähler form
$c_{1}(M)$ is represented by some Kähler form ![]() ${\it\omega}$ on
${\it\omega}$ on ![]() $M$. If we take holomorphic coordinates
$M$. If we take holomorphic coordinates ![]() $(z^{1},\ldots ,z^{n})$ of
$(z^{1},\ldots ,z^{n})$ of ![]() $M$,
$M$, ![]() ${\it\omega}$ and its Ricci form
${\it\omega}$ and its Ricci form ![]() $\text{Ric}({\it\omega})$ are locally written as
$\text{Ric}({\it\omega})$ are locally written as
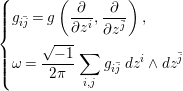 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}g_{i\bar{j}}=g\left({\displaystyle \frac{\partial }{\partial z^{i}}},{\displaystyle \frac{\partial }{\partial z^{\bar{j}}}}\right),\quad \\ {\it\omega}={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\displaystyle \mathop{\sum }_{i,j}g_{i\bar{j}}\,dz^{i}\wedge dz^{\bar{j}}\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}g_{i\bar{j}}=g\left({\displaystyle \frac{\partial }{\partial z^{i}}},{\displaystyle \frac{\partial }{\partial z^{\bar{j}}}}\right),\quad \\ {\it\omega}={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\displaystyle \mathop{\sum }_{i,j}g_{i\bar{j}}\,dz^{i}\wedge dz^{\bar{j}}\quad \end{array}\right.\end{eqnarray}$$and
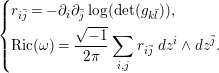 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}r_{i\bar{j}}=-\partial _{i}\partial _{\bar{j}}\log (\det (g_{k\bar{l}})),\quad \\ \text{Ric}({\it\omega})={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\displaystyle \mathop{\sum }_{i,j}r_{i\bar{j}}\,dz^{i}\wedge dz^{\bar{j}}.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}r_{i\bar{j}}=-\partial _{i}\partial _{\bar{j}}\log (\det (g_{k\bar{l}})),\quad \\ \text{Ric}({\it\omega})={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\displaystyle \mathop{\sum }_{i,j}r_{i\bar{j}}\,dz^{i}\wedge dz^{\bar{j}}.\quad \end{array}\right.\end{eqnarray}$$ Since both ![]() ${\it\omega}$ and
${\it\omega}$ and ![]() $\text{Ric}({\it\omega})$ are in
$\text{Ric}({\it\omega})$ are in ![]() $c_{1}(M)$,
$c_{1}(M)$, ![]() $\text{Ric}({\it\omega})-{\it\omega}$ is an exact
$\text{Ric}({\it\omega})-{\it\omega}$ is an exact ![]() $(1,1)$-form. Therefore, there exists a real-valued smooth function
$(1,1)$-form. Therefore, there exists a real-valued smooth function ![]() ${\it\kappa}$ on
${\it\kappa}$ on ![]() $M$ such that
$M$ such that
Let ![]() $\mathfrak{g}$ be the Lie algebra consisting of all holomorphic vector fields on
$\mathfrak{g}$ be the Lie algebra consisting of all holomorphic vector fields on ![]() $M$. Then, any
$M$. Then, any ![]() $V\in \mathfrak{g}$ can be lifted to the anticanonical bundle
$V\in \mathfrak{g}$ can be lifted to the anticanonical bundle ![]() $-K_{M}$ of
$-K_{M}$ of ![]() $M$, and naturally acts on the space of Hermitian metrics on
$M$, and naturally acts on the space of Hermitian metrics on ![]() $-K_{M}$. Let
$-K_{M}$. Let ![]() $h$ be a Hermitian metric on
$h$ be a Hermitian metric on ![]() $-K_{M}$ such that
$-K_{M}$ such that ![]() ${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$, and let
${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$, and let ![]() ${\it\mu}_{h,V}$ be the holomorphy potential of the pair
${\it\mu}_{h,V}$ be the holomorphy potential of the pair ![]() $(h,V)$ defined by this action (cf. Definition 2.2). Then, we can easily check that
$(h,V)$ defined by this action (cf. Definition 2.2). Then, we can easily check that
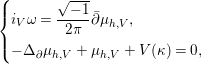 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}i_{V}{\it\omega}={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\bar{\partial }{\it\mu}_{h,V},\quad \\ -{\rm\Delta}_{\partial }{\it\mu}_{h,V}+{\it\mu}_{h,V}+V({\it\kappa})=0,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}i_{V}{\it\omega}={\displaystyle \frac{\sqrt{-1}}{2{\it\pi}}}\bar{\partial }{\it\mu}_{h,V},\quad \\ -{\rm\Delta}_{\partial }{\it\mu}_{h,V}+{\it\mu}_{h,V}+V({\it\kappa})=0,\quad \end{array}\right.\end{eqnarray}$$ where ![]() ${\rm\Delta}_{\partial }=-g^{i\bar{j}}\frac{\partial ^{2}}{\partial z^{i}\partial z^{\bar{j}}}$ denotes the
${\rm\Delta}_{\partial }=-g^{i\bar{j}}\frac{\partial ^{2}}{\partial z^{i}\partial z^{\bar{j}}}$ denotes the ![]() $\partial$-Laplacian with respect to
$\partial$-Laplacian with respect to ![]() ${\it\omega}$. A metric
${\it\omega}$. A metric ![]() ${\it\omega}$ is called a Kähler–Ricci soliton if it satisfies the equation
${\it\omega}$ is called a Kähler–Ricci soliton if it satisfies the equation
for some ![]() $V\in \mathfrak{g}$, where
$V\in \mathfrak{g}$, where ![]() $L_{V}$ denotes the Lie derivative with respect to
$L_{V}$ denotes the Lie derivative with respect to ![]() $V$. This is equivalent to the condition
$V$. This is equivalent to the condition ![]() ${\it\kappa}={\it\mu}_{h,V}$ (up to an additive constant). In particular, in the case when
${\it\kappa}={\it\mu}_{h,V}$ (up to an additive constant). In particular, in the case when ![]() $V\equiv 0$, this metric is a well-known Kähler–Einstein metric. An obstruction to the existence of Kähler–Ricci solitons was first discovered by Tian and Zhu [Reference Tian and ZhuTZ02]. Let
$V\equiv 0$, this metric is a well-known Kähler–Einstein metric. An obstruction to the existence of Kähler–Ricci solitons was first discovered by Tian and Zhu [Reference Tian and ZhuTZ02]. Let ![]() ${\mathcal{F}}$ be a function on
${\mathcal{F}}$ be a function on ![]() $\mathfrak{g}$ defined by
$\mathfrak{g}$ defined by
and define the modified Futaki invariant ![]() $\text{Fut}_{V}(W)$ as the Gâteaux differential of
$\text{Fut}_{V}(W)$ as the Gâteaux differential of ![]() ${\mathcal{F}}$ at
${\mathcal{F}}$ at ![]() $V$ in the direction
$V$ in the direction ![]() $W$, that is,
$W$, that is,
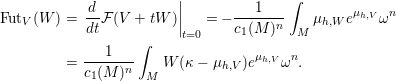 $$\begin{eqnarray}\displaystyle \text{Fut}_{V}(W) & = & \displaystyle \left.\frac{d}{dt}{\mathcal{F}}(V+tW)\right|_{t=0}=-\frac{1}{c_{1}(M)^{n}}\int _{M}{\it\mu}_{h,W}e^{{\it\mu}_{h,V}}{\it\omega}^{n}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{c_{1}(M)^{n}}\int _{M}W({\it\kappa}-{\it\mu}_{h,V})e^{{\it\mu}_{h,V}}{\it\omega}^{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Fut}_{V}(W) & = & \displaystyle \left.\frac{d}{dt}{\mathcal{F}}(V+tW)\right|_{t=0}=-\frac{1}{c_{1}(M)^{n}}\int _{M}{\it\mu}_{h,W}e^{{\it\mu}_{h,V}}{\it\omega}^{n}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{c_{1}(M)^{n}}\int _{M}W({\it\kappa}-{\it\mu}_{h,V})e^{{\it\mu}_{h,V}}{\it\omega}^{n}.\nonumber\end{eqnarray}$$ Hence, if there exists a Kähler–Ricci soliton ![]() ${\it\omega}$ with respect to
${\it\omega}$ with respect to ![]() $V$, then we have
$V$, then we have ![]() ${\it\kappa}={\it\mu}_{h,V}$ (up to an additive constant), and
${\it\kappa}={\it\mu}_{h,V}$ (up to an additive constant), and ![]() $\text{Fut}_{V}(W)$ must vanish. Tian and Zhu showed that
$\text{Fut}_{V}(W)$ must vanish. Tian and Zhu showed that ![]() $\text{Fut}_{V}(W)$ is independent of the choice of
$\text{Fut}_{V}(W)$ is independent of the choice of ![]() ${\it\omega}\in c_{1}(M)$. (In the case when
${\it\omega}\in c_{1}(M)$. (In the case when ![]() $V\equiv 0$, this function coincides with the original Futaki invariant, and its independence was shown in [Reference FutakiFut83].) Recently, Berman and Nyström [Reference Berman and NyströmBN14] generalized this obstruction to arbitrary Fano varieties (i.e., projective normal varieties with log terminal singularities and satisfying the property that
$V\equiv 0$, this function coincides with the original Futaki invariant, and its independence was shown in [Reference FutakiFut83].) Recently, Berman and Nyström [Reference Berman and NyströmBN14] generalized this obstruction to arbitrary Fano varieties (i.e., projective normal varieties with log terminal singularities and satisfying the property that ![]() $-K_{M}$ is an ample
$-K_{M}$ is an ample ![]() $\mathbb{Q}$-line bundle), and introduced the notion of K-stability for the pair
$\mathbb{Q}$-line bundle), and introduced the notion of K-stability for the pair ![]() $(M,V)$. (Wang, Zhou and Zhu [Reference Wang, Zhou and ZhuWZZ14] also defined the slightly modified notion of K-stability inspired by the algebraic formula for the modified Futaki invariant in [Reference Berman and NyströmBN14].) It is important to examine the sign of the modified Futaki invariant, since we can know whether
$(M,V)$. (Wang, Zhou and Zhu [Reference Wang, Zhou and ZhuWZZ14] also defined the slightly modified notion of K-stability inspired by the algebraic formula for the modified Futaki invariant in [Reference Berman and NyströmBN14].) It is important to examine the sign of the modified Futaki invariant, since we can know whether ![]() $c_{1}(M)$ contains a Kähler–Ricci soliton or not if we examine the sign of the modified Futaki invariant on the central fiber for any special test configuration, that is, check the K-polystability.
$c_{1}(M)$ contains a Kähler–Ricci soliton or not if we examine the sign of the modified Futaki invariant on the central fiber for any special test configuration, that is, check the K-polystability.
Chen, Donaldson and Sun [Reference Chen, Donaldson and SunCDS15] and Tian [Reference TianTian15] proved that if ![]() $M$ is K-polystable, there exists a Kähler–Einstein metric. In the case of Kähler–Ricci solitons, Berman and Nyström [Reference Berman and NyströmBN14] showed that if
$M$ is K-polystable, there exists a Kähler–Einstein metric. In the case of Kähler–Ricci solitons, Berman and Nyström [Reference Berman and NyströmBN14] showed that if ![]() $M$ admits a Kähler–Ricci soliton with respect to
$M$ admits a Kähler–Ricci soliton with respect to ![]() $V$, then
$V$, then ![]() $(M,V)$ is K-polystable. They also showed that if
$(M,V)$ is K-polystable. They also showed that if ![]() $M$ is strongly analytically K-polystable and all the higher-order modified Futaki invariants of
$M$ is strongly analytically K-polystable and all the higher-order modified Futaki invariants of ![]() $(X,V)$ vanish, then there exists a Kähler–Ricci soliton with respect to
$(X,V)$ vanish, then there exists a Kähler–Ricci soliton with respect to ![]() $V$, where strongly analytically K-polystable means that the modified K-energy is coercive modulo automorphisms. However, it is still an open question whether the K-polystability of
$V$, where strongly analytically K-polystable means that the modified K-energy is coercive modulo automorphisms. However, it is still an open question whether the K-polystability of ![]() $(M,V)$ leads to the existence of a Kähler–Ricci soliton with respect to
$(M,V)$ leads to the existence of a Kähler–Ricci soliton with respect to ![]() $V$.
$V$.
Motivated by the above reasons, we propose a method of calculating the function ![]() ${\mathcal{F}}$ (therefore, the modified Futaki invariant
${\mathcal{F}}$ (therefore, the modified Futaki invariant ![]() $\text{Fut}_{V}$ as well) for Fano complete intersections in projective spaces. The main theorem of this paper is as follows.
$\text{Fut}_{V}$ as well) for Fano complete intersections in projective spaces. The main theorem of this paper is as follows.
Theorem 1.1. Let ![]() $M$ be a Fano complete intersection in
$M$ be a Fano complete intersection in ![]() $\mathbb{C}P^{N}$, that is,
$\mathbb{C}P^{N}$, that is, ![]() $M$ is an
$M$ is an ![]() $(N-s)$-dimensional Fano variety in
$(N-s)$-dimensional Fano variety in ![]() $\mathbb{C}P^{N}$ defined by homogeneous polynomials
$\mathbb{C}P^{N}$ defined by homogeneous polynomials ![]() $F_{1},\ldots ,F_{s}$ of degree
$F_{1},\ldots ,F_{s}$ of degree ![]() $d_{1},\ldots ,d_{s}$ respectively, and
$d_{1},\ldots ,d_{s}$ respectively, and
is the Fubini–Study metric of ![]() $\mathbb{C}P^{N}$. We suppose that there exists a constant
$\mathbb{C}P^{N}$. We suppose that there exists a constant ![]() $m>0$ such that
$m>0$ such that ![]() $m{\it\omega}\in c_{1}(M)$. Let
$m{\it\omega}\in c_{1}(M)$. Let ![]() $V\in \mathfrak{s}l(N+1,\mathbb{C})$ be a holomorphic vector field on
$V\in \mathfrak{s}l(N+1,\mathbb{C})$ be a holomorphic vector field on ![]() $\mathbb{C}P^{N}$ such that
$\mathbb{C}P^{N}$ such that ![]() $VF_{i}={\it\alpha}_{i}F_{i}$ for some constants
$VF_{i}={\it\alpha}_{i}F_{i}$ for some constants ![]() ${\it\alpha}_{i}~(i=1,\ldots ,s)$. Then, we have
${\it\alpha}_{i}~(i=1,\ldots ,s)$. Then, we have ![]() $m=N+1-d_{1}-\cdots -d_{s}$, and the function
$m=N+1-d_{1}-\cdots -d_{s}$, and the function ![]() ${\mathcal{F}}$ can be written as
${\mathcal{F}}$ can be written as
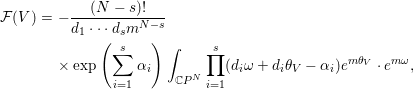 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{(N-s)!}{d_{1}\cdots d_{s}m^{N-s}}\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{(N-s)!}{d_{1}\cdots d_{s}m^{N-s}}\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}},\end{eqnarray}$$ where ![]() ${\it\theta}_{V}:=V\log (\sum _{i=0}^{N}|z^{i}|^{2})$.
${\it\theta}_{V}:=V\log (\sum _{i=0}^{N}|z^{i}|^{2})$.
From the above theorem, we know that ![]() ${\mathcal{F}}(V)$ can be written as a linear combination of the integrals
${\mathcal{F}}(V)$ can be written as a linear combination of the integrals ![]() $I_{0,l}:=m^{l}\int _{\mathbb{C}P^{N}}({\it\theta}_{V})^{l}e^{m{\it\theta}_{V}}{\it\omega}^{N}$ (
$I_{0,l}:=m^{l}\int _{\mathbb{C}P^{N}}({\it\theta}_{V})^{l}e^{m{\it\theta}_{V}}{\it\omega}^{N}$ (![]() $0\leqslant l\leqslant s$).
$0\leqslant l\leqslant s$).
Although we can easily get a method of computing ![]() ${\mathcal{F}}$ using the localization formula for orbifolds in [Reference Ding and TianDT92], our formula (1.1) is still valuable since we need not assume that
${\mathcal{F}}$ using the localization formula for orbifolds in [Reference Ding and TianDT92], our formula (1.1) is still valuable since we need not assume that ![]() $M$ has at worst orbifold singularities. Moreover, we also do not require the explicit geometric knowledge of
$M$ has at worst orbifold singularities. Moreover, we also do not require the explicit geometric knowledge of ![]() $M$,
$M$, ![]() $V$ and
$V$ and ![]() ${\it\omega}$ (local coordinates (uniformization), the zero set of
${\it\omega}$ (local coordinates (uniformization), the zero set of ![]() $V$, curvature, etc.). More concretely, in order to apply the localization formula in [Reference Ding and TianDT92] directly to our case, we have to know the following.
$V$, curvature, etc.). More concretely, in order to apply the localization formula in [Reference Ding and TianDT92] directly to our case, we have to know the following.
(1) The zero set
 $\text{Zero}(V)$ of
$\text{Zero}(V)$ of  $V$, where we assume that
$V$, where we assume that  $\text{Zero}(V)$ consists of disjoint nondegenerate submanifolds
$\text{Zero}(V)$ consists of disjoint nondegenerate submanifolds  $\{Z_{i}\}$.
$\{Z_{i}\}$.(2) The values of integrals
where $$\begin{eqnarray}\int _{Z_{i}}\frac{e^{m({\it\omega}+{\it\theta}_{V})}}{\det (L_{i,V}+K_{i})},\end{eqnarray}$$
$$\begin{eqnarray}\int _{Z_{i}}\frac{e^{m({\it\omega}+{\it\theta}_{V})}}{\det (L_{i,V}+K_{i})},\end{eqnarray}$$ $L_{i,V}(W):=[V,W]$ denotes an endomorphism, and
$L_{i,V}(W):=[V,W]$ denotes an endomorphism, and  $K_{i}$ is the curvature matrix of the normal bundle of
$K_{i}$ is the curvature matrix of the normal bundle of  $Z_{i}$.
$Z_{i}$.
If ![]() $s(=\,\text{codim}(M))=1$ and
$s(=\,\text{codim}(M))=1$ and ![]() $\text{dim}(Z_{i})=0$, the above integral can be computed by taking local coordinates (or uniformization) around
$\text{dim}(Z_{i})=0$, the above integral can be computed by taking local coordinates (or uniformization) around ![]() $Z_{i}$. However, it is very hard to compute in general.
$Z_{i}$. However, it is very hard to compute in general.
The Futaki invariant of complete intersection was first computed by Lu [Reference LuLu99] using the adjunction formula and the Poincaré–Lelong formula. Then, it was also computed by many mathematicians using different techniques (see [Reference Phong and SturmPS04, Reference HouHou08, Reference Arezzo and VedovaAV11]). Lu [Reference LuLu03] also computed the modified Futaki invariant for smooth hypersurfaces in projective spaces. Our formula (Theorem 1.1) extends Lu’s result [Reference LuLu03] for (possibly singular) Fano complete intersections of arbitrary codimension. Compared with the Kähler–Einstein case [Reference LuLu99], our formula has in common that ![]() ${\mathcal{F}}(V)$ is expressed by the degree
${\mathcal{F}}(V)$ is expressed by the degree ![]() $d_{1},\ldots ,d_{s}$ of defining polynomials of
$d_{1},\ldots ,d_{s}$ of defining polynomials of ![]() $M$ and the weights
$M$ and the weights ![]() ${\it\alpha}_{1},\ldots ,{\it\alpha}_{s}$ of the actions induced by the vector field
${\it\alpha}_{1},\ldots ,{\it\alpha}_{s}$ of the actions induced by the vector field ![]() $V$. However, we need more knowledge of
$V$. However, we need more knowledge of ![]() $V$ to compute the integrals
$V$ to compute the integrals ![]() $I_{0,l}$ (
$I_{0,l}$ (![]() $0\leqslant l\leqslant s$) (see Section 5 for more details).
$0\leqslant l\leqslant s$) (see Section 5 for more details).
In this paper, we prove the main theorem (Theorem 1.1) based on the calculations in [Reference LuLu99, Reference Arezzo and VedovaAV11]. In Section 2, we review some fundamental materials and results for Kähler–Ricci solitons. The standard references for (holomorphic) equivariant cohomology theory are [Reference Berline, Getzler and VergneBGV92, Reference HouHou08, Reference LiuLiu95]. We introduce an algebraic formula for ![]() ${\mathcal{F}}$ with reference to the quantization of the modified Futaki invariant studied in [Reference Berman and NyströmBN14]. In Section 3, we give a proof of Theorem 1.1 by the Poincaré–Lelong formula. Then, in Section 4, we also give another proof of Theorem 1.1 using the algebraic formula for
${\mathcal{F}}$ with reference to the quantization of the modified Futaki invariant studied in [Reference Berman and NyströmBN14]. In Section 3, we give a proof of Theorem 1.1 by the Poincaré–Lelong formula. Then, in Section 4, we also give another proof of Theorem 1.1 using the algebraic formula for ![]() ${\mathcal{F}}$ (cf. Proposition 2.8). Finally, we give examples of computation of
${\mathcal{F}}$ (cf. Proposition 2.8). Finally, we give examples of computation of ![]() ${\mathcal{F}}$ in Section 5.
${\mathcal{F}}$ in Section 5.
2 Preminaries
2.1 Holomorphic equivariant coholomogy
Let ![]() $M$ be a complex manifold, and let
$M$ be a complex manifold, and let ![]() $G$ be a Lie group acting holomorphically on
$G$ be a Lie group acting holomorphically on ![]() $M$. Denote
$M$. Denote ![]() $\mathfrak{g}:=\text{Lie}(G)$ the Lie algebra of
$\mathfrak{g}:=\text{Lie}(G)$ the Lie algebra of ![]() $G$. Then, for each
$G$. Then, for each ![]() ${\it\xi}\in \mathfrak{g}$, we denote by
${\it\xi}\in \mathfrak{g}$, we denote by ![]() ${\it\xi}_{M}^{\mathbb{R}}$ the real holomorphic vector field on
${\it\xi}_{M}^{\mathbb{R}}$ the real holomorphic vector field on ![]() $M$ given by
$M$ given by
and by ![]() ${\it\xi}_{M}:=\frac{1}{2}({\it\xi}_{M}^{\mathbb{R}}-\sqrt{-1}J{\it\xi}_{M}^{\mathbb{R}})$ the complex holomorphic vector field on
${\it\xi}_{M}:=\frac{1}{2}({\it\xi}_{M}^{\mathbb{R}}-\sqrt{-1}J{\it\xi}_{M}^{\mathbb{R}})$ the complex holomorphic vector field on ![]() $M$. Let
$M$. Let ![]() $\mathbb{C}[\mathfrak{g}]$ be the algebra of a complex-valued polynomial function on
$\mathbb{C}[\mathfrak{g}]$ be the algebra of a complex-valued polynomial function on ![]() $\mathfrak{g}$. We regard each element in
$\mathfrak{g}$. We regard each element in ![]() $\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ as a polynomial function which takes values in differential forms. The group
$\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ as a polynomial function which takes values in differential forms. The group ![]() $G$ acts on an element
$G$ acts on an element![]() ${\it\sigma}\in \mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ by
${\it\sigma}\in \mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ by
Let ![]() ${\mathcal{A}}_{G}(M)=(\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M))^{G}$ be the space of
${\mathcal{A}}_{G}(M)=(\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M))^{G}$ be the space of ![]() $G$-invariant elements in
$G$-invariant elements in ![]() $\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$. For
$\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$. For ![]() ${\it\sigma}\in \mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$, we define the bidegree of
${\it\sigma}\in \mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$, we define the bidegree of ![]() ${\it\sigma}$ by
${\it\sigma}$ by
where ![]() ${\it\sigma}=P\otimes {\it\varphi}$ (
${\it\sigma}=P\otimes {\it\varphi}$ (![]() $P\in \mathbb{C}[\mathfrak{g}]$ and
$P\in \mathbb{C}[\mathfrak{g}]$ and ![]() ${\it\varphi}\in {\mathcal{A}}^{p,q}(M)$). For instance,
${\it\varphi}\in {\mathcal{A}}^{p,q}(M)$). For instance, ![]() $\text{bideg}({\it\xi})=(1,1)$. Thus,
$\text{bideg}({\it\xi})=(1,1)$. Thus, ![]() ${\mathcal{A}}_{G}(M)=\bigoplus {\mathcal{A}}_{G}^{p,q}(M)$ has the structure of a bigraded algebra. We define the equivariant exterior differential
${\mathcal{A}}_{G}(M)=\bigoplus {\mathcal{A}}_{G}^{p,q}(M)$ has the structure of a bigraded algebra. We define the equivariant exterior differential ![]() $\bar{\partial }_{\mathfrak{g}}$ on
$\bar{\partial }_{\mathfrak{g}}$ on ![]() $\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ as
$\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$ as
Then, ![]() $\bar{\partial }_{\mathfrak{g}}$ increases by
$\bar{\partial }_{\mathfrak{g}}$ increases by ![]() $(0,1)$, the total bidegree on
$(0,1)$, the total bidegree on ![]() $\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$, and preserves
$\mathbb{C}[\mathfrak{g}]\otimes {\mathcal{A}}(M)$, and preserves ![]() ${\mathcal{A}}_{G}(M)$. Hence, we have a complex
${\mathcal{A}}_{G}(M)$. Hence, we have a complex ![]() $({\mathcal{A}}_{G}(M),\bar{\partial }_{\mathfrak{g}})$.
$({\mathcal{A}}_{G}(M),\bar{\partial }_{\mathfrak{g}})$.
Definition 2.1. The holomorphic equivariant cohomology ![]() $H_{\mathfrak{g}}(M)$ of the pair
$H_{\mathfrak{g}}(M)$ of the pair ![]() $(M,G)$ is the cohomology of the complex
$(M,G)$ is the cohomology of the complex ![]() $({\mathcal{A}}_{G}(M),\bar{\partial }_{\mathfrak{g}})$.
$({\mathcal{A}}_{G}(M),\bar{\partial }_{\mathfrak{g}})$.
Let ![]() $E$ be a
$E$ be a ![]() $G$-linearized holomorphic vector bundle over
$G$-linearized holomorphic vector bundle over ![]() $M$, and let
$M$, and let ![]() $\text{Herm}(E)$ be the space of Hermitian metrics on
$\text{Herm}(E)$ be the space of Hermitian metrics on ![]() $E$. The group
$E$. The group ![]() $G$ acts on
$G$ acts on ![]() $\text{Herm}(E)$ by the formula
$\text{Herm}(E)$ by the formula
Hence, for ![]() ${\it\xi}\in \mathfrak{g}$, we define the real Lie derivative of
${\it\xi}\in \mathfrak{g}$, we define the real Lie derivative of ![]() $\mathfrak{g}$ on
$\mathfrak{g}$ on ![]() $\text{Herm}(E)$ by
$\text{Herm}(E)$ by
and the complex Lie derivative of ![]() $\mathfrak{g}$ on
$\mathfrak{g}$ on ![]() $\text{Herm}(M)$ by
$\text{Herm}(M)$ by
We can also define the representation of ![]() $\mathfrak{g}$ on the space of sections
$\mathfrak{g}$ on the space of sections ![]() ${\rm\Gamma}(E)$ in a similar way. Let
${\rm\Gamma}(E)$ in a similar way. Let ![]() ${\rm\nabla}$ be the Chern connection with respect to
${\rm\nabla}$ be the Chern connection with respect to ![]() $h$, and put
$h$, and put
Since ![]() ${\it\mu}_{h,{\it\xi}}(fs)={\it\xi}_{M}f\cdot s+f\cdot L_{{\it\xi}}s-{\it\xi}_{M}f\cdot s-f\cdot {\rm\nabla}_{{\it\xi}_{M}}s=f\cdot {\it\mu}_{h,{\it\xi}}(s)$ for any
${\it\mu}_{h,{\it\xi}}(fs)={\it\xi}_{M}f\cdot s+f\cdot L_{{\it\xi}}s-{\it\xi}_{M}f\cdot s-f\cdot {\rm\nabla}_{{\it\xi}_{M}}s=f\cdot {\it\mu}_{h,{\it\xi}}(s)$ for any ![]() $f\in C^{\infty }(M)$ and
$f\in C^{\infty }(M)$ and ![]() $s\in {\rm\Gamma}(E)$, we have
$s\in {\rm\Gamma}(E)$, we have ![]() ${\it\mu}_{h,{\it\xi}}\in {\rm\Gamma}(\text{End}(E))$. Moreover, one can show that
${\it\mu}_{h,{\it\xi}}\in {\rm\Gamma}(\text{End}(E))$. Moreover, one can show that
where ![]() ${\it\theta}(h)=\partial h\cdot h^{-1}$ is the connection form and
${\it\theta}(h)=\partial h\cdot h^{-1}$ is the connection form and ![]() ${\rm\Theta}(h)=\frac{\sqrt{-1}}{2{\it\pi}}\bar{\partial }(\partial h\cdot h)$ is the curvature form with respect to
${\rm\Theta}(h)=\frac{\sqrt{-1}}{2{\it\pi}}\bar{\partial }(\partial h\cdot h)$ is the curvature form with respect to ![]() $h$. Define the equivariant curvature form
$h$. Define the equivariant curvature form ![]() ${\rm\Theta}_{\mathfrak{g}}(h)$ by
${\rm\Theta}_{\mathfrak{g}}(h)$ by
Then, ![]() ${\rm\Theta}_{\mathfrak{g}}(h)$ is
${\rm\Theta}_{\mathfrak{g}}(h)$ is ![]() $\bar{\partial }_{\mathfrak{g}}$-closed and defines an element in
$\bar{\partial }_{\mathfrak{g}}$-closed and defines an element in ![]() $H_{\mathfrak{g}}^{1,1}(M)$.
$H_{\mathfrak{g}}^{1,1}(M)$.
Now, let us consider the case when ![]() $E=L$ is a
$E=L$ is a ![]() $G$-linearized ample line bundle. Then,
$G$-linearized ample line bundle. Then, ![]() ${\it\mu}_{h,{\it\xi}}$ is a complex-valued smooth function on
${\it\mu}_{h,{\it\xi}}$ is a complex-valued smooth function on ![]() $M$.
$M$.
Definition 2.2. The function ![]() ${\it\mu}_{h,{\it\xi}}$ is said to be the holomorphy potential of the pair
${\it\mu}_{h,{\it\xi}}$ is said to be the holomorphy potential of the pair ![]() $(h,{\it\xi})$.
$(h,{\it\xi})$.
2.2 Kähler–Ricci soliton
Let ![]() $M$ be an
$M$ be an ![]() $n$-dimensional Fano manifold.
$n$-dimensional Fano manifold.
Definition 2.3. A Kähler metric ![]() ${\it\omega}$ on
${\it\omega}$ on ![]() $M$ is a Kähler–Ricci soliton if the metric
$M$ is a Kähler–Ricci soliton if the metric ![]() ${\it\omega}$ solves the equation
${\it\omega}$ solves the equation
for some holomorphic vector field ![]() $V$ on
$V$ on ![]() $M$.
$M$.
If the pair ![]() $({\it\omega},V)$ is a Kähler–Ricci soliton, taking the imaginary part of (2.1) yields
$({\it\omega},V)$ is a Kähler–Ricci soliton, taking the imaginary part of (2.1) yields ![]() $L_{\text{Im}(V)}{\it\omega}=0$, so
$L_{\text{Im}(V)}{\it\omega}=0$, so ![]() ${\it\omega}$ is invariant under the group action generated by
${\it\omega}$ is invariant under the group action generated by ![]() $\text{Im}(V)$. More generally, we have the following proposition.
$\text{Im}(V)$. More generally, we have the following proposition.
Proposition 2.4. [Reference Berman and NyströmBN14, Lemma 2.13]
Let ![]() $M$ be a Fano manifold, and let
$M$ be a Fano manifold, and let ![]() $V$ be a holomorphic vector field on
$V$ be a holomorphic vector field on ![]() $M$. If there exists a Kähler metric
$M$. If there exists a Kähler metric ![]() ${\it\omega}$ that is invariant under the action of
${\it\omega}$ that is invariant under the action of ![]() $\text{Im}(V)$, then there exists a complex torus
$\text{Im}(V)$, then there exists a complex torus ![]() $T_{c}$ acting holomorphically on
$T_{c}$ acting holomorphically on ![]() $M$ such that
$M$ such that ![]() $\text{Im}(V)$ may be identified with an element in the Lie algebra of the corresponding real torus
$\text{Im}(V)$ may be identified with an element in the Lie algebra of the corresponding real torus ![]() $T\subset T_{c}$.
$T\subset T_{c}$.
Proof. First, we check that the isometry group ![]() $K$ of
$K$ of ![]() ${\it\omega}$ is a compact Lie group. This is shown by considering the canonical embedding
${\it\omega}$ is a compact Lie group. This is shown by considering the canonical embedding ![]() $M{\hookrightarrow}H^{0}(M,-kK_{M})$ and the
$M{\hookrightarrow}H^{0}(M,-kK_{M})$ and the ![]() $K$-invariant Hilbert norm
$K$-invariant Hilbert norm
Actually, ![]() $K$ is identified with a subgroup of the group consisting of unitary transformations on
$K$ is identified with a subgroup of the group consisting of unitary transformations on ![]() $H^{0}(M,-kK_{M})$ with respect to
$H^{0}(M,-kK_{M})$ with respect to ![]() $\Vert \cdot \Vert$, which yields that
$\Vert \cdot \Vert$, which yields that ![]() $K$ is compact. Taking the topological closure of the 1-parameter subgroup generated by
$K$ is compact. Taking the topological closure of the 1-parameter subgroup generated by ![]() $\text{Im}(V)$ in
$\text{Im}(V)$ in ![]() $K$, we get a real torus
$K$, we get a real torus ![]() $T$ as desired. In general, any holomorphic action of a real torus on
$T$ as desired. In general, any holomorphic action of a real torus on ![]() $M$ can be naturally extended to the corresponding complex torus action on
$M$ can be naturally extended to the corresponding complex torus action on ![]() $M$.◻
$M$.◻
2.3 Modified Futaki invariant
Let ![]() $M$ be an
$M$ be an ![]() $n$-dimensional Fano variety. For simplicity, let us make the following assumptions.
$n$-dimensional Fano variety. For simplicity, let us make the following assumptions.
(1)
 $M$ is a compact subvariety of a projective manifold
$M$ is a compact subvariety of a projective manifold  $N$.
$N$.(2)
 $L$ is an ample line bundle on
$L$ is an ample line bundle on  $N$ such that on the regular part
$N$ such that on the regular part  $M_{\text{reg}}$ of
$M_{\text{reg}}$ of  $M$ the isomorphism (2.2)holds for some integer
$M$ the isomorphism (2.2)holds for some integer $$\begin{eqnarray}L|_{M_{\text{reg}}}\simeq -kK_{M_{\text{reg}}}\end{eqnarray}$$
$$\begin{eqnarray}L|_{M_{\text{reg}}}\simeq -kK_{M_{\text{reg}}}\end{eqnarray}$$ $k$.
$k$.(3) The Lie group
 $G:=\text{Aut}(M)$ acts on
$G:=\text{Aut}(M)$ acts on  $(N,L)$ such that the isomorphism (2.2) is
$(N,L)$ such that the isomorphism (2.2) is  $G$-equivariant.
$G$-equivariant.
Remark 2.5. In fact, ![]() $M$ can be embedded into
$M$ can be embedded into
for a sufficient large ![]() $k$, and
$k$, and ![]() $(\mathbb{C}P^{N},{\mathcal{O}}(1))$ satisfies the requirement above.
$(\mathbb{C}P^{N},{\mathcal{O}}(1))$ satisfies the requirement above.
We say that ![]() $V$ is a holomorphic vector field on a Fano variety
$V$ is a holomorphic vector field on a Fano variety ![]() $M$ if
$M$ if ![]() $V$ is a holomorphic vector field defined only on its regular part
$V$ is a holomorphic vector field defined only on its regular part ![]() $M_{\text{reg}}$. Then,
$M_{\text{reg}}$. Then, ![]() $V$ induces a local one-parameter family of automorphisms, which extends to a family of
$V$ induces a local one-parameter family of automorphisms, which extends to a family of ![]() $G$ since
$G$ since ![]() $\text{codim}(M\setminus M_{\text{reg}})\geqslant 2$ by the normality of
$\text{codim}(M\setminus M_{\text{reg}})\geqslant 2$ by the normality of ![]() $M$ (cf. [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Lemma 5.2]). Thus, by the assumption (3),
$M$ (cf. [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Lemma 5.2]). Thus, by the assumption (3), ![]() $V$ is given as the restriction of some holomorphic vector field on
$V$ is given as the restriction of some holomorphic vector field on ![]() $N$ to
$N$ to ![]() $M$.Footnote 1
$M$.Footnote 1
Definition 2.6. A Hermitian metric ![]() $h$ on
$h$ on ![]() $-K_{M_{\text{reg}}}$ is said to be admissible if
$-K_{M_{\text{reg}}}$ is said to be admissible if ![]() $h^{k}$ can be extended to a Hermitian metric
$h^{k}$ can be extended to a Hermitian metric ![]() $\tilde{h}_{L}$ on
$\tilde{h}_{L}$ on ![]() $L$ over
$L$ over ![]() $N$ under the isomorphisms (2.2).
$N$ under the isomorphisms (2.2).
Let ![]() $h$ be an admissible Hermitian metric on
$h$ be an admissible Hermitian metric on ![]() $-K_{M_{\text{reg}}}$, and put
$-K_{M_{\text{reg}}}$, and put ![]() ${\it\omega}:=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$. For holomorphic vector fields
${\it\omega}:=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$. For holomorphic vector fields ![]() $V,W$, we define the function
$V,W$, we define the function ![]() ${\mathcal{F}}$ as
${\mathcal{F}}$ as
and the modified Futaki invariant ![]() $\text{Fut}_{V}$ by
$\text{Fut}_{V}$ by
where ![]() ${\it\mu}_{h,V}$ denotes the holomorphy potential of
${\it\mu}_{h,V}$ denotes the holomorphy potential of ![]() $(h,V)$ defined on
$(h,V)$ defined on ![]() $M_{\text{reg}}$. Since the construction of equivariant Chern curvature form is local, if
$M_{\text{reg}}$. Since the construction of equivariant Chern curvature form is local, if ![]() $i:M_{\text{reg}}{\hookrightarrow}N$ is the embedding, we obtain
$i:M_{\text{reg}}{\hookrightarrow}N$ is the embedding, we obtain
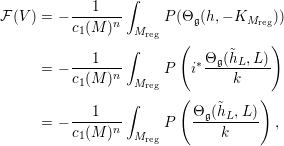 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P({\rm\Theta}_{\mathfrak{g}}(h,-K_{M_{\text{reg}}}))\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P\left(i^{\ast }\frac{{\rm\Theta}_{\mathfrak{g}}(\tilde{h}_{L},L)}{k}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P\left(\frac{{\rm\Theta}_{\mathfrak{g}}(\tilde{h}_{L},L)}{k}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P({\rm\Theta}_{\mathfrak{g}}(h,-K_{M_{\text{reg}}}))\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P\left(i^{\ast }\frac{{\rm\Theta}_{\mathfrak{g}}(\tilde{h}_{L},L)}{k}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{c_{1}(M)^{n}}\int _{M_{\text{reg}}}P\left(\frac{{\rm\Theta}_{\mathfrak{g}}(\tilde{h}_{L},L)}{k}\right),\nonumber\end{eqnarray}$$ where ![]() $P(z):=n!e^{z}$, and this shows that the integral (2.3) is finite. Moreover, using the equivariant Chern–Weil theorem, we can show the following.
$P(z):=n!e^{z}$, and this shows that the integral (2.3) is finite. Moreover, using the equivariant Chern–Weil theorem, we can show the following.
Theorem 2.7. [Reference HouHou08, Section 2.3]
The functions ![]() ${\mathcal{F}}$ and
${\mathcal{F}}$ and ![]() $\text{Fut}_{V}$ are independent of the embedding
$\text{Fut}_{V}$ are independent of the embedding ![]() $M{\hookrightarrow}N$ and the choice of an admissible Hermitian metric
$M{\hookrightarrow}N$ and the choice of an admissible Hermitian metric ![]() $h$ on
$h$ on ![]() $-K_{M_{\text{reg}}}$.
$-K_{M_{\text{reg}}}$.
On the other hand, a pluripotential theoretical formulation of ![]() $\text{Fut}_{V}$ was introduced by Berman and Nyström [Reference Berman and NyströmBN14]. They also introduced the quantized version of the modified Futaki invariant, which is defined more algebraically in terms of the commuting action on the cohomology
$\text{Fut}_{V}$ was introduced by Berman and Nyström [Reference Berman and NyströmBN14]. They also introduced the quantized version of the modified Futaki invariant, which is defined more algebraically in terms of the commuting action on the cohomology ![]() $H^{0}(M,-kK_{M})$. Let
$H^{0}(M,-kK_{M})$. Let ![]() $V$ be a holomorphic vector field on
$V$ be a holomorphic vector field on ![]() $M$ generating a torus action, and put
$M$ generating a torus action, and put
We define the quantization of the function ![]() ${\mathcal{F}}$ at level
${\mathcal{F}}$ at level ![]() $k$ as
$k$ as
where ![]() $(v_{i}^{(k)})$ are the joint eigenvalues for the action of
$(v_{i}^{(k)})$ are the joint eigenvalues for the action of ![]() $\text{Re}(V)$ on
$\text{Re}(V)$ on ![]() $H^{0}(M,-kK_{M})$ defined by the canonical lift of
$H^{0}(M,-kK_{M})$ defined by the canonical lift of ![]() $V$ to
$V$ to ![]() $-K_{M}$. Additionally, let
$-K_{M}$. Additionally, let ![]() $W$ be a holomorphic vector field on
$W$ be a holomorphic vector field on ![]() $M$ generating a
$M$ generating a ![]() $\mathbb{C}^{\ast }$-action and commuting with
$\mathbb{C}^{\ast }$-action and commuting with ![]() $V$. We define the quantization of
$V$. We define the quantization of ![]() $\text{Fut}_{V}(W)$ at level
$\text{Fut}_{V}(W)$ at level ![]() $k$ as
$k$ as
where ![]() $(v_{i}^{(k)},w_{i}^{(k)})$ are the joint eigenvalues for the commuting action of
$(v_{i}^{(k)},w_{i}^{(k)})$ are the joint eigenvalues for the commuting action of ![]() $\text{Re}(V)$ and
$\text{Re}(V)$ and ![]() $\text{Re}(W)$. Then, we have the following.
$\text{Re}(W)$. Then, we have the following.
Proposition 2.8. In the case when ![]() $M$ is smooth, we have the following.
$M$ is smooth, we have the following.
(1) We have the asymptotic expansion of
 ${\mathcal{F}}_{k}(V)$ as
${\mathcal{F}}_{k}(V)$ as  $k\rightarrow \infty$: where
$k\rightarrow \infty$: where $$\begin{eqnarray}{\mathcal{F}}_{k}(V)={\mathcal{F}}^{(0)}(V)\cdot k^{n+1}+{\mathcal{F}}^{(1)}(V)\cdot k^{n}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{k}(V)={\mathcal{F}}^{(0)}(V)\cdot k^{n+1}+{\mathcal{F}}^{(1)}(V)\cdot k^{n}+\cdots \,,\end{eqnarray}$$ ${\mathcal{F}}^{(0)}(V)$ is proportional to
${\mathcal{F}}^{(0)}(V)$ is proportional to  ${\mathcal{F}}(V)$.
${\mathcal{F}}(V)$.(2) We have the asymptotic expansion of
 $\text{Fut}_{V,k}(W)$ as
$\text{Fut}_{V,k}(W)$ as  $k\rightarrow \infty$: where
$k\rightarrow \infty$: where $$\begin{eqnarray}\text{Fut}_{V,k}(W)=\text{Fut}_{V}^{(0)}(W)\cdot k^{n+1}+\text{Fut}_{V}^{(1)}(W)\cdot k^{n}+\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}\text{Fut}_{V,k}(W)=\text{Fut}_{V}^{(0)}(W)\cdot k^{n+1}+\text{Fut}_{V}^{(1)}(W)\cdot k^{n}+\cdots \,,\end{eqnarray}$$ $\text{Fut}_{V}^{(i)}(W)$ is the
$\text{Fut}_{V}^{(i)}(W)$ is the  $i$th-order modified Futaki invariant defined in [Reference Berman and NyströmBN14, Section 4.4], and
$i$th-order modified Futaki invariant defined in [Reference Berman and NyströmBN14, Section 4.4], and  $\text{Fut}_{V}^{(0)}(W)$ is proportional to
$\text{Fut}_{V}^{(0)}(W)$ is proportional to  $\text{Fut}_{V}(W)$.
$\text{Fut}_{V}(W)$.(3) The
 $i$th-order modified Futaki invariant
$i$th-order modified Futaki invariant  $\text{Fut}_{V}^{(i)}(W)$ is the Gâteaux differential of
$\text{Fut}_{V}^{(i)}(W)$ is the Gâteaux differential of  ${\mathcal{F}}^{(i)}$ at
${\mathcal{F}}^{(i)}$ at  $V$ in the direction
$V$ in the direction  $W$, that is,
$W$, that is,  $$\begin{eqnarray}\left.\frac{d}{dt}{\mathcal{F}}_{k}^{(i)}(V+tW)\right|_{t=0}=\text{Fut}_{V}^{(i)}(W).\end{eqnarray}$$
$$\begin{eqnarray}\left.\frac{d}{dt}{\mathcal{F}}_{k}^{(i)}(V+tW)\right|_{t=0}=\text{Fut}_{V}^{(i)}(W).\end{eqnarray}$$In general, when
 $M$ is a (possibly singular) Fano variety, we have the following.
$M$ is a (possibly singular) Fano variety, we have the following.(4)
 $$\begin{eqnarray}{\mathcal{F}}(V)=\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}(V)=\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V).\end{eqnarray}$$(5)
 $$\begin{eqnarray}\text{Fut}_{V}(W)=\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}\text{Fut}_{V,k}(W).\end{eqnarray}$$
$$\begin{eqnarray}\text{Fut}_{V}(W)=\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}\text{Fut}_{V,k}(W).\end{eqnarray}$$
Proof. The statements (2) and (5) were shown in [Reference Berman and NyströmBN14, Section 4.4]. The statement (3) is trivial from the definition of ![]() $\text{Fut}_{k,V}(W)$.
$\text{Fut}_{k,V}(W)$.
(1) As with the proof of (2) (cf. [Reference Berman and NyströmBN14, Section 4.4]) or [Reference Wang, Zhou and ZhuWZZ14, Lemma 1.2], ![]() ${\mathcal{F}}_{k}(V)$ can be calculated by the equivariant Riemann–Roch formula as
${\mathcal{F}}_{k}(V)$ can be calculated by the equivariant Riemann–Roch formula as
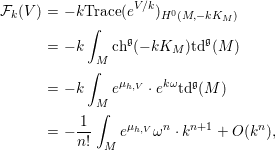 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\text{Trace}(e^{V/k})_{H^{0}(M,-kK_{M})}\nonumber\\ \displaystyle & = & \displaystyle -k\int _{M}\text{ch}^{\mathfrak{g}}(-kK_{M})\text{td}^{\mathfrak{g}}(M)\nonumber\\ \displaystyle & = & \displaystyle -k\int _{M}e^{{\it\mu}_{h,V}}\cdot e^{k{\it\omega}}\text{td}^{\mathfrak{g}}(M)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{n!}\int _{M}e^{{\it\mu}_{h,V}}{\it\omega}^{n}\cdot k^{n+1}+O(k^{n}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\text{Trace}(e^{V/k})_{H^{0}(M,-kK_{M})}\nonumber\\ \displaystyle & = & \displaystyle -k\int _{M}\text{ch}^{\mathfrak{g}}(-kK_{M})\text{td}^{\mathfrak{g}}(M)\nonumber\\ \displaystyle & = & \displaystyle -k\int _{M}e^{{\it\mu}_{h,V}}\cdot e^{k{\it\omega}}\text{td}^{\mathfrak{g}}(M)\nonumber\\ \displaystyle & = & \displaystyle -\frac{1}{n!}\int _{M}e^{{\it\mu}_{h,V}}{\it\omega}^{n}\cdot k^{n+1}+O(k^{n}),\nonumber\end{eqnarray}$$ where ![]() $\text{ch}^{\mathfrak{g}}$ (respectively
$\text{ch}^{\mathfrak{g}}$ (respectively ![]() $\text{td}^{\mathfrak{g}}$) denotes the equivariant Chern character (respectively the equivariant Todd class). Thus,
$\text{td}^{\mathfrak{g}}$) denotes the equivariant Chern character (respectively the equivariant Todd class). Thus, ![]() ${\mathcal{F}}^{(0)}(V)=\frac{c_{1}(M)^{n}}{n!}\cdot {\mathcal{F}}(V)$.
${\mathcal{F}}^{(0)}(V)=\frac{c_{1}(M)^{n}}{n!}\cdot {\mathcal{F}}(V)$.
(4) By definition, ![]() ${\mathcal{F}}(V)$ can be written as
${\mathcal{F}}(V)$ can be written as
where ![]() ${\it\nu}^{V}$ is the push-forward measure of the Monge–Ampère measure
${\it\nu}^{V}$ is the push-forward measure of the Monge–Ampère measure ![]() $\frac{{\it\omega}^{n}}{c_{1}(M)^{n}}$ under
$\frac{{\it\omega}^{n}}{c_{1}(M)^{n}}$ under ![]() ${\it\mu}_{h,V}$. Let
${\it\mu}_{h,V}$. Let ![]() ${\it\nu}_{k}^{V}$ be the spectral measure on
${\it\nu}_{k}^{V}$ be the spectral measure on ![]() $\mathbb{R}$ attached to the infinitesimal action of
$\mathbb{R}$ attached to the infinitesimal action of ![]() $\text{Re}(V)$ on
$\text{Re}(V)$ on ![]() $H^{0}(M,-kK_{M})$:
$H^{0}(M,-kK_{M})$:
where ![]() ${\it\delta}_{v_{i}^{(k)}/k}$ denotes the Dirac measure at
${\it\delta}_{v_{i}^{(k)}/k}$ denotes the Dirac measure at ![]() $v_{i}^{(k)}/k$. Then, by [Reference Berman and NyströmBN14, Proposition 4.1],
$v_{i}^{(k)}/k$. Then, by [Reference Berman and NyströmBN14, Proposition 4.1], ![]() ${\it\nu}_{k}^{V}$ converges to
${\it\nu}_{k}^{V}$ converges to ![]() ${\it\nu}^{V}$ as
${\it\nu}^{V}$ as ![]() $k\rightarrow \infty$ in a weak topology. Hence, we have
$k\rightarrow \infty$ in a weak topology. Hence, we have
as ![]() $k\rightarrow \infty$.◻
$k\rightarrow \infty$.◻
Remark 2.9. When ![]() $M$ is smooth, by the equivariant Riemann–Roch formula, we have an asymptotic expansion as
$M$ is smooth, by the equivariant Riemann–Roch formula, we have an asymptotic expansion as ![]() $k\rightarrow \infty$:
$k\rightarrow \infty$:
Combining with Proposition 2.8(1), we have
as ![]() $k\rightarrow \infty$. In general, when
$k\rightarrow \infty$. In general, when ![]() $M$ is a (possibly singular) Fano variety, we do not know whether we can obtain the expansion (2.8). However, Proposition 2.8(4) allows us to use the equivariant Riemann–Roch formula formally to compute the leading term of (2.8) (i.e., the limit
$M$ is a (possibly singular) Fano variety, we do not know whether we can obtain the expansion (2.8). However, Proposition 2.8(4) allows us to use the equivariant Riemann–Roch formula formally to compute the leading term of (2.8) (i.e., the limit ![]() $\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V)$) even if
$\lim _{k\rightarrow \infty }\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V)$) even if ![]() $M$ has singularities.
$M$ has singularities.
3 The calculation of the function  ${\mathcal{F}}$
${\mathcal{F}}$
Let ![]() $M$ be an
$M$ be an ![]() $n$-dimensional variety in
$n$-dimensional variety in ![]() $\mathbb{C}P^{N}$, and let
$\mathbb{C}P^{N}$, and let ![]() $X$ be a holomorphic vector field on
$X$ be a holomorphic vector field on ![]() $\mathbb{C}P^{N}$. Then,
$\mathbb{C}P^{N}$. Then, ![]() $X$ can be identified with a linear vector field
$X$ can be identified with a linear vector field ![]() $\sum _{i,j=0}^{N}a_{ij}z^{i}\frac{\partial }{\partial z^{j}}$ on
$\sum _{i,j=0}^{N}a_{ij}z^{i}\frac{\partial }{\partial z^{j}}$ on ![]() $\mathbb{C}^{N+1}$, and the traceless matrix
$\mathbb{C}^{N+1}$, and the traceless matrix ![]() $(a_{ij})_{0\leqslant i,j\leqslant N}\in \mathfrak{s}l(N+1,\mathbb{C})$, such that the push-forward of
$(a_{ij})_{0\leqslant i,j\leqslant N}\in \mathfrak{s}l(N+1,\mathbb{C})$, such that the push-forward of ![]() $\sum _{i,j=0}^{N}a_{ij}z^{i}\frac{\partial }{\partial z^{j}}$ with the standard projection
$\sum _{i,j=0}^{N}a_{ij}z^{i}\frac{\partial }{\partial z^{j}}$ with the standard projection ![]() ${\it\pi}:\mathbb{C}^{N+1}-\{0\}\rightarrow \mathbb{C}P^{N}$ is equal to
${\it\pi}:\mathbb{C}^{N+1}-\{0\}\rightarrow \mathbb{C}P^{N}$ is equal to ![]() $X$.
$X$.
For a holomorphic vector field ![]() $X$, we define a complex-valued smooth function on
$X$, we define a complex-valued smooth function on ![]() $\mathbb{C}^{N+1}-0$ by
$\mathbb{C}^{N+1}-0$ by
which descends to a smooth function on ![]() $\mathbb{C}P^{N}$. Let
$\mathbb{C}P^{N}$. Let
be the Fubini–Study metric of ![]() $\mathbb{C}P^{N}$. Then, we have
$\mathbb{C}P^{N}$. Then, we have
We say that ![]() $X$ is tangent to
$X$ is tangent to ![]() $M$ if
$M$ if ![]() $\text{Re}(X)$ leaves
$\text{Re}(X)$ leaves ![]() $M$ invariant. If
$M$ invariant. If ![]() $M$ is a hypersurface defined by a homogeneous polynomial
$M$ is a hypersurface defined by a homogeneous polynomial ![]() $F$ of degree
$F$ of degree ![]() $d$,
$d$, ![]() $X$ is tangent to
$X$ is tangent to ![]() $M$ if and only if
$M$ if and only if ![]() $X$ fixes
$X$ fixes ![]() $[F]\in \mathbb{P}(H^{0}(M,{\mathcal{O}}(d)))$, or, equivalently,
$[F]\in \mathbb{P}(H^{0}(M,{\mathcal{O}}(d)))$, or, equivalently, ![]() $XF={\it\gamma}F$ for some constant
$XF={\it\gamma}F$ for some constant ![]() ${\it\gamma}$. For any
${\it\gamma}$. For any ![]() $X$ that is tangent to
$X$ that is tangent to ![]() $M$, equation (3.2) can be written as
$M$, equation (3.2) can be written as
at some smooth point in local holomorphic coordinates ![]() $(x^{1},\ldots ,x^{n})$ of
$(x^{1},\ldots ,x^{n})$ of ![]() $M$, where
$M$, where ![]() $(g_{i\bar{j}})$ is the matrix of
$(g_{i\bar{j}})$ is the matrix of ![]() ${\it\omega}$.
${\it\omega}$.
Now, let ![]() $M$ be a Fano complete intersection in
$M$ be a Fano complete intersection in ![]() $\mathbb{C}P^{N}$ defined by the homogeneous polynomials
$\mathbb{C}P^{N}$ defined by the homogeneous polynomials ![]() $F_{1},\ldots ,F_{s}$ of degree
$F_{1},\ldots ,F_{s}$ of degree ![]() $d_{1},\ldots ,d_{s}$ respectively, and suppose that
$d_{1},\ldots ,d_{s}$ respectively, and suppose that ![]() $m{\it\omega}\in c_{1}(M)$ for some constant
$m{\it\omega}\in c_{1}(M)$ for some constant ![]() $m>0$. Let
$m>0$. Let ![]() $X$ be a holomorphic vector field tangent to
$X$ be a holomorphic vector field tangent to ![]() $M$, and let
$M$, and let ![]() $G$ be the Lie group generated by
$G$ be the Lie group generated by ![]() $X$. Using the adjunction formula, we know that
$X$. Using the adjunction formula, we know that ![]() $m=N+1-d_{1}-\cdots -d_{s}$ and
$m=N+1-d_{1}-\cdots -d_{s}$ and
where we remark that this isomorphism is not ![]() $G$-equivariant. However, studying the
$G$-equivariant. However, studying the ![]() $G$-action on the normal bundle of
$G$-action on the normal bundle of ![]() $M$, Hou [Reference HouHou08, Section 3] (also refer to [Reference LuLu99, Theorem 4.1]) showed the following.
$M$, Hou [Reference HouHou08, Section 3] (also refer to [Reference LuLu99, Theorem 4.1]) showed the following.
Lemma 3.1. Let ![]() $h$ be the Hermitian metric on
$h$ be the Hermitian metric on ![]() ${\mathcal{O}}(1)$ such that
${\mathcal{O}}(1)$ such that ![]() ${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$ is a Fubini–Study metric of
${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$ is a Fubini–Study metric of ![]() $\mathbb{C}P^{N}$, and let
$\mathbb{C}P^{N}$, and let ![]() $V$ be a holomorphic vector field such that
$V$ be a holomorphic vector field such that
for some constants ![]() ${\it\alpha}_{i}~(i=1,\ldots ,s)$. Then, we have
${\it\alpha}_{i}~(i=1,\ldots ,s)$. Then, we have
where ![]() $h^{m}$ is the Hermitian metric on
$h^{m}$ is the Hermitian metric on ![]() $-K_{M_{\text{reg}}}$ defined via the isomorphism (3.4).
$-K_{M_{\text{reg}}}$ defined via the isomorphism (3.4).
Let ![]() $V$ be a holomorphic vector field defined in Lemma 3.1. We set
$V$ be a holomorphic vector field defined in Lemma 3.1. We set
and ![]() $M_{i}:=N_{1}\cap \cdots \cap N_{i}$ (
$M_{i}:=N_{1}\cap \cdots \cap N_{i}$ (![]() $i=1,\ldots ,s$). Then, we have
$i=1,\ldots ,s$). Then, we have
We define the integrals ![]() $I_{k,l}=I_{k,l}(V)$ (
$I_{k,l}=I_{k,l}(V)$ (![]() $k=0,1,\ldots ,s$;
$k=0,1,\ldots ,s$; ![]() $l\geqslant 0$) by
$l\geqslant 0$) by
Lemma 3.2. For ![]() $k=1,\ldots ,s$,
$k=1,\ldots ,s$, ![]() $I_{k,0}$ satisfies
$I_{k,0}$ satisfies
Proof. We can prove (3.7) in the same way as [Reference LuLu99, Lemma 5.1]. Define a smooth function ![]() ${\it\xi}_{i}$ (
${\it\xi}_{i}$ (![]() $i=1,\ldots ,s$) on
$i=1,\ldots ,s$) on ![]() $\mathbb{C}P^{N}$ by
$\mathbb{C}P^{N}$ by
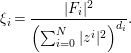 $$\begin{eqnarray}{\it\xi}_{i}=\frac{|F_{i}|^{2}}{\left(\mathop{\sum }_{i=0}^{N}|z^{i}|^{2}\right)^{d_{i}}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\xi}_{i}=\frac{|F_{i}|^{2}}{\left(\mathop{\sum }_{i=0}^{N}|z^{i}|^{2}\right)^{d_{i}}}.\end{eqnarray}$$Using the Poincaré–Lelong formula, we obtain
where ![]() $[N_{k}]$ is the divisor of the zero locus of
$[N_{k}]$ is the divisor of the zero locus of ![]() $F_{k}$. Then, we have
$F_{k}$. Then, we have
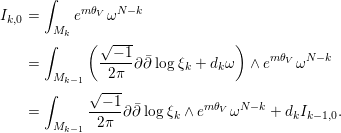 $$\begin{eqnarray}\displaystyle I_{k,0} & = & \displaystyle \int _{M_{k}}e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & = & \displaystyle \int _{M_{k-1}}\left(\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}+d_{k}{\it\omega}\right)\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & = & \displaystyle \int _{M_{k-1}}\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}+d_{k}I_{k-1,0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{k,0} & = & \displaystyle \int _{M_{k}}e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & = & \displaystyle \int _{M_{k-1}}\left(\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}+d_{k}{\it\omega}\right)\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & = & \displaystyle \int _{M_{k-1}}\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}+d_{k}I_{k-1,0}.\nonumber\end{eqnarray}$$On the other hand, using the relation
and integrating by parts, we obtain
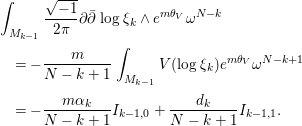 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{M_{k-1}}\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{m}{N-k+1}\int _{M_{k-1}}V(\log {\it\xi}_{k})e^{m{\it\theta}_{V}}{\it\omega}^{N-k+1}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{m{\it\alpha}_{k}}{N-k+1}I_{k-1,0}+\frac{d_{k}}{N-k+1}I_{k-1,1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{M_{k-1}}\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log {\it\xi}_{k}\wedge e^{m{\it\theta}_{V}}{\it\omega}^{N-k}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{m}{N-k+1}\int _{M_{k-1}}V(\log {\it\xi}_{k})e^{m{\it\theta}_{V}}{\it\omega}^{N-k+1}\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{m{\it\alpha}_{k}}{N-k+1}I_{k-1,0}+\frac{d_{k}}{N-k+1}I_{k-1,1}.\nonumber\end{eqnarray}$$Thus, we get the desired result. ◻
If we set ![]() $V\equiv 0$ and
$V\equiv 0$ and ![]() $l=0$, then we obtain the following.
$l=0$, then we obtain the following.
In order to get the explicit expression of ![]() $I_{k,0}$, we show the next lemma.
$I_{k,0}$, we show the next lemma.
Lemma 3.4. For ![]() $k=1,\ldots ,s$, the equation
$k=1,\ldots ,s$, the equation
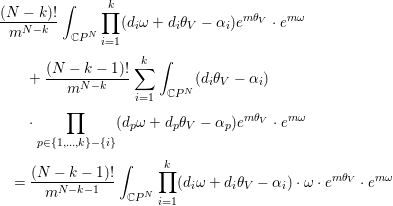 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(N-k)!}{m^{N-k}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\cdot {\it\omega}\cdot e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(N-k)!}{m^{N-k}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\cdot {\it\omega}\cdot e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\end{eqnarray}$$holds.
Proof. For ![]() $i=0,\ldots ,k$, we define integrals
$i=0,\ldots ,k$, we define integrals ![]() $J_{i}$ by
$J_{i}$ by
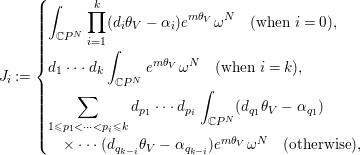 $$\begin{eqnarray}J_{i}:=\left\{\begin{array}{@{}l@{}}\displaystyle \int _{\mathbb{C}P^{N}}\displaystyle \mathop{\prod }_{i=1}^{k}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{when }i=0),\quad \\ d_{1}\cdots d_{k}\displaystyle \int _{\mathbb{C}P^{N}}e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{when }i=k),\quad \\ \displaystyle \mathop{\sum }_{1\leqslant p_{1}<\cdots <p_{i}\leqslant k}d_{p_{1}}\cdots d_{p_{i}}\displaystyle \int _{\mathbb{C}P^{N}}(d_{q_{1}}{\it\theta}_{V}-{\it\alpha}_{q_{1}})\quad \\ \quad \times \cdots (d_{q_{k-i}}{\it\theta}_{V}-{\it\alpha}_{q_{k-i}})e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{otherwise}),\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}J_{i}:=\left\{\begin{array}{@{}l@{}}\displaystyle \int _{\mathbb{C}P^{N}}\displaystyle \mathop{\prod }_{i=1}^{k}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{when }i=0),\quad \\ d_{1}\cdots d_{k}\displaystyle \int _{\mathbb{C}P^{N}}e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{when }i=k),\quad \\ \displaystyle \mathop{\sum }_{1\leqslant p_{1}<\cdots <p_{i}\leqslant k}d_{p_{1}}\cdots d_{p_{i}}\displaystyle \int _{\mathbb{C}P^{N}}(d_{q_{1}}{\it\theta}_{V}-{\it\alpha}_{q_{1}})\quad \\ \quad \times \cdots (d_{q_{k-i}}{\it\theta}_{V}-{\it\alpha}_{q_{k-i}})e^{m{\it\theta}_{V}}{\it\omega}^{N}\quad (\text{otherwise}),\quad \end{array}\right.\end{eqnarray}$$ where ![]() $q_{1}<\cdots <q_{k-i}$ and
$q_{1}<\cdots <q_{k-i}$ and ![]() $\{q_{1},\ldots ,q_{k-i}\}=\{1,\ldots ,k\}-\{p_{1},\ldots ,p_{i}\}$. Then, the direct computation shows that
$\{q_{1},\ldots ,q_{k-i}\}=\{1,\ldots ,k\}-\{p_{1},\ldots ,p_{i}\}$. Then, the direct computation shows that
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \qquad \,\cdot \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{i=0}^{k}\frac{(N-k-1)!(k-i)m^{k-i}}{(N-i)!}J_{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \qquad \,\cdot \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{i=0}^{k}\frac{(N-k-1)!(k-i)m^{k-i}}{(N-i)!}J_{i}.\nonumber\end{eqnarray}$$Hence, the left-hand side of (3.9) is
which is equal to the right-hand side of (3.9).◻
Lemma 3.5. For ![]() $k=1,\ldots ,s$,
$k=1,\ldots ,s$, ![]() $I_{k,0}$ can be written as
$I_{k,0}$ can be written as
Proof. We will prove (3.10) by induction for ![]() $k$. When
$k$. When ![]() $k=1$, equation (3.10) coincides exactly with (3.7), so the statement holds.
$k=1$, equation (3.10) coincides exactly with (3.7), so the statement holds.
Next, we assume that (3.10) holds for a fixed ![]() $k$. Then, by Lemma 3.2, we have
$k$. Then, by Lemma 3.2, we have
Since ![]() ${\it\theta}_{V+tV}={\it\theta}_{V}+t{\it\theta}_{V}$,
${\it\theta}_{V+tV}={\it\theta}_{V}+t{\it\theta}_{V}$, ![]() $(V+tV)F_{i}=({\it\alpha}_{i}+t{\it\alpha}_{i})F_{i}$ and
$(V+tV)F_{i}=({\it\alpha}_{i}+t{\it\alpha}_{i})F_{i}$ and
using the induction hypothesis, we have
and
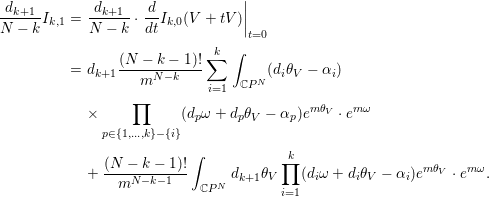 $$\begin{eqnarray}\displaystyle \frac{d_{k+1}}{N-k}I_{k,1} & = & \displaystyle \frac{d_{k+1}}{N-k}\cdot \left.\frac{d}{dt}I_{k,0}(V+tV)\right|_{t=0}\nonumber\\ \displaystyle & = & \displaystyle d_{k+1}\frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \times \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}d_{k+1}{\it\theta}_{V}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d_{k+1}}{N-k}I_{k,1} & = & \displaystyle \frac{d_{k+1}}{N-k}\cdot \left.\frac{d}{dt}I_{k,0}(V+tV)\right|_{t=0}\nonumber\\ \displaystyle & = & \displaystyle d_{k+1}\frac{(N-k-1)!}{m^{N-k}}\mathop{\sum }_{i=1}^{k}\int _{\mathbb{C}P^{N}}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \times \mathop{\prod }_{p\in \{1,\ldots ,k\}-\{i\}}(d_{p}{\it\omega}+d_{p}{\it\theta}_{V}-{\it\alpha}_{p})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}d_{k+1}{\it\theta}_{V}\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}.\nonumber\end{eqnarray}$$Hence, combining with Lemma 3.4, we obtain
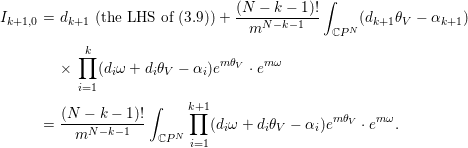 $$\begin{eqnarray}\displaystyle I_{k+1,0} & = & \displaystyle d_{k+1}\text{ (the LHS of (3.9))}+\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}(d_{k+1}{\it\theta}_{V}-{\it\alpha}_{k+1})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k+1}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{k+1,0} & = & \displaystyle d_{k+1}\text{ (the LHS of (3.9))}+\frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}(d_{k+1}{\it\theta}_{V}-{\it\alpha}_{k+1})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{i=1}^{k}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}\nonumber\\ \displaystyle & = & \displaystyle \frac{(N-k-1)!}{m^{N-k-1}}\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{k+1}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}.\nonumber\end{eqnarray}$$ Hence, the statement holds for ![]() $k+1$.◻
$k+1$.◻
Proof of Theorem 1.1.
By Lemma 3.1, ![]() ${\mathcal{F}}$ can be written as
${\mathcal{F}}$ can be written as
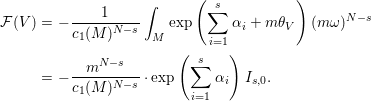 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{1}{c_{1}(M)^{N-s}}\int _{M}\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}+m{\it\theta}_{V}\right)(m{\it\omega})^{N-s}\nonumber\\ \displaystyle & = & \displaystyle -\frac{m^{N-s}}{c_{1}(M)^{N-s}}\cdot \exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)I_{s,0}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{1}{c_{1}(M)^{N-s}}\int _{M}\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}+m{\it\theta}_{V}\right)(m{\it\omega})^{N-s}\nonumber\\ \displaystyle & = & \displaystyle -\frac{m^{N-s}}{c_{1}(M)^{N-s}}\cdot \exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)I_{s,0}.\nonumber\end{eqnarray}$$ Thus, combining with Corollary 3.3 and Lemma 3.5, we get the desired formula for ![]() ${\mathcal{F}}$.◻
${\mathcal{F}}$.◻
4 Another proof of Theorem 1.1
In this section, we give another proof of Theorem 1.1 using the algebraic formula for ![]() ${\mathcal{F}}$ (cf. Proposition 2.8).
${\mathcal{F}}$ (cf. Proposition 2.8).
Lemma 4.1. [Reference Arezzo and VedovaAV11, Lemma 5.1]
Let ![]() $B$ be a holomorphic vector bundle of rank
$B$ be a holomorphic vector bundle of rank ![]() $b$ on a manifold
$b$ on a manifold ![]() $M$, then
$M$, then
Proof. Let ![]() $r_{1},\ldots ,r_{b}$ be the Chern roots of
$r_{1},\ldots ,r_{b}$ be the Chern roots of ![]() $B$. Since
$B$. Since ![]() $\text{ch}(\wedge ^{i}B^{\ast })=\sum _{1\leqslant p_{1}<\cdots <p_{i}\leqslant b}e^{-(r_{p_{1}}+\cdots +r_{p_{i}})}$, we obtain
$\text{ch}(\wedge ^{i}B^{\ast })=\sum _{1\leqslant p_{1}<\cdots <p_{i}\leqslant b}e^{-(r_{p_{1}}+\cdots +r_{p_{i}})}$, we obtain
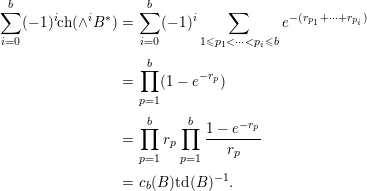 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{b}(-1)^{i}\text{ch}(\wedge ^{i}B^{\ast }) & = & \displaystyle \mathop{\sum }_{i=0}^{b}(-1)^{i}\mathop{\sum }_{1\leqslant p_{1}<\cdots <p_{i}\leqslant b}e^{-(r_{p_{1}}+\cdots +r_{p_{i}})}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p=1}^{b}(1-e^{-r_{p}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p=1}^{b}r_{p}\mathop{\prod }_{p=1}^{b}\frac{1-e^{-r_{p}}}{r_{p}}\nonumber\\ \displaystyle & = & \displaystyle c_{b}(B)\text{td}(B)^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=0}^{b}(-1)^{i}\text{ch}(\wedge ^{i}B^{\ast }) & = & \displaystyle \mathop{\sum }_{i=0}^{b}(-1)^{i}\mathop{\sum }_{1\leqslant p_{1}<\cdots <p_{i}\leqslant b}e^{-(r_{p_{1}}+\cdots +r_{p_{i}})}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p=1}^{b}(1-e^{-r_{p}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p=1}^{b}r_{p}\mathop{\prod }_{p=1}^{b}\frac{1-e^{-r_{p}}}{r_{p}}\nonumber\\ \displaystyle & = & \displaystyle c_{b}(B)\text{td}(B)^{-1}.\nonumber\end{eqnarray}$$ Now, let ![]() $M$ be an
$M$ be an ![]() $(N-s)$-dimensional Fano complete intersection in
$(N-s)$-dimensional Fano complete intersection in ![]() $\mathbb{C}P^{N}$, that is,
$\mathbb{C}P^{N}$, that is, ![]() $M$ is a Fano variety in
$M$ is a Fano variety in ![]() $\mathbb{C}P^{N}$ defined by homogeneous polynomials
$\mathbb{C}P^{N}$ defined by homogeneous polynomials ![]() $F_{1},\ldots ,F_{s}$, and
$F_{1},\ldots ,F_{s}$, and ![]() $V$ is a holomorphic vector field on
$V$ is a holomorphic vector field on ![]() $\mathbb{C}P^{N}$ tangent to
$\mathbb{C}P^{N}$ tangent to ![]() $M$. We adopt the notation of Section 3. We further assume that
$M$. We adopt the notation of Section 3. We further assume that ![]() $V\in \mathfrak{s}l(N+1,\mathbb{C})$ is a Hermitian matrix, so that
$V\in \mathfrak{s}l(N+1,\mathbb{C})$ is a Hermitian matrix, so that ![]() $\text{Im}(V)$ is Killing with respect to the Fubini–Study metric
$\text{Im}(V)$ is Killing with respect to the Fubini–Study metric ![]() ${\it\omega}$.
${\it\omega}$.
Lemma 4.2. [Reference Arezzo and VedovaAV11, Lemma 5.2]
We have the following asymptotic expansion of ![]() $N_{k}$ as
$N_{k}$ as ![]() $k\rightarrow \infty$:
$k\rightarrow \infty$:
Lemma 4.3. We have the following asymptotic expansion of ![]() ${\mathcal{F}}_{k}(V)$ as
${\mathcal{F}}_{k}(V)$ as ![]() $k\rightarrow \infty$:
$k\rightarrow \infty$:
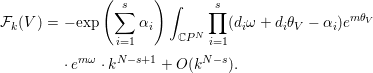 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -\text{exp}\left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,e^{m{\it\omega}}\cdot k^{N-s+1}+O(k^{N-s}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -\text{exp}\left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,e^{m{\it\omega}}\cdot k^{N-s+1}+O(k^{N-s}).\end{eqnarray}$$Proof. This proof is essentially based on the argument in [Reference Arezzo and VedovaAV11, Lemma 5.3]. The only difference between Lemma 4.3 and [Reference Arezzo and VedovaAV11, Lemma 5.3] is the linearization of ![]() $-K_{M}$, to which we have only to pay attention. In order to avoid confusion, let
$-K_{M}$, to which we have only to pay attention. In order to avoid confusion, let ![]() $L(\simeq O(m))$ be a linearized line bundle on
$L(\simeq O(m))$ be a linearized line bundle on ![]() $\mathbb{C}P^{N}$ such that
$\mathbb{C}P^{N}$ such that ![]() $L|_{M}$ is isomorphic to
$L|_{M}$ is isomorphic to ![]() $-K_{M}$ as a linearized line bundle whose linearization is determined by the canonical lift of
$-K_{M}$ as a linearized line bundle whose linearization is determined by the canonical lift of ![]() $V/k$ to
$V/k$ to ![]() $-K_{M}$.
$-K_{M}$.
Let ![]() $\mathbb{C}_{-{\it\alpha}_{i}/k}$ be a trivial bundle on
$\mathbb{C}_{-{\it\alpha}_{i}/k}$ be a trivial bundle on ![]() $\mathbb{C}P^{N}$ with linearization
$\mathbb{C}P^{N}$ with linearization ![]() $t\cdot u=t^{-{\it\alpha}_{i}/k}\cdot u$. Set
$t\cdot u=t^{-{\it\alpha}_{i}/k}\cdot u$. Set ![]() $L_{i}:={\mathcal{O}}(d_{i})\otimes \mathbb{C}_{-{\it\alpha}_{i}/k}$ and
$L_{i}:={\mathcal{O}}(d_{i})\otimes \mathbb{C}_{-{\it\alpha}_{i}/k}$ and ![]() $B:=L_{1}\oplus \cdots \oplus L_{s}$. Then,
$B:=L_{1}\oplus \cdots \oplus L_{s}$. Then, ![]() $\text{rank}\,B=s$, and the section
$\text{rank}\,B=s$, and the section ![]() $F:=(F_{1},\ldots ,F_{s})\in H^{0}(\mathbb{C}P^{N},B)$ is invariant. Since
$F:=(F_{1},\ldots ,F_{s})\in H^{0}(\mathbb{C}P^{N},B)$ is invariant. Since ![]() $M$ is complete, the Koszul complex
$M$ is complete, the Koszul complex
is exact and equivariant, where ![]() ${\mathcal{O}}_{M}$ denotes the structure sheaf of
${\mathcal{O}}_{M}$ denotes the structure sheaf of ![]() $M$. Tensoring by
$M$. Tensoring by ![]() $L^{k}$ preserves the exactness and equivariance, so we obtain
$L^{k}$ preserves the exactness and equivariance, so we obtain
where ![]() ${\it\chi}^{\mathfrak{g}}$ denotes the Lefschetz number. By the equivariant Riemann–Roch formula and Lemma 4.1, we get
${\it\chi}^{\mathfrak{g}}$ denotes the Lefschetz number. By the equivariant Riemann–Roch formula and Lemma 4.1, we get
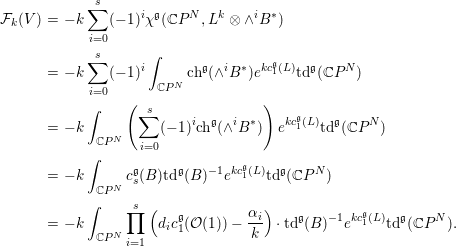 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\mathop{\sum }_{i=0}^{s}(-1)^{i}{\it\chi}^{\mathfrak{g}}(\mathbb{C}P^{N},L^{k}\otimes \wedge ^{i}B^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -k\mathop{\sum }_{i=0}^{s}(-1)^{i}\int _{\mathbb{C}P^{N}}\text{ch}^{\mathfrak{g}}(\wedge ^{i}B^{\ast })e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}\left(\mathop{\sum }_{i=0}^{s}(-1)^{i}\text{ch}^{\mathfrak{g}}(\wedge ^{i}B^{\ast })\right)e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}c_{s}^{\mathfrak{g}}(B)\text{td}^{\mathfrak{g}}(B)^{-1}e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}\left(d_{i}c_{1}^{\mathfrak{g}}({\mathcal{O}}(1))-\frac{{\it\alpha}_{i}}{k}\right)\cdot \text{td}^{\mathfrak{g}}(B)^{-1}e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\mathop{\sum }_{i=0}^{s}(-1)^{i}{\it\chi}^{\mathfrak{g}}(\mathbb{C}P^{N},L^{k}\otimes \wedge ^{i}B^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -k\mathop{\sum }_{i=0}^{s}(-1)^{i}\int _{\mathbb{C}P^{N}}\text{ch}^{\mathfrak{g}}(\wedge ^{i}B^{\ast })e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}\left(\mathop{\sum }_{i=0}^{s}(-1)^{i}\text{ch}^{\mathfrak{g}}(\wedge ^{i}B^{\ast })\right)e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}c_{s}^{\mathfrak{g}}(B)\text{td}^{\mathfrak{g}}(B)^{-1}e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -k\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}\left(d_{i}c_{1}^{\mathfrak{g}}({\mathcal{O}}(1))-\frac{{\it\alpha}_{i}}{k}\right)\cdot \text{td}^{\mathfrak{g}}(B)^{-1}e^{kc_{1}^{\mathfrak{g}}(L)}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N}).\nonumber\end{eqnarray}$$ Let ![]() $h$ be a Hermitian metric on
$h$ be a Hermitian metric on ![]() ${\mathcal{O}}(1)$ such that
${\mathcal{O}}(1)$ such that ![]() ${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$ is the Fubini–Study metric of the
${\it\omega}=-\frac{\sqrt{-1}}{2{\it\pi}}\partial \bar{\partial }\log h$ is the Fubini–Study metric of the ![]() $\mathbb{C}P^{N}$. Then, by Lemma 3.1, the equivariant 1st Chern forms for
$\mathbb{C}P^{N}$. Then, by Lemma 3.1, the equivariant 1st Chern forms for ![]() $(h,V/k)$ and
$(h,V/k)$ and ![]() $(h^{m},V/k)$ are written as
$(h^{m},V/k)$ are written as
respectively. Both ![]() $\text{td}^{\mathfrak{g}}(B)^{-1}$ and
$\text{td}^{\mathfrak{g}}(B)^{-1}$ and ![]() $\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})$ can be written as the form
$\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})$ can be written as the form
where ![]() $A$ (respectively
$A$ (respectively ![]() $B_{i}$) denotes
$B_{i}$) denotes ![]() $2l$-forms (
$2l$-forms (![]() $l\geqslant 1$ (respectively
$l\geqslant 1$ (respectively ![]() $l\geqslant 0$)) not depending on
$l\geqslant 0$)) not depending on ![]() $k$. Hence, we have
$k$. Hence, we have
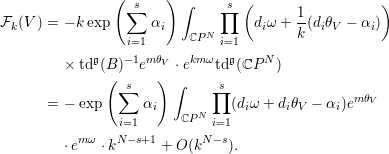 $$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}\left(d_{i}{\it\omega}+\frac{1}{k}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{td}^{\mathfrak{g}}(B)^{-1}e^{m{\it\theta}_{V}}\cdot e^{km{\it\omega}}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,e^{m{\it\omega}}\cdot k^{N-s+1}+O(k^{N-s}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}_{k}(V) & = & \displaystyle -k\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}\left(d_{i}{\it\omega}+\frac{1}{k}(d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\text{td}^{\mathfrak{g}}(B)^{-1}e^{m{\it\theta}_{V}}\cdot e^{km{\it\omega}}\text{td}^{\mathfrak{g}}(\mathbb{C}P^{N})\nonumber\\ \displaystyle & = & \displaystyle -\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})e^{m{\it\theta}_{V}}\nonumber\\ \displaystyle & & \displaystyle \cdot \,e^{m{\it\omega}}\cdot k^{N-s+1}+O(k^{N-s}).\nonumber\end{eqnarray}$$Proof of Theorem 1.1.
By Lemmas 4.2 and 4.3, we have an asymptotic expansion as ![]() $k\rightarrow \infty$:
$k\rightarrow \infty$:
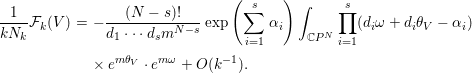 $$\begin{eqnarray}\displaystyle \frac{1}{kN_{k}}{\mathcal{F}}_{k}(V) & = & \displaystyle -\frac{(N-s)!}{d_{1}\cdots d_{s}m^{N-s}}\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \times \,e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}+O(k^{-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{kN_{k}}{\mathcal{F}}_{k}(V) & = & \displaystyle -\frac{(N-s)!}{d_{1}\cdots d_{s}m^{N-s}}\exp \left(\mathop{\sum }_{i=1}^{s}{\it\alpha}_{i}\right)\int _{\mathbb{C}P^{N}}\mathop{\prod }_{i=1}^{s}(d_{i}{\it\omega}+d_{i}{\it\theta}_{V}-{\it\alpha}_{i})\nonumber\\ \displaystyle & & \displaystyle \times \,e^{m{\it\theta}_{V}}\cdot e^{m{\it\omega}}+O(k^{-1}).\nonumber\end{eqnarray}$$ On the other hand, by Proposition 2.8(4), ![]() $\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V)$ converges to
$\frac{1}{kN_{k}}{\mathcal{F}}_{k}(V)$ converges to ![]() ${\mathcal{F}}(V)$ as
${\mathcal{F}}(V)$ as ![]() $k\rightarrow \infty$. Hence, we have the desired formula.◻
$k\rightarrow \infty$. Hence, we have the desired formula.◻
5 Examples
In this section, we compute ![]() ${\mathcal{F}}$ for several examples in [Reference LuLu99, Section 6]. Let
${\mathcal{F}}$ for several examples in [Reference LuLu99, Section 6]. Let ![]() $M$ be a Fano complete intersection in
$M$ be a Fano complete intersection in ![]() $\mathbb{C}P^{N}$. We adopt the notation of Section 3. First, we mention some results obtained as a corollary of the localization formula in holomorphic equivariant cohomology theory (cf. [Reference LiuLiu95, Theorem 1.6]).
$\mathbb{C}P^{N}$. We adopt the notation of Section 3. First, we mention some results obtained as a corollary of the localization formula in holomorphic equivariant cohomology theory (cf. [Reference LiuLiu95, Theorem 1.6]).
Lemma 5.1. If ![]() $V=\text{diag}({\it\lambda}_{0},\ldots ,{\it\lambda}_{N})$ is a diagonal matrix with different eigenvalues
$V=\text{diag}({\it\lambda}_{0},\ldots ,{\it\lambda}_{N})$ is a diagonal matrix with different eigenvalues ![]() ${\it\lambda}_{0},\ldots ,{\it\lambda}_{N}$, then we have
${\it\lambda}_{0},\ldots ,{\it\lambda}_{N}$, then we have
Since the ![]() $I_{0,l}$ are given by the derivatives of
$I_{0,l}$ are given by the derivatives of ![]() $I_{0,0}$, we can compute
$I_{0,0}$, we can compute ![]() $I_{0,l}$ for any integer
$I_{0,l}$ for any integer ![]() $l$. On the other hand, by Theorem 1.1,
$l$. On the other hand, by Theorem 1.1, ![]() ${\mathcal{F}}(V)$ can be written as a linear combination of
${\mathcal{F}}(V)$ can be written as a linear combination of ![]() $I_{0,l}$ (
$I_{0,l}$ (![]() $0\leqslant l\leqslant s$). Hence, we can express
$0\leqslant l\leqslant s$). Hence, we can express ![]() ${\mathcal{F}}(V)$ in terms of the eigenvalues of
${\mathcal{F}}(V)$ in terms of the eigenvalues of ![]() $V$.
$V$.
However, we can calculate ![]() ${\mathcal{F}}(V)$ without using Theorem 1.1 in a special case. We assume that
${\mathcal{F}}(V)$ without using Theorem 1.1 in a special case. We assume that ![]() $M$ has at worst orbifold singularities, and
$M$ has at worst orbifold singularities, and ![]() $V$ satisfies the following conditions.
$V$ satisfies the following conditions.
(1)
 $V$ has isolated zero points
$V$ has isolated zero points  $\{p_{i}\}$.
$\{p_{i}\}$.(2)
 $V$ is nondegenerate at each zero point
$V$ is nondegenerate at each zero point  $p_{i}$, that is, for each local uniformization
$p_{i}$, that is, for each local uniformization  ${\it\pi}:U\rightarrow U/{\rm\Gamma}_{i}\subset M$ with
${\it\pi}:U\rightarrow U/{\rm\Gamma}_{i}\subset M$ with  ${\it\pi}(U)\cap p_{i}\neq \emptyset$,
${\it\pi}(U)\cap p_{i}\neq \emptyset$,  ${\it\pi}^{\ast }V$ vanishes along
${\it\pi}^{\ast }V$ vanishes along  ${\it\pi}^{-1}(p_{i})$ and the matrix
${\it\pi}^{-1}(p_{i})$ and the matrix  $B_{i}=(-\frac{\partial v_{j}^{i}}{\partial z^{k}})_{1\leqslant j,k\leqslant N-s}$ is nondegenerate near
$B_{i}=(-\frac{\partial v_{j}^{i}}{\partial z^{k}})_{1\leqslant j,k\leqslant N-s}$ is nondegenerate near  ${\it\pi}^{-1}(p_{i})$, where
${\it\pi}^{-1}(p_{i})$, where  $(z^{1},\ldots ,z^{N-s})$ are local holomorphic coordinates around
$(z^{1},\ldots ,z^{N-s})$ are local holomorphic coordinates around  ${\it\pi}^{-1}(p_{i})$ and
${\it\pi}^{-1}(p_{i})$ and  $V=\sum _{j=1}^{N-s}v_{j}^{i}\frac{\partial }{\partial z^{j}}$.
$V=\sum _{j=1}^{N-s}v_{j}^{i}\frac{\partial }{\partial z^{j}}$.
In the same way as [Reference Ding and TianDT92, Proposition 1.2], we have the following lemma.
Lemma 5.2. Let ![]() $M$ and
$M$ and ![]() $V$ be as above. Then, we have
$V$ be as above. Then, we have
where ![]() $|{\rm\Gamma}_{i}|$ is the order of the local uniformization group
$|{\rm\Gamma}_{i}|$ is the order of the local uniformization group ![]() ${\rm\Gamma}_{i}$ at a point
${\rm\Gamma}_{i}$ at a point ![]() $p_{i}$.
$p_{i}$.
Remark 5.3. One can extend Lemmas 5.1 and 5.2 to the case when the zero set of ![]() $V$ is the sum of nondegenerate submanifolds, where the word nondegenerate means that the induced actions of
$V$ is the sum of nondegenerate submanifolds, where the word nondegenerate means that the induced actions of ![]() $V$ to the normal bundle of submanifolds are nondegenerate. However, since
$V$ to the normal bundle of submanifolds are nondegenerate. However, since ![]() $I_{0,0}(V)$ and
$I_{0,0}(V)$ and ![]() ${\mathcal{F}}(V)$ are clearly continuous with respect to
${\mathcal{F}}(V)$ are clearly continuous with respect to ![]() $V$, we may think that equations (5.1) and (5.2) hold in the sense of the limit
$V$, we may think that equations (5.1) and (5.2) hold in the sense of the limit ![]() $V_{{\it\epsilon}}\rightarrow V$ of any expression. For instance, we have the following lemma.
$V_{{\it\epsilon}}\rightarrow V$ of any expression. For instance, we have the following lemma.
Lemma 5.4. Let ![]() $m=1$, and let
$m=1$, and let ![]() $V=\text{diag}({\it\lambda}_{0},{\it\lambda}_{1},{\it\lambda}_{2},{\it\lambda}_{2})\in \mathfrak{s}l(4,\mathbb{C})$ be a holomorphic vector field on
$V=\text{diag}({\it\lambda}_{0},{\it\lambda}_{1},{\it\lambda}_{2},{\it\lambda}_{2})\in \mathfrak{s}l(4,\mathbb{C})$ be a holomorphic vector field on ![]() $\mathbb{C}P^{3}$, where
$\mathbb{C}P^{3}$, where ![]() ${\it\lambda}_{0}$,
${\it\lambda}_{0}$, ![]() ${\it\lambda}_{1}$ and
${\it\lambda}_{1}$ and ![]() ${\it\lambda}_{2}$ are different numbers. Then, we have
${\it\lambda}_{2}$ are different numbers. Then, we have
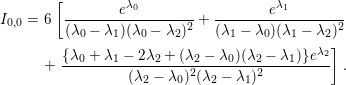 $$\begin{eqnarray}\displaystyle I_{0,0} & = & \displaystyle 6\left[\frac{e^{{\it\lambda}_{0}}}{({\it\lambda}_{0}-{\it\lambda}_{1})({\it\lambda}_{0}-{\it\lambda}_{2})^{2}}+\frac{e^{{\it\lambda}_{1}}}{({\it\lambda}_{1}-{\it\lambda}_{0})({\it\lambda}_{1}-{\it\lambda}_{2})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\{{\it\lambda}_{0}+{\it\lambda}_{1}-2{\it\lambda}_{2}+({\it\lambda}_{2}-{\it\lambda}_{0})({\it\lambda}_{2}-{\it\lambda}_{1})\}e^{{\it\lambda}_{2}}}{({\it\lambda}_{2}-{\it\lambda}_{0})^{2}({\it\lambda}_{2}-{\it\lambda}_{1})^{2}}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{0,0} & = & \displaystyle 6\left[\frac{e^{{\it\lambda}_{0}}}{({\it\lambda}_{0}-{\it\lambda}_{1})({\it\lambda}_{0}-{\it\lambda}_{2})^{2}}+\frac{e^{{\it\lambda}_{1}}}{({\it\lambda}_{1}-{\it\lambda}_{0})({\it\lambda}_{1}-{\it\lambda}_{2})^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{\{{\it\lambda}_{0}+{\it\lambda}_{1}-2{\it\lambda}_{2}+({\it\lambda}_{2}-{\it\lambda}_{0})({\it\lambda}_{2}-{\it\lambda}_{1})\}e^{{\it\lambda}_{2}}}{({\it\lambda}_{2}-{\it\lambda}_{0})^{2}({\it\lambda}_{2}-{\it\lambda}_{1})^{2}}\right].\end{eqnarray}$$Proof. Let ![]() ${\it\epsilon}\neq 0$ be a small number. If we set
${\it\epsilon}\neq 0$ be a small number. If we set ![]() $V_{{\it\epsilon}}:=\text{diag}({\it\lambda}_{0},{\it\lambda}_{1},{\it\lambda}_{2}+{\it\epsilon},{\it\lambda}_{2}-{\it\epsilon})$, then
$V_{{\it\epsilon}}:=\text{diag}({\it\lambda}_{0},{\it\lambda}_{1},{\it\lambda}_{2}+{\it\epsilon},{\it\lambda}_{2}-{\it\epsilon})$, then ![]() $V_{{\it\epsilon}}$ has different eigenvalues. Hence, we can compute
$V_{{\it\epsilon}}$ has different eigenvalues. Hence, we can compute ![]() $I_{0,0}(V)=\lim _{{\it\epsilon}\rightarrow 0}I_{0,0}(V_{{\it\epsilon}})$ directly using (5.1).◻
$I_{0,0}(V)=\lim _{{\it\epsilon}\rightarrow 0}I_{0,0}(V_{{\it\epsilon}})$ directly using (5.1).◻
Example 5.5. Let ![]() $M\subset \mathbb{C}P^{3}$ be the zero set of a cubic polynomial
$M\subset \mathbb{C}P^{3}$ be the zero set of a cubic polynomial ![]() $F:=z_{0}z_{1}^{2}+z_{2}z_{3}(z_{2}-z_{3})$, where
$F:=z_{0}z_{1}^{2}+z_{2}z_{3}(z_{2}-z_{3})$, where ![]() $(z_{0},z_{1},z_{2},z_{3})$ are homogeneous coordinates of
$(z_{0},z_{1},z_{2},z_{3})$ are homogeneous coordinates of ![]() $\mathbb{C}P^{3}$, and let
$\mathbb{C}P^{3}$, and let ![]() $V=\text{diag}(-7t,5t,t,t)$ (
$V=\text{diag}(-7t,5t,t,t)$ (![]() $t\neq 0$) be a holomorphic vector field tangent to
$t\neq 0$) be a holomorphic vector field tangent to ![]() $M$. We compute
$M$. We compute ![]() ${\mathcal{F}}$ by two methods.
${\mathcal{F}}$ by two methods.
(1) The variety ![]() $M$ has a unique quotient singularity at
$M$ has a unique quotient singularity at ![]() $p_{0}:=[1,0,0,0]$. If we restrict
$p_{0}:=[1,0,0,0]$. If we restrict ![]() $V$ to
$V$ to ![]() $M$,
$M$, ![]() $V$ has five zeros,
$V$ has five zeros, ![]() $p_{0}=[1,0,0,0]$,
$p_{0}=[1,0,0,0]$, ![]() $[0,1,0,0]$,
$[0,1,0,0]$, ![]() $[0,0,1,0]$,
$[0,0,1,0]$, ![]() $[0,0,0,1]$ and
$[0,0,0,1]$ and ![]() $[0,0,1,1]$. Let
$[0,0,1,1]$. Let ![]() ${\it\zeta}_{i}:=\frac{z_{i}}{z_{0}}$ (
${\it\zeta}_{i}:=\frac{z_{i}}{z_{0}}$ (![]() $i=1,2,3$) be Euclidean coordinates defined near
$i=1,2,3$) be Euclidean coordinates defined near ![]() $p_{0}$. Then, we can rewrite
$p_{0}$. Then, we can rewrite ![]() $F$ near
$F$ near ![]() $p_{0}$ in the standard form
$p_{0}$ in the standard form
According to [Reference LuLu99, Example 1], we see that there is a uniformization ![]() ${\it\phi}:\mathbb{C}^{2}\rightarrow \mathbb{C}^{2}/{\rm\Gamma}\subset M$ defined by
${\it\phi}:\mathbb{C}^{2}\rightarrow \mathbb{C}^{2}/{\rm\Gamma}\subset M$ defined by
 $$\begin{eqnarray}{\it\phi}:\left\{\begin{array}{@{}l@{}}{\it\zeta}_{1}=uv(u^{4}-v^{4}),\quad \\ {\it\zeta}_{2}=u^{4}+v^{4},\quad \\ {\it\zeta}_{3}=u^{2}v^{2},\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\phi}:\left\{\begin{array}{@{}l@{}}{\it\zeta}_{1}=uv(u^{4}-v^{4}),\quad \\ {\it\zeta}_{2}=u^{4}+v^{4},\quad \\ {\it\zeta}_{3}=u^{2}v^{2},\quad \end{array}\right.\end{eqnarray}$$ where ![]() ${\rm\Gamma}$ is the dihedral subgroup in
${\rm\Gamma}$ is the dihedral subgroup in ![]() $SU(2)$ of type
$SU(2)$ of type ![]() $D_{4}$. Thus, we have
$D_{4}$. Thus, we have ![]() ${\it\phi}^{\ast }(V)=2tu\frac{\partial }{\partial u}+2tv\frac{\partial }{\partial v}$. Since the order of the group
${\it\phi}^{\ast }(V)=2tu\frac{\partial }{\partial u}+2tv\frac{\partial }{\partial v}$. Since the order of the group ![]() $D_{4}$ is
$D_{4}$ is ![]() $8$, applying Lemma 5.2, we obtain
$8$, applying Lemma 5.2, we obtain
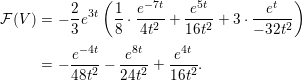 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{2}{3}e^{3t}\left(\frac{1}{8}\cdot \frac{e^{-7t}}{4t^{2}}+\frac{e^{5t}}{16t^{2}}+3\cdot \frac{e^{t}}{-32t^{2}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{e^{-4t}}{48t^{2}}-\frac{e^{8t}}{24t^{2}}+\frac{e^{4t}}{16t^{2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{2}{3}e^{3t}\left(\frac{1}{8}\cdot \frac{e^{-7t}}{4t^{2}}+\frac{e^{5t}}{16t^{2}}+3\cdot \frac{e^{t}}{-32t^{2}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{e^{-4t}}{48t^{2}}-\frac{e^{8t}}{24t^{2}}+\frac{e^{4t}}{16t^{2}}.\nonumber\end{eqnarray}$$(2) By Theorem 1.1, we obtain
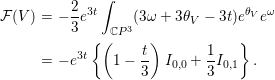 $$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{2}{3}e^{3t}\int _{\mathbb{C}P^{3}}(3{\it\omega}+3{\it\theta}_{V}-3t)e^{{\it\theta}_{V}}e^{{\it\omega}}\nonumber\\ \displaystyle & = & \displaystyle -e^{3t}\left\{\left(1-\frac{t}{3}\right)I_{0,0}+\frac{1}{3}I_{0,1}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{F}}(V) & = & \displaystyle -\frac{2}{3}e^{3t}\int _{\mathbb{C}P^{3}}(3{\it\omega}+3{\it\theta}_{V}-3t)e^{{\it\theta}_{V}}e^{{\it\omega}}\nonumber\\ \displaystyle & = & \displaystyle -e^{3t}\left\{\left(1-\frac{t}{3}\right)I_{0,0}+\frac{1}{3}I_{0,1}\right\}.\nonumber\end{eqnarray}$$By Lemma 5.4, we have
and
Hence, we have
Example 5.6. Let ![]() $M\subset \mathbb{C}P^{4}$ be the zero locus defined by
$M\subset \mathbb{C}P^{4}$ be the zero locus defined by
and let ![]() $V=\text{diag}(-7t,3t,-2t,5t,t)$ (
$V=\text{diag}(-7t,3t,-2t,5t,t)$ (![]() $t\neq 0$) be a holomorphic vector field tangent to
$t\neq 0$) be a holomorphic vector field tangent to ![]() $M$. In the same way as (2) in Example 5.5, we get
$M$. In the same way as (2) in Example 5.5, we get
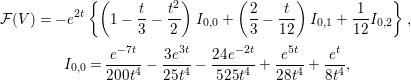 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}(V)=-e^{2t}\left\{\left(1-\frac{t}{3}-\frac{t^{2}}{2}\right)I_{0,0}+\left(\frac{2}{3}-\frac{t}{12}\right)I_{0,1}+\frac{1}{12}I_{0,2}\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{0,0}=\frac{e^{-7t}}{200t^{4}}-\frac{3e^{3t}}{25t^{4}}-\frac{24e^{-2t}}{525t^{4}}+\frac{e^{5t}}{28t^{4}}+\frac{e^{t}}{8t^{4}}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}(V)=-e^{2t}\left\{\left(1-\frac{t}{3}-\frac{t^{2}}{2}\right)I_{0,0}+\left(\frac{2}{3}-\frac{t}{12}\right)I_{0,1}+\frac{1}{12}I_{0,2}\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle I_{0,0}=\frac{e^{-7t}}{200t^{4}}-\frac{3e^{3t}}{25t^{4}}-\frac{24e^{-2t}}{525t^{4}}+\frac{e^{5t}}{28t^{4}}+\frac{e^{t}}{8t^{4}}, & \displaystyle \nonumber\end{eqnarray}$$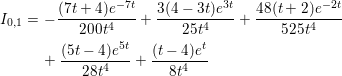 $$\begin{eqnarray}\displaystyle I_{0,1} & = & \displaystyle -\frac{(7t+4)e^{-7t}}{200t^{4}}+\frac{3(4-3t)e^{3t}}{25t^{4}}+\frac{48(t+2)e^{-2t}}{525t^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(5t-4)e^{5t}}{28t^{4}}+\frac{(t-4)e^{t}}{8t^{4}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{0,1} & = & \displaystyle -\frac{(7t+4)e^{-7t}}{200t^{4}}+\frac{3(4-3t)e^{3t}}{25t^{4}}+\frac{48(t+2)e^{-2t}}{525t^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(5t-4)e^{5t}}{28t^{4}}+\frac{(t-4)e^{t}}{8t^{4}}\nonumber\end{eqnarray}$$and
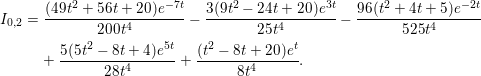 $$\begin{eqnarray}\displaystyle I_{0,2} & = & \displaystyle \frac{(49t^{2}+56t+20)e^{-7t}}{200t^{4}}-\frac{3(9t^{2}-24t+20)e^{3t}}{25t^{4}}-\frac{96(t^{2}+4t+5)e^{-2t}}{525t^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{5(5t^{2}-8t+4)e^{5t}}{28t^{4}}+\frac{(t^{2}-8t+20)e^{t}}{8t^{4}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{0,2} & = & \displaystyle \frac{(49t^{2}+56t+20)e^{-7t}}{200t^{4}}-\frac{3(9t^{2}-24t+20)e^{3t}}{25t^{4}}-\frac{96(t^{2}+4t+5)e^{-2t}}{525t^{4}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{5(5t^{2}-8t+4)e^{5t}}{28t^{4}}+\frac{(t^{2}-8t+20)e^{t}}{8t^{4}}.\nonumber\end{eqnarray}$$Hence, we have
Here, we remark that ![]() $V$ has only three zero points,
$V$ has only three zero points, ![]() $p_{1}=[1,0,0,0,0]$,
$p_{1}=[1,0,0,0,0]$, ![]() $p_{2}=[0,0,0,1,0]$ and
$p_{2}=[0,0,0,1,0]$ and ![]() $p_{3}=[0,0,0,0,1]$, in
$p_{3}=[0,0,0,0,1]$, in ![]() $M$. Actually, the exponents appearing in the above expression of
$M$. Actually, the exponents appearing in the above expression of ![]() ${\mathcal{F}}(V)$ are
${\mathcal{F}}(V)$ are ![]() $-5t={\it\theta}_{V}(p_{1})+2t$,
$-5t={\it\theta}_{V}(p_{1})+2t$, ![]() $7t={\it\theta}_{V}(p_{2})+2t$ and
$7t={\it\theta}_{V}(p_{2})+2t$ and ![]() $3t={\it\theta}_{V}(p_{3})+2t$, and hence correspond to the three zero points of
$3t={\it\theta}_{V}(p_{3})+2t$, and hence correspond to the three zero points of ![]() $V$.
$V$.
Acknowledgements
The author would like to express his gratitude to Professor Ryoichi Kobayashi for his advice on this article, and to the referee for useful suggestions that helped him to improve the original manuscript.