1. Introduction
Mountain glaciers contribute considerably to observed and predicted sea-level rise (e.g. Reference Kaser, Cogley, Dyurgerov, Meier and OhmuraKaser and others, 2006; Reference Lemke and SolomonLemke and others, 2007; Reference MeierMeier and others, 2007). In order to estimate this contribution, it is crucial to know glacier mass balances. Mass-balance measurements are restricted to few glaciers worldwide, in total around 250 (Reference Dyurgerov and MeierDyurgerov and Meier, 2005), and only about 85 data series last longer than 10 years (Reference BraithwaiteBraithwaite, 2002). Most glaciers for which mass balances are measured are chosen for accessibility or by coincidence. However, they might not be representative of the mass balances of all glaciers in a given catchment or mountain range, and simple extrapolation to other glaciers is known to be unreliable (Reference Fountain, Hoffman, Granshaw and RiedelFountain and others, 2009).
Different methods have been used to model the total glacier mass balance of mountain ranges. Reference Machguth, Paul, Kotlarski and HoelzleMachguth and others (2009) used output from regional climate models (RCMs) to run an energy-balance model for all Swiss glaciers, and Reference Schöner and BöhmSchöner and Böhm (2007) applied a statistical approach to model the mass balance of a sample of Austria’s glaciers as far back as the glacier maximum of the Little Ice Age. Reference Hock, de Woul and RadićHock and others (2009) estimate the world’s glaciers’ total contribution to sea-level rise. It has also been shown that reanalysis data can be used successfully to reconstruct the mass-balance history of individual glaciers (e.g. Reference Radić and HockRadić and Hock, 2006; Reference Rasmussen and WengerRasmussen and Wenger, 2009).
The annual surface mass balance of 761 Austrian glaciers is reconstructed for all years between 1969 and 1998, which is an important input for run-off modelling on a catchment or larger scale. A positive degree-day (PDD) model is applied, and its performance validated. Although PDD models are generally viewed as crude because they do not resolve energy-balance terms explicitly, it has been shown in the literature that their performance is comparable to energy-balance models (Reference HockHock, 2003). The scale of the study area, and the computational simplicity required to apply the model to a large number of glaciers over a 30 year timespan, was one reason for choosing a simple approach. Furthermore, the main task is to describe measured volume changes with higher temporal resolution which can be reliably achieved with such a model. However, it is shown that it is necessary to use temporally and spatially varying degree-day factors (DDFs). In order to reproduce directly measured volume changes and their variations, one needs annual resolution, i.e. mean annual DDFs for each elevation band. While the stepwise change from low DDFs of snow and firn to the high DDFs of bare ice moves up-glacier during the season, the annual mean of DDF(h) with altitude becomes a smooth profile which is approached by a linear function of elevation in this study.
The generalizability of directly measured mass balances is addressed, and the relative importance of the main meteorological factors (temperature, precipitation) that control each year’s mass balance is investigated.
2. Study Area
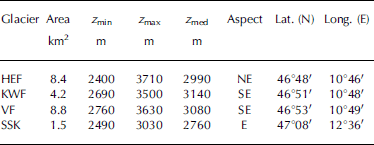
The study area is the Austrian part of the eastern Alps (46˚40ʹ–47˚350 N, 9˚50ʹ–13˚400 E) where, in 1998, 910 glaciers covered a total area of 470 km2 (Reference Lambrecht and KuhnLambrecht and Kuhn, 2007; Reference Kuhn, Lambrecht, Abermann, Patzelt and GrossKuhn and others, 2009). Figure 1 shows a map with the 1998 glacier extent and an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) digital elevation model (DEM) of elevations higher than 2000 m in greyscale. The ASTER DEM is used for illustrative purposes only; our analysis was performed with photogrammetrically derived DEMs (see section 3). Mass balances have been measured over the entire modeled time-span on four glaciers only: Hintereisferner (HEF), Kesselwandferner (KWF), Vernagtferner (VF) and Stubacher Sonnblickkees (SSK) (Reference Schöner and BöhmSchöner and Böhm, 2007). These glaciers’ mass-balance series are used to validate the model; their locations are shown in Figure 1 and basic glaciological parameters are provided in Table 1. More information on the distribution of Austria’s glaciers and its relationship to climate can be found in Reference Abermann, Lambrecht, Fischer and KuhnAbermann and others (2009).
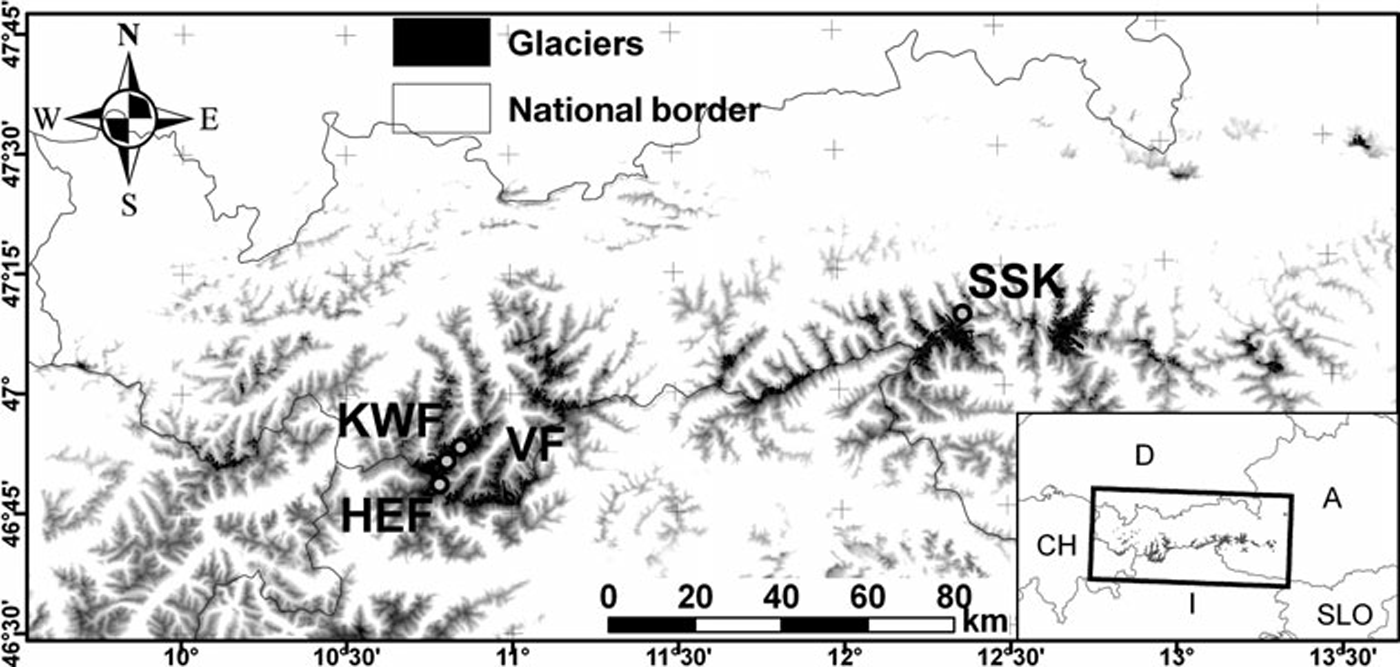
Fig. 1. Glacier cover in Austria according to the glacier inventory of 1998 (Reference Lambrecht and KuhnLambrecht and Kuhn, 2007). The glaciers HEF, KWF, VF and SSK are marked. Elevations higher than 2000 m, derived from an ASTER DEM, are displayed in greyscale in the background.
Table 1. Basic glaciological parameters for the glaciers used to validate the model: area, minimum elevation (z min), maximum elevation (z max), median elevation (z med), main aspect of the ablation area, latitude and longitude as given in Reference Lambrecht and KuhnLambrecht and Kuhn (2007) and Reference Kuhn, Lambrecht, Abermann, Patzelt and GrossKuhn and others (2009) for 1998
3. Data
3.1. Glaciological data
Two glacier inventories serve as glaciological input data for this study. Both were produced by aerial photogrammetry including glacier boundaries and DEMs (e.g. Reference GrossGross, 1987; Reference Lambrecht and KuhnLambrecht and Kuhn, 2007). Glacier area changes, which are necessary to compute annual surface mass balances, are approximated by assuming that the initial area (1969) remains constant until 1985 and then interpolating linearly to the final glacier area (1998). This pattern of area change does not account for glacier growth in the late 1970s and early 1980s but is similar to the mean glacier area changes of the study period (Reference Abermann, Lambrecht, Fischer and KuhnAbermann and others, 2009).
Volume change, ΔV, is calculated by subtracting the 1998 DEMs from the 1969 glacier extent. The total balance,
B, was calculated by
The whole volume change is assumed to have occurred as loss of ice with a density of 900 kgm–3. The resulting B has thus to be taken as the upper bound of the actual mass loss, as some unknown fraction of the total volume change was lost as snow instead of ice. This uncertainty is discussed in section 6.
Directly measured mass-balance data of four glaciers spanning the entire investigation period (Table 1) were used to validate the model. Three of the glaciers are situated very close to each other in the Ötztal valley: HEF, KWF (Reference Hoinkes and LangHoinkes and Lang, 1962; Reference Kuhn, Markl, Kaser, Nickus, Obleitner and SchneiderKuhn and others, 1985, Reference Kuhn, Dreiseitl, Hofinger, Markl, Span and Kaser1999; Reference Fischer and MarklFischer and Markl, 2008; Reference FischerFischer, 2010) and VF (Reference Reinwarth and Escher-VetterReinwarth and Escher-Vetter, 1999; Reference Escher-Vetter, Kuhn and WeberEscher-Vetter and others, 2009). SSK (Slupetz-ky, 1989, 2003; Reference Haeberli, Zemp and HoelzleWGMS, 2007) is located in the Hohe Tauern and thus in a somewhat different climate (generally more precipitation; Reference Abermann, Kuhn and FischerAbermann and others, 2011).
3.2. Meteorological data
The model uses temperature, T, equivalent-potential temperature, θ e, and geopotential, ~, and precipitation as meteorological inputs. T, θ e and Φ and precipitation are taken from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-40 reanalysis project (Reference UppalaUppala and others, 2005). T, θ e and Φ are taken from the 600, 700 and 850 hPa level; precipitation data are the 6 hour forecast from the total precipitation field at the surface. The ERA-40 reanalysis dataset is a dynamically consistent, three-dimensional, gridded dataset with a resolution of 1.25˚ that combines meteorological and satellite observations with a numerical weather-forecast model and covers the period 1957–2002.
The monthly Alps-wide precipitation dataset of the HISTALP project has a spatial resolution of 100 of arc and includes homogenized weather-station data (Reference EfthymiadisEfthymiadis and others, 2006). The dataset was generated with data from valley stations only (Auer and others, 2005) due to well-known problems of precipitation measurement at high altitudes (e.g. Reference Frei and SchärFrei and Schär, 1998). It therefore does not account for an increase in precipitation with altitude and underestimates high-altitude precipitation.
Generally, precipitation anomalies have the same sign at high- and at low-altitude stations (Auer and others, 2005; Reference Bähm, Auer, Granekind and OrlikBöhm and others, 2008). In order to account for the increase in precipitation with elevation, 12mm(100m)–1 were added to each month’s precipitation sum up to a maximum elevation of 3300 m, above which this value is assumed to remain constant. This vertical gradient is larger than annual gradients given by Reference Kuhn, Nickus and PelletKuhn and others (1982) and Reference KuhnKuhn (2003). Winter precipitation mainly consists of advective precipitation (unlike summer precipitation, where convection plays an important role); larger vertical gradients for winter precipitation are therefore expected for winter precipitation than for annual precipitation. Since accumulation is determined by winter precipitation, the chosen gradient best represented the observed vertical balance profile of selected glaciers.
HISTALP and ERA-40 precipitation are combined with the ERA-40 θ e to incorporate a spatially (HISTALP) and temporally (ERA-40) highly resolved precipitation dataset into the model. The higher-spatial-resolution HISTALP dataset is used to determine the total value for a month at a gridpoint and then split into 6 hourly time-steps given by the ERA-40 precipitation data and weighted accordingly. As an example, let HISTALP’s total November precipitation at a glacier’s gridpoint be 90 mm and let ERA-40 show that 30% of the month’s precipitation fell on 6 November and 70% on 20 November. The monthly precipitation is then divided into two time-steps: 27mm on 6 November and 63 mm on 20 November.
The rain–snow boundary is estimated by applying the regression function of Reference SteinackerSteinacker (1983) who related the rain–snow boundary empirically to the equivalent-potential temperature at 850 hPa. He found a relationship of the rain–snow boundary z r/s of
where the equivalent-potential temperature at 850 hPa is inserted in ˚C (Reference SteinackerSteinacker, 1983). If, at a certain point in time, θ e at 850 hPa is 42˚C the rain–snow boundary is assumed to be at 2500 m, applying Equation (2).
4. The Model
A PDD model is applied as widely used in hydrological modelling (e.g. Reference HockHock, 2003, Reference Hock2005; Reference KuhnKuhn, 2003; Reference Huss, Bauder, Funk and HockHuss and others, 2008 and references therein). To estimate the vertical temperature distribution at a certain point in time, temperatures at 600, 700 and 850 hPa and the geopotential there are used. All glacier-covered areas in the study area lie between these pressure levels at all points in time. The geopotential of a certain pressure level, Φ, is converted into geopotential height, z gp, by applying
where ḡ is the mean gravity acceleration (9.81ms–2). z gp is assumed to be equal to the geometrical height, z, with a satisfactory approximation (Reference StullStull, 2000).
If z 1 is located between the 700 and 850 hPa levels, for instance, the temperature there, T z1, is
The same applies analogously for z between 600 and 700 hPa.
To calculate ablation, the relation
is used, where DDF is used for calibration and T >0,day is the daily mean temperature above 0˚C.
Accumulation is estimated by
where P is precipitation and R 0/1 is a value that indicates whether the precipitation has fallen as snow or rain and that can only be 0 (rain) or 1 (snow). If z < z r/s, it is 0, otherwise it is 1. Liquid precipitation is assumed not to contribute to glacier mass gain. Both ablation and accumulation are computed with a 6 hour time-step. Their sum gives the specific mass balance, b.
The spatial and vertical dependence of DDF is a crucial point in the model and needs explanation. In the following, the vertical dependence of DDF (dDDF/dz) is introduced first, and then the spatial dependence.
An energy-balance model, SOMARS (Simulation Of glacier surface Mass balance And Related Sub-surface processes; Reference Greuell and KonzelmannGreuell and Konzelmann, 1994), was applied and validated with in situ measurements of the snow water equivalent at two locations on HEF by Reference SchrottSchrott (2006). With the results of this model (specific balance) an ablation season’s mean DDF at these two weather stations (2650 and 3050 m) is calculated. DDF varies vertically by –0.32mm w.e. (Kd)–1 per 100m of elevation. Over a 1000m height interval this amounts to a difference of –3.2mm(Kd)–1; for example, the lower end may have a DDF of 7.2 mm(Kd)–1 (low albedo) and the upper end one of 4mm(Kd)–1 (high albedo). This vertical gradient of DDFs is extrapolated and used as the vertical dependence of DDF in the model. The vertically changing DDFs are in line with theoretical considerations by Reference HockHock (2003). On average over a melt season, the albedo of lower areas is smaller, so, for a given temperature, the energy added to a surface is higher, as more shortwave radiation is absorbed. This is independent of temperature and would therefore not be reflected in a temperature-index approach with a constant DDF for the whole glacier.
In addition to the vertically varying DDFs, a spatial dependence is introduced. This is found by running the model iteratively with dDDF/dz as described above and with the condition that we must obtain the measured B of each glacier as it had been previously calculated from the glacier inventories. Each individual glacier thus has its own set of DDFs that best represents the measured B. DDFs vary considerably among the individual glaciers and are discussed below.
5. Results
The results of the first calibrated model run (run I) for HEF are shown in Figure 2a. It should be noted that the area changes for the modelled balances are approximated as explained above, whereas the area changes for the measured balances are adjusted each year. This approximation is made so that the method may be applied to unmeasured glaciers as well. Statistical values in Table 2 indicate that a similar quality of results is achieved for the three other glaciers where cross-validation data (i.e. measured mass balance) exist. Figure 2a shows that the model approximates the pattern of glacier change. There is a clear temporal dependence of the differences between measured and modelled balance. Until about 1987, measured balances are more positive than modelled balances; after 1987, this trend is reversed.
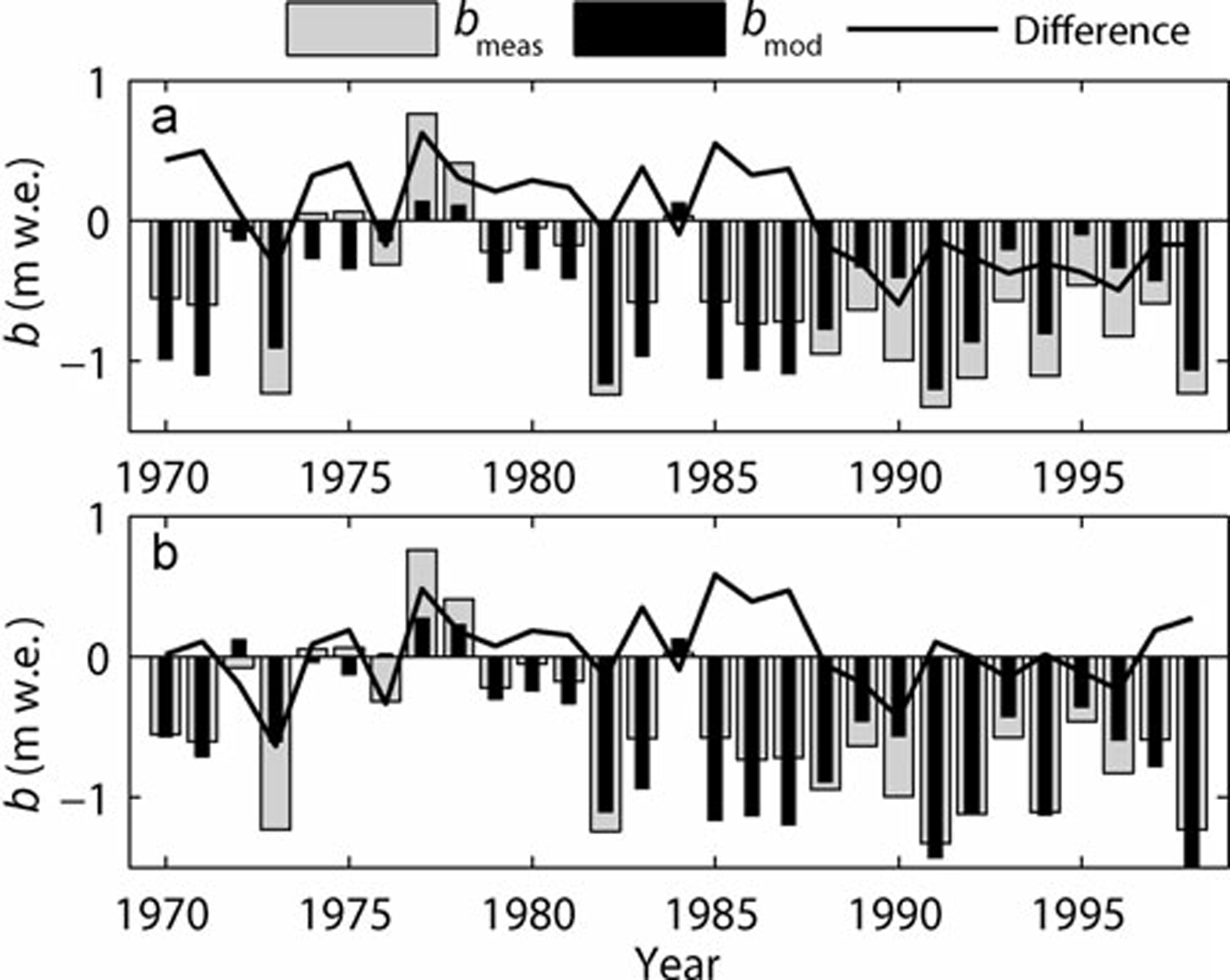
Fig. 2. Measured (b meas) and modelled mean specific surface mass balance (b mod) at HEF for two different model runs. (a) is calculated with constant DDFs over time; in (b), a temporally rising DDF value is introduced based on findings of Figure 3.
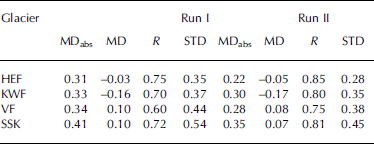
Table 2. Mean absolute difference, MDabs, and the mean signed difference, MD, between annually measured and modelled balances, the correlation coefficient, R, and the standard deviation, STD, of the differences for two model runs (run I: constant DDFs; run II: temporally changing DDFs following the findings of Fig. 3) for 1969–98. MDabs, MD and STD are in mw.e., R is dimensionless
This result is investigated further by asking: which annual values do DDFs have to have averaged over an ablation season to reproduce the measured mass balance of each year on the four glaciers with continuous mass-balance data? This is shown in Figure 3 where mean annual DDFs are plotted over time. The average DDFs are calculated as

Fig. 3. Mean area- and elevation-weighted DDF that best reproduces the measured annual surface mass balance of HEF, KWF, VF and SSK and these glaciers’ mean as calculated according to Equation (4). PF is the polynomial second-order fit that is calculated in order to represent the mean of the glacier’s individual values.
Figure 3 shows that there is an increase in DDFs over the observation period for all glaciers for which measured mass-balance data exist: at a given temperature, more melt occurs in later than in earlier years. The increasing trend is statistically significant and its magnitude is similar for the four glaciers with complete mass-balance data. The absolute values of mean DDFs are largest for VF, followed closely by KWF, significantly lower for HEF and lowest for SSK. For the three glaciers of the Ötztal Alps (HEF, KWF, VF), these differences are likely due to the influence of shortwave radiation. The south-facing VF and southeast-facing KWF receive more shortwave radiation than northeast-facing HEF (Table 1) and therefore have higher DDFs, a result that is consistent with previous research (e.g. Reference HockHock, 2005). SSK also provides a valuable comparison: it is located in a different climate with significantly more precipitation (Reference Abermann, Kuhn and FischerAbermann and others, 2011). More precipitation may cause a higher mean albedo and thus lower mean DDFs. We calculated a second-order polynomial fit (PF) that best represents the mean of all DDF increases, and found that the overall increase is ~1.5mm(Kd)–1 over the 29 years observed.
In the second model run (run II), we introduce a time dependence of DDF for each glacier. The best-fitting set of DDFs as found in run I is altered with time by the rate determined by the polynomial increase according to Figure 3. This altered DDF (DDFII) at any point in time of the study period (dates), which has to be inserted as a serial date number with 0 at 1 January 0000, increasing by 1 each day (amounting for example to 719529 for 1 January 1970), can be expressed by the best-fitting DDF as determined in run I (DDFI):
DDF is now a four-dimensional (3-D: run I; 4-D: run II) function of space and time. Figure 2b shows modelled balances with temporally varying DDFs and measured balances for HEF, as well as their differences. Both the trend and the annual values are better modelled than in the previous run. This is also shown in Table 2 in the mean absolute differences (MDabs), mean signed differences (MD), standard deviations (STD) of the differences between measured and modelled balances and the correlation coefficients, R, between measured and modelled balances. Without exception, the second run gave better results: smaller MDabs, MD and STD, and larger R. The MD values, small in all cases but largest for KWF (0.17mw.e.), suggest that errors largely compensate each other. The correlation coefficients between measured and modelled balance are similar for the four glaciers with directly measured data: they are highest for HEF (0.85) and lowest for VF (0.75) and on average 0.81. The performance of the model using a linear fit versus a second-order polynomial fit is compared: on average the second-order polynomial fit produces slightly higher correlation coefficients, which is why it is used for the final result.
The results of run II are shown in Figure 4 for all Austrian glaciers for which two DEMs exist (761 out of 900 glaciers; 451 out of 470 km2, i.e. 96% of the total glacier area). The evolution of modelled cumulative annual b with time is shown (each black line corresponds to one glacier). In total, 9.4 mw.e. on the ice-covered area of 451 km2 was lost between 1969 and 1998, which amounts to 4.7 km3w.e. The wide spread of the curves is due to differences in glacier type and to the individual glacier's deviation from steady state. The red curves show the cumulative modelled b of the glaciers with directly measured mass balance, and the total, area-weighted cumulative mean specific mass balance is computed and displayed as a green line. Initially, the glaciers' masses remained constant. Starting in 1975, all glaciers show a period of positive mass balances, with a total gain of ~1.3mw.e., corresponding to an ice volume gain of ~1km3. Since 1980, only a few years (e.g. 1984 and 1989) interrupt the generally negative trend. This temporal sequence is in agreement with the cumulative volume change derived from direct surface mass-balance measurements as compiled, for example, in Reference Abermann, Lambrecht, Fischer and KuhnAbermann and others (2009).

Fig. 4. Cumulative mean specific surface mass balance of all modelled glaciers in Austria (black lines) individually; the green line shows their total cumulative mean specific mass balance. The red lines show modelled balances of the glaciers where direct mass-balance measurements exist.
In Figure 5 the set of DDFs that best reproduced the observed glacier mass loss, the glacier’s median elevation (location of the circles) and the mean winter precipitation at the glacier (colours) are displayed. Each thin line represents the DDF(z) of the run with temporally constant DDFs. There is a clear relationship between the median elevation and the DDF at this elevation. The higher the median elevation, the more melt generally occurs at a given temperature and given precipitation. There are two possible explanations for this apparent paradox. First, glaciers usually exist at low median elevations (below 2700ma.s.l.) because they generally accumulate more mass in winter than glaciers with high median elevations do. This is evident in Figure 5, where glaciers with low median elevations show greater precipitation values (blue to yellow colours). However, more wind drift, more avalanching or some combination of these factors can give an additional mass input. As a result, ice is kept under snow cover for a longer part of the ablation season, so the albedo is comparatively high. Second, increasing shortwave radiation with elevation due to less shading and fewer aerosols results in higher general DDF values at higher elevations, as suggested by Reference Lang and BraunLang and Braun (1990) and Reference HockHock (2003).
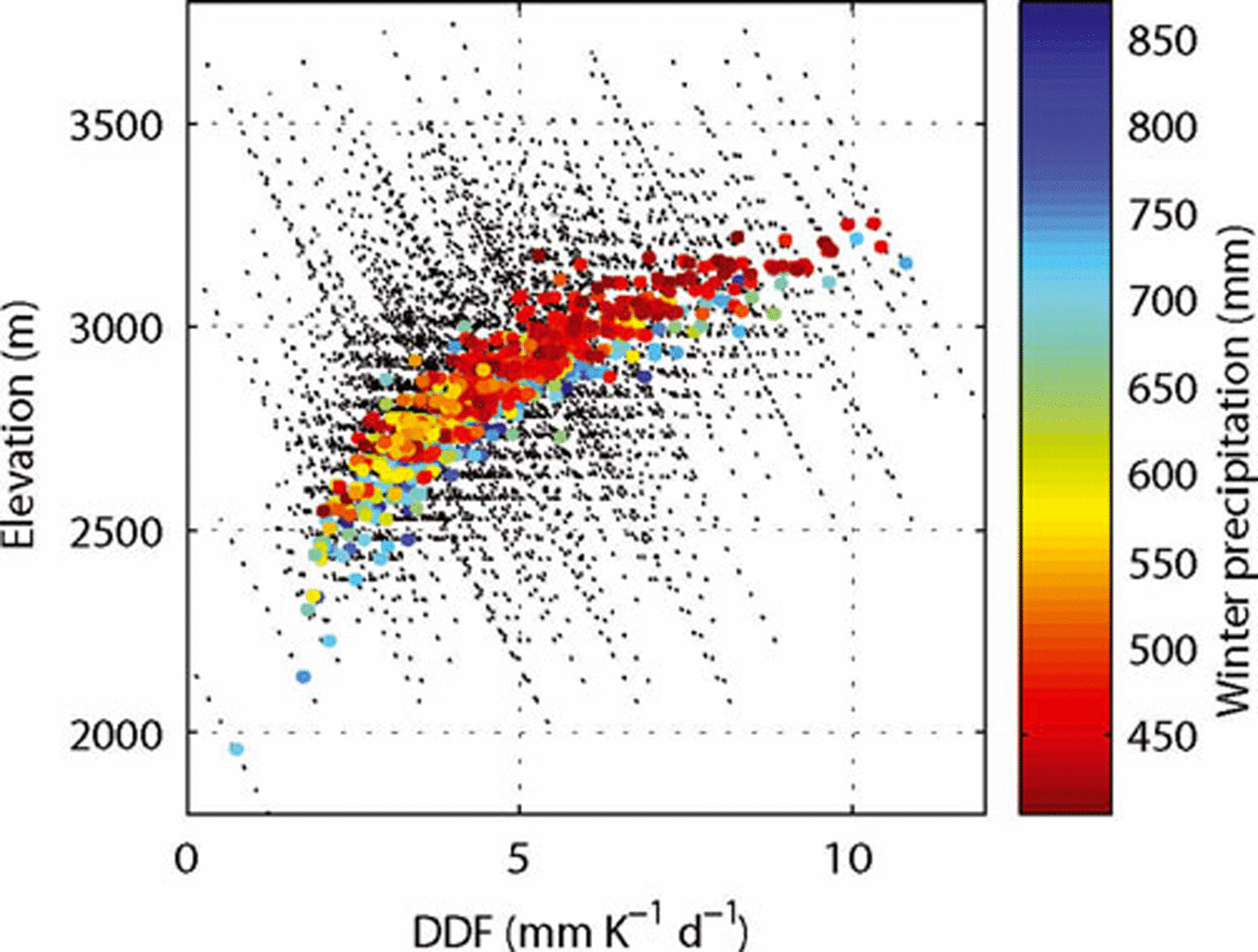
Fig. 5. DDF as a function of elevation for each glacier (thin dashed lines). The colour of the dots shows the mean winter precipitation at the glacier’s coordinate according to HISTALP (October–May, colour scale); their location is determined by the DDF at the glacier’s median elevation (left and bottom scale).
6. Discussion
The dependence of DDF with time is a major challenge when attempting to model future glacier change. For example, consider the problem faced by a hypothetical modeller in 1975 who sought to model future glacier mass balance through 1998 using mass-balance records from Figure 2 since 1969. He could not have known the future time dependence of DDF, and any reasonable assumption would have resulted in a significant underestimation of ice loss, as is obvious from Figure 2.
The subject of temporally changing DDFs was addressed by Reference Huss, Funk and OhmuraHuss and others (2009) who found a decrease in DDFs of ~7% per decade between 1970 and 2008. This seems to contradict the findings of this study but can be explained by the fact that Reference Huss, Funk and OhmuraHuss and others (2009) calculated point mass balance, and thus DDFs at point locations that are all in the accumulation area. The increase in DDFs in our study amounts to ~9% per decade and must be understood as a collective signal for an entire glacier. Since mass balances in recent years have been governed by ablation, it is the ablation area that controls recent glacier-averaged DDF changes. A probable explanation of the glacier-averaged DDF increase could be the increased duration of bare-ice exposure and thus a lower mean surface albedo in later years of the study period. Furthermore, two recent studies show that ice albedo recently decreased significantly as a result of additional dust accumulation after a sequence of negative mass-balance years (Reference Oerlemans, Giesen and van den BroekeOerlemans and others, 2009; Reference FischerFischer, 2010). The recent accelerated glacier retreat may be partly due to this.
An additional explanation for the temporal increase of the DDFs could be found by considering changes of glacier flow velocities in recent years. Less mass accumulated in upper parts of a glacier leads to less mass turnover and thus less ice supply for the glacier tongues. A strong velocity decrease has been found by exploiting long-term velocity measurements on HEF (Reference Span, Kuhn and SchneiderSpan and others, 1997) and KWF (Reference Abermann, Schneider and LambrechtAbermann and others, 2007). Which of these three processes (albedo, decreased mass transport and dynamical thinning) is the strongest component is beyond the scope of this study. A more process-based approach to separate components of the energy balance, combined with a dynamical ice-flow model, is needed.
This study has several simplifications: The fraction of volume change that is a result of basal melt is not accounted for. This volume loss is reflected in measured volume changes but not in the modelled surface balance as too little is known about its magnitude to accurately model it. Locally, this may be an important contribution to a glacier’s mass loss, but on average, and compared to the large surface mass loss, basal melt can be assumed to be negligible (Reference HookeHooke, 2005).
Another simplification is the assumption that all volume was lost as ice. Several aerial photographs were examined qualitatively, indicating that a fraction of the lost volume was snow. For a study of this scale, however, it is not possible to attribute a proportion of volume that was lost as snow to each glacier. Therefore, to estimate the possible impact on the results, the model was run with the exaggerated assumption that half of the lost volume was snow with a density of 550 kgm–3. The resulting total volume loss then amounts to 3.87 km3w.e. or 9% less than calculated with ice density only (i.e. 4.74 km3w.e. loss). The pattern of the cumulative mass balance as well as the modifications of DDF as a function of time and space do not change considerably, so the results would be altered quantitatively but not qualitatively.
The sensitivity of the tuning parameters to the result of this study was investigated by altering them stepwise and comparing the difference between the altered and the best-fitting (run II) mean annual balances. If the DDF is increased systematically by 1 mmK–1 d–1, mean annual balances for all modelled glaciers become more negative by 600 mmw.e. Likewise, the sensitivity of the vertical gradient of the DDFs (i.e. steepening or flattening the slope of the black lines in Fig. 5) is investigated. Model results are not sensitive to changes in DDF gradients: Changing the vertical dependence of DDF from –0.32mm–1(Kd)–1 (100m)–1 to –0.20mm(Kd)–1 (100 m)–1 (i.e. steepening the slope with zero change at the glacier’s median elevation) leads to a reduction of mean annual b by 4 mm. Flattening the slope with zero change at the glacier’s median elevation (i.e. –0.44 mm(Kd)–1 (100m)–1) leads to a reduction of mean annual b by 9 mm.
The data presented in this study allow for an estimation of the relative importance of the main climatic parameters that govern annual glacier mass balances. In Table 3 we summarize correlation coefficients between measured balances of the four well-studied glaciers and anomalies of PDD sums for the whole year, PDD sums for the summer (June–August), winter precipitation (October–May) and summer precipitation, all of which are interpolated to the glacier’s gridpoint. Deviations of winter and summer precipitation correlate only weakly with the measured balance. Annual anomalies of PDD sums correlate much more strongly with surface mass balance than precipitation anomalies do. The strongest correlation between meteorological data and measured balances is found between summer anomalies of PDD sums and the measured balance b (between –0.71 and –0.74), which is consistent with the results of Reference Kuhn, Dreiseitl, Hofinger, Markl, Span and KaserKuhn and others (1999), who examined this for HEF. All four glaciers have similar correlation values, but SSK shows a significantly higher correlation between summer precipitation anomalies and b than the other glaciers, and HEF’s balance is more sensitive than those of the other glaciers to winter precipitation.
Table 3. Correlation coefficients of the four variables’ anomalies (winter (October–May) (δP winter) and summer (June–August) precipitation (δP summer) and annual (δ±PDDyear) and summer (δ±PDDsummer) PDD sums) with measured balances. Bold numbers indicate statistical significance at the 99% confidence level

The results presented in Figure 4 can be taken as an indication of the generalizability of measured mass balances to all Austrian glaciers modelled in this study. HEF has a much more negative mass balance than most other glaciers, so its b is not representative for the overall mass balance of all Austrian glaciers. The specific balances of VF and KWF are close to the average, while SSK’s mean specific balance is more positive than the average.
7. Conclusions
The change over time in the mean annual surface mass balance of all Austrian glaciers for which two DEMs exist between 1969 and 1998 has been investigated in this study. With a PDD model with DDFs that vary in space (3-D) and time, correlation coefficients of >0.8 on average between measured and modelled balances for the four glaciers with direct measurements for validation are reached. Tuning parameters have to be calibrated to each glacier individually to reach a satisfying result. A relation is found between the glacier’s median elevation, mean winter precipitation and the DDF. The general increase in DDFs with time is likely to be due to a larger fraction of the glacier surface that exposes bare ice for an increasingly longer part of the summer, and thus a lower mean albedo. This is consistent with a sequence of negative balance years and an increase in equilibrium-line altitude. Calibrating a PDD model with only a few years of measurements and then extrapolating to the past or future seems extremely unreliable without additional knowledge (e.g. DEMs at various points in time). There are ongoing efforts to extend this study further towards the present and include a new glacier inventory of 2006 (Reference Abermann, Lambrecht, Fischer and KuhnAbermann and others, 2009) in order to investigate how these parameters have evolved in the very recent past. This model could also be used to reproduce mass balances back to the Little Ice Age glacier maximum, for which information on extent and surface elevation could be reconstructed from locations of moraines, thus providing a fascinating picture of >150 years of glacier history.
Acknowledgements
This study was funded by the Commission for Geophysical Research, Austrian Academy of Sciences. We thank the Institute of Meteorology and Geophysics, Innsbruck, the Bavarian Academy of Sciences, Munich, Germany, and H. Slupetzky for providing mass-balance data. The ECMWF/ ERA-40 reanalysis project and the HISTALP database provided the meteorological data. We thank E. Dreiseitl, E. Schlosser, L.A. Rasmussen and S. Kinter for comments and proofreading. Two anonymous reviewers and the editor are acknowledged for helpful suggestions.










