1. Introduction
The generalisation or extension of classical problems from Newtonian viscous fluid mechanics to more rheologically complex situations has a rich heritage in the pages of the Journal of Fluid Mechanics and elsewhere. This operation can, at times, be anticlimactic, with the associated non-Newtonian result appearing qualitatively similar to its Newtonian counterpart. Viscoplastic materials, however, tend not to disappoint: these materials exhibit a non-zero ‘yield stress’  $\tau _Y$, below which they do not flow and above which they do, and the presence of this critical stress can lead to fundamental changes from Newtonian behaviour, with flows exhibiting qualitatively different structures and new phenomenology.
$\tau _Y$, below which they do not flow and above which they do, and the presence of this critical stress can lead to fundamental changes from Newtonian behaviour, with flows exhibiting qualitatively different structures and new phenomenology.
The most common feature of viscoplastic flows is the existence of rigid ‘plug’ regions, where the stress has fallen below the yield stress and the material is either stationary or moves as a solid body. A common example is pipe flow, where the vanishing centreline stress results in a central rigid plug that is carried downstream by lubricating sheared regions against the pipe wall. Other canonical features of viscoplastic flows include extended regions of almost perfectly plastic deformation, where the strain rate is very small and the stress is held very close to the yield stress, and localised narrow layers of high shear which act to lubricate plugs or plastic regions.
These generic features have been explored and described in viscoplastic generalisations of numerous classical flow problems, including lubrication theory (e.g. Balmforth & Craster Reference Balmforth and Craster1999), Stokes’ first and second problems (impulsive lateral motion, or oscillation, of one boundary, respectively; e.g. Balmforth, Forterre & Pouliquen Reference Balmforth, Forterre and Pouliquen2009; Hinton, Collis & Sader Reference Hinton, Collis and Sader2022), flow around a falling cylinder (e.g. Tokpavi, Magnin & Jay Reference Tokpavi, Magnin and Jay2008) and slender-body theory (e.g. Hewitt & Balmforth Reference Hewitt and Balmforth2018). Taylor-West & Hogg (Reference Taylor-West and Hogg2021) have previously considered converging viscoplastic flow in a wedge; in this volume the same authors tackle the problem of viscoplastic corner flow (Taylor-West & Hogg Reference Taylor-West and Hogg2022).
The flow of material past a corner is, of course, a commonplace occurrence. Materials with a yield stress tend to become clogged in the vicinity of corners where the stress is insufficient to yield them; similar clogging occurs near other geometrical features like side branches and local obstructions or expansions. The formation of such clogs or ‘dead zones’ can be problematic in, for example, the food processing or cleaning industries, since no fresh fluid enters these regions. Various studies have also observed the formation of viscoplastic ‘eddies’ or rotating rigid plugs in the vicinity of clogged regions (see e.g. Roustaei & Frigaard Reference Roustaei and Frigaard2013).
Taylor-West & Hogg (Reference Taylor-West and Hogg2022) study the idealised problem of a simple yield-stress fluid (a Bingham fluid) in a wedge, linking their study directly to the equivalent Newtonian problem. Nearly 60 years ago, Moffatt (Reference Moffatt1964) presented a now-classical study demonstrating the existence of an infinite series of counter-rotating inertia-free ‘eddies’ that arise in slow viscous flow in a wedge forced by a disturbance far from the corner. Whilst others have drawn a qualitative analogy with these Moffatt eddies, Taylor-West and Hogg here present the first detailed analysis of the viscoplastic problem. In so doing, they illustrate how to describe the extent of the corner plug or ‘dead zone’ and the adjoining rotating viscoplastic eddy. Their work helps to rationalise the numerous observations of clogged backwaters and rotating eddy ‘plugs’ that have been observed in the literature.
2. Overview
The existence of an infinite set of inertia-free eddies in a Newtonian fluid follows from solving the biharmonic equation in a wedge (with a half-angle  $\alpha \lesssim 73^\circ$) using separation of variables (Moffatt Reference Moffatt1964). A crucial detail of this flow is that the size of the eddies and their rotation rate, and thus the fluid stress, all decay exponentially towards the corner. The decay rate depends on the wedge angle
$\alpha \lesssim 73^\circ$) using separation of variables (Moffatt Reference Moffatt1964). A crucial detail of this flow is that the size of the eddies and their rotation rate, and thus the fluid stress, all decay exponentially towards the corner. The decay rate depends on the wedge angle  $\alpha$, but is in all cases strong: Taylor-West & Hogg (Reference Taylor-West and Hogg2022) note that the strain rate moving away from the corner increases by a factor of at least
$\alpha$, but is in all cases strong: Taylor-West & Hogg (Reference Taylor-West and Hogg2022) note that the strain rate moving away from the corner increases by a factor of at least  $1/0.0078 \approx 128$ between any two neighbouring eddies.
$1/0.0078 \approx 128$ between any two neighbouring eddies.
As such, they are able to predict (a) that the stress will always fall below the yield stress sufficiently close to the corner, leading to a plug there, and (b) that only one eddy immediately neighbouring this plug will feel any appreciable effect from the yield stress of the fluid. That is because – using the Newtonian solution as a guide – the characteristic stain rates in the next eddy out will have increased by at least two orders of magnitude, meaning that the influence of the yield stress will be extremely small. Equivalently, the fluid's yield stress  $\tau _Y$ and viscosity
$\tau _Y$ and viscosity  $\mu$ together define a characteristic rheological strain-rate scale
$\mu$ together define a characteristic rheological strain-rate scale  $\tau _Y/\mu$; this will only be comparable to the Newtonian eddy strain rate in at most one eddy.
$\tau _Y/\mu$; this will only be comparable to the Newtonian eddy strain rate in at most one eddy.
Thus they posit – and then demonstrate the validity of this construction by means of direct numerical simulations – that viscoplastic corner flow in an arbitrarily deep wedge will consist of a clogged corner plug bounded by one viscoplastic eddy, outside of which the flow is essentially well described by the classical Newtonian solution. Of course, in a finite-sized wedge the viscoplastic eddy – or even the clogged corner – may reach sufficiently far up the wedge as to interact with the external flow, which could change some details of the construction.
Based on the Newtonian solution, one can combine the distance  $L$ to the corner with a suitable eddy velocity scale
$L$ to the corner with a suitable eddy velocity scale  $U$ to compare with the plastic strain-rate scale
$U$ to compare with the plastic strain-rate scale  $\tau _Y/\mu$ and determine the location of the ‘critical’ viscoplastic eddy that will divide the plugged corner from the Newtonian outer flow. This eddy can be characterised by a local Bingham number – a dimensionless measure of the importance of the yield stress –
$\tau _Y/\mu$ and determine the location of the ‘critical’ viscoplastic eddy that will divide the plugged corner from the Newtonian outer flow. This eddy can be characterised by a local Bingham number – a dimensionless measure of the importance of the yield stress –  $Bi = \tau _Y L / \mu U = O(1)$.
$Bi = \tau _Y L / \mu U = O(1)$.
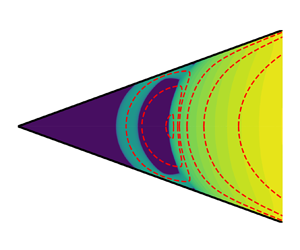
The self-similarity of the underlying Newtonian solution is reflected in the viscoplastic case. Taylor-West & Hogg (Reference Taylor-West and Hogg2022) show that, having defined a suitable local Bingham number as outlined above, there is a critical value below which a new viscoplastic eddy forms, being ‘carved out’ from the existing corner plug. This eddy takes the form of a thin roughly semi-circular shear layer that divides the static clogged corner from a rigidly rotating roughly crescent-shaped plug (see their figure 3a). As  $Bi$ is decreased, the shear layer widens, the rotating plug thins and its rotation rate increases. For sufficiently low
$Bi$ is decreased, the shear layer widens, the rotating plug thins and its rotation rate increases. For sufficiently low  $Bi$, the rotating plug essentially vanishes, and the eddy approaches the Newtonian solution, at which point a new viscoplastic eddy is carved from the remaining corner plug and the process repeats, but at an exponentially smaller length and velocity scale.
$Bi$, the rotating plug essentially vanishes, and the eddy approaches the Newtonian solution, at which point a new viscoplastic eddy is carved from the remaining corner plug and the process repeats, but at an exponentially smaller length and velocity scale.
Taylor-West & Hogg (Reference Taylor-West and Hogg2022) determine, based on a simple torque-balance argument, approximate values for these critical  $Bi$, and roughly determine the associated length of the static corner plug as the yield stress is varied. They go on to analyse the shear layers that bound the rotating viscoplastic eddy, using viscoplastic boundary-layer theory following Balmforth et al. (Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017). When the Bingham number is close to its critical value, these layers essentially act as slip surfaces that separate both the clogged corner and the rigid walls of the wedge from a rotating rigid plug. Generically such shear layers in viscoplastic fluids can be ‘purely viscous’, in the sense that they involve a balance of along-layer pressure gradients and viscous shear stress only, or they can be genuinely viscoplastic, in the sense that some nonlinear plastic stresses also enter this balance. The difference between these two behaviours is typically related to whether the layer is located against a rigid surface (where the velocity must match that of the rigid wall) or is a ‘free shear layer’ linking two rigid plugs (against which, in addition, the stress must fall to equal the fluid's yield stress).
$Bi$, and roughly determine the associated length of the static corner plug as the yield stress is varied. They go on to analyse the shear layers that bound the rotating viscoplastic eddy, using viscoplastic boundary-layer theory following Balmforth et al. (Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017). When the Bingham number is close to its critical value, these layers essentially act as slip surfaces that separate both the clogged corner and the rigid walls of the wedge from a rotating rigid plug. Generically such shear layers in viscoplastic fluids can be ‘purely viscous’, in the sense that they involve a balance of along-layer pressure gradients and viscous shear stress only, or they can be genuinely viscoplastic, in the sense that some nonlinear plastic stresses also enter this balance. The difference between these two behaviours is typically related to whether the layer is located against a rigid surface (where the velocity must match that of the rigid wall) or is a ‘free shear layer’ linking two rigid plugs (against which, in addition, the stress must fall to equal the fluid's yield stress).
Here, the lubricating layer features both behaviours: across the opening of the wedge there is a ‘free shear layer’ linking two rigid plugs, while against the wedge walls the layer is bounded on one side by a rigid surface (see e.g. figure 9(b) in Taylor-West & Hogg Reference Taylor-West and Hogg2022). As such, the dominant balances in the layer vary along its length, as does its width: the free shear layer is asymptotically wider, and has a lower pressure gradient, than that against the wall. More specifically, Taylor-West and Hogg reveal by means of a detailed boundary-layer analysis the manner in which the rotation rate  $\varOmega$ of the plug decays as the Bingham number approaches its critical value, and determine the widths of the two different boundary-layer segments (found to be
$\varOmega$ of the plug decays as the Bingham number approaches its critical value, and determine the widths of the two different boundary-layer segments (found to be  ${\sim }\varOmega ^{1/3}$ and
${\sim }\varOmega ^{1/3}$ and  ${\sim }\varOmega ^{2/3}$, respectively).
${\sim }\varOmega ^{2/3}$, respectively).
The paper ends with an illustration of this behaviour in a ‘real’ flow setting (here flow past a triangular corner region driven by a moving plate; they also illustrate the case of flow past a rectangular opening in an appendix, showing that the same theory can be applied in that case). They find excellent agreement with their theoretical predictions. This comparison nicely demonstrates how one might apply this idealised theory for corner flow to other settings involving flow past any sort of corner or ‘backwater’ region, and thus determine the extent of any stagnant clog that will form in that region.
3. The future
Viscoplastic flow past a corner is a fairly generic scenario, and the question of what controls the extent of any clogged plug that forms there is a natural one. This study goes some way to answer that, at least in cases where the corner is sufficiently deep. A natural question to ask is what happens in cases where the corner is not deep enough to contain the Newtonian solution at all, such that either the rigid corner plug or the rotating viscoplastic eddy reach out to the external flow. While there may be some quantitative differences in such cases, the general approaches of this paper should allow for a way of tackling such problems as well.
The degree to which the qualitative construction outlined here – a clogged corner region bounded by a rotating viscoplastic plug – carries over into different three-dimensional geometries is not obvious, and exploration of this problem would certainly be an interesting extension. The role of inertia on these corner flows would also be worth exploring, since decaying inertial forces in the corner could disrupt the flow and affect the extent of the corner plug. This is presumably an important question in cleaning or batch processing applications where strategies for disturbing clogged corners are desired.
Finally, the rheology of the material could affect the behaviour of the corner flow. The critical wedge angle for the formation of eddies, for example, varies with the power-law index of the fluid (Henriksen & Hassager Reference Henriksen and Hassager1989; Meyer & Creyts Reference Meyer and Creyts2017). This feature is presumably echoed by viscoplastic models with a power-law viscous behaviour (as in the Herschel–Bulkley law), although it seems unlikely that there would be substantive differences in the extent of the plugged-up corner, which is predominantly controlled by the yield stress of the material. More involved rheological models that include time dependence or elastic forces, on the other hand, could result in a disrupted plug structure and more complex dynamics.
1. Introduction
The generalisation or extension of classical problems from Newtonian viscous fluid mechanics to more rheologically complex situations has a rich heritage in the pages of the Journal of Fluid Mechanics and elsewhere. This operation can, at times, be anticlimactic, with the associated non-Newtonian result appearing qualitatively similar to its Newtonian counterpart. Viscoplastic materials, however, tend not to disappoint: these materials exhibit a non-zero ‘yield stress’ $\tau _Y$, below which they do not flow and above which they do, and the presence of this critical stress can lead to fundamental changes from Newtonian behaviour, with flows exhibiting qualitatively different structures and new phenomenology.
$\tau _Y$, below which they do not flow and above which they do, and the presence of this critical stress can lead to fundamental changes from Newtonian behaviour, with flows exhibiting qualitatively different structures and new phenomenology.
The most common feature of viscoplastic flows is the existence of rigid ‘plug’ regions, where the stress has fallen below the yield stress and the material is either stationary or moves as a solid body. A common example is pipe flow, where the vanishing centreline stress results in a central rigid plug that is carried downstream by lubricating sheared regions against the pipe wall. Other canonical features of viscoplastic flows include extended regions of almost perfectly plastic deformation, where the strain rate is very small and the stress is held very close to the yield stress, and localised narrow layers of high shear which act to lubricate plugs or plastic regions.
These generic features have been explored and described in viscoplastic generalisations of numerous classical flow problems, including lubrication theory (e.g. Balmforth & Craster Reference Balmforth and Craster1999), Stokes’ first and second problems (impulsive lateral motion, or oscillation, of one boundary, respectively; e.g. Balmforth, Forterre & Pouliquen Reference Balmforth, Forterre and Pouliquen2009; Hinton, Collis & Sader Reference Hinton, Collis and Sader2022), flow around a falling cylinder (e.g. Tokpavi, Magnin & Jay Reference Tokpavi, Magnin and Jay2008) and slender-body theory (e.g. Hewitt & Balmforth Reference Hewitt and Balmforth2018). Taylor-West & Hogg (Reference Taylor-West and Hogg2021) have previously considered converging viscoplastic flow in a wedge; in this volume the same authors tackle the problem of viscoplastic corner flow (Taylor-West & Hogg Reference Taylor-West and Hogg2022).
The flow of material past a corner is, of course, a commonplace occurrence. Materials with a yield stress tend to become clogged in the vicinity of corners where the stress is insufficient to yield them; similar clogging occurs near other geometrical features like side branches and local obstructions or expansions. The formation of such clogs or ‘dead zones’ can be problematic in, for example, the food processing or cleaning industries, since no fresh fluid enters these regions. Various studies have also observed the formation of viscoplastic ‘eddies’ or rotating rigid plugs in the vicinity of clogged regions (see e.g. Roustaei & Frigaard Reference Roustaei and Frigaard2013).
Taylor-West & Hogg (Reference Taylor-West and Hogg2022) study the idealised problem of a simple yield-stress fluid (a Bingham fluid) in a wedge, linking their study directly to the equivalent Newtonian problem. Nearly 60 years ago, Moffatt (Reference Moffatt1964) presented a now-classical study demonstrating the existence of an infinite series of counter-rotating inertia-free ‘eddies’ that arise in slow viscous flow in a wedge forced by a disturbance far from the corner. Whilst others have drawn a qualitative analogy with these Moffatt eddies, Taylor-West and Hogg here present the first detailed analysis of the viscoplastic problem. In so doing, they illustrate how to describe the extent of the corner plug or ‘dead zone’ and the adjoining rotating viscoplastic eddy. Their work helps to rationalise the numerous observations of clogged backwaters and rotating eddy ‘plugs’ that have been observed in the literature.
2. Overview
The existence of an infinite set of inertia-free eddies in a Newtonian fluid follows from solving the biharmonic equation in a wedge (with a half-angle $\alpha \lesssim 73^\circ$) using separation of variables (Moffatt Reference Moffatt1964). A crucial detail of this flow is that the size of the eddies and their rotation rate, and thus the fluid stress, all decay exponentially towards the corner. The decay rate depends on the wedge angle
$\alpha \lesssim 73^\circ$) using separation of variables (Moffatt Reference Moffatt1964). A crucial detail of this flow is that the size of the eddies and their rotation rate, and thus the fluid stress, all decay exponentially towards the corner. The decay rate depends on the wedge angle  $\alpha$, but is in all cases strong: Taylor-West & Hogg (Reference Taylor-West and Hogg2022) note that the strain rate moving away from the corner increases by a factor of at least
$\alpha$, but is in all cases strong: Taylor-West & Hogg (Reference Taylor-West and Hogg2022) note that the strain rate moving away from the corner increases by a factor of at least  $1/0.0078 \approx 128$ between any two neighbouring eddies.
$1/0.0078 \approx 128$ between any two neighbouring eddies.
As such, they are able to predict (a) that the stress will always fall below the yield stress sufficiently close to the corner, leading to a plug there, and (b) that only one eddy immediately neighbouring this plug will feel any appreciable effect from the yield stress of the fluid. That is because – using the Newtonian solution as a guide – the characteristic stain rates in the next eddy out will have increased by at least two orders of magnitude, meaning that the influence of the yield stress will be extremely small. Equivalently, the fluid's yield stress $\tau _Y$ and viscosity
$\tau _Y$ and viscosity  $\mu$ together define a characteristic rheological strain-rate scale
$\mu$ together define a characteristic rheological strain-rate scale  $\tau _Y/\mu$; this will only be comparable to the Newtonian eddy strain rate in at most one eddy.
$\tau _Y/\mu$; this will only be comparable to the Newtonian eddy strain rate in at most one eddy.
Thus they posit – and then demonstrate the validity of this construction by means of direct numerical simulations – that viscoplastic corner flow in an arbitrarily deep wedge will consist of a clogged corner plug bounded by one viscoplastic eddy, outside of which the flow is essentially well described by the classical Newtonian solution. Of course, in a finite-sized wedge the viscoplastic eddy – or even the clogged corner – may reach sufficiently far up the wedge as to interact with the external flow, which could change some details of the construction.
Based on the Newtonian solution, one can combine the distance $L$ to the corner with a suitable eddy velocity scale
$L$ to the corner with a suitable eddy velocity scale  $U$ to compare with the plastic strain-rate scale
$U$ to compare with the plastic strain-rate scale  $\tau _Y/\mu$ and determine the location of the ‘critical’ viscoplastic eddy that will divide the plugged corner from the Newtonian outer flow. This eddy can be characterised by a local Bingham number – a dimensionless measure of the importance of the yield stress –
$\tau _Y/\mu$ and determine the location of the ‘critical’ viscoplastic eddy that will divide the plugged corner from the Newtonian outer flow. This eddy can be characterised by a local Bingham number – a dimensionless measure of the importance of the yield stress –  $Bi = \tau _Y L / \mu U = O(1)$.
$Bi = \tau _Y L / \mu U = O(1)$.
The self-similarity of the underlying Newtonian solution is reflected in the viscoplastic case. Taylor-West & Hogg (Reference Taylor-West and Hogg2022) show that, having defined a suitable local Bingham number as outlined above, there is a critical value below which a new viscoplastic eddy forms, being ‘carved out’ from the existing corner plug. This eddy takes the form of a thin roughly semi-circular shear layer that divides the static clogged corner from a rigidly rotating roughly crescent-shaped plug (see their figure 3a). As $Bi$ is decreased, the shear layer widens, the rotating plug thins and its rotation rate increases. For sufficiently low
$Bi$ is decreased, the shear layer widens, the rotating plug thins and its rotation rate increases. For sufficiently low  $Bi$, the rotating plug essentially vanishes, and the eddy approaches the Newtonian solution, at which point a new viscoplastic eddy is carved from the remaining corner plug and the process repeats, but at an exponentially smaller length and velocity scale.
$Bi$, the rotating plug essentially vanishes, and the eddy approaches the Newtonian solution, at which point a new viscoplastic eddy is carved from the remaining corner plug and the process repeats, but at an exponentially smaller length and velocity scale.
Taylor-West & Hogg (Reference Taylor-West and Hogg2022) determine, based on a simple torque-balance argument, approximate values for these critical $Bi$, and roughly determine the associated length of the static corner plug as the yield stress is varied. They go on to analyse the shear layers that bound the rotating viscoplastic eddy, using viscoplastic boundary-layer theory following Balmforth et al. (Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017). When the Bingham number is close to its critical value, these layers essentially act as slip surfaces that separate both the clogged corner and the rigid walls of the wedge from a rotating rigid plug. Generically such shear layers in viscoplastic fluids can be ‘purely viscous’, in the sense that they involve a balance of along-layer pressure gradients and viscous shear stress only, or they can be genuinely viscoplastic, in the sense that some nonlinear plastic stresses also enter this balance. The difference between these two behaviours is typically related to whether the layer is located against a rigid surface (where the velocity must match that of the rigid wall) or is a ‘free shear layer’ linking two rigid plugs (against which, in addition, the stress must fall to equal the fluid's yield stress).
$Bi$, and roughly determine the associated length of the static corner plug as the yield stress is varied. They go on to analyse the shear layers that bound the rotating viscoplastic eddy, using viscoplastic boundary-layer theory following Balmforth et al. (Reference Balmforth, Craster, Hewitt, Hormozi and Maleki2017). When the Bingham number is close to its critical value, these layers essentially act as slip surfaces that separate both the clogged corner and the rigid walls of the wedge from a rotating rigid plug. Generically such shear layers in viscoplastic fluids can be ‘purely viscous’, in the sense that they involve a balance of along-layer pressure gradients and viscous shear stress only, or they can be genuinely viscoplastic, in the sense that some nonlinear plastic stresses also enter this balance. The difference between these two behaviours is typically related to whether the layer is located against a rigid surface (where the velocity must match that of the rigid wall) or is a ‘free shear layer’ linking two rigid plugs (against which, in addition, the stress must fall to equal the fluid's yield stress).
Here, the lubricating layer features both behaviours: across the opening of the wedge there is a ‘free shear layer’ linking two rigid plugs, while against the wedge walls the layer is bounded on one side by a rigid surface (see e.g. figure 9(b) in Taylor-West & Hogg Reference Taylor-West and Hogg2022). As such, the dominant balances in the layer vary along its length, as does its width: the free shear layer is asymptotically wider, and has a lower pressure gradient, than that against the wall. More specifically, Taylor-West and Hogg reveal by means of a detailed boundary-layer analysis the manner in which the rotation rate $\varOmega$ of the plug decays as the Bingham number approaches its critical value, and determine the widths of the two different boundary-layer segments (found to be
$\varOmega$ of the plug decays as the Bingham number approaches its critical value, and determine the widths of the two different boundary-layer segments (found to be  ${\sim }\varOmega ^{1/3}$ and
${\sim }\varOmega ^{1/3}$ and  ${\sim }\varOmega ^{2/3}$, respectively).
${\sim }\varOmega ^{2/3}$, respectively).
The paper ends with an illustration of this behaviour in a ‘real’ flow setting (here flow past a triangular corner region driven by a moving plate; they also illustrate the case of flow past a rectangular opening in an appendix, showing that the same theory can be applied in that case). They find excellent agreement with their theoretical predictions. This comparison nicely demonstrates how one might apply this idealised theory for corner flow to other settings involving flow past any sort of corner or ‘backwater’ region, and thus determine the extent of any stagnant clog that will form in that region.
3. The future
Viscoplastic flow past a corner is a fairly generic scenario, and the question of what controls the extent of any clogged plug that forms there is a natural one. This study goes some way to answer that, at least in cases where the corner is sufficiently deep. A natural question to ask is what happens in cases where the corner is not deep enough to contain the Newtonian solution at all, such that either the rigid corner plug or the rotating viscoplastic eddy reach out to the external flow. While there may be some quantitative differences in such cases, the general approaches of this paper should allow for a way of tackling such problems as well.
The degree to which the qualitative construction outlined here – a clogged corner region bounded by a rotating viscoplastic plug – carries over into different three-dimensional geometries is not obvious, and exploration of this problem would certainly be an interesting extension. The role of inertia on these corner flows would also be worth exploring, since decaying inertial forces in the corner could disrupt the flow and affect the extent of the corner plug. This is presumably an important question in cleaning or batch processing applications where strategies for disturbing clogged corners are desired.
Finally, the rheology of the material could affect the behaviour of the corner flow. The critical wedge angle for the formation of eddies, for example, varies with the power-law index of the fluid (Henriksen & Hassager Reference Henriksen and Hassager1989; Meyer & Creyts Reference Meyer and Creyts2017). This feature is presumably echoed by viscoplastic models with a power-law viscous behaviour (as in the Herschel–Bulkley law), although it seems unlikely that there would be substantive differences in the extent of the plugged-up corner, which is predominantly controlled by the yield stress of the material. More involved rheological models that include time dependence or elastic forces, on the other hand, could result in a disrupted plug structure and more complex dynamics.
Declaration of interests
The authors report no conflict of interest.