The conditional Lyapunov exponents and synchronisation of rotating turbulent flows

Abstract

The synchronisation between rotating turbulent flows in periodic boxes is investigated numerically. The flows are coupled via a master–slave coupling, taking the Fourier modes with wavenumber below a given value $k_m$ as the master modes. It is found that synchronisation happens when $k_m$ exceeds a threshold value $k_c$, and $k_c$ depends strongly on the forcing scheme. In rotating Kolmogorov flows, $k_c\eta$ does not change with rotation in the range of rotation rates considered, $\eta$ being the Kolmogorov length scale. Even though the energy spectrum has a steeper slope, the value of $k_c\eta$ is the same as that found in isotropic turbulence. In flows driven by a forcing term maintaining constant energy injection rate, synchronisation becomes easier when rotation is stronger. Here, $k_c\eta$ decreases with rotation, and it is reduced significantly for strong rotations when the slope of the energy spectrum approaches $-3$. It is shown that the conditional Lyapunov exponent for a given $k_m$ is reduced by rotation in the flows driven by the second type of forcing, but it increases mildly with rotation for the Kolmogorov flows. The local conditional Lyapunov exponents fluctuate more strongly as rotation is increased, although synchronisation occurs as long as the average conditional Lyapunov exponents are negative. We also look for the relationship between $k_c$ and the energy spectra of the Lyapunov vectors. We find that the spectra always seem to peak at approximately $k_c$, and synchronisation fails when the energy spectra of the conditional Lyapunov vectors have a local maximum in the slaved modes.

1. Introduction

For some chaotic systems, one may couple two realisations of the system in specific ways to synchronise the states of the two realisations, in the sense that the two realisations remain chaotic, but the difference between them decays over time and approaches zero asymptotically. This phenomenon is called (complete) chaos synchronisation, which was first discussed in Fujisaka & Yamada (1983) and attracted wide attention after Pecora & Carroll (1990) (see e.g. Pecora & Carroll (2015) for a historical account). The phenomenon has applications in e.g. secure communication and parameter estimation, and is used as a paradigm to understand a wide range of phenomena. The research into these applications, as well as the principles behind the phenomenon and other forms of chaos synchronisation, is reviewed in Pecora & Carroll (2015), Eroglu, Lamb & Pereira (2017) and Boccaletti et al. (2002).

In turbulent simulations, chaos synchronisation is closely linked to data assimilation, a practice where observational or measurement data are synthesised with simulation to produce more accurate predictions of turbulent flows. If the aim of data assimilation is to recover the chaotic instantaneous turbulent fields, then it becomes a problem of chaos synchronization. For isotropic turbulence, typically two flows can be synchronised completely by replacing Fourier modes with wavenumbers less than $k_m$ from one flow with those in the other, and synchronisation is achieved only if $k_m$ is larger than a threshold value $k_c$. To the best of our knowledge, Henshaw, Kreiss & Ystróm (2003) are the first to investigate the synchronisation of turbulent flows, where a theoretical estimate of $k_c$ is derived but numerical experiments are conducted to show that synchronisation can be achieved with far fewer Fourier modes. Another early work is Yoshida, Yamaguchi & Kaneda (2005), where it was established numerically that $k_c \eta \approx 0.2$, with $\eta$ the Kolmogorov length scale. Lalescu, Meneveau & Eyink (2013) investigate a similar problem with a different forcing scheme as well as anisotropic grids, and $k_c \eta \approx 0.15$ is found.

When $k_m$ is smaller than $k_c$, Vela-Martin (2021) shows that partial synchronisation can be obtained and that the velocity fields in domains with strong vorticity are better synchronised than those with weaker vorticity. This result suggests that the synchronisation of turbulent flows may have its own specific features pertinent to the physics of turbulence. In Couette flows, Nikolaidis & Ioannou (2022) show that synchronization occurs when streamwise Fourier modes with wavenumber exceeding a threshold value are replicated in the two systems. They also show that synchronisation happens if the conditional Lyapunov exponent is negative, in line with a result known from the synchronisation of low-dimensional chaotic systems (Boccaletti et al. 2002). Channel flows are investigated by Wang & Zaki (2022), where data from layers in the flow domain with different orientations are used to couple two systems. By doing so, scaling of the thickness of the layers needed for synchronisation is established, through numerical experiments as well as analyses of the conditional Lyapunov exponents.

In the aforementioned research, the coupling of the two flows is always achieved by replacing part of the velocity field in one flow by the corresponding part of velocity in the other flow. This type of coupling is termed master–slave coupling. Another common way to couple the two systems is through nudging, where a linear forcing term is introduced in either one or both of the flow fields. The forcing term nudges one flow from the other, hence the name ‘nudging’. Nudging is used in Di Leoni, Mazzino & Biferale (2018, 2020) to synchronise isotropic turbulence with or without rotation. The efficacy of different nudging schemes is compared. In rotating turbulence, they find that synchronisation becomes more effective due to the presence of large-scale coherent vortices, and inverse cascade can be reconstructed when nudging is applied to small scales.

Going beyond the synchronisation between two simulations with identical system parameters, Buzzicotti & De Leoni (2020) consider the synchronisation between large eddy simulations (LES) and direct numerical simulations (DNS), using the nudging method. Because the two systems are different in this case, complete synchronisation is unachievable. However, the authors show that the error between the nudged LES velocity and DNS velocity can be minimised by tuning the parameters in the subgrid-scale models. Thus chaos synchronisation is used to optimise model parameters. Li, Tian & Li (2022) investigate the synchronisation between LES and DNS using the master–slave coupling, with a focus on the threshold wavenumber and the synchronisation error for different subgrid-scale models. They find that the standard Smagorinsky model under certain circumstances produces smaller synchronisation error than the dynamic Smagorinsky model and the dynamic mixed model.

Rotating turbulence, i.e. turbulent flows in a rotating frame of reference, is ubiquitous in atmospheric, oceanic and industrial flows. Rotating turbulence possesses features distinct from non-rotating turbulence, including, for example, the emergence of coherent vortices, steepened energy spectrum, and quasi-two-dimensionalisation of the flow. For detailed reviews on these phenomena, see e.g. Godeferd & Moisy (2015) and Sagaut & Cambon (2008). More recently, it is also noted that some features depend strongly on the forcing scheme (Dallas & Tobias 2016). The synchronisation of rotating turbulence is investigated in Di Leoni et al. (2018, 2020), as mentioned above. These investigations leave some interesting questions unanswered. The most important one is how synchronisation depends on the rate of rotation. For example, how does the threshold wavenumber $k_c$ change with the rotation rate? Also, given the strong effects of the forcing term on the small scales of rotating turbulence (Dallas & Tobias 2016), how the forcing term affects synchronisation in rotating turbulence remains unclear. We intend to address these questions in the present investigation.

We use master–slave coupling instead of nudging. The former does not require specifying the coupling strength, hence reducing the number of control parameters by one. To characterise the synchronised state, we calculate the conditional Lyapunov exponents of the slave system, and quantify their dependence on rotation. Two different forcing mechanisms are considered, to illustrate the effects of the forcing term. As we will show later, rotation has significant impacts on the synchronisation behaviours, and the impacts depend strongly on the forcing term. We believe that these results are a useful addition to our understanding of rotating turbulence, especially concerning how to enhance its predictability via simulations equipped with data assimilation functionalities. The impact of the findings may be found in fields such as numerical weather prediction.

The paper is organised as follows. We introduce the governing equations, the controlling parameters, and the definition of conditional Lyapunov exponents in § 2. The numerical methods and a summary of the numerical experiments are presented in § 3, followed by the results and discussions. Section 4 concludes the paper with the main observations that we make from the numerical experiments.

2. Governing equations

We consider rotating turbulent flows in a $[0,2{\rm \pi} ]^3$ box with ${\boldsymbol {x}} = (x_1, x_2, x_3) = (x,y,z)$ representing the spatial coordinates. The flow satisfies the periodic boundary condition in all three directions. Let ${\boldsymbol {\varOmega }} \equiv \varOmega \hat {\boldsymbol {z}}$ be the rotation rate of a rotating frame of reference, where $\hat {\boldsymbol {z}}$ is the unit vector in the $z$ direction. Let ${\boldsymbol {u}}({\boldsymbol {x}},t)$ be the velocity field. For an observer in the rotating frame, the Navier–Stokes equation (NSE) reads (see e.g. Greenspan 1969)

(2.1)\begin{equation} D_t {\boldsymbol{u}} + 2 {\boldsymbol{\varOmega}} \times {\boldsymbol{u}} ={-} \boldsymbol{\nabla} p + \nu\,\nabla^2 {\boldsymbol{u}} + {\boldsymbol{f}}, \end{equation}

where

(2.2)\begin{equation} D_t \equiv \partial_t + ({\boldsymbol{u}} \boldsymbol{\cdot}\boldsymbol{\nabla}) \end{equation}

is the material derivative, with ${\boldsymbol {u}}$ the velocity, $p = p({\boldsymbol {x}},t)$ the pressure, $\nu$ the viscosity, and ${\boldsymbol {f}} = {\boldsymbol {f}}({\boldsymbol {x}},t)$ the forcing term. The density of the flow has been assumed to be unity. The velocity is assumed to be incompressible, so

(2.3)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{u}} = 0. \end{equation}

Two different forcing terms are considered in this investigation. In the first case,

(2.4)\begin{equation} {\boldsymbol{f}} \equiv (a_f\cos k_f x_2,0,0), \end{equation}

with $a_f = 0.15$ and $k_f =1$. Customarily, the flow driven by forcing terms of this type is called the Kolmogorov flow (Borue & Orszag 1996), therefore we call this forcing term the Kolmogorov forcing. Kolmogorov flow in general is inhomogeneous due to the sinusoidal form of the force, although we do not investigate the effects of the inhomogeneity in what follows. Kolmogorov forcing does not inject energy directly into turbulent velocity fluctuations. Rather, its role is to maintain the unstable mean velocity profile that generates turbulent fluctuations when it loses its stability (Borue & Orszag 1996). The parameter $k_f$ introduces a length scale, which will be at the order of the integral scale of the flow. A velocity scale can be defined from $k_f$ and $a_f$, which determines the order of magnitude of the turbulent kinetic energy of the flow.

In the second case, the forcing term is confined in a range of small wavenumbers in the Fourier space. Specifically, let $\hat {{\boldsymbol {u}}}({\boldsymbol {k}},t)$ be the Fourier transform of ${\boldsymbol {u}}$, and let $\hat {{\boldsymbol {f}}}({\boldsymbol {k}},t)$ be that of ${\boldsymbol {f}}$, with ${\boldsymbol {k}}$ being the wavenumber. The force is defined by

(2.5)\begin{equation} \hat{{\boldsymbol{f}}}({\boldsymbol{k}},t) =\begin{cases} A(t)\,\hat{{\boldsymbol{u}}}({\boldsymbol{k}}, t), & \vert {\boldsymbol{k}}\vert \leqslant k_{f, {max}}, \\ 0, & \vert {\boldsymbol{k}} \vert > k_{f, {max}}, \end{cases} \end{equation}

where $k_{f,{max}} = 2$, and $A(t)$ is given by

(2.6)\begin{equation} A(t) = \frac{ \epsilon_f}{\sum_{\vert {\boldsymbol{k}} \vert \leqslant k_{f,{max}}} \hat{{\boldsymbol{u}}}({\boldsymbol{k}},t)\,\hat{{\boldsymbol{u}}}^*({\boldsymbol{k}},t)}, \end{equation}

with $\epsilon _f = 0.05$, and $^*$ representing the complex conjugate. This forcing term injects kinetic energy into the flow field at a constant rate equal to $\epsilon _f$, via Fourier modes with $\vert {\boldsymbol {k}} \vert \leqslant k_{f,{max}}$. In the stationary stage, the mean energy dissipation rate of the flow would be the same as $\epsilon _f$. We call this forcing term ‘constant power forcing’.

Obviously, the two forcing terms are different in many ways, although both are commonly used in turbulent simulations. As will be shown below, the flow fields driven by the two forces are also different in many ways. To put this observation in context, we note that Dallas & Tobias (2016) investigate the effects of the forcing term on the evolution of rotating turbulence. They used a Taylor–Green forcing with a memory time scale $\tau _m$. With different $\tau _m$, one may obtain different stationary states. For example, the energy spectrum may display different slopes in different stationary states. In our simulations, the Kolmogorov forcing term is a constant, therefore has an infinite memory time. The constant power forcing has a memory time of the order of $(\epsilon _f k_{f, {max}}^2)^{-1/3} \approx 2$. Therefore, it is not surprising to find significant difference between the flows driven by the two different forces. The difference allows us to explore how the forcing terms affect the synchronisability of the flows.

The synchronisation of two flows is investigated by simulating them with same parameters concurrently. Let ${\boldsymbol {u}}^{(1)}$ and ${\boldsymbol {u}}^{(2)}$ be the velocity fields of the two flows, respectively. The velocity fields are initialised with different initial conditions, then evolve over time simultaneously according to the NSE. To synchronise the two flows, the Fourier modes of ${\boldsymbol {u}}^{(2)}$ with $\vert {\boldsymbol {k}}\vert \leqslant k_m$ are replaced by those of ${\boldsymbol {u}}^{(1)}$ at each time step. As such,

(2.7)\begin{equation} \hat{{\boldsymbol{u}}}^{(2)}({\boldsymbol{k}},t) = \hat{{\boldsymbol{u}}}^{(1)}({\boldsymbol{k}},t), \end{equation}

for $\vert {\boldsymbol {k}} \vert \leqslant k_m$ at all times. This way of coupling the two flows is usually termed master–slave coupling (Boccaletti et al. 2002). In this case, ${\boldsymbol {u}}^{(2)}$ is the slave, whereas ${\boldsymbol {u}}^{(1)}$ is the master.

It is expected that under suitable conditions, ${\boldsymbol {u}}^{(1)}$ and ${\boldsymbol {u}}^{(2)}$ will remain turbulent (chaotic) but they will synchronise, i.e. ${\boldsymbol {u}}^{(2)}$ will gradually approach ${\boldsymbol {u}}^{(1)}$. Let the norm of a generic vector field $\boldsymbol {w}$ be

(2.8)\begin{equation} \Vert \boldsymbol{w} \Vert^2 = \frac{1}{(2{\rm \pi})^3} \int_{[0,2{\rm \pi}]^3} \boldsymbol{w} \boldsymbol{\cdot} \boldsymbol{w}\,{\rm d}V. \end{equation}

The synchronisation error

(2.9)\begin{equation} \varDelta(t)\equiv \Vert {\boldsymbol{u}}^{(1)} - {\boldsymbol{u}}^{(2)}\Vert \end{equation}

will decay exponentially towards zero (Henshaw et al. 2003; Yoshida et al. 2005) when the two flows synchronise.

The ability to synchronise the two flows depends crucially on $k_m$, which we will call the coupling wavenumber. The Fourier modes in the two velocity fields with $\vert {\boldsymbol {k}} \vert > k_m$ are the slaved modes, whereas those with $\vert {\boldsymbol {k}} \vert \leqslant k_m$ are the master modes.

Synchronisation depends on various statistics of the flow field, which will be introduced briefly next. As ${\boldsymbol {u}}^{(1)}$ and ${\boldsymbol {u}}^{(2)}$ are both stationary turbulent flows with identical governing equations and control parameters, these statistics can be calculated from either of them. Therefore, we will use only ${\boldsymbol {u}}$ to indicate the velocity field. Let ${\boldsymbol {u}}'\equiv {\boldsymbol {u}} - \langle {\boldsymbol {u}} \rangle$ be the velocity fluctuations, where $\langle \cdot \rangle$ indicates ensemble average. The mean energy dissipation rate $\epsilon$ is defined as

(2.10)\begin{equation} \epsilon = 2 \nu \langle s'_{ij} s'_{ij} \rangle, \end{equation}

where $s'_{ij} = (\partial _j u'_i + \partial _i u'_j)/2$ is the fluctuating strain rate tensor. The small scales of the flow are characterised by the Kolmogorov length scale $\eta$ and the Kolmogorov time scale $\tau _k$, which are defined by (see e.g. Pope 2000)

(2.11a,b)\begin{equation} \eta = (\nu^3/\epsilon)^{1/4} \quad \text{and}\quad \tau_k = (\nu/\epsilon)^{1/2}, \end{equation}

respectively.

When two isotropic turbulent flows are synchronised with the coupling described above, it has been found (Yoshida et al. 2005; Lalescu et al. 2013; Li et al. 2022) that

(2.12)\begin{equation} \varDelta(t) \sim \exp( \alpha t/\tau_k), \end{equation}

where $\alpha$ is the decay rate (note that the error decays only when $\alpha <0$). The decay rate $\alpha$ is a function of $k_m \eta$. The value of $k_m$ for which $\alpha =0$ is the threshold wavenumber and is denoted by $k_c$. The normalised threshold wavenumber $k_c\eta$ is found to be $0.15\unicode{x2013}0.2$ for isotropic turbulence (Yoshida et al. 2005; Lalescu et al. 2013).

For rotating turbulence, it is expected that the Rossby number will play a role. The Rossby number can be defined using the small-scale parameters, leading to the micro-scale Rossby number (Godeferd & Moisy 2015)

(2.13)\begin{equation} Ro_k = \frac{1}{2\varOmega \tau_k}. \end{equation}

The large-scale Rossby number is defined as

(2.14)\begin{equation} Ro_\ell = \frac{u_{rms}}{2\varOmega \ell}, \end{equation}

where $u_{rms}\equiv (\langle u'_i u'_i\rangle /3)^{1/2}$ is the root mean square velocity, and $\ell$ is the integral length scale defined (Yoshida et al. 2005) as

(2.15)\begin{equation} \ell = \frac{\rm \pi}{2 u_{rms}^2}\int_0^\infty k^{{-}1}\,E(k) \,{\rm d}k, \end{equation}

with $E(k)$ the energy spectrum given by

(2.16)\begin{equation} E(k) = \frac{1}{2}\sum_{k\leqslant \vert {\boldsymbol{k}} \vert < k+1} \langle \hat{{\boldsymbol{u}}}({\boldsymbol{k}},t) \boldsymbol{\cdot} \hat{{\boldsymbol{u}}}^*({\boldsymbol{k}},t)\rangle. \end{equation}

Synchronisation of chaotic systems is related to the conditional Lyapunov exponent (CLE) of the slave system. To introduce the concept, let ${\boldsymbol {u}}$ be the master velocity field, and let ${\boldsymbol {u}}^\delta$ be an infinitesimal perturbation to the slaved modes of ${\boldsymbol {u}}$. Thus, by definition,

(2.17)\begin{equation} \hat{{\boldsymbol{u}}}^\delta({\boldsymbol{k}},t) = 0 \quad \text{for}\ \vert {\boldsymbol{k}} \vert \leqslant k_m. \end{equation}

In the meantime, ${\boldsymbol {u}}^\delta$ obeys the linearised NSE

(2.18)\begin{equation} D_t {\boldsymbol{u}}^\delta + ({\boldsymbol{u}}^\delta \boldsymbol{\cdot}\boldsymbol{\nabla}){\boldsymbol{u}} + 2 {\boldsymbol{\varOmega}} \times {\boldsymbol{u}}^\delta ={-} \boldsymbol{\nabla} p^\delta + \nu\,\nabla^2 {\boldsymbol{u}}^\delta + {\boldsymbol{f}}^\delta , \end{equation}

and the continuity equation $\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {u}}^\delta = 0$, where $p^\delta$ and ${\boldsymbol {f}}^\delta$ are the pressure perturbation and the perturbation in the forcing term, respectively.

The CLE, denoted by $\lambda (k_m)$, is defined as (Boccaletti et al. 2002; Nikolaidis & Ioannou 2022)

(2.19)\begin{equation} \lambda(k_m) = \lim_{t\to \infty} \frac{1}{t}\log \frac{\Vert {\boldsymbol{u}}^\delta({\boldsymbol{x}}, t+t_0)\Vert}{\Vert {\boldsymbol{u}}^\delta ({\boldsymbol{x}}, t_0)\Vert}, \end{equation}

where $t_0$ is the initial time. $\lambda (k_m)$ is a function of the coupling wavenumber $k_m$, and $\lambda (k_m=0)$ is the traditional (unconditional) Lyapunov exponent. As the unconditional Lyapunov exponent measures the average growth rate of a generic velocity perturbation over the turbulent attractor, $\lambda (k_m)$ measures the average growth rate of the slaved modes along a generic orbit ${\boldsymbol {u}}({\boldsymbol {x}},t)$. It is known that for canonical chaotic systems, synchronisation occurs only when the CLE is negative (Boccaletti et al. 2002). The same is confirmed for turbulent channel flows (Nikolaidis & Ioannou 2022). One of the questions to be addressed in the present investigation is how the CLE $\lambda (k_m)$ depends on the Rossby number.

For sufficiently large $t$, the velocity field ${\boldsymbol {u}}^\delta$ gives a measure on the most unstable perturbation to the slaved modes, thus is also of interest. This velocity field is called the Lyapunov vector (Ohkitani & Yamada 1989; Bohr et al. 1998), which is another quantity that we will look into.

An equation for $\Vert {\boldsymbol {u}}^\delta \Vert$ can be deduced from (2.18), which reads

(2.20)\begin{equation} \frac{{\rm d}}{{\rm d}t} \frac{\Vert {\boldsymbol{u}}^\delta\Vert^2}{2} = {\mathcal{P}} - {\mathcal{D}} + {\mathcal{F}}, \end{equation}

where

(2.21a,b,c)\begin{equation} {\mathcal{P}} \equiv \overline{- u_i^\delta u_j^\delta s_{ij}}, \quad {\mathcal{D}} \equiv \nu\,\overline{\partial_j u_i^\delta\,\partial_j u_i^\delta}, \quad {\mathcal{F}} \equiv \overline{f_i^\delta u^\delta_i} \end{equation}

are the production term, the dissipation term and the forcing term, respectively, and $s_{ij} = (\partial _j u_i + \partial _i u_j)/2$ is the strain rate tensor. In the above expressions, the overline represents spatial average. The periodic boundary condition has been used when deriving (2.20).

By virtue of (2.20), we obtain

(2.22)\begin{equation} \gamma(k_m,t) \equiv \frac{{\rm d}}{{\rm d}t} \log \Vert {\boldsymbol{u}}^\delta \Vert= \frac{{\mathcal{P}} - {\mathcal{D}} + {\mathcal{F}}}{\Vert {\boldsymbol{u}}^\delta\Vert^2} , \end{equation}

where $\gamma (k_m,t)$ is called the local CLE. Using (2.22), we can write

(2.23)\begin{align} \lambda(k_m) &=\lim_{t\to\infty}\frac{1}{t} \int_{t_0}^{t+t_0} \gamma(k_m,t) \,{\rm d}t \end{align}

(2.24)\begin{align} &=\lim_{t\to\infty}\frac{1}{t} \int_{t_0}^{t+t_0} \frac{{\mathcal{P}} - {\mathcal{D}} + {\mathcal{F}}}{\Vert {\boldsymbol{u}}^\delta\Vert^2} \,{\rm d}t. \end{align}

Therefore, the CLE $\lambda (k_m)$ is the long-time average of $\gamma (k_m,t)$. Whilst $\lambda (k_m)$ is a time-averaged quantity, $\gamma (k_m,t)$ fluctuates over time. Its variance contains information related to the stability of the synchronised state, and as such is also of some interest.

The rotation rate $\boldsymbol {\varOmega }$ does not appear in (2.24). Therefore, the rotation affects $\Vert {\boldsymbol {u}}^\delta \Vert$ only indirectly, through its effects on the production and dissipation terms. Insights into the effects of rotation on $\lambda (k_m)$, hence the synchronisation process, can be obtained from analyses of ${\mathcal {P}}$, ${\mathcal {D}}$ and ${\mathcal {F}}$. For example, the production term ${\mathcal {P}}$ depends crucially on the alignment between ${\boldsymbol {u}}^\delta$ and the eigenvectors of the strain rate tensor $s_{ij}$, as well as the eigenvalues of $s_{ij}$. These aspects will be looked into in our analyses.

The CLEs can be calculated according to (2.19) once ${\boldsymbol {u}}^\delta$ and ${\boldsymbol {u}}$ are available. To find ${\boldsymbol {u}}^\delta$, one might seek to integrate (2.18) numerically. However, this method suffers from the fact that ${\boldsymbol {u}}^\delta$ normally grows exponentially, so the numerics would fail before a sufficiently long time sequence of ${\boldsymbol {u}}^\delta$ could be obtained (which is needed to calculate $\lambda (k_m)$). We thus use a common alternative method (Wolf et al. 1985; Boffetta & Musacchio 2017), where we simulate two coupled flows ${\boldsymbol {u}}^{(1)}$ and ${\boldsymbol {u}}^{(2)}$ concurrently in the same way as described previously, except for two differences. First, ${\boldsymbol {u}}^{(2)}$ is initialised in such a way that the error $\varDelta (0)$ (cf. (2.9)) is a small quantity. Second, ${\boldsymbol {u}}^{(2)}$ is re-initialised repeatedly after each short time interval $\Delta t$, by rescaling ${\boldsymbol {u}}^{(2)}-{\boldsymbol {u}}^{(1)}$ to restore $\Vert {\boldsymbol {u}}^{(2)}-{\boldsymbol {u}}^{(1)} \Vert$ to its initial (small) value. The interval $\Delta t$ is chosen to be short enough such that the evolution of ${\boldsymbol {u}}^{(2)}-{\boldsymbol {u}}^{(1)}$ can be approximated accurately by the linearised NSE. As a result, ${\boldsymbol {u}}^\delta \approx {\boldsymbol {u}}^{(2)}-{\boldsymbol {u}}^{(1)}$. Therefore, we have

(2.25)\begin{equation} \gamma \approx \frac{1}{\Delta t}\log \frac{\Vert {\boldsymbol{u}}^{(2)}({\boldsymbol{x}}, t+\Delta t) - {\boldsymbol{u}}^{(1)}({\boldsymbol{x}}, t+\Delta t) \Vert}{\Vert {\boldsymbol{u}}^{(2)}({\boldsymbol{x}}, t) - {\boldsymbol{u}}^{(1)}({\boldsymbol{x}}, t) \Vert}, \end{equation}

from which we then can calculate $\lambda$ according to (2.23). For more details on the algorithm, see e.g. Boffetta & Musacchio (2017).

We remark that (2.24) gives us a way to calculate the CLEs via ${\mathcal {P}}$, ${\mathcal {D}}$ and ${\mathcal {F}}$, once ${\boldsymbol {u}}^\delta$ has been obtained in the way described above. We used both methods to cross-check the numerics, and found no difference in the results.

Finally, we note that $\varDelta (t)$ is the same as $\Vert {\boldsymbol {u}}^\delta \Vert$ when the two flows are synchronised. However, they are not interchangeable, because they would be significantly different when the two flows do not synchronise.

3. Numerical simulations and results

Equation (2.1) is integrated numerically in the Fourier space with the pseudo-spectral method. As is common for the simulation of rotating turbulence, the Fourier component $\hat {{\boldsymbol {u}}}$ is decomposed into helical modes $a_+({\boldsymbol {k}},t)$ and $a_-({\boldsymbol {k}},t)$, and the equations for $a_+$ and $a_-$ are integrated. Then, $\hat {{\boldsymbol {u}}}$ is reconstructed from $a_\pm$ using the helical decomposition. With this approach, the different components of the Coriolis force are decoupled in the equations for $a_\pm$, so that they (as well as the viscous diffusion term) can be treated with an integration factor that increases the stability of the algorithm.

The advection term is de-aliased according to the two-thirds rule so that the maximum effective wavenumber is $4{\rm \pi} /3N$, where $N^3$ is the number of grid points in the simulations. Time stepping is conducted with an explicit second-order Euler scheme, with a first-order predictor and a corrector based on the trapezoid rule (Li et al. 2020).

Simulations with $N^3=128^3$, $192^3$ and $256^3$ grid points are conducted. The majority of the analyses focus on rotation rates $\varOmega = 0.1$, $0.5$ or $1$. For the flows driven by Kolmogorov forcing, test cases with $\varOmega = 5$ are also simulated to demonstrate that two-dimensionalisation has happened at this rotation rate. Table 1 summarises the parameters for all the cases. We label the cases with a code of the form ‘${\rm F}a{\rm N}b\varOmega cd$’ or ‘${\rm F}a{\rm N}b\varOmega c$’, where letters $a$ to $d$ are numbers. The code records the type of forcing (with $1$ for Kolmogorov forcing, and $2$ for constant power forcing), the number of grid points, and the rotation rate of the case. For each case in table 1, sometimes multiple simulations are conducted with different $k_m$. To differentiate these simulations, we append ‘K’ and the value of $k_m$ to the end of the code. Thus, for example, case F1N128$\varOmega$01K5 is a $128^3$ simulation driven by Kolmogorov forcing with rotation rate $0.1$ and coupling wavenumber $k_m=5$, whereas case F2N256$\varOmega$1K7 is a $256^3$ simulation driven by constant power forcing with rotation rate 1 and $k_m = 7$.

Table 1. Parameters for the cases: $N^3$ is the number of grid points; $\varOmega$ is the rotation rate; $\nu$ is the viscosity; $\delta t$ is the time step size; $u_{rms}$ is the root mean square velocity; $\epsilon$ is the mean energy dissipation rate; $\eta$ is the Kolmogorov length scale; $\lambda$ is the Taylor length scale; $\tau _k$ is the Kolmogorov time scale; $Ro_k$ is the micro-scale Rossby number; $Re_\lambda \equiv u_{rms}\lambda /\nu$ is the Taylor micro-scale Reynolds number; $\ell$ is the integral length scale; and $Re_\ell \equiv u_{rms}\ell /\nu$ is the integral scale Reynolds number.

Multiple realisations of a case are simulated in some cases to obtain convergent statistics for some quantities (e.g. for the variance of the CLEs shown in figure 16).

Since the main focus of this investigation is on the effects of rotation, the simulations have only moderate Reynolds numbers. On the other hand, table 1 shows that the micro-scale Rossby number in some cases is as small as $1.34$ and $1.44$. Therefore the range of cases does cover flows where rotation will have significant impacts on the small scales.

The CLEs are calculated according to the method explained in § 2. The velocity ${\boldsymbol {u}}^{(1)}$ is initialised with a fully developed turbulent velocity field, and ${\boldsymbol {u}}^{(2)}$ is initialised with ${\boldsymbol {u}}^{(1)} + \delta {\boldsymbol {u}}$, where $\delta {\boldsymbol {u}}$ is composed of random numbers distributed uniformly in the interval $[0, 10^{-6} u_{rms}]$. When we calculate the CLEs with a threshold wavenumber $k_m$, ${\boldsymbol {u}}^{(2)}$ is coupled with ${\boldsymbol {u}}^{(1)}$ such that (2.7) is true at all times. The time interval $\Delta t$ between rescaling the magnitude of ${\boldsymbol {u}}^{(2)}-{\boldsymbol {u}}^{(1)}$ is $\Delta t \approx 0.1 \tau _k$. These values are approximately the same as the ones used in Boffetta & Musacchio (2017).

3.1. Basic features of the flow fields

We present some results in this subsection to illustrate the basic features of the flow fields. The energy spectra normalised by Kolmogorov parameters are shown in figure 1. For the flows driven by Kolmogorov forcing shown in figure 1(a), the normalised spectra collapse onto a single curve except for the few lowest wavenumbers. At the lowest wavenumbers, the spectra increase with the rotation rate, which shows increased energetics for the large scales, consistent with our understanding of rotating turbulence.

Figure 1. The energy spectra: (a) cases with Kolmogorov forcing; (b) cases with constant power forcing. The dashed line without symbols indicates the $k^{-2}$ power law. The dash-dotted line without symbols indicates the $k^{-3}$ power law.

The Reynolds number for the flow is relatively small, so no clear inertial range can be identified. Nevertheless, the spectra appear to be consistent with the $k^{-2}$ scaling law that has been reported in previous research (Yeung & Zhou 1998; Dallas & Tobias 2016).

For the flows driven by constant power forcing, similar behaviours are observed for lower rotation rates, as shown in figure 1(b). However, for $\varOmega = 1$, the spectra have steeper slopes in the mid-wavenumber range, and they appear to be more consistent with the $k^{-3}$ power law. The spectra in the dissipation range also appear to drop off at a faster rate. The contrast between figures 1(a) and 1(b) shows that the forcing terms can lead to significant quantitative differences in the flows.

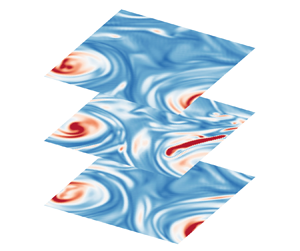
In both flows, energy pile-up is observed at the lowest wavenumber end of the spectra, and the pile-up increases slightly with the rotation rate. The pile-up is an indication of the emergence of large-scale columnar vortices, which is a common feature of rotating turbulence. Columnar vortices are indeed observable visually in our simulations with the larger rotation rates, which are illustrated in figures 2(a,b) for two simulations with $\varOmega = 1$. The figures show snapshots of the distribution of $\vert {\boldsymbol {\omega }}\vert$ on three horizontal cross-sections of the flow domain, where ${\boldsymbol {\omega }} \equiv \boldsymbol {\nabla } \times {\boldsymbol {u}}$ is the vorticity. A columnar vortex is visible at the left corner in both flows. Figure 2(a) shows a simulation with a smaller Reynolds number. In this case, the diameter of the columnar vortex is roughly half of the size of the domain. For the flow with a larger Reynolds number (figure 2b), the background vorticity is stronger, and the columnar vortex appears to be slightly smaller in size but is still clearly visible. We will not show the results for other rotation rates, but we can confirm that columnar vortices are also quite prevalent for $\varOmega = 0.5$, while they are rare for $\varOmega = 0.1$.

Figure 2. Snapshots of the $\vert {\boldsymbol {\omega }}\vert$ distribution taken at three horizontal layers at the same time $t$ for $\varOmega = 1$ with Kolmogorov forcing: (a) from a case with $N=128$; (b) from a case with $N=192$.

The probability density function (p.d.f.) of the vorticity component along the rotation axis is also of interest because it is well known that the p.d.f. displays a positive skewness (Bartello, Mètais & Lesieur 1994; Morize, Moisy & Rabaud 2005) in rotating turbulence, due to the prevalence of cyclonic vortices over the anticyclonic ones. The skewness emerges as rotation is introduced, peaks at an intermediate rotation rate, and then decreases when the rotation rate increases further as the flow is two-dimensionalised under strong rotation. The p.d.f.s for our simulations are plotted in figure 3. The p.d.f.s are indeed skewed towards the positive values, with the corresponding skewness given in parentheses. For flows driven by constant power forcing with $N=128$, the skewness for $\varOmega = 1$ is slightly smaller than that for $\varOmega = 0.5$. In other cases, the skewness increases with the rotation rate. These p.d.f.s show, from another angle, that the effects of rotation are clearly significant.

Figure 3. The p.d.f. of the vorticity component along the rotation axis $\omega _z$: (a) cases with Kolmogorov forcing; (b) cases with constant power forcing.

Table 1 shows that compared with the flows driven by constant power forcing, those driven by Kolmogorov forcing tend to have larger micro-scale Rossby numbers $Ro_k$ for a given rotation rate $\varOmega$. In order to obtain even smaller $Ro_k$ for the latter flows, we computed a few test cases with $\varOmega = 5$, and found that the flows are strongly two-dimensionalised at this rotation rate. Let $E_{2D}(t)$ be the kinetic energy in the two-dimensional Fourier modes with $k_z = 0$, and let $E(t)$ be the total kinetic energy, i.e.

(3.1a,b)\begin{equation} E_{2D}(t) = \frac{1}{2}\sum_{\{{\boldsymbol{k}}:\,k_z = 0\}} \hat{{\boldsymbol{u}}}({\boldsymbol{k}},t) \boldsymbol{\cdot}\hat{{\boldsymbol{u}}}^*({\boldsymbol{k}},t), \quad E(t) = \frac{1}{2}\sum_{{\boldsymbol{k}}} \hat{{\boldsymbol{u}}}({\boldsymbol{k}},t) \boldsymbol{\cdot}\hat{{\boldsymbol{u}}}^*({\boldsymbol{k}},t). \end{equation}

The results for $E_{2D}(t)$ and $E(t)$ for the flows with $\varOmega = 5$ (i.e. cases F1N128$\varOmega$5 and F1N192$\varOmega$5) are shown in figure 4(a). As a comparison, the results for $\varOmega = 1$ are shown in figure 4(b). It can be observed that for $\varOmega = 5$, both $E(t)$ and $E_{2D}(t)$ are an order of magnitude higher than for $\varOmega = 1$, and almost all energy is contained in the two-dimensional modes as $E_{2D}(t)$ deviates from $E(t)$ only slightly. There are regular periods of time in which $E_{2D}(t)$ is indistinguishable from $E(t)$. These behaviours suggest that at $\varOmega = 5$, the flows are quasi-two-dimensionalised with large-scale, two-dimensional columnar vortices, where instability sets in periodically, which leads to temporary small deviation between $E_{2D}(t)$ and $E(t)$. A detailed discussion of this process can be found in Alexakis (2015). The energy spectra for the flow with $\varOmega =5$ at various times are shown in figure 4(c) in green lines, together with those for $\varOmega = 1$ with both forcing terms (shown in black or red). The high-wavenumber ends of the spectra swing violently over time, in a range spanning five orders of magnitude. Though oscillations are also seen in the spectra for the flows with $\varOmega = 1$, the amplitude is much smaller.

Figure 4. (a) Kinetic energy of the flow field and that in the two-dimensional modes for $\varOmega = 5$. (b) The same for cases with $\varOmega = 1$ and $N=128$. (c) Instantaneous energy spectra for cases with $N=128$, plotted every $10\tau _k$ for time spanning $300\tau _k$. Green lines indicate $\varOmega = 5$; red lines indicate $\varOmega = 1$ with constant power forcing; black lines indicate $\varOmega = 1$ with Kolmogorov forcing.

To summarise, the results in this subsection show that for $\varOmega = 0.1$, $0.5$ and $1$, the flows are still predominantly turbulent while displaying strong effects of rotation. The flows where $\varOmega = 5$, on the other hand, appear to be mostly two-dimensionalised and display only weakly turbulent behaviours. We will limit our interest to the synchronisation of flows where turbulence dominates. Therefore, we will focus on the first three rotation rates, and the cases with $\varOmega = 5$ will not be discussed further in what follows.

3.2. Synchronisation error

We now look into the synchronisation of the flows. To obtain smoother results, the data shown in this subsection are the averages of five realisations.

Figure 5 shows the decay of the synchronisation error $\varDelta (t)/\varDelta (0)$ for different $k_m$ and $\varOmega$ with Kolmogorov forcing. Figures 5(a,b,c) correspond to three different Reynolds numbers. There are three common trends across all cases included in these three plots. First, the error decays exponentially when $k_m$ is sufficiently large. Second, the decay rate increases with $k_m$. Third, the error decays only when $k_m$ is greater than some threshold $k_c$, and clearly $k_c$ is different in different cases. For $k_m$ close to but still greater than $k_c$, the error still decays over time, but the rate of decay fluctuates, so exponential functions do not always provide a good fit.

Figure 5. The normalised synchronisation error $\varDelta (t)/\varDelta (0)$ for the cases with Kolmogorov forcing: (a) $N=128$, (b) $N=192$, (c) $N=256$; (d) comparison between cases with different Reynolds numbers.

Comparison across figures 5(a,b,c) shows that the decay rate of the error displays the known dependence on the Reynolds number, namely, everything else being equal, the decay rate decreases as the Reynolds number increases. This trend is illustrated in figure 5(d) with selected cases, with $\varOmega = 0.5$ and $k_m = 9$. As this effect has been reported multiple times in previous research, we will not delve too much into it. For the same reason, we consider only the cases with $N=128$ and $N=192$ for flows with constant power forcing.

More pertinent to our objectives is the observation that rotation has a strong effect on the decay rate. Figure 5 shows that for the same $k_m$, the decay rate decreases with $\varOmega$. The same trend is observed for different Reynolds numbers, as is shown in figures 5(a,b,c).

The results corresponding to constant power forcing are plotted in figure 6. Not surprisingly, $\varDelta (t)$ decays exponentially for sufficiently large $k_m$. Moreover, the dependence of the decay rate on $k_m$ and $Re_\lambda$ is qualitatively similar to that which is observed in figure 5. However, interestingly, the dependence on rotation is significantly different. The black lines in figure 6(a) illustrate the difference clearly. The three black lines correspond to the same $k_m$ but three different rotation rates. While the decay rates for $\varOmega = 0.1$ and $0.5$ show no clear differences, the decay rate for $\varOmega = 1$ is clearly larger. That is, in this case, it appears that the decay rate for $\varDelta (t)$ increases with rotation. The same trend is seen in figure 6(b), which is for flows with a larger Reynolds number. This observation is opposite to the trend that we observe in the cases with Kolmogorov forcing (cf. figure 5), where the decay rate for the same $k_m$ is found to decrease with rotation. The difference in the results for the two forcing terms has not been reported before.

Figure 6. The synchronisation error $\varDelta (t)$ for the cases with constant power forcing: (a) $N=128$, (b) $N=192$.

3.3. Conditional Lyapunov exponents and the threshold wavenumbers

The synchronisability of the slaved flow is related to the CLEs. We calculate the CLEs $\lambda (k_m)$ as well as the local CLEs $\gamma (k_m,t)$ using the algorithm outlined in § 2. The results are presented in terms of the non-dimensionalised CLEs $\varLambda$ and the non-dimensionalised local CLEs $\varGamma$, which are defined as

(3.2a,b)\begin{equation} \varLambda = \lambda \tau_k, \quad \varGamma = \gamma \tau_k. \end{equation}

Here, $\varGamma$ is time dependent and fluctuates over time. Without showing the time sequences, we note that after a period of transience, $\varGamma$ stabilises and fluctuates around a constant value. The magnitude of the fluctuations appears to increase with rotation, but decreases as $k_m$ increases. We will quantify some of these behaviours in what follows, starting with $\varLambda$, which is the average of $\varGamma$ in the stationary stage.

Figure 7 is shown first to establish the relationship between the decay rate of $\varDelta (t)$ and the CLE $\varLambda$. Shown with symbols in the figure are $\varDelta (t)/\varDelta (0)$ for a number of cases already discussed in figures 5 and 6. The lines without symbols represent functions $\exp (\varLambda t/\tau _k)$, where $\varLambda$ is the CLE for the corresponding flow. Some small discrepancies are seen between the two, which we attribute to statistical uncertainty in the data. We note that the discrepancies are in line with those found in previous research (e.g. Nikolaidis & Ioannou 2022). The overall agreement between the two shows that in most cases, the error decays exponentially and the decay rate $\alpha$ equals $\varLambda$. For the case shown with the black line and triangles, $\varDelta (t)$ does not decay exponentially. However, it undulates mildly around the exponential function in such a way that $\varLambda$ appears to capture the long-time mean decay rate. Overall, we may conclude that the decay rate of $\varDelta (t)$ is equal to $\varLambda$, and the synchronisation between two flows can be characterised by $\varLambda$.

Figure 7. Comparison between the decay rates of $\varDelta (t)$ and the CLEs.

As an aside, we note that a larger discrepancy is observed for case F1N128$\varOmega$01K7 than for case F2N192$\varOmega$1K9. This observation appears counter-intuitive at first sight, since $\varOmega$ is larger in the latter case, which should lead to a larger fluctuation in $\varGamma$ hence a larger statistical error in $\varLambda$ (or the corresponding decay rate $\alpha$). However, there is another difference between these two cases, which is that case F2N192$\varOmega$1K9 is computed with a larger $k_m$. As the fluctuation in $\varGamma$ is smaller for larger $k_m$, it is possible that the statistical discrepancy in case F2N192$\varOmega$1K9 is smaller despite the fact that it is computed with a larger $\varOmega$.

We now focus on the results for $\varLambda$. The dependence of $\varLambda$ on the rotation rate $\varOmega$ and the coupling wavenumber $k_m$ is shown in figure 8, including cases with $k_m=0$ where $\varLambda$ represents the unconditional Lyapunov exponent. Figure 8(a) presents the cases with Kolmogorov forcing. In these cases, $\varLambda$ always increases with $\varOmega$, and $\varLambda$ increases with $\varOmega$ quicker for larger $k_m$. The blue lines, which correspond to $k_m=5$ for $N=128$ and $k_m=7$ for $N=192$, are particularly instructive. In these cases, $\varLambda$ increases from a negative value to a positive one as $\varOmega$ increases from $0.1$ to $1$. Therefore, the two flows synchronise when $\varOmega = 0.1$, but they do not when $\varOmega = 1$, which shows emphatically that rotation makes the flows more difficult to synchronise when the flow is driven by Kolmogorov forcing. However, the observation is different for the flows maintained by constant power forcing, which are shown in figure 8(b). In fact, the trend is reversed in this case: here, $\varLambda$ decreases as $\varOmega$ increases, so the flow is easier to synchronise as rotation is increased. Also, the unconditional Lyapunov exponent appears more sensitive to the rotation rate.

Figure 8. Normalised CLEs $\varLambda$ as functions of the rotation rate $\varOmega$ for the cases with (a) Kolmogorov forcing, and (b) constant power forcing. Solid lines indicate $N=128$; dashed lines indicate $N=192$. For $N=128$, squares indicate $k_m=0$, upward triangles indicate $k_m=3$, downward triangles indicate $k_m=5$, and diamonds indicate $k_m=7$. For $N=192$, squares indicate $k_m=0$, upward triangles indicate $k_m=5$, downward triangles indicate $k_m=7$, and diamonds indicate $k_m=9$.

Another observation that we can make from figure 8 is that $\varLambda$ decreases with $k_m$, which can be seen by comparing different curves in the same plot. This trend is investigated further by plotting $\varLambda$ as a function of $k_m\eta$, which is given in figure 9. We first note the values of $\varLambda$ at $k_m = 0$ for $\varOmega = 0.1$. As $\varOmega$ is relatively small, one expects $\varLambda$ to be close to the value found in non-rotating turbulence. Figure 9 shows that $\varLambda$ in this case is approximately $0.1$, though it depends weakly on the Reynolds number as well as the forcing term. This value is indeed close to values found previously for non-rotating turbulence (Boffetta & Musacchio 2017).

Figure 9. Normalised CLEs $\varLambda$ as functions of $k_m\eta$: (a) cases with Kolmogorov forcing; (b) cases with constant power forcing.

Figure 9 shows that for cases with Kolmogorov forcing, $\varLambda$ decreases as $k_m\eta$ increases. More interestingly, the curves corresponding to different cases collapse on each other approximately. The one for $N=192$ and $\varOmega = 1.0$ is slightly larger than the rest. Nevertheless, overall, as a function of $k_m\eta$, $\varLambda$ depends on rotation only weakly. Note that this observation does not contradict the results in figure 8, as the values of $k_m$ in the latter are not non-dimensionalised by $\eta$, and $\eta$ is different for different $\varOmega$.

For the cases with constant power forcing, figure 9(b) shows that $\varLambda$ decreases with $k_m\eta$ in a similar manner. However, the curves corresponding to different $\varOmega$ do not collapse well. In fact, $\varLambda (k_m\eta )$ tends to decrease as $\varOmega$ increases, in particular for stronger rotations.

The threshold wavenumber $k_c$ where $\varLambda$ is zero is of particular interest, as it is the value of $k_m$ for which synchronisation fails. The values of $k_c$ can be found from figure 9, as they are the values of $k_m$ where the curves cross the horizontal axis $\varLambda = 0$, which can be read from the figure directly. The values are plotted as functions of the micro-scale Rossby number $Ro_k$ in figure 10.

Figure 10. Threshold coupling wavenumber $k_c$ as a function of the micro-scale Rossby number $Ro_k$.

Interestingly, figure 10 shows that $k_c\eta$ essentially does not depend on rotation when the flows are driven by Kolmogorov forcing, within the range of rotation rates that we have considered. To two decimal places, $k_c\eta = 0.20$ or $0.19$ for all rotation rates, which is the value obtained in Yoshida et al. (2005) for non-rotating isotropic turbulence.

This result seems to be contradictory to the observation that the decay rate for a given $k_m$ decreases with rotation. However, it can be explained as follows. The decay rates of the synchronisation error are reduced when rotation is introduced, which leads to increased $k_c$. However, as table 1 shows, $\eta$ is decreased by rotation in this type of flow. The end result is that $k_c\eta$ remains roughly a constant.

For the flows driven by constant power forcing, it appears from figure 10 that there is a consistent trend where $k_c\eta$ decreases as $Ro_k$ decreases (i.e. as rotation rate increases). For the smallest $Ro_k$, $k_c\eta$ is reduced to below $0.15$. Therefore, for the flows driven by constant power forcing, rotation does increase the synchronisability of the flow, and this is reflected in both an increased decay rate for the synchronisation error, and a reduced $k_c\eta$.

Di Leoni et al. (2020) reported that rotating turbulence was easier to synchronise, which they attributed to the coherent vortices induced by rotation. Our results for constant power forcing are consistent with their finding, which thus might be explained qualitatively in a similar way. However, the results for Kolmogorov forcing show that the physical picture can depend on the forcing scheme.

It is instructive to cross-check the results for $k_c$ with the energy spectra of the flows. Note that in the majority of cases, the spectra are consistent with a $k^{-2}$ power law (cf. figure 1). Therefore, the dimensionless threshold wavenumber $k_c\eta$ remains approximately unchanged from the value for isotropic turbulence when the spectrum steepens from $k^{-5/3}$ to $k^{-2}$. On the other hand, when the slope of the energy spectra is further steepened, reaching approximately that of the $k^{-3}$ power law, $k_c\eta$ does become smaller, as in the cases with the constant power forcing when $\varOmega = 1$.

To parametrise the decay rate of the synchronisation error with a physical quantity, Yoshida et al. (2005) look into the enstrophy content in the master modes. Let $H_\omega ^m = \sum _{k \leqslant k_m} k^2\,E(k)$ be the enstrophy contained in the master modes, and let $H_\omega = \sum _k k^2\,E(k)$ be the enstrophy of the whole velocity field. They find that in isotropic turbulence, the decay rate $\alpha$ is a universal function of the ratio $H_\omega ^m/H_\omega$, and the ratio at the threshold wavenumber $k_c$, denoted by $H_\omega ^c/H_\omega$, is approximately $0.35$. We plot $H_\omega ^c/H_\omega$ as a function of $Ro_k$ in figure 11 for our simulations. For the largest $Ro_k$, the ratio is approximately $0.36$, which is close to the value found in Yoshida et al. (2005). The ratio increases consistently with rotation for both forcing terms, even for larger values of $Ro_k$ where $k_c\eta$ remains a constant in the flows with Kolmogorov forcing. However, the results for different cases do not collapse on a unique curve. Therefore, it seems that $H^c_\omega /H_\omega$ does not provide a simple way to characterise $k_c$ in rotating turbulence.

Figure 11. Enstrophy ratio $H_\omega ^c/H_\omega$ as a function of the micro-scale Rossby number $Ro_k$.

Another way to characterise $k_c$ is put forward by Di Leoni et al. (2020), who observe that $k_c$ marks approximately the end of the inertial range. The observation is corroborated in Nikolaidis & Ioannou (2022). As the Reynolds numbers for our simulations are relatively small, this observation is not assessed here even though it is highly desirable to do so. Rather, we comment on a potential relationship between $k_c$ and the energy spectrum of the Lyapunov vector ${\boldsymbol {u}}^\delta$, which provides another perspective on the threshold wavenumbers.

Figure 12 plots the energy spectra of ${\boldsymbol {u}}^\delta ({\boldsymbol {x}},t)$ averaged over $t$ in the stationary stage. As the magnitude of ${\boldsymbol {u}}^\delta$ is irrelevant, the energy spectra have been normalised such that the total energy is unity. Also note that included in this figure are the results with $k_m=0$ – they are the spectra of the unconditional Lyapunov vectors.

Figure 12. The energy spectra of the Lyapunov vectors ${\boldsymbol {u}}^\delta$ for $k_m=0$: (a) for the cases with Kolmogorov forcing; (b) for the cases with constant power forcing. The spectra have been normalised in such a way that the total energy is unity.

Figure 12(a) is for the flows driven by Kolmogorov forcing. First, the energy spectra peak at an intermediate wavenumber. That is, the perturbations with energy localised on intermediate wavenumbers are the most unstable. This observation is consistent with Ohkitani & Yamada (1989), where the Lyapunov vector for a shell model is calculated, and they find that the energy spectrum of the Lyapunov vector is localised in the inertial range. Interestingly, the peaks of the spectra here are all found at approximately $k\eta = 0.2$, i.e. at approximately the threshold wavenumber. Similar features are found in figure 12(b), which shows the results for constant power forcing. Again, in most cases, the peaks are found at approximately $k_c\eta$. In particular, for the two cases with $\varOmega = 1$, the peaks are found to shift to lower $k\eta$, consistent with figure 10, which shows that $k_c\eta$ is also reduced in these two cases.

It is desirable to compare the peak wavenumbers with $k_c$ quantitatively. There are some challenges in extracting precise peak wavenumbers due to two factors: first, the spectra of ${\boldsymbol {u}}^\delta$ at lower wavenumbers display stronger statistical fluctuations; second, the gap between two data points on the spectra is $\Delta k = 1$, which is fairly large and potentially introduces error into the reading of the peak wavenumbers. In order to reduce the uncertainty, we average the spectra over five realisations. We then fit a smooth curve to the spectra using cubic splines. The peak wavenumber of the fitted curve is taken to be the peak wavenumber of the spectrum.

The cubic spline fitting is conducted using scipy function UnivariateSpline, with smoothing factor $s$ chosen as $0.01\,\%$ of the maximum of the spectrum, which implies that the 2-norm of the residue of the fitting is smaller than $s$. In other words, only a very small amount of smoothing is allowed.

The peak wavenumbers extracted in the above manner are plotted in figure 13 together with $k_c$, which has been shown in figure 10. The peak wavenumber obtained in this way usually falls between two integer wavenumbers. These two wavenumbers are used to define the error bars in figure 13. The figure confirms the qualitative comments that we made previously. The peak wavenumbers are slightly larger than $k_c$ in most cases. However, they do display the same trends as $k_c$. In particular, for flows driven by constant power forcing, the peak wavenumber clearly drops off significantly for the smallest $Ro_k$, despite the uncertainty in the data.

Figure 13. Comparison between the peak wavenumbers for the spectra of the Lyapunov vectors and $k_c$: (a) cases with $N=128$; (b) cases with $N=192$. Solid lines and solid symbols indicate $k_c\eta$ (same as figure 10). Dashed lines and empty symbols indicate normalised peak wavenumbers of the spectra of the Lyapunov vectors. Lower groups and left-hand $y$-axes are for cases with constant power forcing. Upper groups and right-hand $y$-axes are for cases with Kolmogorov forcing. The error bars correspond to the two adjacent integer wavenumbers.

One plausible explanation for the correlation between $k_c$ and the peak wavenumber of the energy spectrum of ${\boldsymbol {u}}^\delta$ is as follows. Let the coupling wavenumber be $k_m$ in a synchronisation experiment. The peak wavenumber corresponds to the Fourier modes most susceptible to infinitesimal perturbations (on average). One may hypothesise that to synchronise two flows, the perturbations to these most unstable Fourier modes should be suppressed by the coupling in the synchronisation experiments. This suggests that the coupling wavenumber $k_m$ should be larger than the peak wavenumber. However, even though only Fourier modes with wavenumbers up to $k_m$ in the two flows are coupled by design (in fact, they are exact copies of each other), the Fourier modes with wavenumbers slightly larger than $k_m$ are also strongly coupled, due to the fact that they are linked to the master modes through nonlinear inter-scale interactions. The coupling suppresses the growth of the synchronisation errors in these modes. Therefore, synchronisation can still be achieved even if $k_m$ is slightly smaller than the peak wavenumber. As a result, the threshold wavenumber $k_c$ could be slightly smaller than the peak wavenumber in the spectrum of ${\boldsymbol {u}}^\delta$.

The spectra of the Lyapunov vectors corresponding to the conditional CLEs, namely the conditional Lyapunov vectors, are given in figure 14 for the cases where $N=128$, and compared with the unconditional ones. For readability of the figures, only cases where $\varOmega = 0.1$ and $1$ with selected $k_m$ are included. Note that the spectra for the conditional Lyapunov vectors start from wavenumber $k_m+1$ as $\hat {{\boldsymbol {u}}}^{\delta }({\boldsymbol {k}},t) = 0$ for $\vert {\boldsymbol {k}} \vert \leqslant k_m$. The value of $k_m\eta$ for each case is shown in parentheses, which can be compared with the value of $k_c\eta$ to determine if synchronisation is achievable in the case. The interesting observation to note is demonstrated most clearly by both the solid and dashed green lines with triangles in figure 14(a), which correspond to $k_m=3$ for $\varOmega = 0.1$ and $1$, respectively. The flows do not synchronise in these two cases, while they do in all other cases depicted in the plot. The common feature of the spectra in these two cases is that the spectra peak at wavenumbers corresponding to the slaved modes. On the other hand, the spectra for the other cases all peak at $k_m+1$. The same trend can be observed in figure 14(b), and for cases with $N=192$ shown in figure 15. It appears that synchronisation can be achieved only when the energy spectrum of the conditional Lyapunov vector does not have a local maximum among the slave modes.

Figure 14. The energy spectra of the conditional Lyapunov vectors ${\boldsymbol {u}}^\delta$ for different $k_m$ and $N=128$. The values of $k_m\eta$ are shown in parentheses. (a) Cases with Kolmogorov forcing, where $k_c \eta = 0.20$ for both $\varOmega = 0.1$ and $1$. (b) Cases with constant power forcing, where $k_c \eta = 0.19$ for $\varOmega = 0.1$, and $k_c \eta = 0.13$ for $\varOmega = 1$.

Figure 15. Same as figure 14 but for $N=192$. (a) Cases with Kolmogorov forcing, where $k_c \eta = 0.20$ for both $\varOmega = 0.1$ and $1$. (b) Cases with constant power forcing, where $k_c \eta = 0.20$ for $\varOmega = 0.1$, and $k_c \eta = 0.16$ for $\varOmega = 1$.

Although the above results for the conditional Lyapunov vectors are of a qualitative nature, they also suggest that the threshold wavenumber $k_c\eta$ might be associated with the peak of the spectrum of the Lyapunov vector. Given that our simulations cover only a moderate range of Rossby numbers, with relatively low Reynolds numbers, how this observation generalises to a wider range of parameter values requires further investigation.

3.4. The statistics of the local CLEs

As commented previously, the local CLEs $\varGamma$ display significant fluctuations. In this subsection, we present statistics of $\varGamma$ for a few selected cases to highlight the qualitative trends that are shared by the other cases. The statistics in this subsection are all calculated by averaging over time as well as five independent realisations. The average is denoted by $\langle \cdot \rangle$.

The variance of $\varGamma$, ${\rm Var}(\varGamma ) = \langle (\varGamma - \langle \varGamma \rangle )^2\rangle$, is shown in figure 16 for the cases indicated in the figure. The variance clearly increases with rotation in all cases for a given $k_m$, and for a given $\varOmega$, it is smaller for larger $k_m$. The behaviours at high rotation rates are different for the two forcing terms. The variance for constant power forcing seems to increase more slowly at higher rotation rates.

Figure 16. The variance of the normalised local Lyapunov exponent $\varGamma$ for selected cases.

The p.d.f.s of $\varGamma$, shown in figure 17 for the same selected cases, exhibit largely the same behaviours already shown by the mean CLEs and the variances. A common feature is that the width of the p.d.f. increases with the rotation rate. Note that the p.d.f.s are not normalised. The increase in the width is thus a manifestation of increased variance.

Figure 17. The p.d.f.s of the local Lyapunov exponent $\varGamma$ for selected cases: (a) cases with Kolmogorov forcing; (b) cases with constant power forcing. Note that the p.d.f.s are not normalised.

For Kolmogorov forcing (figure 17a), the p.d.f.s of the unconditional $\varGamma$ (with $k_m=0$) do not move significantly with the rotation rate. For $k_m = 7$, the p.d.f. moves towards the positive values as rotation is strengthened, indicating increased mean CLE. These behaviours are consistent with figure 8. The behaviours of the p.d.f.s for constant power forcing (figure 17b) are also consistent with figure 8. One notable difference with the results in figure 17(a) is that the p.d.f.s for the unconditional Lyapunov exponents are affected more strongly by rotation in this case. For example, the p.d.f. for $\varOmega = 1$ is moved to the left significantly, while the same is not observed for the corresponding case in figure 17(a).

At higher rotation rates, the p.d.f.s often have significant probabilities to take both positive and negative values, e.g. those for F1N192$\varOmega$1K7 and F1N192$\varOmega$05K7, and those with constant power forcing and $k_m=5$. Therefore, for these cases, even if synchronisation is achieved in the long term, the synchronisation error $\varDelta (t)$ may increase temporarily when the local CLE is positive. This behaviour is observed in figures 5 and 6 for some $k_m$ values near the threshold wavenumber.

3.5. Statistics of energy production and dissipation

Some understanding of $\varGamma$ and $\varLambda$ can be gained from (2.22). Our calculation shows that the contribution of the forcing term ${\mathcal {F}}$ is always negligible. In what follows, we present only the results related to the production term ${\mathcal {P}}$ and the dissipation term ${\mathcal {D}}$. We use

(3.3a,b)\begin{equation} P \equiv \left\langle \frac{ \tau_k{\mathcal{P}}}{\Vert {\boldsymbol{u}}^\delta \Vert^2} \right\rangle , \quad D \equiv \left\langle \frac{\tau_k{\mathcal{D}} }{\Vert {\boldsymbol{u}}^\delta \Vert^2} \right\rangle \end{equation}

to denote the averaged non-dimensionalised production and dissipation terms, respectively.

The values of $P$ and $D$ are shown in figures 18 and 19. For completeness, results for $N=128$ and $192$ have both been included, but we will comment mainly on those for $N=128$ as the trends are the same for $N=192$. Figure 18 shows the results for the cases with Kolmogorov forcing. We can see that both $P$ and $D$ depend strongly on $k_m$, but are less sensitive to the value of $\varOmega$. The production term $P$ decreases as $k_m$ increases, while the dissipation $D$ increases in the meantime. Thus both contribute to the decrease in $\varGamma$, hence $\varLambda$, as $k_m$ increases. For a given $k_m$, $P$ increases slightly with rotation rate $\varOmega$. On the other hand, $D$ increases slightly with $\varOmega$ for smaller $k_m$, but decreases with $\varOmega$ for larger $k_m$. Overall, $P$ and $D$ change only slightly with $\varOmega$.

Figure 18. The production term $P$ and the energy dissipation term $D$ for cases with Kolmogorov forcing: (a) $N=128$, (b) $N=192$.

Figure 19. Same as figure 18, but for cases with constant power forcing.

For the cases with constant power forcing, figure 19 shows that the main impact of rotation is on the production term $P$. However, in this case $P$ decreases as rotation is increased, i.e. the trend is opposite to what is shown in figure 18. This trend is consistent with the previous observation that in this case synchronisation is easier when $\varOmega$ is larger. Dissipation $D$ does not depend strongly on $\varOmega$.

Further insights into $P$ can be obtained by looking into the alignment between ${\boldsymbol {u}}^\delta$ and $s_{ij}$. Let $s^+_{ij} \equiv \tau _k s_{ij}$ be the dimensionless strain rate tensor. Let ${\boldsymbol {v}} = {\boldsymbol {u}}^\delta /\Vert {\boldsymbol {u}}^\delta \Vert$, and let $\lambda ^s_\alpha \geqslant \lambda ^s_\beta \geqslant \lambda ^s_\gamma$ be the eigenvalues of $s^+_{ij}$, with corresponding eigenvectors ${\boldsymbol {e}}_i$ ($i = \alpha, \beta, \gamma$). Due to incompressibility, we have $\lambda ^s_\alpha + \lambda ^s_\beta + \lambda ^s_\gamma = 0$, with $\lambda ^s_\alpha \geqslant 0$ and $\lambda ^s_\gamma \leqslant 0$. In isotropic turbulence, it is well known that $\lambda ^s_\beta$ is more likely to take positive values, so the magnitude of $\lambda ^s_\gamma$ tends to be the largest among the three.

Letting the angle between ${\boldsymbol {e}}_i$ and ${\boldsymbol {v}}$ be $\theta _i$, we may write

(3.4)\begin{equation} P = P_\alpha + P_\beta + P_\gamma, \end{equation}

where

(3.5a–c)\begin{align} P_\alpha ={-} \left\langle \overline{\lambda^s_\alpha\,\vert {\boldsymbol{v}} \vert^2 \cos^2\theta_\alpha}\right\rangle ,\quad P_\beta ={-} \left\langle \overline{\lambda^s_\beta\,\vert {\boldsymbol{v}} \vert^2 \cos^2\theta_\beta} \right\rangle ,\quad P_\gamma ={-} \left\langle \overline{\lambda^s_\gamma\,\vert {\boldsymbol{v}} \vert^2 \cos^2\theta_\gamma }\right\rangle , \end{align}

with $P_\alpha \leq 0$ and $P_\gamma \geq 0$. The above expressions show that $P$ is closely related to the alignment between ${\boldsymbol {u}}^\delta$ and the eigenvectors of $s^+_{ij}$, the magnitudes of the eigenvalues, and the correlations between them. As ${\boldsymbol {v}}$ is normalised, it is reasonable to expect that its magnitude is insensitive to rotation, and that rotation will affect $P$ mainly through the eigenvalues and $\cos \theta _i$. Since $P$ is always positive in our simulations (cf. figures 18 and 19), $P_\gamma$ is the dominant term in $P$. As a result, we will consider only the statistics of $\cos \theta _\gamma$ and the eigenvalues.

The p.d.f.s of $\cos \theta _\gamma$ are given in figures 20(a,b) for selected cases, showing the results for Kolmogorov forcing and those for constant power forcing, respectively. It is evident that there is a preferable alignment between ${\boldsymbol {e}}_\gamma$ and ${\boldsymbol {u}}^\delta$ when rotation is weak, since the p.d.f.s peak at $\cos \theta _\gamma = 1$. Interestingly, the alignment is weaker for larger $k_m$, and is also weakened by rotation. These trends are observed consistently for both forcing terms. The mean values of the eigenvalues are given in figure 21. Here, the results for the two forcing terms display different trends. For constant power forcing, the mean eigenvalues are almost independent of the rotation rate. For Kolmogorov forcing, the magnitudes of the averaged $\lambda ^s_\alpha$ and $\lambda ^s_\gamma$ both increase significantly with rotation.

Figure 20. The p.d.f.s of $\cos \theta _\gamma$: (a) cases with Kolmogorov forcing; (b) cases with constant power forcing.

Figure 21. The mean values of the eigenvalues of the dimensionless strain rate tensor $s^+_{ij}$. Solid lines indicate cases with Kolmogorov forcing; dashed lines indicate cases with constant power forcing. Squares indicate $\langle \lambda ^s_\alpha \rangle$; triangles indicate $\langle \lambda ^s_\beta \rangle$; diamonds indicate $\langle \lambda ^s_\gamma \rangle$.

Putting the results in figures 20 and 21 together, the physical picture for flows with constant power forcing appears to be simple. The production term $P$ decreases as rotation increases in this case, because the preferable alignment between ${\boldsymbol {e}}_\gamma$ and ${\boldsymbol {u}}^\delta$ is reduced by rotation. For the flows driven by Kolmogorov forcing, the preferable alignment is reduced by rotation, which tends to reduce $P$. However, this trend is opposed by the trend where the eigenvalues of $s^+_{ij}$ increase with rotation. The overall effect is that $P$ increases only slightly with rotation.

3.6. Discussion

The different consequences of the two forcing terms have been made quite obvious from our analysis so far. However, the cause of the difference is not yet elucidated. The Kolmogorov forcing term is inhomogeneous, whereas the constant power forcing is isotropic. However, if rotation is absent, then this difference alone does not lead to significant differences in the statistics that we have examined, notwithstanding the fact that the Reynolds numbers of the flows are not large. This assertion is supported by the various statistics obtained for $\varOmega = 0.1$, i.e. for weakest rotation. For example, figure 20 shows that the alignment is roughly the same for the two forces when $\varOmega = 0.1$. Figure 21 shows that the mean eigenvalues are also almost the same for the two flows when $\varOmega = 0.1$. The same can be said about the (conditional) Lyapunov exponents as well (see e.g. figures 8 and 9). Therefore, if there is no rotation, then the results would be more or less independent of the forcing mechanism even if the Reynolds number is moderate, i.e. even if there is only moderate scale separation between the forced large scales and the small scales.

One may thus conclude that the drastic impacts of the forcing terms originate from the interaction between forcing and rotation. The interaction seems to alter the spectral dynamics profoundly, eluding simple phenomenological explanations (see e.g. Dallas & Tobias (2016) and references therein). A corollary is that it is also unlikely that we can obtain simple mechanical explanations for the difference in the behaviours of the production term, hence those of the Lyapunov exponents, shown in previous subsections. Nevertheless, to shed some light on the physics behind the observations, we look into how different scales of the flow contribute to the production term, and how these contributions depend on the rotation rate.

To do this, we decompose the normalised strain rate tensor $s^+_{ij}$ into a large-scale component $s^{+>}_{ij}$ and a small-scale component $s^{+<}_{ij} \equiv s^+_{ij} - s^{+>}_{ij}$. Here, $s^{+>}_{ij}$ is obtained by applying a low-pass filter on $s^+_{ij}$ (Pope 2000). The production term calculated with $s^{+>}_{ij}$ and ${\boldsymbol {v}}$ is denoted by $P_l$, and that with $s^{+<}_{ij}$ and ${\boldsymbol {v}}$ is denoted by $P_s$, where obviously $P_l + P_s = P$. Here, $P_l$ and $P_s$ represent the contributions from large- and small-scale straining, respectively, to the total production $P$.

We use the Gaussian filter (Pope 2000) to calculate $s^{+>}_{ij}$. The filter length scale $\varDelta$ is chosen to be eight times the grid size, with the corresponding filter wavenumber $k_\varDelta \equiv {\rm \pi}/\varDelta$ being $12$ for $N=192$, and $8$ for $N=128$. The values for $P$, $P_l$ and $P_s$ at different rotation rates are plotted in figure 22 for $k_m=0$. Several observations are evident. First, $P_l$ is larger than $P_s$ for both forcing terms and both Reynolds numbers. That is, large-scale straining makes larger contribution to the total production term, which is consistent with the fact that the spectrum of ${\boldsymbol {u}}^\delta$ peaks at intermediate to low wavenumbers (cf. figure 12). Second, for constant power forcing, both $P_l$ and $P_s$ decrease as $\varOmega$ increases. Both contribute approximately equally to the decrease of the total production. Third, for Kolmogorov forcing, the picture is quite different again. Interestingly, $P_l$ barely increases (or decreases slightly) as $\varOmega$ increases, whereas $P_s$ increases with $\varOmega$ at both Reynolds numbers. Even though $P_l$ makes a bigger contribution to $P$, the change in $P$ with $\varOmega$ comes mainly from $P_s$.

Figure 22. The large-scale ($P_l$) and small-scale ($P_s$) contributions to the production term ($P$): (a) $N=128$, (b) $N=192$.

The results in figure 22 are again non-trivial to interpret fully. If the impacts of forcing are confined in large scales, then the small-scale contributions $P_s$ should behave in similar ways in flows driven by different forcing terms, but this is not supported by figure 22. If the effects of Kolmogorov forcing (coupled with rotation) on smaller scales decrease with increasing scale separation according to naive Kolmogorov phenomenology, then one should reasonably expect $P_l$ to depend more strongly on $\varOmega$ compared with $P_s$, which again is not supported by figure 22. Overall, like previous research (Dallas & Tobias 2016), these observations suggest that large-scale forcing affects the spectral dynamics of rotating turbulence in highly non-trivial ways, which is the root cause of the different synchronisability of the flows.

4. Conclusions

We investigated the synchronisation of rotating turbulence numerically, with a focus on the effects of the rotation rates and the forcing mechanism. The phenomenon is analysed through the decay rate of the synchronisation error, the threshold value of the coupling wavenumber, the conditional Lyapunov exponents (CLEs), the conditional Lyapunov vector, and the dynamical equation for the velocity perturbations.

One main finding is that the ability to synchronise rotating turbulence varies significantly with the forcing mechanism. For Kolmogorov flows, which are driven by a constant sinusoidal forcing term, the CLE for a given coupling wavenumber increases with rotation, which means that the flows are more difficult to synchronise with a given coupling wavenumber. However, the dimensionless threshold value for the coupling wavenumber is essentially independent of rotation within the range of rotation rates that we have investigated, and is unchanged from the value found in isotropic turbulence even though clearly the energy spectrum of the flow is steeper (consistent with the $k^{-2}$ power law).

For a different forcing scheme that is characterised by a prescribed constant energy injection rate, the CLE decreases as rotation is strengthened, so synchronisation is easier to achieve. The dimensionless threshold coupling wavenumber can be significantly smaller when rotation is strong and the slope of the energy spectrum approaches $-3$.

We find that the energy spectra of the Lyapunov vector as well as the conditional Lyapunov vectors have a close relationship with the threshold coupling wavenumber for both forcing schemes. The threshold coupling wavenumber and the wavenumber where the energy spectrum of the Lyapunov vector peaks appear to show the same dependence on rotation. Meanwhile, we find that for both forcing terms, the flows do not synchronise when the energy spectrum of the conditional Lyapunov vector has a peak in the wavenumber range for the slaved Fourier modes.

Rotation is also shown to increase the fluctuation in the local CLE. In some cases, though the long-time CLE is negative, frequently the fluctuating local CLE can become positive. This behaviour explains why for some numerical experiments, the synchronisation error can oscillate about exponential decay, and shows that rotation can reduce the stability of the synchronised state.

An analysis of the production term in the dynamical equation for velocity perturbations shows that rotation tends to reduce the preferential alignment between the perturbation velocity and the eigenvectors of the strain rate tensor. This behaviour tends to reduce the CLE, which is the reason why the flows driven by the second forcing term are easier to synchronise. However, this effect is counterbalanced in the Kolmogorov flows by increased eigenvalues of the strain rate tensor.

A limitation of current investigation is that the Reynolds number is relatively small. Our results indicate that the threshold coupling wavenumber depends on the slope of the energy spectrum of the flow to some extent. To ascertain the relation, simulations with an extended inertial range are needed, which can be achieved only when the Reynolds number of the flow is much higher. The relation between the threshold wavenumber and the energy spectrum of the Lyapunov vector also requires further scrutiny at higher Reynolds numbers. Another limitation is that the anisotropy of rotating turbulence has not yet been accounted for. Due to the formation of columnar vortices along the direction of the rotation axis, the threshold wavenumber can be different in the axial and transversal directions. A two-component threshold wavenumber is likely to provide a more precise description.

The drastically different physical pictures yielded by the two forcings suggest naturally that we might obtain different results again for yet another forcing mechanism (e.g. when the Kolmogorov forcing introduces shearing along the rotating axis). A more extensive investigation is warranted.

Though rotation has profound effects on turbulence, the rotation rate does not appear explicitly in the energy budget of the flow. However, it does enter directly the spectral dynamics and the equations for higher-order statistics. It would be interesting to investigate the behaviours of higher-order statistics such as the generalised Lyapunov exponents (Fujisaka 1983; Cencini, Cecconi & Vulpiani 2010) or the generalised CLEs. They are the natural measures for the strong fluctuations in finite-time amplification of synchronisation errors. Such an investigation would lead to more refined characterisation of the synchronisation process.