No CrossRef data available.
Article contents
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
Published online by Cambridge University Press: 22 December 2022
Abstract
We give an example of an FIID vertex-labeling of 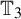 ${\mathbb T}_3$ whose marginals are uniform on
${\mathbb T}_3$ whose marginals are uniform on 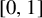 $[0,1]$, and if we delete the edges between those vertices whose labels are different, then some of the remaining clusters are infinite. We also show that no such process can be finitary.
$[0,1]$, and if we delete the edges between those vertices whose labels are different, then some of the remaining clusters are infinite. We also show that no such process can be finitary.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press



