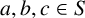TRIPLE-PRODUCT-FREE SETS

Abstract

In this paper, we study triple-product-free sets, which are analogous to the widely studied concept of product-free sets. A nonempty subset S of a group G is triple-product-free if $abc \notin S$ for all $a, b, c \in S$. If S is triple-product-free and is not a proper subset of any other triple-product-free set, we say that S is locally maximal. We classify all groups containing a locally maximal triple-product-free set of size 1. We then derive necessary and sufficient conditions for a subset of a group to be locally maximal triple-product-free, and conclude with some observations and comparisons with the situation for standard product-free sets.

1 Introduction

Triple-product-free sets are one example of a solution-free set. Loosely speaking, a solution-free set in a group is a set whose elements do not satisfy a given equation or collection of equations.

The most extensively studied solution-free sets have been sum-free sets in abelian groups. These are nonempty sets containing no solutions to $x + y = z$ . Interest in sum-free sets dates back to a theorem of Schur [5], which states that for all positive integers k, there exists a positive integer n such that $\{1, 2, \ldots , n\}$ cannot be partitioned into k sum-free sets. This implies that the set of integers cannot be partitioned into finitely many sum-free sets.

A sum-free set is locally maximal if it is not properly contained in any other sum-free set. Such sets relate to another example of a solution-free set: the widely studied concept of caps in finite geometry. A k-cap in the projective space $PG(n, q)$ is a collection of k points with no three collinear. Maximal (by inclusion) caps are known as complete caps. When $q=2$ , complete caps are equivalent to locally maximal sum-free sets of $\mathbb {Z}_2^{n+1}$ . In this context, locally maximal product-free sets for elementary abelian 2-groups of order up to 64 were classified in [4].

In an arbitrary group, we refer not to sum-free sets, but to product-free sets, which contain no solutions to $xy=z$ . As every product-free set is contained in a locally maximal product-free set, it is important to understand the locally maximal product-free sets. Giudici and Hart [3] gave necessary and sufficient conditions for a product-free set to be locally maximal in a group, and investigated groups containing smallest possible locally maximal sum-free sets. They classified all finite groups containing maximal product-free sets of sizes 1 and 2, with the size 3 and 4 case tackled by Anabanti and Hart in [2, 1]. Some general results were also obtained.

In this paper, we focus on locally maximal triple-product-free sets.

Definition 1.1. Let S be a nonempty subset of a finite group G. We say S is triple-product-free if $abc \notin S$ for all $a, b, c \in S$ . Further, S is said to be locally maximal triple-product-free in G if S is triple-product-free and not properly contained in any other triple-product-free set. (If G is an additive group, we refer instead to triple-sum-free sets.)

The following lemma provides infinitely many examples of locally maximal triple-product-free sets.

Lemma 1.2. Let G be a group and let N be a normal subgroup of index 3 in G. Any nontrivial coset of N is locally maximal triple-product-free.

Proof. Suppose $x \notin N$ . Let $a, b, c \in Nx$ . Then $abc \in (Nx)(Nx)(Nx)= (Nx)^3 = N \not = Nx$ . Therefore, $Nx$ is triple-product-free. Moreover, suppose $g\in G\setminus Nx = N \cup Nx^2$ and let $S = \{g\} \cup Nx$ . If $g\in N$ , then $g = (gx^{-3})x\cdot x\cdot x\in (Nx)(Nx)(Nx)$ . If $g\in Nx^2$ , then $g^{-1}\in Nx$ and $g = ggg^{-1}$ . Either way, S is not triple-product-free. Hence, $Nx$ is locally maximal triple-product-free.

The triple-product-free sets provided by Lemma 1.2 are large as a proportion of the group order. At the other extreme are locally maximal triple-product-free sets of smallest size. In Section 2, we determine all groups with locally maximal triple-product-free sets of size 1 (Theorem 2.2). In Section 3, we obtain some results on triple-product-free sets of arbitrary size, including necessary and sufficient conditions for a subset of a group to be locally maximal triple-product-free (Theorem 3.5).

We use the following common notation: for an element a of a group G, the order of a is written $o(a)$ and the centraliser of a in G is $C_G(a)$ . The cyclic group of order n is denoted $C_n$ ; the dihedral group of order $2n$ is denoted $D_{2n}$ , and $Q_8$ is the quaternion group of order 8.

2 Sets of size 1

In this section, we determine all groups with locally maximal triple-product-free sets of size 1.

Lemma 2.1. Suppose $\{a\}$ is a locally maximal triple-product-free set in a group G. Then $o(a) \in \{3, 4, 5\}$ .

Proof. Since $\{a\}$ is triple-product-free, $a^3\notin \{a\}$ , and so $o(a) \geq 3$ . If $\{a\}$ is locally maximal, then $\{a, a^2\}$ cannot be triple-product-free. Therefore, for some $i, j, k, l \in \{1,2\}$ , we have $a^ia^ja^k = a^l$ . Hence, $a^m = 1$ , where $m = i+j+k-l\leq 5$ . Thus, $o(a) \leq 5$ .

Theorem 2.2. Let S be a locally maximal triple-product-free set of size 1 in a group G. Then G is isomorphic to one of $C_3$ , $C_4$ , $C_5$ , $D_{6}$ , $D_{8}$ , $Q_8$ or $D_{10}$ .

Proof. Write $S = \{a\}$ . Then $o(a) \in \{3,4,5\}$ . If S is locally maximal triple-product-free, then for all $x\in G\setminus S$ , the set $\{a,x\}$ is not triple-product-free. That is,

$$ \begin{align*}\{a, x\} \cap \{a^3, a^2x, axa, ax^2, xa^2, xax, x^2a, x^3\} \neq \emptyset.\end{align*} $$

Since $o(a) \geq 3$ , this is equivalent to each x in $G\setminus S$ satisfying

(2.1) $$ \begin{align} x = a^{-1},\ x^2 = 1,\ x=a^3,\ x^3 = a,\ axa^{-1} = x^{-1} \ {\text{or}}\ xax^{-1} = a^{-1}.\end{align} $$

Therefore, if $x\in C_G(a)\setminus \langle a\rangle $ , then $x^2 = 1$ or $x^3=a$ . In the latter case, $x^{-1}$ is neither an involution nor a cube root of a, contradicting the fact that $x^{-1} \in C_G(a)\setminus \langle a\rangle $ . Therefore, $x^2=1$ . Now $ax$ is also in $C_G(a)\setminus \langle a\rangle $ , which forces $(ax)^2 = 1$ . However, $(ax)^2 = a^2x^2 = a^2$ , contradicting Lemma 2.1. Hence, $C_G(a) = \langle a\rangle $ . In particular, every x in G satisfies

(2.2) $$ \begin{align} x \in \langle a \rangle, \ x^2 = 1,\ axa^{-1} = x^{-1} \ {\text{or }} xax^{-1} = a^{-1}.\end{align} $$

We will show that the third possibility in (2.2) is redundant. Suppose $axa^{-1} = x^{-1}$ , and consider $xa$ , which must also satisfy (2.2). If $xa \in \langle a\rangle $ , then $x\in \langle a\rangle $ . We have $(xa)^2 = xaxa = x(axa^{-1})a^2 = a^2$ , and so $(xa)^2 \neq 1$ . If $a(xa)a^{-1} = (xa)^{-1}$ , then $(axa^{-1})a = a^{-1}x^{-1}$ and so $x^{-1}a = a^{-1}x^{-1}$ , which is equivalent to $xax^{-1} = a^{-1}$ . Finally, if $(xa)a(xa)^{-1} = a^{-1}$ , then we again obtain $xax^{-1} = a^{-1}$ . Therefore,

$$ \begin{align*} G = \langle a \rangle \cup \{x\in G : x^2 = 1\} \cup \{x\in G: xax^{-1} = a^{-1}\}.\end{align*} $$

Suppose next that x is an involution. If $xa\in \langle a\rangle $ , then $x\in \langle a \rangle $ . If $(xa)^2 = 1$ , then $xax^{-1}a = xaxa = 1$ , forcing $x \in \{x\in G: xax^{-1} = a^{-1}\}$ . Finally, if $(xa)a(xa)^{-1} = a^{-1}$ , then $xax^{-1} = a^{-1}$ . Thus, we obtain

(2.3) $$ \begin{align} G = \langle a \rangle \cup \{x\in G: xax^{-1} = a^{-1}\}.\end{align} $$

Let $o(a) = n$ . It follows from (2.3) that the conjugacy class of a is either $\{a\}$ or $\{a, a^{-1}\}$ , and hence either $G = \langle a\rangle $ or G is nonabelian of order $2n$ with $\langle a \rangle $ being a normal cyclic subgroup of index 2. Furthermore, by Lemma 2.1, $n \in \{3,4,5\}$ . If $n=3$ , the possibilities are $C_3$ and $D_6$ . If $n=4$ , the possibilities are $C_4$ , $D_8$ and $Q_8$ . If $n=5$ , the possibilities are $C_5$ and $D_{10}$ . A quick check shows that any element of order 3, 4 or 5 in any of these groups does indeed constitute a locally maximal triple-product-free set of size 1.

3 Larger triple-product-free sets

In this section, we obtain some general results about triple-product-free sets. We first need to establish some notation. Let S, T and U be subsets of G and let $g\in G$ . We have

$$ \begin{align*} ST &= \{st: s\in S, t\in T\}\\ STU &= \{stu: s \in S, t \in T, u \in U\}\\ S^{-1} &= \{s^{-1}: s\in S\}\\ S^g & = \{gsg^{-1}: s\in S\}\\ \sqrt S &= \{x\in G: x^2\in S\}\\ \sqrt[3] S&= \{x\in G: x^3\in S\}.\end{align*} $$

A nonempty subset S of a group G is therefore triple-product-free precisely when $S\cap SSS = \emptyset $ .

We begin with a look at the relationship between triple-product-free sets and their inverses.

Lemma 3.1. If S is a triple-product-free set, then $S \cap S^{-1} = \emptyset $ . In particular, triple-product-free sets contain no involutions.

Proof. Let S be a nonempty subset of G. If $S\cap S^{-1} \neq \emptyset $ , then there is some $g \in G$ such that both g and $g^{-1}$ are elements of S. However, $g=ggg^{-1} \in S\cap SSS$ . Thus, S is not triple-product-free.

The following lemma follows immediately from the fact that the inverse map $x\mapsto x^{-1}$ is an anti-automorphism of groups.

Lemma 3.2. Let S be a subset of a group G. Then S is triple-product-free if and only if $S^{-1}$ is triple-product-free. Moreover, S is locally maximal triple-product-free if and only if $S^{-1}$ is locally maximal triple-product-free.

Remark 3.3. Lemma 3.2 implies that there is always an even number of triple-product-free sets of a given cardinality in a finite group. For example, in $Q_8$ , there are six triple-product-free sets of size 1, each consisting of a single element of order 4, and they pair off as inverses of one another.

In the rest of this section, we derive necessary and sufficient conditions for a set to be locally maximal triple-product-free, first in the general case, and then in the special case of abelian groups. For comparison, the following result for product-free sets allowed Giudici and Hart to classify all groups containing locally maximal product-free sets of size 1 or 2.

Theorem 3.4 [3, Lemma 3.1].

Suppose S is a product-free set in the group G. Then S is a locally maximal product-free set if and only if $G = S \cup SS\cup SS^{-1}\cup S^{-1}S \cup \sqrt S$ .

Our characterisation of locally maximal triple-product-free sets, while of a similar flavour, is necessarily more complex. We note that it reduces to (2.1) in the case where $|S| = 1$ .

Theorem 3.5. Let S be a triple-product-free set in a group G. Then S is a locally maximal triple-product-free set if and only if

(3.1) $$ \begin{align} G&=S\cup SSS \cup \{g \in G\setminus S: S^{-1} \cap S^g \not = \emptyset \} \cup S^{-1} \cup S^{-1}S^{-1}S \cup S^{-1}SS^{-1} \nonumber \\ &\quad \cup SS^{-1}S^{-1} \cup \sqrt {S^{-1}S} \cup \sqrt{SS^{-1}} \cup \{g \in G \setminus S: S \cap gSg \not = \emptyset \}\cup \sqrt[3]S. \end{align} $$

Proof. Suppose S is triple-product-free in G. Then S is locally maximal if and only if for all $g \in G\setminus S$ , the set $S\cup \{g\}$ is not triple-product-free. In other words, for all $g \in G\setminus S$ , setting $A= S\cup \{g\}$ , we have $A \cap AAA \neq \emptyset $ . Now,

$$ \begin{align*}AAA = SSS \cup SSg \cup SgS \cup gSS \cup Sg^2 \cup gSg \cup g^2S \cup \{g^3\}.\end{align*} $$

Thus, S is locally maximal if and only if for all $g \in G\setminus S$ , either $g \in AAA$ or there exists $x \in S$ with $x \in AAA$ . That is, at least one of the following occurs.

• • $g \in SSS$ .

• • $g \in SSg \cup gSS$ . Then $1 \in SS$ , which implies $S \cap S^{-1} \not = \emptyset $ . However, this contradicts Lemma 3.1. So $g\notin SSg \cup gSS$ .

• • $g \in SgS$ . Then, there exist $ a, b \in S$ with $ g = a g b$ and thus $a^{-1} = gbg^{-1}$ . It follows that $S^{-1} \cap S^g \not = \emptyset $ .

• • $g \in Sg^2 \cup gSg \cup g^2S$ . Each of these implies that $g \in S^{-1}$ .

• • $g\in \{g^3\}$ . Then $g^2 = 1$ . As by definition S is nonempty, $1\in SS^{-1}$ , and thus $g\in \sqrt {SS^{-1}}$ .

• • $ x \in SSS$ . This is impossible because S is triple-product-free.

• • $x \in SSg$ . Then, there exist $a, b \in S$ with $x= abg$ and so $g \in S^{-1}S^{-1}S$ .

• • $x \in SgS$ . Then there exist $a, b \in S$ with $x= agb$ and so $g \in S^{-1}SS^{-1}$ .

• • $x \in gSS$ . Then, there exist $a, b \in S$ with $x= gab$ and so $g \in SS^{-1}S^{-1}$ .

• • $x \in Sg^2$ . Then, $g^2 \in S^{-1}S$ and so $g\in \sqrt {S^{-1}S}$ .

• • $x \in gSg$ . Then, there exists $a \in S$ with $x= gag$ and so $S \cap gSg \not = \emptyset $ .

• • $x \in g^2S$ . Then $g^2 \in SS^{-1}$ and so $g \in \sqrt {SS^{-1}}$ .

• • $x \in \{g^3\}$ . Then $g \in \sqrt [3]{S}$ .

Hence, S is locally maximal if and only if each g in $G\setminus S$ lies in at least one of the sets indicated. That is, S is locally maximal if and only if

$$ \begin{align*} G&=S\cup SSS \cup \{g \in G\setminus S: S^{-1} \cap S^g \not = \emptyset \} \cup S^{-1} \cup S^{-1}S^{-1}S \cup S^{-1}SS^{-1} \\ &\quad \cup SS^{-1}S^{-1} \cup \sqrt {S^{-1}S} \cup \sqrt{SS^{-1}} \cup \{g \in G \setminus S: S \cap gSg \not = \emptyset \} \cup \sqrt[3]S.\\[-39pt] \end{align*} $$

The situation simplifies considerably in the case of abelian groups, as the next corollary shows.

Corollary 3.6. Let G be an abelian group and S a triple-product-free set in G. Then S is locally maximal triple-product-free if and only if

$$ \begin{align*} G=S\cup SSS\cup S^{-1} \cup SS^{-1}S^{-1} \cup \sqrt {S^{-1}S} \cup \sqrt[3]S. \end{align*} $$

Proof. Suppose S is triple-product-free in G. By (3.1), S is locally maximal triple-product-free if and only if

$$ \begin{align*} G&=S\cup SSS \cup \{g \in G\setminus S: S^{-1} \cap S^g \not = \emptyset \} \cup S^{-1} \cup S^{-1}S^{-1}S \cup S^{-1}SS^{-1} \\ &\quad \cup SS^{-1}S^{-1} \cup \sqrt {S^{-1}S} \cup \sqrt{SS^{-1}} \cup \{g \in G \setminus S: S \cap gSg \not = \emptyset \} \cup \sqrt[3]S. \end{align*} $$

Since G is abelian, $S^{-1} \cup S^{-1}S^{-1}S \cup S^{-1}SS^{-1} \cup SS^{-1}S^{-1} = S^{-1}$ and $ \sqrt {S^{-1}S} = \sqrt {SS^{-1}}$ . Consider the set $\{g {\kern-1pt}\in{\kern-1pt} G\setminus S: S^{-1} {\kern-1pt}\cap{\kern-1pt} S^g \not {\kern-1pt}={\kern-1pt} \emptyset \}$ . Since G is abelian, $S^g {\kern-1pt}={\kern-1pt} S$ for all $g {\kern-1pt}\in{\kern-1pt} G$ . But, S is triple-product-free and so $S^{-1}\cap S = \emptyset $ . Hence, ${\{g \in G\setminus S: S^{-1} \cap S^g \not = \emptyset \} = \emptyset }$ . Finally, suppose $S \cap gSg \not = \emptyset $ . Then there exist $a, b \in S$ such that $a = gbg = bg^2$ . Thus, $g^2 = b^{-1}a$ . Therefore, $\{g \in G \setminus S: S \cap gSg \not = \emptyset \}\subseteq \sqrt {S^{-1}S}$ . Combining all these observations, we see that (3.1) reduces to

$$ \begin{align*} G=S\cup SSS\cup S^{-1} \cup SS^{-1}S^{-1} \cup \sqrt {S^{-1}S} \cup \sqrt[3]S.\\[-37pt] \end{align*} $$

In comparison with standard product-free sets, the criteria for triple-product-free sets being locally maximal are considerably more involved, especially in the nonabelian case. It is interesting to note that the largest possible orders of a group containing a locally maximal product-free set of size k, for $k = 1, 2, 3, 4$ respectively are 8, 16, 24, 40, with computer experiment strongly suggesting 64 for $k=5$ . For locally maximal triple-product-free sets, the largest possible group order for $k=1$ is, as we have seen, 10. Computer testing suggests the maximum orders for $k=2$ and $k=3$ are 32 and 100, respectively. Exact values for the terms of these sequences are probably difficult to obtain, but it would be interesting to have bounds for them. More detail on the experimental calculations is in the first author’s PhD thesis.