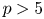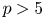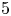1. Introduction
Fano varieties and their log generalizations are one of the basic building blocks of algebraic varieties according to the Minimal Model Program (MMP). In recent years a lot of progress has been made in the study of Fano varieties in characteristic ![]() $0$, notably [Reference BirkarBir19, Reference BirkarBir21]. Less is known about Fano varieties in positive characteristic. It is conjectured that Kodaira type vanishing theorems, which in general fail in positive characteristic, hold for Fano varieties of a given dimension in large enough characteristic [Reference TotaroTot19, Open questions]. This conjecture has been confirmed in dimension
$0$, notably [Reference BirkarBir19, Reference BirkarBir21]. Less is known about Fano varieties in positive characteristic. It is conjectured that Kodaira type vanishing theorems, which in general fail in positive characteristic, hold for Fano varieties of a given dimension in large enough characteristic [Reference TotaroTot19, Open questions]. This conjecture has been confirmed in dimension ![]() $2$ by [Reference Cascini, Tanaka and WitaszekCTW17], where the authors prove the existence of an integer
$2$ by [Reference Cascini, Tanaka and WitaszekCTW17], where the authors prove the existence of an integer ![]() $p_0>0$ such that surfaces of del Pezzo type over perfect fields of characteristic
$p_0>0$ such that surfaces of del Pezzo type over perfect fields of characteristic ![]() $p>p_0$ satisfy the Kawamata–Viehweg vanishing theorem. However, an explicit value for
$p>p_0$ satisfy the Kawamata–Viehweg vanishing theorem. However, an explicit value for ![]() $p_0$ cannot be obtained via the methods of [Reference Cascini, Tanaka and WitaszekCTW17], and in this paper we show that
$p_0$ cannot be obtained via the methods of [Reference Cascini, Tanaka and WitaszekCTW17], and in this paper we show that ![]() $p_0=5$ is both necessary and sufficient.
$p_0=5$ is both necessary and sufficient.
Theorem 1.1 (see Theorem 4.1)
Let ![]() $X$ be a surface of del Pezzo type over a perfect field
$X$ be a surface of del Pezzo type over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $D$ be a Weil divisor on
$D$ be a Weil divisor on ![]() $X$ and suppose that there exists an effective
$X$ and suppose that there exists an effective ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $\Delta$ such that
$\Delta$ such that ![]() $(X, \Delta )$ is a Kawamata log terminal (klt) pair and
$(X, \Delta )$ is a Kawamata log terminal (klt) pair and ![]() $D-(K_X+\Delta )$ is big and nef. Then
$D-(K_X+\Delta )$ is big and nef. Then
The crucial ingredient in the proof of Theorem 1.1 is establishing the following liftability theorem for klt surfaces whose canonical divisor is not pseudo-effective.
Theorem 1.2 (see Theorem 3.4)
Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $X$ be a klt projective surface over
$X$ be a klt projective surface over ![]() $k$ such that
$k$ such that ![]() $K_X$ is not pseudo-effective. Then there exists a log resolution
$K_X$ is not pseudo-effective. Then there exists a log resolution ![]() $\mu \colon V\rightarrow X$ such that
$\mu \colon V\rightarrow X$ such that ![]() $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
In recent years, it has become clear that the understanding of Fano varieties is crucial for the study of klt singularities, in particular in positive characteristics. In characteristic ![]() $0$, Elkik proved that klt singularities are always rational (see [Reference ElkikElk81]). This, however, fails in positive characteristic (see [Reference Cascini and TanakaCT19, Reference BernasconiBer21a, Reference TotaroTot19, Reference YasudaYas19]), and the question is intertwined with the failure of vanishing theorems on Fano varieties. In [Reference Hacon and WitaszekHW19a] the authors prove that klt threefold singularities are rational in large characteristic
$0$, Elkik proved that klt singularities are always rational (see [Reference ElkikElk81]). This, however, fails in positive characteristic (see [Reference Cascini and TanakaCT19, Reference BernasconiBer21a, Reference TotaroTot19, Reference YasudaYas19]), and the question is intertwined with the failure of vanishing theorems on Fano varieties. In [Reference Hacon and WitaszekHW19a] the authors prove that klt threefold singularities are rational in large characteristic ![]() $p>p_0$ where
$p>p_0$ where ![]() $p_0$ is large enough to assure the validity of the Kawamata–Viehweg vanishing theorem for surfaces of del Pezzo type. As a consequence of their work and Theorem 1.1, we can therefore provide an effective bound on the characteristic
$p_0$ is large enough to assure the validity of the Kawamata–Viehweg vanishing theorem for surfaces of del Pezzo type. As a consequence of their work and Theorem 1.1, we can therefore provide an effective bound on the characteristic ![]() $p$ for which klt threefold singularities are rational.
$p$ for which klt threefold singularities are rational.
Corollary 1.3 (see [Reference Hacon and WitaszekHW19a, Theorem 1.1])
Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() ${p>5}$. Let
${p>5}$. Let ![]() $(X, \Delta )$ be a klt threefold over
$(X, \Delta )$ be a klt threefold over ![]() $k$. Then
$k$. Then ![]() $X$ has rational singularities. Moreover, if
$X$ has rational singularities. Moreover, if ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial and
$\mathbb {Q}$-factorial and ![]() $D$ is a Weil divisor on
$D$ is a Weil divisor on ![]() $X$ then
$X$ then ![]() $\mathcal {O}_X(D)$ is Cohen–Macaulay.
$\mathcal {O}_X(D)$ is Cohen–Macaulay.
On the other hand, Theorem 1.1 and Corollary 1.3 have several applications to the birational geometry of threefolds. We mention two: the finiteness of the local étale fundamental group of threefold klt singularities (see [Reference Carvajal-Rojas, Stäbler and KollárCSK20, Theorems A, B and C]) and a refined version of the base-point-free theorem for klt threefolds (see [Reference BernasconiBer21b]). The corollaries below were previously known to hold in large characteristic; we now know them to be true in characteristic ![]() $p>5$.
$p>5$.
Corollary 1.4 (see [Reference Carvajal-Rojas, Stäbler and KollárCSK20, Theorems A, B])
Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $(X, \Delta )$ be a klt threefold over
$(X, \Delta )$ be a klt threefold over ![]() $k$. Let
$k$. Let ![]() $x\in X$ be a closed point. Then the local étale fundamental group of
$x\in X$ be a closed point. Then the local étale fundamental group of ![]() $X$ at
$X$ at ![]() $x$ is finite. Moreover, there exists a quasi-étale cover
$x$ is finite. Moreover, there exists a quasi-étale cover ![]() $\widetilde {X}\rightarrow X$ with prime-to-
$\widetilde {X}\rightarrow X$ with prime-to-![]() $p$ degree such that every quasi-étale cover of
$p$ degree such that every quasi-étale cover of ![]() $\widetilde {X}$ is étale.
$\widetilde {X}$ is étale.
Corollary 1.5 (see [Reference BernasconiBer21b, Theorem 1.1])
Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p> 5$. Let
$p> 5$. Let ![]() $(X, \Delta )$ be a quasi-projective klt threefold log pair and let
$(X, \Delta )$ be a quasi-projective klt threefold log pair and let ![]() $\pi \colon X \to Z$ be a projective contraction morphism of quasi-projective normal varieties over
$\pi \colon X \to Z$ be a projective contraction morphism of quasi-projective normal varieties over ![]() $k$. Let
$k$. Let ![]() $L$ be a
$L$ be a ![]() $\pi$-nef Cartier divisor on
$\pi$-nef Cartier divisor on ![]() $X$ such that:
$X$ such that:
(i)
 $\dim (Z) \geq 1$ or
$\dim (Z) \geq 1$ or  $\dim (Z)=0$ and
$\dim (Z)=0$ and  $\nu (L) \geq 1$;
$\nu (L) \geq 1$;(ii)
 $nL-(K_X+\Delta )$ is a
$nL-(K_X+\Delta )$ is a  $\pi$-big and
$\pi$-big and  $\pi$-nef
$\pi$-nef  $\mathbb {Q}$-Cartier
$\mathbb {Q}$-Cartier  $\mathbb {Q}$-divisor for some
$\mathbb {Q}$-divisor for some  $n>0$.
$n>0$.
Then there exists ![]() $m_0>0$ such that
$m_0>0$ such that ![]() $mL$ is
$mL$ is ![]() $\pi$-free for all
$\pi$-free for all ![]() $m \geq m_0$.
$m \geq m_0$.
In § 5 we construct counterexamples in characteristic ![]() $5$ to Theorem 1.1 and Corollary 1.3 building upon a previous example found by the third author.
$5$ to Theorem 1.1 and Corollary 1.3 building upon a previous example found by the third author.
Theorem 1.6 (see Proposition 5.2 and Theorem 5.4)
Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p=5$. Then:
$p=5$. Then:
(i) there exist a klt del Pezzo surface
 $T$ of Picard rank
$T$ of Picard rank  $1$ and an ample
$1$ and an ample  $\mathbb {Q}$-Cartier divisor
$\mathbb {Q}$-Cartier divisor  $A$ such that
$A$ such that  $H^1(T, \mathcal {O}_T(-A)) \neq 0$;
$H^1(T, \mathcal {O}_T(-A)) \neq 0$;(ii) there exists a
 $\mathbb {Q}$-factorial klt threefold singularity which is not Cohen–Macaulay.
$\mathbb {Q}$-factorial klt threefold singularity which is not Cohen–Macaulay.
This, together with the examples found in [Reference Cascini and TanakaCT19] and [Reference BernasconiBer21a], shows that our assumption on the characteristic in Theorem 1.1 and Corollary 1.3 is optimal.
1.1 Sketch of the proof
We now overview the main techniques and proofs in this paper. In § 3 we prove Theorem 1.2. In order to do this, we first show that we can reduce to the case of such surfaces admitting a Mori fibre space structure (Lemma 2.9). We prove the case of Mori fibre space onto a curve (Proposition 3.2), while the case of klt del Pezzo surfaces of Picard rank ![]() $1$ has been settled by the third author in his PhD thesis [Reference LaciniLac20].
$1$ has been settled by the third author in his PhD thesis [Reference LaciniLac20].
In § 4 we use Theorem 1.2 to prove Theorem 1.1, where the property of the surface being del Pezzo type plays a fundamental role. By running a ![]() $\Delta$-MMP we construct a birational morphism
$\Delta$-MMP we construct a birational morphism ![]() $\pi \colon X \to Y$ which contracts a boundary
$\pi \colon X \to Y$ which contracts a boundary ![]() $N\leq \Delta$ such that
$N\leq \Delta$ such that ![]() $D-(K_X+N)$ is ample and such that the support of
$D-(K_X+N)$ is ample and such that the support of ![]() $N$ coincides with the exceptional locus of
$N$ coincides with the exceptional locus of ![]() $\pi$. Since
$\pi$. Since ![]() $Y$ remains a surface of del Pezzo type, we may apply Theorem 3.4 to construct a log resolution
$Y$ remains a surface of del Pezzo type, we may apply Theorem 3.4 to construct a log resolution ![]() $(V, {\rm Exc}(\mu ))$ of
$(V, {\rm Exc}(\mu ))$ of ![]() $Y$ that lifts to characteristic
$Y$ that lifts to characteristic ![]() $0$ over a smooth base. Since
$0$ over a smooth base. Since ![]() $N$ was contracted by
$N$ was contracted by ![]() $\pi$, after a sequence of blow-ups of points of
$\pi$, after a sequence of blow-ups of points of ![]() $V$, we may find a log resolution of the pair
$V$, we may find a log resolution of the pair ![]() $(X,N)$ lifting to characteristic
$(X,N)$ lifting to characteristic ![]() $0$ over a smooth base. Then we can prove the desired vanishing theorem by applying the logarithmic Deligne–Illusie vanishing theorem (see Lemma 2.10).
$0$ over a smooth base. Then we can prove the desired vanishing theorem by applying the logarithmic Deligne–Illusie vanishing theorem (see Lemma 2.10).
2. Preliminaries
2.1 Notation
In this paper ![]() $k$ denotes a perfect field of characteristic
$k$ denotes a perfect field of characteristic ![]() $p>0$. For
$p>0$. For ![]() $n>0$, we denote by
$n>0$, we denote by ![]() $W_n(k)$ (respectively,
$W_n(k)$ (respectively, ![]() $W(k)$) the ring of Witt vectors of length
$W(k)$) the ring of Witt vectors of length ![]() $n$ (respectively, the ring of Witt vectors).
$n$ (respectively, the ring of Witt vectors).
We say that ![]() $X$ is a variety over
$X$ is a variety over ![]() $k$ or a
$k$ or a ![]() $k$-variety if
$k$-variety if ![]() $X$ is an integral scheme that is separated and of finite type over
$X$ is an integral scheme that is separated and of finite type over ![]() $k$. We say that
$k$. We say that ![]() $X$ is a curve over
$X$ is a curve over ![]() $k$ or a
$k$ or a ![]() $k$-curve (respectively, a surface over
$k$-curve (respectively, a surface over ![]() $k$ or a
$k$ or a ![]() $k$-surface, or a threefold over
$k$-surface, or a threefold over ![]() $k$) if
$k$) if ![]() $X$ is a
$X$ is a ![]() $k$-variety of dimension 1 (respectively, 2, or 3).
$k$-variety of dimension 1 (respectively, 2, or 3).
We say ![]() $(X,\Delta )$ is a log pair if
$(X,\Delta )$ is a log pair if ![]() $X$ is normal variety,
$X$ is normal variety, ![]() $\Delta$ is an effective
$\Delta$ is an effective ![]() $\mathbb {Q}$-divisor and
$\mathbb {Q}$-divisor and ![]() $K_X+\Delta$ is
$K_X+\Delta$ is ![]() $\mathbb {Q}$-Cartier. We say that a pair
$\mathbb {Q}$-Cartier. We say that a pair ![]() $(X, \Delta )$ is log smooth if
$(X, \Delta )$ is log smooth if ![]() $X$ is regular and the support of
$X$ is regular and the support of ![]() $\Delta$ is simple normal crossing (snc). We refer to [Reference KollárKol13] for the basic definitions in birational geometry and of the singularities appearing in the MMP (e.g. klt) and to [Reference Gongyo, Nakamura and TanakaGNT19, Remark 2.7] for birational geometry over perfect fields. We say that a variety is
$\Delta$ is simple normal crossing (snc). We refer to [Reference KollárKol13] for the basic definitions in birational geometry and of the singularities appearing in the MMP (e.g. klt) and to [Reference Gongyo, Nakamura and TanakaGNT19, Remark 2.7] for birational geometry over perfect fields. We say that a variety is ![]() $\mathbb {Q}$-factorial if every Weil divisor is
$\mathbb {Q}$-factorial if every Weil divisor is ![]() $\mathbb {Q}$-Cartier. We recall that klt surface pairs are
$\mathbb {Q}$-Cartier. We recall that klt surface pairs are ![]() $\mathbb {Q}$-factorial (see, for example, [Reference TanakaTan15, Fact 3.4]), so we will often discuss Weil divisors on klt surface pairs without mentioning that they are
$\mathbb {Q}$-factorial (see, for example, [Reference TanakaTan15, Fact 3.4]), so we will often discuss Weil divisors on klt surface pairs without mentioning that they are ![]() $\mathbb {Q}$-Cartier.
$\mathbb {Q}$-Cartier.
Given a proper birational morphism ![]() $\pi \colon X \to Y$ between normal varieties, we denote by
$\pi \colon X \to Y$ between normal varieties, we denote by ![]() ${\rm Exc}(\pi )$ the exceptional locus of
${\rm Exc}(\pi )$ the exceptional locus of ![]() $\pi$. Given a variety
$\pi$. Given a variety ![]() $X$ and a Weil divisor
$X$ and a Weil divisor ![]() $D$, we say that
$D$, we say that ![]() $f \colon Y \to X$ is a log resolution of
$f \colon Y \to X$ is a log resolution of ![]() $(X,D)$ if
$(X,D)$ if ![]() ${\rm Exc}(\pi )$ has pure codimension
${\rm Exc}(\pi )$ has pure codimension ![]() $1$ and the pair
$1$ and the pair ![]() $(Y, {\rm Exc}(\pi )+\pi _*^{-1}D)$ is log smooth.
$(Y, {\rm Exc}(\pi )+\pi _*^{-1}D)$ is log smooth.
2.2 Surfaces of del Pezzo type
In this subsection we collect some properties of surfaces of del Pezzo type.
Definition 2.1 Let ![]() $k$ be a field. We say that a normal
$k$ be a field. We say that a normal ![]() $k$-projective surface
$k$-projective surface ![]() $X$ is a surface of del Pezzo type if there exists an effective
$X$ is a surface of del Pezzo type if there exists an effective ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $\Delta$ such that
$\Delta$ such that ![]() $(X, \Delta )$ is klt and
$(X, \Delta )$ is klt and ![]() $-(K_X+\Delta )$ is ample. The pair
$-(K_X+\Delta )$ is ample. The pair ![]() $(X, \Delta )$ is said to be a log del Pezzo pair. We say
$(X, \Delta )$ is said to be a log del Pezzo pair. We say ![]() $X$ is a klt del Pezzo surface if the pair
$X$ is a klt del Pezzo surface if the pair ![]() $(X,0)$ is log del Pezzo.
$(X,0)$ is log del Pezzo.
Surfaces of del Pezzo type behave nicely from the birational perspective, as the MMP algorithm can be run for any divisor on them and they form a closed class under birational contraction.
Lemma 2.2 Let ![]() $k$ be a perfect field. Let
$k$ be a perfect field. Let ![]() $X$ be a surface of del Pezzo type over
$X$ be a surface of del Pezzo type over ![]() $k$. Then
$k$. Then ![]() $X$ is a Mori dream space, that is, given a
$X$ is a Mori dream space, that is, given a ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $D$ on
$D$ on ![]() $X$ we can run a
$X$ we can run a ![]() $D$-MMP which terminates.
$D$-MMP which terminates.
Proof. Let ![]() $\Delta$ be an effective
$\Delta$ be an effective ![]() $\mathbb {Q}$-divisor on
$\mathbb {Q}$-divisor on ![]() $X$ such that
$X$ such that ![]() $(X, \Delta )$ is a log del Pezzo pair. Choose a sufficiently small rational number
$(X, \Delta )$ is a log del Pezzo pair. Choose a sufficiently small rational number ![]() $\varepsilon >0$ such that
$\varepsilon >0$ such that ![]() $A=\varepsilon D-(K_X+\Delta )$ is ample. By [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.8], there exists an effective
$A=\varepsilon D-(K_X+\Delta )$ is ample. By [Reference Gongyo, Nakamura and TanakaGNT19, Lemma 2.8], there exists an effective ![]() $\mathbb {Q}$-divisor
$\mathbb {Q}$-divisor ![]() $A'$ such that
$A'$ such that ![]() $A' \sim _{\mathbb {Q}} A$ and
$A' \sim _{\mathbb {Q}} A$ and ![]() $(X, \Delta +A')$ is a klt pair. We conclude by noting that a
$(X, \Delta +A')$ is a klt pair. We conclude by noting that a ![]() $D$-MMP coincides with a
$D$-MMP coincides with a ![]() $(K_X+\Delta +A')$-MMP, which exists and terminates by [Reference TanakaTan18, Theorem 1.1].
$(K_X+\Delta +A')$-MMP, which exists and terminates by [Reference TanakaTan18, Theorem 1.1].
Lemma 2.3 Let ![]() $k$ be a field. Let
$k$ be a field. Let ![]() $X$ a surface of del Pezzo type over
$X$ a surface of del Pezzo type over ![]() $k$. Let
$k$. Let ![]() $\pi \colon X \to Y$ be a birational
$\pi \colon X \to Y$ be a birational ![]() $k$-morphism onto a normal surface
$k$-morphism onto a normal surface ![]() $Y$. Then
$Y$. Then ![]() $Y$ is a surface of del Pezzo type.
$Y$ is a surface of del Pezzo type.
Proof. See [Reference Bernasconi and TanakaBT22, Lemma 2.9].
2.3 Lifting to characteristic  $0$ over a smooth base
$0$ over a smooth base
We now collect some notions on liftability we will use in this paper. In this subsection we fix ![]() $k$ to be an algebraically closed field. We start by recalling the definition of liftability to characteristic
$k$ to be an algebraically closed field. We start by recalling the definition of liftability to characteristic ![]() $0$ (see [Reference Cascini, Tanaka and WitaszekCTW17, Definition 2.15]) and to the ring of Witt vectors.
$0$ (see [Reference Cascini, Tanaka and WitaszekCTW17, Definition 2.15]) and to the ring of Witt vectors.
Definition 2.4 Let ![]() $(X,D=\sum _{i=1}^r D_i)$ be a log smooth pair over
$(X,D=\sum _{i=1}^r D_i)$ be a log smooth pair over ![]() $k$. A lifting of
$k$. A lifting of ![]() $(X, D)$ to a scheme
$(X, D)$ to a scheme ![]() $T$ consists of
$T$ consists of
(i) a smooth and separated morphism
 $\mathcal {X}$ over
$\mathcal {X}$ over  $T$,
$T$,(ii) effective Cartier divisors
 $\mathcal {D}_i$ in
$\mathcal {D}_i$ in  $\mathcal {X}$ such that for every subset
$\mathcal {X}$ such that for every subset  $J \subseteq \{1, \ldots, r\}$ the scheme-theoretic intersection
$J \subseteq \{1, \ldots, r\}$ the scheme-theoretic intersection  $\bigcap _{j \in J} \mathcal {D}_j$ is smooth over
$\bigcap _{j \in J} \mathcal {D}_j$ is smooth over  $T$,
$T$,(iii) a morphism
 $\alpha \colon {\rm Spec}(k)\rightarrow T$,
$\alpha \colon {\rm Spec}(k)\rightarrow T$,
such that the base change of the schemes ![]() $\mathcal {X}, \mathcal {D}_1, \ldots, \mathcal {D}_r$ via
$\mathcal {X}, \mathcal {D}_1, \ldots, \mathcal {D}_r$ via ![]() $\alpha$ is isomorphic to
$\alpha$ is isomorphic to ![]() $X, D_1, \ldots, D_n$, respectively.
$X, D_1, \ldots, D_n$, respectively.
If ![]() $T$ is smooth and separated over
$T$ is smooth and separated over ![]() ${\rm Spec}(\mathbb {Z})$ (respectively,
${\rm Spec}(\mathbb {Z})$ (respectively, ![]() $T={\rm Spec}(W(k))$), then we say that
$T={\rm Spec}(W(k))$), then we say that ![]() $(\mathcal {X},\mathcal {D})$ is a lifting of
$(\mathcal {X},\mathcal {D})$ is a lifting of ![]() $(X,D)$ to characteristic
$(X,D)$ to characteristic ![]() $0$ over a smooth base (respectively, a lifting to the ring of Witt vectors).
$0$ over a smooth base (respectively, a lifting to the ring of Witt vectors).
We relate the notions of liftability to characteristic ![]() $0$ and liftability to the ring of Witt vectors.
$0$ and liftability to the ring of Witt vectors.
Proposition 2.5 Let ![]() $(X,D)$ be a log smooth pair over
$(X,D)$ be a log smooth pair over ![]() $k$. Then
$k$. Then ![]() $(X,D)$ admits a lifting to
$(X,D)$ admits a lifting to ![]() $W(k)$ if and only if
$W(k)$ if and only if ![]() $(X,D)$ admits a lifting to characteristic
$(X,D)$ admits a lifting to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Proof. Suppose that ![]() $(X,D)$ admits a lifting
$(X,D)$ admits a lifting ![]() $(\mathcal {X},\mathcal {D})$ to characteristic
$(\mathcal {X},\mathcal {D})$ to characteristic ![]() $0$ over a smooth base
$0$ over a smooth base ![]() $T$. It is sufficient to show that
$T$. It is sufficient to show that ![]() $\alpha \colon {\rm Spec}(k) \to T$ lifts to a section
$\alpha \colon {\rm Spec}(k) \to T$ lifts to a section ![]() $\widetilde {\alpha }\colon {\rm Spec}(W(k)) \to T$ since then the base change of
$\widetilde {\alpha }\colon {\rm Spec}(W(k)) \to T$ since then the base change of ![]() $(\mathcal {X},\mathcal {D})$ along
$(\mathcal {X},\mathcal {D})$ along ![]() $\widetilde {\alpha }$ is a lifting of
$\widetilde {\alpha }$ is a lifting of ![]() $(X,D)$ to
$(X,D)$ to ![]() $W(k)$. The base change
$W(k)$. The base change ![]() $T \times _{\mathbb {Z}} {\rm Spec} (W(k)) \to {\rm Spec}(W(k))$ is a smooth morphism and
$T \times _{\mathbb {Z}} {\rm Spec} (W(k)) \to {\rm Spec}(W(k))$ is a smooth morphism and ![]() $W(k)$ is a complete ring (and thus Henselian). Therefore the section
$W(k)$ is a complete ring (and thus Henselian). Therefore the section ![]() $\alpha \colon {\rm Spec}(k) \to T$ lifts to a section
$\alpha \colon {\rm Spec}(k) \to T$ lifts to a section ![]() ${\rm Spec}(W(k)) \to T$ (see [Reference GrothendieckEGAIV4, Theórème 18.5.17]).
${\rm Spec}(W(k)) \to T$ (see [Reference GrothendieckEGAIV4, Theórème 18.5.17]).
Let ![]() $(\mathcal {X}, \mathcal {D})$ be a lifting of
$(\mathcal {X}, \mathcal {D})$ be a lifting of ![]() $(X,D)$ to
$(X,D)$ to ![]() $W(k)$. As
$W(k)$. As ![]() $\text {Frac}(W(k))$ is a field of characteristic
$\text {Frac}(W(k))$ is a field of characteristic ![]() $0$,
$0$, ![]() ${\rm Spec}(\text {Frac}(W(k))$ is geometrically regular at
${\rm Spec}(\text {Frac}(W(k))$ is geometrically regular at ![]() $\mathbb {Q}$ by [Sta, Tag 038U]. This means that
$\mathbb {Q}$ by [Sta, Tag 038U]. This means that ![]() ${\rm Spec}(W(k))\rightarrow {\rm Spec}(\mathbb {Z})$ is flat with geometrically regular fibres and the morphism
${\rm Spec}(W(k))\rightarrow {\rm Spec}(\mathbb {Z})$ is flat with geometrically regular fibres and the morphism ![]() ${\rm Spec}(W(k))\rightarrow {\rm Spec}(\mathbb {Z})$ is regular (see [Sta, Tag 07R7]). By a theorem of Popescu (see [Reference Conrad and de JongCdeJ02, Theorem 1.3]), the ring
${\rm Spec}(W(k))\rightarrow {\rm Spec}(\mathbb {Z})$ is regular (see [Sta, Tag 07R7]). By a theorem of Popescu (see [Reference Conrad and de JongCdeJ02, Theorem 1.3]), the ring ![]() $W(k)$ is therefore a direct limit of smooth
$W(k)$ is therefore a direct limit of smooth ![]() $\mathbb {Z}$-algebras. By [Reference GrothendieckEGAIV3, Théorème 11.2.6] flatness is preserved under spreading out and thus there exists a smooth and separated
$\mathbb {Z}$-algebras. By [Reference GrothendieckEGAIV3, Théorème 11.2.6] flatness is preserved under spreading out and thus there exists a smooth and separated ![]() $\mathbb {Z}$-scheme
$\mathbb {Z}$-scheme ![]() $T$ such that
$T$ such that ![]() $\mathcal {X}$ and all possible intersection of
$\mathcal {X}$ and all possible intersection of ![]() $\mathcal {D}_i$, for
$\mathcal {D}_i$, for ![]() $1\leq i\leq n$, are defined and smooth over
$1\leq i\leq n$, are defined and smooth over ![]() $T$. Thus we conclude that
$T$. Thus we conclude that ![]() $(X,D)$ admits a lifting to characteristic
$(X,D)$ admits a lifting to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Remark 2.6 As a consequence let us note that if ![]() $(X, D)$ admits a lifting to characteristic
$(X, D)$ admits a lifting to characteristic ![]() $0$ over a smooth base then it admits a lifting over
$0$ over a smooth base then it admits a lifting over ![]() $W_2(k)$ (cf. [Reference Cascini, Tanaka and WitaszekCTW17, Remark 2.16]).
$W_2(k)$ (cf. [Reference Cascini, Tanaka and WitaszekCTW17, Remark 2.16]).
We are interested in understanding how liftability is preserved under blow-ups at smooth points. We therefore introduce the following terminology.
Definition 2.7 Let ![]() $(X, D=\sum _{i=1}^n D_i)$ be a log smooth surface pair over
$(X, D=\sum _{i=1}^n D_i)$ be a log smooth surface pair over ![]() $k$. Let
$k$. Let ![]() $x$ be closed point of
$x$ be closed point of ![]() $X$ and let
$X$ and let ![]() $J \subseteq \{1, \ldots, n\}$ be the subset of maximal cardinality for which
$J \subseteq \{1, \ldots, n\}$ be the subset of maximal cardinality for which ![]() $x \in \bigcap _{j \in J} D_j$ (with the convention that
$x \in \bigcap _{j \in J} D_j$ (with the convention that ![]() $\bigcap _{j \in \emptyset } D_j=X$). Let
$\bigcap _{j \in \emptyset } D_j=X$). Let ![]() $(\mathcal {X}, \mathcal {D}=\sum _{i=1}^n \mathcal {D}_i)$ be a lifting of
$(\mathcal {X}, \mathcal {D}=\sum _{i=1}^n \mathcal {D}_i)$ be a lifting of ![]() $(X,D)$ to a scheme
$(X,D)$ to a scheme ![]() $T$. A lifting
$T$. A lifting ![]() $\overline {x} \subset \mathcal {X}$ of
$\overline {x} \subset \mathcal {X}$ of ![]() $x$ is a subscheme of
$x$ is a subscheme of ![]() $\mathcal {X}$ smooth over
$\mathcal {X}$ smooth over ![]() $T$ such that
$T$ such that ![]() $\overline {x} \times _T {\rm Spec}(k)=x$. We say that a lifting
$\overline {x} \times _T {\rm Spec}(k)=x$. We say that a lifting ![]() $\overline {x}$ is compatible with the snc structure of
$\overline {x}$ is compatible with the snc structure of ![]() $(\mathcal {X}, \mathcal {D})$ if
$(\mathcal {X}, \mathcal {D})$ if ![]() $\overline {x} \subseteq \cap _{j \in J} \mathcal {D}_j$.
$\overline {x} \subseteq \cap _{j \in J} \mathcal {D}_j$.
By possibly changing the base of the lifting, we may always find a lifting of a point to characteristic ![]() $0$ compatible with the snc structure.
$0$ compatible with the snc structure.
Lemma 2.8 Let ![]() $(X,D=\sum _{i=1}^n D_i)$ be a log smooth surface pair over
$(X,D=\sum _{i=1}^n D_i)$ be a log smooth surface pair over ![]() $k$. Let
$k$. Let ![]() $x$ be a closed point of
$x$ be a closed point of ![]() $X$. Suppose that
$X$. Suppose that ![]() $(X, D)$ lifts to characteristic
$(X, D)$ lifts to characteristic ![]() $0$ over a smooth base. Then there exists a lifting of
$0$ over a smooth base. Then there exists a lifting of ![]() $(X,D)$ over a smooth base such that
$(X,D)$ over a smooth base such that ![]() $x$ lifts compatibly with the snc structure.
$x$ lifts compatibly with the snc structure.
Proof. Let ![]() $(\mathcal {X}, \mathcal {D})$ be a lifting of
$(\mathcal {X}, \mathcal {D})$ be a lifting of ![]() $X$ over a
$X$ over a ![]() $\mathbb {Z}$-smooth and separated scheme
$\mathbb {Z}$-smooth and separated scheme ![]() $T$. Then by Proposition 2.5 there exists a lifting
$T$. Then by Proposition 2.5 there exists a lifting ![]() $(\mathcal {X}, \mathcal {D})$ to
$(\mathcal {X}, \mathcal {D})$ to ![]() $W(k)$. Let
$W(k)$. Let ![]() $J \subseteq \{1, \ldots, n\}$ be the subset of maximal cardinality for which
$J \subseteq \{1, \ldots, n\}$ be the subset of maximal cardinality for which ![]() $x \in \bigcap _{j \in J} D_j$. Consider the following diagram.
$x \in \bigcap _{j \in J} D_j$. Consider the following diagram.

Since ![]() $\bigcap _{j \in J}\mathcal {D}_j$ is smooth over
$\bigcap _{j \in J}\mathcal {D}_j$ is smooth over ![]() $W(k)$, by [Reference GrothendieckEGAIV4, Theórème 18.5.17] there exists a lifting
$W(k)$, by [Reference GrothendieckEGAIV4, Theórème 18.5.17] there exists a lifting ![]() $\overline {s} \colon {\rm Spec}(W(k)) \to \bigcap _{j \in J} \mathcal {D}_j$. This shows the existence of a lifting of
$\overline {s} \colon {\rm Spec}(W(k)) \to \bigcap _{j \in J} \mathcal {D}_j$. This shows the existence of a lifting of ![]() $x$ compatible with the snc structure over
$x$ compatible with the snc structure over ![]() $W(k)$. By using Popescu's theorem and a spreading out argument as in the proof of Proposition 2.5, we conclude the existence of a lifting of
$W(k)$. By using Popescu's theorem and a spreading out argument as in the proof of Proposition 2.5, we conclude the existence of a lifting of ![]() $(X,D)$ to characteristic
$(X,D)$ to characteristic ![]() $0$ over a smooth base such that
$0$ over a smooth base such that ![]() $x$ lifts compatibly with the snc structure.
$x$ lifts compatibly with the snc structure.
We now show that liftability is preserved under blow-ups at smooth centres.
Proposition 2.9 Let ![]() $(X,D=\sum _{i=1}^n D_i)$ be a log smooth surface over
$(X,D=\sum _{i=1}^n D_i)$ be a log smooth surface over ![]() $k$ which admits a lifting to characteristic
$k$ which admits a lifting to characteristic ![]() $0$ over a smooth base. Let
$0$ over a smooth base. Let ![]() $x$ be a closed point of
$x$ be a closed point of ![]() $X$ and let
$X$ and let ![]() $\pi \colon X' \to X$ be the blow-up at the point
$\pi \colon X' \to X$ be the blow-up at the point ![]() $x$. Then
$x$. Then ![]() $(X', \pi _*^{-1}D \cup {\rm Exc}(\pi ))$ admits a lifting to characteristic
$(X', \pi _*^{-1}D \cup {\rm Exc}(\pi ))$ admits a lifting to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Proof. Let us choose ![]() $(\mathcal {X},\mathcal {D}=\sum _{i=1}^n \mathcal {D}_i)$ a lifting of
$(\mathcal {X},\mathcal {D}=\sum _{i=1}^n \mathcal {D}_i)$ a lifting of ![]() $(X,D)$ over a smooth and separated scheme
$(X,D)$ over a smooth and separated scheme ![]() $T$ over
$T$ over ![]() ${\rm Spec}(\mathbb {Z})$ such that
${\rm Spec}(\mathbb {Z})$ such that ![]() $x$ lifts compatibly with the snc structure, whose existence is guaranteed by Lemma 2.8. Let
$x$ lifts compatibly with the snc structure, whose existence is guaranteed by Lemma 2.8. Let ![]() $\overline {\pi } \, \colon \mathcal {X'} \to \mathcal {X}$ be the blow-up along
$\overline {\pi } \, \colon \mathcal {X'} \to \mathcal {X}$ be the blow-up along ![]() $\overline {x}$. Then
$\overline {x}$. Then ![]() $\mathcal {X'}$ is a lifting of
$\mathcal {X'}$ is a lifting of ![]() $X'$ because
$X'$ because ![]() $\overline {x}$ is smooth and thus, by [Reference LiuLiu02, § 8, Theorem 1.19],
$\overline {x}$ is smooth and thus, by [Reference LiuLiu02, § 8, Theorem 1.19], ![]() $\mathcal {X'}$ is smooth over
$\mathcal {X'}$ is smooth over ![]() $T$ and the exceptional divisor
$T$ and the exceptional divisor ![]() $\mathcal {E}$ is a
$\mathcal {E}$ is a ![]() $\mathbb {P}^1$-bundle over
$\mathbb {P}^1$-bundle over ![]() $\overline {x}$. We conclude that
$\overline {x}$. We conclude that ![]() $(\mathcal {X'}, \overline {\pi }^{-1}_*\mathcal {D} \cup \mathcal {E})$ is a lifting of
$(\mathcal {X'}, \overline {\pi }^{-1}_*\mathcal {D} \cup \mathcal {E})$ is a lifting of ![]() $(X', \pi _*^{-1}D \cup {\rm Exc}(\pi ))$ over
$(X', \pi _*^{-1}D \cup {\rm Exc}(\pi ))$ over ![]() $T$.
$T$.
Apart from its intrinsic interest, the condition of liftability to characteristic ![]() $0$ over a smooth base is important for its application to vanishing theorems (in fact, for our purposes liftability to
$0$ over a smooth base is important for its application to vanishing theorems (in fact, for our purposes liftability to ![]() $W_2(k)$ would be sufficient). We will apply the machinery developed by Deligne and Illusie (see [Reference Deligne and IllusieDI87] and [Reference HaraHara98] for a logarithmic version) to prove vanishing theorems for liftable surfaces in positive characteristic, of which we recall the following special case.
$W_2(k)$ would be sufficient). We will apply the machinery developed by Deligne and Illusie (see [Reference Deligne and IllusieDI87] and [Reference HaraHara98] for a logarithmic version) to prove vanishing theorems for liftable surfaces in positive characteristic, of which we recall the following special case.
Lemma 2.10 (cf. [Reference Cascini, Tanaka and WitaszekCTW17, Lemma 6.1])
Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p>2$. Let
$p>2$. Let ![]() $(X, \Delta )$ be a two-dimensional projective klt pair over
$(X, \Delta )$ be a two-dimensional projective klt pair over ![]() $k$. Suppose that there exists a log resolution
$k$. Suppose that there exists a log resolution ![]() $\mu \colon V\to X$ of
$\mu \colon V\to X$ of ![]() $(X, \Delta )$ such that
$(X, \Delta )$ such that ![]() $(V, {\rm Exc}(\mu ) \cup \mu _*^{-1} ({\rm Supp} \Delta ))$ lifts to
$(V, {\rm Exc}(\mu ) \cup \mu _*^{-1} ({\rm Supp} \Delta ))$ lifts to ![]() $W_2(k)$. Let
$W_2(k)$. Let ![]() $D$ be a
$D$ be a ![]() $\mathbb {Z}$-divisor on X such that
$\mathbb {Z}$-divisor on X such that ![]() $D - (K_X + \Delta )$ is ample. Then
$D - (K_X + \Delta )$ is ample. Then ![]() $H^i(X, \mathcal {O}_X(D)) = 0$ for any
$H^i(X, \mathcal {O}_X(D)) = 0$ for any ![]() $i > 0$.
$i > 0$.
3. Liftability of klt surfaces whose canonical divisor is not pseudo-effective
In this section we prove that the minimal resolution along with the exceptional locus of a projective klt surface whose canonical divisor ![]() $K_X$ is not pseudo-effective admits a lifting to characteristic
$K_X$ is not pseudo-effective admits a lifting to characteristic ![]() $0$ over a smooth base. First we prove this for klt surfaces admitting a Mori fibre space structure onto a curve (see Proposition 3.2). We then use the classification of klt del Pezzo surfaces of Picard rank
$0$ over a smooth base. First we prove this for klt surfaces admitting a Mori fibre space structure onto a curve (see Proposition 3.2). We then use the classification of klt del Pezzo surfaces of Picard rank ![]() $1$ to deduce the general result.
$1$ to deduce the general result.
3.1 Liftability of Mori fibre spaces
We start by discussing liftability of klt Mori fibre spaces onto a curve.
Lemma 3.1 Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $C$ be a projective smooth curve and let
$C$ be a projective smooth curve and let ![]() $\pi \colon X \to C$ be a minimal ruled surface over
$\pi \colon X \to C$ be a minimal ruled surface over ![]() $k$. Let
$k$. Let ![]() $F_i$ be the fibres over closed points
$F_i$ be the fibres over closed points ![]() $x_i\in C$ for
$x_i\in C$ for ![]() $1\leq i\leq n$. Then
$1\leq i\leq n$. Then ![]() $(X, \sum _{i=1}^n F_i)$ admits a lifting to
$(X, \sum _{i=1}^n F_i)$ admits a lifting to ![]() $W(k)$.
$W(k)$.
Proof. By [Reference HartshorneHart77, V, Proposition 2.2] there exists a vector bundle ![]() $E$ of rank
$E$ of rank ![]() $2$ on
$2$ on ![]() $C$ such that
$C$ such that ![]() $\pi \colon X \to C$ is isomorphic to
$\pi \colon X \to C$ is isomorphic to ![]() $p \colon \mathbb {P}_C(E) \to C$. The curve
$p \colon \mathbb {P}_C(E) \to C$. The curve ![]() $C$ admits a formal lifting
$C$ admits a formal lifting ![]() $\mathcal {C}$ to
$\mathcal {C}$ to ![]() $W(k)$ because the obstruction to the lifting lies in the
$W(k)$ because the obstruction to the lifting lies in the ![]() $H^2(C, T_C)$ by [Reference IllusieIll71, Proposition 3.1.5, p. 248], which vanishes for dimension reasons. Analogously, the obstruction for lifting
$H^2(C, T_C)$ by [Reference IllusieIll71, Proposition 3.1.5, p. 248], which vanishes for dimension reasons. Analogously, the obstruction for lifting ![]() $E$ to a vector bundle
$E$ to a vector bundle ![]() $\mathcal {E}$ over
$\mathcal {E}$ over ![]() $\mathcal {C}$ lies in
$\mathcal {C}$ lies in ![]() $H^2(C, \mathcal {E}nd(E))$ by [Reference IllusieIll71, Proposition 3.1.5, p. 248], which also vanishes. Thus we have a lifting
$H^2(C, \mathcal {E}nd(E))$ by [Reference IllusieIll71, Proposition 3.1.5, p. 248], which also vanishes. Thus we have a lifting ![]() $\mathbb {P}_{\mathcal {C}} (\mathcal {E}) \to \mathcal {C}$. Let
$\mathbb {P}_{\mathcal {C}} (\mathcal {E}) \to \mathcal {C}$. Let ![]() $x_1, \ldots, x_n$ be the closed points on
$x_1, \ldots, x_n$ be the closed points on ![]() $C$ such that
$C$ such that ![]() $\pi ^*x_i=F_i$. By formal smoothness, we can lift
$\pi ^*x_i=F_i$. By formal smoothness, we can lift ![]() $x_1, \ldots, x_n$ to
$x_1, \ldots, x_n$ to ![]() $\mathcal {C}$ and thus the fibres
$\mathcal {C}$ and thus the fibres ![]() $F_1, \ldots, F_n$ admit a formal lifting
$F_1, \ldots, F_n$ admit a formal lifting ![]() $\mathfrak {F}_1, \ldots, \mathfrak {F}_n$ over
$\mathfrak {F}_1, \ldots, \mathfrak {F}_n$ over ![]() $W(k)$. Therefore
$W(k)$. Therefore ![]() $(\mathbb {P}_{\mathcal {C}}(\mathcal {E}), \sum _{i=1}^n \mathfrak {F}_i)$ is a formal lifting of
$(\mathbb {P}_{\mathcal {C}}(\mathcal {E}), \sum _{i=1}^n \mathfrak {F}_i)$ is a formal lifting of ![]() $(X, \sum _{i=1}^n F_i)$ to the formal spectrum
$(X, \sum _{i=1}^n F_i)$ to the formal spectrum ![]() ${\rm Spf}(W(k))$. Since
${\rm Spf}(W(k))$. Since ![]() $H^2(X, \mathcal {O}_X)=H^0(X, K_X)=0$ by Serre duality, the pair is algebraizable by [FGI + Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli05, Corollary 8.5.6 and Corollary 8.4.5].
$H^2(X, \mathcal {O}_X)=H^0(X, K_X)=0$ by Serre duality, the pair is algebraizable by [FGI + Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli05, Corollary 8.5.6 and Corollary 8.4.5].
Proposition 3.2 Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $\pi \colon X \to C$ be a projective morphism such that:
$\pi \colon X \to C$ be a projective morphism such that:
(i)
 $X$ is a projective surface over
$X$ is a projective surface over  $k$ with klt singularities;
$k$ with klt singularities;(ii)
 $C$ is a smooth projective curve;
$C$ is a smooth projective curve;(iii)
 $\pi _*\mathcal {O}_X=\mathcal {O}_C$;
$\pi _*\mathcal {O}_X=\mathcal {O}_C$;(iv)
 $-K_X$ is
$-K_X$ is  $\pi$-ample.
$\pi$-ample.
Let ![]() $\mu \colon V\rightarrow X$ be the minimal resolution. Then the pair
$\mu \colon V\rightarrow X$ be the minimal resolution. Then the pair ![]() $(V, {\rm Exc}(\mu ))$ is log smooth and admits a lifting to characteristic
$(V, {\rm Exc}(\mu ))$ is log smooth and admits a lifting to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Proof. Let us note that the pair ![]() $(V, {\rm Exc}(\mu ))$ is log smooth by the classification of klt surface singularities (see [Reference KollárKol13, § 3.3]). Let us denote by
$(V, {\rm Exc}(\mu ))$ is log smooth by the classification of klt surface singularities (see [Reference KollárKol13, § 3.3]). Let us denote by ![]() $\pi '\colon V\rightarrow C$ the induced fibration. We run a
$\pi '\colon V\rightarrow C$ the induced fibration. We run a ![]() $K_{V}$-MMP over
$K_{V}$-MMP over ![]() $C$. We have the following diagram.
$C$. We have the following diagram.

Note that ![]() $f\colon Y \to C$ is a minimal ruled surface. Every irreducible component
$f\colon Y \to C$ is a minimal ruled surface. Every irreducible component ![]() $E$ of
$E$ of ![]() ${\rm Exc}(\mu )$ is contained in some fibre
${\rm Exc}(\mu )$ is contained in some fibre ![]() $F_i$ of
$F_i$ of ![]() $\pi '$. Let
$\pi '$. Let ![]() $F_1, \ldots F_n$ be the minimal collection of distinct fibres such that
$F_1, \ldots F_n$ be the minimal collection of distinct fibres such that ![]() ${\rm Supp}({\rm Exc}(\mu ))\subset {\rm Supp}(\sum _{i=1}^n F_i).$ Let
${\rm Supp}({\rm Exc}(\mu ))\subset {\rm Supp}(\sum _{i=1}^n F_i).$ Let ![]() $x_i \in C$ be the images of
$x_i \in C$ be the images of ![]() $F_i$ for
$F_i$ for ![]() $i=1, \ldots, n$. Note that we have the inclusion
$i=1, \ldots, n$. Note that we have the inclusion ![]() ${\rm Supp}(g(F_i))\subset {\rm Supp}(F^Y_{i})$ where
${\rm Supp}(g(F_i))\subset {\rm Supp}(F^Y_{i})$ where ![]() $F^Y_{i}$ is the fibre over
$F^Y_{i}$ is the fibre over ![]() $x_i$ of
$x_i$ of ![]() $Y\rightarrow C$. The pair
$Y\rightarrow C$. The pair ![]() $(Y, \sum _{i=1}^n F_i^Y)$ admits a lifting to
$(Y, \sum _{i=1}^n F_i^Y)$ admits a lifting to ![]() $W(k)$ by Lemma 3.1 and admits a lifting to characteristic
$W(k)$ by Lemma 3.1 and admits a lifting to characteristic ![]() $0$ over a smooth base by Proposition 2.5. Since
$0$ over a smooth base by Proposition 2.5. Since ![]() $\sum _{i=1}^n F_i^Y$ is a reduced snc divisor and
$\sum _{i=1}^n F_i^Y$ is a reduced snc divisor and ![]() $g \colon V\rightarrow Y$ can be factored as a sequence of blow-ups of smooth points, the pair
$g \colon V\rightarrow Y$ can be factored as a sequence of blow-ups of smooth points, the pair ![]() $(X, {\rm Exc}(g)+ \sum _{i=1}^n g_*^{-1}F_i)$ admits a lifting to characteristic
$(X, {\rm Exc}(g)+ \sum _{i=1}^n g_*^{-1}F_i)$ admits a lifting to characteristic ![]() $0$ over a smooth base by Proposition 2.9.
$0$ over a smooth base by Proposition 2.9.
3.2 General case
The third author classified all klt del Pezzo surfaces of Picard rank ![]() $1$ in characteristic
$1$ in characteristic ![]() $p>3$ in his PhD thesis [Reference LaciniLac20]. As a consequence of the classification he was able to prove the existence of a log resolution that lifts to characteristic
$p>3$ in his PhD thesis [Reference LaciniLac20]. As a consequence of the classification he was able to prove the existence of a log resolution that lifts to characteristic ![]() $0$ for klt del Pezzo surfaces of Picard rank
$0$ for klt del Pezzo surfaces of Picard rank ![]() $1$ defined over algebraically closed fields of characteristic
$1$ defined over algebraically closed fields of characteristic ![]() $p>5$. This serves as the main ingredient for our results on liftability of surfaces of del Pezzo type.
$p>5$. This serves as the main ingredient for our results on liftability of surfaces of del Pezzo type.
Theorem 3.3 (see [Reference LaciniLac20, Theorem 7.2])
Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $S$ be a klt del Pezzo surface of Picard rank
$S$ be a klt del Pezzo surface of Picard rank ![]() $1$ over
$1$ over ![]() $k$. Then there exists a log resolution
$k$. Then there exists a log resolution ![]() $\mu \colon V\rightarrow S$ such that
$\mu \colon V\rightarrow S$ such that ![]() $(V,{\rm Exc}(\mu ))$ lifts to characteristic
$(V,{\rm Exc}(\mu ))$ lifts to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
With the result above, we are now ready to prove the main result of this section.
Theorem 3.4 Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $X$ be a klt projective surface over
$X$ be a klt projective surface over ![]() $k$ such that
$k$ such that ![]() $K_X$ is not pseudo-effective. Then there exists a log resolution
$K_X$ is not pseudo-effective. Then there exists a log resolution ![]() $\mu \colon V\rightarrow X$ such that
$\mu \colon V\rightarrow X$ such that ![]() $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Proof. Let ![]() $g\colon X\rightarrow Y$ be a
$g\colon X\rightarrow Y$ be a ![]() $K_X$-MMP. There are two cases to distinguish.
$K_X$-MMP. There are two cases to distinguish.
(i)
 $Y$ is a klt del Pezzo surface of Picard rank
$Y$ is a klt del Pezzo surface of Picard rank  $1$. Then
$1$. Then  $Y$ admits a log resolution
$Y$ admits a log resolution  $\mu \colon V\rightarrow Y$ such that
$\mu \colon V\rightarrow Y$ such that  $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic  $0$ over a smooth base by Theorem 3.3.
$0$ over a smooth base by Theorem 3.3.(ii)
 $Y$ is a surface admitting a Mori fibre space structure
$Y$ is a surface admitting a Mori fibre space structure  $\pi \colon Y\rightarrow C$ onto a curve
$\pi \colon Y\rightarrow C$ onto a curve  $C$. Then
$C$. Then  $Y$ admits a log resolution
$Y$ admits a log resolution  $\mu \colon V\rightarrow Y$ such that
$\mu \colon V\rightarrow Y$ such that  $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic  $0$ over a smooth base by Proposition 3.2.
$0$ over a smooth base by Proposition 3.2.
In both cases, ![]() $Y$ admits a log resolution
$Y$ admits a log resolution ![]() $\mu \colon V \rightarrow Y$ such that
$\mu \colon V \rightarrow Y$ such that ![]() $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic ![]() $0$ over a smooth base. Consider the induced rational map
$0$ over a smooth base. Consider the induced rational map ![]() $\mu '\colon V \dashrightarrow X$ and let
$\mu '\colon V \dashrightarrow X$ and let ![]() $\pi \colon V'\rightarrow V$ be a log resolution of the indeterminacy locus of
$\pi \colon V'\rightarrow V$ be a log resolution of the indeterminacy locus of ![]() $\mu '$. Since the morphism
$\mu '$. Since the morphism ![]() $\pi \colon V'\rightarrow V$ can be factored as a composition of blow-ups at points, the pair
$\pi \colon V'\rightarrow V$ can be factored as a composition of blow-ups at points, the pair ![]() $(V',\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi ))$ lifts to characteristic
$(V',\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi ))$ lifts to characteristic ![]() $0$ over a smooth base by Proposition 2.9. The commutative diagram below illustrates the situation.
$0$ over a smooth base by Proposition 2.9. The commutative diagram below illustrates the situation.

We have that the support of ![]() ${\rm Exc}(\tilde {\mu })$ is contained in the support of
${\rm Exc}(\tilde {\mu })$ is contained in the support of ![]() $\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi )$. Therefore
$\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi )$. Therefore ![]() $\tilde {\mu } \colon (V',{\rm Exc}(\tilde {\mu }))\rightarrow X$ is a log resolution that lifts to characteristic
$\tilde {\mu } \colon (V',{\rm Exc}(\tilde {\mu }))\rightarrow X$ is a log resolution that lifts to characteristic ![]() $0$ over a smooth base.
$0$ over a smooth base.
Remark 3.5 One cannot drop the assumption on ![]() $K_X$ being not pseudo-effective and extend the previous result to the class of birationally ruled surfaces with klt singularities. Indeed, for every prime
$K_X$ being not pseudo-effective and extend the previous result to the class of birationally ruled surfaces with klt singularities. Indeed, for every prime ![]() $p>0$, Cascini and Tanaka construct examples of klt rational surfaces
$p>0$, Cascini and Tanaka construct examples of klt rational surfaces ![]() $Y$ of Picard rank
$Y$ of Picard rank ![]() $1$ over
$1$ over ![]() $\mathbb {F}_p$ for which no log resolution along with the exceptional divisors admits a lifting to
$\mathbb {F}_p$ for which no log resolution along with the exceptional divisors admits a lifting to ![]() $W_2(k)$ (see [Reference Cascini and TanakaCT18, Corollary 3.3]). In their examples the canonical divisor
$W_2(k)$ (see [Reference Cascini and TanakaCT18, Corollary 3.3]). In their examples the canonical divisor ![]() $K_Y$ is ample if
$K_Y$ is ample if ![]() $p>2$.
$p>2$.
As a direct application of the previous result, we can prove the Kodaira vanishing theorem for Weil divisors for the class of klt surfaces whose canonical divisor is not pseudo-effective.
Corollary 3.6 Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $X$ be a projective surface over
$X$ be a projective surface over ![]() $k$ with klt singularities such that
$k$ with klt singularities such that ![]() $K_X$ is not pseudo-effective. Then, for an ample Weil divisor
$K_X$ is not pseudo-effective. Then, for an ample Weil divisor ![]() $D$ on
$D$ on ![]() $X$, we have
$X$, we have ![]() $H^i(X, \mathcal {O}_X(K_X+D))=0$ for all
$H^i(X, \mathcal {O}_X(K_X+D))=0$ for all ![]() $i>0$.
$i>0$.
Proof. We can assume ![]() $k$ is algebraically closed by passing to the algebraic closure. Then
$k$ is algebraically closed by passing to the algebraic closure. Then ![]() $X$ is klt and
$X$ is klt and ![]() $(D+K_X)-K_X$ is ample. By Theorem 3.4 and Remark 2.6,
$(D+K_X)-K_X$ is ample. By Theorem 3.4 and Remark 2.6, ![]() $X$ has a log resolution that lifts to
$X$ has a log resolution that lifts to ![]() $W_2(k)$, therefore the result follows from Lemma 2.10.
$W_2(k)$, therefore the result follows from Lemma 2.10.
Remark 3.7 Let us note that Corollary 3.6 was first proven in [Reference ArvidssonArv21, Theorem D] using different techniques.
4. Kawamata–Viehweg vanishing theorem in characteristic  $p>5$
$p>5$
Using the results on liftability obtained in § 3, we are now ready to prove the main result of this paper.
Theorem 4.1 Let ![]() $X$ be a surface of del Pezzo type over a perfect field
$X$ be a surface of del Pezzo type over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>5$. Let
$p>5$. Let ![]() $D$ be a Weil divisor on
$D$ be a Weil divisor on ![]() $X$ and suppose that there exists a boundary
$X$ and suppose that there exists a boundary ![]() $\Delta$ such that
$\Delta$ such that ![]() $(X, \Delta )$ is a klt pair and
$(X, \Delta )$ is a klt pair and ![]() $D-(K_X+\Delta )$ is big and nef. Then
$D-(K_X+\Delta )$ is big and nef. Then
Proof. By taking the base change to the algebraic closure, we may assume ![]() $k$ to be algebraically closed. By possibly perturbing the boundary
$k$ to be algebraically closed. By possibly perturbing the boundary ![]() $\Delta$ we may assume that
$\Delta$ we may assume that ![]() $D-(K_X+\Delta )=A$, where
$D-(K_X+\Delta )=A$, where ![]() $A$ is ample. Since
$A$ is ample. Since ![]() $X$ is a Mori dream space by Lemma 2.2, we can run a
$X$ is a Mori dream space by Lemma 2.2, we can run a ![]() $\Delta$-MMP
$\Delta$-MMP ![]() $g \colon X \to Y$, which terminates with
$g \colon X \to Y$, which terminates with ![]() $\Delta _Y:=g_*\Delta$ being a nef
$\Delta _Y:=g_*\Delta$ being a nef ![]() $\mathbb {Q}$-Cartier divisor. Thus we have
$\mathbb {Q}$-Cartier divisor. Thus we have ![]() $\Delta = g^*\Delta _Y+N$, where
$\Delta = g^*\Delta _Y+N$, where ![]() $N\geq 0$ is effective and exceptional by the negativity lemma [Reference Kollár and MoriKM98, Lemma 3.39]. So we have that
$N\geq 0$ is effective and exceptional by the negativity lemma [Reference Kollár and MoriKM98, Lemma 3.39]. So we have that ![]() $D-(K_X+N)=A+g^*\Delta _Y$ is an ample divisor. Moreover, since
$D-(K_X+N)=A+g^*\Delta _Y$ is an ample divisor. Moreover, since ![]() $N \leq \Delta$, we have that
$N \leq \Delta$, we have that ![]() $(X, N)$ is klt.
$(X, N)$ is klt.
By Lemma 2.3, ![]() $Y$ is a surface of del Pezzo type and therefore there exists a log resolution
$Y$ is a surface of del Pezzo type and therefore there exists a log resolution ![]() $\mu \colon V\rightarrow Y$ such that
$\mu \colon V\rightarrow Y$ such that ![]() $(V, {\rm Exc}(\mu ))$ lifts to characteristic
$(V, {\rm Exc}(\mu ))$ lifts to characteristic ![]() $0$ over a smooth base by Theorem 3.4.
$0$ over a smooth base by Theorem 3.4.
Let us consider the induced rational map ![]() $\mu '\colon V \dashrightarrow X$ and let
$\mu '\colon V \dashrightarrow X$ and let ![]() $\pi \colon V'\rightarrow V$ be a sequence of blow-ups at smooth points such that the induced birational map
$\pi \colon V'\rightarrow V$ be a sequence of blow-ups at smooth points such that the induced birational map ![]() $\widetilde {\mu }\colon V'\dashrightarrow X$ is a morphism. The commutative diagram below illustrates the situation:
$\widetilde {\mu }\colon V'\dashrightarrow X$ is a morphism. The commutative diagram below illustrates the situation:

We have that the support of ![]() ${\rm Exc}(\widetilde {\mu })$ and the support of
${\rm Exc}(\widetilde {\mu })$ and the support of ![]() $\widetilde {\mu }^{-1}_*N$ are contained in the support of
$\widetilde {\mu }^{-1}_*N$ are contained in the support of ![]() $\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi )$. Therefore
$\pi _*^{-1}{\rm Exc}(\mu )+{\rm Exc}(\pi )$. Therefore ![]() $\tilde {\mu }\colon (V',{\rm Exc}(\tilde {\mu })+{\rm Supp}(\tilde {\mu }^{-1}_*N))$ lifts to characteristic
$\tilde {\mu }\colon (V',{\rm Exc}(\tilde {\mu })+{\rm Supp}(\tilde {\mu }^{-1}_*N))$ lifts to characteristic ![]() $0$ over a smooth base, and thus to
$0$ over a smooth base, and thus to ![]() $W_2(k)$ by Remark 2.6. By Lemma 2.10, the result follows.
$W_2(k)$ by Remark 2.6. By Lemma 2.10, the result follows.
Remark 4.2 Motivated by Theorem 3.4, one could ask whether the Kawamata–Viehweg vanishing theorem still holds for the larger class of klt surfaces ![]() $X$ whose canonical bundle is not pseudo-effective, at least in large enough characteristic. However, this is false in general, as shown by the counterexamples in [Reference Cascini and TanakaCT18, Theorem 3.1] and [Reference XieXie10, Theorem 3.1].
$X$ whose canonical bundle is not pseudo-effective, at least in large enough characteristic. However, this is false in general, as shown by the counterexamples in [Reference Cascini and TanakaCT18, Theorem 3.1] and [Reference XieXie10, Theorem 3.1].
5. Counterexamples in characteristic  $p=5$
$p=5$
It is well known that the Kawamata–Viehweg vanishing theorem may fail in positive characteristic. Counterexamples for klt del Pezzo surfaces were found in [Reference Cascini and TanakaCT19] and [Reference BernasconiBer21a] in characteristic ![]() $p=2$ and
$p=2$ and ![]() $p=3$, respectively. As a consequence, in these characteristics there are threefold klt singularities which are not rational. The third author exhibited in [Reference LaciniLac20, Example 7.6] an example of a Picard rank
$p=3$, respectively. As a consequence, in these characteristics there are threefold klt singularities which are not rational. The third author exhibited in [Reference LaciniLac20, Example 7.6] an example of a Picard rank ![]() $1$ klt del Pezzo surface in characteristic
$1$ klt del Pezzo surface in characteristic ![]() $5$ that does not admit a log resolution that lifts to characteristic
$5$ that does not admit a log resolution that lifts to characteristic ![]() $0$ over a smooth base. In this section we show that this example also violates the Kawamata–Viehweg vanishing theorem. In particular, Theorem 1.1 and Corollary 1.3 are sharp.
$0$ over a smooth base. In this section we show that this example also violates the Kawamata–Viehweg vanishing theorem. In particular, Theorem 1.1 and Corollary 1.3 are sharp.
5.1 Construction
We fix an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p=5$ and briefly recall [Reference LaciniLac20, Example 7.6 and B.12]. Consider the following four points in
$p=5$ and briefly recall [Reference LaciniLac20, Example 7.6 and B.12]. Consider the following four points in ![]() $\mathbb {P}^2_k$:
$\mathbb {P}^2_k$:
Let ![]() $L_{ab}$ be the line connecting
$L_{ab}$ be the line connecting ![]() $a$ and
$a$ and ![]() $b$, and similarly define
$b$, and similarly define ![]() $L_{ac}$,
$L_{ac}$, ![]() $L_{ad}$,
$L_{ad}$, ![]() $L_{bc}$,
$L_{bc}$, ![]() $L_{bd}$ and
$L_{bd}$ and ![]() $L_{cd}$. Consider the cubic curves
$L_{cd}$. Consider the cubic curves ![]() $C_0 = L_{ad} + L_{ac} + L_{bc}$ and
$C_0 = L_{ad} + L_{ac} + L_{bc}$ and ![]() $C_{\infty } = L_{ab} + L_{bd} + L_{cd}.$
$C_{\infty } = L_{ab} + L_{bd} + L_{cd}.$
The base locus of the pencil of curves ![]() $\{ C_t = C_0 + tC_{\infty } \}_t$ consists of the points
$\{ C_t = C_0 + tC_{\infty } \}_t$ consists of the points ![]() $a$,
$a$, ![]() $b$,
$b$, ![]() $c$,
$c$, ![]() $d$, counted with multiplicity
$d$, counted with multiplicity ![]() $2$, and of the point
$2$, and of the point ![]() $[0,0,1]$, counted with multiplicity
$[0,0,1]$, counted with multiplicity ![]() $1$. Now resolve the base locus at the points
$1$. Now resolve the base locus at the points ![]() $a$,
$a$, ![]() $b$,
$b$, ![]() $c$ and
$c$ and ![]() $d$. This is done in two steps. First, let
$d$. This is done in two steps. First, let ![]() $S_1$ be the surface obtained by blowing-up once at
$S_1$ be the surface obtained by blowing-up once at ![]() $a$,
$a$, ![]() $b$,
$b$, ![]() $c$ and
$c$ and ![]() $d$. We denote by
$d$. We denote by ![]() $E_a$ the exceptional divisor obtained by the first blow-up over
$E_a$ the exceptional divisor obtained by the first blow-up over ![]() $a$, and we use the analogous notation for the other points. The configuration is illustrated in Figure 1, where the strict transform of
$a$, and we use the analogous notation for the other points. The configuration is illustrated in Figure 1, where the strict transform of ![]() $C_0$ is drawn in grey, the strict transform of
$C_0$ is drawn in grey, the strict transform of ![]() $C_\infty$ is drawn in dark grey and the exceptional divisors are drawn as dotted lines.
$C_\infty$ is drawn in dark grey and the exceptional divisors are drawn as dotted lines.

Figure 1. Configuration of curves on ![]() $S_1$ and images of exceptional locus of
$S_1$ and images of exceptional locus of ![]() $\pi \colon S_2 \to S_1$.
$\pi \colon S_2 \to S_1$.
For simplicity, we use the same notation for a curve and its strict transform under a birational morphism. Notice that, as drawn in the picture, the lines ![]() $L_{ad}$ and
$L_{ad}$ and ![]() $L_{bc}$ meet at infinity, and the same is true for
$L_{bc}$ meet at infinity, and the same is true for ![]() $L_{ab}$ and
$L_{ab}$ and ![]() $L_{cd}$. Next, let
$L_{cd}$. Next, let ![]() $\pi \colon S_2 \to S_1$ be the surface obtained by blowing up the points
$\pi \colon S_2 \to S_1$ be the surface obtained by blowing up the points ![]() $E_a \cap L_{ab}$,
$E_a \cap L_{ab}$, ![]() $E_b \cap L_{bc}$,
$E_b \cap L_{bc}$, ![]() $E_c \cap L_{cd}$ and
$E_c \cap L_{cd}$ and ![]() $E_d \cap L_{ad}$ (in Figure 1 these points are drawn as black circles). We call
$E_d \cap L_{ad}$ (in Figure 1 these points are drawn as black circles). We call ![]() $F_a$,
$F_a$, ![]() $F_b$,
$F_b$, ![]() $F_c$ and
$F_c$ and ![]() $F_d$ the respective exceptional divisors. Notice that on
$F_d$ the respective exceptional divisors. Notice that on ![]() $S_2$ the sets
$S_2$ the sets ![]() $\Gamma _1= \{E_a, L_{ad}, L_{bc}, E_c\}$ and
$\Gamma _1= \{E_a, L_{ad}, L_{bc}, E_c\}$ and ![]() $\Gamma _2= \{ E_d, L_{cd}, L_{ab}, E_b \}$ are chains of four
$\Gamma _2= \{ E_d, L_{cd}, L_{ab}, E_b \}$ are chains of four ![]() $(-2)$ curves. Since we started from
$(-2)$ curves. Since we started from ![]() $\mathbb {P}_k^2$ and performed eight blow-ups, we get that
$\mathbb {P}_k^2$ and performed eight blow-ups, we get that ![]() $K_{S_2}^2 = K_{\mathbb {P}_k ^2} - 8 = 1$. The computations in [Reference LaciniLac20, Example B.12] show that, since the characteristic of
$K_{S_2}^2 = K_{\mathbb {P}_k ^2} - 8 = 1$. The computations in [Reference LaciniLac20, Example B.12] show that, since the characteristic of ![]() $k$ is
$k$ is ![]() $5$, there is a rational cuspidal curve
$5$, there is a rational cuspidal curve ![]() $D=C_2$ in the pencil
$D=C_2$ in the pencil ![]() $\{C_t\} \subset |-K_{\mathbb {P}^2}|$. Note that the strict transform of
$\{C_t\} \subset |-K_{\mathbb {P}^2}|$. Note that the strict transform of ![]() $D$ is disjoint from
$D$ is disjoint from ![]() $\Gamma _1$ and
$\Gamma _1$ and ![]() $\Gamma _2$ and that
$\Gamma _2$ and that ![]() $D \in |-K_{S_2}|$. Starting from
$D \in |-K_{S_2}|$. Starting from ![]() $S_2$, take a log resolution of the cusp of
$S_2$, take a log resolution of the cusp of ![]() $D$ by blowing up three times. We get a surface
$D$ by blowing up three times. We get a surface ![]() $V$ with three exceptional rational curves
$V$ with three exceptional rational curves ![]() $G_1$,
$G_1$, ![]() $G_2$,
$G_2$, ![]() $G_3$ and the following intersection numbers:
$G_3$ and the following intersection numbers:
Note, moreover, that
The configuration of the curves on ![]() $V$ is illustrated in Figure 2. We say that a singular point
$V$ is illustrated in Figure 2. We say that a singular point ![]() $p$ on a surface is of type
$p$ on a surface is of type ![]() $(n)$ if the exceptional divisor of its minimal resolution is a smooth rational curve of degree
$(n)$ if the exceptional divisor of its minimal resolution is a smooth rational curve of degree ![]() $-n$.
$-n$.

Figure 2. Arrangement of curves on ![]() $V$ and the type of singularities on
$V$ and the type of singularities on ![]() $T$.
$T$.
Finally, we consider the birational morphism ![]() $\psi \colon V \to T$ which contracts exactly the curves
$\psi \colon V \to T$ which contracts exactly the curves ![]() $\Gamma _1, \Gamma _2, G_1, G_2$ and
$\Gamma _1, \Gamma _2, G_1, G_2$ and ![]() $D$ also illustrated in Figure 2. We denote
$D$ also illustrated in Figure 2. We denote ![]() $F_{a}^T$,
$F_{a}^T$, ![]() $F^{T}_b$,
$F^{T}_b$, ![]() $F^{T}_c$,
$F^{T}_c$, ![]() $F^{T}_d$ and
$F^{T}_d$ and ![]() $G_3 ^T$ the image via
$G_3 ^T$ the image via ![]() $\psi$ of
$\psi$ of ![]() $F_a$,
$F_a$, ![]() $F_b$,
$F_b$, ![]() $F_c$,
$F_c$, ![]() $F_d$ and
$F_d$ and ![]() $G_3$, respectively.
$G_3$, respectively.
Lemma 5.1 ![]() $T$ is a surface of Picard rank
$T$ is a surface of Picard rank ![]() $1$ with only klt singularities.
$1$ with only klt singularities.
Proof. The singularities on ![]() $T$ are two
$T$ are two ![]() $A_4$ points, one
$A_4$ points, one ![]() $A_1$ point, one
$A_1$ point, one ![]() $(3)$ point and one
$(3)$ point and one ![]() $(5)$ point, so they are klt. As
$(5)$ point, so they are klt. As ![]() $V$ has Picard rank 12, it is clear that
$V$ has Picard rank 12, it is clear that ![]() $T$ has Picard rank
$T$ has Picard rank ![]() $1$. Since the Picard rank is
$1$. Since the Picard rank is ![]() $1$, it is sufficient to compute the intersection of an effective curve with the canonical class to verify
$1$, it is sufficient to compute the intersection of an effective curve with the canonical class to verify ![]() $T$ is del Pezzo. By projection formula
$T$ is del Pezzo. By projection formula
as desired.
5.2 A counterexample to the Kawamata–Viehweg vanishing theorem
In the following we construct a counterexample to the Kodaira vanishing theorem for a Weil divisor ![]() $A$ on
$A$ on ![]() $T$. The choice of the specific Weil divisor was motivated by the fact that it passes through all the singular points and has maximal Cartier index at each point.
$T$. The choice of the specific Weil divisor was motivated by the fact that it passes through all the singular points and has maximal Cartier index at each point.
Using the notation of § 5.1, we start with the following computations:
 \begin{align*} \psi^{*}F_a^T&= F_a+\tfrac{4}{5}E_a+\tfrac{3}{5}L_{ad}+\tfrac{2}{5}L_{bc}+\tfrac{1}{5}E_c+\tfrac{3}{5}E_b+\tfrac{6}{5}L_{ab}+\tfrac{4}{5}L_{cd}+\tfrac{2}{5}E_d+\tfrac{1}{5}D,\\ \psi^*F_b^T&=F_b+\tfrac{3}{5}E_c+\tfrac{6}{5}L_{bc}+\tfrac{4}{5}L_{ad}+\tfrac{2}{5}E_a+\tfrac{1}{5}E_d+\tfrac{2}{5}L_{cd}+\tfrac{3}{5}L_{ab}+\tfrac{4}{5}E_b+\tfrac{1}{5}D,\\ &\psi^*G_{3}^T=G_3+\tfrac{1}{3}G_1+\tfrac{1}{2}G_2+\tfrac{1}{5}D. \end{align*}
\begin{align*} \psi^{*}F_a^T&= F_a+\tfrac{4}{5}E_a+\tfrac{3}{5}L_{ad}+\tfrac{2}{5}L_{bc}+\tfrac{1}{5}E_c+\tfrac{3}{5}E_b+\tfrac{6}{5}L_{ab}+\tfrac{4}{5}L_{cd}+\tfrac{2}{5}E_d+\tfrac{1}{5}D,\\ \psi^*F_b^T&=F_b+\tfrac{3}{5}E_c+\tfrac{6}{5}L_{bc}+\tfrac{4}{5}L_{ad}+\tfrac{2}{5}E_a+\tfrac{1}{5}E_d+\tfrac{2}{5}L_{cd}+\tfrac{3}{5}L_{ab}+\tfrac{4}{5}E_b+\tfrac{1}{5}D,\\ &\psi^*G_{3}^T=G_3+\tfrac{1}{3}G_1+\tfrac{1}{2}G_2+\tfrac{1}{5}D. \end{align*}Proposition 5.2 Let ![]() $A=G_3^T+F_a^T-F_b^T$. Then
$A=G_3^T+F_a^T-F_b^T$. Then ![]() $A$ is an ample
$A$ is an ample ![]() $\mathbb {Q}$-Cartier Weil divisor and
$\mathbb {Q}$-Cartier Weil divisor and
Proof. We first verify that ![]() $A$ is ample. We introduce
$A$ is ample. We introduce ![]() $B:=-A=F_b^T-F_a^T-G_3^T$ and we compute its pullback to
$B:=-A=F_b^T-F_a^T-G_3^T$ and we compute its pullback to ![]() $V$:
$V$:
 \begin{gather*} \psi^*B=F_b-F_a-G_3-\tfrac{2}{5}E_a-\tfrac{3}{5}L_{ab}-\tfrac{2}{5}L_{cd}+\tfrac{2}{5}E_c-\tfrac{1}{5}E_d\\ +\,\tfrac{1}{5}L_{ad}+\tfrac{4}{5}L_{bc}+\tfrac{1}{5}E_b-\tfrac{1}{3}G_1-\tfrac{1}{2}G_2-\tfrac{1}{5}D. \end{gather*}
\begin{gather*} \psi^*B=F_b-F_a-G_3-\tfrac{2}{5}E_a-\tfrac{3}{5}L_{ab}-\tfrac{2}{5}L_{cd}+\tfrac{2}{5}E_c-\tfrac{1}{5}E_d\\ +\,\tfrac{1}{5}L_{ad}+\tfrac{4}{5}L_{bc}+\tfrac{1}{5}E_b-\tfrac{1}{3}G_1-\tfrac{1}{2}G_2-\tfrac{1}{5}D. \end{gather*}
Since ![]() $T$ has Picard rank
$T$ has Picard rank ![]() $1$ and
$1$ and ![]() $B \cdot F_a^T=\psi ^*B \cdot F_a=-\tfrac {1}{5}$ by the projection formula, we conclude
$B \cdot F_a^T=\psi ^*B \cdot F_a=-\tfrac {1}{5}$ by the projection formula, we conclude ![]() $B$ is anti-ample.
$B$ is anti-ample.
We now verify that ![]() $H^1(T, \mathcal {O}_T(B)) \neq 0$, using the Riemann–Roch theorem for surfaces. To this end we write
$H^1(T, \mathcal {O}_T(B)) \neq 0$, using the Riemann–Roch theorem for surfaces. To this end we write
and we compute its intersection numbers with ![]() $\psi$-exceptional divisors:
$\psi$-exceptional divisors:
 \begin{gather*} \lfloor{\psi^*B \rfloor} \cdot L_{ab}=0, \quad \lfloor{\psi^*B \rfloor} \cdot L_{bc}=1, \quad \lfloor{\psi^*B \rfloor} \cdot L_{cd}=0, \quad \lfloor{\psi^*B \rfloor} \cdot L_{ad}=-1,\\ \lfloor{\psi^*B \rfloor} \cdot E_a=1, \quad \lfloor{\psi^*B \rfloor} \cdot E_b=0, \quad \lfloor{\psi^*B \rfloor} \cdot E_c=0, \quad \lfloor{\psi^*B \rfloor} \cdot E_d=1,\\ \lfloor{\psi^*B \rfloor} \cdot D=4, \quad \lfloor{\psi^*B \rfloor} \cdot G_1=2, \quad \lfloor{\psi^*B \rfloor} \cdot G_2=1. \end{gather*}
\begin{gather*} \lfloor{\psi^*B \rfloor} \cdot L_{ab}=0, \quad \lfloor{\psi^*B \rfloor} \cdot L_{bc}=1, \quad \lfloor{\psi^*B \rfloor} \cdot L_{cd}=0, \quad \lfloor{\psi^*B \rfloor} \cdot L_{ad}=-1,\\ \lfloor{\psi^*B \rfloor} \cdot E_a=1, \quad \lfloor{\psi^*B \rfloor} \cdot E_b=0, \quad \lfloor{\psi^*B \rfloor} \cdot E_c=0, \quad \lfloor{\psi^*B \rfloor} \cdot E_d=1,\\ \lfloor{\psi^*B \rfloor} \cdot D=4, \quad \lfloor{\psi^*B \rfloor} \cdot G_1=2, \quad \lfloor{\psi^*B \rfloor} \cdot G_2=1. \end{gather*}
As a consequence one sees that ![]() $\lfloor {\psi ^*B \rfloor }-(K_V+\tfrac {1}{3}G_1+\tfrac {3}{5}D+\tfrac {1}{2}L_{ad})=\lfloor {\psi ^*B \rfloor }-(\psi ^*K_T+\tfrac {1}{2}L_{ad})$ is
$\lfloor {\psi ^*B \rfloor }-(K_V+\tfrac {1}{3}G_1+\tfrac {3}{5}D+\tfrac {1}{2}L_{ad})=\lfloor {\psi ^*B \rfloor }-(\psi ^*K_T+\tfrac {1}{2}L_{ad})$ is ![]() $\psi$-nef and
$\psi$-nef and ![]() $\psi$-big. Thus, by the relative Kawamata–Viehweg vanishing theorem for surfaces (see [Reference TanakaTan18, Theorem 3.3]), we deduce
$\psi$-big. Thus, by the relative Kawamata–Viehweg vanishing theorem for surfaces (see [Reference TanakaTan18, Theorem 3.3]), we deduce ![]() $R^i\psi _*\mathcal {O}_V(\lfloor {\psi ^*B \rfloor })=0$ for
$R^i\psi _*\mathcal {O}_V(\lfloor {\psi ^*B \rfloor })=0$ for ![]() $i>0$ and therefore
$i>0$ and therefore ![]() $h^i(V, \lfloor {\psi ^*B \rfloor })=h^i(T, \mathcal {O}_T(B))$ by the Leray spectral sequence. To apply Riemann–Roch we need the self-intersection of
$h^i(V, \lfloor {\psi ^*B \rfloor })=h^i(T, \mathcal {O}_T(B))$ by the Leray spectral sequence. To apply Riemann–Roch we need the self-intersection of ![]() $\lfloor {\psi ^*B \rfloor }$. To this end we also compute the following intersection numbers:
$\lfloor {\psi ^*B \rfloor }$. To this end we also compute the following intersection numbers:
A straightforward computation now shows ![]() $\lfloor {\psi ^*B \rfloor }^2=-7$, and therefore by the Riemann–Roch theorem we conclude that
$\lfloor {\psi ^*B \rfloor }^2=-7$, and therefore by the Riemann–Roch theorem we conclude that
thus showing that ![]() $h^1(V, \lfloor {\psi ^*B \rfloor })=h^1(T, \mathcal {O}_T(B)) \neq 0$.
$h^1(V, \lfloor {\psi ^*B \rfloor })=h^1(T, \mathcal {O}_T(B)) \neq 0$.
The following corollary shows that the lower bound on the characteristic for the liftability of a log resolution of a klt del Pezzo surface to the ring of second Witt vectors in Theorem 3.4 is optimal.
Corollary 5.3 The surface ![]() $T$ does not admit a log resolution
$T$ does not admit a log resolution ![]() $\mu \colon V \to T$ such that the log pair
$\mu \colon V \to T$ such that the log pair ![]() $(V, {\rm Exc}(\mu ))$ lifts to
$(V, {\rm Exc}(\mu ))$ lifts to ![]() $W_2(k)$.
$W_2(k)$.
Proof. Since ![]() $H^1(T, \mathcal {O}_T(-A))=H^1(T, \mathcal {O}_T(K_T+A)) \neq 0$, the surface
$H^1(T, \mathcal {O}_T(-A))=H^1(T, \mathcal {O}_T(K_T+A)) \neq 0$, the surface ![]() $T$ cannot admit a log resolution lifting to
$T$ cannot admit a log resolution lifting to ![]() $W_2(k)$ by Lemma 2.10.
$W_2(k)$ by Lemma 2.10.
5.3 A klt threefold singularity which is not rational
With the same notation as in § 5.2, we consider the ample ![]() $\mathbb {Q}$-Cartier Weil divisor
$\mathbb {Q}$-Cartier Weil divisor ![]() $A$ on the Picard rank
$A$ on the Picard rank ![]() $1$ klt del Pezzo surface
$1$ klt del Pezzo surface ![]() $T$. Let
$T$. Let
be the affine cone over ![]() $T$ induced by
$T$ induced by ![]() $A$. Let us denote by
$A$. Let us denote by ![]() $v$ the vertex of the cone, that is, the closed subscheme defined by the ideal
$v$ the vertex of the cone, that is, the closed subscheme defined by the ideal ![]() $\bigoplus _{m \geq 1} H^0(T, \mathcal {O}_T(mA))$.
$\bigoplus _{m \geq 1} H^0(T, \mathcal {O}_T(mA))$.
Theorem 5.4 The variety ![]() $X$ is a normal
$X$ is a normal ![]() $\mathbb {Q}$-factorial klt threefold which is not Cohen–Macaulay (and thus not rational).
$\mathbb {Q}$-factorial klt threefold which is not Cohen–Macaulay (and thus not rational).
Proof. By [Reference BernasconiBer21a, Proposition 2.4, (2)], ![]() $X$ is
$X$ is ![]() $\mathbb {Q}$-factorial. By inversion of adjunction (see [Reference Hacon and WitaszekHW19b, Corollary 1.5]), we can apply the proof of [Reference BernasconiBer21a, Proposition 2.5, (3)] to conclude that
$\mathbb {Q}$-factorial. By inversion of adjunction (see [Reference Hacon and WitaszekHW19b, Corollary 1.5]), we can apply the proof of [Reference BernasconiBer21a, Proposition 2.5, (3)] to conclude that ![]() $X$ has klt singularities. Using [Reference BernasconiBer21a, Proposition 2.6], we have
$X$ has klt singularities. Using [Reference BernasconiBer21a, Proposition 2.6], we have
by Proposition 5.2. Thus we conclude that ![]() $X$ is not Cohen–Macaulay.
$X$ is not Cohen–Macaulay.
Acknowledgements
We would like to thank P. Cascini, C.D. Hacon, Zs. Patakfalvi, D.C. Veniani, J. Witaszek and M. Zdanowicz for useful comments on this paper. We are indebted to M. Zdanowicz for several useful discussions on the topic of liftability to the ring of Witt vectors and for providing key arguments used in § 2.3. E.A. was supported by SNF grant no. 200021/169639, F.B. was partially supported by NSF research grant no. DMS-1801851 and by a grant from the Simons Foundation, award no. 256202, J.L. was partially supported by the NSF research grants no. 1265263 and no. 1802460 and by grant no. 409187 from the Simons Foundation.