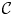1 Introduction
In axisymmetric magnetic confinement fusion devices, zonal flows are poloidal ${\boldsymbol {E}\times \boldsymbol {B}}$![]() flows which are toroidally symmetric but vary in the radial direction (E is the electric field and B is the magnetic field). Electrostatic zonal flows (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998; Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005) (and their electromagnetic counterparts called ‘zonal structures’; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015; Dong et al. Reference Dong, Bao, Bhattacharjee and Lin2019; Zocco et al. Reference Zocco, Mishchenko, Könies, Falessi and Zonca2023) have been widely studied due to their role in regulating drift-wave turbulent transport. Since the poloidal direction is not a symmetry direction in tokamaks, poloidal flows are expected to generate geodesic-acoustic-mode (GAM) oscillations (Winsor, Johnson & Dawson Reference Winsor, Johnson and Dawson1968), which are subject to collisionless Landau damping (Conway, Smolyakov & Ido Reference Conway, Smolyakov and Ido2021). However, Rosenbluth and Hinton (RH) found that the zero-frequency branch of the zonal flow, where the divergence of the poloidal flow is balanced by the divergence of the parallel flow, does not experience collisionless Landau damping, so it can continuously grow while being driven by external source terms (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998). Supposing the source term is axisymmetric, the zero-frequency zonal-flow response is shielded by neoclassical polarization and reduced by a factor $1/(1+1.6q^2\epsilon ^{-1/2})$
flows which are toroidally symmetric but vary in the radial direction (E is the electric field and B is the magnetic field). Electrostatic zonal flows (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998; Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005) (and their electromagnetic counterparts called ‘zonal structures’; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015; Dong et al. Reference Dong, Bao, Bhattacharjee and Lin2019; Zocco et al. Reference Zocco, Mishchenko, Könies, Falessi and Zonca2023) have been widely studied due to their role in regulating drift-wave turbulent transport. Since the poloidal direction is not a symmetry direction in tokamaks, poloidal flows are expected to generate geodesic-acoustic-mode (GAM) oscillations (Winsor, Johnson & Dawson Reference Winsor, Johnson and Dawson1968), which are subject to collisionless Landau damping (Conway, Smolyakov & Ido Reference Conway, Smolyakov and Ido2021). However, Rosenbluth and Hinton (RH) found that the zero-frequency branch of the zonal flow, where the divergence of the poloidal flow is balanced by the divergence of the parallel flow, does not experience collisionless Landau damping, so it can continuously grow while being driven by external source terms (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998). Supposing the source term is axisymmetric, the zero-frequency zonal-flow response is shielded by neoclassical polarization and reduced by a factor $1/(1+1.6q^2\epsilon ^{-1/2})$![]() , where $q$
, where $q$![]() is the safety factor and $\epsilon$
is the safety factor and $\epsilon$![]() is the inverse aspect ratio. This factor is known as the RH residual-flow level, which is important because the residual zonal flow can fully suppress turbulence near the linear instability threshold, which is known as the Dimits shift (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000). The RH residual flow has also been widely simulated to test the validity and accuracy of gyrokinetic simulations (Ye et al. Reference Ye, Xu, Xiao, Dai and Wang2016; Moritaka et al. Reference Moritaka, Hager, Cole, Lazerson, Chang, Ku, Matsuoka, Satake and Ishiguro2019).
is the inverse aspect ratio. This factor is known as the RH residual-flow level, which is important because the residual zonal flow can fully suppress turbulence near the linear instability threshold, which is known as the Dimits shift (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000). The RH residual flow has also been widely simulated to test the validity and accuracy of gyrokinetic simulations (Ye et al. Reference Ye, Xu, Xiao, Dai and Wang2016; Moritaka et al. Reference Moritaka, Hager, Cole, Lazerson, Chang, Ku, Matsuoka, Satake and Ishiguro2019).
Collisionless zonal-flow dynamics has also been studied in stellarators in the context of existing experimental devices such as LHD, W7-X, HSX and TJ-II (Sugama & Watanabe Reference Sugama and Watanabe2006b; Mishchenko, Helander & Könies Reference Mishchenko, Helander and Könies2008; Helander et al. Reference Helander, Mishchenko, Kleiber and Xanthopoulos2011; Xanthopoulos et al. Reference Xanthopoulos, Mischchenko, Helander, Sugama and Watanabe2011; Sánchez et al. Reference Sánchez, Kleiber, Hatzky, Borchardt, Monreal, Castejón, López-Fraguas, Sáez, Velasco and Calvo2013; Monreal et al. Reference Monreal, Calvo, Sánchez, Parra, Bustos, Könies, Kleiber and Görler2016, Reference Monreal, Sánchez, Calvo, Bustos, Parra, Mishchenko, Könies and Kleiber2017; Nicolau et al. Reference Nicolau, Choi, Fu, Liu, Wei and Lin2021; Smoniewski et al. Reference Smoniewski, Sánchez, Calvo, Pueschel and Talmadge2021). It was found that, after the initial GAM oscillations, zonal flows also experience slowly damped oscillations due to radially unconfined trapped particles. The RH level has been derived using both the gyrokinetic and the drift-kinetic formulation, which is written as a velocity-space integral. However, due to the complicated stellarator geometry, numerical calculation is usually required to evaluate the RH residual level.
In quasisymmetric (QS) stellarators (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988; Rodriguez, Helander & Bhattacharjee Reference Rodriguez, Helander and Bhattacharjee2020), the magnitude of the magnetic-field vector $\boldsymbol {B}$![]() , which lies on flux surfaces, can be expressed as $|\boldsymbol {B}|=B(\psi,M\theta -N\varphi )$
, which lies on flux surfaces, can be expressed as $|\boldsymbol {B}|=B(\psi,M\theta -N\varphi )$![]() , where $\psi$
, where $\psi$![]() is the flux-surface label (defined as the toroidal magnetic flux divided by $2{\rm \pi}$
is the flux-surface label (defined as the toroidal magnetic flux divided by $2{\rm \pi}$![]() in this paper), $\theta$
in this paper), $\theta$![]() and $\varphi$
and $\varphi$![]() are the poloidal and toroidal angles in Boozer coordinates (Boozer Reference Boozer1982) and $M$
are the poloidal and toroidal angles in Boozer coordinates (Boozer Reference Boozer1982) and $M$![]() and $N$
and $N$![]() are constant integers. This includes both quasi-axisymmetric (QA) devices where $M\neq 0$
are constant integers. This includes both quasi-axisymmetric (QA) devices where $M\neq 0$![]() and $N=0$
and $N=0$![]() , and quasi-helically (QH) symmetric devices where $M\neq 0$
, and quasi-helically (QH) symmetric devices where $M\neq 0$![]() and $N\neq 0$
and $N\neq 0$![]() . (The quasi-poloidally symmetric devices with $M=0$
. (The quasi-poloidally symmetric devices with $M=0$![]() are not considered in this paper.) Since the drift-kinetic gyrocentre motion in QS stellarators is isomorphic to tokamaks in Boozer coordinates, the collisionless zonal-flow dynamics is expected to be also very similar. However, zonal flows in stellarators can still have geometry-specific properties. For example, a recent study pointed out that, due to the small effective safety factor, a higher level of RH residual flow can be achieved in QH stellarators (Plunk & Helander Reference Plunk and Helander2024) than tokamaks. With the progress in stellarator optimization, QS configurations with great accuracy have been designed (Landreman & Paul Reference Landreman and Paul2022), so the collisional neoclassical transport can be lowered to a level similar to tokamaks, and turbulent transport will be the dominant mechanism controlling confinement times (Guttenfelder et al. Reference Guttenfelder, Lore, Anderson, Anderson, Canik, Dorland, Likin and Talmadge2008; Beurskens et al. Reference Beurskens, Bozhenkov, Ford, Xanthopoulos, Zocco, Turkin, Alonso, Beidler, Calvo and Carralero2021). Since zonal flows often play a crucial role in regulating turbulent transport, we aim to make analytic progress in understanding zonal flows in QS stellarators, which is made easier due to the isomorphism in gyrocentre motion with tokamaks, when expressed in Boozer coordinates.
are not considered in this paper.) Since the drift-kinetic gyrocentre motion in QS stellarators is isomorphic to tokamaks in Boozer coordinates, the collisionless zonal-flow dynamics is expected to be also very similar. However, zonal flows in stellarators can still have geometry-specific properties. For example, a recent study pointed out that, due to the small effective safety factor, a higher level of RH residual flow can be achieved in QH stellarators (Plunk & Helander Reference Plunk and Helander2024) than tokamaks. With the progress in stellarator optimization, QS configurations with great accuracy have been designed (Landreman & Paul Reference Landreman and Paul2022), so the collisional neoclassical transport can be lowered to a level similar to tokamaks, and turbulent transport will be the dominant mechanism controlling confinement times (Guttenfelder et al. Reference Guttenfelder, Lore, Anderson, Anderson, Canik, Dorland, Likin and Talmadge2008; Beurskens et al. Reference Beurskens, Bozhenkov, Ford, Xanthopoulos, Zocco, Turkin, Alonso, Beidler, Calvo and Carralero2021). Since zonal flows often play a crucial role in regulating turbulent transport, we aim to make analytic progress in understanding zonal flows in QS stellarators, which is made easier due to the isomorphism in gyrocentre motion with tokamaks, when expressed in Boozer coordinates.
Here, we explore the collisionless zonal-flow dynamics in QS stellarators, including the GAM oscillation frequency and the RH residual-flow level. The effects from gyroaveraging are not considered in this study, assuming the radial wavelength of zonal flows is much larger than the ion gyroradius. We also assume the adiabatic-electron model since electrons have zero bounce-averaged radial drift in QS stellarators (Mishchenko et al. Reference Mishchenko, Helander and Könies2008), but note that effects from kinetic electrons can be important for non-QS stellarators (Monreal et al. Reference Monreal, Calvo, Sánchez, Parra, Bustos, Könies, Kleiber and Görler2016; Nicolau et al. Reference Nicolau, Choi, Fu, Liu, Wei and Lin2021). It is found that, while the GAM oscillations in QA stellarators are similar to tokamaks, they become non-existent in QH stellarators when the effective safety factor in helical-angle coordinates is small. Compared with concentric-circular tokamaks, the RH residual is also found to be multiplied by a geometric factor $\mathcal {C}$![]() that arises from the flux-surface-averaged classical polarization $\langle {n_{\rm i} m_\textrm {i}|\nabla \psi |^2/B^2}\rangle$
that arises from the flux-surface-averaged classical polarization $\langle {n_{\rm i} m_\textrm {i}|\nabla \psi |^2/B^2}\rangle$![]() , where n i is the ion density and m i is the ion mass. An analytical expression of $\mathcal {C}$
, where n i is the ion density and m i is the ion mass. An analytical expression of $\mathcal {C}$![]() is obtained using the near-axis-expansion (NAE) framework (Garren & Boozer Reference Garren and Boozer1991a,Reference Garren and Boozerb; Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019; Landreman & Sengupta Reference Landreman and Sengupta2019; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020; Rodriguez, Sengupta & Bhattacharjee Reference Rodriguez, Sengupta and Bhattacharjee2022; Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2023), which varies significantly among different configurations. Note that similar modification in the RH level has been found in tokamaks, which is mainly due to the flux-surface elongation (Xiao & Catto Reference Xiao and Catto2006). However, the elongation is limited by the vertical stability, so that typically $\mathcal {C}\lesssim 2.5$
is obtained using the near-axis-expansion (NAE) framework (Garren & Boozer Reference Garren and Boozer1991a,Reference Garren and Boozerb; Landreman, Sengupta & Plunk Reference Landreman, Sengupta and Plunk2019; Landreman & Sengupta Reference Landreman and Sengupta2019; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020; Rodriguez, Sengupta & Bhattacharjee Reference Rodriguez, Sengupta and Bhattacharjee2022; Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2023), which varies significantly among different configurations. Note that similar modification in the RH level has been found in tokamaks, which is mainly due to the flux-surface elongation (Xiao & Catto Reference Xiao and Catto2006). However, the elongation is limited by the vertical stability, so that typically $\mathcal {C}\lesssim 2.5$![]() (Humphreys et al. Reference Humphreys, Casper, Eidietis, Ferrara, Gates, Hutchinson, Jackson, Kolemen, Leuer and Lister2009; Lee et al. Reference Lee, Cerfon, Freidberg and Greenwald2015). Here, a larger $\mathcal {C}$
(Humphreys et al. Reference Humphreys, Casper, Eidietis, Ferrara, Gates, Hutchinson, Jackson, Kolemen, Leuer and Lister2009; Lee et al. Reference Lee, Cerfon, Freidberg and Greenwald2015). Here, a larger $\mathcal {C}$![]() (and the RH level) can be achieved for QA stellarators, provided that they are not subject to the vertical stability. Meanwhile, we found that $\mathcal {C}<1$
(and the RH level) can be achieved for QA stellarators, provided that they are not subject to the vertical stability. Meanwhile, we found that $\mathcal {C}<1$![]() for QH stellarators, but the RH level is still enhanced due to the small effective safety factor (Plunk & Helander Reference Plunk and Helander2024).
for QH stellarators, but the RH level is still enhanced due to the small effective safety factor (Plunk & Helander Reference Plunk and Helander2024).
These analytic results are compared with numerical results from the global gyrokinetic particle-in-cell code GTC. We simulate zonal flows in first-order and second-order NAE configurations, as well as the ‘precise QA’ and ‘precise QH’ configurations reported in Landreman & Paul (Reference Landreman and Paul2022). While the GAM physics is reasonably predicted by the theory, we found that, for the RH residual level, good agreement between analytical and numerical results is achieved only when the amplitude of the QS-breaking magnetic-field component is small enough. As the next step of this research, we will study how the geometric factor $\mathcal {C}$![]() affects the nonlinear interactions between zonal flows and turbulence in QS stellarators.
affects the nonlinear interactions between zonal flows and turbulence in QS stellarators.
The rest of the paper is organized as follows. In § 2, we present our results on the RH level and the GAM frequency. In § 3, we present numerical simulation results. Conclusions and discussions are given in § 4.
2 Theory of collisionless zonal-flow dynamics
2.1 Calculation of Rosenbluth–Hinton residual flow in Boozer coordinates
Consider the time evolution of a zonal electrostatic potential $\varPhi (\psi,t)$![]() and its associated radial electric field $E_r=-\partial _\psi \varPhi |\boldsymbol {\nabla }\psi |$
and its associated radial electric field $E_r=-\partial _\psi \varPhi |\boldsymbol {\nabla }\psi |$![]() . The RH residual flow can be understood from the conservation of toroidal angular momentum, where ‘toroidal’ refers to the symmetric direction of the magnetic field (Sengupta & Hassam Reference Sengupta and Hassam2018). In an electrostatic gyrokinetic plasma, toroidal angular momentum consists of the ${\boldsymbol {E}\times \boldsymbol {B}}$
. The RH residual flow can be understood from the conservation of toroidal angular momentum, where ‘toroidal’ refers to the symmetric direction of the magnetic field (Sengupta & Hassam Reference Sengupta and Hassam2018). In an electrostatic gyrokinetic plasma, toroidal angular momentum consists of the ${\boldsymbol {E}\times \boldsymbol {B}}$![]() -flow part $\mathcal {L}_{{E\times B}}$
-flow part $\mathcal {L}_{{E\times B}}$![]() and the parallel-flow part $\mathcal {L_\parallel }$
and the parallel-flow part $\mathcal {L_\parallel }$![]() (Scott & Smirnov Reference Scott and Smirnov2010; Brizard & Tronko Reference Brizard and Tronko2011; Stoltzfus-Dueck & Scott Reference Stoltzfus-Dueck and Scott2017; Zhu et al. Reference Zhu, Stoltzfus-Dueck, Hager, Ku and Chang2024). The ${\boldsymbol {E}\times \boldsymbol {B}}$
(Scott & Smirnov Reference Scott and Smirnov2010; Brizard & Tronko Reference Brizard and Tronko2011; Stoltzfus-Dueck & Scott Reference Stoltzfus-Dueck and Scott2017; Zhu et al. Reference Zhu, Stoltzfus-Dueck, Hager, Ku and Chang2024). The ${\boldsymbol {E}\times \boldsymbol {B}}$![]() part is defined as $\mathcal {L}_{{E\times B}}=-\iota \langle {\boldsymbol {P}\boldsymbol {\cdot }\boldsymbol {\nabla }\psi }\rangle$
part is defined as $\mathcal {L}_{{E\times B}}=-\iota \langle {\boldsymbol {P}\boldsymbol {\cdot }\boldsymbol {\nabla }\psi }\rangle$![]() , where $\iota$
, where $\iota$![]() is the rotational transform, $\langle {\cdots }\rangle$
is the rotational transform, $\langle {\cdots }\rangle$![]() is the flux-surface average and the classical polarization $\boldsymbol {P}$
is the flux-surface average and the classical polarization $\boldsymbol {P}$![]() is obtained from $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {P}=e(Z_{\rm i} \delta n_{\rm i}-\delta n_{\rm e}$
is obtained from $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {P}=e(Z_{\rm i} \delta n_{\rm i}-\delta n_{\rm e}$![]() ). We have assumed a single gyrocentre ion species with mass $m_{\rm i}$
). We have assumed a single gyrocentre ion species with mass $m_{\rm i}$![]() , charge number $Z_{\rm i}$
, charge number $Z_{\rm i}$![]() , density $n_{\rm i}= n_{{\rm i} 0}+\delta n_{\rm i}$
, density $n_{\rm i}= n_{{\rm i} 0}+\delta n_{\rm i}$![]() and temperature $T_{\rm i}=T_{\rm i0}$
and temperature $T_{\rm i}=T_{\rm i0}$![]() , while electrons are assumed adiabatic so their density perturbation can be written as $\delta n_{\rm e}=n_{{\rm e} 0}e(\varPhi -\langle {\varPhi }\rangle )/T_{\rm e}$
, while electrons are assumed adiabatic so their density perturbation can be written as $\delta n_{\rm e}=n_{{\rm e} 0}e(\varPhi -\langle {\varPhi }\rangle )/T_{\rm e}$![]() , where $e$
, where $e$![]() is the elementary charge. Neglecting effects from gyroaveraging, we obtain $\boldsymbol {P}= -n_{{\rm i} 0} m_{\rm i}\boldsymbol {\nabla }_\perp \varPhi /eB^2$
is the elementary charge. Neglecting effects from gyroaveraging, we obtain $\boldsymbol {P}= -n_{{\rm i} 0} m_{\rm i}\boldsymbol {\nabla }_\perp \varPhi /eB^2$![]() from quasineutrality (see (2.26a,b) below), so that
from quasineutrality (see (2.26a,b) below), so that
The parallel-flow part is defined as $\mathcal {L}_\parallel =\int d\boldsymbol {v}f_{\rm i} m_{\rm i} v_\parallel \hat {\boldsymbol {b}}\boldsymbol {\cdot }\partial \boldsymbol {r}/\partial \varphi$![]() , where $v_\parallel$
, where $v_\parallel$![]() is the parallel velocity, $\hat {\boldsymbol {b}}=\boldsymbol {B}/B$
is the parallel velocity, $\hat {\boldsymbol {b}}=\boldsymbol {B}/B$![]() , $f_{\rm i}(\boldsymbol {r},\boldsymbol {v},t)$
, $f_{\rm i}(\boldsymbol {r},\boldsymbol {v},t)$![]() is the gyrocentre ion distribution and we have neglected the electron contribution. Assuming $\varPhi$
is the gyrocentre ion distribution and we have neglected the electron contribution. Assuming $\varPhi$![]() evolves in time slowly compared with the trapped-ion motion, $\mathcal {L}_\parallel$
evolves in time slowly compared with the trapped-ion motion, $\mathcal {L}_\parallel$![]() can be solved as the neoclassical plasma response to $E_r$
can be solved as the neoclassical plasma response to $E_r$![]() (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Xiao & Catto Reference Xiao and Catto2006; Mishchenko et al. Reference Mishchenko, Helander and Könies2008). We obtain
(Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Xiao & Catto Reference Xiao and Catto2006; Mishchenko et al. Reference Mishchenko, Helander and Könies2008). We obtain
where $\varLambda _1$![]() is given by (2.7) below. Assuming that a zonal-density perturbation is applied to the plasma at $t=0$
is given by (2.7) below. Assuming that a zonal-density perturbation is applied to the plasma at $t=0$![]() such that $E_r$
such that $E_r$![]() is established without parallel flow, then the plasma response will lead to GAM oscillations as well as the generation of parallel flow. For the linear zonal-flow dynamics where the perturbation is small, radial momentum transport (which is nonlinear) can be neglected, so that the toroidal angular momentum is conserved at each flux surface, $\varLambda _0\partial _\psi \varPhi (\psi,t=0)=(\varLambda _1+\varLambda _0)\partial _\psi \varPhi (\psi,t=\infty )$
is established without parallel flow, then the plasma response will lead to GAM oscillations as well as the generation of parallel flow. For the linear zonal-flow dynamics where the perturbation is small, radial momentum transport (which is nonlinear) can be neglected, so that the toroidal angular momentum is conserved at each flux surface, $\varLambda _0\partial _\psi \varPhi (\psi,t=0)=(\varLambda _1+\varLambda _0)\partial _\psi \varPhi (\psi,t=\infty )$![]() , from which we obtain the RH residual level as
, from which we obtain the RH residual level as
Therefore, to evaluate the RH residual level in QS stellarator configurations, we need to quantitatively calculate $\varLambda _1$![]() and $\varLambda _0$
and $\varLambda _0$![]() .
.
A general expression for $\varLambda _1$![]() has been derived by Mishchenko et al. (Reference Mishchenko, Helander and Könies2008) using the Boozer-coordinate representation, where the magnetic field can be written as
has been derived by Mishchenko et al. (Reference Mishchenko, Helander and Könies2008) using the Boozer-coordinate representation, where the magnetic field can be written as
where $G$![]() , $I$
, $I$![]() and $\delta$
and $\delta$![]() are the covariant components of $\boldsymbol {B}$
are the covariant components of $\boldsymbol {B}$![]() . To study both QA and QH configurations, we use a helical angle $\vartheta =\theta -N\varphi$
. To study both QA and QH configurations, we use a helical angle $\vartheta =\theta -N\varphi$![]() as the independent coordinate, where $N$
as the independent coordinate, where $N$![]() is the toroidal mode number of $B$
is the toroidal mode number of $B$![]() , so that the magnetic-field strength depends on $\vartheta$
, so that the magnetic-field strength depends on $\vartheta$![]() but not $\varphi$
but not $\varphi$![]() . Then
. Then
where $\iota _N=\iota -N$![]() and $G_N=G+NI$
and $G_N=G+NI$![]() . Therefore, for QH configurations with $|N|\gg |\iota |$
. Therefore, for QH configurations with $|N|\gg |\iota |$![]() , the effective rotational transform $|\iota _N|$
, the effective rotational transform $|\iota _N|$![]() can be much larger than $|\iota |$
can be much larger than $|\iota |$![]() in helical-angle coordinates. We describe charged-particle gyrocentre orbits using their energy $\mathcal {E}$
in helical-angle coordinates. We describe charged-particle gyrocentre orbits using their energy $\mathcal {E}$![]() and pitch-angle variable $\lambda =\mu /\mathcal {E}$
and pitch-angle variable $\lambda =\mu /\mathcal {E}$![]() , where $\mu$
, where $\mu$![]() is the magnetic moment. In QS stellarators, gyrocentre orbits include passing orbits $\mathcal {E}>\mu B_{\max }$
is the magnetic moment. In QS stellarators, gyrocentre orbits include passing orbits $\mathcal {E}>\mu B_{\max }$![]() and trapped orbits where $\mathcal {E}\leq \mu B_{\max }$
and trapped orbits where $\mathcal {E}\leq \mu B_{\max }$![]() , and we can define the flux-surface average $\langle {\cdots }\rangle$
, and we can define the flux-surface average $\langle {\cdots }\rangle$![]() and the bounce average $\overline {\cdots }$
and the bounce average $\overline {\cdots }$![]() as
as

where $v_\parallel =\pm \sqrt {2(\mathcal {E}-\mu B)/m_{\rm i}}$![]() is the parallel velocity and $\sqrt {g}=(\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla }\vartheta \boldsymbol {\cdot }\boldsymbol {\nabla }\varphi )^{-1}$
is the parallel velocity and $\sqrt {g}=(\boldsymbol {\nabla }\psi \times \boldsymbol {\nabla }\vartheta \boldsymbol {\cdot }\boldsymbol {\nabla }\varphi )^{-1}$![]() is the Jacobian. For the bounce average, the integration is from $\vartheta =0$
is the Jacobian. For the bounce average, the integration is from $\vartheta =0$![]() to $\vartheta =2{\rm \pi}$
to $\vartheta =2{\rm \pi}$![]() for passing particles, and back and forth between bounce points for trapped particles. Then, Mishchenko et al. (Reference Mishchenko, Helander and Könies2008) obtained
for passing particles, and back and forth between bounce points for trapped particles. Then, Mishchenko et al. (Reference Mishchenko, Helander and Könies2008) obtained

Here, $v=\sqrt {2\mathcal {E}/m_{\rm i}}$![]() , $\rho _{\rm i}=\sqrt {T_{\rm i} m_{\rm i}}/Z_{\rm i} e B$
, $\rho _{\rm i}=\sqrt {T_{\rm i} m_{\rm i}}/Z_{\rm i} e B$![]() is the gyroradius at thermal velocity, $f_{{\rm i} 0}$
is the gyroradius at thermal velocity, $f_{{\rm i} 0}$![]() is the Maxwellian distribution function and the integration is only over the passing-orbit velocity space. Also, $\tilde {G}$
is the Maxwellian distribution function and the integration is only over the passing-orbit velocity space. Also, $\tilde {G}$![]() is the solution of
is the solution of
Note that we have simplified (2.7) compared with Mishchenko et al. (Reference Mishchenko, Helander and Könies2008) assuming that the bounce-averaged radial drift velocity is zero, $\overline {\boldsymbol {v}_{\rm d}\boldsymbol {\cdot }\boldsymbol {\nabla }\psi }=0$![]() .
.
We can further carry out the calculation of $\varLambda _1$![]() for QS magnetic fields where $B$
for QS magnetic fields where $B$![]() does not depend on $\varphi$
does not depend on $\varphi$![]() , so that
, so that
so that $\tilde {G}=G_N\rho _\parallel /\iota _N$![]() . Using the relation $\langle {B/|v_\parallel |}\rangle ^{-1}=\overline {|v_\parallel |/B}$
. Using the relation $\langle {B/|v_\parallel |}\rangle ^{-1}=\overline {|v_\parallel |/B}$![]() for passing orbits, we obtain
for passing orbits, we obtain

where $q_N=\iota _N^{-1}$![]() is the effective safety factor. Since the particle motion in QS stellarators is isomorphic to tokamaks in Boozer coordinates (Boozer Reference Boozer1983), the velocity-space integration can be calculated following the existing literature (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Xiao & Catto Reference Xiao and Catto2006). Writing the magnetic-field strength as $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$
is the effective safety factor. Since the particle motion in QS stellarators is isomorphic to tokamaks in Boozer coordinates (Boozer Reference Boozer1983), the velocity-space integration can be calculated following the existing literature (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Xiao & Catto Reference Xiao and Catto2006). Writing the magnetic-field strength as $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$![]() , where $\epsilon \ll 1$
, where $\epsilon \ll 1$![]() is a small parameter, $\varLambda _1$
is a small parameter, $\varLambda _1$![]() is given by
is given by
The evaluation of $\varLambda _0$![]() , however, depends on the geometry. In a large-aspect-ratio concentric-circular tokamak with major radius $R_0$
, however, depends on the geometry. In a large-aspect-ratio concentric-circular tokamak with major radius $R_0$![]() , $G=B_0R_0$
, $G=B_0R_0$![]() and $\psi \approx B_0r^2/2$
and $\psi \approx B_0r^2/2$![]() , where $r=\epsilon R_0$
, where $r=\epsilon R_0$![]() is the radius of the flux surface, we have $\varLambda _0=n_{{\rm i} 0} m_{\rm i} r^2$
is the radius of the flux surface, we have $\varLambda _0=n_{{\rm i} 0} m_{\rm i} r^2$![]() and $\varLambda _1/\varLambda _0=1.6q^2\epsilon ^{-1/2}+O(\epsilon ^0)$
and $\varLambda _1/\varLambda _0=1.6q^2\epsilon ^{-1/2}+O(\epsilon ^0)$![]() , which is the well-known RH result in tokamaks. In QS stellarators, however, $|\boldsymbol {\nabla }\psi |$
, which is the well-known RH result in tokamaks. In QS stellarators, however, $|\boldsymbol {\nabla }\psi |$![]() varies significantly on a flux surface, so that the evaluation of $\varLambda _0$
varies significantly on a flux surface, so that the evaluation of $\varLambda _0$![]() is non-trivial and depends on the geometry. In the following, we use the NAE framework to derive an analytic expression for $\varLambda _0$
is non-trivial and depends on the geometry. In the following, we use the NAE framework to derive an analytic expression for $\varLambda _0$![]() .
.
2.2 Calculation of $\varLambda _0$ from the near-axis expansion theory
from the near-axis expansion theory
The NAE framework provides a systematic approach to constructing QS stellarator configurations. Given a prescribed set of parameters, QS configurations can be generated using NAE expansions up to second order in $\epsilon$![]() (more details on the accuracy of the model can be found in § 3 below). However, since the RH residual is predicted accurately to the lowest order in $\epsilon$
(more details on the accuracy of the model can be found in § 3 below). However, since the RH residual is predicted accurately to the lowest order in $\epsilon$![]() , we focus on parameters required to construct first-order QS configurations. Also, only vacuum fields are considered in the following because $I$
, we focus on parameters required to construct first-order QS configurations. Also, only vacuum fields are considered in the following because $I$![]() does affect $B$
does affect $B$![]() to first order in $\epsilon$
to first order in $\epsilon$![]() . Then, five quantities appear in the calculation of $\varLambda _0$
. Then, five quantities appear in the calculation of $\varLambda _0$![]() and the RH residual, including three from the axis shape $\boldsymbol {r}_0(\varphi )$
and the RH residual, including three from the axis shape $\boldsymbol {r}_0(\varphi )$![]() , and another two quantities $\bar {\eta }$
, and another two quantities $\bar {\eta }$![]() and $\sigma (\varphi )$
and $\sigma (\varphi )$![]() , which determine the flux-surface shaping and rotational transform. In particular, $\sigma (0)=0$
, which determine the flux-surface shaping and rotational transform. In particular, $\sigma (0)=0$![]() for first-order configurations that possess stellarator symmetry (provided the axis also possesses such symmetry), and $\sigma (0)\neq 0$
for first-order configurations that possess stellarator symmetry (provided the axis also possesses such symmetry), and $\sigma (0)\neq 0$![]() for those which do not. Here, stellarator symmetry refers to a property of $\boldsymbol {B}$
for those which do not. Here, stellarator symmetry refers to a property of $\boldsymbol {B}$![]() that $(B_R,B_z,B_\phi )\to (-B_R,B_z,B_\phi )$
that $(B_R,B_z,B_\phi )\to (-B_R,B_z,B_\phi )$![]() under $(R,z,\phi )\to (R,-z,-\phi )$
under $(R,z,\phi )\to (R,-z,-\phi )$![]() with respect to a reference point (chosen to be $z=\phi =0$
with respect to a reference point (chosen to be $z=\phi =0$![]() ) in cylindrical coordinates. Correspondingly, if $(R(\phi ),z(\phi ))$
) in cylindrical coordinates. Correspondingly, if $(R(\phi ),z(\phi ))$![]() is a field line then $(R(-\phi ),-z(-\phi ))$
is a field line then $(R(-\phi ),-z(-\phi ))$![]() is also a field line, including the axis (Dewar & Hudson Reference Dewar and Hudson1998).
is also a field line, including the axis (Dewar & Hudson Reference Dewar and Hudson1998).
Given a magnetic axis $\boldsymbol {r}_0(\varphi )$![]() , we can calculate its arc length $l(\varphi )=\int |{\rm d}\boldsymbol {r}_0/{\rm d}\varphi |{\rm d}\varphi$
, we can calculate its arc length $l(\varphi )=\int |{\rm d}\boldsymbol {r}_0/{\rm d}\varphi |{\rm d}\varphi$![]() , curvature $\kappa (\varphi )$
, curvature $\kappa (\varphi )$![]() and torsion $\tau (\varphi )$
and torsion $\tau (\varphi )$![]() . We can also define orthonormal vectors along the axis, which are the tangent vector $\hat {\boldsymbol {t}}(\varphi )$
. We can also define orthonormal vectors along the axis, which are the tangent vector $\hat {\boldsymbol {t}}(\varphi )$![]() , the normal vector $\hat {\boldsymbol {n}}(\varphi )$
, the normal vector $\hat {\boldsymbol {n}}(\varphi )$![]() and the binormal vector $\hat {\boldsymbol {{\rm b}}}(\varphi )$
and the binormal vector $\hat {\boldsymbol {{\rm b}}}(\varphi )$![]() . These quantities are obtained through the following relations (Mercier Reference Mercier1964; Landreman & Sengupta Reference Landreman and Sengupta2019):
. These quantities are obtained through the following relations (Mercier Reference Mercier1964; Landreman & Sengupta Reference Landreman and Sengupta2019):
where ${\rm d}/{\rm d} l=({\rm d} l/{\rm d} \varphi )^{-1}{\rm d}/{\rm d}\varphi$![]() . Specifically, we obtain $\hat {\boldsymbol {t}}$
. Specifically, we obtain $\hat {\boldsymbol {t}}$![]() from the first equation (which by definition satisfies $|\hat {\boldsymbol {t}}|=1$
from the first equation (which by definition satisfies $|\hat {\boldsymbol {t}}|=1$![]() ), $\kappa$
), $\kappa$![]() and $\hat {\boldsymbol {n}}$
and $\hat {\boldsymbol {n}}$![]() from the second equation assuming $\kappa >0$
from the second equation assuming $\kappa >0$![]() and $|\hat {\boldsymbol {n}}|=1$
and $|\hat {\boldsymbol {n}}|=1$![]() , $\hat {\boldsymbol {{\rm b}}}$
, $\hat {\boldsymbol {{\rm b}}}$![]() from the third equation and $\tau$
from the third equation and $\tau$![]() from the last equation. This procedure can be carried out when $\kappa$
from the last equation. This procedure can be carried out when $\kappa$![]() does not vanish anywhere, which applies to the QA and QH configurations (Landreman & Sengupta Reference Landreman and Sengupta2018). For first-order vacuum QS configurations, the magnetic fields are given by
does not vanish anywhere, which applies to the QA and QH configurations (Landreman & Sengupta Reference Landreman and Sengupta2018). For first-order vacuum QS configurations, the magnetic fields are given by
where $B_0$![]() is the value of the magnetic field on the axis and $2{\rm \pi} R_0$
is the value of the magnetic field on the axis and $2{\rm \pi} R_0$![]() measures the total length of the axis. Also, the Boozer toroidal angle $\varphi$
measures the total length of the axis. Also, the Boozer toroidal angle $\varphi$![]() is defined such that ${\rm d} l/d\varphi$
is defined such that ${\rm d} l/d\varphi$![]() is a constant, namely,
is a constant, namely,
The corresponding equilibria are represented as
Here, $\epsilon =\bar {\eta }\sqrt {2\psi /B_0}$![]() , where $\bar {\eta }$
, where $\bar {\eta }$![]() is a constant in the model that describes the variation of $B$
is a constant in the model that describes the variation of $B$![]() along the flux surface; $\sigma =\sigma (\varphi )$
along the flux surface; $\sigma =\sigma (\varphi )$![]() is the solution of the Riccati equation
is the solution of the Riccati equation
where the on-axis rotational transform $\iota _0$![]() is found together with the solution $\sigma (\varphi )$
is found together with the solution $\sigma (\varphi )$![]() that satisfies the periodic boundary condition in $\varphi$
that satisfies the periodic boundary condition in $\varphi$![]() . From (2.15), flux surfaces with constant $\psi$
. From (2.15), flux surfaces with constant $\psi$![]() are rotating ellipses, which are characterized by their elongation $\tan \zeta$
are rotating ellipses, which are characterized by their elongation $\tan \zeta$![]() and tilt angle $\varTheta$
and tilt angle $\varTheta$![]() with respect to $\hat {\boldsymbol {n}}$
with respect to $\hat {\boldsymbol {n}}$![]() . These two quantities can be obtained from (Rodríguez Reference Rodríguez2023)
. These two quantities can be obtained from (Rodríguez Reference Rodríguez2023)
(Note that $\varTheta$![]() is a geometric poloidal angle measured in configuration space, which is not the same as $\vartheta$
is a geometric poloidal angle measured in configuration space, which is not the same as $\vartheta$![]() .) Therefore, the flux-surface shape is determined by both $\bar {\eta }$
.) Therefore, the flux-surface shape is determined by both $\bar {\eta }$![]() and $\sigma (\varphi )$
and $\sigma (\varphi )$![]() , and $\sigma (0)=0$
, and $\sigma (0)=0$![]() for configurations that also possess stellarator symmetry.
for configurations that also possess stellarator symmetry.
Given a NAE configuration described above, we calculate $\varLambda _0$![]() as follows. Using the relation
as follows. Using the relation
and
we have (to the lowest order in $\epsilon$![]() ) (Jorge & Landreman Reference Jorge and Landreman2021)
) (Jorge & Landreman Reference Jorge and Landreman2021)

and obtain
The RH residual is then calculated as
Compared with concentric-circular tokamaks with the same $\epsilon$![]() and $q$
and $q$![]() , the RH residual in QS stellarators is modified by a geometric factor $\mathcal {C}$
, the RH residual in QS stellarators is modified by a geometric factor $\mathcal {C}$![]() , which is given by
, which is given by
The expected result $\mathcal {C}=1$![]() for concentric-circular tokamaks can be recovered with $\bar {\eta }=\kappa =R_0^{-1}$
for concentric-circular tokamaks can be recovered with $\bar {\eta }=\kappa =R_0^{-1}$![]() and $\sigma =0$
and $\sigma =0$![]() . (Note that, for tokamaks, a non-zero on-axis current density should be included in the first-order NAE equations in order to have non-zero rotational transform.) For stellarator configurations with $\bar {\eta }\neq \kappa$
. (Note that, for tokamaks, a non-zero on-axis current density should be included in the first-order NAE equations in order to have non-zero rotational transform.) For stellarator configurations with $\bar {\eta }\neq \kappa$![]() and $\sigma \neq 0$
and $\sigma \neq 0$![]() , we have $\bar {\eta }^2/\kappa ^{2}+\kappa ^2(1+\sigma ^2)/\bar {\eta }^2>2\sqrt {1+\sigma ^2}>2$
, we have $\bar {\eta }^2/\kappa ^{2}+\kappa ^2(1+\sigma ^2)/\bar {\eta }^2>2\sqrt {1+\sigma ^2}>2$![]() so that the integral is always larger than one, leading to possible enhancement of the RH residual. The denominator $(\bar {\eta } R_0)^2$
so that the integral is always larger than one, leading to possible enhancement of the RH residual. The denominator $(\bar {\eta } R_0)^2$![]() , however, depends on the configuration. Although $\bar {\eta }$
, however, depends on the configuration. Although $\bar {\eta }$![]() is a free parameter in the NAE theory, it is often chosen to maximize $\iota _0$
is a free parameter in the NAE theory, it is often chosen to maximize $\iota _0$![]() while approximately minimizing the flux-surface elongation at the same time (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2023). For the precise QA configuration studied in § 3, we found that $(\bar {\eta } R_0)^2<1$
while approximately minimizing the flux-surface elongation at the same time (Rodríguez et al. Reference Rodríguez, Sengupta and Bhattacharjee2023). For the precise QA configuration studied in § 3, we found that $(\bar {\eta } R_0)^2<1$![]() and $\mathcal {C}>1$
and $\mathcal {C}>1$![]() , leading to enhanced RH residual. For precise QH configuration, $(\bar {\eta } R_0)^2>1$
, leading to enhanced RH residual. For precise QH configuration, $(\bar {\eta } R_0)^2>1$![]() and $\mathcal {C}<1$
and $\mathcal {C}<1$![]() , but the RH residual is still much larger due to the small effective safety factor $|q_N|=|\iota _0-N|^{-1}$
, but the RH residual is still much larger due to the small effective safety factor $|q_N|=|\iota _0-N|^{-1}$![]() (Plunk & Helander Reference Plunk and Helander2024). Also note that $\sigma (0)$
(Plunk & Helander Reference Plunk and Helander2024). Also note that $\sigma (0)$![]() is often chosen to be zero so that the configuration possesses stellarator symmetry. From (2.23), it appears that non-stellarator symmetric configurations with non-zero $\sigma (0)$
is often chosen to be zero so that the configuration possesses stellarator symmetry. From (2.23), it appears that non-stellarator symmetric configurations with non-zero $\sigma (0)$![]() could lead to larger $(1+\sigma ^2)$
could lead to larger $(1+\sigma ^2)$![]() and hence larger RH residual. However, (2.16) indicates that $(\iota _0-N)$
and hence larger RH residual. However, (2.16) indicates that $(\iota _0-N)$![]() scales inversely with $(1+\sigma ^2)$
scales inversely with $(1+\sigma ^2)$![]() at large $\sigma$
at large $\sigma$![]() due to the periodic boundary condition in $\varphi$
due to the periodic boundary condition in $\varphi$![]() , so that the residual level does not necessarily increase with increasing $\sigma (0)$
, so that the residual level does not necessarily increase with increasing $\sigma (0)$![]() .
.
2.3 Geodesic acoustic modes in quasisymmetric stellarators
For numerical verification of the RH residual flow in a gyrokinetic code, one often initiates the simulation with a radially sinusoidal ion gyrocentre density perturbation and observe the time evolution of the corresponding radial electric field $E_r$![]() . For these simulations, $E_r$
. For these simulations, $E_r$![]() exhibits damped GAM oscillations at the beginning and reaches the stationary RH residual at the end. Since GAM oscillations are always present, it is also of interest to understand the GAM frequencies and damping rates. In tokamaks, the elongation is found to affect both the RH residual level (Xiao & Catto Reference Xiao and Catto2006) and the GAM frequency (Gao Reference Gao2010). Here, for QS stellarators, we expect the geometric factor $\mathcal {C}$
exhibits damped GAM oscillations at the beginning and reaches the stationary RH residual at the end. Since GAM oscillations are always present, it is also of interest to understand the GAM frequencies and damping rates. In tokamaks, the elongation is found to affect both the RH residual level (Xiao & Catto Reference Xiao and Catto2006) and the GAM frequency (Gao Reference Gao2010). Here, for QS stellarators, we expect the geometric factor $\mathcal {C}$![]() to play a similar role. In the drift-kinetic regime, a comprehensive analytic derivation of the GAM frequency in circular tokamak geometry has been given by Sugama & Watanabe (Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008), Gao et al. (Reference Gao, Itoh, Sanuki and Dong2008) and Dorf et al. (Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013). Here, we present an outline of the derivation from Sugama & Watanabe (Reference Sugama and Watanabe2006a), which is slightly modified due to the QS stellarator geometry, as well as simplified assuming $\varPhi =\langle {\varPhi }\rangle$
to play a similar role. In the drift-kinetic regime, a comprehensive analytic derivation of the GAM frequency in circular tokamak geometry has been given by Sugama & Watanabe (Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008), Gao et al. (Reference Gao, Itoh, Sanuki and Dong2008) and Dorf et al. (Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013). Here, we present an outline of the derivation from Sugama & Watanabe (Reference Sugama and Watanabe2006a), which is slightly modified due to the QS stellarator geometry, as well as simplified assuming $\varPhi =\langle {\varPhi }\rangle$![]() for reasons discussed below. Under the radially local approximation, we write the ion gyrocentre distribution function as $f_{{\rm i} 0}+{\rm Re}(\delta f\exp ({{\rm i} k_\psi \psi }))$
for reasons discussed below. Under the radially local approximation, we write the ion gyrocentre distribution function as $f_{{\rm i} 0}+{\rm Re}(\delta f\exp ({{\rm i} k_\psi \psi }))$![]() and the potential as ${\rm Re}(\varPhi \exp ({{\rm i} k_\psi \psi }))$
and the potential as ${\rm Re}(\varPhi \exp ({{\rm i} k_\psi \psi }))$![]() , where $k_\psi$
, where $k_\psi$![]() is the wavenumber in $\psi$
is the wavenumber in $\psi$![]() . Neglecting the gyroaveraging operator, the linearized gyrokinetic equation for ions is written as
. Neglecting the gyroaveraging operator, the linearized gyrokinetic equation for ions is written as
where $\omega _{\rm d}=k_\psi \boldsymbol {v}_{\rm d}\boldsymbol {\cdot }\boldsymbol {\nabla } \psi$![]() is the drift frequency and $\hat {\boldsymbol {b}}=\boldsymbol {B}/B$
is the drift frequency and $\hat {\boldsymbol {b}}=\boldsymbol {B}/B$![]() . Note that, here, $\mu$
. Note that, here, $\mu$![]() and $v_\parallel$
and $v_\parallel$![]() are treated as the independent velocity-space variables, namely, $v_\parallel$
are treated as the independent velocity-space variables, namely, $v_\parallel$![]() no longer depends on spatial variables. This simplification is made assuming the GAM frequency $\sim v_{{\rm t}{\rm i}}/R_0$
no longer depends on spatial variables. This simplification is made assuming the GAM frequency $\sim v_{{\rm t}{\rm i}}/R_0$![]() is much larger than the ion transit frequency $\sim v_{{\rm t}{\rm i}}/qR_0$
is much larger than the ion transit frequency $\sim v_{{\rm t}{\rm i}}/qR_0$![]() (Dorf et al. Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013). This assumption is justified for tokamaks with $q>1$
(Dorf et al. Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013). This assumption is justified for tokamaks with $q>1$![]() , where the existing GAM theories have been developed and tested. For QS stellarators, this criterion will be replaced by $q_N/\sqrt {C}>1$
, where the existing GAM theories have been developed and tested. For QS stellarators, this criterion will be replaced by $q_N/\sqrt {C}>1$![]() , as discussed below. For vacuum fields, $\sqrt {g}=G_N/B^2$
, as discussed below. For vacuum fields, $\sqrt {g}=G_N/B^2$![]() , $G_N=G_0=B_0R_0$
, $G_N=G_0=B_0R_0$![]() and $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$
and $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$![]() , we have
, we have
where $\delta _\psi =\epsilon B_0R_0q_N(\rho _\parallel +\mu /Z_{\rm i} ev_\parallel )$![]() represents the neoclassical finite-orbit-width effects and the toroidal derivative $\partial _\varphi$
represents the neoclassical finite-orbit-width effects and the toroidal derivative $\partial _\varphi$![]() has been omitted for the zonal-flow dynamics. The potential $\varPhi$
has been omitted for the zonal-flow dynamics. The potential $\varPhi$![]() is solved from the long-wavelength limit of the gyrokinetic Poisson equation (quasineutrality condition)
is solved from the long-wavelength limit of the gyrokinetic Poisson equation (quasineutrality condition)
Here, $\delta \bar {n}_{\rm i}$![]() is a gyroaveraged version of $\delta n_{\rm i}$
is a gyroaveraged version of $\delta n_{\rm i}$![]() and will be approximated by the latter in the following. For concentric-circular tokamaks, one can Fourier decompose in $\vartheta$
and will be approximated by the latter in the following. For concentric-circular tokamaks, one can Fourier decompose in $\vartheta$![]() , $\delta f=\sum _m\delta f_m\,{\rm e}^{{\rm i} m\vartheta }$
, $\delta f=\sum _m\delta f_m\,{\rm e}^{{\rm i} m\vartheta }$![]() and $\varPhi =\sum _m\varPhi _m\,{\rm e}^{{\rm i} m\vartheta }$
and $\varPhi =\sum _m\varPhi _m\,{\rm e}^{{\rm i} m\vartheta }$![]() , and obtain the following results:
, and obtain the following results:
where $\delta n_m=\int {\rm d}^3 v\,\delta f_m$![]() and $\rho _\psi =\rho _{\rm i}|\boldsymbol {\nabla }\psi |$
and $\rho _\psi =\rho _{\rm i}|\boldsymbol {\nabla }\psi |$![]() , with $\rho _{\rm i}=\sqrt {m_{\rm i} T_{{\rm i} 0}}/Z_{\rm i} eB$
, with $\rho _{\rm i}=\sqrt {m_{\rm i} T_{{\rm i} 0}}/Z_{\rm i} eB$![]() the ion gyroradius. For QS stellarators, however, $|\nabla \psi |^2/B^2$
the ion gyroradius. For QS stellarators, however, $|\nabla \psi |^2/B^2$![]() varies significantly with $\vartheta$
varies significantly with $\vartheta$![]() and $\varphi$
and $\varphi$![]() (2.20), so that different poloidal and toroidal Fourier harmonics are coupled. While the solution for the zonal part $\langle {\varPhi }\rangle$
(2.20), so that different poloidal and toroidal Fourier harmonics are coupled. While the solution for the zonal part $\langle {\varPhi }\rangle$![]() is still given by $\varPhi _0$
is still given by $\varPhi _0$![]() in (2.27a,b) with only a small $O(k_\psi ^2\rho _\psi ^2)$
in (2.27a,b) with only a small $O(k_\psi ^2\rho _\psi ^2)$![]() correction, the solution for the non-zonal part $\varPhi -\langle {\varPhi }\rangle$
correction, the solution for the non-zonal part $\varPhi -\langle {\varPhi }\rangle$![]() can be significantly different from $\varPhi _{m\neq 0}$
can be significantly different from $\varPhi _{m\neq 0}$![]() in (2.27a,b), and solving them correctly can be a non-trivial task. For simplicity, we assume $\varPhi =\langle {\varPhi }\rangle$
in (2.27a,b), and solving them correctly can be a non-trivial task. For simplicity, we assume $\varPhi =\langle {\varPhi }\rangle$![]() and neglect the contribution from the non-zonal potential in the following. This is also consistent with the RH analysis where $\varPhi =\langle {\varPhi }\rangle$
and neglect the contribution from the non-zonal potential in the following. This is also consistent with the RH analysis where $\varPhi =\langle {\varPhi }\rangle$![]() has been assumed for the calculation of $\mathcal {L}_{{E\times B}}$
has been assumed for the calculation of $\mathcal {L}_{{E\times B}}$![]() (2.1a,b), and can be achieved within the adiabatic-electron model assuming $T_{{\rm e} 0}\ll T_{{\rm i} 0}$
(2.1a,b), and can be achieved within the adiabatic-electron model assuming $T_{{\rm e} 0}\ll T_{{\rm i} 0}$![]() .
.
With the assumption that $\varPhi =\langle {\varPhi }\rangle$![]() , the gyrokinetic equation (2.24) does not depend on $\varphi$
, the gyrokinetic equation (2.24) does not depend on $\varphi$![]() , so that the Fourier components $\delta f_m$
, so that the Fourier components $\delta f_m$![]() are well defined. To solve $\delta f_m$
are well defined. To solve $\delta f_m$![]() as a function of $t$
as a function of $t$![]() , we apply Laplace transform in time, $\delta f_{m,\omega }=\int {\rm d} t\,{\rm e}^{{\rm i}\omega t}\delta f_{m}$
, we apply Laplace transform in time, $\delta f_{m,\omega }=\int {\rm d} t\,{\rm e}^{{\rm i}\omega t}\delta f_{m}$![]() and $\varPhi _{0,\omega }=\int {\rm d} t\,{\rm e}^{{\rm i}\omega t}\varPhi _{0}$
and $\varPhi _{0,\omega }=\int {\rm d} t\,{\rm e}^{{\rm i}\omega t}\varPhi _{0}$![]() . The $m=0$
. The $m=0$![]() component of (2.24) is
component of (2.24) is
To obtain $\delta f_{\pm 1,\omega }$![]() as a function of $\varPhi _{0,\omega }$
as a function of $\varPhi _{0,\omega }$![]() , we write (2.24) as
, we write (2.24) as
From the relation $\exp ({{\rm i} k_\psi \delta _\psi \cos \vartheta })=\sum _n{\rm i}^nJ_n(k_\psi \delta _\psi ){\rm e}^{{\rm i} n\vartheta }$![]() , where $J_n$
, where $J_n$![]() are the Bessel functions, we can solve for $\delta f_{ m,\omega }$
are the Bessel functions, we can solve for $\delta f_{ m,\omega }$![]() as (Sugama & Watanabe Reference Sugama and Watanabe2006a)
as (Sugama & Watanabe Reference Sugama and Watanabe2006a)

The above expression can be simplified assuming $|k_\psi \delta _\psi |\ll 1$![]() . Since we only consider the contribution from $\varPhi _{0,\omega }$
. Since we only consider the contribution from $\varPhi _{0,\omega }$![]() , we obtain $\delta f_{1,\omega }$
, we obtain $\delta f_{1,\omega }$![]() as
as

and similarly for $\delta f_{-1,\omega }$![]() . Here, higher-order (in $k_\psi \delta _\psi$
. Here, higher-order (in $k_\psi \delta _\psi$![]() ) terms have been neglected, and $\delta I_1$
) terms have been neglected, and $\delta I_1$![]() is from $\delta f_m(t=0)$
is from $\delta f_m(t=0)$![]() . Note that the gyrokinetic Poisson equation (2.27a,b) shows that $\delta f_0/f_{{\rm i} 0}$
. Note that the gyrokinetic Poisson equation (2.27a,b) shows that $\delta f_0/f_{{\rm i} 0}$![]() is smaller than $e\varPhi _0/T_{{\rm i} 0}$
is smaller than $e\varPhi _0/T_{{\rm i} 0}$![]() by a factor $(k_\psi \rho _\psi )^2$
by a factor $(k_\psi \rho _\psi )^2$![]() . Therefore, $\delta I_1$
. Therefore, $\delta I_1$![]() can be neglected in (2.31) when the initial condition only consists of the $m=0$
can be neglected in (2.31) when the initial condition only consists of the $m=0$![]() component $\delta f_0(t=0)$
component $\delta f_0(t=0)$![]() , as is the common situation for numerical simulations.
, as is the common situation for numerical simulations.
Integrating (2.28) over $(\mu,v_\parallel )$![]() , together with (2.27a,b) and (2.31), one obtains
, together with (2.27a,b) and (2.31), one obtains
Here, $\hat {\omega }=\omega R_0q_N/v_{{\rm t}{\rm i}}$![]() , $v_{{\rm t}{\rm i}}=\sqrt {2T_{{\rm i} 0}/m_{\rm i}}$
, $v_{{\rm t}{\rm i}}=\sqrt {2T_{{\rm i} 0}/m_{\rm i}}$![]() and $K(\hat {\omega })$
and $K(\hat {\omega })$![]() is the GAM dispersion function
is the GAM dispersion function
where $Z(\hat {\omega })$![]() is the plasma dispersion function. Also
is the plasma dispersion function. Also
is from the resonance condition at $\omega =2v_\parallel /R_0q_N$![]() , which was shown to significantly enhance the GAM damping rates. Compared with Sugama & Watanabe (Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008), the geometric factor $\mathcal {C}$
, which was shown to significantly enhance the GAM damping rates. Compared with Sugama & Watanabe (Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008), the geometric factor $\mathcal {C}$![]() appears in the ratio between $\delta _\psi ^2$
appears in the ratio between $\delta _\psi ^2$![]() and $\rho _\psi ^2$
and $\rho _\psi ^2$![]()
Therefore, compared with the tokamak results, here, for QS stellarators, we replace $q$![]() with $q_N/\sqrt {\mathcal {C}}$
with $q_N/\sqrt {\mathcal {C}}$![]() except for the definition of $\hat {\omega }$
except for the definition of $\hat {\omega }$![]() .
.
The evolution of $\varPhi$![]() with $t$
with $t$![]() is obtained through $\varPhi (t)=\int {\rm d}\omega \exp ({-{\rm i}\omega t})\varPhi _{0,\omega }/2{\rm \pi}$
is obtained through $\varPhi (t)=\int {\rm d}\omega \exp ({-{\rm i}\omega t})\varPhi _{0,\omega }/2{\rm \pi}$![]() , where the integration is from $-\infty +{\rm i}\gamma _0$
, where the integration is from $-\infty +{\rm i}\gamma _0$![]() to $+\infty +{\rm i}\gamma _0$
to $+\infty +{\rm i}\gamma _0$![]() with any positive real $\gamma _0$
with any positive real $\gamma _0$![]() . Letting $\omega =\omega _{\rm r}+{\rm i}\gamma$
. Letting $\omega =\omega _{\rm r}+{\rm i}\gamma$![]() and $\hat {\omega }=\hat {\omega }_{\rm r}+{\rm i}\hat {\gamma }$
and $\hat {\omega }=\hat {\omega }_{\rm r}+{\rm i}\hat {\gamma }$![]() , the GAM frequencies are found from $K(\hat{\omega} )=0$
, the GAM frequencies are found from $K(\hat{\omega} )=0$![]() in the lower complex plane. Analytic results can be obtained using the asymptotic expansion of $Z(\hat {\omega })$
in the lower complex plane. Analytic results can be obtained using the asymptotic expansion of $Z(\hat {\omega })$![]() assuming $|\hat {\omega }|\gg 1$
assuming $|\hat {\omega }|\gg 1$![]() and $|\gamma |\ll |\omega _{\rm r}|$
and $|\gamma |\ll |\omega _{\rm r}|$![]() , resulting in (Sugama & Watanabe Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008)
, resulting in (Sugama & Watanabe Reference Sugama and Watanabe2006a, Reference Sugama and Watanabe2008)

Therefore, $\omega _\textrm {r} q_NR_0/v_{\textrm {t}\textrm {i}}\sim q_N/\sqrt {C}$![]() and $|\gamma /\omega _\textrm {r}|\sim (q_N/\sqrt {C})\exp (-q_N^2/\mathcal {C})$
and $|\gamma /\omega _\textrm {r}|\sim (q_N/\sqrt {C})\exp (-q_N^2/\mathcal {C})$![]() , so that GAM oscillations are expected to be heavily damped in QH configurations with small $q_N^2/\mathcal {C}$
, so that GAM oscillations are expected to be heavily damped in QH configurations with small $q_N^2/\mathcal {C}$![]() . Note, however, that the ratio between the GAM frequency and the transit frequency is $q_N/\sqrt {C}$
. Note, however, that the ratio between the GAM frequency and the transit frequency is $q_N/\sqrt {C}$![]() , which should be larger than one in order for the above GAM theory to be valid. While such a criterion is generally satisfied for the QA configurations studied in § 3 below, it is not satisfied for QH configurations where $q_N/\sqrt {C}<1$
, which should be larger than one in order for the above GAM theory to be valid. While such a criterion is generally satisfied for the QA configurations studied in § 3 below, it is not satisfied for QH configurations where $q_N/\sqrt {C}<1$![]() , so that the above GAM theory may not quantitatively describe the heavy GAM damping in QH configurations.
, so that the above GAM theory may not quantitatively describe the heavy GAM damping in QH configurations.
2.4 Application beyond the near-axis expansion
Although the NAE description allowed us to derive an analytical expression of $\mathcal {C}$![]() (2.23), it is not required for the theoretical description of the RH residual and the GAM oscillations. Here, we examine the assumptions behind these theories and their validity for general QS stellarators beyond the NAE description.
(2.23), it is not required for the theoretical description of the RH residual and the GAM oscillations. Here, we examine the assumptions behind these theories and their validity for general QS stellarators beyond the NAE description.
The RH residual flow is a result of the toroidal angular momentum conservation, which is a general result in QS configurations, and the expressions (2.1a,b) and (2.7) for $\varLambda _0$![]() and $\varLambda _1$
and $\varLambda _1$![]() are also general. Therefore, as long as the magnetic-field strength satisfies
are also general. Therefore, as long as the magnetic-field strength satisfies
we will have $\varLambda _0\propto \epsilon ^2$![]() and $\varLambda _1\propto 1.6q_N^2\epsilon ^{3/2}$
and $\varLambda _1\propto 1.6q_N^2\epsilon ^{3/2}$![]() , and then the RH residual can still be written as $(1+1.6q_N^2\epsilon ^{-1/2}/\mathcal {C})$
, and then the RH residual can still be written as $(1+1.6q_N^2\epsilon ^{-1/2}/\mathcal {C})$![]() with a small parameter $\epsilon$
with a small parameter $\epsilon$![]() and a factor $\mathcal {C}$
and a factor $\mathcal {C}$![]() . While $\mathcal {C}$
. While $\mathcal {C}$![]() can be estimated from the axis shape using the NAE result (2.23), it can also be more accurately calculated from direct numerical evaluation of $\varLambda _0$
can be estimated from the axis shape using the NAE result (2.23), it can also be more accurately calculated from direct numerical evaluation of $\varLambda _0$![]() . Suppose the relation (2.37) holds and $\mathcal {C}$
. Suppose the relation (2.37) holds and $\mathcal {C}$![]() is obtained from either the NAE or direct numerical evaluation, the theory of GAM oscillations in § 2.3 can also be carried out without assuming the NAE.
is obtained from either the NAE or direct numerical evaluation, the theory of GAM oscillations in § 2.3 can also be carried out without assuming the NAE.
The relation (2.37) holds for any QS stellarators near the axis where the NAE description is valid, where $\epsilon =\bar {\eta } r$![]() is proportional to the inverse aspect ratio and characterizes the variation of $B$
is proportional to the inverse aspect ratio and characterizes the variation of $B$![]() along field lines. As shown in § 3.5, this relation also holds very well for the precise QA and precise QH configurations, even if they are not obtained from the NAE approach. In fact, a recent work has shown that a large class of QS magnetic fields can be described by the cnoidal solutions of the Korteweg–de Vries equation, which are dominated by the $\cos \vartheta$
along field lines. As shown in § 3.5, this relation also holds very well for the precise QA and precise QH configurations, even if they are not obtained from the NAE approach. In fact, a recent work has shown that a large class of QS magnetic fields can be described by the cnoidal solutions of the Korteweg–de Vries equation, which are dominated by the $\cos \vartheta$![]() component even far away from the axis (Sengupta et al. Reference Sengupta, Nikulsin, Paul, Buller, Nies, Hudson and Bhattacharjee2023). Therefore, we expect our theory of the collisionless zonal-flow dynamics to be applicable to a large class of QS stellarators beyond the NAE.
component even far away from the axis (Sengupta et al. Reference Sengupta, Nikulsin, Paul, Buller, Nies, Hudson and Bhattacharjee2023). Therefore, we expect our theory of the collisionless zonal-flow dynamics to be applicable to a large class of QS stellarators beyond the NAE.
3 Numerical simulations
3.1 Simulation set-up
We use the global gyrokinetic particle-in-cell code GTC (gyrokinetic toroidal codeFootnote 1) to simulate collisionless zonal-flow dynamics. The code utilizes global field-aligned mesh in Boozer coordinates and has been verified for the simulation of microturbulence and zonal flows in the stellarator geometry (Wang et al. Reference Wang, Holod, Lin, Bao, Fu, Liu, Nicolau, Spong and Xiao2020; Fu et al. Reference Fu, Nicolau, Liu, Wei, Xiao and Lin2021; Nicolau et al. Reference Nicolau, Choi, Fu, Liu, Wei and Lin2021; Singh et al. Reference Singh, Nicolau, Nespoli, Motojima, Lin, Sen, Sharma and Kuley2023). We choose a global code because, for the non-axisymmetric stellarator geometry, different radially local flux tubes could lead to different results, whereas a global code provides a simpler and more sharply defined set-up for studying zonal flows. Note that previous studies also showed that flux-tube simulations give reasonable approximations to the global simulation results of the RH residual when the parallel extent of the flux tube is sufficiently long, but the flux-tube length required for convergence is configuration-dependent, for example, 4 poloidal turns for HSX (Smoniewski et al. Reference Smoniewski, Sánchez, Calvo, Pueschel and Talmadge2021), 2 poloidal turns for LHD and at least 6 poloidal turns for W7-X (Sánchez et al. Reference Sánchez, García-Regaña, Bañón Navarro, Proll, Moreno, González-Jerez, Calvo, Kleiber, Riemann and Smoniewski2021).
We use single-species deuterium ions with $m_\textrm {i}=2m_\textrm {p}$![]() , $Z_\textrm {i}=1$
, $Z_\textrm {i}=1$![]() , and uniform $n_{\textrm {i} 0}$
, and uniform $n_{\textrm {i} 0}$![]() and $T_{\textrm {i} 0}$
and $T_{\textrm {i} 0}$![]() . At $t=0$
. At $t=0$![]() , we choose a radial location $\psi _0$
, we choose a radial location $\psi _0$![]() and apply a radially sinusoidal perturbation in the ion weights in a narrow range $\psi \in [\psi _0-\Delta \psi /2,\psi _0+\Delta \psi /2]$
and apply a radially sinusoidal perturbation in the ion weights in a narrow range $\psi \in [\psi _0-\Delta \psi /2,\psi _0+\Delta \psi /2]$![]() so that
so that
In other words, we apply a zonal-density perturbation with wavenumber $k_\psi =2{\rm \pi} /\Delta \psi$![]() at the flux surface $\psi _0$
at the flux surface $\psi _0$![]() , similar to the flux-tube simulations. We can apply the perturbation at different radial locations with varying $\psi _0$
, similar to the flux-tube simulations. We can apply the perturbation at different radial locations with varying $\psi _0$![]() and study the dependence of the RH residual on $\epsilon =\bar {\eta } r$
and study the dependence of the RH residual on $\epsilon =\bar {\eta } r$![]() with $r=\sqrt {2\psi _0/B_0}$
with $r=\sqrt {2\psi _0/B_0}$![]() . We also choose $\Delta \psi =0.2\sqrt {\psi _0\psi _a}$
. We also choose $\Delta \psi =0.2\sqrt {\psi _0\psi _a}$![]() , where $\psi _a$
, where $\psi _a$![]() is the value of $\psi$
is the value of $\psi$![]() at the outermost flux surface of the equilibrium, so that the zonal-flow wavelength $\Delta r\approx 0.1a$
at the outermost flux surface of the equilibrium, so that the zonal-flow wavelength $\Delta r\approx 0.1a$![]() is always 1/10 of the minor radius at the boundary $a=\sqrt {2\psi _a/B_0}$
is always 1/10 of the minor radius at the boundary $a=\sqrt {2\psi _a/B_0}$![]() , and $k_\psi \rho _\psi$
, and $k_\psi \rho _\psi$![]() and $k_\psi \delta _\psi$
and $k_\psi \delta _\psi$![]() (and hence the GAM frequencies) become independent of $\psi _0$
(and hence the GAM frequencies) become independent of $\psi _0$![]() . For each configuration, we choose 8 different values of $\psi _0$
. For each configuration, we choose 8 different values of $\psi _0$![]() corresponding to $r=0.2a, 0.3a$
corresponding to $r=0.2a, 0.3a$![]() ,…, $0.9a$
,…, $0.9a$![]() , which are evenly spaced and away from the inner and outer radial boundaries $\psi _\textrm {in}=0.01\psi _a$
, which are evenly spaced and away from the inner and outer radial boundaries $\psi _\textrm {in}=0.01\psi _a$![]() and $\psi _\textrm {out}=\psi _a$
and $\psi _\textrm {out}=\psi _a$![]() used in the simulations. We note that, as $r$
used in the simulations. We note that, as $r$![]() decreases, the zonal-flow wavelength $\Delta r$
decreases, the zonal-flow wavelength $\Delta r$![]() becomes comparable to $r$
becomes comparable to $r$![]() , so that $\epsilon$
, so that $\epsilon$![]() becomes less well defined and the simulation results are expected to deviate from the theory. For this reason, the radial location $r=0.1 a$
becomes less well defined and the simulation results are expected to deviate from the theory. For this reason, the radial location $r=0.1 a$![]() is not included, even though it is still away from the inner boundary. At $t>0$
is not included, even though it is still away from the inner boundary. At $t>0$![]() , the ion weights are evolved from the delta-$f$
, the ion weights are evolved from the delta-$f$![]() gyrokinetic equation
gyrokinetic equation
with

Here, $\boldsymbol {v}_E=\hat {\boldsymbol {b}}\times \boldsymbol {\nabla }(\hat {J}_0\varPhi )/B$![]() is the ${\boldsymbol {E}\times \boldsymbol {B}}$
is the ${\boldsymbol {E}\times \boldsymbol {B}}$![]() -drift velocity, $\hat {J}_0$
-drift velocity, $\hat {J}_0$![]() denotes gyroaverage on $\varPhi$
denotes gyroaverage on $\varPhi$![]() , $\boldsymbol {B}^*=\boldsymbol {B}(1+\rho _\parallel \boldsymbol {\nabla }\times \hat {\boldsymbol {b}})$
, $\boldsymbol {B}^*=\boldsymbol {B}(1+\rho _\parallel \boldsymbol {\nabla }\times \hat {\boldsymbol {b}})$![]() and $f_{\textrm {i} 0}$
and $f_{\textrm {i} 0}$![]() is chosen to be Maxwellian. With the assumption $T_{\textrm {e} 0}\ll T_{\textrm {i} 0}$
is chosen to be Maxwellian. With the assumption $T_{\textrm {e} 0}\ll T_{\textrm {i} 0}$![]() , the potential $\varPhi =\langle {\varPhi }\rangle$
, the potential $\varPhi =\langle {\varPhi }\rangle$![]() is obtained from the gyrokinetic Poisson equation (2.26a,b).
is obtained from the gyrokinetic Poisson equation (2.26a,b).
In the following, we present simulation results for several first-order and second-order vacuum QA and QH configurations obtained from the NAE approach (Landreman et al. Reference Landreman, Sengupta and Plunk2019; Landreman & Sengupta Reference Landreman and Sengupta2019), as well as the ‘precise QA’ and ‘precise QH’ configurations obtained from global optimization (Landreman & Paul Reference Landreman and Paul2022). These configurations are generated by VMECFootnote 2 . For the NAE configurations, the VMEC input files are generated by pyQscFootnote 3 , which prescribes their fixed outermost flux surfaces at $a=\sqrt {2\psi _a/B_0}=0.1\ \textrm {m}$![]() with $B_0= 1\ \textrm {T}$
with $B_0= 1\ \textrm {T}$![]() . In other words, while their boundaries are described by the NAE, these VMEC equilibria are still global and are not identical to the NAE inside the boundary (Landreman & Sengupta Reference Landreman and Sengupta2019). For the precise QA and precise QH configurations, the corresponding VMEC equilibria are readily available from Landreman (Reference Landreman2021), and the outermost flux surfaces correspond to $a=0.16\ \textrm {m}$
. In other words, while their boundaries are described by the NAE, these VMEC equilibria are still global and are not identical to the NAE inside the boundary (Landreman & Sengupta Reference Landreman and Sengupta2019). For the precise QA and precise QH configurations, the corresponding VMEC equilibria are readily available from Landreman (Reference Landreman2021), and the outermost flux surfaces correspond to $a=0.16\ \textrm {m}$![]() and $a=0.11\ \textrm {m}$
and $a=0.11\ \textrm {m}$![]() , respectively. With the VMEC equilibria, the geometry and the magnetic fields are then converted to Boozer coordinates using BOOZ_XFORMFootnote 4, which coordinates are used for the GTC simulations. Several geometric parameters of these configurations are summarized in table 1, and all these configurations possess stellarator symmetry. For the numerical details, we choose $n_{\textrm {i} 0}=10^{19}\ \textrm {m}^{-3}$
, respectively. With the VMEC equilibria, the geometry and the magnetic fields are then converted to Boozer coordinates using BOOZ_XFORMFootnote 4, which coordinates are used for the GTC simulations. Several geometric parameters of these configurations are summarized in table 1, and all these configurations possess stellarator symmetry. For the numerical details, we choose $n_{\textrm {i} 0}=10^{19}\ \textrm {m}^{-3}$![]() in our simulations, which does not enter our results on the RH residuals and GAM frequencies. The choice of $T_{\textrm {i} 0}$
in our simulations, which does not enter our results on the RH residuals and GAM frequencies. The choice of $T_{\textrm {i} 0}$![]() , however, requires further justification. The RH analysis assumed a small but finite $|k_\psi \delta _\psi |\sim |k_\psi \rho _\psi q_N/\sqrt {\mathcal {C}}|$
, however, requires further justification. The RH analysis assumed a small but finite $|k_\psi \delta _\psi |\sim |k_\psi \rho _\psi q_N/\sqrt {\mathcal {C}}|$![]() , so that $T_{\textrm {i} 0}$
, so that $T_{\textrm {i} 0}$![]() cannot be too large. Since the stellarator configurations presented here have relatively small radius $r\approx 0.1\ \textrm {m}$
cannot be too large. Since the stellarator configurations presented here have relatively small radius $r\approx 0.1\ \textrm {m}$![]() and weak magnetic field $B_0\approx 1\ \textrm {T}$
and weak magnetic field $B_0\approx 1\ \textrm {T}$![]() , we choose $T_{\textrm {i} 0}=1\ \textrm {eV}$
, we choose $T_{\textrm {i} 0}=1\ \textrm {eV}$![]() for the QA configurations and $T_{\textrm {i} 0}=5\ \textrm {eV}$
for the QA configurations and $T_{\textrm {i} 0}=5\ \textrm {eV}$![]() for the QH configurations, which correspond to $|k_\psi \delta _\psi |\approx 0.15$
for the QH configurations, which correspond to $|k_\psi \delta _\psi |\approx 0.15$![]() for the precise QA and precise QH configurations in § 3.5 below. The mesh grids have a radial resolution of $a/200\approx 0.5\ \textrm {mm}$
for the precise QA and precise QH configurations in § 3.5 below. The mesh grids have a radial resolution of $a/200\approx 0.5\ \textrm {mm}$![]() (20 grids per zonal-flow wavelength) and a poloidal resolution of $1\ \textrm {mm}$
(20 grids per zonal-flow wavelength) and a poloidal resolution of $1\ \textrm {mm}$![]() (about $5\rho _\textrm {i}$
(about $5\rho _\textrm {i}$![]() ). In the toroidal direction, we simulate one field period of the configurations with $N_p(N_e+1)$
). In the toroidal direction, we simulate one field period of the configurations with $N_p(N_e+1)$![]() planes. Here, $N_p$
planes. Here, $N_p$![]() planes are used where $\delta n_\textrm {i}$
planes are used where $\delta n_\textrm {i}$![]() is calculated for solving $\varPhi$
is calculated for solving $\varPhi$![]() , and an additional $N_e$
, and an additional $N_e$![]() planes are inserted between each neighbouring two of the $N_p$
planes are inserted between each neighbouring two of the $N_p$![]() planes where magnetic fields are interpolated for pushing particles (Wang et al. Reference Wang, Holod, Lin, Bao, Fu, Liu, Nicolau, Spong and Xiao2020). We use $N_e=2$
planes where magnetic fields are interpolated for pushing particles (Wang et al. Reference Wang, Holod, Lin, Bao, Fu, Liu, Nicolau, Spong and Xiao2020). We use $N_e=2$![]() , and note that GTC prefers $N_p(N_e+1)+1$
, and note that GTC prefers $N_p(N_e+1)+1$![]() to be even for the periodic cubic spline, so we choose $N_p=15$
to be even for the periodic cubic spline, so we choose $N_p=15$![]() for the QA configurations, and $N_p=31$
for the QA configurations, and $N_p=31$![]() for the QH configurations. Approximately 100 marker particles per mesh node are used, and the simulation time step is $0.02 R_0/v_{\textrm {t}\textrm {i}}$
for the QH configurations. Approximately 100 marker particles per mesh node are used, and the simulation time step is $0.02 R_0/v_{\textrm {t}\textrm {i}}$![]() . The simulation results are well converged for these choices of parameters.
. The simulation results are well converged for these choices of parameters.
Table 1. Summary of the configurations studied in this paper. Here, $N_\textrm {fp}$![]() is the field period. The value of $q_N$
is the field period. The value of $q_N$![]() is taken at the axis. The RH residuals are theoretically calculated at $\epsilon =0.1$
is taken at the axis. The RH residuals are theoretically calculated at $\epsilon =0.1$![]() . The GAM frequencies and damping rates are normalized to $v_{\textrm {t}\textrm {i}}/R_0$
. The GAM frequencies and damping rates are normalized to $v_{\textrm {t}\textrm {i}}/R_0$![]() and are independent of $\epsilon$
and are independent of $\epsilon$![]() since $k_\psi \delta _\psi$
since $k_\psi \delta _\psi$![]() does not depend on $\epsilon$
does not depend on $\epsilon$![]() in our simulations. Here, $\omega ^\textrm {ana}_\textrm {r}+\textrm {i}\gamma ^\textrm {ana}$
in our simulations. Here, $\omega ^\textrm {ana}_\textrm {r}+\textrm {i}\gamma ^\textrm {ana}$![]() is the solution of the dispersion function (2.33) and $\omega ^\textrm {num}_\textrm {r}+\textrm {i}\gamma ^\textrm {num}$
is the solution of the dispersion function (2.33) and $\omega ^\textrm {num}_\textrm {r}+\textrm {i}\gamma ^\textrm {num}$![]() is obtained from numerical fitting of the simulation data for QA configurations. Numerical fitting is not applicable to QH configurations where GAM oscillations do not exist.
is obtained from numerical fitting of the simulation data for QA configurations. Numerical fitting is not applicable to QH configurations where GAM oscillations do not exist.

3.2 Concentric-circular tokamak configurations
Before presenting the results in QS stellarators, we first show results in several concentric-circular tokamak configurations with different $q$![]() . Although the theoretical and numerical results have been well established for tokamaks, the results shown here will help give an overall picture on the zonal-flow behaviours, in particular the unusual behaviours at small and large $q$
. Although the theoretical and numerical results have been well established for tokamaks, the results shown here will help give an overall picture on the zonal-flow behaviours, in particular the unusual behaviours at small and large $q$![]() . These tokamak configurations can be described analytically in GTC with major radius $R_0=1\ \textrm {m}$
. These tokamak configurations can be described analytically in GTC with major radius $R_0=1\ \textrm {m}$![]() and minor radius at the outer boundary $a=0.1\ \textrm {m}$
and minor radius at the outer boundary $a=0.1\ \textrm {m}$![]() . The magnetic field is given by $\boldsymbol {B}=G_0\boldsymbol {\nabla }\varphi +q^{-1}\boldsymbol {\nabla }\varphi \times \boldsymbol {\nabla }\psi$
. The magnetic field is given by $\boldsymbol {B}=G_0\boldsymbol {\nabla }\varphi +q^{-1}\boldsymbol {\nabla }\varphi \times \boldsymbol {\nabla }\psi$![]() , with $G_0=B_0R_0$
, with $G_0=B_0R_0$![]() and $B_0=1\ \textrm {T}$
and $B_0=1\ \textrm {T}$![]() , and the Boozer toroidal angle $\varphi$
, and the Boozer toroidal angle $\varphi$![]() is minus the cylindrical toroidal angle, i.e. $\varphi =-\phi$
is minus the cylindrical toroidal angle, i.e. $\varphi =-\phi$![]() . We simulate 1/24 of the torus with 4 planes, and the other simulation parameters are similar to those described above.
. We simulate 1/24 of the torus with 4 planes, and the other simulation parameters are similar to those described above.
Figure 1(a) shows the results at $q=1.0$![]() , $1.4$
, $1.4$![]() and $1.8$
and $1.8$![]() . At $q=1.4$
. At $q=1.4$![]() the zonal flow behaves in the expected way, namely, damped GAM oscillations followed by the RH residual flow. At $q=1.0$
the zonal flow behaves in the expected way, namely, damped GAM oscillations followed by the RH residual flow. At $q=1.0$![]() the GAM is quickly damped, followed by a slow relaxation to the RH residual flow. At $q=1.8$
the GAM is quickly damped, followed by a slow relaxation to the RH residual flow. At $q=1.8$![]() , however, GAM oscillations become persistent and do not damp to zero, even though the theory in § 2.3 still predicts a finite $\gamma <0$
, however, GAM oscillations become persistent and do not damp to zero, even though the theory in § 2.3 still predicts a finite $\gamma <0$![]() . These undamped GAM oscillations occur around $q\approx 1.6$
. These undamped GAM oscillations occur around $q\approx 1.6$![]() , and they have also been observed in GTC simulations in the past (Lin et al. Reference Lin, Hahm, Lee, Tang and White2000) as well as from another global gyrokinetic code COGENT (Dorf et al. Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013).
, and they have also been observed in GTC simulations in the past (Lin et al. Reference Lin, Hahm, Lee, Tang and White2000) as well as from another global gyrokinetic code COGENT (Dorf et al. Reference Dorf, Cohen, Dorr, Rognlien, Hittinger, Compton, Colella, Martin and McCorquodale2013).

Figure 1. Simulation results for concentric-circular tokamaks. (a) The radial electric field $E_r(t)$![]() at $\epsilon =0.05$
at $\epsilon =0.05$![]() normalized to its initial value with increasing $q$
normalized to its initial value with increasing $q$![]() . At $q=1.8$
. At $q=1.8$![]() , GAM oscillations become persistent and do not damp to zero. (b) Same as (a) but with decreasing $q$
, GAM oscillations become persistent and do not damp to zero. (b) Same as (a) but with decreasing $q$![]() . The GAM oscillations indicated by the text arrow are heavily damped and eventually become non-existent. (c) Comparison between analytical (curves) and numerical (markers) results for the RH level.
. The GAM oscillations indicated by the text arrow are heavily damped and eventually become non-existent. (c) Comparison between analytical (curves) and numerical (markers) results for the RH level.
Figure 1(b) shows the results at $q=0.9$![]() , $0.7$
, $0.7$![]() and $0.5$
and $0.5$![]() . As $q$
. As $q$![]() decreases, the GAM oscillations are heavily damped and eventually become non-existent at $q=0.5$
decreases, the GAM oscillations are heavily damped and eventually become non-existent at $q=0.5$![]() , when the initial perturbation relaxes to the residual flow through a slower oscillation. These slower oscillations cannot be described by the GAM theory in § 2.3, since $q<1$
, when the initial perturbation relaxes to the residual flow through a slower oscillation. These slower oscillations cannot be described by the GAM theory in § 2.3, since $q<1$![]() is outside its applicable range.
is outside its applicable range.
Finally, figure 1(c) shows the RH residual level at different $q$![]() , and theory and simulation results agree well (within a $10\,\%$
, and theory and simulation results agree well (within a $10\,\%$![]() difference). This is expected as the RH flow is a result of the toroidal angular momentum conservation regardless of the GAM behaviours. Also note that the theory and simulation results start to deviate at the smallest $\epsilon$
difference). This is expected as the RH flow is a result of the toroidal angular momentum conservation regardless of the GAM behaviours. Also note that the theory and simulation results start to deviate at the smallest $\epsilon$![]() , where the zonal-flow wavelength becomes comparable to the minor radius so that $\epsilon$
, where the zonal-flow wavelength becomes comparable to the minor radius so that $\epsilon$![]() itself becomes less well defined.
itself becomes less well defined.
3.3 First-order NAE configurations
For first-order NAE configurations, we follow the examples presented in Landreman et al. (Reference Landreman, Sengupta and Plunk2019). For QA configurations, the axis shape is chosen to be
where $\phi$![]() is the cylindrical (not Boozer) toroidal angle. To see the effects from $\bar {\eta }$
is the cylindrical (not Boozer) toroidal angle. To see the effects from $\bar {\eta }$![]() , we compare three different configurations with $\bar {\eta }=0.6$
, we compare three different configurations with $\bar {\eta }=0.6$![]() , 0.7 and 0.8, which are labelled by ‘a’, ‘b’, ‘c’ in table 1, respectively. For these configurations, the magnetic-field strength can be written as $B=\sum B_{MN}\cos (M\vartheta -N\varphi )$
, 0.7 and 0.8, which are labelled by ‘a’, ‘b’, ‘c’ in table 1, respectively. For these configurations, the magnetic-field strength can be written as $B=\sum B_{MN}\cos (M\vartheta -N\varphi )$![]() , where $B_{MN}$
, where $B_{MN}$![]() is the Fourier spectrum in Boozer coordinates calculated from BOOZ_XFORM, and only the cosine components are included due to stellarator symmetry. Figure 2 shows the amplitude of the $N=0$
is the Fourier spectrum in Boozer coordinates calculated from BOOZ_XFORM, and only the cosine components are included due to stellarator symmetry. Figure 2 shows the amplitude of the $N=0$![]() components, which are QS, and the amplitude of the $N\neq 0$
components, which are QS, and the amplitude of the $N\neq 0$![]() components, which are QS-breaking. It is seen that $B$
components, which are QS-breaking. It is seen that $B$![]() is dominated by the $(M,N)=(1,0)$
is dominated by the $(M,N)=(1,0)$![]() QS component, but the $N\neq 0$
QS component, but the $N\neq 0$![]() QS-breaking components are also significant; in particular, they remain finite near the axis, which seemingly contradicts the NAE description. As mentioned above, while their boundaries are prescribed by the NAE, these VMEC equilibria are global and not identical to the NAE inside the boundary. Landreman & Sengupta (Reference Landreman and Sengupta2019) showed that, if we prescribe the boundary at $r=a$
QS-breaking components are also significant; in particular, they remain finite near the axis, which seemingly contradicts the NAE description. As mentioned above, while their boundaries are prescribed by the NAE, these VMEC equilibria are global and not identical to the NAE inside the boundary. Landreman & Sengupta (Reference Landreman and Sengupta2019) showed that, if we prescribe the boundary at $r=a$![]() from the first-order NAE theory, the axes of the resulting VMEC equilibria will slightly differ from the original axes assumed by the NAE, resulting in a $O((a/R_0)^2)$
from the first-order NAE theory, the axes of the resulting VMEC equilibria will slightly differ from the original axes assumed by the NAE, resulting in a $O((a/R_0)^2)$![]() QS error even at the axes. Therefore, we do not expect these configurations to be close to QS even near the axes.
QS error even at the axes. Therefore, we do not expect these configurations to be close to QS even near the axes.

Figure 2. The Fourier spectrum of $B$![]() for the first-order NAE QA configurations. Shown is $\sqrt {\sum B_{MN}^2}$
for the first-order NAE QA configurations. Shown is $\sqrt {\sum B_{MN}^2}$![]() , where the summation is over the range in $(M,N)$
, where the summation is over the range in $(M,N)$![]() indicated by the legends.
indicated by the legends.
The GAM oscillations nevertheless behave as expected, and are insensitive to the QS property. As shown in figure 3(a,b), $\mathcal {C}$![]() decreases with increasing $\bar {\eta }$
decreases with increasing $\bar {\eta }$![]() so that the GAM frequency increases. Meanwhile, the GAM damping rate also decreases due to increasing $q_N^2/\mathcal {C}$
so that the GAM frequency increases. Meanwhile, the GAM damping rate also decreases due to increasing $q_N^2/\mathcal {C}$![]() . To compare with the analytic results, the simulation results are often fitted with the following formula (Sugama & Watanabe Reference Sugama and Watanabe2006a):
. To compare with the analytic results, the simulation results are often fitted with the following formula (Sugama & Watanabe Reference Sugama and Watanabe2006a):
where RH is the residual level. However, we found it difficult to achieve a globally good fit, because the initial GAM damping rate is much larger than the late-time damping rate as $E_r$![]() approaches the RH residual. The reason is that, as with the typical Landau-damping process, the initial perturbation is not a GAM eigenstate, which only emerges at large $t$
approaches the RH residual. The reason is that, as with the typical Landau-damping process, the initial perturbation is not a GAM eigenstate, which only emerges at large $t$![]() after the initial fast damping due to phase mixing. Therefore, we ignore the initially large GAM damping rates, and numerically find $(\omega ^\textrm {num}_\textrm {r}, \gamma ^\textrm {num})$
after the initial fast damping due to phase mixing. Therefore, we ignore the initially large GAM damping rates, and numerically find $(\omega ^\textrm {num}_\textrm {r}, \gamma ^\textrm {num})$![]() that matches $E_r$
that matches $E_r$![]() as it approaches the RH level. Comparison with solutions of the dispersion function (2.33) are shown in table 1, and both $\omega _\textrm {r}$
as it approaches the RH level. Comparison with solutions of the dispersion function (2.33) are shown in table 1, and both $\omega _\textrm {r}$![]() and $\gamma$
and $\gamma$![]() agree well with the theoretical prediction. Also note that the GAM oscillations do not completely damp to zero at $\bar {\eta }=0.8$
agree well with the theoretical prediction. Also note that the GAM oscillations do not completely damp to zero at $\bar {\eta }=0.8$![]() where $|q_N|/\sqrt {C}=1.65$
where $|q_N|/\sqrt {C}=1.65$![]() , consistent with the observation in figure 1.
, consistent with the observation in figure 1.

Figure 3. Simulation results for the first-order NAE QA configurations. (a,b) The radial electric field $E_r(t)$![]() at $\epsilon =0.05$
at $\epsilon =0.05$![]() normalized to its initial value. The GAM oscillations and the RH levels are shown separately in two figures for a clearer view. (c) Comparison between analytical (curves) and numerical (markers) results for the RH level. The configurations have the same range in $r$
normalized to its initial value. The GAM oscillations and the RH levels are shown separately in two figures for a clearer view. (c) Comparison between analytical (curves) and numerical (markers) results for the RH level. The configurations have the same range in $r$![]() but different a range in $\epsilon =\bar {\eta } r$
but different a range in $\epsilon =\bar {\eta } r$![]() due to their different $\bar {\eta }$
due to their different $\bar {\eta }$![]() .
.
For the RH level, however, numerical results do not agree with the theoretical predictions. As shown in figure 3(c), theory and simulation results do not show any agreement. Further, as $\epsilon$![]() increases, the numerical RH level actually decreases, in contrast to the theory. This is not a surprise considering the large QS-breaking components shown in figure 2. In fact, Helander et al. (Reference Helander, Mishchenko, Kleiber and Xanthopoulos2011) studied the effects of radially unconfined trapped particles and found the long-time residual level to be
increases, the numerical RH level actually decreases, in contrast to the theory. This is not a surprise considering the large QS-breaking components shown in figure 2. In fact, Helander et al. (Reference Helander, Mishchenko, Kleiber and Xanthopoulos2011) studied the effects of radially unconfined trapped particles and found the long-time residual level to be

where the factor $\beta$![]() comes from the unconfined particles. At small $|k_\psi \rho _\psi |$
comes from the unconfined particles. At small $|k_\psi \rho _\psi |$![]() , $\beta /(k_\psi \rho _\psi )^2$
, $\beta /(k_\psi \rho _\psi )^2$![]() can be large and hence can provide a possible explanation for the observed decrease in the RH level at large $\epsilon$
can be large and hence can provide a possible explanation for the observed decrease in the RH level at large $\epsilon$![]() .
.
For the first-order QH configurations, the example presented in Landreman & Sengupta (Reference Landreman and Sengupta2019) has $a=0.025\ \textrm {m}$![]() , so it is 4 times thinner than the first-order QA configurations. The reason is that, due to the strongly shaped axis, the first-order QH configuration achieves the same level of QS-breaking components in $B$
, so it is 4 times thinner than the first-order QA configurations. The reason is that, due to the strongly shaped axis, the first-order QH configuration achieves the same level of QS-breaking components in $B$![]() at a 4 times smaller $r$
at a 4 times smaller $r$![]() compared with the first-order QA configuration. Therefore, we expect even more significant QS errors for the first-order QH configuration at larger radius $a\sim 0.1\ \textrm {m}$
compared with the first-order QA configuration. Therefore, we expect even more significant QS errors for the first-order QH configuration at larger radius $a\sim 0.1\ \textrm {m}$![]() , so we skip this configuration and proceed to second-order NAE configurations below.
, so we skip this configuration and proceed to second-order NAE configurations below.
3.4 Second-order NAE configurations
We have seen that, for the first-order NAE configurations, the QS-breaking components of $B$![]() are significant, resulting in disagreement in theory and simulation results on the RH level. To see if such deviation can be reduced with reduced QS error, we test the second-order NAE QA and QH configurations from Landreman & Sengupta (Reference Landreman and Sengupta2019). For the second-order QA configuration, the axis is chosen to be
are significant, resulting in disagreement in theory and simulation results on the RH level. To see if such deviation can be reduced with reduced QS error, we test the second-order NAE QA and QH configurations from Landreman & Sengupta (Reference Landreman and Sengupta2019). For the second-order QA configuration, the axis is chosen to be
with $\bar {\eta }=0.632$![]() . For the second-order QH configuration, the axis is
. For the second-order QH configuration, the axis is

with $\bar {\eta }=1.569$![]() . The normal vector $\boldsymbol {n}$
. The normal vector $\boldsymbol {n}$![]() rotates around the axis poloidally four times as the axis is traversed toroidally, resulting in $N=4$
rotates around the axis poloidally four times as the axis is traversed toroidally, resulting in $N=4$![]() . For these configurations, the boundary at $r=a$
. For these configurations, the boundary at $r=a$![]() is carefully chosen so that the axes of the resulting VMEC equilibria are much closer to the original axes assumed by the NAE, which reduces the QS error at the axis to $O((a/R_0)^3)$
is carefully chosen so that the axes of the resulting VMEC equilibria are much closer to the original axes assumed by the NAE, which reduces the QS error at the axis to $O((a/R_0)^3)$![]() . As shown in figure 4, the QS-breaking components of $B$
. As shown in figure 4, the QS-breaking components of $B$![]() are much smaller compared with the first-order configurations near the axis (figure 2). However, a toroidal variation in $B$
are much smaller compared with the first-order configurations near the axis (figure 2). However, a toroidal variation in $B$![]() has to be introduced in order to construct these configurations, which is zero at the axis and increases with $r$
has to be introduced in order to construct these configurations, which is zero at the axis and increases with $r$![]() as $O(r/R_0)^2$
as $O(r/R_0)^2$![]() . Therefore, strictly speaking, the QS-breaking components remain at $O(\epsilon ^2)$
. Therefore, strictly speaking, the QS-breaking components remain at $O(\epsilon ^2)$![]() rather than $O(\epsilon ^3)$
rather than $O(\epsilon ^3)$![]() for the second-order NAE configurations.
for the second-order NAE configurations.

Figure 4. The Fourier spectrum of $B$![]() in helical angle $(\vartheta,\varphi )$
in helical angle $(\vartheta,\varphi )$![]() for the second-order NAE QA and QH configurations. Shown is $\sqrt {\sum B_{MN}^2}$
for the second-order NAE QA and QH configurations. Shown is $\sqrt {\sum B_{MN}^2}$![]() , where the summation is over the range in $(M,N)$
, where the summation is over the range in $(M,N)$![]() indicated by the legends.
indicated by the legends.
Numerical results are shown in figure 5. For the second-order QA configuration, the GAM oscillations are very similar to the first-order QA in figure 3; the numerical fitting formula (3.5) provides a reasonable description at large $t$![]() , and the numerical and theoretical frequencies also agree. Meanwhile, the RH residual agrees much better with theory at small $\epsilon$
, and the numerical and theoretical frequencies also agree. Meanwhile, the RH residual agrees much better with theory at small $\epsilon$![]() , but still deviates from theory at large $\epsilon$
, but still deviates from theory at large $\epsilon$![]() due to the increasing QS error. For the second-order QH configuration, $q_N/\sqrt {\mathcal {C}}=0.48$
due to the increasing QS error. For the second-order QH configuration, $q_N/\sqrt {\mathcal {C}}=0.48$![]() and $E_r$
and $E_r$![]() quickly drop to the RH residual without GAM oscillations, consistent with the result in tokamaks with $q=0.5$
quickly drop to the RH residual without GAM oscillations, consistent with the result in tokamaks with $q=0.5$![]() (figure 1) as well as previous numerical results from simulations of zonal flows in HSX (Smoniewski et al. Reference Smoniewski, Sánchez, Calvo, Pueschel and Talmadge2021). Since GAM oscillations do not exist, the numerical fitting (3.5) is not applicable to the QH configuration. Also, despite the small $\mathcal {C}$
(figure 1) as well as previous numerical results from simulations of zonal flows in HSX (Smoniewski et al. Reference Smoniewski, Sánchez, Calvo, Pueschel and Talmadge2021). Since GAM oscillations do not exist, the numerical fitting (3.5) is not applicable to the QH configuration. Also, despite the small $\mathcal {C}$![]() , the RH level in the QH configuration is still much larger than the QA configuration due to the small $|q_N|$
, the RH level in the QH configuration is still much larger than the QA configuration due to the small $|q_N|$![]() , as predicted by an earlier study (Plunk & Helander Reference Plunk and Helander2024). However, the simulated RH level is still much lower than the theoretical prediction, indicating that the QS-breaking components of $B$
, as predicted by an earlier study (Plunk & Helander Reference Plunk and Helander2024). However, the simulated RH level is still much lower than the theoretical prediction, indicating that the QS-breaking components of $B$![]() are still significant.
are still significant.

Figure 5. Simulation results for the second-order NAE QA and QH configurations. (a,b) Values of $E_r(t)$![]() at $\epsilon =0.05$
at $\epsilon =0.05$![]() for QA and QH. The black dashed curve is from the numerical fit (3.5). (b) Comparison between analytical (curves) and numerical (markers) results for the RH level. The QH configuration has the same range in $r$
for QA and QH. The black dashed curve is from the numerical fit (3.5). (b) Comparison between analytical (curves) and numerical (markers) results for the RH level. The QH configuration has the same range in $r$![]() as the QA configuration, but a larger range in $\epsilon =\bar {\eta } r$
as the QA configuration, but a larger range in $\epsilon =\bar {\eta } r$![]() due to its larger $\bar {\eta }$
due to its larger $\bar {\eta }$![]() .
.
3.5 The precise QA and QH configurations
The precise QA and QH configurations are obtained from global optimization using the software framework SIMSOPT (Medasani et al. Reference Medasani, Landreman, Wechsung, Paul, Jorge, Kaptanoglu, Giuliani, Baillod, Smiet and Qian2024). As shown in figure 6, the QS-breaking components of $B$![]() are very close to zero. Also, the QS components of $B$
are very close to zero. Also, the QS components of $B$![]() are still dominated by $M=1$
are still dominated by $M=1$![]() , so that $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$
, so that $B=B_0[1+\epsilon \cos \vartheta +O(\epsilon ^2)]$![]() holds, even though they are not generated from the NAE approach. Quantities such as $\bar {\eta }$
holds, even though they are not generated from the NAE approach. Quantities such as $\bar {\eta }$![]() and $\sigma$
and $\sigma$![]() can also be obtained near the axis and used to calculate $\mathcal {C}$
can also be obtained near the axis and used to calculate $\mathcal {C}$![]() , which showed good agreement with direct numerical evaluation of $\langle {|\nabla \psi |^2/B^2}\rangle$
, which showed good agreement with direct numerical evaluation of $\langle {|\nabla \psi |^2/B^2}\rangle$![]() . As shown in figure 7, numerical results of the GAM dynamics are qualitatively similar to the NAE configurations. For the RH residual, good agreement between theory and numerical results can be achieved throughout the volume for both the QA and QH configurations, the difference being less than 10 %. Therefore, the theoretical description of the collisionless zonal-flow dynamics can be applicable to actual QS stellarator configurations when the QS-breaking components of $B$
. As shown in figure 7, numerical results of the GAM dynamics are qualitatively similar to the NAE configurations. For the RH residual, good agreement between theory and numerical results can be achieved throughout the volume for both the QA and QH configurations, the difference being less than 10 %. Therefore, the theoretical description of the collisionless zonal-flow dynamics can be applicable to actual QS stellarator configurations when the QS-breaking components of $B$![]() become small enough.
become small enough.

Figure 6. The Fourier spectrum of $B$![]() in helical angle $(\vartheta,\varphi )$
in helical angle $(\vartheta,\varphi )$![]() for the precise QA and QH configurations. Shown is $\sqrt {\sum B_{MN}^2}$
for the precise QA and QH configurations. Shown is $\sqrt {\sum B_{MN}^2}$![]() , where the summation is over the range in $(M,N)$
, where the summation is over the range in $(M,N)$![]() indicated by the legends.
indicated by the legends.

Figure 7. Simulation results for the precise QA and QH configurations. (a,b) Value of $E_r(t)$![]() at $\epsilon =0.1$
at $\epsilon =0.1$![]() . The black dashed curve is from the numerical fit (3.5). (b) Comparison between analytical (curves) and numerical (markers) results for the RH level. The precise QH configuration has a smaller range in $r$
. The black dashed curve is from the numerical fit (3.5). (b) Comparison between analytical (curves) and numerical (markers) results for the RH level. The precise QH configuration has a smaller range in $r$![]() than the precise QA configuration, but still a larger range in $\epsilon =\bar {\eta } r$
than the precise QA configuration, but still a larger range in $\epsilon =\bar {\eta } r$![]() due to its larger $\bar {\eta }$
due to its larger $\bar {\eta }$![]() .
.
4 Conclusions
The linear collisionless plasma response to a zonal-density perturbation in QS stellarators is studied, including the GAM oscillations and the RH residual-flow level. It is found that, while the GAM oscillations in QA configurations are similar to tokamaks, they become non-existent in QH configurations due to the small effective safety factor $q_N$![]() in helical-angle coordinates. Compared with concentric-circular tokamaks, the RH residual is also found to be modified by a geometric factor $\mathcal {C}$
in helical-angle coordinates. Compared with concentric-circular tokamaks, the RH residual is also found to be modified by a geometric factor $\mathcal {C}$![]() , which we derived analytically using the NAE framework. It is found that $\mathcal {C}>1$
, which we derived analytically using the NAE framework. It is found that $\mathcal {C}>1$![]() for the QA configurations and $\mathcal {C}<1$
for the QA configurations and $\mathcal {C}<1$![]() for the QH configurations studied in the paper. Nevertheless, the QH configurations still have much larger RH residual due to the much smaller $q_N$
for the QH configurations studied in the paper. Nevertheless, the QH configurations still have much larger RH residual due to the much smaller $q_N$![]() . These analytic results are compared with numerical simulation results from GTC. While the GAM physics is reasonably predicted by the theory, we found that, for the RH residual level, good agreement between analytical and numerical results is achieved only when the amplitude of the QS-breaking magnetic-field component is small enough. Since zonal flows can be important for regulating turbulent transport, these results suggest a possible relation between the transport level and the stellarator geometric parameters via nonlinear interactions with zonal flows.
. These analytic results are compared with numerical simulation results from GTC. While the GAM physics is reasonably predicted by the theory, we found that, for the RH residual level, good agreement between analytical and numerical results is achieved only when the amplitude of the QS-breaking magnetic-field component is small enough. Since zonal flows can be important for regulating turbulent transport, these results suggest a possible relation between the transport level and the stellarator geometric parameters via nonlinear interactions with zonal flows.
Funding
H.Z. was supported by a grant from the Simons Foundation/SFARI (Grant #560651, AB). This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and the Department of Energy SciDAC HiFiStell project supported by Contract No. DE-SC0024548. H.Z. thanks W. Sengupta, R. Jorge, E. Rodríguez, E. Green, X. Wei for useful discussions.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that supports the findings of this study are openly available at Zenodo (Zhu Reference Zhu2024).