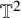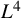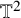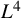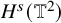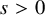Strichartz estimates and global well-posedness of the cubic NLS on $\mathbb {T}^{2}$

Abstract

The optimal $L^4$-Strichartz estimate for the Schrödinger equation on the two-dimensional rational torus $\mathbb {T}^2$ is proved, which improves an estimate of Bourgain. A new method based on incidence geometry is used. The approach yields a stronger $L^4$ bound on a logarithmic time scale, which implies global existence of solutions to the cubic (mass-critical) nonlinear Schrödinger equation in $H^s(\mathbb {T}^2)$ for any $s>0$ and data that are small in the critical norm.

1 Introduction

In the seminal work [1], Bourgain proved Strichartz estimates for the Schrödinger equation on (rational) tori $\mathbb {T}^{d}:=(\mathbf {\mathbb {R}}/2\pi \mathbf {\mathbb {Z}})^{d}$ . More precisely, in dimension $d=2$ , the endpoint estimate in [1] states that there exists $c>0$ such that for all $\phi \in L^2(\mathbb {T}^2)$ and $N \in \mathbf {\mathbb {N}}$ ,

$$\begin{align*}\|e^{it\Delta} P_N \phi \|_{L^4_{t,x}([0,2\pi]\times \mathbb{T}^2)}\leq C_N \|\phi\|_{L^2(\mathbb{T}^2)}, \text{ where } C_N= c\exp\Big(c\frac{\log(N)}{\log\log (N)}\Big). \end{align*}$$

The proof in [1] is based on the circle method and can be reduced to an estimate for the number of divisors function, which necessitates the above constant $C_N$ . However, in the example $\widehat {\phi }=\chi _{[-N,N]^2\cap \mathbf {\mathbb {Z}}^2}$ , we have

(1.1) $$ \begin{align} \|e^{it\Delta} P_N \phi \|_{L^4_{t,x}([0,2\pi]\times \mathbb{T}^2)}\approx (\log N)^{1/4} \|\phi\|_{L^2(\mathbb{T}^2)}; \end{align} $$

see [1, 15, 11].

More recently, the breakthrough result of Bourgain–Demeter on Fourier decoupling [2] provided a more robust approach which has significantly extended the range of available Strichartz estimates on rational and irrational tori. However, the above endpoint $L^4$ estimate has not been improved by this method. Here, we will consider dimension $d=2$ only, but let us remark that in dimension $d=1$ , there is a similar problem concerning the $L^6$ estimate, where it is known from [1] that the best constant is between $c (\log N)^{1/6}$ and $C_N$ , with recent improvements of the upper bound to $c(\log N)^{2+\varepsilon }$ [7, 6] by Fourier decoupling techniques.

In this paper, we obtain the sharp $L^4$ estimate in dimension $d=2$ by using methods of incidence geometry. Set $\log x:=\max \{1,\log _e x\}$ for $x>0$ .

Theorem 1.1. There exists $c>0$ , such that for all bounded sets $S\subset \mathbf {\mathbb {Z}}^{2}$ and all $\phi \in L^{2}(\mathbb {T}^{2})$ , we have

(1.2) $$ \begin{align} \|e^{it\Delta}P_{S}\phi\|_{L_{t,x}^{4}([0,2\pi]\times\mathbb{T}^{2}])}\leq c \left(\log\#S\right)^{1/4}\|\phi\|_{L^{2}}. \end{align} $$

In fact, we prove a stronger result.

Theorem 1.2. There exists $c>0$ , such that for all bounded sets $S\subset \mathbf {\mathbb {Z}}^{2}$ and all $\phi \in L^{2}(\mathbb {T}^{2})$ , we have

(1.3) $$ \begin{align} \|e^{it\Delta}P_{S}\phi\|_{L_{t,x}^{4}([0,\frac{1}{\log\#S}]\times\mathbb{T}^{2}])}\leq c \|\phi\|_{L^{2}}. \end{align} $$

Remark 1.3. Theorem 1.2 implies Theorem 1.1: Applying (1.3) to each interval $[2\pi \frac {k-1}{m},2\pi \frac {k}{m}]$ , $k=1,\ldots ,m$ , for $m\approx \log \#S$ , we obtain (1.2). In particular, (1.1) implies the sharpness of Theorem 1.2 as well.

For the proof of Theorem 1.2, we develop a new method based on a counting argument for parallelograms with vertices in given sets, which relies on the Szemerédi-Trotter Theorem. We remark that the Szemerédi-Trotter Theorem was previously used to bound the number of right triangles with vertices in a given set [13], and it has also been introduced in [2] in connection to Fourier decoupling and discrete Fourier restriction theory. More precisely, if $\widehat {\phi }=\chi _S$ , estimate (1.2) is a corollary of the Pach-Sharir bound in [13]. We point out that in our proof of Theorem 1.2, we also make use of the fourth vertex.

Theorems 1.1 and 1.2 apply to functions with Fourier support in arbitrary sets. Although we make use of the lattice structure, we only use an elementary number theoretic argument in the proof of Theorem 1.2: in the parallelogram $(\xi _1,\xi _2,\xi _3,\xi _4)\in (\mathbf {\mathbb {Z}}^2)^4$ the quantity $\tau =2(\xi _1-\xi _2)\cdot (\xi _1-\xi _4)$ must be a multiple of the greatest common divisor of the two coordinates of $\xi _1-\xi _4$ , which is used to avoid a logarithmic loss in Theorem 1.2.

The $L^4$ -Strichartz estimate plays a distinguished role in the analysis of the cubic nonlinear Schrödinger equation (cubic NLS)

(NLS) $$ \begin{align} iu_{t}+\Delta u=\pm|u|^{2}u, \qquad u|_{t=0}=u_{0}\in H^{s}(\mathbb{T}^{2}), \end{align} $$

which is $L^2(\mathbb {T}^2)$ -critical. (NLS) is known to be locally well-posed in Sobolev spaces $H^s(\mathbb {T}^2)$ for $s>0$ due to [1]. It is also known [11, Cor. 1.3] that the Cauchy problem is not perturbatively well-posed in $L^2(\mathbb {T}^2)$ , which is closely related to the example (1.1) discussed above.

By the conservation of energy, local well-posedness in $H^1(\mathbb {T}^2)$ implies global well-posedness for small enough data [1, Theorem 2]. In the defocusing case, this has been refined to global well-posedness in $H^s(\mathbb {T}^2)$ for $s>3/5$ ; see [4, 5, 14]. Additionally, the result in [3] shows that energy is transferred from small to higher frequencies and therefore causing growth of Sobolev norms $\|u(t)\|_{H^s}$ for $s>1$ .

Theorem 1.2 has the following consequence:

Theorem 1.4. There exists $\delta>0$ such that for $s>0$ and initial data $u_{0}\in H^{s}(\mathbb {T}^2)$ with $\|u_{0}\|_{L^{2}(\mathbb {T}^2)}\leq \delta $ , the Cauchy problem (NLS) is globally well-posed.

The proof is based on an estimate showing that $\|u(t)\|_{H^s(\mathbb {T}^2)}$ can grow only by a fixed multiplicative constant on a logarithmic time scale and because of $\sum _{N\in 2^{\mathbf {\mathbb {N}}}} 1/\log N=\infty $ , any finite time interval can be covered. This argument crucially relies on the sharpness of the estimate in Theorem 1.2. Indeed, if the time interval in Theorem 1.2 were $[0,(\log \#S)^{-\alpha }]$ for $\alpha>1$ instead, the sum would be $\sum _{N\in 2^{\mathbf {\mathbb {N}}}}1/(\log N)^\alpha <\infty $ , which would not yield a global result.

Outline of the paper

In Section 2, we introduce notations and recall the Szemerédi-Trotter Theorem. In Section 3, we provide the proof of Theorem 1.2. Finally, in Section 4, we prove the global well-posedness result (i.e., Theorem 1.4).

2 Preliminaries

We write $A\lesssim B$ if $A\le CB$ for some universal constant $C>0$ , and $A\approx B$ if both $A\lesssim B$ and $B\lesssim A$ . Given a set E, we denote $\chi _{E}$ as the sharp cutoff at E.

For proposition P, denote by $1_{P}$ the indicator function

$$ \begin{align*}1_{P}:=\begin{cases} 1, & {P}\ \text{is true}\\ 0, & \text{otherwise} \end{cases}.\end{align*} $$

For a function $f:\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$ , ${\mathcal {F}}f=\widehat {f}$ denotes the Fourier series of f. For $S\subset \mathbf {\mathbb {Z}}^{2}$ , we denote by $P_{S}$ the Fourier multiplier $\widehat {P_{S}f}:=\chi _{S}\cdot \widehat {f}$ . $2^{\mathbf {\mathbb {N}}}$ denotes the set of dyadic numbers. For dyadic number $N\in 2^{\mathbf {\mathbb {N}}}$ , we denote by $P_{\le N}$ the sharp Littlewood-Paley cutoff $P_{\le N}f:=P_{[-N,N]^{2}}f$ . We denote $P_{N}:=P_{\le N}-P_{\le N/2}$ , where we set $P_{\le 1/2}:=0$ . For function $\phi :\mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$ and time $t\in \mathbf {\mathbb {R}}$ , we define $e^{it\Delta }\phi $ as the function such that

$$\begin{align*}\widehat{e^{it\Delta}\phi}(\xi)=e^{- it\left\vert \xi\right\vert ^{2}}\widehat{\phi}(\xi). \end{align*}$$

For simplicity, we denote $u_{N}=P_{N}u$ and $u_{\le N}=P_{\le N}u$ , for $u:\mathbb {T}^2\rightarrow \mathbf {\mathbb {C}}$ .

Geometric notations on $\mathbf {\mathbb {Z}}^{2}$

For integer point $(a,b)\in \mathbf {\mathbb {Z}}^{2}$ , ${(a,b)}^{\perp }$ denotes $(-b,a)$ .

For integer point $(a,b)\in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $ , $\gcd \left ((a,b)\right )$ denotes $\gcd (a,b)$ .

Given two integer points $\xi _1,\xi _2\in \mathbf {\mathbb {Z}}^2$ , $\overleftrightarrow {\xi _1\xi _2}$ denotes the line through $\xi _1$ and $\xi _2$ .

Figure 2.1 Parallelogram Q.

A parallelogram is a quadruple $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{4}$ such that $\xi _{1}+\xi _{3}=\xi _{2}+\xi _{4}$ . The set of all parallelograms is denoted by ${\mathcal {Q}}$ . Segments and points are two-element pairs and elements of $\mathbf {\mathbb {Z}}^{2}$ , respectively. We call by the edges of Q either the segments $(\xi _{1},\xi _{2}),(\xi _{2},\xi _{3}),(\xi _{3},\xi _{4}),(\xi _{4},\xi _{1})$ , or the vectors $\pm \left (\xi _{1}-\xi _{2}\right ),\pm \left (\xi _{1}-\xi _{4}\right )$ .

For a parallelogram $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}$ (see Fig. 2.1), we denote by $\tau _{Q}$ the number

$$\begin{align*}\tau_{Q}=\tau(\xi_{1},\xi_{2},\xi_{3},\xi_{4})=\left\vert \left\vert \xi_{1}\right\vert ^{2}-\left\vert \xi_{2}\right\vert ^{2}+\left\vert \xi_{3}\right\vert ^{2}-\left\vert \xi_{4}\right\vert ^{2}\right\vert =2\left\vert \left(\xi_{1}-\xi_{2}\right)\cdot\left(\xi_{1}-\xi_{4}\right)\right\vert. \end{align*}$$

For $\tau \in \mathbf {\mathbb {N}}$ , we denote by ${\mathcal {Q}}^{\tau }$ the set of parallelograms $Q\in {\mathcal {Q}}$ such that $\tau _{Q}=\tau $ . Thus, in particular, ${\mathcal {Q}}^{0}$ is the set of rectangles.

Szemerédi-Trotter

The following is a consequence of Szemerédi-Trotter theorem of incidence geometry.

Proposition 2.1 [16, Corollary 8.5].

Let $S\subset \mathbf {\mathbb {R}}^{2}$ be a set of n points, where $n\in \mathbf {\mathbb {N}}$ . Let $k\ge 2$ be an integer. The number m of lines in $\mathbf {\mathbb {R}}^{2}$ passing through at least k points of S is bounded by

(2.1) $$ \begin{align} m\lesssim\frac{n^{2}}{k^{3}}+\frac{n}{k}. \end{align} $$

Remark 2.2. An optimizer S for (2.1) is a lattice $S=\mathbf {\mathbb {Z}}^{2}\cap [-N,N]^{2},N\in \mathbf {\mathbb {N}}$ .

3 Proof of Theorem 1.2

In this section, we prove Theorem 1.2. We will first reduce Theorem 1.2 to Proposition 3.1, then to showing Lemma 3.3. Then we will finish the proof by showing Lemma 3.3.

The proof of Theorem 1.2 will be reduced to the following proposition.

Proposition 3.1. Let $f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$ be a function of the form

$$\begin{align*}f=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}, \end{align*}$$

where $S_{0},\ldots ,S_{m},m\ge 1$ are disjoint subsets of $\mathbf {\mathbb {Z}}^{2}$ such that $\#S_{j}\le 2^{j}$ , and $\lambda _{0},\ldots ,\lambda _{m}\ge 0$ . Suppose that for each $j=0,\ldots ,m$ and $\xi \in S_{j}$ , there exists at most one line $\ell \ni \xi $ such that $\#(\ell \cap S_{j})\ge 2^{j/2+C}$ . Then, we have

(3.1) $$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim m\cdot\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$

and

(3.2) $$ \begin{align} \sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$

Here, $C>0$ is a uniform constant to be specified shortly, and $f(Q)$ denotes $f(\xi _{1})f(\xi _{2})f(\xi _{3})f(\xi _{4})$ for parallelogram $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$ .

Proof of Theorem 1.2 (assuming Proposition 3.1).

Let $S\subset \mathbf {\mathbb {Z}}^{2}$ be a bounded set. Let m be the least integer greater than $\log _{2}\#S$ . Since $\frac {1}{\log \#S}\lesssim \frac {1}{m}$ , to prove Theorem 1.2, we only need to show for $\phi \in L^{2}(\mathbb {T}^{2})$ that

(3.3) $$ \begin{align} \|e^{it\Delta}P_{S}\phi\|_{L_{t,x}^{4}([0,\frac{1}{m}]\times\mathbb{T}^{2})}\lesssim\|\phi\|_{L^{2}(\mathbb{T}^{2})}. \end{align} $$

Decomposing $\widehat {\phi }=\sum _{k=0}^{3}i^{k}\widehat {\phi }_{k}$ , $\widehat {\phi }_{k}\ge 0$ , it suffices to show that for $f:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$ supported in S,

(3.4) $$ \begin{align} \|e^{it\Delta}{\mathcal{F}}^{-1}f\|_{L_{t,x}^{4}([0,\frac{1}{m}]\times\mathbb{T}^{2})}\lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}. \end{align} $$

We define a sequence $\left \{ f_{n}\right \} $ of functions $f_{n}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty ),\mathrm {supp}(f_{n})\subset S$ inductively. Let $f_{0}:=f$ . Given $n\in \mathbf {\mathbb {N}}$ and a function $f_{n}$ , we choose an enumeration $\xi _{1},\xi _{2},\ldots $ of $\mathbf {\mathbb {Z}}^{2}$ (which may depend on n) such that $f_{n}(\xi _{1})\ge f_{n}(\xi _{2})\ge \ldots $ . Let $S_{j}^{0}:=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $ and $\lambda _{j}:=2^{j/2}f_n(\xi _{2^{j}})$ for $j=0,\ldots ,m$ . We have

(3.5) $$ \begin{align} \#S_{j}^{0}=2^{j} \end{align} $$

and

(3.6) $$ \begin{align} \|\lambda_{j}\|_{\ell_{j\le m}^{2}}&=\|2^{j/2}f_{n}(\xi_{2^{j}})\|_{\ell_{j\le m}^{2}}\\& \lesssim f_{n}(\xi_{1})+\|\sum_{j=1}^{m}f_{n}(\xi_{2^{j}})\chi_{\left\{ \xi_{2^{j-1}+1},\ldots,\xi_{2^{j}}\right\} }\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\nonumber \\& \lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$

For $j=0,\ldots ,m$ , we define $E_{j}\subset S_{j}^{0}$ as the set of intersections $\xi \in S_{j}^{0}$ of two lines $\ell _{1},\ell _{2}$ such that

$$\begin{align*}\#\left(\ell_{1}\cap S_{j}^{0}\right),\#\left(\ell_{2}\cap S_{j}^{0}\right)\ge2^{j/2+C}. \end{align*}$$

By the Szemerédi-Trotter bound (2.1) and (3.5), we have

(3.7) $$ \begin{align} \sqrt{\#E_{j}} & \le\#\left\{ \ell\subset\mathbf{\mathbb{R}}^{2}:\ell\text{ is a line and }\#\left(\ell\cap S_{j}^{0}\right)\ge2^{j/2+C}\right\} \\ & \lesssim(\#S_{j}^{0})^{2}/(2^{j/2+C})^3+\#S_{j}^{0}/2^{j/2+C}\nonumber \\ & \lesssim2^{j/2-C}.\nonumber \end{align} $$

Let $f_{n+1}:\mathbf {\mathbb {Z}}^{2}\rightarrow [0,\infty )$ be the function

$$\begin{align*}f_{n+1}:=f_{n}\chi_{E}, \quad E:=\bigcup_{j=0}^{m}E_{j}. \end{align*}$$

Since $f_{n}(\xi )\le f_{n}(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$ holds for $\xi \in E_{j}\subset S_{j}^{0}$ , by (3.7) and (3.6), we have

$$\begin{align*}\|f_{n+1}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}=\|f_{n}\chi_{E}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\lesssim\|\lambda_{j}2^{-j/2}\cdot\sqrt{\#E_{j}}\|_{\ell_{j\le m}^{2}}\lesssim2^{-C}\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}. \end{align*}$$

Fixing $C\in \mathbf {\mathbb {N}}$ as a big number gives

$$\begin{align*}\|f_{n+1}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\le\frac{1}{2}\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}, \end{align*}$$

which implies

(3.8) $$ \begin{align} \|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\le\frac{1}{2}\|f_{n-1}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\le\ldots\le2^{-n} \|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}. \end{align} $$

Let $S_{j}:=S_{j}^{0}\setminus E_{j}$ . By the definition of $E_{j}$ , the function

$$\begin{align*}g_{n}:=\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}} \end{align*}$$

satisfies the conditions for Proposition 3.1. Since $f_n(\xi )\le f_n(\xi _{2^{j}})=\lambda _{j}2^{-j/2}$ holds for $\xi \in S_{j}\subset S_{j}^{0}=\left \{ \xi _{2^{j}},\ldots ,\xi _{2^{j+1}-1}\right \} $ , we have

(3.9) $$ \begin{align} h_{n}:=f_{n}-f_{n+1}=\sum_{j=0}^{m}f_{n}\chi_{S_{j}}\le\sum_{j=0}^{m}\lambda_{j}2^{-j/2}\chi_{S_{j}}=g_{n}. \end{align} $$

Denoting $T_{0}:=\frac {1}{m}$ , by (3.9), we have

$$ \begin{align*} \int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt & \le\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdtdT\\ & \approx\frac{1}{T_{0}}\int_{0}^{2T_{0}}\int_{0}^{T}{\mathcal{F}}\left(\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}\right)(0)dtdT\\ & \approx\frac{1}{T_{0}}\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\mathrm{Re}\int_{0}^{2T_{0}}\int_{0}^{T}e^{it\tau_{Q}}dtdT\\ & \approx\sum_{Q\in{\mathcal{Q}}}h_{n}\left(Q\right)\cdot\frac{1-\cos\left(2T_{0}\tau_{Q}\right)}{T_{0}\tau_{Q}^{2}}\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}h_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}h_{n}(Q)\\ & \lesssim T_{0}\sum_{Q\in{\mathcal{Q}}^{0}}g_{n}(Q)+\sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q) \end{align*} $$

and

$$ \begin{align*} & \sum_{\substack{\tau>0} }\min\left\{ T_{0},\frac{1}{T_{0}\tau^{2}}\right\} \sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sum_{M\in2^{\mathbf{\mathbb{N}}}}\min\left\{ T_{0}M,\frac{1}{T_{0}M}\right\} \frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q)\\ \lesssim{}&\sup_{M\in2^{\mathbf{\mathbb{N}}}}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}g_{n}(Q), \end{align*} $$

concluding by (3.1), (3.2) and (3.6) that

(3.10) $$ \begin{align} \|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L^{4}([0,T_{0}]\times\mathbb{T}^{2})}&=\left(\int_{0}^{T_{0}}\int_{\mathbb{T}^{2}}\left\vert e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\right\vert ^{4}dxdt\right)^{1/4}\\ &\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}\lesssim\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}.\nonumber \end{align} $$

Writing $f=\sum _{n=0}^{\infty }(f_{n}-f_{n+1})=\sum _{n=0}^{\infty }h_{n}$ , by (3.10) and (3.8), we have

$$ \begin{align*} \|e^{it\Delta}{\mathcal{F}}^{-1}f\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)} & \le\sum_{n=0}^{\infty}\|e^{it\Delta}{\mathcal{F}}^{-1}h_{n}\|_{L_{t,x}^{4}\left([0,T_{0}]\times\mathbb{T}^{2}\right)}\\ & \lesssim\sum_{n=0}^{\infty}\|f_{n}\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\\ & \lesssim\sum_{n=0}^{\infty}2^{-n}\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}\lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}, \end{align*} $$

which is (3.4) and therefore completes the proof of Theorem 1.2.

A cross is a triple $(\xi ,\ell _{1},\ell _{2})$ of two mutually orthogonal lines $\ell _{1},\ell _{2}$ and their intersection $\xi $ . For $\{S_j\}_{j=0}^m$ as in Proposition 3.1, we categorize crosses $\left (\xi ,\ell _{1},\ell _{2}\right ),\xi \in \cup _{j=0}^m S_j$ into three types:

$$\begin{align*}\begin{cases} \text{Type 1} & \text{ if } a\ge j/2+C\\ \text{Type 2} & \text{ if } 1\le a<j/2+C\\ \text{Type 3} & \text{ if }a=0, \end{cases} \end{align*}$$

where j is the index such that $\xi \in S_j$ , and a is the number

$$\begin{align*}a=\log_{2}\max\left\{ \#\left(\ell_{1}\cap S_{j}\right),\#\left(\ell_{2}\cap S_{j}\right)\right\}. \end{align*}$$

Note that $a\in \{0\}\cup [1,\infty )$ since $\ell _1\cap S_j$ is nonempty.

Given a rectangle $\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )$ of four distinct vertices, its vertex $\xi _{1}$ is called a vertex of type $\alpha $ , $\alpha =1,2,3$ if the cross $(\xi _{1},\overleftrightarrow {\xi _{1}\xi _{2}},\overleftrightarrow {\xi _{1}\xi _{4}})$ is of type $\alpha $ .

For $\alpha ,\beta =1,2,3$ , we denote by ${\mathcal {Q}}_{\alpha ,\beta }^{0}$ the set of rectangles $\left (\xi _{1},\xi _{2},\xi _{3},\xi _{4}\right )\in {\mathcal {Q}}^{0}$ of four distinct vertices $\xi _1,\xi _2,\xi _3,\xi _4\in \cup _{j=0}^m S_j$ such that $\xi _{1},\xi _{2}$ are type $\alpha $ -vertices and $\xi _{3},\xi _{4}$ are type $\beta $ -vertices. Although the union of ${\mathcal {Q}}_{\alpha ,\beta }^{0}$ is only a proper subcollection of ${\mathcal {Q}}^{0}$ , the following lemma provides a reduction to counting rectangles in ${\mathcal {Q}}_{\alpha ,\beta }^{0}$ .

Lemma 3.2. Let f and $\left \{ S_{j}\right \}_{j=0}^m$ be as in Proposition 3.1. Let $\tau \ge 0$ be an integer. We have

(3.11) $$ \begin{align} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}. \end{align} $$

Proof. For $\xi \in \mathbf {\mathbb {Z}}^{2}\setminus \left \{ 0\right \} $ and $\sigma \in \mathbf {\mathbb {Z}}$ , we denote by ${\mathcal {E}}_{\xi }^{\sigma }$ the set of segments $(\xi _{1},\xi _{4})\in (\mathbf {\mathbb {Z}}^{2})^{2}$ such that $\xi _{1}-\xi _{4}=\xi $ and $\xi _{1}\cdot \xi =\sigma $ .

Since $\tau _{Q}=2\left \vert (\xi _{1}-\xi _{2})\cdot (\xi _{1}-\xi _{4})\right \vert $ is a multiple of $\gcd (\xi _{1}-\xi _{4})$ for any parallelogram $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})$ such that $\xi _{1}-\xi _{4}\neq 0$ , we have

$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q) & \lesssim\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1},\xi_{2}\in\mathbf{\mathbb{Z}}^{2}}f(\xi_{1})^{2}f(\xi_{2})^{2}\\ & \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$

and by Cauchy-Schwarz inequality,

$$ \begin{align*} & \sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{\tau}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\substack{\sigma_{1},\sigma_{2}\in\mathbf{\mathbb{Z}}\\ \sigma_{1}-\sigma_{2}=\pm\tau/2 } }\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma_{1}}\\ (\xi_{2},\xi_{3})\in{\mathcal{E}}_{\xi}^{\sigma_{2}} } }f(\xi_{1})f(\xi_{4})f(\xi_{2})f(\xi_{3})\\& \quad \lesssim\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}}f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\left(\sum_{\substack{(\xi_{1},\xi_{4})\in{\mathcal{E}}_{\xi}^{\sigma}\\ (\xi_1,\xi_1+\xi \mathbf{\mathbb{R}},\xi_1+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\alpha\\ (\xi_4,\xi_4+\xi \mathbf{\mathbb{R}},\xi_4+\xi^\perp \mathbf{\mathbb{R}})\text{ is a cross of type }\beta } }f(\xi_{1})f(\xi_{4})\right)^{2}\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\sum_{\sigma\in\mathbf{\mathbb{Z}}}\sum_{\substack{ (\xi_1,\xi_4)\in{\mathcal{E}}^\sigma_\xi\\(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\text{ or }(\xi_2,\xi_3)=(\xi_1,\xi_4) } }f(\xi_1)f(\xi_4)f(\xi_2)f(\xi_3)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{\xi\in\mathbf{\mathbb{Z}}^{2}\setminus\left\{ 0\right\} \\ \gcd(\xi)\mid\tau } }\left(\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \xi_{1}-\xi_{4}=\xi } }f(Q)+\sum_{\xi_{1}-\xi_{4}=\xi}f(\xi_{1})^{2}f(\xi_{4})^{2}\right)\\& \quad \lesssim\max_{\alpha,\beta=1,2,3}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*} $$

finishing the proof.

There are three main inequalities to be shown.

Lemma 3.3. Let f and $\{\lambda _j\}_{j=0}^m$ be as in Proposition 3.1.

In the cases $(\alpha ,\beta )\neq (2,2)$ , we have

(3.12) $$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$

In case $(\alpha ,\beta )=(2,2)$ , we have

(3.13) $$ \begin{align} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q)\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4} \end{align} $$

and

(3.14) $$ \begin{align} \sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}f(Q)\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}. \end{align} $$

Proof of Proposition 3.1 assuming Lemma 3.3.

We first prove (3.1), which concerns the case $\tau =0$ . By (3.11), (3.12) and (3.13), we have

$$\begin{align*}\sum_{Q\in{\mathcal{Q}}^{0}}f(Q)\lesssim\max_{\alpha,\beta=1,2,3}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*}$$

which is just (3.1).

Now we prove (3.2), which is for $\tau \neq 0$ . By (3.11), for $M\in 2^{\mathbf {\mathbb {N}}}$ , we have

$$\begin{align*}\frac{1}{M}\sum_{\tau\approx M}\sum_{Q\in{\mathcal{Q}}^{\tau}}f(Q)\lesssim\frac{1}{M}\max_{\alpha,\beta=1,2,3}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)+\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}, \end{align*}$$

and for $\alpha ,\beta =1,2,3$ , we have

$$ \begin{align*} & \frac{1}{M}\sum_{\tau\approx M}\sum_{\substack{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}\\ \gcd(\xi_{1}-\xi_{4})\mid\tau } }f(Q)\\& =\frac{1}{M}\sum_{\tau\approx M}\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\cdot f(Q)\\& =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\left(\frac{1}{M}\sum_{\tau\approx M}1_{\gcd(\xi_{1}-\xi_{4})\mid\tau}\right)\cdot f(Q)\\& \lesssim\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{\alpha,\beta}^{0}}\frac{1}{\gcd(\xi_{1}-\xi_{4})}\cdot f(Q), \end{align*} $$

which is $O(\|\lambda _{j}\|_{\ell ^{2}_{j\le m}}^{4})$ by (3.12) and (3.14), and finishes the proof of (3.2).

Before turning to the proof of Lemma 3.3, we consider two preparatory lemmas, where we use the following notation:

For vectors $\overrightarrow {j}=(j_1,j_2,j_3,j_4)\in \mathbf {\mathbb {N}}^4$ and $\overrightarrow {a}=(a_1,a_2,a_3,a_4)\in \mathbf {\mathbb {N}}^4$ , we denote by ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a})$ the set of rectangles $(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}\cap \left (S_{j_{1}}\times S_{j_{2}}\times S_{j_{3}}\times S_{j_{4}}\right )$ of four distinct vertices such that

(3.15) $$ \begin{align} 2^{a_{k}}\le\max\left\{ \#\left(\overleftrightarrow{\xi_{k}\xi_{k+1}}\cap S_{j_{k}}\right),\#\left(\overleftrightarrow{\xi_{k}\xi_{k-1}}\cap S_{j_{k}}\right)\right\} <2^{a_{k}+1}, \end{align} $$

where the cyclic convention on index $\xi _{4l+k}=\xi _{k},l\in \mathbf {\mathbb {Z}}$ is used (see Fig. 3.1).

Figure 3.1 Rectangle $(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^{0}( \overrightarrow{j}, \overrightarrow{a})$ .

Lemma 3.4. Let $\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$ be as in Proposition 3.1. Let $j_{1},j_{2},j_{3},j_{4},a_{3}\ge 0$ be integers. Then, the number of rectangles $(\xi _1,\xi _2,\xi _3,\xi _4)\in {\mathcal {Q}}^0\cap (S_{j_1}\times S_{j_2}\times S_{j_3}\times S_{j_4})$ of four distinct vertices such that

$$\begin{align*}\#\left(\overleftrightarrow{\xi_2 \xi_3}\cap S_{j_3}\right)<2^{a_3+1} \end{align*}$$

is $O(2^{j_{1}+j_{2}+a_{3}})$ .

Proof. There are at most $\#S_{j_1}\cdot \#S_{j_2}=O(2^{j_{1}+j_{2}})$ possible choices of $(\xi _{1},\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$ . Once the pair of two vertices $(\xi _{1,}\xi _{2})\in S_{j_{1}}\times S_{j_{2}}$ is fixed, the third vertex $\xi _{3}$ should lie on the line $\ell _{23}\ni \xi _{2}$ orthogonal to $\overleftrightarrow {\xi _{1}\xi _{2}}$ (see Fig. 3.2), and we require

$$\begin{align*}\#\left(\ell_{23}\cap S_{j_{3}}\right)=\#\left(\overleftrightarrow{\xi_{2}\xi_{3}}\cap S_{j_{3}}\right)<2^{a_{3}+1}, \end{align*}$$

so there are only $O(2^{a_{3}})$ possible choices of $\xi _{3}\in \ell _{23}$ , which then uniquely determines a rectangle. Therefore, we have $O(2^{j_{1}+j_{2}}\cdot 2^{a_{3}})=O(2^{j_{1}+j_{2}+a_{3}})$ such rectangles.

The following lemma is useful in the case that $\xi _{1}$ is a vertex of type $2$ .

Figure 3.2 Choice of $\xi _1,\xi _2,\xi _3$ in the proof of Lemma 3.4.

Lemma 3.5. Let $\left \{ S_{j}\right \} _{j=0}^{m},m\ge 1$ be as in Proposition 3.1. Let $j_{1},j_{2},j_{3},j_{4}$ , $a_{1},a_{2},a_{3},a_{4}\ge 0$ be integers. Assume that

(3.16) $$ \begin{align} 1\le a_{1}<j_{1}/2+C. \end{align} $$

We have

(3.17) $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim 2^{2j_{1}-2a_{1}+a_{2}+a_{4}}, \end{align} $$

(3.18) $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim 2^{2j_{1}-2a_{1}+a_{2}+a_{3}}, \end{align} $$

and

(3.19) $$ \begin{align} \sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim 2^{2j_{1}-2a_{1}+a_{2}+a_{4}/2}. \end{align} $$

We note that the assumption (3.16) is a priori necessary if $\xi _{1}$ is a vertex of type $2$ .

Proof. By (2.1), the number of lines $\ell $ such that $2^{a_{1}}\le \#(\ell \cap S_{j_{1}})<2^{a_1+1}$ is $O(2^{2j_{1}}\cdot 2^{-3a_{1}}+2^{j_{1}}\cdot 2^{-a_{1}})=O(2^{2j_{1}-3a_{1}})$ , and for each such $\ell $ , we have $O(2^{a_1})$ number of points $\xi _1\in \ell \cap S_{j_1}$ . Thus, there exist at most $O(2^{2j_{1}-2a_{1}})$ crosses $(\xi _{1},\ell _{12},\ell _{14})$ such that

$$\begin{align*}2^{a_{1}}\le\max\left\{ \#(\ell_{12}\cap S_{j_{1}}),\#(\ell_{14}\cap S_{j_{1}})\right\} <2^{a_{1}+1}. \end{align*}$$

For such a cross $(\xi _{1},\ell _{12},\ell _{14})$ to be a corner of a rectangle in ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $ , for (3.15), we require further that

(3.20) $$ \begin{align} \#(\ell_{12}\cap S_{j_{2}})<2^{a_{2}+1} \end{align} $$

and

(3.21) $$ \begin{align} \#(\ell_{14}\cap S_{j_{4}})<2^{a_{4}+1}. \end{align} $$

By (3.20), there exist at most $O(2^{a_{2}})$ choices of vertices $\xi _{2}\in \ell _{12}\cap S_{j_{2}}$ .

Figure 3.3 Choice of $\xi _1$ and $\xi _2$ in the proof of Lemma 3.5.

Having fixed $\xi _{1}$ and $\xi _{2}$ , we choose either $\xi _{3}$ or $\xi _{4}$ as follows, which then uniquely determines a rectangle $(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}^{0}$ .

• • Choice of $\xi _{4}$ . Since the choice of $\xi _{4}\in \ell _{14}\cap S_{j_{4}}$ in advance uniquely determines a rectangle, by (3.21), we have (3.17). Also, labeling $\ell _{14}\cap S_{j_{4}}\setminus \left \{ \xi _{1}\right \} =:\left \{ \xi _{4}^{1},\ldots ,\xi _{4}^{l}\right \} ,l<2^{a_{4}+1}$ , we have

  $$\begin{align*}\sum_{r=1}^{l}\frac{1}{\gcd(\xi_{1}-\xi_{4}^{r})}\lesssim\frac{1}{1}+\cdots+\frac{1}{l}\lesssim\log l\lesssim2^{a_{4}/2}, \end{align*}$$
  which implies (3.19).

• • Choice of $\xi _{3}$ . We can also determine a rectangle by choosing $\xi _{3}\in \ell _{23}\cap S_{j_{3}}$ , where $\ell _{23}\ni \xi _{2}$ is the line parallel with $\ell _{14}$ (see Fig. 3.3). To form a rectangle in ${\mathcal {Q}}^{0}(\overrightarrow {j},\overrightarrow {a}) $ , we require

  $$\begin{align*}\#(\ell_{23}\cap S_{j_{3}})=\#(\overleftrightarrow{\xi_{2}\xi_{3}}\cap S_{j_{3}})<2^{a_{3}+1}, \end{align*}$$
  so there are at most $O(2^{a_{3}})$ choices of such vertices $\xi _{3}$ . Thus, we have (3.18).

We can now lay the last brick of the proof of Proposition 3.1.

Proof of Lemma 3.3.

We split the proof into the cases (i) $\alpha =1$ (or $\beta =1$ ), (ii) $(\alpha ,\beta )=(2,2)$ , (iii) $(\alpha ,\beta )=(3,3)$ and (iv) $(\alpha ,\beta )=(2,3)$ (or $(3,2)$ ).

Case I: $\alpha =1$ (or $\beta =1$ ).

For $\xi _{1}\in S_{j_{1}},j_{1}\in \mathbf {\mathbb {N}}$ , by the assumption of Proposition 3.1, there exists at most one line $\ell _{\xi _{1}}\ni \xi _1$ such that $\#(\ell _{\xi _{1}}\cap S_{j_{1}})\ge 2^{j_1/2+C}$ . Thus, for any rectangle $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$ , to which the inequality

$$\begin{align*}\max\left\{ \#\left(\overleftrightarrow{\xi_{1}\xi_{2}}\cap S_{j_{1}}\right),\#\left(\overleftrightarrow{\xi_{1}\xi_{4}}\cap S_{j_{1}}\right)\right\} \ge2^{j_1/2+C}\end{align*}$$

applies since $\xi _{1}$ is of type $\alpha =1$ , we have either $\xi _{2}\in \ell _{\xi _{1}}$ or $\xi _{4}\in \ell _{\xi _{1}}$ . We conclude that for each pair of points $(\xi _{1},\xi _{3})\in (\mathbf {\mathbb {Z}}^{2})^{2}$ such that $\xi _{1}\neq \xi _{3}$ , there is only one possible choice of the other two vertices $\left \{ \xi _{2},\xi _{4}\right \} $ such that $Q=(\xi _{1},\xi _{2},\xi _{3},\xi _{4})\in {\mathcal {Q}}_{1,\beta }^{0}$ , and similar for $(\xi _{2},\xi _{4})$ . By Cauchy-Schwarz inequality, we have

$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{1,\beta}^{0}}f(Q) & =\sum_{Q=(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}_{1,\beta}^{0}}f(\xi_{1})f(\xi_{3})\cdot f(\xi_{2})f(\xi_{4})\\ & \lesssim\sum_{\xi_{1},\xi_{3}\in\mathbf{\mathbb{Z}}^{2}}\left(f(\xi_{1})f(\xi_{3})\right)^{2}\\ & \lesssim\|f\|_{\ell^{2}(\mathbf{\mathbb{Z}}^{2})}^{4}\lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$

which is just (3.12) for the case.

Figure 3.4 Determination of a rectangle from given $\xi _1,\xi _3\in \mathbb {Z}^2$ .

Case II: $(\alpha ,\beta )=(2,2)$ .

Let $j_{1},\ldots ,j_{4},a_{1},\ldots ,a_{4}$ be integers such that $0\le j_{k}\le m$ and $1\le a_{k}<j_{k}/2+C$ for $k=1,\ldots ,4$ . By (3.17), (3.18) and their cyclic relabels of indices $1,2,3,4$ , for non-negative tuple $\left (c_{k,l}\right )_{k\le 4,l\le 2}$ such that $\sum _{k=1}^4\sum _{l=1}^2 c_{k,l}=1$ , we have

$$\begin{align*}\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim2^{\sum_{k=1}^{4}\sum_{l=1}^{2}c_{k,l}\left(2j_{k}-2a_{k}+a_{k+1}+a_{k+1+l}\right)}. \end{align*}$$

The choices $(c_{k,l})_{k\le 4,l\le 2}=\frac {1}{24}\cdot ((2,3),(3,4),(0,6),(3,3))$ and $\frac {1}{12}\cdot ((1,2),(1,2),(3,0),(1,2))$ give

(3.22) $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})-\frac{1}{12}(j_{1}-j_{2})}, \end{align} $$

(3.23) $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})+\frac{1}{6}(a_{1}-a_{2})}, \end{align} $$

respectively. Interpolating (3.22), (3.23) and their dihedral relabelings of indices $1,2,3,4$ , for $\delta =\frac {1}{10000}$ , we have

$$\begin{align*}\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}, \end{align*}$$

from which we conclude by

$$\begin{align*}{\mathcal{Q}}^0_{2,2}\subset\bigcup_{\substack{0\le j_k \le m \\ 1\le a_k\le j_k/2+C \\ k=1,2,3,4}}{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \end{align*}$$

that (using that $f(\xi )=2^{-j/2}\lambda _j$ for $\xi \in S_j$ )

$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,2}^{0}}f(Q) & \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a})\cdot 2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \quad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\\& \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}\cdot\sum_{1\le a_{4}\le m/2+C}1\lesssim m\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$

which is just (3.13).

We pass to showing (3.14), which is just a repeat of the preceding proof. By (3.17), (3.18), (3.19) and their cyclic relabels, for non-negative tuple $\left (c_{k,l}\right )_{k\le 4,l\le 2}$ such that $\sum _{k,l}c_{k,l}=1$ , we have

$$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\sum_{k=1}^{4}\sum_{l=1}^{2}c_{k,l}\left(2j_{k}-2a_{k}+a_{k+1}+a_{k+1+l}\right)}\cdot2^{-c_{1,2}\cdot a_{4}/2}. \end{align*}$$

Plugging the same choices of $\left (c_{k,l}\right )_{k\le 4,l\le 2}$ , we obtain

$$\begin{align*}\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}\lesssim2^{\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert \alpha_{k}-\alpha_{k+1}\right\vert \right)}\cdot2^{-\delta a_{4}}, \end{align*}$$

concluding that

$$ \begin{align*} &\sum_{Q=(\xi_1,\xi_2,\xi_3,\xi_4)\in{\mathcal{Q}}_{2,2}^{0}}\frac{1}{\gcd(\xi_1-\xi_4)}f(Q)\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }\sum_{(\xi_{1},\xi_{2},\xi_{3},\xi_{4})\in{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) }\frac{1}{\gcd(\xi_{1}-\xi_{4})}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ 1\le a_{k}<j_{k}/2+C\\ k=1,2,3,4 } }2^{-\delta\sum_{k=1}^{4}\left(\left\vert j_{k}-j_{k+1}\right\vert +\left\vert a_{k}-a_{k+1}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\sum_{\substack{0\le j_{k}\le m\\ k=1,2,3,4 } }\left(2^{-\delta\left\vert j_{1}-j_{2}\right\vert /2}\lambda_{j_{1}}\lambda_{j_{2}}\cdot2^{-\delta\left\vert j_{3}-j_{4}\right\vert }\lambda_{j_{3}}\lambda_{j_{4}}\right)\\& \qquad \cdot\sum_{\substack{{1\le a_{k}\le m/2} +C\\ k=1,2,3,4 } }2^{-\delta\left(\left\vert a_{1}-a_{2}\right\vert +\left\vert a_{2}-a_{3}\right\vert +\left\vert a_{3}-a_{4}\right\vert \right)}\cdot2^{-\delta a_{4}}\\& \quad \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$

which is just (3.14).

Case III: $(\alpha ,\beta )=(3,3)$ .

For $j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$ , by Lemma 3.4, we have

$$\begin{align*}q_{j_{1},j_{2},j_{3},j_{4}}:=\#{\mathcal{Q}}_{3,3}^{0}\cap\left(S_{j_{1}}\times S_{j_{2}}\times S_{j_{3}}\times S_{j_{4}}\right)\lesssim\min_{k=1,2,3,4}2^{j_{k}+j_{k+1}}. \end{align*}$$

One can check

$$\begin{align*}\min_{k=1,2,3,4}\{j_{k}+j_{k+1}\}-\frac{1}{2}\left(j_{1}+j_{2}+j_{3}+j_{4}\right)\le-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right), \end{align*}$$

and so

$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{3,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-\frac{1}{2}(j_{1}+j_{2}+j_{3}+j_{4})}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$

which is just (3.12) for the case.

Case IV: $(\alpha ,\beta )=(2,3)$ (or $(3,2)$ ).

For $j_{1},j_{2},j_{3},j_{4}\in \mathbf {\mathbb {N}}$ , by Lemma 3.4, we have

(3.24) $$ \begin{align} q_{j_{1},j_{2},j_{3},j_{4}}:=\#{\mathcal{Q}}_{2,3}^{0}\cap\left(S_{j_{1}}\times S_{j_{2}}\times S_{j_{3}}\times S_{j_{4}}\right)\lesssim2^{\min\left\{ j_{1}+j_{4},j_{2}+j_{3},j_{1}+j_{2}\right\} }. \end{align} $$

For $\overrightarrow {a}=(a_1,a_2,0,0)$ with integers $a_{1},a_{2}$ such that $1\le a_{1}<j_{1}/2+C$ and $1\le a_{2}<j_{2}/2+C$ , by Lemma 3.4 and (3.18), we also have

(3.25) $$ \begin{align}\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \lesssim 2^{j_3+j_4+\min\{ a_1,a_2 \}} \lesssim 2^{j_{3}+j_{4}+\frac{1}{2}(a_{1}+a_{2})}\end{align} $$

and

(3.26) $$ \begin{align} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim\min\left\{ 2^{2j_{1}-2a_{1}},2^{2j_{2}-2a_{2}}\right\} \\ & \lesssim2^{j_{1}+j_{2}-(a_{1}+a_{2})}.\nonumber \end{align} $$

Interpolating (3.25) and (3.26), we have

$$ \begin{align*} \#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}+\frac{1}{2}(a_{1}+a_{2})\right)+\frac{2}{5}\left(j_{1}+j_{2}-(a_{1}+a_{2})\right)}\\ &=2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}, \end{align*} $$

which implies

(3.27) $$ \begin{align} q_{j_{1},j_{2},j_{3},j_{4}} & \le\sum_{\substack{1\le a_{1}<j_{1}/2+C\\ 1\le a_{2}<j_{2}/2+C } }\#{\mathcal{Q}}^{0}(\overrightarrow{j},\overrightarrow{a}) \\ & \lesssim\sum_{a_{1},a_{2}\in\mathbf{\mathbb{N}}}2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)-\frac{1}{10}\left(a_{1}+a_{2}\right)}\nonumber \\ & \lesssim2^{\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)}.\nonumber \end{align} $$

By (3.24), (3.27) and the inequality

$$ \begin{align*} & \min\left\{ j_{1}+j_{4},j_{2}+j_{3},j_{1}+j_{2},\frac{3}{5}\left(j_{3}+j_{4}\right)+\frac{2}{5}\left(j_{1}+j_{2}\right)\right\} -(j_{1}+j_{2}+j_{3}+j_{4})/2\\& \quad \le-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right), \end{align*} $$

we conclude

$$ \begin{align*} \sum_{Q\in{\mathcal{Q}}_{2,3}^{0}}f(Q) & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}q_{j_{1},j_{2},j_{3},j_{4}}2^{-(j_{1}+j_{2}+j_{3}+j_{4})/2}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{2},j_{3},j_{4}\ge0}2^{-\frac{1}{100}\left(\left\vert j_{1}-j_{3}\right\vert +\left\vert j_{2}-j_{4}\right\vert \right)}\lambda_{j_{1}}\lambda_{j_{2}}\lambda_{j_{3}}\lambda_{j_{4}}\\ & \lesssim\sum_{j_{1},j_{3}\ge0}2^{-\frac{1}{100}\left\vert j_{1}-j_{3}\right\vert }\lambda_{j_{1}}\lambda_{j_{3}}\cdot\sum_{j_{2},j_{4}\ge0}2^{-\frac{1}{100}\left\vert j_{2}-j_{4}\right\vert }\lambda_{j_{2}}\lambda_{j_{4}}\\ & \lesssim\|\lambda_{j}\|_{\ell_{j\le m}^{2}}^{4}, \end{align*} $$

which is just (3.12) for the case.

Remark 3.6. We thank Po-Lam Yung for the following more conceptional explanation of above interpolation type arguments. For example, in Case IV, $(\frac 12,\frac 12,\frac 12,\frac 12)$ is in the interior of the convex hull C of $(1,0,0,1)$ , $(0,1,1,0)$ , $(1,1,0,0)$ and $(\frac 25,\frac 25,\frac 35,\frac 35)$ . More precisely,

$$ \begin{align*}(\tfrac12,\tfrac12,\tfrac12,\tfrac12) = \tfrac15(1,0,0,1) + \tfrac15(0,1,1,0) + \tfrac{1}{10}(1,1,0,0) + \tfrac12(\tfrac25,\tfrac25,\tfrac35,\tfrac35).\end{align*} $$

All these points lie in the plane $P=\{x_1+x_3 = 1 \text { and } x_2+x_4 = 1\}$ . Hence, for small $\delta> 0$ , the four points

$$ \begin{align*}(\tfrac12\pm_1 \delta, \tfrac12\pm_2\delta, \tfrac12\mp_1\delta, \tfrac12\mp_2\delta), \quad \pm_1,\pm_2\in \{-,+\}\end{align*} $$

are all in $P\cap C$ . Therefore, regardless of the signs of $j_1-j_3$ and $j_2-j_4$ , there exist $c_j\geq 0$ satisfying $c_1+c_2+c_3+c_4 = 1$ so that

$$ \begin{align*} &c_1(j_1+j_4) + c_2(j_2+j_3) + c_3(j_1+j_2) + c_4( \tfrac35(j_3+j_4)+\tfrac25(j_1+j_2) ) \\ & \quad = \tfrac12(j_1+j_2+j_3+j_4) - \delta (|j_1-j_3| + |j_2-j_4|), \end{align*} $$

and in the argument in Case IV above, we have chosen $\delta = \tfrac 1{100}$ .

This completes the overall proof of Theorem 1.2.

4 Proof of Theorem 1.4

We only carry out the proof on the relevant case $0<s\le 1$ , which is most convenient with adapted function spaces. For this purpose, we recall the definition of the function space $Y^{s}$ from [10] and relevant facts. For a general theory, we refer to [12, 10, 8, 9].

Definition 4.1. Let $\mathcal {Z}$ be the collection of finite non-decreasing sequences $\left \{ t_{k}\right \} _{k=0}^{K}$ in $\mathbf {\mathbb {R}}$ . We define $V^{2}$ as the space of all right-continuous functions $u:\mathbf {\mathbb {R}}\rightarrow \mathbf {\mathbb {C}}$ with $\lim _{t\rightarrow -\infty }u(t)=0$ and

$$\begin{align*}\|u\|_{V^{2}}:=\left(\sup_{\left\{ t_{k}\right\} _{k=0}^{K}\in{\mathcal{Z}}}\sum_{k=1}^{K}\left\vert u(t_{k})-u(t_{k-1})\right\vert ^{2}\right)^{1/2}<\infty. \end{align*}$$

For $s\in \mathbf {\mathbb {R}}$ , we define $Y^{s}$ as the space of $u:\mathbf {\mathbb {R}}\times \mathbb {T}^{2}\rightarrow \mathbf {\mathbb {C}}$ such that $e^{it|\xi |^2}\widehat {u(t)}(\xi )$ lies in $V^{2}$ for each $\xi \in \mathbf {\mathbb {Z}}^{2}$ and

$$\begin{align*}\|u\|_{Y^{s}}\:=\left(\sum_{\xi\in\mathbf{\mathbb{Z}}^{2}}\left(1+\left\vert \xi\right\vert ^{2}\right)^{s}\|e^{it|\xi|^{2}}\widehat{u(t)}(\xi)\|_{V^{2}}^{2}\right)^{1/2}<\infty. \end{align*}$$

For time interval $I\subset \mathbf {\mathbb {R}}$ , we also consider the restriction space $Y^s(I)$ of $Y^s$ .

The space $Y^{s}$ is used in [10] and later works on critical regularity theory of Schrödinger equations on periodic domains. Some well-known properties are the following.

Proposition 4.2 [10, Section 2].

$Y^{s}$ -norms have the following properties.

• • Let $A,B$ be disjoint subsets of $\mathbf {\mathbb {Z}}^{2}$ . For $s\in \mathbf {\mathbb {R}}$ , we have

  (4.1) $$ \begin{align} \|P_{A\cup B}u\|_{Y^{s}}^{2}=\|P_{A}u\|_{Y^{s}}^{2}+\|P_{B}u\|_{Y^{s}}^{2}. \end{align} $$

• • For $s\in \mathbf {\mathbb {R}}$ , time $T>0$ and a function $f\in L^{1}H^{s}$ , denoting

  $$\begin{align*}{\mathcal{I}}(f)(t):=\int_{0}^{t}e^{i(t-t')\Delta}f(t')dt', \end{align*}$$
  we have
  (4.2) $$ \begin{align} \|\chi_{[0,T)}\cdot{\mathcal{I}}(f)\|_{Y^{s}}\lesssim\sup_{v\in Y^{-s}:\|v\|_{Y^{-s}}\le1}\left\vert \int_0^T\int_{\mathbb{T}^{2}}f\overline{v}dxdt\right\vert. \end{align} $$

• • For time $T>0$ and a function $\phi \in H^s(\mathbb {T}^2)$ , we have

  (4.3) $$ \begin{align} \|\chi_{[0,T)}\cdot e^{it\Delta}\phi\|_{Y^s}\approx\|\phi\|_{H^s} \end{align} $$
  and for function $u\in Y^s$ , $u\in L^\infty H^s$ and
  (4.4) $$ \begin{align} \|\chi_{[0,T)}u\|_{Y^s}\gtrsim\|u\|_{L^\infty([0,T);H^s)}. \end{align} $$

For $N\in 2^{\mathbf {\mathbb {N}}}$ , denote by ${\mathcal {C}}_{N}$ the set of cubes of size N

$$\begin{align*}{\mathcal{C}}_{N}:=\left\{ (0,N]^{2}+N\xi_{0}:\xi_{0}\in\mathbf{\mathbb{Z}}^{2}\right\}. \end{align*}$$

We transfer (1.3) to the following estimate.

Lemma 4.3. For all $N\in 2^{\mathbf {\mathbb {N}}}$ , intervals $I\subset \mathbf {\mathbb {R}}$ such that $\left \vert I\right \vert \le \frac {1}{\log N}$ , cubes $C\in {\mathcal {C}}_{N}$ , and $u\in Y^{0}$ , we have

(4.5) $$ \begin{align} \|P_{C}u\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}\lesssim\|u\|_{Y^{0}}. \end{align} $$

Proof. We follow the notations in [10, Section 2]. Let u be a $U_{\Delta }^{4}L^2$ -atom; that is,

$$\begin{align*}u(t)=\sum_{j=1}^{J}1_{[t_{j-1},t_{j})}e^{it\Delta}\phi_{j} \end{align*}$$

for $\phi _{1},\ldots ,\phi _{J}\in L^{2}(\mathbb {T}^{2})$ , $t_0\le ...\le t_J$ , $\sum _{j=1}^{J}\|\phi _{j}\|_{L^{2}}^{4}=1$ . By (1.3), we have

(4.6) $$ \begin{align} \|P_{C}u\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|P_{C}e^{it\Delta}\phi_{j}\|_{L^{4}_{t,x}(I\times\mathbb{T}^{2})}^{4}\lesssim\sum_{j=1}^{J}\|\phi_{j}\|_{L^{2}}^{4}\lesssim 1. \end{align} $$

By [10, Proposition 2.3] and (4.6), for $u\in Y^{0}$ , we conclude

$$\begin{align*}\|P_{C}u\|_{L_{t,x}^{4}(I\times\mathbb{T}^{2})}\lesssim\|u\|_{U_{\Delta}^{4}L^2}\lesssim\|u\|_{V_{\Delta}^{2}L^2}\lesssim\|u\|_{Y^{0}}.\\[-37pt] \end{align*}$$

Since we only rely on the $L^4$ estimate, Lemma 4.3 explains why we can work with the $Y^s$ -norm instead of the $U^2$ -based space as was used in [10].

For $N\in 2^{\mathbf {\mathbb {N}}}$ , we set the interval $I_N:=[0,1/\log N)$ . Let $Z_N$ be the norm

$$\begin{align*}\|u\|_{Z_N}:=\|\chi_{I_N}\cdot u\|_{Y^0}+N^{-s}\|\chi_{I_N}\cdot u\|_{Y^s}. \end{align*}$$

We show our main trilinear estimate:

Lemma 4.4. For $0<s\le 1$ and $N\gg 2^{1/s}$ , we have

(4.7) $$ \begin{align} \|{\mathcal{I}}(u_1u_2u_3)\|_{Z_N}\lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}, \end{align} $$

where each $u_j$ could also be replaced by its complex conjugate. The implicit constant is independent from s.

Proof. Let $k_s=\lfloor 1/s \rfloor $ . In this proof, we use $2^{k_s}$ -adic cutoffs: for $N\in 2^{k_s\mathbf {\mathbb {N}}}$ , we denote

$$\begin{align*}P_{\sim N}u=u_{\sim N}=u_{<2^{k_s}N}-u_{<N}. \end{align*}$$

Since $\|\chi _{I_N}\cdot u\|_{Z_{\widetilde {N}}}\approx \|u\|_{Z_N}$ holds for $\widetilde {N}\in [2^{-k_s}N,N]$ , we assume further that $N\in 2^{k_s\mathbf {\mathbb {N}}}$ . (4.7) is reduced to showing

(4.8) $$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{<N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\|v\|_{Y^{0}} \end{align} $$

and

(4.9) $$ \begin{align} \left\vert \int_{I_N\times\mathbb{T}^2}u_1u_2u_3\cdot v_{\ge N}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|u_3\|_{Z_N}\cdot N^{s}\|v\|_{Y^{-s}} \end{align} $$

with implicit constants in (4.8) and (4.9) independent from s.

We prove (4.8) and (4.9). For $M\ge N$ in $2^{k_s\mathbf {\mathbb {N}}}$ and $C\in {\mathcal {C}}_M$ , partitioning $I_N$ to intervals of length comparable to $\frac {1}{\log M}$ and applying (4.5) to each, we have

(4.10) $$ \begin{align} \|\chi_{I_N}\cdot P_C u\|_{L_{t,x}^{4}}\lesssim\left(\frac{\log M}{\log N}\right)^{1/4}\|u\|_{Y^{0}}. \end{align} $$

By (4.10), for $u\in Y^{s}$ , we have

(4.11) $$ \begin{align} \|\chi_{I_N}\cdot u\|_{L_{t,x}^{4}} & \lesssim\|u_{<N}\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\|u_{\sim M}\|_{Y^{0}}\\ & \lesssim\|u\|_{Y^{0}}+\sum_{M\ge N}\left(\frac{\log M}{\log N}\right)^{1/4}\frac{N^{s}}{M^{s}}\cdot N^{-s}\|u\|_{Y^{s}}\nonumber\\ & \lesssim\|u\|_{Y^{0}}+N^{-s}\|u\|_{Y^{s}}\lesssim\|u\|_{Z_N},\nonumber \end{align} $$

which implies (4.8).

We prove (4.9) by partitioning the frequency domain $\mathbf {\mathbb {Z}}^{2}$ into congruent cubes. By (4.10) and (4.1), for $M\in 2^{k_s\mathbf {\mathbb {N}}}$ and $u,v\in Y^{0}$ , we have

(4.12) $$ \begin{align} &\|\chi_{I_N} \cdot P_{\le M}\left(uv\right)\|_{L_{t,x}^{2}}\\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\cdot P_{C_{2}}v\|_{L_{t,x}^{2}}\nonumber \\&\quad \lesssim\sum_{\substack{C_{1},C_{2}\in{\mathcal{C}}_{M}\\ \operatorname{\mathrm{dist}}(C_{1},C_{2})\le M } }\|\chi_{I_N}\cdot P_{C_{1}}u\|_{L_{t,x}^{4}}\|\chi_{I_N}\cdot P_{C_{2}}v\|_{L_{t,x}^{4}}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\left(\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}u\|_{Y^{0}}^2\sum_{C\in{\mathcal{C}}_{M}}\|P_{C}v\|_{Y^{0}}^2\right)^{1/2}\nonumber \\&\quad \lesssim\left(1+\frac{\log M}{\log N}\right)^{1/2}\|u\|_{Y^{0}}\|v\|_{Y^{0}}.\nonumber \end{align} $$

We conclude quadrilinear estimates. By (4.12) and Young’s convolution inequality on $(L,K)$ using that $\sum _{R\in 2^{k_s\mathbf {\mathbb {N}}}}R^{-s}\lesssim 1$ , we have

(4.13) $$ \begin{align} & \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<N}(u_1u_2)P_{<N}(w_{\sim L}v_{\sim K})dxdt\right\vert \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^{s}}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim\|u_1\|_{Y^{0}}\|u_2\|_{Y^{0}} \|w\|_{Y^{s}} \|v\|_{Y^{-s}}\nonumber \end{align} $$

and

(4.14) $$ \begin{align} & \sum_{M\ge N}\sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I\times\mathbb{T}^{2}}P_{\sim M}\left(u_1u_2\right)P_{\sim M}\left(w_{\sim L}v_{\sim K}\right)dxdt\right\vert \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}(\|P_{\ge M/4}u_1\|_{Y^0}\|u_2\|_{Y^0}+\|u_1\|_{Y^0}\|P_{\ge M/4}u_2\|_{Y^0})\nonumber \\&\qquad \cdot\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\sum_{M\ge N}\frac{\log M}{\log N}\frac{N^s}{M^s}\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}\|w_{\sim L}\|_{Y^{0}}\|v_{\sim K}\|_{Y^{0}}\nonumber \\&\quad \lesssim\|u_1\|_{Z_N} \|u_2\|_{Z_N}\sum_{K\ge N}\sum_{L\gtrsim K}(L/K)^{-s}\|w_{\sim L}\|_{Y^s}\|v_{\sim K}\|_{Y^{-s}}\nonumber \\&\quad \lesssim \|u_1\|_{Z_N} \|u_2\|_{Z_N} \|w\|_{Y^s} \|v\|_{Y^{-s}}.\nonumber \end{align} $$

Combining (4.13) and (4.14), we have

(4.15) $$ \begin{align} \sum_{K\ge N}\sum_{L\gtrsim K}\left\vert \int_{I_N\times\mathbb{T}^{2}}(u_1u_2)w_{\sim L}v_{\sim K}dxdt\right\vert \lesssim\|u_1\|_{Z_N}\|u_2\|_{Z_N}\|w\|_{Z_N}N^{s}\|v\|_{Y^{-s}}. \end{align} $$

Note that in (4.12), (4.13), (4.14), (4.15) each function on the left-hand side could be replaced by its complex conjugate. We bound

$$ \begin{align*} & \left\vert \int_{I_N\times\mathbb{T}^{2}}u_1u_2u_3v_{\ge N}dxdt\right\vert \\&\quad \le\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{\ge K/4}u_1\cdot u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{\ge K/4}u_2\cdot u_3\cdot v_{\sim K}dxdt\right\vert \\&\qquad +\sum_{K\ge N}\left\vert \int_{I_N\times\mathbb{T}^{2}}P_{<K/4}u_1\cdot P_{<K/4}u_2\cdot P_{\ge K/4}u_3\cdot v_{\sim K}dxdt\right\vert. \end{align*} $$

Applying (4.15) to each term, we conclude (4.9).

Proof of Theorem 1.4.

Let $s>0$ and $N\gg 2^{1/s}$ . By (4.7), (4.2) and the expansion $|u|^2u-|v|^2v=(|u|^2+\overline {u}v)(u-v)+v^2\overline {(u-v)}$ , we have

(4.16) $$ \begin{align} \|{\mathcal{I}}(|u|^2u-|v|^2v)\|_{Z_N}\lesssim(\|u\|_{Z_N}+\|v\|_{Z_N})^2\|u-v\|_{Z_N}. \end{align} $$

Based on (4.16), we use the contraction mapping principle. Let $B_N\subset H^s$ be the ball

$$\begin{align*}B_N:=\{u_0\in H^s:\|u_0\|_{L^2}+N^{-s}\|u_0\|_{H^s}\le2\delta\}, \end{align*}$$

and $X_N$ be the complete metric space

$$\begin{align*}X_N:=\{u\in C^0(I_N;H^s)\cap Y^s(I_N):\|u\|_{Z_N}\le\eta\} \end{align*}$$

equipped with the norm $Z_N$ , where $\delta ,\eta>0$ are universal constants to be fixed shortly.

By (4.16), there exists $\eta>0$ such that the map

$$\begin{align*}u\mapsto{\mathcal{I}}(|u|^2u) \end{align*}$$

is a contraction map on $X_N$ of Lipschitz constant $1/2$ , which fixes $0$ .

By (4.3), there exists $\delta>0$ such that

(4.17) $$ \begin{align} \|e^{it\Delta}\phi\|_{Z_N}<\eta/4 \end{align} $$

holds for every $\phi \in B_N$ , so that the map

$$\begin{align*}u\mapsto e^{it\Delta}u_0\mp i {\mathcal{I}}(|u|^2u) \end{align*}$$

is a contraction mapping on $X_N$ . Thus, for $u_0\in B_N$ , there exists a solution u to (NLS) in $X_N$ on time interval $I_N$ . Moreover, since the map $u\mapsto {\mathcal {I}}(|u|^2u)$ is a contraction map of Lipschitz constant $1/2$ , given solutions $u,v\in X_N$ to $u_0,v_0\in B_N$ , we have

$$ \begin{align*} \|u-v\|_{Z_N}&\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\|{\mathcal{I}}(|u|^2u)-{\mathcal{I}}(|v|^2v)\|_{Z_N}\\ &\le\|e^{it\Delta}(u_0-v_0)\|_{Z_N}+\frac12\|u-v\|_{Z_N}, \end{align*} $$

which implies that the flow map $u_0\mapsto u\in X_N$ is Lipschitz continuous by (4.3).

We then check uniqueness. Let $u,v\in Y^s\cap C^0H^s$ be solutions to (NLS) on a time interval $[0,T),T>0$ , with common initial data $u_0$ such that $\|u_0\|_{L^2}\le \delta $ . There exists $N_0\gg 2^{1/s}$ such that $I_{N_0}\subset [0,T)$ and

$$\begin{align*}\|u_{>N_0}\|_{Y^0}+N_0^{-s}\|u\|_{Y^s}\le 2N_0^{-s}\|u\|_{Y^s}\le\eta/2, \end{align*}$$

$$\begin{align*}\|v_{>N_0}\|_{Y^0}+N_0^{-s}\|v\|_{Y^s}\le 2N_0^{-s}\|v\|_{Y^s}\le\eta/2. \end{align*}$$

We have

$$ \begin{align*} \|P_{\le N_0}(u-e^{it\Delta}u_0)\|_{Y^0(I_N)}&\lesssim\|P_{\le N_0}(|u|^2u)\|_{L^1(I_N;L^2)}\\ &\lesssim N_0\||u|^2u\|_{L^1(I_N;L^1)}\lesssim N_0\|u\|_{L^4(I_N;L^4)}^3, \end{align*} $$

which shrinks to zero as $N\rightarrow \infty $ since $u\in L^4_{t,x}$ on $I_{N_0}$ by (4.11). Thus, applying the same argument to v, by (4.17), there exists $N\ge N_0$ such that

$$\begin{align*}\chi_{I_N}u,\chi_{I_N}v\in X_N, \end{align*}$$

which implies $u=v$ on $I_N$ . Therefore, the maximal time $t_*\ge 0$ that $u= v$ on $[0,t_*]$ cannot be less than T, implying the uniqueness of solution to (NLS).

In summary, we proved uniform Lipschitz local well-posedness of (NLS) mapping $B_N$ to $X_N$ . It remains to extend the lifespan over arbitrarily large time interval. For $N\gg 2^{1/s},t_0\in \mathbf {\mathbb {R}}$ , and a solution $u\in Y^s$ to (NLS) such that $u(t_0)\in B_N$ and $\|u(t_0)\|_{L^2}\le \delta $ , by (4.4), we have

$$\begin{align*}N^{-s}\|u(t_0+\frac1{2\log N})\|_{H^s}\lesssim\|u\|_{Z_N}\le\eta. \end{align*}$$

Moreover, since $u(t_0)$ is a limit of smooth data in $B_N$ and solutions to (NLS) in $C^0H^2$ conserve their $L^2$ -norms, we have

$$\begin{align*}\|u(t_0+\frac1{2\log N})\|_{L^2}=\|u(t_0)\|_{L^2}\le\delta. \end{align*}$$

Thus, there exists a constant $K\in 2^{\mathbf {\mathbb {N}}}$ such that $u(t_0+\frac {1}{2\log N})\in B_{KN}$ .

Let $u_0\in H^s$ be any function that $\|u_0\|_{L^2}\le \delta $ . Let $N_0\gg 2^{1/s}$ be a dyadic number such that $u_0\in B_{N_0}$ . For $j\in \mathbf {\mathbb {N}}$ , let

$$\begin{align*}N_j:=K^jN_0\text{ and }T_j:=\sum_{k=0}^{j-1}\frac{1}{2\log N_k}. \end{align*}$$

We extend the solution inductively. For $j\in \mathbf {\mathbb {N}}$ , we can extend the solution $u\in Y^s$ to (NLS) on $[0,T_j]$ to $[0,T_{j+1}]$ with $u(T_{j+1})\in B_{N_{j+1}}$ . Since $\lim _{j\rightarrow \infty }T_j=\infty $ , the lifespan of u is infinite.