Introduction
Changes in Himalayan glaciers and their fate have been a matter of debate since the erroneous claim in the 2007 report of the Intergovernmental Panel on Climate Change (Reference Cruz, Parry, Canziani, Palutikof, Van der Linden and HansonCruz and others, 2007) that if the Earth keeps warming at the current rate, Himalayan glaciers could disappear by 2035 (Reference Cogley, Kargel, Kaser and Van der VeenCogley and others, 2010). However, because of the remoteness and high altitudes in the region, relatively few observation data are available regarding the rate at which Himalayan glaciers are shrinking, although some exceptions exist (Reference KulkarniKulkarni, 1992; Reference Fujita, Nakawo, Fujii and PaudyalFujita and others, 1997; Reference WagnonWagnon and others, 2007; Reference Dobhal, Gergan and ThayyenDobhal and others, 2008; Reference Fujita and NuimuraFujita and Nuimura, 2011; Reference Nuimura, Fujita, Fukui, Asahi, Aryal and AgetaNuimura and others, 2011). Other studies have used remote-sensing (RS) data in the Himalaya to assess the changes in mass loss of glaciers by comparing two digital elevation models based on RS data (RS-DEMs) constructed for different years, the accuracy of which relies on an intercomparison of glacier-free terrain (Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007; Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008a, Reference Bolch, Pieczonka and Benn2011).
Reference Nuimura, Fujita, Fukui, Asahi, Aryal and AgetaNuimura and others (2011) reported elevation change in the ablation area of Khumbu Glacier of-0.7 to-1.9 m a-1 for the period 1995-2004, based on differential GPS (DGPS) measurements and an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEM. In the eastern Khumbu region, Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others (2008a, Reference Bolch, Pieczonka and Benn2011) calculated elevation changes of-0.33 ± 0.24 m a-1 for the period 1962-2002, and -0.36 ± 0.07 m a-1 for the period 1970-2007, based on remote-sensing data. Here we calibrate and validate multitemporal RS-DEMs based on the results of a DGPS survey and then we evaluate elevation changes of Himalayan glaciers at the catchment scale using these calibrated RS-DEMs.
We examined the Khumbu region (Fig. 1) of the east Nepal Himalaya, for which annual ASTER images are available. About 36% of the glaciated area in the region is covered by a debris mantle (Reference Fujii and HiguchiFujii and Higuchi, 1977), so temporal changes in glacier length and area do not provide a good indication of glacier health; instead, it is necessary to measure volume (and thus mass) change in this region (Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008a).

Fig. 1. The DGPS-DEM (m a.s.l.) with analyzed glaciers shown in light blue. The grid size of the DGPS-DEM is enlarged to 300m for visibility. The background is an orthorectified ASTER band 3N image taken in November 2004.
Data and Method
GPS survey and calibration of RS-DEM
We performed a single-frequency carrier-phase DGPS survey in 2007 in the Khumbu region (Fig. 1). During the survey, we set a base GPS receiver (CMC All Star receiver) at Syanboche village (star in Fig. 1). Three other receivers of the same type were used for roving. The altitudinal range of the survey was 3400-5500 m a.s.l. and the spatial extent was ~30 km westeast and 25 km north-south (Fig. 1). The field campaign was performed over 25 days. All data were post-processed using Waypoint GrafNav/GrafNet software (NovAtel Inc.). The measurement accuracy of this type of DGPS survey has been reported to be 0.11 m horizontally and 0.17 m vertically, based on a previous study in the Bhutan Himalaya (Reference FujitaFujita and others, 2008). Data processed as unstable or that failed to converge to a solution in the software were excluded from subsequent analysis. Each measured point was projected in Universal Transverse Mercator coordinates (UTM, zone 45 north, WGS84). Finally, a 30 m grid DEM (DGPS-DEM) was generated by a regularized spline with tension, using the open-source software GRASS-GIS. This DEM was used as a reference for calibrating multitemporal RS-DEMs. We used three types of RS-DEM (15 DEMs in total) for the period 1992-2008 (Table 1).
Table 1. Accuracies of adjusted RS-DEMs. The standard deviation (SD) of each RS-DEM and the shift were calculated relative to DGPS-DEM
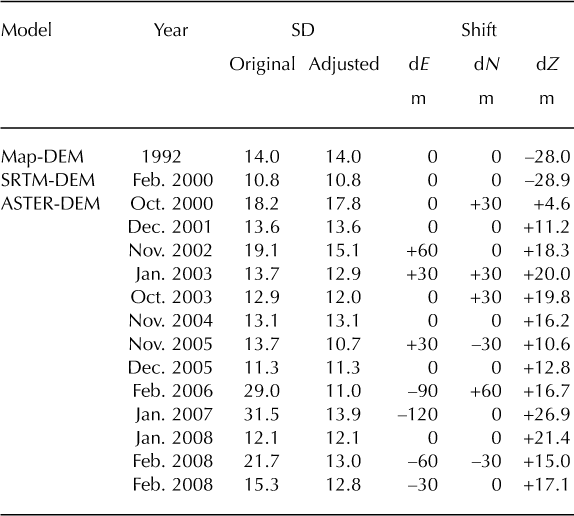
The first DEM type is Map-DEM. The Survey Department of Nepal published 1 : 50000 scale topographic maps from aerial photographs taken in 1992 (Reference Hahn, Baral and SharmaHahn and others, 2003). We digitized the contours (40 m interval) and converted the line data into a 30 m resolution DEM using a regularized spline with tension, employing GRASS-GIS. The estimated horizontal accuracy of the map-derived DEM is 18 m (Reference Salerno, Buraschi, Bruccoleri, Tartari and SmiragliaSalerno and others, 2008).
The second DEM type is a Shuttle Radar Topography Mission-derived DEM (SRTM-DEM) collected in 2000 (http://dds.cr.usgs.gov/srtm/version2_1/SRTM3/; accessed 20 February 2012). The penetration effect of the SRTM C- band radar signal depends on snow condition (dry or wet), which is difficult to determine (Reference Nuth and KääbNuth and Kääb, 2011). Hence, we do not consider the penetration effect of radar waves in this study. We resampled and re-projected the SRTM3 data (3arcsec, ~90m resolution) to a 30m resolution DEM on UTM coordinates (zone 45 north, WGS84) by bilinear interpolation using GIS software.
The third DEM type is ASTER-DEM. We purchased Level 3A01 products of an ASTER orthorectified image with a relative DEM. The orthorectified image from the Level 1A data was produced using stereo images in the VNIR (visible/near-infrared) band. The DEM was generated automatically, without ground control points, by stereophotogrammetry. Details of the algorithm used for DEM generation are provided by Reference Fujisada, Bailey, Kelly, Hara and AbramsFujisada and others (2005), Reference ToutinToutin (2008) and on the ERSDAC (Japanese Earth Remote Sensing Data Analysis Center) website (http://www.gds.aster.ersdac.or.jp/). Accurate estimation of glacier elevation changes requires the co-registration of DEMs (Reference Bolch, Pieczonka and BennBolch and others, 2011; Reference Nuth and KääbNuth and Kääb, 2011). Therefore, each RS-DEM was co-registered against the DGPS-DEM by minimizing the root-mean-square error (rmse) over glacier-free terrain, where no elevation change is expected. Furthermore, the co-registered DEMs were adjusted vertically by subtracting the mean elevation differences against the DGPS-DEM (Table 1).
By then excluding terrain steeper than 30° (which yields poor accuracy (Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007; Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008a; Reference FujitaFujita and others, 2008; Fig. 2)), the rmse and bias among RS-DEMs are significantly improved (Table 1; Fig. 3). Figure 3b also shows that the exclusion of steep terrain has a negligible effect on the altitudinal distribution of glacier area (a decrease in area of 9.7%), because a large proportion of the glacier area has a relatively gentle slope, even in the complex terrain of the Himalaya. In contrast, glacier-free terrain shows a significant reduction in altitude (a decrease in area of 58%).
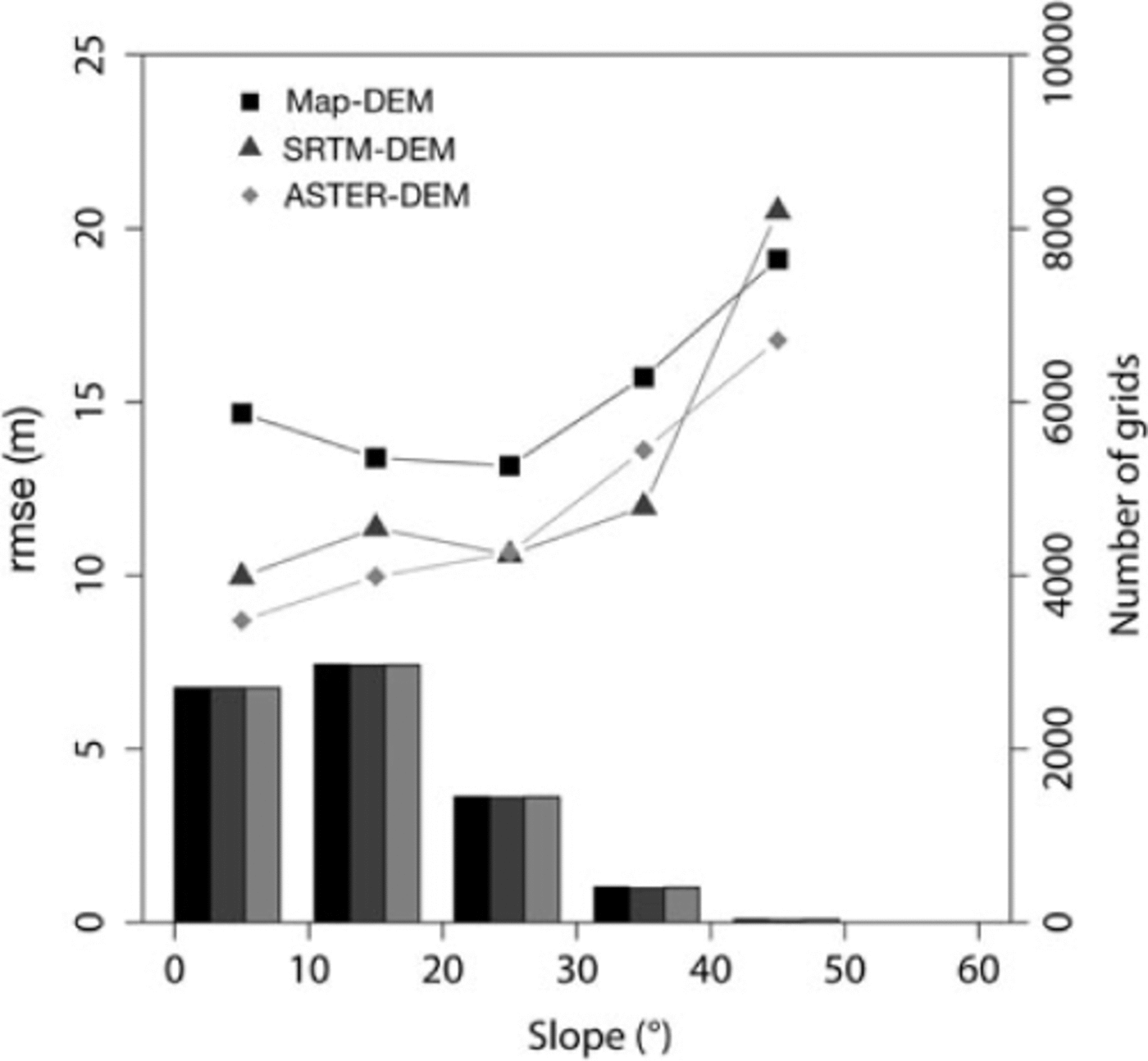
Fig. 2. Root-mean-square error and number of grids of Map-DEM (1992), SRTM-DEM (2000) and the mean of all ASTER-DEMs (2000–08) relative to the DGPS-DEM in each 10_ slope bin on glacier-free terrain.

Fig. 3. (a, b) Altitudinal distribution of (a) elevation differences of SRTM-DEM and ASTER-DEM against the Map-DEM for glacier-free areas and (b) glacier and glacier-free areas in 200m bins for all areas (before screening). (c, d) Altitudinal distribution for areas with slopes less than 30_, of (c) elevation differences of SRTM-DEM and ASTER-DEM against the Map-DEM for glacier-free areas and (d) the glacier and glacier-free areas in 200m bins. The elevation difference of ASTER is the mean value obtained for 13 scenes. Horizontal error bars indicate the standard deviation within each bin.
Delineation of glaciers and debris-covered areas
We delineated the glacier area, the boundary between debris-covered and debris-free area, by manually digitizing using ASTER false-color images taken in October 2003 and November 2004, and obtained an area/altitude profile for each glacier using a gap-filled SRTM-DEM (Reference Jarvis, Reuter, Nelson and GuevaraJarvis and others, 2008). We defined the glacier area as a continuous ice body by excluding areas of thin snow or ice surface covering bedrock on steep slopes. The digitized glacier area shows ~34.8% of debris-covered area, consistent with a previous study (Reference Fujii and HiguchiFujii and Higuchi, 1977).
Elevation change
To obtain the elevation change of Himalayan glaciers, previous studies have computed the difference between two DEMs constructed for different years (Reference Berthier, Arnaud, Kumar, Ahmad, Wagnon and ChevallierBerthier and others, 2007, 2010; Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others, 2008a, Reference Bolch, Pieczonka and Benn2011), meaning that errors in the DEMs have a direct effect on their results, even after an intercomparison over glacier-free terrain. To reduce such scene-dependent errors, we computed the elevation change by generating a weighted least-squares (WLS) linear regression model for each grid. A linear regression is determined to yield the minimum sum of the squared residuals (SSR) at each grid for which the rmse of each RS-DEM is used as the weighting factor, σi . SSR was calculated by

where n is the number of RS-DEMs, ei, is the error between modeled and observed values of each RS-DEM and σi, is the rmse of each RS-DEM (Table 1). Using this procedure, when a linear regression model is calculated, data with a high level of accuracy are heavily weighted, whereas data with a low level of accuracy are lightly weighted. Therefore, the confidence interval of the linear regression, used as an estimate of the error in elevation change, is generally reduced in the case of a larger number of data. Hence, the use of a large number of DEMs results in a lower estimation error. The slope of the linear regression is equivalent to the elevation change (ma-1).
We also excluded outliers with accuracy worse than 5 m a-1, and then recalculated the slope using the remaining data. We finally obtained the spatial distribution of elevation change for glaciers in the Khumbu region (Fig. 4a). We also calculated the 68% confidence level for the regression line. The difference between the regression line and the maximum error slope is used as the error in the grid. Grids with relatively poor accuracy were found at higher altitudes, where the presence of surface snow results in reduced image contrast (Fig. 4b).
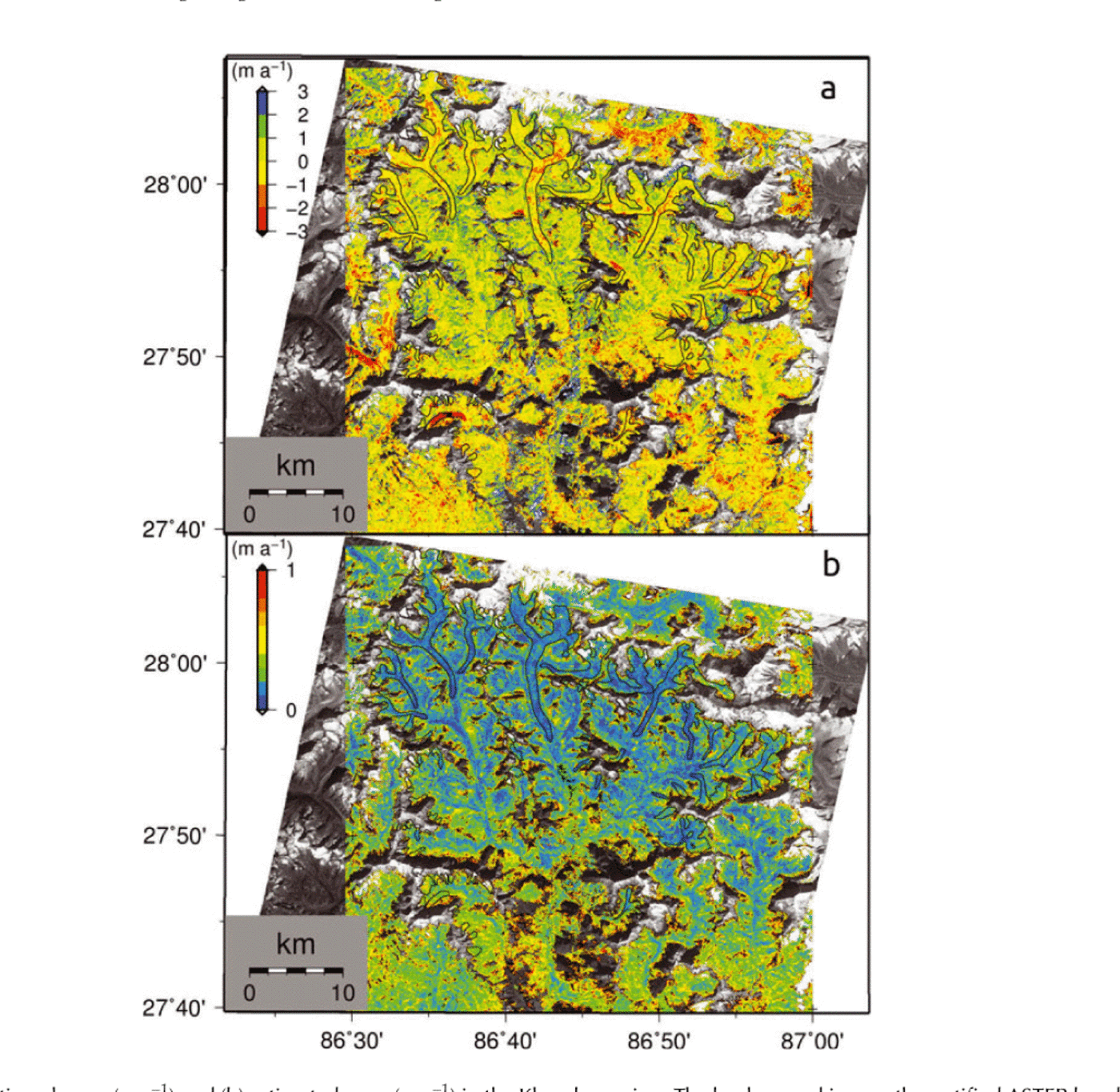
Fig. 4. (a) Elevation change (m a-1) and (b) estimated error (m a-1) in the Khumbu region. The background is an orthorectified ASTER band 3N image taken in November 2004.
The distribution map of elevation change (Fig. 4a) includes many areas with missing data (14% of the total glacier area) due to the variable quality of the original DEMs and the steepness of the terrain. To compute the regional mass balance, we obtained the average elevation change at each 50m altitude band and then calculated the area-weighted average for each glacier. The number of missing data tends to increase with increasing altitude; no data are available for the high-altitude accumulation areas of some glaciers. We extrapolated the elevation change from the uppermost band with valid data to the highest band of each glacier at which no change in elevation was assumed (0 m a-1). The uncertainty at high altitudes has only a minor effect on our estimates because of the small size of high-altitude areas relative to the total glacier area (Fig. 3a). Reference Bolch, Pieczonka and BennBolch and others (2011) used an ice density value of 900 kgm-3 to convert elevation change (ma-1) to regional mass balance (m w.e. a-1), and assigned an additional uncertainty of ±70kgm-3 due to a lack of ice density measurements (Reference ZempZemp and others, 2010). However, we did not use the upper range of the uncertainty because the value is unrealistic. We used an ice density of 865 ± 35 kgm-3.
Results and Discussion
Validation of elevation change of Khumbu Glacier
We used previous field-based studies (Reference Kadota, Seko, Aoki, Iwata and YamaguchiKadota and others, 2000; Reference Nuimura, Fujita, Fukui, Asahi, Aryal and AgetaNuimura and others, 2011) to validate the distribution map of elevation change over Khumbu Glacier (Fig. 5). The field measurements undertaken in four areas on the glacier are consistent with the calculated elevation changes, even considering the spatial variability shown in Figure 5b. The longitudinal profile of elevation changes shows that the surface is lowering in areas 2 and 3. This is also shown for 1995-2004 by Reference Nuimura, Fujita, Fukui, Asahi, Aryal and AgetaNuimura and others (2011). The results of this study are consistent with the survey results for 1995-2004 throughout the debris-covered area. The mean difference between elevation changes in this study and those in previous studies (Reference Kadota, Seko, Aoki, Iwata and YamaguchiKadota and others, 2000; Reference Nuimura, Fujita, Fukui, Asahi, Aryal and AgetaNuimura and others, 2011) for areas 1-4 is 0.30±0.21 m a-1, and the difference for each area is within the estimated error. The very gentle slope (<2°) and heterogeneous topography of debris-covered areas result in a range of surface types, melt rates and elevation changes (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, Reference Sakai, Nakawo and Fujita2002; Reference Mihalcea, Mayer, Diolaiuti, Lambrecht, Smiraglia and TartariMihalcea and others, 2006; Reference QuinceyQuincey and others, 2007).

Fig. 5. (a) Enlargement of the spatial distribution of elevation changes on/around glaciers in the eastern Khumbu region shown in Figure 4a. (b) Longitudinal profile of elevation change along with previous in situ observations on Khumbu Glacier. Vertical bars denote the variability of surveys in previous studies. Horizontal bars show the extent of each area.
Comparison with the DEM subtraction method
We compared elevation changes obtained by linear regression with WLS ('regression method') with those obtained by the classical DEM subtraction method ('subtraction method'). The elevation change by DEM subtraction was calculated from the Map-DEM in 1992 and from the latest ASTER-DEM in 2008. A statistical comparison of the two methods was conducted only for gridpoints available for both methods, and steep slopes (>30°) were excluded from the analysis. The mean and standard deviation of elevation change over the glacier surface for the compared area are -0.75 ± 0.41 and -0.92 ± 0.57 m a-1 for the regression and subtraction methods respectively; the values over glacier-free terrain for the compared area are -0.05 ± 0.53 and -0.20 ± 0.96 m a-1 respectively. That the elevation difference over glacier-free terrain for the subtraction method is not 0 m a-1 is plausible due to the uneven distribution of GPS measurements. If the difference over glacier-free terrain is taken into account, the average elevation change is similar for the regression and subtraction methods (-0.70 ± 0.47 and -0.72 ± 0.77 m a-1 respectively). The standard deviation values for the glacier surface and for glacier-free terrain are smaller for the regression method than for the subtraction method. The results of an F-test for variance at the 95% level show significant difference between the two methods for both glacier and glacier-free terrain. In particular, the standard deviation of the regression method is much smaller than that of the subtraction method over glacier-free terrain.
Although the proposed regression method cannot detect acceleration and deceleration in the same way as the subtraction method (because the regression is linear), the regression method can be used to calculate not only the distribution of elevation change, but also the distribution of uncertainty (Fig. 4b). Small uncertainty is found on gentle valley floors and at lower altitudes, whereas large uncertainty is found on steep slopes and at high altitudes (Fig. 4b). The large uncertainty is consistent with the limitation of stereographically derived DEMs for steeply sloping terrain, as also reported by Reference ToutinToutin (2002) and Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others (2008a). This limitation is also indicated by the large uncertainty in high-altitude accumulation zones, where low contrast is obtained in satellite images. The small uncertainty associated with gentle valley floors is consistent with the areas of large mountainous glaciers. These results show that the regression method can be used to calculate elevation change on large mountainous glaciers on gentle valley floors with small uncertainty.
Comparison of mass-balance results from different approaches in the east Khumbu region
Reference Bolch, Pieczonka and BennBolch and others (2011) reported the accelerated thinning of glaciers in the east Khumbu region after 2002, based on comparisons over a relatively long period (1970-2007) and over a shorter period (2002-07). They also noted the need for further analysis due to the high uncertainty in the recent period (2002-07). We compared the mass balance from the present study with those of Reference Bolch, Pieczonka and BennBolch and others (2011) for ten glaciers in the east Khumbu region. We additionally calculated mass balance for the period 2000-08 without the SRTM-DEM, for comparison with Reference Bolch, Pieczonka and BennBolch and others (2011) (Table 2).
Table 2. Comparison of mass balance (m w.e. a-1) between this study and Reference Bolch, Pieczonka and BennBolch and others (2011)
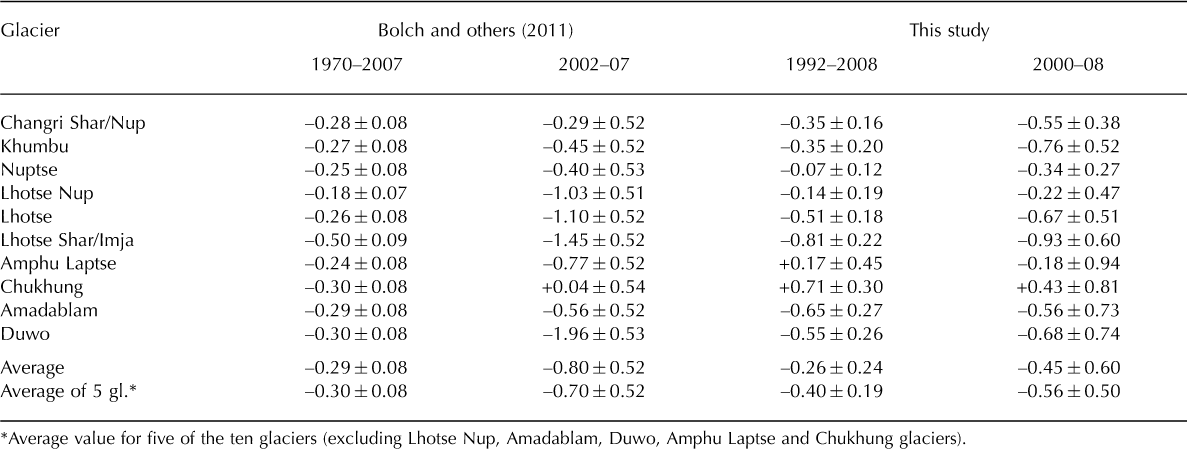
The average mass balances of the ten glaciers for the periods 1970-2007 (Reference Bolch, Pieczonka and BennBolch and others, 2011) and 1992-2008 (this study) show comparable thinning (Table 2). Results for all four periods, 1970-2007, 2002-07, 1992-2008 and 2000-08, show a general tendency of gradually accelerated thinning during recent decades, which is consistent with the results of Reference Bolch, Pieczonka and BennBolch and others (2011). However, considering the temporal changes of mass balance over the four periods, mass loss for the period 2002-07 for Lhotse Nup and Duwo glaciers might be overestimated. Furthermore, the high uncertainties for the period 2000-08 for Amphu Laptse, Chukhung, Amadablam and Duwo glaciers indicate the low reliability of the estimation (Table 2).
Amphu Laptse and Chukhung glaciers are surrounded by steep north-facing slopes, which could degrade the quality of DEMs generated by stereophotogrammetry due to the shadowing effect (Reference KääbKääb, 2002). The average mass balances of five of the ten glaciers (excluding Lhotse Nup, Amadablam, Duwo, Amphu Laptse and Chukhung glaciers) show a gradual increase in the rate of thinning (Table 2) over time. This result is consistent with a recent global trend of negative mass balance (Reference CogleyCogley, 2009). In addition, Figure 6 shows larger dispersion in the mass balance for the three shorter periods (1992-2008, 2000-08 and 2002-07) than for the longer period (1970-2007), reflecting the smaller uncertainty in the case of a longer period. Comparison of the three short periods also indicates a recent acceleration of negative mass balance.
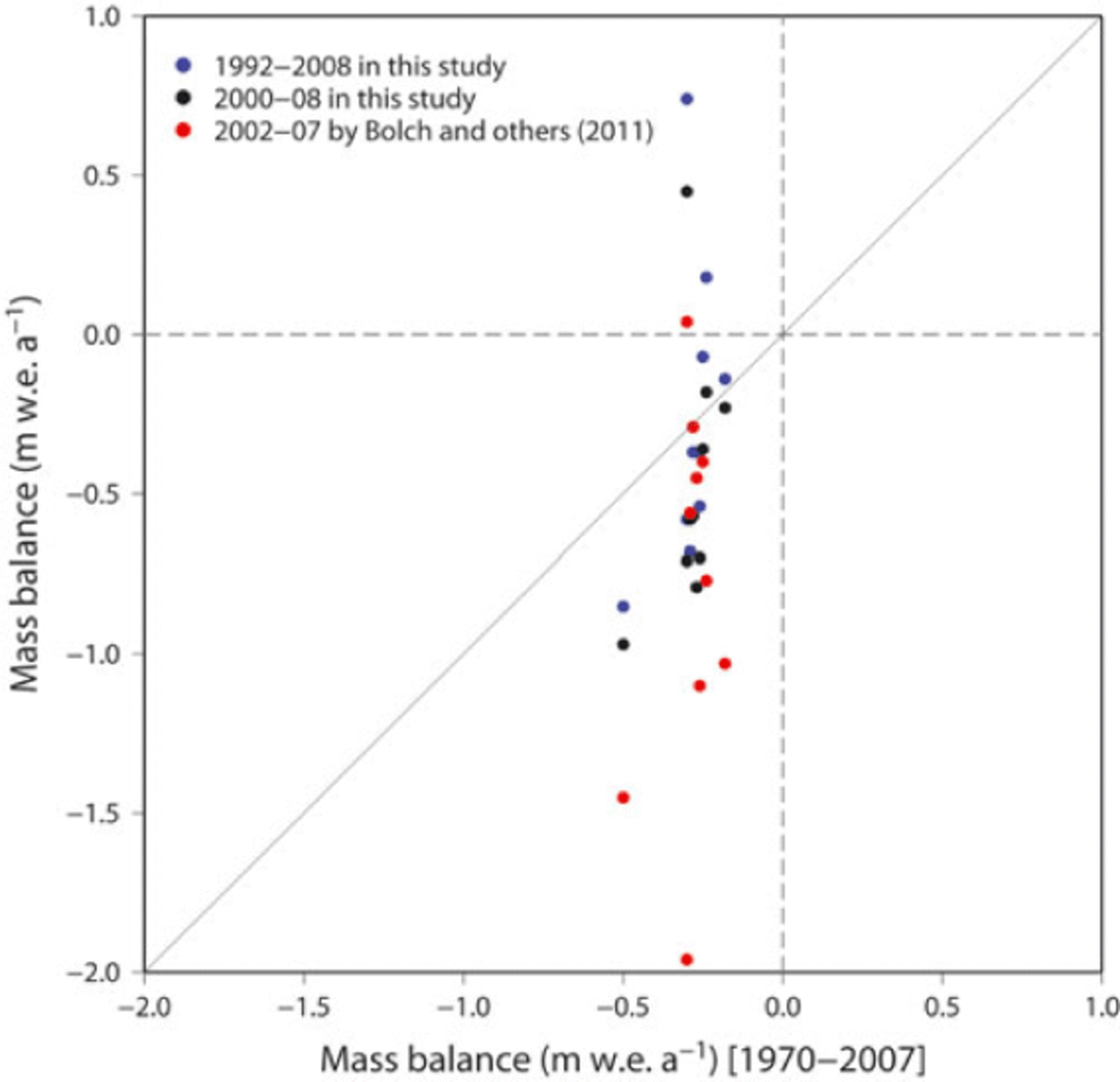
Fig. 6. Comparison of mass balances reported by Reference Bolch, Pieczonka and BennBolch and others (2011) (1970–2007 and 2002–07) and that of the present study (1992–2008). The thin diagonal line is the equivalence line. Dashed lines show no mass change.
Altitudinal distribution of elevation change
Debris-covered glaciers are considered to be less sensitive to climate change because of the insulating effect of their debris mantle (Reference Mattson, Gardner and YoungMattson and others, 1993). However, in the present study, an altitudinal profile of elevation changes for debris-covered areas shows a lowering rate comparable with that of the ablation area of debris-free areas (Fig. 7a). Previous studies have reported that ponds and ice cliffs, which are widely distributed across debris-covered areas, absorb large amounts of heat, so that debris-covered ice melts at a higher rate than previously thought (Reference Sakai, Takeuchi, Fujita and NakawoSakai and others, 2000, 2002). We found thickening of debris-covered surfaces at elevations above 5600 m a.s.l., whereas no thickening was found over debris-free areas (Fig. 7a). However the thickening might be due to uncertainties in the DEM.
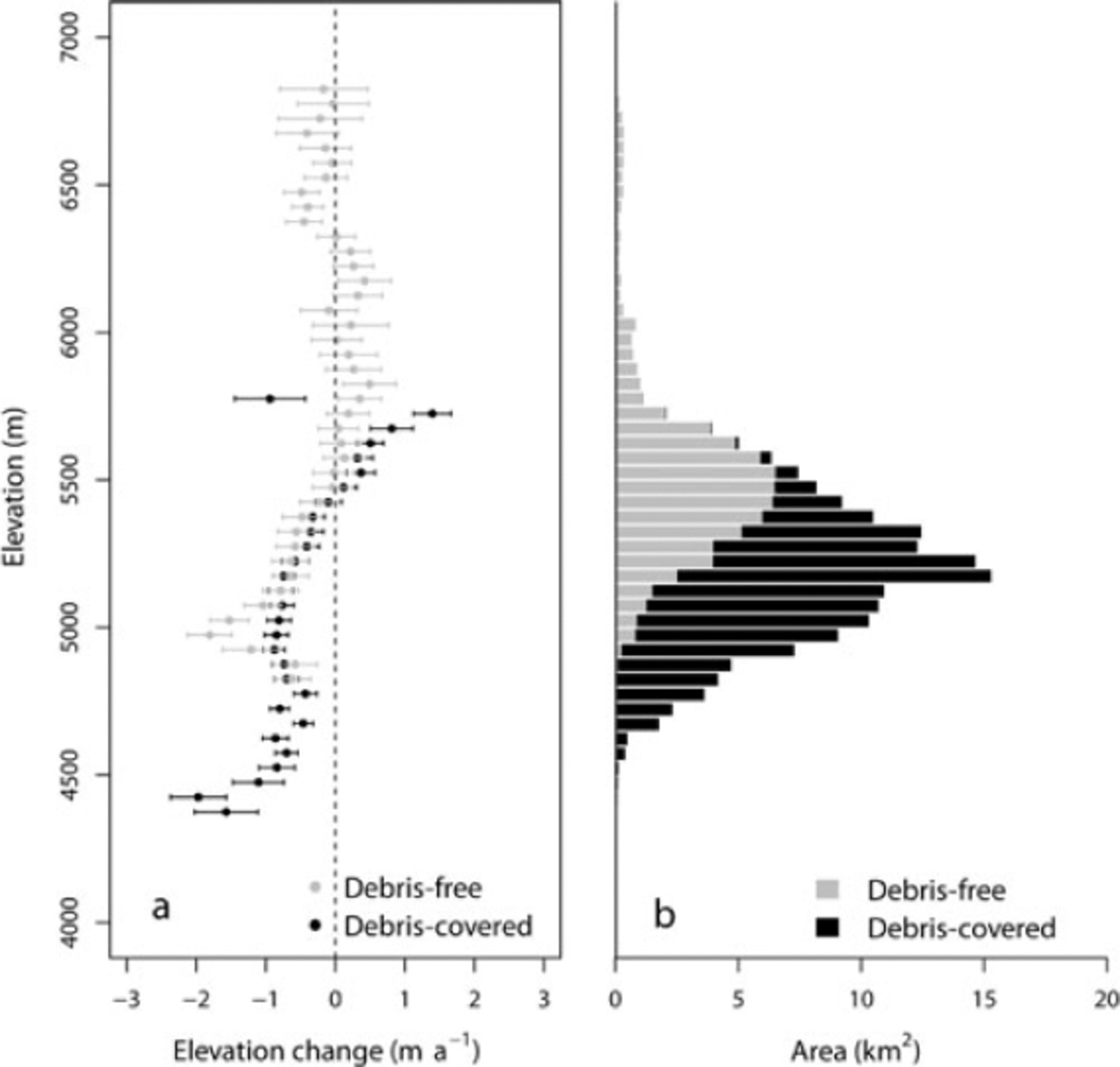
Fig. 7. Altitudinal distribution of (a) elevation change and (b) glacier area in the Khumbu region. The altitudinal distributions are shown for each 50 m bin. Horizontal error bars in (a) indicate the mean uncertainty, calculated by regression method, of each bin.
Regarding the regional mass balance, there is only a small area of debris-covered glaciers above 5600 m a.s.l., so local topographic surface thickening is insignificant relative to the total glacier area. Relatively large errors in elevation data are found above 5600 m a.s.l. for debris-free areas (Fig. 7b), possibly due to the variable quality of the DEMs in snow-covered areas, which show little contrast (Fig. 4b). Although this uncertainty does not affect the regional mass balance (given the small size of debris-free areas relative to the total area), this finding suggests a limitation of stereographically derived DEMs, as also reported by Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others (2008a).
Surface lowering on large debris-covered glaciers
The formation of glacial lakes at the terminus is related to both the slope of the glacier and thinning of the debris-covered area (Reference Sakai and FujitaSakai and Fujita, 2010). In this context, we analyzed the relation between area-weighted elevation change and the slope of debris-covered areas on debris-covered glaciers. The analysis was performed only for glaciers with a debris-covered area larger than 0.5 km2 (Fig. 8). The slope of the debris-covered area was calculated using a linear regression model based on the distance along the flowline upward from the terminus and the surface elevation. A clear lowering (-0.87 m a-1) is found for large glaciers with a slope less than 5° in debris-covered areas. For one of these gently sloping glaciers, Khumbu Glacier, field observations reveal complex, heterogeneous topography (Reference Iwata, Aoki, Kadota, Seko and YamaguchiIwata and others, 2000), characterized by many ponds and ice cliffs. In contrast, relatively low rates of surface lowering (0.35 m a-1) are found for debris-covered areas of small glaciers with a mean slope greater than 5°.

Fig. 8. Elevation change versus the longitudinal slope of debriscovered areas on debris-covered glaciers. Glaciers with a debris-covered area greater than 0.5 km2 are shown. Open and solid circles indicate debris-covered glaciers without and with a glacial lake, respectively. Vertical error bars indicate the standard deviation of elevation change of each debris-covered area.
A study of RS-derived glacier flow velocity in the Khumbu region has suggested that a gentle surface slope (<2°) is related to a smaller gradient in flow speed (Reference QuinceyQuincey and others, 2007). Therefore, a glacier surface height increase as a result of compressive flow (also referred to as emergence velocity) is not expected to compensate for lowering by ablation on a glacier with a gentle slope. The present findings support the relationship between the rate of surface lowering of debris-covered areas and the slope. In addition, the glacier surface connecting two glacial lakes in this region (Imja and Lumding) shows a high rate of lowering (1.14 and 3.41 ma-1) is also consistent with previous study (Reference Bolch, Pieczonka and BennBolch and others, 2011). The lowering of 1.14 m a-1 for Imja Glacier is consistent with that of 1.1 m a-1 for the up-glacier area east of Imja Lake (Reference Lamsal, Sawagaki and WatanabeLamsal and others, 2011), estimated by stereophotogrammetry using Corona and Advanced Land Observing Satellite (ALOS) Panchromatic Remote-sensing Instrument for Stereo Mapping (PRISM) images. The formation of a terminal lake results in reduced compression in the lowermost part of the glacier. In turn, this pressure-free terminus results in a reduction in emergence velocity, leading to further lowering of the glacier surface (Fig. 4a). In addition, Reference Quincey, Luckman and BennQuincey and others (2009) reported that a glacial lake can develop over the short term due to low flow at high elevations and due to the occurrence of stagnant areas around the terminus of glaciers in the Khumbu Himal region. Reference Bolch, Buchroithner, Pieczonka and KunertBolch and others (2008b) also indicated the potential for glacial lake development at the stagnant part of a glacier around the terminus. Although further analysis of temporal changes in flow velocity fields and in thinning rates is required to confirm the feedback mechanism, the clear contrast in thinning rates between lake-contacting and non-contacting glaciers suggests that a similar positive feedback resulted in the accelerated thinning of glaciers in contact with a glacial lake.
Regional mass balance of glaciers
The area-weighted average regional mass balance was calculated to be -0.40 ± 0.25 m w.e. a-1 (Table 3). Table 3 shows that the regional mass balance in the Khumbu region is most affected by debris-covered glaciers, as these glaciers represent a large portion of the area. The debris-covered areas are subjected to higher rates of lowering than are debris-free areas. One possible reason for larger differences between them could be the difference in mean elevation (5102 and 5521 m a.s.l. for debris-covered and debris-free area respectively). The elevation change for debris-free areas (-0.18 ± 0.40 m w.e. a-1; Table 3) is smaller than the observed mass balance of a neighboring debris-free glacier (-0.8 m w.e. a-1 during 1999-2008 for Glacier AX010; Fig. 1 ; Reference Fujita and NuimuraFujita and Nuimura, 2011). We consider that this discrepancy is due mainly to differences in climate (humid in the Shorong region, arid in the Khumbu region; Reference UenoUeno and others, 2001; Reference Bollasina, Bertolani and TartariBollasina and others, 2002; Reference Fujita and NuimuraFujita and Nuimura, 2011) and the limited altitude range of Glacier AX010 (4950-5300 m a.s.l.), for which the RS estimate also shows significant lowering (Fig. 7a). Given the error bar, the regional mass balance is consistent with the global value of about -0.55 m w.e. a-1, calculated from the mass balance during 1996-2005 (Reference CogleyCogley, 2009).
Table 3. Summary of elevation change for glaciers in the Khumbu region

Both observational and numerical studies have reported that the response of glaciers to warming is more pronounced in a humid climate than in an arid climate (Reference MeierMeier, 1984; Reference FujitaFujita, 2008). Precipitation in the Khumbu region is 465 mm at a site adjacent to Khumbu Glacier (5050 m a.s.l.; Reference Bollasina, Bertolani and TartariBollasina and others, 2002) or 950 mm at Syangboche (DGPS base station, 3833 m a.s.l.; Reference UenoUeno and others, 2001). Although the measurement data at 5050 m a.s.l. may not be representative of accumulation areas at higher elevations, a relatively arid environment may suppress the response of glaciers to a warming climate. Asian glaciers affected by the summer monsoon are relatively sensitive to changes in air temperature, via both diminished snow accumulation and surface albedo (Reference Fujita and AgetaFujita and Ageta, 2000; Reference FujitaFujita, 2008). Although a large uncertainty is found at higher altitudes, our evaluation using multitemporal RS data provides information on temporal changes in regional ice resources over recent decades.
Conclusions
We calculated the spatial distribution of elevation change in the Khumbu region for the period 1992-2008 using multitemporal RS-DEMs, which were calibrated using DGPS survey data obtained for glacier-free terrain. The relation between elevation change and the slope of the debris-covered area on large debris-covered glaciers (Fig. 8) shows a marked lowering (>0.5 m a-1) of debris-covered areas with a gentle slope (<5°). The calculated regional mass balance (-0.40 ± 0.25 m a-1) for the period 1992-2008 is consistent with the global value of about -0.55 m w.e. a-1 calculated from the mass balance during 1996-2005 (Reference CogleyCogley, 2009). The proposed method of calculating elevation change, which involves computation of elevation change by a weighted least-squares linear regression model, can reduce the influence of outliers that would remain, even in well-calibrated DEMs, because the use of a large number of DEMs results in reduced uncertainty due to the smaller confidence interval of the linear regression. This method has the advantage of being able to show the distribution of uncertainty (Fig. 4b), although it requires multitemporal DEMs to obtain a statistically significant result, making it difficult to evaluate changes in glacier volume (e.g. accelerated wastage) over short time periods. The addition of an older DEM (e.g. Corona or Hexagon) will improve the statistical significance of the present results. This method is effectively applicable for the regions with satellite DEMs at frequent intervals. The availability of a more precise DEM at a finer spatial resolution (e.g. ALOS3 mission) over a wide region will enable the continuous monitoring of changing ice resources in the Himalayan region. We also note that the stereographic approach is limited in terms of producing a precise DEM from low-contrast images of snow-covered surfaces in accumulation areas at high elevations. Alternative approaches, such as laser altimetry or radar interferometry (e.g. the Tandem-X DLR (German Aerospace Research Center) mission), should be attempted in the future.
Acknowledgements
We thank the staff of the Department of Hydrology and Meteorology of the Ministry of Science and Technology, Nepalese Government, and local Sherpas for generous assistance during fieldwork. We thank T. Bolch, an anonymous reviewer and the Scientific Editor David Rippin for thoughtful comments. Field observations and analyses were supported by grants from MEXT (Japanese Ministry of Education, Culture, Sports, Science and Technology) (No. 19253001), G-4, the 21st Century COE Program of MEXT and the Kurita Water and Environment Foundation (No. 21010).













