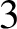1. The error
The published version of [Reference Lusztig and Yun1] contains an error that led to the wrong conclusion on a certain
![]() $3$
-cocycle that appears in the monoidal structure of the monodromic Hecke category.
$3$
-cocycle that appears in the monoidal structure of the monodromic Hecke category.
Below we use notations from [Reference Lusztig and Yun1]. The statement [Reference Lusztig and Yun1, Lemma 10.10] is wrong; that is, the cohomology class of
 $(\lambda ,\mu ^{\natural })\in \textrm {H}^{3}({\Xi ,\overline {\mathbb {Q}}_\ell ^{\times }})$
is not always trivial. The mistake in the ‘proof’ is that, although the character sheaf
$(\lambda ,\mu ^{\natural })\in \textrm {H}^{3}({\Xi ,\overline {\mathbb {Q}}_\ell ^{\times }})$
is not always trivial. The mistake in the ‘proof’ is that, although the character sheaf
![]() $\mathcal {L}$
becomes trivial when restricted to
$\mathcal {L}$
becomes trivial when restricted to
![]() $T(\mathbb {F}_{q})$
, the trivialisation cannot necessarily be made
$T(\mathbb {F}_{q})$
, the trivialisation cannot necessarily be made
![]() $W_{\mathcal {L}}$
-equivariantly. Recall
$W_{\mathcal {L}}$
-equivariantly. Recall
![]() $(\lambda ,\mu )$
comes from a
$(\lambda ,\mu )$
comes from a
![]() $2$
-cocycle
$2$
-cocycle
![]() $c\in Z^{2}(W,T)$
, which in turns comes from the extension
$c\in Z^{2}(W,T)$
, which in turns comes from the extension
Namely, choose a lifting
![]() $\widetilde {w}\in N_{G}(T)$
for each
$\widetilde {w}\in N_{G}(T)$
for each
![]() $w\in W$
, and let
$w\in W$
, and let
![]() $c(w_{1},w_{2})\in T$
be such that
$c(w_{1},w_{2})\in T$
be such that
![]() $\widetilde {w}_{1}\widetilde {w}_{2}=c(w_{1},w_{2})\widetilde {w_{1}w_{2}}$
. On the other hand, the datum of a character sheaf
$\widetilde {w}_{1}\widetilde {w}_{2}=c(w_{1},w_{2})\widetilde {w_{1}w_{2}}$
. On the other hand, the datum of a character sheaf
![]() $\mathcal {L}$
on T gives an extension of abelian groups
$\mathcal {L}$
on T gives an extension of abelian groups
 $$ \begin{align} 1\to \overline{\mathbb{Q}}_\ell^{\times}\to E_{\mathcal{L}}\to T\to 1 \end{align} $$
$$ \begin{align} 1\to \overline{\mathbb{Q}}_\ell^{\times}\to E_{\mathcal{L}}\to T\to 1 \end{align} $$
where
![]() $E_{\mathcal {L}}$
consists of pairs
$E_{\mathcal {L}}$
consists of pairs
![]() $(t,\tau )$
where
$(t,\tau )$
where
![]() $t\in T$
and
$t\in T$
and
![]() $\tau $
is a nonzero element of
$\tau $
is a nonzero element of
![]() $\mathcal {L}_{t}$
. This extension carries an action of
$\mathcal {L}_{t}$
. This extension carries an action of
![]() $W_{\mathcal {L}}$
. Taking
$W_{\mathcal {L}}$
. Taking
![]() $W_{\mathcal {L}}$
-cohomology we get a connecting homomorphism
$W_{\mathcal {L}}$
-cohomology we get a connecting homomorphism
 $$ \begin{align*} \delta_{\mathcal{L}}: \textrm{H}^{2}({W_{\mathcal{L}}, T})\to \textrm{H}^{3}({W_{\mathcal{L}}, \overline{\mathbb{Q}}_\ell^{\times}}). \end{align*} $$
$$ \begin{align*} \delta_{\mathcal{L}}: \textrm{H}^{2}({W_{\mathcal{L}}, T})\to \textrm{H}^{3}({W_{\mathcal{L}}, \overline{\mathbb{Q}}_\ell^{\times}}). \end{align*} $$
Then
![]() $(\lambda ,\mu ^{\natural })=\delta _{\mathcal {L}}(c)$
.
$(\lambda ,\mu ^{\natural })=\delta _{\mathcal {L}}(c)$
.
Now we can always arrange so that c takes values in
![]() $T[2]$
(using Tits liftings). Restricting (1.1) to
$T[2]$
(using Tits liftings). Restricting (1.1) to
![]() $T[2]$
the short exact sequence splits, but not necessarily
$T[2]$
the short exact sequence splits, but not necessarily
![]() $W_{\mathcal {L}}$
-equivariantly. Therefore, the composition
$W_{\mathcal {L}}$
-equivariantly. Therefore, the composition
 $$ \begin{align} \textrm{H}^{2}({W, T[2]})\to \textrm{H}^{2}({W, T})\to \textrm{H}^{2}({W_{\mathcal{L}}, T})\xrightarrow{\delta_{\mathcal{L}}}\textrm{H}^{3}({W_{\mathcal{L}}, \overline{\mathbb{Q}}_\ell^{\times}}) \end{align} $$
$$ \begin{align} \textrm{H}^{2}({W, T[2]})\to \textrm{H}^{2}({W, T})\to \textrm{H}^{2}({W_{\mathcal{L}}, T})\xrightarrow{\delta_{\mathcal{L}}}\textrm{H}^{3}({W_{\mathcal{L}}, \overline{\mathbb{Q}}_\ell^{\times}}) \end{align} $$
is still not necessarily zero.
For example, when
![]() $G=\textrm {SL}(2)$
and
$G=\textrm {SL}(2)$
and
![]() $\mathcal {L}$
has order
$\mathcal {L}$
has order
![]() $2$
, we have
$2$
, we have
![]() $W_{\mathcal {L}}=W\cong \mathbb {Z}/2\mathbb {Z}$
, and the composition (1.2) is nonzero.
$W_{\mathcal {L}}=W\cong \mathbb {Z}/2\mathbb {Z}$
, and the composition (1.2) is nonzero.
2. Correction
The 3-cocycle responsible for the convolution structure on the monodromic Hecke category is the product of two 3-cocycles: one is
![]() $\sigma $
defined in [Reference Lusztig and Yun1, §5.8] and studied in [Reference Yun3], which is often nontrivial; the other one is the
$\sigma $
defined in [Reference Lusztig and Yun1, §5.8] and studied in [Reference Yun3], which is often nontrivial; the other one is the
![]() $\mu ^{\natural }$
mentioned above, which can also be nontrivial. It turns out that the cohomology classes of these two cocycles cancel each other, so their product is cohomologically trivial.
$\mu ^{\natural }$
mentioned above, which can also be nontrivial. It turns out that the cohomology classes of these two cocycles cancel each other, so their product is cohomologically trivial.
In the new version of the paper [Reference Lusztig and Yun2], we give a construction of rigidified minimal IC sheaves that in particular imply the cancellation between
![]() $\sigma $
and
$\sigma $
and
![]() $\mu ^{\natural }$
(although we no longer need
$\mu ^{\natural }$
(although we no longer need
![]() $\sigma $
and
$\sigma $
and
![]() $\mu ^{\natural }$
in the new version of the paper).
$\mu ^{\natural }$
in the new version of the paper).
The idea is to consider a geometric Whittaker model
 $$ \begin{align*}{}_{\psi}\mathcal{M}_{\mathcal{L}}:=D^{b}_{m}((U^{-},\psi)\backslash G/(B,\mathcal{L}))\end{align*} $$
$$ \begin{align*}{}_{\psi}\mathcal{M}_{\mathcal{L}}:=D^{b}_{m}((U^{-},\psi)\backslash G/(B,\mathcal{L}))\end{align*} $$
that is on the one hand a right module for the monodromic Hecke category and, on the other hand, equivalent to mixed sheaves on a point by taking stalks at the identity element
![]() $e\in G$
. See [Reference Lusztig and Yun2, §5.9]. This allows us to rigidify minimal IC sheaves, denoted
$e\in G$
. See [Reference Lusztig and Yun2, §5.9]. This allows us to rigidify minimal IC sheaves, denoted
 $\textrm {IC}(w^{\beta })^{\dagger }_{\mathcal {L}}$
for blocks
$\textrm {IC}(w^{\beta })^{\dagger }_{\mathcal {L}}$
for blocks
![]() $\beta $
. In [Reference Lusztig and Yun2, Lemma 5.12] we show that there are canonical isomorphisms
$\beta $
. In [Reference Lusztig and Yun2, Lemma 5.12] we show that there are canonical isomorphisms
 $$ \begin{align*} \textrm{IC}(w^{\gamma})^{\dagger}_{\mathcal{L}'}\star\textrm{IC}(w^{\beta})^{\dagger}_{\mathcal{L}}\stackrel{\sim}{\to}\textrm{IC}(w^{\gamma\beta})^{\dagger}_{\mathcal{L}} \end{align*} $$
$$ \begin{align*} \textrm{IC}(w^{\gamma})^{\dagger}_{\mathcal{L}'}\star\textrm{IC}(w^{\beta})^{\dagger}_{\mathcal{L}}\stackrel{\sim}{\to}\textrm{IC}(w^{\gamma\beta})^{\dagger}_{\mathcal{L}} \end{align*} $$
for two composable blocks
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
, and these isomorphisms are associative. More generally, in [Reference Lusztig and Yun2, Definition 6.14] we define a rigidified IC sheaf
$\gamma $
, and these isomorphisms are associative. More generally, in [Reference Lusztig and Yun2, Definition 6.14] we define a rigidified IC sheaf
 $\textrm {IC}(w)^{\dagger }_{\mathcal {L}}$
for any w.
$\textrm {IC}(w)^{\dagger }_{\mathcal {L}}$
for any w.
As a result, the main theorems in [Reference Lusztig and Yun1] involving nonneutral blocks can be simplified and no twisting by cocycles appear in the statements. We give the corrected statements below.
Let G be a connected reductive group over
 $k=\overline {\mathbb {F}}_{q}$
. Let
$k=\overline {\mathbb {F}}_{q}$
. Let
![]() $\mathfrak {o}\subset \textrm {Ch}(T)$
. For
$\mathfrak {o}\subset \textrm {Ch}(T)$
. For
![]() $\mathcal {L}\in \mathfrak {o}$
, let
$\mathcal {L}\in \mathfrak {o}$
, let
![]() $H_{\mathcal {L}}$
be the endoscopic group attached to
$H_{\mathcal {L}}$
be the endoscopic group attached to
![]() $\mathcal {L}$
, equipped with a Borel subgroup
$\mathcal {L}$
, equipped with a Borel subgroup
 $B^{H}_{\mathcal {L}}$
and a relative pinning with respect to G. For each
$B^{H}_{\mathcal {L}}$
and a relative pinning with respect to G. For each
![]() $\beta \in {}_{\mathcal {L}'}\underline W_{\mathcal {L}}$
one can define a
$\beta \in {}_{\mathcal {L}'}\underline W_{\mathcal {L}}$
one can define a
![]() $(H_{\mathcal {L}'},H_{\mathcal {L}})$
-bitorsor
$(H_{\mathcal {L}'},H_{\mathcal {L}})$
-bitorsor
 ${}_{\mathcal {L}'}\mathfrak {H}^{\beta }_{\mathcal {L}}$
, so that the disjoint union of
${}_{\mathcal {L}'}\mathfrak {H}^{\beta }_{\mathcal {L}}$
, so that the disjoint union of
 ${}_{\mathcal {L}'}\mathfrak {H}^{\beta }_{\mathcal {L}}$
for all
${}_{\mathcal {L}'}\mathfrak {H}^{\beta }_{\mathcal {L}}$
for all
![]() $\mathcal {L},\mathcal {L}'\in \mathfrak {o}$
and all blocks
$\mathcal {L},\mathcal {L}'\in \mathfrak {o}$
and all blocks
![]() $\beta $
form a groupoid compatible with the convolution of blocks (see [Reference Lusztig and Yun2, §10.3]). Restricting to
$\beta $
form a groupoid compatible with the convolution of blocks (see [Reference Lusztig and Yun2, §10.3]). Restricting to
![]() $\mathcal {L}'=\mathcal {L}$
,
$\mathcal {L}'=\mathcal {L}$
,
 ${}_{\mathcal {L}}\mathfrak {H}_{\mathcal {L}}:=\coprod _{\beta \in {}_{\mathcal {L}}\underline W_{\mathcal {L}}}{}_{\mathcal {L}}\mathfrak {H}^{\beta }_{\mathcal {L}}$
is an algebraic group with neutral component
${}_{\mathcal {L}}\mathfrak {H}_{\mathcal {L}}:=\coprod _{\beta \in {}_{\mathcal {L}}\underline W_{\mathcal {L}}}{}_{\mathcal {L}}\mathfrak {H}^{\beta }_{\mathcal {L}}$
is an algebraic group with neutral component
![]() $H_{\mathcal {L}}$
and component group
$H_{\mathcal {L}}$
and component group
![]() $\Omega _{\mathcal {L}}$
. Let
$\Omega _{\mathcal {L}}$
. Let
 $$ \begin{align*} {}_{\mathcal{L}'}\mathcal{E}_{\mathcal{L}}^{\beta}:=D^{b}_{m}(B^{H}_{\mathcal{L}'}\backslash {}_{\mathcal{L}'}\mathfrak{H}^{\beta}_{\mathcal{L}}/B^{H}_{\mathcal{L}}). \end{align*} $$
$$ \begin{align*} {}_{\mathcal{L}'}\mathcal{E}_{\mathcal{L}}^{\beta}:=D^{b}_{m}(B^{H}_{\mathcal{L}'}\backslash {}_{\mathcal{L}'}\mathfrak{H}^{\beta}_{\mathcal{L}}/B^{H}_{\mathcal{L}}). \end{align*} $$
2.1. Theorem Monodromic-endoscopic equivalence for all blocks, [Reference Lusztig and Yun2, Theorem 10.7]
Under the above notations,
-
1. For
 $\mathcal {L},\mathcal {L}'\in \mathfrak {o}$
and any block
$\mathcal {L},\mathcal {L}'\in \mathfrak {o}$
and any block
 $\beta \in {}_{\mathcal {L}'}\underline W_{\mathcal {L}}$
, there is an equivalence of triangulated categories that sends
$\beta \in {}_{\mathcal {L}'}\underline W_{\mathcal {L}}$
, there is an equivalence of triangulated categories that sends $$ \begin{align*} {}_{\mathcal{L}'}\Psi^{\beta}_{\mathcal{L}}: {}_{\mathcal{L}'}\mathcal{E}_{\mathcal{L}}^{\beta}\stackrel{\sim}{\to} {}_{\mathcal{L}'}\mathcal{D}^{\beta}_{\mathcal{L}} \end{align*} $$
$$ \begin{align*} {}_{\mathcal{L}'}\Psi^{\beta}_{\mathcal{L}}: {}_{\mathcal{L}'}\mathcal{E}_{\mathcal{L}}^{\beta}\stackrel{\sim}{\to} {}_{\mathcal{L}'}\mathcal{D}^{\beta}_{\mathcal{L}} \end{align*} $$
 $\Delta (w)^{H}_{\mathcal {L}}, \nabla (w)^{H}_{\mathcal {L}}$
and
$\Delta (w)^{H}_{\mathcal {L}}, \nabla (w)^{H}_{\mathcal {L}}$
and
 $\textrm {IC}(w)^{H}_{\mathcal {L}}$
in
$\textrm {IC}(w)^{H}_{\mathcal {L}}$
in
 ${}_{\mathcal {L}'}\mathcal {E}^{\beta }_{\mathcal {L}}$
to
${}_{\mathcal {L}'}\mathcal {E}^{\beta }_{\mathcal {L}}$
to
 $\Delta (w)^{\dagger }_{\mathcal {L}}, \nabla (w)^{\dagger }_{\mathcal {L}}$
and
$\Delta (w)^{\dagger }_{\mathcal {L}}, \nabla (w)^{\dagger }_{\mathcal {L}}$
and
 $\textrm {IC}(w)^{\dagger }_{\mathcal {L}}$
in
$\textrm {IC}(w)^{\dagger }_{\mathcal {L}}$
in
 ${}_{\mathcal {L}'}\mathcal {D}^{\beta }_{\mathcal {L}}$
, for
${}_{\mathcal {L}'}\mathcal {D}^{\beta }_{\mathcal {L}}$
, for
 $w\in \beta $
.
$w\in \beta $
.
-
2. The equivalences
 $\{{}_{\mathcal {L}'}\Psi ^{\beta }_{\mathcal {L}}\}$
are compatible with convolutions.
$\{{}_{\mathcal {L}'}\Psi ^{\beta }_{\mathcal {L}}\}$
are compatible with convolutions.
Let G be a connected reductive group over
 $k=\overline {\mathbb {F}}_{q}$
. Let
$k=\overline {\mathbb {F}}_{q}$
. Let
![]() $\mathfrak {o}\subset \textrm {Ch}(T)$
be a W-orbit and
$\mathfrak {o}\subset \textrm {Ch}(T)$
be a W-orbit and
![]() $\mathcal {L}\in \mathfrak {o}$
. Let
$\mathcal {L}\in \mathfrak {o}$
. Let
![]() $\mathbf {c}\subset W^{\circ }_{\mathcal {L}}$
be a two-sided cell and
$\mathbf {c}\subset W^{\circ }_{\mathcal {L}}$
be a two-sided cell and
![]() $\Omega _{\mathbf {c}}$
its stabiliser in
$\Omega _{\mathbf {c}}$
its stabiliser in
![]() $\Omega _{\mathcal {L}}$
. We have the abelian category of semisimple character sheaves
$\Omega _{\mathcal {L}}$
. We have the abelian category of semisimple character sheaves
 $\underline {\mathcal {CS}}^{[\mathbf {c}]}_{\mathfrak {o}}(G)$
on G with semisimple parameter
$\underline {\mathcal {CS}}^{[\mathbf {c}]}_{\mathfrak {o}}(G)$
on G with semisimple parameter
![]() $\mathfrak {o}$
and belonging to the cell
$\mathfrak {o}$
and belonging to the cell
![]() $[\mathbf {c}]\subset W\times \mathfrak {o}$
containing
$[\mathbf {c}]\subset W\times \mathfrak {o}$
containing
![]() $\mathbf {c}$
. Let H be the endoscopic group attached to
$\mathbf {c}$
. Let H be the endoscopic group attached to
![]() $\mathcal {L}$
. To each
$\mathcal {L}$
. To each
![]() $\beta \in \Omega _{\mathcal {L}}$
, we consider the
$\beta \in \Omega _{\mathcal {L}}$
, we consider the
![]() $\beta $
-twisted semisimple unipotent character sheaves category
$\beta $
-twisted semisimple unipotent character sheaves category
![]() $\underline {\mathcal {CS}}^{{\kern1pt}\mathbf {c}}_{u}(H;\beta )$
on H, which carries a
$\underline {\mathcal {CS}}^{{\kern1pt}\mathbf {c}}_{u}(H;\beta )$
on H, which carries a
![]() $\Omega _{\mathbf {c}}$
-action. For more detail, see [Reference Lusztig and Yun2, §11.7,11.9].
$\Omega _{\mathbf {c}}$
-action. For more detail, see [Reference Lusztig and Yun2, §11.7,11.9].
2.2. Theorem Monodromic-endoscopic equivalence for character sheaves, [Reference Lusztig and Yun2, Theorem 11.10]
Under the above notations, there is a canonical equivalence of semisimple abelian categories
 $$ \begin{align*} \underline{\mathcal{CS}}^{[\mathbf{c}]}_{\mathfrak{o}}(G)\cong \bigoplus_{\beta\in \Omega_{\mathbf{c}}}\underline{\mathcal{CS}}^{\mathbf{c}}_{u}(H;\beta)^{\Omega_{\mathbf{c}}}. \end{align*} $$
$$ \begin{align*} \underline{\mathcal{CS}}^{[\mathbf{c}]}_{\mathfrak{o}}(G)\cong \bigoplus_{\beta\in \Omega_{\mathbf{c}}}\underline{\mathcal{CS}}^{\mathbf{c}}_{u}(H;\beta)^{\Omega_{\mathbf{c}}}. \end{align*} $$
Let G be a connected reductive group over
 $k=\overline {\mathbb {F}}_{q}$
with an
$k=\overline {\mathbb {F}}_{q}$
with an
![]() $\mathbb {F}_{q}$
-Frobenius structure
$\mathbb {F}_{q}$
-Frobenius structure
![]() $\epsilon : G\to G$
. Let
$\epsilon : G\to G$
. Let
![]() $\mathfrak {o}\subset \textrm {Ch}(T)$
be a W-orbit stable under
$\mathfrak {o}\subset \textrm {Ch}(T)$
be a W-orbit stable under
![]() $\epsilon $
, and let
$\epsilon $
, and let
![]() $\mathcal {L}\in \mathfrak {o}$
. Let
$\mathcal {L}\in \mathfrak {o}$
. Let
![]() $\mathbf {c},[\mathbf {c}], \Omega _{\mathbf {c}}$
and H be as in Theorem 2.2. Let
$\mathbf {c},[\mathbf {c}], \Omega _{\mathbf {c}}$
and H be as in Theorem 2.2. Let
 $\mathfrak {B}_{\mathbf {c}}=\{\beta \in {}_{\mathcal {L}}\underline W_{\epsilon \mathcal {L}}| w^{\beta }\circ \epsilon $
preserves the cell
$\mathfrak {B}_{\mathbf {c}}=\{\beta \in {}_{\mathcal {L}}\underline W_{\epsilon \mathcal {L}}| w^{\beta }\circ \epsilon $
preserves the cell
![]() $\mathbf {c}$
of
$\mathbf {c}$
of
![]() $W^{\circ }_{\mathcal {L}}\}$
, with the
$W^{\circ }_{\mathcal {L}}\}$
, with the
![]() $\epsilon $
-twisted conjugation action of
$\epsilon $
-twisted conjugation action of
![]() $\Omega _{\mathbf {c}}$
denoted by
$\Omega _{\mathbf {c}}$
denoted by
![]() $\textrm {Ad}_{\epsilon }(\Omega _{\mathbf {c}})$
. Each
$\textrm {Ad}_{\epsilon }(\Omega _{\mathbf {c}})$
. Each
![]() $\beta \in \mathfrak {B}_{\mathbf {c}}$
defines a
$\beta \in \mathfrak {B}_{\mathbf {c}}$
defines a
![]() $\mathbb {F}_{q}$
-Frobenius structure
$\mathbb {F}_{q}$
-Frobenius structure
![]() $\sigma _{\beta \epsilon }$
of H. Moreover, the category
$\sigma _{\beta \epsilon }$
of H. Moreover, the category
![]() $\textrm {Rep}^{\mathbf {c}}_{u}(H^{\sigma _{\beta \epsilon }})$
of unipotent representations of
$\textrm {Rep}^{\mathbf {c}}_{u}(H^{\sigma _{\beta \epsilon }})$
of unipotent representations of
![]() $H^{\sigma _{\beta \epsilon }}$
in the cell
$H^{\sigma _{\beta \epsilon }}$
in the cell
![]() $\mathbf {c}$
carries an action of
$\mathbf {c}$
carries an action of
![]() $\Omega _{\mathbf {c},\beta }$
, the simultaneous stabiliser of
$\Omega _{\mathbf {c},\beta }$
, the simultaneous stabiliser of
![]() $\mathbf {c}$
and
$\mathbf {c}$
and
![]() $\beta $
in
$\beta $
in
![]() $\Omega _{\mathcal {L}}$
. For more detail, see [Reference Lusztig and Yun2, §12.5].
$\Omega _{\mathcal {L}}$
. For more detail, see [Reference Lusztig and Yun2, §12.5].
2.3. Theorem Monodromic-endoscopic equivalence for representations, [Reference Lusztig and Yun2, Corollary 12.7]
Choose a representative for each
![]() $\textrm {Ad}_{\epsilon }(\Omega _{\mathbf {c}})$
-orbit of
$\textrm {Ad}_{\epsilon }(\Omega _{\mathbf {c}})$
-orbit of
![]() $\mathfrak {B}_{\mathbf {c}}$
, and denote this set of representatives by
$\mathfrak {B}_{\mathbf {c}}$
, and denote this set of representatives by
![]() $\dot {\mathfrak {B}}_{\mathbf {c}}$
. There is a canonical equivalence of semisimple abelian categories
$\dot {\mathfrak {B}}_{\mathbf {c}}$
. There is a canonical equivalence of semisimple abelian categories
 $$ \begin{align*} \textrm{Rep}^{[\mathbf{c}]}_{\mathfrak{o}}(G^{\epsilon})\cong \bigoplus_{\beta\in \dot{\mathfrak{B}}_{\mathbf{c}}}\textrm{Rep}^{\mathbf{c}}_{u}(H^{\sigma_{\beta\epsilon}})^{\Omega_{\mathbf{c},\beta}}. \end{align*} $$
$$ \begin{align*} \textrm{Rep}^{[\mathbf{c}]}_{\mathfrak{o}}(G^{\epsilon})\cong \bigoplus_{\beta\in \dot{\mathfrak{B}}_{\mathbf{c}}}\textrm{Rep}^{\mathbf{c}}_{u}(H^{\sigma_{\beta\epsilon}})^{\Omega_{\mathbf{c},\beta}}. \end{align*} $$
Acknowledgement
We thank Gurbir Dhillon, Pavel Etingof, Yau-Wing Li, Ivan Losev and Xinwen Zhu for discussions that led to the discovery of the mistake in the original paper. G.L. is supported partially by the NSF grant DMS-1855773; Z.Y. is supported partially by the Simon Foundation and the Packard Foundation.
Conflict of Interest
None.