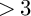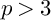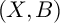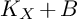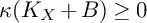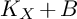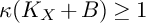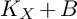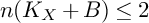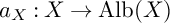1 Introduction
Over the last decade, the minimal model program (MMP) for threefolds over a field of characteristic
![]() $>3$
has been largely established. First, Hacon and Xu proved the existence of minimal models for terminal threefolds over an algebraically closed field k of characteristic
$>3$
has been largely established. First, Hacon and Xu proved the existence of minimal models for terminal threefolds over an algebraically closed field k of characteristic
![]() $> 5$
(see [Reference Hacon and Chenyang13]). Then Cascini, Tanaka, and Xu proved that arbitrary terminal threefold over k is birational to either a minimal model or a Mori fiber space (see [Reference Cascini, Tanaka and Chenyang6]). Base on it, Birkar and Waldron established the MMP for klt threefolds over k (see [Reference Birkar4], [Reference Birkar and Waldron5]). Moreover, there are some generalizations of it in various directions. For example, see [Reference Hashizume, Nakamura and Tanaka15], [Reference Waldron26] for its generalization to log canonical (lc) pairs, [Reference Gongyo, Nakamura and Tanaka10]–[Reference Hacon and Witaszek12] for its generalization to low characteristics, [Reference Das and Waldron9] for its generalization to imperfect base fields, and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and Witaszek3] for its analog in mixed characteristics.
$> 5$
(see [Reference Hacon and Chenyang13]). Then Cascini, Tanaka, and Xu proved that arbitrary terminal threefold over k is birational to either a minimal model or a Mori fiber space (see [Reference Cascini, Tanaka and Chenyang6]). Base on it, Birkar and Waldron established the MMP for klt threefolds over k (see [Reference Birkar4], [Reference Birkar and Waldron5]). Moreover, there are some generalizations of it in various directions. For example, see [Reference Hashizume, Nakamura and Tanaka15], [Reference Waldron26] for its generalization to log canonical (lc) pairs, [Reference Gongyo, Nakamura and Tanaka10]–[Reference Hacon and Witaszek12] for its generalization to low characteristics, [Reference Das and Waldron9] for its generalization to imperfect base fields, and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and Witaszek3] for its analog in mixed characteristics.
Now we can run MMPs for lc threefold pairs over a perfect field of characteristic
![]() $>3$
(see Theorem 2.12). Hence, a central problem remaining is the following conjecture.
$>3$
(see Theorem 2.12). Hence, a central problem remaining is the following conjecture.
1.1 Abundance conjecture
Let
![]() $(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef, then it is semi-ample.
$K_{X}+B$
is nef, then it is semi-ample.
Remark 1.1. The abundance conjecture for lc surface pairs over any field of positive characteristic is proved in [Reference Tanaka24], and for slc surface pairs over any field of positive characteristic, it is proved in [Reference Posva22].
Remark 1.2 (From a perfect field to its algebraic closure).
Many properties of singularities and positivity, for example, klt, lc, semi-ampleness, and Iitaka dimensions, are preserved under the base change from a perfect field to its algebraic closure (see, for example, [Reference Gongyo, Nakamura and Tanaka10, Rem. 2.7]). In this paper, we sometimes do such base changes and assume that we work over algebraically closed fields. However, some conditions need that the base field is algebraically closed, for example, conditions about nef dimensions (see Section 2.8 for definition) and Albanese maps.
When
![]() $K_{X}+B$
is big, Birkar and Waldron proved it in characteristic
$K_{X}+B$
is big, Birkar and Waldron proved it in characteristic
![]() $>5$
(see [Reference Birkar and Waldron5], [Reference Waldron26]), then Hacon and Witaszek proved it in characteristic
$>5$
(see [Reference Birkar and Waldron5], [Reference Waldron26]), then Hacon and Witaszek proved it in characteristic
![]() $5$
(see [Reference Hacon and Witaszek12]). When
$5$
(see [Reference Hacon and Witaszek12]). When
![]() $(X,B)$
is klt and the characteristic of k is greater than
$(X,B)$
is klt and the characteristic of k is greater than
![]() $5$
, Waldron proved it in the case of
$5$
, Waldron proved it in the case of
![]() $\kappa (X,K_{X}+B)= 2$
(see [Reference Waldron25]), Das, Waldron, and Zhang proved it in the case of
$\kappa (X,K_{X}+B)= 2$
(see [Reference Waldron25]), Das, Waldron, and Zhang proved it in the case of
![]() $\kappa (X,K_{X}+B)= 1$
(see [Reference Das and Waldron8], [Reference Zhang29]), Witaszek proved it in the case when the nef dimension
$\kappa (X,K_{X}+B)= 1$
(see [Reference Das and Waldron8], [Reference Zhang29]), Witaszek proved it in the case when the nef dimension
![]() $n(X,K_{X}+B)\leq 2$
(see [Reference Witaszek27]), and Zhang proved it in the case when the Albanese map
$n(X,K_{X}+B)\leq 2$
(see [Reference Witaszek27]), and Zhang proved it in the case when the Albanese map
![]() $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial (see [Reference Zhang30]). In conclusion, the abundance holds when
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial (see [Reference Zhang30]). In conclusion, the abundance holds when
![]() $(X,B)$
is klt, the characteristic of k is greater than
$(X,B)$
is klt, the characteristic of k is greater than
![]() $5$
and one of the following conditions holds:
$5$
and one of the following conditions holds:
-
(1)
 $\kappa (X,K_{X}+B)\geq 1$
,
$\kappa (X,K_{X}+B)\geq 1$
, -
(2) the nef dimension
 $n(X,K_{X}+B)\leq 2$
,
$n(X,K_{X}+B)\leq 2$
, -
(3) the Albanese map
 $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
The above works on the abundance for klt pairs in characteristic
![]() $>5$
can be generalized to the case when the characteristic is greater than
$>5$
can be generalized to the case when the characteristic is greater than
![]() $3$
by some careful modifications (see Section 3). Then it is natural to ask the following question.
$3$
by some careful modifications (see Section 3). Then it is natural to ask the following question.
Question 1.3. How can we generalize a result on the abundance for klt threefold pairs to lc threefold pairs?
In characteristic
![]() $0$
, this is done in [Reference Keel, Matsuki and McKernan18]. However, the approach there needs vanishing theorems and the termination of flips for threefolds. The vanishing theorems may fail in positive characteristic and the termination of flips for threefolds is unknown in positive characteristic for lack of a good understanding of terminal threefold singularities in positive characteristic. In this paper, we propose a new method to solve Question 1.1 and generalize most of results on the abundance for klt pairs in characteristic
$0$
, this is done in [Reference Keel, Matsuki and McKernan18]. However, the approach there needs vanishing theorems and the termination of flips for threefolds. The vanishing theorems may fail in positive characteristic and the termination of flips for threefolds is unknown in positive characteristic for lack of a good understanding of terminal threefold singularities in positive characteristic. In this paper, we propose a new method to solve Question 1.1 and generalize most of results on the abundance for klt pairs in characteristic
![]() $>5$
to lc pairs in characteristic
$>5$
to lc pairs in characteristic
![]() $>3$
. We first prove the nonvanishing theorem for lc threefold pairs over a perfect field k of characteristic
$>3$
. We first prove the nonvanishing theorem for lc threefold pairs over a perfect field k of characteristic
![]() $>3$
.
$>3$
.
Theorem 1.4 (Theorem 4.4).
Let
![]() $(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+ B$
is pseudo-effective, then
$K_{X}+ B$
is pseudo-effective, then
![]() $\kappa (X,K_{X}+B)\geq 0$
.
$\kappa (X,K_{X}+B)\geq 0$
.
As a corollary, we have the following result on termination of flips.
Theorem 1.5 (Theorem 4.5).
Let
![]() $(X,B)$
be a projective lc threefold pair defined over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair defined over a perfect field k of characteristic
![]() $p> 3$
such that
$p> 3$
such that
![]() $K_{X}+B$
is pseudo-effective. Then every sequence of
$K_{X}+B$
is pseudo-effective. Then every sequence of
![]() $(K_{X}+B)$
-flips terminates. In particular, any
$(K_{X}+B)$
-flips terminates. In particular, any
![]() $(K_{X}+B)$
-MMP terminates with a minimal model.
$(K_{X}+B)$
-MMP terminates with a minimal model.
Secondly, we prove the following result which is the main technical result of this paper.
Theorem 1.6 (Theorem 5.1).
Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (X,K_{X}+B)\geq 1$
, then
$\kappa (X,K_{X}+B)\geq 1$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Combined with the results on klt pairs, we deduce the following statements.
Theorem 1.7 (Theorem 6.1).
Let
![]() $(X, B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X, B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. Then the log canonical ring
$>3$
. Then the log canonical ring
is finitely generated.
Theorem 1.8 (Theorem 6.2).
Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and the nef dimension
$K_{X}+B$
is nef and the nef dimension
![]() $n(X,K_{X}+B)\leq 2$
, then
$n(X,K_{X}+B)\leq 2$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Theorem 1.9 (Theorem 6.3).
Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
, then
$\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
It turns out that the following result follows from Theorems 4.4 and 1.6.
Theorem 1.10 (Theorem 6.4).
Let k be an algebraically closed field of characteristic
![]() $>3$
. Assume we have:
$>3$
. Assume we have:
-
(1) abundance for terminal threefolds over k holds, and
-
(2) any effective nef divisor D on any klt Calabi–Yau threefold pair
 $(Y,\Delta )$
(
$(Y,\Delta )$
(
 $(Y,\Delta )$
is klt and
$(Y,\Delta )$
is klt and
 $K_{Y}+\Delta \sim _{{\mathbb Q}}0$
) over k is semi-ample.
$K_{Y}+\Delta \sim _{{\mathbb Q}}0$
) over k is semi-ample.
Then the abundance conjecture for threefold pairs over k holds. In particular, the abundance conjecture for klt threefold pairs over k implies the abundance conjecture for lc threefold pairs over k.
1.2 Outline of the proof of Theorem 1.6
For simplicity, we assume that k is an uncountable algebraically closed field of characteristic
![]() $>3$
(the uncountability is used for defining the nef reduction map). We first prove the nonvanishing theorem for projective lc threefold pairs over k (see Theorem 4.4) as follows. By Theorem 2.20, after replacing, we can assume that
$>3$
(the uncountability is used for defining the nef reduction map). We first prove the nonvanishing theorem for projective lc threefold pairs over k (see Theorem 4.4) as follows. By Theorem 2.20, after replacing, we can assume that
![]() $(X,B)$
is
$(X,B)$
is
![]() ${\mathbb Q}$
-factorial and dlt, and moreover, X is terminal. Then we run a
${\mathbb Q}$
-factorial and dlt, and moreover, X is terminal. Then we run a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial by Definition 2.16. It terminates by Lemma 2.19. If we get a minimal model, then we can use the nonvanishing for klt pairs (see Theorem 3.10) to prove the assertion. Otherwise, we get a Mori fiber space. It implies that the nef dimension
$(K_{X}+B)$
-trivial by Definition 2.16. It terminates by Lemma 2.19. If we get a minimal model, then we can use the nonvanishing for klt pairs (see Theorem 3.10) to prove the assertion. Otherwise, we get a Mori fiber space. It implies that the nef dimension
![]() $n(K_{X}+B)\leq 2$
. We can use Witaszek’s weak canonical bundle formula to handle the case of
$n(K_{X}+B)\leq 2$
. We can use Witaszek’s weak canonical bundle formula to handle the case of
![]() $n(K_{X}+B)= 2$
. The case of
$n(K_{X}+B)= 2$
. The case of
![]() $n(K_{X}+B)= 1$
is trivial by descending
$n(K_{X}+B)= 1$
is trivial by descending
![]() $K_{X}+B$
along the nef reduction map of
$K_{X}+B$
along the nef reduction map of
![]() $K_{X}+B$
. Finally, we need to handle the case of
$K_{X}+B$
. Finally, we need to handle the case of
![]() $n(K_{X}+B)= 0$
. In this case,
$n(K_{X}+B)= 0$
. In this case,
![]() $K_{X}+B$
is numerically trivial. Then the semi-ampleness of
$K_{X}+B$
is numerically trivial. Then the semi-ampleness of
![]() $K_{X}+B$
preserves under any step of MMPs. By Theorem 2.12, we can run a
$K_{X}+B$
preserves under any step of MMPs. By Theorem 2.12, we can run a
![]() $(K_{X}+B-\lfloor B\rfloor )$
-MMP which terminates. It terminates with a Mori fiber space and then we can descend
$(K_{X}+B-\lfloor B\rfloor )$
-MMP which terminates. It terminates with a Mori fiber space and then we can descend
![]() $K_{X}+B$
along the Mori fiber space to prove its semi-ampleness. In conclusion, the nonvanishing holds. As a corollary, we have the termination of flips for pseudo-effective lc threefold pairs over k (see Theorem 4.5).
$K_{X}+B$
along the Mori fiber space to prove its semi-ampleness. In conclusion, the nonvanishing holds. As a corollary, we have the termination of flips for pseudo-effective lc threefold pairs over k (see Theorem 4.5).
Now, let
![]() $(X,B)$
be a projective lc threefold pair over k such that
$(X,B)$
be a projective lc threefold pair over k such that
![]() $K_{X}+B$
is nef. We assume
$K_{X}+B$
is nef. We assume
![]() $\kappa (K_{X}+B)=2$
, which is the most difficult case. Then
$\kappa (K_{X}+B)=2$
, which is the most difficult case. Then
![]() $K_{X}+B$
is endowed with a map
$K_{X}+B$
is endowed with a map
![]() $h:X\to Z$
to a normal proper algebraic space of dimension
$h:X\to Z$
to a normal proper algebraic space of dimension
![]() $2$
by Lemma 5.3. We replace
$2$
by Lemma 5.3. We replace
![]() $(X,B)$
by a
$(X,B)$
by a
![]() ${\mathbb Q}$
-factorial dlt modification by Theorem 2.20. Then one of the following cases holds:
${\mathbb Q}$
-factorial dlt modification by Theorem 2.20. Then one of the following cases holds:
Case I:
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Case II:
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
In Case I, we first prove that
![]() $\lfloor B\rfloor $
must dominate Z (see Proposition 5.5). Then we deduce the semi-ampleness of
$\lfloor B\rfloor $
must dominate Z (see Proposition 5.5). Then we deduce the semi-ampleness of
![]() $K_{X}+B$
by adjunction (see Proposition 5.6).
$K_{X}+B$
by adjunction (see Proposition 5.6).
In Case II, we first modify the pair
![]() $(X,B)$
by running several MMP which are
$(X,B)$
by running several MMP which are
![]() $(K_{X}+B)$
-trivial (see Definition 2.16) so that all h-exceptional prime divisors are connected components of
$(K_{X}+B)$
-trivial (see Definition 2.16) so that all h-exceptional prime divisors are connected components of
![]() $\lfloor B\rfloor $
. Then after further modification we can construct an equidimensional fibration
$\lfloor B\rfloor $
. Then after further modification we can construct an equidimensional fibration
![]() $h_{\varepsilon }:X\to Z_{\varepsilon }$
to a normal projective surface. Finally, we descend
$h_{\varepsilon }:X\to Z_{\varepsilon }$
to a normal projective surface. Finally, we descend
![]() $K_{X}+B$
to
$K_{X}+B$
to
![]() $Z_{\varepsilon }$
and prove its semi-ampleness (see Proposition 5.10).
$Z_{\varepsilon }$
and prove its semi-ampleness (see Proposition 5.10).
1.3 Notation and conventions
![]() $\bullet $
We say that X is a variety if it is an integral and separated scheme which is of finite type over a field k.
$\bullet $
We say that X is a variety if it is an integral and separated scheme which is of finite type over a field k.
![]() $\bullet $
We say that a morphism
$\bullet $
We say that a morphism
![]() $f: X\to Y$
is a contraction if X and Y are normal algebraic spaces (we refer to [Reference Artin1] for definition and basic properties of algebraic spaces),
$f: X\to Y$
is a contraction if X and Y are normal algebraic spaces (we refer to [Reference Artin1] for definition and basic properties of algebraic spaces),
![]() $f_{\ast }{\mathcal O}_{X}={\mathcal O}_{Y}$
, and f is proper.
$f_{\ast }{\mathcal O}_{X}={\mathcal O}_{Y}$
, and f is proper.
![]() $\bullet $
We say that a morphism
$\bullet $
We say that a morphism
![]() $f : X\to Y$
of algebraic spaces is equidimensional if all fibers
$f : X\to Y$
of algebraic spaces is equidimensional if all fibers
![]() $X_{y}$
of f are of the same dimension for
$X_{y}$
of f are of the same dimension for
![]() $y\in Y$
.
$y\in Y$
.
![]() $\bullet $
Let
$\bullet $
Let
![]() $f : X\to Y$
be a surjective morphism of integral algebraic spaces. We say that a
$f : X\to Y$
be a surjective morphism of integral algebraic spaces. We say that a
![]() ${\mathbb Q}$
-divisor D on X is f-exceptional if
${\mathbb Q}$
-divisor D on X is f-exceptional if
![]() $\mathrm {dim}(f(\mathrm {Supp}\ D))<\mathrm {dim}\ Y-1$
.
$\mathrm {dim}(f(\mathrm {Supp}\ D))<\mathrm {dim}\ Y-1$
.
![]() $\bullet $
We call a divisor
$\bullet $
We call a divisor
![]() $D \subseteq X$
vertical with respect to a contraction f if
$D \subseteq X$
vertical with respect to a contraction f if
![]() $f|_{D}$
is not dominant.
$f|_{D}$
is not dominant.
![]() $\bullet $
We call
$\bullet $
We call
![]() $(X,B)$
a pair if X is a normal variety and B is an effective
$(X,B)$
a pair if X is a normal variety and B is an effective
![]() ${\mathbb Q}$
-divisor on X such that
${\mathbb Q}$
-divisor on X such that
![]() $K_{X}+B$
is
$K_{X}+B$
is
![]() ${\mathbb Q}$
-Cartier. For more notions in the theory of MMP such as klt (dlt, lc) pairs, flips, divisorial contractions and so on, we refer to [Reference Kollár, Kollár, Mori, Clemens and Corti20].
${\mathbb Q}$
-Cartier. For more notions in the theory of MMP such as klt (dlt, lc) pairs, flips, divisorial contractions and so on, we refer to [Reference Kollár, Kollár, Mori, Clemens and Corti20].
![]() $\bullet $
Let X be a normal projective variety over a field k, and let D be a
$\bullet $
Let X be a normal projective variety over a field k, and let D be a
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X. If
${\mathbb Q}$
-divisor on X. If
![]() $|mD|=\emptyset $
for all
$|mD|=\emptyset $
for all
![]() $m>0$
, we define the Kodaira dimension
$m>0$
, we define the Kodaira dimension
![]() $\kappa (X,D)=-\infty $
. Otherwise, let
$\kappa (X,D)=-\infty $
. Otherwise, let
![]() $\Phi :X\dashrightarrow Z$
be the Iitaka map (we refer to [Reference Lazarsfeld21, 2.1.C]) of D and we define the Kodaira dimension
$\Phi :X\dashrightarrow Z$
be the Iitaka map (we refer to [Reference Lazarsfeld21, 2.1.C]) of D and we define the Kodaira dimension
![]() $\kappa (X,D)$
to be the dimension of the image of
$\kappa (X,D)$
to be the dimension of the image of
![]() $\Phi $
. Sometimes we write
$\Phi $
. Sometimes we write
![]() $\kappa (D)$
for
$\kappa (D)$
for
![]() $\kappa (X,D)$
. We denote
$\kappa (X,D)$
. We denote
![]() $\kappa (X,K_{X})$
by
$\kappa (X,K_{X})$
by
![]() $\kappa (X)$
. And for a projective variety Y over a field k admitting a smooth model
$\kappa (X)$
. And for a projective variety Y over a field k admitting a smooth model
![]() $\tilde {Y}$
, we define
$\tilde {Y}$
, we define
![]() $\kappa (Y):=\kappa (\tilde {Y})$
.
$\kappa (Y):=\kappa (\tilde {Y})$
.
![]() $\bullet $
Let X be a normal projective variety of dimension n over a field k, and let D be a nef
$\bullet $
Let X be a normal projective variety of dimension n over a field k, and let D be a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X. Then we can define
${\mathbb Q}$
-divisor on X. Then we can define
2 Preliminaries
In this section, we recall some basic results.
2.1 Keel’s results on semi-ampleness
In this subsection, we survey Keel’s work on basepoint free theorem for nef and big
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisors in positive characteristic (see [Reference Keel17]). It is proved that to show the semi-ampleness of a nef and big
${\mathbb Q}$
-divisors in positive characteristic (see [Reference Keel17]). It is proved that to show the semi-ampleness of a nef and big
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor L on a projective variety X, it suffices to show the semi-ampleness of D on
${\mathbb Q}$
-divisor L on a projective variety X, it suffices to show the semi-ampleness of D on
![]() ${\mathbb E}(L)$
, which is a closed subset of X defined below.
${\mathbb E}(L)$
, which is a closed subset of X defined below.
Definition 2.1. Let L be a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on a projective scheme X over a field. An irreducible subvariety
${\mathbb Q}$
-divisor on a projective scheme X over a field. An irreducible subvariety
![]() $Z \subset X$
is called exceptional for L if
$Z \subset X$
is called exceptional for L if
![]() $L|_{Z}$
is not big, that is, if
$L|_{Z}$
is not big, that is, if
![]() $L^{\mathrm {dim}\ Z}\cdot Z = 0$
. The exceptional locus of L, denoted by
$L^{\mathrm {dim}\ Z}\cdot Z = 0$
. The exceptional locus of L, denoted by
![]() ${\mathbb E}(L)$
, is the closure of the union of all exceptional subvarieties.
${\mathbb E}(L)$
, is the closure of the union of all exceptional subvarieties.
Remark 2.2.
![]() ${\mathbb E}(L)$
is actually the union of finitely many exceptional subvarieties by [Reference Keel17, 1.2].
${\mathbb E}(L)$
is actually the union of finitely many exceptional subvarieties by [Reference Keel17, 1.2].
Definition 2.3. A nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor L on a proper scheme X over a field is endowed with a map (EWM)
${\mathbb Q}$
-divisor L on a proper scheme X over a field is endowed with a map (EWM)
![]() $f: X\to Z$
if f is a proper map to a proper algebraic space Z such that it contracts a closed subvariety Y, that is,
$f: X\to Z$
if f is a proper map to a proper algebraic space Z such that it contracts a closed subvariety Y, that is,
![]() $\mathrm {dim}(f(Y))<\mathrm {dim}(Y)$
, if and only if
$\mathrm {dim}(f(Y))<\mathrm {dim}(Y)$
, if and only if
![]() $L|_{Y}$
is not big. We may always assume that such a map has geometrically connected fibers.
$L|_{Y}$
is not big. We may always assume that such a map has geometrically connected fibers.
Remark 2.4. By definition, if L is endowed with a map
![]() $f: X\to Z$
, then a curve
$f: X\to Z$
, then a curve
![]() $C\subseteq X$
is contracted by f if and only if
$C\subseteq X$
is contracted by f if and only if
![]() $L\cdot C=0$
. Moreover, if
$L\cdot C=0$
. Moreover, if
![]() $f^{\prime }:X\to Z^{\prime }$
is a contraction which only contracts L-numerically trivial curves, then by the rigidity lemma (see [Reference Kollár19, II.5.3]) f factors through
$f^{\prime }:X\to Z^{\prime }$
is a contraction which only contracts L-numerically trivial curves, then by the rigidity lemma (see [Reference Kollár19, II.5.3]) f factors through
![]() $f^{\prime }$
.
$f^{\prime }$
.
Lemma 2.5. Let
![]() $p: Y\to X$
be a proper surjective morphism between reduced algebraic spaces of finite type over a field of positive characteristic. Let L be a
$p: Y\to X$
be a proper surjective morphism between reduced algebraic spaces of finite type over a field of positive characteristic. Let L be a
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X such that
${\mathbb Q}$
-divisor on X such that
![]() $p^{\ast }L$
is semi-ample. If X is normal, then L is semi-ample.
$p^{\ast }L$
is semi-ample. If X is normal, then L is semi-ample.
Proof. This lemma follows from [Reference Keel17, Lem. 2.10].
The following theorem is the main result of [Reference Keel17].
Theorem 2.6 [Reference Keel17, Th. 0.2].
Let L be a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on a scheme X, projective over a field of positive characteristic. Then L is semi-ample (resp. EWM) if and only if
${\mathbb Q}$
-divisor on a scheme X, projective over a field of positive characteristic. Then L is semi-ample (resp. EWM) if and only if
![]() $L|_{{\mathbb E}(L)}$
is semi-ample (resp. EWM).
$L|_{{\mathbb E}(L)}$
is semi-ample (resp. EWM).
2.2 Nef reduction map
In this subsection, we recall the notion of nef reduction map.
Definition 2.7. Let X be a normal projective variety defined over an uncountable field, and let L be a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor. We call a rational map
${\mathbb Q}$
-divisor. We call a rational map
![]() $\phi : X \dashrightarrow Z$
a nef reduction map of L if Z is a normal projective variety and there exist open dense subsets
$\phi : X \dashrightarrow Z$
a nef reduction map of L if Z is a normal projective variety and there exist open dense subsets
![]() $U \subseteq X$
,
$U \subseteq X$
,
![]() $V\subseteq Z$
such that:
$V\subseteq Z$
such that:
(1)
![]() $\phi |_{U}: U \to Z$
is proper, its image is V and
$\phi |_{U}: U \to Z$
is proper, its image is V and
![]() $\phi _{\ast }{\mathcal O}_{U} = {\mathcal O}_{V}$
,
$\phi _{\ast }{\mathcal O}_{U} = {\mathcal O}_{V}$
,
(2)
![]() $L|_{F}\equiv 0$
for all fibers F of
$L|_{F}\equiv 0$
for all fibers F of
![]() $\phi $
over V, and
$\phi $
over V, and
(3) if
![]() $x \in X$
is a very general point and C is a curve passing through it, then
$x \in X$
is a very general point and C is a curve passing through it, then
![]() $C\cdot L = 0$
if and only if C is contracted by
$C\cdot L = 0$
if and only if C is contracted by
![]() $\phi $
.
$\phi $
.
It is proved that a nef reduction map exists over an uncountable algebraically closed field.
Theorem 2.8 [Reference Bauer, Campana, Eckl, Kebekus, Peternell, Rams, Szemberg and Wotzlaw2, Th. 2.1].
A nef reduction map exists for normal projective varieties defined over an uncountable algebraically closed field. Furthermore, it is unique up to birational equivalence.
For a nef reduction map
![]() $\phi : X \dashrightarrow Z$
of L, the nef dimension of L is defined to be
$\phi : X \dashrightarrow Z$
of L, the nef dimension of L is defined to be
![]() $\mathrm {dim}\ Z$
and denoted by
$\mathrm {dim}\ Z$
and denoted by
![]() $n(X,L)$
. When the base field is countable and algebraically closed, we can define
$n(X,L)$
. When the base field is countable and algebraically closed, we can define
by [Reference Witaszek27, Prop. 2.16], where K is an uncountable algebraically closed field that contains k, and
![]() $X_{K},L_{K}$
are the base changes of
$X_{K},L_{K}$
are the base changes of
![]() $X,L$
to K. It satisfies
$X,L$
to K. It satisfies
![]() $\kappa (X, L)\leq n(X, L)$
. Sometimes we write
$\kappa (X, L)\leq n(X, L)$
. Sometimes we write
![]() $n(L)$
for
$n(L)$
for
![]() $n(X,L)$
.
$n(X,L)$
.
Lemma 2.9 [Reference Birkar and Waldron5, Lem. 7.2].
Let X be a normal projective variety of dimension
![]() $\leq 3$
over an uncountable algebraically closed field of characteristic
$\leq 3$
over an uncountable algebraically closed field of characteristic
![]() $p> 0$
. Suppose L is a nef
$p> 0$
. Suppose L is a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X with
${\mathbb Q}$
-divisor on X with
![]() $\kappa (L)=n(L)\leq 2$
. Then L is
$\kappa (L)=n(L)\leq 2$
. Then L is
![]() $EWM$
to a proper algebraic space Z of dimension equal to
$EWM$
to a proper algebraic space Z of dimension equal to
![]() $\kappa (L)$
.
$\kappa (L)$
.
The following lemma is very useful for descending a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor along a fibration.
${\mathbb Q}$
-divisor along a fibration.
Lemma 2.10. Let
![]() $f: X\to Z$
be a projective contraction between normal quasi-projective varieties over a field of characteristic
$f: X\to Z$
be a projective contraction between normal quasi-projective varieties over a field of characteristic
![]() $p>0,$
and let L be a f-nef
$p>0,$
and let L be a f-nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X such that
${\mathbb Q}$
-divisor on X such that
![]() $L|_{F} \sim _{{\mathbb Q}} 0$
, where F is the generic fiber of f. Assume
$L|_{F} \sim _{{\mathbb Q}} 0$
, where F is the generic fiber of f. Assume
![]() $\mathrm {dim}\ Z\leq 3$
. Then there exists a diagram
$\mathrm {dim}\ Z\leq 3$
. Then there exists a diagram

with
![]() $\phi ,\psi $
projective birational, and a
$\phi ,\psi $
projective birational, and a
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor D on
${\mathbb Q}$
-divisor D on
![]() $Z^{\prime }$
such that
$Z^{\prime }$
such that
![]() $\phi ^{\ast }L \sim _{{\mathbb Q}} f^{\prime \ast }D$
. Moreover, if Z is
$\phi ^{\ast }L \sim _{{\mathbb Q}} f^{\prime \ast }D$
. Moreover, if Z is
![]() ${\mathbb Q}$
-factorial and f is equidimensional, then we can take
${\mathbb Q}$
-factorial and f is equidimensional, then we can take
![]() $X^{\prime } = X$
and
$X^{\prime } = X$
and
![]() $Z^{\prime } = Z$
.
$Z^{\prime } = Z$
.
Proof. It is an adaptation of a result of Kawamata [Reference Kawamata16, Prop. 2.1]. See [Reference Waldron25, Lem. 3.2] for a proof in this setting.
2.3 Abundance theorem for surfaces
Abundance for slc surfaces over an arbitrary field of characteristic
![]() $>0$
is known.
$>0$
is known.
Theorem 2.11 [Reference Posva22, Th. 1].
Let
![]() $(X,\Delta )$
be a projective slc surface pair over a field of characteristic
$(X,\Delta )$
be a projective slc surface pair over a field of characteristic
![]() $>0$
. If
$>0$
. If
![]() $K_{X}+\Delta $
is nef, then it is semi-ample.
$K_{X}+\Delta $
is nef, then it is semi-ample.
2.4 MMP for threefolds in positive characteristic
In this subsection, we recall the theory of MMP for projective lc threefold pairs over a perfect field of characteristic
![]() $p> 3$
. Moreover, we define a partial MMP over an algebraically closed field of characteristic
$p> 3$
. Moreover, we define a partial MMP over an algebraically closed field of characteristic
![]() $p> 3$
(see Definition 2.16). We will use this construction to study the abundance in Section 5.
$p> 3$
(see Definition 2.16). We will use this construction to study the abundance in Section 5.
Theorem 2.12 [Reference Hashizume, Nakamura and Tanaka15, Th. 1.1] and [Reference Hacon and Witaszek12].
Let
![]() $(X, B)$
be a lc threefold pair over a perfect field k of characteristic
$(X, B)$
be a lc threefold pair over a perfect field k of characteristic
![]() $>3$
and
$>3$
and
![]() $f : X \to Y$
a projective surjective morphism to a quasi-projective variety. If
$f : X \to Y$
a projective surjective morphism to a quasi-projective variety. If
![]() $K_{X}+B$
is pseudo-effective (resp. not pseudo-effective) over Y, then we can run a
$K_{X}+B$
is pseudo-effective (resp. not pseudo-effective) over Y, then we can run a
![]() $(K_{X}+B)$
-MMP over Y to get a log minimal model (resp. Mori fiber space) over Y.
$(K_{X}+B)$
-MMP over Y to get a log minimal model (resp. Mori fiber space) over Y.
We recall the notion of MMP with scaling. Let
![]() $(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
![]() $>3$
and
$>3$
and
![]() $A> 0$
an
$A> 0$
an
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X. Suppose that there is
${\mathbb Q}$
-divisor on X. Suppose that there is
![]() $t_{0}> 0$
such that
$t_{0}> 0$
such that
![]() $(X,B+ t_{0}A)$
is lc and
$(X,B+ t_{0}A)$
is lc and
![]() $K_{X}+B+t_{0}A$
is nef. We describe how to run a
$K_{X}+B+t_{0}A$
is nef. We describe how to run a
![]() $(K_{X}+B)$
-MMP with scaling of A as follows.
$(K_{X}+B)$
-MMP with scaling of A as follows.
Let
![]() $\lambda _{0}=\mathrm {inf} \{t|\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
. Suppose we can find a
$\lambda _{0}=\mathrm {inf} \{t|\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
. Suppose we can find a
![]() $(K_{X}+ B)$
-negative extremal ray
$(K_{X}+ B)$
-negative extremal ray
![]() $R_{0}$
which satisfies
$R_{0}$
which satisfies
![]() $(K_{X}+B+\lambda _{0}A)\cdot R_{0}= 0$
(In general, it is possible that there is no such extremal ray). This is the first ray we contract in our MMP. If the contraction is a Mori fiber contraction, we stop. Otherwise, let
$(K_{X}+B+\lambda _{0}A)\cdot R_{0}= 0$
(In general, it is possible that there is no such extremal ray). This is the first ray we contract in our MMP. If the contraction is a Mori fiber contraction, we stop. Otherwise, let
![]() $X_{1}$
be the result of the divisorial contraction or flip. Then
$X_{1}$
be the result of the divisorial contraction or flip. Then
![]() $K_{X_{1}}+ B_{X_{1}}+\lambda _{0}A_{X_{1}}$
is also nef, where
$K_{X_{1}}+ B_{X_{1}}+\lambda _{0}A_{X_{1}}$
is also nef, where
![]() $B_{X_{1}}$
and
$B_{X_{1}}$
and
![]() $A_{X_{1}}$
denote the birational transforms on
$A_{X_{1}}$
denote the birational transforms on
![]() $X_{1}$
of B and A, respectively. We define
$X_{1}$
of B and A, respectively. We define
![]() $\lambda _{1} =\mathrm {inf} \{t|\ K_{X_{1}}+ B_{X_{1}} + tA_{X_{1}}\ \mathrm {is}\ \mathrm {nef} \}$
. The next step in our MMP is chosen to be a
$\lambda _{1} =\mathrm {inf} \{t|\ K_{X_{1}}+ B_{X_{1}} + tA_{X_{1}}\ \mathrm {is}\ \mathrm {nef} \}$
. The next step in our MMP is chosen to be a
![]() $(K_{X_{1}} + B_{X_{1}})$
-negative extremal ray
$(K_{X_{1}} + B_{X_{1}})$
-negative extremal ray
![]() $R_{1}$
which is
$R_{1}$
which is
![]() $(K_{X_{1}}+B_{X_{1}}+ \lambda _{1} A_{X_{1}})$
-trivial. So long as we can find the appropriate extremal rays, contractions and flips, we can continue this process.
$(K_{X_{1}}+B_{X_{1}}+ \lambda _{1} A_{X_{1}})$
-trivial. So long as we can find the appropriate extremal rays, contractions and flips, we can continue this process.
Proposition 2.13. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and W let be an effective
$>3$
, and W let be an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $K_{X}+B+W$
is nef. Then either:
$K_{X}+B+W$
is nef. Then either:
(1) there is a
![]() $(K_{X}+B)$
-negative extremal ray which is
$(K_{X}+B)$
-negative extremal ray which is
![]() $(K_{X}+B+W)$
-trivial, or
$(K_{X}+B+W)$
-trivial, or
(2)
![]() $K_{X}+B+(1-\varepsilon )W$
is nef for any sufficiently small rational
$K_{X}+B+(1-\varepsilon )W$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. It is an adaptation of [Reference Keel, Matsuki and McKernan18, Lem. 5.1]. Note that the proof there only uses the fact that for any
![]() $(K_{X}+B)$
-negative extremal ray R there is a rational curve C such that C generates R and
$(K_{X}+B)$
-negative extremal ray R there is a rational curve C such that C generates R and
![]() $-(K_{X}+B)\cdot C\leq 6$
, which holds in our setting by [Reference Hashizume, Nakamura and Tanaka15, Th. 1.3] and [Reference Hacon and Witaszek12].
$-(K_{X}+B)\cdot C\leq 6$
, which holds in our setting by [Reference Hashizume, Nakamura and Tanaka15, Th. 1.3] and [Reference Hacon and Witaszek12].
Remark 2.14. The assumption that k is algebraically closed is used for the fact that for any
![]() $(K_{X}+B)$
-negative extremal ray R there is a rational curve C such that C generates R and
$(K_{X}+B)$
-negative extremal ray R there is a rational curve C such that C generates R and
![]() $-(K_{X}+B)\cdot C\leq 6$
.
$-(K_{X}+B)\cdot C\leq 6$
.
Corollary 2.15. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and let A be an effective
$>3$
, and let A be an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $(X,B+A)$
is lc and
$(X,B+A)$
is lc and
![]() $K_{X}+B+A$
is nef. If
$K_{X}+B+A$
is nef. If
![]() $K_{X}+B$
is not nef, then we can run a
$K_{X}+B$
is not nef, then we can run a
![]() $(K_{X}+B)$
-MMP with scaling of A.
$(K_{X}+B)$
-MMP with scaling of A.
Proof. Let
![]() $\lambda := \mathrm {inf} \{t|\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
be the nef threshold. Then the only assertion is that we can find a
$\lambda := \mathrm {inf} \{t|\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
be the nef threshold. Then the only assertion is that we can find a
![]() $(K_{X}+B)$
-negative extremal ray R such that
$(K_{X}+B)$
-negative extremal ray R such that
![]() $(K_{X}+B+\lambda A)\cdot R=0$
. We apply Proposition 2.13 by letting
$(K_{X}+B+\lambda A)\cdot R=0$
. We apply Proposition 2.13 by letting
![]() $W:=\lambda A$
.
$W:=\lambda A$
.
In this paper, we will use the following construction.
Definition 2.16. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and let A be an effective
$>3$
, and let A be an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $(X,B+A)$
is lc and
$(X,B+A)$
is lc and
![]() $K_{X}+B+A$
is nef. We can run a partial
$K_{X}+B+A$
is nef. We can run a partial
![]() $(K_{X}+B)$
-MMP with scaling of A as follows.
$(K_{X}+B)$
-MMP with scaling of A as follows.
Let
![]() $\lambda _{0}=\mathrm {inf} \{t |\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
. If
$\lambda _{0}=\mathrm {inf} \{t |\ K_{X}+B+tA\ \mathrm {is}\ \mathrm {nef} \}$
. If
![]() $\lambda _{0}<1$
, then we stop. Otherwise, by Proposition 2.13, there exists a
$\lambda _{0}<1$
, then we stop. Otherwise, by Proposition 2.13, there exists a
![]() $(K_{X}+ B)$
-negative extremal ray
$(K_{X}+ B)$
-negative extremal ray
![]() $R_{0}$
which satisfies
$R_{0}$
which satisfies
![]() $(K_{X}+B+A)\cdot R_{0}= 0$
. We contract this extremal ray. If the contraction is a Mori fiber contraction, we stop. Otherwise, let
$(K_{X}+B+A)\cdot R_{0}= 0$
. We contract this extremal ray. If the contraction is a Mori fiber contraction, we stop. Otherwise, let
![]() $\mu _{0}: X\dashrightarrow X_{1}$
be the divisorial contraction or flip. Repeat this process for
$\mu _{0}: X\dashrightarrow X_{1}$
be the divisorial contraction or flip. Repeat this process for
![]() $(X_{1},\mu _{0\ast }B), \mu _{0\ast }A$
and so on.
$(X_{1},\mu _{0\ast }B), \mu _{0\ast }A$
and so on.
We call this construction a
![]() $(K_{X}+B)$
-MMP which is
$(K_{X}+B)$
-MMP which is
![]() $(K_{X}+B+A)$
-trivial.
$(K_{X}+B+A)$
-trivial.
The following lemma tells us what the output of this construction is if it terminates.
Lemma 2.17. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and let A be an effective
$>3$
, and let A be an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $(X,B+A)$
is lc and
$(X,B+A)$
is lc and
![]() $K_{X}+B+A$
is nef.
$K_{X}+B+A$
is nef.
If a
![]() $(K_{X}+B)$
-MMP which is
$(K_{X}+B)$
-MMP which is
![]() $(K_{X}+B+A)$
-trivial terminates, then its output is a
$(K_{X}+B+A)$
-trivial terminates, then its output is a
![]() ${\mathbb Q}$
-factorial projective lc pair
${\mathbb Q}$
-factorial projective lc pair
![]() $(X^{\prime }, B^{\prime }+A^{\prime })$
, and either:
$(X^{\prime }, B^{\prime }+A^{\prime })$
, and either:
(1)
![]() $X^{\prime }$
has the structure of a Mori fiber space
$X^{\prime }$
has the structure of a Mori fiber space
![]() $X^{\prime }\to Y$
,
$X^{\prime }\to Y$
,
![]() $K_{X^{\prime }}+B^{\prime }+A^{\prime }$
is the pullback of a
$K_{X^{\prime }}+B^{\prime }+A^{\prime }$
is the pullback of a
![]() ${\mathbb Q}$
-divisor from Y, and
${\mathbb Q}$
-divisor from Y, and
![]() $\mathrm {Supp}\ A^{\prime }$
dominates Y, or
$\mathrm {Supp}\ A^{\prime }$
dominates Y, or
(2)
![]() $K_{X^{\prime }}+B^{\prime }+(1-\varepsilon )A^{\prime }$
is nef for any sufficiently small rational
$K_{X^{\prime }}+B^{\prime }+(1-\varepsilon )A^{\prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Moreover,
![]() $K_{X^{\prime }}+B^{\prime }+A^{\prime }$
is semi-ample if and only if
$K_{X^{\prime }}+B^{\prime }+A^{\prime }$
is semi-ample if and only if
![]() $K_{X}+B+A$
is semi-ample.
$K_{X}+B+A$
is semi-ample.
Proof. We only need to prove that, if a
![]() $(K_{X}+B)$
-MMP which is
$(K_{X}+B)$
-MMP which is
![]() $(K_{X}+B+A)$
-trivial terminates with a Mori fiber space
$(K_{X}+B+A)$
-trivial terminates with a Mori fiber space
![]() $f:(X^{\prime },B^{\prime }+A^{\prime })\to Y$
, then
$f:(X^{\prime },B^{\prime }+A^{\prime })\to Y$
, then
![]() $\mathrm {Supp}\ A^{\prime }$
dominates Y. It is clear since f only contracts curves which have positive intersections with
$\mathrm {Supp}\ A^{\prime }$
dominates Y. It is clear since f only contracts curves which have positive intersections with
![]() $A^{\prime }$
.
$A^{\prime }$
.
We will use the following results on termination of flips.
Theorem 2.18 [Reference Waldron26, Th. 1.6] and [Reference Hacon and Witaszek12].
Let
![]() $(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
![]() $p>3$
. If M is an effective
$p>3$
. If M is an effective
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X, then any sequence of
${\mathbb Q}$
-divisor on X, then any sequence of
![]() $(K_{X}+B)$
-flips which are also M-flips terminates.
$(K_{X}+B)$
-flips which are also M-flips terminates.
Lemma 2.19. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that
$>3$
such that
![]() $K_{X}+B+A$
is nef. If X is terminal, then any
$K_{X}+B+A$
is nef. If X is terminal, then any
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates.
$(K_{X}+B)$
-trivial terminates.
Proof. Since every step of a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial is a step of a
$(K_{X}+B)$
-trivial is a step of a
![]() $K_{X}$
-MMP, the assertion follows from [Reference Kollár, Kollár, Mori, Clemens and Corti20, Th. 6.17].
$K_{X}$
-MMP, the assertion follows from [Reference Kollár, Kollár, Mori, Clemens and Corti20, Th. 6.17].
2.5 Dlt modifications and adjunction
The following result helps us to reduce some problems for lc pairs to
![]() ${\mathbb Q}$
-factorial dlt pairs.
${\mathbb Q}$
-factorial dlt pairs.
Theorem 2.20. Let
![]() $(X, B)$
be a lc threefold pair over a perfect field k of characteristic
$(X, B)$
be a lc threefold pair over a perfect field k of characteristic
![]() $>3$
. Then
$>3$
. Then
![]() $(X, B)$
has a crepant
$(X, B)$
has a crepant
![]() ${\mathbb Q}$
-factorial dlt model. Moreover, we can modify X so that it is terminal.
${\mathbb Q}$
-factorial dlt model. Moreover, we can modify X so that it is terminal.
Proof. For the first assertion, see [Reference Birkar4, Th. 1.6] and [Reference Hacon and Witaszek12]. Let us prove that we can make X terminal. We take a crepant
![]() ${\mathbb Q}$
-factorial dlt model
${\mathbb Q}$
-factorial dlt model
![]() $g: (X^{\prime },B^{\prime })\to (X,B)$
by the first assertion. Hence, by replacing
$g: (X^{\prime },B^{\prime })\to (X,B)$
by the first assertion. Hence, by replacing
![]() $(X, B)$
by
$(X, B)$
by
![]() $(X^{\prime },B^{\prime })$
, we may assume that
$(X^{\prime },B^{\prime })$
, we may assume that
![]() $(X, B)$
is
$(X, B)$
is
![]() ${\mathbb Q}$
-factorial and dlt. Let
${\mathbb Q}$
-factorial and dlt. Let
![]() $U \subseteq X$
be the largest open set such that
$U \subseteq X$
be the largest open set such that
![]() $(U, B|_{U})$
is a snc pair. Then
$(U, B|_{U})$
is a snc pair. Then
![]() $\mathrm {codim}_{ X} (X\backslash U) \geq 2$
. Let
$\mathrm {codim}_{ X} (X\backslash U) \geq 2$
. Let
![]() $f : (X^{\prime }, \Theta ^{\prime })\to (X, 0)$
be a terminal model of
$f : (X^{\prime }, \Theta ^{\prime })\to (X, 0)$
be a terminal model of
![]() $(X, 0)$
as in [Reference Birkar4, Th. 1.7] such that
$(X, 0)$
as in [Reference Birkar4, Th. 1.7] such that
![]() $K_{X^{\prime }} + \Theta ^{\prime }= f^{\ast }K_{X}$
. Then f is an isomorphism over the smooth locus of X; in particular, f is an isomorphism over U. Let
$K_{X^{\prime }} + \Theta ^{\prime }= f^{\ast }K_{X}$
. Then f is an isomorphism over the smooth locus of X; in particular, f is an isomorphism over U. Let
![]() $Z = X\backslash U$
. Define
$Z = X\backslash U$
. Define
![]() $B^{\prime }:= \Theta ^{\prime }+ f^{\ast }B$
on
$B^{\prime }:= \Theta ^{\prime }+ f^{\ast }B$
on
![]() $X^{\prime }$
so that
$X^{\prime }$
so that
and
![]() $(X^{\prime }, B^{\prime })$
is lc.
$(X^{\prime }, B^{\prime })$
is lc.
It remains to show that
![]() $(X^{\prime }, B^{\prime })$
is a dlt pair. Let
$(X^{\prime }, B^{\prime })$
is a dlt pair. Let
![]() $U^{\prime } = f^{-1}(U)$
and
$U^{\prime } = f^{-1}(U)$
and
![]() $Z^{\prime } = X^{\prime }\backslash U^{\prime }$
. Then
$Z^{\prime } = X^{\prime }\backslash U^{\prime }$
. Then
![]() $(U^{\prime }, B^{\prime }|_{U^{\prime }})$
is a snc pair. If E is an exceptional divisor with center in
$(U^{\prime }, B^{\prime }|_{U^{\prime }})$
is a snc pair. If E is an exceptional divisor with center in
![]() $Z^{\prime }$
, then its center in X is contained in Z. Hence
$Z^{\prime }$
, then its center in X is contained in Z. Hence
![]() $a(E, X^{\prime }, B^{\prime })= a(E, X, B)> -1$
. This completes the proof.
$a(E, X^{\prime }, B^{\prime })= a(E, X, B)> -1$
. This completes the proof.
For
![]() ${\mathbb Q}$
-factorial dlt threefold pairs, we have the following result on adjunction.
${\mathbb Q}$
-factorial dlt threefold pairs, we have the following result on adjunction.
Theorem 2.21. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over a perfect field k of characteristic
${\mathbb Q}$
-factorial projective dlt threefold pair over a perfect field k of characteristic
![]() $>0$
. If
$>0$
. If
![]() $(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then
$(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then
![]() $(K_{X}+ B)|_{\lfloor B\rfloor }$
is semi-ample.
$(K_{X}+ B)|_{\lfloor B\rfloor }$
is semi-ample.
Proof. By [Reference Hacon and Witaszek11, Rem. 3.9], we know that all lc centres of
![]() ${\mathbb Q}$
-factorial three-dimensional dlt pairs are normal up to a universal homeomorphism. Hence, we can argue as in [Reference Waldron26, §5] to prove that the
${\mathbb Q}$
-factorial three-dimensional dlt pairs are normal up to a universal homeomorphism. Hence, we can argue as in [Reference Waldron26, §5] to prove that the
![]() $S_{2}$
-fication (see, for example, [Reference Waldron26, 2.2]) of
$S_{2}$
-fication (see, for example, [Reference Waldron26, 2.2]) of
![]() $\lfloor B\rfloor $
is a universal homeomorphism and
$\lfloor B\rfloor $
is a universal homeomorphism and
![]() $(K_{X}+ B)|_{\lfloor B\rfloor }$
is semi-ample.
$(K_{X}+ B)|_{\lfloor B\rfloor }$
is semi-ample.
2.6 Some known results on the abundance
The following theorem collects the recent results toward the abundance conjecture in positive characteristics.
Theorem 2.22. Let
![]() $(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
![]() $>5$
such that
$>5$
such that
![]() $K_{X}+B$
is nef. Assume that one of the following conditions holds:
$K_{X}+B$
is nef. Assume that one of the following conditions holds:
(1)
![]() $\kappa (X,K_{X}+B)\geq 1$
,
$\kappa (X,K_{X}+B)\geq 1$
,
(2) the nef dimension
![]() $n(X,K_{X}+B)\leq 2$
,
$n(X,K_{X}+B)\leq 2$
,
(3) the Albanese map
![]() $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
Then
![]() $K_{X}+ B$
is semi-ample.
$K_{X}+ B$
is semi-ample.
Proof. For (1), the case of
![]() $\kappa (X,K_{X}+B)=3$
is proved in [Reference Birkar and Waldron5, Th. 1.2], the case of
$\kappa (X,K_{X}+B)=3$
is proved in [Reference Birkar and Waldron5, Th. 1.2], the case of
![]() $\kappa (X,K_{X}+B)=2$
is proved in [Reference Waldron25, Th. 1.3] and the case of
$\kappa (X,K_{X}+B)=2$
is proved in [Reference Waldron25, Th. 1.3] and the case of
![]() $\kappa (X,K_{X}+B)=1$
is proved in [Reference Zhang29, Th. 3.1] and [Reference Das and Waldron8, Th. A]. For (2), it is proved in [Reference Witaszek27, Th. 5]. For (3), see [Reference Zhang30, Th. 1.1] and [Reference Witaszek27, Cor. 4.13].
$\kappa (X,K_{X}+B)=1$
is proved in [Reference Zhang29, Th. 3.1] and [Reference Das and Waldron8, Th. A]. For (2), it is proved in [Reference Witaszek27, Th. 5]. For (3), see [Reference Zhang30, Th. 1.1] and [Reference Witaszek27, Cor. 4.13].
Moreover, the nonvanishing theorem for terminal threefolds has been proved in [Reference Xu and Zhang28].
Theorem 2.23 [Reference Xu and Zhang28, Th. 1.1].
Let X be a projective terminal threefold over an algebraically closed field k of characteristic
![]() $>5$
. If
$>5$
. If
![]() $K_{X}$
is pseudo-effective, then
$K_{X}$
is pseudo-effective, then
![]() $\kappa (X, K_{X})\geq 0$
.
$\kappa (X, K_{X})\geq 0$
.
Based on it, the nonvanishing theorem for klt threefold pairs is proved in [Reference Witaszek27].
Theorem 2.24 [Reference Witaszek27, Th. 3].
Let
![]() $(X,B)$
be a projective klt threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective klt threefold pair over a perfect field k of characteristic
![]() $>5$
. If
$>5$
. If
![]() $K_{X}+B$
is pseudo-effective, then
$K_{X}+B$
is pseudo-effective, then
![]() $\kappa (K_{X}+B)\geq 0$
.
$\kappa (K_{X}+B)\geq 0$
.
3 Klt threefold pairs in characteristic
 $>3$
$>3$
In this section, we generalize the results in Section 2.6 to the case when the characteristic is greater than
![]() $3$
. Note that in Section 2.6, we always assume that the characteristic of the base field is greater than
$3$
. Note that in Section 2.6, we always assume that the characteristic of the base field is greater than
![]() $5$
. Actually, the assumption of characteristic
$5$
. Actually, the assumption of characteristic
![]() $>5$
is used for the following assertions. Let k be an algebraically closed field of characteristic
$>5$
is used for the following assertions. Let k be an algebraically closed field of characteristic
![]() $>5$
. Then we have the following propositions hold:
$>5$
. Then we have the following propositions hold:
P 1: (MMP) We can run MMP for lc threefold pairs over k (see, for example, [Reference Hashizume, Nakamura and Tanaka15]).
P 2: (Elliptic fibration) Let
![]() $g: X\to Z$
be a fibration of normal varieties of relative dimension one over k. Assume that the generic fiber
$g: X\to Z$
be a fibration of normal varieties of relative dimension one over k. Assume that the generic fiber
![]() $X_{\eta }$
of g is a curve with arithmetic genus
$X_{\eta }$
of g is a curve with arithmetic genus
![]() $p_{a}(X_{\eta }) = 1$
. Then the geometric generic fiber
$p_{a}(X_{\eta }) = 1$
. Then the geometric generic fiber
![]() $X_{\overline {\eta }}$
of g is a smooth elliptic curve over
$X_{\overline {\eta }}$
of g is a smooth elliptic curve over
![]() $\overline {K(Z)}$
(see [Reference Zhang30, Prop. 2.11]).
$\overline {K(Z)}$
(see [Reference Zhang30, Prop. 2.11]).
P 3: (Dlt adjunction) Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over k. Then every irreducible component of
${\mathbb Q}$
-factorial projective dlt threefold pair over k. Then every irreducible component of
![]() $\lfloor B \rfloor $
is normal. If, moreover,
$\lfloor B \rfloor $
is normal. If, moreover,
![]() $(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then it is semi-ample (see [Reference Das and Hacon7, §2] and [Reference Waldron26, Th. 1.3]).
$(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then it is semi-ample (see [Reference Das and Hacon7, §2] and [Reference Waldron26, Th. 1.3]).
P 4: (Classification of surface F-singularity) Klt surface singularities over k are strongly F-regular (see [Reference Hara14]).
Remark 3.1. These proposition are not independent. For example, the proof of P 1 uses P 4.
Now we assume that the characteristic of k is just greater than
![]() $3$
. Then P 1 and P 2 hold by [Reference Hacon and Witaszek12] and [Reference Zhang30, Prop. 2.11]. Although P 3 may not hold, it is not far from being true. More precisely, if
$3$
. Then P 1 and P 2 hold by [Reference Hacon and Witaszek12] and [Reference Zhang30, Prop. 2.11]. Although P 3 may not hold, it is not far from being true. More precisely, if
![]() $(X,B)$
is a
$(X,B)$
is a
![]() ${\mathbb Q}$
-factorial dlt threefold pair over k, then every irreducible component of
${\mathbb Q}$
-factorial dlt threefold pair over k, then every irreducible component of
![]() $\lfloor B \rfloor $
is normal up to a universal homeomorphism by [Reference Hacon and Witaszek11, Rem. 3.9]. If, moreover,
$\lfloor B \rfloor $
is normal up to a universal homeomorphism by [Reference Hacon and Witaszek11, Rem. 3.9]. If, moreover,
![]() $(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then it is semi-ample by Theorem 2.21. Finally, P 4 may not hold.
$(K_{X}+ B)|_{\lfloor B\rfloor }$
is nef, then it is semi-ample by Theorem 2.21. Finally, P 4 may not hold.
First, we generalize the results on subadditivity of Kodaira dimensions in [Reference Zhang30] to the case when the characteristic is greater than
![]() $3$
(see Theorem 3.4). To do this, we need the following lemmas.
$3$
(see Theorem 3.4). To do this, we need the following lemmas.
Lemma 3.2 (cf. [Reference Zhang30, Lem. 4.10]).
Let
![]() $(\hat {X},\hat {B})$
be a
$(\hat {X},\hat {B})$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and let
$>3$
, and let
![]() $\hat {f}:\hat {X}\to Y$
be a fibration to a normal variety. Assume that
$\hat {f}:\hat {X}\to Y$
be a fibration to a normal variety. Assume that
![]() $K_{\hat {X}}+\hat {B}$
is nef and
$K_{\hat {X}}+\hat {B}$
is nef and
![]() $\hat {B}=G_{1}+G_{2}+\cdots +G_{n}$
is a sum of prime Weil divisors. Denote the normalization of
$\hat {B}=G_{1}+G_{2}+\cdots +G_{n}$
is a sum of prime Weil divisors. Denote the normalization of
![]() $G_{j}$
by
$G_{j}$
by
![]() $G^{\nu }_{j}$
for every
$G^{\nu }_{j}$
for every
![]() $j=1,2,\dots ,n$
. Then for every
$j=1,2,\dots ,n$
. Then for every
![]() $j=1,2,\dots ,n$
,
$j=1,2,\dots ,n$
,
![]() $(K_{\hat {X}}+\hat {B})|_{G_{j}}$
is semi-ample. Moreover, a general fiber
$(K_{\hat {X}}+\hat {B})|_{G_{j}}$
is semi-ample. Moreover, a general fiber
![]() $F_{j}$
of the Iitaka fibration induced by
$F_{j}$
of the Iitaka fibration induced by
![]() $(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
is integral. We denote the image of
$(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
is integral. We denote the image of
![]() $F_{j}$
along the normalization
$F_{j}$
along the normalization
![]() $G^{\nu }_{j}\to G_{j}$
by
$G^{\nu }_{j}\to G_{j}$
by
![]() $\hat {F}_{j}$
.
$\hat {F}_{j}$
.
Assume, in addition, that:
(a) there exist
![]() $N> 0$
and two different effective Cartier divisors
$N> 0$
and two different effective Cartier divisors
![]() $\hat {D}_{i}$
,
$\hat {D}_{i}$
,
![]() $i= 1,2$
such that
$i= 1,2$
such that
for some
![]() $L_{i}\in \mathrm {Pic}^{0}(Y)$
and that
$L_{i}\in \mathrm {Pic}^{0}(Y)$
and that
![]() $\mathrm {Supp}\ \hat {D}_{i}\subseteq \mathrm {Supp}\ \hat {B}$
,
$\mathrm {Supp}\ \hat {D}_{i}\subseteq \mathrm {Supp}\ \hat {B}$
,
(b) there exist effective divisors
![]() $\hat {G}_{1},\hat {G}_{2},\hat {G}^{\prime }_{1},\hat {G}^{\prime }_{2}$
such that
$\hat {G}_{1},\hat {G}_{2},\hat {G}^{\prime }_{1},\hat {G}^{\prime }_{2}$
such that
where
![]() $a_{11}> a_{21}\geq 0$
and
$a_{11}> a_{21}\geq 0$
and
![]() $a_{22}> a_{12} \geq 0$
, and
$a_{22}> a_{12} \geq 0$
, and
(c)
![]() $G_{1}, G_{2}$
are two irreducible components of
$G_{1}, G_{2}$
are two irreducible components of
![]() $\hat {G} _{1}, \hat {G}_{2}$
respectively, such that for
$\hat {G} _{1}, \hat {G}_{2}$
respectively, such that for
![]() $i, j\in \{1, 2\}$
and
$i, j\in \{1, 2\}$
and
![]() $i \neq j$
,
$i \neq j$
,
![]() $\hat {F}_{j}$
dominates Y and
$\hat {F}_{j}$
dominates Y and
Then both
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{2}$
are torsion line bundles.
$L_{2}$
are torsion line bundles.
Furthermore, condition (c) holds, if for
![]() $j = 1, 2$
,
$j = 1, 2$
,
![]() $G_{j}$
is not a component of
$G_{j}$
is not a component of
![]() $\hat {G}^{\prime \prime }_{j}$
and
$\hat {G}^{\prime \prime }_{j}$
and
![]() ${\kappa (F_{j})\geq 0}$
.
${\kappa (F_{j})\geq 0}$
.
Proof. By Theorem 2.21, we have
![]() $(K_{\hat {X}}+\hat {B})|_{\hat {B}}=(K_{\hat {X}}+\hat {B})|_{\lfloor \hat {B}\rfloor }$
is semi-ample. In particular,
$(K_{\hat {X}}+\hat {B})|_{\hat {B}}=(K_{\hat {X}}+\hat {B})|_{\lfloor \hat {B}\rfloor }$
is semi-ample. In particular,
![]() $(K_{\hat {X}}+\hat {B})|_{G_{j}}$
, and hence
$(K_{\hat {X}}+\hat {B})|_{G_{j}}$
, and hence
![]() $(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
are semi-ample for every
$(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
are semi-ample for every
![]() $j=1,2,\dots ,n$
. Moreover, a general fiber
$j=1,2,\dots ,n$
. Moreover, a general fiber
![]() $F_{j}$
of the Iitaka fibration induced by
$F_{j}$
of the Iitaka fibration induced by
![]() $(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
is integral by [Reference Zhang30, Prop. 2.1]. Hence, the first assertion holds.
$(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{j}}$
is integral by [Reference Zhang30, Prop. 2.1]. Hence, the first assertion holds.
Now we assume (a), (b), and (c). Note that
since
![]() $(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{1}}$
is semi-ample and
$(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{1}}$
is semi-ample and
![]() $F_{1}$
is a general fiber of the Iitaka fibration of
$F_{1}$
is a general fiber of the Iitaka fibration of
![]() $(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{1}}$
. We have
$(K_{\hat {X}}+\hat {B})|_{G^{\nu }_{1}}$
. We have
 $$ \begin{align*}\begin{aligned} a_{21}\hat{f}^{\ast}L_{1}|_{F_{1}}&\sim_{{\mathbb Q}} a_{21}(N(K_{\hat{X}} + \hat{B})+ \hat{f}^{\ast}L_{1})|_{F_{1}} \\ &\sim_{{\mathbb Q}} a_{21}\hat{D}_{1}|_{F_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{(by\ (a))} \\ &\sim_{{\mathbb Q}}a_{21}(a_{11}\hat{G}_{1}+a_{12}\hat{G}_{2}+\hat{G}^{\prime}_{1})|_{F_{1}}\ \ \ \mathrm{(by\ (b))}\\ &\sim_{{\mathbb Q}}a_{11}a_{21}\hat{G}_{1}|_{F_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{(by\ (c)).} \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} a_{21}\hat{f}^{\ast}L_{1}|_{F_{1}}&\sim_{{\mathbb Q}} a_{21}(N(K_{\hat{X}} + \hat{B})+ \hat{f}^{\ast}L_{1})|_{F_{1}} \\ &\sim_{{\mathbb Q}} a_{21}\hat{D}_{1}|_{F_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{(by\ (a))} \\ &\sim_{{\mathbb Q}}a_{21}(a_{11}\hat{G}_{1}+a_{12}\hat{G}_{2}+\hat{G}^{\prime}_{1})|_{F_{1}}\ \ \ \mathrm{(by\ (b))}\\ &\sim_{{\mathbb Q}}a_{11}a_{21}\hat{G}_{1}|_{F_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{(by\ (c)).} \end{aligned}\end{align*} $$
Similarly,
![]() $a_{11}\hat {f}^{\ast }L_{2}|_{F_{1}}\sim _{{\mathbb Q}}a_{11}a_{21}\hat {G}_{1}|_{F_{1}}$
. Hence, we have
$a_{11}\hat {f}^{\ast }L_{2}|_{F_{1}}\sim _{{\mathbb Q}}a_{11}a_{21}\hat {G}_{1}|_{F_{1}}$
. Hence, we have
![]() $a_{21}\hat {f}^{\ast }L_{1}|_{F_{1}}\sim _{{\mathbb Q}}a_{11}\hat {f}^{\ast }L_{2}|_{F_{1}}$
. It follows that
$a_{21}\hat {f}^{\ast }L_{1}|_{F_{1}}\sim _{{\mathbb Q}}a_{11}\hat {f}^{\ast }L_{2}|_{F_{1}}$
. It follows that
![]() $a_{21}L_{1}\sim _{{\mathbb Q}}a_{11}L_{2}$
by [Reference Zhang30, Lem. 2.4]. Similarly, we have
$a_{21}L_{1}\sim _{{\mathbb Q}}a_{11}L_{2}$
by [Reference Zhang30, Lem. 2.4]. Similarly, we have
![]() $a_{22}L_{1}\sim _{{\mathbb Q}}a_{12}L_{2}$
. We then deduce that
$a_{22}L_{1}\sim _{{\mathbb Q}}a_{12}L_{2}$
. We then deduce that
![]() $L_{1}\sim _{{\mathbb Q}}L_{2}\sim _{{\mathbb Q}}0$
since
$L_{1}\sim _{{\mathbb Q}}L_{2}\sim _{{\mathbb Q}}0$
since
![]() $a_{11}> a_{21}\geq 0$
and
$a_{11}> a_{21}\geq 0$
and
![]() $a_{22}> a_{12} \geq 0$
. Hence the second assertion holds.
$a_{22}> a_{12} \geq 0$
. Hence the second assertion holds.
It remains to prove the third assertion. As
![]() $\kappa (F_{j})\geq 0$
, we have the canonical divisor
$\kappa (F_{j})\geq 0$
, we have the canonical divisor
![]() $K_{F^{\nu }_{j}}\geq 0$
, where
$K_{F^{\nu }_{j}}\geq 0$
, where
![]() $F_{j}^{\nu }$
is the normalization of
$F_{j}^{\nu }$
is the normalization of
![]() $F_{j}$
. Applying the adjunction formula, we get
$F_{j}$
. Applying the adjunction formula, we get
 $$ \begin{align*}\begin{aligned} 0\sim_{{\mathbb Q}} (K_{\hat{X}} + \hat{B})|_{F_{j}^{\nu}}&\sim_{{\mathbb Q}}((K_{\hat{X}} + \hat{B})|_{G^{\nu}_{j}})|_{F_{j}^{\nu}} \\ &\sim_{{\mathbb Q}}((K_{\hat{X}}+G_{j})|_{G^{\nu}_{j}} + (\hat{B}-G_{j})|_{G^{\nu}_{j}})|_{F_{j}^{\nu}} \\ &\sim_{{\mathbb Q}} (K_{G^{\nu}_{j}}+C_{j})|_{F^{\nu}_{j}} + (\hat{B}-G_{j})|_{F_{j}^{\nu}}\\ &\sim_{{\mathbb Q}}K_{F^{\nu}_{j}}+C_{j}|_{F^{\nu}_{j}} + (\hat{B}-G_{j})|_{F_{j}^{\nu}}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} 0\sim_{{\mathbb Q}} (K_{\hat{X}} + \hat{B})|_{F_{j}^{\nu}}&\sim_{{\mathbb Q}}((K_{\hat{X}} + \hat{B})|_{G^{\nu}_{j}})|_{F_{j}^{\nu}} \\ &\sim_{{\mathbb Q}}((K_{\hat{X}}+G_{j})|_{G^{\nu}_{j}} + (\hat{B}-G_{j})|_{G^{\nu}_{j}})|_{F_{j}^{\nu}} \\ &\sim_{{\mathbb Q}} (K_{G^{\nu}_{j}}+C_{j})|_{F^{\nu}_{j}} + (\hat{B}-G_{j})|_{F_{j}^{\nu}}\\ &\sim_{{\mathbb Q}}K_{F^{\nu}_{j}}+C_{j}|_{F^{\nu}_{j}} + (\hat{B}-G_{j})|_{F_{j}^{\nu}}, \end{aligned}\end{align*} $$
where
![]() $C_{j}\geq 0$
on
$C_{j}\geq 0$
on
![]() $G^{\nu }_{j}$
. It implies that
$G^{\nu }_{j}$
. It implies that
![]() $(\hat {B}-G_{j})|_{F_{j}^{\nu }}\leq 0$
. Since
$(\hat {B}-G_{j})|_{F_{j}^{\nu }}\leq 0$
. Since
![]() $F_{j}$
is general,
$F_{j}$
is general,
![]() $\hat {F}_{j}$
is not contained in
$\hat {F}_{j}$
is not contained in
![]() $\hat {B}-G_{j}$
. Hence,
$\hat {B}-G_{j}$
. Hence,
![]() $\hat {F}_{j}\cap \mathrm {Supp}(\hat {B}-G_{j})=\emptyset $
. By our assumption,
$\hat {F}_{j}\cap \mathrm {Supp}(\hat {B}-G_{j})=\emptyset $
. By our assumption,
![]() $G_{j}$
is not a component of
$G_{j}$
is not a component of
![]() $\hat {G}^{\prime \prime }_{j}$
. Thus,
$\hat {G}^{\prime \prime }_{j}$
. Thus,
![]() $\mathrm {Supp}(\hat {G}^{\prime \prime }_{j})\subseteq \mathrm {Supp}(\hat {B}-G_{j})$
. It follows that
$\mathrm {Supp}(\hat {G}^{\prime \prime }_{j})\subseteq \mathrm {Supp}(\hat {B}-G_{j})$
. It follows that
![]() $\hat {F}_{j}\cap \mathrm {Supp}(\hat {G}^{\prime \prime }_{j})=\emptyset $
.
$\hat {F}_{j}\cap \mathrm {Supp}(\hat {G}^{\prime \prime }_{j})=\emptyset $
.
Lemma 3.3. Let
![]() $(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. Assume that
$>3$
. Assume that
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (X,K_{X}+B)\geq 1$
. Then
$\kappa (X,K_{X}+B)\geq 1$
. Then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. The case of
![]() $\kappa (X,K_{X}+B)=3$
follows from [Reference Hacon and Witaszek12, Th. 1.3]. In the cases of
$\kappa (X,K_{X}+B)=3$
follows from [Reference Hacon and Witaszek12, Th. 1.3]. In the cases of
![]() $\kappa (X,K_{X}+B)= 1\ \mathrm {or}\ 2$
, the assertion is proved when the characteristic of k is greater than
$\kappa (X,K_{X}+B)= 1\ \mathrm {or}\ 2$
, the assertion is proved when the characteristic of k is greater than
![]() $5$
in [Reference Waldron25, Th. 1.3], [Reference Zhang29, Th. 3.1], and [Reference Das and Waldron8, Th. A]. And it uses the assumption of characteristic
$5$
in [Reference Waldron25, Th. 1.3], [Reference Zhang29, Th. 3.1], and [Reference Das and Waldron8, Th. A]. And it uses the assumption of characteristic
![]() $>5$
for P 1. When the characteristic of k is greater than
$>5$
for P 1. When the characteristic of k is greater than
![]() $3$
, by Theorem 2.12, P 1 also holds. Hence, we can argue as in the proofs of [Reference Waldron25, Th. 1.3], [Reference Zhang29, Th. 3.1], and [Reference Das and Waldron8, Th. A] to prove the assertion.
$3$
, by Theorem 2.12, P 1 also holds. Hence, we can argue as in the proofs of [Reference Waldron25, Th. 1.3], [Reference Zhang29, Th. 3.1], and [Reference Das and Waldron8, Th. A] to prove the assertion.
Now we can deduce the following result on subadditivity of Kodaira dimensions in characteristic
![]() $>3$
.
$>3$
.
Theorem 3.4. Let
![]() $f: X\to Y$
be a fibration from a
$f: X\to Y$
be a fibration from a
![]() ${\mathbb Q}$
-factorial projective threefold to a smooth projective variety of dimension
${\mathbb Q}$
-factorial projective threefold to a smooth projective variety of dimension
![]() $1$
or
$1$
or
![]() $2$
, over an algebraically closed field k of characteristic
$2$
, over an algebraically closed field k of characteristic
![]() $p> 3$
. Assume that there is an effective
$p> 3$
. Assume that there is an effective
![]() ${\mathbb Q}$
-divisor B on X such that
${\mathbb Q}$
-divisor B on X such that
![]() $(X, B)$
is klt. Assume that Y is of maximal Albanese dimension. Moreover, we assume that if
$(X, B)$
is klt. Assume that Y is of maximal Albanese dimension. Moreover, we assume that if
![]() $\kappa (X_{\eta }, K_{X_{\eta }}+ B_{\eta }) =\mathrm {dim}\ X-\mathrm {dim}\ Y- 1,$
where
$\kappa (X_{\eta }, K_{X_{\eta }}+ B_{\eta }) =\mathrm {dim}\ X-\mathrm {dim}\ Y- 1,$
where
![]() $X_{\eta }$
is the generic fiber of f and
$X_{\eta }$
is the generic fiber of f and
![]() $K_{X_{\eta }}+ B_{\eta }:=(K_{X}+B)|_{X_{\eta }}$
, then B does not intersect the generic fiber
$K_{X_{\eta }}+ B_{\eta }:=(K_{X}+B)|_{X_{\eta }}$
, then B does not intersect the generic fiber
![]() $X_{\xi }$
of the relative Iitaka fibration
$X_{\xi }$
of the relative Iitaka fibration
![]() $I: X \dashrightarrow Z$
induced by
$I: X \dashrightarrow Z$
induced by
![]() $K_{X}+ B$
on X over Y.
$K_{X}+ B$
on X over Y.
Then
Proof. The case when the characteristic is greater than
![]() $5$
is proved in [Reference Zhang30, Th. 1.4]. Using Theorem 2.12 and Lemma 3.3, we can argue as in the proof of [Reference Zhang30, Th. 1.4] except in the cases when:
$5$
is proved in [Reference Zhang30, Th. 1.4]. Using Theorem 2.12 and Lemma 3.3, we can argue as in the proof of [Reference Zhang30, Th. 1.4] except in the cases when:
(1) Y is an elliptic curve or a simple abelian surface, and
![]() $K_{X}+B$
is f-big, or
$K_{X}+B$
is f-big, or
(2) Y is an elliptic curve,
![]() $\kappa (X_{\eta }, K_{X_{\eta }}+ B_{\eta }) =1$
and B does not intersect the generic fiber
$\kappa (X_{\eta }, K_{X_{\eta }}+ B_{\eta }) =1$
and B does not intersect the generic fiber
![]() $X_{\xi }$
of the relative Iitaka fibration
$X_{\xi }$
of the relative Iitaka fibration
![]() $I: X \dashrightarrow Z$
induced by
$I: X \dashrightarrow Z$
induced by
![]() $K_{X}+ B$
on X over Y.
$K_{X}+ B$
on X over Y.
Now we assume that we are in one of these cases. We first make some reductions as follows. In the case (1), if the characteristic of k is greater than
![]() $5$
, then the proof of [Reference Zhang30, Th. 4.2] reduces the assertion to the case when:
$5$
, then the proof of [Reference Zhang30, Th. 4.2] reduces the assertion to the case when:
![]() $\bullet $
the denominators of coefficients of B are not divisible by p,
$\bullet $
the denominators of coefficients of B are not divisible by p,
![]() $\bullet $
$\bullet $
![]() $K_{X}+B$
is a nef and f-ample,
$K_{X}+B$
is a nef and f-ample,
![]() $\bullet $
$\bullet $
![]() $\nu (K_{X}+B)\leq 2$
,
$\nu (K_{X}+B)\leq 2$
,
![]() $\bullet $
there exist a sufficiently divisible positive integer l and a coherent sheaf
$\bullet $
there exist a sufficiently divisible positive integer l and a coherent sheaf
![]() ${\mathcal F}$
such that
${\mathcal F}$
such that
![]() ${\mathcal F}$
is a subsheaf of
${\mathcal F}$
is a subsheaf of
![]() $f_{\ast }{\mathcal O}_{X}(l(K_{X}+B))$
,
$f_{\ast }{\mathcal O}_{X}(l(K_{X}+B))$
,
![]() $\bullet $
there exists an isogeny
$\bullet $
there exists an isogeny
![]() $\tau :Y_{1}\to Y$
between abelian varieties, some
$\tau :Y_{1}\to Y$
between abelian varieties, some
![]() $P_{i}\in \mathrm {Pic}^{0}(Y_{1})$
and a generically surjective homomorphism
$P_{i}\in \mathrm {Pic}^{0}(Y_{1})$
and a generically surjective homomorphism
In the case (2), if the characteristic of k is greater than
![]() $5$
, the proof of [Reference Zhang30, Th. 4.3] reduces the assertion to the case when:
$5$
, the proof of [Reference Zhang30, Th. 4.3] reduces the assertion to the case when:
![]() $\bullet $
$\bullet $
![]() $K_{X}+B$
is nef,
$K_{X}+B$
is nef,
![]() $\bullet $
there exists a commutative diagram:
$\bullet $
there exists a commutative diagram:

where
![]() $\sigma $
is a log resolution, h is a fibration to a smooth projective surface which is birational to the relative Iitaka fibration induced by
$\sigma $
is a log resolution, h is a fibration to a smooth projective surface which is birational to the relative Iitaka fibration induced by
![]() $\sigma ^{\ast }(K_{X}+B)$
on W over Y,
$\sigma ^{\ast }(K_{X}+B)$
on W over Y,
![]() $\bullet $
there exist a nef and g-big divisor C on Z such that
$\bullet $
there exist a nef and g-big divisor C on Z such that
![]() $\sigma ^{\ast }(K_{X}+B)\sim _{{\mathbb Q}}h^{\ast }C$
,
$\sigma ^{\ast }(K_{X}+B)\sim _{{\mathbb Q}}h^{\ast }C$
,
![]() $\bullet $
the geometric generic fiber of g is either a smooth elliptic curve or a rational curve,
$\bullet $
the geometric generic fiber of g is either a smooth elliptic curve or a rational curve,
![]() $\bullet $
$\bullet $
![]() $\nu (Z,C)=1$
,
$\nu (Z,C)=1$
,
![]() $\bullet $
there exist a sufficiently divisible positive integer l and a nef sub-vector bundle V of
$\bullet $
there exist a sufficiently divisible positive integer l and a nef sub-vector bundle V of
![]() $f_{\ast }{\mathcal O}_{X}(l(K_{X}+B))$
of rank
$f_{\ast }{\mathcal O}_{X}(l(K_{X}+B))$
of rank
![]() $r\geq 2$
,
$r\geq 2$
,
![]() $\bullet $
there exists a flat base change
$\bullet $
there exists a flat base change
![]() $\pi :Y_{2}\to Y$
between elliptic curves such that
$\pi :Y_{2}\to Y$
between elliptic curves such that
where
![]() $L_{i}^{\prime }\in \mathrm {Pic}^{0}(Y_{2}).$
$L_{i}^{\prime }\in \mathrm {Pic}^{0}(Y_{2}).$
When the characteristic of k is greater than
![]() $3$
, using Theorem 2.12 and Lemma 3.3, we can also argue as in the proofs of [Reference Zhang30, Ths. 4.2 and 4.3] to make such reductions.
$3$
, using Theorem 2.12 and Lemma 3.3, we can also argue as in the proofs of [Reference Zhang30, Ths. 4.2 and 4.3] to make such reductions.
If the characteristic of k is greater than
![]() $5$
, then the argument in [Reference Zhang30, Steps 2, 3 of the proof of Th. 4.2 and Steps 2, 3 of the proof of Th. 4.3] implies that there exist an integer
$5$
, then the argument in [Reference Zhang30, Steps 2, 3 of the proof of Th. 4.2 and Steps 2, 3 of the proof of Th. 4.3] implies that there exist an integer
![]() $m_{1}$
and some divisors
$m_{1}$
and some divisors
![]() $D_{i}\in |m_{1}(K_{X}+B)+f^{\ast }L_{i}|$
,
$D_{i}\in |m_{1}(K_{X}+B)+f^{\ast }L_{i}|$
,
![]() $i=1,2,\dots ,r$
for some
$i=1,2,\dots ,r$
for some
![]() $L_{i}\in \mathrm {Pic}^{0}(Y)$
. Moreover, we can construct a pair
$L_{i}\in \mathrm {Pic}^{0}(Y)$
. Moreover, we can construct a pair
![]() $(\hat {X},\hat {B})$
and divisors
$(\hat {X},\hat {B})$
and divisors
![]() $\hat {D}_{1},\hat {D}_{2}$
satisfying all conditions of Lemma 3.2. When the characteristic of k is greater than
$\hat {D}_{1},\hat {D}_{2}$
satisfying all conditions of Lemma 3.2. When the characteristic of k is greater than
![]() $3$
, using Theorem 2.12, we can also argue as in the proofs of [Reference Zhang30, Ths. 4.2 and 4.3] to prove these assertions. By Lemma 3.2,
$3$
, using Theorem 2.12, we can also argue as in the proofs of [Reference Zhang30, Ths. 4.2 and 4.3] to prove these assertions. By Lemma 3.2,
![]() $L_{1}$
and
$L_{1}$
and
![]() $L_{2}$
are torsions. Hence, there exist a sufficiently divisible integer
$L_{2}$
are torsions. Hence, there exist a sufficiently divisible integer
![]() $N>0$
and two different divisors among
$N>0$
and two different divisors among
![]() $D_{i}$
, say,
$D_{i}$
, say,
![]() $D_{1}\neq D_{2}$
such that
$D_{1}\neq D_{2}$
such that
for
![]() $j=1,2$
. Hence we have
$j=1,2$
. Hence we have
![]() $\kappa (X,K_{X}+B)\geq 1$
. In the case (2), it implies that
$\kappa (X,K_{X}+B)\geq 1$
. In the case (2), it implies that
In the case (1), by Lemma 3.3,
![]() $K_{X}+B$
is semi-ample. Thus, for a sufficiently divisible
$K_{X}+B$
is semi-ample. Thus, for a sufficiently divisible
![]() $M>0$
, the linear system
$M>0$
, the linear system
![]() $|M(K_{X}+B)|$
has no base point. Since
$|M(K_{X}+B)|$
has no base point. Since
![]() $K_{X_{\eta }}+B_{\eta }$
is big, the restriction
$K_{X_{\eta }}+B_{\eta }$
is big, the restriction
![]() $|M(K_{X}+B)||_{X_{\eta }}$
on the generic fiber
$|M(K_{X}+B)||_{X_{\eta }}$
on the generic fiber
![]() $X_{\eta }$
defines a generically finite morphism. It implies that
$X_{\eta }$
defines a generically finite morphism. It implies that
In conclusion, the assertion holds.
Using this result on subadditivity of Kodaira dimensions in characteristic
![]() $>3$
, we deduce the following results on the abundance with nontrivial Albanese maps in characteristic
$>3$
, we deduce the following results on the abundance with nontrivial Albanese maps in characteristic
![]() $>3$
.
$>3$
.
Lemma 3.5. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective klt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective klt threefold pair over an algebraically closed field k of characteristic
![]() $> 3$
. Assume that
$> 3$
. Assume that
![]() $K_{X}+B$
is nef, X is non-uniruled and the Albanese map
$K_{X}+B$
is nef, X is non-uniruled and the Albanese map
![]() $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial. Then
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial. Then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. The case when the characteristic of k is greater than
![]() $5$
is proved in [Reference Zhang29, Th. 1.1]. When the characteristic of k is greater than
$5$
is proved in [Reference Zhang29, Th. 1.1]. When the characteristic of k is greater than
![]() $3$
, by the proof of [Reference Zhang29, Th. 1.1], we only need to prove the following assertions.
$3$
, by the proof of [Reference Zhang29, Th. 1.1], we only need to prove the following assertions.
(1) Let
![]() $f_{1}: X_{1}\to Y_{1}$
be a separable fibration from a smooth projective threefold to a smooth projective variety of dimension
$f_{1}: X_{1}\to Y_{1}$
be a separable fibration from a smooth projective threefold to a smooth projective variety of dimension
![]() $1$
or
$1$
or
![]() $2$
over k. Denote by
$2$
over k. Denote by
![]() $\tilde {X}_{1,\overline {\eta }}$
a smooth projective birational model of
$\tilde {X}_{1,\overline {\eta }}$
a smooth projective birational model of
![]() $X_{1,\overline {\eta }}$
, where
$X_{1,\overline {\eta }}$
, where
![]() $X_{1,\overline {\eta }}$
is the geometric generic fiber of
$X_{1,\overline {\eta }}$
is the geometric generic fiber of
![]() $f_{1}$
. Then
$f_{1}$
. Then
(2) Let
![]() $X_{2}$
be a
$X_{2}$
be a
![]() ${\mathbb Q}$
-factorial projective klt threefold over k with
${\mathbb Q}$
-factorial projective klt threefold over k with
![]() $K_{X_{2}} \sim _{{\mathbb Q}} 0$
, and let D be an effective and nef
$K_{X_{2}} \sim _{{\mathbb Q}} 0$
, and let D be an effective and nef
![]() ${\mathbb Q}$
-divisor on
${\mathbb Q}$
-divisor on
![]() $X_{2}$
. Assume that
$X_{2}$
. Assume that
![]() $X_{2}$
has a morphism
$X_{2}$
has a morphism
![]() $f_{2}: X_{2}\to Y_{2}$
to an elliptic curve and that
$f_{2}: X_{2}\to Y_{2}$
to an elliptic curve and that
![]() $X_{2,\overline {\eta }}$
has at most canonical singularities, where
$X_{2,\overline {\eta }}$
has at most canonical singularities, where
![]() $X_{2,\overline {\eta }}$
is the geometric generic fiber of
$X_{2,\overline {\eta }}$
is the geometric generic fiber of
![]() $f_{2}$
. Then either
$f_{2}$
. Then either
![]() $D = 0$
or
$D = 0$
or
![]() $\kappa (X_{2}, D)\geq 1$
.
$\kappa (X_{2}, D)\geq 1$
.
(1) is proved when the characteristic of k is greater than
![]() $5$
in [Reference Zhang29, Cor. 2.9]. It uses the assumption of characteristic
$5$
in [Reference Zhang29, Cor. 2.9]. It uses the assumption of characteristic
![]() $>5$
for the fact that canonical singularities over k are F-pure. This fact holds in characteristic
$>5$
for the fact that canonical singularities over k are F-pure. This fact holds in characteristic
![]() $5$
by [Reference Hara14, Th. 1.2]. Hence, (1) follows from the proof of [Reference Zhang29, Cor. 2.9]. For (2), it suffices to show that if
$5$
by [Reference Hara14, Th. 1.2]. Hence, (1) follows from the proof of [Reference Zhang29, Cor. 2.9]. For (2), it suffices to show that if
![]() $\kappa (X_{2}, D)=0$
, then
$\kappa (X_{2}, D)=0$
, then
![]() $D=0$
. We assume that
$D=0$
. We assume that
![]() $\kappa (X_{2}, D)=0$
. We denote the generic fiber of
$\kappa (X_{2}, D)=0$
. We denote the generic fiber of
![]() $f_{2}$
by
$f_{2}$
by
![]() $X_{2,\eta }$
. Note that
$X_{2,\eta }$
. Note that
and
![]() $(X_{2,\eta },D_{\eta })$
is lc after replacing D by a small multiple. By Theorem 2.11,
$(X_{2,\eta },D_{\eta })$
is lc after replacing D by a small multiple. By Theorem 2.11,
![]() $D_{\eta }$
is semi-ample. Hence
$D_{\eta }$
is semi-ample. Hence
![]() $\kappa (X_{2,\eta },D_{\eta })\geq 0$
. If
$\kappa (X_{2,\eta },D_{\eta })\geq 0$
. If
![]() $\kappa (X_{2,\eta },D_{\eta })\neq 1$
, then by Theorem 3.4, we have
$\kappa (X_{2,\eta },D_{\eta })\neq 1$
, then by Theorem 3.4, we have
![]() $\kappa (X_{2,\eta },D_{\eta })=0$
. Hence
$\kappa (X_{2,\eta },D_{\eta })=0$
. Hence
![]() $D_{\eta }\sim _{{\mathbb Q}}0$
. Note that
$D_{\eta }\sim _{{\mathbb Q}}0$
. Note that
![]() $f_{2}$
is equidimensional since
$f_{2}$
is equidimensional since
![]() $Y_{2}$
is a normal curve. By Lemma 2.10, D descends to an effective
$Y_{2}$
is a normal curve. By Lemma 2.10, D descends to an effective
![]() ${\mathbb Q}$
-divisor on
${\mathbb Q}$
-divisor on
![]() $Y_{2}$
. Hence
$Y_{2}$
. Hence
![]() $D=0$
. Otherwise, we have
$D=0$
. Otherwise, we have
![]() $\kappa (X_{2,\eta },D_{\eta })= 1$
. Then we may apply the proof of [Reference Zhang29, Cor. 2.10] to the case of the characteristic of k is greater than
$\kappa (X_{2,\eta },D_{\eta })= 1$
. Then we may apply the proof of [Reference Zhang29, Cor. 2.10] to the case of the characteristic of k is greater than
![]() $3$
. Therefore, the assertion holds.
$3$
. Therefore, the assertion holds.
Remark 3.6. The non-uniruled assumption is used in the proof of [Reference Zhang29, Th. 1.1].
Theorem 3.7. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective klt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective klt threefold pair over an algebraically closed field k of characteristic
![]() $> 3$
. Assume that
$> 3$
. Assume that
![]() $K_{X}+B$
is nef and the Albanese map
$K_{X}+B$
is nef and the Albanese map
![]() $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial. Denote by
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial. Denote by
![]() $f: X\to Y$
the fibration arising from the Stein factorization of
$f: X\to Y$
the fibration arising from the Stein factorization of
![]() $a_{X}$
and by
$a_{X}$
and by
![]() $X_{\eta }$
the generic fiber of f. Assume, moreover, that
$X_{\eta }$
the generic fiber of f. Assume, moreover, that
![]() $B = 0$
if:
$B = 0$
if:
(1)
![]() $\mathrm {dim}\ Y=2$
and
$\mathrm {dim}\ Y=2$
and
![]() $\kappa (X_{\eta },(K_{X}+B)|_{X_{\eta }})=0$
, or
$\kappa (X_{\eta },(K_{X}+B)|_{X_{\eta }})=0$
, or
(2)
![]() $\mathrm {dim}\ Y=1$
and
$\mathrm {dim}\ Y=1$
and
![]() $\kappa (X_{\eta },(K_{X}+B)|_{X_{\eta }})=1$
.
$\kappa (X_{\eta },(K_{X}+B)|_{X_{\eta }})=1$
.
Then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. The case when the characteristic is greater than
![]() $5$
is proved in [Reference Zhang30, Th. 1.2]. By Lemma 3.5, we can assume that X is uniruled. Moreover, by Lemma 3.3, we can assume that
$5$
is proved in [Reference Zhang30, Th. 1.2]. By Lemma 3.5, we can assume that X is uniruled. Moreover, by Lemma 3.3, we can assume that
![]() $\kappa (X,K_{X}+B)\leq 0$
.
$\kappa (X,K_{X}+B)\leq 0$
.
Since X is uniruled, we have
![]() $\mathrm {dim}\ Y=1\ \mathrm {or}\ 2$
. Note that
$\mathrm {dim}\ Y=1\ \mathrm {or}\ 2$
. Note that
![]() $K_{X_{\eta }}+B_{\eta }$
is semi-ample by the abundance for surfaces (Theorem 2.11) and curves. In particular,
$K_{X_{\eta }}+B_{\eta }$
is semi-ample by the abundance for surfaces (Theorem 2.11) and curves. In particular,
![]() $\kappa (X_{\eta },K_{X_{\eta }}+B_{\eta })\geq 0$
. Therefore by Theorem 3.4, we have
$\kappa (X_{\eta },K_{X_{\eta }}+B_{\eta })\geq 0$
. Therefore by Theorem 3.4, we have
![]() $\kappa (X,K_{X}+B)=0$
, and hence
$\kappa (X,K_{X}+B)=0$
, and hence
![]() $\kappa (Y)=\kappa (X_{\eta },K_{X_{\eta }}+B_{\eta })=0$
. If
$\kappa (Y)=\kappa (X_{\eta },K_{X_{\eta }}+B_{\eta })=0$
. If
![]() $\mathrm {dim}\ Y=1$
, then the assertion is proved when the characteristic of k is greater than
$\mathrm {dim}\ Y=1$
, then the assertion is proved when the characteristic of k is greater than
![]() $5$
in [Reference Zhang30, Th. 4.4]. Using Theorem 3.4, we can argue as in the proof of [Reference Zhang30, Th. 4.4] to prove that
$5$
in [Reference Zhang30, Th. 4.4]. Using Theorem 3.4, we can argue as in the proof of [Reference Zhang30, Th. 4.4] to prove that
![]() $K_{X}+B$
is semi-ample. Otherwise, we have
$K_{X}+B$
is semi-ample. Otherwise, we have
![]() $\mathrm {dim}\ Y=2$
. Then
$\mathrm {dim}\ Y=2$
. Then
![]() $B=0$
by our assumption and f is an elliptic fibration by [Reference Zhang30, Prop. 2.11]. Hence X is non-uniruled. We obtain a contradiction. Thus,
$B=0$
by our assumption and f is an elliptic fibration by [Reference Zhang30, Prop. 2.11]. Hence X is non-uniruled. We obtain a contradiction. Thus,
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Corollary 3.8. Let X be a projective terminal threefold over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}$
is pseudo-effective, then
$K_{X}$
is pseudo-effective, then
![]() $\kappa (X, K_{X})\geq 0$
.
$\kappa (X, K_{X})\geq 0$
.
Proof. The case when the characteristic of k is greater than
![]() $5$
is proved in [Reference Xu and Zhang28, Th. 1.1]. Using Theorem 3.7, we can argue as in the proof of [Reference Xu and Zhang28, Th. 1.1] to prove the assertion.
$5$
is proved in [Reference Xu and Zhang28, Th. 1.1]. Using Theorem 3.7, we can argue as in the proof of [Reference Xu and Zhang28, Th. 1.1] to prove the assertion.
Now we can generalize Theorem 2.22 to the case when the characteristic is greater than
![]() $3$
.
$3$
.
Theorem 3.9. Let
![]() $(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that
$>3$
such that
![]() $K_{X}+B$
is nef. Assume that one of the following conditions holds:
$K_{X}+B$
is nef. Assume that one of the following conditions holds:
(1)
![]() $\kappa (X,K_{X}+B)\geq 1$
,
$\kappa (X,K_{X}+B)\geq 1$
,
(2) the nef dimension
![]() $n(X,K_{X}+B)\leq 2$
,
$n(X,K_{X}+B)\leq 2$
,
(3) the Albanese map
![]() $a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
$a_{X}: X\to \mathrm {Alb}(X)$
is nontrivial.
Then
![]() $K_{X}+ B$
is semi-ample.
$K_{X}+ B$
is semi-ample.
Proof. See Lemma 3.3 for (1). For (2), it is proved when the characteristic of k is greater than
![]() $5$
in [Reference Witaszek27, Th. 5]. Using Theorem 3.7 in the case of
$5$
in [Reference Witaszek27, Th. 5]. Using Theorem 3.7 in the case of
![]() $n(X,K_{X}+B)=0$
, we can argue as in the proof of [Reference Witaszek27, Th. 5] to prove the assertion. For (3), it is proved when the characteristic of k is greater than
$n(X,K_{X}+B)=0$
, we can argue as in the proof of [Reference Witaszek27, Th. 5] to prove the assertion. For (3), it is proved when the characteristic of k is greater than
![]() $5$
in [Reference Witaszek27, Cor. 4.13]. Using Theorem 3.7 and (2), we can argue as in the proof of [Reference Witaszek27, Cor. 4.13] to prove the assertion.
$5$
in [Reference Witaszek27, Cor. 4.13]. Using Theorem 3.7 and (2), we can argue as in the proof of [Reference Witaszek27, Cor. 4.13] to prove the assertion.
Moreover, we can deduce the nonvanishing theorem for klt threefold pairs in characteristic
![]() $>3$
.
$>3$
.
Theorem 3.10. Let
![]() $(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective klt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is pseudo-effective, then
$K_{X}+B$
is pseudo-effective, then
![]() $\kappa (K_{X}+B)\geq 0$
.
$\kappa (K_{X}+B)\geq 0$
.
Proof. It is proved when the characteristic of k is greater than
![]() $5$
in [Reference Witaszek27, Th. 3]. Using Corollary 3.8 and (2) of Theorem 3.9, we can argue as in the proof of [Reference Witaszek27, Th. 3] to prove the assertion.
$5$
in [Reference Witaszek27, Th. 3]. Using Corollary 3.8 and (2) of Theorem 3.9, we can argue as in the proof of [Reference Witaszek27, Th. 3] to prove the assertion.
4 Nonvanishing theorem for lc threefold pairs
In this section, we show the nonvanishing theorem for projective lc threefold pairs. First, we recall a standard lemma on modifying a pair by some birational transform.
Lemma 4.1. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial dlt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial dlt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. Suppose that
$>3$
. Suppose that
![]() $K_{X}+B$
is nef and there exists an effective
$K_{X}+B$
is nef and there exists an effective
![]() ${\mathbb Q}$
-divisor D such that
${\mathbb Q}$
-divisor D such that
![]() $D\equiv K_{X}+B$
. Then there exists a
$D\equiv K_{X}+B$
. Then there exists a
![]() ${\mathbb Q}$
-factorial dlt pair
${\mathbb Q}$
-factorial dlt pair
![]() $(Y,B_{Y})$
such that:
$(Y,B_{Y})$
such that:
(1)
![]() $K_{Y}+B_{Y}$
is nef,
$K_{Y}+B_{Y}$
is nef,
(2)
![]() $n(K_{Y}+B_{Y})=n(K_{X}+B)$
,
$n(K_{Y}+B_{Y})=n(K_{X}+B)$
,
(3)
![]() $\kappa (K_{X}+B)\leq \kappa (K_{Y}+B_{Y})\leq \kappa (K_{X}+B+rD)$
for some
$\kappa (K_{X}+B)\leq \kappa (K_{Y}+B_{Y})\leq \kappa (K_{X}+B+rD)$
for some
![]() $r>0$
,
$r>0$
,
(4)
![]() $K_{Y}+B_{Y}\equiv \Delta $
for an effective
$K_{Y}+B_{Y}\equiv \Delta $
for an effective
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $\Delta $
with
$\Delta $
with
![]() $\mathrm {Supp}\ \Delta \subseteq \lfloor B_{Y}\rfloor $
,
$\mathrm {Supp}\ \Delta \subseteq \lfloor B_{Y}\rfloor $
,
(5)
![]() $(Y\backslash \mathrm {Supp}\ \Delta ,B_{Y})\cong (X\backslash \mathrm {Supp}\ D,B)$
.
$(Y\backslash \mathrm {Supp}\ \Delta ,B_{Y})\cong (X\backslash \mathrm {Supp}\ D,B)$
.
Moreover, if
![]() $D \sim _{{\mathbb Q}} K_{X}+B$
, then
$D \sim _{{\mathbb Q}} K_{X}+B$
, then
![]() $K_{Y}+ B_{Y} \sim _{{\mathbb Q}} \Delta $
in (4).
$K_{Y}+ B_{Y} \sim _{{\mathbb Q}} \Delta $
in (4).
Proof. It follows from Theorem 2.12 and the proof of [Reference Witaszek27, Lem. 4.6].
The following lemma is proved by Witaszek via his weak canonical bundle formula.
Lemma 4.2 [Reference Witaszek27, Lem. 4.8].
Let
![]() $(X,B)$
be a projective
$(X,B)$
be a projective
![]() ${\mathbb Q}$
-factorial threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that the coefficients of B are at most one. Assume that
$>3$
such that the coefficients of B are at most one. Assume that
![]() $L := K_{X}+B$
is nef and
$L := K_{X}+B$
is nef and
![]() $n(L) = 2$
. Then the following hold:
$n(L) = 2$
. Then the following hold:
(1) there exists an effective
![]() ${\mathbb Q}$
-divisor D such that
${\mathbb Q}$
-divisor D such that
![]() $L \equiv D$
,
$L \equiv D$
,
(2) if
![]() $L|_{\mathrm {Supp}\ D} \sim _{{\mathbb Q}} 0$
for some D as above, then
$L|_{\mathrm {Supp}\ D} \sim _{{\mathbb Q}} 0$
for some D as above, then
![]() $\kappa (L) \geq 0$
,
$\kappa (L) \geq 0$
,
(3) if
![]() $L|_{\mathrm {Supp}\ D}\not \equiv 0$
for some D as above, or
$L|_{\mathrm {Supp}\ D}\not \equiv 0$
for some D as above, or
![]() $L|_{\mathrm {Supp}\ D} \sim _{{\mathbb Q}}0$
and
$L|_{\mathrm {Supp}\ D} \sim _{{\mathbb Q}}0$
and
![]() $L\sim _{{\mathbb Q}} D$
, then
$L\sim _{{\mathbb Q}} D$
, then
![]() $\kappa (L)= 2$
.
$\kappa (L)= 2$
.
Then we can deduce the following proposition.
Proposition 4.3. Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $n(X,K_{X}+B)= 2$
, then
$n(X,K_{X}+B)= 2$
, then
![]() $\kappa (K_{X}+B)=2$
.
$\kappa (K_{X}+B)=2$
.
Proof. The proof is similar to the proof of [Reference Witaszek27, Prop. 4.10]. By Theorem 2.20, replacing
![]() $(X,B)$
by a
$(X,B)$
by a
![]() ${\mathbb Q}$
-factorial dlt model, we may assume that
${\mathbb Q}$
-factorial dlt model, we may assume that
![]() $(X,B)$
is
$(X,B)$
is
![]() ${\mathbb Q}$
-factorial and dlt. By Lemma 4.2, there exists an effective
${\mathbb Q}$
-factorial and dlt. By Lemma 4.2, there exists an effective
![]() ${\mathbb Q}$
-divisor D satisfying
${\mathbb Q}$
-divisor D satisfying
![]() $K_{X}+B\equiv D$
. Now by Lemma 4.1, we have a
$K_{X}+B\equiv D$
. Now by Lemma 4.1, we have a
![]() ${\mathbb Q}$
-factorial dlt pair
${\mathbb Q}$
-factorial dlt pair
![]() $(Y,B_{Y})$
such that for some
$(Y,B_{Y})$
such that for some
![]() $r> 0$
,
$r> 0$
,
![]() $\bullet $
$\bullet $
![]() $K_{Y}+B_{Y}$
is nef,
$K_{Y}+B_{Y}$
is nef,
![]() $\bullet $
$\bullet $
![]() $n(K_{Y}+B_{Y}) = n(K_{X}+B)$
and
$n(K_{Y}+B_{Y}) = n(K_{X}+B)$
and
![]() $\kappa (K_{Y}+B_{Y})\leq \kappa (K_{X} +B+rD)$
,
$\kappa (K_{Y}+B_{Y})\leq \kappa (K_{X} +B+rD)$
,
![]() $\bullet $
$\bullet $
![]() $K_{Y}+B_{Y} \equiv E_{Y}$
, where
$K_{Y}+B_{Y} \equiv E_{Y}$
, where
![]() $E_{Y}$
is an effective
$E_{Y}$
is an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $\mathrm {Supp}\ E_{Y}\subseteq \lfloor B_{Y}\rfloor $
.
$\mathrm {Supp}\ E_{Y}\subseteq \lfloor B_{Y}\rfloor $
.
By Theorem 2.21,
![]() $(K_{Y}+B_{Y})|_{\lfloor B_{Y}\rfloor }$
, and hence
$(K_{Y}+B_{Y})|_{\lfloor B_{Y}\rfloor }$
, and hence
![]() $(K_{Y}+B_{Y})|_{\mathrm {Supp}\ E_{Y}}$
are semi-ample. Applying Lemma 4.2 to
$(K_{Y}+B_{Y})|_{\mathrm {Supp}\ E_{Y}}$
are semi-ample. Applying Lemma 4.2 to
![]() $(Y ,B_{Y})$
and
$(Y ,B_{Y})$
and
![]() $E_{Y}$
, we have
$E_{Y}$
, we have
![]() $\kappa (K_{Y} +B_{Y})\geq 0$
.
$\kappa (K_{Y} +B_{Y})\geq 0$
.
We claim that in fact
![]() $\kappa (K_{Y}+B_{Y})\geq 2$
. We apply Lemma 4.1 to
$\kappa (K_{Y}+B_{Y})\geq 2$
. We apply Lemma 4.1 to
![]() $(Y,B_{Y})$
and an effective
$(Y,B_{Y})$
and an effective
![]() ${\mathbb Q}$
-divisor which is
${\mathbb Q}$
-divisor which is
![]() ${\mathbb Q}$
-linearly equivalent to
${\mathbb Q}$
-linearly equivalent to
![]() $K_{Y}+ B_{Y}$
, then we obtain a
$K_{Y}+ B_{Y}$
, then we obtain a
![]() ${\mathbb Q}$
-factorial dlt pair
${\mathbb Q}$
-factorial dlt pair
![]() $(Z,B_{Z})$
satisfying:
$(Z,B_{Z})$
satisfying:
![]() $\bullet $
$\bullet $
![]() $K_{Z}+B_{Z}$
is nef,
$K_{Z}+B_{Z}$
is nef,
![]() $\bullet $
$\bullet $
![]() $n(K_{Z}+B_{Z}) = n(K_{Y}+B_{Y})$
and
$n(K_{Z}+B_{Z}) = n(K_{Y}+B_{Y})$
and
![]() $\kappa (K_{Z}+B_{Z})= \kappa (K_{Y} +B_{Y})$
,
$\kappa (K_{Z}+B_{Z})= \kappa (K_{Y} +B_{Y})$
,
![]() $\bullet $
$\bullet $
![]() $K_{Z}+B_{Z} \sim _{{\mathbb Q}} E_{Z}$
, where
$K_{Z}+B_{Z} \sim _{{\mathbb Q}} E_{Z}$
, where
![]() $E_{Z}$
is an effective
$E_{Z}$
is an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $\mathrm {Supp}\ E_{Y}\subseteq \lfloor B_{Y}\rfloor $
.
$\mathrm {Supp}\ E_{Y}\subseteq \lfloor B_{Y}\rfloor $
.
Similarly, we have
![]() $(K_{Z}+B_{Z})|_{\mathrm {Supp}\ E_{Z}}$
is semi-ample. Therefore, by Lemma 4.2, we have
$(K_{Z}+B_{Z})|_{\mathrm {Supp}\ E_{Z}}$
is semi-ample. Therefore, by Lemma 4.2, we have
![]() $\kappa (K_{Y}+B_{Y})=\kappa (K_{Z}+B_{Z})=2$
. It implies that
$\kappa (K_{Y}+B_{Y})=\kappa (K_{Z}+B_{Z})=2$
. It implies that
![]() $\kappa (K_{X}+B+rD)\geq 2$
. Since
$\kappa (K_{X}+B+rD)\geq 2$
. Since
![]() $K_{X}+B\equiv D$
, it is clear that
$K_{X}+B\equiv D$
, it is clear that
![]() $(K_{X}+B)|_{D}\not \equiv 0$
. Finally, by Lemma 4.2, we have
$(K_{X}+B)|_{D}\not \equiv 0$
. Finally, by Lemma 4.2, we have
![]() $\kappa (K_{X}+B)=2$
.
$\kappa (K_{X}+B)=2$
.
Now we can prove the nonvanishing theorem for projective lc threefold pairs.
Theorem 4.4. Let
![]() $(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair over a perfect field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+ B$
is pseudo-effective, then
$K_{X}+ B$
is pseudo-effective, then
![]() $\kappa (X,K_{X}+B)\geq 0$
.
$\kappa (X,K_{X}+B)\geq 0$
.
Proof. We pass to an uncountable algebraically closed field. Replacing
![]() $(X,B)$
by its log minimal model by Theorem 2.12, we can assume that
$(X,B)$
by its log minimal model by Theorem 2.12, we can assume that
![]() $K_{X}+B$
is nef. By Theorem 2.20, we can take a
$K_{X}+B$
is nef. By Theorem 2.20, we can take a
![]() ${\mathbb Q}$
-factorial dlt model
${\mathbb Q}$
-factorial dlt model
![]() $(X^{\prime },B^{\prime })$
of
$(X^{\prime },B^{\prime })$
of
![]() $(X,B)$
such that
$(X,B)$
such that
![]() $(X^{\prime },B^{\prime })$
is
$(X^{\prime },B^{\prime })$
is
![]() ${\mathbb Q}$
-factorial and dlt, and moreover
${\mathbb Q}$
-factorial and dlt, and moreover
![]() $X^{\prime }$
is terminal. We replace
$X^{\prime }$
is terminal. We replace
![]() $(X,B)$
by
$(X,B)$
by
![]() $(X^{\prime },B^{\prime })$
. If
$(X^{\prime },B^{\prime })$
. If
![]() $\lfloor B\rfloor =0$
, then the proposition follows from Theorem 3.10. Hence we can assume that
$\lfloor B\rfloor =0$
, then the proposition follows from Theorem 3.10. Hence we can assume that
![]() $\lfloor B\rfloor \neq 0$
.
$\lfloor B\rfloor \neq 0$
.
Now, by Definition 2.16, we run a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
$(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
![]() $(X^{\prime \prime },B^{\prime \prime })$
. Note that
$(X^{\prime \prime },B^{\prime \prime })$
. Note that
![]() $(X,(1-\varepsilon )B)$
is klt and every step of a
$(X,(1-\varepsilon )B)$
is klt and every step of a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial is a step of a
$(K_{X}+B)$
-trivial is a step of a
![]() $(K_{X}+(1-\varepsilon )B)$
-MMP for any sufficiently small rational
$(K_{X}+(1-\varepsilon )B)$
-MMP for any sufficiently small rational
![]() $\varepsilon>0$
. Hence we have
$\varepsilon>0$
. Hence we have
![]() $(X^{\prime \prime },(1-\varepsilon )B^{\prime \prime })$
is klt for any sufficiently small rational
$(X^{\prime \prime },(1-\varepsilon )B^{\prime \prime })$
is klt for any sufficiently small rational
![]() $\varepsilon>0$
. If
$\varepsilon>0$
. If
![]() $K_{X^{\prime \prime }}+(1-\varepsilon )B^{\prime \prime }$
is nef for any sufficiently small rational
$K_{X^{\prime \prime }}+(1-\varepsilon )B^{\prime \prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
, then we have
$\varepsilon>0$
, then we have
![]() $\kappa (K_{X^{\prime \prime }}+(1-\varepsilon )B^{\prime \prime })\geq 0$
by Theorem 3.10 since
$\kappa (K_{X^{\prime \prime }}+(1-\varepsilon )B^{\prime \prime })\geq 0$
by Theorem 3.10 since
![]() $(X^{\prime \prime },(1-\varepsilon )B^{\prime \prime })$
is klt. Hence we have
$(X^{\prime \prime },(1-\varepsilon )B^{\prime \prime })$
is klt. Hence we have
Otherwise, by Lemma 2.17, we get a Mori fiber space

and
![]() ${\mathbb Q}$
-divisors C on Z such that
${\mathbb Q}$
-divisors C on Z such that
Hence we have
If
![]() $n(K_{X}+B)= 2$
, by Proposition 4.3, we have
$n(K_{X}+B)= 2$
, by Proposition 4.3, we have
![]() $\kappa (K_{X}+B)=2$
. If
$\kappa (K_{X}+B)=2$
. If
![]() $n(K_{X}+B)= 1$
, then by Theorem 2.8, we get a nef reduction map of
$n(K_{X}+B)= 1$
, then by Theorem 2.8, we get a nef reduction map of
![]() $K_{X}+B$
,
$K_{X}+B$
,
![]() $g: X\to Z^{\prime }$
. Then g is an equidimensional morphism since
$g: X\to Z^{\prime }$
. Then g is an equidimensional morphism since
![]() $Z^{\prime }$
is a normal curve and g is proper over the generic point of
$Z^{\prime }$
is a normal curve and g is proper over the generic point of
![]() $Z^{\prime }$
. By Theorem 2.11, we have
$Z^{\prime }$
. By Theorem 2.11, we have
![]() $(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of g. Hence by Lemma 2.10,
$(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of g. Hence by Lemma 2.10,
![]() $K_{X}+B$
descends to an ample divisor on
$K_{X}+B$
descends to an ample divisor on
![]() $Z^{\prime }$
. Therefore,
$Z^{\prime }$
. Therefore,
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
If
![]() $n(K_{X}+B)= 0$
, then
$n(K_{X}+B)= 0$
, then
![]() $K_{X}+B$
is numerically trivial. By Theorem 2.12, there exists a
$K_{X}+B$
is numerically trivial. By Theorem 2.12, there exists a
![]() $(K_{X}+B-\lfloor B\rfloor )$
-MMP which terminates. Since
$(K_{X}+B-\lfloor B\rfloor )$
-MMP which terminates. Since
![]() $\lfloor B\rfloor> 0$
, this MMP terminates with a Mori fiber space
$\lfloor B\rfloor> 0$
, this MMP terminates with a Mori fiber space

There are
![]() ${\mathbb Q}$
-divisors
${\mathbb Q}$
-divisors
![]() $C^{\prime }$
on
$C^{\prime }$
on
![]() $Z^{\prime \prime }$
,
$Z^{\prime \prime }$
,
![]() $B_{Y}$
on Y such that
$B_{Y}$
on Y such that
![]() $B_{Y}$
is the birational transform of B on Y and
$B_{Y}$
is the birational transform of B on Y and
Now, by Theorem 2.20, we can take a dlt modification
Note that
![]() $\lfloor B_{Y^{\prime }}\rfloor $
dominates
$\lfloor B_{Y^{\prime }}\rfloor $
dominates
![]() $Z^{\prime \prime }$
since
$Z^{\prime \prime }$
since
![]() $f^{\prime }$
only contract curves which have positive intersections with
$f^{\prime }$
only contract curves which have positive intersections with
![]() $\lfloor B_{Y}\rfloor $
. Since
$\lfloor B_{Y}\rfloor $
. Since
![]() $(K_{Y^{\prime }}+B_{Y^{\prime }})|_{\lfloor B_{Y^{\prime }} \rfloor }$
is semi-ample by Theorem 2.21, we deduce that
$(K_{Y^{\prime }}+B_{Y^{\prime }})|_{\lfloor B_{Y^{\prime }} \rfloor }$
is semi-ample by Theorem 2.21, we deduce that
![]() $C^{\prime }$
, and hence
$C^{\prime }$
, and hence
![]() $K_{X}+B$
are semi-ample by Lemma 2.5.
$K_{X}+B$
are semi-ample by Lemma 2.5.
As a corollary, we have the following result on termination of flips.
Theorem 4.5. Let
![]() $(X,B)$
be a projective lc threefold pair defined over a perfect field k of characteristic
$(X,B)$
be a projective lc threefold pair defined over a perfect field k of characteristic
![]() $p> 3$
such that
$p> 3$
such that
![]() $K_{X}+B$
is pseudo-effective. Then every sequence of
$K_{X}+B$
is pseudo-effective. Then every sequence of
![]() $(K_{X}+B)$
-flips terminates. In particular, any
$(K_{X}+B)$
-flips terminates. In particular, any
![]() $(K_{X}+B)$
-MMP terminates with a minimal model.
$(K_{X}+B)$
-MMP terminates with a minimal model.
5 Abundance conjecture for lc threefold pairs
In this section, we show the abundance for lc threefold pairs whose Kodaira dimension
![]() $\geq 1$
. To be precise, we prove the following result.
$\geq 1$
. To be precise, we prove the following result.
Theorem 5.1. Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (X,K_{X}+B)\geq 1$
, then
$\kappa (X,K_{X}+B)\geq 1$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
5.1 Preparation
Before proving Theorem 5.1, we make some preparations.
Lemma 5.2. Let X be a normal projective variety of dimension
![]() $3$
over an algebraically closed field, and let D be a nef
$3$
over an algebraically closed field, and let D be a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X such that
${\mathbb Q}$
-divisor on X such that
![]() $\kappa (X, D) = 2$
. Then
$\kappa (X, D) = 2$
. Then
![]() $n(X,D)= 2$
.
$n(X,D)= 2$
.
Proof. We pass to an uncountable algebraically closed field. Consider the Iitaka map of D. After resolving the indeterminacies and replacing D by its pullback, we can assume that the Iitaka map of D is a morphism. Since D is nef and not big, it has to be numerically trivial on all fibers of the Iitaka map. Hence we have
![]() $n(X,D)\leq 2$
. Then by the equality
$n(X,D)\leq 2$
. Then by the equality
![]() $\kappa (X,D)\leq n(X,D),$
we have
$\kappa (X,D)\leq n(X,D),$
we have
![]() $n(X,D)=2$
.
$n(X,D)=2$
.
Lemma 5.3. Let X be a normal projective variety of dimension
![]() $3$
over an uncountable algebraically closed field of characteristic
$3$
over an uncountable algebraically closed field of characteristic
![]() $>0$
. Assume D is a nef
$>0$
. Assume D is a nef
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor on X such that
${\mathbb Q}$
-divisor on X such that
![]() $\kappa (X, D) = 2$
. Then D is endowed with a map
$\kappa (X, D) = 2$
. Then D is endowed with a map
![]() $h: X\to Z$
to a normal proper algebraic space Z of dimension
$h: X\to Z$
to a normal proper algebraic space Z of dimension
![]() $2$
.
$2$
.
If, moreover,
![]() $D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h, then there exists a commutative diagram:
$D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h, then there exists a commutative diagram:

where
![]() $Z_{1}$
is a smooth projective surface,
$Z_{1}$
is a smooth projective surface,
![]() $X_{1}$
is a normal projective threefold,
$X_{1}$
is a normal projective threefold,
![]() $\phi ,\psi $
are birational morphisms, and
$\phi ,\psi $
are birational morphisms, and
![]() $h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration. Moreover, there exists a nef and big
$h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration. Moreover, there exists a nef and big
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $D_{1}$
on
$D_{1}$
on
![]() $Z_{1}$
such that
$Z_{1}$
such that
![]() $\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
$\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
Proof. By Lemma 5.2, we have
![]() $\kappa (X, D)=n(X,D)= 2$
. Hence, by Lemma 2.9, D is endowed with a map
$\kappa (X, D)=n(X,D)= 2$
. Hence, by Lemma 2.9, D is endowed with a map
![]() $h:X\to Z$
to a normal proper algebraic space Z of dimension
$h:X\to Z$
to a normal proper algebraic space Z of dimension
![]() $2$
.
$2$
.
Assume, moreover,
![]() $D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. By Theorem 2.8, we get a nef reduction map
$D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. By Theorem 2.8, we get a nef reduction map
![]() $f:X\dashrightarrow Y$
of D. Resolving the indeterminacies of f and replacing D by its pullback, we can assume that
$f:X\dashrightarrow Y$
of D. Resolving the indeterminacies of f and replacing D by its pullback, we can assume that
![]() $f:X\to Y$
is a morphism to a normal surface.
$f:X\to Y$
is a morphism to a normal surface.
Now we apply Lemma 2.10 to f and D. Then we get a commutative diagram:

with
![]() $\phi ^{\prime },\psi ^{\prime }$
projective birational, and an
$\phi ^{\prime },\psi ^{\prime }$
projective birational, and an
![]() ${\mathbb Q}$
-divisor C on
${\mathbb Q}$
-divisor C on
![]() $Z^{\prime }$
such that
$Z^{\prime }$
such that
![]() $\phi ^{\prime \ast }D \sim _{{\mathbb Q}} f^{\prime \ast }C$
. Moreover, we can apply the flattening trick [Reference Raynaud and Gruson23, Th. 5.2.2] to
$\phi ^{\prime \ast }D \sim _{{\mathbb Q}} f^{\prime \ast }C$
. Moreover, we can apply the flattening trick [Reference Raynaud and Gruson23, Th. 5.2.2] to
![]() $f^{\prime }$
, and we get the following commutative diagram:
$f^{\prime }$
, and we get the following commutative diagram:

where
![]() $Z_{1}$
is a normal projective surface,
$Z_{1}$
is a normal projective surface,
![]() $X_{1}$
is a normal projective threefold,
$X_{1}$
is a normal projective threefold,
![]() $\phi ^{\prime \prime },\psi ^{\prime \prime }$
are birational morphisms, and
$\phi ^{\prime \prime },\psi ^{\prime \prime }$
are birational morphisms, and
![]() $h_{1}: X_{1}\to Z_{1}$
is a flat fibration. Replacing
$h_{1}: X_{1}\to Z_{1}$
is a flat fibration. Replacing
![]() $Z_{1}$
by a smooth resolution and
$Z_{1}$
by a smooth resolution and
![]() $X_{1}$
by the normalization of main component of the fiber product of
$X_{1}$
by the normalization of main component of the fiber product of
![]() $h_{1}$
and the resolution, we may assume that
$h_{1}$
and the resolution, we may assume that
![]() $Z_{1}$
is smooth.
$Z_{1}$
is smooth.
Let
![]() $\phi :=\phi ^{\prime }\circ \phi ^{\prime \prime }, D_{1}:=\psi ^{\prime \prime \ast }C.$
Then we have
$\phi :=\phi ^{\prime }\circ \phi ^{\prime \prime }, D_{1}:=\psi ^{\prime \prime \ast }C.$
Then we have
Since
![]() $h_{1}$
only contracts curves which are
$h_{1}$
only contracts curves which are
![]() $\phi ^{\ast }D$
-numerically trivial, we know that the morphism
$\phi ^{\ast }D$
-numerically trivial, we know that the morphism
![]() $h\circ \phi : X_{1}\to Z$
factors through
$h\circ \phi : X_{1}\to Z$
factors through
![]() $h_{1}$
. In other words, there exists a natural map
$h_{1}$
. In other words, there exists a natural map
![]() $\psi :Z_{1}\to Z$
making the following diagram commutative:
$\psi :Z_{1}\to Z$
making the following diagram commutative:

This completes the proof of the lemma.
5.2 The case of
 $\kappa (K_{X}+B)=2$
$\kappa (K_{X}+B)=2$
In this subsection, we focus on the case of
![]() $\kappa (K_{X}+B)=2$
, which is the most difficult case.
$\kappa (K_{X}+B)=2$
, which is the most difficult case.
Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that
$>3$
such that
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (K_{X}+B)=2$
. We pass to an uncountable base field. After replacing
$\kappa (K_{X}+B)=2$
. We pass to an uncountable base field. After replacing
![]() $(X,B)$
, we can assume that
$(X,B)$
, we can assume that
![]() $(X,B)$
is
$(X,B)$
is
![]() ${\mathbb Q}$
-factorial and dlt by Theorem 2.20. Then one of the following cases holds:
${\mathbb Q}$
-factorial and dlt by Theorem 2.20. Then one of the following cases holds:
Case I:
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Case II:
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Note that by Lemma 5.3,
![]() $K_{X}+B$
is endowed with a map
$K_{X}+B$
is endowed with a map
![]() $h:X\to Z$
to a normal proper algebraic space Z of dimension
$h:X\to Z$
to a normal proper algebraic space Z of dimension
![]() $2$
. We will run several MMP which are
$2$
. We will run several MMP which are
![]() $(K_{X}+B)$
-trivial. It is clear that every step of such construction is still over Z.
$(K_{X}+B)$
-trivial. It is clear that every step of such construction is still over Z.
5.2.1 Proof of Case I
In this part, we prove Case I (see Proposition 5.6). More precisely, we first prove that
![]() $\lfloor B\rfloor $
must dominate Z in this case. Then we deduce the semi-ampleness of
$\lfloor B\rfloor $
must dominate Z in this case. Then we deduce the semi-ampleness of
![]() $K_{X}+B$
by adjunction.
$K_{X}+B$
by adjunction.
Lemma 5.4. Let
![]() $\phi :Z^{\prime }\to Z$
be a birational morphism from a
$\phi :Z^{\prime }\to Z$
be a birational morphism from a
![]() ${\mathbb Q}$
-factorial projective normal surface to a normal proper algebraic space of dimension
${\mathbb Q}$
-factorial projective normal surface to a normal proper algebraic space of dimension
![]() $2$
. Assume that S is an effective Weil divisor on
$2$
. Assume that S is an effective Weil divisor on
![]() $Z^{\prime }$
. Then we can take a
$Z^{\prime }$
. Then we can take a
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor A such that
${\mathbb Q}$
-divisor A such that
![]() $A\geq S$
and
$A\geq S$
and
![]() $A\cdot E=0$
for any curve E which is
$A\cdot E=0$
for any curve E which is
![]() $\phi $
-exceptional.
$\phi $
-exceptional.
Proof. We will write
![]() $A=S+H+\sum _{\alpha }a_{\alpha }C_{\alpha }$
, where H is a sufficiently ample effective divisor such that
$A=S+H+\sum _{\alpha }a_{\alpha }C_{\alpha }$
, where H is a sufficiently ample effective divisor such that
![]() $S+H$
is ample,
$S+H$
is ample,
![]() $C_{\alpha },\alpha \in I=\{ 1, 2, \ldots , r \}$
are all
$C_{\alpha },\alpha \in I=\{ 1, 2, \ldots , r \}$
are all
![]() $\phi $
-exceptional curves and
$\phi $
-exceptional curves and
![]() $a_{\alpha }$
are some nonnegative rational numbers. It is clear that
$a_{\alpha }$
are some nonnegative rational numbers. It is clear that
![]() $A\geq S$
. We only need to choose appropriate
$A\geq S$
. We only need to choose appropriate
![]() $a_{\alpha }\geq 0$
such that
$a_{\alpha }\geq 0$
such that
![]() $A\cdot E=0$
for any curve E which is
$A\cdot E=0$
for any curve E which is
![]() $\phi $
-exceptional.
$\phi $
-exceptional.
Note that
 $$ \begin{align*}\begin{aligned} A\cdot C_{\beta}&=0, \beta \in I\\ \Longleftrightarrow\ \ \ \ \ \ \ \ \ (\sum_{\alpha}a_{\alpha}C_{\alpha})\cdot C_{\beta} &=-(S+H)\cdot C_{\beta}, \beta\in I\\ \Longleftrightarrow [C_{\beta}\cdot C_{\alpha}]_{\alpha,\beta\in I}[a_{\alpha}]_{\alpha\in I}&=[-(S+H)\cdot C_{\beta}]_{\beta\in I}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} A\cdot C_{\beta}&=0, \beta \in I\\ \Longleftrightarrow\ \ \ \ \ \ \ \ \ (\sum_{\alpha}a_{\alpha}C_{\alpha})\cdot C_{\beta} &=-(S+H)\cdot C_{\beta}, \beta\in I\\ \Longleftrightarrow [C_{\beta}\cdot C_{\alpha}]_{\alpha,\beta\in I}[a_{\alpha}]_{\alpha\in I}&=[-(S+H)\cdot C_{\beta}]_{\beta\in I}, \end{aligned}\end{align*} $$
where
![]() $[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is a matrix with element
$[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is a matrix with element
![]() $C_{\beta }\cdot C_{\alpha }$
at row
$C_{\beta }\cdot C_{\alpha }$
at row
![]() $\beta $
and column
$\beta $
and column
![]() $\alpha $
, and
$\alpha $
, and
![]() $[a_{\alpha }]_{\alpha \in I}, [-(S+H)\cdot C_{\beta }]_{\beta \in I}$
are column vectors with elements
$[a_{\alpha }]_{\alpha \in I}, [-(S+H)\cdot C_{\beta }]_{\beta \in I}$
are column vectors with elements
![]() $a_{\alpha }, -(S+H)\cdot C_{\beta }$
at rows
$a_{\alpha }, -(S+H)\cdot C_{\beta }$
at rows
![]() $\alpha , \beta $
, respectively. Since
$\alpha , \beta $
, respectively. Since
![]() $-(S+H)\cdot C_{\beta }<0$
for
$-(S+H)\cdot C_{\beta }<0$
for
![]() $\beta \in I$
, to get a solution of
$\beta \in I$
, to get a solution of
![]() $[a_{\alpha }]_{\alpha \in I}$
with
$[a_{\alpha }]_{\alpha \in I}$
with
![]() $a_{\alpha }>0$
we only need to prove that the symmetric matrix
$a_{\alpha }>0$
we only need to prove that the symmetric matrix
![]() $[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is negative definite.
$[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is negative definite.
Consider a resolution of singularities
![]() $\phi ^{\prime }:Z^{\prime \prime }\to Z^{\prime }$
. We first prove that the proposition holds for the morphism
$\phi ^{\prime }:Z^{\prime \prime }\to Z^{\prime }$
. We first prove that the proposition holds for the morphism
![]() $\phi \circ \phi ^{\prime }:Z^{\prime \prime }\to Z$
. Let
$\phi \circ \phi ^{\prime }:Z^{\prime \prime }\to Z$
. Let
![]() $C^{\prime }_{\alpha },\alpha \in J$
be all
$C^{\prime }_{\alpha },\alpha \in J$
be all
![]() $\phi \circ \phi ^{\prime }$
-exceptional curves. Since
$\phi \circ \phi ^{\prime }$
-exceptional curves. Since
![]() $\phi \circ \phi ^{\prime }$
is a contraction, for any closed point
$\phi \circ \phi ^{\prime }$
is a contraction, for any closed point
![]() $x\in Z$
,
$x\in Z$
,
![]() $(\phi \circ \phi ^{\prime })^{-1}(x)$
is connected. Hence, different connected components of
$(\phi \circ \phi ^{\prime })^{-1}(x)$
is connected. Hence, different connected components of
![]() $\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
maps to different closed points. We apply [Reference Artin1, Th. 4.5] to the morphism
$\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
maps to different closed points. We apply [Reference Artin1, Th. 4.5] to the morphism
![]() $\phi \circ \phi ^{\prime }$
, then we know that the intersection matrix of any connected component of
$\phi \circ \phi ^{\prime }$
, then we know that the intersection matrix of any connected component of
![]() $\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is negative definite. Note that the intersection matrix of
$\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is negative definite. Note that the intersection matrix of
![]() $\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is the direct sum of intersection matrices of all connected components of
$\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is the direct sum of intersection matrices of all connected components of
![]() $\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
. Hence, the intersection matrix of
$\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
. Hence, the intersection matrix of
![]() $\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is negative definite.
$\bigcup _{\alpha \in J}C^{\prime }_{\alpha }$
is negative definite.
To prove that
![]() $[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is negative definite, we only need to check
$[C_{\beta }\cdot C_{\alpha }]_{\alpha ,\beta \in I}$
is negative definite, we only need to check
![]() $\phi ^{\prime \ast }C_{\alpha },\alpha \in I$
are linearly independent. This is clear since we have
$\phi ^{\prime \ast }C_{\alpha },\alpha \in I$
are linearly independent. This is clear since we have
![]() $\phi ^{\prime \ast }C_{\alpha }=\tilde { C_{\alpha }}+E_{\alpha }$
, where
$\phi ^{\prime \ast }C_{\alpha }=\tilde { C_{\alpha }}+E_{\alpha }$
, where
![]() $\tilde {C_{\alpha }}$
are birational transforms of
$\tilde {C_{\alpha }}$
are birational transforms of
![]() $C_{\alpha }$
and
$C_{\alpha }$
and
![]() $E_{\alpha }$
are
$E_{\alpha }$
are
![]() $\phi ^{\prime }$
-exceptional
$\phi ^{\prime }$
-exceptional
![]() ${\mathbb Q}$
-divisors.
${\mathbb Q}$
-divisors.
Proposition 5.5. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
with
$>3$
with
![]() $\kappa (K_{X}+B)=2$
. Assume
$\kappa (K_{X}+B)=2$
. Assume
![]() $K_{X}+B$
is nef, and it is endowed with a map
$K_{X}+B$
is nef, and it is endowed with a map
![]() $h:X\to Z$
. If
$h:X\to Z$
. If
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
, then
$\varepsilon>0$
, then
![]() $\lfloor B\rfloor $
dominates Z.
$\lfloor B\rfloor $
dominates Z.
Proof. We first prove the case when X is terminal. Since
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any rational
$K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any rational
![]() $\varepsilon>0$
. Then by Definition 2.16, we can run a
$\varepsilon>0$
. Then by Definition 2.16, we can run a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
$(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
![]() $(X^{\prime },B^{\prime })$
since X is terminal. Moreover, since
$(X^{\prime },B^{\prime })$
since X is terminal. Moreover, since
![]() $\kappa (K_{X}+(1-\varepsilon )B)=\kappa (K_{X^{\prime }}+(1-\varepsilon )B^{\prime })$
and
$\kappa (K_{X}+(1-\varepsilon )B)=\kappa (K_{X^{\prime }}+(1-\varepsilon )B^{\prime })$
and
![]() $K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any small rational
$K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any small rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is not nef for any small rational
$K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is not nef for any small rational
![]() $\varepsilon>0$
by Theorem 4.4. Hence this MMP terminates with a Mori fiber space.
$\varepsilon>0$
by Theorem 4.4. Hence this MMP terminates with a Mori fiber space.

Denote the birational transform of B on Y by
![]() $B_{Y}$
. Note that
$B_{Y}$
. Note that
![]() $K_{Y}+B_{Y}$
is endowed with a map
$K_{Y}+B_{Y}$
is endowed with a map
![]() $h_{Y}:Y\to Z$
and
$h_{Y}:Y\to Z$
and
![]() $h_{Y}$
factors through
$h_{Y}$
factors through
![]() $h^{\prime }$
since
$h^{\prime }$
since
![]() $h^{\prime }$
only contracts curves which are
$h^{\prime }$
only contracts curves which are
![]() $(K_{Y}+B_{Y})$
-trivial. In other words, we have a commutative diagram:
$(K_{Y}+B_{Y})$
-trivial. In other words, we have a commutative diagram:

Note that
![]() $h^{\prime }$
is equidimensional,
$h^{\prime }$
is equidimensional,
![]() $Z^{\prime }$
is
$Z^{\prime }$
is
![]() ${\mathbb Q}$
-factorial and
${\mathbb Q}$
-factorial and
![]() $\phi $
is a birational map. Applying Lemma 5.4 to
$\phi $
is a birational map. Applying Lemma 5.4 to
![]() $\phi $
, we get a
$\phi $
, we get a
![]() ${\mathbb Q}$
-Cartier
${\mathbb Q}$
-Cartier
![]() ${\mathbb Q}$
-divisor A on
${\mathbb Q}$
-divisor A on
![]() $Z^{\prime }$
such that
$Z^{\prime }$
such that
![]() $A\geq h^{\prime }(\lfloor B_{Y}\rfloor )$
and
$A\geq h^{\prime }(\lfloor B_{Y}\rfloor )$
and
![]() $h^{\prime }(F)\cdot A=0$
for any
$h^{\prime }(F)\cdot A=0$
for any
![]() $h_{Y}$
-exceptional divisor F. Note that
$h_{Y}$
-exceptional divisor F. Note that
for some integer
![]() $a>0$
. Hence, there exists an effective
$a>0$
. Hence, there exists an effective
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
such that
![]() $M\cdot C=(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )\cdot C$
for any curve C in the fiber of
$M\cdot C=(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )\cdot C$
for any curve C in the fiber of
![]() $h_{Y}$
. In other words, flips of a
$h_{Y}$
. In other words, flips of a
![]() $(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )$
-MMP which is
$(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )$
-MMP which is
![]() $(K_{Y}+B_{Y})$
-trivial are all M-flips. Therefore, by Theorem 2.18, a
$(K_{Y}+B_{Y})$
-trivial are all M-flips. Therefore, by Theorem 2.18, a
![]() $(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )$
-MMP which is
$(K_{Y}+B_{Y}-\lfloor B_{Y}\rfloor )$
-MMP which is
![]() $(K_{Y}+B_{Y})$
-trivial terminates with a Mori fiber space
$(K_{Y}+B_{Y})$
-trivial terminates with a Mori fiber space

such that
![]() $f^{\prime }_{\ast }(\lfloor B_{Y}\rfloor )$
dominates
$f^{\prime }_{\ast }(\lfloor B_{Y}\rfloor )$
dominates
![]() $Z^{\prime \prime }$
by Lemma 2.17. Note that
$Z^{\prime \prime }$
by Lemma 2.17. Note that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
is endowed with a map
$K_{Y^{\prime }}+B_{Y^{\prime }}$
is endowed with a map
![]() $h_{Y^{\prime }}:Y^{\prime }\to Z$
and
$h_{Y^{\prime }}:Y^{\prime }\to Z$
and
![]() $h_{Y^{\prime }}$
factors through
$h_{Y^{\prime }}$
factors through
![]() $h^{\prime \prime }$
since
$h^{\prime \prime }$
since
![]() $h^{\prime \prime }$
only contracts curves which are
$h^{\prime \prime }$
only contracts curves which are
![]() $(K_{Y^{\prime }}+B_{Y^{\prime }})$
-trivial. Therefore
$(K_{Y^{\prime }}+B_{Y^{\prime }})$
-trivial. Therefore
![]() $f^{\prime }_{\ast }(\lfloor B_{Y}\rfloor )$
, and hence
$f^{\prime }_{\ast }(\lfloor B_{Y}\rfloor )$
, and hence
![]() $\lfloor B \rfloor $
dominate Z.
$\lfloor B \rfloor $
dominate Z.
Now we turn to the general case. By Theorem 2.20, we can take a dlt modification
![]() $\mu :(X^{\prime \prime },B^{\prime \prime })\to (X,B)$
such that
$\mu :(X^{\prime \prime },B^{\prime \prime })\to (X,B)$
such that
![]() $(X^{\prime \prime },B^{\prime \prime })$
is
$(X^{\prime \prime },B^{\prime \prime })$
is
![]() ${\mathbb Q}$
-factorial and dlt, and
${\mathbb Q}$
-factorial and dlt, and
![]() $X^{\prime \prime }$
is terminal. If
$X^{\prime \prime }$
is terminal. If
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
, then
$\varepsilon>0$
, then
![]() $K_{X^{\prime \prime }}+B^{\prime \prime }-\varepsilon \lfloor B^{\prime \prime }\rfloor $
is not pseudo-effective for any rational
$K_{X^{\prime \prime }}+B^{\prime \prime }-\varepsilon \lfloor B^{\prime \prime }\rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
, since
$\varepsilon>0$
, since
By the last paragraph,
![]() $\lfloor B^{\prime \prime }\rfloor $
dominates Z. Note that
$\lfloor B^{\prime \prime }\rfloor $
dominates Z. Note that
![]() $\lfloor B^{\prime \prime }\rfloor $
dominates Z if and only if
$\lfloor B^{\prime \prime }\rfloor $
dominates Z if and only if
![]() $\lfloor B\rfloor $
dominates Z since Z is of dimension
$\lfloor B\rfloor $
dominates Z since Z is of dimension
![]() $2$
and
$2$
and
![]() $\mu $
is an isomorphism over a big open subset of X. Hence we have
$\mu $
is an isomorphism over a big open subset of X. Hence we have
![]() $\lfloor B\rfloor $
dominates Z.
$\lfloor B\rfloor $
dominates Z.
Now we can prove Case I.
Proposition 5.6. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that
$>3$
such that
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (K_{X}+B)=2$
. If
$\kappa (K_{X}+B)=2$
. If
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
, then
$\varepsilon>0$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. We pass to an uncountable base field. By Lemma 5.3,
![]() $K_{X}+B$
is endowed with a map
$K_{X}+B$
is endowed with a map
![]() $h:X\to Z$
to a normal proper algebraic space Z of dimension
$h:X\to Z$
to a normal proper algebraic space Z of dimension
![]() $2$
. Now by Proposition 5.5,
$2$
. Now by Proposition 5.5,
![]() $\lfloor B\rfloor $
dominates Z.
$\lfloor B\rfloor $
dominates Z.
Since
![]() $(K_{X}+B)|_{G}\equiv 0$
, where G is the generic fiber of h and G is of dimension
$(K_{X}+B)|_{G}\equiv 0$
, where G is the generic fiber of h and G is of dimension
![]() $1$
, we have
$1$
, we have
![]() $(K_{X}+B)|_{G}\sim _{{\mathbb Q}} 0$
by the abundance for curves. Then we can apply Lemma 5.3 to get a commutative diagram:
$(K_{X}+B)|_{G}\sim _{{\mathbb Q}} 0$
by the abundance for curves. Then we can apply Lemma 5.3 to get a commutative diagram:

where
![]() $Z_{1}$
is a smooth projective surface,
$Z_{1}$
is a smooth projective surface,
![]() $X_{1}$
is a normal projective threefold,
$X_{1}$
is a normal projective threefold,
![]() $\phi ,\psi $
are birational morphisms and
$\phi ,\psi $
are birational morphisms and
![]() $h_{1}: X_{1}\to Z_{1}$
is a fibration. Moreover, there exists a nef and big
$h_{1}: X_{1}\to Z_{1}$
is a fibration. Moreover, there exists a nef and big
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $D_{1}$
on
$D_{1}$
on
![]() $Z_{1}$
such that
$Z_{1}$
such that
![]() $\phi ^{\ast }(K_{X}+B)\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
. To show
$\phi ^{\ast }(K_{X}+B)\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
. To show
![]() $K_{X}+B$
is semi-ample, it suffices to show
$K_{X}+B$
is semi-ample, it suffices to show
![]() $D_{1}$
is semi-ample.
$D_{1}$
is semi-ample.
Let
![]() $B_{1}$
be the birational transform of B on
$B_{1}$
be the birational transform of B on
![]() $X_{1}$
. Since
$X_{1}$
. Since
![]() $\lfloor B\rfloor $
dominates Z, we have
$\lfloor B\rfloor $
dominates Z, we have
![]() $\lfloor B_{1}\rfloor $
dominates
$\lfloor B_{1}\rfloor $
dominates
![]() $Z_{1}$
. Moreover, we have
$Z_{1}$
. Moreover, we have
![]() $\phi ^{\ast }(K_{X}+B)|_{\lfloor B_{1}\rfloor }$
is semi-ample since
$\phi ^{\ast }(K_{X}+B)|_{\lfloor B_{1}\rfloor }$
is semi-ample since
![]() $(K_{X}+B)|_{\lfloor B\rfloor }$
is semi-ample by Theorem 2.21. Hence by Lemma 2.5,
$(K_{X}+B)|_{\lfloor B\rfloor }$
is semi-ample by Theorem 2.21. Hence by Lemma 2.5,
![]() $D_{1}$
, and hence
$D_{1}$
, and hence
![]() $K_{X}+B$
are semi-ample.
$K_{X}+B$
are semi-ample.
5.2.2 Proof of Case II
In this part, we prove Case II (see Proposition 5.10). First, we prove this case when
![]() $K_{X}+B$
is endowed with an equidimensional map
$K_{X}+B$
is endowed with an equidimensional map
![]() $h:X\to Z$
. For the general case, we modify the pair
$h:X\to Z$
. For the general case, we modify the pair
![]() $(X,B)$
by running several MMP which are
$(X,B)$
by running several MMP which are
![]() $(K_{X}+B)$
-trivial so that all h-exceptional prime divisors are connected components of
$(K_{X}+B)$
-trivial so that all h-exceptional prime divisors are connected components of
![]() $\lfloor B\rfloor $
. Then after further modification we can construct an equidimensional fibration
$\lfloor B\rfloor $
. Then after further modification we can construct an equidimensional fibration
![]() $h_{\varepsilon }:X\to Z_{\varepsilon }$
to a normal projective surface. Finally, we descend
$h_{\varepsilon }:X\to Z_{\varepsilon }$
to a normal projective surface. Finally, we descend
![]() $K_{X}+B$
to
$K_{X}+B$
to
![]() $Z_{\varepsilon }$
and prove its semi-ampleness.
$Z_{\varepsilon }$
and prove its semi-ampleness.
Proposition 5.7. Let D be a nef
![]() ${\mathbb Q}$
-divisor on X with
${\mathbb Q}$
-divisor on X with
![]() $\kappa (X,D)=2$
, where X is a
$\kappa (X,D)=2$
, where X is a
![]() ${\mathbb Q}$
-factorial normal projective threefold over an uncountable algebraically closed field k of characteristic
${\mathbb Q}$
-factorial normal projective threefold over an uncountable algebraically closed field k of characteristic
![]() $>0$
. Suppose that D is endowed with an equidimensional map
$>0$
. Suppose that D is endowed with an equidimensional map
![]() $h:X\to Z$
such that
$h:X\to Z$
such that
![]() $D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. Then Z is a projective variety and D is semi-ample.
$D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. Then Z is a projective variety and D is semi-ample.
Proof. By Lemma 5.3, there is a commutative diagram as following:

where
![]() $Z_{1}$
is a smooth projective surface,
$Z_{1}$
is a smooth projective surface,
![]() $X_{1}$
is a normal projective threefold,
$X_{1}$
is a normal projective threefold,
![]() $\phi ,\psi $
are birational morphisms, and
$\phi ,\psi $
are birational morphisms, and
![]() $h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration. Moreover, there exists a nef and big
$h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration. Moreover, there exists a nef and big
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $D_{1}$
on
$D_{1}$
on
![]() $Z_{1}$
such that
$Z_{1}$
such that
![]() $\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
$\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
Since Z is a normal proper algebraic space of dimension
![]() $2$
, there exists an open set
$2$
, there exists an open set
![]() $U\subseteq Z$
such that U is a smooth quasi-projective variety and
$U\subseteq Z$
such that U is a smooth quasi-projective variety and
![]() $T:=Z\backslash U$
consists of finitely many closed points on Z. By Lemma 2.10, we have
$T:=Z\backslash U$
consists of finitely many closed points on Z. By Lemma 2.10, we have
![]() $D|_{h^{-1}(U)}$
is
$D|_{h^{-1}(U)}$
is
![]() ${\mathbb Q}$
-linearly trivial over U since h is equidimensional and
${\mathbb Q}$
-linearly trivial over U since h is equidimensional and
![]() $D|_{G}\sim _{{\mathbb Q}}0$
. Now we take a very ample divisor S on X, which does not contain any component of
$D|_{G}\sim _{{\mathbb Q}}0$
. Now we take a very ample divisor S on X, which does not contain any component of
![]() $h^{-1}(T)$
. Then we have the following commutative diagram:
$h^{-1}(T)$
. Then we have the following commutative diagram:

The
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $D|_{S^{\nu }}$
is nef and big. Consider the exceptional locus
$D|_{S^{\nu }}$
is nef and big. Consider the exceptional locus
![]() ${\mathbb E}(D|_{S^{\nu }})$
. It is, the union of finitely many D-numerically trivial curves on
${\mathbb E}(D|_{S^{\nu }})$
. It is, the union of finitely many D-numerically trivial curves on
![]() $S^{\nu }$
. Note that
$S^{\nu }$
. Note that
![]() $S\cap h^{-1}(T)$
contains no curve by our construction. Hence the image of
$S\cap h^{-1}(T)$
contains no curve by our construction. Hence the image of
![]() ${\mathbb E}(D|_{S^{\nu }})$
, via the natural map
${\mathbb E}(D|_{S^{\nu }})$
, via the natural map
![]() $S^{\nu } \to X$
, is contained in finitely many fibers of h over some closed points in U. Therefore
$S^{\nu } \to X$
, is contained in finitely many fibers of h over some closed points in U. Therefore
![]() $(D|_{S^{\nu }})|_{{\mathbb E}(D|_{S^{\nu }})}$
is semi-ample, and by Theorem 2.6,
$(D|_{S^{\nu }})|_{{\mathbb E}(D|_{S^{\nu }})}$
is semi-ample, and by Theorem 2.6,
![]() $D|_{S^{\nu }}$
is semi-ample.
$D|_{S^{\nu }}$
is semi-ample.
Denote the natural map
![]() $S_{1}^{\nu }\to Z_{1}$
by
$S_{1}^{\nu }\to Z_{1}$
by
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $D|_{S^{\nu }}$
is semi-ample, we know that
$D|_{S^{\nu }}$
is semi-ample, we know that
is semi-ample. Then by Lemma 2.5, we have
![]() $D_{1}$
is semi-ample. Hence
$D_{1}$
is semi-ample. Hence
![]() $\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
is semi-ample. Again by Lemma 2.5 it follows that D is semi-ample. Moreover, D induces the morphism
$\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
is semi-ample. Again by Lemma 2.5 it follows that D is semi-ample. Moreover, D induces the morphism
![]() $h:X\to Z$
. Hence Z is projective.
$h:X\to Z$
. Hence Z is projective.
This proposition proves Case II when
![]() $K_{X}+B$
is endowed with an equidimensional map
$K_{X}+B$
is endowed with an equidimensional map
![]() $h:X\to Z$
by letting
$h:X\to Z$
by letting
![]() $D=K_{X}+B$
. In general, this equidimensionality condition may fail. We need to modify the pair
$D=K_{X}+B$
. In general, this equidimensionality condition may fail. We need to modify the pair
![]() $(X,B)$
. To do this, we need the following lemmas.
$(X,B)$
. To do this, we need the following lemmas.
Lemma 5.8. Let D be a nef
![]() ${\mathbb Q}$
-divisor on X with
${\mathbb Q}$
-divisor on X with
![]() $\kappa (X,D)=2$
, where X is a
$\kappa (X,D)=2$
, where X is a
![]() ${\mathbb Q}$
-factorial normal projective threefold over an uncountable algebraically closed field k of characteristic
${\mathbb Q}$
-factorial normal projective threefold over an uncountable algebraically closed field k of characteristic
![]() $>0$
. Suppose that D is endowed with a map
$>0$
. Suppose that D is endowed with a map
![]() $h:X\to Z$
such that
$h:X\to Z$
such that
![]() $D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. Then any h-exceptional prime divisor F is not nef.
$D|_{G}\sim _{{\mathbb Q}}0$
, where G is the generic fiber of h. Then any h-exceptional prime divisor F is not nef.
Proof. By Lemma 5.3, we have the following commutative diagram:

where
![]() $Z_{1}$
is a smooth projective surface,
$Z_{1}$
is a smooth projective surface,
![]() $X_{1}$
is a normal projective threefold,
$X_{1}$
is a normal projective threefold,
![]() $\phi ,\psi $
are birational morphisms, and
$\phi ,\psi $
are birational morphisms, and
![]() $h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration such that, there exists a nef and big
$h_{1}: X_{1}\to Z_{1}$
is an equidimensional fibration such that, there exists a nef and big
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $D_{1}$
on
$D_{1}$
on
![]() $Z_{1}$
such that
$Z_{1}$
such that
![]() $\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
$\phi ^{\ast }D\sim _{{\mathbb Q}} h^{\ast }_{1}D_{1}$
.
First, by the definition of EWM, we have D is numerically trivial on F. Let
![]() $F_{1}$
be the birational transform of F on
$F_{1}$
be the birational transform of F on
![]() $X_{1}$
. Since
$X_{1}$
. Since
![]() $D_{1}$
is a nef and big
$D_{1}$
is a nef and big
![]() ${\mathbb Q}$
-divisor on
${\mathbb Q}$
-divisor on
![]() $Z_{1}$
, we can write
$Z_{1}$
, we can write
![]() $D_{1}\sim _{{\mathbb Q}}A+E_{1}$
such that A is an ample effective
$D_{1}\sim _{{\mathbb Q}}A+E_{1}$
such that A is an ample effective
![]() ${\mathbb Q}$
-divisor, and
${\mathbb Q}$
-divisor, and
![]() $E_{1}$
is an effective
$E_{1}$
is an effective
![]() ${\mathbb Q}$
-divisor. Moreover, we can choose A such that
${\mathbb Q}$
-divisor. Moreover, we can choose A such that
![]() $\mathrm {Supp}(h_{1}^{\ast }A)$
doesn’t contain any component of
$\mathrm {Supp}(h_{1}^{\ast }A)$
doesn’t contain any component of
![]() $\mathrm {Supp}(\phi ^{\ast }F)\cup \mathrm {Exc}(\phi )$
since A is ample. We take a
$\mathrm {Supp}(\phi ^{\ast }F)\cup \mathrm {Exc}(\phi )$
since A is ample. We take a
![]() ${\mathbb Q}$
-effective divisor
${\mathbb Q}$
-effective divisor
![]() $\Delta $
such that
$\Delta $
such that
![]() $D\sim _{{\mathbb Q}}\Delta $
and
$D\sim _{{\mathbb Q}}\Delta $
and
![]() $\phi ^{\ast }\Delta =h_{1}^{\ast }(A+E_{1})$
.
$\phi ^{\ast }\Delta =h_{1}^{\ast }(A+E_{1})$
.
Now we take a very ample divisor
![]() $H_{1}$
on
$H_{1}$
on
![]() $X_{1}$
. Since
$X_{1}$
. Since
![]() $h_{1}^{\ast }A\cdot F_{1}\cdot H_{1}>0$
, we have
$h_{1}^{\ast }A\cdot F_{1}\cdot H_{1}>0$
, we have
![]() $\mathrm {Supp}(h_{1}^{\ast }A)\cap F_{1}\neq \emptyset $
. Let
$\mathrm {Supp}(h_{1}^{\ast }A)\cap F_{1}\neq \emptyset $
. Let
![]() $A_{X}$
be the birational transform of
$A_{X}$
be the birational transform of
![]() $\mathrm {Supp}(h_{1}^{\ast }A)$
on X. Then its intersection with F is of dimension one by our choice of A. If we take a very ample divisor H on X, it is clear that
$\mathrm {Supp}(h_{1}^{\ast }A)$
on X. Then its intersection with F is of dimension one by our choice of A. If we take a very ample divisor H on X, it is clear that
![]() $A_{X}\cdot F\cdot H>0$
. Note that
$A_{X}\cdot F\cdot H>0$
. Note that
![]() $\Delta \cdot F\cdot H=0$
and
$\Delta \cdot F\cdot H=0$
and
![]() $A_{X}\subseteq \mathrm {Supp}\ \Delta $
. It implies that
$A_{X}\subseteq \mathrm {Supp}\ \Delta $
. It implies that
![]() $F\subseteq \mathrm {Supp}\ \Delta $
and
$F\subseteq \mathrm {Supp}\ \Delta $
and
![]() $F\cdot F \cdot H<0$
.
$F\cdot F \cdot H<0$
.
Lemma 5.9. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
, and let D be an effective
$>3$
, and let D be an effective
![]() ${\mathbb Q}$
-divisor such that
${\mathbb Q}$
-divisor such that
![]() $\mathrm {Supp}\ D\subseteq \mathrm {Supp}\ B$
. Assume that
$\mathrm {Supp}\ D\subseteq \mathrm {Supp}\ B$
. Assume that
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $K_{X}+B-\varepsilon D$
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon D$
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
. Then we have:
$\varepsilon>0$
. Then we have:
(1)
![]() $\kappa (K_{X}+B-\varepsilon D)=\kappa (K_{X}+B)$
for any sufficiently small rational
$\kappa (K_{X}+B-\varepsilon D)=\kappa (K_{X}+B)$
for any sufficiently small rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
(2) if
![]() $D\subseteq \lfloor B\rfloor $
is a reduced divisor, then any
$D\subseteq \lfloor B\rfloor $
is a reduced divisor, then any
![]() $(K_{X}+B- D)$
-MMP which is
$(K_{X}+B- D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates with a pair
$(K_{X}+B)$
-trivial terminates with a pair
![]() $(X^{\prime },B^{\prime })$
such that
$(X^{\prime },B^{\prime })$
such that
![]() $K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
$K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $D^{\prime }$
is the birational transform of D on
$D^{\prime }$
is the birational transform of D on
![]() $X^{\prime }$
,
$X^{\prime }$
,
(3) if
![]() $D\subseteq \lfloor B\rfloor $
is a prime divisor, then D is not contracted by any
$D\subseteq \lfloor B\rfloor $
is a prime divisor, then D is not contracted by any
![]() $(K_{X}+B- D)$
-MMP which is
$(K_{X}+B- D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial.
$(K_{X}+B)$
-trivial.
Proof. Since
![]() $K_{X}+B-\varepsilon D$
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon D$
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
, by Theorem 4.4, we have
$\varepsilon>0$
, by Theorem 4.4, we have
![]() $K_{X}+B-\varepsilon D$
is effective for any sufficiently small rational
$K_{X}+B-\varepsilon D$
is effective for any sufficiently small rational
![]() $\varepsilon>0$
. Hence there exists an effective
$\varepsilon>0$
. Hence there exists an effective
![]() ${\mathbb Q}$
-divisor
${\mathbb Q}$
-divisor
![]() $\Delta _{\varepsilon }\sim _{{\mathbb Q}}K_{X}+B-2\varepsilon D$
for a sufficiently small rational
$\Delta _{\varepsilon }\sim _{{\mathbb Q}}K_{X}+B-2\varepsilon D$
for a sufficiently small rational
![]() $\varepsilon>0$
. Then we have
$\varepsilon>0$
. Then we have
This proves (1) since effective divisors with the same support have the same Kodaira dimension.
Assume that
![]() $D\subseteq \lfloor B\rfloor $
is a reduced divisor. Note that for any sufficiently small rational
$D\subseteq \lfloor B\rfloor $
is a reduced divisor. Note that for any sufficiently small rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $K_{X}+B-\varepsilon D$
is pseudo-effective and every step of a
$K_{X}+B-\varepsilon D$
is pseudo-effective and every step of a
![]() $(K_{X}+B-\varepsilon D)$
-MMP which is
$(K_{X}+B-\varepsilon D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial is a step of a
$(K_{X}+B)$
-trivial is a step of a
![]() $(K_{X}+B-\varepsilon D)$
-MMP. We choose a sufficiently small rational
$(K_{X}+B-\varepsilon D)$
-MMP. We choose a sufficiently small rational
![]() $\varepsilon _{0}>0$
. By Theorem 4.5, we have a
$\varepsilon _{0}>0$
. By Theorem 4.5, we have a
![]() $(K_{X}+B-\varepsilon _{0} D)$
-MMP which is
$(K_{X}+B-\varepsilon _{0} D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates with a pair
$(K_{X}+B)$
-trivial terminates with a pair
![]() $(X^{\prime },B^{\prime })$
such that
$(X^{\prime },B^{\prime })$
such that
![]() $K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
$K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $D^{\prime }$
is the birational transform of D on
$D^{\prime }$
is the birational transform of D on
![]() $X^{\prime }$
. Since any
$X^{\prime }$
. Since any
![]() $(K_{X}+B- D)$
-MMP which is
$(K_{X}+B- D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial is a
$(K_{X}+B)$
-trivial is a
![]() $(K_{X}+B-\varepsilon _{0} D)$
-MMP which is
$(K_{X}+B-\varepsilon _{0} D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial, we have (2) holds.
$(K_{X}+B)$
-trivial, we have (2) holds.
Assume, moreover, that D is a prime divisor. By (2), a
![]() $(K_{X}+B- D)$
-MMP which is
$(K_{X}+B- D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates with a pair
$(K_{X}+B)$
-trivial terminates with a pair
![]() $(X^{\prime },B^{\prime })$
such that
$(X^{\prime },B^{\prime })$
such that
![]() $K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
$K_{X^{\prime }}+B^{\prime }-\varepsilon D^{\prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $D^{\prime }$
is the birational transform of D on
$D^{\prime }$
is the birational transform of D on
![]() $X^{\prime }$
. We take a common resolution of X and
$X^{\prime }$
. We take a common resolution of X and
![]() $X^{\prime }$
$X^{\prime }$

Note that since every step of a
![]() $(K_{X}+B- D)$
-MMP which is
$(K_{X}+B- D)$
-MMP which is
![]() $(K_{X}+B)$
-trivial is a step of a
$(K_{X}+B)$
-trivial is a step of a
![]() $(K_{X}+B- D)$
-MMP, we have
$(K_{X}+B- D)$
-MMP, we have
where E is an effective
![]() $\phi _{2}$
-exceptional
$\phi _{2}$
-exceptional
![]() ${\mathbb Q}$
-divisor. It implies that
${\mathbb Q}$
-divisor. It implies that
Applying the negativity lemma (see [Reference Kollár, Kollár, Mori, Clemens and Corti20, Lem. 3.39]) to
![]() $\phi _{2}$
, we know that
$\phi _{2}$
, we know that
Hence D is not contracted by f, that is, (3) holds.
Now we can prove Case II.
Proposition 5.10. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
${\mathbb Q}$
-factorial projective dlt threefold pair over an algebraically closed field k of characteristic
![]() $>3$
such that
$>3$
such that
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\kappa (K_{X}+B)=2$
. If
$\kappa (K_{X}+B)=2$
. If
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
, then
$\varepsilon>0$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. We pass to an uncountable base field. By Proposition 5.6,
![]() $K_{X}+B$
is endowed with a map
$K_{X}+B$
is endowed with a map
![]() $h:X\to Z$
to an algebraic space Z of dimension
$h:X\to Z$
to an algebraic space Z of dimension
![]() $2$
.
$2$
.
Step 1. We contract all h-exceptional prime divisors which have empty intersection with
![]() $\lfloor B\rfloor $
.
$\lfloor B\rfloor $
.
Let F be a h-exceptional prime divisor such that
![]() $F\cap \lfloor B\rfloor =\emptyset $
, then we can choose a sufficiently small rational
$F\cap \lfloor B\rfloor =\emptyset $
, then we can choose a sufficiently small rational
![]() $\varepsilon $
such that
$\varepsilon $
such that
![]() $(X,B+\varepsilon F)$
is still dlt. Note that by Lemma 5.8, we have
$(X,B+\varepsilon F)$
is still dlt. Note that by Lemma 5.8, we have
![]() $K_{X}+B+\varepsilon F$
is not nef since
$K_{X}+B+\varepsilon F$
is not nef since
![]() $K_{X}+B$
is numerically trivial on F. We run a
$K_{X}+B$
is numerically trivial on F. We run a
![]() $(K_{X}+B+\varepsilon F)$
-MMP as follows.
$(K_{X}+B+\varepsilon F)$
-MMP as follows.
For the first step, the extremal ray is
![]() $(K_{X}+B)$
-numerically trivial since any curve which is
$(K_{X}+B)$
-numerically trivial since any curve which is
![]() $(K_{X}+B+\varepsilon F)$
-negative must be contained in F. If it is a divisorial contraction, then F is contracted and the process terminates. Otherwise, we get a flip
$(K_{X}+B+\varepsilon F)$
-negative must be contained in F. If it is a divisorial contraction, then F is contracted and the process terminates. Otherwise, we get a flip
such that
![]() $F^{+}\neq 0$
. Note that
$F^{+}\neq 0$
. Note that
![]() $K_{X^{+}}+B^{+}+ F^{+}$
is still not nef. By Theorem 4.5, the process must terminate, hence F is contracted after finitely many steps. Since at every step, we only contract
$K_{X^{+}}+B^{+}+ F^{+}$
is still not nef. By Theorem 4.5, the process must terminate, hence F is contracted after finitely many steps. Since at every step, we only contract
![]() $(K_{X}+B)$
-trivial curves, we can replace
$(K_{X}+B)$
-trivial curves, we can replace
![]() $(X,B)$
by the output of this process. Moreover, since the number of h-exceptional prime divisors is finite, we can repeat this process until every h-exceptional divisor intersects
$(X,B)$
by the output of this process. Moreover, since the number of h-exceptional prime divisors is finite, we can repeat this process until every h-exceptional divisor intersects
![]() $\lfloor B \rfloor $
.
$\lfloor B \rfloor $
.
From now on, we can assume that every h-exceptional divisor intersects
![]() $\lfloor B\rfloor $
.
$\lfloor B\rfloor $
.
Step 2. We reduce the proposition to the case when all h-exceptional prime divisors are connected components of
![]() $\lfloor B\rfloor $
.
$\lfloor B\rfloor $
.
To this end, let
![]() $S\subseteq \lfloor B\rfloor $
be a prime divisor such that there exists a h-exceptional divisor F whose intersection with S is of dimension one. By Definition 2.16, we run a
$S\subseteq \lfloor B\rfloor $
be a prime divisor such that there exists a h-exceptional divisor F whose intersection with S is of dimension one. By Definition 2.16, we run a
![]() $(K_{X}+B-S)$
-MMP which is
$(K_{X}+B-S)$
-MMP which is
![]() $(K_{X}+B)$
-trivial. By Lemma 5.9, it terminates with a pair
$(K_{X}+B)$
-trivial. By Lemma 5.9, it terminates with a pair
![]() $(X_{1},B_{1})$
such that
$(X_{1},B_{1})$
such that
![]() $K_{X_{1}}+B_{1}-\varepsilon S_{1}$
is nef for any sufficiently small rational
$K_{X_{1}}+B_{1}-\varepsilon S_{1}$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $S_{1}$
is the birational transform of S on
$S_{1}$
is the birational transform of S on
![]() $X_{1}$
. Moreover,
$X_{1}$
. Moreover,
![]() $S_{1}\neq 0$
.
$S_{1}\neq 0$
.
After replacing
![]() $(X,B), S$
by
$(X,B), S$
by
![]() $(X_{1},B_{1}), S_{1}$
(
$(X_{1},B_{1}), S_{1}$
(
![]() $(X,B)$
may no longer be dlt), we can assume that
$(X,B)$
may no longer be dlt), we can assume that
![]() $K_{X}+B-\varepsilon S$
is nef for any sufficiently small rational
$K_{X}+B-\varepsilon S$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
. Let F be a h-exceptional prime divisor such that it has non-empty intersection with S. Since
$\varepsilon>0$
. Let F be a h-exceptional prime divisor such that it has non-empty intersection with S. Since
![]() $K_{X}+B$
is numerically-trivial on F, we have
$K_{X}+B$
is numerically-trivial on F, we have
![]() $-S$
is nef on F, which implies that
$-S$
is nef on F, which implies that
![]() $S=F$
. It is to say that after this process, there is no h-exceptional divisor F whose intersection with S is of dimension one.
$S=F$
. It is to say that after this process, there is no h-exceptional divisor F whose intersection with S is of dimension one.
Since the number of h-exceptional prime divisors is finite and it decreases strictly under the above process, we can repeat this process until there is no prime divisor
![]() $S\subseteq \lfloor B\rfloor $
such that there exists a h-exceptional divisor F whose intersection with S is of dimension one.
$S\subseteq \lfloor B\rfloor $
such that there exists a h-exceptional divisor F whose intersection with S is of dimension one.
From now on, we can assume that all h-exceptional prime divisors are connected components of
![]() $\lfloor B\rfloor $
.
$\lfloor B\rfloor $
.
Step 3. We further modify
![]() $(X,B)$
and construct an equidimensional fibration
$(X,B)$
and construct an equidimensional fibration
![]() $h_{\varepsilon }:X\to Z_{\varepsilon }$
.
$h_{\varepsilon }:X\to Z_{\varepsilon }$
.
First, let
![]() $F_{h}$
be the reduced h-exceptional divisor and run a
$F_{h}$
be the reduced h-exceptional divisor and run a
![]() $(K_{X}+B-F_{h})$
-MMP which is
$(K_{X}+B-F_{h})$
-MMP which is
![]() $(K_{X}+B)$
-trivial by Definition 2.16. After replacing
$(K_{X}+B)$
-trivial by Definition 2.16. After replacing
![]() $(X,B)$
by the output of this process, we can assume that
$(X,B)$
by the output of this process, we can assume that
![]() $K_{X}+B-\varepsilon F_{h}$
is nef for any sufficiently small rational
$K_{X}+B-\varepsilon F_{h}$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
as at Step 2.
$\varepsilon>0$
as at Step 2.
We choose a sufficiently small rational
![]() $\varepsilon>0$
. Note that by Lemma 5.9, we have
$\varepsilon>0$
. Note that by Lemma 5.9, we have
![]() $\kappa (K_{X}+B-\varepsilon F_{h})=\kappa (K_{X}+B)=2$
. Hence by Lemma 5.3,
$\kappa (K_{X}+B-\varepsilon F_{h})=\kappa (K_{X}+B)=2$
. Hence by Lemma 5.3,
![]() $K_{X}+B-\varepsilon F_{h}$
is endowed with a map
$K_{X}+B-\varepsilon F_{h}$
is endowed with a map
![]() $h_{\varepsilon }:X\to Z_{\varepsilon }$
. We claim that there exists a commutative diagram:
$h_{\varepsilon }:X\to Z_{\varepsilon }$
. We claim that there exists a commutative diagram:

We only need to prove that any curve contracted by
![]() $h_{\varepsilon }$
is contracted by h. Let
$h_{\varepsilon }$
is contracted by h. Let
![]() $C_{1}$
be a curve contracted by
$C_{1}$
be a curve contracted by
![]() $h_{\varepsilon }$
, that is,
$h_{\varepsilon }$
, that is,
![]() $(K_{X}+B-\varepsilon F_{h})\cdot C_{1}=0$
.
$(K_{X}+B-\varepsilon F_{h})\cdot C_{1}=0$
.
If
![]() $C_{1}\cap F_{h}=\emptyset $
, then
$C_{1}\cap F_{h}=\emptyset $
, then
![]() $(K_{X}+B-\varepsilon F_{h})\cdot C_{1}=0$
implies
$(K_{X}+B-\varepsilon F_{h})\cdot C_{1}=0$
implies
![]() $(K_{X}+B)\cdot C_{1}=0$
. Hence
$(K_{X}+B)\cdot C_{1}=0$
. Hence
![]() $C_{1}$
is contracted by h. If
$C_{1}$
is contracted by h. If
![]() $C_{1}\cap F_{h}\neq \emptyset $
and
$C_{1}\cap F_{h}\neq \emptyset $
and
![]() $C_{1}\not \subseteq F_{h}$
, then we have
$C_{1}\not \subseteq F_{h}$
, then we have
![]() $C_{1}\cdot F_{h}>0$
. But
$C_{1}\cdot F_{h}>0$
. But
![]() $K_{X}+B-2\varepsilon F_{h}$
is nef as well, that is,
$K_{X}+B-2\varepsilon F_{h}$
is nef as well, that is,
We obtain a contradiction. Finally, if
![]() $C_{1}\subseteq F_{h}$
, then
$C_{1}\subseteq F_{h}$
, then
![]() $C_{1}$
is always contracted by h.
$C_{1}$
is always contracted by h.
We prove that
![]() $h_{\varepsilon }$
is actually equidimensional. By the above diagram, we know that exceptional divisors of
$h_{\varepsilon }$
is actually equidimensional. By the above diagram, we know that exceptional divisors of
![]() $h_{\varepsilon }$
have to be exceptional divisors of h. Hence, all
$h_{\varepsilon }$
have to be exceptional divisors of h. Hence, all
![]() $h_{\varepsilon }$
-exceptional divisors are supported in
$h_{\varepsilon }$
-exceptional divisors are supported in
![]() $F_{h}$
. If F is a prime
$F_{h}$
. If F is a prime
![]() $h_{\varepsilon }$
-exceptional divisor, we have both
$h_{\varepsilon }$
-exceptional divisor, we have both
![]() $K_{X}+B$
and
$K_{X}+B$
and
![]() $K_{X}+B-\varepsilon F_{h}$
are numerically trivial on F, and hence
$K_{X}+B-\varepsilon F_{h}$
are numerically trivial on F, and hence
![]() $F_{h}$
is numerically trivial on F, which is impossible since F is not nef by Lemma 5.8 and F is a connected component of
$F_{h}$
is numerically trivial on F, which is impossible since F is not nef by Lemma 5.8 and F is a connected component of
![]() $F_{h}$
.
$F_{h}$
.
Step 4. Descend
![]() $K_{X}+B$
to
$K_{X}+B$
to
![]() $Z_{\varepsilon }$
and prove its semi-ampleness.
$Z_{\varepsilon }$
and prove its semi-ampleness.
By Proposition 5.7, we have
![]() $K_{X}+B-\varepsilon F_{h}$
is semi-ample and
$K_{X}+B-\varepsilon F_{h}$
is semi-ample and
![]() $Z_{\varepsilon }$
is a projective variety. Moreover, by Lemma 2.10,
$Z_{\varepsilon }$
is a projective variety. Moreover, by Lemma 2.10,
![]() $K_{X}+B$
descends to a nef and big divisor
$K_{X}+B$
descends to a nef and big divisor
![]() $D_{\varepsilon }$
on
$D_{\varepsilon }$
on
![]() $Z_{\varepsilon }$
since
$Z_{\varepsilon }$
since
![]() $h_{\varepsilon }$
is equidimensional and
$h_{\varepsilon }$
is equidimensional and
![]() $Z_{\varepsilon }$
is
$Z_{\varepsilon }$
is
![]() ${\mathbb Q}$
-factorial by [Reference Waldron25, Prop. 3.3].
${\mathbb Q}$
-factorial by [Reference Waldron25, Prop. 3.3].
By the projection formula for any curve
![]() $\Gamma \subseteq {\mathbb E}(D_{\varepsilon }),$
we have
$\Gamma \subseteq {\mathbb E}(D_{\varepsilon }),$
we have
![]() $K_{X}+B$
is numerically trivial on
$K_{X}+B$
is numerically trivial on
![]() $h_{\varepsilon }^{-1}(\Gamma )$
. However, by our assumption,
$h_{\varepsilon }^{-1}(\Gamma )$
. However, by our assumption,
![]() $h_{\varepsilon }^{-1}(\Gamma )$
has to be contained in
$h_{\varepsilon }^{-1}(\Gamma )$
has to be contained in
![]() $F_{h}$
. Hence it is clear that
$F_{h}$
. Hence it is clear that
Since
![]() $h_{\varepsilon }$
is equidimensional, we have
$h_{\varepsilon }$
is equidimensional, we have
![]() $h_{\varepsilon }^{-1}(h_{\varepsilon }(F_{h}))$
is the union of finitely many prime divisors. All these prime divisors are exceptional divisors of h since
$h_{\varepsilon }^{-1}(h_{\varepsilon }(F_{h}))$
is the union of finitely many prime divisors. All these prime divisors are exceptional divisors of h since
![]() $\psi _{\varepsilon }\circ h_{\varepsilon }(F_{h})$
is of dimension
$\psi _{\varepsilon }\circ h_{\varepsilon }(F_{h})$
is of dimension
![]() $0$
. Hence, we have
$0$
. Hence, we have
We take a dlt modification
![]() $g: (X^{\prime },B^{\prime })\to (X,B)$
such that g only extracts prime divisors E with discrepancies
$g: (X^{\prime },B^{\prime })\to (X,B)$
such that g only extracts prime divisors E with discrepancies
![]() $a(E,X,B)=-1$
by [Reference Birkar4, Lem. 7.7] and [Reference Hacon and Witaszek12]. Then we have
$a(E,X,B)=-1$
by [Reference Birkar4, Lem. 7.7] and [Reference Hacon and Witaszek12]. Then we have
Since
![]() $(K_{X^{\prime }}+B^{\prime })|_{\lfloor B^{\prime }\rfloor }$
is semi-ample by Theorem 2.21, we have
$(K_{X^{\prime }}+B^{\prime })|_{\lfloor B^{\prime }\rfloor }$
is semi-ample by Theorem 2.21, we have
is semi-ample. Then by [Reference Birkar and Waldron5, Lem. 7.1], we have
![]() $D_{\varepsilon }$
, and hence
$D_{\varepsilon }$
, and hence
![]() $K_{X}+B$
are semi-ample.
$K_{X}+B$
are semi-ample.
5.3 Proof of Theorem 5.1
Proof. Case of
![]() $\kappa (X,K_{X}+B)=3$
: In this case,
$\kappa (X,K_{X}+B)=3$
: In this case,
![]() $K_{X}+B$
is nef and big, hence the proposition holds by [Reference Waldron26, Th. 1.1] and [Reference Hacon and Witaszek12].
$K_{X}+B$
is nef and big, hence the proposition holds by [Reference Waldron26, Th. 1.1] and [Reference Hacon and Witaszek12].
Case of
![]() $\kappa (X,K_{X}+B)=2$
: After replacing
$\kappa (X,K_{X}+B)=2$
: After replacing
![]() $(X,B)$
by its dlt modification, we can assume that
$(X,B)$
by its dlt modification, we can assume that
![]() $(X,B)$
is a
$(X,B)$
is a
![]() ${\mathbb Q}$
-factorial dlt pair by Theorem 2.20. Then the proposition follows from Propositions 5.6 and 5.10.
${\mathbb Q}$
-factorial dlt pair by Theorem 2.20. Then the proposition follows from Propositions 5.6 and 5.10.
Case of
![]() $\kappa (K_{X}+B)=1$
: The proof is similar to the case of
$\kappa (K_{X}+B)=1$
: The proof is similar to the case of
![]() $\kappa (K_{X}+B)=2$
but easier.
$\kappa (K_{X}+B)=2$
but easier.
After replacing
![]() $(X,B)$
by its dlt modification, we can assume that
$(X,B)$
by its dlt modification, we can assume that
![]() $(X,B)$
is a
$(X,B)$
is a
![]() ${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Then we have either:
${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Then we have either:
(1):
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
, or
$\varepsilon>0$
, or
(2):
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is pseudo-effective for any sufficiently small rational
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
In the case of (1), since
![]() $K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
$K_{X}+B-\varepsilon \lfloor B \rfloor $
is not pseudo-effective for any rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any rational
$K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any rational
![]() $\varepsilon>0$
. Then by Definition 2.16, we can run a
$\varepsilon>0$
. Then by Definition 2.16, we can run a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
$(K_{X}+B)$
-trivial. By Lemma 2.19, it terminates with a pair
![]() $(X^{\prime },B^{\prime })$
since X is terminal. Moreover, since
$(X^{\prime },B^{\prime })$
since X is terminal. Moreover, since
and
![]() $K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any small rational
$K_{X}+(1-\varepsilon )B$
is not pseudo-effective for any small rational
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is not nef for any small rational
$K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is not nef for any small rational
![]() $\varepsilon>0$
by Theorem 4.4. Hence this
$\varepsilon>0$
by Theorem 4.4. Hence this
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates with a Mori fiber space. Then we have
$(K_{X}+B)$
-trivial terminates with a Mori fiber space. Then we have
![]() $n(K_{X}+B)\leq 2$
. By Proposition 4.3,
$n(K_{X}+B)\leq 2$
. By Proposition 4.3,
![]() $n(K_{X}+B)=1$
since
$n(K_{X}+B)=1$
since
![]() $\kappa (K_{X}+B)=1$
. Then a nef reduction map of
$\kappa (K_{X}+B)=1$
. Then a nef reduction map of
![]() $K_{X}+B$
, which exists by Theorem 2.8, is an equidimensional fibration to a normal curve. Hence we can descend
$K_{X}+B$
, which exists by Theorem 2.8, is an equidimensional fibration to a normal curve. Hence we can descend
![]() $K_{X}+B$
to an ample divisor on the curve by Lemma 2.10.
$K_{X}+B$
to an ample divisor on the curve by Lemma 2.10.
In the case of (2), by Definition 2.16, we run a
![]() $(K_{X}+B-\lfloor B\rfloor )$
-MMP which is
$(K_{X}+B-\lfloor B\rfloor )$
-MMP which is
![]() $(K_{X}+B)$
-trivial which terminates by Lemma 5.9, and replace
$(K_{X}+B)$
-trivial which terminates by Lemma 5.9, and replace
![]() $(X,B)$
by the output.
$(X,B)$
by the output.
![]() $(X,B)$
may no longer be dlt and X may no longer be terminal. However, we can assume that
$(X,B)$
may no longer be dlt and X may no longer be terminal. However, we can assume that
![]() $K_{X}+B-\varepsilon \lfloor B\rfloor $
is nef and
$K_{X}+B-\varepsilon \lfloor B\rfloor $
is nef and
![]() $(X,B-\varepsilon \lfloor B\rfloor )$
is klt for any sufficiently small rational
$(X,B-\varepsilon \lfloor B\rfloor )$
is klt for any sufficiently small rational
![]() $\varepsilon>0$
. By Lemma 5.9, we have
$\varepsilon>0$
. By Lemma 5.9, we have
for any sufficiently small rational
![]() $\varepsilon> 0$
. We choose a sufficiently small rational
$\varepsilon> 0$
. We choose a sufficiently small rational
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $K_{X}+B-2\varepsilon \lfloor B\rfloor $
is nef and
$K_{X}+B-2\varepsilon \lfloor B\rfloor $
is nef and
![]() $\kappa (K_{X}+B-\varepsilon \lfloor B\rfloor )=1$
. Then by Theorem 3.9,
$\kappa (K_{X}+B-\varepsilon \lfloor B\rfloor )=1$
. Then by Theorem 3.9,
![]() $|m(K_{X}+B-\varepsilon \lfloor B\rfloor )|$
induces a fibration
$|m(K_{X}+B-\varepsilon \lfloor B\rfloor )|$
induces a fibration
![]() $h^{\prime }:X\to Z^{\prime }$
for a sufficiently divisible positive integer m since
$h^{\prime }:X\to Z^{\prime }$
for a sufficiently divisible positive integer m since
![]() $(X,B-\varepsilon \lfloor B\rfloor )$
is klt. Denote the generic fiber of
$(X,B-\varepsilon \lfloor B\rfloor )$
is klt. Denote the generic fiber of
![]() $h^{\prime }$
by G. By Theorem 2.11,
$h^{\prime }$
by G. By Theorem 2.11,
![]() $(K_{X}+B-2\varepsilon \lfloor B\rfloor )|_{G}$
is semi-ample. Note that
$(K_{X}+B-2\varepsilon \lfloor B\rfloor )|_{G}$
is semi-ample. Note that
![]() $(K_{X}+B-\varepsilon \lfloor B\rfloor )|_{G}\sim _{{\mathbb Q}}0$
. It implies that
$(K_{X}+B-\varepsilon \lfloor B\rfloor )|_{G}\sim _{{\mathbb Q}}0$
. It implies that
![]() $(K_{X}+B-2\varepsilon \lfloor B\rfloor )|_{G}\sim _{{\mathbb Q}}0$
, and hence
$(K_{X}+B-2\varepsilon \lfloor B\rfloor )|_{G}\sim _{{\mathbb Q}}0$
, and hence
![]() $(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
. Then by Lemma 2.10,
$(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
. Then by Lemma 2.10,
![]() $K_{X}+B$
descends to an ample divisor on
$K_{X}+B$
descends to an ample divisor on
![]() $Z^{\prime }$
. Hence
$Z^{\prime }$
. Hence
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
6 Applications
In this section, we complete the proofs of the statements in the introduction.
Theorem 6.1. Let
![]() $(X, B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X, B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. Then the log canonical ring
$>3$
. Then the log canonical ring
is finitely generated.
Proof. If
![]() $\kappa (K_{X}+B)=0$
or
$\kappa (K_{X}+B)=0$
or
![]() $-\infty $
, the assertion is trivial. Otherwise, we have
$-\infty $
, the assertion is trivial. Otherwise, we have
![]() ${\kappa (K_{X}+B)\geq 1}$
. After replacing
${\kappa (K_{X}+B)\geq 1}$
. After replacing
![]() $(X,B)$
by its log minimal model by Theorem 2.12, we can assume that
$(X,B)$
by its log minimal model by Theorem 2.12, we can assume that
![]() $K_{X}+B$
is nef. Then the assertion follows from Theorem 5.1.
$K_{X}+B$
is nef. Then the assertion follows from Theorem 5.1.
Theorem 6.2. Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $n(X,K_{X}+B)\leq 2$
, then
$n(X,K_{X}+B)\leq 2$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. Case of
![]() $n(K_{X}+B)=0$
: By Theorem 4.4, we have
$n(K_{X}+B)=0$
: By Theorem 4.4, we have
![]() $\kappa (K_{X}+B)\geq 0$
. Hence we have
$\kappa (K_{X}+B)\geq 0$
. Hence we have
Therefore
![]() $K_{X}+B\sim _{{\mathbb Q}}0$
.
$K_{X}+B\sim _{{\mathbb Q}}0$
.
Case of
![]() $n(K_{X}+B)=1$
: Let
$n(K_{X}+B)=1$
: Let
![]() $\phi :X\dashrightarrow Z$
be a nef reduction map, which exists by Theorem 2.8. Since Z is a normal curve, X is normal and
$\phi :X\dashrightarrow Z$
be a nef reduction map, which exists by Theorem 2.8. Since Z is a normal curve, X is normal and
![]() $\phi $
is proper over the generic point
$\phi $
is proper over the generic point
![]() $\mu $
of Z, we have
$\mu $
of Z, we have
![]() $\phi $
is indeed a morphism. Note that
$\phi $
is indeed a morphism. Note that
![]() $(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
by Theorem 2.11, where G is the generic fiber of
$(K_{X}+B)|_{G}\sim _{{\mathbb Q}}0$
by Theorem 2.11, where G is the generic fiber of
![]() $\phi $
. Since
$\phi $
. Since
![]() $\phi $
is equidimensional, we have
$\phi $
is equidimensional, we have
![]() $K_{X}+B\sim _{{\mathbb Q}}f^{\ast }A$
for an ample divisor on Z by Lemma 2.10. Hence
$K_{X}+B\sim _{{\mathbb Q}}f^{\ast }A$
for an ample divisor on Z by Lemma 2.10. Hence
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Case of
![]() $n(K_{X}+B)=2$
: By Proposition 4.3, we have
$n(K_{X}+B)=2$
: By Proposition 4.3, we have
![]() $\kappa (K_{X}+B)=2$
. Then the proposition follows from Theorem 5.1.
$\kappa (K_{X}+B)=2$
. Then the proposition follows from Theorem 5.1.
Theorem 6.3. Let
![]() $(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
$(X,B)$
be a projective lc threefold pair over an algebraically closed field k of characteristic
![]() $>3$
. If
$>3$
. If
![]() $K_{X}+B$
is nef and
$K_{X}+B$
is nef and
![]() $\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
, then
$\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
, then
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Proof. After replacing
![]() $(X,B)$
by its dlt modification, we can assume that
$(X,B)$
by its dlt modification, we can assume that
![]() $(X,B)$
is a
$(X,B)$
is a
![]() ${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Moreover, by Theorems 4.4 and 5.1, we can assume that
${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Moreover, by Theorems 4.4 and 5.1, we can assume that
![]() $\kappa (K_{X}+B)=0$
. By Definition 2.16, we run a
$\kappa (K_{X}+B)=0$
. By Definition 2.16, we run a
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial, which terminates by Lemma 2.19 since X is terminal.
$(K_{X}+B)$
-trivial, which terminates by Lemma 2.19 since X is terminal.
If it terminates with a Mori fiber space, then we have
![]() $n(K_{X}+B)\leq 2$
. Then the semi-ampleness of
$n(K_{X}+B)\leq 2$
. Then the semi-ampleness of
![]() $K_{X}+B$
follows from Theorem 6.2.
$K_{X}+B$
follows from Theorem 6.2.
Otherwise, by Lemma 2.17, this
![]() $K_{X}$
-MMP which is
$K_{X}$
-MMP which is
![]() $(K_{X}+B)$
-trivial terminates with a pair
$(K_{X}+B)$
-trivial terminates with a pair
![]() $(X^{\prime },B^{\prime })$
such that
$(X^{\prime },B^{\prime })$
such that
![]() $K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is nef for any sufficiently small rational
$K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is nef for any sufficiently small rational
![]() $\varepsilon>0$
. Note that for any sufficiently small rational
$\varepsilon>0$
. Note that for any sufficiently small rational
![]() $\varepsilon>0$
we have
$\varepsilon>0$
we have
![]() $(X^{\prime },(1-\varepsilon )B^{\prime })$
is klt since
$(X^{\prime },(1-\varepsilon )B^{\prime })$
is klt since
![]() $(X,(1-\varepsilon )B)$
is klt, and
$(X,(1-\varepsilon )B)$
is klt, and
by Lemma 5.9. Moreover,
![]() $\mathrm {dim}\ \mathrm {Alb}(X^{\prime })\neq 0$
since
$\mathrm {dim}\ \mathrm {Alb}(X^{\prime })\neq 0$
since
![]() $\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
. Hence, by Theorem 3.9,
$\mathrm {dim}\ \mathrm {Alb}(X)\neq 0$
. Hence, by Theorem 3.9,
![]() $K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is
$K_{X^{\prime }}+(1-\varepsilon )B^{\prime }$
is
![]() ${\mathbb Q}$
-linearly trivial for any sufficiently small rational
${\mathbb Q}$
-linearly trivial for any sufficiently small rational
![]() $\varepsilon>0$
. Then
$\varepsilon>0$
. Then
![]() $K_{X^{\prime }}+B^{\prime }$
, and hence
$K_{X^{\prime }}+B^{\prime }$
, and hence
![]() $K_{X}+B$
are
$K_{X}+B$
are
![]() ${\mathbb Q}$
-linearly trivial.
${\mathbb Q}$
-linearly trivial.
Theorem 6.4. Let k be an algebraically closed field of characteristic
![]() $>3$
. Assume we have:
$>3$
. Assume we have:
(1) abundance for terminal threefolds over k holds, and
(2) any effective nef divisor D on any klt Calabi–Yau threefold pair
![]() $(Y,\Delta )$
(
$(Y,\Delta )$
(
![]() $(Y,\Delta )$
is klt and
$(Y,\Delta )$
is klt and
![]() $K_{Y}+\Delta \sim _{{\mathbb Q}}0$
) over k is semi-ample.
$K_{Y}+\Delta \sim _{{\mathbb Q}}0$
) over k is semi-ample.
Then the abundance conjecture for threefold pairs over k holds. In particular, the abundance conjecture for klt threefold pairs over k implies the abundance conjecture for lc threefold pairs over k.
Proof. Let
![]() $(X,B)$
be a projective lc threefold pair over k such that
$(X,B)$
be a projective lc threefold pair over k such that
![]() $K_{X}+B$
is nef. After replacing
$K_{X}+B$
is nef. After replacing
![]() $(X,B)$
by its dlt modification, we can assume that
$(X,B)$
by its dlt modification, we can assume that
![]() $(X,B)$
is a
$(X,B)$
is a
![]() ${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Moreover, by Theorems 4.4 and 5.1, we can assume that
${\mathbb Q}$
-factorial dlt pair and X is terminal by Theorem 2.20. Moreover, by Theorems 4.4 and 5.1, we can assume that
![]() $\kappa (K_{X}+B)=0$
.
$\kappa (K_{X}+B)=0$
.
By Corollary 2.15, we run a
![]() $K_{X}$
-MMP with scaling of B. It terminates by Lemma 2.19 since X is terminal. Hence we have a following sequence:
$K_{X}$
-MMP with scaling of B. It terminates by Lemma 2.19 since X is terminal. Hence we have a following sequence:
such that
![]() $\mu _{i}$
are
$\mu _{i}$
are
![]() $K_{X_{i-1}}$
-MMP which are
$K_{X_{i-1}}$
-MMP which are
![]() $(K_{X_{i-1}}+\lambda _{i-1} B_{i-1})$
-trivial, where
$(K_{X_{i-1}}+\lambda _{i-1} B_{i-1})$
-trivial, where
![]() $\lambda _{i}$
are the smallest numbers such that
$\lambda _{i}$
are the smallest numbers such that
![]() $K_{X_{i}}+\lambda _{i}B_{i}$
are nef and
$K_{X_{i}}+\lambda _{i}B_{i}$
are nef and
![]() $\lambda _{0}>\lambda _{1}>\cdots >\lambda _{r}$
. Moreover,
$\lambda _{0}>\lambda _{1}>\cdots >\lambda _{r}$
. Moreover,
![]() $(X_{r},B_{r})$
is the output of the
$(X_{r},B_{r})$
is the output of the
![]() $K_{X}$
-MMP with scaling of B.
$K_{X}$
-MMP with scaling of B.
If
![]() $(X_{r},B_{r})$
is a minimal model, then
$(X_{r},B_{r})$
is a minimal model, then
![]() $K_{X_{r}}$
is nef. By (1),
$K_{X_{r}}$
is nef. By (1),
![]() $K_{X_{r}}$
is semi-ample. Note that
$K_{X_{r}}$
is semi-ample. Note that
Hence
![]() $K_{X_{r}}\sim _{{\mathbb Q}}0$
. Since
$K_{X_{r}}\sim _{{\mathbb Q}}0$
. Since
![]() $K_{X_{r}}+\lambda B_{r}$
is nef for any
$K_{X_{r}}+\lambda B_{r}$
is nef for any
![]() $\lambda _{r-1}>\lambda > \lambda _{r}=0$
, we have
$\lambda _{r-1}>\lambda > \lambda _{r}=0$
, we have
![]() $B_{r}$
is nef on
$B_{r}$
is nef on
![]() $X_{r}$
. By (2), we have
$X_{r}$
. By (2), we have
![]() $B_{r}$
is semi-ample, and hence
$B_{r}$
is semi-ample, and hence
![]() $B_{r}=0$
since
$B_{r}=0$
since
It implies that
![]() $B=0$
by a standard argument using the negativity lemma (see the proof of Lemma 5.9 for example). Hence
$B=0$
by a standard argument using the negativity lemma (see the proof of Lemma 5.9 for example). Hence
![]() $K_{X}+B=K_{X}\sim _{{\mathbb Q}}0$
by (1).
$K_{X}+B=K_{X}\sim _{{\mathbb Q}}0$
by (1).
Otherwise,
![]() $(X_{r},B_{r})$
is a Mori fiber space. Then we have
$(X_{r},B_{r})$
is a Mori fiber space. Then we have
![]() $n(X_{r}, K_{X_{r}}+\lambda _{r}B_{r})\leq 2$
, where
$n(X_{r}, K_{X_{r}}+\lambda _{r}B_{r})\leq 2$
, where
![]() $\lambda _{r}>0$
. Hence
$\lambda _{r}>0$
. Hence
![]() $K_{X_{r}}+\lambda _{r}B_{r}$
is semi-ample by Theorem 6.2. Moreover,
$K_{X_{r}}+\lambda _{r}B_{r}$
is semi-ample by Theorem 6.2. Moreover,
![]() $K_{X_{r}}+\lambda _{r}B_{r}\sim _{{\mathbb Q}}0$
since
$K_{X_{r}}+\lambda _{r}B_{r}\sim _{{\mathbb Q}}0$
since
If
![]() $\lambda _{r}=1$
, then
$\lambda _{r}=1$
, then
![]() $\lambda _{0}=\lambda _{r}=1$
. It is to say that
$\lambda _{0}=\lambda _{r}=1$
. It is to say that
![]() $K_{X}+B=K_{X_{r}}+\lambda _{r}B_{r}\sim _{{\mathbb Q}}0$
. Therefore, we can assume that
$K_{X}+B=K_{X_{r}}+\lambda _{r}B_{r}\sim _{{\mathbb Q}}0$
. Therefore, we can assume that
![]() $\lambda _{r}<1$
. Then we have
$\lambda _{r}<1$
. Then we have
![]() $K_{X_{r}}+\lambda B_{r}$
is nef for any
$K_{X_{r}}+\lambda B_{r}$
is nef for any
![]() $\lambda _{r-1}>\lambda > \lambda _{r}$
, and hence
$\lambda _{r-1}>\lambda > \lambda _{r}$
, and hence
![]() $B_{r}$
is nef on
$B_{r}$
is nef on
![]() $X_{r}$
. By (2), we have
$X_{r}$
. By (2), we have
![]() $B_{r}$
is semi-ample, and hence
$B_{r}$
is semi-ample, and hence
![]() $B_{r}=0$
since
$B_{r}=0$
since
It is impossible since
![]() $\lambda _{r}>0$
. In conclusion, we have
$\lambda _{r}>0$
. In conclusion, we have
![]() $K_{X}+B$
is semi-ample.
$K_{X}+B$
is semi-ample.
Acknowledgment
I would like to express my gratitude to my advisor Wenhao Ou for his help, encouragement, and support. Further, I would like to thank Jakub Witaszek for answering my question on his paper [Reference Witaszek27]. Finally, I would also like to thank Lei Zhang for his encouragement and helpful advice.